2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9090-1991
測定−校正方式通則
Measurement−General rules for calibration system
1. 適用範囲 この規格は,物理量の測定に用いる計測器の校正方式(1)の定め方及び測定にかかわる誤差
の大きさの求め方について共通事項を規定する。
注(1) 計測器の校正において,必要な事項及び方法を定めたもの。
備考 この規格の引用規格を,次に示す。
JIS Z 8101 品質管理用語
JIS Z 8103 計測用語
2. 用語の定義 この規格で用いる主な用語の定義は,JIS Z 8101及びJIS Z 8103による。
3. 校正方式
3.1
校正
3.1.1
校正の作業 計測器を校正する作業は,次の点検及び(又は)修正の二つから構成する。
(1) 点検 点検では,修正が必要であるか否かを知るために,測定標準(以下,標準という。)を用いて測
定値の誤差を求め,修正限界(3.3.4参照)との比較を行う。
(2) 修正 修正では,計測器の読みと測定量の真の値との関係を表す校正式を求め直すために,標準の測
定を行い,校正式の計算又は計測器の調整を行う。
備考 計測器の読みから測定値を求める式を校正式という。
校正の作業の例
例1. 工程で使われている自動寸法測定器で,1時間に1回,限界ゲージによる点検を行っている。
点検では,測定対象の部品の規格値の上限・下限に相当する限界ゲージの測定を行い,測
定値の誤差が修正限界内ならばそのまま自動寸法測定器を使用して作業を続け,修正限界
を超えたときには,校正式の修正を行う。修正では,上限・下限に相当する限界ゲージの
読みを自動寸法測定器に附属するコンピュータに入力し,校正式の定数を計算し,その結
果に基づいて,計測器の調整を行う。
例2. 電圧計の点検を月1回行っている。点検において,零点の確認をした後,定電圧電源の出力
10Vを測定したところ,測定値は10.04Vとなった。このときの誤差は0.04Vであり,修正
限界D=0.01Vを超えたので,修正を行った。修正では,10Vの測定値が10Vになるよう
に校正式を作り直して,校正表を変更した。
3.1.2
校正の基本 校正方式は,規定される校正の内容によって,次の四つの方式に区分する(表1参照)。
(1) 点検及び修正を行う校正方式 点検の結果によって修正を行う。測定値の誤差が修正限界内の場合は,
修正を行わずそのまま計測器を使用する。測定値の誤差が修正限界を超えた場合は,修正を行い計測
2
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
器を使用する。
(2) 点検だけを行う校正方式 点検の結果によって,測定値の誤差が定められた限界以内の場合は,その
まま計測器を使用する。
例 計測器の修正及び修理を行うには費用がかかりすぎるので,定期的に点検を行って,誤差が定め
られた限界内であれば,そのまま計測器を使用する。
また,定められた限界を超えていれば,計測器を廃棄する。
(3) 修正だけを行う校正方式 点検を行わず,必ず修正を行い,新しい校正式を求め,計測器を使用する。
例 定期的に計測器の零点の修正を必ず行う。すなわち,零点に狂いがあれば,必ず計測器を調整す
る。
(4) 無校正の校正方式 点検及び修正は行わずに,無校正で計測器を使用する。
例 ある計測器の誤差は,その計測器が用いられている工程の製品の公差に対して十分小さいことが
分かっており,校正に費用がかかるので,購入した個々の計測器は無校正でそのまま使い,定期
的に廃棄する。
備考 この規格では,主として(1)の場合について規定し,その他の場合については,必要に応じて規
定する。
表1 校正の内容による校正方式の区分
(1) 点検及び修正を行
う校正方式
(2) 点検だけを
行う校正方式
(3) 修正だけを
行う校正方式
(4) 無校正の校
正方式
点検作業
点検作業
点検作業なし
点検作業なし
↓
↓
↓
↓
点検の結果
点検の結果
修正作業
修正作業なし
↓
↓
↓
結果に応じて修正作業 修正作業なし
↓
↓
↓
↓
↓
使用
使用
廃棄
使用
期限まで使用
3.2
校正における測定
3.2.1
校正における測定の準備 校正における測定のために,次のものを準備しなければならない。
(1) 校正対象の計測器
(2) 測定量の真の値となる標準又は標準器(2)。
注(2) 標準器には,測定量の1点を示す標準器及び多くの点を示す標準器がある(3.3.3参照)。
例 基準分銅,ブロックゲージ,校正された電圧発生器,標準マイクロホンで設定された基準音圧レ
ベル。
(3) その他,校正に必要な機器,装置又は設備。
例 測定用ジグ,荷重発生器,恒温室,恒温恒湿室,無響室。
3.2.2
校正における測定方法 校正における測定方法を,次に示す。
(1) 校正前にあらかじめ値付けされた標準器を,校正対象の計測器によって測定する。
例1. 基準分銅を,校正対象のはかりで測定する。
例2. ブロックゲージを,校正対象のマイクロメータで測定する。
例3. 校正された電圧発生器の出力を,校正対象の電圧計で測定する。
(2) 物理量を発生する機器(以下,発生器という。)が示す測定量を,正確さがよりよい計測器(以下,上
位の計測器という。)及び校正対象の計測器によって測定する。
3
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例1. スピーカの音を,標準マイクロホン及び校正対象の騒音計で測定する。
例2. 荷重発生装置の荷重を,上位の力計及び校正対象の力計で測定する。
(3) 校正対象の計測器によって求めた測定量を,他の計測器によって測定する。
例 校正対象の微量体積計で計り取られた水の量を,校正された天びんで測定する。
3.2.3
校正を行う試験環境の条件 計測器の校正を行う場合の試験環境を,次の二つに区分する。
(1) 計測器を実際に使用する環境のもとで校正を行う。
この場合には,計測器を使用する環境で発生する誤差及び校正の作業の誤差を予測することを必要
とする。
備考 校正に使用する標準について,計測器を使用する環境での標準の表示値の誤差が予測できるこ
とを必要とする。
(2) 特別の環境のもとで校正を行う。
この場合には,計測器を使用する環境で発生する誤差及び校正の作業の誤差のほかに,使用する環
境と校正を行う試験環境との違いによる誤差を予測することを必要とする。
備考1. 特別な試験環境の条件のもとでしか校正できない場合の例
・ 無響室におけるマイクロホンの校正
2. 校正の内容によって,校正を行う試験環境の条件が異なる場合の例
・始業時に行う定点の校正は現場で行うが,1年に1回行う目盛間隔の校正は恒温室で行う。
3.3
校正方式の内容
3.3.1
校正方式で定める事項 校正方式では,次の事項について,4.で示された手順に従って定める。
(1) 校正の種類
(2) 標準及び標準の水準
(3) 校正の間隔及び修正限界
(4) 校正の手順
(5) 校正の作業後の処置
(6) 計測器を使用する条件
(7) 測定の手順
3.3.2
校正の種類 計測器の読みyと標準の値M(真の値とみなされる値)との関係を表す校正のための
関係式の種類により,次によって,校正の種類を定める。
(1) 校正式の基本 yとMとの直線関係を想定した校正のための関係式は,次の二つのことによって成り
立つ。
(a) 定点の校正:yとMからの平均的なずれを修正する。
(b) 傾斜の校正:yとMとの直線関係の感度係数βを修正する。
(2) 校正の種類及びその関係式 校正の種類及びその関係式を,表2に示す。

4
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2 校正の種類及びその関係式
校正の種類
関係式
(a) 点検だけの校正:
修正は行わず,読みをそのまま測定値とする。
y=M
(b) 零点校正:
零点の読みy0で,定点の校正を行う。
y=y0+M
(c) 基準点校正:
基準点M0の読みy0で,定点の校正を行う。
y=y0+ (M−M0)
(d) 目盛間隔校正:
任意の点(その読みがy0である。)を零点として,
傾斜の校正を行う。
y=y0+βM
(e) 零点比例式校正:
零点の読みを零と仮定して,傾斜の校正を行う。
y=βM
(f) 基準点比例式校正:
基準点M0の読みy0で定点の校正を行った後,傾
斜の校正を行う。
y=y0+β (M−M0)
(g) 1次式校正:
読みyの平均値y及び標準の値Mの平均値Mを
用いて,定点の校正及び傾斜の校正を同時に行う。
y=y+β (M−M)
備考1. 高次式及び非線形式による校正については,この規格では取り扱わ
ない。これらの場合,幾つかの範囲に区切って,直線関係を想定し
た校正を行うことができる。
2. 読みをそのまま測定値とするために,目盛を変更又は機械的に調整
することがある。このような場合には,目盛の変更又は機械的な調
整によって修正が行われており,無校正とは区別する。
例1. マイクロメータの零点調整を,かに目スパナでスリーブを回して
行う。
例2. ディジタルスケールの感度係数βの値をカウンタに設定して,表示
値が測定値になるようにする。
(3) 校正の種類の選択 測定範囲,校正の作業の手順,測定の手順など,計測器の使用の実状に即して,
計測器の使用者が,(2)に示した校正の種類の中から必要とするものを選択する。
例 20kg袋詰め工程で,袋詰めの測定に使用しているはかりは,20kg近くのものしか測定しないので,
20kgの分銅を基準点の標準として,基準点比例式の校正を行うこととした。
3.3.3
標準及び標準の水準 校正において値が分かった標準として使用するもの,及びその水準は,次に
よって定める。
(1) 標準の区分 校正に用いる標準を,次の二つに区分する。
(a) 点検のための測定に用いる標準
(b) 修正のための測定に用いる標準
備考1. 点検のための測定に用いる標準のデータを修正に用いるので,改めて修正に用いる標準を用
意する必要がない場合がある。
2. 現場で使う標準で,被測定物と同じような形状・材料で作られた実物を標準として使う場合
がある。
(2) 標準の値付け 標準の値付けは,校正された上位の計測器を用いて行う。標準の値付けには,次の場
合がある。
(a) 標準器に対して,校正前に,上位の計測器によって値付けする。
例1. 基準分銅の値を上位の天びんで決定する。
5
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例2. ブロックゲージの値を上位の測長器で決定する。
例3. 標準電圧発生器の電圧を設定する目盛を校正する。
(b) 校正時に実現した測定量に,上位の計測器によって値付けする。
例1. 校正時に,基準音圧レベルを標準マイクロホンで設定する。
例2. 校正時に,荷重発生装置の荷重を上位の力計で設定する。
例3. 校正対象の微量体積計で計り取られた水の量を,校正された天びんで測定する。
備考1. 測定量の多くの点を示す発生器の値付けは,発生量を設定する目盛と測定量の真の値との関
係から,設定目盛の校正を行うことによって実現する。
2. 校正時に測定量を実現する方法には,測定量の発生器による場合,及び校正対象の計測器に
よる場合がある。校正時に実現した測定量は,上位の計測器で値付けられることによって標
準となる。ただし,備考1.で述べたように,目盛によって測定量の値を実現させる発生器は,
前もって値付けされた標準器の一つである。
(3) 標準の水準
(3.1) 校正に用いる標準の水準を,実際の測定における測定範囲を考慮して,次のいずれかに決める。
(a) 標準1個の場合は,測定範囲の中心に近い値がよい。
(b) 標準2個の場合は,測定範囲の上限及び下限に近い値がよい。
(c) 標準3個以上の場合は,測定範囲の上限及び下限に近い値とその間の値とで水準を決める。
備考 定点の校正を行う場合は,標準1個以上,傾斜の校正を行う場合は標準2個以上を必要とする。
ただし,零点も標準に含めて考える。
(3.2) 点検のための測定に用いる標準の水準の例
・ 最大目盛値の0.8倍の点。
・ 測定範囲の中心点。
・ 零点と測定範囲の中心点との2点。
(3.3) 校正式を求め直す修正作業に用いる標準の水準の例
・ 零点と最大目盛値の間の等間隔の5点。
・ 使用する目盛の上限,下限及び中心の3点。
・ 使用する目盛の上限と下限との2点。
3.3.4
校正の間隔及び修正限界 校正の間隔,及び点検において修正が必要か否かの判断に必要な修正限
界を定める。
校正の間隔は,次に示す点検の間隔と修正の間隔とに区分する。
(1) 点検の間隔 計測器の修正が必要であるか否かを知るために行われる点検と点検との間の時間。
(2) 修正の間隔 点検の結果,計測器を修正する場合の,修正と修正との間の時間。
備考 時間は,校正の実態に即した単位で表してよいが,この規格では生産個数で表す。
校正の間隔及び修正限界の定め方は,附属書1による。
備考 校正の間隔は,計測器の使用条件,定点の校正,傾斜の校正など,校正の種類によって異なる。
例1. ある計測器は,午前・午後の作業開始時に日常的な作業として,零点の修正を必ず行っている。
この場合は修正だけを行う場合に相当しており,修正の間隔は半日に1回となる。
例2. ある計測器の6か月ごとの定期的な校正において,まず,標準5個を用いて計測器を点検する。
点検において,誤差が小さい場合はそのまま合格とし,誤差が大きい場合は,修正において機
械的な調整をしている。現行の校正方式における実績として,調整したもののうち,約半数は6

6
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
か月後の校正時に,また残りの半数は1年後の校正時に修正している。この場合,点検の間隔は
6か月,平均的な修正の間隔は9か月になる。
3.3.5
校正の手順 校正の手順及び校正のための関係式を求め直す計算手順を定める。
点検及び修正の作業の一般的な手順並びに注意事項を次に示す。
なお,校正における測定手順は,個々の計測器の測定方法による。
(1) 点検の手順
(1.1) 点検の一般的な手順及び注意事項は,次による。
手順1 定められた標準を測定し,次の読みのデータを得る。
標準:Mi (i=1, …, k)
読み:yij (i=1, …, k ; j=1, …, n)
手順2 現行の校正式によって,測定値(3)Mˆij(Miの推定値)及びその誤差eijを,次◯
aの及び◯
bの計
算から求める。
注(3) 計測器の目盛によって読み取られた値yは読みであり,校正式に基づいて推定された
測定量の真の値の推定値Mˆが測定値である。
◯
a 測定値Mˆijの計算は,校正の種類によって異なり,表3による。
表3 校正の種類による測定値Mˆijの計算式
校正の種類
測定値Mˆijの計算式
(a) 点検だけの校正
ij
ij
y
M=
ˆ
(b) 零点校正
0
ˆ
y
y
M
ij
ij
−
=
(ただし,y0は零点の読み)
(c) 基準点校正
(
)
0
0
ˆ
y
y
M
M
ij
ij
−
+
=
(ただし,y0は基準点M0
の読み)
(d) 目盛間隔校正
βˆ
ˆ
0
y
y
M
ij
ij
−
=
(ただし,y0は始点の読み)
(e) 零点比例式校正
βˆ
ˆ
ij
ij
y
M=
(f) 基準点比例式校正
βˆ
ˆ
0
0
y
y
M
M
ij
ij
−
+
=
(ただし,y0は基準点M0の
読み)
(g) 1次式校正
βˆ
ˆ
y
y
M
M
ij
ij
−
+
=
備考 βの推定値をβˆと表記する。
備考 修正によって計測器の目盛を変更若しくは調整してある場合,無校正の場合,又は校
正のための関係式の定数が求められていない最初の点検の場合,測定値Mˆijの計算は,
式(1)による。
ij
ij
y
M=
ˆ
·················································································· (1)
◯
b 誤差の計算は,式(2)による。
i
ij
ij
M
M
e
−
=ˆ
············································································ (2)
手順3 計算された誤差eijをあらかじめ定めてある修正限界Dと比較する。誤差eijが,修正限界D
7
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を超えた場合には,(2)の修正を行う。誤差eiiが修正限界Dを超えない場合には,現行の
校正式を採用する。
(1.2) 零点比例式校正の例を,次に示す。
抵抗計の点検の例
手順1 抵抗計の点検のために,標準M=10.00 (kΩ) を測定し,読みy=9.98を得た。
手順2 抵抗計は零点比例式校正を行って使用している。現時点での感度係数の値はβˆ=0.993であ
るから,測定値Mˆは,
993
.0
98
.9
ˆ=
M
=10.05 (kΩ)
となり,また,その誤差eは,
e=10.05−10.00
=0.05 (kΩ)
となる。
手順3 標準M=10.00 (kΩ) の場合,抵抗計の修正限界D=0.04 (kΩ) である。点検のための測定の
結果,誤差e=0.05 (kΩ) が修正限界D=0.04 (kΩ) を超えているので,校正式を求め直す
ために修正を行うこととした。
(1.3) 基準点比例式校正の例を,次に示す。
はかりの点検の例
手順1 はかりの点検のために,標準M=20.10 (kg) を測定し,読みy=20.11を得た。
手順2 はかりは,M0=20.00 (kg) を基準点とした基準点比例式校正を行っている。現時点での感
度係数は
βˆ=1.001,基準点の読みはy0=19.99であるから,測定値Mˆは,
001
.1
99
.
19
11
.
20
00
.
20
ˆ
−
+
=
M
=20.12 (kg)
となり,また,その誤差eは,
e=20.12−20.10
=0.02 (kg)
となる。
手順3 はかりの修正限界D=0.03 (kg) である。点検のための測定の結果,誤差e=0.02 (kg) が修
正限界以内なので,修正は行わないでそのまま使用する。
(2) 修正の手順
(2.1) 修正の一般的な手順及び注意事項を,次に示す。
手順1 定められた標準を測定し,次の読みのデータを得る。
標準:Mi (i=1, …, k)
読み:yij (i=1, …, k ; j=1, …, n)
備考 定点の校正だけの場合,k≧1とする。
傾斜の校正を含む場合,k≧2とする。
手順2 校正のための関係式の定数を計算し,校正式を定める。

8
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
校正式の定数の計算式は校正の種類によって異なり,校正式の求め方は表4による。
表4 校正の種類による校正式の求め方
校正の種類
校正式の求め方
(a) 零点校正及び基準点校正
①零点又は基準点M0での読みの平均
0y次のように求め
る。
n
y
y
j
j0
0
Σ
=
②校正式を次のように求める。
(
)
0
0
y
y
M
M
−
+
=
ただし,零点校正の場合は,M0=0とする。
備考 基準点での読み
0yは,①による他,あらかじ
め定めた方法によって計算する。基準点での
定点校正の方法については,附属書3で規定
する。
(b) 目盛間隔校正
①始点での読みy0を求める。
②感度係数βを次のように求める。
(
)
2
0
ˆ
i
i
i
ij
j
i
M
n
M
y
y
Σ
−
Σ
Σ
=
β
③校正式を次のように求める。
βˆ0y
y
M
−
=
(c) 零点比例式校正
①感度係数βを次のように求める。
2
ˆ
i
i
ij
i
j
i
M
n
y
M
Σ
Σ
Σ
=
β
②校正式を次のように求める。
βˆ
y
M=
(d) 基準点比例式校正
(M0が基準点)
①基準点M0での読みの平均
0yを次のように求める。
n
y
y
j
j0
0
Σ
=
②感度係数βを次のように求める。
(
)(
)
(
)2
0
0
0
ˆ
M
M
n
M
M
y
y
i
i
i
ij
j
i
−
Σ
−
−
Σ
Σ
=
β
③校正式を次のように求める。
βˆ0
0
y
y
M
M
−
+
=
備考 基準点での読み
0yは,①による他,あらかじ
め定めた方法によって計算する。基準点での
定点校正の方法については,附属書3で規定
する。

9
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
校正の種類
校正式の求め方
(e) 1次式校正
①すべての読みの平均y,を次のように求める。
nk
y
y
ij
j
iΣ
Σ
=
②感度係数βを次のように求める。
(
)
(
)2
ˆ
M
M
n
y
M
M
i
i
ij
i
j
i
−
Σ
−
Σ
Σ
=
β
ただし,
k
M
M
i
Σ
=
③校正式を次のように求める。
βˆ
y
y
M
M
−
+
=
(2.2) 零点比例式校正の例を次に示す。
抵抗計の修正の例
手順1 抵抗計の修正のための測定を行い,次のデータを得た。
標準M1=10.00 (kΩ) 読みy1=9.99,
標準M2=40.00 (kΩ) 読みy2=40.08
手順2 抵抗計の零点比例式校正の場合の校正のための関係式の計算を行う。
①感度係数のβを求める。
(
)
2
2
00
.
40
00
.
10
1
08
.
40
00
.
40
99
.9
00
.
10
ˆ
+
×
×
+
×
=
β
=1.002 1
②校正式を求めると,次のようになる。
1
002
.1
y
M=
(2.3) 基準点比例式校正の例を,次に示す。
はかりの修正の例
手順1 はかりの修正のための測定を行い,次のデータを得た。
標準M1=20.00 (kg) 読みy1=19.99,
標準M2=21.00 (kg) 読みy2=21.01,
標準M3=22.00 (kg) 読みy3=22.01
手順2 はかりのM1=20.00kgを基準点M0とする基準点比例式校正の場合の校正のための関係式の
計算を行う。
①基準点M0の読みは
99
.
19
0=
y
である。
②感度係数βを求める。
(
)(
)(
)(
)
(
)
(
)
[
]
012
.1
00
.
20
00
.
22
00
.
20
00
.
21
1
00
.
20
00
.
22
99
.
19
01
.
22
00
.
20
00
.
21
99
.
19
01
.
21
ˆ
2
2
=
−
+
−
×
−
×
−
+
−
×
−
=
β
③校正式を求めると,次のようになる。
021
.1
99
.
19
00
.
20
−
+
=
y
M
10
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.3.6
校正の作業後の処置 校正の作業を行った後の処置について定める。
校正式を求め直す修正を行った場合の処置は,新たに求められた校正式又は校正表を計測器に添付する,
計測器の調整をする,校正表に有効期限を明記する,次の校正時期を明記する,などを行う。
例 抵抗計の修正を行ったときには,読みと測定値との関係を表す校正表を作成し,次回の校正の時
期をその表に書き込むことにした。
3.3.7
校正の間隔内の計測器の使用条件による誤差 計測器を使用する環境条件の,校正の間隔内におけ
る変化による誤差を予測して,計測器の使用条件の範囲を定める。
環境条件の変化による誤差が大きくなると予測されるときには,次に従って対策を決める。
(1) 使用条件の影響が分からない場合は,附属書2によって実験を行い,その影響の大きさを求め,対策
を決める。
(2) 予測した使用条件の影響が無視できず,それに対する対策が可能な場合には,対策を行う。
(3) 予測した使用条件の影響及び対策の結果を合わせて,附属書2及び3によって,測定の誤差の大きさ
を推定し,対策の妥当性の判断を行う。
備考 使用条件に対する対策には,次のようなものがある。
(a) 制御可能な使用条件について,その影響を抑えるため,条件を固定する,又は校正間隔内
の変動の幅を狭くするように制御する。これらの場合には,限定した条件を使用条件とし
て設定する。使用条件を限定した場合の誤差の求め方は,附属書2による。
(b) 制御が難しい使用条件について,その影響をできるだけ避けるために,補助測定による補
正を行う。この場合には,補正式を明記する。このような補正は,広義の校正と考えられ
る。
(c) 使用条件の固定,又は制御を行わない場合には,その条件は誤差の原因となる。
例 計測器の使用条件の例
温度:10〜30℃(5℃以上変化したときは修正を行う。)
湿度:40〜80%
電源電圧:70〜110V
温度の条件は,10〜30℃で使用可能であるが,温度変化が5℃以上あった場合には,その影響
が無視できないので,改めて校正するという対策を取って,計測器を使用することを意味してい
る。
3.3.8
測定の手順 校正をした計測器を使用して,未知試料を測定したときの測定値を求める手順を定め
る。
測定において測定値を求める一般的な手順及び注意事項は,次による。
手順1 未知試料の測定を行い,計測器の目盛による読みyを得る。
手順2 読みyを現行の校正式に代入して,測定値Mˆを計算する。
測定値
ij
Mˆの計算式は,校正の種類によって異なり,表3による。
手順3 測定値を次のように表示する。
T
M
σˆ
2
ˆ±
ただし,
2
ˆT
σは,4.の手順6で求められる誤差分散の推定値とする。
例 基準点比例式校正の例
電圧計による未知試料の測定の例
手順1 電圧計による未知試料の測定における読み
11
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
y=1.754
を得た。
手順2 電圧計は1Vを基準点とする基準点比例式校正をして使用している。現時点での基準点
の読みは
0y=1.002,感度係数βˆ=1.001であるから,未知試料の真の値の推定値(測
定値)は,校正式を用いて,
()
V
751
.1
001
.1
002
.1
754
.1
00
.1
ˆ
=
−
+
=
M
となる。
手順3 電圧計の誤差分散を用いて,未知試料の測定値を次のように表示した。ただし,T
σˆは,
4.の手順6によって求められている。
1.751±0.005 2 (V)
4. 校正方式の定め方 3.に規定された内容について,個々の計測器に対して校正方式を定める。
個々の計測器の校正方式の定め方の一般的な手順及び注意事項は,次による。
手順1 対象とする計測器の現在の使用状態を調べる。
使用状態には,例えば,測定対象の製品又は工程,測定範囲,測定場所の条件,使用頻度,校正
方法,校正の間隔,必要な精度,対応する製品の許容差などがある。
備考 同一の機種であっても,測定対象又は使用状態が異なれば,測定の誤差は異なる場合があ
る。
例 電圧計A1及びA2は同一形式の計測器である。A1は回路の調整工程において,測定範囲が10mV
〜3.16V,正確率が1%の測定に使用している。
また,A2は製品の検査工程において,測定範囲が0.9〜1.1V,正確率が0.5%の測定に使用し
ている。
手順2 計測器の使用状態に合わせ,校正の種類を仮定する。
校正の種類は,測定範囲,現実の校正作業,測定の手順など,使用者の実状に即して,使用者が
選択し,仮定する。
備考 手順3以下の実験及び検討の結果によって,校正式の種類を変えることもある。
例 回路の調整に用いる電圧計A1については0〜3.2Vの範囲で1次式校正を,製品検査に用いる
A2については1Vにおける基準点校正を実状に即して選択した。
手順3 附属書1に従い,使用状態における校正の間隔及び点検における修正限界を求める。
附属書1によって,最適な点検の間隔及び最適な修正限界が求められ,その場合の平均的な修正
の間隔が予測される。
備考 同一の機種であっても,測定対象,校正の内容など,使用する条件によって,校正の間隔
又は修正限界は異なる場合がある。
例 附属書1に従い,校正の間隔を求めたところ,最適な点検の間隔はn=150(個),最適な修正
限界はD=3 (mV) となり,平均的な修正の間隔はu=900(個)と予測された。
手順4 附属書2に従い,校正の間隔内での,計測器の使用における誤差の大きさを,実験によって求め
る。
使用における誤差の大きさは,分散の形で表示する。
Mˆ
12
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
実験結果から,影響量に対する対策を検討する場合は3.3.7による。
例 附属書2に従い,使用における誤差の大きさを求めたところ,使用における誤差分散は
2ˆσ=
3.11 (mV)2となった。
手順5 附属書3に従い,校正の作業の誤差の大きさを,実験によって求める。
校正の作業の誤差の大きさは,分散の形で表示する。
備考 測定対象が標準と同じようなものであり,使用条件が同じであれば,標準を測定したとき
の誤差の大きさは実物を測定したときの誤差の大きさと同じ程度になることから,特に附
属書3の実験を行わなくてもよい。
例 附属書3に従い校正の作業の誤差を求めたところ,校正の作業の誤差分散は
2
ˆc
σ=3.03 (mV)2
となった。
手順6 校正対象の計測器による測定の誤差の大きさを表す誤差分散の推定値σT2を,式(3)によって求める。
2
0
2
2
2
ˆ
ˆ
ˆ
ˆ
σ
σ
σ
σ
+
+
=
c
T
·································································· (3)
ここに,
2
ˆT
σ: 測定の誤差の大きさを表す誤差分散の推定値
2ˆσ: 使用における誤差分散の推定値
2
ˆc
σ: 校正の作業の誤差分散の推定値
2
0ˆσ: 標準の表示値の誤差分散の推定値
ただし,標準の表示値の誤差が不明の場合は,
0ˆσ=0とする
備考 測定値Mˆの測定の誤差eを式(4)で推定する。
T
e
σˆ
2
±
=
·················································································· (4)
ここに, e: 測定の誤差
ただし,手順5において標準と測定対象が同じようなもので,特に,校正作業の誤差の
大きさを求めなかった場合は,近似的に測定の誤差eAを式(5)で推定する。
σˆ
3
±
=
A
e
················································································· (5)
ここに, eA: 近似的な測定の誤差
測定の誤差は,測定量の真の値のおおよその存在範囲を示す。
例 電圧計の校正の作業の誤差分散は
2
ˆc
σ=3.03 (mV)2,使用における誤差分散は
2ˆσ=3.11 (mV)2
であった。標準の表示値の誤差分散を附属書4に従い求めたところ,
2
0ˆσ=0.65 (mV)2となっ
た。したがって,電圧計の測定の誤差の大きさを表す誤差分散
2
ˆT
σは,
2
ˆT
σ=3.11+3.03+0.65
=6.79 (mV)2
となる。
また,測定の誤差は,
65
.0
03
.3
11
.3
2
ˆ
2
+
+
±
=
±
T
σ
=±5.21 (mV)
近似的には,
11
.3
3
ˆ
3
±
=
±σ
=±5.29 (mV)
13
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
となる。
手順7 手順6で求めた測定の誤差の大きさから,校正方式の妥当性を判断し,次によって校正方式を定
める。
(1) 妥当性の判断のために,式(6)によって測定損失の大きさによる定量的な検討を行い,十分であれば,
校正方式を定める。
b
A
L
T+
=
2
2σ
⊿
········································································· (6)
ここに,
L: 測定損失の大きさ
A: 測定対象の製品を不合格としたときの損失(以下,不合格損失
という。)
⊿: 測定対象の製品の許容差
b: 製品1個当たりの測定のコスト
式(6)の右辺の二つの項が同じ程度の大きさにならないときには,(2)において再検討を行う。
例 電圧計について,A=3 000円,⊿=30 (mV),b=21円,また,手順6の誤差分散は
2
ˆT
σ=6.79 (mV)2
であるから,測定の損失の大きさLは,
L=22.6+21
=43.6(円)
となり,損失自体は余り大きくなく,また,右辺の第2項は同じ程度であったので,校正方式
は妥当と判断した。
(2) 検討の結果,妥当性が不十分な場合,次によって校正方式又は測定方法を再検討する。
(a) 使用における誤差が大きいために,測定の誤差分散が大きくなっている場合には,使用条件又は測
定方法の改善のための検討を行う。
(b) 校正の作業の誤差が大きいために,測定の誤差分散が大きくなっている場合には,校正方式の面か
らの検討を行う。
(c) 標準の表示値の誤差が大きいために,測定の誤差分散が大きくなっている場合には,標準の検討を
行う。

14
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1 校正の間隔及び修正限界の定め方
1. 適用範囲 この附属書は,計測器の校正の間隔及び修正限界を定めるための方法の一般的事項につい
て規定する。
2. 校正の間隔及び修正限界の定め方
2.1
校正の間隔及び修正限界を定める手順 校
正の間隔及び修正限界を定める場合の一般的手順
及び注意事項は,次による。
手順1 測定対象の製品の許容差⊿,及び対応す
る製品の不合格損失Aを次のように定め
る。
(1) 測定対象となる製品又は工程条件の許容差⊿
を定める。
備考 工程条件の許容差は,製品の許容差に
対応する工程条件の許容される値の目
標値からの差とする。
(2) 測定対象となる製品又は工程で作られる製品
が,製品の許容差を外れたときに生じる損失
の平均を,製品の不合格損失A(円)として
定める。
手順2 現行における点検の間隔n0及び点検のコ
ストBを次のように定める。
(1) 現行における,計測器の点検の間隔n0(個)
を定める。
(2) 点検のための測定に要するコストを,点検の
コストB(円)として定める。点検のコスト
は,点検のために使用する計測器のコスト,
点検のための測定に用いる標準のコスト,点
検のための人件費などを含む。
適用例
2.ʼ 校正の間隔及び修正限界の定め方 精密抵抗
器を製造する工程で,抵抗値の測定に使用してい
るディジタル抵抗計の校正の間隔及び修正限界を
定める。
2.1ʼ 校正の間隔及び修正限界を定める手順
手順1ʼ 測定対象の製品の許容差⊿,及び対応す
る製品の不合格損失Aを次のように定
める。
(1ʼ) 測定対象の製品の許容差⊿
製造される精密抵抗器の許容差⊿は±0.1%
とする。
⊿=0.1 (%)
(2ʼ) 製品の不合格損失A
精密抵抗器が許容差を超えたときは廃棄処分
となり,その不合格損失Aは1個当たり200
円とする。
A=200(円)
手順2ʼ 現行における点検の間隔n0及び点検のコ
ストBを次のように定める。
(1ʼ) 現行における点検の間隔n0
現在,精密抵抗器は月産30 000個の生産量で
ある。抵抗値の測定に使用するディジタル抵
抗計の点検の間隔n0は毎月1回であるから,
30 000個である。
n0=30 000(個)
(2ʼ) 点検のコストB
ディジタル抵抗計の点検に用いる標準抵抗器
の年間のコストは60 000円,この点検に用い
る割合は5%である(使用比率5%)。年間12
回の点検に使用したとすれば,1回の点検

15
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順3 現行における修正限界D0,平均修正間隔
u0及び修正のコストCを次のように定め
る。
(1) 現行における計測器の修正限界D0を定める。
(2) 現行における計測器の平均的な修正の間隔u0
(個)を定める。
(3) 校正式を求め直す修正に要するコストを,修
正のコストC(円)として定める。修正のコ
ストは,修正に使用する計測器のコスト,修
正のための測定に用いる標準のコスト,修正
のための人件費などを含む。
当たりの標準のコストB1は次のとおりとな
る。
()
円
250
12
05
.0
000
60
1
=
×
=
B
点検に必要な時間を30分,1時間の人件費を
4 000円とすると,点検のための人件費B2は,
B2=4 000×0.5=2 000(円)
となる。
したがって,点検のコストBは
B=B1+B2=250+2 000
=2 250(円)
となる。
手順3ʼ
現行における修正限界D0,平均修正間
隔u0及び修正のコストCを次のように
定める。
(1ʼ) 現行における計測器の修正限界D0
現行のディジタル抵抗計の修正限界D0は,±
0.01%である。
D0=0.01 (%)
(2ʼ) 現行における計測器の平均的な修正の間隔u0
現行のディジタル抵抗計の平均修正間隔u0
は6か月に1回であるから,生産個数で表す
と次のとおりになる。
u0=30 000×6
=180 000(個)
(3ʼ) 校正式を求め直す修正のコストC
ディジタル抵抗計の修正に用いる標準抵抗器
の年間のコストは,60 000円で,この修正に
用いる割合は5%である(使用比率5%)。年
間2回の修正に使用したとすれば,1回の修
正当たりの標準のコストC1は次のとおりと
なる。
()
円
500
1
2
05
.0
000
60
1
=
×
=
C
修正に必要な時間を2時間,1時間の人件費
を4 000円とすると修正のための人件費C2は,
C2=4 000×2=8 000(円)
となる。
16
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順4 最適な点検の間隔n(個),及び最適な
修正限界Dの計算値を次のように求める。
0
0
2
D
A
B
u
n
⊿
×
=
(個)
41
2
0
2
0
3
×
×
=
⊿
u
D
A
C
D
手順5 手順4で計算上求められた最適な点検の
間隔,及び最適な修正限界の計算値につ
いて,実際の作業がやりやすくなるよう
に,その値を管理上分かりやすい値に設
定し,これらを最適な点検の間隔,及び
最適な修正限界とする。
したがって,修正のコストCは
C=C1+C2=1 500+8 000
=9 500(円)
となる。
手順4ʼ
最適な点検の間隔n,及び最適な修正限
界Dの計算値を次のように求める。
計算に必要な値をまとめると,
⊿=0.1 (%),
A=200(円),
B=2 250(円),
C=9 500(円),
n0=30 000(個),
D0=0.01 (%),
u0=180 000(個),
であるから,最適な点検の間隔の計算値
nを次のように求める。
01
.0
1.0
200
250
2
000
180
2
×
×
×
=
n
=20 124(個)
最適な修正限界の計算値Dを次のよう
に求める。
41
2
2
1.0
000
180
01
.0
200
500
9
3
×
×
×
=
D
=0.005 30 (%)
手順5ʼ 最適な点検の間隔,及び最適な修正限界
を管理上分かりやすい値に設定する。
月産30 000個であるから,実働20(日
/月)とすると1日の生産量は,
20
000
30
=1 500(個/日)
となる。最適な点検の間隔nを1日当た
りの生産量で割ると
500
1
124
20
=13.4(日)
となるが,管理を容易にするため,これ
を10日(2週間)に設定する。
したがって,

17
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順6 手順5で設定した最適な値を用いて,予
測される平均的な修正の間隔uを,次の
ように求める。
0
2
0
2
u
D
D
u=
備考 この値は,修正限界を設定したと
きの,平均的な修正の間隔の予測
値である。
uがnより小さくなった場合は,u
=nとする。
2.2
校正の間隔及び修正限界の決定 2.1の手
順によって求められた点検の間隔,及び修正限界
を用いた校正の間隔を決定する。ただし,新しい
校正の間隔,及び修正限界を用いた校正の実績が
2.1の手順6による予測と大きく異なる場合には,
その実績の値に基づいて,改めて最適な点検の間
隔n,最適な修正限界Dを求め直す。
n=1 500×10
=15 000(個)
最適な修正限界の計算値D=0.005 30
(%) を管理しやすい値に設定し,
D=0.005 (%)
とする。
手順6ʼ 平均的な修正の間隔uを予測する。
平均的な修正の間隔uは,
2
2
01
.0
005
.0
=
u
×180 000
=45 000(個)
500
1
000
45
=
u
(日)
=30(日)
と予測される。
2.2ʼ 校正の間隔及び修正限界の決定 ディジタ
ル抵抗計の点検の間隔は10日(2週間),修正限
界は0.005 (%) と設定する。このとき,平均的な
修正の間隔は生産個数45 000個,実働日で約30
日と予測される。校正の間隔,及び修正限界を変
更し,計測器の校正の実績を調べたところ,平均
修正間隔は実働日33日となり,予測とほぼ一致し
た。

18
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2 計測器の使用における誤差の大きさを実験によって求める方法
1. 適用範囲 この附属書は,校正の間隔内における計測器の使用条件又は環境条件によって発生する,
校正では取り除けない使用における誤差の大きさを,あらかじめ実験によって求める方法の一般的事項に
ついて規定する。
2. 誤差の大きさを求める実験の方法
2.1
信号因子及びその水準の選び方 実際に測
定する対象の測定量を信号因子Mとする。信号因
子の水準は,計測器を使用する目盛範囲において,
その上下限近くの値及びその中間の値を選び,間
隔hMの等間隔の3水準に取る。
備考1. 信号因子の水準の絶対値は必ずしも
明らかでなくてもよいが,その場合,
水準の間隔は等間隔であること,及
び実験中は等間隔の状態が再現でき
ることが必要である。
2. 附属書2においては,1次式校正を
想定している。
2.2
誤差因子及びその水準の選び方 現場での
測定作業の条件の中で,測定量以外の,測定結果
に差を与えると思われる条件を,誤差因子 (A, B,
…) として取り上げる。
(1) 誤差因子の数 誤差因子の数は,直交表L18
に割り付けられるように,できるだけ七つ以
内とする。ただし,六つの因子が3水準の場
合,他の一つの因子は2水準の因子とする。
因子が七つを越えそうな場合には,因子の影
響の傾向によって,傾向の異なる代表的な誤
差因子を選び,直交表L18に割り付けられる
ようにする。
適用例
2.ʼ 誤差の大きさを求める実験の方法 (ステー
ジの送りの使用における誤差の場合) XY移動型
ステージは,XY各方向にリニアエンコーダが付
いており,その移動量がディジタルカウンターに
表示される。このXY移動型ステージのX方向の
送りについて,校正の間隔内での使用における誤
差の大きさを求める。
2.1ʼ 信号因子及びその水準の選び方 ステージ
のX方向のストロークは150mmあり,このステ
ージ上に乗せて測定する試料は数mmから150mm
近くのものまであるので,全ストロークを対象と
し,信号因子の水準を次の3水準とする。
M1:25mm,M2:75mm,M3:125mm
信号因子の水準を実現させるものとして,精度
的に上位と考えられるレーザ測長器を使い,ステ
ージを移動させる。その時のステージのカウンタ
ーの読みをデータとして読み取る。
2.2ʼ 誤差因子及びその水準の選び方
(1ʼ) 誤差因子の選択 実際にステージが使用され
る環境条件のうち,測定結果に影響を与える
と考えられる,次の5条件を誤差因子として
取り上げる。
A:室温
B:ステージの傾斜角度
C:試料の質量
D:試料を置く位置
E:ステージ上の高さ

19
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 直交表L18には,2水準の因子一つ,3
水準の因子七つを割り付けることが可
能である。したがって,信号因子及び
誤差因子を併せて,L18に割り付けられ
るように因子を選ぶ。
(2) 誤差因子の水準の設定方法 誤差因子の水準
は3水準,又は2水準を取り上げ,次のよう
な設定を行う。
(2.1) 誤差因子の水準が量的に変わる因子(計量
的な因子という。)の場合
(a) 3水準の場合・水準の間隔
σ
2
3
=
h
とするすな
わち,
第1水準:
,
2
3σ
−
m
第2水準:m,
第3水準:
,
2
3σ
+
m
と設定する。
(b) 2水準の場合,間隔h=2σとする。すなわ
ち,
第1水準:m−σ,
第2水準:m+σ,
と設定する。
(c) 正側だけに2水準をとる場合,
第1水準:m,
第2水準:
,
2σ
+
m
と設定する。
ただし,mは校正の間隔内の誤差因子の
平均値,σは校正の間隔内の誤差因子のば
らつきの標準偏差である。
(2.2) 誤差因子が計量的でない因子の場合 3水
準を取る場合には,第1・第3水準は実際に
起こり得る使用限界と平均的な使用条件と
の幅の半分に近い条件,第2水準は平均的
な使用条件とする。2水準を取る場合には,
3水準の第2水準がない場合と同じにする。
(2ʼ) 誤差因子の水準の設定
(2.1ʼ) 3水準の誤差因子の水準の設定 誤差因子
として取り上げた室温Aの平均値mAが
24℃,室温の校正の間隔内のばらつき(標
準偏差σ)が1.6℃であるので,室温の3水
準を次のように設定した。
誤差因子(室温)
A1:
℃
≒22
6.1
2
3
24
×
−
A2: 24℃
A3:
℃
≒26
6.1
2
3
24
×
+
(2.2ʼ) 計量的でない誤差因子の水準の設定 誤差
因子として取り上げた,ステージ上の試料
の置く位置の水準は,よく使われる中央を
第2水準として,他の水準は,右側と中央
の中間点及び奥と中央の中間点に設定した。
誤差因子(場所)D1:右側
D2:中央
D3:奥
20
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考1. 誤差因子は,できるだけ意図的に水
準値が設定できる計量的な因子であ
ることが望ましい。ただし,反復な
どのように意図的に水準値が設定で
きない因子を取り上げてもよい。
2. 誤差因子の水準の幅を,実際に起こ
り得る現場の条件より大きめで,設
定しやすい値に選び実験した後,4.
の手順によって実際の使用における
誤差を求めることもできる。
附属書2表1 信号因子及び誤差因子の水準
因子
水準
1
2
3
A
−hA
+hA
M
−hM
0
+hM
B
−hB
0
+hB
C
−hC
0
+hC
D
−hD
0
+hD
E
−hE
0
+hE
F
−hF
0
+hF
G
−hG
0
+hG
備考 Mは信号因子,A, B ,…, Gは誤差因子を表す。ま
た,3水準については第2水準を平均的な条件に
とり,これを零とおき,第2水準を中心に第1
水準・第3水準を±hで表した。
2.3
因子の割付け 実験の因子を,附属書2表2
の直交表L18の列番に対して割り付ける。直交表
への因子の割付けにおいて,因子と列番との対応
は任意でよいが,列番1には,2水準の因子を割
り付ける。
なお,列番1〜8のすべての列を用いなくてもよ
い。
備考 因子数が多い場合又は多水準の因子が
ある場合には,L18に限らず,L36など
の他の直交表を用いることもある。
附属書2表2 信号因子及び誤差因子を割り付け
た直交表L18及びデータ
行番
因子 A M B C D E F G データ
列番 1
2
3
4
5
6
7
8
1
1
1
1
1
1
1
1
1
y1
2
1
1
2
2
2
2
2
2
y2
3
1
1
3
3
3
3
3
3
y3
4
1
2
1
1
2
2
3
3
y4
以上のように,因子の水準を設定した。
信号因子,誤差因子の水準をまとめると,
附属書2表1ʼとなる。
附属書2表1ʼ ステージの送りの実験における信
号因子及び誤差因子の水準
因子
水準
1
2
3
M:ステージ移動量
25mm
75mm
125mm
A:室温
22℃
24℃
26℃
B:ステージの傾斜角度 前3°
水平
右3°
C:試料の質量
1kg
2kg
4kg
D:試料を置く位置
右側
中央
奥
E:ステージ上の高さ
30mm
50mm
70mm
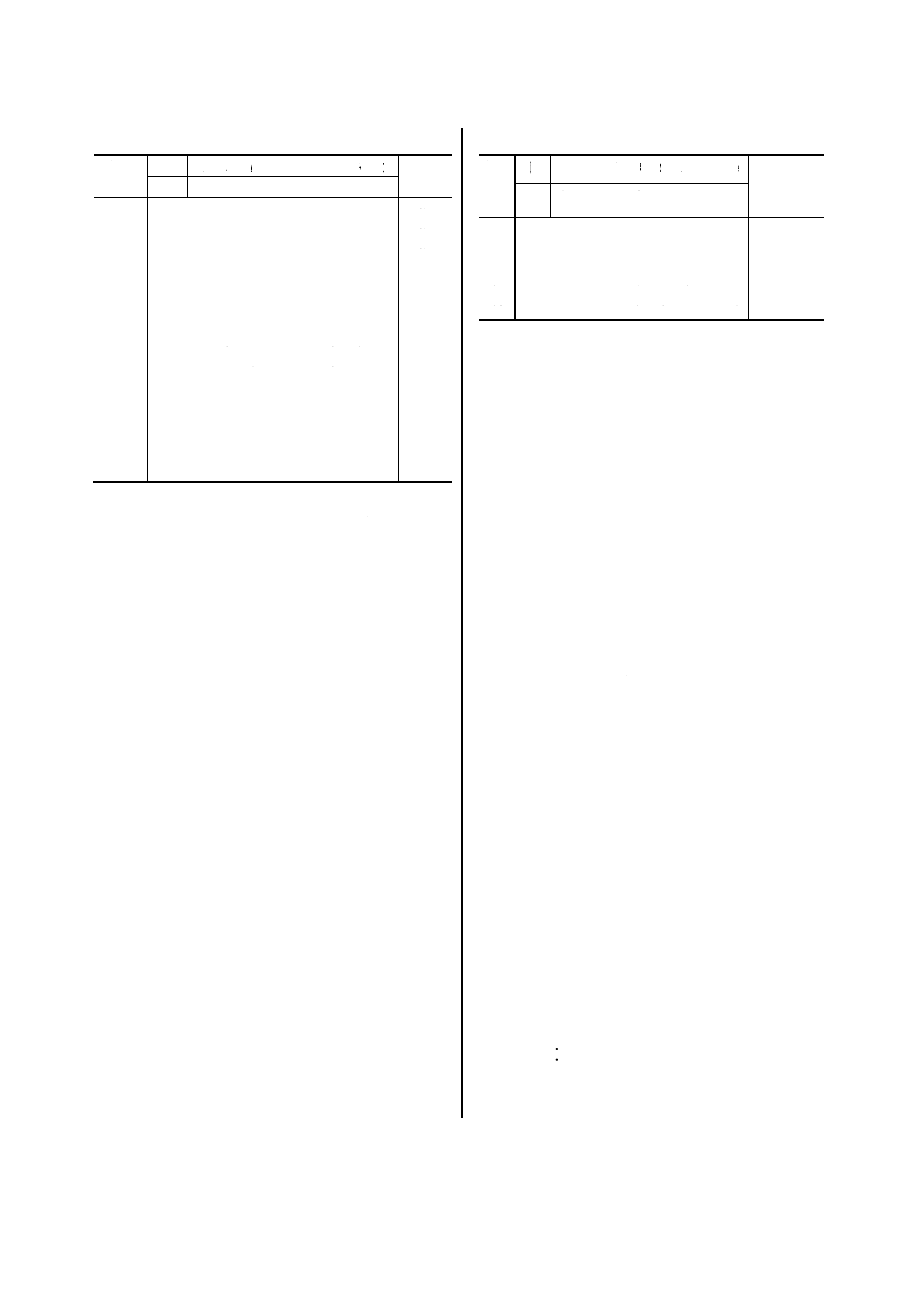
2.3ʼ 因子の割付け 実験に取り上げた附属書2
表1ʼの因子を,附属書2表2'のように,直交表L18
に割り付けた。
附属書2表2ʼ ステージの送りの実験における因
子の割付け及び読みのデータ
行番 因子 e M A B C D E e ステージ・
カウンター
の読み
列番 1 2
3 4 5 6
7 8
1
1 1
1 1 1 1
1 1
24.998 5
2
1 1
2 2 2 2
2 2
24.998 5
3
1 1
3 3 3 3
3 3
24.996 0
4
1 2
1 1 2 2
3 3
74.999 0
5
1 2
2 2 3 3
1 1
74.999 0
6
1 2
3 3 1 1
2 2
74.996 5
7
1 3
1 2 1 3
2 3
124.997 0
8
1 3
2 3 2 1
3 1
124.996 5
9
1 3
3 1 3 2
1 2
124.993 5
10
2 1
1 3 3 2
2 1
24.997 0
11
2 1
2 1 1 3
3 2
24.995 5
12
2 1
3 2 2 1
1 3
24.995 0
13
2 2
1 2 3 1
3 2
74.995 0
21
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
行番
因子 A M B C D E F G データ
列番 1
2
3
4
5
6
7
8
5
1
2
2
2
3
3
1
1
y5
6
1
2
3
3
1
1
2
2
y6
7
1
3
1
2
1
3
2
3
y7
8
1
3
2
3
2
1
3
1
y8
9
1
3
3
1
3
2
1
2
y9
10
2
1
1
3
3
2
2
1
y10
11
2
1
2
1
1
3
3
2
y11
12
2
1
3
2
2
1
1
3
y12
13
2
2
1
2
3
1
3
2
y13
14
2
2
2
3
1
2
1
3
y14
15
2
2
3
1
2
3
2
1
y15
16
2
3
1
3
2
3
1
2
y16
17
2
3
2
1
3
1
2
3
y17
18
2
3
3
2
1
2
3
1
y18
2.4
実験の実施 直交表の行によって決められ
た信号因子,及び誤差因子の組合せの条件におい
て,信号因子Mについて測定を行い,Mに対応す
る計測器の読みyi(iは行番号)を得る。行の実験
の順序は,ランダム化するが,実験のやりやすい
順序で行ってもよい。
3. 使用における誤差の大きさの求め方 2.の実
験において2.2 (2)に従って因子の水準を設定した
場合,次の手順によって計算を行い,使用におけ
る誤差の大きさを求める。
備考 任意の水準設定をして実験を行い,誤
差を換算によって求めようとする場合
の計算手順は,4.による。
手順1 読みのデータを偏差データに変換する。
直交表i行において,信号因子の水準Mj
を測定したときの読みのデータyiについ
て,偏差データ (yi−Mj) を計算し,改め
てyiとおき,附属書2表3を作成する。
備考 必ずしも偏差データに変換する必
要はないが,多くの場合,偏差デ
ータに変換して計算を行うことに
よって,計算の誤差を小さくする
ことができる。
行番 因子 e M A B C D E e ステージ・
カウンター
の読み
列番 1 2
3 4 5 6
7 8
14
2 2
2 3 1 2
1 3
74.994 0
15
2 2
3 1 2 3
2 1
74.990 5
16
2 3
1 3 2 3
1 2
124.994 5
17
2 3
2 1 3 1
2 3
124.992 0
18
2 3
3 2 1 2
3 1
124.991 5
備考 割付けにおいて,1列及び8列には割り付ける因
子がないので,誤差列 (e) とした。
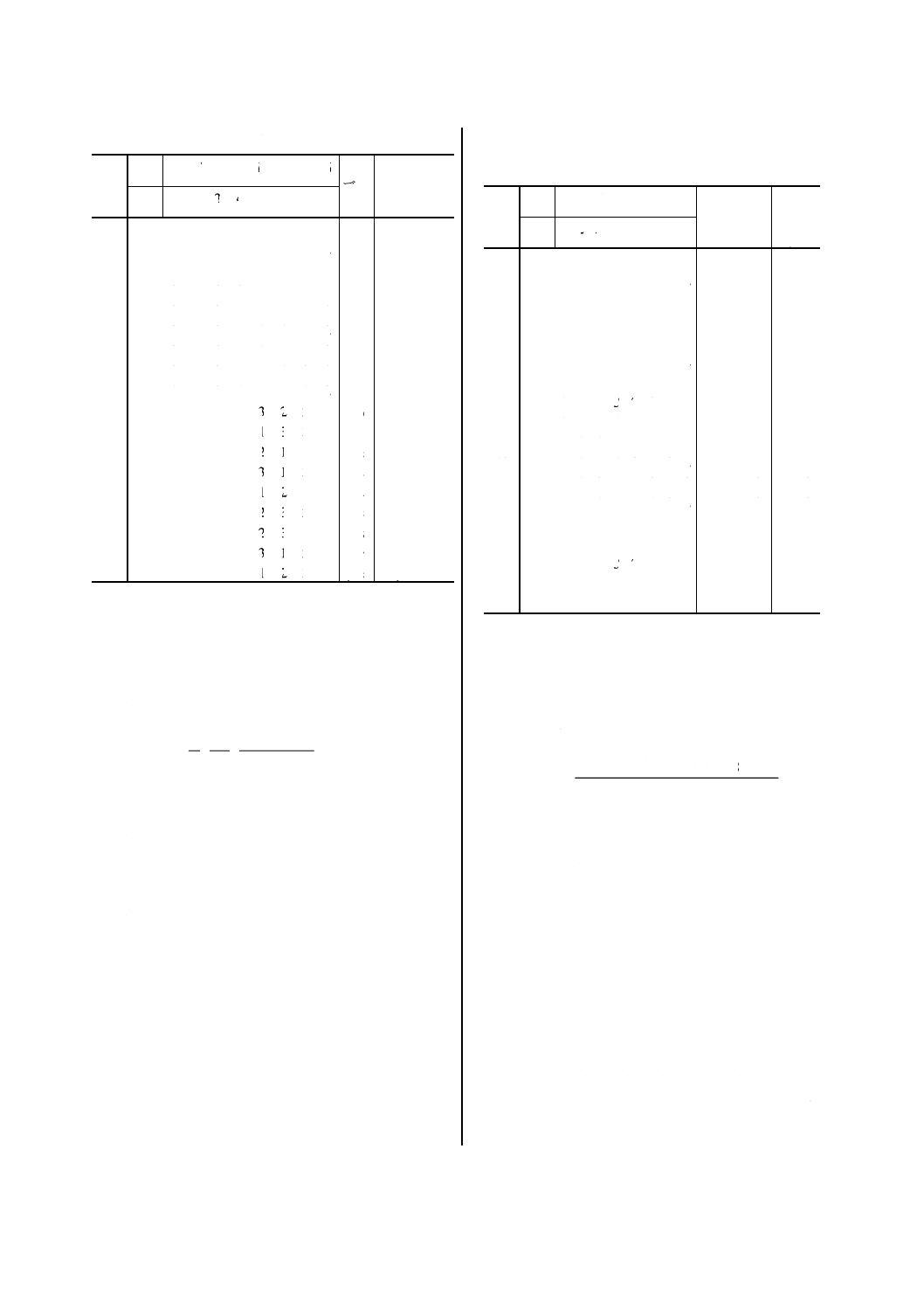
3.ʼ 使用における誤差の大きさの求め方 (ステ
ージの送りの使用における誤差の場合)2.ʼのステ
ージの送りについてのデータを用いて計算を行う。
手順1ʼ 読みのデータを偏差データに変換する。
附属書2表2ʼのデータを次のように変換
する。
ただし,偏差データを1 000倍し,計算
しやすくした。
y1=24.998 5−25.000 0=−0.001 5→−1.5
y2=24.998 5−25.000 0=−0.001 5→−1.5
Μ
y18=124.991 5−125.000 0=−0.008 5→−8.5
まとめると,附属書2表3ʼになる。
22
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2表3 偏差データの表
行番 因子 A M B C D E F G 偏差
デー
タ
計算式
列番 1 2 3 4 5 6 7 8
1
1 1 1 1 1 1 1 1
y1
←y1−M1
2
1 1 2 2 2 2 2 2
y2
←y2−M1
3
1 1 3 3 3 3 3 3
y3
←y3−M1
4
1 2 1 1 2 2 3 3
y4
←y4−M2
5
1 2 2 2 3 3 1 1
y5
←y5−M2
6
1 2 3 3 1 1 2 2
y6
←y6−M2
7
1 3 1 2 1 3 2 3
y7
←y7−M3
8
1 3 2 3 2 1 3 1
y8
←y8−M3
9
1 3 3 1 3 2 1 2
y9
←y9−M3
10
2 1 1 3 3 2 2 1 y10
←y10−M1
11
2 1 2 1 1 3 3 2 y11
←y11−M1
12
2 1 3 2 2 1 1 3 y12
←y12−M1
13
2 2 1 2 3 1 3 2 y13
←y13−M2
14
2 2 2 3 1 2 1 3 y14
←y14−M2
15
2 2 3 1 2 3 2 1 y15
←y15−M2
16
2 3 1 3 2 3 1 2 y16
←y16−M3
17
2 3 2 1 3 1 2 3 y17
←y17−M3
18
2 3 3 2 1 2 3 1 y18
←y18−M3
備考 “←”は,偏差を計算式に従って計算し,改めてyi
とおくことを示す。
手順2 一般平均の効果の大きさSmを求める。
(
)
18
2
18
2
1
y
y
y
Sm
+
+
+
=
Λ
手順3 データの全2乗和STを求める。
ST=y12+y22+…+y182
手順4 信号因子の回帰成分Mβの効果の大きさSβ
と,偏差データの信号因子Mに対する感
度係数βʼ(4)を次のように求める。
yM1=y1+y2+y3+y10+y11+y12
yM2=y4+y5+y6+y13+y14+y15
yM3=y7+y8+y9+y16+y17+y18
信号因子の回帰成分(Mβ)の効果の大き
さSβを次のように求める。
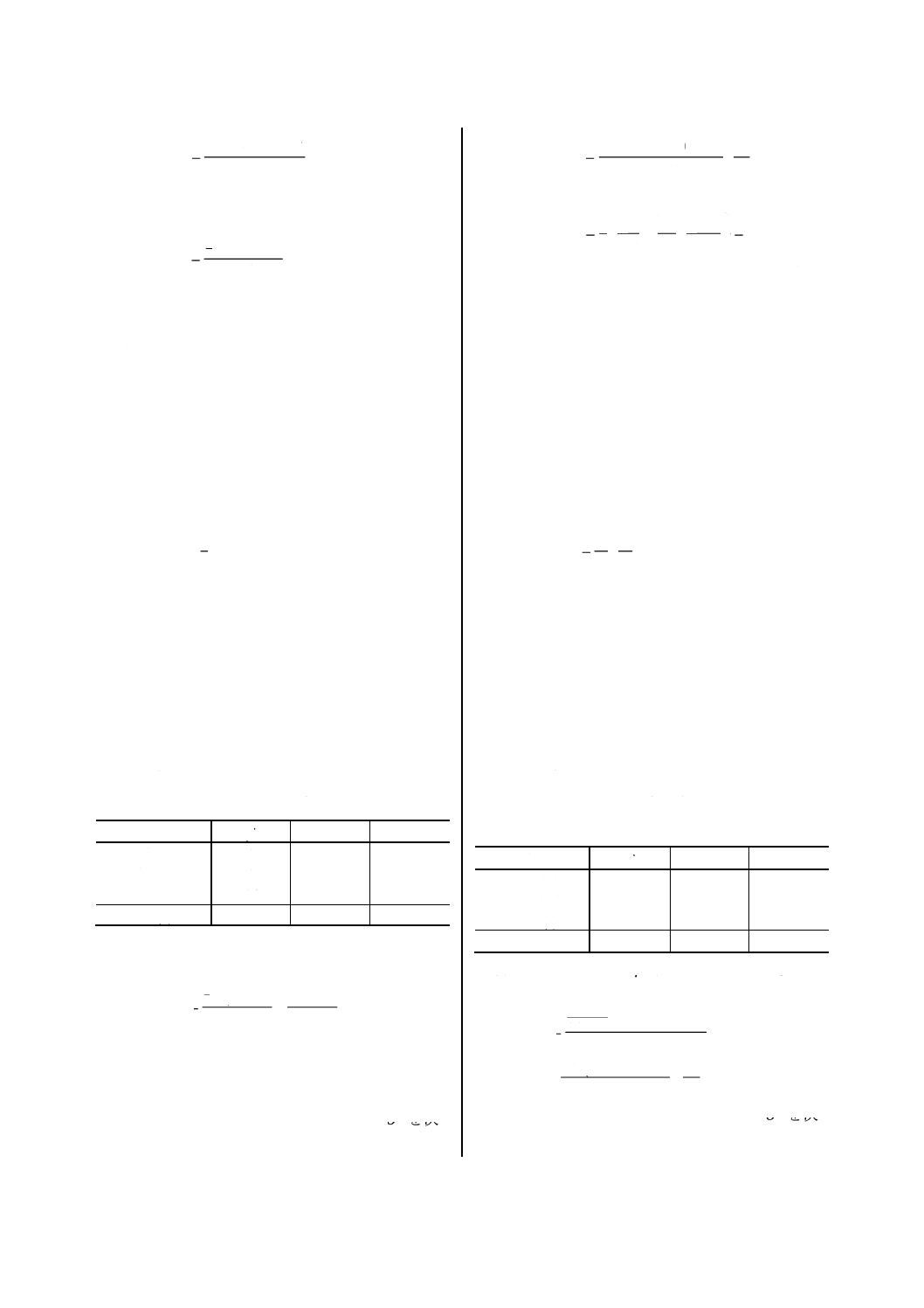
附属書2表3ʼ ステージの送りの実験における読
み及び偏差データ
行番 因子 e M A B C D E e ステージ・
カウンター
の読み
偏差デ
ータ
yi
列番 1 2 3 4 5 6 7 8
1
1 1 1 1 1 1 1 1
24.998 5
−1.5
2
1 1 2 2 2 2 2 2
24.998 5
−1.5
3
1 1 3 3 3 3 3 3
24.886 0
−4.0
4
1 2 1 1 2 2 3 3
74.999 0
−1.0
5
1 2 2 2 3 3 1 1
74.999 0
−1.0
6
1 2 3 3 1 1 2 2
74.996 5
−3.5
7
1 3 1 2 1 3 2 3 124.997 0
−3.0
8
1 3 2 3 2 1 3 1 124.996 5
−3.5
9
1 3 3 1 3 2 1 2 124.993 5
−6.5
10
2 1 1 3 3 2 2 1
24.997 0
−3.0
11
2 1 2 1 1 3 3 2
24.995 5
−4.5
12
2 1 3 2 2 1 1 3
24.995 0
−5.0
13
2 2 1 2 3 1 3 2
74.995 0
−5.0
14
2 2 2 3 1 2 1 3
74.994 0
−6.0
15
2 2 3 1 2 3 2 1
74.990 5
−9.5
16
2 3 1 3 2 3 1 2 124.994 5
−5.5
17
2 3 2 1 3 1 2 3 124.992 0
−8.0
18
2 3 3 2 1 2 3 1 124.991 5
−8.5
備考 偏差は信号因子の水準値である“レーザ測長器
の読み”からステージの移動量の表示値である
“ステージのカウンター読み”を引いたもので
あり,これを偏差データyiとする。
手順2ʼ 一般平均の効果の大きさSmを次のよう
に求める。
(
)(
)
(
)
{
}
18
5.8
5.1
5.1
2
−
+
+
−
−
=
Λ
+
m
S
=360.01
手順3ʼ データの全2乗和STを次のように求める。
ST= (−1.5) 2+ (−1.5) 2+…+ (−8.5)2
=470.25
手順4ʼ 信号因子の回帰成分Mβの効果の大きさ
Sβと,偏差データの信号因子Mに対す
る感度係数βʼを次のように求める。
yM1= (−1.5) + (−1.5) + (−4.0) +
(−3.0) + (−4.5) + (−5.0) =−19.5
yM2= (−1.0) + (−1.0) + (−3.5) +
(−5.0) + (−6.0) + (−9.5) =−26.0
yM3= (−3.0) + (−3.5) + (−6.5) +
(−5.5) + (−8.0) + (−8.5) =−35.0
23
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
2
6
2
3
1
×
+
−
=
M
M
y
y
Sβ
偏差データの信号因子Mに対する感度係
数βʼを次のように求める。
M
M
M
h
y
y
2
6
3
1
×
+
−
=
,
β
注(4) “ʼ”は偏差データに対する計算値
であることを示す。
手順5 誤差の効果の大きさSeを次のように求め
る。
Se=ST−Sm−Sβ
ただし,誤差の効果の大きさの自由度は
16である。
手順6 読みの誤差分散Veを次のように求める。
16
e
e
S
V=
手順7 信号因子の水準の幅hMを用いて,有効除
数γを次のように求める。
γ=6×2×hM2
手順8 附属書2表4の分散分析表に結果をまと
める。
附属書2表4 分散分析表
要因
f
S
V
平均 (m)
1
Sm
Sm
回帰 (Mβ)
1
Sβ
Sβ
誤差 (e)
16
Se
Ve
計 (T)
18
ST
手順9 測定のSN比ηを次のように求める。
(
)
e
e
e
r
V
V
V
S
1
2
,
1
+
+
−
=
β
η
β
備考 ηの式は偏差データからSN比を求め
る式である。
手順10 使用における誤差分散の推定値
2ˆσを次
のように求める。
(
)(
)
{
}
2
6
0.
35
5.
19
2
×
−
+
−
−
=
β
S
=20.02
(
)
(
)
5
3
10
583
.2
10
50
2
6
0.
35
5.
19
,
−
×
−
=
×
×
×
−
+
−
−
=
β
ただし,103は,データを1 000倍し
た計算の変換のための係数である。
手順5ʼ
誤差の効果の大きさSeを次のように求
める。
Se=470.25−360.01−20.02
=90.22
ただし,誤差の効果の大きさの自由度は
16である。
手順6ʼ 読みの誤差分散Veを次のように求める。
16
22
.
90
=
e
V
=5.639
手順7ʼ 信号因子の水準の幅hM (=50mm) を用
いて,有効除数γを次のように求める。
γ=6×2× (50×103) 2=3.0×1010
ただし,103は,信号の単位をμmに合
わせるための係数である。
手順8ʼ 計算結果を附属書2表4ʼの分散分析表に
結果をまとめる。
附属書2表4ʼ ステージの送りの実験における
分散分析表
要因
f
S
V
平均 (m)
1
360.01
360.01
回帰 (Mβ)
1
20.02
20.02
誤差 (e)
16
90.22
5.639
計 (T)
18
470.25
手順9ʼ 測定のSN比ηを次のように求める。
(
)
(
)
639
.5
1
10
583
.2
2
639
.5
639
.5
02
.
20
5
10
0.3
1
10
+
×
−
×
+
−
=
−
×
η
=0.1773
手順10ʼ 使用における誤差分散の推定値
2ˆσを次
のように求める。

24
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
η
σ
1
ˆ2=
4. 誤差因子の水準の幅を変更する場合の使用
における誤差の大きさの求め方 附属書2の2.の
実験において,誤差因子の水準の幅を変更する場
合の誤差の大きさを推定する場合には,3.の計算
に代わって次の手順による。
備考 水準の幅を狭くする場合に,以下の手
順を適用する。水準の幅を広くする場
合に,この実験から推定することは望
ましくない。
例1. 2.2 (2)によって水準の幅を設定すると
狭くなりすぎ,実験がしにくいので,
実験においては水準幅を広く設定した
場合。
例2. 水準の幅を予測してあらかじめ設定す
ることが難しいので,使用における誤
差の大きさを求める実験において,仮
の値を誤差因子の水準として設定した
場合。
手順1 読みのデータを偏差データに変換する。
直交表i行において,信号因子の水準Mj
を測定したときの読みのデータyiについ
て,偏差データyi−Mjを計算し,改めて
yiとおく。
備考 必ずしも偏差データに変換する必
要はないが,多くの場合,偏差デ
ータに変換して計算を行うことに
よって,計算誤差を小さくするこ
とが出来る。
手順2 各因子の各水準の和を,次のように計算
し,附属書2表5の補助表を作成する。
yA1=y1+y2+y3+y4+y5+y6+y7+y8+y9
yA2=y10+y11+y12+y13+y14+y15+y16+y17+
y18
yM1=y1+y2+y3+y10+y11+y12
yM2=y4+y5+y6+y13+y14+y15
yM3=y7+y8+y9+y16+y17+y18
A及びM以外の因子についても同様の計
算を行う。
25
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3
177
.0
1
ˆ2=
σ
=5.640 (μm) 2
4.ʼ 誤差因子の水準の幅を変更する場合の使用
における誤差の大きさの求め方(ステージの送り
の使用における誤差の場合)3.ʼと同じデータ(附
属書2表2ʼ)について誤差因子の水準の幅を変更
した場合の使用における誤差の大きさを計算によ
って求める。
手順1ʼ 読みのデータを偏差データに変換する。
附属書2表2ʼのデータを次のように変換
する。ただし,偏差データを1 000倍し,
計算しやすくした。
y1=24.998 5−25.000 0=−0.001 5→−1.5
y2=24.998 5−25.000 0=−0.001 5→−1.5
Μ
y18=124.991 5−125.000 0=−0.008 5→−8.5
まとめると,附属書2表3ʼになる。
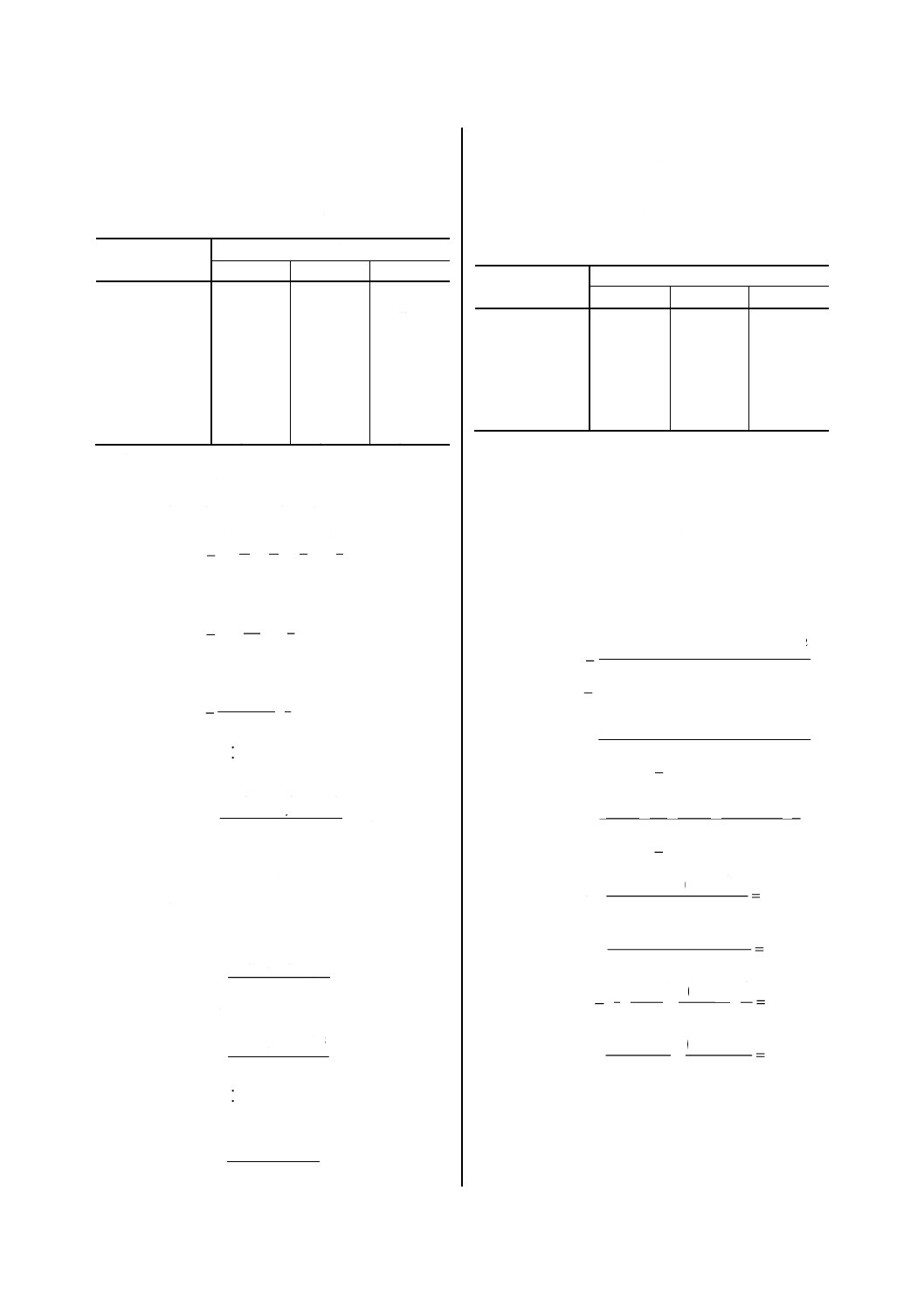
手順2ʼ 各因子の各水準の和を,次のように計算
し,附属書2表5ʼの補助表を作成する。
yM1= (−1.5) + (−1.5) + (−4.0) +
(−3.0) + (−4.5) + (−5.0) =−19.5
yM2= (−1.0) + (−1.0) + (−3.5) +
(−5.0) + (−6.0) + (−9.5) =−26.0
yM3= (−3.0) + (−3.5) + (−6.5) +
(−5.5)+(−8.0)+(−8.5)=−35.0
26
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2表5 因子と水準ごとのykの和
因子
水準
1
2
3
A
yA1
yA2
M
yM1
yM2
yM3
B
yB1
yB2
yB3
C
yC1
yC2
yC3
D
yD1
yD2
yD3
E
yE1
yE2
yE3
F
yF1
yF2
yF3
G
yG1
yG2
yG3
手順3 附属書2表5の結果を用いて,各因子の
効果の計算を次のように行う。
一般平均の効果の大きさ
(
)
18
2
18
2
1
y
y
y
Sm
+
+
+
=
Λ
Aの効果の大きさ
m
A
A
A
S
y
y
S
−
+
=
9
2
2
2
1
Bの効果の大きさ
m
A
A
A
S
y
y
S
−
+
=
9
2
2
21
Μ
Gの効果の大きさ
m
G
G
G
G
S
y
y
y
S
−
+
+
=
6
2
3
2
2
2
1
ただし,計量的な因子であり,かつ,3水
準の誤差因子及び信号因子Mについては,
計算を次のように行う。
Mの回帰成分Mβの効果の大きさ
(
)
2
6
2
3
1
×
+
−
=
M
M
M
y
y
Sβ
Bの回帰成分Bβの効果の大きさ
(
)
2
6
2
3
1
×
+
−
=
M
M
M
y
y
Sβ
Μ
Gの回帰成分Gβの効果の大きさ
(
)
2
6
2
3
1
×
+
−
=
G
G
G
y
y
Sβ
その他の因子 (A, B, C, D, E) につい
ても同様の計算をし,附属書2表5'
にまとめる。
附属書2表5ʼ ステージの送りの実験における因
子の水準ごとのykの和
因子
水準
1
2
3
M
−19.5
−26.0
−35.0
A
−19.0
−24.5
−37.0
B
−31.0
−24.0
−25.5
C
−27.0
−26.0
−27.5
D
−26.5
−26.5
−27.5
E
−25.5
−28.5
−26.5
手順3ʼ 附属書2表5ʼの結果を用いて,各因子の
効果の計算を次のように行う。
一般平均の効果の大きさと,因子B,D
の効果の大きさの計算を行うが,計量的
な因子で,かつ3水準の誤差因子A,C,
E及び信号因子Mについては回帰成分の
効果の大きさを計算する。
(
)
(
)
(
)
[
]
014
.
360
18
5.8
5.1
5.1
2
=
−
+
+
−
+
−
=
Λ
m
S
(
)
(
)
(
)
528
.4
014
.
360
6
5.
25
0.
24
0.
31
2
2
2
=
−
−
+
−
+
−
=
B
S
(
)
(
)
(
)
111
.0
014
.
360
6
5.
27
5.
26
5.
26
2
2
2
=
−
−
+
−
+
−
=
D
S
(
)(
)
[
]
021
.
20
2
6
0.
35
5.
19
2=
×
−
+
−
−
=
β
M
S
(
)(
)
[
]
021
.
20
2
6
0.
35
5.
19
2=
×
−
+
−
−
=
β
M
S
(
)(
)
[
]
021
.
20
2
6
0.
35
5.
19
2=
×
−
+
−
−
=
β
M
S
(
)(
)
[
]
083
.0
2
6
5.
26
5.
25
2=
×
−
+
−
−
=
β
E
S

27
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順4 因子の効果の自由度及び分散の計算を,
次のように行う。
mの自由度fm=1
mの分散Vm=Sm
Aの自由度fA=1
Aの分散VA=SA
Bの自由度fB=2
Bの分散VB=2B
S
Μ
Gの自由度fG=2
Gの分散VG=2G
S
ただし,上記の自由度及び分散の計算に
おいて,計量的な因子であり,かつ,3
水準の誤差因子及び信号因子については,
次のように計算を行う。
Mβの自由度fMβ=1 Mβの分散VMβ=SMβ
Bβの自由度fBβ=1 Bβの分散VBβ=SBβ
Μ
Gβの自由度fGβ=1 Gβの分散VGβ=SGβ
手順5 全2乗和及び誤差の効果の計算を,次の
ように行う。
全2乗和 ST=y12+y22+…+y182
誤差の効果の大きさ
Se=ST−Sm−SM−SA−SB−…−SG
誤差の自由度fe=18−1−fM−fA−fB−…−
fG
ただし,上記の誤差の効果の大きさ及び
誤差の自由度の計算で,計量的な因子で
あり,かつ,3水準の誤差因子の場合は,
SM, SA, …, SGの代わりにSMβ, SAP, …, SGβ
を,fM, fA, …, fGの代わりにfMβ, fAP, …, fGβ
を用いる。
手順6
読みの誤差分散及び分散の合計の計算
を,次のように行う。
誤差分散
e
e
e
f
S
V=
分散の合計
18
T
T
S
V=
各因子の分散Viが誤差分散Veに対して,
2倍以内のものは,誤差分散Veにプール
して,プールした誤差分散Veʼを,次のよ
うに計算する。
,
,
,
e
e
e
e
e
f
S
f
f
S
S
V
=
+
+
=
の和
度
プールする要因の自由
の和
プールする要因の
28
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順4ʼ 因子の効果の自由度及び分散の計算を,
次のように行う。
fm=1
mの分散
Vm=360.014
fMβ=1
Mβの分散
VMβ=20.021
fAβ=1
Aβの分散
VAβ=27.000
fB=2
Bの分散
VB=2.264
fGβ=1
Cβの分散
VCβ=0.021
fD=2
Dの分散
VD=0.056
fEβ=1
Eβの分散
VEβ=0.083
手順5ʼ 全2乗和及び誤差の効果の計算を,次の
ように行う。
ST=(−1.5)2+(−1.5)2+…+(−8.5)2
=470.250
Se=470.250−360.014−20.021−27.000−
4.528−0.021−0.111−0.083=58.472
fe=18−1−1−1−2−1−2−1=9
手順6ʼ
読みの誤差分散及び分散の合計の計算
を,次のように行う。
誤差分散
497
.6
9
472
.
58
=
=
e
V
分散の合計
125
.
26
18
250
.
470
=
=
T
V
各因子の誤差分散がVeの2倍以内のも
のは因子B, C, D, Eであるので
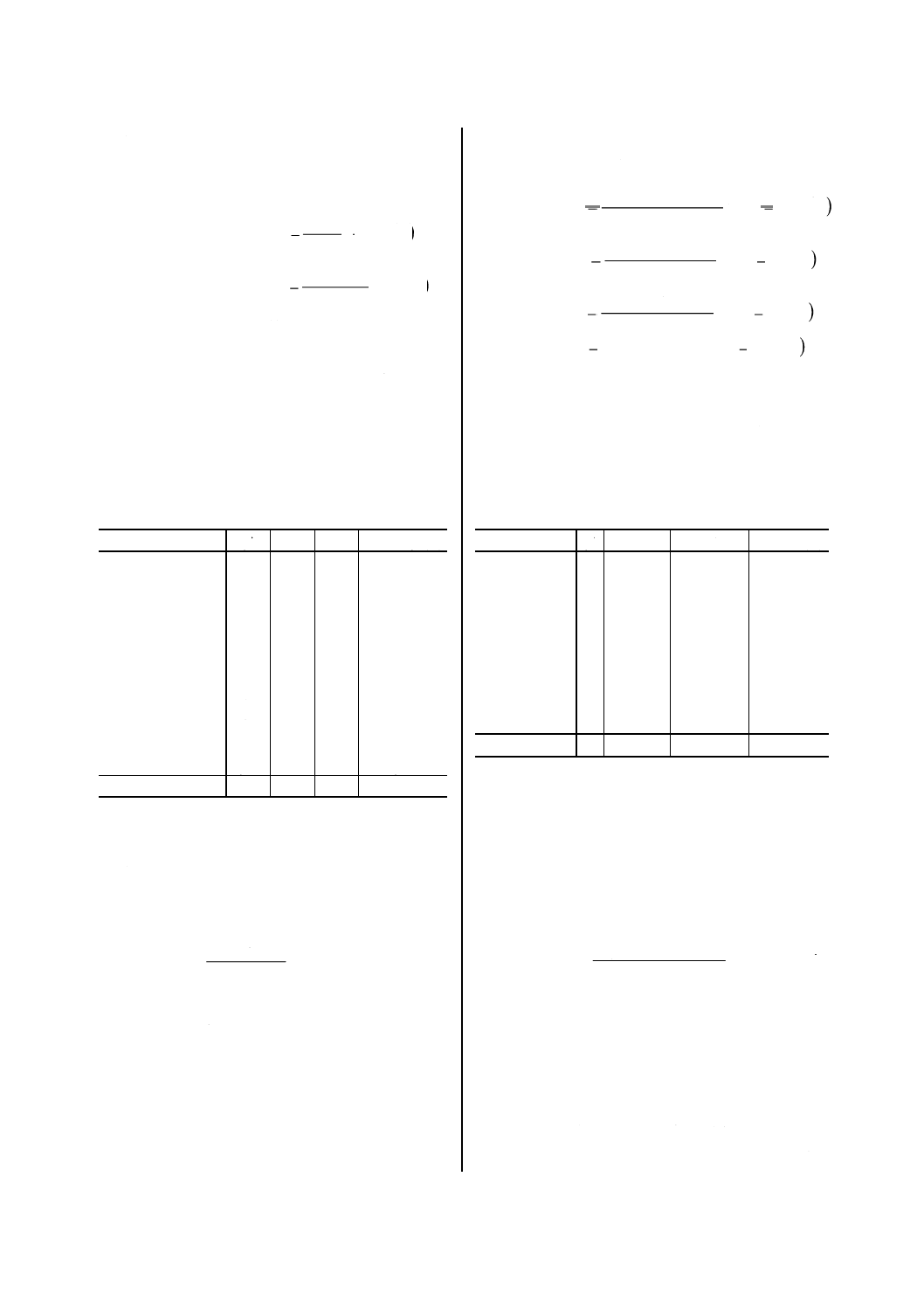
Seʼ=58.472+4.528+0.021+0.111+0.083
=63.215
214
.4
1
2
1
2
9
215
.
63
,
=
+
+
+
+
=
e
V
29
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順7 分散が誤差分散の2倍以上の効果の寄与
率ρの計算を,次のように行う。ただし,
プールした要因についてはρ=0である。
一般平均の寄与率
()
%
100
,
×
−
=
T
e
m
m
S
V
S
ρ
Aの効果の寄与率
()
%
100
,
×
−
=
T
e
A
A
A
S
V
f
S
ρ
以下,同様の計算を行う。プールした誤
差の寄与率ρe'は,次のように100%から
プールしなかった要因の効果の寄与率を
引いて求める。
ρeʼ=100−ρm−ρA−…−ρG
手順8 附属書2表6の分散分析表に計算結果を
まとる。
附属書2表6 分散分析表
要因
f
S
V
寄与率 ρ (%)
m(一般平均)
1
Sʼm
Vʼm
ρm
Aβ
fAβ
SAβ
VAβ
ρAβ
Mβ
fMβ
SMβ
VMβ
ρMβ
Bβ
fBβ
SBβ
VBβ
ρBβ
Cβ
fCβ
SCβ
VCβ
ρCβ
Dβ
fDβ
SDβ
VDβ
ρDβ
Eβ
fEβ
SEβ
VEβ
ρEβ
Fβ
fFβ
SFβ
VFβ
ρFβ
Gβ
fGβ
SGβ
VGβ
ρGβ
e(誤差)
fe
Se
Ve
eʼ(プールした誤差)feʼ
Seʼ
Veʼ
ρeʼ
T(合計)
18
SʼT
VʼT
100.0
備考 各因子の要因について,添え字“β”を付けている
が,計量的な因子ではない誤差因子については,
添え字“β”がないものと考える。
手順9 有効除数γ及び偏差データの信号因子M
に対する感度係数βʼを次のように求める。
γ=6×2hM2
M
M
M
h
y
y
2
6
ˆ
3
1
×
+
−
=
ʼ
β
手順10 回帰成分を誤差分散にプールしない因
子で,新たに水準の幅を設定した計量的
な因子について,換算係数λを次のよう
に求める。
手順7ʼ
分散が誤差分散の2倍以上の効果の寄
与率ρの計算を,次のように行う。
()
%
7.
75
100
250
.
470
214
.4
1
014
.
360
=
×
×
−
=
m
ρ
()
%
4.3
100
250
.
470
214
.4
1
021
.
20
=
×
×
−
=
M
ρ
()
%
8.4
100
250
.
470
214
.4
1
000
.
27
=
×
×
−
=
A
ρ
()
%
1.
16
8.4
4.3
7.
75
100
,
=
−
−
−
=
e
ρ
手順8ʼ 附属書2表6ʼの分散分析表に計算結果を
まとめる。
附属書2表6ʼ ステージの送りの実験における分
散分析表
要因
f
S
V
寄与率 (%)
m(一般平均) 1
360.014
360.014
75.7
Mβ
1
20.021
20.021
3.4
Aβ
1
27.000
27.000
4.8
B
2
4.528
2.264○
Cβ
1
0.021
0.021○
D
2
0.111
0.056○
Eβ
1
0.083
0.083○
e(誤差)
9
58.472
6.497○
e'(誤差プール) 15
63.215
4.214
16.1
T(合計)
18 470.250
26.125
100.0
備考 V欄の“○”は,プールした要因であることを示
す。
手順9ʼ 有効除数γ及び偏差データの信号因子M
に対する感度係数βʼを次のように求め
る。
γ=6×2× (50×103) 2=3.0×1010
(
)
(
)
5
3
10
583
.2
10
50
2
6
0.
35
5.
19
ˆ
−
×
−
=
×
×
×
−
+
−
−
=
ʼ
β
手順10ʼ 回帰成分を誤差分散にプールしない因
子で,新たに水準の幅を設定した計量
的な因子について,換算係数λを次の
ように求める。
誤差因子である室温 (A) の変化を標
準偏差で約半分に抑えるような使用条

30
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A
A
A
h
h,
=
β
λ
ただし,実験における誤差因子の水準の
幅をhAとし,新たに設定した誤差因子
の水準の幅をhAʼとする。
水準の幅を変えない因子については,λ
=1とする。
計量的でない因子については,水準の幅
を狭めることはできないので,λ=1と
する。ただし,条件を固定した場合には,
λ=0とする。
手順11 誤差分散Ve”を次のように求める。
ただし,誤差にプールした要因について
はρ=0とし,和を取らない。
備考 ここで,ρm,及びρMβを落としたの
は,信号因子について1次式校正
することを前提にしたためである。
手順12 測定のSN比ηを次のように求める。
(
)
e
e
e
r
V
V
V
S
′′
′′
′
+
′
+
−
=
1
2
1
β
η
β
備考 ηの式は偏差データからSN比を
求める式である。
手順13 使用における誤差分散の推定値
2ˆσを次
のように求める。
η
σ
1
ˆ2=
5. 使用における誤差の表示 使用における誤差
の大きさを次のように表示する。
使用における誤差の大きさを表す分散
2ˆσ
備考 使用における誤差の大きさを表示する
場合には,使用する条件(誤差因子の
水準の幅など)を付記することが望ま
しい。
件に変更したときの誤差を見積もる。
hAʼ=1
5.0
2
1=
=
A
λ
手順11ʼ 誤差分散Ve”を次のように求める。
(
)
6
519
.4
1.
16
8.4
5.0
100
125
.
26
2
=
+
×
=
′′e
V
手順12ʼ 測定のSN比ηを次のように求める。
(
)
(
)
(
)2-
5
10
0.3
1
m
2
221
.0
5196
.4
1
10
583
.2
2
5196
.4
214
.4
02
.
20
10
μ
=
+
×
−
+
−
=
−
×
η
手順13ʼ 使用における誤差分散の推定値
2ˆσを次
のように求める。
2
221
.0
1
ˆ2=
σ
=4.521 (μm) 2
5.ʼ 使用における誤差の表示 XY移動形ステー
ジのX方向の送りの使用における誤差の大きさを
表す分散は次のとおりである。
2ˆσ=4.521 (μm) 2
ただし,使用する条件は誤差因子の水準の幅で
次のようなときである。
室温:23〜25℃
(
)
e
G
G
B
B
A
A
T
e
V
V
′
′′
+
+
+
+
=
ρ
ρ
λ
ρ
λ
ρ
λ
β
β
β
β
β
β
2
2
2
100
Λ
31
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ステージの傾斜角度:前3〜右3°
試料の質量:1〜4kg
試料を置く位置:右側〜奥
ステージ上の高さ:30〜70mm

32
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3 校正の作業の誤差の大きさを実験によって求める方法
1. 適用範囲 この附属書は,使用者が計測器を校正するとき,校正の作業で発生する誤差の大きさを,
あらかじめ実験によって求める方法の一般的事項について規定する。
2. 誤差の大きさを求める実験の方法
2.1
信号因子及びその水準の選び方 校正に使用する標準を信号因子Mとして用いる。信号因子の水準
は,計測器の使用する目盛範囲において,その上下限の近くを含む3水準以上のk水準とする。
備考 附属書3では,標準の表示値には誤差がないと考えている。標準の表示値の誤差については,
附属書4で規定する。
2.2
誤差因子及びその水準の選び方 校正の作業の中で,信号因子である標準以外の,測定結果に影響
を与えると思われる条件を,誤差因子Nとして取り上げる。誤差因子の水準は,最低限3水準のn水準と
する。
備考 校正の作業では,測定の作業よりは誤差因子が限定されることが多いので,附属書2の使用に
おける誤差を求める場合とは違って,取り上げる誤差因子の数を多くは取り上げていない。誤
差因子の数が多いと判断される場合には,附属書2と同様にL18などの直交表を利用する。
2.3
因子の割付け及び実験の実施 附属書3表1のように,信号因子と誤差因子との組合せに対して,
標準Miの測定を行い,計測器の目盛による読みを得る。
附属書3表1 実験の割付け及び読みのデータ表
誤差
因子
信号因子
M1
M2
M3
・
・
・
Mk
N1
y11
y21
y31
・
・
・
yk1
M
y12
y22
y32
・
・
・
yk2
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
Nn
y1n
y2n
y3n
・
・
・
ykn
備考 誤差因子が多い場合には,附属書2と同様
に,直交表L18に信号因子及び誤差因子を割
り付けてもよい。
3. 校正の作業の誤差の大きさの求め方 附属書3の2.の実験において得られた実験データを基に,次の
手順によって計算を行い,校正の作業の誤差の大きさを求める。
33
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(1) 零点校正及び基準点校正の場合の計算手順
手順1 データの零点校正又は基準点校正を行う。
零点又は基準点での読みの平均
0yを次の
ように求める。
n
y
y
j
i0
0
Σ
=
各データについて,yij−
0y先を計算し,
改めてyijとおく。
また,基準点校正の場合には,Mi−M0を
計算し,改めてMiとおく。
手順2 誤差の効果の大きさSeを次のように求め
る。
Se=ΣiΣj (yij−Mi) 2
ただし,誤差の自由度feはkn-1である。
適用例
(1ʼ) 零点校正の場合の計算手順 0から30mmま
での測定範囲で使用するマイクロメータの校
正作業の誤差の大きさを求めるために,信号
因子として標準ゲージ,
M1=0mm
M2=10mm
M3=20mm
M4=30mm
を測定した。誤差因子Nについて4回行っ
た測定したデータは附属書3表1ʼのとおりで
あった。
附属書3表1ʼ マイクロメータの読み値のデータ
誤差因子
信号
M1
M2
M3
M4
N1
0.01
10.03
20.03
30.10
N2
0.00
9.98
20.00
30.01
N3
0.01
10.00
19.95
29.98
N4
0.02
10.02
20.05
30.08
手順1ʼ データの零点校正を次のように行う。
01
.0
4
04
.0
0
=
=
y
yij−
0yを計算し,改めて附属書3表2ʼ
を作成する。
附属書3表2ʼ マイクロメータの零点校正後のデ
ータ
誤差因子
信号
M1
M2
M3
M4
N1
0.00
10.02
20.02
30.09
N2
−0.01
9.97
19.99
30.00
N3
0.00
9.99
19.94
29.97
N4
0.01
10.01
20.04
30.07
手順2ʼ 誤差の効果の大きさSeを次のように求め
る。誤差yij−Miを計算し,附属書3表3ʼ
作成する。
34
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順3 読みの誤差分散Veを次のように求める。
e
e
e
f
S
V=
手順4 測定のSN比ηcを次のように求める。
e
c
V
1
=
η
手順5 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
c
c
η
σ
1
ˆ2=
(2) 目盛間隔校正の場合の計算手順
附属書3表3ʼ マイクロメータの誤差yij−Miの表
誤差因子
信号
M1
M2
M3
M4
N1
0.00
0.02
0.02
0.09
N2
−0.01
−0.03
−0.01
0.00
N3
0.00
−0.01
−0.06
−0.03
N4
0.01
0.01
0.04
0.07
Se=02+ (−0.01) 2+02+…+ (0.07) 2
=213×10−4
fe=4×4−1=15
手順3ʼ 読みの誤差分散Veを次のように求める。
4
4
10
2.
14
15
10
213
−
−
×
=
×
=
e
V
手順4ʼ 測定のSN比ηcを次のように求める。
4
10
2.
14
1
−
×
=
c
η
=704.2 (mm)−2
手順5ʼ 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
(
)2
4
2
mm
10
2.
14
2.
704
1
ˆ
−
×
=
=
c
σ
(2ʼ) 目盛間隔校正の場合の計算手順 使用範囲0
〜600mmのディジタルスケールの校正作業
の誤差の大きさを求めるために,信号因子と
して,レーザ測長器によって移動量を,
M1=100 000μm, M2=200 000μm,
M3=300 000μm, M4=400 000μm,
M5=500 000μm,
の5水準にとり,附属書3表4ʼのディジタル
スケールの読みの偏差データを得た。
附属書3表4ʼ ディジタルスケールの偏差データ
誤差因子
信号因子
M1
M2
M3
M4
M5
N1
−8
−2
4
−2
4
N2
−10
−4
−3
−1
2
計
−18
−6
1
−3
6

35
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順1 一般平均の効果の大きさSmを次のように
求める。 (
)
kn
y
S
ij
j
i
m
2
Σ
Σ
=
手順2 データの全2乗和STを次のように求める。
ST=ΣiΣjyij2
手順3 有効除数γを次のように求める。
γ=nΣi (Mi−M) 2
手順4 信号因子の効果の大きさSβを次のように
求める。 (
)(
)
[
]
γ
2
M
M
y
S
i
ij
j
i
−
Σ
Σ
=
β
ただし,Mは信号因子の水準の平均値で
ある。
手順5 誤差の効果の大きさSeを次のように求め
る。
Se=ST−Sm−Sβ
ただし,誤差の自由度feはkn−2である。
手順6 読みの誤差分散Veを次のように求める。
e
e
e
f
S
V=
手順7 測定のSN比ηcを次のように求める。
(
)
e
e
c
V
V
S−
=
β
η
γ
1
手順1ʼ 一般平均の効果の大きさSmを次のよう
に求める。
()(
)
[
]
10
2
10
8
2
+
+
−
+
−
=
Λ
m
S
=40.00
手順2ʼ データの全2乗和STを次のように求める。
ST=(−8)2+(−10)2+…+22
=234
手順3ʼ 有効除数γを次のように求める。
5
10
500
10
200
10
100
3
3
3
×
+
+
×
+
×
=
Λ
M
=300×103
γ=2× [ (100×103−300×103) 2+
(200×103−300×103)2+…+(500×
103-300×103) 2]=20×1010
手順4ʼ 信号因子の効果の大きさSβを次のように
求める。
(
)(
)
(
)(
)
(
)
[
]
05
.
130
10
20
10
200
6
10
100
6
10
200
18
10
2
3
3
3
=
×
×
×
+
+
×
−
×
−
+
×
−
×
−
=
Λ
β
S
手順5ʼ 誤差の効果の大きさSeを次のように求め
る。
Se=234−40−130.05
=63.95
fe=5×2−2=8
手順6ʼ 読みの誤差分散Veを次のように求める。
8
95
.
63
=
e
V
=7.99
手順7ʼ 測定のSN比ηcを次のように求める。
まず,偏差データのSN比ηc'を求める。
(
)
99
.7
99
.7
05
.
130
10
10
20
1
,
−
=
×
c
η
=0.764×10−10
測定のSN比ηcに換算するにはηcʼを用い
て次のように計算する。
e
c
c
V
ʼ
+
+
β
β
β
η
η
0
20
,
2×
=

36
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順8 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
c
c
η
σ
1
ˆ2=
(3) 零点比例式校正の場合の計算手順
手順1 データの全2乗和STを次のように求める。
ST=ΣiΣjyij2
手順2 有効除数γを次のように求める。
γ=nΣiMi2
ただし,β0は偏差を求めるために用い
た感度係数で,ここではβ0=1である。
また,β'は偏差データのMに対する感
度係数で,次のように求める。
である。
99
.7
10
54
.2
1
2
1
10
764
.0
5
2
10
−
−
×
×
×
+
+
×
=
c
η
=0.125 163(μm)−2
手順8ʼ 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
163
125
.0
1
ˆ2=
c
σ
=7.99 (μm) 2
(3ʼ) 零点比例式校正の場合の計算手順 回転式流
量計の校正作業の誤差の大きさを求めるため
に,信号因子として,標準流量を,
M1=5L/min, M2=10L/min,
M3=15L/min, M4=20L/min,
の4水準に取り,流量計のパルス出力を読
みとして測定し,附属書3表5ʼのデータを得
た。
附属書3表5ʼ 回転式流量計の割付けとデータ
(パルス/分)
誤差因子
信号因子
M1
M2
M3
M4
N1
38
87
129
171
N2
39
85
126
173
N3
47
97
144
173
計
124
269
399
517
手順1ʼ データの全2乗和STを次のように求める。
ST=382+872+…+1732
=171 729
手順2ʼ 有効除数γを次のように求める。
γ=3× (52+102+152+202)
=2 250
5-
10
3
10
3
3
3
10
2.55
10
20
10
100
5
10
20
)
10
(200
6
10
100
-
6
-
)
10
(-200
(-18)
×
=
×
×
×
×
×
×
×
×
×
=
+
+
)
(
)
(
+
=
ʼ
Λ
β

37
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順3 信号因子の効果の大きさSβを次のよう
に求める。
(
)
[
]
r
M
y
S
i
ij
i
i
2
Σ
Σ
=
β
手順4 誤差の効果の大きさSeを次のように求め
る。
Se=ST−Sβ
ただし,誤差の自由度feはkn−1である。
手順5 読みの誤差分散Veを次のように求める。
e
e
e
f
S
V=
手順6 測定のSN比ηcを次のように求める。
(
)
e
e
c
V
V
S−
=
β
η
γ
1
手順7 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
c
c
η
σ
1
ˆ2=
(4) 基準点比例式校正の場合の計算手順
手順3ʼ 信号因子の効果の大きさSβを次のように
求める。
(
)
250
2
635
19
250
2
517
20
399
15
269
10
124
5
2
2
=
×
+
×
+
×
+
×
=
β
S
=171 348.1
手順4ʼ 誤差の効果の大きさSeを次のように求め
る。
Se=171 729−171 348.1=380.9
fe=4×3−1=11
手順5ʼ 読みの誤差分散Veを次のように求める。
11
9.
380
=
e
V
=34.63
手順6' 測定のSN比ηcを次のように求める。
34.63
34.63
-
348.1
171
250
2
1
)
(
=
c
η
=2.20 (L/min) −2
手順7ʼ 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
20
.2
1
ˆ2=
c
σ
=0.455(L/min)2
(4ʼ) 基準点比例式校正の場合の計算 手順噴射流
量計の校正作業の誤差の大きさを求めるため
に,信号因子として標準流量を
M1=250L/min,
M2=300L/min,
M3=350L/min,
M4=400L/min,
M5=450L/min
の5水準を取り,附属書3表6ʼの流量計の読
みのデータを得た。
また,基準点はM3とした。
附属書3表6ʼ 噴射流量計の読みのデータ
誤差因子
信号因子
M1
M2
M3
M4
M5
N1
251
301
353
400
460
N2
250
299
349
399
448

38
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順1
読みのデータの基準点校正を行う。
基準点M0での読みの平均
0yを次のよ
うに求める。
n
y
y
j
0
0
Σ
=
各データについてyij−
0yを計算し,改め
てyijとおく。
また,Mi−M0を計算し,改めてMiとお
く。
基準点が零点である場合は,零点校正と
同じである。
手順2 データの全2乗和STを次のように求める。
ST=ΣiΣjyij2
手順3 有効除数γを次のように求める。
γ=n∑iMi2
手順4 信号因子の効果の大きさSβを次のように
求める。 (
)
[
]
r
M
y
S
i
ij
j
i
2
Σ
Σ
=
β
手順5 誤差の効果の大きさSeを次のように求め
る。
Se=ST−Sβ
ただし,誤差の自由度feはkn−1である。
手順6 読みの誤差分散Veを次のように求める。
e
e
e
f
S
V=
手順1ʼ
読みのデータの基準点校正を行う。
基準点M3の読みの平均
0yを次のよう
に求める。
(
)
2
349
353
0
+
=
y
=351
各データについてyij−
0yを計算し,改め
てyijとおく。
また,Mi−M0を計算し,改めてMiとお
く。
計算の結果,附属書3表7'の補助表を得
た。
附属書3表7ʼ 流量計の補助表
誤差因子
信号因子
M1
M2
M3
M4
M5
−100
−50
0
50
100
N1
−100
−50
2
49
99
N2
−101
−52
−2
48
97
計
−201
−102
0
97
196
手順2ʼ データの全2乗和STを次のように求める。
ST= (−100) 2+ (−101) 2+…+972
=49 328
手順3ʼ 有効除数γを次のように求める。
γ=2・ [ (−100) 2+ (−50) 2+502+1002]
=50 000
手順4ʼ 信号因子の効果の大きさSβを次のように
求める。
(
)(
)(
)(
)
[
]
000
50
650
49
000
50
196
100
102
50
201
100
2
2=
×
+
+
−
×
−
+
−
×
−
=
Λ
β
S
=49 302.45
手順5ʼ 誤差の効果の大きさSeを次のように求め
る。
Se=49 328−49 302.45
=25.55
fe=5×2−1=9
手順6ʼ 読みの誤差分散Veを次のように求める。
9
55
.
25
=
e
V
=2.839
39
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順7 測定のSN比ηcを次のように求める。
(
)
e
e
c
V
V
S−
=
β
γ
η
1
手順8 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
c
c
η
σ
1
ˆ2=
(5) 1次式校正の場合の計算手順
手順1 一般平均の効果の大きさSmを次のように
求める。 (
)
kn
y
S
ij
j
i
m
2
Σ
Σ
=
手順2 データの全2乗和STを次のように求める。
ST=Σi∑jyij2
手順3 有効除数γを次のように求める。
γ=nΣi (Mi−M) 2
手順7ʼ 測定のSN比ηcを次のように求める。
(
)
839
.2
839
.2
45
.
302
49
000
50
1
−
×
=
c
η
=0.347 (L/min) −2
手順8ʼ 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
347
.0
1
ˆ2=
c
σ
=2.88(L/min)2
(5ʼ) 1次式校正の場合の計算手順 引張試験機の
荷重検出器の校正作業の誤差の大きさを求め
るために,信号因子として,標準荷重検出器
を用いて荷重を,
M1=43.2N, M2=54.0N,M3=64.8N
の3水準に取り,測定したところ,荷重検出
器の読みのデータは附属書3表8'のようにな
った。
附属書3表8ʼ 引張試験機の読みのデータ
誤差因子
信号因子
M1
M2
M3
N1
42.5
53.3
64.2
N2
43.7
54.2
65.7
計
86.2
107.5
129.9
手順1ʼ 一般平均の効果の大きさSmを次のよう
に求める。
(
)
6
7.
65
7.
43
5.
42
2
+
+
+
=
Λ
m
S
6
6.
323
2
=
=17 452.83
手順2ʼ データの全2乗和STを次のように求める。
ST=42.52+43.72+…+65.72
=17932.6
手順3ʼ 有効除数γを次のように求める。
3
8.
64
0.
54
2.
43
+
+
=
M
=54.0
γ=2× [ (43.2−54) 2+ (64.8−54) 2]
=466.56

40
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順4 信号因子の効果の大きさSβを次のように
求める。
(
)(
)
[
]
γ
β
2
M
M
y
S
i
ij
j
i
−
Σ
Σ
=
ただし,Mは信号因子の水準の平均であ
る。
手順5 誤差の効果の大きさSeを次のように求め
る。
Se=ST−Sm−Sβ
ただし,誤差の自由度feはkn−2である。
手順6 読みの誤差分散Veを次のように求める。
e
e
e
f
S
V=
手順7 測定のSN比ηcを次のように求める。
(
)
e
e
r
c
V
V
S−
=
β
η
1
手順8 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
c
c
η
σ
1
ˆ2=
4. 校正の作業の誤差の表示 校正の作業の誤差
の大きさを,次のように表示する。
校正の作業の誤差の大きさを表す分散
2
ˆc
σ
手順4ʼ 信号因子の効果の大きさSβを次のように
求める。
(
)
56
.
466
9.
129
8.
10
2.
86
8.
10
2
×
+
×
−
=
β
S
=477.42
手順5ʼ 誤差の効果の大きさSeを次のように求め
る。
Se=17 932.60−17 452.83−477.42
=2.35
fe=3×2−2=4
手順6ʼ 読みの誤差分散Veを次のように求める。
4
35
.2
=
e
V
=0.588
手順7ʼ 測定のSN比ηcを次のように求める。
(
)
588
.0
588
.0
42
.
477
56
.
4661
−
×
=
c
η
=1.738 (N) −2
手順8ʼ 校正の作業の誤差分散の推定値
2
ˆc
σを次
のように求める。
738
.1
1
ˆ2=
c
σ
=0.575 (N) 2
4ʼ. 校正の作業の誤差の表示 噴射流量計の基準
点比例式校正の作業の誤差の大きさを表す分散は,
次のようになる。
2
ˆc
σ=2.88 (L/min) 2
41
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書4 標準の表示値の誤差の大きさの求め方
1. 適用範囲 この附属書は,校正に使用する標準の表示値の誤差の大きさを求める方法の一般的事項に
ついて規定する。
2. 標準の表示値の決定
2.1
標準器がある場合 一般には,校正に先立って標準器の表示値が決定される。表示値の決定は,上
位の計測器による測定によって行う。
備考 設定目盛の付いた標準発生器の場合には,複数の点における測定量と設定目盛との関係を求め
る校正が標準の表示値の決定に相当する。
例1. 現場の測長器(校正対象の計測器)を校正するためのブロックゲージ(現場校正用の標準)の
表示値を,比較測定器(上位の計測器)によって測定し,決める。
例2. 現場で使用する電圧計の校正の作業において,標準器である電圧発生器の目盛を,前もって上
位の計測器によって校正する。
2.2
校正時に標準となる測定量を発生し測定する場合 校正の作業の中で,発生器又は校正対象の計測
器によって測定量を発生させ,上位の計測器による測定によって表示値を決定する。
例1. 現場で使用する力計の校正の作業において,力を発生させ,上位の計測器である標準力計で測
定することによって,力の値を決定する。
例2. 液体用微量体積計の校正の作業において,校正対象の体積計で所定量の体積の液体をはかり取
り,上位の計測器である天びんで質量をはかり,液体の密度で割って体積の値を決定する。
3. 標準の表示値の誤差
3.1
標準器がある場合 校正に使用する標準の表示値の誤差は,次の誤差成分を含む。
(1) 上位の計測器によって行われる標準器の測定の誤差を,表示値決定の誤差として,表示値の誤差に含
む。
例 比較測定器(上位の測定器)による,ブロックゲージ(現場校正用の標準)の測定の誤差。
(2) 影響量,経時変化などに起因して,校正に使用するときの標準器の値が,表示値を決定したときの値
とは異なることによる誤差を,標準器の安定性の誤差として,表示値の誤差に含む。
備考 影響量による標準の値の変化は,上位の計測器による標準の測定条件と校正作業の測定条件と
が異なる場合に,誤差となる。ただし,条件の違いを補正する場合には,条件の違いによる値
の差は誤差にはならないが,補正の誤差は表示値の誤差として残る。標準の値の経時変化は,
材質が変化したり,摩耗などの劣化が考えられる場合に検討が必要である。ただし,標準器の
校正の間隔内での経時変化だけが誤差となる。
例 現場校正用ブロックゲージの表示値を決めた恒温室と,計測器の校正を行う現場との環境条件の
違いによる誤差,及び表示値を決めた後,現場校正用ブロックゲージを使用したことによる摩耗
などの変化による表示値からの差。
3.2
校正時に標準となる測定量を発生し測定する場合 校正時,上位の計測器の測定による測定量の表
示値決定の誤差を,標準の表示値の誤差とする。
例1. 現場で使用する力計の校正の作業において,上位の計測器である標準力計による測定の誤差。
42
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例2. 液体用微量体積計の校正の作業において,上位の計測器である天びんによる測定の誤差及び使
用した液体の密度の誤差。
4. 標準の表示値の誤差の大きさの求め方
4.1
標準器がある場合 標準器の表示値の誤差の成分の大きさは,次のように求めることができる。
(1) 標準器の表示値決定の誤差の大きさは,標準器の表示値決定に用いる上位の計測器に対して,この規
格の校正方式を適用することによって求める。
すなわち,標準器の表示値決定の誤差の大きさは,上位の計測器の使用における誤差(附属書2参
照),上位の標準による校正作業の誤差(附属書3参照)及び上位の標準の表示値の誤差(附属書4
参照)から,上位の計測器の測定の誤差として推定することができる。
例 現場校正用ブロックゲージの場合,比較測定器(上位の計測器)にこの規格を適用し,上位のブ
ロックゲージ(上位の標準)で校正し,現場校正用ブロックゲージを測定したときの測定の誤差
を,附属書2及び附属書3から求める。
(2) 標準器の安定性の誤差の大きさは,影響量及び時間を誤差因子として,標準器に対して附属書2の方
法を適用することによって,標準器の校正の間隔内の誤差の大きさとして推定することができる。
影響量の補助測定によって補正を行う場合には,値の変化は補正されるが,補正式の誤差を標準器
の表示値の誤差に含む。
例 現場校正用ブロックゲージの場合,温度,湿度及び使用回数を因子として附属書2の実験を行う。
温度の影響が大きいので現場の温度を測定し補正することとした。湿度及び温度補正式の誤差は
標準の表示値の誤差となる。使用回数は,影響はあるが,校正の間隔内ではあまり大きくないの
で誤差と考えることにした。
4.2
校正時に標準となる測定量を発生し測定する場合 標準の表示値決定の誤差の大きさは,標準の表
示値決定に用いる上位の計測器に対して,この規格の校正方式を適用することによって求める。
すなわち,標準の表示値決定の誤差は,上位の計測器の使用における誤差(附属書2参照)及び上位の
標準による校正の作業の誤差(附属書3参照),及び上位の標準の表示値の誤差(附属書4参照)から,
上位の計測器の測定の誤差として推定することができる。
備考 上位の計測器に対しては,校正対象の計測器の校正を行う環境条件が使用条件に相当し,使用
における誤差の大きさを求める場合の誤差因子となる。
5. 標準の表示値の誤差の表示 附属書4の4.において求めた誤差の成分の大きさを,分散の和の形で合
成し,次のように表示する。
標準の表示値の誤差の大きさを表す分散
2
0ˆσ
備考 標準の表示値の誤差を他の誤差成分と合成する場合には,規格本体の4.の手順6で示すように
分散の和の形で合成する。
関連規格 JIS K 0971 液体用微量体積計の校正方法
JIS K 7109 プラスチックの寸法許容差の決め方
43
Z 9090-1991
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS Z 9090 測定−校正方式通則原案作成委員会 構成表
氏名
所属
(委員長)
田 口 玄 一
財団法人日本規格協会
(幹事)
○ 矢 野 宏
工業技術院計量研究所
(委員)
池 田 要
工業技術院標準部
△ 永 田 邦 博
工業技術院標準部
○ 小 池 昌 義
工業技術院計量研究所
○ 櫻 庭 俊 昭
工業技術院電子技術総合研究所
川 村 正 信
財団法人日本規格協会
馬 場 幾 郎
馬場技術士事務所
○ 金 田 知 裕
日本電気ファクトリエンジニアリング株式会社
鎌 田 三 雄
松下電器産業株式会社
○ 斉 藤 晴 司
株式会社ニコン
○ 瀬 戸 修 美
リオン株式会社
○ 塚 越 隆 啓
山武ハネウエル株式会社
中 川 順 彦
株式会社リコー
○ 三 浦 信 行
D.E.A.株式会社
坂 野 進
日本電信電話株式会社
小 泉 正
トヨタ自動車株式会社
(事務局)
飯 塚 敏 之
財団法人日本規格協会
[○印はワーキンググループ (WG) 委員を兼任]
(△印はWG委員)