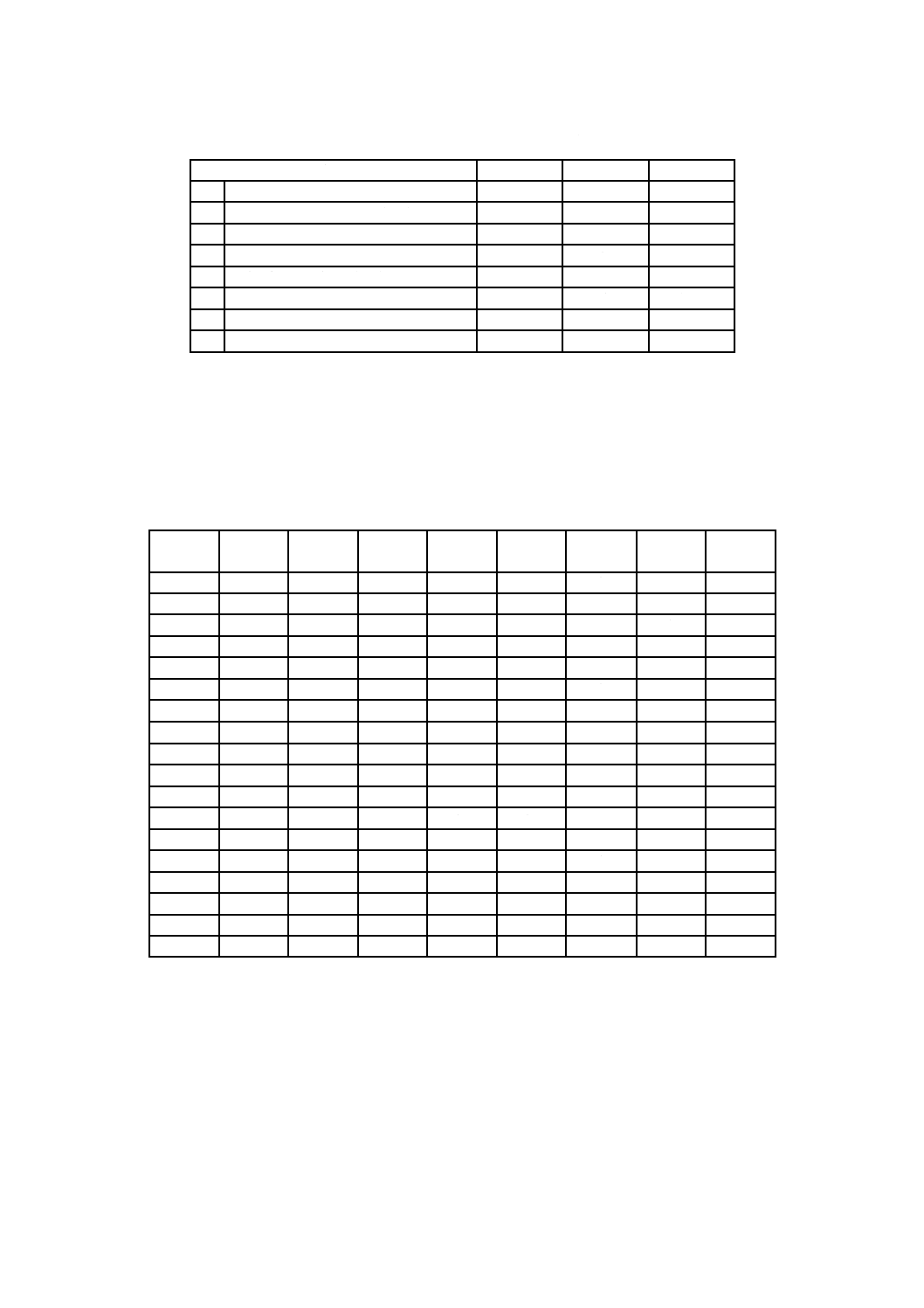Z 9061:2016 (ISO 16336:2014)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 2
2 引用規格························································································································· 2
3 用語及び定義並びに記号 ···································································································· 3
3.1 用語及び定義 ················································································································ 3
3.2 記号 ···························································································································· 5
4 ロバストパラメータ設計の概要 ··························································································· 6
4.1 必要事項 ······················································································································ 6
4.2 システムのロバストネスの評価 ························································································ 6
4.3 SN比によるロバストネスの評価 ······················································································· 8
4.4 技術的なアイデアの評価のための効率的な方法(パラメータ設計) ········································· 8
4.5 二段階設計法(パラメータ設計の戦略)············································································· 9
4.6 最適設計の決定 ············································································································ 11
5 SN比によるロバストネスの評価 ························································································ 12
5.1 SN比の考え方 ·············································································································· 12
5.2 SN比の種類 ················································································································· 13
5.3 ロバストネス定量化の手順 ····························································································· 13
5.4 SN比の計算式:全変動の分解を利用した計算 ···································································· 14
5.5 SN比に関連するトピックス ···························································································· 19
6 パラメータ設計実験の手順 ································································································ 20
6.1 一般 ··························································································································· 20
6.2 (ステップ1)システムの理想機能を明確にする ································································ 20
6.3 (ステップ2)信号因子及びその範囲を選択する ································································ 21
6.4 (ステップ3)出力の測定方法を選択する ········································································· 21
6.5 (ステップ4)ノイズ戦略を作り,ノイズ因子及びその水準を選択する··································· 21
6.6 (ステップ5)設計パラメータから制御因子及びその水準を選択する······································ 21
6.7 (ステップ6)実験に取り上げた因子を内側配列及び外側配列に割り付ける ····························· 22
6.8 (ステップ7)実験を行い,データを収集する ··································································· 23
6.9 (ステップ8)SN比η及び感度Sを計算する ···································································· 23
6.10 (ステップ9)SN比及び感度について,要因効果図を作成する ··········································· 25
6.11 (ステップ10)最適条件を選択する ··············································································· 26
6.12 (ステップ11)利得によって,ロバストネスの改善効果を推定する ······································ 27
6.13 (ステップ12)確認実験を行い,利得及び再現性を調べる ················································· 27
7 事例研究−ランプ冷却システムのパラメータ設計 ·································································· 28
附属書A(参考)SN比を用いたシステムのロバストネスの比較 ··················································· 37
Z 9061:2016 (ISO 16336:2014) 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
附属書B(参考)各技術分野における事例及びSN比 ································································· 44
参考文献 ···························································································································· 65
Z 9061:2016 (ISO 16336:2014)
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人日本規格協会(JSA)から,工
業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済
産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9061:2016
(ISO 16336:2014)
新技術及び新製品開発プロセスのための
統計的方法の応用−ロバストパラメータ設計(RPD)
Applications of statistical and related methods to new technology and
product development process-Robust parameter design (RPD)
序文
この規格は,2014年に第1版として発行されたISO 16336を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
ロバストパラメータ設計(RPD)(以下,パラメータ設計という。)は,技術開発又は製品設計の段階で
活用し,製品の機能のロバストネスの評価を基にして設計パラメータの最適値を求める方法である。ロバ
ストネスの評価は,製品ライフサイクルで生じる全損失を考慮して行う。全損失は,製品ライフサイクル
の各段階で生じるコストと損失とから成り立っている。すなわち,全損失とは,生産段階,使用段階及び
廃棄段階での全てのコストを含めた損失の総和である。
製品がロバストでなければ,出荷されてから廃棄されるまでの使用期間の中で,機能のばらつきによっ
て品質が低下し,結果としてその製品からは,多くの環境的及び社会的な損失(製造業者及び使用者に対
する損失を含む。)が生じる。製品の供給業者には,製品の欠陥に起因した損失及び損害が生じないように,
ロバストな製品を市場に供給する責任及び義務がある。
製品の設計段階でパラメータ設計を適用する目的は,その製品の使用中に生じる可能性がある欠陥,故
障及び品質問題の予防である。パラメータ設計の結果としてのロバストな製品とは,欠陥,故障及び品質
問題で生じる使用者の品質損失を最小にするように設計された製品である。留意する点は,欠陥,故障及
び品質問題は,製品の機能のばらつきによって生じるということである。パラメータ設計では,製品の設
計パラメータを制御因子として扱い,更に,ノイズ因子の存在下でのロバストネスを評価することで,こ
の設計パラメータの最適値の選択を可能にする。パラメータ設計を開発段階及び設計段階で用いれば,製
品を使用環境の下でロバストにする最適な製品の設計を決めることができる。
製造段階で,製品の供給業者は製品仕様と合致した製品を製造する。また,仕様に合致する製品を生産
するために製造工程を最適化することができる。しかし,使用環境,製品劣化などに対するロバストネス
は,製品設計の段階でしか確保できない。
パラメータ設計の方法論は,設計条件の決定を通じてロバストネスを実現する有効な方法を与え,それ
は,市場での多様な損失に対する予防的な対策となる。
実際,多くの欠陥及び故障は,使用環境,劣化,製品のばらつきなどのノイズ条件の変化によって,製
品の特性が目標値から外れたり,又は目標値の近傍で変化したりすることによって生じている。市場での
損失は,製品特性のばらつきの大きさに比例して大きくなるため,ノイズによる製品特性のばらつきをロ
2
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
バストネスの指標として使用できる。このばらつきの指標の逆数であるSN比は,ロバストネスの指標と
して使用できる。すなわち,SN比が大きければ,市場での損失は小さくなる。
パラメータ設計のための実験計画としては,内側配列と外側配列との直積実験計画が提案されており,
制御因子は内側配列に,信号因子及びノイズ因子は外側配列に割り付けられる。直積実験計画を用いるこ
とによって,制御因子とノイズ因子との全ての一次の交互作用が評価できるようになり,ロバストネスの
観点からの最適な制御因子の水準選択ができる。
SN比によるロバストネスの評価がパラメータ設計の要である。外側配列は,内側配列で指示された水
準組合せにおけるSN比,すなわちロバストネスを評価するためのものである。内側配列は,そのSN比
を比較し,製品の設計パラメータの最適な組合せを選ぶためのものである。内側配列としては,直交表L18
が効率的な実験計画として推奨されている。また,この規格では,直交表L18の適用に限定している。直
交表L18以外の実験計画は,参考文献の事例の中に見いだせる。また,内側配列及び外側配列に関する詳
細な資料も参考文献に見いだせる。
この規格が直接対象にしているのは,製品の使用段階で生じる損失である。可能であれば,パラメータ
設計の結果に加えて,他の段階での損失を検討することによって,製品のライフサイクルを通した最適な
設計を行うことができる。
1
適用範囲
この規格は,ロバストな製品を実現するために効率的な,タグチメソッドに基づく最適化の方法論であ
るパラメータ設計を適用する場合の指針を示す。
この規格は,信号対ノイズ比(SN比)をロバストネスの指標として規定し,この指標を用いてロバス
トな製品を設計するパラメータ設計の手順を示す。この規格において,“ロバスト”という用語は,様々な
ノイズ条件の下で製品の機能のばらつきが最小化されていること,すなわち,ノイズレベルが変化しても
製品の機能が変化しないことを意味する。ロバストな製品において,その出力は,信号には敏感となるが
ノイズには鈍感となる。
この規格の方法は,機械,化学製品,電気製品,食品,日用品,ソフトウェア,新材料,サービスなど
を含む,設計・製造する全ての製品に対して適用できる。また,製造技術も製造工程において使う製品で
あるとみなすことができる。さらに,この規格では,適用対象とする製品,技術などを“システム”と表
記している。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 16336:2014,Applications of statistical and related methods to new technology and product
development process−Robust parameter design (RPD)(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8101-1 統計−用語及び記号−第1部:一般統計用語及び確率で用いられる用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: General statistical terms
and terms used in probability(IDT)
3
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ISO 3534-3,Statistics−Vocabulary and symbols−Part 3: Design of experiments
3
用語及び定義並びに記号
3.1
用語及び定義
この規格で用いる用語及び定義は,JIS Z 8101-1及びISO 3534-3によるほか,次による。
注記 ISO 3534-3:2013に対応するJISはないが,ISO 3534-3:1999に対応するJIS Z 8101-3:2006があ
る。ただし,対応国際規格で引用している用語が定義されていないものがあるため,ISO 3534-3
を引用した。
3.1.1
機能(function)
システムが,その目的を達成するために行う働き。
注記 機能は,数学的な入出力関係で表現できる。
3.1.2
ロバストネス(robustness)
様々なノイズ条件の下で,システムの機能のばらつきの小ささの程度。
注記 システムの性能,すなわち機能のばらつきは,ロバストネスによって評価できる。SN比は,ロ
バストネスの定量的指標である。
3.1.3
信号対ノイズ比,SN比(signal-to-noise ratio)
出力の変動のうち,有害な効果に対する有用な効果の比。
注記1 SN比は,一般にデシベル値で表す。ロバストネスの指標としてのSN比の単位記号は,“dB”
ではなく“db”を用いる。
注記2 SN比の真数は,分散又は変動係数のようなばらつきの尺度の逆数であり,経済損失に反比例
する。
注記3 意図的な信号の変化による出力の変化は有用な効果である。理想機能がゼロ点比例式の場合,
ゼロ点を通る直線成分は有用な項である。
注記4 ノイズ条件などによる出力の変化は有害な効果である。例として,ノイズ因子の効果による,
理想機能からのかい(乖)離がある。
注記5 SN比には,ノイズ因子の下でのばらつき及び平均的な使用条件の下での理想機能からのかい
離を含んでいる。
3.1.4
感度(sensitivity)
入力の単位変化に対する出力の変化の大きさ。
注記1 感度は,一般にデシベル(db)値で表す。
注記2 動的特性の場合,線形係数を“β”で表したときに,感度は単位信号に関わる効果の大きさβ2
で表している。
注記3 望目特性の場合,出力の平均を“m”で表したときに,感度は平均値の大きさm2で表してい
る。
3.1.5
ノイズ(noise)
4
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
システムの機能を乱す変数。
注記1 システムの運用及び作動に関する使用者の条件は,信号又はノイズに分類される。
注記2 ノイズは,内乱と外乱とがある。内乱の例として,劣化,疲労などのシステム又はその部品
の時間経過による内部定数の変化,及び製造上のばらつきによる内部定数の違いがある。外
乱の例として,製品の使用条件及び環境条件の変化がある。
注記3 この規格では,実験においてノイズレベルを設定するための因子をノイズ因子(noise factor)
という。ノイズ因子は,誤差因子ともいう。
3.1.6
信号(signal)
システムの入出力関係において,意図した出力を得るために,使用者が意図的に変化させる入力変数。
注記1 システムの運用及び作動に関する使用者の条件は,信号又はノイズに分類される。
注記2 信号には,能動的信号と受動的信号との2種類がある。能動的信号は,使用者が意図した出
力を得るために,使用者によって操作される。例えば,車の方向を変えるためのハンドルの
回転角度がある。受動的信号は,使用者がその出力から入力の値を知るために使用される。
例えば,熱的測定の温度がある。いずれの場合も,出力の値は入力の信号の値が変化するこ
とによって変わる。ただし,能動的な場合には使用者は出力の値を得ることが目的であり,
受動的な場合には使用者は信号の値を知ることが目的である。
3.1.7
動的特性(dynamic characteristics)
信号の値によって変わる目標値をもつ出力。
注記1 動的特性と信号との関係は入出力関数形で示される。多くの場合,システムの機能からの出
力は動的特性である。
注記2 動的特性は,動特性ともいう。
3.1.8
静的特性(static characteristics)
固定された目標値をもつ出力。
注記1 静的特性は,目標値によって,望目特性,望小特性及び望大特性の3種類に分類される。そ
の目標値は,それぞれ,有限値,ゼロ及び無限大である。
注記2 静的特性は,非動的特性(non-dynamic characteristics)又は静特性ともいう。
3.1.9
内側配列(inner array)
設計パラメータが制御因子又は標示因子として割り付けられる実験計画。
注記1 それぞれの実験処理について,SN比及び感度を用いてロバストネスを評価する。
注記2 内側配列としては,直交表を用いるのが望ましい。なぜなら,制御因子として,多くの設計
パラメータを一連の実験の中に取り込むことができるからである。
注記3 実験に用いられる因子をそれらの役割によって分類し,パラメータ設計の中での役割に応じ
て,内側配列又は外側配列に分けて割り付ける。内側配列には制御因子及び標示因子を割り
付ける。
3.1.10
外側配列(outer array)
5
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SN比及び感度を評価するために,使用者の条件である変数がノイズ因子又は信号因子として割り付け
られる実験計画。
注記1 システムの運用及び作動に関する使用者の条件は,信号かノイズかに分類される。
注記2 実験に用いられる因子をそれらの役割によって分類し,パラメータ設計の中での役割に応じ
て,内側配列又は外側配列に分けて割り付ける。外側配列にはノイズ因子及び信号因子を割
り付ける。
3.2
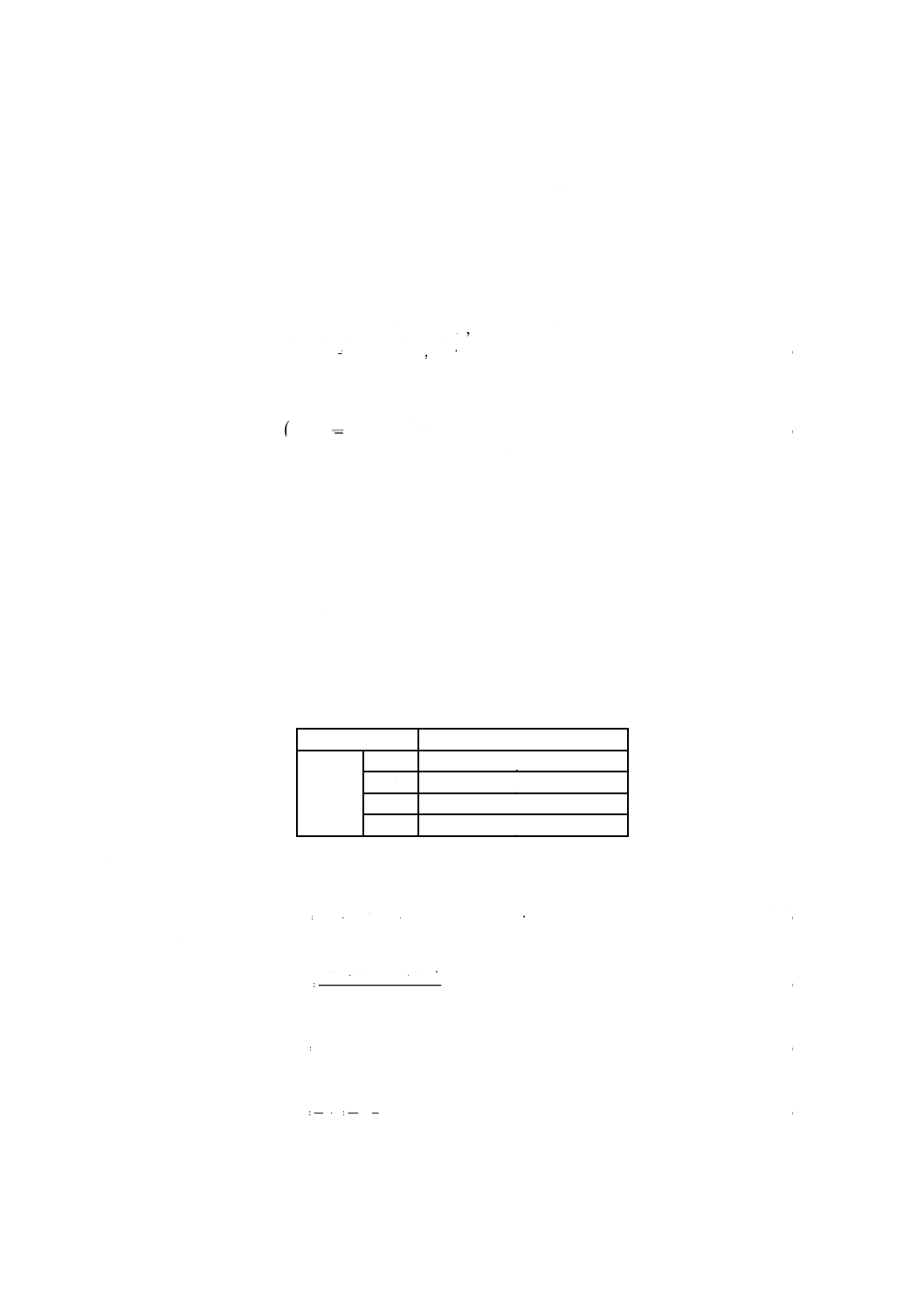
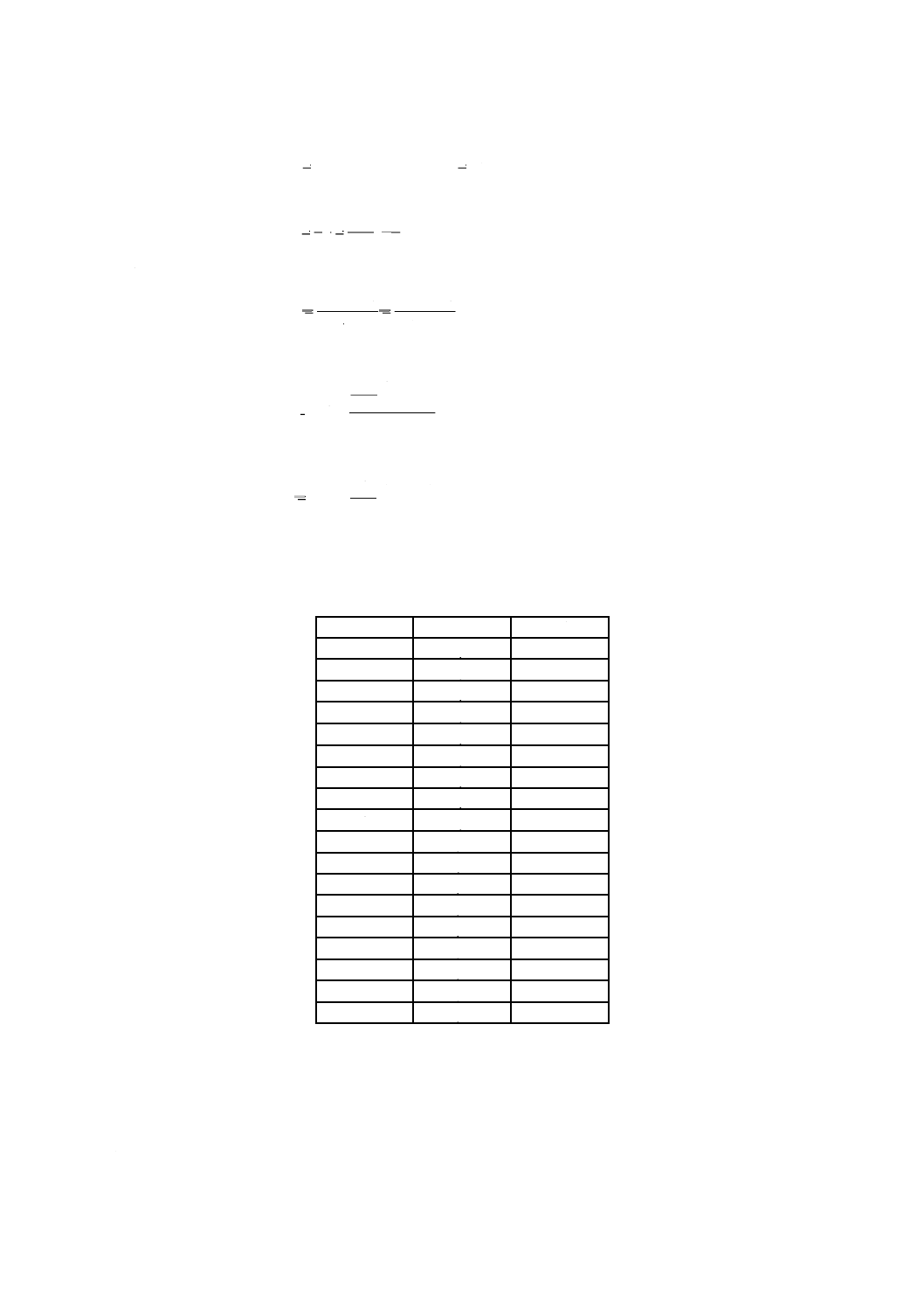
記号
f
:
自由度
(degree of freedom)
k
:
信号因子の水準数
(number of levels of signal factor)
L
:
線形式
(linear form)
Li
:
第i水準の線形式
(linear form for level of i)
M :
信号因子
(signal factor)
Mi :
信号因子の第i水準
(signal level of i)
Mi :
信号因子の第i水準の値 (value of the signal level of i)
N
:
ノイズ因子
(noise factor)
n
:
ノイズ因子の水準数
(number of levels of noise factor)
Ni :
ノイズレベルの第i水準 (noise level of i)
p0
:
標準化誤り率
(standardized error rate)
r
:
有効除数
(effective divisor)
S
:
感度
(sensitivity)
ST :
全変動
(total sum of squares)
Sm :
平均の変動
(sum of squares due to mean)
Sβ :
比例項の変動
(sum of squares due to linear slope β)
SN×β :
比例項の差の変動
(sum of squares due to the variation of linear slope
β between noise levels)
Se
:
誤差の変動
(sum of squares due to error)
Sopt :
最適条件における感度 (estimated value of sensitivity for optimum condition)
Sbase :
比較条件における感度 (estimated value of sensitivity for baseline condition)
Scur :
現行条件における感度 (estimated value of sensitivity for current condition)
Ve :
誤差分散
(error variance)
VN :
総合誤差分散
(variance due to pooled error)
y
:
出力
(output response)
β
:
線形係数
(linear slope)
ΔS :
感度の利得
(gain in sensitivity)
Δη :
SN比の利得
(gain in SN ratio)
η
:
SN比
(SN ratio)
ηopt :
最適条件におけるSN比 (estimated value of SN ratio for optimum condition)
ηbase :
比較条件におけるSN比 (estimated value of SN ratio for baseline condition)
ηcur :
現行条件におけるSN比 (estimated value of SN ratio for current condition)
ρ0
:
標準化寄与率
(standardized contribution ratio)
6
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 対応国際規格では,幾つかの英語表記が併記されているものがあるが,JISでは,代表的な日
本語表記及び英語表記に限定した。
4
ロバストパラメータ設計の概要
4.1
必要事項
ロバストパラメータ設計は,設計プロセスにおいて,ロバストネスを改善する技術的な手段を見いだす
ための合理的かつ効率的な評価方法である。そのため,次の二つの手順を踏まえることが必要である。
a) 正確かつ簡単にロバストネスを評価する手順
b) 複数の技術手段を効率的に比較する手順
この箇条では,ロバストパラメータ設計の概要について規定する。ロバストネスの評価及びパラメータ
設計実験についての詳細かつ具体的な手続きは,箇条5及び箇条6で規定する。
4.2
システムのロバストネスの評価
どのようにして,システムのロバストネスをSN比によって正確に評価できるのかについて考えると,
システムのロバストネスがそのシステムの多くの使用条件に関係しているため,単純な測定によって評価
することはできない。したがって,ロバストネスに関係する隠された要因を明確にするためには,次の二
つの観点で評価をしなければならない。
a) 理想機能の利用 理想機能は,システムが目的とする機能である。ロバストネスの評価において,シ
ステムの実際の機能を測定し,理想機能と比較しなければならない。システムの理想機能を実現する
ためには,欠陥,故障,又は品質問題を避けることが重要である。
b) ノイズ因子の活用 実際の使用状態でのシステムは,様々なノイズ条件の下で働いている。ノイズレ
ベルを変化させて実験の中に意図的にノイズの効果を取り入れるために,あらかじめ決めておいたノ
イズ条件の下でシステムの実際の機能を測定し,評価することが望ましい。ロバストネスの評価は,
ノイズ因子及びその水準の選択に強く依存している。このため,有効なノイズ戦略を立てることが重
要である。
システムの機能とは,目的を実現するために行われるシステムの働きである。例えば,電球の機能は電
気エネルギーを光エネルギーへ変換すること,風車の機能は風のエネルギーを水をくみ上げるなどの仕事
をするための回転エネルギーに変換することである。通常,機能は,入力エネルギーと出力エネルギーと
の関係を表す数学的な関数の形で表される。数学的な関数は様々な形で表される。ゼロ点比例式は,物理
の世界でエネルギー変換を表す関数として一般的である。詳細は,箇条5を参照する。
入力特性及び出力特性は,システムの理想機能によって決まる。入力特性は,入出力関係において信号
とも呼ばれる。実際の使用状態及びパラメータ設計の中では,出力の変化は,使用者が意図的に入力を変
化させることによって得ることができる。信号は,その機能を働かせるために必要なエネルギー又は情報
に関係している。信号因子は,システムの出力を制御するとき,入力を変化させるために使用者が選択す
る条件の一つである。動的特性の実験においては,信号因子は3水準以上をもつことによって,実際の入
出力関係の直線性を評価することができる。静的特性の実験においては,一つの目標出力しかないので,
信号因子は取り上げない。出力特性を単に出力という。
出力の適切な測定方法を決めることは重要である。例えば,時間に依存した現象では,出力を正確に検
出することが困難な場合がある。このような場合,新しい測定方法を開発しなければならない。出力は,
システムの目的に関係している。例えば,イルミネーションの場合では光の強度であり,水のポンプの場
7
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
合では水の量である。
システムの実際の機能を理想機能から外れさせるのが,ノイズ条件である。例えば,実際にシステムが
働く環境条件として,温湿度,使用時の電圧,電気的なノイズの状況,使用頻度,ストレスなどがある。
それらは外乱と呼ばれている。一方,時間経過,疲労など内乱と呼ばれているノイズ条件もある。例えば,
使用時間,アイドリング時間,長時間の使用後の劣化,システム及び/又は部品の製造ばらつきなどがあ
る。これらのノイズ条件は,システムの機能のパフォーマンスを,設計時に期待するレベルより低くする。
ロバストネスの評価の目的はこの低下量を知ることであるため,ロバストネスの評価においては,ノイズ
条件の下でのシステムのばらつきを評価しなければならない。これが,パラメータ設計の実験の中でノイ
ズ条件をノイズ因子として取り上げる理由である。ノイズ因子の三つのカテゴリは,a) 環境,b) 時間経
過及び c) 製造のばらつきである。有効なノイズ戦略のために,実際の使用条件及び環境条件の中で,様々
な種類のノイズを調べることが必要である。
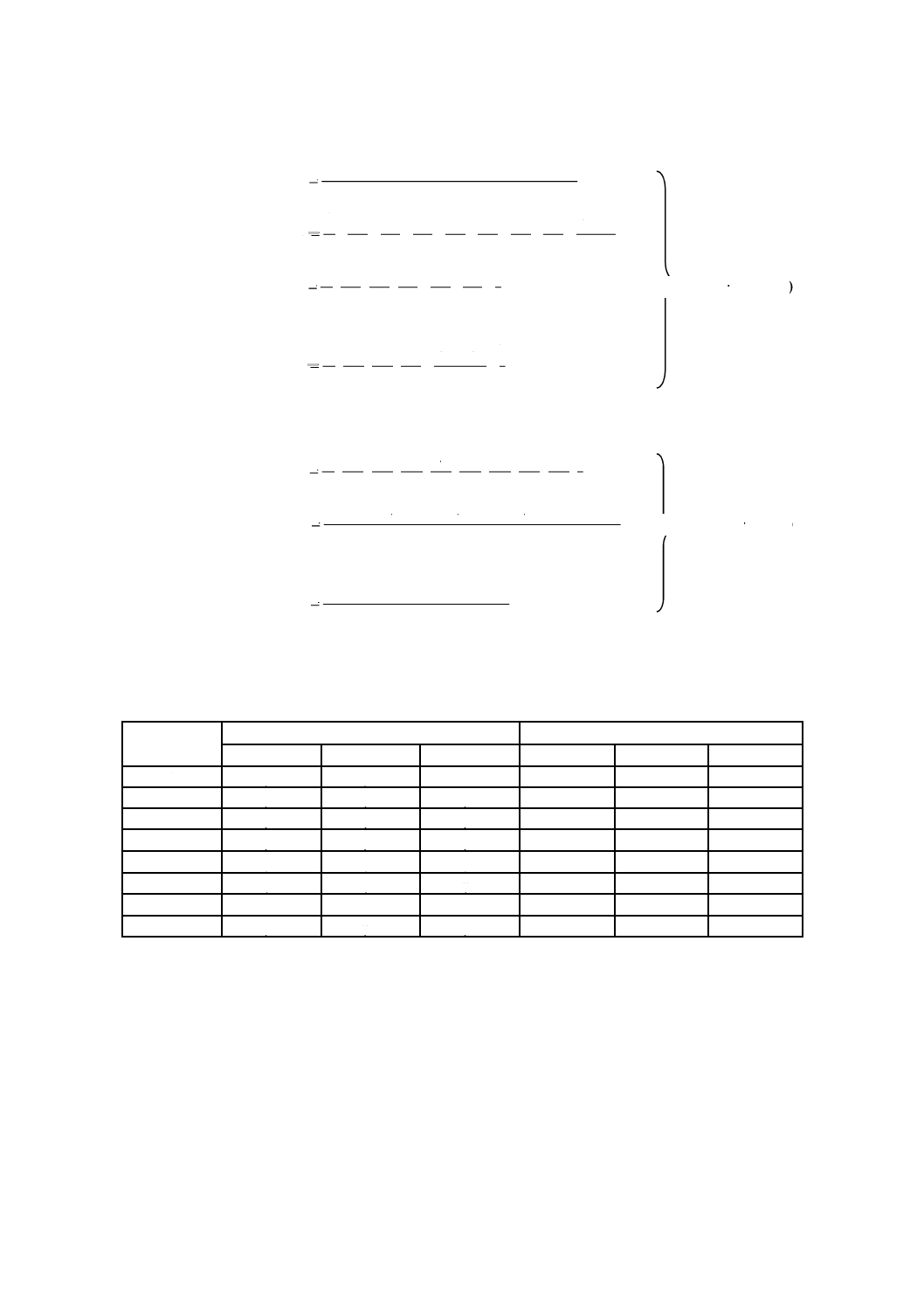
ノイズ因子を用いたロバストネスの評価の概要を図1に示す。ここでは,ノイズレベルN1〜Nnの下で
の複数のデータX1〜Xnが対象システムから得られ,ロバストネスの尺度としてSN比ηを計算する。SN
比の計算式は,箇条5に示す。二つ以上のシステムを比較する場合は,全ての対象システムに同じノイズ
因子で同じノイズレベルを適用することが望ましい。
図1−ノイズ因子によるロバストネスの評価
実験において複数のノイズ因子を適用する場合は,実験のノイズレベルを決めるために直交表を活用す
ることができる。図2では,ノイズレベルN1〜Nnは,直交表によって決まる,A,B,Cなどのノイズ因
子の水準の組合せである。ノイズレベルを決めるために,直交表以外を利用することもできる。
ノイズレベル
N1
N2
…
Nn
SN比
評価されるシステム
X1
X2
…
Xn
η
Ni…ノイズの第i水準
Xi…データ
ノイズ因子
対象システム
データ
8
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2−直交表によって決まるノイズレベルによるロバストネスの評価
4.3
SN比によるロバストネスの評価
理想機能及びノイズ戦略は,ロバストパラメータ設計におけるロバストネスの評価の重要な項目である。
対象システムの実際の機能のばらつき及び効率を測定し,評価することが本質である。そのような評価に
よって,システムが働く際に生じるであろう全ての技術問題をカバーし,技術的な障害を予防することが
できる。ロバストネスの評価では,要求される機能を阻害するノイズ因子の効果の評価も行う。その結果
はSN比及び感度によって示される。
SN比は,複数の設計の間でのロバストネスの差異を明確にする。SN比では,相対的な差異だけに意味
がある。なぜなら,SN比の絶対値は,ノイズレベルの設定によって異なるためであり,したがって,ロ
バストネスの評価においては,ベンチマーキングを行うことが望ましい。
この方法の特徴は,次の点にある。すなわち,SN比の評価に必要な情報は,システムの機能及びノイ
ズ条件に関する知識だけである。対象システムの技術的な細かい情報は必要ない。同じ機能,すなわち,
同じ入出力関係をもっていれば,たとえ技術的な構成が異なっていても,複数のシステムに対して同じよ
うにSN比を計算すればよい。SN比によって複数のシステムのロバストネスが正しく評価されるため,異
なった設計コンセプトをもった様々なシステムであっても,評価し,比較することが可能である。
異なった技術又は異なった設計コンセプトに基づいた複数のシステムは,SN比を通して同じように比
較することができる。従来システムと新開発システム,自社のシステムと競合他社のシステムなど,複数
のシステムは,機能が同じであれば,SN比を通して同じように評価することができる。これが,様々な
設計コンセプトのベンチマーキングにおいて,SN比によるロバストネスの評価を有効に利用できる理由
である。
4.4
技術的なアイデアの評価のための効率的な方法(パラメータ設計)
工業的な製品のシステムを設計する場合,最初に,基本的な技術及びメカニズムを設計コンセプトとし
て選択する。ベンチマークするシステムの設計コンセプトが複数ある場合には,4.3で記載したロバストネ
スの評価は,最適な設計コンセプトを選ぶために適用可能である。
最適な設計コンセプトを選択した後,システムの設計パラメータの値を決めるという詳細設計がある。
この詳細設計の段階で,設計者は,設計対象のシステムの機能が最もロバストで,効率的であるように最
適な公称値を選ぶことによって,システムを最適化することができる。このとき行われる方法をパラメー
タ設計という。なぜなら,この最適化設計では,設計パラメータを最適公称値に設定することによって行
ノイズ因子を割り
付けた直交表
対象システム
データ
直交表によるノイズレベル
1
2
3
4
…
n
A: 周辺温度・湿度
…
B: 新製品と低位製品
…
C: 使用頻度
…
ノイズレベル
N1
N2
N3
N4
…
Nn
SN比
評価されるシステム
X1
X2
X3
X4
…
Xn
η
A,B,C…ノイズ因子
9
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
われるためである。
次のような状況の場合に有意性があると考えられる。システムが最適な状態にあれば,どのような使用
条件の下でも最良のパフォーマンスを実現する。さらに,具体的には,温度及び湿度の広い範囲の条件の
下でも,また,異なった使われ方及び異なった環境の中でも,いつでも,工業的システムは意図した機能
を安定的に働かせることができる。最適な設計条件は,製品のロバストネスが最大になる設計パラメータ
の値の組合せであると考える。パラメータ設計による最適化は,ロバストネスの最大化,すなわち,ばら
つきを最小化し,効率を最大化するための最適化であり,その判断は,ロバストネスの尺度であるSN比
及び感度を用いて行われる。
SN比を用いたロバストネスの評価による最適化は,パラメータ設計における最適化の考え方の基本で
ある。ロバストネスの評価は,設計空間の中で可能な全ての設計について行う必要があるが,現実には不
可能である。なぜなら,設計パラメータの可能な組合せの全てを試験しようとすると,非常に多くの試験
数になるからである。
開発設計段階で用いるために,より現実的な方法として,直交表を用いた実験がある。そこでは,限ら
れた実験処理数の下で,多くの設計パラメータの組合せを試験することができる。直交表を用いた実験計
画は,同じ数の制御因子の多元配置に比べ,実験処理数を削減できるだけでなく,同じ実験処理数で最大
数の制御因子を割り付けることができる。実験結果の信頼性は,再現性を調べるための確認実験によって
確認することができる。再現性を調べるための確認実験を行う方法については,箇条6に示す。
パラメータ設計実験は,次の手順で行う。
− (ステップ1) システムの理想機能を明確にする。
− (ステップ2) 信号因子及びその範囲を選択する。
− (ステップ3) 出力の測定方法を選択する。
− (ステップ4) ノイズ戦略を作り,ノイズ因子及びその水準を選択する。
− (ステップ5) 設計パラメータから制御因子及びその水準を選択する。
− (ステップ6) 実験に取り上げた因子を内側配列及び外側配列に割り付ける。
− (ステップ7) 実験を行い,データを収集する。
− (ステップ8) SN比η及び感度Sを計算する。
− (ステップ9) SN比及び感度について,要因効果図を作成する。
− (ステップ10) 最適条件を選択する。
− (ステップ11) 利得によって,ロバストネスの改善効果を推定する。
− (ステップ12) 確認実験を行い,利得及び再現性を調べる。
4.5
二段階設計法(パラメータ設計の戦略)
これまで示したパラメータ設計の概要を図3に示す。この図の実験は,二つの直交表を含んでいる。一
つは制御因子,すなわち設計パラメータのための直交表(内側配列)であり,もう一つはノイズ因子のた
めの直交表(外側配列)である。このような実験計画を直積実験計画という。実験処理数は,二つの直交
表でそれぞれ指定した数の積となる。例えば,内側配列が直交表L18,外側配列が直交表L12である場合,
それぞれの配列の実験処理数はm=18,n=12となり,全体の実験処理数は18×12=216となる。
10
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3−パラメータ設計のための直積実験計画
信号因子及びノイズ因子のための外側配列には,直交表の代わりに多元配置を使うこともある。実際に
物理的な実験を行う場合,実験処理数を減らすため,多くのノイズ因子を一つの調合ノイズ因子に調合さ
せるのがよい。一方,設計パラメータのための内側配列は,常に直交表を用いることが望ましい。なぜな
ら,多くの設計パラメータを一つの直交表に割り付けることができるためである。
制御因子の水準の組合せそれぞれに対して,ノイズレベルの数に対応した複数の測定データが得られる。
ロバストネスに対する設計パラメータの最適水準を見つけるために,内側配列の各行に対して,すなわち,
設計パラメータの水準の組合せに対して,SN比及び感度を計算する。
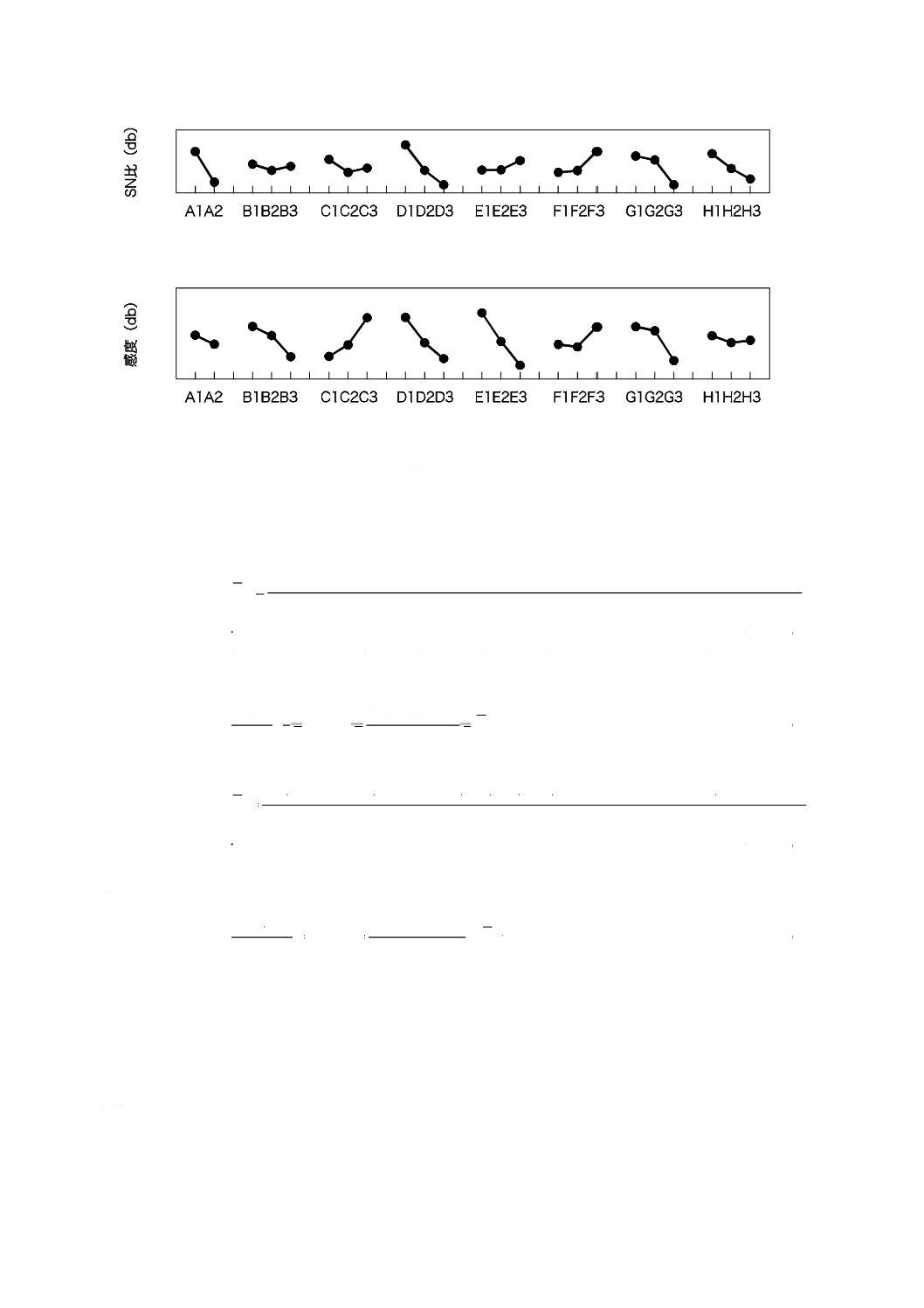
さらに,SN比及び感度に対する個々の制御因子の要因効果を計算し,図4及び図5のような要因効果
図にまとめる。この計算については,箇条6に示す。感度とSN比の要因効果図に基づき,設計パラメー
タの最適値を選択する。望目特性(5.4.4参照)の場合は,感度はデータの平均値を表しており,SN比は
ロバストネスを表している。
要因効果図は,実験で取り上げた設計パラメータがシステムの機能にどのように影響しているかを示し
ている。因子が大きな傾きを示す場合には,その因子はシステムの機能に大きな効果をもつ。SN比及び
感度に対する影響の大きさが,二つの要因効果図で示される。最適水準の選択における重要なポイントは,
感度への要因効果に比べ,SN比への要因効果に,より多くの注意を払うことである。
第1段階で,SN比の要因効果図(図4)からSN比を最大化するように制御因子の最適水準を選択する。
第2段階では,一つの制御因子を用いて,平均値又は線形係数,すなわち感度を目標の値に調整する。こ
の調整においては,感度への効果は最大で,SN比への影響は最小であるような制御因子を選択すること
直交表によるノイズレベル
ノイズ因子
1
2
3
4
…
n
A:温度
B:湿度
C:……
N1
N2
N3
N4
…
Nn
感度
SN比
割り付け
られた設
計パラメ
ータによ
って評価
されるシ
ステム
1
S1
η1
2
S2
η2
3
S3
η3
4
S4
η4
…
…
…
m
S m
η m
ノイズ因子を
割り付けた
外側直交表
制御因子を
割り付けた
内側直交表
データ
11
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
が望ましい。第1段階は,SN比によるロバストネスの最適化であり,第2段階が感度による目標値に対
する出力の大きさの調整である。このような二つの段階による設計は,ロバストネスの設計にとって非常
に重要な手順である。このため,パラメータ設計は二段階設計法又は二段階最適化法ともいう。
二段階設計法の重要性,また,SN比によるロバストネスの最適化と,感度による出力の大きさの調整
との難しさの違いを次に示す。
ロバストなシステムの設計を効率的に行うために,最適化の順序は重要である。例えば,ボイスレコー
ダの場合,周囲の雑音が大きい状態で記録されたデータは,再生のとき,音量を調整することによって記
録された音を聞きやすくすることは難しい。雑音に埋もれた情報を取り出すためには,ノイズの効果を打
ち消すように雑音低減をしたり,周囲の雑音に対して感度の低いマイクロフォンを使ったりするなどの技
術的な対応を取らなければならない。SN比を改善するためには,記録時において高い技術力及び対応策
が必要である。一方,記録時の平均的な録音レベルが低すぎる場合には,再生のときにボリュームを調整
することによって簡単に改善できる。すなわち,出力の大きさの調整は感度によって簡単に行うことがで
きる。
もう一つ,写真及びビデオ動画のような画像の例がある。濃度の平均は簡単に修正できるが,暗い場所
で取られた画像はしばしばノイズが多く,低品質の画像になる。画像処理によって画質を上げることには
限界がある。
出力の大きさを調整するのは,比較的簡単な場合が多い。それは,一つの調整用のパラメータがあれば
よいからである。エネルギーの平均値を調整するのは容易である。一方,ロバストネスを改善するのは容
易ではない。改善するには,できるだけ多くの制御因子があることが望ましい。そのため,システムの設
計において,SN比を最大化できるように設計パラメータを最適値に合わせることをより優先するのがよ
い。これが,SN比によるロバストネスの最適化を第一優先とするという,二段階設計法の思想である。
4.6
最適設計の決定
図4−SN比(ロバストネス)に対する要因効果図の例
図5−感度(平均値又は線形係数)に対する要因効果図の例
12
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
パラメータ実験を行い,要因効果図の中で,どの設計パラメータがSN比に影響し,どの設計パラメー
タが感度に影響するかが明確になれば,ロバストネスを基に,最適な設計パラメータ値の最適値の組合せ
を選択することができる。さらに,コスト,納期などの他の制約を考慮に入れて,最終的な最適設計を決
めることができる。
最終的なシステムの最適設計は,多くの制約の全体的なバランスで決めるのがよいため,実験に取り上
げる因子ができるだけ広い設計空間をカバーできるような実験計画を選択することが望ましい。最適水準
が経験範囲から遠く離れたところにある可能性もあるため,制御因子の水準はできるだけ広い範囲をカバ
ーすることが望ましい。
パラメータ設計において,ロバストネスの最適化はSN比を最大化することによって行われる。SN比は,
ロバストネスがないことによって生じる欠陥,故障及び品質問題による使用者の品質損失の量的な尺度で
ある。使用者の品質損失には,誤動作,故障などによって生じる,余分なメンテナンスのコストなどの損
失も含まれる。
田口玄一の損失関数によれば,SN比を使用者の品質損失の金額に変換することができる。製品が社会
に与える全ての損失は,使用者の品質損失に,例えば,製品開発コスト,材料コスト,製造コスト,輸送
コスト,正規のメンテナンスコスト,廃棄コストなどのコストを加えることによって求めることができる。
社会損失全体は,製品の品質の尺度である。製品設計段階では,設計者は技術の観点からこの社会損失全
体を考慮しなければならない。しかし,設計者が設計段階で社会損失全体を予測することは困難である。
このため,少なくともロバストネスの観点から,製品設計を評価し,最適化することが望ましい。パラメ
ータ設計は,ロバスト工学の観点,すなわち,製品の機能のばらつきの観点から,使用者の品質損失に焦
点を当てている。
5
SN比によるロバストネスの評価
5.1
SN比の考え方
ロバストな製品を設計するためには,システムにおける機能のばらつきをパラメータ設計によって評価
し,最適化しなければならない。このとき,サブシステムのロバストネスを評価する場合であっても,そ
れが組み込まれ,使用者の手にある全体システムのノイズ条件を考慮するのがよい。全体システムレベル
でのロバストネスを保証することが重要である。
システムの機能は,システムの使用状態での入出力関係の関数で定められる。使用者は,システムから
意図した出力を得るために,信号を操作する。信号は,システムの出力を変えるために意図的に設定され
る入力特性である。システムの機能の理想的な入出力関係を示す関数は,システムの理想機能と呼ばれる。
ただし,製造された製品,又は製品の実際の使用条件の下では,製品の理想機能が完全に実現されるわけ
ではない。そこで,パラメータ設計では,理想機能からのずれの大きさを使用条件の下で評価し,SN比
という一つの数値で表す。
システムが実際に使われる場合の使用者の条件には,信号及びノイズがある。信号は,システムの出力
を変化させるために意図的に変化させるシステムへの入力であり,出力に対して大きな効果をもっていな
ければならない。一方,ノイズは,システムの出力をばらつかせる影響をもつ。信号の効果は最大化し,
ノイズの影響は最小化しなければならない。SN比によるロバストネスの評価の実験では,入力特性は信
号因子として,ノイズの原因はノイズ因子として扱う。このように,使用者の条件を区別することは,実
験の目的を明確にする上で重要である。
SN比は,様々なノイズ条件の下での入出力関係がどれだけ理想機能に近いかを定量的に表す尺度であ
13
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。SN比が大きくなれば,入出力関係は理想に近くなり,社会における損失は減少する。その逆の場合
には,理想から遠くなり,社会における損失は増加する。
5.2
SN比の種類
ロバストネスの評価におけるSN比の種類は,対象とする特性によって三つに分類する。すなわち,動
的特性のSN比,静的特性のSN比及びデジタル特性のSN比である。
動的特性のSN比は,信号とそれに対応した出力との関係の安定性を示している。動的特性のSN比は
システムにおける理想機能の関数の形によって,更に三つに分類する。すなわち,ゼロ点比例式の理想機
能,基準点比例式の理想機能及び一次式の理想機能である。理想機能の関数は,対象システムの物理的特
性を基に選択され,多くの場合,ゼロ点比例式が用いられる。
静的特性のSN比は,システムの出力の値の安定性を示している。出力の目標値は固定されており,信
号は一定である。静的特性のSN比は,システムの目標値によって,更に三つに分類する。すなわち,望
目特性,望小特性(5.4.5参照)及び望大特性(5.4.6参照)である。目標値は,システムの種類によって
異なり,望目特性では有限の値,望小特性ではゼロ,望大特性では無限大である。
デジタル特性のSN比は,例えば,0及び1のような二値の入力と出力をもつシステムの性能の評価に
用いる。理想的なデジタルシステムでは,入力が0又は1のとき,システムの出力はそれぞれ0又は1で
ある。この入出力特性の対応がデジタルシステムの理想機能である。デジタルシステムのSN比は,しき
い(閾)値の校正を行った後のデジタルシステムの能力を表す。
5.3〜5.5に,それぞれの種類のSN比を求める手順を示す。
5.3
ロバストネス定量化の手順
SN比及び感度を求める手順は,次のとおりである。
− (ステップ1)システムの理想機能を明確にする。
機能とは,システムがその目的を達成するために行う働きである。動的機能の場合,機能は使用者
の意図を表した信号をもつ。システムの目的を達成するために,信号によってシステムの出力を変化
させる。機能は,入力となる信号と出力との関係を表す関数で表される。
このステップでは,理想機能を定める。すなわち,システムの機能の目的に基づき,信号と出力と
の間の理想関係を定める。理想機能は,期待されるシステムの働きである。
静的特性の場合は,出力を表す特性とシステムの出力の目標値とを明確にし,ステップ3へ進む。
− (ステップ2)信号因子及びその範囲を選択する。
動的特性において,信号は,システムの出力を意図したとおりに変化させるための,能動的又は受
動的に設定される入力である。実験では,信号を操作するための変数を信号因子として用いる。信号
因子は,システムの出力を得るために実験者が設定する変数である。信号因子の範囲は,市場で使用
者が用いる範囲に設定する。
− (ステップ3)出力の測定方法を選択する。
出力を適切に測定する方法を選択する。動的機能の場合,使用者が求める特性の量が出力である。
時間に依存する出力の測定が難しい場合がある。この場合は,ロバストネスの評価のために適切な測
定方法を開発する必要がある。
− (ステップ4)ノイズ戦略を作り,ノイズ因子及びその水準を選択する。
システムの使用条件の下で,理想機能を妨害する条件がノイズ条件である。SN比を評価する実験で
は,ノイズ条件はノイズ因子によって設定する。ノイズ因子は,実際の使用段階での出力を理想状態
から変えてしまう変数である。ロバストネスの評価において,有効で効果的なノイズ条件を決めるた
14
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
めに,可能な限り全てのノイズ条件を検討することが望ましい。ノイズ因子は,使用環境,経時劣化
又は製造ばらつきから選定する。ノイズ因子は,可能な限り異なる種類を含むことが望ましく,また,
平均的な使用者の使用条件を考慮して,できるだけ広い範囲からノイズ因子の水準の値を選択すると
よい。また,長期の使用による劣化のノイズ因子を取り上げることによって,システムの寿命を延ば
すことが可能となる。
− (ステップ5)実験を行い,データを収集する。
SN比によってロバストネスを評価する実験の割り付けを決定する。割り付けは,実験を行う信号因
子の水準とノイズ因子の水準との組合せを示す。一般に,割り付けは,信号因子とノイズ因子との二
元配置が典型的であり,信号因子とノイズ因子との水準を組み合わせた条件で出力を測定する。実験
の割り付けに基づき実験を行い,データを収集すれば,動的SN比の計算ができる。静的特性の場合,
信号因子がないため,ノイズ条件だけのデータとなる。ロバストネスを評価するための割り付けは,
パラメータ設計の直積実験計画のうち,外側配列の部分に相当する。
− (ステップ6)SN比η及び感度Sを計算する。
ステップ5で得られたデータを用いて,SN比η及び感度Sを計算する。計算式を,5.4に示す。計
算式は,ステップ1で定めたシステムの理想機能を基に選択する。SN比は,ノイズ条件による機能
のばらつきを評価したものである。SN比はシステムのロバストネスの指標であり,感度は効率の大
きさの指標である。
5.4
SN比の計算式:全変動の分解を利用した計算
5.4.1
ゼロ点比例式(動的特性)
信号がゼロのとき出力がゼロで,出力が信号に比例して大きくなる状態が理想であれば,理想機能は式
(1)のようなゼロ点比例式で示す。
M
yβ
=
·················································································· (1)
ここに,
y: 出力
β: 線形係数
M: 信号因子
この機能をゼロ点比例式理想機能という。
ゼロ点比例式理想機能のSN比の計算は,次による。
a) ゼロ点比例式理想機能のSN比を計算するデータセット ゼロ点比例式のデータセットを表1に示す。
ここでは,信号因子はk水準,ノイズ因子はn水準である。
表1−ゼロ点比例式理想機能のデータセット
信号
M1
M2
Mk
線形式
ノイズ
レベル
N1
y11
y12
y1k
L1
N2
y21
y22
y2k
L2
…
…
…
…
…
Nn
yn1
yn2
ynk
Ln
b) ゼロ点比例式の場合の全変動の分解
全変動:
)
(T
2
2
12
2
11
T
k
n
f
y
y
y
S
nk
×
=
+
+
=
Λ
··································· (2)
15
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
有効除数:
2
2
2
2
1
k
M
M
M
r
+
+
+
=
Λ
································································ (3)
ノイズレベルごとの線形式:
Λ
Λ
Λ
k
k
k
k
y
M
y
M
y
M
L
y
M
y
M
y
M
L
2
22
2
21
1
2
1
12
2
11
1
1
+
+
+
=
+
+
+
=
nk
k
n
n
n
y
M
y
M
y
M
L
+
+
+
=
Λ
2
2
1
1
····················································· (4)
比例項の変動:
)1
(
)
(
2
2
1
=
×
+
+
+
=
β
β
f
r
n
L
L
L
S
n
Λ
············································ (5)
比例項の差の変動:
)1
(N
2
2
2
2
1
N
−
=
−
+
+
+
=
×
×
n
f
S
r
L
L
L
S
n
β
β
β
Λ
································· (6)
誤差の変動:
)
(
N
T
e
N
T
e
n
k
n
f
f
f
f
S
S
S
S
−
×
=
−
−
=
−
−
=
×
×
β
β
β
β
····························· (7)
誤差分散:
n
k
n
S
f
S
V
−
×
=
=
e
e
e
e
······································································ (8)
総合誤差分散:
e
N
e
N
N
f
f
S
S
V
+
+
=
×
×
β
β
·········································································· (9)
SN比η及び感度S:
N
e)
(
1
log
10
V
V
S
r
n
η
−
×
=
β
····························································· (10)
(
)
e
1
log
10
V
S
r
n
S
−
×
=
β
·······························································(11)
5.4.2
一次式(動的特性)
ゼロ点比例式は汎用性がある特性であり,入力がゼロのとき出力はゼロである。一方,入力と出力の関
係が原点を通らない,及び/又は入力と出力との線形関係だけが必要な場合がある。この場合,式(12)の
ような一次式が理想機能となる。
M
y
β
α+
=
············································································ (12)
ここに,
α: 切片
β: 線形係数
この機能を一次式理想機能という。
一次式理想機能のSN比の計算は,次による。
a) 一次式理想機能のSN比を計算するデータセット 一次式のためのデータセットを表2に示す。ここ
で,信号因子はk水準,ノイズ因子はn水準である。

16
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2−一次式理想機能のデータセット
信号
M1
M2
・・・
Mk
和
ノイズ
レベル
N1
y11
y12
…
y1k
N1
N2
y21
y22
…
y2k
N2
…
…
…
…
…
Nn
yn1
yn2
…
Ynk
Nn
和
Y1
Y2
・・・
Yk
b) 一次式理想機能の場合の全変動の分解
全変動:
)
(T
2
2
12
2
11
T
k
n
f
y
y
y
S
nk
×
=
+
+
+
=
Λ
····································· (13)
平均の変動:
)1
(
)
(
m
2
12
11
m
=
×
+
+
+
=
f
k
n
y
y
y
S
nk
Λ
··········································· (14)
信号の平均値:
k
M
M
M
M
k)
(
2
1
+
+
+
=
Λ
··························································· (15)
有効除数:
2
2
2
2
1
)
(
)
(
)
(
M
M
M
M
M
M
r
k−
+
+
−
+
−
=
Λ
····································· (16)
一次項の変動:
[
]
)1
(
)
(
)
(
)
(
2
2
2
1
1
=
×
−
+
+
−
+
−
=
β
β
f
r
n
Y
M
M
Y
M
M
Y
M
M
S
k
k
Λ
·········· (17)
ノイズ因子の主効果の変動:
)1
(N
m
2
2
2
2
1
N
−
=
−
+
+
+
=
n
f
S
k
N
N
N
S
n
Λ
································· (18)
誤差の変動:
)
1
(e
N
m
T
e
n
k
n
f
S
S
S
S
S
−
−
×
=
−
−
−
=
β
······························· (19)
誤差分散:
n
k
n
S
f
S
V
−
−
×
=
=
1
e
e
e
e
································································ (20)
総合誤差分散:
e
N
e
N
N
f
f
S
S
V
+
+
=
··········································································· (21)
SN比η及び感度S:
N
e)
(
1
log
10
V
V
S
r
n
η
−
×
=
β
····························································· (22)
)
(
1
log
10
eV
S
r
n
S
−
×
=
β
····························································· (23)
注記1 SN比の計算では,単純な繰返しは行わず,他の条件を固定し,ノイズ因子の水準の組合せを
変えた複数のノイズレベルの下で試行を行う。この複数の試行の中に,偶然的なノイズ条件
17
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ではなく,ノイズ因子を意図的に導入している。意図的にノイズレベルを作り出し,多くの
条件の下でばらつきを評価することは,SN比による評価の特徴である。
注記2 理想機能の関数の形によって全変動の分解のための計算式が変わることに注意するのがよい。
例えば,平均の変動(Sm)は,一次式の場合には計算するが,ゼロ点比例式の場合には計算
しない。このこと以外にも,関数の形によって計算式に異なるところがある。
5.4.3
基準点比例式(動的特性)
基準点比例式は,基準点と呼ばれる一つの固定された点を,原点として扱う特性である。基準点比例式
のSN比は,式(24)によって変換を行ったデータ(M ', y ')から計算する。
(
)(
)(
)
0
0,
,
,
y
M
y
M
y
M
−
=
′
′
··························································· (24)
元のデータ(M,y)から基準点(M0,y0)の値を引いたデータを用いて,理想機能を次の式(25)のような
基準点比例式によって表す。 (
)
(
)
0
0
M
M
y
y
−
=
−
β
································································· (25)
この理想機能を基準点比例式理想機能という。係数βは線形係数を表している。
SN比の計算式は,変換後のデータ(M ', y ')を元のデータ(M,y)と同じように扱えば,ゼロ点比例
式の理想機能の場合と同じである。
5.4.4
望目特性(静的特性)
システムの出力が有限の固定された目標値をもっている場合,システムの特性を望目特性という。この
場合,次のa)及びb)で求めた望目特性のSN比をロバストネスの評価に用いる。
a) 望目特性のSN比のためのデータセット 静的特性の場合のデータセットを表3に示す。ここで,ノ
イズ因子はn水準をもち,信号因子はない。データは,例えば,設計Aのような一つの設計仕様の下
で収集する。このようなデータ構造は,全ての静的特性に共通である。
表3−静的特性の場合のデータセット
信号
設計仕様 A
ノイズ
レベル
N1
y1
N2
y2
...
...
Nn
yn
b) 望目特性のSN比の計算のための全変動の分解
全変動:
)
(T
2
2
2
2
1
T
n
f
y
y
y
S
n
=
+
+
+
=
Λ
·············································· (26)
平均の変動:
)1
(
)
(
m
2
2
1
m
=
+
+
+
=
f
n
y
y
y
S
n
Λ
·········································· (27)
誤差の変動:
)1
(e
m
T
e
−
=
−
=
n
f
S
S
S
····················································· (28)
誤差分散:
1
e
e
e
e
−
=
=
n
S
f
S
V
········································································ (29)
18
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SN比η及び感度S:
e
e
m
)
(
1
log
10
V
V
S
n
η
−
=
································································ (30)
)
(
1
log
10
e
mV
S
n
S
−
=
································································ (31)
5.4.5
望小特性(静的特性)
システムの出力が負でない値をもち,ゼロが目標値である場合,システムの特性を望小特性という。こ
の場合,次のa)及びb)で求めた望小特性のSN比をロバストネスの評価に用いる。
a) 望小特性のSN比の計算のためのデータセット 望小特性のデータセットは,静的特性に共通で,表
3の構造をもっている。ここで,ノイズ因子はn水準をもつ。
b) 望小特性のSN比の計算 目標値であるゼロからの偏差の変動は,次の式(32)から求める。
(
)
2
2
2
2
1
2
1
ˆ
n
y
y
y
n
+
+
+
=
Λ
σ
···························································· (32)
ここで,
2ˆσは平均二乗偏差を表す。
SN比ηは,次の式(33)によって計算する。
2
2
ˆ
1
log
10
ˆ
log
10
σ
σ
η
=
−
=
··························································· (33)
5.4.6
望大特性(静的特性)
システムの出力が,大きければ大きいほど望ましく,目標値が無限大である場合には,システムの特性
は望大特性と呼ばれる。この場合,次のa)及びb)で求めた望大特性のSN比をロバストネスの評価に用い
る。
百分率データのように,データに理論的な最大値y0が存在する場合には,最大値からの差分y'=y0−y
へデータを変換し,新しい変数y'を望小特性又は望目特性と考えることができる。この場合の計算式には,
それぞれの場合の計算式を用いることができる。
a) 望大特性のSN比の計算のためのデータセット 望大特性のデータセットは,静的特性に共通で,表
3の構造をもっている。ここで,ノイズ因子はn水準をもつ。
b) 望大特性のSN比の計算 望大特性においては,データyの逆数1/yを望小特性として扱う。したがっ
て,平均二乗偏差の推定値は,次の式(34)から求める。
+
+
+
=
2
2
2
2
1
2
1
1
1
1
ˆ
ny
y
y
n
Λ
σ
························································· (34)
SN比ηは,次の式(35)によって計算する。
2
2
ˆ
1
log
10
ˆ
log
10
σ
σ
η
=
−
=
·························································· (35)
5.4.7
デジタル特性のSN比
デジタルコンピュータ,制御システム,デジタル通信システムなどのように,入力及び出力のデータが,
例えば1又は0のように二値のデジタル値になっている場合がある。このようなデジタル入力及びデジタ
ル出力のシステムでは,次のa)及びb)で求めた標準化SN比をロバストネスの評価に用いる。標準化SN
比は,“しきい(閾)値の調整によって最適化されたあとのSN比”ということを意味している。この調整
を,校正又は水準調整という。
19
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) デジタル特性の標準化SN比計算のためのデータセット 通信機能について考えると,1を送信した
ときに0を受信したとすれば,エラーとなる。このようなエラー率を“p”で表す。0を送信したとき
に1を受信したとすれば,これもエラーである。このようなエラー率を“q”で表す。このようなエラ
ーの状況は,表4にまとめることができる。
表4−2種類のエラー率の表
出力(決定結果)
試行回数
1
0
入力
(サンプル)
1
1−p
p
n1
0
q
1−q
n2
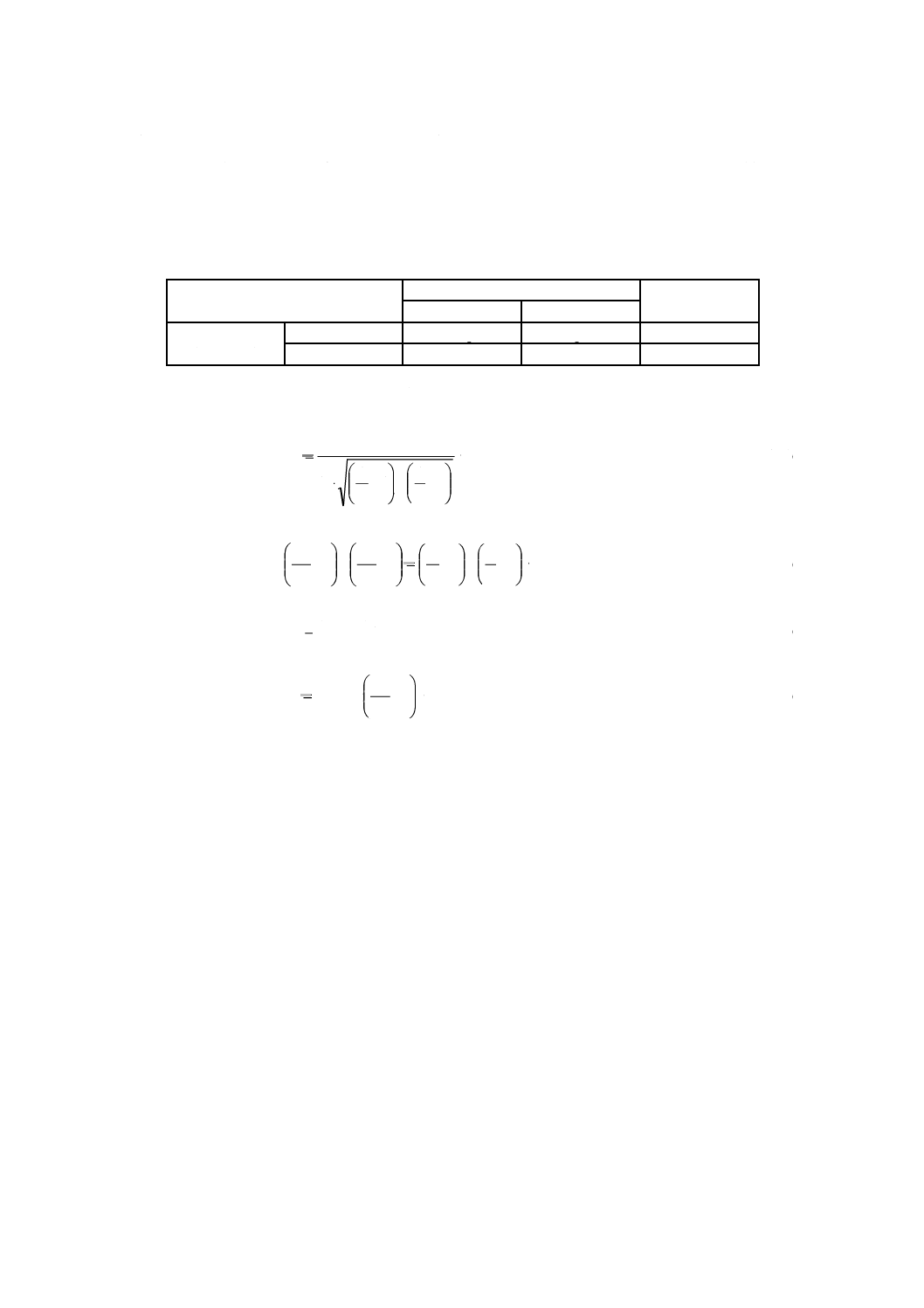
b) デジタル特性の標準化SN比の計算 通信システムを,エラー率p及びqが同じになるようにしきい
(閾)値を調整することによって最適化したとき,標準化誤り率p0は,次の式(36)から求められる。
−
×
−
+
=
1
1
1
1
1
1
0
q
p
p
·························································· (36)
なぜなら,次の式(37)の等式が成立するからである。
−
×
−
=
−
×
−
1
1
1
1
1
1
1
1
0
0
q
p
p
p
············································· (37)
標準化寄与率ρ0は,標準化誤り率p0から,次の式(38)によって計算する。
(
)2
0
0
2
1
p
−
=
ρ
········································································· (38)
デジタル特性の標準化SN比は,次の式(39)のようになる。
−
−
=
1
1
log
10
0
0
ρ
η
································································· (39)
デジタルシステムの標準化SN比は,しきい(閾)値のレベル調整によって最適化した後のデジタ
ルシステムのロバストネスを表している。
5.5
SN比に関連するトピックス
5.5.1
システムの比較におけるSN比の利用
個々のSN比の絶対値には重要な意味はなく,同じノイズレベルの下で評価された二つのシステムのSN
比の差が,システムの比較の尺度となる。同じノイズレベルの下で評価されたSN比の大きさは,システ
ムの非効率性及びばらつきによる市場での損失の指標となる。様々な設計コンセプトによって設計された
複数のシステムのロバストネスの比較が可能となり,これを“ロバストネスアセスメント”という。
SN比は,複数のシステム又は設計コンセプトの間の相対比較に適用可能である。ロバストネスアセス
メントは,技術開発及び製品開発における新しいシステムに適用可能であるだけでなく,ロバストネスに
ついてどの製品が優れているかを明らかにするためのベンチマークにおいて,従来製品及び競合製品を評
価することにも適用可能である。
5.5.2
非線形の場合
信号と出力との間の理想関係が線形でないときであっても,簡単な変数変換によって入出力関係を線形
化できる場合がある。変数変換によって,機能をゼロ点比例式の理想機能で表現することができ,SN比
を計算できる。
例 yを出力,Mを入力,αを定数とする。
20
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
システムの理想機能は
M
e
y
β
α×
=
として,両辺の自然対数を取ると,ln y=ln α+βMとなる。
ln yを新しい変数Yとすれば,Y=ln α+βMとなる。
この場合,一次式のSN比の計算式が適用可能である。
5.5.3
静的特性のSN比
技術開発及び製品開発の上流においては,静的特性のSN比ではなく,動的特性のSN比を適用するこ
とが効果的であり,望ましい。また,静的特性のSN比は,技術開発及び製品開発の下流において適用す
ることができる。
6
パラメータ設計実験の手順
6.1
一般
この箇条は,理想機能がゼロ点比例式の場合におけるパラメータ設計の手順を示す。また,箇条7にそ
の事例を記載する。
設計パラメータを探索するために,内側配列に直交表を適用することが望ましい。なぜなら,直交表は,
同時に多くの設計パラメータの組合せを評価することができるからである。同じ実験処理数であれば,他
の実験計画に比べて,直交表では,取り上げることができる設計パラメータの数は多くなる。このことは,
設計パラメータの最適な水準を選定することによってロバストネスを改善する可能性を大きくすることが
できることを意味している。
6.2〜6.13では,4.4に規定したパラメータ設計の手順を,より詳しく示す。
6.2
(ステップ1)システムの理想機能を明確にする
機能とは,目的を実現するためにシステムが行う働きである。機能は,使用者の意図を指示するために
信号をもつ。信号は,機能に基づいたシステムの目的を実現するために出力を変化させる。機能は,信号
と出力との関係を表した関数で表すことができる。
このステップでは,機能の理想的な状態,すなわち,理想機能を明確にする。理想機能は,システムの
機能に基づいた信号と出力との理想的な関係であり,意図したシステムの働きを表している。
次の問いかけは,理想機能を明確にする助けとなる。
− システムの意図した機能は何か。
− システムは,目的とした出力をどのように実現するか。
− システムが用いる物理現象は何か。
− ハードウェアをシステムとした場合,システムのエネルギー変換は何か。
− ソフトウェア又はサービスをシステムとした場合,情報の変換は何か。
− 出力を変化させる信号は何か。
− システムが実現する出力は何か。
− 入力と出力との理想的な関係は何か。
− 機能を表すために用いられる関数は何か。
信号がゼロのとき出力がゼロ(信号=0で出力=0)で,信号と出力とが比例する場合,機能はゼロ点比
例式で表される。多くの物理的なシステムにおいて,現象は比例的であり,その理想機能に対してゼロ点
比例式が適用される。また,線形のシステムは,使用者にとって,分かりやすく,また,操作しやすい。
このように,信号と出力との関係で示される特性を,動的特性ともいう。
動的特性の理想機能を表す関数には,3種類ある。箇条5で示したように,ゼロ点比例式,基準点比例
式及び一次式である。変数変換を適用すると,入出力関係を簡単な線形式で表すことができる場合がある。
21
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
詳細は,箇条5を参照する。
6.3
(ステップ2)信号因子及びその範囲を選択する
システムの信号を決める。信号は,出力を変化させるために意図的に変化させる変数である。また,シ
ステムに信号を入力するために使用者が操作する変数を,信号因子という。ときには,足踏みペダル,ハ
ンドル,レバーなどによって間接的に,使用者が信号を変化させることもある。信号の選択に基づき,実
験において信号を変化させるための変数を,信号因子として選択する。
信号因子の水準は,使用者の使用範囲を完全にカバーするのがよい。能動的な動的特性の場合,出力は
使用者の要求そのものであるため,出力の範囲はより重要となる。したがって,信号によって変化する出
力が使用者の要求をカバーしているかどうかを確認しなければならない。受動的な動的特性,例えば,温
度計に対する温度のような特性の場合には,実験における信号因子の水準は,実際の信号(温度)の範囲
をカバーする。
実験の結果が広い範囲で適用できるように,信号の範囲は広く取るのがよい。非線形性又は高次のひず
みが信号の残差(ノイズ)として評価できるように,信号の水準数は3以上にするのがよい。また,信号
の水準間の幅を等間隔にすると,変動の分解の計算が容易になる。
6.4
(ステップ3)出力の測定方法を選択する
出力の測定方法を決める。ときには,適切な測定方法が存在しない場合がある。一般に,検証の目的で,
動的特性ではない特性の測定を行っている場合が多いが,理想機能の出力を測定するため,動的特性の効
率的で効果的な測定方法を開発することが重要である。
6.5
(ステップ4)ノイズ戦略を作り,ノイズ因子及びその水準を選択する
実験で用いるノイズ条件を,ノイズ因子として選択する。ノイズ空間でシステムのロバストネスを比較
するには,一つ又は二つのノイズ因子を取り上げれば十分である。ただし,多くのノイズ因子を検討する
ことは必要であり,かつ,その水準の変更が容易なときには,ノイズ因子を直交表に割り付けることがで
きる。
ノイズ因子は,内乱及び外乱の2種類に分類する。内乱は,例えば,経年劣化,部品精度,製造精度,
組立て時のばらつきなど,システムの設計パラメータの値が設計値から外れることによるノイズである。
外乱は,例えば,温度,湿度,振動など,使用の環境条件のようにシステムの外部からくるノイズである。
実験に多くのノイズ因子を取り上げたとき,実験結果はより広い状況で適用可能となるが,実験処理数
は大きくなる。このとき,個々のノイズ因子の出力に対する傾向が分かっている場合,ノイズ因子を調合
する方法がある。調合ノイズ因子では,個々のノイズ因子について,出力が小さくなる水準と出力が大き
くなる水準とにそれぞれまとめて,二つの水準(ノイズレベル)を設定する。これによって,ロバストネ
スは調合ノイズ因子の2水準で評価し,評価実験を効率的に行うことができる。調合ノイズ因子の影響が
小さければ,システムはよりロバストであると言える。
6.6
(ステップ5)設計パラメータから制御因子及びその水準を選択する
実験に用いる設計パラメータを,制御因子として選択する。制御因子は,その水準の一つをベースライ
ンとした3水準が望ましい。最適化の最終ステップでは,制御因子の最適水準の選択及び効果の確認を行
う。設計パラメータの範囲は,どのような範囲を対象に最適化をするかによって決まる。できるだけ広い
範囲を取ることが望ましい。ときには,設計パラメータの最適値は予想した範囲の外側に見つかることも
ある。
制御因子には,設計パラメータの性質によって,長さ及び質量のような連続変数の場合と,材料の種類
及び形状のような定性的な非連続変数の場合とがある。
22
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
制御因子の選択に重要なことは,まず,その値が独立に変化すること,次に,その効果が独立になるこ
とである。ときには,複数の制御因子が交互作用をもつことがある。この場合,水準ずらし法を適用した
り,又はその効果が独立になるように制御因子を選択し直したりする。
例えば,ある実験で,ある部品の体積,比重及び質量を制御因子に選択した場合,それらは相互依存す
るため,独立ではない。この場合,独立な制御因子として,三つのうち二つを選択する。また,例えば,
時間及び温度を制御因子として取り上げる代わりに,加熱エネルギー及び時間を取り上げることもできる
し,時間及び温度プロファイルを取り上げることもできる。
6.7
(ステップ6)実験に取り上げた因子を内側配列及び外側配列に割り付ける
ステップ5で選択された制御因子を内側配列に,ステップ4で選択したノイズ因子及びステップ2で選
択した信号因子を外側配列に割り付ける。内側配列は,例えば,L18のような直交表が望ましく,外側配列
は多元配置でもよい。シミュレーション実験など,外側配列の繰返し実験処理が実施しやすい場合には,
外側配列に直交表を用いてもよい。
直交表L18を,表5に示す。直交表L18には列が8列あり,一つの2水準の制御因子(A)及び七つの3
水準の制御因子(B〜H)を割り付けることができる。2水準の制御因子Aは第1列に割り付ける。直交表
の行は,実験処理の番号を表している。それぞれのセルの中の数字は,列に割り付けられた因子の水準で
ある。例えば,行No.1の実験処理は,A1B1C1D1E1F1G1H1の因子の水準の組合せの条件で実施する。行
No.2の実験処理では,A1B1C2D2E2F2G2H2の因子の水準の組合せの条件で実施する。
表5−直交表L18
No.
1
A
2
B
3
C
4
D
5
E
6
F
7
G
8
H
1
1
1
1
1
1
1
1
1
2
1
1
2
2
2
2
2
2
3
1
1
3
3
3
3
3
3
4
1
2
1
1
2
2
3
3
5
1
2
2
2
3
3
1
1
6
1
2
3
3
1
1
2
2
7
1
3
1
2
1
3
2
3
8
1
3
2
3
2
1
3
1
9
1
3
3
1
3
2
1
2
10
2
1
1
3
3
2
2
1
11
2
1
2
1
1
3
3
2
12
2
1
3
2
2
1
1
3
13
2
2
1
2
3
1
3
2
14
2
2
2
3
1
2
1
3
15
2
2
3
1
2
3
2
1
16
2
3
1
3
2
3
1
2
17
2
3
2
1
3
1
2
3
18
2
3
3
2
1
2
3
1
パラメータ設計の内側配列については,設計空間を効率的に探索するために,直交表を用いるのがよい。
実験処理数が大きくなるという理由で検討する設計パラメータを減らすことは,パラメータ設計の目的か
ら言えば誤りである。したがって,多くの設計パラメータの組合せを同時に評価することが可能になる直
交表による実験を行うことを強く推奨する。設計パラメータの評価は,他の設計パラメータを変化させた
状況の下で行うことが本質的である。
直交表の行の数は,実験処理の数である。列の数は,割り付け可能な因子の数である。制御因子の数が
23
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
直交表の列の数を超えなければ,その直交表に全ての因子を割り付けることができる。効率を考えれば,
全ての列に制御因子を割り付けることが望ましい。
通常,直交表L18を使うことが望ましい。この直交表では,3水準の列の間の交互作用は,他の3水準の
列にほぼ一様に交絡する。この性質は,L12,L18,L36,L54などの直交表に共通であり,特定の交互作用の
影響を受けずに,相対的に大きな効果をもつ主効果を特定することができる。一方,2n,3n,4nなどの系
列の直交表では,2列の交互作用はある特定の列にだけ現れるため,制御因子間に強い交互作用がある場
合には,制御因子の要因効果を誤って判断してしまう場合がある。この問題については,参考文献を参照。
6.8
(ステップ7)実験を行い,データを収集する
内側配列の各行それぞれについて,外側配列のデータを収集する。内側配列の各行のSN比及び感度は,
外側配列のデータから計算する。
外側配列のデータは,内側直交表の各行ごとに収集する。言い換えれば,内側配列によって示された設
計パラメータの各組合せについて,ロバストネスの評価を行う。
内側直交表の各行におけるSN比及び感度によるロバストネスの評価のためのデータの例を,表6に示
す。この例での外側配列は,信号因子とノイズ因子との二元配置であるが,直交表を使うことも可能であ
る。
表6−SN比及び感度の計算のための外側配列の例(2元配置)
信号因子
M1
M2
Mk
線形式
ノイズ因子
N1
y11
y12
y1k
L1
N2
y21
y22
y2k
L2
…
…
…
…
…
Nn
yn1
yn2
ynk
Ln
6.9
(ステップ8)SN比η及び感度Sを計算する
内側直交表L18の各行について,SN比及び感度を計算する。SN比及び感度の計算式は,SN比の種類ご
とに決まっており,5.4に示している。
表6のデータで,ゼロ点比例式の関数を用いる場合の計算は,次による。
全変動:
(
)k
n
f
y
y
y
S
nk
×
=
+
+
+
=
T
2
2
12
2
11
T
Λ
有効除数:
2
2
2
2
1
k
M
M
M
r
+
+
+
=
Λ
ノイズレベルごとの線形式:
k
ky
M
y
M
y
M
L
1
12
2
11
1
1
×
+
+
×
+
×
=
Λ
k
ky
M
y
M
y
M
L
2
22
2
21
1
2
×
+
+
×
+
×
=
Λ
Λ
Λ
nk
k
n
n
n
y
M
y
M
y
M
L
×
+
+
×
+
×
=
Λ
2
2
1
1
比例項の変動:
)1
(
)
(
2
2
1
=
×
+
+
+
=
β
β
f
r
n
L
L
L
S
n
Λ
比例項の差の変動:
)1
(N
2
2
2
2
1
N
−
=
−
+
+
+
=
×
×
n
f
S
r
L
L
L
S
n
β
β
β
Λ
24
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
誤差の変動:
)
(e
N
T
e
n
k
n
f
S
S
S
S
−
×
=
−
−
=
×β
β
誤差分散:
n
k
n
S
f
S
V
−
×
=
=
e
e
e
e
総合誤差分散:
1
N
e
N
e
N
e
N
−
×
+
=
+
+
=
×
×
×
k
n
S
S
f
f
S
S
V
β
β
β
SN比:
(
)
N
e
1
log
10
V
V
S
r
n
−
×
=
β
η
感度:
(
)
e
1
log
10
V
S
r
n
S
−
×
=
β
内側配列の各行のSN比及び感度の計算結果を表7に示す。
表7−内側配列の各行のSN比及び感度
単位 db
No.
SN比
感度
1
η1
S1
2
η2
S2
3
η3
S3
4
η4
S4
5
η5
S5
6
η6
S6
7
η7
S7
8
η8
S8
9
η9
S9
10
η10
S10
11
η11
S11
12
η12
S12
13
η13
S13
14
η14
S14
15
η15
S15
16
η16
S16
17
η17
S17
18
η18
S18
要因効果を見るために,表7に示した内側配列の各行のSN比及び感度から,内側配列の制御因子の各
水準での平均値を式(40)から計算する。
因子Aの第1水準のSN比の平均値は,No.1〜No.9のSN比の平均を取ることによって求める。同様に,
因子Aの第2水準のSN比の平均値は,No.10〜No.18のSN比の平均を取ることによって求める。同様の
計算を制御因子B〜Hについて行う。
25
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
制御因子の各水準のSN比の平均値
(
)
9
9
8
7
6
5
4
3
2
1
1
A
η
η
η
η
η
η
η
η
η
η
+
+
+
+
+
+
+
+
=
(
)
9
18
17
16
15
14
13
12
11
10
2
A
η
η
η
η
η
η
η
η
η
η
+
+
+
+
+
+
+
+
=
(
)
6
12
11
10
3
2
1
1
B
η
η
η
η
η
η
η
+
+
+
+
+
=
·············· (40)
Λ
Λ
(
)
6
17
14
12
7
4
3
3
H
η
η
η
η
η
η
η
+
+
+
+
+
=
感度について,同様の計算を行い,制御因子の各水準での感度の平均値を,次の式(41)から求める。
制御因子の各水準の感度の平均値
(
)
9
9
8
7
6
5
4
3
2
1
1
A
S
S
S
S
S
S
S
S
S
S
+
+
+
+
+
+
+
+
=
(
)
9
18
17
16
15
14
13
12
11
10
2
A
S
S
S
S
S
S
S
S
S
S
+
+
+
+
+
+
+
+
=
················ (41)
Λ
Λ
(
)
6
17
14
12
7
4
3
3
H
S
S
S
S
S
S
S
+
+
+
+
+
=
内側直交表の制御因子の各水準におけるSN比及び感度の平均値を,表8に示す。
表8−SN比及び感度の平均値
単位 db
制御因子
SN比
感度
水準 1
水準 2
水準 3
水準 1
水準 2
水準 3
A
ηA1
ηA2
−
SA1
SA2
−
B
ηB1
ηB2
ηB3
SB1
SB2
SB3
C
ηC1
ηC2
ηC3
SC1
SC2
SC3
D
ηD1
ηD2
ηD3
SD1
SD2
SD3
E
ηE1
ηE2
ηE3
SE1
SE2
SE3
F
ηF1
ηF2
ηF3
SF1
SF2
SF3
G
ηG1
ηG2
ηG3
SG1
SG2
SG3
H
ηH1
ηH2
ηH3
SH1
SH2
SH3
6.10 (ステップ9)SN比及び感度について,要因効果図を作成する
表8に示した平均値のデータを基に,SN比及び感度に対する要因効果を描く。この要因効果図は,そ
れぞれの制御因子がSN比及び感度にどのように影響するかを示している。SN比はばらつきの大きさを,
感度は出力の線形係数又は出力の大きさを,それぞれ表している。
SN比及び感度に対する要因効果図の例を図6に示す。
26
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図6−SN比及び感度に対する要因効果図の例
制御因子の各水準の平均値は直交表から計算するため,SN比及び感度の総平均値は,個々の制御因子
の水準ごとの平均値の平均値と同じになる。この性質を利用し,要因効果図作成のときの,計算ミスの検
査が簡単にできる。
SN比の総平均値は,式(42)となる。
18
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
SN
η
η
η
η
η
η
η
η
η
η
η
η
η
η
η
η
η
η
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
T
······································································································ (42)
SN比について,各制御因子の水準ごとの平均値の平均値は,式(43)に示すように総平均値と同じ値にな
る。
SN
3
H
2
H
1
H
2
A
1
A
3
2
T
η
η
η
η
η
=
+
+
=
=
+
Λ
·················································· (43)
感度の総平均値は,式(44)となる。
18
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
S
T
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
β
······································································································ (44)
感度について,各制御因子の水準ごとの平均値の平均値は,式(45)に示すように総平均値と同じ値にな
る。
β
T
S
S
S
S
S
=
+
+
=
=
+
3
2
3
H
2
H
1
H
2
A
1
A
Λ
·················································· (45)
制御因子が連続変数である場合,因子の効果のプロットが単調に増加又は減少しないときは,制御因子
間に交互作用が存在する可能性があり,その場合は確認実験の再現性が悪くなることがある。制御因子が
連続変数である場合,中間的な水準がロバストでなく,低い水準及び高い水準の両方がロバストであると
いうことは考えにくい。したがって,交互作用の存在を調べる上で,全ての連続変数の制御因子について,
効果が単調に増加又は減少しているかどうかを見るとよい。
6.11 (ステップ10)最適条件を選択する
最適条件を選択するときには,二段階設計法の考え方を用いるのがよい。
まず,SN比に対する要因効果図を見て,それぞれの制御因子について,SN比の平均値の高い水準を最
27
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
適水準として選択する。
次に,感度に対する要因効果図を見る。出力の大きさの調整が必要な場合,SN比の検討後に,感度を,
すなわち,線形係数又は出力の平均値を調整するのに用いることができる因子を選択する。
パラメータ設計は,ロバストネスの最適化を目指しているため,SN比が最も高くなる制御因子の水準
を選択することが本質的である。それによって,結果として得られるシステムは,市場における機能のば
らつきが最小になることが期待できる。
例えば,図6の要因効果図において,最適条件としてA1B1C1D1E3F3G1H1を選択する。制御因子の他
の水準を選んだとき,SN比の値に与える影響が小さい場合,感度又はその他の理由によって,その水準
を選択することもできる。図6では,制御因子EはSN比への効果は小さいが,感度には大きな線形効果
をもっている。したがって,SN比の最適水準である第3水準ではなく,感度の理由によって第2水準を
選択したとしても,SN比すなわちロバストネスの低下は僅かと考えられる。二段階設計法の適用に当た
っては,このようなトレードオフを考慮する。いかなる場合でも,最適条件の組合せは様々な基準を考え
て選択することができるが,その中でも,ロバストネスは最も重要であり,最優先にするのがよい。
6.12 (ステップ11)利得によって,ロバストネスの改善効果を推定する
ロバストネスの改善効果として,制御因子の最適条件におけるSN比と,ベースラインとした比較条件
におけるSN比との差,すなわち,SN比の利得を推定する。
図6の例でいえば,最適条件はA1B1C1D1E3F3G1H1である。
次のように,最適条件におけるSN比の値を式(46)で推定する。
最適条件におけるSN比:
SN
H
G
3
F
3
E
1
D
1
C
1
B
1
A
opt
7
1
1
T
−
+
+
+
+
+
+
+
=
η
η
η
η
η
η
η
η
η
························· (46)
比較条件は,例えば,A1B2C2D2E2F2G2H2であるとして,SN比の値を同じように式(47)で推定する。
比較条件におけるSN比:
SN
2
H
2
G
2
F
2
E
2
D
2
C
2
B
1
A
base
7T
−
+
+
+
+
+
+
+
=
η
η
η
η
η
η
η
η
η
······················· (47)
二つのSN比の差によって,式(48)のとおりSN比の利得を計算する。
SN比の利得:
base
optη
η
η
−
=
∆
········································································ (48)
感度の利得も,同じように式(49)〜式(51)で計算する。
最適条件における感度:
β
T
S
S
S
S
S
S
S
S
S
7
1
H
1
G
3
F
3
E
1
D
1
C
1
B
1
A
opt
−
+
+
+
+
+
+
+
=
························· (49)
比較条件における感度:
β
T
S
S
S
S
S
S
S
S
S
7
2
H
2
G
2
F
2
E
2
D
2
C
2
B
1
A
base
−
+
+
+
+
+
+
+
=
······················· (50)
感度の利得:
base
opt
Δ
S
S
S
−
=
········································································ (51)
6.13 (ステップ12)確認実験を行い,利得及び再現性を調べる
推定された利得を確認するために,比較条件及び最適条件における実験を行うのが望ましい。この実験
を確認実験という。二つの外側配列,すなわち,比較条件及び最適条件の実験を行う。この実験データを
用いて,SN比,感度及び利得を確認値として計算する。
比較条件及び最適条件におけるSN比及び感度について,パラメータ設計実験の要因効果から推定され
た値及び確認実験で確認された値を表9に示す。
28
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表9−確認実験の結果
単位 db
SN比
感度
推定値
確認値
推定値
確認値
最適条件
ηopt
η'opt
Sopt
S'opt
比較条件
ηcur
η'cur
Scur
S'cur
利得
Δη
Δη'
ΔS
ΔS'
SN比及び感度の利得が,それぞれ,推定値と確認値とでほぼ同じであれば,パラメータ設計実験の結
果は再現性が高く,様々な状況で効果が再現すると考えられる。一方,確認値が推定値と異なるときは,
要因効果の加法性がなく,実験結果の再現性に問題が出ると考えられる。その場合は,例えば,理想機能
の設定,入力・出力の特性,SN比の計算式,ノイズ因子の選択,制御因子の選択,測定方法などパラメ
ータ設計の実験計画の項目を見直すことが必要である。
確認実験における利得の結果の再現性が高いときでも,推定値と確認値とで,SN比及び/又は感度の
絶対値が異なる場合がある。そのような場合,まだ知られていない他のノイズ条件が,SN比又は感度に
対して強い効果をもっていることが考えられる。ただし,利得が再現したとすれば,制御因子の効果は再
現し,比較条件に対して,最適条件を選択することによるロバストネスの改善効果は市場でも再現すると
考えられる。
ベースラインとした比較条件の設計から最適条件の設計に改善された利益は,使用者の品質損失の減少
分として表すことができ,改善のために必要なコストと比較することができる。多くの場合,設計パラメ
ータの最適値の選択によるコスト増加はなく,あったとしても小さい。
7
事例研究−ランプ冷却システムのパラメータ設計
この箇条では,ランプ冷却システムにパラメータ設計を適用した事例を記載する。ランプを光源に用い
た照明装置では,過熱状態になることを防ぐために冷却ファンのような冷却システムが必要不可欠である。
冷却性能を評価する実験において,機械内及び周辺温度を正確に測定することは容易ではない。さらに,
熱伝達,輻射及び対流は,冷却システムを構成する材料の影響を受けるが,材料種を実験条件に取り入れ
ると,実験に長い時間及び多大なコストがかかる。この事例は,冷却システムの性能を評価するために,
ファンのモータ電圧と空気の流速との関係に着目した冷却システムの機能を基に,ロバストネスを評価し
たものである。
− (ステップ1)システムの理想機能を明確にする。
冷却システムは,光源であるランプによって発生した熱気を,モータ駆動のファンを用いて機外に
排出することによって,熱源及びその周辺を冷却する。この冷却システムの機能は,“モータ駆動のフ
ァンによって空気の流れを作り,熱気を排出すること”である。これから,理想機能を次のように定
める。すなわち,入力は電圧によって表される電気エネルギーであり,ファンを動かすモータによっ
て消費される。出力は,熱気を取り除くための空気の流速である。このとき,理想機能は,次の式の
ように示すことができる。
M
yβ
=
ここに,
M: 信号:電圧
y: 出力:空気の流速
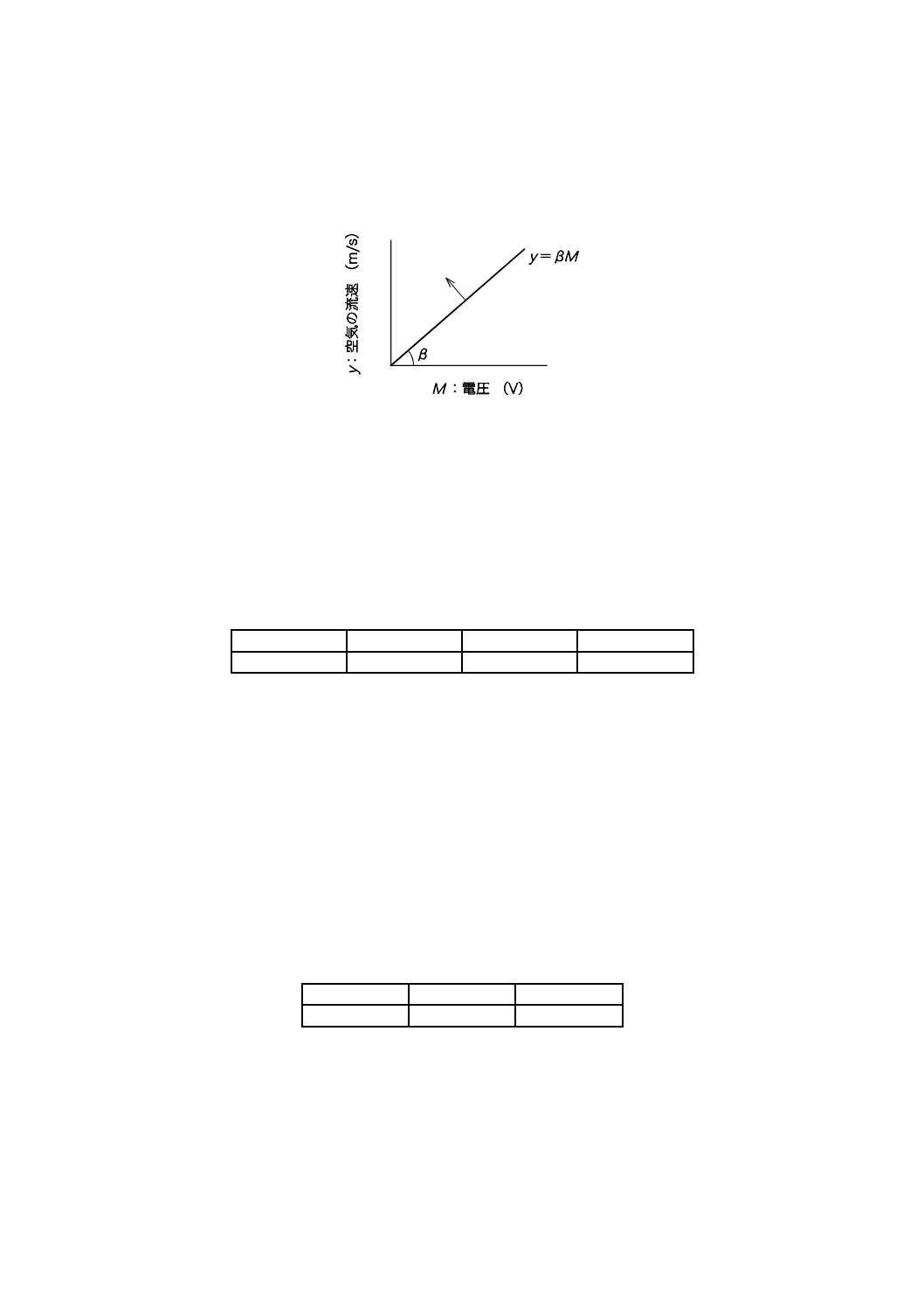
29
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
冷却システムの理想機能を図7に示す。モータの電圧を上げると,空気の流速は電圧に比例して上昇す
る。このとき,乱流,渦又は空気の漏れは,理想機能からのずれ及びエネルギー変換のロスとなり,理想
機能を乱す原因となる。
図7−冷却システムの理想機能
− (ステップ2)信号因子及びその水準を選択する。
冷却システムの信号は,空気の流速を変化させるためにモータに負荷される電圧である。モータ電
圧は,通常0〜25(V)に設定される。したがって,モータ電圧を信号因子に選択し,表10に示すよ
うに5,15及び25(V)の3水準に設定した。
表10−信号因子及びその水準
単位 V
水準
M1
M2
M3
モータ電圧
5
15
25
− (ステップ3)出力の測定方法を選択する。
出力は空気の流速である。空気の流速を風速計によって測定する。
− (ステップ4)ノイズ戦略を作り,ノイズ因子及びその水準を選択する。
ノイズ因子は,市場での使用条件から,機能を乱す要因を選択する。例えば,環境条件,システム
の部品の劣化などである。強い効果をもつノイズ因子であれば,一つ又は二つの典型的なノイズ因子
を選べば十分である。
この事例では,表11に示すように,排気口における障害物の有無をノイズ因子として選択した。排
気口に障害物がある場合,空気の流れは乱されて,冷却効率は落ちる。しかし,排気口に障害物があ
ろうとなかろうと,システムは同じように働くことが望ましい。
表11−ノイズ因子及びその水準
水準
N1
N2
障害物
なし
あり
− (ステップ5)設計パラメータから制御因子及びその水準を選択する。
直交表L18には,一つの2水準因子と七つの3水準因子とを割り付けることができる。選択した制
御因子及びその水準を,表12に示す。
30
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表12−冷却システムにおける制御因子及びその水準
制御因子
水準1
水準2
水準3
A
遮光版
なし
あり
−
B
外装と吸気部との距離(mm)
20
40
60
C
吸気部と熱源との距離(mm)
110
60
40
D
開口部の高さ(mm)
30
15
0
E
排気ダクトの高さ(mm)
30
15
0
F
熱源上部の穴径
大
中
なし
G
熱源下部の穴径
なし
中
大
H
熱源と排気ダクトとの距離(mm)
60
50
40
− (ステップ6)実験に取り上げた因子を内側配列及び外側配列に割り付ける。
制御因子は,内側配列に割り付ける。この事例では,内側配列は直交表L18である。直交表L18の列
への制御因子の割り付けを表13に示す。各行は,No.1〜No.18の各実験処理における制御因子の水準
の組合せを示す。
表13−制御因子の内側配列への割り付け
No.
1
A
2
B
3
C
4
D
5
E
6
F
7
G
8
H
1
なし
20
110
30
30
大
なし
60
2
なし
20
60
15
15
中
中
50
3
なし
20
40
0
0
なし
大
40
4
なし
40
110
30
15
中
大
40
5
なし
40
60
15
0
なし
なし
60
6
なし
40
40
0
30
大
中
50
7
なし
60
110
15
30
なし
中
40
8
なし
60
60
0
15
大
大
60
9
なし
60
40
30
0
中
なし
50
10
あり
20
110
0
0
中
中
60
11
あり
20
60
30
30
なし
大
50
12
あり
20
40
15
15
大
なし
40
13
あり
40
110
15
0
大
大
50
14
あり
40
60
0
30
中
なし
40
15
あり
40
40
30
15
なし
中
60
16
あり
60
110
0
15
なし
なし
50
17
あり
60
60
30
0
大
中
40
18
あり
60
40
15
30
中
大
60
ノイズ因子及び信号因子は,外側配列に割り付ける。この事例では,外側配列は二元配置である。
− (ステップ7)実験を行い,データを収集する。
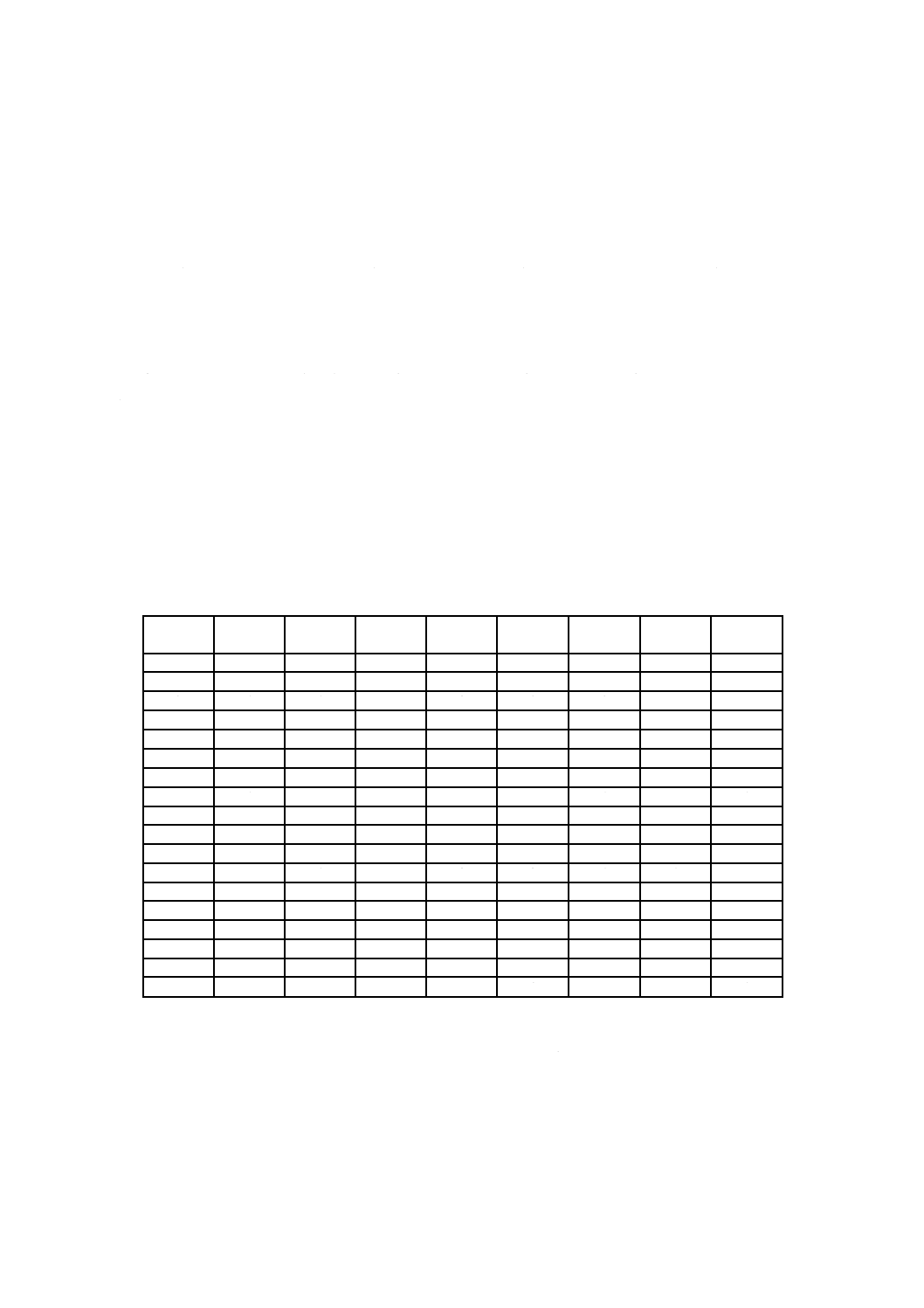
内側配列の各行の実験処理における空気の流速の測定データを表14に示す。

31
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表14−流速の測定結果
単位 m/s
No.
M1
M2
M3
N1
N2
N1
N2
N1
N2
1
0.12
0.09
0.31
0.26
0.44
0.41
2
0.18
0.15
0.28
0.23
0.44
0.32
3
0.36
0.31
1.20
0.96
1.56
1.46
4
0.25
0.22
0.77
0.66
1.24
1.20
5
0.24
0.19
0.84
0.73
1.26
1.08
6
0.23
0.20
0.79
0.67
1.24
1.02
7
0.13
0.08
0.14
0.34
0.30
0.56
8
0.23
0.19
0.57
0.26
0.91
0.56
9
0.24
0.19
0.86
0.68
1.32
1.12
10
0.26
0.17
0.86
0.67
1.30
0.98
11
0.06
0.04
0.23
0.28
0.37
0.27
12
0.36
0.34
1.14
1.04
1.70
1.58
13
0.21
0.12
0.77
0.60
1.18
1.04
14
0.31
0.30
1.12
0.93
1.66
1.42
15
0.10
0.04
0.33
0.24
0.56
0.47
16
0.28
0.23
1.10
0.82
1.66
1.24
17
0.27
0.23
0.83
0.72
1.30
1.08
18
0.28
0.19
0.76
0.57
1.06
0.71
− (ステップ8)SN比η及び感度Sを計算する。
モータ電圧が0のとき,空気の流速は0になる。したがって,箇条6で示したゼロ点比例式の計算
式を,SN比及び感度の計算に適用する。
内側直交表L18の行No.1の測定データによる計算を次に示す。
全変動:
(
)6
900
547
.0
41
.0
44
.0
26
.0
31
.0
09
.0
12
.0
T
2
2
2
2
2
2
T
=
=
+
+
+
+
+
=
f
S
有効除数:
875
25
15
5
2
2
2
=
+
+
=
r
ノイズレベルごとの線形式:
000
600
.
14
41
.0
25
26
.0
15
09
.0
5
000
250
.
16
44
.0
25
31
.0
15
12
.0
5
2
1
=
×
+
×
+
×
=
=
×
+
×
+
×
=
L
L
比例項の変動:
(
)
(
)1
841
543
.0
875
2
60
.
14
25
.
16
2
=
=
×
+
=
β
β
f
S
比例項の差の変動:
(
)1
556
001
.0
875
60
.
14
25
.
16
N
2
2
N
=
=
−
+
=
×
×
β
β
β
f
S
S
誤差の変動:
(
)4
503
002
.0
556
001
.0
841
543
.0
900
547
.0
e
e
=
=
−
−
=
f
S
誤差分散:
32
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
626
000
.0
4
503
002
.0
e
=
=
V
総合誤差分散:
812
000
.0
4
1
556
001
.0
503
002
.0
N
=
+
+
=
V
SN比η及び感度S:
(
)
17
.4
812
000
.0
626
000
.0
841
543
.0
875
2
1
log
10
−
=
−
×
=
η
(
)
08
.
35
626
000
.0
841
543
.0
875
2
1
log
10
−
=
−
×
=
S
同様に内側配列の各行における計算を行う。
内側配列の各行のSN比及び感度の計算結果を表15に示す。
表15−内側配列の各行のSN比及び感度
単位 db
No.
SN比
感度
1
−4.17
−35.08
2
−12.77
−35.86
3
−5.99
−23.94
4
1.76
−26.29
5
−4.81
−26.36
6
−5.35
−26.74
7
−15.93
−35.41
8
−14.45
−30.67
9
−5.35
−26.15
10
−8.82
−26.58
11
−11.40
−37.24
12
−1.08
−23.41
13
−5.57
−27.06
14
−4.92
−23.97
15
−8.00
−33.99
16
−9.13
−24.54
17
−4.89
−26.25
18
−11.99
−28.41
− (ステップ9)SN比及び感度について,要因効果図を作成する。
要因効果図を描くため,内側直交表L18に割り付けた制御因子の各水準でのSN比及び感度の平均値
を,表15のデータに基づき計算する。
内側直交表に割り付けた制御因子の各水準のSN比の平均値は,箇条6で示した計算式によって,
次のように計算する。
(
)
45
.7
9
35
.5
45
.
14
93
.
15
35
.5
81
.4
76
.1
99
.5
77
.
12
17
.4
1
A
−
=
−
−
−
−
−
+
−
−
−
=
η
33
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
31
.7
9
99
.
11
89
.4
13
.9
00
.8
92
.4
57
.5
08
.1
40
.
11
82
.8
2
A
−
=
−
−
−
−
−
−
−
−
−
=
η
(
)
37
.7
6
08
.1
40
.
11
82
.8
99
.5
77
.
12
17
.4
1
B
−
=
−
−
−
−
−
−
=
η
Λ
Λ
(
)
18
.5
6
89
.4
92
.4
08
.1
93
.
15
76
.1
99
.5
3
H
−
=
−
−
−
−
+
−
=
η
感度の平均値も同様に計算する。
平均値の計算結果を表16に示す。
表16−SN比及び感度の平均値
単位 db
制御因子
SN比
感度
水準1
水準2
水準3
水準1
水準2
水準3
A 遮光版
−7.45
−7.31
−
−29.61
−27.94
−
B 外装と吸気部との距離
−7.37
−4.48
−10.29
−30.35
−27.40
−28.57
C 吸気部と熱源との距離
−6.98
−8.87
−6.29
−29.16
−30.06
−27.11
D 開口部の高さ
−5.34
−8.69
−8.11
−30.83
−29.42
−26.07
E 排気ダクトの高さ
−8.96
−7.28
−5.91
−31.14
−29.13
−26.05
F
熱源上部の穴径
−5.92
−7.01
−9.21
−28.20
−27.88
−30.24
G 熱源下部の穴径
−4.91
−9.29
−7.94
−26.58
−30.80
−28.94
H 熱源と排気ダクトとの距離
−8.71
−8.26
−5.18
−30.18
−29.60
−26.55
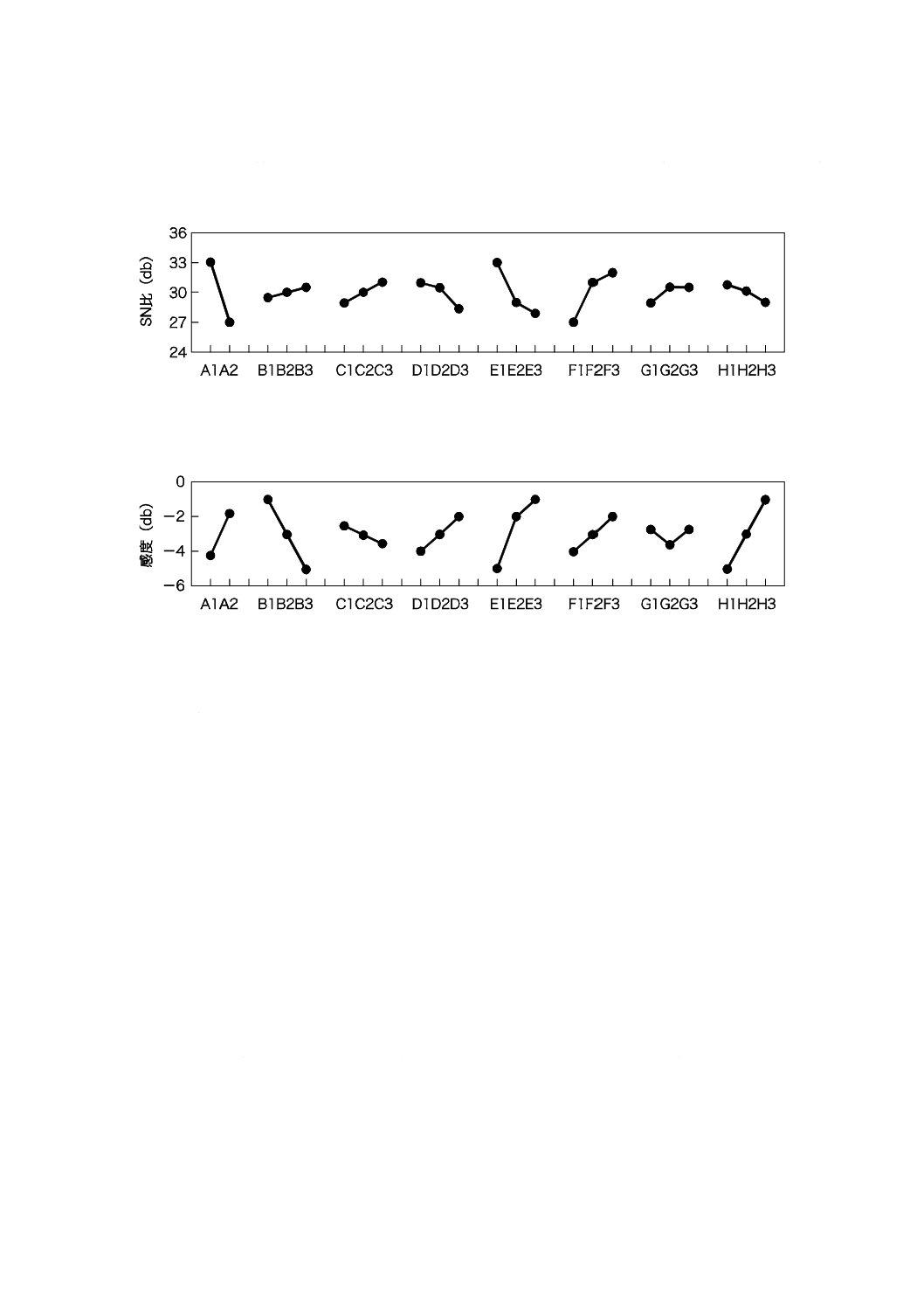
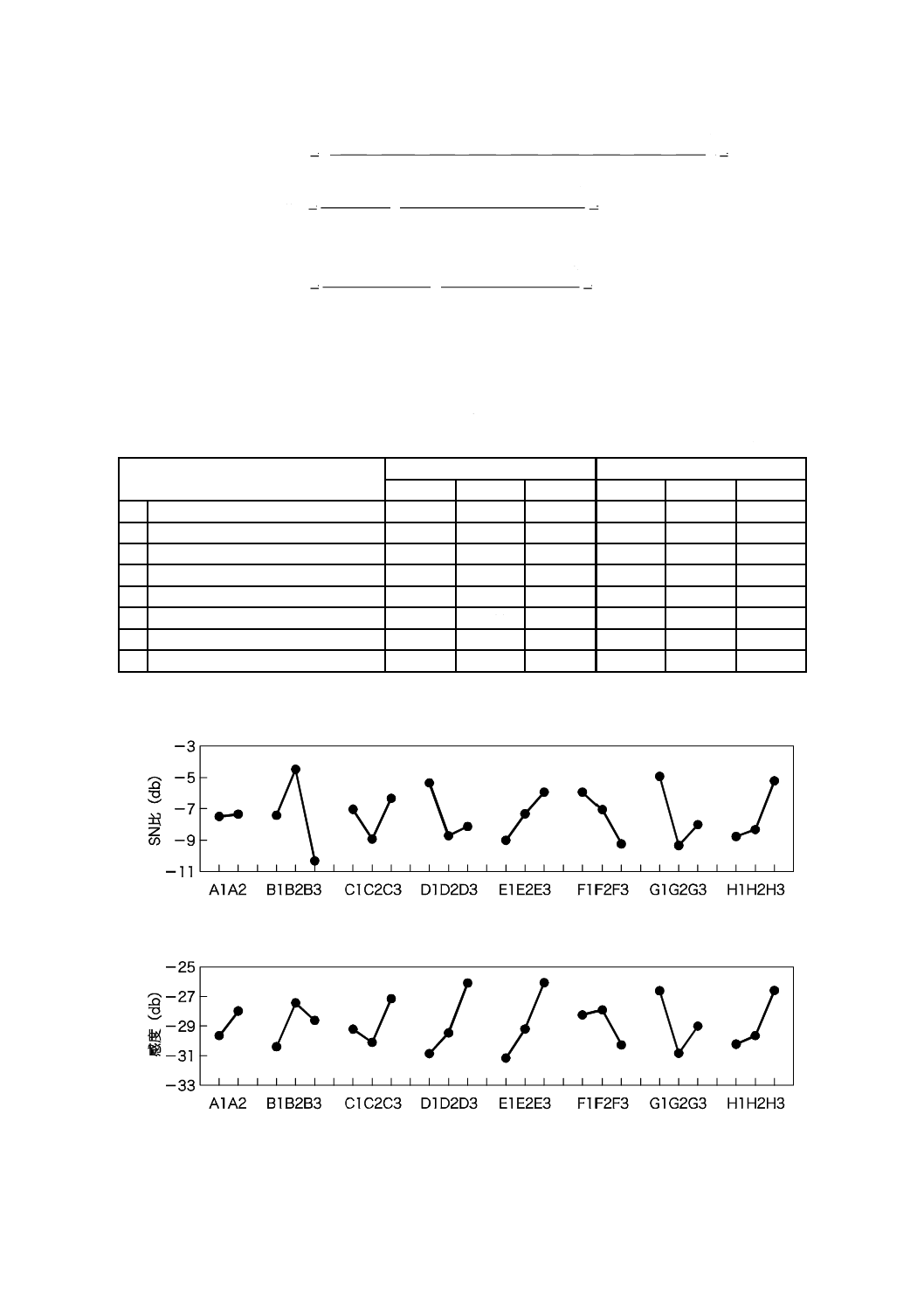
SN比及び感度の要因効果図を図8に示す。
図8−冷却系の要因効果図
34
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− (ステップ10)最適条件を選択する。
SN比を最大にするために,各制御因子の最適水準として,より高いSN比の水準を選択する。SN
比の最適水準の組合せは,A2B2C3D1E3F1G1H3となる。要因効果図から,SN比及び感度の間で最適
水準が異なる因子はDである。感度を高めるために水準D3を選択することも考えられるが,より高
いロバストネスを得ることが冷却システムにとって重要であるため,SN比を優先させ,水準D1を最
適条件として選択した。
− (ステップ11)利得によって,ロバストネスの改善効果を推定する。
最適条件及び比較条件における,SN比及び感度を計算する。
全ての因子の効果を利用した推定は,効果の見積りが過剰になる場合がある。SN比及び感度の適切
な推定のために,効果が相対的に大きい,幾つかの因子を選択する場合もある。
この事例では,SN比を推定するために制御因子のB,D,G及びHを選択した。また,感度を推定
するために制御因子のD,E,G及びHを選択した。
ベースラインとなる比較条件は,冷却システムの初期設計であり,制御因子の水準の組合せは
A1B1C1D1E1F1G1H1である。
表16に示したSN比の平均値を用いて,最適条件及び比較条件におけるSN比の計算を次に示す。
SN比の総平均:
=
SN
T
18個のSN比の平均値=−7.38
最適条件におけるSN比:
23
.2
)
38
.7
(
3
18
.5
91
.4
34
.5
48
.4
3SN
3
H
1
G
1
D
2
B
opt
=
−
×
−
−
−
−
−
=
−
+
+
+
=
T
η
η
η
η
η
比較条件におけるSN比:
19
.4
)
38
.7
(
3
71
.8
91
.4
34
.5
37
.7
3SN
1
H
1
G
1
D
1
B
base
−
=
−
×
−
−
−
−
−
=
−
+
+
+
=
T
η
η
η
η
η
SN比の利得は,最適条件における推定値と比較条件における推定値との差として計算する。
SN比の利得:
42
.6
)
19
.4
(
23
.2
Δ
base
opt
=
−
−
=
−
=
η
η
η
同じように感度の利得も推定される。計算を次に示す。
感度の総平均:
=
β
T
18の感度の平均値=−28.77
最適条件における感度:
70
.
23
)
77
.
28
(
3
55
.
26
58
.
26
05
.
26
83
.
30
3
3
H
1
G
3
E
1
D
opt
−
=
−
×
−
−
−
−
−
=
−
+
+
+
=
β
T
S
S
S
S
S
比較条件における感度:
42
.
32
)
77
.
28
(
3
18
.
30
58
.
26
14
.
31
83
.
30
3
1
H
1
G
1
E
1
D
base
−
=
−
×
−
−
−
−
−
=
−
+
+
+
=
β
T
S
S
S
S
S
感度の利得は,最適条件における推定値と比較条件における推定値との差として計算する。
感度の利得:
72
.8
)
42
.
32
(
70
.
23
base
opt
=
−
−
−
=
−
=
∆
S
S
S
− (ステップ12)確認実験を行い,利得及び再現性を調べる。
比較条件及び最適条件の下で,確認実験を実施した。SN比及び感度の確認値は,確認実験のデータ
から計算する。表17の確認実験の結果から,利得が再現していることを確認する。
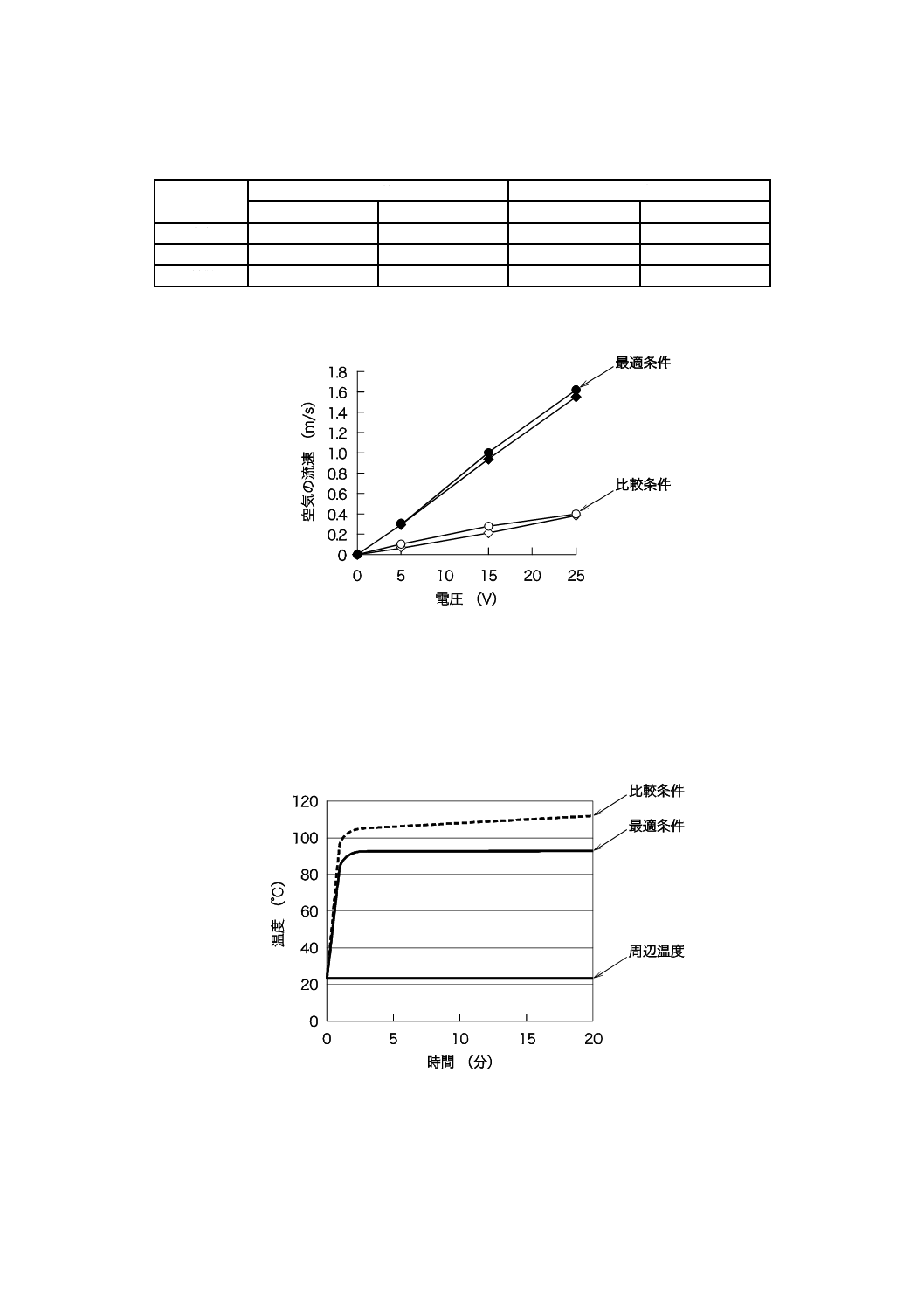
35
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表17−確認実験の結果
単位 db
SN比
感度
推定値
確認値
推定値
確認値
最適条件
2.23
1.66
−23.70
−24.03
比較条件
−4.19
−1.47
−32.42
−35.08
利得
6.42
5.83
8.72
11.05
最適条件の設計及び比較条件の設計における,ノイズ因子の水準ごと入出力関係を,図9に示す。
図9−確認実験の結果
パラメータ設計によって,冷却装置のロバストネス及び効率が大きく改善されたことが分かる。最
適条件では,同じモータ電圧における空気の流れが速くなっており,感度の利得の改善が現れている。
冷却能力の改善によって,照明機器内の温度の低下が期待できる。
最後に,最適条件及び比較条件の設計の下で,温度試験を実施した。温度試験の結果を図10に示す。
図10−高温部分の温度変化
図10で示したように,比較条件の設計では,試験を始めてから20分間温度が上昇し続けている。一方,
最適条件の設計では,温度は3分後に安定し,その後も,危険温度である100 ℃以下に保たれている。
36
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
温度測定によって冷却性能を試験するということは大変であり,時間がかかる。それに対し,この事例
では,空気の流れを生成するという冷却システムの機能と,SN比を指標としたロバストネスの最適化と
に焦点を当てることによって,簡単で素早い評価法を実現した。また,SN比は,その分子はエネルギー
変換の効率を,その分母はエネルギー変換のばらつきを表していることから,エネルギー変換の能力の指
標となっていることに留意する。
37
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
SN比を用いたシステムのロバストネスの比較
A.1 複数の設計コンセプトのロバストネスアセスメント
A.1.1 一般
箇条6に示したように,パラメータ設計では,制御因子とした多くの設計パラメータを直交表による内
側配列に割り付けることによって,一つの設計コンセプトを最適化することができる。一方,製品開発に
おいては,様々な設計コンセプトのロバストネスを比較することが必要となる。例えば,ロバストネスに
ついて,自分自身の設計に対して競争相手の設計をベンチマークすることが必要となる。
そのような場合,製品の機能が同じであれば,(たとえ,異なる設計コンセプトに基づいた複数のシステ
ムがある場合でも)ロバストネスアセスメントを行って異なる設計コンセプトを比較することができる。
箇条5に示した手順は,ロバストネスアセスメントとして適用することができる。基本的に,各設計コン
セプトについて,共通の理想機能に対して同じノイズ戦略の下でSN比及び感度を評価すればよい。
次に二つの例を示す。
A.1.2 事例1:機械部品におけるロバストネスアセスメント
ここでは,玉軸受のロバストネスアセスメントの事例を示す。玉軸受は,各種機械製品の回転部分を構
成しており,軸を支えるとともに回転を滑らかにさせる働き(目的機能)をもっている。従来,軸受の回
転が滑らかに行われているかどうかの評価は,例えば,回転音を耳で聞き分けるという官能評価又は騒音
レベルの評価によって行っていた。この事例では,次のように,軸受の回転機能に基づいて回転の滑らか
さを評価する。
玉軸受の入出力関係を次のように考える。入力は負荷された予圧であり,出力は回転トルクとすれば,
回転トルクyは予圧Mに比例する。理想機能は,次のゼロ点比例式(A.1)から求まる。
M
yβ
=
················································································ (A.1)
ここで,y及びMはそれぞれ回転トルク及び予圧を示す。
全ての使用条件で回転トルクが小さく安定していれば,軸受は高いロバストネスをもち,可聴騒音,振
動及び低信頼性のような品質問題も少なくなる。そこで,軸受の機能として,回転トルクと予圧との関係
を評価することとした。信号因子を予圧として,軸受を使用する範囲を網羅するように,与圧をM1=20 N,
M2=30 N及びM3=40 Nの3水準に変化させて,回転トルクを測定した。
この機能のばらつき及び効率の低下を引き起こす要因をノイズという。ここでのアセスメントでは,ノ
イズ因子として回転速度及び経過時間を選択した。これらの要因は,軸受の劣化に大きな影響を与える。
そこで,次のようにこれら二つのノイズ因子を調合して,ロバストネスアセスメントの中で考慮すること
にした。回転速度は,1 rpm及び3 rpmの2水準とした。経過時間は,開始直後及び開始1分後の2水準と
した。これらのノイズレベルを二つの組合せに調合した。一方は,相対的に劣化が少ない組合せ(相対的
に小さいトルク)であり,他方は相対的に劣化が大きい組合せ(相対的に大きなトルク)である。
− N1:低い回転速度と短い経過時間の水準との組合せ(1 rpmと開始直後との組合せ)
− N2:高い回転速度と長い経過時間の水準との組合せ(3 rpmと開始1分後との組合せ)
個々のノイズ因子の出力への影響の傾向が既知な場合,一つの調合ノイズ因子にノイズ状態を調合する
ことによって,実験の繰返し数を減らすことができる。また,ロバストネスアセスメントにおけるノイズ
38
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
条件は,製品の検査基準又は寿命試験の条件の中から取り上げたり,同じにしたりする必要はない。効率
よく,効果的なノイズ戦略を用いる。回転速度についても実際に使用される高速回転における評価を行う
必要はなく,ロバストネスアセスメントをこのような調合された評価条件で行うことができる。表A.1に
示すように,二つの設計仕様A及び設計仕様Bの例について,一組の回転トルクのデータを取得した。図
A.1に取得したデータのグラフを示す。
表A.1−回転トルクの測定結果
単位 Nm
評価対象
信号因子
M1
20 N
M2
30 N
M3
40 N
設計仕様A
N1
15.0
25.5
39.0
N2
28.5
49.5
65.5
設計仕様B
N1
13.5
24.5
42.5
N2
42.0
65.0
92.5
図A.1−測定データのグラフ
トルクは予圧に比例し,ノイズ因子の影響がないことが理想的である。ノイズ因子の影響がない場合に
は,二つの水準N1及びN2の出力は同じになる。実際には,図A.1に示すように,トルクは必ずしも予圧
と比例せず,ノイズ因子の影響も大きい。SN比は,比例性がどのくらい大きいか,及びノイズ因子の影
響がどのくらい小さいかを,すなわち,ロバストネスを評価している。感度は,線形係数βの大きさを評
価している。この場合,線形係数は予圧当たりのトルクの単位をもち,摩擦係数に相当する量を表してい
る。このため,設計仕様A及び設計仕様Bについて,SN比及び感度の組を同一ノイズ条件の下で求めれ
ば,設計仕様Aと設計仕様Bとのロバストネスの違いを総合的かつ定量的に表現できる。
SN比及び感度は,表A.1のデータから次のように計算する。ここでは,設計仕様Aについてだけ示す。
全変動:
(
)6
00
.
949
9
5.
65
5.
49
5.
28
0.
39
5.
25
0.
15
T
2
2
2
2
2
2
T
=
=
+
+
+
+
+
=
f
S
有効除数:
900
2
40
30
20
2
2
2
=
+
+
=
r

39
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ノイズレベルごとの線形式:
0.
625
2
40
0.
39
30
5.
25
20
0.
15
1
=
×
+
×
+
×
=
L
0.
675
4
40
5.
65
30
5.
49
20
5.
28
2
=
×
+
×
+
×
=
L
比例項の変動:
)1
(
0
931
.
187
9
900
2
2
)0.
675
4
0.
625
2(
r2
)
(
2
2
2
1
=
=
×
+
=
+
=
β
β
f
L
L
S
比例項の差の変動:
)1
(
0
569
.
724
900
2
2
)0.
675
4
0.
625
2(
r2
)
(
N
2
2
2
1
N
=
=
×
−
=
−
=
×
×
β
β
f
L
L
S
誤差の変動:
)4
(
0
500
.
36
0
569
.
724
0
931
.
187
9
00
.
949
9
e
N
T
e
=
=
−
−
=
−
−
=
×
f
S
S
S
S
β
β
誤差分散:
0
125
.9
4
0
500
.
36
e
e
e
=
=
=fS
V
総合誤差分散:
8
213
.
152
1
4
0
569
.
724
0
500
.
36
N
e
N
e
N
=
+
+
=
+
+
=
×
×
β
β
f
f
S
S
V
ここで,誤差分散Veは,N1及びN2内における一次効果を除いたより高次の効果による分散,すなわち
N1及びN2内における入出力関係の比例性からのかい離による分散を表している。総合誤差分散VNは,
誤差及び/又はより高次の効果による分散に加え,N1とN2との間での線形係数の差異による分散をプー
ルした分散を表している。
SN比η及び感度S:
82
.
19
8
213
.
152
)0
125
.9
0
931
.
187
9(
900
2
2
1
log
10
)
(
2
1
log
10
N
e
−
=
−
×
=
−
=
V
V
S
r
β
η
99
.1
)0
125
.9
0
931
.
187
9(
900
2
2
1
log
10
)
(
2
1
log
10
e
=
−
×
=
−
=
V
S
r
S
β
同様の計算を設計仕様Bに対しても行う。両者の計算結果を表A.2に示す。
表A.2−SN比及び感度
単位 db
設計仕様A
設計仕様B
利得
SN比
−19.82
−23.09
3.27
感度
1.99
4.00
−2.01
これらの結果から,設計仕様AのSN比及び感度は,設計仕様Bと比較して,それぞれ,3.27 db高く,
2.01 db低い。真数のスケールを用いると,SN比の3.27 dbの利得は2.12倍に等しいので,設計仕様Aの
ロバストネスは,設計仕様Bのおおよそ2倍であると結論付けることができる。
また,−2.01 dbの感度の利得の真数は0.63であり,その平方根は0.79である。これは,設計仕様Aの
回転トルクの平均値は,同一の予圧に対して,設計仕様Bより約20 %低いことを示している。
40
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
設計仕様A及び設計仕様Bのロバストネス及び線形係数の違いは,SN比及び感度の利得によって量的
に表現できる。さらに,新製品の目標値が,例えば,SN比で−20.0 db及び感度で2.0 dbであるとすれば,
設計仕様Bは目標を満たさないが,設計仕様Aは,目標を満たすことがロバストネスアセスメントの結果
に基づいて結論付けることができる。
A.1.3 事例2:測定システムにおけるロバストネスアセスメント
測定機器の理想機能は,受動的信号の動的特性に関するものであり,関数y=βMで理想機能を示すこと
ができる。ここで,Mは受動的信号としての測定対象量の値であり,yは測定機器が示した値である。こ
の場合の信号は,能動的信号と対比させて,受動的信号という。例えば,自動車のステアリングの場合,
ステアリングの角度は能動的信号である。なぜなら,使用者は,ある回転半径を得るために能動的にステ
アリングを操作し,ステアリングの角度を変化させている。出力である回転半径は,使用者にとって重要
である。測定システムの場合は,測定対象量の値,すなわち信号の値は,測定を始めたときに決まってお
り,使用者が知りたいものである。測定システムの機能は,測定機器が示した値の出力から信号の値を再
現させることである。そのため,この種の信号は受動的信号という。
3次元測定機におけるロバストネスアセスメントの事例を示す。
3次元測定機は,最近,標準室(スダンダードルーム)外の測定にも,広く使われている。3次元測定機
の使用条件は,測定状況によって様々である。3次元測定機に取り付けられたセンサは,測定精度を確保
するために重要であり,いかなる条件下でも十分な性能を発揮することが必要である。3種類のセンサ設
計の中から適切なセンサを選択するために,ロバストネスアセスメントを適用した。
従来の測定機器の評価方法は,ある特定の使用条件下で繰返し測定を行い,標準偏差を求めて機械の測
定誤差の大きさを決定していた。この方法では,他の使用条件下におけるロバストネスを知ることができ
ず,異なる使用条件の下でも同じ性能を発揮するかどうかを保証することはできない。
それとは対照的に,この事例では,ノイズ条件として多くの異なる使用条件の下で測定を行うことによ
って,測定機器の全般的なロバストネスを評価する方法を提示している。センサを含む測定システムの機
能は,ゼロ点比例式y=βMが成立することである。ここで,Mは測定対象量の値を示し,yは測定機器が
示した値を示す。測定システムのロバストネスは,様々なノイズ条件の下での比例関係からのずれの小さ
さによって表され,これは顧客の使用状況での測定誤差の小ささを意味する。
最初に,ノイズ因子を選択するために,測定速度,プローブの回転角などの使用条件について検討した。
結果として,それぞれ三つの水準をもつ四つのノイズ因子を選択した。これら四つの3水準因子を直交表
L9に割り付け,九つのノイズレベルを作成した。効果の大きいノイズ因子の数が多い場合,ノイズ因子を
調合することが容易ではない場合,又はノイズ因子を調合しても意味がない場合には,直交表にノイズ因
子を割り付けることが望ましい。
次に,信号因子Mについて,不確かさが十分で既知の値をもつ三つの異なる試験片を選択し,表A.3に
示すように信号因子の3水準を設定した。
41
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.3−信号因子の水準及びセンサAの測定結果
単位 mm
M1
9.999 6
M2
109.998 9
M3
209.999 2
N1
9.999 0
109.998 9
210.000 1
N2
9.998 7
109.999 1
210.000 6
N3
9.998 0
109.998 6
209.999 6
N4
9.999 1
109.998 7
210.000 3
N5
9.997 0
109.997 0
209.997 8
N6
9.998 9
109.998 8
210.000 0
N7
9.997 3
109.997 1
209.998 8
N8
10.000 6
110.000 5
210.002 3
N9
10.000 0
109.999 9
210.001 4
これらの実験に取り上げた因子の下で,三つの異なるセンサA,センサB及びセンサCを用いて測定し,
三つのセンサのロバストネスを比較した。表A.3にセンサAを用いた測定結果を示す。3水準の受動的信
号及びL9による九つのノイズレベルによる3×9=27のデータを用いて,SN比及び感度を次のように計算
した。
全変動:
)
27
(
29
064
642
.
697
506
4
001
.
210
9
999
.
109
0
000
.
10
1
000
.
210
9
998
.
109
0
999
.9
T
2
2
2
2
2
2
T
=
=
+
+
+
+
+
+
=
f
S
Λ
有効除数:
01
002
414
.
299
56
2
999
.
209
9
998
.
109
6
999
.9
2
2
2
=
+
+
=
r
ノイズレベルごとの線形式:
53
001
597
299
56
2
999
209
1
000
210
9
998
109
9
998
109
6
999
9
0
999
9
1
.
.
.
.
.
.
.
L
=
×
+
×
+
×
=
03
001
721
.
299
56
2
999
.
209
6
000
.
210
9
998
.
109
1
999
.
109
6
999
.9
7
998
.9
2
=
×
+
×
+
×
=
L
Λ
Λ
99
998
989
.
299
56
2
999
.
209
4
001
.
210
9
998
.
109
9
999
.
109
6
999
.9
0
000
.
10
9
=
×
+
×
+
×
=
L
比例項の変動:
)1
(
87
018
642
.
697
506
01
002
414
.
299
56
9
)
99
998
989
.
299
56
03
001
721
.
299
56
53
001
597
.
299
56
(
9
)
(
2
2
9
2
1
=
=
×
+
+
+
=
+
+
+
=
β
β
f
r
L
L
L
S
Λ
Λ
比例項の差の変動:

42
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
)8
(
19
024
000
.0
87
018
642
.
697
506
01
002
414
.
299
56
99
998
989
.
299
56
03
001
721
.
299
56
53
001
597
.
299
56
N
2
2
2
2
9
2
2
2
1
N
=
=
−
+
+
+
=
−
+
+
+
=
×
×
β
β
β
f
S
r
L
L
L
S
Λ
Λ
誤差の変動:
)
18
(
23
021
000
.0
19
024
000
.0
87
018
642
.
697
506
29
064
642
.
697
506
e
N
T
e
=
=
−
−
=
−
−
=
×
f
S
S
S
S
β
β
誤差分散:
18
001
000
.0
18
123
002
000
.0
e
e
e
=
=
=fS
V
総合誤差分散:
75
001
000
.0
8
18
19
024
000
.0
23
021
000
.0
N
e
N
e
N
=
+
+
=
+
+
=
×
×
β
β
f
f
S
S
V
SN比及び感度:
99
024
000
.0
)
18
001
000
.0
87
018
642
.
697
506
(
01
002
414
.
99
562
9
1
log
10
)
(
9
1
log
10
57
.
57
75
001
000
.0
)
18
001
000
.0
87
018
642
.
697
506
(
01
002
414
.
299
56
9
1
log
10
)
(
9
1
log
10
e
N
e
=
−
×
=
−
=
=
−
×
=
−
=
V
S
r
S
V
V
S
r
β
β
η
センサB及びセンサCについても,SN比及び感度を同様に計算した。測定システムにおいて,SN比は
非常に重要である。なぜなら,SN比は測定誤差の小ささを示しているからである。しかし,測定システ
ムは,計量標準があれば簡単に校正することができるため,感度の値そのものはそれほど重要ではない。
すなわち,二段階設計法は,測定システムにも容易に適用可能である。
三つのセンサのSN比の比較を表A.4に示す。これらの結果から,センサAのロバストネスは,センサ
Bより3.14 dbよく,センサCより8.93 dbよい。これは,校正後のセンサAの測定誤差の標準偏差は,セ
ンサBよりも0.68倍小さく,センサCよりも0.35倍小さいことを意味する。このような評価を行うこと
によって,測定システムの総合的なロバストネスアセスメントを行うことができる。
表A.4−SN比の比較
単位 db
センサA
センサB
センサC
SN比
57.57
54.43
48.64
43
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.2 内側配列のための直交表以外の配置
箇条6で説明したように,パラメータ設計において設計パラメータ(制御因子)の数が多い場合,内側
直交表に割り付けて,実験する設計パラメータの水準の組合せを決めることができる。設計パラメータが
四つ以下であっても,直交表に割り付けることができるが,直交表の代わりに,全ての選択可能な組合せ
について評価することも可能である。これを多元配置という。
いずれの場合も,重要なことは,複数の制御因子を一つの実験に同時に取り上げて,それぞれの因子の
水準が一つの固定した条件ではなく,他の因子の水準の様々な組合せの下で評価できるようにすることで
ある。
例として,制御因子A及び制御因子Bは2水準であり,制御因子Cは3水準であるとする。この場合,
多元配置は,次のように2×2×3=12の各因子の水準の組合せとなる。
− No.1:A1B1C1
− No.2:A1B1C2
− No.3:A1B1C3
− No.4:A1B2C1
− No.5:A1B2C2
− No.6:A1B2C3
− No.7:A2B1C1
− No.8:A2B1C2
− No.9:A2B1C3
− No.10:A2B2C1
− No.11:A2B2C2
− No.12:A2B2C3
ロバストネスの評価をそれぞれの組合せについて行い,12個のSN比及び感度を計算する。制御因子の
各水準別平均値を計算して,各パラメータの要因効果を求める。
計算過程は,箇条5及び箇条6と同様である。
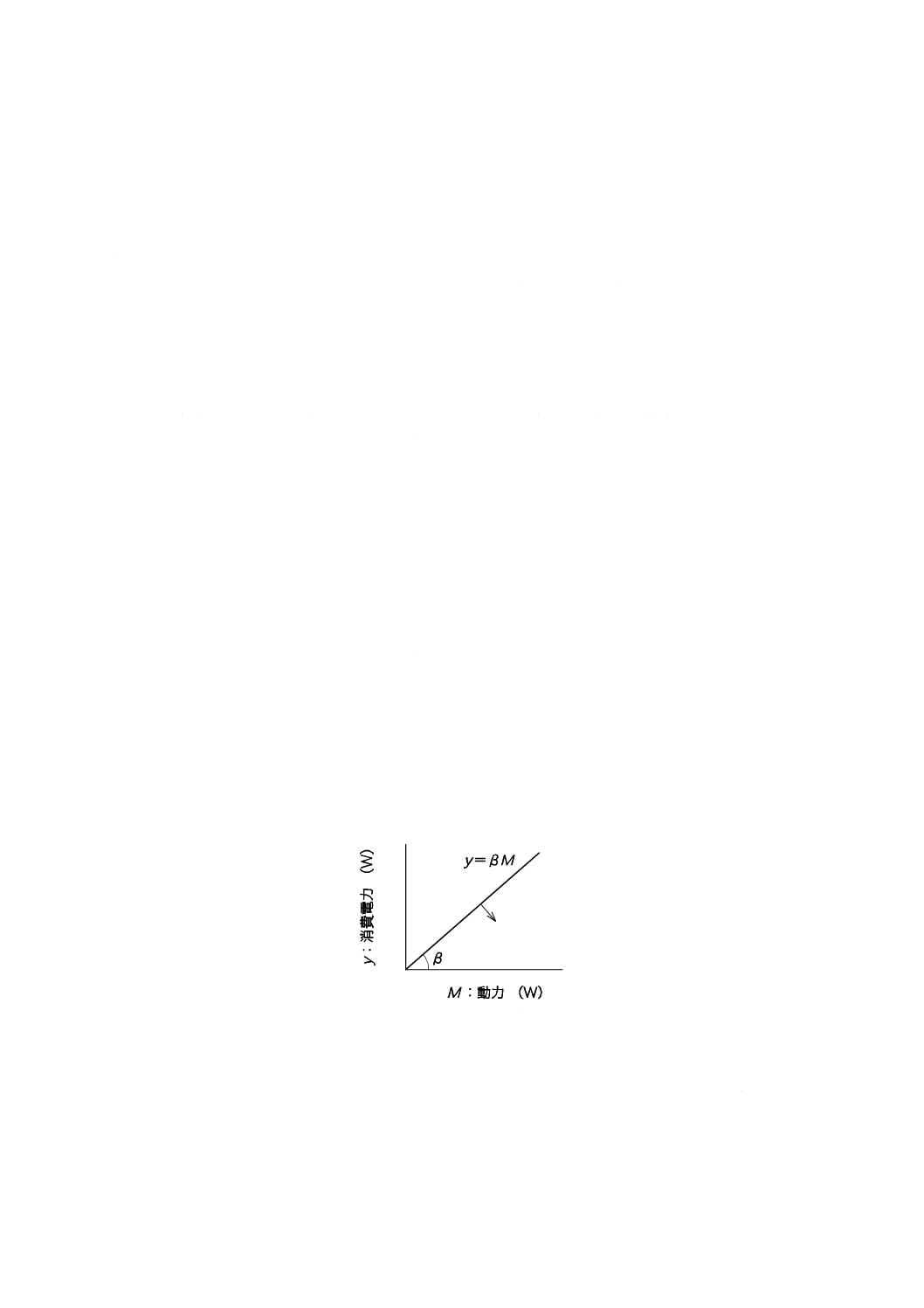
44
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
各技術分野における事例及びSN比
B.1
動的特性の事例
B.1.1 事例1:電機システムにおける動特性の適用(エネルギー変換に基づいた小型直流モータの最適化)
自動車にはウィンドウレギュレータ,ワイパ機構,電子キャリパなどのようないろいろなサブシステム
で多くの小型直流モータが使用されている。発注者は,可聴ノイズ,発熱,トルク,回転数,エネルギー
効率,信頼性などの性能要求及び品質要求の改善を求めている。
典型的モータ試験では,それらの要求が満たされているかどうかを一つずつ検査し,必要があればトレ
ードオフを実施する。これは単に妥当性検証であり,ロバストネスの評価又は最適化ではない。
この事例では,直流モータのエネルギー変換に基づいて,ロバストネスの評価のための理想機能を特定
した。それは,エネルギー効率という今日の強い要望に沿ったものである。
このアプローチが目指すのは,エネルギー変換に基づいた理想機能の最適化を通じて,同時に複数の要
求を改善することである。
− (ステップ1)システムの理想機能を明確にする。
直流モータは,ある作業を行うのに必要な量の回転力を得るために,入力としての電力を消費する。
直流モータの機能は,電力を意図された変位を与えるための回転の動力へ変換することといえる。
エネルギー変換の考え方に基づいて,直流モータの理想機能を“少ない消費電力で必要な回転の動
力を供給すること”とし,エネルギー変換のゼロ点比例式を理想機能とするのがよい。この理想機能
は,次のように表すことができる。
M
yβ
=
ここで,入力Mは必要とされる回転の動力,出力yはある作業を行うために必要な回転の動力を供
給するための消費電力である。線形係数βは,電力消費率として定義し,これは単位動力当たりに必
要な電力に相当する。図B.1に示すように,最適化の基準は,ノイズによるばらつきを低減すること,
すなわち,この関係の“ロバストネス”を高めること及び電力消費率βを最小化することである。
図B.1−直流モータのロバストネス
− (ステップ2)信号因子及びその範囲を選択する。
この実験では,モータは自動車のバッテリに相当する12 V電源に接続しており,駆動負荷をシミュ
レートするために,2 N・m,3 N・m及び4 N・mの三水準のトルクが負荷として与えられる。必要な動
力(回転力)は,機械的エネルギーとして表すこともできる,すなわち,M=2πnTである。ここで,
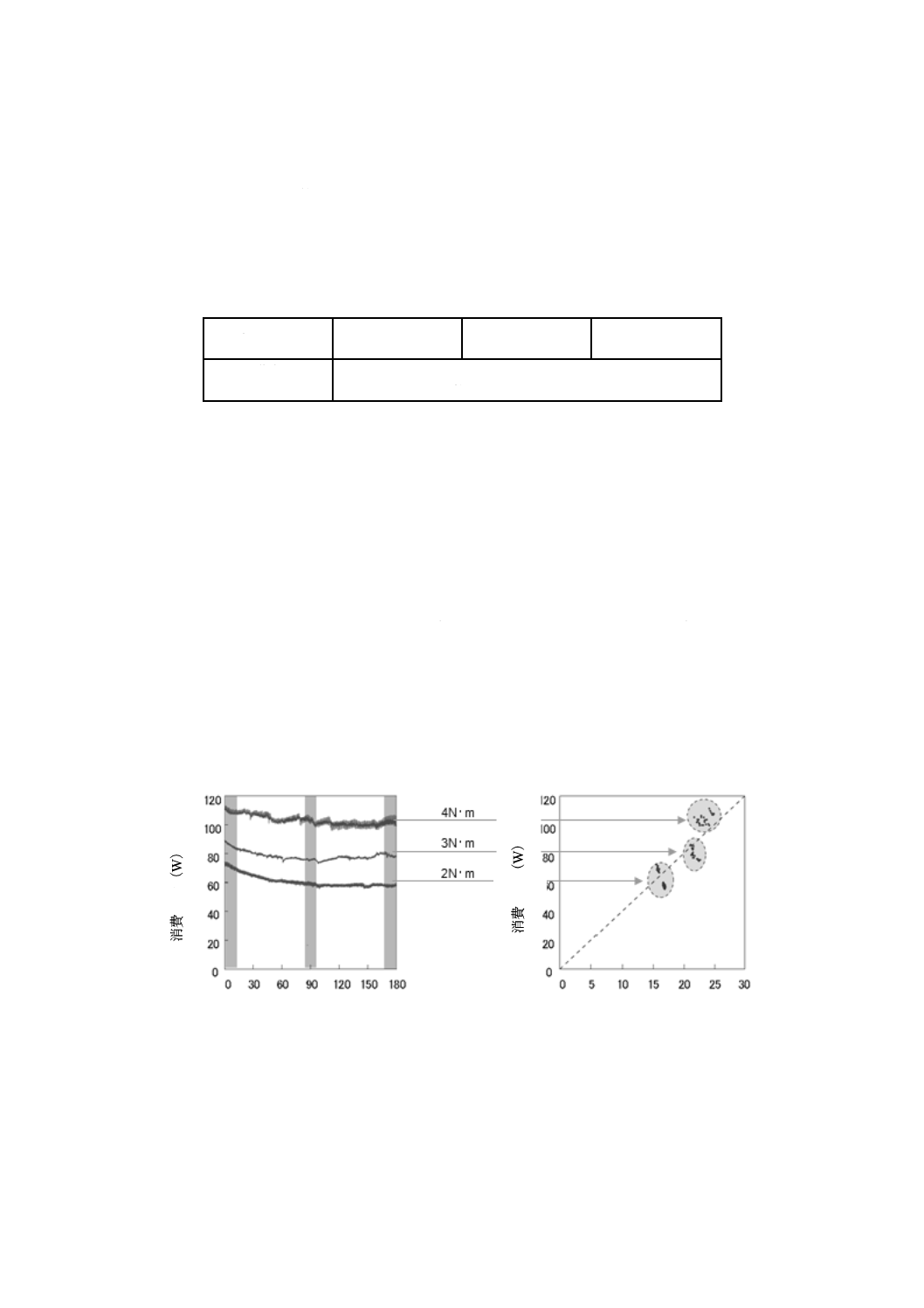
45
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
nは回転速度(rps),Tは負荷トルク(N・m)である。
回転速度(動力)及び内部電流を,0.1秒のサンプリング間隔で180秒間測定した。動力は,信号レ
ベルを同定するために計算した。信号レベルは,表B.1に示すように,回転速度と負荷トルクとの積
として算出される。回転速度を0.1秒のサンプリング間隔で測定したのは,一定のトルク条件下にも
かかわらず,発熱などのノイズの影響によって瞬間速度が変化するためである。
表B.1−直流モータ実験のための信号因子及びその水準
信号因子
M1
負荷トルクT1
M2
負荷トルクT2
M3
負荷トルクT3
動力
(2πnT)
水準値は,回転速度と動作条件に対応する三つの負荷トルク
レベルとの積から算出し,設定する。
− (ステップ3)出力の測定方法を選択する。
出力は電力消費である。消費電力は,電気入力の電流と電圧との積として表すことができる。すな
わち,y=IEである。ここで,Iは電流(A),Eは電圧(V)である。したがって,理想機能は次のよ
うな関係式で表すことができる。
nT
IE
π
2
×
=β
モータの駆動経過時間について,全体の傾向は動作状態が次の三つの経過時間によって特徴付けられる。
すなわち,スタート直後の“初期起動時”,スタートから90秒後及びスタートから180秒後である。それ
ぞれの経過時間で,10秒の間に1.0秒間隔で10データを採取した。各経過時間でのデータサンプルの大き
さは10であり,各々の荷重条件において30個のデータを記録した。したがって,各実験のSN比算出の
ためのデータの大きさは90となる。内側直交表の行No.1の制御因子の組合せにおける実験結果のグラフ
を図B.2に示す。図B.2の左図に各負荷条件で測定された全体の消費電力の時間変化を示し,図B.2の右
図に理想機能の入出力関係とデータとの関係を示す。
図B.2−時間による消費電力の変化と入出力関係
経過時間 (s)
動力 (W)
各負荷条件における消費電力と経過時間
入出力関係
[負荷トルク]
消
費
電
力
(
W
)
消
費
電
力
(
W
)
46
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− (ステップ4)ノイズ戦略を作り,ノイズ因子及びその水準を選択する。
ノイズ因子は,表B.2に示すように,経過時間の三つの水準,すなわち,初期起動時,90秒後及び
180秒後を選択した。
このノイズ因子は,例えば,エネルギーの入出力関係のばらつき,非効率性及び非線形関係のよう
な望ましくない効果をもたらす。
ノイズ因子は,多くの場合,顧客の使用条件,周囲温度,製品の劣化・老化のようなものが考慮さ
れる。しかし,この事例では,ノイズとして意図的に長い時間モータを動作させ,発熱させることに
よって,発熱による効率低下の影響を,積極的にデータに取り入れることにした。この影響は大きく,
実際の使用条件の影響を超えるものである(実際には,誰も180秒間連続でウィンドウレギュレータ
を使用することはない。)。したがって,ノイズ因子として経過時間を選択し,それを3水準に設定し
た。これは,非常に独創的なノイズ戦略である。
表B.2−直流モータ実験のノイズ因子
ノイズ因子
N1
N2
N3
経過時間
初期起動時
90秒後
180秒後
− (ステップ5)設計パラメータから制御因子及びその水準を選択する。
直流モータの設計パラメータから八つの制御因子を選択した。制御因子及びその水準を表B.3に示
す。
表B.3−直流モータ実験の制御因子及びその水準
制御因子
水準1
水準2
水準3
A
部品の固定方法
現行
固い
−
B
部品の板厚
薄い
中位
厚い
C
部品の形状
形状1
形状2
形状3
D
部品の幅
狭い
中位
広い
E
部品の形状
形状1
形状2
形状3
F
部品の内側半径
小さい
中位
大きい
G
部品の形状
形状1
形状2
形状3
H
部品の板厚
薄い
中位
厚い
− (ステップ6)実験に取り上げた因子を内側配列及び外側配列に割り付ける。
表B.4に示すように,内側直交表L18に制御因子を割り付ける。
47
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.4−制御因子の割り付け
No.
1
A
2
B
3
C
4
D
5
E
6
F
7
G
8
H
1
現行
薄い
形状1
狭い
形状1
小さい
形状1
薄い
2
現行
薄い
形状2
中位
形状2
中位
形状2
中位
3
現行
薄い
形状3
広い
形状3
大きい
形状3
厚い
4
現行
中位
形状1
狭い
形状2
中位
形状3
厚い
5
現行
中位
形状2
中位
形状3
大きい
形状1
薄い
6
現行
中位
形状3
広い
形状1
小さい
形状2
中位
7
現行
厚い
形状1
中位
形状1
大きい
形状2
厚い
8
現行
厚い
形状2
広い
形状2
小さい
形状3
薄い
9
現行
厚い
形状3
狭い
形状3
中位
形状1
中位
10
固い
薄い
形状1
広い
形状3
中位
形状2
薄い
11
固い
薄い
形状2
狭い
形状1
大きい
形状3
中位
12
固い
薄い
形状3
中位
形状2
小さい
形状1
厚い
13
固い
中位
形状1
中位
形状3
小さい
形状3
中位
14
固い
中位
形状2
広い
形状1
中位
形状1
厚い
15
固い
中位
形状3
狭い
形状2
大きい
形状2
薄い
16
固い
厚い
形状1
広い
形状2
大きい
形状1
中位
17
固い
厚い
形状2
狭い
形状3
小さい
形状2
厚い
18
固い
厚い
形状3
中位
形状1
中位
形状3
薄い
− (ステップ7)実験を行い,データを収集する。
内側配列の行における外側配列で得られた測定データの例を表B.5に示す。
表B.5−外側配列の測定データ
実験条件
電圧
E(固定)
測定データ
負荷
T1
T3
測定点
起動直後
90秒後
180秒後
起動直後
90秒後
180秒後
回転速度
n1…n10
n11…n20
n21…n30
n61…n70
n71…n80
n81…n90
電流
I1…I10
I11…I20
I21…I30
I61…I70
I71…I80
I81…I90
信号M
動力:W
n1T1…n10T1
n11T1…n20T1
n21T1…n30T1
n61T3…n70T3
n71T3…n80T3
n81T3…n90T3
出力y
電力:W
I1E…I10E
I11E…I20E
I21E…I30E
I61E…I70E
I71E…I80E
I81E…I90E
− (ステップ8)SN比η及び感度Sを計算する。
信号及び出力はエネルギーを表す物理量であるので,ここでは,全変動の分解から得られる要因効
果の加法性を考慮して,各値の平方根をとった。動的な理想機能のゼロ点比例式に対する解析を行っ
た。すなわち,信号2πn1T1…2πn90T3については,M1…M90の平方根を用いる。また,出力I1E…I90Eに
ついては,y1…y90の平方根を用いる。計算手順は,箇条6に示した手順と同じである。
全変動:
(
)
90
T
2
90
2
2
2
1
T
=
+
+
=
f
y
y
y
S
Λ
有効除数:
2
90
2
2
2
1
M
M
M
r
+
+
+
=
Λ
48
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
線形式:
90
90
2
2
1
1
y
M
y
M
y
M
L
+
+
+
=
Λ
比例項の変動:
(
)1
2
=
=
β
β
f
r
L
S
誤差の変動:
(
)
89
e
T
e
=
−
=
f
S
S
S
β
誤差分散:
89
e
e
S
V=
SN比及び感度:
(
)
e
e
1
log
10
V
V
S
r
−
=
β
η
(
)
e
1
log
10
V
S
r
S
−
=
β
以上の計算式で求めたSN比及び感度を表B.6に示す。
表B.6−計算したSN比及び感度
単位 db
No.
SN比
感度
1
11.20
6.00
2
8.99
6.64
3
14.61
5.99
4
14.04
6.46
5
9.33
6.65
6
14.78
5.98
7
11.95
6.21
8
10.86
6.51
9
9.72
6.81
10
7.34
6.78
11
12.22
6.47
12
8.99
6.17
13
11.90
6.21
14
7.92
6.32
15
12.54
6.66
16
9.68
6.64
17
14.92
6.20
18
8.99
6.61
各因子における水準の平均値を表B.7に示す。
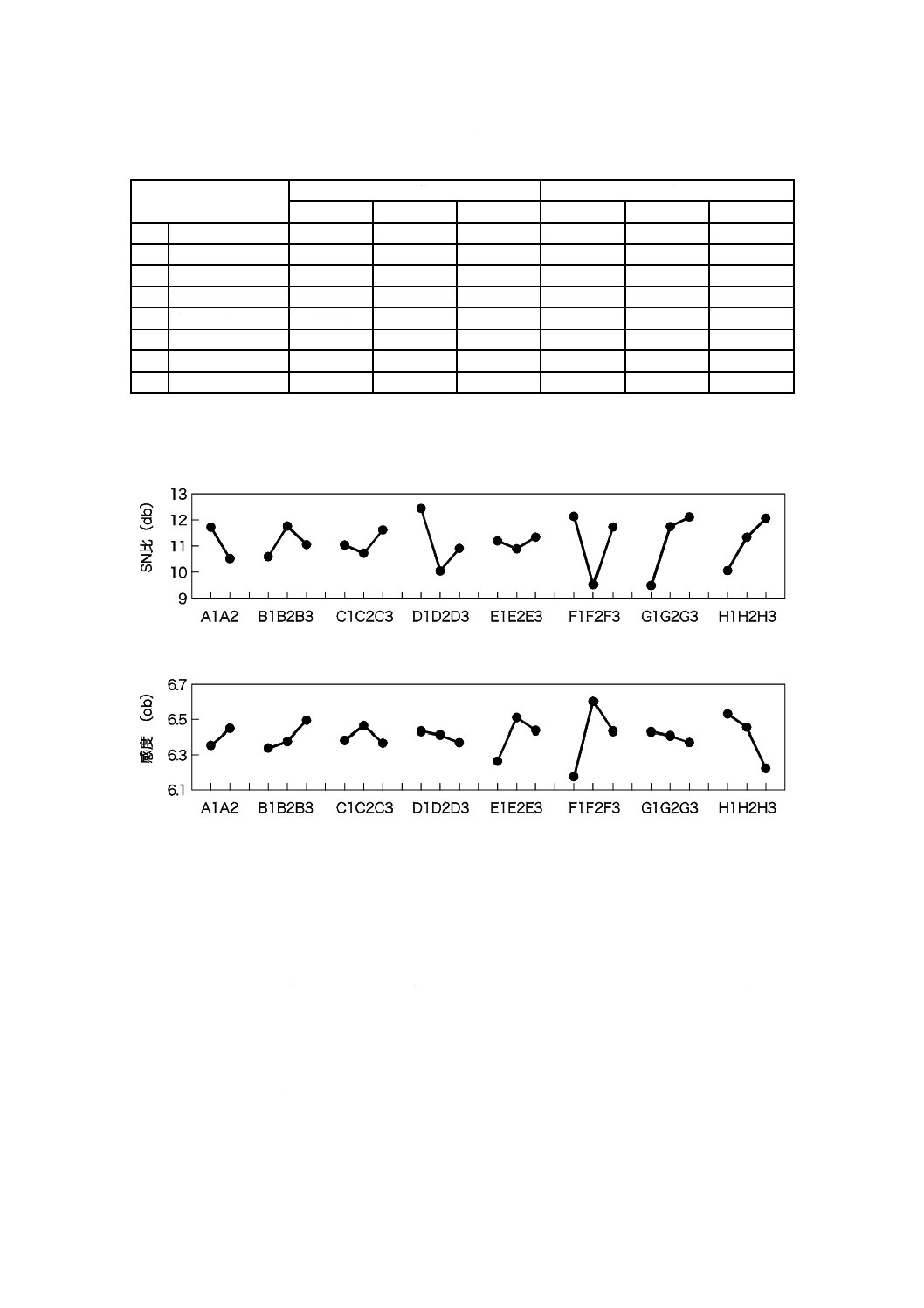
49
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.7−SN比及び感度の平均値
単位 db
制御因子
SN比
感度
水準1
水準2
水準3
水準1
水準2
水準3
A
部品の固定方法
11.72
10.50
−
6.36
6.45
−
B
部品の板厚
10.56
11.75
11.02
6.34
6.38
6.50
C
部品の形状
11.02
10.71
11.61
6.38
6.47
6.37
D
部品の幅
12.44
10.03
10.87
6.43
6.42
6.37
E
部品の形状
11.18
10.85
11.30
6.27
6.51
6.44
F
部品の内側R
12.11
9.50
11.72
6.18
6.60
6.44
G
部品の形状
9.47
11.75
12.10
6.43
6.41
6.38
H
部品の板厚
10.04
11.22
12.07
6.54
6.46
6.23
− (ステップ9)SN比及び感度について,要因効果図を作成する。
直流モータ実験におけるSN比及び感度の要因効果図を図B.3に示す。
図B.3−要因効果図
− (ステップ10)最適条件を選択する。
図B.3の要因効果図は,B及びDを除いた全ての因子について,SN比が高いときに感度が低いこ
とを表している。言い換えれば,予想どおり,ロバストネスが良ければ消費電力は小さくなる。SN
比が最大である最適条件は,A1B2C3D1E3F1G3H3である。ただし,E2とE3との間においてSN比の
差は小さいので,感度及びコストを考慮してE2を選定した。その結果,最適条件として
A1B2C3D1E2F1G3H3を選択した。
− (ステップ11)利得によって,ロバストネスの改善効果を推定する。
確認実験を行う前に,最適条件及び現行条件のSN比及び感度を次のように推定した。ここでは,
全ての因子の効果を計算に用いた。現行条件は,A1B2C1D3E2F1G1H1である。
直交表L18の18個のSN比からSN比の総平均値を計算する。

50
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
SN比の総平均値
174
.
11
18
99
.8
99
.8
20
.
11
18
18
17
2
1
SN
=
+
+
+
=
+
+
+
+
=
Κ
Κ
η
η
η
η
T
最適条件におけるSN比を,次のように計算する。
43
.
16
174
.
11
7
07
.
12
10
.
12
11
.
12
85
.
10
44
.
12
61
.
11
75
.
11
72
.
11
7SN
3
H
3
G
1
F
2
E
1
D
3
C
2
B
1
A
opt
=
×
−
+
+
+
+
+
+
+
=
−
+
+
+
+
+
+
+
=
T
η
η
η
η
η
η
η
η
η
同様に,現行条件におけるSN比を,次のように計算する。
61
.9
174
.
11
7
04
.
10
47
.9
11
.
12
85
.
10
87
.
10
02
.
11
75
.
11
72
.
11
7SN
1
H
1
G
1
F
2
E
3
D
1
C
2
B
1
A
cur
=
×
−
+
+
+
+
+
+
+
=
−
+
+
+
+
+
+
+
=
T
η
η
η
η
η
η
η
η
η
予測されるSN比の利得は,
82
.6
61
.9
43
.
16
cur
opt
=
−
=
−
=
∆
η
η
η
次に,感度の計算を同様に行う。直交表L18の18個の感度から感度の総平均値を計算する。
397
.6
18
61
.6
64
.6
00
.6
18
18
2
1
=
+
+
+
=
+
+
+
=
Κ
ΚS
S
S
Tβ
最適条件における感度を計算する。
06
.6
397
.6
7
23
.6
38
.6
18
.6
51
.6
43
.6
37
.6
38
.6
36
.6
7
3
H
3
G
1
F
2
E
1
D
3
C
2
B
1
A
opt
=
×
−
+
+
+
+
+
+
+
=
−
+
+
+
+
+
+
+
=
β
T
S
S
S
S
S
S
S
S
S
同様に,現行条件の感度を計算する。
37
.6
397
.6
7
54
.6
43
.6
18
.6
51
.6
37
.6
38
.6
38
.6
36
.6
7
1
H
1
G
1
F
2
E
3
D
1
C
2
B
1
A
cur
=
×
−
+
+
+
+
+
+
+
=
−
+
+
+
+
+
+
+
=
β
T
S
S
S
S
S
S
S
S
S
感度の利得を,次のとおりに計算する。
31
.0
37
.6
06
.6
Δ
cur
opt
−
=
−
=
−
=
S
S
S
この場合,感度,すなわち線形係数が小さいことは,消費電力が少ないことを意味する。感度の利
得が負の値であることは,消費電力量に改善がみられたことを示している。
− (ステップ12)確認実験を行い,利得及び再現性を調べる。
最適条件及び現行条件について確認実験を行った。SN比及び感度の結果を表B.8に示す。推定値と
確認値との間では多少の違いがあるものの,最適条件の設計を選択することによってロバストネス及
び消費電力量が改善できることが確認できた。これによって,良い再現性が示されたと結論できる。
表B.8−確認実験の結果
単位 db
SN比
感度
推定値
確認値
推定値
確認値
最適条件
16.43
16.43
6.06
6.11
現行条件
9.61
11.73
6.37
6.93
利得
6.82
4.70
−0.31
−0.82
最適条件及び現行条件における入出力関係を図B.4に示す。
51
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.4−各条件における入出力関係
最適条件において,消費電力のばらつきはかなり小さくなっている。消費電力率βもまた,現行条件の
4.93より約17 %少ない4.08であることが確認された。
これは,電力から機械動力へのエネルギー変換がより効率よく,また円滑に行われたことを意味する。
機能低下によって振動及び可聴ノイズが小さくなることが期待される。別途,同じ回転数において騒音ノ
イズを測定したところ,現行設計に比べて,最適設計では8 (dB)のノイズ低下が見られた。
さらに,消費電力量の削減ということは,同じ出力トルクを出すために少ない電力量でよいことを意味
する。このことは,性能に影響を与えることなくモータを小型化できる機会につながり,年間3 000万円
のコスト削減が見込める。
このロバストネスの最適化事例においては,電力から機械動力の創出というエネルギー変換に基づいて
直流モータの理想機能を定めることによって,消費電力量の改善ができた。その結果,可聴ノイズ及び振
動といった機能低下から起こる現象は徹底的に改善された。消費電力のロバストネス改善が性能の要求を
超えたので,性能の代わりにコスト削減を達成することができた。このような改善は,従来の品質特性及
び性能要件を測定する典型的な1因子実験では達成できない。このような方法による改善は,自然資源及
びエネルギー消費の削減につながり,地球環境に貢献する。
B.1.2 事例2:食品産業における動的特性のSN比の適用(パラメータ設計によるもやし育成の最適化)
もやしは,小豆を水に浸せき(漬)し発芽させ,土のない暗室で育てるという生産過程の中で成長する。
この生産過程の機能は,もやしの質量で表した成長曲線によって示される。動的特性の理想機能のための
SN比を,成長曲線のばらつき及び効率の評価に用いることができる。食品産業でのもやしの生産過程の
最適化に,SN比を用いたパラメータ設計が適用された。
− (ステップ1)システムの理想機能を明確にする。
もやしの成長過程は,小豆を水に浸せきし発芽させ,土のない暗室環境で成長させる。この成長過
程は図B.5に示すように3期に分けられる。それらは発芽期,成長期及び衰退期である。
a) 発芽期 もやしの豆は,一種の大豆,ブラックマッペ(けつるあずき),又はグリーングラムといった
種類の小豆である。小豆は,通常乾燥した冬眠状態にあり,発芽のために一定期間水に浸せきさせ,
熱を与えることが必要である。発芽期の条件は,発芽率及び滅菌効果に対して強く影響する。
b) 成長期 マッペは,発芽後多量の水を吸収することで成長する。発芽機構と成長機構との間に明確な
違いはなく,発芽期と成長期とを区別することは難しい。成長期のもやしの成長を評価するために,
SN比及び感度を用いた。
52
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
c) 衰退期 植物には,成長期の後の成長のためには光合成が必要である。もやしは,その生産環境で光
が供給されないため,豆の栄養素を全て取り入れた後に衰え,腐れを起こす。もやしは,水に浸せき
を始めてから7日又は8日後に始まる衰退期の前に出荷される。
図B.5−もやしの成長曲線(時間による質量倍率の増加)
植物の成長理論に基づいた理想的な成長過程は,次の式(B.1)のように表すことができる。
M
e
Y
Y
β
0
s=
············································································· (B.1)
ここで,Y0は開始時点での豆の初期質量を,Ysは時間Mでのもやしの質量を表す。この式は,もや
し育成の基本機能を表している。この式は,理想機能として使用できる。この式を線形化するために,
自然対数変換を適用する。結果として,この式は次の式(B.2)となる。
M
Y
Y
β
=
0
s
ln
········································································· (B.2)
変数yを次の式(B.3)に置き換えれば,
(
)
0
s/
In
Y
Y
y=
·········································································· (B.3)
式(B.2)は,次の式のように変形できる。
M
yβ
=
このように,もやし成長の理想機能をゼロ点比例式
M
yβ
=
として表すことができる。ここで,信
号Mは時間であり,出力yは初期荷重に対する時間Mでの質量比の自然対数である。もやしの成長
のばらつき及び効率を評価するために,ゼロ点比例式理想機能のSN比及び感度を適用することがで
きる。
− (ステップ2)信号因子及びその範囲を選択する。
ステップ1で記載したように,始点(水浴の開始時点)からの経過時間を信号因子Mとして選択し
た。表B.9に示すように,信号因子Mの3水準は,成長期間の中の3日として,5日目〜7日目を選
択した。一般的に,もやしの収穫に7日間かかる。
表B.9−成長の信号因子の水準
信号の水準
M1
M2
M3
日数 d
5
6
7
53
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− (ステップ3)出力の測定方法を選択する。
出力yiは,時間Miにおける質量Ysから計算される。時間Miでの質量を測定するために,はかり
を使用した。初期質量Y0に対する測定データYsの比を計算し,出力yiを求めるために,その自然対
数を用いた。
− (ステップ4)ノイズ戦略を作り,ノイズ因子及びその水準を選択する。
実験中の制御が容易であるので,育成室の湿度をノイズ因子とし,表B.10のように,その水準を選
択した。ノイズ因子として育成室内の湿度及び温度を同時に選択することが望ましいが,通常,室内
で湿度及び温度を同時に制御することは困難である。発芽条件は,通常,発芽率及び殺菌に強く影響
するので,外乱を避けるために,各行の実験において室内の湿度以外の条件は固定した。
表B.10−ノイズ因子及びその水準
ノイズ因子
N1
N2
湿度 %
60
80
− (ステップ5)設計パラメータから制御因子及びその水準を選択する。
選択された制御因子及びそれらの水準を表B.11に示す。例えば,温度又は気浴時間のような発芽条
件は制御因子として選択しないで,固定した。この事例では,成長期の設計パラメータを制御因子と
して取り上げた。エチレンガスは植物ホルモンのようにもやしの成長に対する効果があり,成長,衰
退,及び腐敗に強い関係があることが知られている。エチレンガス浴に関係する条件を制御因子とし
て選択し,制御因子C及びDとした。制御因子E,F及びGは,散水に関係する条件である。
表B.11−制御因子及びそれらの水準
制御因子
水準 1
水準 2
水準 3
A
種子の種類
ブラックマッペ
グリーングラム
−
B
室温 ℃
18
24
30
C
一日当たりのエチレンガス気
浴回数(時期)
1(朝)
2(朝,昼)
3(朝,昼,夜)
D
エチレンガス濃度 (mL/L)
10
20
30
E
一日当たりの散水回数(時期)
1(朝)
2(朝,昼)
3(朝,昼,夜)
F
1度の散水中の噴霧回数 (回)
1
2
3
G
散水ミネラル添加率 %
0
0.1
1.0
− (ステップ6)実験に取り上げた因子を内側配列及び外側配列に割り付ける。
内側配列すなわち,直交表L18への制御因子の割り付けを,表B.12に示す。内側配列の各行の制御
因子の水準の組合せの下で,外側配列の実験を行う。
54
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.12−内側直交表L18:制御因子の割り付け
No.
1
A
2
B
3
C
4
D
5
E
6
F
7
G
1
ブラックマッペ
18
1
10
1
1
0
2
ブラックマッペ
18
2
20
2
2
0.1
3
ブラックマッペ
18
3
30
3
3
1
4
ブラックマッペ
24
1
10
2
2
1
5
ブラックマッペ
24
2
20
3
3
0
6
ブラックマッペ
24
3
30
1
1
0.1
7
ブラックマッペ
30
1
20
1
3
0.1
8
ブラックマッペ
30
2
30
2
1
1
9
ブラックマッペ
30
3
10
3
2
0
10
グリーングラム
18
1
30
3
2
0.1
11
グリーングラム
18
2
10
1
3
1
12
グリーングラム
18
3
20
2
1
0
13
グリーングラム
24
1
20
3
1
1
14
グリーングラム
24
2
30
1
2
0
15
グリーングラム
24
3
10
2
3
0.1
16
グリーングラム
30
1
30
2
3
0
17
グリーングラム
30
2
10
3
1
0.1
18
グリーングラム
30
3
20
1
2
1
− (ステップ7)実験を行い,データを収集する。
実験は,内側配列及び外側配列の実験計画の下で行った。外側配列の各因子の水準の組合せの下で,
もやしの質量を測定した。直交表L18の各行における出力yのデータを表B.13に示す。ここでは,分
析のための質量比の自然対数変換後の値だけを示す。
表B.13−成長率の測定データ(変換後)
No.
M1(5 d)
M2(6 d)
M3(7 d)
1
1.500
1.625
1.623
1.697
1.692
1.758
2
1.468
1.440
1.569
1.511
1.649
1.782
3
1.502
1.581
1.569
1.579
1.647
1.658
4
2.012
2.167
2.171
2.301
2.230
2.308
5
2.046
2.131
2.175
2.294
2.222
2.254
6
1.937
2.046
2.079
2.177
2.170
2.239
7
1.921
2.063
2.044
2.039
1.991
2.108
8
1.908
2.019
1.991
2.113
1.982
1.989
9
1.870
1.921
1.974
2.041
2.058
2.092
10
1.597
1.690
1.675
1.798
1.758
1.730
11
1.495
1.558
1.591
1.656
1.652
1.696
12
1.575
1.692
1.652
1.714
1.777
1.873
13
1.798
1.901
1.949
2.088
2.078
2.083
14
1.823
1.952
1.978
2.077
2.115
2.162
15
1.723
1.768
1.815
1.887
1.886
1.977
16
1.833
1.826
1.834
1.852
1.852
1.996
17
1.837
1.949
1.883
1.933
1.858
1.981
18
1.707
1.726
1.733
1.873
1.960
1.947
55
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− (ステップ8)SN比η及び感度Sを計算する。
内側配列L18の各行についてSN比及び感度を計算した。ゼロ点比例式理想機能のSN比を適用した。
内側配列の行番号No.1のデータについての計算は次のとおりである。
全変動:
(
)6
796
359
.
16
758
.1
697
.1
625
.1
692
.1
623
.1
500
.1
T
2
2
2
2
2
2
T
=
=
+
+
+
+
+
=
f
S
有効除数:
110
7
6
5
2
2
2
=
+
+
=
r
ノイズレベルごとの線形式:
734
081
.
29
692
.1
7
623
.1
6
500
.1
5
1
=
×
+
×
+
×
=
L
254
616
.
30
758
.1
7
697
.1
6
625
.1
5
2
=
×
+
×
+
×
=
L
比例項の変動:
(
)
(
)1
317
199
.
16
110
2
254
616
.
30
734
081
.
29
2
=
=
×
+
=
β
β
f
S
比例項の差の変動:
(
)
(
)1
034
017
.0
110
2
254
616
.
30
734
081
.
29
N
2
N
=
=
×
−
=
×
×
β
β
f
S
誤差の変動:
(
)4
445
143
.0
034
017
.0
317
199
.
16
796
359
.
16
e
e
=
=
−
−
=
f
S
誤差分散:
861
035
.0
4
445
143
.0
e
=
=
V
総合誤差分散:
096
032
.0
4
1
034
017
.0
445
143
.0
N
=
+
+
=
V
SN比η及び感度S:
(
)
596
.3
096
032
.0
861
035
.0
317
199
.
16
110
2
1
log
10
=
−
×
=
η
(
)
339
.
11
861
035
.0
317
199
.
16
110
2
1
log
10
−
=
−
×
=
S
同様の計算を行った,内側直交表L18の各行におけるSN比及び感度を表B.14に示す。
56
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.14−内側直交表L18のSN比及び感度
単位 db
No.
SN比
感度
1
3.596
−11.339
2
6.176
−11.732
3
2.854
−11.677
4
2.973
−8.854
5
2.681
−8.905
6
3.802
−9.205
7
1.454
−9.586
8
0.948
−9.714
9
3.562
−9.700
10
2.297
−11.058
11
3.551
−11.562
12
4.011
−10.998
13
4.248
−9.729
14
4.657
−9.573
15
3.867
−9.375
16
2.142
−10.297
17
1.068
−10.128
18
4.887
−10.444
制御因子の各水準におけるSN比及び感度の平均値を計算する。
(
)
12
.3
9
562
.3
948
.0
454
.1
802
.3
681
.2
973
.2
854
.2
176
.6
596
.3
1
A
=
+
+
+
+
+
+
+
+
=
η
(
)
41
.3
9
881
.4
068
.1
142
.2
867
.3
657
.4
248
.4
011
.4
551
.3
297
.2
2
A
=
+
+
+
+
+
+
+
+
=
η
(
)
75
.3
6
011
.4
551
.3
297
.2
854
.2
176
.6
569
.3
1
B
=
+
+
+
+
+
=
η
Λ
Λ
(
)
84
.2
6
068
.1
657
.4
011
.4
454
.1
973
.2
854
.2
3
H
=
+
+
+
+
+
=
η
制御因子の各水準におけるSN比及び感度の平均値を表B.15に示す。
表B.15−SN比及び感度の平均値
単位 db
制御因子
SN比
感度
水準1
水準2
水準3
水準1
水準2
水準3
A
種子の種類
3.12
3.41
−
−10.08
−10.46
−
B
室温
3.75
3.70
2.34
−11.39
−9.44
−9.98
C
一日当たりのエチレンガス気
浴回数
2.79
3.18
3.83
−10.14
−10.27
−10.40
D
エチレンガス濃度
3.10
3.91
2.78
−10.33
−10.23
−10.25
E
一日当たりの散水回数
3.66
3.35
2.79
−10.29
−10.33
−10.20
F
1度の散水中の噴霧回数
2.95
4.09
2.76
−10.19
−10.23
−10.40
G
散水ミネラル添加率
3.44
3.11
3.24
−10.14
−10.35
−10.33
H
−
3.05
3.91
2.84
−10.31
−10.37
−10.14
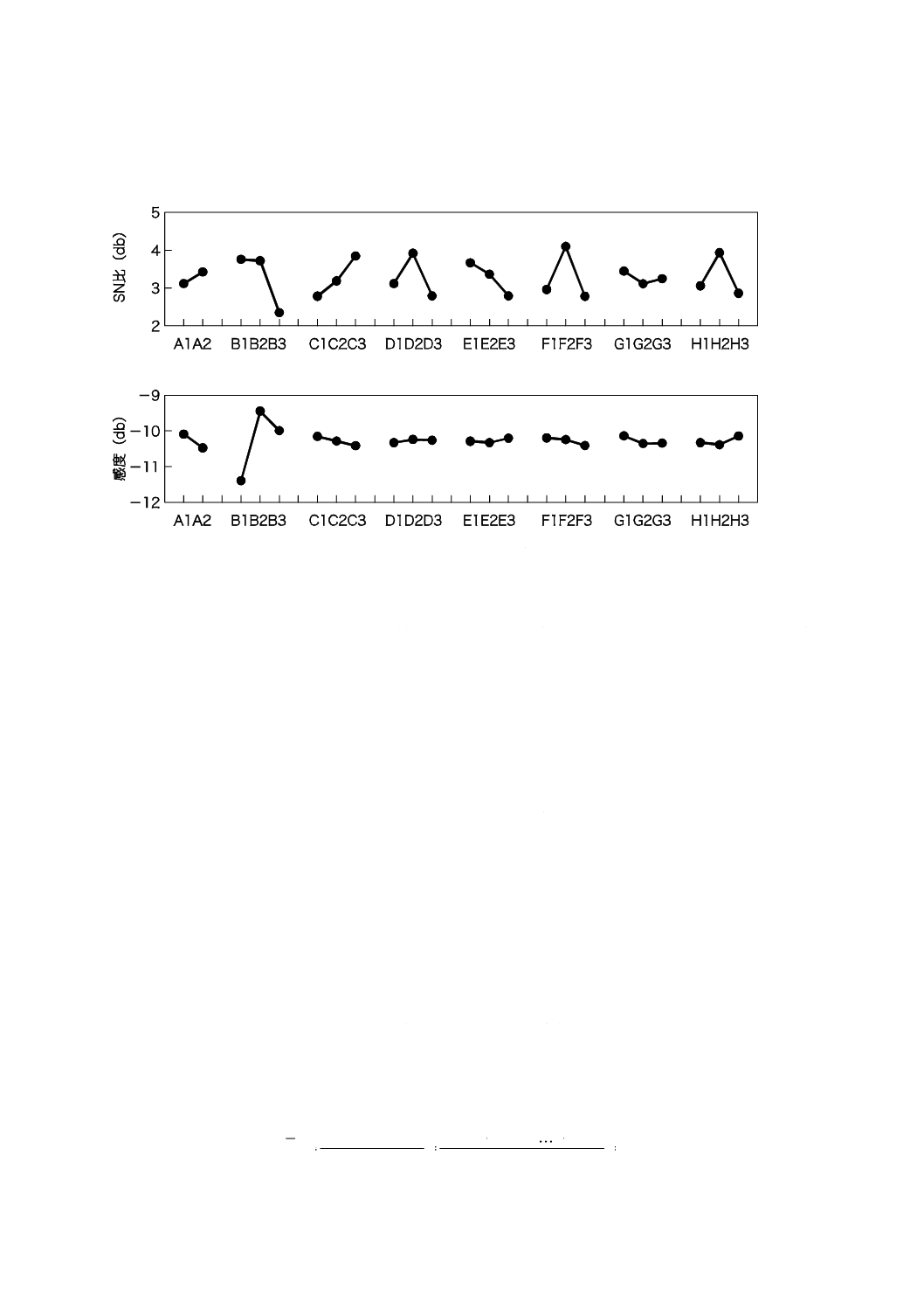
57
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− (ステップ9)SN比及び感度について,要因効果図を作成する。
もやしの育成実験における制御因子の要因効果図を図B.6に示す。
図B.6−豆の発芽に対するSN比及び感度の要因効果図
要因効果については,SN比に対しては制御因子B,D及びFが強く影響し,感度に対しては制御因
子A及びBが強く影響する。SN比を最大にする水準の組合せはA2B1C3D2E1F2G1であり,感度を
最大にする水準の組合せはA1B2C1D2E3F1G1となる。SN比及び感度を同時に最大にする上で,幾つ
かの矛盾が生じている。
− (ステップ10)最適条件を選択する。
SN比がより高いことは,ロバストネスがより高いことを意味する。感度がより高いことは,成長率
がより高いこと,すなわち生産効率が高いことを意味する。
最適化に対する決定プロセスを,次のようにした。第一に,SN比を最大にさせるために制御因子の
水準を選択した。通常,SN比を最大化することはより高い優先性をもっており,SN比に小さい効果
をもつ制御因子を用いて第2段階で感度を調整する。ここで,制御因子Bはロバストネス及び感度に
対して強い効果をもっている。ロバストネスに関してB1が,感度に関してはB2が最適であり,最適
水準が異なっている。ただし,B1とB2との間のSN比の差は0.04(db)だけである。他方,感度で
は1.95(db)の差がある。このことから,制御因子Bの最適水準として,SN比は最大でないが,水
準B2を選択した。最終的に,もやしの成長における最適条件は,A1B2C3D2E1F2G1と設定した。ま
た,ベースライン条件とも呼ばれる現行条件は,A1B1C3D2E1F1G1である。
− (ステップ11)利得によって,ロバストネスの改善効果を推定する。
a) SN比ηの利得の推定 SN比の利得を推定するために,最適条件におけるSN比ηopt及びベースライ
ンとなる現行条件におけるSN比ηcurの推定値の計算を行った。ステップ9で記載したように,SN比
に強い効果をもっている制御因子B,制御因子D及び制御因子FをSN比の推定の計算に用いた。
SN比の総平均:
265
.3
18
887
.4
176
.6
596
.3
18
18
2
1
SN
=
+
+
+
=
+
+
+
=
Κ
Κη
η
η
T
58
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
最適条件におけるSN比の推定値:
17
.5
265
.3
2
09
.4
91
.3
70
.3
2SN
2
F
2
D
2
B
opt
=
×
−
+
+
=
−
+
+
=
T
η
η
η
η
現行条件におけるSN比の推定値:
08
.4
265
.3
2
95
.2
91
.3
75
.3
2SN
1
F
2
D
1
B
cur
=
×
−
+
+
=
−
+
+
=
T
η
η
η
η
SN比の利得:
09
.1
cur
opt
=
−
=
∆
η
η
η
b) 感度Sの利得の推定 感度の利得を予測するために,最適条件における感度Sopt及び現行条件におけ
る感度Scurの推定値の計算を行った。ステップ9で記載したように,感度に強い効果をもっている制
御因子A及び制御因子Bを選択し,表B.15のデータから感度の推定値の計算に用いた。
感度の総平均:
271
.
10
18
444
.
10
732
.
11
339
.
11
18
18
2
1
−
=
−
−
−
−
=
+
+
+
=
Κ
ΚS
S
S
Tβ
最適条件における感度の推定値:
25
.9
)
27
.
10
(
44
.9
08
.
10
2
B
1
A
opt
−
=
−
−
−
−
=
−
+
=
β
T
S
S
S
現行条件における感度の推定値:
20
.
11
)
27
.
10
(
39
.
11
08
.
10
1
B
1
A
cur
−
=
−
−
−
−
=
−
+
=
β
T
S
S
S
感度の利得:
95
.1
Δ
cur
opt
=
−
=
S
S
S
− (ステップ12)確認実験を行い,利得及び再現性を調べる。
実験データを基にした推定値から予測された改善効果を確かめるために,最適条件及び現行条件で
確認実験を行った。
確認実験の結果及び推定の結果を表B.16に示す。
表B.16−確認実験の結果
単位 db
SN比
感度
推定値
確認値
推定値
確認値
最適条件
5.17
5.72
−9.25
−8.93
現行条件
4.08
3.52
−11.20
−11.49
利得
1.09
2.20
1.95
2.56
利得の推定値と利得の確認値とは,SN比及び感度においてそれほど差がなく,利得は再現するといえ
る。ロバストネスにおける改善は,もやしの順調な成長及び成長曲線の制御性の改善につながる。すなわ
ち,成長率,出荷,又は過不足ない量の制御が可能となることを意味している。
感度において2.56(db)の利得が達成された。それは,最適条件下では,現行条件のときより早く,も
やしが成長することを意味する。実際,現行条件では成長するのに7日を要したのに対して,最適条件で
は4日で十分成長することを確認し,生産性において43 %の改善である。
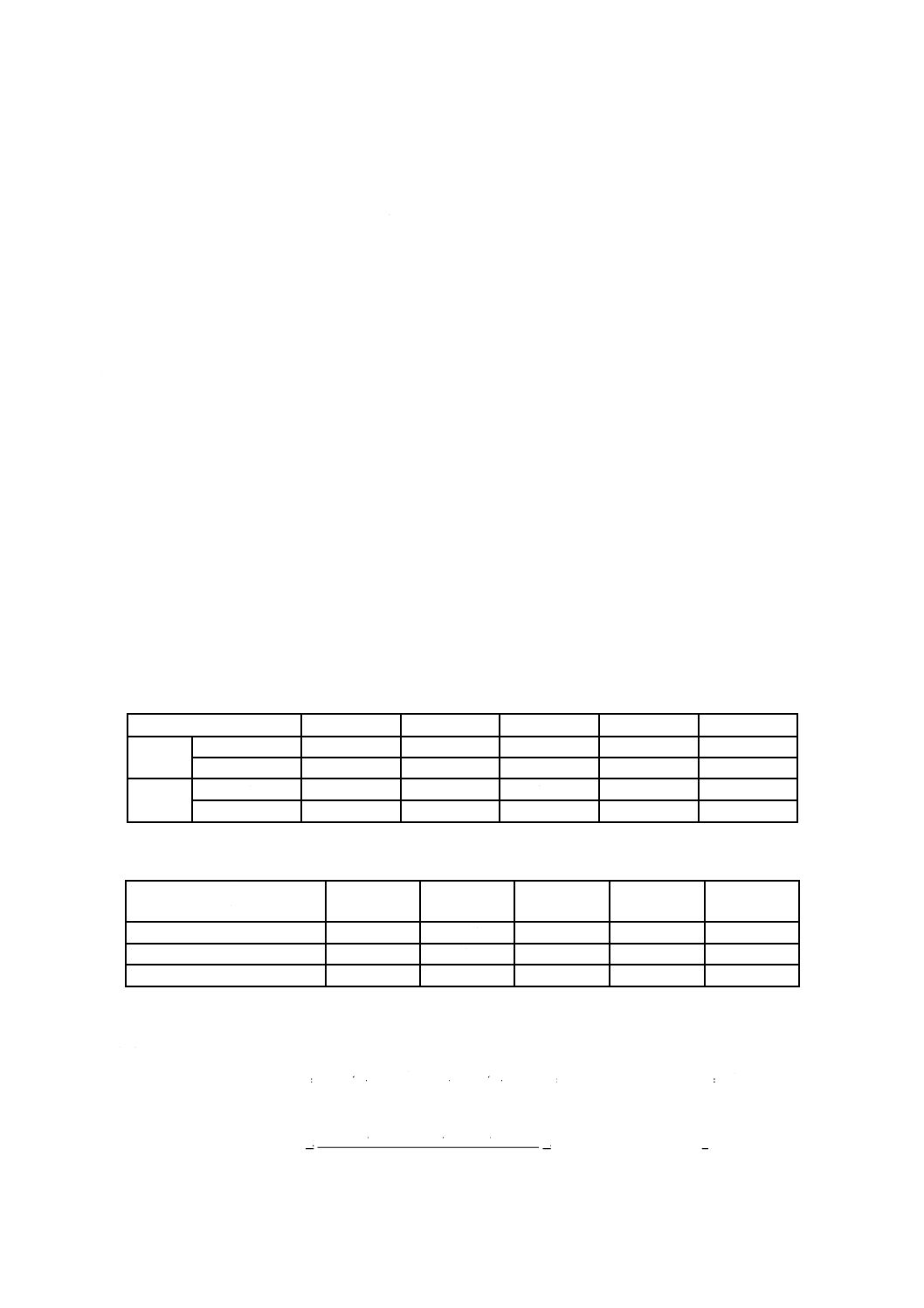
59
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
パラメータ設計の実験によって,ロバストネス及び生産効率の両方で改善が見られた。
B.2
静的特性のSN比
B.2.1 事例1:望目特性のSN比(コンピュータシミュレーションによるカムシャフトの鋳造工程のロバ
ストネスの評価)
B.2及びB.3の目的は,静的特性及び計数特性のSN比の計算を示すことである。ここでの事例では,制
御因子の詳細は議論せず,外側配列のデータからのSN比の計算だけを示す。
自動車のエンジンの重要な部品の一つであるカムシャフトは,通常,鋳造によって製造される。しゅう
(摺)動表面上の鋳造欠陥は,エンジンの性能低下を引き起こす。鋳造条件を最適化するため,CAE
(Computer Aided Engineering) を用いたパラメータ設計を適用した。この箇条では,ロバストネスの評価の
ためのパラメータ設計において,外側配列でのデータセットだけを取り上げて,SN比の計算を示す。
カムシャフトは,金型の鋳型(骨組となる鋳型)に溶融金属(溶湯)を注ぐという鋳造によって生成さ
れる。鋳造欠陥は,溶融金属を注いでいる間にガスを取り除くことによって防ぐことができる。また,ゲ
ートを通過する溶融金属の中の乱流を抑制することは非常に重要である。レイノルズ数Reは乱流の程度
を示し,鋳造における理想レイノルズ数はよく知られている。カムシャフトの鋳造のロバストネスを評価
するために,望目特性のSN比を用いた。内側配列の各行の条件の下で,外側配列でのレイノルズ数のデ
ータを得るために,コンピュータシミュレーションを用いた。
内側直交表L18の第1行の条件下の外側配列でのデータセットの例を表B.17に示す。外側配列のノイズ
因子及びその水準を表B.18に示す。鋳型は,二つのランナー(湯道)をもっており,ノイズ因子の範囲は
生産工程の変動の要求範囲内に設定した。ここでは,制御因子及び最適化の詳細は議論しない。
表B.17−外側配列第1行でのレイノルズ数Reのデータセット
ノイズ因子
K1
K2
K3
K4
K5
I1
J1
5 749
5 900
4 722
4 552
4 070
J2
5 732
5 728
5 484
4 967
4 712
I2
J1
6 162
6 172
6 298
5 138
5 062
J2
6 069
5 278
4 392
3 104
3 879
表B.18−ノイズ因子及びそれらの水準
水準
ノイズ因子
1
2
3
4
5
I:注入時の溶融金属温度
低
標準
−
−
−
J:ランナー
左
右
−
−
−
K:溶融金属の充塡率 %
35
40
45
50
55
第1行のSN比及び感度は,表B.17のデータセットから次のように計算される。
全変動:
)
20
(
058
915
545
879
3
104
3
900
5
749
5
T
2
2
2
2
T
=
=
+
+
+
+
=
f
S
Λ
平均の変動:
(
)
)1
(
028
736
531
20
879
3
104
3
900
5
749
5
m
2
m
=
=
+
+
+
+
=
f
S
Λ
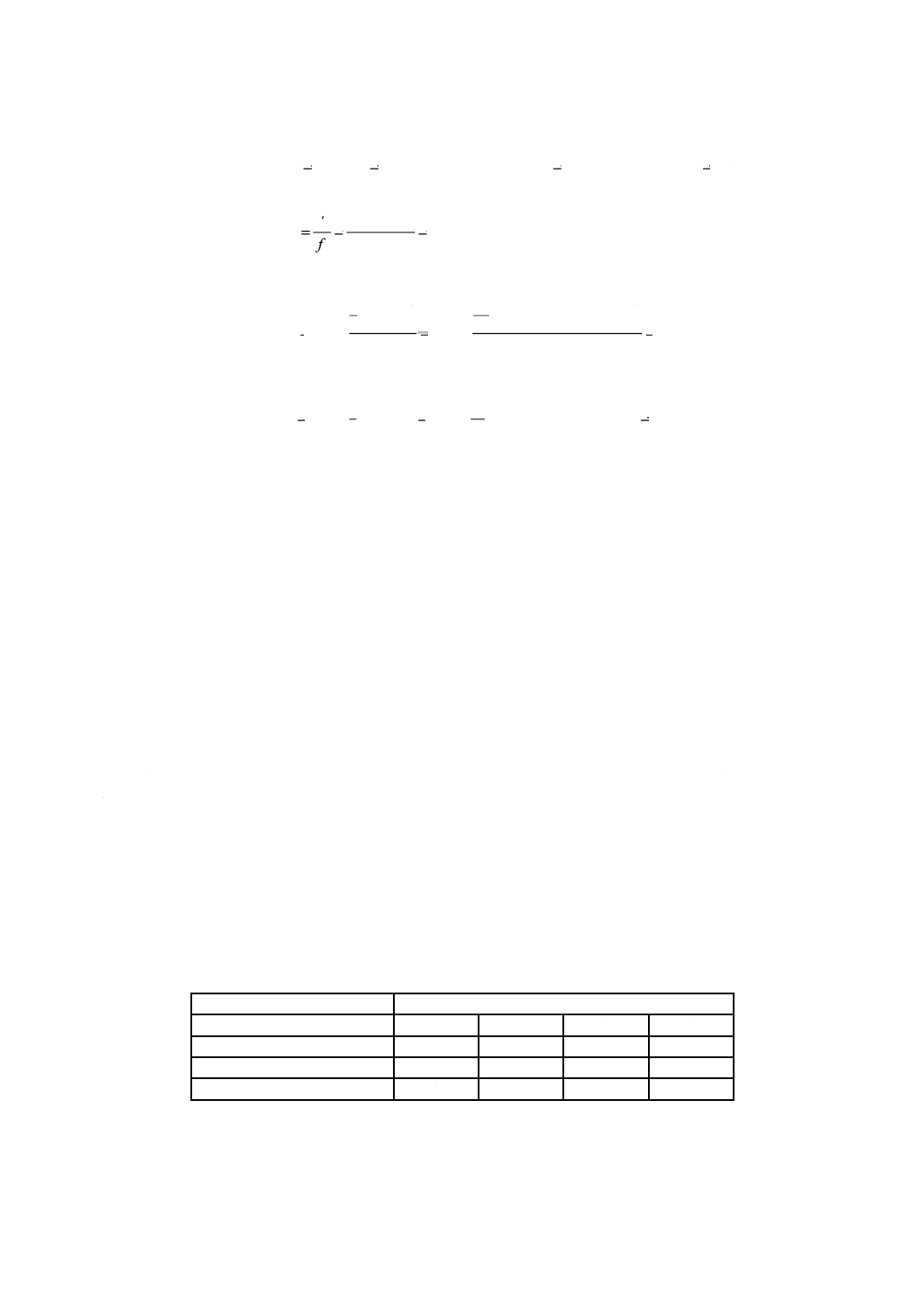
60
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
誤差の変動:
)
19
(
030
179
14
028
736
531
058
915
545
e
m
T
e
=
=
−
=
−
=
f
S
S
S
誤差分散:
265
736
19
030
179
14
e
e
e
=
=
=fS
V
望目特性のSN比:
(
)
(
)
51
.
15
265
736
265
736
028
736
531
20
1
log
10
1
log
10
e
e
m
=
−
=
−
=
V
V
S
n
η
望目特性の感度:
(
)
(
)
24
.
74
265
736
028
736
531
20
1
log
10
1
log
10
e
m
=
−
=
−
=
V
S
n
S
この場合,望目特性のSN比は,出力の安定性,すなわち,(レイノルズ数の平均の二乗)/(誤差分散)
の推定値を表している。感度は,出力の平均の大きさの推定値を示している。感度は,SN比によってロ
バストネスの最適化を行った後,2段階設計法の第2段階である出力の平均を目標値に合わせる調整を行
うために用いられる。
B.2.2 事例2:望小特性のSN比(プリンタの使いやすさにおけるロバストネスの評価)
この事例の目的は,製品開発又は製品企画段階において,顧客が容易に操作できるプリンタカートリッ
ジの最適設計を行うことである。プリンタカートリッジの使いやすさを評価するために,プリンタカート
リッジのイメージスケッチを提示して,10人の顧客による採点を行った。
採点は,次のような3段階で行った。
− 操作が簡単かつ容易:0点
− 操作があまり容易でない:1点
− 操作が困難又は不可能:2点
使いやすさの採点は,点数が低いほど操作が容易なので,望小特性のSN比によって評価することがで
きる。
パラメータ設計のために,制御因子をプリンタカートリッジの操作手順から選択し,内側配列L18に割
り付けた。制御因子及び最適化の詳細についてはここでは議論しない。
外側配列及び採点データを表B.19に示す。顧客の操作方法及び使用環境から,三つのノイズ因子を選択
した。ノイズ因子はいずれも2水準であり,それらを直交表L4に割り付けた。表の合計点のデータは,内
側配列L18の列番号1の設計カートリッジについての10人の顧客による採点の総計である。
表B.19−プリンタカートリッジ設計における外側配列及びデータ
ノイズ因子
水準の組合せ
使用する腕
片手
片手
両手
両手
部屋の明るさ
明るい
暗い
明るい
暗い
プリンタ設置高さ
正面
足元
足元
正面
合計点
3
5
4
5
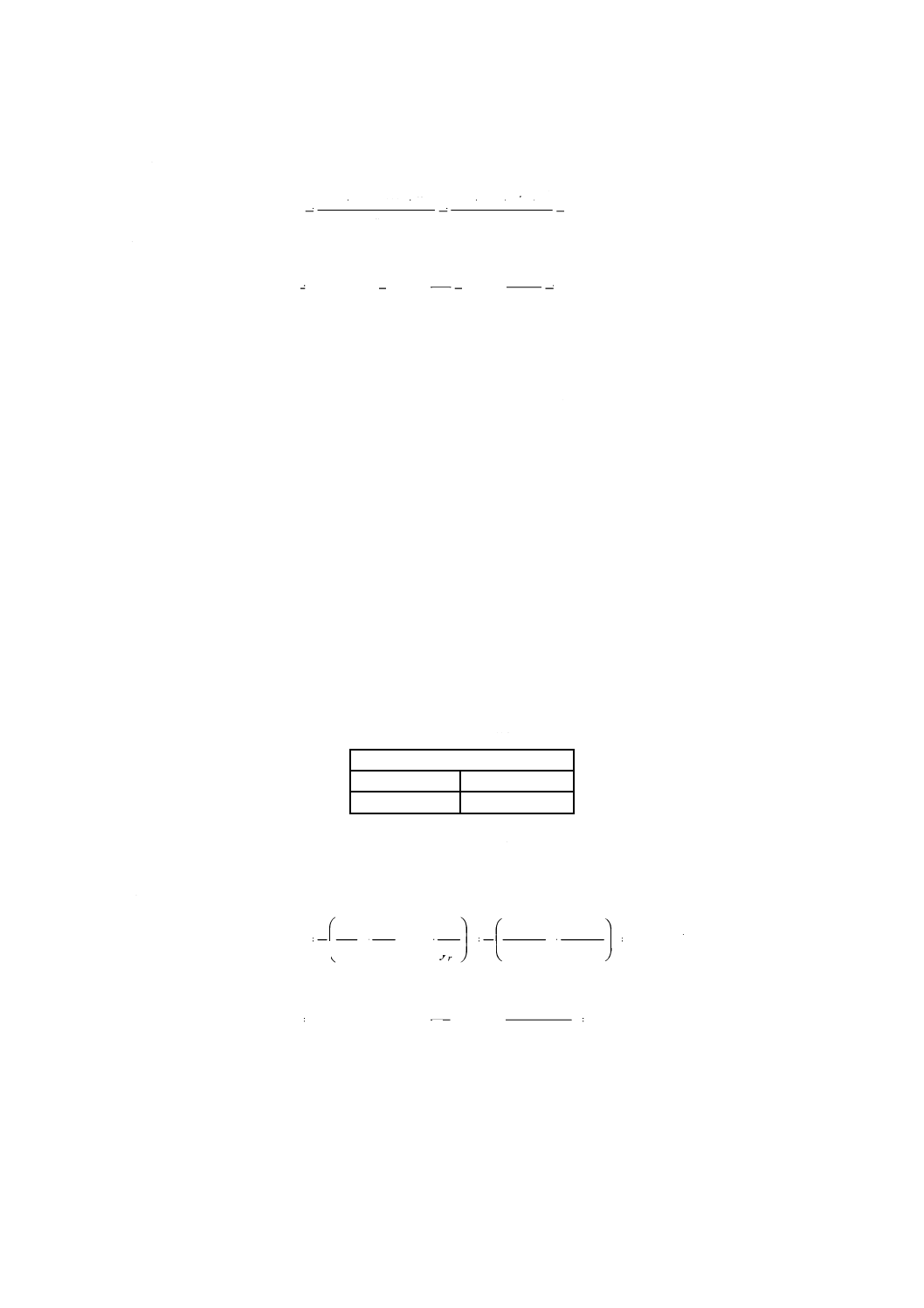
61
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
第1行のSN比は,表B.19のデータから次のように計算する。
平均二乗偏差:
75
.
18
4
5
4
5
3
ˆ
2
2
2
2
2
2
2
2
1
2
=
+
+
+
=
+
+
+
=
r
y
y
y
r
Λ
σ
望小特性のSN比:
73
.
12
75
.
18
1
log
10
ˆ
1
log
10
ˆ
log
10
2
2
−
=
=
=
−
=
σ
σ
η
望小特性のSN比は,0の値からの偏差の二乗平均値,すなわち,目標値からの距離を示す。偏差の二
乗平均は,出力の全分散に相当する。望小特性において,感度は計算しない。
B.2.3 事例3:望大特性のSN比[BRN(酵素)生産菌の培地の改良]
BRNは,微生物が生み出す酵素の一種であり,ある種の成分を分解する能力(力価)をもっている。BRN
生産菌(生産菌である微生物)は,BRN製造用タンク(培地)において培養される。BRNの分解能力(力
価)は生産菌の能力に強く依存しており,高力価の酵素を生み出す菌類を見つけることが重要である。こ
のため,BRN生産菌を培養するための培地を改良するために,パラメータ設計を適用した。制御因子は,
培地組成条件から選択され,内側配列L18に割り付けた。制御因子の詳細は,ここでは議論しない。外側
配列の測定値からのSN比の計算についてだけ示す。
出力は総力価(U/mL)であり,これは1 mL中の規定成分を分解する能力の尺度である。総力価は大き
い程よい,望大特性である。性能及びロバストネスの評価のために,望大特性のSN比を適用した。ノイ
ズ因子は二つの菌株の種類を選択した。最適な培地とは,それぞれの種類の菌株に対して,大きい能力,
しかも,同じ能力をもっていることが望ましい。内側配列L18の第1行における外側配列の測定値を表B.20
に示す。
表B.20−外側配列の値
単位 U/mL
菌株の種類
R1
R2
5 030
5 340
望大特性のSN比は,表B.20の測定値から次のように計算する。
平均二乗偏差:
8
2
2
2
2
2
2
1
2
10
73
.3
340
5
1
030
5
1
2
1
1
1
1
1
ˆ
−
×
=
+
=
+
+
+
=
ry
y
y
r
Λ
σ
望大特性のSN比η:
28
.
74
10
73
.3
1
log
10
ˆ
1
log
10
ˆ
log
10
8
2
2
=
×
=
=
−
=
−
σ
σ
η
B.3
デジタル特性のSN比(自動化された,単語による分類システムの改良)
顧客の声を幾つかのカテゴリに分類するための自動化システムは,多くの製品で音声認識システムの一
つとして使用されている。単語による分類は,そのような分類方法の一つである。例えば,サービス,販
売,競争,ソフトウェアなどの複数のカテゴリについて,分類するか分類しないかの二つの選択肢がある
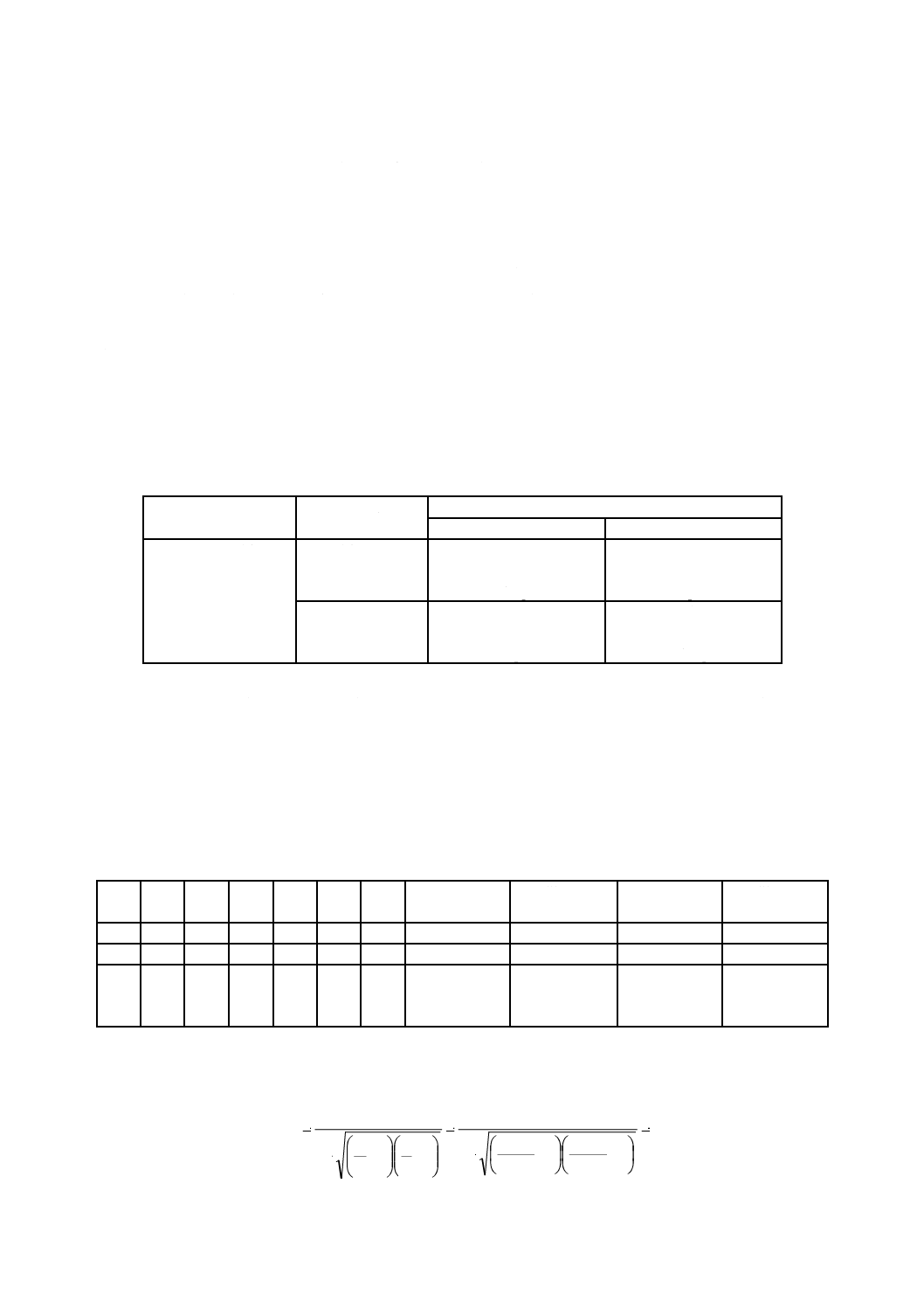
62
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
と仮定する。初めに,一つのカテゴリでよく現れる単語を集め,各カテゴリの単語表に載せる。次に,あ
る顧客の声の中にそのカテゴリの単語表に載せられた単語が発見されたとき,その顧客の声はそのカテゴ
リに分類する。発見されないときには,そのカテゴリには分類しない。
単語が単語表の中に正しく選ばなかった場合,単語による分類には多くの誤りが生じる。ここで,誤り
には次の2種類がある。
− 誤り1(未分類):正しい状態では分類されるものが,単語システムでは分類されない。
− 誤り2(過分類):正しい状態では分類されないものが,単語システムでは分類される。
正しい分類すなわち正解には,次の2種類がある。
a) 正解1(分類する):分類されなければならないものが分類される。
b) 正解2(分類しない):分類されてはならないものが分類されない。
判断の四つのケースを表B.21に示す。単語システムによる分類の性能を評価するために,正しい判断が
必要である。ここでは,人による分類を正しい判断であると仮定した。
表B.21−二つの誤差の分類
分類の方法
分類の結果
単語システムによる分類
分類した
分類しない
人による分類
分類した
正解1
(分類する)
1−p
誤り1
(未分類)
p
分類しない
誤り2
(過分類)
q
正解2
(分類しない)
1−q
2水準直交表を,単語表の中の各単語の分類に対する寄与率を評価するために使用する。各単語は,制
御因子として選択され,内側配列に割り付けられる。その水準については,水準1は単語を使用する場合
とし,水準2は単語を使用しない場合とした。単語の寄与率の大きさは,標準化SN比によって評価する。
SN比は,内側配列の各行について計算する。外側配列は表B.21と同様であり,表B.22の中にも示す。制
御因子の詳細は,ここでは議論しない。ロバストネスの指標であるSN比の計算だけを示す。
表B.22−データ表
No.
単語
1
単語
2
単語
3
単語
4
…
単語
N
正解1
(分類する)
誤り1
(未分類)
正解2
(分類しない)
誤り2
(過分類)
1
1
1
1
1
…
1
0.611
0.389
0.796
0.204
2
0
1
0
1
…
0
0.443
0.557
0.875
0.125
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
…
…
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
デジタル特性の標準化SN比は,外側配列のデータから次のように計算する。
標準化誤り率:
287
.0
1
204
.0
1
1
389
.0
1
1
1
1
1
1
1
1
1
0
=
−
−
+
=
−
−
+
=
q
p
P

63
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
標準化寄与率:
(
)
(
)
180
.0
287
.0
2
1
2
1
2
2
0
0
=
×
−
=
−
=
p
ρ
標準化SN比:
57
.6
1
180
.0
1
log
10
1
1
log
10
0
0
−
=
−
−
=
−
−
=
ρ
η
標準化SN比は,デジタル特性のSN比であり,システムが正しく分類する能力を示している。
B.4
様々な分野におけるロバストパラメータ設計の適用
動的特性の理想機能に対するパラメータ設計の例を,表B.23に示す。
表B.23−パラメータ設計の事例(動的特性)
分野
システム
信号
出力
ノイズ因子
制御因子
機械
はんだ付け
工程[8]
電流
電圧
温度,振動,測定位
置
こて先形状,こて先温度,はんだ線
径,予熱時間,はんだ送り時間,は
んだ送り後の加熱時間,はんだ送り
速度,はんだ送り角度
機械
射出成形機の
可塑化装置[9]
スクリュー
回転時間×
スクリュー
回転速度
溶融樹脂重量
可塑化インターバ
ル
スクリュー圧縮比,スクリューピッ
チ,ヒータゾーン1温度,ヒータゾ
ーン2温度,ヒータゾーン3温度,
スクリュー速度,スクリュー位置
機械
マシニングセ
ンタ[10]
回転時間
累積電力量
モータ+主軸,モー
タ単体
軸受種類,ハウジング寸法,主軸寸
法,間座寸法,間座形状,締め代,
軸受形状,冷却寸法
機械
金型加工(一
刀彫り)[11]
加工体積の
平方根
加工エネルギ
ーの平方根
材料(FC材,SKD61
相当材)
加工法,回転数,1刃体積量,最小
送り制限値,ホルダの種類,工具の
種類,首下長,切削油
機械
感光体クリー
ニングシステ
ム[12]
感光体回転
時間
時間積算トル
ク値
感光体回転の途中
停止の有無,トルク
波形の変動
トナー処方2種,プロセス条件5種,
感光体処方
機械
切削加工[13]
加工時間,
切削重量の
平方根
電力量の平方
根
電力値の変動,切削
回数
切削油希釈,切込み量,チップノー
ズ角,チップすくい角,横切れ刃角,
チップ面ころし,回転数,送り
電気
電子写真ベル
ト定着システ
ム[14]
電圧
電流・断面積
印加電圧の周波数
薬品6種,製造条件2種
電気
光磁気ディス
ク(交換結合
オーバライ
ト)[15]
レーザ発光
時間
記録されたマ
ークの長さ
環境劣化(連続記
録,記録磁界,レー
ザパワー),製造条
件(メモリ組成,記
録層組成,全層膜
厚)
材料,成膜プロセス
電気
電子写真現像
システム[16]
現像電位差
現像トナー量
現像材の劣化
キャリア条件2種,トナー条件1種,
現像器条件5種
薬学
医薬品の噴霧
乾燥[17]
液体投入量
捕集量
溶液濃度
アトマイザ回転数,噴霧角度,気流
流量,排気温度,上部気流流量,下
部気流流量,上部気流噴出し角度,
空気湿度
64
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.23−パラメータ設計の事例(動的特性)(続き)
分野
システム
信号
出力
ノイズ因子
制御因子
薬学
生薬ばい(焙)
煎[18]
加熱時間
生薬全体の質
量変化
原料生薬の水分値
熱風風量,原料仕込量,原料投入量,
焙煎温度,昇温速度,かくはん(攪
拌)温度,熱風温度
薬学
漢方薬配合[19] 時間
血清クレアチ
ンの変化量
ラットの病態(重
度,中度,軽度)
構成生薬5種
食品
耐熱性菌の培
養条件[20]
時間経過
菌数
希釈水のpH
菌種,希釈液の種類,ベンチタイム,
基礎培地の種類,カタラーゼの量,
リゾチームの量,ピルビン酸ナトリ
ウムの量,アラニンの量
静的特性の理想機能に対するパラメータ設計の例を表B.24に示す。
表B.24−パラメータ設計の事例(静的特性)
分野
システム
信号
特性値
ノイズ因子
制御因子
機械
鋳造のシミュ
レーション[21]
−
溶湯のレイノズル数
(望目特性のSN比)
溶湯温度,充塡
率,湯道
チョーク,縦湯道,スワール横湯
道,スワール入口せき(堰),ス
ワール下せき(堰),横湯道,せ
き(堰)下,せき(堰)
機械
プリンタカー
トリッジ交換
作業のユーザ
ビリティ[22]
−
交換作業のしやすさ
の点数付け(望小特性
のSN比)
作業方法,作業
環境
前カバー向き,ロック解除,取手,
持つ場所,ストッパ,ロック
建築
ポリマーセメ
ントモルタル
の塗布[23]
−
ピンホールの合計数
(望小特性のSN比)
塗布速度,塗布
量,温度,材料
粘度,塗布回数
セメント配合比,添加剤の種類,
添加剤の添加量,骨材粒径,骨材
配合比
生物
BRN(酵素)生
産菌のスクリ
ーニング用培
地の改良実験
[24]
−
総力価(望大特性の
SN比)
菌株
培養温度,活性物質量,Zn含有
物質量
市場
調査
テキスト分類
の精度向上[25]
−
2種類の誤り率(デジ
タルのSN比)
−
分類に利用する語
表B.23及び表B.24の文献は,参考文献の項に示す。
65
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] Genichi Taguchi. System of experimental design, UNIPUB. KRAUS INTERNATIONAL PUBLICATION, New
York, 1987
[2] Phadke M.S. Quality engineering using robust design. Prentice-Hall, Inc, 1989
[3] Nair V.N. editor, Taguchiʼs Parameter Design: A Panel Discussion. Technometrics. 1992, 34, pp. 127-161
[4] Jeff Wu C.F., & Hamada M. Experiments: Planning, Analysis, and Parameter Design Optimization. John Wiley
& Sons, Inc, 2000
[5] Taguchi G., Chowdhury S., Taguchi S. Robust Engineering. McGraw-Hill, 2000
[6] Baker T. B. Engineering quality by design: interpreting the Taguchi approach, Marcel Dekker, Inc. and ASQC
Quality Press, 2000
[7] Genichi Taguchi. Subir Chowdhury, and Yuin Wu, Taguchiʼs Quality Engineering Handbook. John Wiley &
Sons, Inc, Hoboken, New Jersey, 2004
[8] 楠本剛史:電流−電圧特性による手はんだ工程条件の最適化,品質工学便覧,日刊工業新聞社,(2007),
pp.195-199
[9] 高橋和仁:射出成形機における可塑化装置の最適化,品質工学便覧,日刊工業新聞社,(2007),
pp.230-235
[10] 玉村郁夫:マシニングセンタ主軸の回転機能,品質工学便覧,日刊工業新聞社,(2007),pp.235-240
[11] 細田剛:金型加工における一刀彫り加工条件の設定,品質工学便覧,日刊工業新聞社,(2007),
pp.240-244
[12] 田村希志臣:感光体クリーニングシステムの最適化,品質工学便覧,日刊工業新聞社,(2007),
pp.249-254
[13] 高橋和仁:切削加工の電力評価の研究,品質工学便覧,日刊工業新聞社,(2007),pp.263-269
[14] 岡林英二:ベルト定着システムにおける電圧−電流特性による金属材料開発,品質工学便覧,日刊工
業新聞社,(2007),pp.297-301
[15] 細川哲夫:交換結合オーバライト光磁気ディスク開発への品質工学の適用,品質工学便覧,日刊工業
新聞社,(2007),pp.301-306
[16] 奥山奥士:テストピースによる電子写真現像システムの技術開発,品質工学便覧,日刊工業新聞社,
(2007),pp.306-310
[17] 矢野耕也:医薬品の噴霧乾燥の機能性のパラメータ設計による評価,品質工学便覧,日刊工業新聞社,
(2007),pp.332-336
[18] 大石芳明:生薬焙煎における製造条件の最適化,品質工学便覧,日刊工業新聞社,(2007),pp.341-346
[19] 矢野耕也:漢方薬の配合比の最適化とモデル動物による薬効評価の検討,品質工学便覧,日刊工業新
聞社,(2007),pp.346-352
[20] 渡部英子:耐熱性菌検出方法の検討,品質工学便覧,日刊工業新聞社,(2007),pp.400-405
[21] 椎野和幸,福本康博:カムシャフト鋳造条件の最適化,品質工学,Vol.9,No.4,(2001),pp.68-73
[22] 坂本信也,河合靖則,田村希志臣,竹田誠:プリンタにおけるユーザビリティの機能性評価,品質工
学,Vol.18,No.1,(2010),pp.96-103
[23] 松井智隆,森義和,中島建夫,下塗り用新規ポリマーセメントモルタルの開発,Vol.17,No.6(2003),
66
Z 9061:2016 (ISO 16336:2014)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
pp.107-113
[24] 後藤孝夫,BRN(酵素)生産菌のスクリーニング用培地の改良実験,Vol.5,No.6(1997),pp.53-59
[25] 小部正人,舘野昌一:品質工学を利用した内容によるテキスト分類の精度向上,第18回品質工学研
究発表大会論文集,(2010),pp.286-289