Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,財団法人日本規格協会(JSA)から,工業標準
原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大
臣が制定した日本工業規格である。
制定に当たっては,日本工業規格と国際規格との対比,国際規格に一致した日本工業規格の作成及び日
本工業規格を基礎にした国際規格原案の提案を容易にするために,ISO 16269-7:2001 Statistical interpretation
of data - Part 7: Median - Estimation and confidence intervalsを基礎として用いた。
JIS Z 9041-5:2003には,次に示す附属書がある。
附属書A(参考)メディアンに対する信頼限界の古典的な決定方法
附属書B(参考)例
JIS Z 9041-5:2003には,次に示す部編成がある。
JIS Z 9041-1 データの統計的な解釈方法―第1部:データの統計的記述
JIS Z 9041-2 データの統計的な解釈方法―第2部:平均と分散に関する検定方法と推定方法
JIS Z 9041-3 データの統計的な解釈方法―第3部:割合に関する検定方法と推定方法
JIS Z 9041-4 データの統計的な解釈方法―第4部:平均と分散に関する検定方法の検出力
Z 9041-5:2003
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 用語,定義及び記号 ········································································································· 2
3.1 用語と定義 ··················································································································· 2
3.2 記号 ···························································································································· 2
4. 適用の条件 ····················································································································· 2
5. 点推定 ··························································································································· 2
6. 信頼区間 ························································································································ 2
6.1 一般 ···························································································································· 2
6.2 古典的な方法 ················································································································ 3
6.3 サンプルサイズが小さい場合···························································································· 3
6.4 サンプルサイズが大きい場合···························································································· 6
附属書A(参考)メディアンに対する信頼限界の古典的な決定方法 ················································ 7
附属書B(参考)例 ·············································································································· 8
B.1 例1····························································································································· 8
B.2 例2···························································································································· 10
1
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9041-5:2003
データの統計的な解釈方法―
第5部:メディアン―推定及び信頼区間
Statistical interpretation of data - Part 5: Median - Estimation and confidence
intervals
序文 この規格は,2001年に第1版として発行されたISO 16269-7:2001,Statistical interpretation of data - Part
7: Median - Estimation and confidence intervalsを翻訳し,技術的内容及び規格票の様式を変更することなく
作成した日本工業規格である。
なお,この規格で側線又は点線の下線を施してある“参考”は,原国際規格にはない事項である。
1. 適用範囲 この規格は,母集団から採取したサンプルサイズnのランダムサンプルに基づき,母集団
が連続確率分布の場合のメディアンに関する点推定値と信頼区間を求める方法を規定する。この方法は分
布に依存しない。すなわち,この方法は母集団分布が属する分布族に関する事前の知識を要しない。類似
した方法によって,四分位点とパーセント点も推定することができる。
備考1. メディアンは第2四分位点及び第50パーセント点である。この規格では,その他の四分位点
及びパーセント点を求める類似の方法については記述しない。
2. この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide21に基づき,IDT(一致している),MOD(修
正している),NEQ(同等でない)とする。
ISO 16269-7:2001,Statistical interpretation of data - Part 7: Median - Estimation and confidence
intervals (IDT)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで,発効年(又は発行年)を付記してあるものは,記載の年の版だけがこの
規格の規定を構成するものであって,その後の改正版・追補には適用しない。発効年(又は発行年)を付
記していない引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 9041-2 データの統計的な解釈方法―第2部:平均と分散に関する検定方法と推定方法
備考 ISO 2602:1980 Statistical interpretation of test results - Estimation of the mean - Confidence
intervalからの引用事項は,この規格の該当事項と同等である。
JIS Z 8101-1 統計―用語と記号―第1部:確率及び一般統計用語
備考 ISO 3534-1 Statistics - Vocabulary and symbols - Part 1: Probability and general statistical termsからの
引用事項は,この規格の該当事項と同等である。
2
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3. 用語,定義及び記号
3.1
用語と定義 この規格で用いる主な用語の定義は,JIS Z 9041-2及びJIS Z 8101-1の用語と定義によ
るほか,次による。
3.1.1
第k順序統計量 あるサンプルについて,観測値を昇順に並べたとき,第k番目の観測値。
備考 サンプルサイズnの観測値を,昇順に並べたときの第k番目の観測値をx[k]とする。ここに,
[]
[]
[]n
x
x
x
≤
≤
≤
Κ
2
1
3.1.2
連続確率分布のメディアン 分布関数が1/2に一致する確率変数の値。
備考 この規格では,連続確率分布のメディアンを母メディアンと呼び,これをMで表す。
参考 用語の定義については,“JIS Z 8101-1,1.10 分位点”に準じて規定した。
3.2
記号
a
母集団内の変数の下限値
b
母集団内の変数の上限値
C
信頼率
c
式(1)においてkの値を決定するために用いる定数
k
下側信頼限界に用いる順序統計量の番号
M
母メディアン
n
サンプルサイズ
T1
サンプルから導かれた下側信頼限界
T2
サンプルから導かれた上側信頼限界
u
標準正規分布の分位点
x[i]
昇順に並べたときの第i番目の観測値(第i順序統計量)
~x
標本メディアン
y
式(1)によってkの値を決定するために計算した中間値
4. 適用の条件 この規格に規定する方法は,サンプルをランダムに採取した場合,いかなる連続的な母
集団にも適用可能である。
備考 母集団分布が近似的に正規分布と考えられる場合,母メディアンは母平均にほぼ等しく,その
信頼限界はJIS Z 9041-2に準拠して計算する。
参考 上記の信頼限界は,JIS Z 9041-2の書式Bを用いて求める。
5. 点推定 母メディアンの点推定値は標本メディアン~xで与えられる。標本メディアンは,観測値を昇
順に並べたとき,次の値によって得られる。
― nが奇数のとき,第[(n+1)/2]番目の順序統計量
― nが偶数のとき,第(n/2)番目の順序統計量と第[n/2+1]番目の順序統計量の算術平均
備考 非対称分布の場合,この推定量は一般に偏りがあり,任意の母集団について不偏な推定量は存
在しない。
6. 信頼区間
6.1
一般 母メディアンに対する両側信頼区間は,[T1, T2](T1<T2)で表される閉区間であり,T1及び
T2をそれぞれ下側信頼限界及び上側信頼限界と呼ぶ。
母集団において,変数の下限値及び上限値がそれぞれa及びbである場合,片側信頼区間は,[T1, b)又
は(a, T2]で表される。
3
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 実際は,負の値とならない変数についてはaをゼロとし,上限値が存在しない変数については
bを無限大にすることが多い。
信頼区間の実際の意味は,指定された小さな確率で誤りが生じることは認めつつ,未知のM が当該区
間内にあることを主張するものである。このようにして計算した区間が母メディアンを含む確率を信頼率
と呼ぶ。
6.2
古典的な方法 附属書Aに,古典的な方法を示す。これは,二つの不等式を解く方法である。ある
信頼率の範囲について,それらの不等式を解く代わりの方法を次に示す。
6.3
サンプルサイズが小さい場合(
100
5
≤
≤n
) サンプルサイズが5から100の場合,最もよく用い
られる八つの信頼率に対し,附属書Aの式を満足するkの値について,片側信頼区間の場合を表1,両側
信頼区間の場合を表2に示す。kの値をこのようにとると,下側信頼限界は次の式で表される。
[]k
x
T=
1
また,上側信頼限界は次の式で表される。
[
]1
2
+
−
=
k
n
x
T
ここに,x[k]は昇順に並べたときの第k番目の観測値である。
nの値が小さいときは,順序統計量に基づく信頼限界が得られない場合がある。
サンプルサイズが小さい場合について,信頼限界の計算例を附属書BのB.1に与え,計算の手順を附属
書B書式Aに示す。
参考 信頼区間については,附属書B書式Bに示されている。
4
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
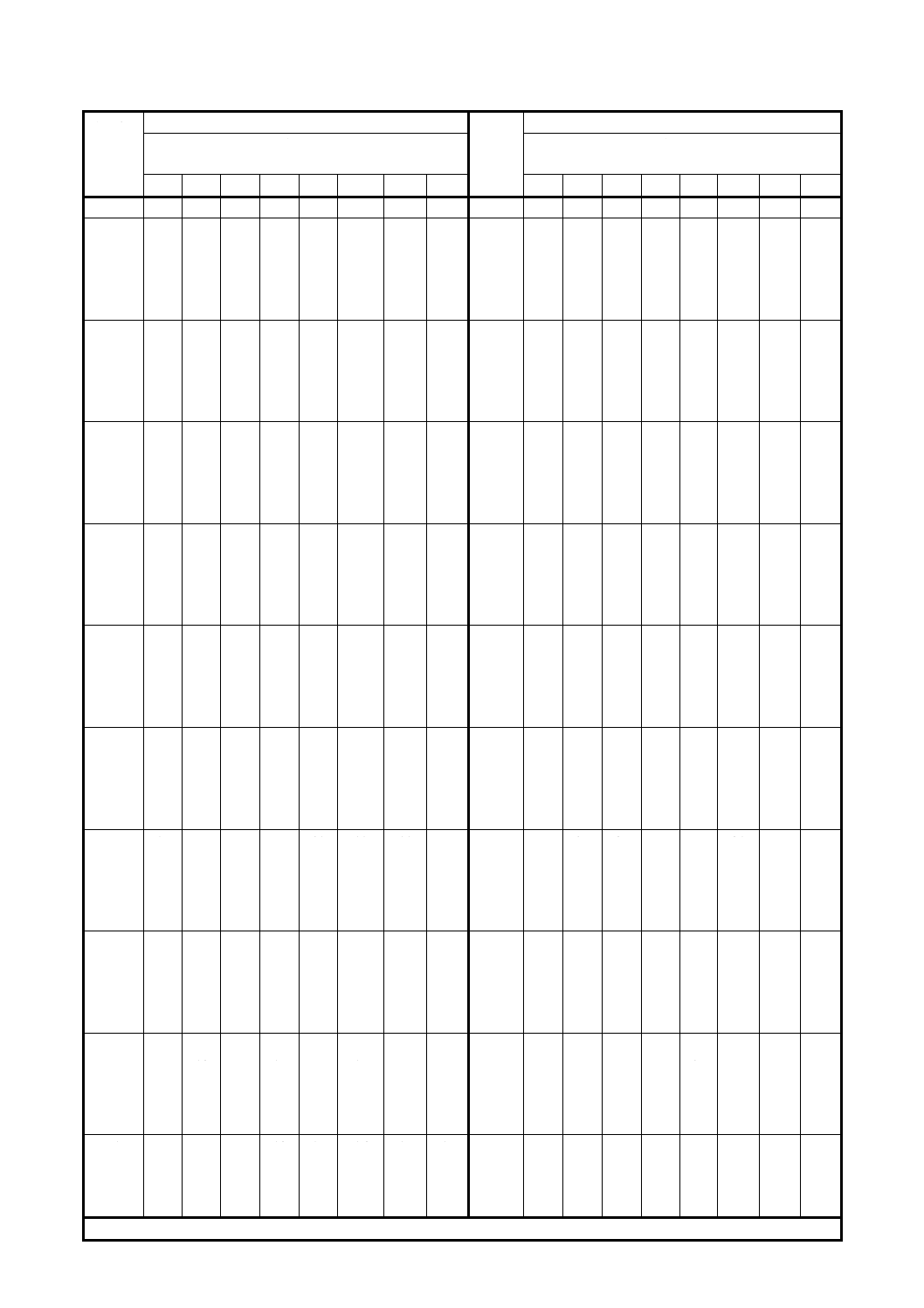
表1 サンプル・サイズが5から100までのkの厳密な値:片側信頼区間の場合
サンプル
サイズ
n
k
サンプル・
サイズ
n
k
信頼率
%
信頼率
%
80
90
95
98
99
99.5
99.8
99.9
80
90
95
98
99
99.5 99.8 99.9
5
2
1
1
a
a
a
a
a
55
24
23
21
20
19
18
17
16
6
7
8
9
10
2
2
3
3
4
1
2
2
3
3
1
1
2
2
2
1
1
1
2
2
a
1
1
1
1
a
a
1
1
1
a
a
a
1
1
a
a
a
a
1
56
57
58
59
60
25
25
26
26
27
23
24
24
25
25
22
22
23
23
24
20
21
21
22
22
19
20
20
21
21
18
19
19
20
20
17
18
18
19
19
17
17
17
18
18
11
12
13
14
15
4
5
5
5
6
3
4
4
5
5
3
3
4
4
4
2
3
3
3
4
2
2
2
3
3
1
2
2
2
3
1
1
2
2
2
1
1
1
2
2
61
62
63
64
65
27
28
28
29
29
25
26
26
27
27
24
25
25
25
26
23
23
23
24
24
21
22
22
23
23
21
21
21
22
22
19
20
20
21
21
19
19
19
20
20
16
17
18
19
20
6
7
7
8
8
5
6
6
7
7
5
5
6
6
6
4
4
5
5
5
3
4
4
5
5
3
3
4
4
4
2
3
3
3
4
2
2
3
3
3
66
67
68
69
70
30
30
31
31
31
28
28
29
29
30
26
27
27
28
28
25
25
26
26
26
24
24
24
25
25
23
23
23
24
24
21
22
22
23
23
21
21
21
22
22
21
22
23
24
25
9
9
9
10
10
8
8
8
9
9
7
7
8
8
8
6
6
7
7
7
5
6
6
6
7
5
5
5
6
6
4
4
5
5
5
4
4
4
5
5
71
72
73
74
75
32
32
33
33
34
30
31
31
31
32
29
29
29
30
30
27
27
28
28
29
26
26
27
27
27
25
25
26
26
26
23
24
24
25
25
23
23
23
24
24
26
27
28
29
30
11
11
12
12
13
10
10
11
11
11
9
9
10
10
11
8
8
9
9
9
7
8
8
8
9
7
7
7
8
8
6
6
7
7
7
5
6
6
6
7
76
77
78
79
80
34
35
35
36
36
32
33
33
34
34
31
31
32
32
33
29
30
30
30
31
28
28
29
29
30
27
27
28
28
29
26
26
26
27
27
25
25
25
26
26
31
32
33
34
35
13
14
14
15
15
12
12
13
13
14
11
11
12
12
13
10
10
11
11
11
9
9
10
10
11
8
9
9
10
10
8
8
8
9
9
7
7
8
8
9
81
82
83
84
85
37
37
38
38
39
35
35
36
36
37
33
34
34
34
35
31
32
32
33
33
30
31
31
31
32
29
29
30
30
31
28
28
28
29
29
27
27
28
28
28
36
37
38
39
40
15
16
16
17
17
14
15
15
16
16
13
14
14
14
15
12
12
13
13
14
11
11
12
12
13
10
11
11
12
12
10
10
10
11
11
9
9
10
10
10
86
87
88
89
90
39
40
40
41
41
37
38
38
38
39
35
36
36
37
37
34
34
34
35
35
32
33
33
34
34
31
32
32
32
33
30
30
31
31
31
29
29
30
30
30
41
42
43
44
45
18
18
19
19
20
16
17
17
18
18
15
16
16
17
17
14
14
15
15
16
13
14
14
14
15
12
13
13
14
14
11
12
12
13
13
11
11
12
12
12
91
92
93
94
95
41
42
42
43
43
39
40
40
41
41
38
38
39
39
39
36
36
37
37
38
34
35
35
36
36
33
34
34
35
35
32
32
33
33
34
31
31
32
32
33
46
47
48
49
50
20
21
21
22
22
19
19
20
20
20
17
18
18
19
19
16
17
17
17
18
15
16
16
16
17
14
15
15
16
16
13
14
14
15
15
13
13
13
14
14
96
97
98
99
100
44
44
45
45
46
42
42
43
43
44
40
40
41
41
42
38
38
39
39
40
37
37
38
38
38
35
36
36
37
37
34
34
35
35
36
33
33
34
34
35
51
52
53
54
22
23
23
24
21
21
22
22
20
20
21
21
18
19
19
19
17
18
18
19
16
17
17
18
15
16
16
17
15
15
15
16
a:このサンプルサイズと信頼率については,信頼区間と信頼限界を決定することはできない。

5
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2 サンプル・サイズが5から100までのkの厳密な値:両側信頼区間の場合
サンプル
サイズ
n
k
サンプル・
サイズ
n
k
信頼率
%
信頼率
%
80
90
95
98
99
99.5 99.8
99.9
80
90
95
98
99
99.5
99.8
99.9
5
1
1
a
a
a
a
a
a
55
23
21
20
19
18
17
16
15
6
7
8
9
10
1
2
2
3
3
1
1
2
2
2
1
1
1
2
2
a
1
1
1
1
a
a
1
1
1
a
a
a
1
1
a
a
a
a
1
a
a
a
a
a
56
57
58
59
60
23
24
24
25
25
22
22
23
23
24
21
21
22
22
22
19
20
20
21
21
18
19
19
20
20
18
18
18
19
19
17
17
17
18
18
16
16
17
17
17
11
12
13
14
15
3
4
4
5
5
3
3
4
4
4
2
3
3
3
4
2
2
2
3
3
1
2
2
2
3
1
1
2
2
2
1
1
1
2
2
1
1
1
1
2
61
62
63
64
65
25
26
26
27
27
24
25
25
25
26
23
23
24
24
25
21
22
22
23
23
21
21
21
22
22
20
20
20
21
21
19
19
19
20
20
18
18
19
19
19
16
17
18
19
20
5
6
6
7
7
5
5
6
6
6
4
5
5
5
6
3
4
4
5
5
3
3
4
4
4
3
3
3
4
4
2
2
3
3
3
2
2
2
3
3
66
67
68
69
70
28
28
29
29
30
26
27
27
28
28
25
26
26
26
27
24
24
24
25
25
23
23
23
24
24
22
22
23
23
23
21
21
21
22
22
20
20
21
21
21
21
22
23
24
25
8
8
8
9
9
7
7
8
8
8
6
6
7
7
8
5
6
6
6
7
5
5
5
6
6
4
5
5
5
6
4
4
4
5
5
3
4
4
4
5
71
72
73
74
75
30
31
31
31
32
29
29
29
30
30
27
28
28
29
29
26
26
27
27
27
25
25
26
26
26
24
24
25
25
25
23
23
23
24
24
22
22
23
23
23
26
27
28
29
30
10
10
11
11
11
9
9
10
10
11
8
8
9
9
10
7
8
8
8
9
7
7
7
8
8
6
6
7
7
7
5
6
6
6
7
5
5
6
6
6
76
77
78
79
80
32
33
33
34
34
31
31
32
32
33
29
30
30
31
31
28
28
29
29
30
27
27
28
28
29
26
26
27
27
28
25
25
25
26
26
24
24
25
25
25
31
32
33
34
35
12
12
13
13
14
11
11
12
12
13
10
10
11
11
12
9
9
10
10
11
8
9
9
10
10
8
8
9
9
9
7
7
8
8
9
7
7
7
8
8
81
82
83
84
85
35
35
36
36
37
33
34
34
34
35
32
32
33
33
33
30
31
31
31
32
29
29
30
30
31
28
28
29
29
30
27
27
28
28
28
26
26
27
27
27
36
37
38
39
40
14
15
15
16
16
13
14
14
14
15
12
13
13
13
14
11
11
12
12
13
10
11
11
12
12
10
10
10
11
11
9
9
10
10
10
8
9
9
9
10
86
87
88
89
90
37
38
38
38
39
35
36
36
37
37
34
34
35
35
36
32
33
33
34
34
31
32
32
32
33
30
30
31
31
32
29
29
30
30
30
28
28
29
29
30
41
42
43
44
45
16
17
17
18
18
15
16
16
17
17
14
15
15
16
16
13
14
14
14
15
12
13
13
14
14
12
12
12
13
13
11
11
12
12
12
10
11
11
11
12
91
92
93
94
95
39
40
40
41
41
38
38
39
39
39
36
37
37
38
38
34
35
35
36
36
33
34
34
35
35
32
33
33
33
34
31
31
32
32
33
30
30
31
31
32
46
47
48
49
50
19
19
20
20
20
17
18
18
19
19
16
17
17
18
18
15
16
16
16
17
14
15
15
16
16
14
14
14
15
15
13
13
13
14
14
12
12
13
13
14
96
97
98
99
100
42
42
43
43
44
40
40
41
41
42
38
39
39
40
40
37
37
38
38
38
35
36
36
37
37
34
35
35
36
36
33
33
34
34
35
32
32
33
33
34
51
52
53
54
21
21
22
22
20
20
21
21
19
19
19
20
17
18
18
19
16
17
17
18
16
16
16
17
15
15
15
16
14
14
15
15
a:このサンプルサイズと信頼率については,信頼区間と信頼限界を決定することはできない。
6
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4
サンプルサイズが大きい場合(
100
>
n
) サンプルサイズが100を超える場合は,次の式で計算
した値の整数部として,信頼率(1−α)におけるkの近似値を用いてよい。
−
+
−
+
=
c
n
n
u
n
y
4.0
1
1
2
1
················································· (1)
ここでuは,標準正規分布の分位点である。片側信頼区間の場合についてuの値を表3に示し,両側信頼
区間の場合についてuの値を表4に示す。
片側信頼区間の場合についてcの値を表3に示し,両側信頼区間の場合についてcの値を表4に示す。
経験式(1)から得たkの値は,表1及び表2の正しい値と完全に一致する。uの小数第8けたまでの数
字が維持されれば,この近似法は極めて正確であり,サンプルサイズが5から280,000以上まで,八つの
信頼率すべてにおける片側信頼区間及び両側信頼区間について,厳密なkの値を得ることができる。
サンプルサイズが大きい場合における信頼限界の計算例を附属書BのB.2に,信頼率の計算方法の手順
を附属書B書式Bに示す。
備考 cの値を簡単に適用するため,表3及び表4におけるcの値の小数点以下の数字は,式(1)
の正確さを保証できる範囲において最小けた数にとどめた。
表3 片側信頼区間の場合のuとcの値
信頼率
%
u
c
80.0
0.84162122
0.75
90.0
1.28155156
0.903
95.0
1.64485364
1.087
98.0
2.05374892
1.3375
99.0
2.32634788
1.536
99.5
2.57582930
1.74
99.8
2.87816173
2.014
99.9
3.09023229
2.222
表4 両側信頼区間の場合のuとcの値
信頼率
%
u
c
80.0
1.28155156
0.903
90.0
1.64485364
1.087
95.0
1.95996400
1.274
98.0
2.32634788
1.536
99.0
2.57582930
1.74
99.5
2.80703376
1.945
99.8
3.09023229
2.222
99.9
3.29052672
2.437
7
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(参考)メディアンに対する信頼限界の古典的な決定方法
この附属書は,本体に関連する事柄を補足するもので,規定の一部ではない。
連続的な母集団からサイズnのランダムにサンプルが採取されたものとする。この条件のもとで,k個
の観測値が母メディアンより小さい確率は二項分布で表される。
n
k
n
k
n
k
n
k
n
k
P
2
1
2
1
1
2
1
2
1
=
−
=
−
,
;
これはまた,正確にk個の観測値が母メディアンより大きい確率でもある。
信頼率(1−α)の両側信頼区間の下側限界及び上側限界は,順序統計量の対(x[k], x[n−k+1]) で与えられ
る。ここに整数kは次の式が成り立つよう決定する。
2
2
1
1
0
α
≤
∑−=
n
k
i
n
i
·········································································· (A.1)
及び
;
2
2
1
0
α
>
∑
=
n
k
i
n
i
······································································· (A.2)
すなわち
∑−=
×
≤
1
0
2
2
k
i
n
n
i
α ······································································ (A.3)
及び
2
2
0
α
×
>
∑=
n
k
i
n
i
······································································ (A.4)
片側信頼区間の場合は,式(A.1)から(A.4)におけるα/2をαで置き替える。
8
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考)例
この附属書は,本体に関連する事柄を補足するもので,規定の一部ではない。
B.1
例1 小形電気製品のコードが,切断するまで繰返し曲げ試験を行う。この試験は,加速試験によっ
て実際の使用状態を再現するものである。コード24個が切断するまでの時間を次に示す。そのうち7件は
中途打切り時間であり,これには星印を付した1)。
57.5
77.8
88.0
96.9
98.4
100.3
100.8
102.1
103.3
103.4
105.3
105.4
122.6
139.3
143.9
148.0
151.3
161.1*
161.2*
161.2*
162.4*
162.7*
163.1*
176.8*
信頼率95%におけるメディアンの推定値とその下側信頼限界を求める。
メディアン寿命時間の点推定値は次のとおりである。
[]
[]
(
)
(
)
0
114
2
6
122
4.
105
2
~
13
12
.
.
=
+
=
+
=
x
x
x
参考 原国際規格では、114.0の後に単位hが付されている。
信頼率95%におけるメディアンに対する下側片側信頼限界は,本体表1において,片側信頼区間の場合
の信頼率95%とn=24に対するkの値と,上の表の第k番目の切断時間から得られる。
本体表1においてk=8,x[8]=102.1である。したがって,信頼率95%における母メディアンは102.1h以上
であることが分かる。
備考 メディアンと下側信頼限界は,サンプルの中の最大値を観測しなくても推定することができる。
メディアンの計算方法を附属書B書式Aの中の表に示す。計算値はイタリックで示す。
1) コードが切断する前に試験から除かれた場合,その時間を“中途打ち切り時間”という。

9
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式A メディアンの推定値の計算
記入前の書式
記入後の書式
データの指定
データ及び観測方法:
単位:
備考:
データの指定
データ及び観測方法:繰返し曲げテストにおける
コード24個の切断時間。テストは実際の使用状
態を促進して模擬する。
単位:時間
備考:最大切断時間のうち7件は中途打ち切りで
あるが,これは全体の半分より少ないため,メデ
ィアンを計算することができる。
予備操作
観測値を昇順に並べる。すなわち,
x[1],x[2],・・・,x[n]
予備操作
観測値を昇順に並べる。すなわち,
x[1],x[2] ,・・・,x[n]
必要な情報
サンプルサイズ,n: n=
a) サンプルサイズは奇数である。 □
b) サンプルサイズは偶数である。 □
必要な情報
サンプルサイズ,n: n=24
a) サンプルサイズは奇数である。 □
b) サンプルサイズは偶数である。
必要な初期計算
a)の場合
m=(n+1)/2:m=
b)の場合
m= n /2:m=
必要な初期計算
a)の場合
m=(n+1)/2:m=
b)の場合
m= n /2:m=12
標本メディアン~xの計算
a) の場合,~xは小さい方(又は大きい方)から第
m番目の観測値である。すなわち,~x=x[m]:~x=
b) の場合,~xは小さい方(又は大きい方)から第
m番目と第m+1番目の観測値の算術平均である。
すなわち,~x=(x[m]+x[m+1])/2:
x[m]=
x[m+1]=
~x=( + )/2
標本メディアン~xの計算
a) の場合,~xは小さい方(又は大きい方)から第
m番目の観測値である。すなわち,~x=x[m]:~x=
b) の場合,~xは小さい方(又は大きい方)から第
m番目と第m+1番目の観測値の算術平均である。
すなわち,~x=(x[m]+x[m+1])/2:
x[m]=105.4
x[m+1]=122.6
~x=(105.4+122.6)/2=114.0
結果
標本メディアン(母メディアンの推定値)は
=
x~
結果
標本メディアン(母メディアンの推定値)は
=
x~
114.0
10
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.2
例2 ナイロン糸120個の切断強さ(ニュートン(N))を,横方向へ昇順に並べて示す。
31.3
33.3
33.5
35.6
36.0
36.2
36.5
37.5
37.8
37.9
38.8
39.1
40.3
40.4
40.8
41.0
41.8
42.4
42.9
43.1
43.2
43.5
43.9
43.9
44.0
44.2
44.2
44.5
44.7
44.7
45.0
45.6
46.0
46.0
46.1
46.1
46.3
46.3
46.3
46.4
46.5
46.7
47.1
47.1
47.1
47.2
47.3
47.4
47.5
47.5
47.8
47.8
47.9
47.9
48.0
48.0
48.2
48.2
48.3
48.3
48.3
48.5
48.6
48.6
48.6
48.6
48.8
48.9
48.9
48.9
49.0
49.0
49.1
49.1
49.1
49.1
49.2
49.2
49.3
49.4
49.4
49.4
49.4
49.5
49.5
49.6
49.7
49.9
49.9
50.0
50.1
50.2
50.2
50.3
50.3
50.3
50.5
50.7
50.8
50.9
50.9
51.0
51.0
51.2
51.4
51.4
51.4
51.6
51.6
51.8
52.0
52.2
52.2
52.4
52.5
52.6
52.8
52.9
53.2
53.3
メディアン切断強さの点推定値と,信頼率99%における両側信頼区間を求める。
メディアン切断強さの点推定値は次のとおりである。
[]
[]
(
)
(
)
3.
48
2
3.
48
3.
48
2
~
61
60
=
+
=
+
=
x
x
x
参考 原国際規格では、48.3の後に単位Nが付されている。
n>100の場合,本体表1及び本体表2には,信頼限界に関して該当するkの値が存在しない。両側信頼
限界が必要であるため,式(1)と本体表4を組み合わせて用いる必要がある。信頼率99%におけるuとc
の値は,本体表4からu=2.57582930,c=1.74である。これらの値とn=120を式(1)に代入するとy=46.448
となる。その整数部をとるとk=46である。
したがって,母メディアンの信頼率99%両側信頼区間は次のとおりである。
[]
[
]
(
)
[]
[]
(
)(
)1.
49
2.
47
75
46
1
,
,
,
=
=
+
−
x
x
x
x
k
n
k
参考 原国際規格では、(47.2, 49.1)の後に単位Nが付されている。
これより,信頼率99%において,切断強さの母メディアンは区間(47.2, 49.1)N内に存在するというこ
とができる。
信頼区間の計算方法を附属書B書式Bの中の表に示す。計算値はイタリックで示した。
11
Z 9041-5:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式B メディアンに対する信頼区間の計算
記入前の書式
記入後の書式
データの指定
データ及び観測方法:
単位:
備考:
データの指定
データ及び観測方法:ナイロン糸120個の切断強さ
単位:ニュートン
備考:99%信頼水準における両側信頼区間を求める。
予備操作
観測値を昇順に並べる。すなわち,
x[1],x[2],・・・,x[n]
予備操作
観測値を昇順に並べる。すなわち,
x[1],x[2] ,・・・,x[n]
必要な情報
サンプルサイズ,n: n=
信頼水準 C: C= %
a) n≤100 片側信頼区間 □
b) n≤100 両側信頼区間 □
c) n>100 片側信頼区間 □
d) n>100 両側信頼区間 □
a)又はc)の下側信頼限界の場合,母集団内にお
けるxの下限値が必要である。 a=
a)又はc)の上側信頼限界の場合,母集団内にお
けるxの上限値が必要である。 b=
必要な情報
サンプルサイズ,n: n=120
信頼水準 C: C=99%
a) n≤100 片側信頼区間 □
b) n≤100 両側信頼区間 □
c) n>100 片側信頼区間 □
d) n>100 両側信頼区間
a)又はc)の下側信頼限界の場合,母集団内におけ
るxの下限値が必要である。 a=
a)又はc)の上側信頼限界の場合,母集団内におけ
るxの上限値が必要である。 b=
kの決定
a)の場合,表1からkを求める。k =
b)の場合,表2からkを求める。k =
c)の場合,表3からuとcを求める。u = c =
d)の場合,表4からuとcを求める。u = c =
c)又はd)の場合,式(1)からyを計算する。y =
そのあと,yの整数部としてkを求める。k =
kの決定
a)の場合,表1からkを求める。k =
b)の場合,表2からkを求める。k =
c)の場合,表3からuとcを求める。u = c =
d)の場合,表4からuとcを求める。
u =2.57582930 c =1.74
c)又はd)の場合,式(1)からyを計算する。y =46.448
そのあと,yの整数部としてkを求める。k =46
信頼限界T1及び/又はT2の決定
a)又はc)の下側限界,及びb)
又はd)の場合,T1=x[k]と置く。 T1=
a)又はc)の上側限界,及びb)
又はd)の場合,m = n−k+1を計算する。m=
そのあと,T2=x[m]と置く。 T2=
信頼限界T1及び/又はT2の決定
a)又はc)の下側限界,及びb)
又はd)の場合,T1=x[k]と置く。 T1=47.2
a)又はc)の上側限界,及びb)
又はd)の場合,m = n−k+1を計算する。m=75
そのあと,T2=x[m]と置く。 T2=49.1
結果
下側信頼限界について,C= %
母メディアンに対する信頼区間は[T1, b)=[ , )
上側信頼限界について,C = %
母メディアンに対する信頼区間は(a, T 2]= ( , ]
両側信頼限界について,C = %
母メディアンに対する対称な信頼区間は
[T1, T 2]=[ , ]
結果
下側信頼限界について,C= %
母メディアンに対する信頼区間は[T1, b)=[ , )
上側信頼限界について,C = %
母メディアンに対する信頼区間は(a, T 2]= ( , ]
両側信頼限界について,C =99%
母メディアンに対する対称な信頼区間は
[T 1, T 2]=[47.2, 49.1]




