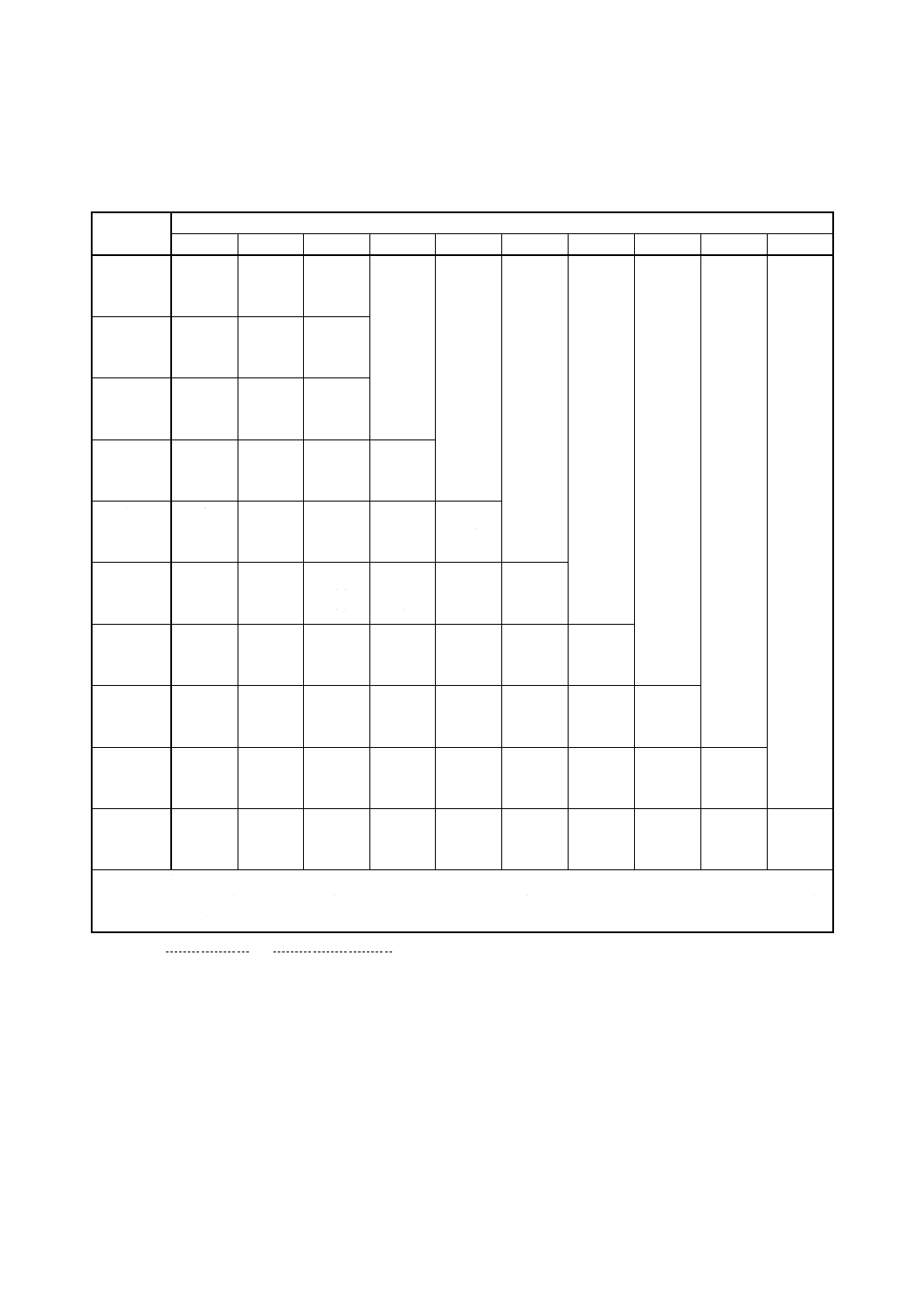Z 9041-3 : 1999 (ISO 11453 : 1996)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。
今回の制定では,国際規格に整合させるために,ISO 11453 : 1996を基礎として用いた。
JIS Z 9041-3には,次に示す附属書がある。
附属書A(規定) 書式Bによる検定の検定特性の計算
附属書B(参考) 書式の使用例
附属書C(参考) 参考文献
JIS Z 9041 : 1999は,一般名称を“データの統計的な解釈方法”として,次の各部によって構成される。
第1部:データの統計的記述
第2部:平均と分散に関する推定方法と検定方法
第3部:割合に関する検定方法と推定方法
第4部:平均と分散に関する検定方法の検出力
Z 9041-3 : 1999 (ISO 11453 : 1996)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 定義 ······························································································································ 2
4. 記号 ······························································································································ 2
5. 割合pの点推定量 ············································································································ 2
6. 割合pの信頼限界 ············································································································ 2
7. 割合pの有意性検定 ········································································································· 3
7.1 一般 ···························································································································· 3
7.2 割合と与えられた値p0との比較 ······················································································· 3
7.3 二つの割合の比較 ·········································································································· 4
8. 書式 ······························································································································ 5
8.1 書式A:割合pの信頼区間 ······························································································· 5
8.2 書式B:割合pと与えられた値p0との比較 ······································································· 10
8.3 書式C:二つの割合の比較 ······························································································ 15
9.1 F分布のパーセント点の表4における内挿 ········································································· 22
9.2 例 ······························································································································ 22
附属書A(規定) 書式Bによる検定の検定特性の計算 ····························································· 39
附属書B(参考) 書式の使用例 ···························································································· 42
附属書C(参考) 参考文献································································································· 54
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9041-3 : 1999
(ISO 11453 : 1996)
データの統計的な解釈方法−
第3部:割合に関する検定方法と
推定方法
Statistical Interpretation of Data−
Part 3 : Tests and confidence intervals relating to proportions
序文 この規格は,1996年に第1版として発行されたISO 11453,Statistical interpretation of data−Tests and
confidence intervals relating to proportions及び1999年に発行されたTechnical Corrigendumを翻訳し,技術的
内容及び規格票の様式を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線が施してある“参考”は,原国際規格にはない事項である。
1. 適用範囲 この規格は,次の問題を扱うための統計的方法について規定する。
a) ある集団からnアイテムのサンプルが抽出され,そのうちのx個がある特定の特性を示しているとき,
その特性の母集団での割合はどのくらいか。(8.1 書式A,参照)
b) a)で推定された割合は,名目上の(指定された)値と異なるのか。(8.2 書式B,参照)
c) 母集団が二つ与えられたとき,二つの母集団でその特性の割合は異なるのか。(8.3 書式C,参照)
d) b)及びc)において,その検定結果が確かであることを十分に保証するためには,母集団からどのくら
いのアイテムを抽出しなければならないのか。(7.2.3及び7.2.4参照)
サンプルを抽出することが母集団に対して実質的な影響を与えないということが重要である。もし,ラ
ンダムに抽出されたサンプルが母集団の10%以下であれば,通常この条件は満たされる。10%を超える場
合には,復元サンプリングを用いていれば,信頼できる結果となっている。
2. 引用規格 次に掲げる規格は,この規格に引用されることによってこの規格の規定の一部を構成する。
これらの引用規格のうちで,発行年を付記してあるものは,記載の年の版だけがこの規格の規定を構成す
るものであって,その後の改正版・追補には適用しない。発効年を付記していない引用規格は,その最新
版(追補を含む)を適用する。
JIS Z 8101-1 統計−用語及び記号−第1部:確率及び一般統計用語
備考 ISO 3534-1 : 1993 Statistics−Vocabulary and symbols−Part 1 : Probability and general statistical
termsからの引用事項は,この規格の該当事項と同等である。
JIS Z 8101-2 統計−用語及び記号−第2部:統計的品質管理用語
備考 ISO 3534-2 : 1993 Statistics−Vocabulary and symbols−Part 2 : Statistical quality control termsか
らの引用事項は,この規格の該当事項と同等である。
2
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3. 定義 この規格で用いる主な用語の定義は,JIS Z 8101-1によるほか,次による。
3.1
該当アイテム (target item) ある特定の特性をもったアイテム。
4. 記号
α
選ばれた有意水準
αʼ
達成された有意水準
1−α
選ばれた信頼係数
β
第2種の誤りの確率
n ; n1 ; n2
サンプルサイズ,サンプル1のサンプルサイズ,サンプル2のサンプルサイズ
X
サンプルにおける該当アイテムの数(確率変数)
x
Xの値
p
母集団における該当アイテムの割合
pu, o
pの片側信頼区間の上限
pl, o
pの片側信頼区間の下限
pu, t
pの両側信頼区間の上限
pl, t
pの両側信頼区間の下限
T
n≦30の場合の信頼限界決定のための表2の値
Cl, o
帰無仮説H0:p≧p0の検定のための棄却限界値
Cu, o
帰無仮説H0:p≦p0の検定のための棄却限界値
Cl, t
帰無仮説H0:p=p0の検定のための下側棄却限界値
Cu, t
帰無仮説H0:p=p0の検定のための上側棄却限界値
p0
与えられたpの値
pʼ
帰無仮説を棄却しない確率 (Pa) を求めるために用いるpの値
Pa
帰無仮説を棄却しない確率
υ1, υ2
F分布の自由度
F1, F2
検定統計量
Fq (v1, v2)
自由度v1, v2のF分布の100q%点(下側確率)
z1, z2
検定統計量
uq
標準正規分布の100q%点(下側確率)
q, η, K
補助的に用いる値のための記号
5. 割合pの点推定量 x個の該当アイテムを含んだnアイテムのサンプルから求められるpの推定量は
n
x
p
/
ˆ=
である。
サンプルがランダムに抽出されていれば,サンプルサイズや母集団の大きさによらず,また,たとえサ
ンプルが母集団のかなりの部分を占めるとしても,この推定量は不偏である。
6. 割合pの信頼限界 pの信頼区間の計算は,書式A-1からA-3に示される。
信頼限界は,サンプルサイズ (n),サンプルにおける該当アイテムの数 (x) 及び選ばれた信頼係数 (1−
α) によって決まる。xの従う確率分布は離散分布なので,選ばれた信頼係数を正確に達成することは一般
3
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
に可能でない。したがって,この方法は, (1−α) 以上で (1−α) に最も近い信頼係数を与える。
選ばれた信頼係数 (1−α) の両側信頼限界を求めるために,この規格で使われる方法では,選ばれた信
頼係数 (1−α/2) の上側及び下側の片側信頼限界のそれぞれを信頼限界として用いる。それゆえ,誤りの
確率は信頼区間のそれぞれの側でα/2以下であることが保証される。
7. 割合pの有意性検定
7.1
一般 実用に配慮して,書式B-1からB-3及びC-1からC-3には,割合に関する帰無仮説と検定を
行うための計画が示されている。方法の最初に,適切な帰無仮説とサンプルサイズn(サンプルサイズn1
及びn2)が決められ,有意水準が選ばれる。標本分布はもともと離散分布なので,方法は選ばれた(名目
上の)水準以下で最も近い有意水準を達成するように計画されている。対立仮説は帰無仮説の補集合とし
て暗黙的に仮定されるので,書式では対立仮説を明示しない。
例 書式B(割合と与えられた値との比較の方法)の最初で,次の三つの帰無仮説H0(対立仮説H1
はH0の補集合)の中から一つを選ぶ。
a) H0 : p≧p0の片側検定
H1 : p<p0
b) H0 : p≦p0の片側検定
H1 : p>p0
c) H0 : p=p0の両側検定
H1 : p≠p0
ただし,p0は与えられた値である。
それぞれの検定結果は,帰無仮説を棄却するか又は棄却しないかのいずれかである。
帰無仮説を棄却するということは,対立仮説を採用することを意味する。帰無仮説を棄却しないという
ことは,必ずしも帰無仮説を許容するということを意味するわけではない。(7.2.2参照)
7.2
割合と与えられた値p0との比較
7.2.1
検定方法
帰無仮説
H0 : p≧p0
H0 : p≦p0
H0 : p=p0
の検定方法(ただし,p0は与えられた値)は,書式B-1からB-3に示されている。もし,n,p及びαの特
定の値に対して棄却限界値が既知であれば,これらの方法を適用することは非常に簡単である。書式Bに
従って検定を繰り返し行うことによって,棄却限界値を決めてもよい。棄却限界値を決めるための別の標
準的な方法が,同じ書式に与えられている。
7.2.2
検定特性 検定特性の計算(第1種の誤りの確率,達成される有意水準及び第2種の誤りの確率を
含んでいる)は,附属書Aに示されている。この目的のために,棄却限界値は既知である必要があり(7.2.1
参照),第2種の誤りの確率を計算するために対立仮説p=p1を選ばなければならない。
7.2.3
サンプルサイズnの決定 もし,サンプルサイズが決められていないならば(例えば,経済的又は
技術的な理由で),与えられた帰無仮説H0(7.2.1参照)に対して有意水準αの達成値が選ばれた又は与え
られた値以下になるように,その最小値に決められなければならない。また,もし,pが特別に選ばれた
又は与えられた値pʼと等しければ,第2種の誤りの確率βの達成値が,近似的にその選ばれた又は与えら
れた値に等しくならなければならない。この目的のために,ラーソン (Larson) のノモグラフ(図2)が用
いられる。ここで,p0とpʼがp尺上に,α, (1−α),α/2, (1−α/2) がp尺上にプロットされ,表1で定
められる直線1と2が引かれる。

4
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1 ラーソン (Larson) のノモグラフ(図2)でサンプルサイズを決定する方法
場合
与えられた値
p0と下の値を結ぶ直線1
p´と下の値を結ぶ直線2
H0 : p≧p0
p´<p0
α
1−β
H0 : p≦p0
p´>p0
1−α
β
H0 : p=p0
p´>p0
1−α/2
β
H0 : p=p0
p´<p0
α/2
1−β
二つの直線の交点でx尺上の値Cl, o (Cu, o) を読み取る。もし,xが整数でなければ,前後の整数に丸め
る。
7.3
二つの割合の比較
7.3.1
検定方法
帰無仮説
H0 : p1≧p2
H0 : p1≦p2
H0 : p1=p2
の検定方法(ただし,p1は母集団1の該当アイテムの割合で,p2は母集団2の該当アイテムの割合であ
る)は,書式C-1からC-3に示されている。これらの方法は,また,一つの母集団におけるアイテムの2
種の属性(2種の2値特性)の独立性を検定するためにも適している。
7.3.2
検定特性 次のことが仮定される。
a) H0 : p1≦p2の片側検定において,検出力 (1−β) は,p1>p2と判断される確率をp1とp2の与えられた
組み合わせに対して計算したものとする。
b) 二つのサンプルサイズが同じ,すなわち,n1=n2=nとする。
有意水準をαとしたとき,検出力のたいへん正確な近似値が,次に示すウォルターズ(Walters [1] に
よって提案された)逆正弦変換によって得られる:
1−β=φ (z−u1−α)
ただし,
φは,標準正規分布の分布関数,
u1−αは,標準正規分布の100 (1−α) %点,
n
z
2
=
[arcsin
(
)
(
)
n
p
n
p
2
/1
arcsin
2
/1
2
1
−
−
−
]
である。
この近似は,また,両側の場合(対立仮説H1 : p1>p2をもつH0 : p1=p2)に対して,αをα/2に置き換え
ることによって用いることができる。
7.3.3
サンプルサイズnの決定 もし,サンプルサイズn1とn2とが前もって決められていない場合には,
有意水準をαとして,検定の検出力が (1−β) 以上となるような,最小の自然数に決められなければならな
い。
帰無仮説をH0 : p1≦p2と仮定する。しかし,次に示す方法は,また,αをα/2に置き換え,制限のついた
対立仮説H1 : p1>p2を用いることによって両側の場合のH0 : p1=p2にも適用する。
サンプルサイズの正確な値は,選ばれたαとβの値に対してヘイスマン(Haseman [2] によって最初に発
表された)表5及び表6で与えられる。これらの表は,二つの母集団に共通のサンプルサイズn=n1=n2
を仮定している。
これらの表に載せられていないα,p1,p2及び (1−β) の値に対して,次の近似式を使うことができる。
5
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
これは,また,サンプルサイズが等しくない場合も適用できる。その場合にはサンプルサイズの比r (n1/n2)
を前もって選んでおく必要がある。
(
)
(
)
2
2
1
1
1
2
1
1
4
−
′
+
+
+
′
=
p
p
n
r
r
n
n
n2=n1/r
ただし,
(
)
(
)
(
)
[
]
{
}
(
)2
2
1
2
2
2
1
1
1
1
1
1
1
p
p
r
p
p
p
rp
u
q
p
r
u
n
−
−
+
−
+
+
=
′
−
−
β
α
1
2
1
+
+
=
r
p
rp
p
p
q
−
=1
である。
8. 書式 適用を簡単にするために,書式で用いられる部分を表している□に印を付ける。(□の水平位置
が,それぞれの部分のその書式の階層における位置を示す。右が上位の階層である。)次に,必要なデータ
を記入し,要求される手順に従う。
8.1
書式A:割合pの信頼区間

6
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.1.1
書式A-1:片側,割合pの信頼区間の上限
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
選択した信頼係数:1−α=
サンプルサイズ:n=
サンプルにおける該当アイテムの数:x=
信頼限界の決定:
a) n≦30のときの方法
□
1) x=nの場合
□
pu, o=1
2) x<nの場合
□
既知の値n,X=x及びq=1−αに対する表2の値を読む。
(この値が信頼限界である。):
T (1-α) (n, x) =pu, o=
b) n>30のときの方法
□
1) x=0の場合
□
計算:
pu, o=1−α1/n
2) x=nの場合
□
pu, o=1
3) 0<x<nの場合
□
q=1−αに対する表3の値を読む:u1-α=
選択した信頼係数に対応するdの値を読む。
計算:
p*= (x+1) / (n+1)
(
)(
)
(
)
(
)
[
](
)=
+
+
−
−
+
+
−
+
=
−
1
/
1
/
1
1
1
/
2
1
*
*
1
*
*
,
n
n
d
p
p
u
n
d
p
p
po
u
α
結果:
p≦pu, o=

7
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.1.2
書式A-2:片側,割合pの信頼区間の下限
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
選択した信頼係数:1−α=
サンプルサイズ:n=
サンプルにおける該当アイテムの数:x=
信頼限界の決定:
a) n≦30のときの方法
□
1) x=0の場合
□
pl, o=0
2) x>0の場合
□
既知の値n,X=n−x及びq=1−αに対する表2の値を読む。
T (1-α) (n, n−x) =
計算:
pl, o=1−T (1-a) (n, n−x) =
b) n>30のときの方法
□
1) x=0の場合
□
pl, o=0
2) x=nの場合
□
計算:
pl, o=α1/n=
3) 0<x<nの場合
□
q=1−αに対する表3の値を読む:u1-a=
選択した信頼係数に対応するdの値を読む。
計算:
p*=x/ (n+1) (
)(
)
(
)
(
)
[
](
)=
+
+
−
−
−
+
−
+
=
−
1
/
1
/
1
1
1
/
2
1
*
*
1
*
*
,
n
n
d
p
p
u
n
d
p
p
po
l
α
結果:
pl, o=
≦p

8
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.1.3
書式A-3:割合pの両側信頼区間
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
選択した信頼係数:1−α=
サンプルサイズ:n=
サンプルにおける該当アイテムの数:x=
信頼限界の決定:
a) n≦30のときの方法
□
1) 上側信頼限界
− x=nの場合
□
pu, t=1
− x<nの場合
□
既知の値n,X=x及びq=1−α/2に対する表2の値を読む。
(この値が信頼限界である。):
T (1−α/2) (n, x) =pu, t=
2) 下側信頼限界
− x=0の場合
□
pl, t=0
− x>0の場合
□
既知の値n,X=n−x及びq=1−α/2に対する表2の値を読む。
T (1-α/2) (n, n−x) =
計算:
pl, t=1−T (1-α/2) (n, n−x) =
b) n>30のときの方法
□
1) 上側信頼限界
− x=0の場合
□
計算:
pu, t=1− (α/2) 1/n=
− x=nの場合
□
pu, t=1
− 0<x<nの場合
□
q=1−α/2に対する表3の値を読む:u1-α/2=
選択した信頼係数に対応するdの値を読む。
計算:p*= (x+1) / (n+1)
(
)(
)
(
)
(
)
[
](
)=
+
+
−
−
+
+
−
+
=
−
1
/
1
/
1
1
1
/
2
1
*
*
2
/
1
*
*
,
n
n
d
p
p
u
n
d
p
p
pt
u
α
2) 下側信頼限界
− x=0の場合
□
pl, t=0
− x=nの場合
□
計算:
pl, t= (α/2) 1/n=
− 0<x<nの場合
□
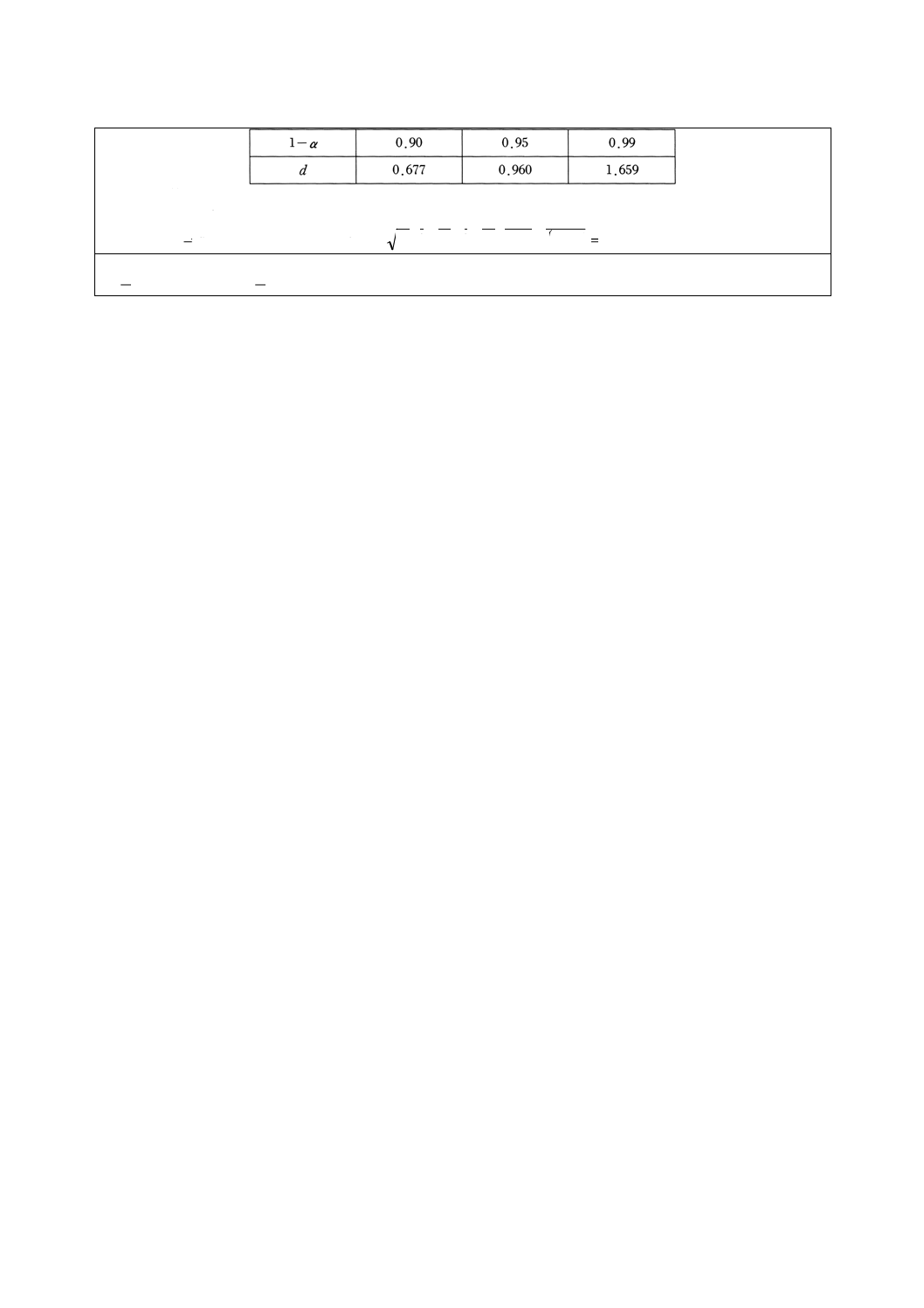
q=1−α/2に対する表3の値を読む:u1-α/2=
選択した信頼係数に対するdの値を読む。
9
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
計算:
p*=x/ (n+1)
(
)(
)
(
)
(
)
[
](
)=
+
+
−
−
−
+
−
+
=
−
1
/
1
/
1
1
1
/
2
1
*
*
2
/
1
*
*
,
n
n
d
p
p
u
n
d
p
p
pt
l
α
結果:
pl, t=
;
pu, t=
;
pl, t≦p≦pu, t

10
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2
書式B:割合pと与えられた値p0との比較
8.2.1
書式B-1:H0 : p≧p0の片側検定を用いた割合pと与えられた値p0との比較
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
与えられた値p0=
選択した有意水準:α=
サンプルサイズ:n=
サンプルにおける該当アイテムの数:x=
検定方法:
I 棄却限界値が既知である(7.2.1参照及び適用可能ならば次に棄却限界値の決定):
□
Cl, o=
もし,x<Cl, oならばH0を棄却;そうでなければ棄却しない。
II 棄却限界値が未知である:
□
a) x≧p0nの場合
□
H0は棄却されない。
b) x<p0nの場合
□
1) n≦30のときの方法
□
n,x及び信頼係数 (1−α) に対する片側の上側信頼限界を書式A-1に従い求める:
pu, o=
もし,pu, o<p0ならばH0を棄却;そうでなければ棄却しない。
2) n>30のときの方法
□
− x=0の場合
□
計算:
pu, o=1−α1/n=
[書式A- 1b)(1)参照]
もし,pu, o<p0ならばH0を棄却;そうでなければ棄却しない。
− 0<x<nの場合
□
q=1−αに対する表3の値を読む:u1-α=
計算:
(
)
(
)(
)
[
]=
−
+
−
−
=
0
0
1
1
1
2
p
x
p
x
n
u
もし,u1>u1-αならばH0を棄却;そうでなければ棄却しない。
検定結果:
H0を棄却する
□
H0を棄却しない
□
棄却限界値の決定:
Cl, oは,書式B-1−IIによる検定でH0を棄却しない最小の非負の整数xである。Cl, oは,xの異なる値に対して書式
B-1−IIを繰り返し適用することによって求められる(1)。それによって,片方は帰無仮説を棄却し,他のものは棄却
しないような値が1異なる二つのxが求まる。もし,xについて出発値が必要ならばxstartを次のように求めることが
できる。
計算:
np0を前後の整数に丸めたものがx*=
pl, o|x=x*= (pl, o|x=x*は書式A-2から求められる)
npl, o|x=x*を前後の整数に丸めたものがxstart=
書式B-1−IIの検定結果の解釈:
x≦Cl, o−1=
のとき,H0を棄却する。
x≧Cl, o=
のとき,H0を棄却しない。
結果:
Cl, o=
注(1) サンプルサイズnがたいへん小さいとき,及び/又はp0が極端な値のとき,棄却限界値は存在しないことがあ
る。

11
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2.2
書式B-2:H0 : p≦p0の片側検定を用いた割合pと与えられた値p0との比較
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
与えられた値p0=
選択した有意水準:α=
サンプルサイズ:n=
サンプルにおける該当アイテムの数:x=
検定方法:
I 棄却限界値が既知である(7.2.1参照及び
適用可能ならば次に棄却限界値の決定):
□
Cu, o=
もし,x>Cu, oならばH0を棄却;そうでなければ棄却しない。
II 棄却限界値が未知である:
□
a) x≦p0nの場合
□
H0は棄却しない。
b) x>p0nの場合
□
1) n≦30のときの方法
□
n,x及び信頼係数 (1−α) に対する片側の下側信頼限界を書式A-2に従い求める:
pl, o=
もし,pl, o>p0ならばH0を棄却;そうでなければ棄却しない。
2) n>30のときの方法
□
− x=nの場合
□
計算:
pl, o=α1/n
[書式A-2b)(1)参照]
もし,pl, o>p0ならばH0を棄却;そうでなければ棄却しない。
− 0<x<nの場合
□
q=1−αに対する表3の値を読む:u1-α=
計算: (
)
(
)
[
]=
+
−
−
−
=
0
0
2
1
1
2
p
x
n
p
x
u
もし,u2>u1-aならばH0を棄却;そうでなければ棄却しない。

12
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検定結果:
H0を棄却する
□
H0を棄却しない
□
棄却限界値の決定:
Cu, oは,書式B-2−IIによる検定で帰無仮説を棄却しない最大の整数xである。Cu, oは,xの異なる値に対して書式
B-2−IIを繰り返し適用することにより求められる(1)。それによって,片方は帰無仮説を棄却し,他のものは棄却し
ないような,値が1異なる二つのxが求まる。もし,必要ならばxについて出発値xstartを次のように求めることがで
きる。
計算:
np0を前後の整数に丸めたものがx*=
pu, o|x=x*= (pu, o|x=x*は書式A-1から求められる)
npu, o|x=x*を前後の整数に丸めたものがxstart=
書式B-2−IIの検定結果の解釈:
x≦Cu, o=
のとき,H0を棄却しない。
x≧Cu, o+1=
のとき,H0を棄却する。
結果:
Cu, o=
注(1) サンプルサイズnがたいへん小さいとき,及び/又はp0が極端な値のとき,棄却限界値は存在しないことがあ
る。

13
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2.3
書式B-3:H0 : p=p0の両側検定を用いた割合pと与えられた値p0との比較
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
与えられた値p0=
選択した有意水準:α=
サンプルサイズ:n=
サンプルにおける該当アイテムの数:x=
検定方法:
I 棄却限界値が既知である(7.2.1参照及び
適用可能ならば次に棄却限界値の決定):
□
Cl, t=
Cu, t=
もし,x<Cl, t又はx>Cu, tならばH0は棄却;
そうでなければ棄却しない。
II 棄却限界値が未知である:
□
a) n≦30のときの方法
□
n,x及び信頼係数 (1−α) に対する両側信頼限界を書式A-3に従い求める:
pl, t=
pu, t=
もし,pl, t>p0又はpu, t<p0ならばH0を棄却;
そうでなければ棄却しない。
b) n>30のときの方法
□
1) x=0の場合
□
計算:
pu, t=1− (α/2) 1/n=
もし,pu, t<p0ならばH0を棄却;そうでなければ棄却しない。
2) x=nの場合
□
計算:
pl, t= (α/2) 1/n=
もし,pl, t>p0ならばH0を棄却;そうでなければ棄却しない。
3) 0<x<nの場合
□
q=1−α/2に対する表3の値を読む:u1-a/2=
計算:
(
)
(
)(
)
[
]=
−
+
−
−
=
0
0
1
1
1
2
p
x
p
x
n
u
(
)
(
)
[
]=
+
−
−
−
=
0
0
2
1
1
2
p
x
n
p
x
u
もし,u1>u1-α/2又はu2>u1-α/2ならばH0を棄却;
そうでなければ棄却しない。
検定結果:
H0を棄却する
□
H0を棄却しない
□
棄却限界値の決定:
書式B-3−IIによる検定でH0を棄却しない最小の非負の整数xがCl, tで,最大の整数がCu, tである。Cl, t及びCu, t
は,xの異なる値に対して書式B-3−IIを繰り返し適用することによって求められる(1)。
それによって,それぞれの側で,片方は帰無仮説を棄却し,他のものは棄却しないような,値が1異なる二つずつ
のxの値が求まる。
もし,必要ならば,xについての出発値xstartを次のように求めることができる。

14
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
計算:
np0を前後の整数に丸めたものがx*=
pl, t|x=x*=
pu, t|x=x*=
pl, t|x=x*及びpu, t|x=x*は書式A-3から求められる。
npl, t|x=x*を前後の整数に丸めたものがxstart (lower) =
npu, t|x=x*を前後の整数に丸めたものがxstart (upper) =
書式B-3−IIの検定結果の解釈:
x≦Cl, t−1=
のとき,H0を棄却する。
x=Cl, t= からx=Cu, t=
のとき,H0を棄却しない。
x≧Cu, t+1=
のとき,H0を棄却する。
結果:
Cl, t=
Cu, t=
注(1) サンプルサイズnがたいへん小さいとき,及び/又はp0が極端な値のとき,棄却限界値は存在しないことがあ
る。

15
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.3
書式C:二つの割合の比較
8.3.1
書式C-1:H0 : p1≧p2の片側検定を用いた二つの割合の比較
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
選択した有意水準:α=
サンプルサイズ1:n1=
サンプルサイズ2:n2=
サンプル1における該当アイテムの数:x1=
サンプル2における該当アイテムの数:x2=
自明なケースの検討:
2
2
1
1
n
x
n
x≧
が真である
□
が真でない
□
真の場合,帰無仮説は棄却されず,検定結果を直ちに得ることができる。
そうでなければ,次の方法でH0を棄却するか否かを決める。
自明でないケースの検定方法:
もし,n1,n2 (x1+x2),(n1+n2−x1−x2) のうち少なくても一つが (n1+n2) /4以下であるならば,2項近似 (I) を適用
すべきである。そうでなければ正規近似 (II) を適用しなければならない。しかし,たとえ上記の条件が満たされた
としても,次の二つの条件が満たされれば,正規近似を適用することができる:
− 2項近似を適用する際に,F分布表での内挿が必要である。
− n1とn2の値が同程度である又は (x1+x2) と (n1+n2−x1−x2) の値が同程度である。
決定:
2項近似を適用する(Iへ進む)。
□
正規近似を適用する(IIへ進む)。
□
I 2項近似
変数:K1,K2,η1,η2の決定:
もし,[n2<n1かつn2<(x1+x2)]又は
[(n1+n2−x1−x2)<n1かつ (n1+n2−x1−x2)<(x1+x2)]
ならば,変数を次のように決定する。
η1=n2=
η2=n1=
K1=n2−x2=
K2=n1−x1=
そうでなければ,以下のように決定する。
η1=n1=
η2=n2=
K1=x1=
K2=x2=

16
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検定統計量の計算と表からの値の求め方:
I a) η1≦K1+K2の場合
□
(
)(
)
(
)(
)=
+
−
−
+
+
+
−
=
1
2
2
1
2
2
1
2
1
1
2
1
1
1
2
K
K
K
K
K
K
F
η
η
η
F分布の自由度:
ν1=2 (K1+1) =
ν2=2 (η1−K1) =
q=1−α,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α) (ν1, ν2) =
I b) η1>K1+K2の場合
□
(
)
(
)(
)=
+
−
+
−
=
1
2
1
2
2
2
1
1
1
2
2
K
K
K
K
F
η
η
F分布の自由度:
ν1=2 (K1+1) =
ν2=2K2
q=1−α,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α) (ν1, ν2) =
2項近似の場合の自明でないケースの結論:
F2≧F (1-α) (ν1, ν2)
ならば,H0を棄却する。そうでなければ,棄却しない。
II 正規近似
検定統計量の計算と表からの値の求め方:
(
)(
)(
)
(
)(
)(
)=
+
−
−
+
+
+
+
−
+
=
2
1
2
1
2
1
2
1
2
1
2
1
1
2
1
1
2
/
2
/1
n
n
x
x
n
n
x
x
n
n
n
n
x
x
x
n
z
q=1−αに対する表3の値を読む:u1-α=
正規近似の場合の自明でないケースの結論:
z2≧u1-α
ならば,H0を棄却する。そうでなければ,棄却しない。
検定結果:
H0を棄却する。
□
H0を棄却しない。
□

17
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.3.2
書式C-2:H0 : p1≦p2の片側検定を用いた二つの割合の比較
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
選択した有意水準:α=
サンプルサイズ1:n1=
サンプルサイズ2:n2=
サンプル1における該当アイテムの数1:x1=
サンプル2における該当アイテムの数2:x2=
自明なケースの検討:
2
2
1
1
n
x
n
x≦
が真である
□
が真でない
□
真の場合,帰無仮説は棄却されず,検定結果を直ちに得ることができる。
そうでなければ,次の方法でH0を棄却するか否かを決める。
自明でないケースの検定方法:
もし,n1,n2, (x1+x2) , (n1+n2−x1−x2) のうち少なくても一つが (n1+n2) /4以下であるならば,2項近似 (I) を
適用すべきである。そうでなければ正規近似 (II) を適用しなければならない。しかし,たとえ上記の条件が満たさ
れたとしても,次の二つの条件が満たされれば,正規近似を適用することができる:
− 2項近似を適用する際に,F分布表での内挿が必要である。
− n1とn2の値が同程度である又は (x1+x2) と (n1+n2−x1−x2) の値が同程度である。
決定:
2項近似を適用する(Iへ進む)。
□
正規近似を適用する(IIへ進む)。
□
I 2項近似
変数:K1,K2,η1,η2の定義:
もし,[n2<n1かつn2<(x1+x2)]又は
[(n1+n2−x1−x2)<n1かつ (n1+n2−x1−x2)<(x1+x2)]
ならば,変数を次のように決定する。
η1=n2=
η2=n1=
K1=n2−x1=
K2=n1−x1=
そうでなければ,次のように決定する。
η1=n1=
η2=n2=
K1=x1=
K2=x2=

18
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検定統計量の計算と表からの値の求め方:
I a) η1≦K1+K2の場合
□
(
)
(
)(
)=
+
+
+
−
−
−
+
=
1
2
1
2
2
2
1
1
1
2
1
2
1
1
1
K
K
K
K
K
K
F
η
η
η
F分布の自由度:
ν1=2 (η1−K1+1) =
ν2=2K1=
q=1−α,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α) (ν1, ν2)=
I b) η1>K1+K2の場合
□
(
)
(
)(
)=
+
−
+
−
=
1
2
1
2
1
1
2
2
2
1
1
K
K
K
K
F
η
η
F分布の自由度:
ν1=2 (K2+1) =
ν2=2K1=
q=1−α,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α) (ν1, ν2) =
2項近似の場合の自明でないケースの結論:
F1≧F (1-α) (ν1, ν2)
ならば,H0を棄却する。そうでなければ,棄却しない。
II 正規近似
検定統計量の計算と表からの値の求め方:
(
)(
)
(
)
(
)(
)(
)=
+
−
−
+
+
+
−
+
−
=
2
1
2
1
2
1
2
1
2
1
2
1
1
2
1
1
1
/
2
/1
n
n
x
x
n
n
x
x
n
n
x
x
n
n
n
x
z
q=1−αに対する表3の値を読む:
u1-α=
正規近似の場合の自明でないケースの結論:
z1≧u1-α
ならば,H0を棄却する。そうでなければ,棄却しない。
検定結果:
H0を棄却する。
□
H0を棄却しない。
□

19
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.3.3
書式C-3:H0 : p1=p2の両側検定を用いた二つの割合の比較
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
選択した有意水準:α=
サンプルサイズ1:n1=
サンプルサイズ2:n2=
サンプル1における該当アイテムの数:x1=
サンプル2における該当アイテムの数:x2=
自明なケースの検討:
2
2
1
1
n
x
n
x=
が真である
□
が真でない
□
真の場合,帰無仮説は棄却されず,検定結果を直ちに得ることができる。
そうでなければ,次の方法でH0を棄却するか否かを決める。
自明でないケースの検定方法:
もし,n1,n2, (x1+x2), (n1+n2−x1−x2) のうち少なくても一つが (n1+n2) /4以下であるならば,2項近似(I)を
適用すべきである。そうでなければ正規近似(II)を適用しなければならない。しかし,たとえ上記の条件が満たされ
たとしても,次の二つの条件が満たされれば,正規近似を適用することができる:
− 2項近似を適用する際に,F分布表での内挿が必要である。
− n1とn2の値が同程度である又は (x1+x2) と (n1+n2−x1−x2) の値が同程度である。
決定:
2項近似を適用する(Iへ進む)。
□
正規近似を適用する(IIへ進む)。
□
I 2項近似
変数:K1,K2,η1,η2の定義:
もし,[n2<n1かつn2<(x1+x2)]又は
[(n1+n2−x1−x2)<n1かつ (n1+n2−x1−x2)<(x1+x2)]
ならば,変数を次のように決定する。
η1=n2=
η2=n1=
K1=n2−x2=
K2=n1−x1=
そうでなければ,以下のように定義する。
η1=n1=
η2=n2=
K1=x1=
K2=x2=

20
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検定統計量の計算と表からの値の求め方:
I a) η1≦K1+K2の場合
□
1)
2
2
1
1
η
η
K
K>
の場合
□
書式C-2から,F1, ν1及びν2を求める:
F1=
ν1=
ν2=
q=1−α/2,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α/2) (ν1, ν2)=
2)
2
2
1
1
η
η
K
K≦
の場合
□
書式C-1から,F2,ν1及びν2を求める:
F2=
ν1=
ν2=
q=1−α/2, ν1, ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α/2) (ν1, ν2)
I b) η1>K1+K2の場合
□
1)
2
2
1
1
η
η
K
K>
の場合
□
書式C-2から,F1,ν1及びν2を求める:
F1=
ν1=
ν2=
q=1−α/2,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α/2) (ν1, ν2) =
2)
2
2
1
1
η
η
K
K≦
の場合
□
書式C-1から,F2,ν1及びν2を求める:
F2=
ν1=
ν2=
q=1−α/2,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-α/2) (ν1, ν2) =
2項近似の場合の自明でないケースの結論:
2
2
1
1
η
η
K
K>
の場合: F1≧F (1-α/2) (ν1, ν2)
2
2
1
1
η
η
K
K≦
の場合: F2≧F (1-α/2) (ν1, ν2)
ならば,H0を棄却する。そうでなければ,棄却しない。
II 正規近似
検定統計量の計算と表の値の決定:
a)
2
2
1
1
n
x
n
x>
の場合
□
書式C-2からz1を求める:
z1=
q=1−α/2に対する表3の値を読む:
u1-α/2=
b)
2
2
1
1
n
x
n
x≦
の場合
□
書式C-1からz2を求める:
z2=
q=1−α/2に対する表3の値を読む:
u1-α/2=

21
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
正規近似の場合の自明でないケースの結論:
2
2
1
1
n
x
n
x>
の場合:
z1≧u1-α/2
2
2
1
1
n
x
n
x≦
の場合:
z2≧u1-α/2
ならば,H0を棄却する。そうでなければ,棄却しない。
検定結果:
H0を棄却する。
□
H0を棄却しない。
□
22
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9. 表及びノモグラフ
9.1
F分布のパーセント点の表4における内挿 Fq (ν, ν2) =F (ν1, ν2) を求めたい場合,ν11<ν1<ν12とし
て,表4には直前直後の値F (ν11, ν2) 及びF (ν12, ν2) が示されているとする。
そのとき
(
)
(
)
(
)
(
)
[
]
−
−
−
−
=
11
12
11
1
1
12
2
12
2
11
2
11
2
1
,
,
,
,
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
F
F
F
F
となる。
もし,ν21<ν2<ν22として,直前直後の値F (ν1, ν21) 及びF (ν1, ν22) が表に与えられているのならば,ν2
に関する内挿も同様な方法で行われる。
(
)
(
)
(
)
(
)
[
]
−
−
−
−
=
21
22
21
2
2
22
22
1
21
1
21
1
2
1
,
,
,
,
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
ν
F
F
F
F
もし,求めたいF値がν1及びν2の両方が表に載っていないならば,内挿は3回必要になる,すなわち,
はじめに二つの自由度のうち一つに関して並行に内挿(2回)を行い,それからもう一方の自由度に関し
て内挿(3回目)を行うことになる。
もし,ν1>30及びν2>30ならば,F分布のパーセント点は次の公式の一つを選んで求められる。
()
g
h
F
527
.0
77
.0
1131
.1
lg
1.0
−
−
=
(
)
g
h
F
681
.0
95
.0
4287
.1
lg
05
.0
−
−
=
(
)
g
h
F
846
.0
14
.1
7023
.1
lg
025
.0
−
−
=
(
)
g
h
F
073
.1
40
.1
0206
.2
lg
01
.0
−
−
=
(
)
g
h
F
250
.1
61
.1
2373
.2
lg
005
.0
−
−
=
(
)
g
h
F
672
.1
09
.2
6841
.2
lg
001
.0
−
−
=
参考 lgは、自然対数を意味する記号であるが、我が国では、loge, lnが通常用いられている。
ただし,
2
1
1
1
ν
ν−
=
g
+
=
2
1
1
1
2
ν
ν
h
Fq (ν1, ν2) =Fq
である。
9.2
例 帰無仮説H0 : p≧p0の検定の棄却限界値を決定する例が太線の入ったノモグラフ(図2)太線で
に示されている(7.2.1参照)。与えられた値は,p0=0.15,α=0.05及びn=35である。ノモグラフからx
の値が1と2の間に読み取れ,それゆえC1, 0=2となる。
サンプルサイズnが決まっておらず,加えてβ=0.10及びpʼ=0.039が与えられているならば,2番目の
線がサンプルサイズを決定するために,pʼから1−βの間に引かれる。ノモグラフの二つの線の交点からn
=50が導かれ,xの値は3となる,すなわち,x≦3のとき,帰無仮説を許容し,そうでないとき,帰無仮
説を棄却し,対立仮説を許容する。
2
3
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2 n≦30のときの割合pの上側の片側信頼限界
n
q=0.950のときのxの値
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1
0,950
2
0,777 0,975
3
0,632 0,865 0,984
4
0,528 0,752 0,903 0,988
5
0,451 0,658 0,811 0,924 0,990
6
0,394 0,582 0,729 0,847 0,938 0,992
7
0,349 0,521 0,659 0,775 0,872 0,947 0,993
8
0,313 0,471 0,600 0,711 0,808 0,889 0,954 0,994
9
0,284 0,430 0,550 0,656 0,749 0,832 0,903 0,959 0,995
10
0,259 0,395 0,507 0,607 0,697 0,778 0,850 0,913 0,964 0,995
11
0,239 0,365 0,471 0,565 0,651 0,729 0,801 0,865 0,922 0,967 0,996
12
0,221 0,339 0,439 0,528 0,610 0,685 0,755 0,819 0,878 0,929 0,970 0,996
13
0,206 0,317 0,411 0,495 0,573 0,646 0,713 0,777 0,835 0,888 0,934 0,972 0,997
14
0,193 0,297 0,386 0,466 0,541 0,610 0,675 0,737 0,794 0,848 0,896 0,939 0,975 0,997
15
0,182 0,280 0,364 0,440 0,511 0,578 0,641 0,701 0,757 0,810 0,859 0,904 0,944 0,976 0,997
16
0,171 0,264 0,344 0,417 0,485 0,549 0,609 0,667 0,722 0,774 0,823 0,868 0,910 0,947 0,978 0,997
17
0,162 0,251 0,327 0,396 0,461 0,522 0,581 0,636 0,690 0,740 0,789 0,834 0,877 0,916 0,951 0,979 0,997
18
0,154 0,238 0,311 0,377 0,439 0,498 0,555 0,608 0,660 0,709 0,757 0,802 0,844 0,884 0,921 0,953 0,980 0,998
19
0,146 0,227 0,296 0,360 0,420 0,476 0,530 0,582 0,632 0,680 0,727 0,771 0,813 0,853 0,891 0,925 0,956 0,981 0,998
20
0,140 0,217 0,283 0,344 0,402 0,456 0,508 0,559 0,607 0,654 0,699 0,742 0,783 0,823 0,861 0,896 0,929 0,958 0,982 0,998
21
0,133 0,207 0,271 0,330 0,385 0,437 0,488 0,536 0,583 0,629 0,672 0,715 0,756 0,795 0,832 0,868 0,902 0,933 0,960 0,983 0,998
22
0,128 0,199 0,260 0,316 0,370 0,420 0,469 0,516 0,561 0,605 0,648 0,689 0,729 0,768 0,805 0,841 0,874 0,906 0,936 0,962 0,984 0,998
23
0,123 0,191 0,250 0,304 0,355 0,404 0,451 0,497 0,541 0,584 0,625 0,665 0,704 0,742 0,779 0,814 0,848 0,880 0,911 0,939 0,964 0,985 0,998
24
0,118 0,183 0,240 0,293 0,342 0,390 0,435 0,479 0,522 0,563 0,604 0,643 0,681 0,718 0,754 0,789 0,823 0,855 0,886 0,915 0,941 0,966 0,985 0,998
25
0,113 0,177 0,232 0,282 0,330 0,376 0,420 0,463 0,504 0,544 0,584 0,622 0,659 0,695 0,731 0,765 0,798 0,830 0,861 0,890 0,918 0,941 0,967 0,986 0,998
26
0,109 0,170 0,223 0,272 0,319 0,363 0,406 0,447 0,487 0,527 0,565 0,602 0,638 0,674 0,708 0,742 0,775 0,807 0,837 0,867 0,895 0,922 0,946 0,968 0,987 0,999
27
0,106 0,164 0,216 0,263 0,308 0,351 0,393 0,433 0,472 0,510 0,547 0,583 0,619 0,654 0,687 0,720 0,753 0,784 0,814 0,844 0,872 0,899 0,925 0,948 0,970 0,987 0,999
28
0,102 0,159 0,209 0,255 0,298 0,340 0,380 0,419 0,457 0,494 0,530 0,566 0,600 0,634 0,667 0,700 0,731 0,762 0,792 0,821 0,850 0,877 0,903 0,927 0,950 0,971 0,988 0,999
29
0,099 0,154 0,202 0,247 0,289 0,329 0,368 0,406 0,443 0,480 0,515 0,549 0,583 0,616 0,648 0,680 0,711 0,742 0,771 0,800 0,828 0,855 0,881 0,906 0,930 0,952 0,972 0,988 0,999
30
0,096 0,149 0,196 0,239 0,280 0,319 0,358 0,394 0,430 0,466 0,500 0,534 0,567 0,599 0,631 0,662 0,692 0,722 0,751 0,779 0,807 0,834 0,860 0,886 0,910 0,932 0,954 0,973 0,989 0,999
(注)
表中の (, ) は小数点を表す。
2
4
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2 n≦30のときの割合pの上側の片側信頼限界(続き)
n
q=0.975のときのxの値
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1
0,975
2
0,842 0,988
3
0,708 0,906 0,992
4
0,603 0,806 0,933 0,994
5
0,522 0,717 0,854 0,948 0,995
6
0,460 0,642 0,778 0,882 0,957 0,996
7
0,410 0,579 0,710 0,816 0,902 0,964 0,997
8
0,370 0,527 0,651 0,756 0,843 0,915 0,969 0,997
9
0,337 0,483 0,601 0,701 0,788 0,864 0,926 0,972 0,998
10
0,309 0,446 0,557 0,653 0,738 0,813 0,879 0,934 0,975 0,998
11
0,285 0,413 0,518 0,610 0,693 0,767 0,833 0,891 0,940 0,978 0,998
12
0,265 0,385 0,485 0,572 0,652 0,724 0,790 0,849 0,901 0,946 0,980 0,998
13
0,248 0,361 0,455 0,539 0,615 0,685 0,749 0,808 0,862 0,910 0,950 0,981 0,999
14
0,232 0,339 0,429 0,508 0,582 0,649 0,712 0,770 0,824 0,873 0,917 0,954 0,983 0,999
15
0,219 0,320 0,405 0,481 0,552 0,617 0,678 0,735 0,788 0,837 0,882 0,923 0,957 0,984 0,999
16
0,206 0,303 0,384 0,457 0,524 0,587 0,646 0,702 0,754 0,803 0,849 0,890 0,928 0,960 0,985 0,999
17
0,196 0,287 0,365 0,435 0,499 0,560 0,617 0,671 0,722 0,771 0,816 0,858 0,897 0,932 0,963 0,986 0,999
18
0,186 0,273 0,348 0,415 0,477 0,535 0,591 0,643 0,693 0,740 0,785 0,828 0,867 0,904 0,936 0,965 0,987 0,999
19
0,177 0,261 0,332 0,396 0,456 0,513 0,566 0,617 0,666 0,712 0,756 0,798 0,838 0,875 0,909 0,940 0,967 0,987 0,999
20
0,169 0,249 0,317 0,379 0,437 0,492 0,543 0,593 0,640 0,685 0,729 0,770 0,809 0,847 0,882 0,914 0,943 0,968 0,988 0,999
21
0,162 0,239 0,304 0,364 0,420 0,472 0,522 0,570 0,616 0,660 0,703 0,743 0,782 0,819 0,855 0,888 0,918 0,946 0,970 0,989 0,999
22
0,155 0,229 0,292 0,350 0,403 0,454 0,503 0,549 0,594 0,637 0,678 0,718 0,757 0,793 0,829 0,862 0,893 0,922 0,949 0,971 0,989 0,999
23
0,149 0,220 0,281 0,336 0,388 0,438 0,485 0,530 0,573 0,615 0,656 0,695 0,732 0,769 0,803 0,837 0,868 0,898 0,926 0,951 0,973 0,990 0,999
24
0,143 0,212 0,270 0,324 0,374 0,422 0,468 0,511 0,554 0,595 0,634 0,672 0,709 0,745 0,779 0,813 0,844 0,874 0,903 0,929 0,953 0,974 0,990 0,999
25
0,138 0,204 0,261 0,313 0,361 0,408 0,452 0,494 0,536 0,575 0,614 0,651 0,687 0,723 0,756 0,789 0,821 0,851 0,880 0,907 0,932 0,955 0,975 0,991 0,999
26
0,133 0,197 0,252 0,302 0,349 0,394 0,437 0,478 0,518 0,557 0,595 0,631 0,667 0,701 0,735 0,767 0,798 0,828 0,857 0,885 0,911 0,935 0,957 0,976 0,991 1
27
0,128 0,190 0,243 0,292 0,338 0,381 0,423 0,463 0,502 0,540 0,577 0,613 0,647 0,681 0,714 0,746 0,777 0,806 0,835 0,863 0,889 0,914 0,937 0,959 0,977 0,991 1
28
0,124 0,184 0,236 0,283 0,327 0,369 0,410 0,449 0,487 0,524 0,560 0,595 0,629 0,662 0,694 0,725 0,756 0,785 0,814 0,842 0,868 0,894 0,918 0,940 0,960 0,978 0,992 1
29
0,120 0,178 0,228 0,274 0,317 0,358 0,398 0,436 0,473 0,509 0-544 0,578 0,611 0,644 0,675 0,706 0,736 0,765 0,794 0,821 0,848 0,873 0,898 0,921 0,942 0,962 0,979 0,992 1
30
0,116 0,173 0,221 0,266 0,308 0,348 0,386 0,423 0,459 0,494 0,529 0,562 0,594 0,626 0,657 0,688 0,717 0,746 0,774 0,801 0,828 0,853 0,878 0,901 0,923 0,944 0,963 0,979 0,992 1
(注)
表中のコンマ (, ) は小数点を表す。
2
5
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2 n≦30のときの割合pの上側の片側信頼限界(続き)
n
q=0.990のときのxの値
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1
0,990
2
0,900 0,995
3
0,785 0,942 0,997
4
0,684 0,860 0,959 0,998
5
0,602 0,778 0,895 0,968 0,998
6
0,536 0,706 0,827 0,916 0,974 0,999
7
0,483 0,644 0,764 0,858 0,930 0,978 0,999
8
0,438 0,590 0,707 0,802 0,880 0,940 0,981 0,999
9
0,401 0,545 0,657 0,750 0,830 0,895 0,947 0,983 0,999
10
0,370 0,505 0,612 0,703 0,782 0,850 0,907 0,953 0,985 0,999
11
0,343 0,470 0,573 0,661 0,738 0,807 0,866 0,917 0,958 0,986 1
12
0,319 0,440 0,538 0,623 0,698 0,766 0,826 0,879 0,925 0,962 0,988 1
13
0,299 0,413 0,507 0,588 0,661 0,728 0,788 0,842 0,890 0,931 0,965 0,989 1
14
0,281 0,390 0,479 0,557 0,628 0,693 0,752 0,806 0,855 0,899 0,936 0,967 0,990 1
15
0,265 0,368 0,454 0,529 0,597 0,660 0,718 0,772 0,821 0,866 0,906 0,941 0,970 0,990 1
16
0,251 0,349 0,431 0,503 0,569 0,630 0,687 0,740 0,789 0,834 0,875 0,913 0,945 0,972 0,991 1
17
0,238 0,332 0,410 0,480 0,544 0,603 0,658 0,710 0,758 0,803 0,845 0,884 0,918 0,949 0,974 0,992 1
18
0,226 0,317 0,392 0,459 0,520 0,578 0,631 0,682 0,729 0,774 0,816 0,855 0,891 0,923 0,952 0,975 0,992 1
19
0,216 0,302 0,375 0,439 0,499 0,554 0,607 0,656 0,702 0,747 0,788 0,827 0,864 0,897 0,928 0,954 0,977 0,992 1
20
0,206 0,289 0,359 0,421 0,479 0,533 0,583 0,631 0,677 0,720 0,762 0,800 0,837 0,871 0,903 0,932 0,957 0,978 0,993 1
21
0,197 0,277 0,344 0,405 0,460 0,512 0,562 0,609 0,653 0,696 0,736 0,775 0,811 0,846 0,878 0,908 0,935 0,959 0,979 0,993 1
22
0,189 0,266 0,331 0,389 0,443 0,494 0,542 0,587 0,631 0,673 0,712 0,750 0,787 0,821 0,854 0,884 0,913 0,938 0,961 0,980 0,994 1
23
0,182 0,256 0,319 0,375 0,427 0,476 0,523 0,567 0,610 0,651 0,690 0,727 0,763 0,797 0,830 0,861 0,890 0,917 0,941 0,963 0,981 0,994 1
24
0,175 0,247 0,307 0,362 0,412 0,460 0,505 0,549 0,590 0,630 0,668 0,705 0,741 0,775 0,807 0,838 0,867 0,895 0,921 0,944 0,965 0,982 0,994 1
25
0,169 0,238 0,296 0,349 0,398 0,445 0,489 0,531 0,572 0,611 0,648 0,684 0,719 0,753 0,785 0,816 0,845 0,873 0,899 0,924 0,946 0,966 0,982 0,994 1
26
0,163 0,230 0,286 0,338 0,385 0,430 0,473 0,515 0,554 0,592 0,629 0,664 0,699 0,732 0,764 0,794 0,824 0,852 0,879 0,904 0,927 0,948 0,967 0,983 0,995 1
27
0,157 0,222 0,277 0,327 0,373 0,417 0,459 0,499 0,538 0,575 0,611 0,646 0,679 0,712 0,743 0,774 0,803 0,831 0,858 0,883 0,908 0,930 0,951 0,969 0,984 0,995 1
28
0,152 0,215 0,268 0,317 0,362 0,404 0,445 0,484 0,522 0,558 0,594 0,628 0,661 0,693 0,724 0,754 0,783 0,811 0,838 0,864 0,888 0,911 0,933 0,952 0,970 0,984 0,995 1
29
0,147 0,208 0,260 0,307 0,351 0,393 0,432 0,470 0,507 0,543 0,577 0,611 0,643 0,675 0,705 0,735 0,764 0,791 0,818 0,844 0,869 0,892 0,914 0,935 0,954 0,971 0,985 0,995 1
30
0,143 0,202 0,252 0,298 0,341 0,381 0,420 0,457 0,493 0,528 0,562 0,594 0,626 0,657 0,687 0,717 0,745 0,773 0,799 0,825 0,850 0,874 0,896 0,918 0,937 0,956 0,972 0,986 0,995 1
(注)
表中のコンマ (, ) は小数点を表す。
2
6
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2 n≦30のときの割合pの上側の片側信頼限界(続き)
n
q=0.995のときのxの値
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1
0,995
2
0,930 0,998
3
0,830 0,959 0,999
4
0,735 0,890 0,971 0,999
5
0,654 0,815 0,918 0,978 0,999
6
0,587 0,747 0,857 0,934 0,982 1
7
0,531 0,685 0,798 0,883 0,945 0,985 1
8
0,485 0,632 0,743 0,831 0,901 0,953 0,987 1
9
0,445 0,585 0,693 0,781 0,854 0,914 0,959 0,988 1
10
0,412 0,545 0,649 0,736 0,810 0,872 0,924 0,963 0,990 1
11
0,383 0,509 0,609 0,694 0,767 0,831 0,886 0,932 0,967 0,991 1
12
0,357 0,478 0,573 0,656 0,728 0,792 0,848 0,897 0,938 0,970 0,992 1
13
0,335 0,450 0,542 0,621 0,692 0,755 0,812 0,862 0,906 0,943 0,973 0,992 1
14
0,316 0,425 0,513 0,590 0,658 0,721 0,777 0,828 0,874 0,914 0,948 0,975 0,993 1
15
0,298 0,402 0,487 0,561 0,628 0,689 0,744 0,795 0,842 0,884 0,920 0,952 0,977 0,993 1
16
0,282 0,382 0,463 0,535 0,600 0,659 0,714 0,764 0,811 0,853 0,892 0,926 0,955 0,978 0,994 1
17
0,268 0,364 0,442 0,511 0,574 0,631 0,685 0,735 0,781 0,824 0,863 0,899 0,931 0,958 0,980 0,994 1
18
0,255 0,347 0,422 0,489 0,550 0,606 0,658 0,707 0,753 0,796 0,836 0,872 0,905 0,935 0,960 0,981 0,995 1
19
0,244 0,332 0,404 0,469 0,528 0,582 0,633 0,681 0,727 0,769 0,809 0,846 0,880 0,911 0,939 0,963 0,982 0,995 1
20
0,233 0,318 0,388 0,450 0,507 0,560 0,610 0,657 0,701 0,743 0,783 0,820 0,855 0,887 0,916 0,942 0,965 0,983 0,995 1
21
0,223 0,305 0,372 0,433 0,488 0,540 0,588 0,634 0,678 0,719 0,758 0,795 0,830 0,862 0,893 0,920 0,945 0,967 0,984 0,995 1
22
0,215 0,293 0,358 0,417 0,470 0,521 0,568 0,613 0,655 0,696 0,735 0,771 0,806 0,839 0,870 0,898 0,924 0,948 0,968 0,985 0,996 1
23
0,206 0,282 0,345 0,402 0,454 0,503 0,549 0,593 0,634 0,674 0,712 0,748 0,783 0,816 0,847 0,876 0,903 0,928 0,950 0,970 0,985 0,996 1
24
0,199 0,272 0,333 0,388 0,438 0,486 0,531 0,574 0,614 0,654 0,691 0,727 0,761 0,794 0,825 0,854 0,882 0,908 0,931 0,953 0,971 0,986 0,996 1
25
0,191 0,262 0,322 0,375 0,424 0,470 0,514 0,556 0,596 0,634 0,671 0,706 0,740 0,772 0,803 0,833 0,861 0,887 0,912 0,934 0,955 0,972 0,987 0,996 1
26
0,185 0,253 0,311 0,363 0,410 0,456 0,498 0,539 0,578 0,615 0,652 0,686 0,720 0,752 0,782 0,812 0,840 0,867 0,892 0,915 0,937 0,956 0,973 0,987 0,996 1
27
0,179 0,245 0,301 0,351 0,398 0,442 0,483 0,523 0,561 0,598 0,633 0,667 0,700 0,732 0,762 0,792 0,820 0,847 0,872 0,896 0,919 0,940 0,958 0,974 0,988 0,997 1
28
0,173 0,237 0,292 0,340 0,386 0,429 0,469 0,508 0,545 0,581 0,616 0,650 0,682 0,713 0,743 0,772 0,800 0,827 0,853 0,877 0,900 0,922 0,942 0,960 0,975 0,988 0,997 1
29
0,167 0,230 0,283 0,330 0,375 0,416 0,456 0,494 0,530 0,566 0,600 0,632 0,664 0,695 0,725 0,754 0,781 0,808 0,834 0,859 0,882 0,904 0,925 0,944 0,961 0,976 0,989 0,997 1
30
0,162 0,223 0,275 0,321 0,364 0,405 0,443 0,480 0,516 0,551 0,584 0,616 0,647 0,678 0,707 0,736 0,763 0,790 0,815 0,840 0,864 0,886 0,908 0,928 0,946 0,963 0,977 0,989 0,997 1
(注)
表中のコンマ (, ) は小数点を表す。
27
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3 標準正規分布のパーセント点uq
q=φ (u)
uq
0, 950
1, 645
0, 975
1, 960
0, 990
2, 326
0, 995
2, 576
(注)
表中のコンマ (, ) は小数点を表す。
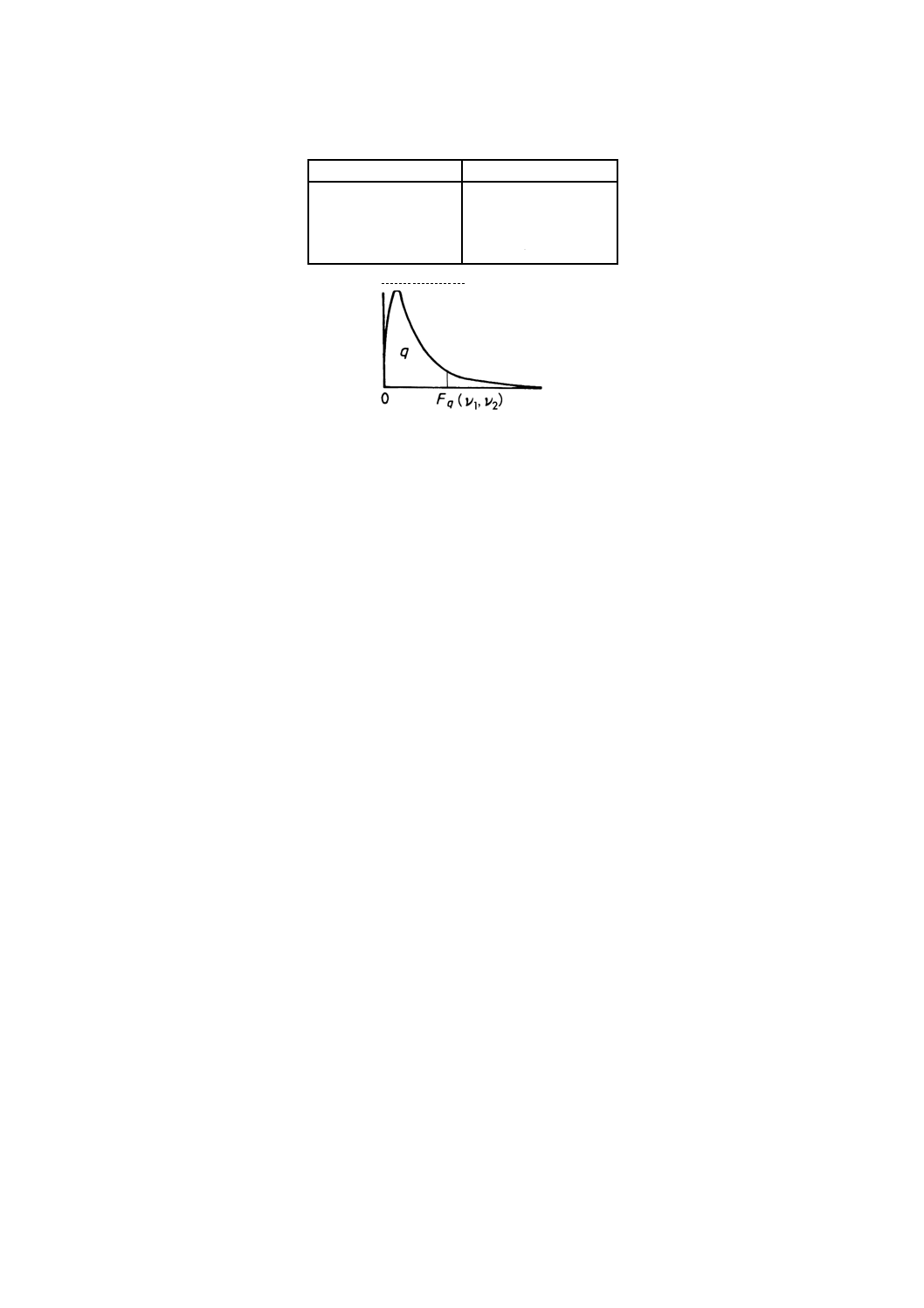
図1 F分布のパーセント点
2
8
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4 F分布のパーセント点(図1参照)
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
1
0,9
39,9 49,5 53,6 55,8 57,2 58,2 58,9 59,4 59,9
60,2 60,7 61,2 61,7 62,3 62,7 63,3
0,95
161
200
216
225
230
234
237
239
241
242
244
246
248
250
252
254
0,975
648
800
864
900
922
937
948
957
963
969
977
985
993
1001
1008
1018
0,990
4052
5000
5403
5625
5764
5859
5928
5981
6022
6056
6106
6157
6209
6261
6303
6366
0,995
16210
20000
21610
22500
23060
23440
23710
23930
24090
24220
24430
24630
24840
25040
25210
25460
0,999
405300
500000
540400
562500
576400
585900
592900
598100
602300
605600
610700
615800
620900
626100
630300
636600
2
0,9
8,53 9,0
9,16 9,24 9,29 9,33 9,35 9,37 9,38 9,39 9,41 9,42 9,44 9,46 9,47 9,49
0,95
18,5
19,0
19,2
19,2
19,3
19,3
19,4
19,4
19,4
19,4
19,4
19,4
19,4
19,5
19,5
19,5
0,975
38,5
39,0
39,2
39,2
39,3
39,3
39,4
39,4
39,4
39,4
39,4
39,4
39,4
39,5
39,5
39,5
0,990
98,5
99,0
99,2
99,2
99,3
99,3
99,4
99,4
99,4
99,4
99,4
99,4
99,4
99,5
99,5
99,5
0,995
199
199
199
199
199
199
199
199
199
199
199
199
199
199
199
199
0,999
999
999
999
999
999
999
999
999
999
999
999
999
999
999
999
999
3
0,9
5,54
5,46
5,39
5,34
5,31
5,28
5,27
5,25
5,24
5,23
5,22
5,20
5,18
5,17
5,15
5,13
0,95
10,1
9,55
9,28
9,12
9,01
8,94
8,89
8,85
8,81
8,79
8,74
8,70
8,66
8,62
8,58
8,53
0,975
17,4
16,0
15,4
15,1
14,9
14,7
14,6
14,5
14,5
14,4
14,3
14,3
14,2
14,1
14,0
13,9
0,990
34,1
30,8
29,5
28,7
28,2
27,9
27,7
27,5
27,3
27,2
27,1
26,9
26,7
26,5
26,4
26,1
0,995
55,6
49,8
47,5
46,2
45,4
44,8
44,4
44,1
43,9
43,7
43,4
43,1
42,8
42,5
42,2
41,8
0,999
167
149
141
37
135
133
132
131
130
129
128
127
126
125
125
123
4
0,9
4,54
4,32
4,19
4,11
4,05
4,01
3,98
3,95
3,94
3,92
3,90
3,87
3,84
3,82
3,80
3,76
0,95
7,71
6,94
6,59
6,39
6,26
6,16
6,09
6,04
6,00
5,96
5,91
5,86
5,80
5,75
5,70
5,63
0,975
12,2
10,6
9,98
9,60
9,36
9,20
3,07
8,96
8,90
8,84
8,75
8,66
8,56
8,46
8,38
8,26
0,990
21,2
18,0
16,7
16,04
15,5
15,2
15,0
14,8
14,7
14,5
14,4
14,2
14,0
13,8
13,7
13,5
0,995
31,3
26,3
24,3
23,2
22,5
22,0
21,6
21,4
21,1
21,0
20,7
20,4
20,2
19,9
19,7
19,3
0,999
74,1
61,2
56,2
53,4
51,7
50,5
49,7
49,0
48,5
48,1
47,4
46,8
46,1
45,4
44,9
44,1
5
0,9
4,06
3,78
3,62
3,52
3,45
3,40
3,37
3,34
3,32
3,30
3,27
3,24
3,21
3,17
3,15
3,10
0,95
6,61
5,79
5,41
5,19
5,05
4,95
4,88
4,82
4,77
4,74
4,68
4,62
4,56
4,50
4,44
4,36
0,975
10,0
8,43
7,76
7,39
7,15
6,98
6,85
6,76
6,68
6,62
6,52
6,43
6,33
6,23
6,14
6,02
0,990
16,3
13,3
12,1
11,4
11,0
10,7
10,5
10,3
10,2
10,1
9,89
9,72
9,55
9,38
9,24
9,02
2
9
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
0,995
22,8
18,3
16,5
15,6
14,9
14,5
14,2
14,0
13,8
13,6
13,4
13,1
12,9
12,7
12,5
12,1
0,999
47,2
37,1
33,2
31,1
29,8
28,8
28,2
27,6
27,2
26,9
26,4
25,9
25,4
24,9
24,4
23,8
6
0,9
3,78
3,46
3,29
3,18
3,11
3,05
3,01
2,98
2,96
2,94
2,90
2,87
2,84
2,80
2,77
2,72
0,95
5,99
5,14
4,76
4,53
4,39
4,28
4,21
4,15
4,10
4,06
4,00
3,94
3,87
3,81
3,75
3,67
0,975
8,81
7,26
6,60
6,23
5,99
5,82
5,70
5,60
5,52
5,46
5,37
5,27
5,17
5,07
4,98
4,85
0,990
13,7
10,9
9,78
9,15
8,75
8,47
8,26
8,10
7,98
7,87
7,72
7,56
7,40
7,23
7,09
6,88
0,995
18,6
14,5
12,9
12,0
11,5
11,1
10,8
10,6
10,4
10,3
10,0
9,81
9,59
9,36
9,17
8,88
0,999
35,5
27,0
23,7
21,9
20,8
20,0
19,5
19,0
18,7
18,4
18,0
17,6
17,1
16,7
16,3
15,7
7
0,9
3,59
3,26
3,07
2,96
2,88
2,83
2,78
2,75
2,72
2,70
2,67
2,63
2,59
2,56
2,52
2,47
0,95
5,59
4,74
4,35
4,12
3,97
3,87
3,79
3,73
3,68
3,64
3,57
3,51
3,44
3,38
3,32
3,23
0,975
8,07
6,54
5,89
5,52
5,29
5,12
4,99
4,90
4,82
4,76
4,67
4,57
4,47
4,36
4,28
4,14
0,990
12,2
9,55
8,45
7,85
7,46
7,19
6,99
6,84
6,72
6,62
6,47
6,31
6,16
5,99
5,86
5,65
0,995
16,2
12,4
10,9
10,1
9,52
9,16
8,89
8,68
8,51
8,38
8,18
7,97
7,75
7,53
7,35
7,08
0,999
29,2
21,7
18,8
17,2
16,2
15,5
15,0
14,6
14,3
14,1
13,7
13,3
12,9
12,5
12,2
11,7
8
0,9
3,46
3,11
2,92
2,81
2,73
2,67
2,62
2,59
2,56
2,54
2,50
2,46
2,42
2,38
2,35
2,29
0,95
5,32
4,46
4,07
3,84
3,69
3,58
3,50
3,44
3,39
3,35
3,28
3,22
3,15
3,08
3,02
2,93
0,975
7,57
6,06
5,42
5,05
4,82
4,65
4,53
4,43
4,36
4,30
4,20
4,10
4,00
3,89
3,81
3,67
0,990
11,3
8,65
7,59
7,01
6,63
6,37
6,18
6,03
5,91
5,81
5,67
5,52
5,36
5,20
5,07
4,86
0,995
14,7
11,0
9,60
8,81
8,30
7,95
7,69
7,50
7,34
7,21
7,01
6,81
6,61
6,40
6,22
5,95
0,999
25,4
18,5
15,8
14,4
13,5
12,9
12,4
12,0
11,8
11,5
11,2
10,8
10,5
10,1
9,80
9,33
9
0,9
3,36
3,01
2,81
2,69
2,61
2,55
2,51
2,47
2,44
2,42
2,38
2,34
2,30
2,25
2,22
2,16
0,95
5,12
4,26
3,86
3,63
3,48
3,37
3,29
3,23
3,18
3,14
3,07
3,01
2,94
2,86
2,80
2,71
0,975
7,21
5,71
5,08
4,72
4,48
4,32
4,20
4,10
4,03
3,96
3,87
3,77
3,67
3,56
3,47
3,33
0,990
10,6
8,02
6,99
6,42
6,06
5,80
5,61
5,47
5,35
5,26
5,11
4,96
4,81
4,65
4,52
4,31
0,995
13,6
10,1
8,72
7,96
7,47
7,14
6,88
6,69
6,54
6,42
6,23
6,03
5,83
5,62
5,45
5,19
0,999
22,9
16,4
13,9
12,6
11,7
11,1
10,7
10,4
10,1
9,89
9,57
9,24
8,90
8,55
8,26
7,81
10 0,9
3,29
2,92
2,73
2,61
2,52
2,46
2,41
2,38
2,35
2,32
2,28
2,24
2,20
2,16
2,12
2,06
0,95
4,96
4,10
3,71
3,48
3,33
3,22
3,14
3,07
3,02
2,98
2,91
2,85
2,77
2,70
2,64
2,54
3
0
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
10 0,975
6,94
5,46
4,83
4,47
4,24
4,07
3,95
3,85
3,78
3,72
3,62
3,52
3,42
3,31
3,22
3,08
0,990
10,0
7,56
6,55
5,99
5,64
5,39
5,20
5,06
4,94
4,85
4,71
4,56
4,41
4,25
4,12
3,91
0,995
12,8
9,43
8,08
7,34
6,87
6,54
6,30
6,12
5,97
5,85
5,66
5,47
5,27
5,07
4,90
4,64
0,999
21,0
14,9
12,6
11,3
10,5
9,93
9,52
9,20
8,96
8,75
8,45
8,13
7,80
7,47
7,19
6,76
11 0,9
3,23
2,86
2,66
2,54
2,45
2,39
2,34
2,30
2,27
2,25
2,21
2,17
2,12
2,08
2,04
1,97
0,95
4,84
3,98
3,59
3,36
3,20
3,09
3,01
2,95
2,90
2,85
2,79
2,72
2,65
2,57
2,51
2,40
0,975
6,72
5,26
4,63
4,28
4,04
3,88
3,76
3,66
3,59
3,53
3,43
3,33
3,23
3,12
3,03
2,88
0,990
9,65
7,21
6,22
5,67
5,32
5,07
4,89
4,74
4,63
4,54
4,40
4,25
4,10
3,94
3,81
3,60
0,995
12,2
8,91
7,60
6,88
6,42
6,10
5,86
5,68
5,54
5,42
5,24
5,05
4,86
4,65
4,49
4,23
0,999
19,7
13,8
11,6
10,3
9,58
9,05
8,66
8,35
8,12
7,92
7,63
7,32
7,01
6,68
6,42
6,00
12 0,9
3,18
2,81
2,61
2,48
2,39
2,33
2,28
2,24
2,21
2,19
2,15
2,10
2,06
2,01
1,97
1,90
0,95
4,75
3,89
3,49
3,26
3,11
3,00
2,91
2,85
2,80
2,75
2,69
2,62
2,54
2,47
2,40
2,30
0,975
6,55
5,10
4,47
4,12
3,89
3,73
3,61
3,51
3,44
3,37
3,28
3,18
3,07
2,96
2,87
2,72
0,990
9,33
6,93
5,95
5,41
5,06
4,82
4,64
4,50
4,39
4,30
4,16
4,01
3,86
3,70
3,57
3,36
0,995
11,8
8,51
7,23
6,52
6,07
5,76
5,52
5,35
5,20
5,09
4,91
4,72
4,53
4,33
4,17
3,90
0,999
18,6
13,0
10,8
9,63
8,89
8,38
8,00
7,71
7,48
7,29
7,00
6,71
6,40
6,09
5,83
5,42
13 0,9
3,14
2,76
2,56
2,43
2,35
2,28
2,23
2,20
2,16
2,14
2,10
2,05
2,01
1,96
1,92
1,85
0,95
4,67
3,81
3,41
3,18
3,03
2,92
2,83
2,77
2,71
2,67
2,60
2,53
2,46
2,38
2,31
2,21
0,975
6,41
4,97
4,35
4,00
3,77
3,60
3,48
3,39
3,31
3,25
3,15
3,05
2,95
2,84
2,74
2,60
0,990
9,07
6,70
5,74
5,21
4,86
4,62
4,44
4,30
4,19
4,10
3,96
3,82
3,66
3,51
3,38
3,17
0,995
11,4
8,19
6,93
6,23
5,79
5,48
5,25
5,08
4,94
4,82
4,64
4,46
4,27
4,07
3,91
3,65
0,999
17,8
12,3
10,2
9,07
8,35
7,86
7,49
7,21
6,98
6,80
6,52
6,23
5,93
5,63
5,37
4,97
14 0,9
3,10
2,73
2,52
2,39
2,31
2,24
2,19
2,15
2,12
2,10
2,05
2,01
1,96
1,91
1,87
1,80
0,95
4,60
3,74
3,34
3,11
2,96
2,85
2,76
2,70
2,65
2,60
2,53
2,46
2,39
2,31
2,24
2,13
0,975
6,30
4,86
4,24
3,89
3,66
3,50
3,38
3,29
3,21
3,15
3,05
2,95
2,84
2,73
2,64
2,49
0,990
8,86
6,51
5,56
5,04
4,69
4,46
4,28
4,14
4,03
3,94
3,80
3,66
3,51
3,35
3,22
3,00
0,995
11,1
7,92
6,68
6,00
5,56
5,26
5,03
4,86
4,72
4,60
4,43
4,25
4,06
3,86
3,70
3,44
0,999
17,1
11,8
9,73
8,62
7,92
7,44
7,08
6,80
6,58
6,40
6,13
5,85
5,56
5,25
5,00
4,60
3
1
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
15 0,9
3,07
2,70
2,49
2,36
2,27
2,21
2,16
2,12
2,09
2,06
2,02
1,97
1,92
1,87
1,83
1,76
0,95
4,54
3,68
3,29
3,06
2,90
2,79
2,71
2,64
2,59
2,54
2,48
2,40
2,33
2,25
2,18
2,07
0,975
6,20
4,77
4,15
3,80
3,58
3,41
3,29
3,20
3,12
3,06
2,96
2,86
2,76
2,64
2,55
2,40
0,990
8,68
6,36
5,42
4,89
4,56
4,32
4,14
4,00
3,89
3,80
3,67
3,52
3,37
3,21
3,08
2,87
0,995
10,8
7,70
6,48
5,80
5,37
5,07
4,85
4,67
4,54
4,42
4,25
4,07
3,88
3,69
3,52
3,26
0,999
16,6
11,3
9,34
8,25
7,57
7,09
6,74
6,47
6,26
6,08
5,81
5,54
5,25
4,95
4,70
4,31
16 0,9
3,05
2,67
2,46
2,33
2,24
2,18
2,13
2,09
2,06
2,03
1,99
1,94
1,89
1,84
1,79
1,72
0,95
4,49
3,63
3,24
3,01
2,85
2,74
2,66
2,59
2,54
2,49
2,42
2,35
2,28
2,19
2,12
2,01
0,975
6,12
4,69
4,03
3,73
3,50
3,34
3,22
3,12
3,05
2,99
2,89
2,79
2,68
2,57
2,47
2,32
0,990
8,53
6,23
5,29
4,77
4,44
4,20
4,03
3,89
3,78
3,69
3,55
3,41
3,26
3,10
2,97
2,75
0,995
10,6
7,51
6,30
5,64
5,21
4,91
4,69
4,52
4,38
4,27
4,10
3,92
3,73
3,54
3,37
3,11
0,999
16,1
11,0
9,01
7,94
7,27
6,80
6,46
6,19
5,98
5,81
5,55
5,27
4,99
4,70
4,45
4,06
17 0,9
3,03
2,64
2,44
2,31
2,22
2,15
2,10
2,06
2,03
2,00
1,96
1,91
1,86
1,81
1,76
1,69
0,95
4,45
3,59
3,20
2,96
2,81
2,70
2,61
2,55
2,49
2,45
2,38
2,31
2,23
2,15
2,08
1,96
0,975
6,04
4,62
4,01
3,66
3,44
3,28
3,16
3,06
2,98
2,92
2,82
2,72
2,62
2,50
2,41
2,25
0,990
8,40
6,11
5,18
4,67
4,34
4,10
3,93
3,79
3,68
3,59
3,46
3,31
3,16
3,00
2,87
2,65
0,995
10,4
7,35
6,16
5,50
5,07
4,78
4,56
4,39
4,25
4,14
3,97
3,79
3,61
3,41
3,25
2,98
0,999
15,7
10,7
8,73
7,68
7,02
6,56
6,22
5,96
5,75
5,58
5,32
5,05
4,78
4,48
4,24
3,85
18 0,9
3,01
2,62
2,42
2,29
2,20
2,13
2,08
2,04
2,00
1,98
1,93
1,89
1,84
1,78
1,74
1,66
0,95
4,41
3,55
3,16
2,93
2,77
2,66
2,58
2,51
2,46
2,41
2,34
2,27
2,19
2,11
2,04
1,92
0,975
5,98
4,56
3,95
3,61
3,38
3,22
3,10
3,01
2,93
2,87
2,77
2,67
2,56
2,44
2,35
2,19
0,990
8,29
6,01
5,09
4,58
4,25
4,01
3,84
3,71
3,60
3,51
3,37
3,23
3,08
2,92
2,78
2,57
0,995
10,2
7,21
6,03
5,37
4,96
4,66
4,44
4,28
4,14
4,03
3,86
3,68
3,50
3,30
3,14
2,87
0,999
15,4
10,4
8,49
7,46
6,81
6,35
6,02
5,76
5,56
5,39
5,13
4,87
4,59
4,30
4,06
3,67
19 0,9
2,99
2,61
2,40
2,27
2,18
2,11
2,06
2,02
1,98
1,96
1,91
1,86
1,81
1,76
1,71
1,63
0,95
4,38
3,52
3,13
2,90
2,74
2,63
2,54
2,48
2,42
2,38
2,31
2,23
2,16
2,07
2,00
1,88
0,975
5,92
4,51
3,90
3,56
3,33
3,17
3,05
2,96
2,88
2,82
2,72
2,62
2,51
2,39
2,30
2,13
0,990
8,18
5,93
5,01
4,50
4,17
3,94
3,77
3,63
3,52
3,43
3,30
3,15
3,00
2,84
2,71
2,49
0,995
10,1
7,09
5,92
5,27
4,85
4,56
4,34
4,18
4,04
3,93
3,76
3,59
3,40
3,21
3,04
2,78
3
2
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
19 0,999
15,1
10,2
8,28
7,27
6,62
6,18
5,85
5,59
5,39
5,22
4,97
4,70
4,43
4,14
3,90
3,51
20 0,9
2,97
2,59
2,38
2,25
2,16
2,09
2,04
2,00
1,96
1,94
1,89
1,84
1,79
1,74
1,69
1,61
0,95
4,35
3,49
3,10
2,87
2,71
2,60
2,51
2,45
2,39
2,35
2,28
2,20
2,12
2,04
1,97
1,84
0,975
5,87
4,46
3,86
3,51
3,29
3,13
3,01
2,91
2,84
2,77
2,68
2,57
2,46
2,35
2,25
2,09
0,990
8,10
5,85
4,94
4,43
4,10
3,87
3,70
3,56
3,46
3,37
3,23
3,09
2,94
2,78
2,64
2,42
0,995
9,94
6,99
5,82
5,17
4,76
4,47
4,26
4,09
3,96
3,85
3,68
3,50
3,32
3,12
2,96
2,69
0,999
14,8
9,95
8,10
7,10
6,46
6,02
5,69
5,44
5,24
5,08
4,82
4,56
4,29
4,00
3,77
3,38
21 0,9
2,96
2,57
2,36
2,23
2,14
2,08
2,02
1,98
1,95
1,92
1,87
1,83
1,78
1,72
1,67
1,59
0,95
4,32
3,47
3,07
2,84
2,68
2,57
2,49
2,42
2,37
2,32
2,25
2,18
2,10
2,01
1,94
1,81
0,975
5,83
4,42
3,82
3,48
3,25
3,09
2,97
2,87
2,80
2,73
2,64
2,53
2,42
2,31
2,21
2,04
0,990
8,02
5,78
4,87
4,37
4,04
3,81
3,64
3,51
3,40
3,31
3,17
3,03
2,88
2,72
2,58
2,36
0,995
9,83
6,89
5,73
5,09
4,68
4,39
4,18
4,01
3,88
3,77
3,60
3,43
3,24
3,05
2,88
2,61
0,999
14,6
9,77
7,94
6,95
6,32
5,88
5,56
5,31
5,11
4,95
4,70
4,44
4,17
3,88
3,64
3,26
22 0,9
2,95
2,56
2,35
2,22
2,13
2,06
2,01
1,97
1,93
1,90
1,86
1,81
1,76
1,70
1,65
1,57
0,95
4,30
3,44
3,05
2,82
2,66
2,55
2,46
2,40
2,34
2,30
2,23
2,15
2,07
1,98
1,91
1,78
0,975
5,79
4,38
3,78
3,44
3,22
3,05
2,93
2,84
2,76
2,70
2,60
2,50
2,39
2,27
2,17
2,00
0,990
7,95
5,72
4,82
4,31
3,99
3,76
3,59
3,45
3,35
3,26
3,12
2,98
2,83
2,67
2,53
2,31
0,995
9,73
6,81
5,65
5,02
4,61
4,32
4,11
3,94
3,81
3,70
3,54
3,36
3,18
2,98
2,82
2,55
0,999
14,4
9,61
7,80
6,81
6,19
5,76
5,44
5,19
4,99
4,83
4,58
4,33
4,06
3,78
3,54
3,15
23 0,9
2,94
2,55
2,34
2,21
2,11
2,05
1,99
1,95
1,92
1,89
1,84
1,80
1,74
1,69
1,64
1,55
0,95
4,28
3,42
3,03
2,80
2,64
2,53
2,44
2,37
2,32
2,27
2,20
2,13
2,05
1,96
1,88
1,76
0,975
5,75
4,35
3,75
3,41
3,18
3,02
2,90
2,81
2,73
2,67
2,57
2,47
2,36
2,24
2,14
1,97
0,990
7,88
5,66
4,76
4,26
3,94
3,71
3,54
3,41
3,30
3,21
3,07
2,93
2,78
2,62
2,48
2,26
0,995
9,63
6,73
5,58
4,95
4,54
4,26
4,05
3,88
3,75
3,64
3,47
3,30
3,12
2,92
2,76
2,48
0,999
14,2
9,47
7,64
6,70
6,08
5,65
5,33
5,09
4,89
4,73
4,48
4,23
3,96
3,68
3,44
3,05
24 0,9
2,93
2,54
2,33
2,19
2,10
2,04
1,98
1,94
1,91
1,88
1,83
1,78
1,73
1,67
1,62
1,53
0,95
4,26
3,40
3,01
2,78
2,62
2,51
2,42
2,36
2,30
2,25
2,18
2,11
2,03
1,94
1,86
1,73
0,975
5,72
4,32
3,72
3,38
3,15
2,99
2,87
2,78
2,70
2,64
2,54
2,44
2,33
2,21
2,11
1,94
3
3
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
24 0,990
7,82
5,61
4,72
4,22
3,90
3,67
3,50
3,36
3,26
3,17
3,03
2,89
2,74
2,58
2,44
2,21
0,995
9,55
6,66
5,52
4,89
4,49
4,20
3,99
3,83
3,69
3,59
3,42
3,25
3,06
2,87
2,70
2,43
0,999
14,0
9,34
7,55
6,59
5,98
5,55
5,23
4,99
4,80
4,64
4,39
4,14
3,87
3,59
3,36
2,97
25 0,9
2,92
2,53
2,32
2,18
2,09
2,02
1,97
1,93
1,89
1,87
1,82
1,77
1,72
1,66
1,61
1,52
0,95
4,24
3,39
2,99
2,76
2,60
2,49
2,40
2,34
2,28
2,24
2,16
2,09
2,01
1,92
1,84
1,71
0,975
5,69
4,29
3,69
3,35
3,13
2,97
2,85
2,75
2,68
2,61
2,51
2,41
2,30
2,18
2,08
1,91
0,990
7,77
5,57
4,68
4,18
3,85
3,63
3,46
3,32
3,22
3,13
2,99
2,85
2,70
2,54
2,40
2,17
0,995
9,48
6,60
5,46
4,84
4,43
4,15
3,94
3,78
3,64
3,54
3,37
3,20
3,01
2,82
2,65
2,38
0,999
13,9
9,22
7,45
6,49
5,89
5,46
5,15
4,91
4,71
4,56
4,31
4,06
3,79
3,52
3,28
2,89
30 0,9
2,88
2,49
2,28
2,14
2,05
1,98
1,93
1,88
1,85
1,82
1,77
1,72
1,67
1,61
1,55
1,46
0,95
4,17
3,32
2,92
2,69
2,53
2,42
2,33
2,27
2,21
2,16
2,09
2,01
1,93
1,84
1,76
1,62
0,975
5,57
4,18
3,59
3,25
3,03
2,87
2,75
2,65
2,57
2,51
2,41
2,31
2,20
2,07
1,97
1,79
0,990
7,56
5,39
4,51
4,02
3,70
3,47
3,30
3,17
3,07
2,98
2,84
2,70
2,55
2,39
2,25
2,01
0,995
9,18
6,35
5,24
4,62
4,23
3,95
3,74
3,58
3,45
3,34
3,18
3,01
2,82
2,63
2,46
2,18
0,999
13,3
8,77
7,05
6,12
5,53
5,12
4,82
4,58
4,39
4,24
4,00
3,75
3,49
3,22
2,98
2,59
35 0,9
2,85
2,46
2,25
2,11
2,02
1,95
1,90
1,85
1,82
1,79
1,74
1,69
1,63
1,57
1,51
1,41
0,95
4,12
3,27
2,87
2,64
2,49
2,37
2,29
2,22
2,16
2,11
2,04
1,96
1,88
1,79
1,70
1,56
0,975
5,48
4,11
3,52
3,18
2,96
2,80
2,68
2,58
2,50
2,44
2,34
2,23
2,12
2,00
1,89
1,70
0,990
7,42
5,27
4,40
3,91
3,59
3,37
3,20
3,07
2,96
2,88
2,74
2,60
2,44
2,28
2,14
1,89
0,995
8,98
6,19
5,39
4,48
4,09
3,81
3,61
3,45
3,32
3,21
3,05
2,88
2,69
2,50
2,33
2,04
0,999
10,9
8,47
6,79
5,88
5,30
4,89
4,59
4,36
4,18
4,03
3,79
3,55
3,29
3,02
2,78
2,38
40 0,9
2,84
2,44
2,23
2,09
2,00
1,93
1,87
1,83
1,79
1,76
1,71
1,66
1,61
1,54
1,48
1,38
0,95
4,08
3,23
2,84
2,61
2,45
2,34
2,25
2,18
2,12
2,08
2,00
1,92
1,84
1,74
1,66
1,51
0,975
5,42
4,05
3,46
3,13
2,90
2,74
2,62
2,53
2,45
2,39
2,29
2,18
2,07
1,94
1,83
1,64
0,990
7,31
5,18
4,31
3,83
3,51
3,29
3,12
2,99
2,89
2,80
2,66
2,52
2,37
2,20
2,06
1,80
0,995
8,83
6,07
4,98
4,37
3,99
3,71
3,51
3,35
3,22
3,12
2,95
2,78
2,60
2,40
2,23
1,93
0,999
12,6
8,25
6,59
5,70
5,13
4,73
4,44
4,21
4,02
3,87
3,64
3,40
3,14
2,87
2,64
2,23
45 0,9
2,82
2,42
2,21
2,07
1,98
1,91
1,85
1,81
1,77
1,74
1,70
1,64
1,58
1,52
1,46
1,35
3
4
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
45 0,95
4,06
3,20
2,81
2,58
2,42
2,31
2,22
2,15
2,10
2,05
1,97
1,89
1,81
1,71
1,63
1,47
0,975
5,38
4,01
3,42
3,09
2,86
2,70
2,58
2,49
2,41
2,35
2,25
2,14
2,03
1,90
1,79
1,59
0,990
7,23
5,11
4,25
3,77
3,45
3,23
3,07
2,94
2,83
2,74
2,61
2,46
2,31
2,14
2,00
1,74
0,995
8,71
5,97
4,89
4,29
3,91
3,64
3,43
3,28
3,15
3,04
2,88
2,71
2,53
2,33
2,16
1,85
0,999
12,4
8,09
6,45
5,56
5,00
4,61
4,32
4,09
3,91
3,76
3,53
3,29
3,04
2,76
2,53
2,12
50 0,9
2,81
2,41
2,20
2,06
1,97
1,90
1,84
1,80
1,76
1,73
1,68
1,63
1,57
1,50
1,44
1,33
0,95
4,03
3,18
2,79
2,56
2,40
2,29
2,20
2,13
2,07
2,03
1,95
1,87
1,78
1,69
1,60
1,44
0,975
5,34
3,97
3,39
3,05
2,83
2,67
2,55
2,46
2,38
2,32
2,22
2,11
1,99
1,87
1,75
1,55
0,990
7,17
5,06
4,20
3,72
3,41
3,19
3,02
2,89
2,78
2,70
2,56
2,42
2,27
2,10
1,95
1,68
0,995
8,63
5,90
4,83
4,23
3,85
3,58
3,38
3,22
3,09
2,99
2,82
2,65
2,47
2,27
2,10
1,79
0,999
12,2
7,96
6,34
5,46
4,90
4,51
4,22
4,00
3,82
3,67
3,44
3,20
2,95
2,68
2,44
2,03
60 0,9
2,79
2,39
2,18
2,04
1,95
1,87
1,82
1,77
1,74
1,71
1,66
1,60
1,54
1,48
1,41
1,29
0,95
4,00
3,15
2,76
2,53
2,37
2,25
2,17
2,10
2,04
1,99
1,92
1,84
1,75
1,65
1,56
1,39
0,975
5,29
3,93
3,34
3,01
2,79
2,63
2,51
2,41
2,33
2,27
2,17
2,06
1,94
1,82
1,70
1,48
0,990
7,08
4,98
4,13
3,65
3,34
3,12
2,95
2,82
2,72
2,63
2,50
2,35
2,20
2,03
1,88
1,60
0,995
8,49
5,79
4,73
4,14
3,76
3,49
3,29
3,13
3,01
2,90
2,74
2,57
2,39
2,19
2,01
1,69
0,999
12,0
7,77
6,17
5,31
4,76
4,37
4,09
3,86
3,69
3,54
3,32
3,08
2,83
2,55
2,32
1,89
80 0,9
2,77
2,37
2,15
2,02
1,92
1,85
1,79
1,75
1,71
1,68
1,63
1,57
1,51
1,44
1,38
1,24
0,95
3,96
3,11
2,72
2,49
2,33
2,21
2,13
2,06
2,00
1,95
1,88
1,79
1,70
1,60
1,51
1,32
0,975
5,22
3,86
3,28
2,95
2,73
2,57
2,45
2,35
2,28
2,21
2,11
2,00
1,88
1,75
1,63
1,40
0,990
6,96
4,88
4,04
3,56
3,26
3,04
2,87
2,74
2,64
2,55
2,42
2,27
2,12
1,94
1,79
1,49
0,995
8,33
5,67
4,61
4,03
3,65
3,39
3,19
3,03
2,91
2,80
2,64
2,47
2,29
2,08
1,90
1,56
0,999
11,7
7,54
5,97
5,12
4,58
4,20
3,92
3,70
3,53
3,39
3,16
2,93
2,68
2,41
2,16
1,72
100 0,9
2,76
2,36
2,14
2,00
1,91
1,83
1,78
1,73
1,69
1,66
1,61
1,56
1,49
1,42
1,35
1,21
0,95
3,94
3,09
2,70
2,46
2,31
2,19
2,10
2,03
1,97
1,93
1,85
1,77
1,68
1,57
1,48
1,28
0,975
5,18
3,83
3,25
2,92
2,70
2,54
2,42
2,32
2,24
2,18
2,08
1,97
1,85
1,71
1,59
1,35
0,990
6,90
4,82
3,98
3,51
3,21
2,99
2,82
2,69
2,59
2,50
2,37
2,22
2,07
1,89
1,74
1,43
0,995
8,24
5,59
4,54
3,96
3,59
3,33
3,13
2,97
2,85
2,74
2,58
2,41
2,23
2,02
1,84
1,49
0,999
11,5
7,41
5,86
5,02
4,48
4,11
3,83
3,61
3,44
3,30
3,07
2,84
2,59
2,32
2,08
1,62
3
5
Z
9
0
4
1
-3
:
1
9
9
9
(I
S
O
1
1
4
5
3
:
1
9
9
6
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ν1
ν2
q
1
2
3
4
5
6
7
8
9
10
12
15
20
30
50
∞
120 0,9
2,75
2,35
2,13
1,99
1,90
1,82
1,77
1,72
1,68
1,65
1,60
1,55
1,48
1,41
1,34
1,19
0,95
3,92
3,07
2,68
2,45
2,29
2,18
2,09
2,02
1,96
1,91
1,83
1,75
1,66
1,55
1,46
1,25
0,975
5,15
3,80
3,23
2,89
2,67
2,52
2,39
2,30
2,22
2,16
2,05
1,94
1,82
1,69
1,56
1,31
0,990
6,85
4,79
3,95
3,48
3,17
2,96
2,79
2,66
2,56
2,47
2,34
2,19
2,03
1,86
1,70
1,38
0,995
8,18
5,54
4,50
3,92
3,55
3,28
3,09
2,93
2,81
2,71
2,54
2,37
2,19
1,98
1,80
1,43
0,999
11,4
7,32
5,78
4,95
4,42
4,04
3,77
3,55
3,38
3,24
3,02
2,78
2,53
2,26
2,02
1,54
∞ 0,9
2,71
2,30
2,08
1,94
1,85
1,77
1,72
1,67
1,63
1,60
1,55
1,49
1,42
1,34
1,26
1,00
0,95
3,84
3,00
2,60
2,37
2,21
2,10
2,01
1,94
1,88
1,83
1,75
1,67
1,57
1,46
1,35
1,00
0,975
5,02
3,69
3,12
2,79
2,57
2,41
2,29
2,19
2,11
2,05
1,94
1,83
1,71
1,57
1,43
1,00
0,990
6,63
4,61
3,78
3,32
3,02
2,80
2,64
2,51
2,41
2,32
2,18
2,04
1,88
1,70
1,52
1,00
0,995
7,88
5,30
4,28
3,72
3,35
3,09
2,90
2,74
2,62
2,52
2,36
2,19
2,00
1,79
1,59
1,00
0,999
10,8
6,91
5,42
4,62
4,10
3,74
3,47
3,27
3,10
2,96
2,74
2,51
2,27
1,99
1,73
1,00
備考 −Fa (ν1, ν2) =1/F (1−α) (ν2, ν1)
(注) 表中のコンマ (, ) は小数点を表す。
36
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5 p1>p2であるp1とp2の様々な組み合わせに対して,H0 : p1≦p2のα=0.05
での片側検定において与えられた検出力1−β(=0.9 ; 0.8又は0.5)を得
るための二つのサンプルの共通のサンプルサイズn1=n2
P2
P1
0.95
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.9
503
371
184
0.8
89
67
38
232
173
87
0.7
42
34
19
74
56
31
338
249
121
0.6
25
20
12
39
30
17
97
73
37
408
302
143
0.5
18
14
9
25
19
11
47
36
19
111
84
43
445
321
155
0.4
13
11
7
17
13
9
30
23
12
53
41
22
116
85
43
445
321
155
0.3
10
9
6
12
10
6
18
15
9
31
23
12
53
41
22
111
84
43
408
302
143
0.2
8
6
5
10
8
5
12
10
6
18
15
9
30
23
12
47
36
19
97
73
37
338
249
121
0.1
6
5
3
8
6
3
10
8
5
12
10
6
17
13
9
25
19
11
39
30
17
74
56
31
232
173
87
0.05
5
5
3
6
5
3
8
6
5
10
9
6
13
11
7
18
14
9
25
20
12
42
34
19
89
67
38
503
371
184
備考 表の各セルにおいて,上段の数値は1−β=0.9を与える共通のサンプルサイズ,中段,下段はそれぞれ,1−β
=0.8, 0.5の場合である。例えば,もし,p1=0.9, p2=0.8ならば,1−β=0.9にするためにはn1=n2=232, 1−β
=0.8にするためにはn1=n2=173, 1−β=0.5にするためにはn1=n2=87だけ採らなければならない
(注)
表中のコンマ (, ) は小数点を表す。
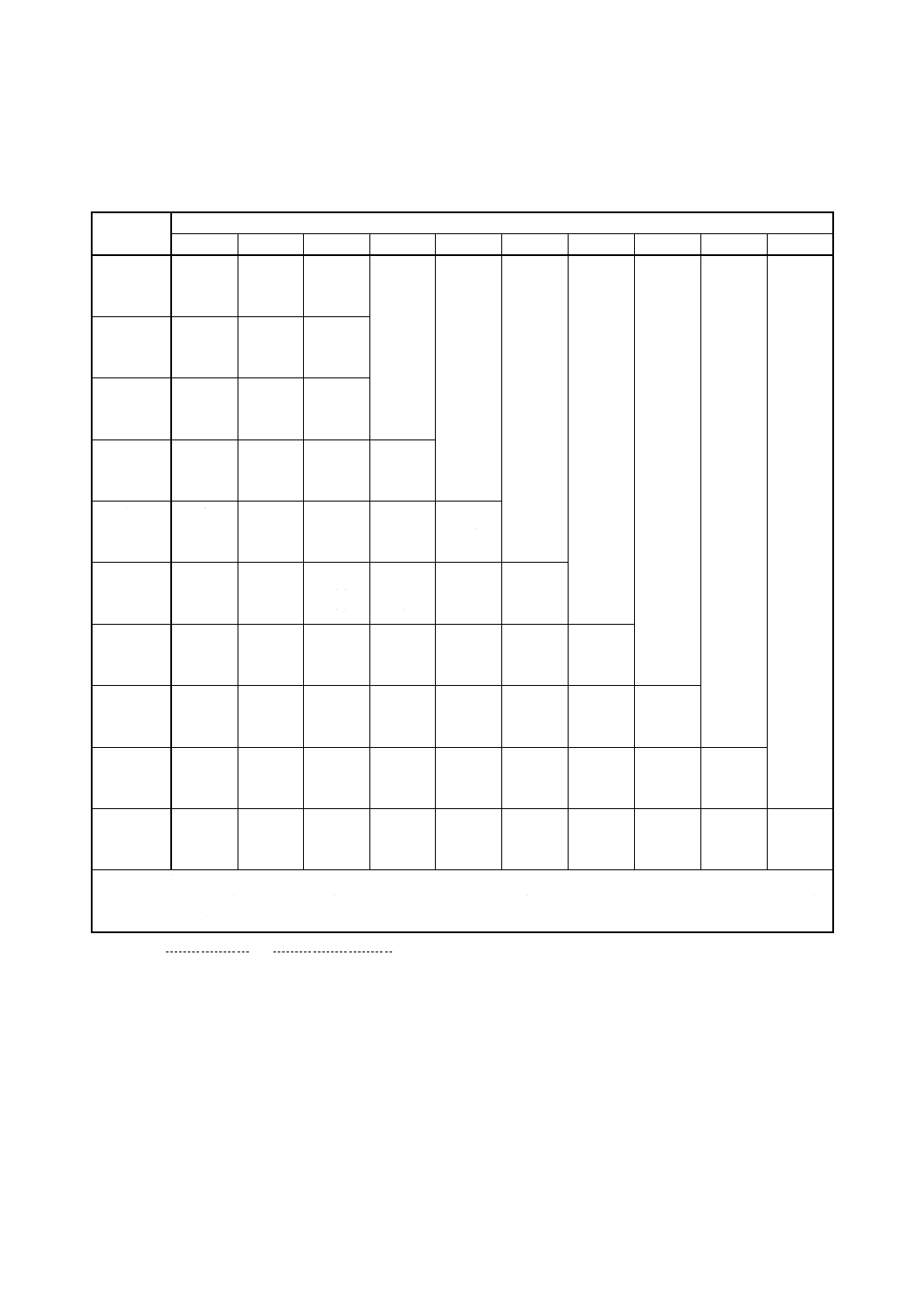
37
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表6 p1>p2であるp1とp2の様々な組み合わせに対してH0 : p1≦p2のα=0.01
での片側検定において与えられた検出力1−β(=0.9 ; 0.8又は0.5)を
得るための二つのサンプルの共通のサンプルサイズn1=n2
P2
P1
0.95
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.9
745
583
333
0.8
130
344
101
269
61
155
0.7
60
108
503
49
86
393
32
52
221
0.6
37
56
143
609
31
46
113
475
18
27
66
265
0.5
25
35
69
163
667
20
29
55
129
519
14
18
34
73
285
0.4
18
24
42
77
171
667
16
20
34
60
137
519
10
13
21
35
78
285
0.3
14
18
28
43
77
163
609
12
15
22
35
60
129
475
9
10
13
22
35
73
265
0.2
12
13
18
28
42
69
143
503
9
12
16
22
34
55
113
393
6
8
9
13
21
34
66
221
0.1
9
9
13
18
24
35
56
108
344
8
9
12
15
20
29
46
86
269
6
6
8
10
13
18
27
52
155
0.05
8
9
12
14
18
25
37
60
130
745
6
8
9
12
16
20
31
49
101
583
5
6
6
9
10
14
18
32
61
333
備考 表の各セルにおいて,上段の数値は1−β=0.9を与える共通のサンプルサイズ,中段,下段はそれぞれ,1−β
=0.8, 0.5の場合である。例えば,もし,p1=0.9, p2=0.8ならば,1−β=0.9にするためにはn1=n2=344単位採
らなければならないが,1−β=0.5にするためにはn1=n2=155だけでよい。
(注)
表中のコンマ (, ) は小数点を表す。
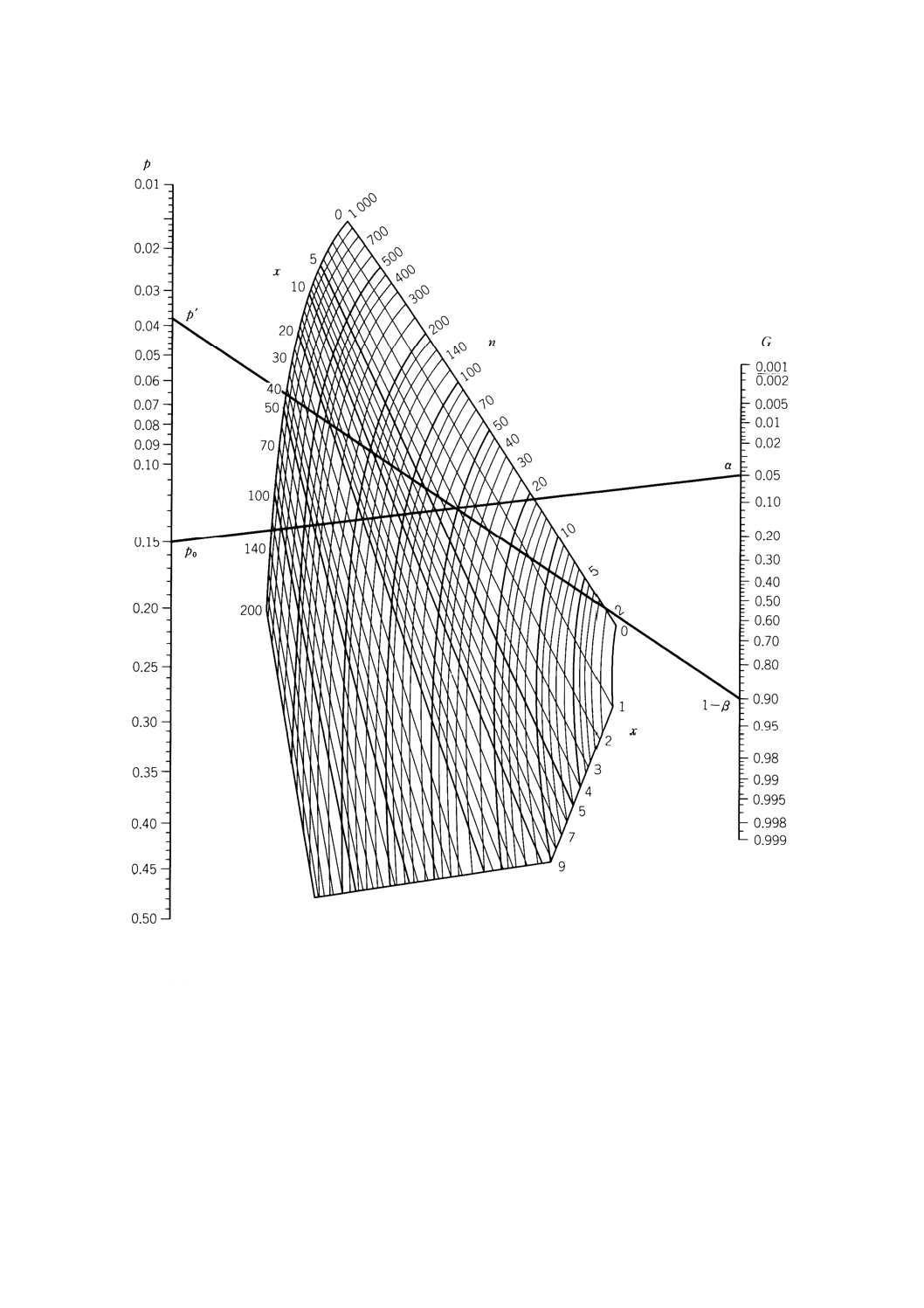
38
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 もし,p<0.01ならばp尺上でpの代わりにλpをマークし,n尺の値をλ倍する。λは0.01/pを
次に大きな整数に丸めて求める。
(注)
表中のコンマ (, ) は小数点を表す。
図2 2項分布のラーソン (Larson) のノモグラフ

39
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) 書式Bによる検定の検定特性の計算
A.1 H0 : p≧p0の片側検定
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
与えられた値p0=
選択した有意水準:α=
サンプルサイズ:n=
検出力を計算したい対立仮説における割合:pʼ=
もし,選択した有意水準αにおけるn及びp0に対応する棄却限界値が未知ならば,書式Bによって計算する。
Cl, o=
H0を棄却しない確率Pαと結果して得られる値の求め方:
もし,H0が真ならば,第1種の誤りの確率は1−Pαになる。達成される有意水準aʼはpʼ=p0のとき,第1種の誤り
の確率と等しくなる。
もし,対立仮説が真ならば,第2種の誤りの確率はPαになる。
計算: (
)(
)
(
)
[
]=
′
−
−
′
−
+
=
′
p
C
n
p
C
u
o
l
o
l
,
,
1
1
2
表3の値を読む:Φ (uʼ) =
結果:
Pα=1−Φ (uʼ) =
もし,pʼ=p0ならば αʼ=Φ (uʼ) =
もし,pʼ<p0ならば β=1−Φ (uʼ) =

40
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.2 H0 : p≦p0の片側検定
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
与えられた値p0=
選択した有意水準:α=
サンプルサイズ:n=
検出力を計算したい対立仮説における割合:p´=
もし,選択した有意水準αにおけるn及びp0に対応する棄却限界値が未知ならば,書式Bによって計算する。
Cu, o=
H0を棄却しない確率Pαと結果として得られる値の求め方:
もし,H0が真ならば,第1種の誤りの確率は1−Pαになる。達成される有意水準αʼはpʼ=p0のとき,第1種の誤り
の確率と等しくなる。
もし,対立仮説が真ならば,第2種の誤りの確率はPaになる。
計算:
(
)
(
)
[
]=
′
+
−
−
′
−
=
′′
p
C
n
p
C
u
o
u
o
u
1
1
2
,
,
表3の値を読む:Φ (uʼʼ) =
結果:
Pa=Φ (uʼʼ) =
もし,pʼ=p0ならば αʼ=1−Φ (uʼʼ) =
もし,pʼ>p0ならば β=Φ (uʼʼ) =

41
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.3 H0 : p=p0の両側検定
特性:
測定方法:
アイテム:
該当アイテムの識別基準:
備考:
与えられた値p0=
選択した有意水準:α=
サンプルサイズ:n=
検出力を計算したい対立仮説における割合:p´=
もし,選択した有意水準αにおけるn及びp0に対応する棄却限界値が未知ならば,書式Bによって計算する。
Cl, t=
Cu, t=
H0を棄却しない確率Pαと結果として得られる値の求め方:
もし,H0が真ならば,第1種の誤りの確率は1−Pαになる。達成される有意水準αʼはpʼ=p0のとき,第1種の誤り
の確率と等しくなる。
もし,対立仮説が真ならば,第2種の誤りの確率はPαになる。
計算: (
)(
)
(
)
[
]=
′
−
−
′
−
+
=
′
p
C
n
p
C
u
t
l
t
l
,
,
1
1
2
(
)
(
)
[
]=
′
+
−
−
′
−
=
′′
p
C
n
p
C
u
t
u
t
u
1
1
2
,
,
表3の値を読む:Φ (uʼ) =
Φ (uʼʼ) =
結果:
Pα=Φ (uʼʼ) −Φ (uʼ) =
もし,pʼ=p0ならば dʼ=1−Φ (uʼʼ) +Φ (uʼ) =
もし,pʼ≠p0ならば β=Φ (uʼʼ) −Φ (uʼ) =

42
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考) 書式の使用例
B.1 書式A
B.1.1 例1:書式A-2 −片側,割合pの信頼区間の下限
特性:家庭にビデオレコーダを保有している
測定方法:インタビュー
アイテム:ある地域の家庭
該当アイテムの識別基準:最低1台のビデオレコーダを保有している
備考:
選択した信頼係数:1−α=0.95
サンプルサイズ:n=20
サンプルにおける該当アイテムの数:x=14
信頼限界の決定:
a) n≦30のときの方法
□
×
1) x=0の場合
□
pl, o=0
2) x>0の場合
□
×
既知の値n,X=n−x及びq=1−αに対する表2の値を読む。
T (1-α) (n, n−x) =0.508
計算:
pl, o=1−T (1-α) (n, n−x) =0.492
b) n>30のときの方法
□
1) x=0の場合
□
pl, o=0
2) x=nの場合
□
計算:
pl, o=α1/n=
3) 0<x<nの場合
□
q=1−αに対する表3の値を読む:u1-α=
選択した信頼係数に対応するdの値を読む。
計算:
p*=x/ (n+1) (
)(
)
(
)
(
)
[
](
)=
+
+
−
−
−
+
−
+
=
−
1
/
1
/
1
1
1
/
2
1
*
*
1
*
*
,
n
n
d
p
p
u
n
d
p
p
po
l
α
結果:
pl, o=0.492
≦p

43
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.1.2 例2:書式A-3 −割合pの両側信頼区間
特性:家庭にビデオレコーダを保有している
測定方法:インタビュー
アイテム:ある地域の家庭
該当アイテムの識別基準:最低1台のビデオレコーダを保有している
備考:
選択した信頼係数:1−α=0.99
サンプルサイズ:n=90
サンプルにおける該当アイテムの数:x=19
信頼限界の決定:
a) n≦30のときの方法
□
1) 上側信頼限界
− x=nの場合
□
pu, t=1
− x<nの場合
□
既知の値n,X=x及びq=1−α/2に対する表2の値を読む。
(この値が信頼限界である。):
T (1-α/2) (n, x) =pu, t=
2) 下側信頼限界
− x=0の場合
□
pl, t=0
− x>0の場合
□
既知の値n,X=n−x及びq=1−α/2に対する表2の値を読む。
T (1-α/2) (n, n−x) =
計算:
pl, t=1−T (1-α/2) (n, n−x) =
b) n>30のときの方法
□
×
1) 上側信頼限界
□
− x=0の場合
□
計算:
pu, t=1−(α/2)1/n=
− x=nの場合
□
pu, t=1
− 0<x<nの場合
□
×
q=1−α/2に対する表3の値を読む:u1-α/2=2.576
選択した信頼係数に対応するdの値を読む。
計算:
p*= (x+1) / (n+1)
(
)(
)
(
)
(
)
[
](
)=
+
+
−
−
+
+
−
+
=
−
1
/
1
/
1
1
1
/
2
1
*
*
2
/
1
*
*
,
n
n
d
p
p
u
n
d
p
p
pt
u
α
0.341

44
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2) 下側信頼限界
− x=0の場合
□
pl, t=0
− x=nの場合
□
計算:
pl, t=(α/2)1/n=
− 0<x<nの場合
□
×
q=1−α/2に対する表3の値を読む:u1-α/2=2.576
選択した信頼係数に対応するdの値を読む。
計算:
p*=x/ (n+1) (
)(
)
(
)(
)(
)
[
](
)=
+
+
−
−
−
+
−
+
=
−
1
/
1
/
1
1
1
/
2
1
*
*
2
/
1
*
*
,
n
n
d
p
p
u
n
d
p
p
pt
l
α
0.111
結果:
pl, t=0.111;
pu, t=0.341;
pl, t≦p≦pu, t

45
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.2 書式B
B.2.1 例1:書式B-2 −H0 : p≦p0の片側検定を用いた割合pと与えられた値p0との比較
特性:家庭にビデオレコーダを保有している
測定方法:インタビュー
アイテム:ある地域の家庭
該当アイテムの識別基準:最低1台のビデオレコーダを保有している
備考:
与えられた値p0=0.48
選択した有意水準:α=0.05
サンプルサイズ:n=20
サンプルにおける該当アイテムの数:x=14
検定方法:
I 棄却限界値が既知である(7.2.1参照及び
適用可能ならば次に棄却限界値の決定):
□
Cu, o=
もし,x>Cu, oならばH0を棄却;そうでなければ棄却しない。
II 棄却限界値が未知である:
□
×
a) x≦p0nの場合
□
H0は棄却しない。
b) x>p0nの場合
□
×
1) n≦30のときの方法
□
×
n,x及び信頼係数 (1−α) に対する片側の下側信頼限界を
書式A-2に従い求める:
pl, o=0.492
もし,pl, o>p0ならばH0を棄却;そうでなければ棄却しない。
2) n>30のときの方法
□
− x=nの場合
□
計算:
pl, o=α1/n= [書式A-2 b)2)参照]
もし,pl, o>p0ならばH0を棄却;そうでなければ棄却しない。
− 0<x<nの場合
□
q=1−αに対する表3の値を読む:u1-a=
計算: (
)
(
)
[
]=
+
−
−
−
=
0
0
2
1
1
2
p
x
n
p
x
u
もし,u2>u1-αならばH0を棄却;そうでなければ棄却しない。
検定結果:
H0を棄却する
□
×
H0を棄却しない
□
棄却限界値の決定:
Cu, oは,書式B.2−IIによる検定で帰無仮説を棄却しない最大の整数xである。Cu, oは,xの異なる値に対して書式
B.2−IIを繰り返し適用することをとおして繰り返し求められる(1)。それゆえ,お互いに1ずつ異なるxの値に対し
て決められ,そのうちの一つは帰無仮説の棄却し,他のものは棄却しない。もし,望めばxについての出発値xstart
を次のように求めることができる。
計算:
np0を次の整数に丸めたものがx*=10
pu, o|x=x*=0.699
pu, 0|x=x*は書式A-1から求められる)
npu, o|x=x*を次の整数に丸めたものがxstart=14
書式B.1−IIの検定結果の解釈:
x≦Cu. o=13
のとき,H0を棄却しない。
x≧Cu, o+1=14
のとき,H0を棄却する。

46
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
結果:
Cu, o=13
注(1) サンプルサイズnがたいへん小さいとき,及び/又はp0が極端な値のとき,棄却限界値は存在しない。

47
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.2.2 例2:書式B-3 −H0 : p=p0の両側検定を用いた割合pと与えられた値p0との比較
特性:家庭にビデオレコーダを保有している
測定方法:インタビュー
アイテム:ある地域の家庭
該当アイテムの識別基準:最低1台のビデオレコーダを保有している
備考:
与えられた値p0=0.33
選択した有意水準:α=0.01
サンプルサイズ:n=90
サンプルにおける該当アイテムの数:x=19
検定方法:
I 棄却限界値が既知である(7.2.1参照及び
適用可能ならば次に棄却限界値の決定):
□
Cl, t=
Cu, t=
もし,x<Cl, t又はx>Cu, tならばH0は棄却;
そうでなければ棄却しない。
II 棄却限度値が未知である:
□
×
a) n≦30のときの方法
□
n,x及び信頼係数 (1−α) に対する両側信頼限界を
書式A-3に従い求める:
pl, t=
pu, t=
もし,pl, t>p0又はpu, t<p0ならばH0を棄却;
そうでなければ棄却しない。
b) n>30のときの方法
□
×
1) x=0の場合
□
計算:
pu, t=1− (α/2) 1/n=
もし,pu, t<p0ならばH0を棄却;そうでなければ棄却しない。
2) x=nの場合
□
計算:
pl, t=(α/2)1/n=
もし,pl, t>p0ならばH0を棄却;そうでなければ棄却しない。
3) 0<x<nの場合
□
×
q=1−α/2に対する表3の値を読む:u1-a/2=2.576
計算:
(
)
(
)(
)
[
]=
−
+
−
−
=
0
0
1
1
1
2
p
x
p
x
n
u
2.359 707
(
)
(
)
[
]=
+
−
−
−
=
0
0
2
1
1
2
p
x
n
p
x
u
−2.613 021
もし,u1>u1-α/2又はu2>u1-α/2ならばH0を棄却;
そうでなければ棄却しない。

48
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検定結果:
H0を棄却する
□
H0を棄却しない
□
×
棄却限界値の決定:
書式B-3−IIによる検定でH0を棄却しない最小の非負の整数xがCl,tで,最大の整数がCu,tである。Cl,t及びCu,tは,
xの異なる値に対して書式B-3−IIを繰り返し適用することを通して繰り返し求められる(1)。それゆえ,それぞれの
組で,お互いに1ずつ値が異なり,一方では帰無仮説を棄却し,他方では棄却しないように決められる。もし,望
めば,xについての出発値Xstartを次のように求めることができる。
計算:
np0を次の整数に丸めたものがx*=30
pl, t|x=x*=0.210
pu, t|x=x*=0.473
(pl, t|x=x*及びpu, t|x=x*は書式A-3から求められる。)
npl, t|x=x*を次の整数に丸めたものがxstart (lower) =19
npu, t|x=x*を次の整数に丸めたものがxstart (upper) =43
書式B-3−IIの検定結果の解釈:
x≦Cl, t−1=18
のとき,H0を棄却する。
x=Cl, t=19
からx=Cu, t=42
のとき,H0を棄却しない。
x≧Cu, t+1=43
のとき,H0を棄却する。
結果:
Cl, t=19
Cu, t=42
注(1) サンプルサイズnがたいへん小さいとき,及び/又はp0が極端な値のとき,棄却限界値は存在しない。

49
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.3 書式C
B.3.1 例1:書式C-1 −H0 : p1≧p2の片側検定を用いた二つの割合の比較
特性:家庭にビデオレコーダを保有している
測定方法:インタビュー
アイテム:
1) 地域Aの家庭
2) 地域Bの家庭
該当アイテムの識別基準:最低1台のビデオレコーダを保有している
備考:
選択した有意水準:α=0.05
サンプル1の大きさ:n1=10
サンプル2の大きさ:n2=15
サンプル1における該当アイテムの数:x1=8
サンプル2における該当アイテムの数:x2=13
自明なケースの検討:
2
2
1
1
n
x
n
x≧
が真である
□
が真でない
□
×
真の場合,帰無仮説は棄却されず,検定結果を直ちに得ることができる。
そうでなければ,次の方法でH0を棄却するか否かを決める。
自明でないケースの検定方法:
もし,n1,n2, (n1+n2) , (n1+n2−x1−x2) のうち少なくても一つが (n1+n2) /4以下であるならば,2項近似(I)を
適用すべきである;そうでなければ正規近似(II)を適用しなければならない。しかし,たとえ上記の条件が満たされ
たとしても,次の二つの条件が満たされれば,正規近似を適用することができる:
− 2項近似を適用する際に,F分布表での内挿が必要である。
− n1とn2の値が同程度であるもしくは (x1+x2) と (n1+n2−x1−x2) の値が同程度である。
決定:
2項近似を適用する(Iへ進む)。
□
×
正規近似を適用する(IIへ進む)。
□
I 2項近似
補助変数:K1,K2,η1,η2の決定:
もし,[n2<n1かつn2< (x1+x2)]又は[(n1+n2−x1−x2) <n1かつ (n1+n2−x1−x2) < (x1+x2)]ならば,補助変数
を次のように決定する。
η1=n2=15
η2=n1=10
K1=n2−x2=2
K2=n1−x1=2
そうでなければ,次のように決定する。
η1=n1=
η2=n2=
K1=x1=
K2=x2=
検定統計量の計算と表からの値の求め方:
I a) η1≦K1+K2の場合
□
(
)(
)
(
)(
)=
+
−
−
+
+
+
−
=
1
2
2
1
2
2
1
2
1
1
2
1
1
1
2
K
K
K
K
K
K
F
η
η
η
F分布の自由度:
ν1=2 (K1+1) =
ν2=2 (η1−K1) =
q=1−α, ν1, ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-a) (ν1, ν2) =

50
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
I b) η1>K1+K2の場合
□
×
(
)
(
)(
)
1
456
982
,0
1
2
1
2
2
2
1
1
1
2
2
=
+
−
+
−
=
K
K
K
K
F
η
η
F分布の自由度:
ν1=2 (K1+1) =6
ν2=2K2=4
q=1−α, ν1, ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-a)( ν1, ν2) =6.16
2項近似の場合の自明でないケースの結論:
F2≧F (1-α) (ν1, ν2)
ならば,H0を棄却する。そうでなければ,棄却しない。
II 正規近似
検定統計量の計算と表からの値の求め方:
(
)(
)(
)
(
)(
)(
)=
+
−
−
+
+
+
+
−
+
=
2
1
2
1
2
1
2
1
2
1
2
1
1
2
1
1
2
/
2
/1
n
n
x
x
n
n
x
x
n
n
n
n
x
x
x
n
z
q=1−αに対する表3の値を読む:u1-α=
正規近似の場合の自明でないケースの結論:
z2≧u1-α
ならば,H0を棄却する。そうでなければ,棄却しない。
検定結果:
H0を棄却する。
□
H0を棄却しない。 □
×

51
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.3.2 例2:書式C-3 −H0 : p1=p2の両側検定を用いた二つの割合の比較
特性:
1) 家庭にブランドAのビデオレコーダを保有している
2) 家庭にブランドBのビデオレコーダを保有している
測定方法:インタビュー
アイテム:ある地域の家庭
該当アイテムの識別基準:
1) 最低1台のブランドAのビデオレコーダを保有している
2) 最低1台のブランドBのビデオレコーダを保有している
備考:
選択した有意水準:α=0.01
サンプル1の大きさ:n1=95
サンプル2の大きさ:n2=95
サンプル1における該当アイテムの数:x1=41
サンプル2における該当アイテムの数:x2=21
自明なケースの検討:
2
2
1
1
n
x
n
x=
が真である
□
が真でない
□
×
真の場合,帰無仮説は棄却されず,検定結果を直ちに得ることができる。
そうでなければ,次の方法でH0を棄却するか否かを決める。
自明でないケースの検定方法:
もし,n1,n2 (x1+x2) , (n1+n2−x1−x2) のうち少なくても一つが (n1+n2) /4以下であるならば,2項近似(I)を適用
すべきである。そうでなければ正規近似(II)を適用しなければならない。しかし,たとえ上記の条件が満たされたと
しても,次の二つの条件が満たされれば,正規近似を適用することができる:
− 2項近似を適用する際に,F分布表での内挿が必要である。
− n1とn2の値が同程度である又は (x1+x2) と (n1+n2−x1−x2) の値が同程度である。
決定:
2項近似を適用する(Iへ進む)。
□
正規近似を適用する(IIへ進む)。
□
×
I 2項近似
変数:K1,K2,η1,η2の決定:
もし,[n2<n1かつn2< (x1+x2)]又は[(n1+n2−x1−x2) <n1かつ (n1+n2−x1−x2) < (x1+x2)]ならば,変数を次
のように決定する。
η1=n2=
η2=n1=
K1=n2−x2=
K2=n1−x1=
そうでなければ,次のように決定する。
η1=n1=
η2=n2=
K1=x1=
K2=x2=

52
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
検定統計量の計算と表からの値の求め方:
I a) η1≦K1+K2の場合
□
1)
2
2
1
1
η
η
K
K>
の場合
□
次のように,F1,ν1及びν2を求める:
(
)
(
)(
)=
+
+
+
−
−
−
+
=
1
2
1
2
2
2
1
1
1
2
1
2
1
1
1
K
K
K
K
K
K
F
η
η
η
F分布の自由度:
ν1=2 (η1−K1+1) =
ν2=2K1=
q=1−α/2,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-a/2) (ν1, ν2) =
2)
2
2
1
1
η
η
K
K≦
の場合
□
次のように,F2,ν1及びν2を求める:
(
)(
)
(
)(
)=
+
−
−
+
+
+
−
=
1
2
2
1
2
2
1
2
1
1
2
1
1
1
2
K
K
K
K
K
K
F
η
η
η
F分布の自由度:
ν1=2 (K1+1) =
ν2=2 (η1−K1) =
q=1−α/2, ν1, ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-a/2) (ν1, ν2) =
I b) η1>K1+K2の場合
□
1)
2
2
1
1
η
η
K
K>
の場合
□
次のように,F1,ν1及びν2を求める:
(
)
(
)(
)=
+
−
+
−
=
1
2
1
2
1
1
2
2
2
1
1
K
K
K
K
F
η
η
F分布の自由度:
ν1=2 (K2+1) =
ν2=2K1=
q=1−α/2,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F (1-a/2) (ν1, ν2) =
2)
2
2
1
1
η
η
K
K≦
の場合
□
次のように,F2,ν1及びν2を求める:
(
)
(
)(
)=
+
−
+
−
=
1
2
1
2
2
2
1
1
1
2
2
K
K
K
K
F
η
η
F分布の自由度:
ν1=2 (K1+1) =
ν2=2K2=
q=1−α/2,ν1,ν2に対する表4の値を(必要ならば内挿して)読む:
F< (1-a/2) (ν1, ν2) =
2項近似の場合の自明でないケースの結論:
2
2
1
1
η
η
K
K>
の場合: F1≧F (1−α/2) (ν1, ν2)
2
2
1
1
η
η
K
K≦
の場合: F2≧F (1−α) (ν1, ν2)
ならば,H0を棄却する。そうでなければ,棄却しない。

53
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
II 正規近似
検定統計量の計算と表からの値の求め方:
a)
2
2
1
1
n
x
n
x>
の場合
□
×
次のように,z1を求める:
(
)(
)
(
)
(
)(
)(
)=
+
−
−
+
+
+
−
+
−
=
2
1
2
1
2
1
2
1
2
1
2
1
1
2
1
1
1
/
2
/1
n
n
x
x
n
n
x
x
n
n
x
x
n
n
n
x
z
z1=2.94
q=1−α/2に対する表3の値を読む:
u (1-α/2) =2.576
b)
2
2
1
1
n
x
n
x≦
の場合
□
次のように,z2を求める:
(
)(
)(
)
(
)(
)(
)=
+
−
−
+
+
+
+
−
+
=
2
1
2
1
2
1
2
1
2
1
2
1
1
2
1
1
2
/
2
/1
n
n
x
x
n
n
x
x
n
n
n
n
x
x
x
n
z
q=1−α/2に対する表3の値を読む:
u(1-α/2)=
正規近似の場合の自明でないケースの結論:
2
2
1
1
n
x
n
x>
の場合:
z1≧u1-α/2
2
2
1
1
n
x
n
x≦
の場合:
z2≧u1-α/2
ならば,H0を棄却する。そうでなければ,棄却しない。
検定結果:
H0を棄却する。
□
×
H0を棄却しない。 □
54
Z 9041-3 : 1999 (ISO 11453 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) 参考文献
[1] Walters, D.E., In defense of the arc sine approximation The Statistician, 28, 1979, pp.219-222.
[2] Haseman, J.K., Exact sample sizes for use with the Fisher−Irwin test for 2×2 tables. Biometrics, 34 (1978)
pp.106-109.
品質管理分野国際整合化分科会
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
今 井 秀 孝
工業技術院軽量研究所
柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
QCコンサルタント
門 山 允
元東京国際大学(故人)
兼 子 毅
武蔵工業大学
◎ 椿 広 計
筑波大学社会工学系
仁 科 健
名古屋工業大学工学部
○ 野 澤 昌 弘
東京理科大学経営学部
三佐雄 武 雄
QCコンサルタント
宮 津 隆
帝京科学大学理工学部
○ 山 田 秀
東京理科大学工学部
○ 岸 本 淳 司
株式会社SASインスティチュートジャパン
横 尾 恒 雄
QCコンサルタント
大 島 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会