Z 9041-2 : 1999
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。これによって,JIS Z 9042 : 1962,JIS Z 9043 : 1962,JIS Z 9044 : 1962,JIS Z 9045 : 1962,
JIS Z 9046 : 1965,JIS Z 9047 : 1979,JIS Z 9048 : 1979,JIS Z 9049 : 1965,JIS Z 9050 : 1963,JIS Z 9051 :
1963,JIS Z 9052 : 1963,JIS Z 9053 : 1963,JIS Z 9054 : 1966,JIS Z 9055 : 1966,JIS Z 9056 : 1979,JIS Z
9057 : 1966,JIS Z 9058 : 1966,JIS Z 9059 : 1966は廃止され,この規格に置き換えられる。
今回の改正では,1976年に第1版として発行されたISO 2854を基礎として用いた。
JIS Z 9041-2には,次に示す附属書がある。
附属書A(規定) 統計数値表
JIS Z 9041 : 1998は,一般名称を“データの統計的な解釈方法”として,次の各部によって構成される。
第1部:データの統計的記述
第2部:平均と分散に関する検定方法と推定方法
第3部:割合に関する検定方法と推定方法
第4部:平均と分散に関する検定方法の検出力
Z 9041-2 : 1999
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 2
3. 定義・記号 ····················································································································· 2
4. 確率変数の平均(,分散(2の推定 ··························································································· 2
5. 正規分布に従う確率変数の期待値及び分散に関する仮説の検定 ················································ 3
6. 正規分布に従う確率変数の期待値及び分散の信頼限界 ···························································· 4
7. 数値例 ··························································································································· 4
8. 書式 ······························································································································ 5
附属書A(規定) 統計数値表 ······························································································ 43
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9041-2 : 1999
データの統計的な解釈方法−
第2部:平均と分散に関する
検定方法と推定方法
Statistical Interpretation of Data
Part 2 : Techniques of estimation and test relating to
means and variances
序文 この規格は,1976年に第1版として発行されたISO 2854 : 1976 Statistical interpretation of data−Tech
niques of estimation and test relating to means and variances, ISO 2602 : 1980 Statistical interpretation of test
results−Estimation of the mean−Confidence intervalを基礎として作成した日本工業規格である。ただし,現
在進行中のISO/TC 69/SC 3/WG 3によるISO 2854の改訂作業方針で,これにISO 2602 : 1980及びISO
3301 : 1975 Statistical interpretation of data−Comparison of two means in the case of paired observationsを統合す
ることが決定されているため,この規格にはISO 2602 : 1980及びISO 3301 : 1975の技術的内容を含めた。
1. 適用範囲
1.1
この規格は,次の統計的な取り扱いに必要な方法について規定する。
a) 確率変数の平均(期待値)又は分散の信頼区間を定める。
b) 確率変数の平均又は分散の値に関する仮説をサンプルによって検定する。
1.2
これらの方法は,測定値が互いに独立な観測から生じたとみなせる場合にだけ有効である。
有限母集団の場合には,データが独立とみなし得るときに適用できる。これは有限母集団に比べてサン
プルサイズが十分に小さければ成立する。経験則から,サンプルサイズが母集団の大きさの1/10より小さ
いことが望ましいといわれている。
1.3
これらの方法の適用に当たっては,確率変数は正規分布に従うと仮定する。対象としているデータ
の集団に関する広はん(汎)な経験からこの仮定が実証可能な場合には,確率変数は正規分布に従うとみ
なすことができる。確率変数が正規分布に従うことを検討する方法は,JIS Z 9041-1又はISO 5479 : 1997
による。
なお,サンプルに基づかない外的な情報に基づいて正規性の仮説を認める場合もある。正規性の仮説が
棄却された場合には,この規格の方法は用いない方がよい。しかし,正規性の仮説が棄却されなかったか
らといって,確率変数が正規分布に従っている保証はない。確率紙を用いれば,正規性に関するグラフィ
カルな検討が可能であり,正規分布からのずれが大きくなれば非正規性を明らかにすることができよう。
確率紙による方法の適用は,正規分布からのずれのタイプを識別できることもあるので,正規分布の数値
的検討の補助として位置づけられる。
2
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
確率変数の正規性が疑われる場合は,この規格の方法を用いずに,正規性の仮定を必要としない方法を
用いることが望ましい。
一方,確率変数の期待値μや分散σ2の不偏推定量として,xやS2を用いる際には正規性の仮定は必要と
しない。
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格は,その最新版(追補を含む)を適用する。
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
備考 ISO 3534-1 : 1993 Statistics−Vocabulary and symbols−Part 1 : Probability and general statistical
termsからの引用事項は,この規格の該当事項と同等である。
JIS Z 9041-1 データの統計的な解釈方法−第1部:データの統計的記述
JIS Z 9041-4 データの統計的な解釈方法−第4部:平均と分散に関する検定方法の検出力
ISO 5479 : 1997 Statistical interpretation of data−Tests for departure from the normal distribution
3. 定義・記号
3.1
用語の定義 この規格で用いる主な用語の定義は,JIS Z 8101-1によるほか,次による。
a) 標準化正規変量 正規分布に従う確率変数を標準化して得られる確率変数。
3.2
記号 この規格で用いる主な記号は,JIS Z 8101-1によるほか,次による。
x 測定値
U 標準化正規変量
uα 標準正規分布の100α%点(下側確率)
ta (ν) 自由度vのt分布の100α%点(下側確率)
X2α (ν) 自由度vのX2分布の100α%点(下側確率)
F (ν1, ν2) 自由度ν1,ν2の分散比統計量
Fα (ν1, ν2) 自由度ν1,ν2の分散比統計量の100α%点(下側確率)
4. 確率変数の平均μ,分散σ2の推定値x及びs2の計算 平均値x及び標本分散s2は,一連の測定値の共通
平均μ及び分散σ2の理論的にも実用的にも有用な推定値である。標本標準偏差sは,標準偏差σの有用な推
定値である。
4.1
n個の測定値xi,i=1,...,nのx及びs2の計算は,次による。
∑
n
i
ix
n
x
1
1
=
=
−
−∑
∑
n
i
n
i
i
i
x
n
x
n
s
1
2
1
2
2
1
1
1
=
=
=
4.2
度数分布において値xjがnj回生じる場合 (j=1,...,k),x及びs2の度数分布からの計算は,次によ
る。
3
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑
k
j
j
n
n
1
=
=
∑
k
j
j
jx
n
n
x
1
1
=
=
−
−∑
∑
k
j
k
j
j
j
j
j
x
n
n
x
n
n
s
1
2
1
2
2
1
1
1
=
=
=
4.3
級分けされた分布からのx及びs2の計算 測定値の個数が十分大きく,例えば50個以上の場合には,
データを級(群)に分割するのが適当なこともある。実際,測定値は,事前に級分けされた形式でだけ利
用可能な場合も多い。級の数をkとし,級jの中心をxjとし,級jに属する測定値の個数をnjとすれば,x
及びs2は4.2の方法で計算できる。この値は,級分けされていない場合の計算の近似値である。
備考 ここで規定した方法は,データの原点及び/又は単位を変更することによって計算を大幅に減
らすことができる場合が多い。特に,精度の低い電卓又はコンピュータで分散を計算するとき
には,十分な精度を得るために原点を変えることが必要な場合がある。
5. 正規分布に従う確率変数の期待値及び分散に関する仮説の検定
5.1
一般的注意 正規分布に従う確率変数の平均,期待値及び分散に関する主要な帰無仮説と検定の実
用的計算手順を書式化して8.(書式)に示した。これらの手順を適用するためには適切な帰無仮説を選択
する必要がある。対立仮説H1はこの書式に与えられていないが,これは対立仮説は帰無仮説に含まれない
μ,σのすべての値を含むことがあるからである。
例えば,分散既知の状況で,平均を与えられた値と比較するために書式Aを用いる際には,次の帰無仮
説のいずれかを対応する対立仮説とともに選ばなくてはならない。
A) 片側検定H0 : μ≧μ0H1 : μ<μ0
B) 片側検定H0 : μ≦μ0H1 : μ>μ0
C) 両側検定H0 : μ=μ0H1 : μ≠μ0
検定の結果は,帰無仮説を棄却するか,棄却できないかのいずれかである。
帰無仮説の棄却は,対立仮説の受容を意味する。一方,帰無仮説を棄却できないことは,必ずしも帰無
仮説を受容することを意味しない。
サンプルサイズnと有意水準αを定めるためには,検定のOC関数,すなわち,検出力関数を参考にす
るのが望ましい。この方法については,JIS Z 9041-4に示されている。
5.2
平均に関する仮説の処置 書式A,Aʼ及びC,Cʼ並びにK,Kʼは,分散が既知であるか否かによっ
て使い分ける。書式中で,分散σ2が既知の場合には標準正規分布の分位点が,未知の場合にはt分布の分
位点が用いられている。ここで規定する方法の適用の便宜を図るため,α=0.05及びα=0.01に対する標準
正規分布の分位点を附属書Aの表1に,t分布の分位点の値を附属書Aの表2に示す。
5.3
分散に関する仮説の処置 書式E〜Hまででは,算術平均が期待値の推定値として用いられている。
算術平均がその期待値で置き換えられる場合には,対応する自由度は1増やすことになる。
ここで規定する方法の適用の便宜を図るため,α=0.05及びα=0.01に対するX2α (ν),X21−α (ν),X2α/2, (ν)
X21−α/2 (ν) の値を附属書Aの表3に,F1−α (ν1, ν2) 及びF1−α/2 (ν1, ν2) の値を附属書Aの表4に示す。
4
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
なお,Fα (ν1, ν2) 及びFα/2 (ν1, ν2) の値は,関係式
Fα (ν1, ν2) =
)
,
(
1
1
2
1
ν
ν
α
−
F
から導出することができる。
6. 正規分布に従う確率変数の期待値及び分散の信頼限界 この規格では,各検定に対応した信頼限界の
決定法も規定している。σ,及びσ1/σ2の信頼限界は,それぞれ,σ2,並びにσ12/σ22の信頼限界の平方根か
ら求めることができる。
7. 数値例
7.1
書式A,Aʼ;B,Bʼ;C,Cʼ,D,Dʼ;E,F,G,Hのための例 8.(書式)を参照する。
特性と観測の方法
特性:2種の糸のサンプルについての切断荷重の測定値データ(単位はN)。
観測の方法:正規性及び外れ値に関する検討が事前に行われている。
アイテム:糸1は,10個,糸2は12個のデータが取られている。
表1 糸の切断荷重 (N) の測定値
糸1
糸2
18.4
18.0
18.8
18.2
19.2
17.0
19.9
18.4
17.2
17.9
20.4
19.6
17.8
17.6
18.2
16.2
19.4
19.0
18.6
16.6
20.0
18.0
7.2
書式K,Kʼ;L,Lʼのための例 取り扱いについては,8.(書式)を参照する。
特性:2種の糸のサンプルについての水分含有率 (%)
アイテム1:n=9の糸のサンプルについて,分析方法1で水分含有率を測定。
アイテム2:アイテム1の同一サンプルを分析方法2で水分含有率を測定。
表2 水分含有率 (%) の測定値
アイテム
分析方法1による
水分含有率
分析方法2による
水分含有率
含有率の差
D=Xi−Yi
Xi
Y1
1
18.2
17.0
1.2
2
20.1
19.1
1.0
3
16.4
17.0
−0.6
4
21.5
23.0
−1.5
5
16.5
16.0
0.5
6
17.4
18.1
−0.7
7
20.1
19.3
0.8

5
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
アイテム
分析方法1による
水分含有率
分析方法2による
水分含有率
含有率の差
D=Xi−Yi
Xi
Y1
8
16.9
17.6
−0.7
9
19.2
17.3
1.9
8. 書式 ここでは,次の統計的方法を規定する。各方法は,書式A,Aʼ,B,Bʼ,C,Cʼ,D,Dʼ,E,F,
G,Hの手順に従って実施するのが望ましい。
a) 与えられた値と平均の比較(分散既知)
手順は,書式Aによる。
b) 与えられた値と平均の比較(分散未知)
手順は,書式Aʼによる。
c) 平均の信頼限界(分散既知)
手順は,書式Bによる。
d) 平均の信頼限界(分散未知)
手順は,書式Bʼによる。
e) 二つの対応のない測定値の平均の比較(分散既知)
手順は,書式Cによる。
f)
二つの対応のない測定値の平均の比較(分散未知。ただし,二つの分散を等しいと仮定してよい場合)
手順は,書式Cʼによる。
g) 二つの対応のない測定値の平均の比較(分散未知。ただし,二つの分散が等しくない場合)
手順は,書式C”による。
h) 二つの対応のない測定値の平均の差の信頼区間(分散既知)
手順は,書式Dによる。
i)
二つの対応のない測定値の平均の差の信頼区間(分散未知。ただし,二つの分散を等しいと仮定して
よい場合)
手順は,書式Dʼによる。
j)
二つの対応のない測定値の平均の差の信頼区間(分散未知。ただし,二つの分散が等しくない場合)
手順は,書式D”による。
k) 分散又は標準偏差と与えられた値との比較
手順は,書式Eによる。
l)
分散又は標準偏差の信頼区間
手順は,書式Fによる。
m) 二つの分散又は二つの標準偏差の比較
手順は,書式Gによる。
n) 二つの分散又は二つの標準偏差の比の信頼区間
手順は,書式Hによる。
o) 二つの対応のある測定値の平均の差と与えられた値の比較(差の分散既知)
手順は,書式Kによる。
p) 二つの対応のある測定値の平均の差と与えられた値の比較(差の分散未知)
6
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
手順は,書式Kʼによる。
q) 二つの対応のある測定値の平均の差の信頼区間(差の分散既知)
手順は,書式Lによる。
r) 二つの対応のある測定値の平均の差の信頼区間(差の分散未知)
手順は,書式Lʼによる。

7
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式A 与えられた値と平均の比較(分散既知)
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ≧μ0 □
B) 片側検定H0 : μ≦μ0 □
C) 両側検定H0 : μ=μ0 □
与えられた値:μ0=
既知の分散の値:σ2=
既知の標準偏差の値:σ=
有意水準:α=
測定値の個数:n=
統計数値表の値(附属書A表1参照)
A),B)の場合 u1−α=
C)の場合
u1−α/2=
計算
x=
D=x−μ0=
A),B)の場合 A=u1−ασ/n
C)の場合
B=u1−α/2σ/n
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

8
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Aの使用例
確率変数と観測方法:
糸の切断荷重
アイテム:糸1の試験片(7.1参照)
帰無仮説と検定のタイプ
A) 片側検定H0 : μ≧μ0 □
B) 片側検定H0 : μ≦μ0 □
C) 両側検定H0 : μ=μ0 □
×
与えられた値:μ0=19.4N
既知の分散の値:σ2=
既知の標準偏差の値:σ=0.85N
有意水準:α=0.05
測定値の個数:n=10
統計数値表の値(附属書A表1参照)
A),B)の場合 u1−α=
C)の場合
u1−α/2=1.960
計算
x=18.79N
D=x−μ0=−0.61 N
A),B)の場合 A=u1−aσ/n
C)の場合
B=u1−a/2σ/n=0.526 8N
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
×
□
糸1の切断荷重の期待値は,与えられた値μ0=19.4Nと有意水準5%で有意な差が検出された。

9
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Aʼ 与えられた値と平均の比較(分散未知)
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ≧μ0 □
B) 片側検定H0 : μ≦μ0 □
C) 両側検定H0 : μ=μ0 □
与えられた値:μ0=
有意水準:α=
測定値の個数:n=
自由度:ν=n−1=
統計数値表の値(附属書A表2参照)
A),B)の場合 t1−α(ν)=
C)の場合
t1−α/2(ν)=
計算
x=
s2=
s=
D=x−μ0=
A),B)の場合 A=t1−a(ν)s/n
C)の場合
B=t1−a/2(ν)s/n
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

10
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Aʼの使用例
確率変数と観測方法:
糸の切断荷重
アイテム:糸1の試験片(7.1参照)
帰無仮説と検定のタイプ
A) 片側検定H0 : μ≧μ0 □
B) 片側検定H0 : μ≦μ0 □
C) 両側検定H0 : μ=μ0 □
×
与えられた値:μ0=19.4N
有意水準:α=0.05
測定値の個数:n=10
自由度:ν=n−1=9
統計数値表の値(附属書A表2参照)
A),B)の場合 t1−α(ν)=
C)の場合
t1−α/2(ν)=2.262
計算
x=18.79N
s2=0.9343N2
s=0.9666N
D=x−μ0=
A),B)の場合 A=t1−α(ν)s/n
C)の場合
B=t1−α/2(ν)s/n=0.691 4N
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
糸1の切断荷重の期待値は,与えられた値μ0=19.4Nと有意水準5%で有意な差が検出されなかった。

11
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式B 平均の信頼限界(分散既知)
確率変数と観測方法:
アイテム:
注:
μの信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
既知の分散の値:σ2=
既知の標準偏差の値:σ=
信頼係数:1−α=
測定値の個数:n=
統計数値表の値(附属書A表1参照)
A),B)の場合 u1−α=
C)の場合
u1−α/2=
計算
x=
A)の場合
u1−ασ/n=
A=x+u1−ασ/n=
B)の場合
u1−ασ/n=
B=x−u1−ασ/n=
C)の場合
u1−α/2−σ/n=
C=x−u1−α/2σ/n=
D=x+u1−α/2σ/n=
信頼限界の報告
A)の場合 μ≦A,
B)の場合 μ≧B,
C)の場合 C≦μ≦D
結果
A)の場合 μ≦
B)の場合 μ≧
C)の場合 ≦μ≦

12
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Bの使用例
確率変数と観測方法:
糸の切断荷重
アイテム:糸1の試験片(7.1参照)
μの信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
既知の分散の値:σ2=
既知の標準偏差の値:σ=0.85N
信頼係数:1−α=0.95
測定値の個数:n=10
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=1.96
計算
x=18.79N
A)の場合
u1−ασ/n=
A=x+u1−ασ/n=
B)の場合
u1−ασ/n=
B=x−u1−ασ/n=
C)の場合
u1−α/2σ/n=0.526 8N
C=x−u1−α/2σ/n=18.263N
D=x+u1−α/2σ/n=19.317N
信頼限界の報告
A)の場合 μ≦A,
B)の場合 μ≧B,
C)の場合 C≦μ≦D
結果
A)の場合 μ≦
B)の場合 μ≧
C)の場合 18.26N≦μ≦19.32N
試験片の切断荷重の平均値は,信頼係数1−α=95%で,18.26Nと19.32Nとの間になる。

13
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Bʼ 平均の信頼限界(分散未知)
確率変数と観測方法:
アイテム:
注:
μの信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
信頼係数:1−α=
測定値の個数:n=
自由度:ν=n−1=
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−α/2 (ν) =
計算
x=
s2=
s=
A)の場合
t1−α (ν) s/n=
A=x+t1−α (ν) s/n=
B)の場合
t1−α (ν) s/n=
B=x−t1−α (ν) s/n=
C)の場合
t1−α/2 (ν) s/n=
C=xt1−α/2 (ν) s/n=
D=x+t1−α/2 (ν) s/n=
信頼限界の報告
A)の場合 μ≦A,
B)の場合 μ≧B,
C)の場合 C≦μ≦D
結果
A)の場合 μ≦
B)の場合 μ≧
C)の場合 ≦μ≦

14
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Bʼの使用例
確率変数と観測方法:
糸の切断荷重
アイテム:糸1の試験片(7.1参照)
注:
μの信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
信頼係数:1−α=0.95
測定値の個数:n=10
自由度:ν=n−1=9
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−a/2 (ν) =t0.975 (9) =2.262
計算
x=18.79 N
s2=0.934 3N2
s=0.966 6 N
A)の場合
t1−α (ν) s/n=
A=x+t1−α (ν) s/n=
B)の場合
t1−α (ν) s/n=
B=x−t1−α (ν) s/n=
C)の場合
t1−α/2 (ν) s/n=0.6914N
C=x−t1−α/2 (ν) s/n=18.099N
D=x+t1−α/2 (ν) s/n=19.481N
信頼限界の報告
A)の場合 μ≦A,
B)の場合 μ≧B,
C)の場合 C≦μ≦D
結果
A)の場合 μ≦
B)の場合 μ≧
C)の場合 18.10N≦μ≦19.48N
試験片の切断荷重の平均値は,信頼係数1−α=95%で,18.10Nと19.48Nとの間になる。

15
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式C 二つの対応のない測定の平均の比較(分散既知)
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1≧μ2 □
B) 片側検定H0 : μ1≦μ2 □
C) 両側検定H0 : μ1=μ2 □
既知の分散の値:σ12=
σ22=
有意水準:α=
測定値の個数:n1=
n2=
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=
計算
1x=
2x=
D=1x−2x=
σD=
2
2
2
1
2
1
n
n
σ
σ+
=
A),B)の場合
A=u1−ασD
C)の場合
B=u1−α/2σD
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

16
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Cの使用例
確率変数と観測方法:
第1確率変数,第2確率変数ともに糸の切断荷重
アイテム:1. 糸1の試験片,2. 糸2の試験片(7.1参照)
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1≧μ2 □
B) 片側検定H0 : μ1≦μ2 □
C) 両側検定H0 : μ1=μ2 □
×
既知の分散の値:σ12=0.722 5N2
σ22=1.000 0N2
有意水準:α=0.05
測定値の個数:n1=10
n2=12
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=1.960
計算
1x=18.79 N
2x=18.04 N
D=1x−2x=0.75 N
σD=
2
2
2
1
2
1
n
n
σ
σ+
=0.3944 N
A),B)の場合
A=u1−ασD
C)の場合
B=u1−α/2σD=0.773 1N
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
二つの糸の切断荷重の平均の間には有意水準5%で有意な差が見出されなかった。

17
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Cʼ 二つの対応のない測定の平均の比較(分散未知。ただし,等しいと仮定してよい場合)
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1≧μ2 □
B) 片側検定H0 : μ1≦μ2 □
C) 両側検定H0 : μ1=μ2 □
有意水準:α=
測定値の個数:n1=
n2=
自由度:ν=n1+n2−2=
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−α/2 (ν) =
計算
1x=
2x=
s12=
s22=
D=1x−2x=
Q= (n1−1) s12+ (n2−1) s22
sD=
ν
2
1
2
1
n
n
Q
n
n+
=
A),B)の場合
A=t1−α (ν) sD
C)の場合
B=t1−α/2 (ν) sD
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

18
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Cʼの使用例
確率変数と観測方法:
第1確率変数,第2確率変数ともに糸の切断荷重
アイテム:1. 糸1の試験片,2. 糸2の試験片(7.1参照)
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1≧μ2 □
B) 片側検定H0 : μ1≦μ2 □
C) 両側検定H0 : μ1=μ2 □
×
有意水準:α=0.05
測定値の個数:n1=10
n2=12
自由度:ν=n1+n2−2=20
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−α/2 (ν) =t0.975 (20) =2.086
計算
1x=18.79 N
2x=18.04 N
s12=0.934 3N2
s22=1.282 7N2
D=1x−2x=0.75 N
Q= (n1−1) s12+ (n2−1) s22=22.518N2
sD=
ν
2
1
2
1
n
n
Q
n
n+
=0.454 3N
A),B)の場合
A=t1−α (ν) sD
C)の場合
B=t1−α/2 (ν) sD=0.947 7N
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
二つの糸の切断荷重の平均の間には有意水準5%では有意な差が見出されなかった。

19
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式C” 二つの対応のない測定の平均の比較(分散未知。ただし,等しくない場合)
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1≧μ2 □
B) 片側検定H0 : μ1≦μ2 □
C) 両側検定H0 : μ1=μ2 □
有意水準:α=
測定値の個数:n1=
n2=
計算
1x=
2x=
s12=
s22=
D=1x−2x=
sD=
2
2
2
1
2
1
n
s
n
s
+
=
C=
2
2
2
1
2
1
1
2
1
n
s
n
s
n
s
+
=
自由度:ν=
1
)
1(
1
1
2
2
1
2
−
−
+
−
n
c
n
c
=
νを切り上げた整数値:
A),B)の場合
t1−α (ν) =
A=t1−α (ν ) sD=
C)の場合
t1−α/2 (ν) =
B=t1−α/2 (ν) sD=
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

20
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式C”の使用例
確率変数と観測方法:
第1確率変数,第2確率変数ともに糸の切断荷重
アイテム:1. 糸1の試験片,2. 糸2の試験片(7.1参照)
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1≧μ2 □
B) 片側検定H0 : μ1≦μ2 □
C) 両側検定H0 : μ1=μ2 □
×
有意水準:α=0.05
測定値の個数:n1=10
n2=12
計算
1x=18.79N
2x=18.04N
s12=0.934 3N2
s22=1.282 7N2
D=1x−2x=0.75N
sD=
2
2
2
1
2
1
n
s
n
s
+
=0.447 6
C=
2
2
2
1
2
1
1
2
1
n
s
n
s
n
s
+
=0.466 4
自由度:ν=
1
)
1(
1
1
2
2
1
2
−
−
+
−
n
c
n
c
=19.98
νを切り上げた整数値:20
A),B)の場合
t1−α (ν) =
A=t1−α (ν) sD=
C)の場合
t1−α/2 (ν) =t0.975 (20) =2.086
B=t1−α/2 (ν) sD=0.933 7
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
二つの糸の切断荷重の平均の間には有意水準5%で有意な差が見出されなかった。

21
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式D 二つの対応のない測定の平均の差の信頼区間(分散既知)
確率変数と観測方法:
アイテム:
注:
△=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
既知の分散の値:σ12=
σ22=
有意水準:1−α=
測定値の個数:n1=
n2=
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=
計算
1x=
2x=
σD=
2
2
2
1
2
1
n
n
σ
σ+
=
A)の場合
u1−ασD=
A=1x−2x+u1−ασD=
B)の場合
u1−ασD=
B=1x−2x−u1−ασD=
C)の場合
u1−α/2σD=
C=1x−2x−u1−α/2σD=
D=1x−2x+u1−α/2σD=
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 ∆≦
B)の場合 ∆≧
C)の場合 ≦∆≦

22
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Dの使用例
確率変数と観測方法:
第1確率変数,第2確率変数ともに糸の切断荷重
アイテム:1. 糸1の試験片,2. 糸2の試験片(7.1参照)
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
既知の分散の値:σ12=0.722 5N2
σ22=1.000 0N2
有意水準:1−α=0.95
測定値の個数:n1=10
n2=12
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=u0.975=1.960
計算
1x=18.79N
2x=18.04N
σD=
2
2
2
1
2
1
n
n
σ
σ+
=0.394 4N
A)の場合
u1−ασD=
A=1x−2x−u1−ασD=
B)の場合
μ1−ασD=
B=1x−2x−u1−ασD=
C)の場合
u1−α/2σD=0.773 1 N
C=1x−2x−u1−α/2σD=−0.023 1N
D=1x−2x+u1−α/2σD=1.523 1N
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 ∆≦
B)の場合 ∆≧
C)の場合 −0.02N≦∆≦1.52N
糸1と糸2との切断荷重の平均の差は,信頼係数1−α=0.95で,−0.02Nと1.52Nとの間になる。

23
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Dʼ 二つの対応のない測定の平均の差の信頼区間(分散未知。ただし,等しいと仮定してよい場合)
確率変数と観測方法:
アイテム:
注:
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
信頼係数:1−α=
測定値の個数:n1=
n2=
自由度:ν=n1+n2−2=
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−α/2 (ν) =
計算
1x=
2x=
s12=
s22=
Q= (n1−1) s12+ (n2−1) s22
sd=
ν
2
1
2
1
n
n
Q
n
n+
=
A)の場合
t1−α (ν) sd=
A=1x−2x+t1−α (ν) sd=
B)の場合
t1−α (ν) sd=
B=1x−2x−t1−α (ν) sd=
C)の場合
t1−α/2 (ν) sd=
C=1x−2x−t1−α/2 (ν) sd=
D=1x−2x+t1−α/2 (ν) sd=
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 ∆≦
B)の場合 ∆≧
C)の場合 ≦∆≦

24
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Dʼの使用例
確率変数と観測方法:
第1確率変数,第2確率変数ともに糸の切断荷重
アイテム:1. 糸1の試験片,2. 糸2の試験片(7.1参照)
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
信頼係数:1−α=0.95
測定値の個数:n1=10
n2=12
自由度:ν=n1+n2−2=20
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−α/2 (ν) =t0.975 (20) =2.086
計算
1x=18.79N
2x=18.04N
s12=0.934 3N2
s22=1.282 7N2
Q= (n1−1) s12+ (n2−1) s22=22.518N2
sd=
ν
2
1
2
1
n
n
Q
n
n+
=0.454 3N
A)の場合
t1−α (ν) sd=
A=1x−2x+t1−α (ν) sd=
B)の場合
t1−α (ν) sd
B=1x−2x−t1−α (ν) sd=
C)の場合
t1−α/2 (ν) sd=0.947 7N
C=1x−2x−t1−α/2 (ν) sd=−0.197 7N
D=1x−2x+t1−α/2 (ν) sd=1.697 7N
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 ∆≦
B)の場合 ∆≧
C)の場合 −0.20N≦∆≦1.70N
糸1と糸2との切断荷重の平均の差は,信頼係数1−α=0.95で,−0.20Nと1.70Nとの間になる。

25
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式D” 二つの対応のない測定の平均の差の信頼区間(分散未知。ただし,等しくない場合)
確率変数と観測方法:
アイテム:
注:
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
有意水準:1−α=
測定値の個数:n1=
n2=
計算
1x=
2x=
s12=
s22=
sd=
2
2
2
1
2
1
n
s
n
s
+
=
C=
2
2
2
1
2
1
1
2
1
n
s
n
s
n
s
+
=
自由度:ν=
1
)
1(
1
1
2
2
1
2
−
−
+
−
n
c
n
c
=
vを切り上げた整数値:
A)の場合
t1−α (ν) =
t1−α (ν) sd=
A=1x−2x+t1−α (ν) sd=
B)の場合
t1−α (ν) =
t1−α (ν) sd=
B=1x−2x−t1−α (ν) sd=
C)の場合
t1−α/2 (ν) =
t1−α/2 (ν) sd=
C=1x−2x−t1−α/2 (ν) sd=
D=1x−2x+t1−α/2 (ν) sd=
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 ∆≦
B)の場合 ∆≧
C)の場合 ≦∆≦

26
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式D”の使用例
確率変数と観測方法:
第1確率変数,第2確率変数ともに糸の切断荷重
アイテム:1. 糸1の試験片,2. 糸2の試験片(7.1参照)
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
有意水準:1−α=0.95
測定値の個数:n1=10
n2=12
計算
1x=18.79N
2x=18.04N
s12=0.934 3N2
s22=1.282 7N2
sd=
2
2
2
1
2
1
n
s
n
s
+
=0.447 6
C=
2
2
2
1
2
1
1
2
1
n
s
n
s
n
s
+
=0.466 4
自由度:ν=
1
)
1(
1
1
2
2
1
2
−
−
+
−
n
c
n
c
=19.98
νを切り上げた整数値:20
A)の場合
t1−α (ν) =
t1−α (ν) sd=
A=1x−2x+t1−α (ν) sd=
B)の場合
t1−α (ν) =
t1−α (ν) sd=
B=1x−2x−t1−α (ν) sd=
C)の場合
t1−α/2 (ν) =t0.975 (20) =2.086
t1−α/2 (ν) sd=0.933 7
C=1x−2x−t1−α/2 (ν) sd=−0.183 7
D=1x−2x+t1−α/2 (ν) sd=1.683 7
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 ∆≦
B)の場合 ∆≧
C)の場合 −0.18N≦∆≦1.68N
糸1と糸2との切断荷重の平均の差は,信頼係数1−α=0.95で,−0.18Nと1.68Nとの間になる。

27
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式E 分散又は標準偏差と与えられた値との比較
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : σ2≧σ02 □
B) 片側検定H0 : σ2≦σ02 □
C) 両側検定H0 : σ2=σ02 □
与えられた値:σ02=
有意水準:α:
測定値の個数:n=
自由度:ν=n−1=
統計数値表の値(附属書A表3参照)
A)の場合
X2α (ν) =
B)の場合
X21−α (ν) =
C)の場合
X21−α/2 (ν) =
X21−α/2 (ν) =
計算
s2=
A=
2
0
2
)1
(
σ
s
n−
検定の解釈
A)の場合 A<X2α (ν),
B)の場合 A>X21−α (ν),
C)の場合 A<X2α/2 (ν) 又はA>X21−α/2 (ν) のとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

28
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Eの使用例
確率変数と観測方法:
糸の切断荷重
アイテム:糸1の試験片(7.1参照)
帰無仮説と検定のタイプ
A) 片側検定H0 : σ2≧σ02 □
B) 片側検定H0 : σ2≦σ02 □
×
C) 両側検定H0 : σ2=σ02 □
与えられた値:σ02=0.600N2
有意水準:α=0.05
測定値の個数:n=10
自由度:ν=n−1=9
統計数値表の値(附属書A表3参照)
A)の場合
X2α (ν) =
B)の場合
X21−α (ν) =X20.95 (9) =16.92
C)の場合
X21−α/2 (ν) =
X21−α/2 (ν) =
計算
s2=0.934 3N2
A=
2
0
2
)1
(
σ
s
n−
=14.015
検定の解釈
A)の場合 A<X2α (ν),
B)の場合 A>X21−α (ν),
C)の場合 A<X2α/2 (ν) 又はA>X21−α/2 (ν) のとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
糸1の切断荷重の分散は,与えられた値σ02=0.600 0N2と有意水準5%で有意な差が検出されなかった。

29
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式F 分散又は標準偏差の信頼区間
確率変数と観測方法:
アイテム:
注:
σ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
信頼係数:1−α=
測定値の個数:n=
自由度:ν=n−1=
統計数値表の値(附属書A表3参照)
A)の場合
X2α (ν) =
B)の場合
X21−α (ν) =
C)の場合
X2α/2 (ν) =
X21−α/2 (ν) =
計算
s2=
A)の場合
A=
)
(
)1
(
2
2
ν
χα
s
n−
B)の場合
B=
)
(
)1
(
1
2
2
ν
χ
α
−
−s
n
C)の場合
C=
)
(
)1
(
2
/
1
2
2
ν
χ
α
−
−s
n
D=
)
(
)1
(
2
/
2
2
ν
χα
s
n−
信頼限界の報告
A)の場合 σ2≦A,
B)の場合 σ2≧B,
C)の場合 C≦σ2≦D
結果
A)の場合 □ σ2≦
B)の場合 □ σ2≧
C)の場合 □ ≦σ2≦
σの信頼限界はσ2の信頼限界の正の平方根となる。

30
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Fの使用例
確率変数と観測方法:
糸の切断荷重
アイテム:糸1の試験片(7.1参照)
σ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
信頼係数:1−α=0.95
測定値の個数:n=10
自由度:ν=n−1=9
統計数値表の値(附属書A表3参照)
A)の場合
X2α (ν) =
B)の場合
X21−α (ν) =
C)の場合
X2α/2 (ν) =X20.025 (9) =2.70
X21−α/2 (ν) =X20.975 (9) =19.02
計算
s2=0.934 3N2
A)の場合
A=
)
(
)1
(
2
2
ν
χα
s
n−
B)の場合
B=
)
(
)1
(
1
2
2
ν
χ
α
−
−s
n
C)の場合
C=
)
(
)1
(
2
/
1
2
2
ν
χ
α
−
−s
n
=0.442 1N2
D=
)
(
)1
(
2
/
2
2
ν
χα
s
n−
=3.114 3N2
信頼限界の報告
A)の場合 σ2≦A,
B)の場合 σ2≧B,
C)の場合 C≦σ2≦D
結果
A)の場合 σ2≦
B)の場合 σ2≧
C)の場合 0.442N2≦σ2≦3.114N2
糸1の切断荷重の分散は,信頼係数1−α=95%で,0.442N2と3.114N2の間にある。
σの信頼限界はσ2の信頼限界の正の平方根となり,ここでは0.66Nと1.75Nとなる。

31
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式G 二つの分散又は標準偏差の比較
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : σ12≧σ22 □
B) 片側検定H0 : σ12≦σ22 □
C) 両側検定H0 : σ12=σ22 □
有意水準:α=
測定値の個数:n1=
n2=
自由度:
ν1=n1−1=
ν2=n2−1=
統計数値表の値(附属書A表4参照)
A)の場合
F1−α (ν2, ν1) =
B)の場合
F1−α (ν1, ν2) =
C)の場合
F1−α/2 (ν1, ν2) =
F1−α/2 (ν2, ν1) =
計算
s12=
s22=
A=
2
2
2
1
s
s
A)の場合 Fα (ν1, ν2) =1/F1−α (ν2, ν1) =
C)の場合 Fα/2 (ν1, ν2) =1/F1−α/2 (ν2, ν1) =
検定の解釈
A)の場合 A<Fα (ν1, ν2)
B)の場合 A>F1−α (ν1, ν2)
C)の場合 A<Fα/2 (ν1, ν2) 又はA>F1−α/2 (ν2, ν1)
のとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

32
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Gの使用例
確率変数と観測方法:
糸の切断荷重
アイテム: 糸1の試験片
糸2の試験片(7.1参照)
帰無仮説と検定のタイプ
A) 片側検定H0 : σ12≧σ22 □
B) 片側検定H0 : σ12≦σ22 □
C) 両側検定H0 : σ12=σ22 □
×
有意水準:α=0.05
測定値の個数:n1=10
n2=12
自由度: ν1=n1−1=9
ν2=n2−1=11
統計数値表の値(附属書A表4参照)
A)の場合
F1−α (ν2, ν1) =
B)の場合
F1−α (ν1, ν2) =
C)の場合
F1−α/2 (ν1, ν2) =F0.975 (9, 11) =3.59
F1−α/2 (ν2, ν1) =F0.975 (11, 9) =3.91
計算
s12=0.934 3N2
s22=1.282 7N2
A=
2
2
2
1
s
s=0.728 4
A)の場合 Fα (ν1, ν2) =1/F1−α (ν2, ν1) =
C)の場合 Fα/2 (ν1, ν2) =1/F1−α/2 (ν2, ν1) =0.256
検定の解釈
A)の場合 A<Fα (ν1, ν2)
B)の場合 A>F1−α (ν1, ν2)
C)の場合 A<Fα/2 (ν1, ν2) 又はA>F1−α/2 (ν2, ν1)
のとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
糸1と糸2の切断荷重の分散は,有意水準5%で有意な差が検出されなかった。

33
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式H 二つの分散又は標準偏差の比の信頼区間
確率変数と観測方法:
アイテム:
注:
σ12/σ22の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
信頼係数:1−α=
測定値の個数:n1=
n2=
自由度: ν1=n1−1=
ν2=n2−1=
統計数値表の値(附属書A表4参照)
A)の場合
F1−α (ν2, ν1) =
B)の場合
F1−α (ν1, ν2) =
C)の場合
F1−α/2 (ν1, ν2) =
F1−α/2 (ν2, ν1) =
計算
s12=
s22=
2
2
2
1
s
s=
A)の場合
A=
2
2
2
1
s
sF1−α (ν2, ν1) =
B)の場合
B=
2
2
2
1
s
s/F1−α (ν2, ν1) =
C)の場合
C=
2
2
2
1
s
s/F1−α/2 (ν1, ν2) =
D=
2
2
2
1
s
sF1−α/2 (ν1, ν2) =
信頼限界の報告
A)の場合 σ12/σ22≦A
B)の場合 σ12/σ22≧B
C)の場合 C≦σ12/σ22≦D
結果
A)の場合□ σ12/σ22≦
B)の場合□ σ12/σ22≧
C)の場合□ ≦σ12/σ22≦
σ1/σ2の信頼限界はσ12/σ22の信頼限界の正の平方根となる。

34
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Hの使用例
確率変数と観測方法:
糸の切断荷重
アイテム: 糸1の試験片
糸2の試験片(7.1参照)
σ12/σ22の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
信頼係数:1−α=0.95
測定値の個数:n1=10
n2=12
自由度:
ν1=n1−1=9
ν2=n2−1=11
統計数値表の値(附属書A表4参照)
A)の場合
F1−α (ν2, ν1) =
B)の場合
F1−α (ν1, ν2) =
C)の場合
F1−α/2 (ν2, ν1) =F0.975 (9, 11) =3.59
F1−α/2 (ν2, ν1) =F0.975 (11, 9) =3.91
計算
s12=0.934 3N2
s22=1.282 7N2
2
2
2
1
s
s=0.728 4
A)の場合
A=
2
2
2
1
s
sF1−α (ν2, ν1) =
B)の場合
B=
2
2
2
1
s
s/F1−α (ν2, ν1) =
C)の場合
C=
2
2
2
1
s
s/F1−α/2 (ν2, ν1) =0.202 9
D=
2
2
2
1
s
sF1−α/2 (ν2, ν1) =2.848
信頼限界の報告
A)の場合 σ12/σ22≦A
B)の場合 σ12/σ22≧B
C)の場合 C≦σ12/σ22≦D
結果
A)の場合 □ σ12/σ22≦
B)の場合 □ σ12/σ22≧
C)の場合 □
× 0.203≦σ12/σ22≦2.848
糸1と糸2の切断荷重の分散比は,信頼係数1−α=95%で0.203と2.848の間にある。
σ1/σ2の信頼限界はσ12/σ22の信頼限界の正の平方根となり,ここでは0.45と1.69となる。

35
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式K 二つの対応のある測定の平均の比較
(二つの対応のある測定の平均の差の期待値に関する検定,差の分散既知)
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1−μ2≧∆0 □
B) 片側検定H0 : μ1−μ2≦∆0 □
C) 両側検定H0 : μ1−μ2=∆0 □
与えられた値:∆0=
既知の値
差の分散:σD2=
差の標準偏差:σD=
有意水準:α=
測定値の個数:n=
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=
計算
差diの平均d
d=
D=d−∆0=
A),B)の場合
A=u1−ασD/n=
C)の場合
B=u1−α/2σD/n=
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

36
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Kの使用例
確率変数と観測方法:
アイテム:
1
n=9の種々の糸素材について,分析方法1で水分含有率を測定。
2
1と同一試料を分析方法2で水分含有率を測定。
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1−μ2≧∆0 □
B) 片側検定H0 : μ1−μ2≦∆0 □
C) 両側検定H0 : μ1−μ2=∆0 □
×
与えられた値:∆0=0%
既知の値
差の分散:σD2=
差の標準偏差:σD=1.00%
有意水準:α=0.05
測定値の個数:n=9
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=u0.975=1.960
計算
差diの平均d
d=0.211%
D=d−∆0=0.211%
A),B)の場合
A=u1−ασD/n=
C)の場合
B=u1−α/2σD/n=0.653%
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
分析方法1と2とでは,水分含有率の期待値が,有意水準5%で有意な差が検出されなかった。
(分析方法1と2との水分含有率の差の期待値と,与えられた値∆0=0%とは,有意水準5%で有意な差が検出されな
かった。)

37
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Kʼ 二つの対応のある測定の平均の比較
(二つの対応のある測定の平均の差の期待値に関する検定,差の分散未知)
確率変数と観測方法:
アイテム:
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1−μ2≧∆0 □
B) 片側検定H0 : μ1−μ2≦∆0 □
C) 両側検定H0 : μ1−μ2=∆0 □
与えられた値:∆0=
有意水準:α=
測定値の個数:n=
自由度:ν=n−1=
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
tν, 1−α/2 (ν) =
計算
差diの平均d
d=
D=d−∆0=
差diの標準偏差:
sd=
A),B)の場合
A=t1−α (ν) sd/n=
C)の場合
B=t1−α/2 (ν) sd/n=
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□

38
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Kʼの使用例
確率変数と観測方法:糸の水分含有率 (%)
アイテム:
1
n=9の種々の糸素材について,分析方法1で水分含有率を測定。
2
1と同一試料を分析方法2で水分含有率を測定。
注:
帰無仮説と検定のタイプ
A) 片側検定H0 : μ1−μ2≧∆0 □
B) 片側検定H0 : μ1−μ2≦∆0 □
C) 両側検定H0 : μ1−μ2=∆0 □
×
与えられた値:∆0=0%
有意水準:α=0.05
測定値の個数:n=9
自由度:ν=n−1=8
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
tν, 1−α/2 (ν) =t0.975 (8) =2.306
計算
差diの平均d
d=0.211%
D=d−∆0=0.211%
差diの標準偏差:
sd=1.125 %
A),B)の場合
A=tν, 1−αsd/n=
C)の場合
B=tν, 1−α/2 sD/n=0.865 %
検定の解釈
A)の場合 D<−A,
B)の場合 D>A,
C)の場合 |D|>Bのとき帰無仮説H0を棄却する。
検定結果
H0は棄却される。
H0は棄却されない。
□
□
×
分析方法1と2とでは,水分含有率の期待値が,有意水準5%で有意な差が検出されなかった。
(分析方法1と2との水分含有率の差の期待値と,与えられた値∆0=0%とは,有意水準5%で有意な差が検出されな
かった。)

39
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式L 二つの対応のある測定の平均の差の信頼限界
(二つの対応のある測定の平均の差の期待値の信頼区間,分散既知)
確率変数と観測方法:
アイテム:
注:
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
既知の値
差の分散:σD2=
差の標準偏差:σD=
信頼係数:1−α=
測定値の個数:n=
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=
計算
差diの平均d
d=
A)の場合
u1−ασD/n=
A=d+u1−ασD/n=
B)の場合
u1−ασD/n=
B=du1−ασD/n=
C)の場合
u1−α/2σD/n=
C=d−u1−α/2σD/n=
D=d+u1−α/2σD/n=
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 ∆≦
B)の場合 ∆≧
C)の場合 ≦∆≦

40
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Lの使用例
確率変数と観測方法:糸の水分含有率 (%)
アイテム:
1
n=9の種々の糸素材について,分析方法1で水分含有率を測定。
2
1と同一試料を分析方法2で水分含有率を測定。
注:
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
既知の値
差の分散:σD2=
差の標準偏差:σD=1.00%
信頼係数:1−α=0.95
測定値の個数:n=9
統計数値表の値(附属書A表1参照)
A),B)の場合
u1−α=
C)の場合
u1−α/2=u0.975=1.960
計算
差diの平均d
d=0.211%
A)の場合
u1−ασD/n=
A=d+u1−ασD/n=
B)の場合
u1−ασD/n=
B=d+u1−ασD/n=
C)の場合
u1−α/2σD/n=0.653 %
C=d−u1−α/2σD/n=−0.442%
D=d+u1−α/2σD/n=0.864%
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 □ ∆≦
B)の場合 □ ∆≧
C)の場合 □
× −0.44%≦∆≦0.86%
両分析方法の水分含有率の差の期待値∆は,信頼係数1−α=0.95で−0.44%と0.86%の間にある。

41
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Lʼ 二つの対応のある測定の平均の差の信頼限界
(二つの対応のある測定の平均の差の期待値の信頼区間,分散未知)
確率変数と観測方法:
アイテム:
注:
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
信頼係数:1−α=
測定値の個数:n=
自由度:ν=n−1=
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−α/2 (ν) =
計算
差diの平均d
d=
A)の場合
t1−α (ν) sd/n=
A=d+t1−α (ν) sd/n=
B)の場合
t1−α (ν) Sd/n=
B=d−t1−α (ν) sd/n=
C)の場合
t1−α/2 (ν) sd/n=
C=d−t1−α/2 (ν) sd/n=
D=d+t1−α/2 (ν) sd/n=
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 □ ∆≦
B)の場合 □ ∆≧
C)の場合 □ ≦∆≦

42
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式Lʼの使用例
確率変数と観測方法:糸の水分含有率 (%)
アイテム:
1
n=9の種々の糸素材について,分析方法1で水分含有率を測定。
2
1と同一試料を分析方法2で水分含有率を測定。
∆=μ1−μ2の信頼区間のタイプ
A) 片側信頼上限 □
B) 片側信頼下限 □
C) 両側信頼限界 □
×
信頼係数:1−α=0.95
測定値の個数:n=9
自由度:ν=n−1=8
統計数値表の値(附属書A表2参照)
A),B)の場合
t1−α (ν) =
C)の場合
t1−α/2 (ν) =t0.975 (8) =2.306
計算
差diの平均d
d=0.211 %
A)の場合
t1−α (ν) sd/n=
A=d+t1−α (ν) sd/n=
B)の場合
t1−α (ν) sd/n=
B=d−t1−α (ν) sd/n=
C)の場合
t1−α/2 (ν) sd/n=0.865 %
C=d−t1−α/2 (ν) sd/n=−0.654%
D=d+t1−α/2 (ν) sd/n=1.076%
信頼限界の報告
A)の場合 ∆≦A,
B)の場合 ∆≧B,
C)の場合 C≦∆≦D
結果
A)の場合 □ ∆≦
B)の場合 □ ∆≧
C)の場合 □
× −0.65%≦∆≦1.08%
両分析方法の水分含有率の差の期待値∆は,信頼係数1−α=0.95で−0.65%と1.08%の間にある。
43
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) 統計数値表
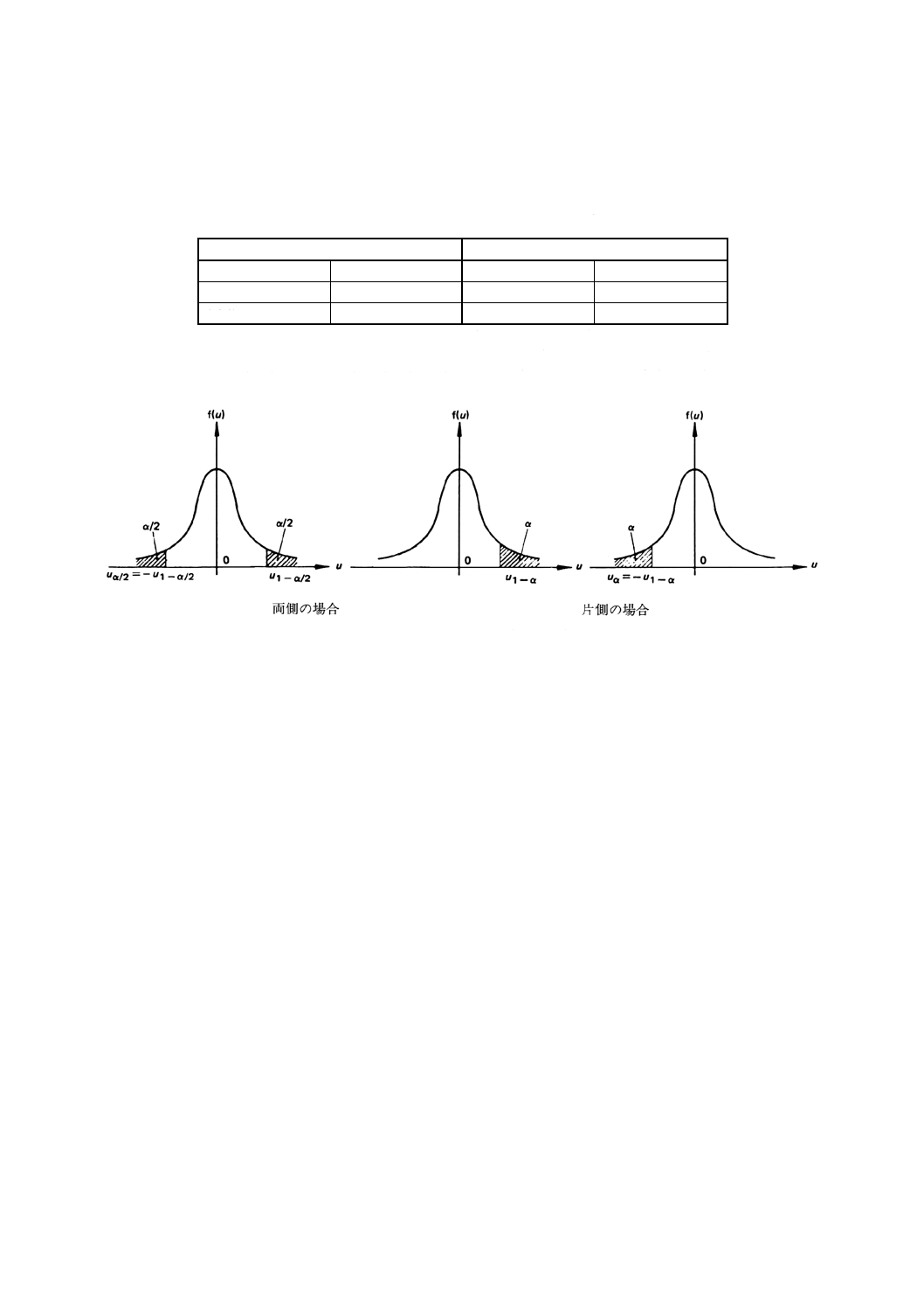
附属書A表1 標準化正規分布の分位点u1−α及びu1−α/2の表
両側の場合
片側の場合
α=0.05
α=0.01
α=0.05
α=0.01
u1−α/2=u0.975
u1−α/2=u0.995
u1−α=u0.95
u1−α=u0.99
1.960
2.576
1.645
2.326
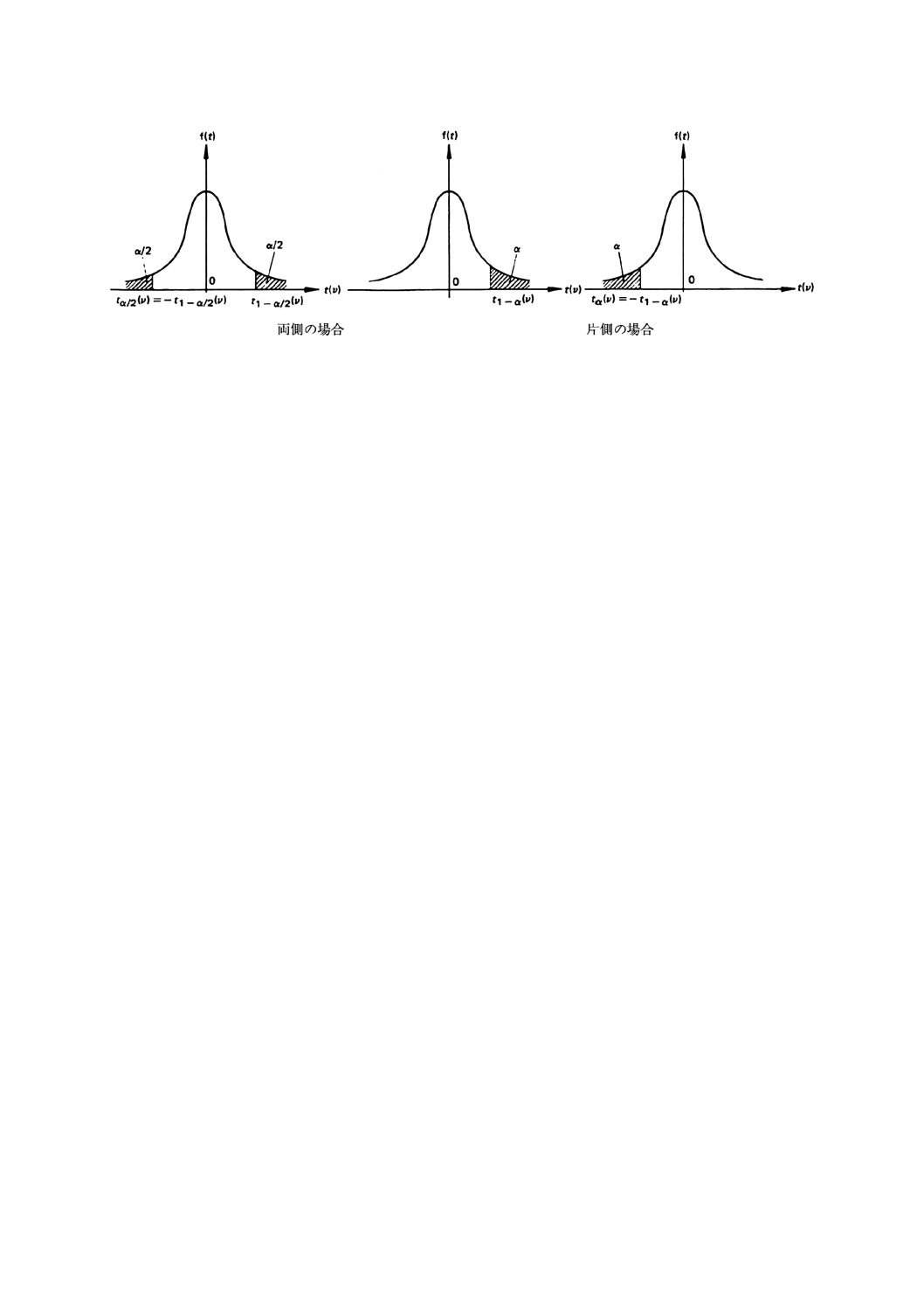
備考 標準化正規変量の分位点uαは,P (U≦uα) =αを満たす点である。Uの分布が
原点0を中心に対称であるため,uα=−u1−αが成り立つ。したがって,P (U
>uα) =1−α,P (uα/2<U<u1−α/2) =1−αが成り立つ。Uの確率密度関数(標
準化正規分布)は,次のようになる(附属書A図1参照)。
附属書A図1 標準化正規分布Uの確率密度
44
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
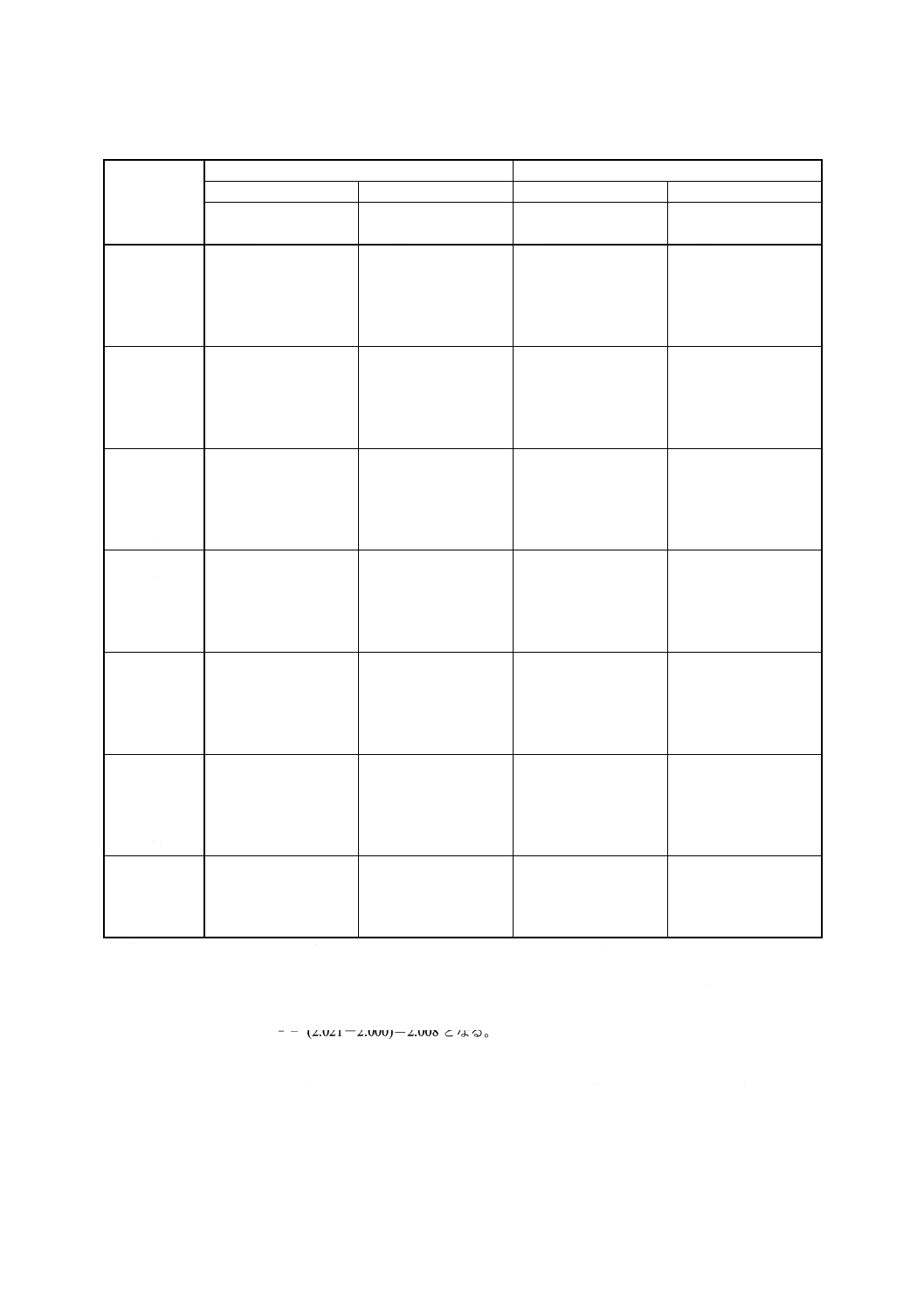
附属書A表2 t分布の分位点t1−α (ν) 及びt1−α/2 (ν) の表
ν
両側の場合
片側の場合
α=0.05
α=0.01
α=0.05
α=0.01
t1−α/2 (ν) =
t1−α/2 (ν) =
t1−α (ν) =
t1−α (ν) =
t0.975 (ν)
t0.995 (ν)
t0.95 (ν)
t0.99 (ν)
1
12.706
63.657
6.314
31.821
2
4.303
9.925
2.920
6.965
3
3.182
5.841
2.353
4.541
4
2.776
4.604
2.132
3.747
5
2.571
4.032
2.015
3.365
6
2.447
3.707
1.943
3.143
7
2.365
3.499
1.895
2.998
8
2.306
3.335
1.860
2.896
9
2.262
3.250
1.833
2.821
10
2.228
3.169
1.812
2.764
11
2.201
3.106
1.796
2.718
12
2.179
3.055
1.782
2.681
13
2.160
3.012
1.771
2.650
14
2.145
2.977
1.761
2.624
15
2.131
2.947
1.753
2.602
16
2.120
2.921
1.746
2.583
17
2.110
2.898
1.740
2.567
18
2.101
2.878
1.734
2.552
19
2.093
2.861
1.729
2.539
20
2.086
2.845
1.725
2.528
21
2.080
2.831
1.721
2.518
22
2.074
2.819
1.717
2.508
23
2.069
2.807
1.714
2.500
24
2.064
2.797
1.711
2.492
25
2.060
2.787
1.708
2.485
26
2.056
2.779
1.706
2.479
27
2.052
2.771
1.703
2.473
28
2.048
2.763
1.701
2.467
29
2.045
2.756
1.699
2.462
30
2.042
2.750
1.697
2.457
40
2.021
2.704
1.684
2.423
60
2.000
2.660
1.671
2.390
120
1.980
2.617
1.658
2.358
∞
1.960
2.576
1.645
2.326
出典:E. S. Pearson and H. O. Hartley, Biometrika Tables for Statisticians, Vol. 1 (1966).
備考1. ν>30のときは,引数をz=120/νとして補間を行う。
例:ν=40 z=120/ν=3 t0.975 (ν) =2.021,ν=60 z=120/ν=2 t0.975 (ν) =2.000,したがって,ν=50 z=
120/ν=2.4のときには,
t0.975 (ν) =2.021−
2
3
4.2
3
−
− (2.021−2.000)=2.008となる。
2. 分位点tα (ν) は,P [t (ν) ≦tα (ν) ]αを満たす点である。ただし,t (ν) は自由度νのt分布に従う確率変数
である。t分布が原点0を中心に対称であるため,tα (ν) =−t1−α (ν) が成り立つ。したがって,P [t (ν) >
tα (ν) ]=1−α,P [tα/2 (ν) <t (ν) <t1−α/2 (ν) ]=1−αが成り立つ。自由度vのt分布に従う確率変数t (ν) の
確率密度関数は,次のようになる(附属書A図2参照)。
45
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A図2 自由度v=n1+n2−2のt分布の確率密度
46
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A表3 カイ二乗分布の分位点X2α/2 (ν),X21−α/2 (ν),X2α (ν) とX21−α (ν) の表
ν
両側の場合
片側の場合
X20.025
X20.975
X20.005
X20.995
X20.05
X20.95
X20.01
X20.99
1
0.001
5.023
0.000 039 3
7.879
0.004
3.841
0.000 2
6.635
2
0.051
7.378
0.010
10.597
0.103
5.991
0.020
9.210
3
0.216
9.348
0.072
12.838
0.352
7.815
0.115
11.345
4
0.484
11.143
0.207
14.860
0.711
9.488
0.297
13.277
5
0.831
12.833
0.412
16.750
1.145
11.071
0.554
15.086
6
1.237
14.449
0.676
18.548
1.635
12.592
0.872
16.812
7
1.690
16.013
0.989
20.278
2.167
14.067
1.239
18.475
8
2.180
17.535
1.344
21.955
2.733
15.507
1.646
20.090
9
2.700
19.023
1.735
23.589
3.325
16.919
2.088
21.666
10
3.247
20.483
2.156
25.188
3.940
18.307
2.558
23.209
11
3.816
21.920
2.603
26.757
4.575
19.675
3.053
24.725
12
4.404
23.337
3.074
28.300
5.226
21.026
3.571
26.217
13
5.009
24.736
3.565
29.819
5.892
22.362
4.107
27.688
14
5.629
26.119
4.075
31.319
6.571
23.685
4.660
29.141
15
6.262
27.488
4.601
32.801
7.261
24.996
5.229
30.578
16
6.908
28.845
5.142
34.267
7.962
26.296
5.812
32.000
17
7.564
30.191
5.697
35.719
8.672
27.587
6.408
33.409
18
8.231
31.526
6.265
37.156
9.390
28.869
7.015
34.805
19
8.907
32.852
6.844
38.582
10.117
30.144
7.633
36.191
20
9.591
34.170
7.434
39.997
10.851
31.410
8.260
37.566
21
10.283
35.479
8.034
41.401
11.591
32.671
8.897
38.932
22
10.982
36.781
8.643
42.796
12.338
33.924
9.542
40.289
23
11.689
38.076
9.260
44.181
13.091
35.173
10.196
41.638
24
12.401
39.364
9.886
45.559
13.848
36.415
10.856
42.980
25
13.120
40.647
10.520
46.928
14.611
37.653
11.524
44.314
26
13.844
41.923
11.160
48.290
15.379
38.885
12.198
45.642
27
14.573
43.194
11.808
49.645
16.151
40.113
12.879
46.963
28
15.308
44.461
12.461
50.993
16.928
41.337
13.565
48.278
29
16.047
45.722
13.121
52.336
17.708
42.557
14.257
49.588
30
16.791
46.979
13.787
53.672
18.493
43.773
14.954
50.892
出典:E. S. Pearson and H. O. Hartley, Biometrika Tables for Statisticians, Vol. 1 (1966)
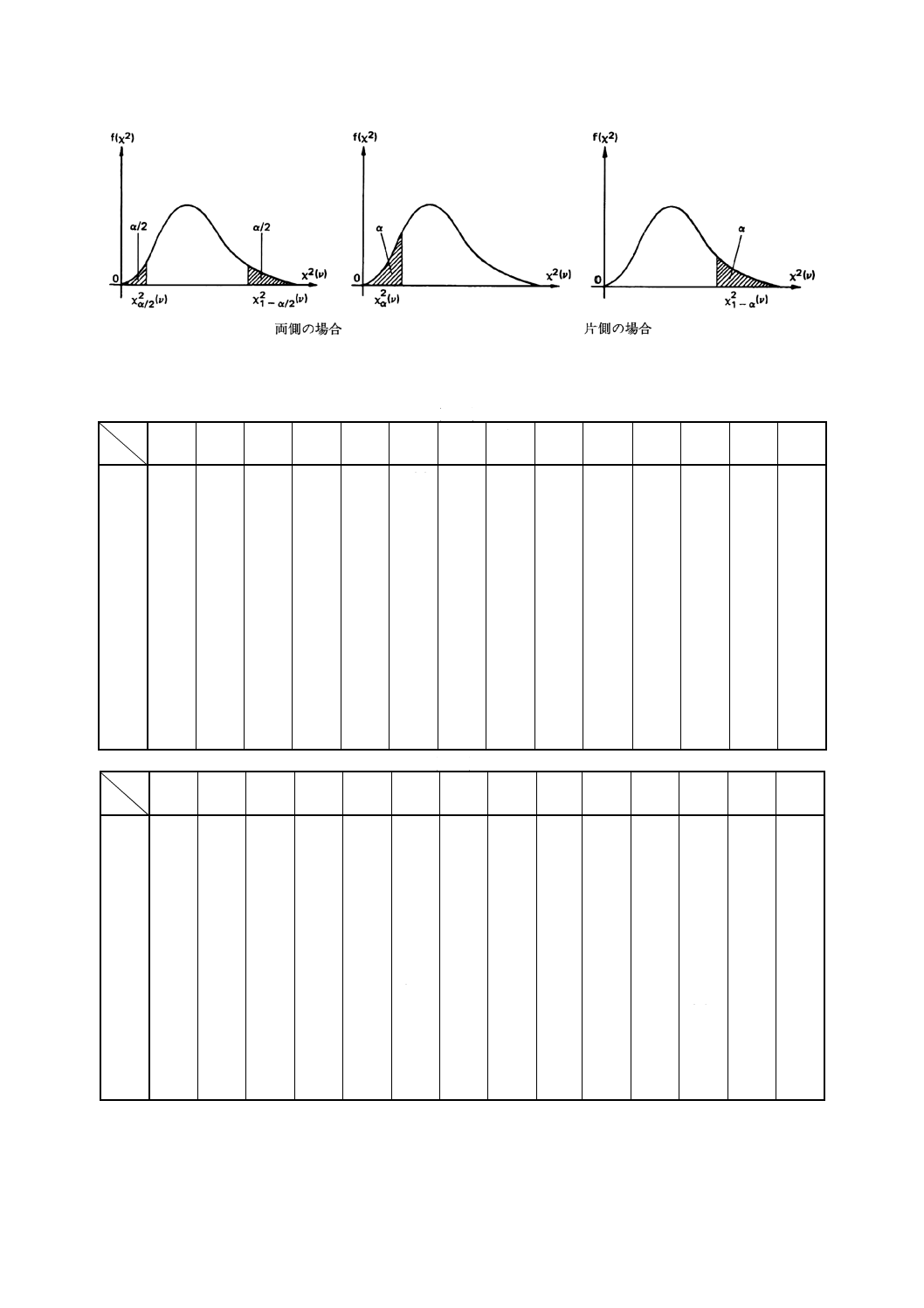
備考 分位点X2α (ν) は,P [X2 (ν) ≦X2α (ν)] =aを満たす点である。ただし,X2 (ν) は自由度νのカイ二乗分布
に従う確率変数である。
P [X2 (ν) >X2α (ν) ] =1−α,P [X2α/2 (ν) <X2 (ν) <X21−α/2 (ν) ] =1−αが成り立つ。
自由度νのカイ二乗分布に従う確率変数X2 (ν) の確率密度関数は,次のようになる(附属書A図3参照)。
47
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A図3 自由度ν=n−1にカイ二乗分布の確率密度
附属書A表4 F分布の上側分位点
F1−α (ν1, ν2), α=0.05
ν1
ν2
4
5
6
7
8
10
12
15
20
24
30
40
60
120
4
6.39
6.26
6.16
6.09
6.04
5.96
5.91
5.86
5.80
5.77
5.75
5.72
5.69
5.66
5
5.19
5.05
4.95
4.88
4.82
4.74
4.68
4.62
4.56
4.53
4.50
4.46
4.43
4.40
6
4.53
4.39
4.28
4.21
4.15
4.06
4.00
3.94
3.87
3.84
3.81
3.77
3.74
3.70
7
4.12
3.97
3.87
3.79
3.73
3.64
3.57
3.51
3.44
3.41
3.38
3.34
3.30
3.27
8
3.84
3.69
3.58
3.50
3.44
3.35
3.28
3.22
3.15
3.12
3.08
3.04
3.01
2.97
10
3.48
3.33
3.22
3.14
3.07
2.98
2.91
2.85
2.77
2.74
2.70
2.66
2.62
2.58
12
3.26
3.11
3.00
2.91
2.85
2.75
2.69
2.62
2.54
2.51
2.47
2.43
2.38
2.34
15
3.06
2.90
2.79
2.71
2.64
2.54
2.48
2.40
2.33
2.29
2.25
2.20
2.46
2.11
20
2.87
2.71
2.60
2.51
2.45
2.35
2.28
2.20
2.12
2.08
2.04
1.99
1.95
1.90
24
2.78
2.62
2.51
2.42
2.36
2.25
2.18
2.11
2.03
1.98
1.94
1.89
1.84
1.79
30
2.69
2.53
2.42
2.33
2.27
2.16
2.09
2.01
1.93
1.89
1.84
1.79
1.74
1.68
40
2.61
2.45
2.34
2.25
2.18
2.08
2.00
1.92
1.84
1.79
1.74
1.69
1.64
1.58
60
2.53
2.37
2.25
2.17
2.10
1.99
1.92
1.84
1.75
1.70
1.65
1.59
1.53
1.47
120
2.45
2.29
2.17
2.09
2.02
1.91
1.83
1.75
1.66
1.61
1.55
1.50
1.43
1.35
F1−α (ν1, ν2), α=0.025
ν1
ν2
4
5
6
7
8
10
12
15
20
24
30
40
60
120
4
9.60
9.36
9.20
9.07
8.98
8.84
8.75
8.66
8.56
8.51
8.46
8.41
8.36
8.31
5
7.39
7.15
6.98
6.85
6.76
6.62
6.52
6.43
6.33
6.28
6.23
6.18
6.12
6.07
6
6.23
5.99
5.82
5.70
5.60
5.46
5.37
5.27
5.17
5.12
5.07
5.01
4.96
4.90
7
5.52
5.29
5.12
4.99
4.90
4.76
4.67
4.57
4.47
4.42
4.36
4.31
4.25
4.20
8
5.05
4.82
4.65
4.53
4.43
4.30
4.20
4.10
4.00
3.95
3.89
3.84
3.78
3.73
10
4.47
4.24
4.07
3.95
3.85
3.72
3.62
3.52
3.42
3.37
3.31
3.26
3.20
3.14
12
4.12
3.89
3.73
3.61
3.51
3.37
3.28
3.18
3.07
3.02
2.96
2.91
2.85
2.79
15
3.80
3.58
3.41
3.29
3.20
3.06
2.96
2.86
2.76
2.70
2.64
2.59
2.52
2.46
20
3.51
3.29
3.13
3.01
2.91
2.77
2.68
2.57
2.46
2.41
2.35
2.29
2.22
2.16
24
3.38
3.15
2.99
2.87
2.78
2.64
2.54
2.44
2.33
2.27
2.21
2.15
2.08
2.01
30
3.25
3.03
2.87
2.75
2.65
2.51
2.41
2.31
2.20
2.14
2.07
2.01
1.94
1.87
40
3.13
2.90
2.74
2.62
2.53
2.39
2.29
2.18
2.07
2.01
1.94
1.88
1.80
1.72
60
3.01
2.79
2.63
2.51
2.41
2.27
2.17
2.06
1.94
1.88
1.82
1.74
1.67
1.58
120
2.89
2.67
2.52
2.39
2.30
2.16
2.05
1.94
1.82
1.76
1.69
1.61
1.53
1.43

48
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
F1−α (ν1, ν2), α=0.01
ν1
ν2
4
5
6
7
8
10
12
15
20
24
30
40
60
120
4
15.98 15.52 15.21 14.98 15.80 14.55 14.37 14.20 14.02 13.93 13.84 13.75 13.65 13.56
5
11.39 10.97 10.67 10.46 10.29 10.05 9.89 9.72 9.55 9.47 9.38 9.29 9.20 9.11
6
9.15 8.75 8.47 8.26 8.10 7.87 7.72 7.56 7.40 7.31 7.23 7.14 7.06 6.97
7
7.85 7.46 7.19 6.99 6.84 6.62 6.47 6.31 6.16 6.07 5.99 5.91 5.82 5.74
8
7.01 6.63 6.37 6.18 6.03 5.81 5.67 5.52 5.36 5.28 5.20 5.12 5.03 4.95
10
5.99 5.64 5.39 5.20 5.06 4.85 4.71 4.56 4.41 4.33 4.25 4.17 4.08 4.00
12
5.41 5.06 4.82 4.64 4.50 4.30 4.16 4.01 3.86 3.78 3.70 3.62 3.54 3.45
15
4.89 4.56 4.32 4.14 4.00 3.80 3.67 3.52 3.37 3.29 3.21 3.13 3.05 2.96
20
4.43 4.10 3.87 3.70 3.56 3.37 3.23 3.09 2.94 2.86 2.78 2.69 2.61 2.52
24
4.22 3.90 3.67 3.50 3.36 3.17 3.03 2.89 2.74 2.66 2.58 2.49 2.40 2.31
30
4.02 3.70 3.47 3.30 3.17 2.98 2.84 2.70 2.55 2.47 2.39 2.30 2.21 2.11
40
3.83 3.51 3.29 3.12 2.99 2.80 2.66 2.52 2.37 2.29 2.20
2.11 2.02 1.92
60
3.65 3.34 3.12 2.95 2.82 2.63 2.50 2.35 2.20 2.12 2.03 1.94 1.84 1.73
120
3.48 3.17 2.96 2.79 2.66 2.47 2.34 2.19 2.03 1.95 1.86 1.76 1.66 1.53
F1−α (ν1, ν2), α=0.005
ν1
ν2
4
5
6
7
8
10
12
15
20
24
30
40
60
120
4
23.15 22.46 21.97 21.62 21.35 20.97 20.70 20.44 20.17 20.03 19.89 19.75 19.61 19.47
5
15.56 14.94 14.51 14.20 13.96 13.62 13.38 13.15 12.90 12.78 12.66 12.53 12.40 12.27
6
12.03 11.46 11.07 10.79 10.57 10.25 10.03 9.81 9.59 9.47 9.36 9.24 9.12 9.00
7
10.05 9.52 9.16 8.89 8.68 8.38 8.18 7.97 7.75 7.65 7.53 7.42 7.31 7.19
8
8.81 8.30 7.95 7.69 7.50 7.21 7.01 6.81 6.61 6.50 6.40 6.29 6.18 6.06
10
7.34 6.87 6.54 6.30 6.12 5.85 5.66 5.47 5.27 5.17 5.07 4.97 4.86 4.75
12
6.52 6.07 5.76 5.52 5.35 5.09 4.91 4.72 4.53 4.43 4.33 4.23 4.12 4.01
15
5.80 5.37 5.07 4.85 4.67 4.42 4.25 4.07 3.88 3.79 3.69 3.58 3.48 3.37
20
5.17 4.76 4.47 4.26 4.09 3.85 3.68 3.50 3.32 3.22 3.12 3.02 2.92 2.81
24
4.89 4.49 4.20 3.99 3.83 3.59 3.42 3.25 3.06 2.97 2.87 2.77 2.66 2.55
30
4.62 4.23 3.95 3.74 3.58 3.34 3.18 3.01 2.82 2.73 2.63 2.52 2.42 2.30
40
4.37 3.99 3.71 3.51 3.35 3.12 2.95 2.78 2.60 2.50 2.40 2.30 2.18 2.06
60
4.14 3.76 3.49 3.29 3.13 2.90 2.74 2.57 2.39 2.29 2.19 2.08 1.96 1.83
120
3.92 3.55 3.28 3.09 2.93 3.71 2.54 2.37 2.19 2.09 1.98 1.87 1.75 1.61
出典:E. S. Pearson and H. O. Hartley, Biometrika Tables for Statisticians, Vol. 1 (1966)
備考1. 補間を行う場合は,
a) ν1,ν2が,10より大きく,20未満の場合には,引数をz=60/νとして補間を行う。
b) ν1,ν2が,20より大きい場合には,引数をzʼ=120/νとして補間を行う。
補間の具体的計算手順については,附属書A表2の備考1.を参照。
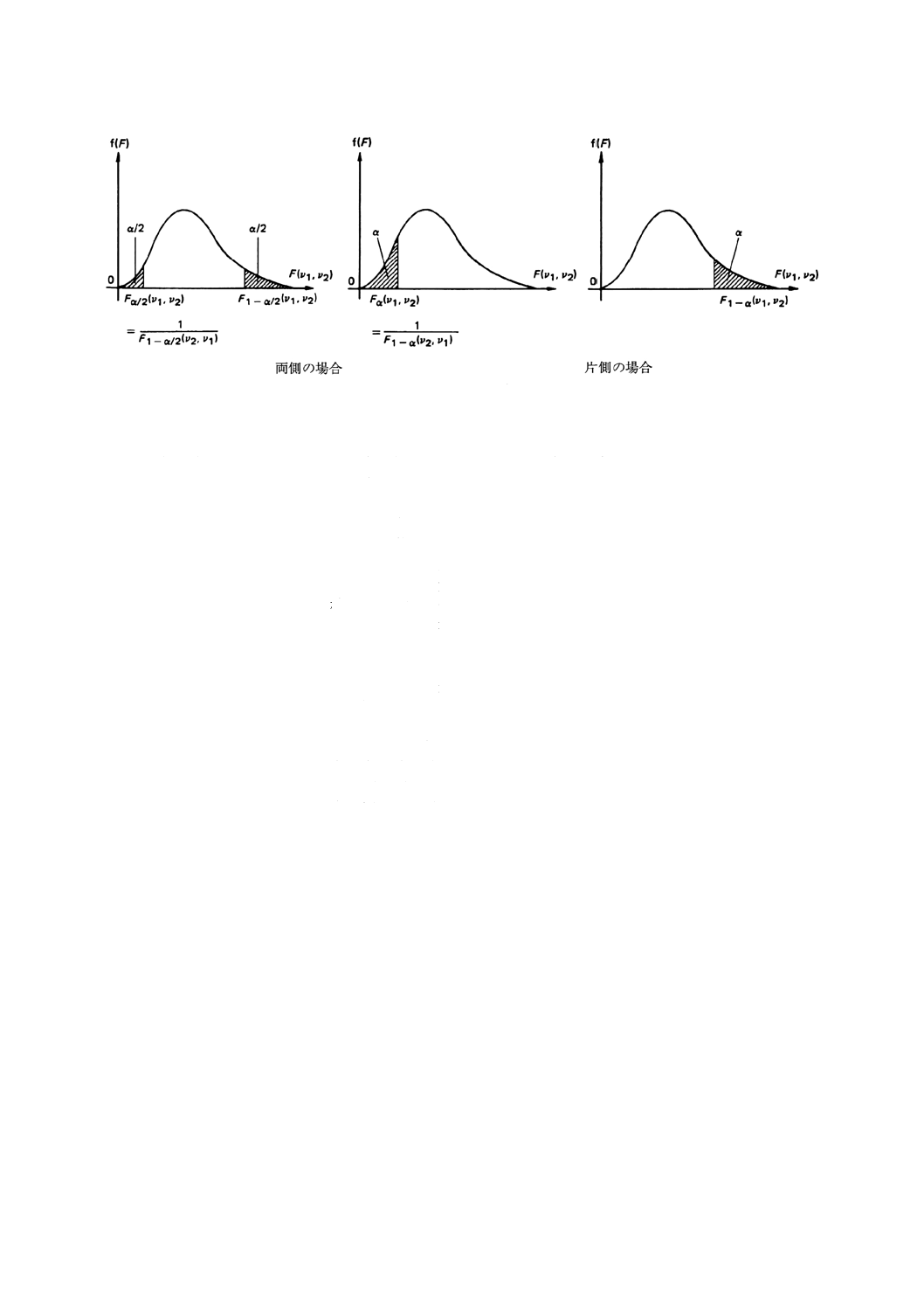
備考2. 分位点Fα (ν1, ν2) は,P [F (ν1, ν2) ≦Fα (ν1, ν2)] =αを満たす点である。ただし,F (ν1, ν2) は分子の自由度ν1,
分母の自由ν2のF分布に従う確率変数である。
したがって,P [F (ν1, ν2) >Fα (ν1, ν2)] =1−α,
P [Fα/2 (ν1, ν2) <F (ν1,ν2) <F1−α/2 (ν1, ν2)] =1−αが成り立つ。
更に,Fα (ν1, ν2) =
)
,
(
1
1
2
1
ν
ν
α
−
F
も成り立つ。
分子の自由度ν1,分母の自由度ν2のF分布に従う確率変数F (ν1, ν2) の確率密度関数は,次のようになる(附
属書A図4参照)。
49
Z 9041-2 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A図4 分子の自由度ν1,分母の自由度ν2のF (ν1, ν2) の確率密度
品質管理分野国際整合化分科会
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
今 井 秀 孝
工業技術院計量研究所
柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
QCコンサルタント
門 山 允
元東京国際大学(故人)
兼 子 毅
武蔵工業大学
◎ 椿 広 計
筑波大学社会工学系
仁 科 健
名古屋工業大学工学部
○ 野 澤 昌 弘
東京理科大学経営学部
三佐雄 武 雄
QCコンサルタント
宮 津 隆
帝京科学大学理工学部
○ 山 田 秀
東京理科大学工学部
○ 岸 本 淳 司
株式会社SASインスティチュートジャパン
横 尾 恒 雄
QCコンサルタント
大 島 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会