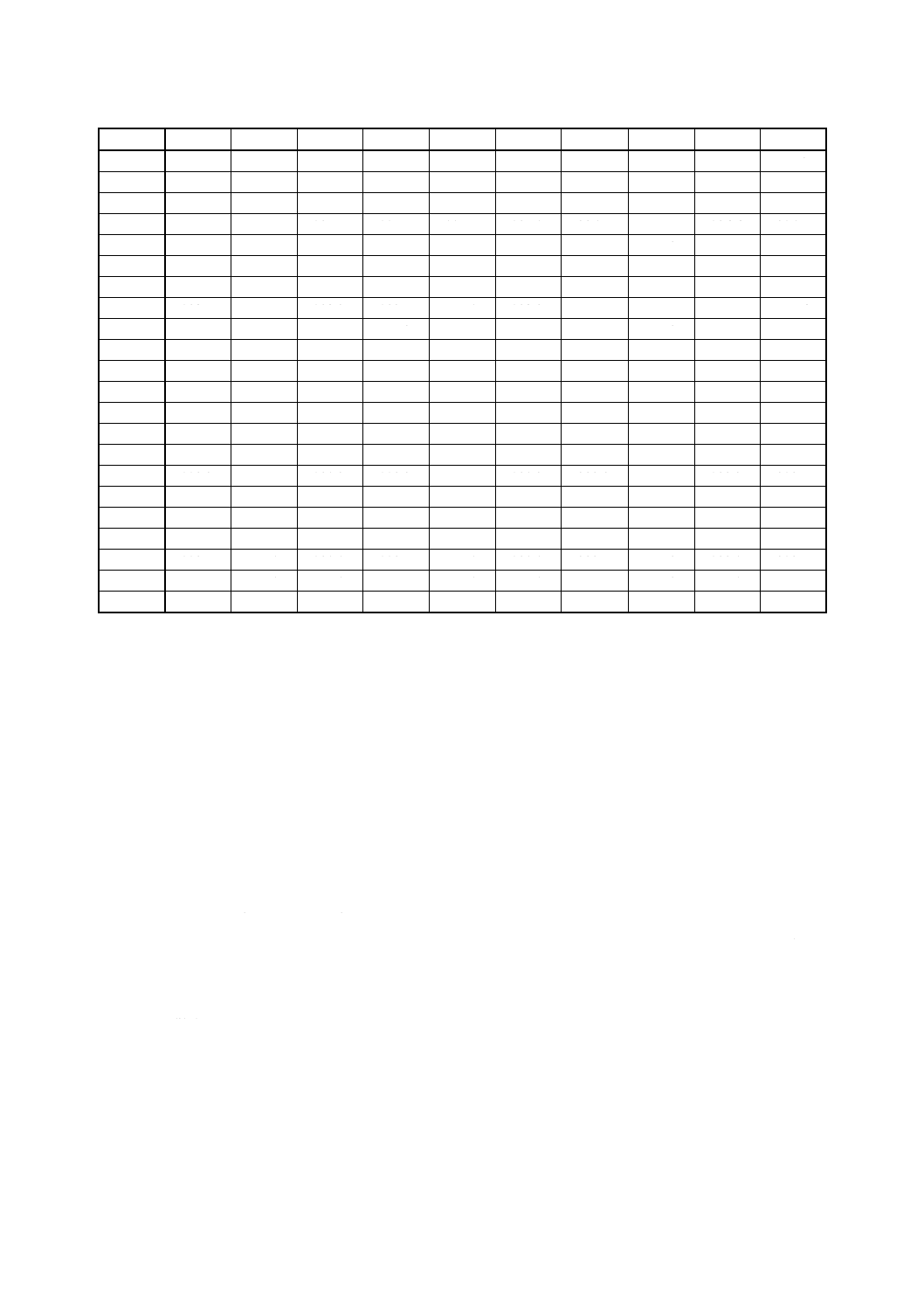Z 9041-1 : 1999
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が制定した日
本工業規格である。これによって,JIS Z 9041 : 1968は廃止され,この規格に置き換えられる。
JIS Z 9041 : 1999は,一般名称を“データの統計的な解釈方法”として,次の各部によって構成する。
第1部:データの統計的記述
第2部:平均と分散に関する検定方法と推定方法
第3部:割合に関する検定方法と推定方法
第4部:平均と分散に関する検定方法の検出力
Z 9041-1 : 1999
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 定義・記号 ····················································································································· 1
3.1 定義 ···························································································································· 1
3.2 記号 ···························································································································· 2
4. 測定値のとり方 ··············································································································· 2
4.1 測定の目的 ··················································································································· 2
4.2 測定値の丸め方 ············································································································· 2
5. 測定値のまとめ方 ············································································································ 4
5.1 測定値の記録 ················································································································ 4
5.2 図による表し方 ············································································································· 4
5.3 数量的な表し方 ············································································································ 11
5.4 測定に関する情報の報告································································································· 16
5.5 層別 ··························································································································· 17
5.6 正規分布 ····················································································································· 19
6. 2変数の場合の測定値のまとめ方 ······················································································· 22
6.1 測定値の記録 ··············································································································· 22
6.2 散布図 ························································································································ 22
6.3 数量的な表し方 ············································································································ 25
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9041-1 : 1999
データの統計的な解釈方法−
第1部:データの統計的記述
Statistical interpretation of data−
Part 1 : Statistical presentation of data
1. 適用範囲 この規格は,工場・実験室などにおけるデータのとり方,まとめ方及び表示方法に関する
統計的方法について規定する。
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格は,その最新版(追補を含む)を適用する。
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
備考 ISO 3534-1 : 1993 Statistics−Vocabulary and symbols−Part 1 : Plobability and general statistical
termsからの引用事項は,この規格の該当事項と同等である。
JIS Z 8101-2 統計−用語と記号−第2部:統計的品質管理用語
備考 ISO 3534-2 : 1993 Statistics−Vocabulary and symbols−Part 2 : Statistical quality controlからの
引用事項は,この規格の該当事項と同等である。
JIS Z 9021 シューハート管理図
備考 ISO 8258 : 1991 Shewhart control chartsからの引用事項は,この規格の該当事項と同等であ
る。
JIS Z 9041-2 データの統計的な解釈方法−第2部:平均と分散に関する検定方法と推定方法
3. 定義・記号
3.1
定義 この規格で用いる主な用語の定義は,JIS Z 8101-1及びJIS Z 8101-2によるほか,次による。
a) 平方和 各測定値と平均値との差の二乗和。
n
x
x
x
x
x
x
x
x
x
x
S
i
i
n
2
2
2
2
3
2
2
2
1
)
(
)
(
)
(
)
(
)
(
∑
∑
+
+
+
+
−
−
=
−
−
−
=
Λ
2変数x及びyに関する平方和は,次の式で計算される。
n
x
x
x
x
x
x
S
i
i
i
2
2
2
)
(
)
(
)
,
(
∑
∑
∑
−
=
−
=
n
y
y
y
y
y
y
S
i
i
i
2
2
2
)
(
)
(
)
,
(
∑
−
∑
∑
=
−
=
b) 工程能力図 工程能力,すなわち,工程のもつ品質に関する能力を図に表したもの。これを工程品質
能力図と呼ぶこともある。
c) 積和 2変数x,yに関するn組の測定値 (x1 , y1), (x2 , y2), …, (xn , yn) についての
)
)(
(
y
y
x
x
i
i
−
−
の合計。
次の式で計算される。
n
y
x
y
x
y
y
x
x
y
x
S
i
i
i
i
i
i
)
)(
(
)
)(
(
)
,
(
∑
∑
−
∑
−
−
∑
=
=
2
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.2
記号 この規格で用いる主な記号は,JIS Z 8101-1によるほか,次による。
f
度数,測定値の存在する範囲を幾つかの級に分けた場合の各級に属する測定値の出現度
数。個々の値はf1, f2, f3, …と書く。
x
測定値。個々の値はx1, x2, x3, …と書く。
x (i)
測定値を大きさの順に並べたとき,小さいほうから数えてi番目の測定値
x~
メディアン(中央値)
xmax
最大値
xmin
最小値
S
平方和
S (x, x)
xの平方和(2変数の場合)
S (y, y)
yの平方和(2変数の場合)
V
不偏分散
h
級の幅
CP
工程能力指数
S (x, y)
xとyとの積和
4. 測定値のとり方
4.1
測定の目的 測定にあたっては,まずその目的を明確にし,その目的に合うように,サンプルのと
り方,測定方法,計測器の選択などを考慮することが望ましい。統計的品質管理における測定の目的を大
別すると次のとおりである。
a) 個々の品物の適合品・不適合品の判定を下すため,個々の品物の品質特性を測定する。
b) ロットの合格・不合格の判定を下すためにロットからランダムに抜き取ったサンプルを測定し,その
平均値や標準偏差を求める。
c) ロットの性質を調べるために,ロットからランダムに抜き取ったサンプルを測定し,その平均値や範
囲などを求める。
d) 工程を管理・解析する管理図を作成するため,工程からランダムに抜き取ったサンプルを測定し,そ
の平均値や範囲などを求める。
e) 要因効果測定のため,複数の因子のいろいろな水準について実験を行った結果を測定し,解析する。
f)
二つの特性の関係を知るため,工程又はロットから対になった測定値を用いて相関関係を調査する。
4.2
測定値の丸め方 平均値・標準偏差のけた数及び数値の丸め方は,次のとおりとする。“丸める”と
は,与えられた大きさの数を一定の丸め間隔の整数倍系列から選んだ大きさの数に置き換えることである。
例1. 丸め間隔:0.1
整数倍:12.1, 12. , 12. , 12.4, ……
例2. 丸め間隔:10
整数倍:1210, 1220, 1230, 1240, ……
4.2.1
平均値及び標準偏差のけた数
a) 平均値 表1のけた数まで出す。
3
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
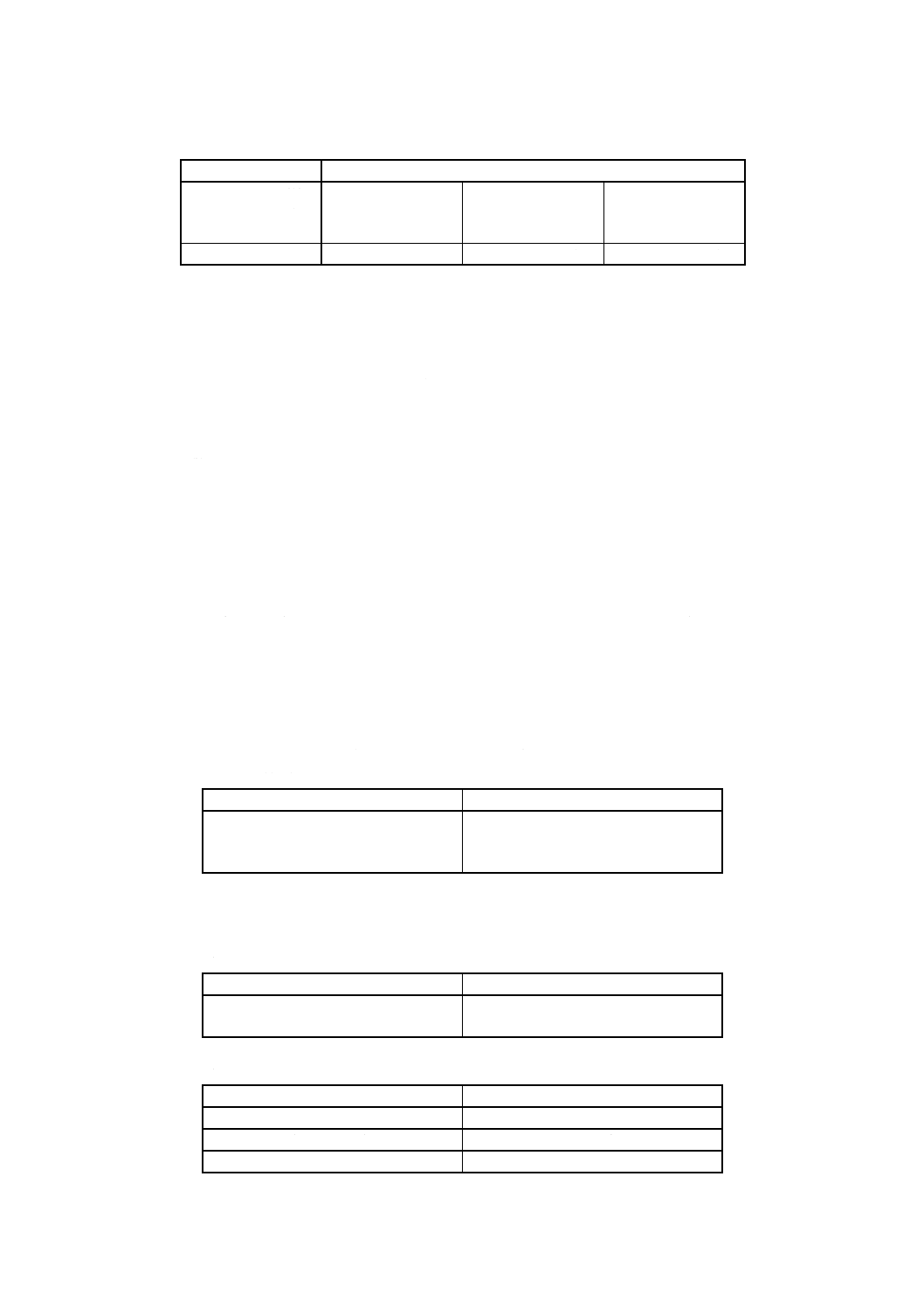
表1
測定値の測定単位
測定値の個数
0.1,1,10などの単位
−
2〜20
21〜200
0.2,2,20などの単位
4未満
4〜40
41〜400
0.5,5,50などの単位
10未満
10〜100
101〜100 0
平均値のけた数
測定値と同じ
測定値より1けた多く
測定値より2けた多く
b) 標準偏差 有効数字を最大3けたまで出す。
例1. 鋼材の厚さを測定して,次の測定値を得た。
2.55 2.63 2.48 2.50 2.52 2.59 2.50 2.46 2.53 2.50 (mm)
この場合,測定単位0.01mm,n=10であるから
x=2.526mm(測定値より1けた多く)
s=0.051 7mm(有効数字3けた)
例2. 0.2sきざみのストップウォッチを用いて,ある作業について時間的測定を行って,次の測定値
を得た。
34.2 35.0 35.8 36.0 36.4 35.6 34.2 (s)
この場合の測定単位は0.2 (s) ,n=7であるから,
x=35.31s(測定値より1けた多く)
s=0.869s(有効数字3けた)
備考 測定値が存在する範囲をx±2sとかx±3sというように推定することがある。このようにxと
sを加減する場合,けた数が不ぞろいのときには,けた数の少ないほうに合わせて丸める。
例2.の場合には
x+2s=35.31+2×0.869=35.31+1.74=37.05
x−2s=35.31−2×0.869=35.31−1.74=37.57
4.2.2
数値の丸め方 ある数値を有効数字nけたの数値に丸める方法は,次のとおりとする。
a) もし,与えられた数に最も近い整数倍が一つしかない場合は,それを丸めた数とする。
例 丸め間隔:0.1
与えられた数
丸めた数
12.223
12.2
12.251
12.3
12.275
12.3
b) もし,与えられた数に等しく近い,二つの隣り合う整数倍がある場合は,規則Aと規則Bのいずれか
による。
規則A 丸めた数として偶数の整数倍を選ぶ。
例 丸め間隔:0.1
与えられた数
丸めた数
12.25
12.2
12.35
12.4
規則B 丸めた数として大きいほうの整数倍を選ぶ。
例 丸め間隔:0.1
与えられた数
丸めた数
12.25
12.3
与えられた数
丸めた数
12.35
12.4
4
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 規則Aが一般には望ましい。例えば,一連の測定をこの方法で処理すると丸め誤差が最小にな
るという利点がある。規則Bは,計算機による計算で広く用いられる規則である。
5. 測定値のまとめ方
5.1
測定値の記録 測定値を記録する場合には,測定の対象となった品物の名称,特性,サンプルのと
り方・サンプルをとった日時,測定の日時,温度,湿度,測定方法,計測器の種類,計測器番号,測定者
など,あとで調査したり解析したりする場合の必要事項を併記することが望ましい。
繰り返して行う測定には,一定の記録用紙を定めておくのがよい。
5.2
図による表し方 多数の測定値を表にしただけでは十分な情報をつかみにくいが,図に表すと情報
がつかみやすくなる。
5.2.1
グラフ化 方眼紙又は適当な用紙の左端に測定値の値,横に測定の順序(又は時間)を目盛り,こ
れに測定値を表す点を記入すると,測定値のばらつき,時間的な動きなど工程の現状がつかみやすくなる。
備考 グラフに測定値の名称と目盛の単位を必ず記載しなければならない。
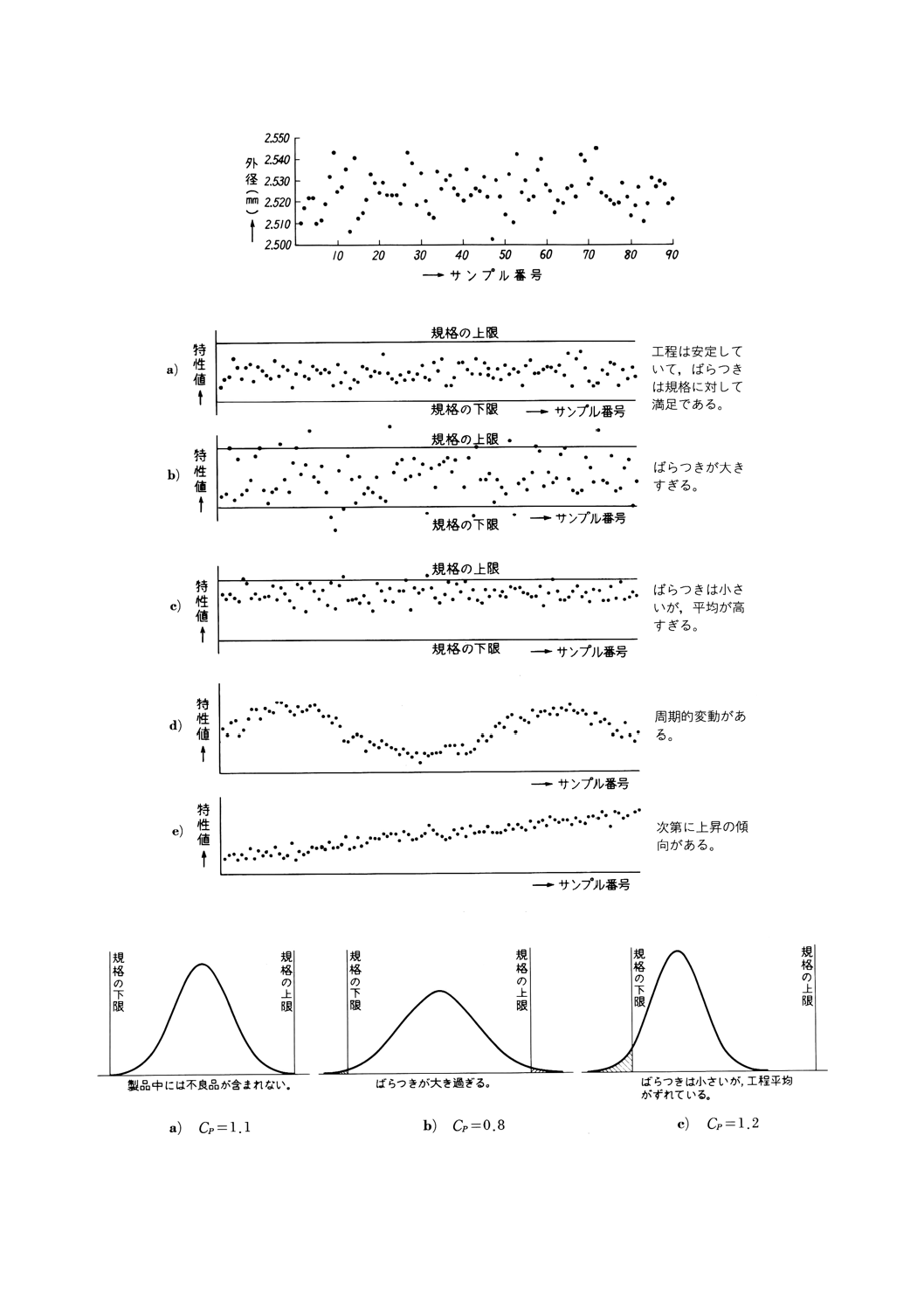
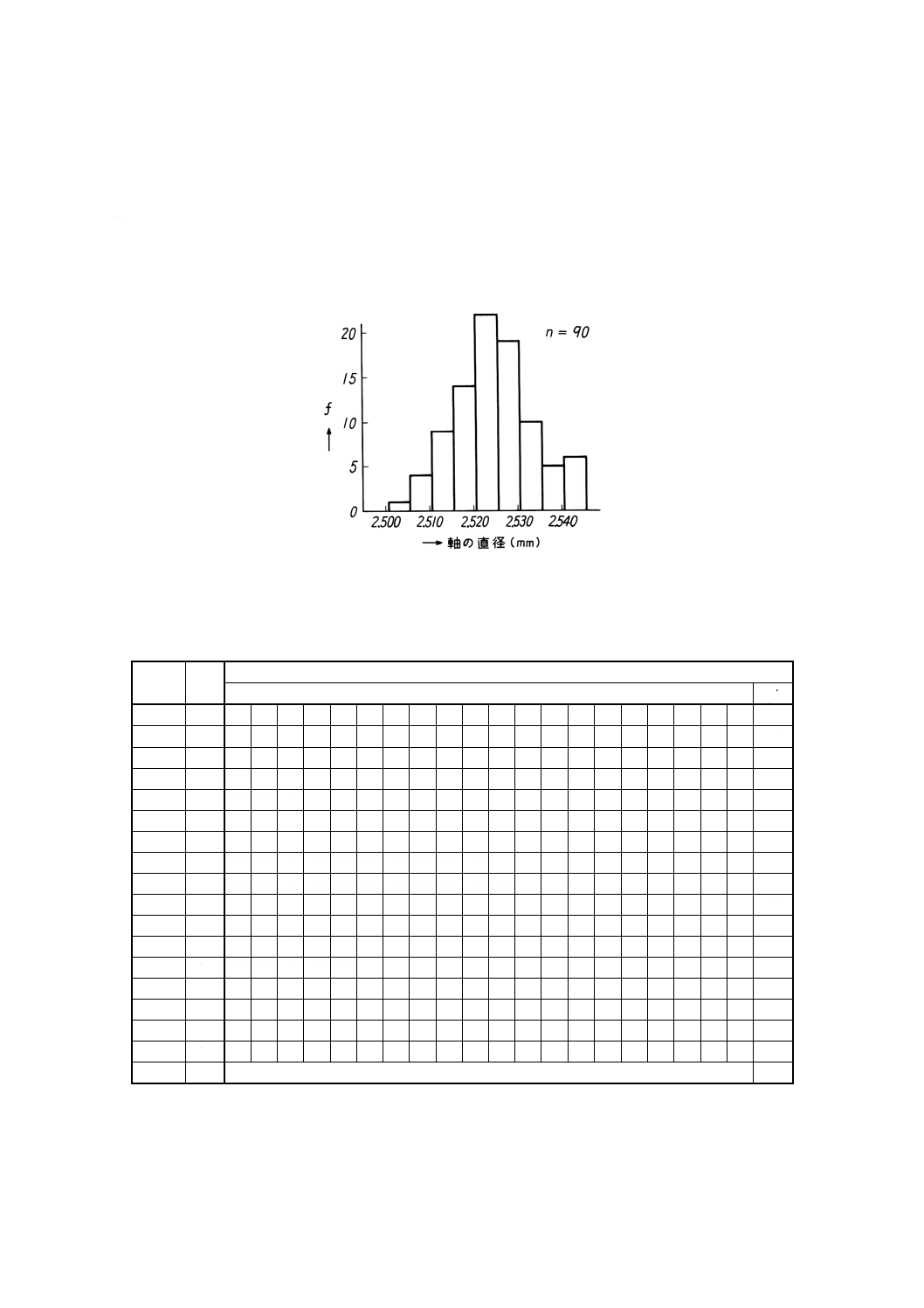
例1. 旋盤で仕上げた軸を加工順に90個抜き取って直径を測定した結果を表2に示す。これをグラフに
表すと図1になる。
このように測定値を時間的な順序に記入したグラフは工程能力図と呼ばれ,工程能力図には,規格が定
められている場合には規格値を表す直線を,規格が定められていない場合には目標値を表す直線を記入す
る。
図2は,工程能力図の例を示したものである。
規格値に対する工程能力を表すため,工程能力指数Cpが使われる(図3参照)。
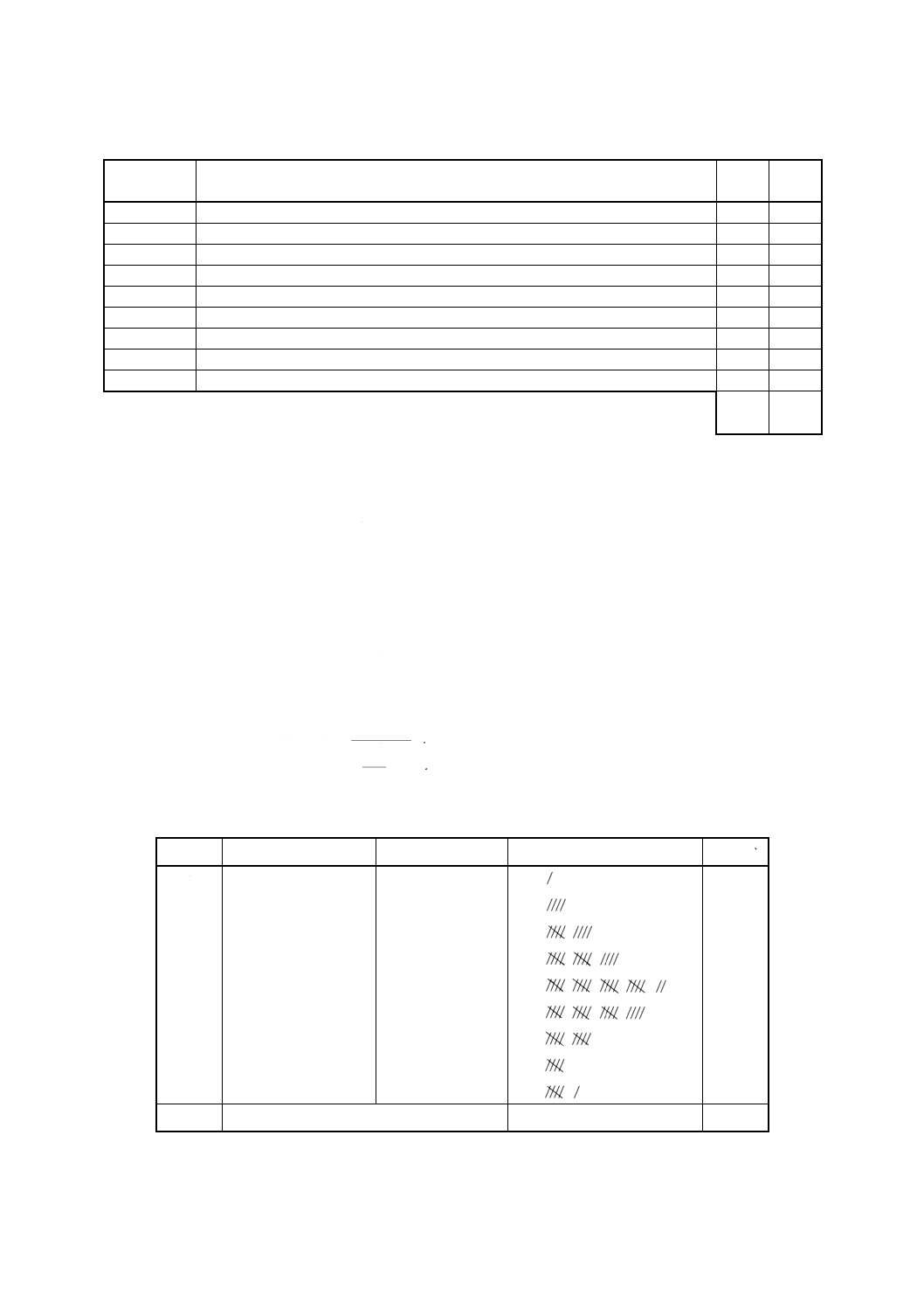
表2
製品名称
XX軸
製造命令番号
BZ-486
期間
99年6月5日
品質特性
外径寸法
職場
A工場第1機械係
99年6月14日
測定単位
0.001mm
基準日産高
10000個
機械番号
JB-21
規格の上限
2.555mm
サンプル 大きさ
n=90
規格の下限
2.495mm
間隔
30分ごと
作業員
鈴木太郎
規格番号
K-52605
測定器番号
M-0052
検査員
加藤次郎
サンプル番号
測定結果
1〜10
2.510
2.517
2.522
2.522
2.510
2.511
2.519
2.532
2.543
2.525
11〜20
2.527
2.536
2.506
2.541
2.512
2.515
2.521
2.536
2.529
2.524
21〜30
2.529
2.523
2.523
2.523
2.519
2.528
2.543
2.538
2.518
2.534
31〜40
2.520
2.514
2.512
2.534
2.526
2.530
2.532
2.526
2.523
2.520
41〜50
2.535
2.523
2.526
2.525
2.523
2.522
2.502
2.530
2.522
2.514
51〜60
2.533
2.510
2.542
2.524
2.530
2.521
2.522
2.535
2.540
2.528
61〜70
2.525
2.515
2.520
2.519
2.526
2.527
2.522
2.542
2.540
2.528
71〜80
2.531
2.545
2.524
2.522
2.520
2.519
2.519
2.529
2.522
2.513
81〜90
2.518
2.527
2.511
2.519
2.531
2.527
2.529
2.528
2.519
2.521
5
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1 表2のデータをグラフに表したもの
図2 工程能力図の例
図3
6
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2.2
度数分布 測定値の存在する範囲を幾つかの級に分け,各級に属する測定値の出現度数を並べると
全体の分布がつかみやすくなる。度数分布は度数表,ヒストグラム,累積度数図などで表す。
a) 度数表 度数表の作り方の手順は,次のとおりとする。
1) 範囲 (R) の計算 測定値の最大値と最小値を求めRを計算する。
R=(測定値の最大値)−(測定値の最小値)
測定値の最大値と最小値は,次のようにすると簡単に求められる。
測定値を記録した表の各行ごとに最大値と最小値を求め,最大値中の最大値,最小値中の最小値
を求める。
これが測定値全体の最大値及び最小値となる。
2) 級幅の決定 最小値と最大値を含む級を5〜20の等間隔の級に分けるように区間の幅を決める。級
幅はRを1, 2, 5(又は10, 20, 50 ; 0.1, 0.2, 0.5など)で除し,その値が5〜20になるものを選ぶ。こ
れが二通りになったときは,サンプルの大きさが100以上の場合は級幅の小さいほうを,99以下の
場合は級幅の大きいほうを用いる。
3) 度数表用紙の準備 表4のように,級,中心,度数マーク,度数などが記入できるような用紙を準
備する。
4) 級の境界の決定 最小値及び最大値を含むように級の境界を決め,度数表に記入する。
まず,第1の級の下限を決め,これに級幅を加えて第1の級と第2の級の境界を求める。このと
き第1の級は最小値を合み,境界は最小測定単位の21のところにくるように決める。以下,順に級
幅を加えて第2,第3,……の境界を求め,最後の級が最大値を含むようにする。
5) 級の中心の計算 次の式によって級の中心を計算し,度数表に記入する。
第1の級の中心=第1の級の境界の合計/2
第2の級の中心=第2の級の境界の合計/2
備考 第2の級,第3の級,……の中心は,次のようにして求めてもよい。
第2の級の中心=第1の級の中心+級幅
第3の級の中心=第2の級の中心+級幅
6) 度数を求める 測定値を順次読みあげ,各級に含まれる測定値の度数を求める。
度数は次の度数マークを用いて記録する。この場合5個ずつにまとめる。
度数
1
2
3
4
5
6
……
度数マーク
……
例2. 度数表の作り方 例1.の測定値について度数表を作る。
1) Rの計算 測定値の最大値及び最小値から求める(表3参照)。
7
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3
サンプル番号
測定結果
行の
最大値
行の
最小値
1〜10
2.510
2.517
2.522
2.522
2.510
2.511
2.519
2.532
2.543
2.525
2.543
2.510
11〜20
2.527
2.536
2.506
2.541
2.512
2.515
2.521
2.536
2.529
2.524
2.541
2.506
21〜30
2.529
2.523
2.523
2.523
2.519
2.528
2.543
2.538
2.518
2.534
2.543
2.518
31〜40
2.520
2.514
2.512
2.534
2.526
2.530
2.532
2.526
2.523
2.520
2.534
2.512
41〜50
2.535
2.523
2.526
2.525
2.523
2.522
2.502
2.530
2.522
2.514
2.535
2.502
51〜60
2.533
2.510
2.542
2.524
2.530
2.521
2.522
2.535
2.540
2.528
2.542
2.510
61〜70
2.525
2.515
2.520
2.519
2.526
2.527
2.522
2.542
2.540
2.528
2.542
2.515
71〜80
2.531
2.545
2.524
2.522
2.520
2.519
2.519
2.529
2.522
2.513
2.545
2.513
81〜90
2.518
2.527
2.511
2.519
2.531
2.527
2.529
2.528
2.519
2.521
2.531
2.511
最大値
2.545
最小値
2.502
最大値=2.545 最小値=2.502
したがって,R=2.545−2.502=0.043
2) 級幅の決定
0.043÷0.002=21.5 切りあげて22
0.043÷0.005=8.6 切りあげて9
0.043÷0.010=4.3 切り捨てて4
したがって,級幅を0.005と決める。
3) 度数表の準備 表4のような度数表を準備する。
4) 級の境界の決定 最小値2.502を含むように級の境界は第1の級2.500 5〜2.505 5,第2の級2.505 5
〜2.510 5……と決め度数表に記入する(表4参照)。
5) 級の中心の計算
503
.2
2
5055
.2
5005
.2
1
=
の級の中心=
第
+
508
.2
2
5105
.2
5005
.2
2
=
の級の中心=
第
+
6) 度数を求める 度数を記録する(表4参照)。
表4 度数表
No.
区間
区間の中心値x
度数マーク
度数f
1
2.500 5〜2.505 5
2.503
1
2
2.505 5〜2.510 5
2.508
4
3
2.510 5〜2.515 5
2.513
9
4
2.515 5〜2.520 5
2.518
14
5
2.520 5〜2.525 5
2.523
22
6
2.525 5〜2.530 5
2.528
19
7
2.530 5〜2.535 5
2.533
10
8
2.535 5〜2.540 5
2.538
5
9
2.540 5〜2.545 5
2.543
6
合計
−
90
備考1. 度数fの合計 (Σf) が測定値の総数 (n) にならなければ度数マークの付け誤りがある。
2. 相対度数が必要なときは,度数fをnで除して求める。
8
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3. 測定値のばらつきの範囲が測定単位の5〜20倍内外で,級に分けたと同じような測定値が得
られたときは,測定値そのものを級の中心としてb)以降の手順をすすめる。
b) ヒストグラム
1) ヒストグラムの書き方 方眼紙又は適当な用紙に図4のように横軸に測定値の級の値,縦軸に度数
を目盛り,各級に属する度数を柱の高さで示す。
図の右上に測定値の総数nを記入する。
例3. 例2.の度数表をヒストグラムに書くと図4のようになる。
図4 ヒストグラム
例4. ある組立部品のすきまの規格は,6.000±0.006mmと定められている。この部品70個の測定結果
をヒストグラムに書くと図5のようになる。測定値のばらつきの幅が最小測定単位の20倍より小
さいので級分けしないで直接ヒストグラムを作る。
x
u
度数
5
10
15
f
5.992
−8
5.993
−7 ×
1
5.994
−6 × ×
2
5.995
−5 ×
1
5.996
−4 × × ×
3
5.997
−3 × × × × ×
5
5.998
−2 × × × × × ×
6
5.999
−1 × × × × × × × × × ×
10
6.000
0 × × × × × × × × × × ×
11
6.001
+1 × × × × × × × × × × ×
11
6.002
+2 × × × × × × × ×
8
6.003
+3 × × × ×
4
6.004
+4 × × × × ×
5
6.005
+5 × ×
2
6.006
+6 ×
1
6.007
+7
6.008
+8
計
70
図5 ヒストグラム
2) ヒストグラムの見方 ヒストグラムを見る場合,次の点に注意する。
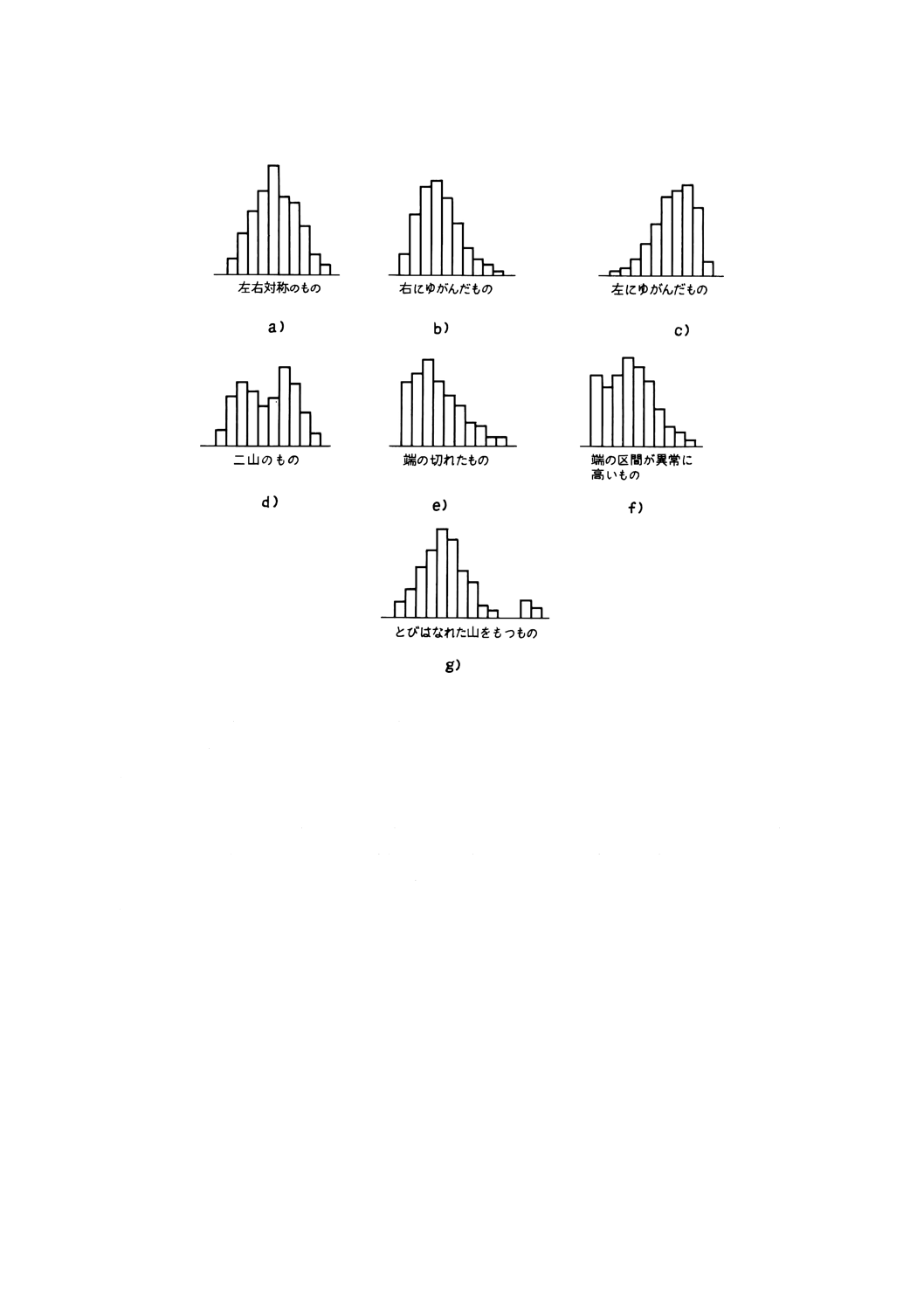
2.1) 多少のでこぼこは無視して大体の姿に着目する。ヒストグラムは中心付近が最も高く,左右に離れ
9
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
るほど低くなる左右対称の形を示す場合が多い。図6に示すようにいろいろの場合がある。
図6 ヒストグラムの例
これらのヒストグラムは,次のような場合に現れる。
a)
一般に多く現れる。
b)
微量成分の含有率など,ある値以下の値をとることができない場合。
c)
純度の高い成分の合有率など,ある値以上の値をとることができない場合。
d)
二つの分布が混じり合っている場合,例えば2台の機械間,2種類の原料間に差がある場合など。
e)
規格以下(又は以上若しくは両方)のものを全数選別してとり除いた場合など。
f)
規格はずれのものを手直ししたり,データを偽って報告した場合など。
g)
測定誤りがあったり,工程に異常があった場合など。
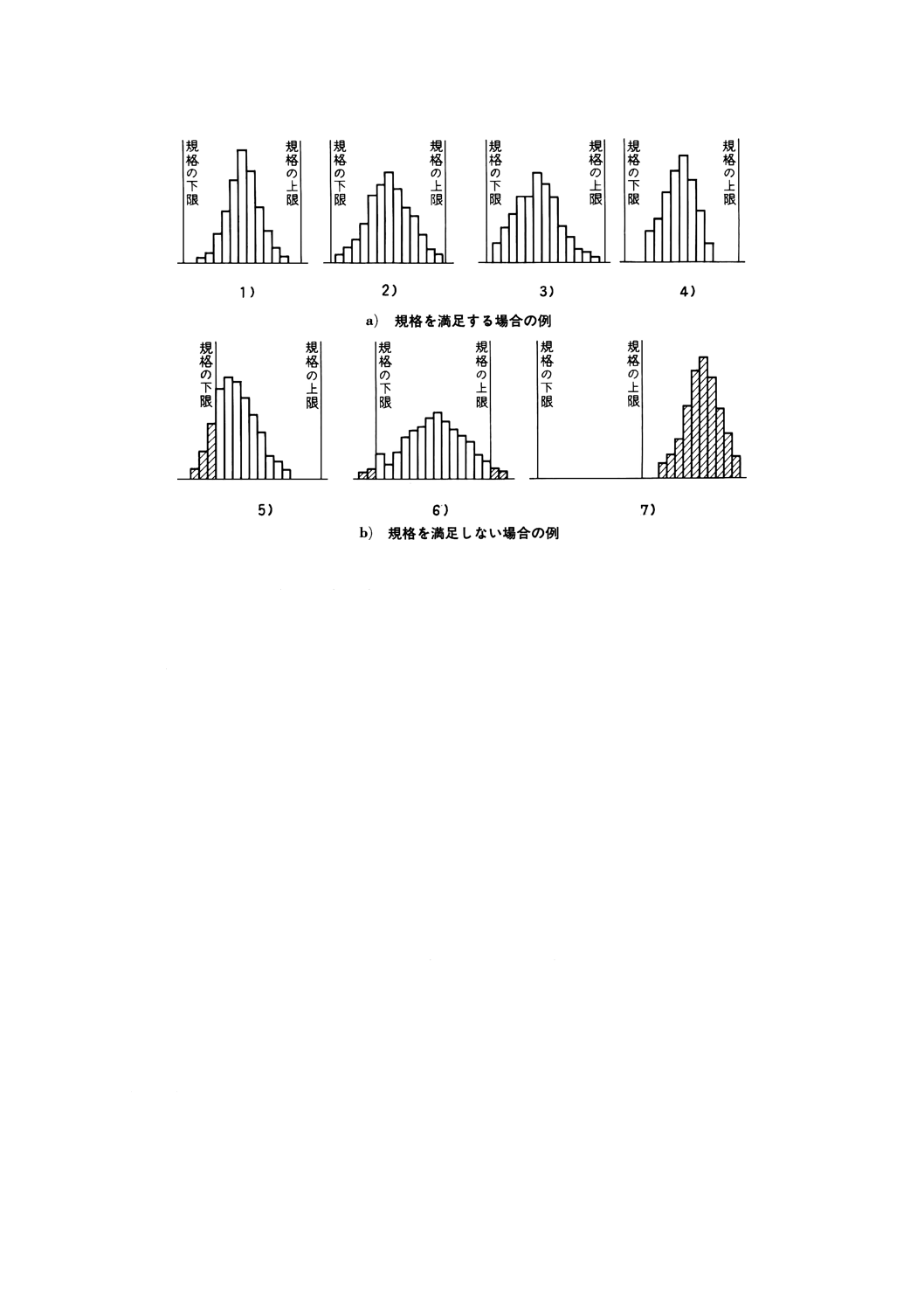
2.2) 規格が定められている場合は,ヒストグラムに規格値のところに線を記入して規格と比較する。ヒ
ストグラムが規格の上限と下限の中に十分なゆとりをもっておさまっているかどうかを見る。規格
が定められていない場合は,目標値のところに線を記入して目標値と比較する。
10
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図7
1) 2) 3) 4)は,いずれも規格を満足している。
ただし,2)と3)は規格に対して余裕がないので注意を要する。
5)と7)は,平均値を規格の中心に近づけるような処置が必要である。5)の場合には,ばらつきを
小さくするのもよい。
6)は,ばらつきを小さくする処置が必要である。
c)
累積度数図 ある値以下の測定値の度数(又は割合),ある値以上の測定値の度数(又は割合)を
求めるには累積度数図が便利である。
累積度数図の作り方の手順は,次による。
1)
累積度数を求める
度数表で第1の級の上側の境界以下の累積度数
− 第1の級の度数
第2の級の上側の境界以下の累積度数
− 第1の級の上側の境界以下の累積度数+第2の級の度数
第3の級の上側の境界以下の累積度数
− 第2の級の上側の境界値以下の累積度数+第3の級の度数
備考1. 最後の級の上側の境界以下の累積度数は,測定値の総数nとなる。
2. 相対累積度数を求めるときは,累積度数をnで除して求める。
2) 累積度数図の作成 方眼紙又は適当な用紙に図8のように方眼紙の横軸に測定値の値,縦軸に累積
度数を目盛り,各上側境界に対応する累積度数を表す点を書き,点を直線で結ぶ。
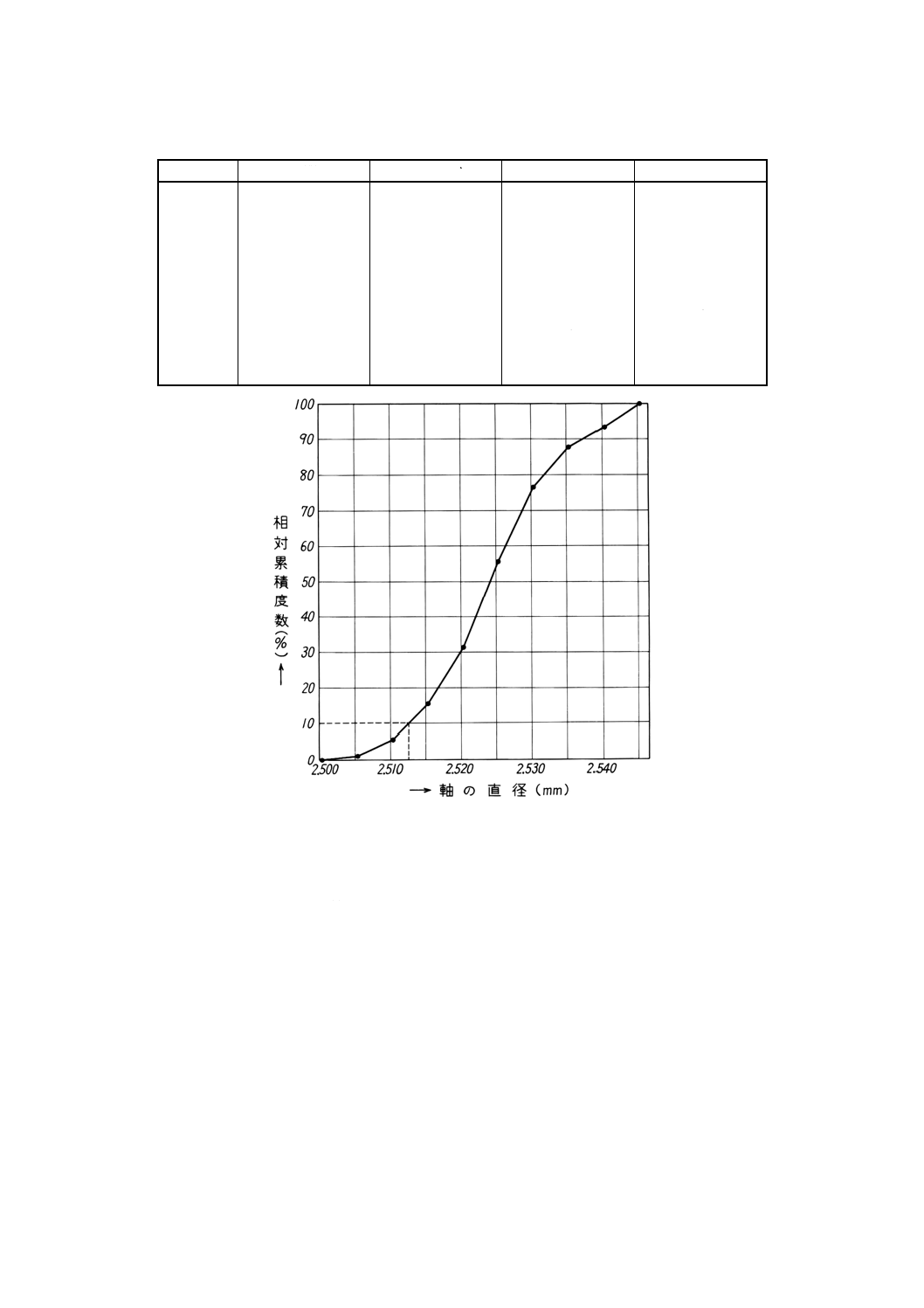
例5. 例2.の度数表を累積度数図に書くと図8のようになる。この図から,例えば2.5125mm以下の測
定値の割合は,10%と読み取ることができる。
11
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5 累積度数表
No.
区間
度数 f
累積度数
相対累積度数 %
1
2.500 5
1
0
0
2
2.505 5
4
1
1.1
3
2.510 5
9
5
5.6
4
2.515 5
14
14
15.6
5
2.520 5
22
28
31.1
6
2.525 5
19
50
55.6
7
2.530 5
10
69
76.7
8
2.535 5
5
79
87.8
9
2.540 5
6
84
93.3
2.545 5
90
100.0
図8 累積度数図
5.3
数量的な表し方
5.3.1
中心の表し方 2個以上の測定値の中心を表すには,平均値又はメディアンが用いられる。
a) 平均値の求め方 平均値を計算する手順は,次のとおりとする。
12
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1) 直接計算する方法
手順
1.1) 測定結果を表6のようにまとめる。
数値例
1.1.1) ある軸について5本のサンプルを抜き取
り,直径を測定し,次の結果を得た。
表6
測定順
測定値
1
x1
2
x2
3
x3
・
・
・
・
・
・
・
・
n
xn
合計
Σu
平均
x
1.2) 測定値の合計Σxを求める。
nx
x
x
x
x
+
+
+
+
∑
Λ
Λ
3
2
1
=
1.3) Σxをサンプルの大きさnで除して平均値を
求める。
n
x
x
∑
=
表6.1
測定順
測定値
1
2.515
2
2.509
3
2.507
4
2.529
5
2.521
合計
12.581
平均
2.516 2
1.2.1)
1
521
.2
925.2
507
.2
509
.2
515
.2
=
=
+
+
+
+
∑x
1.3.1)
)
(2
516
.2
5
581
.
12
mm
x
=
=
2) 変数変換をして計算する方法 測定値xから一定数を減じ,一定数を乗じて(又は一定数で除して)
簡単な数値uに変数変換し,uの平均値を求めてからもとの数値xに換算すると,取り扱う数字が
簡単になり,計算の誤りも少なくなる。
手順
2.1) 変数変換を行う(1)。
表7
測定順
測定値
u= (x−a) ×b
1
x1
u1
2
x2
u2
3
x3
u3
・
・
・
・
・
・
・
・
・
・
・
・
n
xn
un
合計
−
Σu
平均
−
u
2.2) uについての平均値uを求める。
n
u
u
∑
=
2.3) xを求める。
a
b
u
x
+
÷
=
数値例
2.1.1)
表7.1
測定順
測定値
u= (x−2.5) ×1 000
1
2.515
15
2
2.509
9
3
2.507
7
4
2.529
29
5
2.521
21
合計
−
81
平均
−
16.2
2.2.1)
2.
16
5
81
5
21
29
7
9
15
=
=
=
+
+
+
+
u
2.3.1)
2
516
.2
5.2
000
1
2.
16
=
=
+
÷
x
注(1) 減数aは簡単な数を用いると減算の際の誤りが少ない。また,乗数(又は除数)bはuの値を
整数とするように選べばよい。
13
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) メディアンの求め方
1) 測定値が奇数個の場合
手順
1.1) 測定値を大きさの順に並べる。
x(1) , x(2) , x(3) , …… , x(n)
1.2) 中央の値をとってメディアンx~とする。
数値例
1.1.1) ある軸について5本のサンプルを抜き取
り,直径を測定し,次の結果を得た。
2.515 2.509 2.507 2.529 2.521(単位mm)
これを大きさの順に並べる。
2.507 2.509 2.515 2.521 2.529
1.2.1) x~= 2.515 (mm)
2) 測定値が偶数個の場合
手順
2.1) 測定値を大きさの順に並べる
x (1) , x (2) , x (3) , …… , x (n)
2.2) 中央の2個の値をとり,その平均値を求め,
メディアンx~とする。
数値例
2.1.1) ある軸について6本のサンプルを抜き取
り,直径を測定し,次の結果を得た。
2.515 2.509 2.507 2.529 2.521 2.525(単位
mm)
これを大きさの順に並べる。
2.507 2.509 2.507 2.521 2.525 2.525
2.2.1) x~= (2.515+2.521) /2=2.518 (mm)
備考1. メディアンは,測定値を大きさの順に並べたときの中央の値しか使わないから,計算は簡単
であるが,平均値に比べれば精度が劣ることもある。
2. メディアンは,測定値が偶数個の場合は大きさの順に並べたときの中央の二つの平均値を計
算しなければならないので,サンプルの大きさを奇数にしたほうが簡単になる。
3. メディアンを求める場合,サンプルの大きさが大きいと測定値を大きさの順に並べて中央の
値を探し出すことは容易でなくなるので,サンプルの大きさが3又は5,若しくは7くらい
が便利である。
5.3.2
ばらつきの表し方 2個以上の測定値のばらつきを表すには,範囲R,標準偏差s,不偏分散Vな
どが用いられる。
備考 範囲及び標準偏差は,測定値と同じ単位をもつ。不偏分散は測定値の単位の二乗の単位をもつ。
a) 範囲の求め方 範囲の求め方の手順は,次のとおりとする。
手順
1) 測定値の最大値xmaxと最小値xminを求める。
2) xmaxからxminを引いて範囲Rとする。
R=xmax−xmin
数値例
1.1)ある軸について5本のサンプルを抜き取り,
直径を測定し,次の結果を得た。
2.515 2.509 2.507 2.529 2.521(単位mm)
xmax=2.529
14
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
xmim=2.507
2.1) R=2.529−2.507=0.022 (mm)
備考 範囲は,測定値のうち最大値と最小値の2個しか使わないので,標準偏差に比較して,通常精
度が劣るが計算が簡単である。サンプルの大きさが10以下のときに使うと便利である。
b) 不偏分散の求め方
1) 測定結果を表8のようにまとめる。
表8
測定順
測定値x
x2
1
x1
x12
2
x2
x22
3
x3
x32
・
・
・
・
・
・
・
・
・
・
・
・
n
xn
xn2
合計
Σx
Σx2
測定値の合計Σx及び測定値の二乗の合
計Σx2を計算する。
n
x
x
x
x
x
+
+
+
+
∑
Λ
3
2
1
=
2
23
22
21
2
nx
x
x
x
x
+
+
+
+
∑
Λ
=
2) 次の式によって平方和Sを計算する。
n
x
x
S
2
2
)
(∑
−
∑
=
3) 平方和Sを自由度n−1で割って,不偏分散
Vを求める。
1
−
=nS
V
1.1)
表8.1
測定順
測定値x
x2
1
2.515
6.325 225
2
2.509
6.295 081
3
2.507
6.285 049
4
2.529
6.395 841
5
2.521
6.355 441
合計
12.581
31.656 637
581
.
12
521
.2
509
.2
515
.2
=
=
+
+
+
∑
Λ
x
081
6.295
225
6.325
2
+
=
x
∑
31.6
441
6.355
=
+
+Λ
2.1)
8
324
000
.0
5
)
581
.
12
(
637
656
.
31
2
=
−
=
S
3.1)
)
(
2
081
000
.0
1
5
8
324
000
.0
2
mm
V
=
=
−
15
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
c) 不偏分散の求め方(変数変換して計算する方法)
手順
1) 変数変換を行う(2)。
b
a
x
n
×
−)
(
=
表9
測定順
測定値x
u
u2
1
x1
u1
u12
2
x2
u2
u22
3
x3
u3
u32
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
n
xn
un
un2
合計
−
Σu
Σu2
uの合計Σuとu2の合計Σu2を計算する。
n
u
u
u
u
u
+
+
+
+
∑
Λ
3
2
1
=
2
2
3
2
2
2
1
n
u
u
u
u
u
+
+
+
+
∑
Λ
=
2) 次の式によって平方和を計算する。
∑
−
∑
n
u
u
b
S
2
2
2
)
(
1
=
3) 平方和Sを自由度n−1で割って不偏分散V
を求める。
1
−
nS
V=
数値例
1.1)
表9.1
測定順
測定値x
u= (x−2.5) ×1000
u2
1
2.515
15
225
2
2.509
9
81
3
2.507
7
49
4
2.529
29
841
5
2.521
21
441
合計
−
81
1637
81
21
9
15
=
=
+
+
+
∑
Λ
u
1637
441
81
225
2
=
=
+
+
+
∑
Λ
u
2.1)
0003248
.0
5
81
1637
1000
1
2
2
=
=
−
S
3.1)
)
(
0000812
.0
1
5
0003248
.0
2
mm
V
=
=
−
注(2) 減数aは,簡単な数を用いると減算の際の誤りが少ない。また,乗数(又は除数)bはuの値
を整数とするように選べばよい。
d) 標準偏差の求め方 b)及びc)の3)以降を次の手順によって計算して求める。
手順
1) 次の式によって標準偏差sを求める。
V
s=
数値例
1.1)
)
(
00901
.0
0000812
.0
mm
s
=
=
5.3.3
多数の測定値からの平均値x及び標準偏差sの求め方 測定値の個数が多い場合でもxやsは,3.3.1
及び3.3.2の方法で求めることができるが,計算が面倒になるので,測定値の個数が30個以上の場合はこ
こで規定する方法で求めるのがよい。この場合の手順は,次のとおりとする。
計算手順
1) 表10のような計算用紙を用意する。
2) 3.2.2の手順に従って級,中心x,度数fを
記入する。
3) uの欄でfが最大の級の中心をu=0とし,
測定値の小さいほうへ順に−1, −2,……,
大きいほうへ順に1, 2, ……,と記入する。
数値例
1.1) 表4について計算する。
2.1)
3.1) No.5の級のuの中心を0とおく。
備考 xとuとの関係は,次の式で表される。
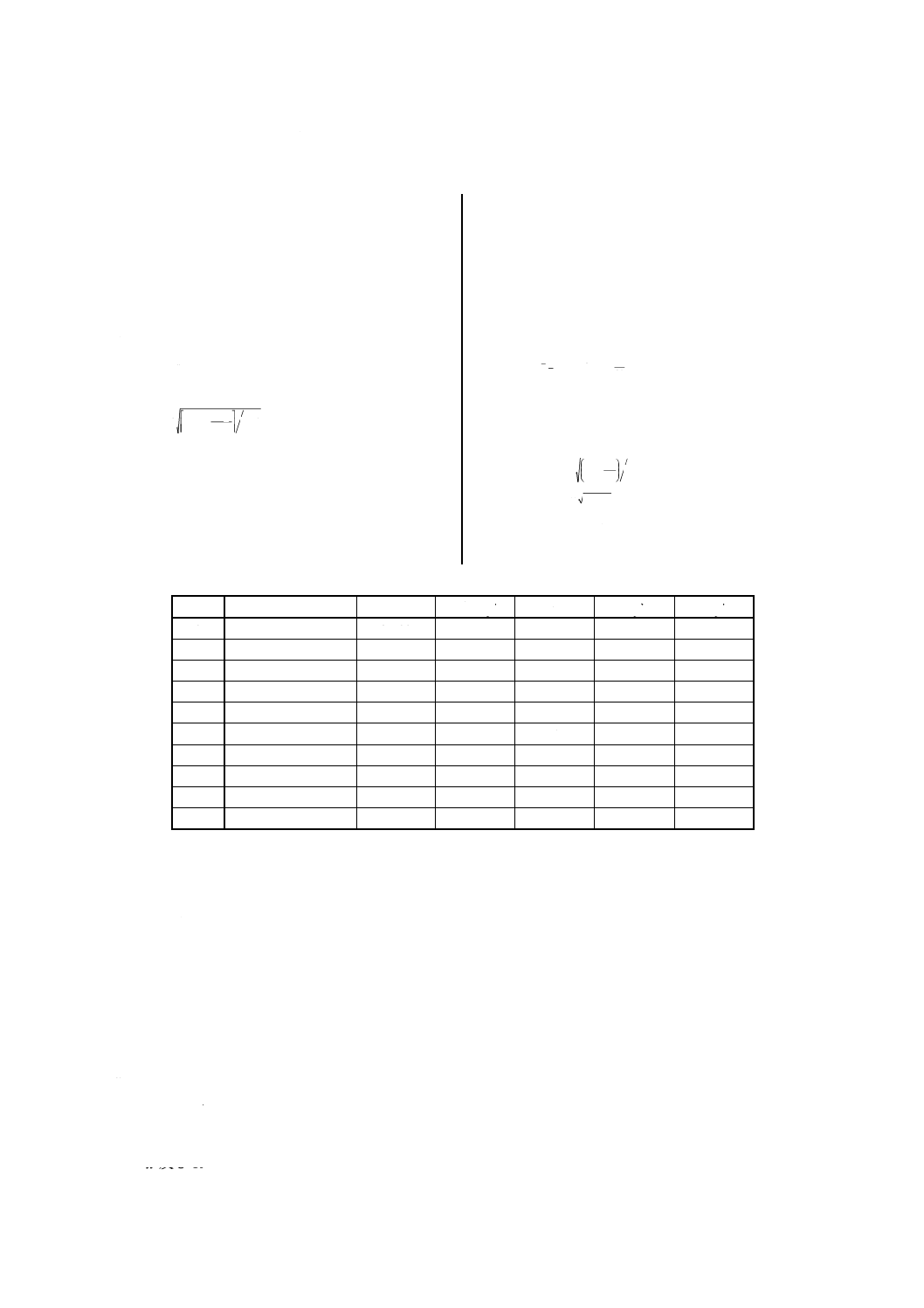
u=[x−(u=0の級の中心)]×1/級幅= (x−a) /h
16
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
a: u=0とおいた級の中心(ここではa=2.523)
h: 級の幅(ここではh=0.005)
4) uとfの積をufの欄に,ufとuの積をu2f
の欄に記入し,これらを加え合わせてufの
合計欄,u2fの合計欄にそれぞれ記入する。
Λ
Λ
+
+
=
∑
2
2
1
1
f
u
f
u
uf
Λ
Λ
+
+
=
∑
2
2
2
1
2
1
2
f
u
f
u
f
u
5) 次の式でxを計算する。
)
/
(
n
uf
h
a
x
∑
+
=
6) 次の式でsを計算する。
)1
(
)
(
2
2
−
∑
−
∑
=
n
n
u
f
u
h
s
4.1)
No.1
uf=−4×1=−4
No.2
uf=−3×4=−12
No.1
u2f=uf×u=−4×−4=16
No.2
u2f=uf×u=−12×−3=36
5.1)
90
30
005
.0
523
.2
×
+
=
x
00167
.0
523
.2
+
)
(
52467
.2
mm
=
6.1)
)1
90
(
90
30
302
005
.0
2
−
−
×
=
s
2809
.3
005
.0
×
=
)
(
00906
.0
mm
=
表10
No.
区間
中心値x
度数f
u
uf
u2f
1
2.500 5〜2.505 5
2.503
1
−4
−4
16
2
2.505 5〜2.510 5
2.508
4
−3
−12
36
3
2.510 5〜2.515 5
2.513
9
−2
−18
36
4
2.515 5〜2.520 5
2.518
14
−1
−14
14
5
2.520 5〜2.525 5
2.523
22
0
0
0
6
2.525 5〜2.530 5
2.528
19
1
19
19
7
2.530 5〜2.535 5
2.533
10
2
20
40
8
2.535 5〜2.540 5
2.538
5
3
15
45
9
2.540 5〜2.545 5
2.543
6
4
24
96
合計
90
−
30
302
5.4
測定に関する情報の報告 測定に関する情報を報告する場合には,少なくとも次の事項を記載する
必要がある。
a) 測定の対象の名称
b) 測定の条件
1) サンプルのとり方
2) サンプルをとった日時
3) 測定の方法,計測器の種類,計測器番号,測定者,測定の環境など。
c) サンプルの大きさn
d) 統計量,次のいずれかを選ぶ。
1)
x及びs
2)
x及びV
3)
x及びR
4)
x~及びR
17
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ただし,Rはサンプルの大きさが10以下の場合に用いてもよい。
e) 分布の形 必要な場合には,度数表又はヒストグラムを記載する。
5.5
層別 測定値を,それが得られた特徴によって,二つ以上の部分集団に分けたとき,その部分集団
を層といい,層に分けることを層別という。
測定値には,必ず大なり小なりのばらつきがある。そこで,そのばらつきを発生させる因子について層
別を行うと,ばらつきの発生原因が分かりやすくなり,ばらつきを減らしたり,工程の平均を好ましい方
向に改善するなど品質の向上に役立てることができる。
通常,原料別,機械別,作業条件別,作業員別などで層別が行われる。
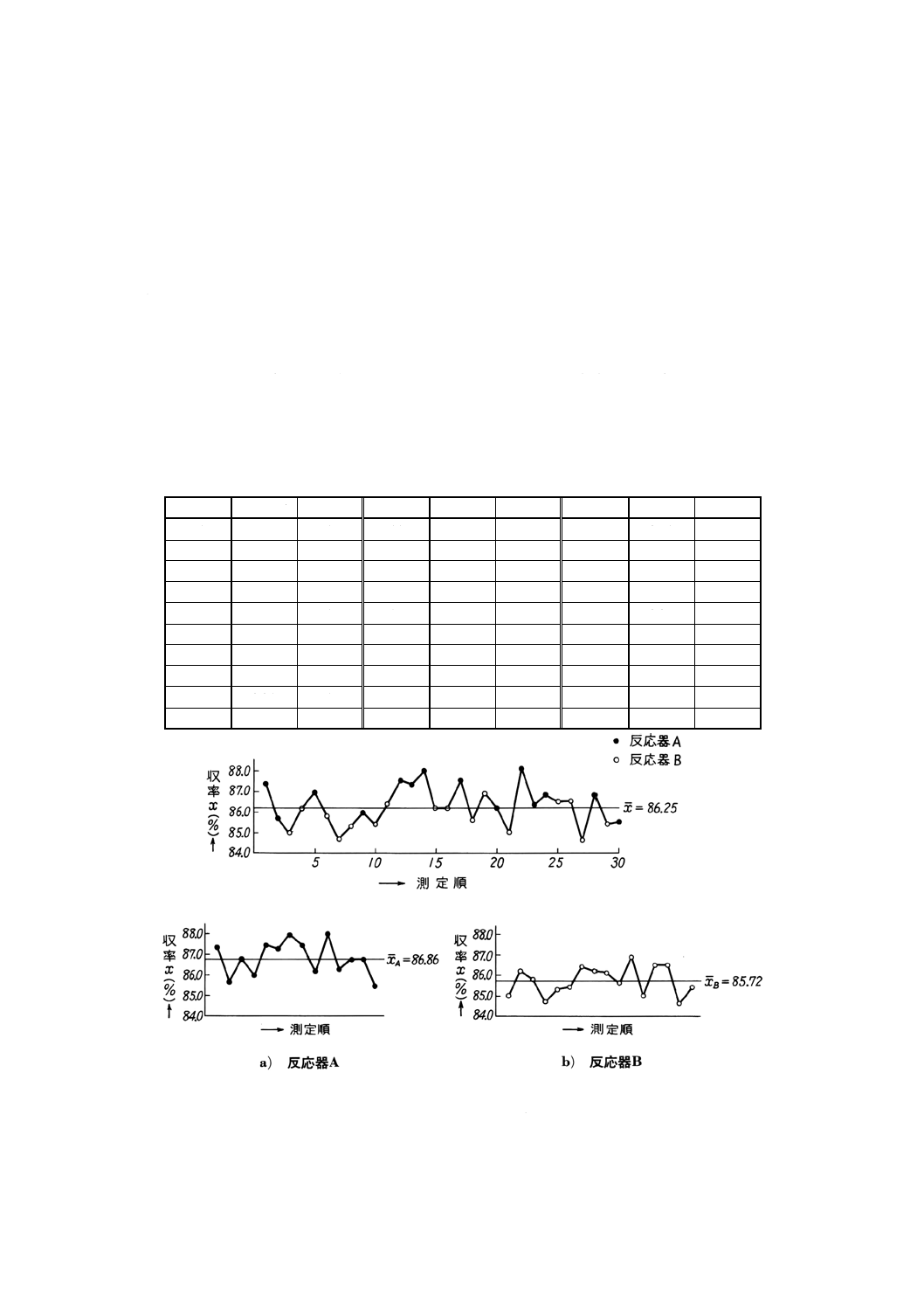
例1. ある化学反応における収率の測定値がある。この反応には,2台の反応器A及びBが使われて
いるので,反応器間に差があるのではないかということに気付き,反応器について層別してみ
た。その結果は図9a)b)のようになり,反応器間に差があることが分かった。
備考 この差が有意であるかどうかの検定は,JIS Z 9041-2の方法による。
表11
単位 %
測定順
収率X
反応器
測定順
収率x
反応器
測定順
収率x
反応器
1
87.4
A
11
86.4
B
21
85.0
B
2
85.7
A
12
87.5
A
22
88.1
A
3
85.0
B
13
87.3
A
23
86.3
A
4
86.2
B
14
88.0
A
24
86.8
A
5
86.9
A
15
86.2
B
25
86.5
B
6
85.8
B
16
86.1
B
26
86.5
B
7
84.7
B
17
87.5
A
27
84.6
B
8
85.3
B
18
85.6
B
28
86.8
A
9
86.0
A
19
86.9
B
29
85.4
B
10
85.4
B
20
86.2
A
30
85.5
A
図9
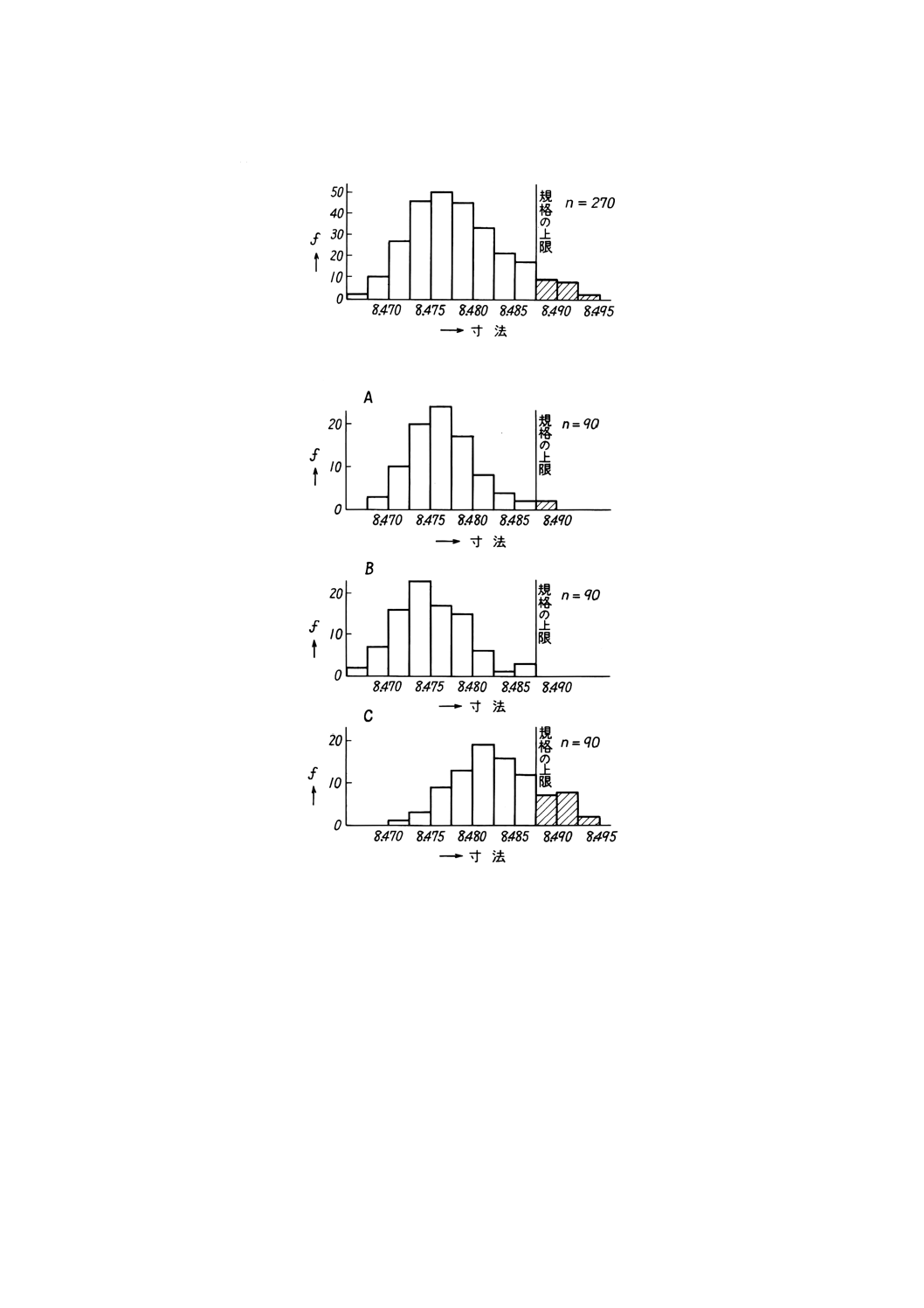
例2. 機械加工されたある部品の寸法について測定した結果をヒストグラムで表したところ,図10a)
のようになった。ところがこの加工は,A,B及びCの3台の機械で平行して加工していて,か
つ,機械間で多少差があることが考えられたので,加工機械別に層別してヒストグラムを書い
18
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
た。結果は図10b)のようになり,A及びBの間にはほとんど差がないが,Cの機械は平均が高
く寸法調整が必要であることが分かった。
図10 a)
図10 b)
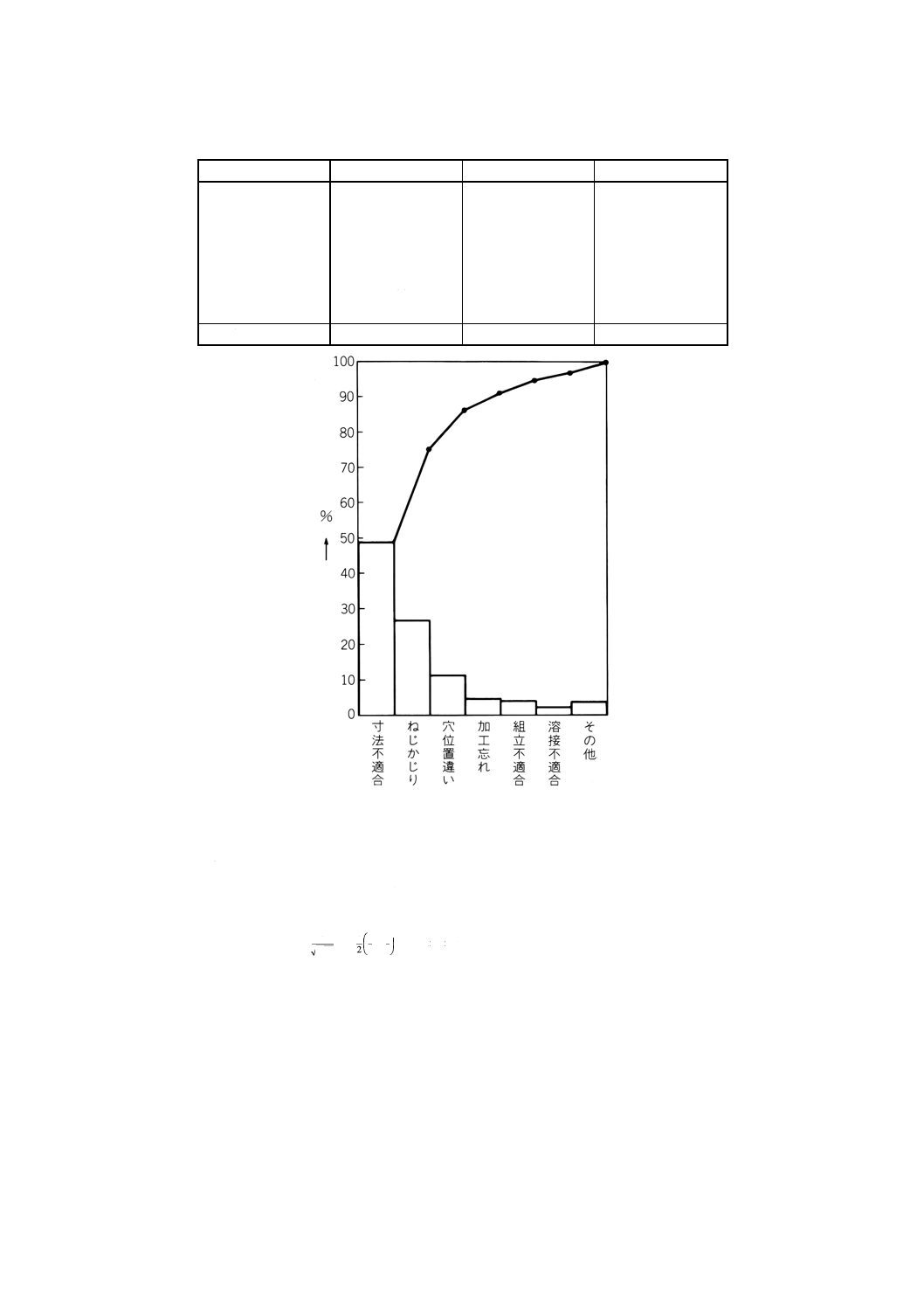
例3. ある組立工程での1か月間の不適合品を,原因別に層別し,原因別度数と,度数の多い原因から
順に合計した累積度数を求めた結果,表12のようになった。これを図示したのが図11である。
この結果,寸法不適合,ねじかじり,穴位置違いによる不適合だけで,不適合全体の86%を
占めていることが分かり,この三つの原因を重点的に対策することにした。
19
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表12
不適合の原因
度数
相対度数 %
相対累積度数 %
寸法不適合
271
48.7
48.7
ねじかじり
147
26.4
75.1
穴位置違い
62
11.1
86.2
加工忘れ
25
4.5
90.7
組立不適合
22
3.9
94.6
溶接不適合
11
2.0
96.6
その他
19
3.4
100.0
合計
557
100.0
図11
備考1. このような図をパレート図といい,不適合などをその原因別,状況別,位置別などに層別し
た結果を表すのに用いられる。
2. 不適合などの損失を金額に換算できるときは,金額でパレート図を書いたほうがよい。
5.6
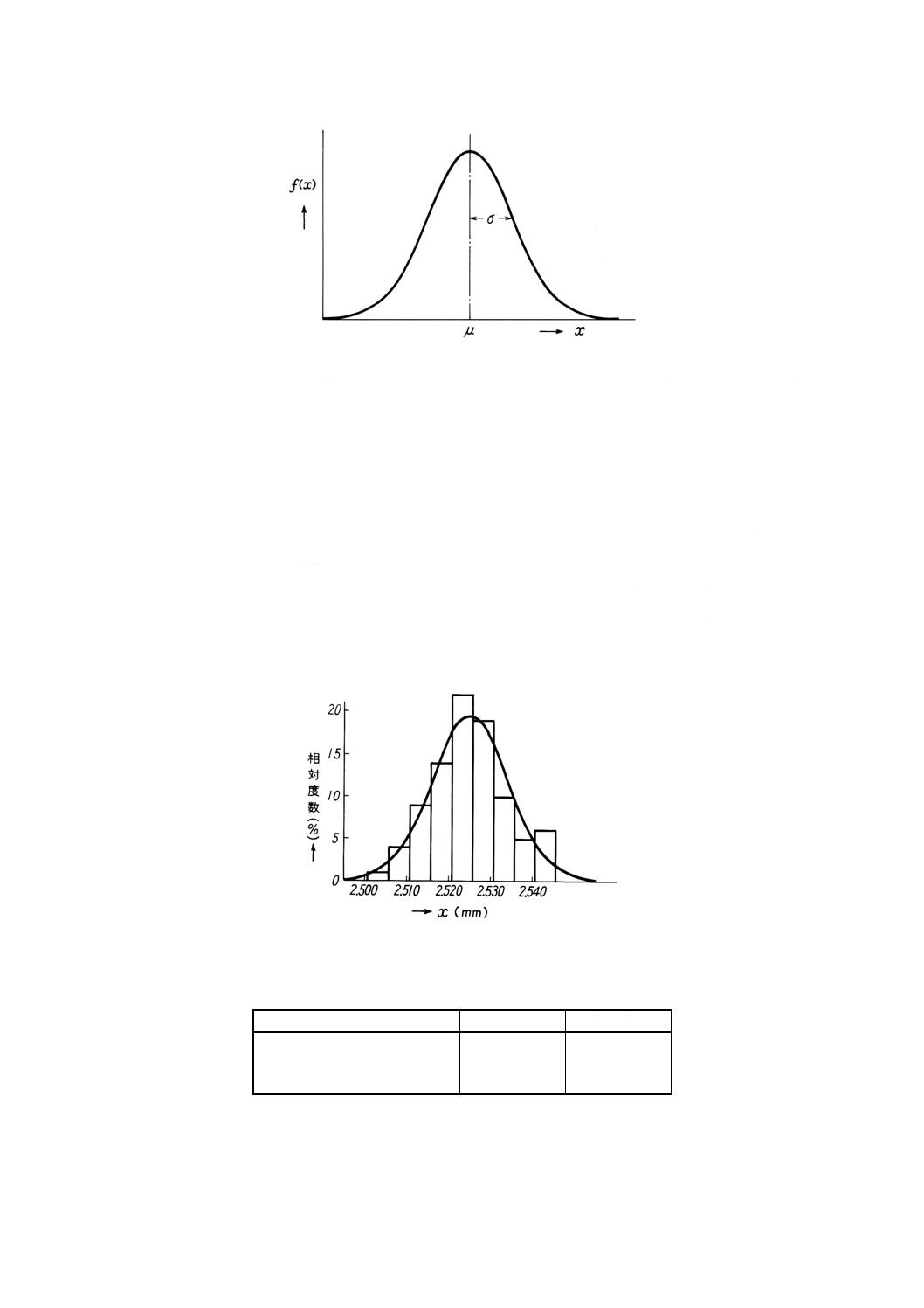
正規分布 次の式で表される曲線を正規分布曲線といい,この分布を正規分布という(図12)。
)
(
21
2
1
)
(
2
∞
<
<
−∞
−
−
x
x
e
x
f
σ
μ
πσ
=
ここに,
x: 連続確率変数
f (x) : 確率密度関数
π: 円周率 π=3.1416
e: 自然対数の底 e=2.7183
σ: 標準偏差
μ: 期待値
20
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図12 正規分布
f (x) はxがμの値をとるとき,最も大きくxがμから離れるほど小さくなり,左右対称の形をとる(正規
分布での期待値はμ, 標準偏差はσとなる。)。
正規分布ではxがμ+kσ以上の値をとる確率は,kの値が等しければその値も一定で,表13のようにな
る。また,左右対称の形であるからμ−kσ以下の値をとる確率,μ±kσの範囲内にある確率なども表13か
ら求めることができる。
一方,ヒストグラムは,サンプルを抜き取った工程(又はロット)の分布の概略の形を示している。図
13は5.2.2b)で作成したヒストグラムの縦軸を相対度数で表したものと5.3.3の度数表から計算したx=
2.524 67 (mm) 及びs=0.009 06 (mm) を期待値及び標準偏差にもつ正規分布を重ねて書いたものである。
図から,このヒストグラムの示す分布は,ほぼ平均2.524 67 (mm) ,標準偏差0.009 06 (mm) の正規分布
になることが分かる。このように工場での測定値の分布は,正規分布とみなせる場合が多い。この場合に
は,度数表から計算したx及びsは工程の測定値の期待値μ及び標準偏差σの推定値となり,かつ,正規分
布の性質を用いてx及びsから工程(又はロット)について種々の情報を得ることができる。
図13
例1. 5.2.1の例1.の測定値のx±s,x±2s,x±3sの範囲外にでる測定値の割合(実測側)と,μ=2.524
67 (mm) ,σ=0.009 06 (mm) の正規分布をするとして,求めた値と比較する。
実測 %
正規分布 %
x±sの範囲外に出る割合
32.2
31.7
x±2sの範囲外に出る割合
5.6
4.5
x±3sの範囲外に出る割合
0
0.27
例2. ある工程で加工された軸の外径寸法の分布は,μ=52.51mm,σ=0.23mmであることが分かって
いる。この工程では直径が53.00以上の軸のできる確率(割合)は,
13
.2
23
.0
51
.
52
00
.
53
=
=
−
k
21
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
であるから正規分布表から0.0166と求められる。
例3. 例2.において軸の直径の規格が52.50±0.40mmと決められた場合,上限規格値=52.90mm,下限
規格値=52.10mmで
70
.1
23
.0
51
.
52
90
.
52
1
=
=
−
k
78
.1
23
.0
51
.
52
10
.
52
2
−
−
=
=
k
であるから,正規分布表から上限規格値を超えるもの0.0446,下限規格値をわるもの0.0375
と求められる。したがって,この工程では不良率が約8%見込まれる。
備考 実際の分布が正規分布でない場合に,測定値がある値以上(又は以下)の値をとる確率を求め
るには,次の方法による。
a) 実際に求めた分布を使って推定する。
b) 測定値を変数変換して正規分布に直し,正規分布表を用いて推定する。例えば,寿命xが正
規分布でなくてもX=logXとおくとXが正規分布に近くなることがある。
表13 正規分布表
k
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
0.0
.500 0
.496 0
.492 0
.488 0
.484 0
.480 1
.476 1
.472 1
.468 1
.464 1
0.1
.460 2
.456 2
.452 2
.448 3
.444 3
.440 4
.436 4
.432 5
.428 6
.424 7
0.2
.420 7
.416 8
.412 9
.409 0
.405 2
.401 3
.397 4
.393 6
.389 7
.385 9
0.3
.382 1
.378 3
.374 5
.370 7
.366 9
.363 2
.359 4
.355 7
.352 0
.348 3
0.4
.344 6
.340 9
.337 2
.333 6
.330 0
.326 4
.322 8
.319 2
.315 6
.312 1
0.5
.308 5
.305 0
.301 5
.298 1
.294 6
.291 2
.287 7
.284 3
.281 0
.277 6
0.6
.274 3
.270 9
.267 6
.264 3
.261 1
.257 8
.254 6
.251 4
.248 3
.245 1
0.7
.242 0
.238 9
.235 8
.232 7
.229 6
.226 6
.223 6
.220 6
.217 7
.214 8
0.8
.211 9
.209 0
.206 1
.203 3
.200 5
.197 7
.194 9
.192 2
.189 4
.186 7
0.9
.184 1
.181 4
.178 8
.176 2
.173 6
.171 1
.168 5
.166 0
.163 5
.161 1
1.0
.158 7
.156 2
.153 9
.151 5
.149 2
.146 9
.144 6
.142 3
.140 1
.137 9
1.1
.135 7
.133 5
.131 4
.129 2
.127 1
.125 1
.123 0
.121 0
.119 0
.117 0
1.2
.115 1
.113 1
.111 2
.109 3
.107 5
.105 6
.103 8
.102 0
.100 3
.098 5
1.3
.096 8
.095 1
.093 4
.091 8
.090 1
.088 5
.086 9
.085 3
.083 8
.082 3
1.4
.080 8
.079 3
.077 8
.076 4
.074 9
.073 5
.072 1
.070 8
.069 4
.068 1
1.5
.066 8
.065 5
.064 3
.063 0
.061 8
.060 6
.059 4
.058 2
.057 1
.055 9
1.6
.054 8
.053 7
.052 6
.051 6
.050 5
.049 5
.048 5
.047 5
.046 5
.045 5
1.7
.044 6
.043 6
.042 7
.041 8
.040 9
.040 1
.039 2
.038 4
.037 5
.036 7
1.8
.035 9
.035 1
.034 4
.033 6
.032 9
.032 2
.031 4
.030 7
.030 1
.029 4
1.9
.028 7
.028 1
.027 4
.026 8
.026 2
.025 6
.025 0
.024 4
.023 9
.023 3
2.0
.022 8
.022 2
.021 7
.021 2
.020 7
.020 2
.019 7
.019 2
.018 8
.018 3
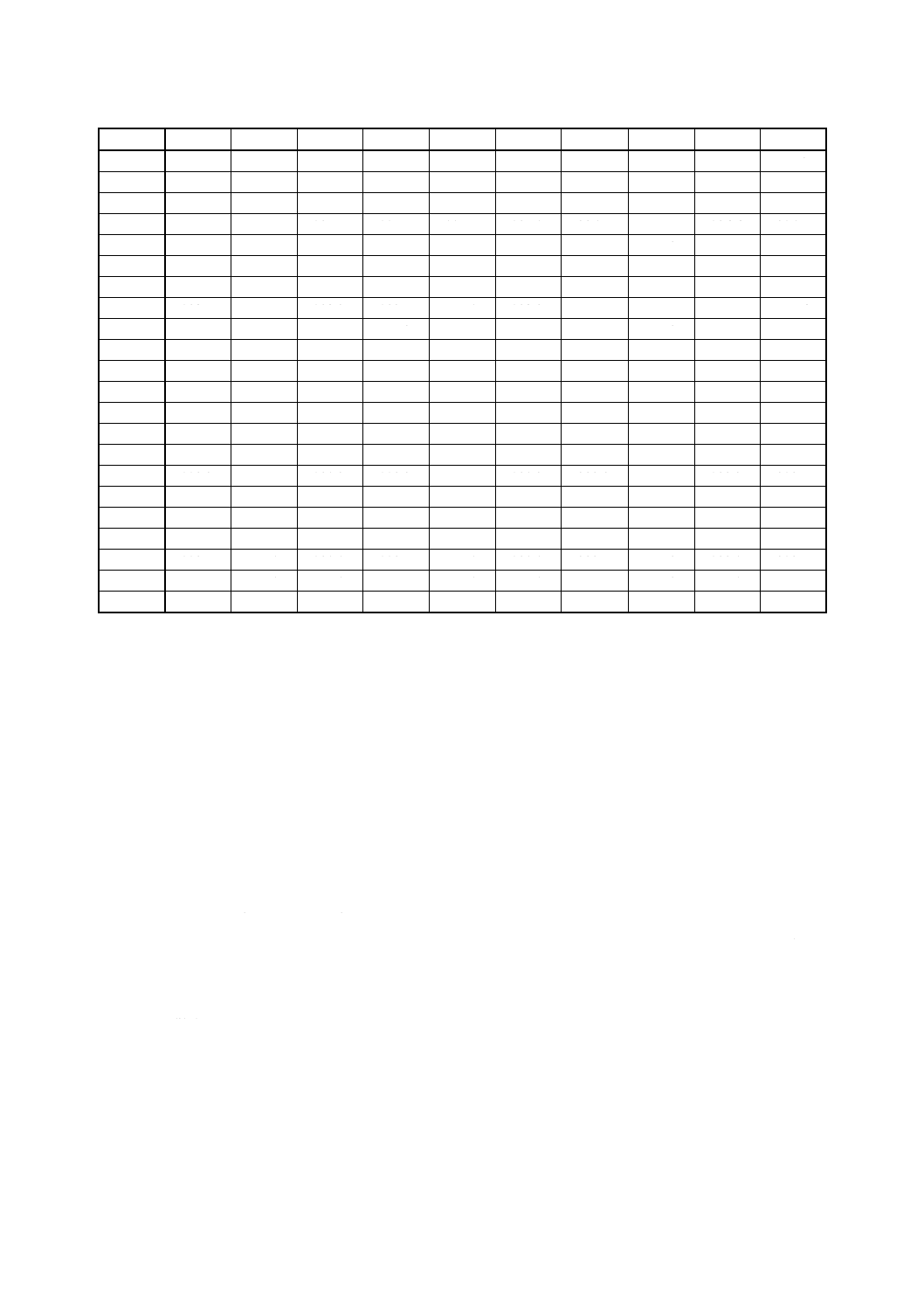
22
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
k
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
2.1
.017 9
.017 4
.017 0
.016 6
.016 2
.015 8
.015 4
.015 0
.014 6
.014 3
2.2
.013 9
.013 6
.013 2
.012 9
.012 5
.012 2
.011 9
.011 6
.011 3
.011 0
2.3
.010 7
.010 4
.010 2
.009 9
.009 6
.009 4
.009 1
.008 9
.008 7
.008 4
2.4
.008 2
.008 0
.007 8
.007 5
.007 3
.007 1
.006 9
.006 8
.006 6
.006 4
2.5
.006 2
.006 0
.005 9
.005 7
.005 5
.005 4
.005 2
.005 1
.004 9
.004 8
2.6
.004 7
.004 5
.004 4
.004 3
.004 1
.004 0
.003 9
.003 8
.003 7
.003 6
2.7
.003 5
.003 4
.003 3
.003 2
.003 1
.003 0
.002 9
.002 8
.002 7
.002 6
2.8
.002 6
.002 5
.002 4
.002 3
.002 3
.002 2
.002 1
.002 1
.002 0
.001 9
2.9
.001 9
.001 8
.001 8
.001 7
.001 6
.001 6
.001 5
.001 5
.001 4
.001 4
3.0
.001 3
.001 3
.001 3
.001 2
.001 2
.001 1
.001 1
.001 1
.001 0
.001 0
3.1
.001 0
.000 9
.000 9
.000 9
.000 8
.000 8
.000 8
.000 8
.000 7
.000 7
3.2
.000 7
.000 7
.000 6
.000 6
.000 6
.000 6
.000 6
.000 5
.000 5
.000 5
3.3
.000 5
.000 5
.000 5
.000 4
.000 4
.000 4
.000 4
.000 4
.000 4
.000 3
3.4
.000 3
.000 3
.000 3
.000 3
.000 3
.000 3
.000 3
.000 3
.000 3
.000 2
3.5
.000 2
.000 2
.000 2
.000 2
.000 2
.000 2
.000 2
.000 2
.000 2
.000 2
3.6
.000 2
.000 2
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
3.7
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
3.8
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
.000 1
3.9
.000 0
.000 0
.000 0
.000 0
.000 0
.000 0
.000 0
.000 0
.000 0
.000 0
6. 2変数の場合の測定値のまとめ方 化学製品の合成反応において,原料中の不純物xと製品の収率y,
鋼材の処理温度xと引張強さy,触媒の活性度xと寿命yというように,対になった測定値xとyとの間の
関係を調べる場合に用いる散布図の書き方及び見方並びに相関係数の計算の手順は,次のとおりとする。
6.1
測定値の記録 測定値を記録する場合には,測定の対象となった品物の名称,特性,サンプルのと
り方,サンプルをとった日時,測定の日時,温度,湿度,測定方法,計測器の種類,計測器番号,測定者
など,あとで調査したり解析したりする場合の必要事項を併記することが望ましい。
繰り返して行う測定には,一定の記録用紙を定めておくとよい。
6.2
散布図 多数の測定値を表にしただけでは十分な情報をつかみにくいが,散布図で表すと情報がつ
かみやすくなる。
6.2.1
散布図の書き方 方眼紙又は適当な用紙の横軸に測定値xの値を目盛り,左端に測定値yの値を目
盛り,対になった測定値 (x , y) の点を記入する。
備考 方眼紙の目盛は,xのばらつきの範囲とyのばらつきの範囲を調べ,それらの長さがほぼ等し
くなるようにとることが望ましい。
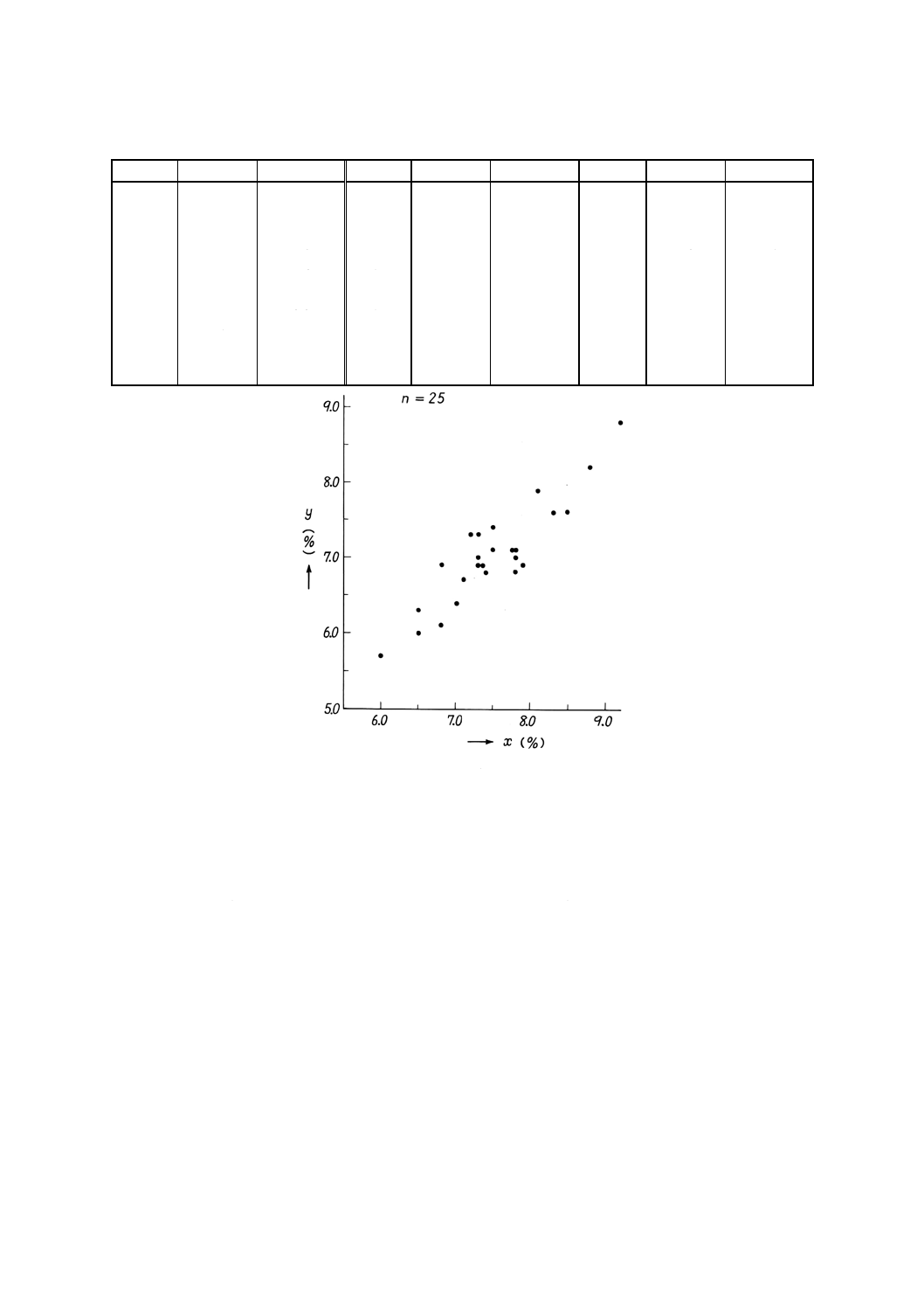
例 原綿の含水率について,加工前の測定結果 (x) と中間工程の測定結果 (y) を表14に示す。これ
を散布図に表すと図14になる。
23
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表14 原綿の含水準
測定順
加工前x
中間工程y
測定順
加工前x
中間工程y
測定順
加工前x
中間工程y
1
6.8
6.1
11
7.8
6.8
21
7.3
7.0
2
7.1
6.7
12
9.2
8.8
22
8.1
7.9
3
6.5
6.3
13
6.0
5.7
23
7.9
6.9
4
7.8
7.1
14
7.5
7.1
24
7.8
7.1
5
7.5
7.4
15
7.8
7.0
25
7.3
6.9
6
8.5
7.6
16
6.8
6.9
7
8.8
8.2
17
7.3
7.3
8
7.0
6.4
18
7.3
6.9
9
7.4
6.8
19
8.3
7.6
10
6.5
6.0
20
7.2
7.3
図14 散布図(表14のデータで書いたもの)
6.2.2
散布図の見方 散布図を見る場合,次の点に注意する。
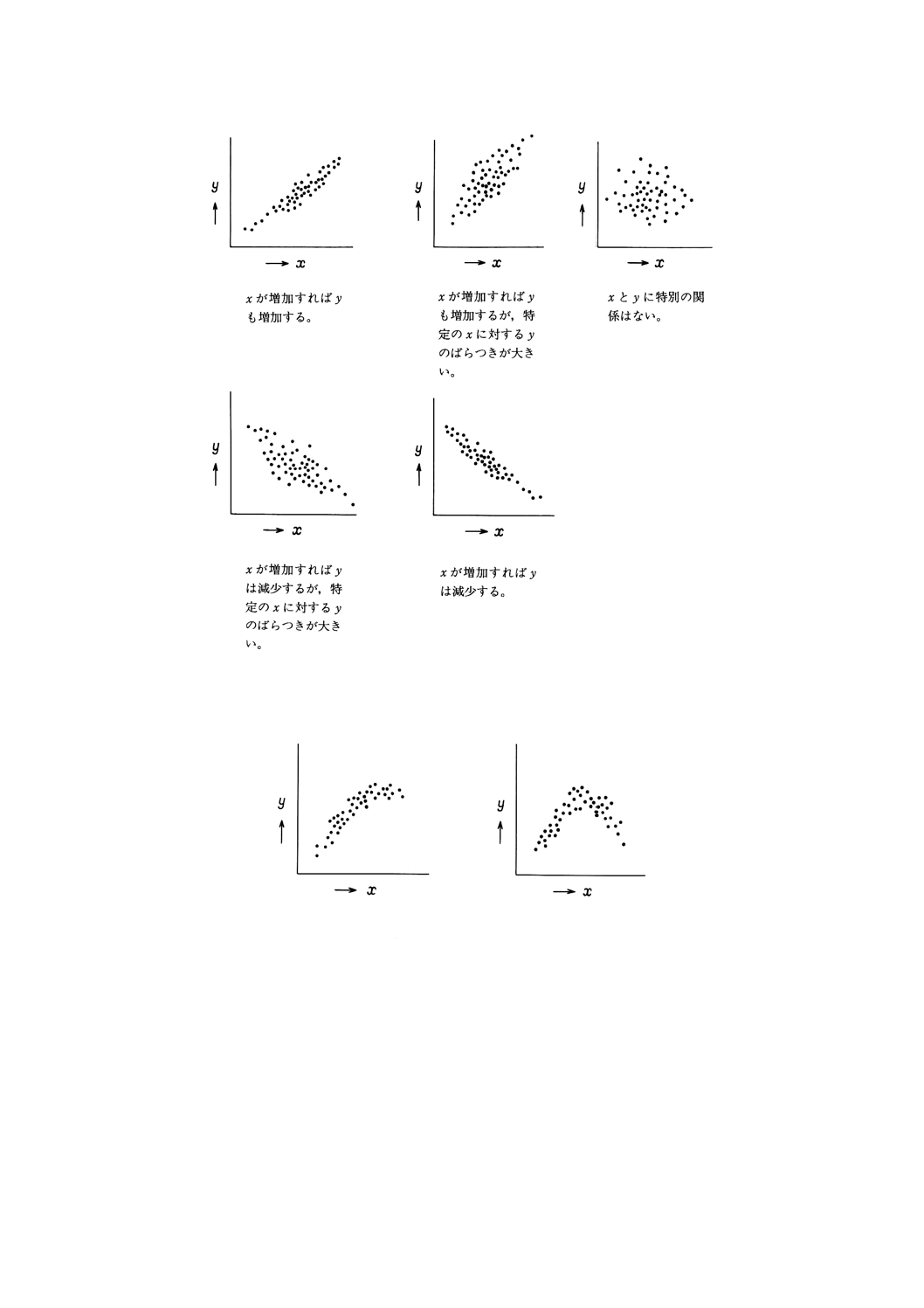
a) 点が右上がりの傾向があるか右下がりの傾向があるかを見る。
1) 右上がりの傾向があるときは,xが増加すればyも増加する関係がある。
2) 右下がりの傾向があるときは,xが増加すればyは減少する関係がある。
b) 点がa)の傾向線からどのくらいばらついているかを見る。傾向線からのばらつきが少ないほどa)の1)
又は2)の関係が強く,傾向線からのばらつきが大きいほどその関係は弱くなる。
24
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図15 散布図の例
備考1. xとyとの関係が,図16のように曲線で表せるような場合には,6.3で説明する相関係数を計
算しても意味がない。
図16
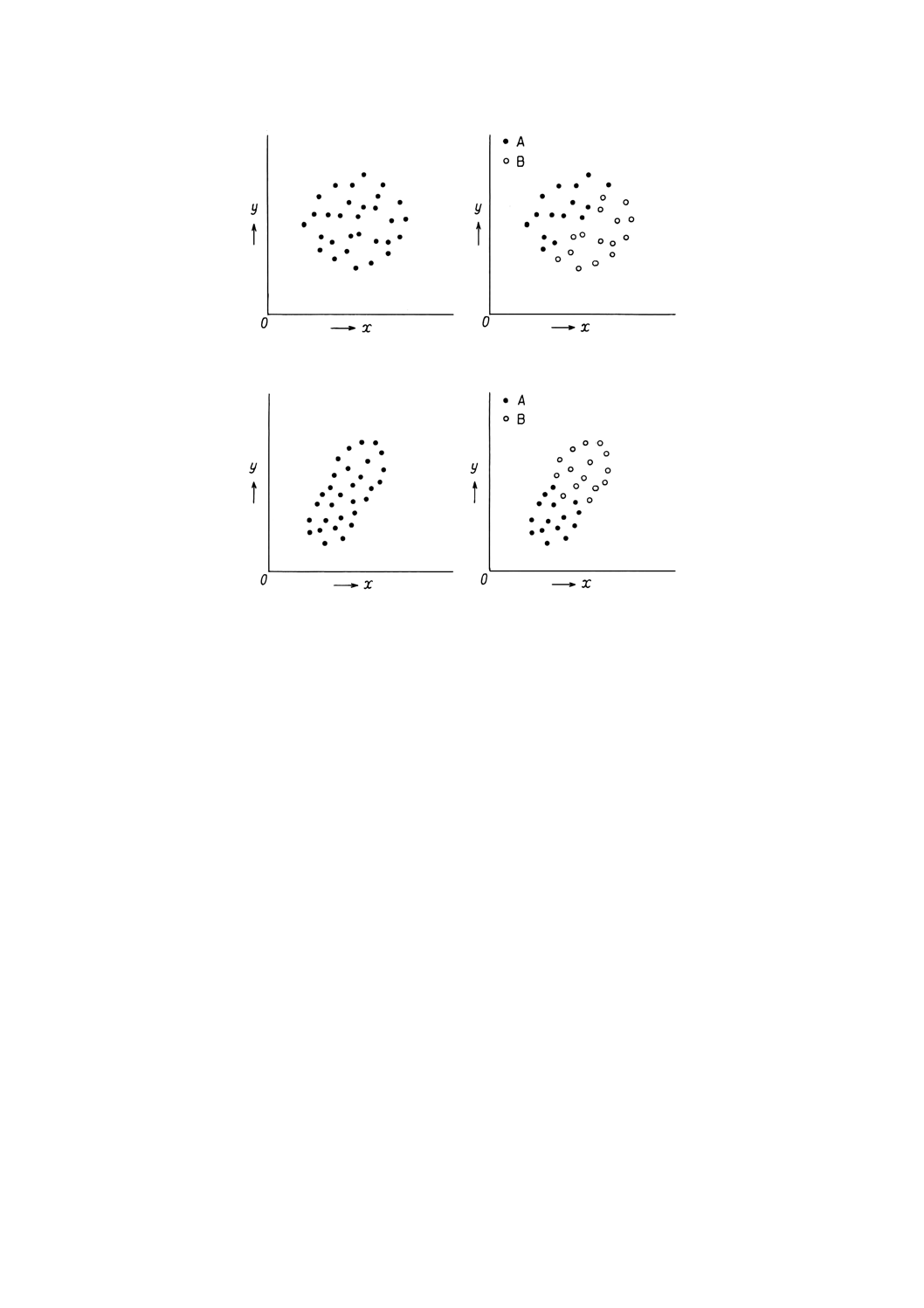
2. 図17のように層別しなければxとyの間に関係が見られないが,層別することによってxと
yの間に関係が見られるようになる場合や,図18のように層別しなければxとyの間に関係
が見られるが,層別することによってxとyの間に関係が見られなくなる場合がある。
25
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図17
図18
6.3
数量的な表し方 対になった測定値 (x , y) の関係を表すには相関係数を用いる。相関係数を計算す
るには,データから直接計算する方法と,相関表から計算する方法とがある。測定値の個数が少ないとき
は,直接計算する方法を,測定値の個数の多い場合は,相関表から計算する方法を用いると便利である。
26
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3.1
相関係数の求め方(直接計算する方法) 相関係数を計算する手順は,次のとおりとする。
手順
1) 測定結果を表15のようにまとめる。
数値例
1.1) 4.2例1.の測定値について計算する(3)。
表15
測定順
測定結果
x2
y2
xy
x
y
1
x1
y1
x12
y12
x1y1
2
x2
y2
x22
y22
x2y2
3
x3
y3
x32
y32
x3y3
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
n
xn
yn
xn2
yn2
xnyn
合計
Σx
Σy
Σx2
Σy2
Σxy
2) 測定値の合計Σx,Σy,測定値の二乗の合計
Σx2, Σy2及び測定値の積の合計Σxyを計算す
る。
Σx=x1+x2+x3+…+xn
Σy=y1+y2+y3+…+yn
Σx2=x12+x22+x32+…+xn2
Σy2=y12+y22+y32+…+yn2
Σxy=x1y1+x2y2+x3y3+…+xnyn
表15.1
測定順
測定結果
x2
y2
xy
x
y
1
6.8
6.1
46.24
37.21
41.48
2
7.1
6.7
50.41
44.89
47.57
3
6.5
6.3
42.25
39.69
40.95
4
7.8
7.1
60.84
50.41
55.38
5
7.5
7.4
56.25
74.76
55.50
6
8.5
7.6
72.25
57.76
64.60
7
8.8
8.2
77.44
67.24
72.16
8
7.0
6.4
49.00
40.96
44.80
9
7.4
6.8
54.76
46.24
50.32
10
6.5
6.0
42.25
36.00
39.00
11
7.8
6.8
60.84
46.24
53.04
12
9.2
8.8
84.64
77.44
80.96
13
6.0
5.7
36.00
32.49
34.20
14
7.5
7.1
56.25
50.41
53.25
15
7.8
7.0
60.84
49.00
54.60
16
6.8
6.9
46.24
47.61
46.92
17
7.3
7.3
53.29
53.29
53.29
18
7.3
6.9
53.29
47.61
50.37
19
8.3
7.6
68.89
57.76
63.08
20
7.2
7.3
51.84
53.29
52.56
21
7.3
7.0
53.29
49.00
51.10
22
8.1
7.9
65.61
62.41
63.99
23
7.9
6.9
62.41
47.61
54.51
24
7.8
7.1
60.84
50.41
55.38
25
7.3
6.9
53.29
47.61
50.37
合計
187.5
175.8
2.1) Σx=6.8+7.1+6.5+…+7.3=187.5
Σy=6.1+6.7+6.3+…+6.9=175.8
Σx2=46.24+50.41+42.25+…+53.29=
1419.25
Σy2=37.21+44.89+39.69+…+47.61=
1247.34
Σxy=41.48+47.57+40.95+…+50.37=
1329.38

27
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3)
n
y
n
x
2
2
)
(,
)
(
∑
∑
及び
n
y
x
)
)(
(
∑
∑
を計算する。
4) 平方和S (x,x) ,S (y,y) ,積和S (x,y) を計
算する。
n
x
x
x
x
s
2
2
)
(
)
,
(
∑
∑
−
=
n
y
y
y
y
s
2
2
)
(
)
,
(
∑
∑
−
=
n
y
x
y
x
y
x
s
)
)(
(
,
)
,
(
∑
∑
∑
−
=
5) 次の式によって相関係数γを計算する。
)
,
(
)
,
(
)
,
(
v
v
S
u
u
S
y
x
S
r=
3.1)
25
.
406
1
25
)5.
187
(
)
(
2
2
=
=゜
n
x
∑
23
.
236
1
25
)8.
175
(
)
(
2
2
=
=
n
y
∑
50
.
318
1
25
8.
175
5.
187
)
)(
(
=
=
×
∑
∑
n
y
x
4.1) S (x, x) =1419.25−1406.25=13.00
S (y, y) =1 247.34−1 236.23=11.11
S (x, y) =1 329.38−1 318.50=10.88
5.1)
91
.0
02
.
12
88
.
10
11
.
11
00
.
13
88
.
10
=
=
=
−
r
注(3) 測定値x及びyからそれぞれ一定数を減じ,一定数を乗じて簡単な数値u及びυに変数変換して
から次の式によって計算すると,計算が簡単にでき,計算誤りも少なくなる。
)
,
(
)
,
(
)
,
(
v
v
S
u
u
S
v
u
S
r=
ここに,
d
c
y
v
b
a
x
u
×
×
−
)
(
,
)
(
−
=
=
6.3.2
相関係数の求め方(相関表の場合) 相関表に表した場合の相関係数の計算手順は,次のとおりと
する。
手順
1) 測定結果をまとめる。
2) x及びyについて,それぞれ5〜20の等間
隔の級に分ける(5.2.2参照)。
3) x及びyの境界を決める(5.2.2参照)。
4) xの級とyの級で区切られる領域に含まれ
る測定値の出現度数fijを記録する。
数値例
1.1) 6.2の例について計算する。
2.1) xの最大値=9.2xの最小値=6.0
R=9.2−6.0=3.2
3.2÷0.2=16
3.2÷0.5=6.4
3.2÷1.0=3.1
したがって,xの級幅を0.5と決める。
yの最大値=8.8 yの最小値=5.7
R=8.8−5.7=3.1
3.1÷0.2=15.5
3.1÷0.5=6.2
3.1÷1.0=3.1
したがって,yの級幅を0.5と決める。
3.1)
xの境界5.75〜6.25, 6.25〜6.75, …………
yの境界5.55〜6.05, 6.05〜6.55, …………
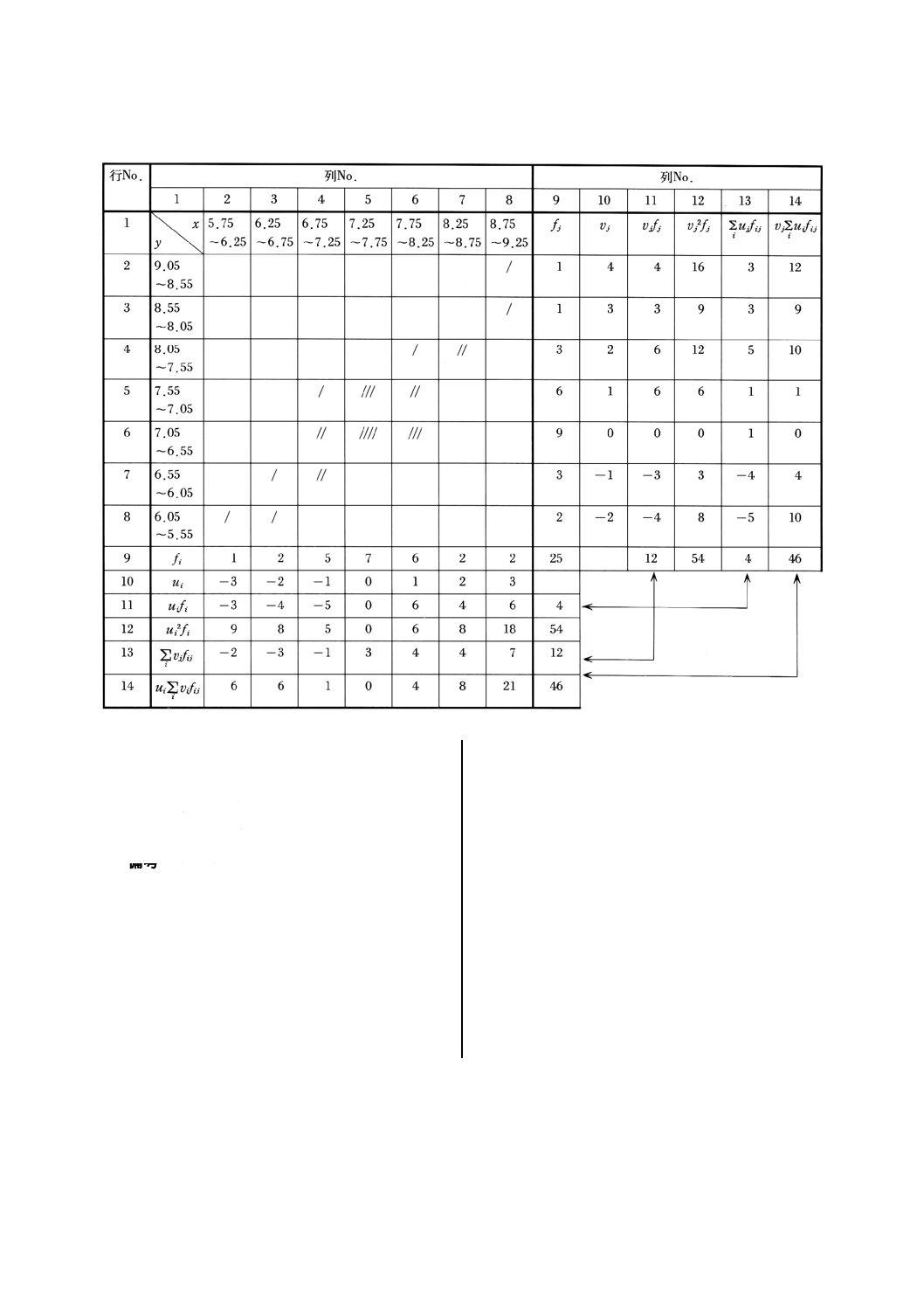
4.1) 表16のようにまとめる。
28
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表16
5) 各列の度数の合計fi及び各行の度数の合計
fj並びに度数の総計nを求める。
∑
+
+
j
i
i
ij
i
f
f
f
f
Λ
Λ
2
1
=
=
∑
+
+
j
j
j
ij
i
f
f
f
f
Λ
Λ
2
1
=
=
備考 ∑
∑
=
j
j
j
i
f
f
となるのでこれによって検算
ができる。
6) fjが最大の級をui=0とし,列No.の小さい
ほうに順に−1 −2 ……,大きいほうに順
に1, 2, ……,と記入する。次にfjが最大の
級をυj=0とし,行No.の大きいほうに順に
−1, −2, ……,小さいほうに順に1, 2, …
…,と記入する。
5.1)
列No.2 f1=1 行No.2 f1=1
列No.3 f2=1+1=2 行No.3 f2=1
n=1+2+5+…+2=1+1+…+2=25
6.1) 列No.5をui=0,行No.6をυj=0とし,ui υj
の値を記入する。

29
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7) uiとfiの積uifi, υjとfiの積υjfj及びそれぞれ
の合計
∑
i
i
if
u並びに∑
j
j
jf
vを計算する。
∑
+
+
i
i
i
f
u
f
u
f
u
Λ
2
2
1
1
=
∑
+
+
j
i
i
f
f
f
Λ
2
2
1
1
υ
υ
υ=
8) uiとuifjの
i
if
u2,υjとυjfjの積
j
2f
j
υ及びそれぞれ
の合計∑
i
j
if
u2並びに∑
j
j
jf
2
υ
を計算する。
∑
+
+
i
i
i
f
u
f
u
f
u
Λ
2
2
2
1
2
1
2=
∑
+
+
j
j
j
f
f
f
Λ
2
2
2
1
2
1
2
υ
υ
υ
=
9) 各列ごとにυjとfijの積の合計∑
j
ijf
jυ及び各行
ごとにuiとfijの積の合計∑
i
ij
if
uを求め,それ
ぞれの合計∑∑
i
j
ij
if
υ並びに∑∑
j
i
ij
if
uを計算する。
備考
∑
∑∑
j
j
i
i
j
ij
i
f
f
υ
υ
=
∑
∑∑
i
i
i
j
i
ij
i
f
u
f
u
=
となるのでこれによって検算ができ
る。
7.1) (行No.11)
列No.2 (−3) ×1=−3
列No.3 (−2) ×2=−4
Μ
列No.9 ∑
i
i
if
u= (−3) + (−4) +……+6
=4
(列No.11)
行No.2 4×1=4
行No.3 3×1=3
Μ
行No.9 ∑
j
i
if
υ=4+3+……+ (−4) =12
8.1) (行No.12)
列No.2 (−3) × (−3) =9
列No.3 (−2) × (−4) =8
Μ
列No.9 ∑
i
i
if
u2=9+8+6+……+18=54
(列No.12)
行No.2 4×4=16
行No.3 3×3=9
Μ
行No.9 ∑
j
ji
jif
2
υ
=16+9+……+8=54
9.1) (行No.13)
列No.2 (−2) ×1=−2
列No.3 (−1) ×1+ (−2) ×1=−3
Μ
列NO.9 ∑∑
i
j
ij
if
υ= (−2) + (−3) +……
=12
(列No.13)
行No.2 3×1=3
行No.3 3×1=3
Μ
行No.9 ∑∑
j
i
ij
if
u=3+3+…+ (−5) =4

30
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
10) uiと∑
j
ij
jf
υ
の積ui
∑
j
ij
jf
υ及びυjと∑
i
ij
if
uの積
ui
∑
i
ij
if
uを求め,それぞれの合計∑∑
i
j
ij
j
i
f
u
υυ並び
に∑∑
j
i
ij
i
j
f
u
υ
を求める。
備考
∑∑
∑∑
=
j
j
ij
i
i
i
j
ij
i
i
f
u
f
u
υ
υ
∑∑
=
i
j
ij
i
if
uυ
となるので,これによって検算がで
きる。
11) 平方和S (u, u) ,S (υ,υ) ,積和S (u, υ) を
計算する。
∑
∑
−
=
i
i
i
i
i
i
n
f
u
f
u
u
u
S
2
2
)
,
(
∑
∑
−
=
j
j
i
i
i
i
n
f
f
S
2
)
,
(
υ
υ
υ
υ
∑∑
∑
∑
−
=
i
j
j
j
i
i
i
i
ij
i
i
n
f
f
u
f
u
u
S
υ
υ
υ)
,
(
12) 次の式によって,相関係数rを計算する。
)
,
(
)
,
(
)
,
(
υ
υ
υ
S
u
u
S
u
S
r=
10.1) (行No.14)
列No.2 (−3) × (−2) =6
Μ
列No.3 (−2) × (−3) =6
Μ
列No.9 ∑∑
i
j
ij
i
i
f
u
υ=6+6+2+…+21=46
(列No.14)
行No.2 4×3=12
行No.3 3×3 : 9
Μ
行No.9 ∑∑
j
i
ij
i
j
f
u
υ
=12+9+……+10=46
11.1)
36
.
534
54
)
,
(
2
−
=
u
u
S
24
.
48
25
12
54
)
,
(
2
−
=
υ
υ
S
08
.
44
2512
4
46
)
,
(
=
−
=
×
υ
u
S
12.1)
87
.0
74
.
5008
.
44
24
.
48
36
.
53
08
.
44
=
=
=
×
r
6.3.3
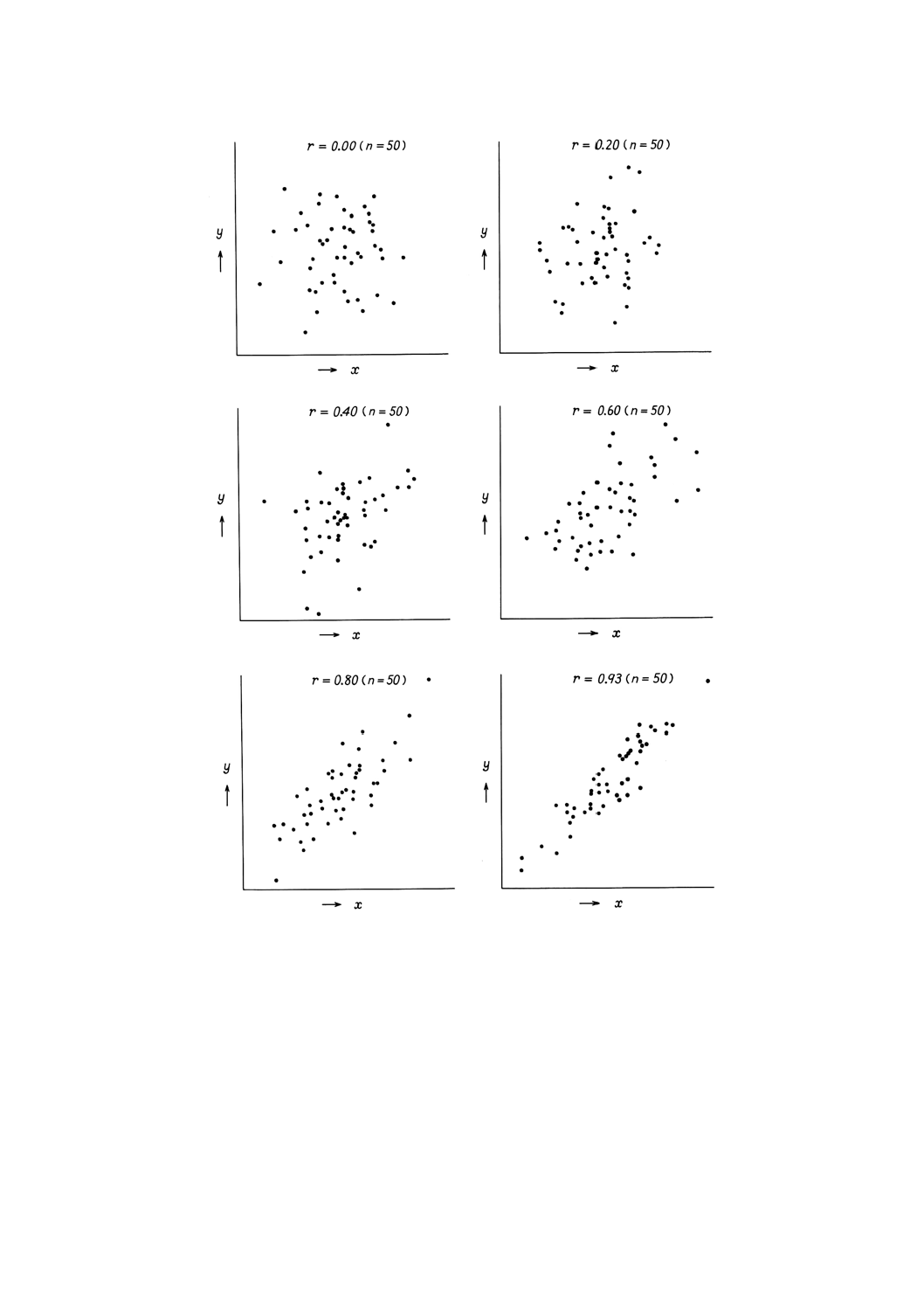
相関係数の意味 相関係数γは,−1≦γ≦1の範囲の値をとる。xが増加すればyも増加する傾向の
ある場合には0<γとなり(正の相関),xが増加すればyは減少する傾向のある場合にはγ<0(負の相関)と
なる。xとyに直線関係のないときはγ≒0となる。
なお,γの値が1又は−1に近い値をとるほど,一定の傾向線からのばらつきは少なくなる。
図19にγのいろいろな場合の散布図を示す。
31
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 γ<0の場合は,右下がりの傾向となる。
図19 散布図の例
32
Z 9041-1 : 1999
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
品質管理分野国際整合化分科会
(主査)
○ 尾 島 善 一
東京理科大学理工学部
(委員)
青 木 茂 雄
財団法人日本科学技術連盟
今 井 秀 孝
工業技術院計量研究所
柿 田 和 俊
社団法人日本鉄鋼連盟
加 藤 洋 一
QCコンサルタント
門 山 允
元東京国際大学(故人)
兼 子 毅
武蔵工業大学
◎ 椿 広 計
筑波大学社会工学系
仁 科 健
名古屋工業大学工学部
○ 野 澤 昌 弘
東京理科大学経営学部
三佐雄 武 雄
QCコンサルタント
宮 津 隆
帝京科学大学理工学部
○ 山 田 秀
東京理科大学工学部
○ 岸 本 淳 司
株式会社SASインスティチュートジャパン
横 尾 恒 雄
QCコンサルタント
大 島 清 治
工業技術院標準部
(事務局)
竹 下 正 生
財団法人日本規格協会
安 田 順 子
財団法人日本規格協会
備考 ○印は「データの統計的な解釈方法」JIS原案作成WGの委員を,◎印は同WGの
主査を兼ねる。