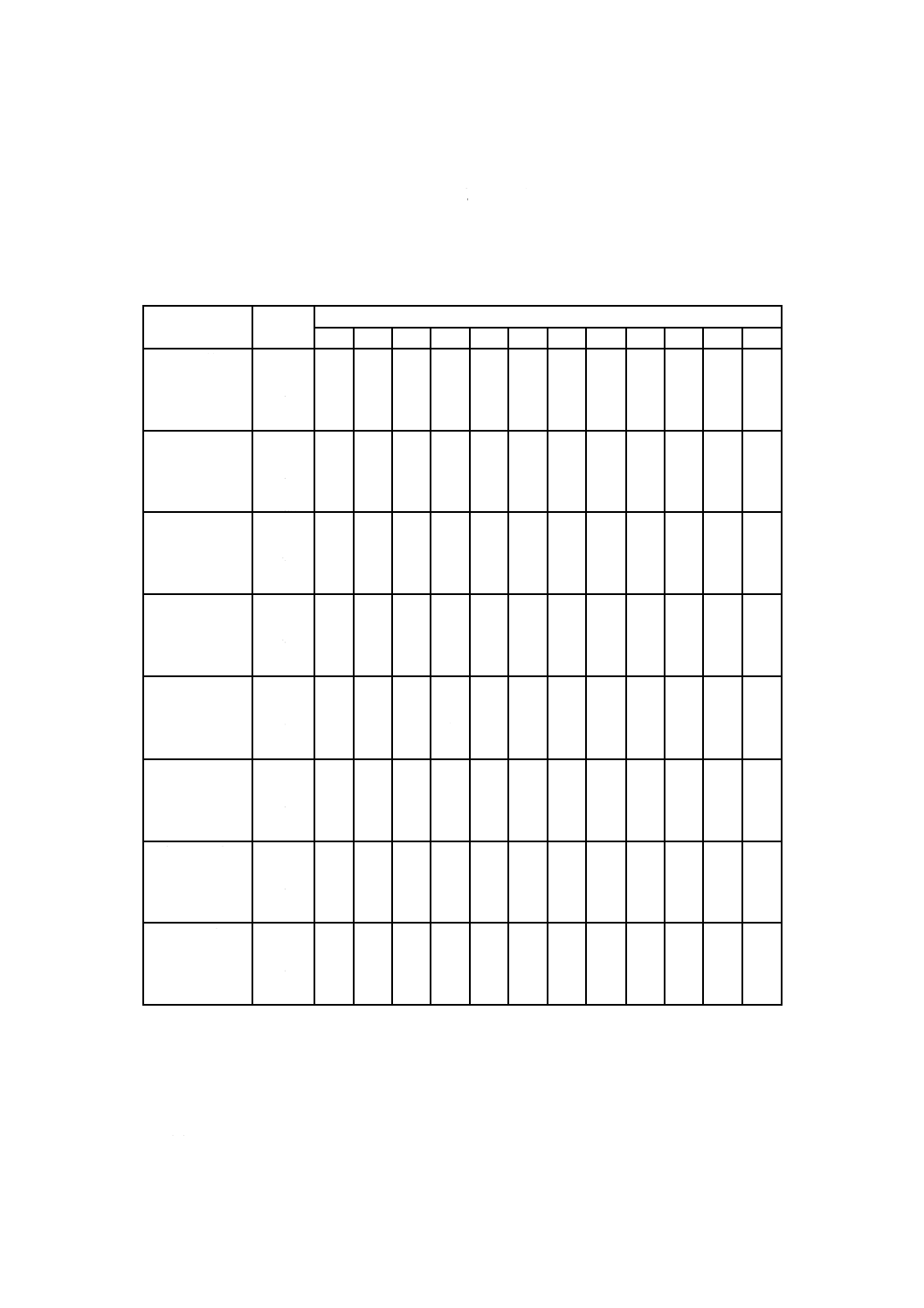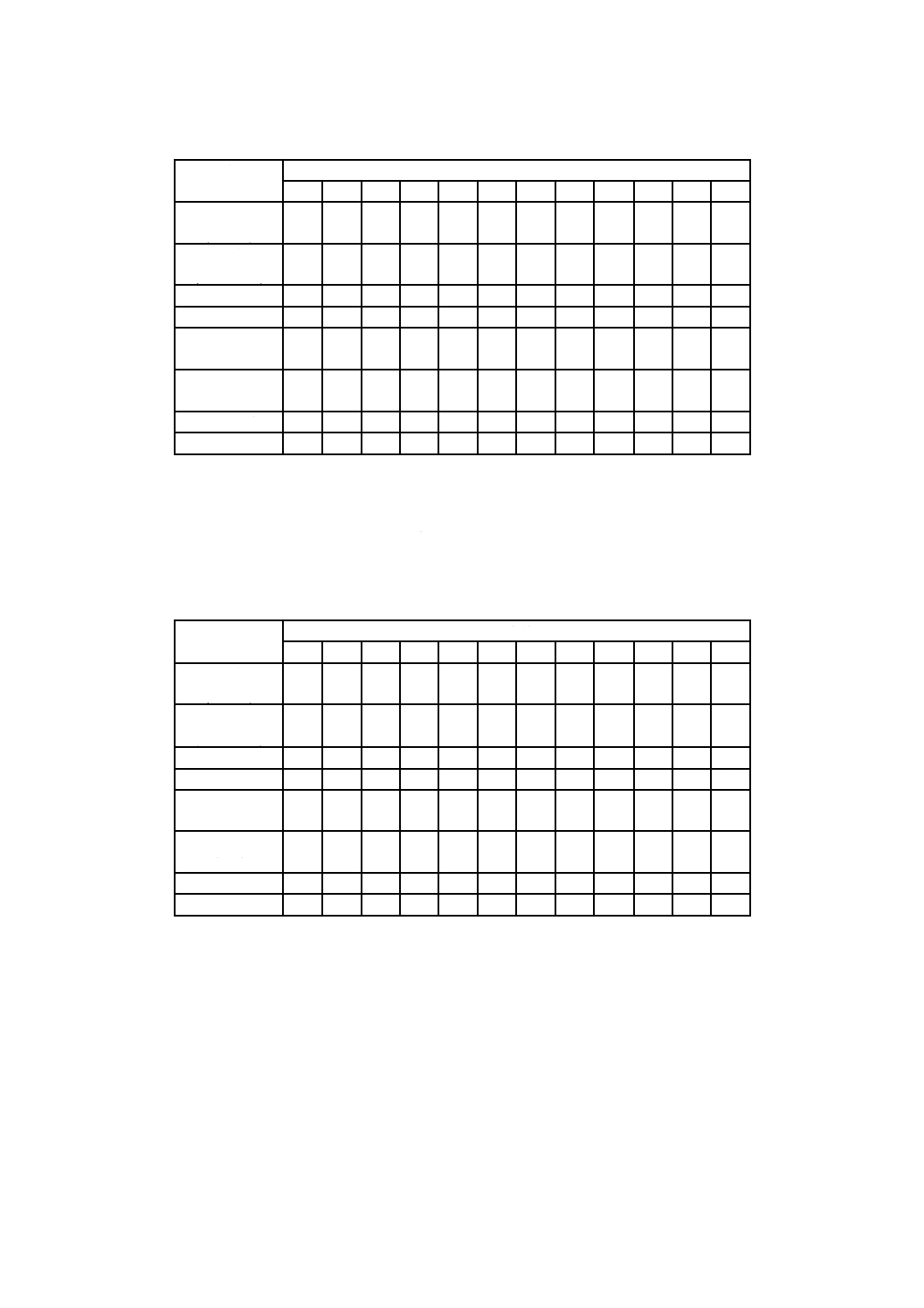Z 9031:2012
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲 ························································································································· 1
2 引用規格 ························································································································· 2
3 用語及び定義 ··················································································································· 2
4 記号及び数学的演算 ·········································································································· 3
4.1 記号 ···························································································································· 3
4.2 数学的演算 ··················································································································· 3
5 乱数······························································································································· 4
5.1 一般 ···························································································································· 4
5.2 疑似一様乱数 ················································································································ 4
5.3 線形合同法 ··················································································································· 5
5.4 M系列法 ······················································································································ 6
6 各種の分布に従う乱数の生成 ····························································································· 10
6.1 一般 ··························································································································· 10
6.2 標準一様分布 ··············································································································· 10
6.3 標準ベータ分布 ············································································································ 11
6.4 三角分布 ····················································································································· 12
6.5 標準指数分布 ··············································································································· 12
6.6 標準正規分布 ··············································································································· 12
6.7 ガンマ分布 ·················································································································· 13
6.8 ワイブル分布 ··············································································································· 14
6.9 対数正規分布 ··············································································································· 15
6.10 ロジスティック分布 ····································································································· 15
6.11 多変量正規分布 ··········································································································· 15
6.12 二項分布 ···················································································································· 16
6.13 ポアソン分布 ·············································································································· 17
6.14 離散一様分布 ·············································································································· 17
7 ランダム化の方法 ············································································································ 18
7.1 ランダム化の目的 ········································································································· 18
7.2 有限母集団からの単純ランダムサンプリングの手順 ····························································· 18
7.3 ランダム割付けの手順 ··································································································· 20
7.4 ランダム化の応用 ········································································································· 21
附属書A(参考)乱数表 ······································································································· 22
附属書B(参考)疑似乱数生成アルゴリズム ············································································· 37
附属書JA(参考)乱数の特性及び検定方法 ·············································································· 74
Z 9031:2012 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
参考文献 ···························································································································· 86
附属書JB(参考)JISと対応国際規格との対比表 ······································································ 88
解 説 ······························································································································· 90
Z 9031:2012
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,財団法人日本規格
協会(JSA)から,工業標準原案を具して日本工業規格を改正すべきとの申出があり,日本工業標準調査
会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによって,JIS Z 9031:2001は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
Z 9031:2012 目次
(4)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
白 紙
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9031:2012
乱数生成及びランダム化の手順
Procedure for random number generation and randomization
序文
この規格は,2010年に第1版として発行されたISO 28640を基に,対応する部分については対応国際規
格を翻訳し,技術的内容を変更することなく作成した日本工業規格であるが,対応国際規格には規定され
ていない規定項目を日本工業規格として追加している。
なお,この規格で側線又は点線の下線を施してある箇所は,対応国際規格を変更している事項である。
変更の一覧表にその説明を付けて,附属書JBに示す。
この規格は,ユーザにとって真の乱数列とみなすことができるような数値の系列を生成する典型的なア
ルゴリズムを規定する。
今日,ほとんどの統計家,科学者,及び技術者は大規模なコンピュータシミュレーションを実行する処
理能力をもつコンピュータを利用できるようになってきたが,これは理論的に妥当な疑似乱数の生成に基
づいていることが重要になってきた。この規格は,ランダム化が必要とされる状況で,正しく,かつ,効
率的にランダム化を実行することを支援するために開発された。
統計的な標準化におけるランダム化が利用される6種類の例を次に示す。
− ランダムサンプルの採取
− サンプルデータの解析
− 規格の開発
− 理論的な結果の確認
− 提案する方法の性能の実証
− 統計学の文献における不確かさの解決
この規格には,乱数を生成するアルゴリズム及びその特徴についての規定にランダム化の手順の規定を
加えている。
1
適用範囲
この規格は,モンテカルロシミュレーションを目的とする一様乱数,正規分布など各種の分布に従う乱
数を生成する方法,及びランダム化を行う方法について規定する。ただし,この規格では,暗号乱数を規
定しない。この規格は,次の者にとって特に有用である。
− 統計的シミュレーションを用いる研究者,技術者,及びオペレーションズマネジメントの専門家
− 統計的品質管理,統計的実験計画,標本調査などに関するランダム化を必要とする統計専門家
− モンテカルロ法の利用を必要とする複雑な最適化法を検討している応用数学者
− 乱数を生成するアルゴリズムを実装するソフトウェア技術者
2
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 28640:2010,Random variate generation methods(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS X 0001 情報処理用語−基本用語
注記 対応国際規格:ISO/IEC 2382-1:1993,Information technology−Vocabulary−Part 1: Fundamental
terms(MOD)
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
注記 対応国際規格:ISO 3534-1:2006,Statistics−Vocabulary and symbols−Part 1: General statistical
terms and terms used in probability(IDT)
JIS Z 8101-2 統計−用語と記号−第2部:統計的品質管理用語
注記 対応国際規格:ISO 3534-2:2006,Statistics−Vocabulary and symbols−Part 2: Applied statistics
(IDT)
JIS Z 8101-3 統計−用語と記号−第3部:実験計画法
JIS Z 8201 数学記号
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS X 0001,JIS Z 8101-1,JIS Z 8101-2及びJIS Z 8101-3によ
るほか,次による。
3.1
乱数(random variate, random number)
特定の確率変数の実現値とみなし得る数。
注記1 “乱数”は,一様分布に従う乱数を意味することが多い。
注記2 数列として与えられた乱数は,乱数列と呼ばれる。
3.2
疑似乱数(pseudorandom number)
アルゴリズムによって生成し,ランダムとみなし得る乱数(3.1)。
注記 誤解がない場合,疑似乱数を単に乱数と呼んでもよい。
3.3
物理乱数(physical random number)
物理的なメカニズムによって生成した乱数(3.1)。
3.4
二値乱数列(binary random number sequence)
0及び1からなる乱数(3.1)の列。
3.5
シード(seed)
3
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
疑似乱数の生成に必要な初期値。
3.6
ランダム化(randomization)
データの採取方法に乱数を用いるプロセスを設ける操作。
3.7
ランダム割付け(random assignment)
実験単位に処置を割り付けるプロセスをランダム化する操作。
4
記号及び数学的演算
4.1
記号
この規格で用いる主な記号は,JIS X 0001,JIS Z 8101-1,JIS Z 8101-2及びJIS Z 8201によるほか,次
による。
X
整数形の一様乱数
U 標準一様乱数
Z
正規乱数
n
乱数列の添え字
4.2
数学的演算
この規格で用いる数学的演算を次に示す。
m (mod k)
整数mを整数kで除した剰余
注記1 この規格の対応国際規格では,整数mを整数kで除した剰余の記号[m (mod k)]にmod (m; k)
を用いている。
m ⊕ k
二進整数m及びkのビットごとの排他的論理和
例1 1 ⊕ 1 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
0 ⊕ 0 = 0
1010 ⊕ 1100 = 0110
m & k
二進整数m及びkのビットごとの論理積
例2 1 & 1 = 1
0 & 1 = 0
1 & 0 = 0
0 & 0 = 0
1010 & 1100 = 1000
注記2 この規格の対応国際規格では,論理積の記号(m & k)にm∧kを用いているが,プログラム
言語によっては排他的論理和の記号として使用されているため,論理積の一般的な記号とし
てm∧kは用いない方がよい。
m←k
kの値をmに代入
m >> k
二進整数mのkビット右シフト
m << k
二進整数mのkビット左シフト
注記3 この規格の対応国際規格では,kの値をmに代入の記号(m←k )にm:= kを用いている。

4
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
R
実数Rの整数部分([R]とも表す。)
R
実数Rを下まわらない最小の整数
gcd (a, b)
自然数aとbとの最大公約数
5
乱数
5.1
一般
この箇条では,疑似一様乱数を生成する幾つかのアルゴリズムについて規定する。
注記1 A.1では乱数表を,A.2では乱数生成に利用した物理乱数を参考として記載している。A.3で
は乱数表の使い方を記載している。
注記2 附属書Bは,ここで述べられた各アルゴリズムのC言語及びBASIC言語による実装コード
例を参考として記載したものである。参考のため,無理数回転法についてはB.6で記載して
いる。
注記3 これらのアルゴリズムの実装コード,及び物理乱数による乱数表が参考文献[23]のホームペ
ージから入手可能である。
注記4 線形合同法は,高精度モンテカルロシミュレーションには用いないほうがよいが,他の疑似
乱数生成法のためのシードの供給,その他の高精度を要しない簡便なモンテカルロシミュレ
ーション等には用いることができる。
5.2
疑似一様乱数
アルゴリズムによって乱数を生成しようとする試みは,コンピュータの発明とほとんど同時に始まり,
以来極めて多数のアルゴリズムが提案されてきた。この規格では,それらのうちから,線形合同法及びM
系列法の二つの類型を選んで規定する。
多数のアルゴリズムが提案されているということは,裏返せば,どれも完全ではないということである。
これは,決定論的なアルゴリズムによってランダムな系列を作り出そうという根本的な矛盾を考えれば明
らかである。各アルゴリズムの長所及び短所はある程度分かっているが,全ての性質が解明されているわ
けではなく,思いがけない欠点がひそんでいる可能性は否定できない。したがって,可能ならば,異なる
類型から複数のアルゴリズムを選んで使用することが望ましい。
この規格で記載する二つの類型の特徴の詳細は,それぞれのアルゴリズムの規定のところで示すが,概
略は,次のとおりである。
a) 線形合同法 現在,多くのコンピュータシステム及びソフトウェアで使用されている。使用メモリが
少なく,高速であるが,周期が短く,あまりランダムでなく,特に高次元のランダム点列を生成する
のには向かないという欠点がある。
b) M系列法 幾つかの変種があるが,いずれもかなり高速であり,周期は実用的観点からすれば無限と
もいえるほど長くできる。使用メモリは,線形合同法と比べると,はるかに多いが,現在のコンピュ
ータでは問題とすべきものではない。高次元のランダム点列の生成にも向いている。
いずれの方法でも,乱数を生成する前にシードを与える必要がある。同じ生成法に同一のシードを与え
ると,同一の疑似乱数列を生成することができるので再実験などの場合に便利である。逆に,同じ生成法
によって異なる疑似乱数列を生成したい場合には,シードを変える必要がある。

5
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.3
線形合同法
5.3.1
定義
次の漸化式を使ってシードX0から数列X1,X2,…を作り出す方法を線形合同法という。
)
,2
,1
(
)
(mod
1
Λ
=
+
=
−
n
m
c
aX
X
n
n
ここで,乗数a及び法mは正の整数であり,加数cは非負の整数である。パラメータa,m,及びcの
値を定めると,一つの線形合同法が確定し,更にシードX0を与えると,作り出される数列が確定する。
注記 漸化式の意味は,次のとおりである。シードX0を使ってaX0+cを計算し,それをmで除した
余りをX1とする。次に,aX1+Cを計算し,それをmで除した余りをX2とする。以下,同様の
操作を繰り返す。
5.3.2
パラメータの値の定め方
a,m及びcの値を勝手に定めたのでは良い疑似乱数列が得られないことが多いので,次のような基準に
従って定めることが望ましい。
法mは,得られる数列の周期の上界となるので,できるだけ大きくするのがよい。1語が32ビットから
なる計算機を使用する場合には,m=232又はm=231−1とすることが望ましい。
乗数aとしては,スペクトル検定で良好な成績を修めたものを使うことが望ましい。
加数cの選び方については,特に厳しい基準はない。ただし,これを0とするか,又は正の整数とする
かによって,生成される数列の周期が異なる場合がある。
注記1 上記の方法でX1,X2,…を計算していくと,いつかはXn=X0となる。このnのことを,この
数列の周期という。n≦mである。
注記2 スペクトル検定は,線形合同法によって生成される数列の1周期全部にわたる性質を調べる
理論的検定であり,その内容は,附属書JAに記載する。
注記3 mが2の整数べき(冪)乗の場合,c=0とすると,周期はm/2以下である。cを奇数,aを4
で除して1余る数,周期はmとなる。
5.3.3
使用するパラメータの例
1語が32ビットの計算機を使用する場合,色々な文献から選んだ表1のパラメータを使用するのがよい。
ただし,2行目及び3行目のパラメータに対してはシードX0は奇数に選ぶ。
6
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−線形合同法で使用するパラメータの例
行番号
a
c
m
μ2
μ3
μ4
μ5
μ6
周期
1
1 664 525
*
232
16.1
10.6
8.0
6.0
5.0
232
2
1 566 083 941
0
232
14.8
9.7
7.5
5.6
4.2
230
3
48 828 125
0
232
14.8
8.8
7.4
5.7
4.9
230
4
2 100 005 341
0
231−1
15.4
10.2
7.7
6.0
5.0
231−2
5
397 204 094
0
231−1
14.8
9.7
7.4
6.0
5.0
231−2
6
314 159 369
0
231−1
15.2
9.9
7.6
5.9
5.1
231−2
注記1 cの列の*印は,任意の奇数を使用してもよいことを表す。
注記2 μ2,…,μ6の列の数値は,スペクトル検定(附属書JA参照)の結果に基づくものである。
生成される数列の連続するk個の要素を使ってk次元(2≦k≦6)の点列を生成する場合,
上位μkビットの精度で見れば,ほぼ一様分布をしているものと考えてよい。それ以上の精度
は保証されない。また,Xn−k+1,Xn−k+2,…,Xn−1の値が与えられたときのXnの条件付き分
布が,上位μkビットの精度でほぼ一様分布となると見ることもできる。したがって,これら
の数値が大きいパラメータを使うことが望ましい。
注記3 1行目のパラメータを使うと,0から232−1までの全ての整数が生成される。2行目,3行
目のパラメータを使うと,生成される数の集合は {4i+1|i=0,1,…,230−1} 又は {4i+
3|i=0,1,…,230−1} である。実際に生成される場合は,シードX0の属する集合である。
4,5,6行目のパラメータを使うと,1から231−2までの全ての正整数が生成される。
注記4 ビット数の少ない乱数列を作りたい場合には,上位ビットを取り出して使うことが望まし
く,下位ビットを取り出して使うことは望ましくない。
5.4
M系列法
5.4.1
定義
pを自然数,c1,c2,…,cp−1を0又は1として,漸化式
)
,3,2
,1
()2
(mod
1
1
2
2
1
1
Λ
Λ
=
+
+
+
+
=
+
−
+
−
−
+
−
+
n
x
x
c
x
c
x
c
x
n
n
p
n
p
p
n
p
p
n
によって生成される0,1の系列x1,x2,…を考える。
xn+N=xnが全てのnについて成り立つ最小の正の整数Nを,この系列の周期という。周期が2p−1であ
るとき,この系列のことをM系列という。
多項式
1
1
1
1
+
+
+
+
−
−
t
c
t
c
t
p
p
p
Λ
のことを上記の漸化式の特性多項式という。
注記1 上記の漸化式からM系列が得られるための条件は,シードx1,x2,…,xpのうちの少なくと
も一つは0でなく,かつ,特性多項式が原始多項式という条件を満たすことである。表2及
び表3は,それぞれ3項,5項の原始多項式の係数を幾つか示したものである。
なお,特性多項式が3項又は5項というのは,特性多項式の0でない項の個数を表してい
る。例えば,表2でp=89,q=38の場合は,特性多項式はt89+t38+1となり,3項である。
注記2 “M系列”という名称のうちの文字Mは,最大を意味する英語のMaximumに由来する。上
記の漸化式によって生成されるいかなる系列の周期も2p−1を超えることはできない。した
がって,周期が2p−1の系列があれば,それは周期が最大の系列である。
注記3 この方法を用いる場合には,上記の漸化式の特性多項式の係数としては,表3の値か,又は
原始多項式であることが文献によって証明されている多項式を使う。
M系列は1ビットからなる系列であるので,これを基にして,もっと桁数の長い疑似乱数列を作る必要

7
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
がある。そのための代表的な方法を5.4.2に規定する。
5.4.2
3項GFSR法
3項GFSR(Generalized Feedback Shift Register)法は,次の漸化式によってwビット二進整数を生成し,
疑似乱数として用いるものである。
)
,3,2
,1
(
Λ
=
⊕
=
+
+
n
X
X
X
n
q
n
p
n
ここに,p>qは整数定数,Xnはwビット二進整数である。この生成法のパラメータは(p, q, w)であり,
シードはX1,…,Xpである。多項式tp+tq+1が特性多項式となる。
注記1 この生成法は,非常に高速で,周期も長くできる。表2の特性多項式を使用すれば,周期は
289−1から29 689−1までの間となる。
注記2 シードとしてX1,X2,…,Xpのp個の値を与える必要があるが,生成される数列の乱数性は
これらのシードに強く依存するので,ユーザが勝手に与えるのは危険である。附属書Bに与
えられているような初期化ルーチンを使用することが望ましい。この手法は,自己相関関数
及びk次元均等分布性(附属書JA参照)を考慮して設計されている。
注記3 pを超えた個数の連続する疑似乱数の組を見ると,各ビットに現れる0の数及び1の数は対
称的に分布しない。特に,ランダムウォーク,パーコレーションなど,過去の長い(p以上
の)履歴に依存する高次元分布が問題となるシミュレーションに使うのは危険である。
8
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2−3項原始特性多項式
p
q
89
38
127
1,7,15,30,63
521
32,48,158,168
607
105,147,273
1279
216,418
2281
715,915,1029
3217
67,576
4423
271,369,370,649,1393,1419,2098
9689
84,471,1836,2444,4187
注記 qは,特性多項式の非零項のべき(冪)を表す。
5.4.3
5項GFSR法
これは,5項の特性多項式を使用するものであり,漸化式
)
,3
,2
,1
(
3
2
1
Λ
=
⊕
⊕
⊕
=
+
+
+
+
n
X
X
X
X
X
n
q
n
q
n
q
n
p
n
でwビットの二進整数の列を生成するものである。3項GFSR法に比べ,1,0の偏りは小さくなっている。
最大周期は2p−1である。(p, q1, q2, q3, w) がパラメータであり,X1,…,Xpがシードである。最大周期を
与えるp,q1,q2,q3の組合せの例を表3に示す。
表3−5項原始特性多項式
P
q1
q2
q3
89
20
40
69
107
31
57
82
127
22
63
83
521
86
197
447
607
167
307
461
1279
339
630
988
2203
585
1197
1656
2281
577
1109
1709
3217
809
1621
2381
4253
1093
2254
3297
4423
1171
2273
3299
9689
2799
5463
7712
注記 q1, q2, q3は,非零項のべき(冪)を表す。
5.4.4
結合トーズワース(Combined Tausworthe)法
0, 1数列x0,x1,x2,x3,…を漸化式
)
,3,2
,1,0
(
)2
(mod
Λ
=
+
=
+
+
n
x
x
x
n
q
n
p
n
によって定義される3項M系列とする。この0, 1数列から連続するw個をつなげたものをw桁の二進整
数とみなす。最初にw桁の二進整数x0x1…xw−1が得られ,次にt個ずらしてw桁の二進整数xtxt+1…xt+p−1
を得る。これを繰り返すとwビット整数の列
)
,3,2
,1,0
(
1
1
Λ
Λ
=
=
−
+
+
n
x
x
x
X
w
nt
nt
nt
n
が得られる。ただし,tは2p−1と互いに素な自然数,wはpを超えない自然数とする。この系列を (p, q, t)
をパラメータとするトーズワース系列という。シードは,x0,…,xp−1である。シードは,どれかは1で
9
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
あるように選ぶ。この系列の周期も2p−1となる。
注記1 二つの自然数が互いに素とは,それらの最大公約数が1であることである。
例 特性多項式として,原始3項式t4+t+1を選んだとする。上記の漸化式でいえば,p=4,q=1と選
んだことになる。もしシードとして(x0,x1,x2,x3)=(1,1,1,1)が漸化式に与えられたとすると,生成さ
れるM系列は1,1,1,1, 0,0,0,1, 0,0,1,1, 1,1,1,0, …であり,その周期は24−1=15である。例えば,15
と互いに素であるt=4を選び,w=4とすると,トーズワース法のパラメータは(4,1,4)で表される。
生成される系列{Xn}は,次のとおりとなる。
X0=x0x1x2x3=1111(=15)
X1=x4x5x6x7=0001(=1)
X2=x8x9x10x11=0011(=3)
X3=x12x13x14x0=0101(=5)
X4=x1x2x3x4=1110(=14)
X5=x5x6x7x8=0010(=2)
…
このトーズワース法で生成された系列は,10進記法で15, 1, 3, 5, 14, 2, 6, 11, 12, 4, 13, 7, 8, 9, 10, 15, 1, 3,
…となり,周期は24−1=15である。
結合トーズワース法は上記のトーズワース系列を複数生成し,排他的論理和で合成して疑似乱数を生成
する手法である。例えばJ個のトーズワース系列{Xn(j)}, j=1,2,…,Jを用意したとする。これらの系列は全
て同じワード長wをもつとする。結合トーズワース法とは,これらの系列の2進表現のビットごとの排他
的論理和
Xn=Xn(1) ⊕ Xn(2) ⊕ … ⊕ Xn(J) (n=0,1,2,…)
によって,一つの系列{Xn}を生成する方法である。
結合トーズワース法のパラメータ,シードはそれぞれのトーズワース法のパラメータ,シードを合わせ
たものである。
注記2 この生成法は,高速で多次元均等分布性(附属書JA参照)のよいものが作れる。附属書B
に添付されたコードの周期は (231−1) (229−1) (228−1) (ほぼ288)であり,メモリも3ワー
ドしか消費しない。また,他に多くの組合せが参考文献の[10]に提案されている。
5.4.5
メルセンヌツイスター(Mersenne Twister)法
Xnをwビット二進整数とする。メルセンヌツイスター法は,整数定数p,q,r及びwビット二進整数定
数aを用い,次の漸化式によってwビット二進整数列Xnを生成し,
)
,3
,2
,1
(
)
(
1
Λ
=
⊕
=
+
+
+
n
A
X
X
X
X
l
n
u
n
q
n
p
n
|
····································· (1)
それを後述の変換によってwビット二進整数疑似乱数列とするものである。ここで,
)
(
1
l
n
u
nX
X
+
|
はXnの上
位w−rビット及びXn+1の下位rビットをこの順に連接して得られる二進整数を表す。Aは,aによって決
まる0及び1からなるw×w行列であり,
⊕
=
の場合)
の最下位ビットが
(
の場合)
の最下位ビットが
(
1
)
(
shiftright
0
)
(
shiftright
X
X
X
X
XA
a
によって積が与えられるものである(ただし,ここではXをw次元の0−1横ベクトルとみなしている)。
10
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここで,shiftrightは1ビットの右シフトを表す。
上位ビットの乱数性を改善するため,Xnに次の変換を施す。
y←Xn
y←y ⊕ (y>>u)
y←y ⊕ ((y<<s) &b)
y←y ⊕ ((y<<t) &c)
y←y ⊕ (y>>l)
最後に得られたyを疑似乱数として出力する。ここに,(y>>u) はyの右uビットシフト,(y<<u) は左u
ビットシフトを表す。b,cは上位ビットの乱数性を改善するための定数ビットマスクである。
このアルゴリズムのパラメータは,(p, q, r, w, a, u, s, t, l, b, c) である。シードはX1の上位w−rビット及
び
X2,…,Xpである。シードとしては,全てが0であるものは選ばない。
注記1 消費されるメモリは,pワードで周期は2pw−r−1となり,前述のGFSR法より効率がよい。
注記2 この生成法は,高速で非常に長い周期と優れた多次元均等分布性(附属書JA参照)をもっ
ている。
6
各種の分布に従う乱数の生成
6.1
一般
整数形の一様乱数Xを使っていろいろな分布に従う乱数Yを生成する方法を示す。目標とする分布の分
布関数をF (y) で表し,それが連続分布の場合は確率密度関数をf (y) で,また,離散分布の場合は確率質
量関数(Y=yとなる確率)をp (y) で表すことにする。
6.2
標準一様分布
6.2.1
確率密度関数
=
その他
≦
≦
,0
1
0
,1
)
(
y
y
f
6.2.2
乱数生成法
箇条5に定める方法で生成される整数形一様乱数Xの取る値の最大値をm−1とすると,
m
X
Y
/
=
とする。
注記1 Xの取る値が離散的なため,Yの取る値も離散的となり,本当の連続分布とはならないこと
に注意する。
注記2 Yの値が1.0となることは決してない。Yの値が0.0となるのは,X=0の場合に限られる。こ
れが起こり得るのは,線形合同法で表1のパラメータを使う場合は,1行目を使うときだけ
である。M系列乱数の場合には,どの生成法でも起こり得る。
注記3 標準一様分布に従う乱数を標準一様乱数と呼び,U, U1, U2などで表す。このように表した場
合,これらは互いに独立であるものとする。
注記4 区間 [a, a+b]上の一様分布に従う乱数Yは,標準一様乱数Uを次の式で変換して生成する。
Y=bU+a
11
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3
標準ベータ分布
6.3.1
確率密度関数
()
(
)
(
)
−
=
−
−
,その他
≦
≦
,
,
0
1
0
1
1
1
y
d
c
B
y
y
y
f
d
c
ここで,(
)
(
)
∫
−
−
−
=
1
0
1
11
,
dx
x
x
d
c
B
d
c
はベータ関数で,パラメータc及びdは正である。
6.3.2
ジェーンク(Jöhnk)の方法
6.2に定める方法で,互いに独立な標準一様乱数U1及びU2を生成し,次の手順で標準ベータ乱数Yを生
成する。
1°
d
cU
U
Y
1
2
1
1
~
+
=
とする。
2°もし不等式 Y~≦1が成り立てば,
Y
U
Y
c~
1
1
=
を採用して終了。
3°上記の不等式が成り立たなければ,U1及びU2を生成し直して1°に戻る。
6.3.3
チェン(Cheng)の方法
6.2に定める方法で,互いに独立な0でない標準一様乱数U1及びU2を生成し,次の手順で標準ベータ乱
数Yを生成する。
[準備]
0°次の式でqを定義する。
(
)
(
)
(
)
−
+
+
−
<
=
その他
,
,
2
2
1
,
min
,
min
d
c
d
c
cd
d
c
d
c
q
[生成]
1°
()
V
c
W
U
U
q
V
exp
,
1
1
1
1
=
−
=
とする。
2°もし不等式
(
)
(
)
(
)
2
2
1
ln
4
ln
ln
U
U
V
q
c
W
d
d
c
d
c
≧
−
+
+
+
+
+
が成り立てば,
Y=W/(d+W)を採用して終了。
3°上記の不等式が成り立たなければ,0でない標準一様乱数U1及びU2を生成し,1°に戻る。
注記1 max(c,d)≦1の場合はJöhnkの方法,そうでない場合はチェンの方法を使うことが望ましい。
注記2 [a,a+b]上の一般のベータ分布に従う乱数Y' は,標準ベータ乱数Yを次の式で変換して生成
できる。
Y'=b Y+a
12
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4
三角分布
6.4.1
確率密度関数
()
+
−
−
−
=
その他
,
≦
≦
,
0
2
b
a
y
b
a
b
y
a
b
y
f
ただしb>0である。
6.4.2
乱数生成法
6.2に定める方法で,互いに独立な標準一様乱数U1及びU2を生成し,Y=a+b(U1+U2−1)とする。
6.5
標準指数分布
6.5.1
確率密度関数
<
=
−
0
,0
0
,
)
(
y
y
e
y
f
y
≧
6.5.2
乱数生成法
標準一様乱数Uを使って
U
Y
ln
−
=
とすることが望ましい。
なお,U=0.0となる可能性のある生成法を使う場合には,
(
)
U
Y
−
−
=
0.1
ln
とすることが望ましい。
注記 区間[a,∞)上の指数分布に従い,平均がa+bの乱数Y' は,標準指数乱数Yを次の式で変換して
生成できる。
Y'=bU+a
6.6
標準正規分布
6.6.1
確率密度関数
∞
<
<
∞
−
=
−
y
e
y
f
y,
2
1
)
(
2
2
1
π
注記 標準正規分布に従う乱数は,標準正規乱数と呼ばれ,Zと表す。
6.6.2
ボックス・ミュラー(Box-Muller)法
標準一様乱数U1, U2を使って,互いに独立な標準正規乱数Y1, Y2を次の式で生成する。
(
)
2
1
1
π
2
cos
ln
2
U
U
Y
−
=
(
)
2
1
2
π
2
sin
ln
2
U
U
Y
−
=
注記1 なお,U1=0.0となる可能性のある生成法を使う場合には,lnU1の代わりにln (1.0−U1) とす
ることが望ましい。
注記2 U1が本当の連続分布をする乱数ではないために,Y1, Y2の取る値も本当の正規分布にはなら
ない。例えば,取り得る値の絶対値の上界は,
m
m
M
ln
2
ln
2
1=
−
=
−
であり,m=232ならばM≈6.660 4,m=231−1ならばM≈6.555 5となる。ただし,真の正規
分布に従う確率変数の絶対値がこれらのMの値を超える確率は10−10程度であるので,この
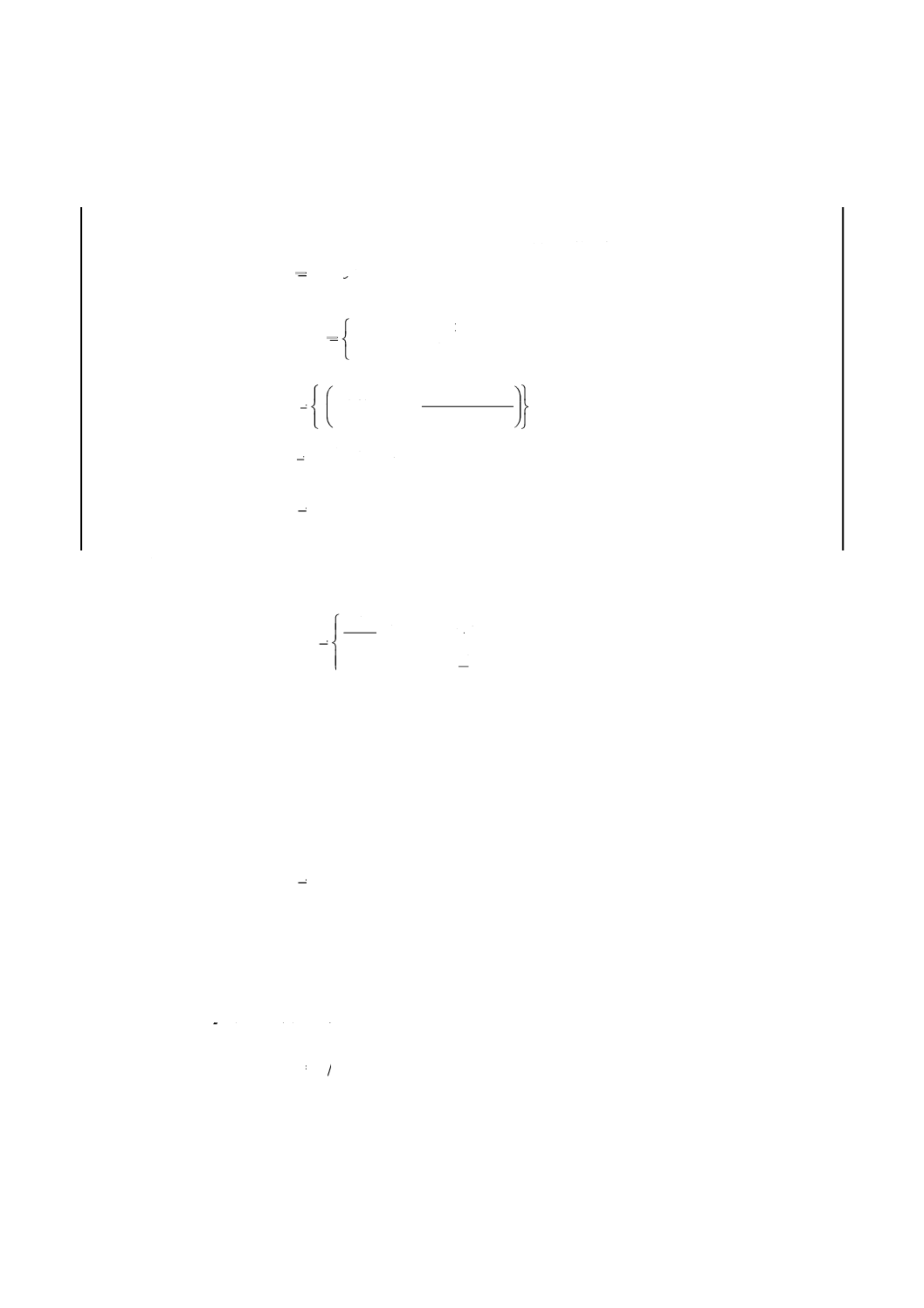
13
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ことが実際上不都合を生じることは,ほとんどない。また,U1, U2を合同法で生成する場合,
U1及びU2が互いに独立でないために,生成されるY1, Y2の分布の裾が真の正規分布からかな
りずれることがある。
6.6.3
逆関数法
6.1の方法で0でない標準一様乱数Uを生成し,分布関数F (y) の逆関数F−1(u) を使って,
)
(
1U
F
Y
−
=
とする。F−1(u) に対する近似式としては,次の山内二郎(参考文献[24]を参照)の近似式を使うとよい。
<
+
<
<
−
=
−
0.1
5.0
,
5.0
0
,
)
(
1
u
w
u
w
u
F
≦
2/1
595
640
.
11
4
220
726
.5
6
178
061
.2
+
−
=
z
z
w
(
)
{
}
u
u
z
−
−
=
1
4
ln
注記 標準正規乱数Zから,平均がμ,分散がσ2の正規乱数Yを作るためには,
Z
Y
σ
μ+
=
とする。
6.7
ガンマ分布
6.7.1
確率密度関数
>
Γ
=
−
−
0
,0
0
,
)
(
1
)
(
1
≦
y
y
e
y
y
f
y
α
α
6.7.2
乱数生成法
6.7.2.1
一般的注意
形状パラメータαの値に応じて,次の4種類の方法を使い分けるのがよい。ただし,生成に要する時間
が長くてもかまわなければ,α>1/3である限り,常に6.7.2.5の方法を用いてもよい。
注記 区間[a,∞)上で尺度パラメータb,形状パラメータαのガンマ分布に従う乱数は,次の各方法で
得られる乱数Yを用いてa+bYとすれば生成できる。
6.7.2.2
α=k(整数)の場合
(
)
k
U
U
U
Y
Λ
2
1
ln
−
=
注記1 2Yは自由度が2kのカイ2乗分布に従う乱数となる。
注記2 標準一様乱数の取る値が0.0となる可能性がある場合には,
Y=−ln{(1−U1)(1−U2)…(1−Uk)}
とする。
6.7.2.3
α=k+21(k:整数)の場合
標準正規乱数Z及び一様乱数U1,U2,…,Ukを使って
(
)
k
U
U
U
Z
Y
Λ
2
1
2
ln
2−
=
とする。
注記1 2Yは,自由度が2k+1のカイ2乗分布に従う乱数となる。
注記2 標準一様乱数の取る値が0.0となる可能性がある場合には,
Y=Z2/2−ln{(1−U1)(1−U2)…(1−Uk)}
14
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とする。
6.7.2.4
αが大きい場合の近似的生成法
標準正規乱数Zを使って,
3
9
1
1
9
−
+
=
α
α
αZ
Y
とする。
注記 これは,ウィルソン・ヒルファーティ(Wilson−Hilferty)の近似に基づくものである。おおむ
ねαが10以上のときに,使うことができる。
6.7.2.5
α (>31) があまり大きくない場合の近似的生成法
0°
r
q
s
p
r
r
r
t
r
s
r
3
3
1
ln
3
1
3
1
−
=
=
−
=
=
−
=
,
,
,
,
α
とする。
1° 標準正規乱数Zを生成する。
2° Z<qならば1°へ
3° Y=(pZ+s) 3,V=Z2/2とし,Uを生成する。
4° (Y−r)2/Y−V≦UならばYを採用して終了
5° W=Y−rlnY−t−Vとする。
6° W≦UならばYを採用して終了
7° W>−ln (1.0−U) ならば1°へ
注記 この算法は,ウィルソン・ヒルファーティの近似に補正を施して得られたものである。近似の
精度はパラメータαの値に依存するが,依存の仕方は複雑である。ごく大雑把には,次のとお
りである。正確なガンマ分布と近似分布のパーセント点との食い違いの絶対値は,0.2を超える
ことはない。
6.7.2.6
チェン の方法(α>1/2の場合に使える正確な生成法)
0°
1
2
4
ln
1
2
1
−
+
=
−
=
−
=
α
α
α
α
C
B
A
,
,
とする。
1° 標準一様乱数U1, U2を生成する。
2° V=Aln{U1/(1−U1)},W=α exp(U1),R=B+CV−W,S=U12U2とする。
3° R≧4.5S−(1+ln4.5)ならばY=Wとして終了
4° R≧lnSならばY=Wとして終了
5° 1°へ戻る。
注記 1°においてU1=0.0となった場合には,生成し直して,0.0と異なるものをU1として採用する。
6.8
ワイブル分布
6.8.1
確率密度関数
<
−
−
=
0
,0
0
),
exp(
1
)
(
y
y
y
y
F
≧
α
6.8.2
乱数生成法
箇条5に定める方法で標準一様乱数Uを生成し,
(
)
{
}α
1
0.1
ln
U
Y
−
−
=
とする。
注記 区間[a,∞)上で尺度パラメータb,形状パラメータαのワイブル分布に従う乱数は,上記の方
法で得られる乱数Y を用いてa+bYとすれば生成できる。
15
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.9
対数正規分布
6.9.1
確率密度関数
>
=
−
0
,0
0
,
2
1
)
(
2
2
1
≦
y
y
e
y
y
f
y
π
6.9.2
乱数生成法
標準正規乱数Zを使って,
Z
e
Y=
とする。
注記 区間[a,∞)上で尺度パラメータbの対数正規分布に従う乱数は,
Y=a+exp(bZ)
として生成する。
6.10 ロジスティック分布
6.10.1 分布関数
∞
<
<
∞
−
+
=
−
y
e
y
F
y,
1
1
)
(
6.10.2 乱数生成法
箇条5に定める方法で,0でない標準一様乱数Uを生成し,
−
=
U
U
Y
1
ln
とする。
注記 位置パラメータ(平均値)がa,尺度パラメータがbのロジスティック分布に従う乱数は,上
記の方法で得られるYを用いてa+bYとすれば生成できる。
6.11 多変量正規分布
平均がμ1,…,μnで,分散及び共分散がσij (1≦i, j≦n) のn次元正規分布に従う乱数Y1,…,Ynは,互
いに独立な標準正規乱数Z1,…,Znから次のようにして作る。
,
1
11
1
1
Z
a
Y
+
=μ
,
2
22
1
21
2
2
Z
a
Z
a
Y
+
+
=μ
…
n
nn
n
n
n
n
Z
a
Z
a
Z
a
Y
+
+
+
+
=
Λ
2
2
1
1
μ
ただし,a11,…,annは定数で,乱数生成を始める前に,分散・共分散から次の手順によって計算してお
く。
1°
)
2(
/
,
11
1
1
11
11
n
i
a
a
a
i
i
≦
≦
σ
σ
=
=
2° j=2,…,nについて,
,
2
/1
1
1
2
−
=
∑
−
=
j
k
jk
jj
jj
a
a
σ
)
1
(
/
1
1
n
i
j
a
a
a
a
jj
j
k
jk
ik
ij
ij
≦
≦
+
−
=
∑
−
=
σ
16
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 この計算は,分散・共分散行列のコレスキー(Cholesky)分解と呼ばれるものである。
6.12 二項分布
6.12.1 確率質量関数
ある事象が1回の試行では確率pで起きるときに,n回の試行でy回起きる確率p (y) は,次の式で与え
られる。
()
(
)
n
y
p
p
y
n
y
p
y
n
y
≦
≦
0
,
1
−
−
=
6.12.2 乱数生成法
6.12.2.1 一般
この分布に従う乱数Yの生成法としては,次のようなものがある。
6.12.2.2 直接法
標準一様乱数をn個生成させて,pより小さいものの個数をYとする。
6.12.2.3 逆関数法
まず,準備として分布関数
()
(
)
n
y
p
p
k
n
y
F
y
k
k
n
k
≦
≦
0,
1
0∑
=
−
−
=
を求める。乱数が必要になるごとに,次の操作をする。標準一様乱数Uを生成し,U≦F(y)を満たす最小
のyをYとする。
6.12.2.4 二者択一法
まず,準備として,n+1個の変数v0,v1,…,vn及び別のn+1個の変数a0,a1,…,anの値を次のよう
にして定める。
1°
n
k
k
p
n
vk
≦
≦
0
),
(
)1
(+
=
2° vk≧1を満たすkの集合をG, vk<1を満たすkの集合をSとする。
3° Sが空集合でない限り,次の3.1°から3.4°までの操作を繰り返す。
3.1° Gの要素を一つ任意に選ぶ(それがiであるものとする。)。Sの要素を一つ任意に選ぶ(そ
れがjであるものとする。)。
3.2° aj=i, vi=vi−(1−vj) とする。
3.3° vi<1ならば,Gの要素iを取り除いてSに移す。
3.4° Sの要素jを取り除く。
以上の準備が完了したら,乱数が必要になるごとに次の操作をする。
1° 標準一様乱数Uを生成し,V=(n+1) Uとする。
2° k=(Vの整数部分),u=V−kとする。
3° u≦vkならばY=k,そうでなければY=akとする。
6.12.2.5 正規近似
nが不等式
10
}
1,
min{
≧
p
p
n
−
を満たす程度に大きいときに使うことができる近似法である。
標準正規乱数Zを生成して
]}
5.0
)
1(
[,0
max{
−
+
−
=
np
p
np
Z
Y
17
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とする。
注記 nが大きい場合には,6.12.2.2及び6.12.2.3の方法は,計算時間が長くかかる。6.12.2.4の方法は,
準備に要する計算時間はnに比例して長くなるが,1組の乱数を生成するのに要する時間は,n
に無関係である。
6.13 ポアソン分布
6.13.1 確率質量関数
平均がμのポアソン分布の確率質量関数は,
)
,2
,1
,0
(
!
)
(
Λ
=
=
−
y
y
e
y
p
y
μ
μ
である。
6.13.2 指数分布との関係を利用する方法
標準一様乱数U1,U2,…を生成し,
μ
−
>e
U
U
U
n
Λ
2
1
を満たす最大のnをYとする。
注記 標準一様乱数の値が0.0になる可能性がある場合には,上記の不等式の左辺を
(
)(
)(
)
n
U
U
U
−
−
−
1
1
1
2
1
Λ
で置き換えた不等式を使う。
6.13.3 正規近似法
μが100以上程度に大きい場合に使うことができる近似法である。
標準正規乱数Zを生成させて,
]}
5.0
[,0
max{
−
+
=
μ
μZ
Y
とする。
6.13.4 二者択一法
μが中程度の大きさ(10から100程度まで)の場合に使うと効率のよい方法である。
まず,Y>nとなる確率が無視できる程度に小さくなる定数nを選ぶ(例えば,
μ
μ6
+
の整数部分をn
とする。)。これ以降の手順は,6.12二項分布の6.12.2.4二者択一法の手順による。ただし,p (y) は,ポア
ソン分布の確率質量関数を使う。
6.14 離散一様分布
M以上でN以下の離散一様乱数を生成するには,箇条5に規定された方法で生成された二進r桁の乱数
列を,次の手順で変換する。ここで,N−M+1は,2rを超えないものとする。
1° 次の不等式を満たす自然数kを見いだす。
k
k
M
N
2
1
1
2
1
≦
≦
+
−
+
−
注記1 このようなkは,2を底とする対数を用いれば,log2(N−M+1)以上の最小の自然数となる。
例 N−M+1=100の場合には,26+1=65≦100≦27=128からk=7となる。
2° 乱数列の上位k桁からなる二進整数にMを加えて十進自然数に変換する。
注記2 k桁の二進数W1W2W3W4…Wkを十進数へ変換すると,2k−1W1+2k−2W2+2k−3W3+2k−4W4+…+
Wkとなる。
例 上位7桁からなる二進整数が1 011 001だとすれば,これに対応する十進数は64+16+8+1=89
である。

18
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3° 変換された十進自然数列でNを超えるものを飛ばして読んだものが,必要な十進乱数列である。
注記3 N−M+1が2rを超えるときには,複数の二進乱数をつないだものを一つの二進乱数とみなす
ことで,必要な乱数を得ることができる。
注記4 この場合には,線形合同法を用いてないことが望ましい。
7
ランダム化の方法
7.1
ランダム化の目的
7.1.1
統計的方法の適用の主たる目的として,考察の対象となる特性の母集団における分布について,母
集団の部分集合であるサンプルを用いて,できるだけ誤差が小さくなるように推論することが挙げられる。
したがって,統計的推論の品質は,その誤差によって評価することができる。このような統計的推論は,
サンプルがランダムであることが必要である。
7.1.2
統計的推論の結論について利害関係者が存在する場合には,推論の基礎となるプロセスの妥当性に
ついて,第三者がその適合性を評価することが可能な品質システムが存在することが望ましい。
7.1.3
サンプルを母集団からランダム化によって構成することの目的は,次のとおりである。
a) 統計的推論の偏りを少なくする。
b) 統計的推論の誤差を評価する。
合否判定検査を適切に適用するときには,ランダムサンプリングと呼ばれる適切なランダム化を行わな
ければならない。同様に,実験計画法の適用に当たってもランダム割付けは,統計的方法を用いて実験結
果の解釈を行うために必要である。
注記1 統計的推論を類似状況に対して繰り返し適用する場合,適切なランダム化は,推論結果の偏
りを平均的に解消することに寄与する。ただし,特定の1回の推論に関しては,測定値に系
統的な影響を与える全ての要因が,ランダム化によって無視できるようになるとは限らない。
このために,必要な調整手順をデータ採取の前までに定める場合がある。この種の調整手順
を,データ採取後に決定するのは,偏りが入る可能性があり,勧められない。
注記2 測定に起因する偏りは,適切なランダム化を行っても一般には解消できない。
注記3 ランダム化を用いずに,恣意的に構成したサンプルに基づく推論結果の方が誤差は小さいと
考えられる場合もある。例えば,適切な系統サンプリングは誤差を多くの場合に減少させる
ことが期待できる。しかし,ランダム化を用いないサンプルからの推論結果の誤差を第三者
が客観的に評価するのは,困難な場合が多い。
注記4 ランダム化には,その実施可能性,推論結果の誤差に対する要求などに応じて,多様な方法
が考えられている。この規格では,それらの中でも最も単純な方法を規定している。しかし,
多段ランダム化,層別ランダム化などの状況でも7.2及び7.3の方法は原理的に適用可能であ
る。
7.2
有限母集団からの単純ランダムサンプリングの手順
7.2.1
有限母集団からサンプルサイズnのサンプルを単純ランダムサンプリングに基づいて構成する手
順は,次のとおりである。この手順を用いることで,サンプリング単位全体,例えば,ロットからある特
定のサンプリング単位が抽出される確率は全て等しくなる。このため,単純ランダムサンプリングは,等
確率ランダムサンプリングとも呼ばれる。
a) サンプリング単位の一覧を作成し,各サンプリング単位に一連番号を1からNまで付ける。
注記1 通常,この一覧に含まれるサンプリング単位全体が,その後に行われる統計的推論の対象

19
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
となる母集団となり,Nが母集団の大きさとなる。この一覧は,サンプリングフレームと
も呼ばれる。サンプリングフレームが,本来の推論の目的と合っていなかったり,不確実
なものであると,実際に推論を行った母集団と,本来推論を行いたかった母集団との間に
かい(乖)離が生じる。このかい離が,推論結果の質を劣化させることがある。このため,
利害関係者の存在する状況では,サンプリングフレームは,適切な品質システムの下で管
理されていることが望ましい。これを母集団管理と呼ぶこともある。
注記2 たるに入ったくぎ,又は1コンサインメントの鉱石のようなものでも,それを移し変える
とき1列に並ぶことを利用して,適切なサンプリング単位を定めることができる。
b) 6.14によって1からNまでの範囲の自然数乱数列を作り,重複を除いて最初のn個の乱数を選ぶ。
注記 ここで規定する単純ランダムサンプリングでは,特定のサンプリング単位が複数回サンプリ
ングされることはない。これは,非復元サンプリングである。特定のサンプリング単位が複
数回サンプリングされることを許すサンプリングは,復元サンプリングである。復元サンプ
リングを行いたい場合には,手順b)において,重複を除かずに最初のn個の乱数を選べばよ
い。対象とする母集団の大きさが有限であっても,復元サンプリングを適用した場合は,無
限母集団からのサンプルとなる。
c) 選んだ数に相当する一連番号が付いたサンプリング単位を抜き取り,考察の対象となる特性を測定す
る。
注記1 選んだ数に相当するサンプリング単位についての測定ができなかった場合には,測定がで
きなかった理由,測定者,測定器など必要な記録を文書として残すことが望ましい。また,
サンプリング単位のもつ特性のために測定が不可能となっている場合には,推論結果に偏
りが生じる場合がある。この場合には,追加検討が必要となる場合もある。この種の偏り
に関して,十分な対処が可能な場合には,測定不能という理由で生じたサンプルの欠損を
追加的なランダムサンプリングで補塡することができる。
注記2 N=nmのときに,1からmまでの範囲の乱数Yを1個生成し,一連番号のYからm番間隔
で周期的にサンプリングを行うことでも,n個のサンプルを抽出できる。このような操作
を系統サンプリングと呼ぶ。系統サンプリングは,その簡便さのためによく用いられてい
る。しかし,サンプリング間隔とデータの値との間に潜在的な関連が存在すると,誤差が
大きくなったり,誤差評価が困難となる。この種の誤差が生じないことが保証できない場
合には,用いることは勧められない。
注記3 一つのサンプリング単位(1次サンプリング単位)が関心のある複数の2次サンプリング
単位からなり,各1次サンプリング単位でその大きさが異なる場合には,単純ランダムサ
ンプリングではなく,1次サンプリング単位の大きさに比例した確率で2次サンプリング
単位をサンプリングする場合がある。これを確率比例サンプリングと呼ぶ。確率比例サン
プリングを行う場合には,1次サンプリング単位に一連番号を付けるのではなく,全ての1
次サンプリング単位に含まれる2次サンプリング単位の全体に一連番号を付け,ある2次
サンプリング単位がサンプリングされた場合には,その2次サンプリング単位が属する1
次サンプリング単位がサンプリングされたとみなせばよい。
7.2.2
利害関係者が存在する場合には,7.2.1の手順が正しく行われ,少なくともサンプリングに起因す
る標本誤差は適切に管理されたことを評価するために,必要な記録を文書化することが望ましい。
注記 文書化が必要なサンプリングの手順には,母集団管理のシステム,適正なサンプリング操作,

20
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
乱数生成の手順(アルゴリズム,パラメータ,初期シード,アルゴリズムによっては乱数生成
後のシード)などが含まれる。
7.3
ランダム割付けの手順
7.3.1
N個の処理をランダムな順序でN個の実験単位に割り付ける手順は,次のとおりである。
注記1 処理とは,実験計画法の用語で,実験に取り上げた因子のそれぞれの水準を実施することを
意味する。したがって,N個の処理とは,水準数がkの因子で繰返し数がrの実験の場合に
は,N=krである。
注記2 N個の処理の中には,同一の処理が繰返し数だけ現れる。
例 繰返しのない直交表実験では,N個の処理は,それぞれ直交表の実験番号に相当する
水準組合せと考えることができる。
注記3 ここでの手順は,N個の品物をランダムに配置する場合などにも適用できる。
a) N個の処理及び実験単位に1からNまでの一連番号を付ける。
注記1 実験単位又は処理の定め方によっては,本来の目的に合致した統計的推論ができない場合
もあるので,実験の計画段階で十分な議論を行い,これらの定め方の論拠を記録しておく
ことが望ましい。また,利害関係者が存在する状況では,事前に定めた実験単位の要件に
合致しない実験単位が実験に混入したり,事前に定めた処理とは異なる処理が実験単位に
施されることを防ぐための,品質システムが確立していることが望ましい。
注記2 実験日を実験単位とするような場合などでは,実験単位は逐次的に実験の場に参入し,実
験を開始する時点では確定していないこともある。その場合には,参入した順番に実験単
位に一連番号を付ければよい。
b) 6.14又はA.3によって乱数列を作り,重複を除いて最初のN個をとる。
c) b)で構成した乱数に大きさの順に番号を付け,その番号の並び方に従って番号付けられた処理を並べ
る。
例 N=12の処理をランダムに並べたい場合には,まず,処理に1から12までの番号を付け,次に
2桁の整数乱数を重複を除いて12個とり,とられた乱数に大きさの順に番号を付ける。仮に,
その結果が,10, 7, 3, 12, 4, 6, 9, 1, 2, 5, 11, 8となった場合には,この順序に処理を並べ変える。
すなわち,一連番号10が付いた処理を先頭に,一連番号8が付いた処理を12番目とするよう
に処理を並べ変える。
d) c)で定めた順番で実験単位に処理を割り付け,考察の対象となる特性の測定を行い,測定値を得る。
注記 実験単位に処理の割付けを行ったが,測定値が得られない場合には,当該実験単位の詳細,
当該処理状況の詳細,測定ができなかった理由,測定者,測定器など必要な記録を文書とし
て残すことが望ましい。また,実験単位と処理との相互作用のために測定が不可能となって
いる場合には,単純な欠測として推論を行うと結果に偏りが生じる場合がある。この場合に
は,追加検討が必要となる場合もある。この種の偏りに関して,十分な対処が可能な場合に
は,測定不能から生じるサンプルの欠損を補塡するために,あらかじめ若干大きな個数の実
験単位を用意しておくことも可能である。
7.3.2
利害関係者が存在する場合には,7.3.1の手順が正しく行われ,少なくとも割付けに起因する誤差
は適切に管理されたことを評価するために,必要な記録を文書化することが望ましい。
注記 文書化が必要なランダム割付けの手順には,適正な割付け操作,乱数生成の手順(アルゴリズ
ム,パラメータ,シード)も含まれる。

21
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.4
ランダム化の応用
7.4.1
層別サンプリング
サンプリング単位の一覧を大きさNiの複数の層に分割し,各層から大きさniのサンプルを7.2の手順に
従って単純ランダムサンプリングする方法を,層別サンプリングと呼ぶ。
注記1 各層の中で2次サンプリング単位の特性のばらつきが小さく,層間では特性のばらつきが大
きい場合には,同じ大きさのサンプルをサンプリングする場合に,層別サンプリングは単純
ランダムサンプリングよりも統計的推論の誤差が小さくなることが期待される。
注記2 母集団における層が階層構造をなしている場合,すなわち,ある層を分割して部分層が形成
されているような場合,層に含まれる部分層を2次サンプリング単位とみなして,単純サン
プリングし,更に抽出された層のサンプリング単位をランダムサンプリングするときがある。
これを2段サンプリングと呼ぶ。2段サンプリングの考え方は,多段サンプリングに拡張す
ることができる。
7.4.2
集落サンプリング
サンプリング単位の一覧を複数のグループ(これを集落という。)に分割し,元のサンプリング単位の代
わりに集落の全体から一部の集落を手順7.2に従って単純ランダムサンプリングし,サンプリングされた
集落に属するサンプリング単位の全てをサンプリングする方法を,集落サンプリングと呼ぶ。
注記 各集落の中でサンプリング単位の特性のばらつきが大きく,集落間では特性のばらつきが小さ
い場合には,同じ大きさのサンプルをサンプリングするときに,集落サンプリングは単純ラン
ダムサンプリングよりも統計的推論の誤差が小さくなることが期待される。

22
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
乱数表
A.1 乱数表
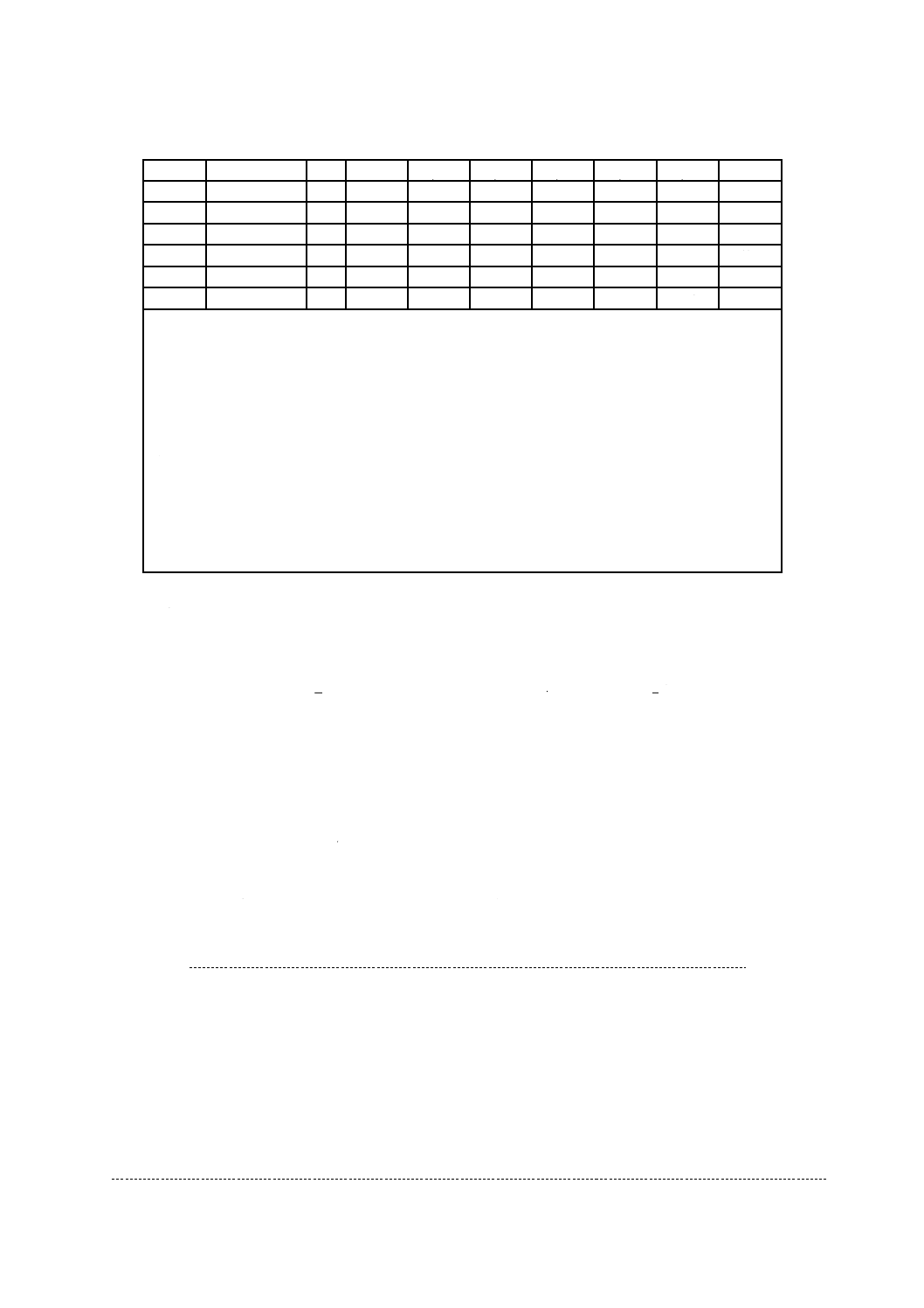
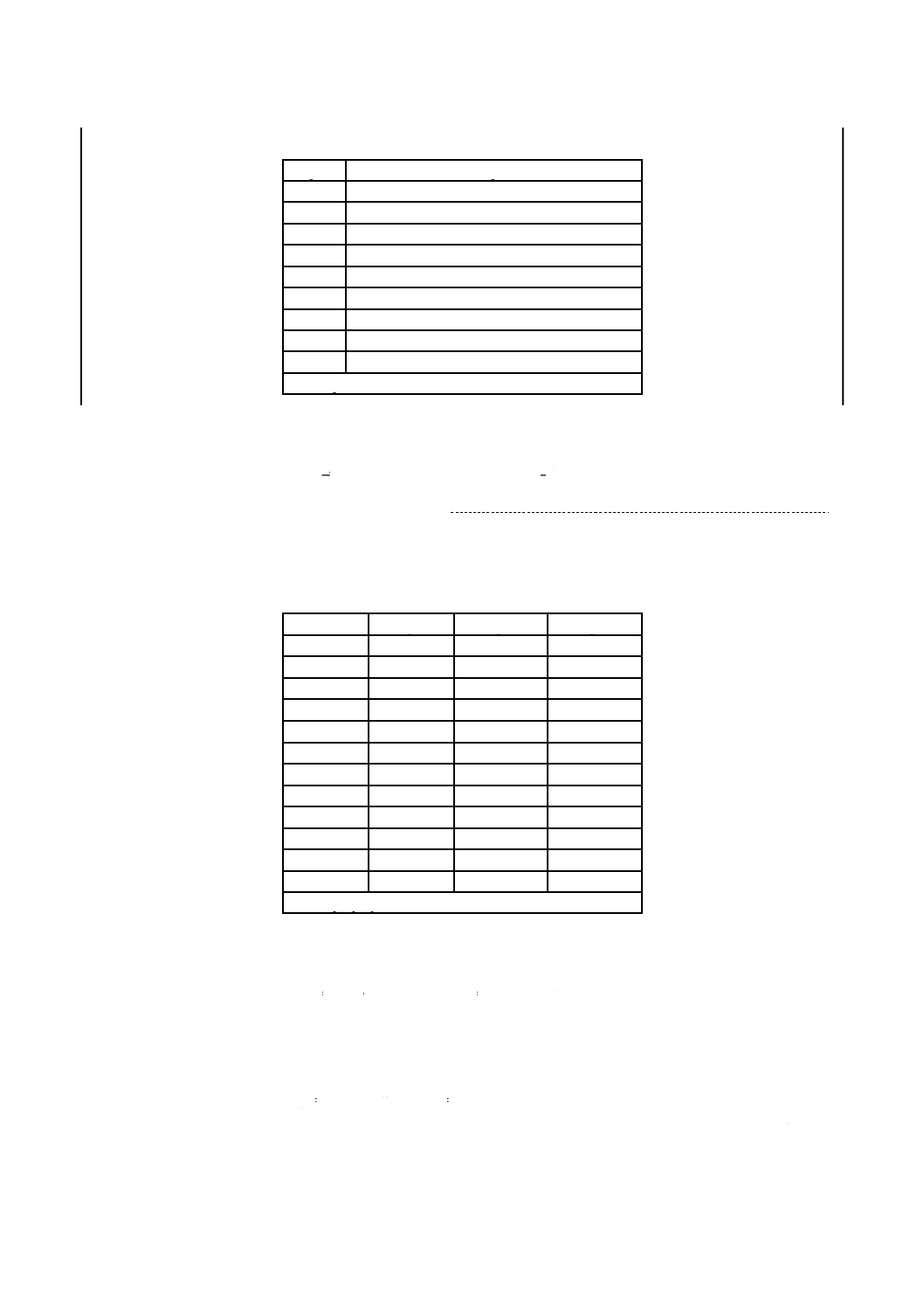
この附属書の乱数表(表A.1)は0から9までの10個の数字をランダムに配置した表であり,物理乱数
を用いて作成した。物理乱数とは,何らかの物理系の示すランダムに変動する量を測定して数値化したも
のである。物理乱数の特徴としては,疑似乱数のような原理的な規則性がなく,また再現性がないことが
挙げられる。
注記 表A.1には,見やすさのために2個ずつの組とし,それを1行に20組印刷されている。これを
左から1〜19列及び0列と呼ぶ。表A.1は,1ページに25行,全体で10ページ250行からな
っており,行番号は左端に印刷されている。
表A.1−乱数表
1 93 90 60 02 17 25 89 42 27 41 64 45 08 02 70 42 49 41 55 98
2 34 19 39 65 54 32 14 02 06 84 43 65 97 97 65 05 40 55 65 06
3 27 88 28 07 16 05 18 96 81 69 53 34 79 84 83 44 07 12 00 38
4 95 16 61 89 77 47 14 14 40 87 12 40 15 18 54 89 72 88 59 67
5 50 45 95 10 48 25 29 74 63 48 44 06 18 67 19 90 52 44 05 85
6 11 72 79 70 41 08 85 77 03 32 46 28 83 22 48 61 93 19 98 60
7 19 31 85 29 48 89 59 53 99 46 72 29 49 06 58 65 69 06 87 09
8 14 58 90 27 73 67 17 08 43 78 71 32 21 97 02 25 27 22 81 74
9 28 04 62 77 82 73 00 73 83 17 27 79 37 13 76 29 90 07 36 47
10 37 43 04 36 86 72 63 43 21 06 10 35 13 61 01 98 23 67 45 21
11 74 47 22 71 36 15 67 41 77 67 40 00 67 24 00 08 98 27 98 56
12 48 85 81 89 45 27 98 41 77 78 24 26 98 03 14 25 73 84 48 28
13 55 81 09 70 17 78 18 54 62 06 50 64 90 30 15 78 60 63 54 56
14 22 18 73 19 32 54 05 18 36 45 87 23 42 43 91 63 50 95 69 09
15 78 29 64 22 97 95 94 54 64 28 34 34 88 98 14 21 38 45 37 87
16 97 51 38 62 95 83 45 12 72 28 70 23 67 04 28 55 20 20 96 57
17 42 91 81 16 52 44 71 99 68 55 16 32 83 27 03 44 93 81 69 58
18 07 84 27 76 18 24 95 78 67 33 45 68 38 56 64 51 10 79 15 46
19 60 31 55 42 68 53 27 82 67 68 73 09 98 45 72 02 87 79 32 84
20 47 10 36 20 10 48 09 72 35 94 12 94 78 29 14 80 77 27 05 67
21 73 63 78 70 96 12 40 36 80 49 23 29 26 69 01 13 39 71 33 17
22 70 65 19 86 11 30 16 23 21 55 04 72 30 01 22 53 24 13 40 63
23 86 37 79 75 97 29 19 00 30 01 22 89 11 84 55 08 40 91 26 61
24 28 00 93 29 59 54 71 77 75 24 10 65 69 15 66 90 47 90 48 80
25 40 74 69 14 01 78 36 13 06 30 79 04 03 28 87 59 85 93 25 73

23
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
26 77 13 56 37 92 36 26 83 84 42 04 39 84 26 00 62 44 97 89 40
27 04 21 84 80 20 09 73 79 62 15 76 81 61 57 16 36 36 29 03 24
28 96 91 94 32 65 59 55 50 79 69 69 61 80 21 43 96 68 83 29 66
29 23 38 06 82 67 25 49 97 72 83 27 70 90 33 89 66 09 23 46 69
30 89 46 08 65 02 88 80 20 29 59 83 30 94 50 43 69 81 38 66 19
31 56 82 84 88 65 52 61 05 43 05 88 61 77 55 79 28 08 94 93 00
32 92 31 75 79 39 82 46 20 97 77 13 15 24 15 05 48 53 99 14 95
33 22 54 74 72 52 51 85 51 01 56 68 42 24 05 98 81 07 40 55 46
34 99 28 79 60 80 00 49 03 39 03 29 84 85 17 48 55 05 51 64 19
35 89 52 48 68 49 44 65 24 36 35 98 74 04 36 05 82 04 50 64 27
36 47 90 08 45 00 04 52 25 76 28 67 01 18 57 74 81 88 96 66 40
37 87 75 05 24 04 49 56 77 04 33 34 01 37 64 23 62 48 32 34 54
38 95 55 93 70 42 10 32 19 00 87 58 49 59 63 48 03 24 48 58 00
39 13 01 12 98 47 81 52 70 76 25 75 66 62 80 18 37 59 39 64 18
40 86 59 37 97 69 19 97 72 80 54 80 06 53 12 96 53 06 13 39 24
41 58 48 01 02 45 49 67 90 87 11 66 39 13 15 62 66 28 18 66 35
42 26 15 97 14 18 31 13 47 94 27 25 78 97 82 13 84 02 31 88 84
43 00 81 06 61 47 24 68 39 69 96 30 88 10 54 85 62 01 89 87 09
44 83 98 33 19 61 92 03 68 42 59 80 75 29 48 24 88 52 69 38 36
45 85 29 95 63 68 73 82 46 10 29 02 81 90 42 44 48 44 72 85 22
46 16 17 01 27 83 36 19 21 94 58 92 67 49 97 16 89 63 54 44 86
47 36 60 31 38 42 86 25 70 35 71 01 04 44 55 35 45 69 46 64 75
48 22 62 18 16 21 04 16 58 65 73 30 44 52 99 88 01 41 82 23 55
49 73 14 32 15 49 02 52 10 56 32 93 04 05 73 62 05 56 91 14 28
50 23 16 88 83 79 38 48 64 19 43 86 75 69 57 65 35 85 04 31 93

24
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
51 26 33 60 08 33 78 27 42 23 22 37 78 41 03 60 09 98 94 14 01
52 22 31 60 76 55 91 10 98 19 83 17 67 97 47 16 57 47 28 27 60
53 24 13 48 08 72 99 31 07 12 67 05 52 84 29 14 34 99 88 76 92
54 75 76 84 41 47 73 82 96 24 29 49 82 04 91 47 81 76 53 00 76
55 80 98 76 48 47 87 97 16 65 76 16 78 88 38 63 03 16 82 69 28
56 40 47 32 31 57 92 18 33 79 47 06 49 15 86 40 24 89 71 14 94
57 66 38 04 09 86 30 66 24 98 53 61 98 65 19 35 91 74 46 39 04
58 95 83 58 88 96 95 89 00 10 19 92 14 48 53 29 11 05 76 60 44
59 48 46 85 87 38 02 25 16 19 30 70 06 91 58 49 89 09 02 45 82
60 08 05 09 34 96 42 68 56 18 70 37 36 37 67 70 85 69 07 66 33
61 98 60 30 35 21 26 65 35 56 30 05 82 22 20 26 79 03 27 95 01
62 36 07 35 77 43 81 75 21 31 38 85 48 31 74 70 85 76 23 49 42
63 41 93 58 87 05 78 72 65 73 78 69 57 33 26 56 86 27 12 00 11
64 17 00 18 97 13 73 86 42 46 10 38 33 03 24 28 88 91 78 50 13
65 02 86 49 24 66 29 53 33 84 56 19 99 36 60 45 78 37 09 64 32
66 00 76 30 20 08 85 92 37 14 94 81 33 67 53 48 55 06 02 69 36
67 71 24 24 69 19 13 39 06 32 82 09 65 75 47 17 52 42 47 17 37
68 91 66 96 78 06 57 42 67 11 09 23 94 15 68 23 65 48 49 11 60
69 78 11 09 12 60 09 74 27 74 90 66 82 11 48 96 60 85 62 42 94
70 59 71 56 70 48 21 28 80 91 49 99 84 89 67 04 58 39 75 50 92
71 26 85 54 20 99 26 09 37 50 89 89 47 04 21 02 25 76 24 82 08
72 36 97 48 76 96 59 95 29 60 78 24 26 32 15 23 42 84 91 39 70
73 19 10 57 55 93 57 85 92 48 73 65 86 32 78 87 80 54 34 78 65
74 96 16 14 42 77 06 89 94 56 28 98 03 21 90 34 01 38 65 41 51
75 48 63 73 08 97 18 99 52 40 32 64 70 62 90 77 74 12 86 93 00

25
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
76 94 21 58 48 37 90 23 50 53 09 98 31 65 34 75 17 98 22 32 91
77 68 12 31 32 38 48 86 73 84 73 66 74 76 83 51 68 13 22 30 37
78 23 15 53 23 99 82 27 82 86 98 81 51 82 99 87 48 32 30 54 85
79 63 66 60 11 20 60 11 20 39 74 95 54 78 66 85 47 12 44 84 55
80 52 21 63 30 56 40 90 52 63 27 02 11 35 39 85 57 23 69 35 16
81 95 10 67 82 95 88 78 26 06 36 50 98 65 48 72 83 38 08 13 15
82 40 67 94 22 00 63 51 36 11 07 45 97 69 20 14 93 46 30 63 74
83 67 95 44 13 44 62 53 51 60 49 27 43 72 91 48 40 79 50 30 88
84 92 34 73 62 65 08 91 99 40 79 33 65 67 37 56 62 45 41 51 25
85 95 16 80 77 21 54 07 80 08 68 92 84 08 57 68 63 46 14 68 22
86 19 79 64 04 19 58 36 36 81 34 03 92 24 76 65 70 92 61 86 34
87 44 58 46 99 75 58 21 55 57 37 75 04 41 59 16 69 71 70 41 39
88 72 61 88 33 27 41 96 04 21 53 34 83 96 00 66 46 04 74 00 90
89 62 09 21 11 46 80 73 61 79 30 04 97 59 88 88 33 72 80 80 07
90 61 87 66 89 12 03 93 93 60 94 50 15 23 12 52 09 69 35 62 70
91 63 29 39 31 11 84 42 51 92 50 30 35 96 67 70 29 85 03 15 98
92 70 24 93 14 21 58 78 59 87 92 97 56 43 69 54 05 61 85 44 78
93 03 24 21 46 71 32 78 41 19 87 83 52 31 17 94 00 39 40 83 79
94 99 27 18 15 33 02 86 01 15 12 70 35 26 94 60 00 17 20 79 01
95 12 96 82 55 86 30 24 86 35 41 10 21 11 36 93 41 97 84 41 23
96 76 44 98 72 29 18 61 51 78 95 88 75 82 11 85 49 97 32 69 62
97 51 43 42 10 41 88 16 54 87 45 09 65 72 91 37 32 16 56 58 96
98 91 20 89 70 96 92 41 89 38 65 02 46 87 52 75 61 62 22 24 36
99 21 86 11 31 96 05 55 47 07 92 11 83 36 27 50 19 41 14 49 21
100 06 57 25 06 99 64 46 37 13 07 64 74 90 93 13 21 92 04 53 41

26
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
101 65 09 79 03 40 61 70 66 12 02 33 21 03 57 89 19 79 70 36 18
102 59 06 64 47 73 52 86 45 85 65 27 96 60 68 26 67 68 64 52 32
103 60 98 10 45 19 77 62 70 49 12 55 89 43 42 26 15 73 82 66 15
104 46 27 13 67 70 15 46 45 16 34 50 62 57 95 33 61 80 03 02 94
105 55 72 44 77 62 96 73 85 96 07 17 60 21 20 02 40 20 30 47 35
106 74 89 44 97 19 11 53 88 78 48 69 42 09 40 48 24 85 09 11 06
107 12 93 47 71 18 38 54 46 10 08 94 98 05 50 94 26 87 89 02 84
108 12 40 99 93 01 58 95 30 03 41 89 96 89 90 10 47 33 10 84 14
109 12 39 82 45 86 40 67 91 18 57 99 84 27 40 11 69 60 01 33 89
110 11 28 80 90 20 67 86 14 79 97 11 25 64 52 60 81 84 51 55 26
111 42 13 43 80 50 92 13 65 93 97 27 77 84 80 12 27 56 00 11 47
112 81 91 76 41 51 41 48 79 45 40 79 09 01 24 50 46 08 11 32 54
113 29 46 68 58 45 92 34 07 88 68 93 47 47 11 25 22 38 48 53 75
114 44 26 11 93 47 20 76 84 00 21 09 41 30 37 54 16 63 30 52 42
115 73 04 00 63 12 42 47 88 15 08 74 65 14 70 97 16 52 99 79 76
116 30 79 52 61 56 28 80 26 27 30 36 62 52 50 10 36 56 26 84 89
117 67 64 55 72 84 45 04 90 57 30 43 00 65 35 34 28 33 52 54 20
118 84 13 25 39 05 64 92 66 76 73 83 18 69 61 38 74 23 64 16 16
119 66 84 65 28 33 39 93 79 58 24 90 74 36 89 37 88 37 81 01 84
120 98 74 89 91 61 67 18 45 71 24 12 52 65 53 48 69 51 32 31 90
121 24 57 07 14 13 92 13 89 41 13 06 54 65 69 71 70 32 10 39 13
122 77 96 47 57 68 65 34 55 43 87 81 85 11 07 18 33 00 69 68 64
123 22 88 51 76 41 55 98 67 95 60 09 85 49 70 12 78 38 14 47 02
124 02 22 74 18 08 12 09 18 27 73 34 18 93 56 44 59 74 03 55 67
125 91 64 46 04 48 25 23 34 52 89 46 85 75 48 80 27 98 89 65 35

27
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
126 63 83 81 67 08 10 53 00 13 74 91 70 70 23 59 04 92 84 13 57
127 92 72 07 33 28 28 56 45 87 27 68 90 22 81 17 68 95 35 79 79
128 07 63 28 69 69 62 18 98 39 59 23 43 72 59 06 56 77 47 89 35
129 57 97 71 03 79 26 34 63 20 72 59 63 53 56 80 44 99 70 73 58
130 80 09 35 76 09 94 46 26 16 24 30 34 40 62 17 70 62 63 62 43
131 56 32 72 17 69 37 95 31 56 46 61 37 15 34 46 28 31 99 88 19
132 32 68 66 05 92 56 46 74 99 44 64 29 52 87 07 24 11 77 65 69
133 07 00 91 81 88 23 29 90 64 62 01 87 64 64 87 63 82 16 41 60
134 42 73 94 06 15 86 13 64 01 00 74 26 36 59 45 76 48 12 29 48
135 96 28 62 38 52 41 03 96 28 84 35 28 05 10 95 85 65 99 27 84
136 06 28 06 37 60 06 21 52 94 37 21 35 83 58 26 68 82 02 88 70
137 51 56 19 62 61 01 73 72 94 30 99 62 52 23 67 06 61 84 22 27
138 38 26 81 98 52 78 73 33 32 68 95 30 39 73 86 72 43 25 18 64
139 54 45 67 29 37 03 58 76 78 46 61 54 76 24 63 53 57 98 86 44
140 35 70 78 20 26 93 82 21 07 85 45 69 19 37 48 94 76 52 81 05
141 21 86 27 29 36 84 60 61 08 61 48 36 60 92 52 00 37 62 23 91
142 80 79 59 52 49 66 77 77 14 42 06 17 17 81 98 62 42 43 59 42
143 84 50 42 01 48 95 42 22 47 61 18 60 59 26 79 46 96 88 57 22
144 74 26 08 09 32 76 91 78 73 99 17 45 23 05 46 26 12 63 21 15
145 67 12 18 96 40 44 88 55 06 46 00 66 26 77 08 38 06 39 21 42
146 83 11 98 04 23 67 06 76 59 77 19 71 47 31 21 23 83 33 20 38
147 21 31 25 53 55 13 88 06 46 00 56 33 90 79 86 08 25 32 83 02
148 82 82 48 75 65 17 67 81 12 16 29 11 85 77 57 92 96 38 69 08
149 63 80 00 00 53 49 80 03 35 40 47 68 34 65 88 00 24 95 15 82
150 96 52 61 06 38 00 45 18 78 30 00 03 31 42 72 18 16 51 20 74

28
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
151 59 35 07 66 40 33 04 75 42 11 97 65 11 40 17 02 45 58 46 84
152 42 14 93 24 70 59 81 13 21 53 98 52 20 92 88 89 83 47 75 27
153 06 04 98 08 13 75 27 46 18 18 72 24 77 56 54 35 56 50 79 72
154 76 45 88 49 18 76 58 49 68 44 97 02 97 59 69 34 44 68 78 86
155 58 43 17 88 86 27 58 27 26 75 41 66 56 25 77 71 73 96 29 06
156 17 69 66 98 88 80 17 96 21 50 59 71 13 79 11 75 33 28 90 02
157 08 56 66 61 89 44 46 22 87 78 69 47 15 06 19 22 39 86 64 43
158 46 78 63 63 53 76 31 19 42 13 40 20 85 67 00 22 68 30 36 74
159 06 16 31 19 37 76 29 23 80 92 77 38 87 16 16 67 87 86 99 57
160 84 07 84 94 91 53 73 30 88 67 96 33 92 74 04 31 52 36 92 21
161 11 73 80 20 33 90 53 37 74 04 46 45 15 82 06 08 77 00 90 68
162 52 30 44 27 96 23 67 04 73 90 06 66 36 65 04 56 19 79 48 71
163 90 32 57 03 68 40 95 05 36 92 17 15 40 01 75 69 22 62 75 27
164 15 84 98 31 33 01 62 44 76 03 02 85 78 80 57 23 30 08 62 60
165 86 41 67 42 72 09 37 31 37 25 86 99 13 76 46 64 97 50 57 86
166 10 26 57 04 11 04 19 67 43 72 83 96 85 90 73 87 58 55 21 82
167 53 04 91 37 70 23 39 92 21 39 89 80 99 99 98 57 17 65 40 69
168 70 47 92 64 03 60 50 83 23 52 34 75 28 04 01 70 34 17 97 27
169 31 50 71 80 37 48 50 01 08 90 02 68 94 39 54 39 70 36 60 78
170 46 13 35 33 17 77 70 39 02 62 74 12 62 49 00 84 91
11 06 57
171 33 71 65 67 88 55 40 80 97 28 81 15 30 65 94 75 70
11 41 91
172 97 48 00 00 68 63 83 70 07 46 52 97 26 31 82 65 09 61 78 20
173 45 32 13 42 96 46 92 91 98 88 68 83 80 97 02 17 78 63 56 98
174 09 43 78 48 98 66 65 14 01 42 33 11 57 39 68 84 74 15 24 60
175 45 75 55 86 92 12 22 26 89 94 17 23 05 18 71 77 26 24 75 25

29
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
176 30 58 50 56 51 33 35 84 07 36 45 31 54 79 19 94 85 61 15 27
177 38 29 53 38 74 01 20 43 33 87 21 36 03 54 07 60 71 97 54 86
178 87 92 34 51 39 18 13 34 24 48 75 84 48 84 79 75 14 81 84 30
179 10 54 99 93 96 30 19 51 07 37 31 90 60 25 68 54 61 21 79 66
180 01 69 43 55 49 67 82 70 85 83 40 65 34 66 34 50 97
11 71 26
181 33 49 13 71 14 29 98 65 16 47 27 92 29 47 71 86 35 66 52 97
182 75 10 33 74 39 65 42 11 92 80 58 13 29 05 85 56 39 15 61 01
183 94 35 83 99 69 53 12 08 26 93 66 93 64 14 63 02 75 55 51 77
184 79 76 46 43 46 06 46 26 35 17 90 86 43 05 58 40 51 78 32 03
185 32 20 12 45 29 40 43 16 69 75 86 42 93 27 92 02 79 30 10 67
186 95 10 59 38 74 84 52 27 61 86 37 55 69 36 21 03 37 53 59 15
187 60 03 81 96 06 53 52 79 00 82 47 35 86 56 93 63 12 40 54 22
188 23 09 08 57 48 58 26 95 00 33 22 17 01 50 62 66 37 53 06 96
189 11 94 28 67 11 22 83 17 73 46 79 37 46 68 62 88 51 48 20 32
190 22 85 98 85 04 95 19 38 01 04 15 83 66 96 95 18 50 92 10 25
191 48 73 80 17 36 84 54 28 02 26 13 65 72 13 93 81 45 39 74 43
192 34 69 71 13 71 34 01 95 10 46 19 16 70 55 96 09 54 24 96 44
193 48 10 86 09 97 64 48 52 57 91 52 13 87 44 26 59 52 01 21 62
194 44 29 83 84 95 40 70 21 06 99 59 34 44 32 94 76 92 64 04 05
195 46 18 02 48 69 77 78 47 78 26 69 31 29 44 00 78 74 82 48 38
196 97 46 36 99 75 77 14 86 73 25 19 04 58 29 62 84 35 32 04 16
197 01 76 22 96 67 70 20 14 25 96 08 89 21 47 24 96 22 49 67 24
198 79 10 66 67 20 12 64 88 50 31 66 80 78 44 50 97 94 54 84 95
199 15 37 42 86 37 42 30 35 20 01 01 33 66 50 45 74 94 02 82 86
200 04 62 14 23 17 37 49 37 60 28 17 97 65 36 36 37 46 18 39 56

30
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
201 06 36 75 55 35 26 33 08 84 97 47 97 91 23 31 42 80 21 65 67
202 57 74 86 33 78 13 15 31 46 01 39 31 99 31 51 13 95 67 41 92
203 99 02 88 16 73 13 80 54 69 94 42 97 10 12 52 48 74 42 75 90
204 55 23 24 18 98 07 50 58 17 02 18 92 18 56 11 85 65 17 14 76
205 02 44 92 69 65 84 98 82 15 12 37 18 90 63 17 95 01 33 05 45
206 67 20 21 25 74 43 92 22 16 80 13 43 15 56 76 70 35 62 68 11
207 53 99 92 52 25 69 32 48 44 64 30 34 10 08 04 24 02 27 34 84
208 13 73 46 61 03 90 82 47 92 40 05 20 59 10 15 00 42 88 31 14
209 30 80 38 29 99 67 67 34 25 53 75 23 90 29 66 30 99 60 75 98
210 30 16 48 47 12 04 37 79 95 44 33 35 30 40 22 16 63 89 03 34
211 60 20 92 59 36 00 22 25 53 60 74 84 21 70 18 29 99 31 12 91
212 79 27 43 90 49 89 75 93 44 31 72 77 61 86 10 58 72 62 48 40
213 04 52 59 98 70 04 86 90 53 43 75 85 36 56 58 96 94 52 12 13
214 59 74 04 66 74 70 30 54 00 61 82 19 27 31 21 15 93 95 69 70
215 60 64 89 92 69 64 85 24 26 83 22 44 04 18 37 71 94 50 22 57
216 20 82 14 78 30 33 21 96 23 47 74 74 56 23 55 40 78 02 22 15
217 96 04 74 74 98 24 08 89 79 86 64 71 73 36 04 36 07 43 04 60
218 24 02 85 77 28 82 68 34 35 89 17 53 02 64 07 83 80 03 25 27
219 16 91 65 66 13 53 86 57 65 43 56 68 22 00 86 15 03 87 61 98
220 78 46 47 80 45 65 72 10 23 82 22 30 68 26 90 79 33 87 53 98
221 37 47 86 62 78 07 40 92 63 35 38 57 54 67 71 96 44 93 12 70
222 22 43 60 81 82 18 47 25 04 57 80 59 48 50 85 97 05 73 13 29
223 48 58 45 04 67 45 96 21 23 19 31 66 47 53 37 93 16 00 97 99
224 13 66 64 65 81 83 49 82 04 35 11 12 73 30 52 34 47 74 72 56
225 81 70 27 16 96 02 61 58 19 87 68 70 26 60 68 16 72 20 44 47

31
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−乱数表(続き)
226 68 19 71 37 99 49 74 70 52 55 62 40 60 88 90 70 29 02 38 14
227 62 82 19 73 28 68 43 89 27 51 56 62 82 75 19 80 51
11 51 86
228 03 98 68 14 33 18 94 07 65 68 61 67 67 39 24 46 43 77 96 62
229 18 99 21 73 42 10 43 28 15 31 20 34 49 94 97 15 74 23 15 13
230 76 84 84 87 17 50 31 81 42 02 95 62 01 11 65 14 85 84 47 24
231 55 58 28 30 19 21 38 37 11 32 31 15 02 54 59 14 55 68 92 12
232 95 36 87 62 50 59 81 23 82 66 28 23 37 91 95 04 24 92 79 93
233 62 56 34 94 09 39 14 83 37 37 68 57 05 58 59 70 56 85 80 06
234 86 97 53 72 02 83 11 32 62 98 85 80 25 53 92 57 94 01 35 37
235 11 93 32 17 84 20 98 93 71 93 81 29 10 14 50 75 77 02 40 07
236 23 55 77 95 59 30 82 16 46 50 37 71 93 03 83 11 73 16 99 14
237 14 26 21 63 83 12 75 45 55 13 52 09 30 97 15 40 61 03 74 65
238 26 09 55 41 19 71 99 06 49 17 99 44 71 37 19 26 47 28 99 40
239 97 48 20 63 93 16 53 85 89 99 19 89 11 43 24 08 25 34 77 62
240 47 65 05 31 63 91 17 55 24 99 64 21 94 05 47 84 67 23 09 86
241 04 06 52 41 99 00 27 64 33 78 91 86 06 65 46 39 47 59 94 61
242 89 45 54 78 24 59 31 20 56 44 71 64 97 21 15 65 09 51 43 97
243 75 97 84 33 16 30 11 92 91 50 70 58 68 50 17 54 98 59 08 16
244 32 46 13 12 85 68 76 59 25 33 20 42 45 87 25 76 31 69 22 37
245 01 70 85 71 19 69 65 11 04 26 94 40 02 45 94 19 03 39 07 48
246 37 78 86 55 37 82 71 98 51 53 71 63 00 84 67 72 86 74 15 59
247 12 89 00 50 61 56 39 83 13 35 87 39 24 66 99 74 58 67 08 24
248 93 80 24 22 36 72 53 86 38 27 02 11 28 26 72 57 83 28 26 50
249 30 00 20 44 24 95 11 58 89 80 37 93 54 66 64 20 52 12 41 15
250 56 16 45 05 73 74 80 21 15 55 73 97 07 86 78 45 76 58 58 66
A.2 乱数表生成に利用した物理乱数
A.2.1 物理乱数生成法
この規格に含まれる乱数表(表A.1)の生成に利用した物理乱数生成法について具体的に示す。まず,
生成源としては,ダイオードの生成するノイズを用いた。ダイオードでは電子なだれ効果によってノイズ
が増幅されるため信号が大きく,安定なノイズが簡易に得られる。このためノイズ源としてよく用いられ
ている。素子としては,米国Noise Com社のNC-2401を用いた。この素子はノイズ源と増幅器とを内蔵し
ており,帯域幅は1 GHz,振幅は160 mVrmsである。
ノイズ信号を数値化する方法としては,
a) ノイズ信号レベルをアナログ/デジタル変換するもの
b) ノイズをパルス列とみなし,単位時間当たりのパルス数を計数するもの
c) ノイズをパルス列とみなし,パルス間隔を測定するもの
などが考えられる。ここでは,アナログ/デジタル変換によるものを利用した。アナログ/デジタル変換
用の装置としてはKeithley Metrabyte社のDAS-4102を用いた。この装置は8ビットの分解能をもち,サン
プリング周波数は最大64 MHzである。実際には64 MHzでサンプリングしても検定で見る以上問題ない
乱数を生成できるが,安全のため表A.1の作成には1 MHzでサンプリングしたものを用いた。分解能3.91
mV/digitで測定を行い,下1ビットだけを乱数源として使用した。
アナログ/デジタル変換装置には装置固有の誤差があるために,変換後の値の頻度分布は一様にならな
い。一様な分布を得るために,同一の乱数源から2ビット (x0, x1) を生成し,

32
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(0, 1)
→ Rn=0
(1, 0)
→ Rn=1
(0, 0), (1, 1) → 棄却
として乱数Rnを生成した。x0,x1の確率分布が等しければ,Rnは一様分布になる。x0,x1の測定間隔は1 μs
と短いので,この間に装置の特性はほとんど変動しない。したがって,x0,x1は同じ確率分布に従うと考
えられる。このほか,あらかじめ確率分布を測定しておいて補正するなどの方法もあるが,装置の特性の
系統的な変動によって影響を受けるので採用しなかった。さらに,32ビットずつまとめてB.5に示した疑
似乱数メルセンヌツイスター(ルーチン名genrand)と排他的論理和をとった。メルセンヌツイスターは,
ルーチンinit̲genrand(19660809UL) によって初期化を行った。メルセンヌツイスターは,論理的に623次
元での一様性をもつことが示されているので,これによって,一様性に関しては一定の保証が得られる。
もし,原乱数列が必要な場合には,再度メルセンヌツイスターと排他的論理和をとることによって原乱数
列を復元することができる。
本体に含まれる乱数表は,このようにして製作した32ビット乱数列の上4ビットをとり,この値が0
以上9以下ならば乱数値として採用し,10以上ならば棄却して次の乱数を生成することによって作成した
十進乱数列である。
A.2.2 バイナリ形式の乱数表ファイルを読み出すプログラムコード
次のプログラムは,バイナリ形式の乱数表ファイルを読み出すための例である。参考文献[23]に記載さ
れたリンク先の乱数表ファイルを記憶媒体(パス)にダウンロードし,次のプログラムを用いて指定した
パスから物理乱数を読み出すことができる。
関数 open̲rndtable(char *filename) はfilenameで指定されたパスに置かれたバイナリ形式の乱数表ファ
イルを開き,乱数取得の準備をする。
関数 init̲rndtable (unsigned long seed) は,seedで指定された乱数表の位置から乱数を取得する。
関数 rndtable() は呼び出されるごとに0以上232−1以下の整数乱数を乱数表から読み取り,その値を
unsigned long形で返す。関数 rndtable̲31() は呼び出されるごとに0以上231−1以下の整数乱数を乱数表か
ら読み取り,その値をlong形で返す。
関数 close̲rndtable() は,乱数表ファイルを閉じる。
物理乱数は原理的に,周期性又は再現性がないことが特徴であるが,乱数表ファイルから読み出す乱数
は,ファイルサイズに等しい周期性及びseedに依存した再現性が存在する。周期性は回避できないので,
ファイルサイズを超える乱数を必要とする場合は,物理乱数を生成する装置から乱数を取得することが望
ましい。再現性は,seedを変えることによって回避することができる。seedの与え方としては,乱数を順
番に使用すること,すなわち,(前回使用したseedの値)+(前回使用した乱数の数)を今回のseedとする
ことが望ましい。
/************************************************************
Random Number Generation from Physical Random Number Tables
************************************************************/
#include <stdio.h>
#include <stdlib.h>

33
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
#define BUFFERSIZE 100000
static long Filesize = -1;
static long Filepos = 0;
static FILE * fp = NULL;
static long Bufsize = BUFFERSIZE;
static unsigned char *Buffer;
static long Bufp = -1;
long open̲rndtable(char * filename)
{
/*** WIN32 ***/
if ( (fp = fopen (filename, "rb" ) ) == NULL ) { /*/
/*** !WIN32 ***
if ( (fp = fopen (filename, "r" ) ) == NULL ) { /*/
perror("init̲rndtable"); exit (1);
}
fseek(fp, 0L, SEEK̲END);
Filesize = ftell(fp);
fseek(fp, 0L, SEEK̲SET);
if (BUFFERSIZE > Filesize)
Bufsize = Filesize;
else
Bufsize = BUFFERSIZE;
Buffer = (unsigned char *)malloc(Bufsize);
if (Buffer == NULL) { perror( "open̲rndtable" ); exit(1); }
Bufp = -1;
return Filesize;
}
void close̲rndtable(void)
{
fclose(fp);
free(Buffer);
Filesize = Bufp = -1;
}

34
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
void init̲rndtable(unsigned long seed)
{
Filepos = (seed * 4) % Filesize;
Bufp = -1;
}
void read̲table (void)
{
long n, nread;
if (Filesize <= 0) {
fprintf (stderr, "read̲table : Random number data file is not opened or
no data in file. ¥n");
exit(1);
}
if (Filesize <= Filepos) Filepos = 0;
if ((Filesize - Filepos) >= Bufsize) {
nread = Bufsize;
}else{
nread = Filesize - Filepos;
}
fseek (fp, Filepos, SEEK̲SET);
n = nread;
do{
n -= fread (Buffer, sizeof(unsigned char) , n, fp);
}while (n > 0);
Filepos += nread;
if (Bufsize > nread) {
Filepos = 0L;
fseek (fp, Filepos, SEEK̲SET);
n = Bufsize-nread;
do {
n -= fread (Buffer + nread, sizeof(unsigned char), n, fp);
}while (n > 0);
}
}
unsigned long rndtable(void)
{
unsigned long x;

35
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
if ((Bufsize - Bufp < 4) || (Bufp < 0)) {
read̲table();
Bufp = 0L;
}
/*** big endian ***/
x = ((unsigned long) Buffer[Bufp + 0] << 24)
+ ((unsigned long) Buffer[Bufp + 1] << 16)
+ ((unsigned long) Buffer[Bufp + 2] << 8)
+ ((unsigned long) Buffer[Bufp + 3]); */
/*** little endian ***
x = ((unsigned long) Buffer[Bufp + 3] << 24)
+ ((unsigned long) Buffer[Bufp + 2] << 16)
+ ((unsigned long) Buffer[Bufp + 1] << 8)
+ ((unsigned long) Buffer[Bufp + 0]); */
Bufp += 4;
return x;
}
long rndtable̲31(void)
{
return (long)(rndtable() >> 1);
}
A.3 乱数表の使い方
表A.1を用いて十進乱数列を作るには,次の方法による。
a) 出発点をランダムに決める ランダムな数列として乱数表を用いるためには,乱数列を取り出す出発
点をランダムに決めることが重要である。
そのため,表A.1の任意のページの上に目をつぶって鉛筆を立てて落とし,当たった点に一番近い
数字を起点として連続3個の数字を読み,その数字を250で除した余りに1を加えた数を行の番号と
する。次にもう一度鉛筆を落として当たった点に一番近い数字を起点として,連続2個の数値を読み,
その数字を20で除した余りを列の番号とする。
例 表A.1の任意のページを開けて,この上に目をつぶって鉛筆を落としたら中間に落ちたのでや
り直した。今度は一番近い数値が3であり,それを起点とした連続3個の数字は370であった。
これを250で除した余りに1を加えると121となるので,第121行をとることとなる。次にも
う一度鉛筆を落としたら9に当たり,それを起点とした連続2個の数字は99であった。これを
20で除した余りは,19なので,第19列をとることとなる。すなわち,乱数表5の第121行19
列の数値39の左端3を乱数列の出発点とする。
b) 乱数列を読み取る 十進1桁の乱数列又は2桁の乱数列が必要な場合は,右へ進む。右端に達したら
36
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
次の行の左端に移る。
十進3桁以上の乱数列が必要な場合は,下に進む。下端に達したら同じページの中で次の列に移る。
ページの右下に達したら次のページの左上に移る。
最後のページの場合には,最初のページに移る。
例1 2桁の乱数列をとりたい場合には,a)の例によって第121行19列の左端から出発すると39, 13,
77, 96, 47, 57, 68, 65,…と進む。
例2 3桁の乱数列をとりたい場合には,同様に第121行19列の左端から出発すると,364, 561, 319,
308, 182, 457, 478, 218, 916, 063, 690, 585,…と進む。
37
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
疑似乱数生成アルゴリズム
B.1
線形合同法
B.1.1 実装上の注意
線形合同法を実装する場合の一つの問題点は,乗算aXを実行するときにしばしばオーバーフロー(桁
あふれ)が起きることである。1語がlビット(典型的なのは,l=32)の計算機を使用する場合に,1語
で表現できる整数Xの範囲は,通常
− 符号なし二進数表現の場合, 0≦X≦2l−1
− 符号付き二進数表現の場合, −2l−1≦X≦2l−1−1
である。したがって,a及びXがいずれもこの範囲内に収まっていてlビットで表現可能だとしても,積
aXはlビットでは表現できないほど(絶対値が)大きくなり,オーバーフローが起きることが多い。オー
バーフローが起きた場合には,あふれた部分を無視して計算が続行されるときと,計算が中断されるとき
とがある。前者のとき,符号付き二進数表現を使っていると,a及びXが共に正整数であっても,乗算の
結果は負整数となってしまうことがある。このような状況に対する対応策が幾つか提案されているので,
そのうちの幾つかを次に示す(l=32と仮定するが,他の場合にも同様な考え方で対処できる。)。
a) 多倍長整数演算(整数の表現及び演算に2lビット以上を使用する計算)を採用して,オーバーフロー
が起きないようにする。
b) オーバーフローによって計算が中断しないならば,オーバーフローを積極的に利用することもできる。
l=32,m=232ならば,オーバーフローした部分を無視して残った部分を符号なし二進数と見ることに
すれば,(mod m) という演算が既に実行されていることになるので好都合である。ただし,符号付き
二進数表現を使用していて,負の整数が2の補数で表現されている場合には,少し事情が異なる。数
学的な意味で,
)
(modm
aX
Y=
であるものとし,Yを符号付き二進数表現として解釈した場合の値をY'とすると,
−
−
<
=
′
1
2
2
2
2
0
,
32
31
32
31
≦
≦
≦
Y
Y
Y
Y
Y
となる。しかし,231≦Y≦232−1の場合でも
)
2
(mod
)
2
)(mod
2
(
)
2
(mod
32
32
32
32
aY
a
aY
Y
a
=
−
=
′
であるので,線形合同法乱数列を生成する演算をこのまま続けていっても不都合を生じない。しかし,
区間 [0, 1) 上の乱数(標準一様乱数)Uを作るときには注意が必要であり,(U=Y'/232ではなくて)
32
2/
5.0 Y
U
′
+
=
としなければならない。
c) a)で示した多倍長の整数演算機能が使えない場合,倍精度の浮動小数点演算を利用して対処すること
もできる。計算時間がかかってもよいのでポータビリティ(同一のプログラムコードを種々の計算環
境の下で使用しても同一の結果が得られること)を重視するならば,この方法を採用することが望ま
しい。次の例は,m=231−1の場合のものである。
38
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
aが比較的小さい1) 場合には,a及びXを倍精度浮動小数点数として表現し,乗算も倍精度で行え
ばよい。
注1) 倍精度浮動小数点数の表現に使用される仮数部の長さは,IBM形ならば56ビット,IEEE形
ならば53ビットである。したがって,aが22ビット以内で表現できる整数,すなわち,a<
4 194 304ならば,上記のいずれの形の表現を使用していても,乗算の結果は正確に表現され
る。
a≧4 194 304の場合には,次のようにすることが望ましい。a1=a (mod 216),a2=a−a1,Y1=a1X (mod
231),Y2=a2X (mod 231) とおく。そうすると,
)1
2
(mod
])
2/
[
]
2/
[
(
31
31
2
2
31
1
1
−
+
+
+
=
=
X
a
Y
X
a
Y
aX
Y
となる。ここで,
1
2
,1
2
62
2
47
1
−
−
≦
≦
X
a
X
a
である。しかし,a2Xの下位16ビットは全て0である。したがって,仮数部に47ビット以上が割り
当てられていれば,Yは正確に計算できる。
B.1.2 プログラムコード
C言語(JIS X 3010参照)及びBASIC言語(JIS X 3003参照)による線形合同法の実装例を次に示す。
BASICコードについては動作の説明を省略し,対応するC言語をコメント文で併記した。また,C言語に
はあるがBASIC言語にはない関数については,B.9にコードを記載した。
法m=232の場合と,m=231−1の場合との2種類のプログラムから構成されている。これは,B.1.1で示
したような問題はなく動作する。特に次の三つの性質が重要である。
− unsigned longの最大値は,232−1以上である。
− unsigned long形の数同士の乗算結果は,乗算結果を(unsigned longの最大値+1)で除した余りと定義
される。
−(unsigned longの最大値+1)は,2のべき(冪)である。
B.1.2.1 m=232の場合
関数lcong32 ( ) は,呼び出されるごとに0以上232−1以下の整数乱数を生成し,結果をunsigned long
形で返す。関数lcong32̲31 ( ) は,呼び出されるごとに0以上231−1以下の整数乱数を生成し,結果をlong
形で返す。初期化関数init̲lcong32 (unsigned long seed) は,unsigned long形の非負整数seedをシードとし
て初期化を行う。加数cが0の場合には,シードX0は奇数でなければならない。このためcが0の場合に
偶数のseedを与えると,seed+1をシードX0として用いる。その他の場合には,seed (mod m) をそのまま
シードX0として用いる。
乗数,加数を変更するには,それぞれプログラム中のMULTIPLIER,INCREMENTの定義を変えればよ
い。この生成法では,lcong32 ( ) の出力を初期化関数init̲lcong32 (seed) の引数として与えれば,そこから
乱数系列を再開することができる。
B.1.2.2 m=231−1の場合
関数lcong31 ( ) は,呼び出されるごとに1以上231−2以下の整数乱数を生成し,結果をlong形で返す。
初期化関数init̲lcong31 (unsigned long seed) は,unsigned long形の非負整数seedをシードとして初期化を
行う。この規格に規定されているパラメータは,全て加数cが0である。このためシードX0は,0であっ
てはならない。seedが0の場合には,特定の数 (19 660 809) をシードX0として用いる。その他の場合に
は,seed (mod m) をそのままシードX0として用いる。
乗数を変更するには,プログラム中のMULTIPLIERの定義を変えればよい。この生成法の状態変数は,
39
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
最後に生成した乱数値そのものである。したがって,lcong31 ( ) の出力を初期化関数init̲lcong31 (seed) の
引数として与えれば,そこから乱数系列を再開することができる。
法がm=231−1の場合には,剰余を計算する必要がある。いま,X=Xhi (m+1) +Xloと分解したとする
と,X (mod m)=(Xhi+Xlo) (mod m) と計算できる。この場合m+1=231であるので,上記の分解は,数が二
進表現されていれば自明である。また,31ビットの整数の積を62ビットで求める必要がある。このプロ
グラムでは,31ビットの整数を上位,下位に分解して積を計算している。多くの計算機には,32ビット(以
上)の数の積を64ビット(以上)で求める命令が備わっているので,機械語などを利用すれば,より高速
なプログラムが得られることもある。
/**********************************************************
C code : Linear Congruential
Modulus = 2^32
Modulus = 2^31-1
The word length of ̀unsigned long' should be larger than 2^32.
The multiplication of ̀unsigned long'
should be defined as multiplication modulus ULONG̲MAX+1.
The value ULONG̲MAX+1 should be a power of 2.
**********************************************************/
/*********************************************************
Part 1. Modulus = 2^32
**********************************************************/
/* Choice 1 */
#define MULTIPLIER 1664525UL
#define INCREMENT 1UL
/* Choice 2 *
#define MULTIPLIER 1566083941UL
#define INCREMENT 0UL */
/* Choice 3 *
#define MULTIPLIER 48828125UL
#define INCREMENT 0UL */
static unsigned long state32;
unsigned long lcong32(void)
{
state32 = (state32 * MULTIPLIER + INCREMENT) & 0xFFFFFFFFUL;
40
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
return state32;
}
long lcong32̲31(void)
{
state32 = (state32 * MULTIPLIER + INCREMENT) & 0xFFFFFFFFUL;
return state32 >> 1;
}
void init̲lcong32(unsigned long s)
{
/* seed should be odd when increment == 0 */
if ((INCREMENT == 0) && (s % 2 == 0)) {
s++;
}
state32 = s;
}
/*********************************************************
Part 2. Modulus = 2^31-1 = 2147483647
**********************************************************/
#undef MULTIPLIER
#undef INCREMENT
#undef NBIT
#define NBIT 15
#define MASK ((1 << NBIT) - 1)
#define MASK2 ((1 << (2 * NBIT)) - 1)
/* Choice 4 */
#define MULTIPLIER 2100005341UL
/* Choice 5 *
#define MULTIPLIER 397204094UL */
/* Choice 6 *
#define MULTIPLIER 314159369UL */
#define MULTIPLIER̲LO (MULTIPLIER & MASK)
#define MULTIPLIER̲HI (MULTIPLIER >> NBIT)
41
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
static unsigned long state31;
long lcong31(void)
{
unsigned long xlo, xhi;
unsigned long z0, z1, z2;
xlo = state31 & MASK;
xhi = state31 >> NBIT;
z0 = xlo * MULTIPLIER̲LO; /* 15bit * 15bit => 30bit */
z1 = xlo * MULTIPLIER̲HI
+ xhi * MULTIPLIER̲LO; /* 15bit * 16bit * 2 => 32bit */
z2 = xhi * MULTIPLIER̲HI; /* 16bit * 16bit => 32bit */
z0 += (z1 & MASK) << NBIT;
z2 += (z1 >> NBIT) + (z0 >> (2 * NBIT));
z0 = (z0 & MASK2) | ((z2 & 1) << (2 * NBIT));
z2 >>= 1;
state31 = z0 + z2;
/* This should not exceed 2*0x7fffffffUL */
if (state31 >= 0x7fffffffUL) state31 -= 0x7fffffffUL;
return (long)state31;
}
void init̲lcong31(unsigned long s)
{
/* seed should not be 0 */
if (s == 0UL) s=19660809UL;
s = s % 0x7fffffffUL;
state31 = s;
}
REM /*********************************************************
REM BASIC code : Linear Congruential
REM **********************************************************/
REM
REM /*********************************************************
REM Part 1. Modulus = 2^32
REM **********************************************************/
42
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
OPTION BASE 0
REM /*********************************************************************/
DECLARE NUMERIC MULTIPLIER
LET MULTIPLIER = 1664525
!#define MULTIPLIER 1664525UL
DECLARE NUMERIC INCREMENT
LET INCREMENT = 1
!#define INCREMENT 1UL
DECLARE NUMERIC state32
!static unsigned long state32;
REM /*********************************************************************/
FUNCTION lcong32
!unsigned long lcong32u( void ) {
LET state32 = And32((state32 * MULTIPLIER) + INCREMENT , MskF̲f)
!
! state32 = ( state32 * MULTIPLIER ;
!
! + INCREMENT ) & 0xFFFFFFFFUL;
LET lcong32 = state32
! return state32;
END FUNCTION
!}
REM /*********************************************************************/
FUNCTION lcong32̲31
!long lcong32( void ) {
!
! state32 = ( state32 * MULTIPLIER
!
! + INCREMENT ) & 0xFFFFFFFFUL;
LET lcong32̲31 = SR32U(lcong32 , 1)
!
! return state32>>1;
END FUNCTION
!}
REM /*********************************************************************/
FUNCTION init̲lcong32(s)
!void init̲lcong32(unsigned long s) {
REM /* seed should be odd when increment == 0 */
IF (INCREMENT = 0) AND (REMAINDER(s , 2) = 0) THEN
!
! if ( (INCREMENT==0) && (s%2 == 0) ) {
LET s = s + 1
! s++;
END IF
! }
LET state32 = s
! state32 = s;
END FUNCTION
!}
REM /*********************************************************
REM BASIC code : Linear Congruential
REM **********************************************************/
REM
43
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
REM /*********************************************************
REM Part 2. Modulus = 2^31-1 = 2147483647
REM **********************************************************/
OPTION BASE 0
DECLARE NUMERIC NBIT
LET NBIT = 15
!#define NBIT 15
DECLARE NUMERIC MASK
LET MASK = SL32U(1 , NBIT) ‒ 1
!#define MASK ((1<<NBIT)-1)
DECLARE NUMERIC MASK2
LET MASK2 = SL32U(1 , 2*NBIT) ‒ 1 !#define MASK2 ((1<<(2*NBIT))-1)
DECLARE NUMERIC MULTIPLIER
LET MULTIPLIER = 2100005341
!#define MULTIPLIER 2100005341UL
DECLARE NUMERIC MULTIPLIER̲LO
LET MULTIPLIER̲LO = And32(MULTIPLIER , MASK)
!
!#define MULTIPLIER̲LO (MULTIPLIER & MASK )
DECLARE NUMERIC MULTIPLIER̲HI
LET MULTIPLIER̲HI = SR32U(MULTIPLIER , NBIT)
!
!#define MULTIPLIER̲HI (MULTIPLIER >> NBIT )
DECLARE NUMERIC state31
!static unsigned long state31;
REM /*********************************************************************/
FUNCTION lcong31
!long lcong31( void ) {
DECLARE NUMERIC xlo, xhi
! unsigned long xlo, xhi;
DECLARE NUMERIC z0, z1, z2
! unsigned long z0, z1, z2;
LET xlo = And32(state31 , MASK)
!
! xlo = state31 & MASK; //1st val:9
LET xhi = SR32U(state31 , NBIT)
!
! xhi = state31 >> NBIT; //1st val:600
LET z0 = xlo * MULTIPLIER̲LO
! z0 = xlo * MULTIPLIER̲LO; /* 15bit * 15bit
=> 30bit */
LET z1 = xlo * MULTIPLIER̲HI
! z1 = xlo * MULTIPLIER̲HI
LET z1 = z1 + xhi * MULTIPLIER̲LO
! + xhi * MULTIPLIER̲LO;

44
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LET z2 = xhi * MULTIPLIER̲HI
! z2 = xhi * MULTIPLIER̲HI;
LET z0 = z0 + SL32U(And32(z1 , MASK) , NBIT)
!
! z0 += (z1 & MASK) << NBIT; //1st val:897833157
LET z2 = z2 + SR32U(z1 , NBIT) + SR32U(z0 , 2 * NBIT)
!
! z2 += (z1 >> NBIT) + (z0 >> (2*NBIT));
LET z0 = Or32(And32(z0 , MASK2) , SL32U(And32(z2 , 1) , 2 * NBIT))
!
! z0 = (z0 & MASK2) | ((z2&1)<<(2*NBIT));
LET z2 = SR32U(Z2 , 1)
! z2 >>=1;
LET state31 = z0 + z2
! state31 = z0 + z2;
REM /* This should not exceed 2*0x7fffffffUL */
IF state31 >= 2147483647 THEN LET state31 = state31 - 2147483647
!
! IF (state31>=0x7fffffffUL)
!
! state31 -= 0x7fffffffUL;
LET lcong31 = state31
! return (long) state31;
END FUNCTION
!}
REM /*********************************************************************/
FUNCTION init̲lcong31(s)
!void init̲lcong31(unsigned long s) {
REM ! /* seed should not be 0 */
IF s = 0 THEN LET s = 19660809 ! if ( s == 0UL ) s=19660809UL;
LET s = REMAINDER(s , 2147483647)
!
! s = s % 0x7fffffffUL;
LET state31 = s
! state31 = s;
END FUNCTION
!}
B.2
3項GFSR法のプログラムコード
C言語(JIS X 3010参照)及びBASIC言語(JIS X 3003参照)による3項GFSR法の実装例を示す。BASIC
コードについては,動作の説明を省略し,対応するC言語をコメント文で併記した。また,C言語にはあ
るがBASIC言語にはない関数については,B.9にコードを記載した。
次のプログラムは,パラメータ (p, q, w)=(1 279, 418, 32) の例であり,周期は21 279−1である。関数gfsr( )
は,呼び出されるごとに0以上232−1以下の整数を生成する。関数gfsr̲31( ) は,呼び出されるごとに0
以上231−1以下の整数を生成する。初期化関数init̲gfsr(s) は,符号なし32ビット整数(0以上232−1以
下の整数)をシードとして初期化を行う。これは,[1 279/32]=39次元の均等分布性をもち,位相差21 279/32
までの自己相関をなくしている。gfsr () ,gfsr̲31 ( ) を呼び出す前に,一度init̲gfsr (s) を実行し初期化を
行わなければならない。
異なる疑似乱数の系列を得るには,init̲gfsr (s) に与えるシードsを変更する。プログラム中のP,Q,
W以外の定数は変えてはならない。周期を変更したい場合はP,QをtP+tQ+1がGF (2) 上で原始的にな

45
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る範囲で変更する。可能なP,Qの値の組については,表2を参照。Wは,生成する整数のビット数を決
定している。Wの値は,マシンのワード長以下で2のべき(冪)乗でなければならない。Wは,マシンに
応じ32又は64といった値が一般的である。例えば,マシンのワード長が64の場合プログラム中の定数
Wを64に変えたときは,gfsr ( ) は0以上264−1以下の整数を生成し,gfsr̲31 ( ) は0以上263−1以下の
整数を生成する。乱数生成を中断し,後に再開したい場合は,中断のとき,サイズPの配列state [P] 及び
整数state̲iを保存し,再開時に保存した値を代入し直せばよい。
なお,このプログラムでは,unsigned long形の大きさは,32ビット以上であると仮定している。
/*************************************************
C code : Trinomial GFSR
*************************************************/
#define P 1279
#define Q 418
#define W 32 /* W should be a power of 2 */
static unsigned long state[P];
static int state̲i;
void init̲gfsr(unsigned long s)
{
int i, j, k;
static unsigned long x[P];
s &= 0xffffffffUL;
for (i = 0; i < P; i++) {
x[i] = s >> 31;
s = 1664525UL * s + 1UL;
s &= 0xffffffffUL;
}
for (k = 0, i = 0; i<P; i++) {
state[i] = 0UL;
for (j = 0; j < W; j++) {
state[i] <<= 1;
state[i] |= x[k];
x[k] ^= x[(k + Q) % P];
k++;
if (k == P) k = 0;

46
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
}
}
state̲i = 0;
}
unsigned long gfsr(void)
{
int i;
unsigned long *p0, *p1;
if (state̲i >= P) {
state̲i = 0;
p0 = state;
p1 = state + Q;
for (i = 0; i < (P-Q); i++)
*p0++ ^= *p1++;
p1 = state;
for (; i < P; i++)
*p0++ ^= *p1++;
}
return state[state̲i++];
}
/* W-1 bit integer */
long gfsr̲31(void)
{
return (long)(gfsr() >> 1);
}
REM /*********************************************
REM BASIC code : Trinomial GFSR
REM **********************************************/
OPTION BASE 0
REM /*********************************************************************/
DECLARE NUMERIC P
LET P=1279
!#define P 1279

47
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
DECLARE NUMERIC Q
LET Q=418
!#define Q 418
DECLARE NUMERIC W
LET W=32
!#define W 32 /* W should be power OF
2 */
DIM state(P)
!static unsigned long state[P];
DECLARE NUMERIC state̲i
!static INT state̲i;
REM
/*****************************************************************************
*******/
FUNCTION init̲gfsr(s)
!void init̲gfsr(unsigned long s){
DECLARE NUMERIC i,j,k
! int i, j, k;
DIM x(P)
! static unsigned long x[P];
LET s = And32(s , MskF̲f)
! s &= 0xffffffffUL;
FOR i = 0 TO P -1
! for (i=0; i<P; i++) {
LET x(i) = SR32U(s , 31)
! x[i] = s>>31;
LET s = Mul32U(1664525 , s) + 1
! s = 1664525UL * s + 1UL;
LET s = And32(s, MskF̲f)
! s &= 0xffffffffUL;
NEXT i
! }
LET k=0
FOR i = 0 TO P -1
! for (k=0,i=0; i<P; i++) {
LET state(i) = 0
! state[i] = 0UL;
FOR j=0 TO W-1
! for (j=0; j<W; j++) {
LET state(i) = SL32U(state(i) , 1)
!
! state[i] <<= 1;
LET state(i) = Or32(state(i) , x(k))
!
! state[i] |= x[k];
LET x(k) = Xor32(x(k) , x(REMAINDER(k + Q , P)))
!
! x[k] ^= x[(k+Q)%P];
LET k = k + 1
! k++;
IF k = P THEN LET k = 0
! if (k==P) k = 0;
NEXT j
! }
NEXT i
! }
LET state̲i = 0
! state̲i = 0;
END FUNCTION
!}
REM
/**************************************************************************/

48
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
FUNCTION gfsr
!unsigned long gfsr(void){
DECLARE NUMERIC i
! int i;
DECLARE NUMERIC p0, p1
! unsigned long *p0, *p1;
IF state̲i >= P THEN
! if (state̲i >= P) {
LET state̲i = 0
! state̲i = 0;
LET p0 = 0
! p0 = state;
LET p1 = Q
! p1 = state + Q;
FOR i=0 TO P-Q-1
! for (i=0; i<(P-Q); i++)
LET state(p0) = Xor32(state(p0) , state(p1))
LET p0 = p0 + 1
LET p1 = P1 + 1
! *p0++ ^= *p1++;
NEXT i
LET p1 = 0
! p1 = state;
FOR i=i TO P-1
! for (; i<P; i++)
LET state(p0) = Xor32(state(p0) , state(p1))
LET p0 = p0 + 1
LET p1 = P1 + 1
! *p0++ ^= *p1++;
NEXT i
END IF
! }
LET gfsr = state(state̲i)
LET state̲i = state̲i + 1
! return state[state̲i++];
END FUNCTION
!}
REM
/**************************************************************************/
REM /* W-1 bit integer */
FUNCTION gfsr̲31
!long gfsr̲31(void){
LET gfsr̲31 = SR32U(gfsr , 1)
! return (long)(gfsr()>>1);
END FUNCTION
!}
B.3
5項GFSR法のプログラムコード
C言語(JIS X 3010参照)及びBASIC言語(JIS X 3003参照)による5項GFSR法の実装例を示す。BASIC
コードについては,動作の説明を省略し,対応するC言語をコメント文で併記した。また,C言語にはあ
るがBASIC言語にはない関数については,B.9にコードを記載した。
次のプログラムは,パラメータが (521, 86, 197, 447, 32) で,周期は2521−1である。このコードの説明
は,3項GFSRのプログラムコードの説明に従う。gfsr5( ) は,呼び出されるごとに0以上232−1以下の整
数を生成する。関数gfsr5̲31( ) は,呼び出されるごとに0以上231−1以下の整数を生成する。初期化ルー
チンinit̲gfsr5 (s) は,符号なし32ビット整数(0以上232−1以下の整数)をシードとし初期化を行う。
gfsr5( ) ,gfsr5̲31( ) を呼び出す前に,一度init̲gfsr5(s) を実行し,初期化を行わなければならない。P,
49
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Q1,Q2,Q3の値の組は,表3に示したものを使用する。
/*************************************************
C code : Pentanominal GFSR
**************************************************/
#define P 521
/* Q1 < Q2 < Q3 */
#define Q1 86
#define Q2 197
#define Q3 447
#define W 32 /* W should be a power of 2 */
static unsigned long state[P];
static int state̲i;
void init̲gfsr5(unsigned long s)
{
int i, j, k;
static unsigned long x[P];
s &= 0xffffffffUL;
for (i = 0; i < P; i++) {
x[i] = s >> 31;
s = 1664525UL * s + 1UL;
s &= 0xffffffffUL;
}
for (k = 0, i = 0; i < P; i++) {
state[i] = 0UL;
for (j = 0; j < W; j++) {
state[i] <<= 1;
state[i] |= x[k];
x[k] ^= x[(k + Q1) % P] ^ x[(k + Q2) % P] ^ x[(k + Q3) % P];
k++;
if (k==P) k = 0;
}
}
50
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
state̲i = 0;
}
unsigned long gfsr5(void)
{
int i;
unsigned long *p0, *p1, *p2, *p3;
if (state̲i >= P) {
state̲i = 0;
p0 = state;
p1 = state + Q1;
p2 = state + Q2;
p3 = state + Q3;
for (i = 0; i < (P - Q3); i++)
*p0++ ^= *p1++ ^ *p2++ ^ *p3++;
p3 = state;
for (; i < (P - Q2); i++)
*p0++ ^= *p1++ ^ *p2++ ^ *p3++;
p2 = state;
for (; i < (P - Q1); i++)
*p0++ ^= *p1++ ^ *p2++ ^ *p3++;
p1 = state;
for (; i < P; i++)
*p0++ ^= *p1++ ^ *p2++ ^ *p3++;
}
return state[state̲i++];
}
/* W-1 bit integer */
long gfsr5̲31(void)
{
return (long)(gfsr5() >> 1);
}
REM /*********************************************
REM BASIC code : Pentanomial GFSR
REM **********************************************/
51
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
OPTION BASE 0
REM /*********************************************************************/
DECLARE NUMERIC P
LET P = 521
!#define P 521
REM /* Q1 < Q2 < Q3 */
DECLARE NUMERIC Q1
LET Q1 = 86
!#define Q1 86
DECLARE NUMERIC Q2
LET Q2 = 197
!#define Q2 197
DECLARE NUMERIC Q3
LET Q3 = 447
!#define Q3 447
DECLARE NUMERIC W
LET W = 32
!#define W 32 /* W should be power of 2 */
DIM state(P)
!static unsigned long state[P];
DECLARE NUMERIC state̲i
!static int state̲i;
REM /*********************************************************************/
FUNCTION init̲gfsr5(s)
!void init̲gfsr5(unsigned long s) {
DECLARE NUMERIC i, j, k
! int i, j, k;
DIM x(P)
! static unsigned long x[P];
LET s = And32(s , MskF̲f)
! s &= 0xffffffffUL;
FOR i=0 TO P-1
! for (i=0; i<P; i++) {
LET x(i) = SR32U(s , 31)
! x[i] = s>>31;
LET s = Mul32U(1664525 , s) + 1
!
! s = 1664525UL * s + 1UL;
LET s = And32(s , MskF̲f)
! s &= 0xffffffffUL;
NEXT i
! }
LET k=0
FOR i=0 TO P-1
! for (k=0,i=0; i<P; i++) {
LET state(i) = 0
! state[i] = 0UL;
FOR j=0 TO W-1
! for (j=0; j<W; j++) {
LET state(i) = SL32U(state(i) , 1)
!
! state[i] <<= 1;
LET state(i) = Or32(state(i) , x(k))
52
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
!
! state[i] |= x[k];
LET x(k) = Xor32(Xor32(Xor32(x(k) , x(REMAINDER(k + Q1 , P))) ,
x(REMAINDER(k + Q2 , P))) , x(REMAINDER(k + Q3 , P)))
!
! x[k] ^= x[(k+Q1)%P]
!
! ^ x[(k+Q2)%P] ^ x[(k+Q3)%P];
LET k = k + 1
! k++;
IF k = P THEN LET K = 0
! if (k==P) k = 0;
NEXT j
! }
NEXT I
! }
LET state̲i = 0
! state̲i = 0;
END FUNCTION
!}
REM /*********************************************************************/
FUNCTION gfsr5
!unsigned long gfsr5(void) {
DECLARE NUMERIC I
! int i;
DECLARE NUMERIC p0, p1, p2, p3 ! unsigned long *p0, *p1, *p2, *p3;
IF state̲i >= P THEN
! if (state̲i >= P) {
LET state̲i = 0
! state̲i = 0;
LET p0 = 0
! p0 = state;
LET p1 = Q1
! p1 = state + Q1;
LET p2 = Q2
! p2 = state + Q2;
LET p3 = Q3
! p3 = state + Q3;
FOR i=0 TO P-Q3-1
! FOR (i=0; i<(P-Q3); i++)
LET state(p0) = Xor32(Xor32(Xor32(state(p0) , state(p1)) , state(p2)) ,
state(p3))
LET p0 = p0 + 1
LET p1 = p1 + 1
LET p2 = p2 + 1
LET p3 = p3 + 1
! *p0++ ^= *p1++ ^ *p2++ ^ *p3++;
NEXT i
LET p3 = 0
! p3 = state;
FOR i=i TO P-Q2-1
! for (; i<(P-Q2); i++)
LET state(p0) = Xor32(Xor32(Xor32(state(p0) , state(p1)) , state(p2)) ,
state(p3))
LET p0 = p0 + 1
LET p1 = p1 + 1
LET p2 = p2 + 1
53
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LET p3 = p3 + 1
! *p0++ ^= *p1++ ^ *p2++ ^ *p3++;
NEXT i
LET p2 = 0
! p2 = state;
FOR i=i TO P-Q1-1
! for (; i<(P-Q1); i++)
LET state(p0) = Xor32(Xor32(Xor32(state(p0) , state(p1)) , state(p2)) ,
state(p3))
LET p0 = p0 + 1
LET p1 = p1 + 1
LET p2 = p2 + 1
LET p3 = p3 + 1
! *p0++ ^= *p1++ ^ *p2++ ^ *p3++;
NEXT i
LET p1 = 0
! p1 = state;
FOR i=i TO P-1
! for (; i<P; i++)
LET state(p0) = Xor32(Xor32(Xor32(state(p0) , state(p1)) , state(p2)) ,
state(p3))
LET p0 = p0 + 1
LET p1 = p1 + 1
LET p2 = p2 + 1
LET p3 = p3 + 1
! *p0++ ^= *p1++ ^ *p2++ ^ *p3++;
NEXT i
END IF
! }
LET gfsr5 = state(state̲i)
LET state̲i = state̲i + 1
! return state[state̲i++];
END FUNCTION
!}
REM /*********************************************************************/
REM /* W-1 bit integer */
FUNCTION gfsr5̲31
!long gfsr5̲31(void) {
LET gfsr5̲31 = SR32U(gfsr5 , 1)
!
! return (long)(gfsr5()>>1);
END FUNCTION
!}
B.4
結合トーズワース法のプログラムコード
C言語(JIS X 3010参照)及びBASIC言語(JIS X 3003参照)による結合トーズワース法の実装例を示
す。BASICコードについては,動作の説明を省略し,対応するC言語をコメント文で併記した。また,C
言語にはあるが,BASIC言語にはない関数については,B.9にコードを記載した。
taus88̲31( ) は,パラメータが (31, 13, 12),(29, 2, 4),及び (28, 3, 17) の三つのトーズワース系列を合
成して,0以上231−1以下の整数を生成する。
54
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
初期化関数init̲taus88(s) は,符号なし32ビット整数(0以上232−1以下の整数)sをシードとして初期
化を行う。異なる疑似乱数の系列を得るには,シードsを変更する。taus88̲31( ) を呼び出す前に,一度
init̲taus88 (s) を実行し,初期化を行わなければならない。初期化は,init̲taus88(s) を使用せずに,使用者
がs1,s2,s3に適切な値を直接代入することによっても行うことができる。ただし,初期化の場合には,
次の三つの条件を満たすようにする必要がある。
− s1の上位31ビットのうちの少なくとも一つは,1である。
− s2の上位29ビットのうちの少なくとも一つは,1である。
− s3の上位28ビットのうちの少なくとも一つは,1である。
s1の下位1ビット,s2の下位3ビット,及びs3の下位4ビットは無視されるので,これらのビットを
変えても生成される乱数列は同じである。
このプログラムにおいて,unsigned long形の大きさは,32ビットであると仮定している。
/*************************************************
C code : Combined Tausworthe
**************************************************/
static unsigned long s1, s2, s3, b;
void init̲taus88(unsigned long s)
{
int i;
unsigned long x[3];
s &= 0xffffffffUL;
i = 0;
while (i < 3) {
if (s & 0xfffffff0UL) {
x[i] = s;
i++;
}
s = 1664525UL * s + 1UL;
s &= 0xffffffffUL;
}
s1 = x[0]; s2 = x[1]; s3 = x[2];
}
/* 31 bit integer */
long taus88̲31(void)
{
55
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b = (((s1 << 13) ^ s1) >> 19);
s1 = (((s1 & 4294967294UL) << 12) ^ b);
b = (((s2 << 2) ^ s2) >> 25);
s2 = (((s2 & 4294967288UL) << 4) ^ b);
b = (((s3 << 3) ^ s3) >> 11);
s3 = (((s3 & 4294967280UL) << 17) ^ b);
return (long)((s1 ^ s2 ^ s3) >> 1);
}
REM /****************************************************
REM BASIC code : Combined Tausworthe
REM ****************************************************/
OPTION BASE 0
REM /*********************************************************************/
FUNCTION init̲taus88(s)
!void init̲taus88(unsigned long s) {
DECLARE NUMERIC i
! int i;
DIM x(3)
! unsigned long x[3];
FOR i = 0 TO 2
! i=0; while (i<3) {
IF And32(s , MskF̲0) <> 0 THEN
!
! if (s & 0xfffffff0UL) {
LET x(i) = s
! x[i] = s; i++;
END IF
! }
LET s = Mul32U(1664525, s) + 1
!
! s = 1664525UL * s + 1UL;
NEXT i
! }
LET s1 = x(0)
LET s2 = x(1)
LET s3 = x(2)
! s1 = x[0]; s2 = x[1]; s3 = x[2];
END FUNCTION
!}
REM /*********************************************************************/
FUNCTION taus88̲31
!long taus88̲31(void) {
REM /***** 31 bit integer *****/
LET b = SR32U(Xor32(SL32U(s1, 13), s1), 19)
!
! b = (((s1 << 13) ^ s1) >> 19);
LET s1 = Xor32(SL32U(And32(s1 , MskF̲e), 12), b)
!
! s1 = (((s1 & 4294967294) << 12) ^ b);
56
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LET b = SR32U(Xor32(SL32U(s2, 2), s2), 25)
!
! b = (((s2 << 2) ^ s2) >> 25);
LET s2 = Xor32(SL32U(And32(s2 , MskF̲8), 4), b)
!
! s2 = (((s2 & 4294967288) << 4) ^ b);
LET b = SR32U(Xor32(SL32U(s3, 3), s3), 11)
!
! b = (((s3 << 3) ^ s3) >> 11);
LET s3 = Xor32(SL32U(And32(s3 , MskF̲0), 17), b)
!
! s3 = (((s3 & 4294967280) << 17) ^ b);
LET taus88̲31 = SR32U(Xor32(Xor32(s1, s2), s3), 1)
!
! return (long)((s1 ^ s2 ^ s3) >> 1);
END FUNCTION
!'}
プログラム中の
b = (((s1 << 13) ^ s1) >> 19) ;
s1 = (((s1 & 4294967294UL) << 12) ^b) ;
は,パラメータが (31, 13, 12) のトーズワース系列をs1に生成し,
b = (((s2 << 2) ^ s2) >> 25) ;
s2 = (((s2 & 4294967288UL) << 4) ^b) ;
及び
b = (((s3 << 3) ^s3) >> 11) ;
s3 = (((s3 & 4294967280UL) << 17) ^b) ;
は,それぞれパラメータが (29, 2, 4),(28, 3, 17) のトーズワース系列をs2,s3に生成する。この三つの二
進整数を,ビットごとの排他的論理和によって合成して,31ビットの疑似乱数列を生成する。
三つのパラメータ (p, q, t) の選択は,合成後の疑似乱数列の多次元均等分布性を最良にするように行わ
れている。上位vビットの精度での多次元均等分布性は,このメモリサイズでの理論上界 [88/v] 次元を達
成している。これらのパラメータは,変えてはならない。異なる疑似乱数列を得るには,シードを変更す
る。
乱数生成を中断し,後に再開して続きを生成したい場合は,中断時にs1,s2及びs3を保存し,再開時
に保存した内容をs1,s2及びs3に代入する。
B.5
メルセンヌツイスター法のプログラムコード
C言語(JIS X 3010参照)及びBASIC言語(JIS X 3003参照)によるメルセンヌツイスター法の実装例
を示す。BASICコードについては,動作の説明を省略し,対応するC言語をコメント文で併記した。また,
C言語にはあるがBASIC言語にはない関数については,B.9にコードを記載した。
このコードの関数genrand ( ) は,32ビット長の符号なし疑似整数乱数(生成される整数の範囲は0以上
232−1以下)を生成する。関数genrand̲31 ( ) は,31ビット長の疑似整数乱数(生成される整数の範囲は
0以上231−1以下)を生成する。init̲genrand (s) は,符号なし32ビット整数(0以上232−1以下の整数)
sをシードとして初期化を行う。genrand ( ) ,genrand̲31 ( ) を呼び出す前に,一度init̲genrand (s) を実行
し,初期化を行わなければならない。異なるシードsに対し異なる出力が得られる。プログラム中のパラ
メータは,変更してはならない。
57
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
これはp=624ワードを使用する例で,パラメータは (624, 397, 31, 32, 0x9908b0df, 11, 7, 15, 18,
0x9d2c5680, 0xefc60000) である。ここに,0xで始まる8桁の数は,16進表記の符号なし32ビット定数で
ある。周期は219 937−1であり,優れた多次元均等分布性をもっている。32ビット精度で623次元に均等
分布しており,また,例えば,上位6ビットは3 115次元均等分布している。
乱数生成を中断し,後に再開して続きを生成したい場合は,中断時に長さPの配列mt [P] 及び整数mti
を保存し,再開時に保存した内容をmt [P]及びmtiに代入する。
なお,このプログラムでは,unsigned long形の大きさは32ビット以上であると仮定している。
/*************************************************
C code : Mersenne Twister
**************************************************/
/* Period parameters */
#define P 624
#define Q 397
#define MATRIX̲A 0x9908b0dfUL /* constant vector a */
#define UPPER̲MASK 0x80000000UL /* most significant w-r bits */
#define LOWER̲MASK 0x7fffffffUL /* least significant r bits */
static unsigned long mt[P]; /* the array for the state vector */
static int mti = P + 1; /* mti==P+1 means mt[P] is not initialized */
/* initializes mt[P] with a seed */
void init̲genrand(unsigned long s)
{
mt[0] = s & 0xffffffffUL;
for (mti = 1; mti < P; mti++) {
mt[mti] = (1664525UL * mt[mti-1] + 1UL);
mt[mti] &= 0xffffffffUL;
}
}
/* generates a random number on [0, 0xffffffff]-interval */
unsigned long genrand(void)
{
unsigned long y;
static unsigned long mag01[2] = {0x0UL, MATRIX̲A};
/* mag01[x] = x * MATRIX̲A for x=0, 1 */
if (mti >= P) { /* generate P words at one time */
58
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
int kk;
if (mti == P + 1) /* if init̲genrand() has not been called, */
init̲genrand(5489UL); /* a default initial seed is used */
for (kk = 0; kk < P - Q; kk++) {
y = (mt[kk] & UPPER̲MASK) | (mt[kk+1] & LOWER̲MASK);
mt[kk] = mt[kk + Q] ^ (y >> 1) ^ mag01[y & 0x1UL];
}
for (; kk < P - 1; kk++) {
y = (mt[kk] & UPPER̲MASK) | (mt[kk+1] & LOWER̲MASK);
mt[kk] = mt[kk + (Q - P)] ^ (y >> 1) ^ mag01[y & 0x1UL];
}
y = (mt[P - 1] & UPPER̲MASK) | (mt[0] & LOWER̲MASK);
mt[P - 1] = mt[Q - 1] ^ (y >> 1) ^ mag01[y & 0x1UL];
mti = 0;
}
y = mt[mti++];
/* Tempering */
y ^= (y >> 11);
y ^= (y << 7) & 0x9d2c5680UL;
y ^= (y << 15) & 0xefc60000UL;
y ^= (y >> 18);
return y;
}
/* generates a random number on [0, 0x7fffffff]-interval */
long genrand̲31(void)
{
return (long)(genrand() >> 1);
}
REM /****************************************************/
REM BASIC code : Mersenne Twister
REM /****************************************************/
59
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
OPTION BASE 0
REM /*********************************************************************/
REM /* Period parameters */
DECLARE NUMERIC P
LET P = 624
!#define P 624
DECLARE NUMERIC Q
LET Q = 397
!#define Q 397
DECLARE NUMERIC MATRIX̲A
LET MATRIX̲A = BVAL("9908b0df" , 16)
!
!#define MATRIX̲A 0x9908b0dfUL
DECLARE NUMERIC UPPER̲MASK
LET UPPER̲MASK = BVAL("80000000" , 16)
!
!#define UPPER̲MASK 0x80000000UL
DECLARE NUMERIC LOWER̲MASK
LET LOWER̲MASK = BVAL("7fffffff" , 16)
!
!#define LOWER̲MASK 0x7fffffffUL
DIM mt(P)
!static unsigned long mt[P];
DECLARE NUMERIC mti
LET mti = P + 1
!static int mti=P+1;
REM /*********************************************************************/
REM /* initializes mt[P] with a seed */
FUNCTION init̲genrand(s)
!void init̲genrand(unsigned long s) {
LET mt(0) = And32(s , MskF̲f) ! mt[0]= s & 0xffffffffUL;
FOR mti = 1 TO P ‒ 1
! for (mti=1; mti<P; mti++) {
LET mt(mti) = Mul32U(1664525 , mt(mti-1)) + 1
!
! mt[mti] = (1664525UL * mt[mti-1] + 1UL);
LET mt(mti) = And32(mt(mti) , MskF̲f)
!
! mt[mti] &= 0xffffffffUL;
NEXT mti
! }
END FUNCTION
!}
REM /*********************************************************************/
REM /* generates a random number ON [0,0xffffffff]-interval */
FUNCTION genrand
!unsigned long genrand(void) {
DECLARE NUMERIC y
! unsigned long y;
DIM mag01(2)
LET mag01(0) = 0
60
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LET mag01(1) = MATRIX̲A
! static unsigned long mag01[2]=
!
! {0x0UL, MATRIX̲A};
REM /* mag01[x] = x * MATRIX̲A for x=0,1 */
IF mti >= P THEN
! if (mti >= P) {
DECLARE NUMERIC kk
! int kk;
IF mti = P + 1 THEN
! if (mti == P+1)
LET y = init̲genrand(5489)
!
! init̲genrand(5489UL);
END IF
FOR kk=0 TO P-Q-1
! for (kk=0;kk<P-Q;kk++) {
LET y = Xor32(And32(mt(kk) , UPPER̲MASK) , And32(mt(kk+1) , LOWER̲MASK))
!
! y = (mt[kk]&UPPER̲MASK)|(mt[kk+1]&LOWER̲MASK);
LET mt(kk) = Xor32(Xor32(mt(kk+Q) , SR32U(y , 1)) , mag01(And32(y , 1)))
!
! mt[kk] = mt[kk+Q] ^ (y >> 1) ^ mag01[y & 0x1UL];
NEXT kk
! }
FOR kk=kk TO P-2
! for (;kk<P-1;kk++) {
LET y = Xor32(And32(mt(kk) , UPPER̲MASK) , And32(mt(kk+1) , LOWER̲MASK))
!
! y = (mt[kk]&UPPER̲MASK)|(mt[kk+1]&LOWER̲MASK);
LET mt(kk) = Xor32(Xor32(mt(kk+Q-P) , SR32U(y , 1)) , mag01(And32(y ,
1)))
!
! mt[kk] = mt[kk+(Q-P)] ^ (y >> 1) ^ mag01[y & 0x1UL];
NEXT kk
! }
LET y = Xor32(And32(mt(P-1) , UPPER̲MASK) , And32(mt(0) , LOWER̲MASK))
!
! y = (mt[P-1]&UPPER̲MASK)|(mt[0]&LOWER̲MASK);
LET mt(P-1) = Xor32(Xor32(mt(Q-1) , SR32U(y , 1)) , mag01(And32(y , 1)))
!
! mt[P-1] = mt[Q-1] ^ (y >> 1) ^ mag01[y & 0x1UL];
LET mti = 0
! mti = 0;
END IF
! }
LET y = mt(mti)
LET mti = mti + 1
! y = mt[mti++];
REM /* Tempering */
LET y = Xor32(y , SR32U(y , 11))
!
! y ^= (y >> 11);
LET y = Xor32(y , And32(SL32U(y , 7) , BVAL("9d2c5680" , 16)))
!
! y ^= (y << 7) & 0x9d2c5680UL;

61
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LET y = Xor32(y , And32(SL32U(y ,15) ,BVAL("efc60000" , 16)))
!
! y ^= (y << 15) & 0xefc60000UL;
LET y = Xor32(y , SR32U(y , 18))
!
! y ^= (y >> 18);
LET genrand = y
! return y;
END FUNCTION
!}
REM /*********************************************************************/
REM /* generates a random number on [0,0x7fffffff]-interval */
FUNCTION genrand̲31
!long genrand̲31(void) {
LET genrand̲31 = SR32U(genrand , 1)
!
! return (long)(genrand()>>1);
END FUNCTION
!}
B.6
無理数回転法
B.6.1 一般
この方式は,この規格の前身であるJIS Z 9031:2001において規格本体に規定されていたが,この規格に
おいては,規格本体からこの附属書のこの箇条に移動して記載する。
B.6.2 定義
無理数α∈[0, 1) 及び自然数mをパラメータとし,0又は1の値をとる数列X1,X2,…を次の式(B.1)で定
義し,これを無理数回転による疑似乱数と呼ぶ。
∑
=
=
+
=
m
i
i
n
n
n
w
d
X
1
)
,2,1
(
)2
(mod
)
(
Λ
α
···································· (B.1)
w∈[0, 1) は,シードである。di (w+nα) は,実数w+nαの二進小数展開における小数点以下第i桁の数
(0又は1)を表す。
注記1 パラメータ及び初期値を明示する必要がある場合には,Xnの代わりにXn(m)(w ; α) と書くこと
にする。
注記2 多くの無理数αについて,mを大きくすれば大きくするほど,乱数列(B.1)の精度は高くなる。
注記3 任意のKに対してK個ごとの系統サンプル列 {XnK+j|n=0, 1,…},j=1,…,K,をそれぞれ
独立,かつ,容易に生成することができる。この性質は,例えば,K台のコンピュータを使
って並列計算をするときに便利である。
注記4 未来(nが増える方向)にも過去(nが減る方向)にも任意に遠くの乱数を,途中の乱数を算
出することなく高速に生成できる。それは,大きいnに対してもnα又はn (1−α) を即座に
計算できるからである。
注記5 この数列は,十分実用になる速さで生成することができる。しかし,これを基に多ビット整
数値の疑似乱数(又は標準一様乱数)を作るには,多くの計算が必要になるため時間がかか
る。
注記6 “無理数回転”という名称は,次のように考えると理解しやすい。単位円周上の回転を考え,

62
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
角度を2πを単位として表すことにする。出発時の位置(角度)をωとし,以後1回に角度α
だけ進むものとすれば,n回進んだときの位置(角度)は,ω+nαの小数部分となる。これ
を二進小数で表現したときに得られるのが,di (ω+nα) である。
B.6.3 パラメータの値の選び方
無理数αとしては,簡単な有理数(桁数の少ない整数の比)では近似しにくいものを選ぶことが望まし
い。mを大きくすれば,疑似乱数(B.1)は幾らでも精度が高くなるが,その代わり生成に時間がかかるよう
になる。精度及び生成時間の双方を考慮して,適切なmを選ぶことが望ましい。
B.6.4 パラメータの値の例
B.6.6に記載されているプログラムコードではパラメータの値として
90
,2/)1
5
(
=
−
=
m
α
としている。このαの値は,有理数近似の困難な無理数として知られている。また,初期値ω∈ [0, 1)に関
しては,特に都合の悪い値はない。
注記 実装においては,無理数を含む計算を有限桁の二進小数で近似しなければならない。B.6.6のプ
ログラムコードでは,無理数α及び初期値ωをそれぞれ,小数点以下150ビットの二進小数で近
似している。
B.6.5 実装の方法
無理数回転による疑似乱数
)
,2,1
(
)2
(mod
)
(
)
;
(
1
)
(
Λ
=
+
=∑
=
n
n
d
X
m
i
i
m
n
α
ω
α
ω
をX1(m) (ω ; α),X2(m) (ω ; α),…,と順次生成するプログラムの実装の方法について示す。ここに,αは無
理数,mは自然数で,これらはパラメータ,ω∈[0, 1) は,シードである。また,x (mod 2) は,整数xを2
で除した余り(すなわち,xが偶数のときは0,奇数のときは1)を表す。di (ω +nα) は,実数ω+nαの二
進小数展開における小数点以下第i桁の数(0又は1)を表す。
無理数は,計算機内部では,有限二進小数によって近似しなければならない。Lをある自然数とする。
無理数αを二進小数で小数点以下 (m+L) 桁まで求め,それに伴い,無理数回転のための足し算を (m+L)
ビットで行い,上位mビットのパリティを疑似乱数として返す。すなわち,具体的には,x0を (m+L) ビ
ットの負でない整数として,整数演算
),
2
(mod
1
L
m
n
n
A
x
x
+
+
+
=
∑
+
+
=
=
L
m
L
i
n
i
n
x
D
y
1
)2
(mod
)
(
によって疑似乱数
∞=1
}
{
n
ny
を得る。ただし,Di (xn) は,(m+L) ビットの負でない整数xnの下位から数えて
第iビットを表す。ここで,A=(2m+Lαの整数部分)である。これによって,ほぼ2L個の {0, 1}−値疑似
乱数を,定義式のとおり,丸め誤差なく生成することができる。
注記1 この実装において,無理数回転の疑似乱数生成法のパラメータは,3個の自然数A,m及びL
である。
注記2 この実装において,シードは,(m+L) ビットの負でない整数x0である。特に,不都合なシ
ードはない。

63
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.6.6 プログラムコード
C言語による無理数回転法の実装例を示し,疑似乱数を生成するための動作について説明する。採用し
たパラメータの値は,それぞれ
60
,
90
],
2
/)1
5
(
2[150
=
=
−
=
L
m
A
··············································· (B.2)
である。すなわち,シードx0を150ビットの負でない整数として,
),
2
(mod
150
1
A
x
x
n
n
+
=
+
∑
=
=
150
61
)2
(mod
)
(
i
n
i
n
x
D
y
······················································· (B.3)
で得られる
∞=1
}
{
n
ny
が生成される疑似乱数である。ただし,Di(xn) は,負でない150ビット整数xnの下位か
ら数えて第iビットを表す。
なお,150ビット整数Aを具体的に書くと,次のとおりである。
A = 882087584457148588530540719149992464804487305
(十進表記)
= 10
0111 1000 1101 1101 1110 0110 1110
01
0111 1111 0100 1010 0111 1100 0001
01
0111 1100 1110 0111 0011 0000 0001
10
0000 0101 1100 1110 1101 1100 1000
00
1101 0000 0100 0010 0000 1000 1001 (二進表記)
次のプログラムでは,上の150ビットの二進数を30ビットずつに分け,それらをunsigned long形配列
alpha [5] に格納している。
式(B.2)のパラメータの値を使用する場合,生成される疑似乱数は,およそ1015個を超えると,これを棄
却する検定が存在することが理論的に分かるので,そのあたりが使用限界である。L=60の場合,ほぼ260
(=およそ1.15×1018)個までの疑似乱数を定義式どおり誤差なく生成できるので,この使用限界をカバ
ーしている。使用限界を延ばすには,mをもっと大きくして疑似乱数の精度を高くする。
この例の生成する疑似乱数の周期は,2150(=およそ1.43×1045)であるが,前述のとおり,1015個を超
える使用は勧められない。
/*============================================================*/
/*
A sample program for Pseudo-random number generator
*/
/*
by means of irrational rotation with m=90 and the
*/
/*
irrational number (sqrt(5)-1)/2.
*/
/*
This program outputs a random {0,1}-sequence.
*/
/*============================================================*/
#define LIMIT 0x3fffffff
#define CARRY 0x40000000
static unsigned long omega[5];
/* Current seeds */

64
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
void m90setseeds(unsigned long s0,
unsigned long s1,
unsigned long s2,
unsigned long s3,
unsigned long s4)
/* Initialization */
{
omega[0] = s0 & LIMIT; omega[1] = s1 & LIMIT;
omega[2] = s2 & LIMIT; omega[3] = s3 & LIMIT;
omega[4] = s4 & LIMIT;
}
char m90randombit(void) /* Returns 0 or 1 at random */
{
static unsigned long alpha[5] = { /* Data of (sqrt(5)-1)/2 */
0x278dde6e, 0x17f4a7c1, 0x17ce7301, 0x205cedc8, 0x0d042089
};
char data̲byte;
union bitarray {
unsigned long of̲32bits;
char of̲8bits[4];
} data̲bitarray;
int j;
for (j=4; j>=1; ){
omega[j] += alpha[j];
if ( omega[j] & CARRY ){
omega[j] &= LIMIT; omega[--j]++;
}
else --j;
}
omega[0] += alpha[0]; omega[0] &= LIMIT;
data̲bitarray.of̲32bits = omega[0] ^ omega[1] ^ omega[2];
data̲byte = data̲bitarray.of̲8bits[0]
^ data̲bitarray.of̲8bits[1]
^ data̲bitarray.of̲8bits[2]
^ data̲bitarray.of̲8bits[3];
data̲byte ^= ( data̲byte >> 4 );
data̲byte ^= ( data̲byte >> 2 );
data̲byte ^= ( data̲byte >> 1 );
return( 1 & data̲byte );

65
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
}
long m90random31()
{
int j;
unsigned long b=0;
for (j=0; j<30; j++) { b |=m90randombit(); b <<= 1; }
b |=m90randombit();
return b;
}
void init̲m90random(unsigned long s) {
int i;
unsigned long x[5];
x[0] = s = s & 0xffffffffUL;
for( i=1; i<5; i++) {
s = 1664525UL * s + 1UL;
x[i] = s = s & 0xffffffffUL;
}
m90setseeds(x[0], x[1], x[2], x[3], x[4]);
}
疑似乱数を使用する前に,ユーザは疑似乱数のシード(unsigned long形の数を5個)を,関数 m90setseeds
を用いてランダムに指定する。
注記1 初期設定m90setseeds (s1,…,s5) では,各sjは0x3fffffff及びXOR(排他的論理和)をとる
ので,実際には,sjとして0〜0x3fffffff=230−1=1073741823の範囲の整数が有効である。
注記2 初期設定m90setseeds (s1,…,s5) 及びm90setseeds (t1,…,t5) において,j=1,…,4に対
しsj=tjでs5≠t5のとき,これら二つの初期設定から生成される疑似乱数列は,最初の230項
が一致する。これは,式(B.3)において上位90ビットだけが関与するからである。m90setseeds
の5個の引数のうち,初めの3個が,疑似乱数の最初の項から計算式(B.3)に関与する。した
がって,主にはじめの3個の引数をランダムに設定することが望ましい。
注記3 初期設定m90setseeds (s1,…,s5) 及びm90setseeds (t1,…,t5) において,j=2,…,5に対
しsj=tjでs1XORt1=0x40000000のとき,これら二つの初期設定から生成される疑似乱数列は,
互いに相手のビットを反転したものになる。これは性質
(
)1
;
)
;
(
21
)
(
)
(
=
+
+
α
ω
α
ω
m
n
m
n
X
X
による。
注記4 状態変数unsigned long omega [5] の内容を保存し,後に,それをシードとして用いれば,疑
似乱数の“続き”を生成することができる。
注記5 関数m90randombit ( ) による二値乱数生成は,十分速い。しかし,mg90random31 ( ) による

66
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
31ビット整数疑似乱数生成は,内部でm90randombit ( ) を31回呼び出すため遅くなる。
B.7
疑似乱数生成の速度
この規格で規定した種々の疑似乱数生成の速度を,この附属書に含まれるコードを用いて評価した。こ
れらは,使用する計算機のアーキテクチュアなどによって変化する。主としてスカラ計算機上で乱数生成
を行うときの性能の目安となるものと考えて欲しい。
全ての疑似乱数について,109個の32bit又は31bitの乱数を生成し,それに要した時間を計測した。ま
た,32bit又は31bitの両方を生成することができる場合には,より高速な方を選択した。使用したルーチ
ンの名称は,表B.1に示されている。他のジョブが割り込まないように注意しながら,実時間で経過時間
を計測した。CPU時間で計測した場合との違いは,1 %以内である。プログラムの起動,乱数の初期化な
どは,計測時間に含めていない。
Platform 1及びPlatform 2は,1998年において比較的上位のデスクトップコンピュータである。Platform 3
は,2008年に入手可能であったノートパソコンである。さらに,プラットフォーム3種及びそれらの環境
で動作するコンパイラを変えて,速度を計測した結果を記載した。
表B.1−乱数の生成速度
生成法
パラメータ
性能(×106個/秒)
(ルーチン名)
Platform1 1)
Platfrom2 2)
Platfrom3 3)
線形合同法
(lcong32)
M=232, a=1 664 525, c=1
7.8
46
66.3
線形合同法
(lcong31)
M=231−1,
a=2 100 005 341, c=0
4.1
9.2
18.4
3項GFSR
(gfsr)
(p, q, w)=(1279, 418, 32)
8.9
31
28.4
5項GFSR
(gfsr5)
(P, q1, q2, q3, w)
=(521, 86, 197, 447, 32)
7.4
26
20.1
結合トーズワース
(taus88̲31)
規格本体に記載のもの
7.3
9.9
31.5
メルセンヌツイスター
(genrand)
規格本体に記載のもの
6.0
17
11.2
無理数回転
(m90random31)
90
,2/)1
5
(
=
−
=
m
α
0.089
0.16
0.02
1) Platform 1
Sun Ultra 30, CPU: UltraSPARC−II 300MHz, Memory: 131M-byte, OS: Solaris 2.6, Compiler: Sun
Workshop Compiler C 4.2, Compiler flags: −x05 -xtarget=ultra
2) Platform 2
CPU: Pentium II 450MHz, Motherboard: AOpen AX6BC, Memory: 256M-byte, OS: Windows NT 4.0,
Compiler: Microsoft Visual C++ 5.0, Compiler flags: /02/GX
3) Platform 3
CPU: Centrino 2 (CoreTM2 Duo SU9300) 1.2GHz, DynabookSS RX2/T7G, Memory: 2G-byte, OS:
Windows Vista, Compiler: Microsoft Visual Studio 2010 C#, Compiler flags: default setting

67
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.1−乱数の生成速度(続き)
プラットフォーム
Windows XP SP 3
HP dc7900 Intel Core2 Duo 3.16GHz
(Platform 3)
コンパイルオプション
なし
なし
/O2 /Ot /GL /FD
/EHsc /MD /W3/c
/Wp64 /Zi /TP
コンパイラ
生成法
gfortran 4.6.0
Intel Visual Fortran
Compler XE 12.0
Microsoft Visual
C++ 2010
線形合同法(lcong32)
148.1 (57.4)
452.0 (173.3)
749.7 (308.2)
線形合同法(lcong31)
25.9 (10.1)
53.9 (21.0)
80.4 (31.4)
3項GFSR
71.1 (29.0)
746.0 (305.2)
270.5 (111.5)
5項GFSR
44.2 (17.4)
507.1 (208.4)
219.0 (88.6)
結合トーズワース
26.3 (10.4)
233.1 (92.5)
190.7 (74.1)
メルセンヌツイスター
28.2 (10.9)
357.9 (140.4)
204.9 (82.7)
無理数回転
0.40 (0.16)
1.76 (0.68)
1.63 (0.63)
プラットフォーム
LINUX : Miracle Linux 3.0
Dell PowerEdge 750 Intel Pentium4 2.8GHz
(RH4 on VMWare Intel Pentium4 3.0GHz)
コンパイルオプション
なし
なし
-O3
コンパイラ
生成法
gfortran 4.6.0
Intel Visual Fortran
Compler XE 12.0
gcc 3.2.3
線形合同法(lcong32)
59.5 (51.6)
199.9 (180.1)
87.1 (230.1)
線形合同法(lcong31)
13.0
(11.1)
32.6 (28.0)
21.5 (53.9)
3項GFSR
46.9 (39.8)
351.7 (299.0)
62.7 (334.2)
5項GFSR
29.2 (24.4)
197.0 (163.7)
56.8 (230.0)
結合トーズワース
17.2 (14.0)
124.5 (115.8)
82.5 (201.3)
メルセンヌツイスター
18.4 (15.6)
173.0 (147.4)
39.9 (176.1)
無理数回転
0.23 (0.15)
0.67 (0.56)
0.32 (0.68)
B.8
乱数出力の例
この規格で規定した乱数生成法について,附属書Bに含まれるコードを用いて出力した例を表B.2に示
す。出力は,全て0以上231−1以下の範囲に収まるようなルーチンを使用して,作成した。最初の5個及
び1 000個目から1 000個おきに5個生成させたものを記載した。これらは,動作確認のための参考として
用意したものである。
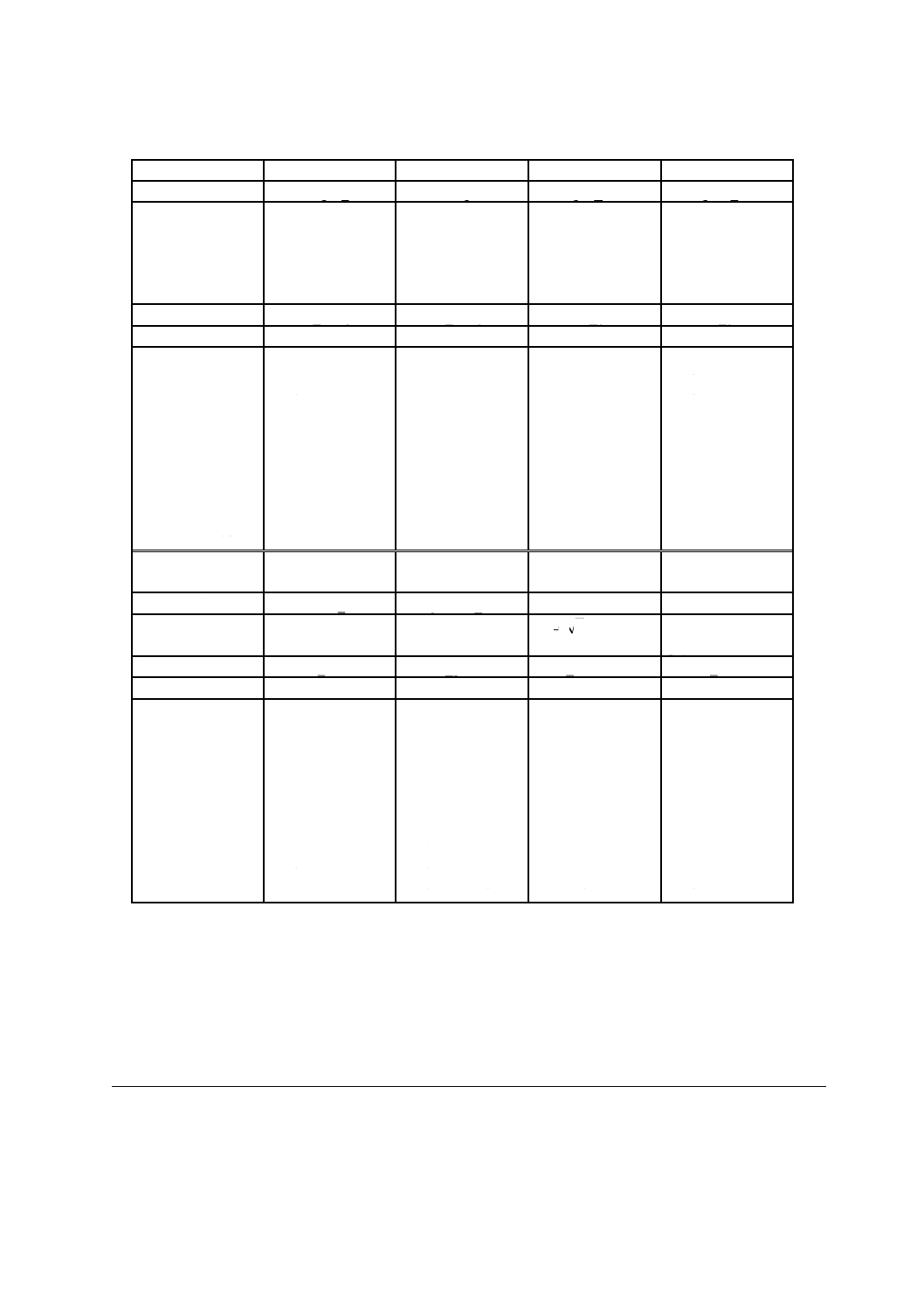
68
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.2−乱数の出力例
生成法
線形合同法
線形合同法
3項GFSR
5項GFSR
ルーチン名
lcong32̲31
lcong31
gfsr̲31
gfsr5̲31
パラメータ
m=232,
M=231−1,
P=1279,
p=521,
a=1 664 525,
a=2 100 005 341,
q=418,
q1=86,
c=1
c=0
w=32
q2=197,
q3=447,
w=32
初期化ルーチン
init̲lcong32
init̲lcong31
init̲gfsr
init̲gfsr5
初期化シード
19 660 809
19 660 809
19 660 809
19 660 809
1
1 276 136 251
1 990 801 112
716 530 710
716 530 710
2
865 096 703
549 424 302
1 004 066 893
1 004 066 893
3
1 405 063 418
2 128 986 934
1 271 815 862
1 271 815 862
4
1 021 835 442
637 203 998
955 533 625
955 533 625
5
1 313 685 521
965 379 446
626 736 785
626 736 785
1000
1 292 340 048
294 652 208
1 588 358 191
1 935 299 389
2000
517 257 756
407 927 492
2 027 766 761
43 898 710
3000
1 420 573 800
216 557 927
1 495 802 935
1 516 572 896
4000
1 195 033 140
919 639 774
1 360 928 075
1 923 029 091
5000
971 701 120
639 093 944
1 950 421 053
2 129 964 021
生成法
統合トーズワース
メルセンヌ
ツイスター
無理数回転
乱数表
ルーチン名
taus88̲31
genrand̲31
m90random31
rndtable
パラメータ
規格本体と同じ
規格本体と同じ
,2
/)1
5
(
−
=
α
ファイル
m=90
phys.bin
初期化ルーチン
init̲taus88
init̲genrand
init̲m90random
init̲rndtable
初期化シード
19 660 809
19 660 809
s0=19 660 809
0
1
116 464 117
652 430 828
1 866 529 801
57 316 494
2
1 350 114 716
769 118 065
734 355 996
905 630 297
3
14 524 262
902 643 984
471 100 209
1 460 801 524
4
565 035 872
1 576 219 271
1 010 760 785
751 624 663
5
1 079 577 460
859 869 705
361 434 904
1 289 292 436
1000
1 404 867 807
1 194 038 620
723 175 118
2 001 042 935
2000
2 022 781 177
563 296 554
1 425 146 035
1 638 049 143
3000
2 098 228 799
1 515 829 663
633 594 956
41 578 219
4000
1 089 352 213
1 803 857 212
352 723 337
87 938 653
5000
262 361 229
1 203 434 155
571 550 544
1 851 047 367
B.9
BASIC言語で記述したC言語に対応する関数
次に示すBASICプログラムコードは,C言語には定義されているが,BASIC言語には定義されていな
い関数を,BASIC言語で記述したものである。附属書Bに記載した疑似乱数生成のためのBASICプログ
ラムコードは,次に示す関数を使用するため,疑似乱数生成プログラムと一緒に読み込んで動作させる必
要がある。
REM /*********************************************
REM BASIC code : FUNCTIONS
REM *********************************************/
69
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
OPTION BASE 0
REM /*******************************************/
DECLARE NUMERIC MskF̲f
DECLARE NUMERIC MskF̲e
DECLARE NUMERIC MskF̲8
DECLARE NUMERIC MskF̲0
LET MskF̲f = BVAL("ffffffff" , 16)
LET MskF̲e = BVAL("fffffffe" , 16)
LET MskF̲8 = BVAL("fffffff8" , 16)
LET MskF̲0 = BVAL("fffffff0" , 16)
REM /*******************************************/
FUNCTION Or32(xA,xB)
DECLARE NUMERIC Ori, OrC
LET OrC = 0
FOR Ori=0 TO 31
LET xA = xA / 2
LET xB = xB / 2
IF (INT(xA) <> xA) OR (INT(xB) <> xB) THEN
LET OrC = OrC + 2 ^ Ori
END IF
LET xA = INT(xA)
LET xB = INT(xB)
IF (xA = 0) AND (xB = 0) THEN EXIT FOR
NEXT Ori
LET Or32 = OrC
END FUNCTION
REM /*******************************************/
FUNCTION And32(xA,xB)
DECLARE NUMERIC Andi, AC
LET AC = 0
IF xA > MskF̲f THEN
LET xA = xA - INT(xA / 4294967296) * 4294967296
END IF
70
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IF xB > MskF̲f THEN
LET xB = xB - INT(xB / 4294967296) * 4294967296
END IF
IF (xA = 0) OR (xB = 0) THEN
LET And32 = 0
ELSEIF xB = MskF̲f THEN !&Hffffffff
LET And32 = xA
ELSEIF xA = MskF̲f THEN !&Hffffffff
LET And32 = xB
ELSEIF xB = MskF̲8 THEN !&Hfffffff8
LET And32 = INT(xA / 8) * 8
ELSEIF xA = MskF̲8 THEN !&Hfffffff8
LET And32 = INT(xB / 8) * 8
ELSEIF xB = MskF̲0 THEN !&Hfffffff0
LET And32 = INT(xA / 16) * 16
ELSEIF xA = MskF̲0 THEN !&Hfffffff0
LET And32 = INT(xB / 16) * 16
ELSE
FOR Andi=0 TO 31
LET xA = xA / 2
LET xB = xB / 2
IF (INT(xA) <> xA) AND (INT(xB) <> xB) THEN
LET AC = AC + 2 ^ Andi
END IF
LET xA = INT(xA)
LET xB = INT(xB)
IF (xA = 0) OR (xB = 0) THEN EXIT FOR
NEXT Andi
LET And32 = AC
END IF
END FUNCTION
REM /*******************************************/
FUNCTION Xor32(xA,xB)
DECLARE NUMERIC Xori, XC
LET XC = 0
FOR Xori=0 TO 31
71
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LET xA = xA / 2
LET xB = xB / 2
IF ((INT(xA) = xA) AND (INT(xB) <> xB)) OR (INT(xA) <> xA) AND (INT(xB) =
xB) THEN
LET XC = XC + 2 ^ Xori
END IF
LET xA = INT(xA)
LET xB = INT(xB)
IF (xA = 0) OR (xB = 0) THEN EXIT FOR
NEXT Xori
LET Xori = Xori + 1
IF (xA =0) AND (xB = 0) THEN
elseIF xA = 0 THEN
FOR Xori=Xori TO 31
LET xB = xB / 2
IF INT(xB) <> xB THEN
LET XC = XC + 2 ^ Xori
END IF
LET xB = INT(xB)
IF xB = 0 THEN EXIT FOR
NEXT Xori
ELSE
FOR Xori=Xori TO 31
LET xA = xA / 2
IF INT(xA) <> xA THEN
LET XC = XC + 2 ^ Xori
END IF
LET xA = INT(xA)
IF xA = 0 THEN EXIT FOR
NEXT Xori
END IF
LET Xor32 = XC
END FUNCTION
REM /*******************************************/
FUNCTION SL32U(xA,xL)
REM 2006-05-31
DECLARE NUMERIC slAH,slAL
72
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IF (xA = 0) OR (xL = 0) THEN
LET SL32U = xA
ELSEIF xL >= 16 THEN
LET slAL = xA - INT(xA / 65536) * 65536
LET slAL = slAL * 2 ^ (xL - 16)
LET slAL = slAL - INT(slAL / 65536) * 65536
LET SL32U = slAL * 65536
ELSE
LET slAL = xA - INT(xA / 65536) * 65536
LET slAH = INT(xA / 65536)
LET slAL = slAL * 2 ^ xL
LET slAH = slAH * 2 ^ xL
LET slAH = slAH - INT(slAH / 65536) * 65536
LET SL32U = slAL + slAH * 65536
END IF
End Function
REM /*******************************************/
FUNCTION SR32U(xA,xL)
REM 2006-06-03
IF xL = 0 THEN
LET SR32U = xA
ELSEIF xA = 0 THEN
LET SR32U = 0
ELSE
LET SR32U = INT(xA / 2 ^ xL)
END IF
End Function
REM /*******************************************/
FUNCTION Mul32U(xA,xB)
REM /***** A,B : unsigned long (32-bit) *****/
REM 2006-06-02
DECLARE NUMERIC MAH, MAL, MBH, MBL
LET MAH = INT(xA / 65536)
LET MBH = INT(xB / 65536)
73
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
IF (xA = 0) OR (xB = 0) THEN
LET Mul32U = 0
ELSEIF (MAH = 0) AND (MBH = 0) THEN
LET Mul32U = xA * xB
ELSE
LET MAL = xA - INT(xA / 65536) * 65536
LET MBL = xB - INT(xB / 65536) * 65536
LET MBH = MAH * MBL + MAL * MBH + INT((MAL * MBL) / 65536)
LET MBH = MBH - INT(MBH / 65536) * 65536
LET MAL = MAL * MBL
LET MBL = MAL - INT(MAL / 65536) * 65536
LET Mul32U = MBL + 65536 * MBH
END IF
END FUNCTION
74
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
乱数の特性及び検定方法
JA.1
乱数の多次元均等分布性
JA.1.1
多次元均等分布及びスペクトル検定
この規格で扱っている疑似一様乱数は,いずれも真の一様乱数[区間 [0, 1) 上の連続な一様分布に従う
乱数]を模擬するものではあるが,離散的な値しかとらないことに注意する必要がある。そこで,離散的
な値をとる真の一様乱数U1,U2,…がもっている一つの性質を考えてみよう。U1,U2,…は互いに独立で,
区間 [0, 1) 上のl桁の二進小数値のいずれかを,等確率でとるものとする。このとき,これらの2l個の二
進小数値の中から,重複を許して任意に選んだk個の数値u1,u2,…,ukと,任意のnに対して
{
}
kl
k
k
n
n
n
u
U
u
U
u
U
2
1
Pr
1
2
1
1
=
=
=
=
−
+
+
,
,
,
Λ
····································· (JA.1)
が成り立つ。
したがって,疑似一様乱数もこれに近い性質をもつことが望ましいが,周期性があるので,確率Prの意
味を“1周期についての相対頻度”と解釈し直すのが適切である。確率Prをこのように解釈するものとし
たとき,疑似乱数列U1,U2,…について式(JA.1)が成り立つならば,この疑似乱数列はk次元均等分布を
するという。
例えば,線形合同法によって生成される疑似乱数列U1,U2,…の1周期分の中には,同じ数値は存在し
ない。したがって,この疑似乱数列は二次元以上の均等分布をしない。実際,この数列を使ってk次元単
位立方体の中に点列 (U1,U2,…,Uk),(U2, U3,…,Uk+1),…を作っていくと,これらは規則的な格子構
造を形成し,全ての点が比較的少ない枚数の等間隔に並んだ(超)平面で覆いつくせることが知られてい
る。この構造のことを,多次元疎結晶構造という。
このような超平面群の間隔の逆数νkを計算によって求め,疑似乱数生成で使うパラメータの良さを判定
することを,スペクトル検定という。νkのことを線形合同法乱数列のk次元精度という。νkのおおよその
意味付けは,次のとおりである。
k
k
ν
μ
2
log
=
とおくと,上記のようにして作ったk次元点列の分布を座標成分の上位μkビットまでの分解能で見るかぎ
り,それらはほぼ一様分布をしているものとみなすことができる。
JA.2
附属書Aのプログラムコードのk次元均等分布性
疑似乱数の上位νビットだけを取り出して得られるνビット二進数列の均等分布の最大次元を,k(v)と
表す。
JA.2.1
3項GFSRのk(v)
3項GFSR法のプログラムコードgfsr ( ) によって生成される整数列の均等分布次元k (v)
(v=1,2,…,32)は,
)
32
,
,2,1
(
39
]
32
/
1279
[
)
(
Λ
=
=
v
v
k
≧
である。
JA.2.2
5項GFSRのk(v)

75
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5項GFSR法のプログラムコードgfsr5 ( ) によって生成される整数列の均等分布次元k (v)
(v=1,2,…,32)は,
)
32
,
,2,1
(
16
]
32
/
521
[
)
(
Λ
=
=
v
v
k
≧
である。
JA.2.3
統合トーズワース法のk(v)
結合トーズワース法のプログラムコードtaus88̲31 ( ) によって生成される整数列の均等分布次元k (v) (v
=1, 2,…,31) は,表JA.1のとおりである。
表JA.1−結合トーズワース乱数列の均等分布の次元
k(1)
k(2)
k(3)
k(4)
k(5)
k(6)
K(7)
k(8)
k(9)
k(10)
k(11)
k(12)
k(13)
k(14)
k(15)
k(16)
k(17)
k(18)
k(19)
k(20)
k(21)
k(22)
k(23)
k(24)
k(25)
k(26)
k(27)
k(28)
k(29)
k(30)
k(31)
88
44
29
22
17
14
12
11
9
8
8
7
6
6
5
5
5
4
4
4
4
4
3
3
3
3
3
3
3
2
2
JA.2.4
メルセンヌツイスター法のk(v)
メルセンヌツイスター法のプログラムコードgenrand ( ) によって生成される整数列の均等分布次元k (v)
(v=1, 2,…,32) は,表JA.2のとおりである。
表JA.2−メルセンヌツイスター乱数列の均等分布の次元
k(1)
k(2)
k(3)
k(4)
k(5)
k(6)
K(7)
k(8)
k(9)
k(10)
k(11)
k(12)
k(13)
k(14)
k(15)
k(16)
k(17)
k(18)
k(19)
k(20)
k (21)
k(22)
k(23)
k(24)
k(25)
k(26)
k(27)
k(28)
k(29)
k(30)
k(31)
k(32)
19937
9968
6240
4984
3738
3115
2493
2492
1869
1869
1248
1246
1246
1246
1246
1246
623
623
623
623
623
623
623
623
623
623
623
623
623
623
623
623
JA.3
乱数の統計的検定
JA.3.1
統計的検定及びその限界
乱数の統計的検定は,乱数の性質を調べるために疑似乱数又は物理乱数から乱数列を実際に生成させ,
この乱数列に対して性質を調べる方法である。実際には,統計的検定は,乱数の部分列の性質のごく一部
分を取り出して見せるにすぎない。乱数の統計的検定には限界があり,理論的に性質を示すことがより重
要である。しかし逆に,疑似乱数の部分列に関しての性質を理論的に知ることは難しいため,ある用途に
実際に使用した乱数列の性質を調べる場合などには,統計的検定が役に立つときもある。
乱数の問題の難しさは,完全な乱数が生成できない点にあるのではなく,ある用途にとって必要な乱数
の性質が分からないことにある。ある用途に必要な検定は,その用途自体であるとしかいいようがないの
である。用途から,必要になる検定の性質が,ある程度推測できる場合もある。例えば,単純サンプリン
グでモンテカルロ数値積分を行う場合には,積分を行う次元での一様性だけから結果の正しさについては,
保証される。しかし,ほとんどの場合には,一部の統計的検定に合格したことをもって,ある用途に十分
76
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
な乱数であるとはいえない。したがって,シミュレーションなどの場合には,複数の乱数を用いて計算を
行うことが望ましい。統計的検定は,乱数生成法が満たすべき最低の条件にすぎないのであるが,驚くべ
きことに,よく利用されている疑似乱数生成法の中には,単純な検定に対し不合格になるものもあるので
ある。
物理乱数の場合でも,事情は同様である。統計的検定によって分かることはごく一部分であるので,で
きる限り生成原理から乱数としての性質を保証するのが望ましい。統計的検定は,最低限の性質を保証す
る程度の意味しかもたない。特に物理乱数の場合には,再現性がないため,例えば,0が続けて100回出
力された場合に,これが故障によるものなのか,それとも偶然なのかは,乱数生成器の内部を検査しない
限り分からない。このようなことから,特にシミュレーションの場合には,物理乱数を使用するときでも,
比較のために疑似乱数を用いた計算も行ったほうがよい。疑似乱数の発展のためにも,こうした計算は望
ましい。もし,乱数によって結果が異なるようなことがあれば,疑似乱数の性質を知る上で重要な情報を
得ることができる。
この附属書では,数多くの統計的検定法のうちのごく一部を紹介するにとどめる。より詳しくは参考文
献[3],[7]などを参照。
注記 “検定のパラドックス”例えば,ある長さの部分列に対して,事象Aが0<P<1になる確率P
で起こるものとする。この場合,事象Aが観測されたときに,これをある危険率で不合格にす
るような検定を考えることができる。しかし,事象Aが有限の確率で起こる以上,部分列の集
合に事象Aが起こるような部分列が含まれる確率は,集合の大きさに応じて幾らでも大きくな
る。したがって,この検定に合格するような部分列の集合は,別の検定“事象Aが起こるよう
な部分列がある確率で含まれる”に不合格になる。つまり,部分列が統計的検定に合格しない
からといって取り除いてしまえば,逆にバイアスを与えることになる。したがって,特に必要
な部分列の性質が分かっている場合を除けば,検定はあくまで生成法全体の良し悪しを調べる
ためのもので,部分列を検定によって排除することは望ましくない。
JA.3.2
基本的な検定
まず,検定のための基本的な道具となるχ2検定及びコルモゴロフ・スミルノフ(Kolmogorov-Smirnov)
検定について簡単に定義しておく。
JA.3.2.1
χ2適合度検定
ある確率変数のとり得る値をk通りの値に分類し,n回の試行の後,それぞれの出現頻度がni (i=1,…,
k) であったとする。χ2適合度検定は,この出現頻度niが,与えられた確率分布pi (i=1,…,k) からの独
立なサンプルで記述できるかどうかを検定する方法である。具体的には,χ2統計量
∑
=
−
=
k
i
i
i
i
np
np
n
1
2
2
)
(
χ
を計算する。仮説が正しい場合,χ2統計量はn→∞のとき,自由度k−1のχ2分布に従う。
注記 この性質を,χ2統計量は漸近的に自由度k−1のχ2分布に従うと呼ぶ。
よって確率
α
χ
χ
α=
}
Pr{
2
2≦
となる
2α
χ(100α %点)を求め,
2
2
α
χ
χ≦
のとき仮説とした確率分布pi (i=1,
…,k) を採択する。
さらに,上記をN回繰り返し,得られたχ2の値を次に示すコルモゴロフ・スミルノフ検定で検定するこ
ともできる。
JA.3.2.2
コルモゴロフ・スミルノフ(Kolmogorov-Smirnov)検定
χ2検定では,有限個に分類されるような確率変数の分布しか扱えない。コルモゴロフ・スミルノフ検定
77
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は,連続的な確率変数の出現頻度が,ある分布と一致しているとみなせるかどうかを検定する手段である。
長さnの乱数列 (x1,…,xn) から,経験分布関数Fn (x)
n
x
x
x
x
F
i
i
n
の個数
となる
≦
=
)
(
が得られる。仮説として想定する分布関数を,Fn (x) とする。このとき,
))
(
)
(
(
max
x
F
x
F
n
K
n
x
n
−
=
+∞
<
<
∞
−
+
))
(
)
(
(
max
x
F
x
F
n
K
n
x
n
−
=
+∞
<
<
∞
−
−
を計算する。
−
,n
nK
K+
の分布関数は,z>0で
{
}
(
)
2
,
2
exp
1
Pr
lim
z
z
Kn
n
−
−
=
−
+
∞
→
≦
であるので,これからパーセント点を求めて検定を行うことができる。nが小さい場合の分布関数につい
ては,参考文献[3],[7]などを参照。
さらに,上記をN回繰り返し,得られたK+,K−の値の分布に対し,更に検定を適用することもできる。
JA.3.3
いろいろな統計的検定法
次に,特に示さない限り乱数は,[0, 1) 上の一様乱数であるとする。
JA.3.3.1
一次元での一様性
一次元での一様性を検定するには,χ2適合度検定及びコルモゴロフ・スミルノフ検定を直接適用する。
− χ2適合度検定
乱数の生成区間をk個の等間隔の区間に分類し,n個の乱数の一次元度数分布n1, n2,…,nkを得る。
このとき,乱数列が一様でランダムであれば,χ2統計量
∑
=
−
=
k
i
i
k
n
k
n
n
1
2
2
/
)
/
(
χ
は,漸近的に自由度k−1のχ2分布に従う。
− コルモゴロフ・スミルノフ検定
[0, 1) 上の一様分布の場合の理論的な分布関数は,
<
<
=
x
x
x
x
x
F
1
,1
1
0
,
0
,0
)
(
≦
≦
となる。これを用いて,長さnの乱数列から得られた経験的な分布関数Fn (x) に対してコルモゴロフ・
スミルノフ検定を適用する。
JA.3.3.2
d次元での一様性
基本的な考え方は,一次元でのχ2適合度検定の場合と同様である。d次元の超立方体を,各次元で幅1/k
ごとに刻み,kd個の等体積の小立方体に分割する。そこでd個の乱数 (x1,…,xd) をn回生成させ,この
点が,各立方体に属する度数分布ni (i=1,…,kd) を得る。このとき,乱数列が一様でランダムであれば,
χ2統計量
∑
=
−
−
−
=
d
k
i
d
d
i
nk
nk
n
1
2
2
)
(
χ
は,漸近的に自由度kd−1のχ2分布に従う。
78
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JA.3.3.3
連の検定
乱数列において,数値が単調に増加する部分列を“上昇”連,単調に減少する部分を“下降”連と呼ぶ。
連の検定は,いろいろな長さの“上昇”連及び“下降”連の度数分布から乱数の性質を調べる方法である。
具体的には,長さnの乱数列から長さ1,…,5の連の度数分布n1,…,n5と,長さ6以上の連の度数分
布n6とを求め,これから統計量V,
∑
−
−
=
6
,
1
)
)(
(
1
≦
≦j
i
ij
j
j
i
i
a
nb
n
nb
n
n
V
を計算する。ここで,
=
2.
860
172
6.
475
139
1.
580
111
57
.
684
83
83
.
788
55
16
.
892
27
6.
475
139
8.
261
113
08
.
470
90
04
.
852
67
82
.
233
45
71
.
614
22
1.
580
111
08
.
470
90
61
.
413
72
27
.
281
54
65
.
186
36
27
.
091
18
57
.
684
83
04
.
852
67
27
.
281
54
33
.
721
40
46
.
139
27
95
.
567
13
83
.
788
55
82
.
233
45
65
.
186
36
46
.
139
27
03
.
097
18
902
.
044
9
16
.
892
27
71
.
614
22
27
.
091
18
95
.
567
13
902
.
044
9
354
.
529
4
)
(ij
a
)
840
/1
,
040
5/
29
,
720
/
19
,
120
/
11
,
24
/5
,6/1(
)
(
=
ib
である。ただし,この値は,乱数列の長さnが十分に長いとき(n>104程度)に近似的に成り立つ式であ
る。一般のnに対するaij, biの正確な値については,参考文献[3],[7]などを参照。
乱数列が一様でランダムであれば,統計量Vは漸近的に自由度6のχ2分布に従う。
JA.3.3.4 衝突検定
χ2適合度検定で高次元の分布の一様性を調べるには,分類の数が多くなるために,非常に多くのサンプ
ルを必要とする。衝突検定は,比較的少ないサンプル数で,高次元の分布の性質を調べることができる方
法である。まず,高次元度数分布の場合と同様に,d次元の超立方体を各次元で幅1/kごとに刻み,m=kd
個の等体積の小立方体に分割する。そこでd個の乱数 (x1,…,xd) をn回生成させ,この点を各立方体に
振り分ける。既に点が属している立方体に更に点が振り分けられた場合に“衝突”が起こったとし,“衝突”
の頻度Nを数える。乱数列が一様でランダムであれば,Nの確率分布は,次の式で与えられる。
{
}
(
)(
)
−
+
+
−
−
=
=
c
n
n
m
c
n
m
m
m
c
N
n
1
1
Pr
Λ
注記 記号{}は,第2種スターリング数を表す。この式から累積確率を計算し,検定を行う。
JA.3.3.5
ランダムウォークを利用した検定
乱数を同時に多く生成させ,その集団としての統計的性質を調べるためには,もちろん今まで述べてき
た方法をそのまま適用することができる。しかし,乱数の数が多くなると,検定を行うのが次第に大変に
なってくる。
大規模な乱数集団の性質の中でも,ランダムウォークを利用した検定は,重要である。この検定で確認
されるような性質は,ファイナンスなどに現れる確率微分方程式,パーコレーションのシミュレーション
などで特に必要になる。ランダムウォークで大規模な乱数集団の性質が現れるのは,ランダムウォークで
はあるステップでの移動の影響が減衰せず,無限に長く残るためである。tステップのランダムウォーク
には,全てのステップでの移動が平等に寄与する。したがって,t回分全ての乱数が平等に関係すること
になり,大規模な乱数集団での統計的な性質を反映することになる。
a) ランダムウォーク検定 d次元のランダムウォーク検定では,
d
2
log
ビットの乱数を生成させ,原点
から始まるd次元立方格子上でのランダムウォークをnステップ行う。これをN回繰り返し,ランダ
79
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ムウォークの終点が2d個のどの象限にあるかの頻度Ni (i=1,…,2d) を計算する。各象限にある確率
は等確率になるはずであるから,χ2統計量
∑
=
−
−
−
=
d
i
d
d
i
N
N
N
2
1
2
2
2
)
2
(
χ
は,自由度2d−1のχ2分布に従うはずである。これをχ2検定で検定する。終点が各象限にある頻度以
外にも,様々な統計量を考えることができる。また,乱数からランダムウォークの動きに変換する方
法によっても結果が変わってくるので,注意する必要がある。
3項GFSR乱数では,nが漸化式の次数を超えた時点で急激にχ2が増大し,検定に不合格になるこ
とが知られている。
b) nブロック検定 nブロック検定は,歩幅を一様乱数で設定する一次元のランダムウォーク検定であ
る。[0, 1) の一様乱数xiをn個生成させ,その平均値xを計算する。これをN回繰り返し,平均値が
1/2以上になる頻度N+を数える。N+の期待値はN/2であるから,χ2統計量
2/
)2/
(
2
2
2
N
N
N−
=
+
χ
は,自由度1のχ2分布に従うはずである。これをχ2検定で検定する。ランダムウォーク検定の場合と
同様に,3項GFSR乱数では,nが漸化式の次数を超えた時点で急激にχ2が増大し,検定に不合格に
なる。
JA.4
乱数の検定結果
疑似乱数又は物理乱数の統計的検定を行った例を示す。疑似乱数の生成には,附属書Aに含まれる乱数
生成コードを利用した。あるシードから始まる疑似乱数系列を12個に区分し,各系列に対して検定を行っ
た。具体的なパラメータ,初期値は表JA.3に示す。物理乱数については,参考文献[23]に保存されたバイ
ナリ形式の乱数表12個を,附属書Bに含まれるコードrndtableを用いて読み取った。初期値の値は,
init̲rndtable (0UL)(ファイルの先頭から読み出す。)で設定した。各検定で“系列”の欄は,乱数ファイル
の番号を表す。表A.1の乱数表の検定については,別個に行ったものをJA.4.8の最後に示してある。

80
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表JA.3−検定を行った乱数
生成法
(ルーチン名)
パラメータ
初期化ルーチン
初期化シード
線形合同法
(lcong32̲31)
m=232,
a=1664525, c=1
init̲lcong32
19 660 809
線形合同法
(lcong31)
m=231−1,
a=2100005341, c=0
init̲lcong31
19 660 809
3項GFSR
(gfsr̲31)
(p, g, w)
=(1279, 418, 32)
init̲gfsr
19 660 809
5項GFSR
(gfsr5̲31)
(p, g1, g2, g3, w)
=(521, 86, 197, 447, 32)
init̲gfsr5
19 660 809
結合トーズワース
(taus88̲int)
附属書Bに記載のもの
init̲taus88
19 660 809
メルセンヌツイスター
(genrand̲31)
附属書Bに記載のもの
init̲genrand
19 660 809
無理数回転
,2/)1
5
(
−
=
α
Init m90random
s0=19 660 809,
(m90random31)
m=90
s1=2 552 272 502,
s2=1 730 193 407,
s3=2 810 126 836,
s4=2 043 670 885
乱数表
(mdtable̲31)
ファイルprnd01〜12. bin
init rndtable
0
JA.4.1
一次元での一様性(コルモゴロフ・スミルノフ検定)
一次元での一様性検定を,コルモゴロフ・スミルノフ検定によって行った。N個の乱数に対するコルモ
ゴロフ・スミルノフ検定を,M回繰り返して得られたM個のコルモゴロフ・スミルノフ統計量
−
+
N
NK
K,
そ
れぞれについて,更にコルモゴロフ・スミルノフ検定を行った。したがって,4種類のコルモゴロフ・ス
ミルノフ統計量K++(
+
N
Kに対するコルモゴロフ・スミルノフ統計量
+
M
K,以下同様),K+−, K−+, K−−が
得られる。疑似乱数については,(N, M)=(104, 104),物理乱数による乱数表に関して,(N, M)=(104, 103) で
検定を行った。結果がどのパーセント値の間にあるかに応じて,次の記号を用いて表JA.4に示す。
99〜
100 %
×
95〜
99 %
△
90〜
95 %
○
0〜
90 %
◎
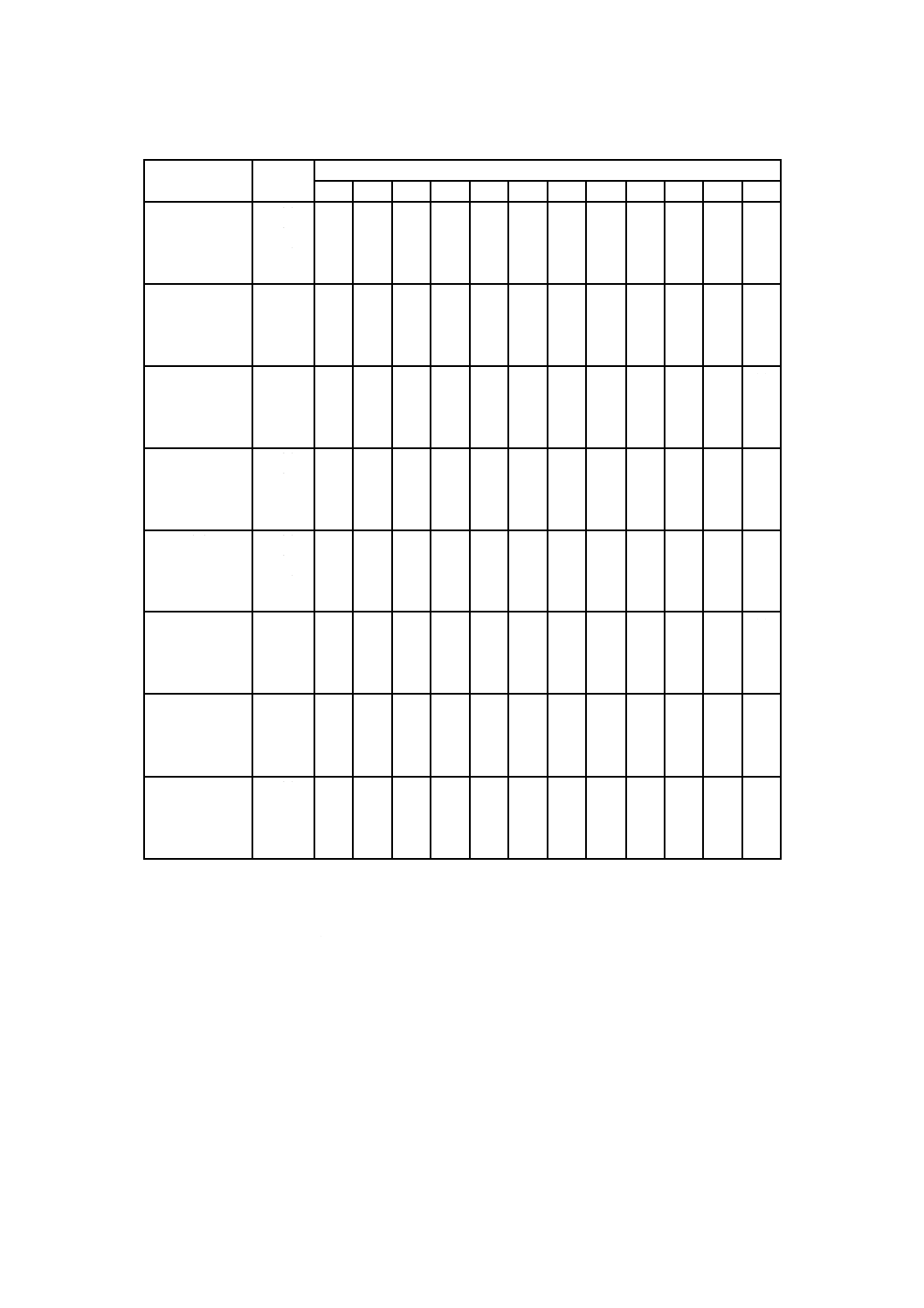
81
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表JA.4−コルモゴロフ・スミルノフ検定の結果
生成法
系列
1
2
3
4
5
6
7
8
9
10
11
12
合同乗算法
K++
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
(m=232)
K+−
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
K−+
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
△
K−−
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
◎
◎
合同乗算法
K++
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
(m=231−1)
K+−
◎
◎
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
K−+
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
K−−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
3項GFSR
K++
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
×
K+−
◎
◎
○
◎
◎
◎
◎
◎
◎
◎
◎
◎
K−+
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K−−
◎
△
○
△
◎
◎
◎
◎
◎
◎
◎
△
5項GFSR
K++
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K+−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K−+
◎
◎
◎
◎
◎
○
◎
◎
◎
○
◎
◎
K−−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
結合
K++
○
○
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
トーズワース
K+−
◎
◎
◎
○
◎
◎
◎
◎
◎
◎
◎
◎
K−+
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
◎
○
K−−
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
メルセンヌ
K++
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
×
ツイスター
K+−
◎
◎
◎
○
◎
○
◎
◎
◎
◎
◎
◎
K−+
◎
◎
○
◎
◎
◎
◎
◎
△
◎
◎
◎
K−−
△
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
○
無理数回転
K++
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K+−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K−+
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
△
K−−
◎
◎
◎
◎
◎
◎
△
○
◎
◎
◎
◎
物理乱数
K++
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K+−
◎
◎
△
◎
◎
◎
○
◎
◎
◎
◎
◎
K−+
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
◎
◎
K−−
◎
○
◎
○
◎
◎
◎
○
◎
◎
◎
◎
JA.4.2
二次元での一様性
二次元での一様性検定を,χ2適合度検定によって行った。正方形 [0, 1)×[0, 1) の各辺を10個に区切り,
100個の正方形に分割する。[0, 1) に規格化した乱数二つを組にして生成した座標点が,分割した各正方形
に属する頻度を乱数2N個に対して求め,χ2を計算した。これをM回繰り返して得られたM個のχ2値に対
し,更にコルモゴロフ・スミルノフ検定を行った結果を表JA.5に示す。疑似乱数については(N, M)=
(104, 104),物理乱数による乱数表に関しては,(N, M)=(104, 5×102) で検定を行った。結果の見方は,一次
元での一様性検定の場合と同じである。
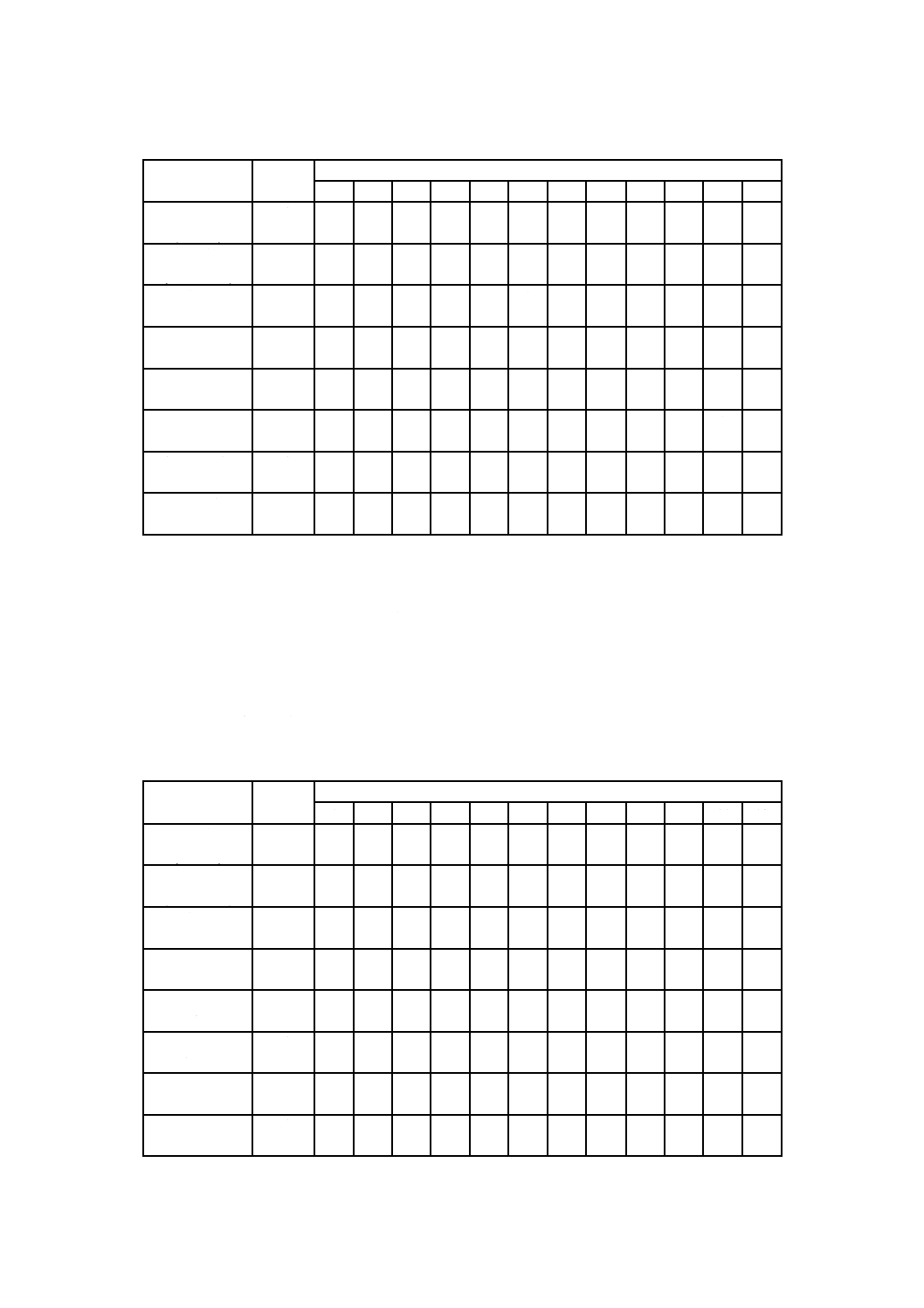
82
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表JA.5−二次元一様性の検定の結果
生成法
系列
1
2
3
4
5
6
7
8
9
10
11
12
合同乗算法
K+
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
(m=232)
K−
◎
○
◎
◎
○
◎
○
◎
◎
◎
◎
◎
合同乗算法
K+
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
(m=231−1)
K−
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
3項GFSR
K+
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
○
◎
K−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
5項GFSR
K+
◎
○
◎
△
◎
◎
△
◎
◎
◎
◎
◎
K−
◎
◎
◎
◎
◎
◎
◎
○
△
◎
◎
◎
結合
K+
◎
◎
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
トーズワース
K−
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
メルセンヌ
K+
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
△
◎
ツイスター
K−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
無理数回転
K+
◎
◎
△
◎
◎
◎
△
◎
◎
◎
◎
◎
K−
◎
◎
◎
◎
◎
○
◎
◎
◎
◎
◎
◎
物理乱数
K+
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K−
△
◎
◎
◎
○
◎
◎
◎
◎
◎
◎
◎
JA.4.3
三次元での一様性
三次元での一様性検定を,χ2適合度検定によって行った。二次元の場合と同様に,立方体の各辺を5個
に区切り,125個の立方体に分割する。[0, 1) に規格化した乱数三つを組にして生成した座標点が,分割し
た各立方体に属する頻度を乱数3N個に対して求め,χ2を計算した。これをM回繰り返して得られたM個
のχ2値に対し,更にコルモゴロフ・スミルノフ検定を行った結果を表JA.6に示す。疑似乱数については (N,
M)=(104, 104),物理乱数による乱数表に関しては,(N, M)=(104, 3×102) で検定を行った。結果の見方は,
一次元での一様性検定の場合と同じである。
表JA.6−三次元一様性の検定の結果
生成法
系列
1
2
3
4
5
6
7
8
9
10
11
12
合同乗算法
K+
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
△
△
(m=232)
K−
◎
◎
△
◎
◎
○
◎
◎
◎
◎
◎
◎
合同乗算法
K+
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
(m=231−1)
K−
○
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
3項GFSR
K+
◎
○
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
K−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
5項GFSR
K+
◎
◎
◎
◎
△
◎
◎
△
◎
△
◎
◎
K−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
結合
K+
◎
◎
◎
◎
○
◎
◎
◎
◎
◎
○
◎
トーズワース
K−
◎
◎
◎
◎
◎
×
◎
◎
◎
◎
◎
◎
メルセンヌ
K+
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
ツイスター
K−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
無理数回転
K+
◎
○
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
K−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
×
◎
物理乱数
K+
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
○
K−
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
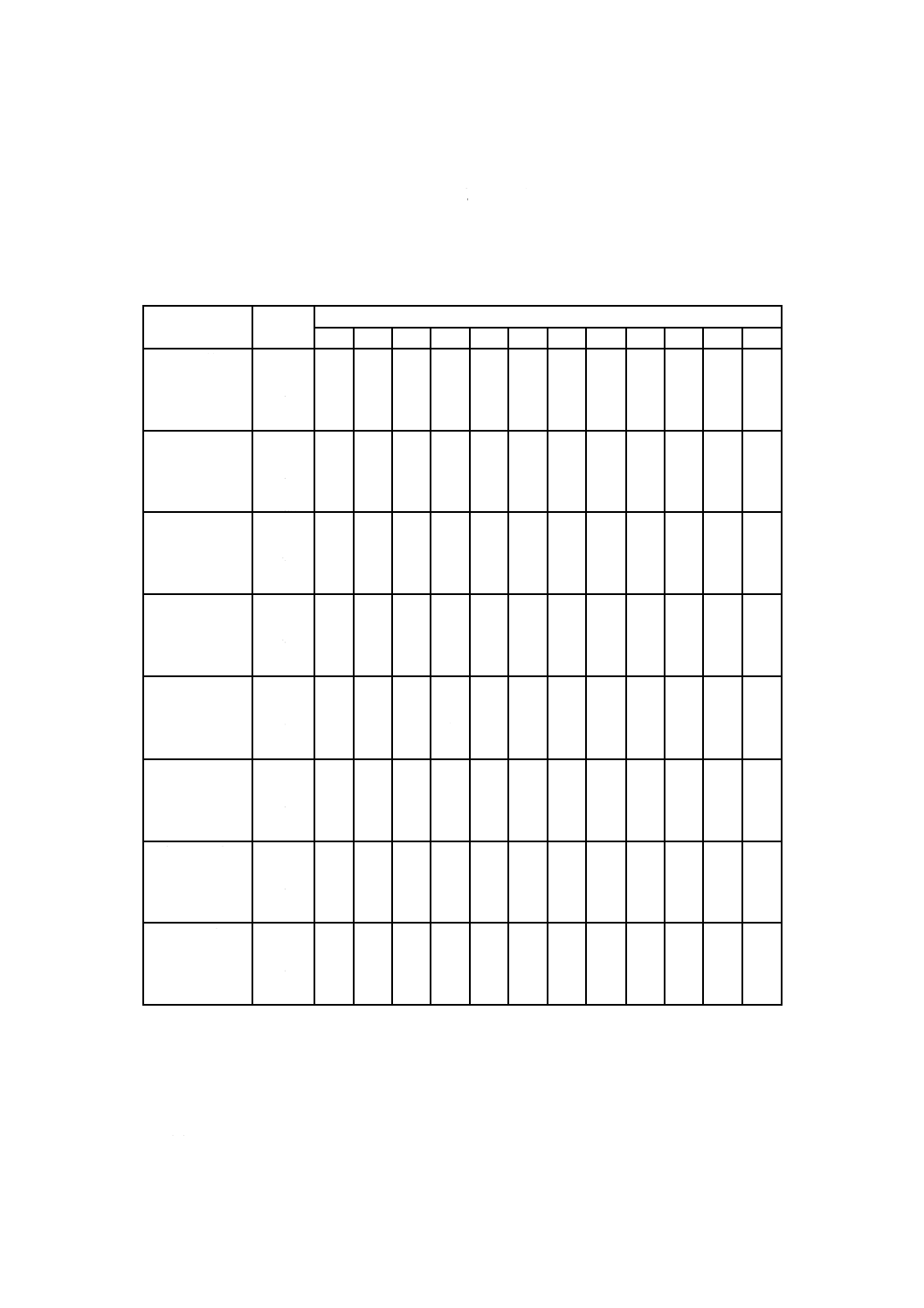
83
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JA.4.4
連の検定
長さNの乱数列に対する統計量Vの計算をM回繰り返し,Vが自由度6のχ2分布に従うとしてコルモ
ゴロフ・スミルノフ検定を行った。
±
up
Kが上昇連,
±
down
K
が下降連のコルモゴロフ・スミルノフ統計量であ
る。疑似乱数については (N, M)=(105, 103),物理乱数による乱数表に関しては,(N, M)=(105, 102) で検定
を行った。結果の見方は,一次元での一様性検定の場合と同じである(表JA.7参照)。
表JA.7−連の検定の結果
生成法
系列
1
2
3
4
5
6
7
8
9
10
11
12
合同乗算法
+
up
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
(m=232)
−
up
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
+
down
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
−
down
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
合同乗算法
+
up
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
(m=231−1)
−
up
K
◎
◎
◎
△
◎
◎
◎
◎
◎
○
◎
◎
+
down
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
−
down
K
◎
◎
◎
△
◎
◎
◎
◎
◎
○
◎
◎
3項GFSR
+
up
K
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
−
up
K
◎
◎
△
△
○
◎
◎
◎
◎
◎
◎
◎
+
down
K
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
−
down
K
◎
◎
△
△
○
◎
◎
◎
◎
◎
◎
◎
5項GFSR
+
up
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
−
up
K
◎
○
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
+
down
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
−
down
K
◎
○
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
結合
+
up
K
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
トーズワース
−
up
K
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
+
down
K
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
−
down
K
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
◎
メルセンヌ
+
up
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
ツイスター
−
up
K
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
◎
+
down
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
−
down
K
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
◎
無理数回転
+
up
K
◎
△
◎
◎
◎
◎
◎
◎
○
◎
◎
△
−
up
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
+
down
K
◎
△
◎
◎
◎
◎
◎
◎
○
◎
◎
△
−
down
K
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
物理乱数
+
up
K
◎
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
−
up
K
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
+
down
K
◎
◎
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
−
down
K
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
JA.4.5
衝突検定
ここでは,十次元の衝突検定を行った。各次元ごとに4等分して,410個の超立方体に分割する。乱数を
10個生成して十次元空間の座標点を定め,乱数N個に対する“衝突”頻度を計算する。これをM回繰り
返し,得られた経験的な衝突確率及び理論確率を,χ2検定を用いて検定する。疑似乱数については (N, M)
=(16 384, 1 000),物理乱数による乱数表に関しては,(N, M)=(16 384, 60) で検定を行った。結果の見方は,
一次元での一様性検定の場合と同じである(表JA.8参照)。
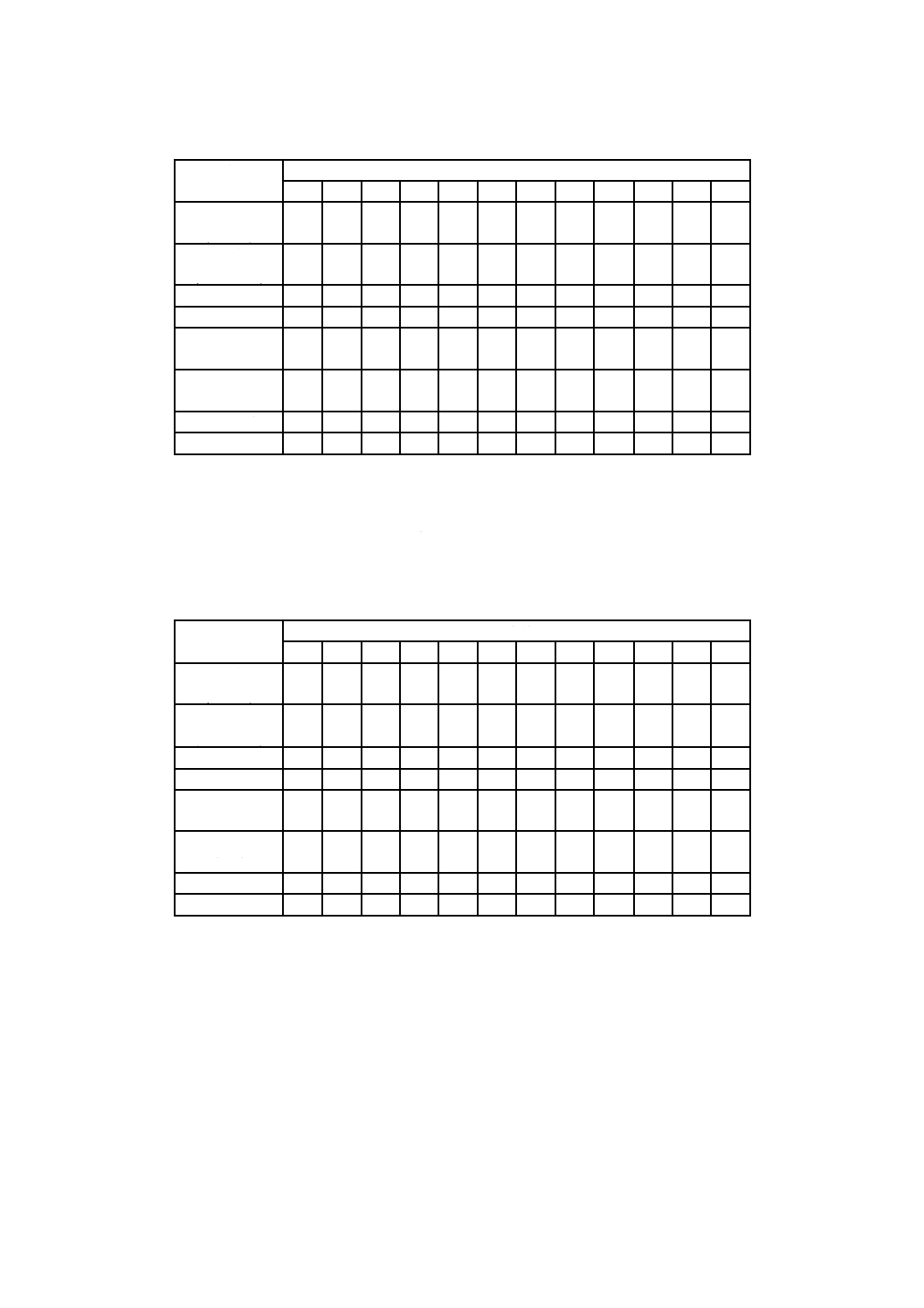
84
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表JA.8−衝突検定の結果
生成法
系列
1
2
3
4
5
6
7
8
9
10
11
12
合同乗算法
(m=232)
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
×
合同乗算法
(m=231−1)
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
3項GFSR
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
5項GFSR
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
◎
結合
トーズワース
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
メルセンヌ
ツイスター
◎
◎
×
×
◎
◎
◎
◎
◎
△
◎
◎
無理数回転
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
物理乱数
◎
◎
◎
◎
◎
◎
◎
◎
◎
×
△
◎
JA.4.6
ランダムウォーク検定
ここでは,二次元のランダムウォーク検定を行った。ステップ数nのランダムウォークをN回繰り返し,
χ2検定で検定を行った。疑似乱数については (n, N)=(104, 105),物理乱数による乱数表に関しては,(n, N)
=(104, 103) で検定を行った。結果の見方は,一次元での一様性検定の場合と同じである(表JA.9参照)。
表JA.9−ランダムウォーク検定の結果
生成法
系列
1
2
3
4
5
6
7
8
9
10
11
12
合同乗算法
(m=232)
△
◎
◎
◎
◎
◎
◎
◎
◎
○
◎
◎
合同乗算法
(m=231−1)
◎
◎
○
○
◎
◎
◎
◎
◎
◎
◎
◎
3項GFSR
×
×
×
×
×
×
×
×
×
×
×
×
5項GFSR
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
△
結合
トーズワース
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
メルセンヌ
ツイスター
△
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
無理数回転
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
○
物理乱数
◎
◎
◎
◎
◎
◎
△
◎
◎
△
◎
◎
JA.4.7
nブロック検定
n個の乱数の平均値の計算をN回繰り返し,平均値が1/2を超える頻度についてχ2検定で検定を行った。
疑似乱数については (n, N)=(104, 105),物理乱数による乱数表に関しては,(n, N)=(104, 103) で検定を行っ
た。結果の見方は,一次元での一様性検定の場合と同じである(表JA.10参照)。
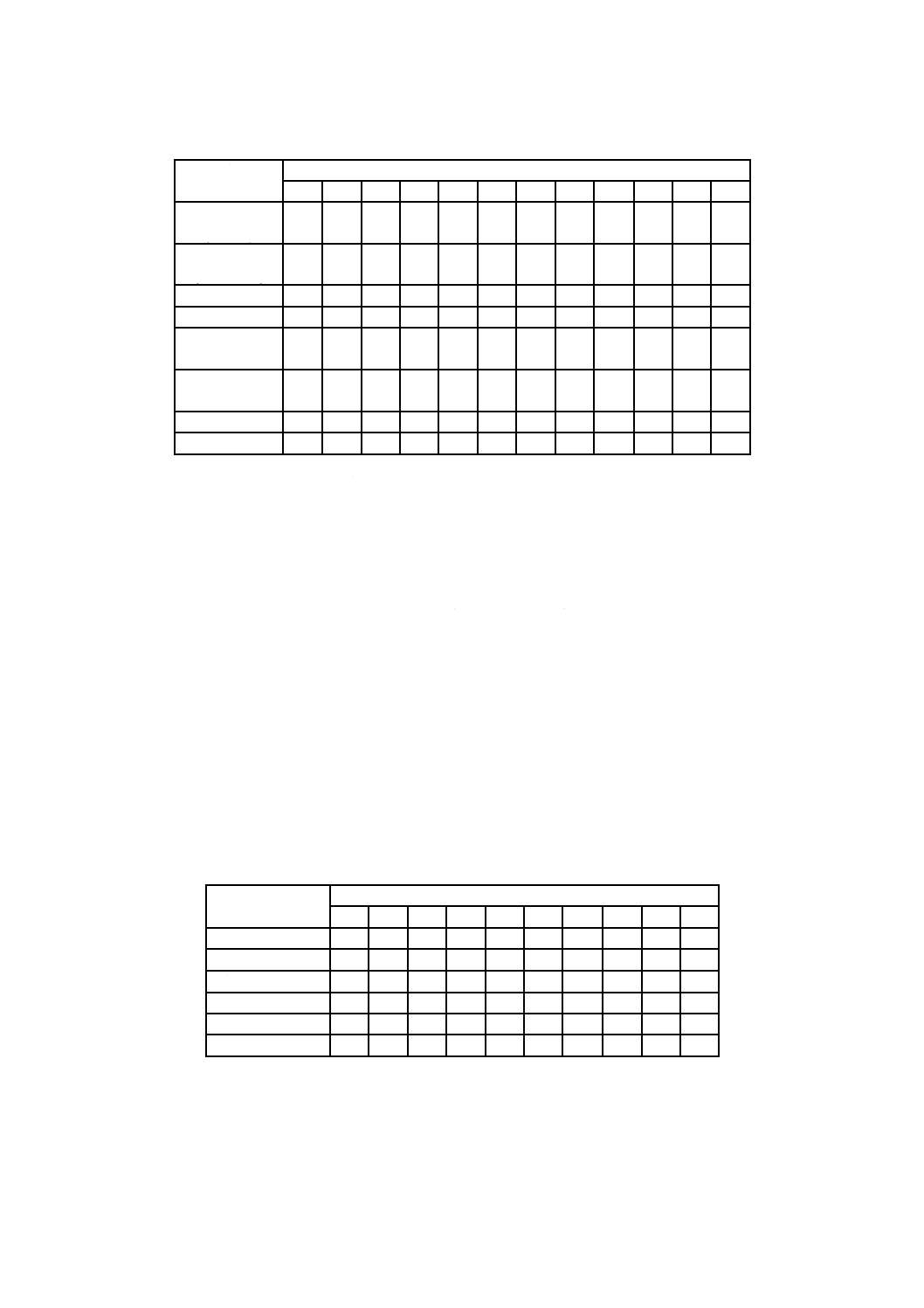
85
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表JA.10−nブロック検定の結果
生成法
系列
1
2
3
4
5
6
7
8
9
10
11
12
合同乗算法
(m=232)
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
合同乗算法
(m=231−1)
◎
◎
◎
◎
◎
○
◎
◎
◎
◎
◎
◎
3項GFSR
×
×
×
×
×
×
×
×
×
△
×
×
5項GFSR
◎
○
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
結合
トーズワース
◎
◎
△
◎
△
◎
◎
◎
◎
◎
◎
◎
メルセンヌ
ツイスター
△
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
◎
無理数回転
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
○
物理乱数
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
JA.4.8
乱数表(表A.1)の統計的検定
乱数表(表A.1)については,乱数の量も少ないため,別個に次の六つの検定を行った。
a) 一次元度数分布 各乱数表に現れる0〜9の数字1 000個の度数分布を,χ2検定によって検定する。
b) 二次元度数分布 相並ぶ2数字を二桁の数字とみなし,各乱数表に現れる500個の数の度数分布を,
χ2検定によって検定する。
c) 横方向系列相関 各乱数表に現れる0〜9の数字1 000個を,横方向に順に読んだときの系列に対し,
自己相関係数を計算し,検定を行う。自己相関係数による検定については,参考文献[7] 参照。
d) 縦方向系列相関 各乱数表に現れる0〜9の数字1 000個を,縦方向に順に読んだときの系列に対し,
自己相関係数を計算し,検定を行う。
e) 横方向間隔検定 各乱数表に現れる0〜9の数字1 000個を,横方向に順に読んだときの系列に対し,
数字0の現れる間隔について,間隔検定を行う。間隔検定については,参考文献[7] 参照。
f)
縦方向間隔検定 各乱数表に現れる0〜9の数字1 000個を,縦方向に順に読んだときの系列に対し,
数字0の現れる間隔について,間隔検定を行う。
10個の乱数表に対する検定結果を,表JA.11に示す。
表JA.11−乱数表(表A.1)の検定結果
検定法
乱数表
1
2
3
4
5
6
7
8
9
10
一次元度数分布
◎
○
◎
◎
◎
△
◎
◎
◎
◎
二次元度数分布
◎
◎
○
◎
◎
◎
◎
◎
◎
◎
横方向系列相関
◎
◎
◎
◎
△
◎
◎
◎
◎
◎
縦方向系列相関
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
横方向間隔検定
◎
◎
◎
◎
◎
◎
◎
◎
◎
◎
縦方向間隔検定
◎
◎
△
◎
◎
◎
◎
◎
◎
◎
86
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1]
JIS X 3003 電子計算機プログラム言語 Full BASIC
[2]
JIS X 3010 プログラム言語C
[3]
伏見正則,乱数,UP応用数学選書,東京大学出版会,1989.
[4]
L. Blum, M. Blum and M. Shub, A Simple Unpredictable Pseudorandom Number Generator, SIAM J.
Comput. , Volume 15, Number 2, (1986) , 364-383.
[5]
A. M. Ferrenberg, D. P. Landau and Y. J. Wong, Monte Carlo Simulations : Hidden Errors from “Good”
Random Number Generators, Physical Review Letters, Volume 69, Number 23, (1992), 3382-3384.
[6]
J. R. Heringa, H. W. J. Blöte and A. Compagner, New Primitive Trinomials of Mersenne-Exponent Degrees
for Random-Number Generation, International Journal of Modern Physics C, Volume 3, Number 3, (1992),
561-564.
[7]
渋谷政昭訳,The Art of Computer Programing (3) - 準数値算法/乱数(第二版),サイエンス社,1981
(原文:D. E. Knuth, Seminumerical Algorithms (The Art of Computer Programming, Volume 2), 2nd. ed.)
[8]
D. E. Knuth, Seminumerical Algorithms (The Art of Computer Programming, Volume 2), 3rd. ed. , Addison
Wesley, 1998. (日本語版:有沢誠訳,The Art of Computer Programming(volume 2) 日本語版,アス
キー・メディアワークス,2004)
[9]
Y. Kurita and M. Matsumoto, Primitive t-nomials (t=3, 5) over GF (2) Whose Degree is a Mersenne
Exponent ≦44497, Mathematics of Computation, Volume 56, Number 194, (1991), 817-821.
[10] P. L'Ecuyer, Maximally Equidistributed Combined Tausworthe Generators, Mathematics of Computation,
Volume 65, Number 213, (1996), 203-213.
[11] T. G. Lewis and W. H. Payne, Generalized Feedback Shift Register Pseudorandom Number Generators,
Journal of the Association for Computing Machinery, Volume 20, Number 3, (1973), 456-468.
[12] M. Luby, Pseudorandomness and Cryptographic Applications. Princeton Univ. Press, 1996.
[13] J. L. Massey, Shift-Register Synthesis and BCH Decoding, IEEE Trans. on Information Theory, Volume
IT-15, Number 1, (1969), 122 127.
[14] M. Matsumoto and T. Nishimura, Mersenne Twister : A 623-Dimensionally Equidistributed Uniform
Pseudo-Random Number Generator, ACM. Trans. Model. Comput. Simul. , Volume 8, Number 1, (1998),
3-30.
[15] A. J. Menezes, P. C. van Ooschot and S. A. Vanstone, Handbook of Applied Cryptography, CRC Press,
1997.
[16] J. von Neumann, Various Techniques Used in Connection with Random Digits, Monte Carlo Method,
Applied Mathematics Series, No.12, U. S. National Bureau of Standards, Washington D. C. , 1951, 36-38.
[17] R. A. Rueppel, Analysis and Design of Stream Ciphers, Springer-Verlag, 1986.
[18] H. Sugita, Pseudo-Random Number Generator by Means of Irrational Rotation, Monte Carlo Methods and
Applications, Volume 1, Number 1, (1995), 35-57.
[19] R. C. Tausworthe, Random Numbers Generated by Linear Recurrence Modulo Two, Mathematics of
Computation, Volume 19, (1965), 201-209.
[20] S. Tezuka and P. L'Ecuyer, Efficient and Portable Combined Tausworthe Random Number Generators, ACM.
87
Z 9031:2012
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Trans. Model. Comput. Simul. , Volume 1, (1991), 99-112.
[21] I. Vattulainen, T. Ala-Nissila and K. Kankaala, Physical Tests for Random Numbers in Simulations, Physical
Review Letters, Volume 73, Number 19, (1994), 2513 2516.
[22] I. Vattulainen, T. Ala-Nissila and K. Kankaala, Physical Models as Tests of Randomness, Physical Review,
Volume E52, (1995), 3205-3214.
[23] 大学共同利用機関法人 情報・システム研究機構 統計数理研究所 乱数ライブラリー
<http://random.ism.ac.jp/>
[24] 山内二郎(編),統計数値表,日本規格協会,1972.
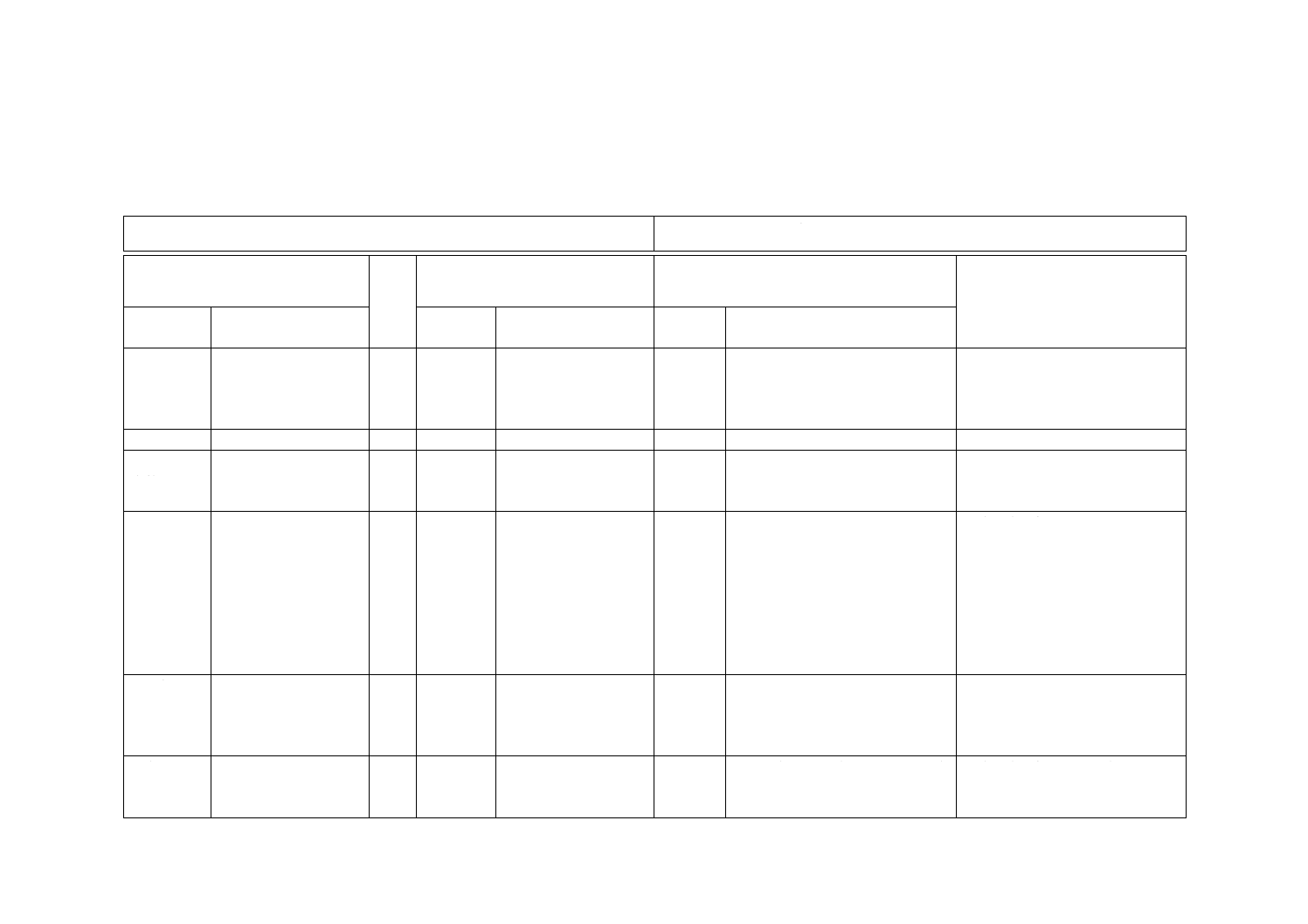
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JB
(参考)
JISと対応国際規格との対比表
JIS Z 9031:2012 乱数生成及びランダム化の手順
ISO 28640:2010 Random variate generation methods
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ご
との評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
1 適用範囲 乱数の生成方法及びラ
ンダム化を行う方法に
ついて規定
1
JISとほぼ同じ
追加
ISO規格では規定していない乱数
の使用方法,すなわちランダム化
を行う方法について旧JISで規定
していた方法を追加。
対応国際規格の定期見直しの際
に,今回のJISと同等な適用範囲
にするよう,拡張改訂を提案して
いく。
2 引用規格
3 用語及び
定義
3
JISとほぼ同じ
追加
現在のISO規格にない“ランダム
化”及び“ランダム割付け”の用
語を追加した。
上記の拡張改訂が実施されれば,
用語及び定義も同等となる。
4 記号及び
数学的演算
4
JISとほぼ同じ
変更
ISO規格では不適切な記号も用い
られているため,旧JISの記号と
置き換えた。また,ISO規格では
規定していない整数の切り上げ,
切り捨て,最大公約数の記号を追
加。
なお,ISO規格で用いている記号
については注記で全て説明した。
対応国際規格で用いている記号が
不適切であるため,この改訂を定
期見直しの際に提案していく。
5 乱数
5
JISとほぼ同じ
追加
旧JISにあり,現在のISO規格で
は規定していない“線形合同法”,
及び一部しか対応していない“3
項GFSR”をM系列法に追加した。
対応国際規格の改訂を提案してい
く。
6 各種の分
布に従う乱
数の生成
6
JISとほぼ同じ
追加
ISO規格では規定していない生成
法について旧JISを追加した。
対応国際規格の不備に起因するた
め,改訂を提案していく。
2
Z
9
0
3
1
:
2
0
1
2
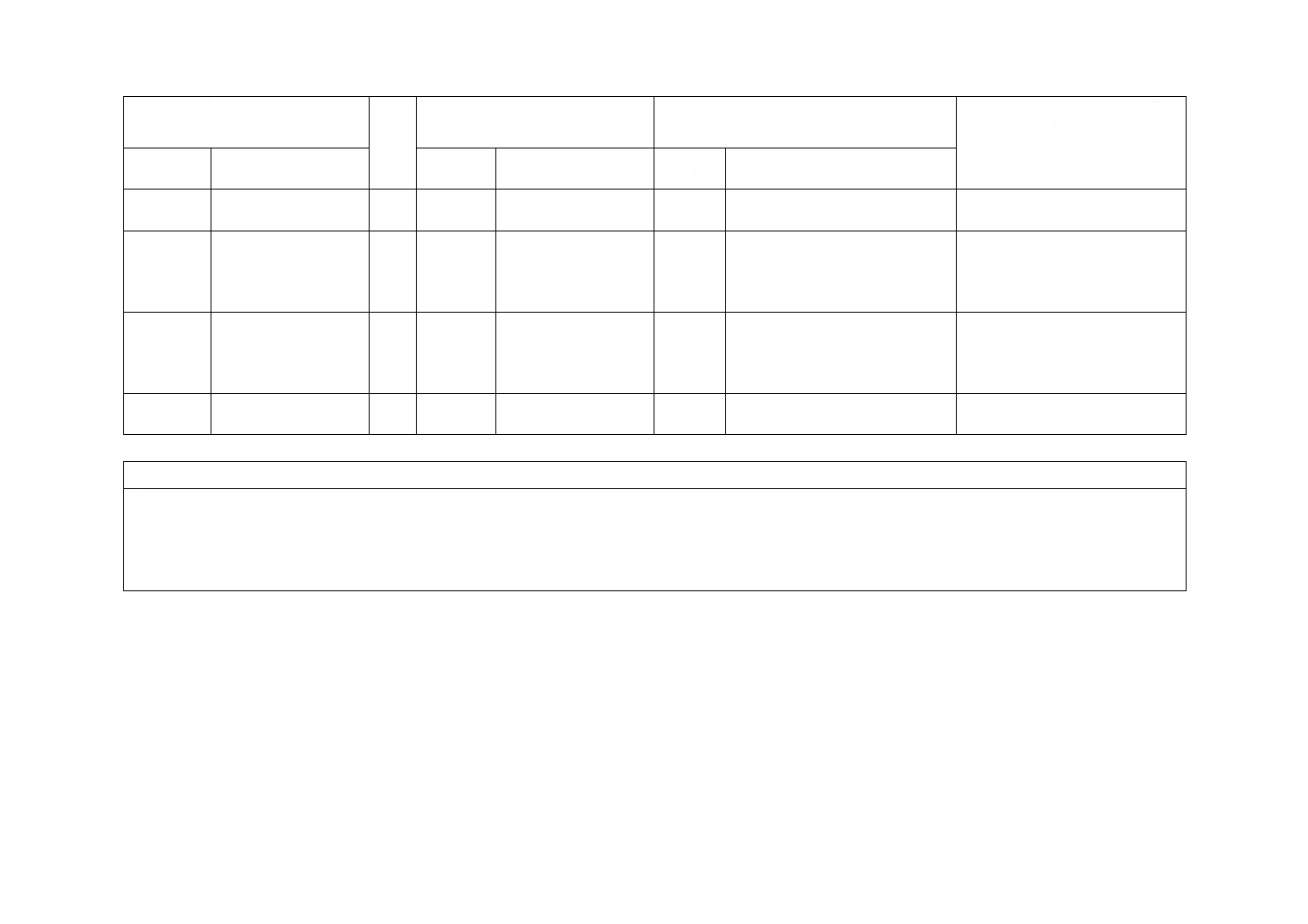
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ご
との評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
7 ランダム
化の方法
−
−
追加
JISとして有用な規定内容なので,
旧JISの規定を追加した。
対応国際規格の改訂を提案してい
く。
附属書A
(参考)
附属書A
JISとほぼ同じ
追加
ISO規格にはない“バイナリ形式
の乱数表ファイルを読み出すプロ
グラムコード”を,A.2.2として旧
JISの記載を追加した。
対応国際規格の不備に起因するた
め,改訂を提案していく。
附属書B
(参考)
附属書B
JISとほぼ同じ
追加
ISO規格には一部しか記載がない
“3項GFSR法”及び“無理数回
転法”について旧JISの記載を追
加した。
対応国際規格の不備に起因するた
め,改訂を提案していく。
附属書JA
−
−
追加
JISとして有用な内容なので,旧
JISの記載を追加した。
対応国際規格の不備に起因するた
め,改訂を提案していく。
JISと国際規格との対応の程度の全体評価:ISO 28640:2010,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 追加 ················ 国際規格にない規定項目又は規定内容を追加している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
2
Z
9
0
3
1
:
2
0
1
2