Z 9020-4:2018 (ISO 7870-4:2011)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 2
2 引用規格························································································································· 2
3 用語及び定義並びに略語及び記号 ························································································ 2
3.1 用語及び定義 ················································································································ 2
3.2 略語 ···························································································································· 3
3.3 記号 ···························································································································· 3
4 累積和図の主な特徴 ·········································································································· 4
5 累積和図の作成の基本ステップ−グラフ表示 ········································································· 5
6 累積和プロットの例−モータ電圧 ························································································ 6
6.1 工程 ···························································································································· 6
6.2 結果の簡易プロット ······································································································· 6
6.3 個々の観測値の標準的な管理図 ························································································ 7
6.4 累積和図−全体像 ·········································································································· 8
6.5 累積和図の作成 ············································································································· 8
6.6 累積和図の解釈 ············································································································· 9
6.7 マンハッタン図 ············································································································ 12
7 累積和による異常判定ルールの基礎 ···················································································· 13
7.1 異常判定ルールの必要性 ································································································ 13
7.2 判定を下すための基礎 ··································································································· 13
7.3 異常判定ルールの有効性の測定 ······················································································· 15
8 異常判定ルールのタイプ ··································································································· 17
8.1 Vマスクのタイプ ········································································································· 17
8.2 Vマスク法 ·················································································································· 17
8.3 代替設計アプローチ ······································································································ 23
8.4 セミパラボリック累積和管理図 ······················································································· 23
8.5 スナブノーズ累積和管理図 ····························································································· 24
8.6 フルVマスク法 ············································································································ 25
8.7 初期値を変更した(FIR)累積和管理図 ············································································ 25
8.8 表形式による累積和管理図 ····························································································· 26
9 工程管理のための累積和管理図 ·························································································· 28
9.1 検出すべき変化の性質 ··································································································· 28
9.2 目標値の選択 ··············································································································· 29
9.3 位置(平均)をモニタリングするための累積和スキーム ······················································· 30
9.4 群内変動のモニタリング用の累積和スキーム ······································································ 39
Z 9020-4:2018 (ISO 7870-4:2011) 目次
(2)
ページ
9.5 特殊な状況 ·················································································································· 47
9.6 離散データ用累積和スキーム ·························································································· 49
附属書A(参考)フォン・ノイマン法 ····················································································· 55
附属書B(参考)表形式による累積和管理図の例 ······································································· 56
附属書C(参考)段階的変化が発生したときの変化点の推定························································ 60
参考文献 ···························································································································· 62
Z 9020-4:2018 (ISO 7870-4:2011)
(3)
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般財団法人日本規格協会(JSA)から,工
業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済
産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS Z 9020の規格群には,次に示す部編成がある。
JIS Z 9020-1 第1部:一般指針
JIS Z 9020-2 第2部:シューハート管理図
JIS Z 9020-3 第3部:工程の合否判定用管理図(予定)
JIS Z 9020-4 第4部:累積和管理図
日本工業規格 JIS
Z 9020-4:2018
(ISO 7870-4:2011)
管理図−第4部:累積和管理図
Control charts-Part 4: Cumulative sum charts
序文
この規格は,2011年に第1版として発行されたISO 7870-4を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
この規格では,意味のある順序に並べられたデータを解釈する,非常に簡易であるが検出能力が高い図
法の適用性及び有用性を実証する。こうしたデータは,売上高,利益又は間接費のような総合的ビジネス
関連数値から,在庫切れ及び欠勤率のような詳細な運用データ,個々の工程パラメータ及び製品特性の管
理に至るまで様々である。データは,連続尺度(例えば,24.60,31.21,18.97…),yes又はno,良又は否,
成功又は失敗などの形式で個々の値として順番に表すこともできれば,要約値(平均,範囲,事象回数な
ど)で表すこともできる。
この方法は,累積和という独特の名称をもっている。この名称は,一系列の観測値から目標値,推奨値,
参照値などの事前に決めた値を差し引き,その差を順々に累積(すなわち,加算)することに由来する。
累積した差を時系列にグラフ化したものを累積和管理図と呼ぶ。このような簡易な演算処理は,次に示す
ように,データの視覚的解釈に顕著な効果をもつ。
累積和管理図は,世界中のゴルファーが意識することなしに使用している。1ラウンドのスコアを“プ
ラス”4又は“マイナス”2と記録することによって,ゴルファーは数字的な意味で累積和管理図を使用し
ている。ゴルファーは,実際のスコアからパーの値を差し引き,その差を加算(累積)する。これは,プ
レー中の累積和管理図である。しかし,この方法は広く知られていることはなく,ビジネス,産業,商業,
行政サービスではあまり使用されていないツールである。これは,通常,累積和管理図が一般に職場の言
語の中というよりは統計的な言語の中で表現されるためである。
ISO 7870-4:2011は,ISO/TR 7871:1997の改正版である。この規格の意図は,広範に予想されるユーザが
容易に理解できるようにして,この方法の広範囲の普及及び理解を促進することである。この方法は,累
積和管理図が検出したい重要な変化量を最大で3倍以上早く検出するため,より一般に使われるシューハ
ート管理図を超えるメリットをもたらしている。さらに,ゴルフの場合のように,ホールごとに目標が変
わるとき,累積和プロットは影響を受けないのに対して,標準的なシューハート管理図の場合は絶えず管
理限界を調整しなければならない。
シューハート管理図に加えて,指数型重み付き移動平均(EWMA)管理図を使用することもできる。
EWMA管理図上に記入する各点は,それまでの全てのサブグループ又は観測値の情報を含んでいるが,指
数的に重みが軽減されることによってサブグループ又は観測値が“徐々に古く”なるので,工程データに
重みが付加されなくなる。累積和管理図の場合と同じように,EWMA管理図は,工程の変化の大きさを検
2
Z 9020-4:2018 (ISO 7870-4:2011)
出するように敏感にできる。これについては,ISO 7870-6で更に考察する。
1
適用範囲
この規格は,量的(測定値)及び質的データを用いる工程及び品質管理の累積和管理図を設計するため
の統計的手順について規定する。この規格は,モニタリング,管理及び解析に累積和(cusum)を用いる
場合の意思決定の汎用的な方法についても規定する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 7870-4:2011,Control charts−Part 4: Cumulative sum charts(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8101-1 統計−用語及び記号−第1部:一般統計用語及び確率で用いられる用語
注記 対応国際規格:ISO 3534-1,Statistics−Vocabulary and symbols−Part 1: General statistical terms
and terms used in probability
JIS Z 8101-2 統計−用語及び記号−第2部:統計の応用
注記 対応国際規格:ISO 3534-2,Statistics−Vocabulary and symbols−Part 2: Applied statistics
3
用語及び定義並びに略語及び記号
この規格で用いる主な用語及び定義は,JIS Z 8101-1及びJIS Z 8101-2によるほか,次による。
3.1
用語及び定義
3.1.1
目標値,T(target value)
平均レベルとの差を検出する必要がある場合の基準となる値。
注記1 累積和管理図では,目標値との差が累積される。
注記2 Vマスクを使用するとき,目標値は,参照値又は公称管理値ということがある。その場合,
目標値は,必ずしも,他の規格に記載されている最も望ましい値又は推奨値ではないと認識
することが望ましい。累積和管理図では,単なる便宜上の目標値でしかない。
3.1.2
基準値(datum value)
<表形式による累積和管理図>差を計算するときの値。
注記1 上方シフトを監視する場合の上限の基準値はT+fσe,下方シフトの場合の下限の基準値は
T−fσeで表される。
注記2 < >の記号は,一つの用語が複数の概念を表す場合に,それぞれの概念に関係する主題又
は分野を表示して対象を限定し,区別するために用いる。
3.1.3
参照シフト値,F,f(reference shift)
<表形式による累積和管理図>目標値(3.1.1)と基準値(3.1.2)との差。
3
Z 9020-4:2018 (ISO 7870-4:2011)
注記 規準化した参照シフト値を表すfと,参照シフト値を表すF(=fσe)とを区別する必要がある。
3.1.4
参照シフト値,F,f(reference shift)
<Vマスク法>Vマスクの判定ラインの傾き(マスク角の正接)。
注記 規準化した参照シフト値を表すfと,参照シフト値を表すF(=fσe)とを区別する必要がある。
3.1.5
決定区間,H,h(decision interval)
<表形式による累積和管理図>異常の検出に必要な基準値(3.1.2)との偏差の累積和。
注記 規準化した決定区間を表すhと,決定区間を表すH=hσeとを区別する必要がある。
3.1.6
決定区間,H,h(decision interval)
<Vマスク法>Vマスクの基準線の1/2の高さ。
注記 規準化した決定区間を表すhと,決定区間を表すH=hσeとを区別する必要がある。
3.1.7
平均連長,L(average run length)
異常を検出するまでに打点される平均サンプル数。
注記 平均連長(L)は,通常,特定の工程の水準に関係しており,適切な下付数字を付ける。例え
ば,L0は,工程が目標レベルにある,すなわち,シフトがゼロのときの平均連長を意味する。
3.2
略語
ARL
平均連長
CS1
シフトがゼロのARLが大きい累積和管理図
CS2
シフトがゼロのARLが比較的小さい累積和管理図
DI
決定区間
EWMA
指数型重み付き移動平均
FIR
初期値を変更した
LCL
下側管理限界(線)
RV
参照値
UCL
上側管理限界(線)
3.3
記号
a
縦軸の目盛係数
C
累積和値
Cr
基準点と異常を示す点との累積和の差
c4
群内の標準偏差を推定するための係数
δ
検出すべき変化量
Δ
規準化した検出すべき変化量
d
リード距離
d2
範囲から群内の標準偏差を推定するための係数
F
参照シフト値
f
規準化した参照シフト値
H
決定区間
4
Z 9020-4:2018 (ISO 7870-4:2011)
h
規準化した決定区間
J
指数
φ
工程調節量
K
離散データの累積和基準値
k
群の数
L0
シフト量がゼロのときの平均連長(ARL)
Lδ
シフト量がδのときの平均連長(ARL)
μ
母平均値
m
母平均発生数
n
群の大きさ
p
“成功”の確率
R
群内の範囲の平均値
r
基準点と異常を示す点との間でプロットされた数
σ
工程の母標準偏差
σ0
群内の母標準偏差
0ˆσ
群内の母標準偏差の推定値
σe
母標準誤差
s
群内の標準偏差
s
群内の標準偏差の平均値
xs
k個の群から求めた標準誤差の推定値
T
目標値
Tm
発生率の参照値又は目標値
Tp
比率の参照値又は目標値
τ
真の変化点
t
観測された変化点
Vavg
平均電圧
avg
ˆV 推定された平均電圧
w
連続する群の平均値間の差
x
個々の観測値
x
群の平均値
x
群の平均の平均値
4
累積和図の主な特徴
累積和図1)は,基本的には,事前に選択した参照値との偏差の累計である。連続した値のグループの平
均は,グラフの最新の傾きによって目で分かるように表示される。累積和図の主な特徴は,次のとおりで
ある。
a) 平均の変化を敏感に検知する。
b) 平均の変化及び変化の大きさは,次のようにグラフの傾きの変化によって分かる。
1) 水平方向のグラフは,平均が目標値又は参照値と同じであることを示す。
2) 下向きの傾きは,参照値又は目標値よりも低い平均を示す。傾きが急になればなるほど,差は大き
5
Z 9020-4:2018 (ISO 7870-4:2011)
い。
3) 上向きの傾きは,参照値又は目標値よりも高い平均を示す。傾きが急になればなるほど,差は大き
い。
c) 累積和図は,管理を続ける上で,調査目的で遡及的に使うこともでき,また,当面の変動を予測する
ために使うこともできる。
上記のb)に関して,累積和図は変化点を明瞭に示す能力をもつ。変化点は,累積和プロットの勾配の変
化によって示される。これは,工程管理に極めて有益である。工程が変化する瞬間を迅速にかつ正確に示
すことができるので,適切な是正処置をとることができる。
累積和の更に有用な特徴は,グラフに打点することなく,すなわち,表形式で取り扱うことができるこ
とである。このことは,プラスチックフィルム製造のように工程パラメータ及び製品特性の数が大きい場
合,高度な技術を扱う工程の監視に累積和図を利用するときに非常に役立つ。こうした工程のデータは,
自動的に捕捉し,累積和ソフトウェアにダウンロードして,自動的に累積和の分析を行える。さらに,多
くの特性の変化を同時に工程管理者に警告することができる。この方法の一例を,附属書Bに示す。
注1) この用語は,箇条6までは単なるグラフとしての表記“累積和図”を用い,箇条7以降は判定
ルールを意識した表記“累積和管理図”を用いて,使い分けをしている。
5
累積和図の作成の基本ステップ−グラフ表示
次のステップを踏んで,個々の値の累積和図を作成する。
ステップ1:参照値,目標値,管理値又は推奨値を選択する。過去の結果の平均は,一般に,優れた選別
手段となる。
ステップ2:意味のある順序(例えば,時間的順序)で結果を表形式にする。各結果から参照値を差し引
く。
ステップ3:ステップ2で得た値を累計する。これらの累計を,累積和図に打点する。
ステップ4:最適な視覚効果が得られるように,記入点間の幅が約2.5 mm以下となるように水平スケー
ルを設定する。
ステップ5:感度が過度に高くなることなく,正しく識別できるように,次のオプションを用いることが
望ましい。
a) 適切な横軸の打点区間を選び,縦軸上の区間の値に応じてその端数を捨てて丸めた,2σ(平均の累積
和を図に記入する場合は2σe)に等しくする。
b) 例えばδなど,既知の変化を検出する必要がある場合は,垂直スケール上のスケール単位を水平スケ
ール上のスケール単位で除した比が,値に応じて端数を捨てて丸めて,σと2σとの間になるように垂
直スケールを選ぶ。
注記 スケールの選択は,視覚上,非常に重要である。スケールが不適切だと,プロットが変わり
やすいという性格のために異常が間近に迫っているという印象を与えたり,又は何も変化し
ていないかのような表示になったりするからである。a)及びb)に記載した手順で,変化を過
大に見せたり過小に見せたりすることなく,適切に表示することが望ましい。
6
Z 9020-4:2018 (ISO 7870-4:2011)
6
累積和プロットの例−モータ電圧
6.1
工程
ある特性に関して,時間的順序で1組40個の値が得られると仮定する。これらの値は,生産順に取り出
させた,生産の初期段階での分数馬力モータの電圧(V)とする。ただし,値は意味のある順序で取り,
連続スケールで表記される個々の値である。その値は,次のようになっている。
9,16,11,12,16,7,13,12,13,11,12,8,8,11,14,8,6,14,4,13,3,9,7,14,2,6,4,
12,8,8,12,6,14,13,12,14,13,10,13,13
参照又は目標電圧値は,10 Vである。
6.2
結果の簡易プロット
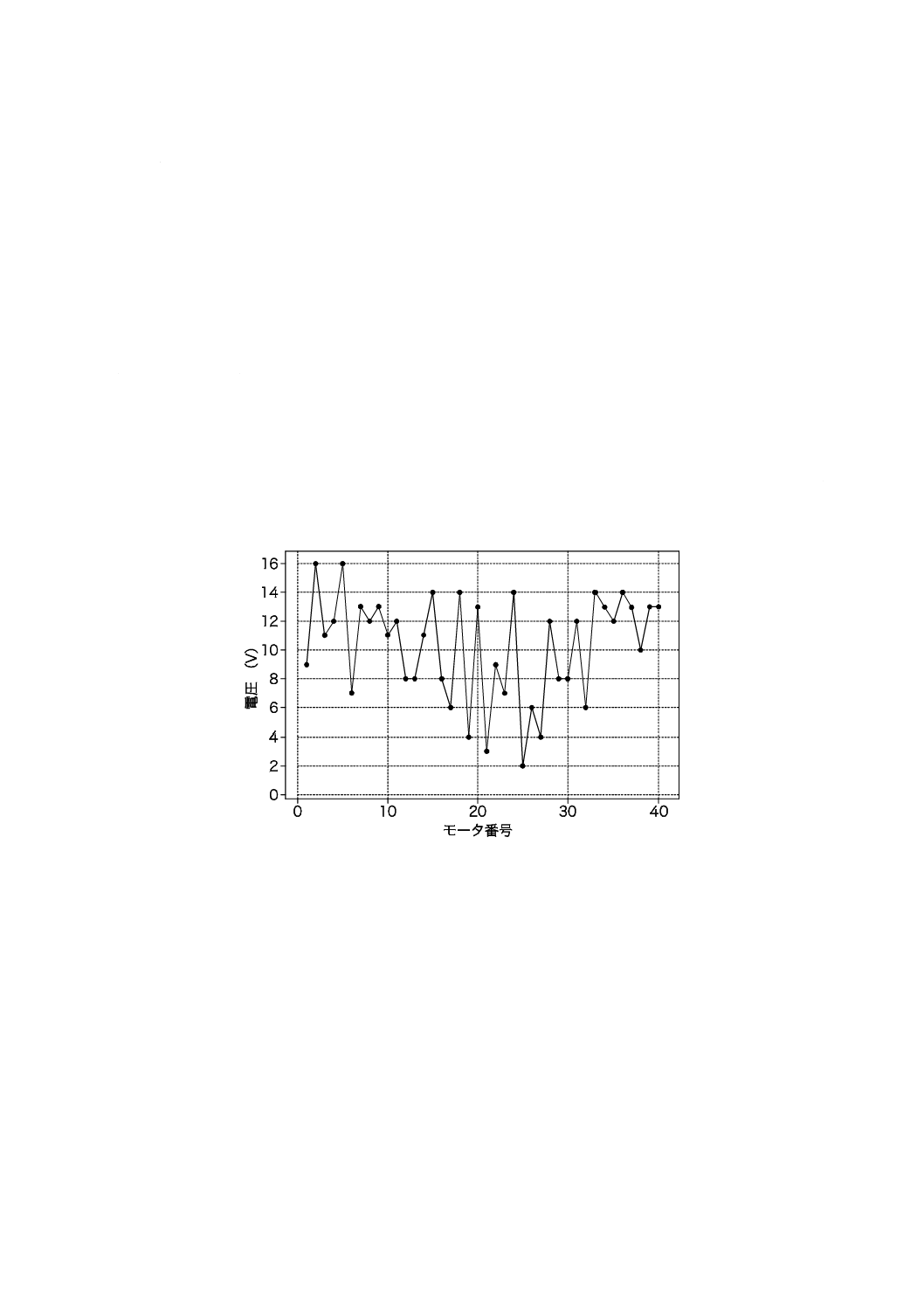
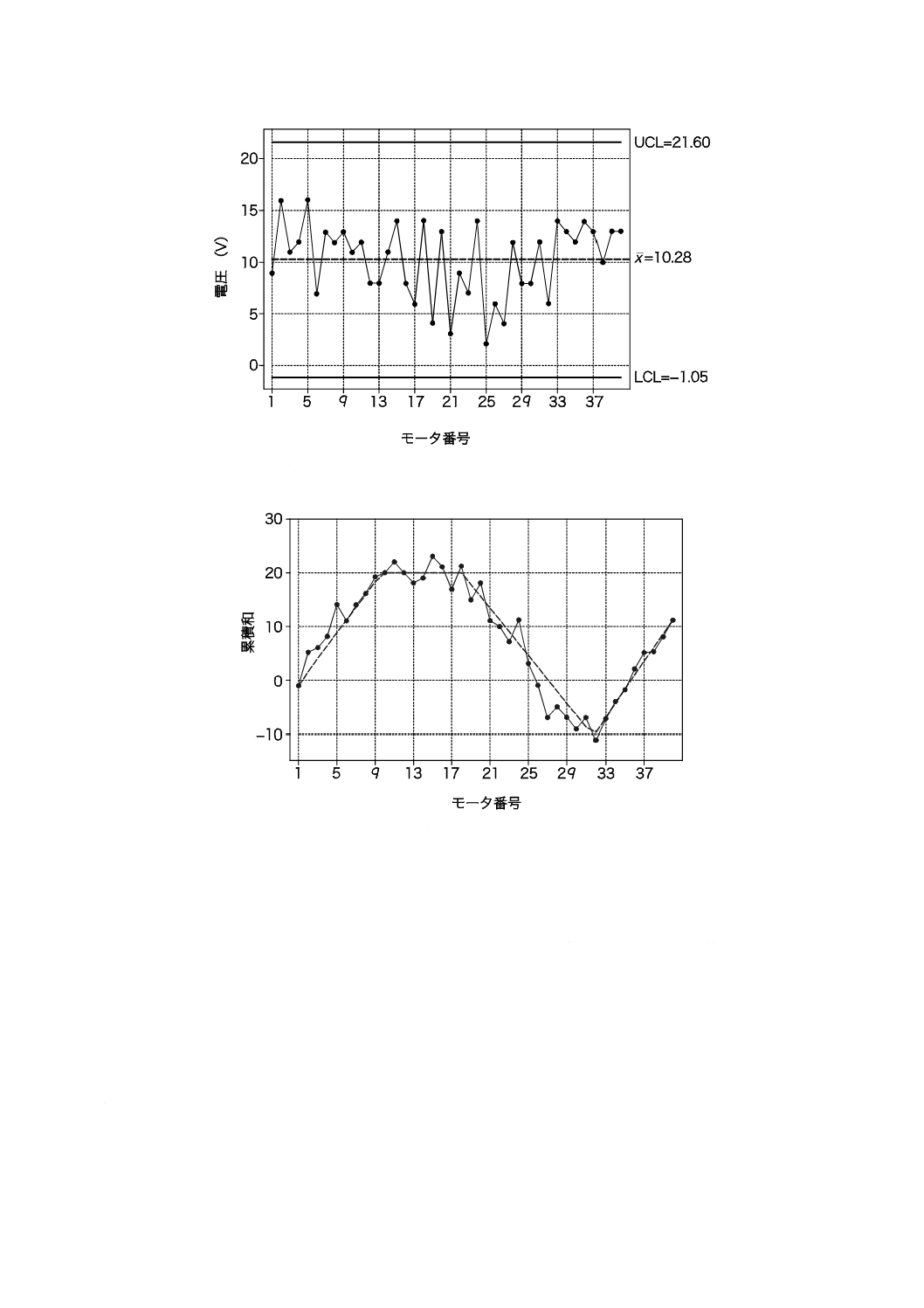
パターン及び傾向を明らかにすることによって,工程の基本的な動きをよりよく理解するための標準的
なアプローチは,図1 a)に示すように,単にこれらの値をそのまま打点することである。
最初が高く,最後が同様に高く,それに比べて中央部分はおおむね降下していることは別にして,図1 a)
は,データが全般に小波が極端に激しいので,特に意味のある現象を表示してはいない。
a) モータ電圧の簡易プロット
図1−モータ電圧の例
7
Z 9020-4:2018 (ISO 7870-4:2011)
b) 個々の観測値の標準的な管理図(例えば,X管理図)
c) 累積和図
図1−モータ電圧の例(続き)
6.3
個々の観測値の標準的な管理図
精巧化の次のレベルは,図1 b)のような個々の観測値の標準的な管理図(例えば,X管理図)を描くこ
とである。
図1 b)は,図1 a)の図と比べても意味をもつわけではない。むしろ,誤解を招きかねない。工程の安定
性及び管理を検証するための標準的な異常判定ルールは,次のとおりである。
a) 上側管理限界(UCL)より上にくる点も,下側管理限界(LCL)より下にくる点もない。
b) 上向き又は下向きに7以上の連がない。
c) 中心線より上又は下に7以上の連がない。
これらの全ての基準への答えは“ノー”である。したがって,これは安定した工程であり,目標値であ
8
Z 9020-4:2018 (ISO 7870-4:2011)
る約10 Vの全平均値の周辺で管理されているという結論が導かれる。更なる標準的な分析で,工程は安定
しているが,仕様要求事項を満たすことができないということが明らかとなる。ただし,この分析そのも
のは,なぜ要求事項を満たすことができないかについての手がかりを与えることはない。
個々の観測値の標準的な管理図(例えば,X管理図)が意義のあるものとなり得ない理由は,管理限界
が工程変動を基準にしていて,望まれる又は指定された要求事項を基準にしていないことである。したが
って,工程が自然に大きな変動を示せば,それに応じて管理限界は広くなる。要求されているのは,変動
の原因を特定又は除去するために,パターン及び傾向を示す,又は変化点を指し示すより優れた方法であ
る。
注記 個々の観測値及び移動範囲管理図(例えば,X-Rm管理図)のようなツールを追加して使用すれ
ば,専門家は他の工程変動の問題に取り組むことができる。
6.4
累積和図−全体像
推奨するもう一つの選択肢は,累積和図をプロットするものである。同じデータを使用する累積和のプ
ロットを,図1 c)に示す。
前の二つの図からは,工程の水準に有意な変化がどこで発生したのか,それとも,そもそも変化が発生
したかどうかがすぐには分からないのに対して,累積和図は,明確なパターンを示している。(目視による)
フィッティングは,10番,18番,それに32番2)のモータの後で,工程の水準に四つの変化が起きている
ことを示している。
箇条4に示すように,上向き又は下向きの傾きは,推奨値よりも高い又は低い値を示し,水平の線は,
推奨値における工程を示している。したがって,この工程は,おおよそ11番〜18番のモータの短い区間
に限って,目標に近いことが見てとれる。1番〜10番のモータは,33番以降のモータと同じように目標値
よりも高く,おおよそ19番〜32番のモータは電圧の低いモータになっている。
こうした変化及びその意味については,6.6で規定し,詳しい解釈を行う。
現実の状況では,生産のこうした点で作業上,何が起きて,このような電圧性能の変化を引き起こした
かを解明することが,次のステップとなる。これは,特に10 Vレベルでの性能の一貫性の改善に向けた一
定の疑問を提起する。例えば,32番のモータの特性が,なぜ33番のモータの特性と異なるものになって
しまったのか,又はこの点で試験歯車の校正に何が起きたのか,シフト又はバッチ変更によるものなのか,
などの疑問である。状況はいかなるものであれ,累積和図をこのように使用すると,優れた診断ツールと
なる。改善への時間的情報を特定しているのである。
注2) 対応国際規格の31番の記載は誤りであり,32番に修正した。
6.5
累積和図の作成
次の例にあるような個別の値を使用する累積和図は,箇条5に示す非常に簡易なステップで作成できる。
ステップ1:参照値RVを選択する。ここでの推奨値又は参照値は,10 Vとなる。
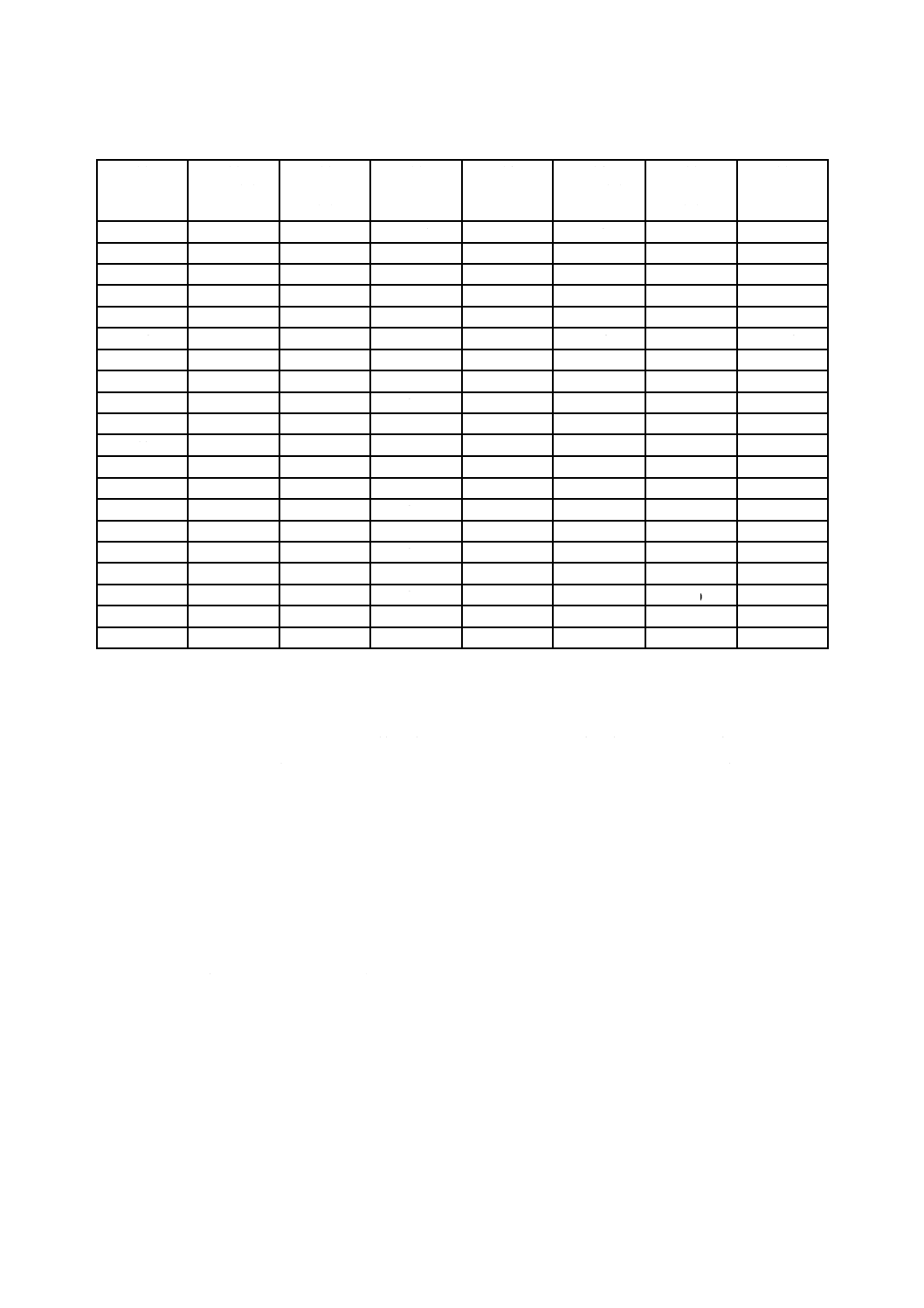
ステップ2:生産順に結果(電圧)を表形式にして,表1にあるようなモータ番号を基準に,第2列(及
び第6列)に電圧を記入する。各結果から参照値の10を差し引いたものを,表1の第3列(及
び第7列)に記入する。
ステップ3:表1の第3列(及び第7列)の値の累積和をとり,それを第4列(及び第8列)に記入する。
第4列(及び第8列)の値を,ステップ4及びステップ5の軸のスケールに関するコメント
に注意しながら,図1 c)に示すように観測(モータ)番号を基準にして打点する。
9
Z 9020-4:2018 (ISO 7870-4:2011)
表1−一系列の個別の値から累積和値を計算するための表
(1)
モータ番号
(2)
電圧(V)
(3)
電圧−10
(V)
(4)
累積和
(5)
モータ番号
(6)
電圧(V)
(7)
電圧−10
(V)
(8)
累積和
1
9
−1
−1
21
3
−7
+11
2
16
+6
+5
22
9
−1
+10
3
11
+1
+6
23
7
−3
+7
4
12
+2
+8
24
14
+4
+11
5
16
+6
+14
25
2
−8
+3
6
7
−3
+11
26
6
−4
−1
7
13
+3
+14
27
4
−6
−7
8
12
+2
+16
28
12
+2
−5
9
13
+3
+19
29
8
−2
−7
10
11
+1
+20
30
8
−2
−9
11
12
+2
+22
31
12
+2
−7
12
8
−2
+20
32
6
−4
−11
13
8
−2
+18
33
14
+4
−7
14
11
+1
+19
34
13
+3
−4
15
14
+4
+23
35
12
+2
−2
16
8
−2
+21
36
14
+4
2
17
6
−4
+17
37
13
+3
5
18
14
+4
+21
38
10
0
5
19
4
−6
+15
39
13
+3
8
20
13
+3
+18
40
13
+3
11
6.6
累積和図の解釈
6.6.1
一般
この例にあるように,累積和図を遡及的な診断に使用するとき,通常は個々の打点を重視するのではな
く,図1 c)に示すようにデータの間を通る,工程の水準ごとに目で見て最も当てはまる直線を引くほうが
よい。
こうした線の傾き又は縦軸を基準にした線の相対的な位置を,通常のデータと同じように解釈しないよ
うに注意しなければならない。縦軸は,もはや実際の電圧を表すものでないことに注意する。
上向き又は下向きの傾きのある直線は,通例のように工程の水準が増大又は減少していることを示すも
のではなく,参照値より大きい又は小さい値で一定であることを示している。傾きが大きくなればなるほ
ど,差は大きくなる。水平の線は,工程の水準が参照値で一定であることを示す。次に,モータの累積和
図の解釈について,詳細に考察する。
6.6.2
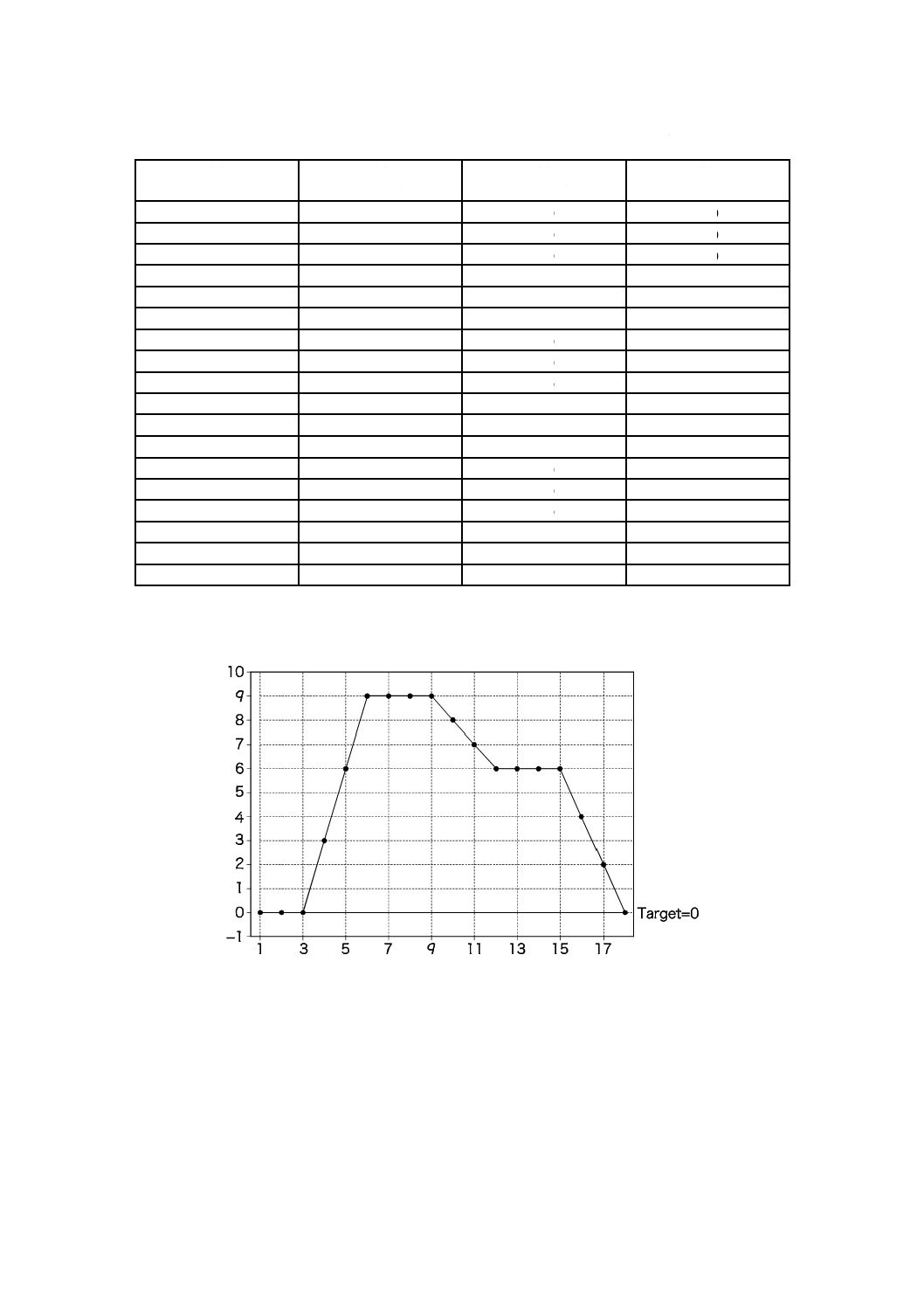
“ノイズを伴わない仮想的”データを用いた累積和図の解釈の基本
1番〜18番のモータの電圧系列が,表2の第2列に示すように10,10,10,13,13,13,10,10,10,
9,9,9,10,10,10,8,8,8となるものと仮定する。参照値は,依然として10 Vである。
10
Z 9020-4:2018 (ISO 7870-4:2011)
表2−累積和図の基本的な解釈を説明するための仮想的モータデータ
(1)
モータ番号
(2)
電圧(V)
(3)
電圧−10(V)
(4)
累積和
1
10
0
0
2
10
0
0
3
10
0
0
4
13
+3
+3
5
13
+3
+6
6
13
+3
+9
7
10
0
+9
8
10
0
+9
9
10
0
+9
10
9
−1
+8
11
9
−1
+7
12
9
−1
+6
13
10
0
+6
14
10
0
+6
15
10
0
+6
16
8
−2
+4
17
8
−2
+2
18
8
−2
+2
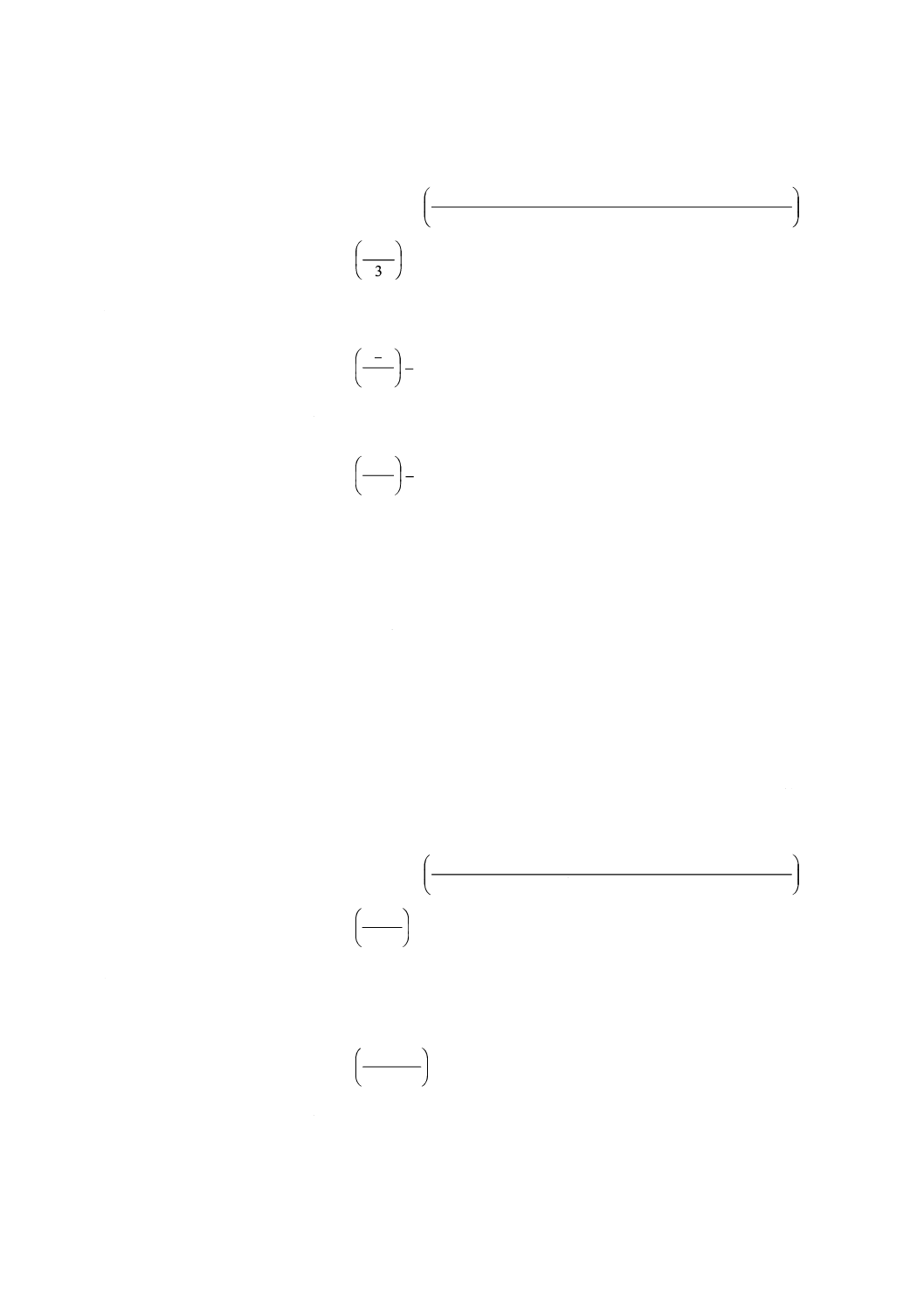
結果としての累積和図は,図2のようになる。
図2−解釈方法を説明するための仮想的モータ電圧の累積和図
表2の第2列の実際の電圧を図2の累積和図と比較すると,次のことが分かる。
a) 1番〜3番,7番〜9番及び13番〜15番のモータは全て,参照値の10 Vになっており,これらのモー
タは累積和図では全て,水平の線で表されている。垂直スケールにおける水平な線の位置は,実際の
モータではなく,それまでの累積和の値に関係していることも分かる。
b) 4番〜6番のモータは,参照値より値が高く,13 Vであり,これらのモータは累積和図では上向きの
傾きによって表されている。問題を複雑にするモータ間の電圧の差がないので,これは明らかである。
11
Z 9020-4:2018 (ISO 7870-4:2011)
ノイズがある場合,特定の傾きからその区間全体で平均値を求める式は,次のようになる。
平均電圧=参照値+
観測間隔の数
積和値
値−直線の先頭部の累
直線の末端部の累積和
Vavg=10+
−30
9
=13
c) 同様に10番〜12番のモータの場合
Vavg=10+
9
3
9
6
=
−
d) 16番〜18番のモータの場合
Vavg=10+
8
3
6
0
=
−
要約すると,累積和図上の異なる傾きは,次のことを示している。
− 1番〜3番,7番〜9番及び13番〜15番のモータでは,電圧は一定で,その値は10である。
− 4番〜6番のモータでは,電圧は一定だが,その値は13である。
− 10番〜12番のモータでは,電圧は一定で,その値は9である。
− 16番〜18番のモータでは,電圧は一定で,その値は8である。
これは,“ノイズのない”データを基準にしているので明らかである。ただし,表1の(2)列及び(6)列に
ある実際の“ノイズのある”データを基準にすると,すぐに明らかというわけにはいかない。
6.6.3
“実際の”データを用いた解釈
図1 c)の累積和図は,次のことを示している。
a) 1番〜10番のモータの平均電圧レベルは,参照電圧より高い値になっている。したがって,計算値は
傾きによって示される。
平均電圧=参照値+
観測間隔の数
積和値
値−直線の先頭部の累
直線の末端部の累積和
Vavg=10+
−
10
0
20
=12
b) 同様に,11番〜18番のモータでは,線が水平なので,平均電圧=10である。
c) 19番〜31番のモータの場合
Vavg=10+
−
−
13
20
12
=7.5
d) 32番〜40番のモータの場合
12
Z 9020-4:2018 (ISO 7870-4:2011)
Vavg=10+
−
−
9
)
12
(
11
=12.6
要約すると,累積和図を使用すると,実際の工程変動に対応した工程平均の変化を計算することができ
る。この点は,一般に広く用いられているあらかじめ定められた柔軟性のない標準的な移動平均によるア
プローチよりも,はるかに進んでいる。結果を要約した推定量を表3に示す。
表3−変動移動平均期間によるモータの平均電圧
モータ番号
モータの平均電圧(V)
1〜10
12.0
11〜18
10.0
19〜31
7.5
32〜40
12.6
この累積和の傾きと平均電圧との関係から計算する方法に代わり,累積和図の各一定レベル部分の部分
的に平均を計算するだけの方法がある。
例えば,1番〜10番のモータの場合は,次によって計算を行う。
Vavg=
+
+
+
+
+
+
+
+
+
10
11
13
12
13
7
16
12
11
16
9
=12.0
個々の電圧の値を使用すると,傾きによる方法とは結果がやや異なることがある。これは,個々の打点
から直線を引くと,データの部分的な変動を平滑化してしまうことから生じる。
6.7
マンハッタン図
電圧レベルの変化点及びその値を推定したら,表現方法を更に簡易化して,実際の電圧を縦軸にとり“ノ
イズを伴わない”形式でデータを表示すると都合がよい。この表現方法は,マンハッタンの直線的な建物
の輪郭を思わせることから,マンハッタン図と呼ばれている。
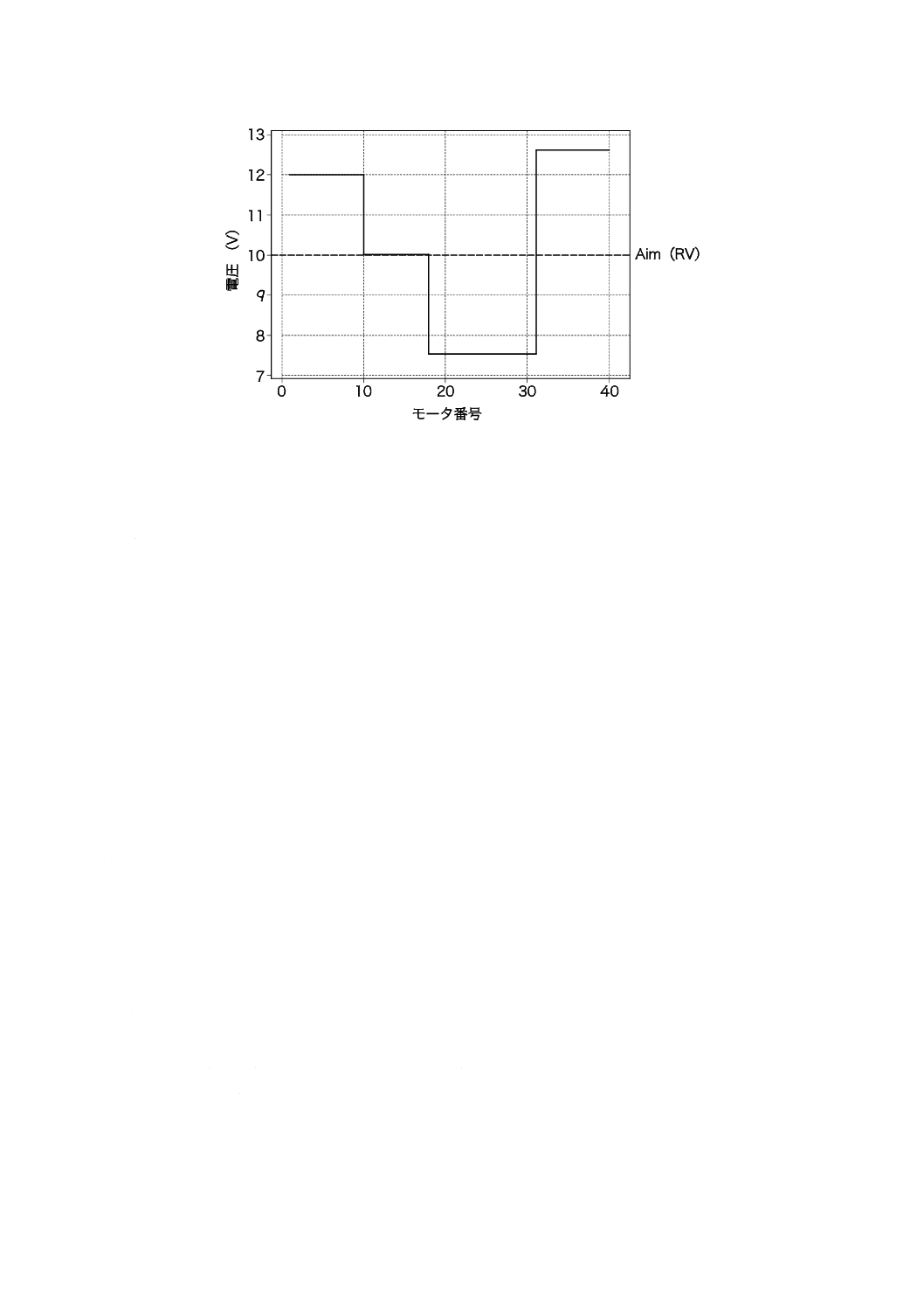
マンハッタン図は,6.6.3のa)〜d)によって計算した電圧をモータの生産順に従来の方法で打点して単純
に表示したものである。これを図3に示す。図3によって,図1 c)の累積和データと図1) a)の本来のノイ
ズのあるデータとの比較ができる。
13
Z 9020-4:2018 (ISO 7870-4:2011)
図3−モータデータのマンハッタン図
図3並びに図1のc)及びa)は,工程解析に用いる累積和図の役割及び価値をまとめたものである。これ
らの図は,数学記号又は正規の統計的表現を用いることなく,容易に理解できる言語及び簡易な視覚に訴
える方法を用いることで何ができるかを示している。
マンハッタン図は簡易で,曖昧なところがないために,累積和図を専門的な中間段階とみなし,データ
をマンハッタン形式で簡単に表記し,専門知識を必要としないコミュニケーション,理解及び応用を促進
するときに役立つことがある。
7
累積和による異常判定ルールの基礎
7.1
異常判定ルールの必要性
累積和管理図の解釈を合理化するためには,異常判定ルールが必要な場合がある。適切な異常判定ルー
ルが異常を示した場合,工程の性質に応じて何らかの処置がとられる。一般的な処置は,次のようなもの
である。
a) 工程管理用の場合,工程条件の調節
b) 改善の場合,変化に対する根本原因の特定
c) 予測の場合,予測モデル又はそのパラメータの分析,及び必要ならば調整
7.2
判定を下すための基礎
判定を下すときの基準を定めることは明らかに必須の条件である。
異常を検出するための有効な基礎を得るためにシステム内の“ノイズ”の適切な定量的尺度が必要であ
る。何がノイズであり,何が異常となるかは,取得する観測値の数及び頻度,サンプル又は群の構成方法
など,採用するモニタリング方法によって決まる。また,変動を定量化するために用いる尺度もこの問題
に影響する。
通常は,次のいずれかの統計的尺度によって,固有の変動を計量する。
a) 標準偏差 個々の観測値の累積和を打点する場合。
標準偏差を計算するための個々の観測値は,工程が均質なセグメントからとることが多い。そのと
き,この操作は,どのような異常を判断するかによって,より面倒なものとなる。一連の平均のシフ
ト若しくはいつもの工程変動の大きさの変化,又はその両方を示すような,固有の偶然変動よりも大
14
Z 9020-4:2018 (ISO 7870-4:2011)
きい異常原因による変動を取り出す。
b) 標準誤差 平均,メディアン,範囲など,観測値の群の幾つかの統計量の累積和を打点する場合。
群分けのコンセプトは,群内の変動は偶然原因で構成され,全ての異常原因による変動は群間で起
こることである。このとき,累積和管理図の第一の役割は,偶然原因による変動と異常原因による変
動とを区別することにある。したがって,群の選択は極めて重要となる。例えば,群を生産工程から
毎時連続して取られた四つのサンプルで構成する場合と,15分ごとに取られた毎時四つのサンプルで
構成する場合とでは,判定の基礎となるばらつきが,非常に異なったものになる。
前者の事例の標準誤差は,後者の事例と比べると小さなものになる。意思決定の基礎として連続し
た部分を用いた累積和管理図ができるが,15分おきの変動の場合は管理図が別のものになる。基本と
なるばらつきの適切な尺度は,いかなる変化を異常とみなすかによる。
しかし,標準偏差又は標準誤差のような,信頼できる定量的尺度を設定するための,十分な期間にわた
り安定性が継続するという必要条件は,累積和管理図に考えられる応用分野の一部では制限が厳しすぎる。
例えば,連続工程の観測値は,小さくて重要ではない平均の水準の変動を示すことがある。こうした変
動を基準にして,系統的又は持続的変化を判定する必要がある。例えば,次のような場合である。
a) 工業プロセスが,サーモスタット又はその他の自動制御装置によって制御されている。
b) 投入された原材料の質が,仕様に反することなく多少の変動を受けることがある。
c) 患者の治療への反応を観察すると,食事,病院又は日常生活によって多少の代謝の変化が生じること
があるが,治療の効果は,全体にわたる一般的な変動を基準にして判断することが望ましい。
その一方で,サンプルは,複数の発生源(行政区域,プラント,機械及びオペレータ)からの出力又は
観測値を含むことがある。そのような場合,局所的な変動が多すぎて,全平均がシフトしているかどうか
を評価するための現実に即した基準が定められない。このために,発生源の組合せから生じるデータは,
注意して取り扱う必要がある。要因となる各発生源内の局所的特異性が見落とされることがあるからであ
る。さらに,情報源間の変動が,時間の進行につれて,全システムで発生する変化を隠してしまうことが
ある。
累積和手順の重要な前提の一つは,工程の標準偏差σが安定していることである。そのため,累積和手
順を構築する前に,いかなる工程についても評価を行って,信頼のできるσの推定値が得られるように,
工程が統計的管理状態にあるかどうかを(R管理図,s管理図又は移動範囲管理図を用いて)調べることが
望ましい。
観測値間の自己相関が現れることもある。すなわち,ある観測値が,次の観測値に多少の影響を与える
場合もある。負の自己相関の一例は,バルク材の使用を推定するために連続的なゲージの読みを使用する
ことで,ある場合の過大な推定値が,次の読みでは過少な推定値を生み出しがちになる。もう一つの例は,
ある月の過大な注文を,翌月の過少な注文で埋め合わせることである。正の自己相関としては,幾つかの
工業プロセスにおいて,あるバッチの材料が,その前のバッチ及び次のバッチのものと部分的に混ぜ合わ
せられることである。
予算及び会計年度末,プロジェクトのマイルストーン及び契約期限が,期間単位のコスト,売上高など
のような連続的な営業成績の配分に影響することがある。
このような側面を考慮すると,データの系列又は順序における変動の定量的尺度,及びそれが適切とな
る状況を検討する必要がある。
15
Z 9020-4:2018 (ISO 7870-4:2011)
累積和を用いた意思決定の基礎となる変動の尺度を,附属書Aに示す。また,状況に応じて,いずれを
選択するかについても,推奨事項を示す。
7.3
異常判定ルールの有効性の測定
7.3.1
基本コンセプト
異常判定ルールの理想的な性能は,最低でも,実際の変化が事前に決めた大きさの場合はそれを直ちに
検出し,実際に変化がない工程の場合は,誤報を発することなく,いつまでもそのまま継続するというも
のである。現実には,これは達成できない。単純で,便利な異常判定ルールの実際に有効な尺度は,平均
連長(ARL)である。
ARLは,現実に変化があるという判定を下すまでに採取するサンプル数の期待値である。
実際に変化がなければ,ARLの理想値は無限である。そうした状況での現実的な目標は,ARLを大きく
することである。反対に,ARLの理想値は1であり,実際に変化があるときは,次のサンプルを採取した
ときに変化が検出される。このように,ARLの選択は,これら二つの相容れない要求事項の妥協点である。
工程が変化していないときに誤った判定を下すと過剰な管理につながり,実際にはばらつきを増加させる。
また,工程が変化したときに適切な処置を講じないと,管理不足につながり,ばらつきを増加させ,生産
コストの増大も招く。
当然,ARLそのものは期待値であり,実現値には統計的変動が存在する。ときには幸運にも,長期にわ
たって誤報を得ることもなく,変化があれば非常に速やかに検出する。ときには,サンプルの不運な連が
誤報を発したり,異常とみなされずに実際の変化を隠してしまったりすることがある。このような変動の
実際のパターンには,時々注意する必要がある。それでも,ARLは,一般に異常判定ルールの有効性の妥
当な尺度とみなされている。これをまとめると,その目的は次のようになる。
真の工程の状態
必要な累積和応答
理想的応答
目標又はその近傍
大きいARL(誤報が少ない)
ARLは無限大
目標からの著しいかい(乖)離
小さいARL(迅速な検出)
ARL=1
7.3.2
ARLの計算例
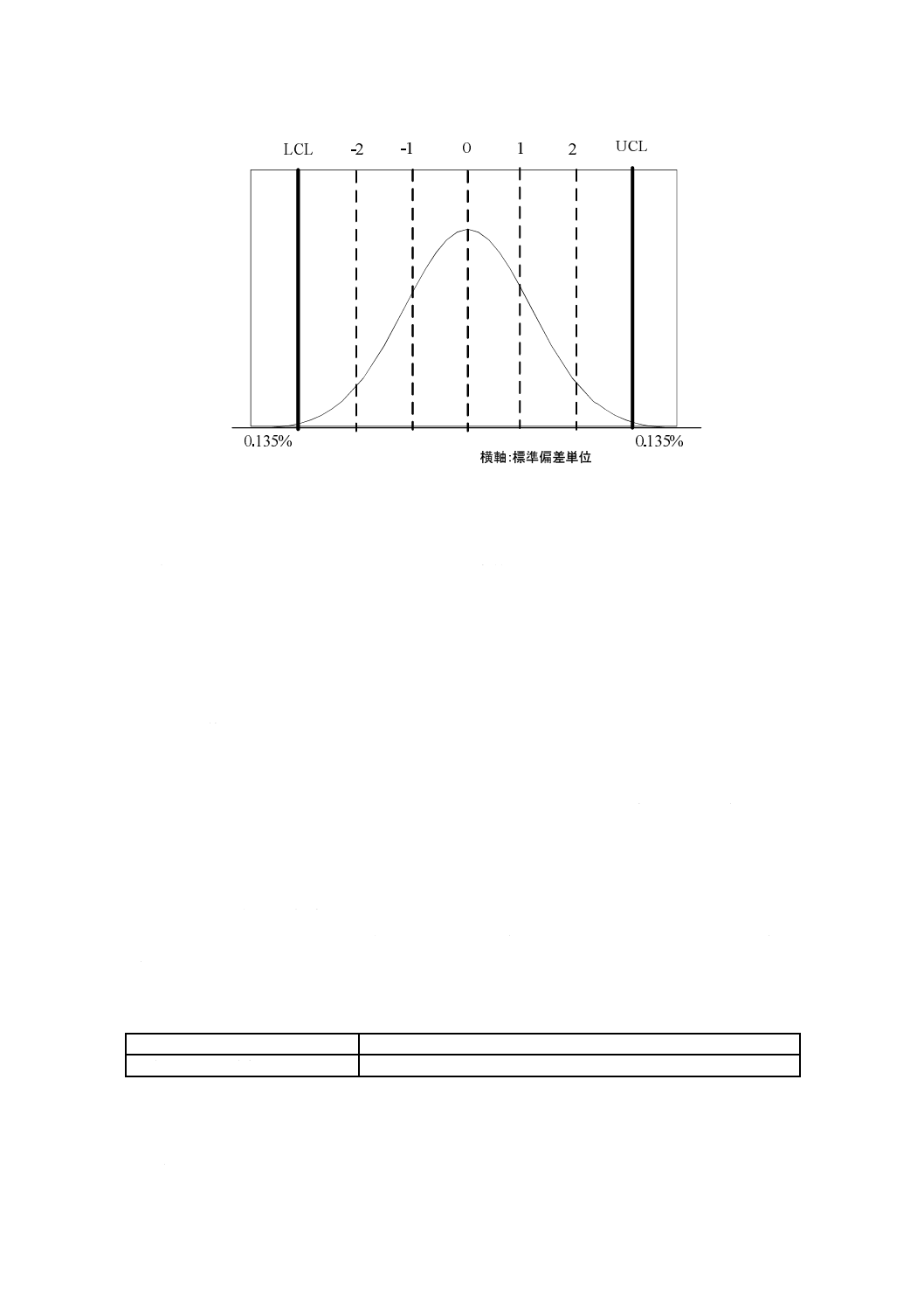
ARLのコンセプトは,累積和管理図固有のものではない。管理限界が中心線から±3の標準偏差に設定
された正規分布をとる標準的なシューハート管理図を例にとる。これを図4に示す。
ここに示す分布は,平均が0で標準偏差が1である。これを“標準正規分布”という。
16
Z 9020-4:2018 (ISO 7870-4:2011)
図4−標準正規分布
工程平均が中心線上又は目標値にあるとき,平均して観測値の約0.135 %が,これらの各限界の外側に
あると予測できることが図4から見てとれる。これより容易に1/0.001 35=741が計算され,平均連長(ARL)
に変換することができる。言い換えれば,上側管理限界を超える値が見られるのは,平均して741の観測
間隔で1回だけと予測される。このような値は,実際に,変化が起きていないレベルにおいても,間違っ
て異常を発する。
したがって,工程が目標値で進行しているとき,高いARLを保証する管理システムを設計する必要があ
る。
工程平均が依然として目標値にあって,両側限界を検討すると,ARLは半分になるので1/(0.001 35+
0.001 35)=370となる。
工程平均が,上側管理限界に向かって1標準偏差単位だけシフトすると仮定する。上側管理限界を超え
るものが,約2.28 %となることが期待される。UCLに関するARLは,この片側限界の場合,1/0.022 8=
44となる。言い換えると,平均して約44の観測間隔で,1標準偏差単位だけ平均がシフトしたことを知ら
せる。
ここで両側限界を検討すると,工程平均がLCLから4標準偏差単位だけ離れているので,LCLの下に
なるのは0.003 2 %だけと予測される。1/(0.000 032+0.228)は片側限界で計算されるARLに実質的には影
響を与えないので,平均が1標準偏差単位をシフトした場合,両側限界のARLは片側限界の場合のARL
とほぼ同じ,すなわち44となる。
まとめると,次のようになる。
平均が目標値
両側限界のARLは片側限界の半分
平均のシフトが増加
両側限界のARLは片側限界のARLに近い
当然,実際には,警戒限界,平均上下の連などを加えた他のシグナルルールで,シフトのより迅速な検
出を確保するが,工程が目標上にあるときに誤報の増加を招く。シューハート管理図は,その簡潔さ,及
び大きなシフトを発生させる独立した異常原因を検出する上での有効性をもつため,極めて魅力的でポピ
ュラーである。
17
Z 9020-4:2018 (ISO 7870-4:2011)
しかし,シューハート管理図では,例え誤報の程度に重大な悪影響を与えることのない小さなシフトが
持続しても,そのシフトを異常とみなすには固有の限外があることが知られている。この点は,目標上に
あるときに長いARLを維持しながら,より迅速にシフトを検出するには,全く別な方法が必要であること
を示している。このような場合に,累積和管理図が適している。
8
異常判定ルールのタイプ
8.1
Vマスクのタイプ
累積和図に異常判定ルールを組み込んだ方法としてVマスク法がある。Vマスク法にはやや形式の異な
る次の四つのタイプがあるが,原理及び効果の点では同一である。その目的について,8.2〜8.6で記載す
る。
a) トランケートVマスク法(truncated V-mask)
b) セミパラボリック累積和管理図(semi-parabolic mask)
c) スナブノーズ累積和管理図(snub-nosed V-mask)
d) フルVマスク法(full V-mask)
注記 この規格では,トランケートVマスク(truncated V-mask)がVマスクの基になるので,以下,
単に“Vマスク法”という。
8.2
Vマスク法
8.2.1
構成及び寸法
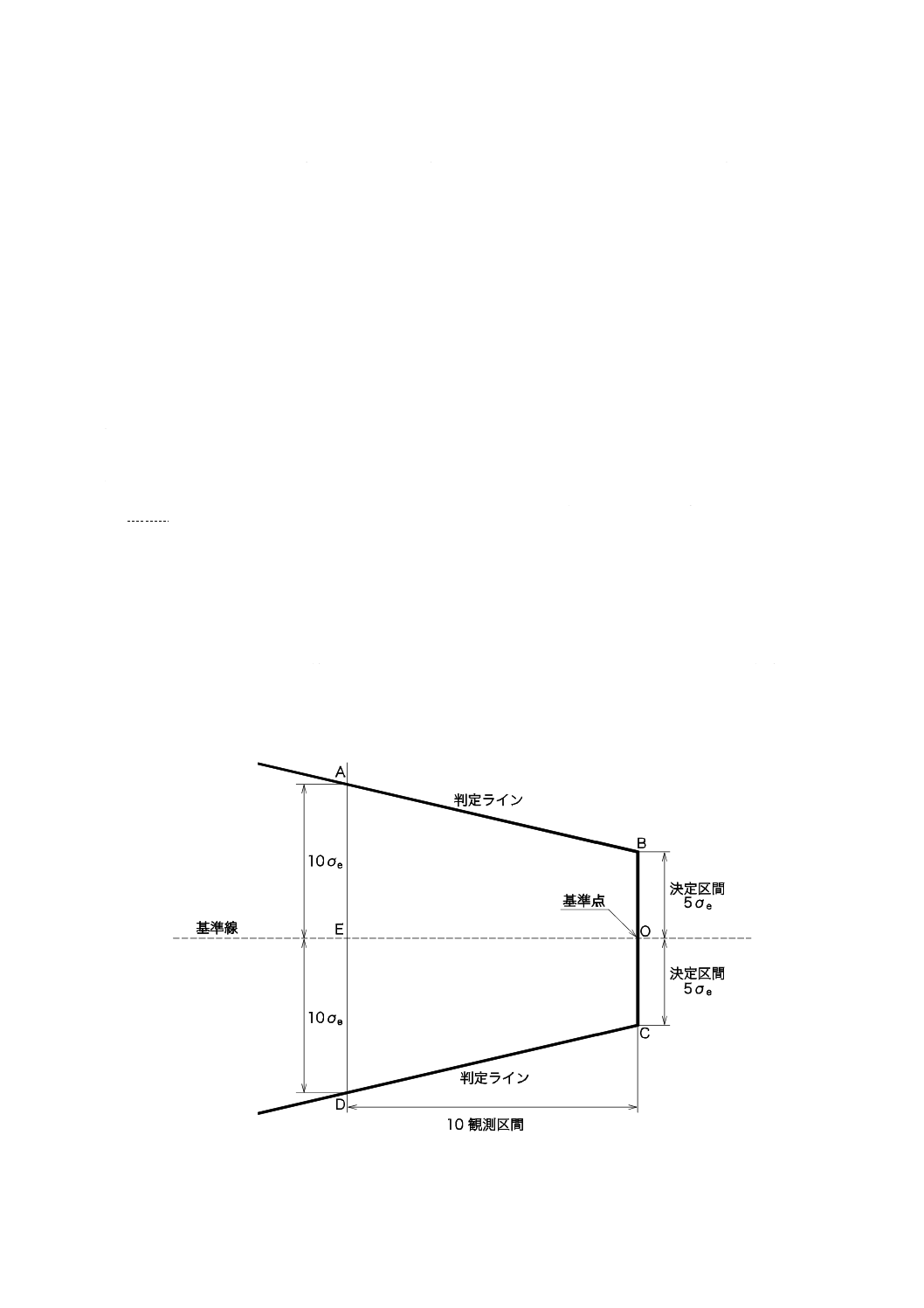
図5に,汎用されるVマスク法を示す。このVマスクは,図中Oで示す基準点を含んでいる。2本の垂
線,OB及びOCが基準点からそれぞれ長さ5σe単位(すなわち,H=5σe)が引かれている。この2本の線
分が決定区間である。2本の斜線,BA及びCDを判定ラインといい,プロットした累積和点を包含するよ
うに,必要に応じて延長してもよい。EOの長さは10観測区間に等しく,垂線EA及びEDの長さはいず
れも10σe単位(すなわち,傾きがF=0.5σeとなるようにする。)となる。
図5−汎用Vマスク法の構成及び寸法
18
Z 9020-4:2018 (ISO 7870-4:2011)
工程変動の標準偏差0.2の,実際のスケールに合わせたVマスク法を図6に示す。ここで標準誤差では
なく標準偏差を使用するのは,平均値でなく個々の観測をモニタリングするように,特定のマスクが作り
出されるからである。
図6−固有の偶然変動のスケールに合わせたVマスク法(標準偏差0.2)
8.2.2
Vマスク法の応用
Vマスク法は,図上に水平な基準線を引き,累積和管理図上に,選択し,プロットする値の上に基準点
を設定して使用する。継続的な管理状況では,この選択し,プロットする値は,通常,最新の点となる。
累積和の経路がVマスクの判定ラインの傾き(又は図5に示すBAの延長線及びCDの延長線)の中に
あれば,そのプロットした点まで,平均的には著しい変化が示されない。工程が管理されている状況下で
は,目標値に関して統計的管理状態にあるという。ただし,累積和の経路がVマスクの判定ラインの傾き
の外側にあれば,目標値から著しくかい(乖)離している。工程管理では,その工程を異常という。
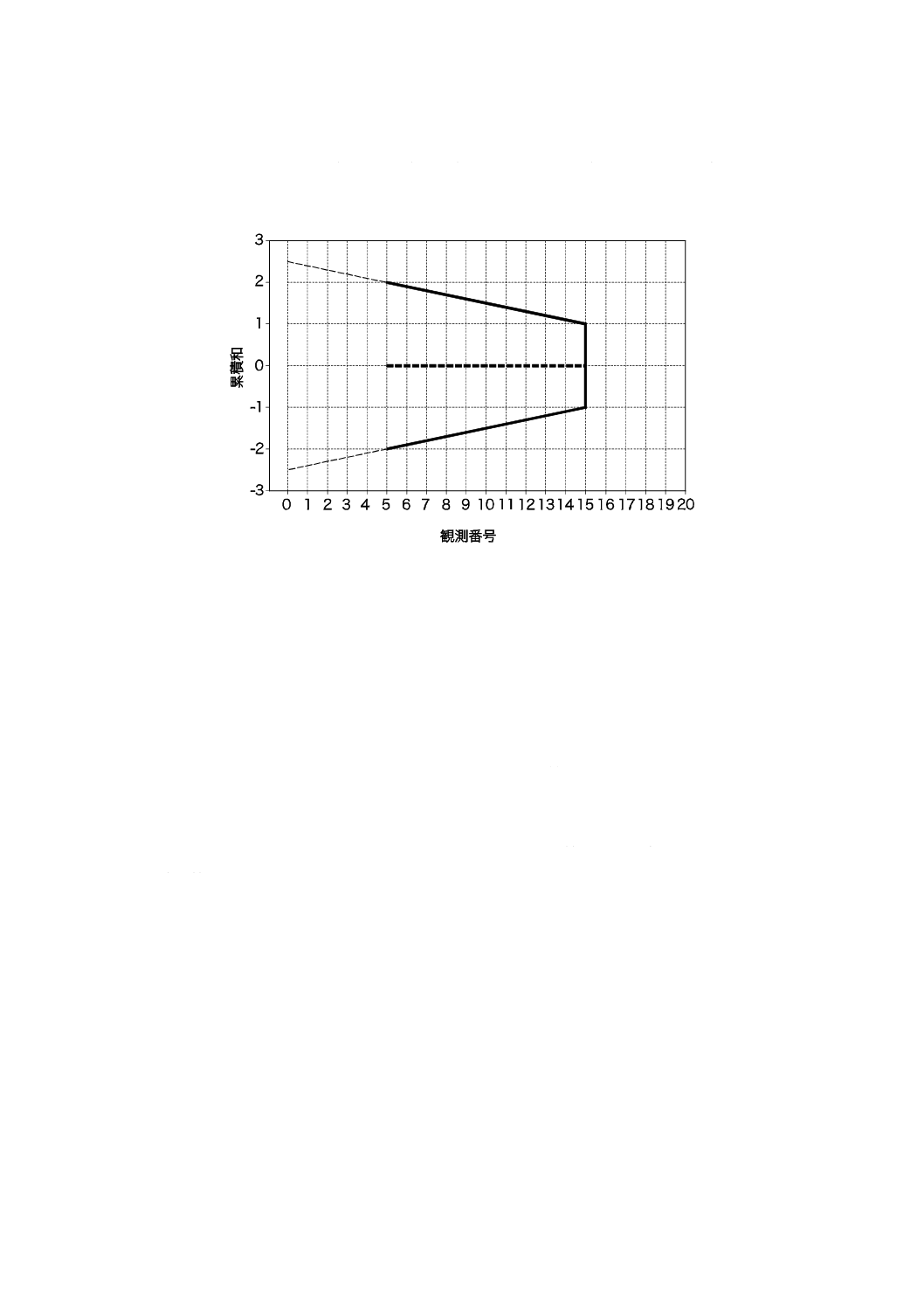
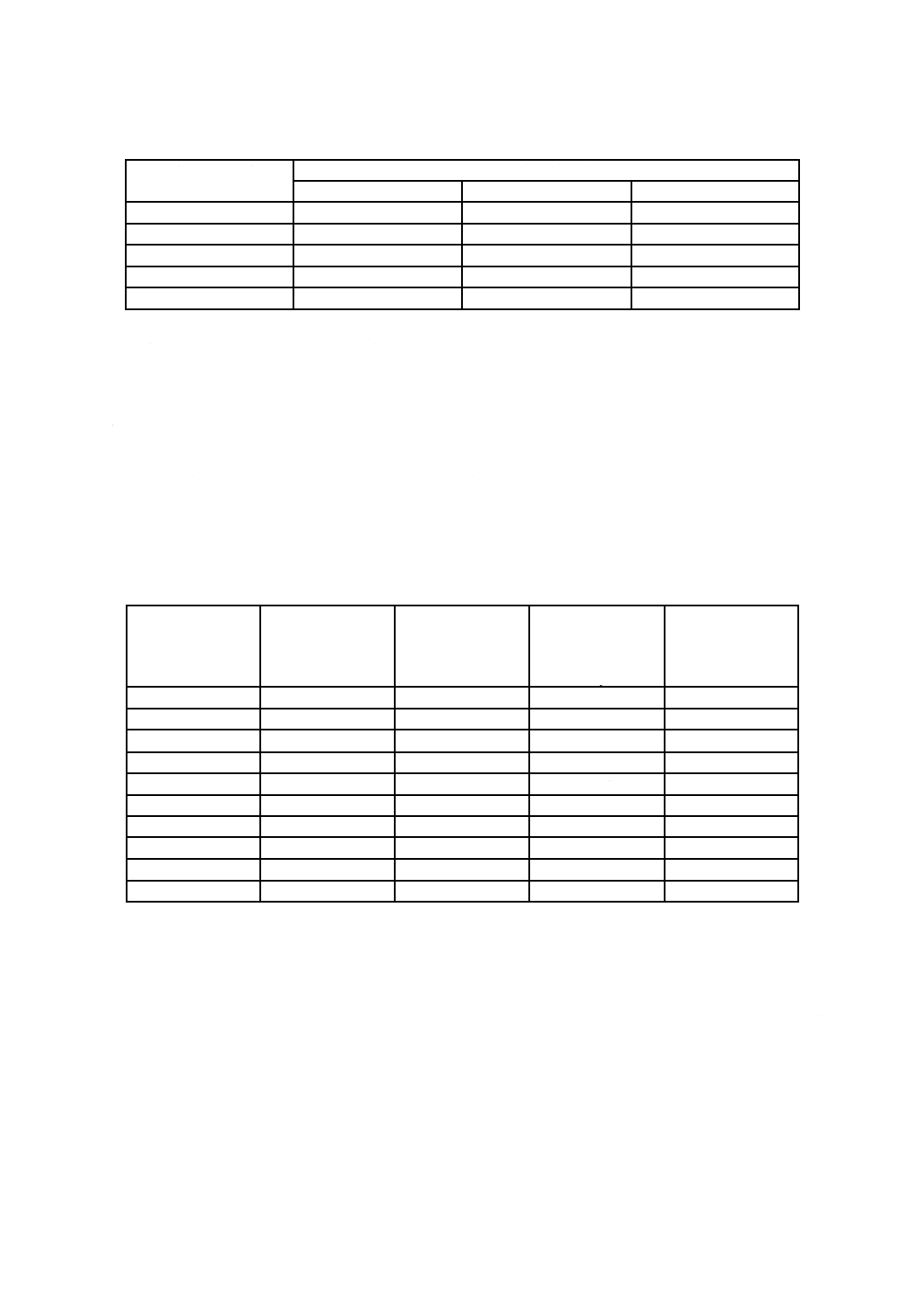
図7は,目標値からの著しいかい(乖)離が検出されない“正常”状況及び二つの“異常”状況(一つ
は表示される値に大きな減少がある状況,さらにもう一つは大きな増大が認められる状況)を示したもの
である。図7の三つの図では,標準偏差を0.2としている。累積和管理図の作成に用いた目標値は,工程
の目標平均に等しい。
現状況の判断は,データの累積和に応じて,Vマスクをかぶせることによって行う。
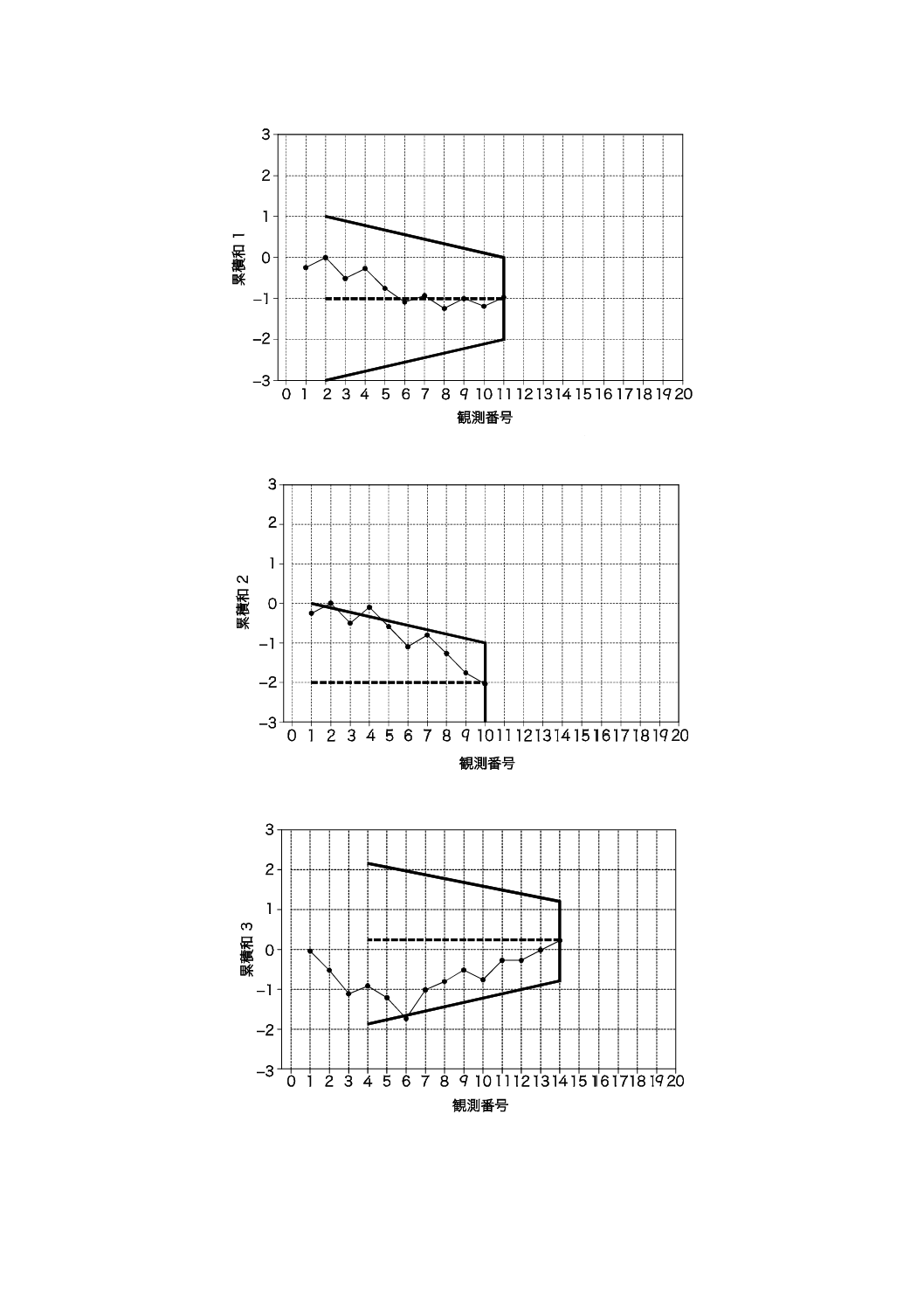
19
Z 9020-4:2018 (ISO 7870-4:2011)
a) 目標値に関して工程平均に有意な変化がない
b) 目標値に関して工程平均が有意に減少
c) 目標値に関して工程平均が有意に増大
図7−工程平均の有意な変化を検出するためのVマスク法の使用の図解
20
Z 9020-4:2018 (ISO 7870-4:2011)
図7 a)は目標値よりも低い工程平均を示しているが,Vマスクはまだ,この変化を有意なかい(乖)離
と認めていない。
図7 b)は,工程平均が目標値よりも有意に低いことを示している。有意なかい(乖)離は観測点10まで
検出されないが,図からは,工程平均が観測点1から早くも低くなっているように見える。観測値を通過
するVマスクの判定ラインの傾きを見れば,工程の実際の平均を評価することができる。これは,工程を
目標値に修復するために必要な修正量の大きさと,観測点1で何が起きたために工程が最初から,このよ
うな低いレベルになったかを特定するための診断情報の手引となる。
図7 c)は,工程平均が目標値よりも有意に高いことを示している。図は,観測点14まで有意であること
を示していない。工程が観測点6まで目標値よりも低い状態で進んでいるように見えるが,これは異常で
あると判断するには十分なものではないと見てとれる。観測点6に続いて,レベルが目標値よりも高いレ
ベルに変化している。観測点6まで線の傾きと観測点6以降の線の傾きとを,原点を含めて計算すること
によって,修正のためのツール及び診断情報が得られる。
上側規格限界又は下側規格限界のいずれかだけを適用するときは,片側管理が適切である。そうすれば,
ハーフマスクを使用することができる。上方又は下方シフトを基準にしてモニタリングするときは,マス
クの下側又は上側部分だけが必要となる。ただし,それでもフルVマスク法を推奨するのは,その簡易さ
及び情報量のためである。無関係な方向へのシフトがあれば,仕様の観点からそのシフトを無視してもよ
いし,より望ましい方向への顕著な移動に注目するように使用してもよい。
8.2.3
平均連長
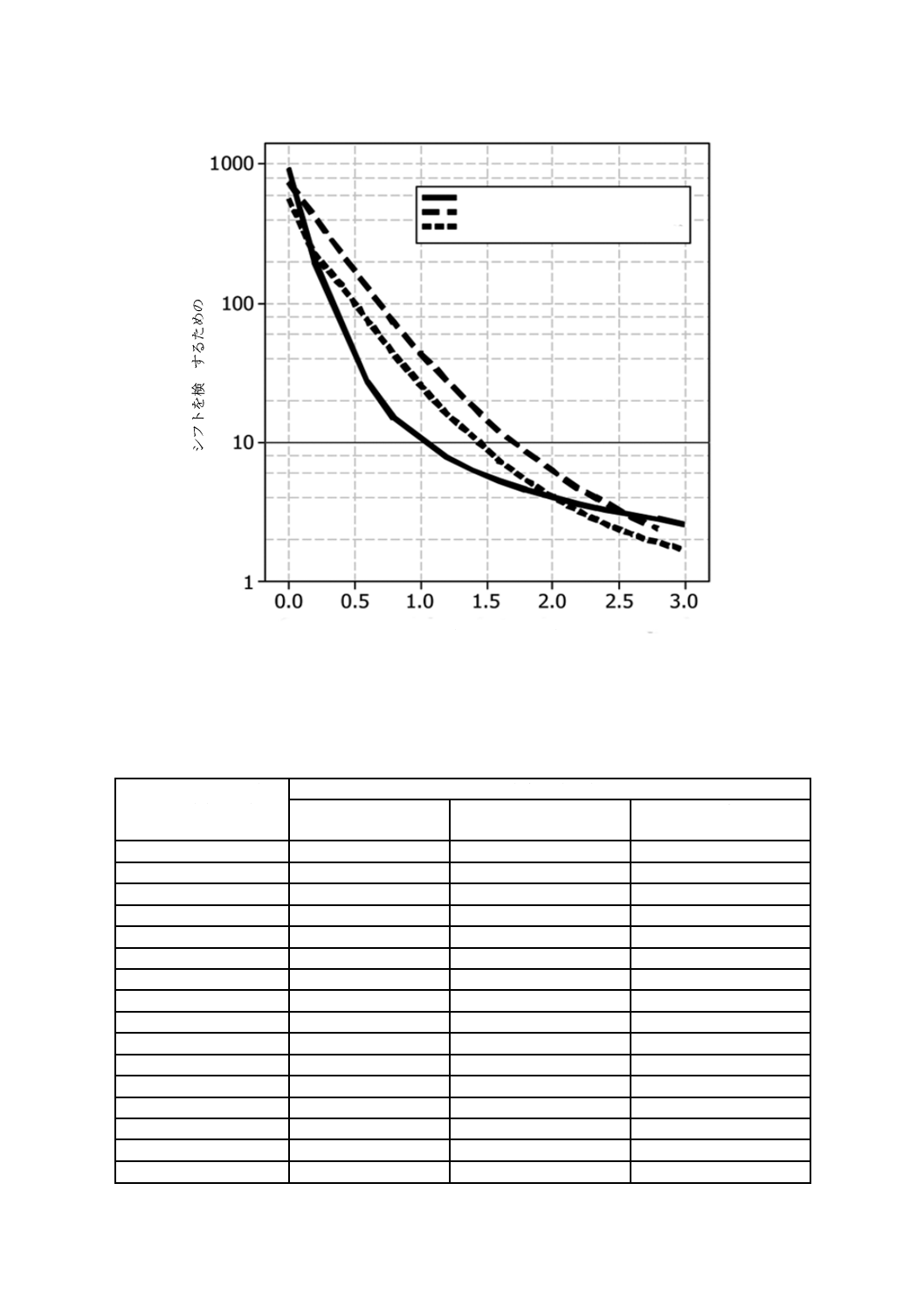
図8に示す範囲内の汎用Vマスク法の平均連長(ARL)特性を,プロットした統計量の標準偏差又は標
準誤差を用いて表4に記載する。累積和管理図のARLを,定着しているシューハート管理図による二つ
の異常判定ルールと比較する。
これらの規則は,次のものである。
− シューハート管理図の異常判定ルール1 中心線から±3の標準偏差外の点,すなわち,処置限界又は
管理限界
− シューハート管理図の異常判定ルール2 中心線から±2の標準偏差外の連続した2点,すなわち,警
戒限界
注記1 プロットした統計量は,標準偏差をσとした正規分布に従うと仮定している。
注記2 平均連長(ARL)は,平均の片側管理を指す。一つの目標値から両側管理を採用する場合は,
目標値のARLを半分にするが(誤報の数は倍になる。),平均のシフトが大きければARLは
影響を受けない。
注記3 ここでいう標準累積和管理図は,図5にあるようにh(決定区間の高さ)=5.0,f(判定ライ
ンの傾き)=0.5である。シューハート管理図の管理限界は,シューハート管理図の異常判定
ルール1だけに関係する。シューハート管理図の管理限界及び警戒限界は,シューハート管
理図の異常判定ルール1と異常判定ルール2とを組み合わせて適用する。
21
Z 9020-4:2018 (ISO 7870-4:2011)
図8−標準的なシューハート管理図と比較した汎用Vマスク法での
目標値からのシフト量による平均連長(ARL)
表4−2組の異常判定ルールを使用する標準シューハート管理図と比較した図5の汎用Vマスク法での
目標値からのシフトによる平均連長(ARL)
目標値からの工程平均の
シフト(単位 σe)
平均連長(ARL)
汎用Vマスク法
3シグマ管理限界の
シューハート管理図
警戒限界線をもつ
シューハート管理図
0.0
931.0
741.0
556.0
0.2
198.0
308.0
223.0
0.4
60.0
200.0
134.0
0.6
27.0
120.0
75.0
0.8
15.0
72.0
43.0
1.0
10.0
44.0
26.0
1.2
7.8
28.0
16.0
1.4
6.3
18.0
11.0
1.6
5.3
12.0
7.4
1.8
4.6
8.7
5.4
2.0
4.0
6.3
4.1
2.2
3.6
4.7
3.2
2.4
3.3
3.7
2.6
2.6
3.0
2.9
2.2
2.8
2.8
2.4
1.9
3.0
2.6
2.0
1.7
汎用Vマスク法
3シグマ管理限界のシューハート管理図
警戒限界線をもつシューハート管理図
シ
フ
ト
を
検
出
す
る
た
め
の
A
R
L
シフト(標準偏差の倍数)
22
Z 9020-4:2018 (ISO 7870-4:2011)
平均連長(ARL)は,次のように異常判定ルールの有効性の指標である。
− 目標値のARLが大きければ大きいほど,誤報の確率が低くなる。
− 目標値の平均からのかい(乖)離点におけるARLが小さければ小さいほど,変化の検出が迅速になる。
図8及び表4は,次のことを示している。
a) 累積和管理図のL0(目標値でのARL)は,±3の管理限界をもつシューハート管理図のものより大き
いのに対して,管理限界及び警報限界をもつシューハート管理図は,L0の値がはるかに小さい。した
がって,三つの管理図のうちで,累積和管理図は誤報率が最も小さく,管理限界処理及び警報限界を
もつシューハート管理図は誤報率が最も高い。
b) 2σe単位までのシフトの場合,累積和管理図のARLは,他のいずれの管理図のARLより小さい。特に
0.4σe単位から1.4σe単位までの区間でそれが顕著である。
c) 2σe単位を超えるシフトの場合,管理限界処理及び警報限界をもつシューハート管理図は,累積和管理
図よりも迅速に応答する。2.4σe単位を超えるシフトの場合,管理限界処理及び警報限界をもつシュー
ハート管理図は,累積和管理図よりも迅速に応答するが,シューハート管理図の迅速な応答は,誤報
率の増大という損失を招くことになる。
8.2.4
平均連長についての概評
第一に,汎用又は標準Vマスク法の寸法は,1標準誤差単位(1σe)のシフトの検出に特化するように設
計されている。これ以外のシフトに注目する場合は,これとは異なるh及びfの値を使用する。構成又は
形状が短縮型とは異なるVマスクを選択し,ARL特性,すなわち,シフト検出性能を挙げてよい。その例
としては,セミパラボリック累積和管理図及びスナブノーズ累積和管理図があるが,この二つについては
それぞれ,8.4及び8.5に記載する。
第二に,補足的な連規則がシューハート管理図と併用されることが多い。そのようなものとしては,“平
均の片側での7連続点”及び“全てが増大又は減少している7連続プロット区間”がある。こうした規則
の問題点は,工程平均が目標値にあるとき,ARLの値を著しく下げること,すなわち,誤報のリスクを増
大させることである。
第三に,ARLの頑健性に影響する要素が幾つかあることが挙げられる。例えば,変動の基本パターンの
形状,σeの値,観測値の独立性などである。表4及び図8に示すARL表は,次の三つの事項を前提にして
いる。
a) 観測値は正規分布している。
b) 標準偏差は既知である。
c) 連続観測は統計的に独立している。
正規分布は対称形である。一般に,片側管理で,シフトする方向と同じ方向に重い裾をもつ分布のわい
(歪)度は,目標値におけるARLを縮めることになるが,平均のシフトが大きい場合は,ARLにほとん
ど影響を与えない。反対に,シフトの方向に分布の裾が軽い場合,目標レベルでのARLは著しく長くなる
が,シフトが大きい場合は,やはりARLに影響することはほとんどない。
標準偏差又は標準誤差は,通常,累積和のプロットに用いたのと同じ観測値の中から選択したもので推
定する。10 %以上の誤差はまれではない。σeを過大に推定するとARLが増加し,過少に推定するとARL
は低下する。このARLへの影響は,目標条件近辺で最も顕著であるが,シフトが大きいところでは影響が
少ない。表5に,σeを推定するときの誤差を10 %とした場合のARLのひず(歪)みを示す。
23
Z 9020-4:2018 (ISO 7870-4:2011)
表5−不正確な値の標準誤差σeがARLに与える影響
目標値からの平均の
シフト(単位 真のσe)
平均連長(ARL)
σeを10 %過大に推定
正しいσeの推定値
σeを10 %過少に推定
0.0
3 000.0
930.0
410.0
0.5
45.0
38.0
35.0
1.0
10.0
10.5
10.0
1.5
6.0
5.8
6.0
2.0
4.4
4.1
4.5
正の自己相関はARLを小さく,負の自己相関はARLを大きくする傾向がある。
ここに挙げた三つの前提の影響は,累積和管理図に特有のものではなく,他の管理図法にも当てはまる
ものであることに注意することが望ましい。
8.3
代替設計アプローチ
平均のシフトの広い範囲にわたって,性能特性の改善を目的にした代替設計アプローチは,セミパラボ
リック累積和管理図(8.4参照),スナブノーズ累積和管理図(8.5参照)又は初期値を変更した(FIR)累
積和管理図(8.7参照)を用いるものである。
これらの代替設計案の性能を標準Vマスク法と比較したものを,表6に示す。
表6−各種累積和マスクの平均連長(ARL)
目標値からの平均
のシフト
(単位 σe)
Vマスク
(h=5,f=0.5)
セミパラボリック
Vマスク
(表7に指定)
スナブノーズ
Vマスク
(h=5,f=0.5及び
h=2.05,f=1.5)
VマスクFIR
(h=5,f=0.5)
0.00
465.0
235.0
300.0
448.0
0.25
142.0
113.0
114.0
125.0
0.50
38.0
36.0
36.0
29.0
1.00
10.0
10.0
10.0
6.4
1.50
5.8
5.3
5.3
3.4
2.00
4.0
3.3
3.3
2.4
2.50
3.1
2.3
2.3
1.9
3.00
2.6
1.7
1.8
1.5
3.50
2.2
1.4
1.5
1.3
4.00
2.0
1.2
1.3
1.2
8.4
セミパラボリック累積和管理図
汎用の,又は標準のVマスク法を,パラメータをh=5,f=0.5として選択した。Vマスク法のパラメー
タh及びfを,これとは別の値にして,特定のサイズの平均のシフトの迅速な応答が得られるようにして
もよい。それ以外のケースでは,食品産業のような業界では,小さなシフトを見逃さないという累積和管
理図の優れた点を残しつつ,より大きなシフトの検出速度を改善する必要がある場合には,マスクタイプ
の変更が必要となる。
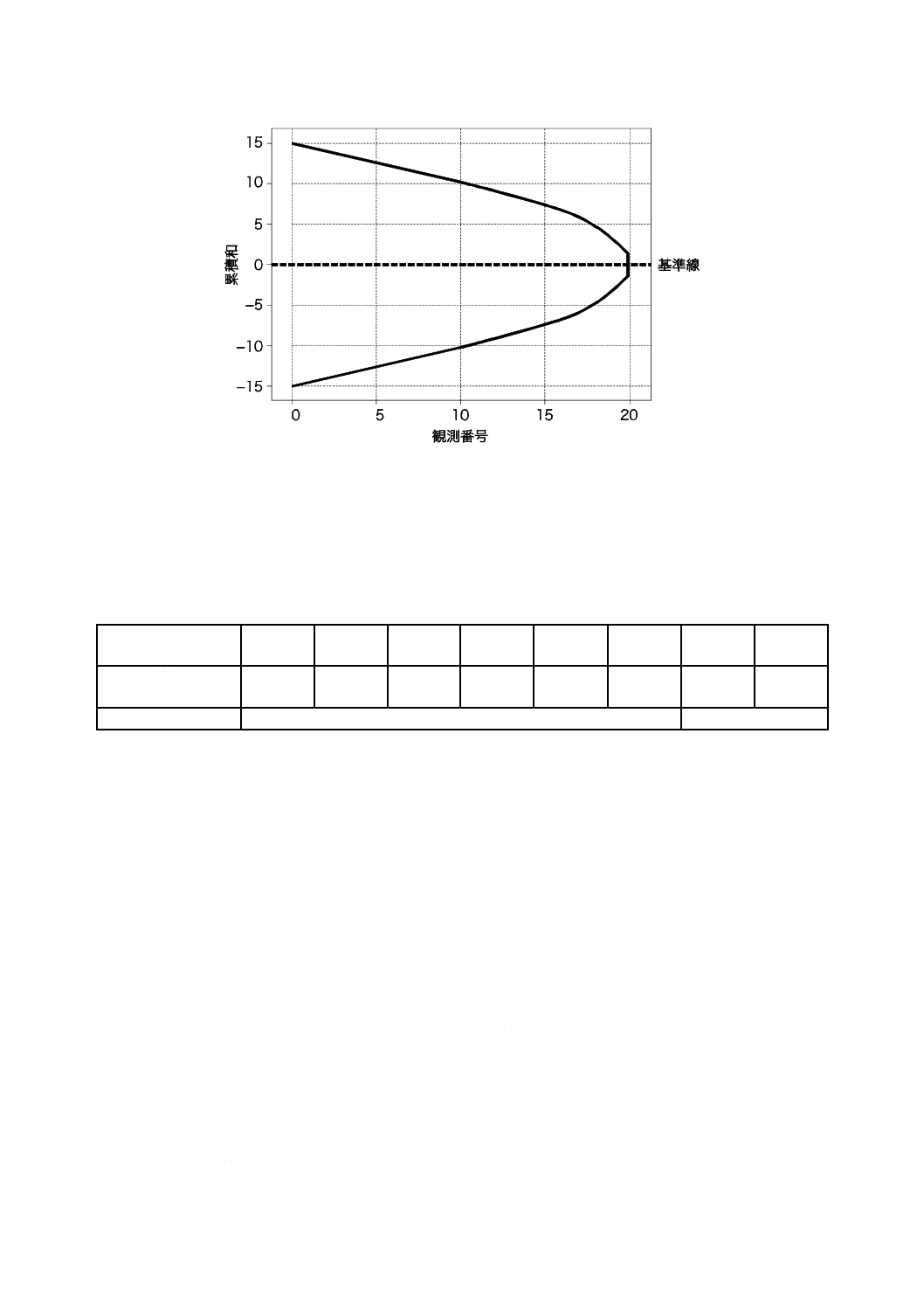
その一つはセミパラボリック累積和管理図で,図9に示すように,狭い端部近辺でVマスクに,曲線形
状が表示される。
24
Z 9020-4:2018 (ISO 7870-4:2011)
図9−セミパラボリック累積和管理図
図9のセミパラボリック累積和管理図の元になっているのは,図5の汎用のVマスク法である。ただし,
狭い端部の最後の五つの観測区間では,マスクが5σeではなく1.25σeの幅になるような曲線となっている。
マスクの作成用データを表7に示す。
表7−セミパラボリック累積和管理図作成用データ
基準(20)からの観
測区間,J
0
1
2
3
4
5
10
20
Jでの半値幅
(単位 σe)
1.25
3.10
4.65
5.90
6.85
7.50
10.00
15.00
作成の詳細
Yhalf-width of mask at J=1.25+2.00J−0.15J2
直線
セミパラボリック累積和管理図の動作性能は,次のとおりである。
a) 平均のシフトの範囲全体で,ゼロを初期値としたVマスク法の性能より優れている。ただし,これは
目標値での誤報率が倍近くなる,という損失を伴っている。
b) 標準偏差0.5より小さい変化を別にして,誤報率の点でも,平均的な変化発生の点でも,標準FIR V
マスク法の性能より劣る。
c) 標準値での誤報率に関しては,スナブノーズ累積和管理図より劣るが,平均的な変化の検出に関して
は性能が同等である。
これらの特徴は,様々な累積和管理図に対して,平均的な変化に関するARLの比較を示した表6に表れ
ている。
8.5
スナブノーズ累積和管理図
スナブノーズ累積和管理図は,セミパラボリック累積和管理図と同じ効果を達成しながら,設定手順が
より簡単になるように意図されたものである。したがって,より大きなシフトに関して,早い応答が必要
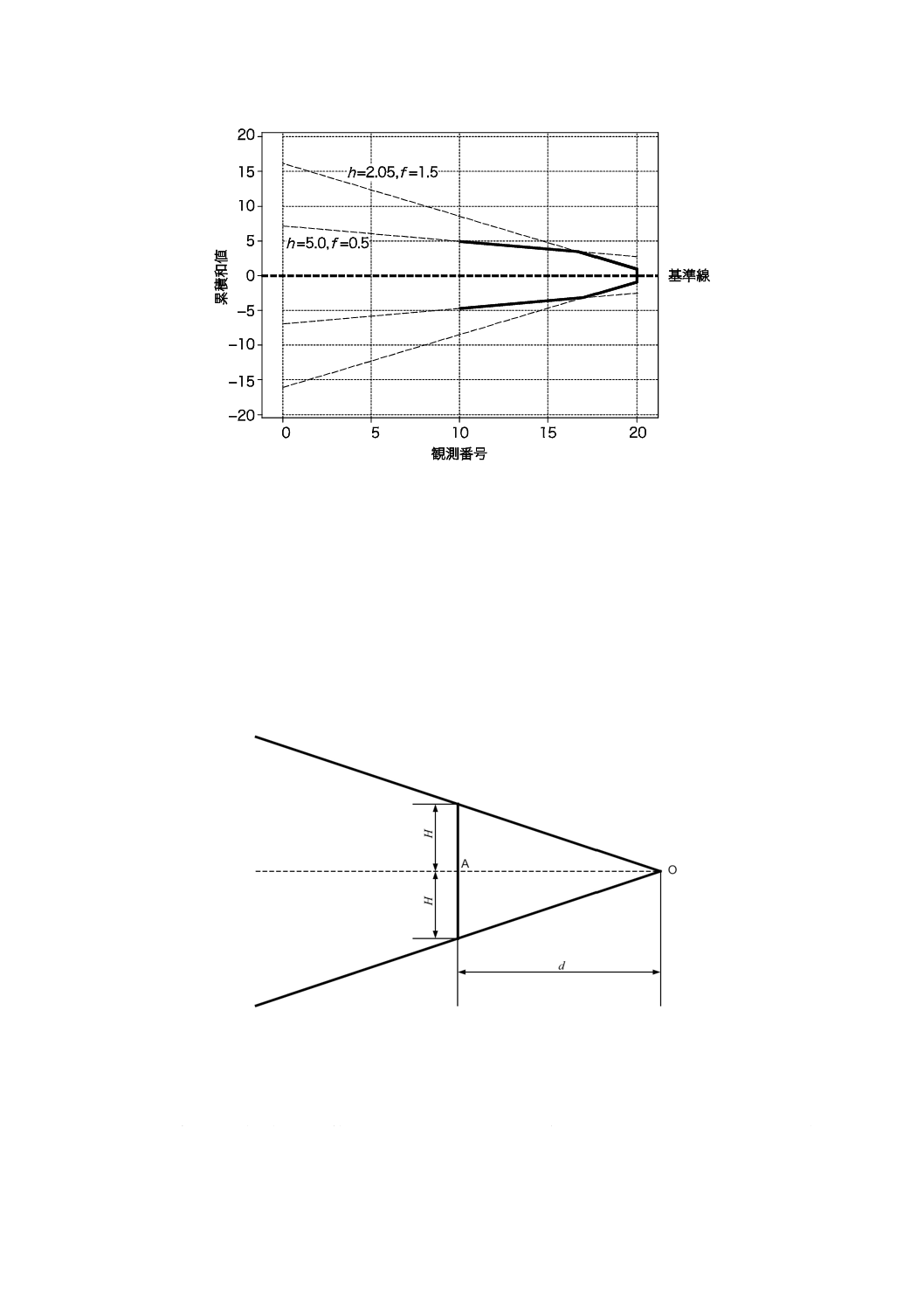
な用途で役立つ。このVマスクは,二つ以上のVマスク法を重ね合わせることによって実現する。h=2.05,
f=1.5のVマスク法をh=5.0,f=0.5の標準マスクの上に重ね合わせたものを,例として図10に示す。表
6は,このスナブノーズ累積和管理図が,広い範囲のシフトで,標準のVマスク法よりも優れた,セミパ
ラボリック累積和管理図に近い性能を示すことを表している。
25
Z 9020-4:2018 (ISO 7870-4:2011)
図10−スナブノーズ累積和管理図
8.6
フルVマスク法
図11に示すように完全なVを元にしたマスクを使用して適用してもよい。このマスクは,Vマスク法
と同一の性能があるので,説明は省略する。
図11は,判定ラインが頂点Oに置かれていることを示している。これは,基準点がないことを意味し,
頂点が累積和管理図の上に置かれているので,頂点は,問題となる最新の観測点より先(右)の距離OA
である。OAは,リード距離dと呼ぶ。特性は既出の標準のVマスク法と同一であり,H=5σe,d=10観
測単位である。
図11−フルVマスク法
8.7
初期値を変更した(FIR)累積和管理図
初期値を変更した(FIR)累積和管理図は,平均がシフトした場合のARLを小さくし,目標上のARL(こ
れは普通の決定基準と同等のもの)を著しく減少させることなく検出できることを目指したものである。
26
Z 9020-4:2018 (ISO 7870-4:2011)
言い換えれば,目的は,誤報率をほぼ変化なく維持しながら,シフトさせて迅速に応答させることにある。
表6の第2列と第5列とを比較すると,初期値を変更した累積和管理図が,範囲全体での平均のシフト
への応答がより迅速に(0.5σeで38でなく29,1σeで10でなく6.4),目標上のARLは448で465とほぼ同
等であることが分かる。
表6は,初期値を変更した累積和管理図が,範囲全体でセミパラボリック累積和管理図又はスナブノー
ズ累積和管理図よりもシフトへの応答が迅速となり,同時に目標上のARLが断然優れていることも示して
いる(初期値を変更した累積和管理図で448,セミパラボリック累積和管理図で235,スナブノーズ累積和
管理図で300)。
初期値を変更した累積和管理図では,ゼロから累算するのではなく,累積和の初期値にアドバンテージ
が与えられる。このアドバンテージに都合のよい値は,一般に決定区間の半分,h/2とすることが認めら
れている。
初期値を変更した累積和管理図の考え方は,累積和が始まる前,又は始まるときに工程に何らかの変化
があるならば,累積和を,それが進む方向にある初期値を設定することは,平均シフトの検出を早めるこ
とになるということである。その一方で,工程に変化がなければ,累積和は当然,ゼロの方に後退し,通
常のゼロスタート累積和と同じ挙動をとる。
表形式による累積和管理図の設計(8.8参照)と併用するときに,上方累積和と下方累積和との両方を一
緒に初期値設定することが多い。
8.8
表形式による累積和管理図
8.8.1
理論的解釈
累積和管理図の主な目的は,ときには,系列データを参考となるように図示することではなく,単に標
準外の状態を検出することにある。そうであれば,累積和を図示する代わりに,表形式で記録するのが望
ましい。この場合は,通常の累積和管理図で用いるVマスクに代わって,数値による異常判定ルールを適
用する。
このようなスキームを,表形式による累積和管理図と呼ぶ。
Vマスクは,傾きで変化を検出する。その決定区間hσeは,累積和点の一定のばらつきを認めている。
マスクの判定ラインの傾きは,“目標値±fσe”の平均の工程レベルに相当する。
表スキームでは,累積及び作図に代わって,次のことを行う。
観測値−目標値
別々に累算し,表にする。
観測値−(目標値+fσe)
上方累積和で平均の増加を検出するために,負になったときに累積和の値をリセットしてゼロにする。
累算し,表にする。
観測値−(目標値−fσe)
下方累積和で平均の減少を検出するために,正になったときに累積和の値をリセットしてゼロにする。
これによって,次のものが得られる。
“±hσe”での決定区間
これはVマスクの場合の次のものに当たる。
Vマスクの基準“hσe”から発散する傾き“fσe”の判定ライン
純粋な統計的意思決定の観点から,その効果は,相当するVマスクで得られるものと同等である。
27
Z 9020-4:2018 (ISO 7870-4:2011)
8.8.2
表形式による累積和管理図法
正規分布に従う測定データ特性の両側累積和決定区間の設定及び解釈は,次のステップを踏む。
ステップ1−累積和パラメータの設定
a) 決定区間hを定める。
b) 判定ラインの傾きfを定める。
c) 目標値Tを定める。
d) 特性の標準誤差σeを推定する。
ステップ2−累積和基準の計算
(T+fσe)及び(T−fσe)を計算する。
ステップ3−平均レベルの増加を検出するために,次の列をもつ上方表形式による累積和管理図の累積和
表を用意する。
e) 観測番号
f)
値
g) 値−(T+fσe)
h) [値−(T+fσe)]の累積和
注記 これは,Tの代わりに,同等のVマスク判定ラインの傾きfσeを加えた(T+fσe)とすることを除
けば通常の累積和プロットに用いる表と似ている。
ステップ4−平均レベルの低下を検出するために,次の列をもつ下方表形式による累積和管理図の累積和
表を用意する。
次の点を除き,ステップ3と同様である。
i)
値−(T−fσe)
j)
[値−(T−fσe)]の累積和
ステップ5−データの記入
k) データを記入し,計算を行う。
l)
累積和の値がプラスの場合 ゼロを起点として,列“[値−(T+fσe)]の累積和”の累積和をとる。累
積和がマイナスになった点で,ゼロにリセットし,累積和が再びプラスになるまでゼロから再度,累
積和をとる。累積和が決定境界hσeに触れるか,それを超えたら上方シフトの異常とする。
m) 累積和の値がマイナスの場合 ゼロを起点として,列“[値−(T−fσe)]の累積和”の累積和をとる。
累積和がプラスになった点で,ゼロにリセットし,累積和が再びマイナスになるまでゼロから再度,
累積和をとる。累積和が決定境界hσeに触れるか,それを下回ったら下方シフトの異常とする。
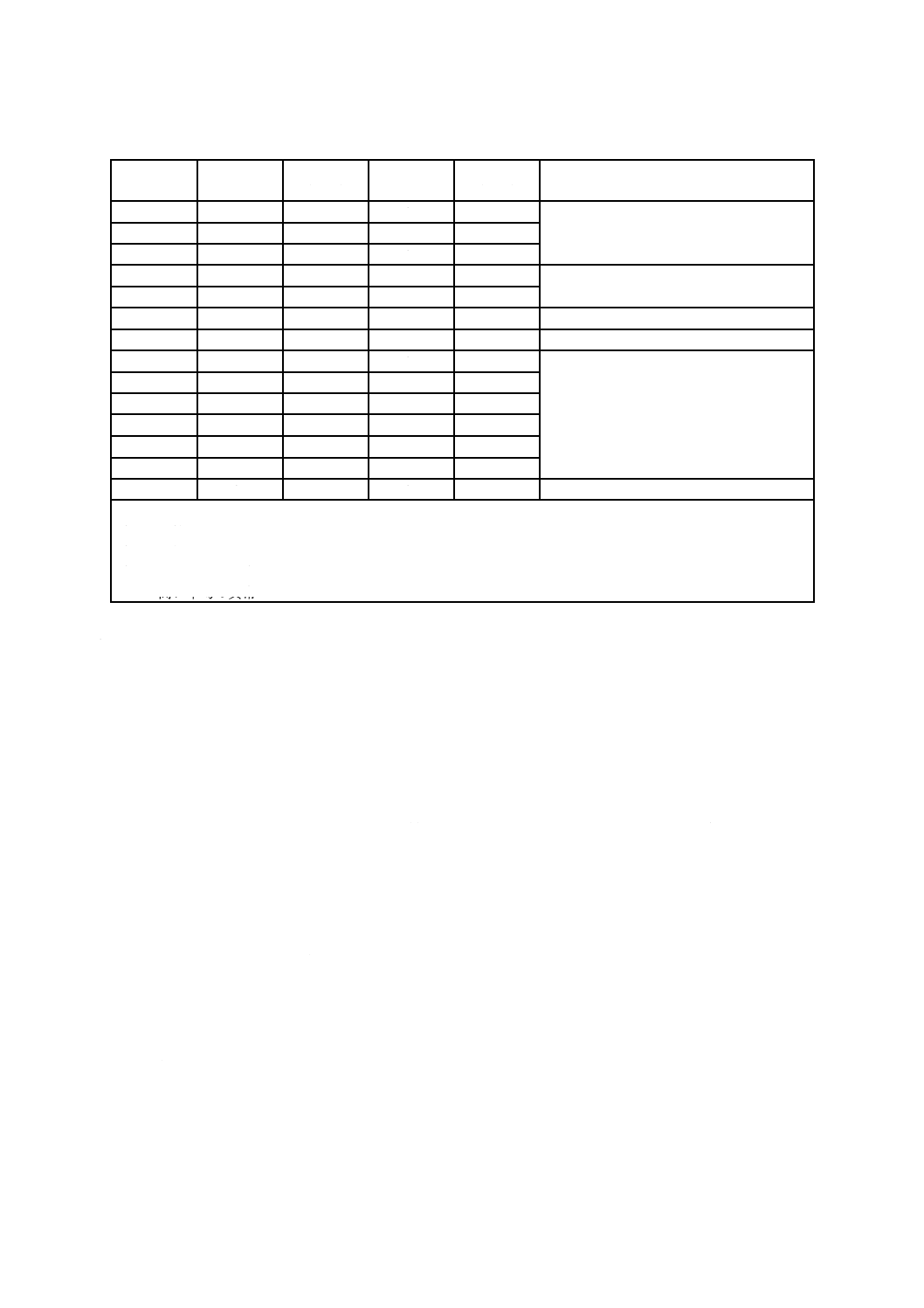
この方法の一例を,表8に示す。表形式による別の例を,附属書Bに示す。
28
Z 9020-4:2018 (ISO 7870-4:2011)
表8−表形式による累積和管理図の設計の例
値
値−11
累積和
(上側)
値−9
累積和
(下側)
参考
10
−1
0
+1
0
いずれの累積和も,工程が目標値にある
ときはゼロ
10
−1
0
+1
0
10
−1
0
+1
0
14
+3
+3
+5
0
目標値より高い工程平均,したがって,
ゼロで低い累積和
14
+3
+6
+5
0
3
−8
0
−6
−6
3
−8
0
−6
−12a)
10
−1
0
+1
−11
10
−1
0
+1
−10
10
−1
0
+1
−9
10
−1
0
+1
−8
10
−1
0
+1
−7
17
+6
+6
+8
0
17
+6
+12b)
+8
0
注記1 目標値=T=10,σe=2,h=5,f=0.5
注記2 第2列=値−(T+fσe)=値−(10+1)=値−11
注記3 第4列=値−(T−fσe)=値−(10−1)=値−9
注a) 低い平均の異常
b) 高い平均の異常
9
工程管理のための累積和管理図
9.1
検出すべき変化の性質
9.1.1
検出すべき変化の大きさ
工程パラメータ又は製品特性のいずれかをモニタリングするための累積和管理図を設計するとき,検出
することが重要となるパラメータ又は特性におけるシフト若しくは変化の大きさに留意することが望まし
い。これは,管理外れを判定するために用いられる“Vマスク”の形状に影響を与える。パラメータ又は
特性を管理するとき,実際は,工程の是正処置が可能である最小のシフトに設定することが多い。検出す
べきシフトをこれより小さくすると,累積和管理図が“ハンティング”(9.1.5参照)現象を引き起こしや
すくなるので,小さくすることにほとんど意味はない。
発生する変化は,“段階的変化”,“ドリフト”又は“周期的”のいずれかに分類することができる。
9.1.2
段階的変化
段階的変化は,ある工程パラメータ又は製品特性で測定したデータが,突然,増加し,新しいレベルに
一段変化することである。以前とは異なるレベルになる変化のことである。このような例は,例えば,今
まで使用していたものとは幾らか異なる原材料のバッチを使用する場合,又は経験のない事務員が管理業
務を引き受け,その人が必要な仕事内容を正しく学習するまでの間に,経験のある人より多くのミスを犯
すような場合である。累積和管理図は,この変化を急勾配で表し,異常であると判定する。
9.1.3
ドリフト
この種の変化は,機器又は工具の摩耗に関連していることが多いが,検査員の基準が時間の経過ととも
に変わる場合に発生する。このパターンは,累積和プロットによって検出され,二次関数的な上昇(又は
下降)として描かれる。
29
Z 9020-4:2018 (ISO 7870-4:2011)
9.1.4
周期的
時間とともに変化し,パターンとして繰り返される変化を,周期的変化という。例えば,3交代制で作
業が行われる工場で,3人の労働者が同じ作業を行っているのに,そのやり方が異なる場合に起こり得る。
シフトBは,必ずシフトAの次に作業を行うというように,シフト順は決まっているので,周期的なパタ
ーンが出現する。累積和管理図では,このパターンが,勾配が一方向に進んでいる区間に続いて,それが
変化して元に戻るといった区間として表示される。
9.1.5
ハンティング
ハンティングは,異常が起こった後,パラメータ又は特性を目標値に正確に調整することができず,行
った調整によって,パラメータ又は特性の中心値が目標の反対側になってしまうときに起きる。そのとき,
累積和管理図では反対方向の勾配を描き,やがて,以前に行った調整とは逆の調整を必要とさせる管理外
れ(異常)を示すようになる。
このようにして,累積和管理図で“ジグザグ”パターンが検出される。これが最も望ましくない状況で
あることは明らかで,最初の“目標値”を慎重に選択し,その後の調整を最小限にとどめることによって
回避することが望ましい。ハンティング対策については,9.3.1のステップ13のc)を参照する。
9.2
目標値の選択
9.2.1
一般
正確な目標値の選択は,累積和管理図を設計する上で最も重要である。
二つの考えられる値の中間にある目標値は,9.1.5に記載する“ハンティング”を発生させる。
9.2.2
目標としての所定値
最も簡易な目標値は,“所定の”又は“事前に割り当てた”値である。このオプションを選択すると,目
標値は,公称値又は許容範囲の中間値のような,何らかの規定値に等しいものに設定することが多い。エ
ンジニアリングの関連分野では,こうした値は仕様書又は図面に記載されている。累積和管理図が製造以
外で使用される場合,所定の目標値は,請求書の処理に要する標準時間か,又は一企業内のある部門の予
算に計上された毎月の支出額のような,ある種の実績レベルとなることがある。
目標そのものが変化することがある。例えば,アイスクリームの売上げを月別に累積和管理図でモニタ
リングする場合,月別の目標値は,何月かによって異なる見込みが高い。アイスクリームの売上げは冬よ
りも夏に高くなると予想されるので,月ごとに異なる目標値を設定するほうがよい。売上パターンの認識
を怠り,月ごとに同じ値を使えば,累積和管理図を示したグラフ用紙に誤ったプロットが記載されてしま
う。累積和値は一年のうちのある期間で上昇し,その後の期間で下降する傾向がある。目標を変更すれば,
アイスクリームの売上げ水準に著しい変化があるか否かを,“季節変動”を除外して正しく示すように累積
和管理図を作成することができる。不適切な目標値は,9.1.5に記載する“ハンティング”現象を招くこと
があるので,この種の目標値を選択するときは,慎重に検討することが望ましい。
基準は,そのパラメータ若しくは特性の期待値,又は平均レベル(中心位置)をモニタリングするとき,
所定(所与)の値を用いるアプローチを採用することである。同じアプローチを用いて,群内の標準偏差
又は範囲のような変動(ばらつき)をモニタリングするための目標値を設定することができるが,この規
格では,この方法を推奨しない。9.2.3及びそれ以降の細分箇条に記載した手引に従って進めることを推奨
する。
9.2.3
実績に基づく目標値
目標値は,現在の実績に基づき設定することができる。このアプローチは,工程パラメータ又は製品特
性の最近の実績履歴に従って管理方法を策定する実績に基づく管理図法である。
30
Z 9020-4:2018 (ISO 7870-4:2011)
中心値又はばらつきのモニタリングに対して,“試行”又は“データ収集”段階でのデータの取り方が極
めて重要な問題である。データを取る区間は,工程固有の偶然変動を完全に観測することのできる十分な
長さに取ることが望ましく,工程の判断が分かれるところである。一般に,試行は累積和プロットに25
点が記入されるだけ,十分に長いものであることが望ましい。これらのデータから,平均値及び標準偏差
の推定を行うことが望ましい。
目標値が決まったら,これを累積和の計算に用いることが望ましいが,累積和がレベルの変化を示して
いる場合は,その後に変更が必要になることがある。そのような変化があってから,工程調節ができない
場合又は新レベルが容認できる場合,講じてもよい処置は目標値の修正だけである。その後,累積和管理
図は,新しい目標値を使用してパラメータ又は特性をモニタリングする。
9.3
位置(平均)をモニタリングするための累積和スキーム
9.3.1
標準スキーム
図12を参照する。
ステップ1−累積和管理図の対象の決定
モニタリングする工程パラメータ又は製品特性を決定する。
注記1 これは,顧客情報からもあれば,主要な工程パラメータ又は重要な製品の特性から決まる
場合もある。対象は,問題解決の中で明らかになることもある。
ステップ2−群の大きさの決定
累積和管理図における合理的な群の決定は,シューハート管理図の作成に用いるものと同一の考え
方で行えばよい。
工程パラメータが選択された累積和管理図の対象であれば,最も適切な群の大きさは通常,1であ
る。これは,溶液の温度又は容器の圧力のようなパラメータが短時間では変化することは,まずない
からである。連続的に繰り返して測定すると,測定値間に差が出ることはまずない。標準偏差及び累
積和マスクの正しい設定値を決めるとき,これは技術的な問題をもたらす。
データが,特定の月の売上高のような真に一度限りのものであれば,合理的な群の大きさは1とな
る。
製品特性が選択されたとき,合理的な群の大きさは1より大きいことが多く,通常は5である。群
の大きさは,工程の確率的変動が入るように選択する。
ステップ3−累積和スキームの選択
表9は,累積和スキームの一般的な要求事項の範囲を定めた標準的スキームを示す。表では二つの
基本スキームを規定し,一つはゼロシフトの平均連長(ARL)が大きいCS1スキーム,もう一つは
ARLが小さいCS2スキームである。すなわち,CS2スキームは工程レベルのシフトをCS1スキーム
より迅速に検出するが誤報が多くなる。スキームの選択担当者は,いずれのシナリオがより重要であ
るかを見極め,適切なスキームを選択しなければならない。表10は,これらの標準的なスキームの性
能の差を示したものである。
31
Z 9020-4:2018 (ISO 7870-4:2011)
表9−群の平均に対する標準的な累積和スキーム
検出される重要な平均のシフトa)
CS1スキーム
CS2スキーム
h
f
h
f
i)<0.75σe
8.0
0.25
5.0
0.25
ii) 0.75〜1.50σe
5.0
0.50
3.5
0.50
iii)>1.50σe
2.5
1.00
1.8
1.00
注記1 実際のシフトがゼロのとき,CS1スキームは,700〜1 000の平均連長L0を示す。
注記2 実際のシフトがゼロのとき,CS2スキームは,140〜200の平均連長L0を示す。
注a) 個々の観測値で(群の大きさ=1),σeは標準偏差を表している。群の大きさが2以上のとき,σeは平
均の標準誤差を表している。
CS1スキーム又はCS2スキームのいずれを選択するのかが決定したら,次に重要なシフトの大きさ
を決める。表9では一般的な三つシフトレベルを示している。この選択に応じて,h及びfの値を読
み取ることができる。
どちらのスキームを選択してよいか明確でない場合,CS1スキームのii),すなわち,h=5.0,f=0.50
を選択することが出発点としてよいことが経験則として分かっている。
表10−群の平均に対する標準的累積和スキームの性能比較
目標値からの平均のシフト
(単位 σe)a)
CS1スキーム
CS2スキーム
(i)
(ii)
(iii)
(i)
(ii)
(iii)
0.00
730.0
930.0
715.0
140.0
200.0
170.0
0.75
16.4
17.0
27.0
10.5
11.5
15.0
1.00
11.4
10.5
13.4
7.4
7.4
8.8
1.50
7.1
5.8
5.4
4.7
4.3
4.0
注記 ここに示す値は平均連長(ARL)である。実際の変化を検出するためにとった実際の連長は変化し,ARL
よりも長くなることもあれば,短くなることもあるので注意する。特に関心があるときは,目標値から特
定のシフトの連長の分布を調べ,遭遇する可能性のある連長の予想範囲を知ることが望ましい。
注a) 個々の観測値で(群の大きさ=1),σeは標準偏差を表している。群の大きさが2以上のとき,σeは平均の標
準誤差を表している。
いずれのスキームを選択するにしろ,これらのパラメータの値に推定された標準偏差σ(又はσe)
を乗じて,マスクの実際のサイズ及び形状を決めることが望ましい。この点についてはステップ8に
記載する。
32
Z 9020-4:2018 (ISO 7870-4:2011)
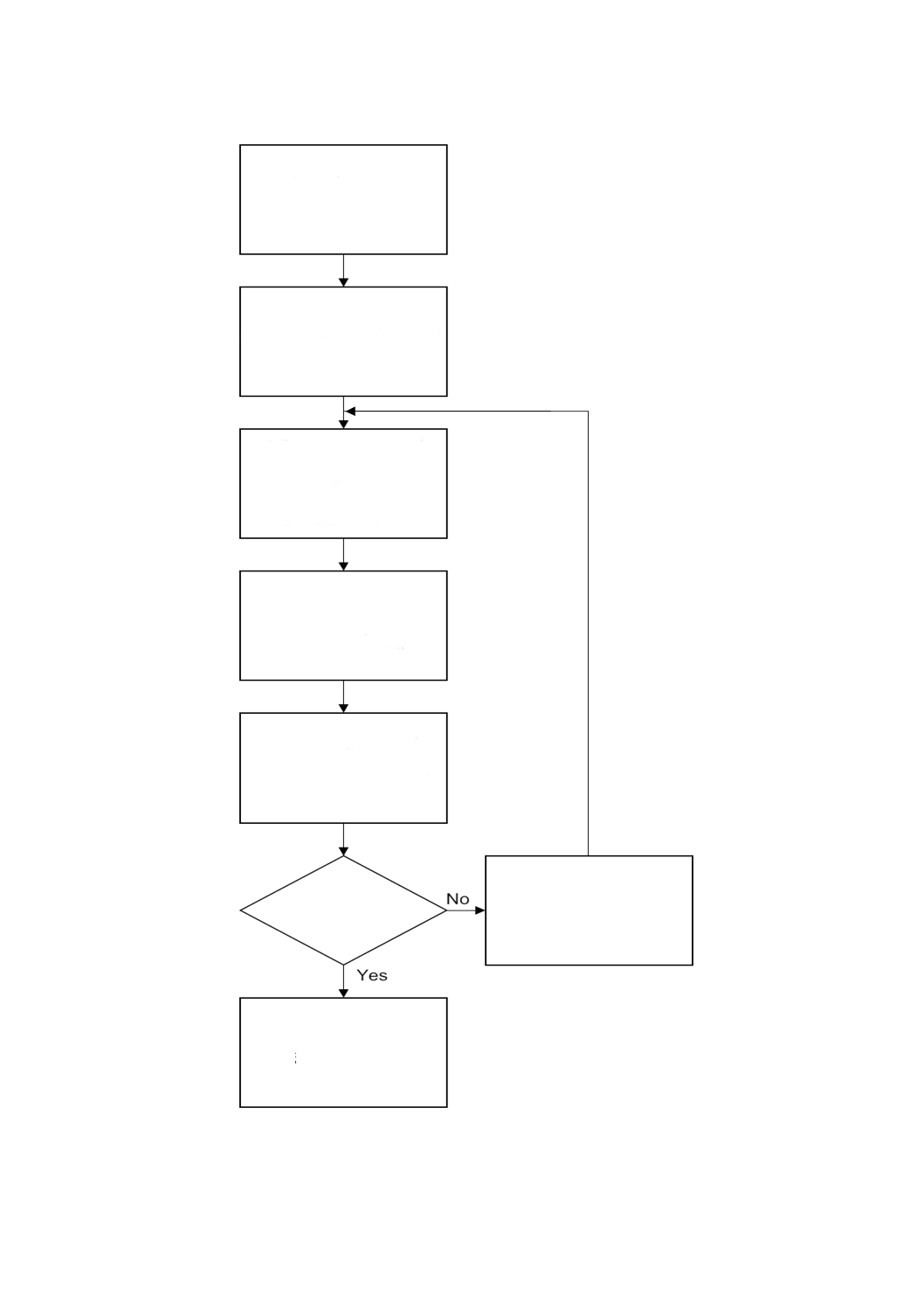
図12−累積和管理図設定プロトコル
1 累積和管理図の
対象の決定
2 群の大きさの決定
3 累積和スキーム
の選択(表9参照)
4 試行期間データの収集
5 試行期間データのσe推定
6 目標値Tの決定
7 累積和管理図のための様
式の作成
8 Vマスクの設定
9 試行データで
累積和を計算
10 試行データの
累積和をプロット
12 “異常原因”の特
定及び除去
13 進行中の図表作成を継
続
11 正常か?

33
Z 9020-4:2018 (ISO 7870-4:2011)
ステップ4−試行期間データの収集
9.2.3に示すように,累積和スキームが適切にチューニングされるように,また,必要ならば,目標
値の設定の手がかりが得られるように工程の変動の特徴を示しているようなデータを取るのが望まし
い。
工程変動の全ての要因が観測されるように,試行期間を決定する。この期間は,少なくとも25個の
群が得られるだけの十分な長さにするか,又は期間を決めた上で十分に高いサンプリング頻度にする
ことが望ましい。
この期間に工程調節のような新たな変動要因が入り込まないように気を付けなければならない。な
ぜならば,変動パターンが崩れてしまうおそれがあるからである。データ収集の中断がある場合,試
行期間を再び設ける必要があるのか,それとも短縮された試行期間に十分なデータが生成されたかを
判定することが望ましい。一般に,集められた群の数が20以上で,考えられる変動要因の全てが20
個の群までの間に観測されたと判断された場合は,その群の数で十分であり,試行期間を終了する。
次に,試行期間時のデータを用いて,累積和管理図が実行されるときの変動のレベルを定めることが
望ましい。この点については,ステップ5及びステップ6に記載する。
ステップ5−試行期間データからのσeの推定
a) 一般 σeを推定する方法の概要を,次のb)及びc)に示す。別のアプローチが必要になる,特殊な状況
が現れることがある。別なアプローチでは,サブグループ平均間の標準偏差を調べて,σeを評価する
必要がある。
b) 群の大きさが2以上の場合(n>1)
i.
各群における範囲(最大値−最小値)を計算する。
ii. 全ての郡における範囲の平均(R)を計算する。
iii. 範囲の平均を表11に示す適切なd2値で除して,群内の標準偏差(
0σ)を推定する。
iv.
0σを群の大きさの平方根で除してσeを推定する。すなわち,σe=
n
σ/
0
。
表11−範囲から群内の標準偏差を推定するための係数d2
群の大きさ,na)
d2
2
1.128
3
1.693
4
2.059
5
2.326
6
2.534
7
2.704
8
2.847
9
2.970
10
3.078
注記 群が10を超える場合,群内の標準偏差の推定には他の方法の方が効率的な場合
がある。
注a) d2の値はn>10の場合でも与えられている。JIS Z 9020-2又はその他の文献若し
くは規格を参照するのがよい。
群の範囲を用いる方法の代わりに,群内標準偏差(s)を用いる方法を使用することができる。Rの
代わりに,群内の標準偏差の平均sを計算する必要があり,σ0はs/c4によって推定される。c4の値を,

34
Z 9020-4:2018 (ISO 7870-4:2011)
表18に記載する。
c) 群の大きさが1の場合(n=1) σの推定に用いられるアプローチは,階差をとる方法(二つの観測
値の移動範囲と呼ぶこともある。)を用いるものである。
試行期間中に収集したデータは,収集した順に入力することが望ましい。最初のデータと次のデー
タとの範囲(差)を計算し,2番目のデータから3番目のデータまでの範囲というように計算をする
ことが望ましい。
k個のサブグループがあれば,範囲の数はk−1となる。これらの範囲の平均(R)を計算する。
σの推定値は,平均範囲を1.128で除して得られる。
ステップ6−目標値Tの決定
9.2に記載したように,目標値は,所定の値又はデータから求めた実績ベースの値である。
a) 所定の値 目標値は指定された値である。仕様書又は図面によって決められることもあれば,製品特
性の場合は公称値,非製造工程の場合はマネジメントの観点から定めたある種の期待されるパフォー
マンスのこともある。
b) 実績ベースの値 ここでは,目標値を,試行期間中に得たデータから次によって決めることが望まし
い。
i.
サブグループ別に平均値(x)を計算する。
ii. これらの平均の平均(x)を計算する。
iii. xを目標値Tとする。
ステップ7−累積和管理図のための様式の作成
a) 一般 累積和管理図のための様式の作成ガイダンスを,箇条5に示す。
b) 累積和表 累積和管理図を作成するために記入でき,読取りができる適切な表を用意する。そのよう
な表の一部を,表12に示す。
表12−累積和管理図を作成するための計算表
サブグループ番号
x
x−T
累積和値,C
以下省略
群の大きさが1の場合は,xを表中の個々のデータxに置き換える。
c) 累積和グラフ用紙 格子線間の間隔が適切な,グラフ用紙を選択する。グラフ用紙の種類の選択は,
壁に貼るか,公示に用いるかなど,用途によって異なる。
適切なスケールを選ぶ。スケールの大きさは,グラフの置かれる場所で異なる。例えば,壁に貼る
又は公示に用いるグラフでは,横軸の群の番号間の間隔は10 mmでよいが,デスク用であれば,間隔
は5 mmでよい。
累積和(C)軸に適切な間隔は,横軸に選択した間隔と同じ約2σeに等しい間隔にすると決まるが,
適宜,数値を丸める。このスケールで顕著な傾向が不自然に平たん(坦)になったり,重要でない傾
向が誇張されたりすることはまずない。
35
Z 9020-4:2018 (ISO 7870-4:2011)
累積和軸の中心点を0とし,グラフ用紙のこの点を通る太字の水平線を引く。グラフ用紙に,垂直
の累積和の目盛を記入する。
このような用紙の例を,図13に示す。
ステップ8−Vマスクの設定
8.2.1に汎用Vマスクの形状を記載し,図5に汎用Vマスクの構成要素及びその目盛の刻み方を示
す。
h,f及びσeの値は,ここに記載するようにして求めることが望ましい。
a) H=hσeを計算する。
b) F=fσeを計算する。
マスクは,累積和管理図用に選択した目盛で描く。事前に決めたサイズの変化が発生したかどうか
について,正しい判断を下す目的でマスクを使用するのであれば,これは不可欠である。
注記2 マスクによっては,アセテートのように透けて見える素材のものがある。マスクの輪郭は,
消えないインクでトレースすることができる。ときには,カードから切り抜いて作ること
もある。この場合でも,H及びFの値は,累積和管理図に用いられる目盛に従って,印を
付ける。
注記3 尺度を自動調整して累積和プロットを表示し,その上にマスクを描くようにしたコンピュ
ータプログラムがある。
ステップ9−試行データでの累積和の計算
ステップ6で決めた目標値及び表12に示すものに類似した表を用いて,試行データの累積和値を計
算する。
ステップ10−試行データでの累積和のプロット
ステップ9までのようにして作成され,表に記載された累積和値は,図13と類似した適切なグラフ
用紙にプロットすることが望ましい。プロットの開始は左側で,そこから右側方向に伸びていく。プ
ロットされた点を全てつなぐ。こうすると,マスクを重ね合わせたときに傾向が読み取りやすくなり,
管理外れの特定に役立つ。
ステップ11−試行データの累積和プロットでの管理外れの検討
累積和プロットの上に,マスクを重ね合わせる。
これは,用紙のゼロ軸に平行なマスクの中心線が変わらないように注意しながら,最後にプロット
された累積和値の上側に,図7 a)に示した“基準点”を合わせて行う。こうすると,マスクが正しい
向きにそろ(揃)うようになる。
最後にプロットされた点が判定ラインの外側ではなくとも,また,最後にプロットされた点が判定
ライン内に戻っている場合でも,判定ラインの外側に点があれば,それは工程に異常があることを示
している。図7 b)を参照する。

36
Z 9020-4:2018 (ISO 7870-4:2011)
+
累
積
和
値
0
-
図13−累積和管理図用紙の例
ステップ12−“異常原因”の特定及び除去
a) 一般 累積和プロットの異常(管理外れ)の点を調べ,“異常原因”を特定することが不可欠である。
b) “異常原因”の特定及び再発防止 異常原因が特定され,再発防止策がとられたら,目標値及び標準
誤差(又は標準偏差)の修正が必要になることがある。観測された異常点が一つだけで,原因に十分
に対処した場合は,それまで目標値,及び標準誤差又は標準偏差に割り当てられていた値を,当初の
試行期間データから異常なサブグループのデータを差し引いたものを使用して修正してもよい。累積
和管理図のグラフ用紙の目盛及びマスクの大きさの計算をやり直し,必要に応じて,用紙及びマスク
の尺度を修正する。
試行データに複数の異常な点がある場合は,どちらかといえば工程に問題があることを示しており,
工程を再検討し,是正し,改めて試行期間を開始し,新しいデータで累積和設定プロトコルをやり直
すことを推奨する。
c) “異常原因”が特定されたが,再発防止策がとれない 経済的又は技術的な問題のために,異常原因
に再発防止策をとれない場合がある。
そのような状況の場合は,全ての試行データに基づいて累積和管理図のパラメータを定め,進行中
のモニタリングに使用する。言い換えれば,このような異常原因を工程の不規則変動の一部とみなす
37
Z 9020-4:2018 (ISO 7870-4:2011)
のである。
d) “異常原因”が特定できない “異常原因”が特定できないでいるままになることがある。これは工
程の改善ができないので,極めて不満足なことである。異常原因の特定にあらゆる努力を払い,他の
統計的手法及び問題解決法を用いて特定に当たることが望ましい。この点に関しては,実験計画法の
ような手法が特に有効である。
異常原因が特定できないでいる場合は,上記c)に記載するステップに従う。
ステップ13−進行中の図表作成の継続
a) 一般 試行データで“統計的管理状態”が得られる場合,又は“異常原因”が満足のいくように解決
されてから新しいデータを収集する場合,累積和管理図は,工程パラメータ又は製品特性の,進行中
のモニタリングを行える準備ができたことになる。用紙の目盛,マスクパラメータ及びマスクの尺度
を使用して,今後,サブグループから得られるデータのモニタリングを行う。
その後に管理外れが出現したら,工程にどういう措置を施すかを検討し,決定することが不可欠で
ある。その措置は,工具などに伴う工程調節から,工程をより好ましい位置に移動させる場合の新し
い目標値の採用に至るまで,様々である。
b) 工程調節 必要な調節量は,次のように累積和プロットから決定することができる。
i)
最後にプロットされた点の累積和の値を求める。
ii) 累積和プロットがマスク上の判定ラインの外に出た場所の,累積和の値を求める。複数の逸脱があ
る場合は,最新の,すなわち,マスク上の基準点に最も近い位置にある管理外れをとる。
iii) これらの2点間の累積和値の差を計算する。
iv) 基準点から異常を示す点との間にプロットされた点の数(r)をカウントする。
v) iii)で計算した差を,iv)でカウントした点の数で除す。すなわち,累積和プロットの局所勾配を計算
する。これは,工程の目標値からのシフト量の推定値である。
vi) 同じ大きさの調節を工程に行ってもよい。行った変更を累積和管理図に記録する。
vii) 累積和値をゼロに戻して,モニタリングを継続する。
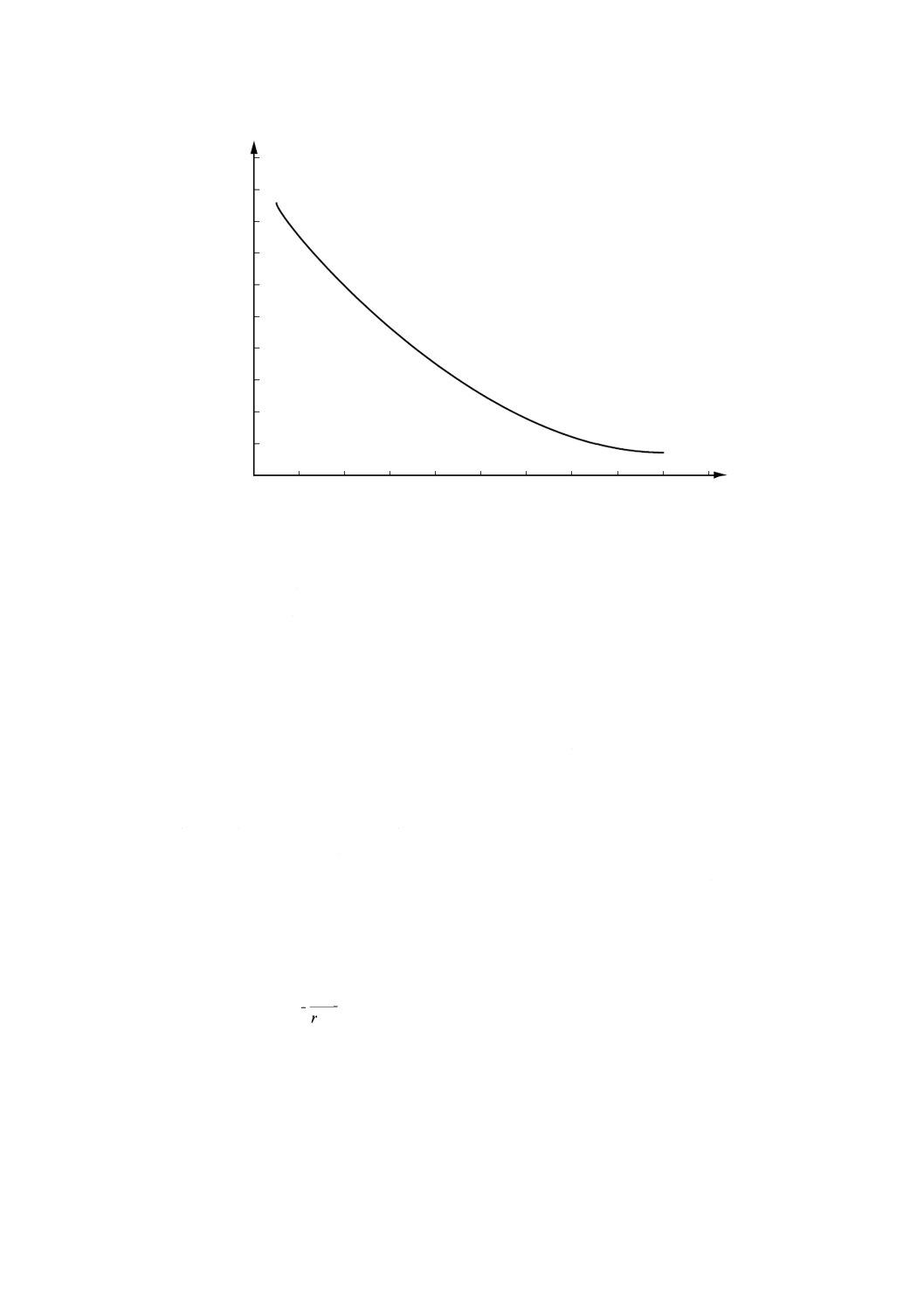
注記4 ここに記載する計算を実行しないで,マスク及び累積和管理図用紙の形状的性質によっ
て,“ルックアップ”グラフを生成し,目標からのシフト量を読み取ることが可能である。
その例を図14に示す。
38
Z 9020-4:2018 (ISO 7870-4:2011)
図14−目標値からのシフトを見るためのルックアップグラフの概略例
c) 工程調節−ハンティング防止 “ハンティング”の概念は,9.1.5で示した。目標値からの計算された
シフト量の100 %を調節値に用いると,ハンティングを引き起こすことが,経験的に分かっている。
そのような調節の後,累積和は,調節が強すぎたかのように,反対方向で管理外れとなり,更に工程
調節が必要なことを示す。工程調節して,最後に示されたシフトに等しい量だけ元に戻すと,その後,
反対方向でまた調節が必要なことを示すことがある。この現象を“ハンティング”という。
ハンティングは,実際のシフトを過大に推定している短期間の累積和勾配によって引き起こされる
ことがあり,マスク設計の修正,又は必要とされる現実的な調節によって直ることがある。
一つの実用的な解決策は,工程調節を示唆されたシフトの100 %未満にとどめることである。この
100 %未満の比率を“ハンティング防止係数”と呼ぶ。これは,累積和のハンティング傾向を弱める。
研究を含めて,経験上,ハンティング防止係数を75 %にするとうまくいくと分かっている。したがっ
て,少なくともはじめは,示唆されたシフトの75 %だけを調節することを推奨する。
図14に示すようなグラフは,ハンティング防止係数を含めて描くことができる。多くの人が累積和
管理図による工程管理の操作に関与する場合,こうすることが望ましい。
他のハンティング防止係数にr/(r+1)があり,rは基準点と異常(管理外れ)を示す点との間の点の
数である。この係数を用いて,工程調節量φは,次のようにして計算する。
1
+
=rCr
ϕ
ここに,Crは,基準点と異常(管理外れ)を示す点との累積和値の差である。
段階的変化が発生した場合,この方法はハンティングの防止に有効である。
9.3.2
標準スキーム−制限事項
9.3.1に記載する基本的な累積和スキームは,大半の用途で良好な値を提供し,多くの場合,それ以上の
変更は必要ない。ただし,少数の用途では,多少の時間が経過すると,重要なサイズのシフトを検出する
δ
r
39
Z 9020-4:2018 (ISO 7870-4:2011)
ためのARLが大きすぎたり,“誤報”の頻度が高すぎたりするという理由で,選択した基本スキームに改
善の余地が出てくることに注意するとよい。
9.3.3
“特定の目標に合った”累積和スキーム
“特定の目標に合った”累積和スキームは,次による。
注記 具体的な累積和スキームの設計には,9.3.1に記載する基本スキームよりも多くの知識及びイン
プットが必要になる。累積和管理図で工程管理をしたい人は,専門家に相談して設計を手伝っ
てもらうとよい。
a) 検出すべき目標値からの(重要な)シフトのサイズを決める。
b) 9.3.1のステップ5のようにして,標準誤差σe(又は,群の大きさが1の場合は標準偏差)を推定する。
c) シフトのサイズが9.3.1のステップ3に示す変化の大きさに対して望ましいARLすなわちLδを指定す
る。
d) シフトがゼロのときの望ましいARL(“誤報”の頻度)すなわちL0を指定する。
e) 標準化シフトΔ=δ/σeを計算する。
f)
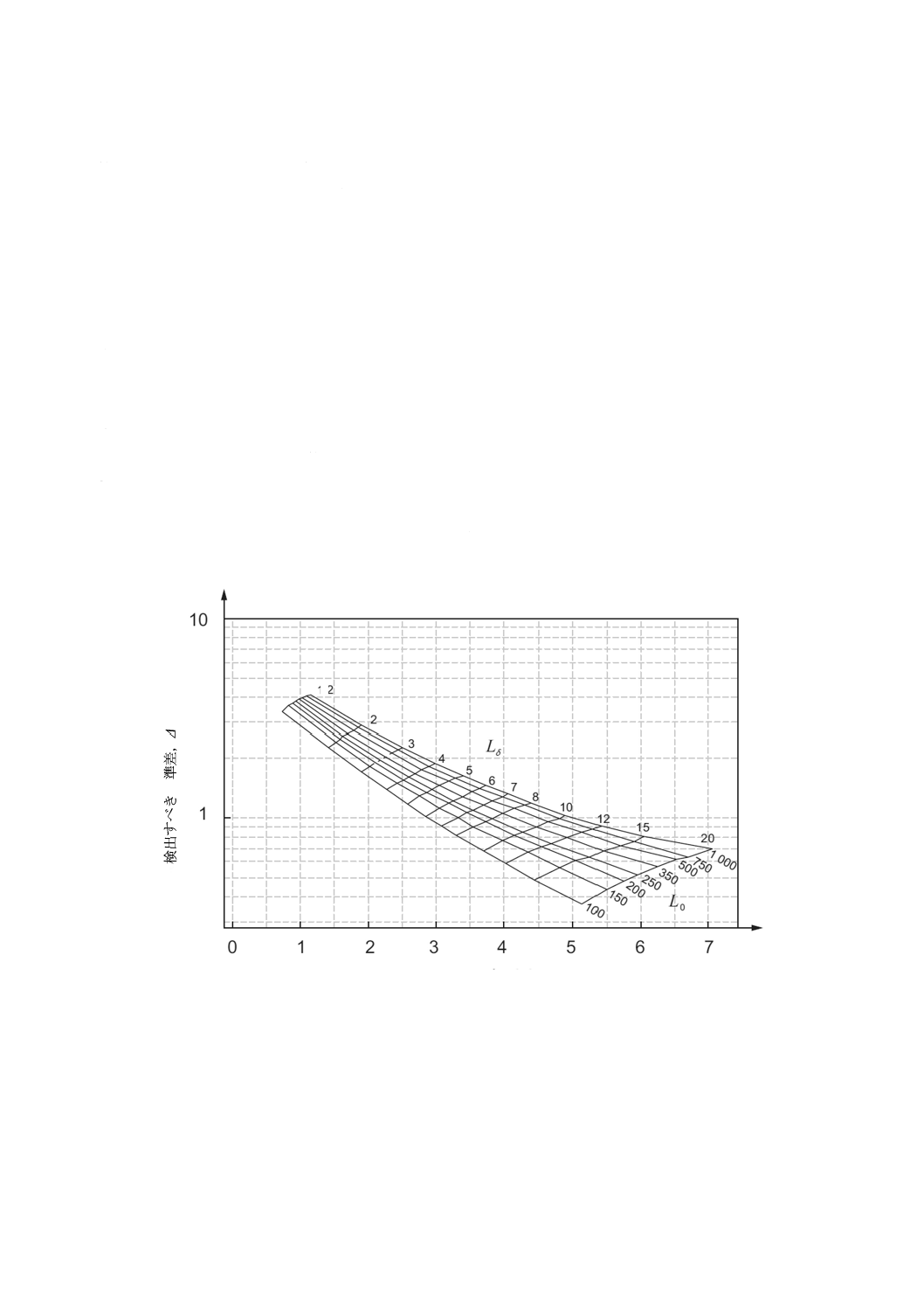
図15のグラフに記入し,Lδ及びL0の値を考慮しながら,計算値Δに対するhを読み取る。
g) fの値は,グラフ上の計算値Δに該当するところから読み取ってもよい。
h) 先に示したh及びfの新しい値に従って,累積和管理図のマスクを修正する。
図15−Vマスクパラメータのインターセプトチャート(正規分布を仮定する。)
9.4
群内変動のモニタリング用の累積和スキーム
9.4.1
一般
工程の平均のモニタリングに加えて,大半のケースで短期的な変動となる工程変動のモニタリングが必
須である。
検
出
す
べ
き
標
準
差
,
Δ
規準化した決定区間,h
.
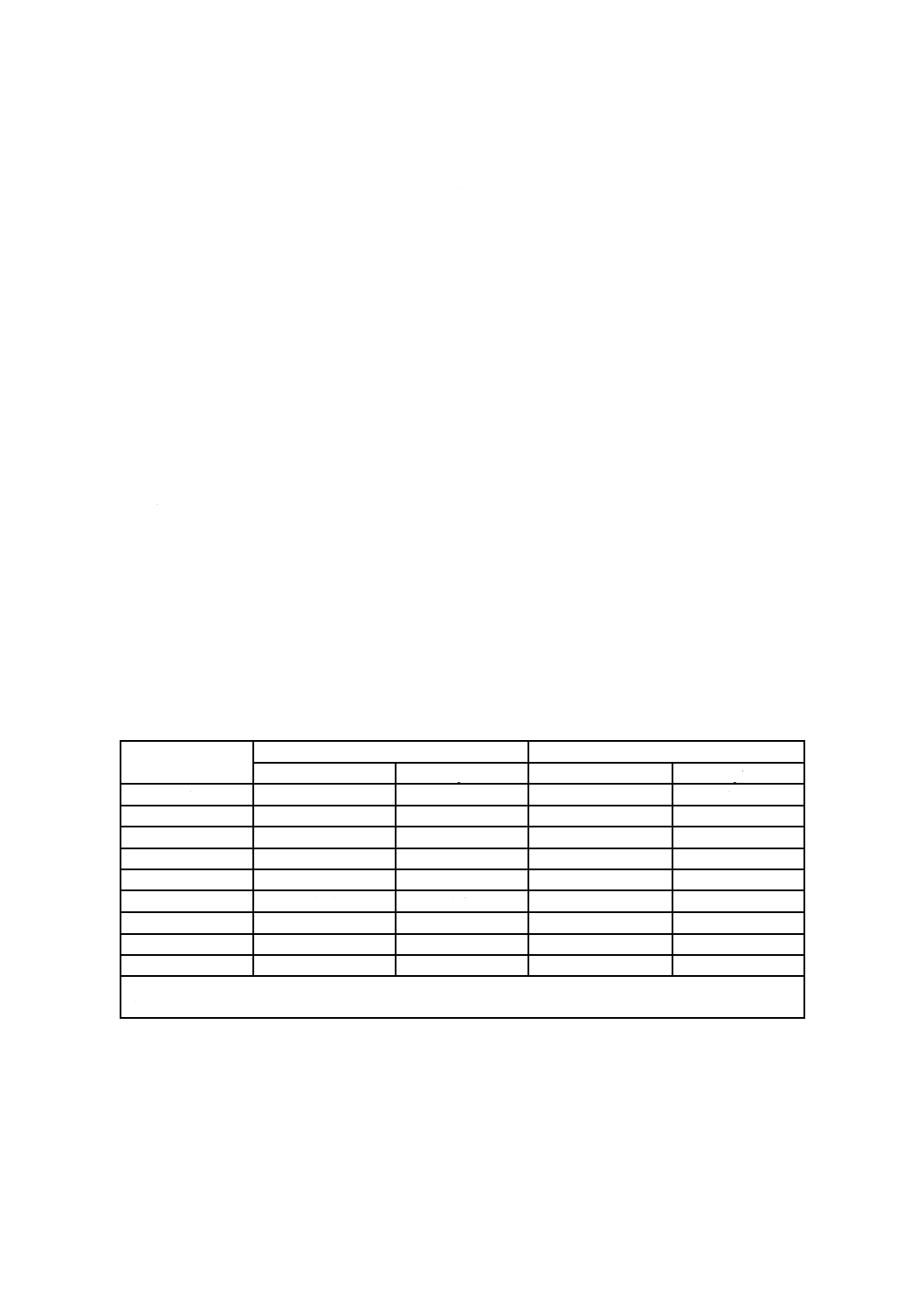
40
Z 9020-4:2018 (ISO 7870-4:2011)
変動の尺度として最も適切なものは,群内の範囲及び群内の標準偏差の二つである。いずれかを選択す
ることが望ましい。その決定は,計算に携わる人々にとっての計算のしやすさ及び尺度の理解水準に左右
される。管理図の操作に携わる人の多くは,その計算のしやすさ及び単純さから範囲を推奨尺度として選
んでおり,しばしば選択される群の大きさ(例えば,5サンプル)においては,その範囲の効率性は標準
偏差とほとんど変わらない。
群の大きさが1の場合,採用する尺度は,連続的な結果間の差を基準にした範囲とすることが望ましい。
9.4.2
群内の範囲用の累積和スキーム
群内の範囲を用いて,工程変動をモニタリングするのに適したスキームを設定するために,次のステッ
プを踏むことが望ましい。ステップの中には,平均値のモニタリング用累積和スキームが実行された場合
に完了するものがある。
ステップ1−累積和管理図の対象の決定
9.3.1のステップ1による。
ステップ2−群の大きさの決定
9.3.1のステップ2による。
ステップ3−範囲用累積和スキームの選択
表13は,範囲用累積和スキームに求められる一般的要求事項を定めた一連の標準スキームについて
規定している。9.3.1に記載したように,表13は二つの基本的スキームを示している。一つは,期待
変動レベルでの平均連長(ARL)が比較的大きいCS1スキームであり,もう一つはARLが比較的小
さいCS2スキームである。CS2スキームは,工程レベルのシフトをCS1スキームよりも迅速に検出す
るが,“誤報”に起因する費用が多くなる。表14は,二つの標準スキームの性能の差を示したもので
ある。
表13−群の範囲用標準累積和スキーム
群の大きさ
CS1スキーム
CS2スキーム
h
f
h
f
2
2.50
0.85
2.50
0.55
3
1.75
0.55
1.75
0.35
4
1.25
0.50
1.25
0.30
5
1.00
0.45
1.00
0.30
6
0.85
0.45
0.85
0.30
7
0.70
0.45
0.70
0.30
8
0.55
0.40
0.55
0.25
9
0.55
0.40
0.55
0.25
10
0.50
0.35
0.50
0.25
注記1 CS1スキームは,600〜1 000の範囲で工程が予想変動レベルで動作するときの,平均連長L0を示す。
注記2 CS2スキームは,150〜210の範囲で工程が予想変動レベルで動作するときの,平均連長L0を示す。
CS1スキーム又はCS2スキームのいずれかを選ぶ。群の平均値と範囲の累積和用スキームとの選択
に用いる選択基準は,同一のものを当てはめることが望ましい。変化が起きていないときに比較的大
きいARLが必要となると場合は,CS1スキームを選ぶ。そうでなければCS2スキームを選ぶ。
いずれのスキームを選ぶにせよ,これらのパラメータの値に推定された変動量Rを乗じて,マスク
の実際のサイズ及び形状を決めることが望ましい。この点については,ステップ8に記載する。

41
Z 9020-4:2018 (ISO 7870-4:2011)
ステップ4−試行期間データの収集
位置について示した指示を,ここにも適用する。
ステップ5−試行期間データによるRの推定
9.3.1のステップ5に記載した方法の一つを用いて,Rを計算する。
表14−群の範囲用標準累積和スキームの性能(ARL)比較
群の大きさ
実際の工程変動レ
ベル
CS1スキーム
CS2スキーム
2
R
779.0
170.0
2R
7.2
5.5
4R
2.3
2.1
3
R
893.0
196.0
2R
4.5
3.6
4R
1.6
1.5
4
R
918.0
157.0
2R
3.3
2.7
4R
1.3
1.2
5
R
771.0
179.0
2R
2.7
2.3
4R
1.2
1.1
6
R
942.0
204.0
2R
2.4
2.0
4R
1.1
1.1
8
R
893.0
162.0
2R
2.0
1.7
4R
1.0
1.0
10
R
635.0
184.0
2R
1.7
1.5
4R
1.0
1.0
注記 ここに示す値は,平均連長(ARL)である。実際の変化を検出するためにとった
実際の連長は変化し,ARLよりも長くなることもあれば,短くなることもあるの
で注意する。特に関心があるときは,目標から特定のシフトの連長の分布を調べ
て,遭遇する可能性のある連長の予想範囲を知ることが望ましい。
ステップ6−目標値Tの決定
a) 所定の値 統計的品質管理又は工程管理の場合,目標値を設定する最も一般的な方法は,次のb)に示
すようなものである。ただし,想定したレベルから目標値を設定することが優先される場合がある。
そうであれば,目標値は範囲内の所定の値に等しくなる。
変動が所定の標準偏差によって記述できる場合,目標範囲はT=d2σとして計算してもよい。d2は採
用する群の大きさに依存する値で,表11を用いる。
b) 実績ベースの値 試行期間中に得たデータから,Rに等しい目標範囲を設定する。
ステップ7−累積和管理図のための様式の作成
累積和表を設定(又は既存の累積和表に追加)し,9.3.1のステップ7に記載するようにして,累積
和グラフ用紙を作成する。
範囲用累積和をプロットする累積和グラフ用紙は,平均値のモニタリングに選択するものに合わせ

42
Z 9020-4:2018 (ISO 7870-4:2011)
て,異なる尺度が必要となることがある。適切な尺度は,次の計算によって得ることができ,最も都
合のよい値に切り上げ又は切り下げる。
範囲用の累積和尺度間隔はaRであり,ここに,aは表15に記載している値である。
表15−範囲用累積和グラフ用紙の目盛係数
群の大きさ
a
2
1.50
3
1.00
4
0.85
5
0.75
6
0.65
8
0.55
10
0.50
ステップ8−累積和マスクの設定
ステップ3で選択した値h及びfを使用して計算する。
a) H=hR
b) F=f R
計算値h及びfを使用してマスクを構成し,累積和グラフ用紙用に選択した尺度に従ってマスクを
拡大縮小する。
ステップ9−試行データでの累積和の計算
ステップ6で求めた目標値及び表12に示すような表を用いて,試行データの範囲で累積和値を計算
する。
ステップ10−試行データの累積和のプロット
範囲の累積和を,9.3.1のステップ7及びステップ10に記載したような範囲について,累積和グラ
フ用紙にプロットする。
ステップ11−異常に対する試行データの累積和プロットの検討
9.3.1のステップ11に記載したように,累積和プロットを検討する。
ステップ12−“異常原因”の特定及び除去
a) 一般 累積和プロット上の異常点を調べ,“異常原因”を特定することが不可欠である。
b)〜d)の一つに従い目標範囲の修正が必要となる場合は,マスクの修正も必要となり,場合によっ
ては,平均値の管理用の累積和グラフ用紙を修正する必要がある。
b) “異常原因”が特定され,再発が防止された 異常原因が特定され,再発防止策がとられたら,目標
範囲値の修正が必要になることがある。観測された異常点が一つだけで,a)に記載するようにして十
分に対処された場合は,それまで目標値に割り当てられていた値を,当初の試行期間データから異常
な群のデータを取り除いたものを使用して修正してもよい。累積和グラフ用紙の尺度及びマスクの寸
法の計算をやり直し,必要に応じて用紙及びマスクの尺度を修正する。
試行データに複数の異常点がある場合は,より多くの工程に関する問題があることを示しており,
工程を再検討し,是正し,改めて試行期間を開始し,新しいデータで累積和設定プロトコルをやり直
すことを推奨する。
43
Z 9020-4:2018 (ISO 7870-4:2011)
c) “異常原因”が特定されたが,再発が防止できない 異常原因が,非経済的状況又は技術関連事項の
ために再発を防止できない場合がある。
そのような状況の場合は,全ての試行データに基づいて累積和パラメータを定め,進行中のモニタ
リングに使用する。言い換えれば,このような異常原因を,工程のランダムな変動の一部とみなすの
である。
d) “異常原因”が特定できない “異常原因”が特定できないままに終わる場合は,c)に従うことが望
ましい。ただし,これは工程の改善ができないので,非常に不満足なことである。異常原因の特定に
あらゆる努力を払うことが望ましい。
ステップ13−進行中の図表作成の継続
a) 一般 9.3.1のステップ13に記載したように,図表作成を継続する。
b) 工程の処置 平均値のモニタリングの場合と同様に,管理外れが観測されたら,発生した変化量を累
積和の勾配から推定してもよい。この場合,管理外れはRで表される変動がどれほど変わったかで判
断する。
累積和の方向が範囲の増加を示している場合,装置又は機械の場合の反応は,保守技術者を呼んで,
装置を修理してもらうことがある。これでうまくいくと分かったら,採用した対策を記録し,累積和
値をゼロにリセットして工程を継続してもよい。工程が以前の変動レベルに戻ったら,累積和は正常
に動作する。
累積和の方向が範囲の減少を示している場合,それは通常,良好な事象とみなすことができるもの
で,その異常原因を特定し,それが残るようにするステップを踏むことが望ましい。これがうまくい
ったら,平均及び範囲(場合によってはグラフ用紙)両方のマスクを,新しい状況を表すように調整
することが望ましい。目標範囲も,新しい低い値に合わせて評価し直すことが望ましい。範囲の累積
和は,プロットを継続する前に再度,ゼロにすることが望ましい。
平均の累積和を再度,ゼロにする必要はないが,その期間だけ以前にプロットされた点の平均の修
正マスクを用いた再検討から,このときの範囲が実際に低いものになっていることが分かる。こうな
れば,平均のプロットについて,新しい異常点を観測することができる。
c) 群内変動の変化の推定値−ハンティング防止 位置(平均)の累積和の場合と同様に,ハンティング
防止のための対策の必要性があると考えられる場合,経験上,推定値の75 %の値を変化量として推奨
する。そのため,計算された変化量の75 %だけを調節することが望ましい。
9.4.3
群内変動をモニタリングするための累積和スキーム
標準偏差をモニタリングするための累積和スキームの設定手順は,群の範囲をモニタリングするための
ものとよく類似している。したがって,この細分箇条では9.4.2と違いだけを示すことから,9.4.2の内容
全体と併読することが望ましい。
群の変動をモニタリングするためのスキームは,群一つ当たりの観測回数が複数かどうかに依存する。
収集するデータが月別売上高のような一度限りのデータの場合,変動のモニタリングには範囲を基準とす
る移動範囲を推奨する。
ステップ3−標準偏差用累積和スキームの選択
表16は,標準偏差をモニタリングするための累積和スキームの一般的な要求事項を定めた,一連の
標準スキームについて規定している。表16は,二つの基本的スキームを規定し,一つは期待される変
動レベルでの平均連長(ARL)が大きいCS1スキーム,もう一つはARLが小さいCS2スキームであ
る。CS2スキームは,CS1スキームより“誤報”がやや多いが,重要な変化をCS1スキームよりやや

44
Z 9020-4:2018 (ISO 7870-4:2011)
早く検出する。表17は,これらの標準的スキームの性能の差を示したものである。
表16−群内の標準偏差用標準累積和スキーム
群の大きさ
CS1スキーム
CS2スキーム
h
f
h
f
2
2.00
0.50
2.00
0.25
3
1.60
0.35
1.60
0.15
4
1.15
0.35
1.15
0.20
4
1.15
0.35
1.15
0.20
5
0.90
0.35
0.90
0.20
6
0.80
0.32
0.80
0.20
7
0.70
0.30
0.70
0.20
8
0.60
0.30
0.60
0.20
9
0.55
0.30
0.55
0.20
10
0.50
0.30
0.50
0.20
12
0.40
0.30
0.40
0.20
15
0.35
0.27
0.35
0.18
20
0.30
0.23
0.30
0.16
注記1 CS1スキームは,700〜1 000の範囲で工程が予想変動レベルで動作するときの,平均連長L0を示
す。
注記2 CS2スキームは,150〜200の範囲で工程が予想変動レベルで動作するときの,平均連長L0を示す。
CS1スキーム又はCS2スキームのいずれかを選ぶ。群の平均用スキームの選択に用いる選択基準は
同一のものを当てはめることが望ましい。変化が起きていないときに長めのARLが必要となる場合は,
CS1スキームを選ぶ。そうでなければCS2スキームを選ぶ。
いずれのスキームを選ぶにせよ,これらのパラメータの値に推定された変動量(
0ˆσ)を乗じて,マ
スクの実際のサイズ及び形状を決めることが望ましい。この点については,ステップ5に記載する。
45
Z 9020-4:2018 (ISO 7870-4:2011)
表17−群標準偏差用標準累積和スキームの性能(ARL)比較
群の大きさ
実際の工程変動
レベル
CS1スキーム
CS2スキーム
2
σ0
920.0
185.0
2σ0
7.4
5.6
4σ0
2.3
2.1
3
σ0
920.0
155.0
2σ0
4.4
3.7
4σ0
1.6
1.5
4
σ0
840.0
180.0
2σ0
3.2
2.6
4σ0
1.3
1.2
5
σ0
820.0
155.0
2σ0
2.6
2.2
4σ0
1.1
1.1
6
σ0
850.0
190.0
2σ0
2.2
1.9
4σ0
<1.1
<1.1
8
σ0
720.0
180.0
2σ0
1.7
1.6
4σ0
1.0
1.0
10
σ0
930.0
200.0
2σ0
1.5
1.4
4σ0
1.0
1.0
12
σ0
840.0
170.0
2σ0
1.3
1.2
4σ0
1.0
1.0
15
σ0
860.0
170.0
2σ0
1.2
1.1
4σ0
1.0
1.0
ここに示した値はARLである。実際の変化を検出するためにとった実際
の連長は変化し,ARLよりも長くなることもあれば,短くなることもあ
るので注意する。特に関心があるときは,目標から特定のシフトの連長
の分布を調べて,遭遇する可能性のある連長の予想範囲を知ることが望
ましい。
ステップ5−試行データからのσ0の推定
a) 群別に群内の標準偏差(s)を計算する。
b) 群内の標準偏差の平均(s)を計算する。
群内の標準偏差を
4
0ˆ
c
s
=
σ
として推定するが,このc4は表18から読み取ることができる。
46
Z 9020-4:2018 (ISO 7870-4:2011)
表18−群内の標準偏差を推定するための係数c4
群の大きさ,n a)
c4
2
0.797 9
3
0.886 2
4
0.921 3
5
0.940 0
6
0.951 5
7
0.959 4
8
0.965 0
9
0.969 3
10
0.972 7
12
0.977 6
15
0.982 3
20
0.986 9
注a) c4の値があるのはn>20のとき。JIS Z 9020-2又はその他の
文献若しくは規格を参照するのがよい。
ステップ6−目標値Tの決定
a) 所定の値 統計的品質管理又は工程管理の場合,目標の群内の標準偏差を設定する最も一般的な方法
は,次のb)に示すようなものである。ただし,想定したσ0のレベルから目標値を設定することが優先
される場合がある。そうであれば,目標の群内の標準偏差はT=c4σ0として計算され,ここに,c4は,
表18にある値である。
b) 実績ベースの値 試行期間中に得たデータから,sに等しい目標値の群内の標準偏差を設定する。
ステップ7−累積和管理図のための様式の作成
累積和表を設定(又は既存の累積和表に追加)し,累積和グラフ用紙を作成する。
群内の標準偏差の累積和をプロットする累積和グラフ用紙は,平均値のモニタリングに選択するも
のに合わせて,異なる尺度が必要となることがある。適切な尺度は,ステップ8の計算によって求め
てもよく,最も都合のよい値に切り上げ又は切り下げる。
群内の標準偏差の累積和尺度間隔はaσ0であり,ここに,aは表19に示している値である。
表19−群内の標準偏差累積和のグラフ用紙の目盛係数
群の大きさ
a
2
1.50
3
1.00
4
0.85
5
0.75
6
0.65
8
0.55
10
0.50
15
0.40
20
0.35
ステップ8−累積和マスクの設定
ステップ3で選択した値h及びfを使用して,計算する。
47
Z 9020-4:2018 (ISO 7870-4:2011)
a) H=h×
0ˆσ
b) F=f×
0ˆσ
計算値H及びFを使用してマスクを構成し,累積和グラフ用紙用に選択した尺度に従って,マスク
を定める。
9.5
特殊な状況
9.5.1
大きな群間変動
状況によっては,平均の群間変動の一部を偶然変動の一部として考慮できるようにすることが重要なこ
とがある。この一例が,累積和管理図で検出されるが,それを除去するプランがない,平均の小さな変動
の場合である。累積和が連続的に異常を表示することを防止するために,これらの小さな変動は,偶然変
動の推定に含めることが望ましい。
群間平均の標準偏差(平均の標準誤差ともいう。)xsを計算する。これらは,試行期間データからとっ
たものでもよいし,変動の代表となる他のデータの期間からとったものでもよい。累積和用紙及びマスク
の尺度設定には,平均の設定に以前用いたσeではなく,値xsを用いる。附属書Aに,このアプローチの
妥当性の確認に役立つ方法を記載する。
この手順によって,累積和プロット上の誤報の数を減らす効果を上げ,より適切な品質管理を行うこと
ができる。
9.5.2
群のデータが一つの場合
累積和モニタリングの対象の中には,その性質上,一度だけ発生するデータを生成するものがあり,そ
うしたデータのサブグループ分けに意味はない。例として,先に挙げたように月別売上高又は製造工程に
用いる化学薬品タンクの温度があり,後者の場合,ほぼ同じ時間に数回繰り返して温度を測定しても,観
測値の変動はない。そうした状況では,群内変動はゼロになり,マスクを引くことができない。
もう一つの例は,ゴルフのスコアを決めるやり方である。ホールごとに期待されるストローク数が異な
っており,ゴルファーは,各ホール別に期待された数を基準にスコアを測定する。差の集計が累積和とな
る。
群の大きさが1のケースは,サンプルの採取及び/又は分析が非常に高額になるときにも発生する。
このとき採用するアプローチは群の大きさを1に設定し,9.3に概説するステップを踏み,その後のステ
ップも群の大きさを1,すなわちn=1として踏むことが望ましい。したがって,位置(平均)は,個々の
観測値そのものでモニタリングされ,一方では,ばらつきが連続した結果の範囲によってモニタリングさ
れる。
平均値の目標は,試行データ区間内で決定されるT=xとするか,又は目標値を所定の値とすることが
望ましい。範囲の目標値は,試行データの逐次差から求められるRとするか,又は標準偏差が所定の値で
ある場合はT=1.128σとすることが望ましい。群の大きさは1であるが,この範囲に限り有効な群の大き
さは2となる。
9.5.3
観測値間の自己相関
いかなる管理図でも同じだが,累積和管理図の基本は観測値の独立性にある。ただし,そうならない工
程又はデータの集合がある。例えば,情報を加熱装置に受け渡すサーモスタットのような閉ループ制御装
置が働いている工程,又は売上高データのような季節性が考えられる工程である。
このような場合,累積和プロットに及ぼす影響は重大で,その性能に著しい影響を及ぼし,場合によっ
ては,誤報が発生し,相当量の変化を見過ごすことになる。
48
Z 9020-4:2018 (ISO 7870-4:2011)
連続するデータに自己相関があるかどうか,その自己相関が正か負かを示す統計的検定がある。最も簡
易な方法は,オリジナルデータの最初の結果と2番目との結果,2番目と3番目…とを比較するというよ
うに,作成順にオリジナルのデータと一つずれた,同じデータとの相関を測定するものである。計算され
た相関係数が0よりもはるかに大きければ,観測値間に正の自己相関を,すなわち,連続する結果は一般
に同方向の変化を示す。相関係数が0よりもはるかに小さければ,負の自己相関が示されたことになり,
結果が一つ手前のものより高ければ,次の結果は反対方向に向かっていることを示し,これは過剰な調節
を受けている工程に共通する特徴である。このような自己相関は,表計算ソフト又はその他の統計のソフ
トウェアパッケージを使用して簡単に計算することができ,そのような分析を行うことを推奨する。
相関係数は−1〜+1の範囲にあり,0と有意に異なる値のしきい(閾)値は,調査に使用するデータ点
がどれほど多いかに依存する。データのサイズが小さければ,見かけ上大きな相関係数は,統計的に有意
ではないことがあるのに対し,データのサイズが大きければ,0に近い相関係数でも統計的に有意と解釈
してもよい。表20に有意となる相関係数に関するおおよその目安を示す。
表20−相関係数の重要区間
ペアデータの数
相関係数の重要区間a)
10
±0.45
15
±0.37
20
±0.33
25
±0.30
注a) 有意水準0.05(両側)における値。
相関係数の計算値が表20に示す区間内にあれば,自己相関があるとする理由はない。サンプルサイズが
小さくて検出できないような,微弱な自己相関が認められる場合がある。
自己相関が発見された場合は,先に進むための最良の方法を決定するために専門家の支援が必要になる
ことがある。対策には,自己相関の原因について,より深い工程解析を行うことを含む。自己相関の原因
が季節性にあれば,期間ごとに目標値を変更することで,これを克服することができる。こうすると,累
積和値は季節性から独立したものとなる。
9.5.4
外れ値
累積和は,外れ値の防止を必要とする。外れ値が発生すれば,それが累積和値に及ぼす影響が大きくな
り,誤報を強く導くことになる。次に示す場合は,累積和の外れ値を防止する簡易だが有効な方法である。
a) 結果を外れ値とみなす場合
1) 群平均が目標値から±3σeより離れている。
2) 個々の観測値が目標値より±3σより大きい。
結果は外れ値として記録するが,次の結果が疑いの限界外にない限り,その値を累積和計算には加
えない。
b) 結果を疑わしい外れ値とみなす場合
1) 群平均が目標値から±2σeより離れている。
2) 個々の観測値が目標値より±2σより大きい。
二つの連続する結果が疑いの限界を超えている場合,その結果の両方を累積和計算に含める。これ
は多くの場合,管理外れになる。
49
Z 9020-4:2018 (ISO 7870-4:2011)
注記 外れ値を検出するより厳格な方法(JIS Z 8402-5参照)があるが,リアルタイムな方法として
は有用ではない。ここに示した方法が簡便で実用的である。
9.6
離散データ用累積和スキーム
9.6.1
事象の頻度データ−ポアソンデータ
9.6.1.1 一般
計数データは事象の頻度に関係し,データは所定の期間又は製品数量ごとの特定の事象の数の頻度であ
る。例としては,月別の事故件数又は欠勤者数,1日当たりの演習又は出撃回数,1分間当たりの電話着信
回数,ユニット又はバッチ当たりの不適合数などが挙げられる。
ポアソン分布は,累積和管理図において次の二つの主たる役割をもつ。
a) nが大きく,pが小さい(例えば,n>20かつp<0.1)の場合,より面倒な二項分布(9.6.2参照)の近
似値となる。
b) 事象が時間又は空間でランダムに発生し,所定の区間で事象の回数について観測が行われる場合,そ
の現象を表現する分布としての役割をもつ。
ポアソンモデルの妥当性は,事象の独立性,及び一定と想定される(異常原因がない場合)平均率にお
ける事象の発生次第で決まる。
一般に,ポアソン分布(及び二項分布)には対称性がないことから,上方及び下方方向へのシフトを評
価する場合に,通常のものとは異なる異常判定ルールを用いることが望ましい。そのため,Vマスク法を
使用する場合,マスクはこれまでと違って対称形ではなく,上半分と下半分とで傾き及び決定区間の値が
異なる。
見かけ上は複雑であるが,計算の簡単さのために導入される分布の中には,他のものによって近似され
る分布がある。例えば,ある種の条件下で,ポアソン又は正規分布は二項分布の近似値として取り扱え,
他の条件下では正規分布がポアソン分布の代わりとなる。
9.3及び9.4では,正規分布データのARLを,平均0,標準偏差を1として,標準正規分布のARLから
単純に決定している。離散分布は,このようにはいかない。各パラメータは個別に計算することが望まし
い。したがって,離散データの累積和管理図の設計のための表は,必然的に,上方向だけの動きが選択さ
れた組合せに限定されている。最近では,ソフトウェアルーチンが入手しやすくなって,離散データに累
積和管理図を選択することが著しく増加している。
9.6.1.2
離散データに関する累積和管理図の一般的な決定ルール
離散データの累積和のスキームは,データの分布の種別の観点から,基準値K及び決定区間Hの二つの
パラメータが一意に特定される。パラメータの選択における主な指標は次のとおりである。
a) 累積和管理図の設計は,基本的に2段階プロセスである。
1) 目標値でのARLが望ましい値を示すための,KとHとの組合せの選択
2) 平均の適切な様々のシフトでの,異常検出の早さの決定
b) 基準値Kは,異常検出の対象となる指定された平均のシフトに基づいて選択することが望ましい。適
切なKは,累積和が最高の感度もつようにするための目標値と検出したい異常平均との間の値である。
Kの値は,データの分布の種別と容認された平均の定義とに依存する。
9.6.1.3
計数データ用の累積和スキーム
ステップ1−実際の平均発生率mを求める。
ステップ2−発生率の参照値又は目標値Tmを選択する。これは値mとなることが多い。
ステップ3−いずれのスキームを当てはめるかを選択して,最も適切な異常判定ルールを決める。推奨す

50
Z 9020-4:2018 (ISO 7870-4:2011)
るスキームは,少なくとも目標1 000のレベルでのARLをもつCS1スキームか,少なくとも目標200のレ
ベルでのARLをもつCS2スキームのいずれかになる。表21を参照。
ステップ4−次のようにH及びKの値を決める。
a) Tm(0.1≦Tm≦25.0)の場合,Tmに最も近い値で表21の値を記入する。Tmが10.0〜25.0の場合は,線
形補間を用いる。
b) Tm>25.0の場合,正規分布によるポアソン分布への近似が適切なものとなるので,σe=
m
Tを用いて,
正規分布に関する9.3に示した該当する表を参照する。
一例として,Tm=25と仮定する。平均25,標準偏差5の正規分布の場合,H=24,K=28である。これ
に対応するARLは約1 500である。H=24,K=28のポアソン変数の真のARLは1 085である。実際の
ARLが正規分布に近似したARLより小さいのは,ポアソン分布のわい(歪)度及び離散性に起因する。
ステップ5−Vマスクを構成して適用するか,表を作成する。
a) 管理図の場合 差(X−Tm)の和をプロットし,決定区間をH,傾きをF(=X−Tm)とするVマスク
法を用いる。
b) 表形式による累積和管理図の場合 差(X−K)の和をとり,累計がマイナスになるたびにゼロに戻す。
Hを基準にして,シフトの異常を検証する。
ステップ6−表22を用いて,該当する公称値からのシフトで選択した累積和管理図のARLを評価する。
例
ステップ2:参照平均率,Tm=4。
ステップ3:CS1のスキームを使用。
ステップ4:Tm=4のときの表21の値を記入する。したがって,H=8,K=6。
ステップ5のa):累積和をプロットし,Vマスクを構成して,それを適用する(H=8,F=2)。
ステップ5のb):表を作成し,表形式による累積和管理図を構成する(H=8,K=6)。
ステップ6:スキームの性能を,次に示す。工程が目標レベルで動作すれば,ARL(L0)は1 736
であるが,率が6.6に増加すれば,ARLは10に下がる。
H
K
Tm
L0
ARL
1 000
500
200
100
50
20
10
5
2
8.0
6.00
4.000 1 736
m
4.160
4.380
4.710
5.000
5.300
5.90
6.60
7.80
11.50
注記 データは表22から抽出。
9.6.2
二分されるデータ−二項データ
9.6.2.1
一般
分類されたデータの場合,データの各項目は,それぞれ多くのカテゴリに所属するものとして分類され
る。カテゴリの数は2であることが多い。すなわち二項で,例えば,結果は通常,0又は1,合否,利益又
は損失,ある特性の有無として表される。
クラスが二つあるデータを“二項”データと呼ぶ。尺度は,利益か損失か,内にいるか外にいるかなど,
本質的に二項である。量的尺度を分類することによって,間接的に二項データとなることがある。例えば,
通話を通話時間が10分を超えるか超えないかとか,6回以内の呼出音で応答があったかなかったかである。

51
Z 9020-4:2018 (ISO 7870-4:2011)
表21−計数(ポアソン)データのCS1及びCS2スキームのTm,H及びK
目標事象率
CS1スキーム
CS2スキーム
Tm
H
K
H
K
0.100
1.5
0.75
2.0
0.25
0.125
2.5
0.50
2.5
0.25
0.160
3.0
0.50
2.0
0.50
0.200
3.5
0.50
2.5
0.50
0.250
4.0
0.50
3.0
0.50
0.320
3.0
1.00
4.0
0.50
0.400
2.5
1.50
3.0
1.00
0.500
3.0
1.50
2.0
1.50
0.630
3.5a)又は4.0
1.50
2.0
2.00
0.800
5.0
1.50
3.5
1.50
1.000
5.0
2.00
5.0
1.50
1.250
4.0
3.00
5.0
2.00
1.600
5.0
3.00
4.0
3.00
2.000
7.0a)又は8.0
3.00
5.0
3.00
2.500
7.0
4.00
5.0
4.00
3.200
7.0
5.00
5.0
5.00
4.000
8.0
6.00
6.0
6.00
5.000
9.0
7.00
7.0
7.00
6.300
9.0
9.00
9.0
8.00
8.000
9.0
11.00
9.0
10.00
10.000
11.0
13.00
11.0
12.00
15.000
16.0
18.00
11.0
18.00
20.000
20.0
23.00
14.0
23.00
25.000
24.0
28.00
17.0
28.00
注記1 CS1スキームは一般に,1 000から2 000までの間の観測値の目標でのARLを示す。CS2スキーム
は,200から400までの間の観測値の目標でのARLを示す。
注記2 Tm<1の場合,個々の観測値が分類するには限られた情報しかないことに気付く。そこで以下に示
すような横軸のスケーリングを推奨する。一つの事象を発生させるのに必要な,平均観測回数1/ Tm
を求める。この値をプロットに都合のよい整数に丸め,それを累積和管理図の横軸の目盛に採用
する。縦軸の累積和の目盛を横軸の尺度と同じ長さの間隔で引き,0より上及び下に,0,+2,+
4など,−2,−4などと連続する偶数の整数を記入する。
注記3 10までのTmの値の選択は,各10ケース中の連続する数値間でほぼ同比率の10の比率を示す標準
値R 10に基づく。
注記4 Tmが10から25までの場合,等間隔の値を示して補間をしやすくする。この区間の中間スキーム
は,H及びKの両方で線形補間によって得ることができ,整数値に丸める。H及びKは同じよう
に丸めることが望ましい。
注a) Hの低い値は1 000よりやや小さいL0を示し,高い値は2 000に近いL0を示す。

52
Z 9020-4:2018 (ISO 7870-4:2011)
表22−計数(ポアソン)データのH及びKに関する累積和スキームのARL特性
パラメータ
CS1スキーム
CS2スキーム
表記値のARLにおける平均発生率
H
K
Tm
L0
Tm
L0
1 000
500
200
100
50
20
10
5
2
2.0
0.25
−
−
0.100
212
0.057 0.072 0.102 0.135 0.179
0.29
0.43
0.74
1.99
2.5
0.25
−
−
0.125
227
0.078 0.097 0.131 0.166 0.220
0.33
0.49
0.82
2.12
2.0
0.50
−
−
0.160
230
0.095 0.121 0.168 0.220 0.280
0.42
0.59
0.91
2.09
1.5
0.75
0.100
1 033
−
−
0.120 0.130 0.181 0.240 0.320
0.46
0.66
0.99
2.11
2.5
0.50
0.125
1 371
0.200
278
0.138 0.167 0.220 0.280 0.350
0.49
0.68
1.05
2.32
3.0
0.50
0.160
1 609
0.250
264
0.179 0.210 0.270 0.330 0.400
0.56
0.77
1.12
2.74
3.5
0.50
0.200
1 461
−
−
0.220 0.250 0.310 0.370 0.440
0.60
0.84
1.31
3.02
4.0
0.50
0.250
966
0.320
271
0.250 0.280 0.340 0.400 0.470
0.65
0.91
1.41
3.37
3.0
1.00
0.320
1 174
0.400
446
0.330 0.390 0.480 0.570 0.690
0.91
1.17
1.63
3.08
2.0
1.50
−
−
0.500
260
0.360 0.420 0.540 0.640 0.780
1.04
1.32
1.78
3.17
2.5
1.50
0.400
1 103
−
−
0.410 0.490 0.610 0.730 0.890
1.15
1.46
1.93
3.37
2.0
2.00
−
−
0.640
221
0.420 0.510 0.650 0.790 0.970
1.27
1.58
2.09
3.44
3.0
1.50
0.500
1 475
−
−
0.540 0.620 0.740 0.860 1.010
1.28
1.60
2.12
3.85
3.5
1.50
0.640
833
0.800
249
0.620 0.700 0.830 0.950 1.100
1.38
1.70
2.26
3.74
4.0
1.50
0.640
1 843
−
−
0.700 0.790 0.920 1.040 1.190
1.47
1.81
2.38
4.44
5.0
1.50
0.800
1 439
1.000
274
0.840 0.920 1.040 1.160 1.310
1.60
1.95
2.64
5.25
5.0
2.00
1.000
1 904
1.250
259
1.090 1.190 1.350 1.500 1.680
2.00
2.37
3.09
5.90
4.0
3.00
1.250
1 867
1.600
354
1.380 1.530 1.750 1.950 2.200
2.61
3.04
3.76
6.35
5.0
3.00
1.600
1 118
2.000
188
1.640 1.770 1.940 2.180 2.420
2.83
3.29
4.07
6.60
7.0
3.00
2.000
894
−
−
1.980 2.110 2.310 2.490 2.710
3.09
3.57
4.59
7.55
8.0
3.00
2.000
1 927
−
−
2.110 2.330 2.430 2.600 2.810
3.23
3.78
4.80
8.40
5.0
4.00
−
−
2.500
300
2.170 2.350 2.600 2.870 3.160
3.63
4.16
5.00
7.60
7.0
4.00
2.500
1 761
−
−
2.620 2.800 3.050 3.260 3.450
3.99
4.53
5.60
8.85
5.0
5.00
−
−
3.200
245
2.730 2.940 3.270 3.560 3.890
4.45
5.00
6.00
8.50
7.0
5.00
3.200
1 318
−
−
3.280 3.480 3.780 4.030 4.320
4.88
5.50
6.50
9.80
6.0
6.00
−
−
4.000
373
3.640 3.880 4.240 5.550 4.930
5.50
6.20
7.20
10.40
8.0
6.00
4.000
1 736
−
−
4.160 4.380 4.710 5.000 5.300
5.90
6.60
7.80
11.50
7.0
7.00
−
−
5.000
348
4.600 4.840 5.200 5.600 5.900
6.60
7.30
8.50
11.60
9.0
7.00
5.000
1 268
−
−
5.100 5.300 5.700 6.000 6.400
6.90
7.70
9.10
13.50
9.0
8.00
−
−
6.400
226
5.800 6.100 6.500 6.800 7.200
7.90
8.60
10.00
14.20
9.0
9.00
6.400
1 351
−
−
6.500 6.800 7.200 7.600 8.100
8.80
9.60
11.10
15.20
9.0
10.00
−
−
8.000
213
7.200 7.600 8.000 8.400 8.900
9.70
10.50
11.90
16.20
9.0
11.00
8.000
946
−
−
8.000 8.300 8.800 9.300 9.800
10.50
11.40
13.00
16.40
11.0
12.00
−
−
10.000
234
9.300 9.600 10.100 10.500 11.000
11.90
12.80
14.60
19.80
11.0
13.00
10.000
1 052
−
−
10.000 10.400 11.000 11.400 11.900
12.70
13.70
15.50
20.30
11.0
18.00
−
−
15.000
214
13.900 14.300 15.100 15.600 16.300
17.40
18.50
20.40
25.90
16.0
18.00
15.000
1 289
−
−
15.100 15.500 16.100 16.500 17.200
18.20
19.40
21.70
29.10
14.0
23.00
−
−
20.000
215
18.800 19.300 20.100 20.700 21.400
22.60
24.00
26.20
32.90
20.0
23.00
20.000
1 140
−
−
20.100 20.500 21.100 21.700 22.300
23.50
24.90
27.60
36.80
17.0
28.00
−
−
25.000
222
23.700 24.300 25.100 25.800 26.500
27.80
29.30
31.90
40.00
24.0
28.00
25.000
1 085
−
−
25.100 25.500 26.200 26.700 27.400
28.70
30.40
33.50
44.90
注記 表は,平均の上方への動きに関係する。
二項分布で満たすべき条件は,次のとおりである。
a) 試行回数は固定,nである。

53
Z 9020-4:2018 (ISO 7870-4:2011)
b) 各試行で,結果は二通りだけである。
c) 試行は独立している。
d) 各試行で,“成功”の確率pは一定である。
e) 変数は,n回の試行での“成功”の総数である。
二項分布は計算が極めて面倒なので,ARL及び異常判定ルールを取り扱うとき,二項分布に近似するも
のとして他の分布を用いてもよい。
二つの二項分布のパラメータn(サンプルサイズに相当することが多い。)及びp(問題の属性をもつ項
目の比率)は,とり得る値の範囲が広いので,全ての組合せの表を作ることが不可能になる。ただし,幅
広い状況に,近似的な手順を当てはめることができる。その手順を次に示す。
− 状況1 Tp<1(目標又は参照比率が10 %より下)の場合,Tm=npとしてポアソン分布を仮定したス
キームを用いる。
− 状況2 Tm>20の(目標条件下で1サンプル当たりの平均事象回数が20を超える)場合,正規分布
を仮定したスキームを用いる。
9.6.2.2
状況1:Tp<0.1−ポアソン分布で近似するスキーム
状況1では二項分布が適切だが,非常に扱いにくいので,ポアソン分布によって近似させるのがよい。
9.6.1.3に記載する段階的な方法を用いる。このときTm=npである。ポアソン分布の場合は,常に二項分
布の場合よりも目標値でのARLが小さくなるが,目標値からかなりシフトした場合のARLは,平均事象
発生率が同じ場合の二項分布のARLにほぼ一致する。
例
ステップ2:n=20,p=0.025だとnp=0.5となり,参照値はTm=0.5となる。
ステップ3:CS1スキームを使用。
ステップ4:Tm=0.5の場合の表21の値を使用。すなわち,H=3,K=1.5。
ステップ5のa):累積和をプロットし,Vマスクを当てはめる(H=3,F=1.0)
ステップ5のb):表を作成し,表形式による累積和管理図を構成する(H=3,K=1.5)。
ステップ6:設計された累積和管理図の性能を次に示す。工程が目標レベルで稼動していれば,
ARL(L0)は1 475である。ただし,率が1.6,すなわちp=0.080に増加すれば,ARLは
10に減少する。
H
K
Tm
L0
ARL
1 000
500
200
100
50
20
10
5
2
3.0
1.50
0.500
1 475
m
0.540
0.620
0.740
0.860
1.010
1.28
1.60
2.12
3.85
注記 データは,表22から抽出。
9.6.2.3
状況2:Tm>20−正規分布で近似するスキーム
状況2では,対応する正規変数に適した対となるパラメータh,fについて,それぞれ例えば,5,0.5を
選ぶ。二項分布の累積和パラメータは,次のようにして得られる。
)
1(
p
p
T
nT
h
H
−
×
=
,Hは最も近い整数に丸める。
[
])
1(
p
p
p
T
nT
f
nT
K
−
×
+
=
,Kは最も近い整数に丸める。
)
1(
p
p
T
nT
f
F
−
×
=
,Fは最も近い整数に丸める。
54
Z 9020-4:2018 (ISO 7870-4:2011)
例
ステップ2:n=80,Tp=0.3,h=5,f=0.5とする。
ステップ4:
20
)3.0
1(3.0
80
5
)
1(
≈
−
×
×
=
−
×
=
p
p
T
nT
h
H
[
]
[
]26
)3.0
1(3.0
80
5.0
)3.0
80
(
)
1(
≈
−
×
×
+
×
=
−
×
+
=
p
p
p
T
nT
f
nT
K
2
)3.0
1(3.0
80
5.0
)
1(
≈
−
×
×
=
−
×
=
p
p
T
nT
f
F
ステップ5のa):累積和をプロットして,Vマスク(H=20,F=2)を当てはめる。
ステップ5のb):表を作り,表形式による累積和管理図を構成する(H=20,K=26)。
ステップ6:工程が目標レベルで動作していれば,ARL(L0)はほぼ930であるが,比率(p)が
0.35に増加している場合,ARLは約10低くなる。

55
Z 9020-4:2018 (ISO 7870-4:2011)
附属書A
(参考)
フォン・ノイマン法
データを図示する目的で累積和管理図を設定するとき,変動を計量する方法は,データの性質,サンプ
リング方法及び計算のしやすさを主な理由として選択してよい。ただし,変化点又は工程平均のシフトの
統計的検定を実施する場合は,選択に注意し,連続する値の自己相関又は周期性の可能性を検討すること
が望ましい。
標準誤差の推定する連続する観測値の異常を調べる一般に有用な検定方法は,次のとおりである。
ステップ1
xsを計算する。
ステップ2 ∑
=
k
i
iw
2
2を計算する。
ステップ3 群の数kをカウントする。
ステップ4 (
)2
2
2
1
2
x
k
i
i
s
k
w
−
∑
=
を計算する。
ステップ5
)2
(
2
1
+
±
k
を計算する。
ステップ4で計算した値がステップ5の大きい値より大きければ,過剰な制御又は交代のような負の自
己相関があることを示す。小さい値より小さければ,例えば,遅れの効果,規則的又は不規則な段階的変
化,ドリフト若しくは傾向など,周期又はその他の正の自己相関があることを示す。
場合によっては,ステップ4の計算値は,表A.1の0.05(両側)パーセント点から評価してもよい。
表A.1−フォン・ノイマン検定のためのパーセント点(両側)
群の数
下限値
上限値
20
0.58
1.42
30
0.65
1.35
50
0.73
1.27
75
0.78
1.22
150
0.84
1.16
200
0.86
1.14
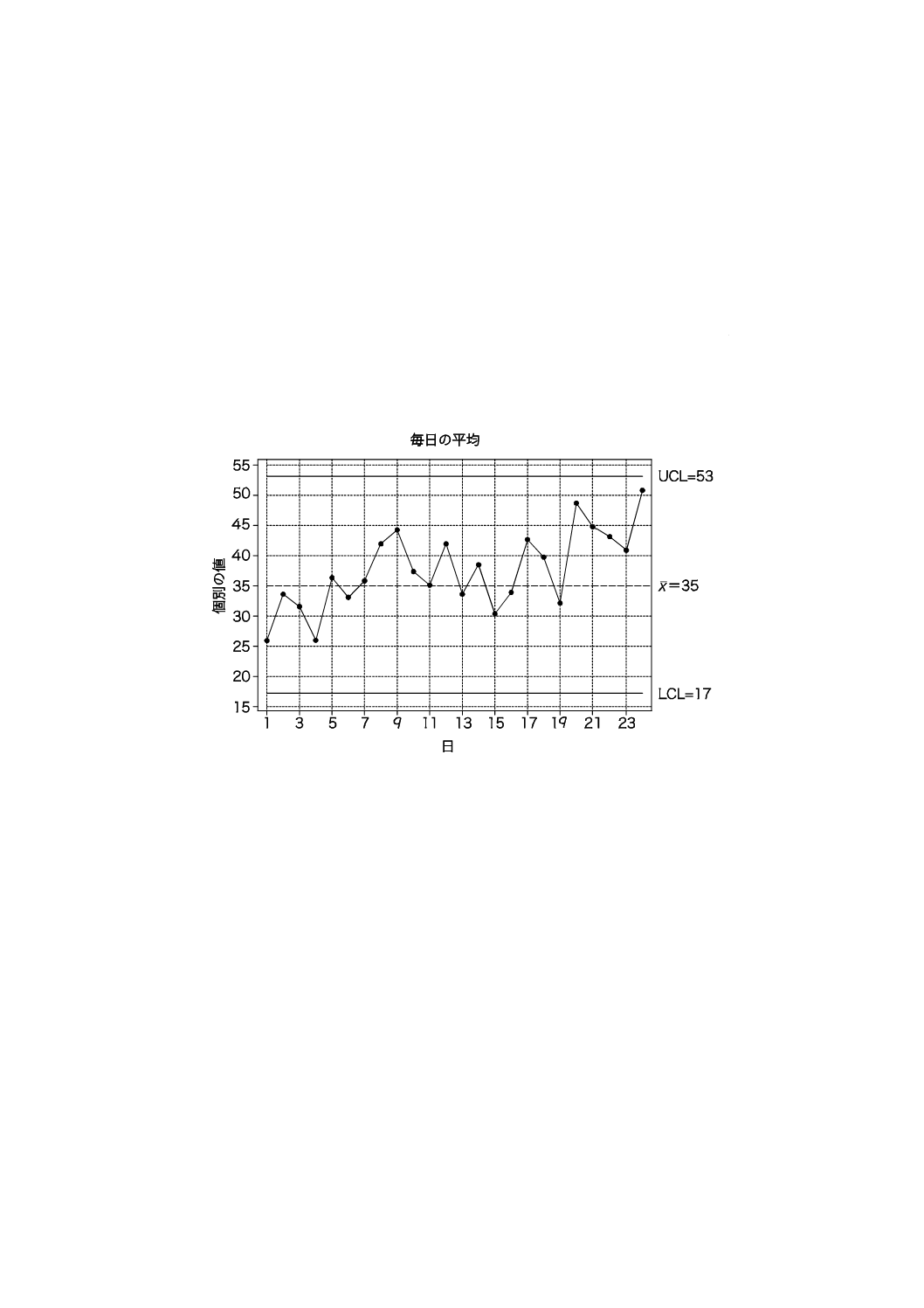
56
Z 9020-4:2018 (ISO 7870-4:2011)
附属書B
(参考)
表形式による累積和管理図の例
シューハート管理図でも累積和管理図でも,過去のデータから求めた平均35及び標準偏差6がパラメー
タとして定められ,用いられてきた。目標値は35に設定されている。
24日間のデータが収集された。データは,25.8,33.4,31.6,26.0,36.4,33.0,35.8,41.8,44.2,37.2,
35.0,41.8,33.4,38.4,30.2,33.8,42.6,39.6,32.0,48.4,44.6,43.0,40.8及び50.6である。
データのシューハート管理図を図B.1に示す。標準シューハート管理図の検定を用いると,異常が検出
されない。
図B.1−毎日の平均値のシューハート管理図
データの累積和点を図B.2に示す。この図は,19日に発生した“異常”が24日に判明したことを示し
ている。図B.1のシューハート管理図では,この変化を検出できない。
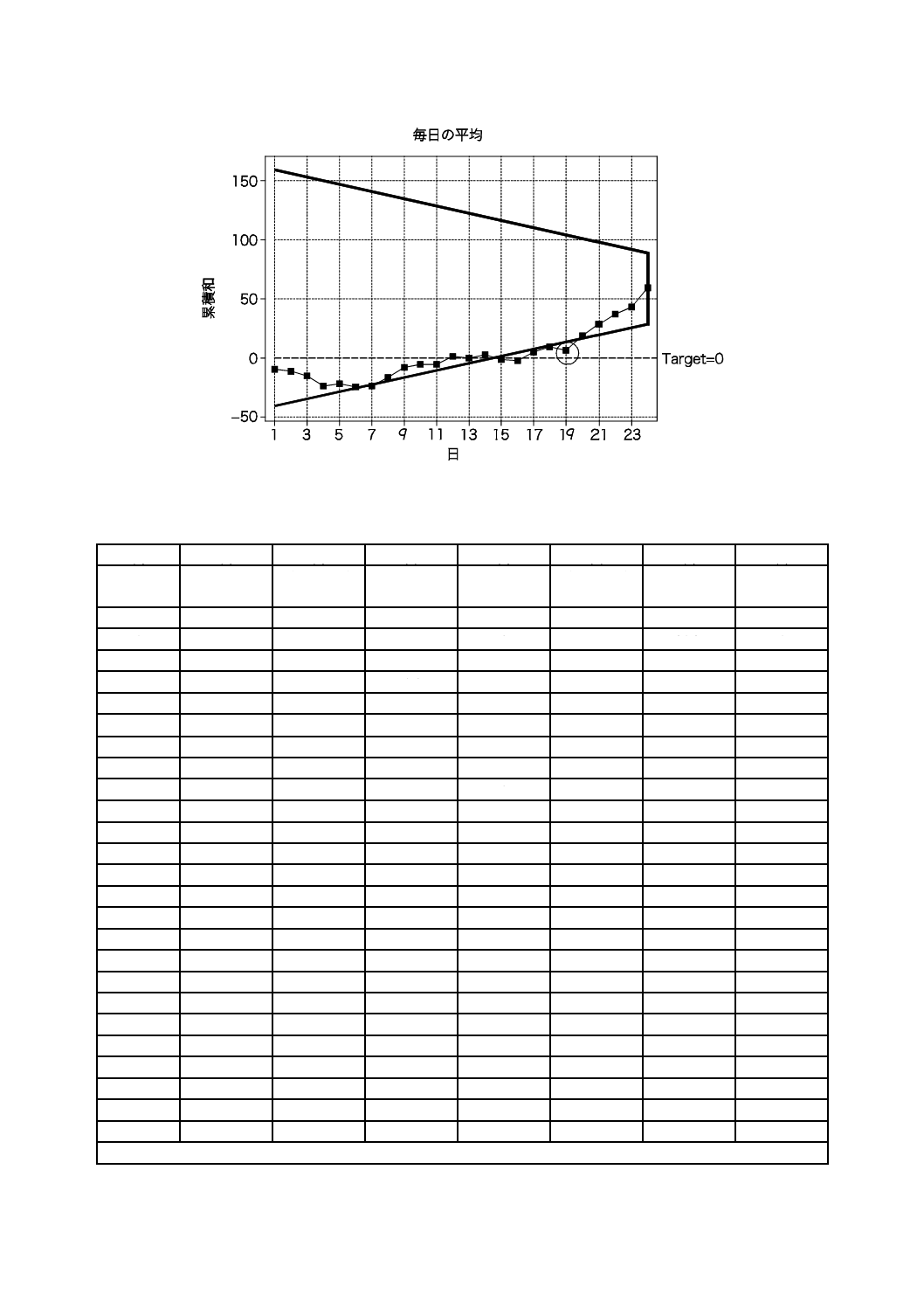
57
Z 9020-4:2018 (ISO 7870-4:2011)
図B.2−毎日の平均値の累積和プロット及びVマスク
表B.1−毎日の平均データの表形式による累積和管理図
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
日
毎日の平均
(X)
(X−T−F)
上側の累積
和値“Hi”
上側の打点
数“Hi”
(X−T+F)
下側の累積
和値“Lo”
下側の打点
数“Lo”
0
15.0
0
−15.0
0
1
25.8
−12.2
2.8
1
−6.2
−21.2
1
2
33.4
−4.6
0.0
0
1.4
−19.8
2
3
31.6
−6.4
0.0
0
−0.4
−20.2
3
4
26.0
−12.0
0.0
0
−6.0
−26.2
4
5
36.4
−1.6
0.0
0
4.4
−21.8
5
6
33.0
−5.0
0.0
0
1.0
−20.8
6
7
35.8
−2.2
0.0
0
3.8
−17.0
7
8
41.8
3.8
3.8
1
9.8
−7.2
8
9
44.2
6.2
10.0
2
12.2
0.0
0
10
37.2
−0.8
9.2
3
5.2
0.0
0
11
35.0
−3.0
6.2
4
3.0
0.0
0
12
41.8
3.8
10.0
5
9.8
0.0
0
13
33.4
−4.6
5.4
6
1.4
0.0
0
14
38.4
0.4
5.8
7
6.4
0.0
0
15
30.2
−7.8
0.0
0
−1.8
−1.8
1
16
33.8
−4.2
0.0
0
1.8
0.0
0
17
42.6
4.6
4.6
1
10.6
0.0
0
18
39.6
1.6
6.2
2
7.6
0.0
0
19
32.0
−6.0
0.2
3
0.0
0.0
0
20
48.4
10.4
10.6
4
16.4
0.0
0
21
44.6
6.6
17.2
5
12.6
0.0
0
22
43.0
5.0
22.2
6
11.0
0.0
0
23
40.8
2.8
25.0
7
8.8
0.0
0
24
50.6
12.6
37.6
8
18.6
0.0
0
T=35,f=0.5s,h=5s
58
Z 9020-4:2018 (ISO 7870-4:2011)
この累積和は,“初期値を変更した(FIR)”累積和管理図を使用しているので,初期値は“上側”及び
“下側”の列の“0日目”に示されている。この値はそれぞれ+2.5s及び−2.5sであり,+15.0及び−15.0
に等しい。同様に0日の“上側の打点数”及び“下側の打点数”は0である。h=5sなので累積和管理図
の管理限界は,それぞれ+30及び−30となる。
“1日目”の値は25.8である。第(3)列目の計算は,次のとおりである。
25.8−35−3=−12.2
この値“−12.2”は一つ上の“上側”の値“15.0”に加算され,和は“2.8”となる。“2.8”は正の値なの
で,“上側の打点数”列の一つ上の値“0”に“1”が加算される。新しい“上側の打点数”のカウントは“1”
となる。
第(6)列の計算は,次のとおりである。
25.8−35+3=−6.2
この値“−6.2”は一つ上の“下側”の値“−15.0”に加算され,和は“−21.2”となる。“−21.2”は負
の値なので,“下側の打点数”列の一つ上の値“0”に“1”が加算される。新しい“下側の打点数”のカウ
ントは“1”となる。
これらの計算は単純に見えるかも知れないが,その実行にはコンピュータの使用が想定されている。
“2日目”の値は“33.4”である。第(3)列の計算は,次のとおりである。
33.4−35−3=−4.6
この値“−4.6”は一つ上の“上側”の値“2.8”に加算され,和は“−1.8”となる。これは負の値なの
で,“上側の打点数”の値は“0”に変わり,“上側の打点数”のカウントも“0”に変わる。すなわち,累
積和のこちら側では“プラス”の累積和値だけが“カウント”される。
第(6)列の計算は,次のとおりである。
33.4−35+3=1.4
この値“1.4”は一つ上の“下側”の値“−21.2”に加算され,和は“−19.8”となる。前と同じように
“−19.8”はマイナスなので,“下側の打点数”列の一つ上の値“0”に“1”が加算され,新しい“下側の
打点数”のカウントは“2”となる。
この手順は“上側”又は“下側”が値h(この例では“30”又は“−30”)を超えるまで続けられる。こ
れは“上側”値が“37.6”となる“24日目”に生じる。
いつ“シフト”が発生したか,及びその“シフト”の量の推定値は,表形式の累積和から得られる。表
B.1から,初期値の変更の影響は工程平均が目標の近辺にあると“上側”及び“下側”の両方で比較的早
くなくなることに注意する。そうでなければ,初期値が“0”の“上側”又は“下側”の累積和が得られる。
この例では,“上側”が30以上になったとき,“下側の打点数”は“8”である。これは“16日目”と“17
日目”の間に変化が起きたことを示唆している(附属書C参照)。推定シフト量は初期値の変更はないと
仮定して,次のようになる。
“上側の打点数”
“上側”
+
F
明示された“シフト”がマイナスであれば,推定値は次の式で表される。
“下側の打点数”
“下側”
+
F
上側はh=30を超えているので,推定シフト量は次のようになる。
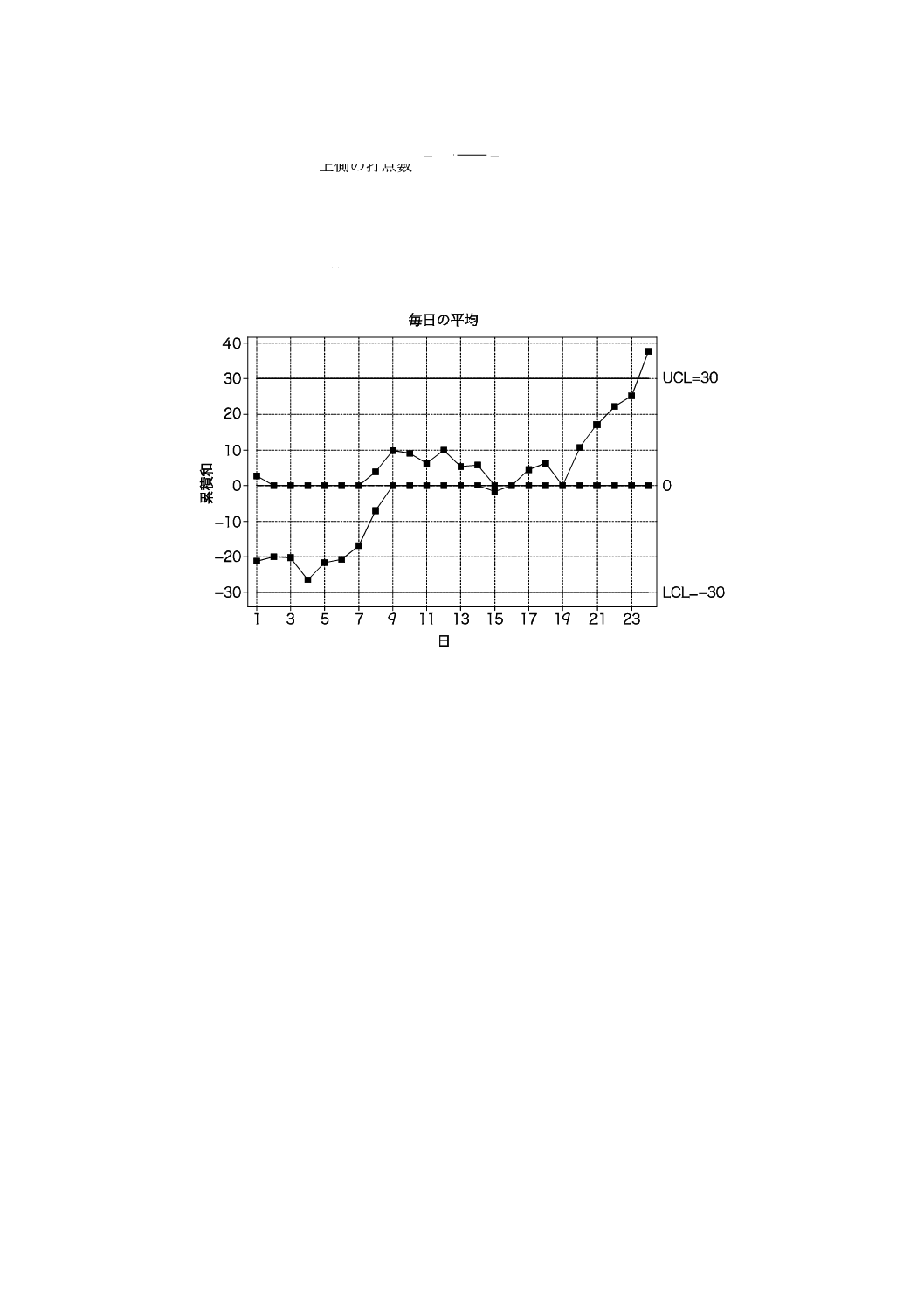
59
Z 9020-4:2018 (ISO 7870-4:2011)
70
.7
8
6.
37
3
=
+
=
+“上側の打点数”
“上側”
F
注記 オリジナルデータの最後の八つの値の母平均は,おおよそ1倍の標準偏差だけ,すなわち,6.0
シフトしている。累積和管理図は,変化点の正確な位置を推定し,推定シフト量を“7.7”と算
定した。これは“6”とそれほどかけ離れていない。
図B.3に,表形式による累積和管理図のグラフを示す。
図B.3−表形式による累積和管理図のプロット
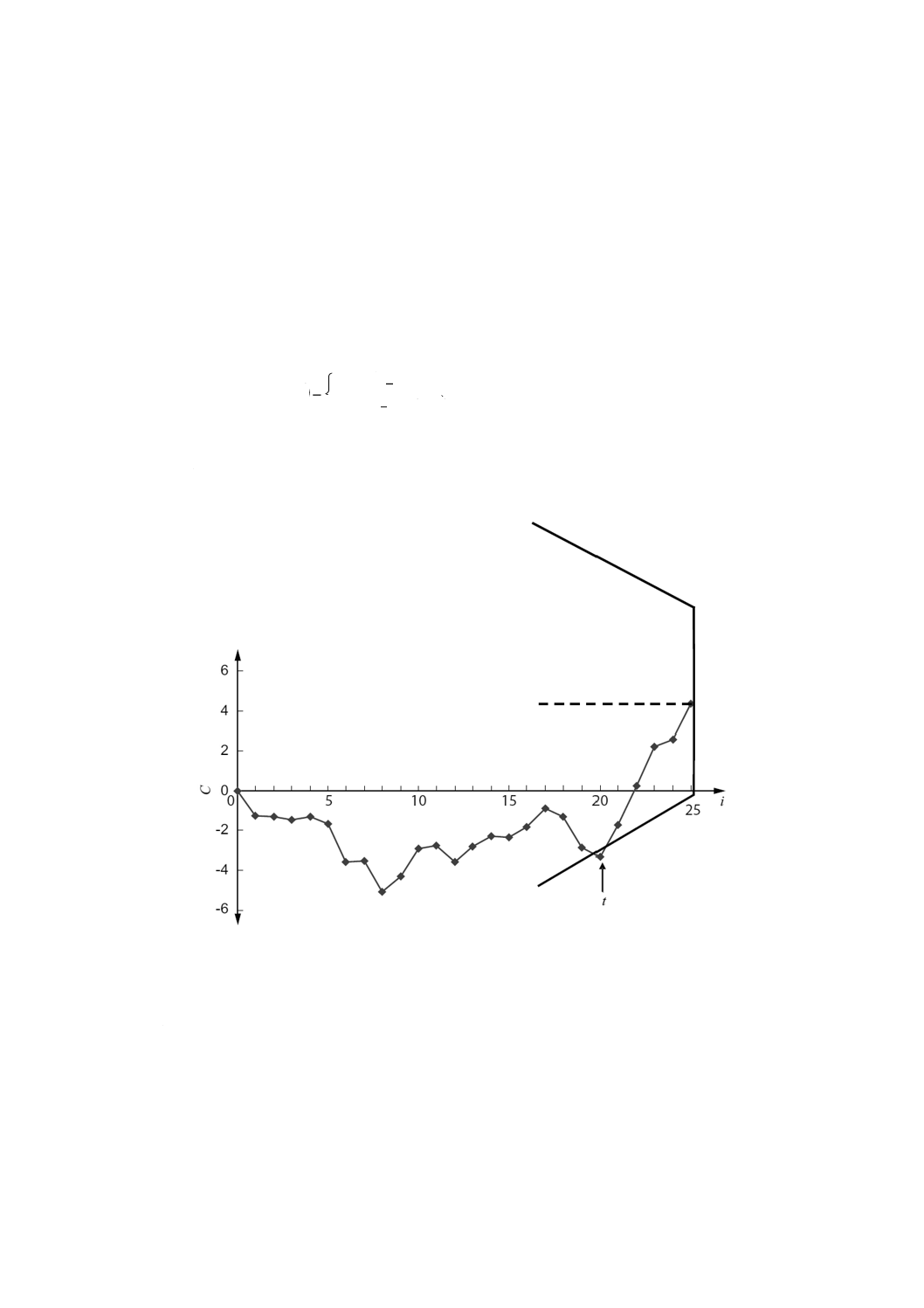
60
Z 9020-4:2018 (ISO 7870-4:2011)
附属書C
(参考)
段階的変化が発生したときの変化点の推定
工程が正常であるか否かは,特定の基準を用いて管理図から判断することができるが,管理図では明確
な原因を特定できない。ただし,管理図の過去の打点の軌跡が,正しい原因を発見するための情報をもた
らすことがある。これが,変化点の推定がもたらす重要な役割である。
T時点の工程平均μ(t)の段階的な変化の場合,真の変化点は次の式のτで表される。
()
(
)
(
)
+
=
+
=
=
Κ
Κ
,1
,
,1
τ
δ
τ
μ
t
T
t
T
t
累積和管理図は,変化点の推定に関しては高い性能をもっている。変化点の推定量は,図C.1に示すよ
うに累積和の経路がVマスクのアーム外に外れ出る時点となる。
図C.1−Vマスク法を用いた変化点の推定
図C.2は,CS1のスキームの場合に(h=0.5,f=0.5),累積和管理図による推定量の分布を示している。
変化点は管理図が異常を示した後にだけ推定できるので,タイプ1のエラーを検討することが望ましい。
そのため,図C.2の分布はタイプ1エラーが発生していないという条件で計算されたものである。
分布は単峰形分布であり,そのモードは真の変化点τ=10と同一である。図C.2の場合,シフト量δ=
1.0σe=Δはそれほど大きくないが,このアプローチを推奨できる。
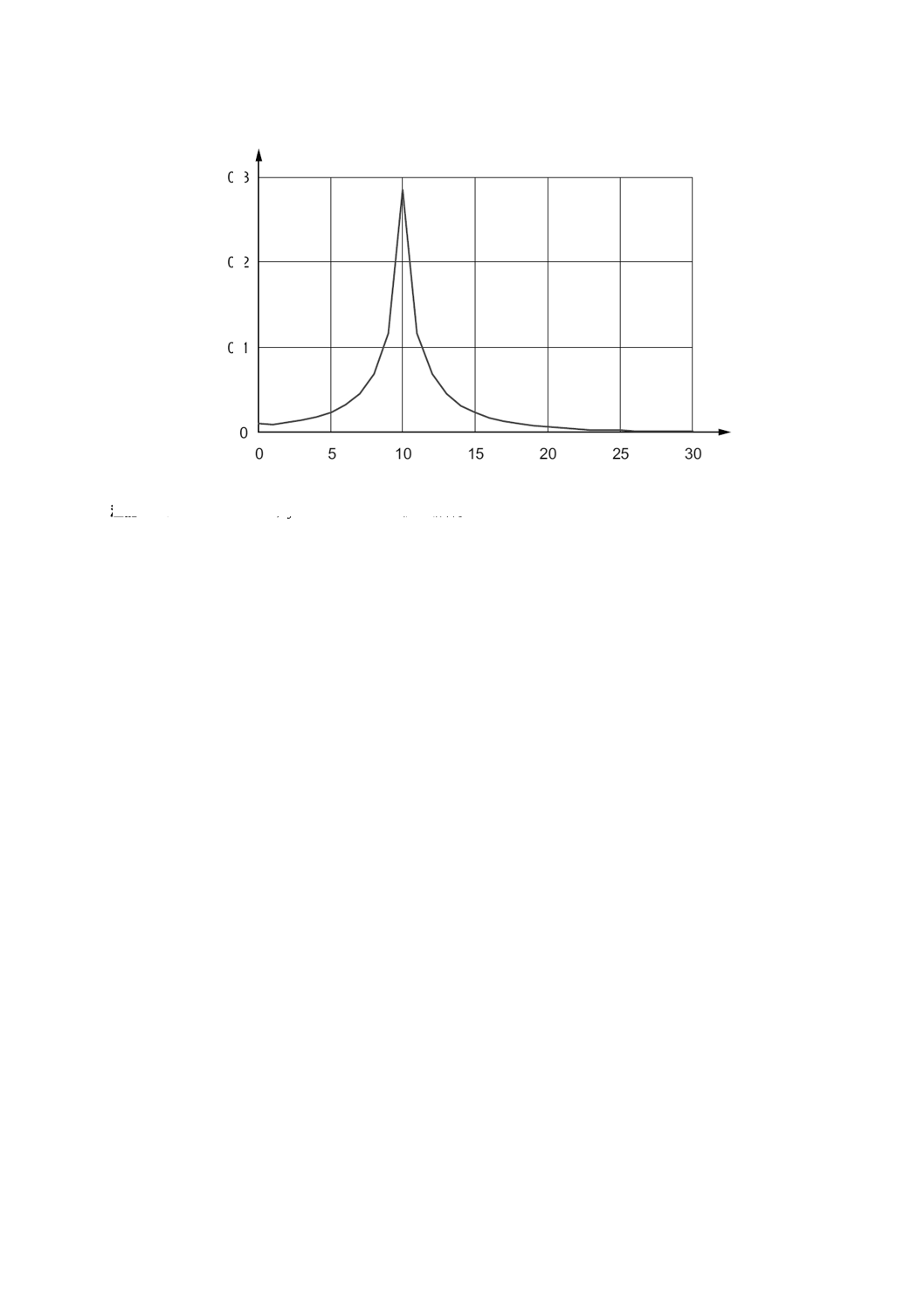
61
Z 9020-4:2018 (ISO 7870-4:2011)
注記 パラメータがh=5.0,f=0.5のVマスク法の場合。
図C.2−累積和による変化点の推定量の分布
P
t
.
.
.
62
Z 9020-4:2018 (ISO 7870-4:2011)
参考文献
[1] Nishina, K. Estimation of the change-point from cumulative sum tests. Reports of Statistical Application
Research, JUSE, 33(4), 1986
[2] Nishina, K. Estimation of the amount of shift using cumulative sum tests. Reports of Statistical Application
Research, JUSE, 35(3), 1988
[3] Nishina, K. A comparison of control charts from the viewpoint of change-point estimation. Quality and
Reliability Engineering International, 8, 1992
[4] JIS Z 8402-5 測定方法及び測定結果の精確さ(真度及び精度)−第5部:標準測定方法の精度を求め
るための代替法
注記 対応国際規格:ISO 5725-5,Accuracy (trueness and precision) of measurement methods and results
−Part 5: Alternative methods for the determination of the precision of a standard measurement
method
[5] JIS Z 9020-1 管理図−第1部:一般指針
注記 対応国際規格:ISO 7870-1,Control charts−Part 1: General guidelines
[6] JIS Z 9020-2 管理図−第2部:シューハート管理図
注記 対応国際規格:ISO 7870-2,Control charts−Part 2: Shewhart control charts
[7] ISO 9000,Quality management systems−Fundamentals and vocabulary
[8] BS 5703,Guide to data analysis, quality control and improvement using cusum techniques
[9] ISO 7870-6:2016,Control charts−Part 6: EWMA control charts