2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9004-1983
計量規準型一回抜取検査
(標準偏差未知で上限又は下限規格値だけ
規定した場合)
Single Sampling Inspection Plans
having Desired Operating Characteristics by Variables
(Standard Deviation Unknown and Single Limit Specified)
1. 適用範囲 この規格は,標準偏差未知で,上限又は下限規格値だけ規定した場合に,ロットの不良率
を保証するときの計量規準型一回抜取検査方式の決め方及び実施の方法について規定する。
引用規格:
JIS Z 9031 ランダム抜取方法
関連規格 JIS Z 8101 品質管理用語
JIS Z 9001 抜取検査通則
JIS Z 9003 計量規準型一回抜取検査(標準偏差既知でロットの平均値を保証する場合及び標
準偏差既知でロットの不良率を保証する場合)
備考 標準偏差未知で上限又は下限規格値だけ規定した場合の計量規準型一回抜取検査とは,ロット
品質をロットの不良率で表した場合に生産者及び消費者の要求する検査特性をもつように設計
した抜取検査であって,一回に抜き取ったサンプルの平均値と標準偏差とを用い,規格値と比
較することによってロットの合格・不合格を判定するものである。
この検査の適用に当たっては,
(1) 検査単位の品質特性は計量値で表され,正規分布をしているとみなせること。
(2) 製品がロットとして処理できること。
(3) 合格ロットの中にも,ある程度の不良品の混在を許せること。
(4) サンプルの抜き取りがランダムにできること。
(5) ロットの大きさは十分大きいこと。
が必要である。
2. 用語及び記号
2.1
用語の意味 この規格で用いる主な用語の意味は,次による。
(1) 検査単位 検査の目的のために選ぶ単位体又は単位量。
(2) 検査ロット 検査の対象とするロット(以下,ロットともいう。)。ロットとは等しい条件下で生産し
た,又は生産したと思われる品物の集まりである。
2
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(3) ロットの大きさ ロット内の検査単位の総数。
(4) ロットの平均値 ロットの検査単位の特性値xの平均値。
m=
N
x
x
x
N
+
…
+
+
...
2
1
(5) ロットの標準偏差 ロットの検査単位の特性値xの標準偏差。
σ=
N
m
x
m
x
m
x
N
2
2
2
2
1
)
(
)
(
)
(
−
+
…
…
+
−
+
−
(6) 不良品 特性値が上限規格値SUを超えるもの,又は下限規格値SLに満たないもの。
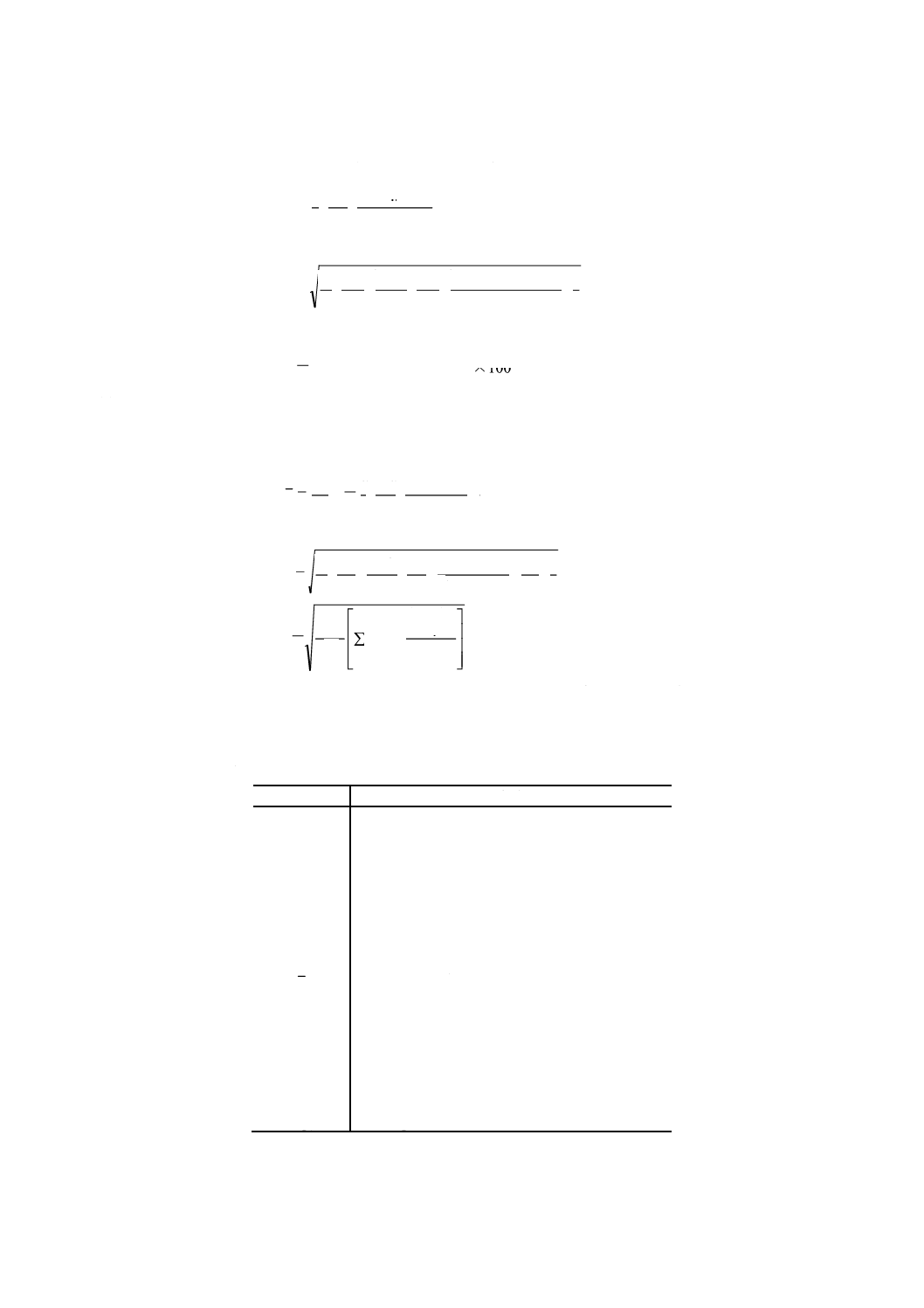
(7) ロットの不良率 p (%) =
ロットの大きさ
ロット内の不良品の数×100
(8) サンプル ロットから抜き取られる検査単位の集まり。
(9) サンプルの大きさ サンプル中の検査単位の数。
(10) サンプルの平均値 サンプルの検査単位の特性値xの平均値。
n
x
x
x
n
i
x
x
n
+
…
…
+
+
∑
2
1
=
=
(11) サンプルの標準偏差 サンプルの検査単位の特性値xの標準偏差。
1
)
(
)
(
)
(
2
2
2
2
1
−
−
+
…
…
+
−
+
−
n
x
x
x
x
x
x
s
n
=
(
)
∑
∑
−
−
n
i
x
i
x
n
2
2
1
1
=
(12) 抜取検査方式 ロットから抜き取るサンプルの大きさとロット判定基準との組合せ。
この規格では,サンプルの大きさnと合格判定係数kとの組合せをいう。
(13) 合格判定係数 合格の判定を下す基準となる係数。
2.2
記号 この規格で用いる記号は,次による。
記号
意味
α
生産者危険
β
消費者危険
N
ロットの大きさ
m
ロットの平均値
σ
ロットの標準偏差
p
ロットの不良率
n
サンプルの大きさ
x
検査単位の特性値
x
サンプルの平均値
s
サンプルの標準偏差
SU
上限規格値
SL
下限規格値
k
合格判定係数
p0
なるべく合格させたいロットの不良率の上限
p1
なるべく不合格としたいロットの不良率の下限
L (p)
不良率pのロットの合格の確率
3. 検査の手順 次の手順によって行う。
3
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(1) 品質特性の基準を設定する。
(2) p0,p1を指定する。
(3) ロットを形成する。
(4) サンプルの大きさと合格判定係数を求める。
(5) サンプルを採る。
(6) サンプルの特性値xを測定し,平均値xと標準偏差sを計算する。
(7) x+ks又はx−ksを計算して,それぞれSU又はSLと比較し,ロットの合格・不合格の判定を下す。
(8) ロットを処置する。
4. 検査の実施
4.1
品質特性の基準の設定 検査単位の特性値xの測定方法を具体的に定め,上限規格値SU又は下限規
格値SLを定める。
4.2
p0,p1の指定 この規格による抜取検査を実施するには,まず品物の受渡し当事者間で協議してp0,
p1を決める。この場合,α=0.05,β=0.10を基準とする。
備考1. α=0.05,β=0.10以外の場合は,参考3によって求めることができる。
2. 参考3を適用できない場合には,参考4を用いて近似的に求めることができる。
4.3
検査ロットの形成 同一条件で生産されたロットをできるだけそのまま検査ロットに選ぶ。ロット
が甚だしく大きい場合は小ロットに区切って検査ロットとしてもよい。
4.4
サンプルの大きさと合格判定係数の求め方 4.2で指定したp0,p1からサンプルの大きさと合格判定
係数を求めるには次による。
(1) 付表を用い,p0を含む行とp1を含む列との交わる欄を求める。
(2) 欄の中の左下の数値(太字)をサンプルの大きさnとし,右上の数字(細字)を合格判定係数kとす
る。
4.5
サンプルの採り方 検査ロットの中から4.4で決めた大きさnのサンプルをJIS Z 9031(ランダム抜
取方法)の3.によってランダムに抜き取る。
4.6
サンプルの試験 大きさnのサンプルについて4.1で定めた測定方法によって,特性値xを測定し,
平均値xと標準偏差sを求める。
4.7
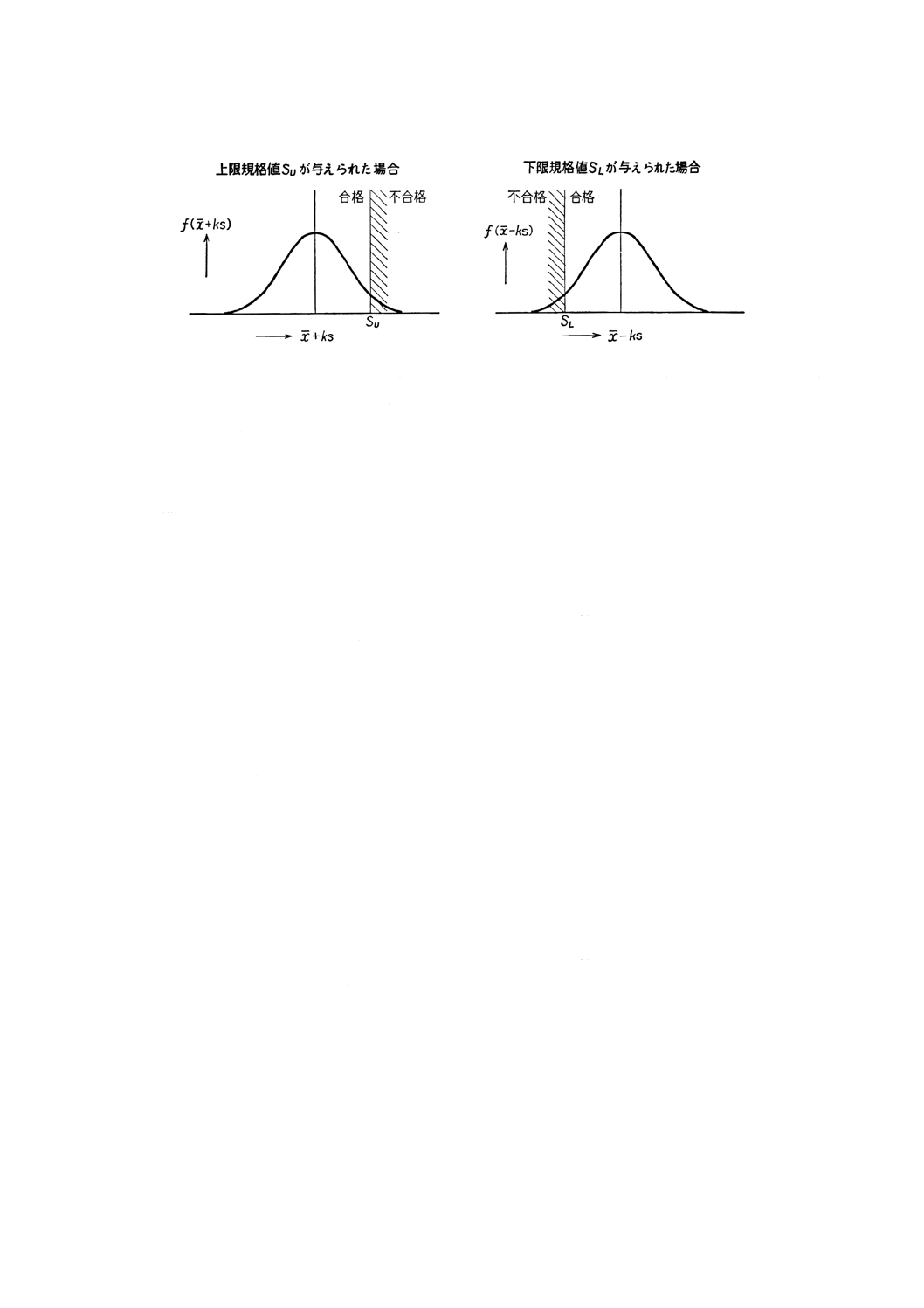
ロットの合否判定 ロットの合否の判定は次による(図参照)。
(1) 上限規格値SUが与えられた場合
x+ks≦SU ならばロットを合格とし,
x+ks>SU ならばロットを不合格とする。
(2) 下限規格値SLが与えられた場合
x−ks≧SL ならばロットを合格とし,
x−ks<SL ならばロットを不合格とする。
4
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図
例1: 金属板の硬さの上限規格値がロックウェル硬さ68と与えられたとき,ロックウェル硬さ68を超
えるものが0.5%以下のロットは合格とし,それが4%以上のロットは不合格としたい。この場合
ロックウェル硬さの値は,ほぼ正規分布に従うものとする。
これから
p0=0.5%,α=0.05;p1=4%,β=0.10
を満足する抜取検査方式を求めるには
(1) p0=0.5%,p1=4%
(2) 付表のp0=0.5%を含む行 (0.451〜0.560%) とp1=4%を含む列 (3.56〜4.50%) との交わる欄
を求める。
(3) この欄からサンプルの大きさn=42,合格判定係数k=2.12を読み取る。
(4) ロットから大きさ42のサンプルを抜き取って,x,sを算出し,
x+2.12s≦68 ならばロットを合格とし,
x+2.12s>68 ならばロットを不合格とする。
例2: 金属板の厚さの下限規格値が2.3mmと与えられたとき,厚さが2.3mm未満のものが1%以下のロ
ットは合格とし,それが9%以上のロットは不合格としたい。この場合,厚さの値はほぼ正規分
布に従うものとする。
これから,
p0=1%,α=0.05;p1=9%,β=0.10
を満足する抜取検査方式を求めるには
(1) p0=1%,p1=9%
(2) 付表のp0=1%を含む行 (0.901〜1.120%) とp1=9%を含む列 (7.11〜9.00%) との交わる欄を
求める。
(3) この欄からサンプルの大きさn=28,合格判定係数k=1.83を読み取る。
(4) ロットから大きさ28のサンプルを抜き取って,x,sを算出し,
x−1.83s≧2.3 ならばロットを合格とし,
x−1.83s<2.3 ならばロットを不合格とする。
4.8
ロットの処置 計量抜取検査による合格ロットはそのまま受け入れ,不合格ロットはあらかじめ定
めた約束に従って処置する。どのような場合でも不合格となったロットをそのままで再提出してはならな
い。
5. 抜取検査表 p0,p1からn,kを求めるための抜取検査表を付表に示す。
5
Z
9
0
0
4
-1
9
8
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
付表 抜取検査表 [p0 (%),p1 (%) を基にしてのサンプルの大きさnと合格判定値を計算するための係数kとを求める表]
左下の数字はn,右上の数字はk (α≒0.05,β≒0.10)
p1 (%)
代表値
0.80
1.00
1.25
1.60
2.00
2.50
3.15
4.00
5.00
6.30
8.00
10.00
12.50
16.00
20.00
25.00
31.50
p0 (%)
範囲
0.71
0.91
1.13
1.41
1.81
2.25
2.81
3.56
4.51
5.61
7.11
9.01
11.30
14.10
18.10
22.50
28.10
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
〜
代表値
範囲
0.90
1.12
1.40
1.80
2.24
2.80
3.55
4.50
5.60
7.10
9.00
11.20
14.00
18.00
22.40
28.00
35.50
0.100
0.090〜 0.112
2.71
87
2.67
68
2.62
54
2.57
42
2.52
34
2.47
28
2.42
23
2.36
19
2.31
16
2.24
13
2.19
11
2.11
9
2.07
8
1.95
6
1.87
5
1.87
5
1.77
4
0.125
0.113〜 0.140
2.64
80
2.59
62
2.54
48
2.49
38
2.44
31
2.39
25
2.32
20
2.28
17
2.21
14
2.16
12
2.10
10
2.02
8
1.97
7
1.90
6
1.82
5
1.72
4
0.160
0.141〜 0.180
2.60
98
2.56
74
2.50
56
2.46
44
2.40
35
2.35
28
2.30
23
2.23
18
2.18
15
2.10
12
2.04
10
2.00
9
1.91
7
1.85
6
1.77
5
1.67
4
0.200
0.181〜 0.224
2.53
90
2.47
66
2.43
51
2.37
40
2.32
31
2.26
25
2.20
20
2.14
16
2.08
13
2.02
11
1.95
9
1.86
7
1.80
6
1.72
5
1.63
4
0.250
0.225〜 0.280
2.44
79
2.39
59
2.34
46
2.28
35
2.23
28
2.17
22
2.12
18
2.04
14
1.99
12
1.93
10
1.86
8
1.75
6
1.67
5
1.53
4
0.315
0.281〜 0.355
2.41
98
2.36
71
2.31
54
2.25
41
2.19
31
2.14
25
2.07
19
2.00
15
1.94
12
1.88
10
1.80
8
1.75
7
1.62
5
1.53
4
0.400
0.356〜 0.450
2.32
89
2.27
65
2.22
48
2.16
36
2.10
28
2.04
22
1.98
17
1.92
14
1.85
11
1.78
9
1.69
7
1.64
6
1.47
4
0.500
0.451〜 0.560
2.23
80
2.18
57
2.12
42
2.07
32
2.00
24
1.94
19
1.88
15
1.81
12
1.72
9
1.64
7
1.58
6
1.51
5
0.630
0.561〜 0.710
2.14
71
2.08
50
2.03
37
1.97
28
1.90
21
1.83
16
1.77
13
1.69
10
1.62
8
1.52
6
1.45
5
0.800
0.711〜 0.900
2.10
92
2.05
62
1.99
44
1.92
32
1.86
24
1.79
18
1.72
14
1.66
11
1.56
8
1.51
7
1.39
5
1.000
0.901〜 1.120
2.01
79
1.95
54
1.89
38
1.83
28
1.76
21
1.69
16
1.62
12
1.53
9
1.45
7
1.33
5
1.250
1.130〜 1.400
1.91
69
1.85
47
1.78
32
1.72
24
1.65
18
1.57
13
1.50
10
1.39
7
1.33
6
1.600
1.410〜 1.800
1.87
95
1.80
60
1.74
40
1.67
28
1.60
20
1.53
15
1.45
11
1.35
8
1.26
6
2.000
1.810〜 2.240
1.76
81
1.69
50
1.63
34
1.56
24
1.48
17
1.40
12
1.32
9
1.19
6
2.500
2.250〜 2.800
1.65
67
1.59
43
1.52
29
1.43
19
1.36
14
1.27
10
1.17
7
3.150
2.810〜 3.550
1.61
96
1.54
57
1.47
36
1.39
23
1.31
16
1.22
11
1.13
8
4.000
3.560〜 4.500
1.49
83
1.42
48
1.34
29
1.25
19
1.17
13
1.08
9
5.000
4.510〜 5.600
1.37
69
1.29
38
1.20
23
1.11
15
1.02
10
6.300
5.610〜 7.100
1.23
53
1.15
30
1.07
19
0.97
12
8.000
7.110〜 9.000
1.18
87
1.10
44
1.00
24
0.89
14
10.000
9.010〜11.200
1.04
68
0.95
34
0.84
18
備考 空欄に対しては抜取検査方式はない。
6
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考1 OC曲線
1. 抜取検査のOC曲線 抜取検査を行う場合,ロット中に不良品が1個もなければ,そのロットは確実
に合格となり,ロットの製品全部が不良品であれば,そのロットは確実に不合格となる。しかし,ロット
の中に良品と不良品とが混じっていれば,ロット品質が良いロットでもある程度不合格となり,ロット品
質が悪いロットでもある程度合格となる。
抜取検査を行ったとき,あるロット品質のロットが長い間には,どのくらいの確率で合格となるか,不
合格となるかを表すのが,OC曲線 (Operating Characteristic Curve) である。
OC曲線は横軸にロットの不良率をとり,縦軸にそのロットが合格する確率をとってある。したがって
ある抜取検査方式で,ある不良率のロットがどれほどの確率で合格となるか,また逆に,ある一定の確率
で合格となるロットの不良率は幾らであるかなどを,この曲線から知ることができる。
例えば検査単位の特性値が上限規格値SU=2.0mm以下のとき,その検査単位は良品とし,SU=2.0mmを
超えるものは不良品とするという規格のもとに製造した製品があり,その製品の検査しようとするロット
の検査単位の特性値はほぼ正規分布に従うものとする。
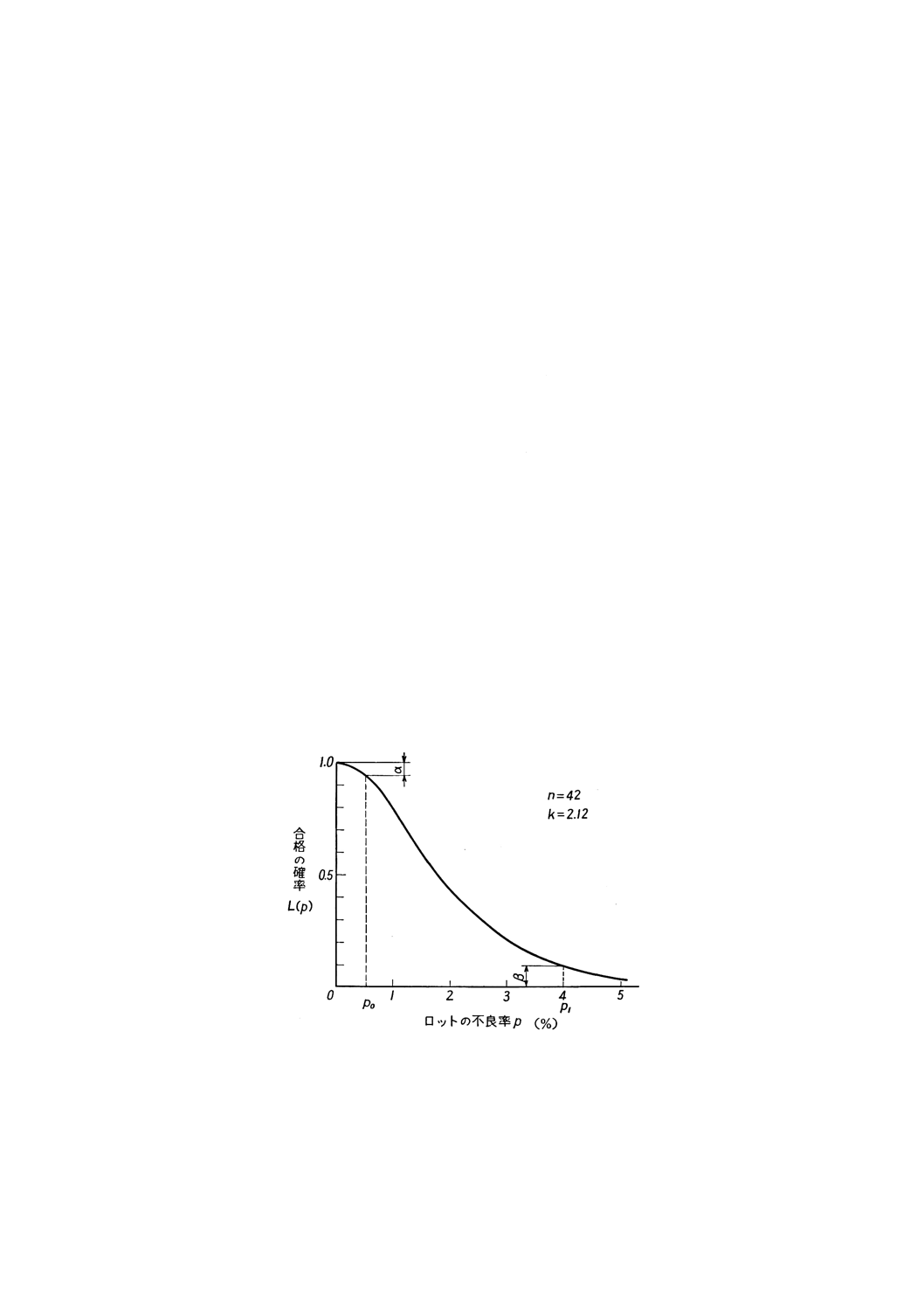
いま,サンプルの大きさn=42,合格判定係数k=2.12という抜取検査方式を繰り返し適用すると,長い
間には不良率0.5%のロットが,この検査で合格する割合は100回のうち95回くらいとなり,5回くらい
は不合格となる。
また,不良率4.0%のロットがこの検査に合格する割合は100回のうち10回くらいとなり,90回くらい
は不合格となる。
この関係を図示すると参考図1のようになる。
参考図1
このようにして,この曲線からn=42,k=2.12という抜取検査方式の場合,検査しようとするロットの
不良率とそのロットが合格となる確率の関係を知ることができる。
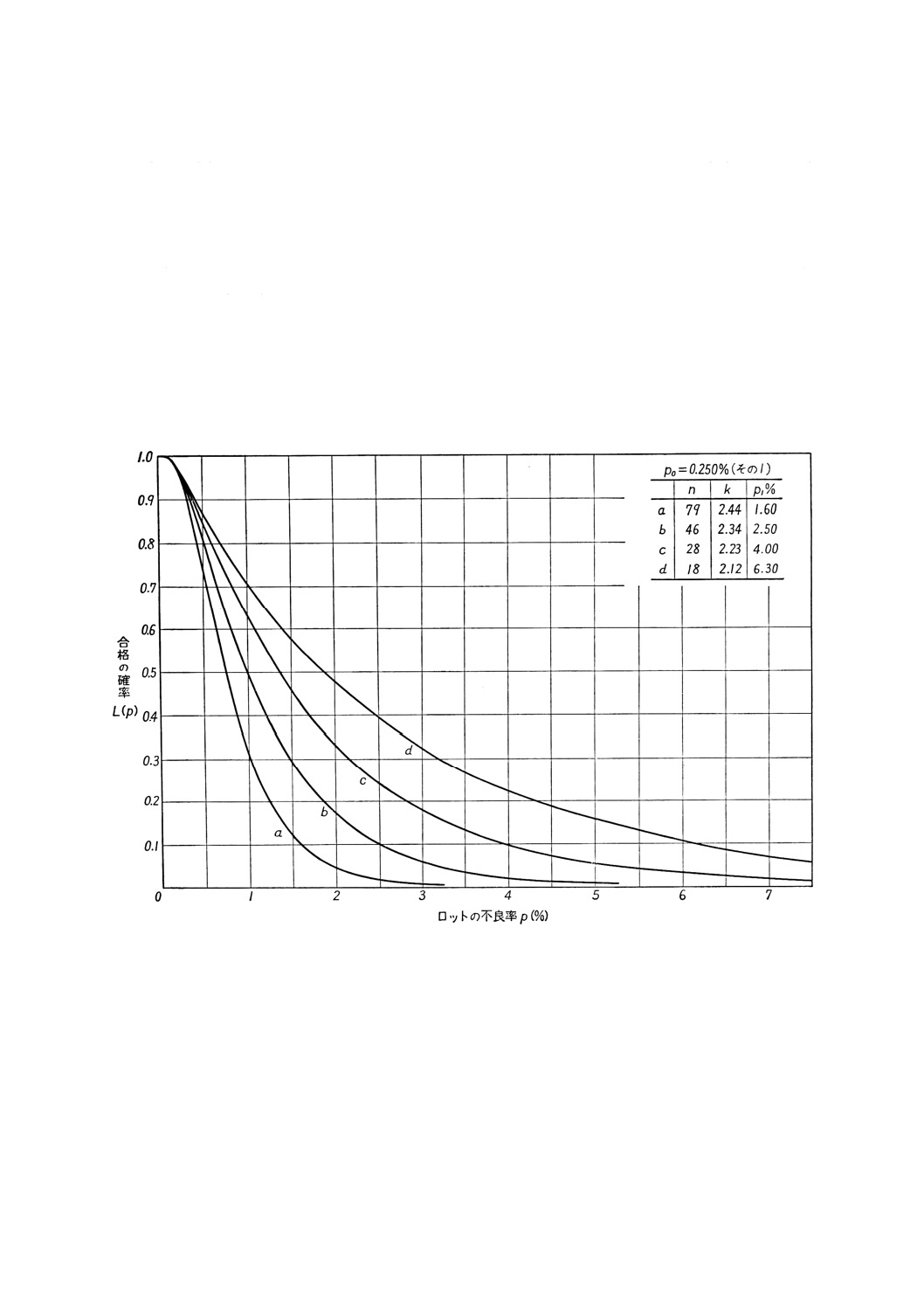
代表的なOC曲線を参考付図1.1〜1.5に示す(OC曲線の書き方は参考3参照)と共に,付表のすべて
の抜取検査方式のそれぞれについてロットの合格の確率L (p) の9個の値に対するロットの不良率p (%)
の値を参考付表に示す。
7
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2. p0,α;p1,βとOC曲線 参考図1からロットの不良率0.5%の点では不合格となる確率は0.05であり,
4.0%の点では合格となる確率は0.10である。したがって,n=42,k=2.12という抜取検査方式を用いれば,
生産者としてはロットの不良率0.5%以下のロット品質の良いロットが不合格とされる確率は0.05以下し
かなく,また消費者としてはロットの不良率4.0%以上のロット品質の悪いロットが合格とされる確率は
0.10以下しかないことがわかる。
この場合に,良いロットの目安となる不良率0.5%をp0=0.5%と表し,その不良率をもつロットが不合格
となる確率を生産者危険といい,α=0.05と表す。
また悪いロットの目安となる不良率4.0%をp1=4.0%と表し,その不良率をもつロットが合格となる確率
を消費者危険といい,β=0.10と表す。
したがって,OC曲線からわかるように,p0より良いロットの場合には,不合格となる危険は0.05より
は小さく,p1より悪いロットの場合には合格となる危険は0.10より小さい。
参考付図1.1 OC曲線 (p0=0.250%,p1=1.60〜6.30%)
8
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
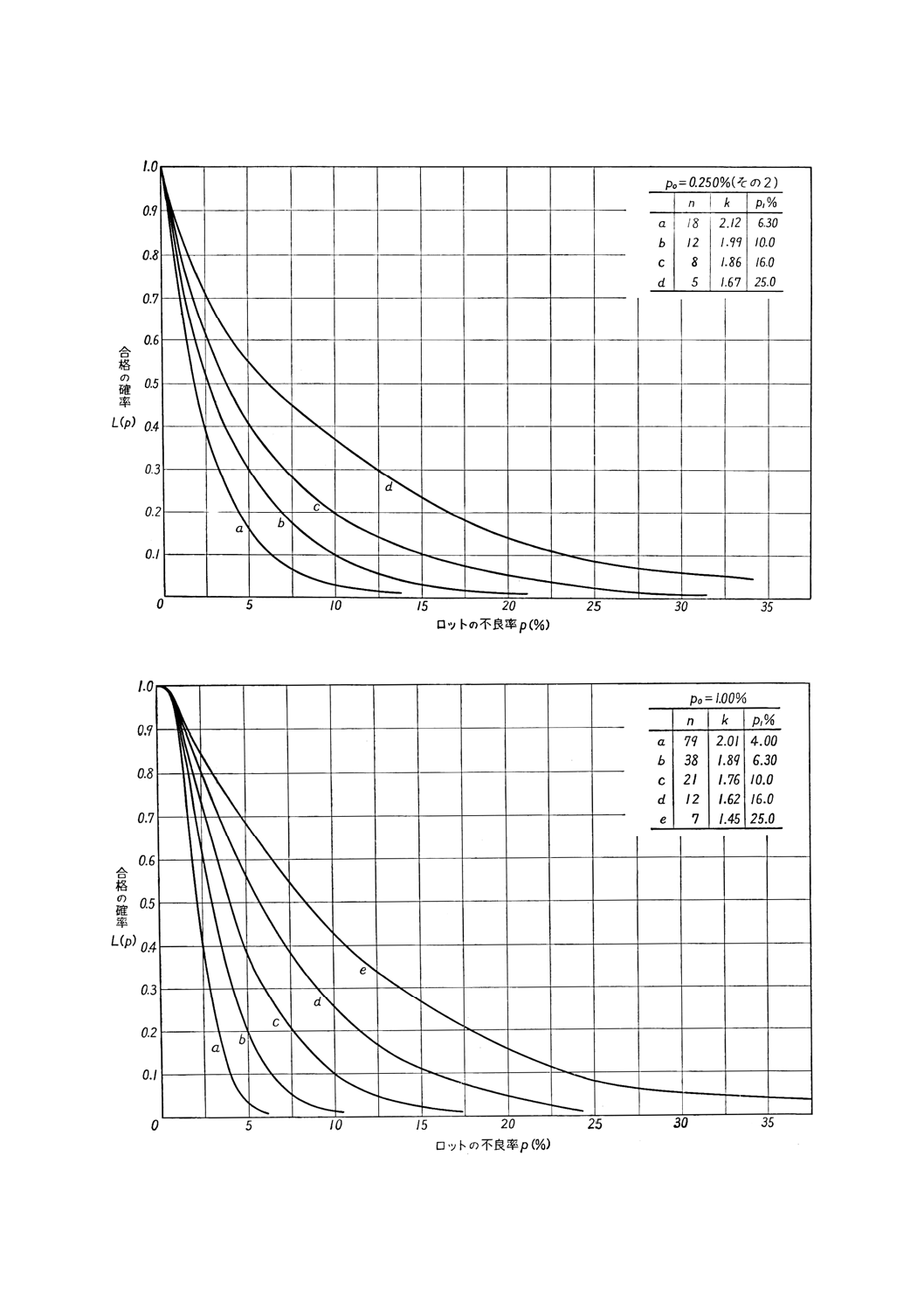
参考付図1.2 OC曲線 (p0=0.250%,p1=6.30〜25.0%)
参考付図1.3 OC曲線 (p0=1.00%,p1=4.00〜25.0%)
9
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
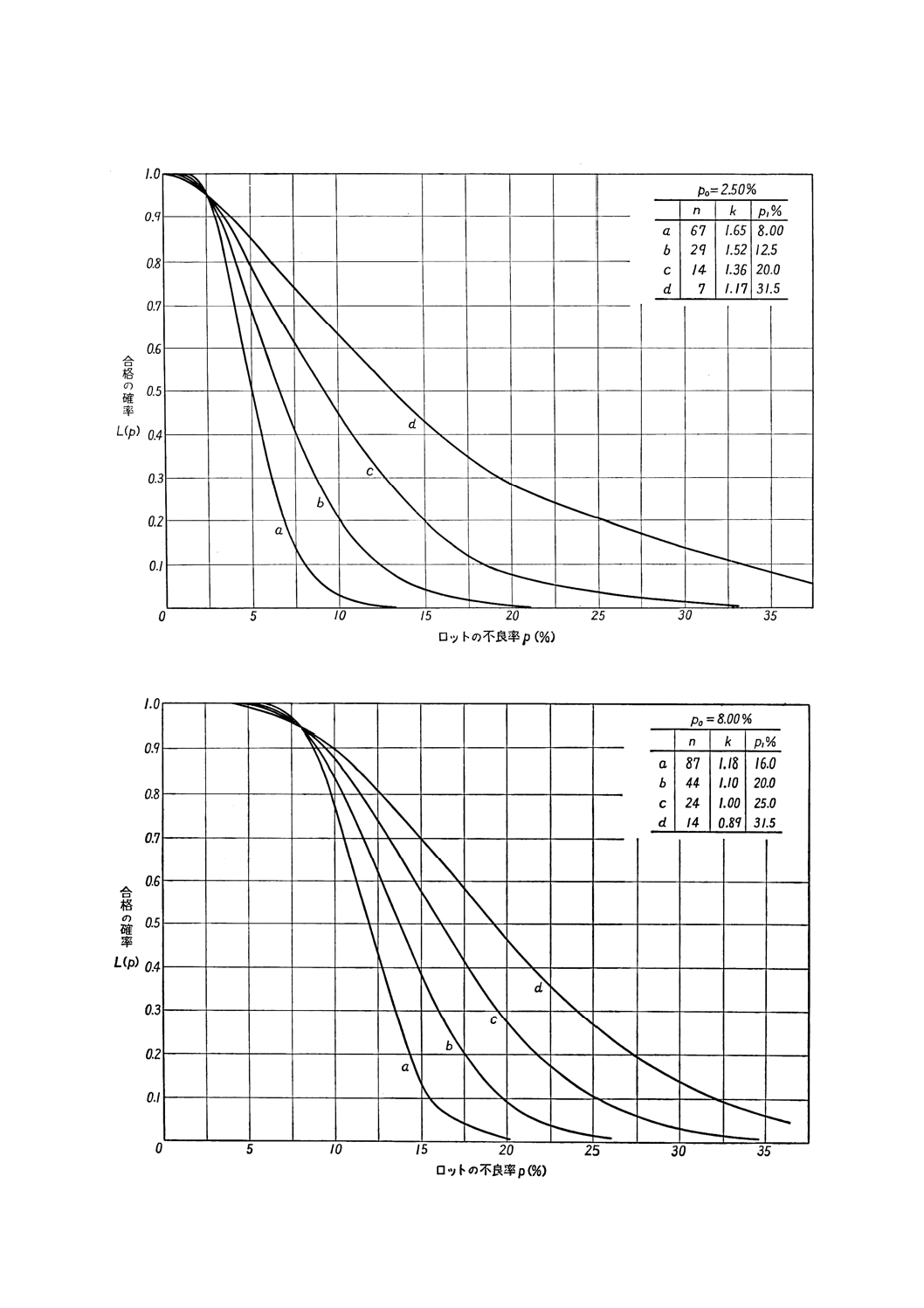
参考付図1.4 OC曲線 (p0=2.50%,p1=8.00〜31.5%)
参考付図1.5 OC曲線 (p0=8.00%,p1=16.0〜31.5%)
10
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考付表 サンプルの大きさnと合格判定係数kのそれぞれの組合せにおける
ロットの合格の確率L (p) に対するロットの不良率p (%)
p0 (%)
p1 (%)
サンプル
合格判
ロットの合格の確率L (p)
の
の
の大きさ
定係数
代表値 代表値
n
k
0.99
0.95
0.90
0.75
0.50
0.25
0.10
0.05
0.01
0.100
0.80
87
2.71
0.06
0.10
0.13 0.21 0.35 0.55 0.81 1.01 1.50
1.00
68
2.67
0.05
0.10
0.14 0.23 0.39 0.65 1.00 1.27 1.94
1.25
54
2.62
0.05
0.10
0.14 0.26 0.46 0.79 1.25 1.62 2.54
1.60
42
2.57
0.04
0.10
0.15 0.28 0.54 0.98 1.60 2.11 3.41
2.00
34
2.52
0.04
0.10
0.16 0.31 0.63 1.19 2.01 2.69 4.44
2.50
28
2.47
0.04
0.10
0.16 0.34 0.73 1.45 2.51 3.40 5.70
3.15
23
2.42
0.03
0.10
0.17 0.38 0.85 1.76 3.14 4.30 7.32
4.00
19
2.36
0.03
0.10
0.18 0.43 1.02 2.18 3.99 5.51 9.46
5.00
16
2.31
0.03
0.10
0.18 0.47 1.18 2.63 4.91 6.84 11.81
6.30
13
2.24
0.03
0.10
0.20 0.55 1.46 3.37 6.41 8.98 15.50
8.00
11
2.19
0.02
0.10
0.20 0.60 1.69 4.06 7.86 11.06 19.05
10.0
9
2.11
0.02
0.10
0.22 0.71 2.13 5.27 10.29 14.45 24.53
12.5
8
2.07
0.02
0.10
0.23 0.76 2.39 6.06 11.92 16.72 28.12
16.0
6
1.95
0.01
0.10
0.25 0.98 3.36 8.83 17.33 24.01 38.83
20.0
5
1.87
0.01
0.10
0.27 1.16 4.20 11.23 21.81 29.83 46.65
25.0
5
1.87
0.01
0.10
0.27 1.16 4.20 11.23 21.81 29.83 46.65
31.5
4
1.77
0.01
0.10
0.30 1.44 5.57 15.03 28.56 38.21 56.92
0.125
1.00
80
2.64
0.07
0.12
0.17 0.26 0.43 0.68 0.99 1.24 1.84
1.25
62
2.59
0.07
0.13
0.17 0.29 0.50 0.82 1.25 1.59 2.43
1.60
48
2.54
0.06
0.12
0.18 0.32 0.58 1.01 1.59 2.06 3.23
2.00
38
2.49
0.06
0.12
0.19 0.35 0.68 1.23 2.01 2.64 4.24
2.50
31
2.44
0.05
0.13
0.19 0.39 0.79 1.49 2.50 3.33 5.45
3.15
25
2.39
0.05
0.12
0.20 0.43 0.92 1.81 3.14 4.25 7.07
4.00
20
2.32
0.04
0.13
0.22 0.49 1.12 2.32 4.13 5.63 9.47
5.00
17
2.28
0.04
0.12
0.22 0.53 1.27 2.72 4.94 6.80 11.53
6.30
14
2.21
0.04
0.13
0.24 0.61 1.55 3.43 6.34 8.77 14.88
8.00
12
2.16
0.03
0.13
0.25 0.68 1.79 4.09 7.66 10.63 18.00
10.0
10
2.10
0.03
0.13
0 26 0.76 2.13 5.03 9.57 13.31 22.40
12.5
8
2.02
0.02
0.12
0.27 0.89 2.67 6.56 12.62 17.53 29.02
16.0
7
1.97
0.02
0.12
0.28 0.98 3.08 7.72 14.89 20.60 33.63
20.0
6
1.90
0.02
0.13
0.31 1.14 3.72 9.46 18.16 24.91 39.72
25.0
5
1.82
0.02
0.13
0.34 1.34 4.63 11.94 22.71 30.76 47.49
31.5
4
1.72
0.01
0.13
0.37 1.66 6.08 15.85 29.49 39.12 57.65
0.160
1.00
98
2.60
0.10
0.16
0.21 0.31 0.48 0.72 1.01 1.23 1.75
1.25
74
2.56
0.09
0.16
0.21 0.33 0.54 0.85 1.24 1.55 2.27
1.60
56
2.50
0.09
0.16
0.23 0.38 0.65 1.06 1.61 2.04 3.09
2.00
44
2.46
0.08
0.16
0.23 0.40 0.73 1.26 1.98 2.55 3.97
2.50
35
2.40
0.07
0.16
0.24 0.46 0.87 1.56 2.53 3.30 5.24
3.15
28
2.35
0.07
0.16
0.25 0.50 1.01 1.90 3.16 4.19 6.78
4.00
23
2.30
0.06
0.16
0.26 0.55 1.17 2.28 3.91 5.23 8.58
5.00
18
2.23
0.05
0.16
0.28 0.63 1.43 2.93 5.16 6.99 11.59
6.30
15
2.18
0.05
0.16
0.28 0.69 1.65 3.52 6.32 8.63 14.39
8.00
12
2.10
0.04
0.16
0.31 0.81 2.06 4.56 8.33 11.42 18.98
10.0
10
2.04
0.04
0.16
0.32 0.91 2.44 5.57 10.33 14.20 23.45
12.5
9
2.00
0.04
0.16
0.34 0.99 2.72 6.32 11.77 16.15 26.49
16.0
7
1.90
0.03
0.16
0.36 1.17 3.49 8.43 15.84 21.65 34.74
11
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p0 (%)
p1 (%)
サンプル
合格判
ロットの合格の確率L (p)
の
の
の大きさ
定係数
代表値 代表値
n
k
0.99
0.95
0.90
0.75
0.50
0.25
0.10
0.05
0.01
20.0
6
1.85
0.02
0.16
0.38 1.32 4.11 10.12 19.02 25.83 40.63
0.160
25.0
5
1.77
0.02
0.16
0.41 1.55 5.09 12.70 23.63 31.70 48.35
31.5
4
1.67
0.02
0.16
0.45 1.90 6.63 16.69 30.44 40.04 58.38
0.200
1.25
90
2.53
0.12
0.20
0.25 0.38 0.58 0.88 1.23 1.50 2.13
1.60
66
2.47
0.11
0.20
0.27 0.43 0.70 1.10 1.60 1.99 2.92
2.00
51
2.43
0.10
0.20
0.27 0.46 0.79 1.30 1.96 2.48 3.75
2.50
40
2.37
0.10
0.20
0.29 0.52 0.94 1.61 2.51 3.21 4.95
3.15
31
2.32
0.09
0.20
0.30 0.57 1.08 1.96 3.16 4.12 6.51
4.00
25
2.26
0.08
0.20
0.32 0.64 1.28 2.41 3.99 5.27 8.43
5.00
20
2.20
0.07
0.20
0.33 0.71 1.52 2.98 5.07 6.76 10.95
6.30
16
2.14
0.07
0.20
0.35 0.79 1.80 3.68 6.44 8.67 14.17
8.00
13
2.08
0.06
0.20
0.36 0.89 2.14 4.54 8.10 10.98 18.00
10.0
11
2.02
0.05
0.20
0.38 1.00 2.51 5.48 9.89 13.43 21.91
12.5
9
1.95
0.05
0.20
0.40 1.14 3.04 6.84 12.49 16.97 27.41
16.0
7
1.86
0.04
0.20
0.43 1.35 3.87 9.06 16.67 22.56 35.68
20.0
6
1.80
0.03
0.20
0.45 1.51 4.54 10.82 19.91 26.78 41.56
25.0
5
1.72
0.03
0.20
0.49 1.78 5.58 13.48 24.57 32.67 49.22
31.5
4
1.63
0.02
0.20
0.53 2.12 7.10 17.40 31.22 40.79 58.98
0.250
1.60
79
2.44
0.15
0.25
0.32 0.49 0.75 1.13 1.60 1.95 2.76
2.00
59
2.39
0.14
0.25
0.34 0.54 0.87 1.37 2.01 2.49 3.64
2.50
46
2.34
0.13
0.25
0.35 0.59 1.01 1.65 2.49 3.14 4.70
3.15
35
2.28
0.12
0.25
0.37 0.66 1.19 2.05 3.20 4.10 6.30
4.00
28
2.23
0.11
0.25
0.38 0.72 1.37 2.46 3.95 5.13 8.02
5.00
22
2.17
0.10
0.25
0.40 0.80 1.63 3.05 5.03 6.62 10.50
6.30
18
2.12
0.09
0.25
0.41 0.88 1.87 3.64 6.16 8.18 13.11
8.00
14
2.04
0.08
0.25
0.44 1.02 2.32 4.71 8.16 10.91 17.54
10.0
12
1.99
0.08
0.25
0.46 1.12 2.65 5.53 9.69 12.99 20.86
12.5
10
1.93
0.07
0.25
0.48 1.25 3.11 6.68 11.86 15.94 25.46
16.0
8
1.86
0.06
0.25
0.50 1.41 3.76 8.39 15.08 20.28 32.02
20.0
6
1.75
0.04
0.25
0.55 1.74 5.00 11.56 20.82 27.75 42.49
25.0
5
1.67
0.04
0.25
0.60 2.04 6.12 14.30 25.54 33.66 50.10
31.5
4
1.58
0.03
0.25
0.64 2.42 7.72 18.30 32.21 41.74 59.74
0.315
1.60
98
2.41
0.20
0.31
0.39 0.56 0.81 1.17 1.58 1.89 2.59
2.00
71
2.36
0.19
0.31
0.40 0.61 0.94 1.41 1.99 2.42 3.42
2.50
54
2.31
0.17
0.31
0.42 0.67 1.08 1.70 2.47 3.05 4.44
3.15
41
2.25
0.17
0.32
0.44 0.75 1.28 2.09 3.15 3.95 5.89
4.00
31
2.19
0.15
0.32
0.46 0.83 1.51 2.59 4.04 5.15 7.85
5.00
25
2.14
0.14
0.32
0.48 0.91 1.73 3.09 4.93 6.38 9.86
6.30
19
2.07
0.12
0.32
0.50 1.03 2.09 3.93 6.46 8.45 13.27
8.00
15
2.00
0.11
0.32
0.53 1.17 2.52 4.92 8.27 10.92 17.22
10.0
12
1.94
0.10
0.31
0.55 1.29 2.96 6.02 10.35 13.76 21.76
12.5
10
1.88
0.09
0.31
0.57 1.44 3.47 7.25 12.61 16.78 26.41
16.0
8
1.80
0.08
0.31
0.62 1.67 4.25 9.17 16.09 21.38 33.20
20.0
7
1.75
0.07
0.32
0.64 1.83 4.83 10.57 18.60 24.65 37.82
25.0
5
1.62
0.05
0.32
0.71 2.32 6.69 15.16 26.54 34.66 51.00
31.5
4
1.53
0.04
0.31
0.76 2.75 8.38 19.24 33.22 42.71 60.51
0.400
2.00
89
2.32
0.26
0.40
0.50 0.71 1.04 1.48 2.01 2.38 3.25
2.50
65
2.27
0.24
0.40
0.52 0.78 1.19 1.78 2.50 3.02 4.25

12
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p0 (%)
p1 (%)
サンプル
合格判
ロットの合格の確率L (p)
の
の
の大きさ
定係数
代表値 代表値
n
k
0.99
0.95
0.90
0.75
0.50
0.25
0.10
0.05
0.01
0.400
3.15
48
2.22
0.22
0.39
0.53 0.84 1.37 2.15 3.12 3.85 5.56
4.00
36
2.16
0.20
0.40
0.55 0.94 1.61 2.64 3.97 4.98 7.37
5.00
28
2.10
0.19
0.40
0.58 1.05 1.89 3.23 4.99 6.34 9.56
6.30
22
2.04
0.17
0.40
0.61 1.17 2.22 3.94 6.25 8.03 12.28
8.00
17
1.98
0.15
0.39
0.63 1.28 2.61 4.85 7.91 10.29 15.93
10.0
14
1.92
0.14
0.40
0.66 1.43 3.04 5.83 9.67 12.64 19.61
12.5
11
1.85
0.12
0.39
0.69 1.61 3.64 7.27 12.29 16.16 25.06
16.0
9
1.78
0.11
0.40
0.74 1.83 4.34 8.90 15.19 19.98 30.72
20.0
7
1.69
0.10
0.40
0.79 2.15 5.42 11.48 19.72 25.84 39.02
25.0
6
1.64
0.08
0.39
0.81 2.33 6.15 13.30 22.94 29.96 44.60
31.5
4
1.47
0.06
0.40
0.95 3.20 9.23 20.41 34.47 43.89 61.43
0.500
2.50
80
2.23
0.33
0.51
0.63 0.91 1.32 1.87 2.53 3.00 4.06
3.15
57
2.18
0.30
0.50
0.65 0.98 1.51 2.25 3.16 3.82 5.35
4.00
42
2.12
0.28
0.50
0.63 1.09 1.77 2.78 4.00 4.93 7.08
5.00
32
2.07
0.25
0.49
0.69 1.18 2.02 3.30 4.94 6.17 9.07
6.30
24
2.00
0.23
0.50
0.74 1.33 2.42 4.14 6.38 8.09 12.10
8.00
19
1.94
0.21
0.50
0.77 1.48 2.83 5.01 7.91 10.12 15.30
10.0
15
1.88
0.19
0.50
0.79 1.63 3.29 6.08 9.82 12.68 19.32
12.5
12
1.81
0.17
0.51
0.85 1.84 3.92 7.47 12.26 15.90 24.22
16.0
9
1.72
0.15
0.50
0.90 2.15 4.89 9.73 16.24 21.12 31.94
20.0
7
1.64
0.12
0.49
0.94 2.45 5.96 12.27 20.69 26.87 40.04
25.0
6
1.58
0.11
0.50
0.99 2.72 6.86 14.34 24.16 31.22 45.78
31.5
5
1.51
0.10
0.50
1.05 3.08 8.09 17.17 28.83 36.95 52.99
0.630
3.15
71
2.14
0.41
0.64
0.80 1.14 1.66 2.35 3.17 3.75 5.07
4.00
50
2.08
0.38
0.64
0.83 1.26 1.94 2.89 4.03 4.87 6.78
5.00
37
2.03
0.34
0.62
0.84 1.36 2.21 3.45 4.98 6.12 8.74
6.30
28
1.97
0.32
0.63
0.88 1.50 2.57 4.19 6.23 7.76 11.31
8.00
21
1.90
0.29
0.63
0.93 1.69 3.07 5.22 7.99 10.07 14.90
10.0
16
1.83
0.26
0.63
0.97 1.89 3.65 6.48 10.17 12.95 19.34
12.5
13
1.77
0.24
0.64
1.02 2.09 4.22 7.73 12.33 15.78 23.63
16.0
10
1.69
0.21
0.64
1.08 2.39 5.12 9.72 15.77 20.26 30.23
20.0
8
1.62
0.19
0.63
1.13 2.63 6.05 11.83 19.41 24.96 36.90
25.0
6
1.52
0.16
0.63
1.21 3.17 7.63 15.42 25.42 32.51 46.98
31.5
5
1.45
0.14
0.64
1.29 3.57 8.95 18.34 30.13 38.23 54.10
0.800
3.15
92
2.10
0.56
0.81
0.98 1.32 1.82 2.46 3.18 3.68 4.80
4.00
62
2.05
0.51
0.79
0.99 1.42 2.07 2.94 3.96 4.69 6.33
5.00
44
1.99
0.47
0.79
1.03 1.56 2.41 3.59 5.00 6.03 8.36
6.30
32
1.92
0.44
0.81
1.10 1.76 2.86 4.46 6.40 7.83 11.09
8.00
24
1.86
0.40
0.80
1.13 1.93 3.32 5.40 7.98 9.90 14.28
10.0
18
1.79
0.36
0.80
1.19 2.16 3.94 6.67 10.14 12.71 18.57
12.5
14
1.72
0.33
0.81
1.25 2.43 4.65 8.16 12.64 15.97 23.44
16.0
11
1.66
0.29
0.79
1.28 2.65 5.37 9.78 15.47 19.66 28.93
20.0
8
1.56
0.25
0.79
1.37 3.11 6.76 12.84 20.61 26.23 38.19
25.0
7
1.51
0.24
0.80
1.44 3.39 7.55 14.52 23.36 29.66 42.76
31.5
5
1.39
0.19
0.80
1.56 4.12 9.87 19.57 31.47 39.55 55.22
4.00
79
2.01
0.68
0.99
1.20 1.64 2.26 3.07 3.98 4.61 6.01
1.00
5.00
54
1.95
0.64
1.00
1.25 1.80 2.63 3.73 5.01 5.92 7.95
6.30
38
1.89
0.58
0.99
1.29 1.97 3.04 4.53 6.30 7.58 10.45

13
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p0 (%)
p1 (%)
サンプル
合格判
ロットの合格の確率L (p)
の
の
の大きさ
定係数
代表値 代表値
n
k
0.99
0.95
0.90
0.75
0.50
0.25
0.10
0.05
0.01
1.00
8.00
28
1.83
0.53
0.99
1.34 2.16 3.52 5.47 7.84 9.57 13.46
10.0
21
1.76
0.50
1.00
1.42 2.42 4.15 6.71 9.86 12.17 17.36
12.5
16
1.69
0.46
1.01
1.49 2.71 4.88 8.19 12.31 15.33 22.07
16.0
12
1.62
0.40
0.99
1.53 3.00 5.75 10.07 15.49 19.45 28.15
20.0
9
1.53
0.35
1.00
1.64 3.46 7.03 12.75 19.91 25.05 36.03
25.0
7
1.45
0.31
1.00
1.73 3.91 8.39 15.66 24.67 31.01 44.06
31.5
5
1.33
0.26
1.00
1.89 4.73 10.86 20.85 32.84 40.90 56.37
5.00
69
1.90
0.86
1.26
1.52 2.07 2.86 3.88 5.01 5.80 7.53
6.30
47
1.85
0.80
1.25
1.57 2.27 3.30 4.69 6.28 7.40 9.89
8.00
32
1.78
0.73
1.25
1.64 2.52 3.90 5.81 8.06 9.68 13.28
10.0
24
1.72
0.67
1.25
1.70 2.75 4.48 6.94 9.89 12.01 16.75
1.25
12.5
18
1.65
0.62
1.26
1.79 3.07 5.25 8.44 12.32 15.12 21.32
16.0
13
1.57
0.55
1.25
1.87 3.45 6.29 10.57 15.82 19.60 27.85
20.0
10
1.50
0.48
1.23
1.93 3.82 7.34 12.78 19.46 24.22 34.40
25.0
7
1.39
0.41
1.23
2.07 4.50 9.30 16.86 26.03 32.40 45.38
31.5
6
1.33
0.39
1.26
2.20 4.96 10.51 19.25 29.70 36.82 50.93
5.00
95
1.87
1.17
1.59
1.86 2.39 3.12 4.01 4.98 5.63 7.04
6.30
60
1.80
1.11
1.62
1.96 2.66 3.67 4.95 6.37 7.35 9.48
8.00
40
1.74
1.00
1.59
2.00 2.89 4.21 5.97 7.97 9.37 12.45
10.0
28
1.67
0.93
1.60
2.10 3.20 4.93 7.30 10.05 12.00 16.28
1.60
12.5
20
1.60
0.84
1.59
2.17 3.54 5.76 8.91 12.62 15.27 21.07
16.0
15
1.53
0.77
1.59
2.27 3.92 6.71 10.75 15.58 19.01 26.44
20.0
11
1.45
0.68
1.58
2.37 4.39 7.96 13.27 19.63 24.11 33.64
25.0
8
1.35
0.62
1.62
2.56 5.09 9.78 16.84 25.23 31.03 42.92
31.5
6
1.26
0.53
1.60
2.69 5.79 11.74 20.81 31.39 38.50 52.43
2.00
6.30
81
1.76
1.49
2.02
2.37 3.05 3.98 5.11 6.34 7.16 8.92
8.00
50
1.69
1.38
2.03
2.46 3.36 4.65 6.29 8.09 9.34 12.01
10.0
34
1.63
1.25
1.99
2.52 3.64 5.31 7.51 10.00 11.73 15.48
12.5
24
1.56
1.16
2.00
2.63 4.02 6.18 9.10 12.46 14.81 19.92
16.0
17
1.48
1.07
2.03
2.77 4.51 7.31 11.22 15.76 18.94 25.78
20.0
12
1.40
0.93
1.98
2.86 5.01 8.65 13.85 19.95 24.21 33.20
25.0
9
1.32
0.84
1.99
3.00 5.60 10.16 16.81 24.58 29.92 40.92
31.5
6
1.19
0.72
2.01
3.28 6.72 13.08 22.45 33.14 40.22 53.95
8.00
67
1.65
1.84
2.53
2.97 3.84 5.02 6.48 8.03 9.08 11.29
10.0
43
1.59
1.68
2.48
3.02 4.14 5.72 7.72 9.92 11.42 14.63
12.5
29
1.52
1.55
2.49
3.14 4.55 6.63 9.34 12.38 14.47 18.96
2.50
16.0
19
1.43
1.42
2.51
3.33 5.15 7.97 11.78 16.11 19.10 25.48
20.0
14
1.36
1.30
2.50
3.45 5.65 9.18 14.05 19.61 23.46 31.55
25.0
10
1.27
1.17
2.52
3.65 6.38 10.95 17.35 24.67 29.67 39.91
31.5
7
1.17
1.01
2.49
3.83 7.26 13.25 21.78 31.41 37.82 50.42
8.00
96
1.61
2.44
3.13
3.55 4.36 5.43 6.67 7.96 8.82 10.59
10.0
57
1.54
2.30
3.15
3.71 4.80 6.28 8.08 9.99 11.27 13.97
12.5
36
1.47
2.12
3.14
3.83 5.24 7.25 9.76 12.49 14.34 18.25
3.15
16.0
23
1.39
1.92
3.12
3.97 5.80 8.51 12.02 15.91 18.56 24.17
20.0
16
1.31
1.76
3.14
4.16 6.44 9.94 14.60 19.79 23.34 30.75
25.0
11
1.22
1.58
3.12
4.35 7.21 11.80 18.02 24.99 29.69 39.32
31.5
8
1.13
1.43
3.15
4.59 8.10 13.91 21.89 30.74 36.61 48.23
4.00
10.0
83
1.49
3.14
4.01
4.54 5.56 6.88 8.42 10.01 11.05 13.19
14
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p0 (%)
p1 (%)
サンプル
合格判
ロットの合格の確率L (p)
の
の
の大きさ
定係数
代表値 代表値
n
k
0.99
0.95
0.90
0.75
0.50
0.25
0.10
0.05
0.01
4.00
12.5
48
1.42
2.90
3.98
4.68 6.05 7.91 10.15 12.51 14.08 17.35
16.0
29
1.34
2.65
3.96
4.85 6.67 9.24 12.44 15.88 18.19 23.02
20.0
19
1.25
2.48
4.05
5.15 7.50 10.93 15.32 20.08 23.29 29.94
25.0
13
1.17
2.23
4.00
5.31 8.23 12.67 18.45 24.78 29.02 37.66
31.5
9
1.08
1.98
3.96
5.52 9.15 14.87 22.46 30.72 36.17 46.96
12.5
69
1.37
3.92
5.02
5.70 6.97 8.63 10.54 12.50 13.79 16.41
16.0
38
1.29
3.59
4.98
5.88 7.64 10.03 12.89 15.88 17.86 21.94
5.00
20.0
23
1.20
3.32
5.02
6.17 8.52 11.81 15.88 20.19 23.06 28.95
25.0
15
1.11
3.05
5.05
6.46 9.47 13.84 19.34 25.23 29.12 37.02
31.5
10
1.02
2.70
4.97
6.67 10.44 16.15 23.47 31.28 36.38 46.45
6.30
16.0
53
1.23
4.92
6.35
7.23 8.90 11.06 13.56 16.09 17.74 21.09
20.0
30
1.15
4.49
6.28
7.44 9.70 12.74 16.36 20.10 22.56 27.56
25.0
19
1.07
4.11
6.24
7.67 10.57 14.61 19.52 24.66 28.03 34.84
31.5
12
0.97
3.74
6.25
8.03 11.79 17.22 23.94 30.97 35.54 44.55
8.00
16.0
87
1.18
6.63
7.96
8.75 10.19 11.98 13.96 15.92 17.17 19.67
20.0
44
1.10
6.14
7.92
9.02 11.08 13.72 16.75 19.81 21.77 25.73
25.0
24
1.00
5.71
8.00
9.47 12.34 16.16 20.64 25.21 28.16 34.09
31.5
14
0.89
5.25
8.08
9.99 13.86 19.18 25.55 32.05 36.22 44.41
20.0
68
1.04
8.24
9.94
10.94 12.76 15.02 17.51 19.96 21.51 24.59
10.0
25.0
34
0.95
7.66
9.94
11.33 13.96 17.31 21.11 24.90 27.32 32.13
31.5
18
0.84
7.02
9.97
11.86 15.55 20.42 26.07 31.73 35.34 42.41
15
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考2 設計の理論
この計量規準型抜取検査の設計の理論は,概略次のとおりである。
上限規格SU値が与えられた場合,ロットから大きさnのサンプルを抜き取り,サンプルの平均値x及び
サンプルの標準偏差sを求め,
x+ks≦SU ならばロットを合格
x+ks>SU ならばロットを不合格
と判定する。このときのサンプルの大きさnと合格判定係数kを求めるのであるが,これは片側許容限界
の問題に帰着する。
すなわち,γをZ=x+ksがSU=m+Kpσを超える確率とし,pをロットの不良率,すなわちp=1−Φ (Kp)
とすれば,
γ=Pr (Z≧SU)
=Pr (x+ks≧m+Kpσ)
=Pr (x−m−Kpσ≧−ks)
=Pr
(
)
k
n
s
K
n
m
x
n
p≧−
−
−
σ
=Pr
k
n
s
K
n
n
x
m
p
≦
+
−
σ
σ
となる。
u=
n
x
m
σ
−
はN (0, 12) に従い,
2
2
)1
(
σ
s
n−
は自由度がn−1のχ2分布に従うので,
y=
σ
σ
s
K
n
n
x
m
p
+
−
は自由度f=n−1,非心度λ=nKpの非心t分布に従う。その分布関数と上側Qパーセント点をそれぞれ,
P (t' ; f, λ) ,t' (Q ; f, λ) と定義すれば,
Pr (x+ks≧m+Kpσ) =P (nk ; n−1,
nKp)
となる。
また,P (t' ; f, λ) =1−P (−t' ; f, λ) であるから,
Pr (x+ks≦SU) =1−P (nk ; n−1,
nKp)
となる。
16
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
不良率p0であるロットの合格の確率が (1−α) であるから,
Pr (x+ks≦SU) =1−α
したがって,
k=
n
K
n
n
t'
p)
,1
;
1(
0
−
−α
である。
一方,任意の合格の確率βとなるロットの不良率pを求めるには,
β=1−P (nk ; n−1, nKp)
を満足しなければならない。

17
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考3 任意のα,βのときの非心t分布による抜取検査方式の求め方
及びOC曲線の書き方
1. 任意のα,βのときの非心t分布による抜取検査方式の求め方
(1) 非心t分布の分布関数の計算 非心t分布の分布関数は,2次元正規分布に関するT関数を用いる。
自由度fが奇数のとき
P (t′ ; f, λ) =Φ (−λB) +2T (λ
,
BA) +2
∑
−
=
−
2
/)1
(
1
1
2
f
i
i
M
………(1)*
自由度fが偶数のとき
P (t′ ; f, λ) =Φ (−λ) +
∑
−
=
2
/)2
(
0
2
2
f
i
i
M
π
………………………………(2)*
ここで,
A=
f
t'
B=
2
t'
f
f
+
であり,Miは,
M0=
)
)
(
B
A
Φ(
B
B
A
λ
λ
φ
M1=B
+
)
(
2
0
λ
φ
π
λ
A
AM
M2=21B (λAM1+M0)
…
…
Mk=k
k1
−B (akλAMk−1+Mk−2)
ただし,a2=1
ak=
1
)2
(
1
−
−
k
a
k
(k=3, 4, ……, f−2)
である。
(2) 非心t分布のパーセント点の計算 x+ksの分布の正規近似から,非心t分布のパーセント点を求め
る近似式を使用する。
t′ (Q ; f, λ) =
f
K
K
f
K
Q
Q
Q
2
1
)
(
2
1
2
2
2
2
2
−
−
−
−
+
λ
λ
λ
…………………(3)*
18
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
式(3)*を初期値として,式(1)*,(2)*から求めた分布関数を使って,ニュートンラフソン法で求める。
(3) n,p0,L (p0) とβを与えてkとp1を求める計算 n,p0とそのp0に対する合格の確率L (p0) =1−α及
びβを与えて,k,p1を求めるには,次の手順で行う。
手順1. λ=nKp0, f=n−1の非心t分布の上側αパーセント点t′ (α ; n−1,
nKp0) を前述の(2)の
方法で求める。
手順2. k=
n
K
n
n
t'
p)
,1
;
(
0
−
α
として,kを求める。
手順3. Kp1=k−Kβ
)1
(2
1
2
−
+
n
k
n
から, (p1, β) を満たす非心度の初期値λ=nKp1を求める。
手順4. 自由度f=n−1,非心度λ=nKp1の非心t分布のパーセント点t' (β ; n−1, nKp1) から,
その上側確率P (t′ ; f, λ) を求め,実現した確率とねらいの値 (1−β) との差をλについて
ニュートンラフソン法で収束させて求める。
(4) 任意のα,β,p0,p1に対する抜取検査方式を求める計算 初期値nは,次の正規近似型で与え,前述
の(3)の方法でp1を求める。
n=
2
1
0
2
2
1
−
+
+
p
p
K
K
K
K
k
β
α
−1
k=
β
α
α
β
K
K
K
K
K
K
p
p
+
+
1
0
この場合,初期値nは真のnより大きくない値であるからL (p1) はβの値より大きくなる。したが
ってこのnを1ずつ増加させて,L (p1) がβに最も近くなるnを求め,その (n, k) を採用する。
2. OC曲線の書き方 抜取検査方式 (n, k) が与えられたとき,ロットの不良率pに対する合格の確率L(p)
は,
L (p) =P (kn ; n−1,
nKp)
で求める。
これにより,不良率pをパラメータとしてL (p) を求めればOC曲線を求めることができる。
3. 例:
p0=1%.α=0.05;p1=10%,β=0.05を満足する抜取検査方式は,1.により初期値n=27,k=1.80から
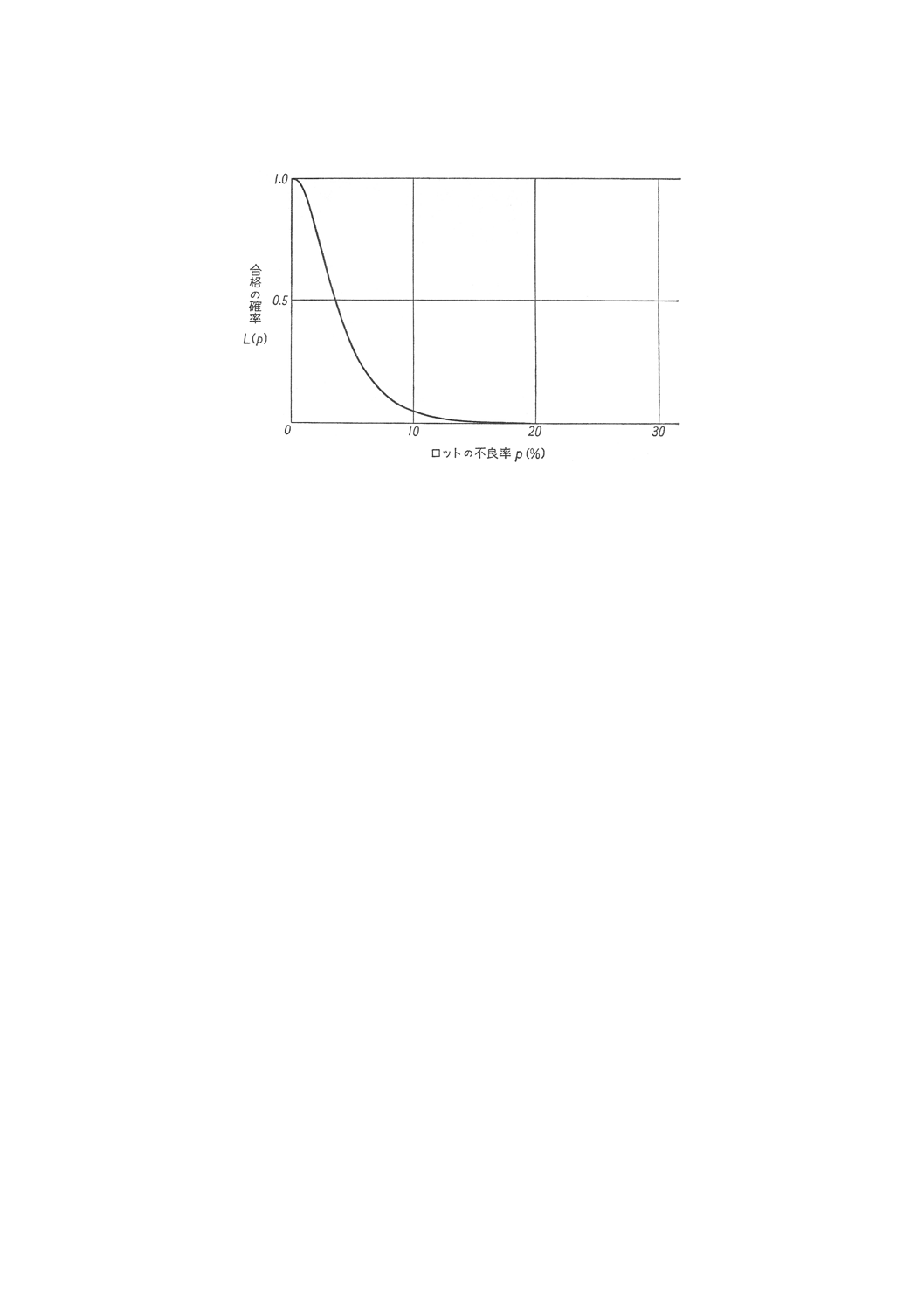
出発し,そしてn=27,k=1.82に収束する。このOC曲線を参考図2に示す。
19
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考図2 OC曲線 (n=27,k=1.82,p0.95=1.00%,p0.05=9.91%)
20
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考4 任意のα,βのときの正規近似による抜取検査方式の求め方
及びOC曲線の書き方
1. 任意のα,βのときの正規近似による抜取検査方式の求め方
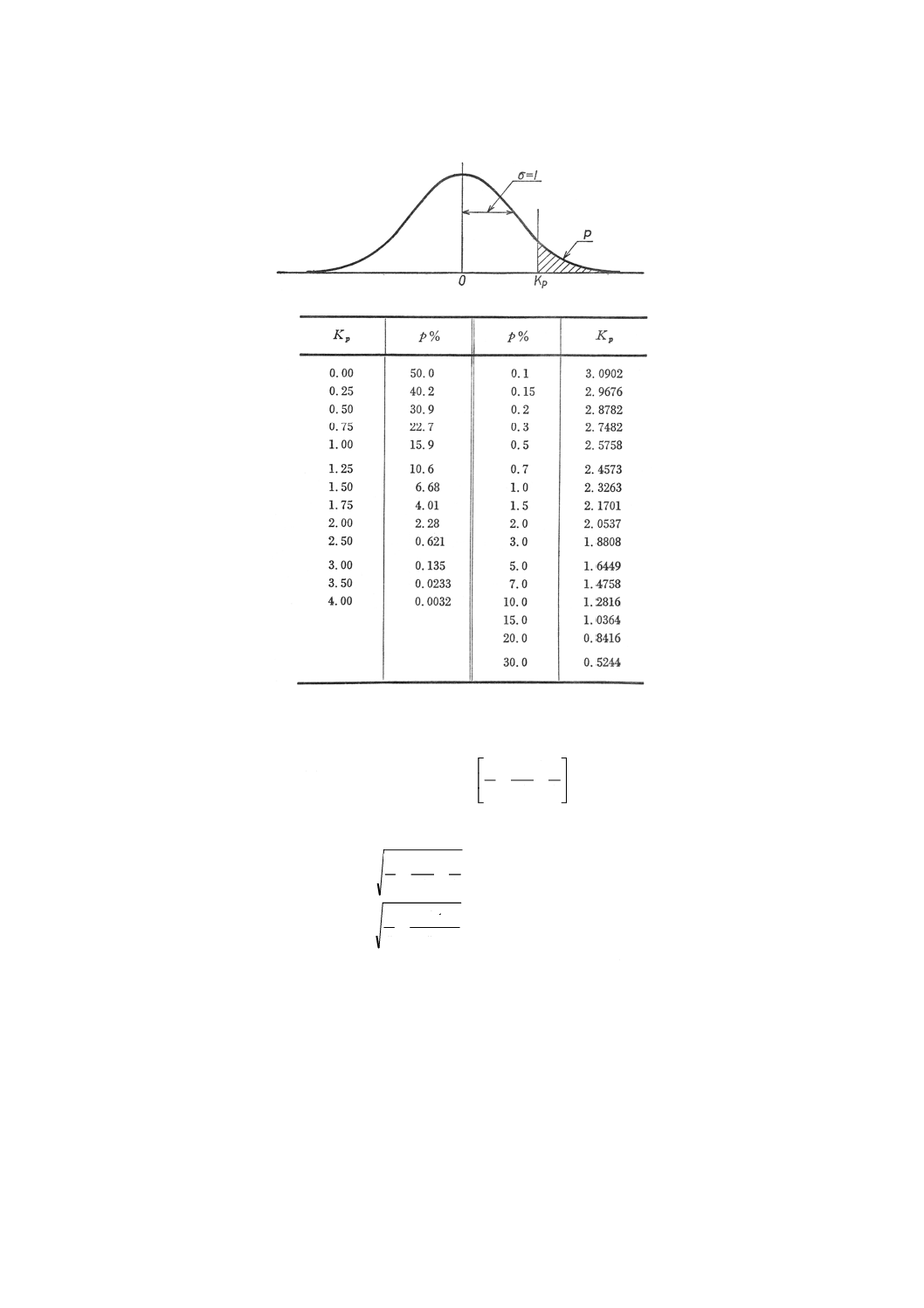
平均値と不良率との関係 検査単位の特性値が正規分布をするとき,そのロットの平均値mi (i=0, 1) 及
び標準偏差σと不良率pとの関係は,次のようになる(参考図3参照)。
上限規格値SUが与えられた場合 SU−mi=Kpσ……………(4)*
下限規格値SLが与えられた場合 SL−mi=−Kpσ…………(5)*
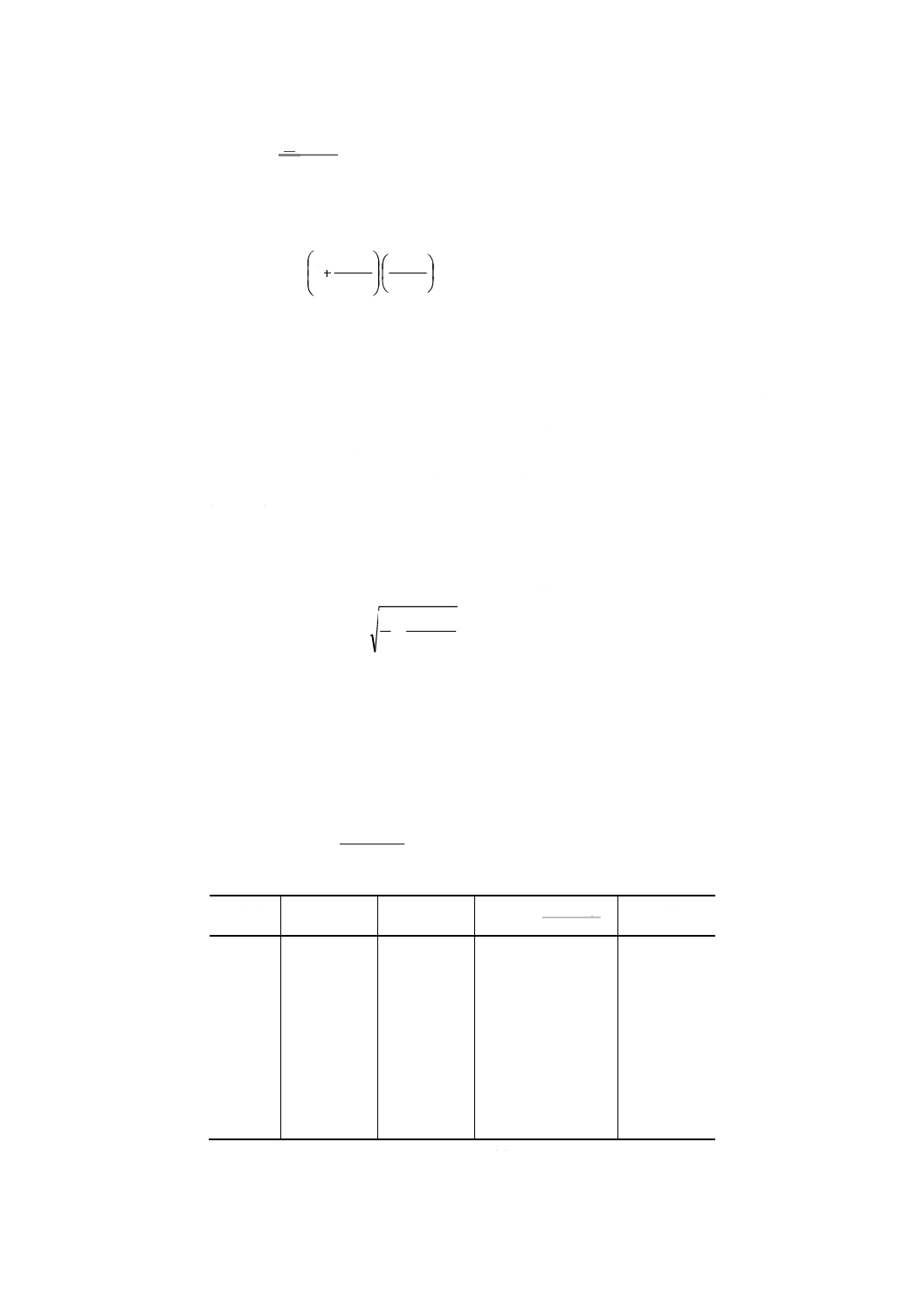
ただし,KPは次の式で定義され,したがって不良率pとKpとの関係は,参考表のようになる。
dt
e
p
p
K
t
∫∞−22
2
1
100
π
=
…………………………………………(6)*
参考図3 ロットの平均値及び標準偏差と不良率との関係
21
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考表 不良率pとKpとの関係
(1) 上限規格値SUが与えられた場合 特性値xが正規分布をしているロットからランダムに大きさnのサ
ンプルを抜き取って,平均値xと標準偏差sを算出すれば,n≧5のとき,x+ksの分布は実用上,
平均値m+kσ 分散σ2
−
+
)1
(2
1
2
n
k
n
の正規分布とみなすことができる。これから次の式の関係が成立する。
m0+kσ+Kασ
)1
(2
1
2
−
+
n
k
n
=SU………………………………(7)*
m1+kσ−Kβσ
)1
(2
1
2
−
+
n
k
n
=SU………………………………(8)*
ただし,Kα,Kβは式(6)*のpとKpをそれぞれαとKα,βとKβで置き換えた式で定義され,したがっ
て参考表によってα及びβからKα,Kβを求めることができる。
一方,(4)*から
m0+Kp0σ=SU……………………………………………………(9)*
m1+Kp1σ=SU……………………………………………………(10)*
である(参考図3参照)。
したがって,式(7)*と(9)*から

22
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
k=Kp0−Kα
)1
(2
1
2
−
+
n
k
n
……………………………………………………(11)*
式(8)*と(10)*から
k=Kp1+Kβ
)1
(2
1
2
−
+
n
k
n
……………………………………………………(12)*
式(11)*と(12)*から
k=
β
α
α
β
K
K
K
K
K
K
p
p
+
+
1
0
…………………………………………………………(13)*
式(11)*と(12)*からn≒n−1として近似的に
n=
2
1
0
2
2
1
−
+
+
p
p
K
K
K
K
k
β
α
························································· (14)*
したがって,ロットから式(14)*で決まるサンプルを抜き取って,平均値x,標準偏差sを算出し,
次のようにする。
x+ks≦SU ならばロットを合格とし,
x+ks>SU ならばロットを不合格とする。
ただし,式(14)*により算出したnが整数でないときはその値より大きくて一番近い整数値をサンプ
ルの大きさnとする。
(2) 下限規格値SLが与えられた場合 (1)と同様にして,サンプルの大きさnは近似的に,
n=
2
1
0
2
2
1
−
+
+
p
p
K
K
K
K
k
β
α
合格判定係数kは,
k=
β
α
α
β
K
K
K
K
K
K
p
p
+
+
1
0
ここでロットから大きさnのサンプルを抜き取って平均値x,標準偏差sを算出し,次のようにす
る。
x−ks≧SL ならばロットを合格とし,
x−ks<SL ならばロットを不合格とする。
ただし,式(14)*により算出したnが整数でないときはその値より大きくて一番近い整数値をサンプ
ルの大きさnとする。
例: p0=1%,α=0.05;p1=4%,β=0.05を満足する抜取検査方式は,次のようにして求めることがで
きる(上限規格値SUが与えられている場合)。
参考表から
Kp0=2.326
Kα=1.645
Kp1=1.751
Kβ=1.645
Kp0−Kp1=0.575
Kα+Kβ=3.290
k=
645
.1
645
.1
645
.1
751
.1
645
.1
326
.2
+
×
+
×
23
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
=
290
.3
707
.6
=2.04
一方,
n=
2
2
575
.0
290
.3
2
04
.2
1
+
=3.08×(5.722)2
=100.8
≒101
したがって抜取検査方式は (n=101,k=2.04) となる。すなわち,ロットからランダムに大き
さ101のサンプルを抜き取って平均値x,標準偏差sを算出し,
x+2.04s≦SU ならばロットを合格
x+2.04s>SU ならばロットを不合格
と判定すればよい。
2. OC曲線の書き方 一般にOC曲線を書く場合には,次の式(15)*を用いる。すなわち不良率p%のロッ
トが与えられた抜取検査方式により長い間に合格する確率をL (p) とすれば,
k=Kp+KL (p)
)1
(2
1
2
−
+
n
k
n
………………………………………………… (15)*
この式(15)*を用いて容易にロットの不良率とそのロットが合格する確率L (p) との関係を書くことがで
きる。
例: p0=1%,α=0.05;p1=4%,β=0.05を満足する抜取検査方式は,n=101,k=2.04である。
この場合のOC曲線を求めるには式(15)*にn=101,k=2.04を代入すれば
2.04=Kp+KL (p)×0.17524
すなわち
KL (p) =
17524
.0
04
.2
p
K
−
この式から,pに種々の値を与えることによりL (p) を求めることができる。
p (%)
Kp
2.04−Kp
KL (P) =
17524
.0
04
.2
p
K
−
L (p)
0.5
2.576
−0.536
−3.058
0.999
1.0
2.326
−0.286
−1.634
0.949
1.5
2.170
−0.130
−0.742
0.771
2.0
2.054
−0.014
−0.078
0.531
2.5
1.960
0.080
0.457
0.324
3.0
1.881
0.159
0.909
0.182
3.5
1.812
0.228
1.302
0.097
4.0
1.751
0.289
1.651
0.049
4.5
1.695
0.345
1.966
0.025
5.0
1.645
0.395
2.255
0.012
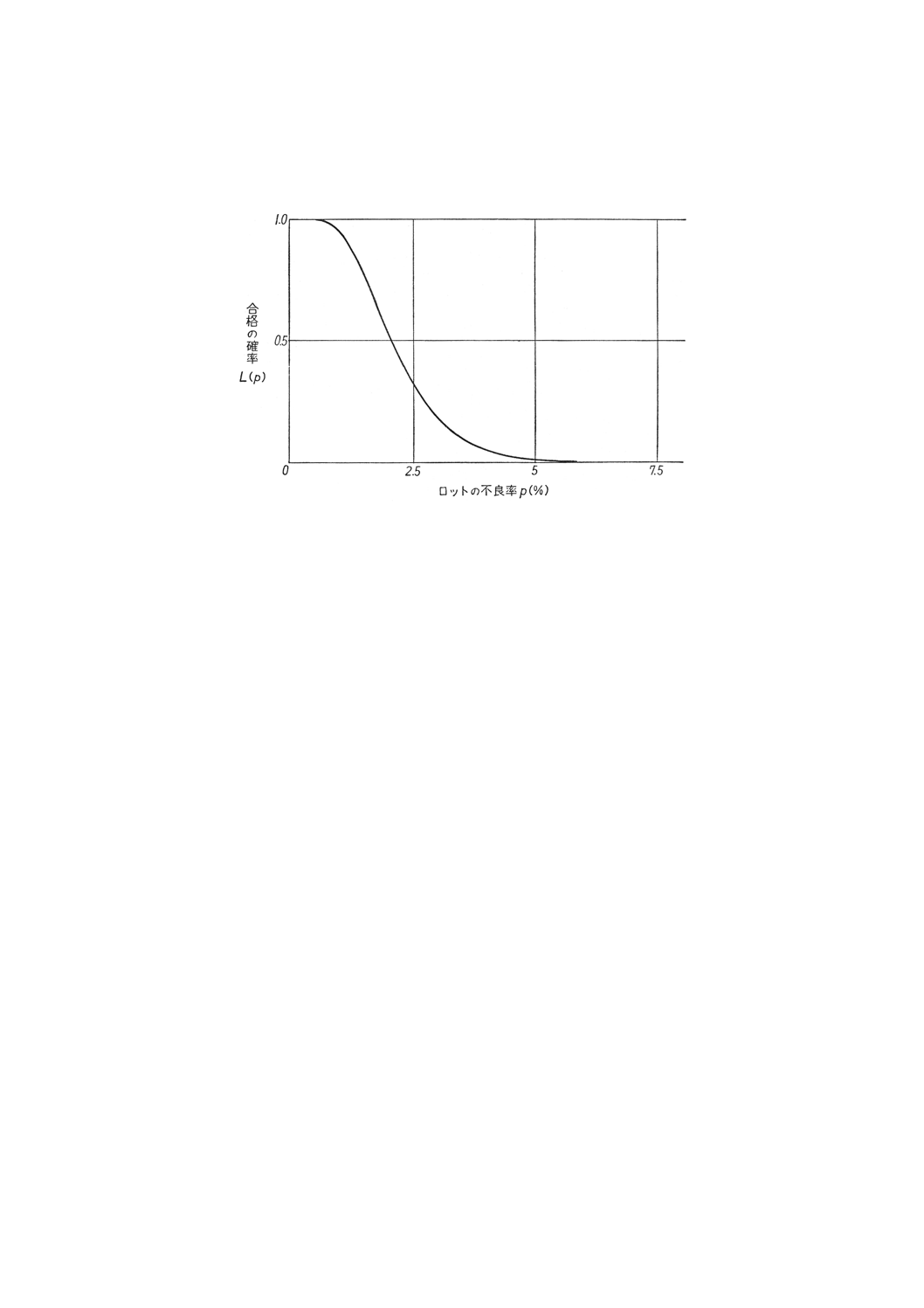
このpを横軸に,L (p) を縦軸にとって,p,L (p) の関係曲線としてOC曲線を求めることがで
24
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
きる。
この場合のOC曲線を参考図4に示す。
参考図4 OC曲線 (n=101,k=2.04)
25
Z 9004-1983
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
基本部会 品質管理専門委員会 構成表
氏名
所属
(委員会長)
朝 香 鐵 一
東京理科大学工学部
石 川 馨
武蔵工業大学
奥 野 忠 一
東京大学工学部
尾 関 和 夫
日本精工株式会社製品技術本部
木 暮 正 夫
玉川大学工学部
田 口 玄 一
財団法人日本規格協会
角 田 克 彦
日本電信電話公社検査部
真 壁 肇
東京工業大学経営工学科
三 浦 新
玉川大学工学部
森 口 繁 一
電気通信大学工学部
森 秀太郎
東京電気株式会社技術本部
山 本 太 郎
日本電気株式会社信頼性品質管理部
山 口 啓 一
新日本製鐵株式会社生産管理部
東 秀 彦
財団法人日本規格協会
横 尾 恒 雄
東洋カーボン株式会社
鷲 尾 泰 俊
慶応義塾大学理工学部
中 村 晴 佳
日産自動車株式会社品質管理部
瀬 倉 久 男
防衛庁装備局
升 山 義 久
日本国有鉄道資材局品質管理部
川 村 正 信
財団法人日本規格協会
卯 木 稔
工業技術院標準部
宮 津 隆
日本鋼管株式会社技術研究所
矢 野 宏
工業技術院計量研究所第一部
上 甲 子 郎
東京理科大学理工学部
(事 務 局)
藤 田 富 男
工業技術院標準部材料規格課
津 金 秀 幸
工業技術院標準部材料規格課
改正原案作成委員会構成表
氏名
所属
(主 査)
上 甲 子 郎*
東京理科大学理工学部
(委 員)
今 田 宏*
日本電気計器検定所東京試験所
梅 村 守*
東京理科大学工学部
押 村 征二郎*
東京理科大学工学部
大 森 志 郎
工業技術院公害資源研究所
川 村 数 増*
ヒロセ電機株式会社品質管理部
岸 暁 男*
武蔵工業大学経営工学科
角 田 克 彦*
日本電信電話公社検査部
林 俊 太*
工業技術院標準部
藤 田 董*
川鉄コンティナー株式会社
真 壁 肇
東京工業大学経営工学科
増 山 良 夫
練馬区立練馬中学校
山 本 太 郎*
日本電気株式会社信頼性品質管理部
(事務局)
竹 下 正 生
財団法人日本規格協会