4
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
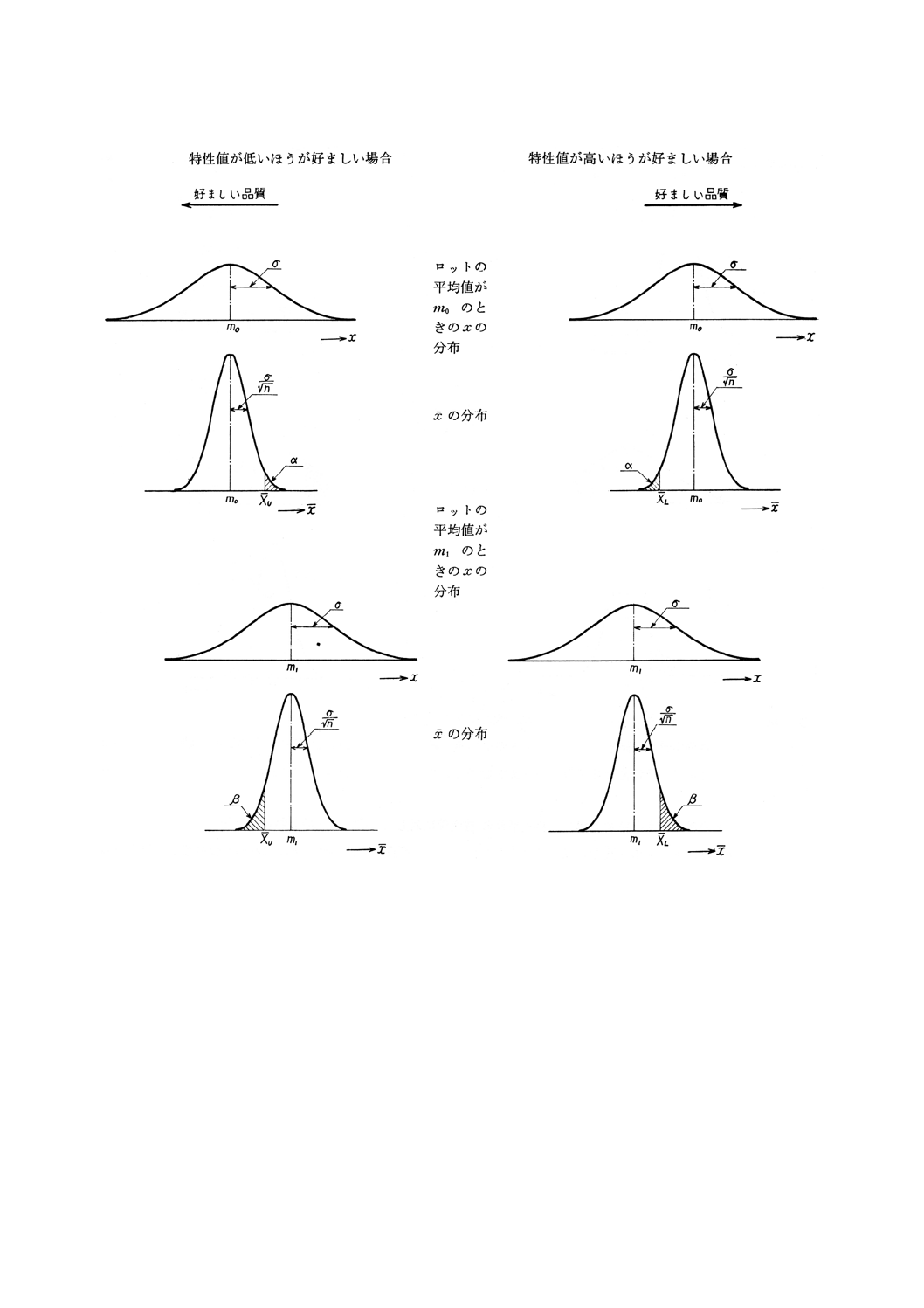
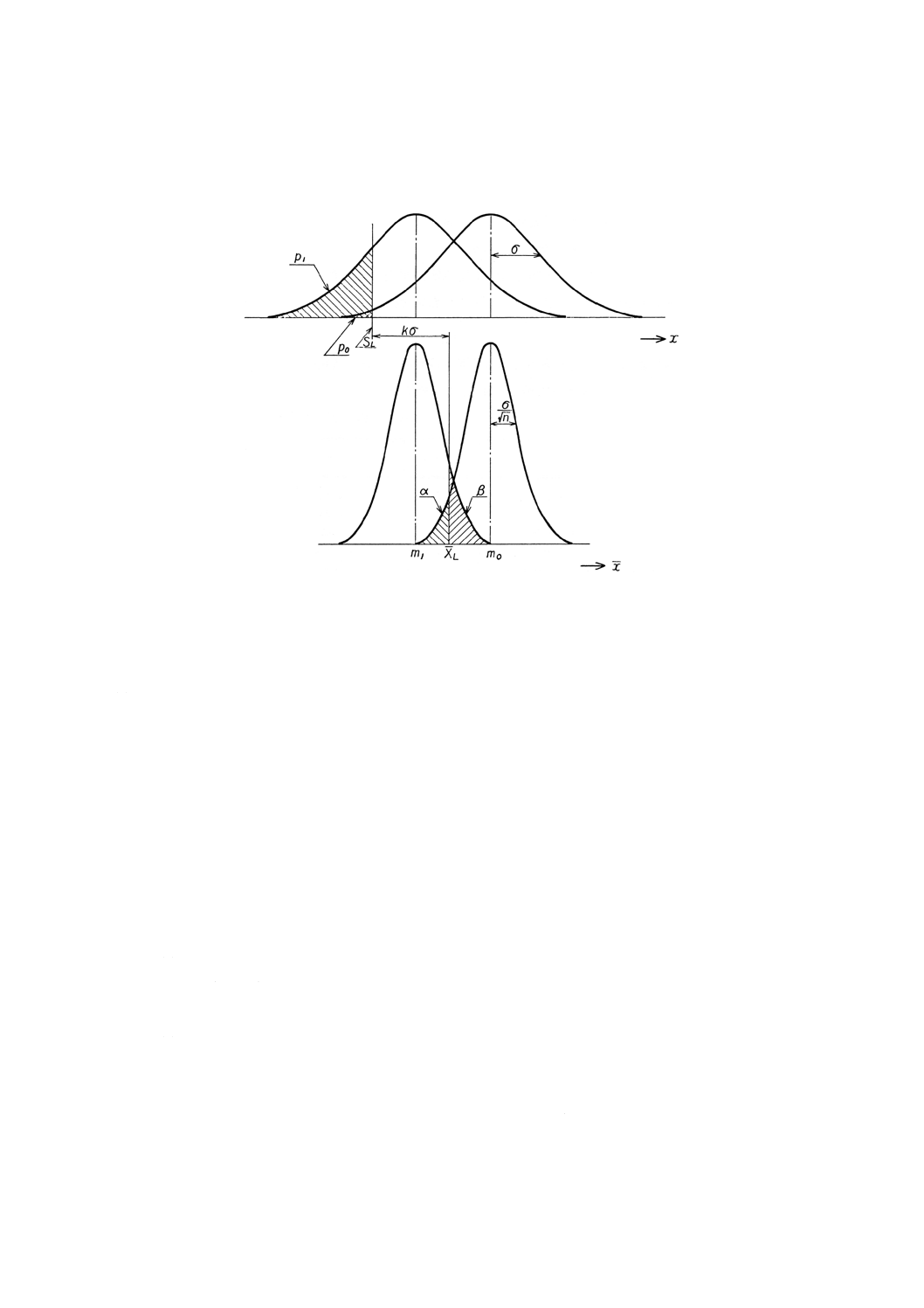
図1 ロットにおけるxとxの分布(平均値を保証する場合)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 9003-1979
計量規準型一回抜取検査
標準偏差既知でロットの平均値を保証する場合及び
標準偏差既知でロットの不良率を保証する場合
Single Sampling Inspection Plans having Desired Operation
Characteristics by Variables (Standard Deviation Known)
1. 適用範囲 この規格は,標準偏差既知でロットの平均値を保証する場合及び標準偏差既知でロットの
不良率を保証する場合の計量規準型一回抜取検査方式の決め方及び実施の方法について規定する。
備考1.
標準偏差既知でロットの平均値を保証する場合及び標準偏差既知でロットの不良率を保証する場合の
計量規準型一回抜取検査とは,ロットの品質をロットの平均値又は不良率で表した場合に生産者及び消
費者の要求する検査特性をもつように設計した抜取検査であって,一回に抜き取った試料の特性値の平
均値に対し既知の標準偏差を使って計算した合格判定値を比較することによって,ロットの合格・不合
格を判定するものである。
この検査の適用に当たっては
(1) 検査単位の品質は,計量値で表し得ること。
(2) 製品がロットとして処理できること。
(3) ロットの特性値の標準偏差がわかっていることが必要である。
(4) 不良率による場合は,特性値が正規分布をしているものとして取り扱われており,不良率をある
限度内に保証するものであるから,合格ロットの中にもある程度の不良品の混入は避けられない。
2.
この規格の中で { } を付けて示してある単位及び数値は,国際単位系 (SI) によるものであって,参
考として併記したものである。
2. 用語及び記号
2.1
用語 この規格で用いる用語の意味は次による。
なお,他の用語については,JIS Z 8101(品質管理用語)の2.(4)を参照。
検査単位
:検査の目的のために選ぶ単位体又は単位量
検査ロット
:検査の対象となるひとまとめの検査単位の集まり(以下,単にロットとい
う。)
ロットの大きさ N
:ロットに含まれる単位体,又は単位量の数
ロットの平均値 m
:ロットの検査単位の特性値xの平均値
N
x
x
x
x
m
N
+
+
+
+
=
Λ
Λ
3
2
1
引用規格:JIS Z 8101 品質管理用語
JIS Z 9004 計量規準型一回抜取検査(標準偏差未知で上限又は下限規格値のみ規定した場合
(抜取検査その4)
JIS Z 9031 ランダム抜取方法関連規格
関連規格:JIS Z 9001 抜取検査通則(抜取検査その1)
2
Z 9003-1979
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ロットの標準偏差 σ
:ロットの検査単位の特性値xの標準偏差
2
2
3
3
2
2
2
1
m
N
x
x
x
x
N−
+
+
+
+
=
Λ
Λ
σ
不良品
:規格に合致しない品物,すなわち特性値が上限規格値SUを超えるもの,又
は下限規格値SLに満たないもの。
ロットの不良率 p (%) :()
100
%
×
=
N
p
数
ロットの中の不良品の
試料
:ロットから抜き取られる検査単位の集まり
試料の大きさ n
:試料中の検査単位の数
試料の平均値 x
:試料の検査単位の特性値xの平均値
n
x
x
x
x
x
n
+
+
+
+
=
Λ
Λ
3
2
1
平方和 S
:試料の特性値と試料の平均値との差の平方和
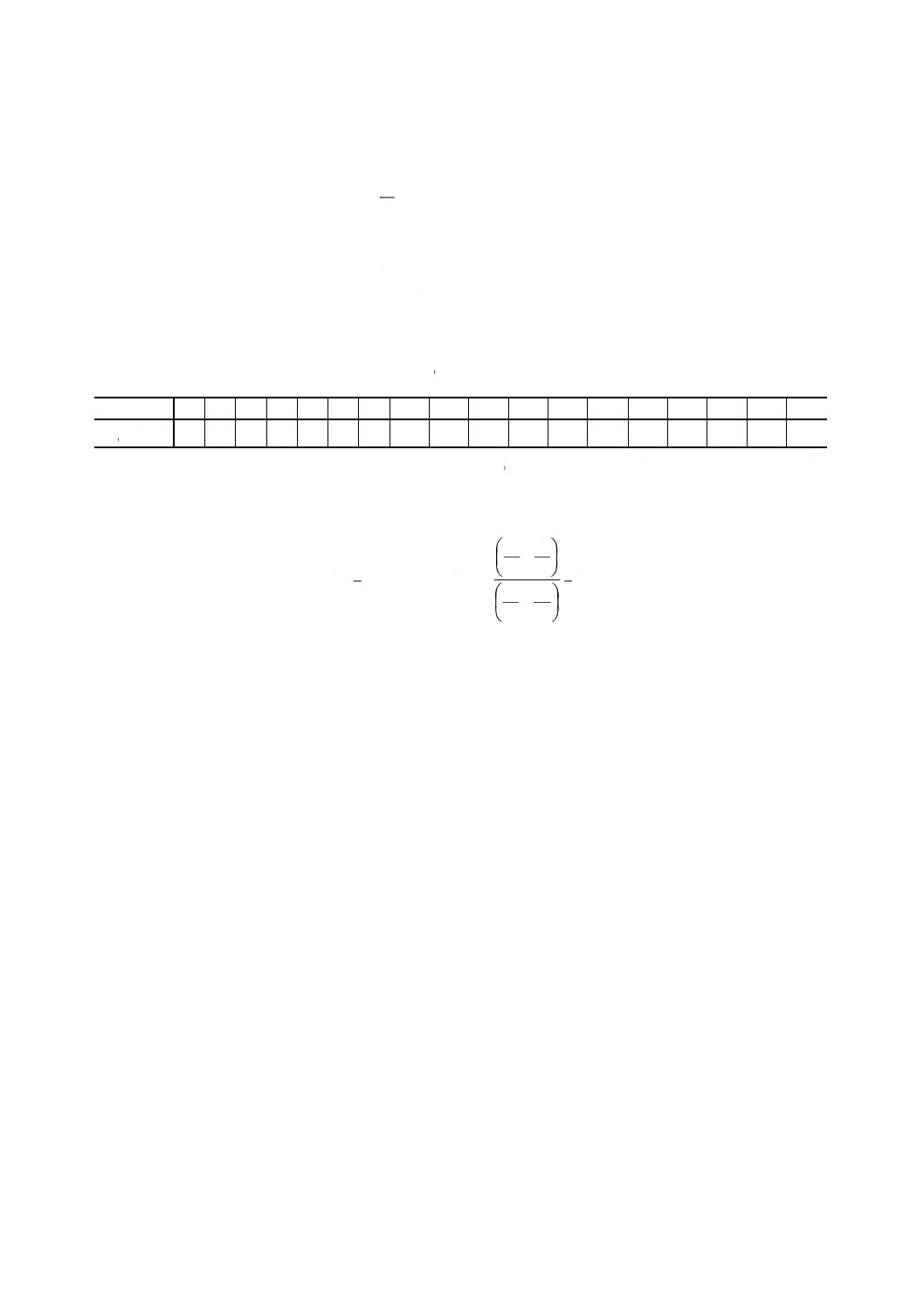
(
)
(
)
(
)
(
)2
2
3
2
2
2
1
x
x
x
x
x
x
x
x
S
n−
+
+
−
+
−
+
−
=
Λ
Λ
(
)(
)
n
x
x
x
x
x
x
x
x
n
n
2
3
2
1
2
2
3
2
2
2
1
+
+
+
+
−
+
+
+
+
=
Λ
Λ
Λ
Λ
不偏分散 V
:平方和をその自由度で割ったもの。すなわち
1
−
=nS
V
不偏分数の平均値 V :試料の大きさnが一定の場合はロットの組数l個のVの平均値は
l
V
V
∑
=
,
nが一定でない場合は
(
)1
−
∑
∑
=
n
S
V
ここに S:各ロットごとの試料の平方和
抜取検査方式
:ロットの合格・不合格をきめる試料の大きさと合格判定値を規定したもの。
合格判定値
:計量抜取検査で合格の判定を下す限界値
合格判定値以下を合格とする場合は,その値を上限合格判定値 (XU) とい
い,合格判定値以上を合格とする場合は,その値を下限合格判定値 (XL)
という。
2.2
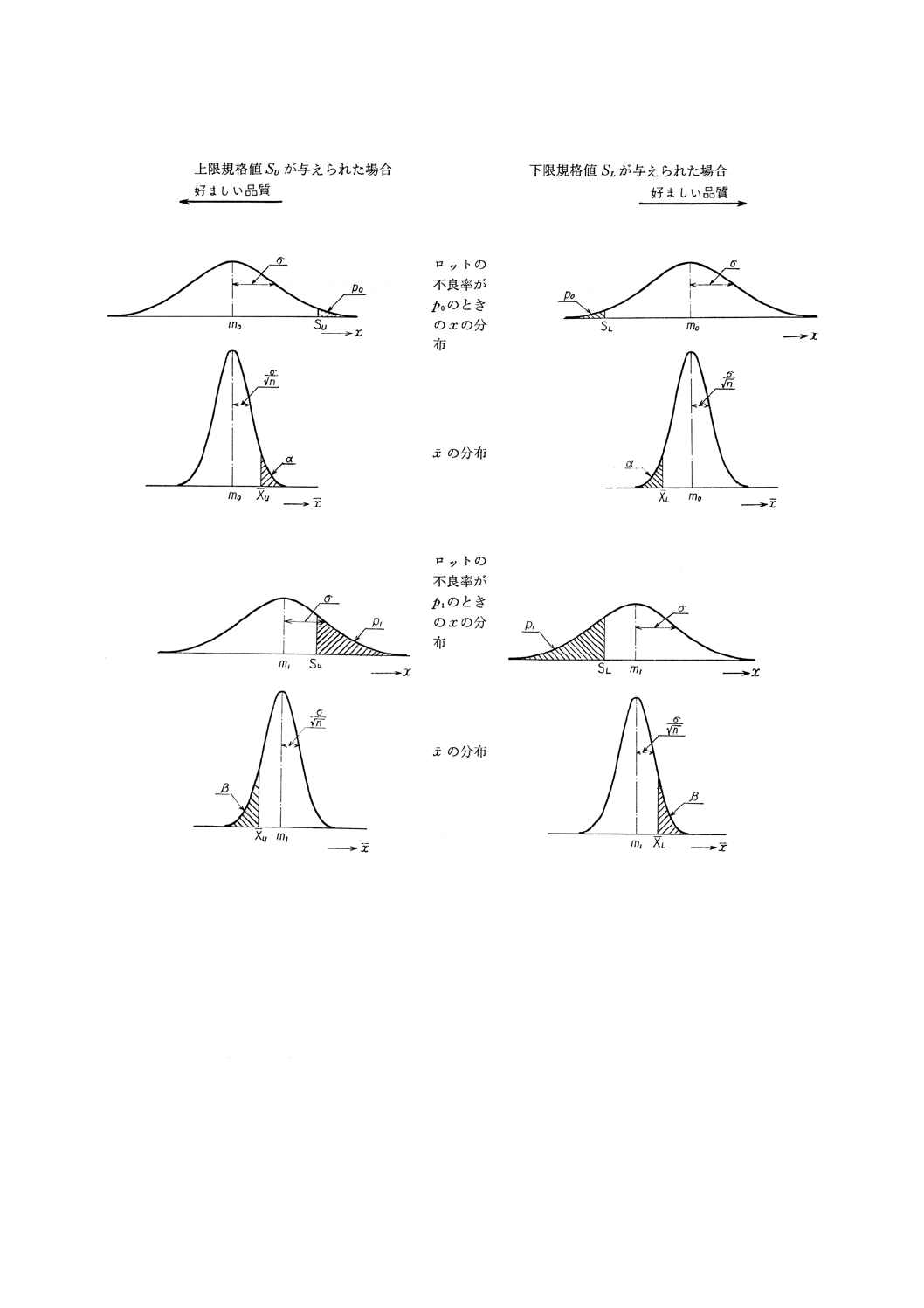
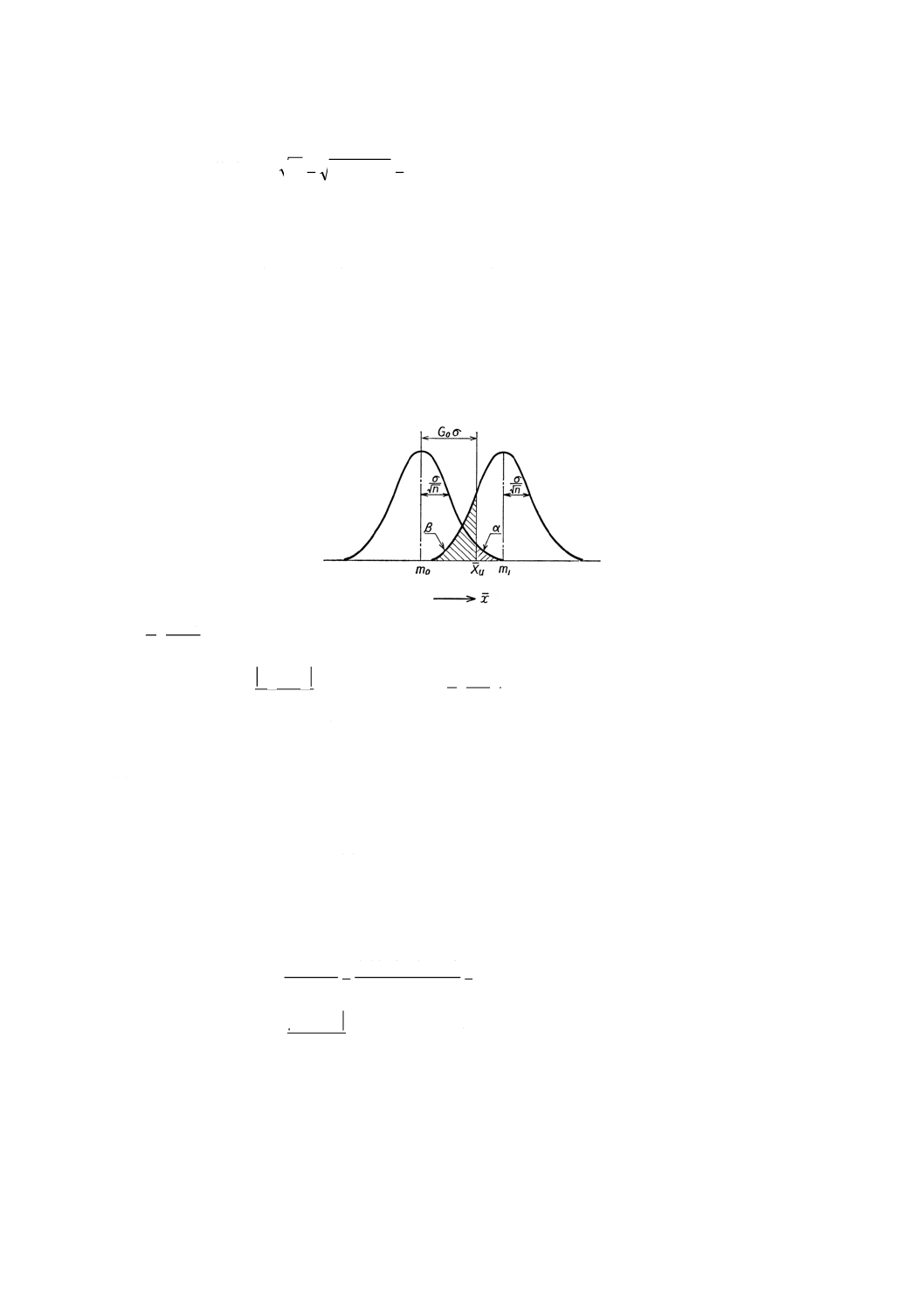
記号 この規格で用いる記号は次による(図1,図2参照)。
x :検査単位の特性値
N :ロットの大きさ
σ :ロットの標準偏差
m :ロットの平均値
m0 :なるべく合格させたいロットの平均値の限界
m1 :なるべく不合格としたいロットの平均値の限界
L (m) :平均値mのロットが合格する確率
p :ロットの不良率 (%)
p0 :なるべく合格させたいロットの不良率の上限
p1 :なるべく不合格としたいロットの不良率の下限
L (p) :不良率pのロットが合格する確率
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
α :生産者危険(平均値m0又は不良率p0のロットが不合格となる確率)
β :消費者危険(平均値m1又は不良率p1のロットが合格となる確率)
n :試料の大きさ
x :試料の平均値
SU :上限規格値
SL :下限規格値
XU :上限合格判定値
XL :下限合格判定値
G0 :ロットの平均値を保証する場合に合格判定値を求めるための係数
k :ロットの不良率を保証する場合に合格判定値を求めるための係数
Kp :標準正規分布の上側確率p%の点
Kα :標準正規分布の上側確率αの点
Kβ :標準正規分布の上側確率βの点
S :平方和
V :不偏分散
V :不偏分散の平均値

4
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1 ロットにおけるxとxの分布(平均値を保証する場合)
5
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2 ロットにおけるxとxの分布(不良率を保証する場合)
3. 種類 この規格に規定する抜取検査には,次の2種類がある。
(1) ロットの平均値を保証する場合 ロットの平均値が好ましい値であればなるべく合格させ,好ましく
ない値であればなるべく不合格とさせるという要求を満足させたい場合に使う。この場合には5.の規
定により実施する。
(2) ロットの不良率を保証する場合 検査単位の特性値に対して規格値(上限規格値・下限規格値)が与
えられた場合には,ロットの品質を不良率で表すことができる。不良率の低いロットはなるべく合格
させ,不良率の高いロットはなるべく不合格とさせるという要求を満足させたい場合に使う。この場
合には6.の規定により実施する。
(1) (2)いずれの場合も,抜取検査を実施する以前に標準偏差は,あらかじめわかっていなければならない
(1)。
注(1) 標準偏差があらかじめわかっていない場合の抜取検査としてはJIS Z 9004〔計量規準型一回抜取検査(標
準偏差未知で上限又は下限規格値のみ規定した場合)(抜取検査その4)〕がある。
6
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4. 検査の手順
手順
ロットの平均値を保証する場合
ロットの不良率を保証する場合
1
測定方法を定める
測定方法を定める
SU,,SLの一方又は両方を規定する
2
m0,m1を指定する
p0,p1を指定する
3
ロットを形成する
ロットを形成する
4
ロットの標準偏差σを指定する
ロットの標準偏差σを指定する
5
試料の大きさと合格判定値を求める
試料の大きさと合格判定値を求める
6
試料をとる
試料をとる
7
試料の特性値xを測定し,平均値xを計算する 試料の特性値xを測定し,平均値xを計算する
8
合格・不合格の判定を下す
合格・不合格の判定を下す
9
ロットを処置する
ロットを処置する
5. ロットの平均値を保証する場合の検査の実施
5.1
測定方法の決定 検査単位の特性値xの測定方法を具体的に定める。
5.2
m0,m1の指定 この規格による抜取検査を実施するには,まず品物を渡す側と受け取る側が合議の
うえm0,m1を決める。この際αは0.05,βは0.10を基準とする。
なお,この規格では,α=0.05,β=0.10の場合の求め方を示す。α=0.05,β=0.10以外の場合は参考5
によって求めることができる。
5.3
ロットの形成 同一条件で生産されたロットをなるべくそのまま検査ロットに選ぶ。ロットがはな
はだしく大きい場合には小ロットに区切って検査ロットとしてもよい。
5.4
σの指定 ロットの標準偏差σがあらかじめわかっている場合,又は品物を渡す側と受け取る側との
間の協定で決められている場合にはその値を用いる。
σが与えられていない場合には過去の検査データから推定したσの値を用いる。各ロットから抜き取った
試料の大きさnが等しい場合は次のとおりとする。nが等しくない場合は参考3による。
(1) 最近の10〜20ロットの検査データについて,次の式により,ロットごとの不偏分散Vを計算する(2)。
(
)(
)
1
2
2
1
2
2
2
2
1
−
+
+
+
−
+
+
+
=
n
n
x
x
x
x
x
x
V
n
n
Λ
Λ
Λ
Λ
注(2) JIS Z 9004〔計量規準型一回抜取検査(標準偏差未知で上限又は下限規格値のみ規定した場合)
(抜取検査その4)〕による検査データが利用できる場合には
V
Se=
を計算する段階としてV
がわかっているから,この値を用いればよい。
(2) (1)で求めた不偏分散Vの平均値Vを計算する。
l
V
V
∑
=
ここに,
ΣV: ロットごとの不偏分散の合計
l: ロットの数
(3) ロット内のばらつきが安定しているかどうか調べる(3)。それにはF分布表(表1)から
1
−
∞n
F
(0.01) を
求め,V・
1
−
∞n
F
(0.01) を計算し,lロットについてこの値を超えるVがなければ,ロット内のばらつ
7
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
きが安定していたと判定する。
表1
1
−
∞n
F
(0.01) の値(4)
n-1
1
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
1
−
∞n
F
(0.01)
6.63 4.61 3.78 3.32 3.02 2.80 2.64 2.51 2.41 2.32 2.18 2.04 1.88 1.79 1.70 1.59 1.47 1.32
注(3) ここではロット内のばらつきが安定しているかどうかを
1
−
∞n
F
(0.01) を用い,危険率1%で調べているが,当事
者間の協定によって更に小さい危険率を使ってもよい。
(4) 求めるn−1の値が表にない場合はFはn−1の逆数に比例して変化するものとしてFの値を補間して求める。
例:n−1=18にたいするFの値を求めるには
(
)
(
)
93
.1
20
1
15
1
18
1
15
1
88
.1
04
.2
04
.2
01
.0
18
=
−
−
×
−
−
=
∞
F
(4) ロット内のばらつきが安定していれば
σの推定値=V
を標準偏差σの値として指定する。
(5) 引き続きこの抜取検査方式を使う場合は,ロットの標準偏差が指定した値とはなはだしい差異がない
ことを(3)の手順を準用して確かめなければならない。
(6) 長期にわたって連続してこの抜取検査方式を使う場合は,最近の20ロット以上の検査データからσの
推定値を求め,σの値を更新する。
例:(1) ある繊維製品のロットからとった大きさn=5の試料について水分を測定したら
1.51%,1.43%,1.39%,1.51%,1.39%
であった。不偏分散は次のようにして求める。
(
)(
)
68
003
.0
1
5
5
23
.7
3
469
.
10
1
5
5
39
.1
51
.1
39
.1
43
.1
51
.1
39
.1
51
.1
39
.1
43
.1
51
.1
2
2
2
2
2
2
2
=
−
−
=
−
+
+
+
+
−
+
+
+
+
=
V
このようにしてl=17ロットからn=5の試料についてVを求めた結果を次の表に示す。
試料
V
1
0.003 68
2
0.006 50
3
0.006 50
4
0.004 42
5
0.002 13
6
0.001 87
7
0.002 88
8
0.006 05
試料
V
9
0.007 33
10
0.002 12
11
0.006 75
12
0.003 35
13
0.000 78
14
0.003 97
15
0.006 33
16
0.003 37
17
0.011 32
(2) これから不偏分散の平均値Vは次のようにして求める。
668
004
.0
17
35
079
.0
=
=
Σ
=lV
V
(3) F分布表から
4∞
F (0.01) =3.32であるから
V・
4∞
F (0.01) = (0.004 668) (3.32) =0.0154 98
8
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
17ロット中Vがこの値を超えるものはないから,ロット内のばらつきは安定している。
(4) σの推定値=
%
3
068
.0
668
004
.0
=
=
V
σの値として指定する。
5.5
試料の大きさと合格判定値の求め方 5.2で指定したm0,m1から試料の大きさと合格判定値を求め
るには,特性値が低いほうが好ましい場合には(1)により,高いほうが好ましい場合には(2)による。
なお,特性値が低すぎても高すぎても好ましくない場合は,高いほうの側,低いほうの側のそれぞれに
ついて(1)又は(2)を準用することができるが,詳細は参考6に示す。この規格では表によって求める手順を
示す。
なお,図によって求めることもできる(参考4参照)。
(1) 試料の大きさnと上限合格判定値XUとを求める場合は,次による(図3参照)。
図3 特性値が低いほうが好ましい場合
(a)
σ
0
1
m
m−
を計算し,小数以下3けたに丸める。
(b) 付表1を用い,
σ
0
1
m
m−
の列で(a)で求めた
σ
0
1
m
m−
の値を含む行を求める。
(c) その行のn及び係数G0を読みとり,
XU=m0+G0σを計算する。
(d) (c)で求めたnとXUについて検査費用などを検討した結果,その値が適当ならばそのまま採用し,
不適当と認めたときはm0,m1の値を修正してnとXUを求めなおす。
例:ドラムかん詰固形かせいソーダ中の酸化鉄分Fe2O3は低いほうが好ましい。ロットの平均値
が0.004 0%以下ならば合格とし,それが0.005 0%以上ならば不合格とするようなnとXUと
を求める。この場合,ロットの標準偏差はσ=0.000 6%とする。α=0.05,β=0.10として抜取
検査方式を求めるには,
(a) m0=0.004 0%,m1=0.00 50%;σ=0.000 6%
667
.1
6
000
.0
0
004
.0
0
005
.0
0
1
=
−
=
−
σ
m
m
(b) 付表1の
σ
0
1
m
m−
の列で1.667を含む行を探していくと,上から3番目に1.463〜1.689
の行がある。
(c) この行からn=4,G0=0.822が求められる。
試料の大きさn=4
上限合格判定値XU=m0+G0σ
9
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
=0.004, 0+0.822×0.0006=0.0045%
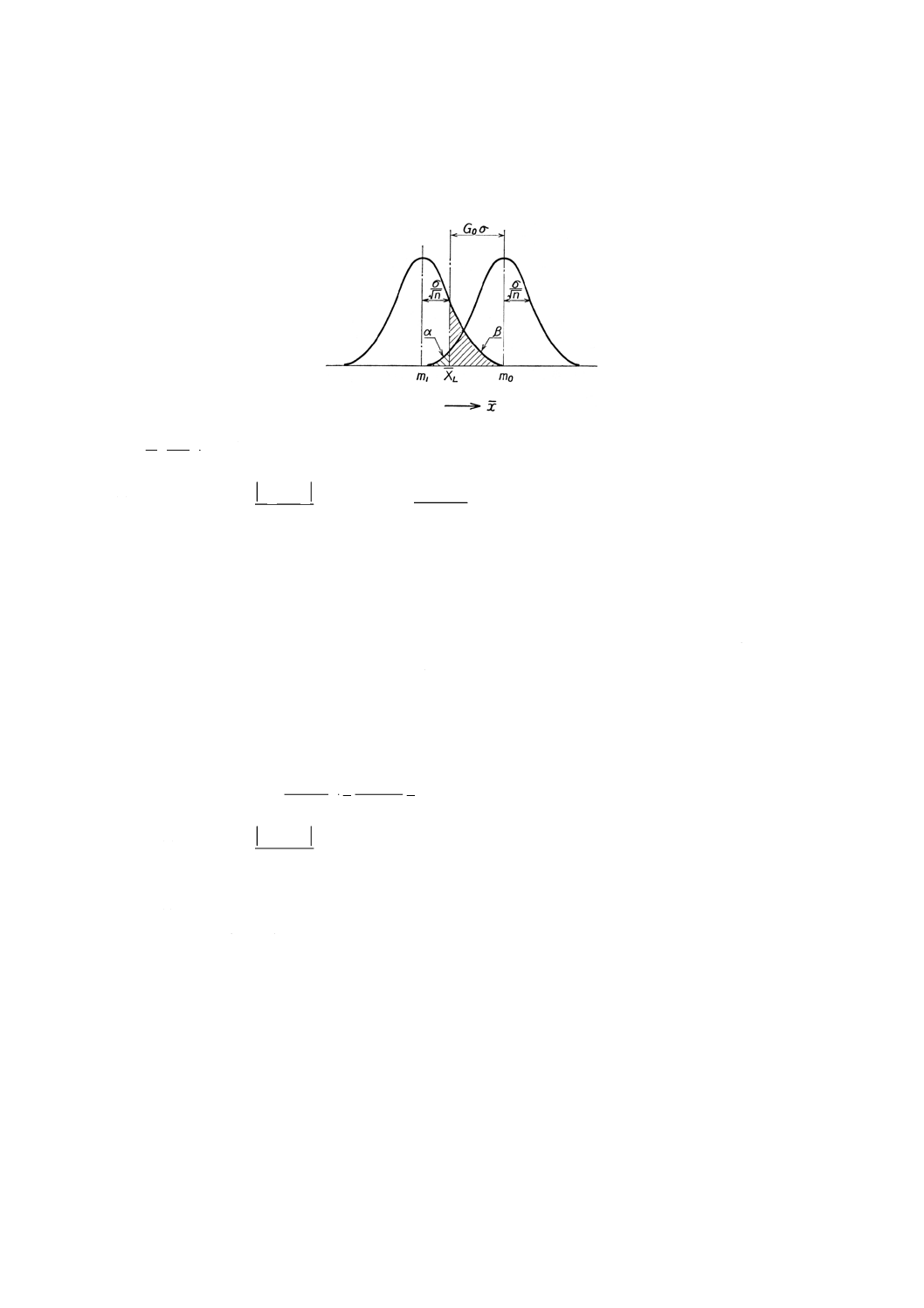
(2) 試料の大きさと下限合格判定値XLとを求める場合は,次による(図4参照)。
図4 特性値が高いほうが好ましい場合
(a)
σ
1
0
m
m−
を計算し,小数点以下3けたに丸める。
(b) 付表1を用い,
σ
0
1
m
m−
の列で求めた
σ
1
0
m
m−
の値を含む行を求める。
(c) その行のn及び係数G0を読みとり,
XL=m0−G0σを計算する。
(d) (c)で求めたnとXLについて検査費用などを検討した結果,その値が適当ならばそのまま採用し,
不適当と認めたときはm0,m1の値を修正してnとXLを求めなおす。
例: 鋼材の引張強さは大きいほうが好ましい。いま平均値が46kgf/mm2 {451.1MPa} 以上のロットは
通し,それが43kgf/mm2 {421.7MPa} 以下のロットは通さないようなnとXUとを求める。この場
合,ロットの標準偏差はσ=4kgf/mm2 {39.2MPa} とする。α=0.05,β=0.10として抜取検査方式
を求めるには
(a) m0=46kgf/mm2 {451.1MPa}, m1=43kgf/mm2 {421.7MPa}, σ=4kgf/mm2 {39.2MPa}
75
.0
4
43
46
1
0
=
−
=
−
σ
m
m
(b) 付表1の
σ
0
1
m
m−
の列で0.75を含む行を探していくと,上から15番目に0.732〜0.755の行
がある。
(c) この行からn=16,G0=0.411が求められる。
試料の大きさ n=16
下限合格判定値XL=m0−G0σ=46−0.411×4
=44.4kgf/mm2 {435.42MPa}
5.6
試料のとり方 検査ロットの中から5.5で決めた大きさnの試料をJIS Z 9031(ランダム抜取方法)
の3.によってランダムに試料を抜き取る。
5.7
試料の試験 大きさnの試料について5.1で定めた測定方法により特性値χを測定し,平均値Xを求
める。
5.8
ロットの判定 ロットの合否判定は次による。
(1) 特性値が低いほうが好ましい場合
10
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.7で求めたxと5.5(1)で求めたXUとを比較し,
χ≦XUならばロットを合格とし,
χ>XUならばロットを不合格とする。
(2) 特性値が高いほうが好ましい場合
5.7で求めたあと5.5(2)で求めたXLとを比較し,
χ≧XLならばロットを合格とし,
χ<XLならばロットを不合格とする。
5.9 ロットの処置 合格又は不合格と判定されたロットはあらかじめ決めた約束にしたがって処置する。
どのような場合でも,不合格となったロットをそのままで再提出してはならない。
6. ロットの不良率を保証する場合の検査の実施
6.1
品質の基準の設定 検査単位の特性値χの測定方法を具体的に定め,上限規格値SU,下限規格値SL
の一方又は両方を定める。
6.2
p0,p1の指定 この規格による抜取検査を実施するには,まず品物を渡す側と受け取る側が合議の
うえp0,p1を決める。この場合,αは0.05,βは0.10を基準とする。
なお,この規格ではα=0.05,β=0.10の場合の求め方を示す。α=0.05,β=0.10以外の場合は参考5に
よって求めることができる。
6.3
ロットの形成 同一条件で生産されたロットをなるべくそのまま検査ロットに選ぶ。ロットがはな
はだしく大きい場合は小ロットに区切って検査ロットとしてもよい。
6.4
σの指定 ロットの標準偏差σがあらかじめわかっている場合,又は品物を渡す側と受け取る側との
間の協定で決められている場合にはその値を用いる。
σが与えられていない場合には,過去の検査データから推定したσの値を用いる。
各ロットから抜き取った試料の大きさnが等しい場合は,次のとおりとする。nが等しくない場合は参
考3による(5.4の例参照)。
(1) 最近の10〜20ロットの検査データについて,次の式によりロットごとの不偏分散Vを計算する(2)。
(
)(
)
1
2
2
1
2
2
2
2
1
−
+
+
+
−
+
+
+
=
n
n
x
x
x
x
x
x
V
n
n
Λ
Λ
Λ
Λ
注(2) JIS Z 9004〔計量規準型一回抜取検査(標準偏差未知で上限又は下限規格値のみ規定した場合)(抜取検査
その4)〕による検査データが利用できる場合には
V
Se=
を計算する段階としてVがわかっているから,
この値を用いればよい。
(2) (1)で求めた不偏分散Vの平均値Vを計算する。
l
V
V
∑
=
ここに
ΣV: ロットごとの不偏分散の合計
l: ロットの数
(3) ロット内のばらつきが安定しているかどうか調べる(3)。それにはF分布表(表1参照)から
1
−
∞n
F
(0.01)
を求め,V・
1
−
∞n
F
(0.01) を計算し,lロットについてこの値を超えるVがなければ,ロット内のばら
11
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
つきが安定していたと判定する。
(4) ロット内のばらつきが安定していれば,
σの推定値=V
を標準偏差σの値として指定する。
(5) 引き続きこの抜取検査方式を使う場合は,ロットの標準偏差が指定した値とはなはだしい差異がない
ことを(3)の手順を準用して確かめなければならない。
表1
1
−
∞n
F
(0.01) の値(4)
n−1
1
2
3
4
5
6
7
8
9
10
12
15
20
24
30
40
60
120
1
−
∞n
F
(0.01) 6.63 4.61 3.78 3.32 3.02 2.80 2.64 2.51 2.41 2.32 2.18 2.04 1.88 1.79 1.70 1.59 1.47 1.32
注(3) ここではロット内のばらつきが安定しているかどうかを
1
−
∞n
F
(0.01) を用い,危険率1%で調べているが,当事
者間の協定によって更に小さい危険率を使ってもよい。
(4) 求めるn-1の値が表にない場合はFはn−1の逆数に比例して変化するものとしてFの値を補間して求める。
例:n−1=18に対するFの値を求めるには
(
)
(
)
93
.1
20
1
15
1
18
1
15
1
88
.1
04
.2
04
.2
01
.0
18
=
−
−
×
−
−
=
∞
F
(6) 長期にわたって連続してこの抜取検査方式を使う場合は,最近の20ロット以上の検査データからσの
推定値を求め,σの値を更新する。
6.5
試料の大きさと合格判定値の求め方 6.2で指定したp0,p1から試料の大きさと合格判定値を求める
には,上限規格値SUが与えられた場合には(1)により,下限規格値SLが与えられた場合には(2)による。
なお,上限規格値SU及び下限規格値SLが与えられた場合は上限規格値の側,下限規格値の側のそれぞ
れについて(1)又は(2)を準用することができるが,詳細は参考6に示す。
この規格では表によって求める手順を示す。
なお,図によって求めることもできる(参考4参照)。
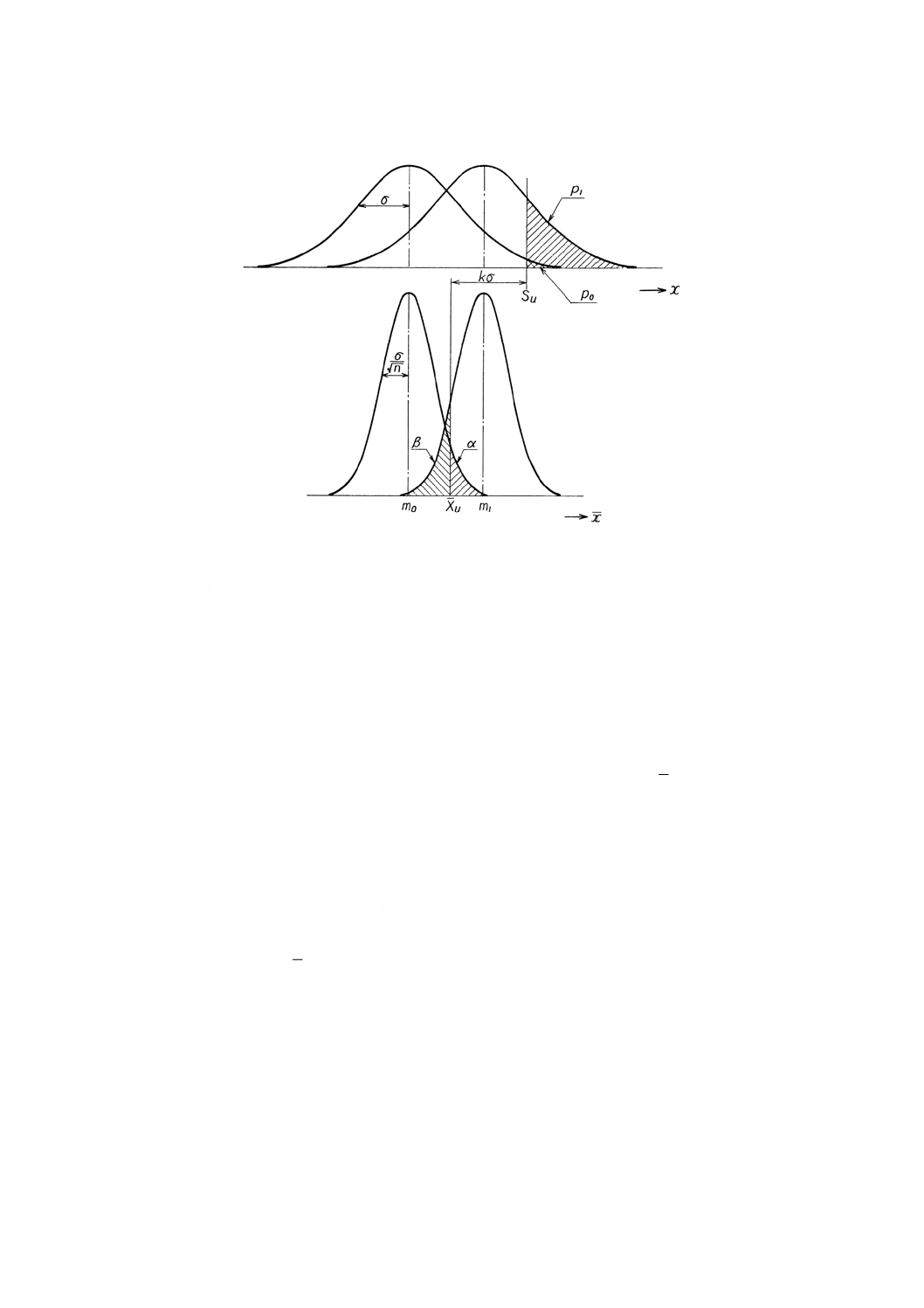
(1) 試料の大きさnと上限合格判定値XUとを求める場合は,次による(図5参照)。
12
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図5 上限規格値が与えられた場合
(a) 付表2を用い,指定されたp0を含む行と,指定されたp1を含む列との交わる欄を求める。
(b) 欄の中の左下の数値(太字)を試料の大きさnとし,右上の数字(細字)を合格判定値を計算する
ための係数kとする。
(c) 上限合格判定値XU=SU−kσを計算する。
(d) (b)で求めたn,kについてOC曲線(付図1)を調べ,検査費用などを検討した結果,その値が適当
ならばそのまま採用し,不適当と認めたときはp0,p1の値を修正して,nとXUを求めなおす。
例:上限規格値が与えられた場合の抜取検査方式の求め方
金属板の硬さの上限規格値がロックウェル硬さ68以下と規定されたとき,ロックウェル硬さ68を超える
ものが0.5%以下のロットは通し,それが4%以上のロットは通さないようなnとXUとを求める。この場合,
ロットの標準偏差はσ=3とする。α=0.05,β=0.10として抜取検査方式を求めるには
(a) p0=0.5% p1=4%
付表2のp0=0.5%を含む行〔0.451〜0.560 (%)〕とp1=4%を含む列〔3.56〜4.50 (%)〕との交わる欄
を求める。
(b) この欄からn=13,k=2.11を読みとる。
試料の大きさn=13とする。
(c) 上限合格判定値XU=SU−kσ=68−2.11×3=61.67
(d) 付図1のOC曲線,参考付図2計量一回抜取検査設計図などにより検査特性を調べた結果満足であり,
また試料の大きさも経済的に見て大きすぎるほどではないので,この方式を採用することにした。
13
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(2) 試料の大きさnと下限合格判定値XLとを求める場合は,次による(図6参照)。
図6 下限規格値が与えられた場合
(a) 付表2を用い,指定されたp0を含む行と指定されたp1を含む列との交わる欄を求める。
(b) その欄の中の左下の数値(太字)を試料の大きさnとし,右上の数値(細字)を合格判定値を計算
する係数kとする。
(c) 下限合格判定値XL=SL+kσを計算する。
(d) (b)で求めたn,kについてOC曲線(付図1)を調べ,検査費用などを検討した結果,必要があれば
p0,p1の値を修正してnとXLを求めなおす。
例:下限規格値が与えられた場合の抜取検査方式の求め方
金属板の厚さの下限規格値が2.3mm以上と規定されたとき,厚さが2.3mmに満たないものが
1%以下のロットは通じ,それが9%以上もあるロットは通さないようなnとXLとを求める。た
だし,ロットの標準偏差はσ=0.2mmとする。α=0.05,β=0.10として抜取検査方式を求めるに
は
(a) p0=1% p1=9%
付表2のp0=1%を含む行〔0.901〜1.12 (%)〕とp1=9%を含む列〔7.11〜9.00 (%)〕との交
わる欄を求める。
(b) この欄からn=10,k=1.81を読みとる。
試料の大きさn=10とする。
(c) 下限合格判定値XL=SL+kσ=2.3+1.81×0.2=2.66
(d) 付図1のOC曲線,参考付図2計量一回抜取検査設計図などにより検査特性を凋べた結果満
足であり,また試料の大きさも経済的に見て大きすぎるほどではないので,この方式を採用
することにした。
6.6
試料のとり方 検査ロットの中から6.5で決めた大きさnの試料をJIS Z 9031の3.によってランダ
ムに試料を抜き取る。
14
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.7
試料の試験 大きさnの試料について6.1で定めた測定方法により特性値χを測定し,平均値xを求
める。
6.8
ロットの合否判定 ロットの合否判定は,次による。
(1) 上限規格値が与えられた場合
x≦XUならばロットを合格とし,
x>XUならばロットを不合格とする。
(2) 下限規格値が与えられた場合
x≧XLならばロットを合格とし,
x<XLならばロットを不合格とする。
6.9 ロットの処置 合格又は不合格と判定されたロットはあらかじめ決めた約束にしたがって処置する。
どのような場合でも,不合格となったロットをそのままで再提出してはならない。
7. 抜取検査表 m0,m1からn,G0を求めるための表を付表1に示す。
またp0,p1からn,kを求めるための表を付表2に示す。
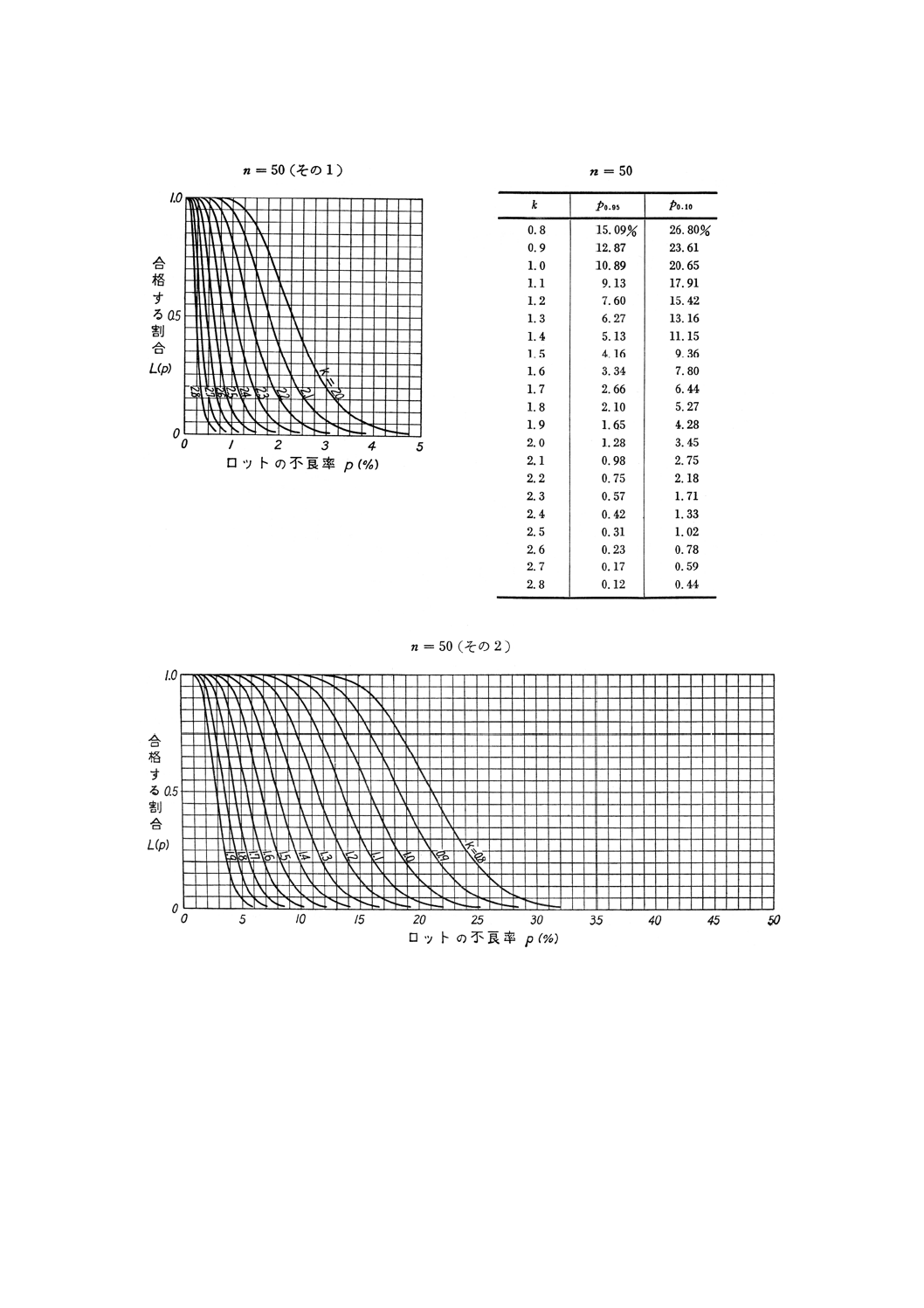
8. OC曲線及び検査設計図 n=3からn=50までのOC曲線を付図1に示す。
また,参考として平均値を保証する場合の抜取検査設計図を参考付図1,不良率を保証する場合の抜取
検査設計図を参考付図2に示す。

15
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
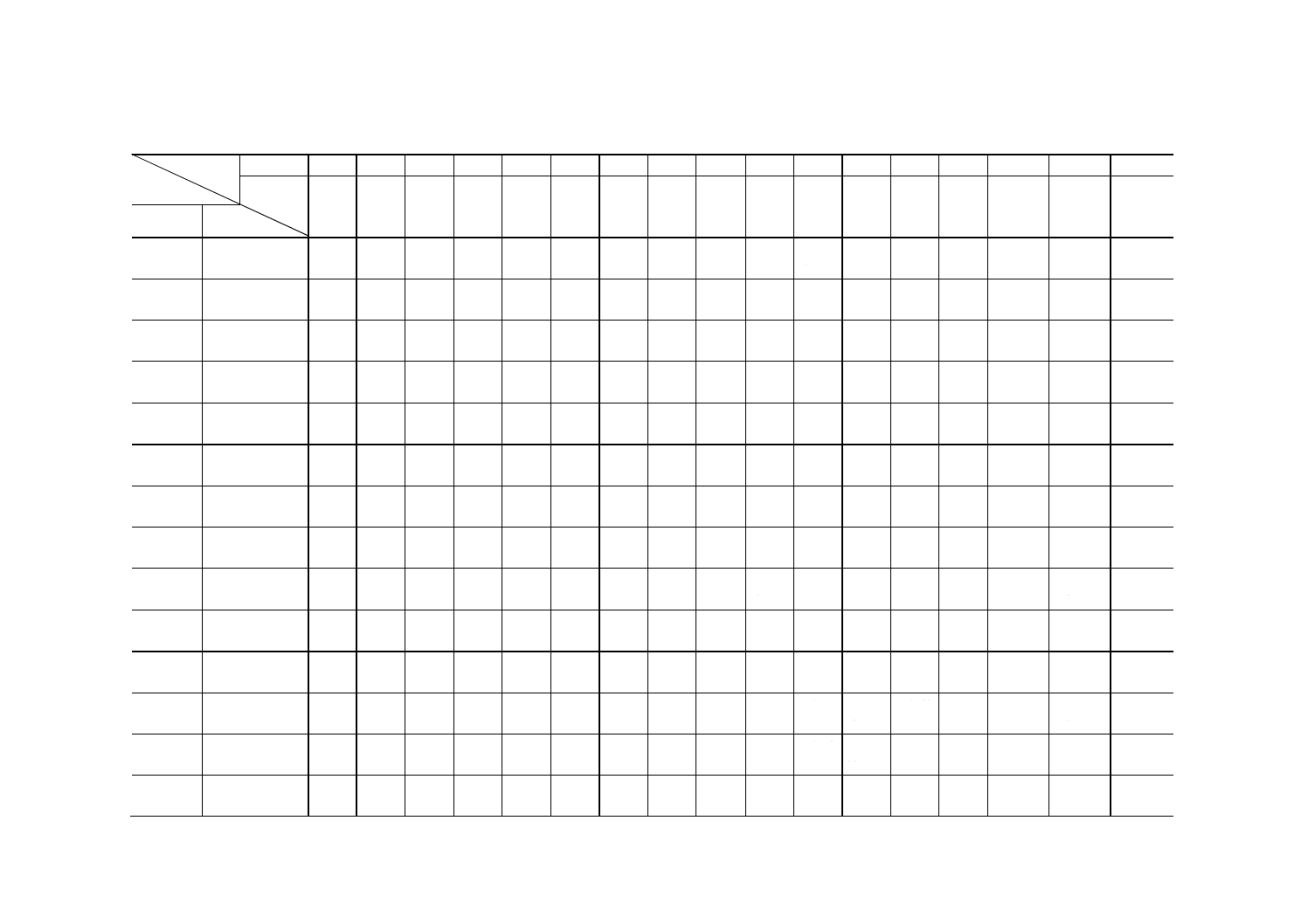
付表1 m0,m1をもとにして試料の大きさnと,合格判定値を
計算するための係数G0を求める表
(α≒0.05,β≒0.10)
σ
0
1
m
m−
n
G0
2.069以上
2
1.163
1.690〜2.068
3
0.950
1.463〜1.689
4
0.822
1.309〜1.462
5
0.736
1.195〜1.308
6
0.672
1.106〜1.194
7
0.622
1.035〜1.105
8
0.582
0.975〜1.034
9
0.548
0.925〜0.974
10
0.520
0.882〜0.924
11
0.496
0.845〜0.881
12
0.475
0.812〜0.844
13
0.456
0.772〜0.811
14
0.440
0.756〜0.771
15
0.425
0.732〜0.755
16
0.411
0.710〜0.731
17
0.399
0.690〜0.709
18
0.383
0.671〜0.689
19
0.377
0.654〜0.670
20
0.368
0.585〜0.653
25
0.329
0.534〜0.584
30
0.300
0.495〜0.533
35
0.278
0.463〜0.494
40
0.260
0.436〜0.462
45
0.245
0.414〜0.435
50
0.233
1
6
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
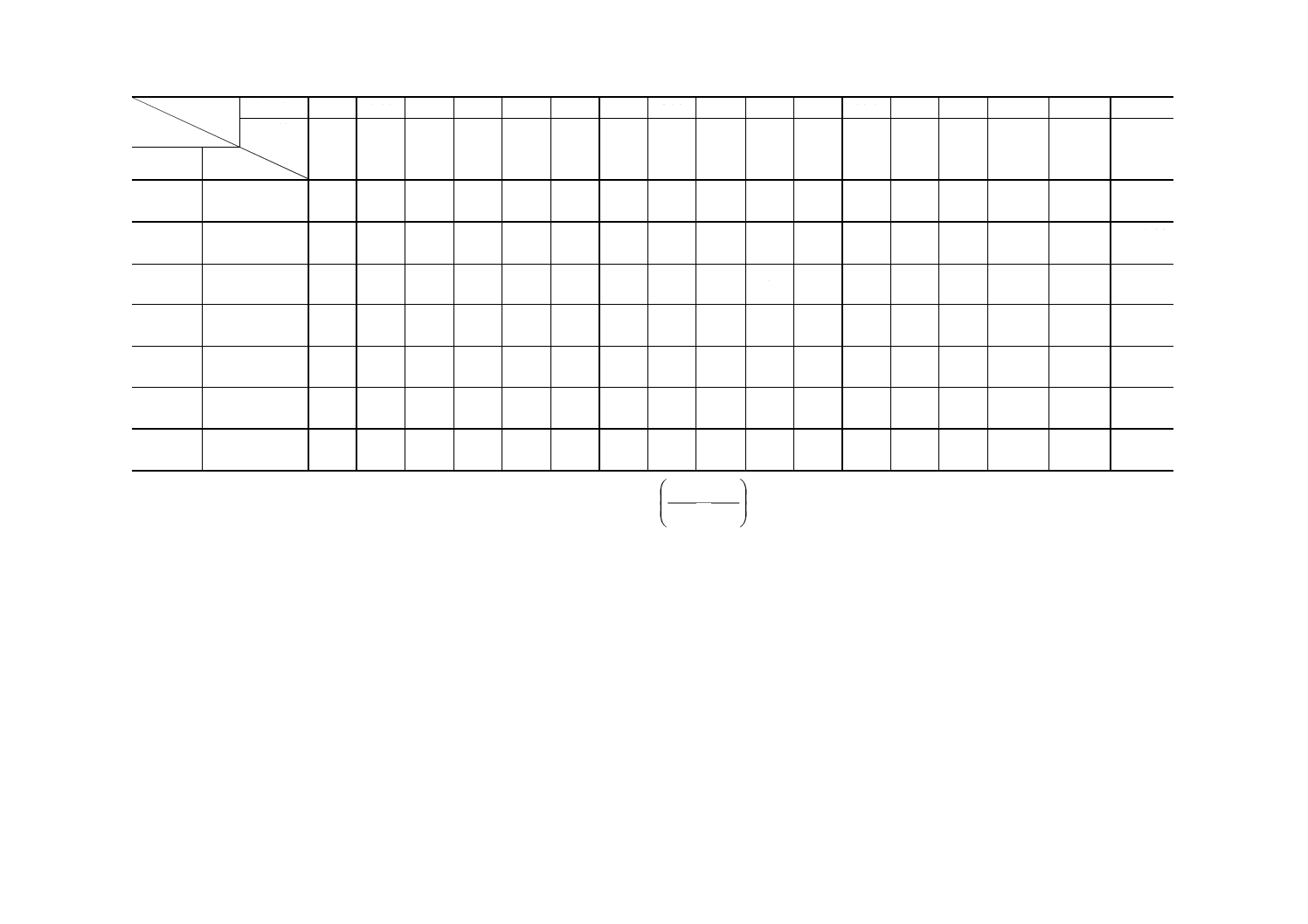
付表2 p0 (%),p1 (%) をもとにしての試料の大きさnと合格判定値を計算するための系数kとを求める表 (α≒0.05 β≒0.10)
左下はn,右上はk
p1 (%)
p0 (%)
代表値
0.80
1.00
1.25
1.60
2.00
2.50
3.15
4.00
5.00
6.30
8.00
10.0
12.5
16.0
20.0
25.0
31.5
範囲 0.71
〜
0.90
0.91
〜
1.12
1.13
〜
1.40
1.41
〜
1.80
1.81
〜
2.24
2.25
〜
2.80
2.81
〜
3.55
3.56
〜
4.50
4.51
〜
5.60
5.61
〜
7.10
7.11
〜
9.00
9.01
〜
11.2
11.3
〜
14.0
14.1
〜
18.0
18.1
〜
22.4
22.5
〜
28.0
28.1
〜
35.5
代表値 範囲
0.100
0.090〜0.112
2.71
18
2.66
15
2.61
12
2.56
10
2.51
8
2.40
7
2.40
6
2.34
5
2.28
4
2.30
4
2.14
3
2.08
3
1.99
2
1.91
2
1.84
2
1.75
2
1.66
2
0.125
0.113〜0.140
2.68
23
2.63
18
2.58
14
2.53
10
2.48
9
2.43
8
2.37
6
2.31
5
2.25
5
2.19
4
2.11
3
2.05
3
1.96
2
1.88
2
1.80
2
1.72
2
1.62
2
0.160
0.141〜0.180
2.64
29
2.60
22
2.55
17
2.50
13
2.45
11
2.39
9
2.35
7
2.28
6
2.22
5
2.15
4
2.09
4
2.01
3
1.94
3
1.84
2
1.77
2
1.68
2
1.59
2
0.200
0.181〜0.224
2.61
39
2.57
28
2.52
21
2.47
16
2.42
13
2.30
10
2.30
8
2.25
7
2.19
6
2.12
5
2.05
4
1.98
3
1.91
3
1.81
2
1.73
2
1.65
2
1.55
2
0.250
0.225〜0.280
*
2.54
37
2.49
27
2.44
20
2.38
15
2.33
12
2.28
10
2.21
8
2.15
6
2.09
5
2.02
4
1.95
4
1.87
3
1.80
3
1.70
2
1.61
2
152
2
0.315
0.281〜0.355
*
*
2.46
36
2.40
25
2.35
19
2.30
14
2.24
11
2.18
9
2.12
7
2.06
6
1.99
5
1.92
4
1.84
3
1.76
3
1.62
2
1.57
2
1.48
2
0.400
0.356〜0.450
*
*
*
2.37
33
2.32
24
2.26
18
2.21
14
2.15
11
2.08
8
2.02
7
1.95
6
1.89
5
1.81
4
1.72
3
1.64
3
1.53
2
1.44
2
0.500
0.451〜0.560
*
*
*
2.33
46
2.28
31
2.23
23
2.17
17
2.11
13
2.05
10
1.99
8
1.92
6
1.85
5
1.77
4
1.68
3
1.60
3
1.50
2
1.40
2
0.630
0.561〜0.710
*
*
*
*
2.25
44
2.19
30
2.09
21
2.08
15
2.02
12
1.95
9
1.89
7
1.81
6
1.74
5
1.65
4
1.56
3
1.46
2
1.36
2
0.800
0.711〜0.900
*
*
*
*
*
2.16
42
2.10
28
2.04
20
1.93
15
1.91
11
1.84
8
1.78
7
1.70
5
1.61
4
1.52
3
1.44
3
1.32
2
1.00
0.901〜1.12
*
*
*
*
*
*
2.06
38
2.00
26
1.94
18
1.88
14
1.81
10
1.74
8
1.66
6
1.58
5
1.50
4
1.42
3
1.30
3
1.25
1.13〜1.40
*
*
*
*
*
*
*
1.97
36
1.91
24
1.84
17
1.77
12
1.70
9
1.63
7
1.54
6
1.45
4
1.37
3
1.26
3
1.60
1.41〜1.80
*
*
*
*
*
*
*
*
1.86
34
1.80
23
1.73
16
1.66
12
1.59
9
1.50
6
1.41
5
1.32
4
1.21
3
2.00
1.81〜2.24
*
*
*
*
*
*
*
*
*
1.76
31
1.69
20
1.62
14
1.54
10
1.46
8
1.37
6
1.28
5
1.16
3
1
7
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p1 (%)
p0 (%)
代表値
0.80
1.00
1.25
1.60
2.00
2.50
3.15
4.00
5.00
6.30
8.00
10.0
12.5
16.0
20.0
25.0
31.5
範囲 0.71
〜
0.90
0.91
〜
1.12
1.13
〜
1.40
1.41
〜
1.80
1.81
〜
2.24
2.25
〜
2.80
2.81
〜
3.55
3.56
〜
4.50
4.51
〜
5.60
5.61
〜
7.10
7.11
〜
9.00
9.01
〜
11.2
11.3
〜
14.0
14.1
〜
18.0
18.1
〜
22.4
22.5
〜
28.0
28.1
〜
35.5
代表値 範囲
2.50
2.25〜2.80
*
*
*
*
1.72
46
1.65
28
1.58
19
1.50
13
1.42
9
1.33
7
1.24
5
1.13
4
3.15
2.81〜3.55
*
*
*
*
1.60
42
1.53
26
1.46
17
1.37
11
1.29
8
1.19
6
1.09
5
4.00
3.56〜4.50
*
*
*
*
1.49
39
1.41
24
1.33
15
1.24
10
1.14
7
1.04
5
5.00
4.51〜5.60
*
*
*
*
1.37
35
1.28
20
1.19
13
1.10
9
0.99
6
6.30
5.61〜7.10
*
*
*
*
1.23
30
1.14
18
1.05
12
0.94
8
8.00
7.11〜9.00
*
*
*
*
1.09
27
1.00
16
0.89
10
10.0
9.01〜11.2
*
*
*
1.03
44
0.94
23
0.83
14
備考 *の欄は付表3によりそれぞれp0,p1の代表値に対するKp0,Kp1を用いてn=
2
1
0
9264
.2
−
p
p
K
K
,k=0.562 073 Kp1+0.437 927Kp0を計算し,nは整数に,kは小数
点以下4けたまで計算し,2けたに丸めたものを用いる。空欄に対しては抜取検査方式はない。
18
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
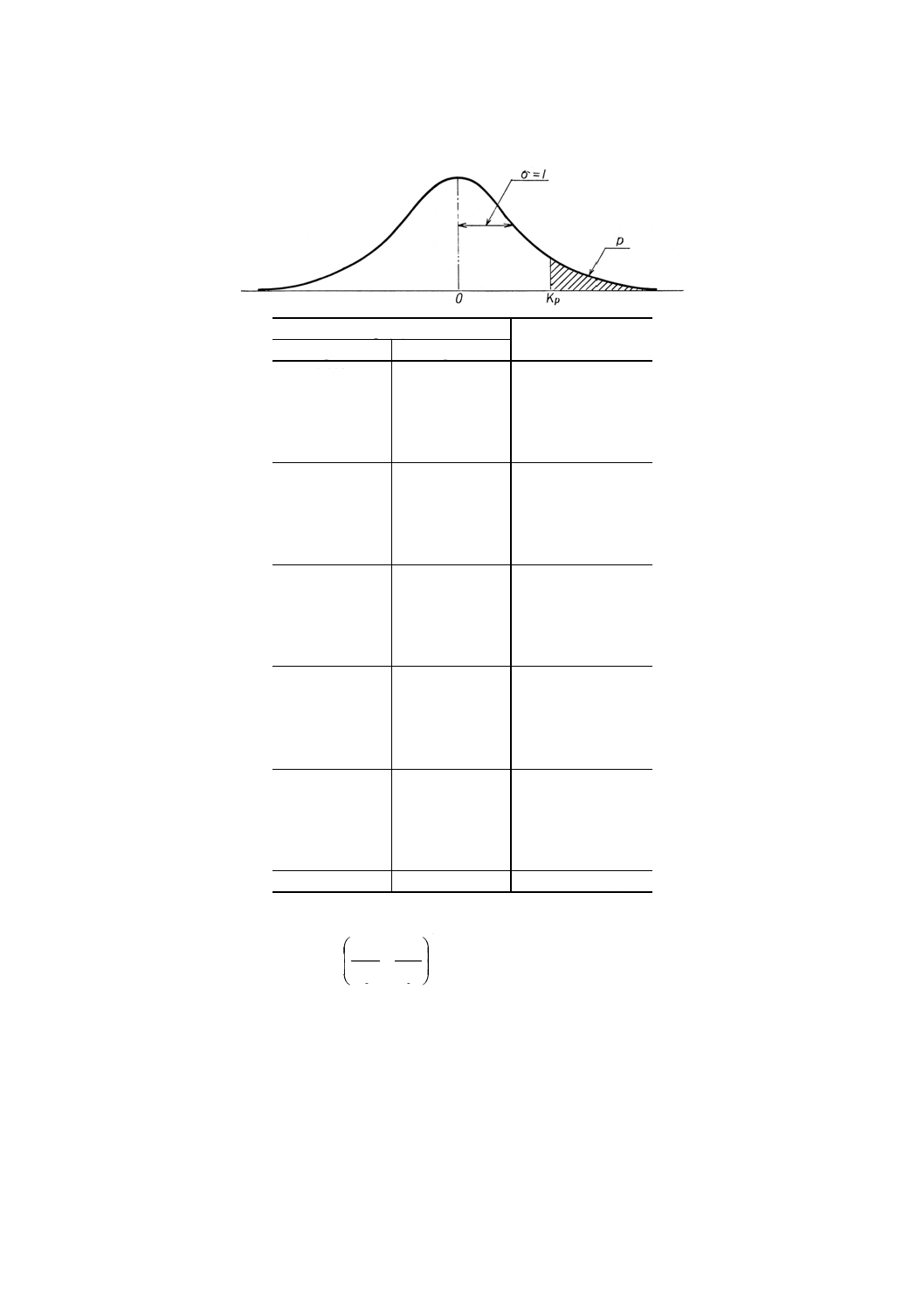
付表3 付表2のpの代表値に対するKp
p (%)
Kp
p0
p1
0.100
−
3.090 23
0.125
−
3.023 34
0.160
−
2.947 84
0.200
−
2.878 16
0.250
−
2.807 03
0.315
−
2.731 74
0.400
−
2.652 07
0.500
−
2.575 83
0.630
−
2.494 88
0.800
0.80
2.408 92
1.00
1.00
2.326 35
1.25
1.25
2.241 40
1.60
1.60
2.144 41
2.00
2.00
2.053 75
2.50
2.50
1.959 96
3.15
3.15
1.859 19
4.00
4.00
1.750 69
5.00
5.00
1.644 85
6.30
6.30
1.530 07
8.00
8.00
1.405 07
10.0
10.0
1.281 55
−
12.5
1.150 35
−
16.0
1.994 46
−
20.0
0.841 62
−
25.0
0.674 49
−
31.5
0.481 73
備考 この表は,標準正規分布における上側確率p (%) を
与える点を示したもので,付表2に示した
n=
2
1
0
9264
.2
−
p
p
K
K
,k=0.562 073Kp1+0.437 927Kp0
によりn,kを計算する際に用いる。
19
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
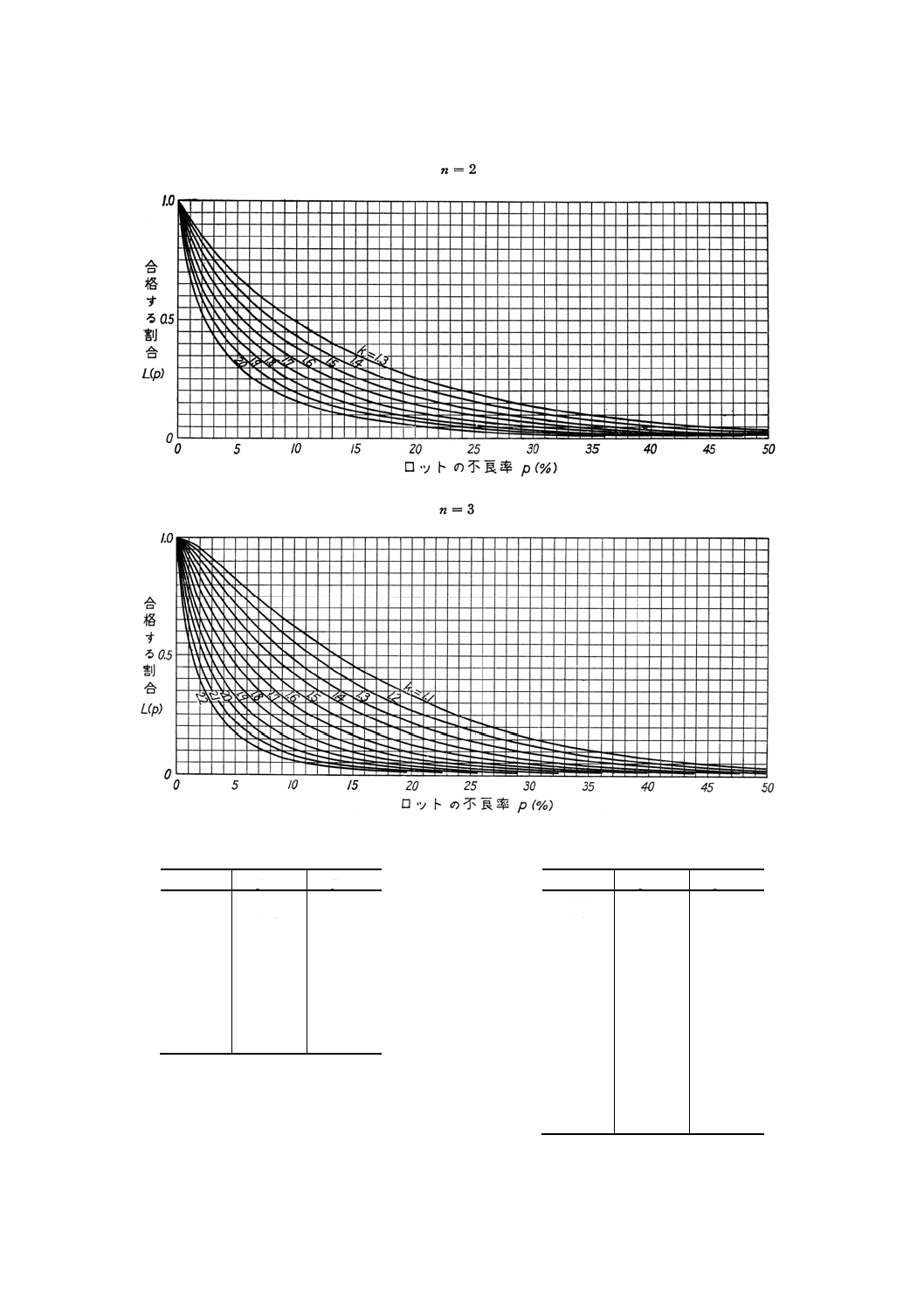
付図1
n=2
k
p0.95
p0.10
1.3
0.69%
34.69%
1.4
0.52
31.07
1.5
0.39
27.63
1.6
0.29
24.39
1.7
0.21
21.37
1.8
0.15
18.57
1.9
0.11
16.02
2.0
0.08
13.70
n=3
k
p0.95
p0.10
1.1
2.02%
35.94%
1.2
1.58
32.27
1.3
1.22
28.77
1.4
0.94
25.46
1.5
0.71
22.36
1.6
0.54
19.49
1.7
0.40
16.85
1.8
0.30
14.45
1.9
0.22
12.30
2.0
0.16
10.38
2.1
0.11
8.69
2.2
0.08
7.21
20
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
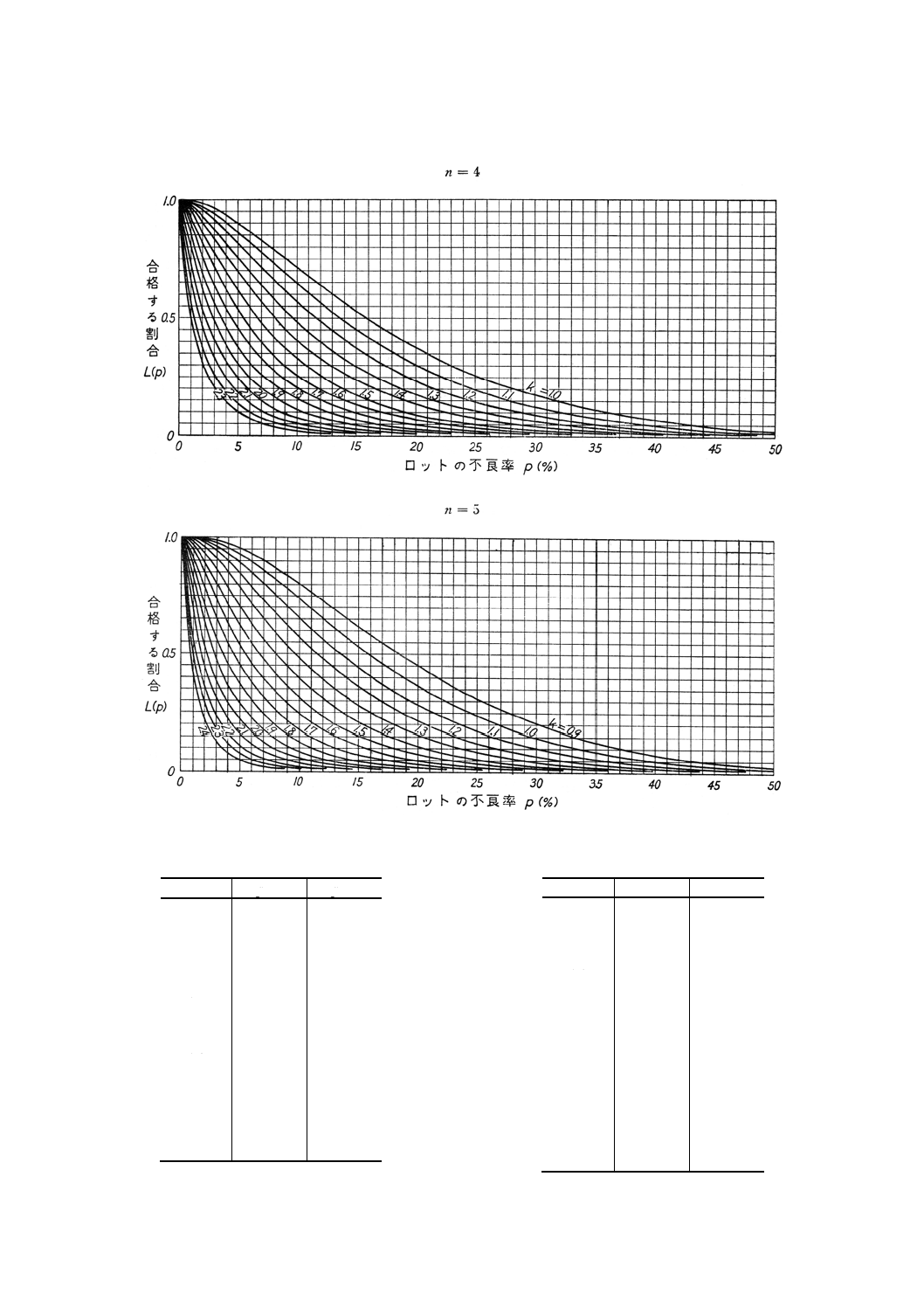
付図1(つづき)
n=4
k
p0.95
p0.10
1.0
3.42%
35.97%
1.1
2.73
32.30
1.2
2.16
28.80
1.3
1.69
25.49
1.4
1.31
22.39
1.5
1.01
19.51
1.6
0.77
16.87
1.7
0.58
14.47
1.8
0.44
12.32
1.9
0.32
10.40
2.0
0.24
8.70
2.1
0.17
7.23
2.2
0.13
5.95
2.3
0.09
4.85
n=5
k
p0.95
p0.10
0.9
5.10%
37.19%
1.0
4.13
33.47
1.1
3.32
29.91
1.2
2.65
26.54
1.3
2.09
23.37
1.4
1.64
20.42
1.5
1.27
17.70
1.6
0.98
15.22
1.7
0.74
12.99
1.8
0.56
10.99
1.9
0.42
9.23
2.0
0.31
7.68
2.1
0.23
6.34
2.2
0.17
5.19
2.3
0.12
4.21
2.4
0.09
3.39
21
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
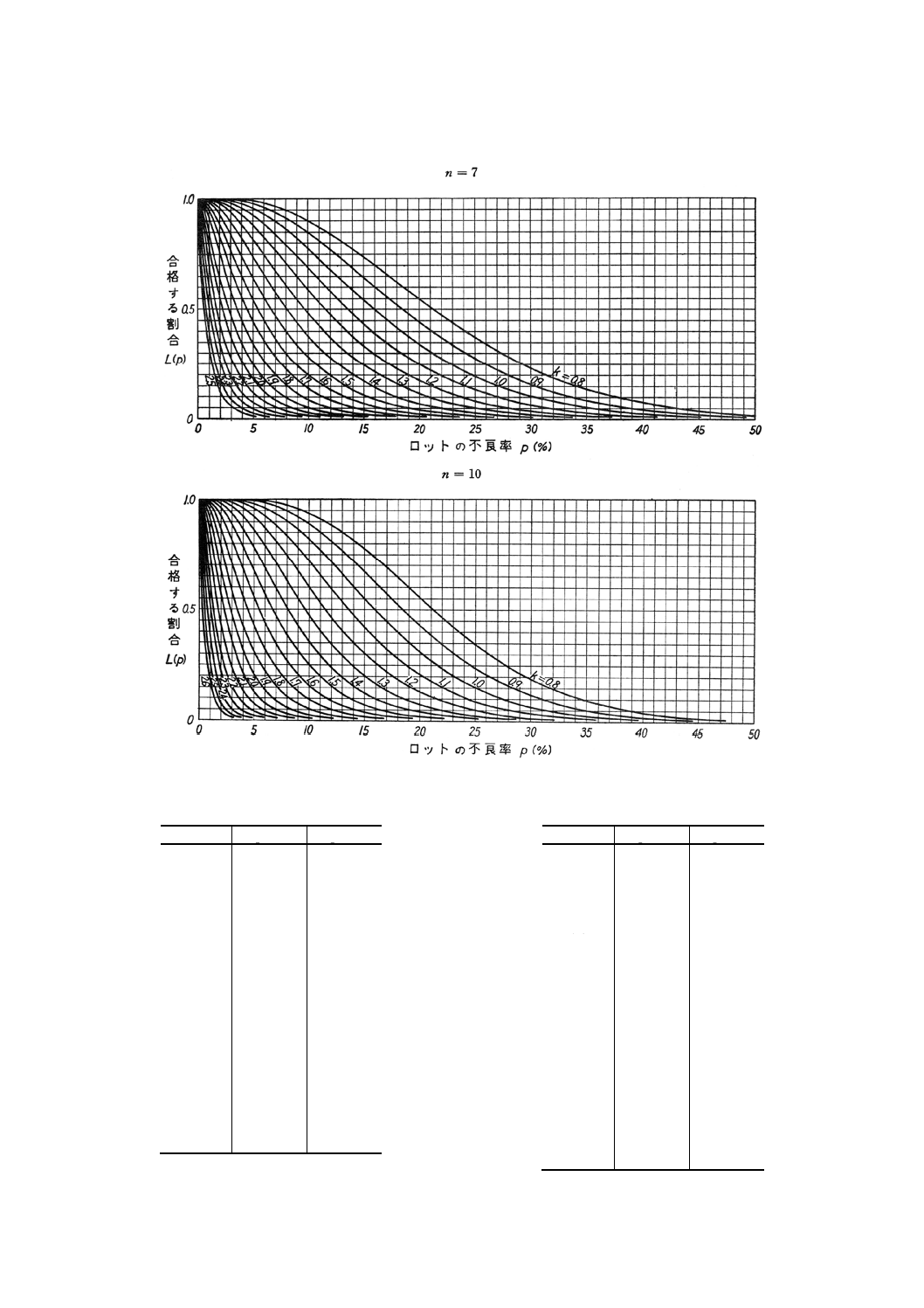
付図1(つづき)
n=7
k
p0.95
p0.10
0.8
7.76%
37.61%
0.9
6.40
33.88
1.0
5.24
30.31
1.1
4.26
26.91
1.2
3.43
23.71
1.3
2.73
20.74
1.4
2.16
17.99
1.5
1.69
15.49
1.6
1.32
13.23
1.7
1.01
11.21
1.8
0.77
9.42
1.9
0.58
7.84
2.0
0.44
6.48
2.1
0.32
5.31
2.2
0.24
4.31
2.3
0.17
3.47
2.4
0.13
2.77
2.5
0.09
2.19
n=10
k
p0.95
p0.10
0.8
9.34%
34.65%
0.9
7.78
31.04
1.0
6.42
27.60
1.1
5.26
24.36
1.2
4.27
21.34
1.3
3.44
18.55
1.4
2.74
15.99
1.5
2.17
13.68
1.6
1.70
11.61
1.7
1.32
9.77
1.8
1.02
8.15
1.9
0.78
6.75
2.0
0.59
5.54
2.1
0.44
4.51
2.2
0.33
3.63
2.3
0.24
2.91
2.4
0.17
2.30
2.5
0.13
1.81
2.6
0.09
1.41
22
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
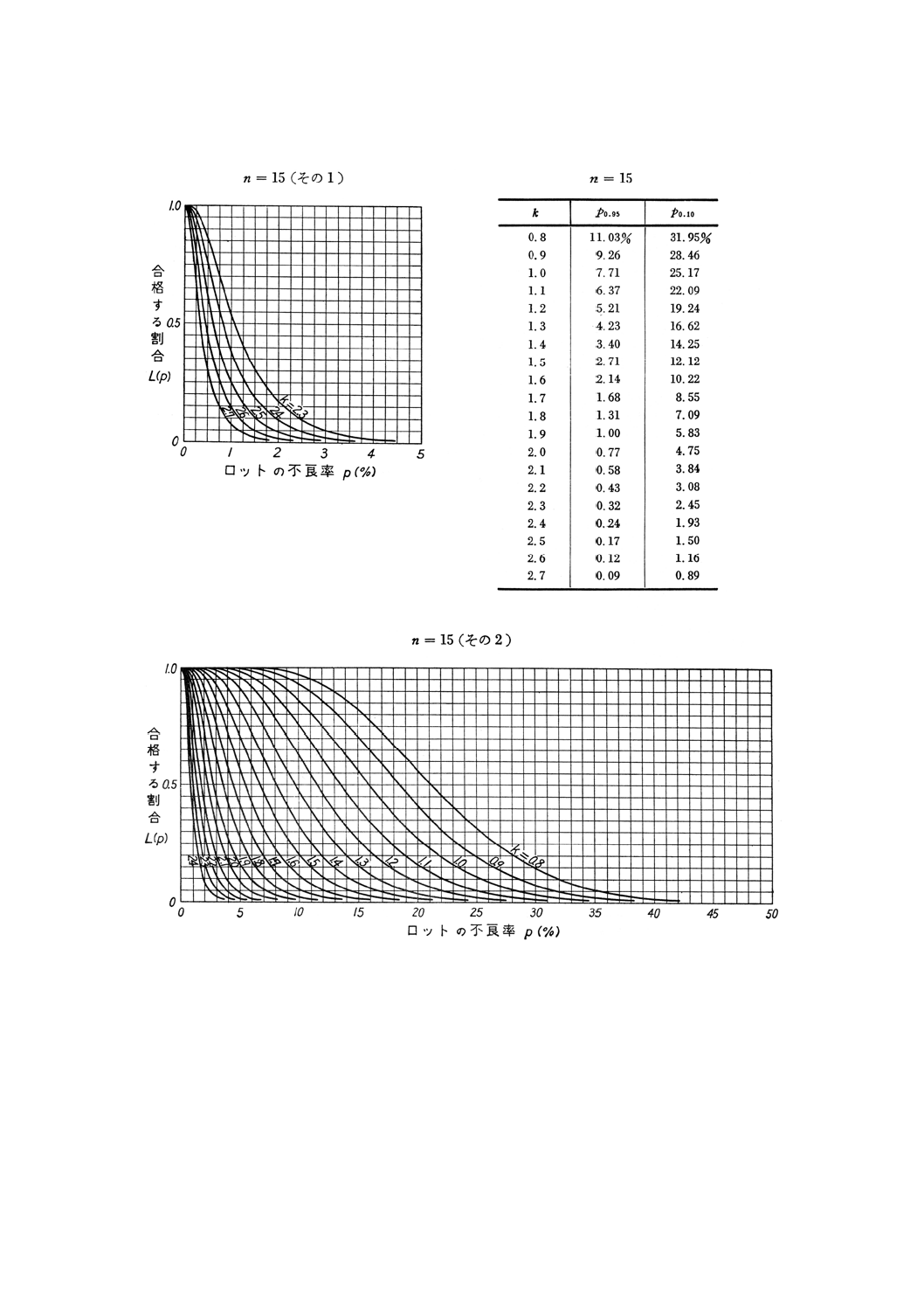
付図1(つづき)
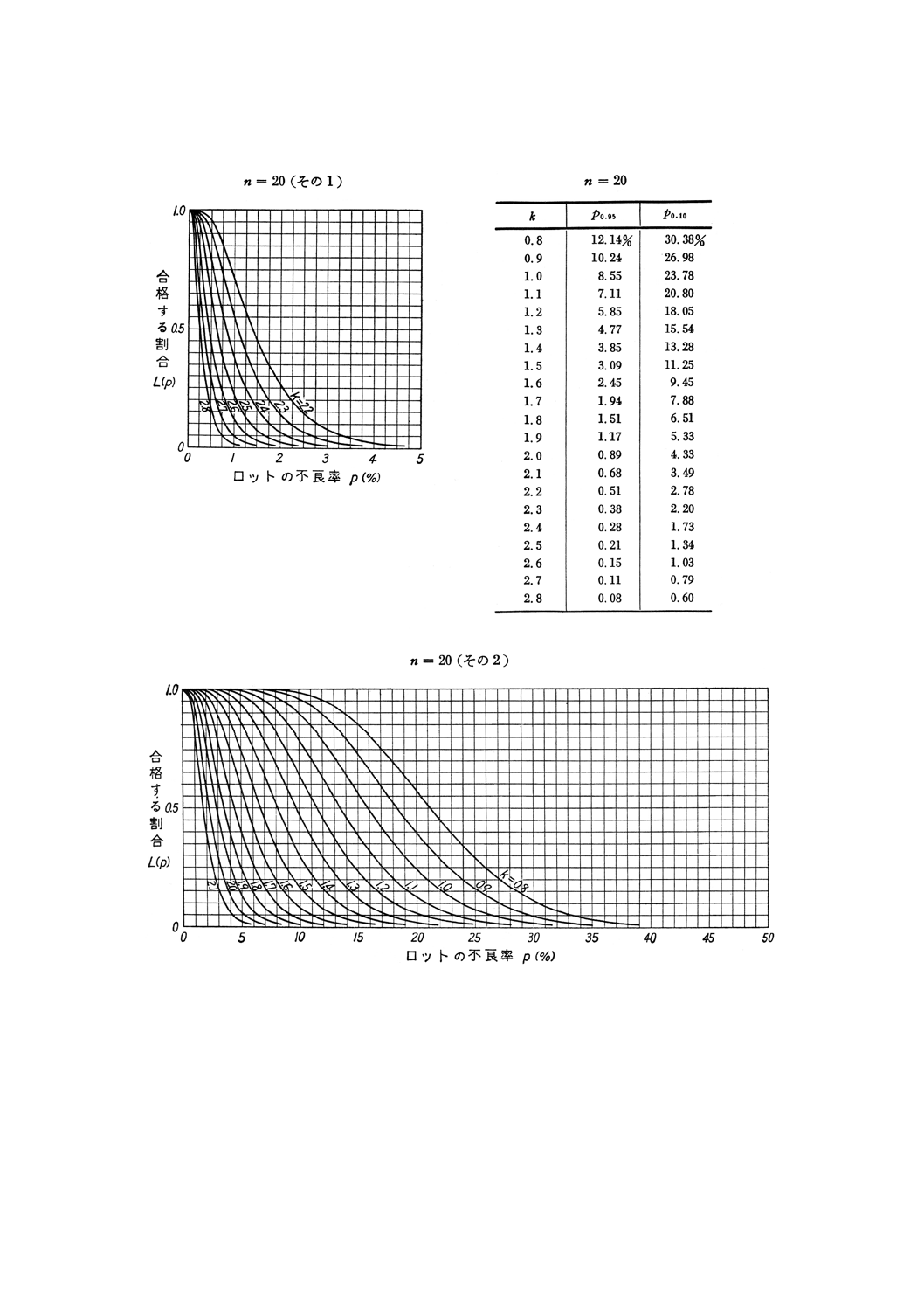
23
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
付図1(つづき)
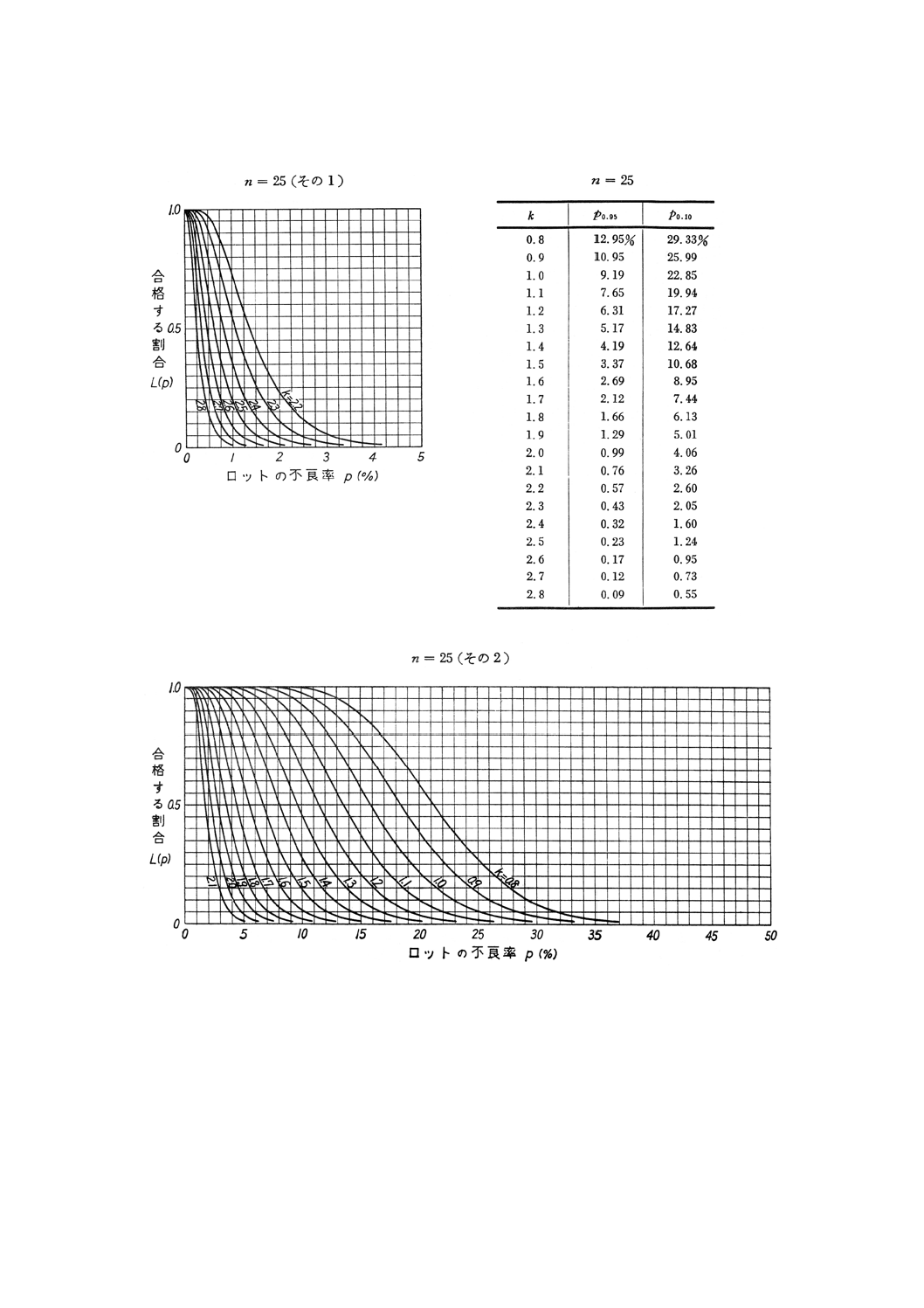
24
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
付図1(つづき)
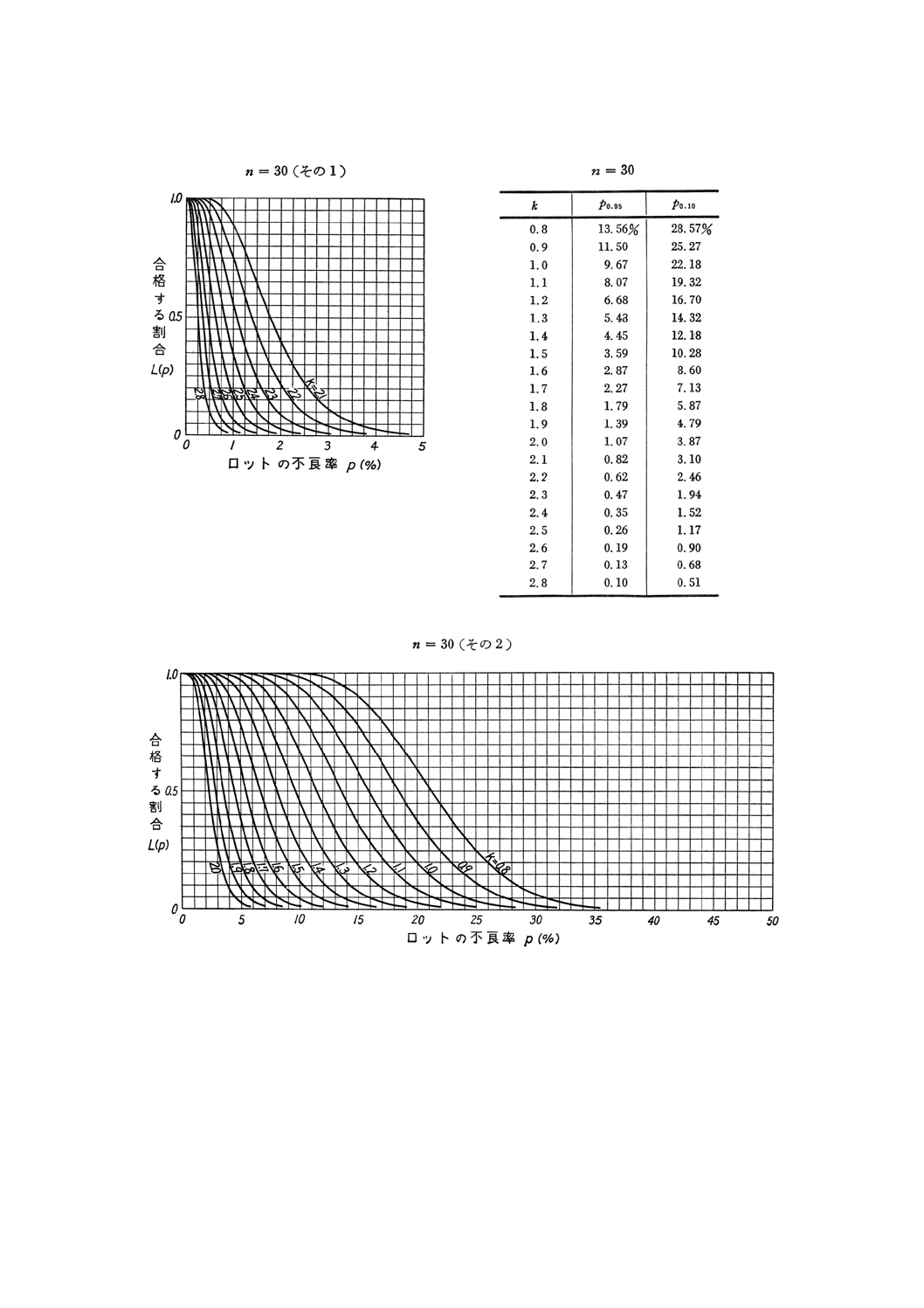
25
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
付図1(つづき)
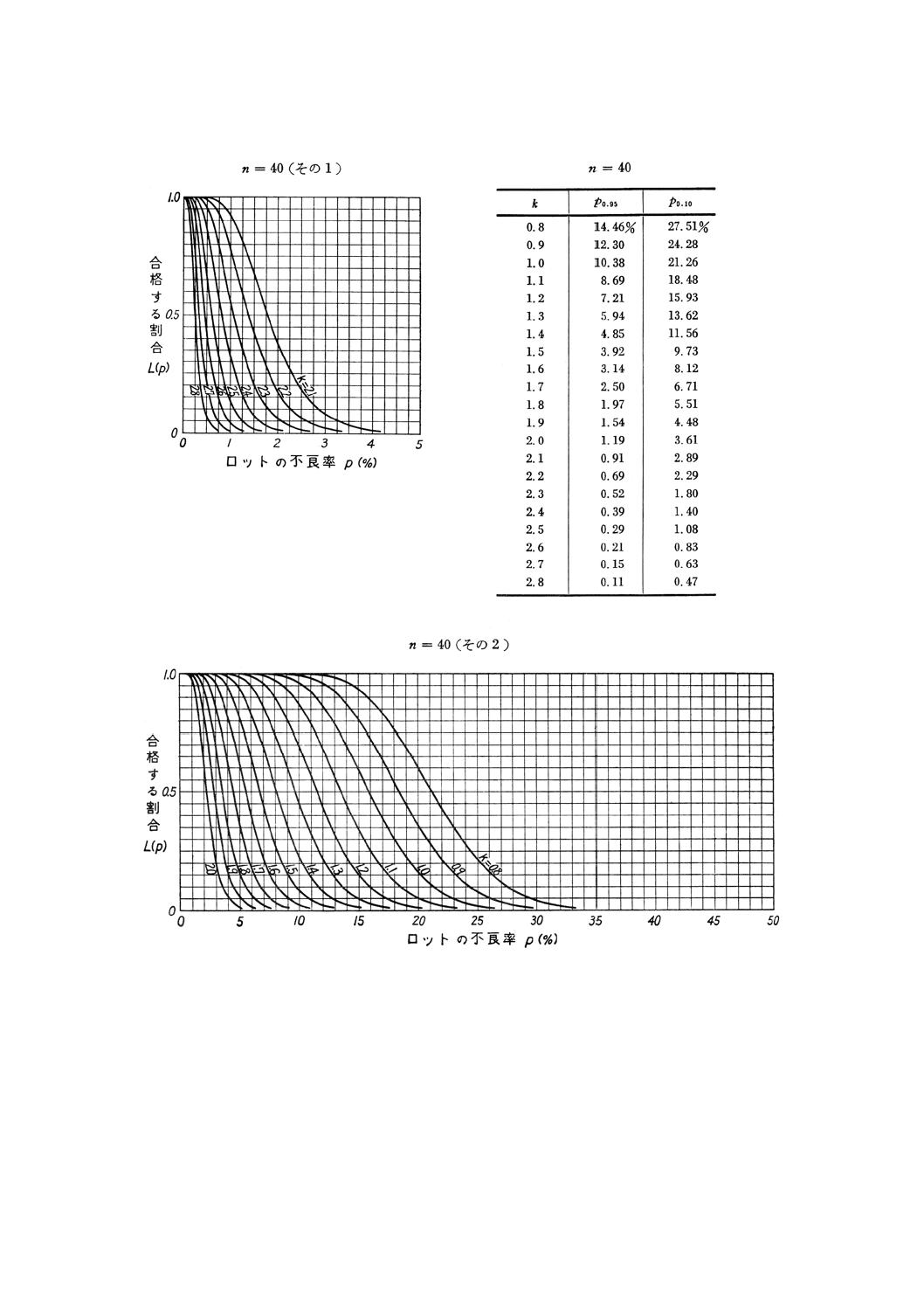
26
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
付図1(つづき)
27
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
付図1(つづき)
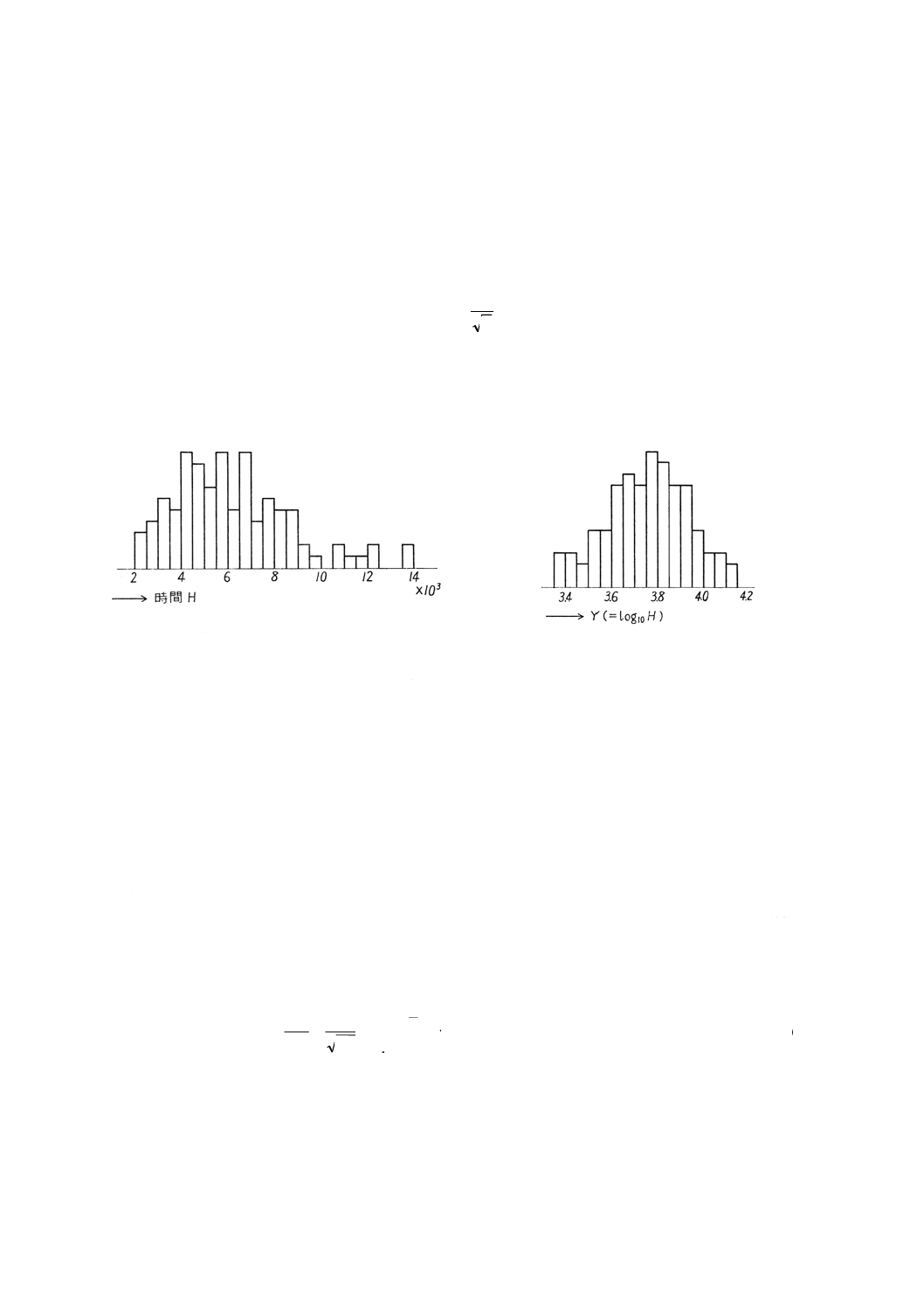
28
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考
1. ロットの特性値の分布 この規格でロットの不良率を保証する場合は,特性値が正規分布をしている
ことを前提条件としている。
もしも特性値が正規分布をしていない場合には変数変換を行って,正規分布となった変数に基づいて計
量抜取検査を適用する。その際,通常の変数変換として,
log10χ,x,log10 (χ+a),
x
1
などが用いられる。
例えば,けい光放電管のあるロットから100本をランダムに抜き取って寿命試験を行い,その結果をヒ
ストグラムにすると参考図1のようになった。
参考図1
参考図2
このヒストグラムは正規分布とみなしがたいが,
Y=log10H
ここに
H: 寿命時間
の変換を各データについて行い,ついで変換した変数Yを横軸としてヒストグラムを作ってみると参考図
2のようになる。
参考図2のヒストグラムは正規分布とみなし得るから,変換した変数Yに基づいて計量抜取検査を適用
できる。
2. 平均値と不良率との関係 検査単位の特性値が正規分布するとき,そのロットの平均値mと不良率p
の関係は次のようになる。
上限規格値が与えられたとき SU−m=Kpσ ·································· (1*)
下限規格値が与えられたとき SL−m=−Kpσ ······························· (2*)
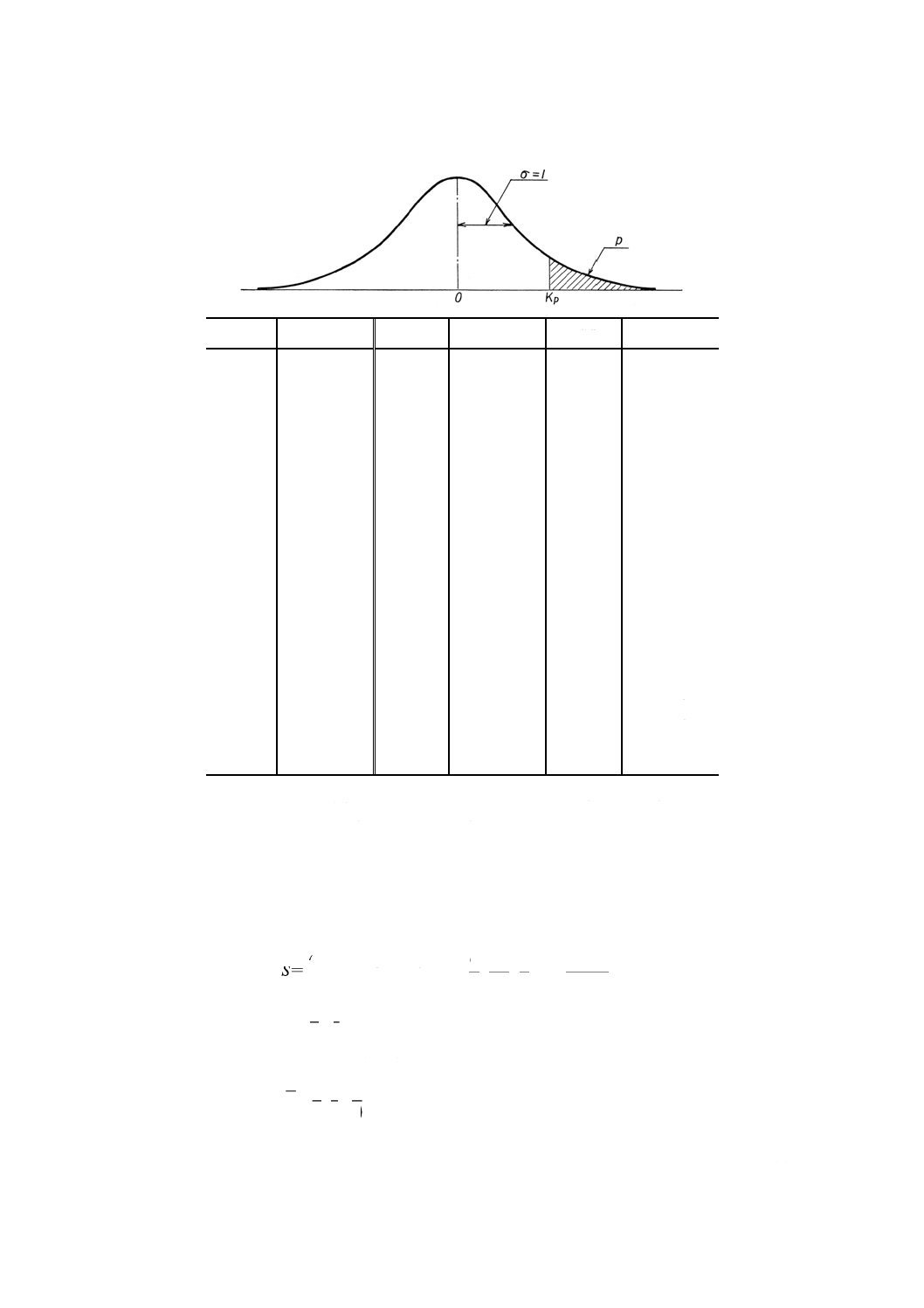
この場合,Kpは次の式で定義され,したがって不良率pとKpとの関係は参考表1のようになる。
∫
−
∞
=
dt
e
p
t
p
2
2
2
1
100
κ
π
······························································ (3*)
29
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考表1 不良率pとKpとの関係
p (%)
Kp
p (%)
Kp
p (%)
Kp
0.0
∞
10
1.281 55
30
0.524 40
0.1
3.090 23
11
1.226 53
31
0.495 85
0.2
2.878 16
12
1.174 99
32
0.467 70
0.3
2.747 78
13
1.126 39
33
0.439 91
0.4
2.652 07
14
1.080 32
34
0.412 46
0.5
2.575 83
15
1.036 43
35
0.385 32
0.6
2.512 14
16
0.994 46
36
0.358 46
0.7
2.457 26
17
0.954 17
37
0.331 85
0.8
2.408 92
18
0.915 37
38
0.305 48
0.9
2.365 62
19
0.877 90
39
0.279 32
1.0
2.326 35
20
0.841 62
40
0.253 35
2.0
2.053 75
21
0.806 42
41
0.227 54
3.0
1.880 79
22
0.772 19
42
0.201 89
4.0
1.750 69
23
0.738 85
43
0.176 37
5.0
1.644 85
24
0.706 30
44
0.150 97
6.0
1.554 77
25
0.674 49
45
0.125 66
7.0
1.475 79
26
0.643 35
46
0.100 43
8.0
1.405 07
27
0.612 81
47
0.075 27
9.0
1.340 76
28
0.582 84
48
0.050 15
29
0.553 38
49
0.025 07
50
0.000 00
備考 付表3と一部重複しているところがある。この表は標準正規分布における
上側確率p (%) を与える点の値を示したもので,指定された任意のα,β
をもつ抜取検査方式を設計する場合その他に使うことができる。
3. 試料の大きさが等しくない場合のσの指定
(1) 最近の10〜20ロットの検査データについて次の式によりロットごとの平方和S及び不偏分散Vを計
算する。
S=(
)(
)
n
x
x
x
x
x
x
n
n
2
2
1
2
2
2
2
1
+
+
+
−
+
+
+
Λ
Λ
Λ
Λ
V=
1
−
n
S
(2) (1)で求めた平方和の合計ΣS及び (n−1) の合計を求め,
(
)1
−
∑
∑
=
n
S
V
を計算する。
(3) ロット内のばらつきが安定しているかどうか調べる。それには各ロットについての (n−1) を用い,F
30
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
分布表(本文5.4の表1参照)からロットごとに
1
−
∞n
F
(0.01) を求め,
V
1
−
∞n
F
(0.01) を計算し,そ
れぞれのVがこれを超えなければロット内のばらつきは安定していると判定する。
(4) ロット内のばらつきが安定していれば
σの推定値=V
を標準偏差σの値として指定する。
(5) 引き続きこの抜取検査方式を使う場合は,ロットの標準偏差が指定した値とはなはだしい差異がない
ことを(3)の手順を準用して確かめなければならない。
(6) 長期にわたって連続してこの抜取検査方式を使う場合は,最近の20ロット以上の検査データからの推
定値を求め,σの値を更新する。
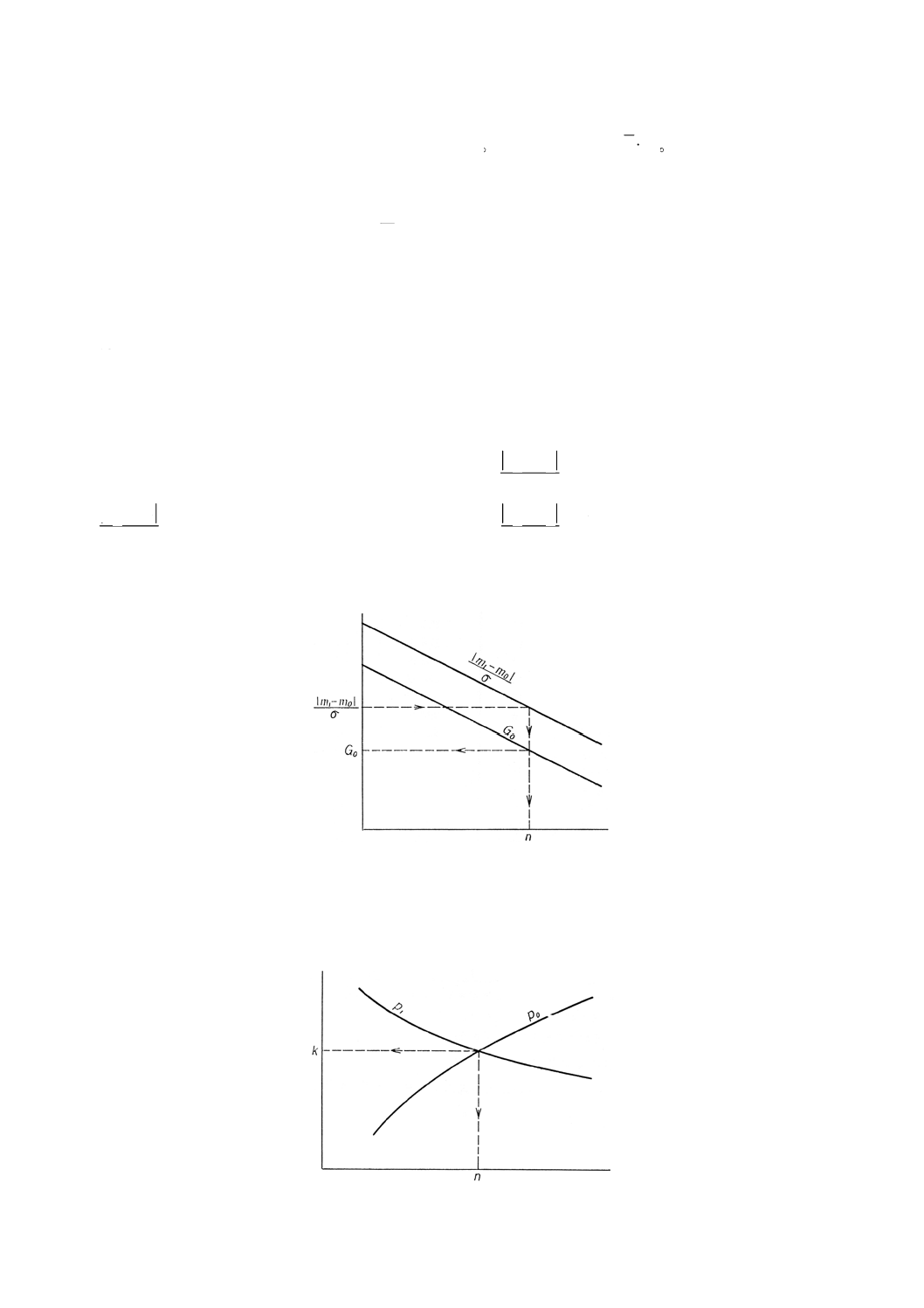
4. 図による抜取検査方式の求め方(α=0.05,β=0.10)
4.1
平均値を保証する場合 指定されたm0,m1,σから
σ
0
1
m
m−
を計算し,参考付図1により縦軸に
σ
0
1
m
m−
の値をとり,これから横軸に平行に右に見ていき
σ
0
1
m
m−
直線との交点をとおる縦軸を下に見て
いき,G0直線との交点の横軸の値が試料の大きさnの値であり,縦軸の値がG0の値である。
参考図3 参考付図1の説明図
4.2
不良率を保証する場合 参考付図2により指定されたp0及びp1の値をもったp0曲線,p1曲線の交点
を見出す。
交点の横軸の値が試料の大きさnの値であり,縦軸の値がkの値である。
参考図4 参考付図2の説明図
31
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5. 抜取検査方式の求め方の根拠
5.1
特性値を保証する場合
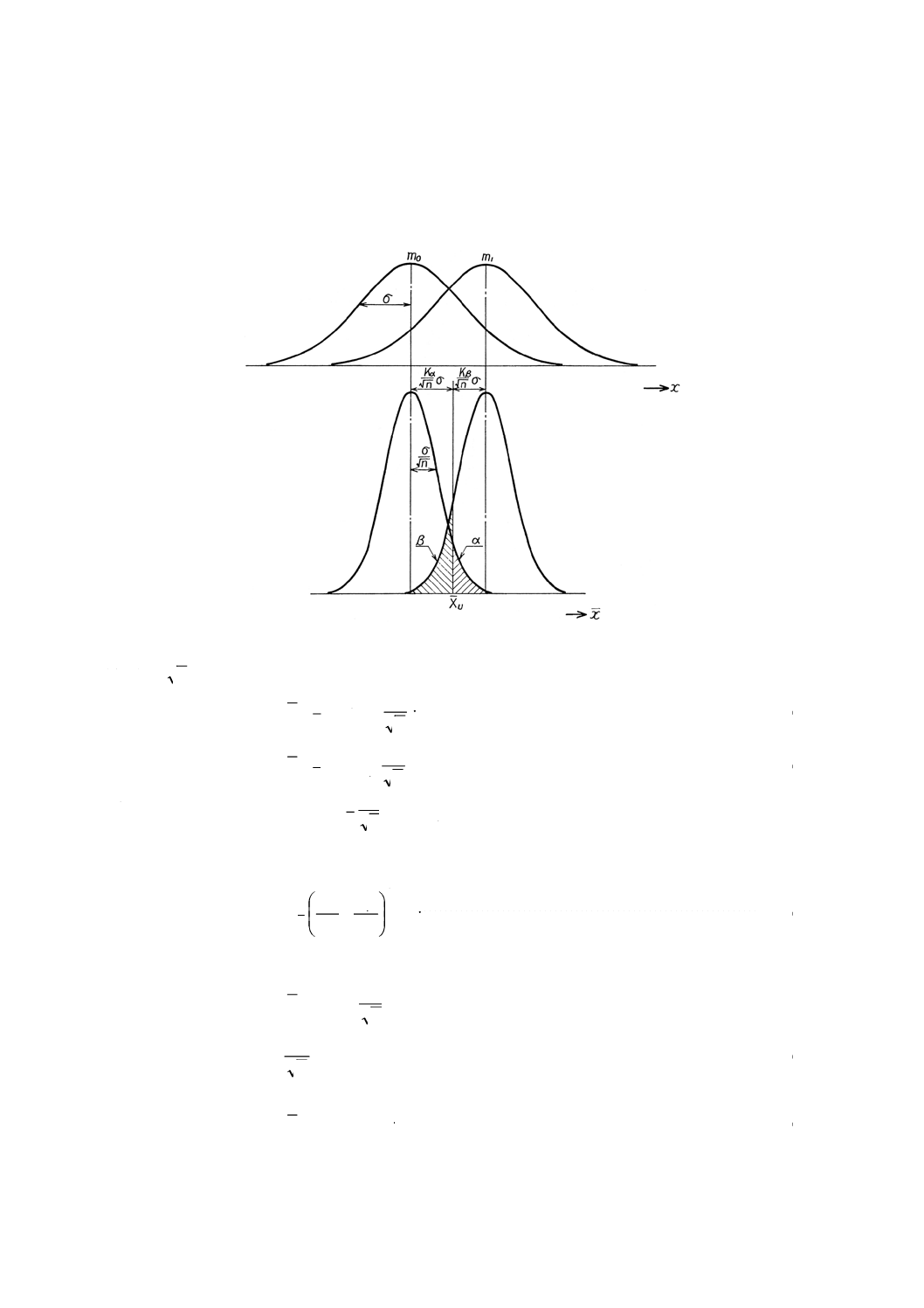
5.1.1
特性値が低いほうが好ましい場合
参考図5
平均値m,標準偏差σのロットから大きさnの試料をとったとき,試料の平均値xの分布は平均値m,標
準偏差
n
/
σ
の正規分布をするから,参考図5から次の関係が得られる。
n
K
m
XU
σ
α
+
=
0
····································································· (1)
n
K
m
XU
σ
β
−
=
1
····································································· (2)
式(1)と(2)から
(
)
β
α
σ
K
K
n
m
m
+
=
−
0
1
試料の大きさnは
2
2
0
1
σ
β
α
−
+
=
m
m
K
K
n
···································································· (3)
上限合格判定値は参考図5から
σ
α
n
K
m
XU
+
=
0
0
G
n
K
=
α
················································································· (4)
とすれば
σ
0
0
G
m
XU
+
=
········································································· (5)
となる。
32
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
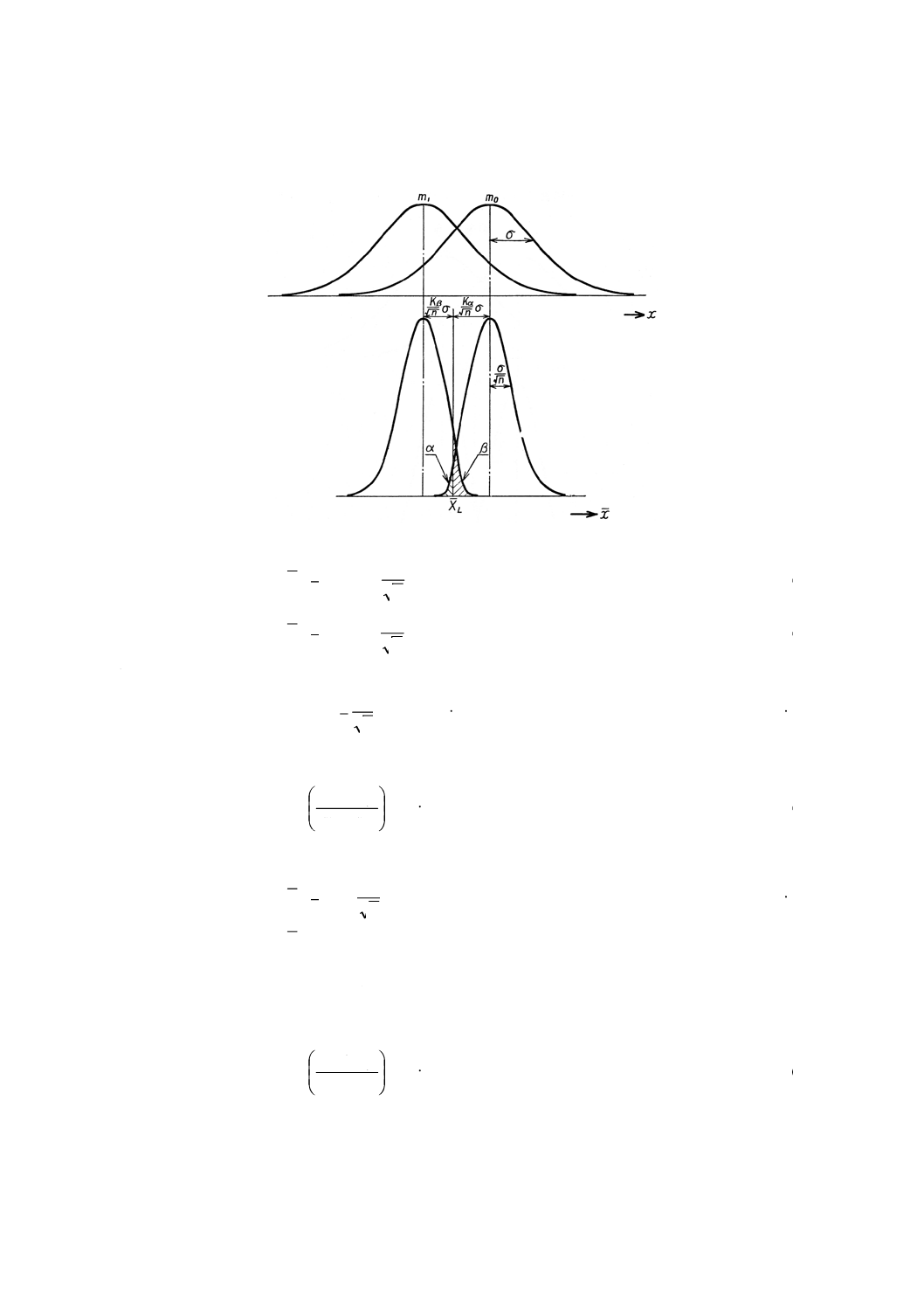
5.1.2
特性値が高いほうが好ましい場合
参考図6
参考図6から5.1.1と同様にして
n
K
m
XL
σ
α
−
=
0
····································································· (6)
n
K
m
XL
σ
β
+
=
1
····································································· (7)
式(6)と(7)から
(
)
β
α
σ
K
K
n
m
m
+
=
−
1
0
·································································
試料の大きさnは
2
2
1
0
σ
β
α
−
+
=
m
m
K
K
n
···································································· (8)
下限合格判定値は参考図6から
σ
α
n
K
m
XL
−
=
0
··········································································
XL=m0−G0σ ··········································································· (9)
となる。
5.1.3
α=0.05,β=0.10の場合の計算式 式(3),(8)から試料の大きさnは特性値が低いほうが好ましい
場合も高いほうが好ましい場合も
2
2
0
1
σ
β
α
−
+
=
m
m
K
K
n
·································································· (10)
となり,
α=0.05,β=0.10
33
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とすれば
Kα=1.64485,Kβ=1.281 55
となるので
2
2
0
1
9264
.2
σ
−
=
m
m
n
···································································· (11)
となる。
上限又は下限合格判定値を求める係数は式(3)から
n
n
K
G
64485
.1
0
=
=
α
·································································· (12)
となる。
備考 α≠0.05,β≠0.10の場合にはそれぞれのα,βに対するKα及びKβの値を用いればよい。
5.2
不良率を保証する場合
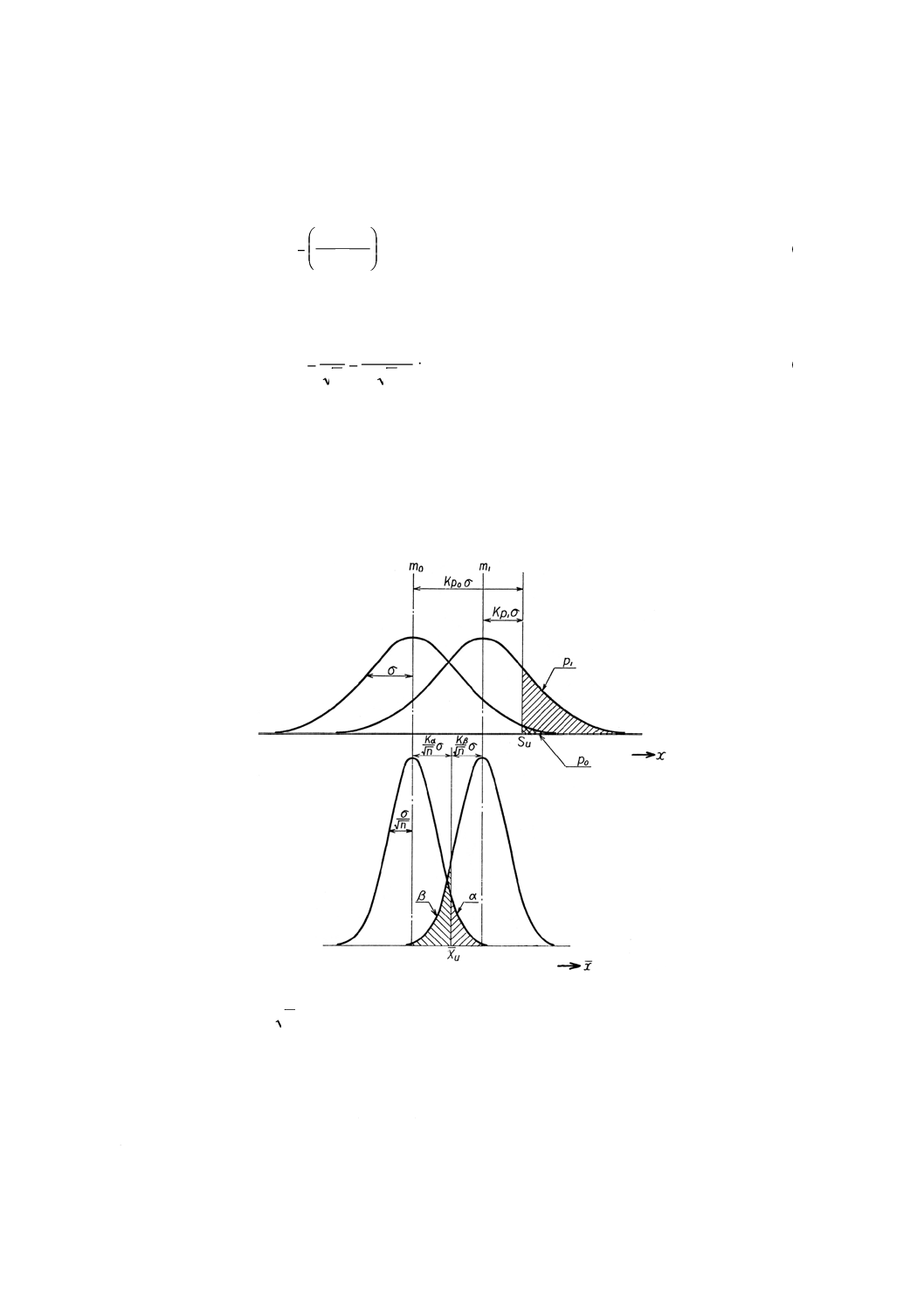
5.2.1
上限規格値が与えられた場合
参考図7
平均値m,標準偏差σの正規分布をなすロットから大きさnの試料をとったときの試料の平均値xの分布
は平均値m,標準偏差
n
/
σ
の正規分布をするから,参考図7から次の関係が得られる。
m0=SU−Kp0σ ·········································································· (13)
m1=SU−p1σ ··········································································· (14)
式(13)と(14)から
m1−m0= (Kp0−Kp1) σ······························································· (15)
式(3)と(15)から
34
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試料の大きさnは
2
1
0
−
+
=
p
p
K
K
K
K
n
β
α
···································································· (16)
上限合格判定値は参考図7により
式(1)と(13)から
n
K
K
S
X
p
U
U
σ
σ
α
+
−
=
0
························································· (17)
式(16)と(17)から
β
α
ασ
σ
K
K
K
K
K
K
S
X
p
p
p
U
U
+
−
+
−
=
1
0
0
β
α
β
ε
K
K
K
K
K
K
S
p
p
U
+
+
−
=
0
1
k
K
K
K
K
K
K
p
p
=
+
+
β
α
β
ε
0
1
································································ (18)
とすれば
XU=SU−kσ ··········································································· (19)
となる。
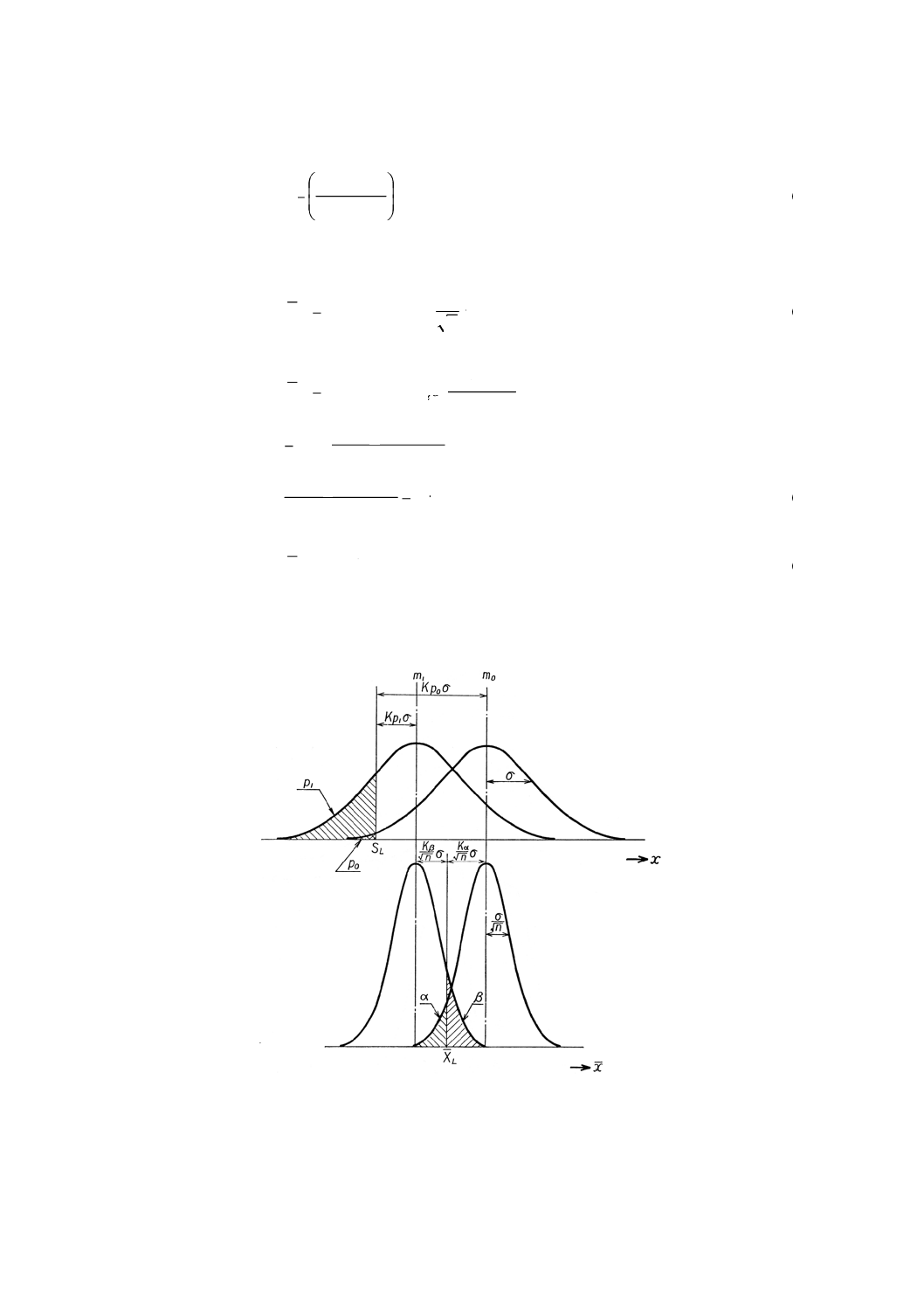
5.2.2
下限規格値が与えられた場合
参考図8
参考図8から5.2.1と同様にして
m0=SL+Kp0σ ·········································································· (20)
m1=SL+Kp1σ ·········································································· (21)
35
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
式(20)と(21)から
mo−m1= (Kp0−Kp1) σ ······························································ (22)
式(3)と(22)から
試料の大きさnは
2
1
0
−
+
=
p
p
K
K
K
K
n
β
α
となり,式(16)と同じになる。
下限合格判定値は参考図8から
式(6)と(20)から
n
K
K
S
X
p
U
L
σ
σ
α
−
+
=
0
························································· (23)
式(16)と(23)から
β
α
ασ
σ
K
K
K
K
K
K
S
X
p
p
p
L
L
+
−
−
+
=
1
0
0
β
α
β
ε
K
K
K
K
K
K
S
p
p
L
+
+
+
=
0
1
式(18)から
XL=SL+kσ ··········································································· (24)
となる。
5.2.3
α=0.05,β=0.10の場合の計算式 式(16)から試料の大きさnは上限規格値が与えられた場合も,
下限規格値が与えられた場合も
2
1
0
−
+
=
p
p
K
K
K
K
n
β
α
であるから,α=0.05,β=0.10とすれば
2
1
0
9264
.2
−
=
p
p
K
K
n
···································································· (25)
上限又は下限合格判定値を求める係数は式(18)から
9264
.2
28155
.1
64485
.1
0
1
0
1
p
p
p
p
K
K
K
K
K
K
K
K
k
+
=
+
+
=
β
α
β
α
k=0.562 073Kp1+0.437 927Kp0 ····················································· (26)
となる。
備考 α≠0.05,β≠0.10の場合には,それぞれのα,βに対するKα及びKβの値を用いればよい。
6. 試料の大きさと上限及び下限合格判定値の求め方
6.1
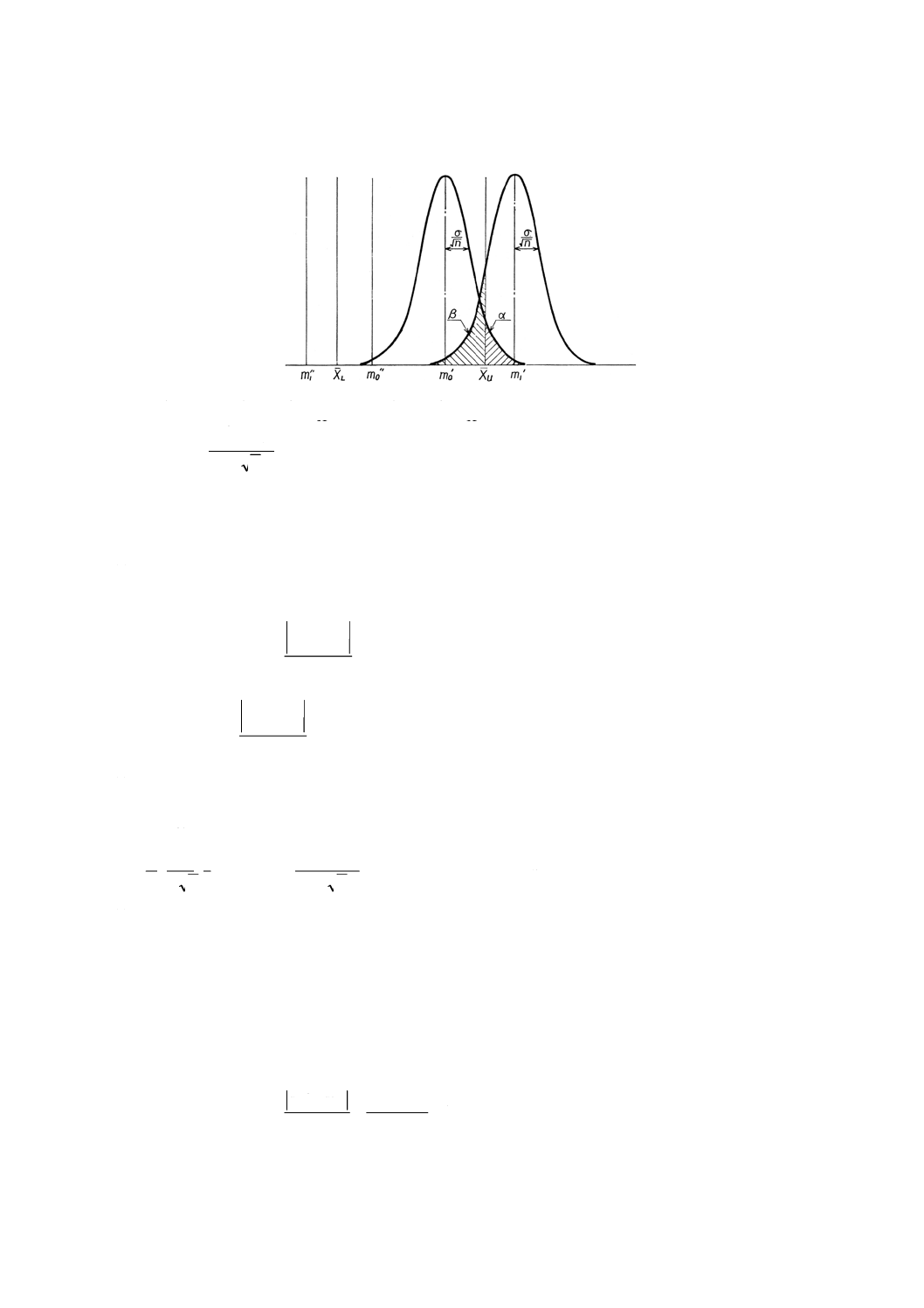
平均値を保証するとき特性値が低すぎても高すぎても好ましくない場合(参考図9参照)
36
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考図9
この場合は,上限合格判定値XU,下限合格判定値XL及び試料の大きさnを,それぞれ5.5(1),5.5(2)
によって求め,
n
m
m
/
0
0
σ
″
−
′
の値が1.7以上のときだけ抜取検査方式を求めることができる。この値が1.7に
満たないときは別の方法による。
ここにm0′,m1′は上限についての値
m0",m1"は下限についての値とする。
(a) m0′,m0"を指定し,この中心に対して対称にm1′,m1"をとる。
したがって │m1′−m0′│ = │m1"−m0"│ となる。
σ
′
−
′
0
1
m
m
を計算する。
(b) 付表1を用い
σ
′
−
′
0
1
m
m
の列で計算値を含む行を求める。
(c) その行のn及び係数G0を読みとり
XU=m0′+G0σ及びXL=m0”−G0σ
を計算する。
(d)
n
m
m
/
0
0
σ
″
−
′
を計算し,
n
m
m
/
0
0
σ
″
−
′
>1.7なら,次の手順に進む。
(e) 求めたnとXU及びXLについて検査費用などを検討した結果,その値が適当ならばそのまま採用
し,不適当と認めたときはm0′,m1′,m0 ", m1" の値を修正してnとXU及びXLを求めなおす。
例:ある金属板の厚さの基本寸法が5mmであり,厚さの平均値が基本寸法から±0.15mmあるロット
は通し,それが±0.4mm以上離れているロットは通さないようなnとXU,XLを求める。この
場合,ロットの標準偏差はσ=0.2mmとする。α=0.05,β=0.10として抜取検査方式を求めるに
は,
(a) m0′=5.15mm,m1′=5.4mm,m0"=4.85mm,m1"=4.6mm,σ=0.2mm
25
.1
2.0
15
.5
4.5
0
1
=
−
=
′
−
′
σ
m
m
37
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(b) 付表1の
σ
′
−
′
0
1
m
m
の列で1.25を含む行を探していくと,上から5番目に1.195〜1.308の行
がある。
(c) この行を右に見ていくと,n=6,G0=0.672を得る。
上限合格判定値XUは
XU=m0′+G0σ=5.15+0.672×0.2=5.28
下限合格判定値XLは
XL=m0"−G0σ=4.85−0.672×0.2=4.72
(d)
7.3
6
/
2.0
85
.4
15
.5
/
0
0
=
−
=
″
−
′
n
m
m
σ
となり1.7より大きいので,次の手順に進む。
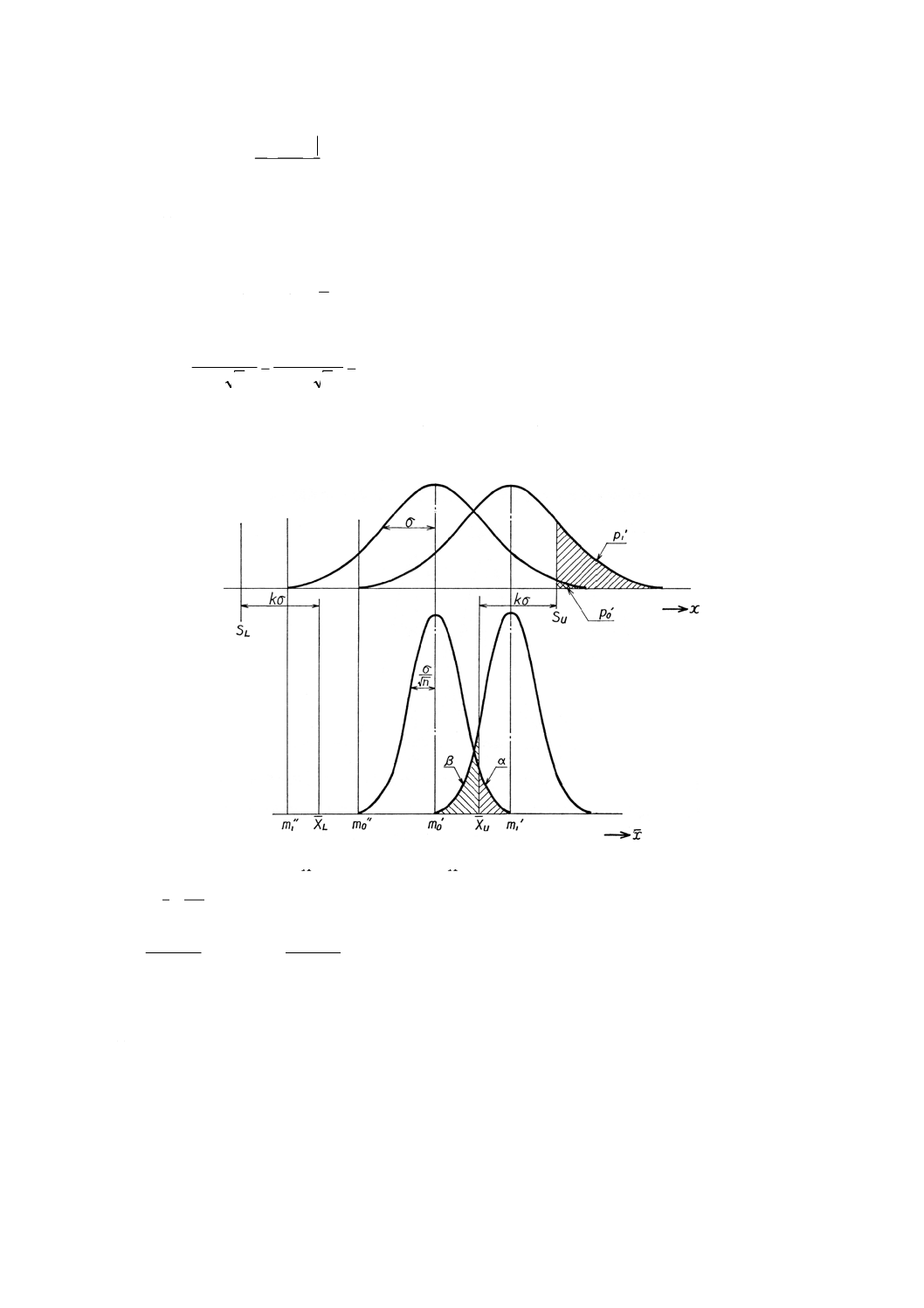
6.2
不良率を保証するとき上限規格値SU及び下限規格値SLが与えられた場合(参考図10参照)
参考図10
この場合は上限合格判定値XU,下限合格判定値XL及び試料の大きさnをそれぞれ6.5(1),6.5(2)によっ
て求め,
σ
L
U
S
S−
の値が参考表2の値以上のときだけ抜取検査方式を求めることができる。
(a)
σ
L
U
S
S−
を計算し,
σ
L
U
S
S−
の値が参考表2の値以上のときは次の手順に進む。
(b) 付表2を用い,指定されたp0を含む行と,指定されたp1を含む列との交わる欄を求める。
(c) その欄のn及び係数kを読みとり,
XU=SU−kσ及びXL=SL+kσを計算する。
(d) 求めたn,kについてOC曲線(付図1)を調べ,あるいはXU及びXLについても検査費用などを
検討した結果,必要があればp0,p1の値を修正してnとXU及びXLを求めなおす。
例:機械部品の軸径の基本寸法が10mmで,その許容差が±0.05mmと与えられたとき,不良率1%のロットは通

38
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
し,不良率10%のロットは通さないようなnとXU,XLを求める。この場合,ロットの標準偏差はσ=
0.015mmとする。α=0.05,β=0.10として抜取検査方式を求めるには
(a) p0=1%,p1=10% : σ=0.015mm ;
SU=10.05mm,SL=9.95mm
7.6
015
.0
95
.9
05
.
10
=
−
=
−
σ
L
U
S
S
であり
参考表2から
p0=1%に対しての値は6.4であるから,次の手順に進む。
(b) 付表2のp0=1%を含む行 〔0.901〜1.12 (%)〕 とp1=10%を含む列 〔9.01〜11.2 (%)〕 との交わる欄 〔n
=8, k=1.74〕 を求める。
(c) この欄からn=8,k=1.74を得る。
上限合格判定値XUは
XU=SU−kσ=10.05−1.74×0.015=10.024
下限合格判定値XLは
XL=SL+kσ=9.95+1.74×0.015=9.976
参考表2 上限及び下限規格値を規定した場合
p0,p1をもとにして抜取検査方式を決め
る条件を示す表 (α=0.05, β=0.10)
p0 (%)
σ
L
U
S
S−
0.1
7.9
0.15
7.7
0.2
7.5
0.3
7.2
0.5
6.9
0.7
6.6
1.0
6.4
1.5
6.0
2.0
5.8
3.0
5.5
5.0
5.0
7.0
4.7
10.0
4.3
15.0
3.8
3
9
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考付図1 計量一回抜取検査設計図
α=0.05
β=0.10

4
0
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
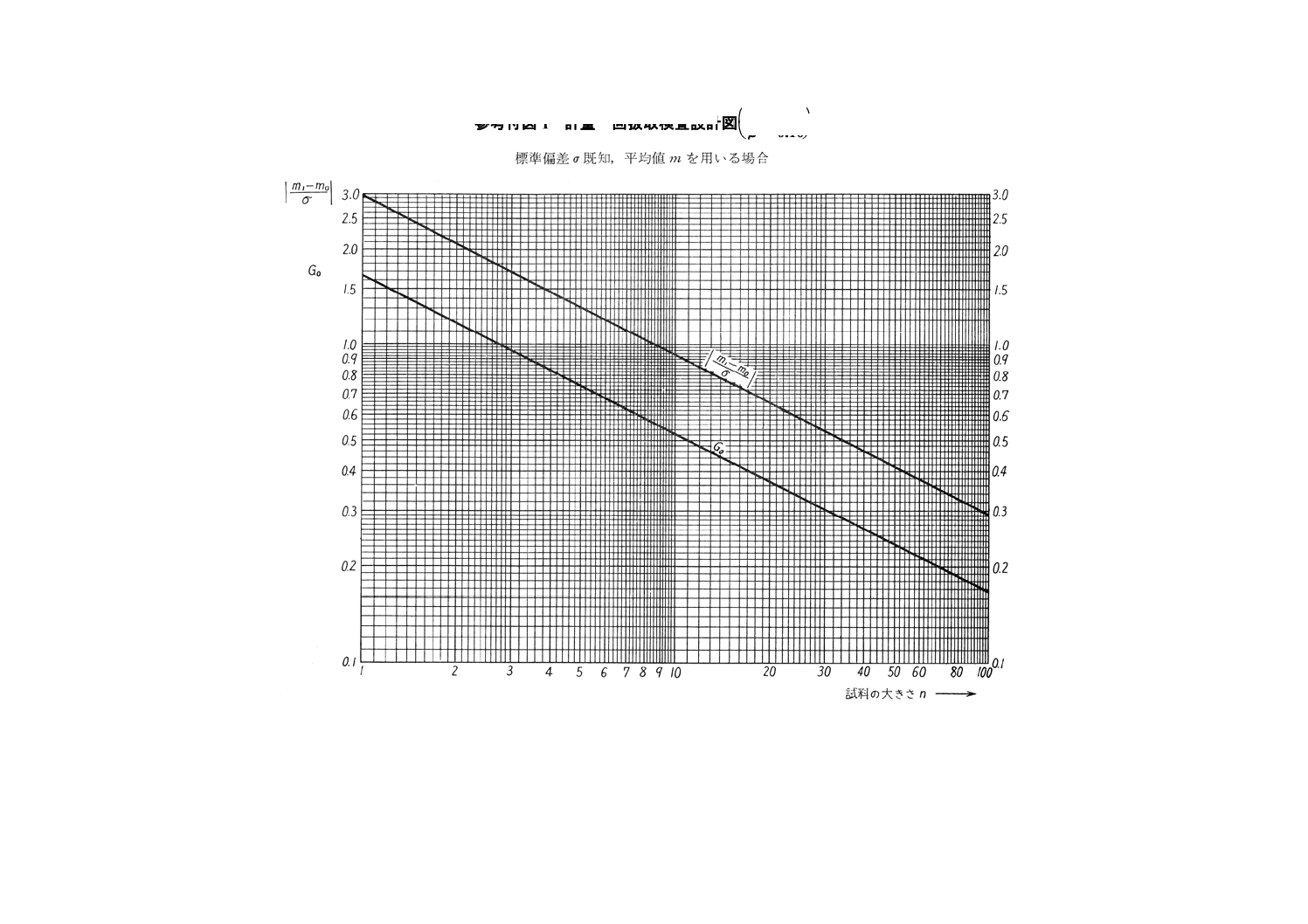
参考付図2 計量一回抜取検査設計図(α=0.05,β=0.10)標準偏差σ既知,不良率pを用いる場合)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
基本部会 抜取検査専門委員会 構成表(昭和32年1月30日改正のとき)
氏名
所属
(委員会長)
山 内 二 郎
東京大学工学部
浅 石 巌
日本電信電話公社技師長室
朝 呑 鉄 一
東京大学工学部
石 川 馨
東京大学工学部
石 田 保 士
東京芝浦電気株式会社製造部
影 木 鹿 吉
日本紡績検査協会
上 山 忠 夫
航空宇宙技術研究所
小 山 正 徳
財団法人日本規格協会
芝 崎 邦 夫
富士製鉄株式会社生産管理部
田 口 玄 一
財団法人日本規格協会
中 込 常 雄
いすゞ自動車株式会社
中曾根 成 雄
防衛庁装備局
中 原 治 夫
日本国有鉄道
三 浦 新
三井化学工業株式会社技術部
森 口 繁 一
東京大学工学部
山 内 道 憲
通商産業省工業品検査所
渡 辺 三 郎
富士重工業株式会社宇都宮製作所
(事務局)
安 達 幸 一
工業技術院標準部運輸航空規格課
宇田川 鉦 作
工業技術院標準部運輸航空規格課
吉 枝 正 明
工業技術院標準部運輸航空規格課
畑 外志夫
工業技術院標準部運輸航空規格課
(事務局)
竹 森 文 夫
工業技術院標準部材料規格課(昭和54年5月1日改正のとき)
市 川 英 雄
工業技術院標準部材料規格課(昭和54年5月1日改正のとき)