Z 8825:2013
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
4 記号······························································································································· 5
5 原理······························································································································· 6
6 レーザ回折・散乱装置 ······································································································· 7
6.1 装置の構成 ··················································································································· 7
6.2 前方散乱光測定のための光学系 ························································································ 8
6.3 種々の装置構成 ············································································································· 9
7 操作手順························································································································· 9
7.1 前提条件 ······················································································································ 9
7.2 試料の検査,調製,分散及び濃度····················································································· 10
7.3 測定 ··························································································································· 11
7.4 精度の評価 ·················································································································· 12
7.5 正確さの評価 ··············································································································· 13
7.6 誤差の要因及びその診断 ································································································ 15
7.7 分解能及び感度 ············································································································ 15
8 測定結果の記録 ··············································································································· 15
附属書A(参考)レーザ回折・散乱の理論的背景 ······································································ 17
附属書JA(参考)試料の分散における留意点 ··········································································· 32
附属書JB(参考)レーザ回折・散乱測定における注意事項 ························································· 34
附属書JC(参考)測定誤差の要因及びその分析 ········································································ 35
附属書JD(参考)レーザ回折・散乱法に用いる標準物質 ···························································· 38
附属書JE(参考)JISと対応国際規格との対比表 ······································································ 39
参考文献 ···························································································································· 45
Z 8825:2013
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本粉体工業技術協会(APPIE)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
これによって,JIS Z 8825-1:2001は廃止され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8825:2013
粒子径解析−レーザ回折・散乱法
Particle size analysis-Laser diffraction methods
序文
この規格は,1999年にISO 13320-1として制定し,2009年に廃止され,同時にこれを包括した第1版と
して発行されたISO 13320を基とし,規格利用者の利便性を図るため技術的内容を変更して作成した日本
工業規格である。
なお,この規格で点線の下線を施してある箇所は,対応国際規格を変更している事項である。変更の一
覧表にその説明を付けて,附属書JEに示す。
レーザ回折・散乱法は,粒子径分布の解析のための主要な方法として,現在広く使用されている。この
技術が普及したのは,様々な粒子系に適用できること,迅速,かつ,自動測定ができること,及び各種の
市販装置があることである。しかし,装置を正しく使い,測定結果を判断するためには必要となる事項が
ある。
1
適用範囲
この規格は,粒子を含む二相系,例えば,粉体,スプレ,エアロゾル,サスペンション,乳液及び液体
中の気泡などの,光散乱強度のパターンの解析による粒子径分布の測定及びそのための装置の要件につい
ての指針を示す。ただし,特定の物質を対象とする,その物質に特有な粒子径測定法について規定する指
針を提供するものではない。
この規格が適用可能な粒子径範囲は,およそ0.1 μm〜3 mm程度である。特別な機器及び条件の場合に
は,適用可能な範囲は3 mm以上及び0.1 μm以下に拡張できる。
非球形粒子の場合には,測定された散乱パターンに対して最もよく一致する散乱パターンを示す球形粒
子の体積基準粒子径分布が,測定結果として得られる。これは,光学モデルに球形粒子を仮定しているた
めである。沈降法,ふるいなどの,他の物理的な原理に基づく測定法による粒子径分布測定結果とは異な
る。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 13320:2009,Particle size analysis−Laser diffraction methods(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS Z 8819-1 粒子径測定結果の表現−第1部:図示方法
2
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 対応国際規格:ISO 9276-1,Representation of results of particle size analysis−Part 1: Graphical
representation(IDT)
JIS Z 8819-2 粒子径測定結果の表現−第2部:粒子径分布からの平均粒子径又は平均粒子直径及びモ
ーメントの計算
注記 対応国際規格:ISO 9276-2,Representation of results of particle size analysis−Part 2: Calculation
of average particle sizes/diameters and moments from particle size distributions(IDT)
JIS Z 8824 粒子径測定のための試料調製−粉体の液中分散方法
注記 対応国際規格:ISO 14887,Sample preparation−Dispersing procedures for powders in liquids
(MOD)
JIS Z 8833 粒子特性を評価するための粉体材料の縮分
注記 対応国際規格:ISO 14488,Particulate materials−Sampling and sample splitting for the
determination of particulate properties(MOD)
ISO 9276-4,Representation of results of particle size analysis−Part 4: Characterization of a classification
process
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
3.1
吸収(absorption)
散乱による以外の光強度の減衰。
3.2
変動係数,CV(coefficient of variation)
標準偏差を平均で除したもの。相対的なバラツキを表す。相対標準偏差とも呼ばれる。
注記1 変動係数は一般的にパーセントで表示される。
注記2 JIS Z 8101-1[1]を適用
3.3
粒子の(複素)屈折率,Np(complex refractive index)
粒子の屈折率。実数部及び虚数部(吸収項)からなる。
注記 粒子の複素屈折率は数学的には次のように表される。
Ip
p
p
n
i
n
N
−
=
ここに,
np: 粒子の屈折率の実数部。
nIp: 粒子の屈折率の虚数部(吸収項)で正の値をとる。
i:
1
−
ISO 80000-7:2008[2],7.5とは異なり,この規格では虚数部にマイナスの符号を付すという慣習に従う。
3.4
相対屈折率,mrel(relative refractive index)
分散媒の屈折率の実数部に対する粒子の複素屈折率の比。
注記1 実際には多くの場合,分散媒は透明であり,したがって,その屈折率の虚数部は無視できる。
注記2 相対屈折率は数学的に次のように表される。
3
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
m
p
rel
n
N
m=
ここに,
nm: 分散媒の屈折率の実数部。
3.5
逆演算(デコンボリューション)(deconvolution)
粒子群全体の粒子径分布を光散乱パターンの測定から推定する数学的手法。
3.6
回折(diffraction)
粒子外表面付近での光散乱。粒子からかなり離れた距離で観測される。
3.7
減衰(extinction)
媒体中を通過する光の散乱及び吸収による減衰。
3.8
モデルマトリックス(model matrix)
各粒子径区間の粒子単位体積に対する散乱光ベクトルによって構成される行列。検出器の寸法及び配置
に応じて調整されており,モデル計算から導かれる。
3.9
多重散乱(multiple scattering)
二つ以上の粒子による連続的な光の散乱。個々の粒子からの散乱光の加算とは異なる散乱パターンを生
じる。
注記 単散乱(3.20)参照
3.10
減衰率,O(obscuration)
粒子の吸光(散乱及び/又は吸収)によって減衰した入射光の割合。
注記1 減衰率はパーセントで表示される。
注記2 割合で示される場合,減衰率と透過率(3.22)との和は1になる。
注記3 ISO 13320:2009では光学濃度(optical concentration)を同義として用いているが,厳密には異
なるため,この規格では減衰率だけを用語として用いる。
3.11
光学モデル(optical model)
光学的に均一で等方的で,また,場合によっては特定の複素屈折率をもつ球のモデルマトリックスの計
算に用いられる理論的モデル。例として,フラウンホーファ回折近似モデル,ミー理論モデル。
3.12
反射(reflection)
波長又は周波数の変化がない表面における光の方向変化。
3.13
屈折(refraction)
光が光学的に不均一な媒体中を透過するとき,又は異なる媒体を分けている表面を通過するとき,光の
伝ぱ速度の変化の結果として放射方向の変化が生じる過程(IEC 60050-845:1987[3])。
注記 次のスネルの法則に従う。
4
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p
p
m
m
sin
sin
θ
θ n
n
=
記号は箇条4を参照。
3.14
繰返し精度(装置)[repeatability (instrument)]
同一の部分試料に対してある特性を複数回,測定した結果における一致の程度。この場合,短い期間に
同一の条件で同じ装置によって同一のオペレータが測定する。
注記 この種の繰返し精度は,サンプリング及び分散による変動を含まない。
3.15
繰返し精度(方法)[repeatability (method)]
異なる部分試料に対してある特性を複数回,測定した結果における一致の程度。この場合,短い期間に
同一の条件で同じ装置によって同一のオペレータが測定する。
注記 この種の繰返し精度は,サンプリング及び分散による変動を含む。
3.16
再現性[reproducibility (method)]
異なる部分試料に対してある特性を複数回,測定した結果における一致の程度。この場合,異なるオペ
レータによって試料は調製され,同一の方法に従って類似した装置で測定される。
3.17
(光)散乱(scattering)
異なる光学的な特性をもつ二つの媒体界面において起きる光の伝ぱの変化。
3.18
散乱角,θ(scattering angle)
入射光軸方向と散乱光の方向との間の角度。
3.19
散乱パターン(scattering pattern)
光散乱強度の角度パターンI(θ) 若しくは半径パターンI(r) 又は,検出器の感度及び配置を考慮した光強
度に対応するエネルギー値のパターン。
3.20
単散乱(single scattering)
粒子群全体による全散乱パターンに対する一つの粒子からの寄与が,他の粒子からの散乱に対して独立
である散乱。
3.21
全量測定(single shot analysis)
容器内の全試料が使用される解析。
3.22
透過率(transmittance)
粒子によって減衰しなかった光の入射光に対する割合。
注記1 透過率はパーセントで表示される。
注記2 割合で表示される場合,減衰率(3.10)と透過率との和は“1”になる。
注記3 ISO 13320:2009では光透過(transmission)を用語として挙げているが,この規格では透過率
5
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を用語として用いる。
3.23
粒子径分布の幅(width of size distribution)
粒子径分布(PSD)の幅。比x90 / x10で与えられる。
注記 正規分布に対しては,標準偏差(絶対値)σ 又は変動係数CVがしばしば用いられる。その場
合,平均から±2 σ の範囲に全体の95 %が,そして,±3 σ の範囲に全体の約99.7 %が入る。
x90とx10との差(x90−x10)は2.6 σ に対応する。
3.24
検出器(光)(detector)
光を電気信号(光電流)に変換する素子。アレイ形検出器など,複数の検出素子からなる検出器の場合
には,個々の検出素子の信号が解析に用いられる。
3.25
標準物質(RM,reference material)
一つ以上の指定された特性について,十分均質かつ安定であり,測定プロセスでの使用目的に適するよ
うに作製された物質。この規格では,測定プロセスの精度を評価するために参照対象として用いる。
注記 JIS Q 0035:2008[4]を適用。
3.26
認証標準物質(CRM,certified reference material)
一つ以上の指定された特性について,計量学的に妥当な手順によって値付けされ,指定された特性の値
及びその不確かさ,並びに計量学的トレーサビリティーを記載した認証書がついている標準物質。この規
格では,測定の正確さを評価するために参照対象として用いる。
注記 JIS Q 0035:2008[4]を適用。
4
記号
この規格で用いる主な記号は,次による。
Aj
粒子径区間jの消散係数
C
粒子濃度,体積分率
CV
変動係数
f
レンズの焦点距離
i
虚数単位
1
−
in
n番目の検出器の光電流
I(θ)
粒子による散乱光強度の角度方向分布
Ih
任意の角度において水平に偏光された光の強度
I(r)
粒子による散乱光強度の検出器上での半径方向分布(検出器によって測定された散乱パターン)
Iv
任意の角度において垂直に偏光された光強度
J1
一次の第一種ベッセル関数
k
媒体中での波数:2 πnm / λ
la
散乱物体から検出器までの距離
lb
粒子が含まれている光の透過長さ(光路長)
Ln
n番目の検出器の信号ベクトル
6
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
mrel
媒体に対する粒子の相対屈折率
M
モデルマトリックス:全ての粒子径区間ごとに粒子単位体積当たりで計算された検出器の信号を含
む。
nIp
粒子の屈折率の虚数部(吸収項)
nm
媒体の屈折率の実数部
np
粒子の屈折率の実数部
Np
粒子の複素屈折率
O
減衰率(=1−透過率)
r
焦点面内における焦点からの動径長
V
粒子径区間に含まれる粒子体積のベクトル(V1, V2, ... Vn)
Vj
粒子径区間jに含まれる粒子体積
v
乾式分散器内における粒子速度
x
粒子径
xj
粒子径区間jの幾何平均径(区間jの代表径)
x50
中位(メジアン)径:ここでは,体積基準。すなわち,粒子の体積で50 %がこの径より小さく,50 %
が大きい。
x10
積算粒子径分布の10 %に対応した粒子径(体積基準)
x90
積算粒子径分布の90 %に対応した粒子径(体積基準)
α
粒子径パラメータ(無次元),πxnm / λ
ΔQ3,j 粒子径区間jの体積分率
θ
光の進行方向に対する散乱角
θm
媒体中での光線と境界面法線との角度:スネルの法則で使用される。3.13,注記参照
θp
粒子中での光線と境界面法線との角度:スネルの法則で使用される。3.13,注記参照
λ
真空中における照射光(源)の波長
σ
標準偏差
ω
角周波数
5
原理
レーザ回折・散乱法による粒子径分布測定は,粒子による光散乱の角度分布(散乱パターン)が粒子径
に依存する現象に基づく。
適正な液体,又はガス中に適正濃度で分散された試料を単色光(通常はレーザ光)ビームが横切るよう
に通過させる。粒子によって様々な角度に散乱された光は複数の光強度検出器で測定され,散乱パターン
に対応する測定値が次の解析のために記録される。測定域における試料濃度などが適正範囲にあれば,粒
子群からの光散乱パターンは,個々の単一粒子からの散乱パターンの総和と等しい。理論的に計算した,
想定される粒子径分画からの散乱パターンの重ね合わせが,測定された散乱パターンに最もよく一致する
ように各分画の寄与率を求める数学的逆問題を解くことで,体積基準の粒子径分布を求める。理論的背景
を附属書Aに示す。
注記1 均一で球形な単一粒子からの散乱パターンは,ミー(Mie)が導出した光散乱理論式によっ
て広い粒子径範囲にわたって記述される(ミー理論の詳細については,参考文献[6-8]参照)。
粒子径が比較的大きい場合(粒子径パラメータα=πxnm / λ>10)において,散乱角の小さい
7
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
範囲(前方小角散乱)では粒子の輪郭での回折が支配的になり,フラウンホーファ
(Fraunhoher)回折式がミー理論式の良い近似式として適用できる(フラウンホーファ回折
近似)。この近似は,粒子及び媒質の光学パラメータ(屈折率)を必要としないという点で便
利である。粒子径が比較的小さい場合,及び/又は,透過性が高い粒子の場合には,一般的
にミー理論を適用する。フラウンホーファ回折近似のほかにも,幾つかの近似がミー理論に
基づく散乱パターンの計算に用いられている。これら,理論的散乱パターン算出法のバリエ
ーションは一般に光学モデルと呼ばれる。適切な光学モデルの選択は,適切な粒子径分布を
得るためには重要である。
注記2 理論的な散乱パターンが,均質な球形粒子の散乱である点に留意が必要である。その点で,
レーザ回折・散乱法で得られる粒子径分布は,球形粒子を前提とした分布(球等価粒子径分
布)である。試料粒子が非球形の場合,仮に単一粒子の解析結果であってさえも(等価)分
布があるような結果が得られる。凝集体を測定する場合には,基本的には凝集体サイズに対
応した結果が得られるが,その凝集構造及び形状も測定結果として得られる(等価)粒子径
分布に影響を与える。
注記3 ミー理論に基づいて散乱パターンを求めるためには,粒子及び媒質の屈折率が必須である。
正しい散乱パターン理論値に基づく粒子径評価のためには正しい屈折率を用いることが必要
であるが,一方,例えば,粒子の屈折率に,バルク材料の屈折率の測定値(参考文献[19-29])
をそのまま用いてよいかどうかは必ずしも自明ではない。屈折率は波長に依存するため,屈
折率測定に用いた光の波長が,粒子径測定で用いられている光源の波長と一致しているとは
限らない点にも留意が必要である。レーザ回折・散乱法において,妥当な屈折率を得るため
のガイドラインは現状でも研究課題ではあるが,幾つかの方法が提案されている(参考文献
[30-33])。
6
レーザ回折・散乱装置
6.1
装置の構成
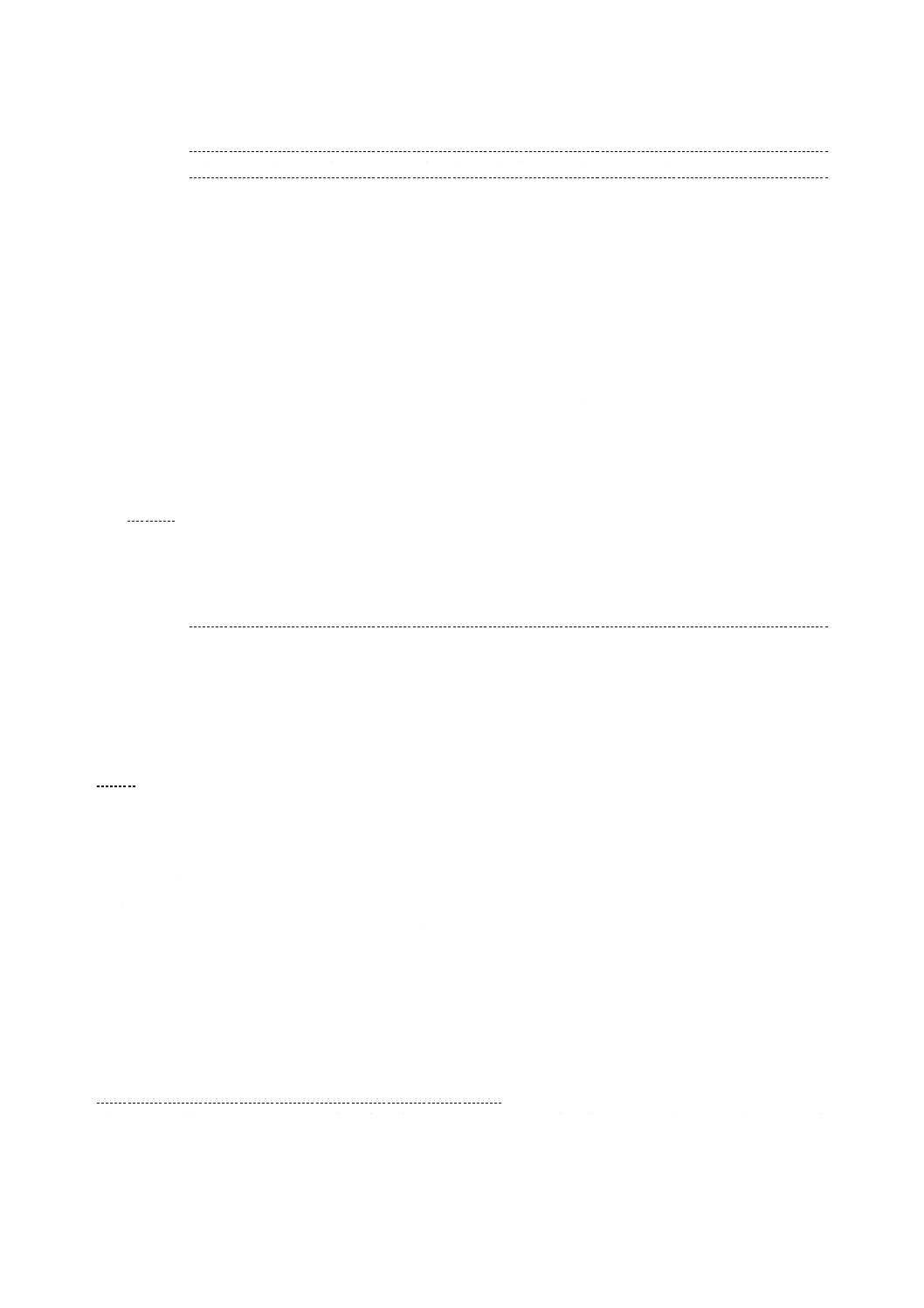
レーザ回折・散乱装置の構成例の概念図を,図1に示す。
光源としては,単一波長で,直進するコヒーレントなビーム(光線)を生成するもの(一般的にはレー
ザ又は他の波長幅の狭い光源)が用いられる。光源から出た光は,照射光学系に入り,これによって分散
粒子系に照射するのに適したビームを得る。
輸送媒体(液体又は気体)中に適正濃度に分散された試料粒子群は,測定領域の光線中を通過する。こ
の測定領域は,使用するレンズのワーキングディスタンスにあることが望ましい。スプレ又はエアロゾル
の測定では,プロセス中の粒子流れが直接,レーザビームを通過するようにする場合もある。乾式粉体の
場合には,乾式粉体分散器を用いることで機械的作用力によって分散させ,エアロゾルにすることもでき
る。この場合,供給器は極力一定の質量流量で試料を分散器に供給する。分散器は圧縮ガス又は減圧系に
よる圧力差のエネルギーを用いて粒子を分散させる。分散器から排出されたエアロゾルは測定領域に吹き
込まれ,通常は集じん(塵)用負圧管に吸引される。比較的サイズの大きい粒子の場合,分散が十分であ
れば,重力沈降によって測定領域へ導入する方法もある。一方,エマルション,ペースト状,粉末などの
試料では,流体中に分散させて測定領域へ導くこともできる。しばしば,分散剤(ぬれ性改良剤,分散安
定剤)及び/又は機械的作用力(かくはん,超音波振動)が,粒子の分散及び分散の安定化のために用い
られる。こうした湿式分散に対しては,循環系を用いるのが最も一般的である。こうした循環系は,光学
8
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定セル,かくはん機及び超音波発生器を備えた分散槽,ポンプ並びに配管で構成される。
記号
1
光源
2
照射光学系
3
測定位置
4
観測光学系
5
前方散乱光検出器
6
透過光検出器
7
広角度(側方)散乱光検出器
図1−レーザ回折・散乱装置の構成例の概念図
粒子による光散乱の角度分布(散乱パターン)の計測には,複数のシリコン検出器又はフォトダイオー
ド,及び/又はピクセルアレイ形検出器が用いられる。加えて,光軸中心に検出器を設置して非散乱光の
強度を測定することによって,減衰率を求めることができる。中心素子から得られる情報に基づき,検出
器又はレンズを移動させ,光軸又は焦点を自動的に再調整するような工夫もある。検出器の設置において
は,内部反射光が再び計測光学系に戻らないようにすることが望ましい。
コンピュータを用いて,測定系の制御,検出したデータの保存及びデータ処理を行う。また,光学モデ
ル(通常は検出器の形状・感度についての補正を加えた,粒子径区間単位体積当たりの散乱パターン行列)
の計算・保存及び粒子径分布計算(逆演算)を行う。コンピュータを用いて自動計測を行わせることもで
きる。
6.2
前方散乱光測定のための光学系
前方の散乱パターンの計測は,散乱光強度が大きいので重要である。特に,フラウンホーファ回折近似
を用いて測定を行う装置では,前方小角散乱光の検出だけで測定が行われる。典型的な2種類の光学系の
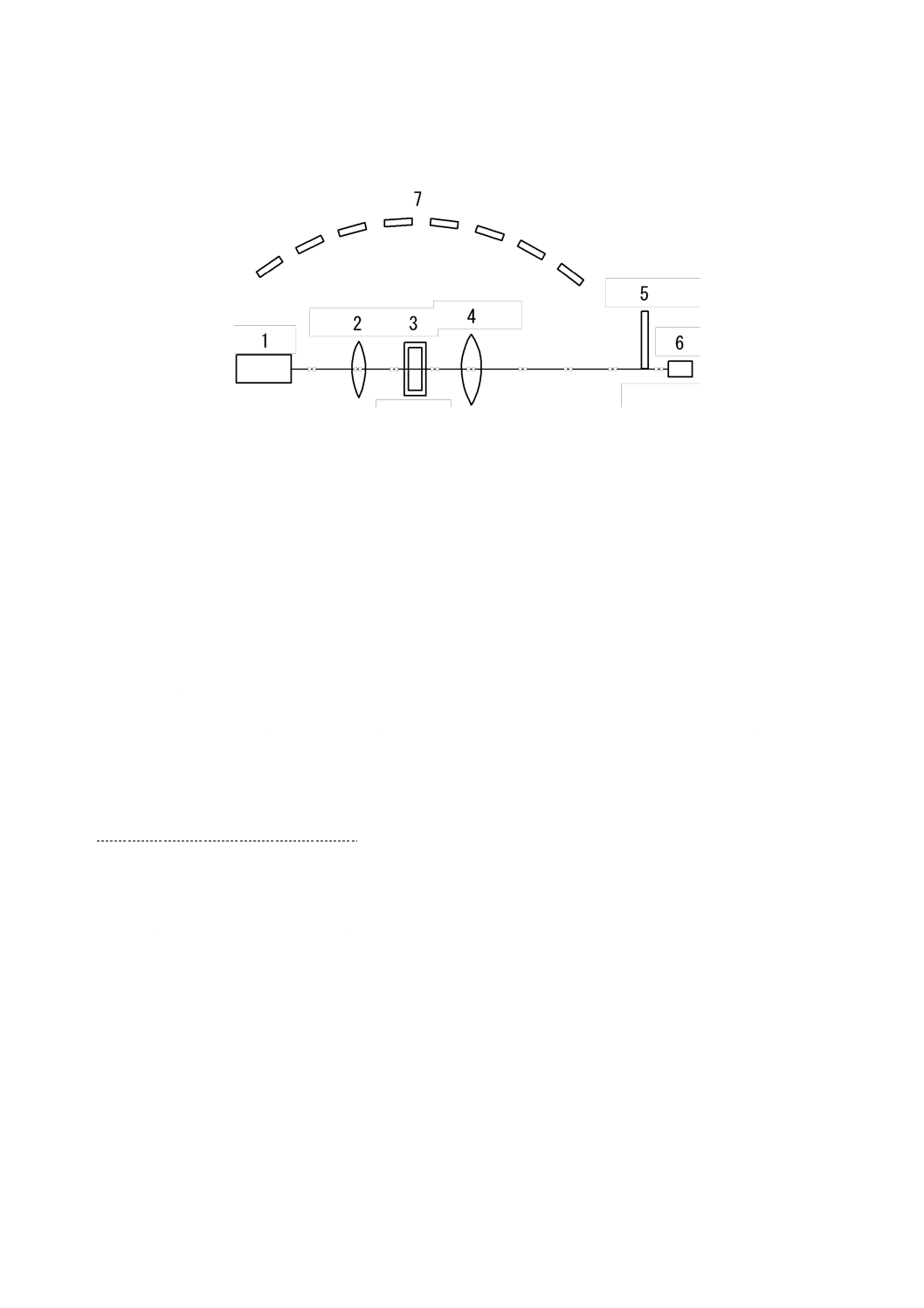
例を図2に示す。
図2 a) はフーリエ光学系,図2 b) は逆フーリエ光学系の模式図である。フーリエ光学系では,平行照
射光中に粒子を導入し,散乱光を集光レンズで検出器へ導く。一方,逆フーリエ光学系では,粒子は照射
光集光レンズの後ろに導入され,散乱光は直接,検出器に入る。逆フーリエ光学系の試料・検出器間距離
は,フーリエ光学系における集光レンズの焦点距離と等価になる。フーリエ光学系の特長は,比較的長い
有効測定域(光路長)を取れる点であり,これによって散乱粒子数を増加させることで散乱光強度を増強
することができる。一方,逆フーリエ光学系では比較的短い光路長範囲の粒子しか測定できないが,散乱
角の大きな散乱光を比較的簡単な光学系を用いて検出できる。
いずれの光学系でも,前方散乱光は複数素子からなる検出器で検出される。このような光学系によって,
一定の制約はあるが基本的に,光軸中の粒子の位置に依存しない散乱パターンが得られる。
9
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
記号
1
検出器
2
集光レンズ(フーリエレンズ)
3
粒子
4
ワーキングディスタンス
5
焦点距離
記号
1
検出器
2
光学測定セル
3
粒子
f
焦点距離
a) フーリエ光学系
b) 逆フーリエ光学系
図2−前方散乱光測定の光学系
6.3
種々の装置構成
粒子径計測性能の向上のために,最近の測定機器では次のような工夫が取り入れられている場合もある。
a) 同じ光学系を用いて,波長の異なる複数光源を用いる。
b) 元の光軸に対して90°以上又は以下の角度に単一又は複数の光源を追加する。
c) 光源及び検出器に偏光フィルタを導入する。
d) 散乱角90°以下の前方散乱領域で,従来の小角前方散乱領域の外側に検出器を追加する。
e) 散乱角90°程度の位置に異なる偏光方向の光強度を独立に計測する検出器を追加する。
f)
散乱角90°以上の後方散乱領域に検出器を追加する。
注記 広角度領域の検出器配置の例を,図1に示す。
7
操作手順
7.1
前提条件
7.1.1
装置の設置場所
装置は,過度な電気的ノイズ,機械的振動及び温度変動がなく,直射日光に当たらない,気流の影響の
少ない清潔な環境に設置することが望ましい。作業場所では,健康,及び安全に関する規則(要求事項)
に従うべきである。光学系を頻繁に再調整するのを避けるために,装置は頑丈な光学定盤をもつものを使
うか,頑丈なテーブル又は定盤の上に設置することが望ましい。
警告 レーザを搭載した装置からのレーザ光でも失明することがある。レーザ光及びその反射光を絶
対に直視してはならない。反射する表面でレーザを遮らない。また,レーザに関する安全衛生
規則を遵守する。
7.1.2
分散用気体
乾式分散及びスプレを適用するときには,圧縮気体がよく用いられる。圧縮気体は油,水及び粒子を含
まないことが必須である。そのため,フィルタ付の乾燥機が必要である。スプレを適用するときには,液
体の蒸気が粒子径の結果に影響しないようにすることが必須である。吸引機は,測定場所から離れた所に
10
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
置いて,高温の排出空気が測定部に影響しないようにすることが望ましい。粒子流れが不安定にならない
ようにするために,空気が流入又は流出する空隙をなくすようにするのがよい。
7.1.3
分散用液体
屈折率が既知の透明な液体ならばいずれも使用可能で,実際に,様々な液体が粉体の分散に使われる。
JA.2に分散液体に対する留意点を記載している。
分散に有機溶媒を用いるときは,健康及び安全に関する法規を遵守しなければならない。蒸気庄の高い
液体を使用するときは,バスの上に有害な蒸気の濃縮層が形成されることを防ぐために,超音波バスには
蓋を用いなければならない。有機溶媒の蒸発によって液体が冷却され,屈折率の変動が起こり,粒子径の
結果に影響する。
警告 有機溶媒に関する安全衛生規則を遵守する。
7.2
試料の検査,調製,分散及び濃度
7.2.1
検査
分析する試料は,試料の粒子径範囲及び粒子の形状を見定め,粒子が適切に分散されているかどうかを
調べるために,肉眼又は顕微鏡で検査しなければならない。測定で得られた粒子径分布は,試料がその粒
子群を代表しており,かつ,十分に分散されているとき,その粒子群の測定結果として妥当である。
注記 試料の分散状態の検査は,現実的には難しく,肉眼又は顕微鏡で検査できない場合もある。
7.2.2
調製
その系を代表する適量の試料を準備する。縮分の方法についてはJIS Z 8833に従うことが望ましい。
液体中に試料を分散する場合には,JIS Z 8824及びJIS Z 8833によって試料を準備する。液中に分散す
る場合,微量の測定試料はよく混合した試料ペーストから切り出すことができる。ペーストが一様であれ
ば,偏析による誤差を最小にすることができる。ペーストは試料をへらで混ぜながら,分散媒を1滴ずつ
加えて作製することができる。適切な粘度は蜂蜜又は歯磨きペースト程度である。誤ってペーストが流動
的になりすぎたときは使用しないで,新たに試料調製をやり直さなければならない。
測定粒子径範囲を超える大きい粒子が含まれる場合は,例えば,ふるいなどで測定範囲外の粒子を取り
除かなければならない。この場合は,その量又は割合を求め,記録しなければならない。
スプレ,エアロゾル及び液体中の気泡は,粒子径分布を変えずにサンプリング又は希釈を行えないので,
適正な濃度(7.2.3及び7.2.4参照)であれば,通常,そのまま測定する。静止空気中に液滴をスプレする
と,小さな液滴は大きな液滴より早く減速され,速度差が生じるので,スプレの流れと同様の速度で適切
に流れる空気中にスプレすることが望ましい。特に,(サブ)ミクロンの液滴では,液滴の蒸発は大きな誤
差の要因となるので,考慮することが望ましい。急速な蒸発で粒子径が小さくなるか又は粒子が消失する
こともある。また,蒸発中の温度低下又は蒸気によって,液滴周囲の屈折率が変化して粒子径分布の測定
結果に影響を与えることもある。
7.2.3
分散
乾燥した粉体は,空気でも液体でも分散できる。分散方法は測定目的に合わせるのがよい。例えば,凝
集粒子のままでよいか又は一次粒子まで分散するかを決めなければならない。
測定領域までの粒子の輸送条件も考慮するとよい。粒子間に相対速度がなく,全ての粒子径の粒子が測
定領域を同じ速度で通過するように,適切な流れを形成することが望ましい。アスペクト比の大きな粒子
は,測定セル中の流れの状態によって特定の方向に配向する傾向がある。乱流の条件であっても,粒子の
配向は完全にはランダムでない。
附属書Aでは,非球形粒子では,粒子の向きによって,散乱パターンが変わり,異なる粒子径の結果に
11
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
なることを解説している。
気体中及び液体中の分散に関する留意点については,附属書JAを参照。
7.2.4
濃度
測定領域での粒子濃度は,適切な検出信号(又は言い換えれば十分なSN比)が得られるような十分な
濃さであることが望ましく,さらに,多重散乱が粒子径分布の測定結果に影響を及ぼさないように十分低
いことが望ましい。
粒子濃度が高い場合には,多重散乱,すなわち,個々の粒子によって散乱した光が,隣接した粒子によ
って更に散乱される現象を無視できない。この多重散乱の影響によって,一般的に,散乱光パターンは大
きな散乱角方向に移動し,解析の結果として最終的に得られる粒子径分布は小さい方にずれる。測定に適
した濃度範囲は,粒子径,粒子径分布の幅,レーザビームの径,及び光路長に依存するので簡単に設定す
ることができない。一つの目安としては,光路長2 mmのセルの場合,直径が1 μmの粒子の場合の典型的
な適正体積濃度は0.002 %程度であり,これに対して100 μmの粒子の場合には0.2 %程度である。減衰率
又は透過率の測定値から指針を得ることができ,上記の例の場合,直径が1 μm,及び,100 μmの粒子試
料の,上記各濃度に対する減衰率は,それぞれ5 %,及び,25 %程度である。一般に,粒子径分布の中で
の小さな粒子径区間の粒子の割合によって,最大許容粒子濃度が決まる。全ての粒子が100 μm以上であ
る場合,減衰率が30 %以下であれば,多重散乱の影響はない。測定に適した濃度範囲を決定するには,何
段階かの異なる濃度で粒子径分布測定を行い,分布の変化を調べる必要がある。附属書Aに,粒子濃度,
粒子径及び減衰率の関係についての情報を示している。更に付随する情報については,個々の装置のマニ
ュアルを参照する。
7.3
測定
7.3.1
手順
7.3.1.1
概要
レーザ回折・散乱法による粒子径の代表的な測定手順は次のとおりである。
a) 装置の立上げ及びブランク測定
b) 試料調製
c) 試料の散乱パターンのデータ収集
d) 適切な光学モデルの選択
e) 散乱パターンの粒子径分布への変換
7.3.1.2
装置の立上げ及びブランク測定
適正な粒子径測定範囲を選び,装置を正しく調整した後,粒子を含まない分散媒だけの試料に対して実
際の試料測定と同じ条件でブランク測定を行う。このデータは,後に粒子だけによる真の信号値を得るた
め,実測データから差し引くので記録しておく。これらのバックグラウンド信号は,装置が適正に機能し
ているかを調べるため,及び試料の測定時の検出信号から差し引くために使われる。
7.3.1.3
試料調製
7.2に従って試料を調製,分散する。規定された信頼区間内試料が製品の粒子群を代表するようにする。
試料の量は,精度を得るのに必要な最小量を満たしていることが望ましい。分散の条件は,粒子を粉砕せ
ずに完全に解きほぐすことができ,多重散乱が起きない程度に十分に低い濃度であることである。
7.3.1.4
散乱パターンのデータ収集測定
測定時間は,統計的に適切な結果を得るのに十分なデータが収集できるように設定する。そのために測
定時間が測定結果に与える影響を調べる。各検出器の信号の平均値を求め,場合によっては標準偏差も求
12
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
める。最終的な信号はバックグラウンド信号を差し引いて計算されることもある。データはコンピュータ
のメモリに保存される。検出器の信号の大きさには,検出面積,光強度,量子効率が大きく影響する。レ
ンズの焦点距離とともに検出器の座標(大きさ及び位置)で各素子の測定散乱角範囲が決まる。一般に,
こうしたパラメータはあらかじめ決められており,コンピュータに保存されている。
多くの装置では,中心位置のレーザビーム強度も測定している。分散試料及びブランク測定の光の強度
差から,減衰率又は透過率が求められ,それは散乱光及び粒子濃度の指標となる。
7.3.1.5
適正な光学モデルの選択
多くの装置では,散乱行列の計算にミー理論又はフラウンホーファ回折近似を使っている。散乱行列は,
それぞれの検出器での,与えられた粒子径区間の粒子の単位体積当たりの信号を表すものである。計算方
法の選択は,測定される粒子の粒子径範囲,光学特性,及び応用に依存する(附属書A参照)。散乱行列
の計算に,他の光散乱理論が使われることもあるが,それは一般的ではない。
ミー理論を使うときは,粒子及び媒質の屈折率,又はその比(相対屈折率)をモデルマトリックスの計
算のために決定し,装置に入力することが望ましい(液体及び固体の屈折率については,参考文献[19-29]
を参照)。表面が,光をランダムに散乱するような粗面である粒子に適用するには,現実的な理由で,屈折
率の虚数部(約0.01i〜0.03i)が必要となる(屈折率については,箇条5の注記3に参考記載がある。)。
ミー理論又はフラウンホーファ回折近似を正しく適用するには,粒子からの光散乱に対する屈折率の影
響をよく理解することが強く推奨される。不適切な光学モデル,又は屈折率の選択は,粒子径分布の結果
に大きな偏りを与えることがある。この偏りは,粒子径分布下限近くの粒子径区間の粒子量として不適切
な値を与える。
測定結果を再確認できるように,屈折率の値は記録して,使用することが大切である。
7.3.1.6
散乱パターンの粒子径分布への変換
逆演算の過程は,粒子径分布から散乱パターンを求める過程の逆である。このために幾つかの数学手法
(アルゴリズム)が開発され,それぞれの機器で使われている(参考文献[7-8],[12-17]参照)。こうした手
法には,測定結果と計算から得た散乱パターンとの差に重みを付ける手法(例えば,最小二乗法),粒子径
分布曲線に拘束条件(例えば,粒子径は負とならないこと)を付ける手法,粒子径分布曲線を平滑化する
手法などがある。測定された検出器信号の変動を用いて,適正な重み付けを求めたり,粒子径分布におけ
る信頼区間(confidence interval)を計算する新しい計算法もある(参考文献[18]参照)。
7.3.2
注意事項
測定開始前及び測定中は,個々の装置のマニュアルで与えられた指示に従う。一般的な注意事項を,附
属書JBに示す。
7.4
精度の評価
7.4.1
標準物質
精度を表すために全ての場合でCVを用いる。評価試験では,x90 / x10の値が1.5〜10の範囲の値をもつ
標準物質(RM)を使用することが望ましい。これらの物質は,粒径分布パラメータに関するバックグラ
ウンドデータをもつとともに,レーザ回折・散乱法に適した,文書化された安定したサンプリング,分散
及び測定のプロトコル(規定)があることが望ましい。さらに,精度及び安定性についての測定結果が文
書化されていることが望ましい。
7.4.2
繰返し精度
適切に装置を立ち上げ,動作条件を正しく設定し,全ての部分を十分に暖機する。
標準物質の測定のプロトコルに従う。
13
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
評価試験用分散試料の同一の部分試料の計測又は全量計測を,少なくとも3回連続して行う。この場合,
適切な濃度及び信号積算時間を確保し,十分多数の粒子を測定するようにする(JIS Z 8833参照)。平均値
を計算し,x10,x50,x90の,及び/又は,x10〜x90の間に他の留意すべきパーセンタイル値があれば,対応
する粒子径のCVを計算する。全ての操作及び結果の詳細を正しく記録する。
粒子径分布のCV,例えば,メジアン径x50のCVが3 %を超えなければ,装置は,この規格を満たすと
考えられる。粒子径分布の両端の数値,例えば,x10及びx90のCVが5 %以下であることが望ましい。10 μm
以下の試料では,これらの最大値は2倍の値としてもよい。
正確に機能する装置を用いて,熟練したオペレータが,特性のよい試料を正しい手順で測定した場合に
は上記各特性値について,1 μm以上の粒子径では 0.5 %,1 μm以下の粒子径では1 %より高い精度を得ら
れる。
もし,大きなCV値が得られたならば,全ての誤差要因(7.6及び附属書JC参照)を調べる。
7.4.3
再現性
再現性の評価試験は,繰返し精度と同じ手順及びプロトコルに従うことが望ましい。それにもかかわら
ず,繰返し精度の場合より大きなCVが得られるときは,サンプリング若しくは分散の手順の差異,又は,
解析者若しくは装置間の差異が考えられる。
7.5
正確さの評価
7.5.1
一般事項
レーザ回折・散乱法は,粒子の特性を理想化してはいるが,基本的には第一原理に基づく測定法である
(附属書A参照)。したがって,校正済の測定システムについて,使用者による妥当性確認は必要ない。
適格性の確認手順(7.5.2〜7.5.5)によって,装置が正しく作動していることを確認する。
7.5.2
標準物質
正確さの認証においては,トレーサブルな球形の認証標準物質(CRM,certified reference materials)を用
いる。例えば,国家計量標準機関に対してトレーサブルな粒子である。これによって,装置が分析プラッ
トフォームとして正しく機能していることが保証される。装置に対して何らかの変更,又は主要な保守が
必要になった場合は,装置の正確さを確保するために再びトレーサブルなCRMを使用する。
正確さの認証に用いられるCRMには,レーザ回折・散乱法にとって適切であると明示されていること,
球形粒子の分布の幅としてx90 / x10の値が少なくとも1.5であるような既知の粒子径分布を構成しているこ
ととともに,全ての粒子が同一の密度及び光学特性をもつことが求められる。CRMの粒子径分布は,国家
計量標準機関によって,又はその指示の下で,絶対的でトレーサブルな方法によって,質量分率又は体積
分率に関して認証されていることが望ましい。ミー理論をデータ解析に用いる場合,その物質に対する屈
折率の実数部及び虚数部を特定しておくことが望ましい。
注記 JIS Z 8900-1[5]に規定されている標準粒子は,上記の要件を満足する認証標準物質である(附
属書JD参照)。
試料の調製,分散及びレーザ回折・散乱測定に関して十分詳細に記載された安定な手順を使えることが
必須である。この手順は,その全体,並びに報告されたタイトル及びバージョンについて追跡可能でなけ
ればならない。
ひとたび装置性能がCRMを基準に比較され,正確さが許容限界内にあることが確認されたならば,又
は,正確さテストが義務付けられていないと考えてよい場合には,これ以降,認証標準物質ではない標準
物質を用いて装置の適格性を確認することができる。さらに,標準物質は球形である必要はない。レーザ
回折・散乱法にとって適切であると明示されていれば,非球形粒子を含む標準物質も使用することが可能
14
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
である。粒子径分布はx90 / x10の値が2以上である既知の範囲から構成されていることが望ましい。非球形
粒子のアスペクト比は1:3以下でなければならない。この粒子径分布は,一定の時間の範囲で適切かつ安
定した結果を与えることが確認された,合意され詳細に記載された操作手順に従い,一つ以上の装置形式
におけるレーザ回折・散乱の解析から得られる,文書化された参照値を有していなければならない。その
参照値がレーザ回折・散乱法以外の方法で得たものである場合,先に示した理由から,重大なバイアスが
かかる可能性がある。
全量測定の場合は,容器の内容物全てを使用する。試料サンプリングが必要な場合は,適切な結果を与
えると証明されている方法を使用するとしても,相応の注意を払う必要がある(JIS Z 8833参照)。
サンプリング,分散,又は測定に関するプロトコルが利用できない場合,使用される手順は,最終結果
と一緒に報告されなければならない。
7.5.3
装置の準備
個々の装置マニュアルに記載されている,装置の準備に関する指示及びアドバイスに従う。装置の機能
は,装置を供給する製造業者による日付及び試験結果の記録を伴う動作適格性の確認(OQ,operational
qualification)試験,又は,相当する試験を通過したものでなければならない。適切な光学系とセルとのア
センブリが組み込まれなければならない。装置は清浄であることが望ましい。測定を通じて粒子フリーな
分散系(気相又は液相)を用いることが望ましい。
解析モードを選択する余地があるならば,モードは行う測定の種類に対して適合していなければならな
い。測定時間及び粒子輸送に関わるガス流速又はポンプ速度を十分なものに設定する。気泡及びコンタミ
ネーションが存在しないことを確実にするには,ブランク(バックグラウンド)測定結果が要求される値
の範囲以内に入らなければならない(製造業者の仕様を参照。)。
熟練したオペレータが装置を準備し,適格性の確認試験を行わなければならない。
結果の表示ソフトは,なるべくJIS Z 8819-1に沿ってふるい下積算分布の出力をするように設定する。
7.5.4
適格性の確認試験
測定を通じてCRMの試験手順に従わなければならない。
通常は全量測定を行う。部分試料のサンプリングが必要な場合,サンプリング手順がよい再現性を与え
ることが証明されている場合だけ,単一試料の分析が許容される。そうでないときには,少なくとも三つ
の部分試料の分析が好ましく,その平均の値を使用しなければならない。
試料量(濃度)は,操作手順に指定されている減衰率又は透過度に達するものでなければならない。
光散乱パターン,又は減衰率値のリアルタイム表示ができることが望ましい。全ての値には重大な変動,
又は突然の変化がないことが望ましい。
7.5.5
適格性の許容基準
CRMでは,各粒子径分布パラメータについて,最大値と最小値の組合せとして, 95 %許容限界が記載
されている。
測定して得られた粒子径分布が次の基準に達しているならば,この規格の要求項目を満足するものとし
て,適格性の確認試験を合格としなければならない。
a) 得られたx10とx30との間の積算量が,この範囲に対して値付けされている標準物質の最大値又は最小
値を,相対値で3 %以上超えない。
b) 得られたx30とx70との間の積算量が,この範囲に対して値付けされている標準物質の最大値又は最小
値を,相対値で2.5 %以上超えない。
c) 得られたx70とx90との間の積算量が,この範囲に対して値付けされている標準物質の最大値又は最小
15
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
値を,相対値で4 %以上超えない。
大きな偏りが出たときは,全ての潜在的な誤差要因を確認し(7.6参照),必要な場合には,専門家のア
ドバイスを求める。
何らかの理由によって,より高度の正確さが求められる場合は,狭い信頼区間をもつCRMを選択する
ことがよい。さらに,最小の偏りを保証するようなサンプリング,分散,及び測定の全プロトコルを使用
することが望ましい。
CRMでない物質(球形及び非球形)に対して,許容基準は装置の供給者から提供されるべきであり,文
書化,安定性及び再現性に関する上記の基準を満たさなければならない。
7.6
誤差の要因及びその診断
系統的測定誤差(偏り)は,次の要因によって発生する可能性がある。
a) 不適切な試料調製
b) 粒子状物質に対する理論的仮定からの逸脱
c) 装置の不適正な操作,又は動作,及び/又はデータの不確定性
附属書JCに参考となる情報を示す。
7.7
分解能及び感度
粒子径分布の分解能,すなわち,異なる粒子径の識別能力及び与えられた粒子径区間の粒子数の僅かな
変化に対する感度は,次の要素で決まる。
a) 検出器の数,位置及び形状
b) 検出器のSN比
c) 測定散乱パターンの微細構造
d) 隣接する粒子径区間の間における散乱パターンの検出可能な差異
e) 測定粒子の実際の粒子径範囲
f)
光学モデルの妥当性
g) 逆演算手順で適用するスムージング
これらの因子は,高分解能のレーザ回折・散乱技術を設計することを難しくしている。各粒子径区間の
最小の幅は通常約1.1〜2(粒子径区間の上限と下限との比)である。特別の場合には,より高い分解能が
可能なことがある。
8
測定結果の記録
測定結果は,JIS Z 8819-1,JIS Z 8819-2及びISO 9276-4に従って報告する。また,次に示す推奨記録事
項については,場所又は測定者が異なっても測定が容易に再現できるように,記録するか,又はプロトコ
ルを定めた文書の形で記載されることが望ましい。
サンプリングの問題及びレーザ回折・散乱法の限界があるため,x5以下及びx95以上の特性値は,追加的
な不確かさ及び/又は系統的誤差の点でぜい弱である。レーザ回折・散乱法によってx100の値を付けるこ
とを,この規格は認めるものではない。
記録には少なくとも次の情報を含めることが推奨される。
注記 対応国際規格では,次の記録項目を含めることを,推奨事項ではなく,必須の要件としている。
a) 試料
1) 試料の完全な同定:化学的情報(性質),バッチ番号及び/又は採取場所,サンプリングの日付け,
時間など。
16
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2) サンプリング手順,すなわち,サンプリング方法及び試料分割手順。
3) 試料の前処理を行う場合(例えば,ふるい分け前処理)には,その方法及び条件
4) 試料量
5) 解析の日付
b) 分散
1) 乾式分散について
1.1) 分散装置の詳細仕様,例えば,輸送管の直径,一次圧
1.2) 供給装置の形式
1.3) 供給速度
1.4) 分散圧力
2) 温式分散について
2.1) 分散液:名称,体積,及び,必要に応じて温度
2.2) 分散剤:種類及び濃度
2.3) 超音波:装置の形式,周波数(エネルギー),照射時間及び測定開始までの休止時間
2.4) ポンプ速度
2.5) 光路長
c) レーザ回折・散乱測定
1) 装置の形式及び番号
2) ソフトウエアのバージョン
3) 分散装置の体積
4) 使用した光学系(レンズの焦点距離など)
5) 最終の光学系調整日
6) 最終の適格性試験日
7) 測定の日及び時間
8) 減衰率
9) 測定開始及び停止のトリガのいき(閾)値(使用した場合)
10) データの取込みのいき(閾)値(使用した場合)
11) 使用した光学モデル
12) (ミー理論を用いた場合)粒子の屈折率の実数部及び虚数部
注記 屈折率の虚数部については,粒子の形状等の影響を考慮して,見かけ上の値を用いる場合
がある。この場合には,見かけ上の値を使用したことを記録する(A.2参照)。
13) (ミー理論を用いた場合)分散媒体の屈折率
注記 対応国際規格では,分散媒体の屈折率は,光学モデルによらず記録することを要求してい
る。
14) (必要に応じて)逆演算の結果得られる最小化残差パラメータ[例えば,対数差分,χ(カイ)2乗
値,相対残差]
d) 測定者
1) 実験室の名前及び場所
2) 測定者の名前又はイニシャル

17
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
レーザ回折・散乱の理論的背景
A.1 はじめに
光と粒子との間には,次の四つの相互作用が働く(参考文献[6-13],[17]参照)。
a) 粒子の輪郭での回折(フラウンホーファ回折)
b) 粒子の内側及び外側の両表面での反射
c) 媒体から粒子へ及びその逆からくる光の界面での屈折
d) 粒子内部での光の吸収
こうした相互作用は,干渉作用を引き起こし,入射光強度の減少(減衰)と同時に散乱角に対する特有
の散乱光強度パターン(散乱パターン)を生じる。散乱パターン及び減衰は,粒子の大きさ,形状及び光
学的特性に依存する。これらの現象はレーザ回折・散乱による粒子径分布測定の基礎をなしている。
一例として,図A.1に5 μm球形粒子に波長633 nmの光を入射したときの光散乱パターンを示す。ただ
しこれは,前方焦点面上で観測された光強度分布である。
記号
x
検出器のx軸
y
検出器のy軸
z
相対光強度
媒体の屈折率 nH20=1.33,波長 λ=633 nm,粒子の屈折率 Np=1.59−0.0i
図A.1−5 μm球形粒子の散乱パターン(前方焦点面での光強度分布)
これは,単一粒子の散乱パターンが次のような特性をもつことを明確に示している。
1) 最大強度は前方(散乱角0°)に位置し,散乱角が大きくなるにつれて徐々に減少する。
2) 粒子径に依存して,異なる角度で特有の極大値及び極小値があり,散乱光強度に大きな差がある。
3) 球形粒子の散乱パターンは円対称を示す。ただし,このような対称性は非球形粒子の場合には生じ
ない。
4) こうした特有の散乱パターンが,粒子径分布測定にレーザ回折・散乱法が応用される基礎となって
いる。レーザ回折・散乱法では,測定領域に存在する粒子の集合に対する粒子径分布が得られる。
単一球形粒子による散乱光は,次の条件が満たされれば,粒子群に対しても拡張できる。
18
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.1) 各粒子はそれぞれ独立に光散乱する。これは多重散乱はほとんどない条件が満たされているとい
うことで,このためには粒子濃度が低いことが望ましい。
4.2) 他の粒子からの散乱光の光学的な干渉はない。全ての粒子が互いに無関係に動き,全体の散乱パ
ターンが何回も測定され平均化される場合,この条件が満たされる。
A.2 減衰
照射光の波長よりも粒子が十分大きい場合,入射光の減衰量は,粒子の幾何学的断面積に入射される量
の2倍になる。これは減衰が粒子から十分な距離をおいて検出される場合であり,遠距離場と呼ばれる。
参考文献[7]は2倍という見かけ上の矛盾を次のように説明している。すなわち,粒子の幾何学的断面積
に入射した光は吸収,又は反射によって,入射光から取り除かれ,反射光量と同量の光は回折によって取
り去られる。これによって,十分な距離(遠距離場)での観測結果が説明される。このことは,大きな粒
子の場合に,散乱断面積と幾何学的断面積との比である散乱係数が1に等しいことを意味している。
照射光の波長が粒子の大きさに比べて十分に小さいという状態ではなくなると,図A.2に示すように,
光の減衰量は粒子の幾何学的断面積の2倍ではなくなる。
一般的に,粒子に対する光線の減衰量は,次の要素に依存する。
a) 粒子径(散乱断面積)
b) 粒子と媒体との相対屈折率
c) 光源の波長
d) 粒子形状
e) 開口角
粒子の屈折率は,実数部をnp,虚数部をnIpとして,複素数Np=np−inIpで表される。
例 高分子ラテックス粒子の屈折率はNp=1.59−0.0iである。虚数部の値が0であることは吸収がな
いことを示している。乳白色に見える懸濁液は可視光での多重散乱によるものである。
吸収項nIpは,通常,正であり,マイナス記号はNpの定義に含まれている。吸収のない分散媒の屈折率
は実数部だけで表される。物質の屈折率の値については参考文献[19-29]などに記載されている。屈折率の
実数部は直接測定することができる(参考文献[22]参照)。屈折率の虚数部については決定的な方法がない。
注記 レーザ回折・散乱法において,妥当な屈折率を得るためのガイドラインは現状でも研究課題で
はあるが,幾つかの方法が提案されている(参考文献[30-33])。
虚数部は,光エネルギーが熱に変換されて失われるときの吸収であると考えられる。さらに,表面に凹
凸のあるような粒子の界面では,全体的な内部反射によってある程度光が失われる。この寄与を含めるた
めに,見かけ上の屈折率として虚数部nIpに0.01から0.03の値を加算することができる。
虚数部nIpが吸収だけに関係していると単純に考えることは物質によっては誤りである。物質系の見かけ
上の吸収を説明するためにnIpの値を,多少調整し,その有効性を確認する必要がある。
見かけ上のnIpの値を使用したことを,測定報告書に明確に記載しておく。
A.3 散乱
散乱光は,屈折境界及び屈折率勾配において発生する。それゆえに,粒子と媒質との相対屈折率mrelは,
散乱光を計算する場合に必須である。もし粒子及び媒質が同じ屈折率であるならば,それらは屈折率整合
ということになり散乱光は発生しない。
レーザ回折・散乱法では,粒子径及び粒子数を測定するために,粒子によって光がどのように散乱した
19
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
か解析する。すなわち,散乱光の,
a) 角度依存性
b) 強度依存性
c) 波長依存性
d) 偏光の影響
を測定に用いる。これらの影響を,装置,場合によっては独立に又は複合的に解析する。
大きな球形粒子の散乱光強度は,粒子の幾何断面積に比例する。
非球形粒子の場合に,その散乱パターンを正確に計算してこれを粒子径解析に用いることはいまだ研究
段階である。
球形粒子はその直径だけで完全に特徴付けられるので,現在のレーザ回折・散乱装置では,球を仮定し
た散乱パターンを基にして,粒子径分布を測定・算出している。このため,不規則形状粒子の測定結果は,
他の測定手法による結果とは同じにはならない。各不規則形状粒子は配向によって断面積が異なり,散乱
パターンも異なる。不規則形状粒子の測定結果は,その散乱パターンが最もよく一致する粒子径分布をも
つ球形粒子として表される。JIS Z 8819-1は,球等価粒子径として表現する慣例を認めている。
大きい粒子においては,散乱光は直径xの2乗に比例して増加する。一方,波長よりも十分小さい粒子
(粒子径x<λ / 10,レイリー領域)では,散乱光は直径xの6乗に比例する。
A.4 光散乱理論
(参考文献[6-10]参照)
レーザ回折・散乱“スペクトル”から粒子径分布への変換については,次の二つの主要操作が重要であ
る。第一に均一粒子の光散乱パターンを与える数学モデルであり,次に測定された散乱パターンから粒子
径分布への逆演算である。
光学的に均一で単一球形粒子による偏光していない入射光に対する散乱光強度の角度方向分布は,次の
式で表すことができる。
()
()
[
]
()
[
]
{
}
2
2
2
1
2
a
2
0
2
θ
θ
θ
S
S
l
k
I
I
+
=
···················································· (A.1)
ここに,
k: 媒質中の波数
la: 散乱体から検出部までの距離
I0: 入射光強度
S1(θ),S2(θ): 一般的に散乱理論から求められる無次元複素関数で,
散乱角θの関数として,それぞれ垂直偏光及び水平偏
光の入射光強度で規格化された振幅を表す(振幅の2
乗が光強度に対応する。)。
1908年,グスタフ・ミーは,定義された境界条件のマクスウェル方程式を解くことによって,既知の波
長をもつ無限平面波に既知の光学的性質をもつ均質な球が照射されるときの光散乱特性を求め,複素関数
のS1(θ) 及びS2(θ) を示した。このミー理論は,全ての大きさの球に有効な厳密解を与える(参照文献[6-8])。
この理論を使用するときの前提は,次による。
a) 全ての粒子が,光学的に均一で,等方性で,球体である(ほかに,均一被覆球のように,解の求まる
特殊な形状,条件もある。)。
b) 粒子は既知の波長の平面波によって照射される。
c) 粒子及び分散媒の屈折率の実数部及び虚数部が既知である。
20
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 粒子表面に電荷又は電流がない。
粒子の散乱パターンは振幅,波長及び偏光に依存して360°全方向で計算できる。これらの関数S1(θ),
S2(θ) 及びI(θ) を,実際にコンピュータで計算するためのアルゴリズムが開発されている(参考文献[10])。
この理論に基づく計算をきちんとするには,光学的特性である粒子の複素屈折率(実数部及び虚数部の
両方を含む),及び分散媒の実数部屈折率が必須である。ただ,これらの情報は簡単には得られない場合が
多い。特に,屈折率の虚数部の値は光の波長に強く依存することが多く,更に,例えば,表面粗さのよう
な粒子特有の表面構造の効果を表すための有限値を加える場合もある。
フラウンホーファ回折近似は,粒子径測定に用いられた最初の光学的モデルである。それは薄い金属板
の開口部を通過した既知波長の平面波について定式化された。バビネの原理によれば,円形開口による回
折パターンと,同じ直径をもつ完全に不透明な円盤による回折パターンは完全に一致する。レーザ回折・
散乱法にこの近似を用いる仮定は,次による。
1) 粒子は光を完全に吸収する。すなわち,粒子の輪郭での回折だけが考慮されている。
2) 全ての粒子が円形断面をもつ(ただし,他の規則的な形状についても計算は可能である。)。
3) 粒子は既知の波長の平面波に照射される。
4) 前方小角範囲の回折だけが考慮されている(θが小さい)。
5) x >> λ
小さい粒子,例えば,フラウンホーファ回折近似での範囲を超えた粒子の場合は,粒子径分布を求める
際の計算誤差を防ぐために物質の光学的特性の正確な値が不可欠になる。
フラウンホーファ回折近似では,偏光及び粒子透過光は考慮しないので,粒子屈折率の値を必要としな
い。
こうした近似に対して,次の式が成り立つ,
(
)2
1
4
2
2
2
1
sin
sin
=
=
θ
α
θ
α
αJ
S
S
·························································· (A.2)
上記の一般式(A.1)は,次の式のように簡略化される。
()
(
)2
1
4
2
a
2
0
sin
sin
=
θ
α
θ
α
α
θ
J
l
k
I
I
······················································· (A.3)
ここに,
α: 無次元粒子径パラメータ,α=πxnm / λ
J1: 一次の第一種ベッセル関数
注記 大きな角度に適用するときは,式(A.3)の右辺に更に項 (1+cos2θ) / 2を乗じる(参考文献[34])。
この式(A.3)の利点は,散乱体の光学的特性に関する情報を必要としないという点で比較的簡単なことで
ある。そのため,光学的性質が未知若しくは変化する材料である場合,又は異なる材料の混合物であるよ
うな場合にしばしば用いられている。実際にはこの近似は,大粒子(直径が波長より大きい場合,すなわ
ち,α >>1のとき)に対して適用可能である。一方,小粒子(フラウンホーファ回折近似の適用範囲を超
える粒子)の場合には,粒子径計測誤差を避けるために粒子の光学的性質を把握することが不可欠になる。
21
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.5 光学モデルの選択
最近の装置では,一般的にはフラウンホーファ回折近似又はミー理論を用いて球形粒子の粒子径を算出
する。前記のように,粒子径の大きさが比較的大きくない場合には,二つのモデルの結果は異なる。適切
な光学モデルを選択する上で測定試料の光学的特性を考慮すべきである。粒子径が50 μmより大きく相対
屈折率が1.2よりも大きな粒子については,ミー理論とフラウンホーファ回折近似とは同様な結果になる
ので光学的特性は必要ない。
a) 透明粒子
b) 不透明粒子
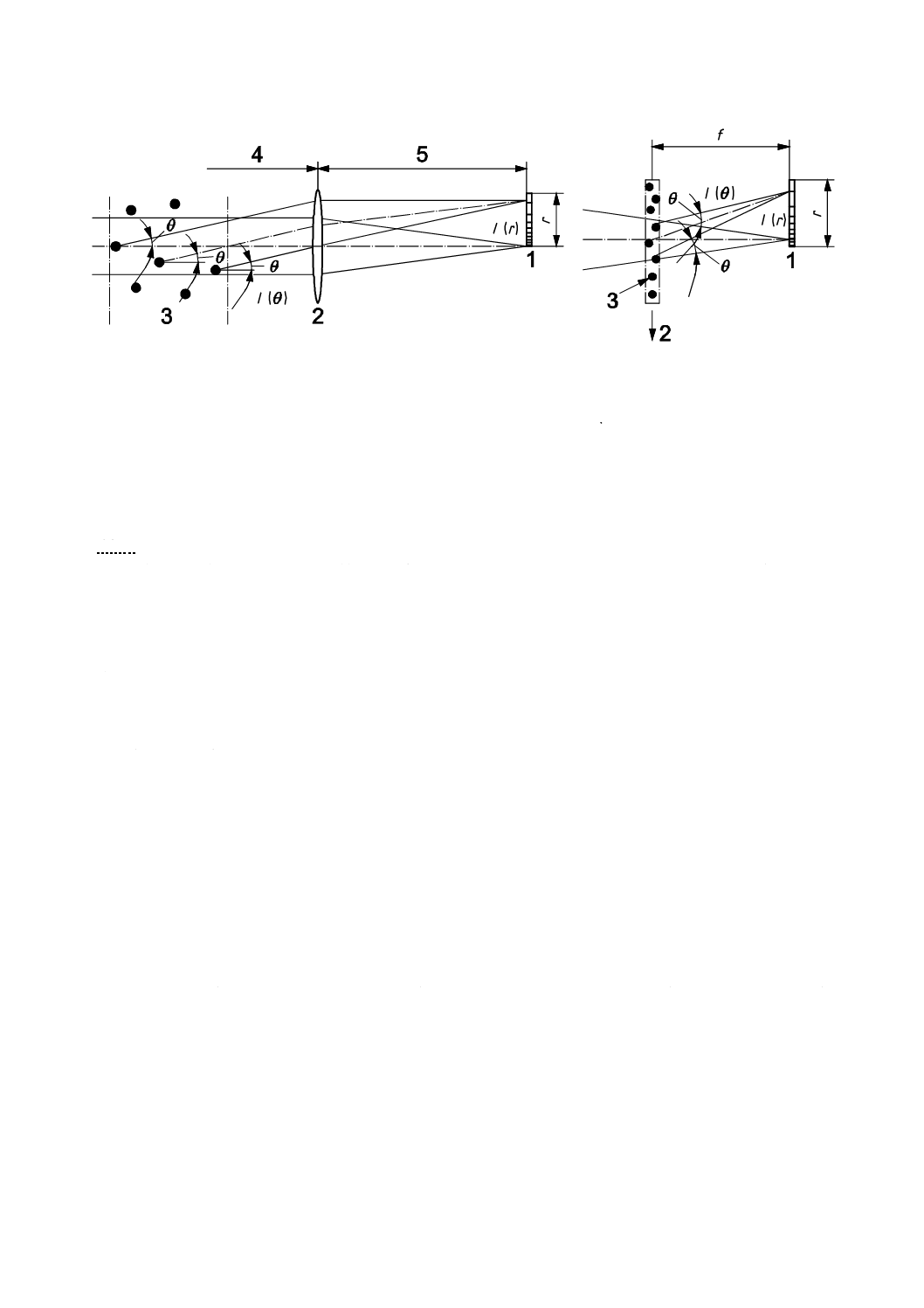
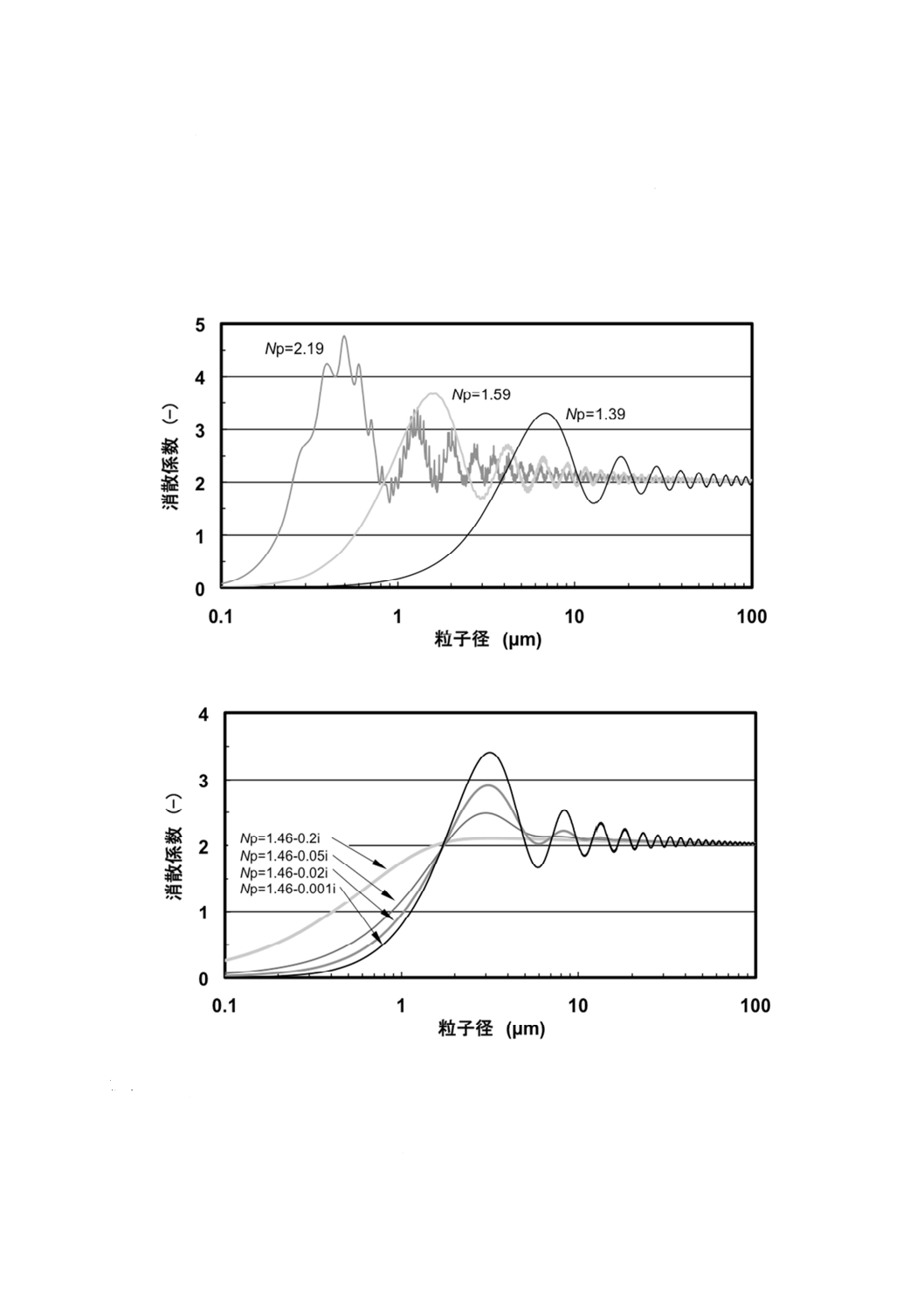
記号
Np :粒子の複素屈折率
計算条件:分散媒屈折率 nH2O=1.33,波長 λ=633 nm
図A.2−ミー理論に基づく粒子径,屈折率による消散係数の変化
22
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ミー理論は,光学的特性が既知の等方性で均質な球形粒子の全ての粒子径に対して,散乱パターンの全
領域について厳密な解を与える。また,光散乱への振幅,波長,及び偏光の影響も計算できる。
フラウンホーファ回折近似は,粒子径が光の波長より大きく,及び/又は不透明な粒子に適用され,粒
子の光学的特性は必要としない。また,前方小角散乱(散乱角が小さい領域)だけに適用され,偏光及び
粒子を透過する光は考慮しない。
図A.2 a) に透明粒子,図A.2 b) に光吸収のある不透明粒子に対する消散係数をミー理論によって計算
した結果を示す。フラウンホーファ回折近似ではこれは全粒子径に対して一定値2になる。
これらのグラフは,約50 μm以上の透明粒子,及び,約2 μm以上の不透明粒子(nIp>0.2)の場合には,
ミー理論及びフラウンホーファ回折近似が一致することを示している。粒子径が2〜50 μmにおいては,
二つのモデルが一致するかどうかは屈折率の実数部及び虚数部の値に依存する。二つのモデルが一致しな
い範囲については,厳密解であるミー理論は50 μm以下(大きさは複素屈折率に依存)の粒子径領域で消
散係数が大きく変動する。また,両グラフはサブミクロン領域で消散係数が急激に減少することを示して
いる。
a) 粒子径3 μm
b) 粒子径100 μm
計算条件:分散媒屈折率 nH2O=1.33,波長 λ=633 nm,粒子屈折率 Np=1.59−0.0i
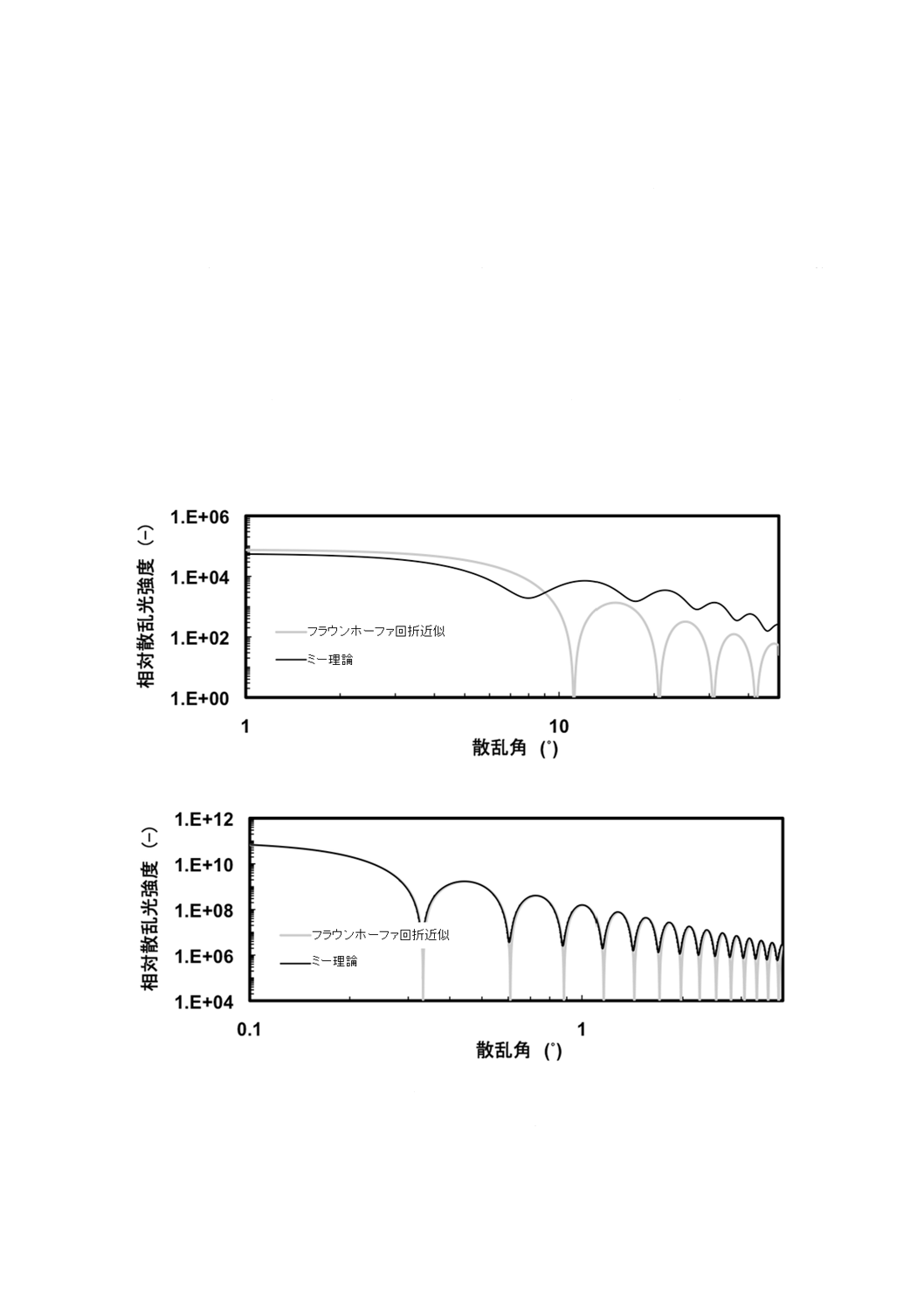
図A.3−フラウンホーファ回折近似及びミー理論に基づく透過粒子の散乱パターンの比較
23
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.2は,約50 μm以下の粒子において,測定試料の光学的特性に依存し,得られる粒子径分布に誤差
が生じることを示している。散乱パターンについても,粒子径又は屈折率によって,二つのモデルが一致
する領域,及び一致しない領域が,同様に存在する。図A.3 a) に3 μm,図A.3 b) に100 μmの透明粒子
について,ミー理論及びフラウンホーファ回折近似から得られる散乱パターンを示す。
粒子径,屈折率の実数部及び虚数部(吸収項)を考慮し,二つのモデルのいずれかを選択する。最小粒
子径が約50 μm以上の粒子径分布をもつ粒子群に対して,フラウンホーファ回折近似及びミー理論に基づ
く結果は通常とてもよく一致する。2〜50 μmの粒子に対して,二つのモデルの一致の程度は,複素屈折率
に強く依存する。不透明な粒子ではよく一致し,透明な粒子では一致しない。小さい粒子の場合は,ミー
理論を用いるのがよい。ミー理論を適用する場合,測定試料の光学的特性がよく知られている必要がある。
この点についての検討及びさらなる測定が必要になる場合もある。
適用した理論モデル及び光学的特性が妥当であるかどうかは,得られた粒子径分布から計算した試料濃
度と実際の濃度とを比較することで一定程度判断できる。光学モデル又は用いた屈折率のいずれかが適切
でないときに,大きな差が生じる。また,他の技術(例えば,顕微鏡,又は沈降法)を用いて,小粒子径
の粒子が測定結果に影響を与えるほど含まれているかどうかを確認することができる。ただし,1個の粗
大粒子と同等の体積になるには,非常に多くの個数の小粒子が必要となる点に注意する必要がある。
A.6 散乱光の検出
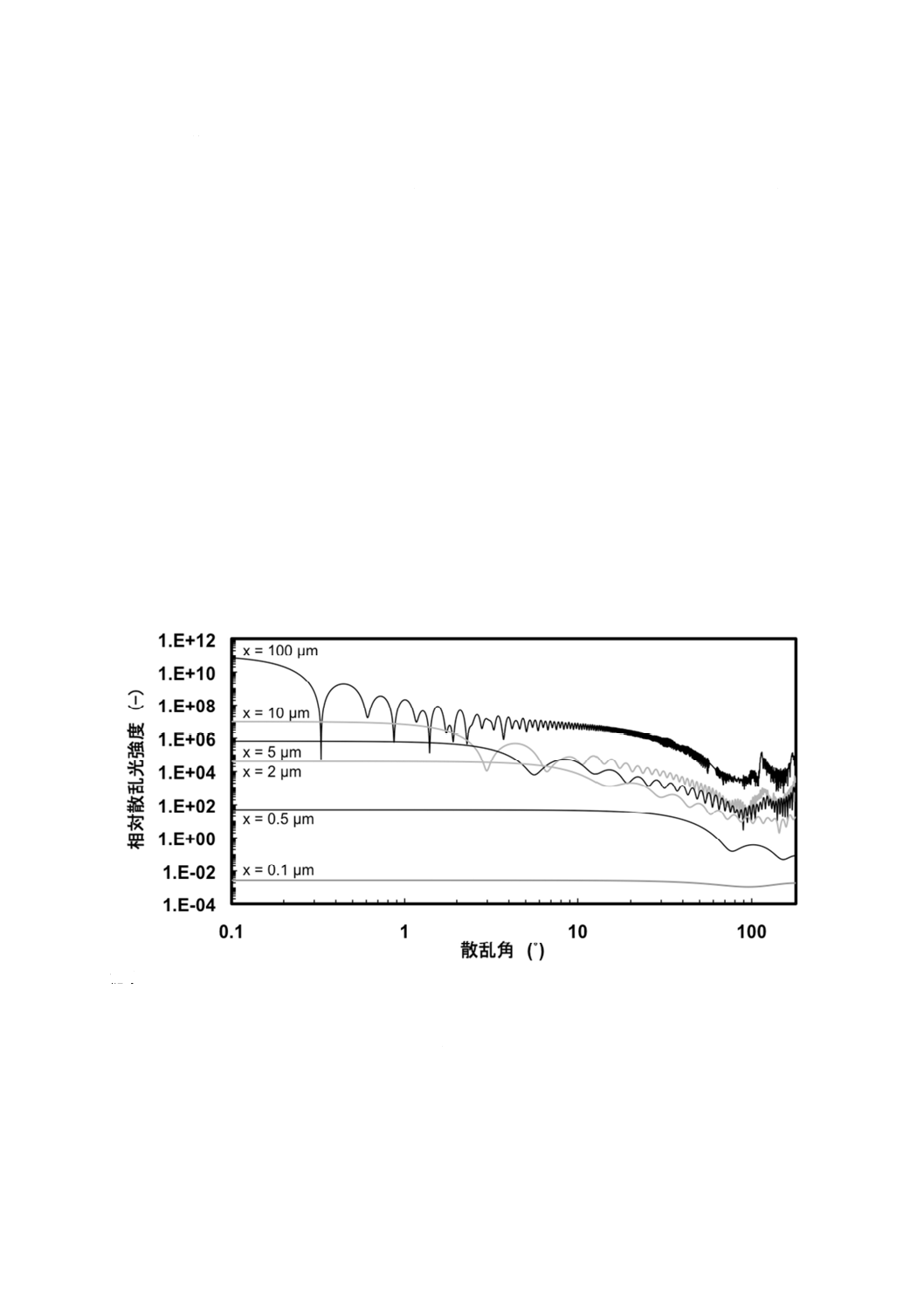
様々なサイズの単一粒子について,散乱光強度の角度変化を図A.4に示す。
記号
x :粒子径
計算条件:分散媒屈折率 nH2O=1.33,波長 λ=633 nm,粒子屈折率 Np=1.59−0.0i
図A.4−ミー理論に基づく散乱パターン(単一粒子)
単一粒子において粒子径0.1 μm及び粒子径100 μmの粒子の散乱光強度のダイナミックレンジ(強度比)
は,約1013である。このダイナミックレンジは,現在使われている検出器に対して非常に大きい。体積は
粒子径xの3乗に比例するので,体積基準の散乱光強度を用いることでダイナミックレンジを小さくでき
24
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
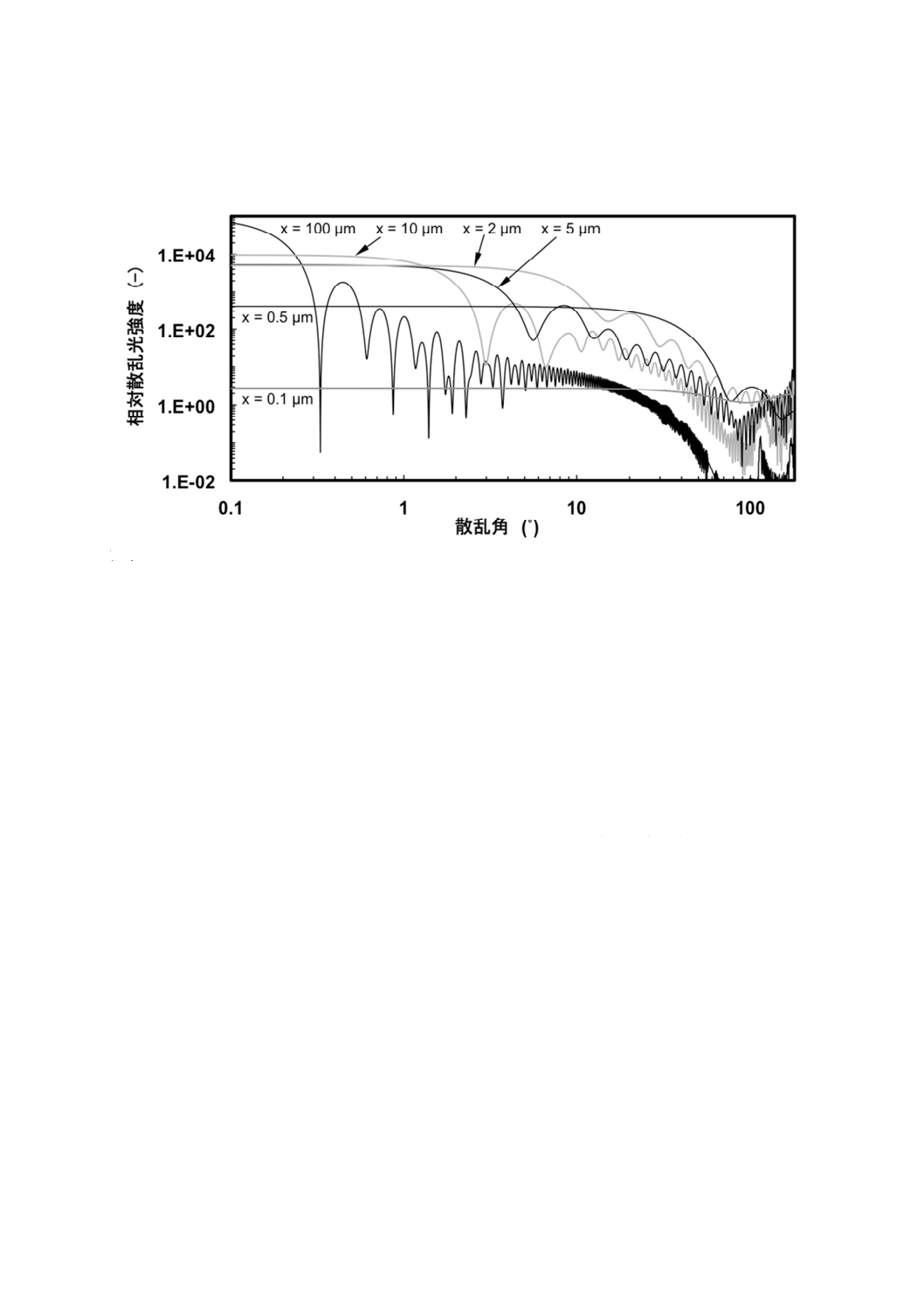
る。したがって,レーザ回折・散乱装置は体積基準の粒子径分布を評価するように設計されている。図A.5
に同一の総体積で比較した場合の粒子径ごとの散乱パターンを示す。
記号
x :粒子径
計算条件:分散媒屈折率 nH2O=1.33,波長 λ=633 nm,粒子屈折率 Np=1.59−0.0i
図A.5−ミー理論に基づく散乱パターン(総粒子体積一定)
各粒子径に対して総体積一定で比較すると,0.1 μm〜100 μmまでの粒子径の散乱光強度のダイナミック
レンジは約104まで減少する。このダイナミックレンジは精密で慎重な検出器設計によって,実質的には
更に改善し得る。
散乱光パターンの特徴を考慮すると,広範囲の角度の散乱光強度を検出することが重要であり,かなり
狭い粒子径分布に対しては,角度について適切な数の検出器を使用することが重要である。一方,各検出
器の信号は,散乱光強度,検出器の面積,及び検出器の感度に比例する。したがって,検出器の面積が減
少すると信号が小さくなり,SN比は悪くなる。このことは,散乱光強度が通常非常に小さくなる散乱角
の大きい領域では特に重要である。実際には,検出器の数及びその面積,その検出器がカバーする散乱角
範囲には,ある程度最適な組合せがあり,装置メーカによってその具体的な設計は異なる。
シリコン光検出器の場合,その電流出力は,検出器面積と散乱光強度との積に比例する。散乱角が小さ
な領域に面積の小さい検出器,散乱角が大きな領域に比較的大きな面積の検出器を配置することによって,
検出器のダイナミックレンジを改善できる。粒子径に対する散乱光強度パターンの特徴によって,大きな
散乱角の場合,小さな散乱角と比べ,単位角度当たりの検出器の数を大幅に減少できる。最適配置された
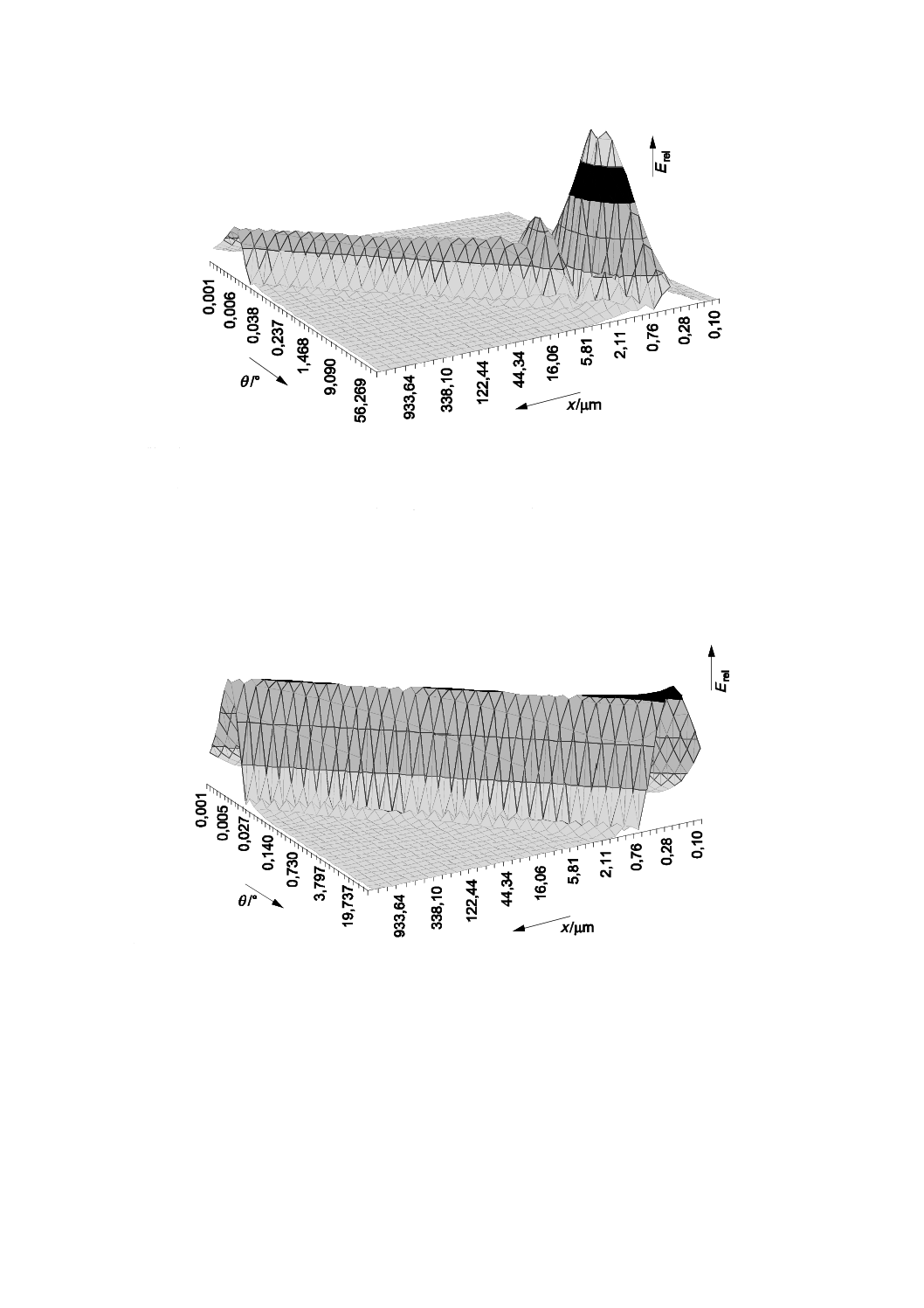
ゲイン一様の検出器の電流出力の一例を散乱角と粒子径とに対してプロットしたグラフを図A.6に示す。
図A.6において,粒子径が大きな場合,粒子径に対する散乱パターンの面積は一定で,散乱光エネルギ
ーはその粒子群の体積に比例する。粒子径が小さい場合,粒子径に対する散乱パターンの面積は一定では
なく,屈折率及び粒子径に依存する。サブミクロン粒子になると散乱光強度は急激に減少する。
25
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
記号
θ :散乱角
Erel :相対エネルギー(光電流値)
x :粒子径
計算条件:分散媒屈折率 nH2O=1.33,波長 λ=633 nm,粒子屈折率 Np=1.59−0.0i
図A.6−最適に配置した検出器の光電流パターン(体積基準。ミー理論に基づく)
散乱角の上限を30°として,条件が図A.6と同じ場合のフラウンホーファ回折近似に基づく散乱光強度
のグラフを図A.7に示す。
記号
θ :散乱角
Erel :相対エネルギー(光電流値)
x :粒子径
図A.7−フラウンホーファ回折近似に基づく最適に配置した検出器の光電流パターン(体積基準)
図A.6及び図A.7は,粒子径の大小によってミー理論及びフラウンホーファ回折近似が一致する領域,
一致しない領域を示す。
26
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
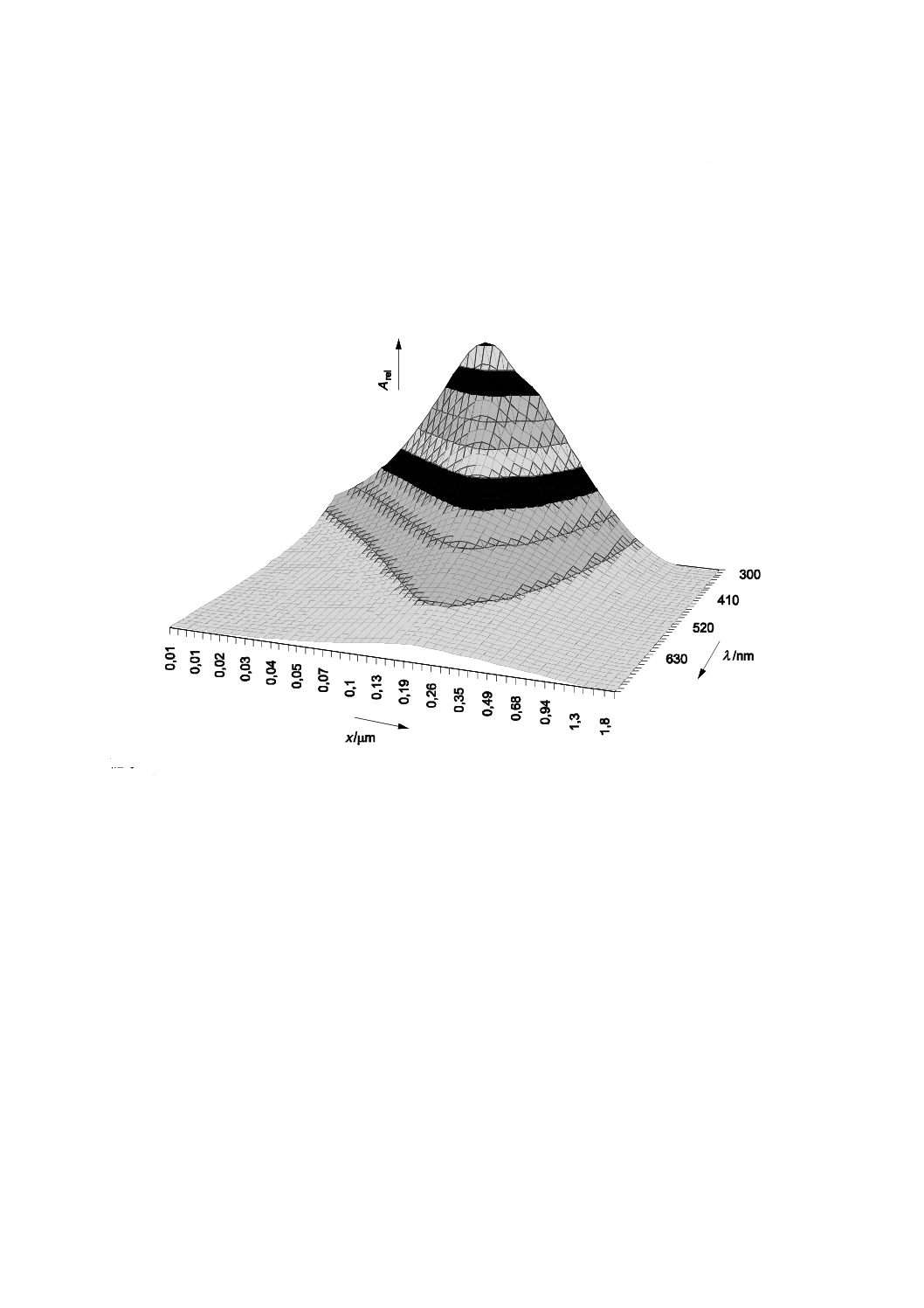
A.7 波長依存性及び偏光差
サブミクロン粒子の光散乱の角度依存性は,0.3 μm以下では少ない。微小な粒子を評価するには,他の
情報が必要である。別の波長の光源を付加的に用いること,及び/又は波長及び偏光の差異を測定するこ
とによって,そうした情報を得ることができる。
微小粒子からの光散乱は,波長に強く依存する。散乱光強度は,波長の4乗に反比例する。レーザ回折・
散乱装置の一部ではこの現象を使っている。光散乱によって生じる相対減衰量について,ミー理論によっ
て計算される波長依存性を図A.8に示す。
記号
λ :波長
Arel :相対減衰量
x :粒子径
計算条件:分散媒屈折率 nH2O=1.33,粒子屈折率 Np=1.59−0.0i
図A.8−減衰の波長,粒子径依存(同一体積基準,水中)
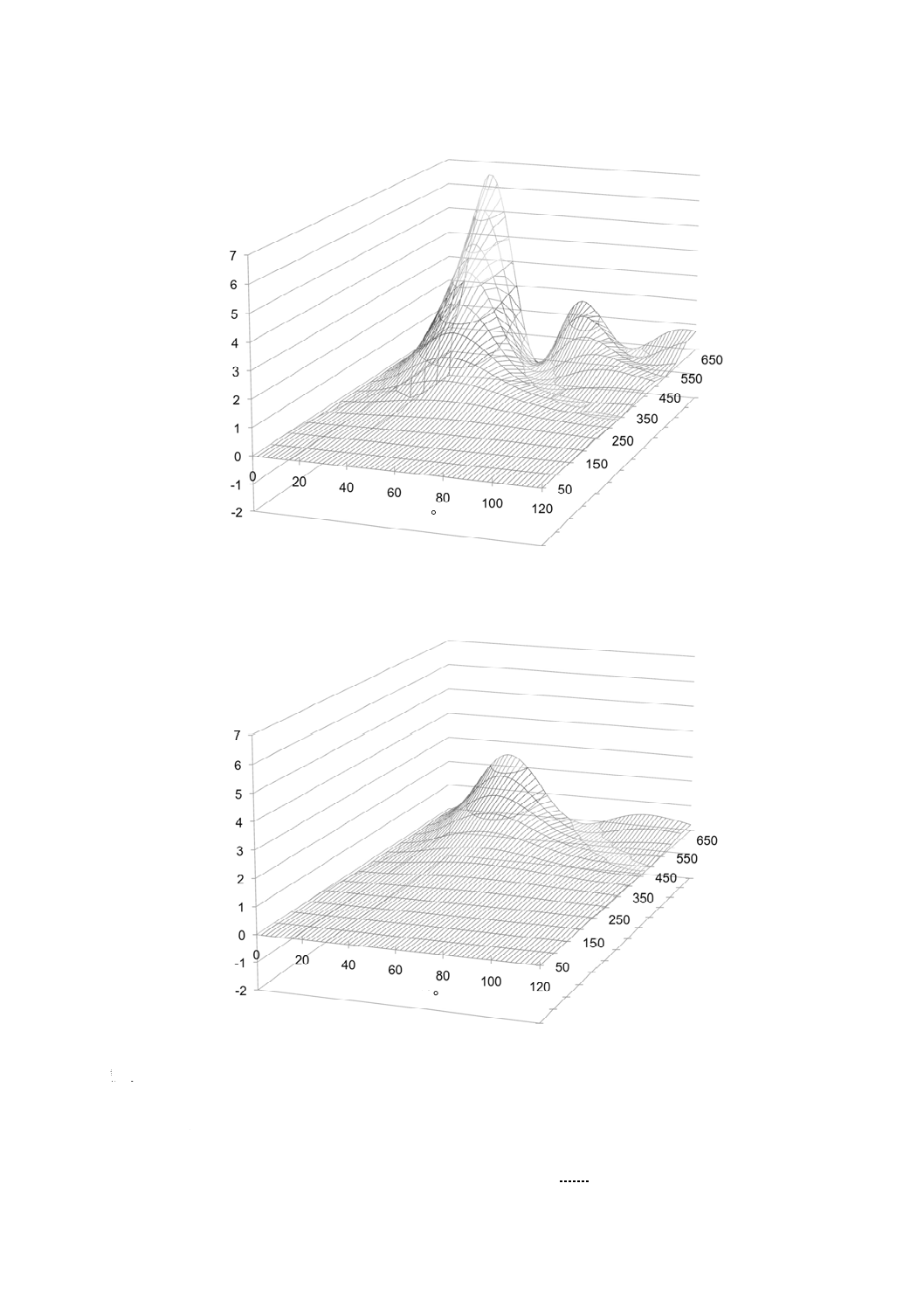
サブミクロン粒子の場合,散乱光の水平及び垂直方向の偏光は粒子径によって大きく変化する。この変
化も波長に依存する。散乱光の偏光の差を,波長450 nm及び633 nmの二つの場合について,図A.9に示
す。
90°付近に波長による違いが顕著に見られる。しかし,このような小さな粒子の光散乱強度は,非常に
小さい。
27
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
θ / °
x / nm
I
v
-I
h
(a
rb
.)
I
v
-I
h
(a
rb
.)
θ / °
x / nm
a) λ=450 nm
b) λ=633 nm
記号:
θ
:散乱角
Iv−Ih :相対偏光強度差
x
:粒子径
図A.9−散乱光の偏光の差[a) 波長450 nm及びb) 633 nmの場合の比較]
28
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
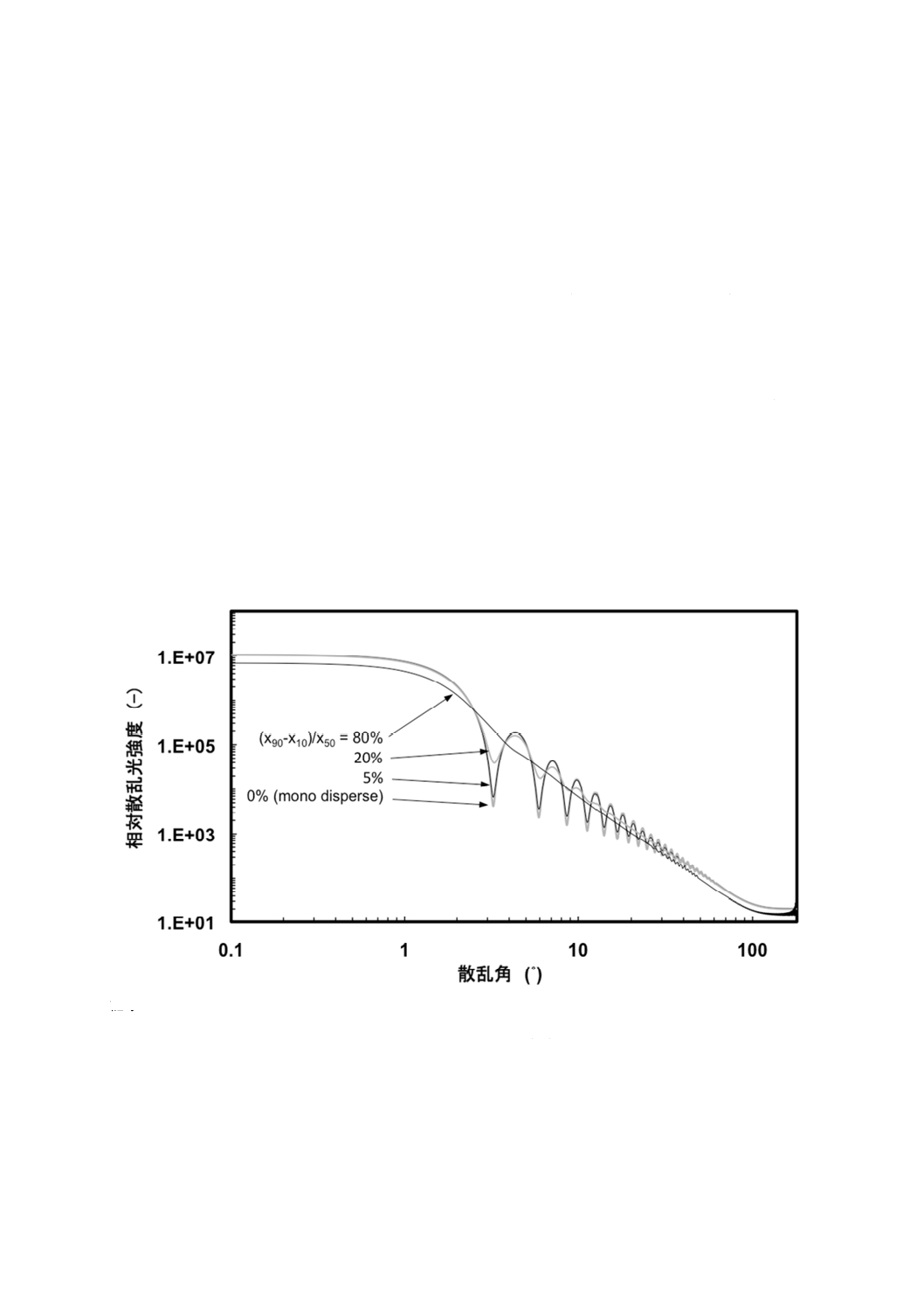
A.8 粒子径分布のための散乱パターン
図A.5には,単分散(単一サイズの)粒子の散乱パターンを示した。散乱強度は,様々に極大・極小を
示し,これらの位置(角度)は主に粒子径,波長,及び屈折率に依存する。同一の粒子総体積で比較する
と,大粒子の散乱光の強度は,小粒子のそれより低角度で大きくなる。これは大粒子の散乱光のエネルギ
ーが一部の角度に制限されるからである。逆に言えば,小粒子の散乱は広い角度に渡る。粒子径分布計測
においては,散乱光強度の相対的角度変化が重要である。なぜならば,散乱光強度の絶対値は,粒子濃度
の影響を強く受けるからである。図A.3〜図A.5は,一般に散乱光強度が広角側へ向かって減少すること,
これが光学モデル又は屈折率の影響を受けることを示している。
実際上,かなり広い粒子径分布をもつ試料を測定する場合がある。図A.10は,散乱光パターンに対する
粒子径分布の幅の影響を示す(対数正規分布を仮定する。)。散乱パターンが様々な極大・極小をもつ複雑
な形状になるのは,単一粒子又は非常に狭い粒子径分布の場合だけであることが分かる。ある程度以上粒
子径分布が広い試料では,こうした細かい構造は消失している。散乱パターンの極大・極小位置が粒子径
によって敏感に移動するので,分布のある試料ではこれらのある種のスムージングが生じている。粒子径
分布の広い試料におけるこうした微細構造の消失は,検出器の信号に誤差をもたらし,これが計測結果に
大きな違いを生じさせる可能性がある。このような誤差の影響の表れ方は,解析に用いる制約条件の設定
の仕方,スムージング,及び逆問題計算アルゴリズム(7.3.1及び7.7参照)によって,相当に異なる。ま
た,広角側の検出器の利用にメリットがあることが分かる。
記号
(x90−x10) / x50:粒子径分布の幅(粒子が単一粒径である場合,この幅は0である。)
計算条件:分散媒屈折率 nH2O=1.33,波長 λ=633 nm,粒子屈折率 Np=1.59−0.0i
図A.10−散乱パターンにおける粒子径分布の幅の影響(x50が10 μmの対数正規分布を仮定)
A.9 濃度
多数個の粒子による散乱光強度は,その粒径をもつ粒子の数に依存して増大する。低濃度の領域ではこ
29
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の関係は比例関係にある。ただし,濃度が高くなると,個々の粒子によって散乱した光のかなりの量が隣
接した粒子によって更に散乱される現象(多重散乱)の効果が無視できない。正確な粒子径分布の決定に
対する最大許容粒子濃度は,この多重散乱の影響が無視できなくなる濃度である。
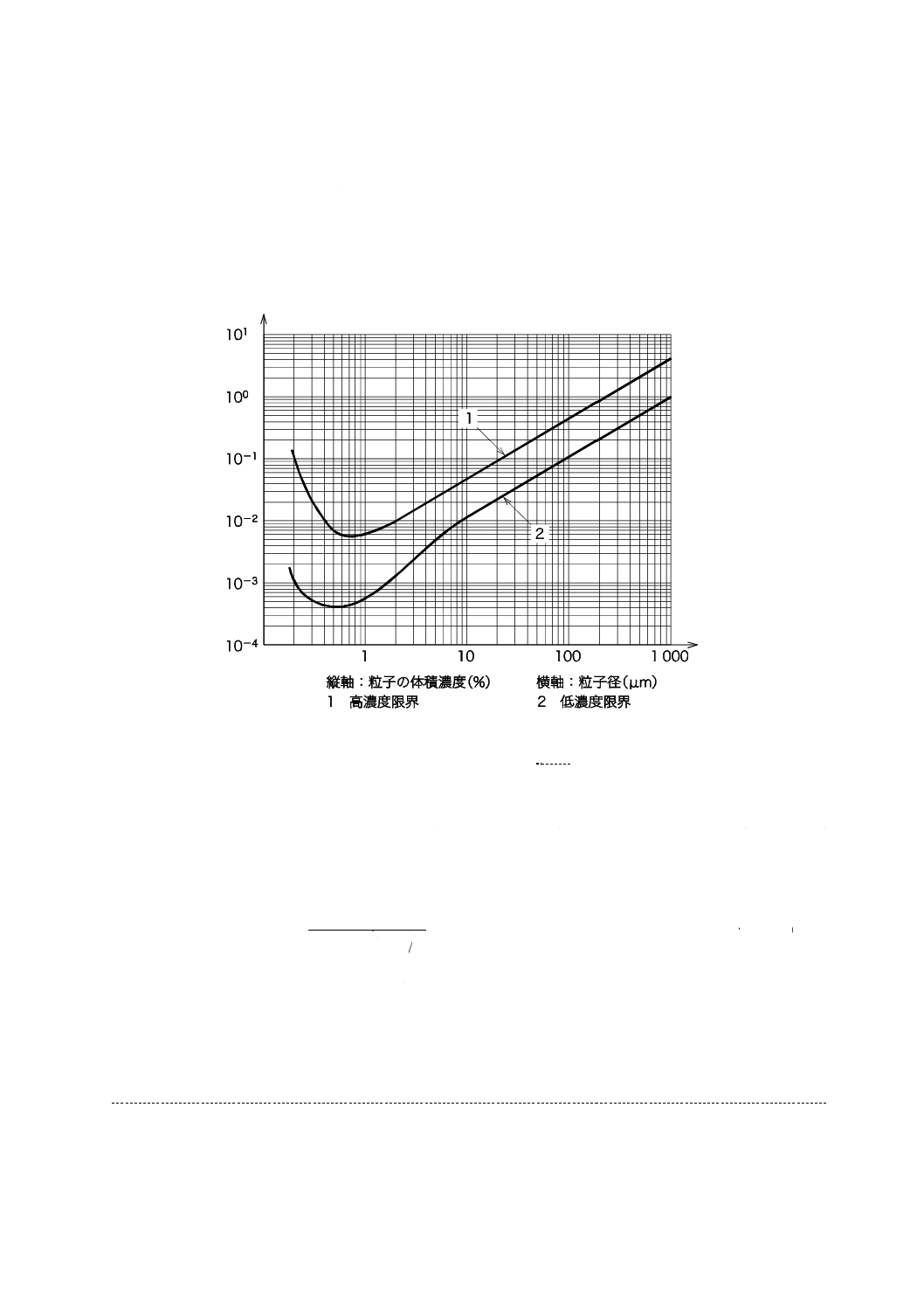
図A.11は,粒子径分布の幅の小さい試料におけるレーザ回折・散乱測定装置の典型的な最大許容粒子濃
度及び最小許容粒子濃度の例である。一例にすぎないが,適切な粒子濃度は,粒子径にほぼ比例すること
を示している。
図A.11−粒子径分布の幅の小さい試料におけるレーザ回折・散乱測定装置の
典型的な最大及び最小許容粒子濃度,光路長 l =2 mm(両対数座標系)
レーザ回折・散乱測定装置には,測定領域の粒子の存在を調べるため,入射レーザビームの減衰を測定
する検出器が備わっていることがある。これは減衰光検出器又は透過光検出器と呼ばれる。減衰率又は透
過率は,多重散乱の著しい影響を避けられる濃度を判定するのに利用できる。
粒子濃度C及び減衰率Oはランベルト-ベールの法則に基づいて,式(A.4)によって関係付けられる。
(
)
(
)
∑
∆
−
−
=
i
j
j
j
x
Q
A
l
O
C
,3
b
3
1
ln
2
···························································· (A.4)
ここに,
Aj: 粒子径区間jの消散係数
lb: 粒子を含む領域の光路長
O: 減衰率
xj: 粒子径区間jの幾何平均粒子径
ΔQ3,j: 粒子径区間jの体積分率
一般的には,多重散乱の影響を受けるかどうかは,試料に含まれる粒子のうち,小さな粒子径区間の粒
子の濃度に支配されるので,どのような分布においても,存在する粒子の最小サイズを考慮して,適切な
濃度を判断しなければならない。粒子径分布の幅が広がると,適切な濃度範囲が変化する。適切な濃度範
囲は,更に,測定光路長,レーザビームの径,及び,検出器感度によって変化する。これらの点について
30
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は個々の装置のマニュアルを参照する。
A.10 データ処理
散乱パターンの計算は,各粒子径区間における単位体積当たりの粒子について,検出器の幾何学的情報
を用いて行う。この計算は,粒子径区間における粒子体積分布が一様であるとして,これらの寄与を積分
し,また,各検出器の受光する角度範囲を積分することで行う。一連の粒子径区間及び検出器に対して,
装置固有のモデル行列が求められる。この行列はn個の粒子径区間それぞれの粒子が単位体積当たりで,
m個の検出器それぞれの信号Ljとしてどのように出力されるか記載している。
•
n
mn
m
n
m
V
V
M
M
M
M
L
L
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
1
1
1
11
1
L
L
L
L
L
L
O
O
O
O
O
O
L
L
L
L
L
L
=
··························· (A.5)
例えば,行列の1行目 (M11 ... M1n) は,n個の粒子径区間の粒子それぞれが単位体積当たりで,1番目の
検出器に検出される信号を示している。一方,最初の列 (M11 ... Mm1) は,第1の粒子径区間の粒子がm個
の検出器それぞれに与える寄与分を表している。異なる測定波長に対しては同様な別の行列を作ることが
できる。行列記号の形で,これを次のように書くことができる。
MV
L=
················································································ (A.6)
この行列形式において,検出器の信号ベクトル(一連の信号の集合)は,離散粒子径分布のベクトルと
モデルマトリックスとの積で表される。しかしながら,実際の測定では,この問題の逆演算が必要になる。
全ての検出器からの信号を測定し,装置固有のモデル行列を用いて,数値的逆演算によって粒子径分布を
求める。
L
M
V
1
−
=
············································································· (A.7)
式(A.7)は,非適切又は悪条件な形式であり,拘束条件がないと僅かな測定誤差も直接逆変換されること
になる。したがって,ある程度の拘束条件は必要である。この拘束条件は製造業者ごとに,装置設計,検
出器数,ノイズレベル及び経験によって相違する。拘束条件の下での逆変換が適切に行えない場合,多分
散試料の粒子径分布データ(グラフ)にゴーストピークが現れるようになる。拘束条件が不足すると,出
力がゼロ又はマイナスになるような不適切な結果となり得る。一方,拘束条件が過剰な場合,分解能を低
下させ,実際の粒子径分布よりも幅の広い分布が出力されることになる。
A.11 粒子形状
球形粒子は,円対称な散乱パターンを示す。これは,一般的に粒子形状と散乱パターンとが関係してい
ることによる。つまり散乱パターンは,粒子と同様な(非)対称性を示す。幾つかの明確な例として,円
形,長方形及び不定形の形状の粒子の示す散乱パターン例を,図A.12に示す。
注記 ただし,フラウンホーファ回折近似の成立する範囲の例である。
非球形粒子の集合体は,同様な散乱パターンを生じる球形粒子の混合体として示される。このような場
合,粒子径分布の測定結果は次の影響を受ける。

31
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 粒子のアスペクト比
b) 測定領域の流れの状態
c) 検出器の配向及び形状
アスペクト比が1に近い粒子群は,測定時にランダムに配向していると仮定することができる。アスペ
クト比が約5以上の粒子群の場合,測定領域の流れ条件が,とり得る配向の確率を決定している。液中分
散している粒子は,レーザ回折・散乱装置の測定領域で通常選択配向していることが示されている(参考
文献[11])。繊維及び薄片試料が,とりわけこうした性質をもっている。このため,粒子のレーザ光照射断
面は,一定の選択配向分布に限定されることになる。
さらに,対応する散乱パターンは,図A.12に示すように円対称性を示さない。このため,検出器の幾何
形状及び方向によって,どの部分の散乱パターンが測定され,粒子径分布に変換されるのかが影響を受け
る。したがって,アスペクト比の大きい粒子の測定結果は,実際に使用する検出器(装置)及び測定部の
流れ条件に依存している。
こうしたことは,得られた粒子径分布についての理解及び解釈のためには,粒子径計測を行う各施設に
おいて高品質の顕微鏡を利用可能にしておくことが必須であることを示している。
図A.12−円形,長方形及び不定形粒子及びその散乱パターン(シミュレーションによる画像)
32
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
試料の分散における留意点
JA.1 気体中の分散(乾式分散)
気体に分散するときは,適切な乾式分散器を使用することが望ましい。大きくて,自由に流れ,重力で
自由落下するような粒子では,通常は十分に分散する。凝集している粒子では,圧縮空気,又は吸引で得
られるせん断応力,粒子どうしの衝突,粒子と壁面との衝突による機械的な破壊分離によって凝集粒子を
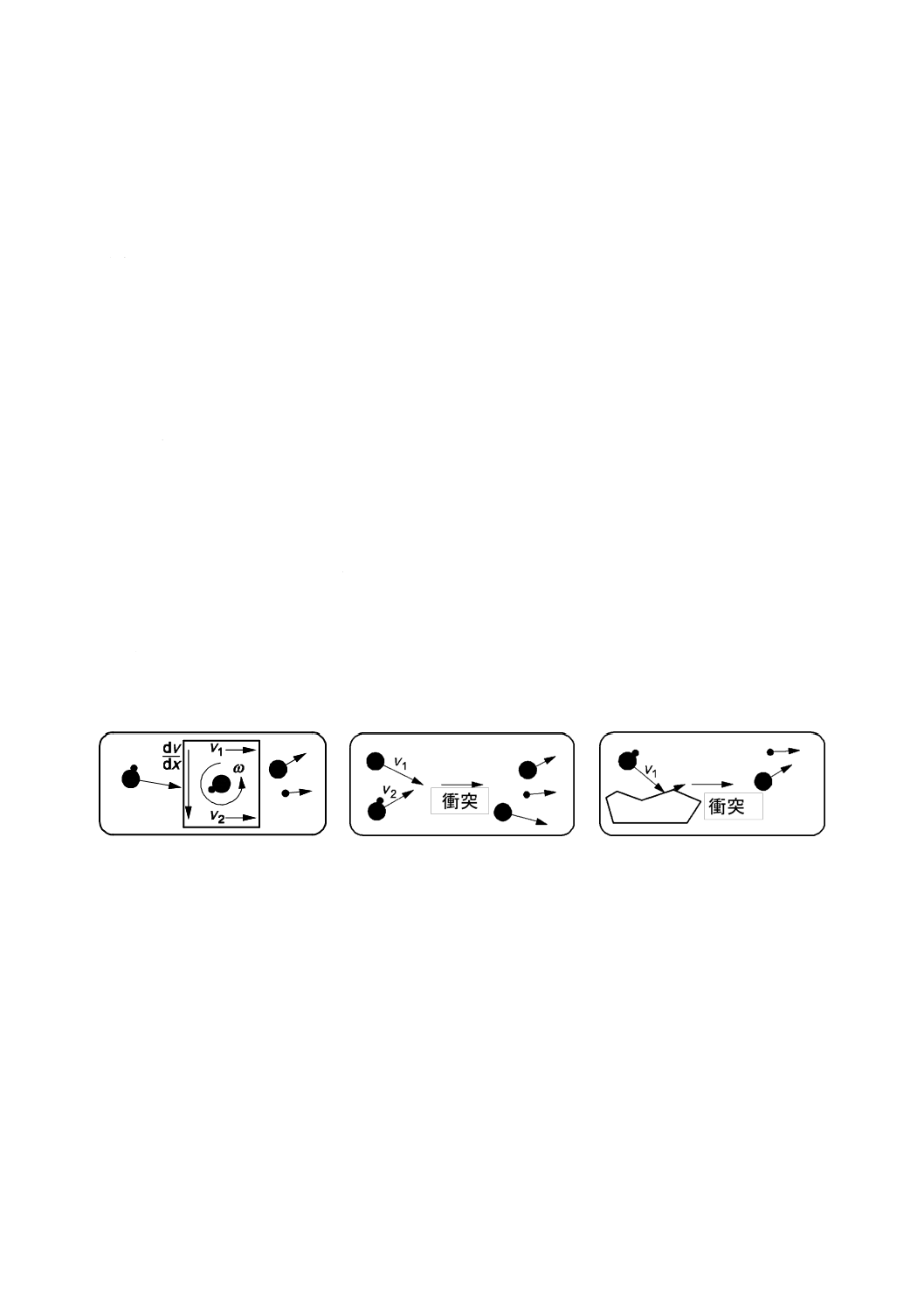
解きほぐして粒子を分散させる(図JA.1)。乾式分散では,縮分試料全部を測定に使う。全ての粒子は測
定領域でほぼ同じ速度であることがよい。粒子径分布が広い粒子群の大粒子径域を適正に測定する目的で,
しばしば多くの試料が使われる。
粒子が粉砕されていないか,また,逆によく分散されているかどうかを確認する。乾式分散と湿式分散
との結果を,直接比較することによって確認する方法がよく用いられる。理想的には,両者の結果が同じ
になることが望ましい。分散又は破砕の度合いを調べるもう一つの方法は,分散エネルギー(例えば,一
次空気圧力)を変化させて,粒子径分布の変化を調べることである。普通,分散エネルギーを大きくして
いくと,最初分散がよくなり,細かい粒子が増加する。その後ある点に達すると,分散エネルギーを大き
くしても粒子径分布が変化せずほぼ一定になる。更に分散エネルギーを大きくすると粒子が破砕されて,
再び細かい粒子が増加することがある。もし,粒子径分布が変化しなくなれば,変化しない範囲の中心が
最適な分散エネルギーとなる。
注記 粒子径分布が変化しない領域は常にあるわけではない。例えば,凝集力が強い粒子,又はもろ
(脆)い粒子等では得られない。
a) 速度勾配によるせん断応力
b) 粒子間の衝突
c) 粒子・壁間の衝突
注記 記号の説明は箇条4を参照。
図JA.1−粉体の乾式分散のプロセス
JA.2 液体中の分散(湿式分散)
液体に分散するときは,JIS Z 8824を参照する。一般に,適正な分散を容易に促進するために,ペース
ト化,かくはん及び超音波照射が用いられる。分散の良否の最初の検査は,肉眼又は顕微鏡による懸樹液
の観察で行う。中くらいの強度で超音波をかけながら,レーザ回折・散乱装置で懸濁液の測定を実施する
ことも可能である。この場合,試料がよく分散されていて,かつ,破砕したり溶解したりする粒子が存在
しないならば,粒子径分布に目立った変化はない。
粒子径分布が広いほど,試料に十分な量の粗粒子が含まれるようにするために,繰り返し測定するため
に必要とする試料の最小量は多くなる(JIS Z 8833参照)。したがって,減衰率が限界となっている場合は,
33
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
これらの試料を懸濁させるのに必要な分散液の量が多くなる。
例えば,JIS Z 8833では,粒子径範囲が約2 μm〜200 μmと広い範囲の粒子を含む試料の場合,x90の粒
子径を3 %の精度で得るには,試料は最低0.3 ml必要であると要求している。
注記 上記はJIS Z 8833で要求している事項であるが,理論上計算される最小試料量は,異なる粒子
の密度などの試料の性状に依存する。
この粒子群からの単散乱を保証するために,最低500 mlの懸濁液が必要になる。また,一回の測定で全
ての粒子径に対して十分な精度を得るために,十分な測定時間,又は十分な積算回数を設定することが望
ましい。適切な測定条件は,要求される測定精度に応じて,実験的に決めるのがよい。
分散に用いる液体は,次の条件を満足することが望ましい。
a) 測定に用いているレーザ光源の波長に対して透明である。
b) 装置に用いられている材料(Oリング,チューブ等)を侵さない。
c) 粒子試料を溶解せず,粒径を変化させない。
d) 気泡及び試料以外の粒子を本来含まない。
e) 粒子試料を容易にかつ安定に分散できる。
f)
粒子試料と大きく異なる屈折率をもつ。
g) 循環(かくはん)が可能な粘度である。
h) 危険物ではなく安全衛生上の要求事項を満足する。
分散に用いる液体には,水がしばしば用いられる。表面張力を低下させる(かつ,これによってぬれ性
を良くする。)ために,低発泡性の表面活性剤を加えてもよく,分散を安定化させるために分散剤(多くの
場合高分子電解質)を加えてもよい。エタノール,2-プロパノール(イソプロピルアルコール),n-ヘクサ
ン,イソオクタンなどの有機溶媒も選択可能である。JIS Z 8824及び参考文献[35-36]を参照。
34
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JB
(参考)
レーザ回折・散乱測定における注意事項
JB.1 一般的注意事項
一般的注意事項について次に示すが,装置,測定対象又は応用によって異なる部分があるので,個々の
装置のマニュアルを参照する。
a) 電源投入前に,システムの各部が適正に接地されていることを確認する。超音波分散槽,乾式分散器,
吸引口及び吸引ホースのような全ての粒子分散装置及び輸送装置は,有機溶媒の引火又は静電気放電
による粉じん爆発を防止するため,必ず接地する。
b) 電源投入後,装置が安定するまで十分な時間待つ。He-Neのようなガスレーザは適切な暖機(通常30
分以上)が必要である。
c) 装置の状態を点検し,必要に応じて所要の測定範囲及びレンズを調整する。手動のシステムでは,検
出器の信号器の散乱光強度を見て,検出器が適正にレンズ焦点面上の中心に位置していることを確認
する。粒子がない状態でのバックグラウンド信号は,装置の構成に応じて指定されるいき(閾)値以
下であることが望ましい(そうでない場合,点検を行い,必要ならば光学部品が適正な性能となるよ
うに清掃する。)。
d) 粒子は全てがレーザビームの照射範囲で,レンズのワーキングディスタンスに的確に投入する。この
ことによって,粒子から発する全ての散乱光が,検出器に焦点を合わせているレンズのアパーチャー
内にきちんと入ることになる。
e) 粒子径分布の分かっている標準試料を用いて,定期的に測定し,精度及び正確さの双方について装置
の動作を確認(検証)し(7.4及び7.5.2参照),日付及び結果を記録する。
f)
湿式分散の場合,分散液中に気泡がないことを確認する。気泡は,分散液の表面で容易に目視できる
か,又は,小さい角度の検出器の不規則な信号の揺らぎとして(リアルタイム表示が可能であれば),
若しくは,透過率又は吸光率の強い揺らぎによって検出できる。泡が発生するような薬剤(例えば,
界面活性剤)は,可能な限り避ける。
g) 乾式分散の場合,目視又は吸光量の点検によって,供給装置が一定の質量流量で動作していることを
確認する。
h) エアロゾル及びスプレの測定で測定領域が装置の内部にない場合には,日光が直接であれ,粒子から
の散乱であれ,いずれにせよ検出器に入らないようにする。また,粒子(液滴も含む。)の流れが一様
であることを確認する。
i)
可能ならば,粒子径分布の結果に及ぼす光学モデルの影響を調べる。
35
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JC
(参考)
測定誤差の要因及びその分析
JC.1 一般
系統的測定誤差(偏り)の発生要因及びその分析方法について,次に示す。
JC.2 試料調製で生じる誤差
試料調製で生じる誤差は,しばしば全体の誤差へ最も大きく寄与し,誤差全体の大部分を占めることが
ある。それらは,次のような要因による。
a) 不適切なサンプリング法を用いた結果,測定領域へ系を代表しない試料が送り込まれることとなる。
この種の誤差は,粒子径分布が広く流動性のよい物質の,大量の試料を不適切なサンプル分割法によ
って分割した場合に,特に顕著になる。装置内において,粒子の大きさによる選択的な輸送によって
も誤差が生じる。例えば,循環ポンプ速度が極端に遅い場合には,循環系内に大きな粒子が沈降する。
不適切なフローシステムによって,測定前に測定系から粒子が失われることがある。
b) 分散手順が不適切で,凝集粒子の分散操作が不完全な場合(不適切な分散媒,分散剤,超音波照射)。
c) 分散中の機械的作用力による粒子の粉砕(例えば,湿式測定中の超音波照射,又は過剰な差圧,及び
/又は乾式測定中の壁との衝突)。これらの影響は,高アスペクト比,かつ,もろい・砕けやすい粒子
に対して,常に,より顕著である。
d) 測定前,又は測定中の粒子(液滴も含む。)の膨潤,再凝集,溶解,又は蒸発。
e) 発泡性の分散剤及び過度のかくはんによる気泡の混入。
f)
例えば,分散液の蒸発又は外部の熱源による温度変化で,分散液又は気体の屈折率が変わってしまう
ことによるばらつき。
JC.3 粒子性状の理論的仮定とのずれ
試料粒子の性状と理論的仮定とのずれによって系統誤差が生じる。ここにも,次の多くの要因がある。
a) 非球形性:多くの実在粒子は球形という仮定を満たさない。非球形粒子の散乱断面積は,光源に対す
る粒子の配向方向に影響される。粒子は全ての可能な配向方向を向いているものと仮定されているが,
この仮定はいつも正しいとは限らない。特に高いアスペクト比の粒子は,配向しやすい方向がある。
b) 表面粗さ:粒子表面は滑らかでなく凹凸がある。それによって表面において拡散的な光散乱が起き,
ランダムな光散乱によって光が消失する。これは粒子内での光吸収としばしば同じ効果がある。
c) 光学的不均一性:凝集,又は多孔質粒子,若しくは異なる成分の混合物のように,粒子が光学的に不
均一である場合がある。結晶性の材料は,観測軸に依存した異なる屈折率を示す。異なる屈折率の材
料の混合物に対して,単一の屈折率の値しか用いることができないにもかかわらずミー理論を適用す
ると,適切な結果が得られないことがある。
d) 蛍光:材料によっては,吸収された光が蛍光として再放射される。蛍光放射の角度分布は粒子径に関
係しないので,粒子径分布の決定を妨げる。
e) 不適切な光学モデル又はパラメータ:最後に最も重要なのが,正しくない(不適切な)光学モデル又
はパラメータが選択されることによる誤差である。例えば,フラウンホーファ回折近似が,小さくて
36
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
透明な粒子をある程度含んでいる試料に適用された場合,小さな粒子径区間の粒子量に重大な誤差が
現れ,多量の小粒子が存在するように計算される(附属書A参照)。一般に正しくないモデル,又は
パラメータの選択を行うと,装置によって計算された粒子濃度と分散媒の体積及び粒子質量から求め
た濃度との間に(大きな)差が現れる(JC.5参照)。
JC.4 操作手順又は装置の機能に起因する誤差
次の場合が考えられる。
a) 測定粒子径範囲外の粒子が存在する場合。この場合,測定範囲を変える(レンズを変える)及び/又
は粗い粒子を前もって,例えば,ふるい分けで除去する。
b) レーザビームの,レンズのワーキングディスタンスの外側領域への試料の投入。
c) 汚れたレンズ又は測定セル。この場合,清掃することが望ましい。
d) 次の要因によるバックグラウンドレベルが高すぎる状態での測定。装置内部でのレーザビームの反射,
集光レーザビームの過大な広がり,集光レーザビームと小角度散乱光検出器との重なり(位置調整ミ
ス),測定体積中の大きな温度変動,又は周囲の光の侵入。
e) 不適切な光学系の位置調整
f)
多重散乱が起こるような高い濃度
g) 信号雑音比が低くなりすぎるほどの低い濃度
h) 光強度から粒子径分布への不適切な逆演算処理 (装置の製造業者に問い合わせる必要がある。)
JC.5 ランダム誤差
JC.4に示されている諸点についての管理が悪いと偶発的な誤差が生じる。さらに,ランダム誤差は,次
のような場合に生じる。
a) 不十分な測定時間,又は検出器からのデータの積算回数不足
b) 大きく外れた減衰率条件(粒子濃度)での測定
c) 装置上の欠陥,例えば,レーザ強度の変動又は検出器の異常ノイズ
JC.6 誤差要因の診断
測定手順の特定部分の誤りは,次の操作で診断される。
a) 少なくとも1時間ブランク状態でレーザ強度を測定する。その値は取扱説明書に与えられている範囲
内で安定していることが望ましい。
b) ブランク測定の間,全検出器の信号を観察する(もし信号のリアルタイム表示が可能であれば)。バッ
クグラウンド信号は,僅かにプラスの値をとるか,又はゼロで安定な挙動を示していることが望まし
い。マイナス又は過負荷出力(100 %)は,検出器の欠陥,電子部品の故障又はセル若しくはレンズ
に汚れかキズがあることを意味することがある。一部の検出器が異常な強度を示すのは,レンズの損
傷,光学セル表面又はレーザ光で照射された他の部品表面からの反射が原因であることが多い。
c) 揮発性の溶媒を用いる場合,その蒸発によって温度変動が起こり,レーザビームが内部の検出器へ曲
げられることで,バックグラウンド測定中の過度の検出信号変動の原因にしばしばなっている。この
結果として,測定範囲の上限に偽のピークが生じる。これらの場合には,温度変動がおさまるまで十
分に長い時間待つのがよい。揮発性の液体系に超音波を照射すると,同じような影響が生じ,変動が
おさまるまでに時間を要する。
37
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 繰り返して試料を測定し,その検出信号を観察する。各素子の平均値及び標準偏差を計算する。全て
の検出器の測定信号を以前に測定されたものと系統的に比較することで一貫性が確実になる。このよ
うにして,信号の精度及び正確さの所見が得られる。信号に系統的な大きな誤差があったり,出力が
ゼロの場合には,通常検出器の欠陥,電子部品の故障,セル又はレンズの汚れ,配置の不良,気泡の
混在,又は,サンプリング及び/又は分散手順に問題があることがある。
e) 試料の粒子濃度が既知であれば,その値と理論値とを比較する。全ての粒子のアスペクト比が4より
小さい粒子系では(参考文献[34]参照),その既知の粒子濃度の試料と式(A.4)に示される式を用いて計
算された粒子濃度とを比較することで,選択した光学モデル及び屈折率の値が適切であることを確認
できる。
f)
アスペクト比が小さな粒子系では,この二つの濃度における僅かな違いから,選択した光学モデル及
び屈折率の正当性が確認できる。これらの値が大きく異なる場合には,原因についての詳細な検討が
必要である。最もよく一致する粒子径分布が得られた後で,全ての検出器に対して測定信号と計算で
求められた値とを比較する。もしも大きい系統誤差があるならば,いずれかの検出器の欠陥,コンタ
ミネーションの存在又は光学モデルが不適切であることを示している。
38
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JD
(参考)
レーザ回折・散乱法に用いる標準物質
JD.1 標準物質
正確さの検証に用いる標準物質としては,“トレーサブルな球形”粒子であり,“分布の幅としてx90 / x10
比が少なくとも1.5であるような既知の粒子径分布を構成しているとともに,通常の密度及び光学的特性
をもつ”ことが必要である。上記の条件を満足する認証標準物質CRMとして,JIS Z 8900-1:2008[5]に規
定されている粒子径範囲の異なる3種類の粒子が入手可能である。
標準物質名:JIS粒子径測定装置検定用粒子
MBP10〜100
MBP3〜30
MBP1〜10
頒布機関: 一般社団法人日本粉体工業技術協会
39
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JE
(参考)
JISと対応国際規格との対比表
JIS Z 8825:2013 粒子径解析−レーザ回折・散乱法
ISO 13320:2009 Particle size analysis−Laser diffraction methods
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
1 適用範
囲
1
JISと同じ
一致
2 引用規
格
3 用語及
び定義
3.1
JISとほぼ同じ
変更
削除
追加
他の関連規格と整合させ,3.2
(記号)については,箇条4
として独立
3.10において“減衰率”に用
語を統一,“光学濃度”は誤用
であるので削除
3.22において“透過率”に用
語を統一
3.24〜3.26に“検出器”,“標
準物質”,“認証標準物質”の
定義を追加
ISO 13320の改訂を働きかける。
ISO TC24/SC4で検討中の用語標
準への反映を図る。
4 記号
3.2
JISとほぼ同じ
変更
他の関連規格と整合させ,記
号については箇条4として独
立
以後の箇条番号を合わせて変
更
ISO 13320の改訂を働きかける。
2
Z
8
8
2
5
:
2
0
1
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
40
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
5 原理
4
JISとほぼ同じ
変更
削除
追加
第2段落と第1段落との順序
を変更
第2段落中回折パターンの図
(図1)及び関連記載を削除
原理についての注記を追加
根本的原理説明から始める方が
理解しやすい。
ISOに引用された図は限定され
た条件のものでありかえって誤
解を招くおそれがある。
6 レーザ
回折・散
乱装置
6.1 装置の構成
5
JISとほぼ同じ
追加
変更
削除
JISで,6.1見出しを追加
第2段落中の""In this Fourier
set-up""を削除
図(図2)を変更
ISOの第3,4段落(試料の導
入に関する記載)については
段落分けせず,第4段落の記
載を第3段落の中間に置くよ
う順序変更
光散乱強度分布から,各検出
素子位置による離散化・光電
変換検出を経るデータまでの
変換に至る記載を削除
第5-8段落は5.2へ移動
光散乱強度分布から,各検出
素子位置による離散化に関す
る記載を削除
第9段落を5.3へ移動
規格の構成を明確化し理解を助
ける。
限定されない一般的な記載であ
るため。
フラウンホーファ回折測定の図
を,ミー理論に基づく測定を含
む,より一般的な図に変更。
理解を助ける。他の部分の記載で
は,まず気体,次いで液体となっ
ているので,合致させた。
正確な説明は難しく,ユーザにと
って不要であり,装置構成によっ
ては必ずしも該当せず,概略説明
はかえって混乱の元となるおそ
れがある。
特定の装置構成の説明を一般的
なものと明確に区別する。
一般的な理解のためには必要な
く,装置構成によっては該当しな
い。
特定の装置構成の説明を一般的
なものと明確に区別する。
2
Z
8
8
2
5
:
2
0
1
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
41
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
6 レーザ
回折・散
乱装置
第10段落を削除
第11,12段落を5.3へ移動
図(図4)を削除
第13段落を削除
4 原理に重複記載がある。
理解を助ける。
図が一般的ではなく,また,図2
に替えて新しく加えた図1と重
複する。
装置の差異を強調する必要はな
く,かえって理解の妨げになる。
6.2 前方散乱光測
定のための光学系
5
JISとほぼ同じ
追加
変更
JISで,6.2見出しを追加
第9段落の記載については,
詳細な記載になるため,注記
に移動
規格の構成を明確化し理解を助
ける。
6.3 種々の装置構
成
5
JISとほぼ同じ
追加
JISで,6.3見出しを追加
規格の構成を明確化し理解を助
ける。
7 操作手
順
7.1 前提条件
6
6.1
JISとほぼ同じ
変更
7.1.2と7.1.3の順序を変更
他の部分の記載では,まず気体,
次いで液体となっているので,合
致させた。
7.2.1 検査
6.2.1
JISとほぼ同じ
追加
注記を追加
試料によっては記載の方法では
検査が困難な場合があるため。
7.2.2 調製
6.2.2
JISとほぼ同じ
変更
引用規格について明記
引用規格との関係を明確化する
ため。
7.2.3 分散
6.2.3
JISとほぼ同じ
削除
変更
対応国際規格の6.2.3.1の記載
を残し,6.2.3.2及び6.2.3.3の
記載を削除(附属書JAに移
動)
記載が参考的であり,詳細な説明
であるが応用範囲が限定的で,液
中分散に関してはJISとの重複
も多いため,本体から削除し,附
属書に移動。
ISO 13320の改訂を働きかける。
7.2.4 濃度
6.2.4
JISとほぼ同じ
変更
付随情報についての記載を節
末に移動
理解を助ける。
2
Z
8
8
2
5
:
2
0
1
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
42
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
7 操作手
順
7.3.1 手順
6.3.1
JISとほぼ同じ
追加
対応国際規格の6.3.1.2〜
6.3.1.6の見出しに相当する手
順概略をJISの7.3.1.1に追加
手順を明確化し,理解を助ける。
ISO 13320の改訂を働きかける。
7.3.2 注意事項
6.3.2
JISとほぼ同じ
削除
変更
対応国際規格の6.3.2.1の記載
を残し,6.3.2.2〜6.3.2.10の記
載を削除(附属書JBに移動)
記載が参考的であり,一般的なが
ら詳細な説明であり,個々の機器
又は応用によっては,不要又は実
行不可能な記載も含まれるため,
附属書に移動。ISO 13320の改訂
を働きかける。
7.4 精度の評価
6.4
JISとほぼ同じ
変更
箇条の題名を変更
ISO 13320の改訂を働きかける。
7.4.3 再現性
6.4.3
JISとほぼ同じ
変更
認証標準物質ではない標準物
質の場合には必ずしも不確か
さについて記載がないことか
ら,記述を削除
ISO 13320の改訂を働きかける。
7.5 正確さの評価
6.5
JISとほぼ同じ
変更
箇条の題名を変更
対応国際規格に規定のない認
証標準粒子がJISに規定され
ているため,記載を追加
ただし,我が国では国家計量
標準機関が認証している認証
標準物質はないため,関連記
述は削除
ISO 13320の改訂を働きかける。
対応国際規格の制定を働きかけ
ている。
7.6 誤差の要因及
びその診断
6.6
JISとほぼ同じ
削除
変更
対応国際規格の6.6.1の記載
を残し,6.6.2〜6.6.6の記載を
削除(附属書JCに移動)
記載が参考的であり,過剰に詳細
であり,個々の機器又は応用によ
っては無関係な記載も含まれる
ため,本体から削除し,附属書に
移動。ISO 13320の改訂を働きか
ける。
2
Z
8
8
2
5
:
2
0
1
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
43
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
7.7 分解能及び感
度
6.7
JISと同じ
一致
−
−
8 測定結
果の記録
7
JISとほぼ同じ
変更
追加
記録項目について,必須事項
ではなく,推奨事項とした。
屈折率の記録につき注記を追
加
必須とされる記録項目の一部に
ついては,利用者が情報を容易に
は入手できないことがあるため。
併せて,この規格を引用し特定の
物質を対象とする個別規格等と
の整合性の確保を容易とするた
め。ISO 13320の改訂を働きかけ
る。
当該記録が重要になる場合を示
し,理解を助ける。
附属書A
(参考)
レーザ回折・散乱の
理論的背景
Annex A
(informative)
変更
図A.2を変更
図A.3を変更
図A.4を変更
図A.5を変更
図A.9を変更
図A.10を変更
図A.11を変更,併せて関係す
るA.9節の記述を変更
式A.5〜A.7を変更
図が分かりにくい,及び/又は計
算結果が正確ではないため。
ISO 13320の改訂を働きかける。
附属書JA
(参考)
試料の分散におけ
る留意点
Annex C
(informative)
追加
対応国際規格の6.2.3.2及び
6.2.3.3の記載と併せて,一つ
の附属書とした。
−
附属書JB
(参考)
レーザ回折・散乱測
定における注意事
項
−
−
追加
対応国際規格の6.3.2.2〜
6.3.2.10の記載を附属書とし
た。
−
附属書JC
(参考)
測定誤差の要因及
びその分析
−
−
追加
対応国際規格の6.6.2〜6.6.6
の記載を附属書とした。
−
2
Z
8
8
2
5
:
2
0
1
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
44
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
附属書JD
(参考)
レーザ回折・散乱法
に用いる標準物質
−
−
追加
対応国際規格の6.5で引用さ
れている標準粒子について附
属書に記載
規格への適合判断の基準となる
標準物質について附属書に明記
した。
−
−
Annex B
(informative)
削除
−
参考記載であり,個々の機器に依
存し,機器構成によっては記載で
きない事項も含まれるため削除
した。
−
−
Annex D
(informative)
削除
−
参考記載であり,また,現在の機
器では使用していない波長によ
るデータが多く,かえって混乱を
招くおそれがあるため削除した。
なお,本記載が引用していたデー
タの記載がある文献については,
附属書Bに掲載した。
−
−
Annex E
(informative)
削除
−
参考記載であり,必ずしも定まっ
たものではなく規格の要求事項
と誤解を生じるおそれがあり,本
体の記載との重複があるため削
除した。
JISと国際規格との対応の程度の全体評価:ISO 13320:2009,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 一致……………… 技術的差異がない。
− 削除……………… 国際規格の規定項目又は規定内容を削除している。
− 追加……………… 国際規格にない規定項目又は規定内容を追加している。
− 変更……………… 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD…………… 国際規格を修正している。
2
Z
8
8
2
5
:
2
0
1
3
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
45
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] JIS Z 8101-1:1999 統計−用語と記号−第1部:確率及び一般統計用語
[2] ISO 80000-7:2008,Quantities and units−Part 7: Light
[3] IEC 60050-845:1987,International electrotechnical vocabulary−Lighting
[4] JIS Q 0035:2008 標準物質−認証のための一般的及び統計的な原則
[5] JIS Z 8900-1:2008 標準粒子−第1部:粒子径測定装置検定用粒子
[6] 松山 達,ミーの散乱理論の導出,粉体工学会誌,2006,43(2),pp.115-129
[7] HULST, H.C. VAN DE. Light scattering by small particles. Dover, New York, NY, 1981. 470 p.
[8] BORN, M., WOLF, E. Principles of optics: Electromagnetic theory of propagation, interference and diffraction
of light, 7th edition. Cambridge University Press, Cambridge, UK, 1999. 1200 p.
[9] BAYVEL, L.P., JONES, A.R. Electromagnetic scattering and its applications. Applied Science, London, 1981.
289 p.
[10] BOHREN, C.F., HUFFMAN, D.R. Absorption and scattering of light by small particles. Wiley, New York, NY,
1983. 530 p.
[11] BERTHOLD, C., KLEIN, R., LÜHMANN, J., NICKEL, K.G. Characterization of fibres and fibre collectives
with common laser diffractometers. Part. Part. Syst. Charact. 2000, 17, pp. 113-116
[12] PHILLIPS, D.L. A technique for the numerical solution of certain integral equations of the first kind. J. Assoc.
Comput. Mach. 1962, 9, pp. 84-97
[13] TWOMEY S. On the numerical solution of Fredholm integral equations of the first kind by the inversion of the
linear system produced by quadrature. J. Assoc. Comput. Mach. 1963, 10, pp. 97-101
[14] PIKE, E.R., MCWHIRTER, J.G., BERTERO, M., DE MOL, C. Generalised information theory for inverse
problems in signal processing. IEE Proc. F: Commun. Radar Signal Proc. 1984, 131, pp. 660-667
[15] HEUER, M., LESCHONSKI, K. Results obtained with a new instrument for the measurement of particle size
distributions from diffraction patterns. Part. Charact. 1985, 2, pp. 7-13
[16] XU, R. Particle characterization: Light scattering methods. Kluwer, Dordrecht, 2000. 397 p. (Powder
Technology Series, Vol. 13.)
[17] HECHT, E. Optics, 4th edition. Addison-Wesley, San Francisco, CA, 2002. 698 p.
[18] BOXMAN, A., MERKUS, H.G., VERHEIJEN, P.J.T., SCARLETT, B. Deconvolution of light-scattering
patterns by observing intensity fluctuations. Appl. Opt. 1991, 30, pp. 4818-4823
[19] LIDE, D.R., editor. CRC handbook of chemistry and physics. CRC Press, Boca Raton, FL, published annually
[20] WASHBURN, E., editor. International critical tables of numerical data: Physics, chemistry and technology:
Index to volumes 1-6. McGraw-Hill, New York, NY for National Research Council, USA, 1933
[21] LANDOLT, H.H., BÖRNSTEIN, R., EUCKEN, A. Zahlenwerte und Funktionen aus Physik, Chemie,
Astronomie, Geophysik und Technik [Numerical values and functions from physics, chemistry, astronomy,
geophysics and technology], 28 volumes, 6th edition. Springer, Berlin, 1950-1980
[22] PALIK, E.D., editor. Handbook of optical constants of solids: Part I. Academic Press, Orlando, FL, 1985;
PALIK, E.D., editor. Handbook of optical constants of solids: Part II. Academic Press, Orlando, FL, 1991;
PALIK, E.D., editor. Handbook of optical constants of solids: Part III. Academic Press, San Diego, CA, 1998.
46
Z 8825:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
999 p. O'Neil Ed. The Merck Index, MERCK & Co., Rahway, N.J, 2006
[23] 化学大辞典編集委員会 編,化学大辞典,共立出版,東京,1964
[24] 飯田 修一編 物理定数表,朝倉書店,東京,1978
[25] ヴェ・エム・ゾロタリョフほか,天然及び人工媒質の光学定数,日ソ通信社,和歌山,1986
[26] 日本化学会編,化学便覧,丸善,東京,2004
[27] 物理学辞典編集委員会編 物理学辞典,培風館,東京,2005
[28] 日本物理学会編 物理データ事典,朝倉書店,東京,2006
[29] HIRLEMAN, E.D., FELTON, P.G., KENNEDY, J. The status of U.S. efforts toward calibration standardization
for laser diffraction instruments. In: Leschonski, K., editor. Proceedings of the 5th European Symposium on
Particle Characterization (PARTEC), pp. 655-671. Nürnberg Messe, Nürnberg, 1992
[30] 早川 修,中平 兼司,椿 淳一郎,レーザー回折・散乱法における最適屈折率の推定法,粉体工学会誌,
1995,30(9),pp. 652-659
[31] 早川 修,安田 佳弘,内藤 牧男,椿 淳一郎,レーザー回折・散乱法における入力光学特性値が粒子
径分布測定結果に及ぼす影響,粉体工学会誌,1995,32(11),pp. 796-803
[32] 木下 健,レーザー回折・散乱法における最適屈折率パラメータの決定法,2000,粉体工学会誌,37(5),
pp.354-361
[33] 木下 健,レーザー回折・散乱法における適正屈折率パラメータ決定用評価関数の検討,2008,粉体工
学会誌,45(2),pp.104-109
[34] JONES, A.R. Error contour charts relevant to particle sizing by forward scattered lobe methods. J. Phys. D:
Appl. Phys. 1977, 10, pp. L163-L165
[35] BERNHARDT, C. Particle size analysis, classification and sedimentation methods, FINKEN, H., translator.
Chapman & Hall, London, 1994. 482 p.
[36] NELSON, R.D. Dispersing powders in liquids. Elsevier, Amsterdam, 1988. 245 p. (Handbook of Powder
Technology, Vol. 7.)




















