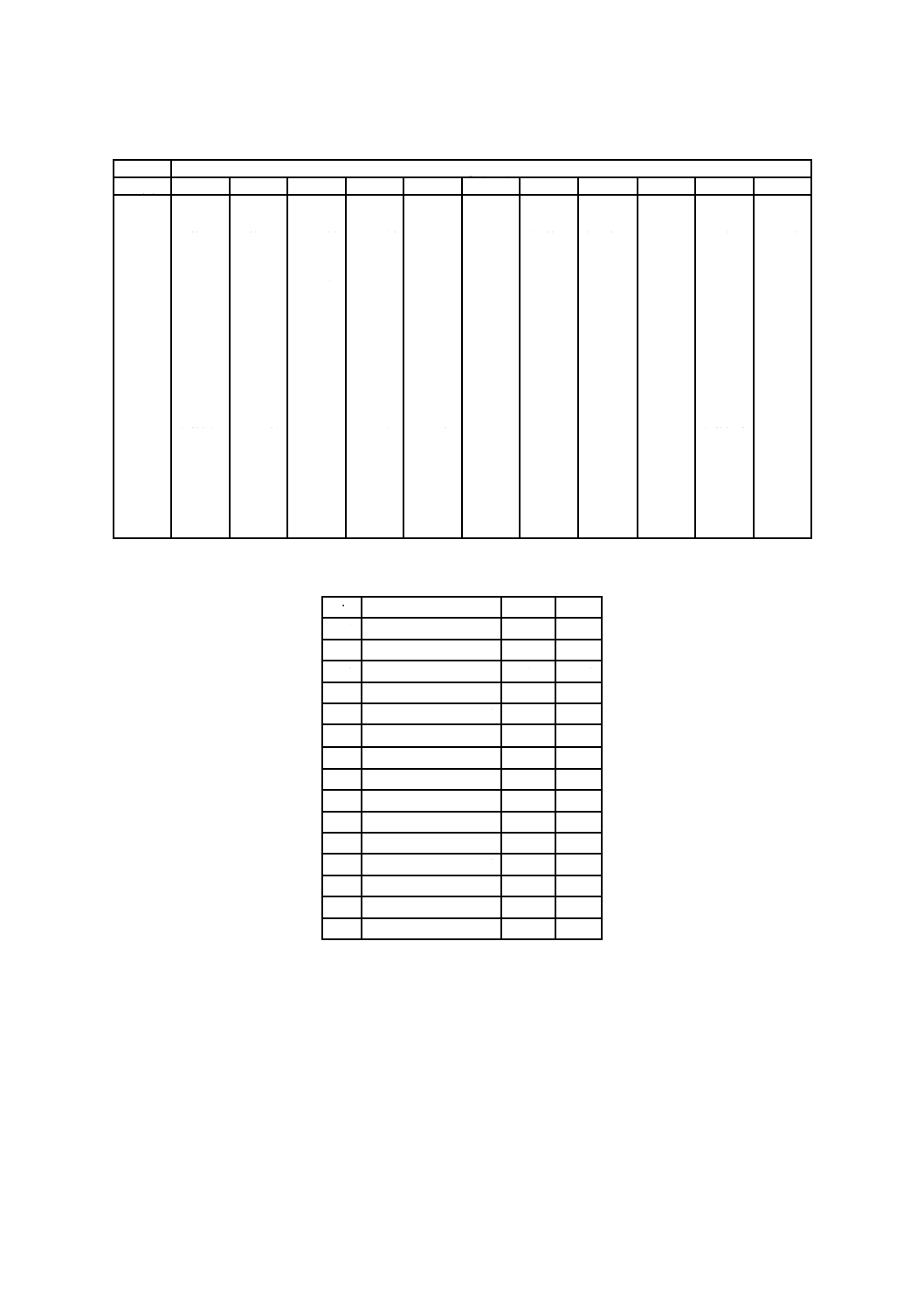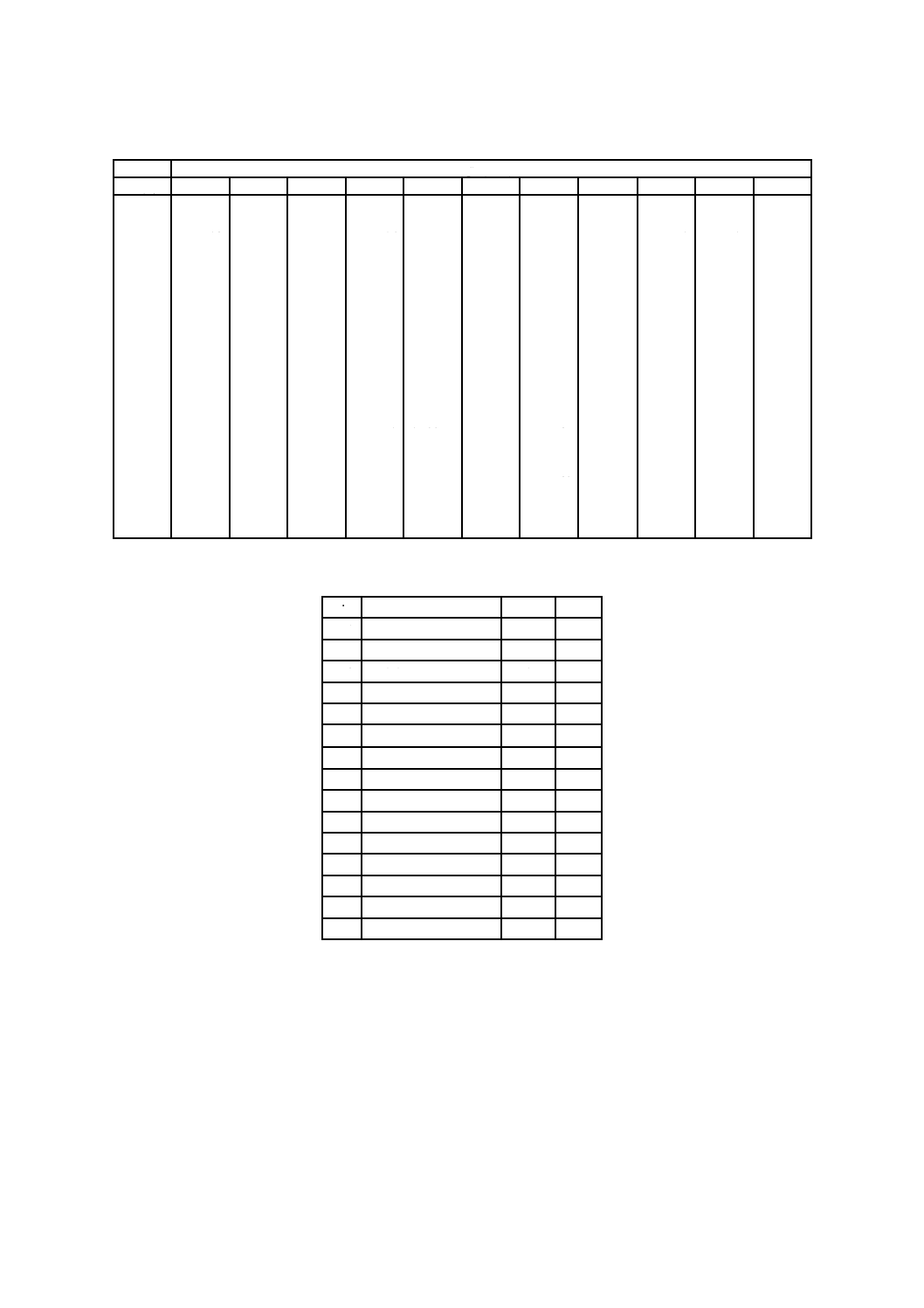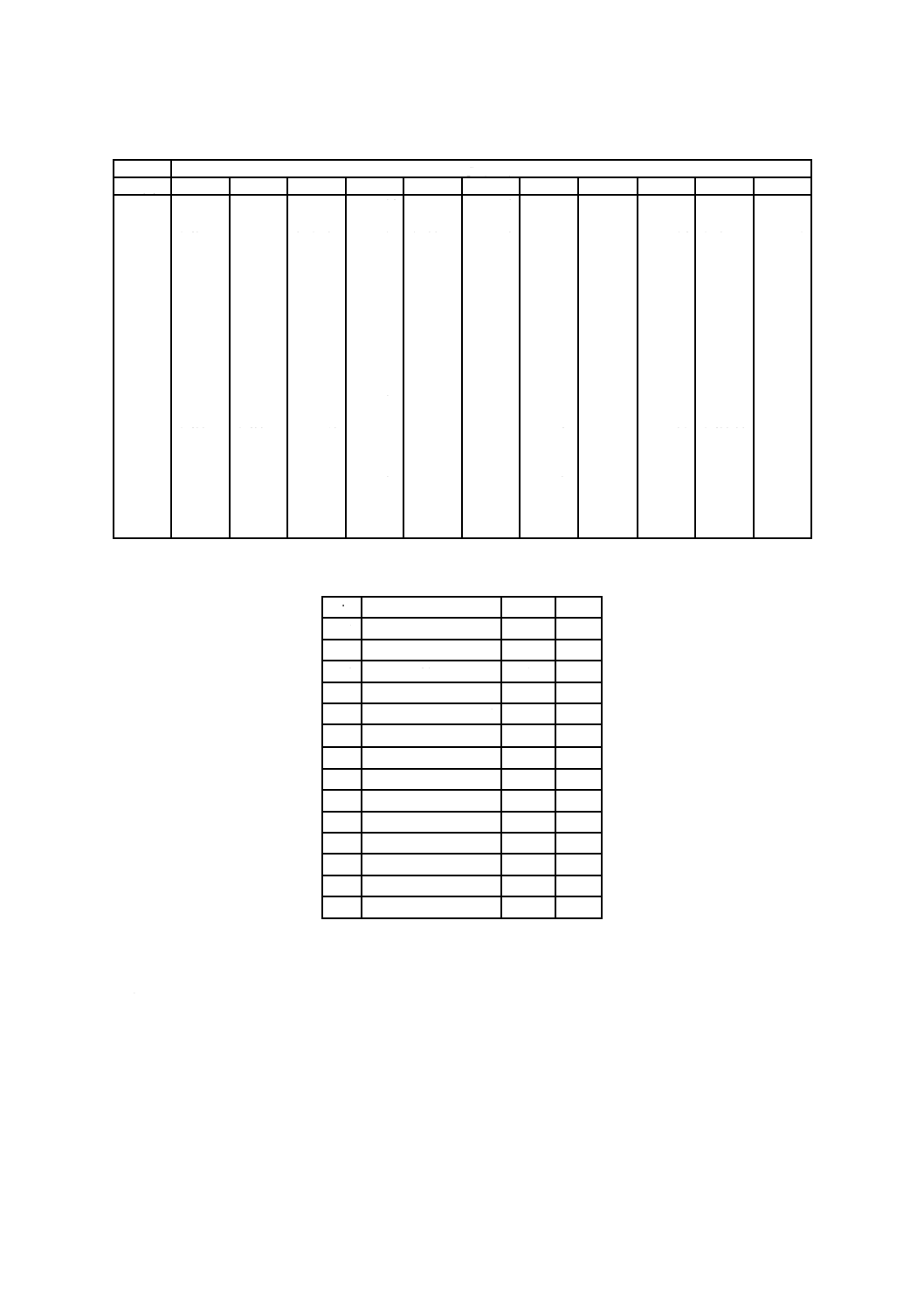Z 8767:2006 (ISO/DIS 9300:2003)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,独立行政法人産業技術総合研究所(AIST)/社
団法人日本計量機器工業連合会(JMIF)から,工業標準原案を具して日本工業規格を制定すべきとの申出が
あり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
制定に当たっては,日本工業規格と国際規格との対比,国際規格に一致した日本工業規格の作成及び日
本工業規格を基礎にした国際規格原案の提案を容易にするために,ISO/DIS 9300:2003,Measurement of gas
flow by means of critical flow Venturi nozzlesを基礎として用いた。
この規格の一部が,技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願公開後の
実用新案登録出願に抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会
は,このような技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願公開後の実用新
案登録出願にかかわる確認について,責任をもたない。
JIS Z 8767には,次に示す附属書がある。
附属書A(規定) ベンチュリノズルの流出係数
附属書B(規定) 様々な気体に関する臨界流れ関数C*の値の表
附属書C(規定) 混合天然ガスの臨界質量束の計算
附属書D(規定) 大気の質量流量補正式
附属書E(規定) ノズルスロートと配管との直径比βが0.25以上の場合の臨界ノズルの臨界質量束
の計算
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 定義 ······························································································································ 2
4. 記号 ······························································································································ 3
5. 基礎式 ··························································································································· 4
5.1 状態方程式 ··················································································································· 4
5.2 理想状態での流量 ·········································································································· 4
5.3 実際の状態における流量 ································································································· 5
5.4 臨界質量束 ··················································································································· 5
6. 適用 ······························································································································ 5
7. 標準臨界ベンチュリノズル(CFVN) ·················································································· 6
7.1 一般要求事項 ················································································································ 6
7.2 形状 ···························································································································· 6
8. 設置に関する要求事項 ······································································································ 9
8.1 一般 ···························································································································· 9
8.2 上流側が配管の場合 ······································································································ 10
8.3 上流側がチャンバの場合 ································································································ 10
8.4 下流側に関する要求事項 ································································································ 10
8.5 圧力測定 ····················································································································· 10
8.6 排水孔 ························································································································ 11
8.7 温度測定 ····················································································································· 11
8.8 密度測定 ····················································································································· 11
8.9 密度の計算 ·················································································································· 11
9. 計算方法 ······················································································································· 12
9.1 質量流量qm ·················································································································· 12
9.2 流出係数Cd ·················································································································· 12
9.3 臨界流れ関数C*及び実在気体臨界流れ係数CR ···································································· 12
9.4 圧力及び温度の測定値のよどみ点状態への変換 ··································································· 12
9.5 下流側に許される最大圧力······························································································ 13
10. 流量測定の不確かさ ······································································································ 14
10.1 一般 ·························································································································· 14
10.2 不確かさの実際の計算 ·································································································· 15
附属書A(規定)ベンチュリノズルの流出係数 ········································································· 16
附属書B(規定)様々な気体に関する臨界流れ関数C*の値の表 ···················································· 17
Z 8767:2006 (ISO/DIS 9300:2003) 目次
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
附属書C(規定)混合天然ガスの臨界質量束の計算···································································· 24
附属書D(規定)大気の質量流量補正式 ·················································································· 28
附属書E(規定)ノズルスロートと配管との直径比βが0.25以上の場合の臨界ノズルの臨界質量
束の計算 ························································································································· 29
参考文献 ···························································································································· 32
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
白 紙
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
Z 8767:2006
(ISO/DIS 9300:2003)
臨界ベンチュリノズル(CFVN)による
気体流量の測定方法
Measurement of gas flow by means of critical flow Venturi nozzles
序文 この規格は,1990年に第1版として発行されたISO 9300:1990,Measurement of gas flow by means of
critical flow Venturi nozzlesの改訂規格であるISO/DIS 9300:2003を翻訳し,技術的内容及び規格票の様式を
変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
1. 適用範囲 この規格は,臨界ベンチュリノズル(以下,CFVNという。)を用い,設備を流れる気体の
質量流量を求めるときの,CFVNの形状及び使用方法(設備への設置及び動作条件)について規定する。
また,その流量計算及び不確かさの評価に必要となる情報も示す。
この規格は,ベンチュリノズルの中で,スロートにおける流速がその位置における臨界流速(これは局
所音速に等しい。)にまで加速されるものについて適用できる。スロートにおいて臨界流速が達成されると,
そのベンチュリノズルの流量は,上流側条件によって決まる最大流量に達する。
この規格は,単相の定常流だけに適用することができる。対象とするCFVNは,例えば,ノズルのスロ
ートと入り口との直径比,スロートレイノルズ数などの指定された仕様範囲内でだけ用いることができる。
また,この規格は,十分な数の実流校正実験が行われ,その結果得られた係数が,ある不確かさの範囲で
使用可能なCFVNだけを対象とする。
この規格は,次の場合について情報を示す。
a) CFVNの上流側にある配管が円断面をもつ場合。
b) CFVN又は一群のCFVNの上流側に大きな空間があり,チャンバとしてみなせる場合。このCFVNの
群としての設置は,CFVNの並列接続によって大流量を発生することを可能とする。低スロートレイ
ノルズ数においては,精密加工ベンチュリノズルを用いた高精度の測定を行うことができる。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide 21に基づき,IDT(一致している),MOD
(修正している),NEQ(同等でない)とする。
ISO/DIS 9300:2003,Measurement of gas flow by means of critical flow Venturi nozzles (IDT)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格のうちで,発行年を付記してあるものは,記載の年の版だけがこの規格の規定を構
成するものであって,その後の改正版・追補には適用しない。
ISO 5167-1:2003,Measurement of fluid flow by means of pressure differential devices inserted in circular
cross-section conduits running full−Part 1: General principles and requirements
2
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ISO 5167-2:2003,Measurement of fluid flow by means of pressure differential devices inserted in circular
cross-section conduits running full−Part 2: Orifice plates
ISO 6976:1995,Natural gas−Calculation of calorific values, density, relative density and Wobbe index from
composition
ISO/TR 5168:1998,Measurement of fluid flow−Evaluation of uncertainties
3. 定義 この規格で用いる主な用語の定義は,次による。
3.1
圧力測定(pressure measurement)
3.1.1
壁面圧力孔(wall pressure tapping) 管路の内面壁にあけられた孔で,孔の周りには段差がなく,そ
の中の圧力がその位置における管路内の静圧に等しくなるようにあけられたもの。
3.1.2
気体の静圧力(static pressure of a gas)p1 壁面圧力孔に圧力計を接続して測定する流れる気体の実
際の圧力。
参考 この規格では,静圧力の絶対値だけを用いる。
3.1.3
気体のよどみ点圧力(stagnation pressure of a gas)po 気体の流れが,等エントロピー過程によって
停止した場合に達するはずである仮想の気体圧力。
参考 この規格では,よどみ点圧力の絶対値だけを用いる。
3.2
温度測定(temperature measurement)
3.2.1
気体の静温度(static temperature of a gas)T1 流れる気体の実際の温度。
参考 この規格では,静温度の絶対値だけを用いる。
3.2.2
気体のよどみ点温度(stagnation temperature of a gas)To 気体の流れが,等エントロピー過程によっ
て停止した場合に達するはずである仮想の気体温度。
参考 この規格では,よどみ点温度の絶対値だけを用いる。
3.3
ベンチュリノズル(Venturi nozzles)
3.3.1
ベンチュリノズル(Venturi nozzles) 流量測定のために設備に設置された収縮管部と拡大管部とを
もつ絞り機構。
3.3.2
普通加工ベンチュリノズル(normally machined Venturi nozzles) 旋盤によって加工され,指定の表
面粗さを達成するために研磨されたベンチュリノズル。
3.3.3
精密加工ベンチュリノズル(accurately machined Venturi nozzles) 超精密旋盤によって,研磨を行
わずに指定の表面粗さが達成されたベンチュリノズル。
3.3.4
スロート(throat) ベンチュリノズルの直径が最小となる断面。
3.3.5
臨界ベンチュリノズル[critical flow Venturi nozzle(CFVN)] スロートにおける流速が臨界に達した
状態で用いるのに適した形状のベンチュリノズルで,臨界状態で用いるもの。
3.4
流量(flow)
3.4.1
質量流量(mass flow-rate)qm CFVNを単位時間当たりに通過する気体の質量。
参考 この規格では,“流量”とは,必ず質量流量を意味する。
3.4.2
スロートレイノルズ数(throat Reynolds number)Red 気体流量と入り口よどみ点とにおける粘性率
から計算される無次元数。特性長さは,よどみ点状態におけるスロート直径とする。スロートレイノルズ
数は,次の式による。
o
m
d
d
q
e
R
μ
π
4
=
3
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.4.3
断熱指数(isentropic exponent)κ 断熱可逆過程(等エントロピー過程)における圧力変化に伴う密
度変化の比。
p
c
d
dp
p
S
2
ρ
ρ
ρ
κ
=
=
ここに, p:
気体の静圧力の絶対値
ρ:
気体の密度
c:
局所音速
S:
(添え字)“等エントロピー過程”であることを示す。
理想気体(1)では,κは比熱比γに等しく,例えば,単原子気体では5/3,二原子気体では7/5,三原子気
体では9/7となる。
注(1) 理想気体では,分子間力及び分子の体積の影響が無視できるが,実在気体では,気体の振舞い
を記述するうえで,分子間力及び分子の体積の影響が無視できなくなる。
3.4.4
流出係数(discharge coefficient)Cd 非粘性気体の一次元等エントロピー流れで発生するはずである
理想的な流量と,同じ上流側条件で実際に発生する流量との比として定義される無次元量。この係数は,
粘性及び壁面の曲がりの影響を補正する。この規格で指定するノズル形状及び設置条件では,この係数は
スロートレイノルズ数だけの関数である。
3.4.5
臨界流量(critical flow) qm 対象とするベンチュリノズルが,これに与えられた上流側条件で達成可
能な最大流量。臨界流量が発生した場合,スロートの流速は,その位置における音波の速度,すなわち微
小圧力の乱れが伝ぱ(播)する速度である局所音速に等しくなる。
3.4.6
臨界流れ関数(critical flow function)C* ベンチュリノズルの入り口とスロートとの間の熱力学的特
性の関係を,一次元等エントロピー流れで求めた無次元数。気体の特性とよどみ点状態(5.2参照)との関
数である。
3.4.7
実在気体臨界流れ係数(real gas critical flow coefficient)CR 臨界流れ関数を別の形で表したもので,
混合ガスでの使用に適したもの。臨界流れ関数と次の関係がある。
1/2
Z
C
C
*
R=
参考 流れ関数との違いに注意する。
3.4.8
臨界圧力比(critical pressure ratio)r* ノズルを流れる質量流量が最大値に達したときの,ノズルス
ロートにおける静圧力のよどみ点圧力に対する比。
3.4.9
背圧比(back-pressure ratio) ノズル出口における静圧のノズル上流側よどみ点圧力に対する比。
3.4.10 ノズルの上流側マッハ数(Mach number)Ma1 ベンチュリノズルの上流側静圧を測定するための壁
面圧力孔の位置における軸方向平均流速の,よどみ点における音速に対する比。
3.4.11 圧縮係数(compressibility factor)Z 取扱う気体の振舞いがどれだけ理想気体の状態方程式からずれ
ているかを表す数値的な関数。温度と圧力との関数であって,次の式で定義する。
RT
pM
Z
ρ
=
3.5
不確かさ(uncertainty)
3.5.1
不確かさ(uncertainty) 約95%の信頼度において測定値が合理的に分布すると予想される範囲。
4. 記号 この規格で用いる記号を,表 1に示す。

4
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 1 記号
記号
量
次元 (2)
SI 単位
A2
ベンチュリノズルの出口の断面積
L2
m2
A*
ベンチュリノズルのスロート断面積
L2
m2
Cd
流出係数
無次元
CR
実在気体の一次元流れにおける臨界流れ係数
無次元
C*
実在気体の一次元流れにおける臨界流れ関数
無次元
C* i
完全気体の一次元等エントロピー流れにおける臨界流れ関数
無次元
D
上流側配管の直径
L
m
d
ベンチュリノズルのスロート直径
L
m
M
分子量
M
kg mol-1
Ma1
ノズルの上流側マッハ数
無次元
P1
ノズル入り口における気体の絶対静圧力
ML-1T-2
Pa
P2
ノズル出口における気体の絶対静圧力
ML-1T-2
Pa
po
ノズル入り口における気体の絶対よどみ点圧力
ML-1T-2
Pa
P*
ノズルのスロートにおける気体の絶対静圧力
ML-1T-2
Pa
P*i
完全気体の一次元等エントロピー流れを仮定したときのスロートにおける
絶対静圧力
ML-1T-2
Pa
(p2/po)i
完全気体の一次元等エントロピー流れを仮定したときのノズル出口におけ
る静圧力と入り口よどみ点圧力との比
無次元
qm
質量流量
MT-1
kg・s-1
qmi
非粘性気体の一次元等エントロピー流れを仮定したときの質量流量
MT-1
kg・s-1
R
普遍気体定数(R=8.314 51)
M L2 T-2 Θ-1
J・mol-1K-1
Red
スロートレイノルズ数
無次元
rc
入り口側絞り半径
L
m
r*
臨界圧力比 p*/po
無次元
U'
相対不確かさ
無次元
T1
ノズル入り口における気体の絶対静温度
Θ
K
To
ノズル入り口における気体の絶対よどみ点温度
Θ
K
T*
ノズルスロートにおける絶対静温度
Θ
K
ν*
スロートにおける局所音速,スロートにおける臨界流速
LT-1
m・s-1
Z
圧縮係数
無次元
β
直径比 d/D
無次元
γ
比熱比
無次元
δ
絶対不確かさ
(3)
(3)
κ
断熱指数
無次元
μo
よどみ点における気体の動粘度
ML-1T-1
Pa・s
μ*
ノズルスロートにおける気体の動粘度
ML-1T-1
Pa・s
ρo
ノズル入り口における気体の密度
ML-3
kg・m-3
ρ*
ノズルスロートにおける気体の密度
ML-3
kg・m-3
注(2) M = 質量, L = 長さ, T = 時間, Θ = 温度
(3) 次元及びSI単位は,対応する量のものとする。
5. 基礎式
5.1
状態方程式 実在気体の振舞いは,次の式で表す。
(
)TZ
M
R
P
=
ρ
········································································ (1)
5.2
理想状態での流量 理想状態の流量は,次の条件下で求める。
5
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 流れは,一次元である。
b) 流れは,等エントロピーである。
c) 気体は,完全(すなわちZ = 1,かつ,κ = γ)である。
この条件下では,臨界流量は次の式で求める。
(
)
[
]2
1
o
o
i
*
*
i
m
T
M
/
R
p
C
A
q=
····································································· (2)
又は
(
)
2
1
o
o
i
*
*
mi
P
C
A
q
ρ
=
··································································· (3)
ここに,
(
)(
)1
2
1
2
1
1
2
−
+
+
=
γ
γ
γ
γ
/
/
i
*
C
······························································ (4)
5.3
実際の状態における流量 実際の状態における臨界流量は,次の式となる。
(
)
[
]
2
1
o
o
*
d
*
m
T
M
/
R
p
C
C
A
q=
····································································· (5)
又は
(
)2
1
o
o
R
d
*
m
P
C
C
A
q
ρ
=
································································· (6)
後者は,
2
1o
*
R
Z
C
C=
··············································································· (7)
から導かれる。ここに,Zoは,入り口側よどみ点状態における圧縮係数である。
o
o
o
o
RT
M
p
Z
ρ
=
······································································· (8)
ここで,気体が完全でないため,C* 及びCRはC*iに等しくないことに注意することが望ましい。また,
流れは一次元でなく粘性の影響によって境界層が発生するため,Cdは1より小さくなる。
5.4
臨界質量束 臨界質量束は,理想状態での流量に対してはqmi /A*となり,実際の状態における流量
に対してはqm /(A* Cd)となる。
6. 適用 それぞれの対象について,CFVNの使用が適しているか,又は他の測定方法が適しているかを
評価することが望ましい。ベンチュリノズルの流れの重要な特徴は,そのベンチュリノズルが臨界状態に
保たれている限り,その流量が下流側圧力に依存しないことである(9.5参照)。
その他の特徴の幾つかを,次に示す。
CFVNの使用で必要となる測定値は,上流側の気体圧力及び温度又は密度だけである。その理由は,ス
ロートにおける状態が熱力学的に導かれるためである。
CFVNのスロートにおける流速がその上流側よどみ点状態によって決まる最大値となるため,設置条件
の影響は,旋回流によるものを除き最小となる。CFVNの使用に当たっては,その入り口側に旋回流があ
ってはならない。
CFVNと亜音速絞り流量計との大きな違いは,CFVNの流量が上流側よどみ点圧力に直接比例し,亜音
速ノズルのように差圧の平方根には比例しないことである。
CFVNの最大流量範囲は,一般に,流れが臨界に達する入り口側圧力以上の範囲で,どれだけ高い圧力
をノズルの入り口側に与えることができるかによって決まる。
CFVNは,試験,校正及び流量制御に最もよく用いられる。
6
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7. 標準臨界ベンチュリノズル(CFVN)
7.1
一般要求事項
7.1.1
検査 CFVNを検査し,この規格の要求事項に適合していることを確認しなければならない。
7.1.2
材質 CFVNの材質は,使用状況に適したものでなければならない。要求事項の幾つかを,次に示
す。
a) この規格で要求する条件を満たす仕上げができることが望ましい。材質によっては,ピット,欠陥,
その他の不均一性によって適していない場合がある。
b) 材質は,必要であれば表面処理を行うことによって,使用中に腐食が起こらないようにしなければな
らない。
c) 材質は,寸法が安定し,使用時における温度がスロート直径測定時と異なる場合には,既知で再現性
のある膨張係数をもち,スロート直径の補正が適切に行えるものが望ましい。
7.1.3
スロート及び入り口の表面仕上げ スロートと円すい(錐)ディフューザとの接点までのトロイダ
ル部分は,その幾何平均表面粗さRaが,普通加工ベンチュリノズルの場合は15×10-6 dを,精密加工ベン
チュリノズルの場合は0.04 μmを超えない仕上げを行う。
スロートと円すい(錐)ディフューザとの接点までのトロイダル部分は,ほこりなどのいかなる汚れも
付着していてはならない。
普通加工CFVNでは,スロート部直径のステップ(段差)が,スロート直径の10%を超えないトロイダ
ルスロートCFVNを使用することができる(参考文献の[10]参照)。
7.1.4
円すい(錐)ディフューザ 用いるCFVNの円すい(錐)ディフューザは,段差,不連続性,凹
凸及び偏心が,局所直径の1%を超えないことを確認しなければならない。円すい(錐)ディフューザの
幾何平均表面粗さRaは,10-4 dを超えてはならない。
7.2
形状
7.2.1
一般 標準CFVNには,次の二つの形状がある。すなわち,トロイダルスロートベンチュリノズ
ル及びシリンドリカルスロートベンチュリノズルである。精密加工ベンチュリノズルは,前者として設計
しなければならない。
7.2.2
トロイダルスロートベンチュリノズル
7.2.2.1
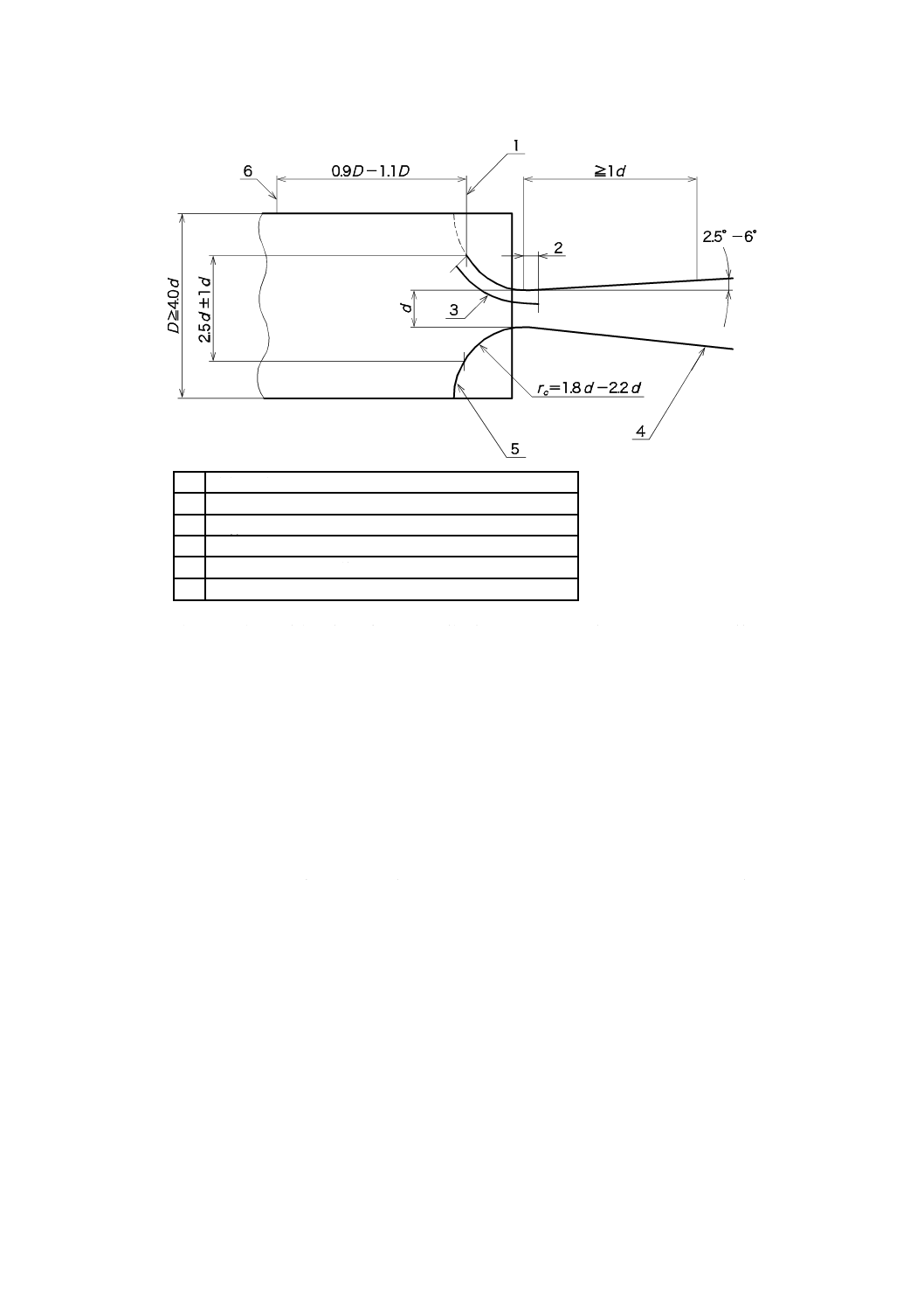
CFVNは,図1に適合しなければならない。
7
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1
入り口面
2
円すい(錐)ディフューザへの接合
3
注(4)参照
4
この範囲の幾何平均表面粗さは10-4dを超えてはならない
5
入り口側表面は,破線の外側になければならない
6
圧力センサ位置
注(4) この範囲の幾何平均表面粗さRaは,普通加工ベンチュリノズルでは15×10-6 dを,精
密加工ベンチュリノズルでは0.04 μmを超えてはならない。また,その形状は,円環
形状よりも±0.001 d以上の誤差があってはならない。
図 1 トロイダルスロートベンチュリノズル
7.2.2.2
CFVNを用いた流量計測システムを構成するその他の要素の設置位置を指定するために,CFVN
の入り口面を基準として用いる。この入り口面は,ノズルの対称軸に垂直な平面が切る流路直径が2.5 d±
0.1 dとなる位置と定義する。
7.2.2.3
CFVNの入り口絞り部分は,円環の一部でなければならない。この円環をなす範囲は,入り口面
から最小面積位置(スロート)を超え,ディフューザと滑らかに接するまでの間でなければならない。入
り口面より上流側の形状は指定しないが,各位置における直径が,円環を延長した形状に一致するか,又
はそれより大きくなければならない(7.2.2.2参照)。
7.2.2.4
入り口面からディフューザまでの円環部分(図1参照)の円環形状からのずれは,0.001 d以下で
なければならない。対称軸を含む平面が切る円環の半径 rcは,1.8 d以上2.2 d以下とする。
7.2.2.5
CFVNのディフューザは,円環形状との接点まで,半頂角が2.5°〜6°の範囲にある円すい(錐)
台とする。ディフューザの長さは,スロート直径より短くてはならない。
7.2.2.6
この規格に従って作製し用いるCFVNが測定する流量の不確かさは,スロート直径の不確かさに
特に大きく依存する。トロイダルスロートCFVNで直径が小さい場合,そのスロート直径を正確に測定す
ることが特に難しい。この点には細心の注意を払うことが望ましい。
7.2.3
シリンドリカルスロートベンチュリノズル
7.2.3.1
CFVNは,図2に適合しなければならない。

8
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1
入り口面
2
注(5)参照
3
注(6)参照
4
推移領域
注(5) この範囲では,幾何平均表面粗さは15×10-6 dを超えてはならない。また,形状は,円環
及び円筒から±0.001 d以上ずれてはならない。
(6) 円すい(錐)ディフューザの幾何平均表面粗さは,10-4dを超えてはならない。
図 2 シリンドリカルスロートベンチュリノズル
7.2.3.2
入り口面は,入り口側絞りの接線が対称軸に垂直になる位置と定義する。
7.2.3.3
CFVNの絞り部分(入り口側)は,円環の1/4とし,その一端は入り口面(7.2.3.2参照)に,も
う一端はシリンドリカルスロートに接するものとする。円環の半径 rc及びシリンドリカルスロートの長さ
は,スロート直径に等しくなければならない。
7.2.3.4
入り口側の円環部分の形状は,円環形状から±0.001 d以上のずれがあってはならない。
7.2.3.5
流量の計算に用いる直径は,シリンドリカルスロートの出口における平均直径とする。この平均
直径は,シリンドリカルスロート出口において,等角度で分布する少なくとも4直径方向に測定した値の
平均値とする。スロート内におけるいかなる直径も,この平均直径から±0.001 d以上ずれてはならない。
スロートの長さは,スロート直径から0.05 d以上ずれてはならない。円環絞り部分とシリンドリカルス
ロートとの接点は,目視によって検査しなければならず,欠陥がないことを確認することが望ましい。接
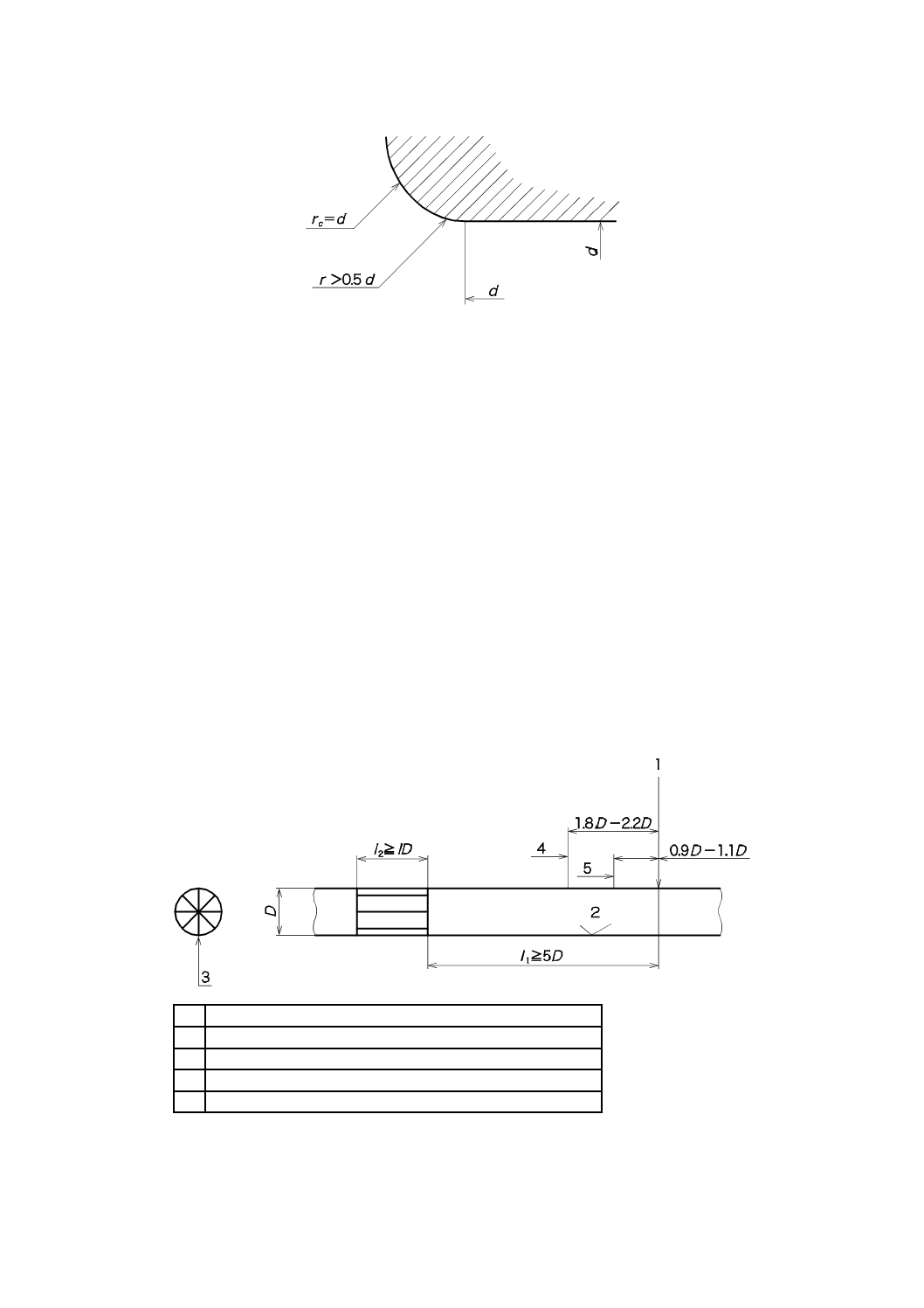
続に欠陥が認められる場合は,ノズルの対称軸を含む平面が切る入り口絞り壁面形状の局所曲率半径が,
入り口形状のいかなる位置(円環部分及びシリンドリカルスロート)においても,0.5 dより大きいことを
確認しなければならない(図3参照)。
入り口側及びスロートの全面は,適切に研磨を行い,その幾何平均表面粗さRaが15×l0-6 dを超えない
ようにしなければならない。
シリンドリカルスロートとディフューザとの接点も,目視によって検査し,欠陥がないことを確認しな
ければならない。
9
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 3 円環部分とシリンドリカルスロートとの接続部(推移領域)詳細
7.2.3.6
ディフューザ形状は,半頂角が3°〜4°の範囲にある円すい(錐)台とする。その長さは,スロ
ート直径より短くてはならない。
8. 設置に関する要求事項
8.1
一般 この規格は,次の二つの設置方法について規定する。
a) CFVNの上流側にある配管が円断面をもつ場合,又は,
b) CFVN又は一群として設置された複数のCFVNの上流側に大きな空間があり,チャンバとみなせる場
合。
a)の場合,CFVNは,8.2に規定する要求事項を満たすシステムに設置しなければならない。b)の場合,
CFVNは,8.3に規定する要求事項を満たすシステムに設置しなければならない。これらの両方の場合にお
いて,CFVNの上流側に旋回流があってはならない。ノズルの上流側に配管系が接続されている場合には,
ノズルの上流側の入り口面からl1 > 5 Dの位置に,図4に示す整流管,又はそれ以上の性能をもつと一般
に認められているその他整流機構(ISO 5167-1/-2参照)を設置することによって,旋回流の可能性を減ら
すことができる。
1
入り口面
2
注(7)参照
3
羽根は,バックリングを避けることのできる厚さとする
4
温度センサ位置
5
圧力センサ位置
注(7) 幾何平均表面粗さは,10-4 Dを超えてはならない。
図 4 ノズルの上流側が配管の場合の設置要求事項
10
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.2
上流側が配管の場合 円断面をもつ直管にCFVNを設置してもよいが,それぞれの中心軸が互いに
±0.02 D以上ずれないようにしなければならない。CFVNの上流側3 Dまでの範囲は,配管断面形状が円
から0.01 D以上ずれてはならず,幾何平均表面粗さRaは,10-4 Dを超えてはならない。入り口配管の直
径は,4 d(β ≦ 0.25)以上としなければならない。
これら上流側条件を満たすことができない場合は,その上流側条件が流量測定の不確かさに及ぼす影響
を調べるための特別な実験を行うのがよい。さらに,可能であれば,一次校正によるCdを実測するのが望
ましい。β > 0.25となる場合の質量流量の補正の一方法を,附属書Eに示す。
8.3
上流側がチャンバの場合 CFVNの対称軸から5d未満,及び,7.2.2.2又は7.2.3.2で定義する入り口
面から5d未満に壁面がない場合,CFVNの上流側はチャンバとみなす。
上流側がチャンバの場合又は流量が大きい場合は,複数のCFVNを使用することができる。
8.4
下流側に関する要求事項 下流側配管に特別な要求はないが,CFVNが臨界に達するために障害と
なるものは避けなければならない。
8.5
圧力測定
8.5.1
CFVNの上流側が円断面配管の場合,上流側の静圧は,ベンチュリノズルの入り口面から0.9 D 〜
1.1 Dの間にあけられた壁面圧力孔を通して測定することが望ましい(図1及び図4参照)。測定圧力を用
いてノズルの入り口側よどみ点圧力を十分正確に求められることが実証できれば,これより上流又は下流
で測定してもよい。
8.5.2
CFVNの上流側がチャンバとみなせる場合は,ノズルの入り口面に垂直な壁面において,入り口面
から10 d±1 d以内の位置で測定することが望ましい。測定圧力を用いてノズルの入り口よどみ点圧力を十
分正確に求められることが実証できれば,これより上流又は下流で測定してもよい。
8.5.3
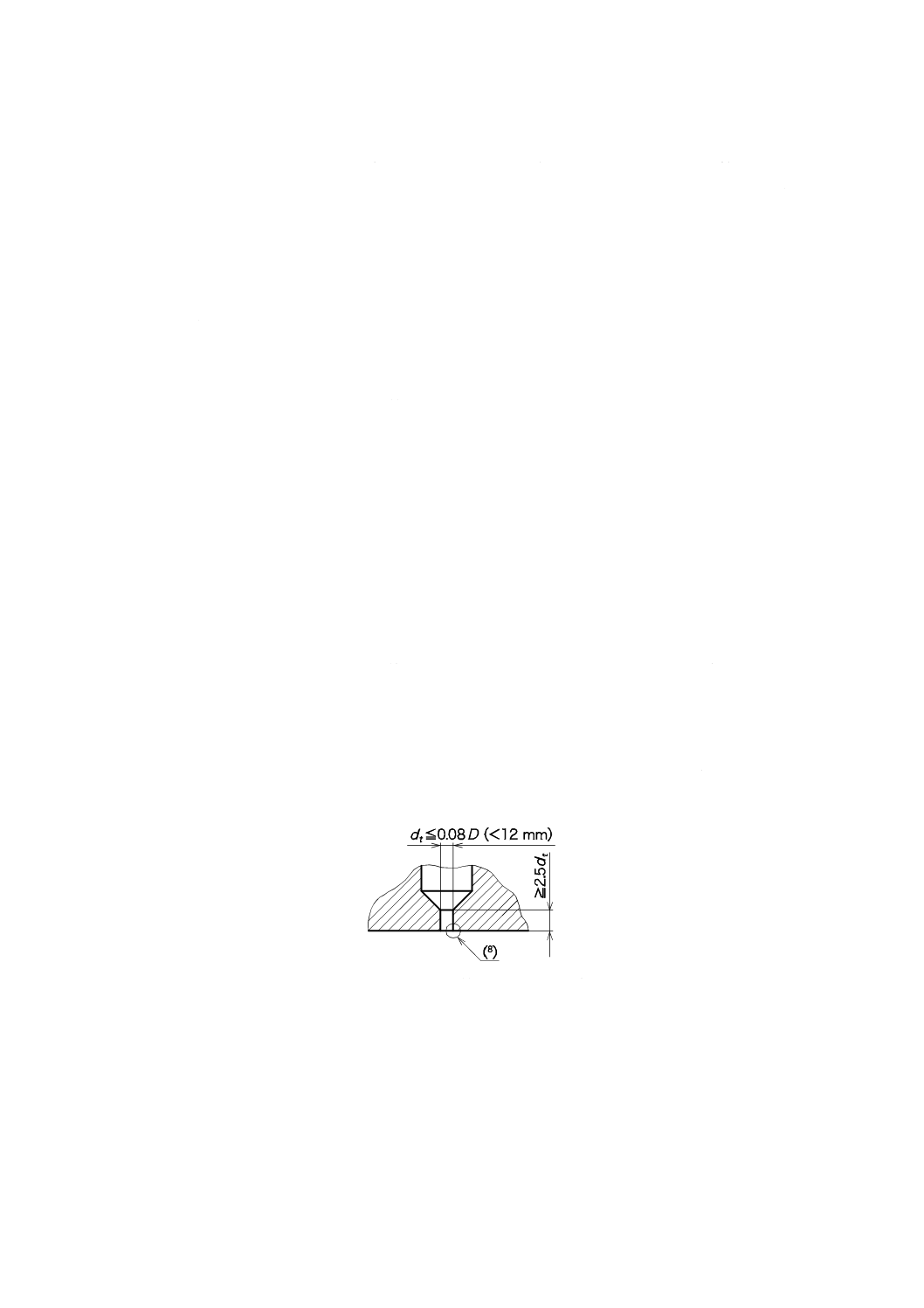
8.5.1で規定する壁面圧力孔の中心線は,可能であれば8.5.2に規定する圧力孔も含め,ノズルの中
心線に垂直に交わらなければならない。測定孔の出口形状は円でなければならない。そのエッジには,ば
りがあってはならない。直角のままか,又は丸みがある場合は,孔の直径の0.1倍を超えてはならない。
目視検査によって,壁面圧力孔がこれらの要求事項を満たしていることを確認しなければならない。上流
側が配管の場合は,壁面圧力孔の直径が0.08 Dを超えず,かつ,12 mm未満でなければならない。壁面圧
力孔は,少なくともその直径の2.5倍以上の長さの範囲では,円筒形状でなければならない(図5参照)。
注(8) 孔のエッジは,その位置が管路の内壁面に一致し,ばりなし
で直角のままか,又は丸みがある場合は,0.1 dを超えては
ならない。
図 5 上流側が配管の場合の壁面圧力孔の詳細
8.5.4
スロート部の流れが臨界に達していることを確認するために,下流側圧力を測定しなければならな
い。この圧力は,ノズルディフューザの出口面から,その位置の管路直径の0.5倍以内にある配管用の壁
面圧力孔を用いて測定しなければならない。
11
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
流れが臨界に達していることは,スロート直下に設けられたステップにおいて壁面圧力を測定すること
によっても確認できる。この方法をによる場合は,CFVNを特別に加工する必要がある(7.1.3参照)。
8.5.5
適用の仕方によっては,出口圧力は,壁面圧力孔を用いずに測定することができる。例えば,CFVN
から直接大気中に,又はその他の一定の圧力中に直接放出することができる。これらの方法では,出口圧
力を測定する必要はない。
8.6
排水孔 適用対象によっては水分の凝縮又は物質が蓄積することがあるため,これを取り除くため
の排水孔を設けることができる。流量測定が行われているときは,この孔を通した流れがあってはならな
い。排水孔が必要な場合は,ノズル上流の壁面圧力孔より上流側に取り付けなければならない。排水孔の
直径は,0.06 D未満とするのがよい。排水孔及びノズル上流側壁面圧力孔の中心軸は,D以上離れていな
ければならない。また,排水孔とノズルの中心軸とが作る平面は,ノズル上流側壁面圧力孔とノズルの中
心軸とが作る平面と異なっていなければならない。
測定の間,ノズルのスロートより上流側では,流れが単相で凝縮がなく,表面がきれいに保たれ,その
仕上げがそのまま保たれなければならない。これが保証できない測定は,この規格に適合するものとはみ
なせない。
8.7
温度測定 ノズル上流側の温度は,ノズル上流側に位置した一つ以上の温度センサで測定しなけれ
ばならない。上流側が配管の場合は,温度センサはCFVNの入り口面から上流側1.8 D〜2.2 Dの間に位置
することが望ましい。温度センサは,直径が0.04 Dよりも小さくなければならず,その位置が壁面圧力孔
と同一面上にあってはならない。測定された温度に基づいてノズルの入り口よどみ点温度を十分正確に求
めることができることが実証できるならば,更に上流側で測定してもよい。
流れる気体のよどみ点温度と配管の環境温度とが5 K以上異なる場合は,温度センサ及び配管の断熱に
特別な考慮が必要である。この場合は,センサには放射熱に鈍感なものを選び,配管には十分に断熱材を
巻いて環境からの熱伝達を最小としなければならない。配管壁と流れる気体の温度とが大きく異なる場合
は,気体温度を正確に測定することは極めて難しくなる。
8.8
密度測定 場合によっては,例えば,気体の分子量が十分な精度で分かっていない場合などには,
ノズル入り口で密度を直接測定することが望ましい。
密度計を用いる場合は,ノズルの上流側壁面圧力孔及び温度センサよりも上流側に設置しなければなら
ない。入り口気体密度を正確に測定するためには,次の点に特別な注意を払わなければならない。
a) 密度計の挿入は,温度及び圧力の測定を乱さないようにしなければならない。
b) 上流側配管から分岐させて密度計に気体を導く場合は,密度計に入る気体が主配管内の気体と同じで
あることを確実にしなければならない。
c) 密度計における圧力及び温度の状態は,補正を可能な限り避けるため,ノズルの入り口状態に可能な
限り近づけることが望ましい。必要であれば,状態方程式を用い,測定した密度を入り口密度に変換
しなければならない。
o
d
o
d
d
o
d
o
Z
Z
T
T
p
p
ρ
ρ=
····································································· (9)
ここに,下付き添え字dは,密度計に関する値であることを示す。Tdは測定することが望ましいが,Pd
は,Poからの差として求めることができる。Zd /Zoは,次の8.9に従って求めるとよい。
8.9
密度の計算 密度を測定する代わりに,気体をガスクロマトグラフで分析し,得られた成分を基に,
ISO 6976: 1995などの確立された方法を用いて密度を計算してもよい。この方法によって得られた密度の
不確かさは,密度計によるものと同等である。
12
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9. 計算方法
9.1
質量流量qm 実際の質量流量は,次のいずれかの式を用いて計算しなければならない。
(
)
[
]2
1
o
o
*
d
*
m
T
M
R
p
C
C
A
q=
又は,
(
)2
1
o
o
R
d
*
m
p
C
C
A
q
ρ
=
A*は,保証されたdの値から計算する。
9.2
流出係数 Cd
9.2.1
流出係数は,CFVNの形状に大きく依存する。ノズルのスロート直径が小さい場合は,その製作と
測定が非常に難しくなることに注意しなければならない(7.2.2.6参照)。
9.2.2
CFVNの流出係数は,次の式から求めてもよい。
n
d
d
bRe
a
C
−
−
=
········································································· (10)
係数a,b 及びnは,それぞれの形状に対し,使用可能なレイノルズ数範囲とともに,表 2に示す。
表 2 係数 a,b及びn
トロイダルスロート
ベンチュリノズル
精密加工トロイダルスロート
ベンチュリノズル
シリンドリカルスロート
ベンチュリノズル
2.1×104 < Red <
3.2×107
a = 0.995 9
b = 2.720
n = +0.5
2.1×104 < Red <
1.4×106
a = 0.998 5
b = 3.412
n = +0.5
3.5×105 < Red < 1.1×107
a = 0.997 6
b = 0.138 8
n = +0.2
9.2.3
9.2.2に示した式(10)を用いて求めた流出係数の95%の信頼度における相対不確かさは,普通加工
ベンチュリノズルでは両形状ともに0.3%,精密加工ベンチュリノズルでは0.2%である。
流出係数の値を附属書Aに示す。
9.3
臨界流れ関数 C* 及び実在気体臨界流れ係数 CR 気体の質量流量の計算に用いるC*の値は,不確
かさの計算ができるのであれば,いかなる方法で計算してもよい。
様々な気体におけるC*を附属書Bに示す。これを用いて計算したC*の不確かさは,95%の信頼度にお
いて0.1 %である。
C*及びCRの計算は,AGA Report No. 8 (1992)(参考文献の [2]参照)に示す状態方程式を,R.C. Johnson
の方法(参考文献の [4]及び[5]参照)に適用して行うこともできる。この方法よって得られたC*の相対不
確かさは,95%の信頼度において0.05%である。
混合天然ガスのC*の臨界質量束に基づいた計算方法を,附属書Cに示す。この方法で得られたqm /(A*Cd)
の不確かさは,95%の信頼度において0.1%である。
9.4
圧力及び温度の測定値のよどみ点状態への変換 入り口よどみ点圧力poは,次の式で計算してもよ
い。
(
)
1
2
1
1
1
2
1
1
−
−
+
=
κ
κ
κ
Ma
p
po
·························································(11)
入り口よどみ点温度Toは,次の式で計算してもよい。
(
)
2
1
1
1
2
1
1
Ma
T
To
−
+
=
κ
································································ (12)
直径比d/Dが0.25に等しいか又はそれ以下の場合(8.2参照),よどみ点温度が測定値に等しいとしても
有意な誤差は発生しない。
13
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9.5
下流側に許される最大圧力 円すい(錐)ディフューザ長さがd以上であるCFVNをスロートレイ
ノルズ数2×105以上で用いる場合,下流側に許される最大圧力は,次の式で求める。
(
)
(
)
[
]
*
*
i
o
max
o
r
r
p
p
.
p
p
+
−
=
2
2
8
0
················································· (13)
ここに,
1
1
2
−
+
=
κ
κ
κ
*r
······································································· (14)
κ は,適切な状態方程式から決定してもよい。
(
)i
o
p
/
p2
は,ディフューザの面積比の関数として,理想気体の等エントロピー関係式から求める。
(
)max
o
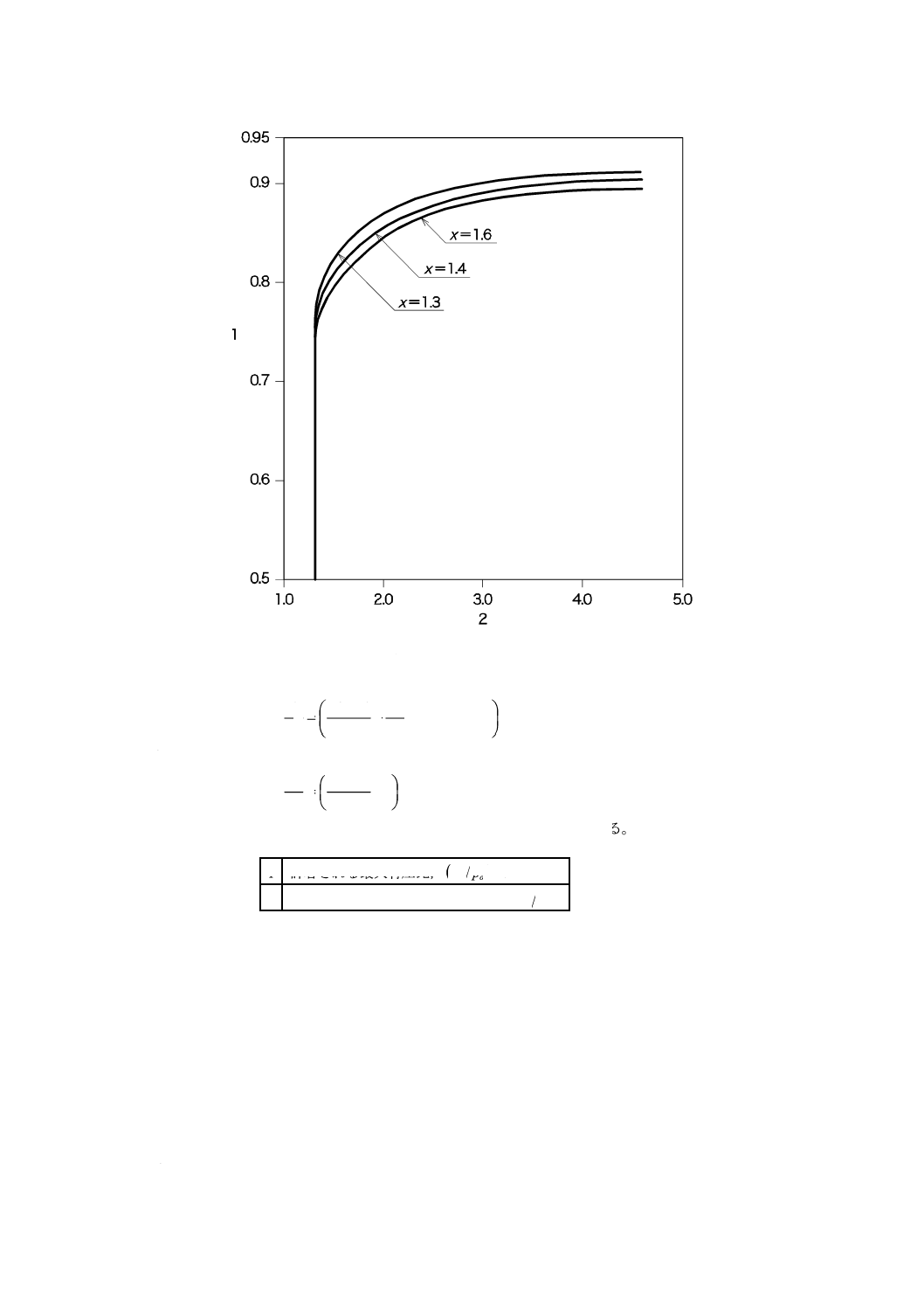
p
/
p2
は,図6から求めてもよい。流れが臨界していることが証明できるのであれば,下流側をこれ
以上高い圧力としてもよい。ディフューザの出口面積がスロート面積の4倍以上の場合,すなわち,ディ
フューザの半頂角が4°である場合に,ディフューザ長さがスロート直径の7倍以上であれば,その長さ
を更に長くしても(
)max
o
p
/
p2
はほとんど変わらない。
スロート及び拡大部を非常に注意深く製作することによって,0.95の圧力比を得ることもできる。
2×105以下のスロートレイノルズ数でCFVNを用いる場合は,圧力比を0.25以下とするか,簡単な非臨
界試験(参考文献の[15]参照)を行うことが望ましい。
14
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考1. レイノルズ数が2×106以上の場合
2. A2/A*は,ベンチュリノズルの形状に依存し,次の式で求められる。
a) トロイダルスロートベンチュリノズルの場合
(
)
2
2
cos
1
2
tan
2
+
−
+
=
a
d
r
d
l
A
A
c
*
θ
θ
b) シリンドリカルスロートベンチュリノズルの場合
2
2
1
tan
2
+
=
d
l
A
A
*
θ
ここに,lは拡大部の長さであり, θ はその半頂角である。
1 許容される最大背圧比,(
)max
op
p2
2 円すい(錐)ディフューザ面積比,
*
A
A2
図 6 CFVNに許容される最大背圧比
10. 流量測定の不確かさ
10.1 一般
10.1.1 この項に対する有用な一般的情報は,ISO/TR 5168による。
10.1.2 この規格に従って流量測定が行われたと表記する場合には,その流量測定の不確かさを計算し,
報告しなければならない。
10.1.3 不確かさは,絶対値又は相対値として記載することができ,次のいずれかの形で表記する。
− qm ± δ qm
− qm [ 1 ± U'(qm) ]
15
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− qm 不確かさ[ 100 U'(qm) ] %以下
ここで,絶対不確かさδ qmは,qm と同じ次元でなければならない。相対不確かさU'(qm) = δ qm/qmは無
次元である。
10.1.4 この規格で定義する流量測定の不確かさ(3.5参照)は,標準偏差の2倍に等しい。この標準偏差
に関しては,流量の計算に用いる各量のもたらす部分不確かさを組み合わせることによって得られる。こ
のとき,この部分不確かさをもたらす要素の数が多く,また,それぞれの部分不確かさが小さく,互いに
独立であると仮定する。単一測定器しか用いない場合及び測定において係数として用いられるものの中に
は,実際には,系統的誤差をもたらすもの(誤差の絶対値の最大値しか評価できない。)もあるが,それら
が組み合わせられる場合には,あたかもラプラス−ガウス分布に従ってランダムに分布する偶然誤差のよ
うに組み合わせることができる。
10.2 不確かさの実際の計算
10.2.1 質量流量qmを計算する基礎式は,次のいずれかである。
(
)2
1
o
o
*
d
*
m
MT
R
p
C
C
A
q=
又は,
(
)2
1
o
o
R
d
*
m
p
C
C
A
q
ρ
=
実際には,右辺に現れる様々な量は,互いに独立ではない。したがって,厳密にいえば,これらの量の
不確かさを組み合わせて直接qmの不確かさを求めることは正しくない。
しかし,ほとんどの応用例において,右辺に現れる各量は互いに独立であるとしても十分である。
10.2.2 質量流量qmの相対不確かさを計算する実用的な式は,次の式となる。
()
()
()
()
()
()
()
[
]2
1
2
2
2
2
2
2
4
1
4
1
o
o
*
*
d
m
'
T
'
U
M
'
U
p
'
U
A
'
U
C
'
U
C
'
U
q
U
+
+
+
+
+
=
······················ (15)
又は,
()
()
()
()
()
()
[
]2
1
2
2
2
2
2
4
1
4
1
o
o
*
R
d
m
'
p
'
U
'
U
A
'
U
C
'
U
C
'
U
q
U
+
+
+
+
=
ρ
································· (16)
入り口気体密度が直接測定されるのではなく,9.に示した式に従って計算するのであれば,そのρoの相
対不確かさは次の式となる。
(){()
(
)(
)
[
]()
(
)(
)
[
]()
o
o
o
d
d
d
d
d
o
'
p
'
U
Z
p
p
Z
p
'
U
Z
p
p
Z
'
U
U
2
2
2
1
1
∂
∂
−
+
∂
∂
−
+
=
ρ
ρ
(
)(
)
[
]()
(
)(
)
[
]()}2
1
2
2
1
1
d
d
d
d
o
o
o
o
T
'
U
Z
T
T
Z
T
'
U
Z
T
T
Z
∂
∂
−
+
∂
∂
−
+
······································· (17)
この式は,次の式に単純化することもできる。
()
()
()
()
()
()
[
]2
1
2
2
2
2
2
d
'
o
'
o
'
d
'
d
'
o
'
T
U
T
U
p
U
p
U
U
U
+
+
+
+
=
ρ
ρ
············································ (18)
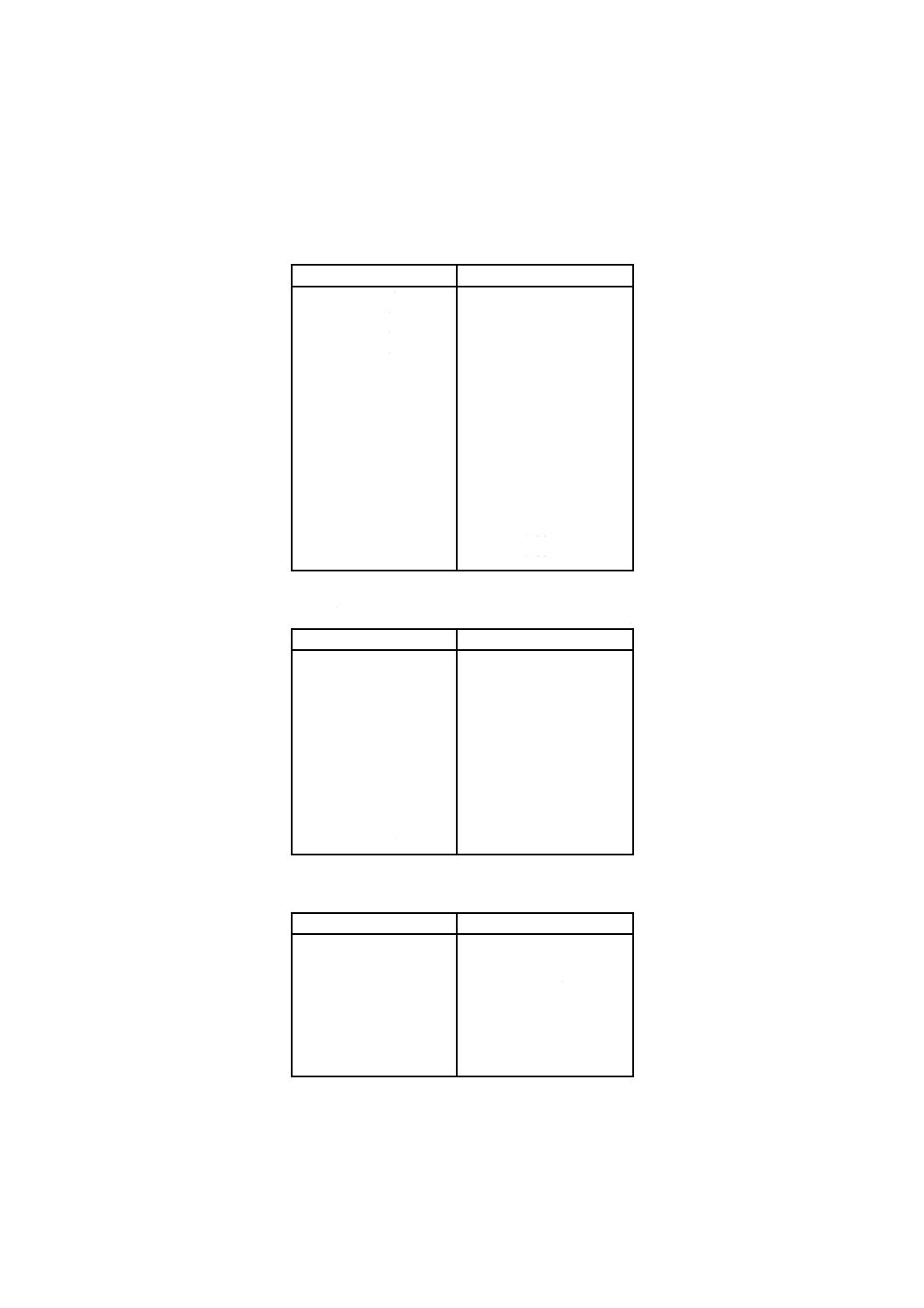
16
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定)ベンチュリノズルの流出係数
附属書A表 1 トロイダルスロートベンチュリノズル
レイノルズ数Red
流出係数Cd
2.1×104
0.977 1
3×104
0.980 2
5×104
0.983 7
7×104
0.985 6
1×105
0.987 3
2×105
0.989 8
3×105
0.990 9
5×105
0.992 1
7×105
0.992 6
1×106
0.993 2
3×106
0.994 3
7×106
0.994 9
1×107
0.995 0
3.2×107
0.995 4
附属書A表 2 精密加工トロイダルスロートベンチュリノズル
レイノルズ数Red
流出係数Cd
2.1×104
0.975 0
3×104
0.978 8
5×104
0.983 2
7×104
0.985 6
1×105
0.987 7
2×105
0.990 9
3×105
0.992 3
5×105
0.993 7
7×105
0.994 4
1.4×106
0.995 6
附属書A表 3 シリンドリカルスロートベンチュリノズル
レイノルズ数Red
流出係数Cd
3.5×105
0.989 8
5×105
0.990 9
7×105
0.992 1
1×106
0.992 6
3×106
0.993 2
7×106
0.994 3
1.1×107
0.995 4
17
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(規定)様々な気体に関する臨界流れ関数C*の値の表
B.1 一般 この附属書は,数種の純気体及び乾燥空気の臨界定数を計算するために必要な情報について示
す。最新の状態方程式の参照が可能な場所では,ISO 9300:1990から値の改訂が行われている。新たな事
実がないところはISO 9300:1990と同じである。幾つかの気体では,2種の方法,すなわち,値の表又は
経験式からC*を求めることができる。この附属書にあるすべての情報は,引用する文献にトレーサブルで
ある。
B.2 表 C*の値の表は,窒素,アルゴン,二酸化炭素を含まない乾燥空気,メタン,二酸化炭素,酸素及
び蒸気に関して与えられる。温度(K)及び圧力(MPa)は,よどみ点での値が用いられる。
B.3 経験式 二酸化炭素,酸素及び蒸気を除き,再帰計算[36]を避けながらも正確に C*が与えられる経
験式を示す。この式は,限られた温度範囲でだけ使用可能である。経験式は,次の形をとる。
∑
=
i
c
b
i
*
i
i
a
C
τ
π
····································································· (B.1)
ここに,
c
o
P
p
=
π
及び,
c
o
T
T
=
τ
この式の係数ai,bi,ci,は,それぞれの気体ごとに附属書B表 2,附属書B表 4,附属書B表 6又は
附属書B表 8に与えられ,臨界パラメータPc及びTcは,それぞれの表の下に与えられる。この式の使用
によって付加される臨界流量の有意な不確かさは全くない。適用可能な温度範囲においては,表の値を内
挿するよりも,式を用いることを推奨する。
B.4 大気 附属書B表5に示すC*の値,又は,附属書B表 6にある係数を用いて式(B.1)で計算したC*
の値は,二酸化炭素が含まれない空気に対してだけ用いることができる。乾燥していない大気を用いてノ
ズルを用いる場合は,その質量流量は大きく湿度の影響を受ける。その場合は,附属書Dに規定の補正係
数を用いることが望ましい。
B.5 ノズルのスロートと配管直径との比,β この項で示す値は,β< 0.25の場合に限って使用できる。
この条件が満たされない場合は,上流側の測定位置で,小さいけれども無視することのできない速度が発
生する。この状態では,使用者は,附属書Eにある質量流量の補正係数を用いることが望ましい。
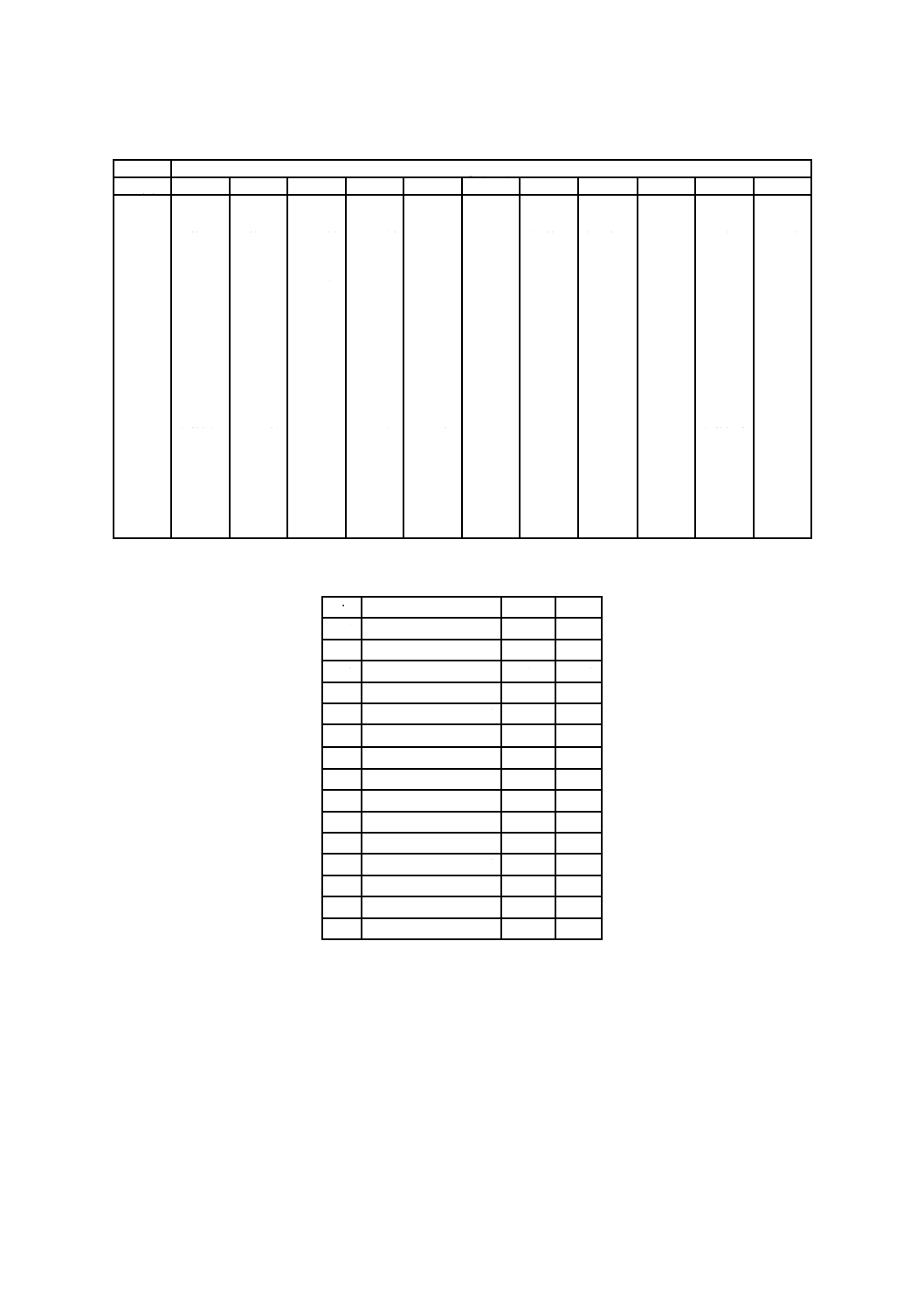
18
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
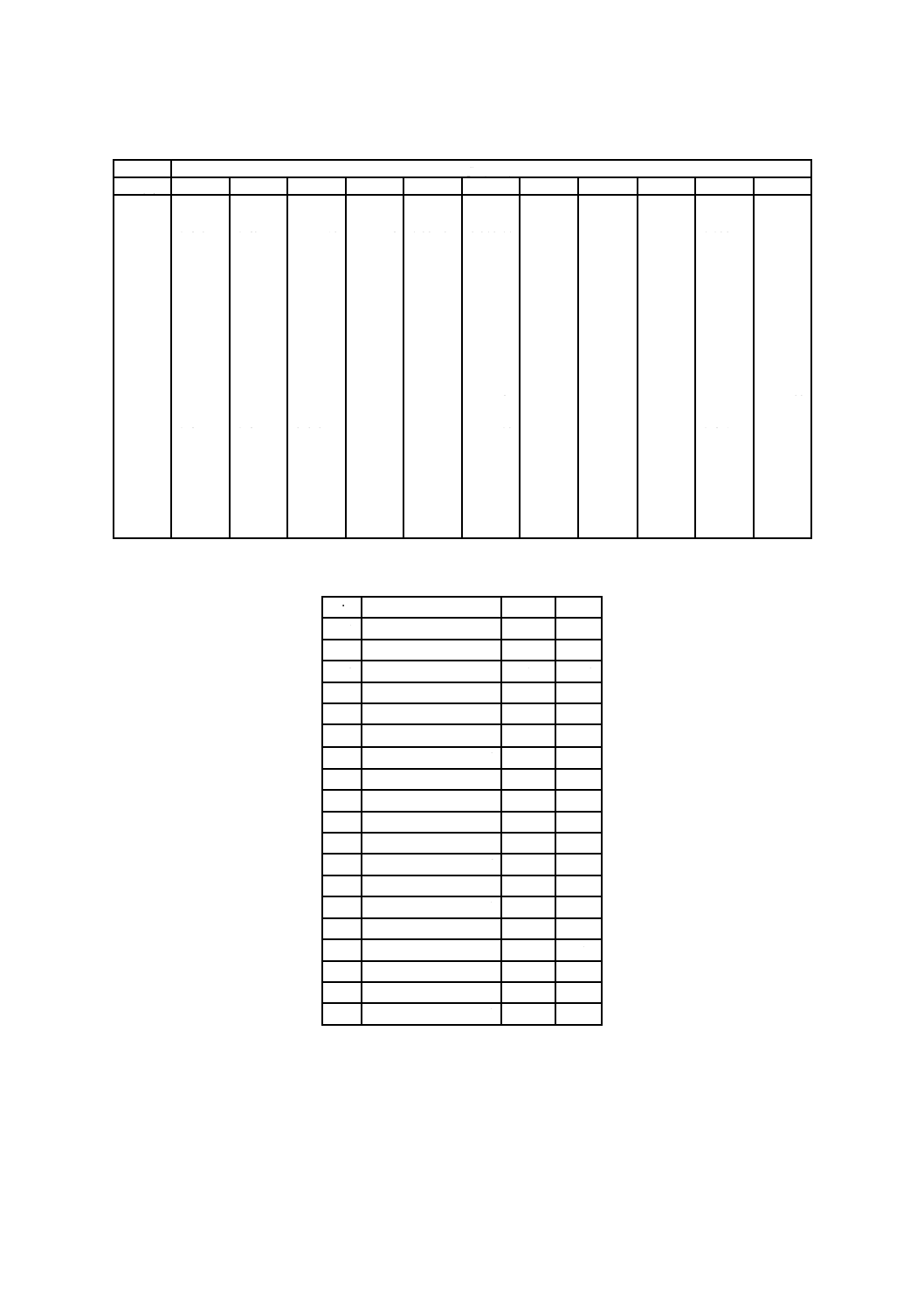
附属書B表 1 窒素のC*の値
po(MPa)
To (K)
0.1
2
4
6
8
10
12
14
16
18
20
200
220
240
260
280
300
320
340
360
380
400
420
440
460
480
500
520
540
560
580
600
0.685 61
0.685 38
0.685 22
0.685 10
0.685 00
0.684 92
0.684 85
0.684 78
0.684 70
0.684 62
0.684 52
0.684 41
0.684 28
0.684 13
0.683 95
0.683 76
0.683 55
0.683 31
0.683 05
0.682 78
0.682 49
0.703 67
0.698 67
0.695 21
0.692 72
0.690 88
0.689 48
0.688 39
0.687 52
0.686 81
0.686 21
0.685 70
0.685 25
0.684 84
0.684 45
0.684 09
0.683 73
0.683 38
0.683 03
0.682 68
0.682 32
0.681 96
0.724 97
0.713 60
0.706 08
0.700 83
0.697 02
0.694 17
0.691 98
0.690 26
0.688 89
0.687 76
0.686 82
0.686 03
0.685 33
0.684 71
0.684 15
0.683 64
0.683 15
0.682 69
0.682 24
0.681 80
0.681 38
0.748 45
0.729 28
0.717 14
0.708 90
0.703 03
0.698 70
0.695 40
0.692 85
0.690 82
0.689 18
0.687 83
0.686 70
0.685 73
0.684 89
0.684 15
0.683 48
0.682 86
0.682 29
0.681 75
0.681 24
0.680 75
0.773 43
0.745 30
0.728 16
0.716 79
0.708 82
0.703 00
0.698 62
0.695 24
0.692 58
0.690 45
0.688 71
0.687 26
0.686 04
0.684 98
0.684 07
0.683 25
0.682 52
0.681 85
0.681 22
0.680 64
0.680 10
0.798 56
0.761 09
0.738 84
0.724 34
0.714 30
0.707 03
0.701 60
0.697 44
0.694 17
0.691 57
0.689 45
0.687 71
0.686 24
0.684 99
0.683 91
0.682 96
0.682 12
0.681 35
0.680 65
0.680 01
0.679 41
0.822 04
0.775 99
0.748 89
0.731 40
0.719 38
0.710 74
0.704 31
0.699 41
0.695 58
0.692 53
0.690 07
0.688 04
0.686 35
0.684 91
0.683 68
0.682 61
0.681 66
0.680 81
0.680 04
0.679 34
0.678 68
0.842 30
0.789 38
0.758 03
0.737 82
0.723 99
0.714 08
0.706 73
0.701 14
0.696 79
0.693 33
0.690 54
0.688 26
0.686 36
0.684 75
0.683 38
0.682 20
0.681 15
0.680 22
0.679 39
0.678 63
0.677 93
0.858 42
0.800 81
0.766 04
0.743 52
0.728 08
0.717 03
0.708 85
0.702 63
0.697 80
0.693 97
0.690 88
0.688 36
0.686 27
0.684 51
0.683 01
0.681 72
0.680 59
0.679 59
0.678 70
0.677 89
0.677 15
0.870 23
0.810 06
0.772 80
0.748 40
0.731 60
0.719 56
0.710 65
0.703 87
0.698 61
0.694 44
0.691 09
0.688 35
0.686 09
0.684 19
0.682 58
0.681 19
0.679 98
0.678 92
0.677 97
0.677 12
0.676 35
0.878 09
0.817 10
0.778 25
0.752 44
0.734 55
0.721 68
0.712 13
0.704 86
0.699 22
0.694 75
0.691 16
0.688 24
0.685 82
0.683 79
0.682 07
0.680 60
0.679 32
0.678 20
0.677 21
0.676 32
0.675 51
附属書B表 2 式(B.1)の係数,窒素
i
ai
bi
ci
1
5.205 142 20 × 10-3
0
−4
2
6.814 027 97 × 10-1
0
0
3
2.377 461 61 × 10-3
0
1
4 −4.519 510 40 × 10-4
0
2
5 −1.374 006 43 × 10-1
1
−7
6
1.499 853 26 × 10-1
1
−3
7 −2.290 164 23 × 10-3
1
0
8
3.299 637 65 × 10-8
1
5
9 −2.026 516 12 × 10-3
1.5
−1
10
3.024 106 16 × 10-4
1.5
0
11
2.837 231 67 × 10-1
2.5
−8
12 −1.129 149 85 × 10-1
3
−8
13 −2.531 933 90 × 10-3
3
−4
14
2.222 006 17 × 10-5
3.5
−2
15
1.190 308 45 × 10-3
4
−6
臨界パラメータ:
Pc = 3.395 8 MPa
Tc = 126.192 K
窒素に関しては,式(B.1)は,圧力は20 MPaまで,温度は250〜600 Kの範囲内で正しい。
参考文献[35]及び[36]。
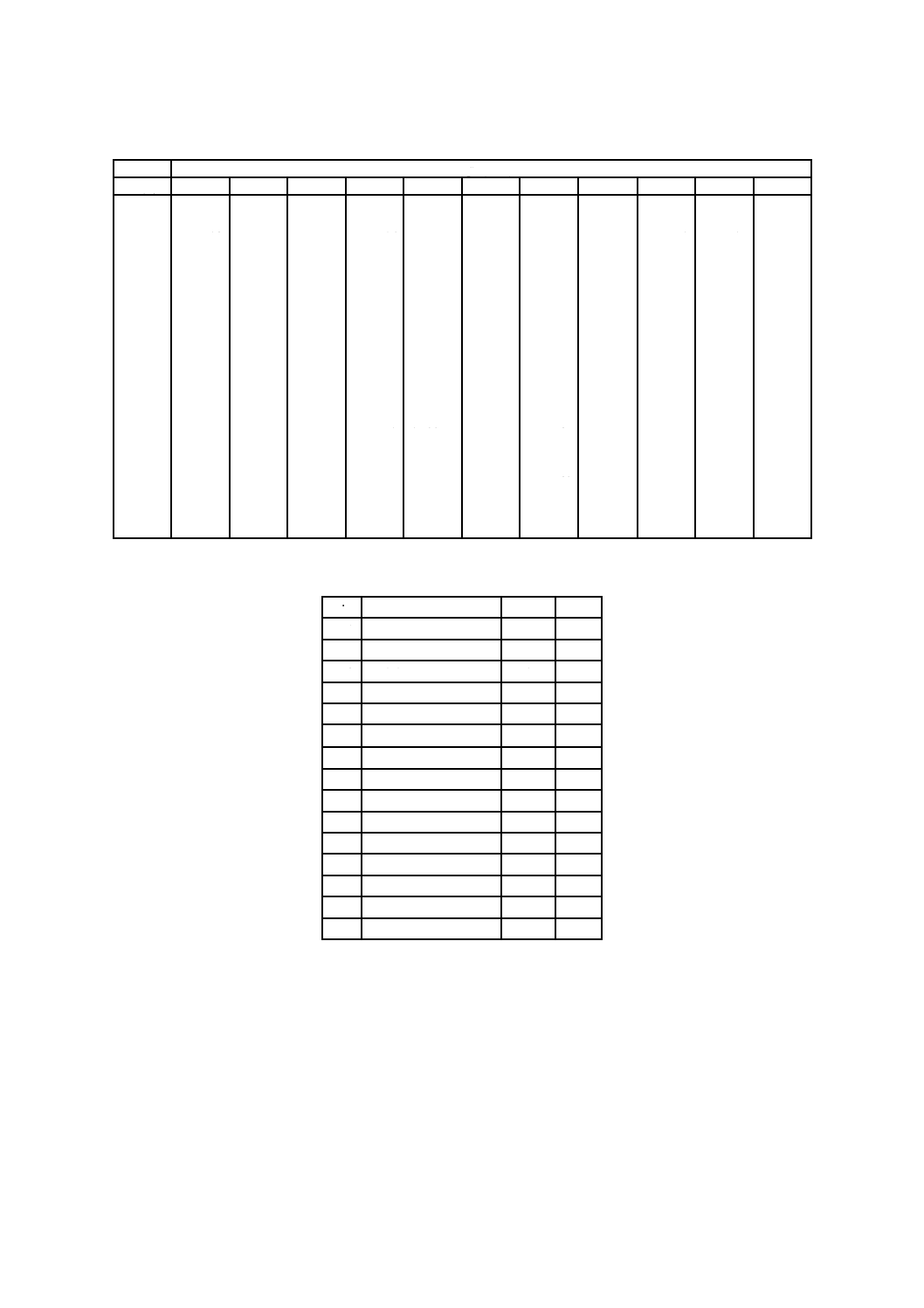
19
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B表 3 アルゴンのC*の値
po (MPa)
To (K)
0.1
2
4
6
8
10
12
14
16
18
20
200
−
−
−
−
−
−
−
−
−
−
−
220
0.727 19 0.747 57 0.771 78 0.799 09 0.829 51 0.862 53 0.896 82 0.930 35 0.960 92 0.986 87 1.007 46
240
0.726 98 0.742 75 0.760 74 0.780 16 0.800 86 0.822 48 0.844 48 0.866 12 0.886 59 0.905 15 0.921 29
260
0.726 82 0.739 26 0.753 08 0.767 56 0.782 56 0.797 87 0.813 20 0.828 21 0.842 53 0.855 83 0.867 83
280
0.726 70 0.736 67 0.747 52 0.758 66 0.769 98 0.781 35 0.792 61 0.803 55 0.814 01 0.823 82 0.832 81
300
0.726 60 0.734 69 0.743 35 0.752 11 0.760 90 0.769 61 0.778 16 0.786 43 0.794 32 0.801 74 0.808 60
320
0.726 53 0.733 14 0.740 15 0.747 15 0.754 09 0.760 92 0.767 57 0.773 97 0.780 06 0.785 79 0.791 11
340
0.726 47 0.731 92 0.737 64 0.743 30 0.748 86 0.754 30 0.759 55 0.764 59 0.769 37 0.773 87 0.778 04
360
0.726 42 0.730 94 0.735 63 0.740 25 0.744 76 0.749 13 0.753 33 0.757 34 0.761 14 0.764 70 0.768 01
380
0.726 38 0.730 14 0.734 02 0.737 80 0.741 48 0.745 02 0.748 41 0.751 63 0.754 67 0.757 51 0.760 14
400
0.726 35 0.729 48 0.732 69 0.735 81 0.738 82 0.741 70 0.744 45 0.747 04 0.749 48 0.751 76 0.753 85
420
0.726 32 0.728 93 0.731 60 0.734 17 0.736 64 0.738 99 0.741 22 0.743 31 0.745 27 0.747 09 0.748 76
440
0.726 30 0.728 48 0.730 69 0.732 81 0.734 83 0.736 74 0.738 55 0.740 24 0.741 81 0.743 26 0.744 59
460
0.726 28 0.728 09 0.729 92 0.731 66 0.733 32 0.734 88 0.736 33 0.737 69 0.738 94 0.740 09 0.741 12
480
0.726 27 0.727 77 0.729 27 0.730 70 0.732 04 0.733 30 0.734 47 0.735 55 0.736 54 0.737 43 0.738 23
500
0.726 25 0.727 49 0.728 72 0.729 88 0.730 97 0.731 97 0.732 90 0.733 74 0.734 51 0.735 19 0.735 79
520
0.726 24 0.727 25 0.728 25 0.729 18 0.730 04 0.730 84 0.731 56 0.732 21 0.732 79 0.733 29 0.733 72
540
0.726 23 0.727 04 0.727 84 0.728 58 0.729 25 0.729 87 0.730 41 0.730 89 0.731 31 0.731 67 0.731 96
560
0.726 22 0.726 87 0.727 49 0.728 06 0.728 57 0.729 03 0.729 43 0.729 77 0.730 05 0.730 27 0.730 44
580
0.726 21 0.726 71 0.727 19 0.727 61 0.727 99 0.728 31 0.728 57 0.728 79 0.728 96 0.729 07 0.729 13
600
0.726 21 0.726 58 0.726 92 0.727 22 0.727 47 0.727 68 0.727 84 0.727 95 0.728 01 0.728 03 0.728 00
附属書B表 4 式(B.1)の係数,アルゴン
i
ai
bi
ci
1
7.261 844 00 × 10-1
0
0
2 −1.173 389 76 × 10-1
1
−4
3 −1.173 389 76 × 10-1
1
−3
4 −2.250 904 86 × 10-3
1
0
5
3.571 311 67 × 10-2
1.5
−4
6
9.236 691 04 × 10-2
2
−9
7 −7.882 951 14 × 10-3
2
−3
8 −4.050 612 00 × 10-3
2
−2
9
9.893 033 93 × 10-5
2
0
10 −1.502 565 89 × 10-1
2.5
−8
11
3.551 149 94 × 10-1
3
−8
12
1.400 857 98 × 10-2
3
−4
13 −1.511 223 06 × 10-1
3.5
−8
14 −2.569 959 78 × 10-2
3.5
−5
15
1.570 106 43 × 10-2
4
−6
臨界パラメータ:
Pc = 4.863 MPa
Tc = 150.687 K
アルゴンに関しては,式(B.1)は,圧力は20 MPaまで,温度は250〜600 Kの範囲内で正しい。
参考文献[35]及び[37]。
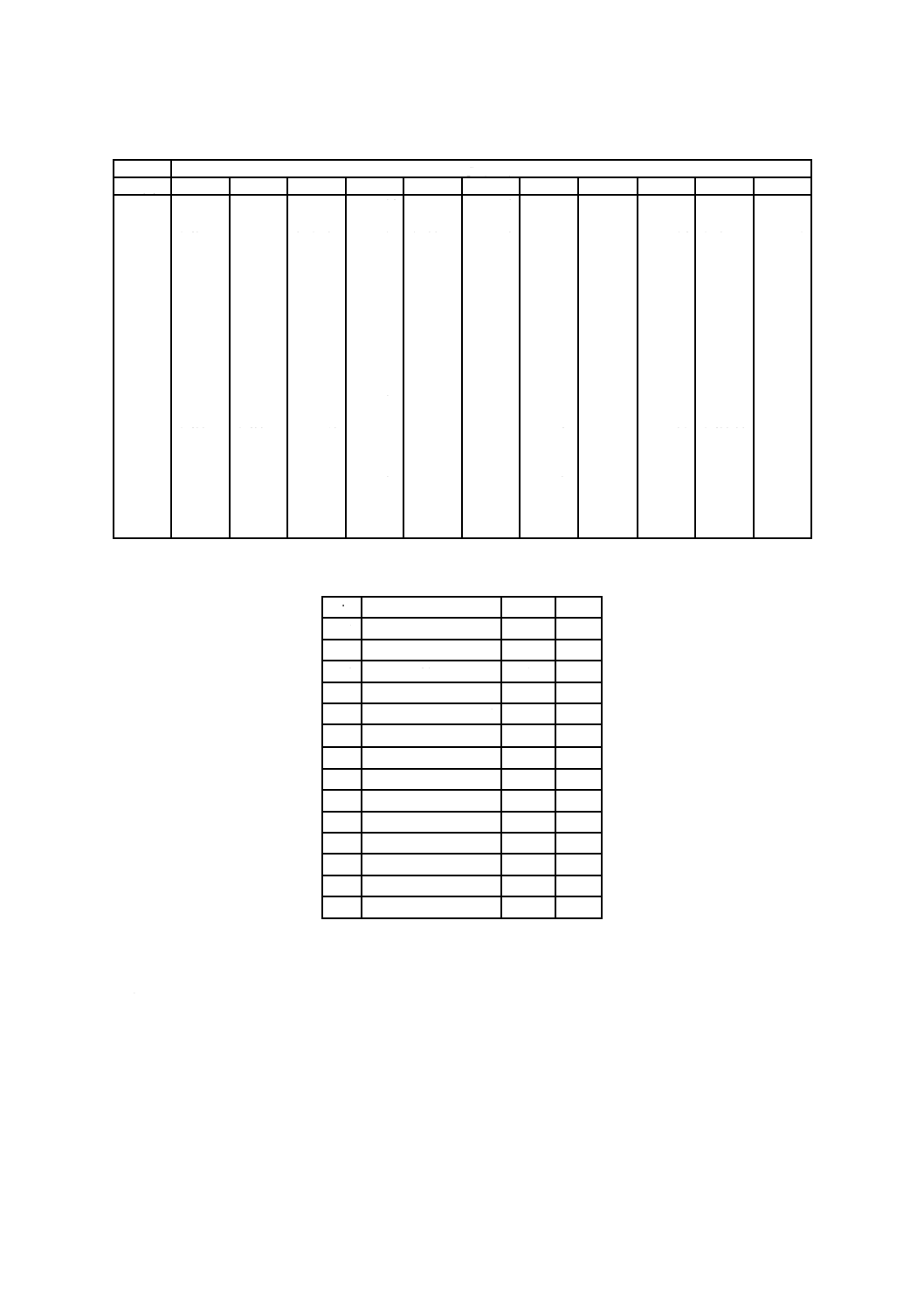
20
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B表 5 乾燥空気のC*の値
po (MPa)
To (K)
0.1
2
4
6
8
10
12
14
16
18
20
200
0.685 90 0.705 14 0.728 11 0.754 14 0.782 77 0.812 51 0.841 06 0.866 13 0.886 30 0.901 24 0.911 32
220
0.685 66 0.699 86 0.715 94 0.733 15 0.751 19 0.769 46 0.787 13 0.803 37 0.817 52 0.829 20 0.838 33
240
0.685 48 0.696 22 0.707 95 0.720 05 0.732 36 0.744 59 0.756 36 0.767 32 0.777 16 0.785 65 0.792 71
260
0.685 34 0.693 60 0.702 38 0.711 22 0.720 02 0.728 63 0.736 88 0.744 57 0.751 55 0.757 70 0.762 96
280
0.685 21 0.691 64 0.698 34 0.704 95 0.711 43 0.717 69 0.723 64 0.729 18 0.734 23 0.738 72 0.742 61
300
0.685 09 0.690 13 0.695 29 0.700 32 0.705 17 0.709 81 0.714 19 0.718 25 0.721 94 0.725 24 0.728 10
320
0.684 97 0.688 93 0.692 94 0.696 79 0.700 46 0.703 93 0.707 18 0.710 18 0.712 89 0.715 31 0.717 40
340
0.684 85 0.687 96 0.691 08 0.694 03 0.696 81 0.699 42 0.701 84 0.704 04 0.706 03 0.707 78 0.709 29
360
0.684 71 0.687 15 0.689 57 0.691 83 0.693 93 0.695 87 0.697 66 0.699 27 0.700 70 0.701 94 0.702 99
380
0.684 55 0.686 46 0.688 31 0.690 02 0.691 59 0.693 03 0.694 32 0.695 46 0.696 46 0.697 31 0.698 00
400
0.684 38 0.685 85 0.687 25 0.688 52 0.689 67 0.690 70 0.691 60 0.692 38 0.693 04 0.693 57 0.693 98
420
0.684 19 0.685 29 0.686 33 0.687 25 0.688 06 0.688 76 0.689 35 0.689 84 0.690 23 0.690 51 0.690 69
440
0.683 97 0.684 78 0.685 52 0.686 15 0.686 68 0.687 12 0.687 46 0.687 72 0.687 89 0.687 97 0.687 96
460
0.683 74 0.684 30 0.684 79 0.685 18 0.685 49 0.685 71 0.685 85 0.685 91 0.685 90 0.685 82 0.685 66
480
0.683 49 0.683 84 0.684 12 0.684 32 0.684 43 0.684 48 0.684 45 0.684 36 0.684 21 0.683 99 0.683 70
500
0.683 22 0.683 39 0.683 50 0.683 53 0.683 49 0.683 39 0.683 23 0.683 01 0.682 73 0.682 40 0.682 02
520
0.682 93 0.682 96 0.682 92 0.682 81 0.682 65 0.682 42 0.682 15 0.681 82 0.681 44 0.681 02 0.680 55
540
0.682 62 0.682 53 0.682 37 0.682 15 0.681 87 0.681 54 0.681 17 0.680 76 0.680 30 0.679 80 0.679 26
560
0.682 30 0.682 10 0.681 84 0.681 52 0.681 15 0.680 74 0.680 29 0.679 80 0.679 27 0.678 71 0.678 11
580
0.681 97 0.681 68 0.681 33 0.680 93 0.680 49 0.680 00 0.679 48 0.678 93 0.678 35 0.677 73 0.677 09
600
0.681 63 0.681 27 0.680 84 0.680 37 0.679 86 0.679 32 0.678 74 0.678 14 0.677 51 0.676 85 0.676 16
附属書B表 6 式(B.1)の係数,乾燥空気
i
ai
bi
ci
1
1.967 947 91 × 10-2
0
−3
2 −2.774 414 35 × 10-2
0
−1
3
7.031 906 83 × 10-1
0
0
4 −3.448 411 43 × 10-3
0
1
5 −1.135 939 77 × 10-1
1
−7
6
1.507 325 95 × 10-1
1
−3
7 −2.403 454 97 × 10-3
1
0
8
1.224 631 76 × 10-6
1
3
9 −3.064 388 30 × 10-3
2
−2
10
2.116 285 54 × 10-1
2.5
−8
11
5.128 802 07 × 10-5
2.5
0
12 −1.666 687 29 × 10-6
3
1
13 −6.554 052 14 × 10-2
3.5
−8
14
1.390 831 40 × 10-2
4
−8
臨界パラメータ:
Pc = 3.786 MPa
Tc = 132.530 6 K
乾燥空気に関しては,式(B.1)は,圧力は20 MPaまで,温度は250〜600 Kの範囲内で正しい。
参考文献[35]及び[38]。
21
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B表 7 メタンのC*の値
po (MPa)
To (K)
0.1
2
4
6
8
10
12
14
16
18
20
200
−
−
−
−
−
−
−
−
−
−
−
220
0.674 04 0.707 10 0.757 33 0.840 96 0.992 20 1.163 38
−
−
−
−
−
240
0.673 23 0.697 96 0.731 18 0.775 54 0.835 85 0.912 11 0.989 36 1.049 30 1.088 02 1.109 75 1.119 53
260
0.672 29 0.691 35 0.715 15 0.743 81 0.778 22 0.818 18 0.861 09 0.902 06 0.936 53 0.962 60 0.980 60
280
0.671 19 0.686 19 0.704 03 0.724 26 0.747 03 0.772 03 0.798 39 0.824 59 0.848 87 0.869 83 0.886 78
300
0.669 92 0.681 89 0.695 66 0.710 68 0.726 91 0.744 13 0.761 92 0.779 64 0.796 56 0.812 00 0.825 46
320
0.668 50 0.678 15 0.688 98 0.700 49 0.712 59 0.725 13 0.737 88 0.750 51 0.762 68 0.774 03 0.784 30
340
0.666 96 0.674 80 0.683 44 0.692 43 0.701 72 0.711 18 0.720 67 0.730 02 0.739 04 0.747 54 0.755 36
360
0.665 32 0.671 73 0.678 69 0.685 82 0.693 08 0.700 39 0.707 64 0.714 75 0.721 59 0.728 06 0.734 06
380
0.663 63 0.668 89 0.674 54 0.680 25 0.686 00 0.691 73 0.697 37 0.702 87 0.708 15 0.713 14 0.717 79
400
0.661 93 0.666 26 0.670 85 0.675 46 0.680 05 0.684 59 0.689 03 0.693 33 0.697 45 0.701 34 0.704 97
420
0.660 25 0.663 81 0.667 56 0.671 29 0.674 97 0.678 59 0.682 11 0.685 50 0.688 73 0.691 78 0.694 63
440
0.658 60 0.661 53 0.664 59 0.667 61 0.670 58 0.673 47 0.676 27 0.678 95 0.681 49 0.683 89 0.686 11
460
0.657 00 0.659 40 0.661 90 0.664 35 0.666 73 0.669 05 0.671 27 0.673 39 0.675 39 0.677 27 0.679 00
480
0.655 47 0.657 43 0.659 46 0.661 44 0.663 35 0.665 19 0.666 95 0.668 62 0.670 18 0.671 64 0.672 98
500
0.654 01 0.655 61 0.657 24 0.658 82 0.660 35 0.661 80 0.663 18 0.664 49 0.665 70 0.666 82 0.667 84
520
0.652 62 0.653 91 0.655 21 0.656 47 0.657 67 0.658 81 0.659 88 0.660 88 0.661 80 0.662 64 0.663 39
540
0.651 31 0.652 33 0.653 36 0.654 34 0.655 27 0.656 14 0.656 96 0.657 70 0.658 39 0.659 00 0.659 53
560
0.650 07 0.650 87 0.651 66 0.652 41 0.653 11 0.653 76 0.654 36 0.654 90 0.655 38 0.655 80 0.656 15
580
0.648 91 0.649 51 0.650 10 0.650 66 0.651 16 0.651 63 0.652 04 0.652 40 0.652 71 0.652 97 0.653 18
600
0.647 80 0.648 24 0.648 66 0.649 05 0.649 39 0.649 70 0.649 96 0.650 17 0.650 34 0.650 46 0.650 54
附属書B表 8 式(B.1)の係数,メタン
i
ai
bi
ci
1 −4.720 546 92 × 10-2
0
−1
2
7.648 102 27 × 10-1
0
0
3 −5.034 818 10 × 10-2
0
1
4
5.707 154 95 × 10-3
0
2
5 −8.628 216 22 × 10-2
0.5
−7
6
2.310 287 94 × 10-3
0.5
−4
7
7.445 647 54 × 10-1
1
−9
8 −4.276 642 05 × 10-1
1
−6
9
3.289 116 00 × 10-1
1
−4
10 −2.068 296 47 × 10-3
1
0
11 −8.178 634 39 × 10-1
1.5
−10
12
1.868 520 89 × 10-4
1.5
−1
13
3.835 357 66 × 10-1
2
−9
14 −2.429 634 03 × 10-3
3
−4
15
2.802 359 69 × 10-1
4
−15
16 −1.226 295 45 × 10-1
5
−15
17
1.706 268 70 × 10-4
5
−6
18
1.582 014 74 × 10-2
6
−14
19 −3.733 935 09 × 10-3
6
−12
臨界パラメータ:
Pc = 4.592 2 MPa
Tc = 190.564 K
メタンに関しては,式(B.1)は,圧力は20 MPaまで,温度は270〜600 Kの範囲内で正しい。
参考文献[35]及び[39]。
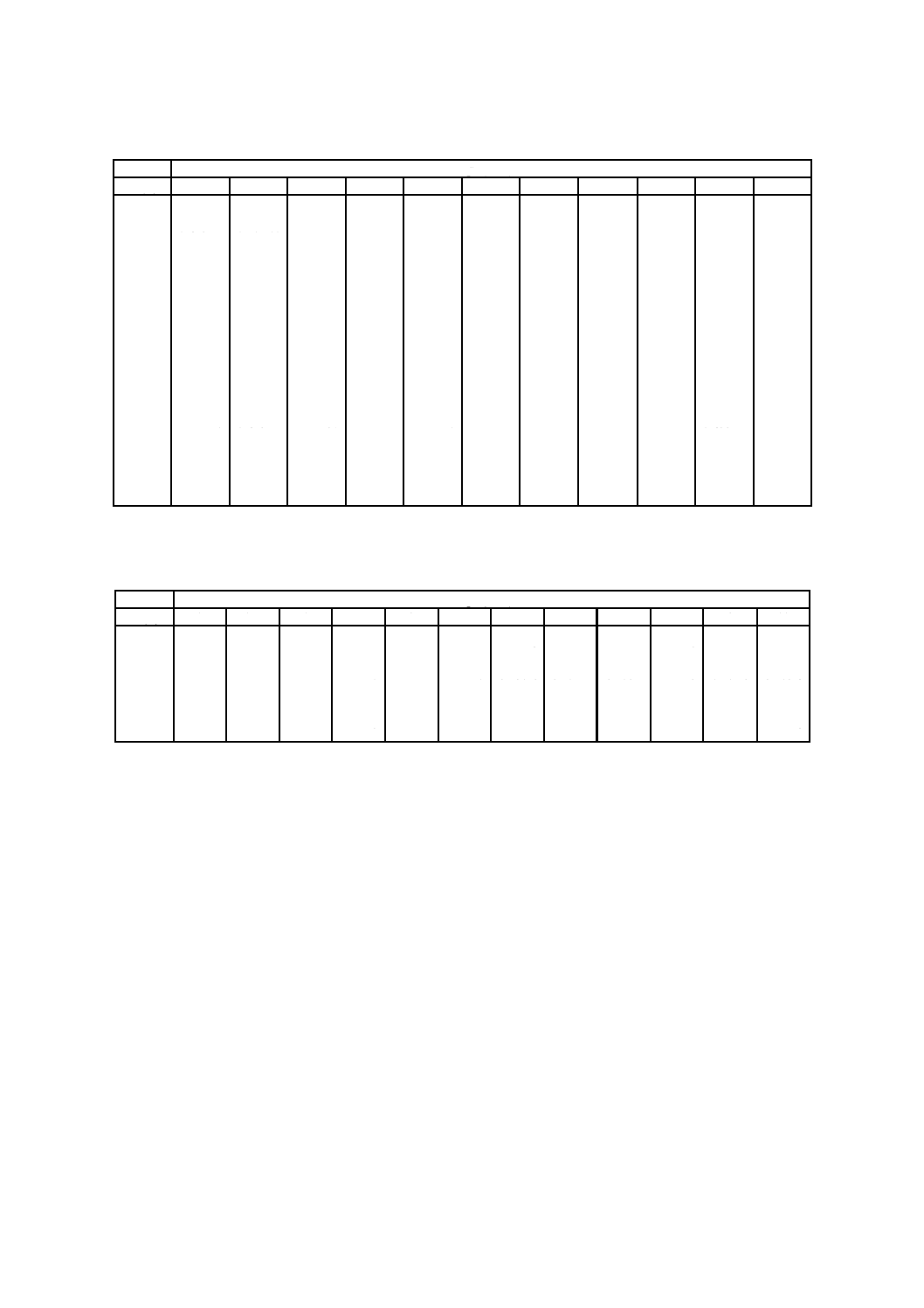
22
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
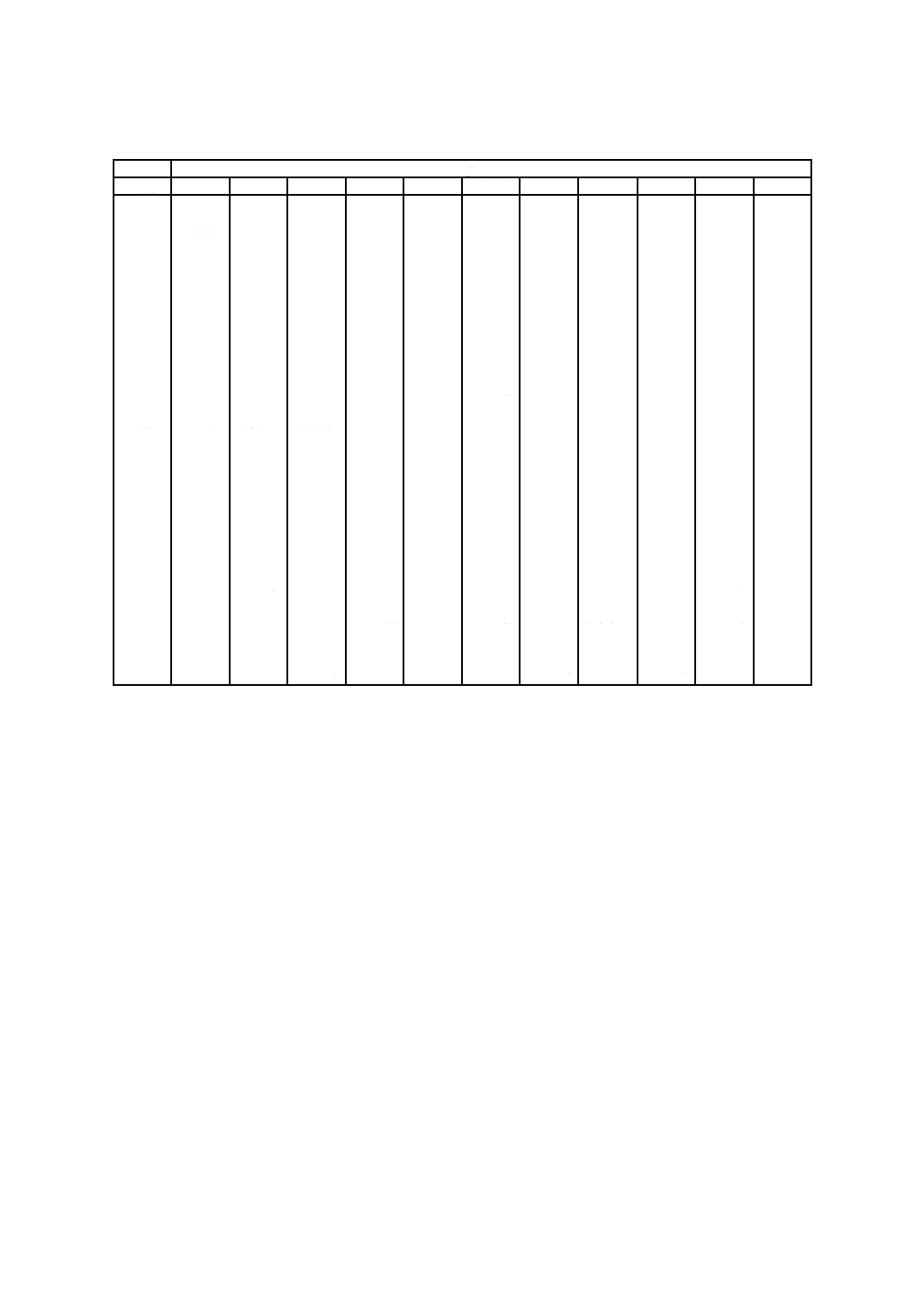
附属書B表 9 二酸化炭素のC*の値
po (MPa)
To (K)
0.1
2
4
6
8
10
12
14
16
18
20
240
−
−
−
−
−
−
−
−
−
−
−
260
0.673 18
−
−
−
−
−
−
−
−
−
−
280
0.670 66 0.715 19
−
−
−
−
−
−
−
−
−
300
0.668 43 0.701 88 0.755 14
−
−
−
−
−
−
−
−
320
0.666 46 0.692 45 0.729 20 0.784 19
−
−
−
−
−
−
−
340
0.664 70 0.685 39 0.712 56 0.748 21 0.797 97
−
−
−
−
−
−
360
0.663 13 0.679 89 0.700 83 0.726 33 0.758 13 0.798 64 0.850 46 0.913 90 0.982 71 1.045 85 1.096 34
380
0.661 71 0.675 50 0.692 09 0.711 34 0.733 88 0.760 41 0.791 55 0.827 36 0.866 73 0.907 11 0.945 22
400
0.660 42 0.671 89 0.685 32 0.700 38 0.717 29 0.736 31 0.757 56 0.780 99 0.806 20 0.832 39 0.858 44
420
0.659 26 0.668 89 0.679 93 0.691 99 0.705 18 0.719 54 0.735 11 0.751 79 0.769 39 0.787 55 0.805 80
440
0.658 19 0.666 34 0.675 53 0.685 38 0.695 92 0.707 16 0.719 08 0.731 60 0.744 61 0.757 91 0.771 28
460
0.657 21 0.664 16 0.671 88 0.680 03 0.688 62 0.697 63 0.707 03 0.716 77 0.726 77 0.736 92 0.747 08
480
0.656 31 0.662 26 0.668 80 0.675 62 0.682 72 0.690 07 0.697 65 0.705 42 0.713 32 0.721 28 0.729 22
500
0.655 48 0.660 60 0.666 18 0.671 93 0.677 86 0.683 94 0.690 15 0.696 45 0.702 82 0.709 20 0.715 54
520
0.654 71 0.659 13 0.663 91 0.668 80 0.673 79 0.678 87 0.684 02 0.689 21 0.694 42 0.699 61 0.704 75
540
0.653 99 0.657 82 0.661 93 0.666 11 0.670 34 0.674 62 0.678 92 0.683 24 0.687 55 0.691 83 0.696 05
560
0.653 32 0.656 65 0.660 19 0.663 77 0.667 38 0.671 00 0.674 63 0.678 25 0.681 85 0.685 40 0.688 90
580
0.652 69 0.655 58 0.658 65 0.661 73 0.664 82 0.667 90 0.670 97 0.674 02 0.677 04 0.680 01 0.682 93
600
0.652 10 0.654 62 0.657 28 0.659 93 0.662 58 0.665 21 0.667 82 0.670 40 0.672 95 0.675 45 0.677 89
参考文献[40]。
附属書B表 10 酸素のC*の値
po (MPa)
To (K)
0
0.5
1
2
3
4
5
6
7
8
9
10
223.15
0.684 6
0.688 6
0.692 7
0.701 3
0.710 4
0.720 1
0.730 4 0.741 3
0.752 8
0.765 0
0.777 9
0.791 4
248.15
0.684 5
0.687 5
0.690 5
0.696 6
0.703 0
0.709 6
0.716 4 0.723 4
0.730 7
0.738 1
0.745 7
0.753 5
273.15
0.684 4
0.686 6
0.688 9
0.693 4
0.698 1
0.702 8
0.707 6 0.712 5
0.717 5
0.722 5
0.727 6
0.732 6
298.15
0.684 2
0.685 9
0.687 6
0.691 1
0.694 6
0.698 1
0.701 6 0.705 2
0.708 7
0.712 3
0.715 9
0.719 4
323.15
0.683 9
0.685 2
0.686 5
0.689 2
0.691 9
0.694 5
0.697 2 0.699 9
0.702 5
0.705 1
0.707 8
0.710 3
348.15
0.683 5
0.684 5
0.685 5
0.687 6
0.689 7
0.691 7
0.693 8 0.695 8
0.697 8
0.699 8
0.701 7
0.703 7
373.15
0.682 9
0.683 7
0.684 5
0.686 1
0.687 7
0.689 3
0.690 9 0.692 5
0.694 0
0.695 5
0.697 0
0.698 4
参考文献[41]。
23
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B表 11 蒸気(単相気体)のC*の値
po (MPa)
To(K)
0.1
2
4
6
8
10
12
14
16
18
20
420
0.673 38
−
−
−
−
−
−
−
−
−
−
440
0.672 72
−
−
−
−
−
−
−
−
−
−
460
0.672 09
−
−
−
−
−
−
−
−
−
−
480
0.671 49
−
−
−
−
−
−
−
−
−
−
500
0.670 91
−
−
−
−
−
−
−
−
−
−
520
0.670 35
−
−
−
−
−
−
−
−
−
−
540
0.669 82 0.689 77
−
−
−
−
−
−
−
−
−
560
0.669 30 0.686 41
−
−
−
−
−
−
−
−
−
580
0.668 79 0.683 58 0.702 47
−
−
−
−
−
−
−
−
600
0.668 30 0.681 19 0.697 15 0.716 39
−
−
−
−
−
−
−
620
0.667 81 0.679 13 0.692 78 0.708 75 0.727 78 0.751 02
−
−
−
−
−
640
0.667 34 0.677 32 0.689 14 0.702 60 0.718 17 0.736 49 0.758 52
−
−
−
−
660
0.666 87 0.675 73 0.686 04 0.697 57 0.710 57 0.725 41 0.742 60 0.762 88 0.787 38
−
−
680
0.666 42 0.674 31 0.683 38 0.693 35 0.704 40 0.716 73 0.730 61 0.746 42 0.764 67 0.786 09 0.811 77
700
0.665 97 0.673 02 0.681 05 0.689 77 0.699 28 0.709 72 0.721 23 0.734 02 0.748 34 0.764 53 0.783 02
720
0.665 52 0.671 86 0.679 00 0.686 67 0.694 95 0.703 92 0.713 65 0.724 28 0.735 92 0.748 77 0.763 01
740
0.665 08 0.670 79 0.677 17 0.683 97 0.691 24 0.699 02 0.707 38 0.716 37 0.726 09 0.736 61 0.748 04
760
0.664 65 0.669 80 0.675 53 0.681 59 0.688 01 0.694 84 0.702 09 0.709 81 0.718 06 0.726 88 0.736 33
780
0.664 22 0.668 89 0.674 05 0.679 47 0.685 18 0.691 21 0.697 56 0.704 27 0.711 37 0.718 89 0.726 86
800
0.663 80 0.668 04 0.672 70 0.677 57 0.682 68 0.688 03 0.693 64 0.699 52 0.705 70 0.712 19 0.719 02
820
0.663 38 0.667 24 0.671 46 0.675 86 0.680 44 0.685 22 0.690 20 0.695 40 0.700 83 0.706 49 0.712 41
840
0.662 96 0.666 48 0.670 32 0.674 30 0.678 43 0.682 72 0.687 17 0.691 79 0.696 59 0.701 57 0.706 75
860
0.662 55 0.665 77 0.669 27 0.672 88 0.676 61 0.680 48 0.684 47 0.688 60 0.692 87 0.697 29 0.701 85
880
0.662 15 0.665 09 0.668 28 0.671 57 0.674 96 0.678 45 0.682 05 0.685 76 0.689 58 0.693 51 0.697 57
900
0.661 75 0.664 45 0.667 37 0.670 37 0.673 45 0.676 61 0.679 87 0.683 21 0.686 64 0.690 17 0.693 79
920
0.661 35 0.663 83 0.666 51 0.669 25 0.672 06 0.674 94 0.677 89 0.680 91 0.684 01 0.687 18 0.690 43
940
0.660 96 0.663 24 0.665 69 0.668 21 0.670 77 0.673 40 0.676 08 0.678 83 0.681 63 0.684 50 0.687 42
960
0.660 57 0.662 67 0.664 93 0.667 23 0.669 58 0.671 98 0.674 43 0.676 93 0.679 47 0.682 07 0.684 72
980
0.660 19 0.662 13 0.664 20 0.666 32 0.668 48 0.670 67 0.672 91 0.675 19 0.677 51 0.679 87 0.682 27
1 000
0.659 81 0.661 60 0.663 51 0.665 46 0.667 44 0.669 46 0.671 51 0.673 59 0.675 71 0.677 86 0.680 04
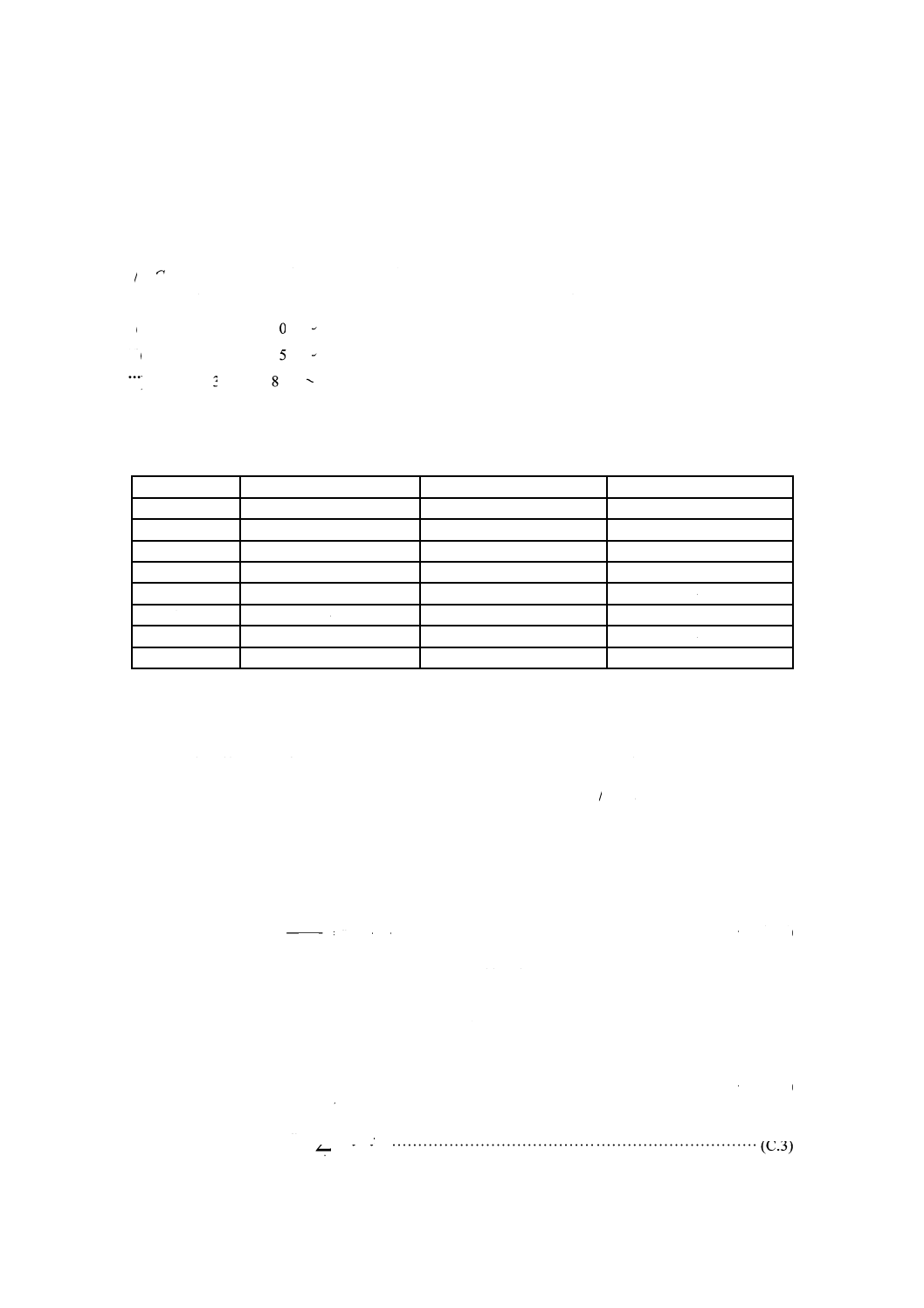
24
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(規定)混合天然ガスの臨界質量束の計算
C.1 一般 この附属書は,混合天然ガスの臨界質量束の計算に必要な情報について示す。相関式は,質量
束
d
*
m
C
A
q
を直接示し,温度,圧力及び気体成分の関数である。
相関式は,成分中のエタンのモル分率の大きさによって次の3領域に分けられる。
i)
レンジ1 0.010 〜 0.045
ii)
レンジ2 0.045 〜 0.080
iii) レンジ3 0.080 〜 0.115
相関式が正しい値を示すためには,モル分率が次の範囲に入っていることが望ましい。
附属書C表 1 モル分率の推奨値
成分
レンジ1
レンジ2
レンジ3
メタン
0.089 〜 0.98
0.84 〜 0.93
0.79 〜 0.88
エタン
0.01 〜 0.045
0.045 〜 0.08
0.08 〜 0.115
プロパン
0.002 〜 0.02
0.008 〜 0.03
0.015 〜 0.04
ブタン
0.0 〜 0.005
0.002 〜 0.01
0.003 〜 0.015
ペンタン
0.0 〜 0.002
0.0 〜 0.002
0.0 〜 0.003
ヘキサン+
0.0 〜 0.001 5
0.0 〜 0.02
0.0 〜 0.03
窒素
0.0 〜 0.03
0.0 〜 0.03
0.0 〜 0.015
二酸化炭素
0.0 〜 0.025
0.0 〜 0.025
0.01 〜 0.025
相関式は,圧力は12 MPaまで,温度範囲は270〜320 Kの間で正しい値を示す。モル分率を加えると1
になることが望ましいことに注意すること。
参考 混合天然ガスの成分が上に示すモル分率範囲に当てはまらない場合は,エタンのモル分率の中
で,最も近い範囲を用いることを推奨する。その場合は,
d
*
m
C
A
q
の不確かさは,95%の信頼
度において,±0.10%から±0.15%に増える。
C.2 相関式 上流側よどみ点における温度 To(K),圧力 po(MPa)であるときの臨界質量束は,次の式から
計算できる。
f
S
q
C
A
q
ref
d
*
m
+
=
·································································· (C.1)
ここに, qref: 基準ガスの質量流量束
S: 成分変化に対する質量束の感度係数
f: 成分の依存係数
これらの項の一般形は,次の式に示す。
∑
=
i
a
i
ref
i
i
a
q
φ
τ
π
···································································· (C.2)
S
bi
i
i
i
=∑πτ
γ
δ ······································································ (C.3)
25
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
[
]
(
)
[
]
ref
CO
CO
CO
CO
N
N
N
N
C
C
i
i
i
C
A
X
C
B
A
X
C
B
A
X
A
X
f
−
−
−
+
−
−
+
+
=
∑
=
2
2
2
2
2
2
2
2
6
3
2
π
τ
π
τ
·············· (C.4)
ref
o
p
p
=
π
及び
ref
o
T
T
=
τ
ここに,pref = 5 MPa及びTref = 200 K
3レンジに対するqref 及びSの係数は,それぞれ,附属書C表 1,附属書C表 2及び附属書C表 3に
示す。
3レンジに対するfの係数は,附属書C表 4に示す。
参考文献[43]。
C.3 ノズルスロートと配管との直径比,β この項に示す値は,β< 0.15の場合に限って正しい。この条
件が満たされない場合は,上流側の測定位置で,小さいけれども無視することのできない流速が発生する。
このような状況では,附属書Eに規定する質量流量の補正係数を用いることが望ましい。
附属書C表 2 qref及びSの係数,式(C.2)及び式(C.3),レンジ1
k
a
α
φ
b
γ
δ
1
0.108 244 635 × 105 1
−0.5
0.484 093 947 ×104 1
−4.5
2
−0.736 494 058 × 102 1
1.5 −0.136 051 287 ×105 1
−2.5
3
−0.287 636 821 × 104 2
−9.5
0.132 819 568 ×105 1
−1.5
4
0.293 505 438 × 104 2
−4.5
0.124 742 840 ×103 1.5
−0.5
5
0.213 321 640 × 103 2.5
−3.5
0.270 400 184 ×104 2
−4.5
6
0.470 680 038 × 104 3.5
−12.5
0.465 931 801 ×104 2.5
−5.5
7
−0.113 603 383 × 101 5
−0.5 −0.522 305 671 ×105 3.5
−15.5
8
−0.949 791 998 × 101 9
−15.5
0.728 305 715 ×105 4
−5.5
9
−
− −
0.626 536 557 ×101 4
−0.5
10
−
− −
0.863 837 290 ×101 6
−8.5
11
−
− −
0.218 148 488 ×101 6
−0.5
12
−
−
−
0.205 507 321 ×103 9
−15.5
13
−
−
−
0.172 829 796 ×101 11
−10.5
14
−
−
−
0.366 195 951 ×10-2 16
−10.5
26
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C表 3 qref及びSの係数,式(C.2)及び式(C.3),レンジ2
k
a
α
φ
b
γ
δ
1
0.110 966 325 × 105 1
−0.5
0.598 807 893 ×100 0
−0.5
2
−0.812 543 416 × 102 1
1.5
0.618 961 744 ×103 1
−1.5
3
−0.297 016 307 × 104 2
−6.5
0.302 809 257 ×104 1
−0.5
4
0.433 774 605 × 104 2
−4.5
0.134 089 681 ×104 1.5
−3.5
5
0.148 426 025 × 104 3
−7.5
0.523 229 697 ×103 2
−1.5
6
0.704 694 512 × 104 4
−15.5
−0.862 689 783 ×104 3
−8.5
7
−0.254 996 358 × 101 4.5
−0.5
0.235 424 200 ×105 3
−7.5
8
−0.224 612 799 × 102 9
−15.5
−0.767 928 108 ×103 3.5
−3.5
9
−
−
−
−0.859 071 767 ×105 4.5
−12.5
10
−
−
−
0.724 778 127 ×104 4.5
−8.5
11
−
−
−
0.153 097 473 ×106 5
−15.5
12
−
−
−
−0.135 420 339 ×104 6
−10.5
13 −
−
−
−0.292 807 154 ×105 7
−20.5
14
−
−
−
0.884 153 806 ×10-1 16
−15.5
附属書C表 4 qref及びSの係数,式(C.2)及び式(C.3),レンジ3
k
a
α
φ
b
γ
δ
1
0.115 572 303 × 105 1
−0.5
0.801 874 088 ×103 1
−1.5
2
−0.249 894 765 × 103 1
0.5
0.264 127 915 ×104 1
−0.5
3
−0.240 531 018 × 104 2
−7.5
0.247 996 282 ×103 1.25
−0.5
4
0.404 006 226 × 104 2
−4.5
0.178 851 521 ×104 2
−8.5
5
0.271 706 092 × 104 3
−7.5
0.101 397 979 ×105 2.5
−5.5
6
−0.126 049 305 × 105 4
−15.5
−0.296 058 326 ×102 3.5
−0.5
7
0.553 331 233 × 105 5
−18.5
−0.680 911 912 ×105 4
−15.5
8
−0.115 934 413 × 103 5
−7.5
0.259 571 626 ×106 5
−18.5
9
−0.262 586 997 × 105 6
−20.5
−0.144 795 597 ×106 7
−25.5
10
−
−
−
−0.110 728 705 ×104 9
−15.5
11
−
−
−
0.144 085 124 ×102 11
−10.5
12
−
−
−
0.901 740 847 ×100 16
−15.5
13
−
−
−
−0.132 368 505 ×100 16
−10.5
附属書C表 5 fの係数,式(C.4)
係数
レンジ 1
レンジ 2
レンジ 3
AC3
2.011 3
2.157 5
2.244 0
AC4
2.751 7
2.803 4
3.123 8
AC5
3.889 8
4.086 0
4.316 1
AC6
4.947 8
5.423 0
5.869 3
AN2
1.014 8
1.041 1
1.107 4
BN2
1.464 3
1.672 1
2.268 9
CN2
0.765 0
0.879 4
1.222 4
ACO2
2.253 3
2.348 8
2.434 7
BCO2
1.673 3
2.002 4
2.125 0
CCO2
0.881 9
1.065 9
1.125 1
Aref
0.066 36
0.136 94
0.217 73
27
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C.4 計算プログラム検算のためのサンプル値 この項では,使用者の作成した計算機による相関式プログ
ラムを検算するためのサンプル値を示す。
附属書C表 6 相関式プログラムの検算例
試験気体1
試験気体2
試験気体3
メタン
0.931 7
0.880 5
0.837 5
窒素
0.024 3
0.010 4
0.003 9
二酸化炭素
0.009 5
0.020 4
0.019 7
エタン
0.026 3
0.062 4
0.093 5
プロパン
0.004 9
0.018 4
0.033 1
ブタン
0.002 0
0.006 1
0.009 7
ペンタン
0.001 3
0.001 5
0.002 0
ヘキサン
0.000 0
0.000 3
0.000 6
附属書C表 7 相関式プログラムの検算例
To (K)
po (MPa)
qref
S
f
qm/A*Cd
試験気体1
280
310
2
10
3 704.50
19 007.4
1 481.33
10 716.5
0.020 94
0.007 07
3 735.52
19 083.2
試験気体2
280
310
2
10
3 805.42
19 749.8
1 402.57
10 905.8
0.042 76
0.028 04
3 865.38
20 055.5
試験気体3
280
310
2
10
3 913.25
20 603.1
1 325.58
11 260.7
0.039 58
0.026 85
3 965.72
20 905.5
28
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D(規定)大気の質量流量補正式
D.1 大気の質量流量補正式 上流側よどみ点における温度がTo(K),圧力がpo(MPa)である大気の質量流量
atmos
m
q,
を,次の式に示す。
(
)
+
+
+
=
−
B
A
RH
.
.
X
q
q
CO
free
CO
dry
,
m
atmos
,
m
100
32
047
0
25
0
1
2
2
π
··············· (D.1)
ここに,
free
CO
dry
,
m
q
−
2
は,二酸化炭素を含まない空気の質量流量,
2
CO
X
は,空気中の二酸化炭素のモル分率(不明な場合は,0.000 4を用いる。),
RHは,空気の相対湿度(%),
18
128
1
66
631
1
422
789
0
828
127
0
2
3
.
.
.
.
A
−
+
−
=
τ
τ
τ
················································ (D.2)
π
π
π
5
999
071
0
36
695
005
0
22
910
001
0
749
288
000
0
2
.
.
.
.
B
−
+
−
−
=
······························ (D.3)
c
o
p
p
=
π
及び
c
o
T
T
=
τ
ここに,pc = 3.786 MPa 及び Tc = 132.530 6 K
D.2 計算プログラム検算のためのサンプル値 この項では,使用者の作成した計算機による相関式プログ
ラムを検算するためのサンプル値を示す。
附属書D表 1 相関式プログラムの検算例
T (K)
p (MPa)
RH (%)
qm,dryCO2-free
qm,atmos
280
0.1
50
241.663
241.403
280
1
100
2 427.42
2 427.11
305
0.1
75
231.501
229.674
305
2
100
4 662.04
4 660.15
29
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E(規定)ノズルスロートと配管との直径比βが0.25以上の場合の
臨界ノズルの臨界質量束の計算
E.1 一般 附属書B及び附属書Cに規定する方法による質量流量の計算で得られる値は,上流側の温度及
び圧力の測定値が真のよどみ点での値であることを仮定している。この仮定は,ノズルのスロートと配管
との直径比βが0.25より小さい場合に当てはまる。β> 0.25の場合は,上流側の測定位置で無視できない
流速が発生し,質量流量に無視できない影響を与える。
上流側の測定位置で無視できない流速が発生している場合は,壁面圧力測定孔は静圧力,すなわち,流
れる気体の圧力を測定するが,流れる気体に温度計を挿入して測定される温度は,気体が温度計に当たる
と減速するため,別の温度Tmとなり,その値は,静温度Tsとは大きく異なり,むしろよどみ点温度Toに
近いが,それらの間の値となる。これらの温度の関係は,温度プローブの回復係数
s
o
s
m
f
T
T
T
T
R
−
−
=
········································································· (E.1)
によって与えられる。
f
Rが0の場合は,プローブは静温度を測定することになり,1の場合は,よどみ点
温度o
Tを測定することになる。実際には,
f
Rは0.5から0.9の間の値をとり,このことは,測定された温
度は静温度ではなく,よどみ点温度に近いことを意味する。
E.2 補正係数 次の補正係数は式(B.1)と同じ気体,すなわち,窒素,アルゴン,二酸化炭素を含まない空
気,及びメタンに用いることができる。適用可能な温度及び圧力の範囲も,附属書Bに規定されるとおり,
250〜600 K(メタンでは270〜600 K),及び20 MPa以下である。この補正は,βが0.25〜0.5の範囲内に
あるときに有効である。
(
)
[
]
1
1
F
R
F
R
q
q
f
o
f
stag
,
m
,
m
+
−
=
β
············································································ (E.2)
ここに, qm,stag:
附属書B又は附属書Cによって計算された質量流量
Rf:
温度プローブの回復係数
補正係数であるFo 及びF1は,次の形をとる。
i
i
C
B
F
+
=1
································································································· (E.3)
ここに,
7
004
0
2
112
0
6
115
1
9
019
6
276
34
693
32
879
25
2
3
4
5
6
.
.
.
.
.
.
.
B
+
−
+
−
+
−
=
β
β
β
β
β
β
············· (E.4)
及び
∑
=
k
t
s
k,i
i
k,i
k,i
n
C
τ
π
·························································································· (E.5)
式(E.5)の係数は,附属書E表1及び附属書E表4に与えられる。臨界パラメータを計算するために必要
となる換算圧力,温度,π及びτは,附属書Bに規定のとおりである。
参考文献[45]。
30
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E表 1 式(E.5)の係数,窒素
i
k
ni,k
pi,k
ti,k
0
1
1.304 619 × 10 -2
0
0
2
−3.666 323 × 10 -5
0
1
3
−3.668 820 × 10 -3
0.5
−5
4
5.024 075 × 10 -4
1
−1
5
2.846 962 × 10 -3
2
−6
6
−7.569 285 × 10 -4
3
−8
1
1
1.516 890 × 10 -2
0
0
2
−2.433 804 × 10 -5
0
1
3
−3.755 322 × 10 -3
1
−3
4
4.068 331 × 10 -3
1
−2
5
9.540 179 × 10 -3
1.5
−6
6
−4.828 687 × 10 -6
5
−6
附属書E表 2 式(E.5)の係数,アルゴン
i
k
ni,k
pi,k
ti,k
0
1
1.359 113 × 10 -2
0
0
2
5.072 601 × 10 -4
1
−1
3
5.776 326 × 10 -4
2
−4
4
4.625 040 × 10 -4
3
−10
5
−3.001 709 × 10 -7
6
−4
1
1
1.702 515 × 10 -2
0
0
2
3.255 007 × 10 -3
1
−2
3
2.029 543 × 10 -4
1
−1
4
6.931 127 × 10 -3
2
−6
5
−1.846 055 × 10 -4
4
−6
附属書E表 3 式(E.5)の係数,二酸化炭素を含まない空気
i
k
ni,k
pi,k
ti,k
0
1
1.307 864 × 10 -2
0
0
2
−4.752 544 × 10 -5
0
1
3
1.760 268 × 10 -2
0.5
−6
4
−1.340 098 × 10 -2
0.5
−5
5
4.672 622 × 10 -4
1
−1
6
1.294 203 × 10 -3
1.5
−4
1
1
1.522 775 × 10 -2
0
0
2
−4.726 879 × 10 -5
0
1
3
−5.958 875 × 10 -3
1
−4
4
3.445 387 × 10 -3
1
−2
5
1.256 916 × 10 -2
1.5
−6
6
−4.775 091 × 10 -5
4
−6
31
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E表 4 式(E.5)の係数,メタン
i
k
ni,k
pi,k
ti,k
0
1
1.068 826 × 10 -3
0
−1
2
1.199 593 × 10 -2
0
0
3
−1.482 920 × 10 -3
0.5
−6
4
2.764 799 × 10 -4
1
−1
5
7.920 711 × 10 -5
2
−2
6
1.111 278 × 10 -3
3
−8
7
−6.815 626 × 10 -5
5
−10
8
3.862 490 × 10 -8
10
−18
1
1
−3.463 148 × 10 -3
0
−3
2
5.286 029 × 10 -3
0
−1
3
1.195 016 × 10 -2
0
0
4
1.664 232 × 10 -3
1
−2
5
1.159 371 × 10 -3
1.5
−4
6
7.260 461 × 10 -3
3
−10
7
−7.541 933 × 10 -4
5
−12
8
2.613 967 × 10 -7
10
−15
32
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
ISO文書
[1] ISO/TR 5168 Measurement of fluid flow−Evaluation of uncertainties
CFVNの一般的事項
[2] K.E. STARLING, J. L. SAVIDGE. Compressibility factors for natural gas and related hydrocarbon gases.
Second edition, Transmission Measurement Committee Report No.8. AGA November 1992, also Errata N°1
issued by AGA June 1993
[3] JAESCHKE, M., AUDIBERT, S., VAN CANEGHEM, P., HUMPHREYS, A. E., JANSSEN-VAN
ROSMALEN, R., PELLEI, Q., MHICHELS, J.P.J., SCHOUTEN, J. A., TEN SELDAM, C. A;, High accuracy
compressibility factor calculation for natural gases and similar mixtures by use of a truncated virial equation,
GERG Technical Monograph TM2 (1988), and Fortschritt-Berichte VDI, Series 6, N°231 (1989)
[4] R.C.JOHNSON. Real gas effects in critical flow through nozzles and tabulated thermodynamic properties.
NASA TN D-2565 (1965)
[5] R.C. JOHNSON. Tables of critical flow functions and thermodynamic properties for methane and
computational procedures for both methane and natural gas. NASA SP-3074, Lewis Research Center, 1972
[6] STEWART, D.G., WATSON, J.T.R., VAIDYA, A.M. Uncertainty in the theoretical mass flow-rate of pure
gases through Critical Flow Nozzles. Int. Fluid Flow Measurement Symposium, Denver 27-30 June, 1999
[7] STEWART, D.G., WATSON, J.T.R., VAIDYA, A.M. The effect of using atmospheric air in Critical Flow
Nozzles. Int. Fluid Flow Measurement Symposium, Denver 27-30 June, 1999
[8] KEGEL, T. A study of the repeatability and reproducibility of the Critical Flow Nozzle. Int. Fluid Flow
Measurement Symposium, Denver 27-30 June, 1999
[9] CARON, R.W., BRITTON, C.L., KEGEL, T. Investigation into the accuracy of multiple Critical Flow Venturis
mounted in parallel within a common plenum. Int. Fluid Flow Measurement Symposium, Denver 27-30 June,
1999
[10] PARK, K.A., CHOI, Y.M., CHOI, H.M., CHA, T.S. YOON, B.H. The evaluation of critical pressure ratios of
sonic nozzle at low Reynolds numbers, released for Flow. Meas. Instrum
[11] STUDZINSKI, W.,WILLIAMSON, I.D., JUNGOWSKI, W., BOTROS, K.K., SAWCHUK, B., STROM, V.,
Novaʼs gravimetric meter prover and sonic nozzle facility, CGA Gas Measurement School, Alberta, Canada,
1994
[12] CHOI, Y.M., PARK, K.A., PARK S.O. Interference effects between sonic nozzles, Flow. Meas. Instrum. 8,
page 113-119, 1997
[13] CHOI, Y.M., PARK, K.A., PARK, J.T., CHOI, H. M., PARK S.O. Interference effects of three sonic nozzles of
different throat diameters in the same meter tube, Flow. Meas. Instrum. 10, page 175-181, 1999
[14] ISHIBASHI, M., TAKAMOTO, Theorical discharge coefficient of a critical circular-arc nozzle with laminar
boundary layer and its verification by measurements using super-accurate nozzles, Flow Measurement and
Instrumentation 11, 305/313, 2000
33
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[15] von LAVANTE, E., NATH, B., DIETRICH, H., Effects of instabilities on flow rates in small sonic nozzles,
9th Conference on Flow Measurement FLOMEKOʼ98, Lund, 1998
[16] CARON, R.W., BRITTON, C.L., KEGEL, T., Investigation into the premature unchocking phenomena of
critical flow venturis, Proceedings of ASME FEDSM 2000-11108, Boston, June 2000
トロイダルスロートベンチュリノズルの流出係数
[17] BRAIN, T. J. S. and MacDONALD, L. M. Evaluation of the performance of small-scale critical flow venturi
using the NEL gravimetric gas flow standard test facility. Fluid Flow Measurement in the Mid 1970s.
Edinburgh: HMSO, 1977, pp. 103-125
[18] BRAIN, T. J. S. and REID, J. Primary calibration of critical flow venturis in high-pressure gas. Flow
Measurement of Fluids, edited by DIJSTELBERGEN, H. H. and SPENCER, E. A. Amsterdam: North Holland
Publishing, 1978, pp. 54-64
[19] SMITH, R. E. and MATZ, R. J. A theoretical method of determining discharge coefficients for Venturis
operating at critical flow conditions. J. Bas. Engng., 1962, vol. 84, No. 4, pp. 434-446
[20] ARNBERG, B. T., BRITTON, C. L. and SEIDL, W. F. Discharge coefficient correlations for circular arc
venturi flowmeters at critical (sonic) flow. Paper No. 73-WA/FM-8. New York: American Society of
Mechanical Engineers, 1973
[21] BRAIN, T. J. S. and REID, J. An investigation of the discharge coefficient characteristics and manufacturing
specification of toroidal inlet critical flow venturi nozzles proposed as standard ISO flowmeters. Proceedings
of the International Conference on Advances in Flow Measurement, Paper C1, University of Warwick.
Cranfield, Bedford: BHRA Fluid Engineering, 1981
[22] SPENCER, E. A., EUJEN, E., DIJSTELBERGEN, H. H. and PEIGNELIN, G. Intercomparison campaign on
high pressure gas flow test facilities. EEC Document No. EUfR 6662. Brussels-Luxembourg: ECSC-EEC-
EAEC, 1980
[23] U.KARNIK, E.B.BOWLES, J.BOSIO, S.CALDWELL. North American Inter-Laboratory Flow Measurement
Testing Program. North Sea Flow Measurement Workshop 1996−Peebles, Scotland. Paper no. 3
[24] M.ISHIBASHI, M.TAKAMOTO. Very Accurate Analytical Calculation of the Discharge Coefficients of
Critical Venturi Nozzles with Laminar Boundary Layer. FLUCOMEʼ97, Hayama
[25] ISHIBASHI, M., TAKAMOTO, M. Discharge coefficient of superaccurate critical nozzle at pressurised
condition. Int. Fluid Flow Measurement Symposium, Denver 27-30 June, 1999
[26] ARNBERG B.T. and ISHIBASHI M., Discharge coefficient equations for critical flow toroidal throat venturi
nozzles, Proceedings of ASME FEDSMʼ01-18030, ASME New Orleans, May 2001
[27] ISHIBASHI, M., TAKAMOTO, M. Discharge coefficient of superaccurate critical nozzle accompanied with
the boundary layer transition measured by reference super-accurate critical nozzles connected in series.
Proceedings of ASME FEDSMʼ01-18036, ASME New Orleans, May 2001
シリンドリカルスロートベンチュリノズルの流出係数
[28] GRENIER, P. Discharge coefficients of cylindrical nozzles used in sonic conditions. NEL fluid Mechanics
Silver Jubilee Conference, Paper No. 1.2. East Kilbride, Glasgow: National Engineering Laboratory,
November 1979
34
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[29] PEIGNELIN, G. and BENZONI, A. Utilisation des Venturi tuyères fonctionnant en régime d'écoulement
sonique comme étalons de débits de gaz sous pression. Note dc Gaz de France, no 67842, 1967
[30] PEIGNELIN, G. and GRENIER, P. Etude du coefficient do décharge des tuyeres fonctionnant en regime
d'ecoule ment sonique au col utilisées comme étalon pour le mesurage de débit de gaz sous pression. Congrès
de I'Association technique du gaz en France, 1978
[31] GRENIER, P. Etude statistique du coefficient de décharge des tuyères a col cylindrique fonctionnant en régime
sonique. Note du Gaz de France, n°81474, August 1981
[32] SPENCER, E. A., EUJEN, E., DIJSTELBERGEN, H. H. and PEIGNELIN, G. Intercomparison campaign on
high pressure gas flow test facilities. EEC Document No. EW 6662. Brussels-Luxembourg: ECSC-EEC-EAEC,
1980
[33] J.BOSIO, J.F.CABROL, P.KERVEVAN. Intercomparison of the calibration results obtained at Gaz de France
Alforville and K-Lab on a critical flow Venturi nozzle. FLOMEL'94. Glasgow, Scotland
[34] VULOVIC, F. Report on the intercomparison carried out on eight European benches using a sonic nozzle as
transfer standard. EUROMET PROJECT No. 307. - M.CERMAP VUL/SZ 97/I/129, 1997
[35] VULOVIC, F., VINCENDEAU, E., VALLET, J.P., WINDENBERGER, C., VILLANGER, O., BOSIO, J.
Influence of the thermodynamics calculations on the flow rate of sonic nozzles. Int. Fluid Flow Measurement
Symposium, Denver 27-30 June, 1999
附属書文献
[36] Stewart D.G., Watson J.T.R., and Vaidya A.M. Improved critical flow factors and representative equations for
four calibration gases. Flow Measurement and Instrumentation,1999; 10(1): 27-34
[37] Span R., Lemmon E.W., Jacobsen R.T., and Wagner W. A Reference Quality Equation of State for Nitrogen.
International Journal of Thermophysics, 1998; 19(4): 1121-1132
[38] Tegeler Ch., Span R., and Wagner W. A new equation of state for argon covering the fluid region from the
triple-point temperature to 700 K at pressures up to 1000 MPa.Paper Presented at 13th Symposium on
Thermophysical Properties, Boulder, June 1997
[39] Panasati M.D., Lemmon E.W., Penoncello S.G., Jacobsen R.T., and Friend D.G.Thermodynamic properties of
air from 60 to 2000 K at pressures up to 2000 MPa. Paper Presented at 13th Symposium on Thermophysical
Properties, Boulder, June 1997
[40] Setzmann U. and Wagner W. A new equation of state and tables of thermodynamic properties for methane
covering the range from the melting line to 625 K at pressures up to 1000 MPa. Journal of Physical and
Chemical Reference Data, 1991; 20(6): 1061-1116
[41] Span R. and Wagner W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the
Triple-Point Temperature to 1100 K at Pressures up to 800 MPa. Journal of Physical and Chemical
Reference Data, 1996; 25(6): 1509-1596
[42] Miller RW. Flow measurement engineering handbook. McGraw-Hill, 1983
[43] IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and
Scientific Use. IAPWS, 1996
[44] Stewart D.G., Watson J.T.R., and Vaidya A.M. A new correlation for the critical mass flux of natural
mixtures. Flow Measurement and Instrumentation, Volume 11 Number 4, December 2000
35
Z 8767:2006 (ISO/DIS 9300:2003)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[45] Stewart D.G., Watson J.T.R., and Vaidya A.M. The effect of using atmospheric air in critical flow
nozzles. Paper presented at the 4th International Symposium on Fluid Flow Measurement, Denver,
une 1999
[46] Stewart D.G., Watson J.T.R., and Vaidya A.M. The effect of high beta values on mass flow through critical
flow nozzles Flow Measurement and Instrumentation, Volume 11 Number 4, December 2000