X 0512:2015
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語,定義,記号及び数学的表記・論理的表記 ······································································ 2
3.1 用語及び定義 ················································································································ 2
3.2 記号 ···························································································································· 3
3.3 数学的表記及び論理的表記 ······························································································ 3
4 シンボルの説明 ················································································································ 3
4.1 基本的な特性 ················································································································ 3
4.2 付加的な機能の要約 ······································································································· 4
4.3 シンボルの構造 ············································································································· 5
5 ECC 200の要求事項 ········································································································· 5
5.1 符号化手順の概要 ·········································································································· 5
5.2 データの符号化 ············································································································· 6
5.3 利用者が考慮すべき事項 ································································································ 13
5.4 ECI ···························································································································· 13
5.5 ECC 200シンボルの属性 ································································································ 15
5.6 構造的連接 ·················································································································· 17
5.7 誤り検出及び誤り訂正 ··································································································· 18
5.8 シンボルの構造 ············································································································ 19
6 ECC 000〜ECC 140シンボルの要件 ···················································································· 20
7 シンボルの寸法 ··············································································································· 21
7.1 寸法 ··························································································································· 21
8 シンボル品質 ·················································································································· 21
8.1 シンボル品質パラメタ ··································································································· 21
8.2 プロセス制御法 ············································································································ 22
9 データマトリックスの参照復号アルゴリズム ········································································ 22
10 利用者ガイドライン ······································································································· 31
10.1 可読文字の印刷 ··········································································································· 31
10.2 自動識別能力 ·············································································································· 31
10.3 システムの検討 ··········································································································· 31
11 送信データ ··················································································································· 32
11.1 FNC1プロトコル(ECC 200専用) ················································································ 32
11.2 第2位置にあるFNC1のプロトコル(ECC 200専用) ························································ 32
11.3 第1位置にあるマクロキャラクタのためのプロトコル(ECC 200専用) ································ 32
X 0512:2015 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
11.4 ECIのプロトコル(ECC 200専用) ················································································ 32
11.5 シンボル体系識別子 ····································································································· 33
11.6 送信データの例 ··········································································································· 33
附属書A(規定)ECC 200コード語の飛び越し配置手順 ····························································· 34
附属書B(規定)ECC 200パターンのランダム化 ······································································ 36
附属書C(規定)ECC 200符号化キャラクタセット ··································································· 38
附属書D(規定)ECC 200位置合せパターン ············································································ 41
附属書E(規定)ECC 200リードソロモン誤り検出及び誤り訂正 ················································· 43
附属書F(規定)ECC 200シンボルキャラクタ配置 ··································································· 48
附属書G(規定)ECC 000〜ECC 140シンボルの属性 ································································ 61
附属書H(規定)ECC 000〜ECC 140データモジュール配置格子 ················································· 62
附属書I(規定)ECC 000〜ECC 140キャラクタ符号化スキーム ··················································· 63
附属書J(規定)ECC 000〜ECC 140 CRCアルゴリズム ····························································· 64
附属書K(規定)ECC 000〜ECC 140誤り検査アルゴリズム及び誤り訂正アルゴリズム ···················· 65
附属書L(規定)ECC 000〜ECC 140主なランダムビット列(16進数) ········································ 66
附属書M(規定)データマトリックス印刷品質−シンボル体系特有の側面 ····································· 67
附属書N(規定)シンボル体系識別子 ····················································································· 75
附属書O(参考)ECC 200の符号化例 ····················································································· 76
附属書P(参考)ECC 200のための最小シンボルデータキャラクタを用いたデータの符号化 ·············· 78
附属書Q(参考)ECC 050を用いたECC 000〜ECC 140符号化例 ················································ 81
附属書R(参考)有用なプロセス制御技術 ··············································································· 82
附属書S(参考)自動識別能力 ······························································································· 84
附属書T(参考)システムの考察 ··························································································· 85
参考文献 ···························································································································· 86
附属書JA(参考)JISと対応国際規格との対比表 ······································································ 87
X 0512:2015
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本自動認識システム協会
(JAISA)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべき
との申出があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
X 0512:2015
情報技術−自動認識及びデータ取得技術−
バーコードシンボル体系仕様−データマトリックス
Information technology-Automatic identification and data capture
techniques-Data Matrix bar code symbology specification
序文
この規格は,2006年に第2版として発行されたISO/IEC 16022,TECHNICAL CORRIGENDUM 1(2008)
及びTECHNICAL CORRIGENDUM 2(2011)を基とし,技術的内容を変更して作成した日本工業規格であ
る。主な変更点は,ISO/IEC 16022のうち,誤り訂正方式がECC 200のシンボルだけを採用し,ISO/IEC
16022で使用を推奨していない誤り訂正方式のECC 000,ECC 050,ECC 080,ECC 100及びECC 140のシ
ンボルを不採用にしたことである。
注記 ECC 000〜ECC 140の記述については,対応国際規格であるISO/IEC 16022を参照。
なお,この規格で点線の下線を施してある箇所は,対応国際規格を変更している事項である。変更の一
覧表にその説明を付けて,附属書JAに示す。
データマトリックスは,正方形のモジュールで構成される二次元マトリックスシンボル体系であり,そ
の周囲には位置検出パターンが置かれる。この規格では,主に,明るい背景(例えば,“白”)上に暗いシ
ンボル(例えば,“黒”)を表示するが,データマトリックスシンボル体系は,暗い背景上に明るいシンボ
ル(一般に,“白黒反転シンボル”という。)として印字することもできる。
バーコード機器の製造業者及び技術系の利用者が,アプリケーション標準の開発及び機器を製造すると
きに参照できるように,シンボル体系仕様を標準化して公開する。
1
適用範囲
この規格は,データマトリックスとして知られているシンボル体系の要件を規定する。データマトリッ
クスシンボル体系の特徴,データキャラクタの符号化,シンボルフォーマット,寸法,印刷品質要件,誤
り訂正規則及び復号アルゴリズム並びに利用者が選択可能なアプリケーションパラメタを規定する。
この規格は,どのような印刷技術又はマーキング技術で作成されたかにかかわらず,全てのデータマト
リックスシンボルに適用する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO/IEC 16022:2006,Information technology−Automatic identification and data capture techniques
−Data Matrix bar code symbology specification,TECHNICAL CORRIGENDUM 1:2008及び
TECHNICAL CORRIGENDUM 2:2011(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS X 0500-1 自動認識及びデータ取得技術−用語−第1部:一般
注記 対応国際規格:ISO/IEC 19762-1,Information technology−Automatic identification and data
capture (AIDC) techniques−Harmonized vocabulary−Part 1: General terms relating to AIDC(IDT)
JIS X 0500-2 自動認識及びデータ取得技術−用語−第2部:光学的読取媒体
注記 対応国際規格:ISO/IEC 19762-2,Information technology−Automatic identification and data
capture (AIDC) techniques−Harmonized vocabulary−Part 2: Optically readable media (ORM)
(IDT)
JIS X 0520 自動認識及びデータ取得技術−バーコードシンボル印刷品質の評価仕様−一次元シンボ
ル
注記 対応国際規格:ISO/IEC 15416,Information technology−Automatic identification and data capture
techniques−Bar code print quality test specification−Linear symbols(IDT)
JIS X 0530 データキャリア識別子(シンボル体系識別子を含む)
注記 対応国際規格:ISO/IEC 15424,Information technology−Automatic identification and data capture
techniques−Data Carrier Identifiers (including Symbology Identifiers)(IDT)
ISO/IEC 646,Information technology−ISO 7-bit coded character set for information interchange
注記 対応日本工業規格:JIS X 0201 7ビット及び8ビットの情報交換用符号化文字集合(MOD)
ISO/IEC 15415,Information technology−Automatic identification and data capture techniques−Bar code
symbol print quality test specification−Two-dimensional symbols
ISO/IEC 8859-1,Information technology−8-bit single-byte coded graphic character sets−Part 1: Latin
alphabet No. 1
ISO/IEC 8859-5:1999,Information technology−8-bit single-byte coded graphic character sets−Part 5:
Latin/Cyrillic alphabet
AIM Inc. ITS/04-001,International Technical Standard: Extended Channel Interpretations−Part 1:
Identification Schemes and Protocol
3
用語,定義,記号及び数学的表記・論理的表記
3.1
用語及び定義
この規格で用いる主な用語及び定義は,JIS X 0500-1及びJIS X 0500-2によるほか,次による。
3.1.1
コード語(codeword)
元データとシンボルに符号化した画像との中間レベルで符号化されるシンボルキャラクタ値。
3.1.2
モジュール(module)
マトリックスシンボル体系で,1ビットを表現するために用いる単一セル。データマトリックスでのモ
ジュール形状は,正方形である。
注記 モジュールの形状は正方形であるが,そこに表現されるビットの形状は,印字方式によっては,
3
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
円形状になる場合がある。
3.1.3
畳込符号(convolutional coding)
(対応国際規格の規定を不採用とした。)
3.1.4
パターンのランダム化(pattern randomising)
コード語領域で,同じパターンの繰返しが続く確率を下げるために,選択されたビットの明暗を反転す
ることで,元のビットパターンを別のビットパターンに変換する手続。
3.2
記号
この規格では,他の指定がない限り,次の数学的記号を用いる。
d
誤り訂正コード語の数
e
消失誤り数
k
(ECC 200では,)誤り訂正コード語の総数
(ECC 000〜ECC 140では,)(対応国際規格の規定を不採用とした。)
m
畳込符号のメモリ次数 (対応国際規格の規定を不採用とした。)
n
(ECC 200では,)データコード語の総数
(ECC 000〜ECC 140では,)(対応国際規格の規定を不採用とした。)
N
符号化スキームでの基数
p
誤り検出のために予約されたコード語の数
S
シンボルキャラクタ
t
誤りの数
u
(対応国際規格の規定を不採用とした。)
v
(対応国際規格の規定を不採用とした。)
X
モジュールの水平幅及び垂直幅
ε
誤り訂正コード語
3.3
数学的表記及び論理的表記
この規格には,次の表記法及び数学的演算を適用する。
div
整数の除算であり,余りは切り捨てる。
mod
除算後の整数剰余
XOR
二つの入力値が異なるときだけ,出力が1になる排他的論理和
LSB
最下位ビット
MSB
最上位ビット
4
シンボルの説明
4.1
基本的な特性
データマトリックスは,マトリックスシンボル体系の二次元シンボルであり,二つの種類がある。
一つは,リードソロモン誤り訂正を用いているECC 200シンボルである。新しいアプリケーションには,
ECC 200シンボルを用いることが望ましい。
もう一つは,レベルの異なる畳込誤り訂正(ECC 000,ECC 050,ECC 080,ECC 100及びECC140)を
用いているECC 000〜ECC 140シンボルである。ECC 000〜ECC 140シンボルは,総合的なシステム性能
4
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
に責任をもてる単一の当事者が,シンボルの生成及び読取りの両方を行うような,クローズされたアプリ
ケーションの中だけで用いるべきである。
注記 この規格では,ECC 000〜ECC 140に関する対応国際規格の規定を不採用とした。
データマトリックスには,次のような特徴がある。
a) 符号化できる文字セット
1) ISO/IEC 646 IRVの値0〜値127
注記1 このバージョンは,ISO/IEC 646 IRVのG0集合並びにそれぞれFS,GS,RS及びUSに修正
した値28〜値31をもつISO/IEC 6429のC0集合から成る。
2) ISO/IEC 8859-1に従った値128〜値255。これらを拡張ASCIIという。
b) データの表し方
暗モジュールがバイナリの“1”であり,明モジュールがバイナリの“0”である。
注記2 この規格では,明るい背景(例えば,“白”)に暗いモジュール(例えば,“黒”)でデータ
マトリックスシンボルを表示する。しかし,4.2に示すように,明暗モジュールの色を反転
させたシンボルを生成してもよい。そのようなシンボルでは,この規格が暗モジュールに
ついて言及するときは,明モジュールを指し,逆も同様である。
c) クワイエットゾーンを含まないモジュール数で表したシンボルサイズ
ECC 200の場合
10×10〜144×144(偶数だけ)
ECC 000〜ECC 140の場合 (対応国際規格の規定を不採用とした。)
d) ECC 200の最大シンボルサイズにおける,シンボル当たりのデータ文字数
1) 英数字
2 335文字まで
2) 8ビットバイト 1 555文字
3) 数字
3 116桁
e) 誤り訂正
ECC 200の場合
リードソロモン誤り訂正
ECC 000〜ECC 140の場合 (対応国際規格の規定を不採用とした。)
f)
コードタイプ
マトリックス形
g) 全方向読取り(全方向とは,リーダからシンボルを見たときのチルト方向に対して360°)
可能
4.2
付加的な機能の要約
データマトリックスで“必須の”又は“任意の”付加的な機能について,概要を次に示す。
a) 反射率の反転(必須)
データマトリックスは,“明るい背景上に暗い画像”又は“暗い背景上に明るい画像”のどちらで表
示されても読み取れるように意図されている(図1参照)。この規格の仕様では,“明るい背景上に暗
い画像”を基本にしている。したがって,反射率反転によって作られたシンボルにおいては,暗モジ
ュールの参照を明モジュールとして,明モジュールの参照を暗モジュールとして,それぞれ読み換え
なければならない。
b) 拡張チャネル解釈[以下,ECI(Extended Channel Interpretations)という。](任意。ECC 200だけで用
いることができる。)
この仕組みは,他の文字セットのキャラクタ(例えば,アラビア文字,キリル文字,ギリシャ文字,

5
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ヘブライ文字)を表すこと,及び,他のデータ解釈又は産業界固有の要件を表すことを可能にする。
c) 長方形シンボル(任意。ECC 200だけで用いることができる。)
長方形フォームとして,六つのシンボル形式がある。
d) 構造的連接機能(任意。ECC 200だけで用いることができる。)
一つのデータを,最大16個のデータマトリックスシンボルに分割して表すことが可能である。シン
ボルがスキャンされる順序に関係なく,元のデータを正しく再構築することができる。
4.3
シンボルの構造
各データマトリックスシンボルは,通常,正方形状のモジュールを規則的に配置したデータ領域で構成
する。大きなECC 200シンボルでは,データ領域が位置合せパターンによって区切られる。データ領域又
はデータ領域及び位置合せパターンのセットを位置検出パターンで囲む。さらに,四辺の周囲をクワイエ
ットゾーンで囲む。2種類のECC 200シンボルを図1に示す。
注記 対応国際規格の図1には,ECC 200シンボル及びECC 140シンボルが表示されているが,この
規格では,ECC 140シンボルの表示を不採用とした。
a) 明背景上に暗モジュール
b) 暗背景上に明モジュール
図1−ECC 200による“A1B2C3D4E5F6G7H8I9J0K1L2”の符号化例
4.3.1
位置検出パターン
位置検出パターンは,1モジュール幅でデータ領域の四方を囲んでいる。左側及び下側に隣接する境界
は,L字形の変化しない暗ラインであり,主に,シンボルの物理的なサイズ,回転及びゆがみを求めるた
めに用いる。二つの反対側(データ領域の右側及び上側に隣接する境界)には,暗モジュール及び明モジ
ュールを交互に配置し,主に,シンボルのセル構造を決めるが,物理的なサイズ及びゆがみを決めるとき
の支援としても用いる。図1では,クワイエットゾーンの範囲をコーナマークで示している。
4.3.2
シンボルサイズ及びデータ容量
ECC 200シンボルは,偶数個の列及び偶数個の行で構成する。正方形のシンボルは,クワイエットゾー
ンを含まずに(10×10)〜(144×144)セルである。長方形のシンボルは,クワイエットゾーンを含まず
に(8×18)〜(16×48)セルである。全てのECC 200シンボルは,右上の角が明モジュールである。ECC
200シンボルの全ての属性を表7に示す。
注記 この細別のECC 000〜ECC 140に関する対応国際規格の規定を不採用とした。
5
ECC 200の要求事項
5.1
符号化手順の概要
ここでは,符号化手順の概要を示す。5.2〜5.2.9.2に詳細な符号化手順を示す。ECC 200の符号化例を附
属書Oに示す。次の手続は,利用者データをECC 200シンボルに変換する。
手続1 データの符号化
符号化に向けて,データ列に含まれる文字の種類を分析する。ECC 200には,多様な符号化

6
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
スキームを含んでおり,デフォルトのスキームよりも効率的にコード語に変換できる,定義済
みの文字セットがある。符号化スキーム及び他機能の実行を切り換えるために,追加コード語
を挿入する。要求されたコード語の数を満たすために,埋め草キャラクタを追加する。利用者
がシンボルサイズを明示しない場合は,データを収容できる最小サイズを選択する。シンボル
サイズの一覧を,表7に示す。
手続2 誤り検査及び誤り訂正コード語の生成
コード語が255個を超えるシンボルは,コード語列を複数のブロックに飛び越し配置するこ
とによって,附属書Aに示す誤り訂正アルゴリズムによる処理を可能にする。各ブロックに誤
り訂正コード語を生成する。この処理の結果,コード語は,誤り訂正コード語の数だけ拡張さ
れる。誤り訂正コード語は,データコード語の後に配置する。
手続3 マトリックス内のモジュール配置
コード語モジュールを,マトリックス内に配置する。位置合せパターンモジュールが必要な
場合は,マトリックス内に挿入する。マトリックスの周囲に,位置検出パターンモジュールを
追加する。
5.2
データの符号化
5.2.1
概要
データは,六つの符号化スキーム(表1参照)の,どのような組合せを用いて符号化してもよい。ASCII
符号化は,基本スキームである。他の全ての符号化スキームは,ASCII符号化スキームから呼び出され,
このASCIIスキームに戻る。表1に示す圧縮の程度は,注意深く解釈する必要がある。与えられたデータ
セットに最適なスキームであっても,データキャラクタ当たりのビット数が,最少にならない場合がある。
もし,最も高い圧縮の程度が必要ならば,符号化スキームの切換え及び符号化スキームの中で用いるコー
ドセットの切換えを考慮しなければならない(附属書P参照)。コード語の数が最小化されても,シンボ
ルを埋めるために,コード語列の拡張が必要になる可能性に注意することが望ましい。この埋める工程に
は,埋め草キャラクタを用いる。
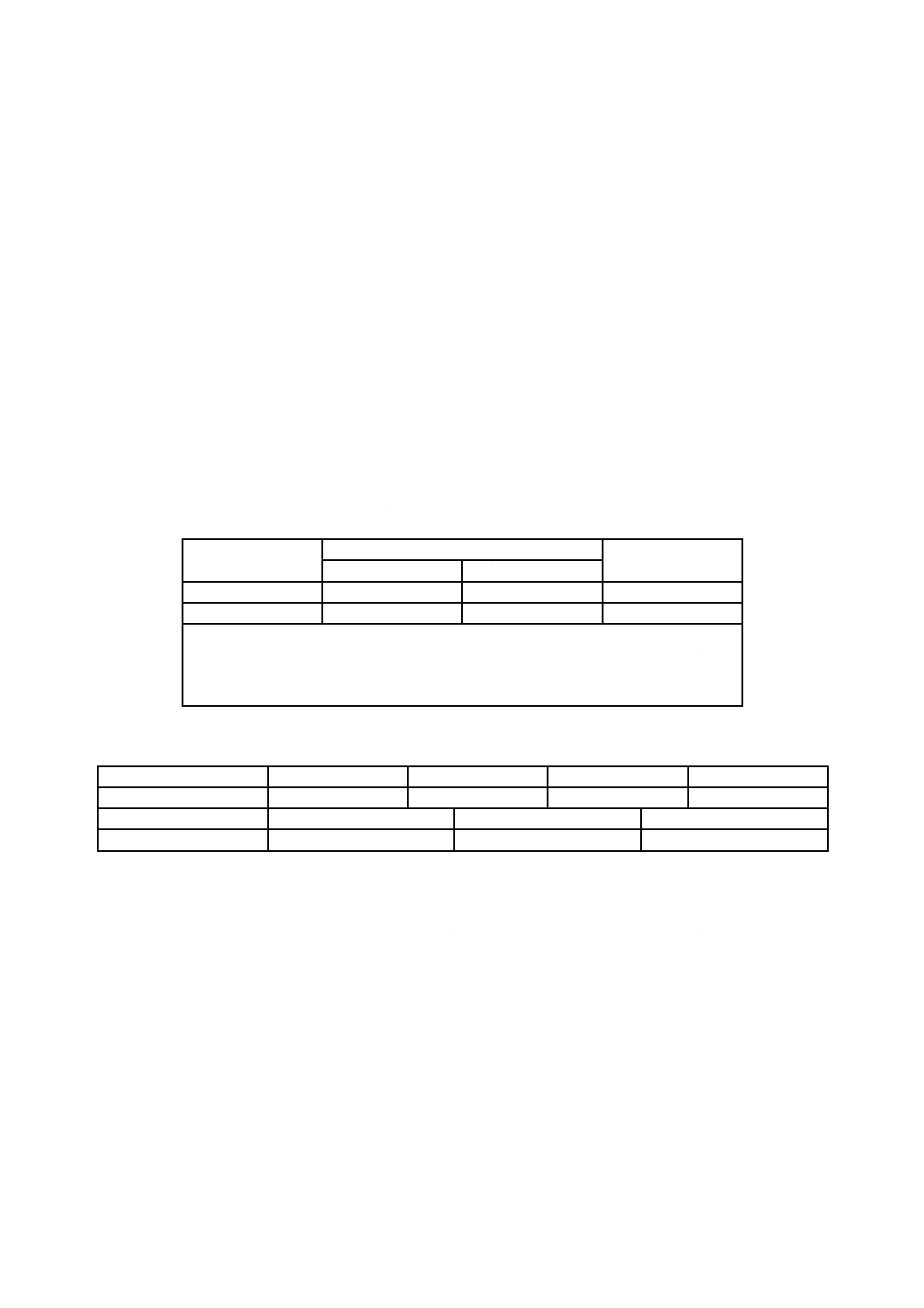
表1−ECC 200のための符号化スキーム
符号化スキーム
キャラクタ
データキャラクタ当たりのビット数
ASCII
2桁の数字組(00〜99)
4
ASCII値 0〜127
8
拡張ASCII値 128〜255
16
C40
大文字英数字
5.33
小文字及び特殊キャラクタ
10.66 a)
テキスト
小文字英数字
5.33
大文字及び特殊キャラクタ
10.66 b)
X12
ANSI X12 EDI データセット
5.33
EDIFACT
ASCII値 32〜94
6
Base 256
全てのバイト値 0〜255
8
注a) シフトキャラクタを用いることによって,二つのC40値として符号化したとき。
b) シフトキャラクタを用いることによって,二つのテキスト値として符号化したとき。
5.2.2
デフォルトキャラクタ解釈
キャラクタ値0〜127のデフォルトキャラクタ解釈は,ISO/IEC 646 IRVに適合していなければならない。
キャラクタ値128〜255のデフォルトキャラクタ解釈は,ISO/IEC 8859-1に適合していなければならない。

7
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この規格でのデータキャラクタの図形表現は,デフォルトの解釈に従う。この解釈は,ECIのエスケープ
シーケンスを用いて変更することができる(5.4参照)。デフォルト解釈は,ECI 000003と一致している。
5.2.3
ASCII符号化
全てのシンボルサイズにおいて,ASCII符号化が第一シンボルキャラクタにデフォルトで設定される。
ASCII符号化は,ASCIIデータ,倍密度数字データ及びシンボル体系制御キャラクタを符号化する。シン
ボル体系制御キャラクタには,ファンクションキャラクタ,埋め草キャラクタ及び他のコードセットへの
切換えキャラクタを含む。ASCIIデータは,コード語1〜128(ASCII値+1)として符号化する。拡張ASCII
(データ値128〜255)は,拡張ASCIIシフトシンボル体系制御キャラクタ(5.2.4.2参照)を用いて符号化
する。2桁の数字組00〜99は,コード語130〜229(数値+130)として符号化する。ASCIIコードの配置
を,表2に示す。
表2−ASCII符号化の値
コード語
データ又は機能
1〜128
ASCIIデータ(ASCII値+1)
129
埋め草
130〜229
2桁の数字組 00〜99 (数値+130)
230
C40符号化への切換え
231
Base 256符号化への切換え
232
FNC1
233
構造的連接
234
リーダの設定
235
拡張ASCIIシフト(拡張ASCIIへの1字切換え)
236
05マクロ
237
06マクロ
238
ANSI X12符号化への切換え
239
テキスト符号化への切換え
240
EDIFACT符号化への切換え
241
ECIキャラクタ
242〜255
ASCII符号化では用いない
5.2.4
シンボル体系制御キャラクタ
ECC 200シンボルには,幾つかの,特別なシンボル体系制御キャラクタがあり,符号化スキームに固有
の意味をもっている。これらのキャラクタは,特定の機能を実行するように復号器に指示するために,又
は,5.2.4.1〜5.2.4.9に規定する固有のデータをホストコンピュータに送信するために用いなければならな
い。これらのシンボル体系制御キャラクタ(値242〜255を除く。)は,ASCII符号化セット(表2参照)
で示されている。
5.2.4.1
切換えキャラクタ
切換えキャラクタは,ASCII符号化から他のいずれかの符号化スキームに切り換えるときに用いる。切
換えキャラクタに続く全てのコード語は,新しい符号化スキームによって圧縮しなければならない。それ
ぞれの符号化スキームは,ASCII符号化セットに戻るための異なる方法をもっている。
5.2.4.2
拡張ASCIIシフトキャラクタ
拡張ASCIIシフトキャラクタは,ASCII値(1〜128)と組み合わせて拡張ASCIIキャラクタ(129〜255)
を符号化するのに用いる。ASCII符号化スキーム,C40符号化スキーム又はテキスト符号化スキームで符
8
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
号化される拡張ASCIIキャラクタには,手前に拡張ASCIIシフトキャラクタを必要とする。さらに,符号
化スキームの規則に従って,拡張ASCIIキャラクタから値128を減じて符号化する。ASCII符号化では,
拡張ASCIIシフトキャラクタをコード語235で表す。ASCII値から128を減じたデータ値に1を加えると
コード語の値になる。例えば,“¥”[通貨記号“円”,ASCII値165。これはASCII値92の“\”(逆スラ
ッシュ)が,JIS X 0201などの文字符号化で通貨記号“円”となるのとは別のものである。]は,拡張ASCII
シフトキャラクタ(コード語235)の後に,値37(165−128)を符号化したコード語38が続く。拡張ASCII
範囲に長い文字列がある場合は,効率を上げるためにBase 256符号化へ切り換えるのが望ましい。
5.2.4.3
埋め草キャラクタ
実行中の符号化スキームに関わりなく,符号化したデータが,シンボルのデータ容量と一致しない場合
は,埋め草キャラクタ(ASCII符号化の値129)を追加して,シンボルのデータ容量と一致させなければ
ならない。埋め草キャラクタは,この用途以外に用いてはならない。符号化モードがASCII符号化モード
以外の場合は,埋め草キャラクタを挿入する前に,ASCII符号化モードに戻さなければならない。253-State
パターンランダム化アルゴリズムは,2番目の埋め草キャラクタから適用し,シンボルの終わりまで続け
る(B.1参照)。
5.2.4.4
ECIキャラクタ
ECIキャラクタは,データの符号化をデフォルト解釈から別のECIへ切り換えるために用いる。ECI手
順は,幾つかのシンボル体系に共通であり,ECI手順のECC 200への適用については,5.4に,より完全
に示す。ECIキャラクタは,適用するECIの識別のために一つ,二つ又は三つのコード語を伴わなければ
ならない。適用中のECIは,符号化されたデータの終わり又は別のECIキャラクタが別のECIを呼び出す
まで継続する。
5.2.4.5
C40符号化及びテキスト符号化におけるシフトキャラクタ
C40符号化及びテキスト符号化では,ASCIIキャラクタ中の英大文字(テキスト符号化では英小文字),
数字及びスペースの37文字を40個ある符号化要素の一つで表し,その他のASCIIキャラクタは,シフト
キャラクタと呼ばれる三つの特別なキャラクタ(40個ある符号化要素値の一つ)と,それに続く40個の
符号化要素値との組で表現する。
5.2.4.6
FNC1代替データ型指定子
GS1及びAIM Inc.が定めた産業標準に従ってデータを符号化するためには,FNC1キャラクタは,第一
シンボルキャラクタ若しくは第二シンボルキャラクタの位置(又は,構造的連接シンボルの最初のシンボ
ルの5番目若しくは6番目の位置)になければならない。それ以外の位置に符号化されたFNC1は,領域
の区切りとして用い,制御キャラクタ“GS”(ASCII値29)として送信しなければならない。
5.2.4.7
マクロキャラクタ
データマトリックスは,産業界で用いる特定のヘッダ及びトレーラを簡略化して,1個のシンボルキャ
ラクタで表現する方法(マクロキャラクタ)を提供する。この機能は,体系化した特定のフォーマットで,
データの符号化に必要なシンボルキャラクタ数を減らすためにある。マクロキャラクタは,シンボルの第
一キャラクタ位置になければならない。それらは,構造的連接機能と一緒に用いてはならない。その機能
を表3に規定する。ヘッダを接頭辞として,トレーラを接尾辞として,それぞれデータ列に加えなければ
ならない。シンボル体系識別子を用いるときは,ヘッダの前に置かなければならない。

9
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3−マクロ機能
マクロコード語
名前
解釈
ヘッダ
トレーラ
236
05マクロ
[)>RS05GS
RS EoT
237
06マクロ
[)>RS06GS
RS EoT
5.2.4.8
構造的連接キャラクタ
構造的連接キャラクタは,シンボルが,5.6で規定する規則に従った構造的連接シーケンスの一部である
ことを示すために用いる。
5.2.4.9
リーダプログラミングキャラクタ
リーダプログラミングキャラクタは,シンボルが,リーダシステムをプログラムするときに用いるメッ
セージを符号化したものである。リーダプログラミングキャラクタは,シンボルの第一コード語でなけれ
ばならない。また,リーダプログラミングを構造的連接とともに用いてはならない。
5.2.5
C40符号化
C40符号化スキームは,英大文字及び数字を効率的に符号化できるように設計されている。他のキャラ
クタは,シフトキャラクタとデータキャラクタとを組み合わせることで符号化できる。
C40キャラクタは,四つのサブセットに分割されている。基本セットと呼ばれる第一キャラクタセット
は,“三つの特別なシフトキャラクタ”,“スペースキャラクタ”,“ASCIIキャラクタのA〜Z”及び“0〜9”
で構成される。それらは,単一のC40値に割り当てられている。他のキャラクタは,三つのシフトキャラ
クタのうちの一つによって,残る三つのサブセットのうちの一つを指定し,C40値の一つを続けることで
符号化する(表C.1参照)。
最初の段階で,個々のデータキャラクタを,それが基本セットのキャラクタの場合は,1個のC40値に,
その他のセットのキャラクタの場合は,2個のC40値に,それぞれ変換する。C40値の列全体を,3個の
値ずつに分解する(一つ又は二つの値が残る場合は,特別な規則が当てはまる。5.2.5.2参照)。各々の組
の3個のC40値(C1,C2,C3)を,計算式(1 600×C1)+(40×C2)+C3+1によって16ビット値に符号化
する。各16ビット値を,上位の8ビット及び下位の8ビットに分けて2個のコード語を得る。
5.2.5.1
C40符号化への切換え及びC40符号化からの切換え
ASCII符号化において,適切な切換コード語(230)を用いてC40符号化に切り換えることができる。
C40符号化からASCII符号化に戻すには,切換解除コード語として,コード語の対に続けてコード語254
を用いる。それ以外では,シンボルに符号化されるデータの終わりまで,C40符号化が有効である。
5.2.5.2
C40符号化の規則
コード語の各対は,16ビット値で表現する。最初のコード語が上位8ビットを表す。3個のC40値(C1,
C2,C3)は,次のように符号化しなければならない。
(1 600×C1)+(40×C2)+C3+1
これによって,1〜64 000の値を生成する。3個のC40値を2個のコード語に圧縮する様子を図2に示す。
シフト1セット,シフト2セット及びシフト3セット中のキャラクタを符号化するには,最初に,適切な
シフトキャラクタを符号化し,続けてデータに対するC40値を符号化しなければならない。C40符号化は,
データを符号化するシンボルの最後のコード語まで有効であってもよい。
次の規則は,誤り訂正コード語の手前に,シンボルキャラクタが1個又は2個だけ残る場合に適用する。
a) 2個のシンボルキャラクタが残り,符号化しなければならないC40値が3個残っている場合(データ
キャラクタ及びシフトキャラクタの両方を含む場合がある。),3個のC40値を最後の2個のシンボル
10
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
キャラクタに符号化する。最後の切換解除コード語は,不要である。
b) 2個のシンボルキャラクタが残り,符号化しなければならないC40値が2個残っている場合(最初の
C40値は,シフトキャラクタ又はデータキャラクタのいずれかの可能性があるが,2番目のC40値は,
データキャラクタでなければならない。),2個残ったC40値の後ろに,埋め草のC40値として“0”(シ
フト1)を補って,終わりの2個のシンボルキャラクタに符号化する。この場合も,最後の切換解除
コード語は,不要である。
c) 2個のシンボルキャラクタが残り,符号化しなければならないC40値(データキャラクタ)が1個だ
け残った場合,最初のシンボルキャラクタとして切換解除キャラクタを符号化し,最後のシンボルキ
ャラクタには,ASCII符号化スキームを用いてデータキャラクタを符号化する。
d) 1個のシンボルキャラクタが残り,符号化しなければならないC40値(データキャラクタ)が1個残
っている場合,最後のシンボルキャラクタは,ASCII符号化スキームを用いてデータキャラクタを符
号化する。切換解除キャラクタは符号化しないが,最後のシンボルキャラクタの前に切換解除キャラ
クタが存在するものとして処理する。
それ以外の場合は,シンボルの終わりの手前でC40符号化スキームから抜け出すために切換解除キ
ャラクタを用いるか,又はそれ以上大きなシンボルサイズでデータを符号化する必要がある。
データキャラクタ
AIM
C40値
14,22,26
16ビット値の計算
(1 600×14)+(40×22)+26+1=23 307
最初のコード語:16ビット値 div 256
23 307 div 256=91
2番目のコード語:16ビット値 mod 256
23 307 mod 256=11
コード語
91,11
図2−C40符号化の例
5.2.5.3
C40符号化での拡張ASCIIシフトの用い方
C40符号化では,拡張ASCIIシフトキャラクタは,シンボル体系の機能キャラクタではなく,符号化セ
ット内での1字切換えである。拡張ASCIIキャラクタ範囲のデータキャラクタの場合,C40符号化の3個
又は4個の値を,次の規則によって符号化する必要がある。
もし,[ASCII値−128]が,基本セットに含まれるときは,
[1(シフト2)][30(拡張ASCIIシフト)][V(ASCII値−128)]
それ以外のときは,
[1(シフト2)][30(拡張ASCIIシフト)][0,1又は2(シフト1,2又は3)]
[V(ASCII値−128)]
とする。
この規則では,[]内の数字は,表C.1のC40値に等しい。Vは,適切なC40値を示すのに用いる。
注記 Vは,“ASCII値−128”が,表C.1のASCII十進値に等しいキャラクタのC40値である。
5.2.6
テキスト符号化
テキスト符号化は,通常の印刷可能なテキストのうち,主に,英小文字を符号化するために設計されて
いる。構造的には,英小文字が直接符号化される(シフトを用いる必要がない)点を除き,C40符号化セ
ットに類似している。英大文字を符号化する場合は,シフト3を前に付ける。テキスト符号化の完全なキ
ャラクタセットの割当てを,表C.2に示す。

11
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2.6.1
テキスト符号化への切換え及びテキスト符号化からの切換え
ASCII符号化において,適切な切換コード語(239)を用いてテキスト符号化に切り換えることができる。
テキスト符号化からASCII符号化に戻すには,切換解除コード語として,コード語の対に続けてコード
語254を用いる。それ以外では,シンボルに符号化されるデータの終わりまで,テキスト符号化が有効で
ある。
5.2.6.2
テキスト符号化の規則
C40符号化の規則を適用する。
注記 ただし,C40符号化の規則の“C40値”を“テキスト符号化値”に読み換える。
5.2.7
ANSI X12符号化
ANSI X12符号化を用いると,標準ANSI X12電子データ交換(EDI)キャラクタを符号化できる。これ
は,C40符号化と同様の方法で,3個のデータキャラクタを2個のコード語に圧縮したものである。これ
で英大文字,数字,スペース及び3個の標準ANSI X12キャラクタ(終了キャラクタ及び分離キャラクタ)
を符号化することができる。ANSI X12コードの配置を,表4に示す。ANSI X12符号化セットには,シフ
トキャラクタが存在しない。
表4−ANSI X12符号化セット
X12値
符号化されたキャラクタ
ASCII値
0
X12 セグメントの終わり
“CR”
13
1
X12 セグメントの分離
“*”
42
2
X12 サブエレメントの分離 “>”
62
3
スペース
32
4〜13
0〜9
48〜57
14〜39
A〜Z
65〜90
5.2.7.1
ANSI X12符号化へ又はANSI X12符号化からの切換え
ASCII符号化において,適切な切換コード語(238)を用いてANSI X12符号化に切り換えることができ
る。ANSI X12符号化からASCII符号化に戻すには,切換解除コード語としてコード語の対に続けてコー
ド語254を用いる。それ以外では,シンボルに符号化されるデータの終わりまで,ANSI X12符号化が有
効である。
5.2.7.2
ANSI X12符号化の規則
ANSI X12データを符号化する最後の部分を除いて,C40符号化の規則を適用する。データキャラクタが
コード語対を完全に使い切らない場合,完全なコード語対として最後のコード語対が終わったところでコ
ード語254を用いてASCIIに切り換え,そのままASCII符号化を用いる。ただし,最初の誤り訂正キャラ
クタの前に1個のシンボルキャラクタだけが残っている場合は,切換解除コード語を必要とせず,その1
個のシンボルキャラクタには,ASCII符号化スキームを用いる。
注記 ただし,C40符号化の規則の“C40値”を“X12値”に読み換える。
5.2.8
EDIFACT符号化
EDIFACT符号化スキームは,63個のASCII値(32〜94までの値)及びASCII符号化に戻るための切換
解除キャラクタ(バイナリで011111)を含む。EDIFACT符号化は,4個のデータキャラクタを3個のコー
ド語に符号化する。この符号化スキームには,EDIFACTのレベルAのキャラクタセットに定義される全
ての数字,アルファベット及び句読点文字を含み,C40符号化で必要とされるシフトキャラクタを含まな
い。
12
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2.8.1
EDIFACT符号化へ及びEDIFACT符号化からの切換え
ASCII符号化において,適切な切換コード語(240)を用いて,EDIFACT符号化に切り換えることがで
きる。ASCII符号化に戻るには,EDIFACT符号化の末尾で,終端としてEDIFACT符号化の切換解除キャ
ラクタを用いなければならない。
5.2.8.2
EDIFACT符号化の規則
EDIFACT符号化キャラクタセットを表C.3に規定する。6ビットEDIFACT値と8ビットASCIIとの間
には,単純な関係がある。図3に示すように,EDIFACTの6ビット値を作成するために,8ビットバイト
の先頭の2ビットを無視する。4個のEDIFACTキャラクタからなる文字列を3個のコード語に符号化する。
簡単な符号化処理では,8ビットバイトの先頭2ビットを除去し,残りの6ビットをEDIFACT値として,
図4に示すように,直接,コード語に符号化しなければならない。EDIFACT符号化が切換解除キャラクタ
で終わる場合,そのシンボルキャラクタの残りのビットをゼロで埋めなければならない。ASCIIモードは,
次のシンボルキャラクタから始まる。最初の誤り訂正キャラクタが現れる直前のシンボルキャラクタまで
EDIFACT符号化が有効であり,かつ,最後の3個がそろった完全なEDIFACTコード語の後に1個又は2
個のコード語だけが残っている場合,これらの残りのコード語は,切換解除キャラクタを必要とせずに,
ASCII符号化スキームで符号化しなければならない。
データキャラクタ
ASCII
EDIFACT値
10進値
8ビットバイナリ値
A
65
01000001
000001
9
57
00111001
111001
注記 復号処理のときに,先頭ビット(6番目のビット)が1の場合,00ビットを前に
付加して8ビットバイトにする。先頭ビット(6番目のビット)が0の場合,01
ビットを前に付加して8ビットバイトにする。ただし,EDIFACT値が011111の,
ASCII符号化に戻るためのシンボル制御用切換解除キャラクタは,例外とする。
図3−EDIFACT値及び8ビットバイト値間の関係
データキャラクタ
D
A
T
A
バイナリ値(表C.3)
00
01
00
00
00
01
01
01
00
00
00
01
3分割8ビットバイト
00
01
00
00
00
01
01
01
00
00
00
01
コード語値
16
21
1
図4−EDIFACT符号化の例
5.2.9
Base 256符号化
Base 256符号化スキームは,ECI及びバイナリデータを含む任意の8ビットバイトデータを符号化する
ときに用いなければならない。デフォルトの解釈を5.2.2に規定する。255-Stateパターンランダム化アル
ゴリズムは,符号化されたデータ内における各Base 256シーケンスに対して適用する(B.2参照)。これは,
Base 256に切り換わった後から始まり,Base 256の領域の長さによって指定される最後のキャラクタで終
わる。
5.2.9.1
Base 256符号化へ又はBase 256符号化からの切換え
適切な切換コード語(231)を用いることによって,ASCII符号化からBase 256符号化に切り換えるこ
とができる。Base 256による符号化が終わると,自動的にASCII符号化に戻る。デフォルト以外の適切な
ECI(5.3.1参照)は,切り換える前に呼び出さなければならない。ただし,Base 256符号化に切り換える
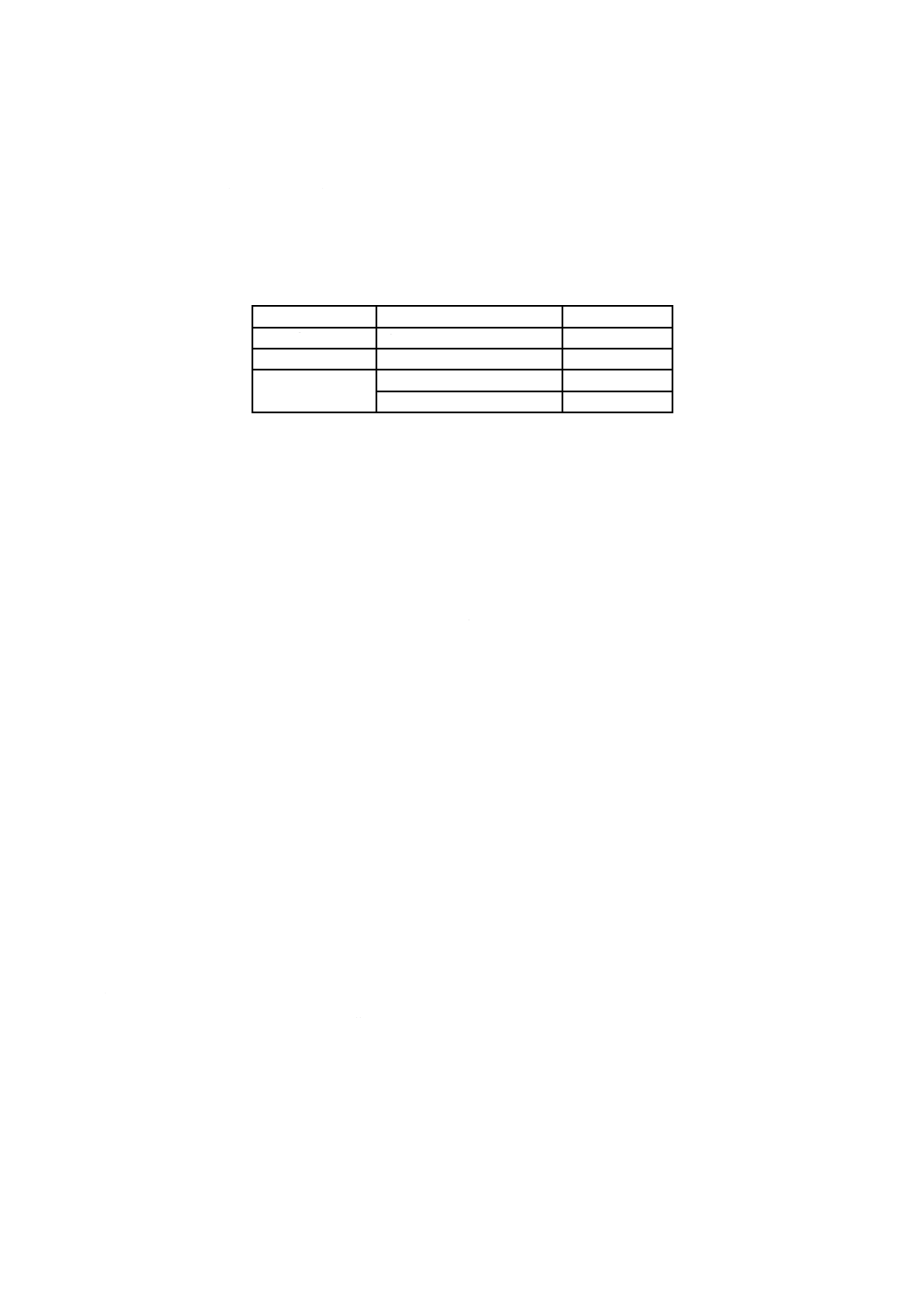
13
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
直前にECIシーケンスがくる必要はない。
5.2.9.2
Base 256符号化の規則
Base 256に切り換えると,切換え後の最初の1個(d1)又は2個(d1,d2)のコード語は,バイト単位
でデータ領域の長さを定義する。表5に,領域の長さを決める仕組みを定義する。これ以降は,全ての符
号化がバイト値で行われなければならない。
表5−Base 256領域の長さ
領域の長さ
d1,d2の値
dの許容値
シンボルの残り
d1=0
d1=0
1〜249
d1=長さ
d1=1〜249
250〜1 555
d1=(長さ DIV 250)+249
d1=250〜255
d2=長さ MOD 250
d2=0〜249
5.3
利用者が考慮すべき事項
ECC 200では,データを符号化する方法が柔軟になっている。ECIプロトコルを用いることによって,
別のキャラクタセットを呼び出すことが可能である。データは,正方形又は長方形のいずれのシンボルに
符号化してもよい。データが単一シンボルの容量を超える場合は,データを構造的連接シーケンスとして
最大16個のシンボルに分けて符号化することができる。それらのシンボルは,互いに論理的に連接された
ECC 200シンボルである(5.6参照)。
5.3.1
ECIの利用者選択
別のECIを用いて特定のコードページ又は特定のデータ解釈を指定する場合は,追加のコード語を用い
て,その機能を呼び出す必要がある。ECIプロトコルを用いると(5.4参照),デフォルト解釈(ECI 000003)
で支援されているラテンアルファベット(ISO/IEC 8859-1ラテンアルファベットNo.1)以外の文字データ
及び記号データを符号化することも可能になる。
5.3.2
シンボルサイズ及びシンボル形状の利用者選択
ECC 200シンボルの形状は,24種類の正方形及び6種類の長方形がある。サイズ及び形状は,利用環境
に適合するように選択する。これらの構成を5.5の技術仕様に示す。
5.4
ECI
ECIプロトコルを用いることによって,出力データ列を,デフォルトのキャラクタセット以外の方法で
解釈することを可能とする。ECIプロトコルは,多数のシンボルにわたって共通の定義がなされている。
データマトリックスでサポートする解釈を大別すると,次の四つになる。
a) 国際キャラクタセット(又はコードページ)
b) データ暗号化,データ圧縮などの汎用解釈
c) クローズド(閉鎖系)システム用の利用者定義解釈
d) バッファなしモードでの構造化連接に対する制御情報
ECIプロトコルについては,“AIM Inc. International Technical Specification−Extended Channel
Interpretations Part 1”に詳しく規定されている。このプロトコルは,印刷前及び復号後のバイト値に,特定
の解釈を指定する一貫した方法を提供する。ECIは,データマトリックスシンボル内に符号化される6桁
の数値(ECIキャラクタに1個〜3個のコード語が続く。)によって識別される。解釈の詳細は,“AIM Inc.
Extended Channel Interpretations Character Set Register”に記載されている。ECIは,シンボル体系識別子を
伝送可能に設定しているリーダだけで用いることができる。シンボル体系識別子を伝送できないように設

14
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定しているリーダは,ECIを含むいかなるシンボルのデータも伝送してはならない。ただし,リーダの内
部でECIを全て処理できる場合は,例外である。
ECIプロトコルは,ECC 200シンボルだけに適用される。指定されたECIは,符号化されたメッセージ
の任意の箇所で呼び出すことができる。
5.4.1
ECIの符号化
ECC 200データマトリックスの様々な符号化スキーム(表1に定義)は,どのECIの下でも適用が可能
である。ECIは,ASCII符号化からだけ呼び出すことができる。一度ECIが呼び出されれば,どのような
符号化スキームとの間でも切換えが可能である。用いる符号化モードは,符号化される8ビットデータ値
によって厳格に決定され,現在有効なECIには依存しない。例えば,48〜57(10進数)までの値は,数値
として解釈されるものではない場合でも,数値モードで符号化するのが最も効率的である。ECI割当ては,
ASCII符号化におけるコード語241(ECIキャラクタ)を用いて呼び出せる。ECI割当て番号を符号化する
には,1個,2個又は3個の追加コード語が用いられる。符号化規則を表6に規定する。
次の例は,符号化の様子を説明したものである。
ECI = 015000
コード語:
[241] [(15 000−127) div 254+128] [(15 000−127) mod 254+1]
= [241] [58+128] [141+1]
= [241] [186] [142]
ECI = 090000
コード語:
[241] [(90 000−16 383) div 64 516+192] [((90 000−16 383) div 254) mod 254+1] [(90 000−16 383)
mod 254+1]
= [241] [1+192] [289 mod 254+1] [211+1]
= [241] [193] [36] [212]
表6−ECC 200におけるECI符号化割当番号
ECI 割当値
コード語シーケンス
コード語値
範囲
000000〜000126
C0
241
C1
ECI̲no+1
C1 = (1〜127)
000127〜016382
C0
241
C1
(ECI̲no−127) div 254+128
C1 = (128〜191)
C2
(ECI̲no−127) mod 254+1
C2 = (1〜254)
0016383〜999999
C0
241
C1
(ECI̲no−16 383) div 64 516+192
C1 = (192〜207)
C2
[(ECI̲no−16 383) div 254] mod 254+1
C2 = (1〜254)
C3
(ECI̲no−16 383) mod 254+1
C3 = (1〜254)
5.4.2
ECI及び構造的連接
データマトリックスシンボルの単体セット又は構造的連接(5.6参照)されたセットに符号化したメッセ
ージには,任意の箇所にECIがあってもよい。呼び出されたどのようなECIも,符号化されたデータが終
了するか又は別のECIに出会うまで,そのECIを適用し続けなければならない。ECIの解釈は,二つ以上
15
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
のシンボルにまたがってもよい。
5.4.3
復号後のプロトコル
ECIデータを伝送するプロトコルは,11.4の規定による。ECIを用いるときは,シンボル体系識別子(11.5
参照)が完全に実装され,適切なシンボル体系識別子をデータの先頭に付加して伝送しなければならない。
5.5
ECC 200シンボルの属性
5.5.1
シンボルサイズ及びデータ容量
ECC 200では,24個の正方形シンボル及び6個の長方形シンボルが利用可能である。これらのシンボル
の内容を表7に示す。
16
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
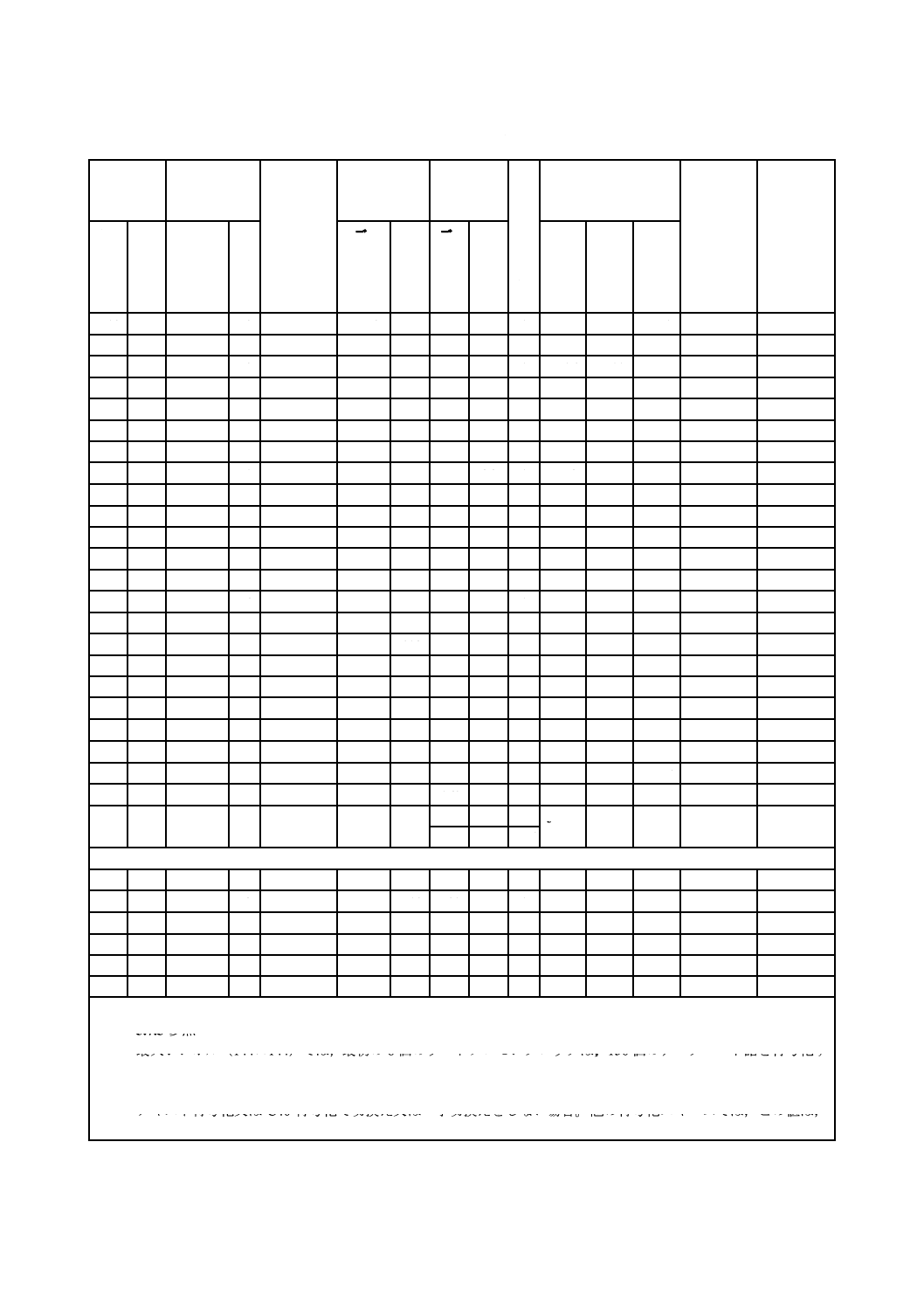
表7−ECC 200シンボルの属性
シンボル
サイズa)
データ
領域
割当て
マトリッ
クス
サイズ
コード語の
合計
リード
ソロモン
ブロック
飛
び
越
し
配
置
ブ
ロ
ッ
ク
最大データ容量
誤り訂正
用コード
語の割合
(%)
最大訂正
コード語
誤り/
消失b)
行
列
基
本
サ
イ
ズ
個
数
デ
ー
タ
誤
り
訂
正
デ
ー
タ
誤
り
訂
正
数
字
英
数
字
バ
イ
ト
10
10
8×8
1
8×8
3
5
3
5
1
6
3
1
62.5
2/0
12
12 10×10
1
10×10
5
7
5
7
1
10
6
3
58.3
3/0
14
14 12×12
1
12×12
8
10
8
10
1
16
10
6
55.6
5/7
16
16 14×14
1
14×14
12
12
12
12
1
24
16
10
50
6/9
18
18 16×16
1
16×16
18
14
18
14
1
36
25
16
43.8
7/11
20
20 18×18
1
18×18
22
18
22
18
1
44
31
20
45
9/15
22
22 20×20
1
20×20
30
20
30
20
1
60
43
28
40
10/17
24
24 22×22
1
22×22
36
24
36
24
1
72
52
34
40
12/21
26
26 24×24
1
24×24
44
28
44
28
1
88
64
42
38.9
14/25
32
32 14×14
4
28×28
62
36
62
36
1
124
91
60
36.7
18/33
36
36 16×16
4
32×32
86
42
86
42
1
172
127
84
32.8
21/39
40
40 18×18
4
36×36
114
48
114
48
1
228
169
112
29.6
24/45
44
44 20×20
4
40×40
144
56
144
56
1
288
214
142
28
28/53
48
48 22×22
4
44×44
174
68
174
68
1
348
259
172
28.1
34/65
52
52 24×24
4
48×48
204
84
102
42
2
408
304
202
29.2
42/78
64
64 14×14
16
56×56
280
112
140
56
2
560
418
277
28.6
56/106
72
72 16×16
16
64×64
368
144
92
36
4
736
550
365
28.1
72/132
80
80 18×18
16
72×72
456
192
114
48
4
912
682
453
29.6
96/180
88
88 20×20
16
80×80
576
224
144
56
4
1152
862
573
28
112/212
96
96 22×22
16
88×88
696
272
174
68
4
1392 1042
693
28.1
136/260
104 104 24×24
16
96×96
816
336
136
56
6
1632 1222
813
29.2
168/318
120 120 18×18
36 108×108
1050
408
175
68
6
2100 1573 1047
28
204/390
132 132 20×20
36 120×120
1304
496
163
62
8
2608 1954 1301
27.6
248/472
144 144 22×22
36 132×132
1558
620
156
62
8 c) 3116 2335 1555
28.5
310/590
155
62
2 c)
長方形シンボル
8
18
6×16
1
6×16
5
7
5
7
1
10
6
3
58.3
3/0
8
32
6×14
2
6×28
10
11
10
11
1
20
13
8
52.4
5/0
12
26 10×24
1
10×24
16
14
16
14
1
32
22
14
46.7
7/11
12
36 10×16
2
10×32
22
18
22
18
1
44
31
20
45.0
9/15
16
36 14×16
2
14×32
32
24
32
24
1
64
46
30
42.9
12/21
16
48 14×22
2
14×44
49
28
49
28
1
98
72
47
36.4
14/25
注a) クワイエットゾーンを含まないシンボルサイズ
b) 5.7.3参照
c) 最大シンボル(144×144)では,最初の8個のリードソロモンブロックは,156個のデータコード語を符号化す
る218個のコード語になる。最後の二つのブロックは,217個のコード語を符号化する(データコード語が155
個)。全てのブロックは,62個の誤り訂正コード語をもっている。
d) テキスト符号化又はC40符号化で切換え又は一字切換えをしない場合。他の符号化スキームでは,この値は,
キャラクタセットのグルーピング及び混合によって変わることがある。
d)
17
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.5.2
大きなシンボルへの位置合せパターンの挿入
表7に示すように,32×32以上の正方形シンボル及び4個の長方形シンボル(8×32,12×36,16×36
及び16×48)には,二つ以上のデータ領域がある。これらのデータ領域は,位置合せパターンで区切られ
ている(附属書D参照)。正方形シンボルは,4,16又は36個のデータ領域に分割される(図D.1,図D.2
及び図D.3参照)。長方形シンボルは,2個のデータ領域に分割される(図D.4参照)。位置合せパターン
の一つおきに現れる暗モジュールは,データ領域の上部及び右側に配置しなければならず,それらは,偶
数列及び偶数行を示す。
5.6
構造的連接
5.6.1
基本原理
ECC 200シンボルは,構造化形式によって最大16個まで連結することができる。最初のシンボルキャラ
クタ位置にコード語233が現れることで,そのシンボルが構造的連接の一部であることを示す。このコー
ド語の直後に3個の構造的連接コード語が続く。最初のコード語は,シンボルシーケンス指示子である。2
番目及び3番目のコード語は,ファイル識別用である。
5.6.2
シンボルシーケンス指示子
このコード語は,構造的に連接された(最大16個の)ECC 200シンボルの中で,“n個のシンボル中の
m番目のシンボル”という形式で,そのシンボル位置を示すものである。このコード語の前半の4ビット
は,(m−1)のバイナリ値として特定のシンボル位置を示す。後半の4ビットは,(17−n)のバイナリ値
として,その構造的連接の中で連結されるシンボルの総数を示す。この4ビットのパターンは,表8で規
定するものに一致しなければならない。
表8−構造的連接におけるシンボル位置を表すビット構造
シンボル位置
m
ビット
1234
シンボルの総数
n
ビット
5678
1
0000
2
0001
2
1111
3
0010
3
1110
4
0011
4
1101
5
0100
5
1100
6
0101
6
1011
7
0110
7
1010
8
0111
8
1001
9
1000
9
1000
10
1001
10
0111
11
1010
11
0110
12
1011
12
0101
13
1100
13
0100
14
1101
14
0011
15
1110
15
0010
16
1111
16
0001
例
7個で構成するシンボルの3番目のシンボルを示すには,次のように符号化する。
3番目の位置
: 0010
合計7個のシンボル : 1010
18
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ビットパターン
: 00101010
コード語値
: 42
5.6.3
ファイル識別
ファイル識別は,二つのコード語値によって表す。各ファイル識別コード語は,1〜254の値をもつこと
ができ,64 516個の異なったファイルの識別を可能にする。ファイル識別の目的は,論理的に関連のある
シンボルだけが,同じメッセージを構成する部分として処理される確率を高めることにある。
5.6.4
FNC1及び構造的連接
構造的連接をFNC1(5.2.4.6参照)と一緒に用いる場合,1番目のシンボルの先頭から四つのコード語は,
構造的連接のために用いなければならない。5番目及び6番目のコード語は,FNC1の用途として利用可能
である。FNC1は,領域区切りとして用いる場合を除き,2番目以降のシンボルの同じ位置に現れてはなら
ない。
5.6.5
バッファあり操作及びバッファなし操作
構造的連接内のメッセージは,メッセージ全体をリーダのバッファ内に蓄積しておいて,全てのシンボ
ルを読んだ時点で伝送することが可能である。別の方法として,リーダが各シンボルを読んだとき,復号
したシンボルのデータを,その都度伝送することも可能である。このようなバッファなし処理では,構造
的連接のためのECIプロトコル(AIM Inc. ITS/04-001,第1部に明示されている。)が,毎回の伝送の先
頭に付加しなければならない制御ブロックを定義する。
5.7
誤り検出及び誤り訂正
5.7.1
リードソロモン誤り訂正
ECC 200シンボルは,リードソロモン誤り訂正を用いている。コード語の総数が255未満のECC 200シ
ンボルでは,飛び越し配置されていないデータコード語から誤り訂正コード語を計算する。コード語の総
数が255以上のECC 200シンボルでは,誤り訂正コード語を,附属書Aで説明する飛び越し配置されたデ
ータコード語から計算する。各ECC 200シンボルには,表7に規定する,特定の数のブロックに分割され
た特定の数のデータコード語及び誤り訂正コード語があり,附属書Aに規定する飛び越し配置手順を適用
する。
ECC 200多項式の演算は,ビットごとのモジュロ2演算及びバイトごとのモジュロ100101101(10進法
の値301)演算を用いて計算しなければならない。これは,この体を表す原始多項式X8+X5+X3+X2+1
を含む28のガロア体である。16個の異なった生成多項式を用いて適切な誤り訂正コード語を生成する。こ
れらをE.1に示す。
5.7.2
誤り訂正コード語の生成
誤り訂正コード語は,データコード語をリードソロモン符号で用いる多項式g(x)で除算した剰余である
(E.1参照)。
注記 長除法によってこの計算を実行する場合,シンボルデータ多項式は,最初にxKを乗算する必要
がある。
データコード語は,多項式の各項の係数であり,最初のデータコード語が次数の一番高い項の係数,最
後のデータコード語が次数の一番低い項の係数,続いて最初の誤り訂正コード語の順番になる。剰余のう
ち,次数の一番高い係数が最初の誤り訂正コード語,0次の係数が最後の誤り訂正コード語になる(コー
ド語列の最後)。これらの演算は,図5に示すような除算回路を用いて実施することができる。レジスタ
b0〜bk−1は,0で初期化される。コードの生成は,二段階で行われる。一段階目では,スイッチが下向きの
状態で,データコード語が出力及び回路の両方を通過することになる。一段階目は,n個のクロックパル
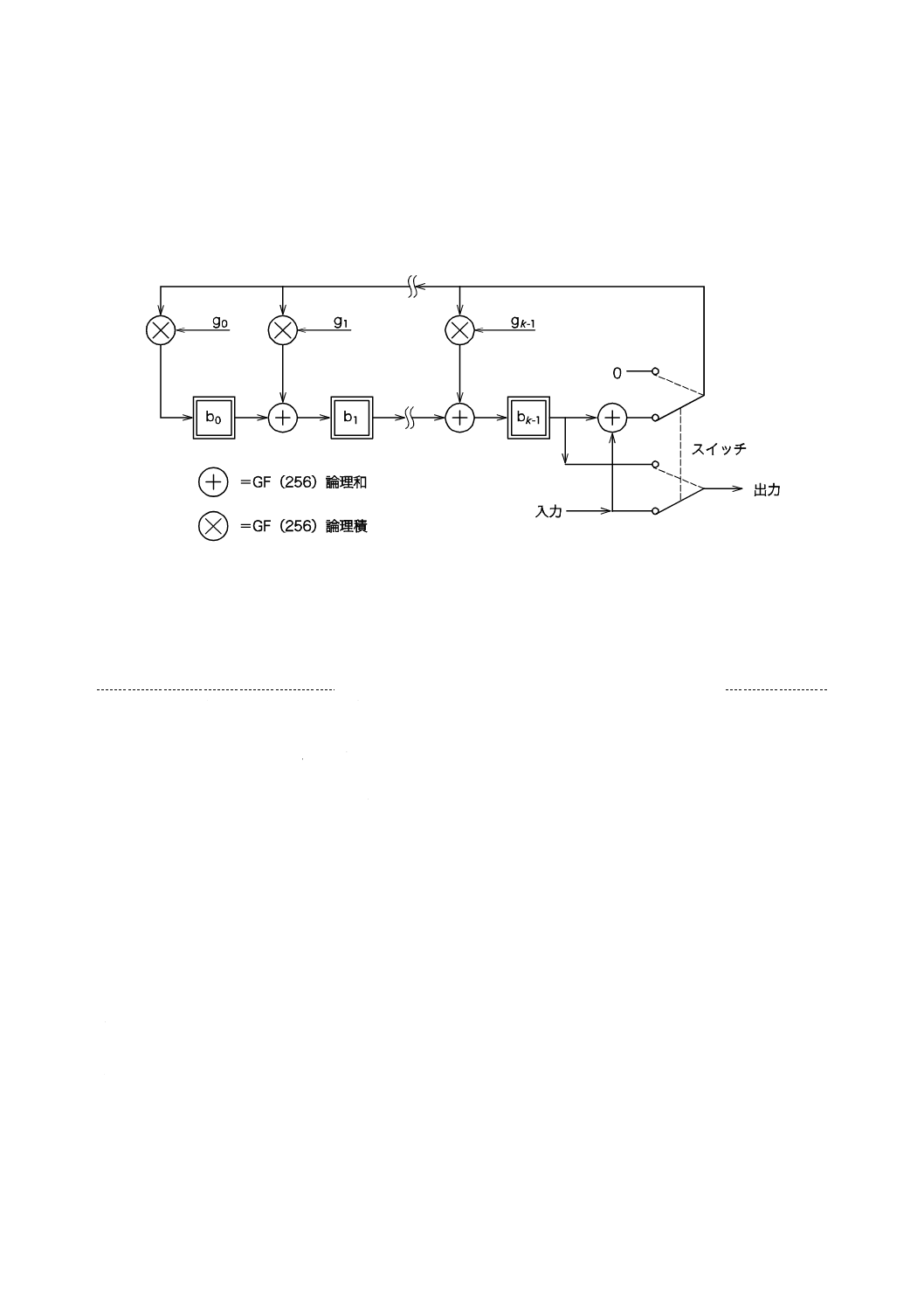
19
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
スの後に終了する。二段階目(n+1...n+k回のクロックパルス)では,スイッチを上向きの状態にしてデ
ータ入力を0で保持している間レジスタを順送りし,誤り訂正コード語εk−1…ε0を生成する。シフトレジ
スタからのコード語は,シンボルに配置される順に従って出力される。もし,飛び越し配置されたならば,
コード語は,連続したシンボルキャラクタとしては配置されない(附属書A参照)。
注記 n及びkは,3.2でデータコード語の総数及び誤り訂正コード語の総数と規定されている。
図5−誤り訂正コード語符号化回路
5.7.3
誤り訂正容量
誤り訂正コード語は,消失誤り(既知の位置における誤ったコード語)及び代入誤り(未知の位置にお
ける誤ったコード語)の2種類の不正なコード語を訂正することができる。消失誤りは,走査不能(シン
ボルの汚れ,シンボルの欠損など)又は復号不能なシンボルキャラクタを指し,代入誤りは,(走査はでき,
復号を試みたが)復号を誤ったシンボルキャラクタを指す。
訂正可能な消失誤り及び代入誤りの数は,次の式で与えられる。
p
d
t
e
−
+
≦
2
ここに,
e: 消失誤りの数
t: 代入誤りの数
d: 誤り訂正コード語の数
p: 誤り検出用に予約されたコード語の数
一般にはp=0である。しかしながら,誤り訂正容量の大半が消失誤りの訂正に費やされると,検出され
ない誤りの数が増えることになる。消失誤りの数が誤り訂正コード語数の半分以上になる場合は,p=3と
する。小さいシンボル(10×10,12×12,8×18及び8×32)では,消失誤りの訂正を用いないのが望まし
い(e=0及びp=1)。
5.8
シンボルの構造
5.7までに得られたコード語シーケンスは,次の手順を用いてECC 200シンボルを構成できる。
a) コード語モジュールを割当てマトリックスに配置する。
b) 位置合せパターンモジュールがある場合は,挿入する。
c) 境界に沿って位置検出パターンモジュールを配置する。
5.8.1
シンボルキャラクタの配置
各シンボルキャラクタは,8個の正方形モジュールで表され,各モジュールがバイナリの1ビットを表
す。暗モジュールが1を表し,明モジュールが0を表す。図6に示すように,8個のモジュールが左から
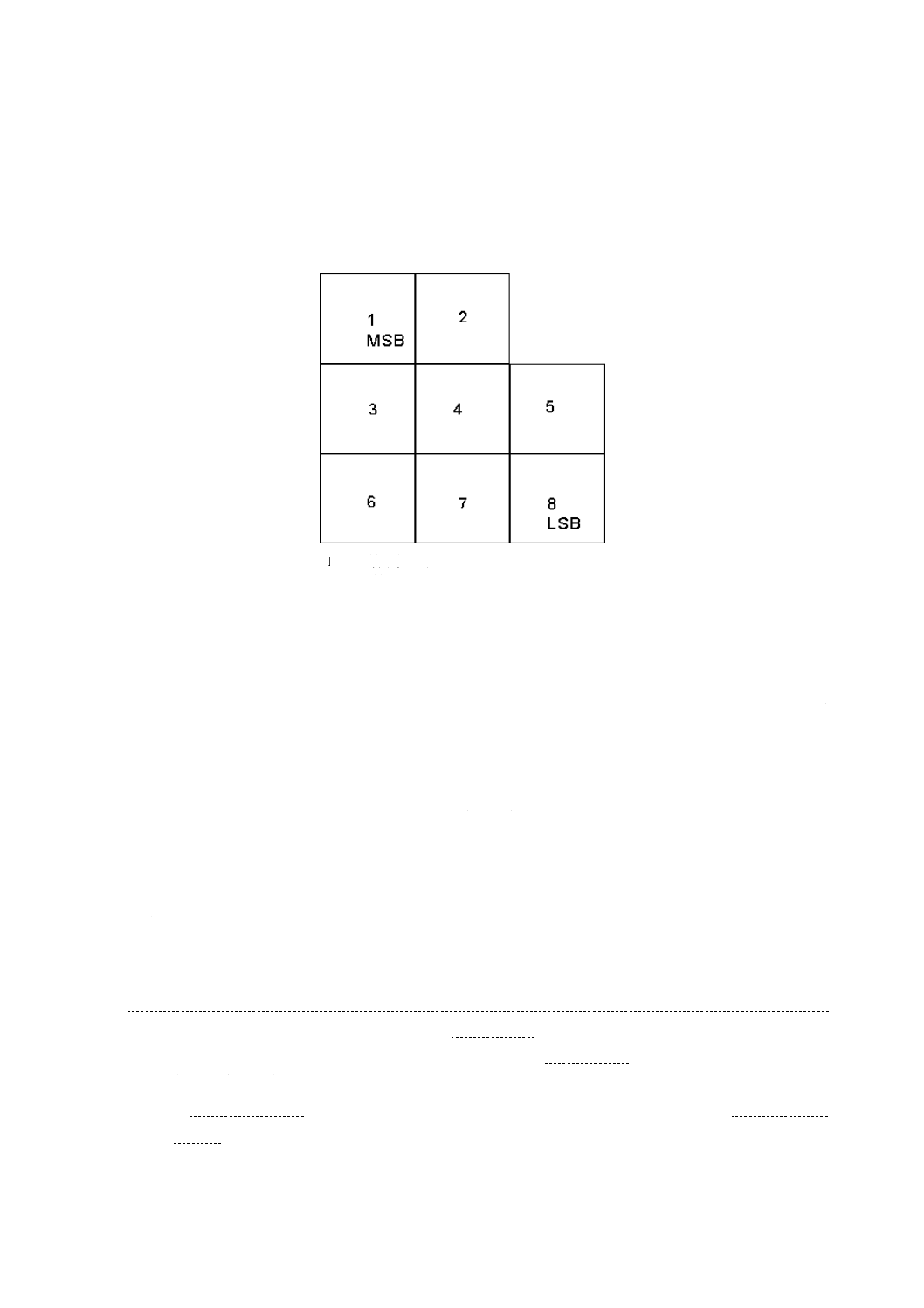
20
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
右に,上から下に向かって順に並ぶことでシンボルキャラクタが形成される。
図6で規定するシンボルキャラクタの形状は,繰り返し配置することによって,広い領域を隙間なく埋
めることはできるが,正方形又は長方形の領域を周辺まで隙間なしに埋めることができないため,図6以
外の分割されたシンボルキャラクタ形が用いられる。シンボルキャラクタの配置について,F.1でC言語
によるプログラムによって規定し,F.2で説明を加え,F.3で図解する。
LSB=最下位ビット
MSB=最上位ビット
図6−ECC 200シンボルキャラクタのコード語表現
5.8.2
位置合せパターンモジュールの配置
次の手順は,正方形の場合は,32×32以上の,長方形の場合は,8×32及び12×36以上のマトリックス
に対してだけ必要である。割当てマトリックスは,表7に規定されるサイズのシンボルフォーマットでデ
ータ領域に分割される。このデータ領域は,2モジュール幅の位置合せパターンによって互いに分離され
ている。この結果として,幾つかのシンボルキャラクタが,隣り合う二つのデータ領域で分割されること
になる。正方形のマトリックスの場合,位置合せパターンは,データ領域の間を水平及び垂直に走る一対
のパターンとして,図D.1〜図D.3に示すように,2個,6個又は10個配置される。長方形マトリックス
の場合,図D.4に示すように,データ領域間に垂直の位置合せパターンが1個だけ配置される。
5.8.3
位置検出パターンモジュールの配置
モジュールは,4.3.1で記述したような位置検出パターンを構成するために,マトリックスの境界に沿っ
て配置される。
6
ECC 000〜ECC 140シンボルの要件
注記 この規格は,誤り訂正方式がECC 000,ECC 050,ECC 080,ECC 100及びECC 140であるシン
ボルに関する規定を不採用にした。ECC 000〜ECC 140シンボルは,JISを作成する時点及びそ
れ以降でも用いることを推奨しない。したがって,ECC 000〜ECC 140に関連する規定である,
細別を含む箇条6も不採用にした。
ECC 000〜ECC 140に関連する規定については,対応国際規格であるISO/IEC 16022:2006を
参照。
21
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7
シンボルの寸法
7.1
寸法
データマトリックスシンボルは,次の寸法に従わなければならない。
a) X寸法
モジュールの幅は,シンボル作成技術及び用いる読取り技術を考慮して,アプリケーションで指定しな
ければならない。
b) 位置検出パターン
位置検出パターンの幅は,X寸法と同じでなければならない。
c) 位置合せパターン
位置合せパターンの幅は,2Xでなければならない。
d) クワイエットゾーン
最小クワイエットゾーンは,四方ともX寸法と同じである。シンボルに隣接した過度な反射ノイズを抑
制する必要があるアプリケーションでは,2X〜4Xのクワイエットゾーンを推奨する。
8
シンボル品質
データマトリックスシンボルは,ISO/IEC 15415で規定する二次元マトリックスシンボルの印刷品質ガ
イドラインに,この後に示す拡張及び修正を施したものを用いて,品質を評価しなければならない。
幾つかのマーキング技術によっては,特別な注意をしないと,この仕様に適合するシンボルを生成でき
ない場合がある。印刷システムを問わず,有効なデータマトリックスシンボルを作るための追加指針を附
属書Tに示す。
8.1
シンボル品質パラメタ
8.1.1
固定パターンの損傷
附属書Mに,固定パターン損傷のための測定及び評価基準を規定する。
注記 ISO/IEC 15415の附属書Aに示すように,ISO/IEC 15415の附属書Aに示す内容よりも,この
規格の附属書Mで規定する測定及び値を優先する。
8.1.2
走査グレード及び総合シンボルグレード
走査グレードは,シンボルの個々の画像における次の各項目についてのグレードの中の最も低いグレー
ドとしなければならない。
− シンボルコントラスト,
− 変位幅,
− 固定パターンの損傷,
− 復号,
− 軸の非均一性,
− グリッドの非均一性,
− 未使用誤り訂正についてのグレード
総合シンボルグレードは,シンボルを試験した画像の総数に対する,個々の走査グレードの算術平均で
ある。
8.1.3
グリッドの非均一性
理想的なグリッドは,各データ領域の四つのコーナポイントを用いて,両方の軸を均等に分割すること
によって計算する。
22
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.1.4
復号
この規格に明記している参照復号アルゴリズムは,復号のためのグレードを決定するために適用しなけ
ればならない。参照復号アルゴリズムを用いて復号を試み,シンボルの復号に失敗したときは,復号のグ
レードを“0”にしなければならない。
8.2
プロセス制御法
データマトリックスシンボルの生成プロセスを監視及び制御するのに有用な測定を行うために,様々な
ツール及び方法を用いることができる。これらを附属書Rに示す。これらの技術は,生成されたシンボル
の印刷品質試験の構成要素としない(8.1及び附属書Mで指定した方法は,シンボルの印刷品質を評価す
るのに必要な方法であった。)。しかし,これらは,シンボルの印刷工程が,有効なシンボルを作成してい
るかどうかのよい指標を,個別に及び全体的に与える。
9
データマトリックスの参照復号アルゴリズム
この参照復号アルゴリズムは,画像の中からデータマトリックスシンボルを見つけて,それを復号する
アルゴリズムである。
a) 次に示す1)〜4)の手続によって,寸法パラメタを決定し,2値化画像を形成する。
1) アプリケーションで規定した開口径の7.5倍の長さをdminとする。これは,“L”パターン側の最小
長さとなる。
注記 ここでいう“開口径”(aperture diameter)は,受光素子面を構成する個々の画素に対応する
ものではない(ISO/IEC 15415参照)。
2) 開口径の7.5倍の長さをgmaxとする。これは,b)の位置検出アルゴリズムによって許容される“L”
パターンの最大間隔となる。
3) 開口径の1.25倍の長さをmminとする。開口径がX寸法の80 %であるとき,これは,公称最小モジ
ュール幅となる。
4) ISO/IEC 15415で規定している方法によって決められたしきい(閾)値を用いて,白黒の画像を形
成する。
b) 次の1)〜9)の手続によって,データマトリックス“L”の二つの外側エッジに対応する,水平及び垂
直の走査ラインを捜す。
1) 画像領域の中央(受光素子面を構成する画素数によっては,1画素分オフセットする場合がある。)
から,水平の両方向に1画素幅の走査ラインを伸ばす。その走査ライン伝いに“白から黒”又は“黒
から白”への変換点(画素の境界)を見つけ,それぞれの変換点について,次の手順を実行する。
1.1) 走査ライン上の各画素の境界箇所(各エッジの開始箇所)から,1画素単位に上に向かってサンプ
リングを行いながらエッジをたどる。この処理を,各エッジの開始箇所から3.5mmin離れた箇所に
達するまで,又は上に向かってたどれなくなるまで続ける。
1.2) 走査ライン上の各画素の境界箇所(各エッジの開始箇所)から,1画素単位に下に向かってサンプ
リングを行いながらエッジをたどる。この処理を,各エッジの開始箇所から3.5mmin離れた箇所に
達するまで,又は下に向かってたどれなくなるまで続ける。
1.3) 上(下方処理の場合は“下”)に向かってたどっている各エッジ列が,各エッジ列の開始箇所から
3.5mminの箇所に達している場合は,それらのエッジ列に対して次の処理をする。
1.3.1) 上(下方処理の場合は“下”)に向かってたどったエッジ列の両端を結ぶ線分Aを引く。
1.3.2) 線分Aの両側0.5mminの範囲内に,エッジ列が収まっているかを検査する。収まっている場合は,
23
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1.3.3)に進む。はみ出している場合は,1.4)に進み,逆方向にエッジをたどる。
1.3.3) はみ出しているエッジが見つかるまで,更に上に向かってエッジをたどる。はみ出しているエッ
ジ箇所からmmin戻り,戻った方向に見て最も近いエッジ箇所を,エッジの終わりとして保存する。
このエッジは,“L”に沿った外側ふち(縁)の候補であろう。
1.3.4) 次に,エッジ開始箇所から下に向かって,はみ出しているエッジが見つかるまでエッジをたどる。
はみ出しているエッジ箇所からmmin戻り,戻った方向に見て最も近いエッジ箇所をエッジの終わ
りとして保存する。このエッジは,“L”に沿った外側ふち(縁)の候補であろう。
1.3.5) 二つの事前手順によって得たエッジ列を基にして,“最も適した”調整済みの新たな線分A1を
計算する。“最も適した”線分は,それぞれのエッジ箇所に線形回帰法(適切な軸を選ぶために
端点を用いる。例えば,もし,水平に近い場合は,その軸をxとする。)を適用して求める。線
分A1の端点をp1及びp2とする。p1及びp2は,線分A1上でエッジの終わりに最も近い箇所
である。
1.3.6) 線分A1の端点であるp1及びp2を保存する。同時に,p1からp2の方向を見たときの,エッジ
の左側の色も保存する。
1.4) もし,1.3)で3.5mminに達しなかった場合,又は1.3.3)で3.5mminを過ぎて上方に拡張できなかった
場合は,エッジ開始箇所から下方向にエッジをたどって,3.5mminの箇所に達するかを検査する。
達する場合は,1.3)内を繰り返す(ただし,逆方向として。)。
注記 対応国際規格では,1.3.4)であったが,間違いであるため1.3.3)に訂正した。
1.5) 1.3)及び1.4)のどちらでも成功しなかった場合,上方エッジ及び下方エッジの両方が,エッジ開始
箇所から少なくとも2mminまで終了したかを検査する。終了している場合は,長さ2mminの上方エ
ッジと下方エッジとを結合した一つのエッジ区分を形成し,そのエッジ区分について1.3)を繰り
返す。
1.6) 画像の境界に達するまで,走査ライン上の次の変換点に進んで1.1)から繰返し処理を続ける。
2) 画像の中心から垂直の両方向に1画素幅の走査ラインを伸ばす。上の1)と同じ論理を用いて,最初
に左に,次に右に各エッジの変換点について線分を探す。
3) 次の四つの判断基準を満たす線分の対を,保存された線分A1群から探す。
3.1) もし,2本の線分(前者,後者)のp1からp2への向きが同じならば,前者のp1から後者のp2
までの距離と前者のp2から後者のp1までの距離との小さい方がgmax未満であるかを確認する。
もし,2本の線分のp1からp2への向きが反対ならば,前者のp1から後者のp1までの距離と前者
のp2から後者のp2までの距離との小さい方がgmax未満であるかを確認する。
3.2) 2本の線分が5°以内に共線的であることを確認する。
3.3) 2本の線分のp1からp2への方向が同じときは,1.3.6)で保存した色が同じであること,又はp1か
らp2の方向が反対方向のときは,1.3.6)で保存した色も互いに異なることを確認する。
3.4) 2本の線分において,他方の線分の遠い方の端点に最も近い箇所に達するまで,それぞれの線分を
伸ばして,2本の仮の線分を形成する。伸ばした2本の線分間の距離が,どの部分でも0.5mmin未
満であることを確認する。
4) 上記3)の基準を満たす短めの線分の対を,その対の四つの端点に“最も適した”一つの長めの線分
A1に置き換える。同時に,新しい長めの線分のp1からp2の方向を見たときの,エッジの左側の色
も保存する。
5) 線分A1の対を結合できなくなるまで,3)及び4)を繰り返す。
24
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6) dmin以上の長さの線分を選択し,“L”側の候補として印を付ける。
7) 次の三つの基準を満たす“L”側候補の対を探す。
7.1) 二つの線分が最も近づく箇所の距離が1.5gmax未満であることを確認する。
7.2) それらの線分がなす角度が90±5°であることを確認する。
7.3) 二つの線分による“L”形の内側の色が同じであることを確認する。もし,一方又は両方の線分が,
それらの交点を通過して伸びるときは,それによって形成された二つ又は四つの“L”パターンを
“L”候補にする前に,色が同じであるだけでなく,交点から先を切り詰めた後の,残りの線分の
長さがdmin以上であることも検査する必要がある。
8) 7)で見つかった“L”の構成要素候補の線分の対を,それらの交点まで延長して“L”候補とする。
9) もし,“L”候補の“L”の内部が白色の線分であった場合は,白黒反転画像として復号する。8)の
“L”候補のうちのそれぞれを“L”形ファインダとして用い,d)から始まる手順で,通常の画像又
は白黒反転の画像としてシンボルの復号を試みる。もし,復号できない場合は,c)に進む。
c) 前の手順での“L”の構成要素候補及び線分A1群を保持する。前回の走査ラインからオフセットした
水平走査ライン及び垂直走査ラインを用いて,“L”の候補を,次の1)〜4)の手順で探し続ける。
1) 中央の水平走査ラインから3mmin上の新しい水平走査ラインを用いて,b) 1)の手順を,中心から3mmin
オフセットした位置から開始することとして繰り返し,続いてb) 3)〜b) 9)を繰り返す。もし,それ
らで復号できない場合は,次の手順に進む。
2) 中央の垂直走査ラインから3mmin左の新しい垂直走査ラインを用いて,b) 2)の手順を,中心から3mmin
オフセットした位置から開始することとして繰り返し,続いて,b) 3)〜b) 9)を繰り返す。もし,そ
れらで復号できない場合は,次の手順に進む。
3) 中央の水平走査ラインから3mmin下の新しい水平走査ラインを用いて,上記1)と同様の処理を繰り
返す。もし,それらで復号できない場合は,中央の垂直走査ラインから3mmin右の新しい垂直走査
ラインを用いて,上記2)と同様の処理を繰り返す。もし,それらで復号できない場合は,4)に進む。
4) シンボルを復号するか,又は画像の端に達するまで,前回プロセスの走査ラインから3mmin上,3mmin
左,3mmin下,3mmin右の水平走査ライン及び垂直走査ラインで1)〜3)の手順を続ける。
d) まず,候補領域に正方形シンボルがあると仮定して処理する。正方形シンボルとして復号できない場
合は,j)で示す長方形シンボルの検出及び復号処理を試みる。正方形シンボルがあると仮定して,最
初に次の1)〜7)の手順を用いて,候補領域の“L”の二辺のそれぞれについて変換点の正規化グラフ
を描き,交互モジュール位置検出パターン(白黒モジュールの単位幅での繰返し)の候補を見つける。
1) 図9に示すように,候補領域の“L”の二辺の内側を二等分する線分を引く。二等分する線分によ
って作られた,面積が等しい二つの領域を,“L”の角から見て右側及び左側と呼ぶ。
2) 図9に示すように,“L”に沿って角からdmin離れた点を通り,もう一方の“L”と平行な,“探索線”
と呼ぶ線分を,それぞれの辺に形成する。
3) 図9に示すように,それぞれの探索線を2本の境界線(“L”及び二等分する線分)が広がるのに合
わせて長くしながら,“L”の交点から離れる方向に動かす。それぞれの探索線は,相対する“L”
の一辺と平行を保つ。それぞれの探索線を画素単位に動かしながら,探索線上の色の変化(黒から
白へ及び白から黒へ)の数を数える。数え始め及び数え終わりは,いずれも“L”の色から逆の色
への変化とする。色の変化を数えるのは,現在の探索線だけでなく,直前及び直後の探索線が,同
じように変化しており,かつ,直前に数えたときの変化と逆の変化のときだけとする。そのときの
探索線の変化の数と“L”の最大長さとの積を,探索線の長さ(そのときの2本の境界線の間隔を
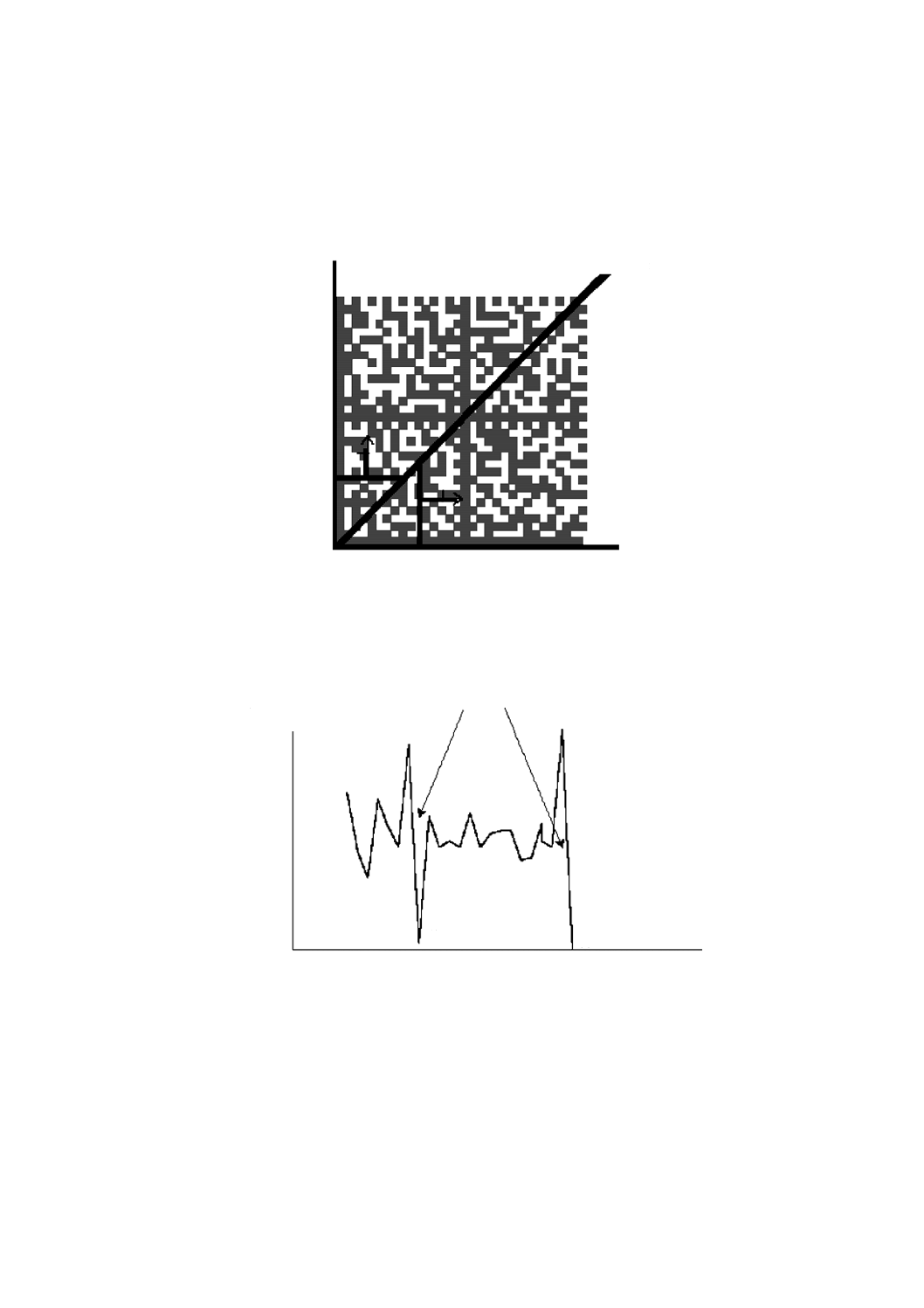
25
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定して得られる。)で除した値を求める。
T=(変換点の数)(“L”の最大長さ)/(探索線の長さ)
この式は,探索線が長くなることで値が増加しないようにTを正規化する。探索線が候補領域+
50 %の最長軸長よりも長くなるまで,Tの値の計算を続ける。
右探索線
“L”側
図9−探索線の広がり
4) それぞれの辺のTの値を描画する。Y軸がTの値で,X軸が“L”の角から探索線までの距離である。
描画の例を図10に示す。
山から谷に降下する候補
X軸−“L”の角からの距離
図10−探索線が広がるときのTの描画例
5) 右側の描画で,最小のXにおけるTの値から始めてXを増やし,Tの値が1よりも大きいという条
件で,先行する局所的な部分におけるTの最大値の15 %よりも小さい最初のTsの値(Tsは,ゼロ
とT−1との大きい方)を見つける。この箇所のXの値を,変換点の数の減少が止まるまで増加さ
せる。変換点の数が増加しなくなった箇所のXの値を,更に一つ増加させる。このXを谷と呼ぶ。
局所的な部分におけるTの最大値となるXの値を,変換点の数が減少するまで増加させ,このXを
山と呼ぶ。山及び谷のX値の平均を,降下線のX値と呼ぶ。山における探索線は,交互位置検出パ
左探索線
“L”側
二等分線
山
山
谷
谷
0
20
10
30
40
50
60
Y軸−T値
26
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ターン側の可能性がある。谷における探索線は,変化しない暗ラインの内側又は明クワイエットゾ
ーンに対応する可能性がある。
6) 左側の描画において,右側の山及び谷の降下線X値に最も一致する降下線X値を与える山及び谷を
見つける。もし,後の手順からこの手順に戻る場合,右側の山及び谷が,どれだけ一致するかとい
う観点から順位をつけて,左側の山及び谷を追加検討する。検討中のどの左側の山及び谷も,右側
及び左側の山のX値の絶対差が,二つの山のX値の平均の15 %未満であること並びに右側及び左
側の谷のX値の絶対差が二つの谷のX値の平均の15 %未満であることを確認しなければならない。
この15 %は,最大許容できる縮小倍率を規定する。
7) 右側の谷探索線,左側の谷探索線及び“L”の二つの辺は,シンボルのデータ領域と考えられる輪
郭を描く。この後,e)以降の手順に従ってデータ領域を処理し,復号を試みる。もし,復号に失敗
した場合は,d) 6)に戻って次の左側の山及び谷を見つける。全ての左側の山及び谷が捨て去られた
場合,右側の山及び谷も捨て去り,d) 5)から,次の右側の山及び谷の探索を続ける。
e) 交互パターンの二つの辺の各々について,交互の明暗モジュールの中央を通る線を,次の1)〜3)の手
順で見つける。
1) 各々の辺について,図11に示すように,長方形の二つの長辺としての山探索線及び谷探索線並びに
二つの短辺としての“L”側及び反対側の谷探索線を境界とする長方形領域を形成する。
図11−長方形領域の作成
2) 長方形領域内の歯状の外側境界に,画素エッジの対を見つける。
2.1) 谷線に平行な試験線を谷線の位置から平行に移動しながら,試験線に直交する方向で反対色とな
る変換点を探す。始めの色は,谷線に沿った画像のうちの最も多い色であり,暗から明へ又は明
から暗へのどちらか一方の変換点だけを選ぶ。
2.2) 見つかった変換点の数が,谷線を構成する画素数の15 %未満の場合,かつ,試験線が山線に到達
他側からの谷線
長方形領域
谷線
山線
Lの境界
Md

27
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
していない場合は,試験線を1画素分だけ山線側に動かし,再度,2.1)から処理を行う。このとき,
新しく見つかった変換点の数を,既に見つけた変換点に加える。15 %の基準を満たした場合又は
山線に到達した場合は,次の手順を続ける。それ以外の場合は,次の残りの山及び谷を用いて,
d) 6)から探索を続ける。
2.3) 線形回帰法によって,選択した画素対の間にあるエッジ上の点を用いて,仮の“最も適した線”
を求める。
2.4) 仮の“最も適した線”からの距離が遠い順に,点の25 %を破棄する。残りの75 %の点を用いて,
線形回帰法によって,最終的な“最も適した線”を求める。この線は,図12“最も適した線”に
示すように,交互パターンの外側を沿うように通る。
図12−交互パターンモジュールの中央線
3) 各々の辺において,“L”の角から山探索線までの距離を山探索線内の変換点の数に1を加えて2倍
にした数で除した距離を,“L”の角に向かって垂直方向にオフセットした,e) 2)で求めた“最も適
した線”と並行な線を作成する。
オフセット=山線までの距離/[(変換点の数+1)×2]
各々の辺において作成した線は,それぞれの辺の,交互モジュールパターンの中央の線に相当す
る(図12参照)。
f)
各辺において,交互パターンのエッジ間の距離を,次の1)〜4)の手続によって測定する。
1) e) 3)で作成した交互パターンの中央の線を“L”の境界との交点及びe) 3)で得た反対側の交互パタ
ーンの中央線との交点で線分化する。この線の長さをMdとする(図11参照)。
2) 線分化した中央線に沿って,全ての隣接エレメント対(すなわち,黒エレメントと白エレメントと
の対)の,全てのエッジ〜類似エッジ間距離を測定する。エッジ間の測定は,“L”の色から反対色
に変わるエッジから始め,“L”の色から反対の色に変わるエッジで終わる。
最も適した線
交互パターンモジュールの
中央線

28
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3) エッジ間距離の中央値を選び,これをエッジ間距離推定値,EE̲Distとする。
4) エッジ間距離がEE̲Distから±25 %を超える全てのエレメント対を破棄する。
g) 各側面について,交互パターンモジュールの中央点を,次の1)〜4)の手続によって見つける。
1) f) 4)で残ったエレメント対の寸法を用いて,エレメント対インクにじ(滲)みの平均によって,(セ
グメント側に依存する垂直又は水平の)平均インクにじみを,次のように計算する。ここでは,残
りのエレメント対中の暗エレメント(幅)をバーとし,明エレメント(幅)をスペースとする。
インクにじ(滲)み=平均[(バー−((バー+スペース)/2))/((バー+スペース)/2)]
2) 中央値を与えたエレメント対の中のバーの中心を,そのバーの外側のエッジから,次の式で与える
オフセットだけ入ったところとして求める。
オフセット=[EE̲Dist×(1+インクにじ(滲)み)]/4
中央値に対応するエレメント対が複数存在するときは,次の手続を用いてエレメント対を一つだ
け選択する。
2.1) “L”ファインダエッジからの距離の順に,エッジ(“L”ファインダエッジを除く。)を並べたエ
ッジリストを作る。エッジが“L”ファインダから離れながら,暗から明への変化点で開始及び終
了するため,それらのエッジ数は,奇数である。
2.2) エッジリストの中央のエッジを中心エッジと呼ぶ。
2.3) (奇数個の)エレメント対のエッジ間距離を計算し,それらの中央値EE̲Distを求める。
2.4) EE̲Dist長さをもつ一つ以上のエレメント対を選択する。
2.5) それらの対の中から,中心エッジに最も近いエッジをもっている一つ又は二つのエレメント対を
選択する。
2.6) 2.5)で二つのエレメント対が選択されたときは,中央エッジに最も近い外側のエッジをもっている
エレメント対を選択する。
2.7) 2.6)でも二つのエレメント対が残ったときは,“L”ファインダに最も近い内側のエッジをもつエレ
メント対を選択する。
3) 次の3.1)〜3.4)の手順を用いて,f) 3)で示した中央値エレメント対のバーの中央から始め,エレメン
ト対のスペース方向に進んで線分化した中央線の終わりに達するまで各エレメント中央を求める
(図13に示す斑点の付いたパターンを参照)。
図13−エレメント中央を見つけるためのエッジ間の測定
(三つのバー及び二つのスペースを図13に示す。もし,スペースが,中央を計算することになっ
ているエレメントであれば,図13は,三つのバー部分がスペースになり,二つのスペース部分がバ
ーになる。中間ラインの終わりのエレメントに隣接した明エレメントの場合,D1又はD4の測定を
行わない。これは,シンボル又はセグメントの測定可能なエレメント境界の範囲外となるためであ
る。)
3.1) 新しいエレメントの方向に,前に計算したエレメントの中央からEE̲Dist/2 である中間ラインに
沿って,点p1を計算する。
29
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.2) d1〜d4の計算は,次のとおり。
d1=D1/2
d2=D2
d3=D3
d4=D4/2
3.3) 値d1〜d4のうちの一つがEE̲Distの25 %以内の場合は,EE̲Distに最も近い一つを選択し,現行
のEE̲Distと選択したd1〜d4の距離との平均値を,新しいEE̲Distとしてセットする。
3.3.1) d1又はd4が選択されるならば,中央を計算することになっているエレメントに最も近いD1エッ
ジ又はD4エッジを選択する。適切な方法[例えば,インクにじ(滲)みがあるときは,オフセ
ットを,距離d1又はd4に含まれたスペース方向に移動する。インクにじ(滲)みがないときは,
オフセットをこのスペースから取り除く。]である[インクにじ(滲)み/2]×(EE̲Dist/2)によ
って,このエッジを相殺する。オフセットエッジ及び計算したエレメント中央に向かって,選択
したd1値又はd4値の0.75倍である中央ラインに沿った点p2を計算する。
3.3.2) d2又はd3が選択されるならば,中央を計算することになっているエレメントに最も近いD2エッ
ジ又はD3エッジを選択する。適切な方法[例えば,インクにじ(滲)みがあるときは,オフセ
ットを,距離d2又はd3に含まれたスペース方向に移動する。インクにじ(滲)みがないときは,
オフセットをこのスペースから取り除く。]である[インクにじ(滲)み/2]×(EE̲Dist/2)によ
って,このエッジを相殺する。オフセットエッジ及び計算したエレメント中央に向かって,選択
したd2値又はd3値の0.75倍である中央ラインに沿った点p2を計算する。
3.3.3) p1及びp2の中間にエレメント中央をセットする。
3.4) d1〜d4の値がEE̲Distの25 %以内でなければ,元の値をEE̲Distとして残し,新しいエレメント
中央p1を用いて,次のエレメントに進む。
4) 中央値エレメント対のバーの中央から始め,3)から逆方向に,線分化した中央線の逆の端に達する
まで,3)の手続を用いて,各エレメントの中央を求める。
h) もし,各側のモジュール数が,最初の有効領域に該当しない場合,次の左の山及び谷のためにd) 6)
から探索を続ける。そうでなければ,拡張交互パターンモジュール中央によって,データ領域にデー
タモジュールサンプリング格子を,次の1)〜3)の手続によって描画する。
1) 2本のほぼ平行している又は平行に伸ばされた線の消失点を形成するために,手順e) 3)の中間線及
び逆の側の“L”線を延長する。
2) それぞれの消失点から,e) 3)線にほぼ垂直でg)モジュールの中心を通過する線を延長する。
3) ほぼ垂直な線の二つのセットの交点は,データ領域内のデータモジュールの中心と一致することが
望ましい(図14参照)。

30
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図14−モジュールサンプリング格子の作成
i)
次の1)〜4)の手順によって,残りのデータ領域を処理する。
1) 一つのデータ領域の処理が終了したとき,次に示す二つのプロセスのいずれかを用いて“左”又は
“上”に,次のデータセクションのための新たな“L”を形成する。
1.1) 新しいデータ領域の一つの側が,手続b)で定めた元の“L”に沿っている場合は,e) 2)から選択し
たポイントのセットと,e) 2)線を越えた位置にある“L”の上のb) 2)によって選択したポイントの
セットを用い,c)からの繰返しによって,新しいデータ領域を処理する。
1.2) もし,新しいデータ領域の両側とも(元の“L”に沿ってはおらず)データ領域に沿っている場合,
新しいデータ領域の両側に隣接するデータ領域に対し,e) 2)によって選択したポイントのセット
を用い,c)からの繰返しによって,新しいデータ領域を処理する。
2) もし,データ領域が,前に処理された領域のモジュール数と一致しない場合,正当なシンボルに対
応した領域の最大数にシンボルを整理する。
3) 一つ以上のデータ領域をもつシンボルの復号は,手順k)で開始する。
4) もし,元のデータ領域が,最後の山及び谷を使い尽くしたとき,前のデータ領域に戻り,そのデー
タ領域の次の左の山及び谷のためにd) 6)から探索を続ける。
j)
長方形シンボルのデータ部分を見つける。
1) “L”の各側面については,側面に垂直な線及び“L”の反対側の長さに沿って走査しながら移動する。
各探索線は,他の“L”側線との平行を保持する。各側面は,画素のサイズによって移動し,“黒か
ら白”及び“白から黒”の変換点の数をカウントし,“L”側の色から反対の色への変換点によって
カウントの開始及び停止をする。一つの色から他の色への移行は,今の探索線のすぐ上下でカウン
トされ,変移色とは反対の色と同じときだけカウントする。各側面が画素によって移動するように,
変換点“T”の数を描く。平行線が“L”+10 %の垂直脚よりも,更に移動するまで続ける。
2) 描画の原点から始めて各方向に,“T値が1よりも大きいとき”及び“先行する局所的な場所の最大
T値の15 %未満のとき”のTs値[Ts=(0及びT−1)の最大]である最初の例を見つける。T値の
減少が停止するまでX値を増加させる。もし,T値が増加できないときは,もう一つX値を増加す
る。このX値を谷とする。T値が減少するまで,局所的な場所の最大X値を増加し,このXを山と
左側の消失点へ
右側の
消失点へ
31
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
する。降下線のX値は,山及び谷のX値の平均とする。この地点の谷線は,シンボル又はデータ領
域の側面を形成する。
3) e)と同様にして,領域の各側面で交互パターン行を探す。
4) f),g)及びh)のようなデータ領域又はシンボル内のモジュールサンプル格子を描く。
5) もし,定義されたデータ領域が無効な長方形シンボルの場合は,更に有効な山から谷の描画変移を
用いて,新しいデータ領域の形成を試みる。
6) i)のように追加の領域を処理する。
7) もし,有効なデータ領域又は二つの領域が検出さた場合,k)及びl)のシンボルの復号を試みる。領
域が有効でない場合又は復号を失敗した場合は,対象領域を無視する。
k) 次の1)〜4)の手続によって,データモジュール数が偶数又は有効な長方形シンボル形式のシンボルの
場合は,リードソロモン誤り訂正を用いて復号する。
1) データモジュールを予測した中央でサンプリングする。“L”と同じ色ならば“1”とし,違う色な
らば“0”とする。
注記 対応国際規格では,第2文は,“Black at the centre is a one and white is a zero.(黒の中央を“1”,
白を“0”とする。)”であるが,白黒反転画像を考慮し,(“L”と同じ色ならば“1”とし,
違う色ならば“0”とする。)とした。
2) 定義されたコード語パターンの八つのモジュールサンプルを,8ビットシンボル文字値に変換する。
3) リードソロモン誤り訂正をシンボルキャラクタ値に適用する。
4) 指定された符号化スキームに従って,データキャラクタにシンボルキャラクタを符号化する。
l)
そうでなければ,データモジュール数が奇数であるため,畳込み誤り訂正を用いてシンボルを復号す
る。
注記 この規格は,誤り訂正方式がECC 000,ECC 050,ECC 080,ECC 100及びECC 140であるシ
ンボルに関する規定を不採用にした。ECC 000〜ECC 140シンボルは,JISを作成する時点及
びそれ以降でも用いることを推奨しない。そのため,対応国際規格の1)〜6)の細別を不採用
とした。ECC 000〜ECC 140の規定については,ISO/IEC 16022を参照。
10 利用者ガイドライン
10.1 可読文字の印刷
データマトリックスシンボルは,何千ものキャラクタを符号化できるので,データキャラクタの可読文
字印刷は,実践的ではない。別の手段として,符号化したテキストではなく,説明的なテキストを併記し
たシンボルにしてもよい。メッセージは,文字サイズ及びフォントを指定せずに,シンボル周辺のどこに
印刷してもよい。可読文字の印刷は,シンボル自体又はクワイエットゾーンを妨げないほうがよい。
10.2 自動識別能力
データマトリックスは,自動識別環境の中で,他のシンボル体系と一緒に用いることができる(附属書
S参照)。
10.3 システムの検討
データマトリックスのアプリケーションは,システム全体のソリューションとして考慮しなければなら
ない(附属書T参照)。
32
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
11 送信データ
ここでは,一般的なバーコードリーダの標準的な送信プロトコルを記述する。これらのリーダには,他
の送信オプションを支援するプログラム機能を備えていてもよい。全ての符号化データキャラクタを送信
データに含む。シンボル体系制御キャラクタ及び誤り訂正キャラクタは,送信しない。より詳細な説明は,
次による。
11.1 FNC1プロトコル(ECC 200専用)
第1シンボルキャラクタ位置(又は,構造的連接シンボルの最初のシンボルの第5シンボルキャラクタ
位置)にあるFNC1は,データがGS1アプリケーション識別子の標準フォーマットに適合していることを
示す。これ以降にあるFNC1は,“領域区切り”として動作する。バーコードリーダは,シンボル体系識別
子の送信を“有効”にしなければならない。最初のFNC1は,送信データに含めてはならないが,その存
在は,シンボル体系識別子の適切な任意選択値“2”(11.5参照)を用いることによって示すことができる。
“領域区切り”として用いるときのFNC1は,ASCIIキャラクタ<GS>(ASCII値29)に置き換えて,送
信メッセージに表現しなければならない。
11.2 第2位置にあるFNC1のプロトコル(ECC 200専用)
FNC1が第2シンボルキャラクタ位置(又は,構造的連接シンボルの最初のシンボルの第6シンボルキ
ャラクタ位置)にあるときは,データが特別な産業標準フォーマットに適合していることをバーコードリ
ーダに通知しなければならない。バーコードリーダは,シンボル体系識別子の送信を“有効”にしなけれ
ばならない。最初のFNC1は,送信データに含めてはならないが,その存在は,シンボル体系識別子の適
切な任意選択値“3”(11.5参照)を用いることによって示すことができる。
最初のシンボルキャラクタに符号化されたデータは,通常,データの先頭に送信しなければならない。
“領域区切り”として用いるときのFNC1は,ASCIIキャラクタ<GS>(ASCII値29)に置き換えて,送信
メッセージに表現しなければならない。
11.3 第1位置にあるマクロキャラクタのためのプロトコル(ECC 200専用)
このプロトコルは,ECC 200シンボルにおいて,二つの特定メッセージを簡略形式で,データの先頭及
びデータの末尾に符号化するのに用いる。
マクロキャラクタが第1位置にあるとき,先頭語及び末尾語を送信しなければならない。第1シンボル
キャラクタが“236(符号化マクロ05)”のとき,先頭語“[)>RS05GS”は,それに続く符号化されたデータ
に先行しなければならない。第1シンボルキャラクタが“237(符号化マクロ06)”のとき,先頭語“[)>RS06GS”
は,それに続く符号化されたデータに先行しなければならない。末尾語“RS EOT”は,いずれの場合も,
データの後に送信しなければならない。
11.4 ECIのプロトコル(ECC 200専用)
ECIを支援しているシステムでは,全ての送信で,シンボル体系識別子を接頭辞として用いなければな
らない。
ECIコード語を検出するごとに,それをエスケープキャラクタ92DEC(又は5CHEX)として送信しなけれ
ばならず,これは,デフォルトの解釈で“¥”(バックスラッシュ又は逆スラッシュ)を表す。次のコード
語は,表6に定義されている規則で6桁の値に逆変換される。6桁の値は,適切なASCII値(48〜57)と
して送信する。¥nnnnnnを識別するアプリケーションソフトウェアは,それに続く全てのキャラクタを,
ECIで定めた6桁のシーケンスとして解釈するのが望ましい。この解釈は,符号化されたデータの最後又
は他のECIシーケンスが検出されるまで有効である。“¥(92DEC)”が符号化データとして必要なときは,
“¥(92DEC)”が発生するごとに,その値の2バイトを送信しなければならない。したがって,1個の“¥”
33
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は,常にエスケープキャラクタであり,“¥”が2個連続した“¥¥”は,真の“¥”データである。
例
符号化データ
: A¥¥B¥C
送信データ
: A¥¥¥¥B¥¥C
シンボル体系識別子を用いると,アプリケーションが正しくエスケープキャラクタを解釈できることを
確実にする。
注記 ISO/IEC 646 IRVでバックスラッシュ又は逆スラッシュを割り当てているコード位置に対し,
JIS X 0201では円記号“¥”を割り当てているので,注意が必要である。ASCII符号化スキーム
などで,円記号“¥”を表す場合は,コード位置165を用いる。
11.5 シンボル体系識別子
JIS X 0530(ISO/IEC 15424)は,シンボルの特別な機能及び復号器で設定したオプションとともに,読
んだシンボル体系を報告するための標準的な手順を提供している。一度,(ECIを用いることを含む)デー
タ構文を識別したときは,復号器によって,適切なシンボル体系識別子を接頭辞として変換データに加え
ることが望ましい。ECIがそのシンボル内に表れた場合,及び11.1又は11.2で規定したFNC1が用いられ
たときは,シンボル体系識別子が必要である。データマトリックスに適応する任意選択値及びシンボル体
系識別子を,附属書Nに示す。
11.6 送信データの例
この例では,2キャラクタメッセージ“¶Ж”は,ASCII符号化スキームを用い,ECC 200に符号化され
る。“¶”は,データマトリックスのデフォルトキャラクタセットで,バイト値が182である(ECI 000003
は,ISO/IEC 8859-1に相当する。)。“Ж”は,ECI 000003にはないキリル文字であるが,同じバイト値で
ある182によってISO/IEC 8859-5(ECI 000007)で表すことが可能である。そのため,完成されたメッセ
ージは,次のように最初のキャラクタの後にECI 000007への切換えを挿入することによって,表示するこ
とができる。シンボルは,次のデータマトリックスコード語の並びで<¶><ECI 000007への切換え><Ж>の
メッセージを [拡張ASCIIシフト] [55] [ECI] [8] [拡張ASCIIシフト] [55] (10進表現では,[235],[55],[241],
[8],[235],[55])のように符号化する。
注記1 値55のコード語に続く拡張ASCIIシフトキャラクタを,182という一つのバイト値で符号化
する。
注記2 ECIは,ECI番号+1としてデータマトリックスで符号化される。
復号器は,任意選択値が4のシンボル体系識別子(ECIであることを示す。)を含む,次のバイト列を送
信する。
93,100,52,182,92,48,48,48,48,48,55,182
これらは,デフォルト解釈で表現すると,次のようになる。]d4¶¥000007¶
復号器は,ECI 000007への切換えを合図するが,結果を解釈することはない。受信側アプリケーション
でのECI対応ソフトウェアは,ECIエスケープシーケンス“¥000007”を削除し,キリル文字“Ж”の扱い
は,そのシステムの仕様による(例えば,DTP用ファイルのフォントの切換え)。最終結果は,“¶Ж”の元
のメッセージと一致する。
34
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
ECC 200コード語の飛び越し配置手順
A.1 概要の図示
72×72シンボルサイズの例では,368個のデータコード語及び144個の誤り訂正コード語は,飛び越し
配置の4レベルを必要とする。それらを,図A.1に示すように,1ブロック当たり128個のコード語(92
個のデータコード語及び36個の誤り訂正コード語)として,四つのブロックの中に分配する。
コード語列
データコード語 d
誤り訂正コード語 ε
1
2
3
4
… … 365 366 367 368 1
2
3
4
…
... 141 142 143 144
ブロック1
データコード語 d
誤り訂正コード語 ε
1
5
… … … 361 365
1
5
… …
137 141
ブロック2
データコード語 d
誤り訂正コード語 ε
2
6
… … … 362 366
2
6
… …
138 142
ブロック3
データコード語 d
誤り訂正コード語 ε
3
7
… … … 363 367
3
7
… …
139 143
ブロック4
データコード語 d
誤り訂正コード語 ε
4
8
… … … 364 368
4
8
… … … 140 144
図A.1−72×72シンボルにおける飛び越し配置の図示
A.2 種々のサイズのシンボルにおける飛び越し配置の開始シーケンス
データコード語及び誤り訂正コード語の飛び越し配置シーケンスを表A.1に示す。
表A.1−種々のシンボルサイズのためのデータコード語及び誤り訂正コード語のシーケンス
シンボルサイズ
リードソロモンブロック
データコード語のシーケンス
誤り訂正コード語のシーケンス
52 × 52
1
1, 3, 5
...
201, 203
1, 3, 5
...
81, 83
2
2, 4, 6
...
202, 204
2, 4, 6
...
82, 84
64 × 64
1
1, 3, 5
...
277, 279
1, 3, 5
...
109, 111
2
2, 4, 6
...
278, 280
2, 4, 6
...
110, 112
72 × 72
1
1, 5, 9
...
361, 365
1, 5, 9
...
137, 141
2
2, 6, 10
...
362, 366
2, 6, 10
...
138, 142
3
3, 7, 11
...
363, 367
3, 7, 11
...
139, 143
4
4, 8, 12
...
364, 368
4, 8, 12
...
140, 144
80 × 80
1
1, 5, 9
...
449, 453
1, 5, 9
...
185, 189
2
2, 6, 10
...
450, 454
2, 6, 10
...
186, 190
3
3, 7, 11
...
451, 455
3, 7, 11
...
187, 191
4
4, 8, 12
...
452, 456
4, 8, 12
...
188, 192

35
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−種々のシンボルサイズのためのデータコード語及び誤り訂正コード語のシーケンス(続き)
シンボルサイズ
リードソロモンブロック
データコード語のシーケンス
誤り訂正コード語のシーケンス
88 × 88
1
1, 5, 9
...
569, 573
1, 5, 9
...
217, 221
2
2, 6, 10
...
570, 574
2, 6, 10
...
218, 222
3
3, 7, 11
...
571, 575
3, 7, 11
...
219, 223
4
4, 8, 12
...
572, 576
4, 8, 12
...
220, 224
96 × 96
1
1, 5, 9
...
689, 693
1, 5, 9
...
265, 269
2
2, 6, 10
...
690, 694
2, 6, 10
...
266, 270
3
3, 7, 11
...
691, 695
3, 7, 11
...
267, 271
4
4, 8, 12
...
692, 696
4, 8, 12
...
268, 272
104 × 104
1
1, 7, 13
...
805, 811
1, 7, 13
...
325, 331
2
2, 8, 14
...
806, 812
2, 8, 14
...
326, 332
3
3, 9, 15
...
807, 813
3, 9, 15
...
327, 333
4
4, 10, 16
...
808, 814
4, 10, 16
...
328, 334
5
5, 11, 17
...
809, 815
5, 11, 17
...
329, 335
6
6, 12, 18
...
810, 816
6, 12, 18
...
330, 336
120 × 120
1
1, 7, 13
...
1039, 1045
1, 7, 13
...
397, 403
2
2, 8, 14
...
1040, 1046
2, 8, 14
...
398, 404
3
3, 9, 15
...
1041, 1047
3, 9, 15
...
399, 405
4
4, 10, 16
...
1042, 1048
4, 10, 16
...
400, 406
5
5, 11, 17
...
1043, 1049
5, 11, 17
...
401, 407
6
6, 12, 18
...
1044, 1050
6, 12, 18
...
402, 408
132 × 132
1
1, 9, 17
...
1289, 1297
1, 9, 17
...
481, 489
2
2, 10, 18
...
1290, 1298
2, 10, 18
...
482, 490
3
3, 11, 19
...
1291, 1299
3, 11, 19
...
483, 491
4
4, 12, 20
...
1292, 1300
4, 12, 20
...
484, 492
5
5, 13, 21
...
1293, 1301
5, 13, 21
...
485, 493
6
6, 14, 22
...
1294, 1302
6, 14, 22
...
486, 494
7
7, 15, 23
...
1295, 1303
7, 15, 23
...
487, 495
8
8, 16, 24
...
1296, 1304
8, 16, 24
...
488, 496
144 × 144
1
1, 11, 21
...
1541, 1551
1, 11, 21
...
601, 611
2
2, 12, 22
...
1542, 1552
2, 12, 22
...
602, 612
3
3, 13, 23
...
1543, 1553
3, 13, 23
...
603, 613
4
4, 14, 24
...
1544, 1554
4, 14, 24
...
604, 614
5
5, 15, 25
...
1545, 1555
5, 15, 25
...
605, 615
6
6, 16, 26
...
1546, 1556
6, 16, 26
...
606, 616
7
7, 17, 27
...
1547, 1557
7, 17, 27
...
607, 617
8
8, 18, 28
...
1548, 1558
8, 18, 28
...
608, 618
9
9, 19, 29
...
1549
9, 19, 29
...
609, 619
10
10, 20, 30
...
1550
10, 20, 30
...
610, 620
36
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(規定)
ECC 200パターンのランダム化
パターンランダム化アルゴリズムは,与えられた位置の入力コード語を新しいランダム化出力コード語
に変換する。
B.1
253-Stateアルゴリズム
このアルゴリズムは,疑似乱数を埋め草コード語値に加える。疑似乱数は,常に1〜253の範囲にあり,
ランダム化された埋め草コード語は,1〜254の範囲にある。
変数“Pad̲codeword̲position”は,符号化データの開始からのデータコード語数である。
B.1.1 253-State ランダム化アルゴリズム
INPUT ( Pad̲codeword̲value, Pad̲codeword̲position )
pseudo̲random̲number = ( ( 149 * Pad̲codeword̲position ) mod 253 ) + 1
temp̲variable = Pad̲codeword̲value + pseudo̲random̲number
IF ( temp̲variable <= 254 )
OUTPUT ( randomised̲Pad̲codeword̲value = temp̲variable )
ELSE
OUTPUT ( randomised̲Pad̲codeword̲value = temp̲variable - 254 )
B.1.2 253-State 逆ランダム化アルゴリズム
INPUT ( randomised̲Pad̲codeword̲value, Pad̲codeword̲position )
pseudo̲random̲number = ( ( 149 * Pad̲codeword̲position ) mod 253 ) + 1
temp̲variable = randomised̲Pad̲codeword̲value - pseudo̲random̲number
IF ( temp̲variable >= 1 )
OUTPUT ( Pad̲codeword̲value = temp̲variable)
ELSE
OUTPUT ( Pad̲codeword̲value = temp̲variable + 254 )
B.2
255-state アルゴリズム
このアルゴリズムは,Base-256符号化コード語値に疑似乱数を加える。疑似乱数は,常に1〜255の範
囲にあり,ランダム化されたBase-256コード語値は,0〜255の範囲にある。
変数“Base256̲codeword̲position”は,符号化データの開始からのデータコード語数である。
B.2.1 255-state ランダム化アルゴリズム
INPUT ( Base256̲codeword̲value, Base256̲codeword̲position )
pseudo̲random̲number = ( ( 149 * Base256̲codeword̲position ) mod 255 ) + 1
temp̲variable = Base256̲codeword̲value + pseudo̲random̲number
IF ( temp̲variable <= 255 )
OUTPUT (randomised̲Base256̲codeword̲value = temp̲variable )
ELSE
37
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
OUTPUT (randomised̲Base256̲codeword̲value = temp̲variable - 256 )
B.2.2 255-state 逆ランダム化アルゴリズム
INPUT ( randomised̲Base256̲codeword̲value, Base256̲codeword̲position )
pseudo̲random̲number = ( ( 149 * Base256̲codeword̲position ) mod 255 ) + 1
temp̲variable=randomised̲Base256̲codeword̲value - pseudo̲random̲number
IF ( temp̲variable >= 0 )
OUTPUT ( Base256̲codeword̲value = temp̲variable )
ELSE
OUTPUT ( Base256̲codeword̲value = temp̲variable + 256 )
38
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(規定)
ECC 200符号化キャラクタセット
表C.1−C40符号化キャラクタセット
C40値
基本セット
Shift 1セット
Shift 2セット
Shift 3セット
キャラクタ
10進値
キャラクタ
10進値
キャラクタ
10進値
キャラクタ
10進値
0
Shift 1
NUL
0
!
33
ʻ
96
1
Shift 2
SOH
1
“
34
a
97
2
Shift 3
STX
2
#
35
b
98
3
space
32
ETX
3
$
36
c
99
4
0
48
EOT
4
%
37
d
100
5
1
49
ENQ
5
&
38
e
101
6
2
50
ACK
6
ʻ
39
f
102
7
3
51
BEL
7
(
40
g
103
8
4
52
BS
8
)
41
h
104
9
5
53
HT
9
*
42
i
105
10
6
54
LF
10
+
43
j
106
11
7
55
VT
11
,
44
k
107
12
8
56
FF
12
-
45
l
108
13
9
57
CR
13
.
46
m
109
14
A
65
SO
14
/
47
n
110
15
B
66
SI
15
:
58
o
111
16
C
67
DLE
16
;
59
p
112
17
D
68
DC1
17
<
60
q
113
18
E
69
DC2
18
=
61
r
114
19
F
70
DC3
19
>
62
s
115
20
G
71
DC4
20
?
63
t
116
21
H
72
NAK
21
@
64
u
117
22
I
73
SYN
22
[
91
v
118
23
J
74
ETB
23
¥
92
w
119
24
K
75
CAN
24
]
93
x
120
25
L
76
EM
25
^
94
y
121
26
M
77
SUB
26
̲
95
z
122
27
N
78
ESC
27
FNC1
{
123
28
O
79
FS
28
|
124
29
P
80
GS
29
}
125
30
Q
81
RS
30
Upper Shift
~
126
31
R
82
US
31
DEL
127
32
S
83
33
T
84
34
U
85
35
V
86
36
W
87
37
X
88
38
Y
89
39
Z
90
注記 ASCII 10進値とC40値との関係は,どのECIが有効かにかかわらず一定である。

39
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.2−テキスト符号化キャラクタセット
テキスト値
基本セット
Shift 1セット
Shift 2セット
Shift 3セット
キャラクタ
10進値
キャラクタ
10進値
キャラクタ
10進値
キャラクタ
10進値
0
Shift
1
NUL
0
!
33
ʻ
96
1
Shift
2
SOH
1
“
34
A
65
2
Shift
3
STX
2
#
35
B
66
3
space
32
ETX
3
$
36
C
67
4
0
48
EOT
4
%
37
D
68
5
1
49
ENQ
5
&
38
E
69
6
2
50
ACK
6
ʻ
39
F
70
7
3
51
BEL
7
(
40
G
71
8
4
52
BS
8
)
41
H
72
9
5
53
HT
9
*
42
I
73
10
6
54
LF
10
+
43
J
74
11
7
55
VT
11
,
44
K
75
12
8
56
FF
12
-
45
L
76
13
9
57
CR
13
.
46
M
77
14
a
97
SO
14
/
47
N
78
15
b
98
SI
15
:
58
O
79
16
c
99
DLE
16
;
59
P
80
17
d
100
DC1
17
<
60
Q
81
18
e
101
DC2
18
=
61
R
82
19
f
102
DC3
19
>
62
S
83
20
g
103
DC4
20
?
63
T
84
21
h
104
NAK
21
@
64
U
85
22
i
105
SYN
22
[
91
V
86
23
j
106
ETB
23
¥
92
W
87
24
k
107
CAN
24
]
93
X
88
25
l
108
EM
25
^
94
Y
89
26
m
109
SUB
26
̲
95
Z
90
27
n
110
ESC
27
FNC1
{
123
28
o
111
FS
28
|
124
29
p
112
GS
29
}
125
30
q
113
RS
30
Upper Shift
~
126
31
r
114
US
31
DEL
127
32
s
115
33
t
116
34
u
117
35
v
118
36
w
119
37
x
120
38
y
121
39
z
122
注記 ASCII 10進値とテキスト値との関係は,どのECIが有効かにかかわらず一定である。

40
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.3−EDIFACT符号化キャラクタセット
データキャラクタ
EDIFACT
バイナリ値
データキャラクタ
EDIFACT
バイナリ値
キャラクタ
10進値
バイナリ値
キャラクタ
10進値
バイナリ値
@
64
01000000
000000
space
32
00100000
100000
A
65
01000001
000001
!
33
00100001
100001
B
66
01000010
000010
“
34
00100010
100010
C
67
01000011
000011
#
35
00100011
100011
D
68
01000100
000100
$
36
00100100
100100
E
69
01000101
000101
%
37
00100101
100101
F
70
01000110
000110
&
38
00100110
100110
G
71
01000111
000111
ʻ
39
00100111
100111
H
72
01001000
001000
(
40
00101000
101000
I
73
01001001
001001
)
41
00101001
101001
J
74
01001010
001010
*
42
00101010
101010
K
75
01001011
001011
+
43
00101011
101011
L
76
01001100
001100
,
44
00101100
101100
M
77
01001101
001101
-
45
00101101
101101
N
78
01001110
001110
.
46
00101110
101110
O
79
01001111
001111
/
47
00101111
101111
P
80
01010000
010000
0
48
00110000
110000
Q
81
01010001
010001
1
49
00110001
110001
R
82
01010010
010010
2
50
00110010
110010
S
83
01010011
010011
3
51
00110011
110011
T
84
01010100
010100
4
52
00110100
110100
U
85
01010101
010101
5
53
00110101
110101
V
86
01010110
010110
6
54
00110110
110110
W
87
01010111
010111
7
55
00110111
110111
X
88
01011000
011000
8
56
00111000
111000
Y
89
01011001
011001
9
57
00111001
111001
Z
90
01011010
011010
:
58
00111010
111010
[
91
01011011
011011
;
59
00111011
111011
¥
92
01011100
011100
<
60
00111100
111100
]
93
01011101
011101
=
61
00111101
111101
^
94
01011110
011110
>
62
00111110
111110
切替解除
01011111
011111
?
63
00111111
111111
注記 ASCII 10進値とEDIFACT値との関係は,どのECIが有効かにかかわらず一定である。
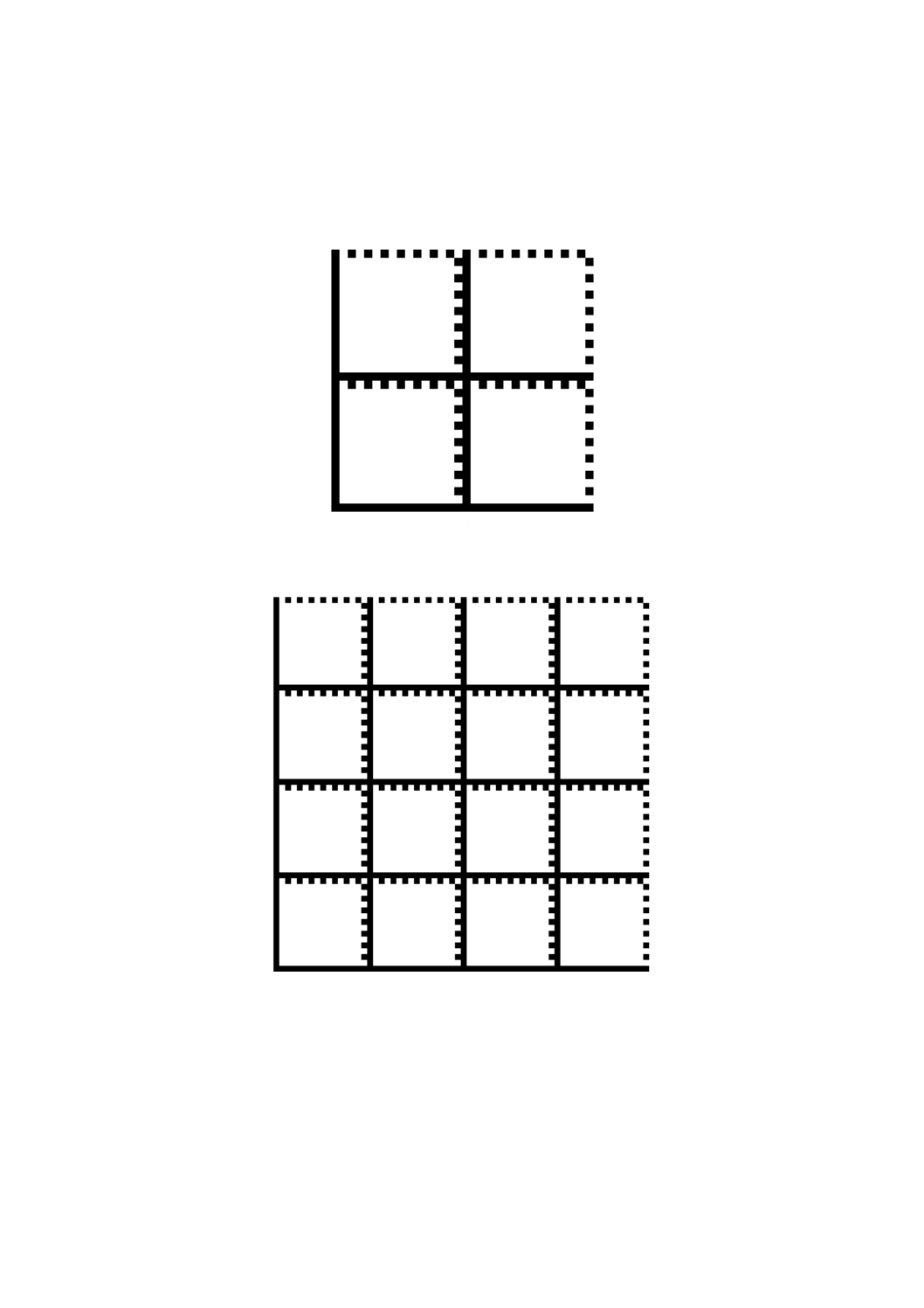
41
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(規定)
ECC 200位置合せパターン
図D.1−32×32正方形シンボルの位置合せパターン構成
図D.2−64×64正方形シンボルの位置合せパターン構成
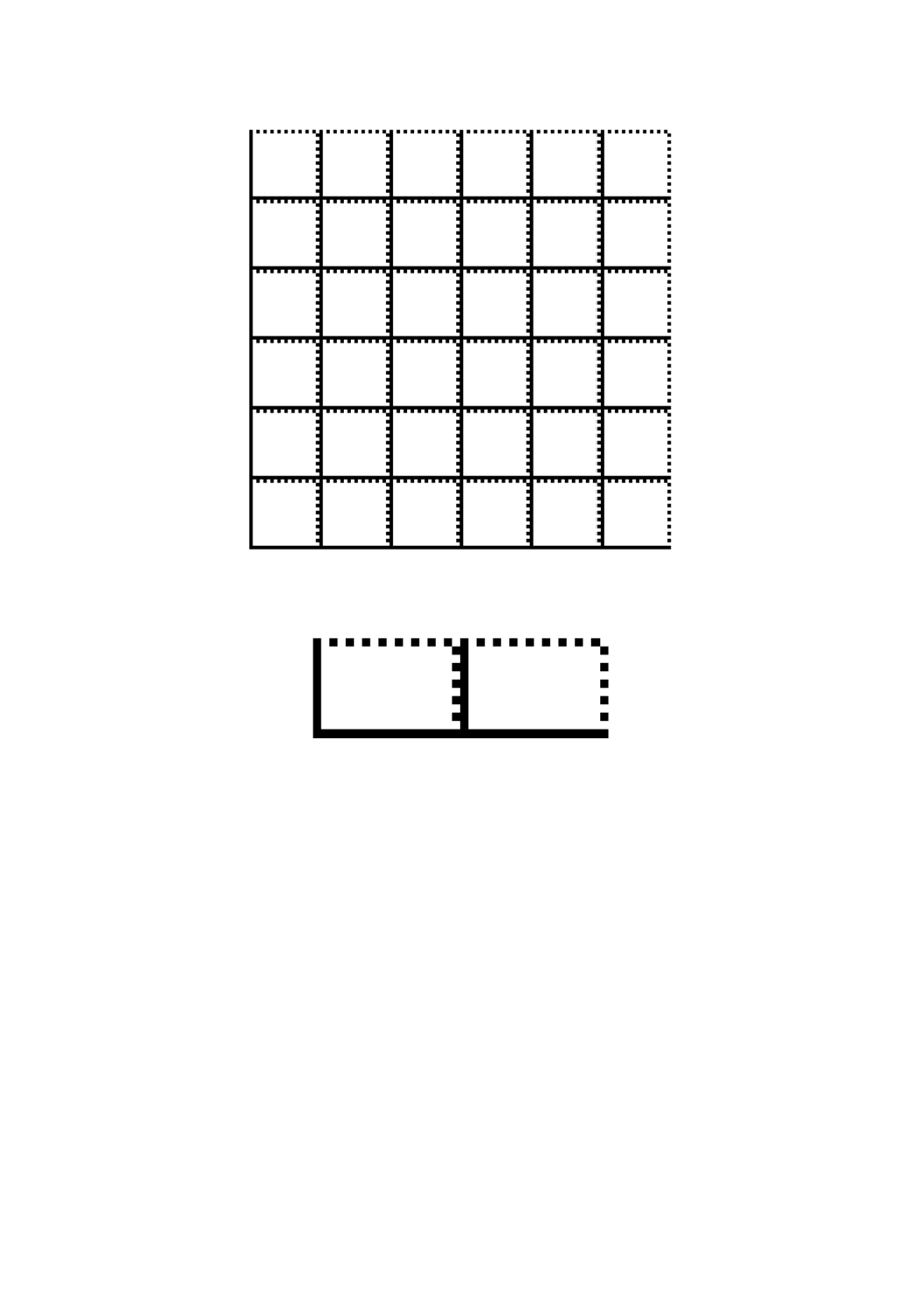
42
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図D.3−120×120正方形シンボルの位置合せパターン構成
図D.4−12×36長方形シンボルの位置合せパターン構成
43
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E
(規定)
ECC 200リードソロモン誤り検出及び誤り訂正
E.1
誤り訂正コード語の生成多項式
誤り訂正コード語は,最初に,シンボルデータ多項式d(x)にxkを乗じ,次に,生成多項式g(x)で除した
剰余の係数である。各生成多項式は,一次多項式x−21, x−22, …, x−2nの積である。ここに,nは,生成
多項式の次数である。
次に,5次多項式の例を示す。
(x+2)(x+4)(x+8)(x+16)(x+32)
=x5+(2+4+8+16+32)x4+((2 * 4)+(2 * 8)+(2 * 16)+(2 * 32)+(4 * 8)+(4 * 16)+(4 * 32)+(8 * 16)+(8 *
32)+(16 * 32))x3+((2 * 4 * 8)+(2 * 4 * 16)+(2 * 4 * 32)+(2 * 8 * 16)+(2 * 8 * 32)+(2 * 16 * 32)+(4 * 8 *
16)+(4 * 8 * 32)+(4 * 16 * 32)+(8 * 16 * 32))x2+((2 * 4 * 8 * 16)+(2 * 4 * 8 * 32)+(2 * 4 * 16 * 32)+(2 * 8 *
16 * 32)+(4 * 8 * 16 * 32))x+(2 * 4 * 8 * 16 * 32)
=x5+62x4+111x3+15x2+48x+228.
注記 このガロア体計算は,通常の整数計算ではない。“−”は,この体では“排他的論理和:XOR”
である“+”と等しく,また,乗算“*”は,二つの2値多項式の乗算結果に対し,モジュロ
100101101(x8+x5+x3+x2+1)をとるものである。
5チェックキャラクタを生成する除数多項式は,
g(x)=x5+62x4+111x3+15x2+48x+228.
7チェックキャラクタを生成する除数多項式は,
g(x)=x7+254x6+92x5+240x4+134x3+144x2+68x+23.
10チェックキャラクタを生成する除数多項式は,
g(x)=x10+61x9+110x8+255x7+116x6+248x5+223x4+166x3+185x2+24x+28.
11チェックキャラクタを生成する除数多項式は,
g(x)=x11+120x10+97x9+60x8+245x7+39x6+168x5+194x4+12x3+205x2+138x+175.
12チェックキャラクタを生成する除数多項式は,
g(x)=x12+242x11+100x10+178x9+97x8+213x7+142x6+42x5+61x4+91x3+158x2+153x+41.
14チェックキャラクタを生成する除数多項式は,
g(x)=x14+185x13+83x12+186x11+18x10+45x9+138x8+119x7+157x6+9x5+95x4+252x3+192x2+97x+
156.
18チェックキャラクタを生成する除数多項式は,
g(x)=x18+188x17+90x16+48x15+225x14+254x13+94x12+129x11+109x10+213x9+241x8+61x7+66x6+
75x5+188x4+39x3+100x2+195x+83.
20チェックキャラクタを生成する除数多項式は,
g(x)=x20+172x19+186x18+174x17+27x16+82x15+108x14+79x13+253x12+145x11+153x10+160x9+188x8
+2x7+168x6+71x5+233x4+9x3+244x2+195x+15.
24チェックキャラクタを生成する除数多項式は,
g(x)=x24+193x23+50x22+96x21+184x20+181x19+12x18+124x17+254x16+172x15+5x14+21x13+155x12+
44
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
223x11+251x10+197x9+155x8+21x7+176x6+39x5+109x4+205x3+88x2+190x+52.
28チェックキャラクタを生成する除数多項式は,
g(x)=x28+255x27+93x26+168x25+233x24+151x23+120x22+136x21+141x20+213x19+110x18+138x17+
17x16+121x15+249x14+34x13+75x12+53x11+170x10+151x9+37x8+174x7+103x6+96x5+71x4+97x3+
43x2+231x+211.
36チェックキャラクタを生成する除数多項式は,
g(x)=x36+112x35+81x34+98x33+225x32+25x31+59x30+184x29+175x28+44x27+115x26+119x25+95x24+
137x23+101x22+33x21+68x20+4x19+2x18+18x17+229x16+182x15+80x14+251x13+220x12+179x11+84x10
+120x9+102x8+181x7+162x6+250x5+130x4+218x3+242x2+127x+245.
42チェックキャラクタを生成する除数多項式は,
g(x)=x42+5x41+9x40+5x39+226x38+177x37+150x36+50x35+69x34+202x33+248x32+101x31+54x30+
57x29+253x28+x27+21x26+121x25+57x24+111x23+214x22+105x21+167x20+9x19+100x18+95x17+175x16
+8x15+242x14+133x13+245x12+2x11+122x10+105x9+247x8+153x7+22x6+38x5+19x4+31x3+137x2+
193x+77.
48チェックキャラクタを生成する除数多項式は,
g(x)=x48+19x47+225x46+253x45+92x44+213x43+69x42+175x41+160x40+147x39+187x38+87x37+176x36
+44x35+82x34+240x33+186x32+138x31+66x30+100x29+120x28+88x27+131x26+205x25+170x24+90x23
+37x22+23x21+118x20+147x19+16x18+106x17+191x16+87x15+237x14+188x13+205x12+231x11+238x10
+133x9+238x8+22x7+117x6+32x5+96x4+223x3+172x2+132x+245.
56チェックキャラクタを生成する除数多項式は,
g(x)=x56+46x55+143x54+53x53+233x52+107x51+203x50+43x49+155x48+28x47+247x46+67x45+127x44
+245x43+137x42+13x41+164x40+207x39+62x38+117x37+201x36+150x35+22x34+238x33+144x32+
232x31+29x30+203x29+117x28+234x27+218x26+146x25+228x24+54x23+132x22+200x21+38x20+223x19
+36x18+159x17+150x16+235x15+215x14+192x13+230x12+170x11+175x10+29x9+100x8+208x7+220x6
+17x5+12x4+238x3+223x2+9x+175.
62チェックキャラクタを生成する除数多項式は,
g(x)=x62+204x61+11x60+47x59+86x58+124x57+224x56+166x55+94x54+7x53+232x52+107x51+4x50+
170x49+176x48+31x47+163x46+17x45+188x44+130x43+40x42+10x41+87x40+63x39+51x38+218x37+
27x36+6x35+147x34+44x33+161x32+71x31+114x30+64x29+175x28+221x27+185x26+106x25+250x24+
190x23+197x22+63x21+245x20+230x19+134x18+112x17+185x16+37x15+196x14+108x13+143x12+189x11
+201x10+188x9+202x8+118x7+39x6+210x5+144x4+50x3+169x2+93x+242.
68チェックキャラクタを生成する除数多項式は,
g(x)=x68+186x67+82x66+103x65+96x64+63x63+132x62+153x61+108x60+54x59+64x58+189x57+211x56
+232x55+49x54+25x53+172x52+52x51+59x50+241x49+181x48+239x47+223x46+136x45+231x44+210x43
+96x42+232x41+220x40+25x39+179x38+167x37+202x36+185x35+153x34+139x33+66x32+236x31+
227x30+160x29+15x28+213x27+93x26+122x25+68x24+177x23+158x22+197x21+234x20+180x19+248x18
+136x17+213x16+127x15+73x14+36x13+154x12+244x11+147x10+33x9+89x8+56x7+159x6+149x5+
251x4+89x3+173x2+228x+220.
45
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
E.2
誤り訂正の計算
“Peterson-Gorenstein-Zierler”アルゴリズムは,符号化されたECC 200シンボルの誤り訂正で用いてもよ
い。
次に示す計算は,この誤り訂正アルゴリズムに従うリードソロモン誤り訂正コード語を用いる。
消失誤りは,削除された箇所を,ダミー値であらかじめ埋めることによって,誤りとして訂正しなけれ
ばならない。
全ての計算は,GF(28)計算を用いて行う。加算及び減算は,バイナリXORに相当する。多項式の乗算の
モジュロとして定義される乗算及び除算は,各多項式がモジュロx8+x5+x3+x2+1下でxのべき乗となっ
ていることを利用し,乗算を加算に変換する対数表及び逆対数表を用いて実行することができる。
シンボルキャラクタ多項式の構造は,C(x)=Cn−1xn−1+Cn−2xn−2+…+C1x1+C0である。ここに,n個の
係数Ciは,Cn−1を最初のシンボルキャラクタとした符号語であり,nは,シンボルキャラクタの総数であ
る。
iがシンボル中の誤り訂正コード語数であるk=1〜iの間で,x=2kのときのC(x)を評価することによっ
て,S0〜Si−1間のシンドローム値を計算する。
jシンドロームを用いて,未知のL0〜Lj−1間のjによるj連立方程式を形成して解く。
S0L0+S1L1+…+Sj−1Lj−1=Sj
S1L0+S2L1+…+SjLj=Sj+1
:
:
Sj−1L0+SjL1+…+S2j−2Lj−1=S2j−1
ここに,jはi/2である。
誤り位置多項式を構築する。
L(x)=Lj−1xj+Lj−2xj−1+...+L0x+1
上記の式で得たLのj値から,k=0〜n−1の間で,x=2kのときのL(x)を評価する。ここに,nはシンボ
ル中のシンボルキャラクタの総数である。
L(2k)=0のときの誤り位置は,n−1−kによって与えられる。誤り位置がj以上見つかったときは,シン
ボルは訂正できない。
見つかった誤り数をmとして,誤り検出位置E0〜Em−1を保存する。ここに,mは,見つかった誤り位
置の数である。最初のmシンドローム及び誤り位置値Eを用いて,未知のX0〜Xm−1(誤りの大きさ)間
のmによるm連立方程式を形成して解く。
E0X0+E1X1+...+Em−1Xm−1=S0
E02X0+E12X1+...+E(m−1)2Xm−1=S1
E03X0+E13X1+...+E(m−1)3Xm−1=S2
:
:
E0mX0+E1mX1+...+E(m−1)mXm−1=Sm−1
誤りを訂正するために,対応する誤りの位置E0〜Em−1で誤りの大きさX0〜Xm−1を,シンボルキャラク
タ値に追加する。
注記 E0 ... Em−1は,誤り位置多項式の根である。
C言語で書かれているこのアルゴリズムは,AIM Inc. ITS/04-001のデータマトリックス開発用フロッピ
46
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ィディスク(参考文献参照)から入手できる。
E.3
誤り訂正コード語の計算
整数配列wd[]に保存された,長さ“nd”のデータコード語列によって与えられる誤り訂正コード語を計
算するために,C言語で書かれた一般的なルーチンの例を次に示す。関数ReedSolomon()は,最初に,原始
多項式“pp”(ECC 200では301)であるサイズ“gf”(ECC 200では28)のガロア体として,対数表及び
逆対数表を生成する。さらに,関数prod()を用い,最初に,位数“nc”の生成多項式の係数を計算し,続
いて“nc”追加チェックコード語を計算してwd[]のデータに追加する。
/* "prod(x, y, log, alog, gf)" returns the product "x" times "y" */
int prod(int x, int y, int *log, int *alog, int gf) {
if (!x || !y) return 0;
else return alog[(log[x] + log[y]) % (gf-1)];
}
/* "ReedSolomon(wd, nd, nc, gf.pp)" takes "nd" data codeword values in wd[] */
/* and adds on "nc" check codewords, all within GF(gf) where "gf" is a */
/* power of 2 and "pp" is the value of its prime modulus polynomial */
void ReedSolomon(int *wd, int nd, int nc, int gf, int pp) {
int i, j, k, *log,*alog,*c;
/* allocate, then generate the log & antilog arrays: */
log = malloc(sizeof(int) * gf);
alog = malloc(sizeof(int) * gf);
log[0] = 1-gf; alog[0] = 1;
for (i = 1; i < gf; i++) {
alog[i] = alog[i-1] * 2;
if (alog[i] >= gf) alog[i] ^= pp;
log[alog[i]] = i;
}
/* allocate, then generate the generator polynomial coefficients: */
c = malloc(sizeof(int) * (nc+1));
for (i=1; i<=nc; i++) c[i] = 0; c[0] = 1;
for (i=1; i<=nc; i++) {
c[i] = c[i-1];
for (j=i-1; j>=1; j--) {
c[j] = c[j-1] ^ prod(c[j],alog[i],log,alog,gf);
}
c[0] = prod(c[0],alog[i],log,alog,gf);
47
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
}
/* clear, then generate "nc" checkwords in the array wd[] : */
for (i=nd; i<=(nd+nc); i++) wd[i] = 0;
for (i=0; i<nd; i++) {
k = wd[nd] ^ wd[i] ;
for (j=0; j<nc; j++) {
wd[nd+j] = wd[nd+j+l] ^ prod(k,c[nc-j-1],log, alog,gf);
}
}
free(c);
free(alog);
free(log);
}
48
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書F
(規定)
ECC 200シンボルキャラクタ配置
F.1
シンボルキャラクタの配置
シンボルキャラクタ配置を生成するC言語プログラムを次に示す。
#include <stdio.h>
#include <alloc.h>
int nrow, ncol, *array;
/* "module" places "chr+bit" with appropriate wrapping within array[] */
void module(int row, int col, int chr, int bit)
{ if (row < 0) { row += nrow; col += 4 - ((nrow+4)%8); }
if (col < 0) { col += ncol; row += 4 - ((ncol+4)%8); }
array[row*ncol+col] = 10*chr + bit;
}
/* "utah" places the 8 bits of a utah-shaped symbol character in ECC200 */
void utah(int row, int col, int chr)
{ module(row-2,col-2,chr,1);
module(row-2,col-1,chr,2);
module(row-1,col-2,chr,3);
module(row-1,col-1,chr,4);
module(row-1,col,chr,5);
module(row,col-2,chr,6);
module(row,col-1,chr,7);
module(row,col,chr,8);
}
/* "cornerN" places 8 bits of the four special corner cases in ECC200 */
void corner1(int chr)
{ module(nrow-1,0,chr,1);
module(nrow-1,1,chr,2);
module(nrow-1,2,chr,3);
module(0,ncol-2,chr,4);
module(0,ncol-1,chr,5);
module(1,ncol-1,chr,6);
module(2,ncol-1,chr,7);
module(3,ncol-1,chr,8);
}
void corner2(int chr)
{ module(nrow-3,0,chr,1);
49
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
module(nrow-2,0,chr,2);
module(nrow-1,0,chr,3);
module(0,ncol-4,chr,4);
module(0,ncol-3,chr,5);
module(0,ncol-2,chr,6);
module(0,ncol-1,chr,7);
module(1,ncol-1,chr,8);
}
void corner3(int chr)
{ module(nrow-3,0,chr,1);
module(nrow-2,0,chr,2);
module(nrow-1,0,chr,3);
module(0,ncol-2,chr,4);
module(0,ncol-1,chr,5);
module(1,ncol-1,chr,6);
module(2,ncol-1,chr,7);
module(3,ncol-1,chr,8);
}
void corner4(int chr)
{ module(nrow-1,0,chr,1);
module(nrow-1,ncol-1,chr,2);
module(0,ncol-3,chr,3);
module(0,ncol-2,chr,4);
module(0,ncol-1,chr,5);
module(1,ncol-3,chr,6);
module(1,ncol-2,chr,7);
module(1,ncol-1,chr,8);
}
/* "ECC200" fills an nrow x ncol array with appropriate values for ECC200 */
void ECC200(void)
{ int row, col, chr;
/* First, fill the array[] with invalid entries */
for (row=0; row<nrow; row++) {
for (col=0; col<ncol; col++) {
array[row*ncol+col] = 0;
}
}
/* Starting in the correct location for character #1, bit 8,... */
chr = 1; row = 4; col = 0;
do {
50
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
/* repeatedly first check for one of the special corner cases, then... */
if ((row == nrow) && (col == 0)) corner1(chr++);
if ((row == nrow-2) && (col == 0) && (ncol%4)) corner2(chr++);
if ((row == nrow-2) && (col == 0) && (ncol%8 == 4)) corner3(chr++);
if ((row == nrow+4) && (col == 2) && (!(ncol%8))) corner4(chr++);
/* sweep upward diagonally, inserting successive characters,... */
do {
if ((row < nrow) && (col >= 0) && (!array[row*ncol+col]))
utah(row,col,chr++);
row -= 2; col += 2;
} while ((row >= 0) && (col < ncol));
row += 1; col += 3;
/* & then sweep downward diagonally, inserting successive characters,... */
do {
if ((row >= 0) && (col < ncol) && (!array[row*ncol+col]))
utah(row,col,chr++);
row += 2; col -= 2;
} while ((row < nrow) && (col >= 0));
row += 3; col += 1;
/* ... until the entire array is scanned */
} while ((row < nrow) || (col < ncol));
/* Lastly, if the lower righthand corner is untouched, fill in fixed pattern */
if (!array[nrow*ncol-1]) {
array[nrow*ncol-1] = array[nrow*ncol-ncol-2] = 1;
}
}
/* "main" checks for valid command line entries, then computes & displays array */
void main(int argc, char *argv[])
{ int x, y, z;
if (argc < 3) {
printf("Command line: ECC200 #̲of̲Data̲Rows #̲of̲Data̲Columns¥n");
} else {
nrow = ncol = 0;
nrow = atoi(argv[1]); ncol = atoi(argv[2]);
if ((nrow >= 6) && (~nrow&0x01) && (ncol >= 6) && (~ncol&0x01)) {
array = malloc(sizeof(int) * nrow * ncol);
ECC200();
for (x=0; x<nrow; x++) {
for (y=0; y<ncol; y++) {
z = array[x*ncol+y];
51
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
if (z == 0) printf(" WHI");
else if (z == 1) printf("BLK");
else printf("%3d.%d",z/10,z%10);
}
printf("¥n");
}
free(array);
}
}
}
F.2
シンボルキャラクタ配置規則
F.2.1
非標準シンボルキャラクタの形
データモジュールの境界及び一部の角では,標準シンボルキャラクタの形を当てはめることができない
ため,非標準形のシンボルキャラクタセットが幾つか必要となる。それらには,六つの場合があり,全て
のシンボルフォーマットに影響する二つの境界線の条件及び特定のシンボルフォーマットに適用される四
つの異なる角の条件である。
a) シンボルキャラクタの形の一部は,片側に置かれ,残りは逆側に置かれる。これは,二つの基本的な
形に適応する(図F.1参照)。これらの配置の変形は,左方及び右方の境界線の間の列と列との関係に
関連する(表F.1参照)。
b) シンボルキャラクタの一部は,上の境界線上に置かれ,残りの部分は,下の境界線上に置かれる。こ
れは,二つの基本的なシンボルキャラクタの形に適応する。これらの配置の変形は,上及び下の境界
線の間の列と列との関係に関連する(表F.1参照)。
c) 四つのシンボルキャラクタの形は,二つ又は三つの角の間に分けられる(図F.3〜図F.6参照)。非標
準のシンボルキャラクタの形は,反対側の境界線上に置かれる。これらの組合せは,一般に,マトリ
ックス配置の周辺の大きさに比例する。基本パターンは,図F.1及び図F.2に図解している。図F.1で
は,モジュールa8及びa7と同様に,モジュールa7及びa6が同じ行にある。図F.2では,モジュー
ルc6及びc3と同様に,モジュールd3及びd1が同じ列にある。境界線配置には,似通った七つの場
合があり,それらは図F.1で図解されているようなシンボルキャラクタの垂直位置,図F.2で図解さ
れているようなシンボルキャラクタの水平位置,及び角配置である。
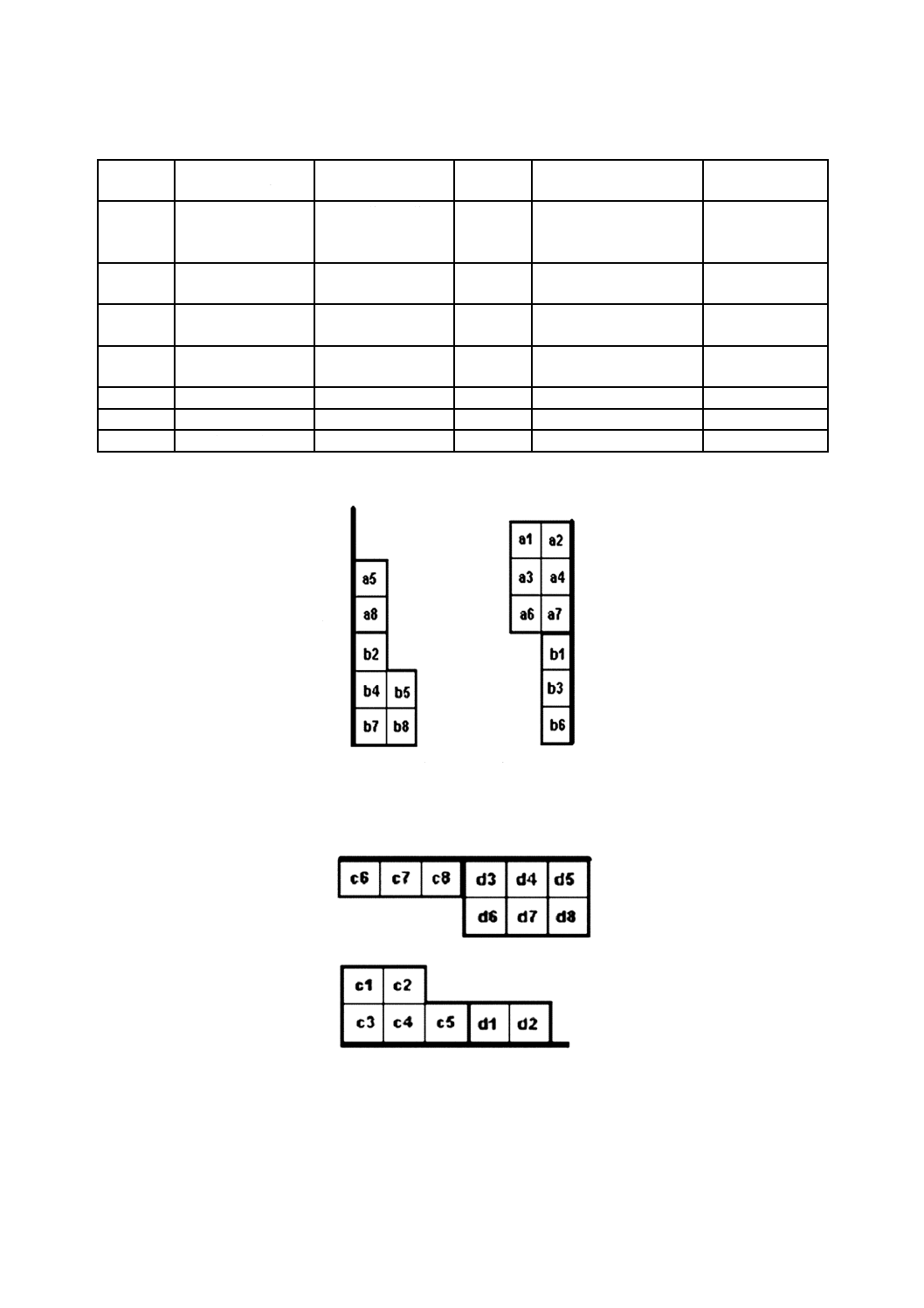
52
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表F.1−境界配置の場合を決定する要素
境界配置
のケース
モジュールa8及び
a7の行関係
モジュールc6及び
c3の列関係
角配置
での図番
影響したマトリックス
配置
参照附属書F
の図番例
1
a7行=a8行
c3列=c6列
なし
正方形:82,162,242,322,
402,482,562,642,722,
802,882,962,& 1202
図F.9及び図F.16
2
a7行=a8行−2
c3列=c6列−2
なし
正方形:102 & 182
図F.10及び図
F.17
3
a7行=a8行+4
c3列=c6列+4
図F.3
正方形:122,202,282,
362,442,1082,& 1322
図F.11及び図
F.18
4
a7行=a8行+2
c3列=c6列+2
図F.4
正方形:142 & 222
図F.12及び図
F.19
5
a7行=a8行
c3列=c6列+2
図F.5
長方形:6×16 & 14×32
図F.13
6
a7行=a8行
c3列=c6列−2
なし
長方形:10×24 & 10×32
図F.14
7
a7行=a8行+4
c3列=c6列+2
図F.6
長方形:6×28 & 14×44
図F.15
左
境
界
右
境
界
図F.1−左及び右のシンボルキャラクタ
上境界
下境界
図F.2−上及び下のシンボルキャラクタ
53
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図F.3−角の状態1
図F.4−角の状態2
図F.5−角の状態3
54
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図F.6−角の状態4
注記1 分割が起きるシンボルキャラクタ番号は,シンボルフォーマットによって異なるため,シン
ボルキャラクタを示すのに,a,b,cなどの代用的記法を用いている。
注記2 左下及び右上の角の位置検出パターンモジュールによって,角のキャラクタが識別される。
F.2.2
シンボルキャラクタの配置
シンボルキャラクタは,次の方法によってマトリックスに配置する。
a) 配置マトリックスを作成
1) 1データ領域だけの小形シンボルは,これが配置マトリックスに相当する。
2) 1データ領域よりも大きい大形シンボルの場合,配置マトリックスは,隣接するデータ領域サイズ
の領域に等しい。実際,配置マトリックスは,区切り配置パターンがない。例えば,36×36のシン
ボルは,四つの16×16データ領域がある。これらが接して,32×32の配置マトリックスを形成す
る。各シンボルフォーマットの配置マトリックスの大きさを表7に示す。境界配置の場合を表F.1
に示す。
b) シンボルキャラクタ2は,図11で規定しているビット(又はモジュール)シーケンスに従って,一番
左上の位置に配置する。シンボルキャラクタ2のモジュール1を識別するために,表記2.1を用いる。
全ての配置マトリックスの一番左上に,このモジュールがある。図F.7にあるモジュール配置シーケ
ンスは,全ての配置マトリックスについて一定である。
2.1
2.2
3.6
3.7
3.8
4.3
4.4
4.5
2.3
2.4
2.5
5.1
5.2
4.6
4.7
4.8
2.6
2.7
2.8
5.3
5.4
5.5
1.a
6.1
6.2
5.6
5.7
5.8
1.b
6.3
6.4
6.5
6.6
6.7
6.8
図F.7−モジュール配置の開始シーケンス
注記 a及びbの値は,配置マトリックスの大きさで決まる。
c) 角に配置する形は,表F.1及び適切な図F.3〜図F.6に従って配置される。標準シンボルキャラクタに
55
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ついては,上に図示しているシンボルキャラクタ2,5及び6のような同じ形が連続して組み合わされ
る。非標準的なシンボルキャラクタの配置を,表F.1に示す。この処理の結果として,シンボルキャ
ラクタで完全にカバーされている配置マトリックスになるが,大部分の配置図を表示していない。
d) シンボルキャラクタのシーケンスは,次のとおりに決められる。左下及び右上間の斜線上にシンボル
キャラクタが配置され,通常は,各シンボルキャラクタのモジュール8の中心を通ってつな(繋)が
っている。
e) 最初の斜線は,シンボルキャラクタ1のモジュール8を通る線で始まる。例外として,6×28配置マ
トリックスではモジュール8ではなく,図F.6で決められた角の状態によってシンボルキャラクタ内
のモジュールの値を判断する(すなわち,図F.7で1.bと識別されたモジュールは,モジュール1.2を
意味する。)。斜線は続いてモジュール2.8及び3.8を通っていく。
f)
この時点で,斜線は,最上列の境界線と交差する。次の斜線は,最上列の右方4モジュールの位置又
は8×8配置マトリックスの場合は,右方3モジュール,下方1モジュールの位置から始まる。すなわ
ち,斜線は,常に4モジュール分移動する。モジュール8と交差する配置経路に基づいて,シンボル
キャラクタは,順番に番号が付けられる。モジュール4.8,5.8,6.8,…と交差する下降斜線によって
次のキャラクタが決まる。
g) 図F.8に示している配置経路は,元の斜線よりも4モジュール右(又は4モジュール下,又はそれら
の組合せ)の位置にある斜線に続く。一番目及び奇数である全ての斜線は,シンボルキャラクタシー
ケンスを,左下〜右上に向かって配置する。2番目及び偶数である全ての斜線は,シンボルキャラク
タシーケンスを右上〜左下に向かって配置する。
図F.8−シンボルキャラクタ配置シーケンス
h) 配置経路が,配置マトリックスの境界線内に完全に納まっていない非標準的なシンボルキャラクタの
形に遭遇すると,そのシンボルキャラクタは,マトリックスの反対側に続けられる。この効果として,

56
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
これらのシンボルキャラクタの反対部分は,配置経路が,その位置と交差する前に番号が付けられる。
例えば,配置マトリックスの図(図F.8参照)では,シンボルキャラクタ3及び7の他の部分は,配
置経路がそれらと交差する前に,あらかじめ番号が付けられる。配置経路は,番号がないシンボルキ
ャラクタだけに番号を付ける。これらの境界線及び角の条件を,表F.1に示す。シンボルキャラクタ
1,3,4及び7について,図F.8に示す。角の状況は,番号付けシーケンスに影響する。次に,左下
角の表示を示す。
図F.3では,その上のシンボルキャラクタの前に番号が付けられる(図F.12及び図F.19の例を参照)。
図F.4では,その上のシンボルキャラクタの前に番号が付けられる(図F.12及び図F.19の例を参照)。
図F.5では,その右のシンボルキャラクタの後に番号が付けられる(図F.13の例を参照)。
図F.6では,その上のシンボルキャラクタの前に番号が付けられる(図F.15の例を参照)。
角の残りのモジュールは,配置経路のそれらと交差する前に番号が付けられる。
i)
この配置法は,全てのシンボルキャラクタが配置されるまで続き,配置マトリックスの右下で終わる。
四つの大きさの配置マトリックス(10×10,14×14,18×18及び22×22)では,右下の角に2×2の
領域が残っている。この領域の左上及び右下のモジュールは,黒である(通常バイナリの1として符
号化する。)。これを図F.8に示す。
この方法に従う典型的な配置マトリックスをF.3に示す。図F.9〜図F.15は,境界線配置の1〜7の
ケースを網羅する。図F.16〜図F.19は,別の例であり,ケース1〜4についてのものである。F.1は,
全ての符号化されたビットを,適切な配置マトリックスに配置することが可能な,C言語プログラム
である。
F.3
ECC 200のシンボルキャラクタ配置例
図F.9−サイズ8の正方形マトリックスのコード語配置

57
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図F.10−サイズ10の正方形マトリックスのコード語配置
図F.11−サイズ12の正方形マトリックスのコード語配置

58
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図F.12−サイズ14の正方形マトリックスのコード語配置
図F.13−6×16長方形マトリックスのコード語配置
図F.14−10×24長方形マトリックスのコード語配置

59
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図F.15−6×28長方形マトリックスのコード語配置
図F.16−サイズ16の正方形マトリックスのコード語配置
図F.17−サイズ18の正方形マトリックスのコード語配置

60
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図F.18−サイズ20の正方形マトリックスのコード語配置
図F.19−サイズ22の正方形マトリックスのコード語配置
61
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書G
(規定)
ECC 000〜ECC 140シンボルの属性
(対応国際規格の規定を不採用とした。)
62
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書H
(規定)
ECC 000〜ECC 140データモジュール配置格子
(対応国際規格の規定を不採用とした。)
63
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書I
(規定)
ECC 000〜ECC 140キャラクタ符号化スキーム
(対応国際規格の規定を不採用とした。)
64
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書J
(規定)
ECC 000〜ECC 140 CRCアルゴリズム
(対応国際規格の規定を不採用とした。)
65
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書K
(規定)
ECC 000〜ECC 140誤り検査アルゴリズム及び誤り訂正アルゴリズム
(対応国際規格の規定を不採用とした。)
66
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書L
(規定)
ECC 000〜ECC 140主なランダムビット列(16進数)
(対応国際規格の規定を不採用とした。)
67
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書M
(規定)
データマトリックス印刷品質−シンボル体系特有の側面
シンボル体系の構造及び参照復号アルゴリズムに違いがあるため,シンボルの読取り評価上の特定パラ
メタの効果は,一つのシンボル体系から別のものにわたって変化してもよい。ISO/IEC 15415は,特定の
シンボル体系仕様が,その体系特有の属性のグレードを決めることに対応している。この附属書では,
ISO/IEC 15415をデータマトリックスに適用するときに用いる,固定パターンの損傷グレードを定義する。
M.1 データマトリックス固定パターン損傷
M.1.1 評価される機能
評価の対象となる固定パターンの一つである外側固定パターンの特徴は,シンボルの1モジュール幅の
周囲部分及びシンボル外の最小1モジュール幅(又はアプリケーションによって決める場合は,それ以上)
のクワイエットゾーンに含まれている。内部位置合せパターンを備えている大きなシンボル(正方形シン
ボルの32×32又はそれ以上。長方形シンボルの8×32,12×36又はそれ以上)では,位置合せパターンは,
固定パターンの一部である。シンボルの左側及び下側は,1モジュール幅の変化しない“L”状であり,右
側及び上側には単一の明暗モジュールが交互に繰り返して配置される(クロックトラックとして知られて
いる。)。位置合せパターン内の位置合せバー及び内部クロックトラックは,それぞれ1モジュール幅であ
り,変化しないバー及び単一の明暗モジュールを交互に繰り返した配置である。固定パターン損傷のグレ
ードは,損傷モジュールの総数だけでなく,損傷の集中も考慮する。
M.1.2 外側固定パターン“L”のグレード付け
“L”のそれぞれの側への損傷は,それを構成している個々のモジュールの変位幅に基づいてグレード
付けしなければならない。これらの測定は,“L”の二つの側の全長及び関連したクワイエットゾーンに適
用する。
図M.1に四つの区分L1,L2,QZL1及びQZL2を示す。区分L1は,“L”の垂直部分及び“L”の角に
隣接したクワイエットゾーンのモジュールに拡張した部分である(図M.1のL1参照)。区分L2は,“L”
の水平部分及び“L”の角に隣接したクワイエットゾーンのモジュールに拡張した部分である(図M.1の
L2参照)。区分QZL1及び区分QZL2は,L1及びL2に隣接したクワイエットゾーンの部分,及びL1と
L2との端から1モジュール越えた拡張部分である(それぞれ,図M.1の影付き部分を参照)。L1及びL2
が交差している角のモジュールは,両方の区分に含んでおり,QZL1及びQZL2の交差している部分も同
じである。
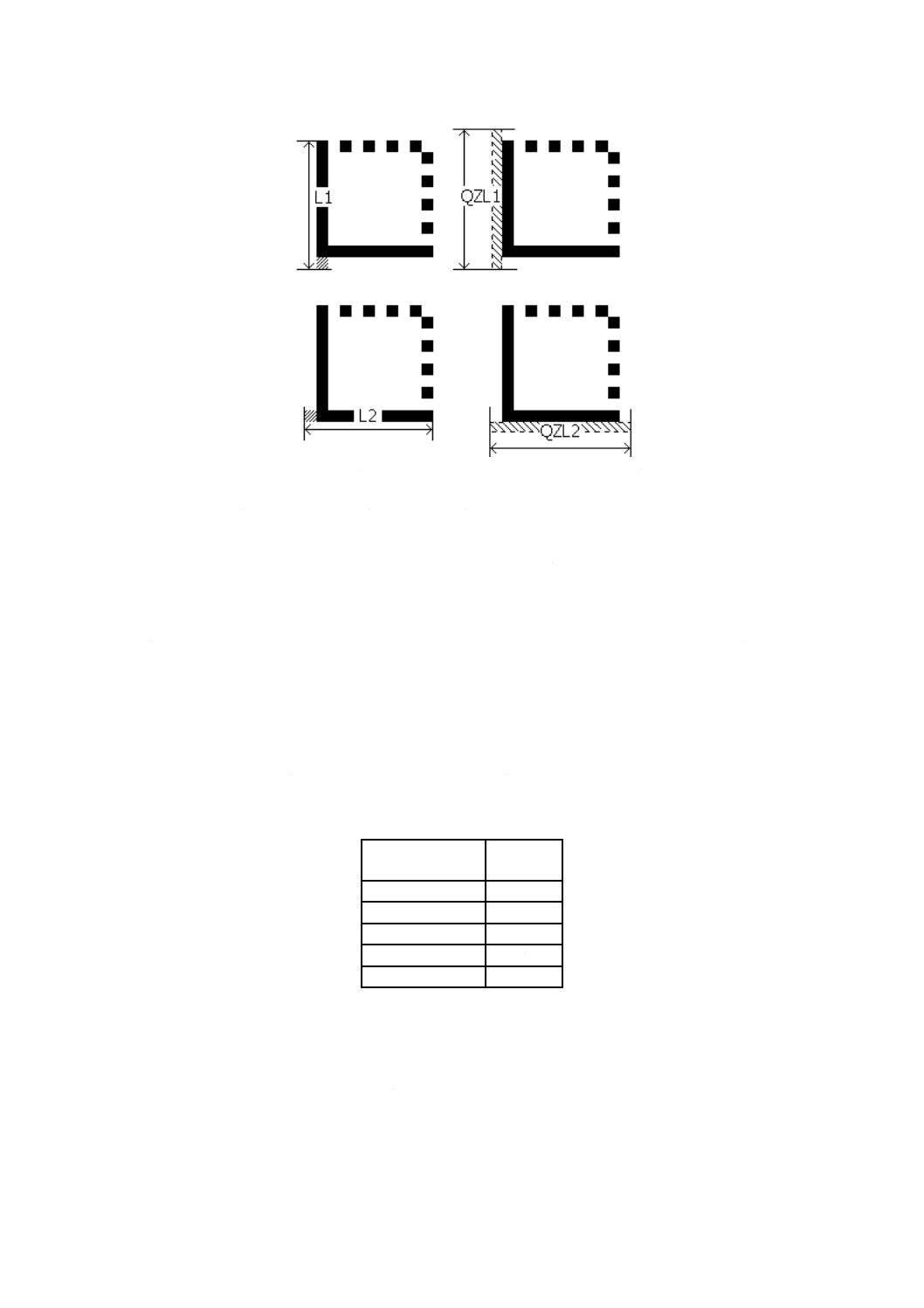
68
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図M.1−外側L及び対応する固定パターンのクワイエットゾーン部分
次に示す手続は,各区分に,順番に適用しなければならない。
a) ISO/IEC 15415の値に基づいて,各モジュールの変位幅グレードを求める。各モジュールがとるべき
明暗の値は分かっているので,暗であるべきモジュールで反射率が全域的しきい(閾)値よりも上の
もの,及び明であるべきモジュールで反射率が全域的しきい(閾)値よりも下のものについては,変
位幅グレードを“0”にしなければならない。
b) 各変位幅のグレードレベルには,ISO/IEC 15415に記載しているパラメタグレード重ね合わせ技術を
適用する。
1) “L”の二つの側(図M.1のL1及びL2)及びこれらに接するクワイエットゾーン領域(図M.1の
L1及びL2のそれぞれに隣接するQZL1及びQZL2)については,そのグレードに満たない全ての
モジュールをモジュール誤りと想定し,表M.1に示すグレードしきい(閾)値に基づいて想定損傷
グレードを求める。変位幅グレードレベルと想定損傷グレードとの低い方を採用する。
表M.1−想定損傷のためのグレードしきい(閾)値
モジュール損傷
の割合
グレード
0 %
4
≦9 %
3
≦13 %
2
≦17 %
1
>17 %
0
2) 各区分のグレードは,全ての変位幅グレードレベルの最上位結果グレードでなければならない。
c) さらに,二つ以上のデータ領域をもった正方形シンボル及び長方形シンボルについては,上のa)及び
b)を一部変更した手続を適用する。一部変更の内容は,L1区分及びL2区分として,クワイエットゾ
ーンのモジュールから始まり,同じデータ領域のクロックトラック領域で終わるものをとり,QZL1
区分及びQZL2区分として,図M.1と同様に,L1区分及びL2区分に隣接するクワイエットゾーンを
とることである。すなわち,左下のデータ領域一つだけを,一つしかデータ領域をもたないシンボル
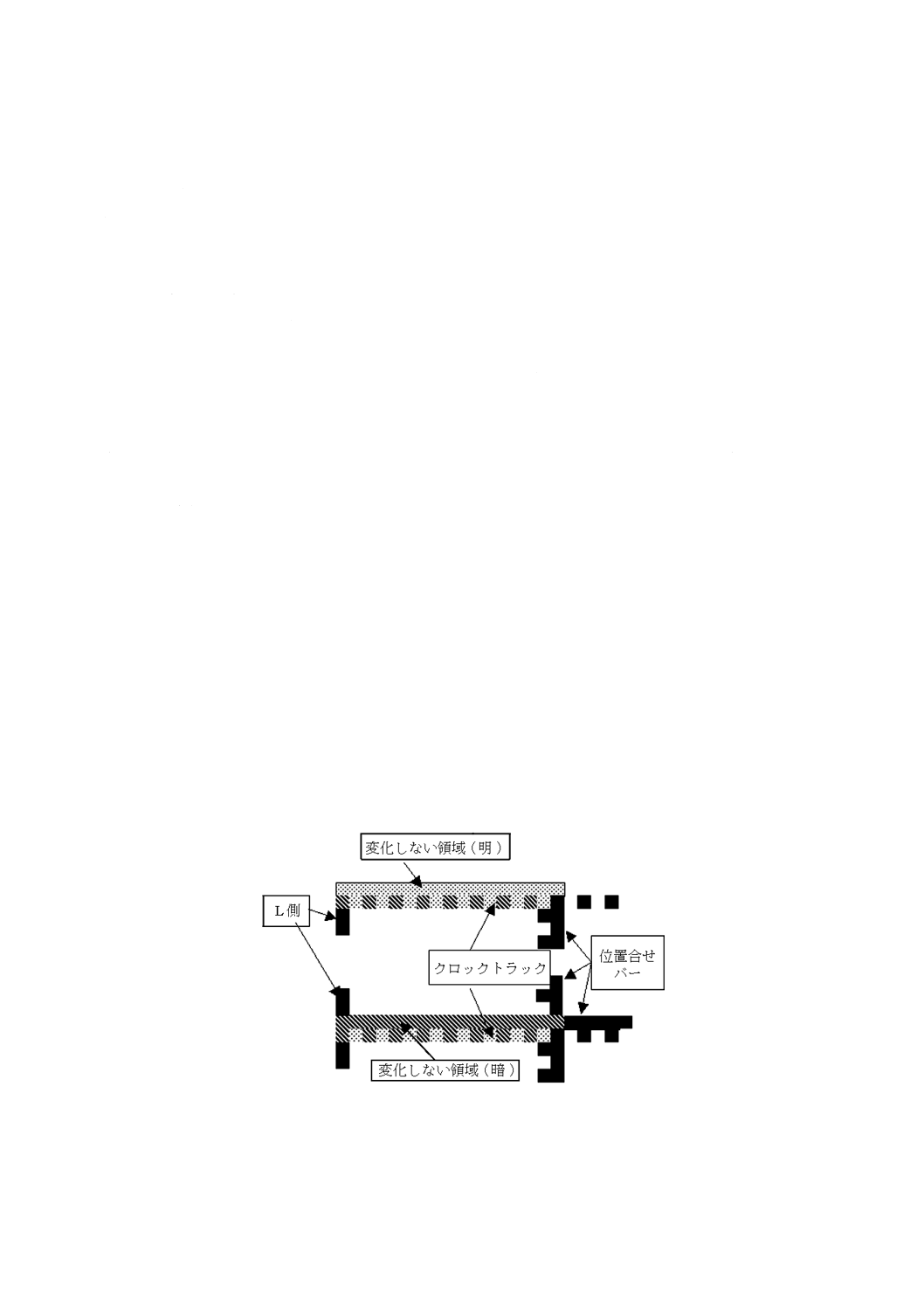
69
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
であるかのように扱うことである。この変更手続で得られたグレードが,元の手続a)及びb)を用いて
L1,L2,QZL1及びQZL2から得た値よりも低い場合は,a)及びb)で得たグレードをこの変更手続値
で置き換える。
d) さらに,区分L1及び区分L2で,全ての損傷モジュール連続が,少なくとも長さ4モジュール以上の
正常モジュール連続で離されており,どの損傷モジュール連続も,3モジュールより長くないことを
確認する。もし,この試験が不合格の場合は,上の手順で得たグレードを,変位幅グレードレベル“0”
に下げなければならない。
e) 区分の固定パターン損傷のグレードは,全ての変位幅グレードレベルの最上位結果グレードでなけれ
ばならない。
M.1.3 クロックトラック及び隣接する変化しない領域部分のグレード
ここでは,内部位置合せパターン(もし,あれば),外部クロックトラック及び関連するクワイエットゾ
ーン領域での損傷の測定法を定義する。これらの試験は,内部位置合せパターン,クロックトラック及び
データ領域の境界に関連するクワイエットゾーン領域,又はより大きなシンボルの個々のデータ領域に適
用する。各区分は,クロックトラック部分及び変化しない領域部分(クワイエットゾーン又は内部位置合
せバーの一部)からなる。
クロックトラック部分は,“L”側又は内部位置合せバー内の暗モジュールから垂直に始まり,クワイエ
ットゾーン又は次の内部位置合せバーのいずれかの前にある明モジュールに続く。
クワイエットゾーンに隣接していない位置合せバーをもった変化しない領域部分は,関連するクロック
トラック部分の最初のモジュールに隣接したモジュールで始まり,関連するクロックトラック部分の最後
のモジュールを過ぎて,1モジュール先まで続く。図M.4 a)にこれらの区分の構成を示す。外部クワイエ
ットゾーン部分に対応する変化しない区分は,これと同じ方法で定義する(図M.2参照)。
クワイエットゾーンに隣接している位置合せバーをもった変化しない領域部分は,関連するクロックト
ラック部分の最初のモジュールに隣接したモジュールを用いて開始し,関連するクロックトラック部分の
最後のモジュールに隣接したモジュールに続く。図M.4 b)にこれらの区分の構成を示す。
注記 内部位置合せパターンがないシンボルでは,外部クロックトラック区分は,シンボルの全幅又
は全高さまで伸びる。
注記 この図は,内部位置合せパターン区分が,同色の他の内部位置合せ区分に
(1モジュール分)重なることを示している。
図M.2−外部クロックトラック区分及び内部位置合せパターン区分の構造
70
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
シンボル(データ領域が複数の)内の各外部クロックトラック区分又は内部位置合せパターン区分につ
いて,次の手順に従って損傷を測定する。
a) 変換点率試験 2値化画像内の全てのクロックトラック区分[外部(クワイエットゾーンに隣接。)及
び内部(内部位置合せバーに隣接。)の両方]で,クロックトラック側の変換点の数Tc及び変化しな
いライン側変換点の数Tsをカウントし,次の式で変換点率グレードTRを計算する(表M.2参照)。
Tsʼ=Max (0, Ts−1)
TR=Tsʼ/Tc
表M.2−変換点率のグレード
TR
グレード
TR<0.06
4
0.06≦TR<0.08
3
0.08≦TR<0.10
2
0.10≦TR<0.12
1
TR≧0.12
0
注記 変換点をカウントする区間の両端は,クロックトラック又は変化しない領域の最初及び最後
のモジュール内にある。参照復号アルゴリズムによって描かれた格子の交点である(図M.3
参照)。
参照復号アルゴリズムに基づいたモジュールの中央を結ぶ格子
A−A' 変化しない領域の始め及び終わりを定めている交点
B−B' クロックトラックの始め及び終わりを定めている交点
図M.3−完全なシンボル(左)及び損傷のあるシンボル(右)の変換点
b) 想定損傷グレード ISO/IEC 15415の値に基づいて,各モジュールの変位幅グレードを求める。各モ
ジュールがとるべき明暗の値は分かっているので,暗であるべきモジュールで反射率が全域的しきい
(閾)値よりも上のもの,及び明であるべきモジュールで反射率が全域的しきい(閾)値よりも下の
ものについては,変位幅グレードを“0”にしなければならない。
c) 各変位幅グレードに対して そのグレード以上のグレードを達成していない全てのモジュールをモジ
ュール誤りと仮定し,次の三つの評価に基づいて,想定損傷グレードを推測する。
1) クロックトラックの均整試験 クロックトラックの各区分で,五つの隣接するモジュールのグルー
プを取って,区分の長手方向に1モジュールずつ進み,五つの隣接するモジュールの任意のグルー
プに,二つまでのモジュール誤りがないか確認する。この状況を満たすならば,クロックトラック
の均整グレードは“4”でなければならず,他の場合は“0”でなければならない。
2) クロックトラック損傷試験 各区分のクロックトラックにある,誤ったモジュールの数をカウント
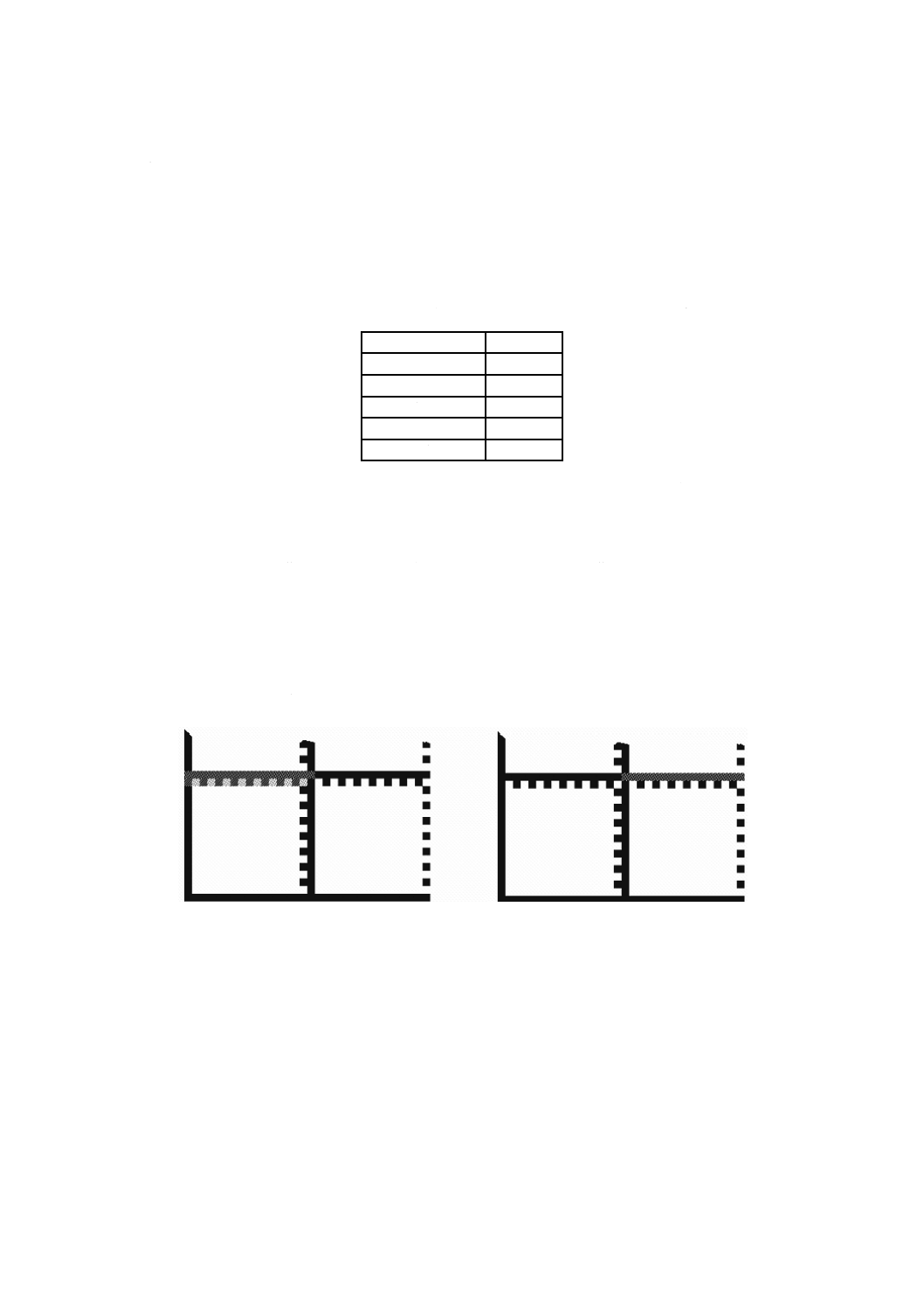
71
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
する。領域の長さに対する,誤ったモジュールの割合Pから,表M.3に示す損傷割合のグレードを
求める。
3) 変化しない領域の固定パターン試験 各区分で,クロックトラックに隣接する変化しない領域(内
部位置合せバー又は外部クワイエットゾーン領域)にある,誤ったモジュールの数をカウントする。
領域の長さにわたって誤ったモジュールの割合Pは,表M.3に示した損傷割合のグレードでなけれ
ばならない。
表M.3−クロックトラック区分及び変化しない領域区分の損傷割合のグレード
P
グレード
P<10 %
4
10 %≦P<15 %
3
15 %≦P<20 %
2
20 %≦P<25 %
1
P≧25 %
0
d) 変位幅グレードレベル,クロックトラック均整グレード,クロックトラック損傷割合グレード及び変
化しない固定ターン損傷割合グレードの各グレードレベルは,最小の値をとる。
e) 区分の想定損傷グレードは,全ての変位幅グレードレベルの最高グレードでなければならない。
f)
区分の固定パターン損傷グレードは,変換点率グレード及び想定損傷グレードの最小グレードでなけ
ればならない。
g) クロックトラック及び変化しない領域区分の総合固定パターン損傷グレードは,個々の区分のそれぞ
れで得たグレードの最小グレードである。
図M.4の網掛け部分は,次のクロックトラック部分及び変化しない領域部分の変換点率,均整及び変化
しない固定パターン試験を含む,内部位置合せパターン区分の例を示している。
a)
b)
図M.4−外部クワイエットゾーンで終わる内部位置合せパターン区分
図M.5の網掛け部分は,次の外部クロックトラック及びそれに関連するクワイエットゾーンの変換点率,
均整試験及び変化しない領域の固定パターン試験が適用される例を示している。
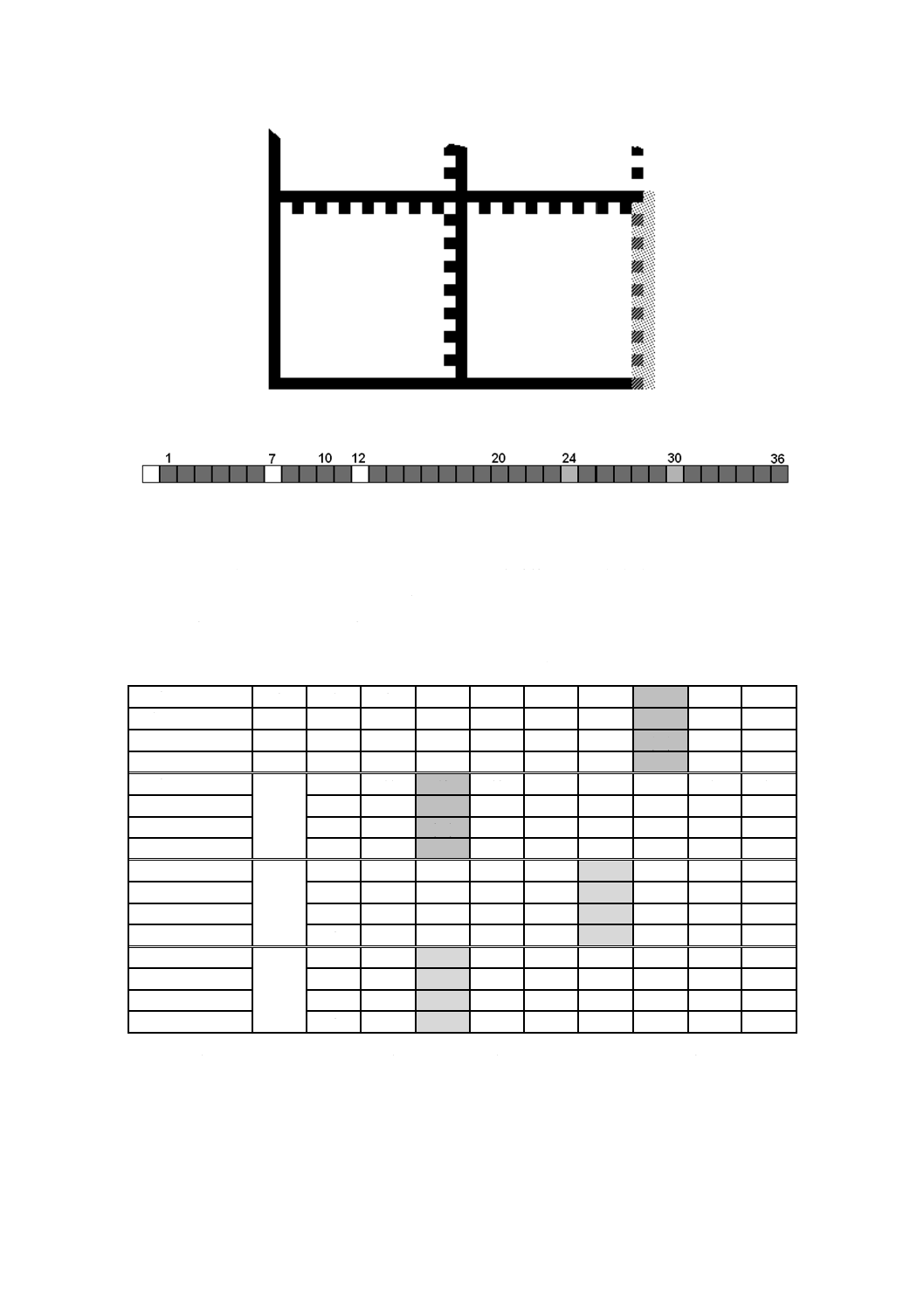
72
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図M.5−外部クロックトラック区分
図M.6−36×36シンボルのL側のためにグレード分けされる37モジュールの例
例 図M.6は,36×36シンボルのL1区分のグレード化に基づいたSC(Symbol Contrast:シンボルコ
ントラスト)=89 %及びGT[Global Threshold:全域的しきい(閾)値]=51 %の例である。区
分の0〜36モジュールに対する,反射率,変位幅の値及び変位幅グレードを表M.4に示す。Lの
角に隣接したクワイエットゾーン上の拡張されたモジュールは,モジュール“0”として示される。
表M.4−36モジュール区分の変位幅グレード化の例
モジュール
0
1
2
3
4
5
6
7
8
9
反射率(%)
84
15
13
13
13
9
11
84
11
10
変位幅
74
80
86
86
86
94
90
(74)
90
92
変位幅グレード
4
4
4
4
4
4
4
0
4
4
モジュール
10
11
12
13
14
15
16
17
18
反射率(%)
9
11
70
13
12
15
11
11
11
変位幅
94
90
(42)
86
88
80
90
90
90
変位幅グレード
4
4
0
4
4
4
4
4
4
モジュール
19
20
21
22
23
24
25
26
27
反射率(%)
27
11
14
10
12
50
12
11
14
変位幅
54
90
83
92
88
2
88
90
83
変位幅グレード
4
4
4
4
4
0
4
4
4
モジュール
28
29
30
31
32
33
34
35
36
反射率(%)
13
12
37
13
12
13
11
13
12
変位幅
86
88
31
86
88
86
90
86
88
変位幅グレード
4
4
2
4
4
4
4
4
4
注記 モジュール0, 7及び12は,明瞭な“明”。モジュール24及び30は,低い変位幅である。
これらの値に基づいた区分グレードを,表M.5に示す。
73
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表M.5−グレード化区分の例
MOD
グレード
レベル
モジュール
の数
モジュール
の累積数
損傷 モジュ
ールの残り
損傷 モジュ
ールの%
想定損傷
グレード
低い
グレード
4
33
33
4
10.8
2
2
3
0
33
4
10.8
2
2
2
1
34
3
8.1
3
2
1
0
34
3
8.1
3
1
0
3
37
0
0
4
0
区分の最終グレードは,最終列の高いグレードである。
2
M.1.4 平均グレードの計算及びグレード化
個々のセグメントの評価に加え,AG(平均グレード)の計算は,個別のセグメントにおいては比較的影
響が小さいものの,複数のセグメントに影響を与える損傷が累積したときの効果を考慮して行う。これは,
区分L1,L2,QZL1,QZL2と,全てのクロックトラック及びそれに隣接する変化しない領域を合わせた
区分との,5区分のグレードの平均値を基準にする。
全ての区分がグレード化された後で,平均グレードAGを計算する。
AG=(区分グレード値の合計)/5
表M.6に従って,AGの値にグレードを割り当てる。
シンボルの固定パターン損傷グレードは,5区分のそれぞれのグレード及びAGのグレードのうち,最
も低いものを採用する。
表M.6−AGのグレード化
5区分グレードの
平均
グレード
4
4
≧3.5
3
≧3.0
2
≧2.5
1
<2.5
0
例1
五つの区分のうちの四つの区分がグレード4,及び一つのグレードが1のとき,
(4×4)+(1×1)=17
AG=17/5=3.4
表M.6から,平均値3.4のときのグレードが2となる。六つのグレードのうち,1が最も低
いため,シンボルの固定パターン損傷グレードは,1である。
例2
五つの区分のうちの三つの区分がグレード4,一つのグレードが3及びもう一つのグレード
が1のとき,
(3×4)+(1×3)+(1×1)=16
AG=16/5=3.2
表M.6から,平均値3.2のときのグレードが2となる。六つのグレードのうち,1が最も低
74
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
いため,シンボルの固定パターン損傷のグレードは,1である。
例3
五つの区分の全てがグレード3のとき,
5×3=15
AG=15/5=3.0
表M.6から,平均値3.0のときのグレードが2となる。六つのグレードのうち,2が最も低
いため,シンボルの固定パターン損傷のグレードは,2である。
M.2 走査グレード
ISO/IEC 15415に従って評価された標準パラメタのグレード及びこの附属書Mに従って評価された固定
パターン損傷グレードのうちの最小値を走査グレードとする。
75
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書N
(規定)
シンボル体系識別子
JIS X 0530(ISO/IEC 15424)は,読んだシンボル体系,バーコードリーダに設定した任意設定及びバー
コードの特殊な特徴を報告するために,定型化した方法を規定している。
データマトリックスのシンボル体系識別子は,次のとおりである。
]dm
ここに,
] は,シンボル体系識別フラグ(ASCII値93)
d は,データマトリックスシンボル体系のコードキャラクタ
m は,表N.1に規定する,いずれかの値をもつ変更子キャラクタ
表N.1−データマトリックスのシンボル体系識別子オプション値
mの値
内容
0
ECC 000−140
1
ECC 200
2
ECC 200でFNC1が第1又は第5キャラクタ位置
3
ECC 200でFNC1が第2又は第6キャラクタ位置
4
ECC 200でECIプロトコルを支援
5
ECC 200でFNC1が第1又は第5キャラクタ位置+ECIプロトコル
6
ECC 200でFNC1が第2又は第6キャラクタ位置+ECIプロトコル
注記 許されるmの値は,0,1,2,3,4,5,6である。
76
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書O
(参考)
ECC 200の符号化例
この例で符号化する利用者データは,“123456”(6桁の数字)である。
手順1:データの符号化
ASCII表現では,
データキャラクタ:
“1”
“2”
“3”
“4”
“5”
“6”
10進値:
49
50
51
52
53
54
ASCII符号化は,上記六つのキャラクタを3バイトに変換する。これは,数字対に対して,次の式を用
いることによって完成する。
コード語=(数字対の数値)+130
この計算の具体例は,次のとおりである。
“12”=12+130=142
“34”=34+130=164
“56”=56+130=186
データ符号化後のデータ列は,次のようになる。
10進値:142 164 186
表7によると,三つのデータコード語が10×10シンボルに納まり,五つの誤り訂正コード語を追加する
必要がある。符号化されたデータが,データ領域を正しく満たさないときは,埋め草コード語を追加する。
手順2:誤り検査及び誤り訂正
誤り訂正コード語は,リードソロモンアルゴリズムを用いて生成され,符号化データ列に付加される。
得られたデータ列は,次のとおりになる。
コード語
1
2
3
4
5
6
7
8
10進
142
164
186
114
25
5
88
102
16進
8E
A4
BA
72
19
05
58
66
データコード語
誤り訂正コード語
附属書Eは,ECC 200誤り訂正処理を記載し,E.3は,誤り訂正コード語の計算を実行するルーチンの
例を示している。
手順3:マトリックスへのモジュール配置
手順2からの最終的なコード語は,5.8.1に記述しているアルゴリズムに従って,シンボルキャラクタと
してバイナリマトリックスの中に配置する(図O.1参照)(図F.1も参照)。

77
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図O.1−マトリックス内のモジュール位置
手順4:実際のシンボル
最終的なデータマトリックスシンボルは,位置検出パターンモジュールを付加し,バイナリの“1”を黒
に,バイナリの“0”を白に変換することによって生成される(図O.2参照)。
図O.2−“123456”を符号化した最終データマトリックスシンボル
78
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書P
(参考)
ECC 200のための最小シンボルデータキャラクタを用いたデータの符号化
同じデータでも,異なるコードセットを用いることによって,異なるデータマトリックスシンボルとし
て表現してもよい。
次のアルゴリズムは,通常,最短のコード語列を生成する。
a) ASCII符号化で開始
b) ASCII符号化の間は,
1) 次のデータシーケンスが,少なくとも二つの連続したアラビア数字のとき,二つの数字をASCIIモ
ードの2桁の数字として符号化する。
2) 先読み試験[手順j)で始まる。]が異なるモードを示すときは,そのモードに切り換える。
3) Base 256符号化が示された場合,Base 256符号化モードへの切換えキャラクタが符号化される。さ
らに,現段階では定義されない長さ領域が符号化される。手順g)又は手順i)で,長さ領域が埋めら
れる(二つ目の長さ領域を付加することが必要な場合がある。)。
4) 次のデータキャラクタが拡張ASCII(127よりも大きい値)のときは,最初に上段1字切換えキャ
ラクタ(値:235)を用いて,ASCIIモードでそれを符号化する。
5) そうでなければ,次のデータキャラクタをASCII符号化で処理する。
c) C40符号化の間は,
1) C40符号化が,新しい二つのシンボルキャラクタを始める時点にあるとき,先読み試験[手順j)で
始まる。]が,他のモードを表示しているときは,そのモードに切り換える。
2) そうでなければ,次のキャラクタをC40符号化で処理する。
d) テキスト符号化の間は,
1) テキスト符号化が,新しい二つのシンボルキャラクタを始める時点にあるとき,先読み試験[手順
j)で始まる。]が,他のモードを表示しているときは,そのモードに切り換える。
2) そうでなければ,次のキャラクタをテキスト符号化で処理する。
e) X12符号化の間は,
1) X12符号化が,新しい二つのシンボルキャラクタを始める時点にあるとき,先読み試験[手順j)で
始まる。]が,他のモードを表示しているときは,そのモードに切り換える。
2) そうでなければ,次のキャラクタをX12符号化で処理する。
f)
EDIFACT (EDF)符号化の間は,
1) EDIFACT(EDF)符号化が,新しい三つのシンボルキャラクタを始める時点にあるとき,先読み試
験[手順j)で始まる。]が,他のモードを表示しているときは,そのモードに切り換える。
2) そうでなければ,次のキャラクタをEDF符号化で処理する。
g) Base 256(B256)符号化の間は,
1) 先読み試験[手順j)で始まる。]が,他のモードを表示しているときは,そのモードに切り換える。
2) そうでなければ,次のキャラクタをB256符号化で処理する。
h) データの最後まで,手順b)から繰り返す。
i)
データの最後で,B256符号化の状態にあった場合は,長さを0に設定する(0は,B256符号化が,
79
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
そのシンボルを終わらせることを表す。)。
先読み試験[手順j)〜s)]
先読み試験は,最適なモードを探すために,符号化されるデータを走査する。
j)
各モードのシンボルキャラクタカウントを初期化する。
1) 現在のモードがASCIIのときの初期化は,
ASCIIカウント=0,C40カウント=1,テキストカウント=1,X12カウント=1,
EDFカウント=1,B256カウント=1.25
そうでないときの初期化は,
ASCIIカウント=1,C40カウント=2,テキストカウント=2,X12カウント=2,
EDFカウント=2,B256カウント=2.25
2) 現在のモードがC40符号化のときの初期化は,C40カウント=0
3) 現在のモードがテキスト符号化のときの初期化は,テキストカウント=0
4) 現在のモードがX12符号化のときの初期化は,X12カウント=0
5) 現在のモードがEDF符号化のときの初期化は,EDFカウント=0
6) 現在のモードがB256符号化のときの初期化は,B256カウント=0
k) データの最後に,
1) 全てのカウントを整数に切り上げる。
2) ASCIIカウントが小さいか,又は他の全てのカウントが同じときは,ASCII符号化を表す試験から
戻る。
3) B256カウントが,他の全てのカウントよりも小さいときは,B256符号化を表す試験から戻る。
4) EDFカウントが,他の全てのカウントよりも小さいときは,EDF符号化を表す試験から戻る。
5) テキストカウントが,他の全てのカウントよりも小さいときは,テキスト符号化を表す試験から戻
る。
6) X12カウントが,他の全てのカウントよりも小さいときは,X12符号化を表す試験から戻る。
7) C40符号化を表示する試験から戻る。
l)
ASCIIカウントの処理
1) データキャラクタがアラビア数字のときは,ASCIIカウントに1/2を加える。
2) データキャラクタが拡張ASCII(127よりも大きい値)のときは,ASCIIカウントを切り上げて2
を加える。
3) そうでなければ,ASCIIカウントを切り上げて,1を加える。
m) C40カウントの処理
1) データキャラクタがC40固有のものであるとき,C40カウントに2/3を加える。
2) データキャラクタが拡張ASCII(127よりも大きい値)のときは,C40カウントに8/3を加える。
3) そうでなければ,C40カウントに4/3を加える。
n) テキストカウントの処理
1) データキャラクタがテキストキャラクタの固有のものであるとき,テキストカウントに2/3を加え
る。
2) データキャラクタが拡張ASCII(127よりも大きい値)のときは,テキストカウントに8/3を加える。
3) そうでなければ,テキストカウントに4/3を加える。
o) X12カウントの処理
80
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1) データキャラクタがX12の固有のものであるときは,X12カウントに2/3を加える。
2) データキャラクタが拡張ASCII(127よりも大きい値)のときは,X12カウントに13/3を加える。
3) そうでなければ,X12カウントに10/3を加える。
p) EDFカウントの処理
1) データキャラクタがEDFの固有のものであるとき,EDFカウントに3/4を加える。
2) データキャラクタが拡張ASCII(127よりも大きい値)のときは,EDFカウントに17/4を加える。
3) そうでなければ,X12カウントに13/4を加える。
q) B256カウントの処理
1) キャラクタが機能キャラクタのとき(FNC1,構造的連接,リーダプログラム又はコードページ),
B256カウントに4を加える。
2) そうでなければ,B256カウントに1を加える。
r) この試験ループで,少なくとも四つのデータキャラクタが処理された場合
1) ASCIIカウントに1を加えたときに,他のカウントと同じか又はそれより小さい場合は,ASCII符
号化を表す試験から戻る。
2) B256カウントに1を加えたとき,ASCIIカウントと同じか又は他のカウントよりも小さい場合は,
B256符号化を表す試験から戻る。
3) EDFカウントに1を加えたものが,他の全てのカウントよりも小さいときは,EDF符号化を表す試
験から戻る。
4) テキストカウントに1を加えたものが,他の全てのカウントよりも小さいときは,テキスト符号化
を表す試験から戻る。
5) X12カウントに1を加えたものが,他の全てのカウントよりも小さいときは,X12符号化を表す試
験から戻る。
6) C40カウントに1を加えたものが,ASCII,B256,EDF及びTextカウントよりも小さいときは,
6.1) C40カウントが,X12カウントよりも小さいときは,C40符号化を表す試験から戻る。
6.2) C40カウントが,X12カウントと等しい場合
6.2.1) 三つあるX12カウントの終端,区切りキャラクタのうちの一つが,非X12キャラクタの前にあ
る,まだ処理されていないデータの中の最初にあるときは,X12符号化を表す試験から戻る。
6.2.2) そうでなければ,C40符号化で戻る。
s)
戻り状態が起こるまで,手順k)から繰り返す。
81
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書Q
(参考)
ECC 050を用いたECC 000〜ECC 140 符号化例
(対応国際規格の規定を不採用とした。)

82
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書R
(参考)
有用なプロセス制御技術
この附属書では,読取り可能なデータマトリックスシンボルの作成プロセスを監視及び制御するために
有効なツール及び手順を記述する。これらの技術は,作成されるシンボルの印刷品質チェックを構成する
ものではない(箇条8及び附属書Nで定義される手法は,シンボルの品質評価に要求される手法である。)
が,これらの技術は,個別に,総合的に,シンボル生成プロセスで使用可能なシンボルが作成されるかど
うかのよい指針となる。
R.1 シンボルコントラスト
多くの一次元シンボル用検証器は,静的に反射率を計測するモード又は走査しながら反射率を描画する
モード及び/又は復号不能な走査のシンボルコントラストを出力するモードのいずれかを備えている。特
殊な照明構成が要求されるシンボルを除き,波長が660 nmで0.150 mm又は0.250 mmの測定開口径で得
られるシンボルコントラスト(又は,最大スキャン反射率から最小スキャン反射率を通して得られるシン
ボルコントラスト値又は静的反射率計測で得られる最大値と最小値との差のいずれか)は,画像に起因す
るシンボルコントラスト値と相互関係があることが分かっている。特に,このような読取りは,シンボル
コントラストが意図するシンボル品質グレードで許容される,最小値を十分に超えるものであることを検
査するのに用いることができる。
R.2 特別な参照シンボル
プロセス制御の目的のために,“30Q32434343079<OQQ”を符号化した16×16 ECC 200参照シンボルを
印刷したものを用いることができる。図R.1で表されるように,この参照シンボルは,一次元的に走査し,
JIS X 0520(ISO/IEC 15416)のエッジ計測方法を用いて印刷拡張を測定評価することが可能な,平行なバ
ー及びスペースの領域をもつ。
図R.1−“30Q324343430794<OQQ”を符号化したECC 200参照シンボル
多くの一次元シンボル用検証器は,復号できない走査の場合でも,JIS X 0520の方法によって測定され
たエレメント幅のリストを出力するように,プログラムすることが可能である。ECC 200参照シンボルの
83
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
上半分を通過する,どのような一次元の試験走査の左方部分も,四つのバー及び四つのスペースの対(b1
〜b4,s1〜s4で示される。)を含む。
水平方向の印刷太りは,次のように計算される。
(b1+b2+b3+b4)/(b1+s1+b2+s2+b3+s3+b4+s4)
この値は,データマトリックスにおいては50 %を目標とするのが望ましい。また,実測値は,35 %〜65 %
の範囲内に納まらなければならない。
この測定値は,参照シンボルのエレメントが長く連続することが多い方向の印刷変動をあまり反映しな
いことに注意が必要である。印刷プロセスのより完成度の高い評価が必要ならば,データマトリックス参
照シンボルは,両方向で印刷して評価することが望ましい。
R.3 軸の非均一性評価
どのシンボルにおいても,“L”形の位置検出パターンの二つの側の長さを測る。各長さを,そのモジュ
ール数で除す。例えば,12×36のシンボルは,12及び36で除す。
これらの正規化された二つの寸法XAVG及びYAVGは,次の計算式において,軸性不均一性のグレードを計
算するために用いられる。
AN=abs(XAVG−YAVG)/[(XAVG+YAVG)/2]
ANの値が0.12よりも大きい場合,シンボルは,ISO/IEC 15415によってグレード“0”になる。0.06ま
での値では,このパラメタのグレード“4”に一致する。
R.4 シンボルのゆがみ及び欠陥の目視検査
印刷されたシンボルのサンプルの周辺パターンを目視で検査することによって,印刷プロセスの二つの
重要な側面をモニターすることができる。
第一に,マトリックス格子の局所的なゆがみによって引き起こされる誤りに,二次元マトリックスシン
ボルは影響を受けやすい。このようなゆがみは,“L”形位置検出パターン上の曲がった角か,シンボルの
二つのクワイエットゾーン沿いに見られる,交互パターン内の不均衡なスペーシングの,いずれかの形で
現れる。より大きなECC 200シンボルに含まれる位置合せパターンで,直線性及び均一性が目視でチェッ
クできる。このような方法によって,参照復号に失敗する可能性の高いシンボルが容易に見つかる。
第二に,2本の位置検出パターン及び隣接するクワイエットゾーンの反射率は,常に反対の状態(黒/
白)にすることが望ましい。印刷機構の欠陥は,位置検出パターン又はクワイエットゾーンを白又は黒の
線が侵す位置を目視で確認することで見つけることができる。
これらの印刷プロセスにおけるシステム上の欠陥は,修正されることが望ましい。
84
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書S
(参考)
自動識別能力
データマトリックスは,他のシンボルと自動識別するように設計された復号器を適切にプログラムする
ことで読み取ることができる。読取り安全性を最大にするために,復号器で有効にするシンボル体系は,
与えられたアプリケーションが必要とするものだけに制限するのがよい。
85
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書T
(参考)
システムの考察
どのようなデータマトリックスのアプリケーションでも,総合的なシステムソリューションとして捉え
ることが望ましい。シンボルの符号化及び復号を構成するコンポーネント(マーカ又はプリンタ,ラベル,
リーダ)が,1個のシステムとして機能することが重要である。いずれかのコンポーネントが動作不良を
起こしたとき及びコンポーネント間の相性が悪いときは,システム全体の性能低下を招くことになる。
a) 仕様を遵守することは,システム全体の成功を確実にする一つの鍵であるが,それ以外にも,性能に
影響する要因が幾つか存在する。次に示すガイドラインは,バー又はマトリックスコードシステムの
仕様を定め,機器の選定をするとき考慮することが望ましい。
b) 用いるマーキング及び印刷技術によって達成することが可能な許容値が得られるような,印字密度を
選択する。
c) 印刷技術によって生成されたシンボル密度及び品質に適した解像度をもつリーダを選択する。
d) 印刷されたシンボルの光学特性は,スキャナの光源及びセンサの波長に互換性があることを確認する。
e) 最後に,ラベル又はパッケージ構成におけるシンボルへの適合を確認する。ラベルの重なり,透き通
し,曲面及び凸凹面は,全てのシンボルの可読性に影響を与え得る。
連続モジュールを1本のベタ線で,一貫して作り出すことができないマーキング技術(例えば,ドット
ピン,インクジェット)で,アプリケーションが明示した開口径を用いるシンボルの復号と干渉すること
がないように,通常,モジュール間の間隔に特別な注意をすることを要求する。さらに,モジュールと水
平軸及び垂直軸との相対的な位置は,ISO/IEC 15415で指定する軸方向の均一性の要件に適合する必要が
ある。アプリケーション仕様は,開口径,照明光の波長,印刷品質総合グレードなどの仕様に対する手引
きについて,ISO/IEC 15415を参照する必要がある。
走査システムは,明及び暗からの拡散反射光の変化を受け取る必要がある。走査角度によっては,鏡面
反射成分が大きくなり,必要な拡散成分を超える場合は,読取りが困難になる。部品又は材料の表面を変
更することができる場合は,つや消し,非光沢などの仕上げが,鏡面反射の影響を最小限に抑えることが
できる。このオプションが利用できない場合は,目的のコントラストを得るために,読み込むマークのた
めの照明を最適化する必要がある。
86
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
(1) Lin and Costello, "Error Control Coding: Fundamentals and Applications," Prentice Hall, 1983
(2) C. Britton Rorabaugh, "Error Coding Cookbook," McGraw Hill, 1996.
(3) AIM Inc. "Data Matrix Developer's Diskette" (AIM Inc., 125 Warrendale-Bayne Road, Suite 100, Warrendale,
PA 15086, USA)
(4) ISO/IEC 6429,Information technology−Control functions for coded character sets
87
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
JISと対応国際規格との対比表
JIS X 0512:2015 情報技術−自動認識及びデータ取得技術−バーコードシンボ
ル体系仕様−データマトリックス
ISO/IEC 16022:2006,Information technology−Automatic identification and data capture
techniques−Data Matrix bar code symbology specification,TECHNICAL
CORRIGENDUM 1:2008及びTECHNICAL CORRIGENDUM 2:2011
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差異
の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
3 用語,定義,
記号及び数学
的表記・論理
的表記
3.1.3 畳込符号
3.1.3
畳込符号の定義
削除
データマトリックスシンボルの
誤り訂正方式がECC 000,ECC
050,ECC 080,ECC 100及びECC
140だけで用いている。
この規格では,データマトリックス
シンボルの誤り訂正方式がECC 200
であるシンボルだけを採用した。誤
り訂正方式がECC 000〜ECC 140で
あるシンボルは,JISを作成する時
点及びそれ以降でも用いることを推
奨しないため,それらに関する規定
を不採用にした(推奨しない理由:
現状の二次元シンボル用リーダに
は,データマトリックスシンボルの
誤り訂正がECC 000〜ECC 140の復
号ソフトウェアが組み込まれていな
いため,読み取ることができない。)。
3.2 記号
3.2
JISとほぼ同じ
変更
誤り訂正方式がECC 200のシン
ボルで用いる記号だけを定義し,
それ以外の記述を削除した。
同上
4 シンボルの
説明
4.1 基本的な特性
c),e)
4.1
c),e)
JISとほぼ同じ
変更
誤り訂正方式がECC 200のシン
ボルだけを規定し,それ以外の規
定を削除した。
同上
4.3 シンボルの構造
4.3
JISとほぼ同じ
変更
誤り訂正方式がECC 200のシン
ボルだけを表示し,ECC 140シン
ボルを削除した。
同上
3
X
0
5
1
2
:
2
0
1
5
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
88
X 0512:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差異
の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
4 シンボルの
説明
4.3.2 シンボルサイ
ズ及びデータ容量
4.3.2
JISとほぼ同じ
変更
誤り訂正方式がECC 200のシン
ボルだけを規定し,それ以外の規
定を削除した。
同上
6 ECC 000〜
ECC 140シン
ボルの要件
6
ECC 000〜ECC 140シンボ
ルの要件
削除
−
同上
9 データマト
リックスの参
照復号アルゴ
リズム
l)
1)〜6)
l)
1)〜
6)
参照復号アルゴリズムの
中で,誤り訂正方式が畳込
方式の復号手順部分
削除
誤り訂正方式がECC 200のシン
ボルだけを規定し,それ以外の規
定を削除した。
同上
附属書G
(規定)
附属
書G
ECC 000〜ECC 140シンボ
ルの属性
削除
−
同上
附属書H
(規定)
附属
書H
ECC 000〜ECC 140データ
モジュール配置格子
削除
−
同上
附属書I
(規定)
附属
書I
ECC 000〜ECC 140キャラ
クタ符号化スキーム
削除
−
同上
附属書J
(規定)
附属
書J
ECC 000〜ECC 140 CRC
アルゴリズム
削除
−
同上
附属書K
(規定)
附属
書K
ECC 000〜ECC 140誤り検
査アルゴリズム及び誤り
訂正アルゴリズム
削除
−
同上
附属書L
(規定)
附属
書L
ECC 000〜ECC 140主なラ
ンダムビット列(16進数)
削除
−
同上
JISと国際規格との対応の程度の全体評価:ISO/IEC 16022:2006,TECHNICAL CORRIGENDUM 1:2008,TECHNICAL CORRIGENDUM 2:2011,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 削除 ················ 国際規格の規定項目又は規定内容を削除している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3
X
0
5
1
2
:
2
0
1
5