X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て,通商産業大臣が改正した日
本工業規格である。これによってJIS X 0016 : 1987は改正され,この規格に置き換えられる。
今回の改正では,情報通信技術の進展に伴って,既存用語の拡充,新技術及び新しい概念に対する用語
の追加を行った。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
X 0016 : 1997
(ISO/IEC 2382-16 : 1996)
情報処理用語(情報理論)
Glossary of terms used in
information processing
(Information Theory)
序文 この規格は,1996年に第2版として発行されたISO/IEC 2382-16, Information technology−Vocabulary
−Part 16 : Information theoryを翻訳し,技術的内容を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
1. 適用範囲 この規格は,情報処理における情報理論用語,定義及び対応英語について規定する。
2. 分類 用語は,次のとおり分類する。
a) 一般用語(16.01参照)
b) 通報及び通信系(16.02参照)
c) 基本量に関する用語(16.03参照)
d) 導出量に関する用語(16.04参照)
3. 表記法 この規格は,各用語を番号,用語,定義及び対応英語の四つの欄に分けて規定する。それぞ
れの欄における表記法及び解釈を,次に示す。
a) 番号 番号は,6個の数字によって表す。最初の2けたの数字は,情報処理用語の規格番号の末尾2
けたを示す。次の2けたの数字は,この規格での分類を示す。最後の2けたは,同一分類内の一連番
号を示す。
b) 用語
1) 同一の意味を示す用語が二つ以上ある場合は,表記した順に従って優先使用する。
2) 用語の一部が丸括弧( )で囲まれている場合は,その部分を省略してもよいことを表す。この場
合は,括弧内を省略したときとしないときとの間に優先順位はない。
3) 用語の使用分野を限定する場合には,用語に引き続く丸括弧( )内にそのことを示す。
例 “情報(情報理論における)”(16.01.03参照)
c) 定義
1) 文中で下線の引いてある語は,情報処理用語に関する日本工業規格に規定されていることを示す。
2) 丸括弧( )の使い方は,b)と同様とする。
d) 対応英語
1) この欄の英語は,対応国際規格に規定されている用語であって,規定されている定義と対応する。
2
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2) 対応英語について使用上の注意がある場合には対応英語に引き続く丸括弧( )内に示す。
3) 対応英語に付けられた括弧内の注記の意味は,次のとおりとする。
(使用しないほうがよい。) 国際規格及びこの規格では,この英語を使用しないので,使用しな
いほうがよいことを示す。
例 16.03.03 negentropy(使用しないほうがよい)
(使用してはいけない。) 国際規格及びこの規格では,用語統一の見地から,この英語を使用し
てはいけないことを示す。
(この意味では使用しないほうがよい。) 国際規格及びこの規格では,他の意味で使われている
ため,この英語を使用しないほうがよいことを示す。
(××だけ) この英語は××(国名)だけで通用することを示す。
4) 使用分野を限定する丸括弧( )の用法は,b)と同様とする。
4. 情報処理用語(情報理論)
16.01 一般用語
番号
用語
定義
対応英語
16.01.01
情報理論
情報の定量的な尺度を取り扱う理論分野。
information theory
16.01.02
通信理論
雑音,その他の妨害の影響下における通報の伝送に関す
る性質を取り扱う理論分野。
commumication theory
16.01.03
情報(情報理論にお
ける)
事象の集合から生起する事象に関する不確実さを減らし
たり取り除いたりする知識。
備考 情報理論において,“事象”は,確率論で使用
されるものと同様である。事象の例には次の
ようなものがある。
− ある要素 集合の中に特定の要素が存在する
こと。
− ある通報の中又はある通報の特定の位置に,
ある文字又はある語が存在すること。
− ある実験から得られる結果の一つ。
information
16.02 通報及び通信系
番号
用語
定義
対応英語
16.02.01
通報(情報理論及び
通信理論におけ
る)
情報の伝達を目的とする,順序付けられた文字列。
message (in information
theory and
communication
theory)
16.02.02
情報源
通信系において通報が発生する部分。
message source,
information source
16.02.03
通報受端
通信系において通報を受け取る部分。
message sink,
information sink
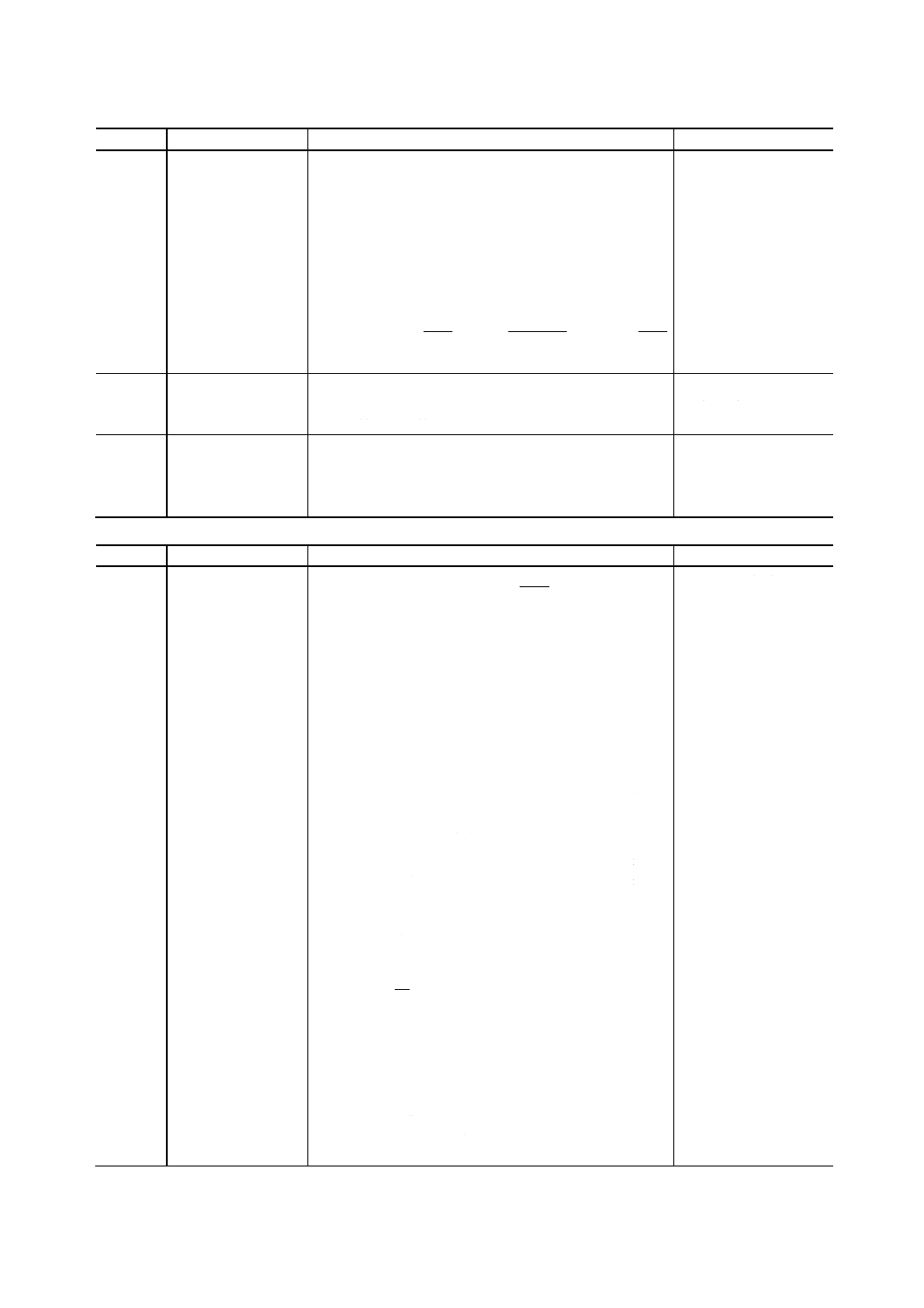
3
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語
16.02.04
通信路(通信理論に
おける)
通信系において情報源と通報受端とを結ぶ部分。
備考1. 符号器が情報源と通信路入力との間に,ま
た復号器が通信路出力と通報受端との間に
存在してもよい。一般に,符号器及び復号
器は,通信路の一部とはみなさない。しか
し,情報源及び通報受端の一部とみなす場
合がある。
2. シャノンの情報理論においては,情報源か
らの通報に対して通報受端が受け取る通報
の条件付き生起確率で,通信路は特徴付け
られる。
channel (in
communication
theory)
16.02.05
2元対称通信路
2進文字から成る通報を伝送する通信路であり,伝送し
たある文字がもう一方の文字に変化してしまう条件付き
確率が等しい性質をもつもの。
symmetric binary
channel
16.02.06
定常情報源
通報の生起確率が時刻に依存しない情報源。
stationary message
source,
stationary information
source
16.03 基本量に関する用語
番号
用語
定義
対応英語
16.03.01
選択情報量
互いに排反な事象から成る有限集合中の事象の数の対
数。数学的には,この選択情報量は,
H0=log n
で表される。ここで,nは事象の数である。
備考1. 16.01.03の備考参照。
2. 対数の底によって単位が定まる。よく使わ
れる単位には次のものがある。
対数の底が2のときはシャノン(記号は
Sh)。
対数の底がeのときはナット(記号は
nat)。
対数の底が10のときはハートレー(記号
はHart)。
単位の変換表を次に示す。
1Sh =0.693nat=0.301Hart
1nat =1.443Sh =0.434Hart
1Hart=3.322Sh=2.303nat
3. 選択情報量は,事象の生起確率に対して独
立である。
4. 有限個の互いに排反な事象から成る有限集
合の中から,特定の事象を選択するために
必要な,b個の選択肢からの選択回数は,b
を底とする対数で定義した選択情報量の小
数部分を切り上げた整数に等しい。ただし,
bは整数とする。
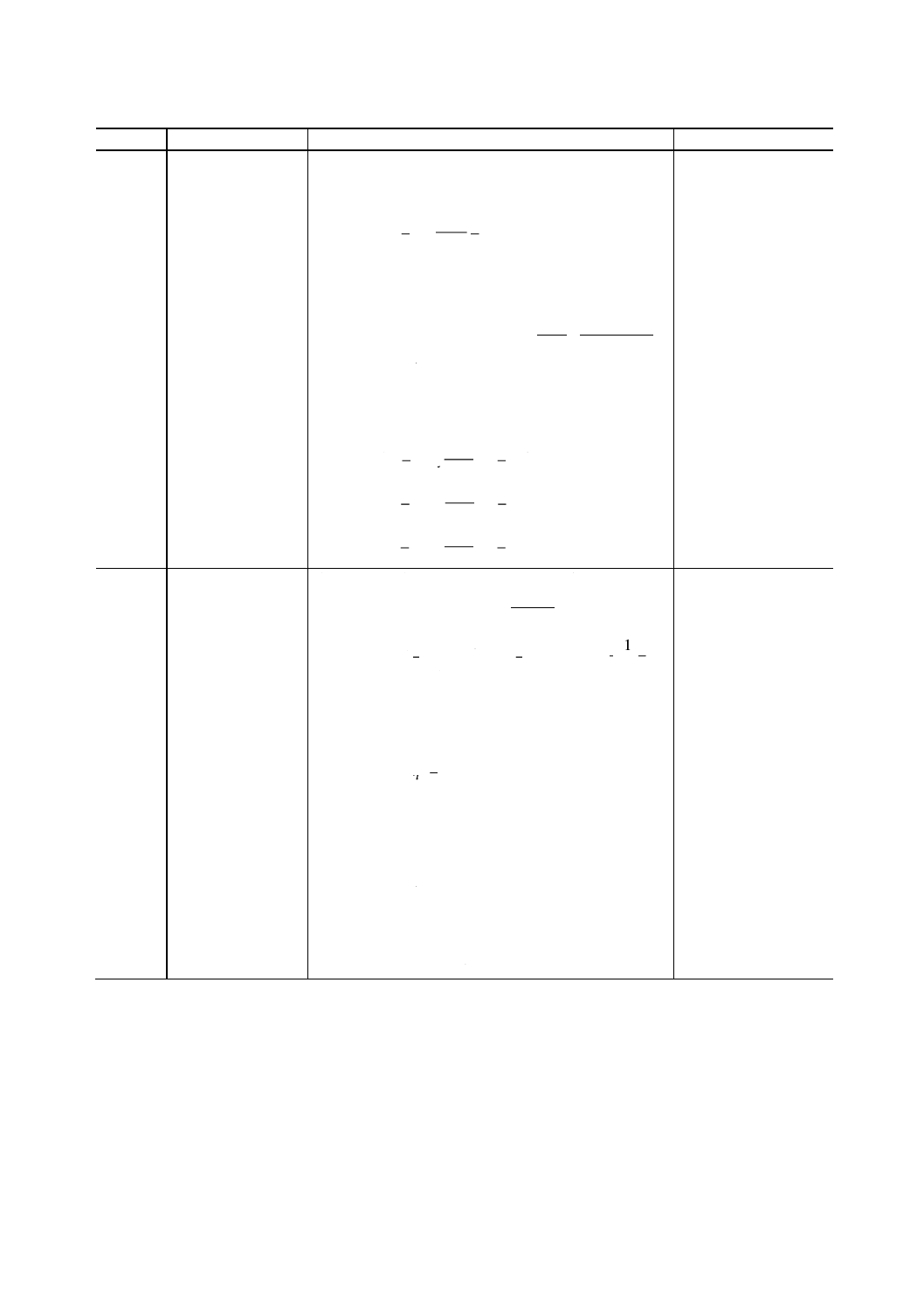
例 {a, b, c} を三つの事象から成る集合とすると,
この集合の選択情報量は次のとおり。
H0= (log2 3) Sh =1.585Sh
= (loge 3) nat =1.098nat
= (log10 3) Hart=0.477Hart
decision content
4
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語
16.03.02
情報量
確率事象の生起を知ることによって伝えられる情報の尺
度。この尺度はその事象の生起確率の逆数の対数に等し
く,数学的には,
)
(
log
)
(
1
log
)
(
x
p
x
p
x
I
−
=
=
で表される。ここで,p (x) は事象xの生起確率である。
備考1. 16.01.03の備考参照。
2. 生起確率が等しい事象から成る集合では,
各事象の情報量はその集合の選択情報量に
等しい。
例 {a, b, c} を三つの事象から成る集合とし,各事
象の生起確率をp (a) =0.5, p (b) =0.25及びp
(c) =0.25とする。これらの事象の情報量は次の
とおり。
Sh
1
Sh
50
.0
1
log
)
(
2
=
=
a
I
Sh
2
Sh
25
.0
1
log
)
(
2
=
=
b
I
Sh
2
Sh
25
.0
1
log
)
(
2
=
=
c
I
information content
16.03.03
エントロピー,
平均情報量
有限の完全事象系の中から,いずれの事象が生起したか
を知ることによって伝えられる情報量の平均値。数学的
には,
)
(
1
log
)
(
)
(
)
(
)
(
1
1
i
n
i
i
i
n
i
i
x
p
x
p
x
I
x
p
X
H
∑
∑
=
=
=
=
で表される。ここで,X= {x1,……,xn} は事象xi(i=1,
……,n)の集合, I (xi) は事象の情報量,及びp (xi) は事
象xiの生起確率であって,
1
)
(
1
=
∑
=
n
i
ix
p
を満たすものとする。
備考 完全事象系とは,それを構成する事象が互い
に排反であり,すべての事象の和集合が全事
象に一致する事象系をいう。
例 {a, b, c} を三つの事象から成る集合とし,各事
象の生起確率をp (a) =0.5, p (b) =0.25及びp
(c) =0.25とする。この集合のエントロピーは次
のとおり。
H(X)=p(a) I(a)+p(b) I(b)+p(c) I(c)=1.5 Sh
entropy,
average information
content,
negentropy(使用しない
ほうがよい)
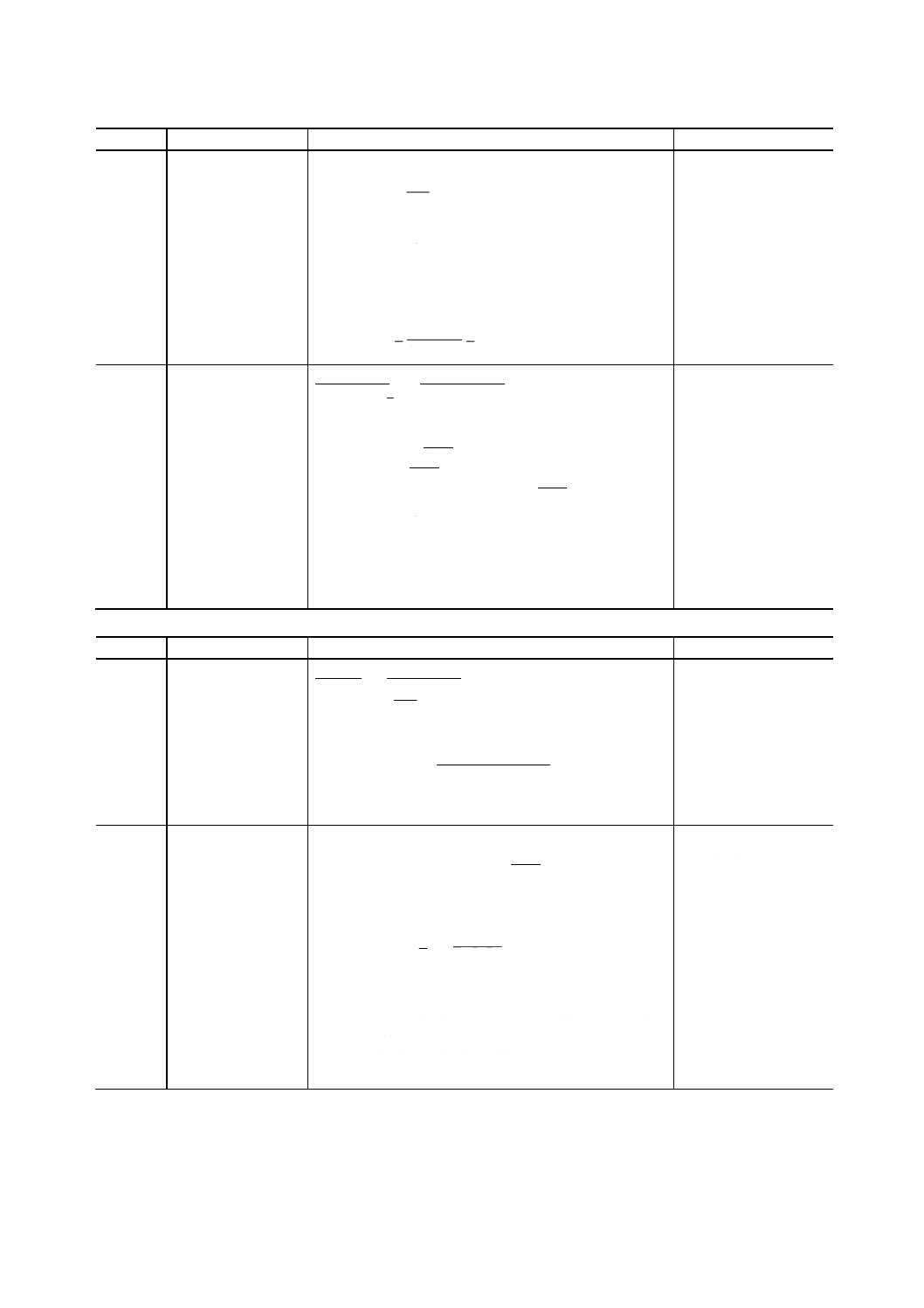
5
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語
16.03.04
相対エントロピー
エントロピーHと選択情報量H0との比Hr。数学的には,
0
H
H
Hr=
で表される。
例 {a, b, c} を三つの事象から成る集合とし,各事
象の生起確率をp (a) =0.5, p (b) =0.25及びp
(c) =0.25とする。この集合の相対エントロピー
は次のとおり。
95
.0
Sh
585
.1
Sh
5.1
=
=
r
H
relative entropy
16.03.05
冗長量(情報理論に
おける)
選択情報量H0とエントロピーHとの差R。数学的には,
H
H
R
−
=
0
で表される。
備考 通常,通報は,適切な符号を用いて,より少
ない文字数で表現できる。冗長量は,その符
号化によって達成される通報の平均長の減少
量と考えられる。
例 {a, b, c} を三つの事象から成る集合とし,各事
象の生起確率をp (a) =0.5, p (b) =0.25及びp
(c) =0.25とする。この集合の冗長量は次のとお
り。
R=1.585 Sh−1.500 Sh=0.085Sh
redundancy(in
information theory)
16.04 導出量に関する用語
番号
用語
定義
対応英語
16.04.01
冗長度(情報理論に
おける)
冗長量Rと選択情報量H0との比r。数学的には,
0
H
R
r=
で表される。
備考 冗長度は相対エントロピーHrの1の補数に等
しい。すなわち,
r=1−Hr
である。
relative redundancy
16.04.02
条件付き情報量
ある事象yが生起したという条件下で他の事象xの生起
を知ることによって伝えられる情報の定量的な尺度。こ
の尺度は事象yが生起したという条件下の事象xの条件
付き確率p(x | y)の逆数に等しい。数学的には,この尺度
I (x | y) は,
)
|
(
1
log
)
|
(
y
x
p
y
x
I
=
で表される。
備考 条件付き情報量I (x | y) は,x及びyの結合情
報量I (x, y) からyの情報量I (y) を引いた差に
等しい。すなわち,
I (x | y) =I (x, y) −I (y)
である。
conditional information
content
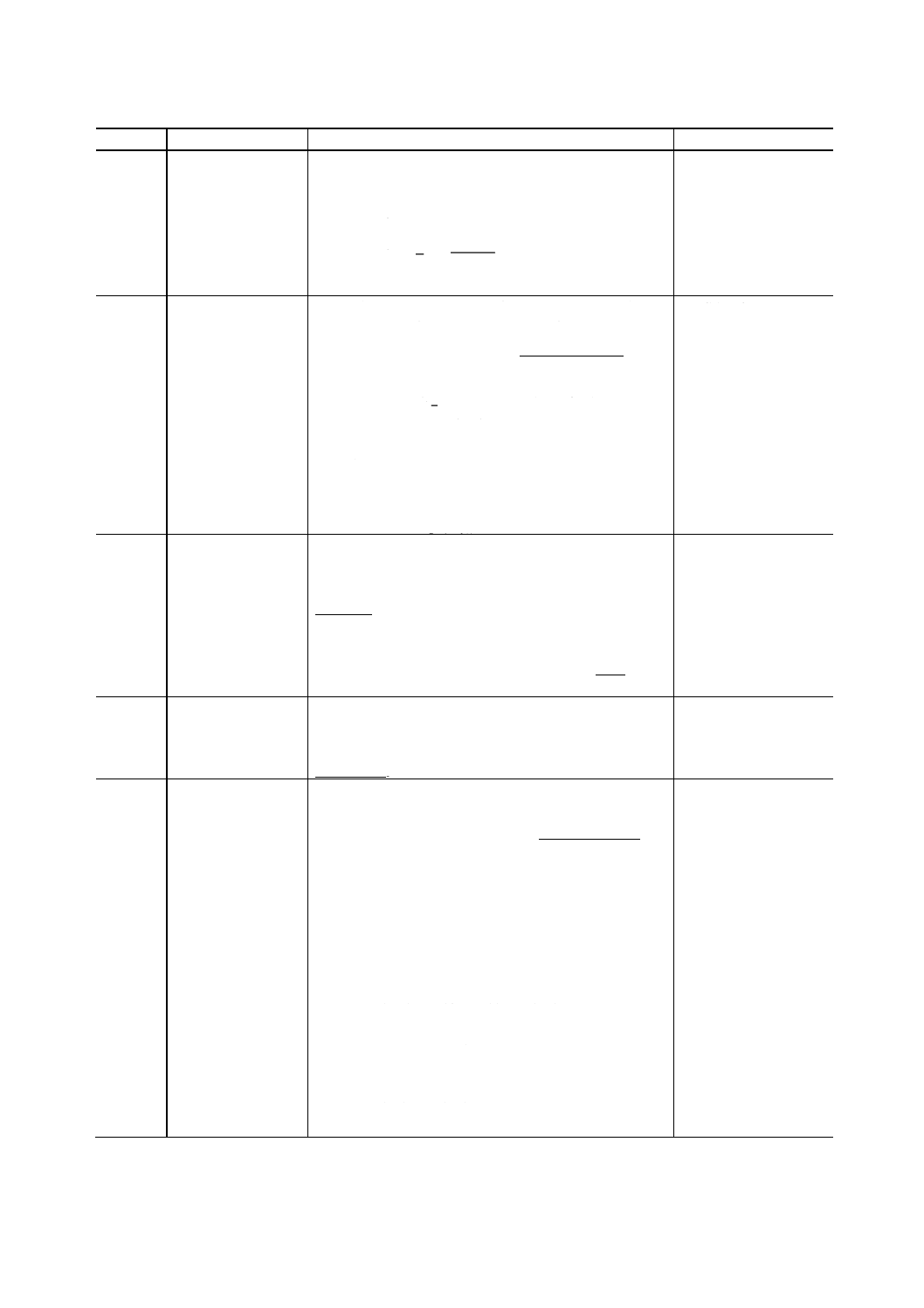
6
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語
16.04.03
結合情報量
二つの事象x及びyが同時に生起したことを知ることに
よって伝えられる情報の定量的な尺度。この量は両事象
の結合確率p (x, y) の逆数の対数に等しい。数学的には,
この尺度I (x, y) は,
)
,
(
1
log
)
,
(
y
x
p
y
x
I
=
で表される。
joint information content
16.04.04
条付きエントロピ
ー,
条件付き平均情報
量
完全事象系の中から一つの事象が生起したという条件下
で,他の完全事象系の中から一つの事象が生起したこと
を知ることによって伝えられる条件付き情報量の平均
値。数学的には,この尺度は,
)
|
(
)
,
(
)
|
(
1
1
j
i
n
i
m
j
j
i
y
x
I
y
x
p
Y
X
H
∑∑
=
=
=
で表される。
ここで,X={x1,……,xn} は事象xi (i=1,……,n) の
集合, Y={y1,……,ym} は事象yj (j=1,……,m) の
集合, I (xi | yj) はyjが生起したという条件下でxiの条件
付き情報量,及びp (xi, yj) は両事象の結合確率である。
conditional entropy,
mean conditional
information content,
average conditional
information content
16.04.05
あいまい量,
あいまい度,
一つの通信路によって情報源に接続されている通報受端
において特定の通報の集合が生起したという条件下で,
情報源においてある通報の集合が生起する条件付きエン
トロピー。
備考 あいまい量は,雑音のある通信路で影響を受
けた受信通報を訂正するために,通報受端に
おいて供給しなければならない1通報当たり
の付加的情報量の平均値である。
equivocation
16.04.06
散布量,
散布度
一つの通信路によって通報受端に接続されている情報源
において特定の通報の集合が生起したという条件下で,
通報受端においてある通報の集合が生起する条件付きエ
ントロピー。
irrelevance,
prevarication,
spread
16.04.07
伝達情報量,
相互情報量
事象xの生起を知ることによって伝えられる情報量I (x)
と,他の事象yが生起したという条件下で同じ事象xの
生起を知ることによって伝えられる条件付き情報量I (x |
y) との差。
数学的には,この尺度T (x, y) は,
T (x, y) =I (x) −I (x | y)
で表される。
備考1. 二つの事象x及びyの例として,ある通信
路の情報源での通報,及び通報受端での通
報があげられる。
2. 伝達情報量は
T (x , y) =I (x) +I (y) −I (x, y)
とも表せる。ここで,I (y) は事象yの情
報量,I(x, y) は両事象の結合情報量である。
このことから,伝達情報量がx及びyに関
して対称であって,
T (x, y) =T (y, x)
であることがわかる。
transinformation
(content) ,
transferred information,
transmitted information,
mutual information
7
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語
16.04.08
平均伝達情報量
完全事象系の中から一つの事象が生起したという条件下
で,他の完全事象系の中から一つの事象が生起したこと
を知ることによって伝えられる伝達情報量の平均値。数
学的には,この尺度は
)
,
(
)
,
(
)
,
(
1
1
j
i
n
i
m
j
j
i
y
x
T
y
x
p
Y
X
T
∑∑
=
=
=
で表される。
ここで,X= {x1,……,xn} は事象xi (i=1,……,n) の
集合,Y= {y1,……,ym} は事象yj (j=1,……,m) の
集合,T (xi, yj) はxi並びにyjの伝達情報量,及びp (xi, yj)
は両事象の結合確率である。
備考1. 平均伝達情報量はX及びYに関して対称で
ある。二つの事象集合X及びYがあったと
き,平均伝達情報量は,Xのエントロピーと,
Yに関するXの条件付きエントロピーとの
差に等しい。すなわち,
T (X, Y) =H (X) −H (X | Y) =H (Y) −H(Y | X)
=T (Y, X)
である。
2. Xを情報源での特定の通報の集合とし,Yを
通報受端での特定の通報の集合としたと
き,平均伝達情報量は,その通信路を通し
て送られる情報の尺度である。平均伝達情
報量は,情報源でのエントロピーとあいま
い量との差に等しく,通報受端でのエント
ロピーと散布量との差にも等しい。
mean transinformation
content,
average transinformation
content
16.04.09
1文字当たりの平均
エントロピー,
1文字当たりの平均
情報量,
1文字当たりの情報
速度
定常情報源から出されるすべての通報に対する1文字当
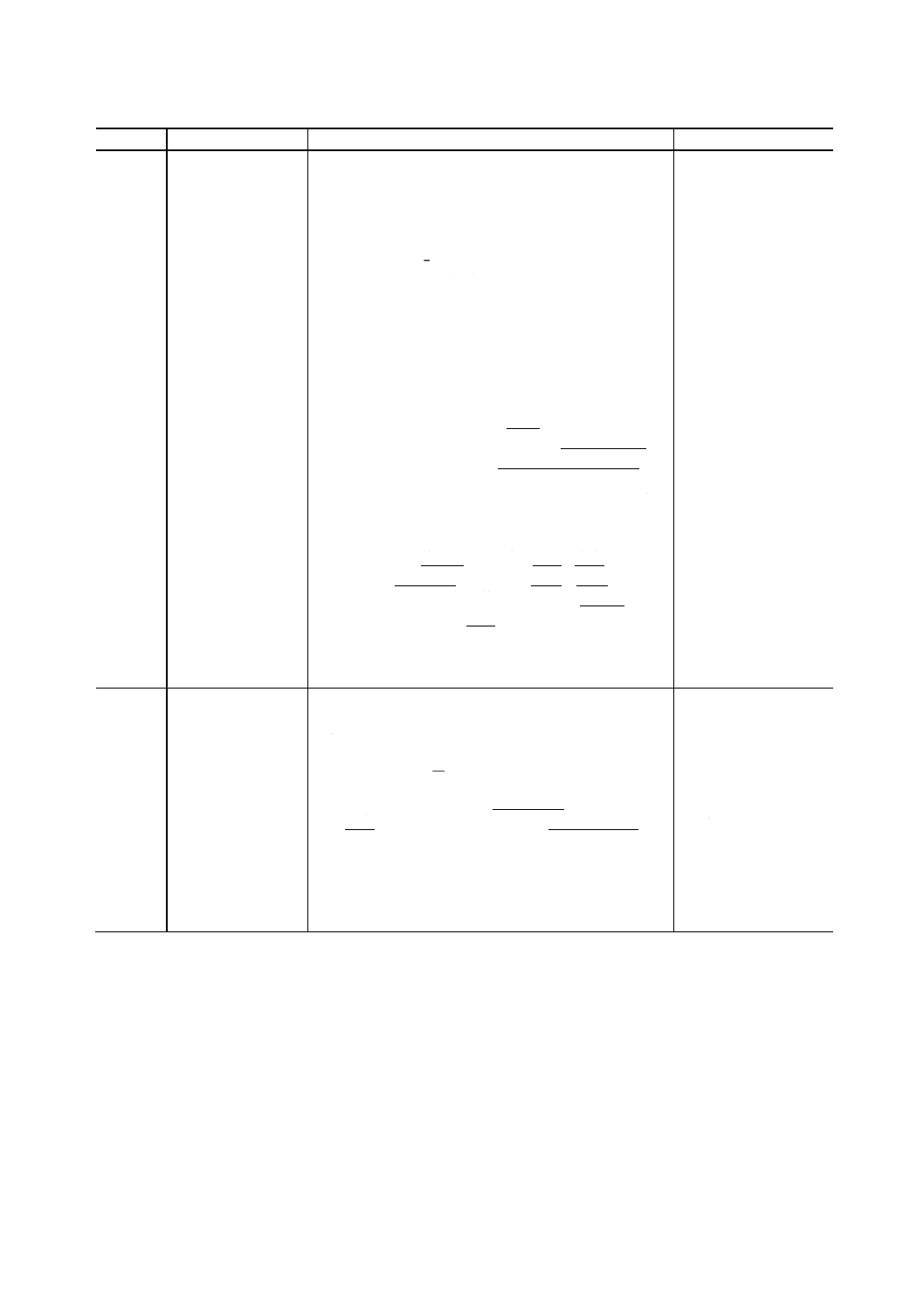
たりのエントロピーの平均値。数学的には,この尺度H'
は極限値
m
H
H
m
m∞
→
=
′
lim
で表される。ここで,Hmは定常情報源から出されるm
個の文字から成る全系列についてのエントロピーであ
る。
備考1. 1文字当たりの平均エントロピーは,Sh/文
字などの単位で表現される。
2. 情報源が定常でないならば,この極限値は
存在しない場合がある。
character mean entropy,
character mean
information content,
character average
information content,
character information
rate
8
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語
16.04.10
(平均)情報速度
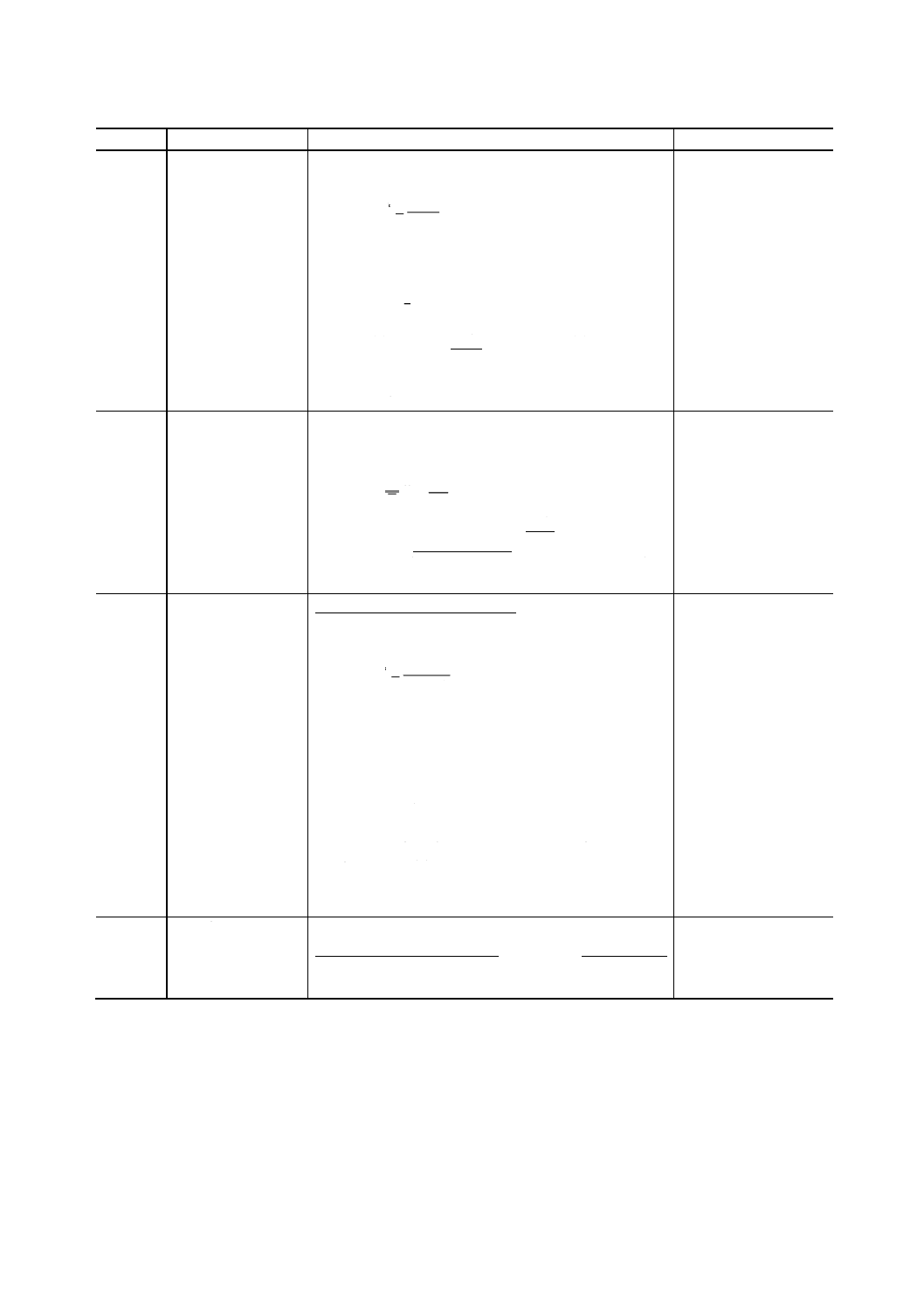
1文字当たりの平均エントロピーH'を文字の時間長さの
平均値で割ったもの。数学的には,この尺度H*は
)
(X
t
H
H
′
=
で表される。ここで,X={x1,……,xn} は文字xi(i=1,
……,n)の集合であり,
∑
=
=
n
i
i
ix
t
x
p
X
t
1
)
(
)
(
)
(
は確率p (xi) で生じる文字xiの時間長さt (xi) の平均値で
ある。
備考 平均情報速度はSh/秒などの単位で表現され
る。
(average) information
rate
16.04.11
1文字当たりの平均
伝達情報量
定常情報源から出されるすべての通報に対する平均伝達
情報量の1文字当たりの平均値。数学的には,この尺度
T'は,極限値
m
T
T
m
m∞
→
=
′
lim
で表される。ここで,Tmはm個の文字から成る入力及び
出力の系列間の平均伝達情報量である。
備考 1文字当たりの平均伝達情報量は,Sh/文字な
どの単位で表現される。
character mean
transinformation
content
16.04.12
平均伝達情報速度
1文字当たりの平均伝達情報量T'を,入力文字及び出力
文字の対の時間の平均値で割ったもの。数学的には,こ
の尺度T*は,
)
,
(
Y
X
t
T
T
′
=
で表される。
ここで,X= {x1,……,xn} は入力文字xi (i=1,……,
n)の集合, Y= {y1,……,ym} は出力文字yj (j=1,…
…,m)の集合,及び
)
,
(
)
,
(
)
,
(
1
1
j
i
n
i
m
j
j
i
y
x
t
y
x
p
Y
X
t
∑∑
=
=
=
は結合確率p (xi,yj) で生起する文字の組 (xi, yj) の時間
長t (xi, yj) の平均値である。
備考 平均伝達情報速度は,Sh/秒などの単位で表
現される。
average transinformation
rate
16.04.13
通信路容量
情報源から通報を伝送する際の通信路の能力の尺度。1
文字当たりの平均伝達情報量の最大値又は平均伝達情報
速度の最大値で表現される。この最大値は適当な符号を
用いれば,任意の小さな誤り確率で達成できる。
channel capacity
9
X 0016 : 1997 (ISO/IEC 2382-16 : 1996)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
情報処理用語−情報理論用語JIS原案作成委員会 構成表
氏名
所属
(委員長)
大 野 義 夫
慶應義塾大学理工学部電気工学科
飯 田 実
三菱電機株式会社
今 井 秀 樹
東京大学生産技術研究所
魚 木 五 夫
産能大学経営情報学部
小 川 正 純
株式会社日立製作所
兼 谷 明 男
通商産業省工業技術院
金 子 敏 信
東京理科大学理工学部電気工学科
下 田 宏 一
日本ユニシス株式会社
高 橋 行 俊
国際電信電話株式会社研究所
中 川 正 雄
慶應義塾大学理工学部電気工学科
比田井 裕
株式会社東芝
森 宗 正
規格調整専門委員
因 幸二郎
財団法人日本規格協会
(事務局)
及 川 清
社団法人情報処理学会