R 1674:2007
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,社団法人日本ファインセラミックス協会(JFCA)
/財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,日
本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
JIS A 1674には,次に示す附属書がある。
附属書1(規定)等分散検定(F検定)の方法
附属書2(参考)数値例
附属書3(規定)記録様式
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 2
3. 記号 ······························································································································ 2
4. 用語の定義 ····················································································································· 2
5. 試験装置及び器具 ············································································································ 3
6. 試験片及び試験片の加工手順 ····························································································· 3
7. 試験方法 ························································································································ 5
8. 統計的方法 ····················································································································· 6
9. 結果の記録 ····················································································································· 9
附属書1(規定)等分散検定(F検定)の方法 ·········································································· 12
附属書2(参考)数値例 ········································································································ 16
附属書3(規定)記録様式 ····································································································· 18
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
R 1674:2007
ファインセラミックスの加工損傷による
強度変化の統計的判定方法
Statistical analysis for influence of
machining damage on strength of fine ceramics
序文 この規格は,ファインセラミックス製の機械部品又は構造部材の品質に大きな影響を及ぼす加工損
傷について,それが強度に及ぼす影響を客観的に比較する方法を提供することによって,製品の品質管理
を容易にし,信頼性の向上に資することを目的として制定された。これらの目的が達成されることによっ
て,我が国のファインセラミックス製品の技術的競争力は更に高まり,その市場拡大に寄与することが期
待される。
なお,この規格に対応する国際規格は現在制定されていない。
1. 適用範囲 この規格は,ファインセラミックス製の機械部品又は構造部材が,その製造工程において
加工を行った場合,加工によって生じる強度差の有意性を,統計的に判定する方法について規定する。
備考 この規格でいう“強度”とは,通常用いられる“強さ”と同義であって,ここでは簡潔な表記
を行うことを目的に用いられる。
1.1
適用対象とする加工法 この規格は,基本的には同一の加工法を用いて,異なる2種類の加工条件
の下で加工を行った場合に生じる強度差を定量的に求める場合に用いる。
備考1. 加工法とは,機械部品又は構造部材の製造工程において,成形,切断,除去,仕上げなどの
目的で用いる手段のことをいう。セラミックスの加工による表面仕上げにおいては,研削加
工,ラッピング・ポリシングなどの遊離と(砥)粒加工,放電加工,レーザ加工などが用い
られる。
2. 加工条件とは,各々の加工法において加工能率,加工後の表面性状などを支配する設定条件
のことをいい,通常は幾つかの設定値の組合せによって表される。
3. この規格は,強度差を求める簡便な方法(例えば,平均値の相対比較などの方法)では,有
意性の判定が困難な場合に用いる。強度差が明らかに有意とみなせる場合は,この規格を適
用する必要はない。
1.2
強度差の有意性判定 有意性の判定は,比較優位の強度が得られると考えられる一方の加工条件を
基準として,他方の加工条件における強度低下が有意であるか否かを調べることによって行う。
1.3
加工損傷の有無の判定 また,加工の影響がない場合を基準としたときの強度差すなわち強度に影
響を及ぼす加工損傷の有無の判定にも用いることができる。
なお,この場合,基準となる試験片の加工法・加工条件については,この規格の中で規定する。
1.4
研削加工に関する推奨値 この評価法を適用するに当たっては,1.3の場合を除いて加工法は特に規
定しないが,セラミックスに用いられることの多い研削加工については,加工条件などに関する推奨値を
2
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
規格の中に示す。
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0601 製品の幾何特性仕様(GPS)−表面性状:輪郭曲線方式−用語,定義及び表面性状パラメ
ータ
JIS B 0621 幾何偏差の定義及び表示
JIS B 7502 マイクロメータ
JIS R 1601 ファインセラミックスの曲げ強さ試験方法
JIS R 1625 ファインセラミックスの強さデータのワイブル統計解析法
JIS Z 8101-1 統計−用語と記号−第1部:確率及び一般統計用語
JIS Z 8401 数値の丸め方
3. 記号 記号の定義は,次による。
表 1 記号とその定義
記号
定義
a
連続切れ刃間隔
D
と(砥)石直径
f,f1,f2,fw
自由度
fd
平面研削におけると(砥)石軸方向送り量
g
最大と粒切込み深さ
l,L
4点曲げ内スパン及び外スパン
m
ワイブル係数又は形状母数
n,na,nb
試験片の数
Ra
中心線平均粗さ
Sa,Sb
平方和
V,Va,Vb
測定強度値の分散
Vw
と(砥)石周速
vw
加工物速度
w,h
試験片の幅及び高さ
Xai,Xbi
測定強度値
X,
a
X,
b
X
測定強度値の平均
α,αF
危険率又は有意水準
1−αc
信頼係数
Δ
と(砥)石切込み深さ
μ,μa,μb
母平均
σ
母標準偏差
2
σ,
2a
σ,
2b
σ
母分散
4. 用語の定義 この規格で用いる主な用語の定義は,統計的仮説検定に関しては,JIS Z 8101-1に,ワ
イブル統計解析については,JIS R 1625 によるほか,次による。
4.1
加工損傷 セラミックスを加工したとき,加工表面の欠け,表面又は表面直下の微細なき裂,微小
なボイド状の欠陥,残留応力など,機械的又は熱的な原因によって被加工物に生じる変質。
参考 特に研削加工においては,加工方向に依存した方向性をもつき裂が残留することが知られてい
3
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
4.2
研削と(砥)石の目直し 研削と(砥)石表面に分布する摩耗・鈍化した切れ刃から,スティック
と(砥)石,軟鋼などを研削して鋭利な切れ刃を創生する作業。
4.3
研削と(砥)石の形直し 加工に伴うと粒の破砕・脱落で崩れたと(砥)石形状を,スティックと
(砥)石,軟鋼などを研削して修正する作業
参考 セラミックスの研削加工では切れ刃の摩耗・鈍化が進みやすく,これによって被加工物に対す
る機械的,熱的負荷が増大する場合があることから,これを避けるために研削と(砥)石の目直
し,形直しが行われる。
4.4
横軸平面研削盤 水平主軸に取り付けた平形と(砥)石の外周面を用いる研削方式の研削盤をいい,
テーブルの形状・動作の違いによって,角テーブル往復動形と円テーブル回転形の2種類がある。前者の
方がより一般的で加工条件の設定が容易なことから,この規格では,角テーブル往復動形が望ましい。
4.5
レジノイドボンド・ダイヤモンドホイール フェノール樹脂などの熱硬化性合成樹脂でダイヤモン
ドと粒を結合したと(砥)石。無機質又はメタル結合材に比べ被加工物に対するあたりが柔らかい。
4.6
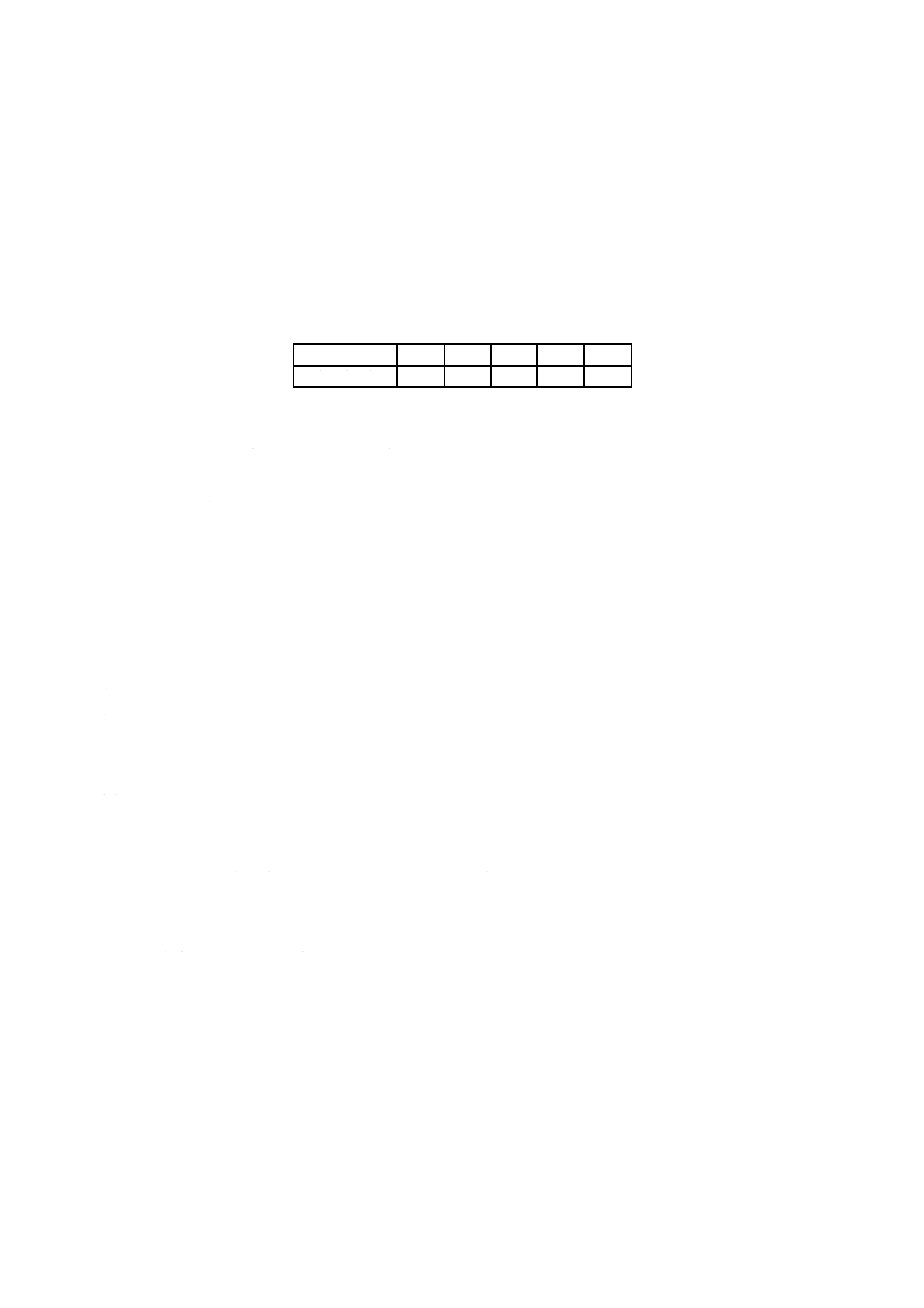
最大と粒切込み深さ と(砥)石表面における個々のと(砥)粒切れ刃による切込み深さの最大値。
横軸平面研削では連続切れ刃の間隔をa,工作物速度及びと(砥)石周速をvw及びVw,毎回のと(砥)石
切込み量をΔ,と(砥)石直径をDとすれば
D
V
v
a
g
∆
×
=
w
w
2
で表せるが,と(砥)石表面の切れ刃はその
間隔,高さとも不ぞろいでgは通常大きく変動する。
4.7
スパークアウト 研削抵抗によると(砥)石軸などの弾性変形で生じる切り残しを,仕上げ面性状
の向上を目的に,と(砥)石切込みを与えることなく数回研削して除去する作業。
4.8
曲げ試験ジグ 材料試験機のテーブルと負荷ロッドとの間に設置し,曲げ試験を高精度,かつ,効
率的に行うための装置。曲げ試験では負荷点,支点の位置決め,試験片の形状など各種の誤差要因が存在
する。曲げ試験ジグはこれらによる測定誤差を極力低減できる構造及び位置決めの容易さが要求される。
4.9
Welchの検定 二組のデータの平均値の差の検定で,統計量
b
2
b
a
2
a
b
a
n
n
X
X
σ
σ
+
−
は,分散が未知ではあ
るが等しいとみなせる場合にはt分布に従い,t検定を行うことができる。しかし,分散が等しいとみなせ
ない場合は,上式の
2
a
σ,
2
b
σをそれぞれの標本分散で置き換えた統計量が,近似的に自由度(f)
)1
(
)
(
)1
(
)
(
)
(
b
2
b
b
a
2
a
a
2
b
b
a
a
−
+
−
+
=
n
n
V
n
n
V
n
V
n
V
f
のt分布に従うことを利用して検定を行うことができる。この検定方法をWelchの検定という。
5. 試験装置及び器具
5.1
研削盤 試験片表面をこの規格に示す条件で加工できる横軸平面研削盤。
5.2
試験機 JIS R 1601に示す4点曲げ試験ができる材料試験機。
5.3 曲げ試験ジグ JIS R 1601 に示す4点曲げ試験及びこの規格で要求する仕様を満たす曲げ試験ジグ。
6. 試験片及び試験片の加工手順
6.1
試験片の数 この規格で用いる試験片は,比較を行う二つの加工条件に対してそれぞれ同数を準備
することを基本とする。ただし,同数の試験片を用意できない場合については,8.7に示すような近似的な
4
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
評価を行う。このとき各加工条件に対して必要な試験片の数は,当事者間の協議により定めることとする
が,統計的評価が可能なように十分な数の試験片を用意しなければならない。
参考 各加工条件に対して同数の試験片を用意する場合,その数は,統計的仮説検定における危険率,
検出すべき強度差,用いる材料のワイブル係数などを基に算出することができる。一般には,
危険率,検出すべき強度差を小さくすると,より多くの試験片を必要とするようになる。表2
に示す数値は,母平均の5 %に相当する強度変化を検出する場合に必要な試験片の数を,危険
率を8.2で規定するα=0.1とし,表3に示すt分布表を用いて計算した例である。
表 2 試験片の数
ワイブル係数
20
15
10
8
5
試験片の数
20
35
75
115
275
6.2
試験片の形状,寸法 試験片の形状は断面が長方形の角柱とし,その寸法は長さが36 mm以上で,
幅は4.0±0.1 mm,厚さは3.0±0.1 mmとする。
6.3
試験片は製造条件が同一と認められる素材から同一の加工法を用いて異なる二つの加工条件で作製
し,強度が比較優位にあると予想される一方をA試験片,他方をB試験片と呼ぶ。
6.4
A試験片及びB試験片は,6.1〜6.3を満たすことができれば実部品から切り出して作製してもよい。
試験片を切り出す場合には,次の点に注意する。
a) 切り出しなどの作業過程で損傷を受けないよう十分注意する。
b) 試験片の切り出しは,実部品の該当箇所に推定される最大引張り応力の方向を試験片の長手方向と一
致させる。
c) b)を満足しない場合は,推定される最大引張り応力の方向と試験片の長手方向との関係を記録する。
d) 最大引張り応力の方向が推定できない場合は,切り出し方向を記録する。
e) 複数の試験片を切り出すに当たり,部位によって加工条件などが異なる可能性がある場合には,その
内容を記録する。
6.5
加工は,6.2に規定した試験片の幅4.0 mmの一つの面について行う。
6.6
試験片の幅4.0 mmの二つの面の平行度は,JIS B 0621に規定された定義に従い0.015 mm以下とす
る。
6.7
A試験片,B試験片とも,それぞれの数の試験片を同時に加工することが望ましい。
6.8
研削加工を評価対象とする場合には,次の点に配慮することが望ましい。
a) 実部品で推定される最大引張り応力の方向とその部位の研削加工方向との関係を再現する。
b) 最大引張り応力の方向が推定できない場合は,加工によって生じる条こん(痕)が試験片の長手方向
と直角方向になるように加工する。
c) 上記のa)およびb)のいずれにも該当しない場合は,その内容及び理由を記録する。
d) 研削加工は,前加工の影響を除くため,あらかじめ両端面を除く4面を,JIS B 0601に準拠した測定
で,表面粗さが0.20 μmRa以下になるように仕上げた長方形断面の試験片を用いる。
e) 加工による表面除去量は100 μm程度とする。
6.9
加工の影響がない場合を基準としたときの強度変化について評価する場合には,次のような条件で
A試験片の加工を行わなければならない。
a) 横軸平面研削盤によって,レジノイドボンド・ダイヤモンドホイールを用いて試験片の長手方向に湿
式研削する。
5
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 砥石は粒度600を標準とし,これより過度に粗粒又は細粒のと(砥)石の使用は避ける。
c) と(砥)石の形直し及び目直しを行わなければならない。その方法としては,低炭素鋼を0.1〜0.2
mm3/mm2研削することを推奨する。ただし,加工条件は,と石切込みを2〜5 μmとし,それ以外は次
のd) と同程度とする。
d) 研削加工条件は,と石周速Vw=1 500 m/min,テーブル速度vw=10 m/min,と石切込みΔ=2 μm,と石
軸方向送りfd=2 mm,スパークアウト2回(と石直径D=200 mmの場合)が望ましい。
備考 直前の目直しからの単位面積当たりの累積研削量が0.2 mm3/mm2以上となると石は目直しを行
ってから使用するのが望ましい。
参考 加工条件と加工損傷との関係については,最大と粒切込み深さ
D
V
v
a
g
Δ
2
w
w
=
(a:連続切れ刃
間隔)を大まかな指標とすることができる。すなわち,gが大きいほど損傷は大きくなる。
6.10 JIS R 1601 に準拠し,表面加工の影響がないことが明らかな4点曲げ強度が測定されている場合に
は,それらの値を7.3のA試験片の強度測定結果とみなすことができる。また,これらのデータはそのま
ま8. のA試験片の強度測定値として使用することができる。
6.11 加工を行った試験片は,りょう(稜)を丸めるか又は面取りをする。
6.12 りょうの加工は,6.9のA試験片の加工に準じる。と石は粒度600を標準とし,試験片の長手方向に
研削する。りょうを面取りした後,評価対象となる加工を行った面の両側の二つのりょうに有害なチッピ
ングがないことを確認する。
7. 試験方法
7.1
強度の測定はJIS R 1601に規定する曲げ試験による。
7.2
測定誤差をできるだけ小さくするため,次の点に配慮することが望ましい。
a) 6.において仕上げられた試験片は,試験片に付着した研削液,水分などをエチルアルコールなどで洗
浄,除去した後,十分乾燥させる。
b) すべての試験片の幅及び厚さを JIS B 7502に規定するマイクロメータなどによって,0.005 mmの精
度以上で測定する。
c) 曲げ試験は4点曲げ負荷とする。支持点スパンは30 mm又は40 mmとし,負荷スパンは前者の場合
は10 mm,後者の場合は20 mmとする。この規格では後者によるのがよい。
d) 曲げ試験に使用するジグは,試験片の幅方向の平行度の不足を補正できる自由度をもつこと。このた
め,例えば,負荷側にボール(球)などを介し,負荷ローラが試験片の幅方向とに均一な線接触を維
持できる構造とする。
e) 曲げ負荷時に,支点及び負荷点で,試験片の長手方向への変移が拘束されることを避けるため,支持
ローラ及び負荷ローラは回転自由度をもつことが望ましい。このとき,4点曲げの内側ローラ(通常
は負荷ローラ)は内方向に,外側ローラ(通常は支持ローラ)は外方向に転動することを考慮し,曲
げ試験ジグはこれを妨げない構造とする。
f)
負荷ローラ,支持ローラなどの曲げジグの構成要素は負荷による塑性変形を回避できる硬度をもたせ
る。
g) 負荷軸に対する曲げジグ(負荷ローラ,支持ローラなど)及び試験片の設置精度は 0.1 mm 以内にす
る。
7.3
強度は,試験片破壊時の最大荷重Pを測定し,次の式にこの値と負荷(内)スパンl,支持(外)ス
6
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
パンL及び個々の試験片の幅w及び高さhを代入して求め,JIS Z 8401に準拠し有効数字3けたに丸める。
(
)
2
3
2
PLl
X
wh
−
=
8. 統計的方法
8.1
左片側検定 この規格では加工後の試験片の強度が比較優位にあると推定される試験片すなわちA
試験片を基準にしたときのB試験片の強度低下の有意性を評価することによって,両者の強度の相対比較
又はA試験片が無損傷とみなせる場合には,損傷の有無の判定を行うことを目的とする。したがって,統
計的仮説検定の手法として左片側検定を採用する。
8.2
危険率 α 検定の危険率はα=0.1とする。
参考 統計的仮説検定では危険率を0.05又はそれより小さい値とすることが多いが,この規格では,
過度に小さい危険率は,強度差の検出に必要な試験片本数の著しい増加を招くことから,通常
よりも高めの値とした。
8.3
A及びB試験片の強度測定値
)
1
(
a
a
n
i
Xi
~
=
,
)
1
(
b
b
n
i
Xi
~
=
から,それぞれの平均
a
X,
b
X,強度値
の平方和Sa,Sb,分散Va,Vbを次式で求める。
∑
=
i
X
n
X
a
a
a
1
∑
=
i
X
n
X
b
a
b
1
(
)2
a
a
2a
a
1∑
∑
−
=
i
i
X
n
X
S
(
)2
b
b
2b
b
1∑
∑
−
=
i
i
X
n
X
S
1
a
a
a
−
=nS
V
1
b
b
b
−
=nS
V
ただし,na,nbはそれぞれの強度値の数で,同数であることを標準とする。
8.4
試験片の数が同数の場合は,8.6の手順に従う。
8.5
試験片の数が異なる場合は,附属書1に示す等分散検定(F検定)を行う。その結果,
a) 等分散の場合は8.6の手順に従う。
b) 等分散が棄却された場合は,8.7の手順に従う。
8.6
8.4及び8.5 a) に該当する場合は,次の手順(t検定)に従う。
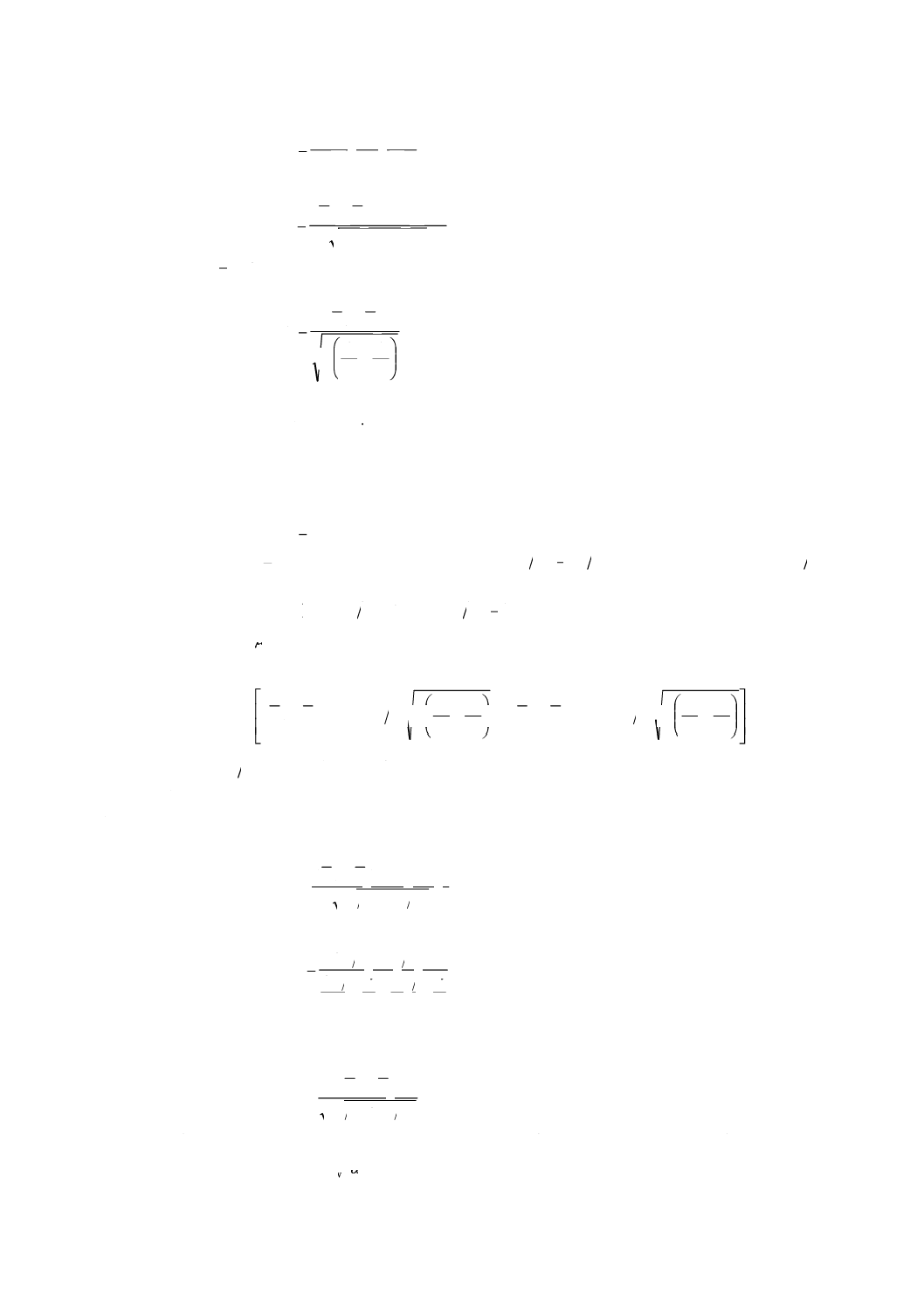
a) 強度の差に関する統計量(u)
b
2b
a
2a
a
b
a
b
)
(
)
(
n
n
X
X
u
σ
σ
μ
μ
+
−
−
−
=
において,母分散
2
a
σ,
2
b
σが,未知ではあるが等しいとみなせる場合には,その母分散に共通の分散
の推定値(V)
7
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1)
(
)1
(
b
a
b
a
−
+
−
+
=
n
n
S
S
V
を用いた統計量(ts)
)
1
1(
)
(
)
(
b
a
a
b
a
b
s
n
n
V
X
X
t
+
−
−
−
=
μ
μ
が,自由度
2
b
a
−
+
=
n
n
f
のt分布に従うことを用い,帰無仮説を
b
a
μ
μ=
として二組の強度データから
次の検定統計量t0を計算する。
+
−
=
b
a
a
b
0
1
1
n
n
V
X
X
t
b) αを危険率として,t分布上で確率
α
α=
>
)]
,
(
[
r
f
t
t
P
を与えるt軸上の点を
)
,
(α
f
t
とする。
)
,
(α
f
t
t −
>
······························································(左片側検定)
が帰無仮説の採択域となる。
c) t分布表(表3)から,
)
,
(α
f
t
を求め,測定値から求めたt0と比較する。
)
,
(
0
α
f
t
t
−
>
−
ならば,平均強度に差があるとはいえない。
)
,
(
0
α
f
t
t
−
≤
ならば,平均強度に差があるといえる。
d) 信頼係数は,
9.0
1
C=
−α
とする。t分布上で,
2
)]
2
,
(
[
C
C
r
α
α
=
>
f
t
t
P
を与えるt軸上の点を
)2
,
(
C
α
f
t
とする。上記a) の統計量tSについて,
C
C
S
C
r
1
)]
2
,
(
)2
,
(
[
α
α
α
−
=
<
<
−
f
t
t
f
t
P
から,強度差
a
bμ
μ−
の100 (1−αC) %信頼区間を求める。信頼区間の上限及び下限は次によって計算
する。
+
+
−
+
−
−
b
a
C
a
b
b
a
C
a
b
1
1
)2
,
(
)
(
,
1
1
)2
,
(
)
(
n
n
V
f
t
X
X
n
n
V
f
t
X
X
α
α
なお,
)2
,
(
C
α
f
t
は,t分布表から求める。
8.7
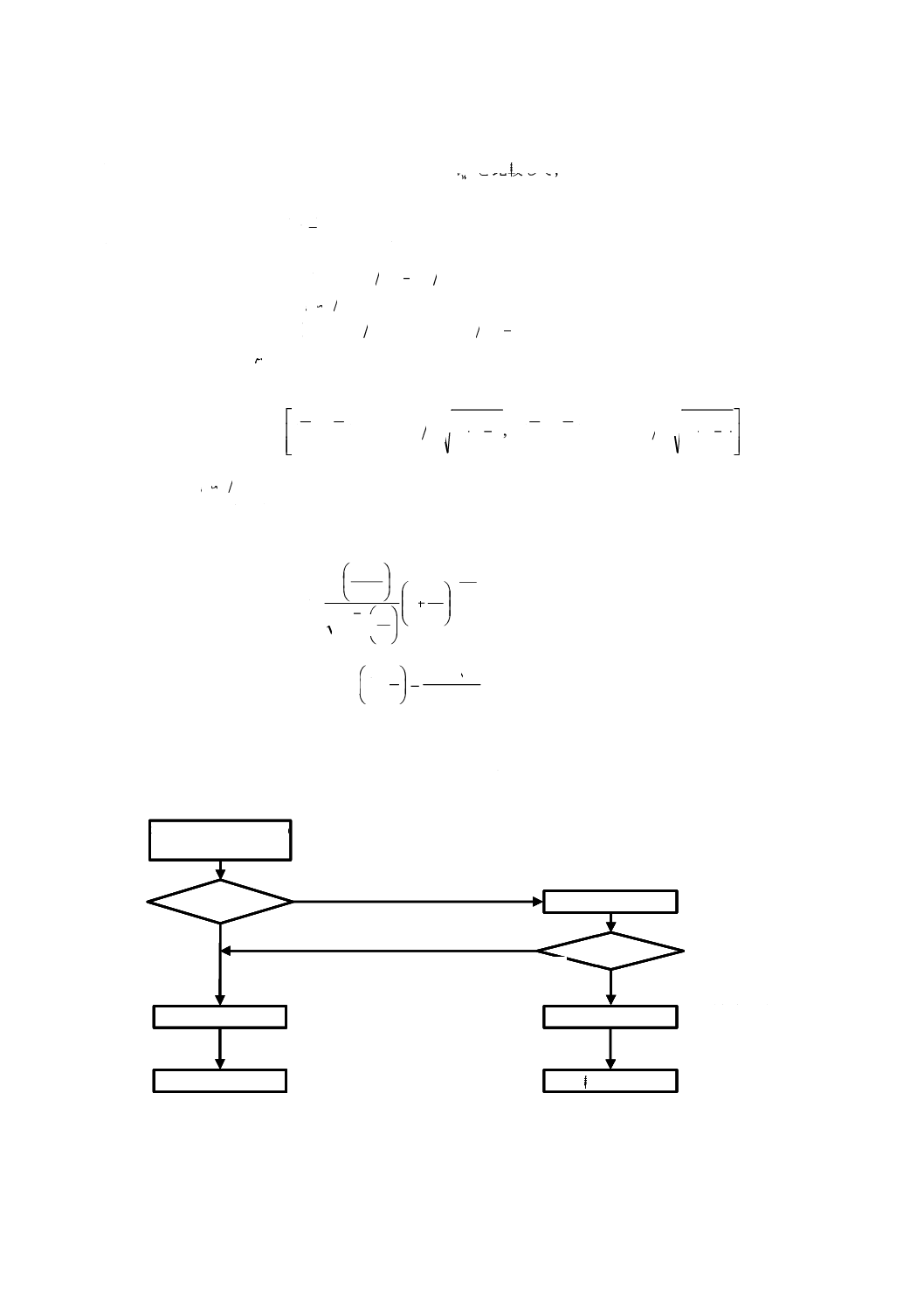
8.5 b) に該当し,t検定が適用できない場合。
a) 8.6 a) の統計量uにおいて,母分散が未知で等しいとはいえない場合には,その母分散に個別に推定
した分散Va,Vbを用いた統計量
b
b
a
a
a
b
a
b
S
)
(
)
(
n
V
n
V
X
X
t
+
−
−
−
=
μ
μ
が,近似的に自由度
1
)
(
1
)
(
)
(
b
2
b
b
a
2
a
a
2
b
b
a
a
w
−
+
−
+
=
n
n
V
n
n
V
n
V
n
V
f
のt分布に従うことを用い,帰無仮説を
b
a
μ
μ=
として二組の強度データから次の検定統計量tw0を計
算する。
b
b
a
a
a
b
w0
n
V
n
V
X
X
t
+
−
=
b) αを危険率として,t分布上で
α
α=
>
)]
,
(
[
w
r
f
t
t
P
を与えるt軸上の点を
)
,
(wα
f
t
とすれば,
)
,
(
wα
f
t
t−
>
····························································(左片側検定)
8
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
が帰無仮説の採択域となる(Welchの検定)。
c) t分布表から
)
,
(wα
f
t
を求め,測定値から求めた
0
wtと比較して,
)
,
(w
0
w
α
f
t
t
−
>
ならば,平均強度に差があるとはいえない。
)
,
(w
0
w
α
f
t
t
−
≤
ならば,平均強度に差があるといえる。
d) 信頼係数は,
9.0
1
C=
−α
とする。t分布上で,
2
)]
2
,
(
[
C
C
w
r
α
α
=
>
f
t
t
P
を与えるt軸上の点を
)2
,
(
C
wα
f
t
とする。上記a) の統計量tSについて,
C
C
w
S
C
w
r
1
)]
2
,
(
)2
,
(
[
α
α
α
−
=
<
<
−
f
t
t
f
t
P
から,強度差
a
bμ
μ−
の100 (1−αC) %信頼区間を求める。信頼区間の上限及び下限は次に基づいて計
算する。
+
+
−
+
−
−
b
b
a
a
C
w
a
b
b
b
a
a
C
w
a
b
)2
,
(
)
(
,
)2
,
(
)
(
n
V
n
V
f
t
X
X
n
V
n
V
f
t
X
X
α
α
なお,
)2
,
(
C
wα
f
t
はt分布表から求める。
8.8
t分布表から
)
,
(α
f
t
などの読み取る手順を計算機で行う場合は,次に示すt分布の確率密度関数を数
値積分する。
()
2
1
2
1
2
Γ
2
1
Γ
+
−
+
+
=
f
f
t
f
f
f
t
p
π
ここで,
()
2
2!
1
2
2
!
k
k
k
k
π
Γ
+
=
(ただし,kは整数)
8.9
8.1〜8.8の手順を附属書2に示す数値を用いた使用例とともに書式化したものを,附属書3に示す。
これらの書式は,解析結果の記録様式としても用いる。
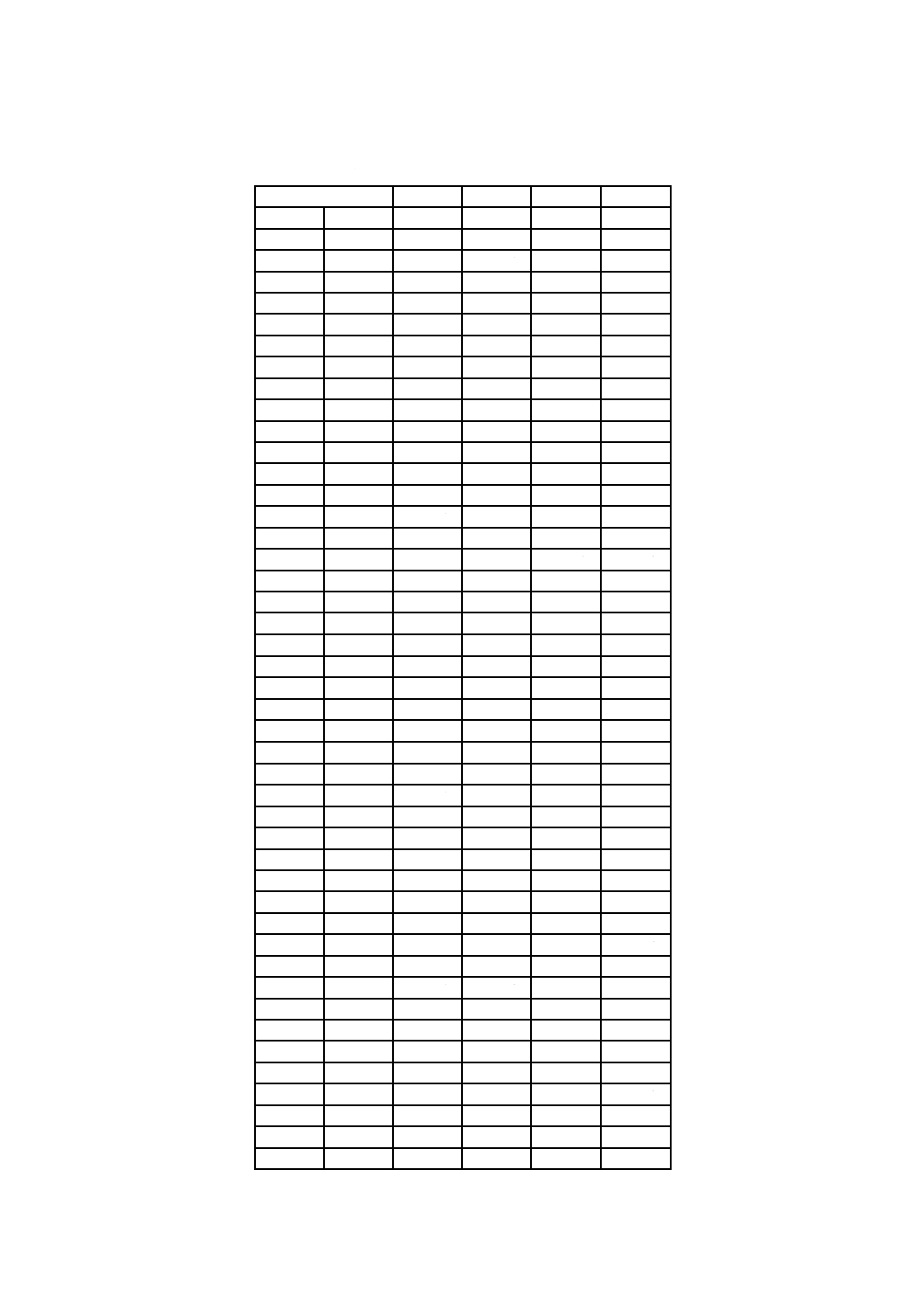
8.10 8.1〜8.8の手順をフローチャート化するとともに,各手順で用いる書式を図1に示す。
注*
図中の書式は附属書3に規定されたものを用いる。
図 1 統計的方法の手順フローチャート
有意水準、信頼係数
の選択
等分散検定
t検定
Welchの検定
A,B同数
0.1
α=
1
0.9
c
α
−
=
【様式2-1】
A,B同数か
A,B同数でない
【様式1】
等分散か
分散に差がない
分散に差がある
【様式2-2】
信頼区間推定
信頼区間推定
【様式3-2】
【様式3-1】
有意水準、信頼係数
の選択
有意水準、信頼係数
の選択
等分散検定
等分散検定
t検定
t検定
Welchの検定
Welchの検定
A,B同数
0.1
α=
1
0.9
c
α
−
=
【様式2-1】
A,B同数か
A,B同数か
A,B同数でない
【様式1】
等分散か
等分散か
分散に差がない
分散に差がある
【様式2-2】
信頼区間推定
信頼区間推定
信頼区間推定
信頼区間推定
【様式3-2】
【様式3-1】
(書式1)*
(書式3-1)*
(書式3-2)*
(書式2-2)*
(書式2-1)*
有意水準,信頼係数の
選択
α=0.1
1−αC=0.9
9
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
9. 結果の記録 結果は,この規格に規定された方法に従って得られたことを明記するとともに,次の項
目について記録しなければならない。
a) A試験片の加工法,加工条件
b) B試験片の加工法,加工条件
c) 切出し試験片の場合,実部品の形状及び切出し部位
d) 試験片の形状及び寸法
e) 強度の試験方法及び試験雰囲気
f)
試験者又は記録者
g) 解析結果
附属書3の書式に従い,次の結果について記録する。
1) 試験片の数na,nb
2) 強度測定値Xai,Xbi
3) 強度の平均
a
X,
b
Xと平均値差
b
a
X
X−
4) 自由度f又はfw
5) 危険率α又はαF
6) 分散Va,Vbと分散比
b
aV
V
7) 強度差の有無の評価結果
8) 信頼係数1−αC及び100 (1−αC)% 信頼区間
10
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
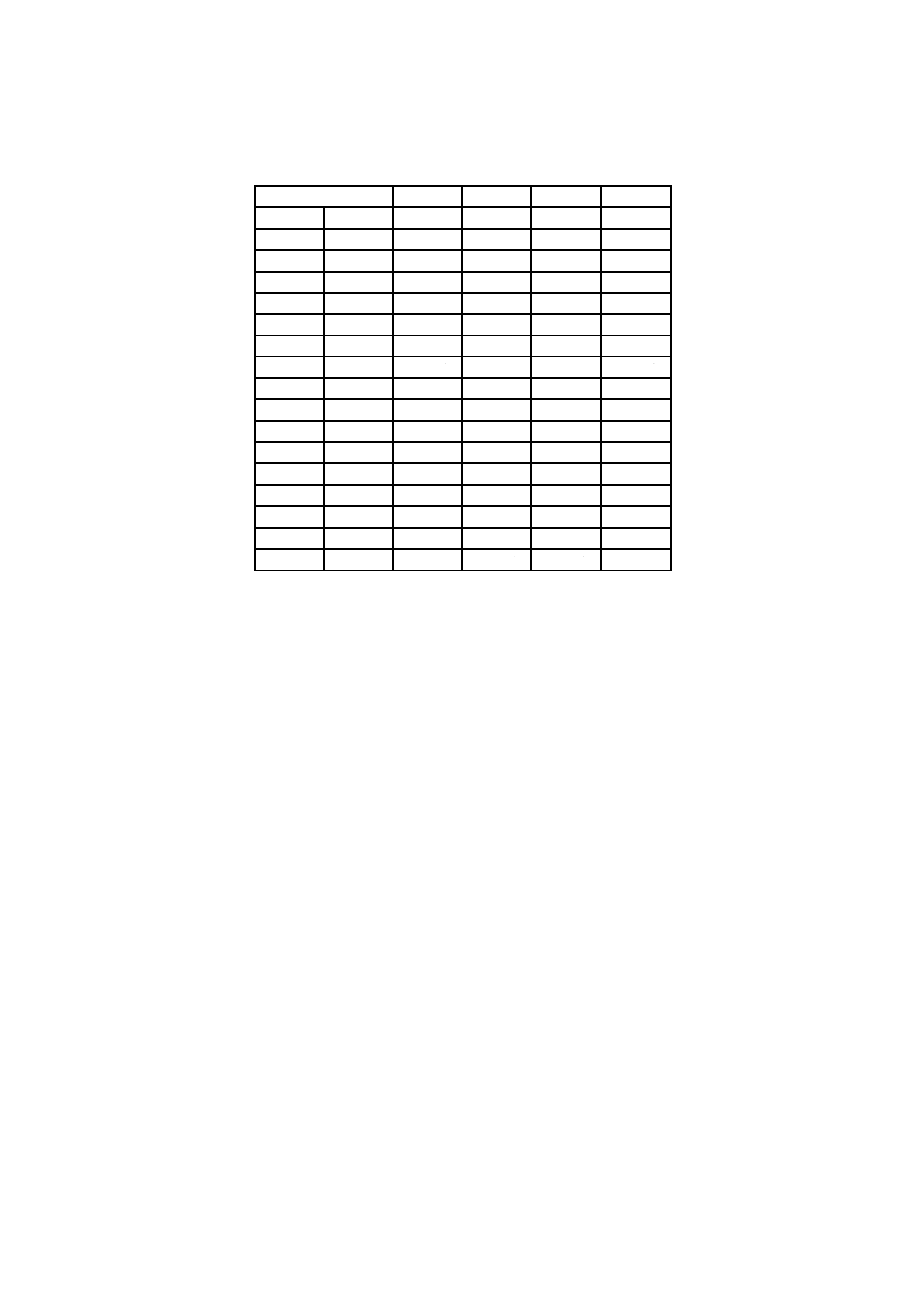
表3 t分布表
α
α=
>
)]
,
(
[
r
f
t
t
P
を満足する
)
,
(α
f
t
の値
α=
0.01
0.025
0.05
0.1
n
f
5
8
2.896 5
2.306 0
1.859 5
1.396 8
6
10
2.763 8
2.228 1
1.812 5
1.372 2
7
12
2.681 0
2.178 8
1.782 3
1.356 2
8
14
2.624 5
2.144 8
1.761 3
1.345 0
9
16
2.583 5
2.119 9
1.745 9
1.336 8
10
18
2.552 4
2.100 9
1.734 1
1.330 4
11
20
2.528 0
2.086 0
1.724 7
1.325 3
12
22
2.508 3
2.073 9
1.717 1
1.321 2
13
24
2.492 2
2.063 9
1.710 9
1.317 8
14
26
2.478 6
2.055 5
1.705 6
1.315 0
15
28
2.467 1
2.048 4
1.701 1
1.312 5
16
30
2.457 3
2.042 3
1.697 3
1.310 4
17
32
2.448 7
2.036 9
1.693 9
1.308 6
18
34
2.441 1
2.032 2
1.690 9
1.307 0
19
36
2.434 5
2.028 1
1.688 3
1.305 5
20
38
2.428 6
2.024 4
1.686 0
1.304 2
21
40
2.423 3
2.021 1
1.683 9
1.303 1
22
42
2.418 5
2.018 1
1.682 0
1.302 0
23
44
2.414 1
2.015 4
1.680 2
1.301 1
24
46
2.410 2
2.012 9
1.678 7
1.300 2
25
48
2.406 6
2.010 6
1.677 2
1.299 4
26
50
2.403 3
2.008 6
1.675 9
1.298 7
27
52
2.400 2
2.006 6
1.674 7
1.298 0
28
54
2.397 4
2.004 9
1.673 6
1.297 4
29
56
2.394 8
2.003 2
1.672 5
1.296 9
30
58
2.392 4
2.001 7
1.671 6
1.296 3
31
60
2.390 1
2.000 3
1.670 6
1.295 8
32
62
2.388 0
1.999 0
1.669 8
1.295 4
33
64
2.386 0
1.997 7
1.669 0
1.294 9
34
66
2.384 2
1.996 6
1.668 3
1.294 5
35
68
2.382 4
1.995 5
1.667 6
1.294 1
36
70
2.380 8
1.994 4
1.669 9
1.293 8
37
72
2.379 3
1.993 5
1.666 3
1.293 4
38
74
2.377 8
1.992 5
1.665 7
1.293 1
39
76
2.376 4
1.991 7
1.665 2
1.292 8
40
78
2.375 1
1.990 8
1.664 6
1.292 5
41
80
2.373 9
1.990 1
1.664 1
1.292 2
42
82
2.372 7
1.989 3
1.663 6
1.292 0
43
84
2.371 6
1.988 6
1.663 2
1.291 7
44
86
2.370 5
1.987 9
1.662 8
1.291 5
45
88
2.369 5
1.987 3
1.662 4
1.291 2
46
90
2.368 5
1.986 7
1.662 0
1.291 0
47
92
2.367 6
1.986 1
1.661 6
1.290 8
48
94
2.366 7
1.985 5
1.661 2
1.290 6
11
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3 t分布表(続き)
α
α=
>
)]
,
(
[
r
f
t
t
P
を満足する
)
,
(α
f
t
の値
α=
0.01
0.025
0.05
0.1
n
f
49
96
2.365 8
1.985 0
1.660 9
1.290 4
50
98
2.365 0
1.984 5
1.660 6
1.290 3
55
108
2.361 4
1.982 2
1.659 1
1.289 4
60
118
2.358 4
1.980 3
1.657 9
1.288 8
80
158
2.350 2
1.975 1
1.654 6
1.286 9
100
198
2.345 3
1.972 0
1.652 6
1.285 8
120
238
2.342 1
1.970 0
1.651 3
1.285 1
150
298
2.338 9
1.968 0
1.650 0
1.284 4
200
398
2.335 8
1.965 9
1.648 7
1.283 7
400
798
2.331 0
1.962 9
1.646 8
1.282 6
600
1 198
2.329 5
1.961 9
1.646 1
1.282 3
800
1 598
2.328 7
1.961 4
1.645 8
1.282 1
1 000
1 998
2.328 2
1.961 2
1.645 6
1.282 0
2 000
3 998
2.327 3
1.960 6
1.645 2
1.281 8
10 000
19 998
2.326 5
1.960 1
1.644 9
1.281 6
∞
2.326 4
1.960 0
1.644 9
1.281 6
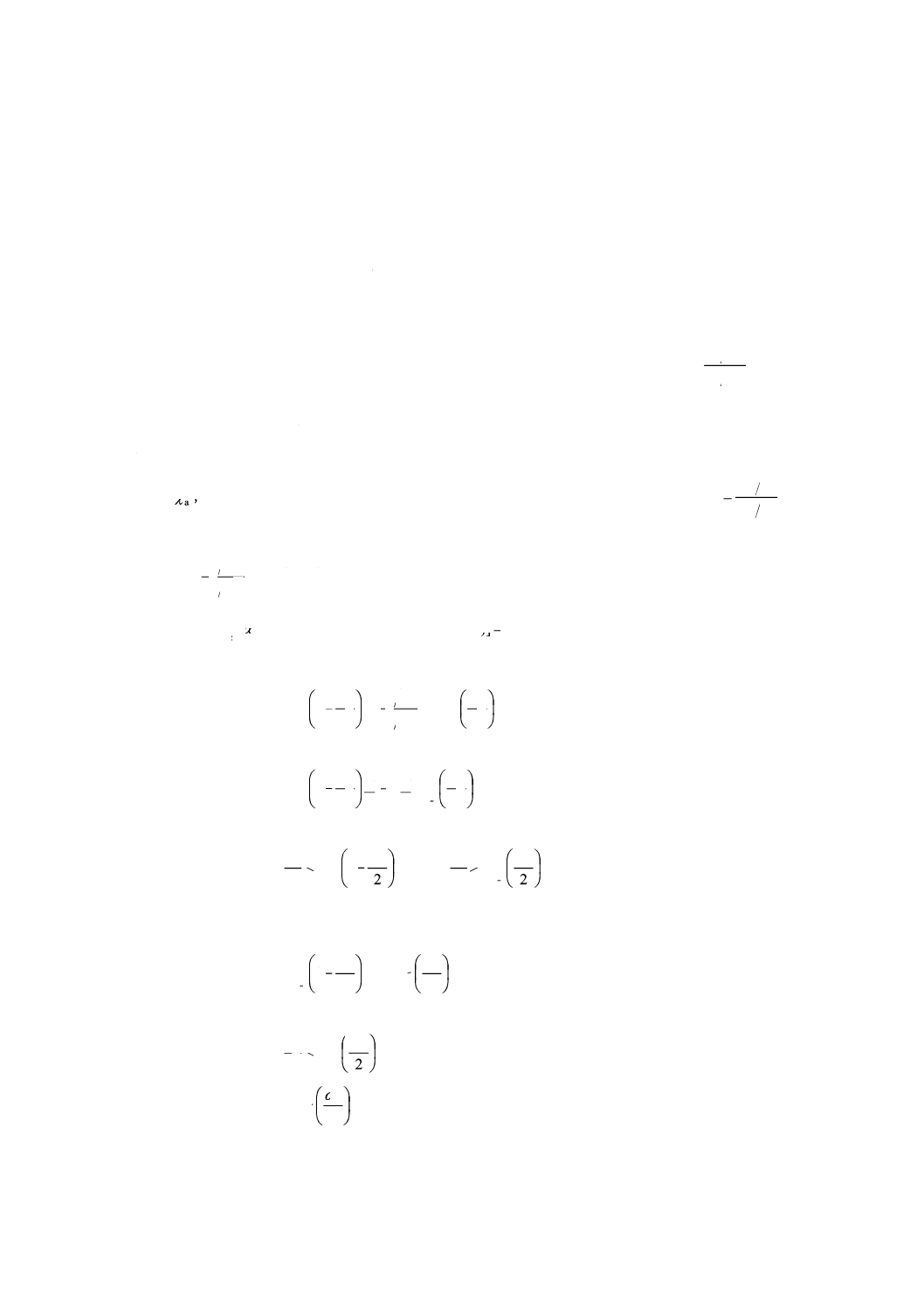
12
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1(規定)等分散検定(F検定)の方法
この規格では二組の強度データは同数であることを標準としている。一方,データ数が異なる場合は,
等分散検定を行い,等分散の場合は t 検定,等分散でない場合はWelchの検定を用いる。次にその手順
を示す。
1. 二組の強度値Xai,Xbiのそれぞれの母分散を
2
a
σ,
2
b
σ標本分散をVa,Vbとすれば,
2b
b
2a
a
σ
σ
V
V
はF分布(1)
に従うことを用いて統計的仮説検定を行う。帰無仮説Xai,Xbiのそれぞれの母分散が等しい。すなわち,
2
a
σ=
2
b
σ
とおく。
注(1)
2
aχ,
2
b
χが互いに独立して,それぞれ自由度fa,fb のχ二乗分布に従うとき,
b
2b
a
2a
f
f
F
χ
χ
=
がなす
分布を自由度(fa,fb )のF分布という。二組のデータの母分散と標本分散との比に関し,
2b
b
2a
a
σ
σ
V
V
F=
は,自由度(na−1,nb−1)のF分布に従う。
αFを危険率,
)
(
F
1
2α
f
f
F
をαF点{F分布で
F
F)]
(
[
1
2
α
α
=
f
f
F
F
P>
となる点}におけるF軸上の値,f1,f2 を分
子及び分母の自由度(Va>Vbの場合)とするとき,次の式が満足されるか否かを判定する。
−
2
2
1
F
2b
b
2a
a
F
1
2
1
2
α
σ
σ
α
f
f
f
f
F
V
V
F
<
<
したがって,
−
2
2
1
F
b
a
F
1
2
1
2
α
α
f
f
f
f
F
V
V
F
≦
≦
が帰無仮説の採択域となり,
−2
1
F
b
a
1
2
α
f
f
F
V
V<
及び
2F
b
a
1
2
α
f
f
F
V
V>
が棄却域となる。
なお,棄却域の前者は,
−
2
/1
2
1
F
F
2
1
1
2
α
α
f
f
f
f
F
F
=
を用いれば,
2F
b
a
2
1
α
f
f
F
V
V<
であり,これはVa>Vb では
1
2
F
2
1
≧
α
f
f
F
を考慮すれば常に不成立となる。したがって,標本分散の大きい
方を分子にして,

13
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2F
b
a
1
2
α
f
f
F
V
V>
だけを評価対象とすればよい。
2. 二組の強度データの分散比
0Fを本体8.3の結果を用い,次の式によって求める。
Va>Vbのとき
b
a
0
V
V
F=
Va<Vbのとき
a
b
0
V
V
F=
3. 自由度f1,f2を次によって求め,これを用いて
2F
2
1
α
f
f
F
をF分布表(附属書1表1)から求める。た
だし,α F=0.1とする。
4. F0と
2F
2
1
α
f
f
F
との比較によって分散の差の有意性を検定する。
Va>Vbのとき
1
a
1
−
=n
f
1
b
2
−
=n
f
Va<Vbのとき
1
b
1
−
=n
f
1
a
2
−
=n
f
2F
0
2
1
α
f
f
F
F<
ならば,分散に差があるとはいえない。
2F
0
2
1
α
f
f
F
F≧
ならば,分散に差があるといえる。
5. 1.〜 4.の手順を計算機で行う場合は,F分布表を用いる代わりに,次のF分布の密度関数を数値積分
する。
()
+
+
=
+
−
−
2
Γ
2
Γ
2
Γ
1
2
1
2
1
2
2
1
1
2
2
2
1
2
1
1
1
f
f
f
f
x
f
f
x
f
f
x
p
f
f
f
f
ここで,
()
2
2!
1
2
2
!
k
k
k
k
π
Γ
+
=
(k は整数)とする。

14
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1表1 F分布表
2
2
F
F
r
1
2
α
α
=
f
f
F
F
P
>
を満足する
2F
1
2
α
f
f
F
の値,
1.0
F=
α
f2
f1
1
2
3
4
5
6
7
8
9
10
12
1
161
199
216
225
230
234
237
239
241
242
244
2
18.5
19.0
19.2
19.2
19.3
19.3
19.4
19.4
19.4
19.4
19.4
3
10.1
9.55
9.28
9.12
9.01
8.94
8.89
8.85
8.81
8.79
8.74
4
7.71
6.94
6.59
6.39
6.26
6.16
6.09
6.04
6.00
5.96
5.91
5
6.61
5.79
5.41
5.19
5.05
4.95
4.88
4.82
4.77
4.74
4.68
6
5.99
5.14
4.76
4.53
4.39
4.28
4.21
4.15
4.10
4.06
4.00
7
5.59
4.74
4.35
4.12
3.97
3.87
3.79
3.73
3.68
3.64
3.57
8
5.32
4.46
4.07
3.84
3.69
3.58
3.50
3.44
3.39
3.35
3.28
9
5.12
4.26
3.86
3.63
3.48
3.37
3.29
3.23
3.18
3.14
3.07
10
4.96
4.10
3.71
3.48
3.33
3.22
3.14
3.07
3.02
2.98
2.91
11
4.84
3.98
3.59
3.36
3.20
3.09
3.01
2.95
2.90
2.85
2.79
12
4.75
3.89
3.49
3.26
3.11
3.00
2.91
2.85
2.80
2.75
2.69
13
4.67
3.81
3.41
3.18
3.03
2.92
2.83
2.77
2.71
2.67
2.60
14
4.60
3.74
3.34
3.11
2.96
2.85
2.76
2.70
2.65
2.60
2.53
15
4.54
3.68
3.29
3.06
2.90
2.79
2.71
2.64
2.59
2.54
2.48
16
4.49
3.63
3.24
3.01
2.85
2.74
2.66
2.59
2.54
2.49
2.42
17
4.45
3.59
3.20
2.96
2.81
2.70
2.61
2.55
2.49
2.45
2.38
18
4.41
3.55
3.16
2.93
2.77
2.66
2.58
2.51
2.46
2.41
2.34
19
4.38
3.52
3.13
2.90
2.74
2.63
2.54
2.48
2.42
2.38
2.31
20
4.35
3.49
3.10
2.87
2.71
2.6
2.51
2.45
2.39
2.35
2.28
21
4.32
3.47
3.07
2.84
2.68
2.57
2.49
2.42
2.37
2.32
2.25
22
4.30
3.44
3.05
2.82
2.66
2.55
2.46
2.40
2.34
2.30
2.23
23
4.28
3.42
3.03
2.80
2.64
2.53
2.44
2.37
2.32
2.27
2.20
24
4.26
3.40
3.01
2.78
2.62
2.51
2.42
2.36
2.30
2.25
2.18
25
4.24
3.39
2.99
2.76
2.60
2.49
2.40
2.34
2.28
2.24
2.16
26
4.23
3.37
2.98
2.74
2.59
2.47
2.39
2.32
2.27
2.22
2.15
27
4.21
3.35
2.96
2.73
2.57
2.46
2.37
2.31
2.25
2.20
2.13
28
4.20
3.34
2.95
2.71
2.56
2.45
2.36
2.29
2.24
2.19
2.12
29
4.18
3.33
2.93
2.70
2.55
2.43
2.35
2.28
2.22
2.18
2.10
30
4.17
3.32
2.92
2.69
2.53
2.42
2.33
2.27
2.21
2.16
2.09
31
4.16
3.30
2.91
2.68
2.52
2.41
2.32
2.25
2.20
2.15
2.08
32
4.15
3.29
2.90
2.67
2.51
2.40
2.31
2.24
2.19
2.14
2.07
33
4.14
3.28
2.89
2.66
2.50
2.39
2.30
2.23
2.18
2.13
2.06
34
4.13
3.28
2.88
2.65
2.49
2.38
2.29
2.23
2.17
2.12
2.05
35
4.12
3.27
2.87
2.64
2.49
2.37
2.29
2.22
2.16
2.11
2.04
36
4.11
3.26
2.87
2.63
2.48
2.36
2.28
2.21
2.15
2.11
2.03
37
4.11
3.25
2.86
2.63
2.47
2.36
2.27
2.20
2.14
2.10
2.02
38
4.10
3.24
2.85
2.62
2.46
2.35
2.26
2.19
2.14
2.09
2.02
39
4.09
3.24
2.85
2.61
2.46
2.34
2.26
2.19
2.13
2.08
2.01
40
4.08
3.23
2.84
2.61
2.45
2.34
2.25
2.18
2.12
2.08
2.00
41
4.08
3.23
2.83
2.60
2.44
2.33
2.24
2.17
2.12
2.07
2.00
42
4.07
3.22
2.83
2.59
2.44
2.32
2.24
2.17
2.11
2.06
1.99
43
4.07
3.21
2.82
2.59
2.43
2.32
2.23
2.16
2.11
2.06
1.99
44
4.06
3.21
2.82
2.58
2.43
2.31
2.23
2.16
2.10
2.05
1.98
45
4.06
3.20
2.81
2.58
2.42
2.31
2.22
2.15
2.10
2.05
1.97
46
4.05
3.20
2.81
2.57
2.42
2.30
2.22
2.15
2.09
2.04
1.97
47
4.05
3.20
2.80
2.57
2.41
2.30
2.21
2.14
2.09
2.04
1.96
48
4.04
3.19
2.8
2.57
2.41
2.29
2.21
2.14
2.08
2.03
1.96
49
4.04
3.19
2.79
2.56
2.40
2.29
2.20
2.13
2.08
2.03
1.96
50
4.03
3.18
2.79
2.56
2.40
2.29
2.20
2.13
2.07
2.03
1.95
55
4.02
3.16
2.77
2.54
2.38
2.27
2.18
2.11
2.06
2.01
1.93
60
4.00
3.15
2.76
2.53
2.37
2.25
2.17
2.10
2.04
1.99
1.92
70
3.98
3.13
2.74
2.50
2.35
2.23
2.14
2.07
2.02
1.97
1.89
80
3.96
3.11
2.72
2.49
2.33
2.21
2.13
2.06
2.00
1.95
1.88
100
3.94
3.09
2.70
2.46
2.31
2.19
2.10
2.03
1.97
1.93
1.85
150
3.90
3.06
2.66
2.43
2.27
2.16
2.07
2.00
1.94
1.89
1.82
200
3.89
3.04
2.65
2.42
2.26
2.14
2.06
1.98
1.93
1.88
1.80
500
3.86
3.01
2.62
2.39
2.23
2.12
2.03
1.96
1.90
1.85
1.77
1 000
3.85
3.00
2.61
2.38
2.22
2.11
2.02
1.95
1.89
1.84
1.76
∞
3.84
3.00
2.60
2.37
2.21
2.10
2.01
1.94
1.88
1.83
1.75

15
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1表1 F分布表(続き)
2
2
F
F
r
1
2
α
α
=
f
f
F
F
P
>
を満足する
2F
1
2
α
f
f
F
の値,
1.0
F=
α
f2
f1
15
20
24
30
40
50
75
100
200
500
∞
1
246
248
249
250
251
252
253
253
254
254
254
2
19.4
19.4
19.5
19.5
19.5
19.5
19.5
19.5
19.5
19.5
19.5
3
8.70
8.66
8.64
8.62
8.59
8.58
8.56
8.55
8.54
8.53
8.53
4
5.86
5.80
5.77
5.75
5.72
5.70
5.68
5.66
5.65
5.64
5.63
5
4.62
4.56
4.53
4.50
4.46
4.44
4.42
4.41
4.39
4.37
4.37
6
3.94
3.87
3.84
3.81
3.77
3.75
3.73
3.71
3.69
3.68
3.67
7
3.51
3.44
3.41
3.38
3.34
3.32
3.29
3.27
3.25
3.24
3.23
8
3.22
3.15
3.12
3.08
3.04
3.02
2.99
2.97
2.95
2.94
2.93
9
3.01
2.94
2.90
2.86
2.83
2.80
2.77
2.76
2.73
2.72
2.71
10
2.85
2.77
2.74
2.70
2.66
2.64
2.60
2.59
2.56
2.55
2.54
11
2.72
2.65
2.61
2.57
2.53
2.51
2.47
2.46
2.43
2.42
2.40
12
2.62
2.54
2.51
2.47
2.43
2.40
2.37
2.35
2.32
2.31
2.30
13
2.53
2.46
2.42
2.38
2.34
2.31
2.28
2.26
2.23
2.22
2.21
14
2.46
2.39
2.35
2.31
2.27
2.24
2.21
2.19
2.16
2.14
2.13
15
2.40
2.33
2.29
2.25
2.20
2.18
2.14
2.12
2.10
2.08
2.07
16
2.35
2.28
2.24
2.19
2.15
2.12
2.09
2.07
2.04
2.02
2.01
17
2.31
2.23
2.19
2.15
2.10
2.08
2.04
2.02
1.99
1.97
1.96
18
2.27
2.19
2.15
2.11
2.06
2.04
2.00
1.98
1.95
1.93
1.92
19
2.23
2.16
2.11
2.07
2.03
2.00
1.96
1.94
1.91
1.89
1.88
20
2.20
2.12
2.08
2.04
1.99
1.97
1.93
1.91
1.88
1.86
1.84
21
2.18
2.10
2.05
2.01
1.96
1.94
1.90
1.88
1.84
1.83
1.81
22
2.15
2.07
2.03
1.98
1.94
1.91
1.87
1.85
1.82
1.80
1.78
23
2.13
2.05
2.01
1.96
1.91
1.88
1.84
1.82
1.79
1.77
1.76
24
2.11
2.03
1.98
1.94
1.89
1.86
1.82
1.80
1.77
1.75
1.73
25
2.09
2.01
1.96
1.92
1.87
1.84
1.80
1.78
1.75
1.73
1.71
26
2.07
1.99
1.95
1.90
1.85
1.82
1.78
1.76
1.73
1.71
1.69
27
2.06
1.97
1.93
1.88
1.84
1.81
1.76
1.74
1.71
1.69
1.67
28
2.04
1.96
1.91
1.87
1.82
1.79
1.75
1.73
1.69
1.67
1.65
29
2.03
1.94
1.90
1.85
1.81
1.77
1.73
1.71
1.67
1.65
1.64
30
2.01
1.93
1.89
1.84
1.79
1.76
1.72
1.70
1.66
1.64
1.62
31
2.00
1.92
1.88
1.83
1.78
1.75
1.70
1.68
1.65
1.62
1.61
32
1.99
1.91
1.86
1.82
1.77
1.74
1.69
1.67
1.63
1.61
1.59
33
1.98
1.90
1.85
1.81
1.76
1.72
1.68
1.66
1.62
1.60
1.58
34
1.97
1.89
1.84
1.80
1.75
1.71
1.67
1.65
1.61
1.59
1.57
35
1.96
1.88
1.83
1.79
1.74
1.70
1.66
1.63
1.60
1.57
1.56
36
1.95
1.87
1.82
1.78
1.73
1.69
1.65
1.62
1.59
1.56
1.55
37
1.95
1.86
1.82
1.77
1.72
1.68
1.64
1.62
1.58
1.55
1.54
38
1.94
1.85
1.81
1.76
1.71
1.68
1.63
1.61
1.57
1.54
1.53
39
1.93
1.85
1.80
1.75
1.70
1.67
1.62
1.60
1.56
1.53
1.52
40
1.92
1.84
1.79
1.74
1.69
1.66
1.61
1.59
1.55
1.53
1.51
41
1.92
1.83
1.79
1.74
1.69
1.65
1.61
1.58
1.54
1.52
1.50
42
1.91
1.83
1.78
1.73
1.68
1.65
1.60
1.57
1.53
1.51
1.49
43
1.91
1.82
1.77
1.72
1.67
1.64
1.59
1.57
1.53
1.50
1.48
44
1.90
1.81
1.77
1.72
1.67
1.63
1.59
1.56
1.52
1.49
1.48
45
1.89
1.81
1.76
1.71
1.66
1.63
1.58
1.55
1.51
1.49
1.47
46
1.89
1.80
1.76
1.71
1.65
1.62
1.57
1.55
1.51
1.48
1.46
47
1.88
1.80
1.75
1.70
1.65
1.61
1.57
1.54
1.50
1.47
1.46
48
1.88
1.79
1.75
1.70
1.64
1.61
1.56
1.54
1.49
1.47
1.45
49
1.88
1.79
1.74
1.69
1.64
1.60
1.56
1.53
1.49
1.46
1.44
50
1.87
1.78
1.74
1.69
1.63
1.60
1.55
1.52
1.48
1.46
1.44
55
1.85
1.76
1.72
1.67
1.61
1.58
1.53
1.50
1.46
1.43
1.41
60
1.84
1.75
1.70
1.65
1.59
1.56
1.51
1.48
1.44
1.41
1.39
70
1.81
1.72
1.67
1.62
1.57
1.53
1.48
1.45
1.40
1.37
1.35
80
1.79
1.70
1.65
1.60
1.54
1.51
1.45
1.43
1.38
1.35
1.32
100
1.77
1.68
1.63
1.57
1.52
1.48
1.42
1.39
1.34
1.31
1.28
150
1.73
1.64
1.59
1.54
1.48
1.44
1.38
1.34
1.29
1.25
1.22
200
1.72
1.62
1.57
1.52
1.46
1.41
1.35
1.32
1.26
1.22
1.19
500
1.69
1.59
1.54
1.48
1.42
1.38
1.31
1.28
1.21
1.16
1.11
1 000
1.68
1.58
1.53
1.47
1.41
1.36
1.30
1.26
1.19
1.13
1.08
∞
1.67
1.57
1.52
1.46
1.39
1.35
1.28
1.24
1.17
1.11
1.00
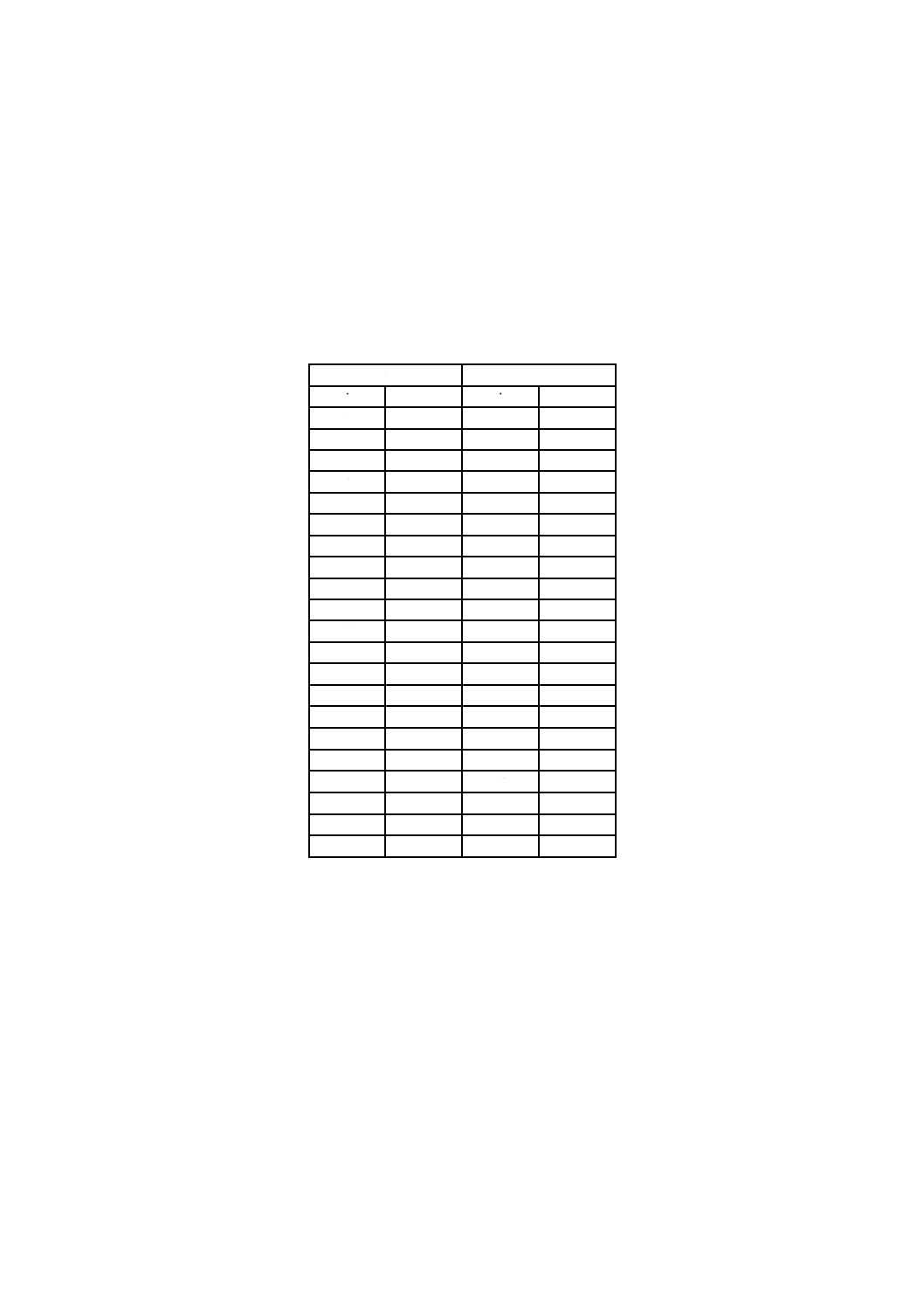
16
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2(参考)数値例
この附属書は,本体及び附属書(規定)に関連する事柄を補足するもので,規定の一部ではない。
1. 附属書3の書式1及び書式3-1のための例
附属書2表1 強度データ(20本,20本)
単位 MPa
A
B
i
Xai
i
Xbi
1
889
1
786
2
780
2
795
3
783
3
679
4
808
4
777
5
816
5
774
6
778
6
782
7
856
7
707
8
817
8
780
9
737
9
816
10
828
10
748
11
857
11
825
12
827
12
806
13
760
13
729
14
837
14
743
15
685
15
729
16
743
16
797
17
790
17
748
18
825
18
804
19
824
19
826
20
834
20
824
na=
20
nb=
20
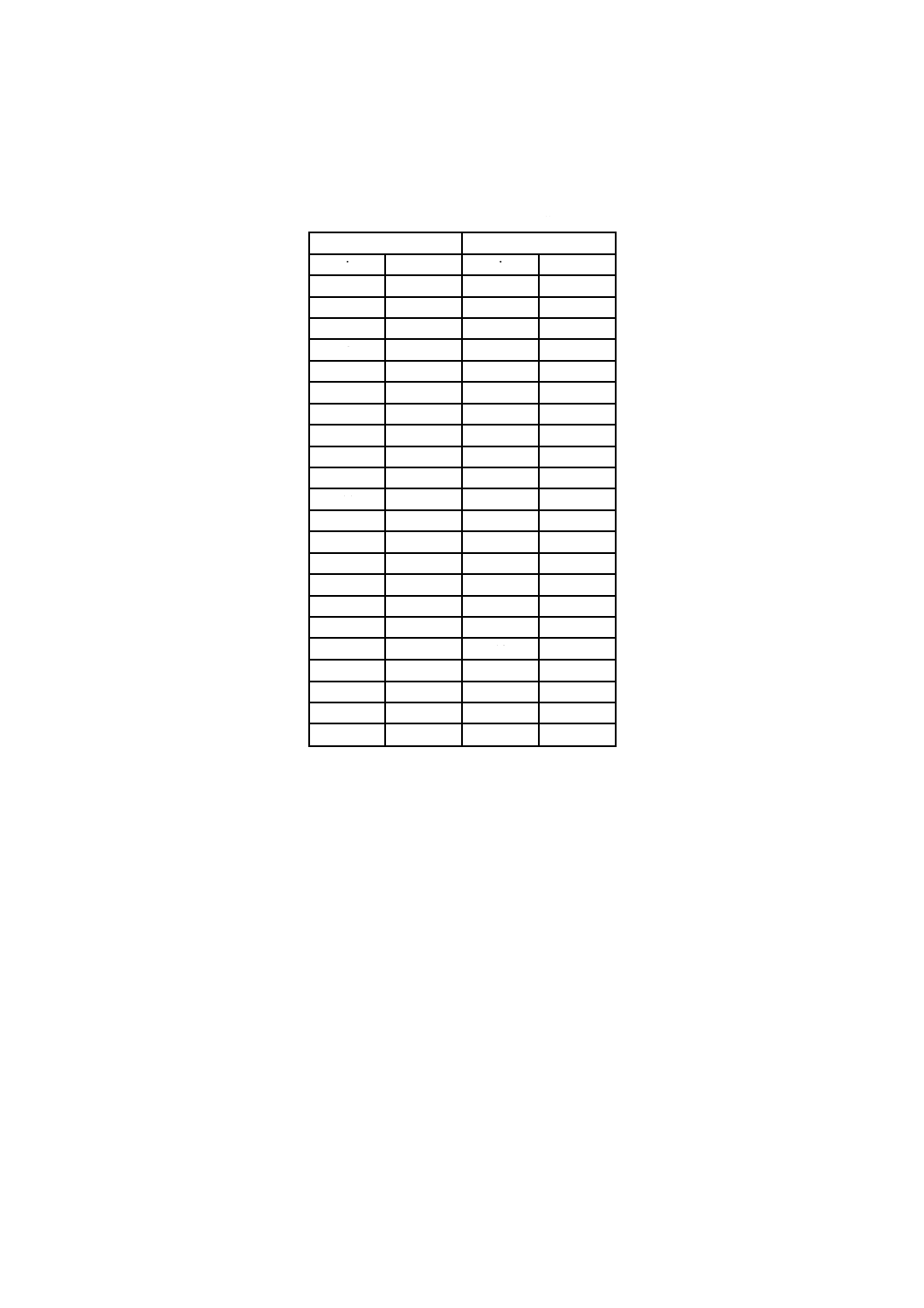
17
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2. 附属書3の書式2-1,書式2-2及び書式3-1のための例
附属書2表2 強度データ(21本,18本)
単位 MPa
A
B
i
Xai
i
Xbi
1
288
1
220
2
304
2
255
3
322
3
260
4
325
4
285
5
333
5
301
6
338
6
314
7
365
7
323
8
366
8
342
9
374
9
353
10
376
10
384
11
383
11
389
12
402
12
401
13
407
13
429
14
411
14
432
15
412
15
460
16
417
16
484
17
431
17
495
18
439
18
525
19
443
20
465
21
488
na=
21
nb=
18
18
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3(規定)記録様式
ここでは,次の評価方法を規定する。各方法は,書式1,書式2-1,書式2-2,書式3-1及び書式3-2に
示す手順に従って実施しなければならない。これらの書式は,解析結果を記入することによって,記録様
式として用いることができる。
a) A,B同数の場合又はA,B同数でなく,かつ,等分散の場合の平均強度の比較(t検定)
解析手順及び記録は書式1による。
b) A,B同数でない場合の分散の比較(F検定)
解析手順及び記録は書式2-1による。
c) A,B同数でなく,かつ,等分散でない場合の平均強度の比較(Welchの検定)
解析手順及び記録は書式2-2による。
d) 平均強度の差の信頼区間(A,B同数の場合又は,A,B同数でなく,かつ,等分散の場合)
解析手順及び記録は書式3-1による。
e) 平均強度の差の信頼区間(A,B同数でなく,かつ,等分散でない場合)
解析手順及び記録は書式3-2による。

19
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式1 A,B同数の場合又はA,B同数でなく,かつ,等分散の場合の平均強度の比較(t検定)
A試験片:加工の影響のない試験片又は相対的に高強度と予想される試験片
B試験片:任意の条件で加工された試験片又は相対的に低強度と予想される試験片
危険率:α=
測定値の個数:
=
an
=
bn
自由度:
=
−
+
=
2
b
an
n
f
統計数値表(表3)から読み取り
=
)
,
(α
f
t
計算
=
a
X
=
b
X
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
=
−
+
−
+
=
1)
(
)1
(
b
a
b
a
n
n
S
S
V
=
+
−
=
b
a
a
b
0
1
1
n
n
V
X
X
t
検定の解釈
)
,
(
0
α
f
t
t
−
>
ならば,平均強度に差があるとはいえない。
)
,
(w
0
w
α
f
t
t
−
≦
ならば,平均強度に差があるといえる。
検定結果
平均強度に差があるといえる。 平均強度に差があるとはいえない。

20
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式1 の使用例
A試験片:附属書2表1 A列
B試験片:附属書2表1 B列
危険率:α=0.1
測定値の個数:
=
an
20
=
bn
20
自由度:
=
−
+
=
2
b
an
n
f
38
統計数値表(表3)から読み取り
=
)
,
(α
f
t
1.304 2
計算
=
a
X
803.70
=
b
X
773.75 (
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
43 196
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
32 592
=
−
+
−
+
=
1)
(
)1
(
b
a
b
a
n
n
S
S
V
1 994.4
=
+
−
=
b
a
a
b
0
1
1
n
n
V
X
X
t
−2.120 7
検定の解釈
)
,
(
0
α
f
t
t
−
>
ならば,平均強度に差があるとはいえない。
)
,
(w
0
w
α
f
t
t
−
≦
ならば,平均強度に差があるといえる。
検定結果
平均強度に差があるといえる。 平均強度に差があるとはいえない。

21
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式2-1 A,B同数でない場合の分散の比較(F検定)
A試験片:加工の影響のない試験片又は相対的に高強度と予想される試験片
B試験片:任意の条件で加工された試験片又は相対的に低強度と予想される試験片
危険率:
=
F
α
測定値の個数:
=
an
=
bn
計算
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
=
−
=
1
a
a
a
n
S
V
=
−
=
1
b
b
b
n
S
V
b
aV
V>
ならば
=
=
b
a
0
V
V
F
=
−
=
1
a
1n
f
=
−
=
1
b
2
n
f
b
aV
V<
ならば
=
=
a
b
0
V
V
F
=
−
=
1
b
1n
f
=
−
=
1
a
2
n
f
統計数値表(附属書1表1)から読み取り
=
2F
1
2
α
f
f
F
検定の解釈
2F
0
1
2
α
f
f
F
F<
ならば,分散に差があるとはいえない。
2F
0
1
2
α
f
f
F
F≧
ならば,分散に差があるといえる。
検定結果
分散に差があるといえる。 分散に差があるとはいえない。
→書式2-2へ進む →書式1へ進む

22
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式2-1 の使用例
A試験片:附属書2表2 A列
B試験片:附属書2表2 B列
危険率:
=
F
α
0.1
測定値の個数:
=
an
21
=
bn
18
計算
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
58 025
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
13 581
=
−
=
1
a
a
a
n
S
V
2 901.3
=
−
=
1
b
b
b
n
S
V
7 989.1
b
aV
V>
ならば
=
=
b
a
0
V
V
F
=
−
=
1
a
1n
f
=
−
=
1
b
2
n
f
b
aV
V<
ならば
=
=
a
b
0
V
V
F
2.75
=
−
=
1
b
1n
f
17
=
−
=
1
a
2
n
f
20
統計数値表(附属書1表1)から読み取り
=
2F
1
2
α
f
f
F
2.23
検定の解釈
2F
0
1
2
α
f
f
F
F<
ならば,分散に差があるとはいえない。
2F
0
1
2
α
f
f
F
F≧
ならば,分散に差があるといえる。
検定結果
分散に差があるといえる。 分散に差があるとはいえない。
→書式2-2へ進む →書式1へ進む

23
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式 2- 2 A,B同数でなく,かつ,等分散でない場合の平均強度の比較(Welchの検定)
A試験片:加工の影響のない試験片又は相対的に高強度と予想される試験片
B試験片:任意の条件で加工された試験片又は相対的に低強度と予想される試験片
分散の検定は書式2-1に従う
危険率:α=
測定値の個数:
=
an
=
bn
計算
=
a
X
=
b
X
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
=
−
=
1
a
a
a
n
S
V
=
−
=
1
b
b
b
n
S
V
=
−
+
−
+
=
1
1
b
2
b
b
a
2
a
a
2
b
b
a
a
w
n
n
V
n
n
V
n
V
n
V
f
=
+
−
=
b
b
a
a
a
b
w0
n
V
n
V
X
X
t
統計数値表(表3)から読み取り
=
)
,
(wα
f
t
検定の解釈
)
,
(w
0
w
α
f
t
t
−
>
ならば,平均強度に差があるとはいえない。
)
,
(w
0
w
α
f
t
t
−
≦
ならば,平均強度に差があるといえる。
検定結果
平均強度に差があるといえる。 平均強度に差があるとはいえない。

24
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式2-2 の使用例
A試験片:附属書2表2 A列
B試験片:附属書2表2 B列
分散の検定は書式2-1に従う
危険率:α=0.1
測定値の個数:
=
an
21
=
bn
18
計算
=
a
X
385.2
=
b
X
369.6
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
58 025
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
13 581
=
−
=
1
a
a
a
n
S
V
2 901.3
=
−
=
1
b
b
b
n
S
V
7 989.1
=
−
+
−
+
=
1
1
b
2
b
b
a
2
a
a
2
b
b
a
a
w
n
n
V
n
n
V
n
V
n
V
f
27.0
=
+
−
=
b
b
a
a
a
b
w0
n
V
n
V
X
X
t
−0.648
統計数値表(表3)から読み取り
=
)
,
(wα
f
t
1.314
検定の解釈
)
,
(w
0
w
α
f
t
t
−
>
ならば,平均強度に差があるとはいえない。
)
,
(w
0
w
α
f
t
t
−
≦
ならば,平均強度に差があるといえる。
検定結果
平均強度に差があるといえる。 平均強度に差があるとはいえない。

25
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
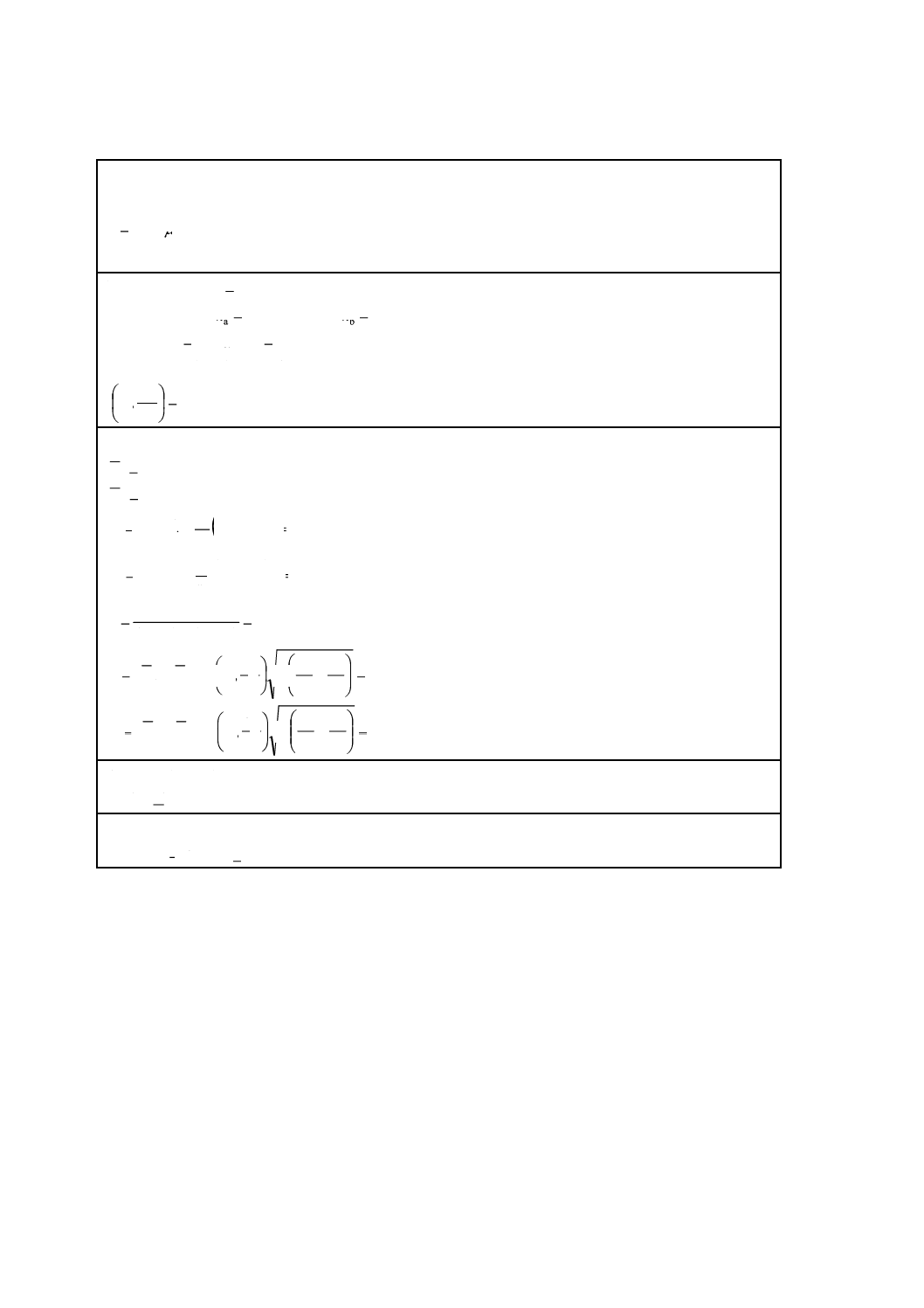
書式3-1 平均強度の差の信頼区間(A,B同数の場合又はA,B同数でなく,かつ,等分散の場合)
A試験片:加工の影響のない試験片又は相対的に高強度と予想される試験片
B試験片:任意の条件で加工された試験片又は相対的に低強度と予想される試験片
A
Bμ
μ−
=
d
の信頼区間
信頼係数:
=
−
C
1α
測定値の個数:
=
an
=
bn
自由度:
=
−
+
=
2
b
an
n
f
統計数値表(表3)から読み取り
=
2
,
C
α
f
t
計算
=
a
X
=
b
X
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
=
−
+
−
+
=
1)
(
)1
(
b
a
b
a
n
n
S
S
V
=
+
−
−
=
b
a
C
a
b
1
1
2
,
)
(
n
n
V
f
t
X
X
C
α
=
+
+
−
=
b
a
C
a
b
1
1
2
,
)
(
n
n
V
f
t
X
X
D
α
∆の100 (1−αC) %信頼区間
D
d
C
≦
≦
結果
≦
≦d
26
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式3-1 の使用例
A試験片:附属書2表1 A列
B試験片:附属書2表1 B列
A
Bμ
μ−
=
d
の信頼区間
信頼係数:
=
−
C
1α
0.9
測定値の個数:
=
an
20
=
bn
20
自由度:
=
−
+
=
2
b
an
n
f
38
統計数値表(表3)から読み取り
=
2
,
C
α
f
t
1.686
計算
=
a
X
803.70
=
b
X
773.75 (
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
43 196
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
32 592
=
−
+
−
+
=
1)
(
)1
(
b
a
b
a
n
n
S
S
V
1 994.4
=
+
−
−
=
b
a
C
a
b
1
1
2
,
)
(
n
n
V
f
t
X
X
C
α
−53.8
=
+
+
−
=
b
a
C
a
b
1
1
2
,
)
(
n
n
V
f
t
X
X
D
α
−6.14
∆の100 (1−αC) %信頼区間
D
d
C
≦
≦
結果
MPa
1.6
8.
53
−
−
≦
≦d

27
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式3-2 平均強度の差の信頼区間(A,B同数でなく,かつ,等分散でない場合)
A試験片:加工の影響のない試験片又は相対的に高強度と予想される試験片
B試験片:任意の条件で加工された試験片又は相対的に低強度と予想される試験片
A
Bμ
μ−
=
d
の信頼区間
信頼係数:
=
−
C
1α
測定値の個数:
=
an
=
bn
計算
=
a
X
=
b
X
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
=
−
=
1
a
a
a
n
S
V
=
−
=
1
b
b
b
n
S
V
=
−
+
−
+
=
1
1
b
2
b
b
a
2
a
a
2
b
b
a
a
w
n
n
V
n
n
V
n
V
n
V
f
=
+
−
=
b
b
a
a
a
b
w0
n
V
n
V
X
X
t
統計数値表(表3)から読み取り
=
2
,
C
w
α
f
t
=
+
−
−
=
b
b
a
a
C
w
a
b
2
,
)
(
n
V
n
V
f
t
X
X
C
α
=
+
+
−
=
b
b
a
a
C
w
a
b
2
,
)
(
n
V
n
V
f
t
X
X
D
α
∆の100 (1−αC) %信頼区間
D
d
C
≦
≦
結果
≦
≦d

28
R 1674:2007
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
書式3-2 の使用例
A試験片:附属書2表2 A列
B試験片:附属書2表2 B列
A
Bμ
μ−
=
d
の信頼区間
信頼係数:
=
−
C
1α
0.9
測定値の個数:
=
an
21
=
bn
18
計算
=
a
X
385.2
=
b
X
369.6
(
)=
−
=
∑
∑
2
a
a
2a
a
1
i
i
X
n
X
S
58 025
(
)=
−
=
∑
∑
2
b
b
2b
b
1
i
i
X
n
X
S
13 581
=
−
=
1
a
a
a
n
S
V
2 901.3
=
−
=
1
b
b
b
n
S
V
7 989.1
=
−
+
−
+
=
1
1
b
2
b
b
a
2
a
a
2
b
b
a
a
w
n
n
V
n
n
V
n
V
n
V
f
27.0
=
+
−
=
b
b
a
a
a
b
w0
n
V
n
V
X
X
t
−0.648
統計数値表(表3)から読み取り
=
2
,
C
w
α
f
t
1.703
=
+
−
−
=
b
b
a
a
C
w
a
b
2
,
)
(
n
V
n
V
f
t
X
X
C
α
−56.7
=
+
+
−
=
b
b
a
a
C
w
a
b
2
,
)
(
n
V
n
V
f
t
X
X
D
α
25.4
∆の100 (1−αC) %信頼区間
D
d
C
≤
≦
結果
MPa
4
25
7
56
.
d
.
≦
≦
−