R 1625:2010
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲 ························································································································· 1
2 引用規格 ························································································································· 1
3 用語及び定義 ··················································································································· 1
4 原理······························································································································· 2
5 統計解析に関するワイブル分布関数 ····················································································· 3
6 統計解析方法 ··················································································································· 3
6.1 強さ試験データ ············································································································· 3
6.2 形状母数及び尺度母数の推定法························································································· 3
7 記録······························································································································· 6
附属書A(参考)最ゆう法を用いた母数推定の解析事例······························································· 7
附属書JA(参考)JISと対応国際規格との対比表 ······································································ 12
R 1625:2010
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,社団法人日本ファ
インセラミックス協会(JFCA)から,工業標準原案を具して日本工業規格を改正すべきとの申出があり,
日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによって,JIS R 1625:1996は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権及び出願公開後の実用新案登録出願にかかわる確認について,責
任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
R 1625:2010
ファインセラミックスの強さデータの
ワイブル統計解析法
Weibull statistics of strength data for fine ceramics
序文
この規格は,2003年に第1版として発行されたISO 20501:2003を基とし,単一モード・2母数ワイブル
統計解析法に対応するため,技術的内容を変更して作成した日本工業規格である。
なお,この規格で側線又は点線の下線を施してある箇所は,対応国際規格を変更している事項である。
変更の一覧表にその説明を付けて,附属書JAに示す。
1
適用範囲
この規格は,ファインセラミックスの室温及び高温における曲げ強さ試験及び引張強さ試験から得られ
る即時破壊強さデータの,形状母数(ワイブル係数)及び尺度母数を求める方法の一つである単一モード・
2母数ワイブル統計解析法について規定する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 20501:2003,Fine ceramics (advanced ceramics, advanced technical ceramics)−Weibull statistics
for strength data(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS R 1600 ファインセラミックス関連用語
JIS R 1601 ファインセラミックスの室温曲げ強さ試験方法
JIS R 1604 ファインセラミックスの高温曲げ強さ試験方法
JIS R 1606 ファインセラミックスの室温及び高温引張強さ試験方法
JIS Z 8401 数値の丸め方
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS R 1600によるほか,次による。
3.1
単一モードワイブル分布
統計処理の対象とする強度データ群のもつ分布の種類であり,破壊原因が1種類だけであり,かつ,ぜ
2
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
い(脆)性破壊を起こした強度データからなる。
3.2
形状母数(ワイブル係数:m)
ワイブル分布における確率密度関数の形状を決めるパラメータで,推定値として扱う。この値が大きい
ほど強さ分布の広がりは小さい。
3.3
尺度母数(β)
2母数ワイブル分布において累積破壊確率が63.2 %となる強さで,推定値として扱う。
3.4
2母数ワイブル分布
形状母数,尺度母数及び位置母数の三つのパラメータのうち,位置母数を0としたワイブル分布。
3.5
最ゆう(尤)法
強さデータから母数を推定する一つの方法。得られた観測値が実現する確からしさ(ゆう度)を最大に
するように母数を決定する方法。
3.6
ワイブルプロット
強さデータを,たて軸lnln (1−F )−1,横軸lnσ に目盛られたグラフにプロットすること。ここでFは累
積破壊確率,σ は強さである。
3.7
データのランク法
強さ又は破壊応力データの順序数[6.2 e) 1)]から累積破壊確率を計算する方法。
3.8
信頼区間
強さデータから推定したパラメータθˆの真値(母数)θ が,あらかじめ定められた一定の確率1−α 以
上で含まれる区間(L
θˆ,U
θˆ)のこと。ここで1−α は信頼係数,α は危険率で,この規格では0.1だけを
用いる。L
θˆ及びU
θˆは,それぞれ下側信頼限界及び上側信頼限界である。
4
原理
この規格は,別途得られたファインセラミックスの室温及び高温における曲げ強さ試験及び引張強さ試
験から得られる即時破壊強さデータを使用し,その材料の強度及びそのばらつきを他の材料と比較したり,
部材設計を行う場合に必要となる破壊確率及び強度の関係を明らかにする統計データを求めることができ
る。統計分布の適用性を厳密にするために,強度試験は破壊起点近傍での単一引張応力場の得られる曲げ
及び引張試験結果に限定し,破壊源も1種類であることを要件にしている。統計量であるから,元となる
強度試験データは多いことが望ましいが,材料のもつばらつきも加味して,得られた結果の確からしさを
表す“信頼区間”も求めることができる。
強度データセットはこの規格の手順に則り,小さい順に並べられ,強度の順位を示すランクを算出する。
その後,最ゆう法といわれる繰り返し計算法によって単一モードワイブル分布の特性を表す,形状母数及
び尺度母数を求める。得られた形状母数,尺度母数及びデータ数によって,信頼区間が算出される。得ら
れた結果は,数値データとともに,図示することで強さと破壊確率との関係が分かりやすく示される。

3
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
統計解析に関するワイブル分布関数
強さデータの解析には,次の式で表す単一モード・2母数ワイブル分布関数を用いる。
()
−
−
=
m
F
β
σ
σ
exp
1
ここに,
F (σ): 単一モード・2母数ワイブル分布関数
m: 形状母数
σ: 強さ又は破壊応力(Pa又はN/mm2)
β: 尺度母数(Pa又はN/mm2)
6
統計解析方法
6.1
強さ試験データ
統計解析の対象とするデータは,曲げ強さ試験データ及び引張強さ試験データとし,その試験方法は,
通常次による。
a) 曲げ強さ試験方法は,JIS R 1601又はJIS R 1604の規定による。
b) 引張強さ試験方法は,JIS R 1606の規定による。
c) 強さ試験は,いずれも30本以上の試験片について行うことが望ましい。
6.2
形状母数及び尺度母数の推定法
ワイブル分布関数の未知母数である形状母数m及び尺度母数βを,最ゆう法によって求め,ワイブルプ
ロット図も作成する。
手順は,次による。
a) ワイブル分布関数又はその確率密度関数に最ゆう法を適用することによって得られる次の式(1)によ
って,形状母数の仮推定値
t
mˆを算出する。
(
)
0
ˆ
1
ˆ
1
ˆ
1
=
×
−
+
∑
∑
∑
=
=
=
n
i
m
i
n
i
i
m
i
n
i
i
t
t
tln
n
ln
m
n
σ
σ
σ
σ
················································ (1)
ここに,
σi (i=1〜n): i番目の試料の強さデータ
n: 強さデータの数
b) 尺度母数の仮推定値
tβˆは,次の式(2)によって算出し,JIS Z 8401の規定によって有効数字3けたに丸
める。また,式(2)において,t
mˆの代わりに式(3)で算出したmˆを代入したときの尺度母数の推定値を,
バイアス補正を行った推定値βˆとする。
t
t
m
n
i
m
i
t
n
ˆ
/1
1
ˆ
1
ˆ =∑
=
σ
β
··································································· (2)
ここに,
t
mˆ: 形状母数の仮推定値
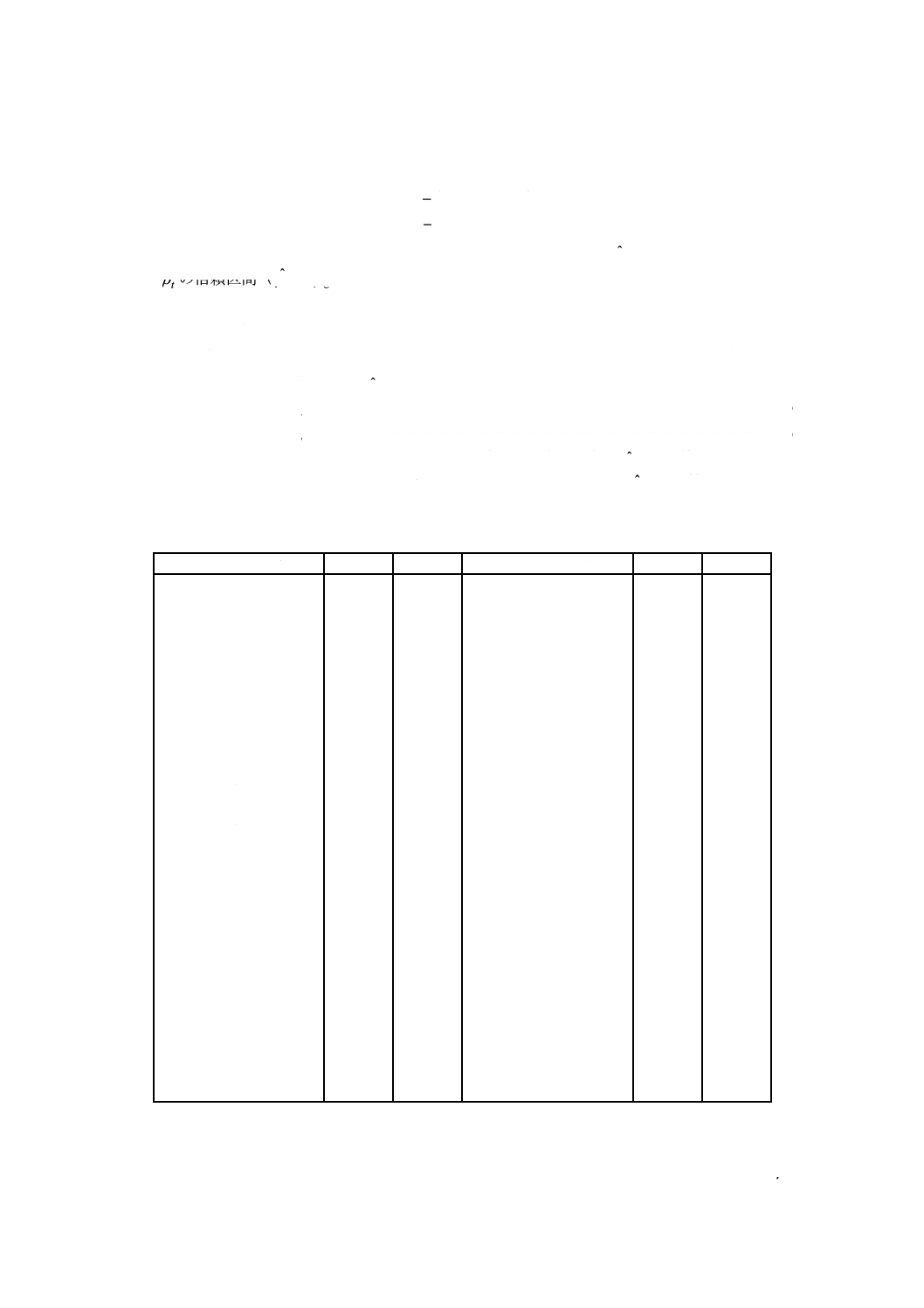
c) 形状母数の推定値mˆは,次の式(3)によって統計上のバイアス補正を行うことによって算出し,JIS Z
8401の規定によって有効数字3けたに丸める。
t
nm
B
m
ˆ
ˆ
×
=
··············································································· (3)
4
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
Bn: バイアスの補正係数
ただし,Bnは試験片本数nの関数とし,次の式による。
n ≦120の場合
1
1.1
)1
04
.2(
−
−
+
×
=
n
Bn
n <120の場合
1
=
n
B
d) 信頼区間 形状母数の仮推定値
t
mˆ(バイアス補正なし)の信頼区間(
L
mˆ,U
mˆ)及び尺度母数の仮推
定値
tβˆの信頼区間(
L
βˆ,U
βˆ)の算出は,次による。
なお,この規格では,危険率は0.1だけを扱う。
1) 形状母数の仮推定値の信頼区間の求め方 信頼係数100×(1−α)=90 %の信頼区間は,表1に規定し
た試験片個数がNのときのq0.05及びq0.95の値を用いて,式(4)及び式(5)によって下側信頼限界
L
mˆ及
び上側信頼限界
U
mˆを算出し,(
L
mˆ,
U
mˆ)と記述する。
95
.0
/
ˆ
ˆ
q
m
m
t
L=
··········································································· (4)
05
.0
/
ˆ
ˆ
q
m
m
t
U=
··········································································· (5)
ここに,
q0.05: 5 %累積出現確率を与える
m
mt/
ˆ
の値
q0.95: 95 %累積出現確率を与える
m
mt/
ˆ
の値
表1−最ゆう法で求めた形状母数の90 %信頼区間に対応する上下信頼限界を与えるq値
試験片数,N
q0.05
q0.95
試験片数,N
q0.05
q0.95
5
0.683
2.779
42
0.842
1.265
6
0.697
2.436
44
0.845
1.256
7
0.709
2.183
46
0.847
1.249
8
0.720
2.015
48
0.850
1.242
9
0.729
1.896
50
0.852
1.235
10
0.738
1.807
52
0.854
1.229
11
0.745
1.738
54
0.857
1.224
12
0.752
1.682
56
0.859
1.218
13
0.759
1.636
58
0.861
1.213
14
0.764
1.597
60
0.863
1.208
15
0.770
1.564
62
0.864
1.204
16
0.775
1.535
64
0.866
1.200
17
0.779
1.510
66
0.868
1.196
18
0.784
1.487
68
0.869
1.192
19
0.788
1.467
70
0.871
1.188
20
0.791
1.449
72
0.872
1.185
22
0.798
1.418
74
0.874
1.182
24
0.805
1.392
76
0.875
1.179
26
0.810
1.370
78
0.876
1.176
28
0.815
1.351
80
0.878
1.173
30
0.820
1.334
85
0.881
1.166
32
0.824
1.319
90
0.883
1.160
34
0.828
1.306
95
0.886
1.155
36
0.832
1.294
100
0.888
1.150
38
0.835
1.283
110
0.893
1.141
40
0.839
1.273
120
0.897
1.133
2) 尺度母数の仮推定値の信頼区間の求め方 信頼係数(1−α)=90 %の信頼区間は,表2に規定した
試験片個数がNのときのt0.05及びt0.95の値を用いて,式(6)及び式(7)によって下側信頼限界
L
βˆ及び

5
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
上側信頼限界U
βˆを算出し,(
L
βˆ,U
βˆ)と記載する。
)
ˆ
/
(
exp
ˆ
ˆ
95
.0
t
t
L
m
t
−
×
=β
β
······························································· (6)
)
ˆ
/
(
exp
ˆ
ˆ
05
.0
t
t
U
m
t
−
×
=β
β
······························································ (7)
ここに,
t0.05: 5 %累積出現確率を与える
β
β/
ˆt
の対数値に
t
mˆを乗じた値
t0.95: 95 %累積出現確率を与える
β
β/
ˆt
の対数値に
t
mˆを乗じた値
表2−最ゆう法で求めた尺度母数の90 %信頼区間に対応する上下信頼限界を与えるt値
試験片数,N
t0.05
t0.95
試験片数,N
t0.05
t0.95
5
−1.247
1.107
42
−0.280
0.278
6
−1.007
0.939
44
−0.273
0.271
7
−0.874
0.829
46
−0.266
0.264
8
−0.784
0.751
48
−0.260
0.258
9
−0.717
0.691
50
−0.254
0.253
10
−0.665
0.644
52
−0.249
0.247
11
−0.622
0.605
54
−0.244
0.243
12
−0.587
0.572
56
−0.239
0.238
13
−0.557
0.544
58
−0.234
0.233
14
−0.532
0.520
60
−0.230
0.229
15
−0.509
0.499
62
−0.226
0.225
16
−0.489
0.480
64
−0.222
0.221
17
−0.471
0.463
66
−0.218
0.218
18
−0.455
0.447
68
−0.215
0.214
19
−0.441
0.433
70
−0.211
0.211
20
−0.428
0.421
72
−0.208
0.208
22
−0.404
0.398
74
−0.205
0.205
24
−0.384
0.379
76
−0.202
0.202
26
−0.367
0.362
78
−0.199
0.199
28
−0.352
0.347
80
−0.197
0.197
30
−0.338
0.334
85
−0.190
0.190
32
−0.326
0.323
90
−0.184
0.185
34
−0.315
0.312
95
−0.179
0.179
36
−0.305
0.302
100
−0.174
0.175
38
−0.296
0.293
110
−0.165
0.166
40
−0.288
0.285
120
−0.158
0.159
e) 強さデータのワイブルプロットは,次の手順で行う。
1) 統計解析を行おうとするn個の強さデータを,強さの小さい順に並べ替える。
2) 各順位i (i=1〜n) のデータに対して次の式(8)(メジアン・ランク法)を用いて累積破壊確率Fiを
算出し,i,σ i,Fiの対応表を作成する。
4.0
3.0
+
−
=ni
Fi
·············································································· (8)
ここに,
n: 強さデータの数(試験片の総数)
6
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
i: 小さい順に並べ替えた順位
Fi: i番目の累積破壊確率
3) 2) の強さの順位iに従って,σ i及びFiの組を,たて軸lnln (1−F )−1,横軸lnσ に目盛られたグラフ
にプロットする。
4) 式(2)及び式(3)で得られた形状母数の推定値mˆ及び尺度母数の推定値βˆを次の式(9)に代入し,ワイ
ブルプロットの回帰直線を引く。
β
σ
ˆ
ˆ
ˆ
)
1(
1
ln
m
ln
m
F
lnln
−
=
−
−
························································· (9)
ここに,
F: 累積破壊確率
mˆ: 式(3)で得られた形状母数の推定値
σ: 強さ又は破壊応力(Pa又はN/mm2)
βˆ: 式(2)で得られた尺度母数の推定値(Pa又はN/mm2)
5) 4) で引いた回帰直線の左右に信頼区間を示す2本の折線を図示することが望ましい。
それらはたて軸をlnln (1−F )−1とし,次のとおりである。
(
0
,
ˆL
lnβ
)を通り,傾きが
L
mˆ及び
U
mˆの線
(
0
,
ˆU
lnβ
)を通り,傾きが
L
mˆ及び
U
mˆの線
7
記録
記録は,次の事項について記載しなければならない。
a) 強さの試験方法
1) 3点曲げ試験,4点曲げ試験,引張試験の別
b) 強さ試験条件
1) 曲げ試験の場合は上下スパン
2) 高温,室温の別,高温下の試験の場合は試験温度
c) 試験片の形状及び寸法
d) 試験片の個数
e) 強さデータ
f)
強さデータの平均値
g) 解析結果
1) 形状母数の推定値mˆ
2) 尺度母数の推定値βˆ
3) 信頼区間(
L
mˆ,
U
mˆ),(
L
βˆ,U
βˆ)
4) ワイブルプロット図
h) 記録者
7
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
最ゆう法を用いた母数推定の解析事例
A.1 使用データ
この解析例で使用する,測定されたデータの例を,表A.1に示す。
A.2 手順
手順を,次に示す。
a) 表A.1の強さデータを,6.2 a) に示す式(1)を用いて,計算機によって数値解析を行い,形状母数の仮
推定値
t
mˆを算出する。
この場合,
t
mˆ=25.5となる。
b) a) で得られた
t
mˆ及び表A.1の強さデータを,6.2 b) に示す式(2)に代入し,尺度母数の仮推定値
tβˆを
算出する。
a) で算出した
t
mˆを用いると,
tβˆ=975.7となる。
c) a) で得られた
t
mˆは,最ゆう法に特有の試験片数に依存する偏りを含むため,6.2 c) に示す式(3)を用
いて,試験片の数に応じて補正係数Bnを算出し,これを仮推定値
t
mˆに乗じてバイアス補正を行った
形状母数の推定値mˆを算出する。n=30の場合,Bn=0.953 8となり,a) で算出した
t
mˆを用いると,mˆ
=24.3となる。さらにバイアス補正を行った尺度母数の推定値βˆは,6.2 b) に示す式(2)にmˆを代入し,
βˆ=974.9となる。
d) 次に,得られた形状母数の仮推定値,尺度母数の仮推定値及び試験片数から信頼区間を算出する。6.2
d) にあるとおり,形状母数の信頼係数90 %の信頼区間を求めるには,表1に規定したq0.05及びq0.95
の値を用い,
t
mˆ(バイアス補正なし)をそれぞれの値で除することによって,次のとおり求める。
1.
19
334
.1/5.
25
/
ˆ
ˆ
95
.0
=
=
=
q
m
m
t
L
1.
31
820
.0/5.
25
/
ˆ
ˆ
05
.0
=
=
=
q
m
m
t
U
同様に,尺度母数の信頼係数90 %の信頼区間を求めるには,表2に規定したt0.05及びt0.95の値を用
い,
tβˆ=975.7から,次のとおり求める。
0.
963
)5.
25
/
334
.0
exp(
7.
975
)
ˆ
/
exp(
ˆ
ˆ
95
.0
=
−
×
=
−
×
=
t
t
L
m
t
β
β
[
]
7.
988
5.
25
/)
338
.0
(
exp
7.
975
)
ˆ
/
exp(
ˆ
ˆ
05
.0
=
−
−
×
=
−
×
=
t
t
U
m
t
β
β
したがって,信頼区間は次のとおりである。
)1.
31
,1.
19
(
)
ˆ,
ˆ(
=
U
Lm
m
)7.
988
,0.
963
(
)
ˆ
,
ˆ
(
=
U
Lβ
β
e) 次の手順で,ワイブルプロット図を作成する。
1) 表A.1の強さデータを,強さの小さい順に並び替え,順位iを付す。
結果を,表A.2の左3列に示す。
2) 6.2 e) 2) に示す式(8)を用いて,順位iに対する累積破壊確率Fiを算出し,更に,
1
)
/1(
−
=
i
i
F
lnln
Y
,
i
iln
X
σ
=
を算出する。得られた結果を,表A.2の右3列に示す。
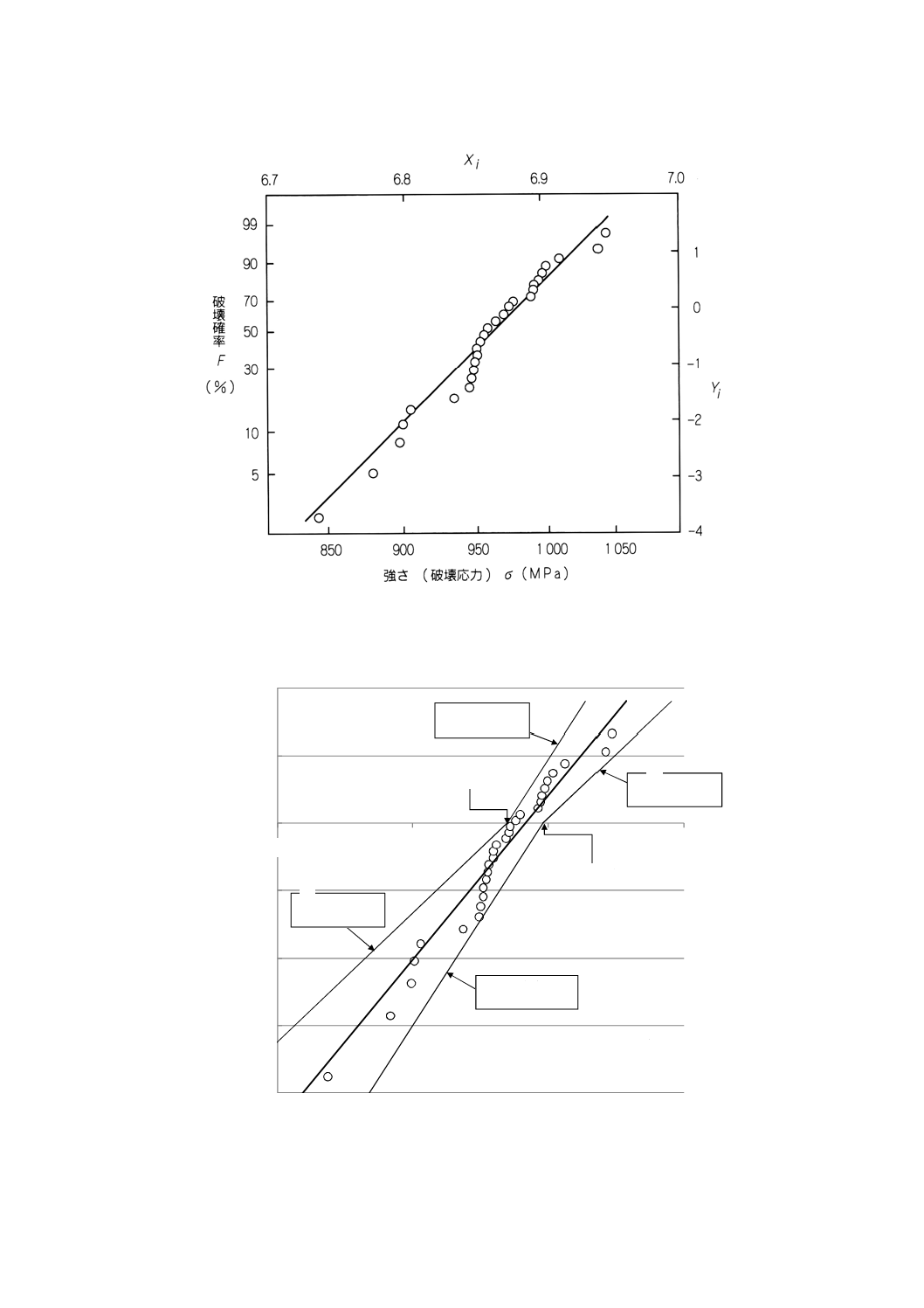
3) Xi及びYiの組を,グラフにプロットする。
表A.2のデータを用いた例を,図A.1及び図A.2に示す。
8
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4) b) 及びc) で得られたmˆ及びβˆを,6.2 e) 4) に示す式(9)に代入した後,二つの任意の累積破壊確率
Fに対し,それぞれの強さσ を算出し,二組の点[lnσ, lnln (1−F)−1]を直線で結び,回帰直線とす
る。
5) 次にワイブルプロット及び回帰直線の左右に90 %信頼区間を表す2本の折線を引く。プロットの左
側に位置する折線は,たて軸,すなわちlnln (1−F)−1がゼロとなる,F=63.2 %におけるよこ軸の値
がlnL
βˆであり,そこから傾きが
U
mˆ及び
L
mˆの折線となる。同様に,プロットの右側に位置する折
線は,たて軸ゼロでのよこ軸の値がlnU
βˆであり,そこから傾きが
U
mˆ及び
L
mˆの折線となる。これ
ら4本の直線を引くには,
β
σ
ln
m
ln
m
F
lnln
−
=
−
−1
)
1(
において,m及びβに,d) で求めた
)1.
31
,1.
19
(
)
ˆ,
ˆ(
=
U
Lm
m
)7.
988
,0.
963
(
)
ˆ
,
ˆ
(
=
U
Lβ
β
のそれぞれの値を代入し,任意の累積破壊確率Fに対して求められる点及び(
L
lnβˆ,0)又は(
U
lnβˆ,0)
を結べばよい。
以上から,プロットした回帰直線の例を,図A.1及び図A.2に示す。
f)
a)〜c) の手順をニュートン・ラプソン法によって数値解析し,補正計算を行うFORTRANによるプロ
グラムの例及びこれに表A.1の強さデータを入力したときの計算結果の出力例を,次に示す。
ニュートン・ラプソン法による数値解析では,たて軸g (m),横軸mに目盛られたグラフにおいて,
mの仮設定値miに対して,g (mi) における接線とm軸との交点のm座標mi+1を求め,これをmiに置
き換える。この計算を繰り返すことによって,有効数字3けたを得るのに十分な精度のm値を計算す
ることができる。このときのmiとmi+1との関係は,次の式で示される。
なお,miの初期設定値には,例えば,強さデータの最大値及び最小値からmを概算し,これを用い
れば収束が速い。
また,式中のσimは,計算機によってはオーバーフローの可能性があるが,強さデータの平均値σm
を求め,ΣσimをσmmΣ (σi / σm) mに置き換えて式を整理することによって避けることができる。
()
()
i
i
i
i
m
g
m
g
m
m
′
−
=
+1
ただし,()
(
)
[
]
(
)
2
1
2
1
1
1
2
2
×
−
×
−
×
−
=
′
∑
∑
∑
∑
=
=
=
=
−
n
i
m
i
n
i
i
m
i
n
i
m
i
n
i
i
m
i
ln
n
ln
n
m
n
m
g
σ
σ
σ
σ
σ
σ
9
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[プログラムの概要]
DOUBLE PRECISION D1, D2, D3, D4, WM, WM1, AS, S(500)
DATA ER/0.0001/, SS/0.0/, SMIN/9999.0/, SMAX/0.0/
ER:ワイブル係数の設定推定精度
DO 10 N=1,500
WRITE(6,100) N
READ(5.*) S(N)
S:強さデータの入力
IF (S(N).EQ,0.0) GO TO 20
全データ入力終了後:0
SS=SS+S(N)
IF (S(N).LT.SMIN) SMIN=S(N)
SMIN:最小強さ
IF (S(N).GT.SMAX) SMAX=S(N)
SMAX:最大強さ
10 CONTINUE
20 N=N−1
N:強さデータの数
AS=SS/N
AS:平均強さ
WM=ALOG (ALOG(N+1.0)/ALOG(1.0+1.0/N)/ALOG(SMAX/SMIN) WM:ワイブル係数の初期設定値
40 D1=0.0
最ゆう法によるワイブル係数の数値解析
D2=0.0
(以下13行)
D3=0.0
D4=0.0
WM1=WM
DO 30 I=1,N
D1=D1+(S(I)/AS)**WM*DLOG(S(I))
D2=D2+(S(I)/AS)**WM
D3=D3+DLOG(S(I))
D4=D4+(S(I)/AS)**WM*(DLOG(S(I)))**2
30 CONTINUE
WM=WM−(1.0/WM+D3/N−D1/D2)/(−(D4*D2−D1**2)/D2**2− mi+1=mi−g(mi)/gʼ(mi)の計算
WM**(−2))
IF (DABS(WM−WM1).GT.ER) GO TO 40
推定精度の確認
SO1=AS*(D2/N)**(1/WM)
SO1:尺度母数の推定値
WM2=WM*(2.04*N**(−1.1)+1.0)**(−1.0)
ワイブル係数の偏り補正
WRITE(6,200)N
N:強さデータの数の出力
WRITE(6,300)AS
AS:平均強さの出力
WRITE(6,400)SO1
SO1:尺度母数の出力
WRITE(6,500)WM2
WM2:偏り補正後のワイブル係数の出力
100 FORMAT(1H+, 2Hi=, 14,5H S=)
200 FORMAT(27H NUMBER OF SPECIMENS = , I 4)
300 FORMAT(27H MEAN STRENGTH = , F8.3)
400 FORMAT(27H WEIBULL SCALE PARAMETER= , F8.3)
500 FORMAT(27H WEIBULL MODULUS = , F8.3)
STOP
END
[表A.1のデータ入力による計算結果の出力例]
NUMBER OF SPECIMENS = 30
MEAN STRENGTH = 956.467
WEIBULL SCALE PARAMETER = 975.720
WEIBULL MODULUS = 24.319
10
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.1−強さデータの例
試験片番号
強さ
σ
(MPa)
試験片番号
強さ
σ
(MPa)
試験片番号
強さ
σ
(MPa)
1
969
11
992
21
899
2
1 005
12
962
22
964
3
946
13
1 040
23
955
4
946
14
953
24
944
5
843
15
996
25
965
6
1 035
16
988
26
883
7
985
17
950
27
948
8
943
18
990
28
949
9
953
19
897
29
987
10
903
20
932
30
972
表A.2−計算結果
強さの順位
I
試験片
番号
強さ
σi
(MPa)
Fi= i−0.3
n+0.4
Yi=
lnln(1−F )−1
Xi=ln σi
1
5
843
0.023
−3.759
6.737
2
26
883
0.056
−2.855
6.783
3
19
897
0.089
−2.375
6.799
4
21
899
0.122
−2.042
6.801
5
10
903
0.155
−1.784
6.806
6
20
932
0.188
−1.572
6.837
7
8
943
0.220
−1.390
6.849
8
24
944
0.253
−1.231
6.850
9
3
946
0.286
−1.087
6.852
10
4
946
0.319
−0.956
6.852
11
27
948
0.352
−0.835
6.854
12
28
949
0.385
−0.722
6.855
13
17
950
0.418
−0.615
6.856
14
9
953
0.451
−0.512
6.860
15
14
953
0.484
−0.414
6.860
16
23
955
0.516
−0.319
6.862
17
12
962
0.549
−0.227
6.869
18
22
964
0.582
−0.136
6.871
19
25
965
0.615
−0.046
6.872
20
1
969
0.648
0.043
6.876
21
30
972
0.681
0.133
6.879
22
7
985
0.714
0.224
6.893
23
29
987
0.747
0.317
6.895
24
16
988
0.780
0.414
6.896
25
18
990
0.813
0.515
6.898
26
11
992
0.845
0.624
6.900
27
15
996
0.878
0.744
6.904
28
2
1 005
0.911
0.884
6.913
29
6
1 035
0.944
1.059
6.942
30
13
1 040
0.977
1.327
6.947
11
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.1−強さデータのワイブルプロットの例
図A.2−強さデータのワイブルプロットの例(信頼区間表示あり)
-4
-3
-2
-1
0
1
2
6.7
6.8
6.9
7.0
を通り
傾きmU
ln
ln
(1
-F
)
-1
lnσ
を通り
傾きmL
を通り
傾きmU
を通り
傾きmL
参考付図2強さデータのワイブルプロットの例(信頼区間表示あり)
)0
,
ˆ
(ln
L
β
)0
,
ˆ
(ln
U
β
)0
,
ˆ
(ln
U
β
)0
,
ˆ
(ln
L
β
)0
,
ˆ
(ln
U
β
)0
,
ˆ
(ln
L
β
)7.
988
,0.
963
(
ˆ
,
ˆ
(
)1.
31
,1.
19
(
ˆ
,
ˆ
(
=
=
U
L
U
Lm
m
β
β
ln
ln
ln
ln
ln
ln
12
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
JISと対応国際規格との対比表
JIS R 1625:2010 ファインセラミックスの強さデータのワイブル統計解析法
ISO 20501:2003 Fine ceramics (advanced ceramics, advanced technical ceramics)−
Weibull statistics for strength data
(I)JISの規定
(II)
国際規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差異の
理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
1適用範
囲
破壊強さデータの,
形状母数(ワイブル
係数)及び尺度母数
を求める方法の一
つである単一モー
ド・2母数ワイブル
統計解析法につい
て規定。
1
単一モード(単一欠陥分
布に対する最ゆう推定)
だけでなく,多重モード
(競合欠陥分布に対する
最ゆう推定)についても
規定。
削除
JISは単一モードだけを規定。 単一モードの方が簡便さがあり,使
いやすく実用性がある。
2引用規
格
3 用語及
び定義
2
用語及び定義
削除
JISは単一モードだけを規定。 JISは競合欠陥分布に対する最ゆう
推定を規定していないので記載は不
要。
4原理
−
−
追加
JISでは原理を規定。
原理について説明するため。
−
−
3
記号
削除
JISでは記載なし。
2定義と用語に記載しているため。
−
−
4
有意性及び使用
削除
JISは単一欠陥分布に対する最
ゆう推定を規定。ISO規格では
Method A単一欠陥分布に対す
る最ゆう推定及びMethod B競
合欠陥分布に対する最ゆう推
定を規定。
単一モードの方が簡便さがあり,使
いやすく実用性がある。
1
2
R
1
6
2
5
:
2
0
1
0
13
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規
格番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇
条ごとの評価及びその内容
(V)JISと国際規格との技術的差異
の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
5 ワイブ
ル分布関
数
2.4.1
単一欠陥分布に対する
最ゆう推定
一致
−
−
6
競合欠陥分布に対する
最ゆう推定
削除
JISでは記載なし。
単一モードの方が簡便さがあり,使
いやすく実用性がある。
6統計解
析方法
6.1 強さ試験デー
タ
6.2 形状母数及び
尺度母数の推定法
a),b)
c)
d) 信頼区間
e)
−
5.3
5.4
5.5.2
7.3.1
統計解析方法
統計解析方法
追加
一致
一致
一致
一致
JISの試験方法を引用した。
7記録
8
報告
変更
附属書A
(参考)
最ゆう法を用いた
母数推定の解析事
例
附属書A
(informative)
附属書B
(informative)
附属書C
(informative)
附属書D
(informative)
変更
JISと国際規格との対応の程度の全体評価:ISO 20501:2003,MOD
1
3
R
1
6
2
5
:
2
0
1
0

14
R 1625:2010
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 一致……………… 技術的差異がない。
− 削除……………… 国際規格の規定項目又は規定内容を削除している。
− 追加……………… 国際規格にない規定項目又は規定内容を追加している。
− 変更……………… 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD…………… 国際規格を修正している。
1
4
R
1
6
2
5
:
2
0
1
0