M 8709:2006 (ISO/DIS 3086:2005)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,社団法人日本鉄鋼連盟(JISF)/財団法人日本
規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査
会の審議を経て,経済産業大臣が制定した日本工業規格である。
制定に当たっては,日本工業規格と国際規格との対比,国際規格に一致した日本工業規格の作成及び日
本工業規格を基礎にした国際規格原案の提案を容易にするために,ISO/DIS 3086:2005,Iron ores−
Experimental methods for checking the bias of samplingを基礎として用いた。
この規格の一部が,技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願公開後の
実用新案登録出願に抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会
は,このような技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願公開後の実用新
案登録出願にかかわる確認について,責任をもたない。
JIS M 8709には,次に示す附属書がある。
附属書A(規定)統計的解析のフローシート
附属書B(参考)実験例
M 8709:2006 (ISO/DIS 3086:2005)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 定義 ······························································································································ 2
4. 原理 ······························································································································ 2
5. 一般事項 ························································································································ 2
5.1 実験の測定データの組数 ································································································· 2
5.2 実験の判定基準 ············································································································· 2
5.3 実験の品質特性 ············································································································· 2
6. サンプリング及び試料調製方法 ·························································································· 2
6.1 サンプリング ················································································································ 2
6.2 試料調製及び測定 ·········································································································· 2
7. 実験データの解析 ············································································································ 3
7.1 差の計算 ······················································································································ 3
7.2 差の平均値及び標準偏差の決定 ························································································ 3
7.3 異常値の検定−グラッブス検定 ························································································ 3
7.4 偏りの検定に用いるデータの選定······················································································ 4
7.5 偏りの検定 ··················································································································· 5
8. 実験報告書 ····················································································································· 6
附属書A(規定)統計的解析のフローシート ············································································· 7
附属書B(参考)実験例 ······································································································· 10
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
M 8709:2006
(ISO/DIS 3086:2005)
鉄鉱石−サンプリングの偏りを調査する実験方法
Iron ores-Experimental methods for checking the bias of sampling
序文 この規格は,2005年に第4版として発行されたISO/DIS 3086,Iron ores−Experimental methods for
checking the bias of samplingを翻訳し,技術的内容及び規格票の様式を変更することなく作成した日本工業
規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
1. 適用範囲 この規格は,JIS M 8702に規定する方法によって鉄鉱石をサンプリングするときに,停止
ベルトサンプリング方法を基準として,その他のサンプリング方法での偏りを調査するための実験方法に
ついて規定する。
備考1. 偏り調査実験の前に機械式サンプリングシステムの点検をするのが望ましい。
2. JIS M 8702に完全には準拠していないサンプリングシステムに偏りが発生するとは必ずしも
いえない。したがって,JIS M 8702の条件を満たしていない点について意見の相違がある場
合は,偏りの調査を行うのがよい。当事者の一方が,ある特定の条件において偏りが存在す
ると主張するときは,その条件での偏りの調査を行うのがよい。
3. この規格に規定した実験データの解析方法は,次の場合にも適用してよい。
a) JIS M 8702に規定した試料調製方法を基準として,鉄鉱石の試料調製の偏りを調査する
場合。
b) JIS M 8706に規定した手動粒度分析方法を基準として,その他の粒度分析方法の偏りを
調査する場合。
c) 異なる場所,例えば,積地と揚地とで採取した同一ロットの試料から得た結果の有意差
を調査する場合。
4. この規格の対応国際規格を,次に示す。
なお,対応の程度を表す記号は,ISO/IEC Guide 21に基づき,IDT(一致している),MOD
(修正している),NEQ(同等でない)とする。
ISO/DIS 3086:2005,Iron ores−Experimental methods for checking the bias of sampling (IDT)
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格は,その最新版(追補を含む。)を適用する。
JIS M 8700 鉄鉱石及び還元鉄−用語
備考 ISO 11323:2002, Iron ore and direct reduced iron−Vocabularyからの引用事項は,この規格の
該当事項と同等である。
JIS M 8702 鉄鉱石―サンプリング及び試料調製方法
2
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 ISO 3082:2000, Iron ores−Sampling and sample preparation proceduresからの引用事項は,こ
の規格の該当事項と同等である。
JIS M 8708 鉄鉱石−サンプリング,試料調製及び測定の精度を確認する実験方法
備考 ISO 3085:2002, Iron ores−Experimental methods for checking the precision of sampling, sample
preparation and measurementが,この規格と一致している。
3. 定義 この規格で用いる主な用語の定義は,JIS M 8700による。
4. 原理 実験の対象とする方法(以下,方法Bという。)から得た結果と,技術的及び経験的観点から実
質的に偏りがない結果が得られると判断される基準方法(以下,方法Aという。)の結果とを比較する。方
法Bから得た結果と方法Aから得た結果との間に統計的に有意差がないと判断した場合,方法Bを日常
の方法として採用してよい。有意差の評価は,実測の偏りと基準とする偏り(δ)(5.2参照)とを,90 %の
信頼区間で比較して行う。
5. 一般事項
5.1
実験の測定データの組数 実験に必要な測定データの組の数は,10以上とする。最小10組の測定デ
ータで実施した異常値検定及び実測の偏りに対する信頼区間の統計解析の結果によっては,追加の実験が
必要となる。
参考 測定データの組とは,同一対象物を方法A及び方法Bで採取し,それぞれの試料を分析して得
た一対のデータをいう。
5.2
実験の判定基準 基準とする偏りの値(δ)は,その値まで低減するための費用効果があるかを考慮
し,あらかじめ決定する。目安としてδは,JIS M 8708によって求めたサンプリング,試料調製及び測定
の標準偏差σSPMよりも小さい値が望ましい。
備考 実験が試料調製の調査だけを目的とする場合は,δの値はJIS M 8708によって求めたσPM より
も小さい値が望ましい。
5.3
実験の品質特性 品質特性には,全鉄分,水分,粒度分布,物理特性などがある。
6. サンプリング及び試料調製方法
6.1
サンプリング サンプリングの偏りを調査するための方法Aは,JIS M 8702に規定する停止ベルト
サンプリング方法とする。
方法A:停止ベルトコンベア上の採取位置から,最大粒度の3倍以上か,又は30 mmのいずれか大きい
方の長さで,鉱石の流れの全幅・全厚からインクリメントを採取する。
方法B:方法Bの例として,運転中のベルトコンベアからの機械式サンプラによるサンプリング,船若
しくは貨車への,又は船又若しくは貨車からの鉱石の移動中に行うサンプリングなどがある。
方法Bは,通常JIS M 8702によって行うが,同一対象物で行った方法Aと比較しなければならない。
方法A及び方法Bのサンプル採取は,極力近い位置で行う。このことは特に品質特性が変化しやすい鉱
石で重要となる。
6.2
試料調製及び測定
6.2.1
1ロットから方法A及び方法Bによって採取したインクリメントを2個の大口試料A及びBにま
とめる。
3
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.2.2
大口試料A及びBをJIS M 8702によって,同じ方法で調製し,品質特性を規定する規格によって
それぞれを測定して一組の測定データを得る。
6.2.3
このような手順を10ロット以上について行う(5.1参照)。
備考1. 方法A及び方法Bのインクリメントを,互いにごく近い位置で採取できる場合は,試料調製
及び測定は各インクリメントごとに行うか,又は隣接する数個のインクリメントをまとめて
行うのがよい。これによって,1ロット全体から一組の測定データを得るよりも迅速に,10
組以上の測定データを得ることができる。この方法は,数ロットから採取したインクリメン
トの組について,同種の鉱石について行うのが望ましい。ただし,インクリメント及び大口
試料の両方からなる数組の結果を一つにして取り扱うことはできない。この場合,インクリ
メントからの組か,又は大口試料からの組かのいずれかにすべきである。
2. 実験費用に制限があること,停止ベルトサンプリングは作業負荷がかかることなどから,停
止ベルトサンプリングの数は少なくするのが経済的である。このため試料調製及び測定は慎
重に行い,かつ,複数回行うのがよい。
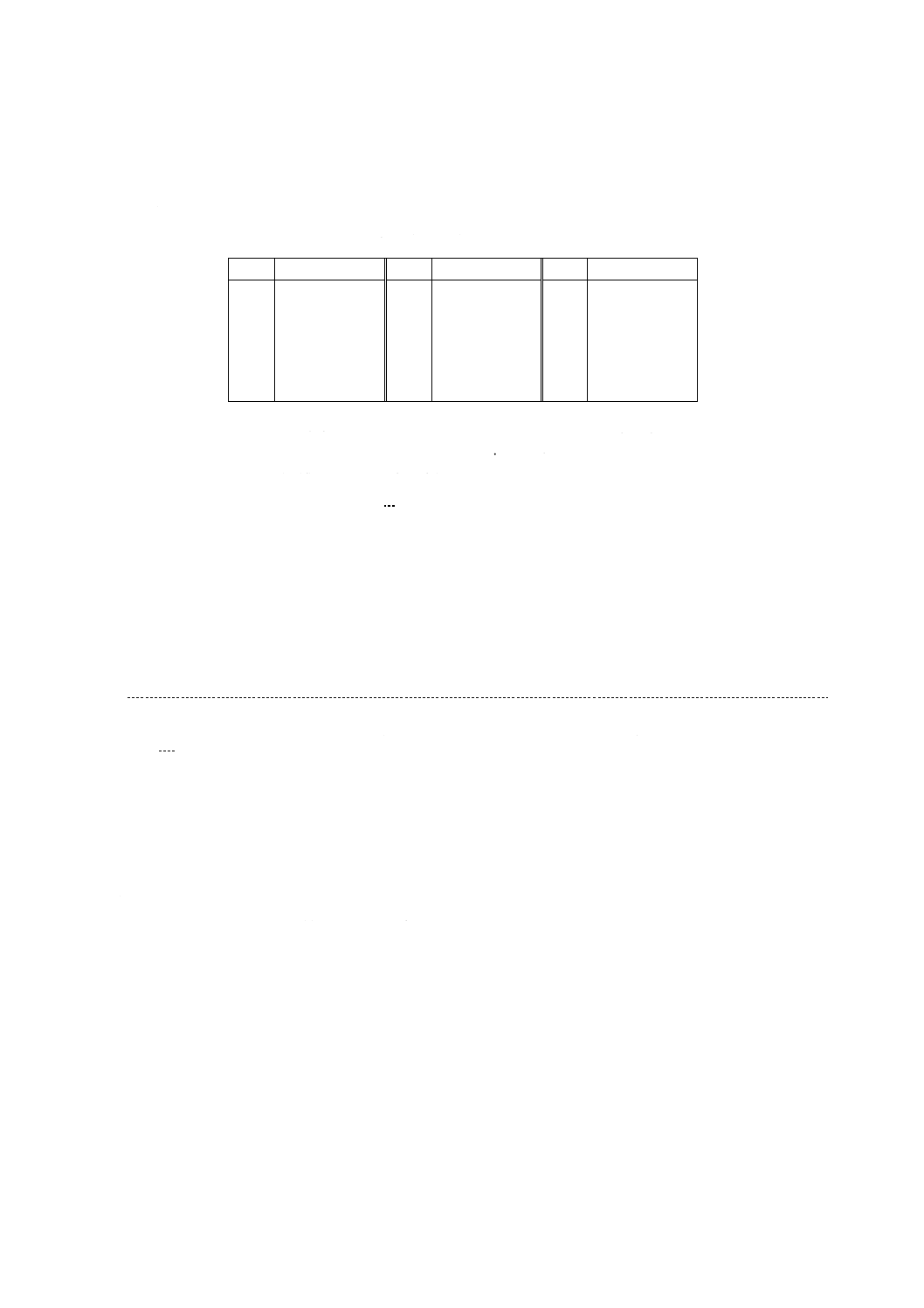
7. 実験データの解析 実験データの解析は,7.1〜7.5に示す手順によって行う(附属書Aのフローシー
ト参照)。
7.1
差の計算
7.1.1
方法Aによって得た各々のデータを
Ai
x,方法Bによって得た各々のデータを
Bi
xとする。試料調
製と測定とを複数回実施した場合は,平均値を採用する。
7.1.2
Ai
xと
Bi
xとの差
idを式(1)によって計算する。
Ai
Bi
i
x
x
d
−
=
i=1,2,...,k ············································· (1)
ここに, k: 測定データの組の数
7.2
差の平均値及び標準偏差の決定
7.2.1
差の平均値(d)を,測定データのけた数より一つ多いけた数まで計算する。
∑
=
id
k
d
1
············································································ (2)
7.2.2
差の平方和(SSd)及び標準偏差(Sd)を,測定データのけた数より一つ多いけた数まで計算する。
2
2
)
(
1∑
−
∑
=
i
i
d
d
k
d
SS
······························································· (3)
)1
(−
=
k
SS
S
d
d
········································································· (4)
7.3
異常値の検定−グラッブス検定
7.3.1
diを小さい順に並べる。
7.3.2
次の式によってグラッブス検定の統計値,Gk及びG1を計算する。
d
k
k
S
d
d
G
−
=
··········································································· (5)
d
S
d
d
G
1
1
−
=
············································································ (6)
ここに, dk: diの最大値
4
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d1: diの最小値
7.3.3
Gk又はG1のいずれか大きい方を選ぶ。
7.3.4
Gk又はG1のいずれか大きい方の値と表1の5 %有意水準でのグラッブス検定の限界値とを比較す
る。手順はa)及びb)による。
表 1 グラッブス検定の限界値
k
限界値(5 %)
k
限界値(5 %)
k
限界値(5 %)
6
7
8
9
10
11
1.887
2.020
2.126
2.215
2.290
2.355
12
13
14
15
16
17
2.412
2.462
2.507
2.549
2.585
2.620
18
19
20
21
22
23
2.651
2.681
2.709
2.733
2.758
2.781
参考 kの値が表1の値より大きい場合のグラッブス検定の限界値,及び
他の有意水準での限界値については,Grubbs, F.E. and Beck, G.
(1972)“Extension of sample sizes and percentage points for
significance tests of outlying observations”, Technometrics 14,
847-854及びJIS Z 8402-2:1999, 表5に規定されている。
a) Gk又はG1のいずれか大きい方の値が限界値より小さいか,又は同じ場合は,異常値はない。7.5に進
む。
b) Gk又はG1のいずれか大きい方の値が限界値より大きい場合は,次の判断による。
1) Gkが大きいとき,差の最大値dkを異常値とする。
2) G1が大きいとき,差の最小値d1を異常値とする。
7.3.5
異常値diを除外して,7.2〜7.3.3までの手順を繰り返す。
参考1. 繰り返して検定を行うと実際の有意水準が所定の値よりも大きくなるので,統計的には好ま
しくない。
2. 異常値を除外した場合,以降で用いるkは,残った有効な測定データの組の数となる。
7.3.6
Gk又はG1のいずれか大きい方の値と表1の5 %有意水準でのグラッブス検定の限界値とを比較す
る。手順はa)及びb)による。
a) Gk又はG1のいずれか大きい方の値が限界値より小さいか,又は同じ場合は,異常値はない。7.4に進
む。
b) Gk又はG1のいずれか大きい方の値が限界値より大きい場合,次の判断による。
1) Gkが大きいとき,差の最大値dkを異常値とする。
2) G1が大きいとき,差の最小値d1を異常値とする。
7.3.7
60 %以上のデータが残っている場合は,7.3.5に戻る。
7.3.8
60 %以上のデータが残っていない場合は,検定を中止し,削除した全データを戻し,7.5に進む。
7.4
偏りの検定に用いるデータの選定
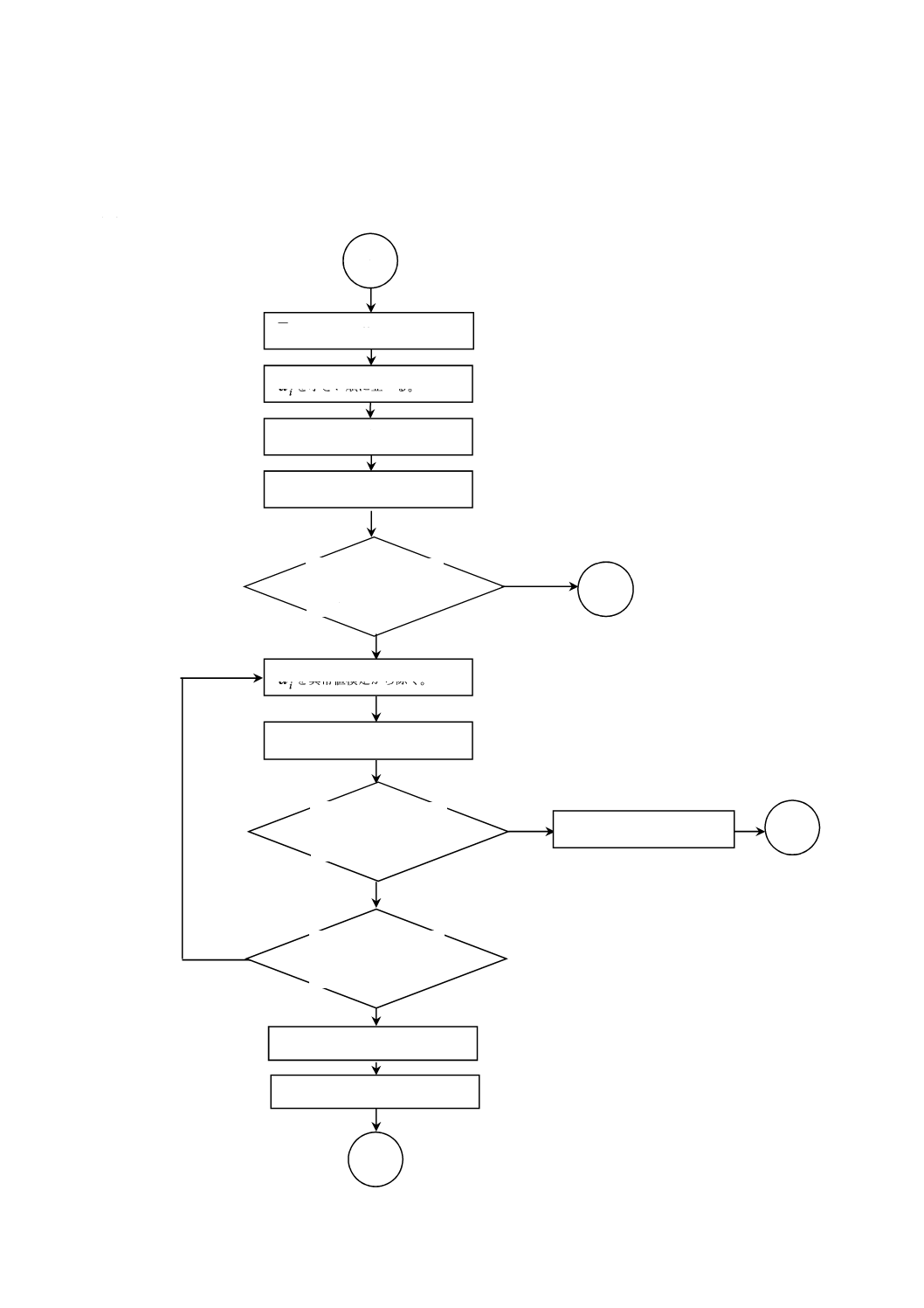
7.4.1
原因が特定可能な異常値の処置 グラッブス検定で異常値を検出した場合は,水分の変化,カッタ
開口部の部分的な閉塞,サンプルの特性の変化など,原因について検討するのが望ましい。異常値の原因
が特定され,将来においても再発の可能性がある場合は,その異常値は除去せず元に戻し,7.5に進む。
再発する可能性がない場合は,異常値を以後の解析から除く。この場合10組の測定データが残っている
ときは,7.5に進む。10組の測定データがない場合は,少なくとも10組がそろうようにサンプリング及び
測定を実施し,7.1〜7.3.8の手順を繰り返す。
5
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.4.2
原因が特定できない異常値の処置 異常値の原因が特定されない場合は,その異常値は除く。10
組の測定データが残っている場合は,7.5に進む。10組の測定データが残っていない場合は,データを追
加して少なくとも10組をそろえる。最初異常と判断したデータは,追加したデータを含むグラッブス検定
において必ずしも異常になるとは限らない。したがって,除いた異常値も含めて7.1〜7.3.8までの手順を
繰り返す。
7.5
偏りの検定
7.5.1
dの信頼区間の決定 手順はa)及びb)による。
a) 異常値として除外しなかった組の差の平均値及び標準偏差を計算する。
b) 次の式によって信頼限界の下限値LL及び上限値ULを測定値と同じ有効数字で求める。
k
S
t
d
LL
d
−
=
········································································· (7)
k
S
t
d
UL
d
+
=
·········································································· (8)
ここに, t: 表2に示した自由度(k-1)のスチューデントのt分布の数
値
k: 異常値として除去されなかった測定データの組の数
表2では測定データの組の数がkの場合,対応するtの値は,既に自由度(k-1)で示している。
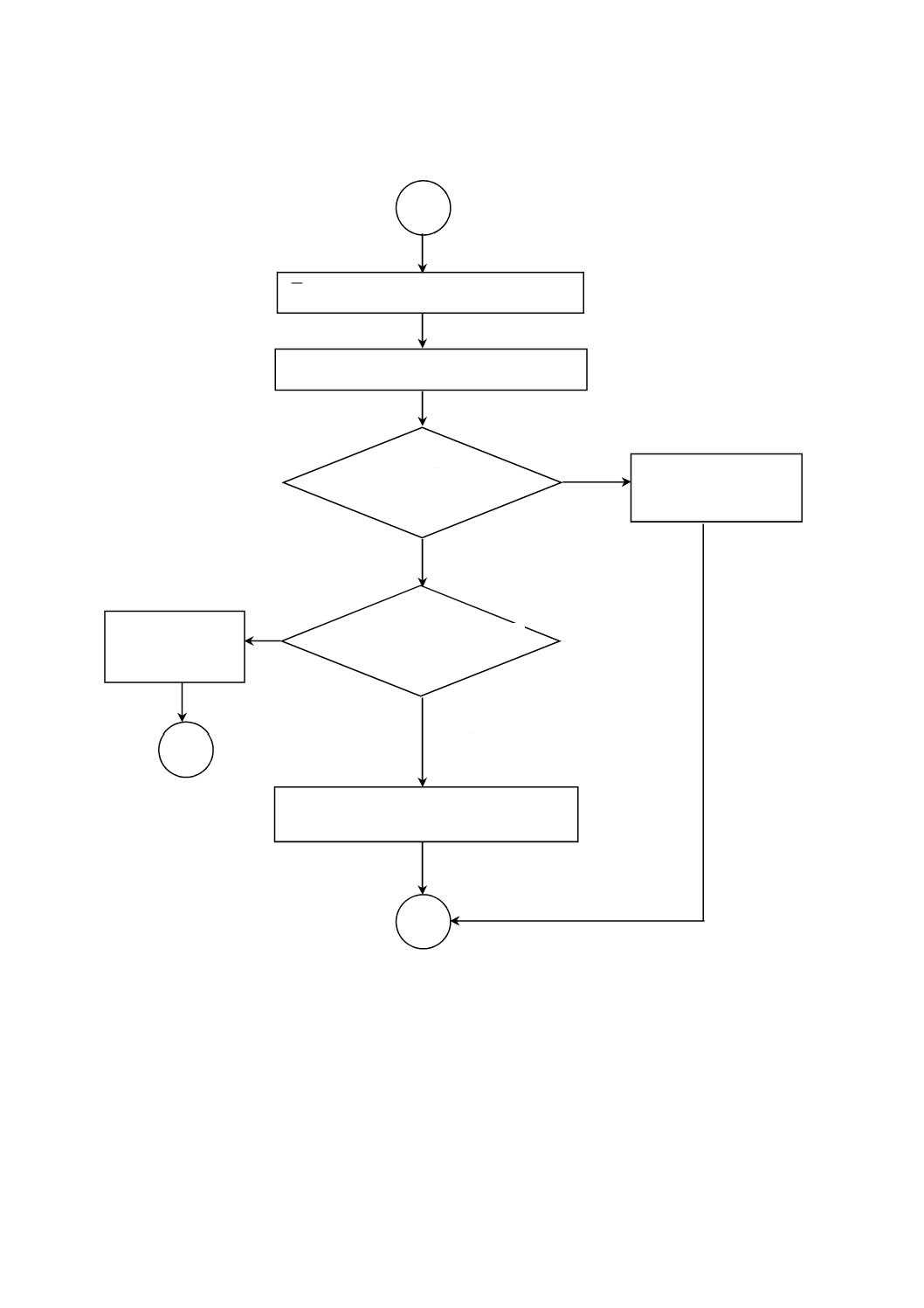
7.5.2
信頼区間の統計的解析 横線の中心をゼロ(0)とし,LL,UL,−δ及び+δの値をプロットする。
LLからULまでの範囲が−δから+δまでの範囲に完全に含まれているかを調べる(附属書A参照)。
a) −δから+δまでの範囲に含まれている場合,偏りは基準内である。方法Bは日常の方法として適用
できると判定し,実験を終了する(附属書B.2,B.4及びB.5参照)。
b) LLからULまでの範囲が−δから+δまでの範囲に完全に含まれていない場合,LLからULまでの範
囲にゼロ(0)が含まれているかを調べる。
1) ゼロ(0)が含まれていない場合は,方法Bは日常の方法として適用することはできず,サンプリン
グシステムを調整しなければならない(附属書B.1参照)。
2) ゼロ(0)が含まれている場合は,更にサンプリング及び測定が必要となる。新たな測定データの組,
できれば数組の測定データを追加し,7.1〜7.5の手順を,日常の方法として採用できるかどうか分
るまで繰り返す(附属書B.3参照)。

6
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 2 有意差水準10 %のtの値(両側検定)
測定の組の数
k
t
測定の組の数
k
t
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
1.740
1.734
1.729
1.725
1.721
1.717
1.714
1.711
26
27
28
29
30
31
32
33
34
35
40
50
81
121
241
∞
1.708
1.706
1.703
1.701
1.699
1.697
1.696
1.694
1.692
1.691
1.685
1.677
1.664
1.658
1.651
1.645
備考1. 表2は,ISO 2602:1980 測定結果の統計的解釈−平均の推定−
信頼区間から引用した。
2. t表は一般の統計の教科書で入手することができる。
8. 実験報告書 実験報告書には,次の情報を含む。
a) 実験の統括者及び実施者の氏名
b) 実験場所
c) 実験報告書の発行日
d) 実験期間
e) 測定品質特性及び適用規格
f)
調査対象ロットの詳細
g) サンプリング及び試料調製の詳細
h) 異常値検定の結果及び判定
i)
t値及び判定
j)
実験統括者の解説及び意見
k) 実験結果に基づいた処置
7
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定)統計的解析のフローシート
A.1 グラッブスの異常値検定のフローシート
はい
はい
いいえ
いいえ
C
はい
いいえ
C
Step 1
Step 2
Step 3
Step 4
A
d及び
d
Sを計算する。
idを小さい順に並べる。
k
G及び
1
Gを計算する。
k
G又は
1
Gの大きい方を選ぶ。
k
G又は
1
Gの大きい方
がグラッブスの限界値
より大きいか?
idを異常値検定から除く。
Step1〜4を繰り返す
異常値検定を中止する。
異常値を元に戻す。
少なくとも60%以上の
元データの組が残って
いるか?
B
k
G又は
1
Gの大きい方
がグラッブスの限界値
より大きいか?
異常値を除く。
8
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A
.2
異
常値
の
処置
の
フ
ロー
シ
ート
はい
はい
C
異常値を個々に調査する。
異常値の原因が特定で
きるか?
はい
いいえ
いいえ
A
B
異常値を再編入する。
すべての異常値につ
いて調査したか?
k≧10か?
異常値を除く。
はい
異常値を除く。
その原因は将来も起こ
る可能性はあるか?
すべての異常値につ
いて調査したか?
A
追加のサンプリング
と測定を行い少なく
とも10組の測定デ
ータを得る。
いいえ
いいえ
すべての異常値につ
いて調査したか?
k≧10か?
追加のサンプリング
と測定を行い少なく
とも10組の測定デ
ータを得る。
先に除いた異常値を
再編入する。
いいえ
いいえ
はい
いいえ
はい
はい
はい
8
M
8
7
0
9
:
2
0
0
6
(I
S
O
/D
IS
3
0
8
6
:
2
0
0
5
)
9
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.3 偏りの検定のフローシート
dの信頼限界LL及びULを計算する。
横軸にLL,UL,0,−δ及び+δをプロットする。
LLからULまでの範囲が−δから
+δまでの範囲に含まれるか?
実験終了。
方法Bを日常の方法とし
て適用してよい。
更にサンプリング
及び測定を実施す
る。
方法Bは日常法として採用できない。
サンプリングシステムを調整する。
はい
はい
いいえ
いいえ
C
終了
A
LLからULまでの範囲にゼロ(0)
が含まれるか?
10
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考)実験例
表B.1〜B.5に示したデータは,実際の実験で得た数値であるが,データの出所を保護するために,二つ
の方法(A法及びB法)で得た結果に定数を加えて変換している。しかし,実験の条件及び偏りの基準値
は単なる例とする。
B.1
数値例1 (δ:全鉄分で0.10 %)
表B.1に示す数値例は,機械式サンプリング(方法B)と基準方法Aとを比較した実験の結果である。
実験によって検出しようとする偏りの大きさは,全鉄分で0.10 %とする。
表 B.1 実験データ
ロット
全鉄分(%)
di=xBi−xAi
di2
xBi
xAi
1
2
3
4
5
6
7
8
9
10
63.71
62.98
63.24
63.77
60.01
63.82
63.85
64.20
64.08
64.07
63.75
62.95
63.70
63.93
60.82
63.99
64.09
64.21
64.12
64.27
−0.04
0.03
−0.46
−0.16
−0.81
−0.17
−0.24
−0.01
−0.04
−0.20
0.001 6
0.000 9
0.211 6
0.025 6
0.656 1
0.028 9
0.057 6
0.000 1
0.001 6
0.040 0
合計
−2.10
1.024 0
210
.0
10
10
.2
1
−
=
∑
−
=
=
id
k
d
(
)
583
.0
10
)
10
.2
(
024
.1
1
2
2
2
=
−
−
=
∑
−
∑
=
i
i
d
d
k
d
SS
255
.0
9
589
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えたdiの値:−0.81,−0.46,−0.24,−0.20,−0.17,−0.16,−0.04,−0.04,−0.01,0.03
941
.0
255
.0
)
210
.0
(
03
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
353
.2
255
.0
)
81
.0
(
210
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:2.353
表1から10組の測定データに対するグラッブス検定の限界値は,2.290となる。
G1>2.290であり,di=−0.81は異常値となる。
11
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
したがって,残りの9組について異常値検定を実施する。
143
.0
9
29
.1
1
−
=
∑
−
=
=
id
k
d
(
)
183
.0
9
)
29
.1
(
368
.0
1
2
2
2
=
−
−
=
∑
−
∑
=
i
i
d
d
k
d
SS
151
.0
8
183
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えたdiの値:−0.46,−0.24,−0.20,−0.17,−0.16,−0.04,−0.04,−0.01,0.03
146
.1
151
.0
)
143
.0
(
03
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
099
.2
151
.0
)
46
.0
(
143
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:2.099
表1から9組の測定データに対するグラッブス検定の限界値は,2.215となる。
G1<2.215であり,新たな異常値はない。
異常値の考察:
考察の結果,異常値(di=−0.81)には特定された原因があり,サンプリングした試料の品質特性に変化
があることが分った。将来とも起こり得る原因であることから,この一組のデータは保持するのがよい。
したがって,最初のデータ(表B.1)を偏りの検定にかけるものとする。
偏りの検定:
測定データの組に変更がなく,d,SSd及びSdの値は変わらない。
dに対する信頼限界は,次のとおりとなる。
36
.0
10
255
.0
833
.1
210
.0
−
=
×
−
−
=
−
=
k
S
t
d
LL
d
06
.0
10
255
.0
833
.1
210
.0
−
=
×
+
−
=
+
=
k
S
t
d
UL
d
表2からt=1.833を得る。
水平軸にプロットする。
12
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
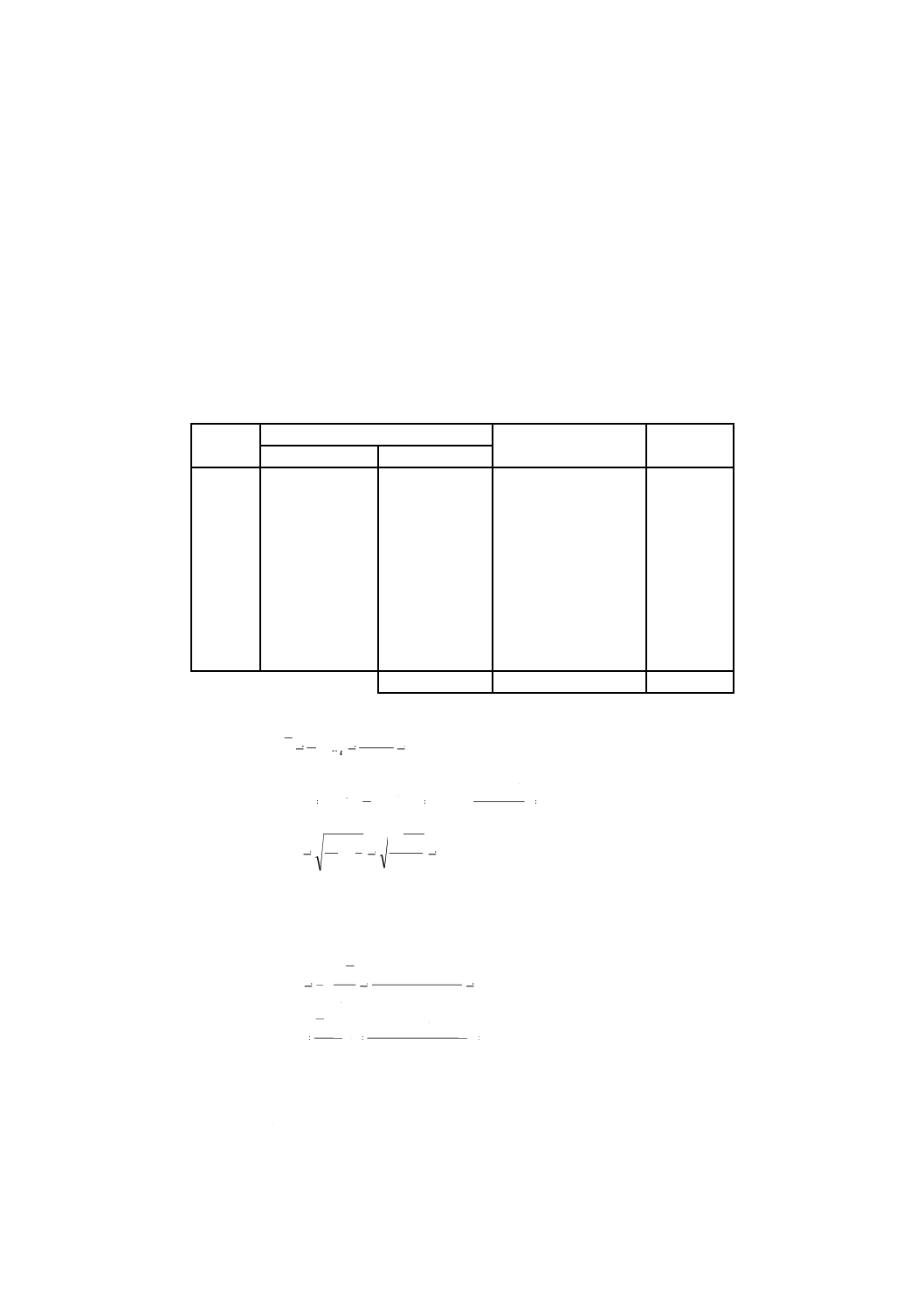
LLからULまでの範囲は−δから+δまでの範囲に完全には含まれず,しかもゼロ(0)を含んでいない。
この場合,方法Bには有意な偏りがあり,日常の方法として適用できない。サンプリング設備を調整しな
ければならない。
B.2
数値例2 (δ:全鉄分で0.20 %)
表B.2.a,表B.2.b及び表B.2.cに示す数値例は,JIS M 8702に従って行った機械式サンプリング(方法
B)と基準方法Aとを比較した実験の結果である。
実験によって検出しようとする偏りの大きさは,全鉄分で0.20 %とする。
表 B.2.a 実験データ
ロット
全鉄分(%)
di=xBi−xAi
di2
xBi
xAi
1
2
3
4
5
6
7
8
9
10
62.36
62.18
62.22
62.32
62.43
62.72
63.58
63.64
63.85
63.21
62.36
62.21
62.44
62.27
62.51
62.74
63.79
63.77
64.15
63.93
0
−0.03
−0.22
0.05
−0.08
−0.02
−0.21
−0.13
−0.30
−0.72
0
0.000 9
0.048 4
0.002 5
0.006 4
0.000 4
0.044 1
0.016 9
0.090 0
0.518 4
合計
−1.66
0.728 0
166
.0
10
66
.1
1
−
=
∑
−
=
=
id
k
d
(
)
452
.0
10
)
66
.1
(
0
728
.0
1
2
2
2
=
−
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
224
.0
9
452
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えた
idの値:−0.72,−0.30,−0.22,−0.21,−0.13,−0.08,−0.03,−0.02,0.00,0.05
964
.0
224
.0
)
166
.0
(
05
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
LL=−0.36
UL=−0.06
−δ=−0.10
0
+δ=+0.10
13
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
473
.2
224
.0
)
72
.0
(
166
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
k
G又は
1
Gのいずれか大きい方の値:2.473
表1から10組の測定データに対するグラッブス検定の限界値は,2.290となる。
G1>2.290であり,di=−0.72を異常値と判定して除去し,残りの9組に対し異常値検定を実施する。
残りの9組の測定データについて,d及び
d
Sを計算する。
104
.0
9
94
.0
1
−
=
∑
−
=
=
id
k
d
(
)
111
.0
9
)
94
.0
(
6
209
.0
1
2
2
2
=
−
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
118
.0
8
111
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えた
idの値:−0.30,−0.22,−0.21,−0.13,−0.08,−0.03,−0.02,0.00,0.05
305
.1
118
.0
)
104
.0
(
05
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
661
.1
118
.0
)
30
.0
(
104
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:1.661
表1から9組の測定データに対するグラッブス検定の限界値は,2.215となる。
G1<2.215であり,新たな異常値は存在しない。
異常値の考察:
考察の結果,異常値(di=−0.72)には特定される原因がないことが分った。少なくとも10組のデータ
をそろえるために追加のサンプリング及び測定が必要である。 第10番目のロットデータは,新たな検定
の組では必ずしも異常値になるとは限らないため,データに復帰させる(表B.2.b参照。)。

14
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 B.2.b 実験データ
ロット
全鉄分(%)
di=xBi−xAi
di2
xBi
xAi
1
2
3
4
5
6
7
8
9
10
11
62.36
62.18
62.22
62.32
62.43
62.72
63.58
63.64
63.85
63.21
63.53
62.36
62.21
62.44
62.27
62.51
62.74
63.79
63.77
64.15
63.93
63.50
0
−0.03
−0.22
0.05
−0.08
−0.02
−0.21
−0.13
−0.30
−0.72
0.03
0
0.000 9
0.048 4
0.002 5
0.006 4
0.000 4
0.044 1
0.016 9
0.090 0
0.518 4
0.000 9
合計
−1.63
0.728 9
148
.0
11
63
.1
1
−
=
∑
−
=
=
id
k
d
(
)
487
.0
11
)
63
.1
(
9
728
.0
1
2
2
2
=
−
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
221
.0
10
487
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えたdiの値:−0.72, −0.30,−0.22,−0.21,−0.13,−0.08,−0.03, −0.02,0.00,0.03, 0.05
896
.0
221
.0
)
148
.0
(
05
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
588
.2
221
.0
)
72
.0
(
148
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:2.588
表1から11組の測定データに対するグラッブス検定の限界値は,2.355となる。
G1>2.355であり,di=−0.72は,この場合も異常値とみなして,異常値検定から外し,検定は残り10
組について実施する。

15
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 B.2.c 実験データ
ロット
全鉄分(%)
di=xBi−xAi
di2
xBi
xAi
1
2
3
4
5
6
7
8
9
10
11
62.36
62.18
62.22
62.32
62.43
62.72
63.58
63.64
63.85
削除
65.53
62.36
62.21
62.44
62.27
62.51
62.74
63.79
63.77
64.15
削除
63.50
0
−0.03
−0.22
0.05
−0.08
−0.02
−0.21
−0.13
−0.30
0.03
0
0.000 9
0.048 4
0.002 5
0.006 4
0.000 4
0.044 1
0.016 9
0.090 0
0.000 9
合計
−0.91
0.210 5
091
.0
10
91
.0
1
−
=
∑
−
=
=
id
k
d
(
)
128
.0
10
)
91
.0
(
5
210
.0
1
2
2
2
=
−
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
119
.0
9
128
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えた
idの値:−0.30,−0.22,−0.21,−0.13,−0.08,−0.03, −0.03,−0.02,0.00,0.05
185
.1
119
.0
)
091
.0
(
05
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
756
.1
119
.0
)
30
.0
(
091
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:1.756
表1から10組の測定データに対するグラッブス検定の限界値は,2.290となる。
G1<2.290であり,新たな異常値は存在しない。
偏りの検定:
測定データの組に変更がなく,d,SSd及びSdの値は変わらない。
dに対する信頼限界は,次のとおりとなる。
16
.0
10
119
.0
833
.1
091
.0
−
=
×
−
−
=
−
=
k
S
t
d
LL
d
02
.0
10
119
.0
833
.1
091
.0
−
=
×
+
−
=
+
=
k
S
t
d
UL
d
16
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2からt=1.833を得る。
水平軸にプロットする。
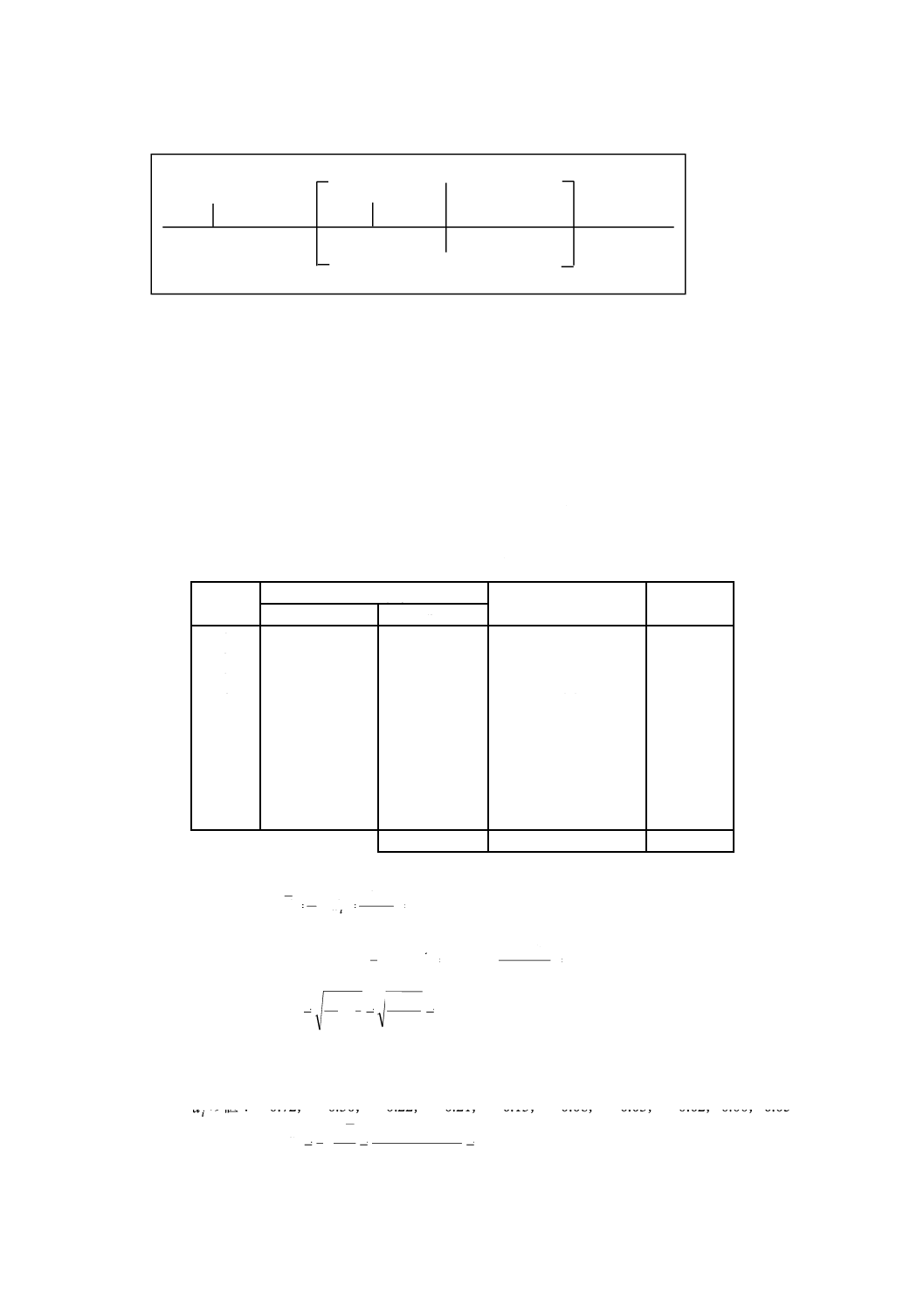
LLからULまでの範囲は,−δから+δまでの範囲に完全に含まれる。この場合,偏りは基準内であり,
方法Bは日常の方法として適用してよい。
B.3
数値例3 (δ:+6.3 mm粒度区分で0.30 %)
表B.3に示す数値例は,機械式サンプリング(方法B)と基準方法Aとを比較した実験の結果である。
実験によって検出しようとする偏りの大きさは,+6.3 mm粒度区分で0.30 %である。
表 B.3 実験データ
ロット
+6.3 mm粒度区分(%)
di=xBi−xAi
di2
xBi
xAi
1
2
3
4
5
6
7
8
9
10
2.62
3.76
1.75
3.08
1.80
2.38
2.64
2.25
2.35
2.31
2.63
2.79
1.83
4.04
2.33
2.82
3.21
2.08
2.48
2.34
−0.01
0.97
−0.08
−0.96
−0.53
−0.44
−0.57
0.17
−0.13
−0.03
0.000 1
0.940 9
0.006 4
0.921 6
0.280 9
0.193 6
0.324 9
0.028 9
0.016 9
0.000 9
合計
−1.61
2.715 1
161
.0
10
61
.1
1
−
=
∑
−
=
=
id
k
d
(
)
456
.2
10
)
61
.1
(
1
715
.2
1
2
2
2
=
−
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
522
.0
9
456
.2
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えた
idの値:−0.96,−0.57,−0.53,−0.44,−0.13,−0.08,−0.03,−0.01,0.17,0.97
167
.2
522
.0
)
161
.0
(
97
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
531
.1
522
.0
)
96
.0
(
161
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
LL=−0.16
UL=−0.02
−δ=−0.20
0
+δ=+0.20
17
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Gk又はG1のいずれか大きい方の値:2.167
表1から10組の測定データに対するグラッブス検定の限界値は,2.290となる。
G1<2.290であり,異常値はない。
偏りの検定:
異常値がなく,d,SSd及びSdの値は,変わらない。
dに対する信頼限界は,次のとおりとなる。
46
.0
10
522
.0
833
.1
161
.0
−
=
×
−
−
=
−
=
k
S
t
d
LL
d
14
.0
10
522
.0
833
.1
161
.0
=
×
+
−
=
+
=
k
S
t
d
UL
d
表2からt=1.833を得る。
水平軸にプロットする。
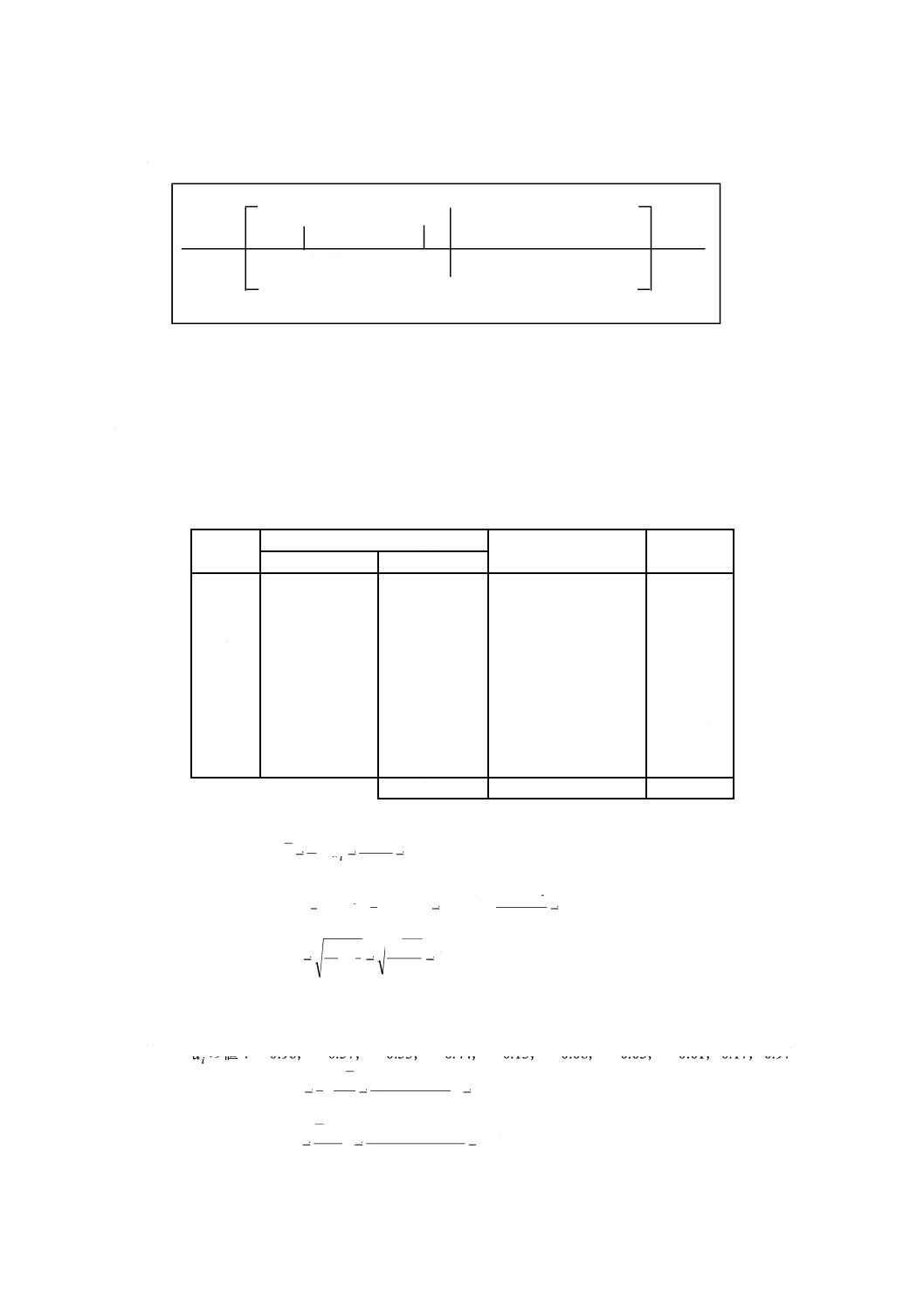
LLからULまでの範囲は,−δから+δまでの範囲に完全には含まれないが,ゼロ(0)を含んでいる。
この場合,更にサンプリング及び測定が必要となる。
B.4
数値例4 (δ:水分で0.30 %)
表B.4に示す数値例は,測定試料の粒度及び質量が水分に及ぼす影響を調べた実験の結果である。この
実験では,質量1 kgで粒度−10 mmの試料(方法B)と質量5 kgで粒度−22.4 mmの試料(方法A)とを比較
した。実験によって検出しようとする偏りの大きさは,水分で0.30 %とする。
LL=−0.46
UL=+0.14
−δ=−0.30
0
+δ=+0.30

18
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 B.4 実験データ
ロット
銘柄
水分(%)
Ai
Bi
i
x
x
d
−
=
2
id
Bi
x
Ai
x
1
2
3
4
5
6
7
8
9
10
A
A
A
B
B
C
C
D
E
C
1.89
1.64
1.80
5.34
5.22
3.27
3.75
4.36
4.08
3.70
2.00
1.68
1.67
5.42
5.29
3.04
3.90
4.65
4.00
3.89
−0.11
−0.04
0.13
−0.08
−0.07
0.23
−0.15
−0.29
0.08
−0.19
0.012 1
0.001 6
0.016 9
0.006 4
0.004 9
0.052 9
0.022 5
0.084 1
0.006 4
0.036 1
合計
−0.49
0.243 9
049
.0
10
49
.0
1
−
=
∑
−
=
=
id
k
d
(
)
220
.0
10
)
49
.0
(
9
243
.0
1
2
2
2
=
−
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
156
.0
9
220
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えた
idの値:−0.29,−0.19,−0.15,−0.11,−0.08,−0.07,−0.04,0.08,0.13,0.23
788
.1
156
.0
)
049
.0
(
23
.0
=
−
−
=
−
=
d
k
k
S
d
d
G
545
.1
156
.0
)
29
.0
(
049
.0
1
1
=
−
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:1.788
表1から10組の測定データに対するグラッブス検定の限界値は,2.290となる。
Gk<2.290であり,異常値はない。
偏りの検定:
異常値がなく,d,SSd及びSdの値は変わらない。
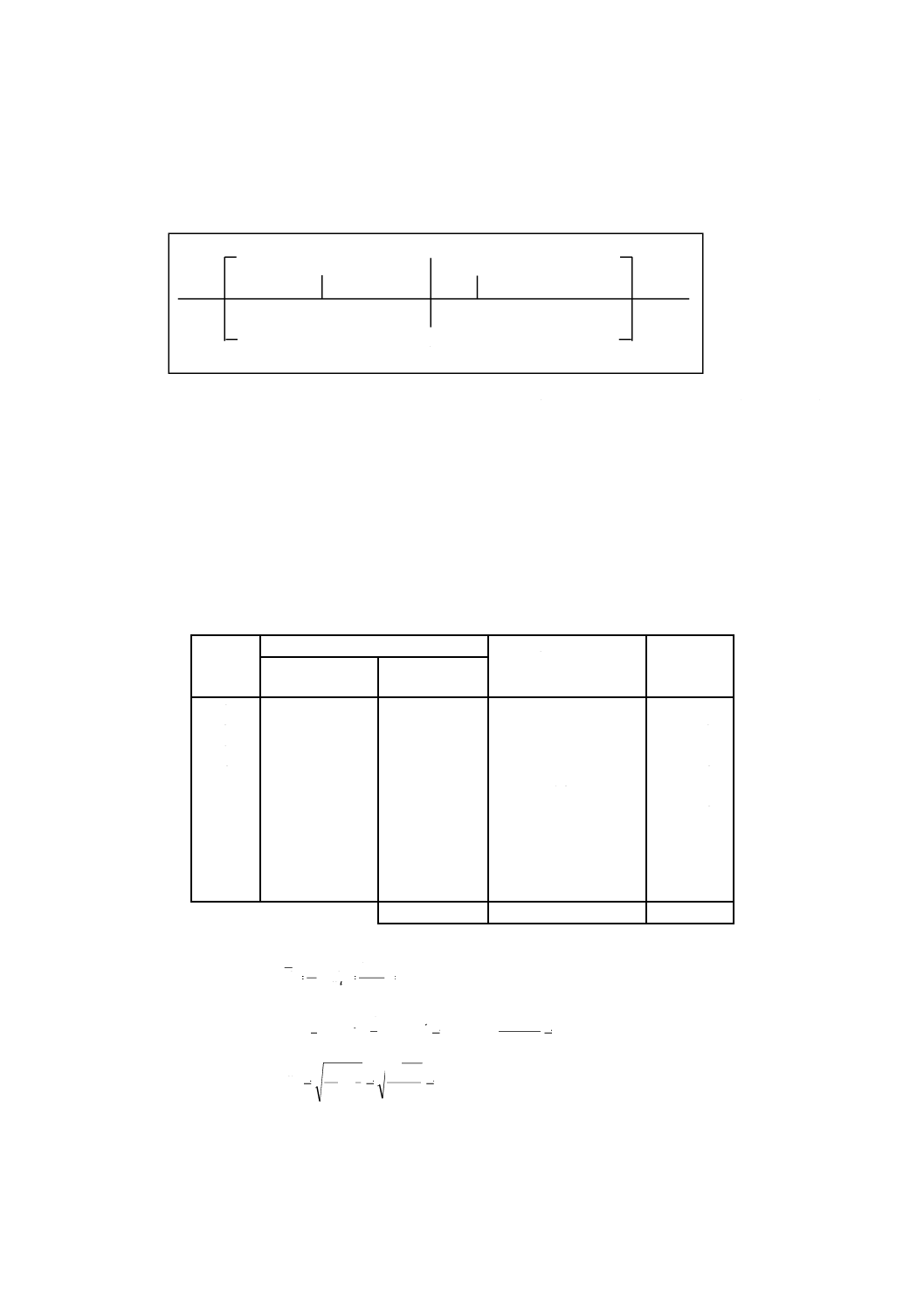
dに対する信頼限界は,次のとおりとなる。
14
.0
10
156
.0
833
.1
049
.0
−
=
×
−
−
=
−
=
k
S
t
d
LL
d
04
.0
10
156
.0
833
.1
049
.0
=
×
+
−
=
+
=
k
S
t
d
UL
d
19
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2からt=1.833を得る。
水平軸にプロットする。
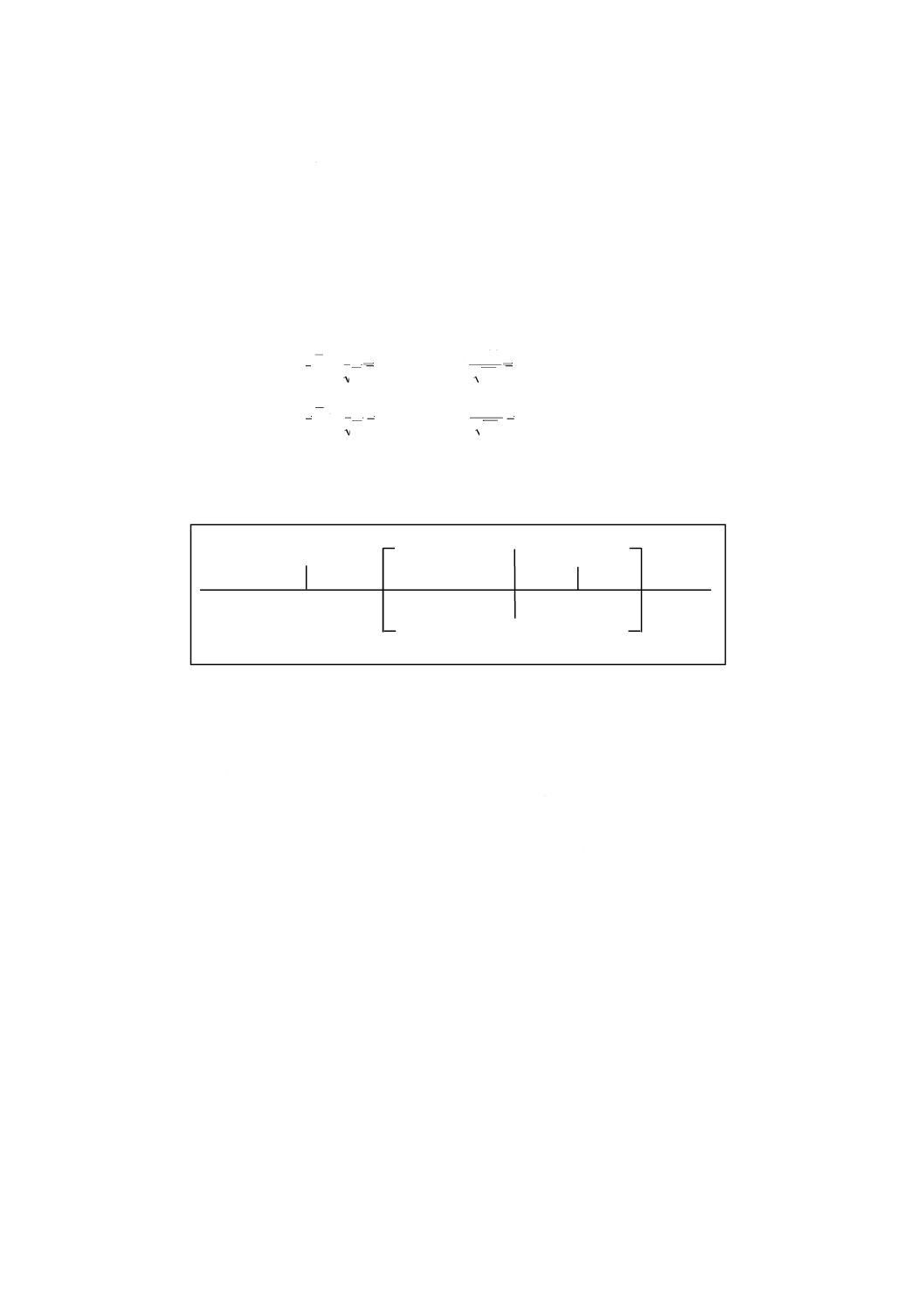
LLからULまでの範囲は,−δから+δまでの範囲に完全に含まれる。この場合,二つの条件の間に有
意差はないと判定する。
B.5
数値例5 (δ:全鉄分で0.30 %)
表B.5.a及び表B.5.bに示す数値例は,JIS M 8702に従って行った機械式サンプリング(方法B)と基準
方法Aとを比較した実験の結果である。
実験によって検出しようとする偏りの大きさは,全鉄分で0.30 %とする。
表 B.5.a 実験データ
ロット
全鉄分(%)
di=xBi−xAi
di2
xBi
xAi
1
2
3
4
5
6
7
8
9
10
66.88
67.53
65.20
68.35
66.57
66.14
66.19
66.35
67.00
66.40
66.68
67.24
64.96
68.13
66.84
66.16
65.96
66.32
66.70
66.26
0.20
0.29
0.24
0.22
−0.27
−0.02
0.23
0.03
0.30
0.14
0.040 0
0.084 1
0.057 6
0.048 4
0.072 9
0.000 4
0.052 9
0.000 9
0.090 0
0.019 6
合計
1.36
0.466 8
136
.0
10
36
.1
1
=
∑
=
=
id
k
d
(
)
282
.0
10
)
36
.1(
8
466
.0
1
2
2
2
=
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
177
.0
9
282
.0
)1
(
=
=
−
=
k
SS
S
d
d
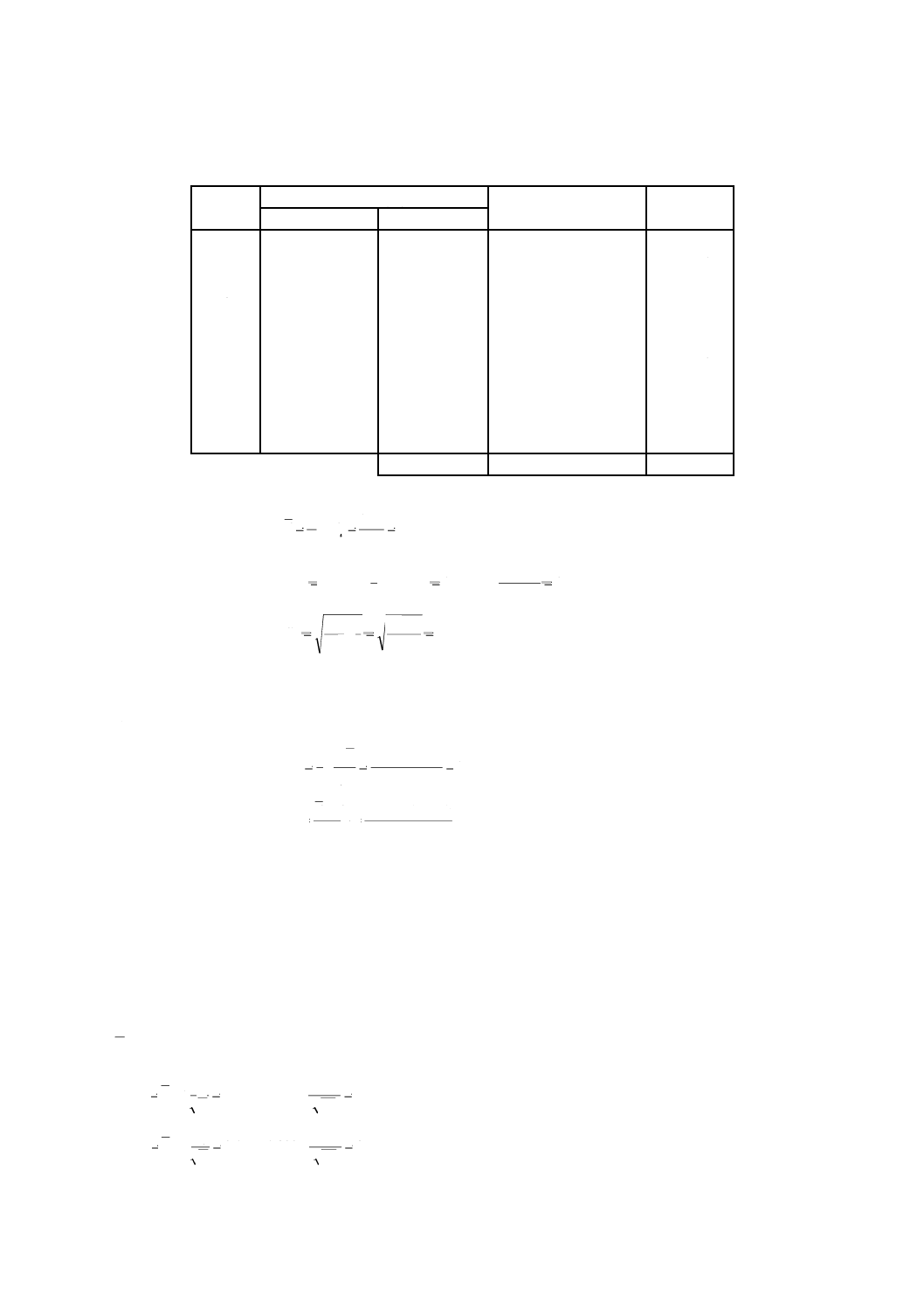
異常値の検定:
LL=−0.14
UL=+0.04
−δ=−0.30
0
+δ=+0.30
20
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
並び替えた
idの値:−0.27,−0.02,0.03,0.14,0.20, 0.22, 0.23, 0.24, 0.29, 0.30
927
.0
177
.0
136
.0
30
.0
=
−
=
−
=
d
k
k
S
d
d
G
294
.2
177
.0
)
27
.0
(
136
.0
1
1
=
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:2.294
表1から10組の測定データに対するグラッブス検定の限界値は,2.290となる。
G1>2.290であり,di=−0.27を異常値と判定して除去し,残りの9組に対し異常値検定を実施する。
181
.0
9
63
.1
1
=
∑
=
=
id
k
d
(
)
099
.0
9
)
63
.1(
394
.0
1
2
2
2
=
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
111
.0
8
099
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えたdiの値:−0.02,0.03,0.14,0.20, 0.22, 0.23, 0.24, 0.29, 0.30
072
.1
111
.0
181
.0
30
.0
=
−
=
−
=
d
k
k
S
d
d
G
811
.1
111
.0
)
02
.0
(
181
.0
1
1
=
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:1.811
表1から9組の測定データに対するグラッブス検定の限界値は,2.215となる。
G1<2.215であり,新たな異常値はない。
異常値の考察:
考察の結果,異常値(di=−0.27)には原因があり,サンプリングされた試料に異物が混入したことが分
った。将来とも起こり得る原因でないため,このロット5のデータは除去するのがよい。この場合は,サ
ンプリング及び測定を行い,表B.5.bに示すように新しい一組を追加する。
21
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表 B.5.b 実験データ
ロット
全鉄分(%)
di=xBi−xAi
di2
xBi
xAi
1
2
3
4
5
6
7
8
9
10
11
66.88
67.53
65.20
68.35
削除
66.14
66.19
66.35
67.00
66.40
66.83
66.68
67.24
64.96
68.13
削除
66.16
65.96
66.32
66.70
66.26
66.91
0.20
0.29
0.24
0.22
−0.02
0.23
0.03
0.30
0.14
−0.08
0.040 0
0.084 1
0.057 6
0.048 4
0.000 4
0.052 9
0.000 9
0.090 0
0.019 6
0.006 4
合計
1.55
0.400 3
155
.0
10
55
.1
1
=
∑
=
=
id
k
d
(
)
160
.0
10
)
55
.1(
3
400
.0
1
2
2
2
=
−
=
−
=
∑
∑
i
i
d
d
k
d
SS
133
.0
9
160
.0
)1
(
=
=
−
=
k
SS
S
d
d
異常値の検定:
並び替えたdiの値:−0.08,−0.02,0.03,0.14,0.20, 0.22, 0.23, 0.24, 0.29, 0.30
090
.1
133
.0
155
.0
30
.0
=
−
=
−
=
d
k
k
S
d
d
G
767
.1
133
.0
)
08
.0
(
155
.0
1
1
=
−
−
=
−
=
d
S
d
d
G
Gk又はG1のいずれか大きい方の値:1.767
表1から10組の測定データに対するグラッブス検定の限界値は,2.290となる。
G1<2.290であり,新たな異常値はない。
偏りの検定:
測定データの組に変更がなく,d,SSd及びSdの値は変わらない。
dに対する信頼限界は,次のとおりとなる。
08
.0
10
133
.0
833
.1
155
.0
=
×
−
=
−
=
k
S
t
d
LL
d
23
.0
10
133
.0
833
.1
155
.0
=
×
+
=
+
=
k
S
t
d
UL
d
22
M 8709:2006 (ISO/DIS 3086:2005)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
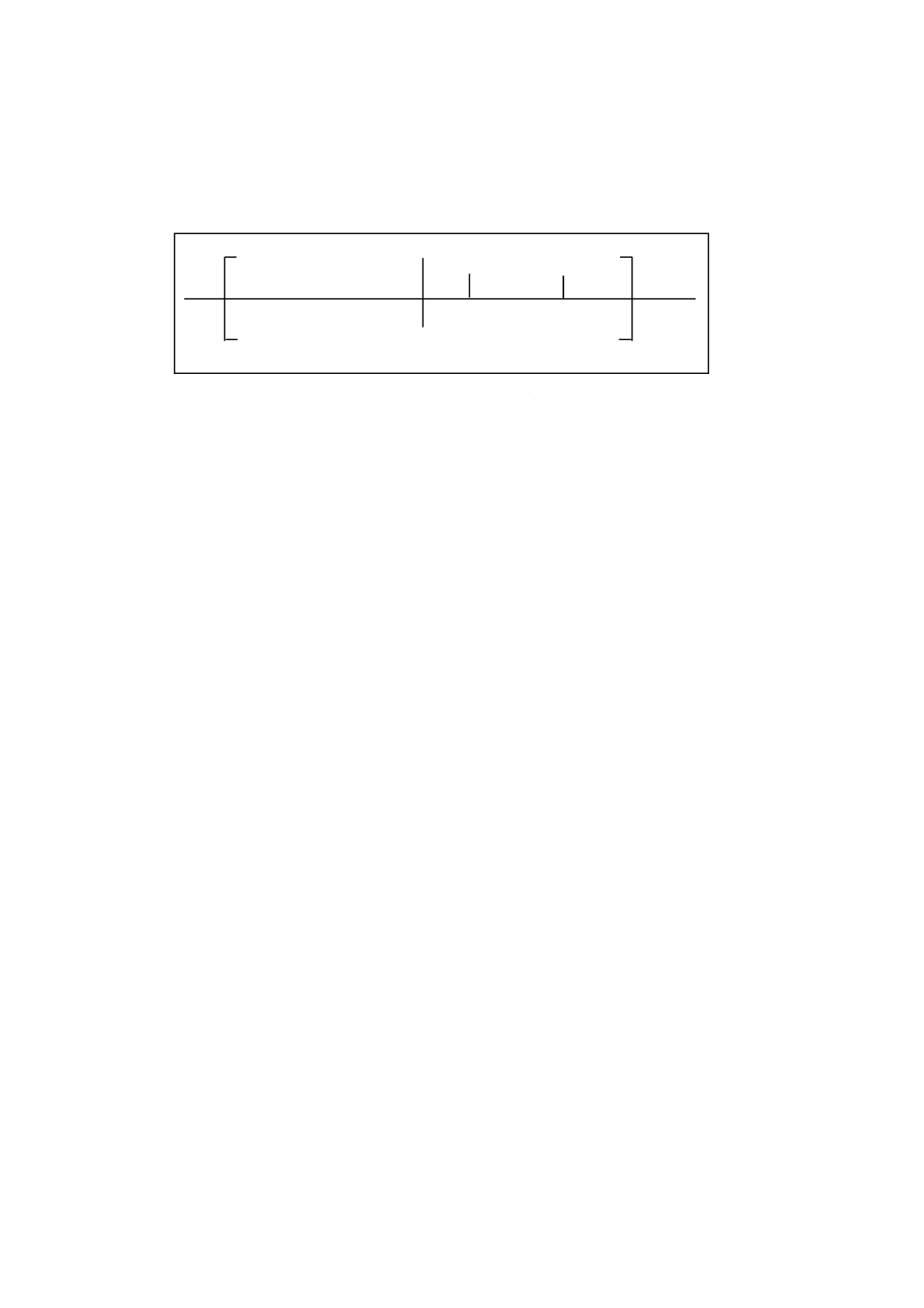
表2からt=1.833を得る。
水平軸にプロットする。
LLからULまでの範囲は,−δから+δまでの範囲に完全に含まれる。この場合,偏りは基準内であり,
方法Bは日常の方法として適用してよい。
LL= 0.08
UL=0.23
−δ=−0.30
0
+δ=+0.30














