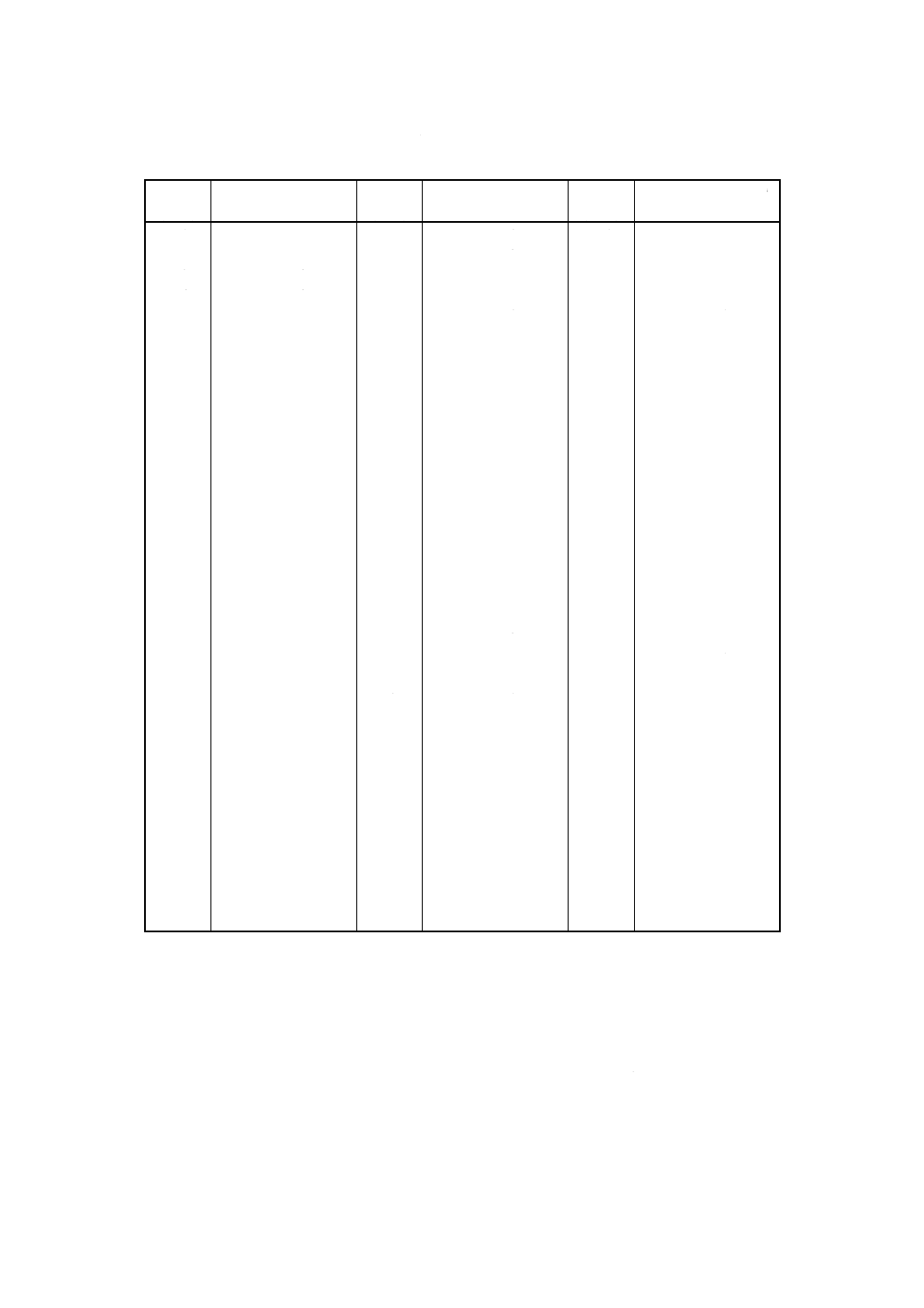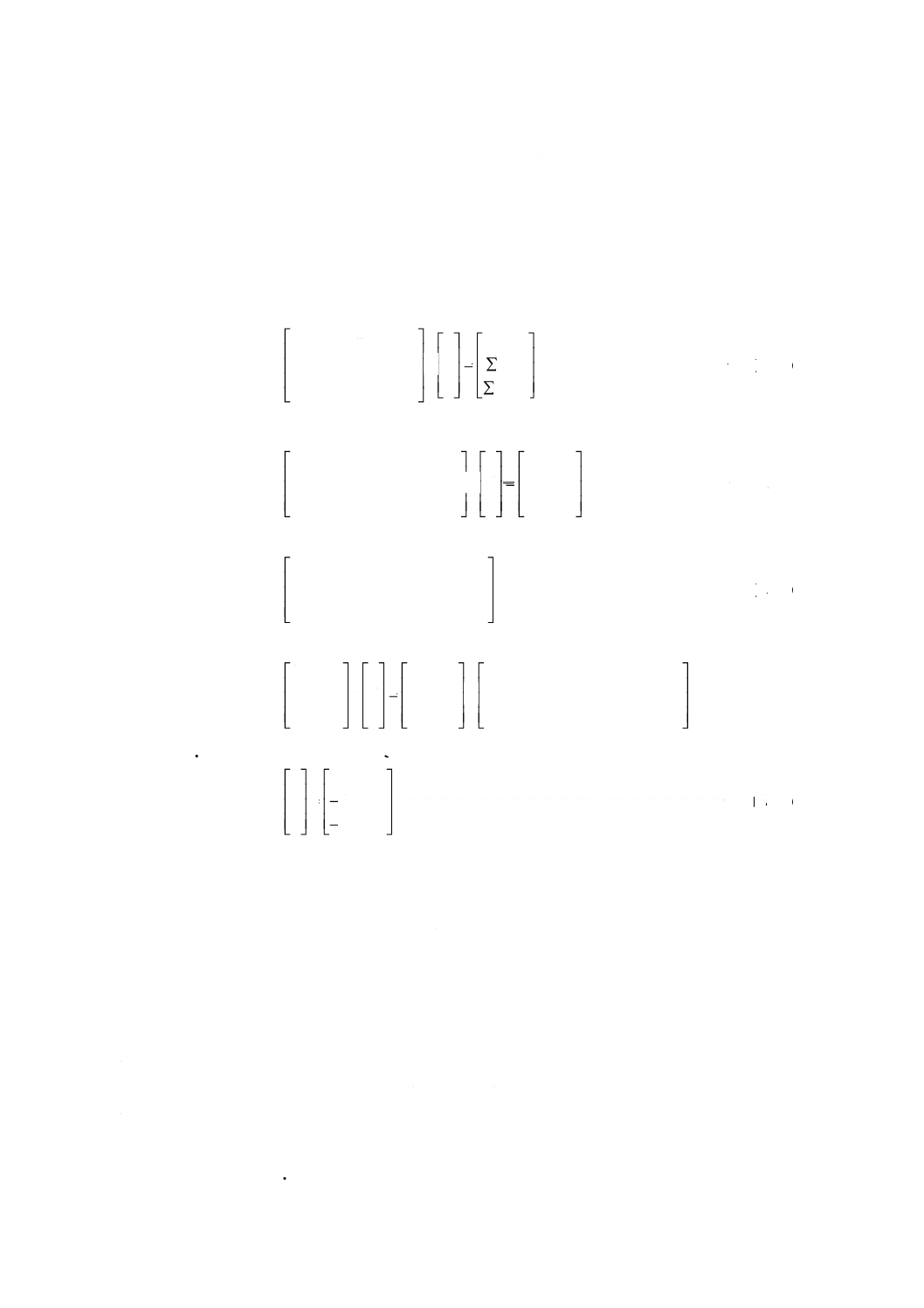K 7020 : 1998 (ISO 10928 : 1997)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づいて,日本工業標準調査会の審議を経て通商産業大臣が制定した日本
工業規格である。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
K 7020 : 1998
(ISO 10928 : 1997)
ガラス強化熱硬化性プラスチック
(GRP) 管及び継手−回帰分析法
及びその使用
Glass-reinforced thermosetting plastics (GRP) pipes and fittings
−Methods for regression analysis and their use
序文
この規格は,1997年に第一版として発行された,ISO 10928, Plastics piping systems−Glass-reinforced
thermosetting plastics (GRP) pipes and fittings−Methods for regression analysis and their useを翻訳し,技術的内
容及び規格票の様式を変更することなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある“参考”は,原国際規格にはない事項である。
この規格は,通常,時間に依存する試験データの回帰分析を行い,設計の結果と要求性能に対する一致を
評価する手順を示すために作成したものである。この規格の適用は,試料による試験から得られたデータ
を使用する場合だけに限定する。個別規格は周方向引張強さ,変位及びクリープによって得られる管の長
期特性に対する推定値を必要とする。
原国際規格では,破壊試験によって得られた試験データを解析する際に適用可能な統計手法の範囲が検討
された。これらの単純な統計手法の多くは,次のような結果を得るために,データに対する対数変換を必
要とする。
a) 正規分布をする;
b) 負の傾きをもつ回帰直線が得られ;かつ
c) 十分に高い相関回帰関係がある(表1参照)
b),c)2条件を満足する一方,解析結果において分布がひずみを示す場合もあり,a)の条件を満たさない結
果があった。このひずみのある分布の解析を取り扱うことのできる手法を検討した結果,この規格では相
関分析法を採用することとした。
非破壊試験による試験結果,例えば,クリープ又は時間による変位の変化は,多くの場合上記3条件を満
足するので,この規格に準拠し,独立変数として時間を用いるより単純な手法を用いることができる。
1. 適用範囲
この規格は,正規分布又はひずみのある分布の数値を対数に変換したとき,データの解析に適用可能な
計算手順について規定する。この規格は,ガラス強化プラスチック管及び継手の,通常,時間の関数とし
ての特性を解析する試験方法及び個別規格について適用することを目的とする。ただし,他のいかなるデ
ータ類の解析にも適用が可能である。
2
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
データの性質に対応して,適用するために3種類の方法を規定する。これらの手法に用いる外挿法は,
50年間の特性を予測するために,おおむね期間10 000時間について収集されたデータから求めた傾向を延
長する。
参考 規格を適用する場合の配慮について“解説”の1.1(適用条件)を参照。
2. 原理
データは,最小二乗法に基づく回帰分析によって解析する。これによってひずみのある分布及び/又は
正規分布並びに一次又は二次の多項式関係に対する適用が可能となる。
3種類の解析手法は,次のとおり。
− 方法A:一次の関係を扱う相関分析法
− 方法B:独立変数を時間とし,一次の関係を扱う最小二乗法(一次回帰分析)
− 方法C:独立変数を時間とし,二次の関係を扱う最小二乗法(二次回帰分析)
これらの方法は,データの相関及び外挿の妥当性についての統計的検定を含む。
3. 関数関係を求める手順
3.1
線形関係−方法A及びB
3.1.1
方法A及びBに共通する手順
直線式の形に当てはめる場合は,方法A(3.1.2参照)又は方法B(3.1.3)を用いる。
y=a+b×x ··············································································· (1)
ここに,
y: 観察特性値の対数 (log)
a: y軸の切片
b: 直線の傾き
x: 時間,t (h) の対数 (log)
3.1.2
方法A−相関分析法
3.1.2.1
一般
方法Aについては,3.1.2.2から3.1.2.5に従い,次の変数を計算する。
(
)
n
Y
y
Q
i
y
2
−
∑
=
········································································ (2)
(
)
n
X
x
Q
i
x
2
−
∑
=
······································································· (3)
(
)(
)
[
]
n
Y
y
X
x
Q
i
i
xy
−
×
−
∑
=
··························································· (4)
ここに,
Qy: y軸に平行なyiの偏差の二乗和をデータの数nで除した値
Qx: x軸に平行なxiの偏差の二乗和をデータの数nで除した値
Qxy: 直線に直交するxi, yiの偏差の積和をデータの数nで除した値
Y: データyの算術平均,すなわち,
n
y
Y
i
∑
=
X: データxの算術平均,すなわち,
n
x
X
i
∑
=
xi, yi: 個々のデータの値
3
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
n: 全データ(xi, yiの対の)数
備考 Qxyが,0より大きい場合,直線の傾きは正であり,Qxyが,0より小さい場合,直線の傾きは負
である。
3.1.2.2
データの当てはまり度
次の式を用いて,相関係数r又はr2を求める。
y
x
xy
Q
Q
Q
r
×
=
··········································································· (5)
y
c
xy
Q
Q
Q
r
×
=
2
2
············································································ (6)
r2又はrの値nの関数として表1に示される適用可能な最小値以下の場合は,解析に不適切なデータと
みなす。
表1 n対のデータに対応するr2又はrの選択可能な最小値
自由度
(n−2)
最小値
自由度
(n−2)
最小値
r2
r
r2
r
11
0.641 6
0.801 0
23
0.381 6
0.617 7
12
0.608 4
0.780 0
24
0.368 9
0.607 4
13
0.578 1
0.760 3
25
0.356 9
0.597 4
14
0.550 6
0.742 0
30
0.307 0
0.554 1
15
0.525 0
0.724 6
35
0.269 3
0.518 9
16
0.501 8
0.708 4
40
0.239 7
0.489 6
17
0.480 5
0.693 2
45
0.216 0
0.464 8
18
0.460 6
0.678 7
50
0.196 5
0.443 3
19
0.442 5
0.665 2
60
0.166 3
0.407 8
20
0.425 6
0.652 4
70
0.144 3
0.379 9
21
0.409 9
0.640 2
80
0.127 3
0.356 8
22
0.395 3
0.628 7
90
0.113 9
0.337 5
100
0.103 1
0.321 1
備考 表1及びこの規格の他の箇所において,式並びにr2及びrに対応する値は,使用
の便宜上,r2及びrについてだけは,他の出版物に示されている参照値を引用し
ている。
3.1.2.3
関数関係
関数関係を表す直線の,a及びbは,次の式によって求める。
y=a+b×x ··············································································· (1)
最初に,Γを次のように置く。
x
y
Q
Q
Γ=
··················································································· (7)
次いで,次の式を用いて,a及びbを算出する。
x
xy
Q
Q
b=
··················································································· (8)
a=Y−b×X ·············································································· (9)
3.1.2.4
分散の計算
tuが破壊時間に適用可能であれば,xuを次のように置く。
xu=logtu ················································································· (10)
4
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
式(11),(12)及び(13)を用いて,i=1からnまで次の統計量をそれぞれ計算する。
− 真のxiに対する,最適推定値xi'
− 真のyiに対する,最適推定値yi'
− xに対する誤差分散の値,σb2
(
)
Γ
a
y
b
x
Γ
x
i
i
i
×
−
×
+
×
=
′
2
······························································· (11)
yi'=a+b×xi' ··········································································· (12)
(
)
(
)
(
)Γ
n
x
x
Γ
y
y
i
i
i
i
b
×
−
′
−
∑
×
+
′
−
∑
=
2
2
2
2
σ
················································ (13)
次の量を計算する。
xy
b
Q
b
E
×
×
=2
2
σ
············································································ (14)
xy
b
Q
n
b
Γ
D
×
×
×
×
=
2
2
σ ··································································· (15)
次の式によって傾き,bの分散,Cを計算する。
C=D×(1+E) ········································································· (16)
3.1.2.5
外挿に対するデータの当てはまり度の検討
直線を外挿する場合には,次の式を用いてTを計算する。
(
)
5.0
5.0
C
b
b
b
T
=
=
の分散
····························································· (17)
Tの絶対値|T|(すなわち,符号を無視する。)が,表2に示す自由度 (n−2) のスチューデントのtの対
応する値に等しいか又は大きい場合,外挿に適切なデータとみなす。
5
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2 スチューデントのt分布のパーセント点
(信頼係数の片側上方確率2.5%点;両側の信頼確率5%水準,信頼係数97.5%のtv)
自由度
(n−2)
スチューデントのt
tv
自由度
(n−2)
スチューデントのt
tv
自由度
(n−2)
スチューデントのt
tv
1
12.706 2
36
2.028 1
71
1.993 9
2
4.302 7
37
2.026 2
72
1.993 5
3
3.182 4
38
2.024 4
73
1.993 0
4
2.776 4
39
2.022 7
74
1.992 5
5
2.570 6
40
2.021 1
75
1.992 1
6
2.446 9
41
2.019 5
76
1.991 7
7
2.364 6
42
2.018 1
77
1.991 3
8
2.306 0
43
2.016 7
78
1.990 8
9
2.262 2
44
2.015 4
79
1.990 5
10
2.228 1
45
2.014 1
80
1.990 1
11
2.201 0
46
2.012 9
81
1.989 7
12
2.178 8
47
2.011 2
82
1.989 3
13
2.160 4
48
2.010 6
83
1.989 0
14
2.144 8
49
2.009 6
84
1.988 6
15
2.131 5
50
2.008 6
85
1.988 3
16
2.119 9
51
2.007 6
86
1.987 9
17
2.109 8
52
2.006 6
87
1.987 6
18
2.100 9
53
2.005 7
88
1.987 3
19
2.093 0
54
2.004 9
89
1.987 0
20
2.086 0
55
2.004 0
90
1.986 7
21
2.079 6
56
2.003 2
91
1.986 4
22
2.073 9
57
2.002 5
92
1.986 1
23
2.068 7
58
2.001 7
93
1.985 8
24
2.063 9
59
2.001 0
94
1.985 5
25
2.059 5
60
2.000 3
95
1.985 3
26
2.055 5
61
1.999 6
96
1.985 0
27
2.051 8
62
1.999 0
97
1.984 7
28
2.048 4
63
1.998 3
98
1.984 5
29
2.045 2
64
1.997 7
99
1.984 2
30
2.042 3
65
1.997 1
100
1.984 0
31
2.039 5
66
2.039 5
32
2.036 9
67
2.036 9
33
2.034 5
68
2.034 5
34
2.032 2
69
2.032 2
35
2.030 1
70
2.030 1
3.1.2.6
計算例による統計手法の有効性の確認
計算例とともに表3に示すデータは,ユーザがこの規格に規定する計算方法以外の統計手法を用いても
この規格の式から得られるのと同等の結果を得ることを証明するものである。例証の目的として問題とな
る特性,Vによって表される量は,代表的な大きさで特殊な単位ではない。丸めの誤差によって結果が正
確に一致するとは限らないが,得られたr,r2,b,a及びVの平均値,Vmは,この計算例に示す値と±0.1%
の範囲内にあるはずで,適用が可能である。その他の統計量は,手法の確認を支援するためのものである。

6
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3 計算例用基礎データ及び統計解析の確認
n
V
y (log V)
時間,t (h)
x (log t)
1
3.08
0.488 6
5 184
3.714 7
2
3.08
0.488 6
2 230
3.348 3
3
3.15
0.498 3
2 220
3.346 4
4
3.15
0.498 3
12 340
4.091 3
5
3.15
0.498 3
10 900
4.037 4
6
3.15
0.498 3
12 340
4.091 3
7
3.15
0.498 3
10 920
4.038 2
8
3.22
0.507 9
8 900
3.949 4
9
3.22
0.507 9
4 173
3.620 4
10
3.22
0.507 9
8 900
3.949 4
11
3.22
0.507 9
878
2.943 5
12
3.29
0.517 2
4 110
3.613 8
13
3.29
0.517 2
1 301
3.114 3
14
3.29
0.517 2
3 816
3.581 6
15
3.29
0.517 2
669
2.825 4
16
3.36
0.526 3
1 430
3.155 3
17
3.36
0.526 3
2 103
3.322 8
18
3.36
0.526 3
589
2.770 1
19
3.36
0.526 3
1 710
3.233 0
20
3.36
0.526 3
1 299
3.113 6
21
3.50
0.544 1
272
2.434 6
22
3.50
0.544 1
446
2.649 3
23
3.50
0.544 1
446
2.668 4
24
3.50
0.544 1
684
2.835 1
25
3.64
0.561 1
104
2.017 0
26
3.64
0.561 1
142
2.152 3
27
3.64
0.561 1
204
2.309 6
28
3.64
0.561 1
209
2.320 1
29
3.85
0.585 5
9
0.954 2
30
3.85
0.585 5
13
1.113 9
31
3.85
0.585 5
17
1.230 4
32
3.85
0.585 5
17
1.230 4
平均:Y=0.530 1, X=2.930 5
分散
Qx = 0.798 12
Qy = 0.000 88
Qxy =−0.024 84
相関係数
r
=−0.938 08
r2
= 0.879 99
関数関係
Γ = 0.001 10
b
=−0.031 12
a
= 0.621 29
分散の計算(3.1.2.4参照)
E = 7.659 8×10−2
D = 1.053 7×10−5
7
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C = 1.134 4×10−5(bの分散)
σb2 = 1.222 7×10−1(xに関する誤差の分散)
外挿の適用可能性の検討(3.1.2.5参照)
n
= 32
tv
= 2.042 3
T
=−0.031 12/ (1.134 4×10−5) 0.5=−9.239 53
|T|
= 9.239 53>2.042 3
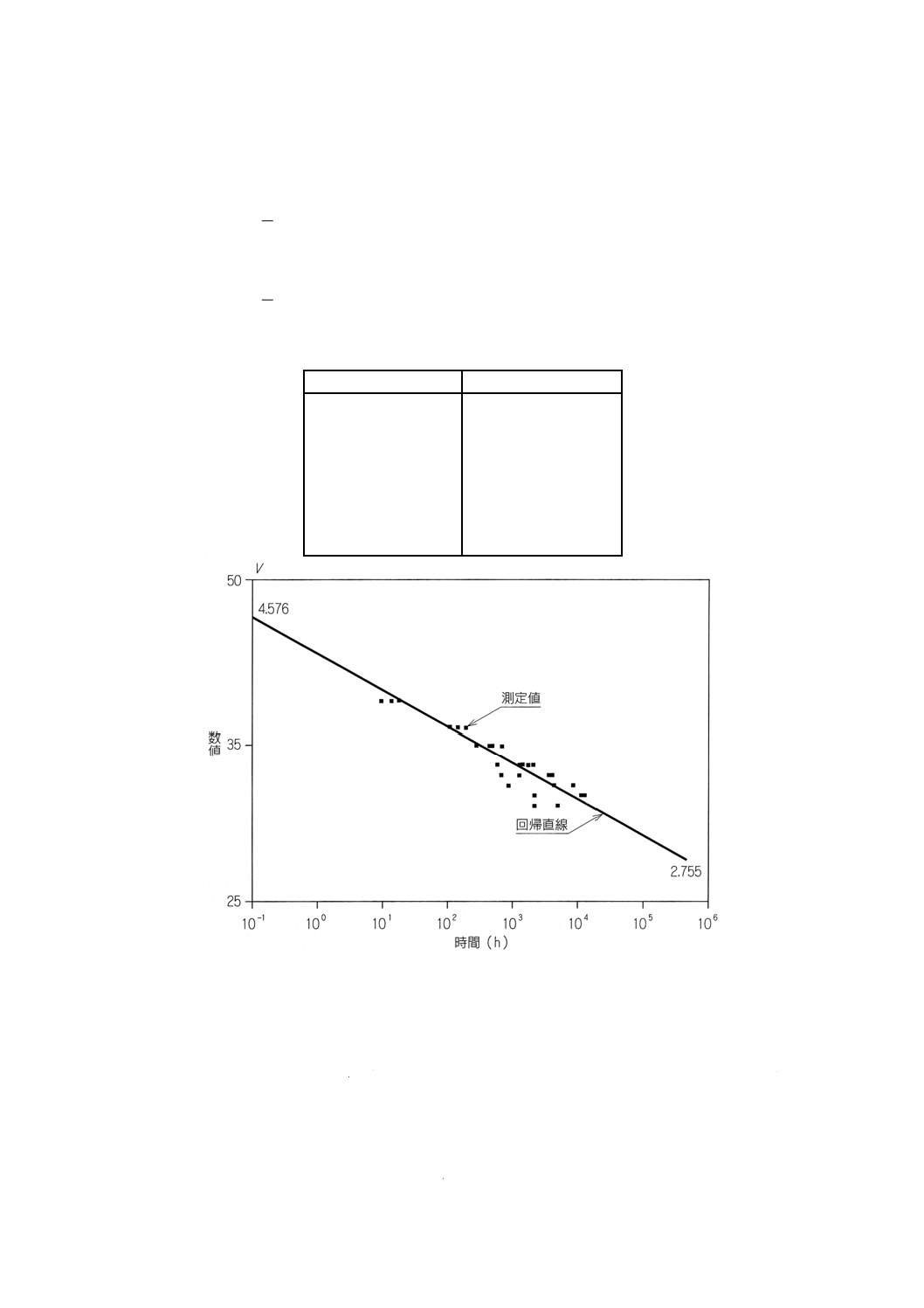
各時間における,Vの平均,Vmの推定値を表4及び図1に示す。
表4 Vの平均,Vmの推定値
時間,t (h)
Vm
0.1
4.492
1.0
4.181
10.0
3.892
100.0
3.623
1 000
3.372
10 000
3.139
100 000
2.922
438 000
2.791
図1 表4の結果による回帰直線
3.1.3
方法B−時間を独立変数とする回帰直線
3.1.3.1
一般
方法Bでは,まず次の変数を計算する。
Sy=Σ (yi−Y) 2·········································································· (18)
(y軸に平行な偏差の二乗和)
Sx=Σ (xi−X) 2 ········································································· (19)
(x軸に平行な偏差の二乗和)
Sxy=Σ (xi−X) × (yi−Y) ···························································· (20)
8
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(直線に直交する偏差の二乗和)
ここに,
Y: データyの算術平均,すなわち,
n
y
Y
i
∑
=
X: データxの算術平均,すなわち,
n
x
X
i
∑
=
xi, yi: 個々のデータの値
n: 全データ(xi, yiの対の)数
備考 Sxyが,0より大きい場合,直線の傾きは正であり,Sxyが,0より小さい場合,直線の傾きは負
である。
3.1.3.2
データの妥当性
次の式を用いて,相関係数,r又はr2を求める。
y
x
xy
S
S
S
r
×
=
·········································································· (21)
y
x
xy
S
S
S
r
×
=
2
2
··········································································· (22)
r2又はrの値がnの関数として表1に示される適用可能な最小値以下の場合は,解析に不適切なデータ
とみなす。
3.1.3.3
関数関係
直線関係を示す関数[式(1)参照]の,a及びbは,次の順に求める。
x
xy
S
S
b=
················································································· (23)
a=Y−b×X ············································································ (24)
3.1.3.4
外挿に対するデータの妥当性の検討
直線を外挿する場合には,次の式を用いてMを計算する。
(
)
(
)
2
2
2
2
2
2
y
xy
y
x
xy
x
S
n
S
S
S
t
S
S
M
×
−
−
×
×
−
=
ν
··················································· (25)
tvは,スチューデントのtの適用可能な値であって,表2によって求める。
Mの値が,0に等しいか又はそれ以下の場合,外挿に適用不可能なデータとみなす。
3.1.3.5
計算例による統計手法の有効性の確認
表5に示すデータを用い,3.1.3.2から3.1.3.4までに示す計算手順によって,得られたr, r2, b, a及びV
の平均値Vmが,この計算例に示す値と±0.1%の範囲内にあることを確認する。
9
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表5 計算例用基礎データ及び統計解析の確認
n
時間,t (h)
x (log t)
V
y (log V)
1
0.10
−1.000 0
7 114
3.852 1
2
0.27
−0.568 6
6 935
3.841 0
3
0.50
−0.301 0
6 824
3.834 1
4
1.00
0
6 698
3.825 9
5
3.28
0.515 9
6 533
3.815 1
6
7.28
0.862 1
6 453
3.809 8
7
20.0
1.301 0
6 307
3.799 9
8
45.9
1.661 8
6 199
3.792 3
9
72.0
1.857 3
6 133
3.787 7
10
166
2.220 1
5 692
3.755 2
11
219
2.340 4
5 508
3.741 0
12
384
2.584 3
5 393
3.731 8
13
504
2.702 4
5 364
3.729 5
14
3 000
3.477 1
5 200
3.716 0
15
10 520
4.022 0
4 975
3.696 8
平均:X=1.445 0,Y=3.781 9
二乗和
Sx
=
31.681 1
Sy
=
0.034 7
Sx
y
= −1.024 2
相関係数
r
= −0.977 5
r2
=
0.955 6
関数関係(3.1.3.3参照)
a
=
3.828 6
b
= −0.032 3
外挿の適用可能性の検討(3.1.3.4参照)
tv
=
2.160 4
M
=
942.21
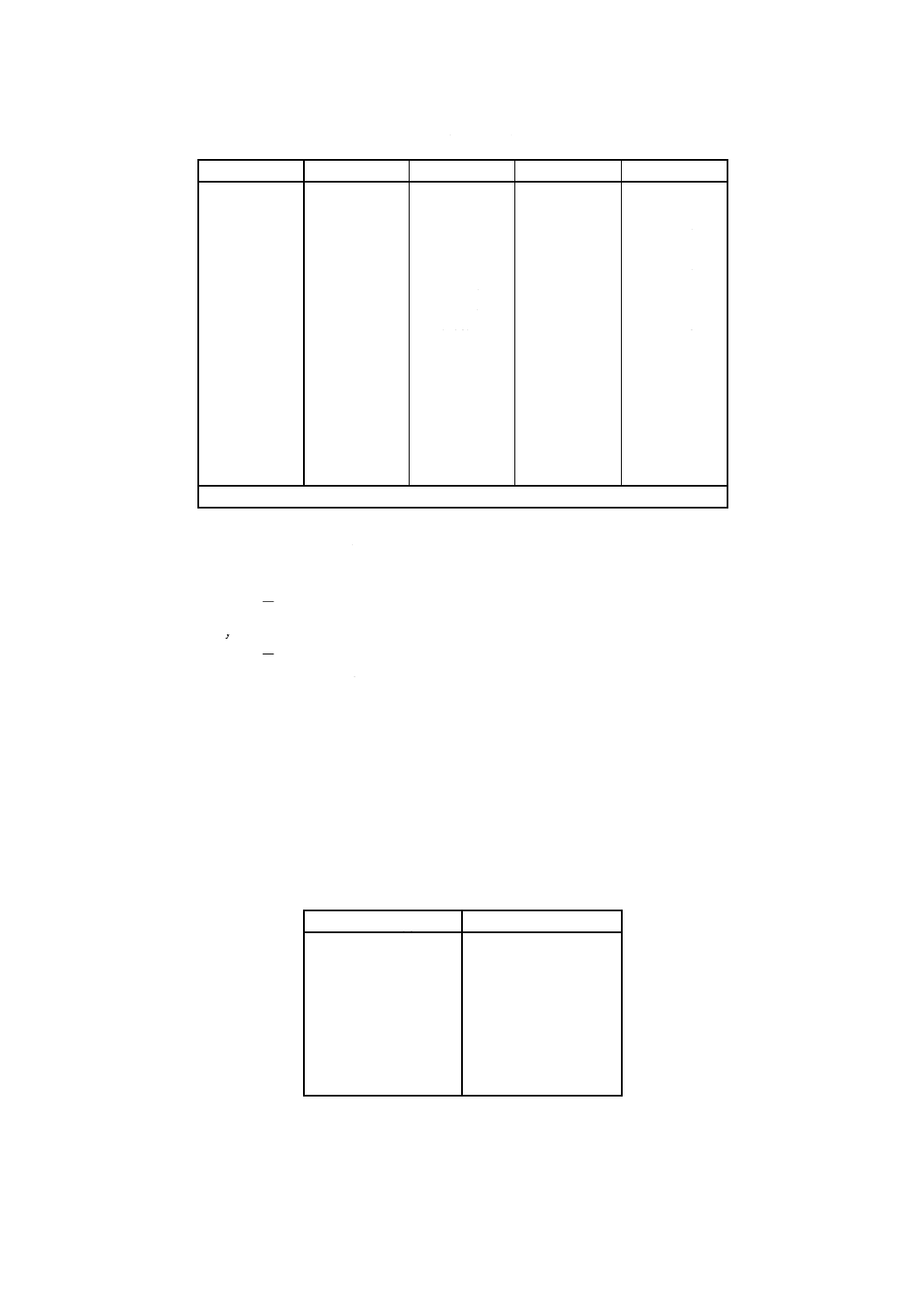
各時間における,Vの平均,Vmの推定値を表6に示す。
表6 Vの平均,Vmの推定値
時間,t (h)
Vm
0.1
7 259
1.0
6 739
10.0
6 256
100.0
5 808
1 000
5 391
10 000
5 005
100 000
4 646
438 000
4 428
3.2
二次多項式−方法C
3.2.1
一般
この方法は,次の曲線の当てはめに適用する。
10
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
y=c+d×x+e×x2 ···································································· (26)
ここに,
y: 観察特性値の対数 (log)
c: y軸の切片
d, e: xの一次及び二次の係数
x: 時間,t (h) の対数 (log)
3.2.2
変数
C法では,次の変数を計算する。
Σxi
個々のデータxの和
Σxi2
個々のデータxの二乗和
Σxi3
個々のデータxの三乗和
Σxi4
個々のデータxの四乗和
Σyi
個々のデータyの和
(Σyi)2
個々のデータyの和の二乗
Σyi2
個々のデータyの二乗和
Σ (xiyi)
個々のデータxi,yiの積の和
Σ (xi2yi)
個々のデータxi2,yiの積の和
Sx=Σ (xi−X) 2
一次の項に関するx軸に平行な偏差の二乗和
Sxx=Σ (xi2−X2) 2
二次の項に関するx軸に平行な偏差の二乗和
Sy=Σ (yi−Y) 2
一次の項に関するy軸に平行な偏差の二乗和
(
)2
ˆ
ˆ
ˆ
Y
y
S
i
y
−
∑
=
回帰曲線の一次の項に関するy軸に平行な偏差の二乗和
Sxy=Σ [ (xi−X) × (yi−Y) ]
一次の項に関する一次曲線に直角な偏差の二乗和
Sxxy=Σ [ (xi2−X2) × (yi−Y) ]
二次の項に関する二次曲線に直角な偏差の二乗和
(
)(
)
Y
y
Y
y
S
i
i
y
y
ˆ
ˆ
ˆ
−
×
−
∑
=
回帰曲線の一次の項に関する一次曲線に直角な偏差の二乗和
ここに,
Y: データyの算術平均,すなわち,
n
y
Y
i
∑
=
Yˆ: 回帰直線データyˆの算術平均,すなわち
n
y
Y
iˆ
ˆ
∑
=
X: データxの算術平均,すなわち,
n
x
X
i
∑
=
3.2.3
解法
次の行列を用いて,c,d,及びe(3.2.1参照)を求める。
Σyi=c×n+d×Σxi+e×Σxi2 ······················································· (27a)
Σ (xi×yi) =c×Σxi+d×Σxi2+e×Σxi3 ··········································· (27b)
Σ (xi2×yi) =c×Σxi2+d×Σxi3+e×Σxi4 ········································· (27c)
備考 計算手順の詳細例を附属書Aに示す。
3.2.4
データの妥当性
相関係数,r又はr2を次の式を用いて計算する。
11
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
y
y
y
y
S
S
S
r
ˆ
ˆ
×
=
·········································································· (28)
y
y
y
y
S
S
S
r
ˆ
ˆ
2
2
×
=
·········································································· (29)
r2又はrの値がnの関数として表1に示される適用可能な最小値以下の場合は,解析に不適切なデータ
とみなす。
3.2.5
外挿に対するデータの妥当性の検討
直線を外挿する場合は,次の式を用いて,Mを計算する。
(
)
(
)
2
2
2
2
2
2
2
2
y
xxy
y
xx
xy
y
x
v
xxy
xx
xy
x
S
n
S
S
S
S
S
S
t
S
S
S
S
M
×
−
−
×
+
−
×
×
−
+
=
·························· (30)
Mが,0又は0以下の場合,外挿に不適当とみなす。
3.2.6
計算例による統計手法の有効性の確認
3.2.2から3.2.5に示す統計計算手順に従い,表5に示すデータ例を用いて,r, r2, a, b及びVmを計算した
結果,その値が,±0.1%以内に入ることを確認する。
二乗和及びその他の変数
Σxi
=
21.671
Σxi2
=
62.989
Σxi3
=
180.623
Σxi4
=
584.233
Σyi
=
56.728
(Σyi)2
=
3 218.09
Σyi2
=
214.574
Σ (xiyi)
=
80.932
Σ (xi2yi)
=
235.175
Sx
=
31.681
Sxx
=
386.638
Sy
=
0.034 7
y
Sˆ
=
0.033 4
Sxy
=
− 1.024 2
Sxxy
=
− 3.041 8
y
y
Sˆ
=
0.033 4
解析結果(3.2.3参照)
c
=
3.828 8
d
=
− 0.026 2
e
=
− 0.002 2
相関係数(3.2.4参照)
r
=
0.982 2
r2
=
0.964 7
12
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
外挿の適用可能性の検討(3.2.5参照)
tv
=
2.160 4
M
=
15 853.7
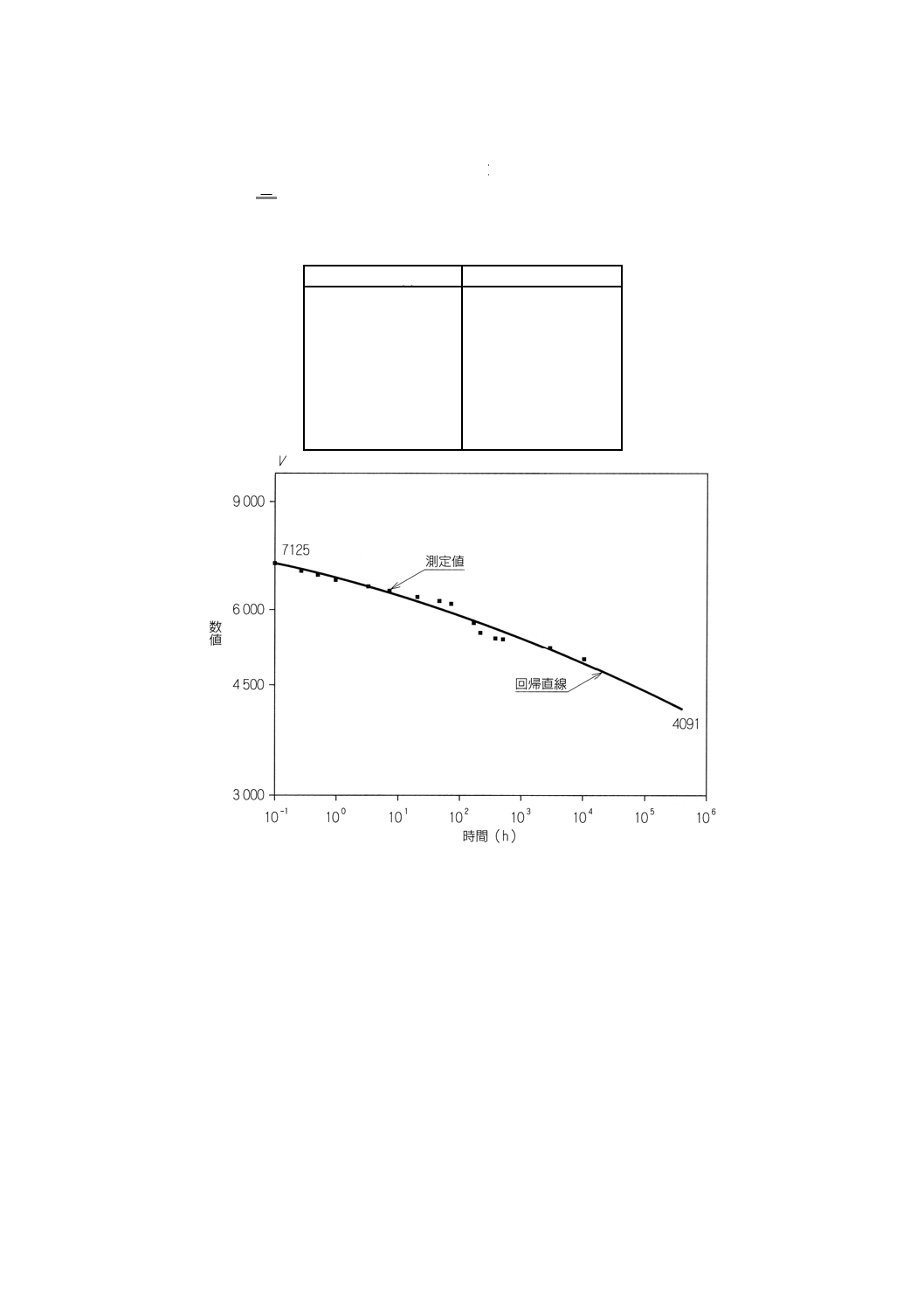
各時間における,Vの平均,Vmの推定値を表7及び図2に示す。
表7 Vの平均,Vmの推定値
時間,t (h)
Vm
0.1
7 125
1.0
6 742
10.0
6 315
100.0
5 856
1 000
5 375
10 000
4 884
100 000
4 393
438 000
4 091
図2 表7の結果による回帰直線
4. 製品設計及び試験方法への適用
4.1
一般
製品の特性及び性能は,個別規格の定める要求からの制約を受ける。ある場合にそれは破壊試験,例え
ば,周方向引張強さ,またある場合は,実際又は推定による物性,例えば,剛性などである。
求める物性値が方法B及び方法Cの援用を可能にする場合,両方法の計算による結果を確認しなければ
ならない。それぞれの方法において,r2及び/又はrの計算結果を比較し,高い方の値を用いて物性を決
定しなければならない。個別規格が,一つの方法を特定している場合は,その方法に従わなければならな
い。
いずれの場合でも,これら物性値については,要求性能と比較の上長期の値(例えば,50年間)を外挿
して求めなければならない。この外挿については,必要な場合,3.1又は3.2を援用して求めた,a, b, c, d
13
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
及びeの値を,それぞれ次の式(31)又は(32)に代入して求める。
log y=a+b×tL ········································································ (31)
log y=c+d×tL+e×tL2 ······························································ (32)
ここに,
tL: 時間,t (h) で示す長時間の対数 (log) [50年間 (438 000h) , tL
=5.641 47]
式(31)及び(32)を解き,yに関する外挿値を求め,個別規格に規定する要求値と比較する。これらを補足
する手順として設計上の要求を得るための計算結果の援用に関しては,4.2を参照すること。また,その実
際の適用例として4.3に計算の妥当性を示す。
製品を試験し,規定の要求に合致するかどうかを予測し並びに確認するためには,4.4を参照すること。
またその実際の適用例として4.3に計算の妥当性を示す。
4.2から4.5までの記述は,最小値,50年間の長期性能及び6分間の短期性能に限り適用が可能である。
最大値又はその他の期間を含む適用に関しては,適切な調整を図る必要がある。
個別規格が規定するこの規定に一致しない製品の数量及び証明又は品質計画における試料の要求とその
許容可能な水準の限界に関しては,これらの方法は品質管理を目的とする適用が望ましい。
4.2
設計
4.2.1
回帰値
4.2.1.1
得られた長期の値
設計における管の初期の短期試験から,特性の平均値,V0, mと標準偏差,σを得たとした場合,個別規
格の要求に合致した設計手順は,次のとおりとなる。
いま安全率,Fsを特定すれば,長期(50年間)特性の最小値(図4参照),V50, minは,次の式を用いて
計算する。
V50, min=Fs×V50, s, min ·································································· (33)
又は,
V50, min=V50, s, min ······································································· (34)
ここに,
V50, s, min: 長期(50年間)特性の最小要求値
4.2.1.2
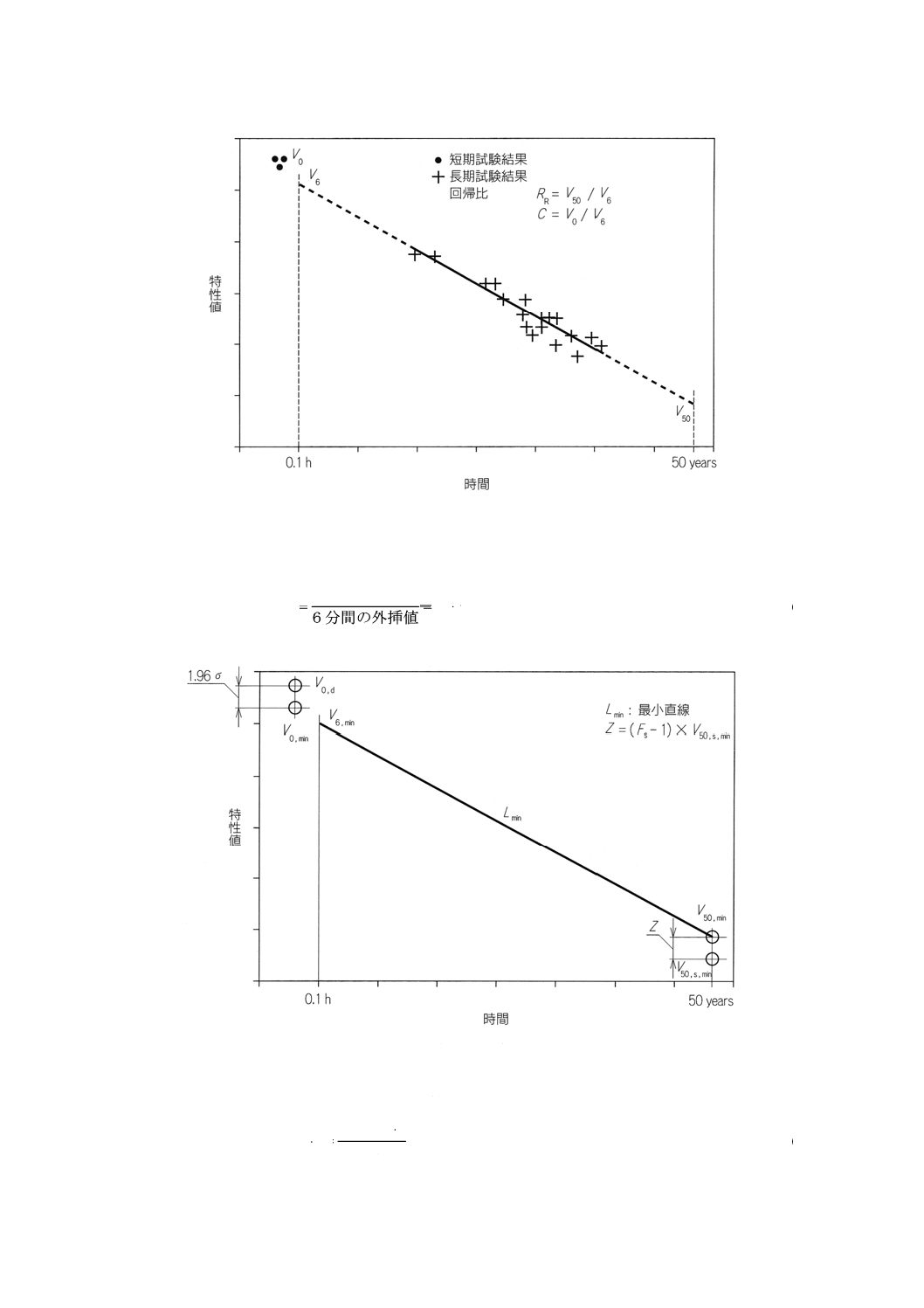
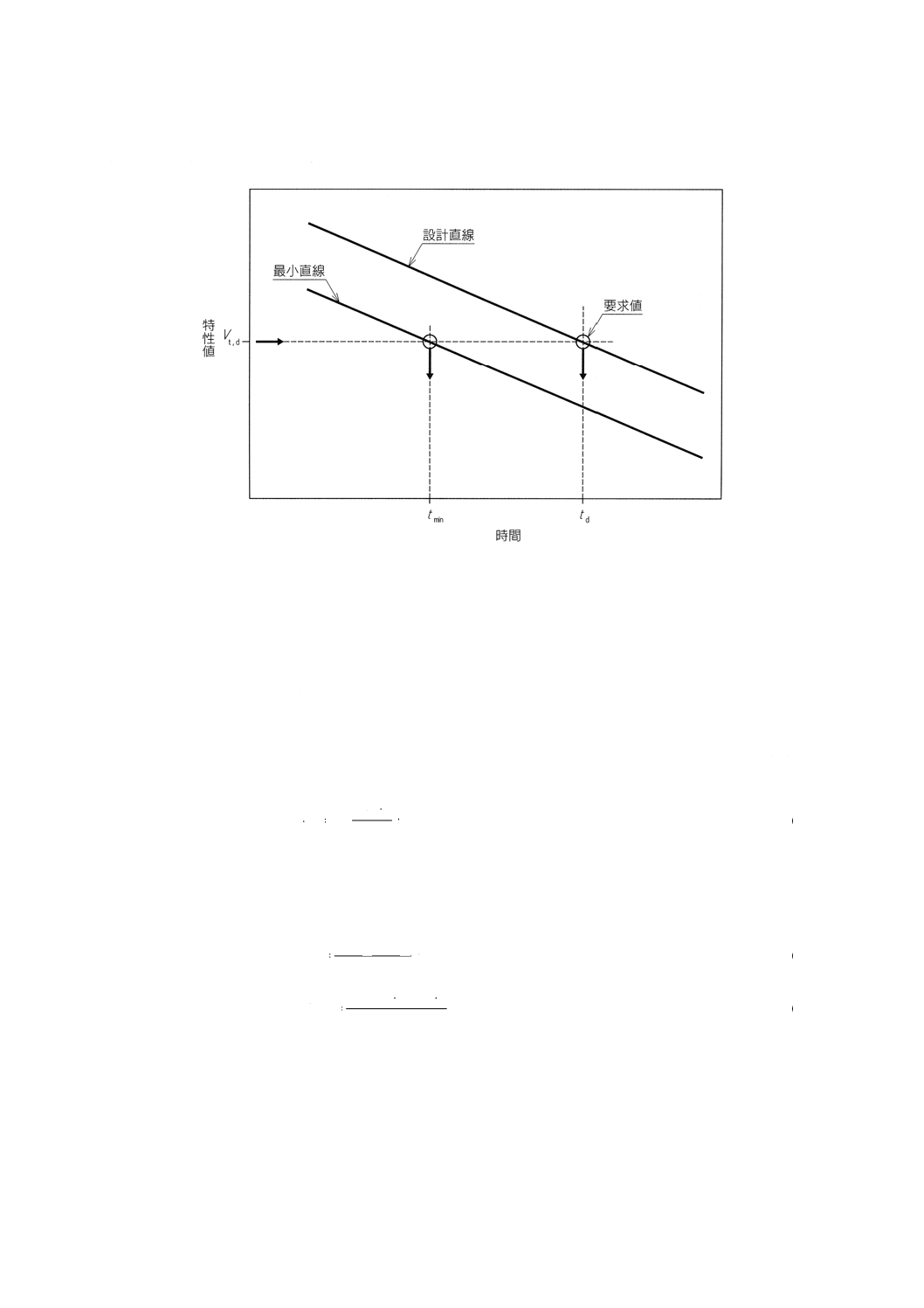
回帰比(図3参照)
回帰比,RRは,次の式を用いて計算する。
6
50
6
50
V
V
RR
=
=
分間)の特性値
外挿した短期(
年間)の特性値
外挿した長期(
······························· (35)
ここで,50年間及び6分間の外挿特性値は,式(31)及び(32)を用いて計算する。ただし,0.1時間(6分
間)の対数値は,−1,50年間の対数値は,5.641 47とする。
14
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3 外挿値
4.2.1.3
要因C(図3参照)
管の初期試験の結果による6分間の外挿値に関連して,因子,Cを次の式を用いて計算する。
6
0
V
V
C
=
=6分間の外挿値
初期特性値
·························································· (36)
4.2.2
初期値
図4 得られた結果
4.2.2.1
初期特性の最小値 (V0. min)
初期特性の最小値,V0. minを次の式を用いて計算する。
R
R
V
C
V
min
,
50
min
,0
×
=
··································································· (37)
15
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
C: 式(36)による計算値
V50, min: 式(33)又は(34)による計算値
RR: 式(35)による計算値
4.2.2.2
特性の設計値
初期特性の設計値,V0, dを次の式を用いて計算する。
V0, d=V0, min+1.96×σ ································································ (38)
ここに,
σ: 初期試験結果における特性値の標準偏差
1.96は,推定の危険率,2.5%を想定した値である。個別規格において,これ以外の危険率を特定してい
る場合は,標準となる統計処理から得られる危険率を,1.96に代替することができる。
備考 標準偏差は,特性の平均値が増大するにつれて大きくなることが考えられる。またその逆もあ
る。したがって,バリエーションに対する一定の係数を用いることによって,特性値の各種水
準に対する設計上の特性値を得ることができる。
短期(6分間)及び長期(50年間)の設計特性値を定め,設計直線を次のように定める。
− 6分間の設計特性値,V6, dは次の式を用いて計算する。
C
V
V
d
d
,0
,6
=
············································································· (39)
ここに,Cは,4.2.1.3に従って決定する。
− 50年間の設計特性値,V50, dは次の式を用いて計算する。
V50, d=RR×V6, d ········································································ (40)
ここに,RRは,4.2.1.2に従って定めた回帰比である。
− 適用が可能であれば,次の式に従って設計一次直線を決定する。
log Vt, d=ad+ (b×log t) ····························································· (41)
ここに,
Vt, d: 時間,tにおける設計特性値
b: 最小及び平均回帰直線の傾き
ad: 設計直線の定数
更にまた,
ad=a+δd ··············································································· (42)
ここに,
a: 特性値の平均直線の定数[式(1)参照]
また,
m
d
d
V
V
,0
,0
log
=
δ
·········································································· (43)
− 適用が可能であれば,次の式に従って設計二次曲線を決定する。
log Vt, d=cd+ (d×log t) + [e× (log t)2 ] ······································· (44)
ここに,
Vt, d: 時間,tにおける設計特性値
d, e: 設計曲線及び二次の平均回帰曲線の係数
cd: 設計二次曲線の定数
cd=c+δd················································································ (45)
ここに,
c: 二次の平均回帰曲線の定数[式(26)参照]
m
d
d
V
V
,0
,0
log
=
δ
·········································································· (43)
4.3
設計に対する計算手順の有効性の確認例
4.3.1
一般

16
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
適用可能であれば,4.3.2及び4.3.3に示すデータを用い,計算手順を確認し,a,b,c,d,e,r2,r,V50,
min,V6, min,V0, min及びV0, dの計算結果が,計算例の±0.1%以内にあることを確認する。
4.3.2
例1:線形関係;破壊試験による破壊挙動
4.3.2.1
問題
計算にあたり次を仮定する;
a) 表3に示すデータは,管の長期破壊試験の結果で,単位をMPaで示す。
b) 表4は,この管の長期破壊試験結果の回帰分析から得られた結果である。
c) 同等の管の断面構成からなる管について,a)及びb)の条件下で短期破壊試験を行った結果を表8に示
す。いま公称圧力 (PN) 1.0の管について,安全率,1.8を用い,設計値を計算せよ。
表8 短期破壊試験結果
単位 MPa
5.20
4.45
4.90
5.03
4.67
5.11
4.73
4.97
5.33
5.11
4.60
5.03
4.59
4.91
4.88
4.67
4.98
5.36
破壊試験の平均値
p0=4.918
標準偏差
σ=0.259
4.3.2.2
計算及び最終結果
表3のデータについて(3.1.2.6参照)
a=0.621 29
b=−0.031 12
ゆえに(表4)から,
p6 =4.492MPa
p50=2.791MPa
式(35)を用いて
3
621
.0
492
.4
791
.2
6
50
=
=
=p
p
RR
式(36)を用いて,
9
094
.1
492
.4
918
.4
6
,0
=
=
=p
p
C
m
公称圧力 (PN) 1.0の管について,安全率,1.8を用い,設計値を計算した結果は,式(33)を用いて,
p50, min=Fs×p50, s, min=1.8×1.0=1.8MPa
MPa
90
.2
3
621
.0
8.1
min
,
50
min
,6
=
=
=
R
R
p
p
及び式(35),式(37)を用いて,
p0, min=C×p6, min=1.094 9×2.90=3.17MPa
式(38)を用いて
p0, d=p0, min+1.96×σ=3.17+1.96×0.259=3.679MPa
このようにして,6分間及び50年間の設計値は,式(39)及び(40)を用いて次のとおりとなる。
MPa
36
.3
9
094
.1
679
.3
,0
,6
=
=
=C
p
p
d
d
P50, d=RR×P6, d=0.621 3×3.36=2.088MPa
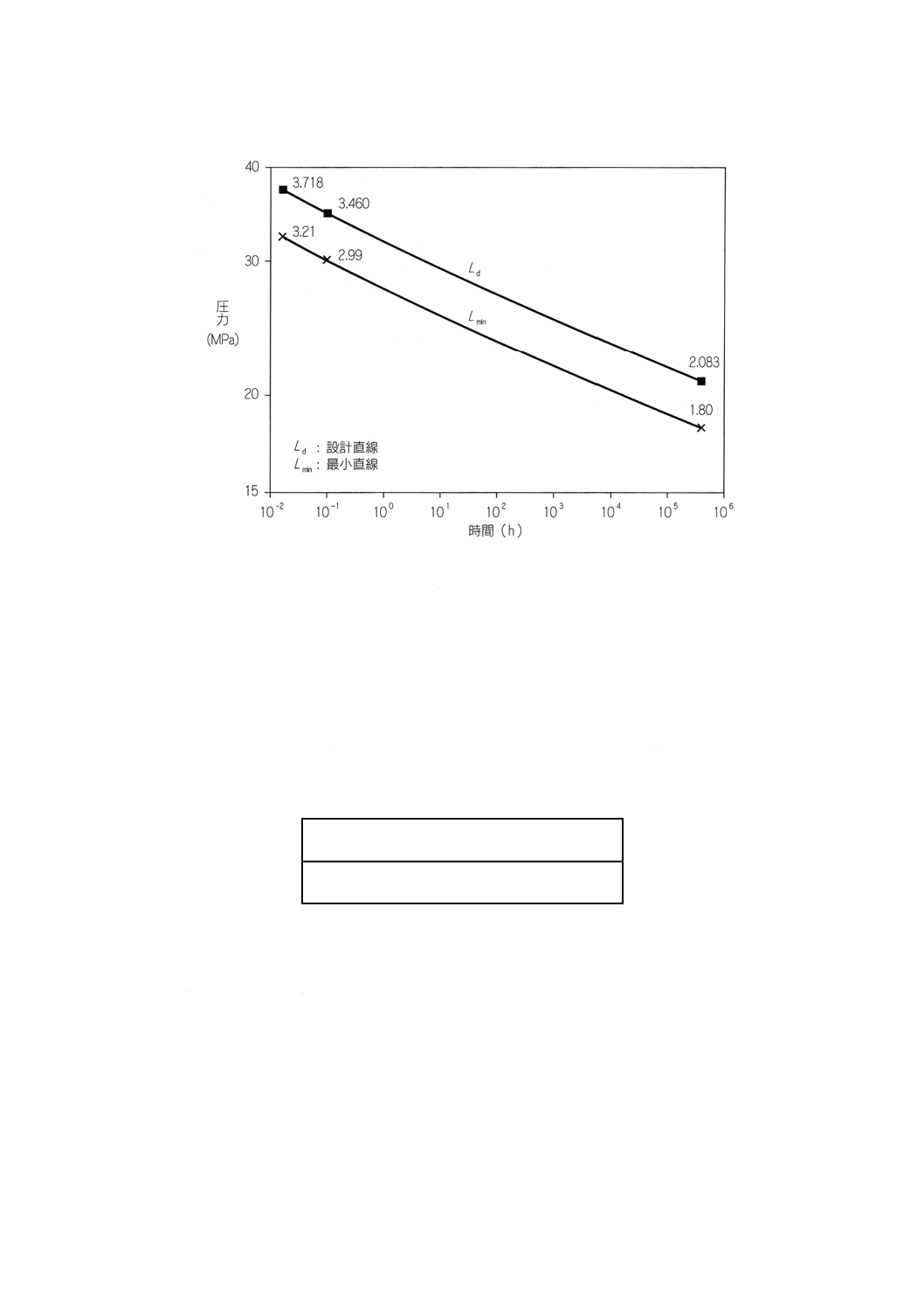
17
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
これらの計算結果を図5に示す。
図5 圧力の例
4.3.3
例2:二次の関係−非破壊試験(クリープ)挙動
4.3.3.1
問題
計算にあたり次を仮定する。
a) 表5に示すデータは,リングの長期剛性試験の結果で,単位を,N/m2で示す。
b) 表6及び表7は,この剛性試験結果の回帰分析から得られた結果である。
c) 同等の管の断面構成からなる管について,a)及びb)の条件下で短期剛性試験を行った結果を表9に示
す。いま公称圧力 (PN) 1.0の管について,安全率,1.8を用い,設計値を計算せよ。
表9 短期剛性試験結果
単位 N/m2
7 540
7 200
6 970
7 190
7 760
7 170
7 100
7 310
6 990
7 180
短期剛性試験の平均値
S0, m=7 241
標準偏差
σ=243
4.3.3.2
計算及び最終結果
方法Bを用いて(線形関係,3.1.3.2及び3.1.3.5参照)
r
=−0.977 5
r2
= 0.955 6
方法Cを用いて(二次多項式関係,3.2.4及び3.2.6参照)
r
= 0.982 2
r2
= 0.964 7
方法Cによって得た,r,r2は,方法Bによって得た値よりも大きいから,方法Cによって得られる曲
線の方が適切である。それゆえ,表5に示すデータから計算し,3.2.6に示した結果は,次のとおりとなる。
c
=
3.828 8
18
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d
=
−0.026 2
e
=
−0.002 2
ゆえに(表7),
S6
=
7 125N/m2
S50
=
4 091N/m2
これらの結果から次のとおりとなる。
式(35)を用いて,
3
574
.0
125
7
091
4
6
50
=
=
=SS
RR
式(36)及び表9に示す結果を用いて,
3
016
.1
125
7
241
7
6
,0
=
=
=S
S
C
m
いま,2 000N/m2の最小長期リング剛性をもつSN5 000の管を安全率1.0で設計するとすれば,式(34)を
用いて,
S50, min=S50, s, min=2 000N/m2
2
min
,
50
min
,6
N/m
483
3
2
574
.0
000
2
=
=
=
R
R
S
S
また,式(35)及び(37)を用いて,
S0, min=C×S6, min=1.016 3×3 483N/m2=3 540N/m2
初期要求値 (5 000N/m2) から,S0, minの値は,長期要求値 (3 540N/m2) よりも大きいから,適切なS0,min
の値は,
S0, min=5 000N/m2
ゆえに,式(38)及び表9に示す結果を用いて,
S0, d=S0, min+1.96×σ=5 000+1.96×243=5 476N/m2
6分間及び50年間の設計値は,式(39)及び(40)を用いて,次のとおりとなる。
2
2
,0
,6
N/m
388
5
N/m
3
016
.1
476
5
=
=
=C
S
S
d
d
S50, d=RR×S6, d=0.574 2×5 388N/m2=3 094N/m2
初期要求値 (5 000N/m2) に基づき,6分間及び50年間の最小値は,同様に式(39)及び(40)を用いて,
2
2
2
min
,0
min
,6,0
N/m
825
2
N/m
920
4
N/m
3
016
.1
000
5
=
=
=
=
C
S
S
S0.5, min=RR×S0.6, d=0.574 2×4 920N/m2=2 825N/m2
これらの式から図6に示す曲線のプロットを得る。
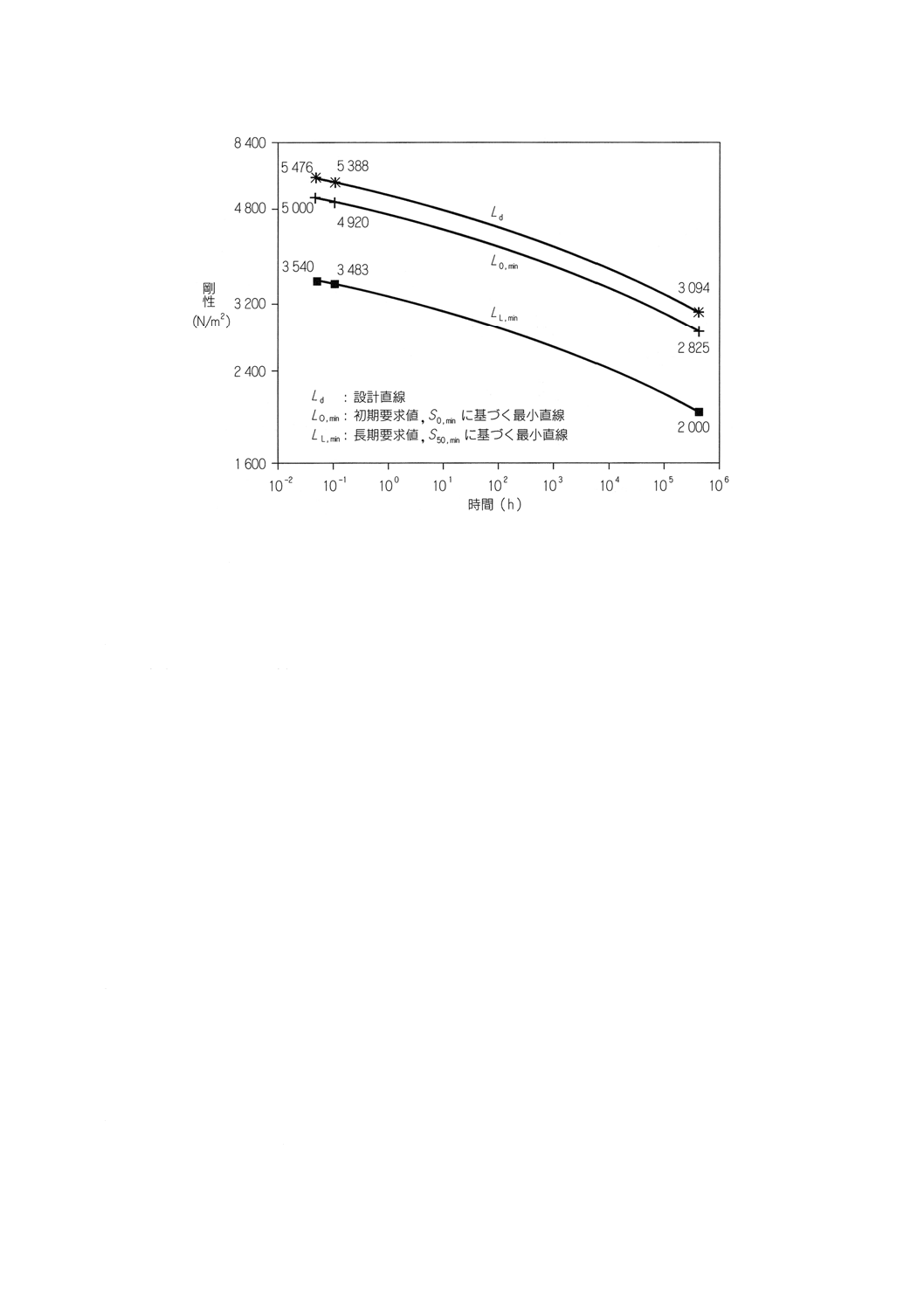
19
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図6 偏平剛性の例
4.4
製品設計及び性能値に対する一致を確認する方法
4.4.1
一般
次の仮定に基づくものとする。
a) 管の設計は,製品に関する短期試験又は短期及び長期試験の両方によって確認される。
b) 調査される特性の設計値,V0, dは,4.2による。
次の手順に従い,適用可能な場合,製品が設計要求に合致することを示す。
ここで,
− 方法1(4.4.2参照)は破壊試験の挙動について有効
− 方法2(4.4.3参照)は非破壊試験の挙動について有効
4.4.2
方法1−破壊試験データによる確認
4.4.2.1
設計及び最小直線又はそのいずれか及び製品の試験結果間の関係4.2.2.2に準拠して求めた特性
設計値を用い,又は個別規格の規定に従い,次の要求が基準と合致しているかどうかを評価しなければな
らない。
大集団,すなわち,20個以上の連続的な結果を用いる場合,個別規格との合致を確認するために次の条
件を満足しなければならない。
a) 結果の平均値は,設計値に等しいか又は大きくなければならない(4.2参照)。
b) 個々の結果に,最小値の80%より小さい値があってはならない(4.2参照)。小集団,すなわち5個又
はそれ以下の連続的な結果を用いる場合,次の条件を満足するか,個別規格の規定に従わなければな
らない。
c) 試料の平均値が,設計値を求めるために使用した標準偏差を設計値から差し引いた値より小さくては
ならない(4.2参照)。
d) 個々の結果に,最小値の80%より小さい値があってはならない(4.2参照)。
4.4.2.2
設計直線と製品データ間の関係
20
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0以外の時間,6分間又は50年間が個別規格中に特定されている場合,設計値,Vt, dを求めるため,式(41)
(4.2.2.2参照)を用いなければならない。
図7 特性試験値
4.4.2.3
最小直線と製品データ間の関係(図7参照)
0以外の時間,6分間又は50年間が個別規格中に特定されている場合,設計の最小値,Vt, minを求めるた
め,次の式を用いなければならない。
log Vt, min=amin+ (b×log t) ························································· (46)
ここに,
Vt, min: 与えられた時間,tに対する最小特性値
b: 最小及び平均直線の傾き
amin: 最小直線の定数
amin=a+δmin ··········································································· (47)
ここに,
a: 平均特性値直線の定数[式(1)参照]
m
V
V
,0
min
,0
min
log
=
δ
······································································ (48)
4.4.2.4
特定の時間,t経過後の設計特性値,Vt, dの一致(図7参照)
設計直線に対する破壊に至るまでの時間,td,又は最小直線に対する破壊に至るまでの時間,tminは,次
の式のうち適切な一つを用いて確認しなければならない。
b
a
V
t
t
d
d,
d
log
log
−
=
·································································· (49)
b
a
V
t
t
min
min
,
min
log
log
−
=
··························································· (50)
4.4.3
方法2−非破壊試験データによる確認
備考 長期設計又は物性挙動の確認に対する非破壊試験には,通常クリープ試験を用いる。試験時間,
tcの期間及び関連する特性要求は個別規格の規定に従うものとする(4.4.1参照)。
4.4.3.1
設計及び/又は最小直線及び製品の試験結果間の関係
これらの関係には,4.4.2.1に規定する仮定及び要求が適用可能である。
21
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.4.3.2
設計直線と製品データ間の関係
0以外の時間,6分間又は50年間が個別規格中に特定されている場合,設計値,Vt, dを求めるため,式(41)
及び(44)同じく式(46),(47)及び(48)(4.2.2.2参照)を用いなければならない。
4.4.3.3
最小直線と製品データ間の関係
4.4.3.3.1
線形関係(図7参照)
線形関係の場合,仮定,手順及び式については4.4.2.3の規定が適用可能である。
4.4.3.3.2
二次多項式関係(原理は図7参照)
0以外の時間,6分間又は50年間が個別規格中に特定されている場合,設計の最小値,Vt, minを求めるた
め,次の式を用いなければならない。
log Vt, min=Cmin+ (d×log t) + [e× (log t) 2] ·································· (51)
ここに,
Vt, min: 与えられた時間,tに対する最小特性値
d, e: 最小及び平均回帰直線に関する係数
cmin: 最小直線の定数
cmin=c+δmin ··········································································· (52)
ここに,
c: 平均特性値直線の定数[式(26)参照]
m
V
V
,0
min
,0
min
log
=
δ
······································································ (53)
4.4.3.4
特定の時間,t経過後の設計特性値,Vt, dの一致(図7参照)
製品が個別規格に定める時間,tcの後,設計値,Vt, d又はVt, minに一致することを確認するため,tをtc
に置きかえたとき,次の式を用いて対応する値を求めなければならない。
線形関係の場合,
log Vt, d=ad+ (b×log t) ····························································· (41)
log Vt, min=amin+ (b×log t) ························································· (46)
二次多項式曲線関係の場合,
log Vt, d=cd+ (d×log t) + [e× (log t) 2] ······································ (44)
log Vt, min=cmin+ (d×log t) + [e× (log t) 2] ·································· (51)
4.5
設計と製品性能値の有効性を計算する手順の検証例
4.5.1
一般
4.5.2及び4.5.3に示すデータを用い,計算手順を確認し,pt, d,tmin,St, d及びSt, minの計算結果が,計算例
の±0.1%以内にあることを確認する。
4.5.2
例3:線形関係−破壊試験による破壊挙動
4.5.2.1
問題
一連の管が,4.3.2に規定する設計を基に製造された。試験片の特性は,短期(初期破壊)及び長期(100
時間)圧力強さ試験によって測定された。短期試験結果を表10に示す。試験圧力,pt, dによって実施し,
4.5.2.3によって求めた3個の試験片から得られた長期試験の結果を表11に示す。この管は,4.4.2.1及び
4.4.2.4に合致することを確認する。
4.5.2.2
計算及び最終結果
4.5.2.2.1
初期破壊圧力要求値に対する一致の求め方

22
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表10 試験片に対する短期破壊圧力
単位 MPa
3.86
3.85
3.19
3.84
3.67
3.98
3.92
4.01
3.26
3.75
3.49
3.83
3.69
4.00
3.94
4.17
3.86
3.85
3.19
3.84
3.67
3.77
3.92
3.78
平均初期破壊圧力
p0, m
=3.76
最小初期破壊圧力
p0, min =3.19
表10から,p0, m(試料)=3.76MPa,P0, min(試料)=3.19MPa,4.3.2.2から,p0, d=3.68MPa及びp0, min
(設計)=3.17MPa;それゆえ,P0, m(試料)>P0, d及びP0, minとなる。(試料)>0.8×P0, min(設計) (=2.54MPa)
で,製品試験片は,4.4.2.1a)及び4.4.2.1b)に合致する。
4.5.2.2.2
長期(100時間)圧力強さに対する一致の求め方
設計直線の式を次のように求める。
a) 式(43)を用いて
2
121
.0
918
.4
18
.
37
log
log
,0
,0
−
=
=
=
m
d
d
p
p
δ
b) 式(42)を用いて,
ad=a+δd=0.627 31+ (−0.117 8) =0.506 1
c) 式(41)を用いて,
log pt, d:0.506 1− (0.033 17×log t) ·············································· (58)
最小直線の式を次のように求める。
d) 式(48)を用いて,
9
184
.0
918
.4
21
.3
log
log
,0
min
,0
min
−
=
=
=
m
p
p
δ
e) 式(47)を用いて,
amin=a+δmin=0.627 31+ (−0.184 9) =0.442 4
f)
式(50)を用いて,
17
033
.0
4
442
.0
log
log
,
min
−
−
=
d
tp
t
·························································· (55)
個別規格が,100時間の圧力試験を要求する場合,試験圧力,pt, dを求めるとき,試料を1個試験し,破
壊に至る最小時間,tminを次のように求める。
g) 式(58)を用いて,
logpt, d=0.439 7
ゆえに,
pt, d=2.752MPa
h) 式(55)を用いて,
log tmin=−0.081 36
ゆえに,
tmin=1.206h

23
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この2.75MPaの圧力,すなわち,pt, dを使って3個の試験片について実際の試験を行ったとき,表11に
示す結果が得られた。
表11 試験片の破壊に至る時間
単位 h
125.3
101.3
97.4
破壊に至る平均時間
tm =
108
破壊に至る最小時間
tmin =
97.4
表11から,tm(試料)=108h,及びtmin(試料)=97.4h,4.5.2.1から,td=100h及び4.5.2.2h)からtmin
=1.206 h;それゆえ,tm(試料)>td及びtmin(試料)>tminで,製品は,4.4.2.1c)及び4.4.2.1d)に一致する。
4.5.3
例4:二次の関係−非破壊試験(クリープ)挙動
4.5.3.1
問題
一連の管が,4.3.3に規定する設計を基に製造された。試験片の特性は,短期(初期偏平剛性)及び長期
(1 000時間クリープ)試験によって測定された。短期試験結果を表12に,長期試験結果を表13に示す。
この管は,4.4.3.1及び4.4.3.7に一致するかを確認する。
4.5.3.2
計算及び最終結果
4.5.3.2.1
管の初期剛性要求値に対する一致の求め方
表12 試験片の試験による初期偏平剛性の結果
単位 N/m2
5 600
4 980
5 720
5 620
5 690
5 695
5 550
5 980
5 020
5 720
5 600
5 295
5 560
5 680
5 550
5 620
5 795
5 570
平均初期偏平剛性
S0, m
=5 569
最小初期偏平剛性
S0, min =980
表12から,S0, m(試料)=5 569N/m2,及びS0, min(試料)=4 980N/m2,4.3.3.2から,S0, d=5 476N/m2
及びS0, min=5 000N/m2。それゆえS0, m(試料)>S0, d及びS0, min(試料)>0.8×S0, min(設計)で,製品は,
4.4.2.1a)及び4.4.2.1b)に一致する。
4.5.3.2.2
長期(1 000時間)偏平剛性の要求に対する一致の求め方
設計直線の式を次のように求める。
a) 式(46)を用いて,
5
120
.0
241
7
476
5
log
log
,0
,0
−
=
=
=
m
d
d
S
S
δ
b) 式(45)を用いて,
cd=c+δd=3.828 8+ (−0.120 5) =3.708 3
c) 式(44)を用いて,
log St, d=3.708 3− (0.026 2×log t) −0.002 2× (log t) 2 ···················· (56)
最小直線の式を次のように求める。
d) 式(53)を用いて,
8
160
.0
241
7
000
5
log
log
,0
min
,0
min
−
=
=
=
m
S
S
δ
e) 式(52)を用いて,
cmin=c+δmin=3.828 8+ (−0.160 8) =3.668

24
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
f)
式(51)を用いて,
log St, min=3.668−0.026 2×log t-0.002 2× (log t) 2 ···························· (57)
管理手順が,1 000時間の偏平剛性試験を要求するので,設計剛性,St, d及び最小偏平剛性,St, minを次の
ように求める。
g) 式(56)を用いて,
log St, d=3.609 9
ゆえに,
St, d=4 073N/m2
h) 式(57)を用いて,
log St, min=3.569 6
ゆえに,
St, min=3 712N/m2
3個の試験片について1 000時間の偏平剛性試験を行ったとき,表13に示す結果が得られた。
表13 試験片の1 000時間剛性試験の結果
単位 N/m2
4 012
4 205
4 161
平均長期偏平剛性
Sm
=4 126
最小長期偏平剛性
Smin
=4 012
表13から,Sm(試料)=4 126N/m2及びSmin(試料)=4 012N/m2;g)から,St,d=4 073N/m2及びh)から,
St, min=3 712N/m2。それゆえSm(試料)>St, d及びSt, min(試料)>tminで,製品は,4.4.2.1c)及び4.4.2.1d)
に一致する。
25
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) 数学的手順
A.1 行列の演算
3.2.3(解法)に示す式(27a),(27b)及び(27c)を用いるとき,行列(マトリックス)による解法を記述する。
これらの式に基づき,行列(A : 1)をつくる。
∑∑∑
=
×
∑
∑
∑
∑
∑
∑
∑
∑
i
i
i
i
i
i
i
i
i
i
i
i
i
y
x
y
x
y
e
d
c
x
x
x
x
x
x
x
x
n
2
4
3
2
3
2
2
······································· (A : 1)
それぞれの変数に対し3.2.6に示す数値を代入すれば,行列(A : 1)は次の式(A : 2)となる。
=
×
175
.
235
932
.
80
728
.
56
233
.
584
623
.
180
989
.
62
623
.
180
989
.
62
671
.
21
989
.
62
671
.
21
15
e
d
c
······························ (A : 2)
数学の公式に従い,式(A : 2)の左辺第一項の3×3の行列の逆行列をつくれば次の (A: 3) のようになる。
−
−
−
−
−
−
1
015
.0
7
042
.0
7
001
.0
7
042
.0
5
152
.0
8
040
.0
7
001
.0
8
040
.0
7
132
.0
··············································· (A : 3)
行列(A : 2)と(A : 3)の両辺を乗じて,次の新しい式(A : 4)を得る。
−
−
−
−
−
−
×
=
×
1
015
.0
7
042
.0
7
001
.0
7
042
.0
5
152
.0
8
040
.0
7
001
.0
8
040
.0
7
132
.0
175
.
235
932
.
80
728
.
56
1
0
0
0
1
0
0
0
1
e
d
c
·········· (A : 4)
この行列(A : 4)を解けば,結果は式(A : 5)となる。
−−
=
2
002
.0
2
026
.0
8
828
.3
e
d
c
··································································· (A : 5)
このベクトル行列から3.2.3及び3.2.6に示す変数,c,d,eの解を得る。
A.2 代入による計算
同一セットの式(3.2.3参照)及び3.2.6に示すデータについて上記の解法に代替する解き方を次に示す。
備考 次の部分は数値を丸めてあるので異なる計算機で計算すると結果は,わずかながら相違する可
能性がある。
式(27a)から,
56.728=15.000×c+21.671×d+62.989×e ·································· (A : 6)
式(27b)から,
80.932=21.671×c+62.989×d+180.623×e ································ (A : 7)
式(27c)から,
235.175=62.989×c+180.623×d+584.233×e ····························· (A : 8)
式(A : 8)を解いて,式(A : 9)を得る。
26
K 7020 : 1998 (ISO 10928 : 1997)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
e=0.402 5−0.107 8×c−0.309 2×d ··········································· (A : 9)
式(A : 9)を式(A : 6)及び(A : 7)に代入して式(A : 10)及び式(A : 11)を得る。
31.375=8 210×c+2.195×d ··················································· (A : 10)
8.231=2.200×c+7.140×d ····················································· (A : 11)
式(A : 11)を解いて式(A : 12)を得る。
d=1.152 8−0.308 1×c ·························································· (A : 12)
式(A : 12)のdを式 (A : 10)に代入すれば,式(A : 13)を得る。
7.533 7×c=28.844 6 ····························································· (A : 13)
したがって,
c=3.828 8 ·········································································· (A : 14)
式(A : 14)の結果を式(A : 13)のcに代入すれば,式(A : 15)によってdを得る。
d=−0.026 2 ······································································· (A : 15)
式(A : 14)のc,式(A : 15)のdの値をそれぞれ式(A: 9)に代入すれば,eの値を得る。
e=−0.002 2 ······································································· (A : 16)
このようにして,両法はいずれも同じ結果を与える(ただし,A.2の備考を参照)。
JIS K 7020 原案作成委員会 構成表
氏名
所属
(委員長)
宮 入 裕 夫
東京医科歯科大学医用器材研究所
宗 宮 詮
慶應義塾大学理工学部機械工学科
安 宅 信 行
昭和女子大学大学院生活機構研究科
西 出 徹 雄
通商産業省基礎産業局化学課
(増 田 優)
大 嶋 清 治
通商産業省工業技術院標準部材料規格課
橋 本 繁 晴
財団法人日本規格協会技術部国際規格整合室
青 木 茂
青木技術事務所
磯 貝 智 彦
東京電力株式会社原子力技術部
(山 本 晋 児)
西 本 直 樹
三井化学株式会社生産技術本部エンジニアリング部
鳥 山 義
興和化成株式会社化成品本部
中 井 邦 彦
富士化工株式会社技術部
野間口 兼 政
日立化成工業株式会社山崎工場
河 内 秀 二
栗本化成株式会社湖東工場技術部
北 村 達 人
社団法人強化プラスチック協会
(事務局)
田 村 正 勝
日本プラスチック工業連盟
備考 ( ) 内は,前任者