C 2143-3:2013 (IEC 60216-3:2006)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語,定義,記号及び略語 ································································································· 2
3.1 用語及び定義 ················································································································ 2
3.2 記号及び略語 ················································································································ 3
4 計算の原理 ······················································································································ 5
4.1 一般原理 ······················································································································ 5
4.2 予備的な計算 ················································································································ 6
4.3 分散の計算 ··················································································································· 7
4.4 統計検定 ······················································································································ 7
4.5 結果 ···························································································································· 7
5 有効な計算を行うための要求事項及び推奨事項 ······································································ 8
5.1 試験データに関する要求事項 ··························································································· 8
5.2 計算の精度 ··················································································································· 8
6 計算手順························································································································· 8
6.1 予備的な計算 ················································································································ 8
6.2 本計算 ························································································································ 11
6.3 統計検定 ····················································································································· 13
6.4 熱的耐久グラフ ············································································································ 14
7 計算及び結果に対する要求事項 ·························································································· 15
7.1 熱的耐久性の計算 ········································································································· 15
7.2 統計検定の取りまとめ及び報告 ······················································································· 15
7.3 結果の報告 ·················································································································· 15
8 試験報告························································································································ 15
附属書A(規定)熱的耐久性計算の判定フローチャート ····························································· 17
附属書B(規定)判定表 ······································································································· 18
附属書C(参考)統計表 ······································································································· 19
附属書D(参考)実施例 ······································································································· 28
附属書E(参考)コンピュータプログラム················································································ 35
C 2143-3:2013 (IEC 60216-3:2006)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人電気学会(IEEJ)及び一般財団
法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本
工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS C 2143の規格群には,次に示す部編成がある。
JIS C 2143-1 第1部:劣化処理手順及び試験結果の評価
JIS C 2143-2 第2部:熱的耐久性の測定−評価指標の選択
JIS C 2143-3 第3部:熱的耐久性の計算の手引き
JIS C 2143-5 第5部:相対熱的耐久性指数(RTE)の求め方
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
C 2143-3:2013
(IEC 60216-3:2006)
電気絶縁材料−熱的耐久性−
第3部:熱的耐久性の計算の手引き
Electrical insulating materials-Properties of thermal endurance-
Part 3: Instructions for calculating thermal endurance characteristics
序文
この規格は,2006年に第2版として発行されたIEC 60216-3を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で側線又は点線の下線を施してある参考事項は,対応国際規格にない事項である。
1
適用範囲
この規格は,JIS C 2143-1及びJIS C 2143-2に従って,複数の一定温度で試験片を劣化処理したとき,
時間経過によって得られる特性変化を基に,熱的耐久性を導く計算手順について規定する。
試験データは,非破壊試験,破壊試験又は保証試験によって求める。非破壊試験又は保証試験では,終
点に到達した試験片の個数が試験片の中央値を超えた時点で残りの試験を打ち切ることがあるため,不完
全データであってもよい。
この規格は,計算手順を実施例によって説明している(附属書D参照)。
注記1 対応国際規格では,計算を容易にするためのコンピュータプログラムを推奨している(附属
書E参照)。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 60216-3:2006,Electrical insulating materials−Thermal endurance properties−Part 3:
Instructions for calculating thermal endurance characteristics(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS C 2143-1 電気絶縁材料−熱的耐久性−第1部:劣化処理手順及び試験結果の評価
注記 対応国際規格:IEC 60216-1:2001,Electrical insulating materials−Properties of thermal endurance
−Part 1: Ageing procedures and evaluation of test results(IDT)
JIS C 2143-2 電気絶縁材料−熱的耐久性−第2部:熱的耐久性の測定−評価指標の選択
注記 対応国際規格:IEC 60216-2:2005,Electrical insulating materials−Thermal endurance properties
2
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−Part 2: Determination of thermal endurance properties of electrical insulating materials−Choice of
test criteria(IDT)
IEC 60493-1:1974,Guide for the statistical analysis of ageing test data−Part 1: Methods based on mean values
of normally distributed test results
3
用語,定義,記号及び略語
3.1
用語及び定義
この規格で用いる主な用語及び定義は,次による。
3.1.1
順序データ(ordered data)
データの要素の並びを増加の方向とし,各要素がその前の要素より大きいか又は等しくなるように並べ
替えたデータグループ。
注記1 この規格で増加の方向とは,データをこの方向で順序付けたとき,最初の要素の大きさが最
小であることを意味している。
注記2 “グループ”という用語は,統計理論上の文献では,全データセットのサブセットを表す場
合にも用いられる。グループは,セットのパラメータの一つが同じ値をもつ(例えば,劣化
処理温度など)データからなる。グループは,それ自身,他のパラメータ(例えば,破壊試
験の場合の時間など)によって特徴付けられる幾つかのサブグループからなる。
3.1.2
順序統計量(order-statistic)
順序データで,一連の中の数で表した位置によって同じものとみなすことができるセットのそれぞれの
値。
3.1.3
不完全データ(incomplete data)
ある境界位置から上及び/又は下の値が未知である順序データ。
3.1.4
打切りデータ(censored data)
打ち切って測定をしていない値の数が分かっている不完全データ。
注記1 打切りが規定の数値の上又は下から始まる場合は,打切りはタイプ1である。規定の順序統
計量の上又は下から始まる場合は,タイプ2である。この規格は,タイプ2だけを扱う。
注記2 規定する劣化処理時間後に試験を終了するとき,“定時打切り”又は“タイプ1途中打切り”
といい,規定する試験片数が故障した後に試験を終了するとき,“定数打切り”又は“タイプ
2途中打切り”という。
3.1.5
自由度(degrees of freedom)
データの数からパラメータの数を減じた数。
3.1.6
データグループの不偏分散(variance of data group)
一つ以上のパラメータによって定義した照合水準からのデータ偏差の平方の和を自由度の数で除したも
の。
3
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記1 この規格では,不偏分散を単に分散という。
注記2 照合水準は,例えば,平均値(パラメータが一つの場合),直線(パラメータが二つの場合:
勾配及び切片)などである。
3.1.7
データグループの中央2次モーメント(central second moment of a data group)
データグループの要素の平均からの偏差の平方の和をグループ中のデータ数で除したもの。
3.1.8
データグループの共分散(covariance of data groups)
等しい要素数の二つのデータグループにおいて,対応する要素の間で各グループ平均からの偏差を乗算
し,その合計を自由度で除したもの。
3.1.9
回帰分析(regression analysis)
二つのデータグループの対応する要素の間の関係を示す回帰直線を推定し,この直線と各要素との偏差
の平方の和が最小となるように回帰直線を導く過程。
注記 最適直線のパラメータを,回帰係数と呼ぶ。
3.1.10
相関係数(correlation coefficient)
二つのデータグループの要素間の関係の完璧さの度合いを示す統計的指標。相関係数は,共分散を二つ
のデータグループの分散を乗じた数の平方根で除したものに等しい。
注記 この平方の値は,0(相関なし)と1(完全な相関)との間である。
3.1.11
終点ライン(end-point line)
特性−時間グラフにおいて,規定の特性変化(終点)を示す値で時間軸に平行に引いた直線。
3.2
記号及び略語
この規格で用いる主な記号及び略語は,次による。
箇条番号
a
回帰係数(y切片)
4.3,6.2
ap
破壊試験の計算のための回帰係数(p切片)
6.1
b
回帰係数(x−y図の勾配)
4.3,6.2
bp
破壊試験の計算のための回帰係数(x−p図の勾配)
6.1
br
中間定数(
c
Xˆの計算)
6.3
c
中間定数(
2
χの計算)
6.3
f
自由度の数
表C.2〜表C.5
F
フィッシャー分布した統計的変数
4.2,6.1,6.3
F0
Fの表中の値(熱的耐久グラフの直線性)
4.4,6.3
F1
Fの表中の値(特性グラフの直線性−有意差 0.05)
6.1
F2
Fの表中の値(特性グラフの直線性−有意差 0.005)
6.1
g
破壊試験の劣化処理時間の順位数
6.1
h
破壊試験の特性値の順位数
6.1
HIC
TIと等しい温度での半減温度幅
4.3,箇条7
4
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
HICg
TIgに対応する半減温度幅
7.3
i
暴露温度の順位数
4.1,6.2
j
終点到達時間の順位数
4.1,6.2
k
劣化処理温度の数
4.1,6.2
M
不完全データでの試験片の全数
6.2.2
mi
温度
iϑで劣化処理した試験片の数
4.1,6.1
N
終点到達時間の全数
6.2
ng
時間τgで劣化処理したグループでの特性値の数
6.1
ni
温度
iϑにおけるy値の数
4.1,6.1
p
該当するグループの特性の平均値
6.1
p
特性値
6.1
P
2
χ分布の有意水準
4.4,6.3.1
pe
破壊試験での終点の値
6.1
g
p
時間τgでの劣化処理グループの特性の平均値
6.1
pgh
個々の特性値
6.1
q
対数の底
6.3
r
計算に含まれる設定した劣化処理時間の数(破壊試験)
6.1
r2
相関係数の二乗
6.2.3
s2
2
1sと
2
2sとの重み付き平均
6.3
2
1s
2
1isの重み付けをした平均で,対象グループ中のプールした分散
4.3,6.1〜6.3
()a
s21
2
1sの調整値
4.4,6.3
2
1g
s
時間τgを劣化処理したグループの特性値の分散
6.1
2
1is
温度
iϑでのyij値の分散
4.3,6.2
2
2s
回帰直線についての分散
6.1〜6.3
2
as
s2を調整した値
6.3
2
rs
中間定数
6.3
2
Ys
Yの分散
6.3
t
スチューデント分布する確率論的変数
6.3
tc
tを修正した値(不完全データ)
6.3
TC
TIの下側95 %信頼限界
4.4,箇条7
TCa
TCの調整値
7.1
TI
温度指数
4.3,箇条7
TI10
10 000時間(10 kh)での温度指数
7.1
TIa
TIの調整値
7.3
TIg
グラフ的手段又は明確な信頼限界なしに求めた温度指数
7.3
x
独立変数:熱力学的温度の逆数
4.1
x
xの重み付き平均値
6.2
X
yの推定に関するxの特定の値
6.3
Xˆ
yの特定の値におけるxの推定値
6.3
c
Xˆ
Xˆの上側95 %信頼限界
6.3

5
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
xi
iϑに対応する熱力学的温度の逆数
4.1,6.1
y
yの重み付き平均値
6.2
y
従属変数:終点到達時間の対数
4.1
Yˆ
特定のxの値におけるyの推定値
6.3
Y
xの推定に関するyの特定の値
6.3
Yc
Yˆの下側95 %信頼限界
6.3
iy
温度
iϑにおけるyijの平均値
4.3,6.2
yij
τijに対応するyの値
4.1,6.1
z
zgの平均値
6.1
zg
破壊試験での劣化処理時間の対数−グループg
6.1
α
分散についての打切りデータ係数
4.3,6.2
β
分散についての打切りデータ係数
4.3,6.2
ε
打切りデータの平均分散の係数
4.3,6.2
Θ0
熱力学的目盛上の0 ℃に対応する温度(273.15 K)
4.1,6.1
ϑˆ
温度指数に関する推定温度
6.3.3
c
ϑˆ
ϑˆの信頼限界
6.3.3
iϑ
グループiの劣化処理温度(℃)
4.1,6.1
μ
平均値についての打切りデータ係数
4.3,6.2
μ2(x)
x値の中央2次モーメント
6.2,6.3
ν
一つの劣化処理温度で取り出された特性値の全数
6.1
τf
温度推定のための選定時間
6.3
τg
グループgの劣化処理時間
6.1.4
τij
終点到達時間
6.4
χ2
χ2分布した確率論的変数
6.3
4
計算の原理
4.1
一般原理
一般的な計算手順及び箇条6の指示は,IEC 60493-1に規定する原理に基づいている。その原理の概略
を次に示す(IEC 60493-1の3.7.1参照)。
a) 規定の終点に到達するまでの時間(終点到達時間)の対数の平均と熱力学的(絶対)温度の逆数との
間の関係は,直線的である。
b) 直線関係からの終点到達時間の対数の偏差の値は,劣化処理温度に関係なく一定の分散で正規分布す
る。
一般の計算手順で用いるデータは,予備的な計算によって試験データから導く。この計算の詳細は,判
定試験の種類すなわち非破壊試験,保証試験又は破壊試験による(4.2参照)。全ての場合において,デー
タはx,y,m,n及びkからなる。
ここに, xi=1/(
iϑ+Θ0): 劣化処理温度iϑ(℃)の熱力学的数値の逆数
yij=log τij: 温度
iϑにおけるj番目の終点到達時間τijの対数
ni: 温度
iϑで劣化処理したグループ番号i中のy値の数
mi: 温度
iϑで劣化処理したグループ番号i中の試験片の
6
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
数(打切りデータではniと異なる。)
k: 劣化処理温度又はy値のグループの数
注記 計算を通して一貫していれば,対数の底には,いかなる数値を用いてもよい。ほとんどのコン
ピュータ言語及び計算機では,自然対数(底がe)を使用しているので,自然対数を用いるこ
とが望ましい。
4.2
予備的な計算
4.2.0A 一般
全ての場合に,劣化処理温度の熱力学的数値の逆数をxiの値として計算する。
4.2.1〜4.2.3によって求めた各終点到達時間τijの対数をyijの値として計算する。
多くの非破壊試験及び保証試験の場合,経済的な理由によって(例えば,データのばらつきが大きい場
合),全ての試験片が終点に到達する前に,少なくとも幾つかの温度グループでの劣化処理を中止するのが
よい。このような場合,得られたx及びyのデータを基に打切りデータの計算を行う(6.2.1.2参照)。
完全データ及び不完全データが混在するグループ,又はそれぞれの劣化処理温度ごとに異なる時点で打
ち切った打切りデータのグループは,いずれも6.2.1.2の計算に用いてもよい。
4.2.1
非破壊試験
非破壊試験(例えば,劣化処理中の質量減少)では,各試験片の判定特性の値は,劣化処理周期ごとに,
直接得られる。したがって,終点到達時間τijは,直接的に又は連続した測定値の間の直線的な内挿によっ
て得られる。
4.2.2
保証試験
保証試験では,個々の試験片の終点到達時間τijは,終点に到達した劣化処理周期とその直前の周期との
中間点として求める[JIS C 2143-1の6.3.2(保証試験)参照]。
4.2.3
破壊試験
破壊試験では,特性値を得るときに試験片が破壊されるため,各試験片の終点到達時間は直接測定でき
ない。
終点到達時間を推定するため,終点近傍に次の仮定を置く。
a) 特性の平均値と劣化処理時間の対数との関係は,おおよそ直線的である。
b) この直線関係からの各特性値の偏差の値は,劣化処理時間に関係なく一定の分散で正規分布している。
c) 個々の試験片に関して,特性の曲線と時間の対数との関係は,a) の関係で示す線に平行な直線である。
これらの仮定を適用するために,それぞれの劣化処理時間で求めたデータについて劣化曲線を描く。曲
線は,その劣化処理時間の対数に対して各試験片グループの特性値の平均をプロットして得られる。
グループ平均の一つ以上が終点レベルを超えるまで,各温度の劣化処理を続けるのがよい。この曲線の
おおよその直線になる範囲の終点ラインの近傍に直線を引く(図D.2参照)。
選択範囲の直線性からの偏差が許容できるかどうかを決定するため,統計検定(F検定)を行う(6.1.4.4
参照)。許容できる場合,同じグラフの上に,各試験片の特性値をプロットする。個々の試験片のプロット
した点を通り,劣化直線に平行な直線を引く。その試験片についての終点到達時間の対数yijの推定値は,
終点ラインと直線との交点に対応する時間の対数の値となる(図D.2参照)。
グループ平均の一つ以上が終点レベルを超えない場合でも,幾つかの制限付きで,平均値から求めた直
線部分を終点レベルまで外挿をしてもよい(6.1.4.4参照)。
上記の操作は,6.1.4に規定する計算の中で数値的に実行できる。
7
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.3
分散の計算
分散は,4.2.0Aで得たx及びyを用い,次によって計算する。
yijの値のそれぞれのグループについて,平均
iy及び分散
2
1isを計算し,21isにグループサイズに従った重み
付けをしてプールした分散
2
1sを求める。
不完全データについては,Sawが導き(参考文献[1]参照),それを基に発展させた6.2.1.2に規定する
計算式を用いる。必要な係数(平均に関するμ,分散に関するα及びβ並びにグループの分散からの平均
の分散を求めるためのε)は,表C.1に記載してある。多数のグループに関して,グループサイズに応じ
て重み付けし,分散をプールする。εのグループ値の平均値は,重み付けなしでプールした分散を乗じて
求める。
注記 ここでは,グループサイズによる重み付けは,Sawによる最初の提案に同じく,εの定義の中
に暗に含まれている。このことは,幾つかの式の表現をより簡単にしている。
係数a及びb(xとyとの間の最適直線の係数)は,平均値
iy及びxiの値から単回帰分析によって計算
する。
温度指数TI及び半減温度幅HICの値は,回帰係数から計算する。回帰直線からの偏差の分散は,回帰
係数及びグループ平均から計算する。
4.4
統計検定
統計検定は,次による。
a) 終点到達時間を推定する計算の前に,破壊試験データの直線性に関するフィッシャー検定(F検定)
を行う(4.2.3参照)。
b) yの値のグループ中の分散が著しく異なるかどうかを確認するため,分散の同等性の検定(バートレ
ットのχ2検定)を行う。
c) 回帰直線からの偏差の,グループ内のプールした分散に対する比が,基準値F0より大きいかどうかを
確認するためのF検定を行う。すなわち,試験データにアレニウス則を適用することの妥当性を検定
する。
ばらつきが非常に小さいデータの場合,実際にはほとんど意味のない非直線性が統計的に有意として検
出されることがある。
このようにF検定を満足しない場合であっても,結果が得られるように次のような手順を含む。
1) F検定がちょうど受入可能な結果を与えるように,グループ中のプールした分散
2
1sの値に係数
F/F0を乗じ増やす(6.3.2参照)。
2) この調整した値()a
s21
を用いて,結果の下側信頼限界TCaを計算する。
3) 下側信頼区間(TI−TCa)が受入可能とみなせる場合は,非直線性は実用上重要でないと判断する
(6.3.2参照)。
4) データのばらつきの成分
2
1s及び
2
2sから,回帰方程式を用いておおよその信頼区間を計算する。
温度指数TI,その下側信頼限界TC及び半減温度幅HICを計算し(7.1参照),次の式(1)の条件が成り立
つ場合,結果は受入可能とする。
TI−TC≦0.6 HIC ······································································· (1)
下側信頼区間(TI−TC)が僅かに限界0.6 HICを超えている場合でも,温度指数TIの値に(TC+0.6 HIC)
を代入してF≦F0が成り立っている場合は,結果は有効とする。
4.5
結果
上記のように,統計検定に規定する結果からの多少のずれを許容し,温度指数TI,その半減温度幅HIC
8
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
及びその下側95 %信頼限界TCは回帰方程式から計算する。
温度指数及び半減温度幅の報告の形式は,統計検定の結果によって決まる(7.2及び7.3参照)。
ただ一つの数値的な結果であるTI(HIC)だけでは試験データの定性的な全体像を表せない場合,及び
データの評価が熱的耐久グラフ(6.4参照)以外では完全にできない場合は,報告の重要な要素として熱的
耐久グラフの添付が必要である。
5
有効な計算を行うための要求事項及び推奨事項
5.1
試験データに関する要求事項
この規格の計算手順に従う試験データは,JIS C 2143-1の箇条5(試験手順の詳細)の要求事項に適合し
なければならない。
5.1.1
非破壊試験
この試験におけるほとんどの特性については,グループの試験片の数は5個が適切である。ただし,デ
ータのばらつき(信頼区間,6.3.3参照)が大き過ぎる場合は,試験片の数を増やすことによって,より満
足できる結果が得られる。このことは,全ての試験片が終点に到達する前に劣化処理を終える必要がある
場合に,特に当てはまる。
5.1.2
保証試験
いずれのグループでも,最初の劣化処理周期に2個以上の試験片が終点に到達してはならない。また,
二つ以上のグループがこのような試験片を含んでいる場合は,実験の手順を注意深く調査し(6.1.3参照),
試験報告書にそのことを記載することが望ましい。
それぞれのグループの試験片の数は5個以上とし,現実的に取扱いが可能な最大の個数は31個までとす
る(表C.1)。ほとんどの目的のための適切な試験片の数は21個である。
5.1.3
破壊試験
それぞれの試験温度について,一つ以上のグループの特性平均値が終点レベルより上になり,かつ,一
つ以上のグループの特性平均値が終点レベルより下になるまで劣化処理を続けることが望ましい。場合に
よっては,特別な条件の下に,終点レベルを超えて特性の平均値を僅かに外挿して求めてもよい(6.1.4.4
参照)。ただし,このような取扱いは,一つの温度グループ以外に適用してはならない。
5.2
計算の精度
多くの計算の段階が,数値自体に比べて一般にその値は小さいとはいえ,数値の差の合計又はこれらの
差の平方和を含んでいる。このような状況から,計算結果に有効数字3桁の精度を求めるためには,6桁
以上の有効数字の内部精度で計算を行う必要がある。計算において同じことの繰返しが単調に続くことを
考慮して,コンピュータの利用が望ましい。この場合は,内部精度10桁以上の有効数字による計算が容易
に行える。
6
計算手順
6.1
予備的な計算
6.1.1
温度及びx値
全ての種類の試験で,それぞれの劣化処理温度は,熱力学的温度(K)で表し,その逆数をxiとして,
次の式(2)によって計算する。
0
1
Θ
x
i
i
+
=ϑ
·············································································· (2)
9
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
Θ0: 273.15 K
6.1.2
非破壊試験
i番目のグループのj番目の試験片について,それぞれの劣化処理周期の終了後の特性値が得られる。こ
れらの値から,直線による内挿によって終点到達時間τijを求めてその対数をyijとして計算する。
6.1.3
保証試験
i番目のグループのj番目の試験片について,終点に到達した劣化処理周期とその直前の周期との中間点
の時間を求め,この時間の対数をyijとする。
試験片の1個が,最初の劣化処理周期で終点に到達した場合は,無効として扱い,次のいずれかの処置
をとる。
a) その試験片グループはなかったものとし,新しい試験片グループによって試験を再開する。
b) その試験片はなかったものとして,グループの平均及び分散の計算のときにグループmiの中の試験片
の数から1を減じる(6.2.1.2参照)。
最初の劣化処理周期に,2個以上の試験片が終点に達した場合,そのグループを捨てて,試験手順の全
ての段階に十分注意を払いながら,新しいグループを試験する。
6.1.4
破壊試験
6.1.4.0A それぞれの温度
iϑで劣化処理した試験片のグループについて,6.1.4.1〜6.1.4.5に規定する処理を
行う。
注記 添字iは,多数の添字の組合せによる混乱を避けるため,6.1.4.2〜6.1.4.4の式から省いている。
これらの細分箇条における計算は,それぞれの劣化処理温度からのデータについて個別に行う。
6.1.4.1 それぞれの劣化処理時間ごとのデータグループについて特性の平均値を計算する。これらの値を,
特性値pを縦軸とし,劣化処理時間の対数zを横軸としたグラフ上にプロットする(図D.2参照)。目視に
よって,特性の平均値をプロットした点を通る平滑な曲線を描く。
6.1.4.2
この曲線が,ほぼ直線となる時間領域を選ぶ(6.1.4.4参照)。この時間領域内で,平均値は終点
ラインp=peの両側に1点以上が位置し,かつ,3点以上の特性の平均値を含む必要がある。このような条
件が満たされず,また,例えば試験片が残っていないなどの理由で,それ以上の測定ができない場合は,
6.1.4.4の条件に従って若干の外挿をしてもよい。
直線に該当するとして選び出した特性の平均値(又は対応するグループ)の数をr,個々の劣化処理時
間の対数をzg,個々の特性値をpghとおく。
ここに, g=1… r: 時間τgで試験した試験対象のグループの順位数
h=1… ng: g番目のグループの中での特性値の順位数
ng: グループ番号gの中での特性値の数
ほとんどの場合,それぞれの劣化処理時間ごとのグループの試験片の数ngは同数であるが,これは必要
条件ではなく,グループ間でngの値が異なる場合についても計算を行うことができる。
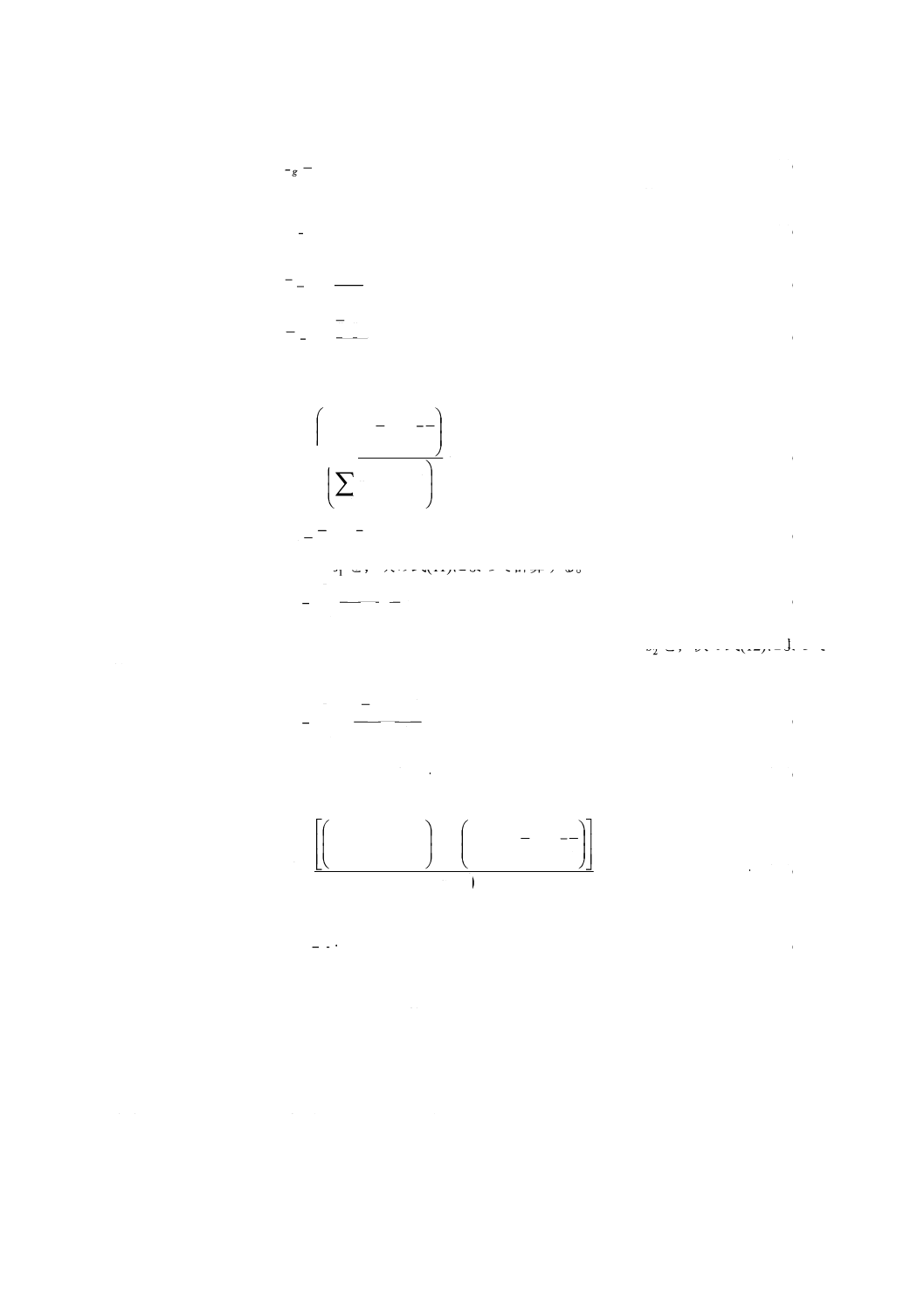
選び出したそれぞれの特性値のグループについて,平均値
g
p及び分散
2
1g
sを,それぞれ次の式(3)及び式
(4)によって計算する。
∑
=
=
g
n
h
g
gh
g
n
p
p
1
············································································· (3)
(
)1
1
2
2
2
1
−
−
=∑
=
g
n
h
g
g
gh
g
n
p
n
p
s
g
······························································· (4)
10
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
τgの対数を,次の式(5)によって計算する。
g
gz
τ
log
=
················································································ (5)
6.1.4.3
ν,z及びpの数値を,それぞれ次の式(6),式(7)及び式(8)によって計算する。
∑
=
=
r
g
g
n
1
ν
················································································ (6)
∑
=
=
r
g
g
g
v
n
z
z
1
············································································· (7)
∑
=
=
r
g
g
g
v
n
p
p
1
············································································ (8)
回帰式p=ap+bpzの係数を,次の式(9)及び式(10)によって計算する。
−
−
=∑
∑
=
=
r
g
g
g
r
g
g
g
g
p
z
z
n
p
z
p
z
n
b
1
2
2
1
ν
ν
······························································ (9)
z
b
p
a
p
p
−
=
··········································································· (10)
特性グループのプールした分散
2
1sを,次の式(11)によって計算する。
(
)
(
)
∑
=
−
−
=
r
g
g
g
r
v
s
n
s
1
2
1
2
1
1
·····································································(11)
回帰直線からのグループの特性値の平均のばらつきについて,重み付き分散
2
2sを,次の式(12)によって
計算する。
(
)
(
)
∑
=
−
−
=
r
g
g
g
g
r
p
p
n
s
1
2
2
2
2
ˆ
································································ (12)
ここに,
g
p
p
g
z
b
a
p
+
=
ˆ
································································ (13)
また,式(12)は次の式(14)のように表すことができる。
(
)2
1
2
1
2
2
2
−
−
−
−
=
∑
∑
=
=
r
p
z
v
p
z
n
b
p
v
p
n
s
r
g
g
g
g
p
r
g
g
g
······························· (14)
6.1.4.4
次の式(15)によってFを求め,有意水準0.05での非直線性のF検定を行う。
2
1
2
2
s
s
F=
·················································································· (15)
Fの計算値が自由度fn=r−2及びfd=ν−rの表中の値F1[F1=F(0.95, r−2, ν−r),表C.2参照]を超え
る場合は,6.1.4.2における選択を変更して計算を繰り返す。
r≧3で有意水準0.05のF検定を満足できない場合は,計算値Fを表中の自由度fn=r−2,fd=ν−r及び
有意水準0.005の値F2[F2=F(0.995, r−2, ν−r),表C.3参照]と比較して,F検定を行う。
この水準での検定を満足する場合,計算は続けてもよいが,7.3.2による温度指数の調整はできない。
有意水準0.005でのF検定(すなわち,F≦F2)を満足できないか,又は6.1.4.1に従ってプロットする
特性点が全て終点ラインの片側にあるときには,次の条件の下に外挿することができる。
全ての平均値
g
pが,終点の値peの同じ側にあり,かつ,選び出した平均値の数が3以上で有意水準0.05
11
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
のF検定を満足する場合,終点の値peと終点に最も近い平均値
g
p(通常,rp)との差の絶対値が,差(
)
rp
p−
1
の絶対値の25 %未満であれば,外挿してもよい。
この場合,計算は続行できるが,7.3.2による温度指数の調整はできない。
6.1.4.5
選定したグループの各特性値について,推定終点到達時間の対数yijを,次の式(16)及び式(17)に
よって計算する。
(
)
p
e
gh
g
ij
b
p
p
z
y
−
−
=
··································································· (16)
ni=ν ····················································································· (17)
ここに, j=1... ni: 温度に対して推定したy値のグループ中でのy値の順位数
iϑ: 劣化処理温度
zg: 劣化処理時間の対数
yijのni値: 6.2.1の計算に用いるlog(時間)値
6.1.5
不完全データ
不完全データの場合は,y値のグループを昇順に並び替える(3.1.1参照)。
6.2
本計算
6.2.1
グループの平均及び分散の計算
それぞれの温度
iϑで得たy値yijのグループの平均及び分散を計算する。
6.2.1.1
完全データ
データが完全な試験では,通常の式(18)及び式(19)を使用できる。
∑
=
=
in
j
i
ij
i
n
y
y
1
············································································· (18)
(
)1
1
2
1
2
2
1
−
−
=∑
=
i
n
j
i
ij
i
n
y
n
y
s
i
································································· (19)
これらの代わりに,この目的に便利さでは劣るが,不完全なデータのための式(6.2.1.2参照)を用いる
こともできる。そのとき,係数は次の式(20),式(21)及び式(22)の値となる。
(
)1
1
−
=
i
i
n
α
············································································ (20)
(
)1
1
−
−
=
i
i
i
n
n
β
·········································································· (21)
i
i
n
1
1−
=
μ
·············································································· (22)
注記 これらの式は,簡単な代数学によって導かれる。平均又は分散についての式[式(18)及び式(19)
参照]が,式(23)及び式(24)を用いて得たものと同等の場合は,それぞれの結果として得られた
式の未知数は,式(20)〜式(22)の結果を用いて,その式に当てはめることができる。εの値は,
明らかに1である。
6.2.1.2
不完全データ
データが不完全な試験では,式(18)及び式(19)に代えて,次の式(23)及び式(24)を用いる。
(
)
(
)
∑
−
=
−
+
−
=
1
1
1
1
i
i
n
j
i
ij
i
in
i
i
n
y
y
y
μ
μ
······················································ (23)
12
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
(
)
∑
∑
−
=
−
=
−
+
−
=
1
1
2
1
1
2
2
1
i
i
i
i
n
j
n
j
ij
in
i
ij
in
i
i
y
y
y
y
s
β
α
········································ (24)
αi,βi及びμiの値は,表C.1(劣化処理した試験片の数m及びy値の数nに対応した行)から読み取る。
データが部分的に不完全(すなわち,一つ以上の温度グループが完全で,かつ,一つ以上の温度グループ
が不完全)なときには,式(20)〜式(22)を用いて値を導く。
6.2.2
平均及び分散
yijの値の全数N,xの重み付平均値x及びyの重み付平均値yを,次の式(25)〜式(27)によって計算する。
∑
=
=
k
i
in
N
1
·············································································· (25)
∑
=
=
k
i
i
i
N
x
n
x
1
············································································ (26)
∑
=
=
k
i
i
i
N
y
n
y
1
············································································ (27)
不完全データについては,試験片の全数Mを,次の式(28)によって計算する。
∑
=
=
k
i
i
m
M
1
············································································· (28)
完全データでは,M=Nである。
不完全データでは,εiの値を表C.1から読み取る。完全なデータ,又は一部不完全なデータにおいて
ni=miならば,εiの値は1でなければならない。
平均分散の係数を,次の式(29)によって計算する。
∑
=
=
k
i
i
k
1
ε
ε
··············································································· (29)
データグループのプールした分散
2
1sを,次の式(30)によって計算する。
(
)
(
)
∑
=
−
−
=
k
i
i
i
k
N
s
n
s
1
2
1
2
1
1
ε
··································································· (30)
x値の中央2次モーメントμ2(x)を,次の式(31)によって計算する。
()
N
x
N
x
n
x
k
i
i
i
−
=∑
=1
2
2
2
μ
··························································· (31)
6.2.3
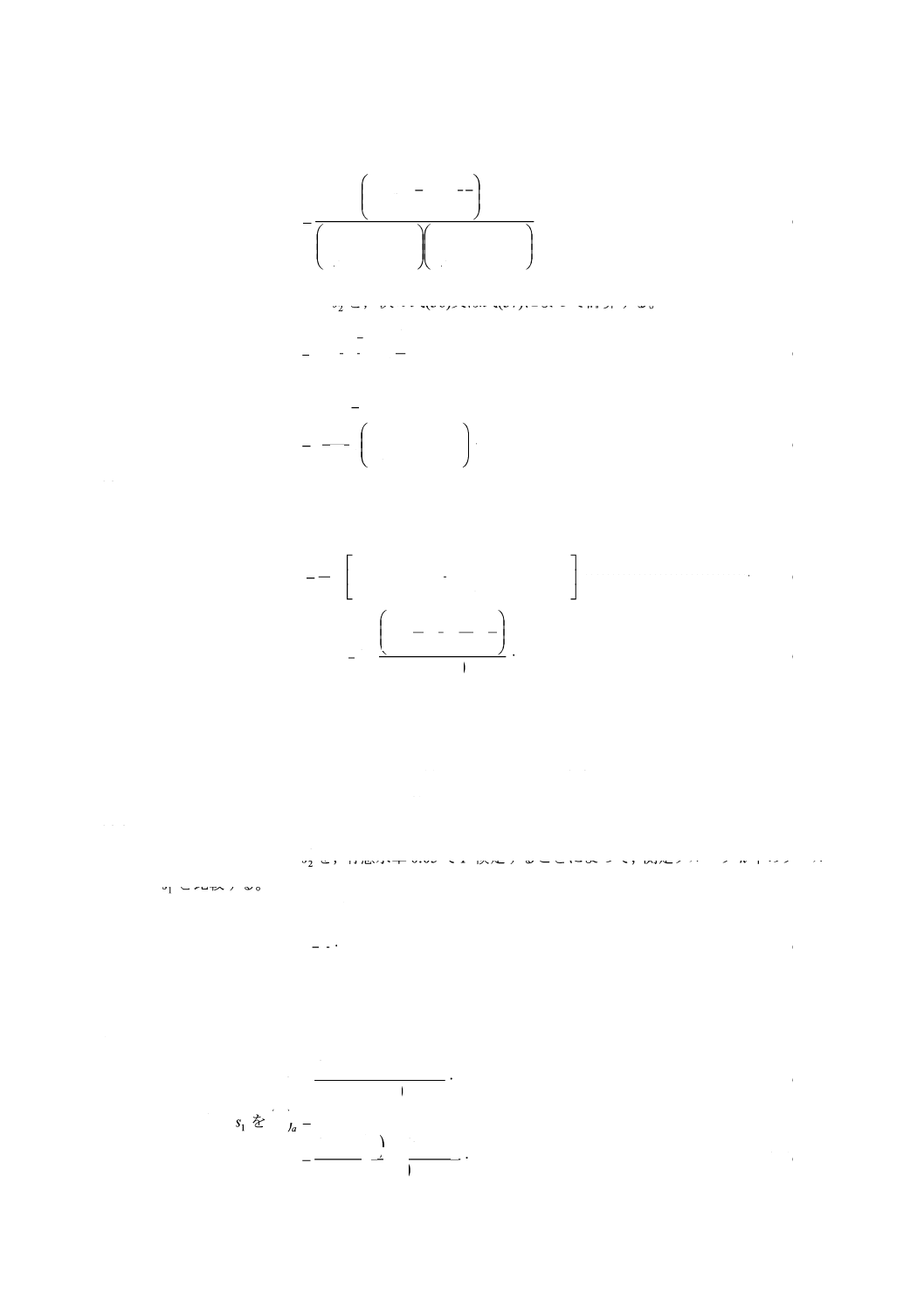
回帰計算
回帰直線は,次の式(32)によって表す。
bx
a
y
+
=
·············································································· (32)
直線の勾配bは,次の式(33)によって計算する。
−
−
=∑∑=
=
k
i
i
i
k
i
i
i
i
x
N
x
n
y
x
N
y
x
n
b
1
2
2
1
······························································ (33)
y軸上の切片aは,次の式(34)によって計算する。
x
b
y
a
−
=
·············································································· (34)
13
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
相関係数の二乗は,次の式(35)によって計算する。
−
−
−
=
∑
∑
∑
=
=
=
k
i
i
i
k
i
i
i
k
i
i
i
i
y
N
y
n
x
N
x
n
y
x
N
y
x
n
r
1
2
2
1
2
2
2
1
2
·········································· (35)
回帰直線からのyの平均の分散
2
2sを,次の式(36)又は式(37)によって計算する。
(
)
(
)
∑
=
−
−
=
k
i
i
i
i
k
Y
y
n
s
1
2
2
2
2
ˆ
··································································· (36)
ここに,
i
i
bx
a
Y
+
=
ˆ
(
)
(
)
−
−
−
=
∑
=
k
i
i
i
y
N
y
n
k
r
s
1
2
2
2
2
2
2
1
······················································· (37)
6.3
統計検定
6.3.1
分散の同等性の検定
バートレットのχ2関数の値を,次の式(38)によって計算する。
(
)
(
)
−
−
−
=
∑
=
k
i
i
q
i
q
s
n
s
k
N
c
q
1
2
1
2
1
2
log
1
log
ln
ε
χ
·································· (38)
ここに,
(
)1
3
1
1
1
1
1
−
−
−
−
+
=
∑
=
k
k
N
n
c
k
i
i
················································ (39)
qは,この式の中で用いる対数の底である。他の細分箇条で計算に用いた底と同じである必要はない。
q=10のときはln q=2.303,q=eのときはln q=1である。
χ2の値を表C.5中の自由度f=k−1の値と比較する。χ2の値が有意水準0.05の表中の値より大きい場合
は,χ2の値,及びχ2より小さく,かつ,表中で最も大きい値を示す有意Pの値を報告する。コンピュータ
プログラムを用いてχ2及びその有意水準を計算する場合は,それらを報告する。
6.3.2
直線性の検定(F検定)
回帰直線からの偏差の分散
2
2sを,有意水準0.05でF検定することによって,測定グループk中のプール
した分散
2
1sと比較する。
その比を,次の式(40)によって計算する。
2
1
2
2
s
s
F=
·················································································· (40)
この値を表中の自由度fn=k−2及びfd=N−kのF0[F0=F(0.95, k−2, N−k),表C.2及び表C.3参照]の
値と比較する。
a) F≦F0の場合,プールした分散を,次の式(41)によって計算する。
(
)
(
)
(
)2
2
2
2
2
1
2
−
−
+
−
=
N
s
k
s
k
N
s
···························································· (41)
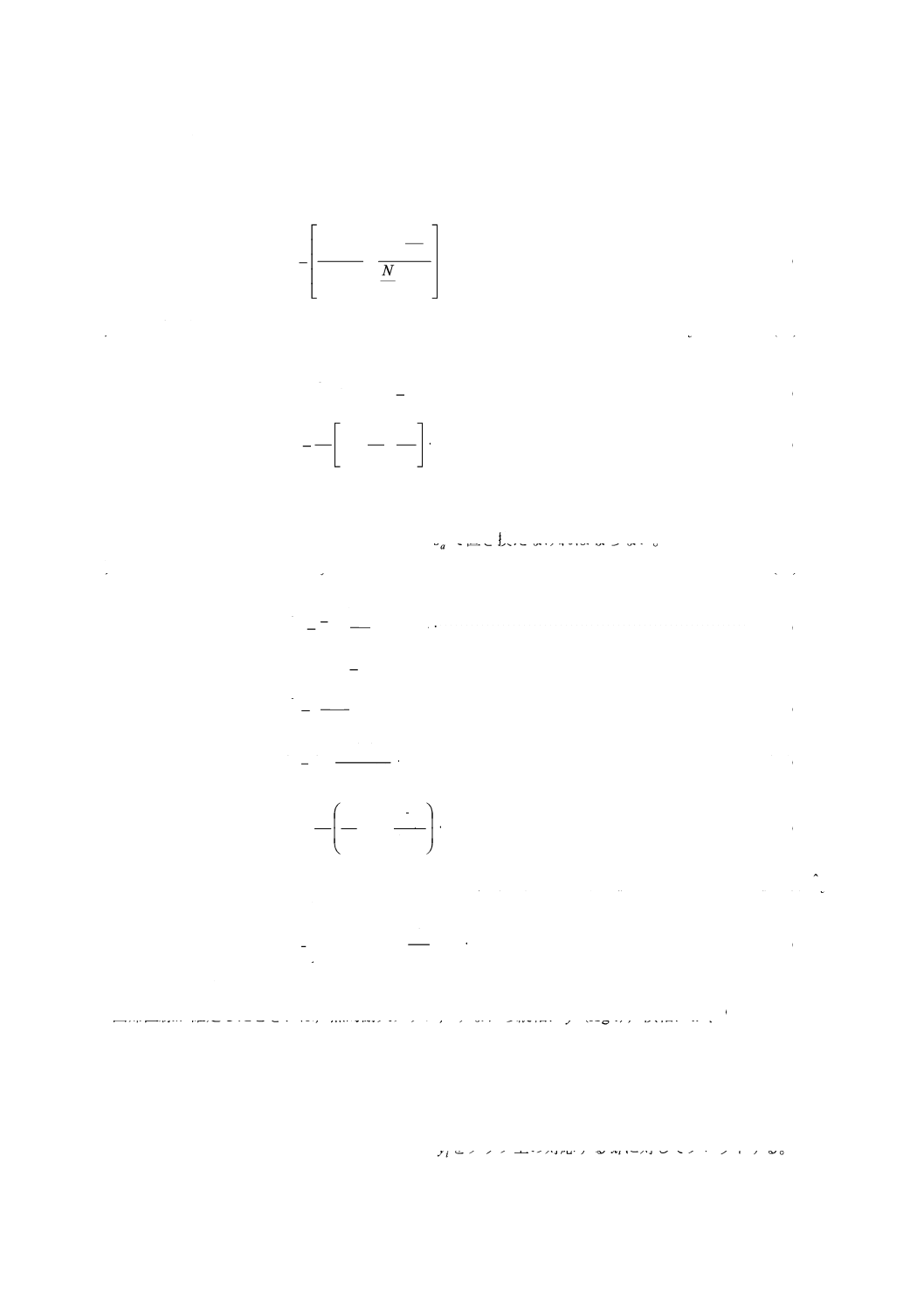
b) F>F0の場合,
2
1sを()
(
)
0
2
1
2
1
F
F
s
s
a=
に調整し,s2の調整した値を,次の式(42)によって計算する。
(
)()
(
)
(
)2
2
2
2
2
1
2
−
−
+
−
=
N
s
k
s
k
N
s
a
a
························································· (42)
14
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.3.3
X及びYの推定値の信頼限界
信頼水準0.95で自由度N−2におけるスチューデントのt表(表C.4参照)にある値t0.95, N−2を求める。
データの不完全な量に応じて,修正したtの値tcを,次の式(43)によって計算する。
1
2
,
95
.0
5.4
8
1
1
−
−
+
−
−
=
NM
N
t
t
N
c
··························································· (43)
a) Yの推定値 与えられたXに対応するYの推定値Yˆ及びその下側95 %信頼限界cYˆを,次の式(44)及び
式(45)によって計算する。
Y
c
c
s
t
Y
Y
−
=ˆ
ˆ
,
bx
a
Y
+
=
ˆ
··························································· (44)
(
)
()
−
+
=
x
x
X
N
s
sY
2
2
2
2
1
μ
································································ (45)
熱的耐久グラフの信頼限界曲線(6.4参照)は,対象とする範囲にわたり,幾つかの(X,Y)の組
についてYcを計算し,グラフにプロットした点(X,Yc)を通る曲線を描くことによって得られる。
F>F0の場合は,式(42)によってs2の値を
2
asで置き換えなければならない。
b) Xの推定値 終点到達時間τfに対応するXの推定値Xˆ及びその上側95 %信頼限界を,次の式(46)〜式
(49)によって計算する。
(
)
r
r
c
r
c
b
s
t
b
y
Y
x
X
+
−
+
=
ˆ
······························································· (46)
ここに,
f
Y
τ
log
=
(
)
b
a
Y
X
−
=
ˆ
············································································ (47)
()
x
Nb
s
t
b
b
c
r
2
2
2
μ
−
=
······································································ (48)
(
)
()
−
+
=
x
x
X
b
b
N
s
s
r
r
2
2
2
2
ˆ
μ
······························································ (49)
温度の推定値ϑˆ及びその下側95 %信頼限界
c
ϑˆを,対応するXの推定値Xˆ及びその上側信頼限界
c
Xˆ
から次の式(50)によって計算する。
0
ˆ
1
ˆ
Θ
X−
=
ϑ
,
0
ˆ
1
ˆ
Θ
Xc
c
−
=
ϑ
························································· (50)
6.4
熱的耐久グラフ
回帰直線が確定したときには,熱的耐久グラフ,すなわち縦軸にy(log τ),横軸にx[(
)
0
1
Θ
+
ϑ
]をと
ったグラフにその直線を引く。通常,xは右から左に増すようにプロットし,劣化処理温度(℃)の値を
この軸上に記す[図D.1のa)及びb)参照]。この目的のために市販のグラフ用紙を用いてもよい。
この計算をコンピュータで行う場合は,プログラムによって適切な不等間隔目盛上にグラフをプロット
することができる。
yij=log τijの個々の値及び6.2.1で求めた平均値
iyをグラフ上の対応するxiに対してプロットする。
xiは,次の式(51)による。
15
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
0
1
Θ
x
i
i
+
=ϑ
·········································································· (51)
熱的耐久グラフは,下側95 %信頼限界曲線を描くことよって完成する(6.3.3参照)。
7
計算及び結果に対する要求事項
7.1
熱的耐久性の計算
回帰直線の式(52)(係数a及びbは,6.2.3に従って計算する。)を用い,終点到達時間20 000時間(20 kh)
に対応する温度(℃)を計算する。
y=a+bx ················································································ (52)
この温度の数値が,温度指数TIである。
同じ方法で,終点到達時間10 000時間(10 kh)に対応する温度の数値TI10を計算する。半減温度幅HIC
は,次の式(53)となる。
HIC=TI10−TI ········································································· (53)
6.3.3 b) の方法で,y=log 20 000におけるTIの下側95 %信頼限界TC,又は調整した値
2
asを用いた場合
はTCaを計算する。
その結果から(TI−TC)/HIC又は(TI−TCa)/HICを求める。
また,熱的耐久グラフにプロットする(6.4参照)。
7.2
統計検定の取りまとめ及び報告
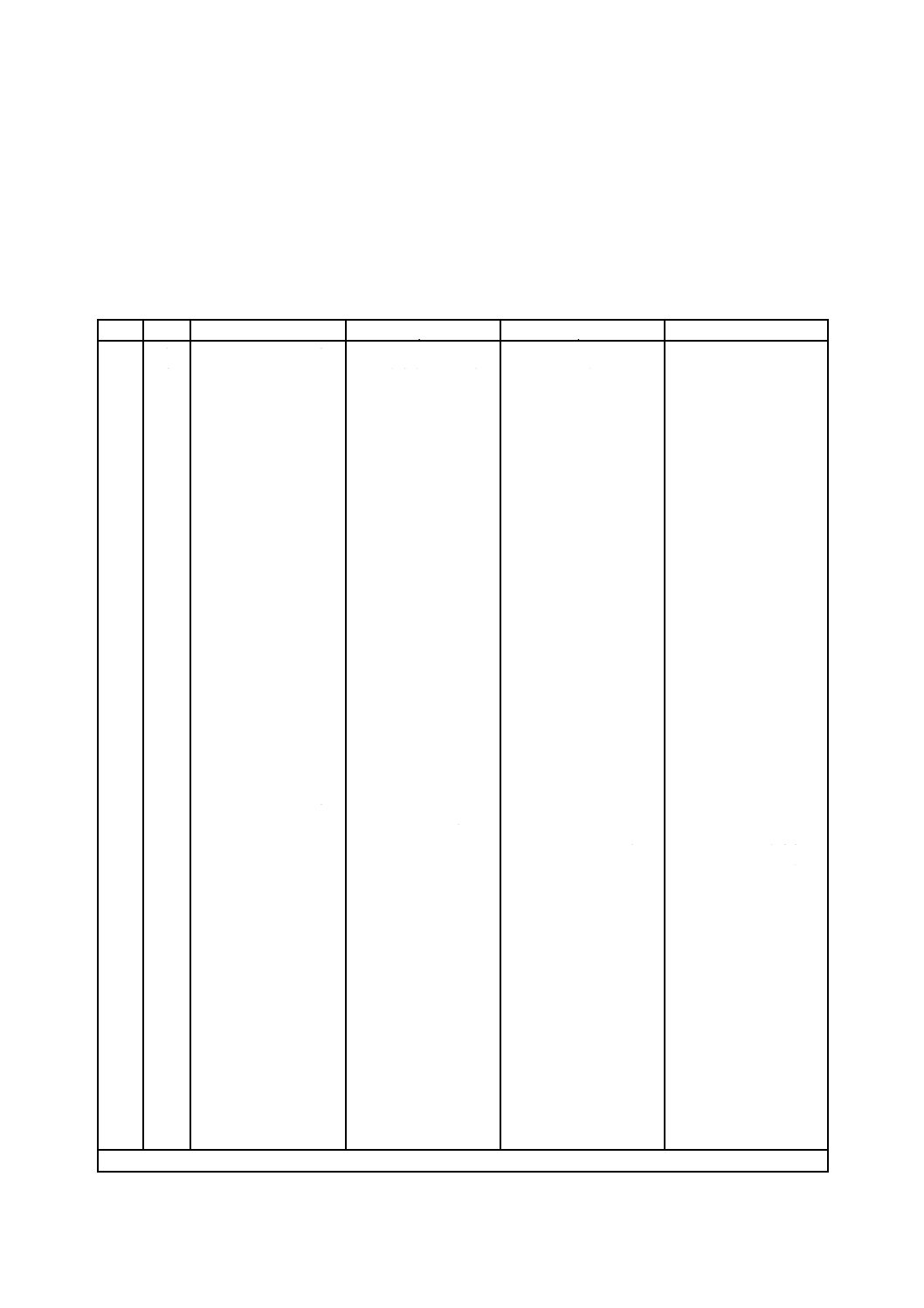
統計検定の判定表を附属書Bに示す。表B.1において,見出欄の“検定又は処理”の条件に合致しない
場合は,表の右端の欄に示すように処理する。条件に合致する場合は,次の段階に示すように処理する。
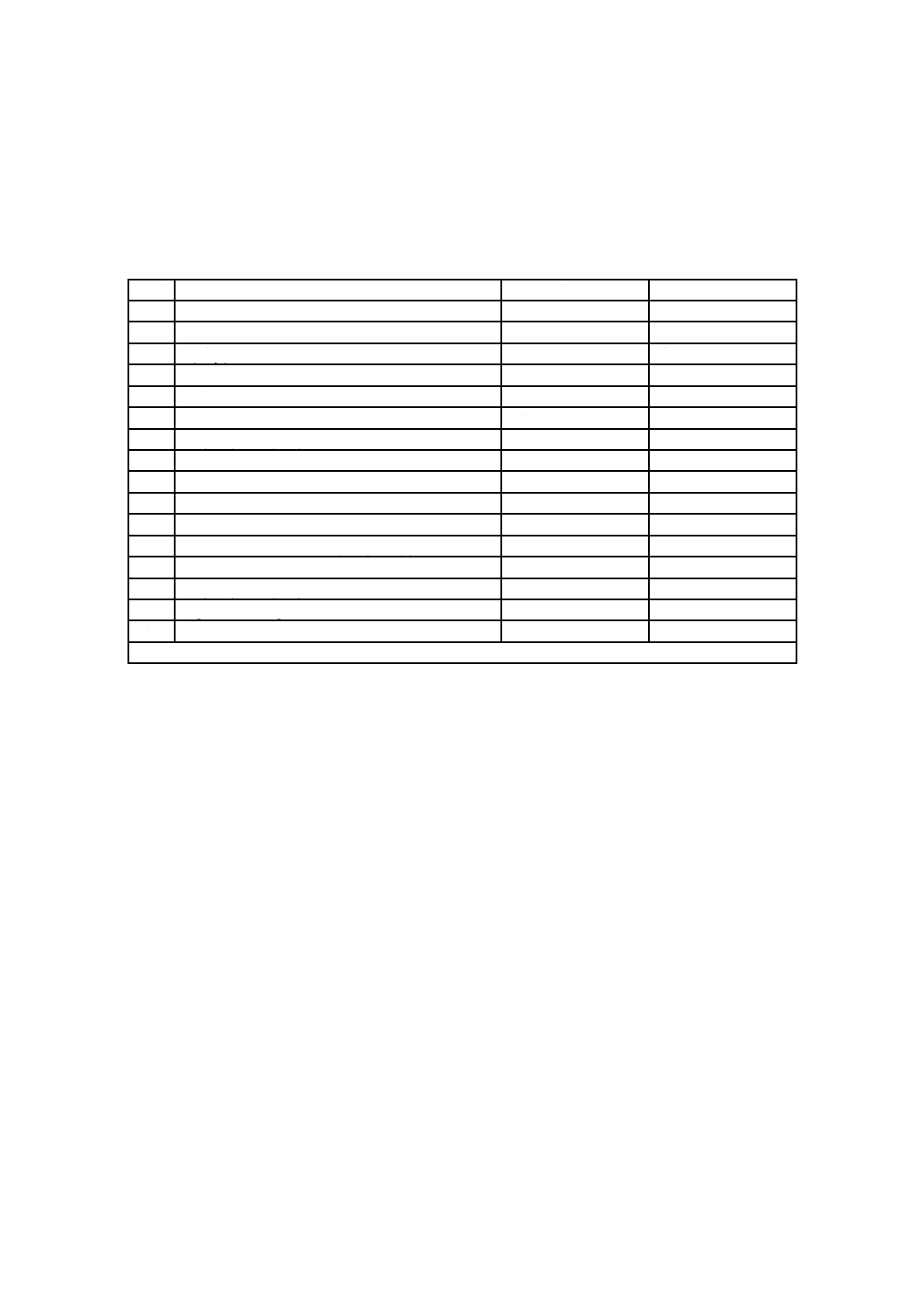
同様な手順を,熱的耐久性計算の判定フローチャートに示す(附属書A参照)。
7.3
結果の報告
7.3.1
(TI−TC)/HIC≦0.6の場合は,試験結果はJIS C 2143-1の6.8(試験報告書)に従って,次の形式(54)
で報告する。
TI(HIC): xxx(xx.x) ···································································· (54)
7.3.2
0.6<(TI−TC)/HIC≦1.6で,同時にF≦F0(6.3.2参照)の場合は,HICとともに,次の式(55)で求
めたTIaの値を,形式(54)で報告する。
TIa=TC+0.6 HIC ···································································· (55)
7.3.3
その他の全ての場合は,結果を次のように報告する。
TIg=…, HICg=… ···································································· (56)
8
試験報告
試験報告には,次の事項を含める。
a) 試験片の寸法及び状態調節を含む試験した材料の説明
b) 調べた特性,選定した終点,及び必要な場合は特性の初期値
c) 特性の測定に用いた試験方法(例えば,参照した規格など)
d) 試験手順に関連する情報(例えば,劣化処理雰囲気など)
e) 個々の劣化処理温度及び対応する次のデータ
1) 非破壊試験では,個々の終点到達時間
2) 保証試験では,劣化処理周期の数,経過時間及びその周期の間に終点に到達した試験片の数
16
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3) 破壊試験では,劣化処理時間及び個々の特性値並びに劣化処理時間での特性変化のグラフ
f)
熱的耐久グラフ
g) 7.3で規定した書式に従った温度指数及び半減温度幅
h) 6.3.1で要求があった場合は,χ2及びPの値
i)
保証試験では,5.1.2に従った最初の劣化処理周期に終点に到達した試験片数
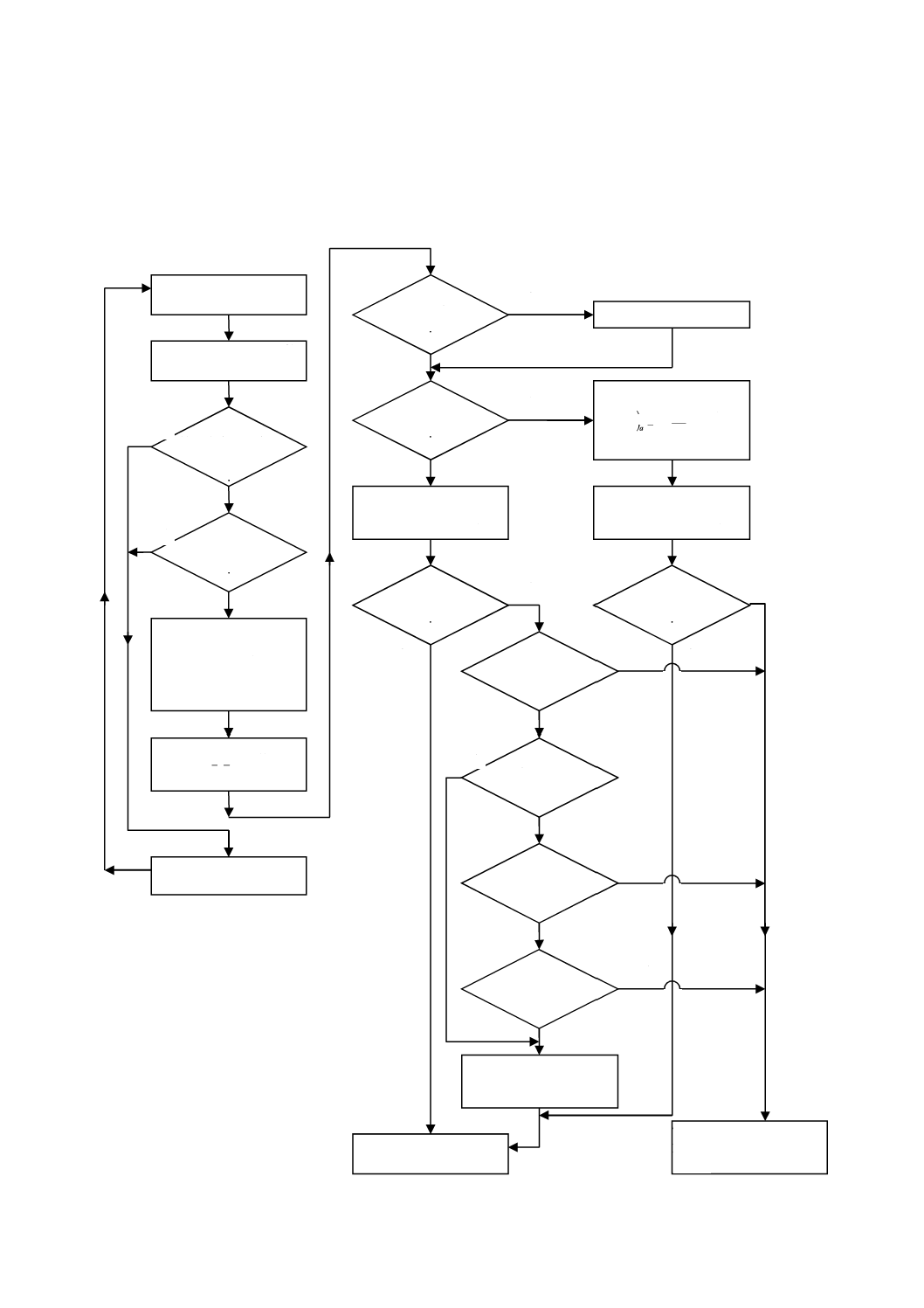
17
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
熱的耐久性計算の判定フローチャート
選定した劣化処理温度
での試験片グループ
終点到達平均時間の計算
TIの計算
最長推定平均時間
≧5 000 h
?
外挿
≦25 k
?
推定値の計算:
分散:s1i2
χ2
の計算
s12
の計算
s22
の計算
2
1
2
2
s
s
F=
の計算
新たなグループでの
より低温での試験
P(χ2, k−1)≧0.05
?
F≦F0
?
はい
いいえ
はい
いいえ
はい
いいえ
はい
いいえ
s2の計算
(s12とs22とのプール)
TI,TC,HICの計算
TI−TC≦0.6 HIC
?
はい
いいえ
TI−TC≦1.6 HIC
?
はい
いいえ
破壊試験
?
はい
いいえ
外挿なし
?
はい
いいえ
全てF≦F1
?
はい
いいえ
TI の調整
↓
TIa=TC+0.6 HIC
報告
TI(HIC) xxx(xx.x)
χ2及びPの報告
TI−TCa≦0.6 HIC
?
はい
いいえ
s2の計算
[(s12)aとs22とのプール]
TI,TC,HICの計算
s12の調整
()
0
2
1
2
1
F
F
s
s
a=
の計算
TIg=xxx
TIを除く
HICg=xx.x 又は 試験デー
の報告
タの報告
18
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(規定)
判定表
表B.1−検定に伴う判定及び処理
段階
検定又は処理a)
参照
検定不合格時の処理
1
最長終点到達平均時間≧5 000 h
JIS C 2143-1の5.5
段階15へ
2
外挿≦25 K
JIS C 2143-1の5.5
段階15へ
3
P( χ2, f )≧0.05
6.3.1
χ2及びPを報告
−
段階4へ
4
F≦F0
6.3.2
段階12へ
5
TI−TC≦0.6 HIC
7.3
段階7へ
6
TI (HIC): xxx (xx.x)を報告
7.3
−
7
TI−TC≦1.6 HIC
7.3
段階14へ
8
破壊試験の判定
6.1.4.4
段階11へ
9
外挿なしのデータ処理
6.1.4.4
段階14へ
10
F≦F1
6.1.4.4
段階14へ
11
TIa=TC+0.6 HICをTI (HIC): … (..)として報告
7.3
−
12
TI−TCa≦0.6 HIC
6.3.2
段階14へ
13
TI (HIC): xxx (xx.x)を報告
7.3
−
14
TIg=xxx,HICg=xx.xを報告
7.3
−
15
新たなグループでのより低温における試験
−
−
注a) 太字は,処理を表す。
19
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
統計表
注記 表C.1〜表C.5は,対応国際規格の表を記載している。
表C.1−不完全データ計算用の係数
m
n
α
β
μ
ε
5
3
614.470 506 172 8
−100.380 198 559 7
0.000 000 000 0
860.448 288 888 9
5
4
369.315 310 001 2
−70.671 293 489 9
472.493 715 084 2
874.074 589 444 7
6
4
395.414 213 960 5
−58.270 118 352 3
222.691 521 846 8
835.765 030 646 5
6
5
272.528 723 805 2
−44.098 885 093 6
573.512 612 381 5
887.106 668 142 6
7
4
415.588 035 156 3
−46.540 155 273 4
0.000 000 000 0
841.774 673 437 5
7
5
289.191 447 008 9
−38.006 043 810 7
364.264 215 381 5
837.368 126 781 9
7
6
215.514 679 687 5
−30.136 366 210 9
642.234 560 615 2
898.799 440 429 7
8
5
302.255 954 330 4
−32.045 551 009 5
173.745 192 558 9
823.132 502 297 0
8
6
227.132 033 490 0
−26.714 924 272 0
462.394 689 655 8
845.589 167 341 7
8
7
178.019 204 785 1
−21.890 905 564 9
692.008 291 149 8
908.717 523 176 5
9
5
312.981 200 000 0
−26.384 270 000 0
0.000 000 000 0
830.502 200 000 0
9
6
236.385 800 000 0
−23.298 610 000 0
296.052 630 000 0
821.317 260 000 0
9
7
186.640 100 000 0
−19.789 890 000 0
534.460 180 000 0
855.209 670 000 0
9
8
151.512 000 000 0
−16.614 080 000 0
729.711 990 000 0
917.058 320 000 0
10
6
244.119 156 089 0
−20.004 774 072 9
142.373 900 284 7
815.821 088 682 6
10
7
193.620 588 004 7
−17.666 360 481 4
386.952 601 761 8
825.759 043 775 3
10
8
158.230 060 832 0
−15.243 793 158 2
589.634 132 230 7
864.621 929 488 4
10
9
131.803 038 236 3
−13.034 762 797 6
759.253 366 384 2
924.098 919 253 1
11
6
250.685 932 098 8
−16.853 035 429 5
0.000 000 000 0
822.972 912 731 5
11
7
199.469 546 848 7
−15.583 654 537 4
249.259 995 307 9
812.630 898 625 4
11
8
163.699 612 133 7
−13.837 118 255 7
457.209 096 574 3
832.548 816 179 9
11
9
137.229 924 382 7
−12.100 190 779 3
633.229 292 467 8
873.335 541 088 0
11
10
116.591 321 046 4
−10.496 956 971 8
783.017 794 944 4
930.088 037 299 4
12
7
204.534 992 422 9
−13.576 711 024 4
120.574 855 492 1
810.980 305 184 0
12
8
168.329 219 660 0
−12.443 988 079 5
332.551 955 767 4
814.726 902 133 0
12
9
141.642 522 967 4
−11.121 946 667 6
513.149 341 538 3
840.062 504 581 7
12
10
121.088 479 244 8
−9.835 950 775 4
668.539 265 126 9
881.240 032 296 2
12
11
104.506 080 037 5
−8.633 379 584 8
802.544 129 235 6
935.228 223 004 9
13
7
208.940 611 828 4
−11.645 614 282 7
0.000 000 000 0
817.592 186 339 0
13
8
172.346 425 140 0
−11.086 526 420 1
215.202 335 515 1
807.269 942 297 3
13
9
145.417 868 782 7
−10.147 234 899 2
399.323 652 033 8
819.318 009 509 0
13
10
124.737 192 422 5
−9.130 008 532 8
558.746 158 905 5
847.590 859 692 6
13
11
108.301 805 863 3
−8.151 081 966 3
697.715 856 087 3
888.359 118 118 9
13
12
94.679 614 970 6
−7.225 211 787 4
818.869 702 877 8
939.679 419 663 9
注記 α,β,μ及びεの単位は,1×10−3

20
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.1−不完全データ計算用の係数(続き)
m
n
α
β
μ
ε
14
8
175.901 842 209 0
−9.774 682 609 8
104.554 351 698 0
807.510 679 332 7
14
9
148.706 654 321 0
−9.189 143 374 5
291.514 076 584 4
807.927 394 074 1
14
10
127.881 689 678 0
−8.422 450 692 9
454.060 900 206 5
825.039 882 806 3
14
11
111.381 769 972 9
−7.626 697 130 2
596.623 583 260 4
854.823 830 446 3
14
12
97.927 824 691 4
−6.863 605 925 9
722.224 918 847 7
894.761 415 308 6
14
13
86.536 307 523 1
−6.135 526 882 2
832.719 252 448 7
943.566 894 197 6
15
8
179.051 340 576 2
−8.507 153 076 2
0.000 000 000 0
813.556 818 212 9
15
9
151.627 445 154 0
−8.256 692 317 2
189.315 731 952 4
803.657 234 619 6
15
10
130.638 736 267 4
−7.722 878 628 9
354.390 697 378 5
810.944 133 571 3
15
11
114.045 779 796 6
−7.097 395 186 3
499.752 662 880 0
831.192 011 019 8
15
12
100.571 888 183 6
−6.464 822 448 7
628.585 928 820 5
861.635 264 831 5
15
13
89.346 612 386 1
−5.857 855 430 9
743.099 738 270 9
900.526 205 166 5
15
14
79.679 695 687 0
−5.275 139 366 7
844.614 393 863 7
946.988 901 484 6
16
9
154.251 868 908 5
−7.352 734 812 9
92.286 597 662 4
804.890 154 565 0
16
10
133.092 655 230 3
−7.037 490 348 3
259.470 300 502 6
803.417 948 946 8
16
11
116.397 190 014 4
−6.571 880 798 3
407.107 444 694 2
815.225 911 951 0
16
12
102.862 022 796 0
−6.059 026 278 1
538.470 351 887 8
837.405 616 491 7
16
13
91.647 511 041 4
−5.548 523 480 8
655.915 300 372 3
867.986 413 358 9
16
14
82.133 483 929 8
−5.057 399 050 1
761.089 730 468 5
905.730 213 237 4
16
15
73.828 121 853 0
−4.583 976 609 5
854.940 091 579 0
950.022 975 937 6
17
9
156.610 475 842 1
−6.476 460 274 5
0.000 000 000 0
810.419 011 339 7
17
10
135.306 977 099 1
−6.369 862 523 4
168.979 564 112 2
801.066 074 880 2
17
11
118.497 493 348 7
−6.054 318 734 9
318.520 886 724 6
805.318 062 739 4
17
12
104.894 493 937 6
−5.654 673 321 1
451.948 602 041 3
820.151 369 194 9
17
13
93.641 407 943 0
−5.231 044 716 6
571.696 183 063 2
843.486 177 866 0
17
14
84.157 807 920 1
−4.813 301 797 2
679.548 045 681 0
873.880 335 131 3
17
15
75.987 691 268 4
−4.410 061 254 4
776.751 703 284 6
910.442 891 855 0
17
16
68.776 185 039 1
−4.020 399 239 0
863.986 627 489 9
952.730 802 137 3
18
10
137.319 690 100 1
−5.720 840 122 8
82.592 591 372 5
802.835 654 113 7
18
11
120.396 550 341 6
−5.547 705 212 4
233.762 521 677 5
800.258 419 848 3
18
12
106.717 957 142 0
−5.254 869 270 6
368.923 773 992 3
808.487 834 862 6
18
13
95.417 915 235 3
−4.913 521 939 3
490.558 207 272 5
825.357 995 890 6
18
14
85.912 982 279 7
−4.560 657 091 3
600.519 390 056 5
849.333 989 100 0
18
15
77.784 669 734 1
−4.214 502 545 1
700.184 082 553 0
879.339 504 407 5
18
16
70.690 282 324 6
−3.879 229 298 2
790.508 013 638 6
914.725 238 932 5
18
17
64.370 690 391 9
−3.554 819 683 0
871.976 998 724 4
955.161 899 362 0
注記 α,β,μ及びεの単位は,1×10−3
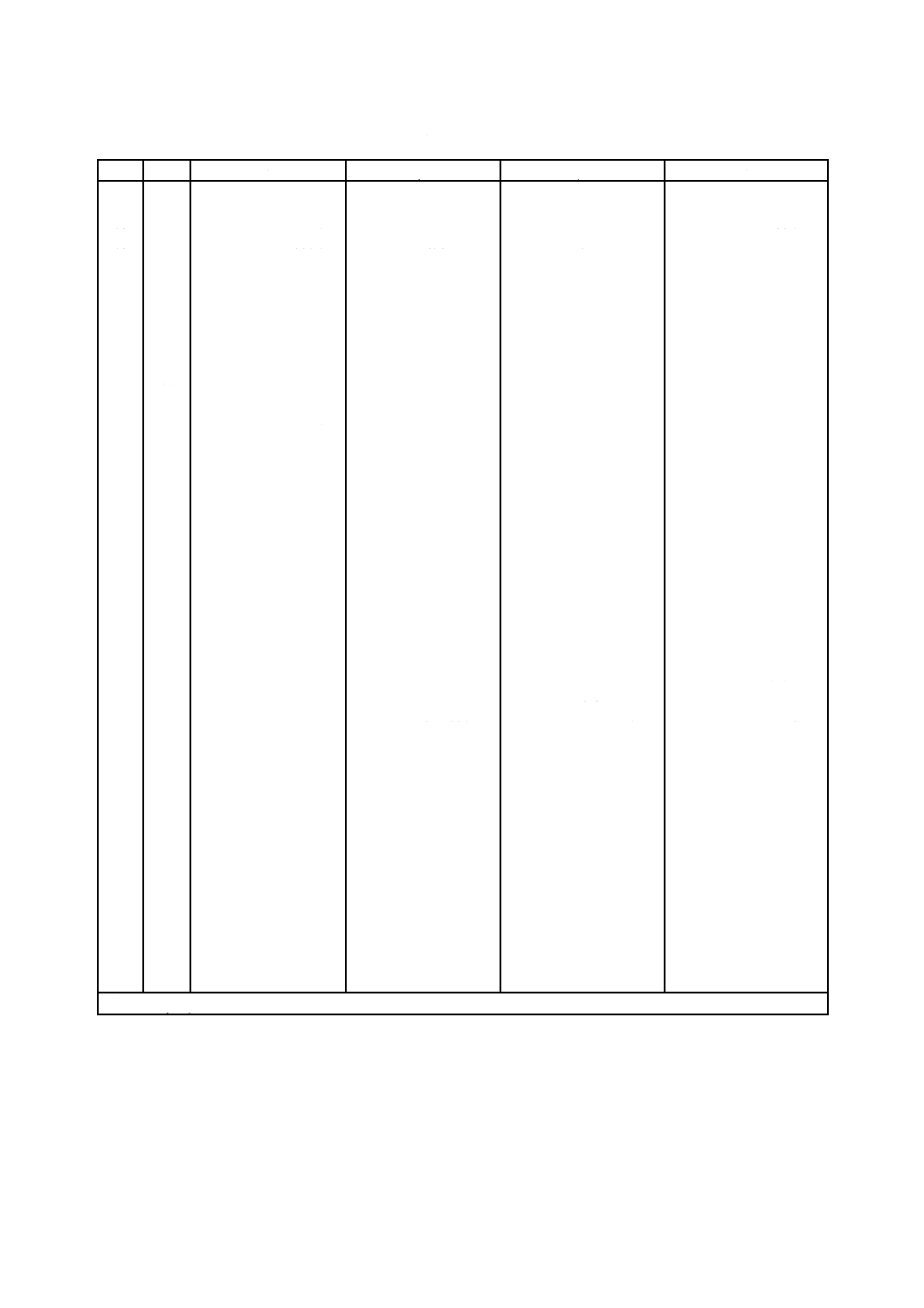
21
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
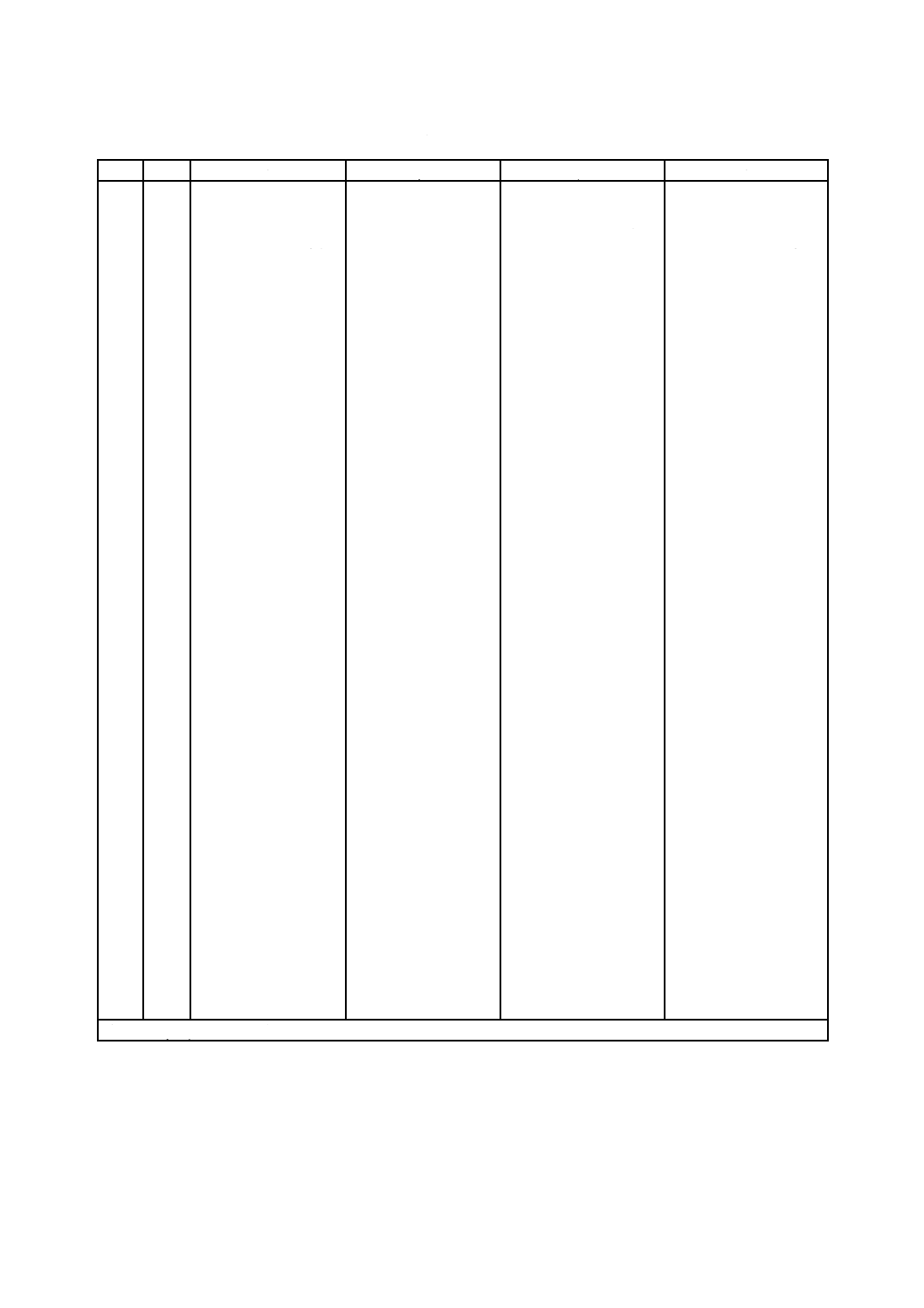
表C.1−不完全データ計算用の係数(続き)
m
n
α
β
μ
ε
19
10
139.149 625 000 0
−5.090 018 125 0
0.000 000 000 0
807.909 618 750 0
19
11
122.130 237 500 0
−5.053 480 937 5
152.583 847 187 5
799.119 842 812 5
19
12
108.370 456 250 0
−4.861 845 937 5
289.231 816 562 5
801.360 262 500 0
19
13
97.018 825 000 0
−4.598 604 062 5
412.455 355 937 5
812.396 743 437 5
19
14
87.480 900 000 0
−4.306 963 437 5
524.150 835 000 0
830.631 200 000 0
19
15
79.344 375 000 0
−4.010 505 625 0
625.758 673 437 5
854.902 153 125 0
19
16
72.297 331 250 0
−3.720 423 750 0
718.357 160 937 5
884.394 535 000 0
19
17
66.078 087 307 1
−3.438 596 529 0
802.684 840 281 0
918.630 065 987 3
19
18
60.495 123 456 8
−3.165 752 232 4
879.085 324 747 8
957.356 388 289 5
20
11
123.720 724 690 7
−4.571 903 849 4
74.739 952 689 8
801.179 011 626 4
20
12
109.882 247 113 5
−4.477 035 548 8
212.683 662 366 2
797.948 281 173 8
20
13
98.473 823 238 1
−4.287 939 233 2
337.273 238 927 2
803.677 721 219 6
20
14
88.899 384 983 5
−4.054 686 452 3
450.433 824 821 7
816.713 086 237 3
20
15
80.740 119 043 3
−3.804 781 413 9
553.643 825 389 0
835.843 732 032 9
20
16
73.694 598 203 3
−3.553 609 281 2
648.041 435 461 8
860.173 538 768 6
20
17
67.524 357 313 6
−3.308 057 336 8
734.481 449 050 2
889.078 451 004 8
20
18
62.027 051 120 2
−3.068 869 206 8
813.538 080 764 9
922.202 807 269 0
20
19
57.059 331 163 4
−2.837 292 341 8
885.449 527 637 9
959.347 069 438 1
21
11
125.180 504 268 8
−4.102 787 081 4
0.000 000 000 0
805.857 221 187 1
21
12
111.274 858 447 6
−4.101 040 726 7
139.085 614 417 5
797.605 437 620 2
21
13
99.807 327 895 4
−3.982 732 403 3
264.868 574 231 4
798.472 591 530 8
21
14
90.192 703 419 5
−3.805 109 379 9
379.291 522 952 8
806.763 785 482 7
21
15
82.006 895 840 0
−3.599 696 102 2
483.858 887 792 2
821.225 961 821 7
21
16
74.946 575 450 5
−3.384 632 353 4
579.743 276 288 7
840.921 205 171 3
21
17
68.784 814 683 3
−3.170 115 019 5
667.856 652 288 5
865.147 773 729 6
21
18
63.335 741 064 5
−2.960 377 331 2
748.883 265 049 3
893.423 810 538 9
21
19
58.441 207 543 7
−2.755 639 453 1
823.271 305 249 0
925.482 471 420 9
21
20
53.992 487 284 4
−2.557 464 289 7
891.180 261 676 2
961.160 991 780 3
22
12
112.562 249 376 3
−3.733 942 654 3
68.249 899 230 9
799.813 456 437 8
22
13
101.038 358 565 9
−3.683 676 456 5
195.088 306 477 2
796.200 753 033 8
22
14
91.380 460 456 0
−3.559 186 854 7
310.616 120 426 8
800.134 506 430 3
22
15
83.165 536 713 6
−3.396 328 281 6
416.355 757 299 6
810.324 221 550 3
22
16
76.085 740 665 3
−3.215 758 572 9
513.502 991 079 9
825.800 027 083 5
22
17
69.915 447 090 2
−3.029 759 742 9
603.001 704 223 8
845.821 800 161 5
22
18
64.479 595 568 7
−2.845 164 997 2
685.591 100 846 1
869.833 743 632 6
22
19
59.631 110 650 6
−2.664 566 007 3
761.823 205 764 4
897.461 327 883 1
22
20
55.245 182 109 6
−2.487 974 468 3
832.048 472 778 3
928.502 565 642 9
22
21
51.238 188 548 3
−2.317 111 964 4
896.367 325 561 6
962.820 644 707 6
注記 α,β,μ及びεの単位は,1×10−3

22
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.1−不完全データ計算用の係数(続き)
m
n
α
β
μ
ε
23
12
113.753 114 824 5
−3.375 661 462 4
0.000 000 000 0
804.147 498 958 3
23
13
102.180 592 915 5
−3.391 035 253 9
127.779 779 922 2
796.393 802 656 5
23
14
92.478 714 378 2
−3.317 568 453 9
244.286 853 730 7
796.302 286 039 9
23
15
84.232 065 039 4
−3.195 430 410 7
351.054 316 620 9
802.558 394 510 6
23
16
77.130 671 601 8
−3.047 956 733 6
449.294 709 215 6
814.162 196 954 9
23
17
70.946 228 319 6
−2.889 128 739 5
539.972 715 916 5
830.348 307 946 7
23
18
65.506 773 051 7
−2.727 427 071 3
623.857 738 790 5
850.523 990 198 2
23
19
60.674 543 903 7
−2.567 467 256 7
701.554 759 605 1
874.245 203 107 7
23
20
56.331 747 664 1
−2.410 824 975 7
773.511 902 625 0
901.219 290 370 3
23
21
52.378 971 244 4
−2.257 458 807 1
840.003 110 782 9
931.291 926 725 9
23
22
48.750 967 330 6
−2.109 138 220 4
901.084 347 837 2
964.344 871 037 5
24
13
103.243 347 881 9
−3.104 836 192 9
62.796 296 393 4
798.667 677 335 2
24
14
93.499 899 161 3
−3.080 597 976 9
180.179 665 703 1
794.841 653 545 8
24
15
85.219 822 400 0
−2.997 560 243 2
287.859 544 598 4
797.456 360 640 0
24
16
78.094 848 041 1
−2.881 836 788 2
387.060 117 227 4
805.486 809 924 8
24
17
71.894 122 886 0
−2.749 128 344 1
478.761 192 082 8
818.144 554 412 7
24
18
66.444 704 304 8
−2.609 144 801 8
563.751 195 249 6
834.815 363 694 5
24
19
61.612 691 563 3
−2.467 829 940 8
642.664 080 518 4
855.018 951 419 5
24
20
57.287 908 800 0
−2.328 319 155 2
715.998 983 808 0
878.398 189 184 0
24
21
53.375 054 194 3
−2.191 560 665 7
784.121 449 345 2
904.723 395 218 0
24
22
49.794 229 859 7
−2.057 530 704 7
847.245 055 046 6
933.875 440 847 1
24
23
46.493 767 000 5
−1.927 973 165 6
905.392 264 548 8
965.749 572 297 4
25
13
104.232 885 613 2
−2.825 050 151 1
0.000 000 000 0
802.701 301 544 1
25
14
94.453 143 892 0
−2.848 396 832 3
118.172 687 883 0
795.402 438 793 7
25
15
86.139 657 001 5
−2.803 071 458 2
226.670 678 353 7
794.630 540 737 9
25
16
78.989 382 024 2
−2.717 860 940 0
326.724 816 668 1
799.346 648 224 3
25
17
72.770 823 174 3
−2.610 275 202 5
419.326 141 499 8
808.740 684 495 8
25
18
67.309 061 167 5
−2.491 180 827 8
505.276 666 008 1
822.180 644 398 6
25
19
62.470 447 683 2
−2.367 461 361 3
585.228 093 541 2
839.166 598 102 9
25
20
58.148 780 157 1
−2.243 330 943 3
659.707 591 544 9
859.305 787 476 1
25
21
54.254 772 141 2
−2.120 927 932 5
729.129 747 248 1
882.309 499 023 6
25
22
50.710 634 469 5
−2.000 815 184 9
793.793 828 693 6
907.996 803 098 9
25
23
47.451 582 466 4
−1.883 013 652 0
853.865 474 685 9
936.274 654 862 4
25
24
44.436 084 435 5
−1.769 195 964 9
909.341 937 225 5
967.048 258 250 8
26
14
95.344 951 652 9
−2.620 976 346 5
58.149 346 185 6
797.692 105 701 4
26
15
87.000 011 060 1
−2.612 140 016 6
167.386 495 331 3
793.760 045 585 9
26
16
79.823 556 347 0
−2.556 356 239 1
268.207 052 434 6
795.387 979 746 5
26
17
73.585 712 493 3
−2.472 950 569 9
361.609 787 669 1
801.749 088 924 2
26
18
68.110 255 082 3
−2.373 992 685 8
448.407 042 544 8
812.194 055 876 7
26
19
63.262 342 617 2
−2.267 184 422 5
529.262 848 347 4
826.208 688 490 2
26
20
58.936 792 778 9
−2.157 486 675 1
604.721 224 122 4
843.381 329 569 6
26
21
55.048 042 936 4
−2.047 914 524 5
675.223 991 890 1
863.388 484 003 6
26
22
51.522 935 221 6
−1.939 929 951 9
741.117 446 777 6
885.995 805 567 7
26
23
48.297 466 480 8
−1.833 861 504 0
802.647 219 753 4
911.060 297 192 9
26
24
45.318 643 413 4
−1.729 780 273 4
859.940 670 651 4
938.508 290 093 4
26
25
42.552 583 209 7
−1.629 261 554 1
912.976 149 171 2
968.252 478 710 8
注記 α,β,μ及びεの単位は,1×10−3
23
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
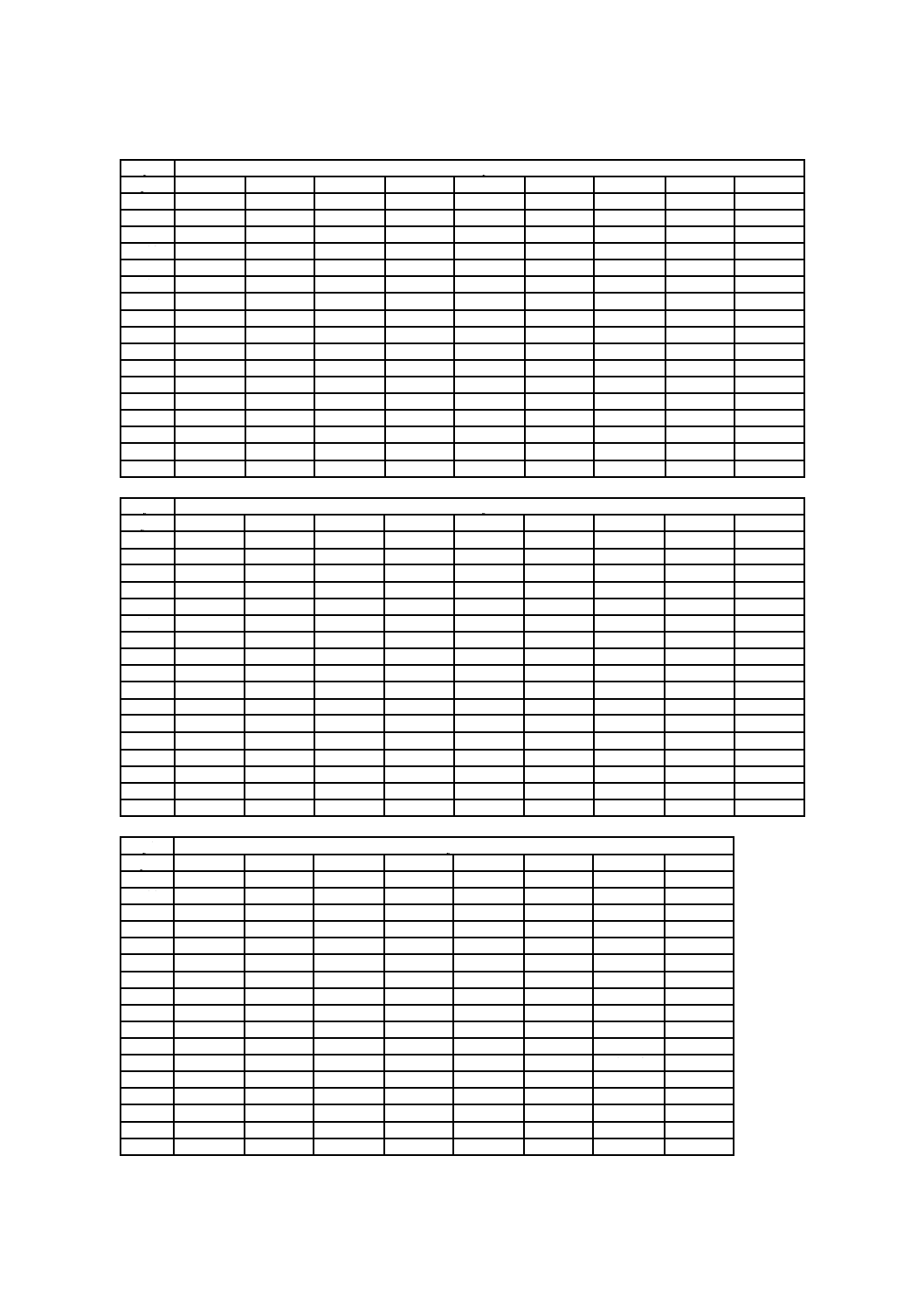
表C.1−不完全データ計算用の係数(続き)
m
n
α
β
μ
ε
27
14
96.179 952 415 7
−2.398 330 795 0
0.000 000 000 0
801.462 097 378 7
27
15
87.807 233 951 0
−2.424 824 879 2
109.908 447 002 3
794.576 240 291 9
27
16
80.604 908 585 4
−2.397 518 691 3
211.422 762 924 1
793.315 879 921 6
27
17
74.346 695 559 0
−2.337 441 207 8
305.545 934 609 8
796.846 398 872 9
27
18
68.856 363 573 0
−2.257 899 609 6
393.098 036 470 7
804.502 877 056 5
27
19
63.997 827 886 1
−2.167 418 784 4
474.752 453 008 4
815.757 617 370 5
27
20
59.665 408 004 9
−2.071 567 175 3
551.064 568 013 3
830.186 793 990 7
27
21
55.774 966 628 5
−1.973 967 843 6
622.492 414 801 3
847.448 219 212 0
27
22
52.256 650 509 1
−1.876 793 609 6
689.408 781 849 6
867.273 947 639 7
27
23
49.049 953 893 3
−1.781 045 141 6
752.104 268 197 1
889.473 159 384 9
27
24
46.101 825 203 4
−1.686 910 857 4
810.780 782 969 1
913.932 486 779 3
27
25
43.368 537 622 7
−1.594 507 505 2
865.534 983 389 9
940.592 671 976 3
27
26
40.822 044 246 6
−1.505 300 292 0
916.331 145 646 2
969.372 165 667 9
28
15
88.566 025 912 5
−2.241 132 818 2
54.142 478 801 1
796.851 152 756 7
28
16
81.339 370 105 7
−2.241 441 397 0
156.288 646 095 9
792.882 432 527 5
28
17
75.060 373 981 7
−2.203 940 607 0
251.064 797 130 7
793.761 059 837 3
28
18
69.554 150 197 3
−2.143 147 145 2
339.296 241 903 9
798.810 986 602 2
28
19
64.683 999 121 8
−2.068 438 756 0
421.663 641 341 7
807.491 370 564 5
28
20
60.343 313 763 4
−1.985 966 124 9
498.730 858 604 3
819.367 766 769 3
28
21
56.447 978 854 4
−1.899 822 629 5
570.966 583 043 2
834.086 917 498 6
28
22
52.929 720 988 9
−1.812 683 033 9
638.759 337 098 7
851.362 210 800 1
28
23
49.730 866 708 1
−1.726 122 211 5
702.425 476 425 6
870.970 736 294 0
28
24
46.800 965 426 3
−1.640 824 982 1
762.209 793 536 6
892.756 725 488 4
28
25
44.095 734 093 7
−1.556 898 149 9
818.278 335 252 4
916.630 022 383 7
28
26
41.578 780 488 7
−1.474 495 826 6
870.703 044 247 0
942.542 088 687 8
28
27
39.226 562 034 9
−1.394 969 127 3
919.437 834 977 3
970.415 906 516 9
29
15
89.279 883 950 6
−2.061 068 353 9
0.000 000 000 0
800.388 437 037 0
29
16
82.031 509 834 9
−2.088 154 781 9
102.724 036 530 3
793.877 036 548 2
29
17
75.732 129 652 0
−2.072 559 754 0
198.095 960 802 7
792.263 582 227 8
29
18
70.209 350 617 3
−2.029 914 279 8
286.943 773 786 0
794.868 014 074 1
29
19
65.326 705 651 2
−1.970 453 580 3
369.953 573 812 1
801.138 249 032 6
29
20
60.976 857 817 2
−1.900 926 199 3
447.695 899 552 2
810.629 267 057 7
29
21
57.075 122 222 2
−1.825 852 469 1
520.647 203 374 5
822.979 169 012 3
29
22
53.553 594 979 1
−1.748 283 440 2
589.206 152 039 4
837.890 741 721 5
29
23
50.356 178 834 6
−1.670 211 381 3
653.704 451 693 1
855.122 458 451 0
29
24
47.434 795 061 7
−1.592 782 963 0
714.411 894 115 2
874.488 236 049 4
29
25
44.747 071 219 0
−1.516 466 229 5
771.535 321 180 3
895.860 662 948 3
29
26
42.255 794 376 7
−1.441 322 471 7
825.211 204 490 1
919.167 805 180 3
29
27
39.930 419 412 0
−1.367 534 108 1
875.491 537 135 3
944.369 090 532 7
29
28
37.750 921 973 1
−1.296 339 683 3
922.322 734 544 5
971.391 163 917 5
注記 α,β,μ及びεの単位は,1×10−3

24
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.1−不完全データ計算用の係数(続き)
m
n
α
β
μ
ε
30
16
82.684 820 885 4
−1.937 664 400 8
50.652 014 573 0
796.118 572 279 5
30
17
76.366 256 465 8
−1.943 349 624 5
146.570 247 501 8
792.158 476 319 7
30
18
70.826 762 953 8
−1.918 317 017 4
235.981 114 359 5
792.461 131 587 5
30
19
65.930 930 098 6
−1.873 623 032 8
319.574 313 579 2
796.467 129 928 9
30
20
61.571 167 864 8
−1.816 627 096 1
397.925 628 146 2
803.721 454 578 9
30
21
57.662 159 653 0
−1.752 277 838 5
471.517 592 025 1
813.853 822 773 7
30
22
54.135 742 160 1
−1.683 950 682 5
540.756 077 379 4
826.559 615 528 3
30
23
50.936 394 609 4
−1.613 946 311 8
605.982 564 971 8
841.586 818 964 2
30
24
48.017 520 085 7
−1.543 759 560 3
667.481 860 128 2
858.730 910 242 0
30
25
45.338 701 707 0
−1.474 228 249 3
725.485 016 653 2
877.836 129 828 8
30
26
42.864 116 365 2
−1.405 671 510 2
780.167 231 081 2
898.798 090 502 7
30
27
40.562 288 770 8
−1.338 127 121 8
831.640 469 649 9
921.559 182 169 8
30
28
38.407 368 531 3
−1.271 797 397 1
879.940 590 381 4
946.084 740 241 1
30
29
36.382 112 999 3
−1.207 813 151 8
925.008 722 656 2
972.304 453 992 4
31
16
83.301 992 538 5
−1.789 978 738 8
0.000 000 000 0
799.449 240 316 8
31
17
76.966 136 087 7
−1.816 327 048 7
96.420 883 672 2
793.277 568 074 3
31
18
71.410 327 810 5
−1.808 419 671 8
186.348 933 495 6
791.408 319 114 9
31
19
66.500 911 757 5
−1.778 059 755 9
270.475 566 988 6
793.280 391 567 8
31
20
62.130 594 837 7
−1.733 208 979 2
349.380 454 238 2
798.430 692 473 8
31
21
58.213 650 031 6
−1.679 255 477 3
423.551 017 869 7
806.480 582 844 0
31
22
54.681 451 819 7
−1.619 889 288 3
493.398 689 540 3
817.118 733 927 4
31
23
51.478 457 936 1
−1.557 665 638 7
559.271 735 187 4
830.086 415 779 9
31
24
48.558 751 556 4
−1.494 336 391 4
621.464 461 258 2
845.168 568 248 7
31
25
45.883 258 032 6
−1.431 029 978 5
680.222 614 151 8
862.191 333 503 9
31
26
43.417 750 283 1
−1.368 360 139 7
735.744 785 101 6
881.024 058 266 6
31
27
41.131 756 949 6
−1.306 543 790 7
788.179 632 726 8
901.581 102 905 3
31
28
38.998 487 430 7
−1.245 608 341 8
837.618 735 482 7
923.816 123 588 4
31
29
36.995 887 902 7
−1.185 768 788 8
884.084 886 238 3
947.698 822 700 0
31
30
35.108 942 438 4
−1.128 054 899 5
927.515 641 210 7
973.161 491 746 6
注記 α,β,μ及びεの単位は,1×10−3
25
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.2−F−分布表抜粋,F(0.95,fn,fd)
f
fn
fd
1
2
3
4
5
6
7
8
9
10
4.965
4.103
3.708
3.478
3.326
3.217
3.135
3.072
3.02
11
4.844
3.982
3.587
3.357
3.204
3.095
3.012
2.948
2.896
12
4.747
3.885
3.49
3.259
3.106
2.996
2.913
2.849
2.796
13
4.667
3.806
3.411
3.179
3.025
2.915
2.832
2.767
2.714
14
4.6
3.739
3.344
3.112
2.958
2.848
2.764
2.699
2.646
15
4.543
3.682
3.287
3.056
2.901
2.79
2.707
2.641
2.588
16
4.494
3.634
3.239
3.007
2.852
2.741
2.657
2.591
2.538
17
4.451
3.592
3.197
2.965
2.81
2.699
2.614
2.548
2.494
18
4.414
3.555
3.16
2.928
2.773
2.661
2.577
2.51
2.456
19
4.381
3.522
3.127
2.895
2.74
2.628
2.544
2.477
2.423
20
4.351
3.493
3.098
2.866
2.711
2.599
2.514
2.447
2.393
25
4.242
3.385
2.991
2.759
2.603
2.49
2.405
2.337
2.282
30
4.171
3.316
2.922
2.69
2.534
2.421
2.334
2.266
2.211
40
4.085
3.232
2.839
2.606
2.449
2.336
2.249
2.18
2.124
50
4.034
3.183
2.79
2.557
2.4
2.286
2.199
2.13
2.073
100
3.936
3.087
2.696
2.463
2.305
2.191
2.103
2.032
1.975
500
3.86
3.014
2.623
2.39
2.232
2.117
2.028
1.957
1.899
f
fn
fd
10
11
12
13
14
15
16
17
18
10
2.978
2.943
2.913
2.887
2.865
2.845
2.828
2.812
2.798
11
2.854
2.818
2.788
2.761
2.739
2.719
2.701
2.685
2.671
12
2.753
2.717
2.687
2.66
2.637
2.617
2.599
2.583
2.568
13
2.671
2.635
2.604
2.577
2.554
2.533
2.515
2.499
2.484
14
2.602
2.565
2.534
2.507
2.484
2.463
2.445
2.428
2.413
15
2.544
2.507
2.475
2.448
2.424
2.403
2.385
2.368
2.353
16
2.494
2.456
2.425
2.397
2.373
2.352
2.333
2.317
2.302
17
2.45
2.413
2.381
2.353
2.329
2.308
2.289
2.272
2.257
18
2.412
2.374
2.342
2.314
2.29
2.269
2.25
2.233
2.217
19
2.378
2.34
2.308
2.28
2.256
2.234
2.215
2.198
2.182
20
2.348
2.31
2.278
2.25
2.225
2.203
2.184
2.167
2.151
25
2.236
2.198
2.165
2.136
2.111
2.089
2.069
2.051
2.035
30
2.165
2.126
2.092
2.063
2.037
2.015
1.995
1.976
1.96
40
2.077
2.038
2.003
1.974
1.948
1.924
1.904
1.885
1.868
50
2.026
1.986
1.952
1.921
1.895
1.871
1.85
1.831
1.814
100
1.927
1.886
1.85
1.819
1.792
1.768
1.746
1.726
1.708
500
1.85
1.808
1.772
1.74
1.712
1.686
1.664
1.643
1.625
f
fn
fd
19
20
25
30
40
50
100
500
10
2.785
2.774
2.73
2.7
2.661
2.637
2.588
2.548
11
2.658
2.646
2.601
2.57
2.531
2.507
2.457
2.415
12
2.555
2.544
2.498
2.466
2.426
2.401
2.35
2.307
13
2.471
2.459
2.412
2.38
2.339
2.314
2.261
2.218
14
2.4
2.388
2.341
2.308
2.266
2.241
2.187
2.142
15
2.34
2.328
2.28
2.247
2.204
2.178
2.123
2.078
16
2.288
2.276
2.227
2.194
2.151
2.124
2.068
2.022
17
2.243
2.23
2.181
2.148
2.104
2.077
2.02
1.973
18
2.203
2.191
2.141
2.107
2.063
2.035
1.978
1.929
19
2.168
2.155
2.106
2.071
2.026
1.999
1.94
1.891
20
2.137
2.124
2.074
2.039
1.994
1.966
1.907
1.856
25
2.021
2.007
1.955
1.919
1.872
1.842
1.779
1.725
30
1.945
1.932
1.878
1.841
1.792
1.761
1.695
1.637
40
1.853
1.839
1.783
1.744
1.693
1.66
1.589
1.526
50
1.798
1.784
1.727
1.687
1.634
1.599
1.525
1.457
100
1.691
1.676
1.616
1.573
1.515
1.477
1.392
1.308
500
1.607
1.592
1.528
1.482
1.419
1.376
1.275
1.159

26
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.3−F−分布表抜粋,F(0.995,fn,fd)
f
fn
fd
1
2
3
4
5
6
7
8
9
10
12.826
9.427
8.081
7.343
6.872
6.545
6.302
6.116
5.968
11
12.226
8.912
7.6
6.881
6.422
6.102
5.865
5.682
5.537
12
11.754
8.51
7.226
6.521
6.071
5.757
5.525
5.345
5.202
13
11.374
8.186
6.926
6.233
5.791
5.482
5.253
5.076
4.935
14
11.06
7.922
6.68
5.998
5.562
5.257
5.031
4.857
4.717
15
10.798
7.701
6.476
5.803
5.372
5.071
4.847
4.674
4.536
16
10.575
7.514
6.303
5.638
5.212
4.913
4.692
4.521
4.384
17
10.384
7.354
6.156
5.497
5.075
4.779
4.559
4.389
4.254
18
10.218
7.215
6.028
5.375
4.956
4.663
4.445
4.276
4.141
19
10.073
7.093
5.916
5.268
4.853
4.561
4.345
4.177
4.043
20
9.944
6.986
5.818
5.174
4.762
4.472
4.257
4.09
3.956
25
9.475
6.598
5.462
4.835
4.433
4.15
3.939
3.776
3.645
30
9.18
6.355
5.239
4.623
4.228
3.949
3.742
3.58
3.45
40
8.828
6.066
4.976
4.374
3.986
3.713
3.509
3.35
3.222
50
8.626
5.902
4.826
4.232
3.849
3.579
3.376
3.219
3.092
100
8.241
5.589
4.542
3.963
3.589
3.325
3.127
2.972
2.847
500
7.95
5.355
4.33
3.763
3.396
3.137
2.941
2.789
2.665
f
fn
fd
10
11
12
13
14
15
16
17
18
10
5.847
5.746
5.661
5.589
5.526
5.471
5.422
5.379
5.34
11
5.418
5.32
5.236
5.165
5.103
5.049
5.001
4.959
4.921
12
5.085
4.988
4.906
4.836
4.775
4.721
4.674
4.632
4.595
13
4.82
4.724
4.643
4.573
4.513
4.46
4.413
4.372
4.334
14
4.603
4.508
4.428
4.359
4.299
4.247
4.2
4.159
4.122
15
4.424
4.329
4.25
4.181
4.122
4.07
4.024
3.983
3.946
16
4.272
4.179
4.099
4.031
3.972
3.92
3.875
3.834
3.797
17
4.142
4.05
3.971
3.903
3.844
3.793
3.747
3.707
3.67
18
4.03
3.938
3.86
3.793
3.734
3.683
3.637
3.597
3.56
19
3.933
3.841
3.763
3.696
3.638
3.587
3.541
3.501
3.465
20
3.847
3.756
3.678
3.611
3.553
3.502
3.457
3.416
3.38
25
3.537
3.447
3.37
3.304
3.247
3.196
3.151
3.111
3.075
30
3.344
3.255
3.179
3.113
3.056
3.006
2.961
2.921
2.885
40
3.117
3.028
2.953
2.888
2.831
2.781
2.737
2.697
2.661
50
2.988
2.9
2.825
2.76
2.703
2.653
2.609
2.569
2.533
100
2.744
2.657
2.583
2.518
2.461
2.411
2.367
2.326
2.29
500
2.562
2.476
2.402
2.337
2.281
2.23
2.185
2.145
2.108
f
fn
fd
19
20
25
30
40
50
100
500
10
5.305
5.274
5.153
5.071
4.966
4.902
4.772
4.666
11
4.886
4.855
4.736
4.654
4.551
4.488
4.359
4.252
12
4.561
4.53
4.412
4.331
4.228
4.165
4.037
3.931
13
4.301
4.27
4.153
4.073
3.97
3.908
3.78
3.674
14
4.089
4.059
3.942
3.862
3.76
3.698
3.569
3.463
15
3.913
3.883
3.766
3.687
3.585
3.523
3.394
3.287
16
3.764
3.734
3.618
3.539
3.437
3.375
3.246
3.139
17
3.637
3.607
3.492
3.412
3.311
3.248
3.119
3.012
18
3.527
3.498
3.382
3.303
3.201
3.139
3.009
2.901
19
3.432
3.402
3.287
3.208
3.106
3.043
2.913
2.804
20
3.347
3.318
3.203
3.123
3.022
2.959
2.828
2.719
25
3.043
3.013
2.898
2.819
2.716
2.652
2.519
2.406
30
2.853
2.823
2.708
2.628
2.524
2.459
2.323
2.207
40
2.628
2.598
2.482
2.401
2.296
2.23
2.088
1.965
50
2.5
2.47
2.353
2.272
2.164
2.097
1.951
1.821
100
2.257
2.227
2.108
2.024
1.912
1.84
1.681
1.529
500
2.075
2.044
1.922
1.835
1.717
1.64
1.46
1.26
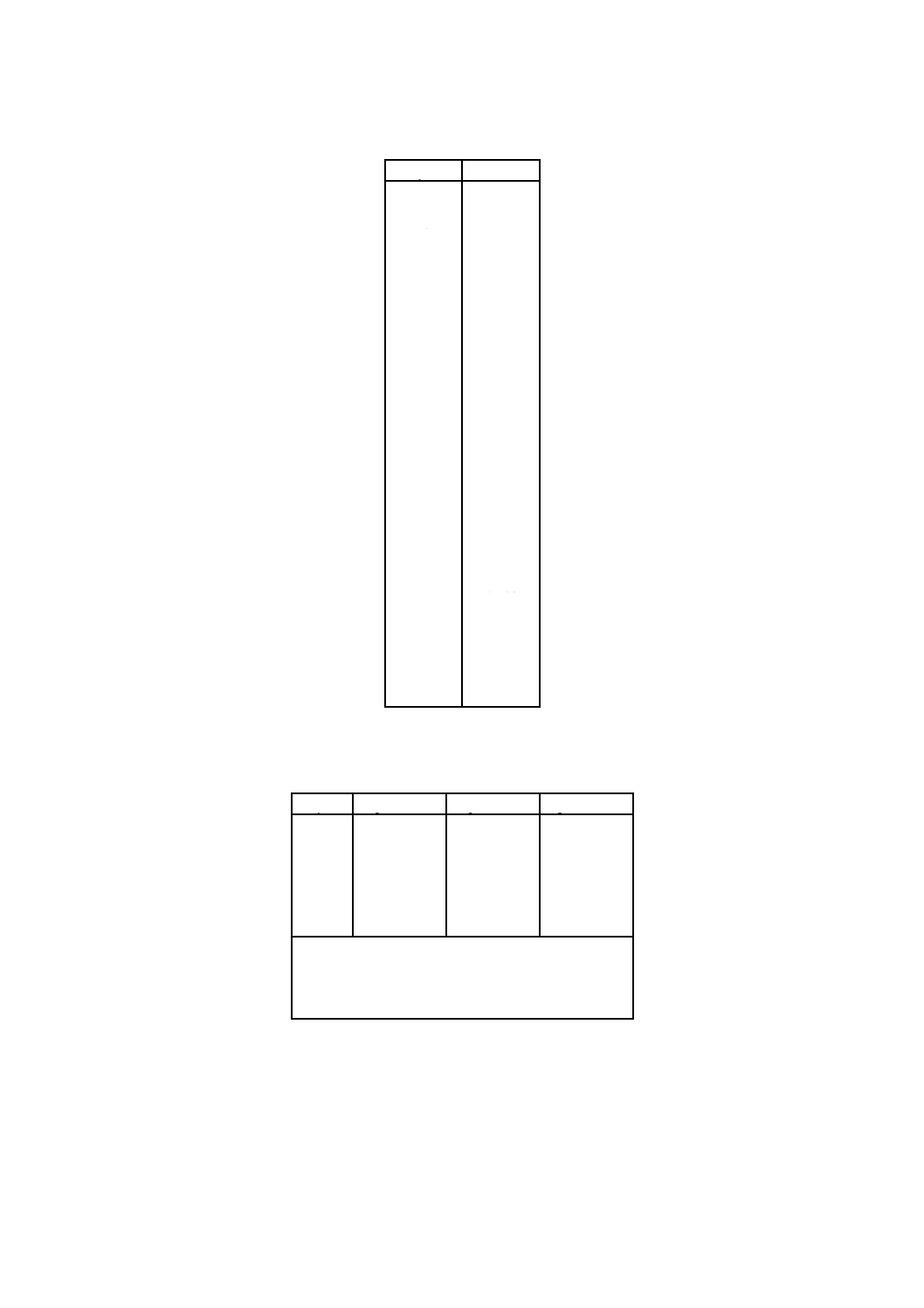
27
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.4−t−分布抜粋表,t0.95
f
t
1
6.314
2
2.920
3
2.353
4
2.132
5
2.015
6
1.943
7
1.895
8
1.860
9
1.833
10
1.812
11
1.796
12
1.782
13
1.771
14
1.761
15
1.753
16
1.746
17
1.740
18
1.734
19
1.729
20
1.725
25
1.708
30
1.697
40
1.684
50
1.676
100
1.660
500
1.64
表C.5−χ2分布表抜粋
f
p=0.95
p=0.99
p=0.995
1
3.8
6.6
7.9
2
6.0
9.2
10.6
3
7.8
11.3
12.8
4
9.5
13.3
14.9
5
11.1
15.1
16.7
6
12.6
16.8
18.5
注記 有意水準Pは,(1−p)に等しい。例えば,有意
水準0.05はp=0.95に対応する。
ここで用いるpは,本体で用いるpとは異な
る。

28
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
実施例
注記 表D.1〜表D.3は,対応国際規格の表を記載している。
表D.1−実施例1−不完全データ(保証試験)
ϑi
240
260
280
xi
0.001 948 747 929
0.001 875 644 753
0.001 807 827 895
j
τij
yij
τij
yij
τij
yij
1
1 764
7.475 339 237
756
6.628 041 376
108
4.682 131 227
2
2 772
7.927 324 360
924
6.828 712 072
252
5.529 429 088
3
2 772
7.927 324 360
924
6.828 712 072
324
5.780 743 516
4
3 780
8.237 479 289
1 176
7.069 874 128
324
5.780 743 516
5
4 284
8.362 642 432
1 176
7.069 874 128
468
6.148 468 296
6
4 284
8.362 642 432
2 184
7.688 913 337
612
6.416 732 283
7
4 284
8.362 642 432
2 520
7.832 014 181
684
6.527 957 918
8
5 292
8.573 951 525
2 856
7.957 177 323
756
6.628 041 376
9
7 308
8.896 724 917
2 856
7.957 177 323
756
6.628 041 376
10
7 812
8.963 416 292
3 192
8.068 402 959
828
6.719 013 154
11
7 812
8.963 416 292
3 192
8.068 402 959
828
6.719 013 154
12
3 864
8.259 458 195
972
6.879 355 804
13
4 872
8.491 259 809
1 428
7.264 030 143
14
5 208
8.557 951 184
1 596
7.375 255 778
15
5 544
8.620 471 541
1 932
7.566 311 015
16
5 880
8.679 312 041
1 932
7.566 311 015
17
5 880
8.679 312 041
2 100
7.649 692 624
18
5 880
8.679 312 041
2 268
7.726 653 665
19
2 604
7.864 804 003
20
2 772
7.927 324 360
mi
21
21
21
ni
11
18
20
αi
0.125 180 504 27
0.063 335 741 06
0.053 992 487 28
βi
−0.004 102 787 08
−0.002 960 377 33
−0.002 557 464 29
μi
0
0.748 883 265 05
0.891 180 261 68
εi
0.805 857 221 19
0.893 423 810 54
0.961 160 991 78
∑
−
=
1
1
in
j
ijy
83.089 487 275 2
133.285 066 669
127.452 728 95
(
)
∑
−
=
−
1
1
2
i
i
n
j
ij
in
y
y
6.127 249 075 70
19.955 744 346 8
41.422 442 313 8
iy
8.963 416 292
8.050 988 496
6.840 720 748 66
2
1is
0.591 278 355 53
0.661 652 813 85
0.863 951 396 023
29
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.1−実施例1−不完全データ(保証試験)(続き)
∑
=
k
i
ik
1
ε
0.886 814 007 835
(29)
∑
=
k
i
i
ix
n
1
2
0.000 170 463 415 664
∑
=
k
i
i
iy
n
1
2
2986.411 838 81
∑
=
k
i
i
i
iy
x
n
1
0.711 293 042 041
∑
=
=
k
i
i
m
M
1
63
(28)
∑
=
=
k
i
in
N
1
49
(25)
∑
=
k
i
i
i
N
x
n
1
0.001 864 375 319 83
(26)
∑
=
k
i
i
i
N
y
n
1
7.761 832 390 07
(27)
b
15327.985 78
(33)
a
−20.815 286 004 4
(34)
2
1s
0.647 296 300 122
(30)
2
2s
0.395 498 398 826
(36)
F
0.611 000 555 311
(40)
χ2
0.554 692 947 413
(38)
c
1.031 619 329 65
(39)
t0.95, N−2
1.677 926 722
(43)
tc
1.738 953 340 31
(43)
μ2(x)
2.949 884 440 3×10−9
(31)
s2
0.641 938 897 967
(41)
ϑˆ
TI=
225.827 791 333
(50)
c
ϑˆ
TC=
214.550 619 764
(50)
HIC
11.518 995 303 8
(53)
(TI−TC)/HIC
0.979 006 525 432
TIa
221.462 017 221
(55)
結果
TI (HIC): 221.5 (11.5)

30
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.2−実施例2−完全データ(非破壊試験)
ϑi
180
200
220
xi
0.002 206 774 799
0.002 113 494 663
0.002 027 780 594
j
τij
yij
τij
yij
τij
yij
1
7 410
8.910 585 718
3 200
8.070 906 089
1 100
7.003 065 459
2
6 610
8.796 338 933
2 620
7.870 929 597
740
6.606 650 186
3
6 170
8.727 454 117
2 460
7.807 916 629
720
6.579 251 212
4
5 500
8.612 503 371
2 540
7.839 919 360
620
6.429 719 478
5
8 910
9.094 929 520
3 500
8.160 518 247
910
6.813 444 599
mi
5
5
5
ni
5
5
5
εi
1
1
1
∑
=
i
n
j
ijy
1
44.141 811 66
39.750 189 92
33.432 130 93
∑
=
i
n
j
ijy
1
2
389.835 529 1
316.113 013 5
223.741 618
iy
8.828 362 332
7.950 037 984
6.686 426 187
2
1is
0.033 905 452 03
0.002 437 344 2
0.005 003 578 14
31
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.2−実施例2−完全データ(非破壊試験)(続き)
∑
=
k
i
ik
1
ε
1
(29)
∑
=
k
i
i
ix
n
1
2
6.724 304 421 1×10−5
∑
=
k
i
i
iy
n
1
2
929.256 902 85
∑
=
k
i
i
i
iy
x
n
1
0.249 215 878 14
∑
=
=
k
i
i
m
M
1
15
(28)
∑
=
=
k
i
in
N
1
15
(25)
∑
=
k
i
i
i
N
x
n
1
2.116 016 685 4×10−3
(26)
∑
=
k
i
i
i
N
y
n
1
7.821 608 834 4
(27)
b
11929.077 582
(33)
a
−17.420 518 37
(34)
2
1s
0.036 104 891 8
(30)
2
2s
0.188 563 697 29
(36)
F
5.222 663 409
(40)
F0
4.747
χ2
0.466 116 435 248
(38)
c
1.111 111 111 1
(39)
t0.95, N−2
1.770 933 396 2
(43)
tc
1.770 933 396 2
(43)
μ2(x)
5.343 001 171 0×10−9
(31)
2
as
0.051 199 586 08
(42)
ϑˆ
TI=
163.428 648 665
(50)
c
ϑˆ
TCa=
158.670 330 155
(50)
HIC
11.363 255 775 6
(53)
(TI−TCa)/HIC
0.418 746 053 44
結果
TI (HIC): 163 (11.4)
(54)
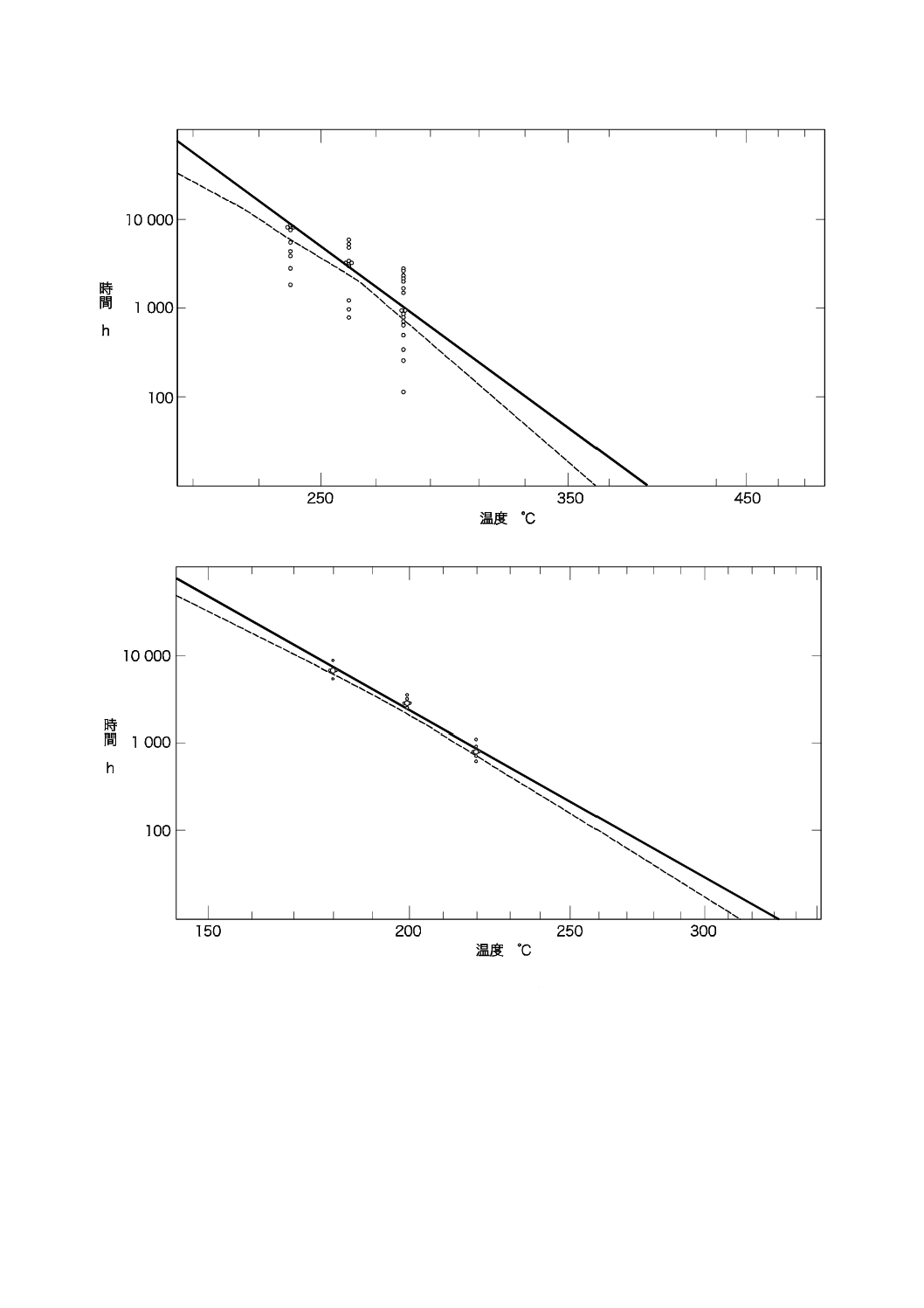
32
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 実施例1
b) 実施例2
注記 a)の図では,直線は回帰方程式を,破線は推定温度の下側95 %信頼限界を示している。b)の図は,コンピュー
タ処理によって作成した。
図D.1−熱的耐久グラフ
33
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.3の実施例は,破壊試験データに特有の計算の例証を与え,単一の試験温度との関連を説明する。
この計算からのデータ及びその他の試験温度からのデータは,実施例2(表D.2参照)と同様の計算に取
り込まれている。
表D.3−実施例3−完全データ(破壊試験)
終点70.0
τg
288
336
432
624
720
pgh
139.5
121.9
101.2
77.8
69.6
125
109.3
99.5
74.6
69.4
120.8
98.3
98.4
71.4
67.2
112.7
96.5
92.4
68.2
60.4
112
93
78.1
60.5
59.4
ng
5
5
5
5
5
g
p
122.00
103.80
93.92
70.50
65.20
2
1g
s
125.795
139.510
89.197
44.050
24.420
log τg
5.662 96
5.817 111
6.068 426
6.436 15
6.579 251
ni
25
z
6.112 8
p
91.084
bp
−59.493 7
ap
454.756
2
1s
84.594
2
2s
77.266
F
0.913
F1
3.098
zgh
6.831 151
6.689 472
6.592 851
6.567 257
6.572 528
6.587 428
6.477 685
6.564 276
6.513 469
6.569 166
6.516 832
6.292 792
6.545 787
6.459 682
6.532 187
6.380 683
6.262 536
6.444 936
6.405 895
6.417 89
6.368 917
6.203 707
6.204 574
6.276 47
6.401 081
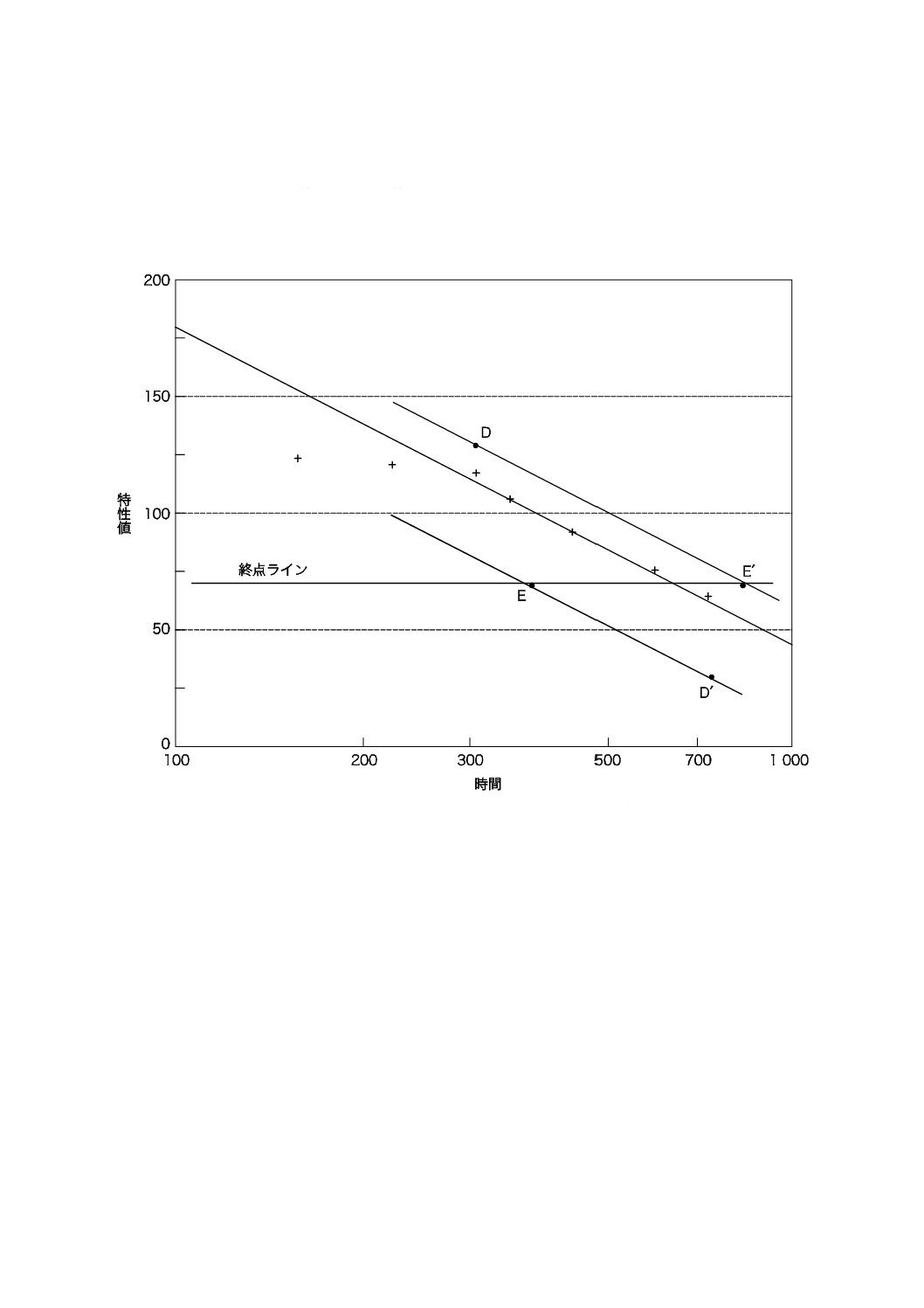
34
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表D.3の実施例3のデータを図示したグラフを図D.2に示す。点E及び点E'を通る直線は選定した終点
を示す。点D及び点D'は,このデータ処理の理解のために,実際のデータにはない仮想の点を追加したも
のであり,この点から回帰直線に平行な直線を引いて,点E及び点E'において終点ラインと交差する時間
がそれぞれ想定される終点到達時間である。グラフ上に印したその他の幾つかの点は,それぞれ特性値グ
ループの平均値である。
図D.2−実施例3(破壊試験データ)の特性−時間グラフ
表D.3のデータセットで,劣化処理時間624時間までだけが有効であった場合は,70.5>70.0であるた
め,劣化曲線は終点ラインと交差していない。この場合,必要となる外挿は次のとおりになる。
(70.5−70.0)/(122.0−70.5)=0.009 7
この外挿は,6.1.4.4の他の制限に触れないことを条件として許容できる。

35
C 2143-3:2013 (IEC 60216-3:2006)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E
(参考)
コンピュータプログラム
対応国際規格では,この規格で用いる計算用プログラムをCD-ROMの形で提供している。対応国際規格
の附属書Eの記述はプログラムの解説であって,その実行には直接関係しないと判断したため,この規格
では不採用とした。
このCD-ROMは,一般財団法人日本規格協会からIEC 60216-3を購入すると,入手することができる。
この規格にはCD-ROMを添付しない。また,動作環境(OS,プログラム言語など)は,我が国の現状
に照らしてやや旧版に属するものを前提としている。現在は,最新のOS上で動作する市販の統計計算用
ソフトウェアが種々存在するため,比較的容易に計算を行うことができる。
参考文献
[1] SAW. J. G., Estimation of the Normal Population Parameters given a Singly Censored Sample, Biometrika 46,
150, 1959
[2] PRESS. W.H. et al., Numerical Recipes. FORTRAN Version, Cambridge University Press, Cambridge 1989
[3] JIS C 2143-5 電気絶縁材料−熱的耐久性−第5部:相対熱的耐久性指数(RTE)の求め方
注記 対応国際規格:IEC 60216-5,Electrical insulating materials−Thermal endurance properties−Part
5: Determination of relative thermal endurance index (RTE) of an insulating material(IDT)