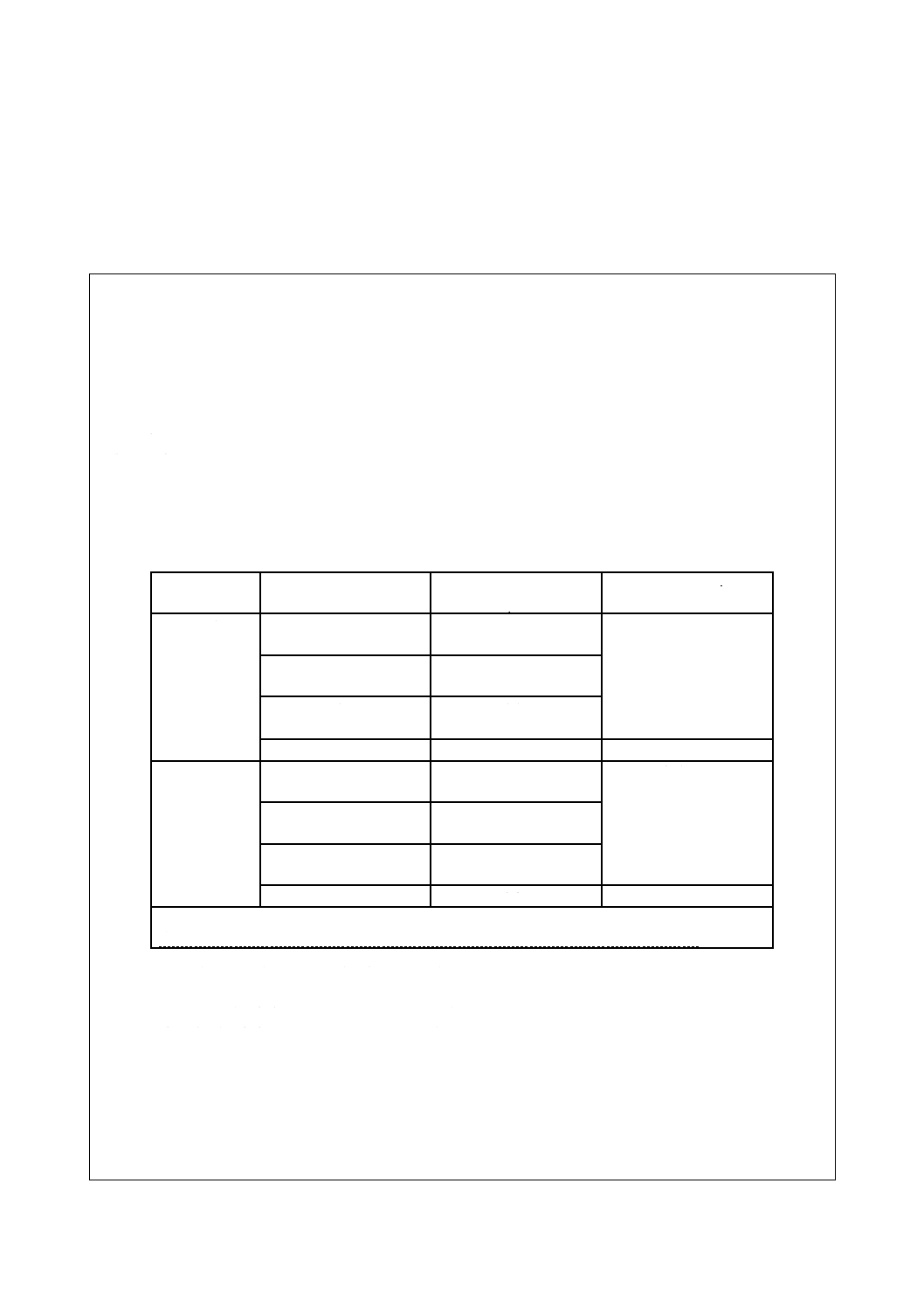C 1911:2013 (IEC 62110:2009)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
4 電界及び磁界の測定原理 ···································································································· 2
4.1 一般的事項 ··················································································································· 2
4.2 測定器 ························································································································· 2
4.3 高調波成分 ··················································································································· 3
4.4 測定結果の記録 ············································································································· 3
4.5 測定時の留意点 ············································································································· 4
5 電界及び磁界の基本的測定手順 ··························································································· 5
5.1 一般的手順 ··················································································································· 5
5.2 1点測定 ······················································································································· 5
5.3 3点測定 ······················································································································· 6
5.4 5点測定 ······················································································································· 6
6 電界への最大ばく露レベルを探すための測定手順 ··································································· 7
6.1 架空送配電線 ················································································································ 7
6.2 地中ケーブル ················································································································ 7
6.3 変電所及びその他の電力システム機器················································································ 7
7 磁界への最大ばく露レベルを探すための測定手順 ··································································· 8
7.1 架空電力線 ··················································································································· 8
7.2 地中ケーブル ················································································································ 8
7.3 変電所及びその他の電力システム機器················································································ 9
附属書A(参考)交流架空送配電線から発生する電界の特性························································ 10
附属書B(参考)交流電力システムが発生する磁界の特性 ··························································· 21
附属書C(参考)平均ばく露レベルに関する3点測定の概念························································ 34
附属書D(参考)電界及び磁界測定報告書の書式例 ··································································· 39
附属書E(参考)参考文献 ···································································································· 41
C 1911:2013 (IEC 62110:2009)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人電気学会(IEEJ)及び一般財団
法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本
工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
C 1911:2013
(IEC 62110:2009)
交流電力システムから発生する電界及び磁界の強さ
−公衆の人体ばく露を考慮した測定手順
Electric and magnetic field levels generated by AC power systems-
Measurement procedures with regard to public exposure
序文
この規格は,2009年に第1版として発行されたIEC 62110を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,交流電力システムから発生する電界及び磁界の,人体へのばく露レベルを評価するための
測定手順について規定する。この規格は,直流電力システムには適用しない。
この規格は,居住環境及び公衆が立入り可能な場所における公衆の人体ばく露に適用する。
この規格は,電界及び磁界の基本的な測定手順について規定するとともに,人体ばく露に関しては,人
体が占める空間平均に相当する電界及び磁界の強さを得るための基本的な測定手順について規定する。
この規格は,電力システムの運用及び/又は保守に関連するような職業的ばく露には適用しない。その
ようなばく露は,配電用変電所,送電用変電所若しくは発電所の内部,地中ケーブル用のマンホール若し
くはトンネルの内部,又は架空送電鉄塔上若しくは電柱上での作業時に生じることが考えられる。
注記1 鉄道用電気設備は別の規格で規定されているため,この規格の対象外である(3.7参照)。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 62110:2009,Electric and magnetic field levels generated by AC power systems−Measurement
procedures with regard to public exposure(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。この引用
規格は,その最新版(追補を含む。)を適用する。
JIS C 1910 人体ばく露を考慮した低周波磁界及び電界の測定−測定器の特別要求事項及び測定の手
引き
注記 対応国際規格:IEC 61786,Measurement of low-frequency magnetic and electric fields with regard
to exposure of human beings−Special requirements for instruments and guidance for measurements
(IDT)
2
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS C 1910によるほか,次による。
注記 “磁束密度”と“磁界強度”とを区別することは,磁性材料中の磁界を考える場合だけに意味
がある。空気中については,両方の量を表す共通の用語として“磁界”を用いることが一般的
である。
3.1
1点測定(single-point measurement)
均一な電界及び磁界の場合に適用する,規定する高さでの電界及び磁界の強さを測定する手順。
注記 電界及び磁界を均一とみなすことができる条件を,5.1に規定する。
3.2
3点測定(three-point measurement)
不均一な電界及び磁界の場合に適用する,ある地点の規定する三つの高さでの電界及び磁界の強さを測
定する手順。
3.3
5点測定(five-point measurement)
床下又は地面下にある発生源から発生する不均一な電界及び磁界の場合に適用する,規定する高さでの
5点の電界及び磁界の強さを測定する手順。
3.4
平均ばく露レベル(average exposure level)
人体がばく露される電界及び磁界の,全身にわたる空間平均値。
3.5
3点平均ばく露レベル(three-point average exposure level)
3点測定で得られた三つの値の算術平均値,又は5点測定で得られたうちの大きい方から三つの値の算
術平均値。
注記 この算術平均値は,ある地点における平均ばく露レベルの推定値として用いる。
3.6
最大ばく露レベル(maximum exposure level)
測定対象区域における1点測定の最大値,又は平均ばく露レベルの最大値。
3.7
電力システム(power system)
架空送配電線,地中ケーブル,変電所及びその他の送配電機器からなるシステム。ただし,鉄道用電気
設備は別の規格で規定されているため,この規格の対象外である。
4
電界及び磁界の測定原理
4.1
一般的事項
電界及び磁界の測定に関する一般的情報及び要求事項については,JIS C 1910によるほか,参考事項と
してCIGRE(国際大電力システム会議)技術冊子[6][8],IEEE(米国電気電子学会)規格[7][9]など,その
他の技術文書を参照する。
4.2
測定器
電界及び磁界を測定するための測定器は,JIS C 1910に規定した校正及び仕様に対する要求事項を満足
3
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
しなければならない。このような測定器は,特に電磁両立性,温度及び湿度に関し,製造業者が推奨する
適切な条件下で使用することが望ましい。
3軸の測定器では,合成電界及び合成磁界の実効値Frを測定する。単軸の測定器では,Fx,Fy及びFz
を測定することによって,式(1)からFrを求めることができる。
2
z
2
y
2
x
r
F
F
F
F
+
+
=
·································································· (1)
ここに, Fx,Fy及びFz: 電界又は磁界の直交する3軸の各成分の実効値
電界及び磁界に高調波が含まれない場合には,Fmax及びFminを測定することによって,式(2)からFrを求
めることもできる。
2
min
2
max
r
F
F
F
+
=
····································································· (2)
ここに, Fmax: 電界及び磁界だ円の半長径の実効値
Fmin: 電界及び磁界だ円の半短径の実効値
4.3
高調波成分
高調波は一般的に,非線形の機器から発生する。高調波は,送電線及び配電線で検出されることがある。
通常,交流配電システムにおける電圧の全高調波ひずみ([3]及び[4]を参照)は僅かであり,ばく露レベル
に対して実質的な影響を及ぼすことはないため,高調波成分を定量化する必要はない。交流送電システム
では更に高調波成分が少ない。
電界及び磁界の高調波成分を無視できない可能性がある場合には,JIS C 1910によって,電界及び磁界
の高調波成分を推定する既存の手法を用いることが望ましい。高調波の周波数を考慮に入れた電界及び磁
界は,適用する規格(例えば[5])が定めた手順に従って評価することが望ましい。
4.4
測定結果の記録
測定報告書には,次の情報を記録することが望ましい。
− 測定を行った日付,時刻及び天候(例えば晴れ,雨,雪,風況など)
− 温度及び湿度(電界測定の場合)
− 入手できる場合には,電力システムの種類(架空送配電線,ケーブル,変電所など)及び公称電圧,
並びに電界及び磁界を発生する架空導体及び/又は地中ケーブルの配列及び相順
− 入手できる場合には,測定器に関する情報[測定器製造業者,形式,プローブの寸法及び形状,種類
(浮遊電位形電界測定器,接地式電界測定器,フラックスゲート式磁界測定器,コイルプローブ又は
ホール効果プローブ),強度範囲,通過帯域幅及び最終校正日]
− 測定における不確かさの推定
注記1 測定における不確かさは,例えばJIS C 1910が規定している手順によって推定することが
できる。
− 測定を実施した人及び機関の名称
− 測定を実施した点の地表からの高さ又は床面からの高さ
− 対象となる電力システムと測定位置との関係
− 測定を建築物内で行った場合には,室内における測定位置
− 測定した電界又は磁界の強さ
− どの電界及び磁界量を報告しているかの明示。例えば電界及び磁界の合成値,電界及び磁界の直交す
る3軸の各成分の実効値,電界及び磁界だ円の半長径又は半短径の実効値など
4
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 測定位置近くにある他の電界及び磁界の発生源の種類,位置及び運転条件
− 測定位置及び他の電界及び磁界の発生源を含む測定区域の図及び/又は写真
− 電界測定の場合,固定した物体及び移動可能な物体の種類,材質,寸法及び位置
− 磁界測定の場合,磁性体又は非磁性の導体から成る固定した物体及び移動可能な物体の種類,材質,
寸法及び位置
− 必要に応じ,磁界測定時の電流値
注記2 こうした負荷電流値を得るのが困難な場合もあり得る。また低電圧の配電システムの場合
には,零相電流の方がより意味のあるパラメータである可能性もある。
注記3 負荷電流の変動を調査する一つの可能な方法として,別の磁界測定器を固定位置に設置す
ることが考えられる([6]参照)。
− 顕著な場合には,高調波成分
測定結果を計算値及び/又は他の測定結果と比較する場合に,上記の情報が重要となる。
測定報告書の例を,附属書Dに示す。
4.5
測定時の留意点
4.5.1
電界及び磁界の向き
4.5.1.1
電界
電界測定器には,単軸及び3軸があるが,3軸を用いるのが望ましい。
導体表面近くの電界は,表面と直交する。したがって,特に架空送配電線から生じる電界の場合,地表
面の近くでは,水平成分を無視することができる。そのため地表近くでは単軸測定(垂直成分)で十分で
ある。架空送配電線下の地表からの高さ1.0 mの地点で計算した電界の強さの例をA.3.3に示す。これら
の例から,地表面からの高さ1.0 mにおける垂直成分は,合成値とほぼ同じであることが分かる(図A.9
及び図A.10を参照)。
導電性の物体が存在している場合(4.5.2.1参照),又は地表面と架空送配電線との間隔が小さい場合には,
特に注意を払わなければならない。
4.5.1.2
磁界
磁界の測定は,3軸の測定器を用いて合成磁界を求めることが望ましいが,単軸測定器を使用する特別
の理由がある場合はその限りではない(単軸測定器を使用する理由とは,磁界の方向及び磁界だ円の半長
径の実効値を知りたい場合,磁界だ円の方向と形状を調べたい場合及び直線磁界の方向が既知である場合
である。ただし,これらの場合の測定手順はこの規格では取り扱わない。)。適切な3軸測定器が入手でき
ない場合,測定を行った時間中に磁界の強さが変化していなければ,単軸測定器を用いて式(1)又は式(2)
によって合成磁界を算出してもよい。この場合,非導電性材料でできた固定具を利用して,プローブを直
交する3方向に向けることで,測定時間を短縮できる。
注記 3軸測定器は,三つの成分を順番に測定することが多く,磁界が変化している場合には,この
点に留意することが望ましい。
一般に,送電線下の磁界だ円の半短径の実効値は,半長径の実効値に比べてかなり小さい。このような
場合には,単軸測定器を使用してもよい(B.3.3参照)。
4.5.2
測定位置
4.5.2.1
電界
ある位置においてひずみのない1) 電界を測定するためには,周辺に他の電力線,鉄塔,樹木,フェンス,
背の高い草木又はその他の物体ができる限り存在しないことが望ましい。測定位置は比較的平たん(坦)
5
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
であることが望ましい。電界の強さは植物に大きく影響される点に留意することが望ましい。一般に,個々
の植物の上方では電界が強まり,植物の側面近くでは電界は減衰する。電界がどれほど乱れるかは,植物
の水分含有量によって大きく左右される。
可能であれば,移動可能な物体は全て取り除くことが望ましい。それができない場合には,プローブと
その物体との距離を,物体の高さの3倍以上(固定していない物体)又は1.0 m以上(固定した物体)に
することが望ましい[6]。
これらの推奨を実現することができない場合には,その旨を測定報告書に明示することが望ましい。
注1) ここでは,“空間的に乱れがない”ことを意味しており,“高調波によって波形がひずんでいる”
こととは異なる。
4.5.2.2
磁界
ひずみのない磁界の値を測定するには,磁性材料又は非磁性導体を含んでいる固定していない物体を,
測定位置からその物体の最大寸法の3倍以上の距離に離しておくことが望ましい。ひずみのない磁界を正
確に測定するためには,プローブと固定した磁性物体との距離は1.0 m以上とするのがよい[7]。
これらの推奨を実現することができない場合には,その旨を測定報告書に明示することが望ましい。
4.5.3
電界測定における測定者によるひずみの影響
測定する電界のひずみを低減するため,電界測定器と測定者との距離を1.5 m以上,できれば3 m確保
するのがよい[6]。これは,非導電性の支持物に取り付けたプローブとモニターとを光ファイバーケーブル
で接続することによって実現できる。
4.5.4
磁界測定における他の発生源の影響
電力システム以外の磁界発生源が,測定地点近くに存在している場合,測定結果に及ぼす影響を最小化
するため,可能であればそうした磁界発生源の電源を切るか又は移動することが望ましい。これが困難な
場合,これらの磁界発生源に関する必要な情報,例えば磁界発生源の種類,測定地点に対する相対位置な
どを測定報告書に記録することが望ましい。
4.5.5
電界測定における湿度条件
相対湿度が70 %を上回る場合,プローブ及び支持物への結露によって,正しく電界が測定できなくなる
可能性がある[6]。湿度による影響は電界測定器によって異なるため,そうした条件下で電界測定器が正し
く作動するかどうかを測定前に確認しておくことが望ましい。
5
電界及び磁界の基本的測定手順
5.1
一般的手順
ここでは1点測定,3点測定及び5点測定のそれぞれの測定手順を定める。
架空送配電線下で電界及び磁界の強さを測定する場合,地表近くの電界及び磁界は均一と考えられる(そ
の根拠についてはB.3.2.1参照)。したがって,その場合は1点測定で十分である。地中ケーブル,屋内変
電所などの近くでは,電界及び磁界は不均一と考えられ 2) ,3点測定又は5点測定を用いなければならな
い。
注2) 本文では“地中ケーブル,屋内変電所などの近くでは,電界及び磁界は不均一と考えられ”と
あるが,地中ケーブルについては,その構造及び地下に埋設されていることから,事実上地上
に電界を作り出すことはない。
5.2
1点測定
電界又は磁界が均一と考えられる場合,対象地点における電界又は磁界の強さは,地表又は建築物内の
6
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
床面から1.0 mの高さで測定することが望ましい。この測定によって得られた電界又は磁界の強さを“平
均ばく露レベル”とする(附属書A及び附属書Bを参照)。
必要があれば1.0 m以外の高さで測定してもよいが,その場合には実際の測定した高さを測定報告書に
明示することが望ましい。
5.3
3点測定
電界又は磁界が不均一と考えられる場合,対象地点における電界又は磁界の強さは,地表面又は建築物
内の床面から0.5 m,1.0 m及び1.5 mの高さの3点で測定することが望ましい。電力設備の近傍又は建築
物内では,電力設備の表面,境界又は壁面から水平に0.2 m離れた位置で測定することが望ましい。この
測定によって得られた電界又は磁界の強さの“3点平均ばく露レベル”を“平均ばく露レベル”とする(附
属書C参照)。
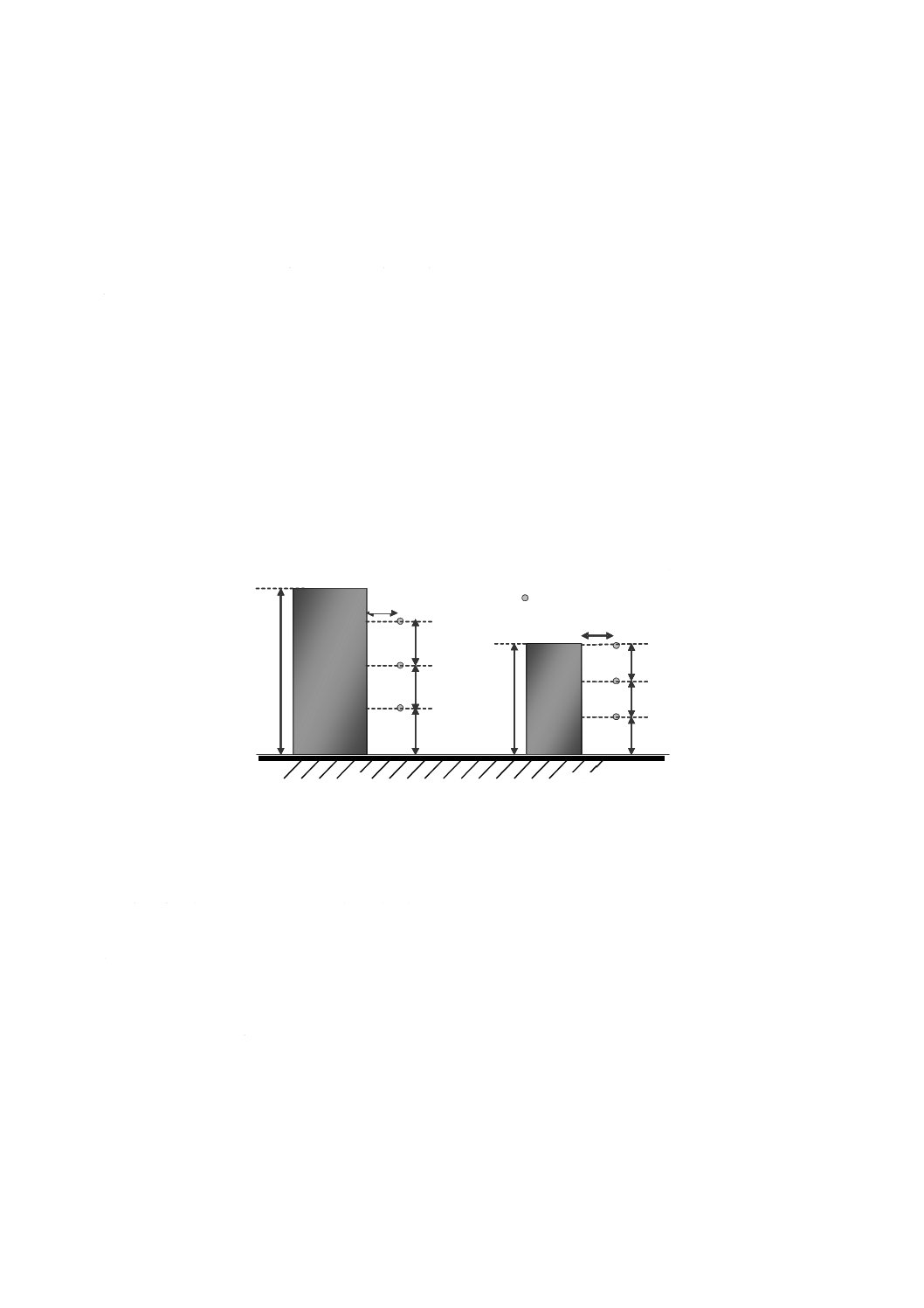
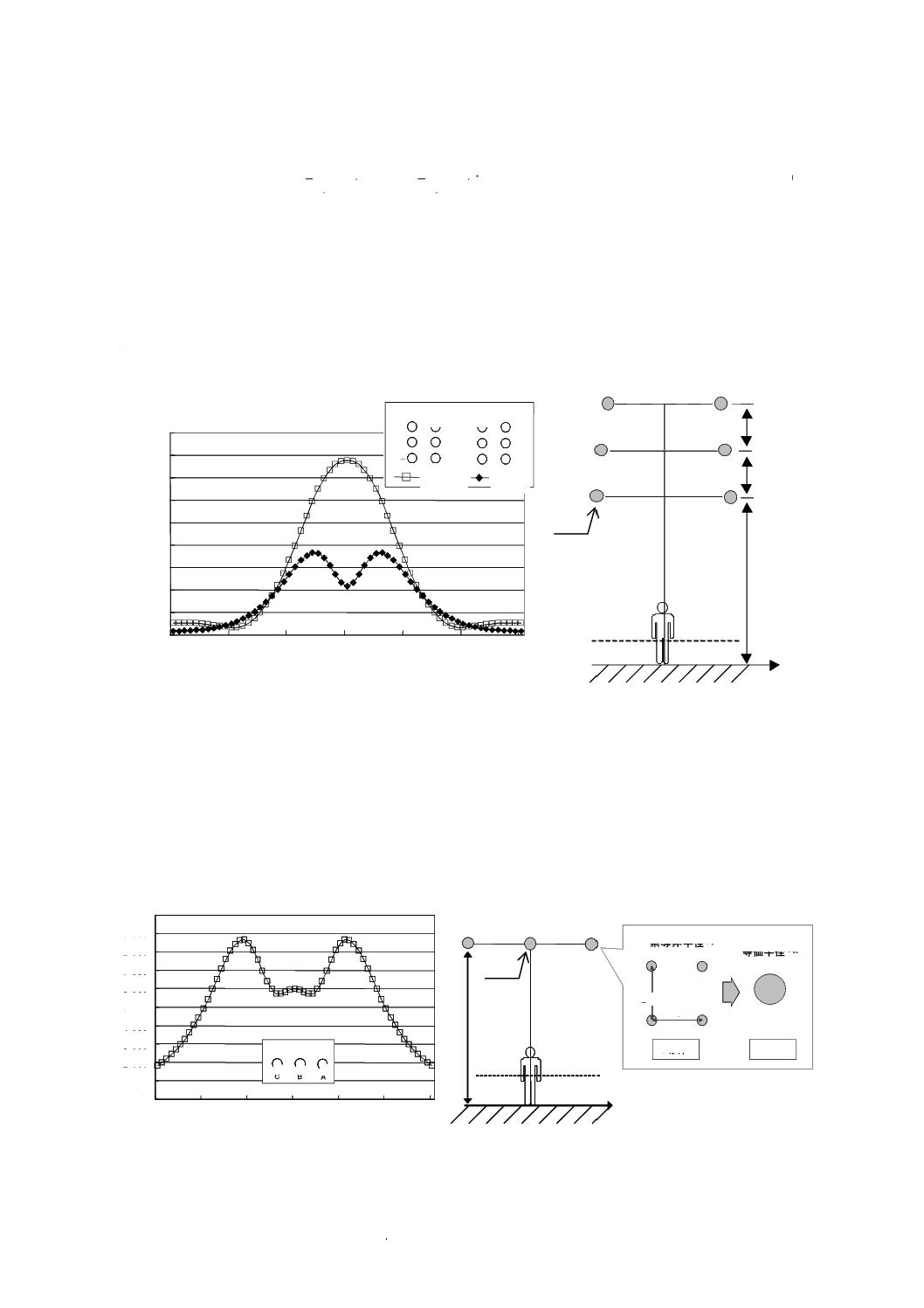
設備の高さが1.5 m未満の場合,3点測定は設備の最上部の高さと同じ高さを最も高い位置とする等間
隔の三つの高さで行わなければならない(図1参照)。
必要があれば0.5 m,1.0 m及び1.5 m以外の高さで測定してもよいが,その場合には実際の測定した高
さを測定報告書に明示することが望ましい。
注記 適用する規格が空間平均を認めていない場合(例えば[2]の場合),3点の測定値の中で最大の値
を用いることが望ましい。
単位 m
図1−3点測定の高さ
5.4
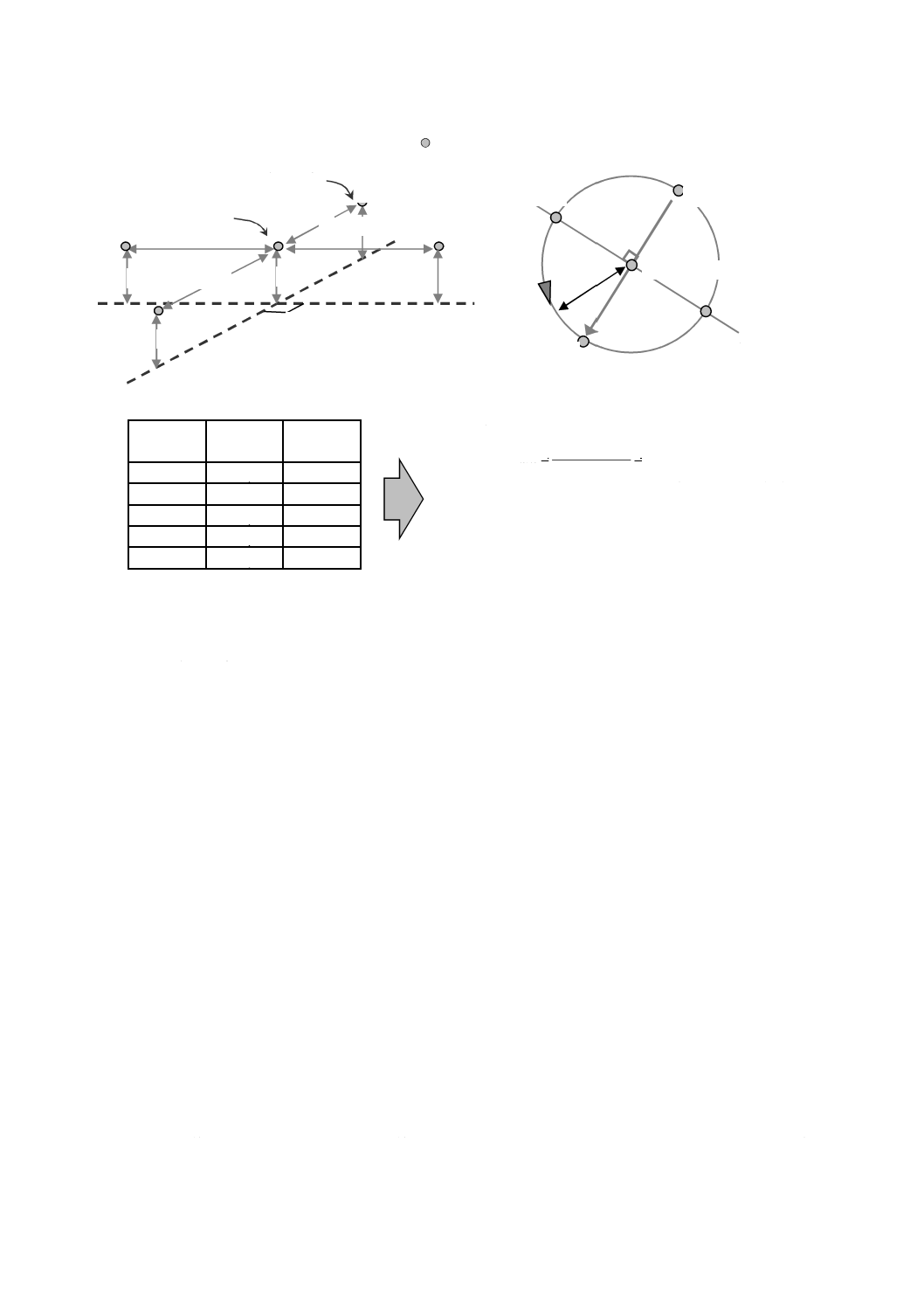
5点測定
電界及び磁界発生源が地下又は床下にあり,人がその上方に横たわる可能性が高い場合には,次のとお
り5点測定を行うことが望ましい(図2参照)。
a) 最大磁界の値及び位置を検出するために,地表面又は床面から0.2 mの高さで磁界の強さを走査する。
b) 2番目に大きい磁界の値及び位置を,最大磁界の位置を中心とする半径0.5 mの円周上で探す。
c) この2番目に大きい値の位置及び円周上で対称になる位置においても測定を行う。
d) ここまでに測定した3点を結ぶ直線と,最大磁界の位置で直交する直線とが,円周と交わる点2か所
で,それぞれ測定を行う。
ここまで測定した5点の測定値のうち,大きい方から三つ目までの値の平均値を算出する。この平均値
を“平均ばく露レベル”とする。
注記 実際には,動かすことのできない家具,部屋の壁などがある場合には,それらを考慮してこの
手順を適用する必要がある。
人が地表又は床の上に横たわる可能性が低い場合には,5.3の3点測定を行う。
0.2
0.2
0.5
0.5
0.5
H
H
H/3
H/3
H/3
H
H
H/3
H/3
H/3
測定点
H< 1.5
1.5
≧
7
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
破線は地表面又は床面を表す。
測定点
測定値
(例)
採用する
点
平均ばく露レベルの計算例
(
)
6
3
5
P
2
P
1P
average
=
+
+
=
B
ここに,Baverage
:平均ばく露レベル(μT)
P1,P2,P5 :それぞれ測定点P1,P2,
P5の測定値
P1
10 µT
○
P2
5 µT
○
P3
1 µT
−
P4
2 µT
−
P5
3 µT
○
図2−5点測定
6
電界への最大ばく露レベルを探すための測定手順
6.1
架空送配電線
架空送配電線下の電界の強さは,導体からの距離,導体間隔及び相順を含む多くの要因,並びに線路電
圧によって変化する(附属書A参照)。
最大電界の強さは,径間において,導体が地表に最も近くなる地点の導体下に見られる。したがって,
電界の強さが最大となる位置を見つけるために,まず架空送配電線に平行な直線を想定し,その直線上で
可能であれば適当な間隔を置きながら,地表面から1.0 mの高さで電界の強さを測定することが望ましい
(線路方向の分布)。次に,別のピークがあるかどうかを確認するため,線路方向の分布が最大になる位置
で架空送配電線に直交する直線を想定し,その直線に沿って地表面から1.0 mの位置で測定を行うことが
望ましい(断面方向の分布)。
対象区域内において電界の強さが最大となる位置が既に分かっている場合には,その位置で1点測定を
行うことが望ましい。
導体が対象区域外の上空を通過している場合であっても,最大ばく露レベルを見つけるプロセスは同様
で,その導体と平行な線路方向の分布を測定することが望ましい。
[6],[7] などの幾つかの文献は,架空送配電線周囲における電界の強さの分布を得るための詳細な手順
を示している。
6.2
地中ケーブル
地中ケーブルが地上に電界を作り出すことはなく,したがって電界測定は不要である。
6.3
変電所及びその他の電力システム機器
架空送配電線(6.1参照)及び架空送配電線が接続される変電所を除き,電力システム機器は一般公衆が
立入り可能な区域に電界を発生することはなく,したがって電界測定は不要である。
0.5 m
0.5 m
0.5 m
0.5 m
0.2 m
0.2 m
0.2 m
P1
P3
P4
0.2 m
最大点
90 °
2番目に大きい点
P2
P5
測定点(P1〜P5)
直交線上の点(P4)
2番目に大きい点(P2)
(円周上の最大点)
最大点(P1)
直交線上の点(P5)
P2の対称点(P3)
0.5 m
円周
8
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
架空送配電線が接続される変電所については,対象区域内で電界の強さが最大である地点を検出するた
めに,変電所周囲において適当な間隔を置きながら,地表面から1.0 mの高さ,かつ,変電所から水平に
0.2 m離れた位置で,電界の強さを測定することが望ましい。
最大電界の強さを検出した位置において,3点測定を行うことが望ましい(5.3参照)。
対象区域内において電界の強さが最大となる位置が既に分かっている場合には,その位置で3点測定を
行うことが望ましい。
変電所の場合,最大電界は通常,架空送配電線が変電所に到達した位置の線下に生じる。このような架
空送配電線下での電界測定は,6.1に示した手順に従って行うことが望ましい。
7
磁界への最大ばく露レベルを探すための測定手順
7.1
架空電力線
架空送配電線下の磁界の強さは,導体からの距離,導体間隔及び相順を含む多くの要因並びに線路の電
流によって変化する(附属書B参照)。
最大磁界の強さは,径間において,導体が地表に最も近くなる地点の導体下に見られる。したがって,
磁界の強さが最大となる位置を見つけるためには,まず架空送配電線に平行な直線を想定し,その直線上
で,可能であれば適当な間隔を置きながら,地表面から1.0 mの高さで磁界の強さを測定することが望ま
しい(線路方向の分布)。次に,別のピークがあるかどうかを確認するため,線路方向の分布が最大になる
位置で架空送配電路に直交する直線を想定し,その直線に沿って地表面から1.0 mの位置で測定を行うこ
とが望ましい(断面方向の分布)。
架空送配電線下の磁界は,均一と考えられる(5.1参照)。
対象区域内において磁界の強さが最大となる位置が既に分かっている場合には,その位置で1点測定を
行うことが望ましい。
導体が対象区域外の上空を通過している場合であっても,最大ばく露レベルを見つけるプロセスは同様
で,その導体と平行な線路方向の分布を測定することが望ましい。
[6],[7] などの幾つかの文献は,架空送配電線周囲における磁界の強さの分布を得るための詳細な手順
を示している。
7.2
地中ケーブル
地中ケーブルに直交する直線を想定し,その直線に沿って適当な間隔を置きながら地表面から1.0 mの
高さで磁界の強さを測定することが望ましい(断面方向の分布)。最大磁界の強さを検出した位置において,
3点測定を行うことが望ましい(5.3参照)。
磁界は,地中ケーブルに沿っておおむね一定であるが,ケーブル処理空間,マンホールなどの特殊な場
所又は埋設深さが変化している場合はその限りではない。ケーブル経路に沿って高さ1.0 mで測定を行い,
最大磁界の強さを求めることによってこのような場所を検出することができる(線路方向の分布)。最大磁
界の強さを検出した位置において,上記(断面方向の分布)と同じ手順で測定を行うことが望ましい。
特に詳細な調査を必要とする対象区域がある場合 3) には,上記(線路方向及び断面方向の分布)と同一
の手順による測定を繰り返してもよい。
対象区域内において磁界の強さが最大となる位置が既に分かっている場合には,その位置で3点測定を
行うことが望ましい。
注3) 例えば,地中ケーブルの埋設状況が不明確な場合。
9
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3
変電所及びその他の電力システム機器
電力システム機器又は変電所の周囲において,機器表面又は変電所境界から水平に0.2 m離れた位置で,
適当な間隔を置きながら地表面から1.0 mの高さで磁界の強さを測定することが望ましい。機器の高さが
1.5 m未満である場合には,1.0 mの代わりに,機器の最上部の高さで磁界の強さの測定を行うことが望ま
しい。最大磁界の強さを検出した位置において,3点測定を行うことが望ましい(5.3参照)。
対象区域内において磁界の強さが最大となる位置が既に分かっている場合には,その位置で3点測定を
行うことが望ましい。
変電所の場合,最大磁界は通常,架空送配電線又は地中ケーブルが変電所に到達した位置の線下又は地
中ケーブル上に生じる。このような位置での磁界測定は,7.1及び7.2にそれぞれ示した手順に従って行う
ことが望ましい。
機器表面又は変電所境界により近付いたところでは,局所的により高い磁界の強さが検出される場合が
ある。しかし,このような磁界の強さは,通常の状況における一般公衆の平均ばく露レベルを代表する値
とは考えられない。
屋内変電所の上方区域が利用されており,人がその床に横たわる可能性が高い場合,5点測定を行うこ
とが望ましい(5.4参照)。
人が床に横たわる可能性が低い場合には,3点測定を行うことが望ましい。
10
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
交流架空送配電線から発生する電界の特性
A.1 一般的事項
一般に,考慮する必要がある電界を発生するのは高電圧の架空送電線だけである。低電圧の架空配電線
若しくは配電設備の近く,又は変電所の周囲における電界の強さは低い。地中ケーブルはシールドされて
いるため,外部に電界を発生させることはない。
この附属書は,架空送電線から発生する電界の空間分布の計算例を示す。
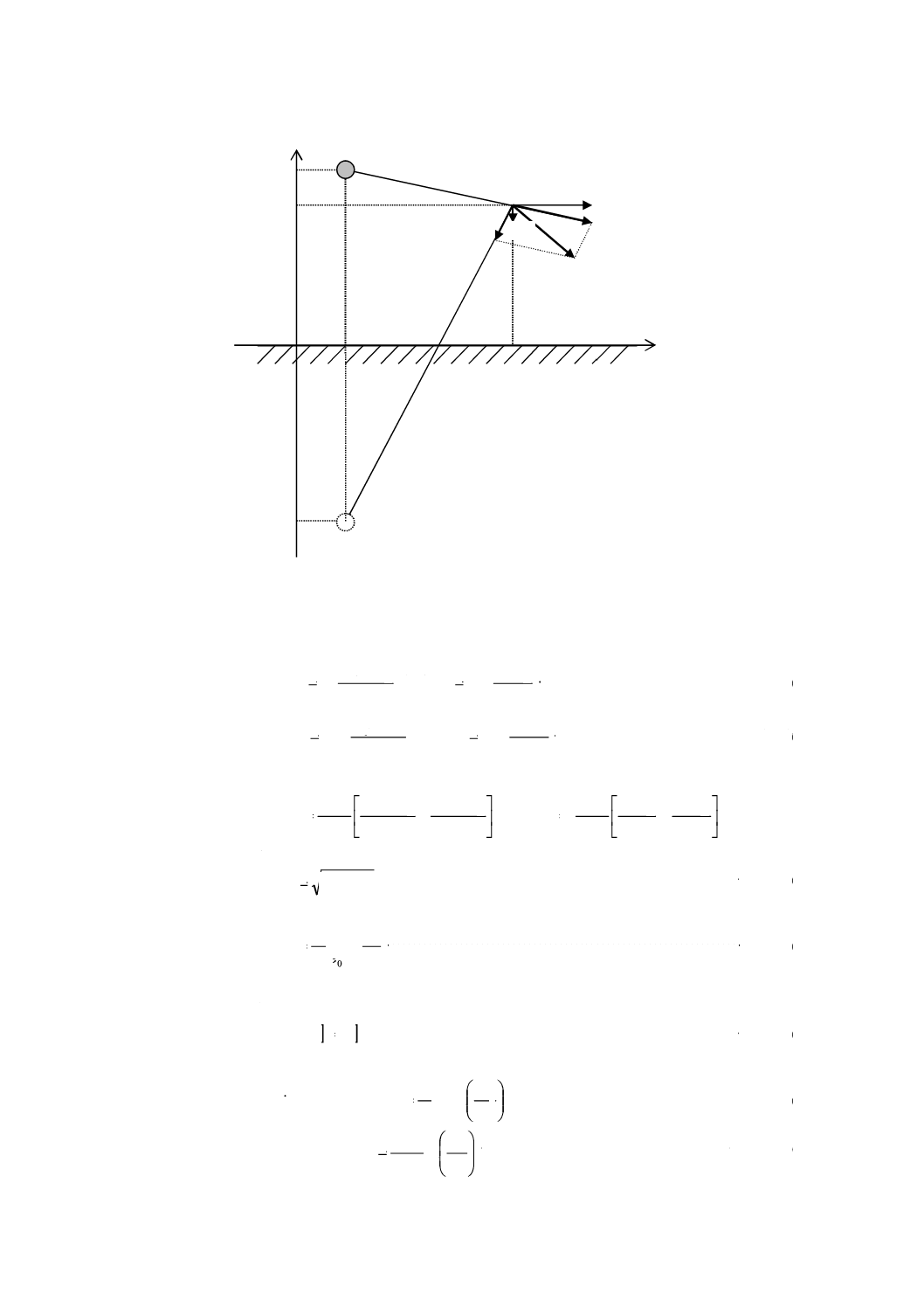
A.2 電界の強さの一般的な計算手順
線電荷密度がλで地表面に平行な直線導体から距離rにおける電界強度Eは,式(A.1)によって表す。
r
E
1
2
0ε
λ
π
=
··········································································· (A.1)
ここに,
ε0: 真空の誘電率。8.854×10-12 F/mに等しい。
大地の導電性を考慮すると,図A.1に示すとおり,高さ−hにおける鏡像線電荷密度−λの直線導体を用
いて,任意の点PにおけるEを式(A.2)によって計算することができる。
1
0
1
1
2
R
E
ε
λ
π
=
及び
2
0
2
1
2
R
E
ε
λ
π
=
················································· (A.2)
ここに,
E1: λの直線導体によって点Pに生じる電界強度
E2: −λの直線導体によって点Pに生じる電界強度
R1: λの直線導体から点Pまでの距離。式(A.3)による。
R2: −λの直線導体から点Pまでの距離。式(A.3)による。
2
p
2
p
c
1
)
(
)
(
Y
h
X
X
R
−
+
−
=
及び
2
p
2
p
c
2
)
(
)
(
Y
h
X
X
R
+
+
−
=
············ (A.3)
ここに,
Yp: 点Pの高さ
Xc: λ及び−λの直線導体のX座標
Xp: 点PのX座標
11
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
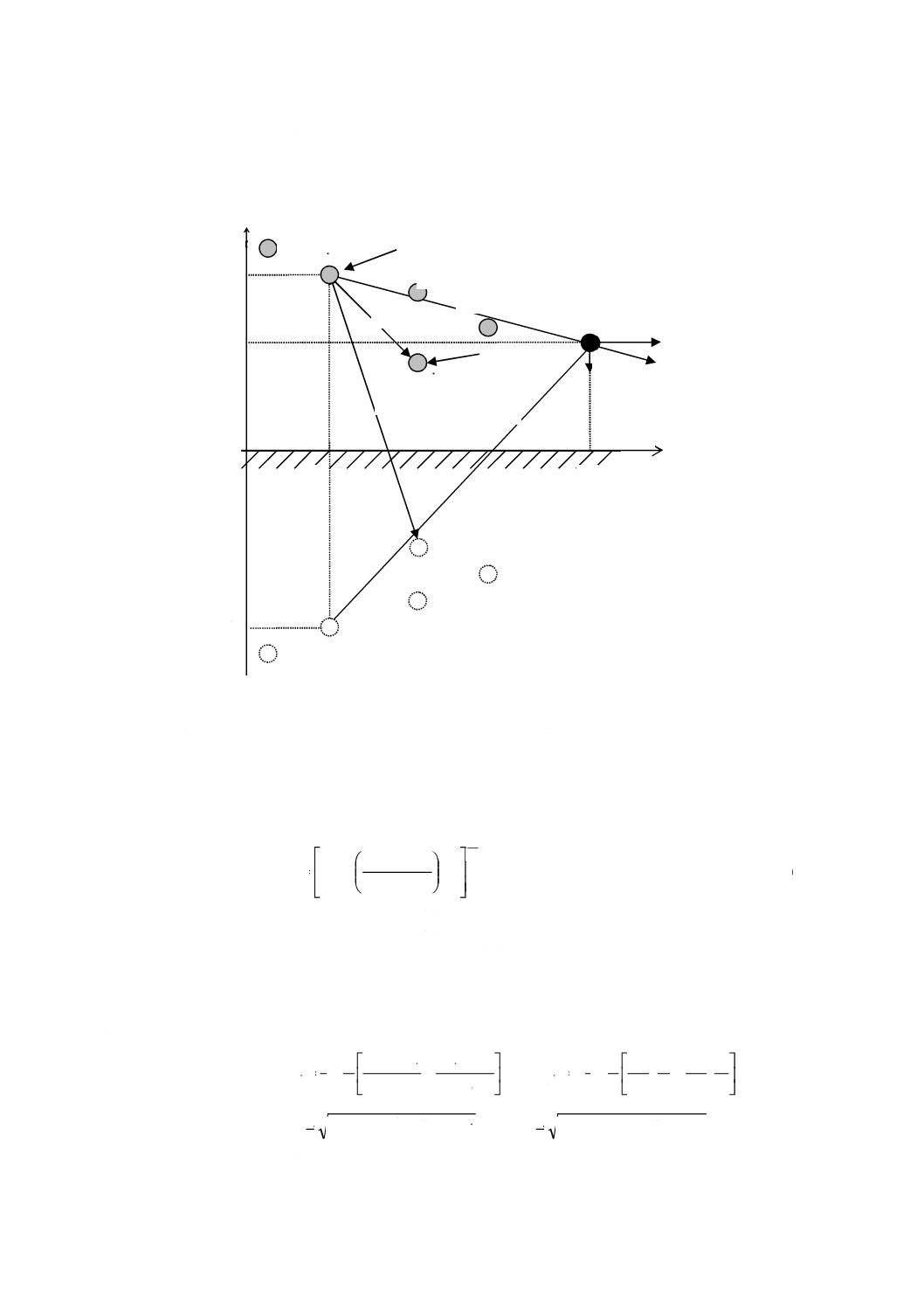
図A.1−線電荷による電界
電界ベクトルE1及びE2は,直交成分E1x及びE1y,並びにE2x及びE2yに分解でき,式(A.4)及び式(A.5)
で表される。
1
c
p
1
1
R
X
X
E
Ex
−
=
及び
1
p
1
1
R
Y
h
E
Ey
−
−
=
·········································· (A.4)
2
c
p
2
2
R
X
X
E
Ex
−
−
=
及び
2
p
2
2
R
Y
h
E
Ey
+
−
=
······································· (A.5)
したがって,電界ベクトルEの直交成分Ex及びEyは式(A.6)となる。
−
−
−
π
=
2
2
c
p
2
1
c
p
0
2
R
X
X
R
X
X
Ex
ε
λ
及び
+
+
−
π
−
=
2
2
p
2
1
p
0
2
R
Y
h
R
Y
h
Ey
ε
λ
······ (A.6)
点Pにおける電界強度Eは式(A.7)で表される。
2
2
y
x
E
E
E
+
=
········································································ (A.7)
導体表面の電位Vは式(A.8)となる。
a
h
V
2
ln
2
0ε
λ
π
=
······································································· (A.8)
ここに,
a: 導体の半径
図A.2に示すように複数の導体がある場合,式(A.8)は行列になる。
[][][]
V
P
=
λ
··········································································· (A.9)
行列[P]は,電位係数行列であり,式(A.10)及び式(A.11)で表される。
i = 1〜nのとき
π
=
i
i
0
ii
2
ln
2
1
r
h
P
ε
··············································(A.10)
i ≠ jのとき
π
=
ij
ij
0
ij
ln
2
1
d
D
P
ε
···················································· (A.11)
E1x
E1
E
E2
P
−λ
Yp
Xc
Xp
R1
R2
h
E1y
X
O
−h
Y
λ
地表
12
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
n: 導体数
Dij: 導体iと導体jの鏡像との距離
dij: 導体iと導体jとの距離
ri: 導体iの半径
図A.2−地表面を含む一般的な多相導体系
架空送電線下の電界の強さを計算する場合には,図A.2に示す線電荷の分布系を利用することができる。
交流電力線の場合,導体iが各相の導体に対応する。相導体iが素導体の束で構成され,その素導体の数
がnbで,各素導体が正多角形の各頂点に位置している場合,riは式(A.12)によって等価な幾何学的半径rei
に置き換えることができる(図A.4参照)。
(
)
b
b
1
1
b
0
b
ei
sin
2
n
n
n
S
r
n
r
π
=
−
···················································(A.12)
ここに,
nb: 素導体の数
r0: 素導体の半径
S: 隣接する素導体間の距離
線電荷密度λiは線形連立方程式(A.9)で求めることができる。
導体iが発生する電界ベクトルの点Pにおける成分Exi及びEyiは,式(A.14)を用いて,式(A.13)で表され
る。
−
−
−
π
=
2
i2
p
ci
2
i1
ci
p
0
i
xi
2
R
X
X
R
X
X
E
ε
λ
及び
+
+
−
π
−
=
2
i2
p
i
2
i1
p
i
0
i
yi
2
R
Y
h
R
Y
h
E
ε
λ
··(A.13)
2
p
i
2
p
ci
i1
)
(
)
(
Y
h
X
X
R
−
+
−
=
及び
2
p
i
2
p
ci
i2
)
(
)
(
Y
h
X
X
R
+
+
−
=
········(A.14)
ここに,
Xci: λi及び−λiの直線導体のX座標
2
j
i
n
相導体
dij
Dij
半径, rj
Xci
Xp
R1i
R2i
鏡像導体
Ei
Exi
Eyi
X
P
地表
1
半径, ri
Y
O
hi
−hi
Yp
13
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
架空送電線全体では,点Pにおける各成分の総和は式(A.15)となる。
∑
=
=
n
i
E
E
1
xi
x
及び
∑
=
=
n
i
E
E
1
yi
y
·····················································(A.15)
A.3 架空送電線が発生する電界の例
A.3.1 電界の空間分布
図A.3は,2回線垂直配列の77 kV架空送電線が発生する電界の強さの空間分布を計算した例である。
各導体の半径は,12.65 mmである。順相及び逆相の両方を考慮している(図A.3参照)。電界の強さは,
地上1.0 mの高さにおいて,送電線の中心からの距離の関数として計算している。
図A.3−架空送電線下における電界の強さの空間分布(77 kV,2回線垂直配列)
図A.4は,1回線水平配列の500 kV架空送電線が発生する電界の強さの空間分布を計算した例である。
各導体の半径は14.25 mmである。電界の強さは,地上1.0 mの高さにおいて,送電線の中心からの距離の
関数として計算している。各相は,それぞれ半径14.25 mmの導体4本で構成されており,隣接する導体
の間隔は400 mmである。したがって,式(A.12)によって得られる等価な幾何学的半径189.5 mmを計算に
用いる。
図A.4−導体束をもつ架空送電線下における電界の強さの空間分布(500 kV,1回線水平配列)
3.2 m
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
距離(m)
11.0 m
0
100
200
300
400
500
600
700
800
900
-
-
-
0
A
B
C
A
B
C
Untransposed
A
B
C
C
B
A
transposed
phase sequence
0
100
200
300
400
500
600
700
800
900
-
-
-
0
30
20
10
10
20
30
距離(m)
電界(V/m)
A
B
C
A
B
C
順相
A
B
C
C
B
A
逆相
位相配列
導体
0
1 000
2 000
3 000
4 000
5 000
6 000
7 000
8 000
9 000
10 000
-
-
-
距離(m)
-
-
-
0
30
20
10
10
20
30
10.0 m
10.0 m
地表
距離(m)
11.0 m
1.0 m
14.25 mm
189.5 mm
4導体
素導体半径 ri
等価半径rei
換算
単導体
400 mm
S
S
導体
C
B
A
位相配列
電界(V/m)
14
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
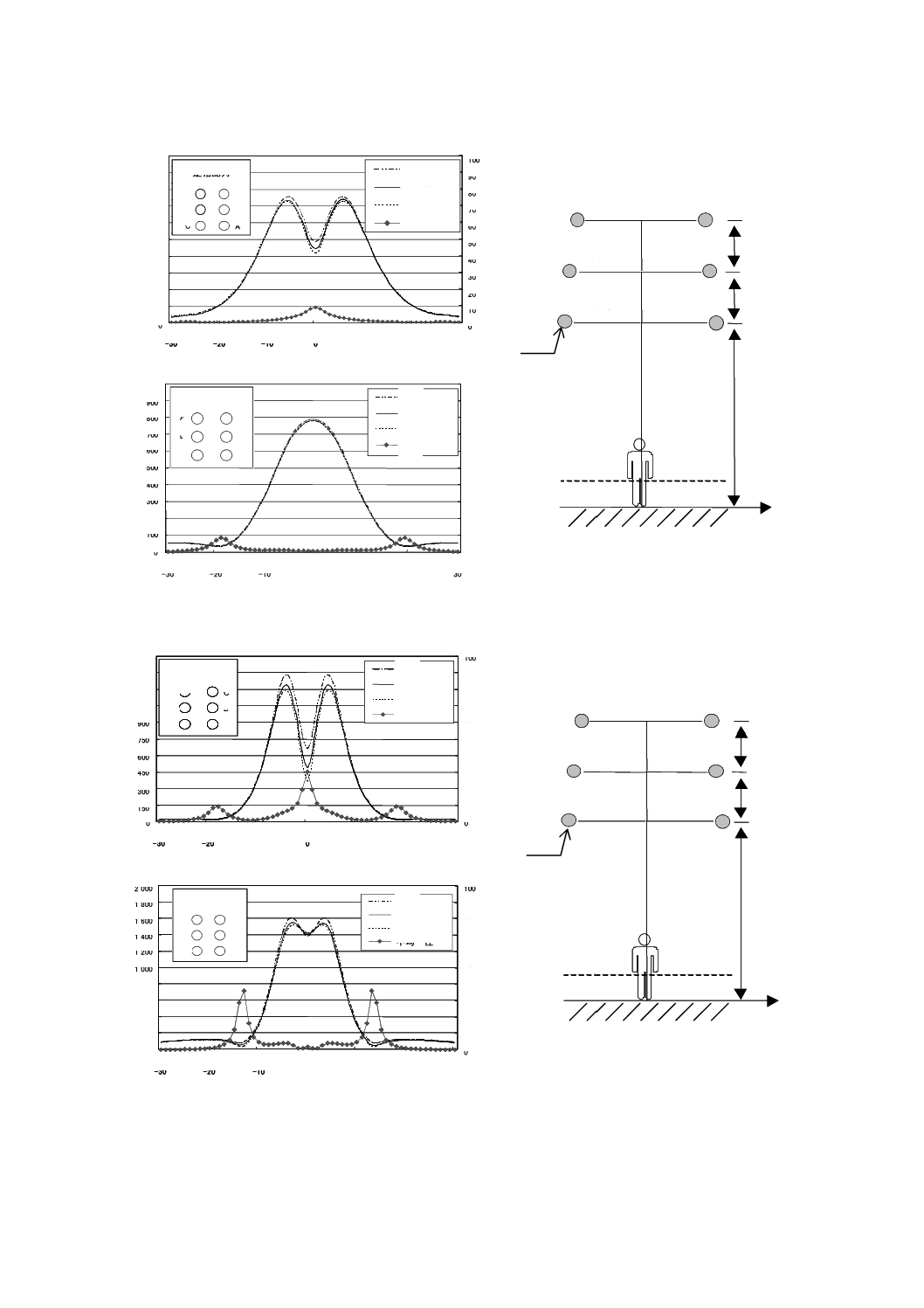
A.3.2 電界に影響を及ぼす要因
A.3.2.1 最低位置の導体と地表との間隔
図A.5は,2回線垂直配列の77 kV架空送電線が発生する電界の強さの空間分布を計算した二つの例で
ある。一方の例では,最低位置にある導体と地表との間隔を11.0 mと想定し,他方の例ではそれを6.0 m
と想定した。順相及び逆相の両方を考慮している。電界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さ
において,送電線の中心からの距離の関数として計算している。各導体の半径は12.65 mmである。
図A.5は,不均一性の計算結果も示しており,不均一性は式(A.16)の最大値として定義している。
100
avg
avg×
−
=
E
E
E
N
h
································································(A.16)
ここに,
N: 不均一性(%)
Eh: 地上0.5 m,1.0 m及び1.5 mの高さにおける電界の強さ
Eavg: 三つの高さにおける電界の強さの算術平均値
この方法は,電界の不均一性を評価し定義する近似的な方法と考えることができる。
図A.6は,1回線水平配列の500 kV架空送電線が発生する電界の強さの空間分布を計算した二つの例で
ある。図A.6には不均一性の計算結果も示した。一方の例では,最低位置にある導体と地表との間隔を11.0
mと想定し,他方の例ではそれを6.0 mと想定した。電界の強さは,地上0.5 m,1.0 m及び1.5 mの高さ
において,送電線の中心からの距離の関数として計算している。各相は,それぞれ半径14.25 mmの導体4
本で構成されており,隣接する導体の間隔は400 mmである。したがって,式(A.12)によって得られる等価
な幾何学的半径189.5 mmを計算に用いる。
15
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 最低位置にある導体と地表との間隔が11.0 mの場合
b) 最低位置にある導体と地表との間隔が6.0 mの場合
図A.5−架空送電線下における電界の強さ及び不均一性の空間分布−導体の高さの影響
(77 kV,2回線垂直配列)
0
50
100
150
200
250
300
350
400
450
500
- 30
- 20
- 10
0
10
20
30
0
10
20
30
40
50
60
70
80
90
100
不均一性[%]
- 30
- 20
- 10
0
10
20
30
電界(V/m)
0 - 30
- 20
- 10
0
10
20
30
距離(m)
0
10
20
30
40
50
60
70
80
90
100
Non
-
1,5 m
1,0 m
0,5 m
Non-
A
B
C
A
B
C
100
200
300
400
500
700
800
1000
0
600
900
- 30
- 20
- 10
0
10
20
30
0
10
20
30
40
50
60
70
80
90
100
1.5 m
1.0 m
0.5 m
不均一性
untransposed
A
B
A
B
A
B
C
A
B
C
順相配列
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
距離(m)
11.0 m
3.2 m
距離(m)
不均一性[%]
電界(V/m)
導体
C
A
A
B
C
B
逆相配列
C
A
1,5 m
1,0 m
0,5 m
1.5 m
1.0 m
0.5 m
不均一性
3.2 m
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
距離(m)
6.0 m
- 30
- 20
-10
0
10
20
30
0
10
20
30
40
50
60
70
80
90
100
不均一性[%]
1,5 m
1,0 m
0,5 m
750
900
1 050
1 200
1 350
1 500
0
150
300
450
600
- 30
- 20
-10
0
10
20
30
1.5 m
1.0 m
0.5 m
A
B
C
B
transposed phase
sequence
A
B
C
C
B
A
逆相配列
0
200
400
1 000
1 400
1 800
2 000
- 30
- 20
- 10
0
10
20
30
0
10
20
30
40
50
60
70
80
90
100
1,5 m
1,0 m
0,5 m
A
B
A
B
untransposed
600
800
1 200
1 600
- 30
- 20
- 10
0
10
20
30
1.5 m
1.0 m
0.5 m
不均一性
A
B
C
A
B
C
順相配列
不均一性
距離(m)
電界(V/m)
不均一性[%]
電界(V/m)
導体
距離(m)
16
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 最低位置にある導体と地表との間隔が11.0 mの場合
b) 最低位置にある導体と地表との間隔が6.0 mの場合
図A.6−架空送電線下における電界の強さ及び不均一性の空間分布−導体の高さの影響
(500 kV,1回線水平配列)
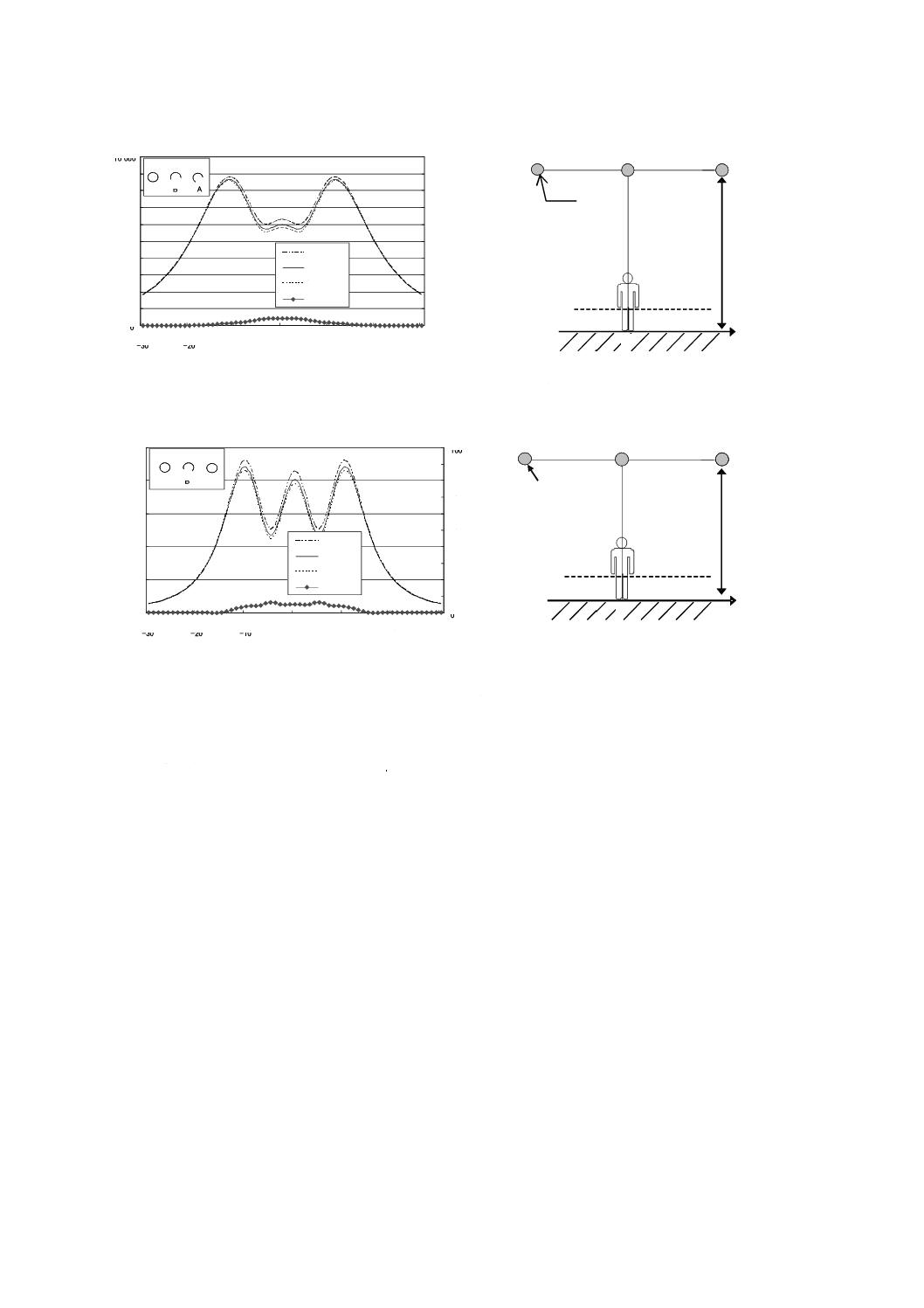
A.3.2.2 各導体間の距離
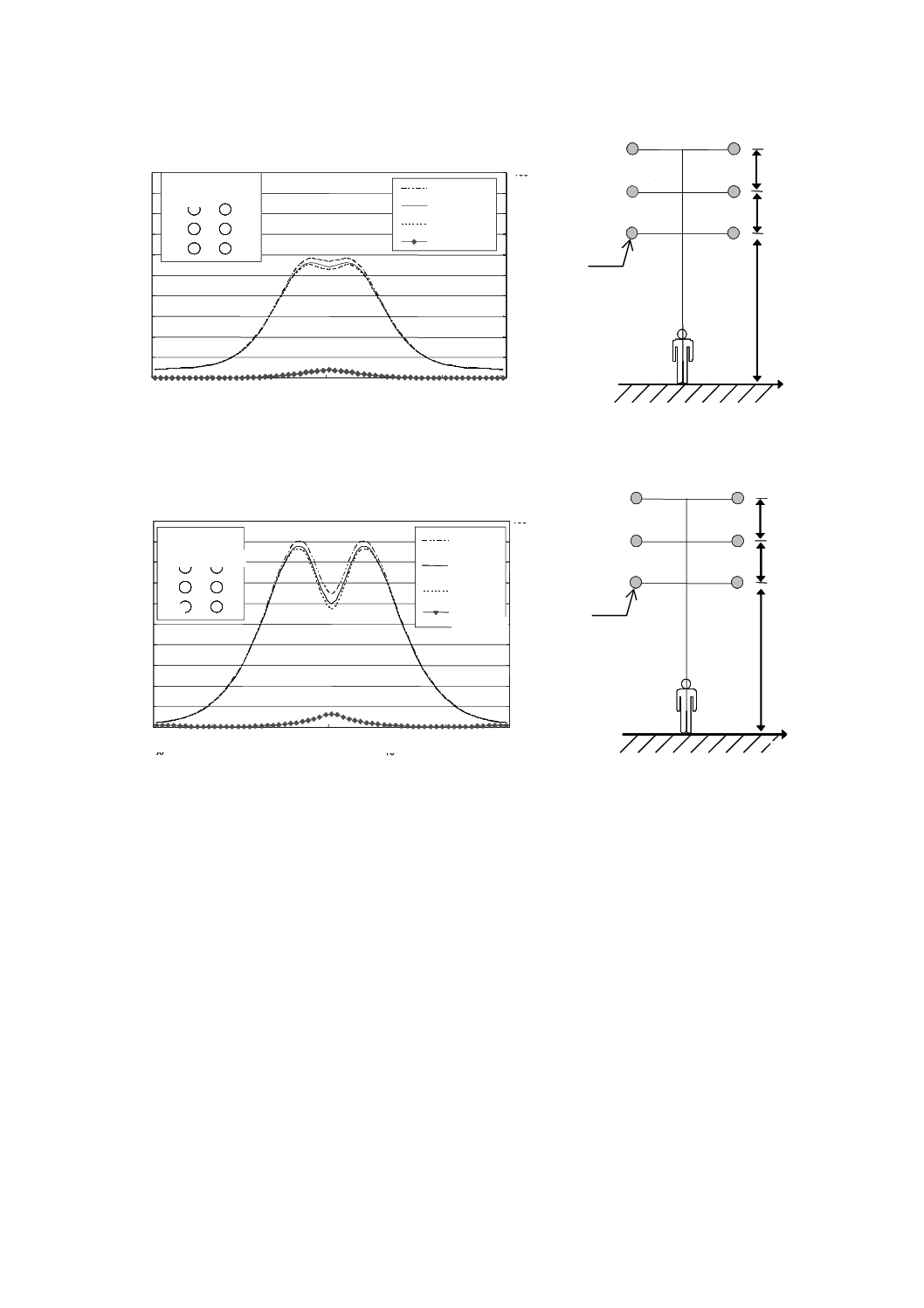
図A.7は,2回線垂直配列の77 kV架空送電線が発生する電界の強さの空間分布を計算した二つの例で
ある。図A.7には,不均一性の計算結果も示した。二つの架空送電線はいずれも同じ電圧であると想定し,
一方は導体間の距離が短く,他方はそれが長い。相配列は逆相であり,各導体の半径は12.65 mmである。
電界の強さは,地上1.0 mの高さにおいて送電線の中心からの距離の関数として計算している。
0
1 000
2 000
3 000
4 000
5 000
6 000
7 000
8 000
9 000
10 000
0
-30
-20
-10
10
20
30
距離(m)
電
界
0
10
20
30
40
50
60
70
80
90
100
不均一性[%]
1.5m
1.0m
0.5m
不均一性
C
B
A
位相配列
10.0m
10.0m
地表
距離(m)
11.0m
1.0m
0
導体
距離(m)
0
5000
10000
15000
20000
25000
0
-30
-20
-10
10
20
30
電界(V/m)
0
10
20
30
40
50
60
70
80
90
100
1,5m
1,0m
0,5m
不均一性
C
B
A
位相配列
不均一性[%]
導体
10.0m
10.0m
地表
距離(m)
6.0m
0
1.0m
17
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 導体間の距離が短い場合
b) 導体間の距離が長い場合
図A.7−77 kV架空送電線下における電界の強さの空間分布−導体間の距離の影響
(77 kV,2回線垂直配列)
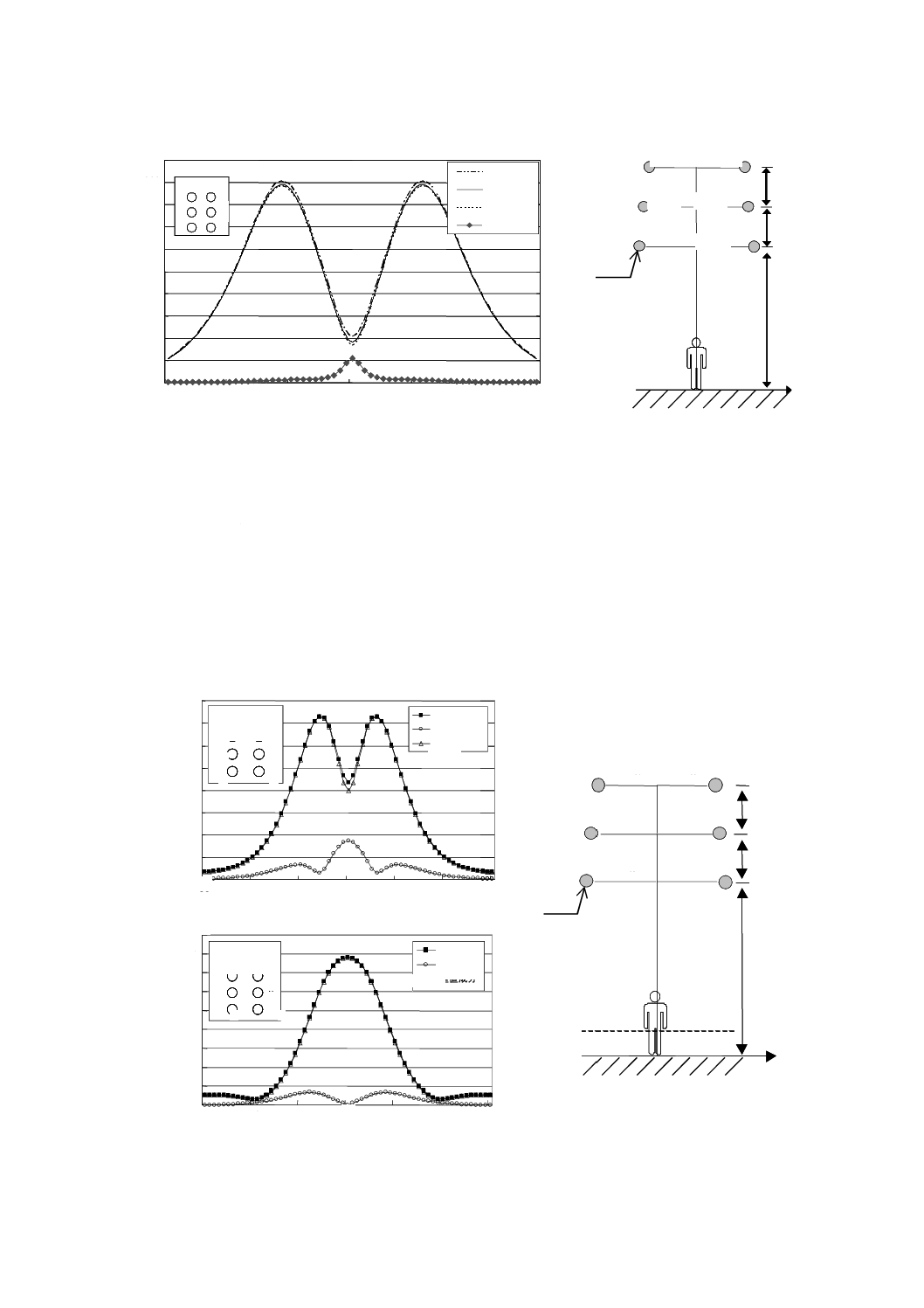
図A.8は,2回線垂直配列の500 kV架空送電線が発生する電界の強さの空間分布を計算した例である。
図A.8には不均一性の計算結果も示した。相配列は逆相である。電界の強さは,地上1.0 mの高さにおい
て,送電線の中心からの距離の関数として計算している。各相は,半径14.25 mmの導体4本で構成され
ており,隣接する導体の間隔は400 mmである。したがって,式(A.12)によって得られる等価な幾何学的半
径189.5 mmを計算に用いる。
0
50
100
150
200
250
300
350
400
450
500
-
-
-
0
電界(V/m)
0
10
20
30
40
50
60
70
80
90
100
不均一性[%]
A
B
C
B
transposed phase
sequence
-
-
-
0
30
20
10
10
20
30
1,5 m
1,0 m
0,5 m
1.5 m
1.0 m
0.5 m
不均一性
A
B
C
C
B
A
逆相配列
2.0 m 2.0 m
3.0 m
3.0 m
地表
11.0 m
2.0 m
2.0 m
2.0 m
2.0 m
距離(m)
導体
距離(m)
5.0 m
5.0 m
地表
距離(m)
11.0 m
3.5 m
3.5 m
3.8 m
3.8 m
0
50
100
150
200
250
300
350
400
450
500
-
-
-
0
30
0
10
20
30
40
50
60
70
80
90
100
Non
-
0,5 m
-uniformity
A
B
C
C
B
A
untransposed
phase sequence
0
50
100
150
200
250
300
350
400
450
500
-30
-20
-10
0
10
20
30
0
10
20
30
40
50
60
70
80
90
100
1.5 m
1.0 m
0.5 m
不均一性
A
B
C
C
B
A
逆相配列
不均一性[%]
距離(m)
導体
電界(V/m)
3.2 m
3.2 m
18
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.8−架空送電線下における電界の強さ及び不均一性の空間分布−導体間の距離の影響
(500 kV,2回線垂直配列)
A.3.3 垂直成分及び水平成分
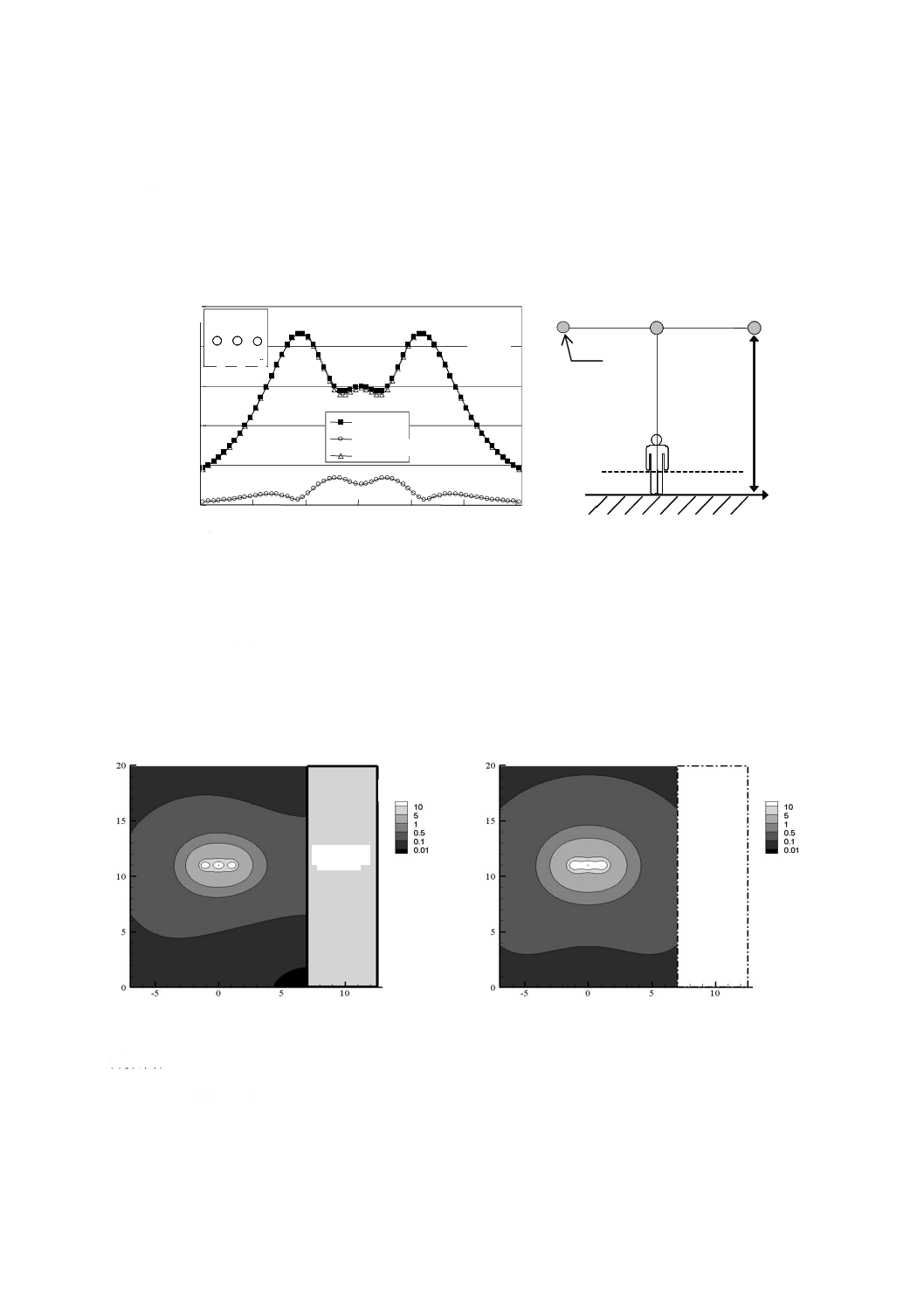
図A.9は,2回線垂直配列の77 kV架空送電線が発生する電界の強さの垂直成分及び水平成分の空間分
布を計算した例である。各導体の半径は12.65 mmである。順相及び逆相の両方の相配列を考慮している。
電界の強さは,地上1.0 mの高さにおいて,送電線の中心からの距離の関数として計算している。最低位
置にある導体と地表との間隔は11.0 mである。
図A.9−77 kV架空送電線下における電界の強さの垂直成分及び水平成分
0
1 000
2 000
3 000
4 000
5 000
6 000
7 000
8 000
9 000
10 000
-
-
-
0
0
10
20
30
40
50
60
70
80
90
100
不均一性 [%]
-30
-20
-10
0
10
20
30
10.25 m10.25 m
10.50 m 10.50 m
11.00 m 11.00 m
13.50 m
13.50 m
地表
11.00 m
導体
A
B
C
B
A
B
C
B
逆相配列
C
A
1,5 m
1,0 m
0,5 m
1.5 m
1.0 m
0.5 m
不均一性
電界(V/m)
距離(m)
距離(m)
0
50
100
150
200
250
300
350
400
-30
-20
-10
0
10
20
30
vertical
A
B
C
C
B
A
transposed
phase sequence
0
50
100
150
200
250
300
350
-30
-20
-10
0
10
20
30
resultant
horizontal
合成
水平成分
垂直成分
A
B
C
C
B
A
逆相配列
0
100
200
300
400
500
600
700
800
900
-
-
-
0
vertical
C
C
0
100
200
300
400
500
600
700
800
900
-
-
-
0
30
20
10
10
20
30
resultant
horizontal
合成
水平成分
垂直成分
A
B
A
B
untransposed
phase sequence
A
B
C
A
B
C
順相配列
3.2 m
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
距離(m)
11.0 m
電界(V/m)
距離(m)
距離(m)
導体
電界(V/m)
400
19
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.10は,1回線水平配列の500 kV架空送電線が発生する電界の強さの垂直成分及び水平成分の空間
分布を計算した例である。電界の強さは,地上1.0 mの高さにおいて,送電線の中心からの距離の関数と
して計算している。最低位置にある導体と地表との間隔は11.0 mである。各相は,半径14.25 mmの導体
4本で構成されており,隣接する導体の間隔は400 mmである。したがって,式(A.12)によって得られる等
価な幾何学的半径189.5 mmを計算に用いる。
図A.10−500 kV架空送電線下における電界の強さの垂直成分及び水平成分
A.3.4 近接効果
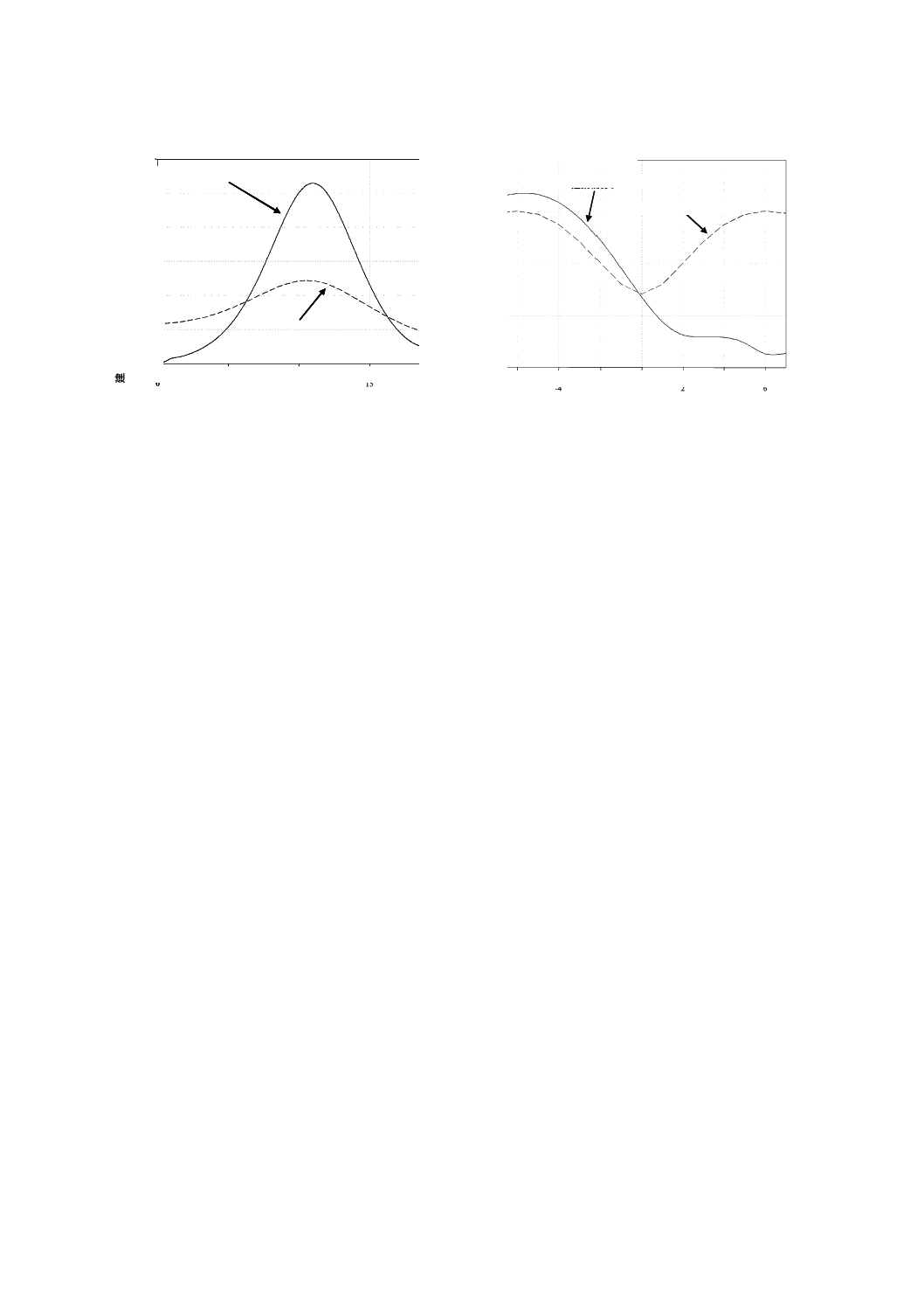
図A.11は,高い建築物に近接した25 kV架空送電線が発生する電界を計算し,等高線図に示した例であ
る。建築物の壁面における最大電界は,その導体と同じ高さで発生している。地表では,電界は建築物に
よって低下している(図A.12参照)。
a) 建築物あり
b) 建築物なし
計算条件
導体の高さ
11.0 m
導体の間隔
1.12 m
建築物の高さ
20.0 m
架空送電線の中心から建築物までの距離
7.0 m
図A.11−25 kV架空送電線の電界等高線
0
2000
4000
6000
8000
10000
-
-
-
0
vertical
C
B
A
phase
0
2 000
4 000
6 000
8 000
10 000
-
-
-
0
20
30
10
10
20
30
resultant
horizontal
合成
水平成分
垂直成分
C
B
A
位相配列
10.0 m
10.0 m
地表
距離(m)
11.0 m
1.0 m
距離(m)
導体
電界(V/m)
Building
Building
location
建築物あり
建築物なし
送電線中心からの距離(m)
送電線中心からの距離(m)
高さ(m)
高さ(m)
電界(kV/m)
電界(kV/m)
地表
地表
20
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.12−建築物の壁面位置に沿った電界分布,及び地上1 mの高さにおける電界分布
地表からの高さ(m)
0
5
10
15
20
0.00
0.05
0.10
0.15
0.20
0.25
0.30
建築物あり
建築物なし
0
5
-6
-4
-2
0
2
4
6
Electric Field at 1m from the ground (kV/m)
0,00
0,02
0,04
0,06
0,08
With the effect of the building
Without the effect of the building
-6
-4
-2
0
2
4
6
0.00
0.02
0.04
0.06
0.08
建築物あり
建築物なし
地
表
面
か
ら
1
m
の
高
さ
に
お
け
る
電
界
分
布
(k
V
/
m
)
送電線中心からの距離(m)
建
築
物
の
壁
面
位
置
に
沿
っ
た
電
界
分
布
(k
V
/
m
)
21
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
交流電力システムが発生する磁界の特性
B.1
一般的事項
磁界が均一であれば,磁界への平均ばく露レベルは1点測定で求めることができる。しかし磁界が不均
一な場合,平均ばく露レベルを推定するには適切な測定方法が必要である。このためには,電力システム
周辺の磁界の空間分布を理解しなければならない。
磁界の空間分布は,発生源の種類によって,例えば架空送電線,地中ケーブル,配電設備又は変電所の
いずれであるかによって異なる。また各系統の回線配列によっても異なる。
この附属書では,磁界の強さの一般的な計算手順,及び多様な電力システムが発生する磁界の空間分布
を計算した例を示す。
B.2
磁界の強さの一般的な計算手順
B.2.1 合成磁界
合成磁束密度Brは,式(B.1)で示す磁界ベクトルB及びBの内積の,周期Tにわたる平均値の平方根と
して定義することができ,式(B.2)で表す。
(
)
(
)
(
)k
j
i
k
j
i
B
γ
ω
β
ω
α
ω
+
+
+
+
+
=
+
+
=
t
B
t
B
t
B
t
B
t
B
t
B
sin
2
sin
2
sin
2
)(
)(
)(
z
y
x
z
y
x
·············· (B.1)
ここに, i,j,k: 直交3方向の単位ベクトル
(
)
(
)
(
)
[
]
∫
∫
∫
π
π
−
π
π
−
−
+
+
+
+
+
π
=
π
=
=
ω
ω
ω
ω
γ
ω
β
ω
α
ω
ω
ω
t
t
B
t
B
t
B
t
t
T
B
T
T
d
sin
2
sin
2
sin
2
2
d
2
d
1
2
2
z
2
2
y
2
2
x
2
2
2
2
r
B
B
· (B.2)
ここで式(B.3)の関係を用いると,式(B.2)を式(B.4)のように大幅に簡素化することができる。
(
)
(
)
{
}
ω
α
ω
α
ω
ω
ω
ω
ω
π
=
+
−
=
+
∫
∫
π
π
−
π
π
−
t
t
t
t
d
2
cos
1
2
1
d
sin2
····························· (B.3)
2
z
2
y
2
x
r
B
B
B
B
+
+
=
······························································· (B.4)
このBrを単純に合成磁界と呼ぶ。これは,各軸成分間の位相差によって影響されることはなく,磁界の
各軸成分の実効値だけで決定される。
人体の磁界ばく露を評価する場合には,Brを用いることが望ましい。
B.2.2 単一周波数の交流磁界における最大及び最小の実効値
磁界ベクトルBの絶対値|B|が最大又は最小になる条件は,次のようになる。
0
d
d
=
t
B
·············································································· (B.5)
|B|は式(B.6)によって表すことができる。

22
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
(
)
(
)
γ
ω
β
ω
α
ω
+
+
+
+
+
=
=
t
B
t
B
t
B
2
2
z
2
2
y
2
2
x
sin
2
sin
2
sin
2
B
B
B
············· (B.6)
式(B.6)において式(B.5)を満足する条件は式(B.7)となる。
2ωt+δ=π又は2ωt+δ=0························································· (B.7)
ここで,δは式(B.8)で与えられる。
γ
β
α
γ
β
α
δ
2
cos
2
cos
2
cos
2
sin
2
sin
2
sin
tan
2
z
2
y
2
x
2
z
2
y
2
x
1
B
B
B
B
B
B
+
+
+
+
=
−
··································· (B.8)
式(B.7)を式(B.6)に代入すると,式(B.6)の|B|は式(B.9)で表される。よって,|B|の最小の実効値Bmin,及び
|B|の最大の実効値Bmaxは,それぞれ式(B.10)及び式(B.11)で求めることができる。
(
)
(
)
(
)
(
)
{
}
δ
γ
δ
β
δ
α
−
+
−
+
−
±
+
+
=
2
cos
2
cos
2
cos
2
z
2
y
2
x
2
z
2
y
2
x
B
B
B
B
B
B
B
············· (B.9)
(
)
(
)
(
)
(
)
{
}
δ
γ
δ
β
δ
α
−
+
−
+
−
+
+
+
=
=
2
cos
2
cos
2
cos
2
1
Max
2
1
2
z
2
y
2
x
2
z
2
y
2
x
max
B
B
B
B
B
B
B
B
······ (B.10)
(
)
(
)
(
)
(
)
{
}
δ
γ
δ
β
δ
α
−
+
−
+
−
−
+
+
=
=
2
cos
2
cos
2
cos
2
1
Min
2
1
2
z
2
y
2
x
2
z
2
y
2
x
min
B
B
B
B
B
B
B
B
······ (B.11)
磁界の最大の実効値及び最小の実効値であるBmax及びBminは,それぞれだ円磁界の長径及び短径に対応
している。Bmax≦Brの関係は常に成り立ち,直線磁界ではBmax=Brとなる。
さらにBmax,Bmin及びBrの間には,式(B.12)の関係が成り立つ。
2
min
2
max
r
B
B
B
+
=
································································· (B.12)
高調波を含む磁界では,Bmax及びBminを決定することは困難であるため,4.3に規定する方法でBrを測
定する。
B.3
架空送電線が発生する磁界の例
B.3.1 磁界の空間分布
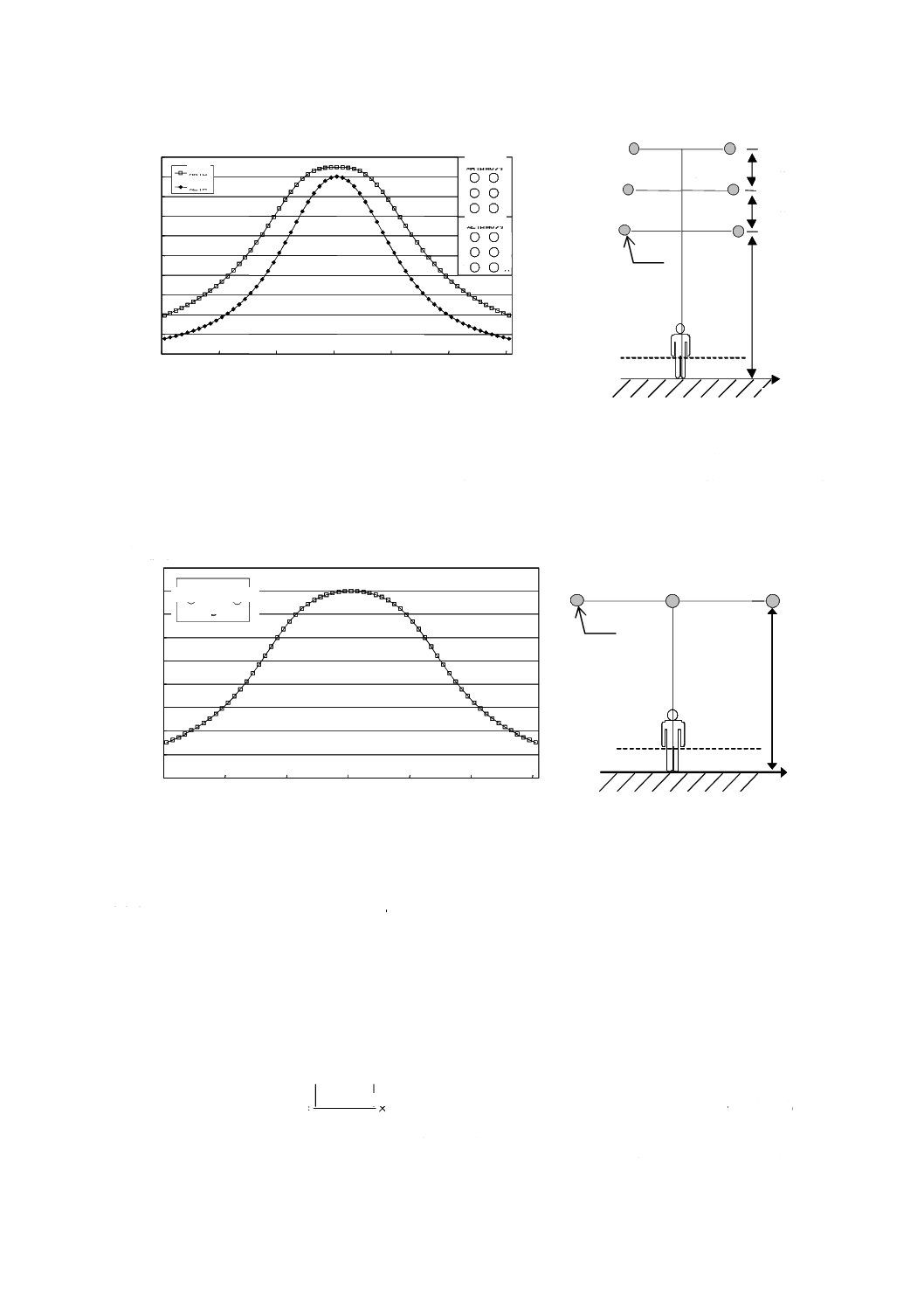
図B.1は,2回線垂直配列の77 kV架空送電線が発生する磁界の強さの空間分布を計算した例である。
順相及び逆相の両方を考慮している。磁界の強さは,地表上1.0 mの高さにおいて,送電線の中心からの
距離の関数として計算している。各回線を流れる電流値は,平衡で200 Aと仮定した。
23
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.1−77 kVの架空送電線下における磁界の強さの空間分布(77 kV,2回線垂直配列)
図B.2は,1回線水平配列の500 kV架空送電線が発生する磁界の強さの空間分布を計算した例である。
磁界の強さは,地表上1.0 mの高さにおいて,送電線の中心からの距離の関数として計算している。回線
を流れる電流値は,平衡で200 Aと仮定した。
図B.2−500 kV架空送電線下における磁界の強さの空間分布(500 kV,1回線水平配列)
B.3.2 磁界に影響を及ぼす要因
B.3.2.1 最低位置の導体と地表との間隔
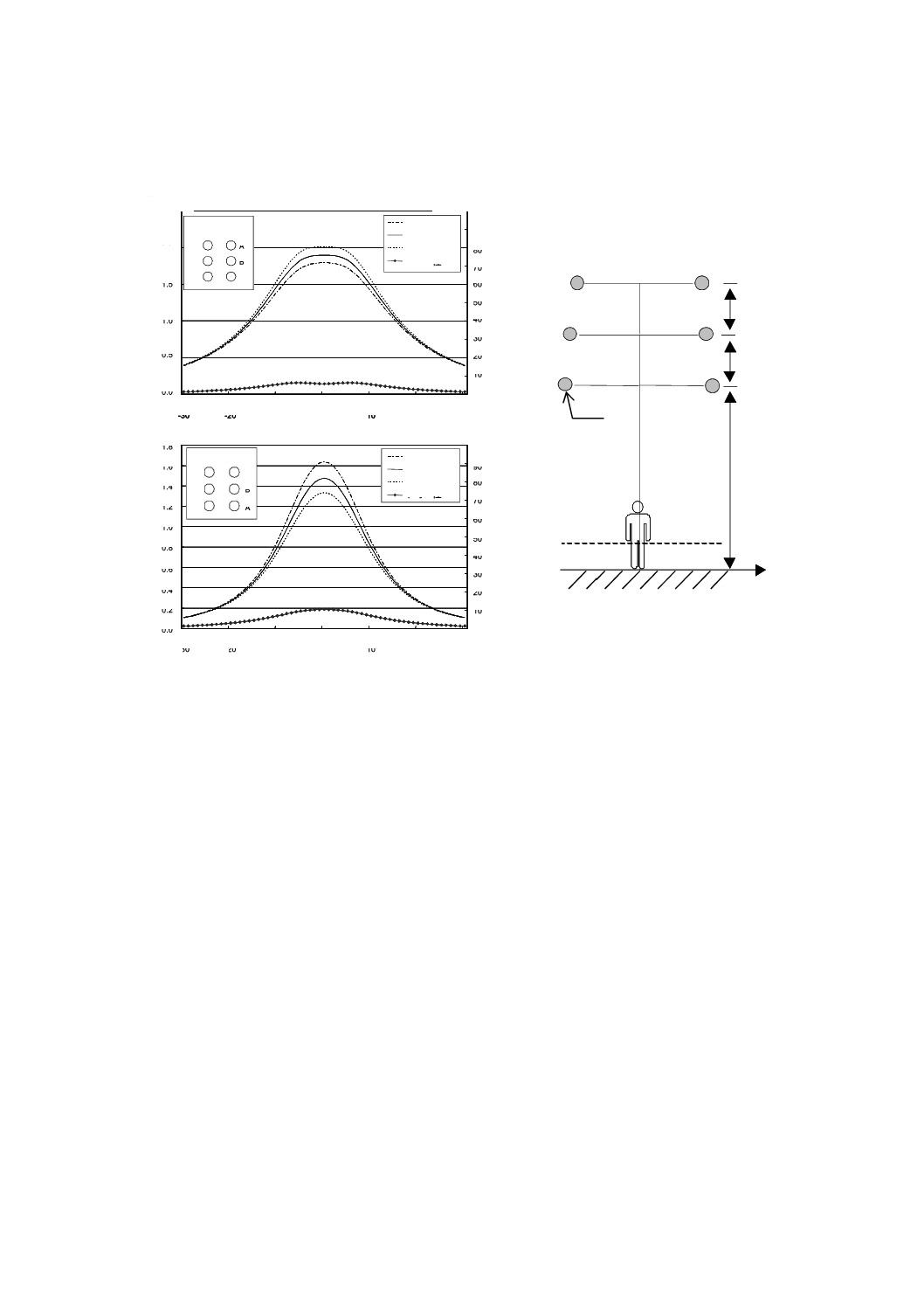
図B.3は,2回線垂直配列の77 kV架空送電線が発生する磁界の強さの空間分布を計算した二つの例で
ある。一方の例では,最低位置にある導体と地表との間隔を11.0 mと想定し,他方の例ではそれを6.0 m
と想定した。順相及び逆相の両方を考慮している。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さ
において,送電線の中心からの距離の関数として計算している。各回線を流れる電流値は,平衡で200 A
と仮定した。
図B.3には,不均一性の計算結果も示しており,不均一性は式(B.13)の最大値として定義している。
100
avg
avg×
−
=
B
B
B
N
h
································································ (B.13)
ここに,
N: 不均一性(%)
Bh: 地表上0.5 m,1.0 m及び1.5 mの高さにおける磁界の強さ
3.2 m
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
11.0 m
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
-
-
-
0
30
20
10
10
20
30
距離(m)
磁界(μT)
-
-
-
0
A
B
A
B
A
B
C
A
B
C
順相配列
順相
逆相
導体
A
B
C
B
A
B
C
B
逆相配列
C
A
距離(m)
10.0 m
10.0 m
地表
距離(m)
11.0 m
1.0 m
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
-
-
-
0
30
20
10
10
20
30
距離(m)
phase sequence
-
-
-
0
位相配列
C
B
A
導体
磁界(μT)
24
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Bavg: 三つの磁界の強さの算術平均値
この方法は,磁界の不均一性を推定し定義する近似的な方法と考えることができる。
a) 最低位置にある導体と地表との間隔が11.0 mの場合
図B.3−架空送電線下における磁界の強さの空間分布−導体高さの影響(77 kV,2回線垂直配列)
3.2 m
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
11.0 m
0.0
0.5
1.0
1.5
-30
-20
-10
0
10
20
30
0
10
20
30
40
50
60
70
80
1,5 m
1,0 m
0,5 m
-
-30
-20
-10
0
10
20
30
距離 (m)
1.5 m
1.0 m
0.5 m
不均一性
A
B
C
A
B
C
順相配列
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
-
-
-
0
30
20
10
10
20
30
距離(m)
0
10
20
30
40
50
60
70
80
90
100
-
-
-
0
1,5 m
1,0 m
0,5 m
1.5 m
1.0 m
0.5 m
不均一性
A
B
C
C
B
A
逆相配列
不均一性(%)
磁界(μT)
導体
不均一性(%)
磁界(μT)
100
2.0
2.5
90
距離 (m)
25
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
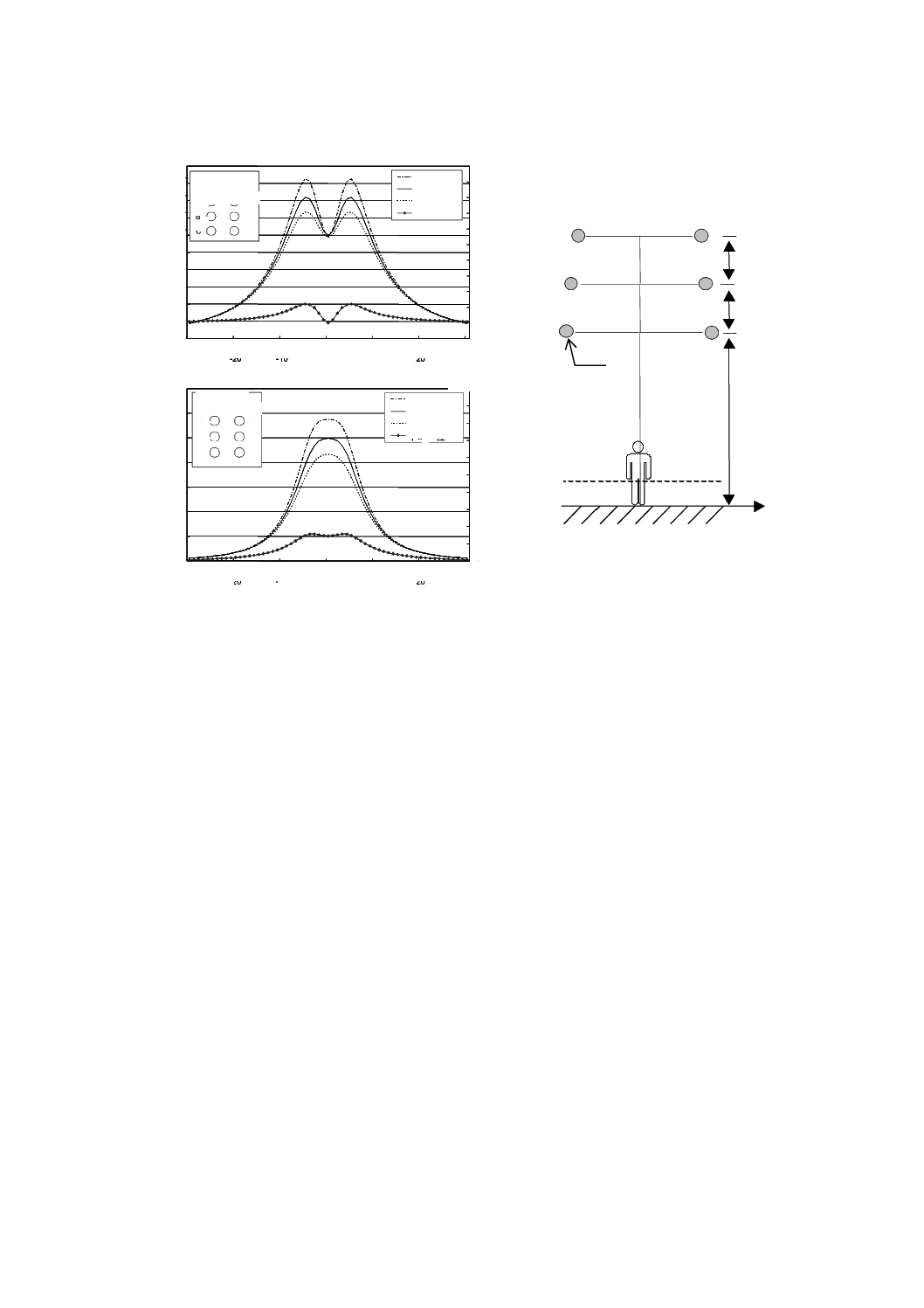
b) 最低位置にある導体と地表との間隔が6.0 mの場合
図B.3−架空送電線下における磁界の強さの空間分布−導体高さの影響(77 kV,2回線垂直配列)(続き)
3.2 m
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
距離(m)
6.0 m
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
-30
-20
- 10
0
10
20
30
距離 (m)
-10
0
10
20
30
40
50
60
70
80
1,5 m
1,0 m
0,5 m
-30
-20
- 10
0
10
20
30
1.5 m
1.0 m
0.5 m
不均一性
A
B
A
B
untransposed
phase sequence
A
B
C
A
B
C
順相配列
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
-
-
-
0
30
20
10
10
20
30
距離(m)
0
10
20
30
40
50
60
70
80
90
100
不均一性(%)
1,5 m
1,0m
0,5 m-
-
-
-
0
1.5 m
1.0m
0.5 m
不均一性
-
A
B
C
B
transposed
phase sequence
A
B
C
C
B
A
逆相配列
磁界(μT)
導体
磁界(μT)
不均一性(%)
90
100
26
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.4は,1回線水平配列の500 kV架空送電線が発生する磁界の強さの空間分布を計算した二つの例で
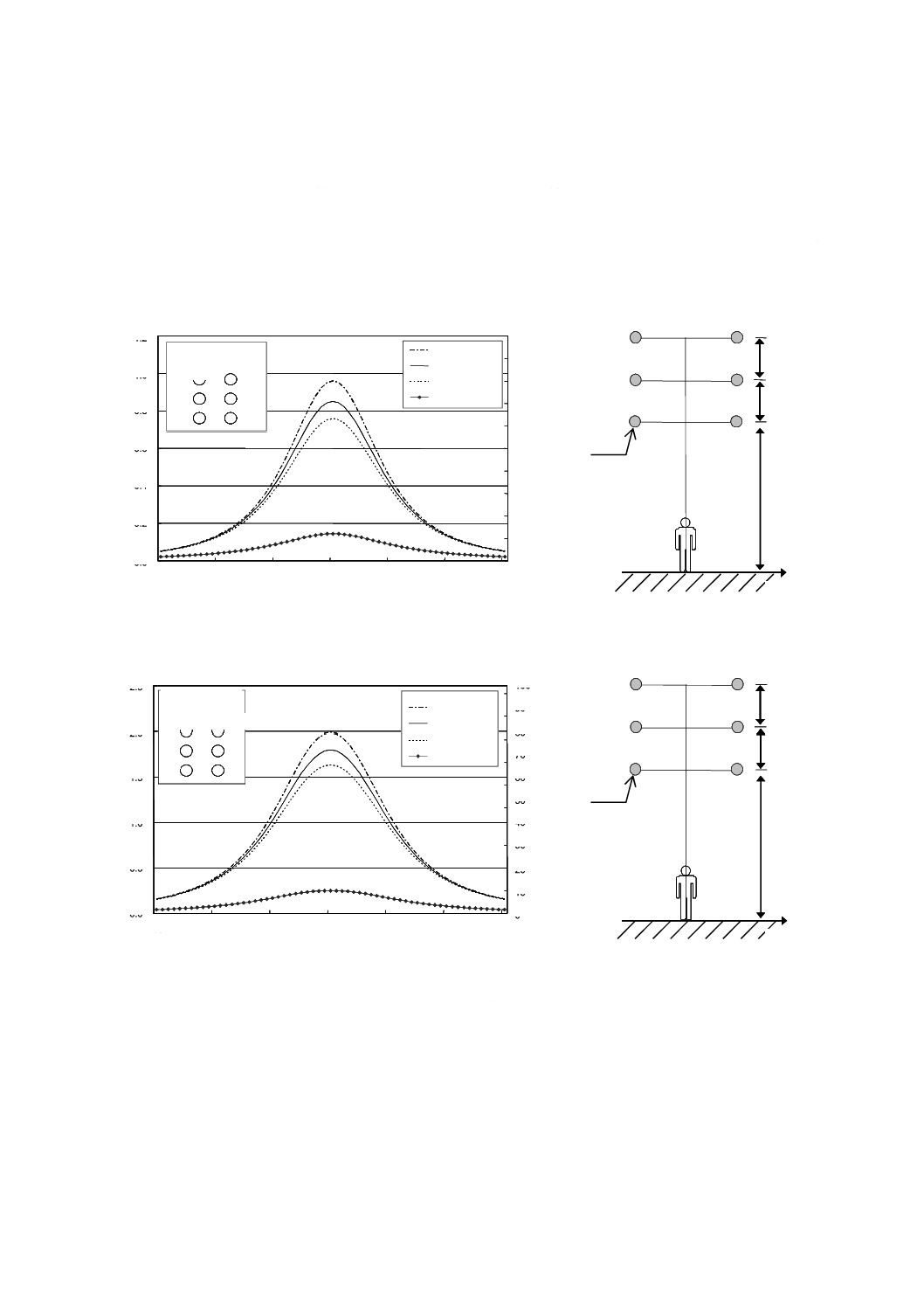
ある。図B.4には不均一性の計算結果も示した。一方の例では,最低位置にある導体と地表との間隔を11.0
mと想定し,他方の例ではそれを6.0 mと想定した。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高
さにおいて,送電線の中心からの距離の関数として計算している。回線を流れる電流値は,平衡で200 A
と仮定した。
a) 最低位置にある導体と地表との間隔が11.0 mの場合
b) 最低位置にある導体と地表との間隔が6.0 mの場合
図B.4−500 kV架空送電線下における磁界の強さ及び不均一性の空間分布−導体高さの影響
(500 kV,1回線水平配列)
10.0 m
10.0 m
地表
距離(m)
11.0 m
1.0 m
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
-
-
-
0
30
20
10
10
20
30
距離(m)
0
10
20
30
40
50
60
70
80
90
100
1,5 m
1,0 m
0,5 m
-
-
-
0
1.5 m
1.0 m
0.5 m
不均一性
位相配列
C
B
A
導体
磁界(μT)
不均一性(%)
10.0 m
10.0 m
地表
距離(m)
6.0 m
1.0 m
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
-
-
-
0
30
20
10
10
20
30
距離(m)
0
10
20
30
40
50
60
70
80
90
100
1,5 m
1,0 m
0,5 m
-
-
-
0
1.5 m
1.0 m
0.5 m
不均一性
位相配列
導体
磁界(μT)
不均一性
A
B
C
27
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.3.2.2 各導体間の距離
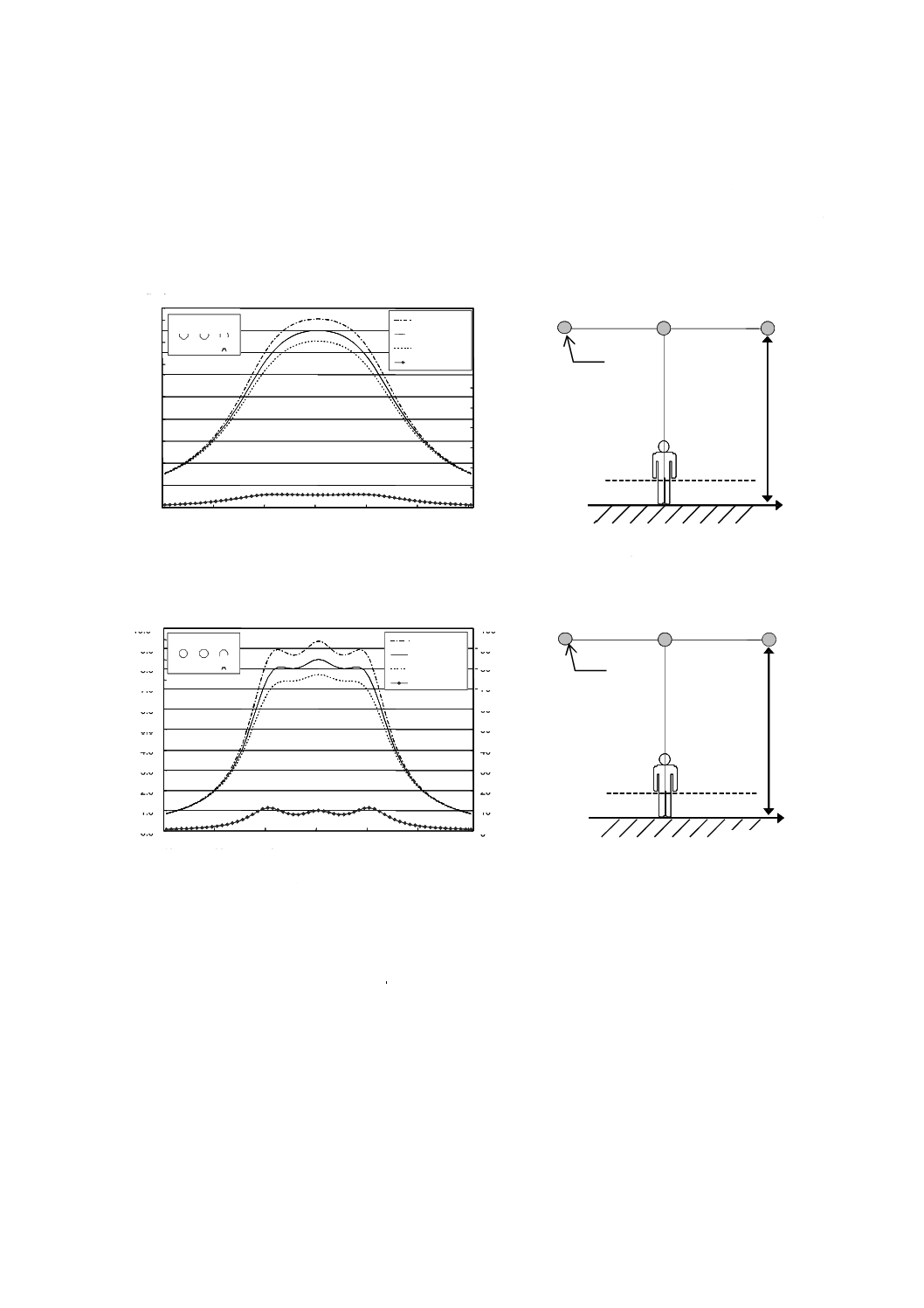
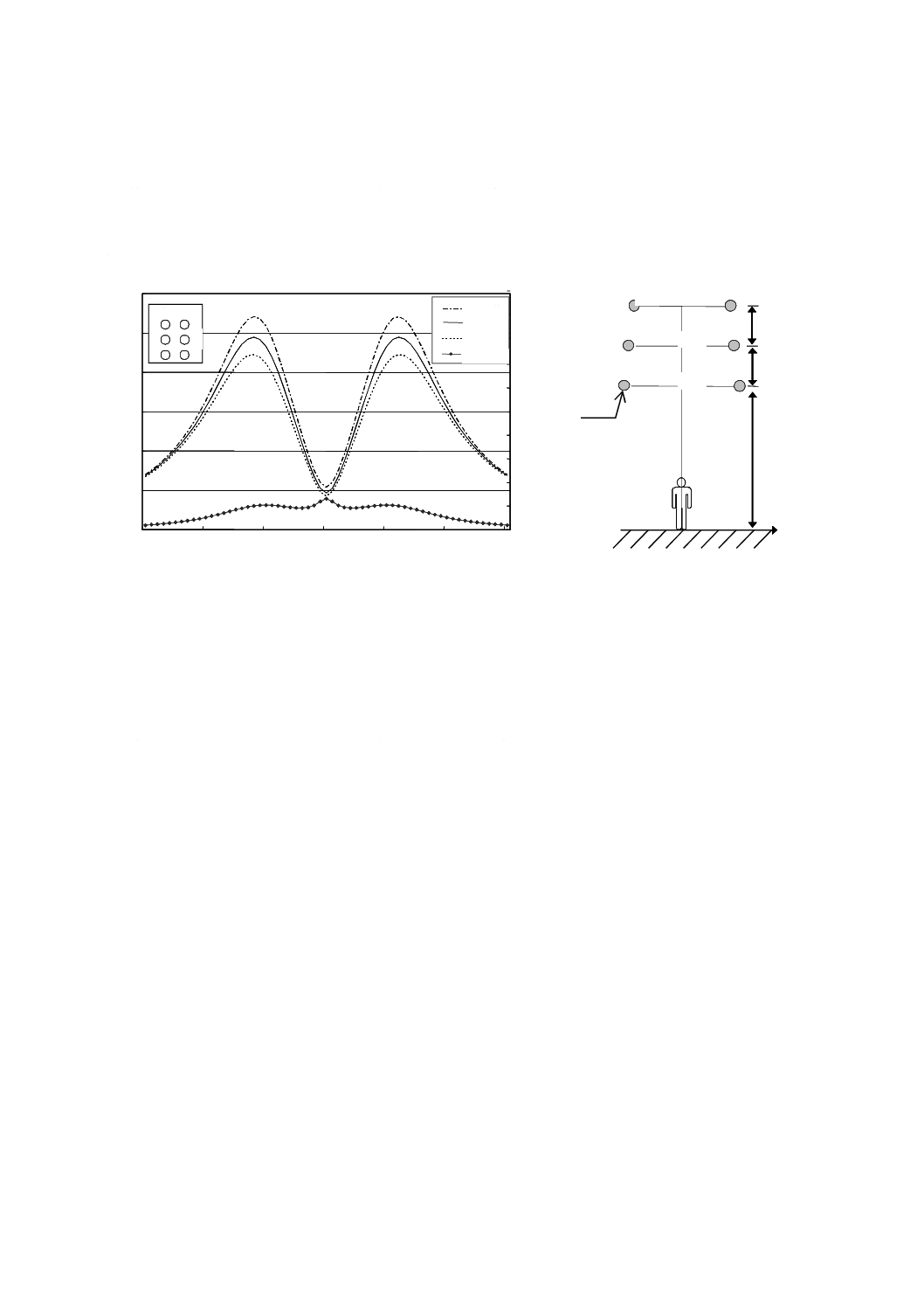
図B.5は,2回線垂直配列の77 kV架空送電線が発生する磁界の強さの空間分布を計算した二つの例で
ある。図B.5には不均一性の計算結果も示した。二つの架空送電線はいずれも同じ電圧であると想定し,
一方は導体間の距離が短く,他方はそれが長い。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さに
おいて,送電線の中心からの距離の関数として計算している。回線を流れる電流値は,平衡で200 Aと仮
定し,また逆相の相配列と仮定した。
a) 導体間の距離が短い場合
b) 導体間の距離が長い場合
図B.5−77 kV架空送電線下における磁界の強さ及び不均一性の空間分布−導体間の距離の影響
(77 kV,2回線垂直配列)
2.0 m 2.0 m
3.0 m
3.0 m
地表
距離(m)
11.0 m
2.0 m 2.0 m
2.0 m 2.0 m
0.0
0.2
0.4
0.6
0.8
1.0
1.2
-
-
-
0
30
20
10
10
20
30
距離(m)
0
10
20
30
40
50
60
70
80
90
100
1,5 m
1,0 m
0,5 m
-
-
-
0
1.5 m
1.0 m
0.5 m
不均一性
A
B
C
B
transposed phase
sequence
A
B
C
C
B
A
逆相配列
導体
不均一性(%)
磁界(μT)
3.2 m 3.2 m
5.0 m
5.0 m
地表
距離(m)
11.0 m
3.5 m
3.5 m
3.8 m
3.8 m
距離(m)
0.0
0.5
1.0
1.5
2.0
2.5
-
-
-
0
30
20
10
10
20
30
0
10
20
30
40
50
60
70
80
90
100
1,5 m
1,0 m
0,5 m
-
-
-
0
1.5 m
1.0 m
0.5 m
不均一性
A
B
C
B
untransposed
phase sequence
A
B
C
C
B
A
逆相配列
導体
不均一性(%)
磁界(μT)
28
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
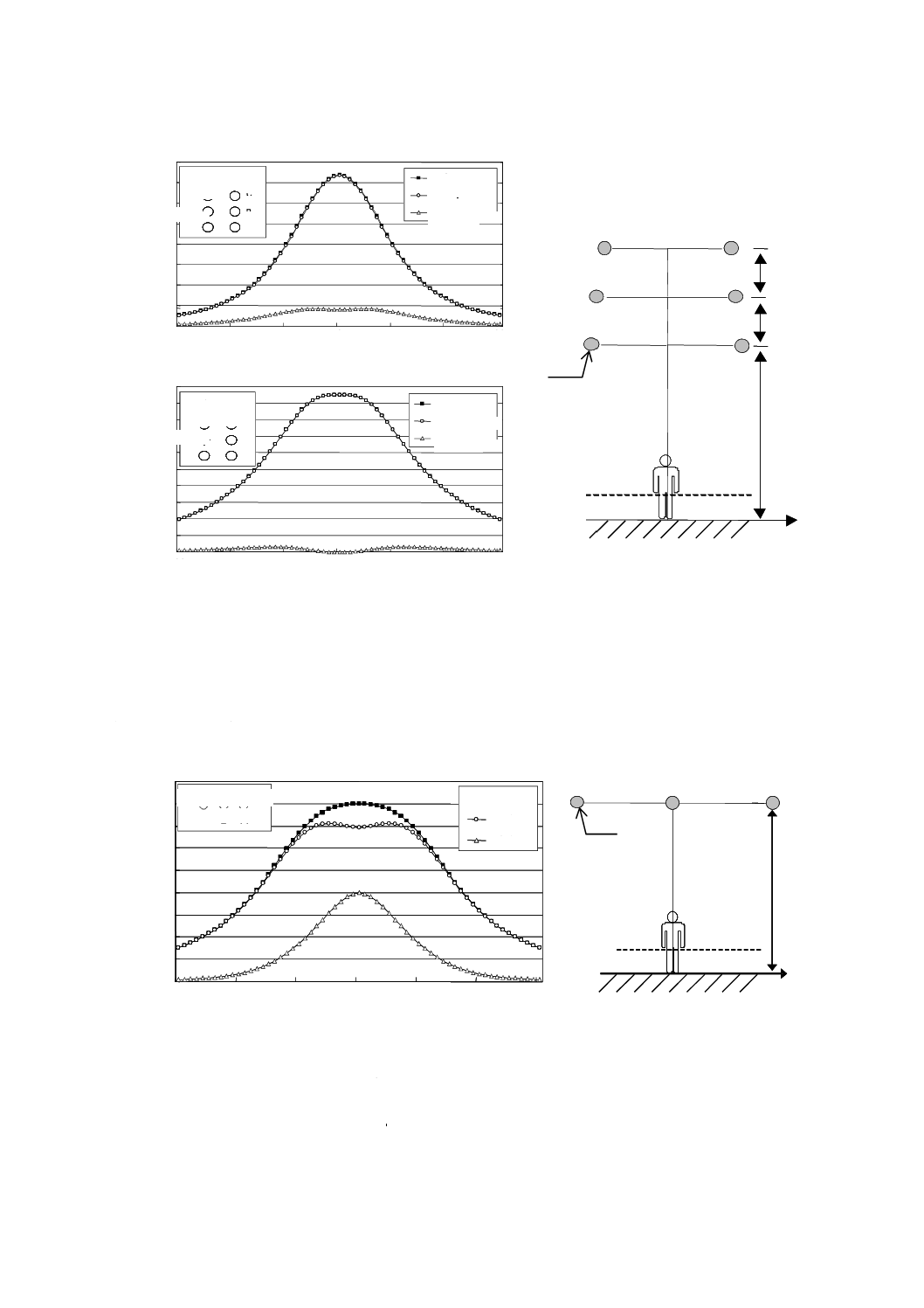
図B.6は,2回線垂直配列の500 kV架空送電線が発生する磁界の強さの空間分布を計算した例である。
図B.6には不均一性の計算結果も示した。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さにおいて,
送電線の中心からの距離の関数として計算している。回線を流れる電流値は,平衡で200 Aと仮定し,ま
た逆相の相配列と仮定した。
図B.6−500 kV架空送電線下における磁界の強さの不均一性の空間分布−導体間の距離の影響
(500 kV,2回線垂直配列,逆相)
B.3.3 だ円の半長径及び半短径成分
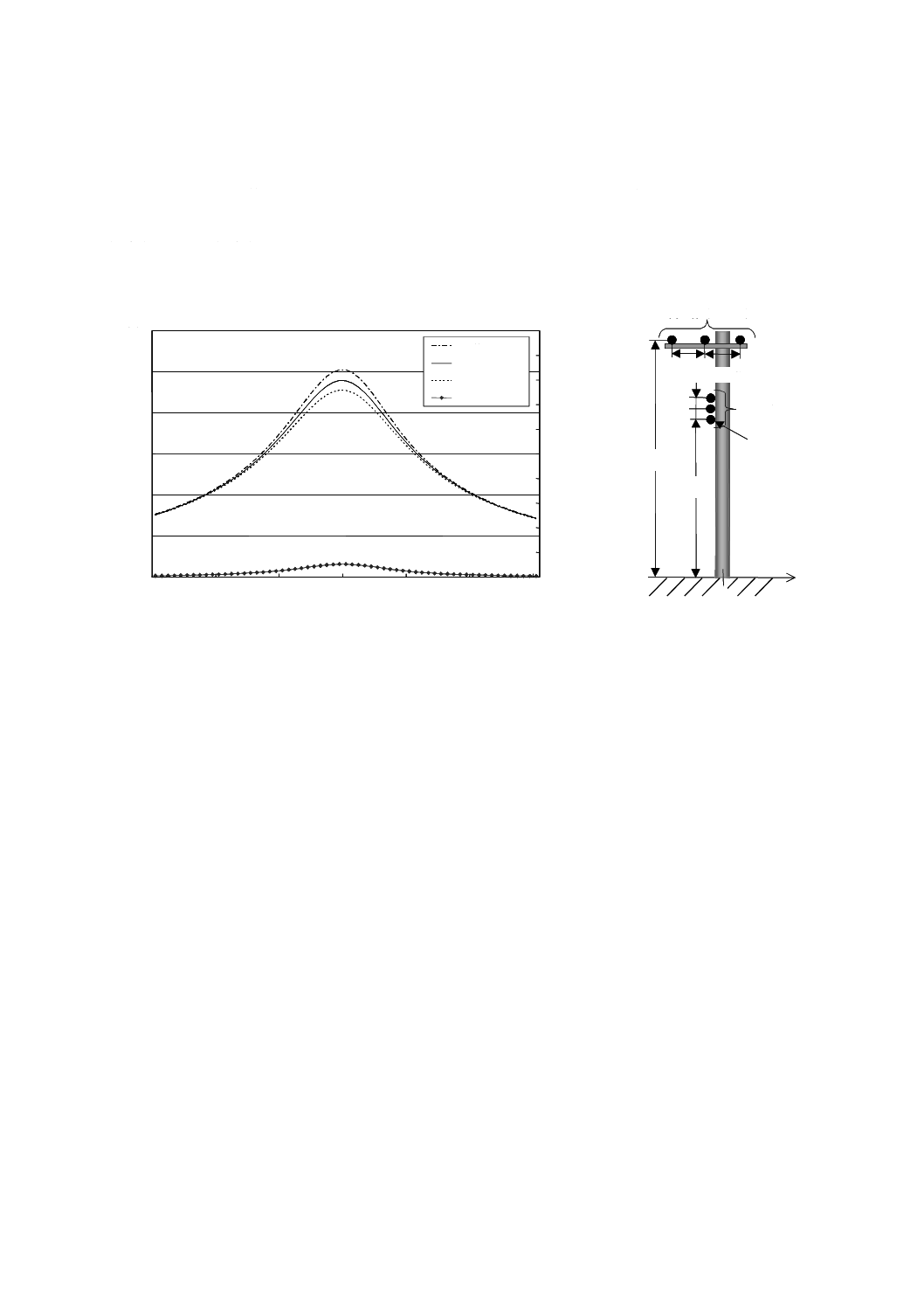
図B.7は,2回線垂直配列の77 kV架空送電線が発生する磁界の強さの半長径及び半短径成分の空間分
布を計算した例である。順相及び逆相両方を考慮している。磁界の強さは,地表上1.0 mの高さにおいて,
送電線の中心からの距離の関数として計算している。各回線を流れる電流値は,平衡で200 Aと仮定した。
10.25 m 10.25 m
10.5 m 10.5 m
11.0 m 11.0 m
13.50 m
13.50 m
地表
11.00 m
0.0
0.1
0.2
0.3
-
-
-
0
30
20
10
10
20
30
距離(m)
0
10
20
30
40
50
60
70
80
90
100
-
-
-
0
1.5 m
1.0 m
0.5 m
不均一性
A
導体
A
B
C
B
A
B
C
B
逆相配列
C
A
距離(m)
不均一性(%)
磁界(μT)
29
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.7−77 kV架空送電線下における磁界の強さの半長径成分及び半短径成分の実効値
(77 kV,2回線垂直配列)
図B.8は,1回線水平配列の500 kV架空送電線が発生する磁界の強さの半長径及び半短径成分の空間分
布を計算した例である。磁界の強さは,地表上1.0 mの高さにある送電線の中心からの距離の関数として
計算している。回線を流れる電流値は,平衡で200 Aと仮定した。
図B.8−500 kV架空送電線下における磁界の強さの半長径成分及び半短径成分の実効値
(500 kV,1回線水平配列)
3.2 m
3.2 m
3.5 m
3.5 m
3.8 m
3.8 m
3.0 m
3.0 m
1.0 m
地表
距離(m)
11.0 m
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
-30
-20
-10
0
10
20
30
Magnetic Field (
µT)
resultant
semi-
semi-minor axis
0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
-30
-20
-10
0
10
20
30
合成
半長径
半短径
A
B
C
B
transposed phase
sequence
A
B
C
C
B
A
逆相配列
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
-
-
-
0
Magnetic Field (
µT)
resultant
semi-major axis
semi-minor axis
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
-
-
-
0
30
20
10
10
20
30
合成
半長径
半短径
A
B
C
B
untransposed
phase sequence
A
B
C
C
B
A
逆相配列
距離(m)
磁界(μT)
距離(m)
1.6
導体
磁界(μT)
10.0 m
10.0 m
地表
距離(m)
11.0 m
1.0 m
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
-
-
-
0
距離(m)
Magnetic Field (
µ
T)
resultant
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
-
-
-
0
30
20
10
10
20
30
合成
半長径
半短径
phase sequence
C
B A
位相配列
導体
磁界(μT)
30
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.4
架空配電線路が発生する磁界の例
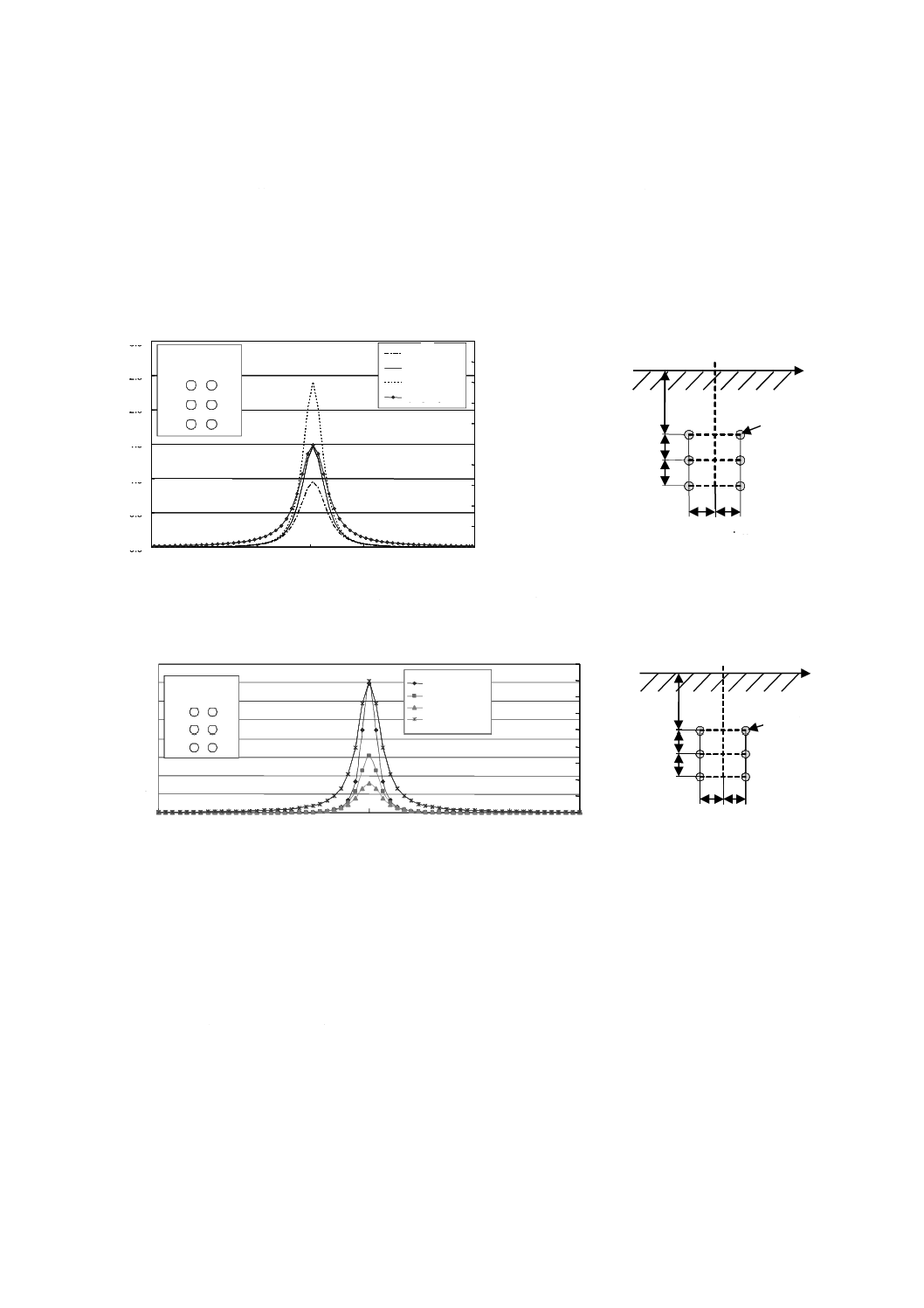
図B.9は,6 600 V及び100 Vの架空配電線路が発生する磁界の強さの空間分布を計算した例である。図
B.9には不均一性の計算結果も示した。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さにおいて,
配電線の中心からの距離の関数として計算している。回線を流れる電流は,6 600 V線路については200 A
(A相),190 A(B相)及び150 A(C相)の不平衡電流を仮定し,100 V線路については中性線を除いて
100 Aの平衡電流と仮定した。
図B.9−架空配電線路(6 600 V/100 V)下における磁界の強さ及び不均一性の空間分布
0.0
1.0
2.0
3.0
4.0
5.0
6.0
-
-
-
0
0
10
20
30
40
50
60
70
80
90
100
1,5 m
1,0 m
0,5 m
-
-
-
0
30
20
10
10
20
30
距離(m)
磁界(μT)
不均一性(%)
1.5 m
1.0 m
0.5 m
不均一性
0
地表
0.85 m
高圧線 (6 600 V)
低圧線 (100 V)
中性線
0.3 m
0.3 m
12.3 m
10.3 m
0.85 m
距離(m)
31
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.5
地中ケーブルが発生する磁界の例
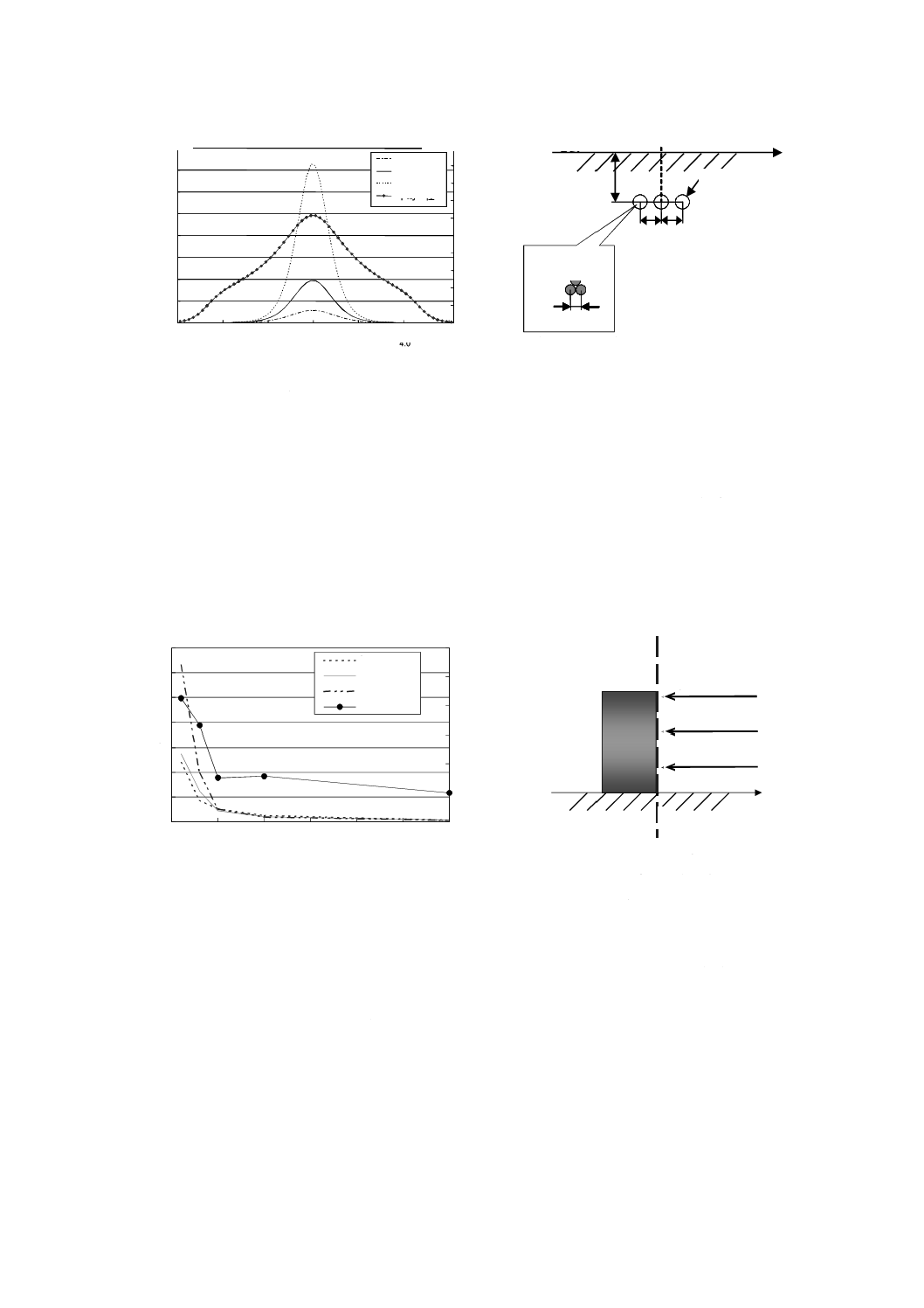
図B.10は,2回線垂直配列の地中ケーブルが発生する磁界の強さの空間分布を計算した例である。図
B.10には不均一性の計算結果も示した。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さにおいて,
ケーブルの中心からの距離の関数として計算している。回線を流れる電流は,平衡で200 Aと仮定し,ま
た逆相の相配列と仮定した。深く埋設したケーブル及び浅く埋設したケーブルの,磁界の強さ及び不均一
性を比較した。
a) 深く埋設されたケーブル
b) 浅く埋設されたケーブル
図B.10−地中ケーブル上方における磁界の強さ及び不均一性の空間分布−埋設深さの影響
図B.11は,よ(撚)りピッチ3.0 mの3本よ(撚)りケーブル(トリプレックスケーブル)を用いた3
回線の地中ケーブルが発生する磁界の強さの空間分布を計算した例である。図B.11には不均一性の計算結
果も示した。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さにおいて,ケーブルの中心からの距離
の関数として計算している。回線を流れる電流は,平衡で200 Aと仮定した。
0.0
0.5
1.0
1.5
2.0
2.5
3.0
-
-
-
0
距離(m)
0
10
20
30
40
50
60
70
80
1,5 m
1,0 m
0,5 m
-
-
-
0
30
20
10
10
20
30
1.5 m
1.0 m
0.5 m
不均一性
0
0.5 m0.5 m
距離(m)
ケーブル
0.35 m
1.85 m
地表
0.35 m
transposed
A
B
C
A
逆相配列
C
B
不均一性(%)
磁界(μT)
90
100
transposed
A
逆相配列
0
2
4
6
8
10
12
14
16
-
-
-
0
距離(m)
0
10
20
30
40
50
60
70
80
90
0,5 m
1,0 m
1,5 m
-
-
-
0
30
20
10
10
20
30
0,5 m
1,0 m
1,5 m
0
0.5 m
0.5 m
ケーブル
0.35 m
0.60 m
地表
0.35 m
B
C
C
A
B
不均一性
距離(m)
磁界(μT)
不均一性(%)
32
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.11−地中ケーブル上方における磁界の強さの不均一性の空間分布−導体の間隔の影響
B.6
配電設備が発生する磁界の例
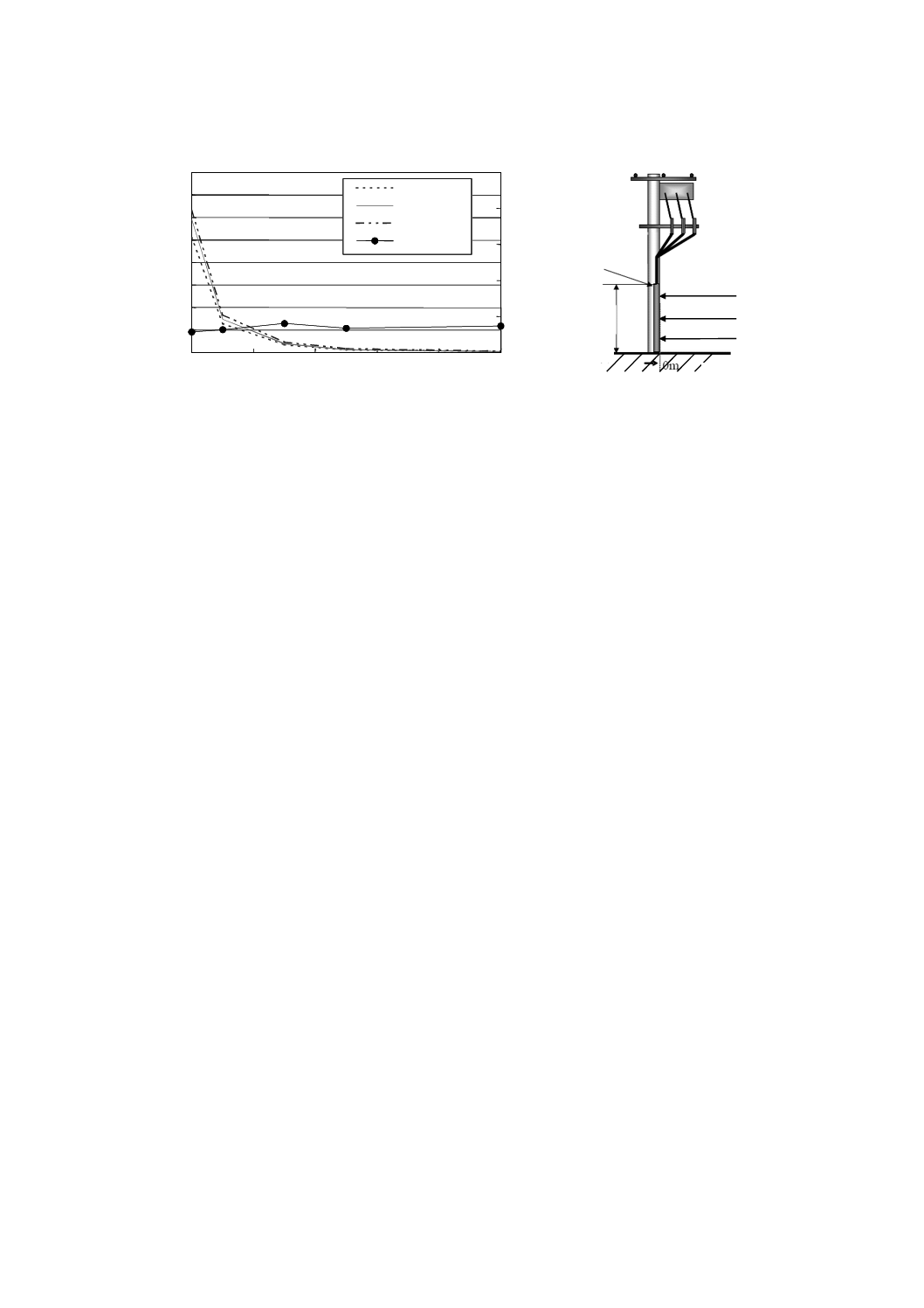
図B.12は,配電設備(6 600 Vの地上設置形変圧器)が発生する磁界の強さの空間分布を測定した例で
ある。図B.12には不均一性の計算結果も示した。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの高さに
おいて,設備の表面からの距離を変えて測定した。測定値が最大となった点は,二次側回路の前,高さ1.5
mの位置であった。負荷電流の測定値は,6 600 V(一次)側回路で3.6 A,100 V/200 V(二次)側回路で
39 Aであった。
図B.12−6 600 Vの地上設置形変圧器周囲で測定した磁界の強さ及び不均一性の空間分布
B.7
垂直ケーブルが発生する磁界の例
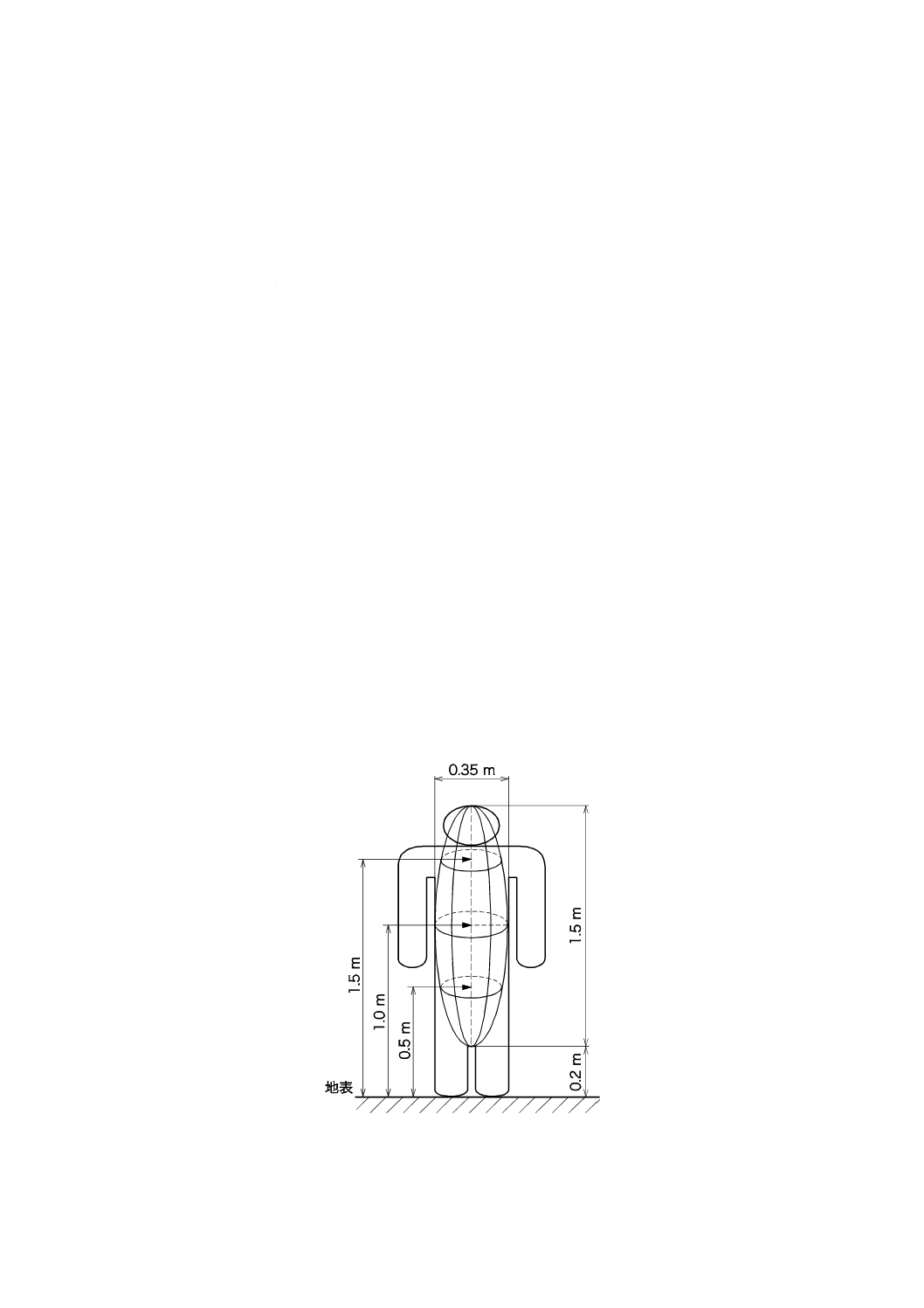
図B.13は,3本よ(撚)りケーブル[トリプレックスケーブル,断面積325 mm2,よ(撚)りピッチ1.35
m,スパイラル半径22.5 mm]で6 600 Vの1回線垂直ケーブルが発生する磁界の強さの空間分布を測定し
た例である。図B.13には不均一性の計算結果も示した。磁界の強さは,地表上0.5 m,1.0 m及び1.5 mの
高さにおいて,ケーブルの表面からの距離を変えて測定した。各相のケーブルを流れる電流の測定値は,
142 A,128 A及び139 Aであった。
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
-6.0
-4.0
-2.0
0.0
2.0
4.0
6.0
0
20
40
60
80
100
120
140
160
180
200
1.5 m
1.0 m
0.5 m
不均一性
0.6m
0.25 m
管路
3 cm
A
B
C
距離(m)
トリプレックスケーブル
A
B
C
0
相
0. 25 m
地表
磁界(μT)
不均一性(%)
距離(m)
0
1
2
3
4
5
6
7
0
0.5
1
1.5
2
2.5
3
-20%
0%
20%
40%
60%
0.5 m
1.0 m
1.5 m
不均一性
距離(m)
H = 1.5 m
H = 0.5 m
H = 1.0 m
0
距離(m)
H=0.5 m
H=1.0 m
H=1.5 m
地表
不均一性
磁界(μT)
80%
100%
6.6 kV:(3.6 A)
100/200 V:(39 A)
33
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.13−6 600 Vの垂直ケーブル周囲で測定した磁界の強さと不均一性の空間分布
0
5
10
15
20
25
30
35
40
0.0
0.2
0.4
0.6
0.8
1.0
距離(m)
0%
20%
40%
60%
80%
100%
0.5 m
1.0 m
1.5 m
不均一性
スイッチ
鋼管
トリプレックスケーブル
不均一性(%)
磁界(μT)
地表
2.0 m
H=1.5 m
H=1.0 m
H=0.5 m
距離(m)
6.6 kV線
(142 A) (128 A) (139 A)
34
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
平均ばく露レベルに関する3点測定の概念
C.1 3点測定の概念
この規格においては,均一な磁界に対し高さ1.0 mで測定した磁界の強さ(1点測定)を平均ばく露レ
ベルとみなす。一方,不均一な磁界については,地表上0.5 m,1.0 m及び1.5 mの高さで行った3点測定
の算術平均値を,3点平均ばく露レベルと定義している。
したがって,3点平均ばく露レベルが人体の全身における平均ばく露レベルに対応することを示す必要
がある。こうして評価した値は,ICNIRPガイドラインにおける公衆に対するばく露の参考レベルとの比
較を意図したものである。C.2及びC.3の記述に従い,平均ばく露レベルと3点平均ばく露レベルとが同
等であることを説明できれば,参考レベルとの比較が可能である。ただし,中枢神経系における電流密度
として表現されている基本制限との比較はできない。なぜならば,この規格が誘導電流を考慮していない
ためである。同様に,3点測定ではIEEE規格が規定しているような局所の最大値を推定することもできな
い。
この附属書においては,平均ばく露レベルをある仮定のもとで算出し,3点平均ばく露レベルと比較し
ている。
C.2 平均ばく露レベルの計算
計算を単純化するため,人体モデルを仮定する。使用する人体モデルは,垂直軸の長さが1.5 m,水平
軸の長さが0.35 mで地表上0.2 mに位置する回転だ円体であり,人体形状に重ね合わせた図を図C.1に示
す。磁界はこの回転だ円体内の0.05 m間隔の格子点で計算し,算出した値の平均値を人体の平均ばく露レ
ベルとする。
図C.1−回転だ円体の人体モデル
35
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C.3 平均ばく露レベルと3点平均ばく露レベルとの比較
C.3.1 磁界の強さの計算
磁界の強さの計算は,ビオ・サバールの法則を用いて行う。
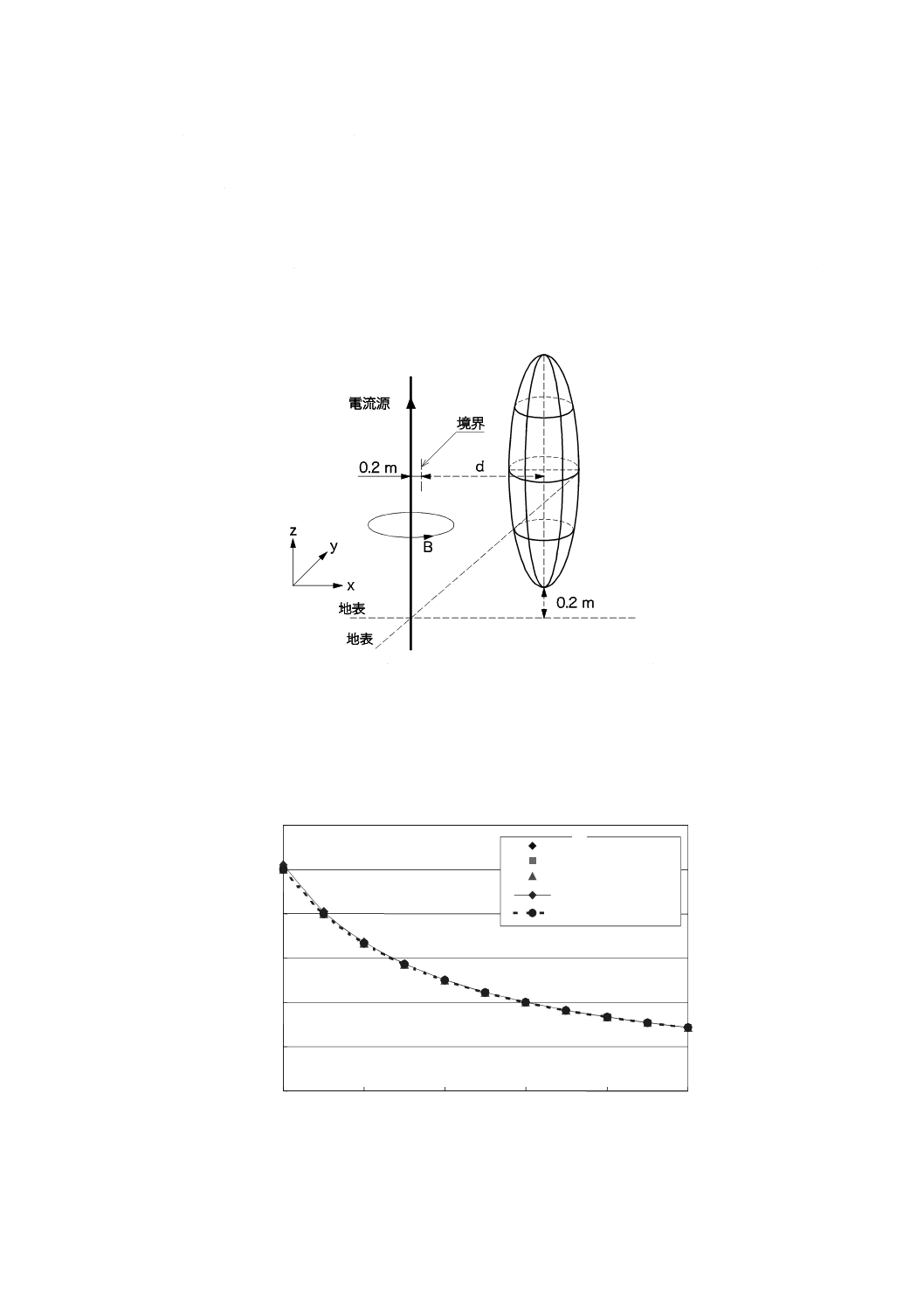
C.3.2 無限長の単一直線ケーブル
磁界発生源として,500 Aの交流電流が流れる無限長の単一直線ケーブルを考える。ケーブルは地面に
対して垂直であり,人体モデルの中心は磁界発生源との境界から距離dの位置にある(図C.2参照)。導体
の太さ・絶縁層の厚さ・ケーブルと防護管との間の空間・防護管の厚さなどを考慮し,磁界発生源との境
界は,ケーブルの中心から0.2 mの位置にあると仮定した。
図C.2−直線ケーブルが発生する磁界中における人体モデル
計算した磁界分布を,図C.3に示す。
この場合,磁界の高さ方向の分布は均一であり,3点平均ばく露レベルは平均ばく露レベルにほぼ一致
する。
図C.3−直線ケーブルが発生する磁界の強さ
0
50
100
150
200
250
300
0.2
0.4
0.6
0.8
1.0
1.2
境界からの距離(m)
0.5 m
1.0 m
1.5 m
平均ばく露レベル
3点平均ばく露レベル
磁界(μT)
36
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
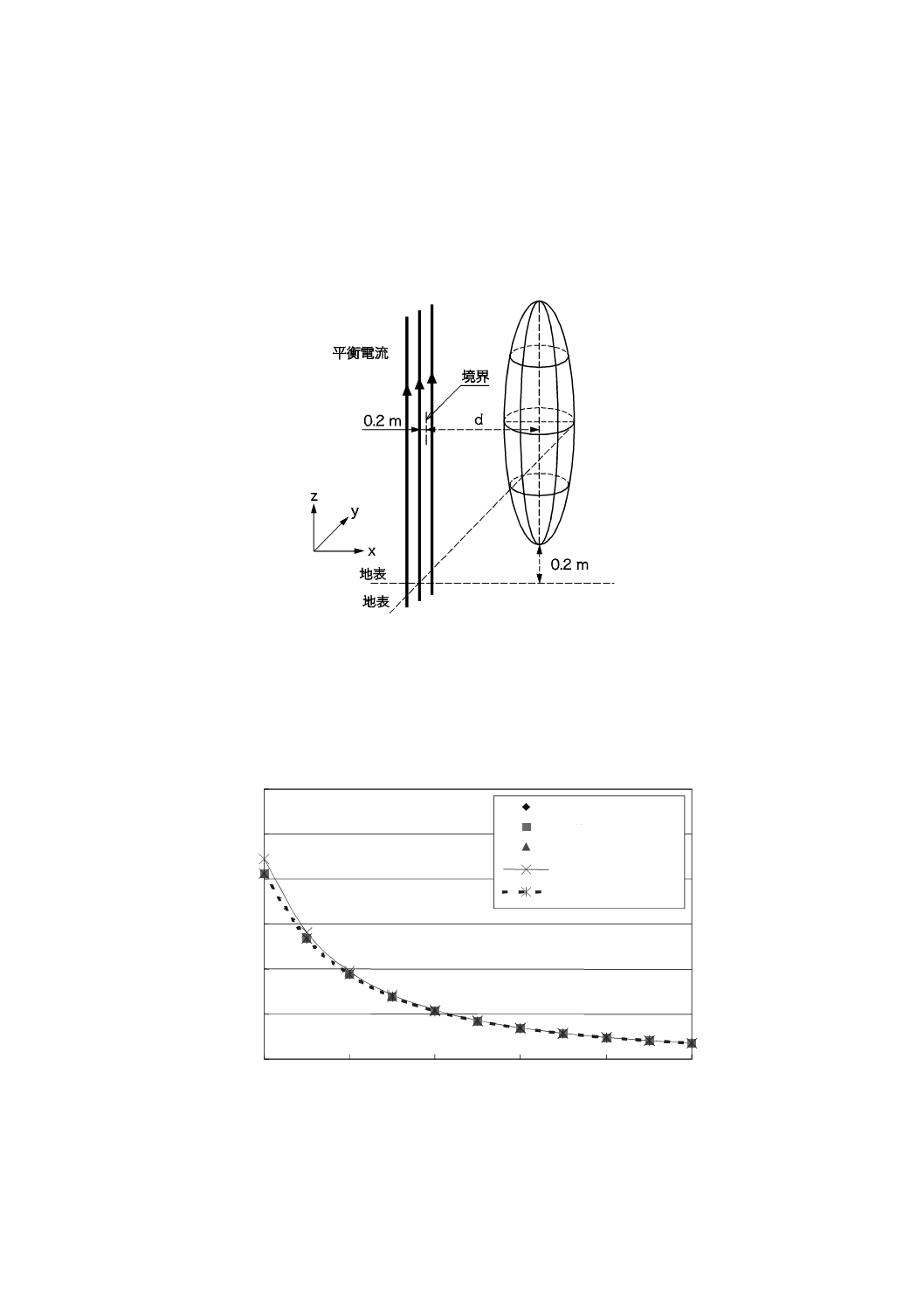
C.3.3 平衡電流が流れる3本の平行ケーブル
磁界発生源として,500 Aの三相平衡電流が流れる3本の無限長の直線ケーブルを考える。ケーブルは
互いに平行で,地面に対して垂直な同一平面内にある。ケーブル間隔は0.1 m,0.2 m及び0.3 mの3通り
を考える。人体モデルの中心は磁界発生源との境界から距離dの位置にある(図C.4参照)。導体・絶縁層
の厚さ・ケーブルと防護管との間の空間・防護管の厚さなどを考慮し,磁界発生源との境界は,ケーブル
の中心から0.2 mの位置にあると仮定した。
図C.4−3本の平行ケーブルが発生する磁界中における人体モデル
計算した磁界分布のうち,ケーブル間隔が0.1 mの場合を図C.5に示す。
この場合,磁界の高さ方向の分布は均一であり,3点平均ばく露レベルは平均ばく露レベルにほぼ一致
する。
図C.5−平衡電流が流れる3本の平行ケーブルが発生する磁界の強さ
磁界(μT)
0
25
50
75
100
125
150
0.2
0.4
0.6
0.8
1
1.2
境界からの距離(m)
0.5 m
1.0 m
1.5 m
平均ばく露レベル
3点平均ばく露レベル
ケーブル間隔 = 0.1 m
37
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
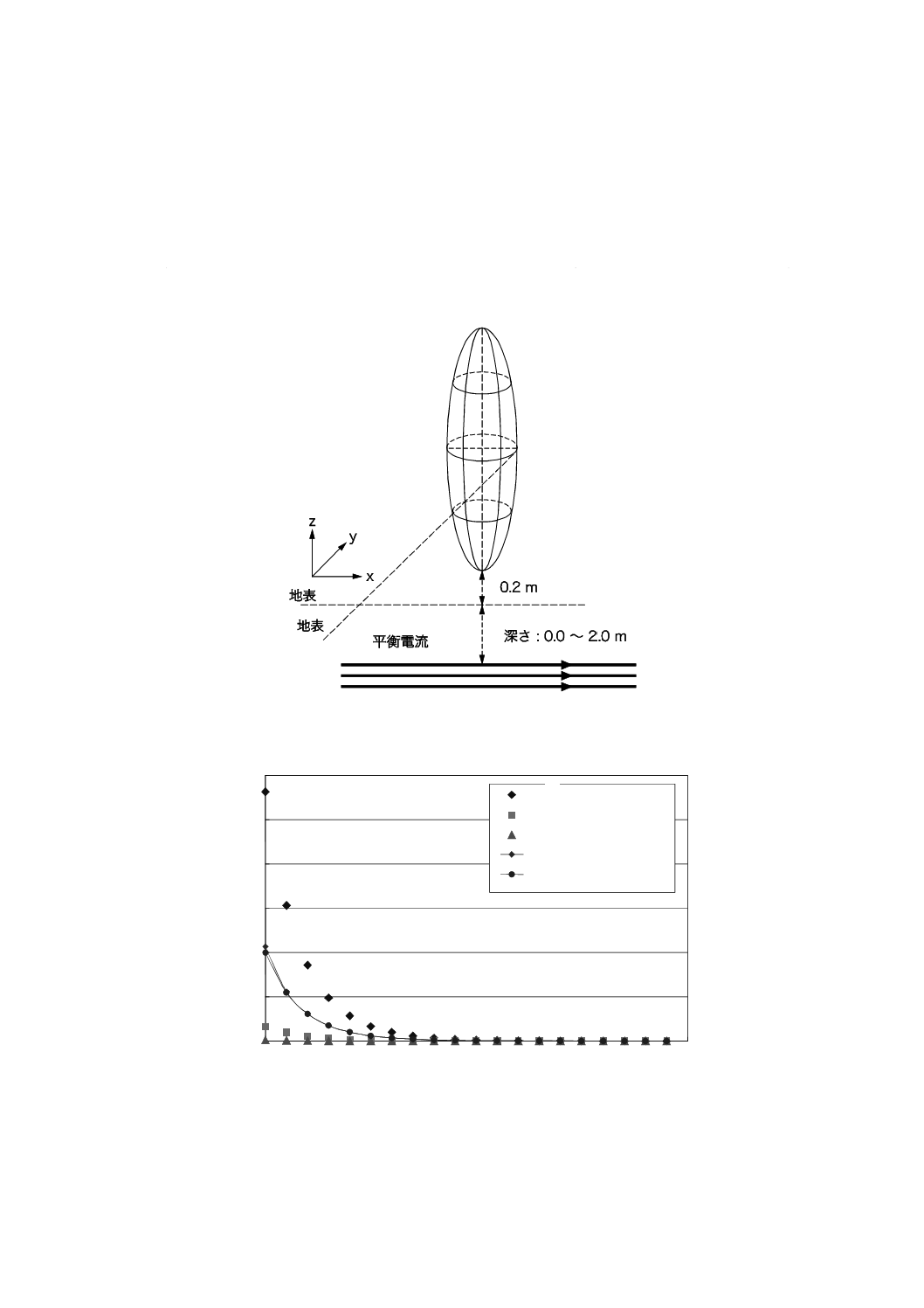
C.3.4 平衡電流が流れる地中ケーブル
磁界発生源として,500 Aの三相平衡電流が流れる無限長の直線ケーブルを考える。ケーブルは地中に
ある。3本よ(撚)りケーブル(トリプレックスケーブル)であり,断面積が325 mm2,よ(撚)りピッ
チが1.35 m,スパイラル半径が22.5 mmである(図C.6参照)。
計算した磁界分布を図C.7に示す。
この場合,高さ方向の分布での不均一性が顕著であり,特にケーブルが地表近くの地中にある場合にそ
れが顕著であるが,3点平均ばく露レベルは平均ばく露レベルにほぼ一致する。
図C.6−地中ケーブルが発生する磁界中における人体モデル
図C.7−地中ケーブルが発生する磁界の強さ
0
2
4
6
8
10
12
0.0
0.5
1.0
1.5
2.0
地表からの深さ(m)
0.5 m
1.0 m
1.5 m
平均ばく露レベル
3点平均ばく露レベル
磁界(μT)
38
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
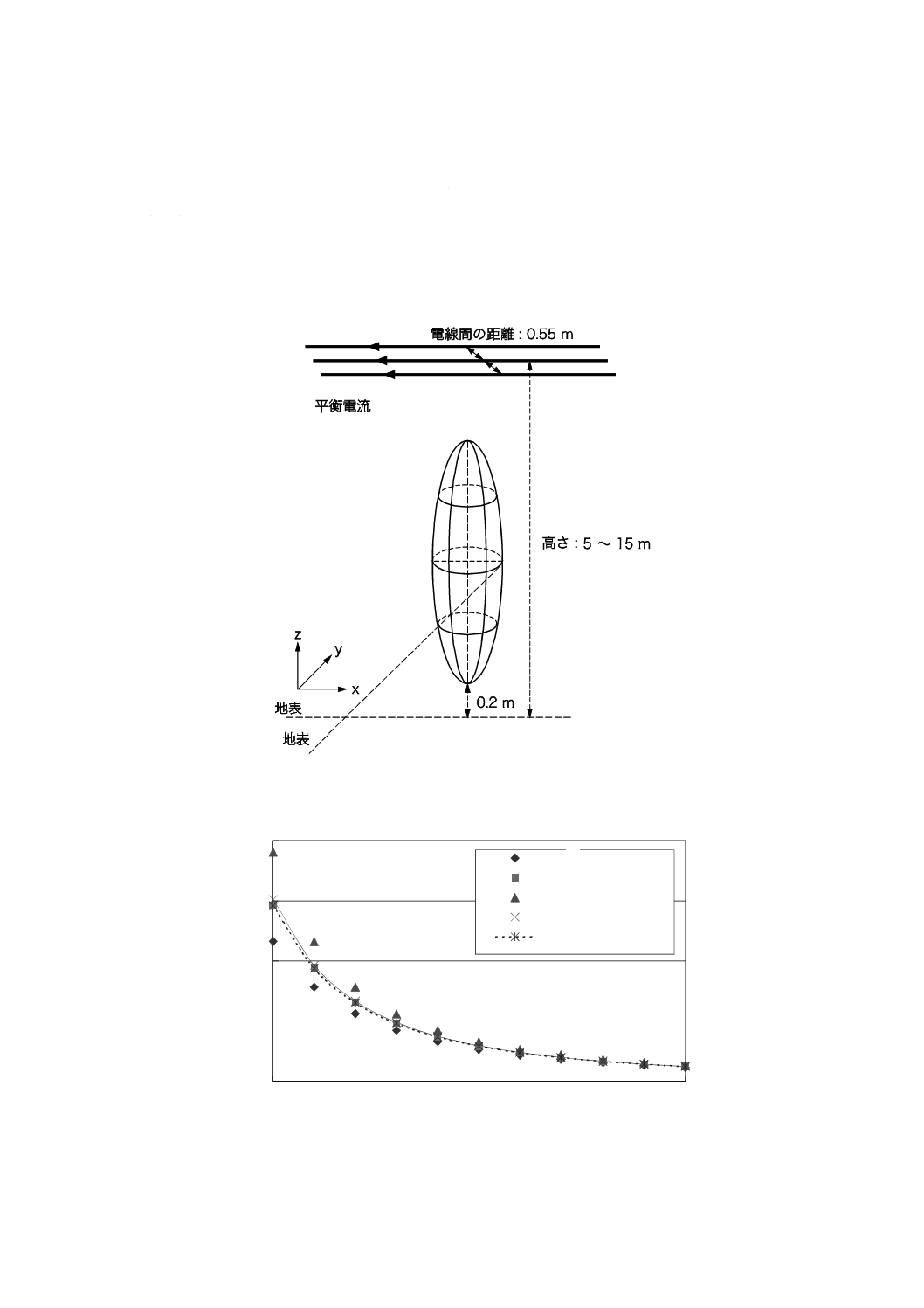
C.3.5 平衡電流が流れる架空線
磁界発生源として,500 Aの三相平衡電流が流れる3本の無限長の直線電線を考える。電線は互いに平
行で,地面に対して平行な同一平面上にある。電線間の距離として0.55 mを仮定した。3本の各線の高さ
は,地表から5 m〜15 mとした(図C.8参照)。
計算した磁界分布を図C.9に示す。
この場合,磁界の高さ方向の分布は均一であるとみなされ,3点平均ばく露レベル,及び地表上1.0 m
における1点測定で得られたばく露レベルは平均ばく露レベルにほぼ一致する。
図C.8−架空線が発生する磁界中における人体モデル
図C.9−平衡電流の流れる架空線が発生する磁界の強さ
0.0
2.0
4.0
6.0
8.0
5
10
15
地表からの高さ(m)
0.5 m
1.0 m
1.5 m
平均ばく露レベル
3点平均ばく露レベル
磁界(μT)
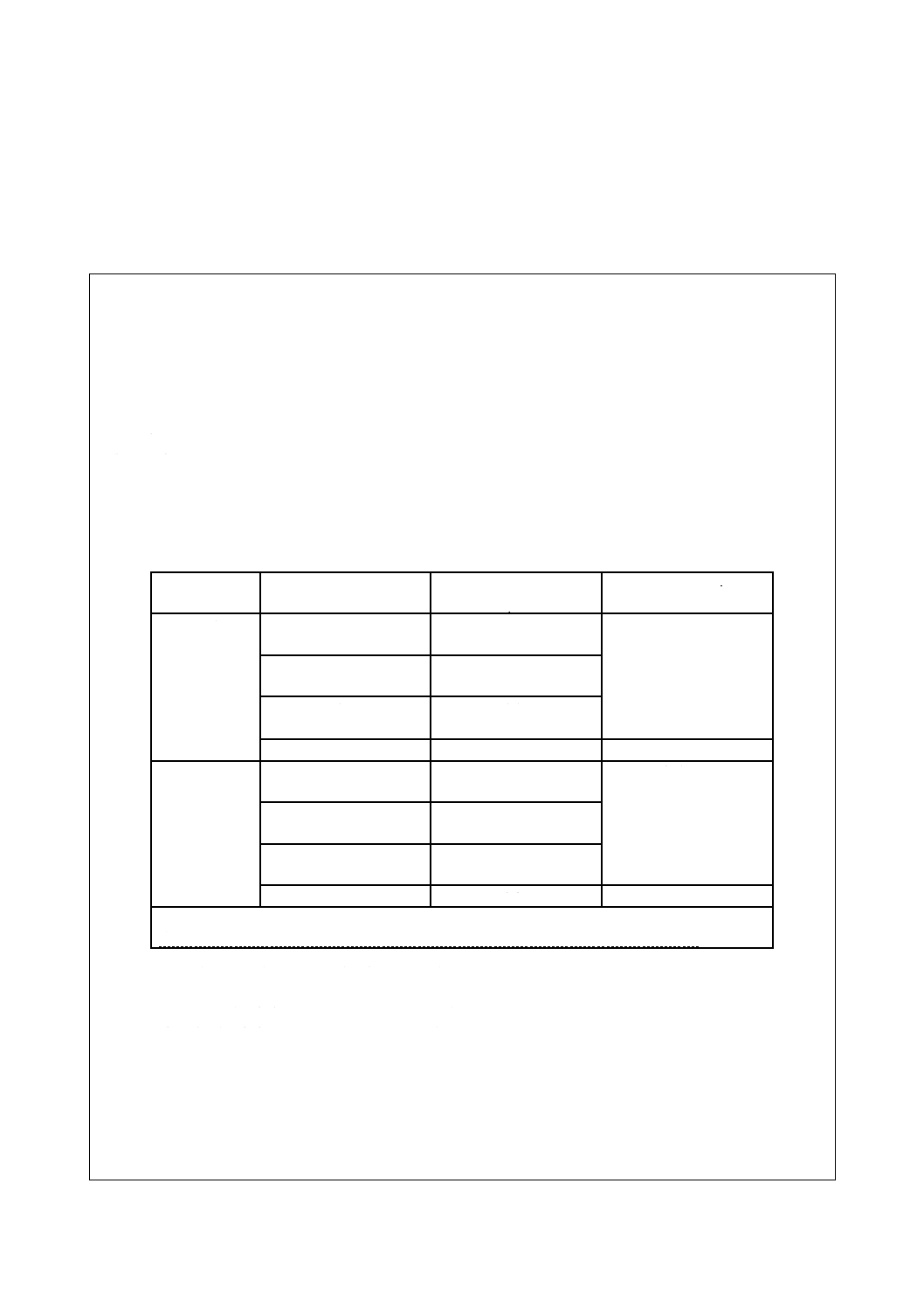
39
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
電界及び磁界測定報告書の書式例
電界及び磁界測定報告書の書式例を,次に示す。
測定結果
1. 日付,時刻,気象条件,温度,湿度
2006年7月27日,14:00〜14:15,曇り,25 ℃,60 %
2. 電力システムの種類(公称電圧,測定中の負荷条件)
地中送電ケーブル(77 kV,100 A〜105 A/1回線)
架空配電線路(6 600 V/100 V,負荷条件は不明)
3. 所在地(住所)“住所”
4. 測定器
製造業者:XXX社
型式:ABC-MF2000
プローブの種類:3軸空心コイル,各コイルの直径は不明
測定可能な範囲:10 nT〜1 mT
周波数帯域:40 Hz〜800 Hz
最終校正日:2006年5月3日
5. 測定実施者:“氏名”,“所属”
6. 測定結果
地点番号
測定高
m
磁界の強さ
μT
磁界の量 a)
No.1
(屋外)
0.5
(地表上)
0.13
合成磁界
1.0
(地表上)
0.40
1.5
(地表上)
1.17
−
0.57
3点平均ばく露レベル
No.2
(屋内)
0.5
(床上)
0.03
合成磁界
1.0
(床上)
0.12
1.5
(床上)
0.65
−
0.27
3点平均ばく露レベル
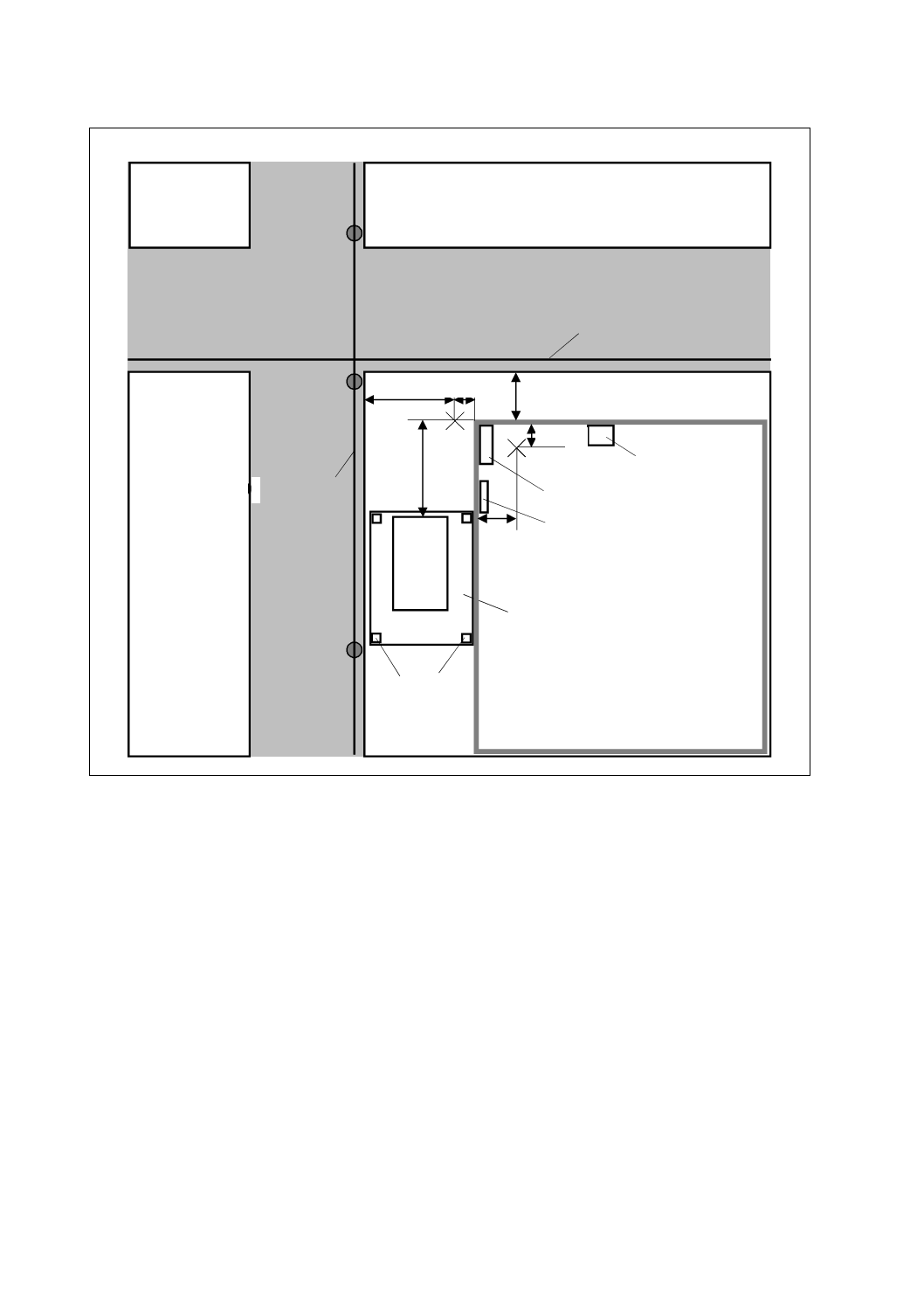
測定点は添付シートに記載する。
注a) 合成磁界,3点平均ばく露レベル,長軸成分の実効値,X軸成分の実効値 など
7. その他の電界及び磁界発生源(動作中のもの)
No.1:なし
No.2:エアコン(測定点からおよそ2.0 mの位置)
冷蔵庫(測定点からおよそ5.0 mの位置)
8. 留意すべき物体
No.1:自動車,金属製の支柱,車庫の屋根
(測定点からおよそ6.0 mの位置)
No.2:金属製の棚(測定点からおよそ1.8 mの位置)
9. 高調波成分
無視できる。
40
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
平面図
1.0 m
77 kV 地中送電線
6 600 V / 100 V
架空配電線
住居
自
動
車
No.1
1.5 m
4.5 m
3.0 m
No.2
6.0 m
3.0 m
車庫
金属棚
冷蔵庫
エアコン
YY 大通り
XX 通り
金属ポール
屋根
41
C 1911:2013 (IEC 62110:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E
(参考)
参考文献
[1] ICNIRP, Guidelines for limiting exposure to time-varying electric, magnetic, and electromagnetic fields (up to
300 GHz); Health Phys. 74, 494-522, 1998
[2] IEEE Std C95.6-2002, IEEE Standard for Safety Levels With Respect to Human Exposure to Electromagnetic
Fields, 0-3 kHz
[3] IEC 61000-2-2, Electromagnetic compatibility (EMC)−Part 2-2: Environment−Compatibility levels for
low-frequency conducted disturbances and signalling in public low-voltage power supply systems, March 2002
[4] CEATI International, Inc., T984700-5103: Canadian Power Quality (PQ) Survey 2000, report, Montreal,
Canada.
[5] ICNIRP, Guidance on determining compliance of exposure to pulsed and complex non-sinusoidal waveforms
below 100 kHz with ICNIRP guidelines. Health Physics, March 2003, Vol. 84, No. 3, 383-387
[6] CIGRE TF C4.2.03, Technical guide for measurement of low frequency electric and magnetic fields near
overhead power lines, International Council on Large Electrical Systems (in press)
[7] IEEE Std 644-1994, IEEE Standard Procedures for Measurement of Power Frequency Electric and Magnetic
Fields from AC Power Lines
[8] CIGRE TF C4.2.05, Technical Brochure Nr 320: Characterisation of ELF Magnetic Fields−April 2007,
International Council on Large Electrical Systems
[9] IEEE Std PC95.3.1, Draft recommended practice for measurements and computations of human exposure to
electric and magnetic fields, 0 Hz to 100 kHz