C 1612 : 2000
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項に基づき,社団法人日本電気計測器工業会 (JEMIMA) 及び財
団法人日本規格協会 (JSA) から工業標準原案を具して日本工業規格を改正すべきとの申出があり,日本工
業標準調査会の審議を経て,通商産業大臣が改正した日本工業規格である。これによって,JIS C 1612 : 1988
は改正され,この規格に置き換えられる。
今回の改正では,放射温度計の性能の表し方及び試験方法について規定した。
JIS C 1612には,次に示す附属書がある。
附属書1(規定) 校正方法
附属書2(規定) 標準放射温度計
附属書3(参考) 放射温度計の特性及び校正
C 1612 : 2000
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目次
ページ
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 定義 ······························································································································ 1
4. 性能 ······························································································································ 3
4.1 測定範囲 ······················································································································ 3
4.2 精度定格 ······················································································································ 3
4.3 基準動作条件 ················································································································ 3
4.4 標的サイズ ··················································································································· 3
4.5 面積効果 ······················································································································ 3
4.6 指数n ·························································································································· 3
4.7 再現性 ························································································································· 3
4.8 分解能 ························································································································· 3
4.9 応答時間 ······················································································································ 3
4.10 温度ドリフト ··············································································································· 3
4.11 ウォームアップ時間 ······································································································ 3
4.12 変換器負荷抵抗 ············································································································ 3
4.13 使用温度範囲 ··············································································································· 3
4.14 使用湿度範囲 ··············································································································· 3
4.15 絶縁抵抗 ····················································································································· 3
4.16 耐電圧 ························································································································ 3
5. 試験 ······························································································································ 3
5.1 試験の種類 ··················································································································· 3
5.2 試験項目 ······················································································································ 3
5.3 試験条件 ······················································································································ 4
5.3.1 放射温度計の設置 ········································································································ 4
5.3.2 試験条件の設定 ··········································································································· 4
5.4 試験実施方法 ················································································································ 4
5.4.1 精度定格試験 ·············································································································· 4
5.4.2 面積効果試験 ·············································································································· 5
5.4.3 再現性試験 ················································································································· 5
5.4.4 分解能試験 ················································································································· 5
5.4.5 応答時間試験 ·············································································································· 5
5.4.6 温度ドリフト試験 ········································································································ 5
5.4.7 絶縁抵抗試験 ·············································································································· 5
5.4.8 耐電圧試験 ················································································································· 6
C 1612 : 2000 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6. 表示 ······························································································································ 6
附属書1(規定) 校正方法 ··································································································· 7
1. 適用範囲 ························································································································ 7
2. 放射温度計の校正 ············································································································ 7
3. 校正用具 ························································································································ 7
3.1 黒体炉 ························································································································· 7
3.2 標準温度計 ··················································································································· 8
4. 校正方法 ························································································································ 8
4.1 校正手順 ······················································································································ 8
4.2 放射率補正 ··················································································································· 9
4.3 空洞放射率の評価 ········································································································· 10
附属書2(規定) 標準放射温度計 ························································································· 11
1. 適用範囲 ······················································································································· 11
2. 試験 ····························································································································· 11
3. 特性 ····························································································································· 11
4. 校正 ····························································································································· 11
4.1 0.9(m単色放射温度計 ····································································································· 11
4.2 0.65(m単色放射温度計 ··································································································· 11
5. 定点黒体炉 ···················································································································· 12
6. 精度維持 ······················································································································· 12
7. 指数n ··························································································································· 12
附属書3(参考) 放射温度計の特性及び校正 ·········································································· 13
1. 幾何光学的な装置定数 ····································································································· 13
1.1 放射温度計の基本原理···································································································· 13
1.2 標的サイズ ·················································································································· 14
1.3 距離係数と視野角 ········································································································· 15
1.3.1 距離係数F ················································································································· 15
1.3.2 視野角2( ··················································································································· 15
1.4 標的の確認機構(照準)································································································· 15
1.4.1 ファインダー方式 ······································································································· 15
1.4.2 マーカ方式 ················································································································ 16
1.4.3 その他の方式 ············································································································· 16
2. 放射温度計の出力特性及び精度定格の確認方法 ···································································· 17
2.1 放射温度計の特性式 ······································································································ 17
2.2 定数算出方法 ··············································································································· 19
2.3 温度目盛の誤差 ············································································································ 19
2.4 温度目盛の最大誤差 ······································································································ 20
C 1612 : 2000 目次
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2.5 精度定格の確認 ············································································································ 21
2.6 リニアライザ出力の精度定格の確認 ·················································································· 22
3. 放射温度計の指数n ········································································································· 23
3.1 指数nの利用 ··············································································································· 23
3.2 指数nの定数算出法 ······································································································ 24
3.3 定数値 ························································································································ 25
3.4 指数nの定数による放射率補正 ························································································ 25
4. 黒体炉の種類及び構成例 ·································································································· 26
5. 空洞放射率・空洞反射率及び空洞の実効温度 ······································································· 28
5.1 実効温度 ····················································································································· 29
5.2 空洞反射率の測定 ········································································································· 32
5.3 空洞放射率の評価 ········································································································· 32
6. 0.65(m単色放射温度計の2 000〜3 000℃の温度域における校正 ················································ 33
6.1 減光装置による校正 ······································································································ 33
6.2 非線形性測定による校正································································································· 33
7. 単色放射温度計の構成及び特性例 ······················································································ 35
8. 単色放射温度計特性式の定数決定方法 ················································································ 36
9. 定点黒体炉の種類及び構成例 ···························································································· 37
10. 構造の表示 ·················································································································· 38
10.1 構成 ·························································································································· 38
10.2 光学系 ······················································································································· 38
10.3 照準 ·························································································································· 39
10.4 フィルタ ···················································································································· 39
10.5 検出素子 ···················································································································· 39
10.6 信号処理系 ················································································································· 39
10.7 入出力系 ···················································································································· 39
10.8 附属品 ······················································································································· 39
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
C 1612 : 2000
放射温度計の性能試験方法通則
Test Methods for Radiation Thermometers
1. 適用範囲 この規格は,標的の放射輝度を測定し,温度に換算して表示する放射温度計の性能の表し
方及び試験方法について規定する。ただし,分光感度特性に関しては,パラメータによる表し方が未確立
であって,この規格からは除く。
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの規格は,その最新版を適用する。
JIS Z 8750 ガラス製温度計による温度測定方法
JIS Z 8710 温度測定方法通則
3. 定義 この規格で用いる主な用語の定義は,次による。
a) 種類
1) 単色放射温度計 狭い波長帯域における放射エネルギーだけを測定する形式の放射温度計。
2) 部分放射温度計 比較的広い波長帯域におけるエネルギーを測定する形式の放射温度計。
3) 全放射温度計 広い波長帯域における放射エネルギーを測定する形式の放射温度計。
4) 多色放射温度計 互いに異なる複数の波長帯域における放射エネルギー間の関係を利用する形式の
放射温度計。
5) 走査式放射温度計 測定物体を順次走査測定する形式の放射温度計で,測定する波長帯域は1)〜4)
のいずれかに属する。
b) 放射温度計にかかわる用語
1) 検出素子 放射に感応し,そのエネルギーに対応した電気信号を発生する素子。
2) 光学系 標的からの放射を集光又は結像させる機構。
3) レンズ式 光学系にレンズを用いる方式。
4) ミラー式 光学系にミラーを用いる方式。
5) ライトガイド式 光学系にライトガイドを用いる方式。
6) ファイバ式 光学系に光ファイバを用いる方式。
7) 測定距離 放射温度計の先端又は基準点から標的までの距離。
8) 標的サイズ ある測定距離において,放射温度計の測定対象と規定した標的の大きさ(直径などで
表す。)。
9) 距離係数 測定距離と標的サイズの比。
10) 面積効果 測定物体の面積の違いによって,放射温度計の出力が変化すること。
11) 視野 放射温度計で測定することのできる範囲。
2
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
12) 視野角 光学系の主点から角度で表現した視野の大きさ。
13) 視定 標的などを見定めること。
14) 照準 標的を正しく視定する機構。
15) 測定波長 放射温度計が応答する波長。
16) 実効波長 放射温度計で測定される実効的な波長。
17) 指数n 標的の温度と放射温度計の検出器の出力信号との関係を表す指数。
18) 半値幅 バンドパス形光学フィルタにおける最大透過率の1/2に対応する波長の差。
19) 検出器 標的の放射輝度を検出して電気信号に変換する装置で,光学系,検出素子及び電気系で構
成する。
20) 変換器 検出器の出力信号を計測制御に使用するための電気信号に変換する装置。
21) 許容負荷抵抗 性能が保証される範囲で接続できる負荷抵抗。
22) 基準動作条件 周囲条件の変化による装置への影響が無視できる範囲。
23) 正常動作条件 周囲条件の影響を補正すれば正常な測定値が得られる範囲。
24) 精度定格 基準動作条件の下で放射温度計に許容される最大誤差の限界。
25) 再現性 同一の方法で同一の測定対象を同じ条件で繰り返し測定した場合,個々の測定値が一致す
る性質。
26) 分解能 識別可能な温度差。
27) 応答時間 ステップ応答において,出力が最終値の決められた割合に達するまでの時間。一般に最
終値の63.2%,90%,95%又は98%の値で示される。
28) ウォームアップ時間 機器を始動してから機器が正常に動作するまでに必要な時間。
29) 温度ドリフト 周囲温度が変化することによって生じる放射温度計の出力変動。
c) 測定にかかわる用語
1) 測定物体 測定の対象となる物体。
2) 標的 測定物体上の測定が行われる領域。
3) 放射エネルギー 放射の形態で放出,伝搬又は授受されるエネルギー。
4) 放射輝度 与えられた方向の放射源の単位時間,単位立体角当たりの放射エネルギーをその方向の
放射源の正射影面積で割った値。
5) 黒体 入射した放射を,波長,入射方向及び偏光状態に関係なくすべて吸収する理想的な熱放射体。
これは同一温度の熱放射体の中で,どの方向,どの波長でも最大の分光放射輝度をもつ。完全放射
体ともいう。
6) 黒体空洞 黒体を近似的に実現するために,不透明な壁で形成した空洞で,測定用の開口をもつ。
7) 黒体炉 黒体空洞と加熱又は冷却機構をもつ装置。
8) 輝度温度 特定の波長又は波長帯において,測定物体の放射輝度に等しい放射輝度をもつ黒体の温
度。
9) 分光放射輝度 放射輝度の分光密度。
10) 放射率 物体の放射輝度と,物体と同じ温度にある黒体の放射輝度との比。
11) 空洞放射率 黒体空洞壁が均一な温度にある場合の黒体空洞の開口の特定な方向への放射率。
12) 空洞反射率 特定の方向から黒体空洞の開口に入射した放射のうち,黒体空洞内で反射して開口か
ら再び出てくる放射の割合。
3
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4. 性能
4.1
測定範囲 測定温度の下限値と,上限値の範囲で表す。レンジ切換え機能をもつときには,レンジ
ごとの範囲を表示する。
4.2
精度定格 保証する精度定格を温度± [ ] ℃で,又は表示温度に対する百分率± [ ] %で表す。
表示方法がこれと異なるとき及び精度定格が測定レンジ又は測定温度で異なるときは,これを明示する。
また,温度表示と温度出力をもつもの,又は複数の温度出力をもつ場合には,いずれに関する精度定格か
を明示する。
4.3
基準動作条件 周囲温度23±5℃,相対湿度35〜75%とする。これと異なるときには,その条件を
明示する。
4.4
標的サイズ 標的の大きさで表すものとし,そのサイズを実現する測定距離で表す。標的サイズと
測定距離の関係を式又は図で示してもよい。必要に応じて視野角,距離係数,対物レンズ又は対物鏡の有
効径などを併記する。
4.5
面積効果 標的サイズ及びその1.4倍サイズ(面積2倍)で試験して得た示度の差及びその試験温度
で表す。他のサイズで値を併記する場合には,標的サイズに対する試験サイズの倍率を明示する。
4.6 指数n 検出器の出力特性から求まる指数nを式で表すか,又は光学特性から求まる実効波長で示す。
必要に応じて測定波長範囲を併記する。
4.7
再現性 試験して得た値及びその試験温度で表す。
4.8
分解能 試験して得た値及びその試験温度で表す。
4.9
応答時間 示度が測定範囲の0%から50%に変化する熱放射を,視野にステップ的に与えた状態にお
ける95%応答時間で表す。ただし,条件を明示する場合には,これと異なる値を表示してもよい。
4.10 温度ドリフト 正常動作条件における温度係数又は変動幅及びその試験温度(輝度温度)で表す。
4.11 ウォームアップ時間 1分以上のウォームアップ時間を必要とする場合には,その時間で表す。
4.12 変換器負荷抵抗 アナログ出力において,変換器負荷抵抗で表す。
4.13 使用温度範囲 使用可能な周囲温度の下限値から上限値の範囲で表す。
4.14 使用湿度範囲 使用可能な周囲湿度の下限値から上限値の範囲で表す。
4.15 絶縁抵抗 試験した部位,試験して得た値及び試験電圧で表す。
4.16 耐電圧 外部電源を使用する場合には,試験した部位及び試験電圧で表す。ただし,外部電源を使
用しない場合には表示しない。
5. 試験
5.1
試験の種類 試験の種類は,次による。
a) 形式試験 放射温度計の一形式について,試作又は生産初期段階で実施するもので,主として意図さ
れた性能の達成度を確認することを目的とする試験。この試験の結果に基づき製品の一般仕様を定め
性能を表示する。
b) 個別試験 個々の製品について,出荷前に実施するもので製品の良否を確認することを目的とする試
験。
なお,立会試験においては,特に規定がない限りこの個別試験を適用する。
5.2
試験項目 試験は,表に示す○印の項目について行う。
4
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1 試験の種類と試験項目
試験項目
試験の種類
外部電源を使用するもの
外部電源を使用しないもの
形式
個別
形式
個別
精度定格試験
○
○
○
○
面積効果試験(1)
○
−
○
−
再現性試験
○
−
○
−
分解能試験
○
−
○
−
応答時間試験
○
−
○
−
温度ドリフト試験
○
−
○
−
絶縁抵抗試験(2)
○
○
○
○
耐電圧試験
○
−
−
−
注(1) 走査式放射温度計には適用しない。
(2) 外部電源を使用しないもので出力端子をもたないものについては適用
しない。
5.3
試験条件
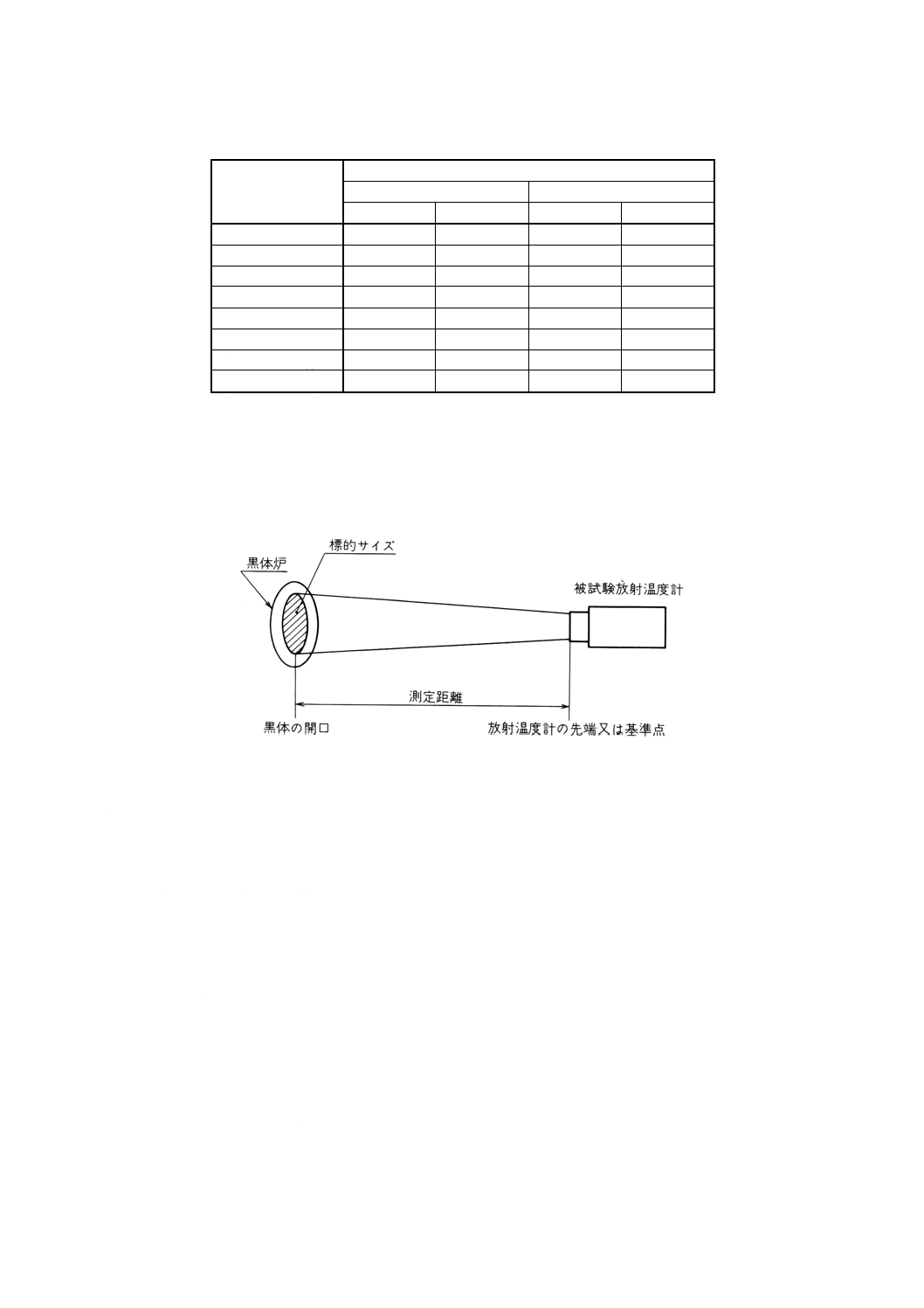
5.3.1
放射温度計の設置 黒体炉の放射エネルギーを適正に得るために,原則として図1の関係に放射温
度計を設置する(附属書1及び2参照)。
図1放射湿度計の設置
5.3.2
試験条件の設定
a) 4.3で規定された基準動作条件で試験する。
b) 測定距離は,所定の値に設置する。
c) 標的サイズは,所定の大きさを確保する。
d) 照準合わせは,適正に調節する。
e) 黒体炉は,附属書1に規定されたものを使用する。
f)
標準温度計は,附属書2に規定されたものを使用する。
5.4
試験実施方法
5.4.1
精度定格試験 所定の試験温度を与え,そのときの示度を調べる。
a) 示度の測定は,一体形の場合は附属の指示計を読み,分離形で指示計のないものは,出力値をディジ
タル電圧計で測定する。ただし,ディジタル電圧計を使用する場合は,被試験放射温度計の精度定格
に対して十分な精度をもつものを用意する。
b) 形式試験においては,被試験放射温度計の測定範囲のほぼ0%,0〜20%,20〜40%,40〜60%,60〜
80%,80〜100%及びほぼ100%の各々から一温度を黒体炉で実現して標準温度計の示度との誤差を調
べる。
5
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
c) 個別試験においては,被試験放射温度計の測定範囲の0〜30%,30〜70%及び70〜100%の各々から一
温度を,最大誤差を生じる温度が把握されている場合にはその温度を,黒体炉で実現して標準温度計
の示度との誤差を調べる。ただし,使用目的及び試験条件によって試験温度を変更することができる。
5.4.2
面積効果試験 次の方法で試験する。
a) 被試験放射温度計に規定される標的サイズの1.5倍以上の直径の開口をもつ黒体炉又は熱源で,被試
験放射温度計の測定範囲の中間付近温度 (30〜70%) に設定できるものを用意する。
b) 標的の大きさを変化させるためには,規定の標的サイズに相当する開口の絞り(以下,標準絞りとい
う。)と標的サイズの1.4倍以上の開口径をもつ絞りを用意する。
c) 5.3によって被試験放射温度計を設置し,2種の絞りを重ね合わせて標的の前面に設置する。黒体炉又
は熱源を被試験放射温度計の測定範囲の中間付近温度に設定し,十分に温度が安定した後,被試験放
射温度計の示度を調べる。引き続き,標準絞りを抜き取りそのときの示度を調べ,両者の示度を比較
して差を求める。
d) 示度の測定は,5.4.1 a)と同様に行う。
5.4.3
再現性試験 被試験放射温度計の視野に,黒体炉の放射エネルギーを遮断する遮へい板を出し入
れして示度の変化を調べる。
a) 黒体炉を,被試験放射温度計の測定範囲の50%の示度とほぼ等しい温度に設定する。
b) 遮へい板は,視野を完全に遮る大きさをもち,被試験放射温度計の示度が安定した後,遮へい板を視
野に入れ,そこで示度が平衡状態になるまでおく。この操作を10回繰り返す。
c) 毎回測定時,黒体炉温度に相当する被試験放射温度計の示度を調べ,示度変化の標準偏差σを求めて,
その2σで変化量を表す。
5.4.4
分解能試験 黒体炉を5.4.3 a)のとおりに設定して,被試験放射温度計の示度を調べ,出力に含ま
れるノイズから分解能 (N) を求める。示度の変化幅をNppとし,
2
2
PP
N
N=
を分解能とする。
ディジタル表示でノイズを無視できる場合は,表示分解能で表示してよい。
5.4.5
応答時間試験 次の方法で試験する。
a) 黒体炉を5.4.3 a)のとおりに設定して,黒体炉の温度が正しく測定できるよう被試験放射温度計を設置
する。
b) 被試験放射温度計の視野の一部を遮へい板で遮り,示度がほぼ0%になるよう遮へい板の位置を調整
する。
c) 被試験放射温度計の出力変化から応答時間を求める。ここで,遮へい板の操作は,応答時間を求める
のに支障のない速さで実行する。
5.4.6
温度ドリフト試験 次の方法で試験する。
a) 黒体炉又は輝度温度が安定な熱源を被試験放射温度計の測定範囲の中間付近温度 (30〜70%) に設定
する。
b) 被試験放射温度計の周囲温度を,正常動作条件で変化させ,ほぼ10℃間隔で示度の変化を調べる。
5.4.7
絶縁抵抗試験 電源及び入出力端子と外箱間の抵抗を500V DCで測定する。ただし,電源回路の
一部がコンデンサなどの接地要素を介して接地されている場合には,製造業者指定の電圧によって試験を
行ってもよい。
6
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.4.8
耐電圧試験 電源端子と外箱との間に,周波数50Hz又は60Hzの正弦波に近い交流電圧1 000Vを
1分間加えて試験を行う。ただし,電源電圧 (E) が150Vを超える場合には (2E+1 000) Vで試験する。
なお,電源回路の一部がコンデンサなどの接地要素を介して接地されている場合には,製造業者指定の
電圧によって試験を行ってもよい。
6. 表示 放射温度計の適当な箇所に,次の事項を表示する。
a) 製造業者の定める形式
b) 製造業者名又はその略号
c) 製造番号又は製造年月
関連規格 JIS B 0155 工業プロセス計測制御用語及び定義
JIS T 1141 医用赤外撮像装置
JIS Z 8103 計測用語
JIS Z 8113 照明用語
JIS Z 8120 光学用語
JIS Z 8706 光高温計による温度測定方法

7
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1(規定) 校正方法
1. 適用範囲 この附属書は,放射温度計の校正方法について規定する。
2. 放射温度計の校正 黒体空洞の温度を,校正しようとする放射温度計と標準として用いる温度計(以
下,標準温度計という。)とで測定し,相互の示度を比較する。
3. 校正用具 標準温度計は,放射温度計,白金抵抗温度計又はガラス製温度計を用いる。黒体炉は,標
準黒体炉と比較黒体炉との2種類とし,使用する標準温度計の種類によって分類する。
a) 標準黒体炉:標準温度計にガラス製温度計,白金抵抗温度計を用いる黒体炉。
b) 比較黒体炉:標準温度計に放射温度計を用いる黒体炉。
黒体炉の種類と校正できる温度範囲及び使用する標準温度計を,附属書1表1に示す。
附属書1表1 黒体炉の種類と温度範囲及び標準温度計
黒体炉の種類
黒体炉の温度範囲
標準温度計の種類
標準
黒体炉
低温域
−50〜300℃
ガラス製温度計
白金抵抗温度計
中温域
50〜500℃
白金抵抗温度計
比較
黒体炉
中温域
400〜1 100℃
0.9μm単色放射温度計
高温域
800〜1 500℃
0.9μm単色放射温度計
0.65μm単色放射温度計
超高温域
1 000〜3 000℃
0.9μm単色放射温度計(2 000℃以下)
0.65μm単色放射温度計
3.1
黒体炉 黒体炉の構造及び性能は,次による。
a) 黒体空洞の開口径は,校正する放射温度計の距離係数から求められる標的サイズの1.5倍以上とする
(附属書3参照)。
b) 黒体空洞は,開口径の2倍以上の深さをもち,内壁の表面放射率が0.7以上の,波長による放射率の
変化が少ない材質で構成し,その空洞反射率が0.02以下であることを確認する。ただし,同一波長域
の放射温度計相互を比較する場合,又は校正精度に対する要求が低い場合には,この条件が緩和され
る(附属書3参照)。
c) 黒体炉は,温槽又は電気炉によって黒体空洞の温度を所定の温度に保つことができ,その定常状態に
おける1分間の安定性は,±0.5℃以内とする。
d) 黒体炉が定常状態にあるときの黒体空洞の底面の温度分布(底面の中心からの温度差),及び底面の温
度に対する開口部の温度の降下又は上昇の割合は,黒体炉の種類によって,附属書1表2の値以内と
する。ただし,校正精度に対する要求が低い場合には,この条件が緩和される。(附属書3参照)。

8
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1表2 黒体炉の種類及び黒体空洞の温度分布
黒体炉の種類
底面の温度分布 開口部温度の底面温度に対する割合
標準黒体炉
±1℃
− 2%〜+0.4%
中温域比較黒体炉
±2.5℃
−10%〜+2%
高温域比較黒体炉
±5℃
−10%〜+2%
超高温域比較黒体炉
±10℃
−20%〜+4%
備考1. 底面の温度分布は,中心からの温度差で表す。
2. 開口部温度の底面温度に対する割合 (%) はケルビンで表される温度
の割合を示す。
3. 開口絞りのない円筒黒体空洞の場合には,空洞壁面の温度が附属書1
表2の割合に達する位置を開口部とみなす。
4. 絞り率の大きい開口絞りをもつ黒体空洞及び球形黒体空洞において
は,開口部温度の底面温度に対する割合を表の割合の1/2とする。
e) 黒体炉には,温槽又は電気炉における黒体空洞の開口位置又は底面位置を表示する。
f)
標準黒体炉は標準温度計が着脱でき,その設置位置が再現できる構造であって,標準温度計の示度と
黒体空洞の底面の温度は,温槽で±0.2℃以内,電気炉では±0.5℃以内で一致し,その一致を保証し得
るものでなければならない。
g) 比較黒体炉においては,黒体空洞の温度が1 500℃以下のとき,その温度を熱電温度計で測定し,定期
的に附属書2に基づく標準温度計で校正する方法を準用することができる。
3.2
標準温度計 標準温度計は,黒体炉の種類によって次のものを使用する。
a) 標準黒体炉 温槽を用いる黒体炉の場合には,±0.5℃よりもよい精度で校正された標準温度計を使用
し,電気炉を用いる黒体炉の場合には,±0.2℃よりもよい精度で校正された標準温度計を使用する。
標準温度計の校正は,JIS Z 8705及びJIS Z 8710を準用する。
b) 比較黒体炉 附属書2に基づく標準放射温度計を使用する。
4. 校正方法
4.1
校正手順
a) 放射温度計の設置及び視定方法は,黒体炉の形式によって次のとおりとする。ただし,いずれの場合
も視野欠けがあってはならない。
1) 標準黒体炉においては,光軸を合わせて開口部ないし炉底面を視定する。
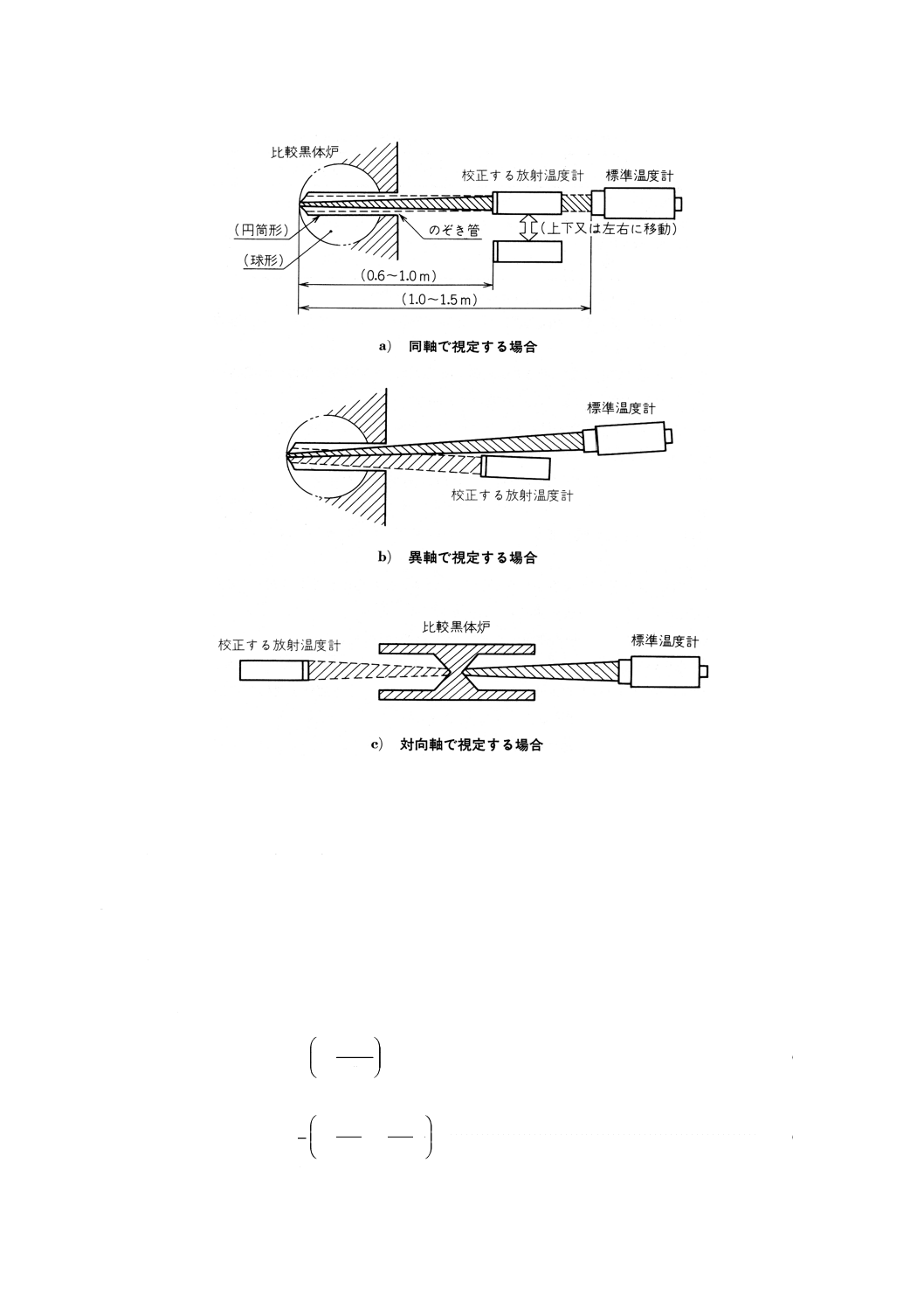
2) 中温域及び高温域の比較黒体炉においては,標準温度計及び校正する放射温度計を附属書1図1 a),
b)に示すように同一光軸上又は異軸のいずれかで設置し,開口部又は底面を視定する。
3) 高温域及び超高温域の比較黒体炉においては,前項2)による。ただし,前後が対称な構造の比較黒
体炉であって,前後の温度差が許容誤差内であることが確認されている黒体炉の場合には,標準温
度計と校正する放射温度計を附属書1図1 c)のように対向して設置し,互いの底面を視定する方法
を採用してもよい。
9
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1図1 放射温度計の配置
b) 周囲温度及び相対湿度を本体4.3に定める基準動作条件に維持する。
c) 光路を背景光や浮遊塵のない状態に維持する。
d) 黒体炉を校正する温度に設定し,3.1 c)に規定する範囲内に温度が安定することを確認する。
e) 校正する放射温度計に通電し,本体4.11に示されたウォームアップ時間を経過したことを確認する。
f)
標準温度計及び校正する放射温度計の示度を交互に,ほぼ等しい時間間隔で各2回以上読み取り,相
互の平均値の差から誤差を求める。黒体炉に温度変動がある場合には,その変動の誤差に及ぼす影響
が無視できる状態で測定する。
4.2
放射率補正 校正する放射温度計の示度は,黒体空洞の空洞放射率を用いて次のように補正する。
a) 標準黒体炉による校正の場合
T
n
S
c
−
−
=
ε
1
1
········································································ (1)
b) 比較黒体炉による校正の場合
T
n
n
S
c
s
c
−
−
−
+
=
ε
ε
1
1
1
······························································ (2)
ここに,
S: 校正する放射温度計に対する輝度温度 (K)
10
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
T: 標準温度計で測定される温度 (K)
n: 校正する放射温度計の指数n(附属書3参照)
ns: 標準温度計の指数n
εc: 黒体空洞の空洞放射率
4.3
空洞放射率の評価 黒体空洞の空洞放射率は,その空洞反射率の測定から評価することができる(附
属書3参照)。
11
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2(規定) 標準放射温度計
1. 適用範囲 この附属書は,放射温度計を標準温度計として用いる校正方法について規定する。
2. 試験
a) 0.9μm形:測定波長帯域の中心波長が0.85μmから0.95μmまでの範囲にある単色放射温度計で,中心
波長から0.1μm以上離れた波長領域における分光感度が中心波長の0.02%以下とする。
b) 0.65μm形:測定波長帯域の中心波長が0.64μmから0.66μmまでの範囲にある単色放射温度計で,中
心波長から0.1μm以上離れた波長領域における分光感度が中心波長の0.01%以下とする。
3. 特性 特性は式(1)で表し,輝度温度は式(2)で求める。
+
−
=
B
AT
c
C
V
2
exp
································································· (1)
A
B
V
C
A
c
T
−
−
=
ln
ln
/
2
····································································· (2)
ここに,
T: 輝度温度 (K)
V: 単色放射温度計の出力 (V)
c2: 0.014 388m・K(放射の第二定数)
A,B,C: 単色放射温度計固有の定数で校正によって決定する。
4. 校正
4.1
0.9μm単色放射温度計 亜鉛点,アルミニウム点,銀点,金点及び銅点黒体炉のうち3種類以上の
定点黒体炉を用い,次の方法で校正して特性式の定数を決定する。
a) 校正に先立ち単色放射温度計を乾燥した雰囲気,又は乾燥剤を交換して48時間以上おく。
b) 附属書1の4.1を準用して各定点での校正を行う。
c) 各定点における測定値の最小値と最大値の差は,亜鉛点では0.3℃,それ以外の定点では0.15℃とし,
これを超えた場合は再測定を行う。ただし,1 500℃以下の温度でだけ使用する場合は亜鉛点を0.5℃,
それ以外の定点を0.2℃まで許容する。
d) 各定点測定値を用いて,連立方程式又は最小二乗法によって式(1)の定数A,B及びCを決定する(附
属書3参照)。このときB=0.5×10−5±0.5×10−5m・Kが満たされない場合は,再度校正を行うものと
する。ただし,1 500℃以下の温度でだけ使用する場合は,B=0.75×10−5±1.0×10−5m・Kが満たされ
ない場合に再校正する。
4.2
0.65μm単色放射温度計 実効波長0.65μmの輝度温度,又は分光放射輝度の比が値付けされた光高
温計用標準電球及び銅点黒体炉を用い,次の方法で校正して特性式の定数を決定する。
a) 校正の手順は,4.1 a),b)を準用する。
b) 光高温計用標準電球で目盛特性付けを行い,4.1 d)を準用して定数を決定する。
c) 銅点黒体炉で校正し,4.2 b)で決定した定数を式(1)に代入して求まる銅点出力の計算値と比較して,
計算値が校正値と一致するように定数Cを再決定する。
d) 2 000℃以上の温度範囲は,減光装置などを用いて校正する(附属書3参照)。
12
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
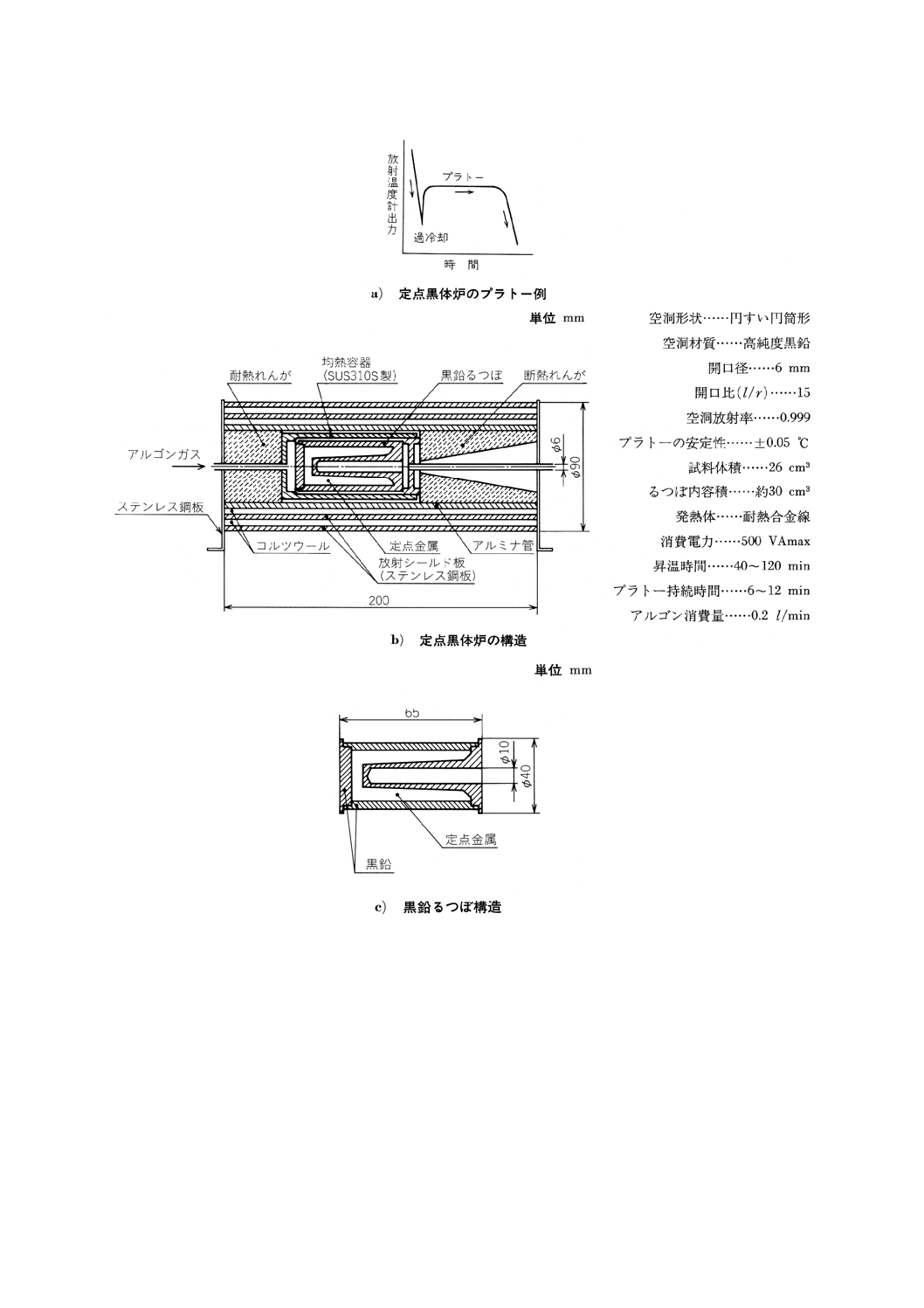
5. 定点黒体炉 中央部に黒体空洞をもつ高純度の黒鉛製るつぼに純度99.999%以上の定点用金属を鋳込
み,その潜熱によって,黒体空洞を一定期間,定点金属の凝固点温度に保つ機能をもつ黒体炉で,開口径
は6mm以上,空洞放射率は0.999以上,プラトーの持続時間は5分以上で,そのときの温度変動は0.1℃
以内とする(附属書3参照)。
6. 精度維持 単色放射温度計の精度を維持するために,同一定点黒体炉で定期的に校正し,4.による校
正値との差が出力にして0.5%以下であることを確認する。出力の変化が0.5%以上,2%未満の場合には,
その差に応じて定数Cを補正する。出力の変化が2%以上の場合には,4.に従って再校正を行うものとする。
7. 指数n 単色放射温度計の指数nは,式(1)の定数A,Bを用いて,次の式から求める。
B
AT
c
B
AT
ATc
n
2
)
(
2
2
2
+
+
=
≒
···························································· (3)
13
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3(参考) 放射温度計の特性及び校正
序文 この附属書(参考)は,本体及び附属書(規定)に関連する事柄を補足するもので,規定の一部で
はない。
1. 幾何光学的な装置定数
1.1
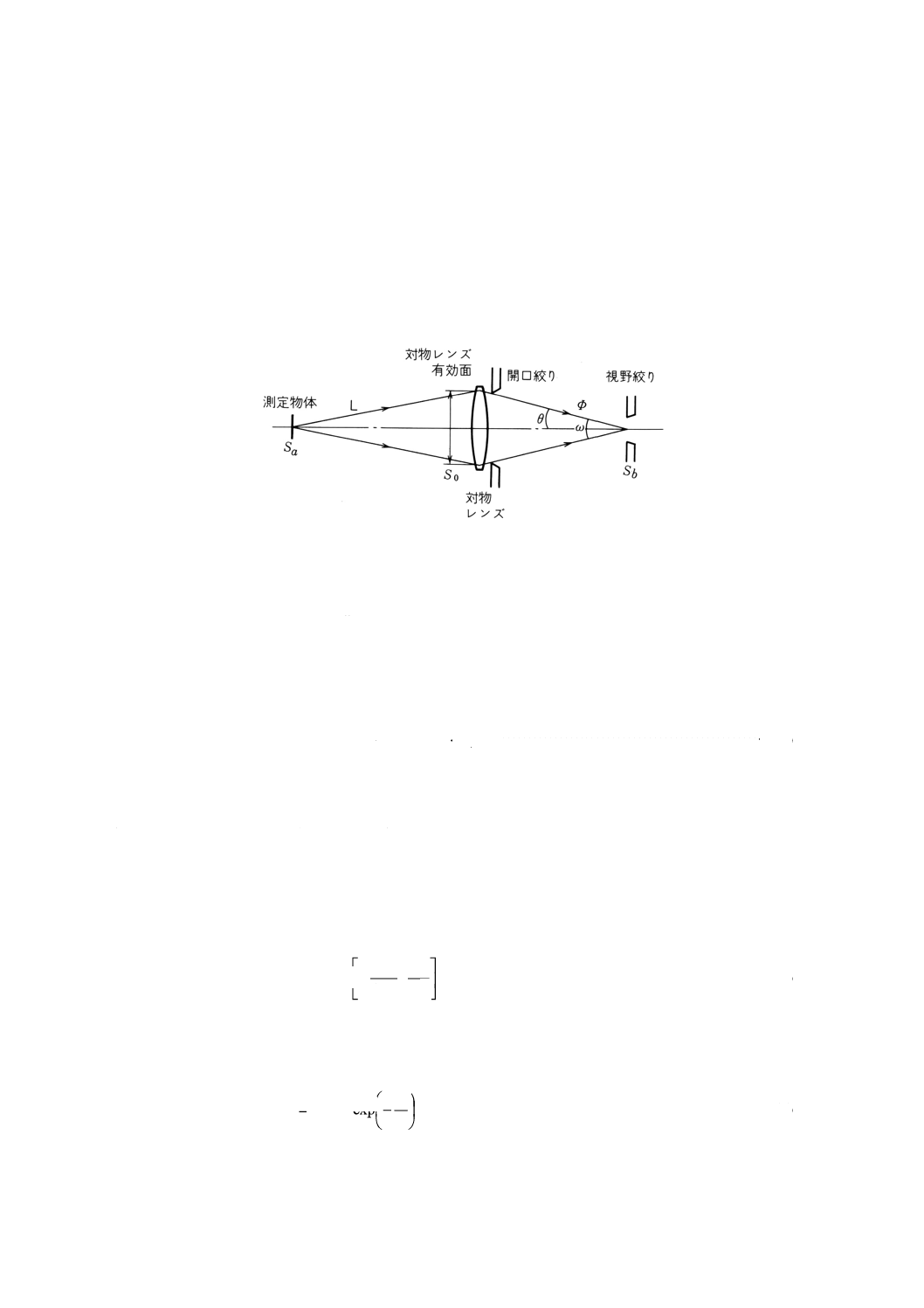
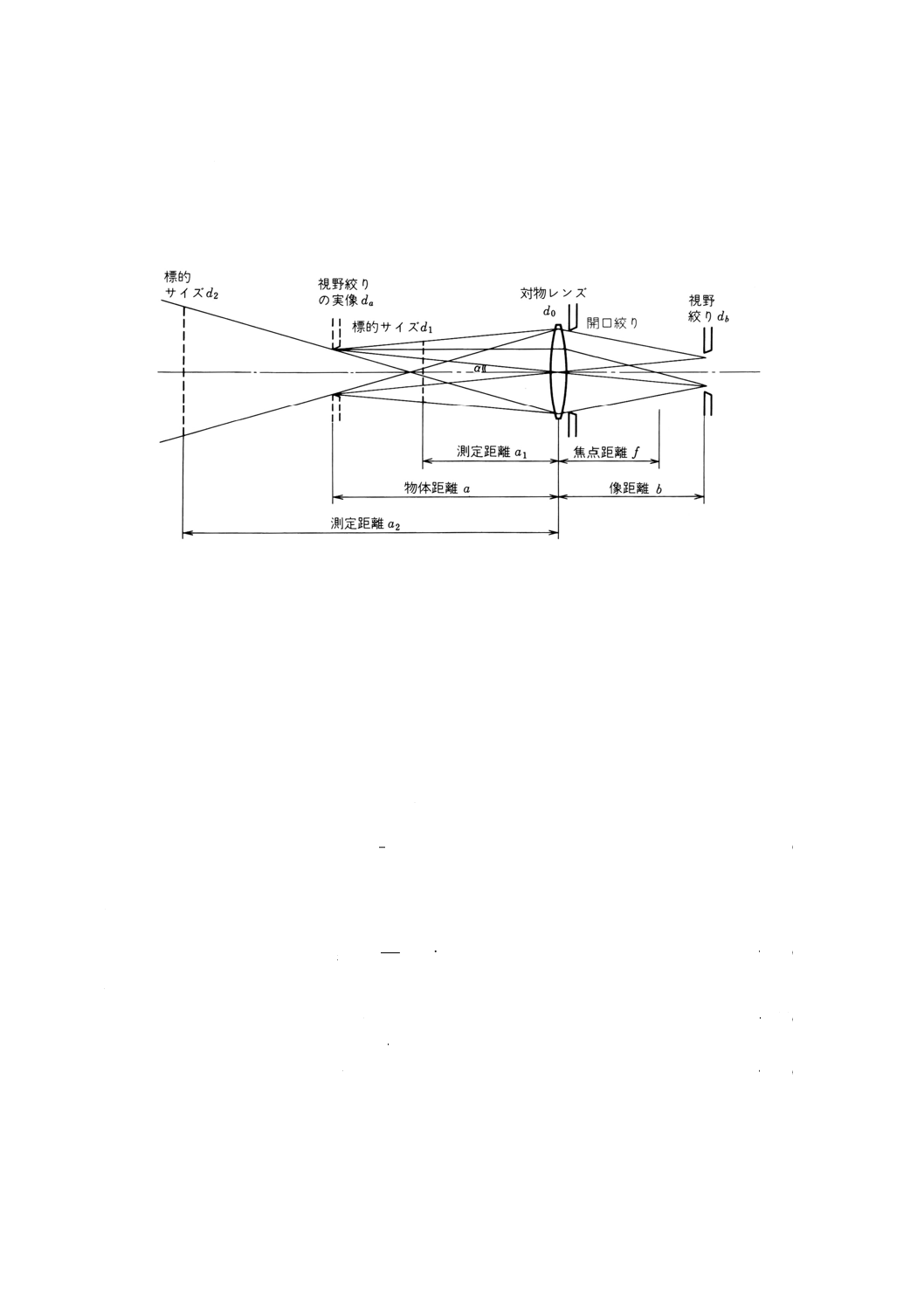
放射温度計の基本原理
附属書3図1 放射温度計の基本構成
附属書3図1のような光学系で,分光放射輝度Lλの物体の実像が,面積Sbの視野絞り(又は検出素子)
を完全に覆う状態では,視野絞りを通過する分光放射束Φλは,
Φλ=ω・Sb・τλ・Lλ
で与えられる。ここで,ωは視野絞り面の中心に対して対物レンズの有効面が張る立体角,τλは対物レンズ
の分光透過率を表す。放射温度計の検出素子の分光感度特性をSλ,光学系を含めた全体の透過帯域をWと
すると,検出器からの出力信号電圧Vは,Lλ=0でV=0となる条件下では,
∫
=
λ
τ
ω
λ
λ
λ
d
L
S
S
K
V
w
b
1
····················································· (1)
と表すことができる。ここで,K1は放射のエネルギーから電圧への変換係数である。
[式(1)は,実像が絞りの面とは異なる位置に結像していても,測定物体面が十分に大きく,それからの
放射が視野絞りSbを完全に覆っている場合にはそのままで成立する。]
放射温度計が単色放射温度計の場合,式(1)は
V=K1・ω・Sb・Sλ・τλ・Lλ・∆λ
と表される。ここで,∆λは透過帯域幅である。この電圧Vは,測定物体が黒体の場合,その温度Tと附属
書2の特性を用いて
+
−
=
)
(
exp
2
B
AT
c
C
V
······························································· (2)
となる関係で結び付けられる。ここで,A,B,Cは,各放射温度計固有の定数。このようにして,Tは出
力電圧Vから非線形変換によって求められることが分かる。
帯域幅の広い放射温度計では式(2)よりもむしろ次の式が優れている。
−
=
T
B
T
C
V
Aexp
··································································· (3)
ここで,A,B,Cは各放射温度計固有の定数である。ただし,真温度が求められるのは,測定物体が黒
14
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
体のときだけであり,一般には,放射率の補正を施してはじめて真温度が得られる。
1.2
標的サイズ 実計器における標的サイズは,面積効果を考慮して規定される。以下では,幾何光学
的関係だけから決定できるとして,その大きさを示す。
式(1)が成立するためには,測定物体の像が視野絞り(又は検出素子)を完全に覆う必要がある。この条
件を満たす最小の領域が標的であり,その大きさ(標的サイズ)は,測定距離によって異なる。
附属書3図2 標的サイズの決定
附属書3図2に,幾つかの測定距離における標的サイズの決定法を示す。図で視野絞りを対物レンズで
逆に投影して得られる実像を点線で示してある。この像がこの距離(物体距離a)での標的を表し,像の
大きさdaが標的サイズに等しくなる。
対物レンズの開口絞りが対物レンズに接近して設置されている場合には,対物レンズから物体距離まで
の標的は,視野絞りの実像の外周とレンズの有効面の外周とを結んで形成される空間を,各測定距離にお
いて,光軸に垂直に切った断面に等しい。このとき,標的サイズは標的の外接円の直径で定める。
測定距離a1,a2及びaにおける標的サイズd1,d2及びdaは,対物レンズの有効径をd0とするとき,次
のとおり算出する。
a) 測定距離が物体距離より小さい場合 (a1≦a)
0
1
0
1
)
(
d
a
a
d
d
d
a
+
−
=
·································································· (4)
ここで,d0は物体距離aにおける標的サイズである。
b) 測定距離が物体距離よりも大きい場合 (a2≧a)
0
2
0
2
)
(
d
a
a
d
d
d
a
−
+
=
································································· (5)
c) 測定距離が物体距離に等しい場合
da=a/F ···················································································· (6)
=2a tanα ················································································· (7)
=2aa ······················································································ (8)
ただし,Fは距離係数,αは視野角の1/2値である。また,式(8)は視野角2αが0.25rad (14.3°) 以下
の場合とする。
15
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1.3
距離係数と視野角 距離係数F及び視野角2αは,物体距離aと標的サイズdaの関係を表す係数であ
る。
1.3.1
距離係数F 対物レンズの焦点距離fを,視野絞りの径をdbとすると物体距離aにおける距離係数
Faは,次の式で示される。
b
a
d
f
a
f
F
−
=
1
1
······································································· (9)
物体距離aが焦点距離fに対して十分大きくf/a≪1とみなせる場合は,
b
d
f
F=
················································································· (10)
となって,距離係数Fは物体距離に関係なく固定される。
1.3.2
視野角2α 対物レンズの中心から標的サイズdaを見込む視野角2αは,距離係数Fを用いて次の
ように示される。
=
−
F
2
1
tan1
α
········································································ (11)
F
2
1
=
················································································ (12)
ただし,式(12)は視野角2αが0.25rad (14.3°) 以下の場合とする。
1.4
標的の確認機構(照準) 標的の確認機構は,使用目的に合わせて実用化されている。主な標的の
確認機構を次に例示する。
1.4.1
ファインダー方式 放射温度計本体に標的サイズを確認できるファインダーを備えている機構。た
だし,標的サイズを示す指標を備えていることが条件で,指標がないものは除く。
なお,取扱説明書などに標的サイズと測定距離の関係又は距離係数が記載される。
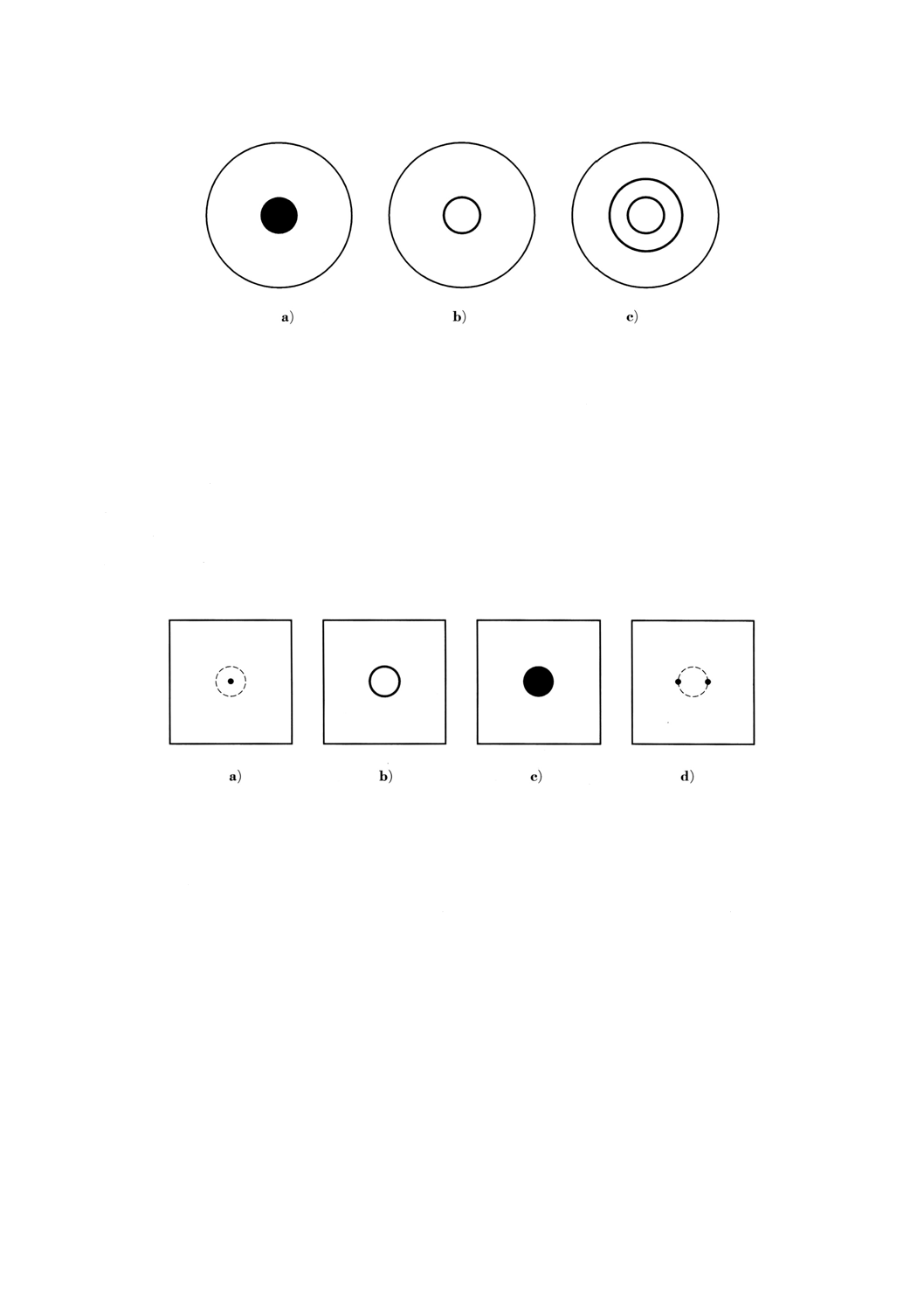
a) 黒丸方式 ファインダーを通して測定物を視定したとき,標的サイズに相当する部分を附属書3図3
のa)のような指標で視野を黒く覆うことで確認する機構。
なお,標的サイズを黒く覆うため,測定している像の確認ができない。原理的には光軸のずれが発
生しないため,ピント合わせ機構と組み合わせることで,主に標的サイズの小さな放射温度計に使用
される。
b) 一重円方式 ファインダーを通して測定物を視定したとき,標的サイズに相当する部分を附属書3図
3のb)のような指標で確認する機構で,原理的には光軸の調整機構が必要となる。
c) 二重円方式 一般的に固定焦点式の放射温度計に用いられ,ファインダーを通して測定物を視定した
とき,標的サイズに相当する部分を附属書3図3のc)のように二重の指標で確認する機構で,測定距
離が近い場合は内側の指標を用い,測定距離が遠い場合に外側の指標を使い分ける。
なお,測定距離によって標的サイズと指標の間に誤差が生じるため,標的サイズが大きい放射温度
計に用いられる。
16
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図3 ファインダー視野内の指標
1.4.2
マーカ方式 マーカ方式は測定物体にレーザ又はLEDなどを使用して光を照射し,標的又は標的
サイズを示す機構で,測定距離が比較的短い固定焦点の放射温度計に多く用いられる。
なお,取扱説明書などに標的サイズと測定距離の関係又は距離係数が記載される。
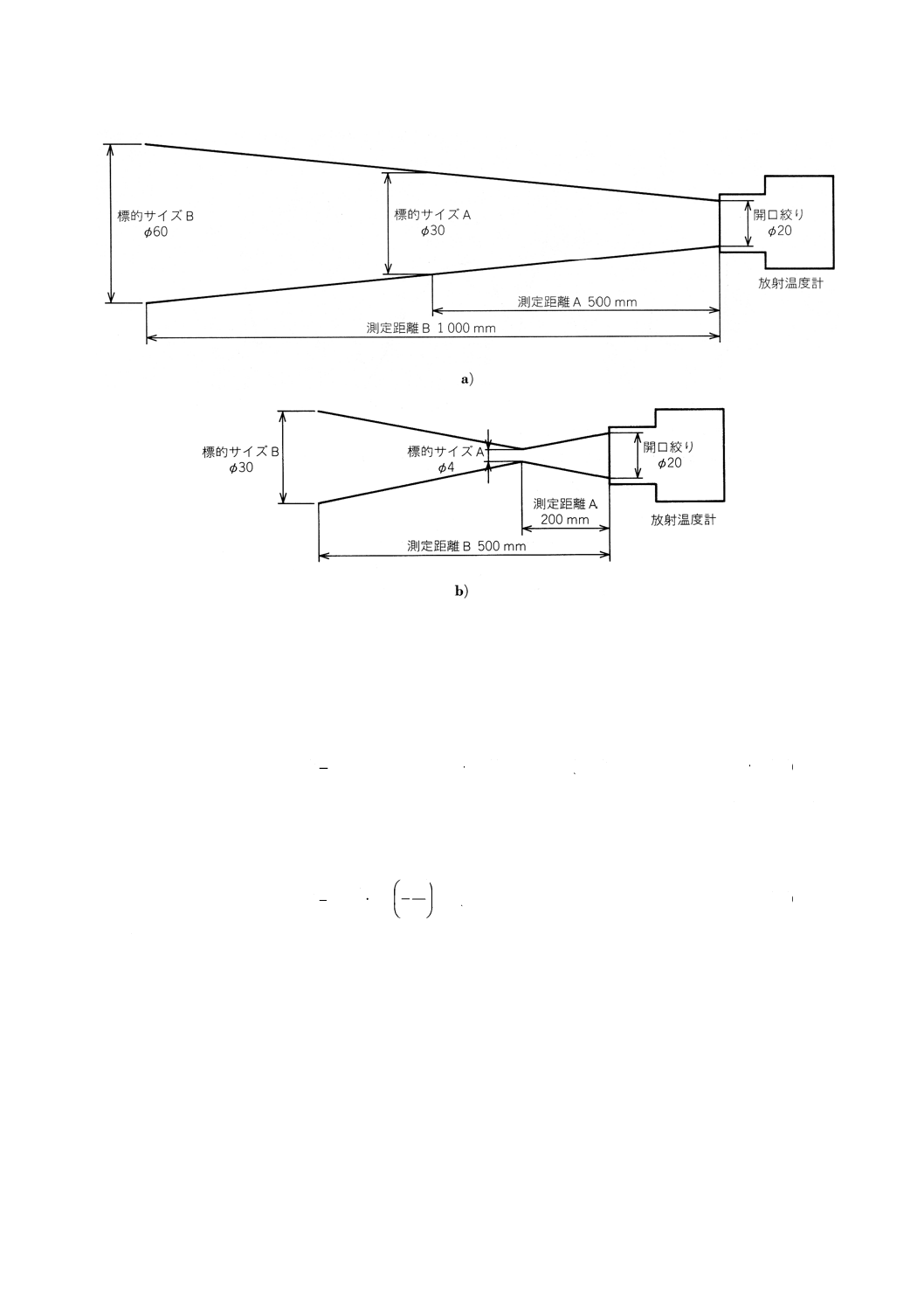
a) 測定位置照射方式 レーザ又はLEDなどを使用し,附属書3図4のa)のように標的サイズの一部に
ドットを照射し指示するため,標的サイズは分からない。
b) 標的サイズ照射方式 レーザ又はLEDなどを使用し,附属書3図4のb)及びc)のように標的サイズ
を線又は面で照射し指示するため,測定物体の標的が確認できる。
c) 標的サイズ簡易照射方式 レーザ又はLEDなどを使用し,附属書3図4のd)のように標的サイズの
二点をドットで照射し指示するため,測定物体の標的が確認できる。
備考 点線は標的サイズを示すためのもので,マーカが照射されているわけではない。
附属書3図4 マーカの照射表示の例
1.4.3
その他の方式
a) ライトガイド又はファイバ方式 温度計本体と光学系に分離できる構造で,光学系にライトガイド又
はファイバを用い,照準に当たって光学系の射出側に光源をセットし,その光学系を透過した光によ
って視定する方式。ただし,照射光に広がりがあるため標的サイズは,確認できない。
b) 温度計と照準器を交換する方式 検出器固定用架台又は水冷ジャケットから温度計を取り外し,照準
器を検出器固定用架台又は水冷ジャケットに取り付け,標的を確認する方式。
c) 照準を備えていない温度計 温度計本体には,標的サイズ又は測定位置を示す機構がないため,附属
書3図5のように取扱説明書などに測定距離と測定径の関係を記載し,標的サイズ又は距離係数を示
す。
17
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図5 取扱説明書の一例
2. 放射温度計の出力特性及び精度定格の確認方法
2.1
放射温度計の特性式 検出素子の線形性がよい場合には,温度Tの黒体に対する検出器の出力V (T)
は附属書3の式(1)と同様に次の式で求まる。
∫
+
=
)
0(
)
,
(
)
(
1
K
V
d
T
L
S
S
K
T
V
b
w
b
λ
λ
τ
ω
λ
λ
···························· (13)
ここで,Lb (λ, T) は温度Tの黒体の波長λでの分光放射輝度,V (0K) はT=0Kでの出力(オフセット)
である。これに対して,実用放射温度計の特性は,検出器の線形性がよい場合には,附属書3の式(3)と同
様に次の式
)
0(
exp
)
(
K
V
T
B
CT
T
V
A
+
−
=
·················································· (14)
で近似できる。
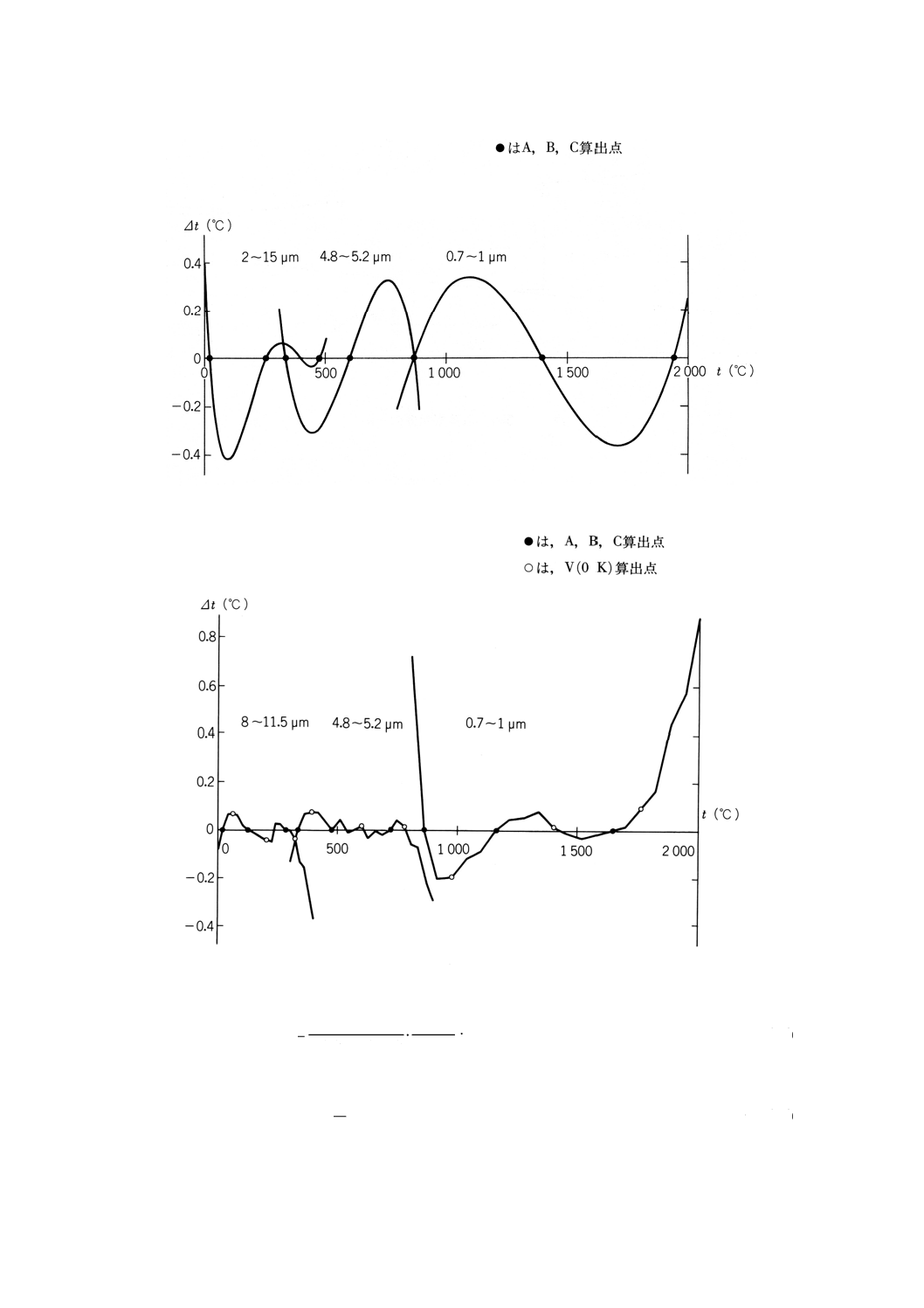
附属書3図6は,Sλ=1,フィルタの透過波長帯域Wではτλ=1,その他では,τλ=0とおき,式(13)で求
めた特性式と,これを式(14)に当てはめて得られる特性式との偏差曲線を示す。式(14)は,波長帯域が広く,
かつ温度範囲が広い場合に近似の精度が若干落ちる傾向にあるが,一般の放射温度計に対して実用的に十
分な精度の近似となる。附属書3図7は,実データに基づく例示である。
18
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図6 理想特性に対する偏差曲線
附属書3図7 実データに対する偏差曲線
放射温度計の指数nを次の式で定義する。
dT
T
dV
K
V
T
V
T
n
)
(
)
0(
)
(
−
=
·························································· (15)
出力特性が式(14)で表されるとき,指数nは
T
B
A
n
+
=
·············································································· (16)
となる。
19
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
式(14)は帯域幅の広い放射温度計,及び2色温度計の特性式として有効であり,指数nの評価,形式試
験における特性のばらつきの評価,精度定格の決定,精度定格試験における確認温度の決定などに利用で
きる。ただし,この特性式は,TをVの関数として表すことが困難で,かつ補外領域で近似の精度が低下
する欠点があって,短波長領域の単色放射温度計の特性式としては附属書2の式(1)が優れている。
2.2
定数算出方法 式(14)は,
Y (T) =V (T) −V (0K) ······························································ (17)
とおけば,
1
2
1
3
1
3
1
2
1
2
1
3
1
3
1
2
ln
1
1
ln
1
1
ln
ln
ln
ln
T
T
T
T
T
T
T
T
Y
Y
T
T
Y
Y
T
T
B
−
−
−
×
−
×
=
············································ (18)
1
3
1
3
1
3
ln
ln
1
1
T
T
T
Y
T
T
B
A
+
−
=
·················································· (19)
=
1
1
1expTB
T
Y
C
A
······································································ (20)
となって,3点の温度T1,T2,T3でのY1,Y2,Y3が与えられれば,定数A,B,Cが求まる。この関係を
利用して,V (0K) に仮の値を入れて3測定値によってA,B,Cを算出し,他の温度T4,T5,…での測定
値,V4,V5,…に対する偏差の重み付き二乗和が最低となる定数を,仮の値を与えたV (0K) を逐次変えて
計算して求める。
この逐次計算方式では,V (0K) の可変範囲をV (0K) の最終到達値付近に限定することが必要で,その
限定プログラムが重要な役割を果たす。附属書3図7の例示は,この計算方式によって,T1,T2,T3に目
盛範囲の5%,30%,70%の温度を,T4,T5,T6に15%,50%,80%の温度を取って計算したもので,黒丸
がT1,T2,T3,白丸が最小二乗法を適用したT4,T5,T6であることを表す。この方法では,T1,T2,T3の
温度の選定が得られる特性式の精度に影響を及ぼし,特に,補外領域でその影響が顕著である。
2.3
温度目盛の誤差 標準特性V0 (T) が
V0 (T) =C0・F (A0, B0, T) +D0 ····················································· (21)
である放射温度計の実際の特性V (T) が
V (T) =C・F (A, B, T) +D ·························································· (22)
であって,V (T) がT1,T2の二つの温度でV0 (T) と一致するようにC(感度)及びD(零点)を調節した
状態を想定する。すなわち,
V (T1) =V0 (T1), V (T2) =V0 (T2)··················································· (23)
この場合の任意の温度TでのV (T) とV (T0) との差∆V (T) は,式(21),(22),(23)から
∆V (T) =C [F (A, B, T) −F (A, B, T1)]
−C0 [F (A0, B0, T) −F (A0, B0, T1)] ················································ (24)
ただし,
0
2
1
2
0
0
1
0
0
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
C
T
B
A
F
T
B
A
F
T
B
A
F
T
B
A
F
C
−
−
=
·········································· (25)
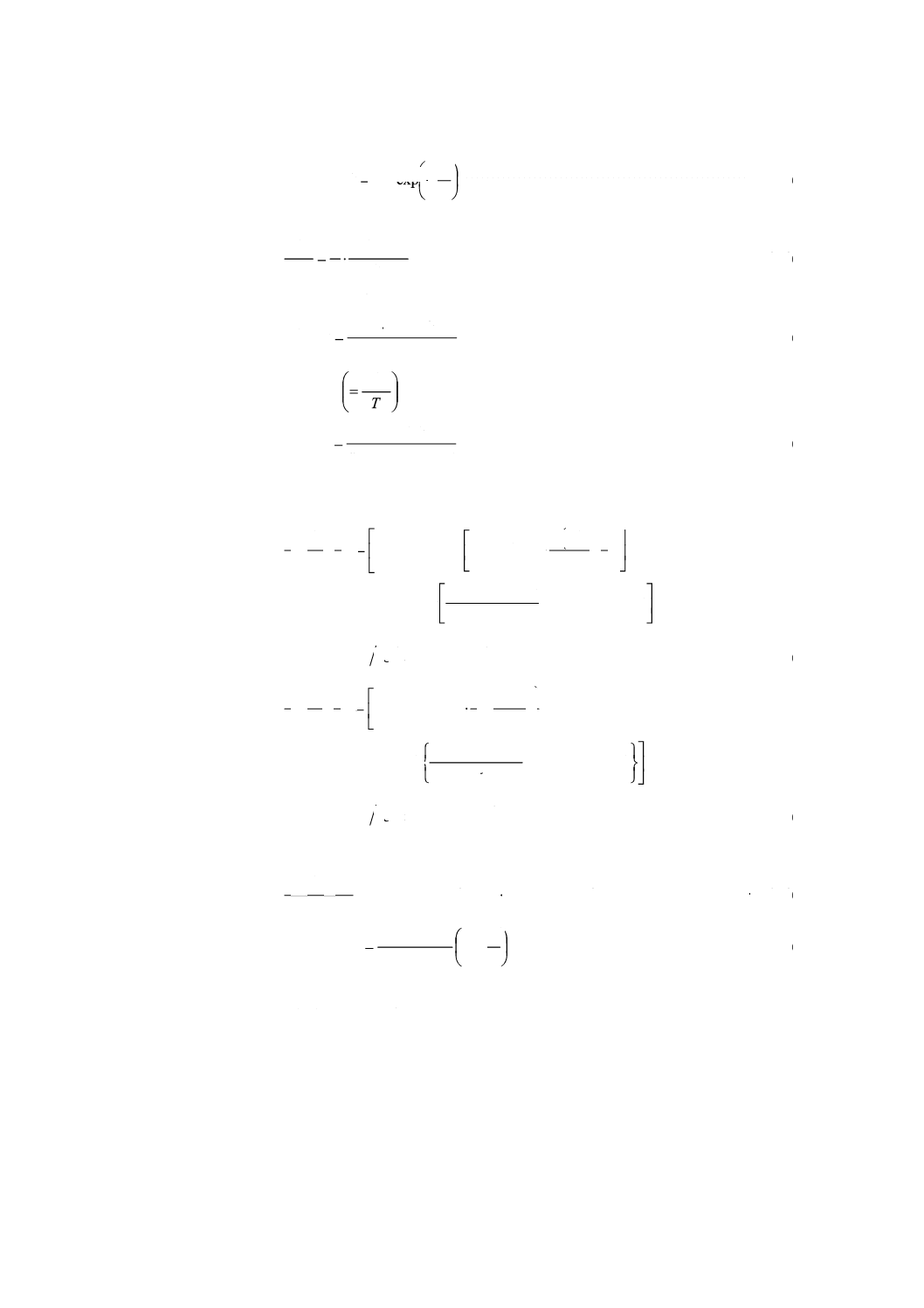
式(24)を利用すると,定数A,Bが標準特性A0,B0からずれたときに,それが温度目盛の誤差にどのよ
うに影響を及ぼすかを求めることができる。
20
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
式(22)は式(14)に等しく
−
=
T
B
T
T
B
A
F
Aexp
)
,
,
(
························································· (26)
とおける。式(15)の指数nと∆T,∆Vとの関係は,
D
T
V
T
V
n
T
T
−
=
)
(
)
(
1
⊿
⊿
··································································· (27)
となり,これから式(24)の∆V (T) を温度差∆T (T) に換算すれば
)
,
,
(
)
(
)
(
T
B
A
F
C
n
T
V
T
T
T
=
⊿
⊿
························································· (28)
が得られる。温度に対する比率
=TT
R
⊿
⊿
に換算すれば
)
,
,
(
)
(
)
(
T
B
A
F
C
n
T
V
T
R
=
⊿
⊿
························································· (29)
となる。
2.4
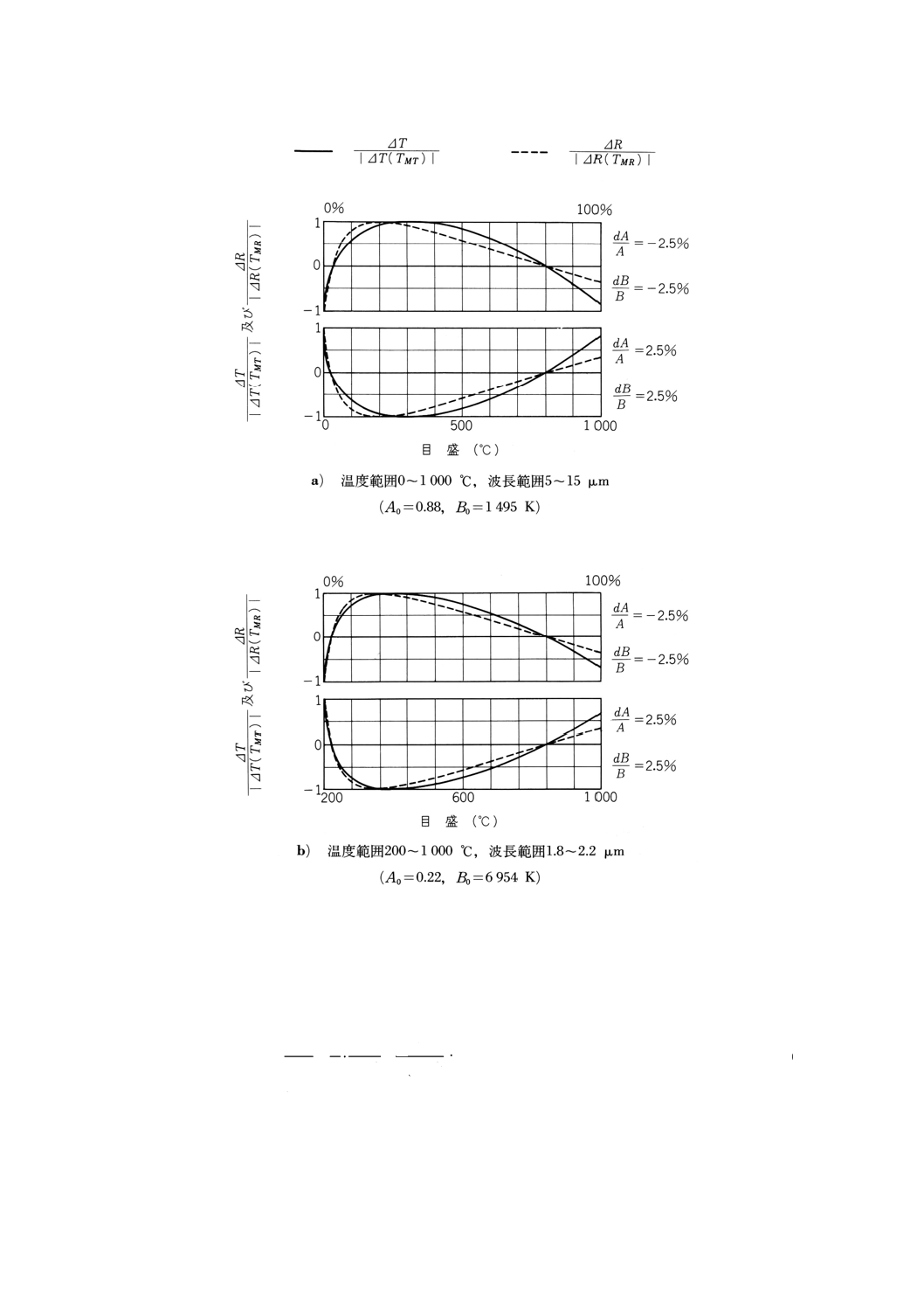
温度目盛の最大誤差 式(28)及び式(29)をTで微分すると次のようになる。
{
}
{
}
+
=
dT
T
V
d
T
T
V
T
B
A
F
n
dT
T
T
d
)
(
)
(
)
,
,
(
)
(
⊿
⊿
⊿
′
−
+
)
,
,
(
)
,
,
(
)
(
2
T
B
A
F
n
T
T
B
A
F
B
T
V
T⊿
{
}]
)
,
,
(
[
2
T
B
A
F
n
C
················································ (30)
{
}
{
}
=
dT
T
V
d
T
B
A
F
n
dT
T
R
d
)
(
)
,
,
(
)
(
⊿
⊿
′
−
+
)
,
,
(
)
,
,
(
)
(
2
T
B
A
F
n
T
T
B
A
F
B
T
V
⊿
{
}]
)
,
,
(
[
2
T
B
A
F
n
C
················································ (31)
ただし,
{
}
)
,
,
(
)
,
,
(
)
(
0
0
0
T
B
A
F
C
T
B
A
F
C
dT
T
V
d
′
−
′
=
⊿
······························ (32)
+
=
′
T
B
A
T
T
B
A
F
T
B
A
F
)
,
,
(
)
,
,
(
··············································· (33)
式(30),式(31)がT1,T2の間で零になる温度TMT,TMRを数値計算によって算出すれば,各々はT1,T2間
の温度範囲において∆T (T) 及び∆R (T) の絶対値が最大となる温度となる。この温度を式(28),式(29)に代
入すれば,T1,T2間でそれぞれに対する最大誤差が求まる。
全目盛範囲においての最大誤差は,表示が目盛範囲の0%及び100%となる温度での誤差を式(28),式(29)
から求めて∆T (TMT) 及び∆R (TMR) と比較し,絶対値の最も大きいものとして得られる。|∆T (TMT)|,|
∆R (TMR)|を全目盛範囲の最大誤差とするには,調節温度T1,T2を表示が目盛範囲の0%及び100%の温度
に近い条件で選ぶことが必要である。

21
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2.5
精度定格の確認 各々の放射温度計の特性を表す定数A,Bの標準特性A0,B0からの偏差をδA=A
−A0,δB=B−B0とおけば
F (A, B, T) =F (A0, B0, T) ・F (δA, δB, T) ········································· (34)
+
+
+
=
+
T
B
A
T
B
A
T
B
A
δ
δ
0
0
···················································· (35)
と表すことができる。ここでは,このδA,δBを用いて式(28),式(29)の右辺を
∆T (δA, δB, T) =∆T (T) ······························································ (36)
∆R (δA, δB, T) =∆R (T) ····························································· (37)
とおく。δA及びδBの変動に起因する∆T (δA, δB, T),∆R (δA, δB, T) の変動δ (∆T),δ (∆R) は,δA,δBの相
互が独立した原因だけによる変動の場合
{
}{
}2
2
)
,
,0(
)
,0
,
(
)
(
T
B
T
T
A
T
T
δ
δ
δ
⊿
⊿
⊿
+
=
································ (38)
{
}{
}2
2
)
,
,0(
)
,0
,
(
)
(
T
B
R
T
A
R
R
δ
δ
δ
⊿
⊿
⊿
+
=
································· (39)
その他の場合
δ (∆T) =|∆T (δA, 0, T) |+|∆T (0, δB, T) | ········································· (40)
δ (∆R) =|∆R (δA, 0, T) |+|∆R (0, δB, T) | ········································· (41)
で求まるとみなせ,最大誤差は式(30),式(31)から求まるTMT,TMRをTに代入することによって得られる。
精度定格は,製造条件のばらつきを反映するサンプルを選んで各々の特性を調べ,前述の方法を利用し
た検討に基づいて最大誤差の限界を評価して決定する。
精度定格試験には,最大誤差が限界値となる条件でのTMT,TMRを測定点に選ぶ。TMT,TMRには,δA,
δBの相乗効果が現れ変動するが,最大誤差が限界値を超えないことを確認する目的の試験では,前記条件
によって一温度による精度定格試験でもよいことになる。
附属書3表1にT1,T2を目盛範囲の2.5%と80%の温度にとって,式(40),式(41)を適用してδA=±0.025A0,
δB=±0.025B0とおいて得られた計算例を示す。T1,T2間の最大誤差|∆T (TMT)|,|∆R (TMR)|は,
0
A
A
δ及
び
0
B
B
δが等しい条件では,温度,波長及び波長帯域幅の影響は比較的小さく,温度目盛範囲に依存しその範
囲にほぼ比例して増大する。また,δA,δBの影響は,同率ではδBの影響が大きく,AA
δ<0.1,BB
δ<0.1で
の最大誤差は,AA
δ,BB
δにほぼ比例する。
TMT,TMRは目盛の低温側に片寄って現れ,数指nが大きい放射温度計はその傾向が顕著である。附属書
3図8に式(28),式(29)から求まる∆T (T) /|∆T (TMT)|,∆R (T) /|∆R (TMR)|の誤差曲線を例示する。精度
定格試験温度の選定には,このような∆T (T),∆R (T) 曲線による検討がむしろ有効である。
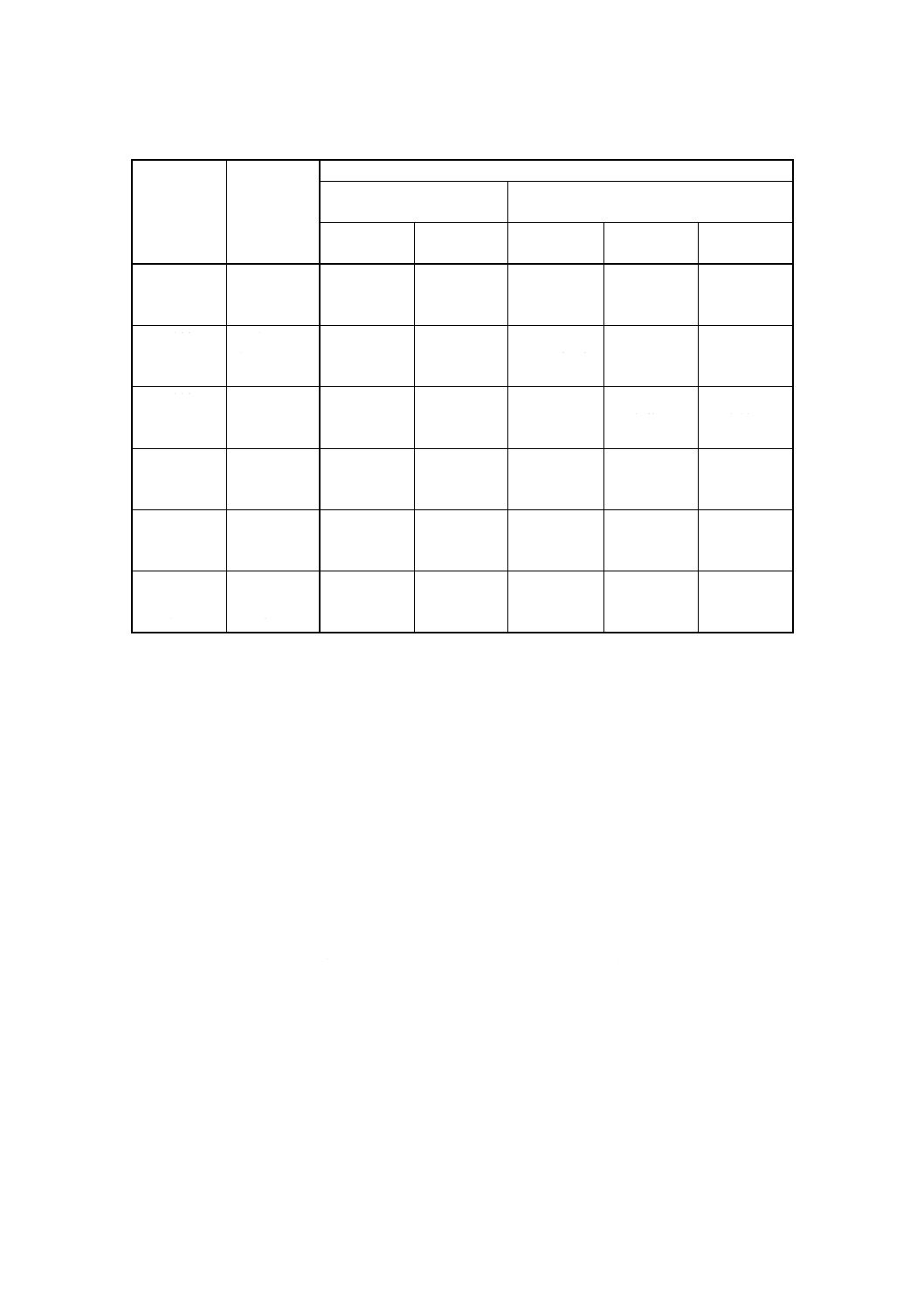
22
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3表1 最大誤差の計算例
温度範囲
及び
T1,T2
℃
波長範囲
(μm) 及び
A0,B0
K
δ (∆T) K(上段)及びδ (∆R) %(下段)
δA=2.5%
δB=2.5%
T1,T2間最大誤差
( ) はその発生温度℃
0%目盛
100%目盛
δA=2.5%
δB=0%
δA=0%
δB=2.5%
δA=2.5%
δB=2.5%
0〜500
T1=12.5
T2=400
5〜15
A0=1.04
B0=1 371
1.03
0.38
2.51
0.32
−0.95 (171)
−0.23 (126)
− 2.18 (148)
− 0.55 (110)
− 3.13 (153)
− 0.77 (113)
0〜1 000
T1=25
T2=800
5〜15
A0=0.88
B0=1 495
3.27
1.20
5.38
0.42
−2.11 (358)
−0.38 (212)
− 4.38 (279)
− 0.90 (164)
− 6.45 (302)
− 1.28 (174)
0〜1 000
T1=25
T2=800
9〜11
A0=0.83
B0=1 060
2.16
0.79
5.08
0.40
−2.39 (366)
−0.42 (231)
− 3.49 (297)
− 0.69 (182)
− 5.83 (323)
− 1.11 (196)
200〜1 000
T1=220
T2=840
1〜3
A0=2.28
B0=4 203
3.85
0.81
4.28
0.34
−2.11 (423)
−0.32 (358)
− 4.50 (384)
− 0.71 (337)
− 6.66 (392)
− 1.05 (341)
200〜1 000
T1=220
T2=840
1.8〜2.2
A0=0.22
B0=6 954
5.34
1.13
4.40
0.35
−0.17 (430)
−0.03 (349)
− 6.48 (371)
− 1.05 (323)
− 6.66 (372)
− 1.08 (323)
500〜2 000
T1=537.5
T2=1 700
0.75〜0.95
A0=1.41
B0=15 916
10.13
2.60
8.28
0.36
−0.45 (923)
−0.04 (721)
−12.59 (753)
− 1.29 (675)
−13.08 (755)
− 1.34 (675)
2.6
リニアライザ出力の精度定格の確認 リニアライザの構成や特性は,放射温度計の形式によって異
なっていて,それを個々に議論することはできない。ここでは,検出器とリニアライザを分離して評価す
る場合と,一体として総合評価する場合について一般的なガイドラインを示す。
a) 分離評価 リニアライザが放射温度計検出器出力を忠実に温度目盛に変換し,変換誤差が検出器特性
のばらつきに比べて無視でき,そのことが確認される場合には,検出器出力特性だけに着目して,精
度定格を決定し,精度定格試験を行うことができる。この場合は,リニアライザ出力を対象として精
度定格試験を実施しても結果は同じである。
リニアライザ特性のばらつきが無視できない場合には,各々の精度の和が両者を総合した精度とな
る。この場合には各々精度定格試験を実施して,最大誤差が精度定格内にあることの確認が必要であ
る。
b) 総合評価 リニアライザ出力だけに着目して総合的に精度定格試験を実施する場合には,3点以上の
温度の試験で最大誤差が評価できるようにリニアライザを構成することが望ましい。この条件が満た
されない構成のリニアライザ出力に対する精度定格試験では,さらに多くの測定点が必要である。
23
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図8 誤差曲線
3. 放射温度計の指数n
3.1
指数nの利用 黒体の温度の増加の割合∆T/Tと,それに対する放射温度計の出力の増加の割合∆V (T)
/V (T) との関係は,式(15)で定義されるnを用いて次の式で表される。
)
0(
)
(
)
(
1
K
V
T
V
T
V
n
T
T
−
=
⊿
⊿
···························································· (42)
この関係を面積効果,放射率の影響,光路吸収の影響,温度分解能などの評価のために利用することが
できる。
標的の面積効果に関しては,標的の放射輝度が同じでも,放射温度計の検出素子に入射する放射束が標
24
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
的のサイズによって変化する。標的のサイズを変化させたとき,放射温度計の出力がV (T1) からV (T1) +
∆V (T1) に増加し,そのときの示度がT1からT1+∆T1に増加したとする。温度T1における指数をn1とすれ
ば,出力増加の割合と示度増加とは,次の関係になる。
)
0(
)
(
)
(
1
1
1
1
1
1
K
V
T
V
T
V
n
T
T
−
=
⊿
⊿
························································· (43)
一方,異なる温度の標的に対して,標的サイズを前と同じだけ変化させたとき,出力がV (T2) からV (T2) +
∆V (T2) へ,示度がT2からT2+∆T2へ増加したとすると,温度T2における指数をn2として次の関係が得ら
れる。
)
0(
)
(
)
(
1
2
2
2
2
2
K
V
T
V
T
V
n
T
T
−
=
⊿
⊿
························································ (44)
標的の温度が異なっても,標的のサイズが同じだけ変化した場合には,出力増加の割合は同じと考えら
れる。すなわち,
)
0(
)
(
)
(
)
0(
)
(
)
(
2
2
1
1
K
V
T
V
T
V
K
V
T
V
T
V
−
=
−
⊿
⊿
················································· (45)
したがって,式(43),(44),(45)から
1
1
2
1
2
2
T
T
n
n
T
T
⊿
⊿
=
····································································· (46)
が得られる。式(46)を用いれば,特定の温度T1において標的の面積効果∆T1/T1が与えられていれば,他の
温度T2における標的の面積効果∆T2/T2を指数nを利用して求めることができる。
放射率の影響に関しては,出力V (T) が放射率に比例することに着目すれば,式(42)と同様の関係が成り
立つ。ここで∆Tを (T−S),∆Vを (1−εc),V=1として,黒体炉の空洞放射率の補正を与える附属書1の
式(1)及び式(2)が導かれる。
光路吸収の影響や温度分解能に関しても,対応する量を式(42)の∆VとVに代入して,温度変化と関係付
けることができる。
3.2
指数nの定数算出法 指数nは,式(14)に示す放射温度計の特性式が決定されている場合には,その
定数AとBを式(16)に代入して求められ,その定数は次に示す方法で概略値を求めることもできる。
a) 測定温度の上限と下限における指数nからの算出 製造業者が表示した,測定温度の上限Tuと下限
Tlにおける指数nu及びnlを次の式に代入し,連立方程式を解いて定数AとBを決定する。
+
=
+
=
l
l
u
u
T
B
A
n
T
B
A
n
··········································································· (47)
b) 放射率補正機構を利用する算出 放射率補正目盛上の設定位置εにおいて,設定位置をわずかな量∆ε
だけ増加させたときの示度の増加は,次の式で表される。
ε
ε
⊿
⊿
−
=
n
T
T
1
······································································· (48)
放射温度計の測定温度の上限と下限とのそれぞれの近傍において,放射率補正の設定をεからε+∆εに増
加させたとき,示度がTuからTu+∆Tuへ,及びTlからTl+∆Tlへ増加したとする。これらの値を式(48)に代
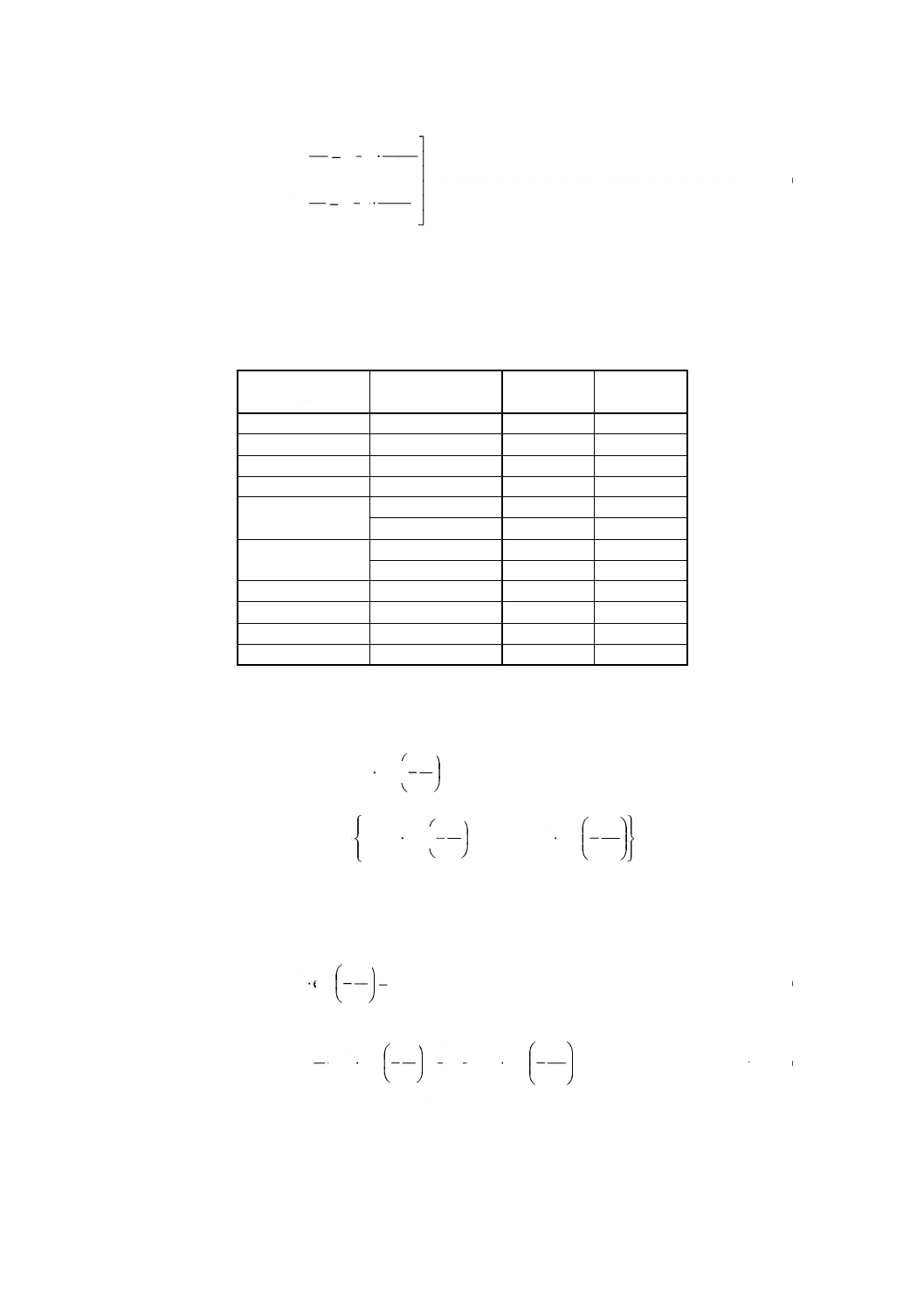
入し,nが式(15)によって定数AとBで表されることから,次の連立方程式を解いてAとBを決定する。
25
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−
=
+
−
=
+
l
l
l
u
u
u
T
T
T
B
A
T
T
T
B
A
⊿
⊿
⊿
⊿
ε
ε
ε
ε
································································ (49)
ただし,折線近似のリニアライザを使っている場合,TuとTlとしては折れ点付近を避ける必要がある。
3.3
定数値 式(16)によって各種放射温度計の指数nを求めるためのおおよその定数A,Bを附属書3表
2に例示する。定数値は測定波長帯域によって大きく変化し,測定波長帯域が同じであっても分光感度特
性の違いや温度範囲で若干変化するので,機種ごとに評価する必要がある。
附属書3表2 測定波長範囲及び温度範囲による定数A,Bの数値例
測定波長範囲
μm
測定温度範囲
℃
A
B
K
0.65
800〜2 000
0.01
22 120
0.90
400〜2 000
0.06
15 860
0.7〜 1.0
400〜2 000
0.89
14 400
0.9〜 1.8
400〜2 000
1.17
8 550
0.7〜 2.2
200〜 600
0.70
6 210
300〜 800
1.91
4 540
2.0〜 2.2
200〜 600
0.09
6 770
300〜 800
0.08
6 780
3.2〜 4.0
100〜1 500
0.43
3 678
4.8〜 5.2
0〜1 500
0.53
2 569
8.0〜11.5
0〜1 000
0.78
1 179
2 〜15
0〜1 000
3.06
681
3.4
指数nの定数による放射率補正 放射率ε,温度Tの測定物体が温度Trの壁に囲まれた状態の放射温
度計の温度指示(輝度温度)をSとする。この条件下でのε,T,Sの関係は,式(14)を利用すれば次の式に
よって表せる。
0
exp
)
(
V
S
B
S
C
S
V
A
+
−
=
0
exp
)
1(
exp
V
T
B
T
T
B
T
C
r
A
r
A
+
−
−
+
−
=
ε
ε
·················· (50)
ここで,温度Sが黒体で校正された値,A,Bが放射温度計の指数nの定数として既知であるとし,ε及
びTrがなんらかの方法で求められているとする。以上の処置がなされていて,測定物体の温度Tが放射温
度計温度表示範囲の下限値Tminと上限値Tmaxとの間にあれば,式(50)の第2項と第3項とから,
X
T
B
TA
=
−
exp
··································································· (51)
ただし,
−
−
−
−
=
r
A
r
A
T
B
T
S
B
S
X
exp
1
exp
1
ε
ε
ε
··································· (52)
X (Tmin) ≦X≦X (Tmax) ································································ (53)
式(53)は放射率補正した温度値の表示可能なXの範囲に当たり,X (Tmin),X (Tmax) は式(51)から求める。式
(52)から求めたXが式(53)を満たしていれば,測定物体の温度Tは,このXを式(51)に代入して,Tmax,Tmin
26
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を上下限値とする数値計算によって電卓でも容易に計算できる。
この方法では,放射率補正用に評価された指数nの定数A,Bが与えられていれば,放射輝度に対応す
る出力が取り出せない温度表示だけの放射温度計であっても,放射率が既知な測定物体であれば,放射温
度計による測定輝度温度だけによって放射率補正値を算出でき,測定物体を囲む壁の温度がほぼ一様であ
れば,放射温度計で測定して評価したTrを用いた測定物体周囲壁面温度の補正も可能になる。ただし,式
(50)の適用は,測定する波長・温度領域がλT>2×10−3m・Kの放射温度計に適し,λT<3×10−3m・Kの領域
の放射温度計に対しては,式(2)の利用がむしろ適する。
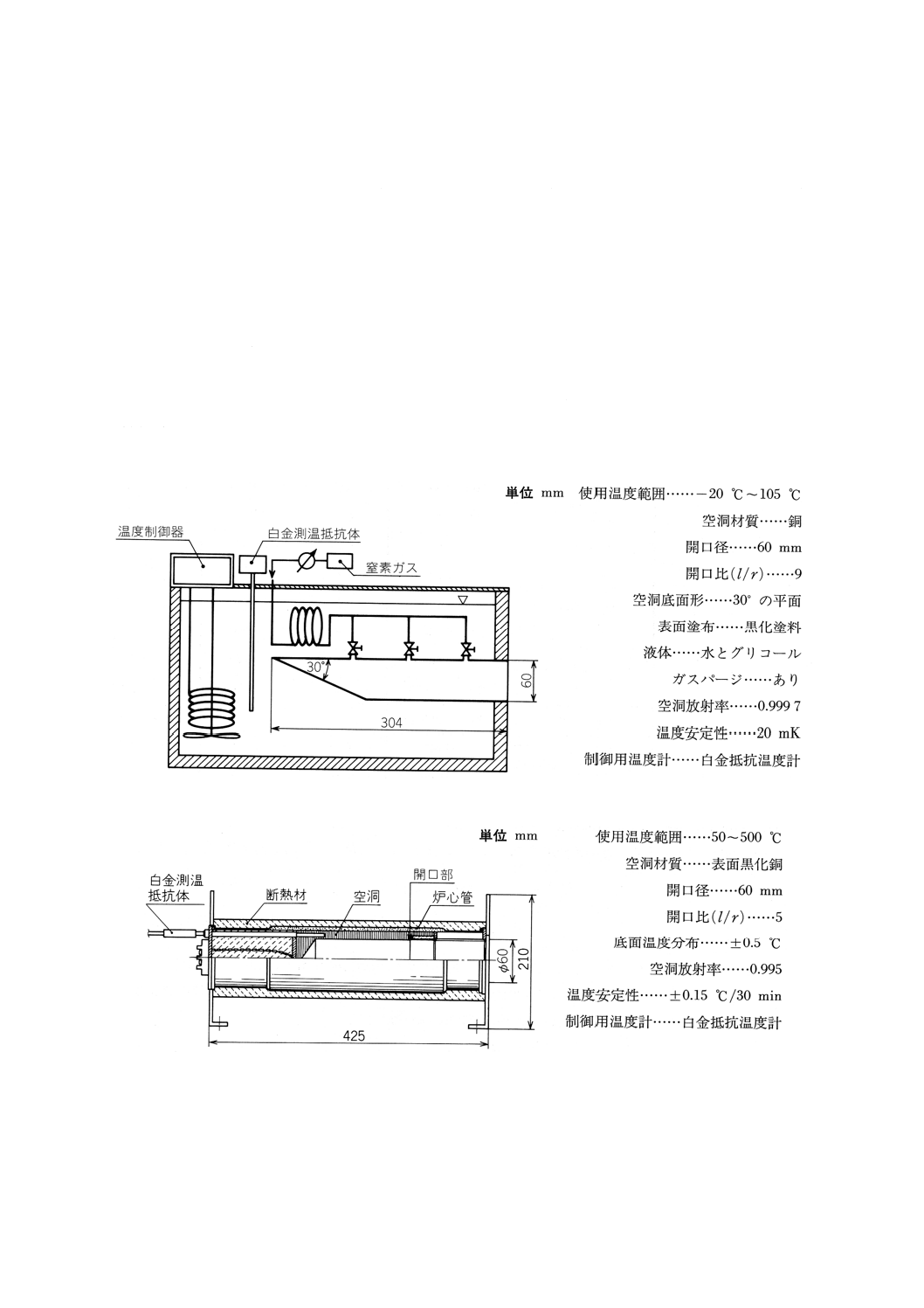
4. 黒体炉の種類及び構成例 黒体炉は,温度範囲によって利用できる発熱体や炉材などが限定され,
200℃以下の温度範囲では温槽が,1 050℃までは金属発熱体を用いた電気炉が,1 550℃までは炭化けい素
(SiC) の電気炉が,そして,3 000℃までは不活性雰囲気中で黒鉛円筒を直接通電加熱するタンマン形電気
炉が用いられる。
附属書3図9〜15に各々の温度範囲で使用できる黒体炉を,種々の空洞形状について例示する。
附属書3図9 低温域標準黒体炉
附属書3図10 中温域標準黒体炉(二重円すい形)
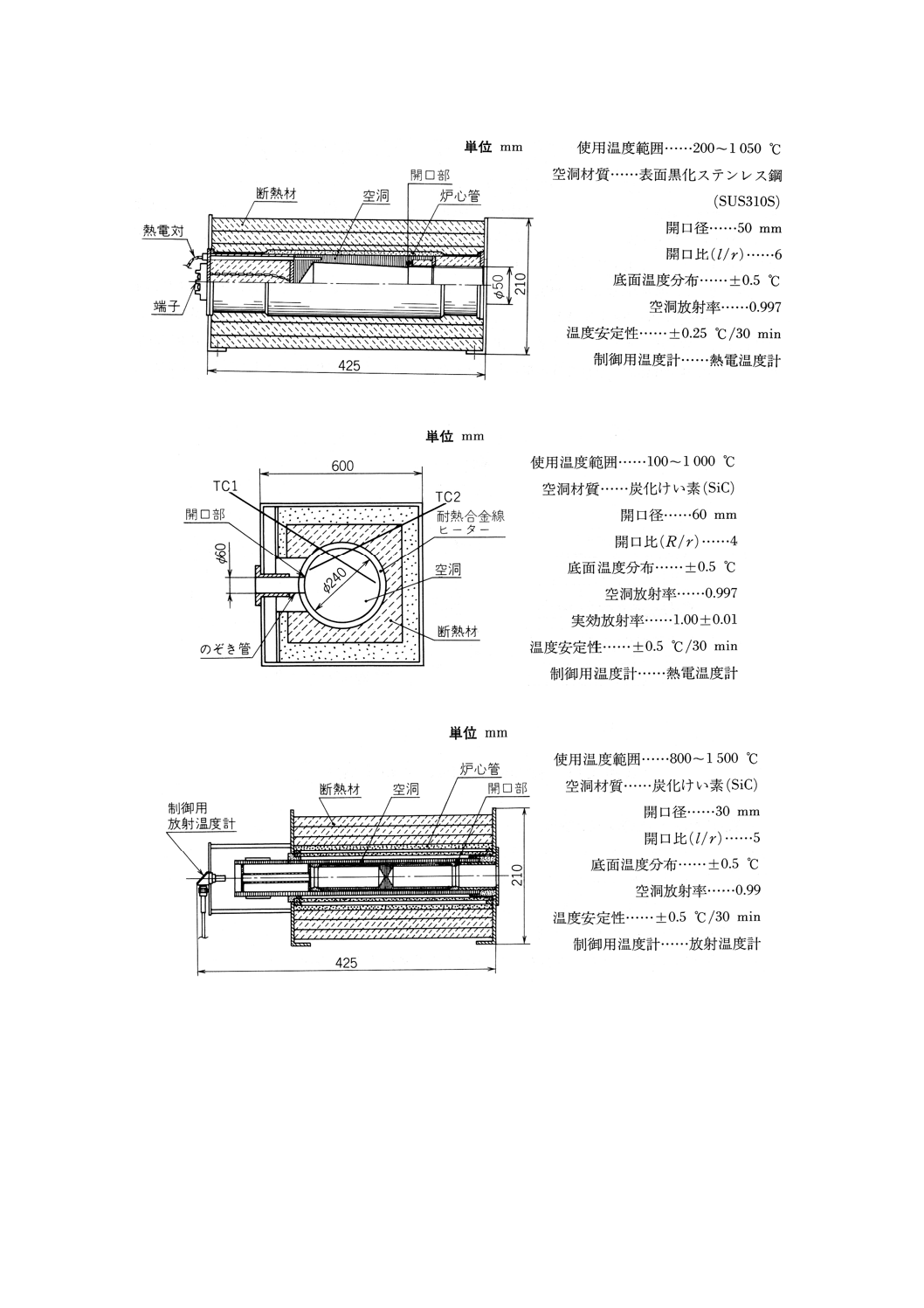
27
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図11 中温域比較黒体炉(二重円すい形)
附属書3図12 中温域比較黒体炉(球形)
附属書3図13 高温域比較黒体炉(円すい円筒形)
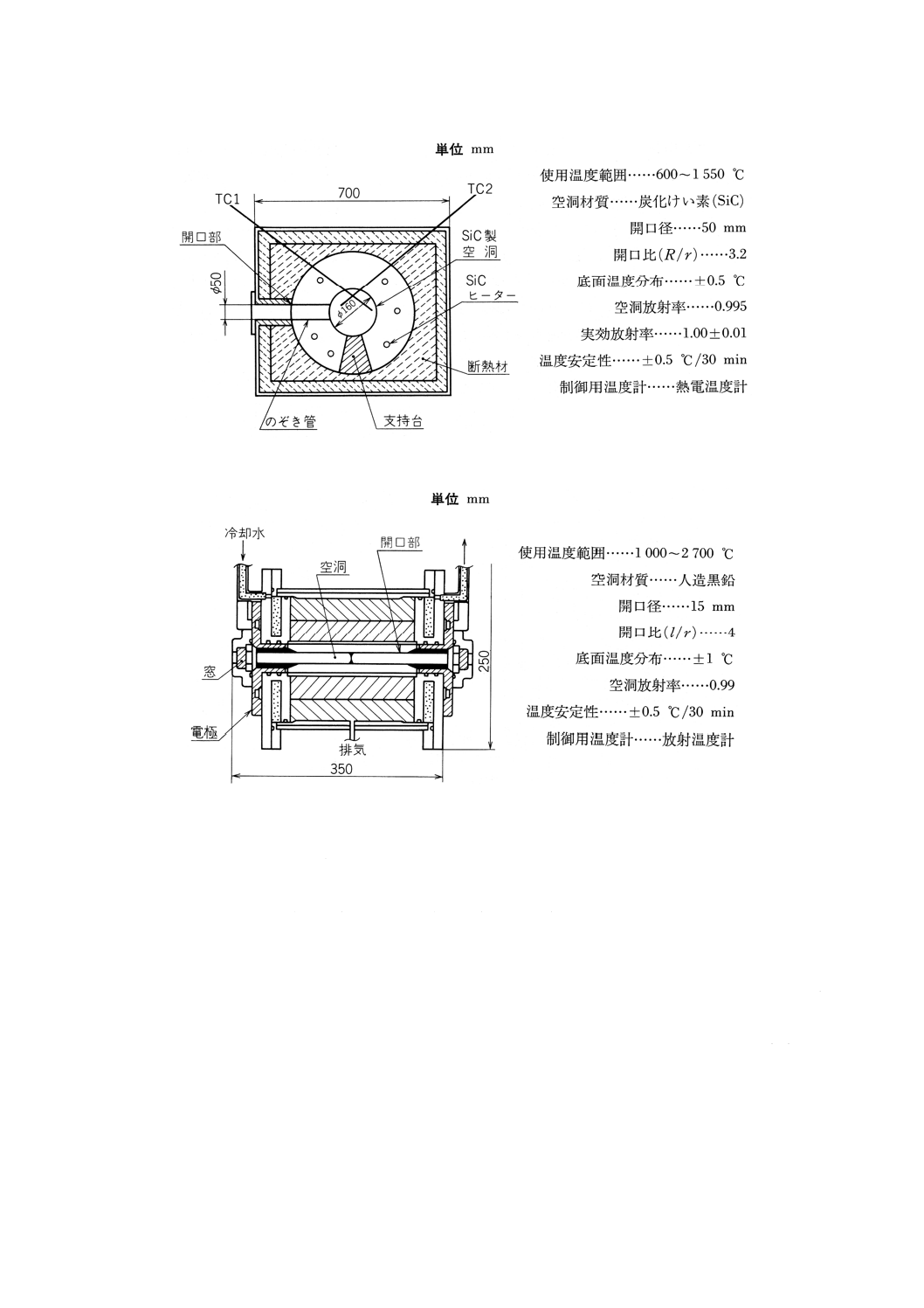
28
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図14 高温域比較黒体炉(球形)
附属書3図15 超高温域比較黒体炉(円すい円筒形)
5. 空洞放射率・空洞反射率及び空洞の実効温度 物体の放射率εは,その吸収率αに等しい (ε=α)。この
関係をキルヒホッフの法則という。この関係と放射エネルギーの保存則(吸収率α,反射率ρ及び透過率τ
の和は1となる。)から,物体の放射率とその物体の反射率及び透過率との間には,次の関係が成立する。
ε+ρ+τ=1 ············································································· (54)
物体がその内部に空洞をもち,空洞壁面上の各面素が互いに放射エネルギーを交換しているような場合
について考える。その物体が一様な温度T0にある場合,空洞壁面上のある地点の分光放射輝度L (λ) を次
の式で表す。
L (λ) =εc・Lb (λ, T0) ·································································· (55)
ここでεcは一様な温度にある空洞の放射率であり,これを空洞放射率という。壁の表面が互いに放射エ
ネルギーを交換しているような空洞の場合にも,それが一様な温度にある限り,キルヒホッフの法則が成
立する。すなわち,空洞放射率εcはその空洞の実効吸収率αcに等しい (εc=αc)。空洞壁に対して放射の透
過が無視できる場合 (τc=0) には,空洞吸収率αcと空洞反射率ρcの和は,放射エネルギーの保存則から1
29
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
となる (αc+ρc=1)。したがって,空洞放射率と空洞反射率との間には,式(54)と同様の関係が成立するこ
とになる。
εc+ρc=1 ··············································································· (56)
黒体放射を近似的に実現するために,観測用の開口をもち,不透明な壁で形成された空洞(これを黒体
空洞という。)を製作し,これを高温に加熱又は低温に冷却して所定の温度に設定することが行われる。こ
のようにして製作された黒体空洞の特性は,次の二つの要因から,理想的な黒体の特性からずれることに
なる。第一の要因は,空洞が壁によって完全に囲まれているわけではなく,開口をもつこと,第二の要因
は,空洞壁が必ずしも一様な温度でないことである。
従来は,上記二つの要因が,黒体空洞の特性に及ぼす効果をまとめて“実効放射率”によって表してい
たが,この規格では二つの要因による効果をそれぞれ別個に表すこととする。すなわち,黒体空洞が開口
をもっている効果は“空洞放射率”によって表し,空洞壁の温度が一様でないことの効果は,次に述べる
“実効温度”によって表す。
5.1
実効温度 黒体空洞の実効温度Teは,次の式で定義される。
L (λ) =εc・Lb (λ, Te) ·································································· (57)
ここでL (λ) は,いま考えている黒体空洞の分光放射輝度である。式(55)と式(57)とを比較して,温度が
一様な黒体空洞では,実効温度は空洞の温度に等しい (Te=T0) ことが分かる。
一般に放射温度計は,黒体空洞の底面を観測するから,空洞底面の分光放射輝度に着目する。空洞内で
は壁面の各点から出射された熱放射が多重反射を行っており,結果としてその総和が観測される。したが
って,空洞底面の分光放射輝度は,壁面の各点から出射された放射を,ある割合で重み付けした総和とし
て次の式のように表される。
∫
=
ds
T
L
W
L
x
b
x
)
,
(
)
(
λ
λ
··························································· (58)
ここでTxは,位置xでの空洞壁の温度,Wxは位置xから出射した放射が分光放射輝度に寄与する割合を
表す重み関数で,壁面の放射率と空洞の形状によって決まるものであり,dsは壁面上の面積素片で,積分
は空洞の壁面上で行う。
一様な温度 (T0) の黒体空洞の場合,式(58)は
∫
=
ds
W
T
L
L
x
b
)
,
(
)
(
0
λ
λ
··························································· (59)
となる。式(55)と式(59)とを比較することによって,空洞放射率と重み関数とは,次の関係にあることが
分かる。
∫
=
ds
Wx
c
ε
············································································ (60)
温度が一様でない黒体空洞の場合,T0を参照温度(普通空洞底面の温度を参照温度にとる。)として,
実効温度 (Te) と位置xでの空洞壁の温度 (Tx) をT0から差分で表す。
∆Te=Te−T0 ············································································ (61)
∆Tx=Tx−T0
式(61)を用いて,式(57)と式(58)のそれぞれの右辺をテーラー展開すれば,
+
+
=
e
b
c
b
c
T
dT
T
dL
T
L
L
⊿
0
0
0
)
,
(
)
,
(
)
(
λ
ε
λ
ε
λ
···································· (62)
30
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
+
+
=
∫
∫
ds
T
W
dT
T
dL
ds
T
L
W
L
x
x
b
b
x
⊿
0
0
0
)
,
(
)
,
(
)
(
λ
λ
λ
······················ (63)
となって,式(62)と式(63)の右辺の第1項は互いに等しく,式(62)と式(63)が第2項まで近似できる条件
においては次の式を得る。
∫
=
ds
T
W
T
x
x
c
e
⊿
⊿
ε
1
··························································· (64)
式(64)は,温度だけの関数であって,波長は依存しない。すなわち,Wxの波長による変化が無視できる
条件では,∆Te(したがって実効温度)は,波長によらず一定と考えることができる。
式(64)は,∆Tx/T0が十分小さい場合に成立する。これに対して∆Tx/T0が相対的に大きい場合は,式(62)及
び式(63)のそれぞれの右辺の第3項以上の項が有意となって,Teは波長依存性をもつことになる。
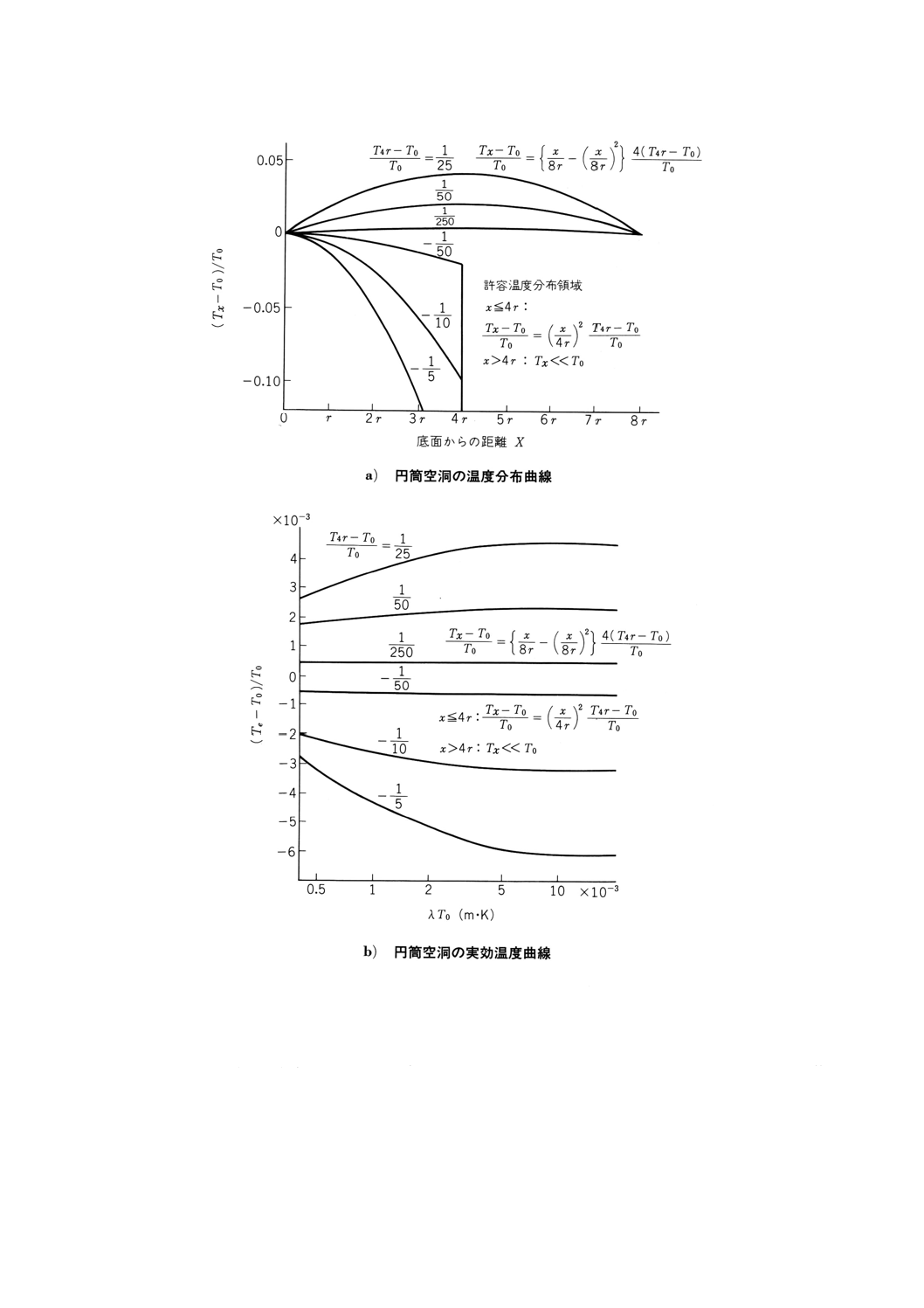
附属書3図16に温度分布をもつ円筒空洞の実効温度を示す。空洞壁を完全拡散性の壁面と仮定しその放
射率を0.75とした計算例である。附属書3図16 a)は,計算において用いた円筒空洞の温度分布を示す。r
は円筒の半径である。図中のパラメータは空洞底面から4rの位置における温度上昇の割合 [(T4r−T0) /T0]
を示す。温度分布は,いずれも二次式で表されるとし,その関数形を図中に示した。
31
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図16 円筒空洞の実効温度計算例
附属書3図16 b)には,温度上昇の割合をパラメータとし,波長と温度の積に対する実効温度を示す。温
度上昇の割合が附属書1表2の標準黒体炉に許容されている−2%から+0.4%の間では,実効温度と空洞底
面の温度差の割合 [(Te−T0) /T0] は±0.1%以内に入っている。これは,T0=1 000Kとしたとき,標準黒体
炉の実効温度と標準温度計が示す空洞底面の温度との差が±1℃以内であることを示すものである。
温度上昇の割合が附属書1表2の中温域及び高温域比較黒体炉に許容されている−10%から+2%の間で
は,λT0が0.5×10−3から10×10−3m・Kまで変化したとき,実効温度は,T0に対する割合で0.1%以内の変
32
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
化である。また,波長0.9μmの標準放射温度計とT0=1 000Kの比較黒体炉を用いて,他の波長の放射温度
計を校正する場合の誤差は,実効温度の差の割合で表すと±0.05%以内に入っている。すなわち,実効温
度の誤差は±0.5℃以内と評価される。
温度上昇の割合が附属書1表2の超高温域比較黒体炉に許容されている−20%から+4%の間ではλT0が
0.5×10−3から10×10−3m・Kまで変化したとき,実効温度は,T0に対する割合で0.3%以内の変化である。
また,波長0.65μmの標準放射温度計とT0=2 000Kの比較黒体炉を用いて,他の波長の放射温度計を校正
する場合の誤差は,実効温度の差の割合で表すと±0.15%以内に入っている。すなわち,実効温度の誤差
は±3℃以内と評価される。
実効放射率εeとεc,Teとの関係は
εe・Lb (λ・T0) =εc・Lb (λ・Te) ·························································· (65)
で表され, (Te−T0) /T0がλT0によって変化する領域では,εeが大きく変化する。そのために,実効放射率
を表示する場合は,εeとλ,T0との関係を明示することが必要である。
なお,εeに対してはキルヒホッフの法則は一般的には成立しない。
5.2
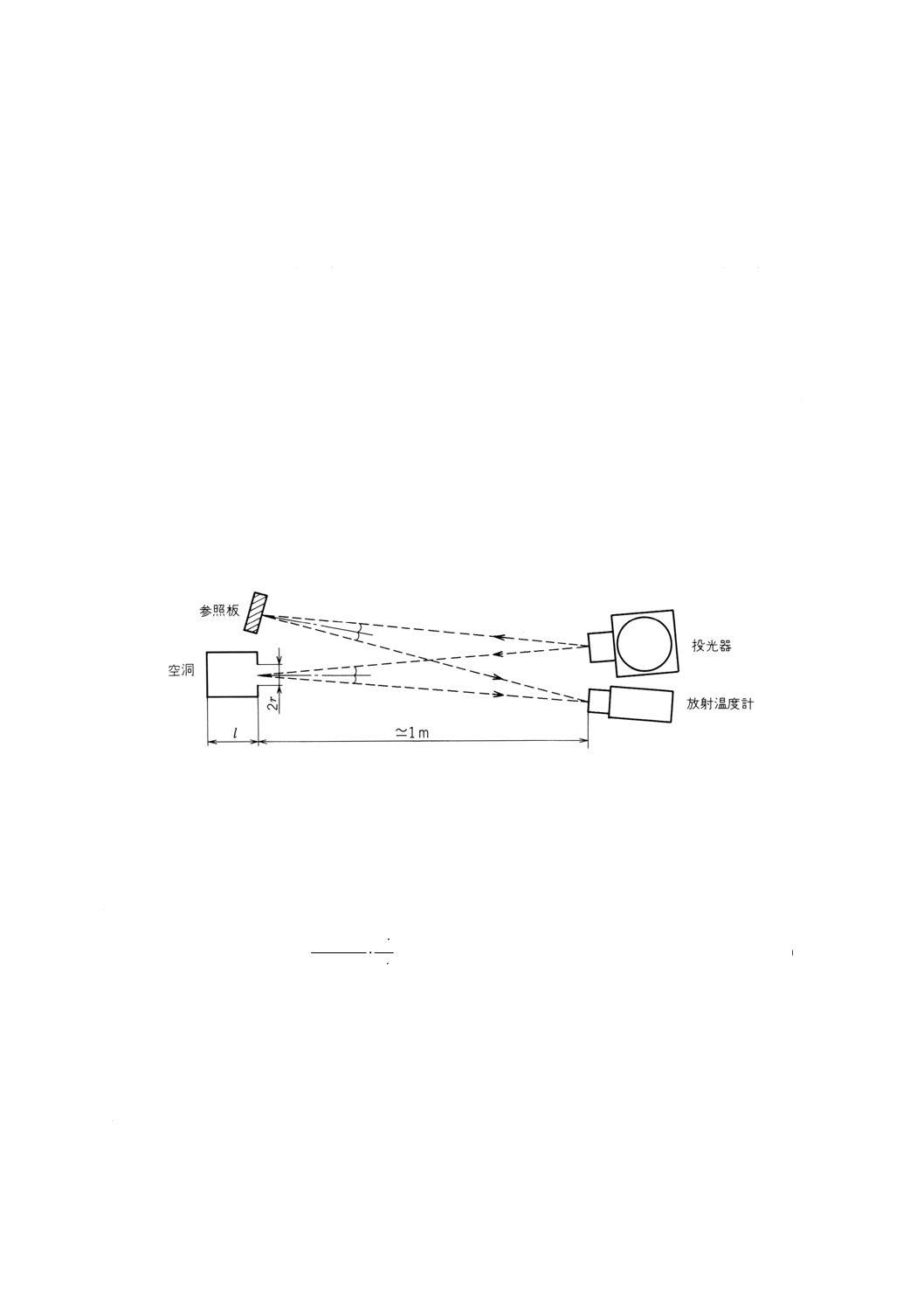
空洞反射率の測定 黒体空洞の空洞反射率は,次の方法によって測定して求める。
反射率が0.95以上の完全拡散面とみなせる石こう又は硫酸バリウムで作った参照板及び空洞体の開口を,
放射温度計と点灯した投光器(スライドの投影機で可)から約1m以上離して附属書3図17のようにセッ
トし,次の手順で計測する。
附属書3図17 空洞反射率の測定
a) 投光器と放射温度計を空洞の開口に視定し,そのときの放射温度計の読みをV1とする。
b) a)の状態で,投光器の全面を完全に遮光し,このときの放射温度計の読みをV10とする。
c) 次に投光器と放射温度計を参照板に視定し,そのときの放射温度計の読みをV2とする。
d) c)の状態で投光器の全面を完全に遮光し,このときの放射温度計の読みをV20とする。
e) a)〜d)の測定値を用いて次の式によって,空洞の反射率を求める。
2
2
20
2
10
1
l
r
V
V
V
V
−
−
=
ρ
······································································ (66)
ここで,lは空洞の深さ,rは空洞開口の半径である。
開口絞りがない円筒空洞及び円すい円筒空洞の場合は,附属書1表2の備考2.によって求まる開口
部の位置と空洞底面との距離をlとする。
f)
このとき円筒空洞では,1.4ρ<0.02,球形空洞で1.6ρ<0.02,頂角120°の円すい円筒空洞及び二重円
すい空洞で2.0ρ<0.02であることを確認する。
5.3
空洞放射率の評価 5.2で求めた空洞反射率ρを用い,空洞放射率εcを空洞の形式によって次の式で
評価する。
33
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 絞りが炉内にある円筒空洞
εc= (1−1.1ρ) ±0.3ρ ······························································· (67)
b) 球状空洞
εc= (1−1.2ρ) ±0.4ρ ······························································· (68)
c) 絞りが炉内にある円すい円筒及び二重円すい空洞
εc= (1−1.5ρ) ±0.5ρ ······························································· (69)
d) 絞りが炉内にない円筒空洞
04.1
1+−
=
ρ
εc
·············································································· (70)
e) 絞りが炉内にない円すい円筒空洞
02
1+−
=
ρ
εc
··············································································· (71)
ただし,二重円すい空洞は,その開口を絞りとみなす。
6. 0.65μm単色放射温度計の2 000〜3 000℃の温度域における校正
6.1
減光装置による校正 2 000〜3 000℃の温度域の校正は,光高温計で用いられる高温測定の方法を準
用し,0.65μm単色放射温度計に減光装置(NDフィルタなど)を挿入して行う。真温度Th (K) は,得られ
た見掛けの温度(測定値)T (K) を次の式に示す関係を用い補正して求める。
T
D
Th
1
1
+
=
············································································ (72)
ここで,Dは弱めの度合いの定数 (pyrometric attenuation value) である。光高温計用標準電球を用いて1
000〜2 000℃の範囲で見掛け温度Tiと真温度Thiの数組を測定し,この値を式(72)に代入してDiを求めその
平均値でDを決定する。
6.2
非線形性測定による校正 放射温度計の特性式の目盛をそのままより高温に補外する場合,入射輝
度と出力が比例すること(線形性)を確認しなければならない。放射温度計の応答度に非線形性を生じる
ほとんどの要因は検出器であり,非線形性を測定する場合,検出器だけの非線形性を測定することが多い
が,ここでは放射温度計のシステムとしての応答度の非線形性を測定する。また,光を重ね合わせる方法
としては,二つの光源の放射をビームコンジュゲータなどを用いて同じ光路で合わせる方法と,一つの光
源の放射を二つの独立した開口を用いて,別の角度から検出器に重ね合わせる方法の2通りがあり,一般
的には前者が精度が高い。ここでは後者を示す。
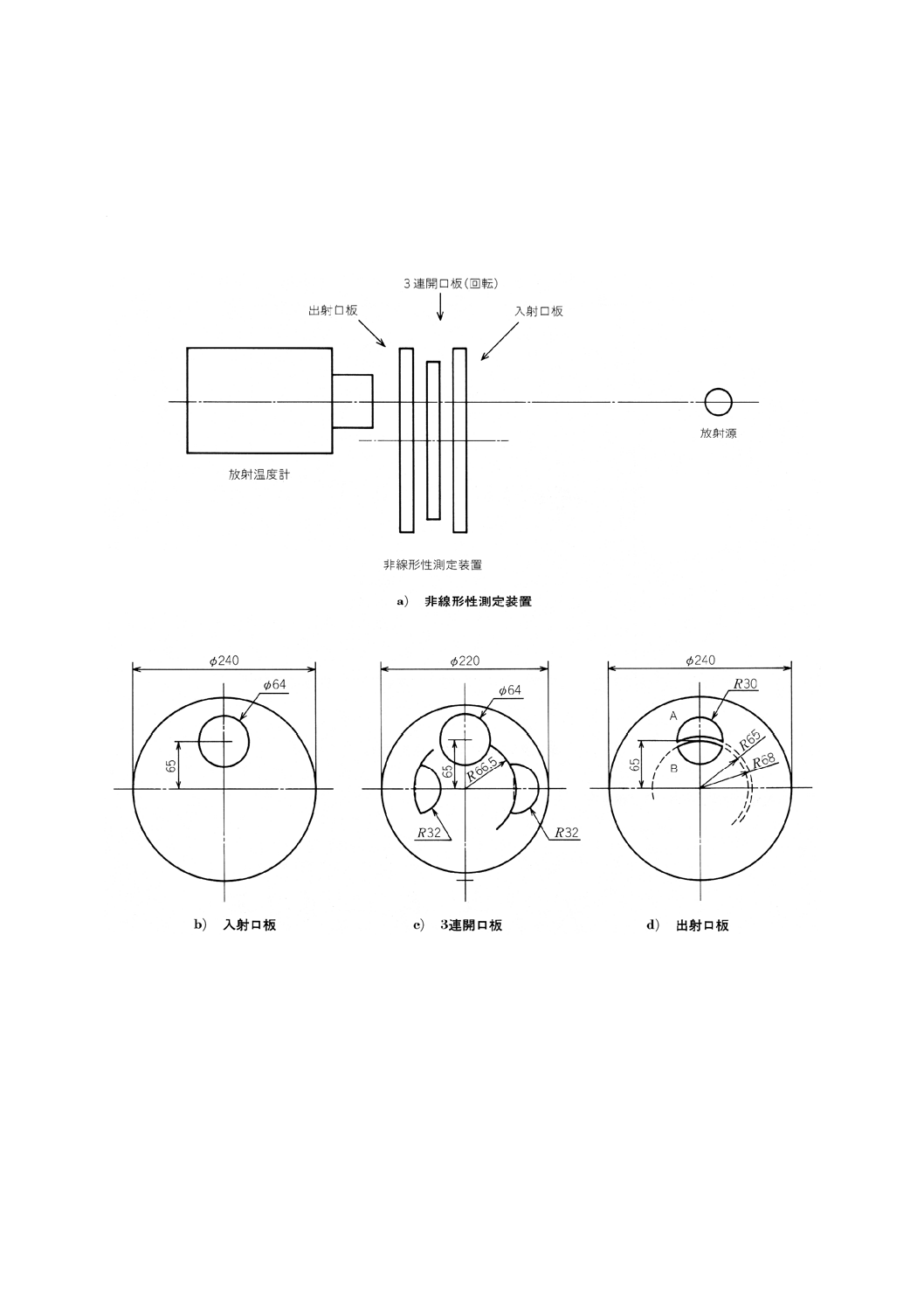
非線形性測定の原理を附属書3図18 a)に示す。放射温度計のすぐ前に二つの開口を開閉する装置をおく。
その装置は附属書3図18 b)からd)に示す三つの円盤からなる。附属書3図18 b)の入射口板は光源側の入
り口である。附属書3図18 c)の3連開口板は開口を選択する円板を90°ずつ回転させて,附属書3図18 d)
の出射口板の二つの月形の開口の部分を独立に開閉する。こうして放射温度計に入射する光量を足し合わ
せ,入射光量が2倍になったときの出力の2倍からの偏差を調べるものである。
開口AとBの状態が開と閉,開と開,閉と開,閉と閉に対応する出力をそれぞれA,A・B,B,Zとして
Z
B
A
B
A
Z
B
A
NL
−
+
−
+
=
)
(
)
(
··························································· (73)
によって非線形性NLを定義する。
光源には,標準電球を用いることによって2 000℃まで,ハロゲン電球を用いることによって2 700℃ま
34
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
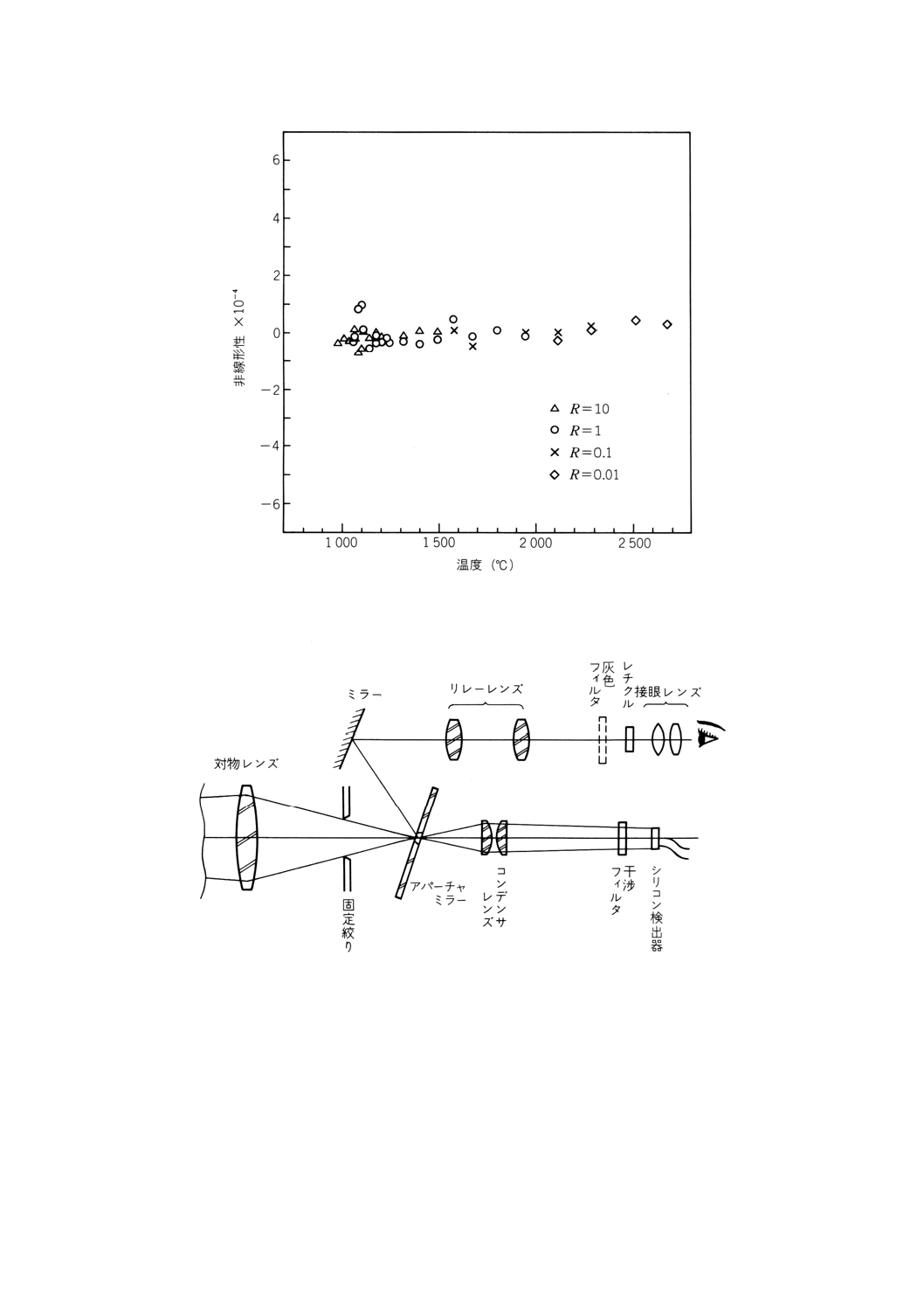
での輝度が得られる。今回使用した0.65μmシリコン単色放射温度計の非線形性を附属書3図19に示す。
横軸は,放射温度計の出力A・B−Zの輝度温度で目盛り,縦軸は式(73)のNLを10−4で示した。1 000℃〜2
700℃までNLが0.01%以下であり,この温度までは非線形性を補正をする必要がなく,特性式を補外でき
る。
なお,2 700℃での光電流は0.01mA以下である。
附属書3図18 非線形測定の測定原理及び配置例
35
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図19 非線形性測定例
7. 単色放射温度計の構成及び特性例
附属書3図20 単色放射温度計の構成例
36
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3表3 単色放射温度計の特性例
項目
0.65μm単色放射温度計
0.9μm単色放射温度計
測定波長
650nm
900nm
半値幅
15nm
80nm
視野角
0.215°
0.537°
測定距離
250mm〜∞
400mm〜∞
標的サイズ
1mm (at 250mm)
3mm (at 400mm)
(直径)
2mm (at 400mm)
測定範囲
900〜1 500℃
400〜850℃
(レンジ切換えによる)
1 050〜1 900℃
500〜1 100℃
1 250〜2 550℃
600〜1 450℃
1 550〜3 700℃
700〜2 000℃
分解能
0.1℃ (at 900℃)
0.2℃ (at 400℃)
0.01℃ (at 1 000℃)
0.01℃ (at 600℃)
面積効果
0.1%以下
0.1%以下
(出力の差)
8. 単色放射温度計特性式の定数決定方法 0.9μm単色放射温度計及び0.65μm単色放射温度計の定数は,
次の方法によって決定する。
a) 3組の校正値による場合 3組の校正値 (T1, V1), (T2, V2), (T3, V3) の場合には,次の算出式から式(2)
の定数A,B,Cを決定する。
2
1
1
T
T
X
−
=
3
1
2
T
T
X
−
=
)
/
ln(
1
2
1
2
1
V
V
X
c
Y =
)
/
ln(
1
3
2
2
2
V
V
X
c
Y =
)
)(
(
)
(
2
1
1
2
2
1
2
2
1
Y
X
Y
X
X
X
Y
Y
A
−
−
−
=
1
2
1
2
1
AT
X
X
Y
Y
B
−
−
−
=
+
=
B
AT
c
V
C
1
2
1exp
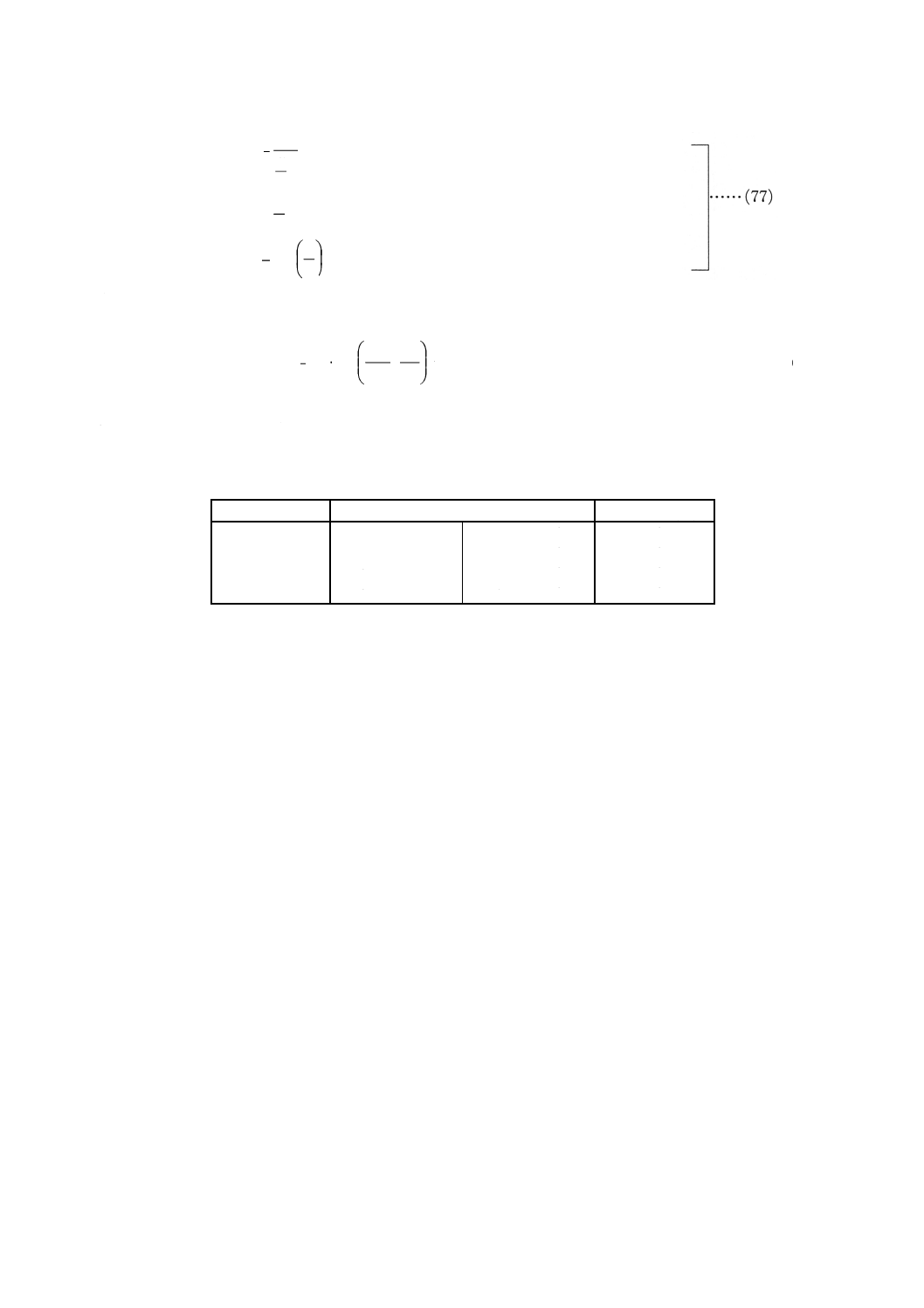
b) 3組以上の校正値による場合 各組の校正値が (T1, V1), (T2, V2),…… (Tm, Vm) の場合は,次の式に
示す正規方程式から連立方程式を解いてx,y,zを求め,これを式(77)に代入することによって,定数
A,B,Cを最小二乗法で決定する。
zm
V
y
V
T
x
T
m
i
i
m
i
i
i
m
i
i
+
+
=
∑
∑
∑
=
=
=
1
1
1
ln
ln
∑
∑
∑
∑
=
=
=
=
+
+
=
m
i
i
i
i
m
i
i
m
i
i
i
m
i
i
i
V
T
z
V
T
y
V
T
x
V
T
1
2
1
1
2
1
2
ln
)
(ln
)
ln
(
ln
∑
∑
∑
∑
=
=
=
=
+
+
=
m
i
i
m
i
i
m
i
i
i
m
i
i
i
V
z
V
y
V
T
x
V
T
1
1
2
1
2
1
ln
)
(ln
)
(ln
ln
37
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
z
x
y
c
x
A
+
=
2
A
x
y
B=
=
x
C
1
exp
c) 銅点又は銀点黒体炉での校正値による定数Cの再決定 附属書2の4.1 d)又は4.2 b)で求めた定数A,
Bを用い,銅点又は銀点(温度Tc)黒体炉による校正値をVcとして定数Cを次の式で再決定する。
+
=
B
AT
c
V
C
c
c
2
exp
······························································· (78)
9. 定点黒体炉の種類及び構成例 定点黒体炉の種類と凝固温度及び標準温度計による測定値のばらつき
は,次による。
附属書3表4 定点黒体炉の種類
種類
凝固温度
ばらつき (2σ)
亜鉛点
692.677 K
419.527 ℃
±0.5℃
アルミニウム点
933.473 K
660.323 ℃
±0.2℃
銀点
1 234.93 K
961.78 ℃
±0.2℃
銅点
1 357.77 K
1 084.62 ℃
±0.2℃
38
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書3図21 定点黒体炉の構成例
10. 構造の表示
10.1 構成 検出器と変換器が分離した分離形,検出器と表示器機能が一体となった一体形のいずれかを
表示する。手持ち測定するものは,携帯形を表示する。
10.2 光学系 集光方式はレンズ式,ミラー式,ライトガイド式,光ファイバ式又はこれらを併用した方
式のいずれかを表示する。必要に応じて,レンズなどの材質及び構成を併記する。結像方式は,レンズ又
はミラーと検出素子の距離が固定されている固定焦点式又はその距離を調節できる可動焦点式のいずれか
を表示する。
39
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
10.3 照準 標的を正しく視定する機構(附属書3の1.4参照)をもつ場合は,その方式を表示する。
10.4 フィルタ フィルタを使用している場合には,種類,構成及び主な特性を表示する。主な特性とし
て,帯域フィルタは中心波長及び半値幅を,カットフィルタは遮断波長を表示し,必要に応じて透過率を
併記する。
10.5 検出素子 検出素子の名称又は略称を表示する。名称又は略称は,熱電形検出素子のサーモパイル,
サーミスタ・ボロメータ,焦電素子及び光電形検出素子のSi,InGaAs,Ge,PbS,PbSe,InAs,InSb,HgCdTe
などとする。
10.6 信号処理系 放射率補正機構,信号の一定時間内の最高値,平均値,最低値などの保持機構,外部
同期機構,設定値に対する制御,警報などの電気信号発生機構及び検出信号のリニアライザの有無を表示
する。
10.7 入出力系 温度表示及び電気信号の有無並びにそれぞれについてアナログ,ディジタルの別とその
形態を表示する。ディジタルの場合は通信方式を明示する。
10.8 附属品 次に示す附属品のうち,採用しているものの名称を表示する。必要に応じて機能又は性能
を併記する。
a) 検出器固定用金具及び架台
b) 検出器保護筒
c) 水冷ジャケット
d) エアパージ機構
e) のぞき筒(サイティングチューブ)
f)
その他,補助光学系など
40
C 1612 : 2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
原案作成委員会 構成表
氏名
所属
(委員長)
藤 村 貞 夫
東京大学工学部
(副委員長)
小 野 晃
工業技術院計量研究所
(主査)
後 藤 昌 彦
玉川大学工学部
大 塚 美枝子
東亜大学大学院総合技術専攻
永 松 荘 一
通商産業省機械情報産業局
橋 爪 邦 隆
工業技術院標準部
橋 本 進
財団法人日本規格協会技術部
佐久間 史 洋
工業技術院計量研究所
斉 藤 尚 子
日本電気計器検定所
堀 友 繁
雪印乳業株式会社技術研究所
平 本 一 男
住友金属工業株式会社システム事業部
上 義 明
松下電子工業株式会社技術本部電子総合研究所
福 高 善 己
川崎製鉄株式会社水島製鉄所
高 田 章
旭硝子株式会社中央研究所
小 川 実 吉
株式会社横河総合研究所
(幹事)
高 橋 克 友
大倉電気株式会社計測制御事業部
笠 井 豊
NEC三栄株式会社技術本部
芝 田 智 夫
川惣電機工業株式会社計測第一事業部
服 部 晋
株式会社チノー品質管理本部
佐々木 正 直
東京精工株式会社生産部
野 村 俊 行
株式会社堀場製作所分析システム統括部
村 田 敏 廣
ミノルタ株式会社計測機器事業部
若曽根 和 之
社団法人日本電気計測器工業会
(事務局)
勝 田 敏 江
社団法人日本電気計測器工業会