C 1400-3:2014 (IEC 61400-3:2009)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲 ························································································································· 1
2 引用規格 ························································································································· 2
3 用語及び定義 ··················································································································· 2
4 記号及び略語 ··················································································································· 9
4.1 記号及び単位 ················································································································ 9
4.2 略語 ··························································································································· 10
5 主要要素 ························································································································ 11
5.1 一般 ··························································································································· 11
5.2 設計方法 ····················································································································· 11
5.3 安全クラス ·················································································································· 13
5.4 品質保証 ····················································································································· 13
5.5 ロータ ナセル・アセンブリ(RNA)の銘板 ······································································· 13
6 外部条件 ························································································································ 14
6.1 一般 ··························································································································· 14
6.2 風車クラス ·················································································································· 14
6.3 風条件 ························································································································ 15
6.4 海洋環境条件 ··············································································································· 15
6.5 その他の環境条件 ········································································································· 23
6.6 電力系統条件 ··············································································································· 24
7 構造設計 ························································································································ 24
7.1 一般 ··························································································································· 24
7.2 設計方法 ····················································································································· 25
7.3 荷重 ··························································································································· 25
7.4 設計条件及び荷重ケース ································································································ 26
7.5 荷重計算及び荷重効果計算······························································································ 38
7.6 終極(終局)限界状態解析······························································································ 41
8 制御及び保護システム ······································································································ 44
9 機械システム ·················································································································· 44
10 電気システム ················································································································ 44
11 基礎の設計 ··················································································································· 45
12 洋上風車サイトにおける外部条件の評価 ············································································ 45
12.1 一般 ·························································································································· 45
12.2 気象海象データベース ·································································································· 46
12.3 風況精査 ···················································································································· 46
C 1400-3:2014 (IEC 61400-3:2009) 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
12.4 波の評価 ···················································································································· 48
12.5 水流の評価 ················································································································· 49
12.6 水位,潮せき(汐)及び高潮の評価 ················································································ 49
12.7 海氷の評価 ················································································································· 49
12.8 海洋付着生物の評価 ····································································································· 50
12.9 海底変形及び洗掘 ········································································································ 50
12.10 隣接風車からの後流の影響評価····················································································· 50
12.11 その他の環境条件の評価 ······························································································ 50
12.12 地震条件の評価 ········································································································· 51
12.13 ウェザウィンドウ及びウェザダウンタイムの評価 ····························································· 51
12.14 電力系統条件の評価 ··································································································· 51
12.15 地盤条件の評価 ········································································································· 51
13 組立,据付及び建設 ······································································································· 52
13.1 一般 ·························································································································· 52
13.2 計画 ·························································································································· 53
13.3 設置状態 ···················································································································· 53
13.4 サイトへのアクセス ····································································································· 53
13.5 環境条件 ···················································································································· 54
13.6 提出文書 ···················································································································· 54
13.7 受取り,取扱い及び保管 ······························································································· 54
13.8 基礎/アンカシステム ·································································································· 54
13.9 洋上風車の組立 ··········································································································· 54
13.10 洋上風車の建設 ········································································································· 54
13.11 締結部品及びアタッチメント ························································································ 55
13.12 クレーン,ホイスト及び揚重装置 ·················································································· 55
14 試運転,運転及び保守 ···································································································· 55
14.1 一般 ·························································································································· 55
14.2 安全運転,検査及び保守に対する設計要求 ······································································· 55
14.3 試運転に関する指示書 ·································································································· 56
14.4 運転要員への指示マニュアル ························································································· 57
14.5 保守マニュアル ··········································································································· 59
附属書A(参考)洋上風車の主要設計パラメータ ······································································ 60
附属書B(参考)波のスペクトルの定式化 ················································································ 63
附属書C(参考)浅水の流体力学及び砕波 ··············································································· 67
附属書D(参考)流体力荷重の計算に関する指針 ······································································ 73
附属書E(参考)氷荷重に対する洋上風車支持構造物の設計に関する推奨 ······································ 84
附属書F(参考)洋上風車の基礎の設計 ··················································································· 93
附属書G(参考)発電時における終極(終局)強度解析のための気象海象パラメータの統計的外挿 ····· 94
附属書H(参考)防食 ·········································································································· 99
C 1400-3:2014 (IEC 61400-3:2009)
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
附属書JA(参考)波浪統計及び波浪スペクトル定式化 ······························································ 103
附属書JB(参考)浅水の流体力学及び砕波 ············································································· 107
C 1400-3:2014 (IEC 61400-3:2009) 目次
C 1400-3:2014 (IEC 61400-3:2009) 目次
(4)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本電機工業会(JEMA)から,
工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経
済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS C 1400の規格群には,次に示す部編成がある。
JIS C 1400-0 風力発電システム−第0部:風力発電用語
JIS C 1400-1 風車−第1部:設計要件
JIS C 1400-2 風車−第2部:小形風車の設計要件
JIS C 1400-3 風車−第3部:洋上風車の設計要件
JIS C 1400-11 風力発電システム−第11部:騒音測定方法
JIS C 1400-12-1 風車−第12-1部:発電用風車の性能試験方法
JIS C 1400-21 風力発電システム−第21部:系統連系風車の電力品質特性の測定及び評価
JIS C 1400-22 風車−第22部:風車の適合性試験及び認証
JIS C 1400-24 風車−第24部:雷保護
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
C 1400-3:2014
(IEC 61400-3:2009)
風車−第3部:洋上風車の設計要件
Wind turbines-Part 3: Design requirements for offshore wind turbines
序文
この規格は,2009年に第1版として発行されたIEC 61400-3を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
この規格の目的は,洋上風車の最低限の設計要求事項を規定することであり,完全な設計仕様又は指示
マニュアルとして用いることを意図したものではない。
なお,この規格で側線又は点線の下線を施してある参考事項,並びに附属書JA及び附属書JBは,対応
国際規格にない事項である。
1
適用範囲
この規格は,JIS C 1400-1の要求事項に加え,洋上風車サイトの外部条件の評価に関する追加要求事項
を規定するとともに,洋上風車の工学的健全性を達成するための基本的な設計要求事項について規定する。
この規格の目的は,設計寿命においてあらゆる危険性による損傷に対して適切な保護レベルを示すことで
ある。この規格は,JIS C 1400-1と併せて用いなければならない。
この規格は,洋上風車の構造部品の工学的健全性に焦点を置いているが,制御機構並びに保護機構,内
部電気システム,機械的システムのようなサブシステムも考慮している。
風車の支持構造物が海洋の流体力による荷重にさらされる場合は,洋上風車とみなす。
注記1 この規格では,“荷重”は,“力又はモーメント”の意味で用いる。
この規格に規定する設計要求事項は,浮体式洋上風車の工学的健全性を達成するには,必ずしも十分で
はない。
この規格は,箇条2に規定した該当するJIS,ISO規格及びIEC規格を併せて用いる。特に,この規格
で対象とする洋上風車は,JIS C 1400-1の要求事項を満足していることを前提とする。この規格に従って
設計した洋上風車の安全性レベルは,JIS C 1400-1に規定の同等レベル以上となる。箇条によっては,要
求事項の詳細な規定によって明確になるように,JIS C 1400-1の本文をそのまま規定している部分がある。
洋上風車の設計,製造,組立,据付,建設,試運転,運転及び保守の各種要素の実施,並びにこの規格
の要求事項が満たされていることの確認には,様々な関係者が責任を負う場合がある。これらの関係者間
における責任の分担は,契約上の問題であり,この規格の適用範囲外である。
洋上風車の安全性が損なわれないことが適切に実証される場合,この規格のどの要求事項を修正しても
よい。この規格に従っても,いかなる個人,組織又は企業がほかの関連する規則を遵守する責任を免れる
ものではない。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 61400-3:2009,Wind turbines−Part 3: Design requirements for offshore wind turbines(IDT)
2
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS C 1400-1:2010 風車−第1部:設計要件
注記 対応国際規格:IEC 61400-1:2005,Wind turbines−Part 1: Design requirements(IDT)
JIS Q 9001:2008 品質マネジメントシステム−要求事項
注記 対応国際規格:ISO 9001:2000,Quality management systems−Requirements(IDT)
JIS W 0201:1990 標準大気
注記 対応国際規格:ISO 2533:1975,Standard Atmosphere(IDT)
ISO 2394:1998,General principles on reliability for structures
ISO 19900:2002,Petroleum and natural gas industries−General requirements for offshore structures
ISO 19901-1:2005,Petroleum and natural gas industries−Specific requirements for offshore structures−Part
1: Metocean design and operating considerations
ISO 19901-4:2003,Petroleum and natural gas industries−Specific requirements for offshore structures−Part
4: Geotechnical and foundation design considerations
ISO 19902,Petroleum and natural gas industries−Fixed steel offshore structures
ISO 19903:2006,Petroleum and natural gas industries−Fixed concrete offshore structures
IEC 60721-2-1:2002,Classification of environmental conditions−Part 2-1: Environmental conditions
appearing in nature−Temperature and humidity
注記 IEC 61400-3:2009では,1982年版及び追補1(1987)を引用している。
IEC 61400-13:2001,Wind turbine generator systems−Part 13: Measurement of mechanical loads
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS C 1400-1:2010によるほか,次による。
3.0A
砕波(breaking waves)
波が水深の深い所から水深の浅い所に進んだ場合などに,波面勾配が安定限界を超えて,波が砕ける現
象,又はその砕けた波。
3.1
(風及び波の)同一方向[co-directional (wind and waves)]
同じ方向の作用。
3.2
水流(current)
通常,流れの速度及び方向を用いて示す,特定の場所を通過する水の流れ。
3.3
設計波(design wave)
3
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
海洋構造物の設計に用いる,波高,周期及び波向を定義した決定論的な波。設計波は,特定の規則波理
論の使用に関する必要条件が付随してもよい。
3.4
設計者(designer)
洋上風車の設計に責任を負う者。
3.5
環境条件(environmental conditions)
風車の挙動に影響を与える可能性がある環境の特性(風,波,海の流れ,水位,海氷,海洋付着生物,
洗掘,全体的な海底変形など)。
3.6
(風車の)外部条件[external conditions (wind turbines)]
環境条件,電力系統条件,その他の気象要素(温度,雪,氷など)を含む,洋上風車の運転に影響を与
える要素。
3.7
極値有義波高(extreme significant wave height)
年間超過確率1/N(“再現期間”:N年)の,3時間にわたって平均した最高有義波高の期待値。
注記 観測時間の制限などで3時間にわたる平均値が取得できない場合,安全側の値になる限りにお
いて3時間より短い時間での平均値を用いてもよい。
3.8
極値波高(extreme wave height)
個別波の最高波高(一般にゼロアップクロス法による波の波高)の年間超過確率1/N(“再現期間”:N
年)の期待値。
3.9
定着氷板(fast ice cover)
固く連続的に覆われた動かない氷。
3.10
吹送距離(fetch)
風がほぼ一定の風速及び風向で海上を吹き抜ける距離。
3.11
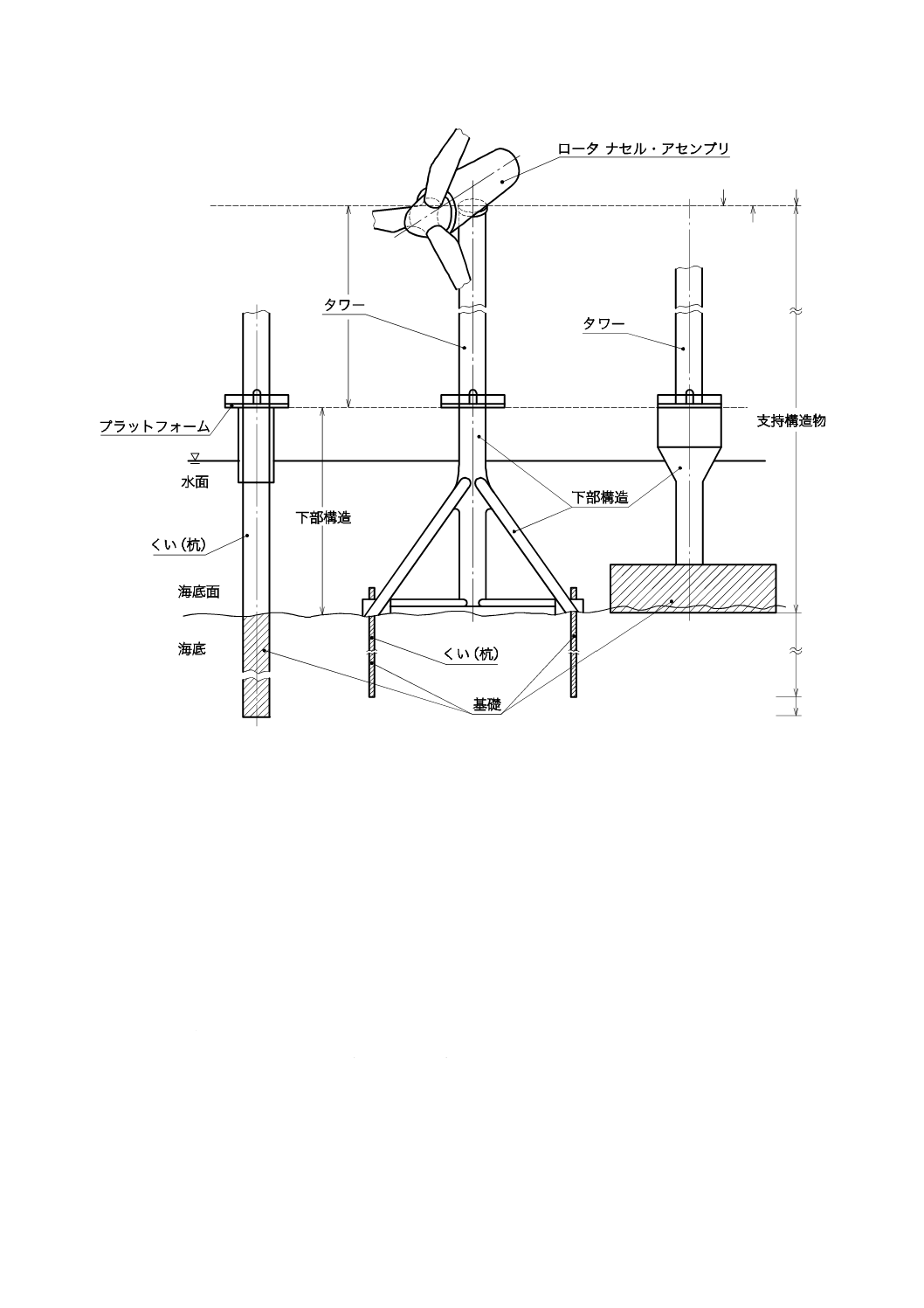
基礎(foundation)
洋上風車支持構造物のうち,構造物に作用する荷重を海底に伝える部分。図1に基礎の様々な例を洋上
風車のほかの部分と併せて示す。
4
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1−洋上風車の各部
3.12
最高天文潮位(highest astronomical tide)
あらゆる天文学的条件の組合せ及び平均的な気象条件において,発生が予測できる最高静水位。気象学
的に発生し,かつ,基本的に不規則な高潮は,潮位の変化に重なるため,全体的な静水位は,最高天文潮
位より高くなることもある。
3.13
波の推算(hindcasting)
数値モデリングによって特定地域の時系列的な(気象海象)データをシミュレーションする手法。
3.14
(風車の)ハブ高さ[hub height (wind turbines)]
風車ロータの受風面積の中心の平均潮位からの高さ。
3.15
氷丘氷(hummocked ice)
大きな氷盤が互いにぶつかったとき,又は大きな氷盤が洋上風車支持構造物などの固い障害物にぶつか
ったとき,氷片及び氷盤が起伏状に積み重なったもの。
5
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.16
氷盤(ice floe)
大きさが数メートルから数キロメートルの板状の氷で,海岸にしっかりと凍り付いているのではなく,
静止又は移動しているもの。
3.17
着氷(icing)
洋上風車の一部が氷又は霜で覆われ,それが堆積したもので,荷重の増加及び/又は特性変化につなが
る可能性があるもの。
3.18
陸地で囲まれた水(land-locked waters)
ほとんど又は完全に陸地で囲まれた水。
3.19
荷重効果(load effect)
単独荷重又は組合せ荷重の構造部品又はシステムに対する影響。内力,応力,ひずみ,運動など。
3.20
最低天文潮位(lowest astronomical tide)
あらゆる天文学的条件の組合せと平均的な気象条件において,発生が予測できる最低静水位。気象学的
に発生し,かつ,基本的に不規則な高潮は,潮位の変化に重なるため,全体的な静水位は,最低天文潮位
より低くなることもある。
3.21
製造業者(manufacturer)
洋上風車の製造及び建設の責任を負う者。
3.22
海洋環境条件(marine conditions)
海洋環境の特性(波,海の流れ,水位,海氷,海洋付着生物,洗掘,全体的な海底変形など)であって,
風車の挙動に影響を与える可能性があるもの。
3.23
海洋付着生物(marine growth)
植物,動物及び微生物による構造部品(部材を含む。)の表面被覆。
3.24
平均潮位(mean sea level)
波,潮せき(汐)及び高潮による変動を除外するのに十分な期間にわたる海面の平均水位。
3.25
平均ゼロクロス周期(mean zero crossing period)
ある海況におけるゼロクロス法による波(基準線を上方又は下方へ越える波)の平均周期。
3.26
気象海象(metocean)
気象及び海象を合わせた略語。
3.27
(風及び/又は波の)多方向[multi-directional (wind and/or wave)]
6
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
方向の分布。
3.28
洋上風車(offshore wind turbine)
支持構造物が流体力荷重にさらされる風車。
3.29
洋上風車サイト(offshore wind turbine site)
単独又はウィンドファーム内の個々の洋上風車の位置又は計画された位置。この規格では,単に“サイ
ト”ともいう。
3.30
貫入深さ(pile penetration)
海底からくい(杭)の一番下までの鉛直距離。
3.31
(風車の)集電設備[power collection system (wind turbines)]
1台以上の風車から電力を集電する電気システム。集電設備には風車接続端と電力系統の接続端との間
を接続する全ての電気設備を含む。洋上ウィンドファームでは,海岸への接続端も集電設備に含む場合が
ある。
3.32
評価時間(reference period)
風速,海面高さ,応答など,与えられた統計的過程に対して定常性が仮定できる期間。
3.33
屈折(refraction)
水深及び/又は流速の変化によって波の伝ぱ(播)速度が変化した結果,波のエネルギーが再分配され
る過程。
3.34
恒流(residual currents)
潮流以外の水流成分。最も重要なものとして高潮流がよく挙げられる。
3.35
ロータ ナセル・アセンブリ(rotor-nacelle assembly)
支持構造物によって支えられる洋上風車の一部(図1参照)。
3.36
海底面(sea floor)
海と海底との境界面。
3.37
海底勾配(sea floor slope)
砂浜から連想されるような,海底面の局部的な傾斜。
3.38
海況(sea state)
統計的に定常的な海の状態。
3.39
海底(seabed)
7
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
海底面の下で,支持構造物を埋め込む所。
3.40
海底変形(seabed movement)
自然の地質作用によって海底が移動すること。
3.41
洗掘(scour)
水流及び波による,又は海底面より上の自然流況を妨げる構造要素による海底地盤の除去。
3.42
有義波高(significant wave height)
ある海況における波の高さの統計的指標。海面高さの標準偏差をσηとしたとき,4×σηと定義する。波
周波数が狭帯域に限られる海況では,有義波高は,ゼロアップクロス法による波全体の波高値の大きい方
から1/3までの平均波高に近似的に等しい。
注記 ゼロアップクロス法による波全体の波高値の大きい方から1/3の平均波高H1/3は,深海の海面
では,波スペクトルの形にかかわらず,平均でH1/3=0.95 Hsとなる。
3.43
飛まつ(沫)帯(splash zone)
支持構造物の中で,波及び潮せき(汐)の変化によって頻繁に水にぬ(濡)れる外側部分。次の二つの
レベルに挟まれた領域である。
− 再現期間1年の最高静水位に再現期間1年の有義波高に等しい波高の波の波頂高を加えたレベル。
− 再現期間1年の最低静水位から再現期間1年の有義波高に等しい波高の波の谷を差し引いたレベル。
3.44
静水位(still water level)
波による変化を除外したうえで,潮せき(汐)及び高潮の影響を考慮して計算した概念上の水位面。静
水位は,平均潮位より高い場合,等しい場合,又は低い場合があり得る。
3.45
高潮(storm surge)
風及び大気圧の変化によってもたらされる不規則な海の動き。
3.46
下部構造(sub-structure)
洋上風車の支持構造物のうち,海底より上方に突き出し,かつ,基礎をタワーに接続する部分(図1参
照)。
3.47
支持構造物(support structure)
タワー,下部構造及び基礎で構成する洋上風車の部分(図1参照)。
3.48
うねり(swell)
局地的に発生したものではなく,サイトから離れた場所の風によって発生した波がサイトまで伝ぱ(播)
してきた海況。
3.49
潮流(tidal current)
8
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
潮せき(汐)による水流。
3.50
潮差(tidal range)
最高天文潮位と最低天文潮位との差。
3.51
潮せき(汐)(tides)
天文学的な力によって発生する規則的,かつ,予測可能な海の運動。
3.52
タワー(tower)
洋上風車支持構造物のうち,下部構造とロータ ナセル・アセンブリとの間にある部分。(図1参照)。
3.53
津波(tsunami)
海底面の急激な鉛直運動によって起きる長周期の海の波。
3.54
(風及び/又は波の)単一方向[uni-directional (wind and/or waves)]
単一の方向への作用。
3.55
水深(water depth)
海底面と静水位との鉛直距離。
注記 静水位には幾つかの場合があるため(3.44参照),水深の値も一つとは限らない。
3.56
波頂高(wave crest elevation)
波頂及び静水位との鉛直距離。
3.57
波向(wave direction)
波が伝ぱ(播)してくる平均方向。
3.58
波高(wave height)
ゼロアップクロス法による個々の波の水面における点の最高点と最低点との間の鉛直距離。
3.59
波の周期(wave period)
ゼロアップクロス法による波を区切る二つのゼロアップクロス点間の時間間隔。
3.60
波のスペクトルのピーク周波数(wave spectral peak frequency)
波のスペクトルの最大エネルギーの周波数。
3.61
波のスペクトル(wave spectrum)
ある海況における波のエネルギー分布の周波数領域での表現。
注記 “二次元波のスペクトル”と記載する場合は,エネルギー分布の周波数領域及び方向領域での
表現を意味する。
9
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.62
波形勾配(wave steepness)
波長に対する波高の比。
3.63
ウェザダウンタイム(weather downtime)
環境条件が厳しすぎるため所定の洋上作業が実行できない時間。
3.64
ウェザウィンドゥ(weather window)
所定の洋上作業の実行が可能な環境条件が続く期間。
3.65
ウィンドプロファイル−ウィンドシア法則(wind profile−wind shear law)
静水位からの高さ方向の風速変化を与える数学的表現。
注記 通常用いるウィンドプロファイルは,対数法則の式(1)及び指数法則の式(2)である。
)
/
(
)
/
(
)
(
=
)
(
o
r
o
r
In
In
・
z
z
z
z
z
V
z
V
································································ (1)
α
=
r
r・zz
z
V
z
V
)
(
)
(
····································································· (2)
ここに,
V(z): 高さzにおける風速
z: 静水位からの高さ
zr: プロファイルをフィッティングするための静水位からの
基準高さ
zo: 粗度長
α: ウィンドシア(又は指数法則)の指数
3.66
ゼロアップクロス法による波(zero up-crossing wave)
ゼロアップクロス点の間の水面変動の時系列波形の部分。ゼロアップクロス点とは,海面が静水位より
(下降するのではなく)上昇するときの点である。
4
記号及び略語
この規格で用いる主な記号及び略語は,JIS C 1400-1:2010によるほか,次による。
4.1
記号及び単位
AC
チャーノック定数
(−)
d
水深
(m)
fp
波のスペクトルのピーク周波数
(s−1)
g
重力加速度
(m/s2)
h
海氷の厚さ
(m)
hN
再現期間N年の海氷の厚さ
(m)
hm
氷がある冬季の年間最大氷厚の長期平均値に等しい氷厚
(m)
H
個別波高(個々の波の波高)
(m)
HB
砕波波高
(m)
10
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
HD
設計波高
(m)
HN
再現期間N年の個別波高
(m)
Hs
有義波高
(m)
HsN
再現期間N年の有義波高
(m)
HredN
再現期間N年の低減波高
(m)
H1/3
ゼロアップクロス波が高い方から1/3の有義波高
(m)
k
波数
(−)
Kmax
氷結した日数の累積温度
(℃)
p (Vhub)
ハブ高さ風速の確率密度関数
(−)
Rd
部品耐力の設計値
(−)
Rk
部品耐力の特性値
(−)
s
海底勾配
(°)
Sd
荷重効果の設計値
(−)
Sk
荷重効果の特性値
(−)
Sη
波の片側スペクトル
(m2/Hz)
t
時間
(s)
T
波の周期
(s)
TD
波の設計周期
(s)
Tp
ピークスペクトル周期
(s)
Tz
ゼロクロス波の平均周期
(s)
T1/3
ゼロアップクロス波が高い方から1/3の平均周期
(s)
Uss
海潮流速度
(m/s)
Uw
吹送流速度
(m/s)
Ubw
砕波によって引き起こされる沿岸流速度
(m/s)
Ve
極値風速
(m/s)
VN
再現期間N年の極値風速(10分間の平均)の期待値
(m/s)
VredN
再現期間N年の低減極値風速(3秒間の平均)
(m/s)
η
静水面(SWL)に対する海面高さ
(m)
κ
カルマン定数
(−)
λ
波長
(m)
θw
波向
(°)
θwm
平均波向
(°)
θc
水流方向
(°)
ση
海面高さの標準偏差
(m)
τ
温度
(℃)
4.2
略語
COD
同一方向(co-directional)
CPT
コーン貫入試験(cone penetration test)
DLC
設計荷重ケース(design load case)
ECD
方向変化を伴う極値コヒーレントガスト(extreme coherent gust with direction change)
11
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ECM
極値流速モデル(extreme current model)
EDC
極値方向変化(extreme direction change)
EOG
運転時の極値突風(extreme operating gust)
ESS
極値海況(extreme sea state)
ETM
極値乱流モデル(extreme turbulence model)
EWH
極値波高(extreme wave height)
EWLR 極値水位範囲(extreme water level range)
EWM
極値風速モデル(extreme wind speed model)
EWS
極値ウィンドシア(extreme wind shear)
HAT
最高天文潮位(highest astronomical tide)
LAT
最低天文潮位(lowest astronomical tide)
MIC
微生物腐食(microbiologically influenced corrosion)
MIS
方向偏差(misaligned)
MSL
平均潮位(mean sea level)
MUL
多方向(multi-directional)
NCM
通常流速モデル(normal current model)
NSS
通常海況(normal sea state)
NTM
通常乱流モデル(normal turbulence model)
NWH
通常波高(normal wave height)
NWLR 通常水位範囲(normal water level range)
NWP
通常ウィンドプロファイルモデル(normal wind profile model)
RNA
ロータ ナセル・アセンブリ(rotor-nacelle assembly)
RWH
低減波高(reduced wave height)
RWM
低減風速モデル(reduced wind speed model)
SSS
高波浪時海況(severe sea state)
SWH
高波浪時波高(severe wave height)
SWL
静水位(still water level)
UNI
単一方向(uni-directional)
5
主要要素
5.1
一般
この箇条では,洋上風車の構造,機械,電気及び制御装置の安全を確保するための工学的及び技術的要
求事項を規定する。この要求事項は,洋上風車の設計,製造,据付及び運転・保守マニュアル,並びに関
連する品質管理プロセスに適用する。さらに加えて,洋上風車の据付,運転及び保守の様々な経験に基づ
いて作成した安全のための手続きも考慮している。
5.2
設計方法
この規格では,設計荷重を決定するために構造動力学モデルを用いる。設計荷重については,箇条6に
規定する外部条件,及び箇条7に定義する設計条件に該当する全ての組合せについて,荷重を考慮しなけ
ればならない。この規格では,その組合せの最小のものを設計荷重として規定する。
洋上風車の支持構造物は,サイト固有の外部条件に基づいて設計しなければならない。これらの外部条
12
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
件は,箇条12に規定する要求事項に従って決定する。その外部条件は,設計基準にまとめておかなければ
ならない。
JIS C 1400-1:2010の6.2で規定する標準風車クラスに基づいて初期段階に設計されたロータ ナセル・ア
センブリ(RNA)の場合,洋上風車のサイト固有の外部条件が,構造の健全性を失わせるものではないこ
とを実証しなければならない。この実証は,固有の洋上風車サイト条件について計算した荷重及び変形を,
初期設計時の計算結果と比較することによって行わなければならない。このとき,構造物の耐力及び適切
な材料の選定には,耐力の余裕及び環境の影響を考慮する。荷重計算の場合は,サイト固有の地盤の特性
が,洋上風車の動的特性に及ぼす影響も考慮しなければならない。また,同時にこれらの動的特性が,海
底変形及び洗掘によって長期的に変化する潜在的可能性も考慮に入れる。
注記 ここでの“風車クラス”は,JIS C 1400-1:2010の“風車カテゴリ”を指す。
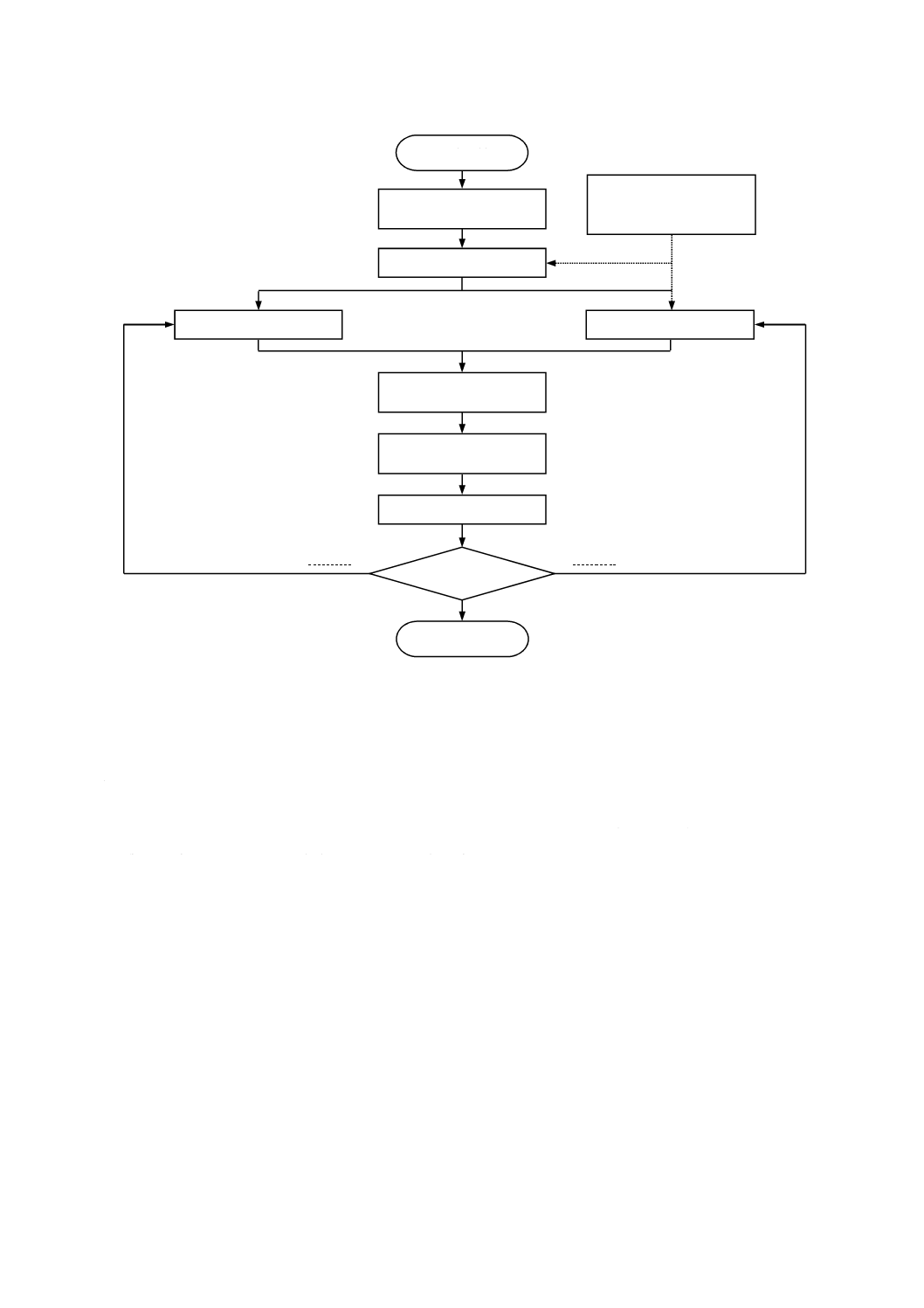
洋上風車の設計手順は,図2による。この図は,設計手順の主な要素を示すとともに,各要素がこの規
格のどの箇条に対応しているかも示している。設計手順は,繰り返し計算によるものであり,一体形支持
構造物及びロータ ナセル・アセンブリからなる風車全体について,荷重及び荷重効果の計算を実施しなけ
ればならない。構造的健全性を7.6に規定する限界状態解析に基づいて確認した段階で,洋上風車の構造
設計は完了したとみなしてもよい。
想定した設計値において信頼性を向上させ,構造動力学モデル及び設計条件が正しいことを検証するた
めに,フルスケールの試験から得られたデータを使用してもよい。フルスケールの試験に対する機械的荷
重の測定の指針は,IEC 61400-13:2001による。
設計の妥当性の検証は,計算及び/又は試験で行わなくてはならない。この検証を試験で行う場合,試
験中の外部条件にはこの規格に規定する特性値及び設計条件が反映されていることを示さなければならな
い。また,試験荷重を含む試験条件の選定には,該当する安全率も考慮しなければならない。
13
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2−洋上風車の設計プロセス
5.3
安全クラス
洋上風車の設計は,次の二つの安全クラスのいずれかに従って行わなければならない。
・ 通常安全クラスは,故障が人身事故,又は社会的若しくは経済的に影響が大きいリスクとなる場合に
適用する。
・ 特殊安全クラスは,安全要求事項がその地域の規則によって決まる場合,及び/又は安全要求事項が
製造業者と顧客との間で合意されている場合に適用する。
通常安全クラスの風車に対する部分安全率は,7.6による。
特殊安全クラスの風車に対する部分安全率は,製造業者と顧客との間で合意しなければならない。特殊
安全クラスに従って設計した洋上風車は,6.2に定義するクラスSの風車とする。
5.4
品質保証
品質保証は,洋上風車及びその全ての部品の設計,調達,製造,据付,運転及び保守における不可欠な
要素でなければならない。
品質システムは,JIS Q 9001:2008の要求事項に適合することが望ましい。
5.5
ロータ ナセル・アセンブリ(RNA)の銘板
ロータ ナセル・アセンブリ(RNA)の銘板には,少なくとも次の事項を明瞭に,かつ,容易に消えな
いように表示しなければならない。
・ 製造業者名及び生産国名
設計完了
設計開始
サイト特有の外部条件
(箇条6及び箇条12)
設計条件及び荷重ケース
(7.4)
荷重及び荷重効果の計算
(7.5)
限界状態解析(7.6)
構造的健全性
RNA設計
支持構造物の設計
RNA設計
(例:JIS C 1400-1,
標準風車クラス)
いいえ
いいえ
はい
洋上風車の設計基準
14
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ 形名及び製造番号
・ 製造年
・ 定格出力
・ 基準風速 Vref
・ ハブ高さの運転風速範囲 Vin−Vout
・ 運転周囲温度範囲
・ IEC風車クラス(JIS C 1400-1:2010参照)
・ 風車接続端での定格電圧
・ 風車接続端の周波数,又は公称変動範囲が2 %より大きい場合にはその周波数の範囲
6
外部条件
6.1
一般
この箇条では,洋上風車の設計において考慮しなければならない外部条件を規定する。
洋上風車の荷重,耐久性及び運転は,環境条件及び電気条件の影響を受ける可能性がある。適切な水準
の安全性及び信頼性を確保するため,環境,電気及び地盤条件のパラメータを考慮して設計し,これらの
パラメータを設計文書に明記しなければならない。
環境条件は,風の条件,海洋環境条件(波,海の流れ,水位,海氷,海洋付着生物,海底変形及び洗掘),
及びその他の環境条件に分けられる。電気条件は,電力系統の条件を示す。
サイトの地盤の特性も考慮しなければならない。地盤については,海底変形,洗掘及びその他の海底の
不安定性要素による地盤の時間的変化も含めて考慮する。
ロータ ナセル・アセンブリ(RNA)の構造的健全性に対し考慮する第一の外部条件は,風の条件であ
る。ただし,支持構造物の動的特性によっては,海洋環境条件の影響も考えられる。ロータ ナセル・アセ
ンブリ(RNA)の設計で,海洋環境条件の影響が無視できる程度であることが示された場合も含め,あら
ゆる場合において,後に洋上風車を据付ける個々のサイトの海洋環境条件を適切に考慮したうえで,構造
的健全性を実証しなければならない。
その他の環境条件も,設計の仕様,例えば,制御装置の機能,耐久性,腐食などに影響する。
外部条件は,更に通常外部条件及び極値外部条件に細分される。通常外部条件は,一般に再現性がある
構造荷重条件に関するものである。一方,極値外部条件は,まれな設計外部条件を表す。設計荷重ケース
は,これらの外部条件と,風車の運転モード及びほかの設計条件との,潜在的に重要と考えられる組合せ
によって構成しなければならない。
設計で考慮しなければならない通常条件及び極値条件は,6.2〜6.6に規定する。
6.2
風車クラス
設計において考慮する外部条件は,洋上風車を据付けるサイト候補地又はサイトの種類によって異なる。
JIS C 1400-1:2010では,風車クラスを風速及び乱流のパラメータによって定義している。これらのクラス
によって,陸上のほとんどの風車を対象にしている。
風速及び乱流のパラメータによる風車クラスの定義は,洋上風車のロータ ナセル・アセンブリ(RNA)
の設計基準としても適切である。
さらに,設計者及び/又は顧客によって特殊な風の条件若しくはほかの外部条件又は特殊な安全クラス
(5.3参照)が要求される場合のための別の風車クラスとして,クラスSを定義する。
洋上風車の設計に用いる外部条件を全て特定するには,風車クラスを定義する風速及び乱流強度に加え
15
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
て幾つかの重要なパラメータ,特に海洋環境条件が必要となる。これらの追加パラメータの値は,6.3,6.4,
6.5及び6.6による。
設計寿命は,20年以上としなければならない。
製造業者は,用いたモデル及び主要な設計パラメータの値を設計文書に明記しなければならない。この
箇条のモデルを用いた場合には,パラメータの値を記載するだけでよい。設計文書には,附属書Aに示す
設計情報を記載することが望ましい。
この箇条では,細分箇条の題名の括弧内に示す略語は,7.4に規定する設計荷重ケースの風条件を示す場
合に用いる。
6.3
風条件
洋上風車は,設計基準として採用した風条件に安全に耐え得るように設計しなければならない。
荷重及び安全を考慮する場合の風の種類は,洋上風車の通常の運転状態で1年に1回よりも頻繁に発生
する通常風条件と,再現期間を1年又は50年で規定する極値風条件とに区分する。
洋上風車の支持構造物の設計は,洋上風車サイトを代表する風条件に基づかなければならない。この風
条件は,箇条12に規定する要求事項に従って評価しなければならない。
ロータ ナセル・アセンブリ(RNA)に関しては,設計のときに仮定する風条件は,サイト固有として
もよいし,又はJIS C 1400-1:2010に規定するモデル及びパラメータ値の定義を用いてもよい。ただし,後
者の場合,サイト固有の外部条件によって構造的健全性が損なわれないことを,別途実証しなければなら
ない。JIS C 1400-1:2010に規定する風条件をロータ ナセル・アセンブリ(RNA)の設計基準として用い
る場合は,モデル及びパラメータ値について,次の例外事項を仮定してもよい。
・ 水平面に対する平均流れの傾斜はゼロである。
・ ウィンドプロファイルV (z) は,平均風速を静水位からの高さzの関数で表す。標準風車クラスの場合,
通常のウィンドプロファイルは,式(3)の指数法則で算出する。
()
α
×
=
hub
hub
z
z
V
z
V
···································································· (3)
ここに,
α: 通常風条件に対する指数法則の指数。α=0.14
Vhub: ハブ高さ風速
zhub: 静水位からのハブ高さ
3秒平均の極値風速(Ve50及びVe1)の発生と極値波高(H50及びH1)の発生との間には相関関係はない
と仮定し,両者の同時発生を想定するのは現実的ではない。したがって,次の低減極値風速モデル(RWM)
を極値波高と併せて用いる。
()
11
.0
hub
ref
50
red
1.1
×
=
z
z
V
z
V
··························································· (4)
()
()z
V
z
V
red50
1
red
8.0
=
···································································· (5)
6.4
海洋環境条件
洋上風車は,設計基準として採用した海洋環境条件に安全に耐え得るように設計しなければならない。
この箇条に示す海洋環境条件には,波,海の流れ,水位,海氷,海洋付着生物,洗掘及び海底変形を含む。
洋上環境に関するその他の外部条件は,6.5に規定する。
洋上風車の支持構造物の設計は,洋上風車サイトを代表する海洋環境条件を含む環境条件に基づかなけ
16
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ればならない。
設計者は,海洋環境条件がロータ ナセル・アセンブリ(RNA)に及ぼす影響を考慮しなければならな
い。ほとんどのケースにおいて,洋上風車のロータ ナセル・アセンブリ(RNA)は,特定のサイトを対
象とするのではなく,広範な海象環境に適したものとして設計する。したがって,設計者は,風車の使用
に当たり想定される程度以上の厳しい環境を反映した一般的な海洋環境条件を仮定してもよい。支持構造
物の動的特性及び仮定した設計海洋環境条件によっては,海洋環境条件がロータ ナセル・アセンブリ
(RNA)の構造的健全性に及ぼす影響が無視できる程度のものであることを,設計者は必要に応じて適切
な解析によって実証してもよい。
荷重及び安全を考慮する場合の海洋環境条件は,洋上風車の通常の運転状態で1年に1回よりも頻繁に
発生する通常海洋環境条件と,再現期間が1年又は50年と定義される極値海洋環境条件とに区分する1)。
注1) ただし,この規格では,水位の通常範囲は再現期間1年の水位の変化と規定している(6.4.3.1
参照)。
6.4.1
波
波は形状が不規則であり,波高,波長及び伝ぱ(播)速度も変化する。また,一方向又は複数の方向か
ら同時に洋上風車に打ち寄せることもある。実際の海の特徴は,確率論的波浪モデルによって海況を表現
することで,最もよく反映させることができる。この確率論的波浪モデルは,個々の小さな周波数成分を
多数重ね合わせたものとして海況を表現する。それぞれの成分は,固有の振幅,周波数及び伝ぱ(播)方
向をもつ周期的な波であり,互いの位相は不規則である。設計海況は,有義波高Hs,ピークスペクトル周
期Tp及び平均波向θwmとともに,波の片側スペクトルSηを用いて表さなければならない。ここで,必要に
応じて,波のスペクトルに方向分布関数を適用してもよい。波の標準的なスペクトルの式を,参考として
附属書Bに示す。
注記 波の標準的なスペクトルの式については,附属書JAを参考としてもよい。
場合によっては,実際の海を表す概念として周期的又は規則的な波を設計に用いることができる。決定
論的な設計波は,その波高,周期及び波向によって規定する。
洋上風車の設計では,風と波浪条件との相関関係を考慮に入れなければならない。この相関関係は,次
のパラメータの長期的な結合確率分布について考慮しなければならない。
・ 平均風速:V
・ 有義波高:Hs
・ ピークスペクトル周期:Tp
これらのパラメータの結合確率分布は,吹送距離,水深,海底地形などの現地のサイト条件に影響され
る。したがって,結合確率分布は,適切な長期測定データに,適宜,数値的な波の推算を補足して求めな
ければならない(12.4参照)。
通常風条件と波との相関関係には,平均風向及び平均波向を考慮してもよい。風向及び波向の分布(多
方向)は,支持構造物に作用する荷重に重要な影響をもたらすことがある。この影響の度合いは,風及び
波の方向性,並びに支持構造物の軸対称性の程度によって異なる。風及び波の方向が同一方向で,これら
を単一の方向から作用させることが最悪ケースになるという仮定は安全側であり,それゆえ許容できるの
で,そのように仮定して差し支えないことを設計者は必要に応じて適切な解析によって実証してもよい。
風向及び波向に関する仮定は,7.4の設計荷重ケースごとに考慮する。
風及び波の方向偏差を考慮する場合,方向関連のデータ及び風車設計のためのモデル化手法の信頼性の
確保に特に注意しなければならない(7.5参照)。
17
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
それぞれ波浪モデルを,確率論的な海況表現及び規則的な設計波の両方について,6.4.1.1〜6.4.1.8に規
定する。確率論的海況モデルは,洋上風車の設置予定サイトに適した波のスペクトルに基づかなければな
らない。
6.4.1.1
通常海況(NSS)
それぞれ通常海況に対して,有義波高,ピークスペクトル周期及び波向を,関連する平均風速と併せて
選定しなければならない。選定は,設置予定のサイトに適した気象海象パラメータの長期的な結合確率分
布に基づくものとする。
疲労荷重計算において,設計者は,考慮する通常海況(データ)の個数及び分解能が,十分に長期間の
気象海象パラメータの分布から想定される疲労損傷の計算をするのに十分であることを確認しなければな
らない。
終極(終局)荷重計算では,通常海況は,7.4.1に規定する例外事項を除き,与えられた平均風速の値を
条件とする有義波高Hsの期待値で表現した海況としなければならない。設計者は,それぞれの有義波高に
対応したピークスペクトル周期Tpの範囲を考慮しなければならない。設計計算は,洋上風車に作用する荷
重が最大となるピークスペクトル周期値に基づくものとしなければならない。
6.4.1.2
通常波高(NWH)
決定論的な通常設計波高HNWHは,与えられた平均風速の値を条件とする有義波高の期待値Hs.NSSに等し
いと仮定しなければならない。
設計者は,それぞれの通常波高に対応した波の周期Tの範囲を考慮する。通常波高と併せて用いる波の
周期は,式(6)で算出する範囲内と仮定してもよい。
g
g
)
(
3.
14
)
(
1.
11
NSS
s,
NSS
s,
V
H
T
V
H
≦
≦
············································· (6)
NWHに基づく設計計算では,この範囲内で洋上風車に作用する荷重が最大となる波の周期値を仮定し
なければならない2)。
注2) 波の周期の下限値は,砕波の波高限界から求められる(附属書C参照)。
なお,波の周期には深さに依存する下限はなく,低周波数成分の発達によって砕波帯内で伸
長する傾向があることに注意する。
6.4.1.3
高波浪時海況(SSS)
発電中の洋上風車の終極(終局)荷重の計算では,高波浪時海況の確率論的モデルを通常風条件と併せ
て考慮しなければならない。高波浪時海況モデルは,発電に対応する風速範囲のそれぞれの風速に対して
一つの高波浪時海況を関連付けるものである。それぞれの高波浪時海況の有義波高Hs,SSS (V) は,一般にサ
イト固有の気象海象データに外挿法を適用して決定する。このとき,有義波高と風速との組合せの再現期
間は50年とする3)。全ての風速に対して,風条件によらない再現期間50年の極値有義波高Hs50をHs,SSS (V)
の安全側に見積もった値として用いてもよい。
注3) 気象海象データの外挿は,いわゆる逆一次信頼性解析法(Inverse First Order Reliability Method:
IFORM)を用いて行うことが望ましい。この方法を,附属書Gに記載する。附属書Gでは,
サイト固有の環境条件からHs,SSS (V) を求める指針についても説明する。
設計者は,それぞれの有義波高に対応するピークスペクトル周期Tpの範囲を考慮する。この範囲内で,
設計計算は,洋上風車に作用する荷重が最大となるようなピークスペクトル周期の値に基づかなければな
らない。
6.4.1.4
高波浪時波高(SWH)
18
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
発電中の洋上風車の終極(終局)荷重の計算では,高波浪時の決定論的な設計波を通常風条件と併せて
考慮しなければならない。高波浪時波高モデルは,発電に対応する風速範囲のそれぞれの平均風速に対し
て一つの高波浪時波高を関連付けている。高波浪時波高HSWH (V) は,一般に,サイト固有の気象海象デー
タに外挿法を適用して求める。このとき,有義波高と平均風速との組合せの再現期間は50年とする4)。全
ての平均風速に対して,風条件によらない再現期間50年の極値波高H50をHSWH (V) の安全側に見積もっ
た値として用いてもよい。
注4) 6.4.1.3に記載した高波浪時海況モデルに関しては,附属書Gに記載するIFORMを使用するこ
とが望ましい。附属書Gには,Hs,SSS (V) からHSWH (V) を求める指針も記載している。
設計者は,それぞれの高波浪時波高に対応する波の周期Tの範囲を考慮しなければならない。高波浪時
波高と併せて用いる波の周期は,式(7)で算出する範囲内と仮定してもよい。
g
g
)
(
3.
14
)
(
1.
11
SSS
s,
SSS
s,
V
H
T
V
H
≦
≦
·············································· (7)
SWHに基づく設計計算では,この範囲内で洋上風車に作用する荷重が最大となる波の周期値を仮定しな
ければならない。
6.4.1.5
極値海況(ESS)
確率論的な極値海況モデルは,再現期間50年の極値有義波高Hs50及び再現期間1年の極値有義波高Hs1
の両方について考慮しなければならない。Hs50及びHs1の値は,12.4を参照し,洋上風車サイトの測定値
及び/又は波の推算データの解析から求める。設計者は,Hs50及びHs1に対応するピークスペクトル周期
Tpの範囲をそれぞれ考慮する。設計計算は,洋上風車に作用する荷重が最大となるようなピークスペクト
ル周期値の基準としなければならない。
極値風及び極値波の長期的な結合確率分布を定義する情報がない場合,再現期間50年の3時間極値海況
の状態で,再現期間50年の10分間平均極値風速が発生すると仮定する。同様の仮定を,再現期間がそれ
ぞれ1年の3時間極値海況と10分間極値風速との組合せに適用する。
6.4.1.6
極値波高(EWH)
決定論的な極値設計波は,再現期間50年の極値波高H50及び再現期間1年の極値波高H1の両方につい
て考慮しなければならない。H50及びH1の値並びに対応する波の周期は,12.4を参照し,洋上風車サイト
の測定値の解析から求めてもよい。別の方法として,波高のレイリー分布を仮定し,式(8)及び式(9)のよう
に仮定してもよい。
H50=1.86Hs50 ············································································ (8)
H1=1.86Hs1 ·············································································· (9)
ここに,
Hs50: 3時間の評価時間に対する再現期間50年の極値有
義波高H50の値
Hs1: 3時間の評価時間に対する再現期間1年の極値有
義波高H1の値
これらの極値波高と組み合わせる波の周期は,式(10)で与えられる範囲内と仮定してもよい。
g
g
)
(
3.
14
)
(
1.
11
s.ESS
s.ESS
V
H
T
V
H
≦
≦
············································ (10)
EWHに基づく設計計算では,この範囲内で洋上風車に作用する荷重が最大となる波の周期値を仮定し
なければならない。水深が浅いサイトでは,極値波高H50及びH1並びに対応する波の周期をサイト固有の
測定値の解析から求めなければならない。利用できる測定値がない場合,上記のレイリー分布の関係から
19
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
求めたH50及びH1の各値よりも砕波波高が小さい場合,H50及びH1は,砕波波高に等しいと仮定しなけれ
ばならない。参考として附属書Cに,サイト条件に基づく砕波の性質及び大きさの求め方の指針を示す。
附属書Cには,水深が浅い海岸付近の波高分布の経験的モデルも示す。
6.4.1.7
低減波高(RWH)
決定論的な低減設計波は,50年に1回発生する事象と定義される低減波高Hred50及び1年に1回と定義
される低減波高Hred1の両方を考慮しなければならない。Hred50及びHred1の各値は,3秒平均の極値風速(Ve50
及びVe1)と同時発生する組合せが,極値波高(H50及びH1)と低減極値風速(Vred50及びVred1)との組合
せと同じ確率か,又は更に条件の悪い組合せとなるように決定する。
Hred50,Hred1及び対応する波の周期は,洋上風車サイトの測定値の解析から求めてもよい(12.4参照)。
別の方法として,波高のレイリー分布を仮定し,式(11)及び式(12)のように仮定してもよい。
Hred50=1.3Hs50 ··········································································(11)
Hred1=1.3Hs1 ··········································································· (12)
ここに,
Hs50: 3時間の評価時間に対する再現期間50年
の極値有義波高H50の値
Hs1: 3時間の評価時間に対する再現期間1年の
極値有義波高H1の値
式(11)及び式(12)は,10分平均風速の確率分布及び個別波高の確率分布による結合確率分布を考慮して
導き出された式である。この導出過程で,風速変動についてはガウスの確率分布を,波高についてはレイ
リー分布を仮定している。砕波が発生するような水深が浅い場所では,波高のレイリー分布は必ずしも有
効ではない。浅水サイトでは,低減波高Hred50及びHred1並びに対応する波の周期をサイト固有の測定値の
解析から求めなければならない。利用できる測定値がない場合は,上記のレイリー分布の関係式から求め
たHred50及びHred1の各値よりも砕波波高が小さい場合,Hred50及びHred1は砕波波高に等しいと仮定しなけ
ればならない。参考として附属書Cに,浅水域における波高分布の経験的モデルを示す。
6.4.1.8
砕波
洋上風車の設計では,砕波の影響を評価しなければならない。砕波は,崩れ波,巻き波又は砕け寄せ波
に分類される。崩れ波又は巻き波が,洋上風車に適したサイトで見られる砕波である。水深,海底勾配及
び波の周期によって,砕波が崩れ波又は巻き波となるかが決まる。
附属書Cに,浅水の流体力学及びサイト特性が砕波の性質及び大きさに及ぼす影響についての指針を参
考として示す。また,附属書Dには,洋上風車の支持構造物に対する砕波荷重の計算に関する指針を参考
として示す。
6.4.2
海の流れ
海の流れは,通常空間的及び時間的に変化するものの,一般には,速度及び方向が一定の水平面内で一
様な流れであり,深さだけの関数と考えることができる。海流速については,次の成分を考慮しなければ
ならない。
・ 潮せき(汐),高潮,大気圧の変化などによって生じる海潮流
・ 風によって生じる海面付近の流れ
・ 沿岸において,波によって引き起こされる沿岸に平行に流れる海浜流(沿岸流及び離岸流)
全体的な流速は,これらの成分のベクトル和である。波によって引き起こされる水粒子速度及び流速は
ベクトル的に加算しなければならない。海の流れが波長と波の周期との関係に及ぼす影響は,一般に小さ
いため,無視してもよい。
20
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
波によって引き起こされる波頂の水粒子速度に比べて全体的な流速が遅い場合,及び渦放出又は移動氷
盤による支持構造物の振動が発生しにくい場合は,海の流れが洋上風車の流体力学的疲労荷重に及ぼす影
響は考えなくてもよい。設計者は,サイト固有のデータを適切に評価することによって,疲労荷重の計算
に対して海の流れを無視してもよいかどうかを判断しなければならない。
6.4.2.1
海潮流
海潮流プロファイルは,流速Uss (z) をSWLからの高さzの関数と定義したとき,水深dに対する単純
な指数法則の式(13)によってその特性を表してもよい。
7
1
ss
ss
)0(
)
(
×
d
d
z
U
z
U
+
=
··························································· (13)
海面流速Uss(0)の1年再現値及び50年再現値は,12.5を参照し,洋上風車サイトの測定値を解析して求
めてもよい。
一般に,海潮流の方向は,波向と同じと仮定してもよい。
6.4.2.2
吹送流
吹送流は,水面流速Uw(0)から静水位の下20 mの深さでゼロに減少する速度Uw(z)の線形分布の式(14)
としてその特性を表してもよい。
×
20
1
)0(
)
(
w
w
z
U
z
U
+
=
···························································· (14)
水深が20 m未満のサイトでは,吹送流の海底面での流速はゼロにはならない。
吹送流の海面流速は,方向が風向と一致していると仮定して,式(15)から推定してもよい。
Uw (0)=0.01 V1-hour (z=10 m) ······················································· (15)
ここに, V1-hour (z=10 m): SWLから10 mの高さにおける風速の1時間平均値
V1-hour (z=10 m) の1年再現値及び50年再現値は洋上風車サイトの測定値を解析して求めてもよい。こ
れらの風速を式(15)に代入し,吹送流の海面流速の1年再現値及び50年再現値を推定してもよい。
6.4.2.3
砕波によって引き起こされる海浜流
海岸の砕波帯付近又はその範囲内に洋上風車を設置する場合,砕波のせん断力によって引き起こされる
海浜流を考慮しなければならない。
砕波によって引き起こされる海浜流の大きさは,波の運動及び水流の運動の連成を十分に考慮した適切
な数値モデル(ブシネスク方程式モデルなど)を用いて求めてもよい。ただし,海岸線に平行に流れる海
浜流については,砕波点における設計速度Ubwを式(16)から推定してもよい。
B
bw
2
H
s
U
g
=
········································································ (16)
ここに,
HB: 砕波波高
s: 海底勾配
g: 重力加速度
砕波波高は,附属書Cに記載するサイト特性に基づいて推定してもよい。
注記 砕波及び沿岸潮流の扱いは,附属書JBを参照。
6.4.2.4
通常流速モデル(NCM)
通常流速モデルは,通常波浪条件に対応した吹送流と,砕波によって引き起こされる水流(必要な場合)
とのサイト固有の組合せとして定義する。通常流速モデルには,潮せき(汐)及び高潮によって生じる海
21
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
潮流は含まない。
通常流速モデルは,通常及び高波浪時波浪条件(NSS,NWH,SSS及びSWH)を含む終極(終局)荷
重ケースにおいて仮定しなければならない。6.4.2.2を参照し,それぞれの荷重ケースで,吹送流の速度は
対応する平均風速から推定してもよい。
6.4.2.5
極値流速モデル(ECM)
極値流速モデルは,再現期間1年及び50年の,海潮流,吹送流及び砕波によって引き起こされる水流(必
要な場合)のサイト固有の組合せとして定義する。
極値流速モデルは,極値波浪条件又は低減波浪条件(ESS,EWH及びRWH)を含む終極(終局)荷重
ケースであると仮定する。波と同じ再現期間の海の流れを,これらの荷重ケースについて仮定しなければ
ならない。
6.4.3
水位
洋上風車の流体力荷重の計算では,サイトにおける水位の変化(顕著な場合)を考慮しなければならな
い。ただし,通常波浪条件(NSS及びNWH)を伴う終極(終局)荷重ケースでは,次の6.4.3.1に規定す
る例外を除き,平均潮位(MSL)に等しい一定水位を想定してもよい。
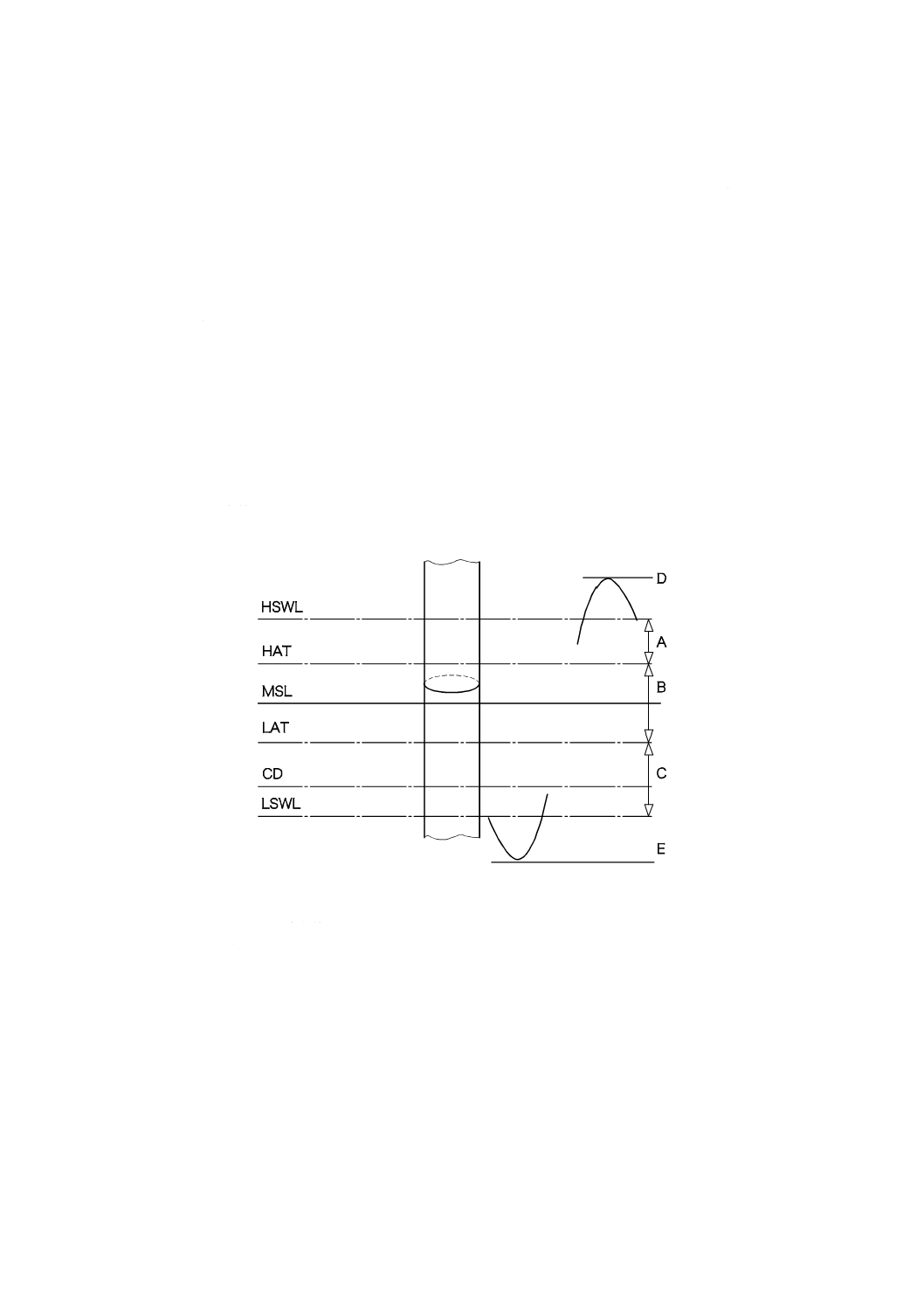
図3は,水位の定義を示す。
HSWL 最高静水位
A 高潮による水位上昇
HAT
最高天文潮位
B 潮差
MSL
平均潮位
C 高潮による水位低下
LAT
最低天文潮位
D 最高波頂高
CD
海図基準水位(LATに等しい場合が多い) E 最低波底高
LSWL 最低静水位
図3−水位の定義
6.4.3.1
通常水位範囲(NWLR)
通常水位範囲は,再現期間1年の水位の変化に等しいと仮定しなければならない。水位の長期的な確率
分布を表すサイト固有のデータが存在しない場合,通常水位範囲は,最高天文潮位(HAT)から最低天文
潮位(LAT)までの差に等しいと仮定してもよい。
22
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
通常水位範囲は,海況及び風速の結合確率分布(Hs,Tp及びVhub)に基づく通常海況(NSS)の疲労荷
重ケース及び終極(終局)荷重ケースにおいて仮定しなければならない。また,次の条件の終極(終局)
荷重ケースでも通常水位範囲を仮定しなければならない。
・ 高波浪時海況(SSS)モデル及び高波浪時波高(SWH)モデル
・ 再現期間1年の波浪条件
終極(終局)荷重の計算は,荷重が最大となる通常水位範囲内の水位に基づくか,又は通常水位範囲内
の水位の確率分布を適切に考慮して実施しなければならない。
確率論的な高波浪時海況(SSS)モデル及び高波浪時波高(SWH)モデルに関連した終極(終局)荷重
ケースにおいて,通常水位範囲に対応する水位では波高が水深によって制限される場合がある。この場合,
波高が水深によって制限されることを回避するためには,極値水位範囲(EWLR)内で,より高めの水位
を仮定しなければならない。
流体力学的疲労荷重の計算では,設計者は,水位の変化が疲労荷重に及ぼす影響が無視できるか,又は
平均潮位以上の一定水位を仮定することで,その影響を安全側に見積もることができることを,場合によ
っては適切な解析によって実証してもよい。
6.4.3.2
極値水位範囲(EWLR)
極値水位範囲は,再現期間50年の波浪条件に対応する終極(終局)荷重ケースに対して仮定しなければ
ならない。荷重計算は,洋上風車に作用する荷重が最大になるような水位を基準として行わなければなら
ない。支持構造物の流体力荷重,氷荷重及び浮力の計算のために,対応する設計に必要な変動水位を求め
なければならない。
水位を含む気象海象パラメータの長期的な結合確率分布が存在しない場合,設計者は,少なくとも次の
水位に基づいて計算を実施しなければならない。
・ 再現期間50年の最高静水位(最高天文潮位と高潮による水位上昇との適切な組合せに基づく。)
・ 再現期間50年の最低静水位(最低天文潮位と高潮による水位低下との適切な組合せに基づく。)
・ 砕波の最大荷重に対応した水位
6.4.4
海氷
場所によっては,海氷による洋上風車の支持構造物の荷重が重要となる場合がある。氷の荷重は,定着
氷板による静的荷重に関係している場合,又は風及び水流によって引き起こされる氷盤の動きによる動的
荷重に関係している場合がある。移動氷盤が長期間にわたって支持構造物に衝撃を与えた結果,顕著な疲
労荷重を引き起こすこともある。海氷の発生及び特性に関するサイト固有の評価は,12.7の規定によって
実施しなければならない。
氷荷重の計算に関する指針を附属書Eに示す。
6.4.5
海洋付着生物
海洋付着生物は,洋上風車の支持構造物の質量,形状及び表面状態に影響する。その結果,海洋付着生
物が支持構造物の流体力による荷重,動的応答,アクセス性及び腐食速度に影響する場合がある。
場所によっては,海洋付着生物が顕著になることがあり,支持構造物の設計において考慮しなければな
らない。
海洋付着生物は,“硬質”(一般に,貝類及びフジツボ)及び“軟質”[のり(海苔)及びコンブ類]に大
分される。硬質の付着物は,一般に軟質の付着物より厚さは薄いが粗度が大きい。一般に,構造物を設置
すると間もなく海洋生物が群生するが,数年後には成長速度が鈍る。
海洋付着生物の性質及び厚さは,構造部材の潮位に対する位置,卓越水流に対する向き,年月及び保守
23
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の方針によって異なるが,塩分,酸素濃度,pH値,水流,温度のようなその他のサイト条件にも依存する。
腐食環境は,通常,支持構造物の上部浸水部分及び飛まつ帯の下部に付着した海洋付着生物による影響
を受ける。海洋付着生物の種類及びその他の局部条件によって,実質的な影響は腐食性を進行させる場合
又は遅らせる場合がある。海洋付着生物によって腐食プロセスが進行する場合(例えば,腐食性代謝物質
によって),一般に“微生物腐食”(Microbiologically influenced corrosion:MIC)と呼ばれる。さらに,海
洋付着生物は,コーティング/ライニング及び電気防食を含む腐食抑制のシステムに影響を及ぼすことも
ある。
海洋付着生物について仮定するのは不確かさが伴うため,海洋付着生物の検査及び除去に関する方策を
支持構造物の設計の一環として計画することが望ましい。実施間隔,検査方法及び海洋付着生物の除去基
準は,洋上風車の構造信頼性に対する海洋付着生物の影響,及びサイト固有の条件下で海洋付着生物の経
験の程度を基準としなければならない。
6.4.6
海底変形及び洗掘
洋上風車の支持構造物は,海底変形及び洗掘の影響を考慮に入れて設計しなければならない。海底変形
及び洗掘の解析,並びに適切な洗掘防止工の設計は,ISO 19901-4:2003の要求事項に適合しなければなら
ない。海底条件の評価に関する要求事項は,12.9による。
6.5
その他の環境条件
風及び海洋環境条件以外の種々の環境(気象)条件は,熱,光化学,腐食,機械,電気,その他の物理
的作用によって,洋上風車の健全性及び安全性に影響することがある。さらに,気象パラメータが組み合
わさるとその作用が増大することがある。
少なくとも,次に示す環境条件を考慮し,施した対応を設計文書に記載しなければならない。
・ 気温
・ 湿度
・ 空気密度
・ 太陽の放射
・ 雨,ひょう(雹),あられ(霰),雪及び氷結
・ 化学的活性物質
・ 活動粒子[浮遊じんあい(塵埃)など]
・ 腐食を引き起こす塩分
・ 雷
・ 地震
・ 海水密度
・ 水温
・ 船舶などの往来
設計で考慮する気象条件は,変化する条件の代表値又は限界値によって指定する。設計値を選定する場
合は,幾つかの気象条件が同時に発生する確率も考慮する。
再現期間1年かそれ以上頻発する,気象条件の通常限界内の変化が,洋上風車の設計に用いた通常運転
(条件)を阻害してはならない。
相関関係が存在しない限り,6.5.2のその他の極値環境条件は,JIS C 1400-1:2010の通常風条件及び6.4
の通常海洋環境条件とを組み合わせなければならない。
6.5.1
その他の通常環境条件
24
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
考慮しなければならないその他の通常環境条件の値は,次の値を用いることが望ましい。
・ 気温範囲5)
−10 ℃〜+40 ℃
・ 相対湿度
100 %まで
・ 太陽の放射強度
1 000 W/m2
・ 空気密度
1.225 kg/m3
・ 海水密度
1 025 kg/m3
・ 水温範囲5)
0 ℃〜+35 ℃
注5) 気温範囲及び水温は,1時間平均値とする。
設計者がその他の外部条件を指定する場合は,それらのパラメータ及びその値を設計文書に記載する。
また,それらはIEC 60721-2-1:2002の要求事項に適合しなければならない。
6.5.2
その他の極値環境条件
洋上風車の設計で考慮しなければならないその他の極値環境条件は,温度,雷,氷結及び地震とする。
6.5.2.1
温度
標準風車クラスの洋上風車に対する極値気温範囲は,−20 ℃〜+50 ℃であることが望ましい。
6.5.2.2
雷
JIS C 1400-1:2010で要求している雷保護に関する規定は,標準風車クラスの洋上風車に対しても十分で
あると考えてもよい。
6.5.2.3
氷結
標準風車クラスの洋上風車に対しては,氷結に関する最低要求事項は,規定しない。風車各部の氷結と
して,次によるものを考慮しなければならない。
・ 温度0 ℃前後及び0 ℃以下では,湿度及び氷の堆積物
・ 温度0 ℃以下では,波頂の波しぶき
6.5.2.4
地震
標準風車クラスの洋上風車に対しては,地震に関する最低要求事項は規定しない。地震の条件及び影響
に関しては,JIS C 1400-1:2010を参照する。
6.6
電力系統条件
洋上風車接続端における通常の条件は,次による。
すなわち,パラメータが次の範囲内にある場合は,通常の電力系統条件を適用する。
・ 電圧 公称値±10 %(公称値自体は,IEC 60038参照)
・ 周波数 公称値±2 %
・ 電圧不平衡 電圧の逆相成分の比が2 %以下。
・ 自動再閉路周期 自動再閉路の周期は,初回の再閉路では0.1秒〜5秒,2回目の再閉路では10秒〜
90秒を考慮しなければならない。
・ 供給停止 電力系統の供給停止は,年間20回発生すると仮定する。6時間以下6) の供給停止は,通常
の供給停止状態であるとみなす。3か月以下の供給停止は,極値状態とみなさなければならない。
注6) 6時間の運転を,暴風の最も厳しい地域の持続時間に相当すると仮定している。
7
構造設計
7.1
一般
洋上風車構造物の荷重を受ける部品が健全であることを検証し,安全性レベルが許容水準にあることを
25
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
確認する。適切な安全性レベルをもつ洋上風車の構造的健全性を立証するために,構造部材の終極(終局)
強度及び疲労強度を,計算及び/又は試験によって検証しなければならない。
構造解析は,ISO 2394:1998に基づいて行う。
計算は,適切な方法を用いて実施する。計算方法の説明を設計文書に記載しなければならない。説明に
は,計算方法の妥当性の根拠を盛り込むか,又は適切な検証研究を参照しなければならない。
なお,強度検証試験の荷重レベルは,7.6による特性荷重に適した安全率に対応していなければならない。
7.2
設計方法
風車を設計するに当たっては,限界状態を超えないことを検証しなければならない。また,ISO 2394:1998
に規定するように,計算の代わりに模型試験及び試作機試験によって構造設計を検証してもよい。
7.3
荷重
設計計算では,7.3.1〜7.3.6に規定する荷重を考慮しなければならない。
7.3.1
重力荷重及び慣性荷重
重力荷重及び慣性荷重は,重力,振動,回転及び地震によって生じる静的及び動的荷重をいう。
7.3.2
空力荷重
空力荷重とは,空気流,並びに空気流と風車の静止部及び可動部との相互作用によって生じる静的及び
動的な荷重をいう。
空気の流れは,ロータ面を通過する平均風速及び乱れ,ロータの回転速度,空気密度並びに風車構成部
品の空力形状及び空力弾性効果を含むそれらの部品の相互作用効果に依存する。
7.3.3
作動荷重
作動荷重は,風車の運転及び制御によって生じる。また,作動荷重には,発電機及びインバータからの
トルク制御,ヨー及びピッチのアクチュエータの荷重,並びに機械ブレーキの荷重を含む幾つかの区分が
ある。それぞれのケースにおいて,応答及び荷重の計算では,利用可能なアクチュエータ力の範囲を考慮
することが重要である。特に,機械ブレーキでは,あらゆる制動時の応答及び荷重を確認する場合,温度
及び経年変化の影響を受ける摩擦,ばね力又は圧力の範囲を考慮しなければならない。
7.3.4
流体力荷重
流体力荷重は,水の流れ及び水の流れと洋上風車の支持構造物との相互作用によって生じる動的荷重で
ある。
流体力荷重は,水の流れの運動,水の密度,水深,支持構造物の形状及び流力弾性効果を含むそれらの
相互作用効果に依存する。
洋上風車の支持構造物のうち,流体力荷重を受けるものとして設計していない部分は,再現期間50年の
最高波頂高の期待値に最小間隔を加えた高さに位置していなければならない。このとき,最高天文潮位,
高潮による水位上昇,極値波の波頂高及び支持構造物の動きを考慮する。最小間隔はエアギャップと呼ば
れるが,これは0.2* Hs50とする。ただし,最小値は1 mとしなければならない。
特に,附属物の設計においては,波の“打上げ”によって生じる流体力荷重を考慮することが望ましい。
7.3.5
海氷荷重
洋上風車に作用する海氷荷重は,静的荷重及び動的荷重の両方がある。静的荷重は,定着氷板の温度変
動又は水位変化のいずれかによって生じる。動的荷重は,風及び潮流による氷盤の動き,並びに氷盤が支
持構造物と接触することによって生じる。
海又は湖における氷荷重と,支持構造物の設計との関連性は,洋上風車の具体的な設置場所及び特性に
依存する。氷荷重の計算に関する指針を附属書Eに示す。
26
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.6
その他の荷重
風車後流荷重,衝撃荷重,氷荷重などのその他の荷重が発生する可能性があるため,適宜,考慮する。
必要に応じて,JIS C 1400-1:2010に従って地震荷重を考慮しなければならない。このほか,海底地震で
生じた波(津波)による流体力荷重について考慮が必要な場合もある。
内圧及び外圧,並びにそれらから生じる浮力によって支持構造物に作用する静水圧荷重を,適宜,考慮
しなければならない。
7.4
設計条件及び荷重ケース
この細分箇条では,洋上風車の設計荷重ケースを示し,考慮しなければならない最小限の条件を規定す
る。
設計では,洋上風車の寿命は,洋上風車がさらされると考えられる最も顕著な状態までを含んだ設計条
件の組合せによって代表させることができる。
荷重ケースは,運転モード又は洋上風車特有の組立,建設若しくは保守の条件のようなその他の設計条
件と外部条件との組合せによって決定しなければならない。適切な発生確率での全ての該当する荷重ケー
スを制御及び保護システムの挙動と併せて考慮する。洋上風車の構造的健全性の検証に用いる設計荷重ケ
ースは,次の組合せから計算する。
・ 通常設計条件,及び適切な通常又は極値外部条件
・ 故障設計条件,及び適切な外部条件
・ 輸送,据付及び保守の設計条件,並びに適切な外部条件
極値外部条件と故障条件との間に相関関係がある場合は,両者の現実的な組合せを設計荷重ケースとし
て考慮しなければならない。
それぞれの設計条件において,数種類の設計荷重ケースを考慮する。少なくとも,表1の設計荷重ケー
スを考慮しなければならない。表1では,設計荷重ケースは,それぞれの設計条件について,風条件,海
洋環境条件,電気系統条件及びその他の外部条件によって規定している。さらに,海氷の発生が予想され
るサイトに洋上風車を設置する場合には,表2に示す海氷の設計荷重ケースを考慮しなければならない。
決定論的な風モデルによる設計荷重ケースにおいて,最大ヨー角及び/又は最大風速に達する前に,洋
上風車の制御によって風車を停止することがあり得る場合,同じ決定論的な風条件の変化による乱流条件
の下で,風車が確実に停止できることを示さなければならない。
特定の風車設計の構造的健全性に関連する場合は,その他の設計荷重ケースも考慮しなければならない。
それぞれの設計荷重ケースに対して,適切な解析タイプを,表1に“F”及び“U”で示す。“F”は,疲
労強度の評価に用いる疲労荷重の解析を意味する。“U”は,材料強度,翼端たわみ及び構造安定性に関係
した終極(終局)荷重の解析を意味する。
“U”で示す設計荷重ケースは,通常状態(N),異常状態(A)又は輸送及び建設状態(T)に分類され
る。通常設計荷重ケースは,風車の寿命を通じて頻繁に発生することが予想される。風車は,通常な状態,
又は軽度の故障若しくは異常状態の場合がある。異常設計条件は,発生頻度が低いと予想されるものであ
る。これは,通常,保護システムの作動に至る重大な故障を伴った設計条件に相当する。設計条件の分類
N,A又はTによって,終極(終局)荷重に適用する部分安全率γfを決定する。この安全率は,表3によ
る。
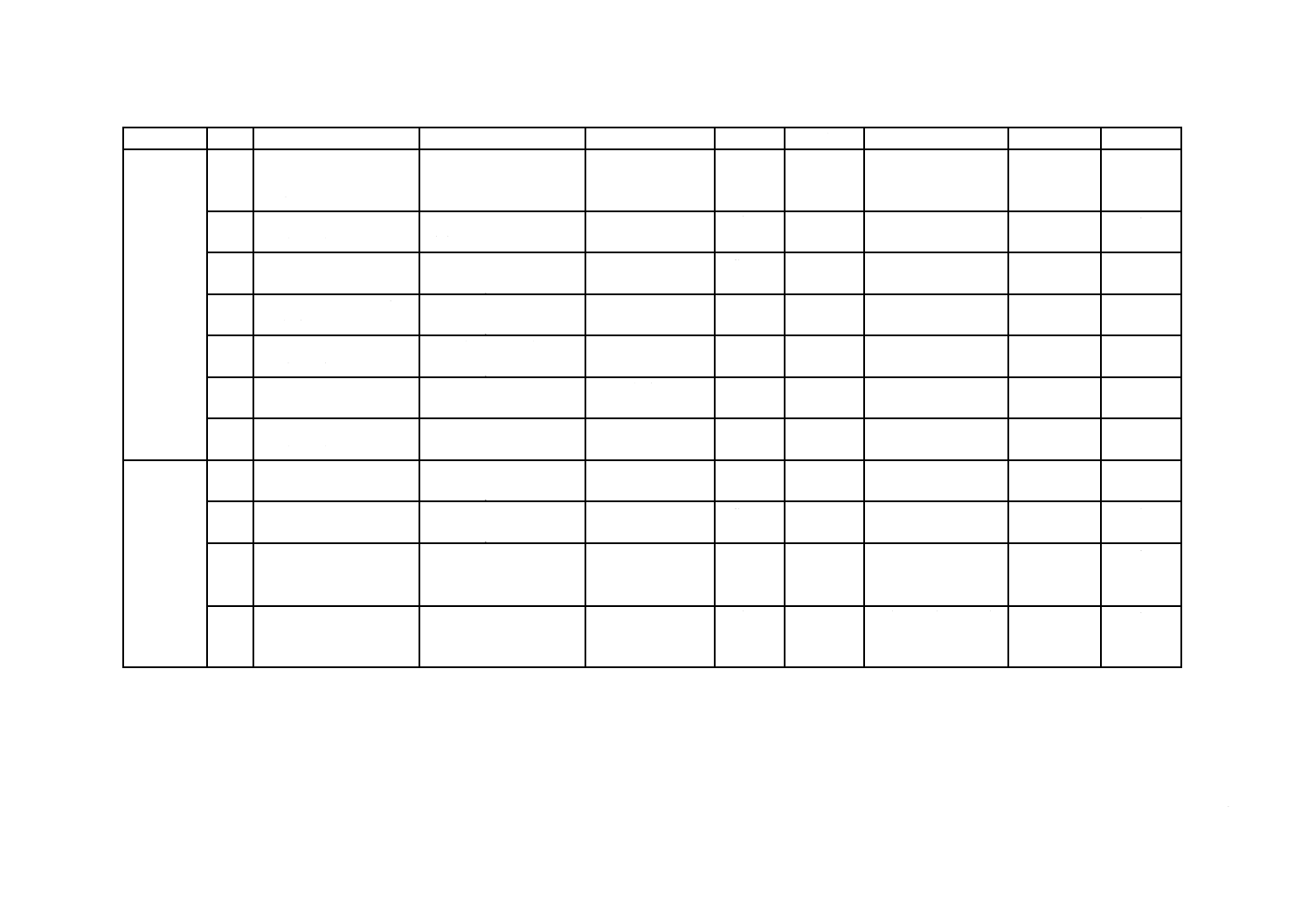
表1−設計荷重ケース(DLC)
設計条件
DLC
風条件
波
風及び波の方向性
海流
水位
その他の条件
解析のタイプ 部分安全率
1) 発電
1.1
NTM
Vin<Vhub<Vout
RNA
NSS
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
RNAに対する極値
荷重の外挿時
U
N
(1.25)
1.2
NTM
Vin<Vhub<Vout
NSS Hs,Tp及びVhubの
結合確率分布
COD及びMUL
水流なし NWLR又は
MSL以上
F
*
1.3
ETM
Vin<Vhub<Vout
NSS
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
U
N
1.4
ECD Vhub=Vr−2 m/s,
Vr及びVr+2 m/s
NSS(又はNWH)
Hs=E[Hs|Vhub]
MIS及び風向変化 NCM
MSL
U
N
1.5
EWS
Vin<Vhub<Vout
NSS(又はNWH)
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
U
N
1.6a
NTM
Vin<Vhub<Vout
SSS
Hs=Hs.SSS
COD及びUNI
NCM
NWLR
U
N
1.6b
NTM
Vin<Vhub<Vout
SWH
H=HSWH
COD及びUNI
NCM
NWLR
U
N
2) 発電中
の故障発
生
2.1
NTM
Vin<Vhub<Vout
NSS
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
制御装置の故障又は
ネットワークロス
U
N
2.2
NTM
Vin<Vhub<Vout
NSS
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
保護装置又は先行す
る内部の電気故障
U
A
2.3
EOG
Vhub=Vr±2 m/s及びVout
NSS(又はNWH)
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
外部又は内部の電気
故障(ネットワーク
ロスを含む。)
U
A
2.4
NTM
Vin<Vhub<Vout
NSS
Hs=E[Hs|Vhub]
COD及びUNI
水流なし NWLR又は
MSL以上
制御,保護又は電気
装置の故障(ネット
ワークロスを含む。)
F
*
2
7
C
1
4
0
0
-3
:
2
0
1
4
(I
E
C
6
1
4
0
0
-3
:
2
0
0
9
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
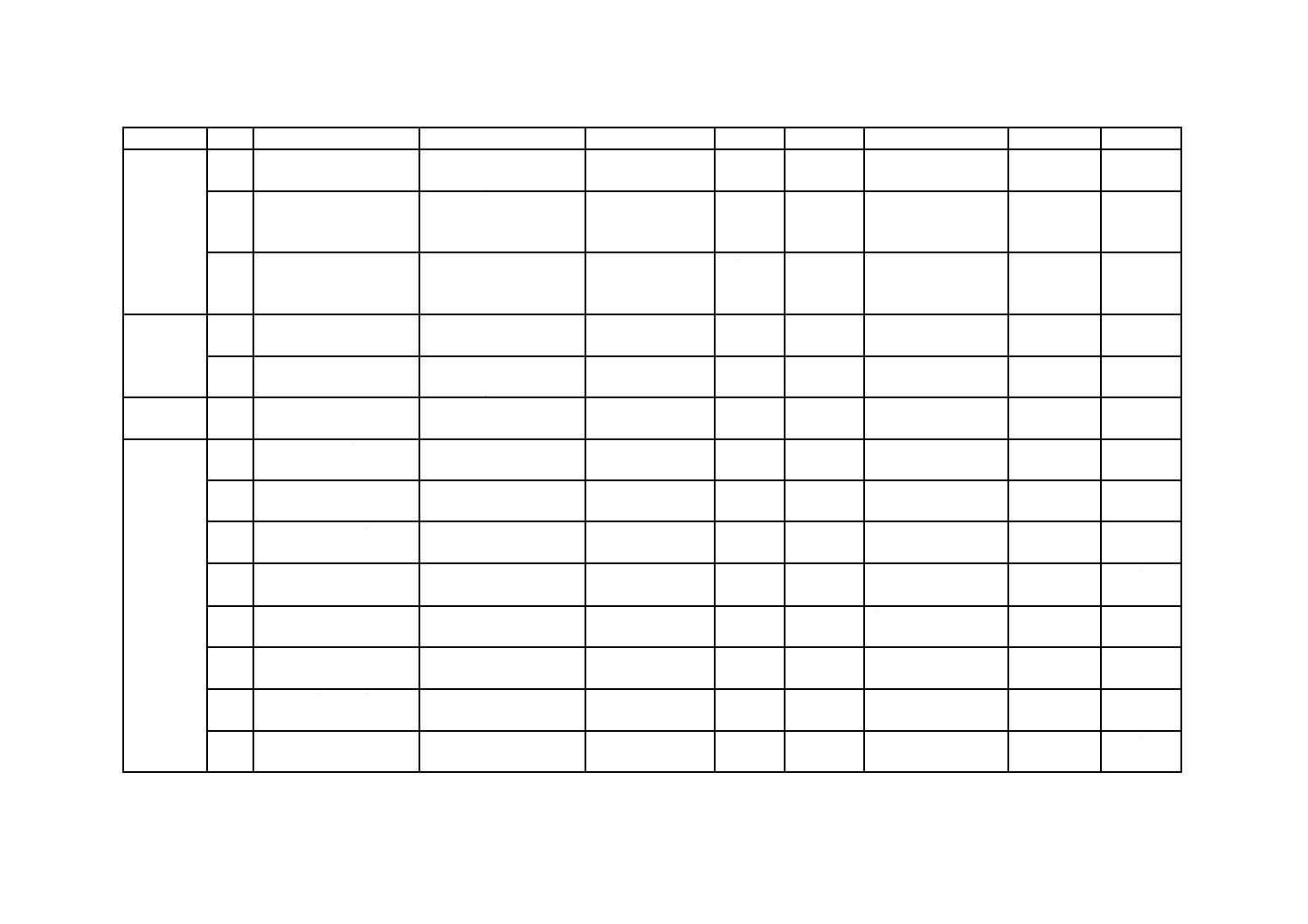
表1−設計荷重ケース(DLC)(続き)
設計条件
DLC
風条件
波
風及び波の方向性
海流
水位
その他の条件
解析のタイプ 部分安全率
3) 起動
3.1
NWP
Vin<Vhub<Vout
NSS(又はNWH)
Hs=E[Hs|Vhub]
COD及びUNI
水流なし NWLR又は
MSL以上
F
*
3.2
EOG
Vhub=Vin,Vr±2 m/s及び
Vout
NSS(又はNWH)
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
U
N
3.3
EDC1
Vhub=Vin,Vr±2 m/s及び
Vout
NSS(又はNWH)
Hs=E[Hs|Vhub]
MIS及び風向変化 NCM
MSL
U
N
4) 通常停
止
4.1
NWP
Vin<Vhub<Vout
NSS(又はNWH)
Hs=E[Hs|Vhub]
COD及びUNI
水流なし NWLR又は
MSL以上
F
*
4.2
EOG
Vhub=Vr±2 m/s及びVout
NSS(又はNWH)
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
U
N
5) 緊急停
止
5.1
NTM
Vhub=Vr±2 m/s及びVout
NSS
Hs=E[Hs|Vhub]
COD及びUNI
NCM
MSL
U
N
6) 待機中
(静止又は
遊転)
6.1a
EWM乱流モデル
Vhub=k1Vref
ESS
Hs=k2Hs50
MIS及びMUL
ECM
EWLR
U
N
6.1b
EWM定常風モデル
V(zhub)=Ve50
RWH
H=Hred50
MIS及びMUL
ECM
EWLR
U
N
6.1c
RWM定常風モデル
V(zhub)=Vred50
EWH
H=H50
MIS及びMUL
ECM
EWLR
U
N
6.2a
EWM乱流モデル
Vhub=k1Vref
ESS
Hs=k2Hs50
MIS及びMUL
ECM
EWLR
ネットワークロス
U
A
6.2b
EWM定常風モデル
V(zhub)=Ve50
RWH
H=Hred50
MIS及びMUL
ECM
EWLR
ネットワークロス
U
A
6.3a
EWM乱流モデル
Vhub=k1V1
ESS
Hs=k2Hs1
MIS及びMUL
ECM
NWLR
極値ヨーミスアライ
メント
U
N
6.3b
EWM定常風モデル
V(zhub)=Ve1
RWH
H=Hred1
MIS及びMUL
ECM
NWLR
極値ヨーミスアライ
メント
U
N
6.4
NTM
Vhub<0.7Vref
NSS Hs,Tp及びVhubの
結合確率分布
COD及びMUL
水流なし NWLR又は
MSL以上
F
*
2
8
C
1
4
0
0
-3
:
2
0
1
4
(I
E
C
6
1
4
0
0
-3
:
2
0
0
9
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
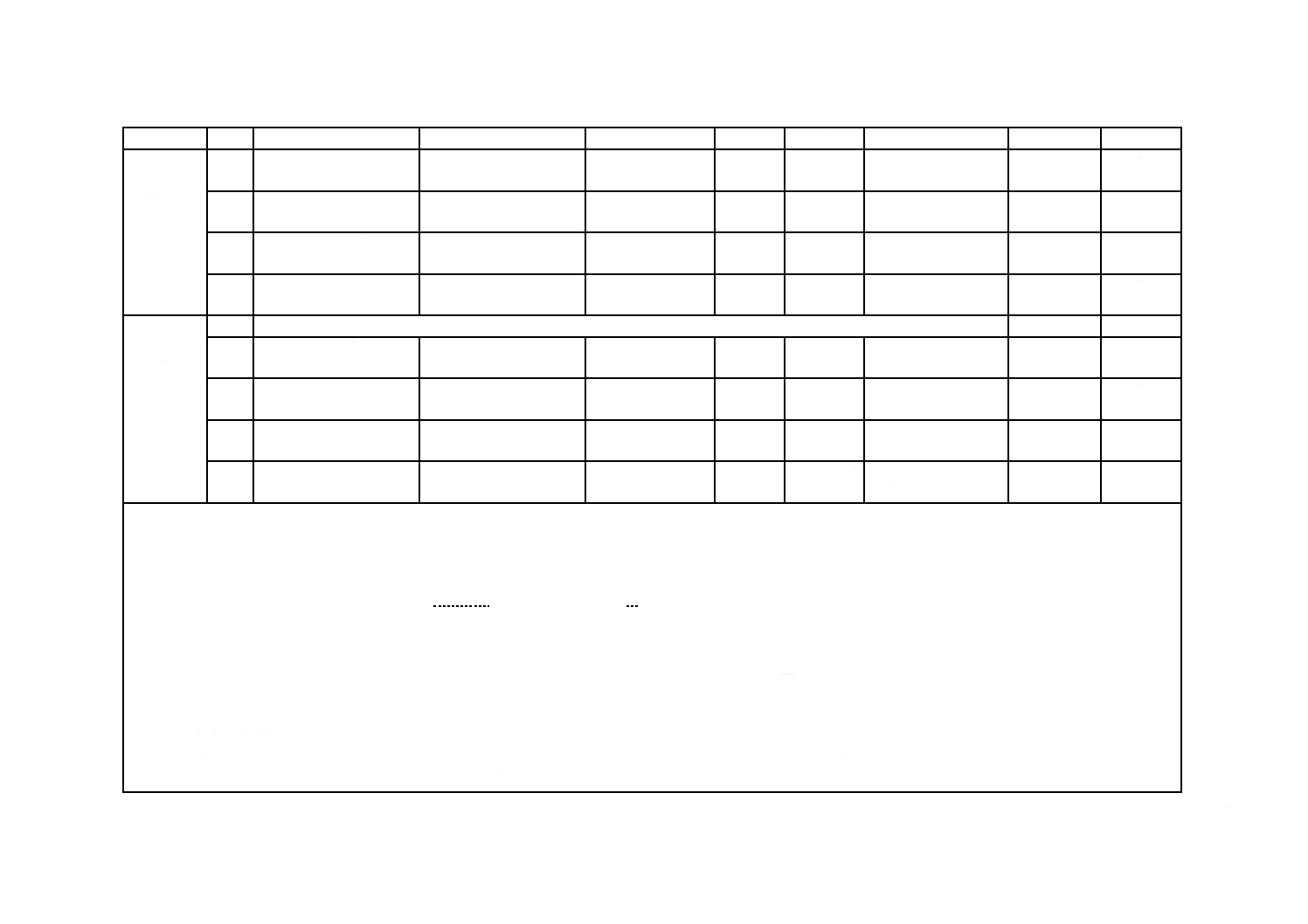
表1−設計荷重ケース(DLC)(続き)
設計条件
DLC
風条件
波
風及び波の方向性
海流
水位
その他の条件
解析のタイプ 部分安全率
7) 待機中
に故障の
発生
7.1a
EWM乱流モデル
Vhub=k1V1
ESS
Hs=k2Hs1
MIS及びMUL
ECM
NWLR
U
A
7.1b
EWM定常風モデル
V(zhub)=Ve1
RWH
H=Hred1
MIS及びMUL
ECM
NWLR
U
A
7.1c
RWM定常風モデル
V(zhub)=Vred1
EWH
H=H1
MIS及びMUL
ECM
NWLR
U
A
7.2
NTM
Vhub<0.7Vref
NSS Hs,Tp及びVhubの
結合確率分布
COD及びMUL
水流なし NWLR又は
MSL以上
F
*
8) 輸送,
組立,保守
及び修理
8.1
製造業者が指定
U
T
8.2a
EWM乱流モデル
Vhub=k1V1
ESS
Hs=k2Hs1
COD及びUNI
ECM
NWLR
U
A
8.2b
EWM定常風モデル
Vhub=Ve1
RWH
H=Hred1
COD及びUNI
ECM
NWLR
U
A
8.2c
RWM定常風モデル
V(zhub)=Vred1
EWH
H=H1
COD及びUNI
ECM
NWLR
U
A
8.3
NTM
Vhub<0.7Vref
NSS Hs,Tp及びVhubの
結合確率分布
COD及びMUL
水流なし NWLR又は
MSL以上
据付け期間中は電気
系統なし。
F
*
“Vr±2 m/s”は,この範囲内の全ての風速に対する感度を解析しなければならない。
注記 略語を,次に示す。
COD
同一方向(6.4.1参照)
DLC
設計荷重ケース
ECD
方向変化を伴う極値コヒーレントガスト(JIS C 1400-1)
ECM
極値流速モデル(6.4.2.5参照)
EDC
極値方向変化(JIS C 1400-1)
EOG
運転時の極値突風(JIS C 1400-1)
ESS
極値海況(6.4.1.5参照)
ETM
極値乱流モデル(JIS C 1400-1)
EWH
極値波高(6.4.1.6参照)
EWLR 極値水位範囲(6.4.3.2参照)
EWM
極値風速モデル(JIS C 1400-1)
EWS
極値ウィンドシア(JIS C 1400-1)
MIS
方向の偏差(6.4.1参照)
MSL
平均海潮位(6.4.3参照)
MUL
多方向(6.4.1参照)
NCM 通常流速モデル(6.4.2.4参照)
NTM
通常乱流モデル(JIS C 1400-1)
NWH
通常波高(6.4.1.2参照)
NWLR 通常水位範囲(6.4.3.1参照)
NWP
通常ウィンドプロファイルモデル
NSS
通常海況(6.4.1.1参照)
(JIS C 1400-1)
RWH 低減波高(6.4.1.7参照)
RWM
低減風速モデル(6.3参照)
SSS
高波浪時海況(6.4.1.3参照)
SWH
高波浪時波高(6.4.1.4参照)
UNI
単一方向(6.4.1参照)
F
疲労(7.6.3参照)
U
終極強度(7.6.2参照)
N
通常
A
異常
T
輸送及び建設
*
疲労に対する部分安全率(7.6.3参照)
2
9
C
1
4
0
0
-3
:
2
0
1
4
(I
E
C
6
1
4
0
0
-3
:
2
0
0
9
)
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
30
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1に風速範囲が規定されている場合は,風車設計に対して最も厳しい条件になる風速を考慮する。風
速範囲は,幾つかの風速の値で表してもよい。この場合,計算精度を確保するために,十分な分解能をも
たなければならない7)。設計荷重ケースを定義することにおいて,箇条6の風条件及び海洋環境条件を基
準とする。
注7) 一般に,風車の間隔は2 m/sで十分である。
RNAに作用する荷重の計算では,一般に波は風と同一方向であり,風も波も一つの方向(単一方向)か
ら作用すると仮定してもよい8)。ただし,平均風向の過渡的変化を伴う設計荷重ケース(DLC 1.4及びDLC
3.3)は除く。
注8) DLC 1.4及びDLC 3.3では,平均風向の過渡的変化の前は,風及び波は,同一方向,かつ,単
一方向であると仮定してもよい。
一般に,平均風向の過渡的変化を伴う設計荷重ケース(DLC 1.4及びDLC 3.3)及び待機状態(静止又は
遊転)設計条件の風車に対する設計荷重ケースを除く全ての設計荷重ケースにおいて,支持構造物に作用
する荷重の計算では,風及び波の方向は,同一と仮定してもよい。
幾つかのケースにおいては,多方向からの風及び波は,支持構造物に作用する荷重に重大な影響を及ぼ
すことがある。これは主に,支持構造物の非軸対称性の程度に依存する。表1に示す幾つかの設計荷重ケ
ースでは,風及び波が最も厳しいケースである一つの方向(単一方向)から作用すると仮定して荷重計算
を実施してもよい。ただし,この場合,計算した最も厳しいケースの荷重を支持構造物の該当方向に適用
することによって,構造的健全性を検証しなければならない。
それぞれの設計荷重ケースについて考慮しなければならない平均又は極値ヨーミスアライメントは,JIS
C 1400-1:2010による。ヨーミスアライメントは,風車主軸の風向に対する水平面内の偏差と定義する。
7.4.1
発電(DLC 1.1〜DLC 1.6)
この設計条件では,洋上風車は運転中であり,電気負荷に接続している。想定する風車の形状には,ロ
ータのアンバランスを考慮する。また,ロータの製造過程で規定されている最大質量のアンバランス及び
空力アンバランス(例えば,ブレードピッチ及びねじれの偏差)を設計計算に用いる。また,ヨーミスア
ライメント及び制御装置のトラッキング(目標値追従)誤差などの理論的な最適運転条件からの偏差も,
運転荷重の解析で考慮しなければならない。
DLC 1.1及びDLC 1.2では,洋上風車の寿命を通じて通常運転条件で発生する通常乱流モデル(NTM)
及び確率論的な通常海況(NSS)から生じる荷重の要求事項を具体化した。
DLC 1.1の解析は,RNAに作用する終極(終局)荷重の計算だけに要求する。DLC 1.1の計算は,ある
平均風速範囲に対する確率論的海況,及び乱流流入風の複数の応答解析による荷重応答結果の統計的外挿
に基づかなくてはならない。それぞれの個別海況に対する有義波高は,該当する平均風速を条件とする有
義波高の期待値としなければならない。
DLC 1.2では,それぞれの該当する平均風速に対して,一つの有義波高の値を考慮してもよい。ただし,
設計者は考慮する通常海況の個数及び分解能が,気象海象パラメータの十分に長期間の分布に関連した疲
労荷重の計算に対して十分なものとしなければならない。それぞれの通常海況では,有義波高,ピークス
ペクトル周期,波向及び水位は,気象海象パラメータの長期結合確率分布を基に,関連する平均風速とと
もに考慮する。
DLC 1.2では,通常海況(NSS)を想定しなければならない。それぞれの通常海況に対して有義波高,
ピークスペクトル周期及び方向を設置予定のサイトに適した気象海象パラメータの長期結合確率分布を基
に,関連する平均風速とともに選定しなければならない。設計者は,気象海象パラメータの十分に長期間
31
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の分布に関連した疲労損傷に対して,考慮する通常海況の個数及び分解能を,十分に確保しなければなら
ない。
DLC 1.3は,極値乱流条件において生じる終極(終局)荷重の要求事項を具体化したものである。この
設計荷重ケースに対しては,通常海況(NSS)を想定し,それぞれの個別海況に対する有義波高は,該当
する平均風速を条件とする有義波高の期待値としなければならない。
DLC 1.4及びDLC 1.5は,洋上風車の寿命中に発生し得るその影響が重大な事象となり得る過渡的なケ
ースを規定している。これらの荷重ケースでは,通常海況(NSS)を想定し,それぞれの個別海況に対す
る有義波高は,該当する平均風速を条件とする有義波高の期待値としなければならない。決定論的な通常
波高(NWH)を用いた応答解析で代替してもよいが,この場合には,波高が該当する平均風速を条件とす
る有義波高の期待値に等しいと仮定しなければならない。
DLC 1.4では,過渡的な風向変化の前は,風及び波は同一方向であると仮定してもよい。
DLC 1.6aは,通常乱流モデル(NTM)及び高波浪時海況(SSS)条件において生じる終極(終局)荷重
の要求事項を具体化したものである。それぞれの個別海況に対する有義波高は,6.4.1.3の規定により,該
当する平均風速の有義波高の条件付き分布から計算しなければならない。
DLC 1.6bでは,それぞれの平均風速に対する決定論的な高波浪時波高(SWH)は,6.4.1.4の規定により
計算しなければならない。
なお,DLC 1.6aの扱いにおいて,確率論的な高波浪時海況の動的シミュレーションで波の非線形運動が
適切に表現されている場合は,DLC 1.6bの計算は省略してもよい。
RNAに作用する荷重の計算では,DLC 1.1の応答解析結果の統計解析は,翼根の面内モーメント及び面
外モーメントの極値,並びに翼端たわみの計算を含まなければならない。DLC 1.3による極値設計値がこ
れらのパラメータの極値を上回った場合は,DLC 1.1の詳細な解析は省略してもよい。これらのパラメー
タの極値設計値がDLC 1.3による極値設計値以下である場合,DLC 1.3に用いる極値乱流モデル(JIS C
1400-1参照)の係数cは,DLC 1.3で計算した極値設計値がDLC 1.1で計算したこれらのパラメータの極
値設計値以上になるまで引き上げてもよい。
7.4.2
発電中の故障発生又は電力系統の喪失(DLC 2.1〜DLC 2.4)
この設計条件は,風車の発電中に故障又は電力系統の喪失が発生した場合に引き起こされる過渡的な事
象を扱う。風車の荷重に顕著に影響する制御及び保護システムのあらゆる故障又は電気システムの内部故
障(例えば,発電機の短絡)を考慮しなければならない。DLC 2.1では,制御機能関連の故障又は電力系
統の喪失の発生は,通常事象として考慮する9)。DLC 2.2では,保護機能又は内部電気システムに関連し
た故障を含むまれな事象は異常として考慮する。DLC 2.3では,重大な影響になり得る風事象であるEOG
を,内部又は外部電気システムの故障(電力系統の喪失を含む。)と関連させ,異常事象として考慮する。
このケースでは,荷重が最悪となるように,これら二つの事象が発生するタイミングを選定しなければな
らない。故障又は電力系統の喪失が直ちに停止には至らないものの,それによる荷重が顕著な疲労損傷に
つながる可能性がある場合,この状況の継続時間及び通常乱流モデル(NTM)による疲労損傷をDLC 2.4
にて評価しなければならない。
注9) DLC 2.1では,電力系統における故障に対するライドスルーに関する設計条件についても考慮
することが望ましい。
DLC 2.1,DLC 2.2,DLC 2.3及びDLC 2.4では,通常海況(NSS)条件を想定し,それぞれの個別海況
に対する有義波高は,該当する平均風速を条件とする有義波高の期待値としなければならない。DLC 2.3
の場合は,決定論的な通常波高(NWH)を用いた応答解析で代替してもよいが,この場合には波高が,該
32
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
当する平均風速を条件とする有義波高の期待値に等しいと仮定しなければならない。
7.4.3
起動(DLC 3.1〜DLC 3.3)
この設計条件は,静止状態又は遊転状態から発電に至る過渡時に洋上風車に作用する荷重の要因となる
全ての事象を含む。発生回数は,制御システムの挙動に基づいて推定しなければならない。
DLC 3.1,DLC 3.2及びDLC 3.3では,通常海況(NSS)条件を想定し,それぞれの個別海況に対する有
義波高は,該当する平均風速を条件とする有義波高の期待値としなければならない。決定論的な通常波高
(NWH)を用いた応答解析で代替してもよいが,この場合には,波高が該当する平均風速を条件とする有
義波高の条件付き分布の期待値に等しいと仮定しなければならない。
DLC 3.3では,風向が過渡的に変化する前の状態では,風及び波は同一方向であると仮定してもよい。
7.4.4
通常停止(DLC 4.1〜DLC 4.2)
この設計条件は,発電状態から静止状態又は遊転状態に至る通常の過渡状態において,洋上風車に作用
する荷重の要因となる全ての事象を含む。発生回数は,制御システムの挙動に基づいて推定しなければな
らない。
DLC 4.1及びDLC 4.2では,通常海況(NSS)を想定し,それぞれの個別海況に対する有義波高は,該
当する平均風速を条件とする有義波高の期待値としなければならない。決定論的な通常波高(NWH)を用
いた応答解析で代替してもよいが,この場合には,波高が該当する平均風速を条件とする有義波高の期待
値に等しいと仮定しなければならない。
7.4.5
緊急停止(DLC 5.1)
緊急停止によって生じる荷重を考慮しなければならない。
DLC 5.1では,通常海況(NSS)条件を想定し,それぞれの個別海況に対する有義波高は,該当する平
均風速を条件とする有義波高の期待値としなければならない。
7.4.6
待機状態(静止又は遊転)(DLC 6.1〜DLC 6.4)
この設計条件では,待機状態の風車のロータは静止状態又は遊転状態のいずれかである。この条件の終
極(終局)荷重は,DLC 6.1,DLC 6.2及びDLC 6.3の解析によって,求めなければならない。これに対し
て,DLC 6.4は,疲労荷重に関する規定である。
DLC 6.1及びDLC 6.2では,極値風条件と極値波浪条件との組合せは,全体的な極値環境が再現期間50
年となるようなものでなければならない。極値風条件及び極値波浪条件の長期結合確率分布を求めるデー
タがない場合,再現期間50年の極値海況において,再現期間50年の10分間平均極値風速が発生すると仮
定しなければならない。DLC 6.3では,再現期間1年の極値海況及び10分間平均極値風速の組合せについ
て同じ仮定を適用しなければならない。
DLC 6.1,DLC 6.2及びDLC 6.3は,乱流流入風及び確率論的な海況の応答解析によって,又は定常的な
風モデルを決定論的な設計波と組み合わせて処理することによって解析してもよい。これらの2種類の方
法に基づく,DLC 6.1,DLC 6.2及びDLC 6.3に関する荷重ケースを,表1に定義する。風条件を極値風速
モデル(EWM)で定義する設計荷重ケースでは,定常的な極値風速モデル又は乱流極値風モデルのいずれ
かを,表1のとおり用いなければならない。定常的な極値風速モデル又は定常的な低減風速モデル(RWM)
を用いる場合は,これを決定論的な設計波と組み合わせ,動的応答に対する適切な補正を行って準定常解
析から応答を推算しなければならない(附属書D参照)。
DLC 6.1,DLC 6.2及びDLC 6.3では,風向及び波向の角度偏差を考慮して支持構造物に作用する荷重を
計算しなければならない。風向及び波向について,サイト固有の適切な測定値が利用できる場合は,これ
を用いて,これらの設計荷重ケースの極値風条件と極値波浪条件との組合せについて,方向の角度偏差の
33
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
範囲を求める。荷重計算は,この範囲内で支持構造物に作用する荷重が最大となるような角度偏差の値に
基づかなければならない。
サイト固有の適切な風向及び波向のデータが存在しない場合は,支持構造物に作用する荷重が最大とな
る角度偏差を考慮しなければならない。この角度偏差が30°を超える場合,偏差を発生させた風向変化に
関連した期間内で海況の厳しさが減衰するため,極値波高を低減させてもよい10)。極値波高の低減分は,
水深,吹走距離及びその他の該当するサイト固有の条件を考慮して計算しなければならない。
注10) 極値風条件及び極値波浪条件は,最初は同一方向と仮定してもよい。暴風域が風車サイト上を
通過すると,風向が変化して波向との角度偏差が生じる可能性がある。顕著な風向変化を考慮
する間は,波の状態の厳しさは緩和される。
特性荷重において,風車のヨーシステムに滑りが発生する可能性がある場合は,平均ヨーミスアライメ
ントに対して考えられる最も好ましくない滑りを加味しなければならない。極値風条件でヨー運動が予測
されるヨーシステム(例えば,フリーヨー,受動ヨー又はセミフリーヨー)をもつ場合には,乱流風モデ
ルを用いなければならない。このとき,ヨーミスアライメントは,乱流風向変化及び風車の動的ヨー応答
に依存する。また,通常運転から極値条件まで風速が増大するときに,風車が大きなヨー運動又はつりあ
い状態の変化を受ける場合は,この挙動を解析に含めなければならない。
DLC 6.1において,能動的にヨー制御を行う洋上風車の場合,定常的な極値風速モデルにおいては±15°,
乱流極値風モデルにおいては±8°の平均ヨーミスアライメントを想定しなければならない。ただし,この
場合,ヨーシステムの滑りがないことを保証できなければならない。
DLC 6.1aでは,乱流極値風モデルを極値海況(ESS)条件と併せて用いなければならない。応答計算に
は,極値風速と極値海況との各組合せに対して,六つ以上の1時間の再現を基準とした動的シミュレーシ
ョンを用いなければならない。この場合,ハブ高さの平均風速,乱流標準偏差及び有義波高を,それぞれ
の1時間の応答解析期間に対して50年再現値としなければならない。50年再現平均風速の1時間値は,
表1の換算法を用いて10分間平均から式(17)のように求めてもよい。
min
10
.
50
1
hour
1.
50
−
−
=V
k
V
··································································· (17)
ここに,
k1=0.95
乱流標準偏差の1時間値は,10分間値から式(18)のように求めてもよい。
b
+
=
−
−
min
10
.i
hour
1.i
σ
σ
·································································· (18)
ここに,
b=0.2 m/s
JIS C 1400-1:2010の附属書Bに示した乱流モデルを式(17)及び式(18)で算出する50年再現平均風速及び
乱流標準偏差の1時間値とともに用いてもよい。
1時間の応答解析期間に対する有義波高は,表1の換算法を用いて3時間評価時間に対する値から求め
てもよい。このとき,水深の深いサイトでは,式(19)となる。
k2=1.09 ················································································· (19)
水深が浅いサイトでは,式(19)のk2の値は,安全側であると考えてもよいし,調整してもよい。
設計者が,再現時間を1時間未満とした場合でも推定した極値応答が減少することはないことを実証で
きる場合には,1時間未満の再現を仮定してもよい。この場合は,附属書Dを参照し,拘束波による解法
を用いてもよい。この手法については,応答解析期間10分間を基準とした拘束波による解法では,ハブ高
さの平均風速は再現期間50年の10分間値とし,有義波高は再現期間50年の3時間値としなければならな
い。また,組み込む規則波の波高は,再現期間50年の極値波高の大きさH50としなければならない。
DLC 6.1bでは,定常的な極値風速モデルを再現期間50年の低減波高Hred50の決定論的な低減波高(RWH)
34
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
と併せて用いなければならない。
DLC 6.1cでは,定常的な低減風速モデル(RWM)を決定論的な極値波高(EWH)と併せて用いなけれ
ばならない。この場合,風速はVred50を仮定し,波高は再現期間50年の極値波高H50に等しいものと仮定
しなければならない。
DLC 6.1b及びDLC 6.1cは,DLC 6.1aの扱いにおいて,確率論的な極値海況の動的シミュレーションで
波の非線形運動が適切に表現されている場合,省略してもよい。
DLC 6.2では,極値風条件を含む暴風の初期段階における電力系統の喪失を想定しなければならない。
風車の制御装置及びヨーシステムを6時間運転できる容量のバックアップ電力が備わっていない限り,±
180°までの風向変化の影響を解析しなければならない。
DLC 6.2aでは,乱流極値風モデルを極値海況(ESS)条件と併せて用い,ハブ高さ平均風速及び有義波
高を50年再現値としなければならない。極値応答の推定には,DLC 6.1aと同じ方法を用いなければなら
ない。
DLC 6.2bでは,定常的な極値風速モデルを再現期間50年の低減波高Hred50の決定論的な低減波高(RWH)
と併せて用いなければならない。DLC 6.2bは,DLC 6.2aの扱いにおいて,確率論的な極値海況の動的シミ
ュレーションで波の非線形運動が適切に表現されている場合,省略してもよい。
DLC 6.3では,再現期間1年の極値風を極値ヨーミスアライメントと組み合わせなければならない。定
常的な極値風速モデルにおいてはヨー誤差±30°まで,又は乱流風モデルにおいては平均ヨーミスアライ
メント±20°までを仮定しなければならない。
DLC 6.3aでは,乱流極値風モデルを極値海況(ESS)条件と併せて用いなければならない。この場合,
ハブ高さ平均風速及び有義波高は1年再現値としなければならない。極値応答の推定には,上記のDLC 6.1a
と同じ方法を用いなければならない。
DLC 6.3bでは,定常的な極値風速モデルを,再現期間1年の低減波高Hred1の決定論的な低減波高(RWH)
と併せて用いなければならない。DLC 6.3bは,DLC 6.3aの扱いにおいて,確率論的な極値海況の動的シミ
ュレーションで波の非線形運動を適切に表現している場合,省略してもよい。
DLC 6.4では,任意の部品に対して顕著な疲労損傷が発生する可能性がある場合(遊転状態のブレード
の質量などによる),変動荷重時の発電していない期間内の時間推定値を各風速について考慮しなければな
らない。特に,波の励振による影響,及び静止状態又は遊転状態のロータからの低モードの空力減衰の影
響を受けた支持構造物の共振による荷重を考慮しなければならない。海の状態は,通常海況(NSS)を想
定しなければならない。それぞれの通常海況に対する有義波高,ピークスペクトル周期及び波向を関連す
る平均風速と併せて選定しなければならない。選定は,設置予定のサイトに適した気象海象パラメータの
長期結合確率分布を基準としなければならない。設計者は,気象海象パラメータの十分に長期間の分布に
関連した疲労損傷に対して,考慮する通常海況の個数及び分解能を,十分に確保しなければならない。
7.4.7
待機中に故障が発生した場合(DLC 7.1〜DLC 7.2)
待機中の風車の挙動が電力系統又は風車の故障によって通常挙動から逸脱する場合について,解析をし
なければならない。電力系統の喪失時以外の故障によって待機状態の風車が通常挙動から逸脱する場合は,
起こり得る事態を特に解析の対象としなければならない。
ヨーシステムの故障の場合は,±180°のヨーミスアライメントを考慮しなければならない。それ以外の
故障に対しては,ヨーミスアライメントをDLC 6.1と同じにしなければならない。
DLC 7.1では,故障条件と,極値風条件及び極値波浪条件との組合せは,全体的な極値環境が再現期間1
年とならなければならない。極値風条件及び極値波浪条件の長期結合確率分布を求めるデータが存在しな
35
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
い場合は,再現期間1年の極値海況において,再現期間1年の10分間平均極値風速が発生すると仮定しな
ければならない。
DLC 7.1は,乱流流入風及び確率論的な海況の応答解析によって,又は定常的な風モデルを決定論的な
設計波と組み合わせて処理することによって解析してもよい。これらの2種類の方法に基づく,DLC 7.1
の補助的な荷重ケースを,表1に定義する。極値風速モデル(EWM)によって風条件を定義する設計荷重
ケースでは,定常的な極値風速モデル又は乱流極値風モデルのいずれかを表1のとおり用いなければなら
ない。定常的な極値風速モデル又は定常的な低減風速モデル(RWM)を用いる場合は,これを決定論的な
設計波と組み合わせ,動的応答に対する適切な補正を行って準定常解析から応答を推定しなければならな
い(附属書D参照)。
DLC 7.1では,風向と波向との角度偏差を考慮して,支持構造物に作用する荷重を計算しなければなら
ない。風向及び波向について,サイト固有の適切な測定値が利用できる場合は,これを用いてこれらの設
計荷重ケースの極値風条件と極値波浪条件との組合せについて,方向の角度偏差範囲を求めなければなら
ない。荷重計算は,この範囲内で支持構造物に作用する荷重が最大となるような角度偏差の値を基準とし
なければならない。
サイト固有の適切な風向及び波向のデータが存在しない場合は,支持構造物に作用する荷重が最大とな
る角度偏差を考慮しなければならない。この角度偏差が30°を超える場合,偏差を発生させた風向変化に
関連した期間は海況の厳しさが減衰するため,極値波高を低減させてもよい。極値波高の低減分は,水深,
吹走距離及びその他の該当するサイト固有の条件を考慮して計算しなければならない。
DLC 7.1にみられる特性荷重においてヨーシステムに滑りが発生する可能性がある場合は,考えられる
最も好ましくない滑りを考慮しなければならない。
DLC 7.1aでは,乱流極値風モデルを極値海況(ESS)条件と併せて用いなければならない。極値応答の
推定は,上記のDLC 6.1aと同じ方法を用いなければならない。
DLC 7.1bでは,定常的な極値風速モデルを再現期間1年の低減波高Hred1の決定論的な低減波高(RWH)
と併せて用いなければならない。
DLC 7.1cでは,定常的な低減風速モデル(RWM)を決定論的な極値波高(EWH)と併せて用いなけれ
ばならない。この場合,風速はVred1と仮定し,波高は再現期間1年の極値波高H1に等しいものと仮定し
なければならない。
DLC 7.1b及びDLC 7.1cは,DLC 7.1aの扱いにおいて,確率論的な極値海況の動的シミュレーションで
波の非線形運動が適切に表現されている場合,省略してもよい。
DLC 7.2では,任意の部品に対して顕著な疲労損傷が発生する可能性がある場合,各風速及び海況につ
いて電力系統の故障又は風車の故障による発電していない期間内の時間推定値を考慮しなければならない。
特に,波の励振による影響,及び静止状態又は遊転状態のロータからの低モードの空力減衰の影響を受け
た支持構造物の共振による荷重を考慮しなければならない。海の状態は,通常海況(NSS)条件を想定し
なければならない。それぞれの通常海況に対する有義波高,ピークスペクトル周期及び波向を関連する平
均風速と併せて選定しなければならない。選定は,設置予定のサイトに適した気象海象パラメータの長期
結合確率分布を基準としなければならない。設計者は,気象海象パラメータの完全長期分布に関連した疲
労損傷に対して,考慮する通常海況の個数及び分解能を,十分に確保しなければならない。
7.4.8
輸送,組立,保守及び修理(DLC 8.1〜DLC 8.3)
DLC 8.1では,製造業者は,洋上風車の輸送,現地組立,アクセス,保守及び修理に対して想定される
全ての風条件,海洋環境条件及び設計条件を記載しなければならない。記載した最大限の風条件及び海洋
36
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
環境条件が風車に対して顕著な荷重を発生させ得る場合は,これらの条件を設計において考慮しなければ
ならない。製造業者は,記載した条件と,設計で考慮する風条件及び海洋環境条件との間には十分なマー
ジンを与え,許容し得る安全性レベルを確保しなければならない。この十分なマージンは,記載した風条
件に5 m/sを加えて求めてもよい。
洋上風車の輸送,組立,アクセス,保守及び修理時に発生する荷重は,次のものを考慮に入れなければ
ならない。
・ 工具及び携行機材の質量
・ クレーン操作による荷重
・ 風車の作業船による係留荷重及び防舷荷重
・ 該当する場合,ヘリコプタ作業に関連した荷重
専用作業船による支持構造物への衝撃を考慮して,ISO 19902の要求事項及び指針に沿って解析を実施
しなければならない。
設計者は,設計条件,作業船の最大寸法及び作業船が洋上風車に接岸する場合の限界外部条件を記載し
なければならない。設計者は,作業船が0.5 m/sの速度で支持構造物に接触するとき以上の衝撃を考慮しな
ければならない。このときの質量の割増し係数は,作業船が横向きに衝突する場合は1.4,船首又は船尾で
衝突する場合は1.1とする。この場合,衝撃に関連した全運動エネルギーが防舷設備によって吸収される
ものと仮定しなければならない。作業船によるアクセスが可能な最大風条件及び最大海洋環境条件による
荷重には,作業船の衝撃による荷重を組み合わせなければならない。
支持構造部が吸収するエネルギーは,作業船の衝撃が作用する部分の剛性と比較したときの支持構造物
の剛性に依存する。コンクリート構造のような剛性が非常に高い支持構造物の場合は,エネルギーは主に
作業船によって吸収される。作業船による衝突後に重要となるのは,衝撃力によって発生する支持構造物
への何らかの損傷を調べることである。そのうえで,支持構造物の所定の耐荷重を維持するために修理が
必要な場合,その内容を特定しなければならない。
設計者に作業船に関する情報がない場合,衝撃力には,通常,支持構造物の全幅にわたって分布する5 MN
の水平分布荷重を適用することができる。この荷重は,動的増幅を含めて考慮しなければならない。衝突
部分の鉛直範囲は,作業船の喫水並びに作業船のアクセスが可能な最大波及び最大潮せき(汐)に基づい
て評価しなければならない。実際には,作業船の位置は,平均潮位(MSL)に対して+3 m〜−5 mで変化
する。局部圧力の計算では,鉛直方向は2 mの範囲を仮定してもよい。
ヘリコプタ作業による洋上風車の荷重は,必要に応じて考慮しなければならない。設計条件,ヘリコプ
タの最大寸法及びヘリコプタが洋上風車に着陸する場合の限界外部条件を,事業者又は設計者が記載し,
荷重計算において考慮しなければならない。
このほか,DLC 8.2には,1週間以上続く可能性のある全ての輸送,組立,保守及び修理の風車状態を含
めなければならない。該当する場合,この荷重ケースには,一部完成した支持構造物,RNAなしで建つ支
持構造物及びブレードを1本以上外した状態のRNAを含めなければならない。これらの状態のいずれに
おいても,電力系統は接続していないものと仮定しなければならない。これらの状態では,電力系統接続
を必要としないことを前提に,荷重を低下させてもよい。
ロック装置は,DLC 8.1の該当条件から生じる荷重に耐えることができなければならない。特に,アク
チュエータの設計最大駆動力の妥当性を考慮に入れなければならない。
DLC 8.2aでは,乱流極値風モデルを極値海況(ESS)条件と併せて用いなければならない。極値応答の
推定には,上記のDLC 6.1aと同じ方法を用いなければならない。
37
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
DLC 8.2bでは,定常的な極値風速モデルを再現期間1年の低減波高Hred1の決定論的な低減波高(RWH)
と併せて用いなければならない。
DLC 8.2cでは,定常的な低減風速モデル(RWM)を決定論的な低減波高(RWH)と併せて用いる。こ
の場合,風速はVred1と仮定し,波高は再現期間1年の極値波高H1に等しいものと仮定しなければならな
い。
DLC 8.2b及びDLC 8.2cは,DLC 8.2aの扱いにおいて,確率論的な極値海況の動的シミュレーションで
波の非線形運動が適切に表現されている場合,省略してもよい。
DLC 8.3では,洋上ウィンドファームの建設期間中において,電力系統に接続するまでの間に,任意の
部品に対して顕著な疲労損傷が発生する可能性がある場合,各風速及び海況について,発電していない期
間内の時間推定値を考慮しなければならない。また,部分設置された洋上風車の疲労荷重についても考慮
しなければならない。例えば,一部完成した支持構造物,RNAなしで建つ支持構造物及びブレードを1本
以上外した状態でのRNAで,この状況がかなりの長期間継続すると予測される場合が,これに当たる11)。
海の状態は,通常海況(NSS)条件を想定しなければならない。それぞれの通常海況に対する有義波高,
ピークスペクトル周期及び波向を,関連する平均風速と併せて選定しなければならない。選定は,設置予
定のサイトに適した気象海象パラメータの長期結合確率分布を基準としなければならない。設計者は,気
象海象パラメータの十分に長期間の分布に関連した疲労損傷に対して,考慮する通常海況の個数及び分解
能を,十分に確保しなければならない。
注11) 部分設置した洋上風車の風及び/又は波,並びに水流による渦励振による感度を考慮すること
が望ましい。
7.4.9
海氷設計荷重ケース
海氷が発生すると予測されるサイトに設置する洋上風車では,支持構造物の設計において表1の荷重ケ
ースに加えて表2の荷重ケースも考慮しなければならない。海氷設計荷重ケースE1〜E7については,該
当する荷重計算方法の指針と併せて附属書Eに示す。
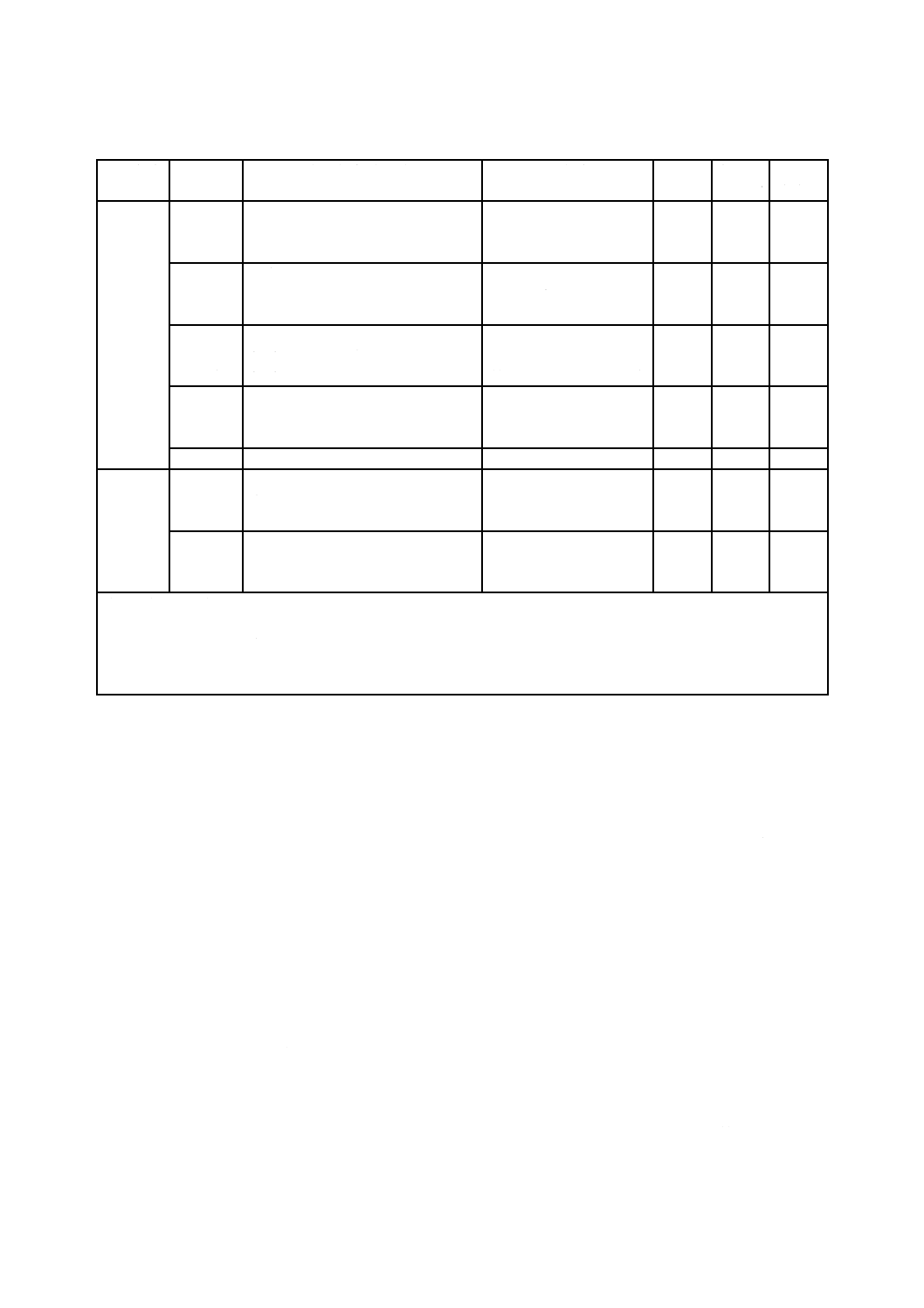
38
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2−海氷の設計荷重ケース
設計条件
DLC
海氷条件(荷重)
風条件
水位
解析の
タイプ
部分
安全率
発電
E1
温度変動による水平荷重
NTM
Vhub=Vr±2 m/s及びVout
最大スラストとなる風速
NWLR
U
N
E2
温度変動又はアーチ効果による水平
荷重
NTM
Vhub=Vr±2 m/s及びVout
最大スラストとなる風速
NWLR
U
N
E3
極値事象
の外挿
該当速度の移動氷盤による水平荷重
h=h50 外洋の場合
h=hm 内陸にある湖の場合
NTM
Vhub=Vr±2 m/s及びVout
最大スラストとなる風速
NWLR
U
N
E4
該当速度の移動氷盤による水平荷重
h=h50 外洋の場合
h=hm 内陸にある湖の場合
Vin<Vhub<Vout
NWLR
F
*
E5
水位変動による結氷板の垂直荷重
風荷重は適用しない
NWLR
U
N
待機状態 E6
氷丘氷及び氷りょう(稜)からの圧
力
EWM
乱流風モデル
Vhub=V1
NWLR
U
N
E7
該当速度の移動氷盤からの水平荷重
h=h50 外洋の場合
h=hm 内陸にある湖の場合
NTM
Vhub<0.7Vref
NWLR
F
*
注記 略語を,次に示す。
DLC
設計荷重ケース
EWM
極値風速モデル(JIS C 1400-1)
NTM
通常乱流モデル(JIS C 1400-1)
NWLR
通常水位範囲(6.4.3.1参照)
F
疲労(7.6.3参照)
U
終極強度(7.6.2参照)
N
通常
*
疲労の部分安全率(7.6.3参照)
7.5
荷重計算及び荷重効果計算
荷重及び荷重効果の計算は,該当する外部条件の組合せに対して洋上風車の構造の動的応答を適切に考
慮した方法を用いて行わなければならない。
7.5.1
流体力荷重の関連性
洋上風車の支持構造物に作用する流体力荷重が,支持構造物の動的振動の結果としてロータ ナセル・ア
センブリ(RNA)に間接的にのみ影響することがある。このロータ ナセル・アセンブリ(RNA)に対す
る流体力荷重の間接的影響は,一般に小さく,支持構造物の動的特性によっては無視できることもある。
設計者は,このような荷重の影響が無視できることを実証できる場合は,ロータ ナセル・アセンブリ
(RNA)への流体力荷重の影響を考慮しなくてもよい。ロータ ナセル・アセンブリ(RNA)の設計で流
体力荷重の影響を考慮しない場合も含めた全てのケースにおいて,各洋上風車サイトの海洋環境条件を適
切に考慮して構造的健全性を実証しなければならない。
洋上風車の支持構造物の設計に関連した荷重計算では,7.3.1〜7.3.6に規定する全ての荷重を考慮に入れ
なければならない。荷重計算は,洋上風車サイトを代表する外部条件に基づかなければならない。
7.5.2
流体力荷重の計算
洋上風車の支持構造物に作用する流体力荷重の計算は,適切な方法を用いて実施しなければならない。
附属書Dに,構造物に対する流体力荷重を,附属物及び海洋付着生物の影響を考慮して計算するための指
針を参考として示す。
39
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
海洋付着生物が支持構造物への流体力荷重に及ぼす影響を考慮しなければならない。影響の考慮は,構
造部材の外径に“硬質”の海洋付着生物の予測平均厚さを加えるとともに,構造部材を海洋付着生物の予
測量及び予測厚さに応じて“滑らかな”表面と,“粗い”表面とに分類して行わなければならない。
なお,最高天文潮位(HAT)より高い位置にある構造要素は,流体力学的に滑らかとみなすことができ
る。
ある特定の部品組立体が完全に覆われるほど,海洋付着生物の厚さがある場合は,その影響を支持構造
物の流体力荷重のモデリングに適切に組み込まなければならない。
7.5.3
海氷荷重の計算
海氷による静的荷重及び動的荷重の計算のための指針を,附属書Eに示す。
7.5.4
シミュレーションに関する要求事項
通常,風車の荷重効果の計算では,構造動力学モデルを利用した動的シミュレーションを用いる。ある
特定の荷重ケースには,対応した確率論的な風及び/又は波の情報を入力する。これらのケースでは,特
性荷重効果の推定結果の統計的信頼性を確保するために,荷重データの総期間は十分に長くなければなら
ない。一般には,応答解析で考慮するそれぞれの平均ハブ高さ風速及び海況には,10分間の確率論的再現
を6個以上(又は連続1時間を1個)を必要としなければならない。ただし,次のようにある特定の設計
荷重ケースでは,荷重計算への要求事項は更に複雑である。
・ DLC 2.1,DLC 2.2及びDLC 5.1では,与えられた風速及び海況の事象ごとに12個以上の10分間応答
解析を実施しなければならない。
・ DLC 1.1では,平均風速と海況との組合せごとに行う応答解析個数及び期間は,特性荷重効果の外挿
から信頼できる極値の長期確率分布を求めるのに十分なものでなければならない。
・ DLC 1.6a,DLC 6.1a,DLC 6.2a,DLC 6.3a及びDLC 7.1aでは,応答解析で考慮するそれぞれの平均風
速及び海況に対して,1時間の確率論的再現を6個以上必要としなければならない。ただし,計算時
間を短くすることにより,推定される極値応答が1時間の解析による実現で得られるものを下回らな
いことを設計者が実証できる場合は,この要求事項を緩和し,これより短い解析時間を想定してもよ
い。この目的においては,拘束波による解法を用いてもよい(附属書D参照)。
動的シミュレーションを必要とする荷重ケースの入力として用いる平均風速,乱流標準偏差及び有義波
高の値は,選定された応答解析期間に適したものでなければならない。
DLC 1.6a,DLC 6.1a,DLC 6.2a,DLC 6.3a及びDLC 7.1aを除いて,動的シミュレーションを必要とする
荷重ケースの入力として用いる平均風速,乱流標準偏差及び有義波高の値は,入力パラメータの評価時間
が選定された応答解析期間に一致するよう,必要に応じて調節しなければならない。異なる評価時間に対
する風速,乱流標準偏差及び海況の各パラメータを調節する必要性及びその方法に関する指針は,12.3及
び12.4による。DLC 6.1a,DLC 6.2a,DLC 6.3a及びDLC 7.1aでは,7.4.6に示す換算を適用しなければな
らない。DLC 1.6aの場合は,指針を附属書Gに示す。
通常,動的シミュレーションに用いる初期条件は,応答解析期間の初期において荷重効果の統計値に影
響するため,確率論的な風及び/又は波の入力を用いた解析期間の考慮対象からデータの最初の5秒間(又
は必要に応じてそれより長く)は除外しなければならない。
風速範囲が与えられる確率論的な海況及び乱流流入風の応答解析に関係する荷重ケースでは,特性荷重
効果の超過確率を,洋上風車を設置するサイトに固有の通常海況条件と風速との結合確率分布を考慮して
計算しなければならない。荷重計算の多くは限定された持続期間の確率論的応答解析を伴うため,要求さ
れる再現期間に対して求めた特性荷重効果は,応答解析で求めた値より大きくなってもよい。
40
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
決定論的風速場及び波浪事象が指定された荷重ケースでは,荷重効果の特性値は最悪のケースで計算し
た過渡値としなければならない。乱流流入風を不規則海況と併せて用いる場合,それぞれの確率論的再現
の中の最悪のケースで計算した荷重効果の平均値を用いなければならない。ただし,DLC 2.1,DLC 2.2及
びDLC 5.1は除く。これらのケースでは,荷重効果の特性値は最大荷重効果が大きい方から半分までのも
のの平均値としなければならない。
7.5.5
その他の要求事項
7.3.1〜7.3.6に規定した荷重をそれぞれの設計荷重ケースで考慮に入れなければならない。該当する場合
は,次の内容も併せて考慮に入れる。
・ 風車そのものによる風速場のじょう(擾)乱(風車後流による誘導速度,タワー後流など)
・ ブレードの空力特性に対する三次元流の影響(例えば,三次元失速及び空力翼端損失)
・ 否定上な空力効果
・ 構造動力学と振動モードの連成
・ 空力弾性効果
・ 風車の制御及び保護システムの挙動
・ 洋上風車のブレード又はその他の部品の氷結による空力特性及び動的特性に対する影響
・ 基礎と海底との相互作用の静的特性及び動的特性。設計者は,特に,基礎と海底との相互作用の非線
形性並びに洗掘,サンドウェーブなどによる動的特性の不確かさ,及びそれが長期的に変化する可能
性について注意しなければならない。支持構造物の固有振動数の変化及び基礎荷重の変化に対する洋
上風車の設計のロバスト性を評価しなければならない。
・ 堆積した海洋付着生物の質量が支持構造物の固有振動数及び動的荷重に及ぼす影響
・ 空力荷重と流体力荷重との組合せに対する風車の動的応答
・ 附属書Cに示す,非線形な波の運動
・ 附属書Dに示す,回折力
疲労荷重を計算するための荷重ケースを定義するのに用いる気象海象パラメータ(有義波高,ピークス
ペクトル周期及び平均風速)は,気象海象パラメータの十分に長期間の分布に対する疲労損傷を明らかに
十分な分解能を確保しなければならない。
風向と波向との間の角度偏差が大きく異なることを考慮した動的シミュレーションでは,横方向の空力
弾性減衰が非常に小さくなるため,波力による支持構造物の共振による応答が増大する場合がある。設計
者は,支持構造物の横方向運動の空力弾性減衰のモデリング及び方向データの両方の信頼性の確保に特に
注意しなければならない。
多くの場合で,風車部品の重要箇所における局所ひず(歪)み又は局所応力は,同時に作用する多軸荷
重によって支配される。このような場合,設計荷重を規定するのに,直交方向荷重の時系列データには,
動的シミュレーションから得られたデータを用いることもある。このような直交方向成分の時系列データ
を用いて疲労荷重及び終極(終局)荷重を計算する場合,位相及び大きさの両方が保たれるように,風向
方向成分の時系列データを組み合わせなければならない。この直接法からは,顕著な応力の時刻歴データ
が求められる。そのうえで,荷重組合せの問題を避けるため,この極値予測法及び疲労予測法を一つの時
刻歴データに適用することができる。
終極(終局)荷重成分は,最も好ましくない成分値と同時に発生すると仮定した,安全側に見積もった
手法によって組み合わせてもよい。
コンクリートのひび割れ評価と地盤沈下の評価について設計条件を定義することが望ましい。発電荷重
41
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ケース(DLC 1.2)に基づき,次のいずれかを用いることが望ましい。
・ 時間超過確率1 %に対応する曲げモーメントによる荷重
・ 最大平均推力に標準偏差の1.28倍を加算した曲げモーメントによる荷重(90 %分位値)
7.6
終極(終局)限界状態解析
7.6.1
方法
この規格は,部分安全率の形式を用いて荷重及び材料の不確かさ及びばらつき,解析方法の不確かさ並
びに破壊が発生した場合の構造部品の重要性を示す。
洋上風車のロータ ナセル・アセンブリ(RNA)の終極(終局)限界状態解析は,JIS C 1400-1:2010に
規定した要求事項を満たさなければならない。支持構造物の設計では,次の細分箇条による。
7.6.1.1
部分安全率法
構造物又は構造部品の安全性レベルは,式(20)のように設計荷重効果Sdが設計耐力Rd以下の場合に,満
足されるとみなす。
Sd≦Rd ··················································································· (20)
式(20)は,設計基準であり,設計不等式ともいう。対応する等式Sd=Rdは,設計等式という。
7.6.1.1.1
設計荷重効果
特定の荷重Fiに関連した設計荷重効果を設定するには,次の2種類の方法がある。
・ 方法1 設計荷重効果は,特性荷重効果に所定の荷重係数を乗じて式(21)によって求める。
Sdi=γfiSki ················································································ (21)
ここに,
Sdi: 特定の荷重Fiに対する設計荷重効果
γfi: 荷重係数
Ski: 特定の荷重Fiに対する特性荷重効果
・ 方法2 設計荷重効果は,設計荷重の構造解析から求める。このとき,設計荷重は,特性荷重に所定
の荷重係数を乗じて式(22)によって求める。
Fdi=γfiFki················································································ (22)
ここに,
Fdi: 特定の荷重Fiに対する設計荷重
Fki: 特定の荷重Fiに対する特性荷重
動的応答を適切に表現することが重要な場合,一般には,方法1を用いて設計荷重効果を求める。一方,
方法2は,一般には,材料の非線形挙動若しくは幾何学的非線形性又はその両方を適切に表現することが
重要な場合に用いる。一般に,方法1は,タワーを含めた支持構造物の設計荷重効果を風車に作用する風
荷重から計算する場合に適用する。一般に,方法2は,タワーの荷重効果を境界条件として用いる支持構
造物及び基礎の設計に用いる。これら二つの方法の相違点は,図4による。
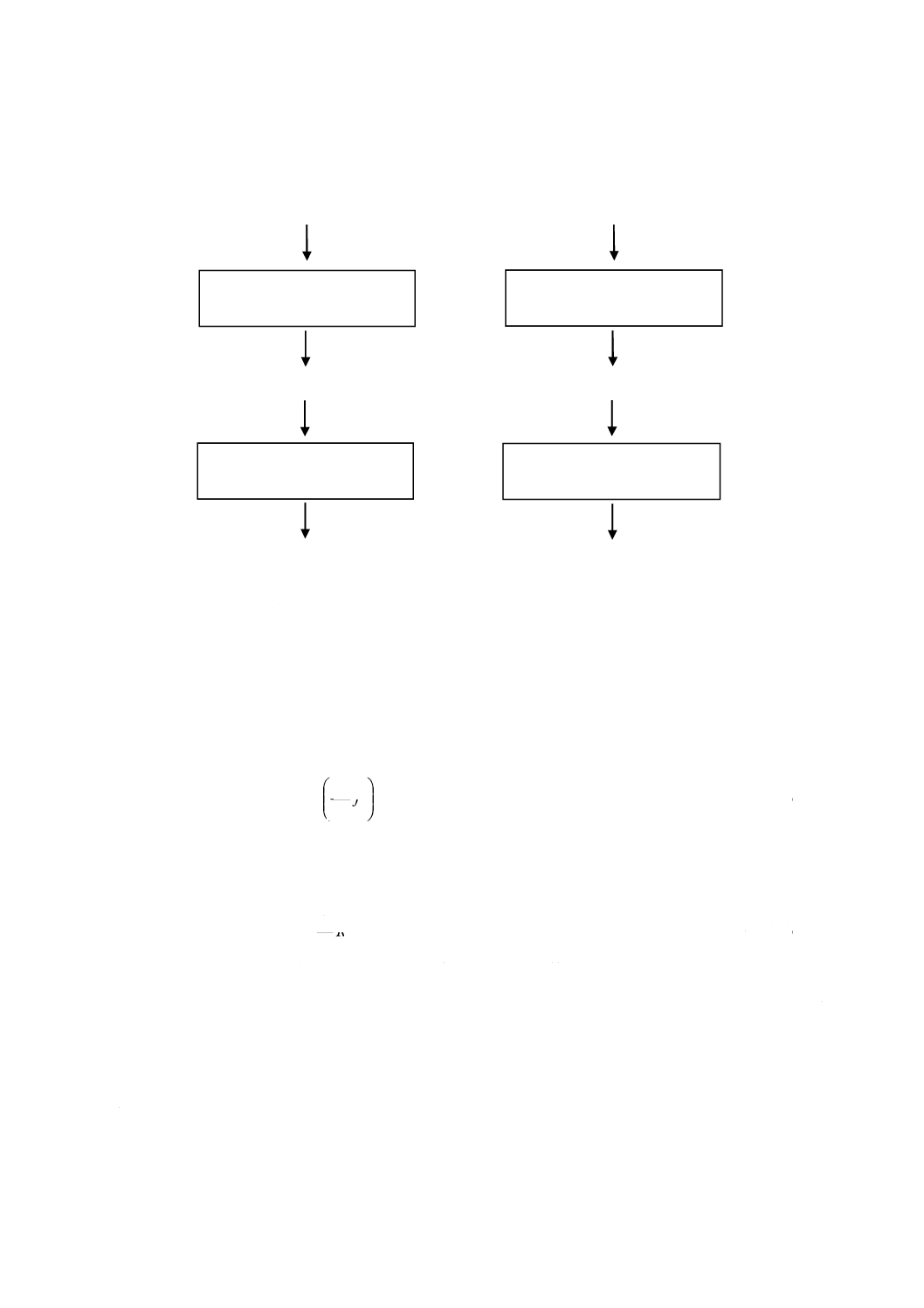
42
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4−設計荷重効果の2種類の計算方法
7.6.1.1.2
設計耐力
特定の構造部品の設計耐力Rdを設定するには,2種類の方法がある。
・ 方法1 式(23)を用いて特性材料強度から設計耐力を求める。
k
m
d
1f
R
R
γ
=
········································································· (23)
ここに,
γm: 材料強度に対する材料係数
fk: 材料強度の特性値
・ 方法2 式(24)を用いて特定の構造部品の特性耐力から設計耐力を求める。
k
m
d
1R
R
γ
=
·············································································· (24)
ここに,
Rk: 部品耐力の特性値
JIS C 1400-1:2010の規定では,式(22)を式(24)とともに用いる。一部の規格,例えば,ISO 19902は,式
(21)を式(23)と組み合わせて用いることを要求している。一方,ISO 19903:2006などの規格は,式(22)を式
(24)と組み合わせて用いることを要求している。
7.6.2
終極(終局)強度解析
支持構造物のシステム及び部品の設計耐力は,ISOの海洋構造物設計規格又はその他の一般に認知され
た海洋規格に従って求めなければならない。ただし,タワーの設計耐力については,JIS C 1400-1:2010の
7.6.2に従って求めてもよい。終極(終局)強度設計荷重ケース及び関連する荷重安全率については,この
a) 方法1
動的解析及び/又は
非線形解析
特性荷重
特性荷重効果
設計荷重効果
b) 方法2
荷重係数に乗じる
特性荷重
設計荷重
設計荷重効果
荷重係数に乗じる
動的解析及び/又は
非線形解析
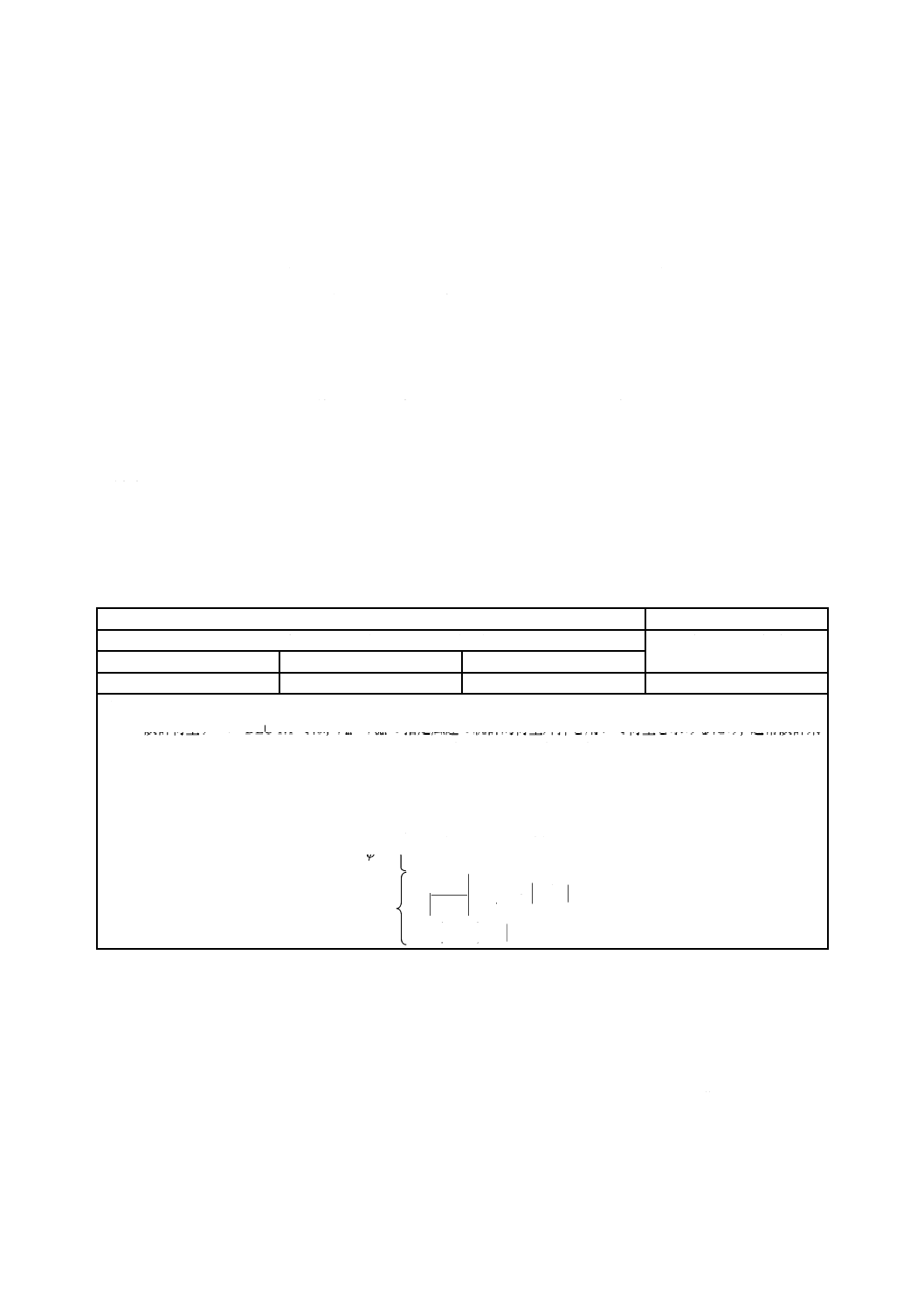
43
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
規格(JIS C 1400-3)に規定する値を用いて,支持構造物を設計しなければならない。
評価対象の支持構造物部品ごとに,かつ,表1の終極(終局)強度解析が要求される荷重ケースごとに,
マージンが最も少ない最も重要な限界状態について式(22)の設計基準を検証する。
下部構造及び基礎の構造設計を類似した設計原則に基づいたISO規格又はその他の一般に認知された海
洋規格に従って実施する場合は,7.6.1.1.1の方法2を用いて地盤の非線形性の影響を適切に考慮しなけれ
ばならない。一般的な設計条件では,主な荷重は固定荷重に加えて風荷重及び流体力荷重となる。基礎及
び下部構造の設計荷重効果は,流体力荷重及び固定荷重の設計値に加え,設計風荷重効果をタワーフラン
ジ又は海底面のような適切な境界面における外部荷重として適用した構造解析から求めてもよい。
7.6.1.1.1の方法1を用いて,特性風荷重,流体力荷重及び固定荷重を組み合わせて統合的に動的解析を
行った結果の特性荷重効果に,同じ荷重安全率を適用して設計荷重効果を求めてもよい。この場合,地盤
及び下部構造の応答における非線形性のモデリングが欠落していることを補正するために,部分安全率を
補正することに注意する必要がある。この補正によって,関連するISO設計規格に対する参照も含め,こ
の規格の規定と同等レベルの構造的信頼性を確認する必要がある。
7.6.2.1
荷重に対する部分安全率
荷重に対する部分安全率は,JIS C 1400-1:2010に規定した値以上でなければならない。これらの値を参
考として表3に掲載する。
表3−荷重に対する部分安全率γf
好ましくない荷重
好ましい荷重b)
設計状態のタイプ(表1及び表2参照)
全ての設計条件
通常(N)
異常(A)
輸送及び建設(T)
1.35 a)
1.1
1.5
0.9
注a) 全体の荷重応答を顕著に緩和する初期張力及び重力荷重は望ましい荷重として考慮する。
b) 設計荷重ケースDLC 1.1では,Vin〜Voutの指定風速の統計的荷重外挿を用いて荷重を求めるため,通常設計条
件に対する部分荷重係数は,γf=1.25としなければならない。通常設計条件において重力による荷重応答の特
性値Fgravityを当該の設計条件に対して計算することができ,かつ,重力が“好ましくない荷重”の場合,重
力,その他の荷重発生源による複合荷重の部分荷重係数は次の値としてもよい。
γf=1.1+ϕς2
ここに,
ϕ = 0.15(DLC 1.1の場合)
0.25(上記以外の場合)
ς =
k
gravity
1
F
F
−
,(
k
gravity
F
F
≦
の場合)
1,(
k
gravity
F
F
>
の場合)
7.6.2.2
耐力及び材料に対する部分安全率
支持構造物のシステム及び部品の設計耐力は,ISOの海洋構造物設計規格又はその他の一般に認知され
た海洋設計規格に従って求めなければならない。したがって,終極(終局)設計耐力,それに関連した材
料強度及び/又は耐力の特性値,並びにそれらに関連した材料及び/又は耐力の安全率を評価する公式は,
上記の規格のものを用いなければならない。ただし,タワーの設計耐力については,JIS C 1400-1:2010の
7.6.2に従って求めてもよい。
7.6.3
疲労破壊
44
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
支持構造物のシステム及び部品の設計耐力は,ISOの海洋構造物設計規格又はその他の一般に認知され
た海洋設計規格に従って求めなければならない。したがって,疲労設計耐力,それに関連した材料強度及
び/又は耐力の特性値,並びにそれらに関連した材料及び/又は耐力の安全率を評価する公式は,上記の
規格のものを用いなければならない。ただし,タワーの設計耐力については,JIS C 1400-1:2010の7.6.3
によって求めてもよい。疲労設計荷重ケース及び関連する荷重安全率については,この規格(JIS C 1400-3)
に規定する値を用いて,支持構造物を設計しなければならない。
評価対象の支持構造物部品ごとに,かつ,疲労強度解析が要求される表1及び表2の荷重ケースごとに,
マージンが最も少ない最も重要な限界状態について設計基準を検証しなければならない。
7.6.4
特殊部分安全率
測定又は測定によって検証された解析によって,荷重の大きさが通常のレベルの信頼性より高いことが
確かめられている場合は,荷重に対して低めの部分安全率を用いてもよい。ここで用いる全ての部分安全
率の値は,設計文書に記載しなければならない。
8
制御及び保護システム
洋上風車の運転及び安全性は,JIS C 1400-1:2010の箇条8に規定した要求事項を満たした制御及び保護
システムで管理しなければならない。
制御及び保護システムの全ての部品を海洋環境の影響から適切に保護するための対策を施さなければな
らない。腐食防止に関する指針を附属書Hに示す。
9
機械システム
この規格における機械システムとは,単に静的構造部品又は電気部品で構成するシステムだけではなく,
軸,リンク,軸受,スライド,歯車及びその他の装置の組合せによって使われるか,又は相対運動を伝達
する全てのシステムを指す。風車内部におけるこのようなシステムには,増速機,軸及び,カップリング
などの動力伝達装置の機械要素,並びにブレーキ,ブレードピッチ制御装置及びヨー駆動装置などの補助
装置を含む場合がある。補助装置は,電気,油圧又は空圧によって駆動される場合がある。
洋上風車内部の全ての機械システムの設計は,JIS C 1400-1:2010の箇条9に規定した要求事項を満たさ
なければならない。
全ての機械システムを海洋環境の影響から適切に保護するための対策を施さなければならない。腐食防
止に関する指針を附属書Hに示す。
10
電気システム
洋上風車の“電気システム”は,風車接続端を含むそれぞれの洋上風車に設置する全ての電気設備で構
成する。
集電設備は,この規格の対象ではない。
洋上風車の電気システムの設計は,JIS C 1400-1:2010の箇条10に規定した要求事項を満たさなければ
ならない。ただし,要求事項が明らかに陸上サイトだけに関連するものは除く。
全ての電気部品を海洋環境の影響から適切に保護するための対策を施さなければならない。対策は,該
当する国内及び国際的な設計に関する規約及び規則による適切な腐食クラス,気候クラス,環境クラス,
汚損クラス及び外郭による保護等級(IPコード)を選定することによって行わなければならない。腐食防
止に関する指針を附属書Hに示す。
45
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
設計者は,絶縁要件,塩分雰囲気,湿度及び温度,換気要件,水分及び/又は結露の存在,雨漏りの可
能性,機械的衝撃又は振動,並びに風車電気システムの健全性を維持するための保守要件について,適切
に配慮しなければならない。
11
基礎の設計
洋上風車の基礎の設計及び構造解析は,ISOの海洋構造物設計規格又はその他の一般に認知された海洋
設計規格に従って実施しなければならない。ISO規格以外の海洋設計規格を用いる場合は,終極(終局)
強度及び疲労について同等レベル以上の構造的信頼性が得られることを実証する必要がある。この規格の
表1及び表2に規定する設計荷重ケース及び関連する荷重安全率を,基礎の設計基準として用いなければ
ならない。
一般に,設計及び解析は,ISO 19900:2002に適合しなければならない。広範囲の海洋構造物に適用可能
な地球科学及び基礎工学の観点での地盤工学及び基礎特有の要求事項は,ISO 19901-4:2003に基づいてい
る。従来の固定式鋼構造物に関連したくい(杭)基礎の設計については,ISO 19902に詳細がある。従来
の固定式コンクリート構造に関連した浅い重力基礎の設計に関する特有の要求事項の詳細は,ISO
19903:2006による。
基礎は,静的作用及び動的作用(繰返し及び過渡的)を構造物に過剰な変形又は振動を生じることなく
伝達するよう設計しなければならない。繰返し作用及び過渡的作用の構造応答に対する影響とともに,支
持地盤の強度に対する影響について特に注意しなければならない。また,海底面が基礎部材に対して移動
する可能性について調査しなければならない。このような移動による荷重が予測される場合は,設計にお
いて考慮しなければならない。
輸送及び据付の場合に,基礎に作用する荷重を考慮に入れなければならない。くい(杭)構造の場合(図
1参照),海底に打設されるくい(杭)には疲労損傷12) を計算するための解析を実施しなければならない。
疲労解析では,くい(杭)を打ち込む場合に,衝撃に関連した荷重を考慮する。このとき,くい(杭)の
構造動力学,くい(杭)の詳細設計,及びくい(杭)の打ち込み工程による応力増加を考慮に入れる。
注12) くい(杭)の打込み時に累積する疲労損傷が,洋上風車の寿命を通じて,くい(杭)によって
累積する全体的な損傷のかなりの部分を占めることもある。
風車支持構造物の全ての部品を腐食の影響から適切に保護するための対策を施さなければならない(附
属書H参照)。
洋上風車の基礎の設計に関する更に詳細な指針を,附属書Fに示す。
12
洋上風車サイトにおける外部条件の評価
12.1
一般
洋上風車は,環境条件及び電気的条件にさらされる他,場合によっては近隣の風車が負荷,耐久性及び
運転に影響を及ぼすこともある。これらの条件に加えて,洋上風車サイトの地震,海底地形及び地盤に関
する条件を考慮する必要がある。
洋上風車サイトにおける外部条件は,次の各細分箇条の要求に従い,設計及び/又は設計検証の基準と
して評価しなければならない。また,設計文書には,洋上風車の設計の基準となる外部条件を明記しなけ
ればならない。設計根拠となることができる主要な外部条件パラメータの要約リストを,附属書Aに指針
として示す。
7.6.2.1に規定した各荷重に対する部分安全率は,サイトにおける通常風況条件及び極値風況条件の評価
46
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
が,この箇条に規定した最小限の要求事項に従って実施されたことを仮定している。
12.2
気象海象データベース
サイト固有の気象海象データベースの構築に当たっては,次の情報を含まなければならない。
・ 風速及び風向
・ 有義波高,波の周期及び波向
・ 風の統計値と波の統計値との相関
・ 水流の速度及び方向
・ 水位
・ 海氷の発生及びその特性
・ 着氷の発生
・ 気温,水温,空気密度,海水密度,海水塩分濃度,サイトの海底地形,海洋付着生物など,該当する
その他の気象海象パラメータ
サイト固有の測定結果からデータベースを構築し,必要に応じて数値シミュレーション(推算)で補っ
てもよい。サイト固有の測定を行う場合は,一般にその測定結果と長期間にわたる測定が行われている近
傍の地点におけるデータとの相関を確認しなければならない。ただし,測定結果が安全側であることを示
す場合は,この限りではない。サイト固有の測定を行うモニタリング期間は,個々のパラメータとともに
これらのパラメータの結合確率分布について信頼できる統計値を確保するのに十分な期間でなければなら
ない13)。近隣地点で得られた適切な長期データとの相関を確認した場合又はその長期データを風車サイト
に適用するに当たり,信頼性の高い数値計算手法を適用する場合には,サイト固有の長期測定は,一般に
要求しない。
注13) 測定データの相関解析だけが行われる場合は,予定されている洋上風車サイトから長期測定が
行われている地点までの距離が50 kmよりも近いことが望ましく,両地点での水深,吹送距離
及び海底地形が類似していることが望ましい。長期データを風車サイト固有の短期データから
相関処理によって求める場合は,相関関係が適切かどうか及び相関解析の不確さが推定できる
かどうかについて,注意を払うことが望ましい。予定している風車サイトから長期測定地点ま
での距離が50 kmよりも遠い場合は,サイトの気象海象統計値を推定するために数値シミュレ
ーション(推算)も行うことが望ましい。
浅水域のサイトにおける波高,周期及び波のスペクトルの特徴を明らかにするに当たり,時系列での測
定が特に重要な場合がある。
計測の実施に当たり,データの質及び量を極めてまれな事象を外挿して得られるかどうかについて,特
別な注意を払い設定することが望ましい。
12.3
風況精査
風車サイトでは,次の各パラメータ値を推定しなければならない。
・ ハブ高さにおける再現期間50年の10分間平均極値風速
・ 風速の確率密度関数p(Vhub)
・ 周囲乱流標準偏差σˆ[主方向成分の標準偏差の平均値として推定する14)。],及びVhubがVinとVoutとの
間にあり,かつ,VhubがVrefに等しい場合におけるσˆの標準偏差
σ
σˆ
注14) 乱流の主方向成分は,水平方向成分で近似してもよい。
・ ウィンドシア15)
注15) ある特定の地域では,強安定成層流又は厳しい粗度変化に付随して,長期にわたり強いウィ
47
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ンドシアがあることが報告されている。箇条6に規定する外部条件は,このような場合を含
むことは,意図していない。
・ 空気密度
上記の統計処理で用いる風速ビンの間隔は2 m/s以下とし,風向方位区分の間隔は30°以下とする。空
気密度を除く全てのパラメータは,10分間平均で与えられ,風向別に得られなければならない。
サイトの風のパラメータは,次のいずれか一方としなければならない。
・ 0.2 Vref〜0.4 Vrefの範囲で測定し,かつ,それを外挿した値
・ サイトで得られた短期モニタリング測定値,地域の気象観測所又は地域の規約若しくは規格とから得
られる長期間の記録に基づいて,相関解析で求めた値
サイト固有の極値平均風速が10分間を超える平均化時間でしか得られない場合は,表4に規定した換算
係数を用いて10分間平均の極値風速を推定してもよい。表中の係数は,与えられた平均化時間の極値風速
と,10分間平均極値風速の比を表す。
表4−様々な平均化時間の極値風速の換算
平均化時間
10分間
1時間
3時間
10分間平均の極値風速に対する補正係数
1.00
0.95
0.90
平均風速Vhubの長期確率分布は,10分間〜3時間の範囲では平均化時間に依存しないものと仮定しても
よい16)。
注16) 長期確率分布の裾部分では,平均風速がVoutを超えるため,この仮定を適用できない。
乱流標準偏差の値は,測定データに対して適用する適切な統計手法を用いて求めなければならない。可
能な場合,トレンド除去を行ったデータを用いることが望ましい。地形的効果(海岸線)又はその他の局
所的な効果が乱流強度に影響を及ぼす可能性がある場合は,これらの影響をデータで示さなければならな
い。乱流強度を評価する場合は,測定データの取得時に用いられる風速計の特性,サンプリング間隔及び
平均化時間を考慮しなければならない。
乱流に関するサイトのデータがない場合は,チャーノック(Charnock)の式(25)から得られる表面粗度
パラメータz0を用いて,乱流標準偏差σ1を推定してもよい。
2
0
hub
hub
C
0
)
/
(
In
×
z
z
V
A
z
κ
g
=
······························································· (25)
ここに,
g: 重力加速度
κ=0.4: カルマン(Karman)定数
AC: チャーノック定数
外洋では,AC=0.011とすることが望ましい。沿岸地域では,AC=0.034を用いてもよい17)。
注17) 外洋条件では,表面粗度パラメータ及び表面粗度から式(25)で計算される乱流標準偏差を適用す
る。沿岸地域の地勢及び海岸の粗度が乱流標準偏差を増大させる原因となり得る場合は,注意
することが望ましい。
海面粗度は,風速とともに増大し,このため乱流強度も風速の関数として増加する。式(25)の陰的な方
程式を解くことによって粗度パラメータを求め,同様に,式(26)により風速の主方向成分についての標準
偏差を計算してもよい。
48
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
15
0
hub
hub
1
44
.1
28
.1
)
/
(
In
I
z
z
V
×
×
+
=
σ
··················································· (26)
ここに,
I15: Vhub=15 m/sのときに得られる,ハブ高さにおける乱流強度の
平均値18)
注18) 式(26)における標準偏差1.44 I15は,JIS C 1400-1:2010と矛盾しない。しかしながら,幾つかの
洋上地点においては,これよりも顕著に大きな標準偏差が記録されている。ゆえに,特定のサ
イトについては,類似のサイト又は近隣のサイトから得られる情報を考慮して,このパラメー
タを注意して評価することが望ましい。
平均化時間1時間で乱流標準偏差を推定するに当たり,適切なサイト固有データがない場合は,式(27)
の関係を仮定して,10分間平均の乱流標準偏差を求めてもよい。
b
+
=
−
−
min
10
.i
hour
1.i
σ
σ
·································································· (27)
ここに,
b=0.2 m/s
サイトでの空気密度データがない場合は,JIS W 0201:1990で規定の空気密度の値を年間平均気温に対し
て適切に補正して仮定しなければならない。
12.4
波の評価
次のパラメータを推定しなければならない。
・ 評価時間を3時間と仮定した再現期間50年の有義波高Hs.50,及びそれに関連する波のピークスペク
トル周期の範囲
・ 評価時間を3時間と仮定した再現期間1年の有義波高Hs.1,及びそれに関連する波のピークスペクト
ル周期の範囲
・ 再現期間50年の個々の波の極値波高H50
・ 再現期間1年の個々の波の極値波高H1
・ 再現期間50年の個々の波の低減波高Hred50
・ 再現期間1年の個々の波の低減波高Hred1
・ 再現期間50年の極値波頂高
ISO 19901-1:2005を参照し,極値有義波高は有義波高の長期分布の裾部分の外挿により求めた気象海象
データベースから求めてもよい。個々の波の極値波高は,有義波高Hs及び波のピークスペクトル周期Tp
の長期分布と,有義波高Hsの条件の下で個々の波高Hの短期分布との畳み込みによって評価してもよい。
ただし,極値波高は水深による制限を受ける場合もある。
水深,海底勾配,波高,波の周期及び波形勾配に応じて,洋上風車サイトで砕波が生じる可能性がある。
これらのパラメータの評価結果を踏まえ,サイトの条件に基づく砕波の性質及び規模を求めるに当たり,
附属書Cに記載されている指針に従ってもよい。
次の各パラメータの長期結合確率分布は,サイト固有の気象海象データベースを解析して設定しなけれ
ばならない。
・ ハブ高さにおける平均風速Vhub
・ 有義波高Hs
・ 波のピークスペクトル周期Tp
定義上,Hs及びTpは平均化時間に依存しないため,長期の周辺確率分布は平均化時間によって変化しな
い。Vhub,Hs及びTpの結合確率分布を求めるに当たり,有義波高及び波のピークスペクトル周期と関係付
ける相関をとる平均風速を定義するために,平均化時間を選定しなければならない。平均化時間は,1時
49
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
間としなければならない。Vhub,Hs及びTpを利用できる結合統計データが別々の平均化時間を用いた値で
ある場合は,当該データを平均化時間1時間の風速に基づく値に換算しなければならない。風の影響下で
は,何時間単位というかなりの時間をかけて波浪が形成されるため,平均化時間が長くなるとVhub,Hs及
びTp相互の相関が高くなることがある。しかし,サイト固有の特性によっては,平均化時間によって相関
が顕著には変化しない場合もある。したがって,Vhub,Hs及びTpの長期結合確率分布は,平均化時間に依
存しないものと仮定するのが合理的な場合もある。
必要に応じて,結合確率分布の範囲を拡大し,風向及び波向も含めなければならないが,この五つのパ
ラメータの結合出現確率を導出できるようなサイト固有の測定値は,存在しないことが多い19)。結合確率
分布の分解能は,風速ビンの間隔が2 m/s以下,有義波高ビンの間隔が0.5 m以下及び波の周期ビンの間隔
が0.5 s以下でなければならない。方向データもある場合は,風向及び波向の方位区分を30°以下としな
ければならない。
注19) 同一方向の風及び波を仮定することは,安全側に見積もっていない場合もあるが,ある特定の
サイト及び洋上風車構造によっては,これとは逆に,同一方向であると安全側となり過ぎるこ
ともある。
サイト固有の波のスペクトル及び方向分布の評価についての要求がないときは,附属書Bの標準関数を
仮定してもよい。
ただし,適切かつ信頼できる測定値がある場合は,洋上風車の設計及び/又は設計検証の基準としてサ
イト固有の波のスペクトル及び方向分布関数を評価してもよい。
12.5
水流の評価
水流は,洋上風車の支持構造物に作用する荷重への影響に加えて,船舶の接舷及び防舷材の位置及び方
向にも影響を及ぼし,海底洗掘を発生させることもある。
潮流,高潮,吹送流及び海浜流が風車サイトに関係する場合,これらの成分を考慮して海の流れを評価
しなければならない。サイトで卓越している海の流れのそれぞれの顕著な成分の速度及び方向特性は,そ
れぞれ個別に評価を行わなければならない。
再現期間が1年及び50年の極値表層流速度は,サイト固有の気象海象データベースを解析することによ
って求めなければならない。
サイト固有の水流速度の深さ方向への変化については,評価のための要件がなく,6.4.2に規定した標準
流速プロファイルを仮定してもよい。ただし,適切かつ信頼できる測定値がある場合,洋上風車の設計及
び/又は設計検証の基準としてサイト固有の水流速度プロファイルを用いてもよい。
12.6
水位,潮せき(汐)及び高潮の評価
次のパラメータを求めるため,風車サイトにおける水位の平均値及び変動を評価しなければならない。
・ 平均潮位(MSL)
・ 最高天文潮位(HAT)及び最低天文潮位(LAT)
・ 高潮による水位上昇を含む,最高静潮位(HSWL)
・ 高潮による水位低下を含む,最低静潮位(LSWL)
これらのパラメータは,サイト固有の気象海象データベースから求めなければならない。高潮を正確に
推定するためには,長期にわたる一連のデータセットが必要である。サイト固有の高潮の特性を求めるた
めには,近隣地点で入手可能な長期にわたる測定値又は推算値を相関手法とともに用いてもよい。
12.7
海氷の評価
海氷の発生が予想される場所に設置する洋上風車支持構造物を設計する場合は,海氷の影響を評価しな
50
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ければならない。評価を行うに当たり,洋上風車サイトにおける海氷の特性について,詳細な情報が必要
となる。製造業者は,仮定した海氷の特性値を設計文書内に記載しなければならない。次の各パラメータ
は,海氷地図又は類似資料に記載されている統計データから求めなければならない。
・ 再現期間50年の氷厚h
・ 海氷破壊強度σc
・ 水流又は風によって生じる氷盤に関するリスク
・ 水位変動によって誘起される力に関するリスク
・ 海氷密接度の程度
12.8
海洋付着生物の評価
適用できる指針類,その地域における経験,及び既存の測定値に基づき,海洋付着生物の厚さ及び水面
下の深度に対する依存関係を評価しなければならない。海洋付着生物の性質,想定し得る厚さ,及び深度
依存関係を明確にするに当たり,サイト固有の調査が必要な場合がある20)。
注20) 海洋付着生物に関する情報は,幾つかの地域(北海,ペルシャ湾,西アフリカ海岸部,メキシ
コ湾,カリフォルニア海岸部及びカナダの東海岸)について入手できる(ISO 19901-1参照)。
12.9
海底変形及び洗掘
海底の安定性について評価を行わなければならない。サイトの海底地形及び地盤構成から,斜面の崩壊,
地滑り,陥没又は浸食現象が発生する可能性を考慮する必要があるか否かを決定しなければならない。重
力式基礎の設計では,一般に,沈下及び地盤の液状化に対して配慮しなければならない。
観測結果によれば,海底面の変化は,一般に,次の各事象の組合せとして表すことができる。
・ くい(杭),群くい(杭)などの構造要素周辺が水流で急しゅん(峻)に掘り込まれることを特徴とす
る,局所洗掘。
・ 構造物の周りに浅く洗掘された領域があることを特徴とする広域洗掘。構造物全体の影響,複数の構
造物の相互作用,又は波と地盤と構造物の相互作用に起因する可能性がある。
・ 構造物がなくても発生する,サンドウェーブ,サンドリッジ,砂洲などの全体的な海底変形。このよ
うな変形は,海底面の上昇,下降又は上昇及び下降の繰り返しをもたらすこともある。人工構造物を
追加することによって局所的な土砂輸送の相が変化する可能性があり,この変化は侵食を進行させた
り,堆積の原因となったりすることがあるが,全く影響がない場合もある。
海底変形及び洗掘が発生する場合,基礎に対する鉛直方向及び横方向の支持が失われる結果となる可能
性があり,浅い基礎の場合,望ましくない沈下及び変位を引き起こし,基礎要素に過大な応力を作用させ,
風車構造の動的特性を変化させる結果となることがある。洗掘が発生する可能性がある場合は,洗掘の発
生を設計上考慮するか,洗掘を抑えるか,又はこの両方を考慮しなければならない。
風車サイトにおける洗掘範囲及び洗掘防止工は,次のいずれかの方法で求めなければならない。
・ 近隣のサイト又は海底面の特性が類似したサイトにおける既往の記録に基づいて求める。
・ 水理模型実験から求める。
・ 試作機又は模型実験によって校正された計算から求める。
12.10 隣接風車からの後流の影響評価
隣接する風車からの後流に対する影響評価は,JIS C 1400-1:2010の要求事項によらなければならない。
12.11
その他の環境条件の評価
次の環境条件を評価して,洋上風車の設計のために立てた仮定と比較しなければならない。
・ 通常気温範囲及び極値気温範囲
51
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ ひょう(雹),あられ(霰)及び雪
・ 湿度
・ 雷
・ 太陽光の放射
・ 化学的活性物質
・ 塩分
・ 海水密度
・ 水温範囲
12.12 地震条件の評価
地震条件に対する評価は,JIS C 1400-1:2010の要求事項によらなければならない。
12.13 ウェザウィンドウ及びウェザダウンタイムの評価
洋上風車の輸送,据付及び保守を実施するに当たり,ウェザウィンドウ及びウェザダウンタイムが重要
となる。ウェザウィンドウ及びウェザダウンタイムに対する評価は,洋上風車のサイトについて行わなけ
ればならない。
12.14 電力系統条件の評価
電気的な設計条件との適合性を確実にするために,サイト候補地における風車接続端から見た外部の電
気的状態を評価しなければならない。外部の電気的状態には,次の各項目を含める21)。
注21) 風車の設計者は,電力系統の適合条件に配慮する必要がある場合もある。上記の各項目は,最
低限の要求をまとめたものである。我が国の電力系統に対する適合性要件は,設計段階で対応
する必要がある。
・ 規定された電圧範囲及び継続時間による,接続維持又は解列要件を含む,通常電圧及び範囲
・ 規定された周波数範囲及び継続時間による,接続維持又は解列要件を含む,通常周波数,範囲及び変
化率
・ 平衡故障及び非平衡故障時にパーセント逆相電圧として規定する電圧不平衡
・ 中性点接地方式
・ 地絡検出方式及び地絡保護方式
・ 電力系統の停電回数
・ 寿命内における電力系統の合計供給停止時間
・ 自動再閉路周期
・ 所定の無効電力補償運転スケジュール
・ 故障電流及び継続時間
・ 風車接続端における短絡インピーダンス及び地絡インピーダンス
・ 電力系統の電源高調波電圧ひずみ
・ 電力線搬送信号の有無及びその周波数
・ ライドスルー要件のための故障プロファイル
・ 力率制御要件
・ 出力変化率要件
・ その他の電力系統適合性要件
12.15 地盤条件の評価
サイト候補地における地盤の特性は,専門資格をもつ地質工学の技術者による評価を行わなければなら
52
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ない。
基礎構造に影響を及ぼす深さ及び面積,又は基礎構造によって影響を受ける深さ及び面積にわたり,地
盤の特性を明確にする適切な情報を取得するため,地盤調査を実施しなければならない。一般に,地盤調
査には,次の各項目を含めなければならない。
・ サイトの地質学的調査
・ 海底面にある巨れき(礫),サンドウェーブ又は障害物などの記録も含めた海底地形調査
・ 地球物理学的調査
・ 原位置試験及び実験室での試験からなる地質工学的調査
基礎の設計で必要となるパラメータを当該地域の浅い部分の地質評価と併せて,調査によって取得した
データを考慮しなければならない。現実的には,物理探査結果を精査してから土壌採取及び試験計画を決
定することが望ましい。
工学的特性を求めるために適したデータを決定するための原位置試験及び実験室での試験に土質サンプ
ルを提供するため,地盤調査には地盤ボーリングを1回以上実施しなければならない。必要なボーリング
の本数及び深さは,洋上ウィンドファーム内における風車基礎の数及び位置,サイト付近の地盤分布,基
礎の方式,並びに事前の物理探査結果によって決定しなければならない。地盤調査においては,地盤ボー
リングを補うためにコーン貫入試験(CPT)及び小深度振動式ボーリングを利用してもよい。サイト固有
の地盤データは,原則として,ウィンドファーム内のそれぞれの基礎に対して確認しなければならない。
この目的のために,CPTを地盤ボーリングが実施されない風車位置で用いてもよい。CPTの校正を行うた
め,地盤ボーリング箇所のうち1地点のすぐ近くでCPTを1回実施しなければならない。
地盤調査では,基礎設計の根拠として次のデータを取得しなければならない。
・ 地盤の分類に対するデータ及び地盤の説明
・ せん断強度パラメータ
・ 圧密パラメータを含む変形特性
・ 透水性
・ 風車構造の動的特性を予測するための剛性及び減衰パラメータ
適切な原位置試験及び実験室での試験によって,それぞれの土質層についてこれらの工学的特性を十分
に評価しなければならない。
地盤条件の評価では,地盤の液状化に関する潜在的可能性,基礎構造及び周辺地盤の長期的な沈下及び
変位,並びに流体力学的安定性及び地盤安定特性についても考慮しなければならない。
13
組立,据付及び建設
13.1
一般
洋上風車の製造業者は,洋上風車構造及び機材について,設置に関する要求事項を明記した据付マニュ
アルを提供しなければならない。洋上風車の据付は,これらの作業について訓練を受けた要員又は指導を
受けた要員によって実施しなければならない。
洋上風車施設のサイトは,作業が安全かつ効率的な方法で実施できるように準備,保守,運営及び管理
を行わなければならない。必要に応じて,関係者以外立入禁止の措置もその中に盛り込むことが望ましい。
オペレータは,存在する危険及び潜在的な危険を認識し,それを取り除くことが望ましい。
設置工事は,綿密に施工しなければならない。建設中及び設置完了時のデータを取得するための試運転
中は,計画した作業のチェックリストを準備し,全てにわたって記録を取り続けなければならない。
53
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
据付要員は,適宜,目,足,聴覚,頭部などの防護のために,認可を受けた個人用保護具を用いなけれ
ばならない。タワーに登る要員,又は地上若しくは水位よりも高所で作業を行う要員は,当該作業に関す
る訓練を受けることが望ましく,認可を受けた安全帯及び安全昇降補助具を用いなければならない。安全
保護具には,このほか,サバイバルスーツ及び浮き具を含む。
全ての機材は,十分に整備し,使用対象の作業に適したものでなければならない。クレーン,ホイスト
及び揚重装置は,スリング,フック及びその他の器具を全て含め,安全な揚重作業に適したもので,かつ,
認可を受けたものでなければならない。
ひょう(雹),あられ(霰),雷,強風,地震,結氷,高波,潮せき(汐)極大時などの特異な条件下で
は,洋上風車の据付に対して特に配慮することが望ましい。
据付手順は,作業要員に危険を与えたり,構造物に許容外の荷重を作用させることなく,必要に応じて
作業を中断できるようなものでなければならない。ナセル取り付け前のタワーだけを据付けた状態の場合,
原因が風又は水流であるかにかかわらず,タワーからの渦放出によって生じる流れに直交方向の振動を回
避するような適切な方策をとらなければならない。据付マニュアルには,作業できる上限風速及び対策方
法を記載しなければならない。
洋上風車施設のサイトにおける建設作業を実施する前に,航行及び飛行の障害になると判断される一時
的又は恒久的な予定建造物については,十分な事前通知をもって公表し,関連する地図及びデータベース
に位置,範囲及び高さを示さなければならない。航空障害灯及び障害標識は,関連する国内及び国際的な
規則及び規約に適合したものでなければならない。
ヘリコプタの運用は,着陸プラットフォームの構造安全性,離隔距離,防火,表示などに関するあらゆ
る面について,関連する国内及び国際規則及び規約に適合したものでなければならない。
13.2
計画
風車及び関連設備の組立,建設及び据付は,作業が安全に,かつ,我が国の規則に従って実施されるよ
うに計画しなければならない。計画には,品質保証手順のほか,必要に応じて次の各項目を考慮する。
・ 作業及び検査計画に関する詳細な図面及び仕様書
・ 掘削作業,発破のほか,例えば,くい(杭)打設,洗掘防止工敷設工事,ケーブル敷設などの,並び
に基礎工事及び水面下の建設作業に関連するその他の作業を安全に実施するための規則
・ 基礎,ボルト,アンカ及び鉄筋鋼材などの埋込物の適切な取扱いに関する規則
・ コンクリートの混合,送出,サンプリング,注入,仕上げ及び導管の埋設に関する規則
・ タワー及びその他のアンカの据付手順
・ 潜水時の安全規則を含む,洋上作業時の健康,安全及び環境に関する規則
・ 避難手順(風況及び海況のモニタリング,並びにいつ避難が必要かの情報を含む。)
13.3
設置状態
洋上風車の据付中は,サイトを安全上又は航行上の危険を及ぼさないような状態に保たなければならな
い。
13.4
サイトへのアクセス
サイトには安全にアクセスできなくてはならず,次の各項目を考慮しなければならない。
・ 障害物及び輸送経路
・ 立入禁止区域
・ 交通
・ 運搬物資の質量限度
54
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ サイトにおける機材の移動
・ 船舶から風車へのアクセス手段
・ ヘリコプタから風車へのアクセス手段
13.5
環境条件
据付作業中は,製造業者が指定する環境基準値を監視しなければならない。次の各項目などについて考
慮することが望ましい。
・ 風速
・ 氷及び雪
・ 周囲温度
・ 雷
・ 視程
・ 雨
・ 波高
・ 水深の不足
13.6
提出文書
洋上風車の製造業者は,洋上風車の組立手順,据付,建設に関する図面,仕様書及び指示書を用意しな
ければならない。製造業者は,全ての荷重,質量,荷揚地点及び特殊工具の詳細,並びに洋上風車を安全
に取り扱い,据付けるために必要な手順についての詳細を提供しなければならない。製造業者は,あらゆ
る危険作業について,リスク評価書を作成しなければならない。
13.7
受取り,取扱い及び保管
据付作業中の洋上風車機材の取扱い及び輸送は,当該作業に適していることが確認された機材を用いて,
製造業者が推奨する方法に従って実施しなければならない。
風によって誘起される運動に起因する,損傷のリスクを伴うような危険性がある場合には,ブレード,
ナセル,その他の空力部品,及び軽量な部品の安全に配慮しなければならない。
13.8
基礎/アンカシステム
据付又は組立を安全に行うために,製造業者が指定している場合は,特殊工具,ジグ及び固定具,並び
にその他の器具を用いなければならない。
13.9
洋上風車の組立
洋上風車は,製造業者の指示書に従って組立を行わなければならない。全ての部品について,検査を実
施し,適切に注油し,供用前調整が行われていることを確認しなければならない。
13.10
洋上風車の建設
洋上風車の建設は,洋上における建設作業を,適切かつ安全に行うための訓練指導を受けた要員によっ
て実施しなければならない。風車の据付作業に関する特殊な訓練のほかに,訓練には少なくとも次の内容
を含めなければならない。
・ 救急法
・ 洋上特有の手順(例えば,救命ボート,救命胴衣,特殊スーツ及び洋上でのサバイバル生活方法)
・ 負傷者又は意識不明者も対象とした避難手順
・ ボート,ヘリコプタ及び洋上のアクセスシステムの使用法(夜間に安全に乗り移る手順については特
に注意を要する。)
全ての作業は,適切な通信手段をもつ2名以上の要員で行わなければならない。
55
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
建設工程に必要である場合を除き,建設作業中には,洋上風車の電気システムのどの部位にも,通電し
てはならない。この場合,建設工程に通電が必要である場合は,風車の納入業者によって用意された書面
による手順に従って,当該機材への通電を行わなければならない。
建設中は,動くこと(回転又は並進)が潜在的な危険をもたらすことがある全ての要素について,不測
の動作が発生しないように配慮しなければならない。
13.11
締結部品及びアタッチメント
洋上風車は,製造業者が推奨するトルク及び/又はほかの指示書に従って,緊張材の締結部品及びその
他の取付け部品を取り付けなければならない。極めて重要であるとされている締結部品は,点検を励行し,
締付けトルク及びほかの要求に対する確認手順を入手して適用する。
検査は,特に次の項目を確認する目的で実施しなければならない。
・ 支線,ケーブル,ターンバックル,ジンポール,並びにその他の器具及び機器の組立及び接続を適切
に行う。
・ 建設作業を安全に実施するために必要な揚重機材を正しく取り付ける。
13.12 クレーン,ホイスト及び揚重装置
クレーン,ホイスト及び揚重装置は,スリング,フック及び建設作業を安全に行うために必要なその他
の器具を全て含め,安全な揚重作業及び載荷物の最終配置作業に適したものでなければならない。建設作
業及び取扱いに関する製造業者の指示書及び説明文書には,部品及び/又は組立品についての予想荷重及
び安全なリフティングポイントに関する情報を記載することが望ましい。ホイスト機材,スリング及びフ
ックは,全て安全荷重に対する試験及び確認が行われていなければならない。
14
試運転,運転及び保守
14.1
一般
試運転,運転,検査及び保守の各手順は,要員の安全を考慮のうえ,洋上風車のマニュアルに記載しな
ければならない。
洋上風車の設計は,全ての構成部品について,検査及び保守のための安全なアクセス手段を組み込まな
ければならない。そのアクセス手段は,我が国の規則に適合しなければならない。
箇条10の要求は,洋上風車内に測定目的で一時的に取り付けた電気測定装置も対象とする。
運転要員及び保守要員は,適宜,目,足,聴覚,頭部防護のために,認可を受けた個人用保護具を用い
なければならない。タワーに登る要員,又は地上若しくは水位よりも高所で作業を行う要員は,当該作業
に関する訓練を受けなければならず,認可を受けた安全帯,安全昇降補助具を用いなければならない。安
全保護具には,このほか,ライフジャケット,ウェットスーツ及び浮き具を含まなければならない。
14.2
安全運転,検査及び保守に対する設計要求
運転要員による洋上風車の通常運転は,プラットフォームの位置で運転可能でなければならない。自動
/遠隔制御システムより優先するように,標識で表示した現場での手動操作装置を備えなければならない。
電気的負荷の一時的な喪失などが原因であるような,故障であっても,洋上風車のその後の安全性にと
って重要ではない外部事象の場合,一連の運転停止動作が完了後に通常運転へ自動復帰してもよい。
要員が誤って可動部品に接触することを防ぐように設計した保護部材は,固定しなければならないが,
頻繁にアクセスすることが予測されない場合には,可動式でもよい。
この保護部材は,次の要件を満たさなければならない。
・ 堅ろう(牢)な構造である。
56
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ 容易には通り抜けできない。
・ 可能な限り,保護部材を取り外さずに主要な保守作業を実施できる。
洋上風車の支持構造物上に設けられた通路又はプラットフォームは,飛まつ帯も上方に配置しなければ
ならない。安全のため,海洋付着生物の除去も検討することが望ましい。サイトにおいて着氷のリスクが
ある場合には,着氷条件下におけるはしご(梯子)及びプラットフォームへのアクセス制限も考慮しなけ
ればならない。氷の落下によって構造物が損傷するリスクについても考慮しなければならない。
回転中のブレード先端部と,通路又はプラットフォームとの間には,垂直方向に適切な最小の距離を確
保しなければならない。
故障を発見する診断装置を利用できるような設計上の措置を講じなければならない。
点検要員及び保守要員の安全を確保するため,設計には次の各項目を盛り込まなければならない。
・ 検査及び日常点検を実施するための,安全なアクセス通路及び作業場所
・ 回転部品又は可動部品に作業要員が誤って接触しないための適切な防護手段
・ プラットフォームよりも高所に登るか,又は高所で作業を行う場合の,命綱及び安全帯若しくはその
他の安全保護具の用意
・ 点検又は保守作業を実施する間,風況及びDLC 8.1に規定する設計条件に従って,ロータ及びヨー機
構の回転,又はブレードのピッチ角変化のようなその他の機械的運動などを固定する措置,並びにブ
ロックを安全に解除するための措置。
・ 活線に対する警告標識
・ 蓄電された電気を除去するための適切な機器
・ 作業要員を火災から保護する適切な防火対策
・ ナセルから脱出するための代替避難経路
・ 非常時に洋上風車から脱出するための代替避難経路に関する措置
・ 洋上風車内に1週間滞在するための備蓄(食料,水,暖房,衣服/毛布)
・ 洋上用安全装備(救命胴衣,救命ボート,灯火類,信号拳銃,照明弾など)
保守手順には,ハブ又はブレード内部などの閉鎖された作業区域に入る作業要員について,危険な状況
にあることを待機要員が認識した場合に,“直ちに救助を開始できる安全措置を必要に応じて盛り込まなけ
ればならない。
航行及び飛行に関する障害灯及び障害標識は,我が国の規則及び規約に適合したものでなければならな
い。
14.3
試運転に関する指示書
製造業者は,試運転に関する指示書を提供しなければならない。
14.3.1
通電
製造業者の指示書には,洋上風車の電気システムの初期通電手順を記載しなければならない。
14.3.2
試運転試験
製造業者の指示書には,全ての機器,制御系及び装置が適切,安全,かつ,機能的に作動することを確
認するために,据付後に実施する,洋上風車の試験手順を記載しなければならない。この試験手順は,次
の事項を含めなければならない。
・ 安全な起動
・ 安全な停止
・ 安全な緊急停止
57
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ 過回転又は過回転の代表的な模擬状態からの安全な停止
・ 保護システムの機能試験
14.3.3
記録
製造業者の指示書には,保管しなければならない適切な記録の情報,試験実施,試運転,制御パラメー
タ及び結果を記載しなければならない。
14.3.4
試運転後の業務
据付が完了し,製造業者が推奨する慣し運転期間に引き続き,製造業者が要求する特定の作業を完了し
なければならない。
この作業には,締結部品の予荷重,潤滑油の交換,その他の部品の適切な設置及び作動の点検,並びに
制御パラメータの適切な調整などがある。
14.4
運転要員への指示マニュアル
14.4.1
一般
運転要員用の指示マニュアルは,洋上風車の製造業者が提供し,必要に応じて試運転実施時の特殊な現
場状況に関する情報を追加補足しなければならない。マニュアルは,運転員が読んで理解できる言語で,
運転要員及び保守要員に提供しなければならない。マニュアルには,次の内容を含めなければならない。
・ 以下の作業について適切な訓練を受けた要員又は指導を受けた要員が運転を実施しなければならない
ことについての要求事項
・ 安全運転のための制限事項及びそのシステムの記載
・ 起動及び停止手順
・ 警報動作一覧
・ 緊急時の手順計画
・ 安全な洋上アクセス手順
・ 必要に応じて規定する次の要求事項
− 目,足,聴覚,頭部防護のように,認可を受けた個人用保護具を用いなければならない。
− タワーに登る要員,又は水位よりも高所で作業を行う要員は全て,適宜,当該作業に関する訓練を
受けなければならず,かつ,認可を受けた安全帯,安全昇降補助具又はその他の安全補助具を用い
なければならない。
14.4.2
運転記録及び保守記録についての指示書
マニュアルには,運転記録及び保守記録を保管することについて記載しなければならなず,次の項目を
含んでいることが望ましい。
・ 風車の識別名称
・ 発電量
・ 運転時間
・ 停止時間
・ 故障が報告された日時
・ 整備及び修理の日時
・ 故障又は整備の種類
・ 対策した内容
・ 交換された部品
14.4.3
計画外の自動停止に関する指示書
58
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
故障又は機能不良に起因する計画外の自動停止の後,運転マニュアル又は指示書でほかの方法を指定し
ていない限り,洋上風車の再起動前に運転員が原因調査しなくてはならないことを,マニュアルに記載す
る。計画外の自動停止は,全て記録することが望ましい。
3か月を超えて発電を行わなかった後に,洋上風車を再起動する場合は,特別な注意を払わなければな
らない。再起動前に,全ての部品及びシステムに対して検査を行い,工学的観点からの健全性を評価しな
ければならない。長期にわたり発電を行わなかったことによる影響のため,設計要求を満足しないと判定
された部品及びシステムは,修理又は交換を行わなければならない。重要な部品及びシステムの状態につ
いては,風車が再起動して発電状態に復帰した後,監視しなければならない。
14.4.4
信頼性低下に関する指示書
マニュアルには,異常の兆候若しくは警報,又は信頼性低下について,その根本原因を排除するための
措置を講じなくてはならないことを記載しなければならない。
14.4.5
作業手順計画
マニュアルには,次の各項目を考慮し,安全な作業手順に従って洋上風車を運転することを記載しなけ
ればならない。
・ 電気システムの運転
・ 運転と保守との調整
・ 各種設備の撤去手順
・ タワーに登る手順
・ 機器の取扱手順
・ 悪天候時の作業
・ 通信手順及び緊急時の対応計画
・ 風車へのアクセス手順
14.4.6
緊急時手順計画
想定される緊急事態を運転マニュアルにおいて特定し,運転要員に要求される対応方法を定めなければ
ならない。
マニュアルには,火災の場合,又は明らかに洋上風車若しくは部品が構造的に損傷している場合は,当
該リスクが明確に評価されない限り,誰も洋上風車に近付かないことが望ましいことを記載しなければな
らない。
緊急時手順計画を作成するときには,以下の項目では,構造的損傷が増大する可能性があることを考慮
しなければならない。
・ 過回転
・ 着氷状態
・ 雷雨
・ 地震
・ 支線の破損又は緩み
・ ブレーキ故障
・ ロータのアンバランス
・ 締結部品の緩み
・ 潤滑不良
・ 火災及び洪水
59
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ 船舶の衝突
・ その他の部品の故障
14.5
保守マニュアル
それぞれの洋上風車には,保守マニュアルを用意し,その保守マニュアルには,最低限,風車製造業者
が指定した保守に関する要求事項及び緊急時手順を記載しなければならない。マニュアルには,計画外保
守についても記載しなければならない。
保守マニュアルでは,摩耗,損傷,腐食及び海洋付着生物の被害を受ける部品を特定し,交換基準を示
さなければならない。
保守マニュアルで記載することが望ましい事項は,以下のとおりである。
・ 風車の保守マニュアルで指定し,かつ,そのマニュアルで指示した間隔で,適切な訓練又はこの作業
において指導を受けた要員が点検及び保守を実施しなければならないという要求事項
・ 洋上風車の予備システム及びその運転の説明
・ 注油頻度,並びに潤滑油又はほかの特殊液体の種類の指定
・ 試運転手順
・ 保守点検間隔及び手順
・ 保護用予備システムの機能確認手順
・ 内部配線図及び単線結線図
・ 張力及びトルク荷重を含めた,支線の点検及び再締付け計画,並びにボルトの検査及び予荷重計画
・ アクセスシステムの保守,例えば,業務用船舶の衝突などが原因で損傷が発生した後などの修理手順
・ 診断手順及びトラブルシューティング指針
・ 推奨予備品一覧
・ 現場での組立及び据付に関する図面
・ 工具一覧
・ 海洋付着生物の検査,及び考えられる除去方法
・ 洗掘防止工の保守
60
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
洋上風車の主要設計パラメータ
A.1 洋上風車の識別
洋上風車について,設計文書に含まれる要約に,次の情報を記載することが望ましい。
・ 風車の名称及び形式(説明)
・ 位置座標
A.1.1 ロータ ナセル・アセンブリ(機械)に関するパラメータ
次の情報を記載することが望ましい。
・ 定格出力
(kW)
・ ロータ直径
(m)
・ 回転数範囲
(min−1)
・ 出力制御(ストール方式/ピッチ方式)
・ ハブ高さ[平均潮位(MSL)上]
(m)
・ ハブ高さにおける風速範囲Vin〜Vout
(m/s)
・ 設計寿命
(年)
・ 運転時の質量(最小値,最大値)
(kg)
・ ロータ ナセル・アセンブリの防食方式(説明)
A.1.2 支持構造物に関するパラメータ
次の情報を記載することが望ましい。
・ 基礎に関する説明。(必要な場合)洗掘防止工の説明も含む。
・ 設計水深
(m)
・ 風車周辺の海底地形
・ 風車位置における地盤条件(説明。12.15参照)
・ 支持構造物の固有振動数(最小値,最大値)
− 通常運転条件時
(Hz)
− 極値運転条件時
(Hz)
・ 腐食許容量
(mm)
・ 防食方式(説明)
・ アクセスプラットホームの高さ[平均潮位(MSL)上]
(m)
A.1.3 風況(基準時間10分を基本とし,ウィンドファームの後流効果を適宜含む)
次の情報を記載することが望ましい。
・ NTM及びETMに用いる,平均風速の関数として表された乱流強度。
・ 年間平均風速(位置はハブ高さ)
(m/s)
・ 風の平均吹上/吹下角
(deg)
・ 風速分布(ワイブル分布,レイリー分布,測定分布など)
・ 通常のウィンドシアモデル及びパラメータ
・ 乱流モデル及びパラメータ
61
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ ハブ高さにおける極値風速Ve1及びVe50
(m/s)
・ 再現期間1年及び50年の極値突風モデル及びパラメータ
・ 再現期間1年及び50年の極値風向変化モデル及びパラメータ
・ コヒーレントな極値突風モデル及びパラメータ
・ 風向変化を伴うコヒーレントな極値突風モデル及びパラメータ
・ 極値ウィンドシアモデル及びパラメータ
・ 風向分布(風配図)
A.1.4 海洋環境条件(適宜,基準時間3時間を基本とする)
次の情報を記載することが望ましい。
・ 潮せき(汐)変化及び/又は高潮(再現期間50年)
(m)
・ 最高天文潮位(HAT)
(m)
・ 最低天文潮位(LAT)
(m)
・ 最高静水位(HSWL)
(m)
・ 最低静水位(LSWL)
(m)
・ 再現期間1年及び50年の有義波高
(m)
・ 再現期間1年及び50年の波のピーク周期の範囲
(s)
・ 再現期間1年及び50年の個別極値波高
(m)
・ 再現期間1年及び50年に対応する波の周期の範囲
(s)
・ 再現期間1年及び50年の極値波頂高
(m)
・ 再現期間1年及び50年の極値表層流
(m/s)
・ 方向も考慮した,風及び波の結合確率分布(Hs,Tp及びV)
・ 波のスペクトル及びパラメータ
・ 決定論的な波モデル及びパラメータ
・ 砕波モデル及びパラメータ
・ 海氷条件(12.7参照)
・ 局所洗掘量及び,広域洗掘量,又は両者の合計(最大許容値)
(m)
・ 海底面変化量(最大許容値)
(m)
・ 海洋付着生物の外形及び厚さ
(mm)
A.1.5 風車における電力系統条件
次の情報を記載することが望ましい。
・ 通常電圧及び範囲
(V)
・ 通常周波数及び範囲
(Hz)
・ 電圧不平衡
(V)
・ 電力系統供給停止の最大継続時間
(日)
・ 電力系統の年間停止回数
(1/年)
・ 寿命内の電力系統供給停止の合計時間
(h)
・ 自動再閉路周期(説明)
・ 外部の平衡故障及び非平衡故障発生時の挙動(説明)
62
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.2 その他の環境条件
次の情報を記載することが望ましい。
・ 通常気温範囲及び極値気温範囲
(℃)
・ 通常海水温度範囲及び極値海水温度範囲
(℃)
・ 空気密度
(kg/m3)
・ 海水密度
(kg/m3)
・ 太陽光の放射
(W/m2)
・ 湿度
(%)
・ 雨,ひょう(雹),あられ(霰),雪及び着氷
・ 化学的活性物質
・ 活動粒子[浮遊じんあい(塵埃)など]
・ 雷保護システムの説明
・ 地震モデル及びパラメータ(説明)
・ 塩分
(g/m3)
・ DLC 6.4の場合に想定される持続期間及び環境条件
・ DLC 7.2の場合に想定される持続期間及び環境条件
・ DLC 8.3の場合に想定される持続期間及び環境条件
A.3 輸送,建設,保守及び修理の制限条件
次の情報を記載することが望ましい。
・ 最大風速
(m/s)
・ 最大有義波高
(m)
・ 水位の最大変化量
(m)
・ 許容気温
(℃)
・ 保守における最大風速
(m/s)
・ 輸送船の排水量
(t)
63
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
波のスペクトルの定式化
B.1
一般
海況は,波のスペクトルを特定して線形ランダム波モデルで表すと便利なことが多い。海洋工学の場合,
通常は,2変数スペクトル式を選定する。すなわち,波のスペクトルを定義するために必要なパラメータ
は,有義波高Hs及びピークスペクトル周期Tpである。
最も使用に適したスペクトル式は,地理的位置,モデル化する海況の厳しさ及びスペクトル式の適用対
象によって決まる。ただし,風によって引き起こされる海象に対して最もよく用いるスペクトルは,十分
発達した海象ではピアソン・モスコビッツスペクトル(PMスペクトル),発達途中の海象ではJONSWAP
(Joint North Sea Wave Project:北海での波浪共同観測計画)スペクトルである。うねりのスペクトルに関
する情報は,ISO 19901-1 [1]で得られる。
スペクトルをサイト固有のパラメータとともに用いれば,吹送距離及び浅水影響における実際の制約を
もともと考慮していることになるため,最も良好な結果が得られる。
B.2
ピアソン−モスコビッツスペクトル
PMスペクトルは,十分に発達した波の場合,すなわち,波の成長が吹送距離に制限されない場合に適
用できる。多くの水域では大抵の場合,このケースに該当するため,PMスペクトルを疲労解析のために
用いることが多い。海面上昇のスペクトル密度SPM(f)は,式(B.1)で算出する。
×
×
×
×
4
p
5
4
p
2
s
PM
25
.1
exp
5
312
.0
)
(
f
f
f
f
H
f
S
−
=
−
·························· (B.1)
ここに,
Hs: 有義波高(m)
fp: ピーク周波数
p
1
T
=
(Hz)
f: 周波数(Hz)
図B.1に,Hs=2.25 m及びTp=7.13秒で与えられる海況に関するPMスペクトルを示す。
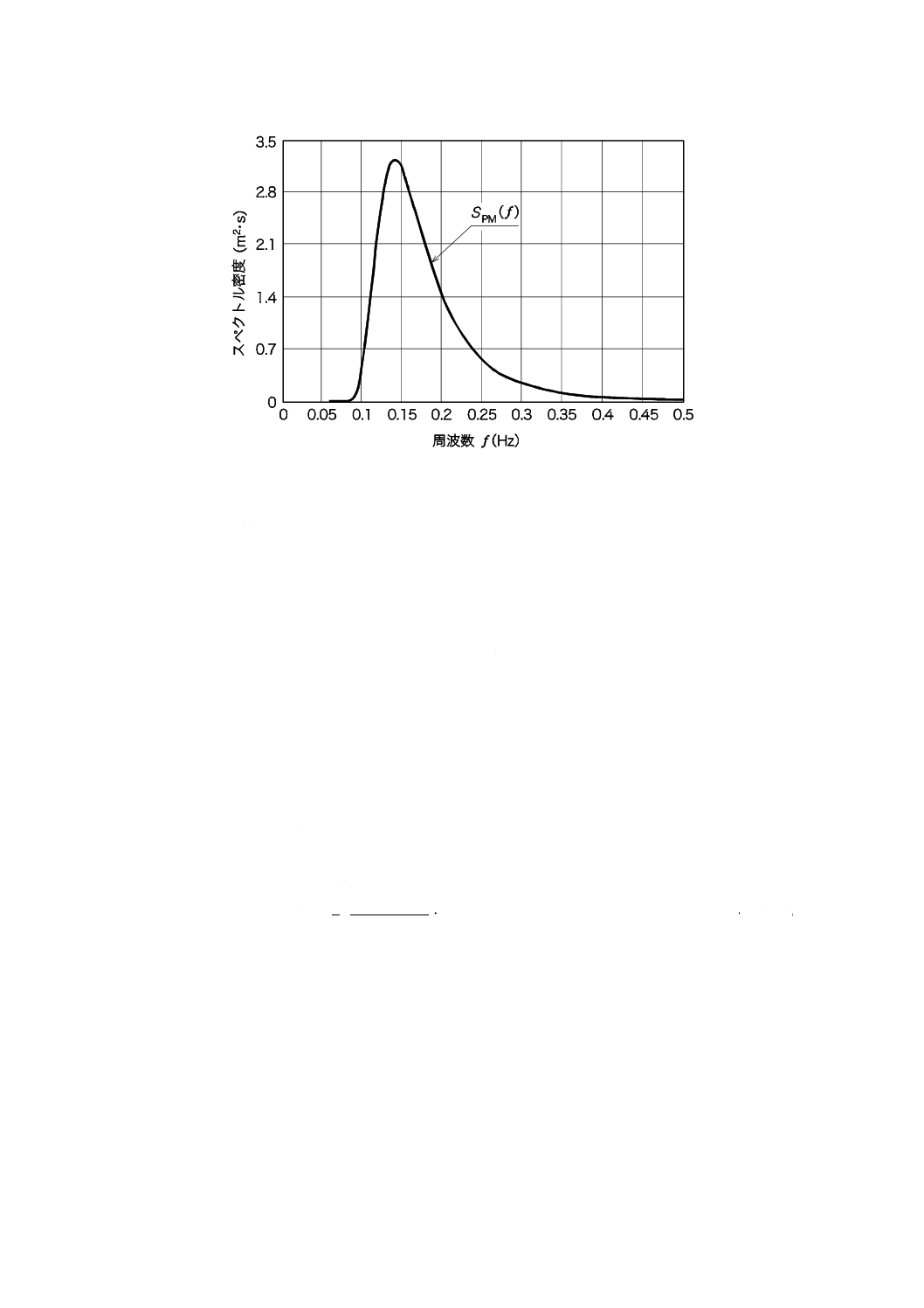
64
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.1−PMスペクトル
B.3
JONSWAPスペクトル
JONSWAPスペクトルは,限られた吹送距離の下での発達中の波を対象に,PMスペクトルの修正式とし
て定式化されたものである。全エネルギーが同じPMスペクトルと比較すると,このスペクトルは,荒天
条件でPMスペクトルよりもピークが高く,かつ,スペクトル幅が狭くなるように導出される。したがっ
て,JONSWAPスペクトルは,極値事象の解析を行う場合に用いることが多い。
ピーク増幅係数γα及び正規化係数C(γ) という二つの補正係数を導入する。前者は,ピークを増大しス
ペクトル幅を減少するもので,後者は,両スペクトル式で必ず同じHs(エネルギー)となるようにするた
め,スペクトル密度を低減するものである。そのためγ=1でPMスペクトルとなるように定式化方法が選
ばれている。
海面上昇のスペクトル密度は,式(B.3)の係数を用いて式(B.2)で算出する。
SJS(f )=C(γ)×SPM(f )×γα ··························································· (B.2)
ここに,
γ: ピーク増幅係数
C(γ): 正規化係数
∫
∫
∞
∞
0
α
PM
0
PM
)
(
)
(
)
(
df
f
S
df
f
S
C
γ
γ=
······························································ (B.3)
一例として,北海の代表的な荒天時海況(Hs=14.4 m,Tp=15.4秒及びγ=3.3)に関するJONSWAPス
ペクトルとPMスペクトルとの比較を,図B.2に示す。
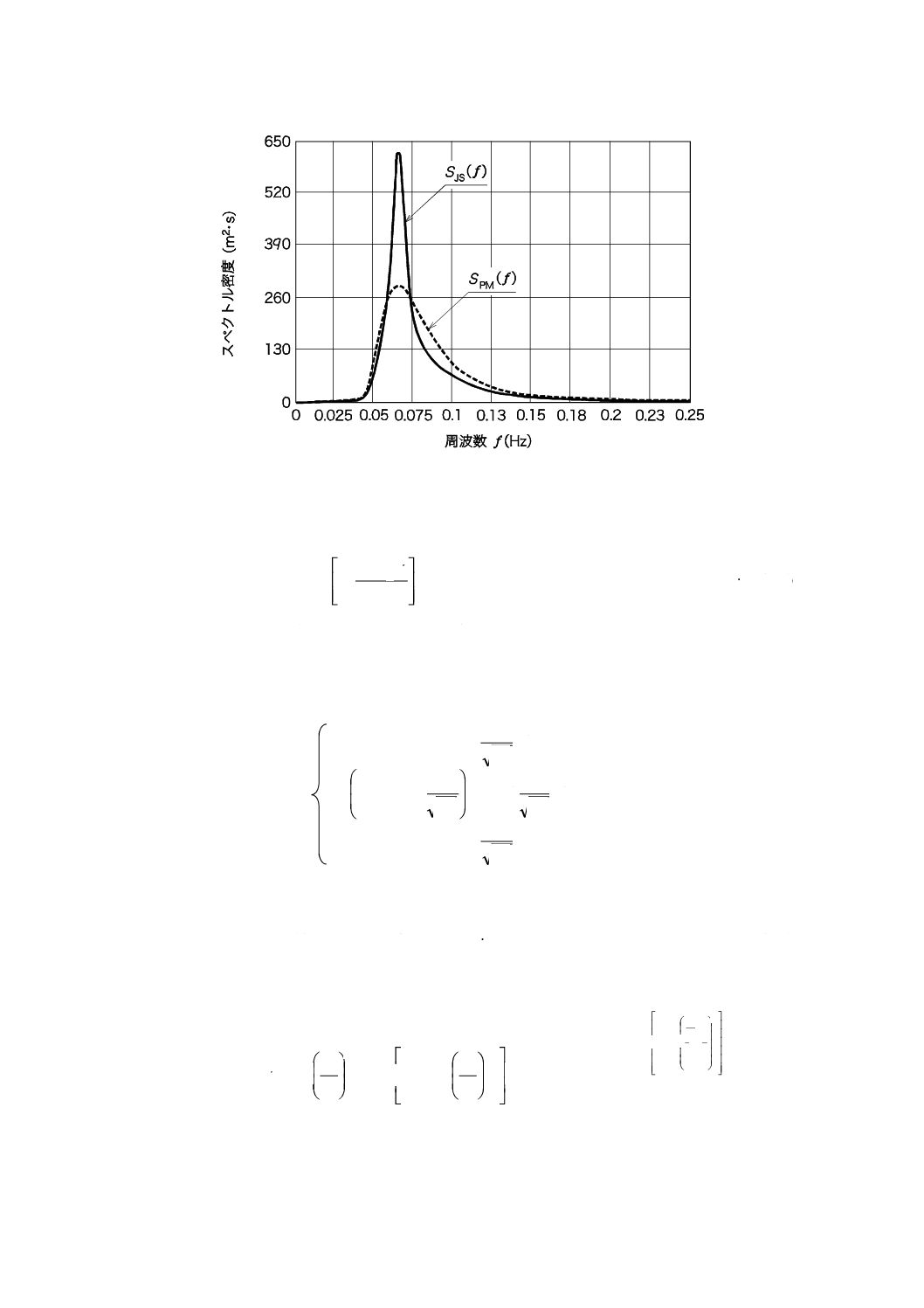
65
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.2−北海の代表的な荒天時海況に対するJONSWAPスペクトル及びPMスペクトル
より詳細な情報の代わりに,式(B.4)の値を用いてもよい。
2
p
2
2
p
2
)
(
exp
f
f
f
σ
α
−
−
=
································································ (B.4)
ここに,
σ=0.07: f ≦fp
σ=0.09: f >fp
ピーク増幅係数は,式(B.5)による。
の場合
≧
の場合
<
<
の場合
≦
5
1
5
6.3
15
.1
75
.5
exp
6.3
5
s
p
s
p
s
p
s
p
H
T
H
T
H
T
H
T
−
=
γ
······················ (B.5)
Hsの単位はメートルで,Tpは秒である。
正規化係数は,式(B.6)による。
C(γ)=1−0.287×lnγ ······························································· (B.6)
γ=1の場合には,正規化係数は,1となる。
上記の値を用いて,JONSWAPスペクトルを式(B.7)に示すように表現することが多い。
−
×
×
×
×
×
×
×
×
×
2
1
p
0.5
exp
4
p
5
p
p
2
s
JS
)
ln
287
.0
1(
25
.1
exp
5
312
.0
)
(
σ
γ
γ
f
f
f
f
f
f
T
H
f
S
−
−
−
−
−
=
······ (B.7)
JONSWAPスペクトルは,浅水域の波に対して用いられる,最も良いモデル化スペクトルである。
66
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.4
ピークスペクトル周期とゼロクロス周期との関係
ピークスペクトル周期Tpとゼロクロス周期Tzとの間には,式(B.8)の近似的関係が存在する。この関係
は,PMスペクトル及びJONSWAPスペクトルの両方に対して適当である。
γ
γ
+
+
=
11
5
p
z
×
T
T
····································································· (B.8)
γ=1の場合,PMスペクトルでは式(B.9)の関係がある。
Tp=1.41×Tz ·········································································· (B.9)
B.5
波の方向分布
海洋構造物の設計では,通常,全ての波が一方向,すなわち,風が吹く方向に伝ぱ(播)すると仮定す
る。したがって,どの波も波頂が長い長波頂波(二次元)と仮定する。先に求めた一次元波のスペクトル
は,この状況を表している。
しかし,実際の海は,通常様々な方向に伝ぱ(播)する数多くの大波及び小波で構成される。すなわち,
ある一点における波のエネルギーは,角度分布及びある範囲で拡がる周波数分布をもつ。このような波は,
波頂が長くないため,短波頂波と呼ばれる。長波頂波と比較すると,短波頂波は波の作用が低下している
ことを示しており,これを式(B.10)の二次元波のスペクトルS(f, θ ) で表してもよい。θは,風向に対する
相対方向である。
S(f, θ )=S(f )×D(f, θ ) ····························································· (B.10)
ここに,
S(f ): 一次元波のスペクトル
D(f, θ ): 方向分布関数
方向分布関数D(f, θ ) は,一般に未知であるため,通常は,波の主な進行方向の両側に広がる方位区分
について,対称で周波数が独立である関数D(θ ) によって代替し,式(B.11)の関係を適用する。
∫
=
π
π
θ
θ
−
1
)
(d
D
······································································· (B.11)
通常,方向についての情報は,測定及び妥当性の検証が困難である。このため,固定式海洋構造物の実
設計では,特に浅水域内の場合,単一方向の海況を用いることが望ましい。
B.6
ほかの周波数単位を用いることによる影響
この附属書では,波のスペクトルの周波数単位は,Hzを用いている。波のスペクトルを単位rad/sで扱
うこともでき,この場合,式(B.12)及び式(B.13)の関係を適用する。
T
π
ω2
=
··············································································· (B.12)
S(f )=2π×S(ω) ····································································· (B.13)
B.7
参考文献
[1] ISO 19901-1,Petroleum and natural gas industries−Specific requirements for offshore structures−Part 1:
Metocean design and operating considerations, ISO TC 67/SC 7, Date: 2003-08-14
[2] Guidelines for Design of Wind Turbines, 2nd edition 2002, Det Norske Veritas and Risø National Laboratory
[3] DNV-OS-J101,Design of Offshore Wind Turbine Structures, October 2007, Det Norske Veritas
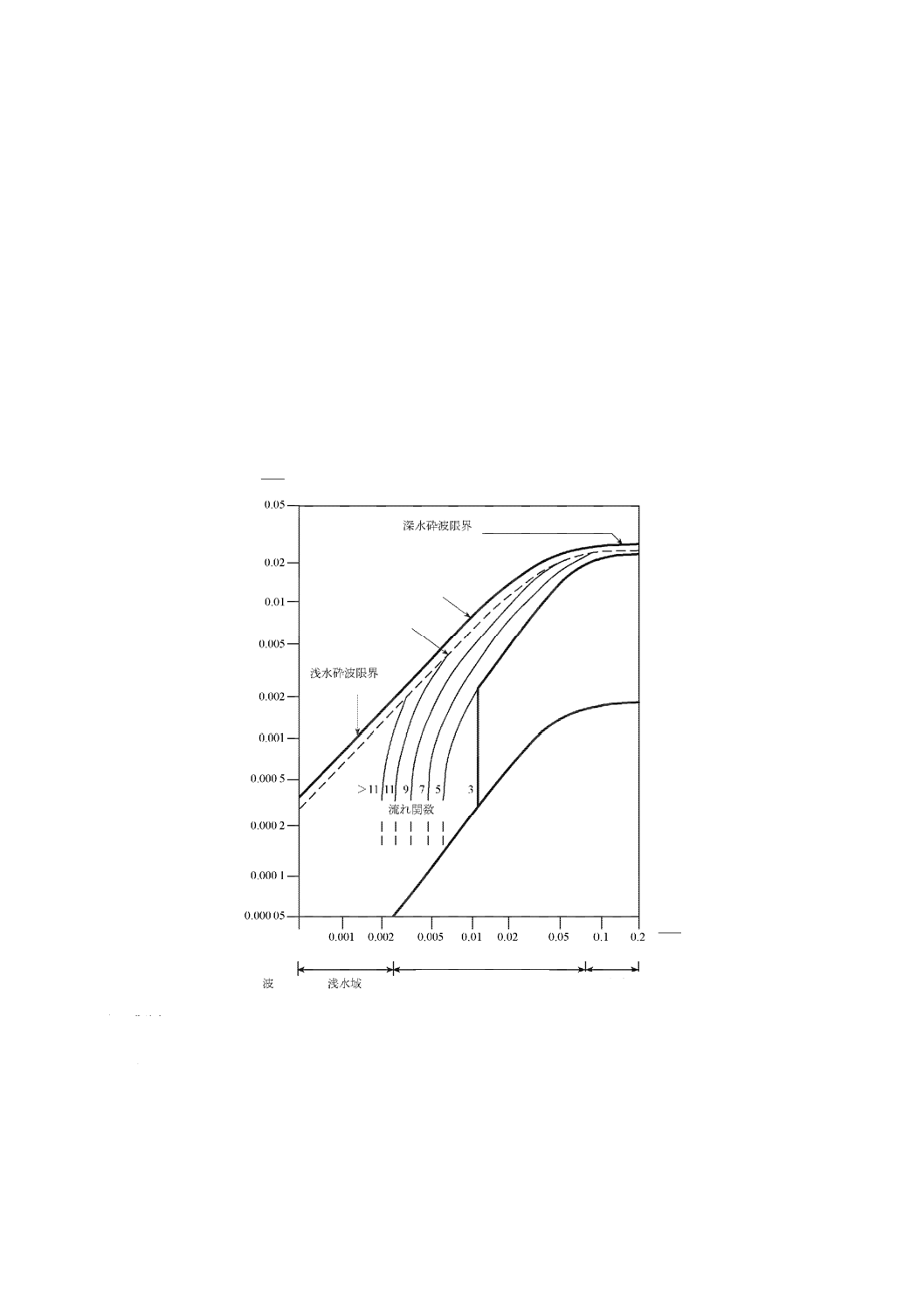
67
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
浅水の流体力学及び砕波
C.1 適切な波理論の選択
二次元規則波の運動を予測するに当たり,規則波に関する幾つかの理論を用いることができる。各種の
理論は,いずれも,適切な境界条件を用いて,同じ微分方程式の近似解を得るものである。どの理論も,
波頂に関して対称で,かつ,形状が変化することなく伝ぱ(播)する波形について計算を行うものである。
これらの理論は,関数形における差異,並びに波面の非線形運動及び動的境界条件の満足の程度に差異が
ある。図C.1は,適切な規則波理論を選定するための指針を正規化した波高及び水深の関数として示した
図である。
H=波高
L=波長
T=波の周期
d=水深
g=重力加速度
図C.1−規則波理論の選定に関する図
深水域における波高が小さい波は,実質的に線形近似する。この領域における規則波は,波形が正弦波
中間水域
深水域
線形エアリ波
又は流れ関数
ストークス五次
又は流れ関数3
H/L=0.14
Hb
0.9Hb
H/d=0.78
2
T
H
g
2
T
d
g
68
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
状であり,かつ,線形エアリ波理論又は低次の流れ関数解を用いてモデル化してもよい。
波高が増大する又は水深が減少すると,波形の勾配が増し,静水位より上の波頂高の値が,同じ静水位
より下の波の谷の深さよりも大きくなる。波形及び水粒子運動は,もはや線形波理論では正確に表現でき
なくなる。解の次数を正しく選定すれば,幅広い水深範囲を対象として流れ関数理論を適切に適用できる。
深水域における波形勾配が大きい波をモデル化するに当たり,ストークス5次近似理論を用いてもよい。
波高が更に増大する又は水深が更に減少すると,波頂における水粒子の水平速度がある時点で波速を超
えて,波が崩れる。水粒子が波頂から前方に向けて放出され,砕波が起きるといわれている。
波理論及びその適用範囲に関する更に詳しい説明は,ISO 19901-1を参照してもよい。
C.2 不規則波列のモデル化
不規則波列は,ランダムな海況に相当し,エアリ波理論で表現されるそれぞれの正弦波成分の和として
モデル化してもよい。中間水域又は浅水域では,エアリ波理論の精度を評価することが望ましい。
線形エアリ波理論では,海底面から静水位までの水粒子運動が定義されている。水位の変化を考慮する
に当たり,波動ストレッチ解法を適用してもよい。適切な手法としては,ウエラ及びデルタストレッチの
二つがあり,ISO 19901-1に規定されている(ISO 19901-1のA.8.4及びA.9.4.1参照)。
波浪場に構造物が密に存在すると,構造物に接近する波の性質に顕著な影響を与えることがある。この
ような場合は,回折解析を実施する必要がある。構造物に作用する荷重に対して波の回折が及ぼす影響を
考慮するに当たり,MacCamy-Fuchs補正を用いてもよい。
浅水域では,海面上昇分布はガウス分布から逸脱し,個別波高の分布もレイリー分布から逸脱すること
となる。この場合,浅水域についてバチェス(Battjes)及びグルーネダイグ(Groenendijk)が考案した波
高分布[1]を用いてもよい。バチェス・グルーネダイクモデルは,次のような条件下で行った水理実験を基
にして開発された。その条件とは,流れがない場における勾配が一定の海底上の二次元波であり,それた
め,適用上の制約がある22)。波向分布係数が1.0以下の場合に,バチェス・グルーネダイクモデルを併用
しないほうがよい。
注22) バチェス・グルーネダイクモデルを用いる場合は,次の条件を満足していることが望ましい。
a) 波の進行方向が最も大きい海底勾配の方向の30°以内にある。
b) 風車位置から波の来る方向へ深水波の波長の1倍又は3倍に相当する距離にわたる平均海
底勾配のうち,いずれか大きい方が正値であって,かつ,その値が0.05 rad以下であるこ
とが望ましい。
c) 風車位置から波の来る方向へ深水波の波長の10倍に相当する距離にわたる海底勾配を求
めたとき,1波長相当の距離ごとの10区間のそれぞれの平均海底勾配がb) で算定した勾
配から0.02 rad以上は異ならないことが望ましく,かつ,隣接する区間同士の勾配は0.005
rad以上異ならないことが望ましい。
d) 流速が1.5 m/s未満であることが望ましい。
バチェス・グルーネダイクモデルの波高分布は,局所水深及び海底面の局所勾配の関数であり,式(C.1)
となる。

69
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の場合
≧
,
−
−
=
の場合
≦
,
−
−
=
=
<
=
tr
6.3
2
2
tr
2
1
1
exp
1
)
(
exp
1
)
(
)
(
)
(
h
h
h
h
h
F
h
h
h
h
h
F
h
h
Pr
h
F
·········· (C.1)
ここで,定数h1及びh2は,表C.1による値である。波高の二乗平均平方根Hrmsは,式(C.2)による。
d
m
m
H
0
0
rms
×
24
.3
×
69
.2
+
=
······················································· (C.2)
ここに,
d: 局所水深(m)
m0: 海面上昇の分散(m2)
過渡状態の波高Htr(m)は,式(C.3)による。
Htr=(0.35+5.8×tanα)d ·························································· (C.3)
ここに,
α: 海底面の局所勾配(rad)
過渡状態の正規化波高htrは,式(C.4)による。
rms
tr
tr
H
H
h=
·············································································· (C.4)
最終的に,超過確率x %の個別波高は,式(C.5)による。
Hx %=hx %Hrms ······································································· (C.5)
ここに,
hx %: xの様々な値に対して,表C.1で与えられる値
表C.1−Htrに対する定数h1,h2及び正規化波高hx %
htr
h1
h2
h2 %
h1 %
h0.1 %
0.05
12.209
1.060
1.549
1.621
1.814
0.10
7.012
1.060
1.549
1.621
1.814
0.15
5.070
1.060
1.549
1.621
1.814
0.20
4.028
1.060
1.549
1.621
1.814
0.25
3.369
1.060
1.549
1.621
1.814
0.30
2.912
1.060
1.549
1.621
1.814
0.35
2.575
1.061
1.549
1.621
1.814
0.40
2.315
1.061
1.549
1.621
1.815
0.45
2.108
1.061
1.550
1.622
1.815
0.50
1.939
1.062
1.551
1.623
1.816
0.55
1.799
1.062
1.552
1.624
1.817
0.60
1.682
1.064
1.554
1.626
1.820
0.65
1.582
1.065
1.556
1.628
1.823
0.70
1.497
1.068
1.560
1.632
1.827
0.75
1.424
1.071
1.564
1.637
1.832
0.80
1.361
1.075
1.570
1.643
1.839
0.85
1.308
1.080
1.577
1.650
1.847
0.90
1.261
1.086
1.586
1.659
1.857
0.95
1.222
1.093
1.596
1.670
1.869
1.00
1.188
1.100
1.607
1.682
1.882
70
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.1−Htrに対する定数h1,h2及び正規化波高hx %(続き)
htr
h1
h2
h2 %
h1 %
h0.1 %
1.05
1.159
1.109
1.620
1.695
1.898
1.10
1.134
1.119
1.635
1.710
1.914
1.15
1.113
1.130
1.650
1.726
1.932
1.20
1.096
1.141
1.666
1.744
1.952
1.25
1.081
1.153
1.684
1.762
1.972
1.30
1.068
1.165
1.702
1.781
1.993
1.35
1.057
1.178
1.721
1.801
2.016
1.40
1.048
1.192
1.741
1.821
2.038
1.45
1.040
1.205
1.761
1.842
2.062
1.50
1.033
1.219
1.781
1.864
2.086
1.55
1.028
1.234
1.802
1.885
2.110
1.60
1.023
1.248
1.823
1.907
2.135
1.65
1.019
1.262
1.844
1.930
2.160
1.70
1.016
1.277
1.865
1.952
2.184
1.75
1.013
1.292
1.887
1.974
2.209
1.80
1.011
1.306
1.908
1.996
2.234
1.85
1.009
1.321
1.929
2.019
2.259
1.90
1.007
1.335
1.951
2.041
2.284
1.95
1.006
1.350
1.972
2.063
2.309
2.00
1.005
1.364
1.987
2.085
2.334
2.05
1.004
1.379
1.985
2.107
2.358
2.10
1.003
1.393
1.984
2.129
2.383
2.15
1.002
1.407
1.983
2.151
2.407
2.20
1.002
1.421
1.982
2.150
2.431
2.25
1.002
1.435
1.981
2.149
2.455
2.30
1.001
1.449
1.980
2.149
2.479
2.35
1.001
1.463
1.980
2.148
2.502
2.40
1.001
1.476
1.979
2.148
2.525
2.45
1.001
1.490
1.979
2.147
2.548
2.50
1.000
1.503
1.979
2.147
2.571
2.55
1.000
1.516
1.979
2.147
2.594
2.60
1.000
1.529
1.978
2.147
2.616
2.65
1.000
1.542
1.978
2.146
2.629
2.70
1.000
1.555
1.978
2.146
2.629
2.75
1.000
1.568
1.978
2.146
2.629
2.80
1.000
1.580
1.978
2.146
2.629
2.85
1.000
1.593
1.978
2.146
2.628
2.90
1.000
1.605
1.978
2.146
2.628
2.95
1.000
1.617
1.978
2.146
2.628
3.00
1.000
1.630
1.978
2.146
2.628
浅水域に対して,再現期間50年の極値波高(EWH)H50を求めるために,式(C.5)を表C.1と併せて用い
る場合,低減波高(RWH)は,式(C.6)を用いて推定してもよい。
rms50
red50
×
2
×
1.1
H
H
=
······························································ (C.6)
71
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここで,Hrms50は,再現期間50年の海況に対する海面上昇の分散から求められる値である。再現期間1
年の低減波高の推定にも,同じ手法を用いてもよい。
バチェス・グルーネダイクモデルの波高分布の適用例として,水深がd=21 m,有義波高測定値(標準
偏差の4倍)がHm0=7.1 m,海底勾配がtanα=0.01である場所について検討する。超過確率0.1 %の波高
H0.1 %を求めると,次のとおりである。
波高の標準偏差:
0
m=Hm0/4=1.775 m
過渡状態の波高:
Htr=(0.35+5.8×0.01)×21=8.57 m
波高の二乗平均平方根:
Hrms=2.69×1.775+3.24×1.7752/21=5.26 m
過渡状態の正規化波高:
htr=Htr/Hrms=8.57/5.26=1.63
表C.1を用いて調べた値:
htr=1.63の場合,h1=1.021及びh2=1.256
正規化したh0.1 %を求めるに当たり,分布関数Fを用いる場合は,次による。
・ F1使用時:h0.1 %=h1[−ln(0.001)]1/2=1.021×[−ln(0.001)]1/2=2.68
・ F2使用時:h0.1 %=h2[−ln(0.001)]1/3.6=1.256×[−ln(0.001)]1/3.6=2.15
h0.1 %>htr=1.63なのでF2を用いなければならず,この結果h0.1 %=2.15となる。
最終的に,超過確率0.1 %の波高は,次の式のとおりとなる。
H0.1 %=2.15×Hrms=2.15×5.26=11.3 m
従来のレイリー分布波高では,次の値が得られる。
H0.1 %=1.86×7.1=13.2 m
C.3 砕波
波の砕け方にはいろいろあり,主として海底勾配に対する深水波の波形勾配の比によって決まる。
浅水減では,波高の砕波限界は経験的に局所水深のおよそ78 %である。海底勾配[静水深が波の伝ぱ(播)
方向に減少]が存在することによって砕波が発生し,その波高は,同じ局所水深における規則波の限界波
高(0.78 d)よりも顕著に高くなる可能性がある。Barltrop及びAdamsによって指針が提示されている[2]。
波高Hの規則波に伴う波の周期Tには,水深に依存する下限値が存在し,砕波波高限界から求められる。
周期Tは,式(C.7)で近似してもよい。
×
d
H
h
d
T
78
.0
tan
2
14
.0
78
.0
1
−
<
π
g
,H<0.78 dの場合 ························· (C.7)
ここに,
d: 水深23)
注23) この式中の定数0.14は,均一で水平な海底の上方における砕波を対象とした理論に基づくもの
である。海底面に起伏及び/又は勾配がある場合には,この定数は変化し得ることに注意する。
深水域では,波形勾配が1/7を超えた場合,すなわち,波高が波長の14 %よりも大きくなると砕波が発
生する可能性がある。
砕波波高HBは,式(C.8)から推定してもよい。
)
tan
19
exp
1
6.1
)]
tan
19
exp(
1[
44
/
/1
2
b
B
α
α
(−
+
=
−
−
=
+
=
b
a
T
a
d
b
H
g
··························································· (C.8)
72
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
Tb: 砕波周期
α: 海底勾配
砕波特性は,風と波との相互作用,波同士の相互作用及び水流との相互作用にも影響される。
砕波は,崩れ波,巻き波又は砕け寄せ波のいずれかに分類すると便利である。
崩れ波は,与えられた条件だけが砕波の原因となり,とがった波形を保持し続ける波である。波形及び
波の運動は,高次の流れ関数解を用いて適切に表現してもよい。
巻き波は,初期波形勾配が一般に中程度である波が,海底勾配を遡上しながら伝ぱ(播)することによ
って突然崩れるときに発生する。局地水深に対する規則波の限界波高よりも十分大きい波高に成長し,波
頂では水がほとばしり出る。この噴出された水が固定構造物に衝突すると,大きな衝撃荷重及び高い局所
圧力が発生する可能性がある。
巻き波を数値的にモデル化することは困難である。一つの方法を参考として附属書Dに示す。静水位よ
りも下方では,高次流れ関数を解くことによって,波形及び運動を表してもよい。
砕け寄せ波は,波高が低く非常に長い波が海岸のような海底勾配と遭遇したときに発生する。この砕波
の特性は,崩れ波及び巻き波と相当異なっており,洋上風車の設計に対しては重要ではないと考えられる。
予想される砕波の種類は,海底勾配α(rad)及び波形勾配の平方根の関数に基づき,表C.2から求めて
もよい。パラメータξは,深水波の波高H0又は砕波波高Hb及びじょう(擾)乱を受けていない波の波長
λ0に基づいて式(C.9)によって計算してもよい。
0
b
b
0
0
0
/
tan
/
tan
λ
α
ξ
λ
α
ξ
H
H
=
=
········································································ (C.9)
表C.2−砕波の種類
崩れ波
巻き波
砕け寄せ波
ξ0<0.45
0.45<ξ0<3.3
3.3<ξ0
ξb<0.40
0.40<ξb<2.0
2.0<ξb
砕波の発生及びその種類は,構造物の有無によっても影響される場合があり,特に密集した構造物の場
合に顕著である。
C.4 参考文献
[1] Battjes, J. A., and Groenendijk, H. W., “Wave height distributions on shallow foreshores,” J. of Coastal
Engineering, Vol. 40 (2000) pp.161-182.
[2] Barltrop, N. D. P., and Adams, A. J., “Dynamics of Fixed Marine Structures,” Butterworth Heinemann, ISBN 0
7506 1046 8.
[3] Ochi, M. K.,“Ocean Waves−The Stochastic Approach”, Cambridge University Press, 1998.
73
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
流体力荷重の計算に関する指針
D.1 一般
適切な波理論を選択した場合は(附属書C参照),波及び水流に伴う水粒子の運動,並びにその結果発
生する構造荷重を計算してもよい。
不規則波列の水粒子運動は,次の手法を用いて生成してもよい。
a) ホワイトノイズフィルタ処理 この手法では,波のスペクトルを表現するフィルタによって,ガウス
性ホワイトノイズが時間領域でフィルタ除去される。
b) ランダム係数法 この手法では,海面が多くの正弦関数と余弦関数との和として近似される。それぞ
れの正弦及び余弦関数の振幅は,波のスペクトルに応じて,ランダムかつ正規分布に従う。
c) ランダム位相角法 この手法では,海面が多く正弦(余弦)関数の和として近似され,それぞれの正
弦(余弦)関数は,波のスペクトルに応じた固定振幅及びランダムな位相角をもつ。
計算方式又は検討対象の設計荷重ケースに応じて,自然現象を可能な限り良好に模擬した一つ以上の特
性をもつように海面をモデル化することが,重要である。模擬する特性の例としては,次のとおりである。
・ 波のスペクトルの複雑性
・ 波群の長さ
・ 1波群当たりの波数
・ 実事象の再現不確実性
ランダム位相角法を用いるときは,この手法は,用いる要素数が無限の場合にだけ,正規のガウス過程
を模擬して(かつ,正しい“波群特性”を与えて)いるという事実に注意することが望ましい。実際には,
1 000個以上の成分を用いて検討することが望ましい[1]。
海洋構造物に作用する流体力荷重は,次のとおり分類することができる。
・ 粘性抵抗荷重 水流が部材を通過するときに,水流中に発生する渦によって生じる荷重。粘性抵抗力
は,流入速度の二乗に比例する。
・ 慣性荷重 加速流体中の圧力勾配,及び部材と加速流体との局所的な相互作用によって生じる荷重。
慣性力は,流体の加速度に比例する。
・ 回折波荷重 構造物があることによって波のパターンが変化し,その結果,構造物に作用する荷重が
変化するという原理に基づく荷重。
・ 波浪打込み及びスラミングによる荷重 部材が水面を通過するときのように,慣性力が発生する荷重。
この慣性力は,相対速度の二乗に比例する。
・ 放出渦による荷重 抵抗荷重を発生させるそれぞれの渦が構造物から離れるときに,変動力が構造物
に作用する荷重。構造の固有振動数が渦放出周波数に近い場合には,大きな振動に発達する場合があ
る。
・ 放射波による荷重 構造物の振動運動によって生じるもので,構造物から離れる方向に伝ぱ(播)す
る自由表面波が生成される荷重。この荷重は,構造物の振動速度に線形比例し,運動履歴に依存する。
振動運動が小さい場合,例えば,海底中に基礎が設置されている大半の洋上風車の支持構造物の場合
は,放射波による荷重を無視できる。放射波の減衰は,ポテンシャル理論の回折法/屈折法によって
74
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
計算できる。
上述の荷重に加えて,静水圧に起因する荷重も考慮しなければならない。この荷重は,中空の部材にと
って特に重要である。
部材が波長と比べて小さい場合,水粒子の運動は,部材による影響を局所的に受けるにとどまり,この
ときの荷重は,モリソン(Morison)式を用いて抵抗成分及び慣性成分から計算できる。これについては,
D.2に記載する。部材寸法が波長の約1/5よりも大きい場合は,D.3に記載しているように回折効果が重要
である。
D.2 モリソン(Morison)式
モリソン(Morison)式[2]は,フレーム構造に作用する粘性抵抗及び慣性荷重を計算するに当たり,一
般に用いられる表現である。静的部材に対する式は,式(D.1)による。
U
A
C
U
U
D
C
F
&
ρ
ρ
m
d
2
1
+
=
························································· (D.1)
ここに,
F: 部材単位長当たりの力
Cd: 抵抗係数
Cm: 慣性係数
ρ: 水の密度
D: 部材の直径
A: 部材断面積
U: 流体速度の部材に対する法線方向成分
U&: 流体加速度の部材に対する法線方向成分
構造物が顕著に運動する場合,相対速度によって抵抗力が変わるため,流体力学的減衰が生じ得る。相
対加速度によって慣性力と同様の力が発生し,この力は,構造物と一緒に運動する付加水質量を考えるこ
とによって,大抵はうまく解析できる。この場合,モリソン(Morison)式は,式(D.2)になる。
s
a
w
m
r
r
d
2
1
U
A
C
U
A
C
U
U
D
C
F
&
&
ρ
ρ
ρ
−
+
=
········································ (D.2)
ここに,
Ur: 相対速度の部材に対する法線方向成分
w
U&: 流体加速度の部材に対する法線方向成分
s
U&: 構造物加速度の部材に対する法線方向成分
Ca: 付加質量係数(Ca=Cm−1,細長い柱状の固定部材の場
合)
Cd及びCmの値は,レイノルズ数,表面粗度,クーリガン・カーペンタ(Keulegan-Carpenter)数及び流
速と波速との比の関数として変化する。数多くのサイトで実施された実験の結果によれば,同じ基準条件
において,Cd及びCmの値にかなりのばらつきがある。結果として,海洋構造物向けの妥当なCd値及び
Cm値には,まだかなり不確定性がある。Cd値及びCm値の選定に関する指針として,設計者は,文献[3]
を参照する。
非柱状部材については,Cd値及びCm値の選定に関する指針を文献[4]で得てもよい。非円形断面の場合
は,Cdが流れの入射角の関数であることに注意することが望ましい。
D.3 回折
波の回折が発生するのは,構造物が波のパターンを変化させるためである。構造物の断面寸法が波長と
比べて大きい場合,一般にはD>0.2 λである場合に波の回折が発生する。この場合には,モリソン(Morison)
75
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
式を適用できない。
波の回折効果を計算するためには,回折を起こす構造物を通り抜ける流れがないという境界条件を追加
し,波理論の手順に従う必要がある。一般に,線形波理論を仮定して,吸込み・湧出し法又は有限要素流
体解析に基づく数値解析法を用いなければならない。吸込み・湧出し法で得られる結果は,不規則な周波
数が確実に排除されていることを確認することが望ましい。新しい構造概念が導入され,かつ,最先端の
数値解析法でも荷重を適切に表現できない場合は,模型実験の実施が望ましい。
ある特定の単純な事例の場合,例えば,鉛直な円柱が海底から伸びて自由表面から突き出ている場合に
は,回折問題を解析的に解いてもよい。中間水深で自由表面から突き出た円柱に対する解は,MacCamy
及びFuchsによって示されている[5]。波の伝ぱ(播)方向において,半径aの円柱に作用する単位軸方向
長さ当たりの正味荷重は,式(D.4)のパラメータを用いて式(D.3)で算出する。
)
cos(
)
(
1
)
(
cos
)
(
cos
2
1
x
α
ω
ρ
−
=
t
ka
A
kd
h
ks
h
k
H
f
g
······································ (D.3)
ここに,
)
(
'
)
(
'
)
(
2
1
2
1
1
ka
Y
ka
J
ka
A
+
=
)
('
)
('
tan
1
1
1
ka
Y
ka
J
−
=
α
··································································· (D.4)
単位軸方向長さ当たりの水平力は,モリソン(Morison)式の慣性項に相当する式(D.5)で記述してもよ
い。
α
ρπu
a
C
f
&
2
m
x=
········································································ (D.5)
式(D.5)で,α
u&は,海底面からsだけ上方において,位相遅れがαである水粒子の加速度であり,式(D.6)
で算出する。
1
2
m
)
(
4
)
cos(
)]
(
cos
/)
(
)[cos
2/
(
A
ka
C
t
kd
h
ks
h
Hk
u
π
α
ω
α
=
−
=g
&
·································· (D.6)
この解析解は,モノパイル,重力式基礎などの柱状基礎に作用する波力の予測に用いることができる。
ただし,例えば,氷荷重を低減する目的で波飛まつ帯に円すい(錐)状の部位がある場合など,想定して
いる円形断面から構造の形状が大きく外れていると,その公式から間違った結果が導かれることもある。
D.4 波浪打込み及びスラミングによる荷重
部材が急に水中に沈むと,波浪打込み力及びスラミング力が発生する。波のスラミングは,ほぼ水平な
部材が,波通過時の水面の隆起に飲み込まれたときに発生する。最大スラミング力は,平均水位にある部
材に対して発生し,スラミング力の方向はほぼ鉛直である。波浪打込みは,砕波に伴うもので,波向に直
角な平面内で,任意の傾斜角の部材に対して作用する。最大力は,平均水位よりも上方で発生する。いず
れの場合も力が衝撃的に作用するため,構造の動的応答が重要である。
実際,スラミングの流体力学は非常に複雑である。部材の形状,水面の正確な形及びスラミングが発生
したときの巻き込み空気の存在が,スラミング力に大きな影響を与える。単位軸方向長さ当たりのスラミ
ング力は,一般に式(D.7)で表現される。
2
s
2
1
DU
C
F
ρ
=
········································································ (D.7)
ここに,
Cs: スラミング係数
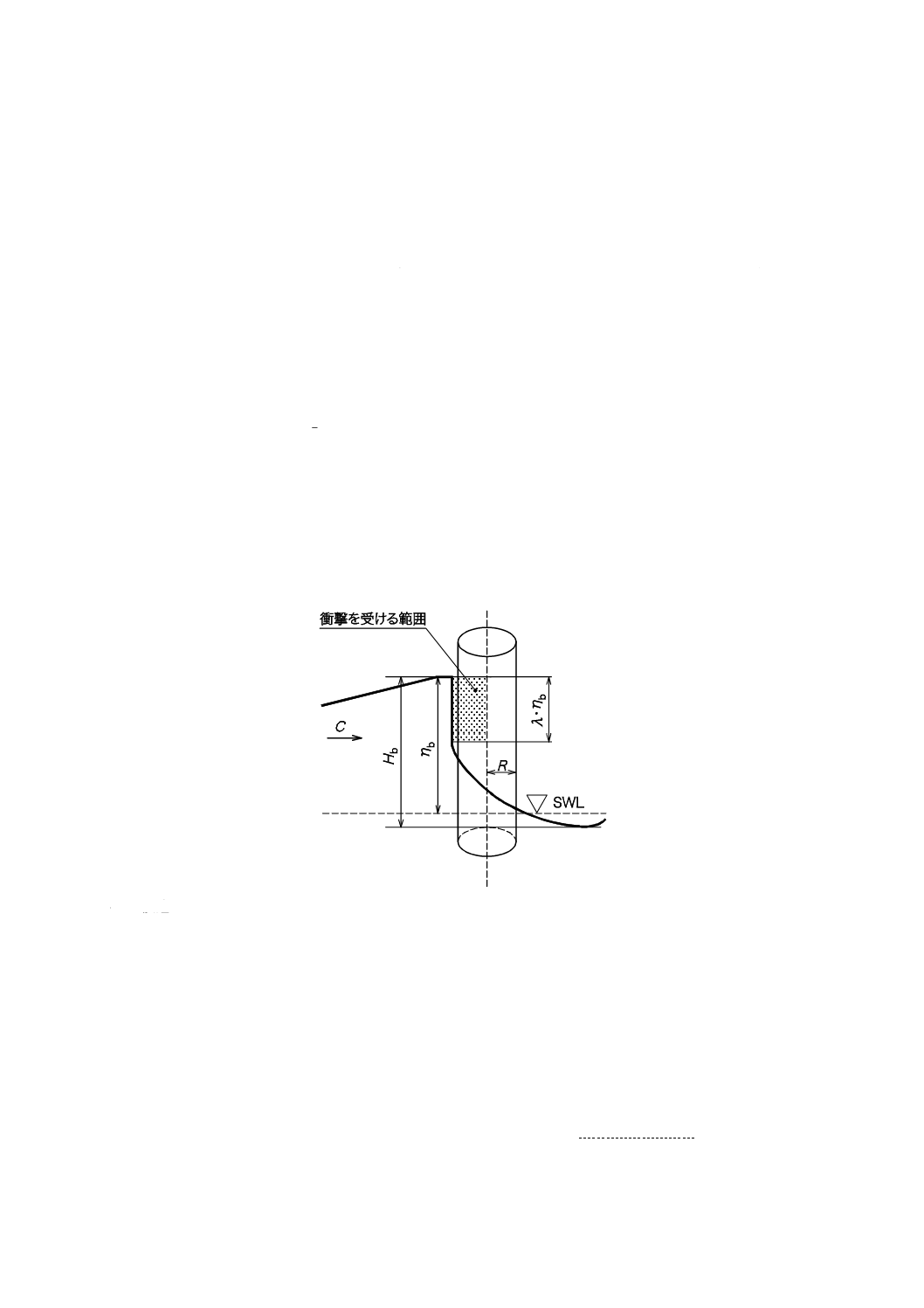
76
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
円柱に対するCsの測定値は,一般に3〜7である。
波によるスラミング又は波浪打込みにおいて,速度Uは,単に水粒子の速度ではない。衝撃発生位置の
粒子速度のうち,まず水面に対して垂直な速度,次に部材に対して垂直な速度を求めることによって,波
理論からUを求めることができる。理論上は,スラミング方程式(D.7)においてU2の代わりに|Us|Upを用い
る方が正確であり,ここで,Usは水面が円柱直径を横切る速さ,Upは円柱に垂直方向の水粒子速度である。
波浪打込み及びスラミングによって,非常に高い圧力が発生する可能性がある。この圧力は推定可能で
あるが,計算がかなり不確実である。周りを囲まれていない水に関しては,実用上,スラミング又は波浪
打込みを受ける面について,1 MPaの圧力を考えるのが妥当である[4]。
鉛直及び傾いた柱状構造物に作用する砕波について,Wienkeが測定した結果[6]によると,追加の波力成
分として衝撃力FIを式(D.8)のとおりモリソン(Morison)式に付け加えてもよい。
Fwave̲break=FD+FM+FI ····························································· (D.8)
ここに,
FD: 波力のうち抵抗成分
FM: 波力のうち慣性成分
FI: 砕波力による衝撃成分
抵抗力及び慣性力は,波の周期運動に伴う水面の上昇によって変化し,高次の波理論を用いて解析して
もよい。
砕波環境内にある円柱を考えると衝撃を受ける範囲は,図D.1のように定義できる。
C :波速
Hb :砕波地点での波高
ηb :自由水表面の最大上昇量
R :円柱の半径
λ :巻き込み率 ≈ 0.5
図D.1−砕波及び円柱のパラメータ
水塊が円柱に対して垂直ではなく傾斜角γで衝突する場合,円柱断面は真円断面ではなくだ(楕)円断
面で表現する必要がある。傾斜した円柱又は巻込みが進んだ砕波の先端部が鉛直な円柱に対して斜め,す
なわち,波頂よりも下方で衝突する場合にも,この表現は有効である(図D.2参照)。
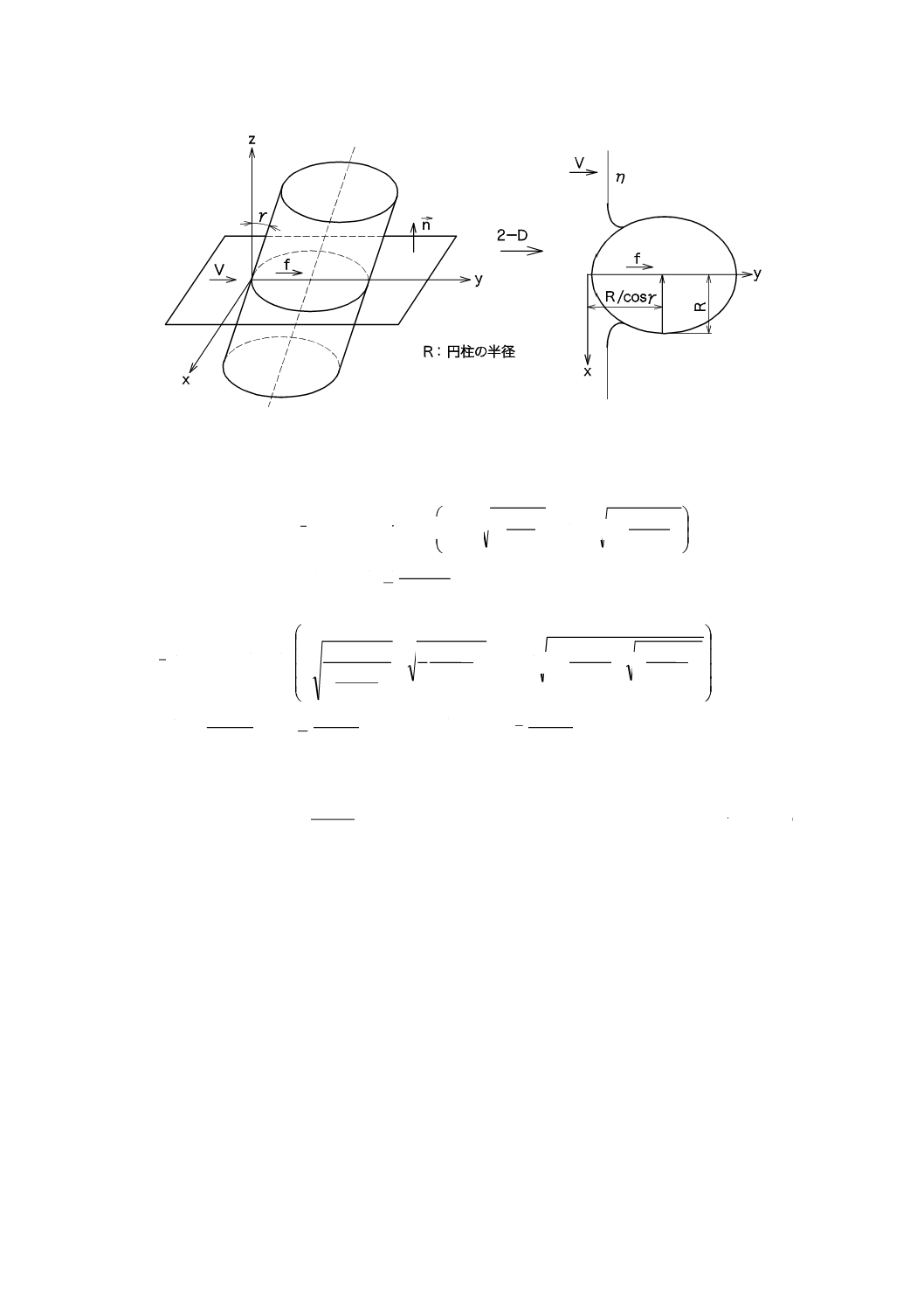
77
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図D.2−斜めに流入するときのパラメータ
衝撃力FIは,式(D.9)及び式(D.10)のとおりに計算してもよい。
γ
γ
γ
π
γ
ρ
λη
cos
8
0
4
cos
1
arctan
cos
2
2
cos2
2
water
b
I
V
R
t
t
R
V
h
t
R
V
RV
F
≦
≦
ここに,
−
−
=
············ (D.9)
γ
γ
γ
γ
γ
γ
γ
π
γ
ρ
λη
cos
32
'
cos
32
12
'
cos
32
3
'
cos
6
'
4
cos
1
arctan
'
cos
3
8
'
cos
6
1
cos
4
2
2
water
b
I
V
R
t
t
V
R
t
V
R
t
R
V
t
R
V
h
t
R
V
t
R
V
RV
F
−
=
ただし,
≦
≦
ここに,
−
=
−
·······(D.10)
衝撃の継続時間は,式(D.11)で算出する。
γ
cos
32
13
V
R
T=
········································································ (D.11)
ここに,傾斜角γは,水塊の運動方向と円柱軸に対する垂線とがなす角度であり,鉛直な円柱における
砕波の場合,cosγ=1である。この場合の衝撃力の高さ方向分布(γ=0°)を,図D.3に示す。
巻込みが進んだ砕波の先端部が鉛直な円柱に衝突する場合,又は傾斜円柱における砕波の場合,cosγ<1
である。
波向に対する円柱の傾きとともに,巻き込み率λ(図D.1参照)が増加することに注意することが望ま
しい。最大衝撃力は,波向に対する傾斜角が約25°の場合に発生する。
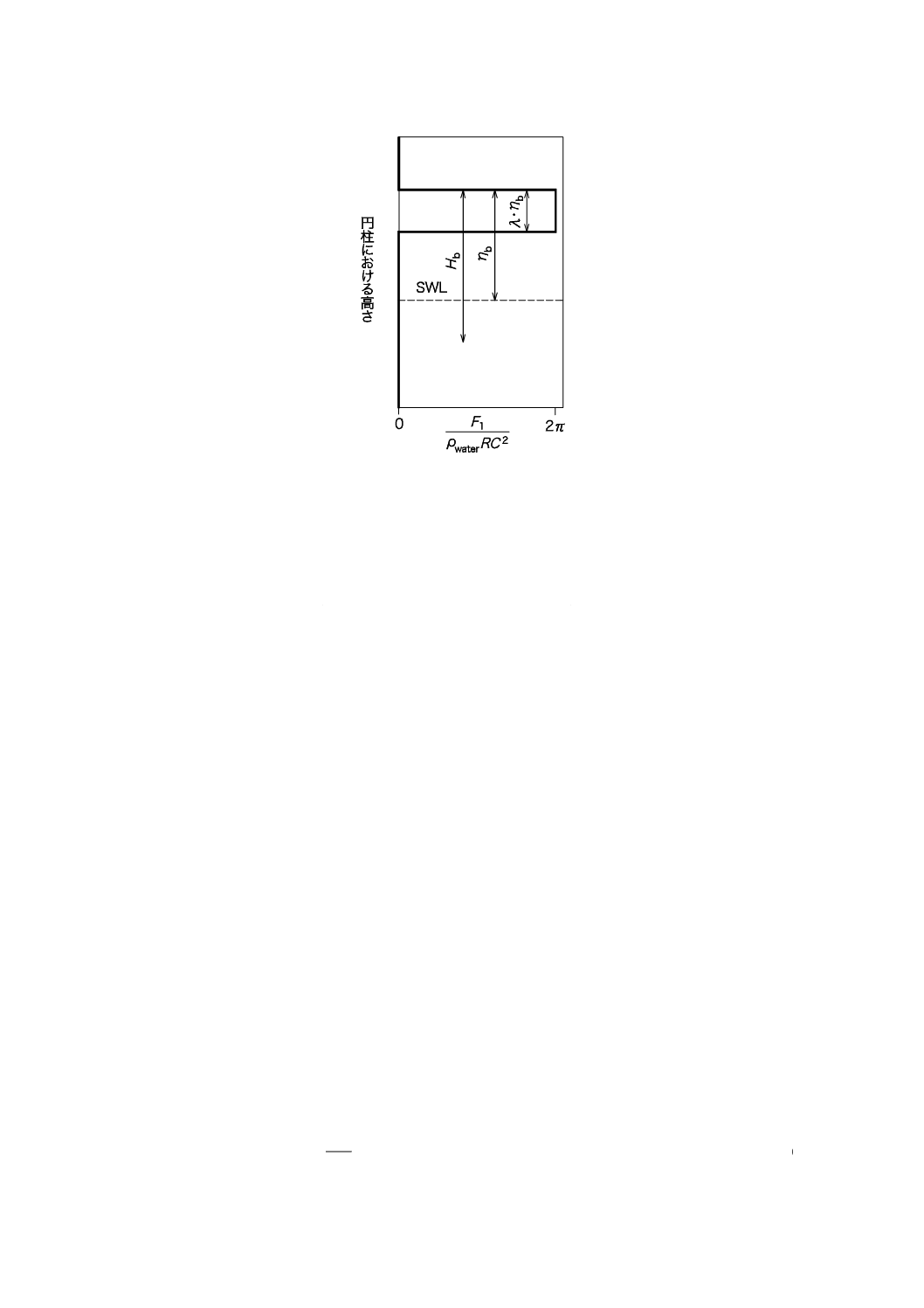
78
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図D.3−衝撃力の高さ方向分布(γ=0)
D.5 渦誘起振動
円柱パイルなどの鈍頭体を通過する流れの中で発生し放出される渦は,その物体に動的荷重を与える。
この種の荷重の危険性は,主として,構造物の固有振動数と励振周波数との間で共振が起こる可能性に起
因する。広範な条件で発生する複雑な共振メカニズムによって,損傷を招く大きな振動振幅が引き起こさ
れる可能性がある。この場合,流れと構造物運動との相互作用によって励振周波数が固有振動数に支配さ
れ,かつ,励振周波数が固有振動数に固定される。
渦放出による励振は,物体後流中の渦の運動に伴う圧力変動によって発生する。変動力は,主として水
流方向に対して直角だが,渦放出は,水流方向の動的な力も発生させる。また,渦放出によって誘起され
る構造物の運動が,時間平均の抵抗力を著しく増大させる可能性がある。渦放出による力は,複雑な流体
力学現象の結果として生じるもので,水流及び構造の特性を表す広範囲のパラメータに大きく依存する。
多くの研究活動が行われているにもかかわらず,プロセス全体の解明は不完全であり,荷重及び応答の予
測は不確実性を免れない。渦放出に起因する流体力荷重の計算に関しては,幾つかの指針が文献[7],[8],
[9]及び[10]で示されている。
共振現象に耐えるように設計できる構造部材は,ほとんどない。したがって,一般的には,共振が起こ
り得る条件を回避するか,又は特別な方法を用いて励振メカニズムを抑制することが重要である。大きな
振動振幅が見込まれる周波数については,荷重又は応答よりもはるかに確実に予測可能である。
渦誘起振動は,定常流又は長周期波[高クーリガン・カーペンタ(Keulegan-Carpenter)数]による水流
速度によって発生する可能性がある。
D.5.1 クロスフロー運動の危険速度
変動揚力の周波数は,流速とともに増大する。危険速度において揚力変動の周波数flが部材の固有振動
数と等しい場合は,共振の発生が予想される。系の構造減衰レベルによっては,大振幅の振動が発生する
場合がある。流れが近似的に定常流である場合,すなわちクーリガン・カーペンタ(Keulegan-Carpenter)
数Kcが高い場合,危険速度は,式(D.12)で算出する。
t
n
crit
S
D
f
U=
············································································(D.12)
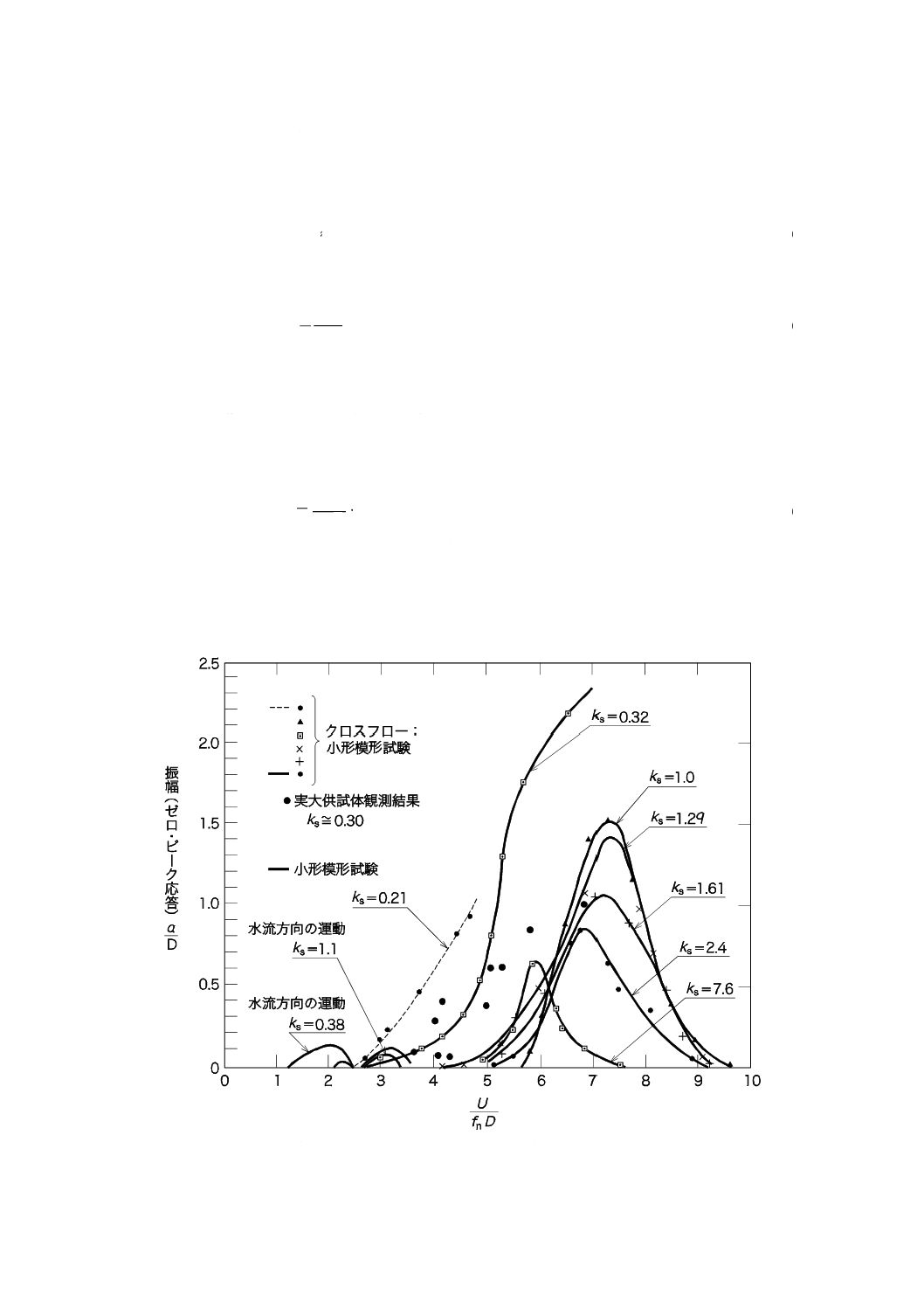
79
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
fn: 構造物の固有振動数(Hz)
St: ストローハル数
円柱の場合は,ストローハル数が約0.2であるから,クロスフロー振動のピークに対して,式(D.13)とな
る。
D
f
U
n
crit
5
≈
··········································································(D.13)
振動は,これよりも低い流速で始まることがある。流速は,換算速度Urを用いて式(D.14)で表現しても
よい。
D
f
U
U
n
r=
·············································································(D.14)
ストローハル数が約0.2であるレイノルズ数では,換算危険速度の値が振幅のピーク部でおよそ5であ
る。超臨界レイノルズ数では,大振幅のクロスフロー振動が始まる流速が,Ur ≈ 3.7で与えられる。減衰の
小さい構造物は,僅かに低いUrで応答する場合がある。
顕著なクロスフロー運動が始まる流速は,一般に構造物の質量及び減衰,並びに排除質量によって決ま
る。これらの影響を組み合わせた無次元“質量減衰パラメータ”ksは,式(D.15)で定義される。
2
e
s
2
D
m
k
ρ
δ
=
·············································································(D.15)
ここに,
me: 単位長当たりの等価質量[4]
δ: 対数構造減衰率
図D.4は,顕著なクロスフロー振動が予想される条件をks及びUrで示した図である。これらの条件を避
けられない場合は,ストレーク,シュラウド,フェアリングなどの手段によって励振を抑制してもよい。
図D.4−水流方向及びクロスフロー方向の円柱模型及び実物大円柱の応答(文献[4]から)
80
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
D.5.2 水流方向運動の危険速度
交互渦が周波数flで放出されると,水流方向の動的荷重が周波数2 flで発生する。したがって,この励振
モードに対する換算危険速度は,式(D.16)のとおりである。
5.2
r≈
U
···············································································(D.16)
水流方向振動の発生につながる,ほかの渦放出モードも観測されている。主なモードは,通常の交互放
出パターンではなく,二つ一組で同時に放出される渦に関するもので,式(D.17)に示す更に低い危険速度
となる。
0.2
r≈
U
···············································································(D.17)
任意の構造物について水流方向振動の振幅は,一般にクロスフロー方向における振幅の20 %以下である。
D.6 附属物
構造物の附属物,例えば,J字管,ボート・フェンダ,はしご(梯子),通路などに作用する流体力荷重
も考慮することが望ましい。J字管及びフェンダのような大形の附属物は,個別の部材としてモデル化で
きることが多い。一方,小形の附属物については,モデル化された要素の寸法及び/又は力係数によって
省略された要素に作用する力の寄与を考慮できる場合は,明確にモデル化する必要はない。
等価流体力係数の計算によって附属物に作用する荷重をモデル化する場合について,簡易な方法を次に
記載する。
D.6.1 附属物及びモノパイル表面の海洋付着生物を含んだ場合の流体力係数の推定に対する代替手段
全体の荷重解析に対する簡易な方法の一つは,主としてAPI推奨案2A-WSD[11]に基づくもので,等価
流体力係数を計算することによって附属物に作用する荷重をモデル化する場合について,次に記述する。
これらの方法は,等価流体力抵抗係数及び等価流体力慣性係数(Cdeq及びCmeq)を求めるものである。
この等価流体力係数について,モノパイルの基本寸法(直径)と併せてモリソン(Morison)式を用いると,
附属物,海洋付着生物などを含む断面全体に作用する全流体力が得られる。
等価流体力係数は,次の変数の関数となる。
・ レイノルズ数(R)
・ 表面粗度(e)
・ 海洋付着生物の厚さ(tMG)
・ クーリガン・カーペンタ(Keulegan-Carpenter)数(K)
・ 合成速度(Um),波速(Uw)及び流速(Uc)
・ 附属物の寸法(di)
・ 波向及び水流方向に対する,モノパイル表面における附属物の相対角度(φ i)
・ モノパイルと附属物との間隔
附属物,すなわち,J字管,フェンダ,ボート接舷部などは鉛直な円柱(筒)で近似され,文献[11]で提
案されている等価直径diで表される。
この方式全体の原理は,個々の部材に作用する荷重の合計として等価流体力係数を計算し,それをモノ
パイルの直径で正規化するというものである。
したがって,任意の断面に関する等価流体力係数は,式(D.18)及び式(D.19)で計算される。
×
×
×
×
∑
N
i
K
IF
K
WAF
e
R
C
D
d
K
WAF
e
R
C
D
D
C
1
i
i
di
i
di
i
dsi
i
d
ds
deq
)
,
(
)
(
)
,
(
'
)
(
)
,
(
'
=
+
=
φ
·············(D.18)
81
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[
]
{
}
×
×
∑
N
i
K
IF
C
K
C
D
d
C
K
C
D
D
C
1
i
i
mi
dsi
i
mi
2
i
ds
m
2
2
meq
)
,
(
1
)
,
(
1
'
)
,
(
)'
(
=
−
+
+
=
φ
·················(D.19)
ここに,
'
'
'
'
'
m
i
m
i
i
m
i
m
D
k
e
D
T
U
K
d
T
U
K
v
d
U
R
v
D
U
R
≡
×
≡
×
≡
×
≡
×
≡
di'=di+2tMG D'=D+2tMG
ここに,
Cds(R,e): 定常状態(水流だけ)の抵抗係数
WAFd: 後流増幅係数
IFd及びIFm: モノパイルが存在することで附属物に関する流体力係
数が変動することを表す干渉係数
D≫diのときには,附属物がモノパイルに及ぼす干渉を考慮しない。
多くの実用例では,流体力係数のR依存性を無視できるが,附属物又は疲労解析の場合には必ずしも当
てはまらない。したがって,流体力係数のR依存性を考慮することが望ましい。
浅水域の場合は,波の運動が水深をそれほど大きくは超えず,自由表面における波の運動に基づいてR
及びKを計算できる。しかし,一般には,各断面について局所的なR及びKの値を計算する方がより正確
である。
干渉係数IFdi及びIFmiは,次の三つの現象について考慮する。すなわち,(1) モノパイルの陰で附属物
に作用する流体力荷重が減少する後流効果,(2) 附属物とモノパイルとの間にある隙間が小さいときに,
附属物に作用する流体力荷重が増大する隙間効果,及び (3) モノパイル側面の増速効果の三つである。
後流効果を計算するには,API推奨案2A-WSD[11]を利用してもよい。隙間効果を計算する手法は存在
しないが,鉛直な無限壁に近接する円柱の流体力係数を計算するための有益な方法が,DNV Classification
Notes No.30.5[7]に幾つか示されている。円柱構造物側面の増速効果は,多くの場合,二次元ポテンシャル
流理論によって計算される。
D.7 計算方法
幾つかの設計荷重ケース,特に極値事象を表している荷重ケースについては,風及び波による荷重の確
率論的特性,構造の柔軟性及び波の非線形特性の影響を全て考慮することが重要である。これらの影響を
同時に考慮するため,D.7.1に記載するとおり,非線形不規則波モデルが必要となる。このモデルは,工学
的用途ではまだ一般的でないことから,代わりに以下のD.7.2,D.7.3及びD.7.4で示す3種類の方法が提
案されている。
D.7.1 陽解法
最も厳密な方法では,次のパラメータを陽的にモデル化する。
・ 構造の柔軟性
・ 乱流風
・ 低波頂の非線形不規則波
この場合は,ブシネスク(Boussinesq)解法などの不規則で非線形なモデルを用いて,波の運動を計算
する。乱流風場及び構造動力学の計算モデルは,陸上風車の時間領域シミュレーションに用いるモデルと
同様である。この方法は,設計荷重ケースによっては,最大荷重を得るために長時間のシミュレーション
82
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を要し,また,波動解の収束が遅い場合がある。
D.7.2 波の非線形係数による解法
この方法を用いる場合は,次のパラメータの影響をシミュレーションで考慮する。
・ 構造の柔軟性
・ 乱流風
・ 線形不規則波
波の非線形性による影響は,対象となっている特定の風車及び条件について考慮した,荷重係数一式を
用いて計算する。一連の時間領域シミュレーション結果から,最大荷重に対応する風速及び波高が同定さ
れる。これらの条件を用いて,それぞれの荷重の“波の非線形係数”を計算するために,剛構造並びに (a)
非線形規則波及び (b) 線形規則波について追加のシミュレーションを実施する。次に,これらの係数を最
初のシミュレーションで同定した最大荷重に乗じる。この代わりに,スケーリングした線形波について最
初のシミュレーションを繰り返してもよい。この場合は,(b) によってスケーリングした規則波で得られ
る最大荷重が,(a) による非線形波のそれと一致するようにスケール係数を選ぶ。
ほかに考慮するものがない場合は,二次元波運動理論の水平成分に方向分布係数を適用することによっ
て,方向分布の影響を不規則波及び規則波に含めることが可能である。方向分布係数に関する説明は,ISO
19901-1:2005のA.8.7.2を参照する。
D.7.3 規則波による解法
この手法を用いる場合は,次の項目の影響をシミュレーションで考慮する。
・ 構造の柔軟性
・ 定常風
・ 非線形規則波
対象部材の最大空力荷重を同定するため,静穏な海における乱流風によるシミュレーションを最初に実
施する。次に,非線形規則波によるシミュレーションを定常風モデルによって行うが,空力荷重の大きさ
が最低でも先ほど乱流風モデルで求めた値と一致するまで,風速を設計値を超えて増加させる。物理的に
あり得ない限界状態に対する支持構造物の応答が結果に影響しないようにするため,シミュレーションを
波の周期の3周期分以下にすることが望ましい。
方向分布係数を二次元規則波運動理論の水平成分に適用することによって,規則波による解法に方向分
布の影響を含めることが可能である。方向分布係数に関する説明は,ISO 19901-1:2005のA.8.7.2を参照す
る。
D.7.4 拘束波による解法
この手法を用いる場合は,次の項目の影響をシミュレーションで考慮する。
・ 構造の柔軟性
・ 乱流風
・ 線形不規則波
・ 非線形規則波
この場合は,一連の線形不規則波の中に非線形規則波を一つ交ぜることによって,波の運動を計算する。
乱流風場及び構造動力学の計算モデルは,陸上風車の時間領域シミュレーションに用いるモデルと同様で
ある。別の方法としては,拘束した“新しい波”による解法をストレッチ法と併せて,用いることも可能
である。
方向分布係数を二次元波運動理論の水平成分に適用することによって,拘束波による解法に方向分布の
83
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
影響を含めることが可能である。方向分布係数に関する説明は,ISO 19901-1:2005のA.8.7を参照する。
D.8 参考文献
[1] Elgar, S., Guza, R.T., and Seymour, R.J., 1985, “Wave group statistics from numerical simulations of a random
sea”, Applied Ocean Research 7 (1985) 2, p93-96.
[2] Morison, J.R., O' Brien, M.P., Johnson, J.W. and Schaf, S.A., 1950, “The forces exerted by surface waves on
piles”, Petroleum Transactions, AIME, Vol. 189, pp 149-157.
[3] ISO 13819-2,“Petroleum and natural gas industries−Offshore structures−Part 2: Fixed steel structures”
[4] Barltrop, N.D.P., and Adams, A.J., 1977, “Dynamics of fixed marine structures”, Butterworth Heinemann, ISBN
0 7506 1046 8.
[5] MacCamy, R.C., and Fuchs R.A., 1954, “Wave forces in piles: A diffraction theory”, Technical memorandum no.
69, Beach Erosion Board, US Navy Corps of Engineers.
[6] Wienke, J., “Druckschlagbelastung auf Schlanke Zylindrische Bauwerke durch Brechende Wellen−Slamming
an Offshore Windkraftanlagen-” Dissertation, Technische Universität Carolo-Wilhelmina zu Braunschweig.
[7] Det Norske Veritas, CN 30.5: “Environmental Conditions and Environmental Loads”, Classification Notes No.
30.5, March 2000.
[8] UK Department of Energy, “Fluid Loading on Fixed Offshore Structures−Background to the the 4th edition of
Offshore Installations: Guidance on Design and Construction”, Offshore Technology Report OTH 90322, 1990.
[9] DS410: “Code of Practice for Loads for the Design of Structures (Norm for last pa° konstruktioner)”, Danish
Standards Association, 2004.
[10] Germanischer Lloyd, Rules and Guidelines IV-Part 8 Pipelines, 1 “Rules for Subsea Pipelines and Risers”,
2004.
[11] API Recommended Practice 2A-WSD (RP 2A-WSD) Twentieth Edition,July 1,1993, “Recommended Practice
for Planning, Designing and Constructing Fixed Offshore Platforms−Working Stress Design”.
84
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E
(参考)
氷荷重に対する洋上風車支持構造物の設計に関する推奨
E.1
はじめに
氷荷重は,冬季気候の水域において,厳しく,かつ,決定的要因となる荷重ケースである。北米,北ヨ
ーロッパ及び北方アジアの湖及び海水面上のサイトにおいては氷の発生を評価することが望ましい。移動
氷によって,極めて厳しい荷重が支持構造物に発生し,洋上風車の壊滅的な破壊を招く可能性がある。
この附属書は,おおむね参考文献[1]及び[2]に基づいている。
氷荷重の大きさは,氷の動きのほかにも局所的な氷の状態及び水位を,支持構造物の寸法及び形状に対
して考慮しつつ推定することが望ましい。次の氷荷重について,評価を行うことが望ましい。
・ 定着氷板に生じる温度変化による水平荷重(熱的な氷圧力)
・ 水位の変動を受ける定着氷板による荷重で,アーチ効果を用いて求まる水平荷重
・ 移動氷盤から受ける水平荷重
・ 沈込み及び押上げの両プロセスに起因して発生する,氷丘及び氷脈から受ける圧力
・ 水位の変動を受ける定着氷板による鉛直荷重
E.2
一般
詳細な統計分析を実施していない場合,氷荷重は,一般に通常水位範囲(NWLR)内の任意の水位で発
生すると想定されている。水位の影響を受けやすい円すい(錐)体部をもつ構造物については,すい(錐)
体の高さを決定する設計水位を特定するため,冬季条件における水位変動に対する統計データを収集する
ことが望ましい。この附属書で扱う支持構造物は,コンクリート又は鋼製の鉛直円柱部及び円すい(錐)
体部を備え,水線における断面が円又は長方形の構造物を想定している。
湖又は海岸線に近い海では,通常,ある特定の厚さまで成長した氷床は移動していない。移動氷に由来
する荷重は,移動氷の厚さを確認することが望ましい。さらに,成長して厚さを増した氷板に対しては,
熱的圧力,アーチ効果及び鉛直方向の隆起による荷重を確認することが望ましい。
移動氷が予想される水域では,全ての季節について移動氷から受ける荷重を計算し,その荷重が卓越流
及び風ベクトルの方向に作用するとみなすことが望ましい。風向が氷の移動方向と無関係である可能性に
ついても,考慮することが望ましい。通常は,荷重ケースに対して動的時間シミュレーションが要求され
る。風車の固有振動数,及びウィンドファーム内のほかの風車の固有振動数が,氷が砕ける振動数にロッ
クインする可能性を調査することが望ましい。評価の一部として,模型試験を利用することも可能である。
E.3
氷厚の選定
氷厚hは,現地の海氷地図又は類似資料に記載されている統計データを解析して設定することが望まし
い([7]参照)。この附属書の末尾に,データベースに関する参考資料を記載した。多くの事例では,氷厚
及び氷破壊強度を組み合わせた解析を実施することになる。外洋の風車については,再現期間50年に相当
する区分で氷厚を選定してもよい。群島部及び陸地に囲まれた水域の風車については,移動氷の厚さとし
て“通常の冬”に相当する値を選定し,定着氷板の厚さとしては再現期間50年の値を選定してもよい。
式(E.1)は,凍結期の終わりにおける氷厚(m)を推定する式である。
85
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
50
9.0
032
.0
max−
×
K
h=
··························································· (E.1)
ここに,
Kmax: 凍結期において0 ℃未満であった24時間平均気温の
絶対値の合計値(℃・日)24)
注24) 例 5日間の平均気温が−12,−19,+2,−3及び−4(℃)の場合は,Kmax=38
E.4
荷重ケース
E.4.1〜E.4.6の荷重ケースが風車サイトに関係する場合は,この荷重ケースを適用することが望ましい。
風況及び水位条件を7.4.9の表2に規定する。これら表2の荷重ケースについて,海氷荷重と組み合わせ
るサイト固有の適切な値を求めるため,箇条12の要求に従ってこれらの条件を評価することが望ましい。
波に関する検討は要求されない。荷重ケースDLC E1,DLC E2,DLC E3,DLC E5及びDLC E6は,終極
(終局)荷重ケースである。また,DLC E4及びDLC E7は,疲労荷重ケースである。動的荷重負荷につい
ては,E.4.6に記載する。
E.4.1 温度変化に由来する定着氷板による荷重(DLC E1)
熱的な氷圧力は,湖域及び汽水域においてだけ検討することが望ましい。北海のような塩水性の外洋で
は,熱的な氷圧力を無視できる。
ウィンドファーム内では,ウィンドファーム外縁部に位置する洋上風車の支持構造物において,熱によ
る一方向性の氷圧力が最大となり,陸地から外洋に向けて又はウィンドファームの中心から半径方向外向
きに作用すると仮定することが望ましい。砕氷船が熱的圧力下にある定着氷板を通って水路を開く場合は,
開水路に向かって氷が膨張することとなり,式(E.2)に対応する力が発生する。
この熱的力は,式(E.2)で求められる。
Ft=ftD ·················································································· (E.2)
ここに,
D: 水線における支持構造物の直径
D<4 mの場合は,Dを4 mとする。
ft: 支持構造物の単位幅当たりの力
ウィンドファーム内に単独で配置した支持構造物,又は
外縁に配置した支持構造物に対しては,ftを300 kN/mに
設定する。外縁の列の内側,又はウィンドファーム内側
の支持構造物に対しては,ft値を100 kN/mとする。
E.4.2 水位変動及びアーチ効果に由来する定着氷板による水平荷重(DLC E2)
風車の支持構造物間,又は支持構造物と岸との間で,アーチ効果によって生じる一方向の水平圧力は,
式(E.3)によって推定可能である。
Fv=fvD ················································································· (E.3)
ここに,
D: 水線における支持構造物の直径
D<4 mの場合は,Dを4とする。
fv: 200 kN/m
E.4.3 移動氷から受ける水平荷重(DLC E3,DLC E4及びDLC E7)
大きな移動氷盤から受ける力は,E.4.3.1又はE.4.3.2に記載する方法に従って推定することが望ましい。
極値風とDLC E3の氷荷重との組合せの外挿が要求されることについては,E.6に記載する。
DLC E7は,風車が待機状態で,かつ,移動氷によって支持構造物及びタワーに疲労荷重が発生し得る
86
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
という状況である。
E.4.3.1 鉛直柱状断面
これは[1]及び[3]から取り入れた方法で,柱状断面をもつ鉛直構造物について考慮する。氷が破砕される
ことによる最大静的力は,式(E.4)から推定してもよい。
Fd=k1k2k3hDσc ······································································ (E.4)
ここに,
k1: 氷衝突面における支持構造物の形状に関する形状係数
k2: 支持構造物に対して氷が接触する場合の接触係数
k3: 氷厚と支持構造物直径との間の比率に関する,アスペク
ト比係数
D: 水線における支持構造物の直径
σc: 氷の破壊強度
・ 氷の破壊強度σc 氷の破壊強度値は,氷の破壊強度又は積σchの統計データから求めることが望まし
い。基準破壊強度の統計解析を実施するため,[7]を参照し,実温度及びブライン(高濃度塩水)量を
補正することが望ましい。
現地の氷のデータがない場合は,北バルト海及び北極域カナダにおいて典型的な値である,次の値
から選択可能である25)。
− 年間で最も寒い時期に,風及び水流によって移動する氷については,σc=3.0 MPa
− 熱膨張又は熱収縮によって,非常にゆっくりと移動中の氷については,σc=2.5 MPa
− 温度が融点に近い春季の氷については,σc=1.5 MPa
− 部分的に弱くなり,温度が融点に近い氷については,σc=1.0 MPa
− 北海などの外洋における1年氷については,σc=0.5 MPa
注25) 上記の参照値は,カナダ政府橋等標準規格(1978)に従ったものであり,当該規格では0.7
MPa〜2.8 MPaの範囲の値が示されている。ソビエト連邦標準規格(1976)では,0.44 MPa
〜1.47 MPaの範囲が記載されている。上記で与えられていた値は,安全側であるといえる。
・ 形状係数k1 形状係数k1には,次の値が与えられる。
− 長方形断面の場合は,k1=1
− 円形断面の場合は,k1=0.9
・ 接触係数k2 接触係数は,連続的に破砕している氷が,支持構造物に対して完全に凍り付いている状
態から移動を始めた時点を除き,支持構造物の公称面積Dh全体には接触していないという事実を考慮
している。
− 氷が連続的に移動しているときは,k2=0.5
− 氷が移動し始めた時点で,氷が支持構造物表面に凍りついているときは,k2=1
− 凍りついた氷が支持構造物の周りで局所的に厚くなっているときは,k2=1.5
3番目のケースに関する別の方法は,損傷を受けていない氷原を調べる代わりに,支持構造物のす
ぐ近くでは,厚さhを氷厚で置き換えている。
・ アスペクト比係数k3 アスペクト比係数は,接触点における三次元応力状態を考慮している。氷厚に
比べてパイル又はタワーが細い場合は,応力状態が二次元であるとみなせる。したがって,次の式で
表す。
D
h
k
/
5
1
3
+
=
87
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ 荷重作用高さ 支持構造物付近に氷が堆積するリスクがある場合は,6 m未満の水深について,その
0.2倍分だけ荷重作用高さを増やすことが望ましい。
・ 模型試験の校正 荷重レベル及び種類は,砕氷の発生が連続的か又は非静的な座屈が生じたかどうか
に大きく依存することが,模型試験で示されている([9]参照)。また,氷の速度に起因するピーク荷
重レベルには,顕著には依存しないことがわかっている。模型試験については,更にE.6に記載する。
E.4.3.2 傾斜断面
Ralstonが1977年に発表した式が,[2]で提案されており,アイスコーンを備えた洋上風車などの傾斜し
た構造物について有効である。また,[5]では,この式がAPIによって推奨案として選定されている。引用
された式は,0<α<70の範囲にある傾斜に対して有効であり,ここでαは,水平面から測定した傾斜であ
る。[9]で紹介されている模型試験は,コーンに作用する氷荷重に関して,氷盤速度1 m/sまではRalston
式が安全側の値を与えることを示している。
コーンによって上方に曲げられている氷から受ける水平荷重は,式(E.5)による。
)
(
2
T
2
w
3
2
w
2
2
b
1
4
h
D
D
h
A
hD
A
h
A
A
F
−
+
+
=
g
g
ρ
ρ
σ
································ (E.5)
鉛直下向きの荷重は,式(E.6)による。
)
(
2
T
2
w
2
1
V
D
D
h
B
H
B
F
−
+
=
g
ρ
······················································· (E.6)
ここに, A1,A2,A3,A4,
B1及びB2:
無次元の係数で,氷とアイスコーンとの間の摩擦率
μ,及びすい(錐)角αの関数である。係数の値は,
図E.1を参照する。
σb: 氷の曲げ強度。0.26 σc以上とする。
h: 氷床の厚さ
ρw: 水の密度
g: 重力加速度
D: 水線におけるコーン直径
DT: コーン上部の直径(=タワーの直径)
コーンが氷を下向きに曲げている場合は,ρwをρw/9に代えて同じ式を適用する。また,コーンが氷を上
向きに曲げている場合の鉛直方向の力も同様である。
コーンが氷を上向きに曲げている場合,氷の最上部から氷厚分だけ高い位置よりもコーン高さが高いと
きは,上記の式を用いてもよい。また,コーンが氷を下向きに曲げている場合,氷の最下部から氷厚分だ
け高い位置よりもコーン高さが高いときは,上記の式を用いてもよい。コーンの設計では,一般に,コー
ン以外の支持構造物のどの部分においても氷の破砕が発生条件で設計することが望ましい。すい(錐)状
構造以外の部位で氷破砕荷重が作用する(例えば,水位変動が原因で)ことによるリスク及び結果につい
て,評価を行うことが望ましい。
上下にコーンが付いている場合は,先端部に直接作用する力を除き,上記のとおり推定してもよい。先
端が鋭い場合は,[9]を参照し,水平力を2倍に増加することが望ましく,先端が丸い場合は,水平力を3
倍に増加することが望ましい。
氷とコーンとの間の動摩擦係数μは,次の値に設定してもよい。
− コンクリート/腐食した鋼のコーンについては,μ=0.15
− 新品又は塗装した鋼のコーンについては,μ=0.10
E.4.3.3 局部氷圧力
支持構造物は,次の局部氷圧力に対して設計することが望ましい。
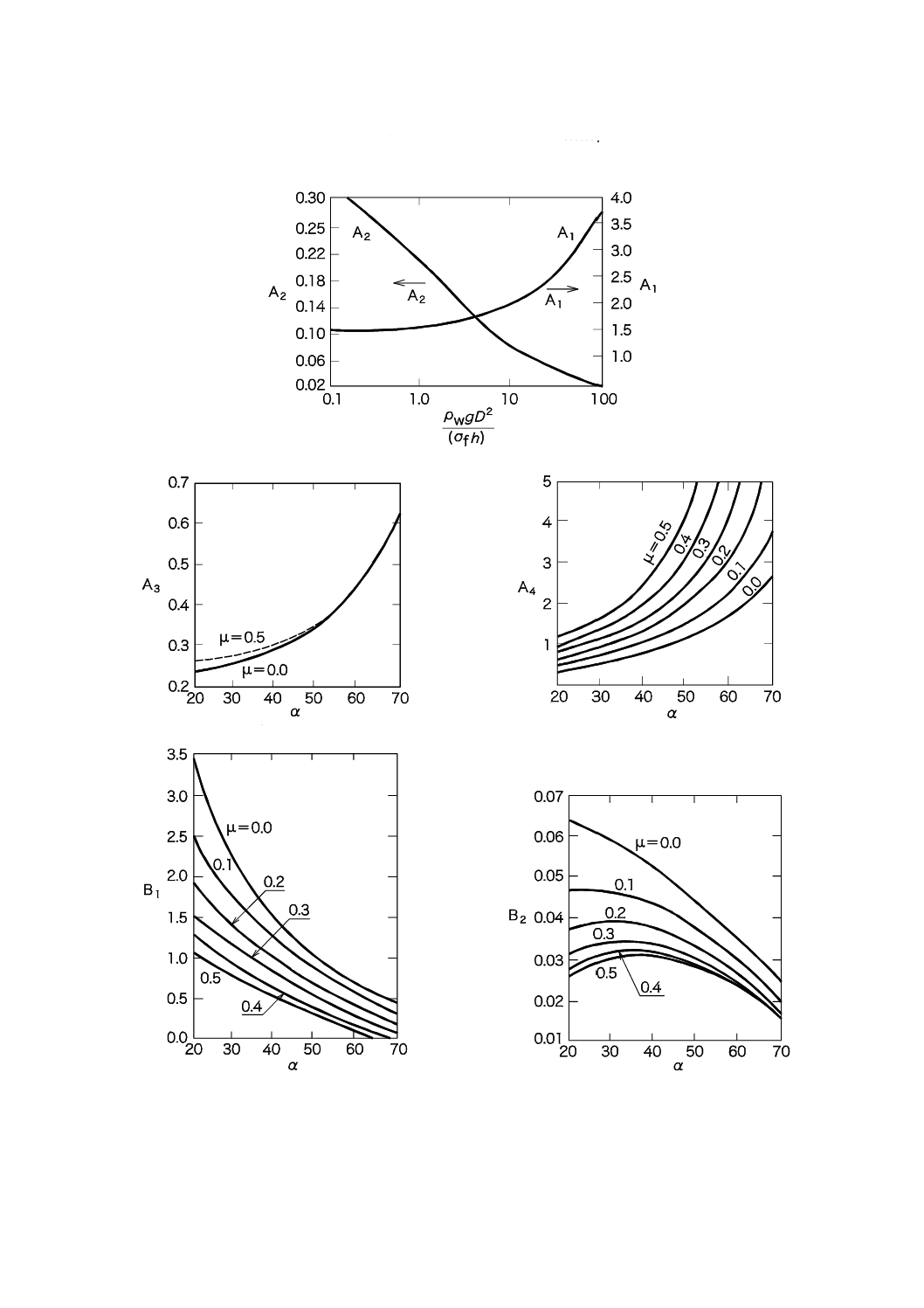
88
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
σc.local=σc (5 h2/Alocal−1)0.5<20 MPa ············································ (E.7)
ここに,
Alocal: 検討対象の局所面積
a) A1及びA2
b) A3
c) A4
d) B1
e) B2
図E.1−塑性限界解析の氷荷重係数([6]参照)
E.4.3.4 風及び水流によって誘起される荷重
波又は水流によって氷盤に作用する荷重は,式(E.8)で推定可能である。
89
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A
U
C
F
2
2
d
f
ρ
=
········································································ (E.8)
ここに,風の場合は,
Cd: 0.004
ρ: 1.3 kg/m3
U: 氷表面の10 m上方の風速
また,水の場合は,
Cd: 0.006
ρ: 1 000 kg/m3
U: 氷の底面の1 m下方を流れる自由流の速度
A: 氷盤面積
風及び/又は水流による荷重は,氷の破壊強度が上限となる。風及び水流による複合漂流力は,サイト
データの統計解析に基づくことが望ましい。
E.4.4 定着氷板による鉛直荷重(DLC E5)
水位が変動する場合に,支持構造物に凍りついた定着氷板によって発生する鉛直荷重は,式(E.9)の支持
構造物表面の付着部におけるせん断強度Vτに制限されるか,又は氷が支持構造物の周りで環状に割れてい
る場合は,式(E.10)の曲げ強度Vbによって制限される。この二つの荷重のうち低い方によって制限が決ま
り,その値を用いることが望ましい。
τ
τ
A
V=
················································································ (E.9)
ここに,
τ: 付着せん断強度
A=πDh: 円柱状の鉛直支持構造物における接触面積
付着せん断強度τは,次のいずれかを用いる。
− 鋼製で淡水氷の場合,0.8 MPa
− 鋼製で海氷の場合,0.3 MPa [12]
− コンクリート製で海氷の場合,1 MPa [8]
z
A
V
∆
g
ρ
σb
b
6.0
=
·································································· (E.10)
ここに,
A: 接触面積
σb: 氷の曲げ強度。0.26 σc以上とする。
ρ: 水の密度
g: 重力加速度
Δz: 水位差
E.4.5 氷脈による圧力(DLC E6)
DLC E6は,極値氷荷重が再現期間1年の極値風条件と組み合わされた状況を対象としている。支持構
造物に最大せん断荷重を与える風荷重を適用することが望ましい。
移動中の氷床に囲まれた氷脈が支持構造物を押している場合は,非常に大きな荷重が発生する可能性が
ある。そのような氷脈は,氷片で構成されており,氷片が一緒に凍りついて2〜3 mの厚さで固められた
ものが含まれる。押し固められた氷の上下にある,押し固められていない氷塊は,氷荷重に対してほとん
ど寄与しない。
氷荷重は,氷が破砕される場合又は氷脈が水平面内で曲げられて破壊する場合のいずれの仮定について
も概算される。氷脈によるリスクを伴う海域については,通常は風車を設置しないほうがよい。
E.4.6 動的荷重
風車に対して,氷荷重による動的な影響の確認を行うことが望ましい。統計データ又は測定値がない場
合に用いられる動的荷重シミュレーションに関する,幾つかの単純化された式を,次に示す。
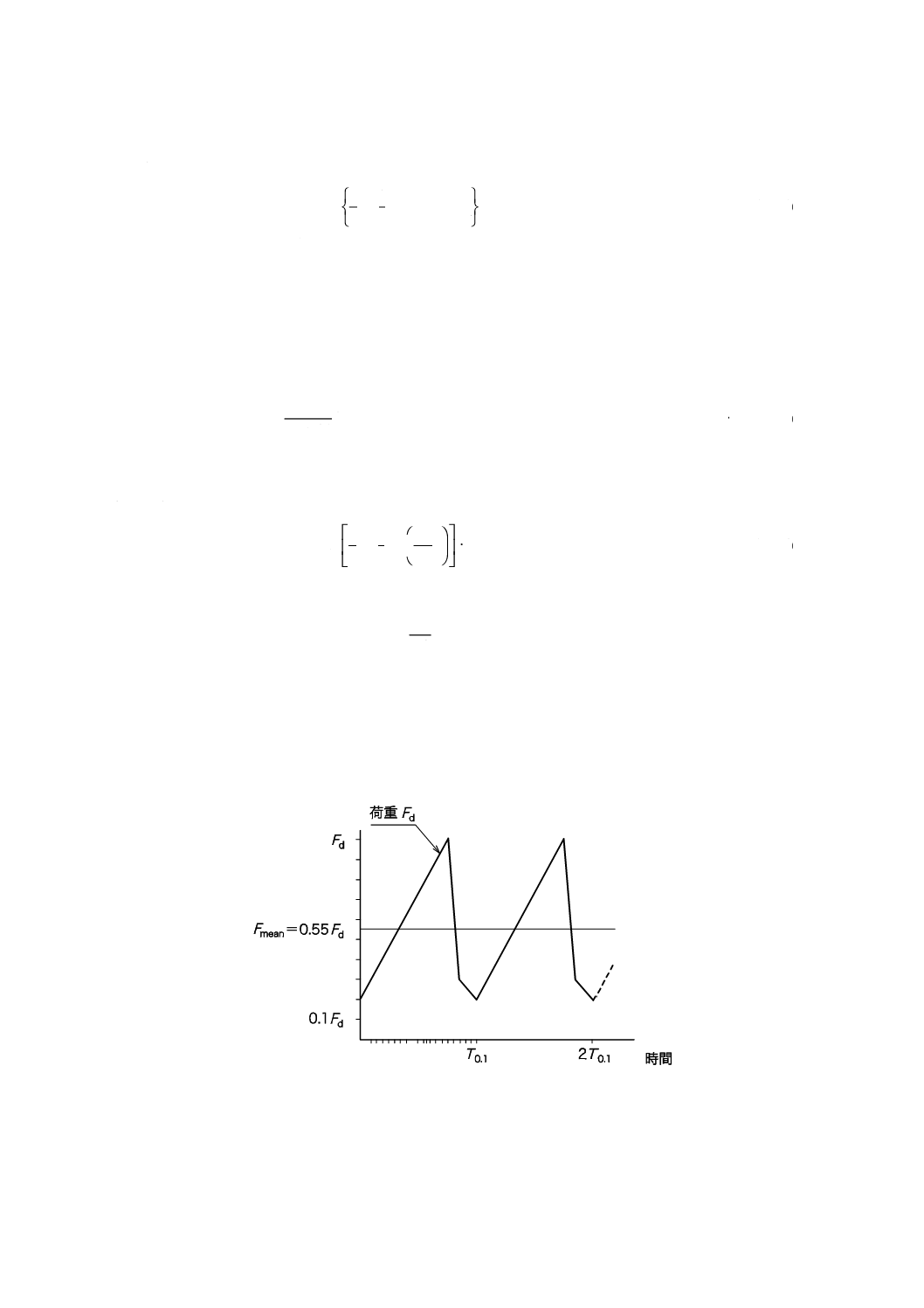
90
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
移動氷によって鉛直支持構造物に作用する荷重の変動は,式(E.11)のとおり,プラス側にずらした正弦関
数で近似してもよい。
[
]
)
2
/(
sin
4
1
4
3
N
d
dynv
π
t
f
F
F
+
=
··················································· (E.11)
ここに,
Fd: 式(E.4)で得られる,移動氷による水平荷重
t: 時間
fN: 風車の固有振動数。一次モード及び二次モードの両方に
ついて検討することが望ましい。
動的効果は,座屈形破壊の発生時に最大となり,この破壊によって氷荷重の大きな変動が発生する([9]
及び[11]参照)。
同調に関する基準は,[10]に従う。
3.0
)
(
N
>
f
h
U
×
········································································· (E.12)
ここに,
U: 氷盤の速度
移動氷によってすい(錐)状(α≧30 °)の支持構造物に作用する荷重の変動は,プラス側にずらし正弦
関数で近似してもよい。
t
f
F
F
π
2
sin
4
1
4
3
b
d
dynk
+
=
························································ (E.13)
ここに,
Fd: 式(E.4)で得られる,移動氷による水平荷重
t: 時間
fb:
Kh
U
ここで,Uは,氷盤の実速度であり,4≦K≦7である。
K値は,最大荷重が得られる値を選択することが望
ましい。
別の方法としては,動的荷重に関して三角形の波形を仮定してもよい[鉛直の柱状物体及びすい(錐)
の両方に適用する。](図E.2参照)。
図E.2−きょし(鋸歯)状の荷重プロファイル(T0.1=1/fN又は1/fb)
大きな氷盤が衝突した衝撃による荷重については,式(E.14)に示すとおり,過渡荷重を考慮した方法で
確認することが望ましい。
91
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の場合
>
又は
=
の場合
≦
=
kU
F
t
F
t
F
kU
F
t
kUt
t
F
d
d
d
,
0
)
(
,
)
(
·················································· (E.14)
ここに,
U: 衝突速度
t: 衝突による衝撃の持続時間
k: 水線における構造物の剛性
E.5
確率論的シミュレーションにおける要求
氷原に対して質が高い観測を行うにあたり,現地での実際の観測は制約を受けるため,通常は,E.6に
示すように,主として氷の模型試験における応答シミュレーションを根拠とすることが要求される。こう
した模型試験では,確率論的な氷荷重を表した時系列データが得られる。氷の模型試験では,通常は,数
分程度の試行荷重に相当する荷重時系列データだけが生成されるので,統計的にほぼ独立な10分間の動的
氷荷重シミュレーション結果を得るために,[9]に記載された手法によって測定時系列データを拡大するこ
とが要求される。
したがって,動的風車モデルでは,独立な氷荷重時系列データ及び風荷重データが模擬されている。運
転可能な風荷重及び極値氷荷重の複合荷重状態における10分間の事象の個数(N)が見積もられ,次に,
JIS C 1400-1:2010の附属書Fで概要が記載されているとおり,外挿した極値荷重を推定できる。この推定
では,JIS C 1400-1:2010の式(F.6)を用いることが望ましい。得られる値は,50年間における10分間事象
の個数の逆数ではなく,氷盤が50年間移動する間における,運転可能な風荷重を伴う10分間事象の数の
逆数である,という修正が行われている。
E.6
模型試験における要求
模型試験は,人工氷を用いて実施してもよい。通常は,力をλ3倍,曲げ強度及び破壊強度をλ倍,時間
をλ0.5倍にするFroude則に基づいて試験結果をスケーリングする。
氷荷重と構造物との間における動的な相互作用をモデル化するためには,氷荷重を受ける構造物の固有
振動数,減衰及び剛性を正確にモデル化することが望ましい。
すい(錐)状構造の場合は,動的相互作用の発生が制約されるので,支持構造物に対する動的氷荷重の
入力値を生成するに当たり,剛体模型試験の結果を用いてもよい。鉛直構造物の場合は,氷荷重と構造振
動との間で厳しい動的相互作用が発生することがあるため,このような側面をモデル化時に盛り込むこと
が望ましい。この場合,氷盤速度と構造振動の速さとの比が正確にモデル化されるように,関連する固有
振動数,減衰及び剛性がモデル化されることは極めて重要である。典形的な風車支持構造物の場合,氷荷
重との動的な相互作用を生じ得るモードは,通常は二次固有振動モードである。
模型試験に関する代表的な要求事項,結果及び設計手順は,[9]で解説されている。
E.7
参考文献
[1] Bergdahl, Lars: Islaster på vindkraftverk till havs, Dimensioneringsrekommendationer (in Swedish) Department
of Water, Environment Transport, Chalmers, Rapport nr 2002:1. (Ice Loads on Wind Turbines at Sea,
Recommendations for Design).
92
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[2] Christensen, Flemming Thunbo and Gravesen, Helge: Determination of Extreme Ice Forces, Lecture Notes.
2003.
[3] Haapanen, E, Määttänen, M and Koskinen, P: Offshore Wind Turbine Foundations in Ice Infested Waters.
Proceedings OWEMES conference 1997.
[4] Löfquist, Bertil: Istryck mot bropelare (in Swedish), Vägverket 1987. (Ice pressures at bridge columns.
[5] American Petroleum Institute, API: Planning, Designing and Constructing Fixed Offshore Structures in Ice
Environments. Bulletin 2N, API, Second Edition, 1995.
[6] Ralston, T: Ice Force Design Considerations for Conical Offshore Structures. POAC 1977
[7] Christensen, F.T. and Skourup, J: Extreme ice properties, Journ. of Cold Regions Engineering, Vol. 5, No. 2,
June, 1991, pp 51-68.
[8] Cammaert, A.B. and Muggeridge, D.B: Ice interaction with offshore structure. Van Nostrand Reinhold. New
York, 1988
[9] Gravesen, H., Petersen, B., Sørensen, S.L., and Vølund, P: Ice forces to wind turbine foundations in Denmark.
POAC' 03, Trondheim. Norway, 2003.
[10] Singh, S.K., Timco, G.W., Frederking, R.M.W., and Jordam, L.J: Test of ice crushing on a flexible structure.9th
Int. Conf. on Offshore Mechanics and Arctic Engng, Vol. IV, pp 89-94, 1990.
[11] Yue, Q., & Bi, X.,: Ice-Induced Jacket Structure Vibrations in Bohai Sea, Journal of Cold Regions Engineering,
Vol. 14, No. 2, June 2000, ASCE.
[12] Oksanen P: Adhesion strength of ice, VTT, Espoo, Finland 1982
E.8
氷況に関するデータベース
氷況に関するデータベースには,次がある。
・ Climatological Ice Atlas for the Baltic Sea, Kattegat, Skagerak and Lake Vänern. Sjöfartsverket, S-601 78
Norrköping, Sweden
・ The National Ice Center, USA (NATICE): www.natice.noaa.gov
・ The National Snow and Ice Data Center, USA (NSIDC): www.nsidc.org
・ NOAA Atlas, An Electronic Atlas of Great Lakes Ice Cover: www.glerl.noaa.gov/data/ice/atlas
・ Canadian Ice Service: http://ice-glaces.ec.gc.ca/ 26)
注26) このウェブサイトは,海氷及びカナダ海域の氷山に関する,環境省の公式オンライン情報源
である。
93
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書F
(参考)
洋上風車の基礎の設計
洋上風車の基礎の設計に関する詳細な指針は,次の刊行物に記載されている。
a) ジャーマンロイド風力エネルギー社,規則及び指針:IV−工業サービス,Part 2−洋上風車の認証に関
する指針
b) DNV洋上標準,DNV-OS-J101及び洋上風車構造の設計
94
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書G
(参考)
発電時における終極(終局)強度解析のための
気象海象パラメータの統計的外挿
G.1
一般
この附属書では,気象海象環境パラメータの外挿について検討する。長期間の気象海象パラメータを外
挿して再現期間50年に相当する値を推定するに当たり,与えられた気象海象パラメータに対する応答の変
動は無視される。すなわち,与えられた平均風速,乱流強度及び有義波高について,例えば,1時間にお
ける最大の応答の不規則な変動は無視される。したがって,長期気象海象パラメータを最初に外挿し,次
に再現期間50年の応答を求めるため応答計算に進む場合は,関連する全気象海象パラメータに対する応答
計算を実施し,その次に気象海象パラメータの長期分布を正しく考慮して応答を外挿することによって得
られる結果と比較すると,通常は異なる結果が得られる。ただし,DLC 1.6a及び1.6bで要求されているよ
うに外部条件の外挿だけを行うことで,DLC 1.1で要求されている全応答の外挿に関して,有益な補足情
報が得られる。この附属書では,気象海象パラメータの一般的な外挿法,すなわち,逆一次信頼性解析法
(IFORM)(参考文献[1]参照)について記載する。この手法は,DLC 1.3で用いた極値乱流モデル用の乱
流強度を求めるために適用したものである。
IFORMはある意味,平均風速Vと有義波高Hsとの再現期間50年の組合せを定義する環境等値線を生成
する手法であるといえる。環境等値線を求めた場合は,次のステップは,条件付きの極値応答の期待値が
極大となる点を,等値線に沿って探すことである。この点における極値応答が,再現期間50年の応答に関
する推定値である。非線形波の運動及び波荷重の動的増幅の重要度に依存して,動的シミュレーションに
よる擬似ランダムな応答時系列データを幾つか用いる,及び/又は規則波に基づく準静的な応答計算を用
いることによって,条件付き極値応答の期待値が求まることもある。これについては,高波浪時波高(SWH)
が6.4.1.4で規定されている。また,この附属書の最後では,SWHの評価について検討している。
G.2
平均風速で条件付けられた50年間の有義波高を求めるためのIFORMの利用
IFORMでは,適切な平均化時間による平均風速V及び有義波高Hsの結合分布モデルを利用することが
要求される。IFORMの計算結果は,その結合分布の環境等値線である。この環境等値線を構築するため,
相関がない二つの標準正規分布変数U1及びU2から,式(G.1)の結合分布の組(V,Hs)に確率変数変換す
る必要がある。
(V,Hs)=ϕ (U1,H2) ······························································ (G.1)
上記の変換を行う一般的な方法の一つとして,いわゆる式(G.2)のRosenblatt変換の適用が挙げられる。
)
(
)
(
)
(
)
(
s
Hs
2
V
1
V
H
F
U
V
F
U
=
=
Φ
Φ
··································································· (G.2)
ここに,
Ф: 標準正規累積分布関数(CDF)
FV(V): 平均風速の周辺CDF
FHs(Hs|V): 平均風速における条件付き有義波高の分布
Rosenblatt変換の利点は,単純であること,及びFV(V)とFHs(Hs|V)との二つの分布によって結合分布の
表現が容易になることである。したがって,所要の確率変数変換は,式(G.3)のとおりとなる。
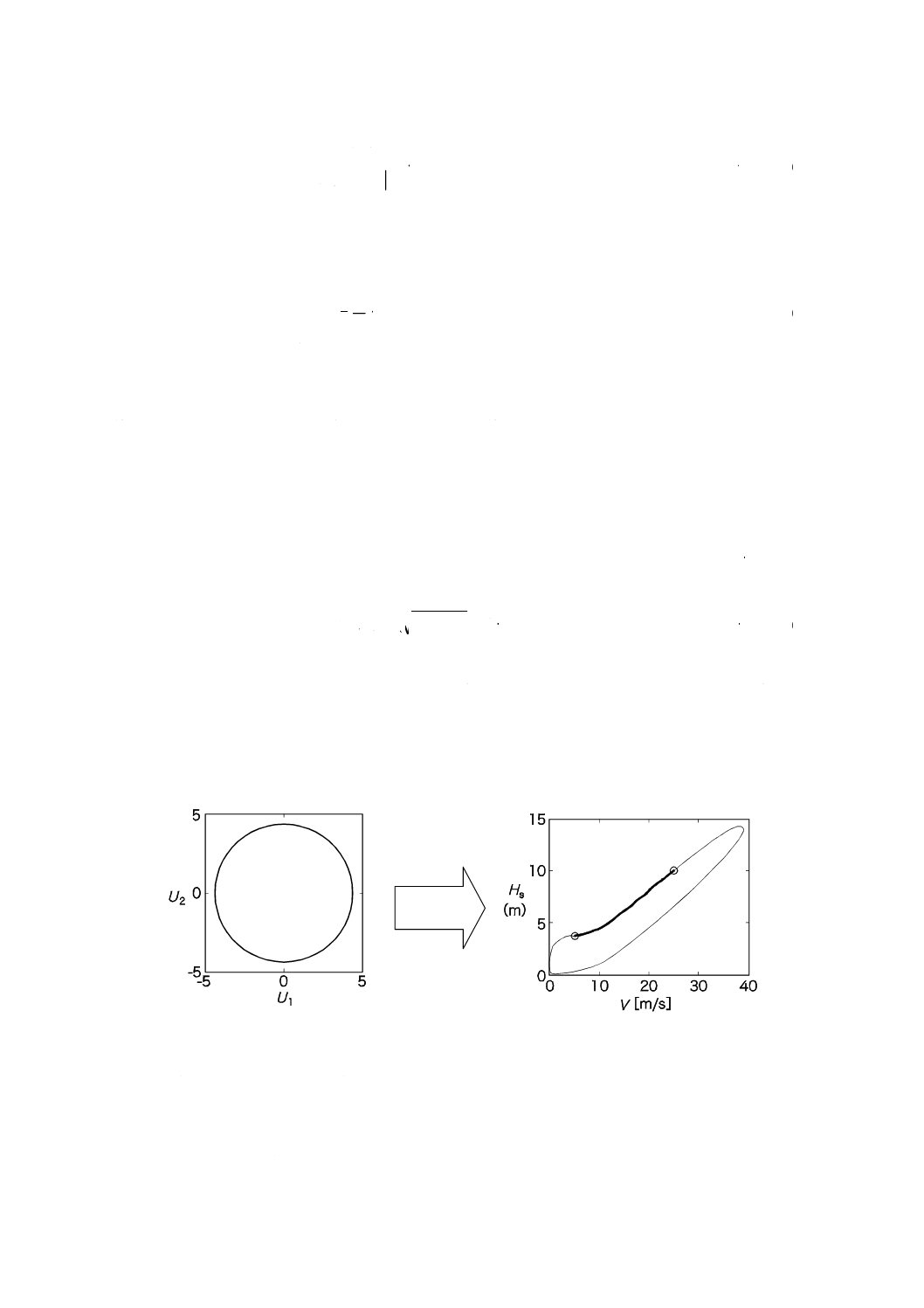
95
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
]
)
(
[
)]
(
[
2
1
s
H
s
1
1
V
V
U
F
H
U
F
V
Φ
Φ
−
−
=
=
··································································· (G.3)
式(G.3)の変換を用いることによって,次の手順で直ちに環境等値線が得られる。U1−U2平面における半
径βの円,すなわち,式U12+U22=β2を満たす点は,V−Hs平面上の曲線に変換される。この曲線が環境
等値線である。半径βは,式(G.4)で定義される。
N
1
1
)
(
−
=
β
Φ
·········································································· (G.4)
ここに,
N: 50年間における独立な海況の個数
海況の継続時間が3時間の場合,N=50×365×24/3=1.46×105のときは,β ≈ 4.35である。海況の継続
時間が1時間の場合は,β ≈ 4.60となる。海況継続時間が3時間の例は,図G.1による。通常は,環境等
値線全体を求める必要はない。対象とするのは環境等値線のうち,運転範囲内にあり,与えられた平均風
速について最大有義波高が得られる部分[高波浪時海況(SSS)と呼ばれる。]である。この範囲では,最
も高い平均極値応答が得られる。環境等値線のこの部分は,近似を用いずに次のとおり求めることが可能
である。運転範囲内のそれぞれの平均速度Vについて,まず,式(G.5)によって標準化された変数U1を求
める。
U1=Ф−1[FV(V)] ···································································· (G.5)
次に,このVを用いてHs.SSS (V) で表される有義波高が,式(G.6)によって得られる。
]
)
2
(
[
)
(
2
1
1
s
H
s.SSS
V
U
F
V
H
−
=
−
β
Φ
·················································· (G.6)
図G.1で小円に挟まれた環境等値線の太線部分は,式(G.5)及び式(G.6)から得たものである。
この方法は,平均風速及び有義波高の結合分布モデルへの依存度がかなり高いため,このモデルの適合
度について統計的又は視覚的な検定を実施しなければならない。また,結合分布モデルには,有義波高の
上限値の影響が含まれていることが望ましい。この影響がモデルに含まれているか不明である場合は,
Hs,SSS (V) 推定値が過大とならないように環境等値線を求めた後に上限を追加してもよい。
図G.1−3時間分の海況に対する50年分の環境等値線の構築例
G.3 V及びHsの結合分布の例及び環境等値線の近似例
多くの事例においてデータを適切に近似できる,二つの結合分布モデルを次に示す。この二つのモデル
の利点は,式(G.5)及び式(G.6)を近似する,単純な解析的表現を得られることである。これらの表現は幾つ
かの統計パラメータに依存しており,このパラメータは大抵の場合,確実に推定可能なものである。ここ
96
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
で強調すると,これらの僅かな統計パラメータを確実に推定できるからといって,環境等値線を確実に推
定できるか否かは保証されない。これを保証するためには,選定したモデルの適合度の検定を実施する必
要がある。これらの検定でそのモデルが合格すれば,ここで示す解析表現によって,信頼できる環境等値
線が推定される。
最初に示した分布モデルは,HsがVに関する条件付き正規分布に従うと仮定している。この意味は,式
(G.7)のとおりである。
(
)
Φ
)
(
)
(
s
H
s
H
s
s
s
H
V
V
H
V
H
F
σ
μ
−
=
······················································· (G.7)
ここで,μHs (V)=E (Hs|V) 及びσHs (V)=D (Hs|V) は,それぞれVに関するHsの条件付き平均偏差及び
標準偏差である。この場合,式(G.6)は,式(G.8)になる。
)
(
)
(
s
H
2
1
2
s
H
SSS
s,
V
U
V
H
σ
β
μ
−
+
=
················································· (G.8)
式(G.8)に対する安全側の近似値は,U1の二乗の項を切り捨てることによって得られる。これによって,
式(G.9)の単純な表現となる。
)
(
)
(
s
H
s
H
SSS
s,
V
V
H
βσ
μ
+
≈
························································· (G.9)
VとHsとの相関が強くなるほど,また,カットアウト平均風速と再現期間50年の平均風速との差が大
きくなるほど,式(G.9)が式(G.8)を良好に近似することになる。
ここで示す2番目の分布モデルは,HsがVに関する条件付き対数正規分布に従うと仮定している。この
意味は,式(G.10)及び式(G.11)のとおりである。
Φ
)
(
)
(
log
)
(
s
log
s
log
s
s
s
H
V
V
H
V
H
F
H
H
σ
μ
−
=
·············································· (G.10)
)
(
)
(
)
(
]
)
(
1
log[
)
(
1
log
)
(
log
s
H
s
H
s
H
2
s
H
s
H
log
2
s
H
s
H
s
H
log
V
V
V
CoV
V
CoV
V
CoV
V
μ
σ
σ
μ
μ
=
+
=
+
−
=
········································ (G.11)
式(G.10)を用いると,式(G.6)は,式(G.12)のとおりとなる。
)]
(
)
(
exp[
s
logH
2
1
2
s
logH
SSS
s,
V
U
V
H
σ
β
μ
−
+
=
····································· (G.12)
式(G.12)に対する安全側の近似は,式(G.11)にテイラー展開を用いるとともに,式(G.12)でU1の二乗の項
を切り捨てることによって得られる。
)]
(
exp[
)
(
s
H
s
H
SSS
s,
V
CoV
V
H
β
μ
×
≈
················································ (G.13)
VとHsとの相関が強くなるほど,また,カットアウト平均風速と再現期間50年の平均風速との差が大
きくなるほど,式(G.13)が式(G.12)を良好に近似することになる。式(G.13)は,U1の二乗を再び導入するこ
と,すなわち,βを
21
2U
−
β
で置換することによって顕著に改善される。
条件付き平均μHs (V)=E (Hs|V) 及び標準偏差σHs (V)=D (Hs|V) は,大抵の場合,確実に推定すること
が可能である。視覚的又は統計的な適合度検定を実施するためには,μHs (V) 及びσHs (V) を推定するとき
よりも多くのデータが必要であるが,結局は判断に頼って安全側であることを保証することになる。対数
97
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
正規分布モデルは,同じデータセットを与えられた正規分布モデルに比べて,安全側であることが注目さ
れる。E (Hs|V) 及びD (Hs|V) の推定及び/又は分布モデルを保守側に選定することが不可能な場合は,
Hs.SSS (V) に関する安全側の推定として,平均風速とは独立な極値有義波高Hs50を用いてもよい。Hs50は,
Hsの周辺分布から再現期間50年で定義され,かつ,海況継続時間が環境等値線の構築に用いた海況継続
時間と同一の値である。
正規分布及び対数正規分布は,どちらも,より高い平均風速において予想される有義波高の上限を適切
に説明しにくい場合がある。したがって,Hs,SSS (V) を過大に見積もることがないように上限を定義する場
合があることに注意を要する。上限の例としては,海況継続時間が環境等値線の構築に用いた海況継続時
間と同じで,再現期間50年の極値有義波高Hs50などである。
G.4
海況継続時間の選定
何が適切な選択であるかは,サイトに依存することから,海況継続時間の選定について指針を示すこと
は困難である。ただし,この件についての簡単な考察をこの箇条で提示する。
海況は,海面上昇過程が静的であると仮定できる間の状態として定義する。海況の継続時間は,一般に
1時間以上であるため,海況の継続時間として風速の基準時間と一致する僅か10分を選定した場合は,幾
つか問題が発生することになる。継続時間10分を選択した場合は,求める極値応答,すなわち,風車が発
電状態のときに通常風条件の下で発生する再現期間50年である応答が,SSSではないにもかかわらず,10
分間海況中に発生し得る有意確率がある。したがって,この場合,SSSに対する有義波高を相当かさ(嵩)
上げする(増加させる)必要がある。海況の実際の持続状態に近くなるように,より長い継続時間を選定
すれば,この問題が軽減される。重要な設計条件の一つは,暴風雨が終了した時点である。これは波が厳
しいままだが,風車を起動できるまで風速が低下している状況である。この状況における運転中の空力荷
重と流体力荷重との組合せは,環境等値線を決めることによって解析できる。継続時間として10分間を選
択し,かつ,Hs,SSSが適切にかさ(嵩)上げされていない場合,重要な荷重ケースに寄与する波荷重を過小
評価する場合がある。
気象海象データの測定は,推算に加えて実施し,1時間のデータとして取得することが多い。すなわち,
気象海象データは毎時1回ずつ観測する。風のデータの場合,1時間の取得データは,通常,1時間平均値
である。すなわち,風の1時間データとは,平均化時間が1時間の平均風速である。一方,10分間平均の
風速データもあり,これを1時間データ又は3時間データへ変換するよう要求される場合もある。このよ
うな変換がV及びHsの結合分布に与える影響について,次に簡単に記載する。平均風速の長期周辺分布を
考えた場合,平均化時間が10分,1時間及び3時間である風速分布の間に,幾らか違いがある。周辺分布
の標準偏差は,基準時間の増加とともに僅かに低下するが,平均値は変化しない。Hsの長期周辺分布は,
定義上,サンプリング間隔及び適用時の基準時間とは独立であるため,不変である。
風の影響下では,数時間単位というかなりの時間をかけて波が形成されるため,VとHsとの相関は,基
準時間の増加とともに強まる場合がある。ただし,サイト固有の特性によっては,平均化時間に応じて相
関が顕著には変化しないこともあるため,Vhub,Hs及びTpの長期結合確率分布が基準時間に対して独立で
あると仮定するのが合理的な場合がある。
G.5
高波浪時波高(SWH)の算出
高波浪時波高HSWH (V) とは,有義波高がHs,SSS (V) となる高波浪時海況(SSS)における,極値波高であ
る。SSSの定義上,環境等値線上の各点において,この海況の最大応答の期待値が必要である。したがっ
98
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
て,HSWHは,あるSSSの海況における最大波高の期待値であることが望ましい。洋上における多くの事例
では,最大波高分布の最頻値が極値波高であるとみなされる。最頻値は期待値よりも幾らか小さいが,現
在の用法では,期待値の代わりに最頻値を用いることを許容している。
波高分布F (H|Hs) が既知である場合は,HSWHに関する式(G.14)を解くことでHSWH (V) を算出してもよ
い。
M
V
H
H
H
F
1
1
)]
(
[
SSS
s,
s
SWH
−
=
=
··················································· (G.14)
ここに,
M: SSSにおける波の平均の個数
式(G.14)は,分布の最頻値を示す。波高分布F (H|Hs) が未知である場合は,(深水域における,狭帯域
海面上昇過程の仮定に基づき)波高がレイリー分布に従うと仮定することによって,Hs,.SSS (V) からHSWH
(V) を算出してもよい。海況継続時間が3時間の場合は,HSWH (V) は,式(G.15)のとおりとなる。
HSWH (V)=1.86 Hs,.SSS (V) ························································· (G.15)
Hsに関する条件付き波高分布が,例えば,水深の制約が原因でレイリー分布モデルによって十分に説明
できない場合は,式(G.15)が有効ではないこともある。式(G.14)又は式(G.15)を用いてHSWH (V) を算出する
に当たり,十分なデータがない場合は,HSWH (V) の安全側の値として,Vに対して独立で再現期間が50
年の,条件なし極値波高H50を用いてもよい。
G.6
参考文献
[1] Winterstein, S.R., Ude, T., Cornell, C.A., Bjergager, P. and Haver, S.: “Environmental parameters for extreme
response: Inverse FORM with omission factors”, ICOSSAR' 93, Insbruck, 1993.
99
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書H
(参考)
防食
H.1 一般
洋上風車は,非常に腐食しやすい海洋環境にさらされており,アクセス性の制約を受けるため,検査及
び修理の実施時期が制限されることが多い。そのため,洋上風車には独自の防食策が必要であり,例えば,
材料選定,設計上の配慮,防食システム,適切な検査,修理計画などが挙げられる。
腐食損傷は,構造の健全性に影響を及ぼし,様々な点で耐荷重能力を損なう可能性がある。防食の目的
は,疲労荷重及び極限荷重の影響を受けやすい部位について,そのような損傷の発生を防止することであ
る。疲労では,疲労亀裂の発生に対して腐食損傷部に応力集中する。極値荷重に対しては,防食は,構造
部材の耐荷重機能が低下する可能性を防ぐ。疲労設計を行う場合,完全な防食システムが配置されており,
当該システムについて検査及び修理が適切に計画されている場合,支持構造部材には腐食損傷がないもの
と仮定される。洋上風車の構造部品,機械部品及び電気部品の設計では,腐食が機能性に与える影響,例
えば,さ(錆)びた継ぎ手部の固着又はセンサの故障などを考慮することが望ましい。
洋上風車用の防食システムは,認知された規約及び規格に従って設計されることが望ましいが,異なる
規格にある解析方法を誤って混用しないように注意する。
H.2 海洋環境
腐食は,酸化と呼ばれる電気化学的プロセスにおいて,金属表面がイオン化して分解することが特徴で
ある。このプロセスは,導電性をもつイオン性電解質の存在に依存し,イオン性電解質は,海洋環境中の
海水によって供給される。腐食プロセスは,主に,海水に関する次の要素に影響を受ける。
・ 溶存している塩分及び汚染物質の種類及び質量
・ 溶存酸素
・ 温度
・ 運動及び流れ
海洋環境との関係について理解を助けるため,洋上風車構造物を次の区画に分けることができる。
・ 海上大気部
・ 飛まつ部又は中間部
・ 海中部
・ 海底土中部
海上大気部には,飛まつ部上方の完全に大気暴露された区画及び一部覆われた区画がある。
飛まつ部は,想定される海面上昇分布によって断続的にぬ(濡)れる構造区画として定義され,場所に
よる差が大きい。
海中部は,飛まつ部の下方に伸びた部分で海水が流入する内部区画も含まれる。
海底土中部には,構造で海底堆積物中に埋没した部分又は配置された固形物に覆われた部分もある。
海中部の上部及び飛まつ部の下部は,海洋付着生物の影響も受ける。海洋付着生物の種類及び範囲並び
に局所条件によっては,海洋付着生物の影響で腐食の進行が進んだり又は遅くなったりする可能性がある。
また,海洋付着生物はコーティング,ライニング,電気防食などの防食システムの働きも妨げる。
100
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
極寒条件では,腐食を抑制する酸化被膜,防食コーティング及び海洋付着生物が氷によって剝がれるこ
とで腐食速度が増加する可能性がある。
熱帯条件では,平均温度及び湿度が高いため海洋環境は更に厳しく,防食システムに関する考慮が一層
重要となる。
H.3 防食に関する考慮
防食システムは,構造に対する腐食損傷の割合をその設計寿命を通して防止又は極小化するために用い
る。実際には,腐食を完全に防止することは困難なことが多いが,腐食速度を可能な限り遅くすることは
可能である。
腐食損傷は,次の防食方法によって極小化できる。
・ 認知された設計に関する規則及び規格を用いることによる,適切な構造材料の選定
・ アクセス性,適切な排水,角部及び欠陥の除去,ほかの検討事項などの,適切な設計手法の利用
・ コーティングシステムによる金属材料と電解液との間の絶縁
・ 防食システムの定期検査及び定期修理の実施
・ 陰極防食などの電気化学的保護
H.4 防食システム
洋上風車基礎構造物のための防食システムは,コーティングシステム及び陰極防食という2大分野にグ
ループ化することが可能である。この2大分野について,支持構造物の各区画と照らし合わせて論じる。
海上大気部及び飛まつ部については,認知された規約又は規格に従って,全ての金属表面に適切なコー
ティングシステムを適用することが望ましい。飛まつ部に対しては,特に注意することが望ましい。この
部位では海況の環境に合わせてコーティングシステムを指定することが望ましい。コーティングシステム
を構造物の運用条件に適合させ,かつ,その効果について評価することが望ましい。
海中部及び海底土中部も,適切な防食システムで保護することが望ましい。この防食システムは,構造
物の設計寿命まで耐えることを意図したもので,そうでない場合は,更新又は修理の実施が可能であるこ
とが望ましい。更新が予想される場合は,コーティングのあらゆる破壊を検出するために,独自の調査期
間を設けることが望ましい。
箱桁内部の空間,管ソケットなど恒久的に密封シールしている部位については,内部の防食は要求しな
い。組立時には,シール処理の実施前に,空洞が確実に清浄で乾燥しているよう,特別な注意を払うこと
が望ましい。水の出入りがほとんどないか又は皆無の恒久的に浸水している空間についても,防食に関す
る要求を低減してもよい。
設計寿命を通じての健全性の維持を確保するために,全てのコーティングシステムについて,検査及び
修理計画を課すことが望ましい。検査の頻度を減らす場合は,認知された標準に対するコーティングの適
格性を更に重視することが望ましい。コーティング適格性だけで設計寿命中の性能が保証されるわけでは
なく,類似の適用例で実証された製品の経験に基づいてコーティングを選定する必要があることに注意す
ることが望ましい。
さらに,海中部では常時,陰極防食を行うことが望ましい。陰極防食は,通常,ガルバニ陽極(犠牲陽
極)か又は外部電源システムのいずれかを備えている。陰極防食システムによって,構造の各部位で好ま
しくない電流分布が生じた場合は,その領域に追加コーティングを施すことが望ましい。陰極防食の効果
がない間隙及び領域は,なくすか又は追加コーティングで補うことが望ましい。徹底的な検査及び修理を
101
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
実施するに当たり,ドックに入れることができる浮体構造物については,この要求を見直してもよい。
防食システムの代わりに,腐食しろを用いるのは,重要度が低い部品,設計寿命が短い部品,定期検査
又は定期修理作業が予定されている部位に限ることが望ましい。例えば,ISO 19902では,北海における,
防食されていない低合金鋼又は非合金鋼の腐食速度が,飛まつ部で年間0.3 mm,海中部で年間0.1 mmに
指定されている。設計寿命が20年の場合,腐食は飛まつ部で6 mm,海中部で2 mmとなり,限界状態解
析において,この値を腐食しろとして見込むことが望ましい。
H.5 ロータ ナセル・アセンブリ(RNA)における防食
ナセルも海上大気部に配置されており,支持構造物の場合と同様の海洋環境による腐食というストレス
にさらされる。防食に関しても,支持構造用と同様の一般的な配慮をすることが望ましい。追加の防食方
法としては,ナセルを海上大気部から分けて密閉する方法がある。
ナセルにある全金属表面について,認知された規則又は規格に従ったコーティングシステムを適用する
ことが望ましい。ISO 12944-2に従った次の環境分類とすることが望ましい。
・ 外部部品,金具,センサなどは,クラスC5-Mに応じた防食を行うことが望ましい。
・ 外部の空気に直接さらされる内部表面は,クラスC4に応じた防食を行うことが望ましい。
・ 外気に対して密閉された内部表面は,クラスC3に応じた防食を行うことが望ましい。
80 %よりも高い相対湿度では,顕著な腐食の発生が一般に容認されているため,環境シーリング及び空
調によって,ナセル内部の環境を制御することが望ましい。環境制御システムについては,風車制御シス
テムによって監視し,通常の定期整備を実施することが望ましい。
さらに,外気と直接又は間接的に接触しているその他の内部部品(例えば,軸受又は増速機の通気孔)
及び運転用資材(例えば,潤滑油及び作動油)は,ナセル外側の外部部品(例えば,シール,ゴム製品及
びホース)と同様に,洋上の海洋環境に耐えるように仕様を定めて設計を行うことが望ましい。指針とし
て,JIS C 60721-3-3に従って当該環境を説明することが望ましい。
H.6 参考文献
[1] DNV-OS-C101,Design Of Offshore Steel Structures, General (LRFD Method), April 2004.
[2] DNV-OS-J101,Design Of Offshore Wind Turbine Structures. June 2004.
[3] DNV RP-B401,Cathodic Protection Design
[4] Germanischer Lloyd WindEnergie GmbH, Rules and Guidelines: IV−Industrial Services,Part 2−Guideline
for the Certification of Offshore Wind Turbines, 2005.
[5] Germanischer Lloyd, VI−Additional Rules and Guidelines, Part 9 Materials and Welding, 6 Guideline for
Corrosion Protection and Coating Systems
[6] ISO 12944-2,Paints and varnishes−Corrosion protection of steel structures by protective paint systems−Part
2: Classification of environments
[7] ISO/DIS 12495,Cathodic protection for fixed steel offshore structures, 2000
[8] ISO 19902,Petroleum and natural gas industries−Fixed steel offshore structures
[9] NACE Standard RP0176-2003,Corrosion Control of Steel Fixed Offshore Structures Associated with
Petroleum Production.
[10] NORSOK Standard M-501,Surface Preparation and Protective Coating, Rev.4, 1999
[11] NORSOK Standard M-503,Cathodic Protection, Rev.2, 1997
102
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[12] STG-Richtlinie Nr. 2215,Korrosionsschutz für Schiffe und Seebauwerke
[13] ZTV-KOR,Zusätzliche technische Vertragsbedingungen und Richtlinie für den Korrosionsschutz von
Stahlbauten
[14] ZTV-W,Zusätzliche technische Vertragsbedingungen und Richtlinie Wasserbau für Korrosionsschutz im
Stahlwasserbau
[15] ZTV-RHD-ST,Zusätzliche technische Vertragsbedingungen und Richtlinie reaktionsharzgebundene
Dünnbelege auf Stahl
[16] Korrosionsschutz in der maritimen Technik Tagungsband zur 1. Tagung, Korrosionsschutz von Offshore-
Windenergieanlagen, Nils Hunold und Dr. Bernhard Richter
[17] W. v. Baeckmannn und W. Schwenk (1999): “Handbuch des kathodischen Korrosionschutzes”, 4. Auflage,
Wiley-VCH Verlag
[18] Egon Kunze (2001): “Korrosion und Korrosionsschutz”, Band 4 Korrosion und Korrosionsschutz in
verschiedenen Gebieten, Wiley-VCH Verlag
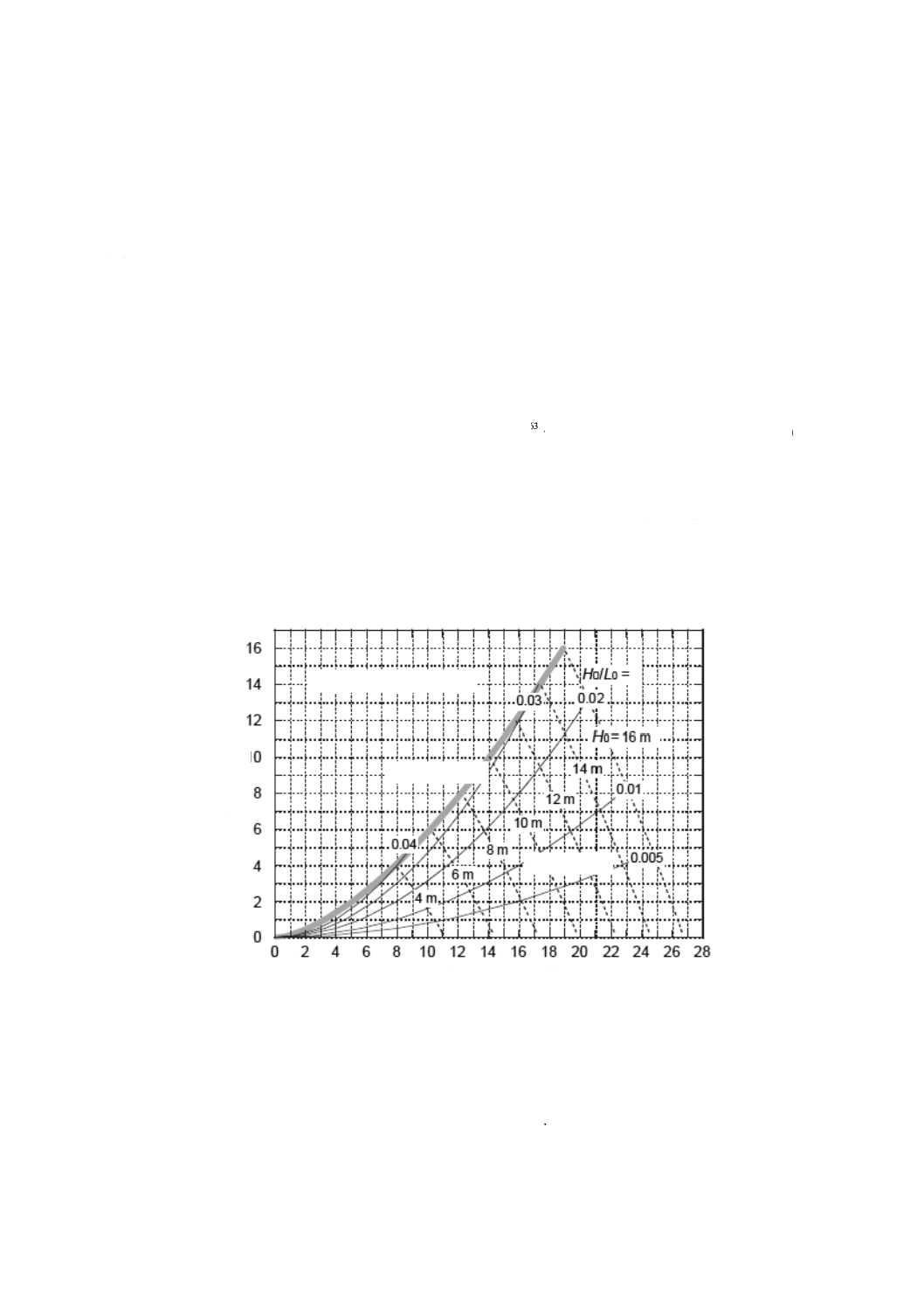
103
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
波浪統計及び波浪スペクトル定式化
JA.1 波浪統計
JA.1.1 有義波高と波の周期との関係
海洋における波の特性は,通常,有義波高H1/3又はHs,及びピークスペクトル周期Tp又は有義波周期
T1/3を用いて記述する。波を発生させ,発達させる風の直接の影響下にある場合,波は風浪と呼ばれる。
発生領域の外へ移動した後は,風浪はうねりと呼ばれる。風浪の特性周期は波の成長とともに増大し,式
(JA.1)の公式によって近似的に表わされる([1]参照)。
63
.0
3/1
3/1
)
(3.3H
T≅
又は,
()63
.0
s
p
5.3 H
T≅
········································ (JA.1)
ここで,TpとHsとの関係はTp≅1.1T1/3及びH1/3≅0.95Hsを用いて,T1/3とH1/3との関係から導かれる。
うねりが発生領域の外へ移動するとともに,その高さは減少し始めるのに対し,周期は長くなる。図JA.1
は,所定の波高に対する波の周期の範囲を示す。外洋の沿岸では,うねりは波条件の支配的要因になるこ
とがある。サイトにおける有義波高,波の周期,風速との関係は気象海象データベースによって求めるこ
とが望ましい。
図JA.1−波高と周期との関係
JA.1.2 有義波高と最大波高との関係
深海域における波高分布は,式(JA.2)のレイリー分布を用いて近似的に記述される。
p(x)=4.01×x exp(−2.005×x2) ··············································· (JA.2)
ここに, x=H/H1/3
無波浪帯
風浪帯
うねり帯
波
高
H
1
/
3
(
m
)
波の周期 T1/3(s)
104
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
レイリー分布では,統計的有義波高H1/3は,スペクトル有義波高Hsに等しい。しかし,実際の波高の分
布はレイリーよりも僅かながら狭く,JA.2で記載するスペクトル形状にかかわらず,H1/3=0.95 Hsという
近似的関係が,大部分の波浪条件で成り立つ([3]参照)。
個別波記録のHmaxは,その確率密度関数に応じて統計的に変化する。1 000個の波にわたる長さ(平均
周期10.8秒で3時間に相当)の記録の中で最も頻繁な値27) は,式(8)及び式(9)に示すとおり,Hmax=1.86Hs
によって算出する。最大波高の確率的性質については[2]を参照。
注27) ISO 19901-1の3.19では,この値を“最確最大値(most probable maximum)”と呼んでいる([5]
参照)。
JA.2 波スペクトル定式化
JA.2.1 一般
海況は,線形ランダム波浪スペクトルで表すと便利なことが多い。これは,方向波浪スペクトルと呼ば
れ,式(JA.3)のように,周波数スペクトルS(f )と方向分布関数D(f, θ )との積で表す。
S(f, θ )=S(f )×D(f, θ ) ······························································· (JA.3)
ここに,
f: 周波数(Hz)
θ: 平均波向に関する方位角(rad)
方向スペクトルS(f, θ )は,二次元波浪スペクトルと呼ばれることがあり,周波数スペクトルS(f )は,一
次元波浪スペクトルと呼ばれる。いずれも長さの次元を二乗して,周波数(単位Hz)の次元を乗じるのに
対して,方向分布関数は次元が1/ラジアンとなる。
JA.2.2 周波数スペクトルの定式化
JA.2.2.1 修正ブレットシュナイダー・光易スペクトル
設計波高及び周期が統計的有義波高H1/3及び有義波周期T1/3を用いて与えられている場合,式(JA.4)の
修正ブレットシュナイダー・光易スペクトルが用いられることが多い([4]参照)。
4
3/1
5
43/1
23/1
)
(
75
.0
exp
205
.0
)
(
−
−
−
−
=
f
T
f
T
H
f
S
································· (JA.4)
修正ブレットシュナイダー・光易スペクトルは,H1/3 ≈ 0.956HsかつTp ≈ 1.136T1/3という条件下で,ピア
ソン・モスコビッツスペクトル(B.2参照)から導かれている。
JA.2.2.2 修正JONSWAPスペクトル
JONSWAPスペクトル(B.3参照)を,統計的有義波高H1/3,有義波周期T1/328)及びピーク増幅係数γ の
項で指定する場合は,式(JA.5)のような修正JONSWAPスペクトルを用いることができる([2]参照)。
()
()
[
]
(
)
−
−
−
−
−
−
=
2
2/2
1
p
exp
4
p
5
4
p
2
3/1
J
25
.1
exp
σ
γ
β
f
T
f
T
f
T
H
f
S
······················· (JA.5)
ここで,パラメータは式(JA.6),式(JA.7)及び式(JA.8)で算出する。
)
ln
01915
.0
094
.1(
)
9.1(
185
.0
0336
.0
230
.0
0624
.0
1
J
γ
γ
γ
β
×
×
×
−
+
−
+
=
−
·········· (JA.6)
559
.0
3/1
p
)2.0
(
132
.0
1
−
+
−
γ
T
T≅
······················································· (JA.7)
105
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
>
≅
の場合
,
の場合
≦
,
p
p
09
.0
07
.0
f
f
f
f
σ
··················································· (JA.8)
ここで,fp=1/Tpは,ピークスペクトルにおける周波数を表す。
注28) ゼロアップクロス法によって波の高い方から1/3の平均周期と定義される有義波周期は,スペ
クトルモーメントmによって定義した平均周期Tm−1,0=m−1/m0にほぼ等しい。
ピーク増幅係数γ は,JONSWAPスペクトルの原著では1〜7の値をとるが,式(JA.5)を用いるときには,
γ の値は波浪特性に応じて1〜10の中から選ぶことができる。十分に成長した風浪については,γ =1とな
り,JONSWAPスペクトルは,ピアソン・モスコビッツスペクトルになる。うねりについては,移動距離
に比例して値を増大させればよい。数千キロメートルを移動してきたうねりについては,γ =10が適切と
考えられる([2]参照)。
JA.2.3 方向分布関数
波スペクトルエネルギーの方向分布については,幾つかの定式化がある。その中でも,式(JA.9)の光易
による定式化が野外観測データによって実証されてきた([4]参照)。
2
cos
)
(
0
s
2
0
θ
θ
θ
−
=
,
D
f
D
······················································· (JA.9)
ここに,D0は式(JA.10)で算出する。
0
0
1
2s
0
0
cos
2
D
d
πθ
πθ
θθ
θ
+
−+
∫
−
−
=
················································ (JA.10)
また,θ0は与えられた方向軸から測定された主波向を表し,sは式(JA.11)に示すように周波数とともに
変化する分散度パラメータである。
の場合
≧
,
の場合
≦
,
=
−
p
max
5.2
p
p
max
5
p
f
f
s
f
f
f
f
s
f
f
s
··········································· (JA.11)
分散度パラメータのピーク値smaxは,風浪成長の状態に応じて変化する([4]参照)。十分に成長した風
浪のsmaxの代表値は,約10である。smax値の増大とともに,方向分散の程度は小さくなる。減衰距離が短
いうねりについてはsmax=25,深海波に見られる減衰距離が長いうねりについてはsmax=75が提案されて
いる([2]参照)。
JA.3 参考文献
[1] Goda, Y. 2003. Revisiting Wilsonʼs formulas for simplified wind-wave prediction, Journal of Waterway, Port,
Coastal and Ocean Engineering,Vol.129, No.2,pp. 93-95
[2] Goda, Y. 2010. Random Seas and Design of Maritime Structures (3rd Edition), World Scientific, Singapore.
[3] Goda, Y and Kudaka, M. 2007. On the role of spectral width and shape parameters in control of individual wave
height distribution, Coastal Engineering Journal, Vol. 49, No. 3, 2007, pp. 311-335
[4] H. Mitsuyasu, F. Tasai, T. Suhara, S. Mizuno, M. Ohkusu, T. Honda, and K. Rikiishi. 1975. Observation of the
directional spectrum of ocean waves using a cloverleaf buoy, Journal of Physical Oceanography, Vol. 5, No. 4,
pp.750--760
106
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
[5] ISO 19901-1:2005,Petroleum and natural gas industries−Specific requirements for offshore structures−Part
1: Metocean design and operating considerations
107
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JB
(参考)
浅水の流体力学及び砕波
JB.1 浅水域における波浪変形
波は,深海から岸に向かって移動する間に様々な変形過程をたどる。そうした過程には,浅水変形,屈
折,回折,砕波などがある。波が,ある程度の強さの流れがある区域に広がっていくと,波高及び波向が
変化する。風車の支持構造物に対する波の作用を評価する前に,こうした波の変形過程を考慮することが
望ましい。
浅水変形とは,水深の減少に伴う波の周期及び波高の変化の過程のことをいう。この過程は,通常,線
形エアリ波理論によって評価される。不規則波については,各スペクトル成分の浅水変形過程を計算し,
これらを合成して全体としての変形を評価する。砕波帯の外側の単一最大波の作用に対して支持構造物を
設計する場合には,非線形波浅水変形理論(例 [1]参照)を用いることが望ましい。これは,波高の増大
が,線形エアリ波理論による予測よりもかなり大きくなる可能性があるためである。
波の屈折とは,海底上の水深の二次元的変化に伴う波の伝ぱ(播)速度の変化によって,波高及び波向
が変化する過程のことをいう。単純な海底地形の場合には,規則波を用いて解析することができるが,波
の屈折は同時に回折過程を伴うため,方向波浪スペクトルを用いて分析することが望ましい。
波の回折とは,島などの障害物の裏の幾何学的影の領域へ波エネルギーが伝達される過程をいう。波の
回折の度合いは,回折波高の入射高に対する比である回折係数で表す。回折係数は,波の入射角度に非常
に敏感であるため,方向波浪スペクトル計算を用い,方向分布特性を十分に考慮して評価することが望ま
しい。
JB.2 浅水域における砕波
JB.2.1 砕波限界
風によって生成される波には,いわゆるホワイトキャッピング(白波)という,深海域における波の動
的不安定性に起因する砕波の上限がある。規則波の場合,砕波波高は式(JB.1)の公式によって表される([2]
及び[3]参照)。
4/3
b
0
0
0.17
1exp
1.5
(115tan
)
d
H
L
L
π
α
×
×
=
−
−
+
··························· (JB.1)
ここに,
Hb: 砕波波高
d: 水深
L0: 深海波長=g T2/(2π)(T:波の周期)
tanα: 海底勾配
また,自由水表面の最大上昇量
b
ηは式(JB.2)の公式によって表される([4]参照)。
(
)
[
]1
exp
tan
2
1
−
=
f
d
f
b
α
η
·························································· (JB.2)
ここに,
(
)
2
2
1
/
2.44
9.24
3.18
10
b
b
b
b
H
H
H
fHd
d
d
d
−
=
−
+
×
······················ (JB.3)
108
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
2
1
2
1.93
1.05
5.58
10
b
b
b
b
H
H
H
fHd
d
d
d
−
=
−
+
+
×
····················· (JB.4)
JB.2.2 浅水域における代表波高の変化
一様に傾斜した海底の浅瀬については,有義波高H1/3及びHmaxの変化は,式(JB.5)及び式(JB.6)の実験式
([1]参照)を用いて近似的に評価することができる。
s
r
0
0
1/3
0
r
0
1
max
r
0
s
r
0
0
/
0.2
min[(
)
]
/
0.2
KKH
dL
H
KH
d
KH
KKH
dL
β
β
β
,
≧
の場合
=
+
,
,
,
<
の場合 ······················ (JB.5)
s
r
0
0
max
*
*
*max
0
r
0
1
r
0
s
r
0
0
1.95
/
0.2
min[(
)
1.95
]
/
0.2
KKH
dL
H
KH
d
KH
KKH
dL
β
β
β
×
×
,
≧
の場合
=
+
,
,
,
<
の場合 ······· (JB.6)
ここに, 記号min[a, b, c]: a,b,cの中の最小値
Ks: 浅水係数
Kr: 屈折係数
H0: 深海域有義波高
d: 水深
係数β0,β1,… は,式(JB.7)及び式(JB.8)のように定式化されている。
0.38
1.5
0
0
0
1
0.29
max
0
0
0.028(
/
)
exp(20tan
)
0.52exp(4.2tan)
max0.92
0.32(
/
)
exp(2.4tan)
r
r
kHL
kHL
β
α
β
α
β
α
×
×
×
×
×
−
−
=
=
=
,
················ (JB.7)
*
0.38
1.5
0
0
0
*
1
*
0.29
max
0
0
0.056(
/
)
exp(20tan
)
0.68exp(3.8tan)
max1.79
0.57(
/
)
exp(2.4tan)
r
r
kHL
kHL
β
α
β
α
β
α
×
×
×
×
×
−
−
=
=
=
,
················· (JB.8)
式(JB.5)及び式(JB.6)の適用性は,“CLASHデータベース”という大きなデータセットに含まれるデータ
によって確認されている([5]参照)。
JB.3 沿岸流
波が,岸に対して斜めに入射すると,砕波が岸に平行な流れを引き起こすが,これは沿岸流と呼ばれる。
沿岸流は,海岸線の近くでは非常に弱く,砕波帯の中ほどで最も強くなり,砕波帯の外側で急速に減衰す
る。
一様に傾斜した海辺での不規則波砕波及び潮流発生の数値シミュレーションに基づく沿岸潮流のピーク
速度について,式(JB.9)が提案されている([6]参照)。
(
)
b
3/1
f
bw
2
sin
115
.0
θ
b
H
s
C
U
g
≈
··················································· (JB.9)
ここに,
Cf: 底面摩擦係数
s: 海底勾配
θb: 砕波点の波向角
式(JB.9)でCf=0.01と設定すると,式(JB.10)が導かれる。
(
)
b
3
/1
bw
2
sin
5.
11
θ
b
H
s
U
g
=
·····················································(JB.10)
109
C 1400-3:2014 (IEC 61400-3:2009)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.2.3の式(16)は,θb=10°及び (H1/3)b=Hbとした場合に導かれる。
JB.4 参考文献
[1] Goda, Y. 1975. Irregular wave deformation in the surf zone, Coastal Engineering in Japan,Vol.18, SCE, 1975,
pp.13-26.
[2] Goda, Y. 2010. Random Seas and Design of Maritime Structures(3rd edition), World Scientific,Singapore,
Section 3.1.1.
[3] Goda, Y. 2009. Random Wave Breaking and Nonlinear Wave Evolution across the Surf Zone, Chapter 4 of
Handbook of Coastal and Ocean Engineering ed. by Y. C. Kim, World Scientific, Singapore.
[4] 桂川哲行,服部昌太郎 1988.浅水変形波動場の計算法,第35回海岸工学講演会論文集,pp.73-77
[5] Goda, Y. 2009. A performance test of nearshore wave height prediction with CLASH datasets, Coastal
Engineering, Vol. 56, No. 3, pp. 220-229.
[6] Goda, Y. 2008. Wave setup and longshore currents induced by directional spectral waves: Prediction formulas
based on numerical computation results, Coastal Engineering Journal,Vol.50, No.4, pp. 397-440