C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 3
4 記号及び略語 ·················································································································· 10
4.1 記号及び単位 ··············································································································· 10
4.2 略語 ··························································································································· 12
5 主要構成要素 ·················································································································· 13
5.1 一般事項 ····················································································································· 13
5.2 設計方法 ····················································································································· 13
5.3 安全カテゴリ ··············································································································· 13
5.4 品質保証 ····················································································································· 13
5.5 風車銘板 ····················································································································· 13
6 外部条件························································································································ 14
6.1 一般事項 ····················································································································· 14
6.2 風車クラス ·················································································································· 14
6.3 風条件 ························································································································ 15
6.4 その他の環境条件 ········································································································· 23
6.5 電力系統条件 ··············································································································· 24
7 構造設計························································································································ 25
7.1 一般事項 ····················································································································· 25
7.2 設計方法 ····················································································································· 25
7.3 荷重 ··························································································································· 25
7.4 設計条件及び設計荷重ケース ·························································································· 25
7.5 荷重計算 ····················································································································· 30
7.6 終極限界状態解析 ········································································································· 31
8 制御システム及び保護システム ·························································································· 37
8.1 一般事項 ····················································································································· 37
8.2 制御機能 ····················································································································· 37
8.3 保護機能 ····················································································································· 37
8.4 ブレーキシステム ········································································································· 38
9 機械システム ·················································································································· 38
9.1 一般事項 ····················································································································· 38
9.2 取付け誤り ·················································································································· 39
9.3 油圧又は空気圧によるシステム ······················································································· 39
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010) 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
9.4 メインギヤボックス(増速機) ······················································································· 39
9.5 ヨーシステム ··············································································································· 39
9.6 ピッチシステム ············································································································ 40
9.7 保護機能機械ブレーキ ··································································································· 40
9.8 転がり軸受 ·················································································································· 40
10 電気システム ················································································································ 41
10.1 一般事項 ···················································································································· 41
10.2 電気システムの一般要求事項 ························································································· 41
10.3 保護装置 ···················································································································· 41
10.4 断路装置 ···················································································································· 41
10.5 接地システム ·············································································································· 41
10.6 雷保護 ······················································································································· 41
10.7 電気ケーブル ·············································································································· 41
10.8 自己励磁 ···················································································································· 42
10.9 雷電磁インパルスに対する保護 ······················································································ 42
10.10 電力品質 ·················································································································· 42
10.11 電磁両立性················································································································ 42
11 サイトの固有条件に対する風車の評価 ··············································································· 42
11.1 一般事項 ···················································································································· 42
11.2 サイトの地形的複雑さの評価 ························································································· 42
11.3 評価に必要な風条件 ····································································································· 43
11.4 隣接風車の後流の影響評価 ···························································································· 44
11.5 その他の環境条件の評価 ······························································································· 44
11.6 地震条件の評価 ··········································································································· 44
11.7 電力系統条件の評価 ····································································································· 45
11.8 土壌条件の評価 ··········································································································· 45
11.9 風のデータを参照した構造的な健全性の評価 ···································································· 45
11.10 サイト固有の条件に関する荷重計算による構造的な健全性の評価 ········································ 47
12 組立て,据付け及び建設 ································································································· 47
12.1 一般事項 ···················································································································· 47
12.2 計画 ·························································································································· 47
12.3 据付条件 ···················································································································· 48
12.4 サイトへのアクセス ····································································································· 48
12.5 環境条件 ···················································································································· 48
12.6 文書 ·························································································································· 48
12.7 受取り,取扱い及び保管 ······························································································· 48
12.8 基礎又はアンカによるシステム ······················································································ 48
12.9 風車の組立て ·············································································································· 49
12.10 風車の建設 ··············································································································· 49
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010) 目次
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
12.11 締結部品及びアタッチメント ························································································ 49
12.12 クレーン,ホイスト及びつり上げ装置············································································ 49
13 試運転,運転及び保守 ···································································································· 49
13.1 一般事項 ···················································································································· 49
13.2 安全運転,点検及び保守に関する設計要件 ······································································· 49
13.3 試運転に関する指示書 ·································································································· 50
13.4 運転要員への指示マニュアル ························································································· 51
13.5 保守マニュアル ··········································································································· 52
附属書A(規定)風車クラスSを規定する設計パラメータ ·························································· 54
附属書B(参考)乱流モデル ································································································· 56
附属書C(参考)地震荷重の評価 ··························································································· 61
附属書D(参考)風車後流乱流及びウィンドファーム乱流 ·························································· 62
附属書E(参考)測定−相関−予測[measure-correlate-predict (MCP)]法による
風車サイトの風分布の予測 ······························································································ 64
附属書F(参考)終極強度解析のための荷重の統計的外挿 ··························································· 66
附属書G(参考)荷重外挿に関するMiner則を用いる疲労解析 ···················································· 74
附属書H(参考)同時荷重 ···································································································· 79
附属書JA(参考)風車クラス及び乱流カテゴリの追加 ······························································· 81
参考文献 ···························································································································· 83
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010) 目次
(4)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般社団法人日本
電機工業会(JEMA)から,工業標準原案を具して日本工業規格を改正すべきとの申出があり,日本工業
標準調査会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによって,JIS C 1400-1:2010は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS C 1400の規格群には,次に示す部編成がある。
JIS C 1400-0 第0部:風力発電用語
JIS C 1400-1 第1部:設計要件
JIS C 1400-2 第2部:小形風車の設計要件
JIS C 1400-3 第3部:洋上風車の設計要件
JIS C 1400-11 第11部:騒音測定方法
JIS C 1400-12-1 第12-1部:発電用風車の性能試験方法
JIS C 1400-21 第21部:系統連系風車の電力品質特性の測定及び評価
JIS C 1400-22 第22部:風車の適合性試験及び認証
JIS C 1400-24 第24部:雷保護
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
C 1400-1:2017
(IEC 61400-1:2005, Amd.1:2010)
風力発電システム−第1部:設計要件
Wind Energy Generation systems-Part 1: Design requirements
序文
この規格は,2005年に第3版として発行されたIEC 61400-1及びAmendment 1:2010を基に,技術的内
容を変更することなく作成した日本工業規格である。ただし,追補(amendment)については,編集し,
一体とした。
なお,附属書JA及びこの規格で点線の下線を施してある参考事項は,対応国際規格にはない事項であ
る。
この規格は,風車に関する最小限の設計要件を概説する。
この規格は,完全な設計仕様書又は指示マニュアルとして用いることを意図したものではない。風力発
電システムの安全性が損なわれないことを適切に実証することができる場合,この規格のどの要求事項を
変更してもよい。ただし,これは箇条6の風車クラス及び外部条件の関連定義には適用しない。この規格
を遵守しても,いかなる個人,組織又は企業は,その他の関連する規則を遵守する責任から免れられるわ
けではない。
1
適用範囲
この規格は,風車の技術的な健全性を確保するために不可欠な設計要件について規定する。その目的は,
設計寿命を通じて生じる全ての危険要因による損傷に対して,適切なレベルの保護措置を講じることであ
る。
この規格は,制御及び保護機構,内部電気システム,機械システム,支持構造物など,風車の全てのサ
ブシステムに関係している。
この規格は,全てのサイズの風車に適用する。ただし,小形風車の場合には,JIS C 1400-2を適用して
もよい。
注記1 洋上風車の設計要件については,JIS C 1400-3を参照する。
この規格は,箇条2に規定する適切な引用規格と一緒に用いることが望ましい。
注記2 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 61400-1:2005,Wind turbines−Part 1: Design requirements及びAmendment 1:2010(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
2
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS B 1518 転がり軸受−動定格荷重及び定格寿命
注記 対応国際規格:ISO 281,Rolling bearings−Dynamic load ratings and rating life(MOD)
JIS B 1519:2009 転がり軸受−静定格荷重
注記 対応国際規格:ISO 76:2006,Rolling bearings−Static load ratings(IDT)
JIS B 9960-1 機械類の安全性−機械の電気装置−第1部:一般要求事項
注記 対応国際規格:IEC 60204-1,Safety of machinery−Electrical equipment of machines−Part 1:
General requirements(MOD)
JIS B 9960-11 機械類の安全性−機械の電気装置−第11部:交流1 000 V又は直流1 500 Vを超え36
kV以下の高電圧装置に対する要求事項
注記 対応国際規格:IEC 60204-11,Safety of machinery−Electrical equipment of machines−Part 11:
Requirements for HV equipment for voltages above 1 000 V a.c. or 1 500 V d.c. and not exceeding 36
kV(MOD)
JIS C 1400-2 風車−第2部:小形風車の設計要件
注記 対応国際規格:IEC 61400-2,Wind turbines−Part 2: Design requirements for small wind turbines
JIS C 1400-21 風力発電システム−第21部:系統連系風車の電力品質特性の測定及び評価
注記 対応国際規格:IEC 61400-21,Wind turbines−Part 21: Measurement and assessment of power
quality characteristics of grid connected wind turbines(MOD)
JIS C 1400-24 風車−第24部:雷保護
注記 対応国際規格:IEC 61400-24,Wind turbines−Part 24: Lightning protection(MOD)
JIS C 60364(規格群)低圧電気設備
注記 対応国際規格:IEC 60364 (all parts),Low-voltage electrical installations(MOD)
JIS C 60364-5-54 建築電気設備−第5-54部:電気機器の選定及び施工−接地設備,保護導体及び保
護ボンディング導体
注記 対応国際規格:IEC 60364-5-54,Low-voltage electrical installations−Part 5-54: Selection and
erection of electrical equipment−Earthing arrangements, protective conductors and protective
bonding conductors
JIS C 60721-2-1 環境条件の分類 自然環境の条件−温度及び湿度
注記 対応国際規格:IEC 60721-2-1,Classification of environmental conditions−Part 2-1: Environmental
conditions appearing in nature−Temperature and humidity
JIS C 61000-6-1 電磁両立性−第6-1部:共通規格−住宅,商業及び軽工業環境におけるイミュニテ
ィ
注記 対応国際規格:IEC 61000-6-1,Electromagnetic compatibility (EMC)−Part 6-1: Generic standards
−Immunity for residential, commercial and light-industrial environments(IDT)
JIS C 61000-6-2 電磁両立性−第6-2部:共通規格−工業環境におけるイミュニティ
注記 対応国際規格:IEC 61000-6-2,Electromagnetic compatibility (EMC)−Part 6-2: Generic standards
−Immunity for industrial environments(MOD)
JIS Z 9290-3 雷保護−第3部:建築物等への物的損傷及び人命の危険
注記 対応国際規格:IEC 62305-3,Protection against lightning−Part 3: Physical damage to structures
and life hazard(MOD)
3
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS Z 9290-4 雷保護−第4部:建築物等内の電気及び電子システム
注記 対応国際規格:IEC 62305-4,Protection against lightning−Part 4: Electrical and electronic systems
within structures(IDT)
IEC 61000-6-4,Electromagnetic compatibility (EMC)−Part 6-4: Generic standards−Emission standard for
industrial environments
IEC 61400-4:2012,Wind turbines−Part 4: Design requirements for wind turbine gearboxes
ISO 2394:1998,General principles on reliability for structures
ISO 2533:1975,Standard Atmosphere
ISO 4354:1997,Wind actions on structures
ISO 6336-2,Calculation of load capacity of spur and helical gears−Part 2: Calculation of surface durability
(pitting)
ISO 6336-3:2006,Calculation of load capacity of spur and helical gears−Part 3: Calculation of tooth bending
strength
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
3.1
年平均(annual average)
十分な期間にわたって集めた十分な量の測定データセットを平均した値であって,測定対象の期待値を
推定できるもの。平均を計算する期間は,季節差などの非定常効果をならすため,1年単位の整数倍とす
ることが望ましい。
3.2
年平均風速(annual average wind speed),Vave
年平均の定義に従って平均した風速。
3.3
自動再閉路周期(auto-reclosing cycle)
系統故障の後に開放された遮断器が自動的に再閉路し,電路が系統に再接続されるまでの約0.01秒から
数秒間変化する期間。
3.4
(風車の)ロック装置[blocking (wind turbines)]
例えば,ロータ又はヨー機構の運動を防止するために,誤って始動できないようにする機械的ピン,そ
の他の装置(ただし,通常の機械式ブレーキ装置は除く。)。
3.5
(風車の)ブレーキ装置[brake (wind turbines)]
ロータ速度を緩めるか,又は回転を静止させることができる装置。
注記 ブレーキ装置は,例えば,空力,機械又は電気的原理で作動してもよい。
3.6
特性値(characteristic value)
達成されない所定の確率(すなわち,所定の量以下の超過確率)をもつ値。
4
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.7
複雑な地形(complex terrain)
地形が変化に富み又は障害物が存在し,それらによって気流がゆがめられやすい周辺地形。
3.8
(風車の)制御機能[control functions (wind turbines)]
風車及び/又は周囲の状態の情報に基づいて,風車の動作限界値内に保つように調整する制御システム
及び保護システムの機能。
3.9
カットイン風速(cut-in wind speed),Vin
乱流がない定常風の場合に,風車が動力を発生し始めるハブ高さにおける最小の風速。
3.10
カットアウト風速(cut-out wind speed),Vout
乱流がない定常風の場合に,風車が動力を発生するように設計されたハブ高さにおける最大の風速。
3.11
設計限界値(design limits)
設計に用いられる最大値又は最小値。
3.12
潜在的な欠陥(dormant failure)
通常の運転中には検知できない部品又はシステムの故障。
3.13
風下(downwind)
主となる風の方向(主風向)。
3.14
電力系統(electrical power network)
送配電用の特定設備,変電所,送電線又はケーブル。
注記 この系統の区分は,地理的な条件,所有権,電圧などの適切な基準によって定義される。
3.15
(風車の)緊急停止[emergency shutdown (wind turbines)]
保護機能又は手動操作によって風車を速やかに停止させること。
3.16
環境条件(environmental conditions)
風車の挙動に影響を与える可能性がある環境(風,高度,温度,湿度など)の特性。
3.17
(風車の)外部条件[external conditions (wind turbines)]
環境条件(温度,雪,氷など)及び電力系統の条件を包含する風車の運転に影響を与える因子。
3.18
極値風速(extreme wind speed)
t秒間で平均した最大風速で,年超過確率1/N(“再現期間”:N年)をもつ。
注記 この規格では,再現期間N=50年及びN=1年,並びに平均時間t=3秒及びt=10分を用いる。
平易な言葉では,耐風速という,あまり正確ではない用語がしばしば用いられる。しかし,こ
5
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の規格では,風車は,設計荷重ケースとして極値風速を用いて設計される。
3.19
フェイルセーフ(fail-safe)
故障の発生が重大な障害につながることを防止する設計上の特質。
3.20
ガスト(gust)
風速の瞬間的な増加。突風ともいう。
注記 ガストは,立ち上がり時間,振幅及び継続時間で特徴付けてもよい。
3.21
水平軸風車(horizontal axis wind turbine)
ロータの回転軸がほぼ水平な風車。
3.22
(風車の)ハブ[hub (wind turbines)]
翼又は翼組立品をロータ軸に取り付ける固定部品。
3.23
(風車の)ハブ高さ[hub height (wind turbines)],zhub
風車ロータの受風面中心の地上からの高さ(3.51参照)。
3.24
(風車の)アイドリング[idling (wind turbines)]
低速回転しているが,電力を発生していない風車の状態。
3.25
慣性小領域(inertial sub-range)
風の乱流スペクトルの周波数間隔であって,渦が等方性になった後,次々に小さなスケールになる過程
におけるエネルギー散逸が無視できるもの。
注記 風速10 m/sの場合,慣性小領域は,約0.2 Hzから1 kHzまでである。
3.26
限界状態(limit state)
構造物及びそれに作用する荷重の状態であって,それを超えると構造物が設計要件に満足しなくなる状
態(ISO 2394の2.2.9を修正)。
注記 設計計算(すなわち,限界状態に対する設計要件)の目的は,限界状態になる確率を対象の構
造物の種類に対して規定されたある値以下に抑えることである(ISO 2394の2.2.9参照)。
3.27
ウィンドシアーの対数則(logarithmic wind shear law)
3.62参照。
3.28
平均風速(mean wind speed)
数秒から数年を変数とする所定期間内で平均化した風速の瞬時値の統計的平均。
3.29
ナセル(nacelle)
水平軸風車において,タワーの頂部に配置され,動力伝達装置,その他の構成要素を格納するもの。
6
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.30
(風車の)電力系統への接続端[network connection point (wind turbines)]
単一風車の場合,ケーブル端子。風力発電所の場合,サイトの集電設備の母線との接続点。
3.31
電力系統の喪失(network loss)
風車制御システムの事故時運転継続(FRT)の規定時間を超える停電。
3.32
(風車の)通常停止[normal shutdown (wind turbines)]
全ての段階が制御システムの制御下にある停止。
3.33
動作限界値(operating limits)
風車設計者によって設定された,制御システム及び保護システムの動作を支配する条件のセット。
3.34
待機中の風車(parked wind turbine)
静止又はアイドリングのいずれかの状態の風車。静止又はアイドリングのいずれかは,風車の設計によ
る。
3.35
集電設備[power collection system (wind turbines)]
1台以上の風車から電力を集める集電システム。これには,風車接続端と電力系統への接続端との間を
接続する全ての電気設備を含む。
3.36
ウィンドシアーの指数則(power law for wind shear)
3.62参照。
3.37
出力(power output)
特定の形態で,かつ,特定の目的のために,装置によって供給される電力。
注記 風車の場合,風車によって供給される電力をいう。
3.38
保護機能[protection functions (wind turbine)]
風車を設計限界値内に保つことを保証する制御システム及び保護システムの機能。
3.39
定格出力(rated power)
部品,デバイス又は機器の特定の運転条件に対して,一般に製造業者が指定する出力の値。
注記 風車の場合,通常の運転条件及び外部条件下で供給するよう設計されている(風車の)最大連
続電気出力をいう。
3.40
定格風速(rated wind speed),Vr
乱流がない定常風の場合に,風車の定格出力に到達するハブ高さにおける最小の風速。
3.41
レイリー分布(Rayleigh distribution),PR
7
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
確率分布関数の一つ(3.63参照)。
3.42
基準風速(reference wind speed),Vref
風車クラスを定義するために用いる風速の基本パラメータ。その他の設計に関係する気象パラメータは,
基準風速,その他の基本風車クラスパラメータから導かれる(箇条6参照)。
注記 基準風速Vrefの風車クラスで設計された風車は,風車のハブ高さにおける再現期間50年の10
分平均極値風速がVref以下の風速に耐えるように設計する。
3.43
回転サンプル風速度(rotationally sampled wind velocity)
回転する風車ロータのある点から見た風速度。
注記 回転サンプル風速度の乱流スペクトルは,通常の乱流スペクトルとは異なる。回転中に,翼は
風の流れを切るが,流れは空間的に変化している。そのため,その結果としての乱流スペクト
ルは,回転周波数及びその高調波において相当量の分散を含んでいる。
3.44
ロータ回転数[rotor speed (wind turbines)]
風車ロータの軸回りの回転数。
3.45
粗度長(roughness length),z0
鉛直方向の風速プロファイルが,高さに対して対数的に変化すると仮定した場合,平均風速が0となる
外挿高さ。
3.46
計画保守(scheduled maintenance)
指定の計画に従って実施する予防的保守。
3.47
サイトのデータ(site data)
風車サイト(設置場所)の環境,地震,土壌及び電力系統のデータ。風のデータは,特に記載がない場
合,10分サンプルの統計とする。
3.48
静止(standstill)
風車が止まっている状態。
3.49
(風車の)支持構造物[support structure (wind turbines)]
タワー及び基礎からなる風車の一部。
3.50
耐風速(survival wind speed)
構造物が耐えるよう設計されている最大風速に対する慣用名称。
注記 この規格では,この用語は用いていない。設計条件では,その代わりに“極値風速”を用いる
(3.18参照)。
3.51
受風面(swept area)
8
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ロータが1回転中に描く平面を,風向に対して垂直に投影した面。
3.52
乱流強度(turbulence intensity),I
平均風速に対する風速の標準偏差の比。この比は,指定する時間内に取得した風速測定データサンプル
と同一のデータセットから決定する。
3.53
乱流尺度パラメータ(turbulence scale parameter),Λ1
主方向無次元パワースペクトル密度が0.05に等しい場合の波長。
注記 この波長は,f0S1(f0)/σ12=0.05で定義される。ここに,Λ1=Vhub/f0 。
3.54
乱流標準偏差(turbulence standard deviation),σ1
ハブ高さにおける乱流風速度の主方向成分の標準偏差。
3.55
終極限界状態(ultimate limit state)
一般に最大耐荷重能力に相当する限界状態(ISO 2394の2.2.10を修正)。
3.56
計画外保守(unscheduled maintenance)
指定の計画保守ではなく,ある項目の状態に関して指摘を受けて実施する保守。
3.57
風上(upwind)
風下(主風向)と反対の方向。
3.58
垂直軸風車(vertical axis wind turbine)
ロータ軸が風の流れに対して,おおむね垂直な風車。
3.59
ワイブル分布(Weibull distribution),PW
確率分布関数の一つ(3.63参照)。
3.60
ウィンドファーム(wind farm)
3.61参照。
3.61
風力発電所(wind power station)
一群又は多群の風車。通常は,ウィンドファームという。
3.62
(ウィンドシアー則における)風速プロファイル(wind profile-wind shear law)
地上高さに対する風速の変化に対して仮定される数学表現。
注記 通常,プロファイルは,ウィンドシアーの対数則では式(1),又はウィンドシアーの指数則では
式(2)が用いられる。
9
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
=
0
r
0
r
ln
ln
)
(
)
(
z
z
z
z
z
V
z
V
·································································· (1)
α
z
z
z
V
z
V
=
r
r)
(
)
(
····································································· (2)
ここに,
V(z): 高さzにおける風速
z: 地上高さ
zr: プロファイルを合わせるために用いられる基準地上高さ
z0: 粗度長
α: ウィンドシアー(指数則)の指数
3.63
風速分布(wind speed distribution)
ある長時間内の風速の分布を記載するのに用いる確率分布関数。
注記 よく用いられる分布関数は,式(3)に示すレイリー分布関数PR(V0)及びワイブル分布関数PW(V0)
である。
=
=
k
C
V
V
P
V
V
V
P
0
0
W
2
ave
0
0
R
exp
1
)
(
2
π
exp
1
)
(
−
−
−
−
························································ (3)
ただし,
=
=
の場合)
(
+
2
2
π
1
1
ave
k
C
k
CΓ
V
································· (4)
ここに, P(V0): 累積確率関数,すなわち,V<V0の確率
V0: 限界風速
Vave: 風速Vの平均値
C: ワイブル分布関数の尺度パラメータ
k: ワイブル分布関数の形状パラメータ
Γ: ガンマ関数
C及びkは,実際のデータから求めてもよい。レイリー分布関数は,k=2,かつ,C及びVave
がk=2の場合の式(4)で表す条件を満足する場合のワイブル分布関数に等しい。
分布関数は,風速がV0よりも小さい累積確率を表す。したがって,[P(V1)−P(V2)]は,指定し
た範囲V1とV2との間で求めた場合,風速がこれらの範囲内にあるのは時間にしてどのくらい
の割合かを示す。分布関数を微分することで,それに対応する確率密度関数が得られる。
3.64
ウィンドシアー(wind shear)
風向に対して垂直な面上の風速変化。
3.65
ウィンドシアーの指数(wind shear exponent),α
10
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ウィンドシアーの指数則の指数(3.62参照)。
3.66
風速(wind speed),V
空間中の指定する点において,その指定点周りの微小量の大気の運動速度。
注記 風速は,また,局所の風速度(ベクトル)の大きさである(3.69参照)。
3.67
風力発電システム(風車)[wind turbine generator system (wind turbine)]
風の運動エネルギーを電気エネルギーに変換するシステム。
3.68
風車サイト(wind turbine site)
単独又はウィンドファーム内の個々の風車の位置。
3.69
風速度(wind velocity)
対象点の微小量の大気の運動の方向を示すベクトル。その大きさは,この大気の“かたまり”の運動速
度に等しい。
注記 したがって,任意点の速度は,その点を通って移動する大気のかたまりの位置ベクトルの時間
微分である。
3.70
風車の電気システム(wind turbine electrical system)
接地,ボンディング及び通信機器を含む,風車接続端に至るまでの風車内部の全ての電気設備。特に,
風車に接地回路を提供する風車近くに配置された導体を含む。
3.71
風車接続端(wind turbine terminals)
風車が集電設備に接続でき,風車の供給者によって特定される接続点。これは,電力の伝送及び通信の
ための接続を含む。
3.72
ヨー運動(yawing)
鉛直軸周りのロータ軸の回転(水平軸風車だけに適用)。
3.73
ヨーミスアラインメント(yaw misalignment)
風車のロータ軸の風向に対する水平偏向量。
4
記号及び略語
4.1
記号及び単位
この規格で用いる記号の意味及び単位は,次による。
C
ワイブル分布関数の尺度パラメータ
(m/s)
CCT
乱流構造補正パラメータ
(−)
CT
スラスト(thrust)係数
(−)
Coh
コヒーレンス(coherence)関数
(−)
D
ロータ直径
(m)
11
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
f
周波数
(Hz)
fd
材料強度の設計値
(−)
fk
材料強度の特性値
(−)
Fd
荷重の設計値
(−)
Fk
荷重の特性値
(−)
Iref
10分平均風速15 m/sでのハブ高さにおける乱流強度の期待値
(−)
Ieff
有効乱流強度
(−)
k
ワイブル分布関数の形状パラメータ
(−)
K
修正ベッセル関数
(−)
L
等方性乱流積分尺度パラメータ
(m)
Le
コヒーレンス尺度パラメータ
(m)
Lk
速度成分積分尺度パラメータ
(m)
m
Wöhler曲線(材料のS-N曲線)の指数
(−)
ni
荷重ビン(bin)iの疲労サイクルのカウント数
(−)
N(.)
引数によって与えられる範囲(すなわち,S-N曲線)で,一定の大きさの荷重に対し
て破損に至るまでのサイクル数
(−)
N
極値状態の再現期間
(年)
p
生存確率
(−)
PR(V0)
レイリー分布,すなわち,V<V0となる確率
(−)
PW(V0)
ワイブル分布
(−)
r
投影された距離ベクトルの大きさ
(m)
si
ビンi内のサイクル数に関連する応力(又はひずみ)レベル
(−)
S1(f)
風速度の主方向成分パワースペクトル密度関数
(m2/s)
Sk
風速度の一方向成分スペクトル
(m2/s)
T
ガスト特性時間
(秒)
t
時間
(秒)
V
風速
(m/s)
V(z)
高さzにおける風速
(m/s)
Vave
ハブ高さにおける年平均風速
(m/s)
Vcg
ロータの全受風面における極値コヒーレントガストの大きさ
(m/s)
VeN
極値風速の3秒間平均期待値,再現時間間隔N年。Ve1及びVe50は,それぞれ1年
及び50年に対応する。
(m/s)
Vgust
期待再現期間50年におけるガストの大きさの最大値
(m/s)
Vhub
ハブ高さにおける風速
(m/s)
Vin
カットイン風速
(m/s)
V0
風速分布モデルにおける限界風速
(m/s)
Vout
カットアウト風速
(m/s)
Vr
定格風速
(m/s)
Vref
基準風速
(m/s)
V(y, z, t) 水平ウィンドシアーの時間変化として記述する風速度の主方向成分
(m/s)
12
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
V(z,t)
極値ガスト及びシアー条件の時間変化として記述する風速度の主方向成分
(m/s)
x, y, z
風の流れ場の記述に用いる座標系。風の方向(主方向),風と直角方向(横方向)及
び鉛直方向に対応する。
(m)
zhub
風車のハブ高さ
(m)
zr
基準地上高さ
(m)
z0
対数風速プロファイルの粗度長
(m)
α
ウィンドシアーの指数
(−)
β
極値風向変化モデルのパラメータ
(−)
δ
変動係数
(−)
Γ
ガンマ関数
(−)
γf
荷重の部分安全率
(−)
γm
材料の部分安全率
(−)
γn
損傷結果に対する部分安全率
(−)
θ(t)
風向の時間変化
(°)
θcg
ガスト時における平均風速方向からの最大角度偏差
(°)
θeN
再現期間N年の極値風向変化
(°)
Λ1
主方向無次元パワースペクトル密度fS1(f)/σ12が0.05に等しくなる場合の波長として定
義する乱流尺度パラメータ
(m)
σˆ
予想乱流標準偏差
(m/s)
eff
ˆσ
有効予想乱流標準偏差
(m/s)
σwake
風車後流乱流標準偏差
(m/s)
Tˆσ
最大風車後流中心乱流標準偏差
(m/s)
σ
σˆ
予想乱流標準偏差σˆの標準偏差
(m/s)
σ1
ハブ高さにおける風速度の主方向成分の標準偏差
(m/s)
σ2
ハブ高さにおける風速度の横方向成分の標準偏差
(m/s)
σ3
ハブ高さにおける風速度の上方向成分の標準偏差
(m/s)
E〈 〉
括弧内のパラメータの期待値
(−)
Var〈 〉 括弧内のパラメータの分散
(−)
4.2
略語
この規格で用いる略語の意味は,次による。
A
(部分安全率の)異常設計条件(abnormal)
a.c.
交流
d.c.
直流
DLC
設計荷重ケース(design load cases)
ECD
風向変化を伴う極値コヒーレントガスト(extreme coherent gust with direction change)
EDC
極値風向変化(extreme direction change)
EOG
運転中の極値ガスト(extreme operating gust)
ETM
極値乱流モデル(extreme turbulence model)
EWM
極値風モデル(extreme wind speed model)
EWS
極値ウィンドシアー(extreme wind shear)
13
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
F
疲労(fatigue)荷重の解析
N
(部分安全率の)通常又は極値の設計条件(normal and extreme)
NWP
通常風速プロファイルモデル(normal wind profile model)
NTM
通常乱流モデル(normal turbulence model)
S
風車クラスS(special wind turbine category)
T
(部分安全率の)輸送及び建設の設計条件(transport and erection)
U
終極(ultimate)荷重の解析
5
主要構成要素
5.1
一般事項
風車の構造,機械システム,電気システム及び制御システムの安全性を確保するための工学的及び技術
的要求事項を,5.2〜5.5に規定する。この要求事項からなる仕様書は,風車の設計,製造,据付け,運転・
保守マニュアル,及びそれらに関連した品質マネジメントプロセスに適用する。さらに,風車の据付け,
運転及び保守に用いる様々な方法において確立されている安全手順を考慮する。
5.2
設計方法
この規格は,設計上の荷重を予測するために構造動力学モデルの使用を要求する。そのようなモデルは,
箇条6に規定する乱流条件などの風条件及び箇条7に規定する設計条件を用いて,風速範囲にわたって荷
重を決定するために用いる。関係する外部条件と設計条件との組合せの全てを解析する。この規格におい
ては,この組合せの最小セットを設計荷重ケースとして定義する。
予測設計値の信頼性を高め,かつ,構造動力学モデル及び設計条件を検証するために,風車のフルスケ
ール試験データを用いることができる。
設計の妥当性の検証は,計算及び/又は試験で行う。この検証で試験結果を用いる場合,この規格中で
定義する特性値及び設計条件を反映するために,試験中の外部条件を示す。試験条件を選択する場合には,
試験荷重を含む,関連する安全率を考慮する。
5.3
安全カテゴリ
風車は,次の二つの安全カテゴリのいずれかに従って設計する。
− 通常安全カテゴリ 故障が人身の傷害又は経済的及び社会的影響を起こすリスクのある場合に適用す
る。
− 特別安全カテゴリ 安全要求事項が我が国の法規制によって決まる場合及び/又は追加の安全要求事
項が受渡当事者間で合意される場合に適用する。
通常安全カテゴリの風車に対する部分安全率は,7.6の規定による。
特別安全カテゴリの風車に対する部分安全率は,受渡当事者間の合意による。特別安全カテゴリに基づ
いて設計された風車は,6.2に定義する風車クラスSの風車である。
5.4
品質保証
品質保証は,風車及びその全ての部品の設計,調達,製造,据付け,運転及び保守において不可欠であ
る。
品質システムは,JIS Q 9001の要求事項に適合することが望ましい。
5.5
風車銘板
風車の銘板には,次の事項を明瞭で,かつ,消えないように表示する。
− 風車製造業者名及び国名
14
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 形名及び製造番号
− 製造年
− 定格出力
− 基準風速,Vref
− ハブ高さの運転風速範囲,Vin〜Vout
− 運転周囲温度範囲
− 風車クラス(表1参照)
− 風車接続端での定格電圧
− 風車接続端での周波数又は公称変動範囲が2 %を超える場合には,その周波数の範囲。
6
外部条件
6.1
一般事項
風車の設計においては,この箇条に記載する外部条件を考慮する。
風車は,荷重,耐久性及び運転に影響する,環境条件及び電気的条件の影響を受ける。適切なレベルの
安全性及び信頼性を確保するために,環境,電気及び土壌のパラメータを考慮して設計し,これらのパラ
メータは,設計文書に明確に記載する。
環境条件は,風条件,その他の環境条件に分けられる。電気的条件は,電力系統の条件に関係する。土
壌特性は,風車の基礎の設計に関係する。
各外部条件は,通常及び極値の条件に分けられる。通常外部条件とは,一般的に周期的に起きる構造荷
重条件に関係するものである。一方,極値外部条件とは,頻度としてはまれに起きる外部設計条件を示す。
設計荷重ケースは,風車の運転モードなどの設計条件とこれらの外部条件との潜在的に危険な組合せであ
る。
風条件は,構造的な健全性に影響する主な外部条件である。その他の環境条件は,制御システム機能,
耐久性,腐食などの設計仕様に影響する。
風車クラス別の設計に必要な通常条件及び極値条件を,6.2〜6.5に示す。
6.2
風車クラス
設計において考慮する外部条件は,風車を据付けしようとするサイト又はサイトの種類によって異なる。
風車のクラスは,風速及び乱流パラメータによって定義する。この分類の目的は,大多数のサイトをカバ
ーすることである。風速及び乱流パラメータの値は,多くの異なるサイトを代表するために定めており,
個々のサイトの固有条件を正確に表現するためのものではない(11.3参照)。風車のクラス分けは,風速及
び乱流パラメータによって,明確に定義された風車全体の強度範囲を提供する。表1は,風車クラスを定
義する基本パラメータを示している。
特殊な風条件などの外部条件又は特別安全カテゴリ(5.3参照)が設計者又は顧客によって要求される場
合には,追加のクラスとして,風車クラスSを設定する。風車クラスSに対する設計値は,設計者が定め,
設計文書に記載して指定する。このような特殊設計の場合には,風車を用いる上で想定される苛酷さと同
程度以上の環境条件を,設計条件として選択する値に反映させる。
注記 洋上条件,又はハリケーン,サイクロン,台風のような熱帯性低気圧が発生する場合で,風車
クラスI,II及びIIIとして定義された風条件から逸脱する条件に対しては,風車クラスS又は
附属書JAの風車クラスTの設計が必要な場合がある。さらに,高乱流カテゴリAとして定義
する風条件から逸脱する条件に対しては,附属書JAの極高乱流カテゴリA+が必要な場合があ

15
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
表1−風車クラスの基本パラメータa)
パラメータ
風車クラス
I
II
III
S
Vref(m/s)
50
42.5
37.5
設計者が指
定する数値
乱流カテゴリAにおけるIref(−)
0.16
乱流カテゴリBにおけるIref(−)
0.14
乱流カテゴリCにおけるIref(−)
0.12
この表の値は,ハブ高さにおいて適用する。
Vref
:10分平均基準風速
A
:高乱流カテゴリの場合に選定
B
:中乱流カテゴリの場合に選定
C
:低乱流カテゴリの場合に選定
Iref
:風速が15 m/sのときの乱流強度b) の期待値
注記 風車クラスは,乱流カテゴリと組み合わせて用いられる(例 乱流カテゴリAを想
定したクラスIの場合,クラスIA)。
注a) 年平均風速Vaveは,この規格の風車クラスの基本パラメータとして用いない。これ
らのクラスの風車設計に対する年平均風速は,式(9)で表す。
b) Irefは,この規格では代表値ではなく,平均値として定義されていることに注意する。
風車クラスSを除く,クラスIAからIIICまでを,標準風車クラスと呼ぶ。
風車設計で用いる外部条件を全て特定するには,これらの基本パラメータのほかに,幾つかの重要な追
加パラメータが必要である。標準風車クラスに対する追加パラメータは,6.3〜6.5に示す。
風車クラスI〜IIIの設計寿命は,20年以上とする。
風車クラスSの風車については,製造業者は設計文書に,用いたモデル及び設計パラメータの値を記載
する。この箇条6に規定するモデルを採用する場合には,パラメータの値を記載するだけでよい。風車ク
ラスSの設計文書には,附属書Aに規定する情報を記載する。
6.3内の細分箇条の見出しに括弧書きで追加した略語は,7.4で定義する設計荷重ケースの風条件を記載
するときに用いる。
6.3
風条件
風車は,選択した風車クラスで定義された風条件に対して,安全に耐えるように設計する。
風条件の設計値は,設計文書に明確に記載して指定する。
荷重及び安全を考慮する場合,風条件は,風車の通常の運転中に頻繁に発生する通常風条件と,1年又
は50年の再現期間で定義される極値風条件とに分類される。
風条件は,多くの場合,一定の平均流と,変動する決定論的なガストプロファイル又は乱流のいずれか
との組合せで表現される。全てにおいて,水平面に対して最大8°までの平均流の傾斜角による影響を考
慮する。なお,この傾斜角は,高さ方向に変化しないものと仮定する。
“乱流”とは,10分間の平均値からの,風速度のランダムな変化を意味する。乱流モデルを用いる場合,
モデルは変動する風速,ウィンドシアー及び風向の影響を含み,かつ,ウィンドシアーを変化させること
によって回転サンプリング(風車の回転時の検出ポイント)を考慮できるものとする。
なお,乱流の風速度の3方向成分は,次のように定義する。
− 主方向−平均風速度の方向
− 横方向−水平かつ主方向に直角
16
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 上方向−主方向及び横方向に対して直角方向,すなわち,鉛直方向から平均流の傾斜角分だけ傾いた
方向。
標準風車クラスの場合,乱流モデルにおけるランダムな風の速度場は,次の条件を満足させる。
a) 6.3.1及び6.3.2で与える値をもつ乱流標準偏差σ1は,高さによって不変であると仮定する。平均風向
に直角な成分は,次に示す標準偏差1) とする。
− 横方向成分:σ2≧0.7σ1
− 上方向成分:σ3≧0.5σ1
注1) 実際の値は,乱流モデルの選択及びb)の要求事項に依存する。
b) ハブ高さzにおける主方向乱流尺度パラメータΛ1は,式(5)による。
m
60
m
42
m
60
7.0
1
≧
≦
=
z
z
z
Λ
······························································· (5)
パワースペクトル密度の三つの直交成分S1(f),S2(f)及びS3(f)は,慣性小領域中の周波数の増加に伴
って,式(6)及び式(7)に漸近する。
3
5
3
2
hub
1
2
1
1
05
.0
)
(
−
−
=
f
V
Λ
σ
f
S
·························································· (6)
)
(
3
4
)
(
)
(
1
3
2
f
S
f
S
f
S
=
=
······························································· (7)
c) 既知のコヒーレンスモデルを用いる。コヒーレンスモデルは,自己スペクトルによって分割された,
主方向に直角な面において空間的に離れた2点での主方向速度成分のコスペクトルの大きさによって
定義する。
これらの要求事項を満たす推奨乱流モデルとして,附属書Bに記載するMannの一様シアー乱流モデル
がある。これらの要求事項を満たす,よく用いられる他のモデルも,附属書Bに記載する。これら以外の
乱流モデルの使用を選択する場合には,荷重に大きく影響することがあるため,慎重に行うことが望まし
い。
6.3.1
通常風条件
6.3.1.1
風速分布
風速分布は,通常設計条件におけるそれぞれの荷重条件の発生頻度を決定するため,風車設計において
重要である。10分間の風速の平均値は,式(8)で表すハブ高さにおけるレイリー分布に従うと仮定する。
−
=
2
ave
hub
hub
R
2
π
exp
1
)
(
V
V
V
P
−
······················································ (8)
ここに,標準風車クラスでは,Vaveは,式(9)によって選定する。
Vave=0.2 Vref ·············································································· (9)
6.3.1.2
通常風速プロファイルモデル(NWP)
風速プロファイルV(z)は,平均風速を地上高さzの関数で表したものである。標準風車クラスの場合,
通常風速プロファイルは,式(10)の指数法則による。
α
z
z
V
z
V
=
hub
hub
)
(
···································································· (10)
17
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ウィンドシアーの指数αは,0.2とする。
仮定した風速プロファイルを用いて,ロータの受風面の高さ方向の平均鉛直ウィンドシアーを定義する。
6.3.1.3
通常乱流モデル(NTM)
通常乱流モデル(NTM)では,乱流標準偏差σ1の代表値は,所定のハブ高さにおける風速の90 %分位
値2) によって与える。標準風車クラスに対するこの値は,式(11)による。
σ1=Iref(0.75 Vhub+b) ここに,b=5.6(m/s) ······························(11)
注2) 追加の荷重計算において他の分位値が必要な場合には,標準風車クラスに対しては対数正規分
布を仮定することによって近似してもよい。
2
ref
hub
1
hub
ref
hub
1
)]
s
m
4.1(
[
m/s
8.3
)
75
.0(
/
I
V
σ
Var
c
c
V
I
V
σ
E
=
〉
〈
=
=
〉
〈
)
(
ここに,
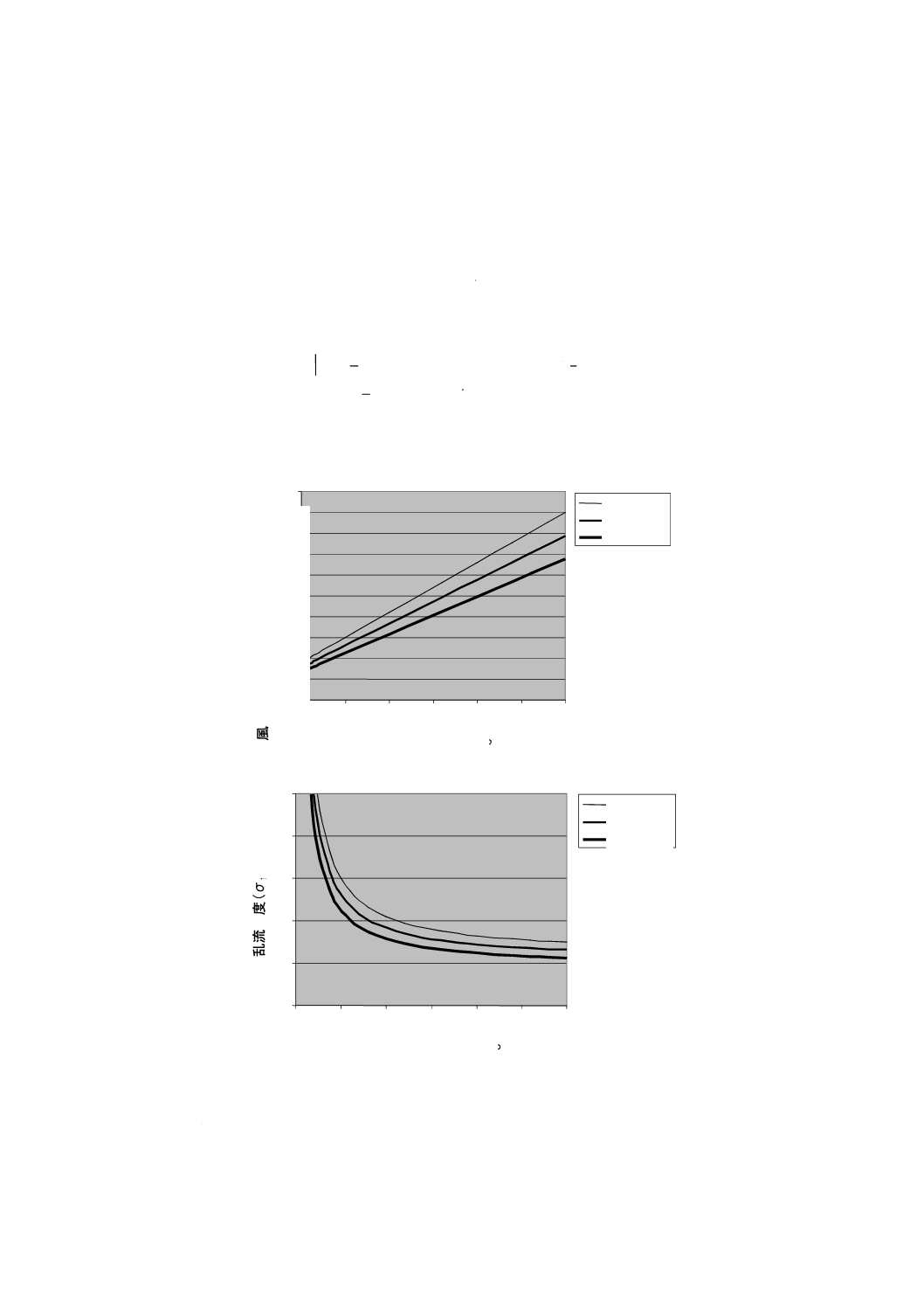
+
乱流標準偏差σ1及び乱流強度σ1/Vhubの値を,図1 a)及び図1 b)に示す。
Irefは,表1の値を用いる。
0
0.5
1
15
2
2.5
3
3.5
4
4.5
5
0
5
10
15
20
25
30
ハブ高さにおける風速Vhub (m/s)
風
速
度
の
主
方
向
成
分
の
標
準
偏
差
σ
1
(
m
/s
)
カテゴリA
カテゴリB
カテゴリC
a) 通常乱流モデル(NTM)の乱流標準偏差
0
0.1
0.2
0.3
0.4
0.5
0
5
10
15
20
25
30
ハブ高さにおける風速Vhub (m/s)
カテゴリA
カテゴリB
カテゴリC
乱
流
強
度
(
σ
1
/Vh
u
b
)
b) 通常乱流モデル(NTM)の乱流強度
図1−通常乱流モデル(NTM)
6.3.2
極値風条件
極値風条件には,暴風による極大風速,風速及び風向の急激な変化などのほか,ウィンドシアーに関す
18
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る事象も含む。
6.3.2.1
極値風モデル(EWM)
極値風モデルは,定常又は乱流いずれかの風モデルとする。ここで,風モデルは,基準風速Vref及びあ
る一定の乱流標準偏差σ1に基づいている。
定常極値風モデルにおいて,再現期間50年の極値風速Ve50及び再現期間1年の極値風速Ve1を,高さz
の関数として式(12)及び式(13)を用いて計算する。
11
.0
hub
ref
50
e
4.1
zz
V
z
V
=
)
(
···························································· (12)
Ve1(z)=0.8 Ve50(z)······································································ (13)
定常極値風モデルでは,±15°の範囲で一定のヨーミスアラインメントを仮定することによって,短時
間の平均風向からの偏向を設定する。
乱流極値風モデルでは,10分平均風速は,zの関数として,50年及び1年の再現期間で式(14)及び式(15)
による。
11
.0
hub
ref
50)
(
zz
V
z
V
=
································································ (14)
V1(z)=0.8 V50(z) ······································································· (15)
主方向乱流標準偏差3) は,式(16)による。
σ1=0.11 Vhub············································································ (16)
注3) 乱流極値風モデルの乱流標準偏差は,通常乱流モデル(NTM)又は極値乱流モデル(ETM)に
関係付けられない。定常極値風モデルは,約3.5のピーク係数によって,乱流極値風モデルに
関係付けられる。
6.3.2.2
運転中の極値ガスト(EOG)
ハブ高さにおける極値ガストの大きさVgust 4) は,標準風車クラスでは,式(17)による。
(
)
=
1
1
hub
1
e
gust
1.0
1
3.3
;
35
.1
Min
Λ
D
σ
V
V
V
+
−
································· (17)
ここに,
σ1: 式(11)による。
Λ1: 式(5)による乱流尺度パラメータ
D: ロータ直径
注4) この式においてガストの大きさは,起動及び停止のような運転事象の発生頻度とともに,50年
再現期待値を考慮して校正した。
風速は,式(18)に定義する。
=
)
上記以外の場合
(
)
の場合
≦
≦
(
−
−
)
(
0
π
2
cos
1
π
3
sin
37
.0
)
(
)
,
(
gust
z
V
T
t
T
t
T
t
V
z
V
t
z
V
······· (18)
ここに,
V(z): 式(10)に定義する。
T= 10.5(秒)
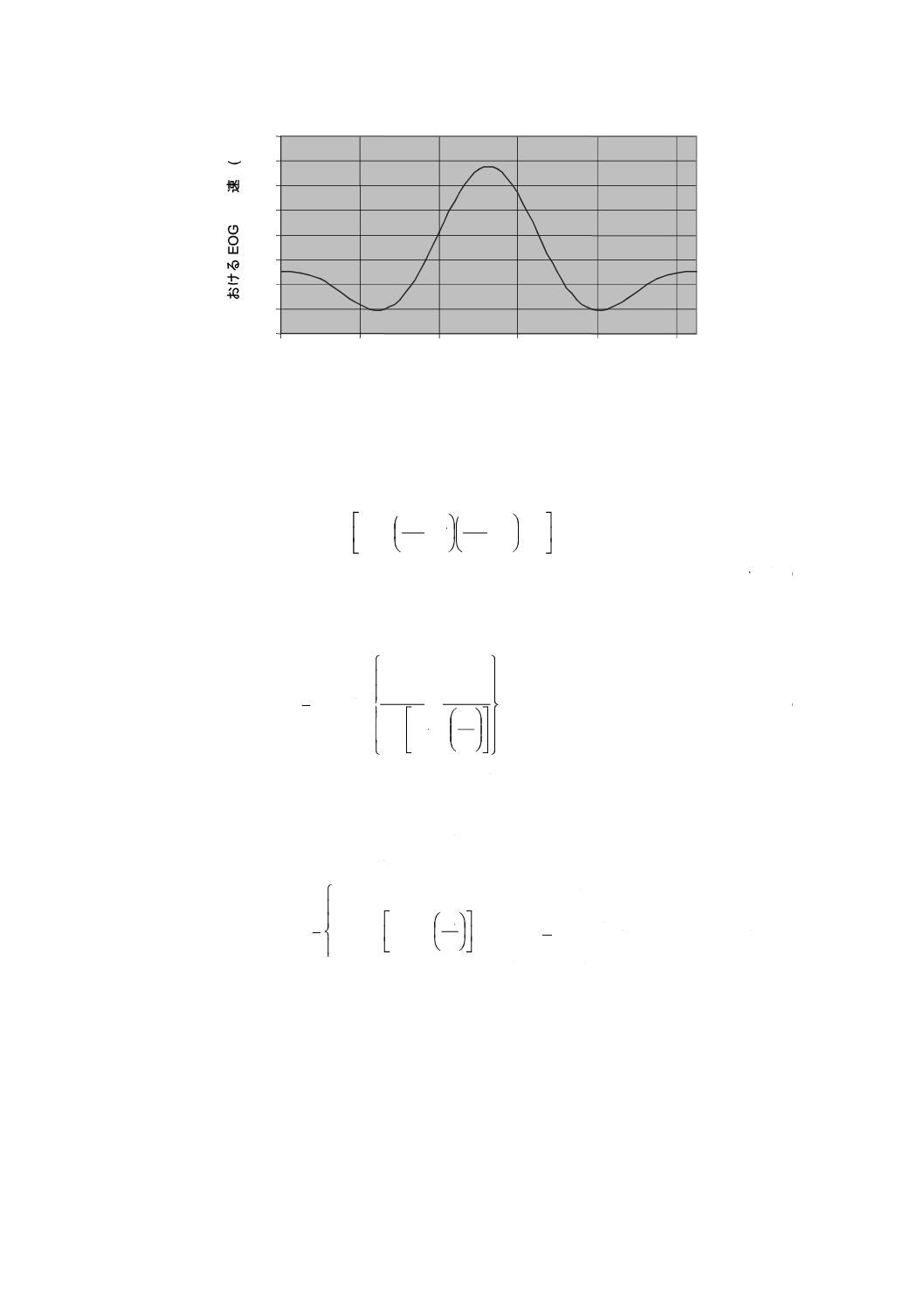
運転中の極値ガストの例[Vhub=25(m/s),クラスIA,D=42(m)]を,図2に示す。
19
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
20
22
24
26
28
30
32
34
36
0
2
4
6
8
10
時間 t (s)
ハ
ブ
高
さ
に
お
け
る
E
O
G
の
風
速
(m
/s
)
図2−運転中の極値ガストの例
6.3.2.3
極値乱流モデル(ETM)
極値乱流モデルは,6.3.1.2の通常風速プロファイルモデルと主方向との標準偏差が,式(19)による乱流
を用いる。
10
4
3
072
.0
hub
ave
ref
1
+
−
+
=
c
V
c
V
I
c
σ
ここに,c=2(m/s)································································ (19)
6.3.2.4
極値風向変化(EDC)
極値風向変化の大きさθeは,式(20)を用いて計算する。
+
±
=
1
hub
1
e
1.0
1
arctan
4
Λ
D
V
σ
θ
················································· (20)
ここに,
σ1: 通常乱流モデルの式(11)による。
θe: ±180°の間に制限される。
Λ1: 式(5)による乱流尺度パラメータ
D: ロータ直径
過渡的な極値風向の時間変化θ (t)は,式(21)による。
±
°
=
)
の場合
>
(
)
の場合
≦
≦
(
−
)
の場合
<
(
T
t
θ
T
t
T
t
θ
t
t
θ
e
e
0
π
cos
1
5.0
0
0
)
(
··························· (21)
ここに,T=6秒は,極値風向変化の継続時間である。また,符号は最悪の過渡的荷重が生じるように選
択する。風向変化の過渡的状態が終了した後は,風向は変わらないものと仮定する。風速は,6.3.1.2に規
定する通常風速プロファイルモデルに従う。
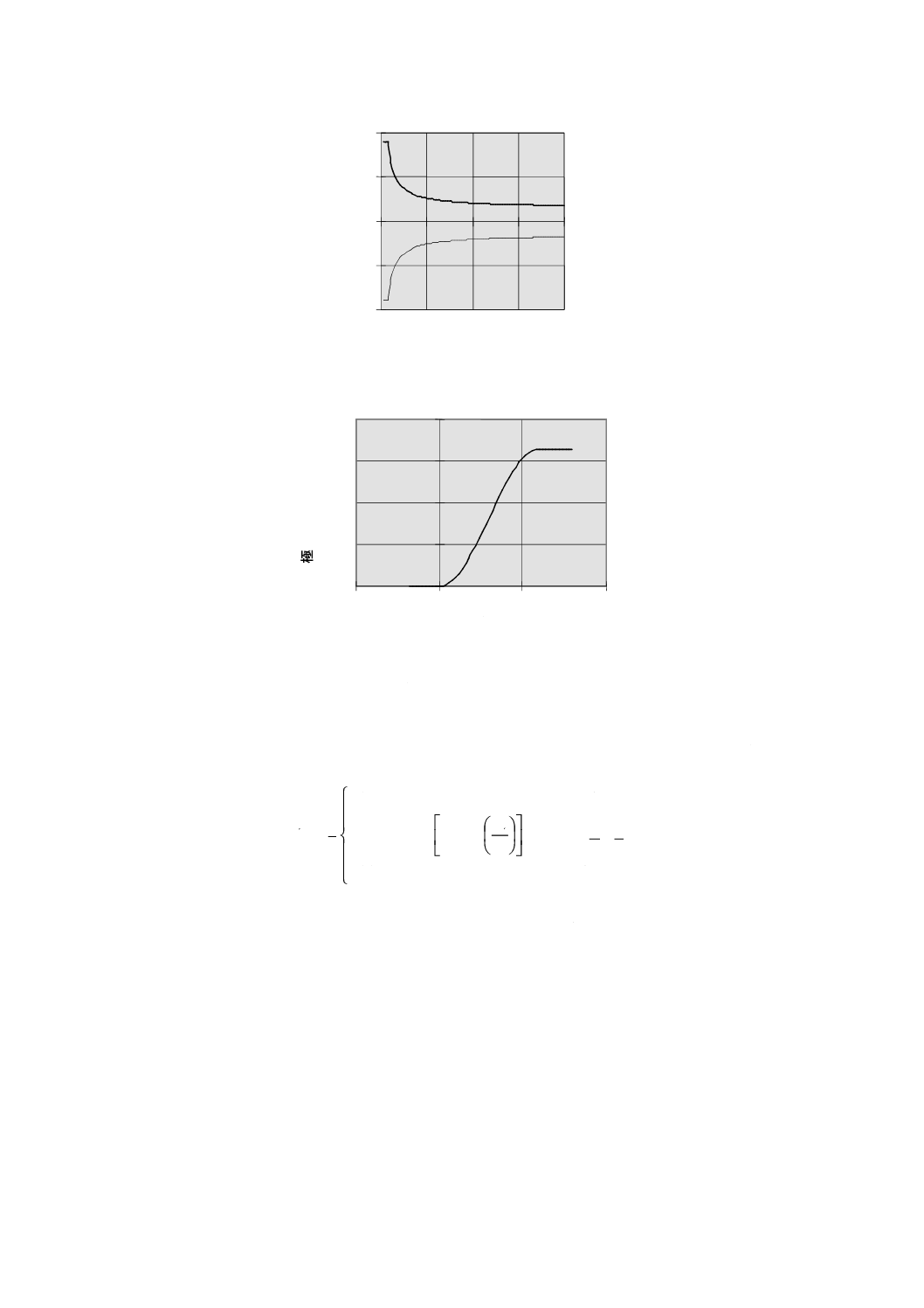
ここで,例として,乱流カテゴリA,D=42(m),zhub=30(m)におけるVhubの変化に対する極値風向
変化の大きさを,図3に示す。また,Vhub=25(m/s)における風向変化の時間変化を,図4に示す。
20
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
‒200
‒100
0
100
200
0
10
20
30
40
風速 Vhub (m/s)
極
値
風
向
変
化
θ
e
(
°)
図3−極値風向変化の大きさの例
0
10
20
30
40
‒5
0
5
10
時間 t (s)
極
値
風
向
変
化
θ
(t
)
(
°)
図4−極値風向変化の時間変化の例
6.3.2.5
風向変化を伴う極値コヒーレントガスト(ECD)
風向変化を伴う極値コヒーレントガストは,式(22)で表す大きさをもつ。
Vcg=15(m/s) ········································································ (22)
風速の時間変化は,式(23)に定義する。
=
の場合)
>
(
+
の場合)
≦
≦
(
−
+
の場合)
<
(
T
t
V
z
V
T
t
T
t
V
z
V
t
z
V
t
z
V
cg
cg
)
(
0
π
cos
1
5.0
)
(
0
)
(
)
,
(
············· (23)
ここに,T=10(秒)は,立ち上がり時間で,風速V(z)は,6.3.1.2に規定する通常風速プロファイルモデ
ルによる。Vhub=25(m/s)における極値コヒーレントガスト中の風速の立ち上がり例を,図5に示す。
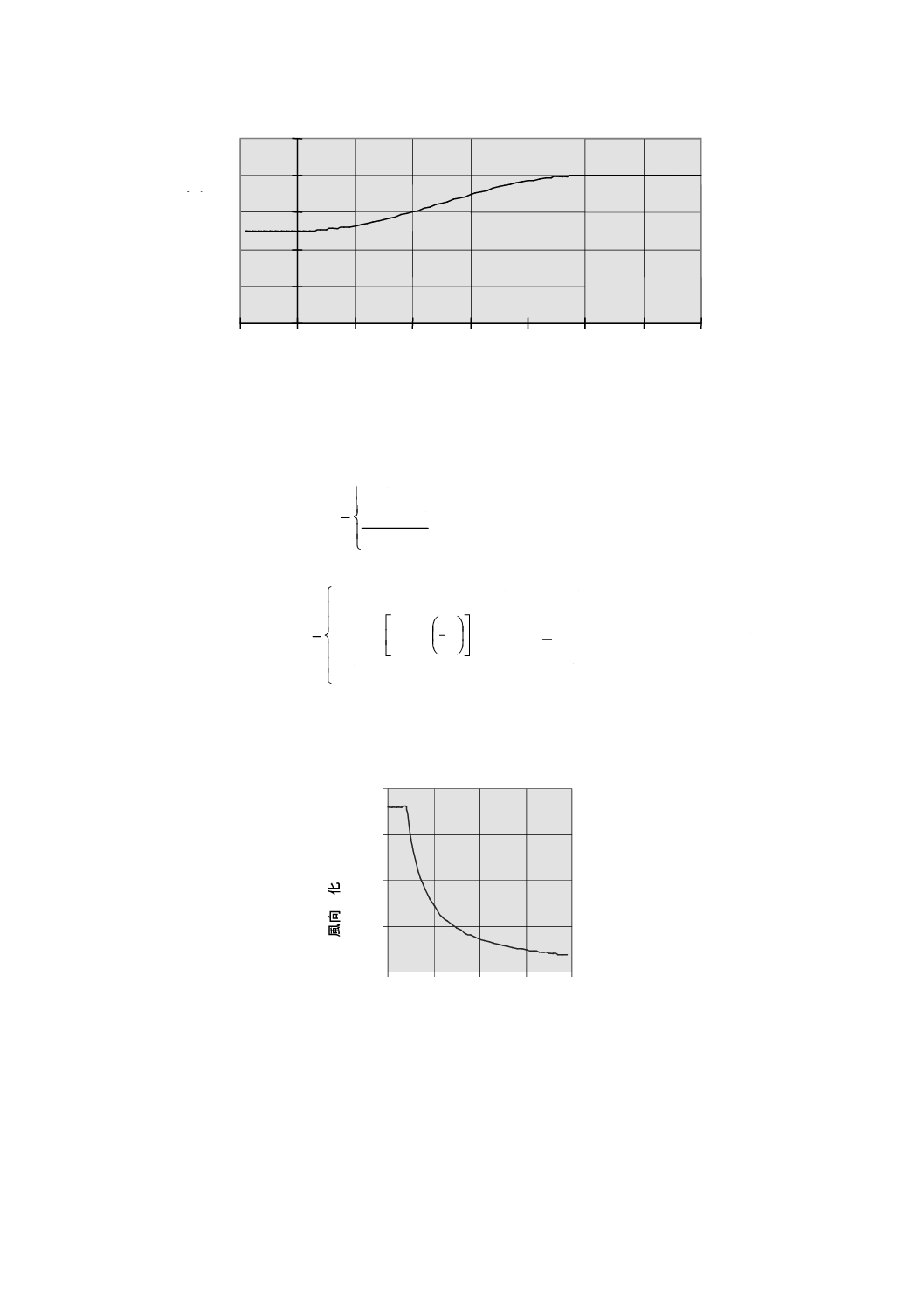
21
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0
10
20
30
40
50
‒2
0
2
4
6
8
10
12
14
時間 t (s)
風
速
V
(z
,
t)
(
m
/s
)
図5−極値コヒーレントガスト(ECD)の大きさの例
風速の立ち上がりは,0°からθcgまでの風向変化θと同時に発生すると仮定し,ここにθcgは,式(24)
に定義する。
°
°
=
の場合]
<
)<
(
[
)
(
)の場合]
(
<
[
ref
hub
hub
hub
hub
cg
s/
m
4
s/
m
720
s/
4
180
)
(
V
V
V
V
V
θ
m
················· (24)
同時に発生する風向変化は,式(25)による。
±
±
°
=
の場合)
>
(
の場合)
≦
≦
(
−
の場合)
<
(
T
t
T
t
T
t
t
t
θ
cg
cg
0
π
cos
1
5.0
0
0
)
(
θ
θ
··························· (25)
ここに,立ち上がり時間を,T=10(秒)とする。
Vhubに対する風向変化の大きさθcg及びVhub=25(m/s)における時間変化に対する風向変化θ(t)を,それ
ぞれ図6及び図7に示す。
0
50
100
150
200
0
10
20
30
40
風速 Vhub (m/s)
風
向
変
化
θ
c
g
(°
)
図6−極値コヒーレントガスト(ECD)の風向変化
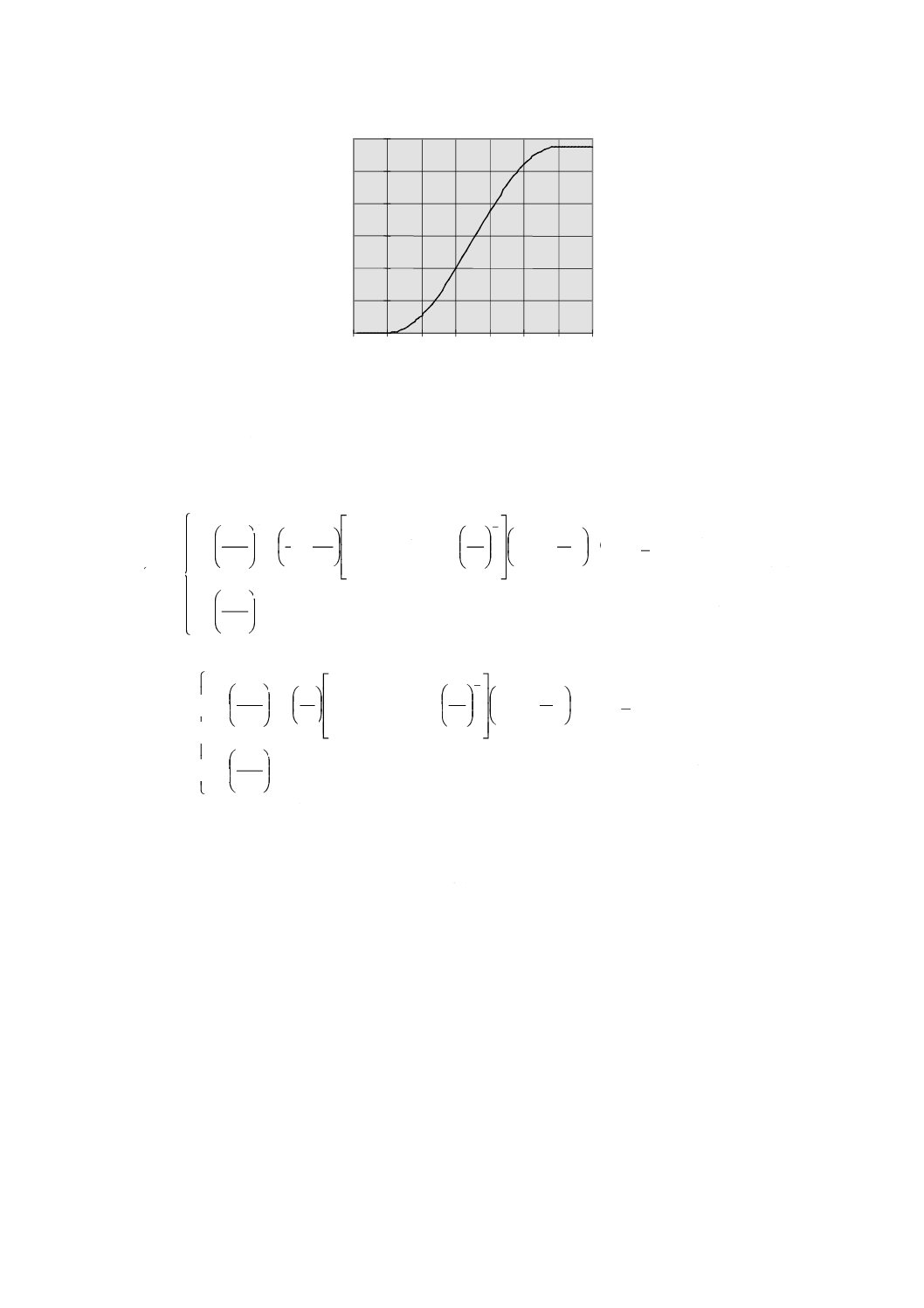
22
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0
5
10
15
20
25
30
‒2
0
2
4
6
8
10
12
時間 t (s)
風
向
変
化
θ
(t
)
(
°)
図7−風向の時間変化の例
6.3.2.6
極値ウィンドシアー(EWS)
極値ウィンドシアーは,式(26)及び式(27)で表す風速変化を用いて計算する。
(正及び負の)鉛直方向シアー変化は,式(26)による。
±
)
上記以外の場合
(
)
の場合
≦
≦
(
−
+
−
=
α
α
z
z
V
T
t
T
t
Λ
D
βσ
D
z
z
z
z
V
t
z
V
hub
hub
4
1
1
1
hub
hub
hub
0
π
2
cos
1
2.0
s)
/
m
(5.2
)
,
(
······· (26)
水平方向シアー変化は,式(27)による。
±
)
上記以外の場合
(
)
の場合
≦
≦
(
−
+
=
α
α
z
z
V
T
t
T
t
Λ
D
βσ
D
y
z
z
V
t
z
y
V
hub
hub
4
1
1
1
hub
hub
0
π
2
cos
1
2.0
s)
/
m
(5.2
)
,
,
(
··········· (27)
ここに, 鉛直及び水平方向シアー両方に対して,
α=0.2,β=6.4,T=12(秒)
σ1: 通常乱流モデルの式(11)による。
Λ1: 式(5)による乱流尺度パラメータ
D: ロータ直径
水平方向のウィンドシアー変化の符号は,過渡状態で最も厳しい荷重が生じるように選択する。二つの
極値ウィンドシアーは,同時には適用しない。
23
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0
0.5
1.0
1.5
2.0
0
10
20
30
40
風速 V(z, t) (m/s)
z
/z
h
u
b
t=0の場合
t=T/2のプラス側
t=T/2のマイナス側
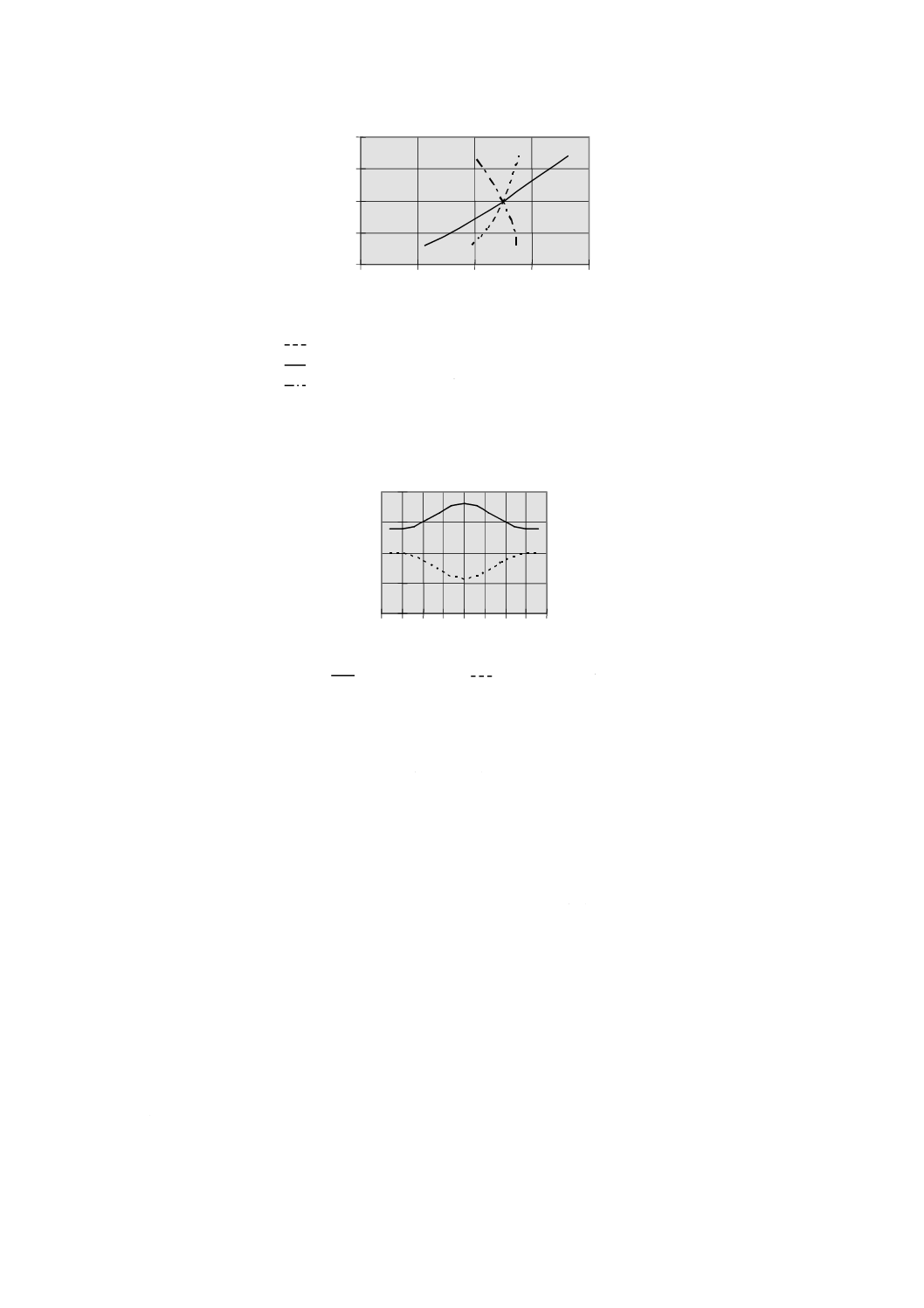
図8−開始前(t=0,波線)及び最大シアー(t=6秒,実線)における
正及び負の極値鉛直ウィンドシアー,風速プロファイルの例
0
10
20
30
40
‒2 0
2
4
6
81012 14
時間 t (s)
風
速
V
(z
,
t)
ロータ上端, ロータ下端
図9−正のウィンドシアーの時間的変化に対するロータ頂部及び底部における風速の例
ここで,一例として,極値鉛直ウィンドシアー[乱流カテゴリA,zhub=30(m),Vhub=25(m/s),D=
42(m)]を,図8に示す。図8では,極値事象の開始前(t=0秒)及び最大シアー(t=6秒)の状態にお
ける風速プロファイルを示している。また,図9では,ロータの頂部及び底部において,シアーが時間と
ともに発達するときの風速を示している(図8の場合と仮定は同じ。)。
6.4
その他の環境条件
風以外の種々の環境(気象)条件は,熱,光化学,腐食,機械,電気,その他の物理的作用によって風
車の健全性及び安全性に影響することがある。さらに,幾つかの気象条件が組み合わさる場合,これらの
作用が増大することがある。
次に示す環境条件を考慮し,施した対応を設計文書に記載する。
− 温度
− 湿度
− 空気密度
− 日射
− 雨,あられ,雪及び氷
− 化学的活性物質
− 機械的活性粒子
24
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 大気中塩分濃度
− 雷
− 地震
洋上環境では,更に考慮する環境条件がある。
気象条件は,変化する条件の代表値又は限界値によって定義する。設計値を選ぶ場合は,幾つかの気象
条件が同時に起きる可能性を考慮する。
再現期間1年に対応する通常域内の気象条件の変化では,風車設計上における通常の運転を妨げない。
相関が存在しない場合には,6.4.2に規定する“その他の極値環境条件”は,6.3.1に規定する“通常風条
件”と組み合わせる。
6.4.1
その他の通常環境条件
風以外の通常の環境条件値で考慮するものを,次に示す。
− 周囲温度範囲:−10 ℃〜+40 ℃
− 相対湿度:95 %
− 大気成分:内陸の非汚染大気と同等(JIS C 60721-2-1参照)
− 日射強度:1 000 W/m2
− 空気密度:1.225 kg/m3
設計者がその他の外部条件パラメータを指定する場合は,これらのパラメータ及びその値を設計文書に
記載する。また,それらはJIS C 60721-2-1の要求事項に適合させる。
6.4.2
その他の極値環境条件
風以外の極値環境条件で風車設計に考慮するものは,温度,雷,氷及び地震(地震条件の評価について
は11.6参照)とする。
6.4.2.1
温度
標準風車クラスに対して極値温度範囲は,少なくとも,−20 ℃〜+50 ℃とする。
6.4.2.2
雷
標準風車クラスの風車の場合には,10.6に規定する雷保護の装備で十分とみなす。
6.4.2.3
着氷
標準風車クラスの風車には,着氷に関する最低限の要求事項は規定しない。
6.4.2.4
地震
標準風車クラスの風車には,地震に関する最低限の要求事項は規定しない。
地震条件及び作用を検討する場合には,11.6及び附属書Cを参照する。
6.5
電力系統条件
設計で考慮する風車接続端における通常条件を,次に示す。
パラメータが次に規定する範囲内にある場合には,通常の電力系統条件であるとみなす。
− 電圧:公称値(IEC 60038に準拠)±10 %
− 周波数:公称値±2 %
− 電圧不平衡:逆相成分の正相成分に対する比が2 %以下
− 自動再閉路周期:初回の再閉路に対して0.1秒〜5.0秒,2回目に対しては10秒〜90秒
− 停電:電力系統の停電は,年間20回起きると仮定する。6時間以内の停電5) は,通常条件とみなす。
最長1週間の停電は,極値条件と考える。
注5) 6時間以内の停電は,最も厳しい暴風の継続時間に対応すると仮定して設定されている。
25
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7
構造設計
7.1
一般事項
風車の構造物の荷重を受ける部品は,構造的な健全性を検証し,満足できる安全レベルであることを確
認する。風車の構造的な健全性が適切な安全レベルにあることを検証するために,風車の構造部品の終極
強度及び疲労強度は,計算及び/又は試験によって検証する。
構造解析は,ISO 2394に基づいて行う。
計算は,適切な方法を用いて行う。計算方法は,設計文書に記載する。設計文書には,計算方法が正し
いことの根拠又は適切な検証実験の言及を含める。強度検証のための全ての試験に用いる荷重レベルは,
7.6の荷重の特性値に適切な安全率を含める。
7.2
設計方法
風車の設計に当たっては,規定する限界状態を超えないことを検証する。計算の代わりに,モデル試験
及び試作機試験を行って,ISO 2394に規定する構造設計で検証してもよい。
7.3
荷重
7.3.1〜7.3.4に規定する荷重は,設計計算の場合に考慮する。
7.3.1
重力荷重及び慣性荷重
重力荷重及び慣性荷重は,重力,振動,回転及び地震によって生じる静的及び動的荷重である。
7.3.2
空力荷重
空力荷重は,静的及び動的荷重であって,大気流と風車の静止部及び可動部との空力干渉によって生じ
る。
大気流は,ロータを横切る平均風速及び乱流,ロータの角速度,空気密度,並びに風車部品の空力的形
状及び空力弾性効果を含む相互作用効果に左右される。
7.3.3
作動荷重
作動荷重は,風車の運転及び制御によって生じる。作動荷重は,発電機及びインバータのトルク制御,
ヨー及びピッチの駆動荷重並びに機械ブレーキの荷重を含む種々のカテゴリのものからなる。各ケースで
駆動装置の力の範囲を考えることは,応答及び荷重の計算では重要である。特に機械ブレーキ装置におい
て,ブレーキ事象中の応答及び荷重を検討する場合,温度及び経年変化によって影響を受ける摩擦,ばね
力又は圧力の範囲を考慮する。
7.3.4
その他の荷重
その他の荷重,例えば,後流荷重,衝撃荷重,着氷による荷重などが起きることがあり,適切にこれら
を含める(11.5参照)。
7.4
設計条件及び設計荷重ケース
この箇条では風車の設計荷重ケースの構成を述べ,最小限考慮することを規定する。
風車の寿命は,設計において,風車が経験すると思われる最も重要な状態を代表する一連の設計条件に
よって表すことができる。
設計荷重ケースは,運転モード,又は規定の組立て,建設,保守などの設計条件を外部条件と組み合わ
せて決定する。関係する全ての設計荷重ケースは,妥当な発生確率で考慮する。そのとき,制御システム
及び保護システムの動作も考慮する。風車の構造的な健全性を検証するために用いる設計ケースは,次の
組合せから計算する。
− 通常設計条件及び適切な通常又は極値の外部条件
− 故障設計条件及び適切な外部条件
26
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 輸送,据付け,保守のための設計条件及び適切な外部条件
極値外部条件と故障条件との間に相関関係がある場合は,両者の現実的な組合せを一つの設計荷重ケー
スとみなす。
各設計条件の中で複数の設計荷重ケースを考慮する。少なくとも,表2の設計荷重ケースを考慮する。
この表では,設計荷重ケースの各々の設計条件について,風条件,電気的外部条件,その他の外部条件に
記載することを規定している。
例えば,決定論的な風モデルにおける設計荷重ケースの間,風車コントローラが最大ヨー角及び/又は
風速に到達する前に風車を停止させる場合,風車が同じ決定論的な風条件の変化において乱流条件の下で
安全に停止できることを示している。
特定の風車の設計の構造的な健全性に必要な場合には,その他の設計荷重ケースも考慮する。
各設計荷重ケースに対する適切な解析タイプを,表2において,“F”又は“U”で示す。“F”は,疲労
強度の評価に用いる疲労荷重の解析を意味する。“U”は,材料強度,翼先端変位及び構造安定性(座屈)
の解析などの終極荷重の解析を意味する。
“U”で示される設計荷重ケースの場合には,通常(N),異常(A)又は輸送及び建設(T)のいずれか
の設計条件に分類する。通常設計条件は,風車の寿命期間において,頻繁に生じるものである。風車は通
常の状態にあり,軽度の故障又は異常状態の経験を含む。異常設計条件は,生じる可能性が非常に少ない
ものである。これは通常,システムの保護機能の動作などの厳しい故障が生じた設計条件に対応するもの
である。N,A又はTによる設計条件の分類によって,終極荷重に適用される部分安全率γfが決定される。
部分安全率は,表3による。
27
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2−設計荷重ケース
設計条件
DLC
番号
風条件
その他の条件
解析の
タイプ
部分
安全率
1) 発電
1.1
NTM
Vin<Vhub<Vout
極値事象の外挿
U
N
1.2
NTM
Vin<Vhub<Vout
F
*
1.3
ETM
Vin<Vhub<Vout
U
N
1.4
ECD
Vhub=Vr−2(m/s),Vr,
Vr+2(m/s)
U
N
1.5
EWS
Vin<Vhub<Vout
U
N
2) 発電中の故障
発生
2.1
NTM
Vin<Vhub<Vout
制御システムの故障又は電力
系統の喪失
U
N
2.2
NTM
Vin<Vhub<Vout
保護システムの故障又は先行
する内部電気故障
U
A
2.3
EOG
Vhub=Vr±2(m/s)及びVout 電力系統の喪失を含む,内外
の電気故障
U
A
2.4
NTM
Vin<Vhub<Vout
電力系統の喪失を含む,制御
システム,保護システム又は
電気システムの故障
F
*
3) 起動
3.1
NWP
Vin<Vhub<Vout
F
*
3.2
EOG
Vhub=Vin,Vr±2(m/s)及び
Vout
U
N
3.3
EDC
Vhub=Vin,Vr±2(m/s)及び
Vout
U
N
4) 通常停止
4.1
NWP
Vin<Vhub<Vout
F
*
4.2
EOG
Vhub=Vr±2(m/s)及びVout
U
N
5) 緊急停止
5.1
NTM
Vhub=Vr±2(m/s)及びVout
U
N
6) 待機中(静止
又はアイドリ
ング)
6.1
EWM
再現期間50年
U
N
6.2
EWM
再現期間50年
電力系統の喪失
U
A
6.3
EWM
再現期間1年
極値ヨーミスアラインメント
U
N
6.4
NTM
Vhub<0.7 Vref
F
*
7) 待機中の故障
7.1
EWM
再現期間1年
U
A
8) 輸送,組立て,
保守及び修理
8.1
NTM
Vmaint:製造業者が指定
U
T
8.2
EWM
再現期間1年
U
A
注記 この表で用いる略語は,次による。
DLC
設計荷重ケース(以下,DLC番号を表す場合は,略語“DLC”を用いる。例 DLC 1.1)
ECD
風向変化を伴う極値コヒーレントガスト(6.3.2.5参照)
EDC
極値風向変化(6.3.2.4参照)
EOG
運転中の極値ガスト(6.3.2.2参照)
EWM
極値風モデル(6.3.2.1参照)
EWS
極値ウィンドシアー(6.3.2.6参照)
NTM
通常乱流モデル(6.3.1.3参照)
ETM
極値乱流モデル(6.3.2.3参照)
NWP
通常風速プロファイルモデル(6.3.1.2参照)
Vr±2(m/s) この範囲の全ての風速に対する感度を解析することを意味する。
F
疲労(7.6.3参照)
U
終極(7.6.2参照)
N
通常設計条件[における部分安全率(表3参照)]
A
異常設計条件[における部分安全率(表3参照)]
T
輸送及び建設の設計条件[における部分安全率(表3参照)]
*
疲労に対する部分安全率(7.6.3参照)
28
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2で風速範囲を示している場合,風車設計に対して最悪条件となる風速を考慮する。風速の範囲は,
一組の不連続な値によって代表できる。その場合,分解能は,計算精度6) を保証するのに十分なものとす
る。設計荷重ケースの定義において,風条件は,箇条6を参照する。
注6) 一般に,2 m/sの分解能は十分と考えられる。
7.4.1
発電(DLC 1.1〜1.5)
この設計条件では,風車は運転中であり,電気負荷に接続されている。想定する風車の形状に,ロータ
の不平衡を考慮する。設計計算には,ロータの製造に指定されている最大質量及び空力不平衡(例えば,
翼ピッチ及びねじれの偏差)を用いる。
さらに,運転荷重の解析には,ヨーミスアラインメント,制御システムのトラッキング誤差などの理論
的な最適運転条件からの偏差を考慮する。
DLC 1.1及びDLC 1.2は,寿命期間における風車の通常の運転中に現れる大気の乱れから生じる要求事
項を具体化している(NTM)。DLC 1.3は,極値乱流条件から生じる終極荷重に対する要求事項を具体化し
ている。DLC 1.4及びDLC 1.5は,風車の寿命期間に発生する危機的な事象として選択された過渡的なケ
ースを規定している。
DLC 1.1におけるシミュレーションデータの統計解析には,少なくとも,翼根面内曲げモーメント,面
外曲げモーメント及び翼先端変形の極値計算を含める。これらのパラメータの設計極値よりもDLC 1.3に
よって得られた極値の方が大きい場合は,DLC 1.1の更なる解析は省略してもよい。
DLC 1.3において導き出した設計極値がこれらのパラメータの設計極値を超えない場合には,DLC 1.3
の極値乱流モデルに用いる式(19)の係数cを,DLC 1.1において計算したこれらのパラメータの設計極値以
上に引き上げてもよい。
7.4.2
発電中の故障発生又は電力系統の喪失(DLC 2.1〜2.4)
この設計条件は,風車の発電中の故障又は電力系統の喪失によって引き起こされる過渡事象を意味する。
制御システム及び保護システムの故障又は電気システムの内部故障は,風車にかかる荷重に大きく影響す
るので(例えば,発電機の短絡),これらが発電中に起きるものと想定する。
DLC 2.1の場合,制御機能の故障又は電力系統の喪失の発生は,通常の事象として解析する。
DLC 2.2の場合,保護機能又は内部電気システムの故障など,まれな故障の発生は,異常な事象として
解析する。
DLC 2.3の場合,運転中の極値ガスト(EOG)などの潜在的に重大な風の事象は,内部又は外部の電気
システムの故障(電力系統の喪失を含む。)の事象と組み合わさるため,異常な事象と考えられる。この場
合は,これらの二つの事象の発生タイミングは,最悪荷重が得られるように選ぶ。
故障又は電力系統の喪失によって風車が即時停止にならず,その結果引き起こされる荷重が重大な疲労
破壊をもたらす場合には,通常乱流モデル(NTM)において生じる疲労破壊に加えて,この状況が予想さ
れる継続時間をDLC 2.4において評価する。
DLC 2.3は,表2の風条件の代替としての,統計的な風のシミュレーション(NTM:Vin<Vhub<Vout)を
用いて分析する通常の事象(すなわち,荷重に対する部分安全率1.35)を,内部又は外部の電気システム
の故障(電力系統の喪失を含む)と組み合わせてもよい。この場合,考慮する各平均風速に対して,12回
の応答シミュレーションを行う。それぞれの応答シミュレーションにおいて,電気システムの故障が起き
た後の極値応答を計算する。ただし,初期条件の影響が無視できるようになった後に,故障について考慮
する。各平均風速において,見かけの極値応答は,12個のサンプリングされた極値応答の平均値に12個
のサンプルの標準偏差の3倍を加算して求める。DLC 2.3の特性応答値は,見かけの極値応答の中の極値
29
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
として決定する。
7.4.3
起動(DLC 3.1〜3.3)
この設計条件は,静止又はアイドリング状態から発電に至るまでの過程で風車に作用する荷重の原因と
なる全ての事象を含んでいる。発生回数は,制御システムの挙動に基づいて予想する。
7.4.4
通常停止(DLC 4.1〜4.2)
この設計条件は,発電状態から静止又はアイドリング状態に至るまでの通常の過程において,風車に荷
重をもたらす全ての事象を含む。発生回数は,制御システムの挙動に基づいて予想する。
7.4.5
緊急停止(DLC 5.1)
緊急停止によって生じる荷重を考慮する。
7.4.6
待機中(静止又はアイドリング)(DLC 6.1〜6.4)
この設計条件では,待機中の風車のロータは,静止又はアイドリング状態にある。DLC 6.1,DLC 6.2及
びDLC 6.3においては,この条件は極値風モデル(EWM)を考慮する。DLC 6.4においては,通常乱流モ
デル(NTM)を考慮する。
風条件が極値風モデル(EWM)によって定義される設計荷重ケースの場合,定常又は乱流のいずれの風
モデルを用いてもよい。乱流極値風モデルを用いる場合,完全な動的応答又はISO 4354で明確に規定して
いるガスト及び動的応答の適切な補正付きの準定常解析のいずれかを用いて推定する。
定常極値風モデルを用いる場合,共振応答の作用を上記の準定常解析から推定する。共振応答と背景応
答との比(R/B)が5 %未満の場合,定常極値風モデルによる静的解析を用いてもよい。風車ヨーシステム
の滑りが荷重の特性値で起きる場合,起こる可能性のある不都合な最大滑りを平均ヨーミスアラインメン
トに加算する。風車が,極値風条件においてヨー運動が予測されるヨーシステムをもつ場合(例えば,フ
リーヨー,受動ヨー又はセミフリーヨー)には,乱流極値風モデルを用いる。
なお,ヨーミスアラインメントは,乱流の風向変化及び乱流ヨーの動的応答によって支配される。また,
風車が大きなヨー運動又は通常の運転から極値条件への風速増加中の平衡変化にさらされる場合,この挙
動はこの解析に含める。
DLC 6.1において,アクティブヨーシステムをもつ風車にヨーシステム中の滑りに対する制限が設けら
れている場合には,定常極値風モデルを用いるときは±15°までのヨーミスアラインメント,又は乱流極
値風モデルを用いるときは±8°の平均ヨーミスアラインメントを課す。
DLC 6.2において,極値風条件を含む暴風の初期段階における電力系統の喪失を仮定する。制御システ
ム及びヨーシステムに対して,少なくとも6時間の容量をもつ電力のバックアップが与えられない限り,
±180°までの風向変化の作用を解析する。
DLC 6.3において,1年の再現期間をもつ極値風を極値ヨーミスアラインメントと組み合わせる。定常極
値風モデルを用いる場合には±30°までの極値ヨーミスアラインメント,又は乱流極値風モデルを用いる
場合には,±20°の平均ヨーミスアラインメントを仮定する。
DLC 6.4において,無視できない疲労損傷が生じるような変動荷重がいずれかの部品に生じる場合には
(例えば,アイドリング状態の翼の自重による),その風速における非発電状態の予想時間数を考慮する。
7.4.7
待機中の故障(DLC 7.1)
電力系統又は風車の故障によって,待機中の風車の挙動が通常状態から変化した場合には,解析する。
電力系統の喪失以外の何らかの故障による場合には,起こる可能性のある事態を特に解析の対象とする。
故障状態は,極値風モデル(EWM)と1年の再現期間との組合せとする。故障状態は,乱流,又はガスト
及び動的応答を補正した準定常のいずれかとする。
30
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ヨーシステムの故障の場合,±180°のヨーミスアラインメントを考慮する。他の故障の場合のヨーミス
アラインメントは,DLC 6.1による。
DLC 7.1中に,ヨーシステム中の滑りが荷重の特性値で起こる可能性がある場合,最も厳しい滑りを考
慮する。
7.4.8
輸送,組立て,保守及び修理(DLC 8.1〜8.2)
DLC 8.1において,製造業者は,風車の輸送,組立て,保守及び修理の間に発生する可能性がある全て
の風条件及び設計条件を記載する。この最大許容条件が風車に重大な荷重をもたらす場合には,この条件
を考慮して設計する。製造業者は,満足できる安全レベルを付与するために,記載した条件と風条件との
間に十分な設計マージンをとる。十分なマージンは,記載した風条件に5 m/sを加えることで得てもよい。
さらに,DLC 8.2においては,1週間を超える可能性がある風車の輸送,組立て,保守及び修理の条件を
含める。これには,部分的に完成したタワー,ナセルなしで立つタワー及び複数本の翼が欠けた風車も含
む。全ての翼が同時に取り付けられることを仮定してもよい。これらの全ての条件において,電力系統は
接続されないと仮定する。電力の供給を必要としない場合には,これらの全ての状態でも,荷重を減らす
対策をとることができる。
ロック装置は,DLC 8.1の該当する条件で発生する荷重に耐えることを要求する。特に,最大設計駆動
力の印加を考慮する。
7.5
荷重計算
7.3.1〜7.3.4に規定する荷重を,各設計荷重ケースに考慮する。関連する場合には,次の事項を考慮する。
− 風車自体に起因した風の流れ場のじょう(擾)乱(風車後流による誘導速度,タワーシャドウなど)
− 三次元の流れが翼の空力特性に及ぼす影響(例えば,三次元ストール,空力チップロスなど)
− 非定常空力効果
− 構造の動特性及び振動モードの連成
− 空力弾性効果
− 風車の制御システム及び保護システムの挙動
風車荷重の計算には,通常,構造動力学モデルを用いる動的シミュレーションを用いる。ある設計荷重
ケースでは,乱流を含む風が入力される。このケースの場合,荷重の特性値の推定に統計的な信頼性を確
保するために荷重データの全期間は十分長くとる。少なくとも6回の10分間統計データ(又は連続60分
間)を,シミュレーション用の各ハブ高さにおける平均風速に対して要求する。ただし,DLC 2.1,DLC 2.2
及びDLC 5.1の場合には,少なくとも12回のシミュレーションを所定の風速における各事象に対して実施
する。動的シミュレーションに用いる初期条件は,通常,シミュレーション期間の初期において荷重統計
に影響を与えるので,最初の5秒間のデータ(又は必要な場合,より長く)は,乱流を含む風の入力を含
む解析間隔の検討から除外する。
動的シミュレーションに乱流を含む風を用いる場合,空間分解能7) 及び時間分解能に注意することが望
ましい。
注7) 空間分解能については,隣接する点の間の最大距離が,Λ1[式(5)参照]の25 %未満,及びロー
タ直径の15 %以下であることが望ましい。この距離は,四つの点で構成される各格子セルの点
を結ぶ対角線の長さとする。非一様な格子の場合,ロータ表面における格子間距離の平均値を,
代表的な空間分解能とみなしてもよいが,この格子間距離は,翼端に向かうに従って短くする
ことが望ましい。
31
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
多くの場合,所定の風車部品の重要な部位の局所ひずみ又は応力は,同時に起きる多軸荷重によって支
配される。この場合,シミュレーションからのアウトプットである直交荷重の時刻歴データは,荷重の設
計値を指定するのにしばしば用いられる。このような直交成分の時刻歴データを用いて疲労荷重及び終極
荷重を計算する場合には,位相及び大きさの両方を維持するように,時刻歴データを組み合わせる。すな
わち,この直接法では,重要な応力値を時刻歴データから導くことになる。また,極値及び疲労を予測す
る方法では,荷重の組合せによる問題を避けて,単一のデータを適用してもよい。
終極荷重成分も,極値成分値が同時に生じるものと仮定して,安全側に組み合わせてもよい。この選択
を行う場合,安全側でない考えの取り入れを避けるために,最小及び最大の極値成分の値について,可能
なあらゆる組合せを適用する。
数多くの実現確率から得られた,同時荷重から極値設計荷重を導くための指針を,附属書Hに示す。
7.6
終極限界状態解析
7.6.1
方法
部分安全率は,荷重及び材料の不確かさ及び偏差,解析方法に含まれる不確かさ並びに損傷結果に関す
る構造部品の重要性を考慮する。
7.6.1.1
荷重及び材料の部分安全率
荷重及び材料の不確かさ及び偏差の安全設計値を保証するために,式(28)及び式(29)に定義するように部
分安全率を取り入れる。
Fd=γf Fk ················································································· (28)
ここに,
Fd: 合計内部荷重又は所定の設計荷重ケースの種々の発生源から
同時に発生する多重荷重成分に対する荷重応答の設計値
γf: 荷重の部分安全率
Fk: 荷重の特性値
k
m
d
1f
f
γ
=
·············································································· (29)
ここに,
fd: 材料の設計値
γm: 材料の部分安全率
fk: 材料物性の特性値
この規格では,荷重の部分安全率は,次を考慮する。
− 荷重の特性値からの好ましくない逸脱及び/又は不確かさの可能性
− 荷重モデルにおける不確かさ
この規格では,材料の部分安全率は,ISO 2394と同様,次を考慮する。
− 材料強度の特性値からの好ましくない逸脱及び/又は不確かさの可能性
− 断面耐力又は構造部位の耐荷重能力の不正確な評価の可能性
− 幾何学的パラメータにおける不確かさ
− 構造物の材料物性と管理標本による試験で測定した材料物性との間の関係の不確かさ
− 換算率の不確かさ
これらの異なる不確かさは,個々の部分安全率によって説明が付くこともあるが,この規格では他の大
部分の規定と同様に,荷重に関係する要因は安全率γfに結び付け,かつ,材料に関係する要因は安全率γm
に結び付ける。
7.6.1.2
損傷結果及び部品クラスに対する部分安全率
次の部品クラスを区別するため,損傷結果に対する部分安全率γnを導入する。
32
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 部品クラス1 故障しても風車の重要部分の不具合には結び付かない,“フェイルセーフ”の構造部品
に用いられるもの(監視付きの交換可能軸受など)。
− 部品クラス2 故障すると風車の重要部分の不具合につながる可能性がある,“非フェイルセーフ”の
構造部品に用いられるもの。
− 部品クラス3 8.3に規定する風車の非冗長保護機能の実行のため,駆動装置及びブレーキ装置を主な
構造部品に結び付ける“非フェイルセーフ”の機械部品に用いられるもの。
損傷結果に対する部分安全率は,実翼試験などの試験を実施する際の試験荷重の中に含める。
風車の終極限界状態解析のため,必要に応じて次の4種類の解析を行う。
− 終極強度解析(7.6.2参照)
− 疲労破壊解析(7.6.3参照)
− 安定性解析(座屈など)(7.6.4参照)
− 臨界変形解析(翼及びタワーの機械的干渉など)(7.6.5参照)
いずれの種類の分析も,限界状態関数の異なる定式化が必要で,安全率を用いることで異なる原因の不
確かさに対処する。
7.6.1.3
公認の材料基準の適用
風車の要素の構造的な健全性を求める場合,関連する材料に対して我が国又は国際的な基準を採用して
もよい。我が国又は国際的な設計基準に規定する部分安全率を,この規格に規定する部分安全率と併用す
る場合には,特別な注意が必要である。最終的な安全レベルが,この規格において意図する安全レベルを
下回らないことを確認する。
基準によっては,材料の部分安全率γmを,材料強度の固有のばらつき,生産管理の範囲,生産方法など,
不確かさの異なる要因を考慮して,幾つかの材料係数に分離することがある。この規格に規定する材料係
数は,強度パラメータの固有のばらつきを考慮した“材料に対する一般的な部分安全率”と呼ばれるもの
に相当する。用いる基準が,部分安全率を規定するか又は他の不確かさを説明するために特性値の減少係
数を用いる場合には,これらも考慮する。
基準によっては,設計検証の荷重及び材料部品に対する部分安全率について様々に分化させることがあ
る。ここで意図する安全率の分化とは,ISO 2394に定義されるものである。選択した基準における安全率
の分化がISO 2394におけるものと異なる場合には,選択した基準とこの規格に規定する検証との間で適切
な調整を行う。
7.6.2
終極強度解析
限界状態関数は,式(30)の条件によって,荷重の関数S及び耐力の関数Rに分離することができる。
γn・S(Fd)≦R(fd) ········································································· (30)
耐力関数Rは,一般には材料耐力の最大許容設計値に対応するため,R(fd)=fdである。一方,終極強度
解析に対する関数Sは通常,構造応答の最高値として定義されるため,S(Fd)=Fdである。したがって,式
は,式(31)になる。
k
m
n
k
f
1
1
f
F
γ
γ
γ
≦
····································································· (31)
ここで,γnは,損傷結果に対する部分安全率であり,材料の安全率として扱われないことに注意する。
評価対象の各風車部品,及び表2における各終極強度解析に該当する設計荷重ケースについて,式(31)
の限界状態条件として最小のマージンをもつ最も危険な限界状態に対して検証する。
風速の範囲を規定する乱流を含む設計荷重ケースの場合には,荷重の特性値の超過確率は,6.3.1.1に規
33
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定する風速分布を考慮して計算する。多くの荷重計算は,限られた継続時間の統計的シミュレーションを
含むので,要求される再現期間に対して決定する荷重の特性値は,シミュレーションで計算するいずれの
値よりも大きいことが想定される。乱流を用いる荷重の特性値の計算に関する指針は,附属書Fに記載す
る。
DLC 1.1では,荷重の特性値は統計的な荷重外挿によって決定し,いずれの10分間の最大値についても,
通常の設計条件では3.8×10−7(すなわち,50年の再現期間)以下の超過確率に相当する。
外挿法で用いるデータは,DLC 1.1の風車の運転範囲における長さが少なくとも10分の風車シミュレー
ションの時刻歴から抽出する。[Vr−2(m/s)]からカットアウトまでの各風速に15個以上のシミュレーシ
ョンが必要であり,[Vr−2(m/s)]未満の各風速には6個のシミュレーションが必要である。データを抽
出する際,設計者は,外挿に対するピーク間の非依存性の影響を考慮し,なるべく依存性を最小限に抑え
る。設計者は,データ及び確率分布を集計して一貫性のある長期間の分布を作成する。長期間の荷重の安
定的な評価を確保するため,収束判定基準は,短期的又は長期的な超過分布の場合のデータのモードより
も小さい確率分位値を適用する。収束判定基準の指針については,附属書Fを参照する。
翼根面内曲げモーメント,面外曲げモーメント及び翼先端変形の特性値は,単純化した手順8) で決定し
てもよい。したがって,この特性値は,統計的な荷重外挿における部分荷重係数を維持しながら,各10
分間における極値の平均値を計算し,その最大値に外挿係数1.5を乗じて求めてもよい(表3参照)。
注8) このアプローチは,3枚翼のアップウィンド風車において用いられてきた。他の風車形式に用
いる場合には,注意することが望ましい。
指定された決定論的な風モデルによる設計荷重ケースの場合,荷重の特性値は,過渡状態の中で計算し
たうち,最も厳しい値とする。乱流を用いる場合は,荷重の特性値を計算した10分間の計算値の中での最
大値の平均値とする。ただし,DLC 2.1,DLC 2.2及びDLC 5.1においては,最大荷重の上位50 %の標本
の平均値とする。
7.6.2.1
荷重の部分安全率
荷重の部分安全率は,表3に規定する値以上とする。

34
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3−荷重の部分安全率γf
好ましくない荷重
好ましい荷重b)
設計条件のタイプ(表2参照)
全ての設計条件
通常(N)
異常(A)
輸送及び建設(T)
1.35 a)
1.1
1.5
0.9
注a) DLC 1.1において,荷重がVinとVoutとの間の規定の風速で統計的な荷重外挿を用
いて決定する場合,通常設計条件の部分安全率はγ f=1.25とする。
通常設計条件の場合,重力による荷重応答の特性値Fgravityが問題の設計条件に
対して計算でき,かつ,重力が好ましくない荷重の場合,重力と他の発生源との
組合せ荷重に対する部分安全率は,次の値をもつ場合がある。
γ f=1.1+φ・ζ2
=
(上記以外の場合)
の場合)
(
0.25
1.1
DLC
15
.0
ϕ
>
=
k
gravity
k
gravity
k
gravity
0
1
F
F
F
F
F
F
ζ
;
≦
;
−
b) 全荷重応答を大きく軽減する見掛け及び重力荷重は,好ましい荷重とみなす。好
ましい荷重及び好ましくない荷重の両方の場合,式(30)は,次になる。
γnS(γ f, unfavFk,unfav,γ f,favFk,fav)≦R(fd)
荷重の部分安全率を荷重応答に適用する7.6.1.1のアプローチは,動的応答の特有な表現が主要な関心事
であると仮定する。風車の基礎,材料の非線形挙動若しくは幾何学的な非線形性又はこれら両方の特有な
表現が主要な関心事である場合,荷重応答の設計値Sdは,荷重の設計値Fdの組合せに関する構造解析か
ら得る。ここで,荷重の設計値Fdは,荷重の特性値Fkと,好ましい荷重及び好ましくない荷重に対して
規定する荷重の部分安全率γfとの乗算によって得られる。
Fd=γfFk
表3からγfで因数分解されるタワー界面における荷重応答(せん断力及び曲げモーメント)は,境界条
件として適用する。
重力による基礎の場合,全体の安定性を考慮した限界状態(土壌に不具合がない状態での剛体運動),並
びに土壌及び基礎の支持力は,公認の基準に従って考慮し計算する。一般的に,好ましくない不変荷重の
場合には荷重の部分安全率γf=1.1を,好ましい不変荷重の場合には荷重の部分安全率γf=0.9を,基礎の
荷重,座屈及び浮力に適用する。それぞれのサイトの品質マネジメント及び監視によって,設計文書で指
定する基礎材料の密度を満たしていることを証明できる場合,不変基礎荷重の部分安全率γf=1.0を土壌及
び基礎の支持力に関する限界状態に用いることができる。計算の結果,浮力が地下水位に等しい場合,浮
力の部分安全率γf=1.0を適用することができる。
代替として,土壌及び基礎の支持力を確認する場合には,好ましい不変荷重の部分安全率及び好ましく
ない不変荷重の部分安全率は,γf=1.0に基づいて行うことができ,全体の安定性の確認の場合には,好ま
しくない不変荷重のとき,γf=1.1,及び好ましい不変荷重のとき,γf=0.9の荷重の部分安全率に基づいて
行うことができる。全ての場合において,5 %/95 %の分位値として定義する質量又は密度の安全側の評価
を用いる。好ましい荷重の場合,下位の方の分位値を用いる。その他の場合,上位の方の分位値を用いる。
表3に規定する通常設計条件及び異常設計条件に対する荷重の部分安全率の使用は,荷重計算モデルは
荷重測定によって確認する必要がある。これらの測定は,空力,制御及び動的応答について考慮して,評
価対象の風車の設計と十分に近似した風車において行う。
35
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.6.2.2
公認の設計基準がない場合の材料の部分安全率及び損傷結果に対する部分安全率
材料の部分安全率は,用いることができる材料特性に関する試験データから適切に決定する。強度パラ
メータの固有のばらつきを考慮した一般的な材料の部分安全率の値γmは,式(32)による。
γm≧1.1 ·················································································· (32)
ここでは,95 %の信頼限界9) において,生存確率pが95 %の材料特性に適用する。この値は,材料の
破壊が風車の主要部品,例えば,溶接した円筒タワー,タワーフランジ接続部,溶接機械フレーム又は翼
接続部の故障につながる延性挙動10) をもつ部品に適用する。破壊のモードには,次を含む。
− 延性材料の降伏
− 十分な数によるボルト結合が一つのボルトの欠陥によって強度が1/γmになるボルト破断
注9) 特性強度パラメータは,95 %分位値(95 %信頼限界で決定される。)として選択するか又は代表
サンプルの試験に対して確立されたルーチンで証明書の値として選択することが望ましい。
10) 延性挙動は延性材料だけでなく,例えば,内部的冗長によって延性材料のように振る舞う部品
も含む。
材料の破壊が風車の主要部品の故障に急速につながる,ぜい(脆)性挙動の“非フェイルセーフ”の機
械部品又は構造部品の場合,一般的な材料の部分安全率は,次の値以上とする。
− 円筒タワー及び翼のような曲面シェル構造の全体的な座屈に対して,1.2
− 引張強度又は圧縮強度を超える破壊に対して,1.3
この一般的な材料の部分安全率から全体的な材料の部分安全率を求めるには,寸法効果,許容誤差,紫
外線,湿度などの外部作用による劣化,通常では検知されない欠陥などを考慮することが必要である。
この場合の損傷結果に対する部分安全率は,次による。
− 部品クラス1:γn=0.9
− 部品クラス2:γn=1.0
− 部品クラス3:γn=1.3
7.6.2.3
公認の設計基準がある場合の材料の部分安全率
荷重,材料及び損傷結果に対する合成部分安全率γf,γm及びγnは,7.6.2.1及び7.6.2.2に規定する値以上
とする。
7.6.3
疲労破壊解析
疲労破壊は,適切な疲労破壊計算を用いて予測する。例えば,Miner則の場合,累積損傷が1を超えた
とき,限界状態に到達したとする。そのため,風車の設計寿命の範囲内での累積損傷は1以下である。疲
労破壊計算は,サイクル範囲と平均ひずみ(又は応力)レベルとの両方の作用を加味して公式化を考える。
全ての部分安全率(荷重,材料及び損傷結果)は,各疲労サイクルに関係する損傷の増加を評価するため
に,各疲労サイクルひずみ(又は応力)の範囲に適用する。定式化の例は,附属書GにMiner則として示
す。
7.6.3.1
荷重の部分安全率
荷重の部分安全率γfは,全ての通常設計条件及び異常設計条件に対して,1.0とする。
7.6.3.2
公認の設計基準がない場合の材料の部分安全率及び損傷結果に対する部分安全率
材料の部分安全率γmは,S-N曲線が50 %の生存確率及び15 %未満の変動係数に基づく場合,1.5以上と
する。疲労強度11) の変動係数が,例えば,15 %〜20 %と大きい部品の場合(強化コンクリート,ファイ
36
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
バ複合材などの複合物からなる多くの部品),材料の部分安全率γmはそれに応じて増やす必要があり,1.7
以上とする。
注11) ここでは,疲労強度は,いずれかのサイクル数に伴う応力範囲と定義している。
疲労強度は,統計的に意味がある数の実験から求める。特性値の設定は,寸法効果,許容誤差,紫外線
などの外部作用による劣化,通常では検知されない欠陥などを考慮する。
溶接構造鋼の場合,伝統的に97.7 %の生存確率がS-N曲線のベースとして用いている。この場合,γmは
1.1としてもよい。定期的な点検プログラムの導入によって危険なクラックの進展を検出することが可能な
場合,より低い値のγmを用いてもよい。全ての場合において,γmは0.9より大きくする。
ファイバ複合材の場合,強度分布は実際の材料の試験データから確定する。S-N曲線のベースとして,
95 %信頼レベルにおける95 %の生存確率を用いる。この場合,γmは1.2としてもよい。他の材料に対して
も,同じアプローチを用いてもよい。
この場合の損傷結果に対する部分安全率は,次による。
− 部品クラス1:γn=1.0
− 部品クラス2:γn=1.15
− 部品クラス3:γn=1.3
7.6.3.3
公認の設計基準がある場合の部分安全率
荷重,材料及び損傷結果に対する合成部分安全率は,基準に規定する分位値を十分に考慮するとともに,
7.6.3.1及び7.6.3.2に規定する値以上とする。
7.6.4
安定性解析
設計荷重の下では,“非フェイルセーフ”の構成要素の耐荷重部品は,座屈を生じさせない。その他の全
ての構成要素については,荷重の設計値で弾性座屈が生じてもよい。全ての構成要素は,荷重の特性値で
は座屈を生じさせない。
設計値を得るために,荷重の部分安全率γfの最小値は,7.6.2.1に基づいて選択する。材料の部分安全率
は,7.6.2.2に規定する値以上とする。
7.6.5
臨界変形解析
7.6.5.1
一般事項
表2に示す設計条件において,構造的な健全性に影響をもたらす変形が生じないことを検証する。
好ましくない方向への最大弾性変形は,表2に示す設計荷重ケースに対して,特性荷重を用いて決定す
る。結果として生じる変形に,次の荷重,材料及び損傷結果に対する合成部分安全率を乗算する。
a) 荷重の部分安全率 γfの値は,表3から選択する。
b) 材料の弾性的性質に対する部分安全率 γmの値は,次による。
− 該当する部品の弾性的性質を試験及び監視によって決定した場合を除き,γmの値は1.1とする。
− 上記について,試験及び監視によって決定した場合,低減してもよい。ただし,形状的な不確かさ
及び変形の計算方法の精度には,特別の注意を払う。
c) 損傷結果に対する部分安全率 γnの値は,次による。
− 部品クラス1:γn=1.0
− 部品クラス2:γn=1.0
− 部品クラス3:γn=1.3
弾性変形を変形が生じていない位置で最も好ましくない方向に加え,その結果生じた位置を非干渉の要
37
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
求事項(7.6.5.2参照)と対比する。
7.6.5.2
翼(先端)の変形
最も重要な検討事項は,翼とタワーとの間に機械的な干渉が生じないことを検証することである。
一般的に,翼の変形は,終極荷重及び疲労荷重のケースについて計算する必要がある。終極荷重のケー
スで生じた変形は,はりモデル,有限要素モデルなどに基づき計算することが可能である。表2に該当す
る全ての設計荷重ケースは,該当する荷重の部分安全率とともに考慮する必要がある。
さらに,DLC 1.1については,7.4.1に従って翼先端変形の外挿が不可欠となる。ここでは,直接的な動
的変形解析を利用することができる。最も好ましくない方向における超過確率は,特性変形の場合と荷重
の特性値の場合とでは同じとする。さらに,特性変形は,荷重,材料及び損傷結果に対する合成部分安全
率を乗じ,変形が生じていない位置において最も好ましくない方向に加え,その結果生じた位置を非干渉
の要求事項と対比する。
7.6.6
特別な場合の部分安全率
荷重の大きさを,測定又は測定による解析によって,通常の信頼度より高く確立されている場合には,
荷重に対して,より低い部分安全率を用いてもよい。用いた部分安全率の値は,全て設計文書に記載する。
8
制御システム及び保護システム
8.1
一般事項
風車の運転及び安全性は,この箇条の要求事項を満たす制御システム及び保護システムによる。
いかなる手動又は自動による介入でも,保護機能を確保する。手動による介入を認める装置は,必要に
応じて,明確に適切な標識によって識別可能とする。
制御システム及び保護システムの設定は,部外者が変更できないように防護する。
8.2
制御機能
風車の制御機能は,能動的又は受動的方法で運転を制御し,運転パラメータを通常限界内に維持する。
例えば,保守の場合などのように,制御モードの選択ができる場合には,各モードにおける制御は他の全
ての制御に優先する。ただし,緊急停止ボタンを除く。モードの選択は,単一モードに対応した各位置で
ロックできるセレクタによって支配する。特定の機能を数値的に制御している場合には,機能を適切に選
択できるようにアクセスコードを与える。
制御機能は,次のような機能又はパラメータを支配又は制限してもよい。
− 出力
− ロータ回転数
− 電気負荷の接続
− 起動及び停止手順
− ケーブルのねじれ
− 風向への整列
8.3
保護機能
風車の保護機能は,制御機能の故障,内部又は外部故障,危険な事象などの結果,動作する。保護機能
は,風車を安全な状態に維持する。保護機能が動作するレベルは,設計限界値を超えないように設定する。
保護機能は,制御機能よりも高い優先順位をもたせるが,指令によって系統を遮断するブレーキシステ
ム及び装置にアクセスする場合の緊急停止ボタンよりも優先順位を高くしない。
保護機能は,次のような場合に動作させる。
38
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 過速度
− 発電機の過負荷又は故障
− 過大振動
− ケーブルの異常なねじれ(ヨー運動によってナセルが回転することに起因するもの)
保護機能は,フェイルセーフの動作をするように設計する。保護機能は,一般的に,保護機能を提供す
るシステム内のいかなる電源又は交換部品の単一故障又は不良からも風車を保護する。制御機能を提供す
るシステムの検出部品又は交換構造部分の単一故障は,保護機能の故障につながらないようにする。
複数の故障が相互に独立でない場合又は共通の原因によって発生する場合には,単一故障として扱う。
潜在的な欠陥によるリスクを減らすために,対策をとる。保護機能を提供するシステム内の交換部品は,
安全状態のままで故障させるか,又は交換部品の状態を自動的に監視する。いずれの場合でも,風車を停
止させる。非交換部品は,適切な間隔で点検する。
非冗長保護機能の実行において,全ての非フェイルセーフの部品は,7.6に定義する損傷結果に対する部
分安全率に関して,部品クラス3の部品とみなす。このような保護システムの全ての重要部品は,終極強
度,疲労,座屈及び危険な変形に対して解析する。
保護機能と制御機能とが相反する場合,保護機能が制御機能に優先する。
風車が安全性に重要な影響を及ぼす内部の故障又はトリップによって停止した場合,風車を自動又は遠
隔によって再始動できないようにする。電力系統の遮断又は負荷喪失の後に,このような故障又はトリッ
プが引き続いた場合でも,電力系統又は負荷の回復後に自動的に再始動できないようにする。
制御機能に優先する緊急停止ボタンによって,ロータを,保守及び修理に対して定義する風速限界(7.4.8
参照)を下回る風速において完全に停止にもっていく。少なくとも,運転状態からアイドリングモードに
もっていく。さらに,緊急停止ボタンの動作によって,中電圧及び高電圧システムを遮断する。緊急停止
ボタンは,全ての主要な作業場所(例えば,ナセル及びタワー底部)に設置する。用いた後に緊急停止ボ
タンを復帰させるには,適切な作業を必要とする。復帰後,手動解除することで,自動的に再始動できる
ようにする。
8.4
ブレーキシステム
ブレーキシステムによって,ロータをいかなる運転状態からもアイドリングモード又は完全停止にもっ
ていく。保守及び修理に対して定義する風速限界(7.4.8参照)を下回る風速において,ロータを危険なア
イドリング状態から完全に停止させる手段を設ける。
少なくとも一つのブレーキシステムは,直接ロータに働くような空力原理によって作動させることを推
奨する。この推奨に満足しない場合には,少なくとも一つのブレーキシステムを,ロータシャフト又は風
車のロータに作用させる。
ブレーキ装置は,外部電源がなくなっても働くように設計する。ブレーキ装置は,ブレーキ装置が加え
られた後,少なくとも1時間は定義する風条件に対して,ロータを安全停止位置に保つようにする。長い
時間電力が喪失している場合には,補助電源又は手動操作のいずれかによってブレーキ装置を働くように
する。
9
機械システム
9.1
一般事項
この規格における機械システムは,静的構造部品又は電気部品だけではなく,軸,リンク,軸受,スラ
39
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
イド,歯車,その他の装置の組合せによって用いる又は相対運動を伝える,全てのシステムを指す。風車
内のシステムには,ギヤボックス,軸,カップリングなどの動力伝達装置,及びブレーキ装置,翼ピッチ
制御装置,ヨー駆動装置などの補助装置を含む。補助装置は,電気,油圧又は大気圧によって駆動するこ
ともある。
動力伝達装置並びに制御システム及び保護システム中の全ての機械システムは,利用可能な場合,関連
するJIS,IEC規格及びISO規格に従って設計する。該当する場合には,その他の認められた規格を用い
る。システムの部品が部品クラス3に属さない場合には,部分安全率は,7.6.1.2の部品クラス2とする。
冷却及びろ過システムは,指定する保守手順がある場合,所定の運転温度範囲において,適切な運転条
件を維持できるように,特に注意する。
ブレーキ装置の中の摩耗しやすい部品の残存寿命は,自動的に監視し,かつ,定期的に点検する。緊急
停止に対して不十分な材料がある場合,風車は待機状態にする。全てのブレーキ装置は,応答時間を許容
レベル内に保つように設計し,保守する。
荷重計算は,平均ブレーキレベル及び設計に対して予測される最小の摩擦力及び加圧力を考慮に入れた
最小ブレーキレベルの両方を含むシミュレーションに基づく。ブレーキをかけたとき,ブレーキ装置が最
小ブレーキレベルでスリップする可能性がある場合,過熱,ブレーキ性能の低下及び火災のリスクを避け
るように設計する。
9.2
取付け誤り
リスク源となる可能性のある部品の取付け又は再取付け時に生じる誤りは,これらの部品の設計によっ
て防止する。設計による対応ができない場合には,部品自体及び/若しくはハウジングに対して情報を与
える。この情報は,リスクを避けるために,運動の方向が知られている可動部及び/又はそのハウジング
にも与える。さらに,必要となる追加の情報を,オペレータの指示書及び保守用マニュアルに記載する。
間違った接続がリスク源となる可能性がある場合には,間違った接続ができないように設計する。設計
による対応ができない場合には,パイプ,ホース又は接続ブロックに対して,情報によって,不完全な接
続をしないように注意を促す。
9.3
油圧又は空気圧によるシステム
油圧又は空気圧のエネルギーによって補助装置を駆動させている場合には,システムは,これらの種類
のエネルギーがもつ全ての潜在的な危険を避けるように,設計,構成及び装備を行う。蓄圧されたエネル
ギーを隔離又は放出するための手段を,システムに取り入れる。加圧油又は圧縮空気を送る全てのパイプ
及び/又はホース,並びにこれらの接続器具は,予見される内部及び外部の応力に耐えるように設計する
か,又はこの応力から保護する。破裂の結果生じる負傷などのリスクを最小限にするための注意を促す。
9.4
メインギヤボックス(増速機)
メインギヤボックスは,IEC 61400-4に従って設計する。
注記 対応国際規格では,“ISO 81400-4と同等の規格がIEC 61400の規格群として発行されるまで,
ISO 81400-4に従って設計する。”と記載しているが,ISO 81400-4は廃止され,IEC 61400-4に
置き換えられた。
9.5
ヨーシステム
ヨーシステムは,固定したナセル方位角を維持する手段(油圧ブレーキ装置など),そのナセル方位角を
変える手段(電気モータ,ギヤボックス,ピニオンなど)及び回転をガイドする手段(例えば,軸受)か
らなる。
全てのモータは,箇条10の関連部分に適合させる。
40
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
最終ヨー歯車などのギヤシステムの非冗長部品は,部品クラス2の部品とみなす。複数のヨー駆動装置
がヨーギヤシステムにおいて十分な冗長性を確保し,交換を容易に行うことが可能である場合,減速ギヤ
ボックス及び最終駆動ピニオンは,部品クラス1の部品とみなすことができる。
ピッチングの安全率は,ISO 6336-2に従って計算する。ISO 6336-2の図6において,限定的なピッチン
グに許容される寿命係数ZNTの上限曲線(1)を適用してもよい。さらに,ISO 6336-3に従って,歯の曲げ
強さが十分であることを証明する。ギヤの歯にかかる反対方向の曲げ荷重は,ISO 6336-3の附属書Bに従
って考慮する。表4にSH(ピッチングに対する表面耐久性の安全率)及びSF(歯の破損に対する曲げ強さ
の安全率)の最小値を規定する。これらの値は,荷重の特性値Fkを用いて計算する。つまり,これらの値
には,損傷結果に対する部分安全率γn,材料の部分安全率γm及び荷重の部分安全率γfが含まれる。
表4−必要とするヨーギヤシステムの安全率SH及びSFの最小値
項目
部品クラス1
部品クラス2
表面耐久性(ピッチング)
SH≧1.0
SH≧1.1
歯の曲げ疲労に対する強さ
SF≧1.1
SF≧1.25
静的な曲げに対する強さ
SF≧1.0
SF≧1.2
効率的なモニタリングを実施する場合,より低い安全率を適用することが可能である。1.0未満の安全率
を適用する場合,予測される交換間隔を保守マニュアルに記載する。
9.6
ピッチシステム
ピッチシステムは,翼ピッチ角を調整する手段(油圧駆動装置,電気モータ,ギヤボックス,ブレーキ
装置,ピニオンなど)及び回転をガイドする手段(軸受など)で構成することができる。
全てのモータは,箇条10の関連部分に適合させる。十分な冗長性が確保された個別のピッチ駆動装置を
もつピッチシステムのモータは,部品クラス2とみなすことができる。
9.7
保護機能機械ブレーキ
保護機能のために用いる機械ブレーキ装置は,一般的に油圧又は機械的ばね圧によって加えられる摩擦
(力)装置である。摩擦パッドなどの摩耗部品の残存寿命は,制御システム及び保護システムによって監
視する。このシステムには,緊急停止機構に必要な材料が不足している場合,タービンを待機状態に入れ
る機能をもたせる。
荷重の計算においては,適切な範囲のブレーキレベルを考慮してシミュレーションを行う。ブレーキ装
置によって風車が静止状態を維持している場合でも,このブレーキ装置が最小ブレーキレベルにおいて静
止状態から滑る可能性があるときは,乱流風におけるスリップ時間は,過熱,ブレーキ性能の低下及び火
災のリスクを十分に避けられる短さとする。
9.8
転がり軸受
転がり軸受の定格解析は,JIS B 1518及びJIS B 1519に従って行う。軸を支持する軸受(メイン軸,ギ
ヤボックスなど)については,(生存確率90 %の場合の)軸受の寿命は,20年以上とする。計算方法には,
運転条件を考慮する。JIS B 1518による調整係数[すなわち,a1係数(信頼度係数)]を適用する場合には,
十分に注意して適用する。
冷却及びろ過システムは,指定する保守手順によって,運転温度範囲の全体において適切な運転条件態
を確実に維持できるように,特に注意する。
軸受の設計荷重は,7.4に規定する各種の設計荷重ケースで決定した荷重及び7.6に規定する適切な安全
率を反映させる。軸受の設計に当たっては,その寿命期間中に予測される回転数,並びにその回転がメイ
41
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ン軸の軸受のような連続性の回転か,又はピッチベアリング及びヨーベアリングのような変動性の回転か
を考慮する。さらに,動きが小さいことによる潤滑不足の潜在的な影響にも注意する。
旋回輪軸受については,設計荷重における静定格荷重の係数は,JIS B 1519に従って1.0以上とする。
接続部品の柔軟性によって,荷重の分散を慎重に考慮する。
10 電気システム
10.1 一般事項
風車設備の電気システム(以下,風車の電気システムという。)は,個々の風車から風車接続端に至るま
でに据え付ける全ての電気機器からなる。
集電設備は,この規格の対象には含まない。
10.2 電気システムの一般要求事項
電気システムは,箇条6に定義する全ての通常及び極値の外部条件において,風車の運転及び保守を行
っている間に風車及び外部電気システムに生じるおそれがある損害だけでなく,人畜に及ぼす危険性を最
小限にするように設計する。
全ての電気機器及び部品を含む電気システムは,関連するIEC規格に適合させる。特に風車の電気シス
テムの設計は,JIS B 9960-1の要求事項に適合させる。交流1 000 V又は直流1 500 Vを超える公称電圧の
回路を含む風車の電気システムの設計は,JIS B 9960-11の要求事項に適合させる。機械設備以外の固定設
備は,JIS C 60364規格群の要求事項に適合させる。製造業者は,用いる設計規格を宣言する。電気システ
ムは,風車からの発電出力が変動する性質のものであることを考慮して設計する。
10.3 保護装置
風車の電気システムは,JIS C 60364規格群の要求事項に加えて,不安全な条件又は状態につながる風車
及び外部電気システムの機能不良に対して保護する適切な装置を含める。
10.4 断路装置
風車の電気システムは,保守又は試験時に全ての電源から切り離せるように設計する。
半導体装置は,単独では断路装置として用いてはならない。
照明,その他の電気システムが保守中の安全のために必要な場合には,これらの回路は,その他の全て
の回路が通電されていないときにも通電できるように,独自の断路装置をもつ補助回路を備える。
10.5 接地システム
風車の設計には,JIS C 60364規格群の要求事項及びJIS Z 9290-3の要求事項に適合する現地の接地極シ
ステムを含める。接地極システムが適切となる土壌条件の範囲は,設計文書に記載する。他の土壌条件で
起きることに関しての勧告も記載することが望ましい。
接地設備(接地極,接地導体,主接地端子及び接地棒)の選定及び施工は,JIS C 60364-5-54及び地域
電気規制当局の要求事項に適合しなければならない。
交流1 000 V又は直流1 500 Vを超えて運転する電気システムの場合には,保守期間中の接地に関する条
項を提供する。
10.6 雷保護
風車の雷保護は,JIS Z 9290-3に従って設計する。安全性が損なわれない場合には,保護措置を風車全
ての部品まで拡大させる必要はない。JIS C 1400-24に指針が示されている。
10.7 電気ケーブル
げっ歯類,その他の動物がケーブルをきず付ける可能性がある場合には,外装ケーブル又は電線管を用
42
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
いる。地下ケーブルは,作業車又は農耕機によって損傷を受けないように,適切な深さに埋設する。地下
ケーブルを電線管又はダクトで防護しない場合には,ケーブルカバー又は適切なマーキングテープで印を
付ける。
10.8 自己励磁
自励式の風車の電気システムは,電力系統が停電した場合でも遮断することができ,かつ,安全に遮断
状態を維持させる。
コンデンサバンクが誘導発電機に並列に接続されている(すなわち,力率改善のため)場合,電力系統
が喪失しても,発電機の自己励磁を回避するためにコンデンサバンクを遮断する適切な開閉器を設ける。
コンデンサが自己励磁の原因とならないことを十分示すことができる場合は,この限りではない。
10.9 雷電磁インパルスに対する保護
過電圧保護は,JIS Z 9290-4の要求事項に従って設計する。
保護の限度値は,電気設備に伝ぱ(播)する雷電磁インパルスが機器の絶縁レベルによって規定する限
度値を超えないように設計する。
10.10 電力品質
風車の電力品質特性は,JIS C 1400-21に従って評価する。
JIS C 1400-21に規定する手順は,公的な配電又は送電系統の運用者の要求事項に従っていることを証明
するために用いることができる。
10.11 電磁両立性
伝導妨害のエミッションは,10.9で規定する。
放射妨害のエミッションは,IEC 61000-6-4の要求事項に満足させる。
伝導妨害に対するイミュニティは,10.6で規定する。
放射妨害に対するイミュニティは,JIS C 61000-6-1又はJIS C 61000-6-2の要求事項に満足させる。風車
の製造業者は,これら二つの規格のいずれを風車設計に適用したかを宣言する。
11 サイトの固有条件に対する風車の評価
11.1 一般事項
風車は,環境条件及び電気的条件にさらされ,これには風車の荷重,耐久性及び運転に作用する隣接風
車の影響が含まれる。これらの条件に加えて,風車サイトの地震条件,地形条件及び土壌条件を考慮する。
サイトの固有条件によって,構造的な健全性を損なわないことを示す。これを証明するためには,サイト
の複雑性の評価(11.2参照)及びサイトの風条件の評価(11.3参照)が必要である。構造的な健全性の評
価に対して,次の二つのアプローチのいずれを用いてもよい。
a) これらの条件の全ては,風車の設計で仮定する条件よりも過酷でないことの証明(11.9参照)。
b) サイトの固有条件以上の厳しい条件に対する構造的な健全性の証明(11.10参照)。
全ての条件が設計で仮定する条件よりも厳しい場合には,構造的及び電気的の適合性は,b)のアプロー
チを用いて証明する。
7.6.2.1の荷重の部分安全率は,通常風条件及び極値風条件のサイト評価がこの箇条の最低限の要求事項
に従って行ったことを仮定して設定している。
11.2 サイトの地形的複雑さの評価
サイトの地形的複雑さは,平面に対する地形の傾斜及び地形の変化によって特徴付ける。
風車を取り囲む全ての風向方位区分に対して,タワー基礎を通過し,一定の距離及び方位区分幅におい

43
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
て地形を近似する平面を定義し,この平面によって地形の傾斜を求める。表5において,傾斜は,方位区
分内でタワー基礎を通過する近似平面内における平均線の傾斜とする。近似平面からの地形変化は,地表
面上の点から近似平面までの鉛直距離とする。
表5−地形的複雑さの判定基準
風車からの距離範囲
方位区分幅
近似平面の最大傾斜
最大地形変化a)
5 zhub未満
360°
<10°
0.3 zhub未満
10 zhub未満
30°
0.6 zhub未満
20 zhub未満
30°
1.2 zhub未満
注a) 指標を満たさない部分の合計面積が5 zhub2未満の場合,指標を満足するとみなす。
地形的複雑さの評価に用いる地表面格子の分解能は,1.5 zhub又は100 mのどちらか小さい方よりも粗く
しない。
表5の指標を満足しない方位区分から流入する風力エネルギーが全体の15 %以上の場合には,このサイ
トは複雑であるとみなし,満足しない方位区分から流入する風力エネルギーが全体の5 %に満たない場合
には,このサイトは平たんであるとみなす。
ここで,地形的複雑さを示す複雑度指標icを次のように定義する。複雑と判定した方位区分から流入す
るエネルギーが5 %未満である場合,ic=0とする。複雑と判定した方位区分からの流入エネルギーが15 %
以上である場合,ic=1とする。複雑と判定した方位区分からの流入エネルギーが5 %以上15 %未満の場合,
icを0〜1まで線形に変化させる。
11.3 評価に必要な風条件
風車サイトにおける,次のパラメータの値を評価する。
− 再現期間50年のハブ高さにおける極値10分平均風速
− VinとVoutとの間の風速の確率分布関数p(Vhub)
− 周囲乱流標準偏差σˆ[主方向成分12) の標準偏差の平均値と推定された],VinとVoutとの間のVhubにお
けるσˆの標準偏差
σ
σˆ及びVrefに等しいVhubにおけるσˆの標準偏差
σ
σˆ
− 流れの傾き
− ウィンドシアー13)
− 空気密度
注12) 乱流の主方向成分は,水平成分によって近似してもよい。
13) 長期間の高いシアー値は,強い密度成層流れ又は激しい粗度変化に関係して,ある地域で報告
されている。箇条6の外部条件は,このケースを扱っていない。
空気密度についてサイトのデータがない場合,空気密度は年平均温度で適切に補正したISO 2533に一致
するISO標準大気と仮定する。
上記に用いる風速ビンの間隔は,2 m/s以下とし,風向方位区分は30°以下とする。空気密度以外の全
てのパラメータは,10分平均とし,風向ごとに取り扱う。
サイトの風のパラメータ14) は,次のいずれかとする。
− 0.2 Vref〜0.4 Vrefの範囲で測定し,かつ,外挿したもの。
− サイトで行った測定によって計算したもの,現地の気象観測所の長期記録,又は現地の規則若しくは
規格によるもの。
注14) 風車からの距離が構造物の特性長さの20倍の範囲内にある重要な構造物からの後流にも注意
44
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
を払うのがよい。
測定値を用いる場合,他の適切な方法が示されていない限り,サイトの固有条件は,入手可能な現地の
気象観測所の長期データと関係付ける。測定期間は,6か月間以上の信頼できるデータを得ることで十分
とみなす。季節的な変化が風条件に大きく影響する場合には,測定期間は十分に長くして,これらの影響
を含める。
主方向成分の標準偏差の値は,適切にトレンド除去した測定データを統計的に処理して決定する。地形,
その他の現地の影響が乱流強度に影響すると考えられる場合,これらの影響はデータで示す。乱流強度を
評価する場合,測定データを得るために用いる風速計の特性,サンプリング速度及び平均時間を考慮する。
11.4 隣接風車の後流の影響評価
発電中の隣接風車の後流の影響を考慮する。ウィンドファームにおける風車の適切さの評価は,風上に
位置する風車からの単一又は複数の後流を考慮した決定論的な乱流の風特性を,風車間の間隔の影響を含
めて,発電に関係する全ての周囲風速及び風向に対して考慮する。
一般的に後流の影響に起因することが想定される荷重の増加は,有効乱流強度を用いることで説明して
もよい。この場合には,周囲乱流及び離散し乱れた後流が及ぼす荷重への影響を適切に説明する。
疲労計算に関する有効乱流強度Ieffは,附属書Dに基づいて導いてもよい。
一般的に,各種終極荷重条件における乱流強度は,疲労に対する有効乱流強度と同一であるとみなすこ
とはできない。
11.5 その他の環境条件の評価
風車の設計のために立てた仮定と比較するために,次に示す環境条件を評価する。
− 通常及び極値の温度範囲
− 着氷,あられ及び雪
− 湿度
− 雷
− 日射
− 化学的活性物質
− 大気中塩分濃度
11.6 地震条件の評価
世界で地震の影響を受ける地域は限定されるため,標準風車クラスの風車には耐震に対する要求事項は
ない。地震活動が弱いため,適用可能な特定地域の地震規定によって除外されるサイトに対しては,地震
評価の解析は要求しない。次に示す地震荷重ケースが重要な場所では,風車サイトの固有条件に対して技
術的な健全性を証明する。この評価は,附属書Cに基づくのがよい。荷重評価は,地震荷重とその他の大
きく頻繁に生じる運転荷重との組合せを考慮する。
地震荷重は,特定地域の規定に定義されるように,地表面加速度及び応答スペクトルに対する要求事項
によって決まる。特定地域の規定が利用できないか又は規定が地表面加速度及び応答スペクトルを提示し
ていない場合には,これらのパラメータの適切な評価を実施する。
地表面加速度は,再現期間475年に対して評価する。
地震荷重は,次のいずれか高い方の値に等しい運転荷重に重ね合わせる。
a) 寿命期間を平均化した通常発電中の荷重
b) 停止前の荷重がa) で得られる値に等しくなる風速に対して緊急停止する間の荷重
45
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
全ての荷重成分に対する荷重の部分安全率は,1.0とする。
地震荷重評価は,周波数領域法によって行ってもよい。この場合,運転荷重は,地震荷重に直接加算す
る。
地震荷重評価は,時間領域法によって行ってもよい。この場合,運転荷重が上記の時間平均値を代表す
ることを確保するために十分なシミュレーションをする。
上記のいずれかの評価に用いるタワーの固有振動モード数は,公認の地震規定に従って選定する。この
ような規定がない場合,全体質量の85 %の全モード質量による連続モードを用いる。
構造物の耐震性の評価は,弾性応答だけ又は延性によるエネルギー散逸を仮定してもよい。ただし,後
者は特定の種類の構造,特に格子構造及びボルト締結に対して正しく評価することが重要である。
地震計算及びタワー上の荷重の組合せに対する従来の解析方法を,附属書Cに示す。地震がタワーとは
別の構造物に大きな荷重を引き起こす可能性がある場合には,この手法は用いない。
11.7 電力系統条件の評価
計画されているサイトにおける風車接続端の外部電気条件について,電気設計条件との適合性を確実に
するために評価する。外部電気条件には,次を含める15)。
− 通常の電圧及び範囲。指定する電圧範囲及び継続時間にわたって接続されたままとするか又は遮断す
るかに関する要求事項を含む。
− 通常の周波数,範囲及び変化率。指定する周波数範囲及び継続時間にわたって接続されたままとする
か又は遮断するかに関する要求事項を含む。
− 対称故障及び非対称故障における逆相電圧の比(%)として指定する電圧不平衡
− 中性点接地の方式
− 地絡故障の検出及び保護の方法
− 電力系統の年間停電回数
− 自動再閉路周期
− 必要な無効電力補償時間
− 故障における電流及び継続時間
− 風車接続端における相間及び対地間の短絡インピーダンス
− 電力系統のバックグラウンド高調波電圧ひずみ
− (ある場合)電力線搬送波の存在及びその搬送波の周波数
− ライドスルーの要求事項のための故障特性
− 力率制御の要求事項
− ランプ率の要求事項
− その他の電力系統両立性の要求事項
注15) 風車設計者は,電力系統との両立性条件を考慮する必要がある場合がある。上記は,一連の最
低限の要求事項を規定したものである。設計の段階では,特定地域及び我が国の電力系統との
両立性条件も想定する必要がある。
11.8 土壌条件の評価
計画されているサイトの土壌特性は,入手可能な特定地域の建築基準を参照して,専門の有資格土質工
学技術者によって評価する。
11.9 風のデータを参照した構造的な健全性の評価
風車の構造的な健全性は,設計に用いたサイトの実測風況パラメータの値と比較することによって評価
46
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
してもよい。この場合,次に示す条件を全て満たすとき,風車はサイトに適するとみなす。
− 再現期間50年のハブ高さにおける極値10分平均風速のサイトの推定値は,Vref 16) 未満である。
− Vhubの確率密度関数のサイトの値は,風速が0.2 Vref〜0.4 Vrefの全てのVhubの値における設計確率密度
関数(6.3.1.1参照)未満である。
− 乱流標準偏差σ1[式(11)参照]の代表値は,風速0.2 Vref〜0.4 Vrefの全てのVhubの値において推定され
る乱流標準偏差の90 %分位値のサイトの値以上である。すなわち,乱流標準偏差は,式(34)となる。
σ
σ
.
σ
σ
ˆ
28
1
ˆ
1
+
≧
········································································ (34)
注16) 代わりに,再現期間50年のハブ高さにおける極値3秒平均風速の風車サイトの主要推定値は,
Ve50未満としてもよい。
地形が複雑である場合,乱流の主方向成分の標準偏差の推定値は,乱流のゆがみを考慮して大きくす
る 17)。サイトの気流の傾きは,全方向の最大をとり,6.3の規定値未満とする。気流の傾きに関するサイ
トのデータ又は計算値がなく,かつ,地形が複雑な場合には,気流は,風車から5 zhubの距離の範囲内に
おいて近似平面(11.2参照)に常に平行であると仮定する。
注17) 複雑な地形の影響は,次の式に規定する乱流構造補正パラメータCCTを追加して乗じることに
よって加味してもよい。
(
)
(
)
375
.1
ˆ
ˆ
ˆ
ˆ
1
2
1
3
2
1
2
CT
σ
σ
σ
σ
C
+
+
=
ここに,推定標準偏差
iˆσの比は,ハブ高さの値に対応する。乱流成分に関するサイトのデー
タがなく,かつ,地形が複雑である場合,モデル計算の結果又はCCT=1+0.15 icを用いてもよ
い。icは,11.2に定義する複雑度指標をいう。
方向に対するサイトの平均鉛直ウィンドシアーの指数αは,6.3.1.2に規定する値未満で,かつ,0より
も大きくする。ウィンドシアーに対するサイトのデータがない場合,地形及び粗度を考慮して計算する。
サイトの平均空気密度は,Vr以上の風速では6.4.1の規定値未満とする。
風車後流の影響は,通常乱流モデル(NTM)における乱流標準偏差σ1が,風速0.2 Vref〜0.4 Vref(又は風
車の特性が明らかとなっている場合には,0.6 Vr〜Vout)において,サイトにおいて推定される乱流標準偏
差の90 %分位値(周囲乱流及び後流乱流の両方を含む。)以上であることを検証することによって,適切
に評価することができる18)。すなわち,乱流標準偏差は,式(35)となる。
σ1≧Ieff・Vhub ············································································· (35)
注18) このアプローチは,方位区分とともに変化する単独の周囲乱流又は後流乱流と組み合わせた乱
流の評価にも使用することができる。σˆの標準偏差
σ
σˆは,方位区分での値の平均値として決め
てもよい。
Ieffの計算に関する指針は,附属書Dに示す。
さらに,部分後流によるサイト固有の水平方向シアーが,6.3.2.6に規定するEWSを超えず,後流の影
響を含むサイト固有の極値乱流19) が,6.3.2.3に規定するETMを超えないことを証明する。サイト固有の
乱流の証明に当たって,サイト固有の条件,後流の影響を受ける頻度及びウィンドファームの配置状況を
考慮する。
注19) サイト固有の極値乱流は,最も厳しい方向における後流の中心における最大乱流としてもよい。
47
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
11.10
サイト固有の条件に関する荷重計算による構造的な健全性の評価
風車の構造的な健全性は,風車サイト固有の条件値を用いて計算した荷重及び変形を,設計時の計算値
と比較することで証明する。この場合,構造耐力に対する設計裕度及び周辺環境に及ぼす影響を考慮する。
計算には,平均的な風向及び風速,後流の影響などを含む風条件の変化を考慮する。
乱流成分に関するサイトのデータがなく,かつ,地形が複雑な場合には,主流方向成分に対する横方向
及び上方向の乱流標準偏差の比率は,それぞれ1.0及び0.7と仮定する。
風車後流の影響を受ける場合には,終極限界状態及び疲労限界状態において,構造的な健全性が損なわ
れないことを検証する。通常乱流モデル(NTM)のDLC 1.2における疲労限界状態に対して,σ1は,附属
書Dに定義するIeffなどの適切な後流乱流モデルで置き換える。
終極限界状態の解析においては,適切なモデルによって計算した後流の影響を含むサイト固有の条件に
対して,DLC 1.1又はDLC 1.3,及びDLC 1.5を適用する。終極限界状態(ULS)の荷重を求めるための通
常乱流モデル(NTM)は,附属書Dの式(D.4)に定義する大規模なウィンドファーム内部の特性周囲乱流
として設定してもよい。
疲労荷重の計算において,附属書Dに定義するIeffは,評価対象の構成部品の材料のWöhler曲線指数m
に依存するため,異なる材料の特性をもつ構造部品にかかる荷重は,材料に適するmの値を用いて再計算
又は評価する。
12 組立て,据付け及び建設
12.1 一般事項
風車の製造業者は,据付マニュアルを提供し,そこに風車の構造物及び設備に関する据付けの要求事項
を明確に記載する。風車の据付けは,その業務の訓練及び指示を受けた者が行う。
風車の施設のサイトは,業務が安全かつ効率的な方法で行えるように整備,保守,運用及び管理する。
これには,関係者以外の立入禁止の処置も含むことが望ましい。運転者は,現存する危険及び潜在的な危
険を識別し,取り除くことが望ましい。
計画した業務の点検表を,準備する。完了報告及び点検記録は,保管することが望ましい。
該当する場合,据付け要員は,認証を受けた目,足,聴力及び頭部の防護具を装着する。タワーに登る
又は地面若しくは水面よりも高い場所で作業する全ての要員は,これらの作業の訓練を受けることが望ま
しく,作業に当たっては,認証を受けた安全ベルト,落下防止器具又はその他の安全器具を用いる。該当
する場合,水域では浮き具を用いることが望ましい。
全ての設備は,よく整備し,使用目的に適するようにしておく。クレーン,ホイスト及びリフト(ワイ
ヤ,フック,その他の器具を含む。)は,安全なつり上げ作業に十分な状態とする。
あられ,雷,強風,地震,着氷などの異常な条件下で行う風車設備の据付けには,特別の注意を払うこ
とが望ましい。
ナセルなしで建っているタワーの場合には,危険な風速下で,渦による横方向の振動発生を防止する手
段を講じる。危険な風速及び対策方法は,据付マニュアルに記載する。
12.2 計画
作業を安全に,かつ,特定地域及び我が国の規則に基づいて行うために,風車及び関連設備の組立て,
建設及び据付けは,計画的に実施する。計画書には,品質保証手順に加えて,適宜,次の検討事項を含め
る。
− 掘削作業を安全に実施するための規則
48
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 詳細図面,作業仕様書及び検査計画
− 基礎,ボルト,アンカ,鉄筋鋼材などの埋設物に関する適切な取扱規則
− コンクリート成分,運搬,サンプリング,注入,仕上げ及び導管配置に関する規則
− 発破に関する安全規則
− タワーその他のアンカの据付手順
12.3 据付条件
風車の据付け中,サイトは安全面で危険がないように維持する。
12.4 サイトへのアクセス
サイトへのアクセスは,安全を維持する。次の事項を考慮する。
− 防護壁及び輸送ルート
− 交通
− 道路表面
− 道幅
− クリアランス
− 道路の耐荷重
− サイトにおける設備の移動
12.5 環境条件
据付け中は,製造業者が指定する環境条件の制限を遵守する。次の事項を考慮することが望ましい。
− 風速
− 雪及び氷
− 周囲温度
− 砂じん(塵)
− 雷
− 視界
− 雨
12.6 文書
風車の製造業者は,風車の組立手順,据付け及び建設に関する図面,仕様書及び指示書を提供する。製
造業者は,風車の取扱い及び据付けに必要な全ての荷重,質量,つり上げ点,特殊工具及び手順の詳細を
提供する。
12.7 受取り,取扱い及び保管
据付け中の風力発電装置の取扱い及び輸送は,業務に適した装置を用いて,製造業者の推奨する方法で
行う。
風車はしばしば丘陵地に設置される。そのため,重機は,ずれないように設置する。全ての取扱い及び
組立作業のためには,適切な広さの水平な土地が望ましい。これができない場合には,全ての重機は,安
定する位置にしっかりと固定する。
風によって動くことで,損傷するおそれがある場合には,翼,ナセル,その他の空力部品及び軽いこん
包箱は,ロープ,くい及び/又はグランドアンカで固定する。
12.8 基礎又はアンカによるシステム
製造業者が安全な据付け又は組立作業のために特に指定する場合には,特殊工具,ジグ,固定具,その
他の器具を用いる。
49
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
12.9 風車の組立て
風車は,製造業者の指示書に従って組み立てる。検査を行い,適切な潤滑及び使用前の調整が,全ての
部品に行われているかを確認する。
12.10
風車の建設
風車の建設は,適切かつ安全な建設手順について訓練及び指示を受けた要員が行う。
建設工程上必要な場合を除き,風車の電気システムのいかなる部分も,建設中に通電しない。この場合,
これらの設備の通電は,風車の供給者が提供する文書による手順に基づいて行う。
動くこと(回転又は移動)によって潜在的な危険がある全ての要素は,建設期間中の不測の動作を防止
する。
12.11
締結部品及びアタッチメント
ねじ締結部品,その他のアタッチメントは,風車の製造業者が推奨するトルク及び/又はその他の指示
書に従って取り付ける。重要と識別された締結部品は点検し,取付けトルク,その他の要求事項を確認す
るために手順書を入手し用いる。
特に,次の事項を確認するため,検査を実施する。
− 支線,ケーブル,ターンバックル,ジンポール,その他の機器及び装置が,適切に組み立てられ,接
続されている。
− 安全な建設作業を行うために必要なつり上げ装置が,適切に取り付けられている。
12.12
クレーン,ホイスト及びつり上げ装置
クレーン,ホイスト及びつり上げ装置(安全な建設作業のために必要な,全てのホイスト用ワイヤ,フ
ック,その他器具を含む。)は,安全なリフト作業及び荷物の最終設置のために適切なものとする。建設及
び取扱いに関する製造業者の指示書及び文書には,部品及び/又は組立品の予想荷重及び安全なつり下げ
点を指示することが望ましい。全てのホイスト,ワイヤ及びフックは,安全荷重を確認するために試験す
る。
13 試運転,運転及び保守
13.1 一般事項
試運転,運転,検査及び保守に関する手順は,要員の安全を念頭に計画し,風力発電システムのマニュ
アルに記載して指定する。
全ての部品の検査及び保守のため,安全にアクセスできるように設計する。
箇条10の要求事項は,測定の目的で風車に一時的に据え付ける電気計測機器も対象とする。
該当する場合,運転及び保守要員は,認証を受けた目,足,聴力及び頭部の防護具を装着する。タワー
に登る又は地面若しくは水面よりも高い場所で作業する全ての要員は,これらの作業の訓練を受けること
が望ましく,作業に当たっては,認証を受けた安全ベルト,落下防止器具又はその他の安全器具を用いる。
該当する場合,水域では浮き具を用いることが望ましい。
13.2 安全運転,点検及び保守に関する設計要件
運転要員による風車の通常の運転は,地上で可能とする。自動及び/又は遠隔制御システムに優先する,
標識で表示した現地手動操作装置を備える。
電気負荷の喪失及び復帰のような,故障として検出されるが,風車のその後の安全性にとって重大でな
い外部事象は,停止サイクルの終了後に通常の運転に自動的に復帰してもよい。
可動部への不慮の接触から要員を保護するために設計した保護部材は,移動式であるために頻繁な接触
50
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
が予測される場合を除き,固定式とする。
保護部材は,次のとおりとする。
− 堅固な構造とする。
− 簡単に通り抜けができない配置とする。
− 可能な限り,取外しをしないで必要不可欠な保守作業ができるようにする。
故障を見付ける診断機器が利用できるように設計する。
検査及び保守の要員の安全性を確保するために,設計には,次の項目を取り入れる。
− 検査及び日常の保守のための安全なアクセス通路及び作業場所
− 回転部品又は可動部への不慮の接触から要員を保護するための適切な手段
− 高所に登る又は作業する要員のための認証を受けた命綱,安全ベルト又はその他の安全器具の設置
− DLC 8.1に規定する風条件及び設計条件に従った点検中,ロータ及びヨー運動機構の回転又は翼のピ
ッチ機構のようなその他の機械的機構の動きを拘束する手段,及び安全にこれらの拘束を外す手段の
設置
− 活線への警告標識
− 蓄積された電気を放電させる適切な装置
− 要員を火災から保護する適切な手段
− ナセルからの代替避難路
保守手順には,ハブ又は翼の内部などの閉じた作業区域に入る要員が危険な状況であることを待機して
いる作業員が確認でき,即座に救助活動を開始できるようにするための安全手順を記載する。
13.3 試運転に関する指示書
製造業者は,試運転に関する指示書を提供する。
13.3.1 通電
製造業者の指示書には,風車の電気システムの初回通電手順を記載する。
13.3.2 試運転試験
製造業者の指示書には,全ての装置,制御部及び機器が適切,安全かつ機能的に運転できることを確認
するために,据付後の風車試験の手順を含める。試験項目は,次のとおりである。ただし,これらに限定
しない。
− 安全な起動
− 安全な停止
− 安全な緊急停止
− 過速度又はこれを代表する模擬状態からの安全な停止
− 保護システムの機能試験
13.3.3 記録
製造業者の指示書には,試験,試運転,制御パラメータ及び結果を記載する,適切な記録を保管するこ
との指示を含める。
13.3.4 試運転後の業務
据付けが完了し,製造業者が推奨する一定期間の慣らし運転の後で,製造業者が要求する特定の作業を
実施する必要がある。
51
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この作業には,締結部品の締め直し,潤滑油の交換,並びにその他の部品に対する制御パラメータが適
切に設定され機能していることの確認及びその後の適切な調節を含める。ただし,これらに限定しない。
風車サイトは,危険を取り除き,侵食を防止するために整地することが望ましい。
13.4 運転要員への指示マニュアル
13.4.1 一般事項
風車の製造業者は,運転マニュアルを提供する。運転マニュアルには,適宜,試運転時にサイトの特別
な条件に基づいて必要事項を補足する。マニュアルの内容には,次を含める。ただし,これに限定しない。
− 風車の運転の業務は適切に訓練又は指導を受けた運転要員が行うという要求事項
− 安全な動作限界値及びシステムの記載
− 起動及び停止の手順
− 警報動作の一覧表
− 緊急時の手順計画
− 次の要求事項の明確な記載
・ 該当する場合,認証を受けた目,足,聴力及び頭部の防護具を装着する。
・ 該当する場合,タワーに登る又は地面若しくは水面よりも高い場所で作業する全ての要員は,これ
らの作業の訓練を受け,認証を受けた安全ベルト,落下防止器具又はその他の安全器具を用いる。
・ 該当する場合,水域では浮き具を用いることが望ましい。
・ 運転マニュアルは,運転要員及び保守要員が読んで理解できる言語を用いて,利用できるようにす
る。
13.4.2 運転及び保守の記録に対する指示書
マニュアルには,運転及び保守の記録を保管することを記載する。記録には,次の事項を含めることが
望ましい。
− 風車の識別名称
− 発電量
− 運転時間
− 停止時間
− 報告された故障の日付及び時刻
− 整備又は修理の日付及び時刻
− 故障又は整備の内容
− 実施した対策
− 交換した部品
13.4.3 計画外の自動停止に対する指示書
マニュアルには,運転マニュアル又は指示書に別途指定しない限り,計画外の自動停止が故障又は機能
不良によって生じた場合,運転者は風力発電システムを再起動する前に原因を調査することを記載する。
全ての計画外の自動停止は,記録することが望ましい。
13.4.4 信頼性の低下に対する指示書
マニュアルには,異常又は信頼性の低下について徴候又は警報があった場合,根本原因を除去する処置
を講じることを記載する。
13.4.5 作業手順計画
マニュアルには,風車は,次のことを考慮した安全作業手順に従って運転することを記載する。
52
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 電気システムの運転
− 運転と保守との調整
− 電力系統との解列手順
− タワーに登る手順
− 機器の取扱手順
− 悪天候のときの作業
− 意思伝達の手順及び緊急時の計画
13.4.6 緊急時の手順計画
運転マニュアルには,予想される緊急状態及び運転要員の必要な手順を規定する。
運転マニュアルには,風車又はその部品の火災又は明らかな構造上の損傷の危険性がある場合,危険の
性格が特定できない限り,誰も風車に近付かないほうがよいことをマニュアルに記載する。
緊急時の手順計画を作成する場合,構造上の損傷の危険性が,次の事項によって増大する可能性を考慮
する。
− 過速度
− 着氷の状態
− 雷雨
− 地震
− 支線の損傷又は緩み
− ブレーキ装置の故障
− ロータの不平衡
− 締結部品の緩み
− 潤滑不良
− 砂嵐
− 火災又は洪水
− その他部品の故障
13.5 保守マニュアル
各風車には,保守マニュアルを装備する。このマニュアルには,少なくとも,風車の製造業者が指定す
る保守要求事項及び緊急時の手順を含める。マニュアルには,計画外保守も含める。
保守マニュアルには,摩耗する部品を特定し,交換の基準を記載する。
保守マニュアルに含めることが望ましい事項を,次に示す。
− 点検及び保守の業務は,適切に訓練又は指導を受けた要員によって,指定する間隔で,風車保守マニ
ュアルの指示書に従って実施する。
− 風車のサブシステム及びその運転の記載
− 潤滑の頻度及び潤滑剤,その他特殊液体の種類を記載した潤滑計画
− 再試運転の手順
− 保守検査の周期及び手順
− 保護用サブシステムの機能点検の手順
− 内部配線図及び単線結線図
− 張力を含む支線検査及び張力再調整のスケジュール,並びにトルク荷重を含むボルト検査及び締め直
しのスケジュール
53
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 診断の手順及びトラブルシューティングの指針
− 推奨する予備品一覧表
− サイトの組立て及び据付けの図面一式
− 工具リスト
54
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
風車クラスSを規定する設計パラメータ
風車クラスSの風車の設計文書には,次の情報を記載する。
風車仕様
定格出力
(kW)
ハブ高さにおける運転風速範囲Vin−Vout
(m/s)
設計寿命
(年)
風条件
NTM及びETMで用いる平均風速の関数としての乱流強度
年平均風速
(m/s)
気流の平均吹上角
(°)
風速分布(ワイブル分布,レイリー分布,実測値,その他)
風速プロファイルモデル及びパラメータ
乱流モデル及びパラメータ
ハブ高さにおける極値風速Ve1及びVe50
(m/s)
1年及び50年の再現期間における極値ガストモデル及びパラメータ
1年及び50年の再現期間における極値風向変化モデル及びパラメータ
極値コヒーレントガストモデル及びパラメータ
風向変化を伴う極値コヒーレントガストモデル及びパラメータ
極値ウィンドシアーモデル及びパラメータ
電力系統の条件
通常の供給電圧及び範囲
(V)
通常の供給周波数及び範囲
(Hz)
電圧不平衡
(V)
電力系統の停電の最大継続期間
(日)
電力系統の停電の回数
(回/年)
自動再閉路周期(説明)
対称及び非対称の外部故障中の挙動(説明)
その他の環境条件(考慮する場合)
洋上風車の場合の設計条件(水深,波浪条件など)
通常及び極値の温度範囲
(℃)
大気中の相対湿度
(%)
空気密度
(kg/m3)
日射
(W/m2)
雨,あられ,雪及び着氷
化学的活性物質
55
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
機械的活性粒子
雷保護システムの説明
地震モデル及びパラメータ
大気中塩分濃度
(g/m3)
56
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
乱流モデル
荷重の設計値の計算に用いる二つの乱流モデルを,次に示す。乱流速度の変動は,その成分がゼロ平均
ガウス統計量をもつ定常ランダムのベクトル場と仮定する。a)のモデルを推奨する。
a) Mann一様シアーモデル
b) Kaimalのスペクトル及び指数コヒーレンスモデル
これらのモデルのパラメータは,6.3に規定する一般的な乱流に対する要求事項を満足するように選択さ
れている。
B.1
Mann(1994) 一様シアー乱流モデル
このモデルの記載は,三次元速度スペクトルテンソルを定義した点で,従来のモデルとは幾分異なる。
モデルはvon Karman(1948)の等方性エネルギースペクトルが一様の平均速度シアーによって急速にゆが
(歪)むと仮定する。その条件から結果として生じるスペクトルテンソル成分は,式(B.1)〜式(B.6)で与え
られる。
}
)
(
]
)
(
[
2
{
π
4
)
(
)
,
,
(
2
1
2
2
2
1
1
1
3
1
2
1
2
0
4
0
0
3
2
1
11
ζ
k
k
ζ
k
k
β
k
k
k
k
k
k
E
k
k
k
Φ
+
+
+
−
−
=
·········· (B.1)
}
)
(
]
)
(
[
2
{
π
4
)
(
)
,
,
(
2
2
2
2
2
1
2
1
3
2
2
2
2
0
4
0
0
3
2
1
22
ζ
k
k
ζ
k
k
β
k
k
k
k
k
k
E
k
k
k
Φ
+
+
+
−
−
=
········ (B.2)
)
(
π
4
)
(
)
,
,
(
2
2
2
1
4
0
3
2
1
33
k
k
k
k
E
k
k
k
Φ
+
=
··················································· (B.3)
}
)
(
]
)
(
[
]
)
(
[
{
π
4
)
(
)
,
,
(
2
1
2
2
2
1
1
1
3
2
2
1
3
1
2
1
4
0
0
3
2
1
12
ζ
ζ
k
k
ζ
k
k
β
k
k
ζ
k
k
β
k
k
k
k
k
k
E
k
k
k
Φ
+
+
+
−
+
−
−
=
··························································································· (B.4)
}
)
(
]
)
(
[
{
π
4
)
(
)
,
,
(
1
2
2
2
1
1
3
1
2
2
0
0
3
2
1
13
ζ
k
k
k
k
β
k
k
k
k
k
E
k
k
k
Φ
+
+
+
−
=
······················ (B.5)
}
)
(
]
)
(
[
{
π
4
)
(
)
,
,
(
2
2
2
2
1
1
3
2
2
2
0
0
3
2
1
23
ζ
k
k
k
k
β
k
k
k
k
k
E
k
k
k
Φ
+
+
+
−
=
····················· (B.6)
ここに,
〉
〈
=
=
∫∫∫
+∞
∞
−
+∞
∞
−
+∞
∞
−
−
−
−
)
,
,
(
)
,
,
(
1
)
,
,
(
)
,
,
(
π
8
1
)
,
,
(
)
,
,
(
3
3
2
2
1
1
j
3
2
1
i
2
iso
3
2
1
ij
3
2
1
3
2
1
ij
3
3
2
1
ji
*
3
2
1
ij
3
3
2
2
1
1
δ
x
δ
x
δ
x
u
x
x
x
u
E
σ
δ
δ
δ
R
dδ
dδ
dδ
e
e
e
δ
δ
δ
R
k
k
k
Φ
k
k
k
Φ
δ
k
δ
k
δ
k
λ
λ
λ
+
+
+
=
ι
ι
ι
: 無次元相関テンソル
u1, u2, u3: それぞれ主方向,横方向及び上方向の速度成分
δ1, δ2, δ3: 無次元空間距離ベクトル成分
k1, k2, k3: 三つの成分方向の無次元空間波数
2
3
2
2
2
1
k
k
k
k
+
+
=
:無次元波数ベクトルの大きさ
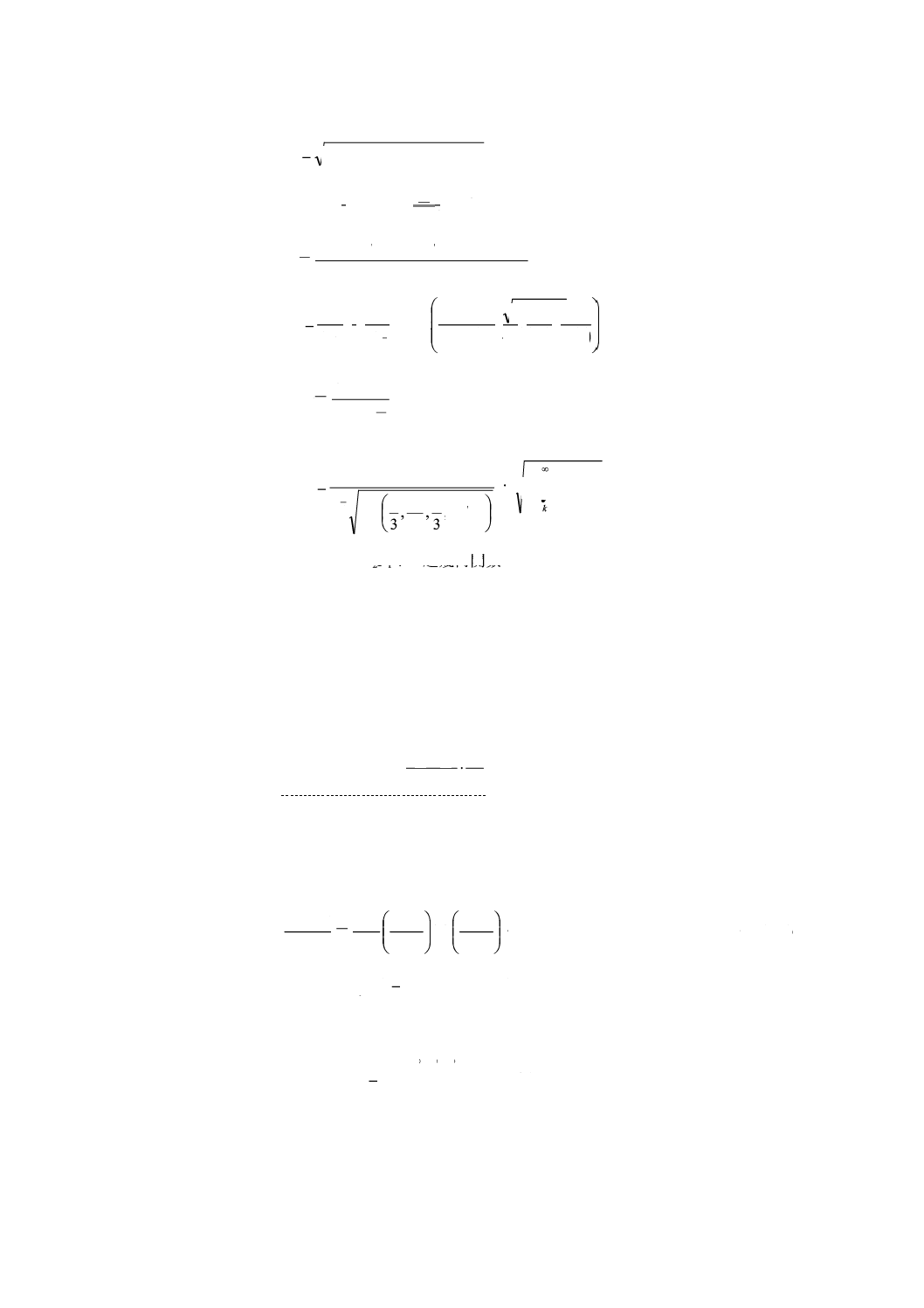
57
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
3
1
2
0
]
)
(
[
)
(
2
k
k
β
k
k
k
β
k
k
+
+
=
:シアーゆがみ前の大きさ
,
+
=
,
−
=
2
1
1
2
2
2
1
2
1
1
C
C
k
k
ζ
C
k
k
C
ζ
)
(
]}
)
(
[
{
)
(
2
2
2
1
2
1
3
3
2
2
2
1
2
1
1
k
k
k
k
k
β
k
k
k
k
k
k
β
C
+
+
−
+
=
(
)
()
()
(
)
()
+
−
+
+
=
k
β
k
k
k
β
k
k
k
k
k
k
β
k
k
k
k
C
1
1
3
2
0
2
2
2
1
1
2
3
2
2
2
1
2
0
2
2
arctan
6
17
2
4
)
1(
453
.1
)
(
k
k
k
E
+
=
:無次元von Karmanの等方性エネルギースペクトル
=
−2
1
2
3
2
,34,
6
17
,31
)
(
k
F
k
γ
k
β
−
:
∫∞k
dp
p
E
k
)
(
2
に逆比例する無次元ゆがみ時間
ここに,
2F1: 超幾何関数
λ,
2
iso
σ
: それぞれ非等方性分散及び尺度パラメータ
γ: 無次元シアーゆがみパラメータ
このモデルはvon Karmanの等方性モデルよりも複雑であるが,一つの追加パラメータ,すなわち,シア
ーゆがみパラメータγを含むだけである。このパラメータが0のとき,等方性モデルとなる。このパラメ
ータが増加するにつれて,主方向及び横方向速度成分の分散は増し,一方,上方向速度成分の分散は減少
する。その結果生じる乱流渦構造は,主方向に引き伸ばされ,かつ,1−2平面に関して傾く。
注記 超幾何関数2F1は,次のとおり定義される。
∑
∞
=0
1
2
!
)
(
)
(
)
(
)
,
,
,
(
n
n
n
n
n
n
z
c
b
a
z
c
b
a
F
=
ここに,(a)n=a(a+1)(a+2)…[a+(n−1)]
上記モデルによって作られるランダム速度場がハブ高さにおける風速において風車を通り過ぎて対流に
よって伝達されると仮定し,ある点で観測される速度成分スペクトルは,スペクトルテンソル成分を積分
することによって計算してもよい。特に,無次元の片側スペクトルは,式(B.7)で与えられる。
hub
ij
hub
2
1
2
iso
2
1
i
π
2
π
4
)
(
V
f
Ψ
V
f
σ
σ
σ
f
S
f
λ
λ
=
················································ (B.7)
ここに,
∫∫
∞
∞
−
∞
∞
−
=
3
2
3
2
1
ij
1
ij
)
,
,
(
)
(
dk
dk
k
k
k
Φ
k
Ψ
ただし,i=jの場合,Ψij(k1): 一次元波数自己スペクトル,
i≠jの場合,Ψij(k1): 一次元波数相互スペクトル
∫∫∫
+∞
∞
−
+∞
∞
−
+∞
∞
−
=
3
2
1
3
2
1
ij
2
iso
2
i
)
,
,
(
dk
dk
dk
k
k
k
Φ
σ
σ
:成分分散
同様に,主方向に直角の空間距離に対するコヒーレンスは,式(B.8)で与えられる。

58
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∫∫
+∞
∞
−
+∞
∞
−
−
−
hub
jj
hub
ii
3
2
3
2
hub
ij
3
2
ij
π
2
π
2
,
,
π
2
)
,
,
(
3
3
2
2
V
f
Ψ
V
f
Ψ
dk
dk
e
e
k
k
V
f
Φ
δ
δ
f
Coh
δ
ik
δ
ik
λ
λ
λ
λ
λ
=
················· (B.8)
ただし,この積分の解析式は知られていない。積分は,パラメータγの特定の値に対して数値的に行う。
Mann(1998)はこの積分を実行し,その結果をKaimalスペクトルモデルと比較した。Kaimalモデルに対
する最小二乗近似によって,シアーパラメータγは式(B.9)で与えられる。
γ=3.9 ··················································································· (B.9)
この結果,次の式(B.10)の分散関係式が得られる。
≈
≈
⇒
5.0
7.0
85
.0
65
.1
25
.3
1
3
1
2
2
iso
2
3
2
iso
2
2
2
iso
2
1
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
=
=
=
························································ (B.10)
上記で得られた横方向分散は,表B.1が示す値よりも僅かに小さいことに注意する。尺度パラメータは,
漸接慣性小領域主方向スペクトルを平均化することで求めることができる。つまり,式(B.11)から得られ
る。
1
3
5
3
2
hub
1
2
1
3
5
3
2
hub
2
iso
1
8.0
05
.0
π
2
475
.0
)
(
Λ
f
V
Λ
σ
f
V
σ
f
S
≈
⇒
=
→
−
−
−
−
λ
λ
········· (B.11)
要約すると,Mannモデルの三つのパラメータは,式(B.12)で与えられる。
γ=3.9
σiso=0.55σ1 ··········································································· (B.12)
ℓ=0.8Λ1
ここに,σ1及びΛ1は,6.3の規定による。
三方向乱流速度シミュレーションの場合,速度成分はスペクトルテンソルの分解及び離散フーリエ変換
による近似によって決定する。したがって,三次元空間領域は等間隔の離散点に分けられ,各点の速度ベ
クトルは,式(B.13)で与えられる。
=
∑
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
3
2
1
3
3
2
1
2
3
2
1
1
3
2
1
,
,
3
2
1
3
2
1
3
2
1
k
k
k
n
k
k
k
n
k
k
k
n
k
k
k
C
e
z
y
x
u
z
y
x
u
z
y
x
u
k
k
k
zk
yk
xk
i
λ
+
+
·················· (B.13)
ここに,
≈
0
)
(
π
2
)
,
,
(
2
1
2
0
2
2
2
0
1
2
1
1
3
2
2
2
1
1
1
3
1
2
4
0
3
3
2
1
0
3
2
iso
3
2
1
−
−
−
−
−
+
−
k
k
k
k
k
k
k
ζ
k
k
β
k
ζ
k
k
k
β
ζ
k
k
ζ
k
k
Δ
N
N
N
k
E
σ
k
k
k
C
λ
u1, u2, u3: 実数部及び虚数部が乱流速度場の独立した実現値である
複素ベクトル成分
n1, n2, n3: それぞれ異なる波数に対して独立しており,かつ,単位
分散をもつ実数部及び虚数部をもつ複素ガウスランダム
値
x, y, z: 空間格子点の座標

59
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
N1, N2, N3: 三方向の空間格子点の数
Δ: 空間的な格子分解能
この式(B.13)において,∑
3
2
1
,
,
k
k
k
の表記は,格子中の全ての無次元波数にわたる総和を意味し,FFT手法を
用いて計算することができる。空間領域が全ての次元において8ℓより小さい場合,スペクトルテンソルの
因数分解[C(k1, k2, k3)]が推奨される。この手順は,Mann(1998)の論文に記載されている。
B.2
Kaimal(1972)20) のスペクトル及び指数コヒーレンスモデル
風速の成分パワースペクトル密度は,式(B.14)によって無次元の形式で与えられる。
3
5
hub
k
hub
k
2
k
k
6
1
4
)
(
=
V
fL
V
fL
σ
f
fS
+
····························································· (B.14)
ここに,
f: 周波数(Hz)
k: 速度成分の方向を示す指数(すなわち,1=主方向,2=横方
向,3=上方向)(表B.1参照)
Sk: 風速度の一方向成分スペクトル
σk: 速度成分標準偏差[式(B.15)参照]
Lk: 速度成分積分尺度パラメータ
∫∞0
k
2
k
)
(df
f
S
σ=
······································································· (B.15)
乱流スペクトルのパラメータは,表B.1で与えられる。
表B.1−Kaimalモデルの乱流スペクトルのパラメータ
速度成分指数(k)
1
2
3
標準偏差 σk
σ1
0.8 σ1
0.5 σ1
積分尺度 Lk
8.1 Λ1
2.7 Λ1
0.66 Λ1
注記 σ1は乱流の標準偏差,Λ1は積分尺度パラメータを表す(6.3参照)。
主方向速度成分の空間の相関構造を考慮するため,Kaimalの自己スペクトルと併せて,式(B.16)による
指数コヒーレンスモデルを用いることができる。
−
5.0
2
C
2
hub
12
.0
12
exp
)
,
(
L
r
V
r
f
f
r
Coh
+
=
································· (B.16)
ここに,
Coh(r, f): 自己スペクトル関数によって空間的に分離された二つ
の地点における,風速度の主方向成分の相互スペクトル
密度の絶対値によって定義されるコヒーレンス関数
r: 平均風向に直角な面上への,2点間の分離ベクトルの投
影の大きさ
f: 周波数(Hz)
LC=8.1Λ1: コヒーレンス尺度パラメータ
注20) 表B.1の乱流成分分散比及び上方向速度成分に対する式の形は,元のKaimalスペクトルのモデ
ルと幾分異なっている。主方向尺度は,元のKaimalスペクトルに近似するように選ばれており,
60
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
また,横方向及び上方向尺度は,漸近慣性小領域及び表B.1で与えられる分散比に対して,6.3
のスペクトルの要求事項を満足するように選ばれている。
B.3
参考文献
J.C. Kaimal, J.C. Wyngaard, Y. Izumi, and O.R. Cote, “Spectral characteristics of surface-layer turbulence”, Q.J.R.
Meteorol. Soc., v. 98, 1972, pp. 563-598
T. von Karman, “Progress in the statistical theory of turbulence”, Proc. Nat. Acad. Sci., v. 34, 1948, pp. 530-539
J. Mann, “The spatial structure of neutral atmospheric surface-layer turbulence”, J. of Fluid Mech., v. 273, 1994,
pp. 141-168
J. Mann, “Wind field simulation”, Prob. Engng. Mech., v. 13, n. 4, 1998, pp. 269-282
61
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
地震荷重の評価
複雑な解析の必要性を容易に判別できない場合に用いるために,地震荷重の計算の簡易的従来手法を示
す。
主要な単純化は,一次タワー曲げモードよりも高い振動モードを無視することにあり,そのため全体構
造はこれと同じ加速度を受けると仮定する。二次モードの無視は非安全側の重大な単純化であるので,タ
ワー質量をタワー頂部質量に組み入れ,さらに,従来の空力荷重を加えることで,この単純化を埋め合わ
せる。
地表面加速度を導く方法は,11.6と一致させる。詳細なサイトのデータがない場合,従来手法の仮定を
採用する。用語は,ISO 3010をベースに用いる。
手順には,次のステップを含める。
− 我が国の関連する規格によって要求されるサイト及び土壌条件を評価又は推定する。
− 正規化された設計応答スペクトル及び地震災害地域区分ファクタを用いて,臨界ダンピングの1 %ダ
ンピングを仮定し,一次タワー曲げ固有周波数における加速度を求める。
− ロータ全体,ナセル及びタワー質量の50 %がタワー頂部に集中しているシステムが上記の加速度を受
けた場合の荷重を計算する。
− この結果を,定格風速における緊急停止機構に対して計算した特性荷重に加える。
− この結果を,設計荷重又は風車の設計抵抗力と比較する。
タワーがこの合成荷重に耐えられる場合,これ以上の検討は不要である。合成荷重に耐えられない場合,
11.6に従って,徹底的な検討を行う。
62
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
風車後流乱流及びウィンドファーム乱流
D.1 後流効果
疲労計算では,通常の運転中の有効乱流強度Ieff,Frandsen(2007),を用いて隣接風車による風車後流効
果を考慮してもよい。ハブ高さにおける平均風速に条件付けられる有効乱流強度は,式(D.1)のように定義
してもよい。
(
)
(
)(
)
m
m
dθ
V
θ
I
V
θ
p
V
I
1
π
2
0
hub
hub
hub
eff
=∫
········································ (D.1)
ここに, Vhub: ハブ高さにおける風速
p: 風向の確率密度関数
I: 風向θによって変わる周囲及び後流が組み合わさった乱流強度
m: 評価対象の材料のWöhler(S-N曲線)指数
次に,一様分布P(θ/Vhub)を仮定する。一様分布以外の場合には,式を調整してもよい21)。ウィンドファ
ーム内部では,平均風速は低下しないと仮定する。
注21) ウィンドファームにおける風車の配置が,非一様又は非格子状である場合,式(D.1)に含まれて
いる概念を維持して,式を適宜修正することが望ましく,影響を及ぼす近接風車,後流によっ
てじょう(擾)乱を受ける風向方位区分,及びハブ高さにおける平均風速に条件付けした風向
方位区分の発生確率を考慮しなければならない。
通常の運転中の有効乱流強度Ieffは,式(D.2)又は式(D.3)による。min{dI}≧10Dの場合,式(D.2)による。
hub
eff
ˆ
V
σ
I
c
=
············································································ (D.2)
min{dI}<10Dの場合,式(D.3)による。
(
)
()
06
.0
;
ˆ
ˆ
1
1
ˆ
W
T
W
W
1
1
i
hub
hub
eff
eff
=
+
−
=
=
∑
=
p
d
σ
p
σ
p
N
V
V
σ
I
m
N
i
m
m
c
············ (D.3)
ここに,
σˆ
28
.1
ˆ
ˆ
σ
σ
σc
+
=
: 特性周囲乱流標準偏差
σˆ: 予想周囲乱流標準偏差
σ
σˆ: 予想周囲乱流標準偏差の標準偏差
2
2
T
i
2
hub
T
ˆ
8.0
5.1
ˆ
c
σ
C
d
V
σ
+
+
=
: 後流中心でのハブ高さにおける最大乱流
標準偏差の特性値
CT: 対応するハブ高さにおける風速度での風
車スラスト係数の特性値。隣接する風車
のスラスト係数が不明である場合,一般
値CT=7c/Vhubを用いることができる。
di: ロータ直径によって正規化した隣接風車
No. iまでの距離
c: 定数。c=1(m/s)
Ieff: 有効乱流強度
63
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
N: 隣接風車の数
m: 評価対象の構造部品の材料に対応する
Wöhler曲線指数
他の風車の背後に“隠れた”風車からの後流効果を考慮する必要はない。例えば,1列に並んだ風車の
場合,評価対象の風車に最も近い二つの風車からの後流だけを考慮する。ウィンドファームの構成にも依
存するが,Ieffの計算に含まれる最近接風車の数を,表D.1に示す。
“横3列以上のウィンドファーム内部”のケースにおけるウィンドファーム構成を,図D.1に示す。
表D.1−考慮する最近接風車の数
ウィンドファームの構成
N
2基の風車
1
1列
2
2列
5
3列以上のウィンドファーム内部
8
大規模なウィンドファーム内部では,風車は風車自身の周囲乱流を発生させる傾向がある。したがって,
次のいずれかの周囲乱流の場合は,上記の
Tˆσの式の場合を除き,
cσˆの代わりに次の式(D.4)で表す特性周
囲乱流を仮定する。
a) 評価対象の風車からウィンドファームの“端”までの風車の数が,5基を超える。
b) 卓越風向に対して,垂直な列中の間隔が3D未満である。
(
)
σ
c
σ
σ
σ
σ
σ
′
+
′
+
′
+
=
′
ˆ
28
.1
ˆ
ˆ
ˆ
2
1
ˆ
2
2
W
···················································· (D.4)
ここに,
T
f
r
hub
W
2.0
1
36
.0
ˆ
C
d
d
V
σ
+
=
······························································· (D.5)
ここに,
dr: 風車直径で正規化した列中の風車間隔
df: 風車直径で正規化した列間の距離
図D.1−構成−横3列以上のウィンドファーム内部
D.2 参考文献
FRANDSEN S. (2007), Turbulence and turbulence generated loading in wind turbine clusters, Risø report R-1188
64
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E
(参考)
測定−相関−予測[measure-correlate-predict (MCP)]法による
風車サイトの風分布の予測
特定のサイトに対する風車の適合性の評価には,サイトにおける設計限界風速パラメータの評価が必要
となる。往々にしてウィンドファームの単一の設置点でさえ,評価を行うためのデータが不十分である。
ただし,他の場所の長期記録に基づく外挿によって,総合的にデータ記録を拡張することができる。MCP
法は,この拡張された記録を作成する手段である。次に示す説明は,East Anglia大学の国立風力・気象研
究部門の“Prediction of extreme wind speed at wind energy sites,a set of guidelines prepared under ETSU contract
W/11/00427/00”からとられている。
E.1
測定−相関−予測(MCP)
MCP法は,データの平均化期間及び方位特性が変化する多くの形態をとる。ここでは,風車サイト及び
近くの基準気象観測所の一時間間隔の同時刻データに基づく一つのバージョンを記載する。これらのデー
タは,クロスプロットされ,方位区分方向に直線回帰式を導くのに用いられる。方位区分は,気象観測所
によって用いられる方位区分と同じとし,一般的には30°方位区分である。回帰式を導くのに用いられる
データセットは,可能な限り長い期間が必要である。少なくとも,全ての季節的変化をカバーすることが
望ましい。
E.2
年平均風速及び分布への適用
上記の回帰式は,短期間変化を除外するのに十分に長い期間,おそらく少なくとも7年間にわたる長期
の気象観測所記録に対して,方位区分ごとに適用する。この結果がサイトの1時間平均記録であり,サイ
ト評価のために確率分布としてデータ処理される。
E.3
極値風速への適用
極値風速の予測に対する古典的方法は,精度を改善するために修正されたGumbel解析[例えば,“The
designers guide to wind loading of building structures”NJ Cook,Butterworths,1995に述べられているBest
Leiblein Unbiased Estimators(BLUE)手法]である。推奨されるデータの最小長さは10年間である。
このほかに,Gumbel法から派生した,独立暴風法(MIS)を適用することも可能である。これもCook
が述べた方法で,データセットから1年間当たりの複数のデータ点を用いている。この方法は,7年間の
短いデータセットを用いることができる。MIS法では,全ての値が独立事象の値であることを保証するた
めに,しきい値及び時間フィルタを適用して,独立した暴風のピーク風速を選択する。
方位区分固有の回帰係数は,Gumbel基準の年,MISの暴風事象及び方位区分に基づいて,気象観測所の
最大時間風速表に適用する。したがって,類似の表を,風車サイトに対して作成する。Gumbel解析では,
候補地の各年の最大値を抽出して用いる。
この係数は時間平均データから作られ,時間平均データに適用されるので,ここでの係数の使用は適切
である。この方法では,候補地の最大値が基準サイトの最大値と同じ方位区分で生じるとは仮定しない。
候補地の最大値は,方位固有の回帰係数を用いることによってサイト間の関係を考慮して,より正確に決
65
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
定することができる。
極値解析における適切な再現期間の選択には,年間に起きる事象数を考慮することが望ましい。
ガスト率は,サイト観測データ又は理論的方法によって推定することが望ましい。
E.4
参考文献
N J Cook, The designers guide to wind loading of building structures, Butterworths, 1995
National Wind Power and Climatic Research Unit of the University of East Anglia, Prediction of extreme wind
speed at wind energy sites,a set of guidelines prepared under ETSU contract W/11/00427/00
R I Harris, Gumbel re-visited-a new look at extreme value statistics applied to wind speeds,Journal of Wind
Engineering and Industrial Aerodynamics, Volume 59 (1996) pp. 1-22
D C Quarton, Wind Farms in Hostile Terrain,Final Report,A report prepared under ETSU contract
W/43/00501/00/00, July 1999
R.I. Harris, The accuracy of design values predicted from extreme value analysis, Journal of Wind Engineering
and Industrial Aerodynamics, 89 (2001) pp. 153-164
66
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書F
(参考)
終極強度解析のための荷重の統計的外挿
F.1
一般事項
構造物の破壊は,危険部位の応力が部品材料の抵抗力を超える場合に起きる。荷重が増加するとともに
応力が次第に増加するように,局所応力が荷重に関係すると仮定する場合,構造部品の強度は,破壊を引
き起こす終極荷重によって定義することができる。運転荷重を与えた上で,荷重の極値と許容終極荷重と
を適切な安全率を適用して比較することで,構造の適合性を評価することができる。
風車の荷重は,種々の風条件における乱れた流入風に依存する。したがって,適切な特性荷重を決定す
るために,統計に基づいて荷重の極値を解析することが必要である。
与えられた風条件に対して,短期間の荷重応答を定常不規則過程でモデル化するのが合理的である。次
に,荷重をこの過程で表すことができると仮定した場合の,外挿のためのデータ抽出の方法及び荷重の外
挿方法を説明する。さらに,収束判定基準を提案し,逆一次信頼性法(IFORM)を用いて,長期間の荷重
を評価する代替手法を説明する。
これらの方法は,3枚翼水平軸アップウィンド風車に対して検証されている。その他の風車のコンセプ
ト,及び/又は荷重フィードバックを含む制御方式においては,特別な注意が必要となる可能性がある。
詳細な情報及び指針は,参考文献[1] 22) に記載されている。
注22) この附属書の角括弧内の参考文献番号は,F.6による。
F.2
外挿のためのデータ抽出
外挿法で用いるデータは,指定する風条件において,風車の運転範囲における時刻歴の風車シミュレー
ションから抽出する。データは,各シミュレーション,シミュレーションを均等時間間隔のブロックに分
けて作るサブセット又は極値間の最小時間間隔を確保して作るサブセットから,グローバルな個別応答極
値を選択することによって抽出してもよい。
個々の荷重応答極値の間に独立性を確保することは,幾つかの外挿法において重要である。抽出を行う
とき,設計者は外挿におけるピーク間の独立性がもたらす影響を考慮し,可能な限り依存性を最小限に抑
える必要がある。外挿のために選択した方法(例えば,時間基準の間で確率関数の変換を含む方法)が独
立仮定の影響を受けやすい場合,設計者は独立性を統計学的に検証することが望ましい。
独立性を確保するための単純なアプローチとしては,各10分間シミュレーションにおける最大値又は三
つの応答サイクルよりも長い区間からの局所的極値が独立し,三つの応答サイクル(ブロック サイズにわ
たって三つの平均交差によって定義する。)の個別応答極値の間の最小時間間隔を必要とすると仮定する方
法がある。系統的,統計学的なアプローチが必要な場合,設計者は,標準的な評価技術(参考文献[5],[6]
など参照)を用いて独立性を検証し,制御された方法で依存性を最小限に抑えてもよい。
POT法(しきい値法)を用いてもよいが,設計者は,しきい値による切捨て誤差及び相関性が経験的な
分布形状に大きな影響を与えないように注意する必要がある。
67
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
F.3
荷重外挿法
F.3.1
一般事項
50年間にわたる風車の荷重を判定するための極値事象の外挿について提案するアプローチは,次の手法
に分けることができる。
a) パラメータフィッティング後に集計処理する手法 風車の運転範囲を,通常乱流モデル(NTM)のレ
ベルにおける時間領域シミュレーションの離散風速と離散発電性能とに区分する。それぞれの風速の
実現のための極値(パラメトリック)分布を推定する(参考文献[2]参照)。平均風速の長期分布関数
に応じた全ての分布を集計する。集計した分布関数の50年再現値を予測する。10分間のシミュレー
ションからの最大値において,50年再現荷重の確率は,3.8×10−7となる。
b) データ集計後にパラメータフィッティングする手法 風車の運転範囲を,通常乱流モデル(NTM)の
レベルにおける時間領域シミュレーションの離散風速と離散発電性能とに区分する。風車の運転範囲
内における平均風速の長期分布関数に応じて,全ての時刻歴から,該当する極値を集計する。全ての
極値に対する単一の(集計された)分布関数を推定する。得られた分布関数から50年再現値を予測す
る。
特定の観測期間Tにおいてシミュレーションした極値の短期分布の集計から,同じ期間における長期間
の極値の経験分布への集計に当たっては,最大値からの外挿及び局所的極値からの外挿の2種類のケース
が考えられる。
F.3.2
最大値
観測期間Tにおける最大値の短期分布を,次の式(F.1)に示す。
(
)
T
V
s
F
term
short
;
−
······································································· (F.1)
このとき,sは荷重応答を意味する。また,平均風速の長期分布を用いることで,極値の長期分布を求
めることができる。
(
)
(
)()dV
V
f
T
V
s
F
T
s
F
out
in
V
V
term
short
term
long
∫
−
−
=
;
|
;
····································· (F.2)
要求する再現期間Trの終極荷重応答srは,次の式(F.3)を用いて求めることができる。
(
)
T
T
N
N
T
s
F
r
r
term
long
=
−
=
−
,
1
1
;
··················································· (F.3)
これらの式を実際に用いる場合,通常は離散的な風速値を用いることになる。したがって,次のように
なる。
(
)
(
)
()
out
M
in
k
k
k
k
M
k
k
term
short
term
long
V
V
V
V
V
V
f
p
p
T
V
s
F
T
s
F
≦
<
<
≦
Κ
1
1
,
Δ
,
;
|
;
=
≈∑
=
−
−
··· (F.4)
分布F short-termは,経験分布へのフィッティングによって求めることができる。
(
)
k
k
i
k
ki
term
short
n
i
n
r
V
S
F
,
,1
,1
Κ
=
+
=
−
··············································· (F.5)
このとき,skiは風速kからi番目の極値サンプルを示し,riは風速kから生じるnk極値におけるskiのラ
ンクである。以降の展開のために,総和による経験分布の等価表現は次のとおりとなることに注目する。
(
)
(
)
k
ki
kj
n
j
k
k
ki
term
short
n
i
S
S
I
n
V
S
F
k
,
,1
,
‒
1
1
1
Κ
=
+
=∑
=
−
······························· (F.6)
このとき,指標関数I(x)は次の式(F.7)のように表現する。
68
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
=
0
1
0
1
)
(
>
≦
x
for
x
for
x
I
··································································· (F.7)
指標関数の役割は,ski以下の値をもつ経験的確率に寄与するようにski以下の全ての値を抽出することで
ある。指標関数の具体的な定義が,同一の極値を実現するための事象を含むことを保証することに注意す
る。
F.3.3
局所的極値
観測期間Tにおける最大値の短期分布を,その期間における独立な局所的極値n(V)から求める(極値は
正の値であると仮定している,負の値では符号を逆転させる)。
(
)
(
)
)
(
;
|
;
|
V
n
local
term
short
T
V
s
F
T
V
s
F
=
−
················································ (F.8)
式(F.9)に定義する長期分布,及び要求する再現期間Trの終極荷重応答srを,F.3.2に説明のとおり確立す
る。厳密には,nは,Vに依存する分布が仮定されている乱数である。ただし,風車への適用において,n
は,平均値と比較して変動が限られている。このため,上記で暗示的に行っているように,nを平均値(V
に条件付きの)で置き替えることで十分な精度が得られる。式(F.9)及び式(F.10)を適用するときに,考慮す
る特定の荷重応答に最も寄与する風速の代表値sを用いる場合,近似を許容してもよい。この近似に基づ
き,次のように表すことができる。
(
)
(
)()dV
V
f
T
V
s
F
T
s
F
out
in
V
V
n
local
term
long
∫
=
−
;
|
;
········································ (F.9)
(
)
T
T
N
N
T
s
F
r
r
term
long
=
−
=
−
,
1
1
;
················································· (F.10)
F.3.4
長期経験分布
全ての風速からのデータを集計し,合成したデータに分布をフィッティングすることは,利点がある。
このための一つの方法は,ビンごとのシミュレーションの数を風速のワイブル分布(又は他の適切な分布)
によって決定し,数多くのシミュレーションを計算することである。
()
()
out
M
in
k
k
k
k
total
k
sims
V
V
V
V
V
V
f
p
p
N
V
N
≦
<
<
≦
Κ
1
,
Δ
,
=
≈
························· (F.11)
シミュレーションが完了し,最大値を抽出した後,全ての風速の全ての最大値を単一の分布に合成し,
次のようにランク付けする。
()
total
k
i
i
term
long
n
i
n
r
S
F
,...,
1
,1 =
+
=
−
················································· (F.12)
このとき,siは全ての風速のi番目の極値サンプルを示し,riは合成した分布から生じるntotal極値におけ
るsiのランクを示す。
この方法の潜在的な短所として,高い風速が卓越することによる荷重を経験分布の裾部における大きな
極値としてを抽出する手段が,非常に僅かなシミュレーションしか存在しない点が挙げられる。この問題
に対応するため,低確率の風速ビンに対する追加的なシミュレーションを用いて追加的な長期分布を計算
することができる。ビンごとの総シミュレーション時間は,元の風速分布に従う必要があるが,全てのビ
ンからランダムにブートストラップしたデータを用いて,数多くの新しい経験的な長期分布を形成するこ
とができ,そこにおいては数多くのシミュレーションが利用できる。数多くの長期分布を形成することに
よって,単一の総計の長期分布を形成するためにこれらを平均化する。これは,確率水準を下げるための
外挿に用いることができる。
69
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
F.4
収束判定基準
F.4.1
一般事項
風車の終極荷重の解析では,風速の重要性が,外挿する荷重に依存して変化する。ある荷重では,定格
に近い風速が支配的である一方,カットアウト付近又はその他の風速が支配的となる荷重も存在する。設
計者は,支配的な風速を詳しく検証して,方法の安定性を確保するために十分な数のシミュレーションを
実施することが重要である。[Vr−2(m/s)]からカットアウトまでの各風速においては,15以上のシミュ
レーションが必要であり,Vが[Vr−2(m/s)]未満の各風速においては6個のシミュレーションが必要で
ある。
[Vr−2(m/s)]からカットアウトまでの風速に必要なシミュレーションの最小数に加え,7.6.2に従っ
て追加的な収束判定基準も適用する。推奨するシミュレーション数は,結果として得た経験的な分布の信
頼区間を計算することによって決める。十分であるとみなすシミュレーション数は,最大値(global maxima)
の経験荷重分布の84 %分位値に対する90 %の信頼区間の幅が,84 %分位値の推定値の15 %よりも低くな
る数である。この区間は,ブートストラップ法(参考文献[3]参照)若しくは二項検定(参考文献[4]参照)
を用いて評価するか,又は採用する外挿法の一部として推定することができる。
10分シミュレーションごとの極値mに帰結するその他の方法(ブロック最大値など)を用いて極値を求
める場合,84 %以上の分位値を式(F.13)による,p*に置き換える必要がある。
(
)m
p
1
84
.0
*=
········································································· (F.13)
フィッティングの前に風速データの集計結果を用いて長期間の分布を確立するか,又は集計処理
(aggregation)の前にそれぞれの風速のデータに対するパラメータ分布のフィッティングを実施するかに
応じて,収束判定基準を各短期荷重分布に個別に適用することが望ましい。
フィッティングの前の集計処理を含む手順において,全ての風速ビンの集計後における荷重の経験的な
長期分布は,短期分布に対して提案した上記の基準に類似した収束判定基準を利用することで確立するこ
とができる。この経験分布の裾部において収束を確認することを保証するため,収束判定基準を課す適切
な分位値を,経験的な長期分布に見られる明らかな“折れ曲がり(knee)”(しばしば観察される)に対応
する分位値よりも高くすることが望ましい。
F.4.2
荷重分位値の推定
非超過確率pに対応する,所望の荷重分位値
p
Lˆは,次の方法で推定する。
シミュレーションから値がm個得られた場合,S1≦S2≦…≦Smのように全ての荷重データをランク順に
並べる。最大値を用いる場合,mはシミュレーションの個数に等しくなることに注意する。
指定されたpについては,式(F.14)によって整数iを見出す方法を確保することが必要である。
1
1
1
+
+
−
m
i
p
m
i
≦
≦
·································································· (F.14)
ここに,2≦i≦m。
式(F.14)の不等式の解及びiの値が見つかるように,十分な数のmの極値を得る必要がある(このために,
十分な数のシミュレーションを実行する必要がある)。
次に,補間(線形補間)によって,荷重分位値の推定値を式(F.15)によって計算する。
p
Sˆ=Si−1+[p(m+1)−(i−1)](Si−Si−1)········································· (F.15)
ここに,2≦i≦m。
70
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
F.4.3
信頼限界
84 %分位値に対する90 %の信頼区間
0.84
ˆS
が次のとおりになるように,信頼限界を推定する。
15
.0
ˆ
ˆ
‒
ˆ
84
.0
95
.0,
84
.0
05
.0,
84
.0
<
S
S
S
··························································· (F.16)
ここに,区間
95
.0,
84
.0
0.05
0.84,
ˆ
,
ˆ
S
S
は,求められる90 %の信頼区間を表す。
F.4.4
ブートストラップに基づく信頼区間
信頼区間を形成するためのブートストラップ手順(参考文献[3]及び[7]参照)を用いて,非超過確率p,
最大値(m1, m2, m3, m4, m5, … mp)の初期データセットを取り,新しいセット(m1, m2, m3, m4, m5, … mp)を
形成するために,これらのデータをランダムに再サンプリングするか,又は元のサンプルと同じサイズの
ブートストラップによって再サンプリングすることで始める。それぞれの再サンプリングにおいて,デー
タをランダムに再サンプリングするため,ブートストラップの再サンプリングは,元のサンプルからの繰
返し値によって構成されることに注意する。この過程は,大量なNb個のブートストラップ再サンプリング
を形成するために繰り返す。これらのpのデータセットのそれぞれから,84 %分位値に対する個別の評価
値を得る。セット(l1, l2, l3, l4, l5, … lNp)を形成するこれらのNb個の推定値から,データに順序付けを行う
ことで,通常の方法によって信頼区間を見つけることができる。これらを式(F.16)の分子に用いることがで
きる。元々のデータから得られる84 %分位値の推定値は,式(F.16)の分母を表す。
信頼限界の合理的な推定値を判断するためには,最小25個のブートストラップ再サンプリングで十分で
ある可能性がある。ただし,より大きな5 000個程度の再サンプリングによって,より高い信頼性の推定
値を得ることができることがある。
F.4.5
二項分布に基づく信頼区間
二項分布(参考文献[7]参照)に基づく信頼区間では,ブートストラップ法を用いた計算の信頼区間より
も,計算負荷は軽減する。この計算負荷の軽減は,最も一般的な状況において生じる二項信頼区間を計算
するために,パラメータを表にすることによって達成する。84 %荷重分位値における90 %の信頼区間にお
いて,表F.1は,式(F.17)で推定信頼限界を補間するために必要なk*,l*,A及びBの値を与える。シミュ
レーションの数は,各風速ビンにおいて,15〜35である。

71
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表F.1−二項分布に基づく信頼区間を確立するために必要なパラメータ
(84 %分位値の荷重における90 %信頼区間)
シミュレーションの数
k*
l*
A
B
15
9
14
0.50
0.32
16
10
15
0.27
0.19
17
11
16
0.10
0.03
18
11
16
0.87
0.96
19
12
17
0.58
0.90
20
13
18
0.35
0.83
21
14
19
0.16
0.76
22
14
20
1.00
0.69
23
15
21
0.69
0.60
24
16
22
0.45
0.50
25
17
23
0.25
0.39
26
18
24
0.08
0.26
27
18
25
0.85
0.12
28
19
25
0.58
0.98
29
20
26
0.36
0.91
30
21
27
0.18
0.83
31
22
28
0.02
0.75
32
22
29
0.75
0.66
33
23
30
0.51
0.56
34
24
31
0.31
0.44
35
25
32
0.13
0.32
表F.1は,10分間最大値の84 %分位値における90 %信頼区間を与えるように調整した設計式とともに
用いる。設計式は,式(F.17)によって表すことができる。
(
)(
)
(
)(
)
(
)
(
)
*
*
*
*
*
*
1
1
k
k
l
l
k
l
k
l
x
x
A
x
x
B
x
x
x
x
−
−
−
+
−
=
−
+
+
··························· (F.17)
ここに,l*,k*,A,及びBは,実施するシミュレーション数の関数として表F.1に示すとおりであり,
xl*,x(l+1)*,xk*,及びx(k+1)*は,ランク順にしたシミュレーションによる極値から得る。収束判定基準を満
たすか否かを判断するために,この推定値の式(F.18)を式(F.16)に挿入する。
k
l
x
x
S
S
−
≈
−
95
.0
,
84
.0
05
.0
,
84
.0
ˆ
ˆ
························································ (F.18)
F.5
逆一次信頼性法(IFORM)
荷重外挿法の代替方法として,長期間の荷重を推定することを目的としたIFORMがある。この方法は,
通常乱流モデル(NTM)の条件において,乱流及び風車応答のシミュレーションを実施する。[Vr−2(m/s)]
からカットアウト風速まで,最小で15以上のシミュレーションを実施することが望ましい。さらに,最も
高い荷重を生じる風速を特定する。短期間の荷重分布から50年の再現期間の定義に一致した確率水準への
外挿によって,DLC 1.1の再現期間50年の荷重を得る。
設計者が,特定した重要な風速(しばしば一つだけ)による荷重分布の推定信頼区間を必要とする場合
を除き,IFORMの収束判定基準は,他の外挿法の収束判定基準と同じであることが望ましい。
逆一次信頼性法(IFORM)技術(物理ランダム変数を標準的な正規ランダム変数へ変換することに依存
72
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
する。参考文献[8]参照。)の使用に関する理論は,文書にまとめられている(例えば,参考文献[9]を参照
する。)。この理論を,通常乱流モデル(NTM)の条件下における長期間の風車荷重を推定するために適用
することができる。
次の手順を用いて,風車の終極荷重に対してIFORMを実行する。
a) [Vr−2(m/s)]からカットアウト風速までの風速ビンにおいて,15のシミュレーションを実行する。
b) どの風速ビンにおいて最大の荷重極大値が生じるかを特定する。
c) b)で特定した風速ビンについて,更に15のシミュレーションを実施して探索を実施する。再び,最大
荷重が発生する設計風速v*を特定する。経験荷重分布の最大値の84 %分位値に対する90 %信頼区間
の幅が,84 %分位値の推定値の15 %未満となるように,重要な風速におけるシミュレーション数が十
分であるかを確認する。
d) c)で特定した風速ビンに対して短期間の解析を実施する。この風速ビンにおける荷重分布に望まれる
分位値を導出する。この分位値は,目標確率水準に依存する。
なお,分位値は,次のように算出する。
− レイリー分布の累積分布関数(CDF)を用いて,U1=Φ−1[FV(v*)]を計算する。
− 50年に一度の10分間の超過確率は,pT=3.8×10−7である。これはβ=4.95に対応する。
− U2=[β2−U12]1/2を解く。
− 荷重分位値PS=Φ(U2)を導き出す(表F.2参照)。
長期間の荷重は,風速ビンv*の短期間の分布のPS分位値となる。適切な分位値を得るためには,外挿
が必要となる場合がある。

73
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表F.2−IFORM手順での使用を目的とした,異なる風車クラスのハブ高さの風速を関数とした
短期間の荷重超過確率
v*
(m/s)
1-PS,クラスI
1-PS,クラスII
1-PS,クラスIII
5
5.77E-07
4.74E-07
4.16E-07
6
3.85E-07
3.72E-07
3.73E-07
7
3.87E-07
4.14E-07
4.55E-07
8
5.13E-07
5.93E-07
7.02E-07
9
8.50E-07
1.05E-06
1.33E-06
10
1.71E-06
2.25E-06
3.03E-06
11
4.14E-06
5.79E-06
8.24E-06
12
4.83E-07
4.14E-07
3.81E-07
13
3.71E-07
3.80E-07
4.07E-07
14
4.52E-07
5.22E-07
6.22E-07
15
7.66E-07
9.73E-07
1.27E-06
16
1.71E-06
2.37E-06
3.37E-06
17
4.93E-06
7.41E-06
1.14E-05
18
1.81E-05
2.95E-05
4.93E-05
19
4.32E-07
3.85E-07
3.71E-07
20
3.81E-07
4.14E-07
4.73E-07
21
5.64E-07
7.02E-07
9.10E-07
22
1.23E-06
1.71E-06
2.48E-06
23
3.72E-06
5.79E-06
9.31E-06
24
1.55E-05
2.67E-05
4.76E-05
25
8.80E-05
1.68E-04
3.34E-04
F.6
参考文献
[1] Wind Energy, Vol. 11, Number 6, November-December 2008, Special Issue on Design Load Definition
[2] MORIARTY, P.J., HOLLEY, W.E., BUTTERFIELD, S.P. (2004), “Extrapolation of Extreme and Fatigue Loads
Using Probabilistic Methods”, NREL-NWTC, Golden, CO
[3] EFRON, B. and TIBSHIRANI, R. J., (1993), “An Introduction to the Bootstrap”, Chapman and Hall, New York
[4] HOGG, R. V. and CRAIG, A. T., (1995), “Introduction to Mathematical Statistics”, 5th Ed., Prentice Hall,
Englewood Cliffs, New Jersey
[5] HOEFFDING, W., (1948), “A Non-Parametric Test of Independence”, The Annals of Mathematical Statistics,
Vol. 19, No. 4, pp. 546-557
[6] BLUM, J.R., KIEFER, J. and ROSENBLATT, M., (1961), “Distribution Free Tests of Independence based on
the Sample Distribution Function”, The Annals of Mathematical Statistics, Vol. 32, No. 2, pp. 485-498
[7] FOGLE, J. AGARWAL, P. and MANUEL, L. (2008), “Towards an Improved Understanding of Statistical
Extrapolation for Wind Turbine Extreme Loads”
[8] ROSENBLATT, M. (1952), “Remarks on a Multivariate Transformation”, Ann. Math. Stat., Vol. 23, pp.
470-472
[9] SARANYASOONTORN, K. and MANUEL, L.,“Design Loads for Wind Turbines using the Environmental
Contour Method”, Journal of Solar Energy Engineering including Wind Energy and Building Energy
Conservation, Transactions of the ASME, Vol. 128, No. 4, pp. 554-561, November 2006
74
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書G
(参考)
荷重外挿に関するMiner則を用いる疲労解析
G.1
疲労解析
疲労破壊は,変動荷重による損傷の蓄積から生じる。この種の疲労に関する巨視的な見解については,
損傷の増大は局所の応力−ひずみ線図で示される,個々のヒステリシスサイクルから生じるということが
一般的に理解されている。したがって,荷重時刻歴の極大値は,局所の最小値と対になって一つの全サイ
クルを描く(レインフローサイクルカウント,Matsuishi & Endo,1968,又はDowling,1972参照)。これ
らの各々のサイクルは一組の極値によって特徴付けられる(又は範囲及び中間値によって,等価となる。
すなわち,二つの対となるサイクル極値間の差及び平均によって特徴付けられる)。損傷が線形的で,かつ,
各サイクルに独立に蓄積する場合(Palmgren,1924及びMiner,1945),損傷の合計は,式(G.1) 23) によっ
て得られる。
()
∑
=
i
iS
N
D
1
········································································ (G.1)
ここに,
Si: i番目のサイクルの荷重範囲
N(・): 引数によって与えられる範囲(すなわち,S-N曲線)で,一定
の大きさの荷重に対して破損に至るまでのサイクル数
注23) 式を簡素化するために,各サイクルの中間点荷重レベルの変動の影響は無視している。この制
限は,等価サイクル範囲の使用によって中間点荷重レベルを変える問題が後から取り込まれた
場合,除外される場合がある。
さらに,式(G.1)において,破壊部位の局所応力は,荷重と線形関係にあると仮定している。疲労解析の
場合,一般的に,設計に選ばれるS-N曲線は,材料データから曲線を決定する場合の,所定の生存確率(し
ばしば95 %)及び信頼レベル(しばしば95 %)に関係付けられる。
したがって,損傷が合計して1になる場合に,望まれる最小レベルの信頼度を与えると期待される。
風車の寿命の場合,風条件の広い範囲で生じるサイズが変わる多くのサイクルに見舞われる。したがっ
て,設計のために,荷重スペクトルを推定する必要がある。
このスペクトルの最大サイクルは,シミュレーションによって得られるデータ又は風車寿命より著しく
短い(継続)時間の試験結果の近似によって推定する。
各風条件に対して,荷重は定常的なランダムプロセスによってモデル化されると仮定することができる。
したがって,所定の風速V及び特定時間間隔Tに対して予想される損傷の期待値は,式(G.2)で得られる場
合がある。
∫∞0
ST
)
(
)
,
(
,
dS
S
N
T
V
S
n
T
V
D
E
=
······················································· (G.2)
ここに, nST(S|V,T): サイクル数に対する密度関数として定義される短時間
荷重スペクトル
この場合,時間間隔T中の荷重範囲間隔(SA,SB)中の予想サイクル数は∫B
A
)
,
(
ST
S
S
dS
T
V
S
n
で得られる。
75
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
全風車寿命間の通常運転荷重による予想される損傷の期待値は,時間間隔を全寿命時間に延長し,かつ,
運転風速範囲にわたって積分することで得られる。これは,式(G.3)から得られる。
∫
∫∫∞
out
in
out
in0
ST
)
(
)
(
)
,
(
)
(
,
V
V
V
V
dSdV
V
p
S
N
T
V
S
n
T
Lifetime
dV
V
p
T
V
D
E
T
Lifetime
D
E
=
=
··· (G.3)
ここに, p(V): 6.3.1.1の標準風車クラスに規定されるハブ高さ風速に対する
確率密度関数
長時間荷重スペクトルを,式(G.4)のように定義すると,式(G.5)が得られる。
∫
out
in
)
(
)
,
(
)
(
ST
LT
V
V
dV
V
p
T
V
S
n
T
Lifetime
S
n
=
·········································· (G.4)
∫∞0
LT
)
(
)
(
dS
S
N
S
n
D
E
=
·································································· (G.5)
多くの場合,荷重及び風速値の範囲を離散的なビンに分割することは実際上都合がよい。この場合,予
想される損傷は,式(G.6)で近似できる。
∑
≈
j,k
k
jk
S
N
n
D
E
)
(
··································································· (G.6)
ここに,
njk: j番目の風速及びk番目の荷重ビン中の寿命荷重サイクルの予
想数
Sk: k番目の荷重ビンの中央値
したがって,上記の定義から式(G.7)が得られる。
∫
∫
2
2
2
2
ST
+
)
(
)
,
(
j
j
j
j
k
k
k
k
ΔV
V
ΔV
V
ΔS
S
ΔS
S
jk
dSdV
V
p
T
V
S
n
T
Lifetime
n
+
−
−
=
······························· (G.7)
ここに, ΔVj: j番目風速ビンの中
ΔSk: k番目荷重ビン
これらの結果を用いて,安全率を荷重に適用するという7.6.3の要求事項を考慮する場合,疲労解析の限
界状態関係式は,式(G.8)となる。
1
)
(
)
(
0
LT
≦
dS
S
γ
N
S
n∫∞
······································································· (G.8)
ここに, γ=γf γm γn: それぞれ荷重,材料及び損傷結果に対する三つの一般部
分安全率の積
離散的記述では,この式は,式(G.9)となる。
(
)
∑k
j
k
jk
S
γ
N
n
,
1
≦ ······································································· (G.9)
大きな損傷が表2の複数の設計荷重ケースで起きる場合,全ての設計荷重ケースに対する損傷の各部分
は,式(G.9)の左辺を用いて計算されるが,合計しても1以下とする。
上記の公式化は,各荷重サイクルの中間点荷重レベルの変化の影響を無視している。この変化を扱う一
つの単純な方法は,固定の中間点値でもって等価荷重サイクルによる損傷を定義することである。この場
76
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
合,等価サイクルによる損傷は,変化する中間点をもつサイクルによる損傷と正確に同じである。したが
って,破壊は,所定のサイクル範囲及び中間点値におけるサイクルの場合と同じである,等価サイクル範
囲Seqの一定の大きさサイクル数で(平均して)起きるものとする。したがって,変化する中間点値N(S, M)
に対する,S-N曲線の一群N(S, M)を定義する場合,等価損傷の式(G.10)が得られる。
N(Seq, M0)=N(S, M) ································································· (G.10)
したがって,S,Mの所定の値及び選択された一定の中間点荷重レベルM0を与えることで,Seqが得られ
る。数学的にこれは,式(G.11)のように表される。
Seq=N−1[N(S, M), M0] ······························································ (G.11)
ここに,逆関数は第2の独立変数の関数N中の第1独立変数の解に適用される。典型的にM0は,荷重
データ中で直接観測される範囲の値の中央にある等価荷重サイクルに対して,R値(最大荷重と最小荷重
との比)を与えるように選ばれる。
しばしば,全ての運転風速を考慮した平均荷重が受容される。幸いにも,S-N曲線が解析的(例えば,
べき乗又は指数形式)に定義される大抵の場合,等価サイクル荷重範囲は容易に計算できる。ただし,範
囲が大きくなるにつれて,注意が必要になる。中間点値にもよるが,所定のサイクルに対する最大又は最
小荷重値は,静的強度に近くなる可能性がある。その場合,単純な高サイクルS-N曲線を適用しないほう
がよい。また,より大きな範囲の値では,局所の応力又はひずみは,圧縮−圧縮が,又は引張り−引張り
が支配的なケースから,引張り−圧縮のケースに遷移する可能性がある。これは異なる解析的なS-N曲線
表現をもつことになる。このため,等価サイクル範囲を決定するとき,適切なS-N関係式を用いることが
重要である。所定の荷重時刻歴の場合,まずレインフローサイクルを確認し決定する。この決定によって
一組の等価中間点が一定のサイクルの一組が,各サイクルに対して適切なS-N関係式を考慮して計算する。
これらの等価サイクルの分布は,新しい短時間等価荷重スペクトルを与えると推定される。この新しいス
ペクトルは,各荷重及び風速ビンに対して,損傷に対して用いられるサイクル数を定義するために用いら
れる。この方法を用いる主な利点は,中間点荷重レベルを独立変数として追跡するよりも,等価スペクト
ルの推定が統計的に正確なことである。この利点は,中間点ビンを別々に追跡するよりももっと多くの荷
重サイクルが各荷重及び風速ビンに対する典型的な時間シリーズの荷重データから計算することから生じ
る。
短時間荷重スペクトルを決定するときに生じる追加的で実際的な問題は,レインフロー法によって決定
される,膨大な量の小さいサイクルである。これらの小さいサイクルは接近した時点で発生するため,相
互に関係する可能性がある。さらに,小さいサイクルは,分布の末端部の解析的近似の形をゆが(歪)ま
せる可能性がある。したがって,短時間分布の端を近似する場合,しきい値を上回るサイクルだけを考慮
することが推奨される。少なくとも,95 %分位値のしきい値が実際上うまく働く。小さいサイクルを除く
か又は大きな追加的で統計的な信頼度を生むために一致させるためにもっと多くのデータ点が必要な場合,
より低いしきい値が適切なことがある。
実際の風車設計に応用する場合,動的シミュレーションデータから短時間等価荷重スペクトルを推定し
た後,寿命損傷を計算することが必要である。これを完遂する方法の一つに,次の手順がある。
a) 全ての風速を考えて,平均荷重レベルとして,基準中間点荷重レベルを選択する。
b) 所定の風速に対するシミュレーションデータから局所の一連の最大値及び最小値を抽出する。同一風
条件に対する多くの時間シリーズから得られた局所の一連の最大値及び最小値を単一のシリーズに連
結させる。
c) レインフロー法を用いて,各模擬荷重サイクルに対する中間点及び範囲を同定する。
77
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
d) 選択された基準中間点荷重レベルに関係して各荷重サイクルに対する等価範囲を決定する。
e) 選択されたしきい値を超えるデータに対して,等価荷重サイクルの短時間確率分布FST(S|V, T)の解析
近似を決定する。分布を近似する方法に対する一つの指針として,Moriarty及びHolley,2003を参照
することが望ましい。データに対する近似が満足できるかどうか及びデータに比べて分布の末端部の
挙動を信頼度高く推定するのに十分なデータがあるかどうかを調べるために,選択した分布の形を確
認する。
f)
荷重ビンがしきい値を下回る場合は,そのデータを用いて各ビンの寿命サイクルの予想数を決定する。
荷重ビンがしきい値を超える場合は,その近似荷重分布を決定する。これによって,式(G.12)が得ら
れる。
−
−
+
≈
る場合
番目のしきい値を超え
が
場合
番目のしきい値以下の
が
j
S
T
V
ΔS
S
F
T
V
ΔS
S
F
M
j
S
m
P
T
Lifetime
n
k
j
k
k
j
k
k
j
k
jk
j
jk
,
2
,
2
(G.12)
ここに,
mjk: しきい値以下の場合,j番目の風速ビンとk番目の荷重ビンと
に対するデータで計算したシミュレーション疲労サイクル数
Mj: しきい値を超える場合,シミュレーションで計算した疲労サ
イクル数
なお,
ave
ave
2
2
π
2
2
π
V
ΔV
V
V
ΔV
V
j
j
j
j
j
e
e
P
+
−
−
−
−
=
は,仮定した風速のレイリー分布に対するビンj中にある時間割合を示
す。
これに基づき,寿命損傷を次のとおり,計算する。
− 式(G.9)の左側を用いて,損傷を合計する。
− 全て疲労荷重ケースから,全寿命損傷を合計する。
この手順を用いる場合には,次の課題に注意する。
− 風速及び荷重範囲ビンの解像度は,所望の数値精度に対して十分なものとする。
− 荷重範囲の十分に大きな値は,長時間荷重分布の端を適切に表すものを用いる。
最初の課題は,残りの全ての風速又は荷重範囲からデータをスキップさせて二つの異なるビン解像度に
よって計算した結果の差の半分として誤差を近似することによって処理できる。代替としては,結果を制
限するために,中心値の代わりにビン値の末端部の点を用いて損傷の合計を計算する方法がある。
二つ目の課題は,寿命損傷の増加が無視できるまで,最高の荷重範囲ビン値を漸次増やすことで処理で
きる。
ただし,比,
T
Lifetimeは大きな数なので,最大の必要な荷重ビンは,シミュレーションデータで観測さ
れる最大サイクルよりも著しく大きいことに注意を払う。これは,全模擬荷重時刻歴は風車の寿命よりは
るかに小さいために考えられ,統計的な外挿は,長時間荷重分布の末端部から損傷を正確に推定すること
が必要となる。
G.2
参考文献
Dowling, N.E., Fatigue Failure Predictions for Complicated Stress-strain Histories, J. of Materials, v.7, n.1, Mar.,
1972, pp. 71-87
78
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Matsuishi, M. and Endo, T., Fatigue of Metals Subjected to Varying Stress, Proc. Japan Soc. of Mech. Engrs., n.
68-2, 1968, pp. 37-40
Miner, M.A., Cumulative Damage in Fatigue, J. of Applied Mech., v.12, 1945, pp. A159-A164
Moriarty, P. J. and Holley, W. E., Using Probabilistic Models in Wind Turbine Design,Proc. ICASP9, San
Francisco, CA, July 6-9, 2003
Palmgren, A., Die Lebensdauer von Kugellagern, Zeitschrift der Vereines Deutcher Ingenieure, v. 68, n. 14, 1924,
pp. 339-341
79
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書H
(参考)
同時荷重
H.1 一般事項
部品に作用する荷重によって生じる局所応力又は局所ひずみを判断するため,風車部品の詳細な構造計
算には,有限要素法又は他の適切なモデルを一般的に用いる。通常,この計算において,荷重が作用する
適切な断面を定義する(例 タワー頂部の荷重を定義するヨーベアリングの界面)。この場合,荷重の境
界条件を定義する六つの荷重成分,すなわち,Fx,Fy,Fzの三つの力,及びMx,My,Mzの三つのモーメ
ントが存在する。ここでは,便宜上,x軸及びy軸は荷重面内,z軸は荷重面に垂直であると想定する。極
値荷重状態を説明するために,表H.1に示すような荷重マトリクスで定義することが多い。
表H.1−極値荷重マトリクス
Fx
Fy
Fz
Mx
My
Mz
FR
θF
MR
θM
Fx
最大
最小
Fy
最大
最小
Fz
最大
最小
Mx
最大
最小
My
最大
最小
Mz
最大
最小
FR
最大
MR
最大
この表では,上部の見出しに示すとおり,各列は,荷重成分の値を表す。各行は,同時値(同時に発生
する全ての値)を示し,陰影が付いたセルは,左側の見出しに示すように,最大値又は最小値のいずれか
をもつ特定の成分を示す。これらの最大値及び最小値は,特定の荷重成分において,全範囲の値を網羅す
ることを意図している。詳細な構造モデルの解析を各行を用いて実施し,結果として生じる局所応力又は
局所ひずみの値を決定し,適切な破壊基準と比較する。平面内の荷重に応じて,構造的剛性及び強度が異
なる荷重方向において類似している場合,x及びyの両方の成分の絶対値が大きいが,各成分がその最大
値付近でないときに,最大の極値荷重が生じる可能性がある。したがって,面内ベクトルの合成値を右側
に追加した列及びその下部に追加した行にも記載する。
これらの面内合成荷重を,式(H.1)に定義する。
2
2
y
x
R
F
F
F
+
=
及び
2
2
y
x
R
M
M
M
+
=
·········································· (H.1)
これらの合成荷重の方向を,式(H.2)に定義する。
θF=arctan(Fx/Fy)及びθM=arctan(Mx/My) ········································ (H.2)
表中の値は,風車全体の動的シミュレーションコードのアウトプットである六つの荷重成分の時刻歴デ
80
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ータをポスト処理することによって決定する。この解析では,時刻歴から各成分の最大値及び最小値並び
に合成値の最大値を探索する。それぞれに対応する時間ポイントに関連した同時値を,表の行に記載する。
このようにして箇条7で規定するそれぞれの荷重ケースを解析し,異なる荷重ケースから各行の極値荷重
を,各風車部位の荷重範囲を決定するために用いる。
H.2及びH.3に,二つのアプローチを紹介する。ただし,安全側の同時荷重を得るためには,注意が必
要である。
H.2 スケーリング
このアプローチは,次の手順で構成される。
a) それぞれの断面及び荷重成分について,考慮する荷重ケースの一つのビンから,最大の特性荷重を抽
出する。
b) 特性荷重に対して±5 %以内の付近に最大値があるビンから,時刻歴データを選択する。
c) この時刻歴の最大値を,特性荷重に合わせてスケーリングする。これによるスケーリング率を,この
時刻歴において選択した最大値に対して,全ての同時荷重の成分に適用する。
d) 各荷重成分について,極値設計荷重解析に用いるための一つの荷重ケースの時刻歴データを選定する。
e) 最小値についてもこの手順を行う。
H.3 平均化
このアプローチは,次のような手順で構成される。
a) 複数の事象で構成される荷重ケースについて,正の終極荷重を,各事象の最大値の平均として計算す
る。
b) 同時荷重を,各事象の同時値の絶対値の平均として計算する。同時荷重の符号は,最大荷重をもつ事
象の同時荷重の符号と合わせる。
c) 負の終極荷重を,各事象の最小値の平均として計算する。同時荷重は,正の場合と同じ方法によって
計算する。
d) 絶対終極荷重は,最大値の平均,又は対応する同時値と上記の最小荷重の平均との絶対値のうち大き
い方の値とする。
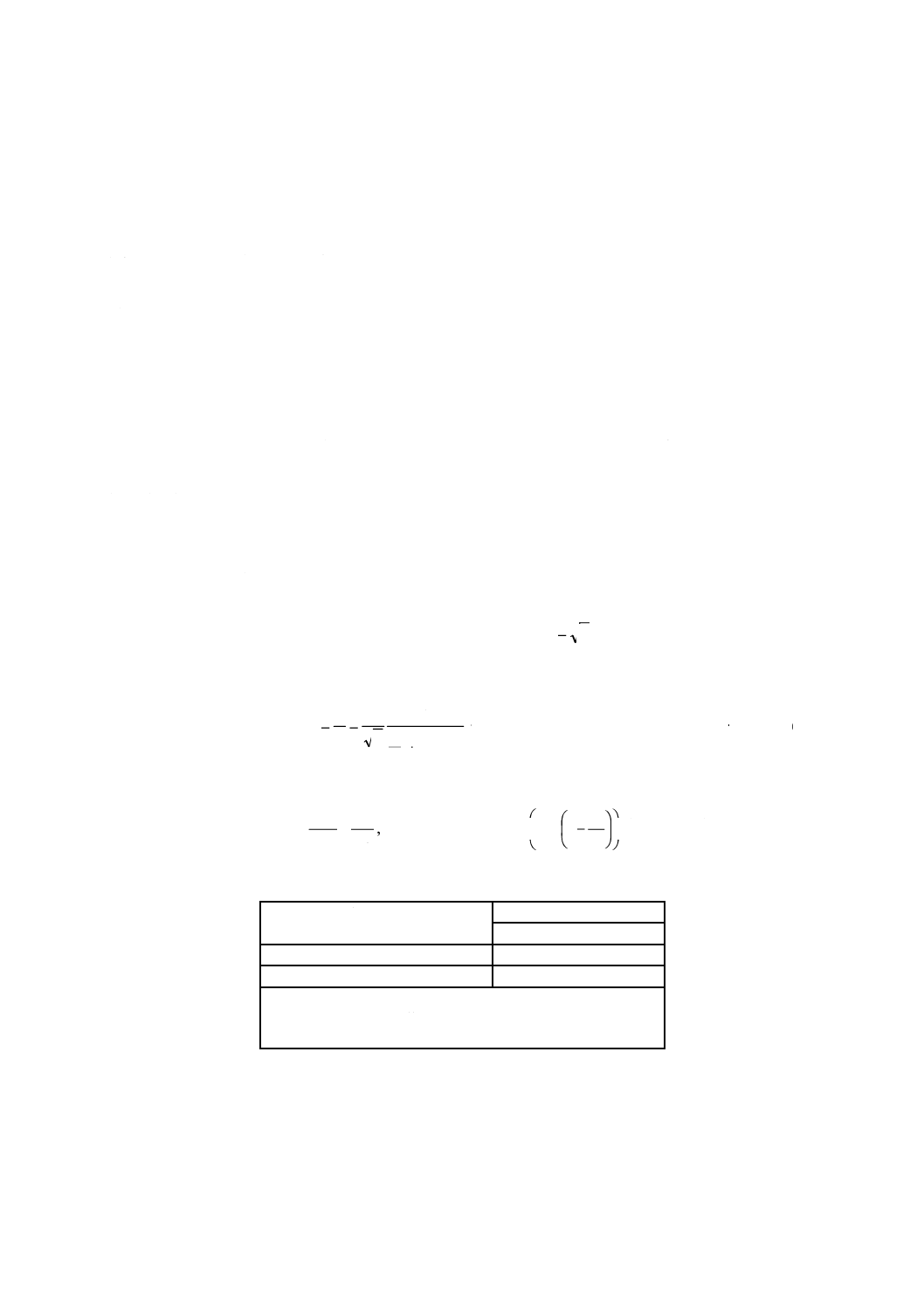
81
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
風車クラス及び乱流カテゴリの追加
JA.1 風車クラス及び乱流カテゴリの追加
風車を建設するサイトが,熱帯性低気圧襲来地域で,風条件が,6.2に規定する風車クラスI,II及びIII
を逸脱する場合には,表JA.1(表1参照)の風車クラスTの基準風速Vref,Tを用いてもよい。ただし,風
車クラスTに対する年平均風速Vaveは,式(9)によらず,10 m/s,8.5 m/s又は7.5 m/sのいずれかから選択
して組み合わせる。式(9)以外の風条件については,6.3に従うものとする。
なお,熱帯性低気圧襲来地域における10分平均基準風速の評価は,“風力発電設備支持物構造設計指針・
同解説”及びIshiharaらによる文献を参考にするとよい。
風条件が高乱流カテゴリAを逸脱する場合には,表JA.1の極高乱流カテゴリA+を用いることが望まし
い。極高乱流カテゴリA+を追加した通常乱流モデル(NTM)の乱流標準偏差及び乱流強度の分布を図JA.1
(図1参照)に示す。
例えば,年平均風速がクラスII,基準風速がクラスT及び乱流カテゴリA+の場合,風車クラスは“IIA +,
T”となる。
注記 DLC 6.1及びDLC 6.2に対する荷重の部分安全率は,年最大風速の変動係数COVが15 %未満
であると仮定して設定されている。COVが15 %以上の場合には,50年再現極値風速V50をCOV
=15 %〜30 %に比例した係数η=1〜1.15を用いて,
50
50
~
V
η
V=
の関係によって補正してもよい。
年最大風速のCOVは,Gumbel分布から仮定して,風速の50年及び100年の再現期待値U50及
びU100から求めることができる。COVは式(JA.1)のように示す。
2
577
.0
1
6
π
+
=
=
α
β
μ
σ
COV
······················································ (JA.1)
ここに,
(
)
100
,
50
,
1
1
ln
ln
,
,
50
50
50
100
50
100
=
−
−
=
+
=
−
−
=
N
N
p
αp
U
β
p
p
U
U
α
N
······· (JA.2)
表JA.1−日本における風車クラス及び乱流カテゴリの追加
パラメータ
風車クラス
T
Vref,T(m/s)
57
乱流カテゴリA+におけるIref(−)
0.18
この表の値は,ハブ高さにおいて適用する。
Vref,T :熱帯性低気圧襲来地域に適用する10分平均基準風速
A+
:極高乱流カテゴリの場合に選定
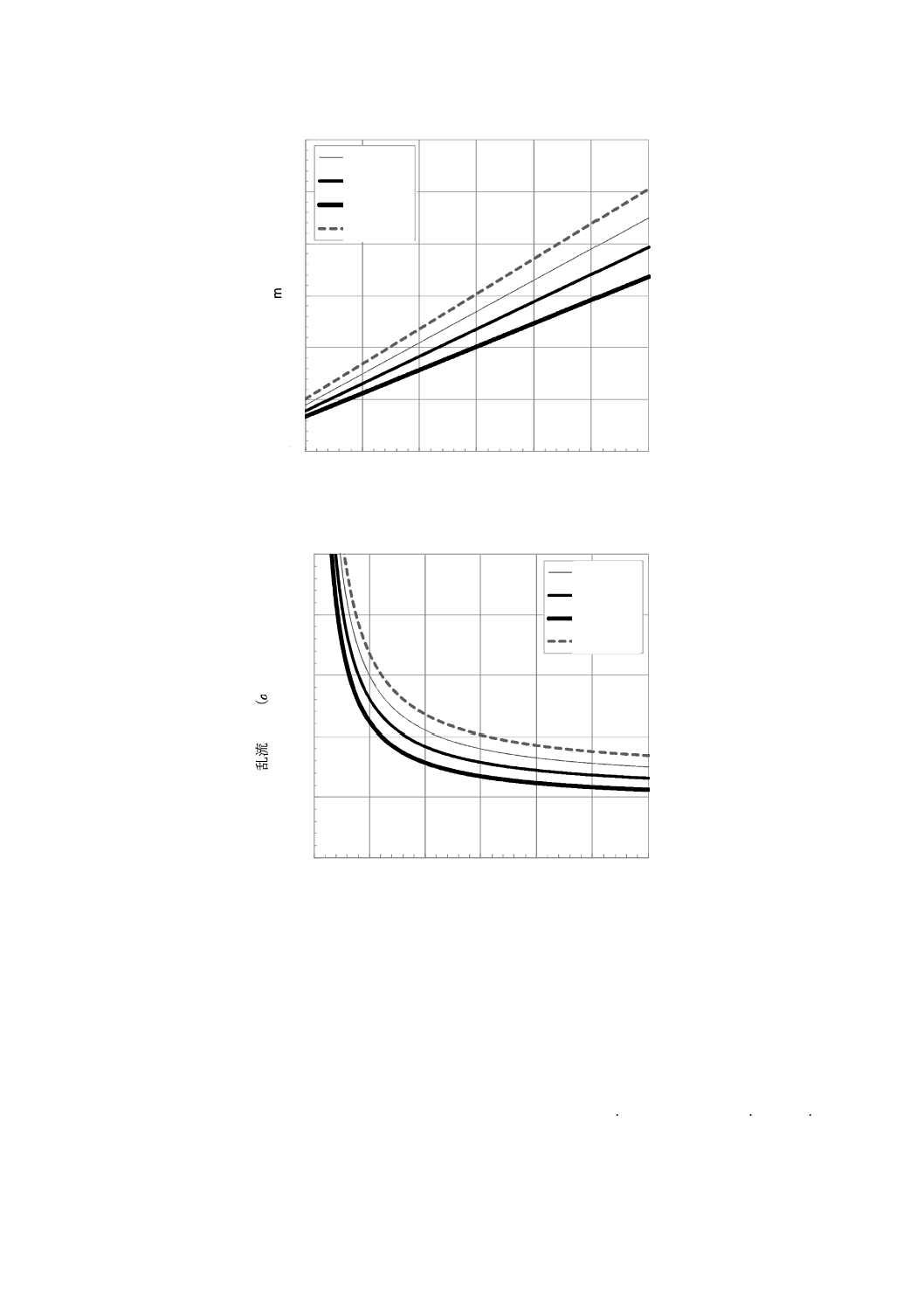
82
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0
1
2
3
4
5
6
0
5
10
15
20
25
30
σ
1
m
/s
Vhub[m/s]
category A
category B
category C
category H
a) 通常乱流モデル(NTM)の乱流標準偏差
0
0.1
0.2
0.3
0.4
0.5
0
5
10
15
20
25
30
T
u
rb
u
le
n
ce
in
te
n
s
ity
Vhubm/s
category A
category B
category C
category H
b) 通常乱流モデル(NTM)の乱流強度
図JA.1−極高乱流カテゴリA+を追加した通常乱流モデル(NTM)
風車クラスTは,標準風車クラスとは考えない。ただし,風車クラスTのVaveは,標準風車クラスI〜
IIIに対応したVaveから選択するのが望ましい。
JA.2 参考文献
土木学会,風力発電設備支持物構造設計指針・同解説[2010年版],2010
Ishihara, T. and Yamaguchi, A. (2014), Prediction of the extreme wind speed in mixed climate region by using
Monte Carlo simulation and Measure-Correlate-Predict method, Wind Energy
カテゴリA
カテゴリB
カテゴリC
カテゴリA+
カテゴリA
カテゴリB
カテゴリC
カテゴリA+
乱
流
強
度
(
σ
1
/V
hu
b
)
83
C 1400-1:2017 (IEC 61400-1:2005,Amd.1:2010)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
JIS B 9706-1:2009 機械類の安全性−表示,マーキング及び操作−第1部:視覚,聴覚及び触覚シグナ
ルの要求事項
注記 対応国際規格:IEC 61310-1:2007,Safety of machinery−Indication, marking and actuation−Part 1:
Requirements for visual, acoustic and tactile signals(IDT)
JIS B 9706-2:2009 機械類の安全性−表示,マーキング及び操作−第2部:マーキングの要求事項
注記 対応国際規格:IEC 61310-2:2007,Safety of machinery−Indication, marking and actuation−Part 2:
Requirements for marking(IDT)
JIS C 0617(規格群) 電気用図記号
注記 対応国際規格:IEC 60617,Graphical symbols for diagrams
JIS C 1400-0 風力発電システム−第0部:風力発電用語
JIS C 1400-3:2014 風車−第3部:洋上風車の設計要件
JIS C 3662(規格群) 定格電圧450/750 V以下の塩化ビニル絶縁ケーブル
注記 対応国際規格:IEC 60227 (all parts),Polyvinyl chloride insulated cables of rated voltages up to and
including 450/750 V
JIS C 3663(規格群) 定格電圧450/750 V以下のゴム絶縁ケーブル
注記 対応国際規格:IEC 60245 (all parts),Rubber insulated cables−Rated voltages up to and including
450/750 V
JIS C 4034(規格群) 回転電気機械
注記 対応国際規格:IEC 60034 (all parts),Rotating electrical machines
JIS C 8211:2004 住宅及び類似設備用配線用遮断器
注記 対応国際規格:IEC 60898,Electrical accessories−Circuit-breakers for overcurrent protection for
household and similar installations(MOD)
JIS C 8269(規格群) 低電圧ヒューズ
注記 対応国際規格:IEC 60269 (all parts),Low-voltage fuses
JIS Q 9001 品質マネジメントシステム−要求事項
注記 対応国際規格:ISO 9001,Quality management systems−Requirements(IDT)
ISO 3010:2001,Basis for design of structures−Seismic actions on structures
ISO 8930:1987,General principles on reliability for structures−List of equivalent terms
IEC 60038,IEC standard voltages
IEC 60146 (all parts),Semiconductor converters
IEC 60173:1964,Colours of the cores of flexible cables and cords
IEC 60287 (all parts),Electric cables−Calculation of the current rating
IEC 60439 (all parts),Low-voltage switchgear and controlgear assemblies
IEC 60446:2007,Basic and safety principles for man-machine interface, marking and identification−
Identification of conductors by colours or alphanumerics
IEC 60529:1989,Degrees of protection provided by enclosures (IP Code)
IEC/TR 60755:2008,General requirements for residual current operated protective devices