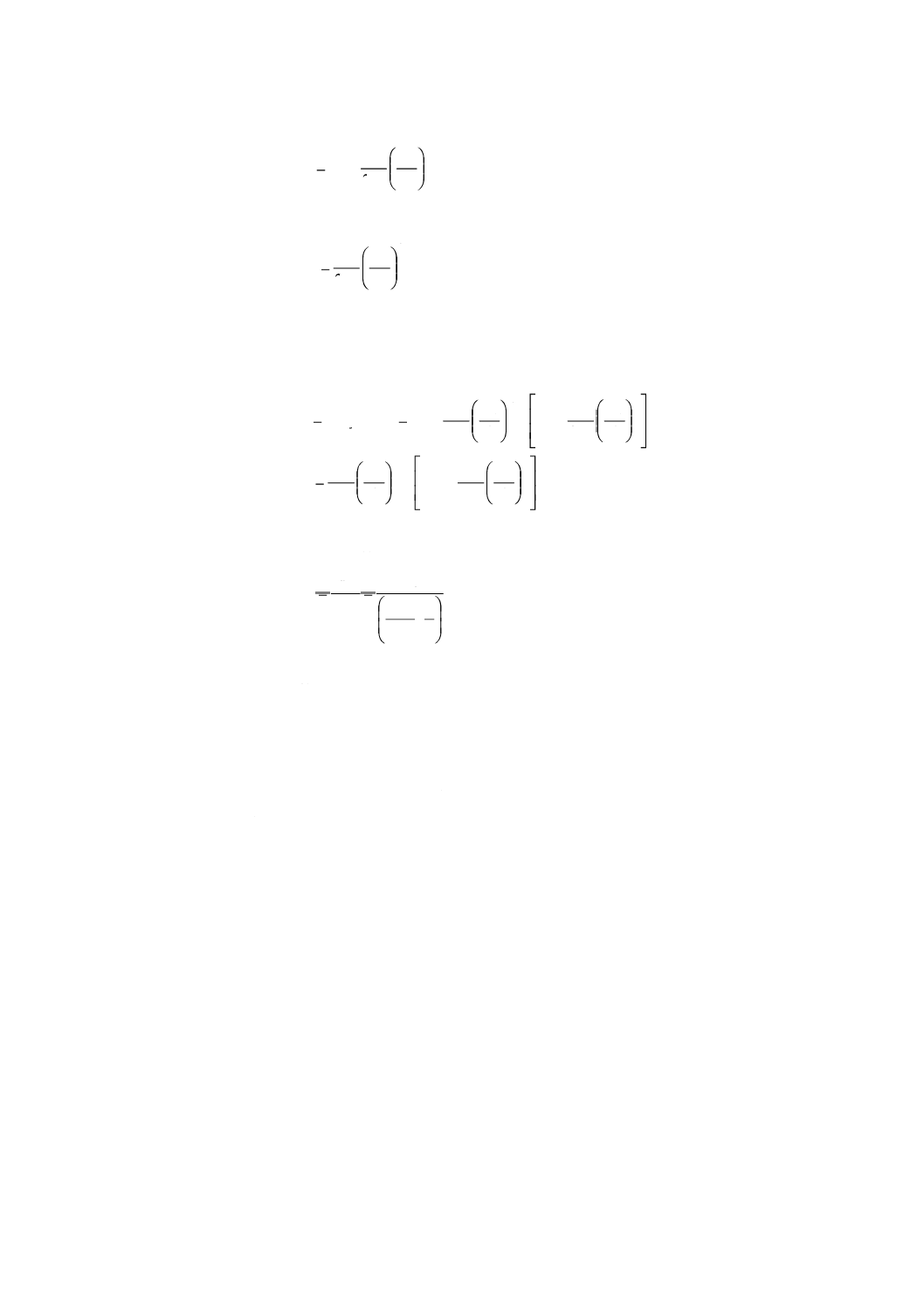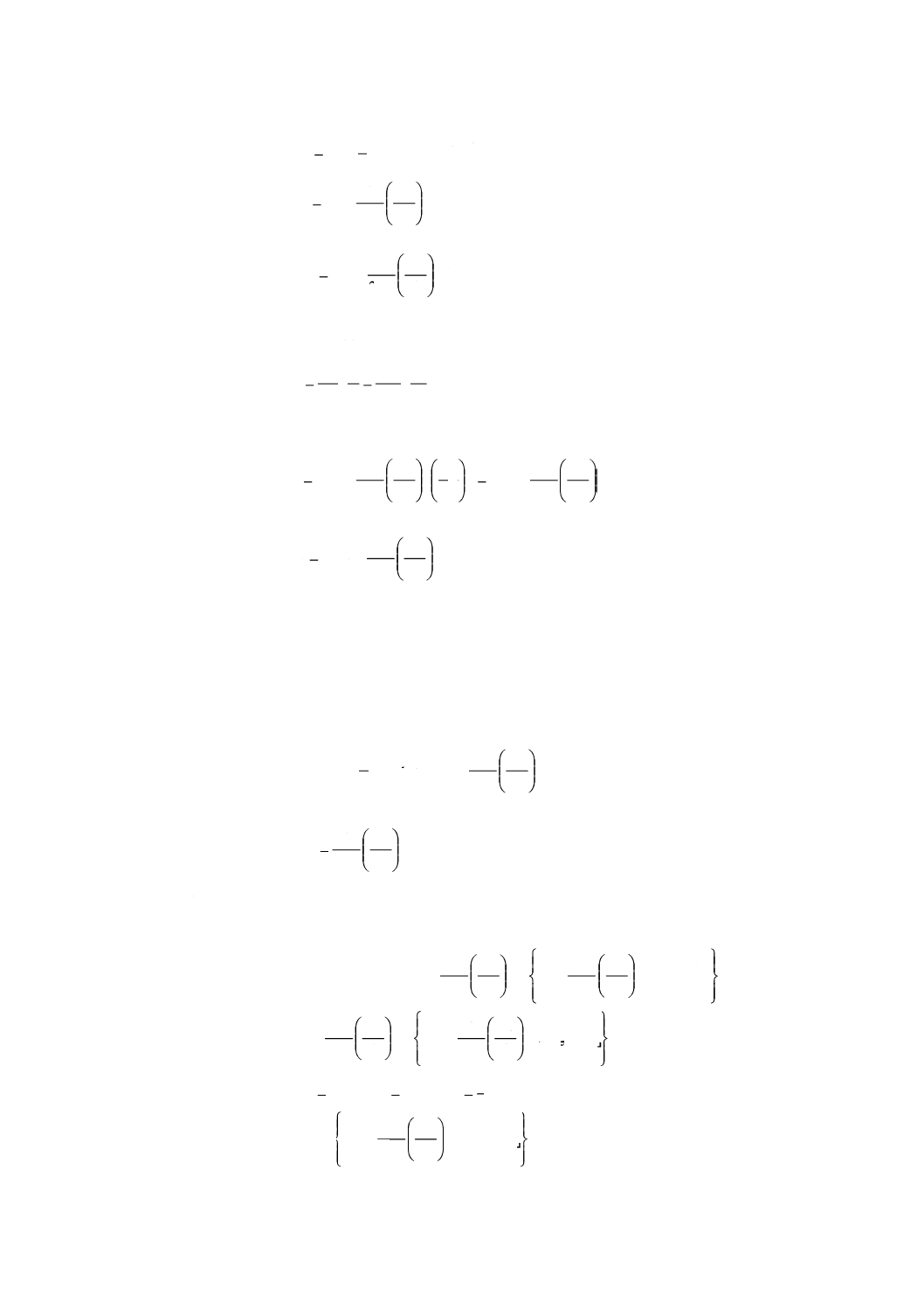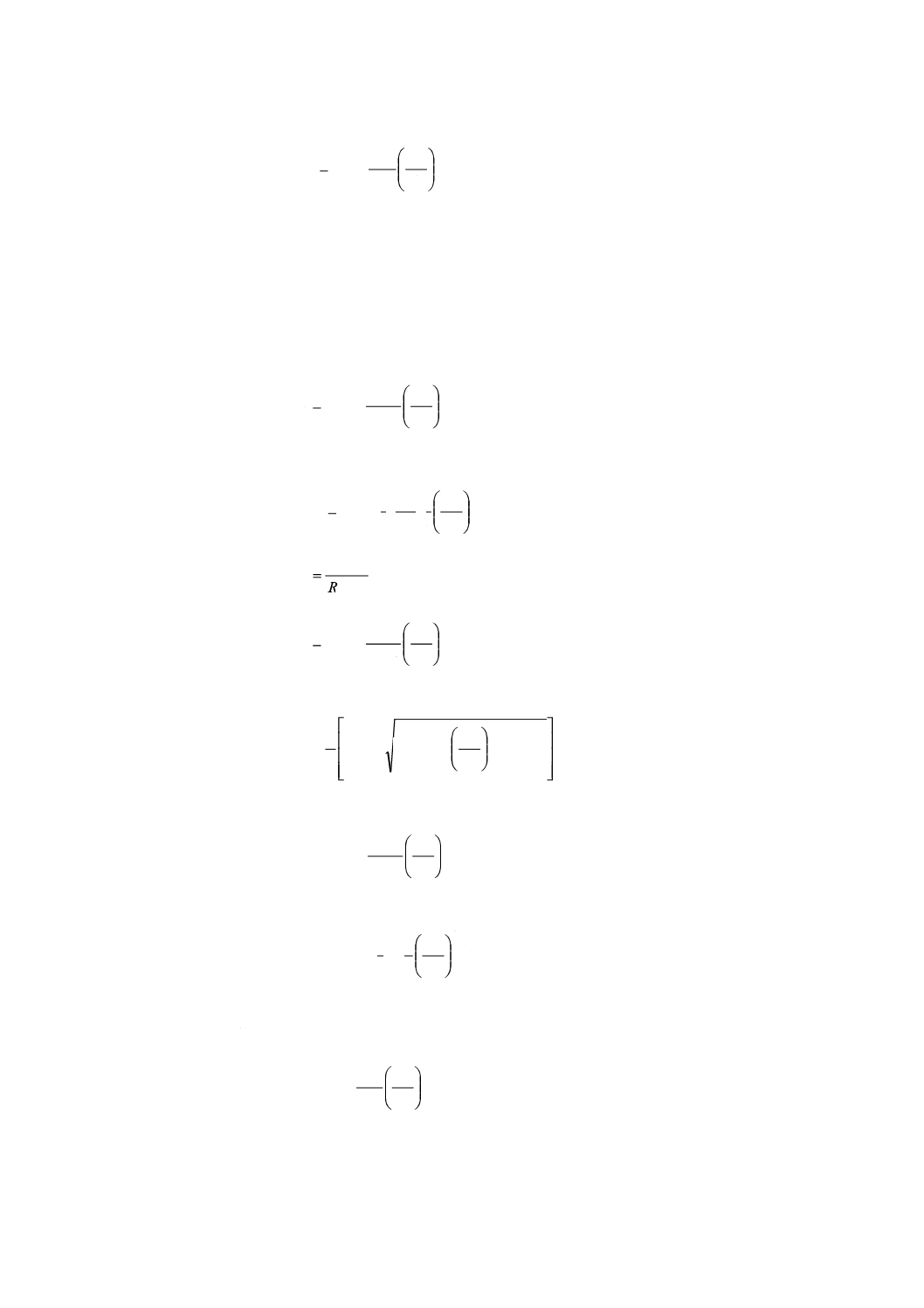
113
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図29 ピトー静圧管(続き)
27.3 空気速度の限界
管を通過する流れのマッハ数は,0.25(大気で85m・s−1)を超えてはならない。
ピトー静圧管のせき止め圧測定孔の孔径di(単位mm)に対するレイノルズ数は200以上とする。すな
わち,大気で試験する場合には,速度 (m・s−1) は,次式以上でなければならない。
v=3/di
114
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
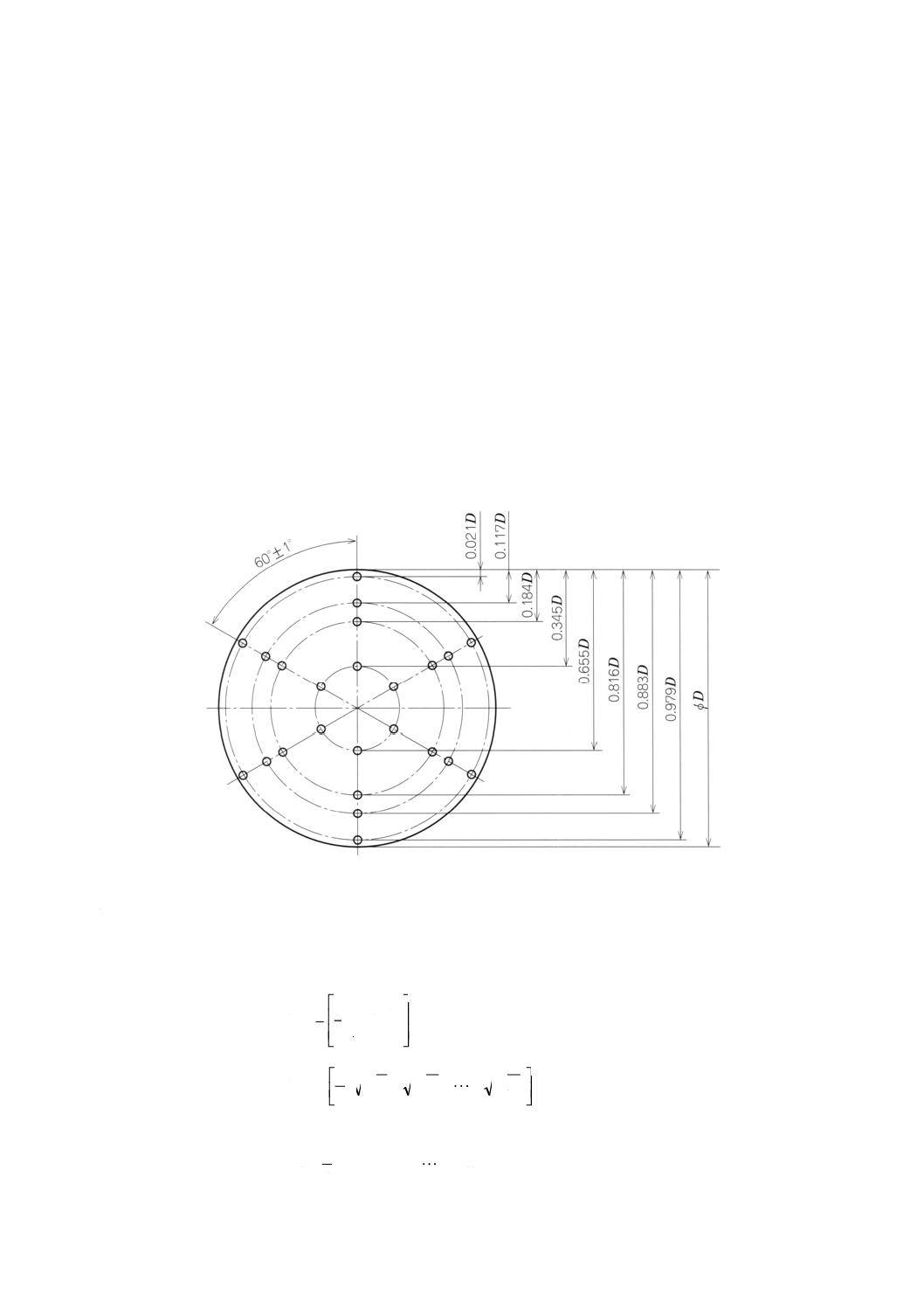
27.4 測定点の位置
ピトー静圧管の先頭の中心は,附属書図30に示すように,通風路に対称に配置された三つの直径に沿っ
て規定の間隔で24点以上連続して配列する。
ピトー静圧管の頭部は±2゚の範囲内で通風路の軸に平行にする。
通風路の片側の内壁からの測定位置(直径当たり8点の場合)は,次の許容差内にあるものとする。
ここに,最小許容差は±1mm以内とする。
0.021D±0.000 6D
0.117D±0.003 5D
0.184D±0.005D
0.345D±0.005D
0.655D±0.005D
0.816D±0.005D
0.883D±0.003 5D
0.979D±0.000 6D
附属書図30 標準通風路におけるトラバースによる測定位置
27.5 流量の算出
それぞれの測定点において,ピトー静圧管によって差圧∆pjを測定する。
測定断面における平均差圧∆pmは,n個の差圧∆pjの平方根の平均の2乗であり,次の式に示す。
2
1
5.0
1
∆
=
∆
∑
=
n
j
j
m
p
n
p
2
2
1
)
(
1
∆
+
+
∆
+
∆
=
∆
n
m
P
P
P
n
p
流量測定断面xの平均空気密度ρxは平均静圧から算出する。
)
(
1
2
1
exn
ex
ex
ex
p
p
p
n
p
+
+
+
=
115
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
px=pex+pa
静温度Θxは次の式に示す。
1−
∆
+
Θ
=
Θ
κ
κ
m
x
x
sgx
x
p
p
p
x
w
x
x
R
p
Θ
=
ρ
質量流量qmは次の式に示す。
m
x
x
m
p
D
q
∆
=
ρ
αεπ
2
4
2
ここに,
5.0
2
2
6
1
2
1
1
∆
+
+
∆
−
=
x
m
x
m
p
p
p
p
κ
κ
κ
ε
は空気の膨張による修正係数である。αは,27.6記載の補正係数又は流量係数である。
27.6 流量係数
流量係数αは,この規格の大気中の試験方法に従って求められた測定値の平均値に対して,ISO 3966に
規定されたそれぞれの補正係数を適用して算出される。係数αは,次に示すように,直径Dx及び断面にお
ける平均速度vmxから算出されるレイノルズ数に依存する。
x
m
x
m
x
mx
x
Dx
D
q
D
q
D
v
3
10
71
4
Re
×
≈
=
=
μ
π
μ
ρ
大気に対し,SI単位で示すと次のとおりである。
ReDx
3×104
105
3×105
106
3×106
α
0.986
0.988
0.990
0.991
0.992
27.7 測定の不確かさ
αの平均値を使用すると,体積又は質量流量の±0.8%にもなる算出過程の誤差を無視することになる。
測定の偶然誤差の合計は,±1.1%となる。したがって,流量測定の不確かさは,±2%とみなすことができ
る。
ここに,マノメータの校正の不確かさを,±1.0%と仮定している。この条件を満たすためには,低い空
気速度においても高感度なマノメータが必要であり,密度が1.2kg・m−3の空気の場合に必要なマノメータ
の校正を示す。
±1.5Pa
±1Pa
±0.5Pa
±0.25Pa
16m・s−1
13m・s−1
9m・s−1
6m・s−1
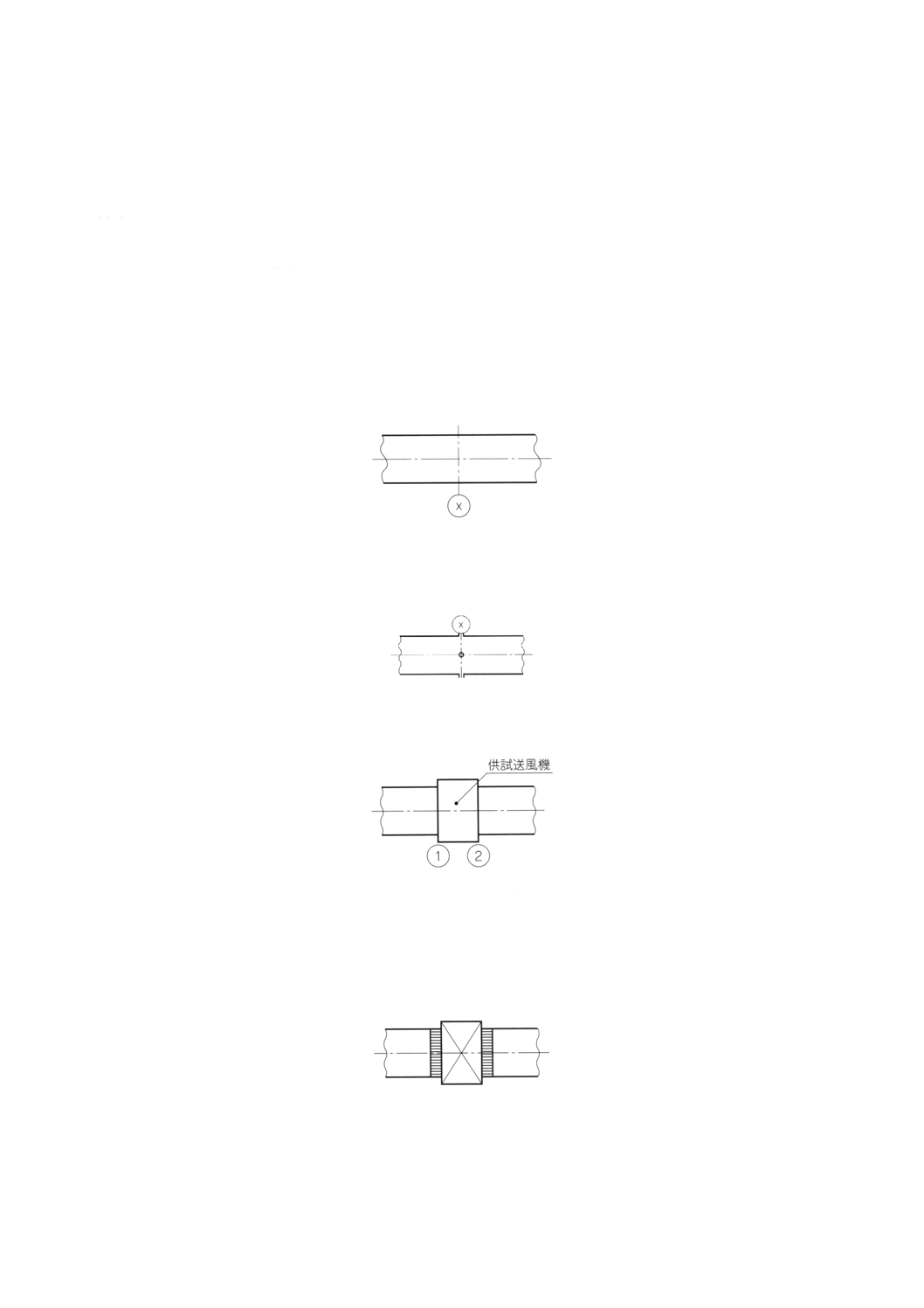
28. 接続形式
送風機に使用される現地の接続形式には,次の4種類がある。
A:吸込管と吐出し管の両方をもたない場合
B:吸込管はもたず,吐出し管だけをもっている場合
C:吐出し管はもたず,吸込管だけをもっている場合
D:吸込管と吐出し管の両方をもっている場合
116
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
送風機の試験は,上記の接続条件を可能な限り再現するものとし,次の4種類の試験接続形式を定義す
る。
28.1 接続形式A:吸込管と吐出し管の両方をもたない場合
接続形式Aの場合には,送風機は吸込ベルマウス,吐出し管などの補助装置なしで試験する。
ただし送風機に附属している補助装置(保護金網,吸込ベルマウスなど)は装備する。
この場合には,31.3及び31.4の規定のように吸込又は吐出し側空気槽を使用する。
28.2 接続形式B:吸込管はもたず,吐出し管だけをもっている場合
接続形式Bの場合は,整流格子つきの吐出し管を使用する。送風機の吐出し口に旋回流がない場合には
管路の長さは短くてもよい。
送風機に附属する補助装置を除いて,送風機の吸込側に補助装置を取り付けて試験してはならない。
通常,吐出し圧力は旋回流防止装置の後の吐出し管路において測定する。測定管路及び旋回流防止装置
は,送風機吐出し側の共通部分を使用する(30.2参照)。
特に遠心送風機において,吐出し側空気槽を使用し,かつ送風機の吐出し口に旋回流がない場合には,
送風機と空気槽との間に短い試験管路[30.2f)参照]を使用することができる。
28.3 接続形式C:吐出し管はもたず,吸込管だけをもっている場合
接続形式Cの場合は,吸込管路の模擬を使用するものとし,送風機に附属する補助装置(保護金網,デ
ィフューザなど)を除いて,吐出し管又は補助装置は使用しない。
吸込管路で吸込圧力を測定する場合には,送風機吸込側の共通部分を使用する(30.3参照)。
送風機の吐出し側に短い管路がある場合には,吸込側空気槽を使用してもよい(31.3参照)。
この管路は,長さが非常に短く(例えば0.5D),事実上流れの全抵抗が吸込側にある場合でも,送風機
の性能にかなりの影響を与える。
したがって,現地において送風機の吐出し管路が短い場合には,この管路も試験通風路とみなす。
試験に使用する測定管路長さは,試験報告書に記載する。
送風機の性能については,他の試験と同様に算出する。
28.4 接続形式D:吸込管と吐出し管の両方をもっている場合
接続形式Dの場合には,吸込管路の模擬を使用し,吐出し管を使用するものとする。
通常,吸込及び吐出し管路は,30.2及び30.3に規定した共通部分でなければならない。
吸込側空気槽又は吐出し側空気槽を使用する場合には,吐出し管路は,送風機吐出し側に旋回流がなけ
れば,30.2f)に記載の短いものでよい。
大形送風機(直径800mm以上)の場合には,吐出し側で,整流装置を含む標準共通通風路による試験
の実施が困難な場合がある。この場合には,関係者の協定に基づき,吐出し側に2Dhの長さの管路を用い
て,30.2f)及び30.4に記載の方法によって,送風機の性能を決定してもよい。
このようにして得られた結果は,送風機が大きな旋回流を発生することもあり,吸込側と吐出し側との
両方に共通通風路を使用する場合に得られる結果と,ある程度の差を生じることがある。
どちらの方法が最も代表的な値を与えるかについては,今後の研究を待たなければならない。
この場合には,吐出し静圧は吐出し管路で測定せず,大気圧に等しいとみなす。
28.5 試験の接続形式表示
性能を識別するために,特性を示す記号として,次のような試験の接続形式を示す文字を追加する。
pFA,pFB,pFC又はpFD
psFA,psFB,psFC又はpsFD
117
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ηrA,ηrB,ηrC又はηrD
29. 標準通風路の構成部品
29.1 記号
次の記号を使用して,30.,32.,33.,34.,及び35.に規定する標準通風路の構成部品を定める。各部品は,
29.2に規定する関連項に適合するものとする。
29.2 構成部品
29.2.1 附属書図31は,11.に従って断面xにおいて測定した内径Dxの円形管路を示す。
通風路部間の接合部はできるだけ少なくし,内部の突出部をなくし,位置は正確に合わせる。また漏れ
は試験対象の流量に比べ無視できる程度でなければならない。特に測定に,ピトー管又は温度計を挿入す
る場合には注意を要す。
附属書図31 内径Dxの円形管路記号
29.2.2 附属書図32は,断面xにおける平均静圧pexの集合管壁静圧測定孔(管壁静圧孔)を示す。
管壁静圧孔とマノメータとの接続は,7.に適合しなければならない。
附属書図32 管壁静圧孔の集合管記号
29.2.3 附属書図33は,18.及び19.に従って配置,運転される試験対象の送風機を示す。
附属書図33 試験中の送風機記号
29.2.4 附属書図34は,試験通風路内の流体抵抗の解消用に設計された補助送風機を示す。流量の調整は,
速度制御,ピッチ制御,制動装置及びその他の方法で行うが,どの方法においても一定の流量が確保され
なければならない。
旋回防止装置は,補助送風機とそれが接続される試験通風路の間に挿入する。
附属書図34 補助送風機記号
29.2.5 附属書図35は,試験通風路の吸込口又は吐出し口における流量の絞り装置を示す。
装置は管路の中心に対し,旋回流又は偏流を発生させないものとする。装置の一部に補助送風機を使用
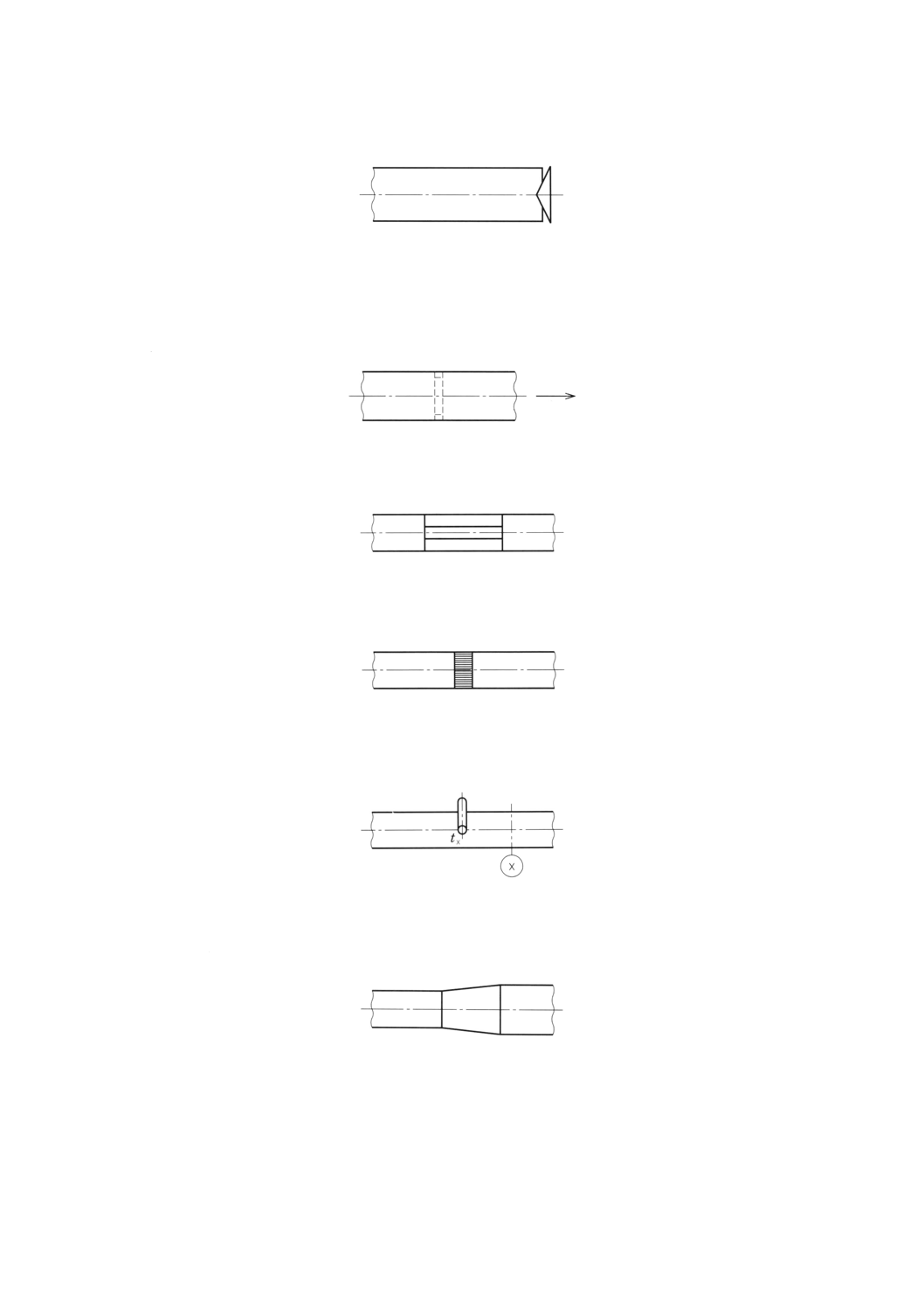
118
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
してもよい。
附属書図35 吸込又は吐出し口の流量絞り装置記号
29.2.6 附属書図36は,試験管路中の整流装置を示し,金網又は金属製の多孔板で構成される。
孔は,一様かつ0.05D以下の一様間隔であいていなければならない。整流板は正確に切断し,管壁面で
の漏れをなくすために,半径方向の厚みが,最大0.012d又は6mm,最小0.008d又は3mm,長さが0.05d
以下の支持リングの取付又は他の方法をとるものとする。
附属書図36 管路中の整流装置記号
29.2.7 附属書図37は,送風機吐出し口における旋回エネルギーを分散させるために設計された標準整流
格子を示す。
附属書図37 標準整流格子
29.2.8 附属書図38は,軸直角方向旋回流の成長を防止するために設計された整流装置,又は旋回エネル
ギーを分散させるために設計された整流格子を示す。
附属書図38 旋回防止装置又は整流格子記号
29.2.9 附属書図39は,断面xにおける平均温度を測定するために,空気槽又は管路に挿入された温度計
を示す。温度計の位置は,管壁静圧孔又は試験設備に流入する流れに影響を与えない位置とする。
附属書図39 試験空気槽に挿入された温度計記号
29.2.10 附属書図40は,二つの円形管路又は円形の送風機吐出し口と試験管路を接合する円形の接続管を
示す。この接続管形状は,30.に規定する角度,面積及び長さに適合していなければならない。
附属書図40 円形管路の接続管記号
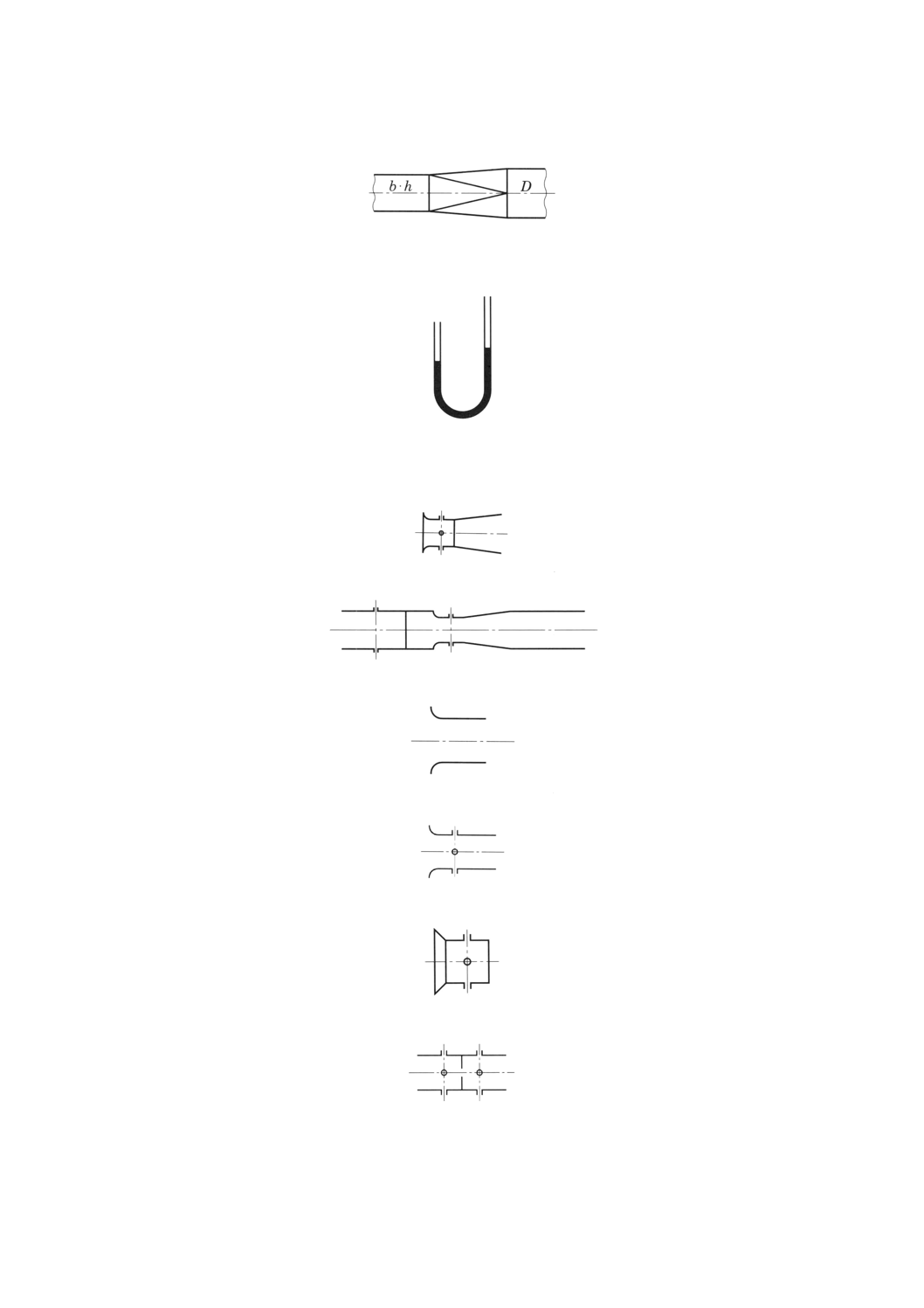
29.2.11 附属書図41は,長方形断面の送風機吐出し口に接合される円形試験管路,又は寸法b・hの試験管
路から円形試験管路への接続管を示す。
この接続管形状は,30.に規定する面積比及び長さに適合するものとし,附属書図58に示すような単一
119
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
形状曲線とする。
附属書図41 長方形断面と円形断面管路との接続管記号
29.2.12 附属書図42は,6.2の要求に適合する静圧又は差圧測定用のマノメータを示す。
附属書図42 マノメータ
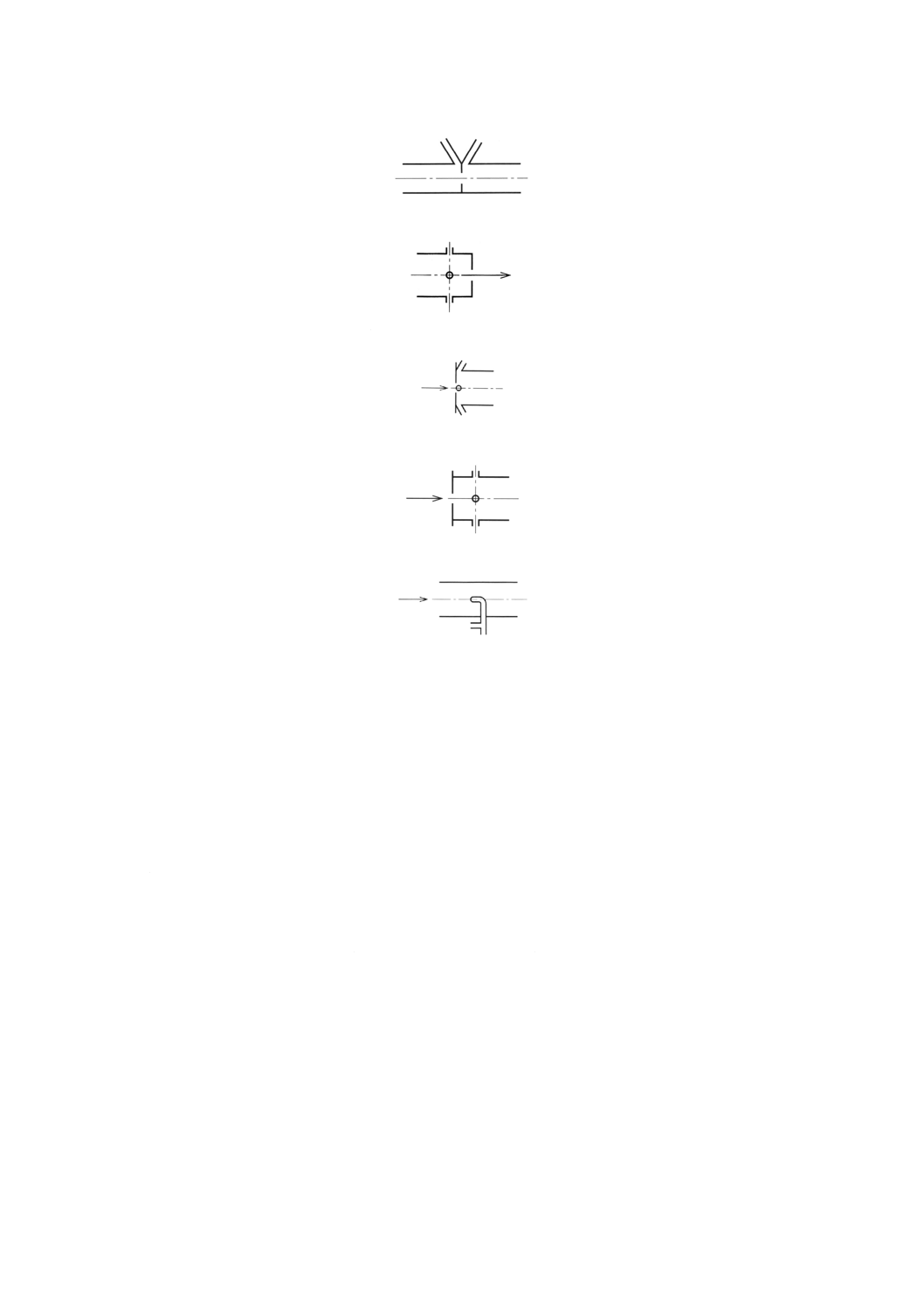
29.3 流量測定器具
以下に示す各器具は,寸法,寸法の公差,及び測定方法について,関連する箇条に適合するものとする。
附属書図43 吸込側ISOベンチュリノズル(22.参照)
附属書図44 管路内ISOベンチュリノズル(22.及び23.参照)
附属書図45 試験空気槽に使用するノズル(23.参照)
附属書図46 四分円インレットノズル(24.参照)
附属書図47 コニカルインレットノズル(25.参照)
附属書図48 D・D/2タップをもつ管路内オリフィス板(26.参照)
120
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図49 コーナタップをもつ管路内オリフィス板(26.参照)
附属書図50 管壁静圧孔をもつ吐出し側オリフィス板(26.参照)
附属書図51 コーナタップをもつ吸込側オリフィス板(26.参照)
附属書図52 管壁静圧孔をもつ吸込側オリフィス板(26.参照)
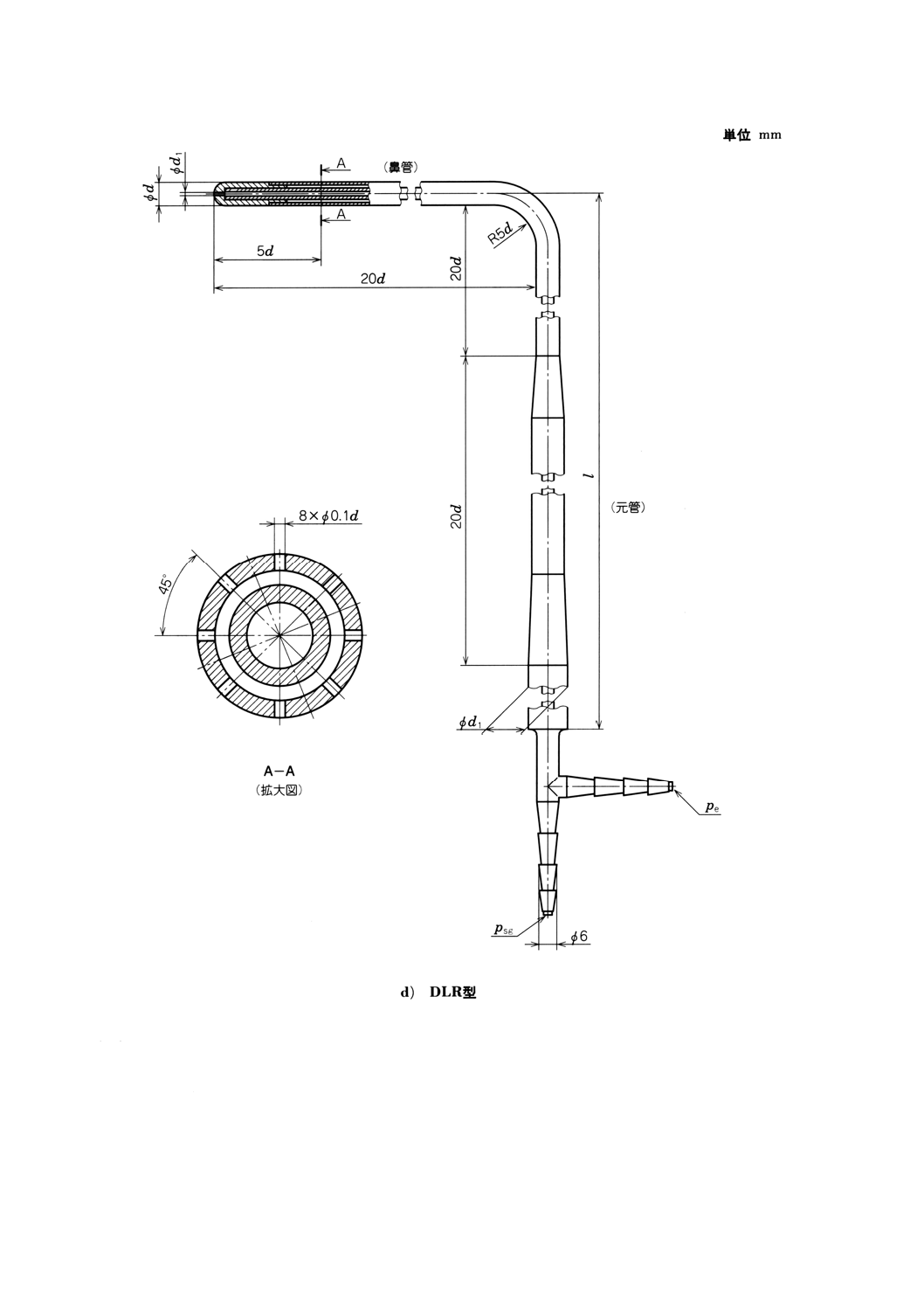
附属書図53 ピトー静圧管トラバース(27.参照)
30. 管路接続送風機の共通通風路
30.1 共通部分
接続形式B,C又はDの送風機の場合には,標準通風路は,送風機の吸込口及び/又は吐出し口に接続
する共通部分から構成される。この項ではその共通部分について説明する。
圧力測定は,これらの共通部分の外側端部において行う。測定される送風機の圧力がいかなる接続形式
に対しても一貫性を保つように,管路形状は厳密に制限されている。
30.2 送風機吐出し側の共通部分
これは送風機に接続する試験通風路の吐出し側に相当する。7.に適合する管壁静圧孔とともに,附属書
図54のように円形断面の中央部に29.2.7に適合する整流格子を含むものとする。次のb)及びc)の図に示
す限度内で,面積及び/又は形状の違いを吸収するため,接続管を使用できる。
附属書図54,附属書図55及び附属書図56に推奨装置を示す。これとは別に,附属書図57に示す代替
装置,また附属書図59に示すような特殊な場合がある。
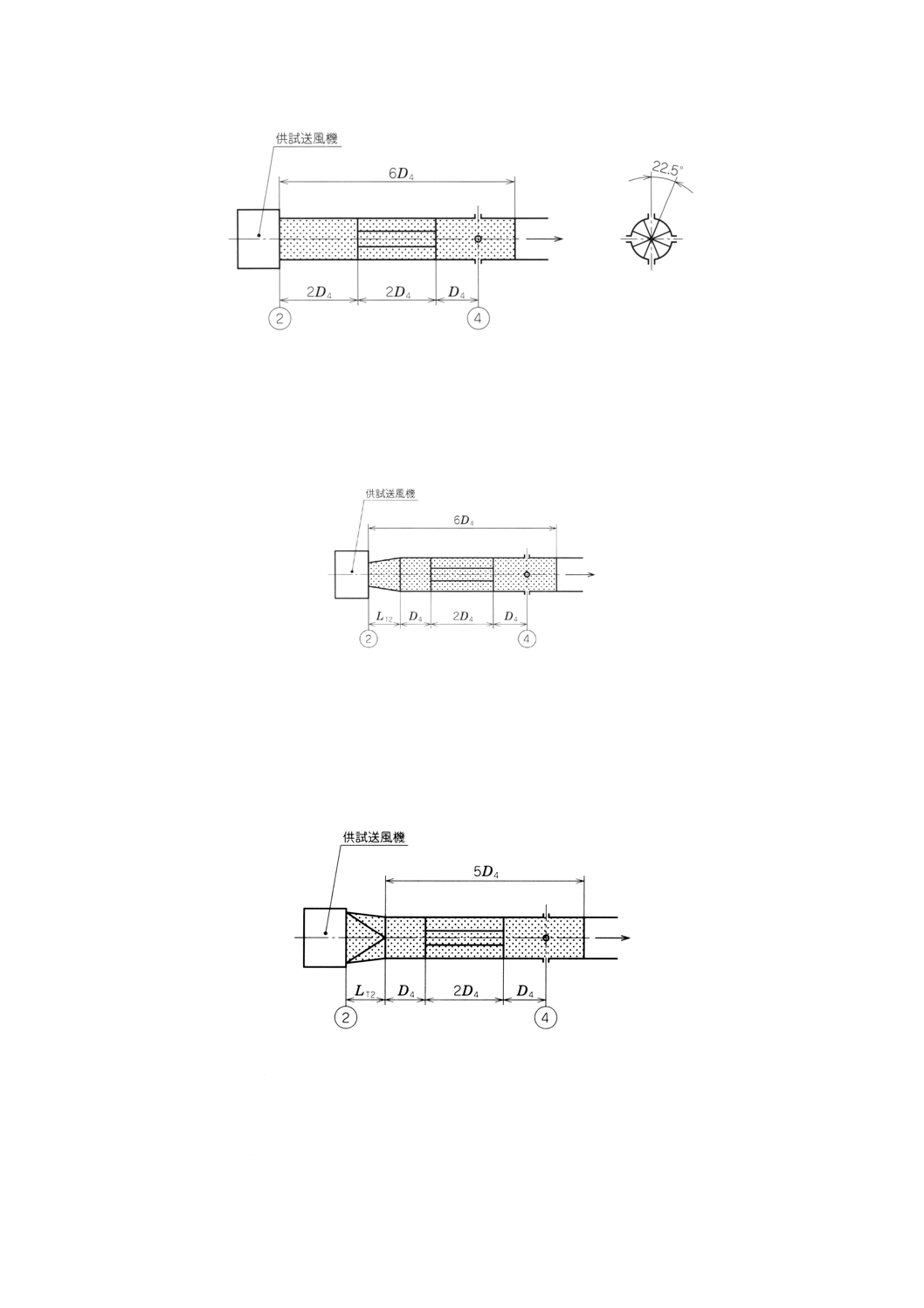
a) 送風機の吐出し口が円形でD4=D2の場合(附属書図54参照)
星形整流格子は,断面4の管壁静圧孔と角度22.5°をなす位置に,等間隔に配置された8枚の放射
状羽根から構成される。羽根の厚みは,0.007D4以下とする。
整流格子の長さは2D4±1%とする。
121
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図54 送風機の吐出し口が円形でD4=D2の場合
b) 送風機の吐出し口が円形でD4≠D2の場合
0.95≦ (D4/D2) 2≦1.07
LT2=D4
備考41. 接続管は円錐形で,摩擦損失係数は長さD4直径D4の管路の損失係数と同一とする。
附属書図55 送風機の吐出し口が円形でD4≠D2の場合
c) 送風機の吐出し口が長方形 (b×h) の場合。ただし,b>hとする。(附属書図56参照)
0.95≦πD42/4bh≦1.07
b≦4h/3の場合 LT2=1.0D4
b>4h/3の場合 LT2=0.75 (b/h) D4
備考42. 接続部は,図のように単一形状曲線とする。
附属書図56 送風機の吐出し口が長方形 (b×h) の場合。ただし,b>hとする。
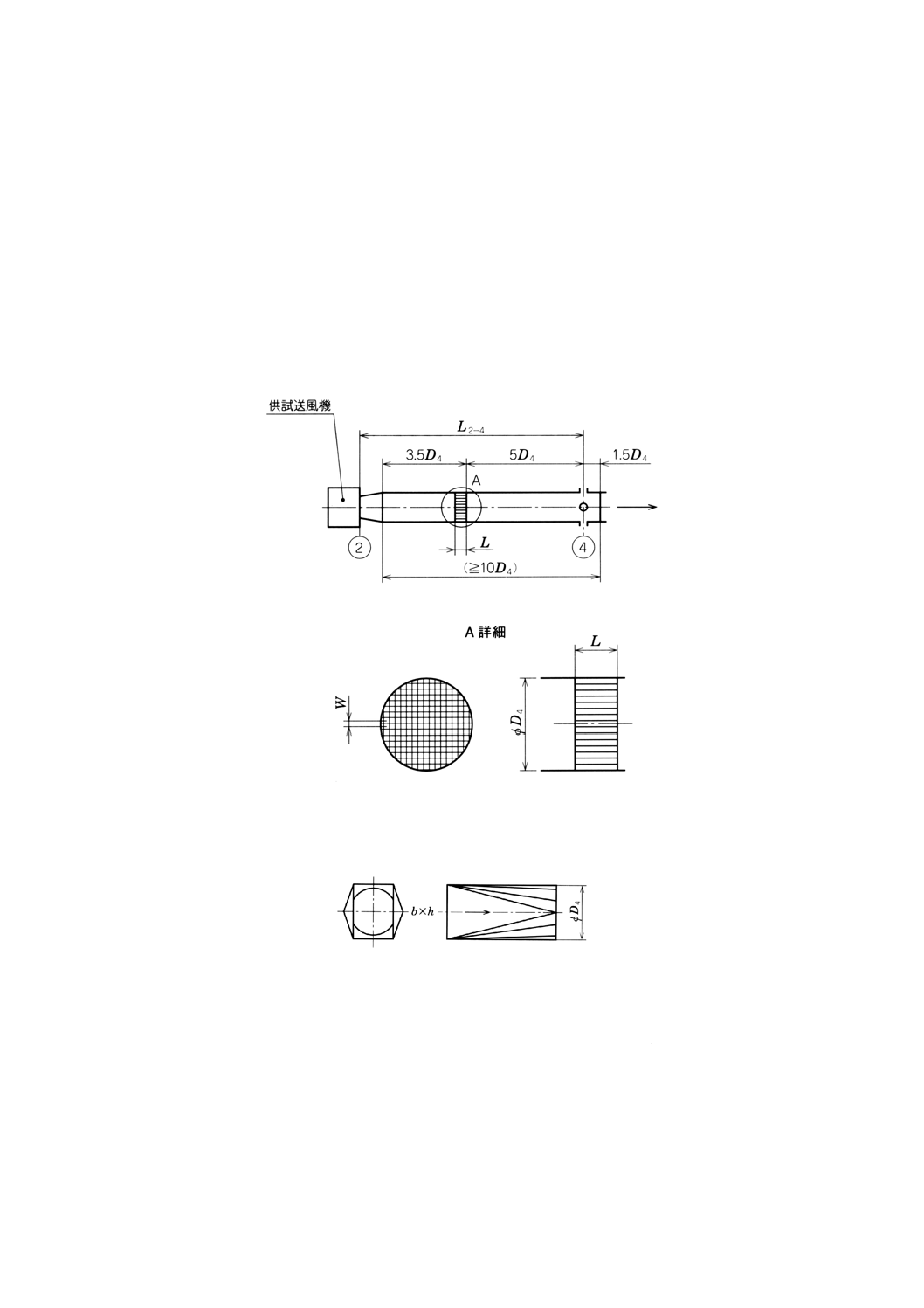
d) 送風機の吐出し口が円形又は長方形で,0.95≦A2/A4≦1.05の場合(附属書図57参照)
吐出し管の整流装置がセル型整流格子の場合
整流格子はおのおののセルが幅W,長さLの,正方形,六角形などの等断面セルにより構成されて
いる。ベーンの厚み (e) は0.005Dを超えてはならない。
122
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1) 標準整流格子の規格は,次による。
W=0.075D4
L=0.45D4
e≦0.005D4
eを除いて,寸法精度はすべて0.005D以内とする。
2) 管壁静圧孔をもつ吐出し側オリフィス板上流側の整流格子は,次による[26.9及び附属書図23e), g)
参照]。
W=0.15D4
e≦0.003D4
L=0.45D4
附属書図57 送風機の吐出し口が円形又は長方形で,0.95≦A2/A4≦1.05の場合
e) 接続部形状(附属書図58参照)
接続管は,附属書図58及び30.2 c)に記載するように単一形状曲線とする。
附属書図58 接続部形状
f)
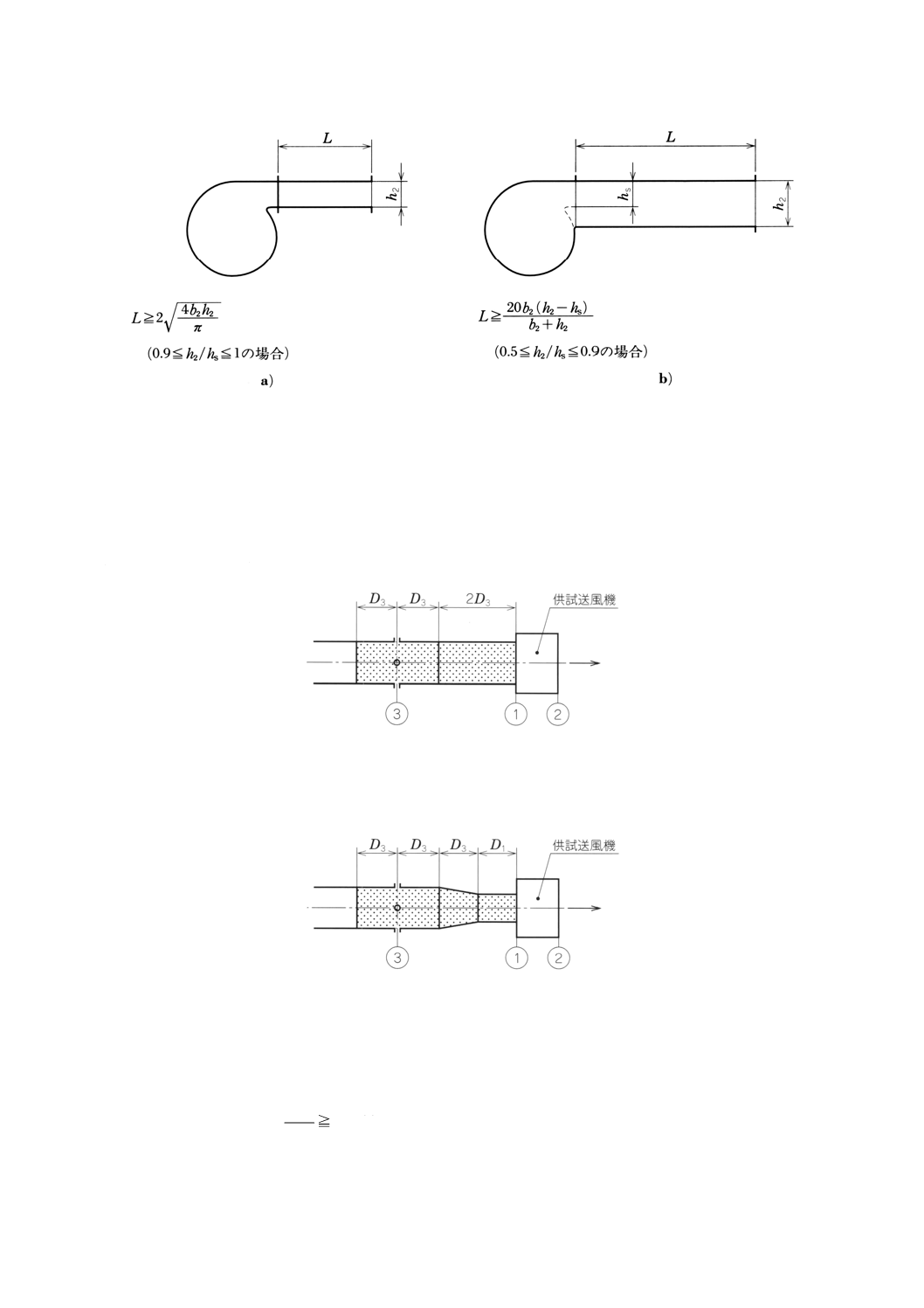
特殊な場合(附属書図59参照)
接続形式B,又はDの送風機(吐出し口における旋回流が小さい遠心ボリュート又は横流送風機な
ど)の試験で,大気又は空気槽に吐出す特殊な場合は,簡略化された吐出し管路で代替試験ができる。
この吐出し管は,送風機吐出し口と同じ断面をもち,その長さは附属書図59a)又はb)記述の式によ
って定められる。
123
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図59 特殊な場合
管断面の許容公差は,送風機吐出し口面積の±0.01 (1%) である。
30.3 送風機吸込側の共通部分
この共通部分は,送風機に接続する試験通風路の吸込側に相当し,附属書図60に示すように,7.に適合
する管壁静圧孔をもつものとする。
下記b)及びc)に規定する限度内で,面積又は/及び形状の差を吸収するために,接続管が使用できる。
a) 送風機の吸込口が円形で,D3=D1の場合(附属書図60参照)
附属書図60 送風機の吸込口が円形で,D3=D1の場合
b) 送風機の吸込口が円形で,0.975D1≦D3≦1.5D1の場合(附属書図61参照)
備考43. 接続管は円錐形で,摩擦損失係数は直径D3及び長さD3の管路の摩擦係数と同一とする。
附属書図61 送風機の吸込口が円形で,0.975D1≦D3≦1.5D1の場合
c) 送風機の吸込口が長方形 (b×h) の場合(附属書図62参照)
送風機吸込口に接続する部分は,送風機吸込口と同じ長方形断面 (b×h) とし,その長さLs1は次の
式に示す。
bh
D
95
.0
4
23≧
π
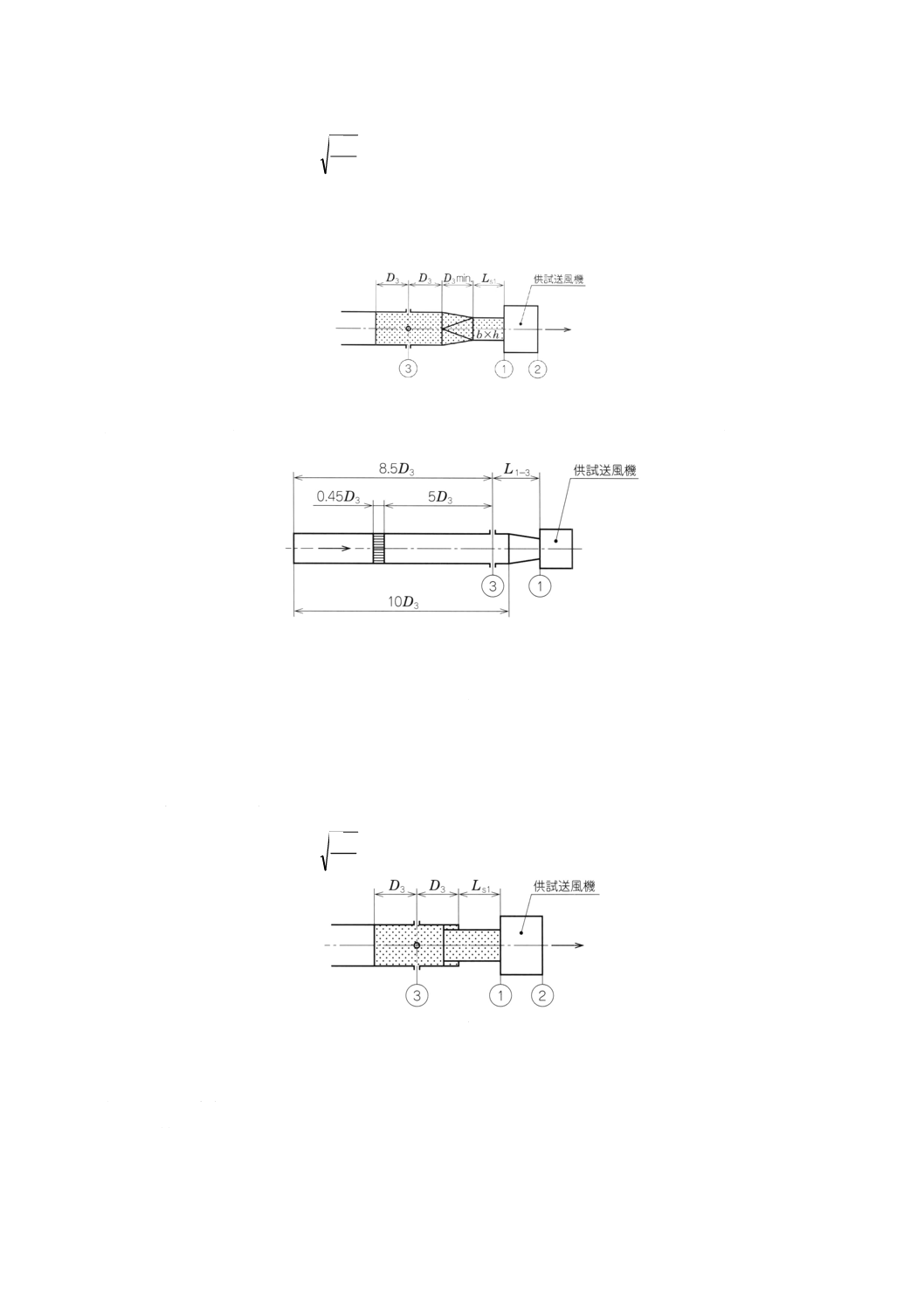
124
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
π
bh
Ls
4
1=
D3又は縦横比b/h(ただしb>h)に上限はないが,短い側の間の広がり角度は15°を超えてはなら
ず,また長い側の間の細まり角度は30°を超えないこととする。接続管は,30.2e)に記載の形状とす
る。
附属書図62 送風機の吸込口が長方形の場合
d) 送風機吸込口が円形又は長方形断面で,0.925≦A3/A1≦1.125の場合[附属書図63及び30.2 d)1)参照]
附属書図63 送風機吸込口が円形又は長方形断面で,0.925≦A3/A1≦1.125の場合
e) 送風機吸込口が円形又は長方形断面の場合
付属書図64に示すような30.5に適合する吸込管路の模擬を使用できる。この方法は,直径D3の試
験通風路が,吸込ベルマウス全体を含むのに十分な大きさがある場合に適切である。
30.5a) 記載の条件の下で,送風機吸込口が円形断面の場合:
Ls1=D1
長方形断面の場合:
π
bh
Ls
4
1=
附属書図64 送風機吸込口が円形又は長方形断面の場合
30.4 吐出し管路の模擬
吐出し管をもたない送風機は,その吐出し側に吐出し管路の模擬をつけることによって吐出し管をもつ
送風機として試験することができる。
吐出し管路の模擬形状は,適宜30.2a),b),c),d)1)又はf)規定の共通部分の形状とする。共通部分の吐
出し口は大気に開放されているが,吐出し側の圧力は断面4の管壁静圧孔で測定する[30.2f)を除く。]。
125
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
大形送風機(800mm以上)の場合には,整流装置を含み,吐出し側の共通通風路によって,試験を実施
することが困難な場合がある。
このような場合には,関係者の協定に基づき,送風機の性能は,長さ2Dhの吐出し管路によって,測定
することができる。
このようにして得られる結果は,特に送風機から大きな旋回流が発生する場合には,吸込側と吐出し側
の両方で共通通風路を使用した場合に得られる結果とある程度の差が生じることがある。
この場合には,静圧pe4は,2D吐出し管路の管壁で測定しない。この静圧は大気圧に等しいとみなす。
30.5 吸込管路の模擬
吸込管をもたない送風機は,その吸込側に吸込管路の模擬をつけることによって,吸込管をもつ送風機
として試験することができる。
a) 送風機の吸込口が円形断面の場合
模擬は送風機の吸込口と同じ直径をもつ円形通風路とし,入口には吸込ベルマウスをつける。
吸込管の長さLs1は,通常Ls1=D1で,定格運転範囲すべてにわたって,吸込管をもつ送風機の正し
い特性を与える。ただし,特別の場合で,風量ゼロ又はゼロ付近の送風機圧力を,吸込管をもつ送風
機と等しくするためには,試験管路をさらに長くする必要がある。このように完全な送風機特性が要
求される場合には,必要に応じてこの模擬を伸ばしたり,吸込ベルマウスをその吸込端に設けて,30.3
a)の共通部分を使用してもよい。
b) 送風機の吸込口が長方形断面の場合
模擬の断面は,送風機吸込口と同じ長方形断面 (b×h) でなければならない。管路長さは次の式に
示す。
π
bh
Ls
4
1=
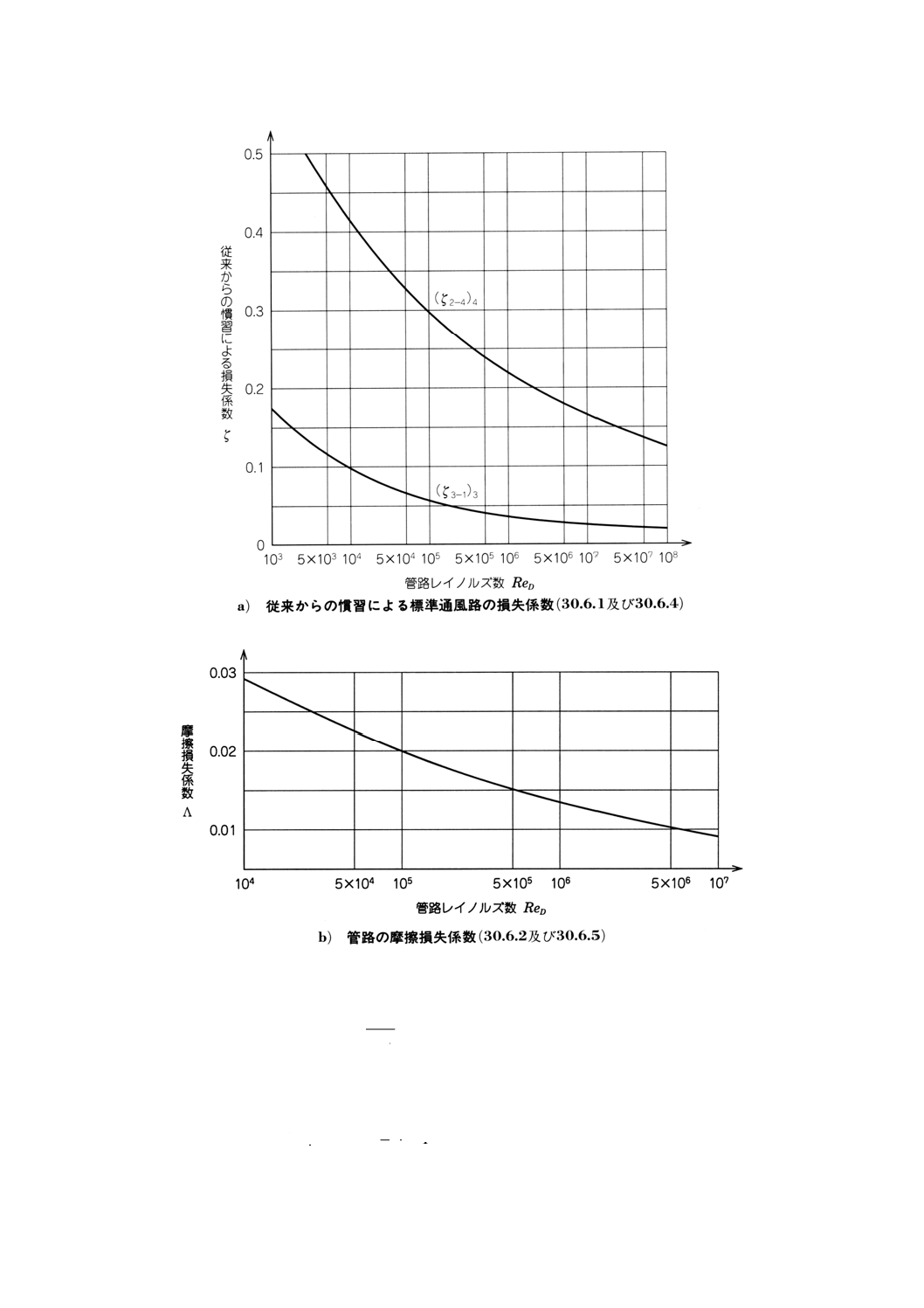
30.6 標準通風路における損失の考慮
ここに記載する従来からの慣習による損失は,標準通風路による試験時の管路摩擦に対し適用され,附
属書図65に摩擦係数を示す。
これらの摩擦係数は試験通風路内の流れのレイノルズ数Re0に依存し,送風機によって生ずる実際の速
度分布とは関係なく,滑らかな管路内における理想流れに基づいている。
摩擦損失は,30.2及び30.3記載の送風機吐出し口又は吸込口と圧力測定断面との間の共通部分について
計算する。接続管を取り付けたり,30.5に記載の吸込管路の模擬を使用する場合(この場合吸込ベルマウ
スの損失も含む)にも,同じ摩擦係数を適用する。
30.6.1 30.2a),b)及びc)記載の吐出し側共通部分の損失
直線管路の直径分の長さにおける摩擦係数は,次の式に示す。
Λ=0.005+0.42 (ReD4) −0.3
外側の管路を含む整流格子の従来からの慣習による損失係数は,次の式に示す。
ζs=0.95 (ReD4) −0.12
送風機吐出し口と測定断面4の間との従来からの慣習による損失係数 (ζ2−4) 4は,次の式に示す。
(ζ2−4) 4=3Λ+0.95 (ReD4) −0.12
=0.015+1.26 (ReD4) −0.3+0.95 (ReD4) −0.12
ここに,標準空気の場合
126
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6
4
4
4
4
4
4
4
10
15
Re
×
≈
=
D
D
m
V
m
V
D
μ
ρ
附属書図65a)にレイノルズ数に対して図示した損失係数 (ζ2−4) 4を示す。
断面2及び4の間の損失は,次の式で示される。
4
24
4
4
4
2
4
2
2
)
(
M
mF
v
p
ρ
ζ−
−=
∆
30.6.2 30.2d)1)に記載の吐出し側共通部分の損失
摩擦係数Λは,次の式に示す。
Λ=0.14 (ReDh4) −0.17
この曲線を附属書図65b)に示す。
セル型整流格子の等価長さと水力直径Dhとの比(円形管路の場合 (Dh=D4) は,次の式に示す。
83
.1
2
6.
184
65
.
26
1
04
.
15
+
−
=
h
h
h
e
D
e
D
e
D
L
30.2d)1)記述の吐出し側の共通部分の従来からの慣習による損失係数は,次の式に示す。
(
)
+
Λ
=
−
−
4
4
4
2
4
4
2
h
e
h
D
L
D
L
ζ
ここに,L2−4は送風機吐出し口と測定断面間との管路長さである。
30.6.3 30.2f)記述の短い吐出し管路の損失
管路の摩擦は考慮しない。
30.6.4 30.3a),b)及びc)記述の吸込共通部分の損失
摩擦損失係数Λは,次の式に示す。
Λ=0.005+0.42 (ReD3) −0.3
及び
(ζ1−3) 3=0.015+1.26 (ReD3) −0.3
ここに,標準空気の場合
6
3
3
3
3
3
3
3
10
15
Re
×
≈
=
D
v
D
v
m
m
D
μ
ρ
従来からの慣習による損失係数 (ζ1−3) 3=− (ζ1−3) 3は,常に負であり,これを附属書図65a)に示す。
断面3と断面1との間のエネルギー損失は,次の式に示す。
(
)
3
23
3
3
1
3
1
3
2
M
mF
v
p
ρ
ζ−
−=
∆
30.6.5 30.3d)記載のセル型整流格子つき吸込側共通部分の損失
摩擦損失係数Λは,30.6.2と同じ式で示す。
Λ=0.14 (ReDh3) −0.17
ここに,標準空気の場合
6
3
3
3
3
3
3
3
10
15
Re
×
≈
=
h
m
V
h
m
V
h
D
D
D
μ
ρ
127
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図65 損失係数
この結果,断面1と断面3との間の従来からの慣習による損失係数は次の式に示す。
(
)
3
3
1
3
1
3
h
D
L−
−
Λ
−
=
ζ
これを附属書図65a)に示す。
断面3と断面1の損失は,次の式に示す。
(
)
3
23
3
3
1
3
1
3
2
M
mF
v
p
ρ
ζ−
−=
∆
128
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
30.6.6 30.5記述の吸込管路模擬の損失
30.3a)d)などの共通部分に対応する吸込管路が要求される場合を除いて,この吸込管路模擬には損失は許
されない。
31. 標準試験空気槽
31.1 試験空気槽
測定箇所の設定,又は送風機が実際に使用されると想定される条件を模擬するため,若しくはその両方
のために,試験設備に空気槽を設置することができる。
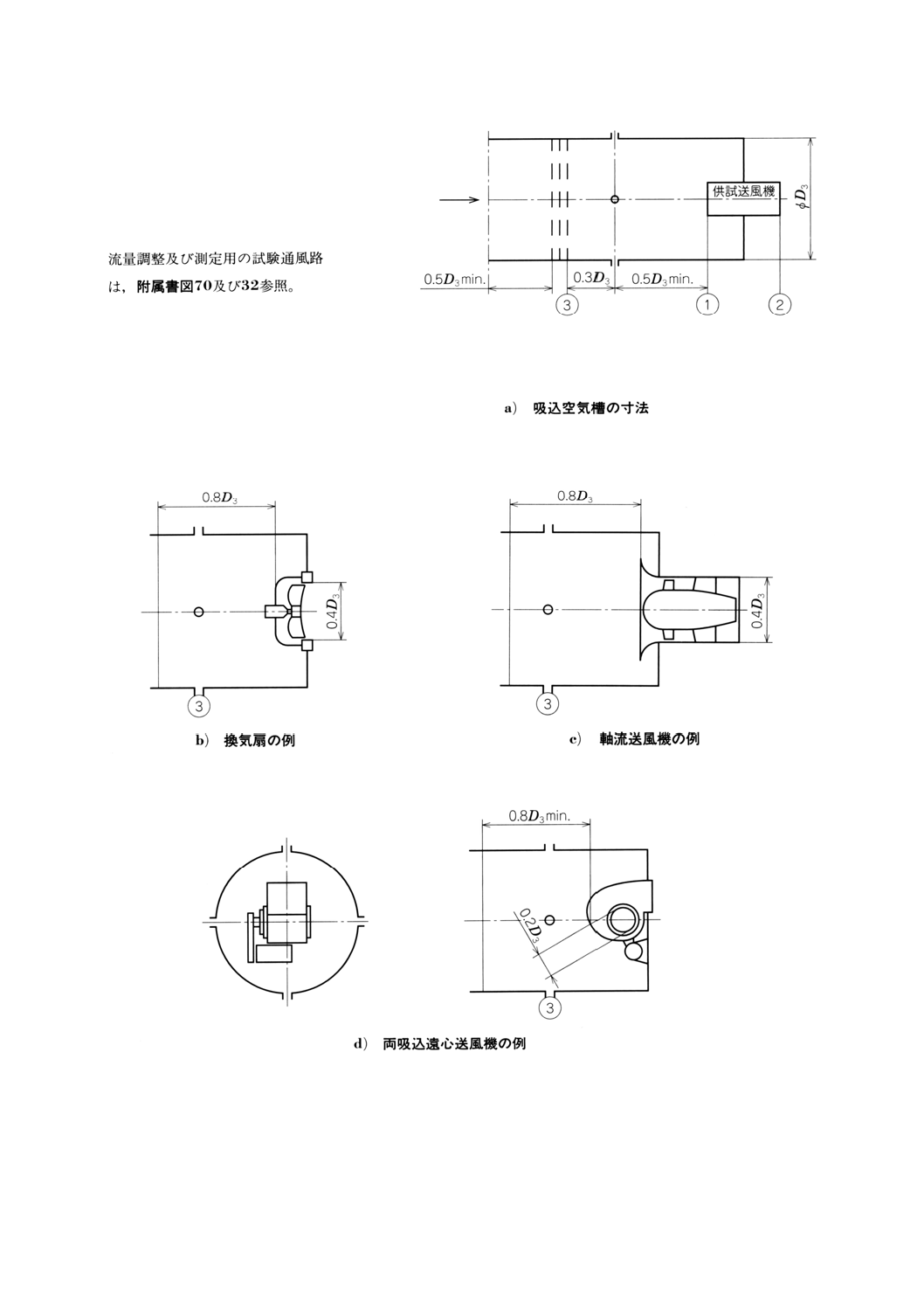
31.1.1 寸法
試験空気槽の断面は,円形,正方形又は長方形のいずれでもよい。
長さに関しては,附属書図66及び67に示す最小距離以上で,試験対象の送風機を収容するのに十分な
長さが必要である。
31.1.2 管壁静圧測定孔(管壁静圧孔)
測定断面の管壁静圧孔は,7.の要求項目に適合するものとし,円形空気槽の周囲,正方形又は長方形空
気槽の側面の中心に,等間隔に取り付けるものとする。
31.1.3 整流装置
正しい速度分布を得るために,測定装置図に示す位置で,空気槽内に整流装置を設ける。
測定断面が整流装置の下流にある場合には,整流装置は測定断面の前方で実質的に一様な流れをつくる。
金網の下流0.1Dhの距離における最大速度は,最大速度が2m・s−1以上の場合には,平均速度の25%を超え
てはならない。
測定断面が整流装置の上流側にある場合には,整流金網の目的は,上流側の噴流運動エネルギーを吸収
して無限空間におけるような正常な膨張をさせることである。これには,噴流の境界に,混合空気を供給
する逆流が必要になるが,逆流の最大速度は,計算平均噴流速度の10%を超えてはならない。
測定断面が空気槽内の整流装置の両側にある場合には,上記の各場合の要求に適合するものでなければ
ならない。
これらの要求に適合する整流装置は,金網又は多孔板を任意に組み合わせて使用できるが,一般に両方
の要求を満たすためには,規定に合った空気槽長さが必要である。
この条件に適合する流れを確実に得るために空気槽壁面に隙間のないように,流れの方向に連続して,
60%, 50%及び45%の開口面積をもつ3枚の一様な金網又は多孔板を,0.1Dh間隔で,取り付ける。
整流装置は,汚れによる詰まりがあってはならない。
正しい速度分布が得られることを確認するために,整流装置の性能を検査する必要がある。
129
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図66 吸込側試験空気槽:形式1
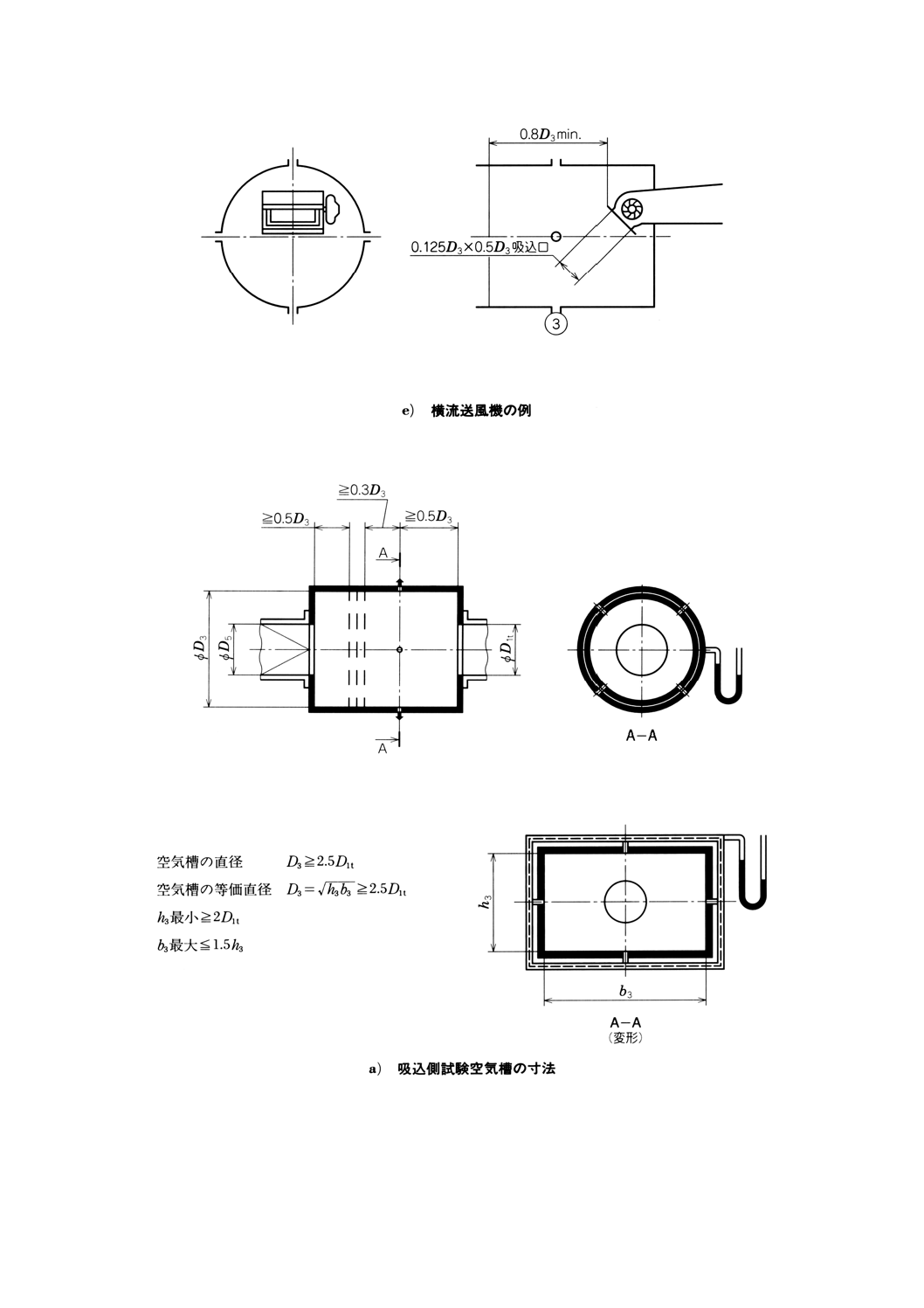
130
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注) 図の送風機寸法は最大許容寸法を示す。
附属書図66 吸込側試験空気槽:形式1(続き)
附属書図67 吸込側試験空気槽:形式2
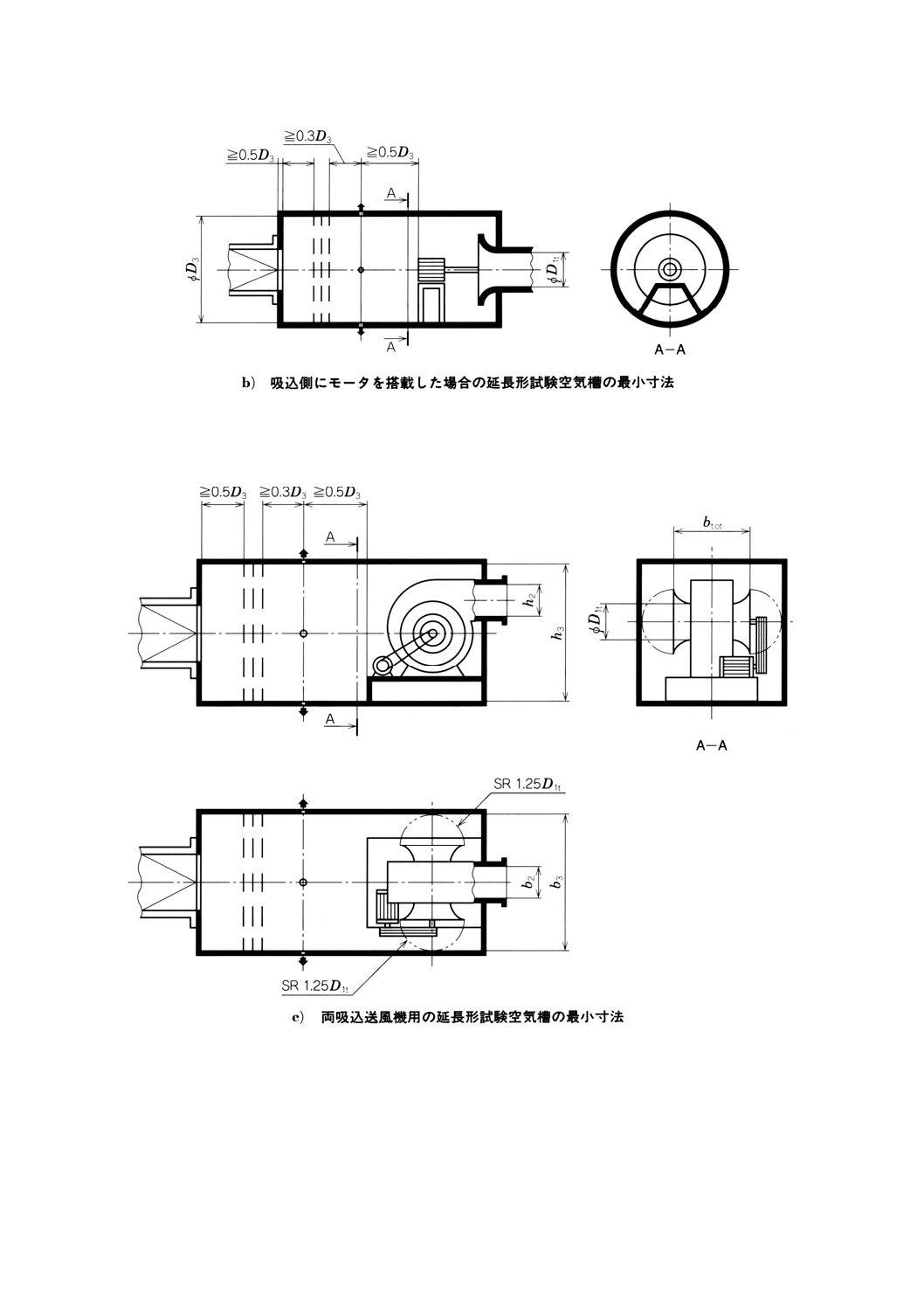
131
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図67 吸込側試験空気槽:形式2(続き)
31.1.4 マルチノズル
マルチノズルは,可能な限り対称的に配置する。各ノズルの中心線は,空気槽の壁面からノズルのスロ
ート直径の1.5倍以上離れていなければならない。
同時に使用する任意の2本のノズルの中心間の最小距離は,最大ノズルのスロート直径の3倍とする。
132
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
最大ノズルの出口面から下流の整流装置までの距離は,最小でも最大ノズルのスロート直径の2.5倍と
する。
ノズルの入口面と上流及び下流の管壁静圧孔と間の距離は,38±6mmとする。
31.1.5 空気槽内のオリフィス板
オリフィス板は,±1°及び±0.005Dhの範囲内で,空気槽と同心でなければならない(26.2参照)。オリ
フィス板の上流面と上流側整流装置の出口との距離は,最小0.4Dhとする。
ここに,Dhは空気槽の空力直径である。
オリフィス板の出口面と下流側整流装置の出口との距離は,最小0.5Dhとする。
オリフィス板の入口断面と上,下流側圧力測定孔との距離は,0.05Dh±0.01Dhとする。
オリフィス板は26.2に適合するものでなければならない。
31.2 可変給気システム及び排気システム
試験設備の測定装置には,運転点を変化させる手段を装備するものとする。
31.2.1 絞り装置
送風機の運転点を調整するために,絞り装置が使用できる。絞り装置は,管路又は試験空気槽の端部に,
管路又は空気槽の中心に対称となるように設置する。
31.2.2 補助送風機
試験送風機の運転点を調整するために補助送風機が使用される。補助送風機は,定格流量が試験装置を
通過するのに十分な圧力をもった設計でなければならない。ダンパ制御,ピッチ制御又は速度制御などの
流量調節手段が必要になる場合がある。補助送風機は,試験中に急激に大きく動揺したり,脈動してはな
らない。
31.3 標準吸込側試験空気槽
31.3.1 試験空気槽
本附属書では,3種類の吸込空気槽について規定する(附属書図66,67及び68参照)。
31.3.1.1 吸込側試験空気槽:形式1
試験空気槽の断面は,内径D3の円形,D3×D3の正方形又は短い方の辺がD3の長方形にすることができ
る。
試験空気槽の長さは,附属書図66に示すように,圧力測定孔と送風機のケーシング又はモータとの間の
最小距離を保ち,試験対象の送風機を収容するのに,十分な長さであることが望ましい。
31.3.1.2 吸込側試験空気槽:形式2
試験空気槽の断面は,内径D3の円形,D3×D3の正方形,又はb3×h3 (b3≦1.5h3) の長方形とすることが
できる。ここに,D3は空気槽の等価直径で,
3
3
3
h
b
D=
吸込側に駆動機をもつ送風機,又は両吸込送風機の場合には,接続条件に応じて,空気槽の圧力測定孔
と送風機近接部分の間に,対応する最小距離が必要である。最小寸法に相当する長さに延長した試験空気
槽を使用する必要がある(附属書図67を参照)。
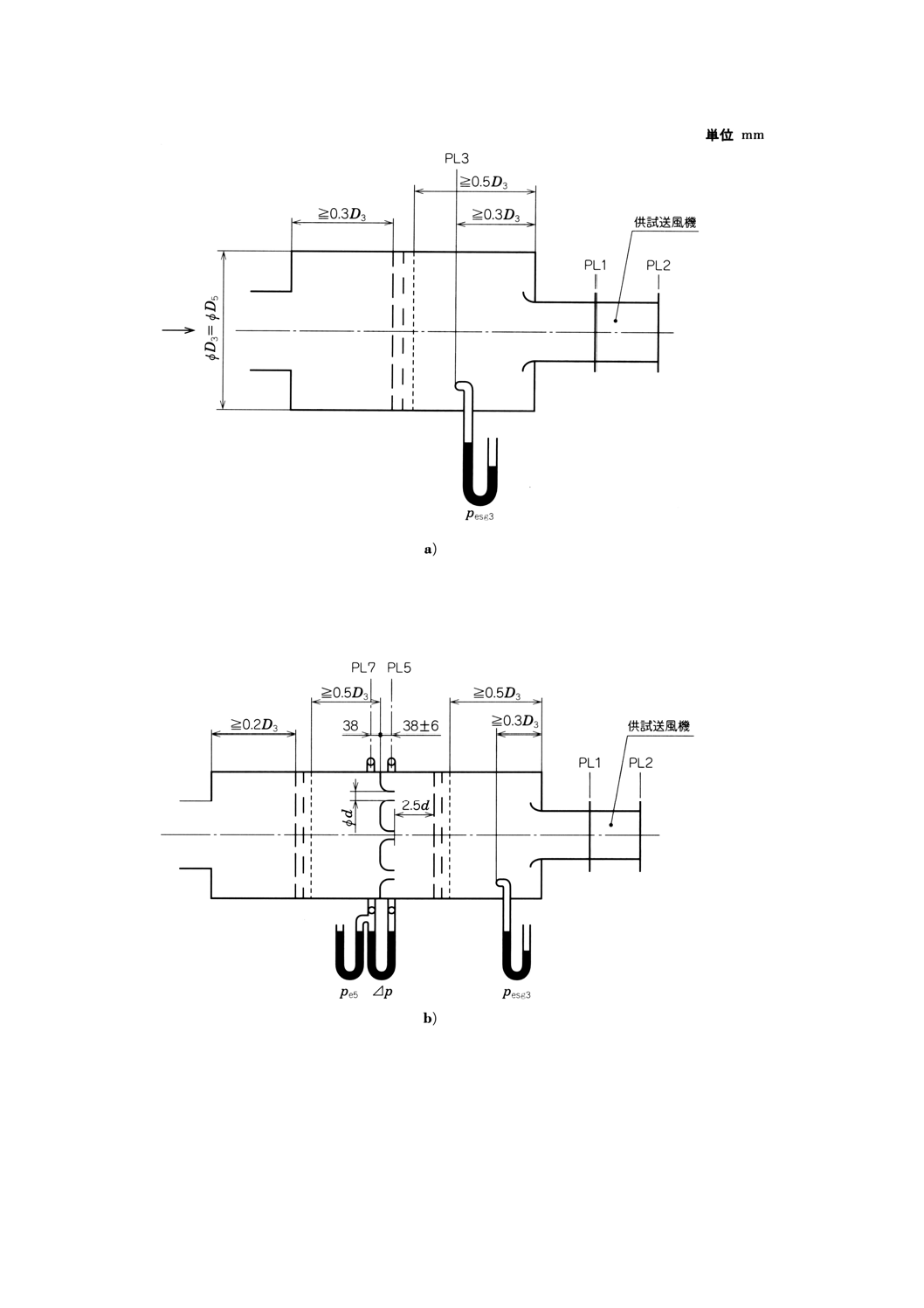
133
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図68 吸込側試験空気槽:形式3
31.3.1.3 吸込側試験空気槽:形式3
吸込側試験空気槽:形式3の寸法D3は,円形試験空気槽の内径,又は内側の断面寸法h1,b3をもつ長
方形試験空気槽の等価直径である。
ここに,
134
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
π
3
3
3
4b
h
D=
圧力測定断面3の位置は次による。
・空気槽の下流端の上流
:0.3D3以上
・整流装置の下流
:0.2D3以上
吸込側空気槽:形式3には,流量測定用のノズルをつけることができる(附属書図68参照)。
31.3.2 試験対象の送風機
31.3.2.1 吸込側空気槽:形式1
円形空気槽の場合には,試験対象の送風機の吸込口スロート面積A1tは,
D32/8を超えてはならない。
D32>8A1tとする。
ここに,A1tは吸込口が空気槽と同心の場合の吸込口スロート面積である。
これに当てはまらない場合には,吸込口スロート総面積は,D32/16を超えてはならない。
附属書図66,67に,最大吸込口をもつ送風機例を示す。
31.3.2.2 吸込側空気槽:形式2
試験対象の送風機は,吸込口スロート直径D1tが,D3/2.5を超えてはならない。
又はA1t≦A3/6.25
又はA3≧6.25A1t
両吸込送風機を試験する場合には,試験空気槽の幅は両方の吸込部を収容できる幅以上でなければなら
ない。
正方形又は長方形断面をもつ空気槽を選択すると便利である。空気槽の合計幅b3は,送風機の幅bと附
属書図67に示すように1.25D1tに等しい半径の半球に対応する二つの吸込開口部の周囲の開放空間の合計
である。
31.3.2.3 吸込側空気槽:形式3
吸込側空気槽の断面積は,送風機の吸込口スロート面積の5倍とする。
A3≧5A1
この場合には,流量測定にマルチノズルを使用してもよい(附属書図68参照)。
31.4 標準吐出し側試験空気槽
31.4.1 試験空気槽(附属書図69参照)
空気槽の断面は,内径D6の円形, (D6×D6) の正方形, (h6×b6) の長方形が可能である。
空気槽の内径D6は,円形空気槽の内径,又は内側の寸法がh6とb6の長方形空気槽の等価直径である。
ここに,
π
6
6
6
4b
h
D=
送風機の吐出し圧力Pe4は,送風機吐出し管路又は空気槽内で測定できる。吐出し空気槽は,流量測定
にマルチノズルを使用してもよい(附属書図30参照)。
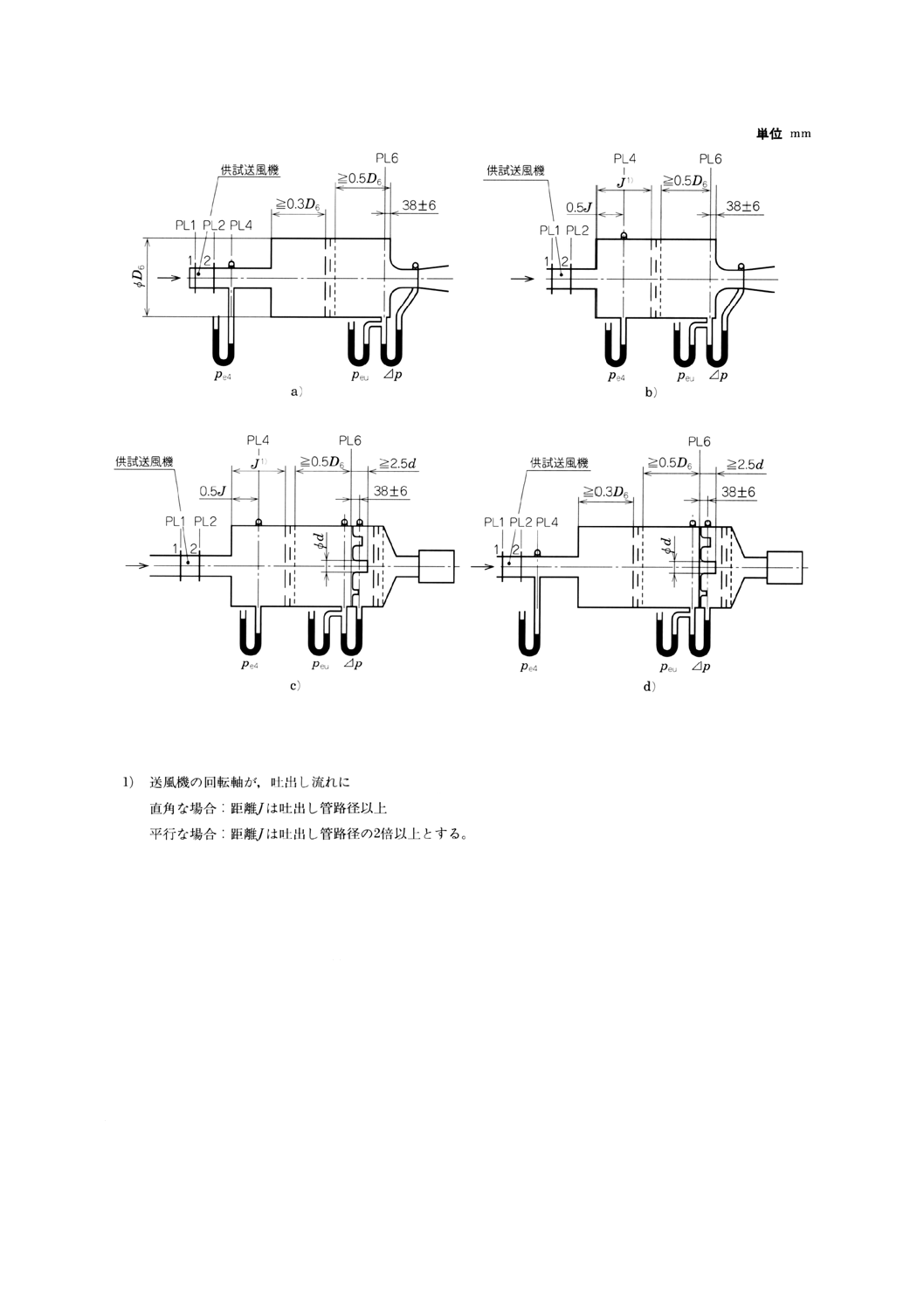
135
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図69 吐出し側試験空気槽
31.4.2 試験対象の送風機
吐出し側空気槽(附属書図69)の断面積は,送風機の回転軸が吐出し流れに対し直角な場合には,送風
機吐出し口,又は吐出し管路面積の9倍以上 (A6≧9A2),送風機回転軸が吐出し流れに対し平行な場合に
は,送風機吐出し口,又は吐出し管路面積の16倍以上 (A6≧16A2) でなければならない。
32. 試験空気槽を使用する場合の標準試験方法−接続形式A
32.1 送風機装置の形式
送風機を空気槽に設置するのに,一般的に次の2種類がある。
a) 吸込側に空気槽を設置した場合
b) 吐出し側に空気槽を設置した場合
流量を調節及び測定する方法を,吸込側に空気槽を設置した場合について11種類,吐出し側に空気
136
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
槽を設置した場合について2種類示す。それぞれについて流量測定方法を規定し,あわせてその詳細
を説明する項目及び図を示す。
接続形式Aで性能試験を行う際の測定,計算などの共通する方法を,吸込側に空気槽を設置した場
合の11種類,及び吐出し側に空気槽を設置した場合の2種類に対し,32.2と32.3に示す。
空気槽は,マッハ数の影響が無視できるほど十分な大きさをもつとみなす。
この方法は,この附属書に適合するすべての送風機に対して,おおむね有効である。
ただし,次の二つの場合は簡略法でもよい。
− 送風機吐出し口の基準マッハ数Ma2refが0.15未満で,圧力比が1.02を超える場合
− 基準マッハ数Ma2refが0.15未満で,圧力比が1.02未満の場合
これらの場合の計算方法を,32.2.4.1及び32.2.4.2に示す。
32.2 吸込側の試験空気槽
32.2.1 流量の測定
流量は次の方法で測定する。
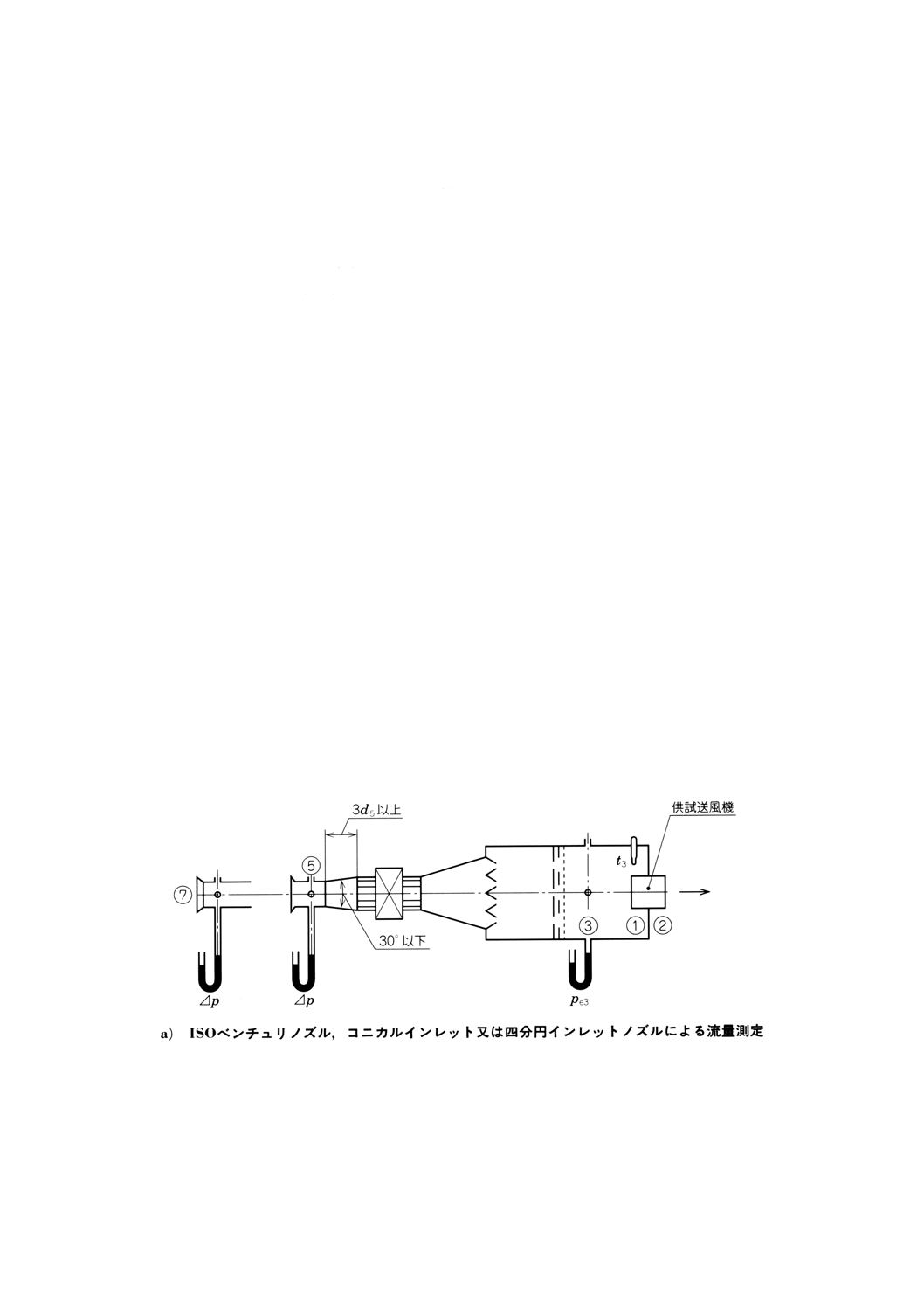
− 吸込側ISOベンチュリノズルによる[附属書図70a)参照]
− 四分円インレットノズルによる(附属書図70a)参照)
− コニカルインレットによる(附属書図70a)参照)
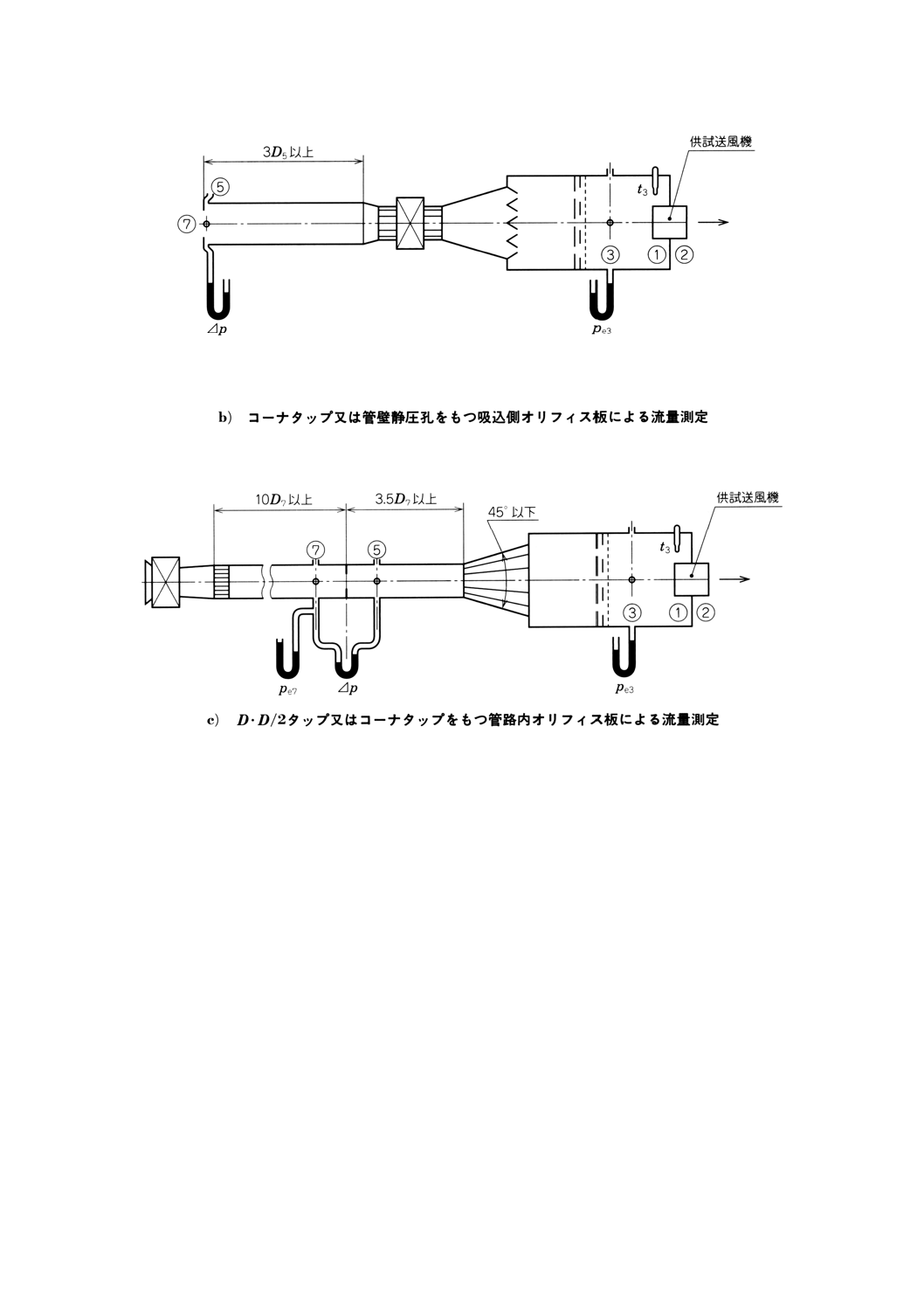
− コーナタップをもつ吸込側オリフィス板による(附属書図70b)参照)
− 管壁静圧孔をもつ吸込側オリフィス板による(附属書図70b)参照)
− D・D/2タップをもつ管路内オリフィス板による(附属書図70c)参照)
− コーナタップをもつ管路内オリフィス板による(附属書図70c)参照)
− 管路内ISOベンチュリノズルによる(附属書図70d)参照)
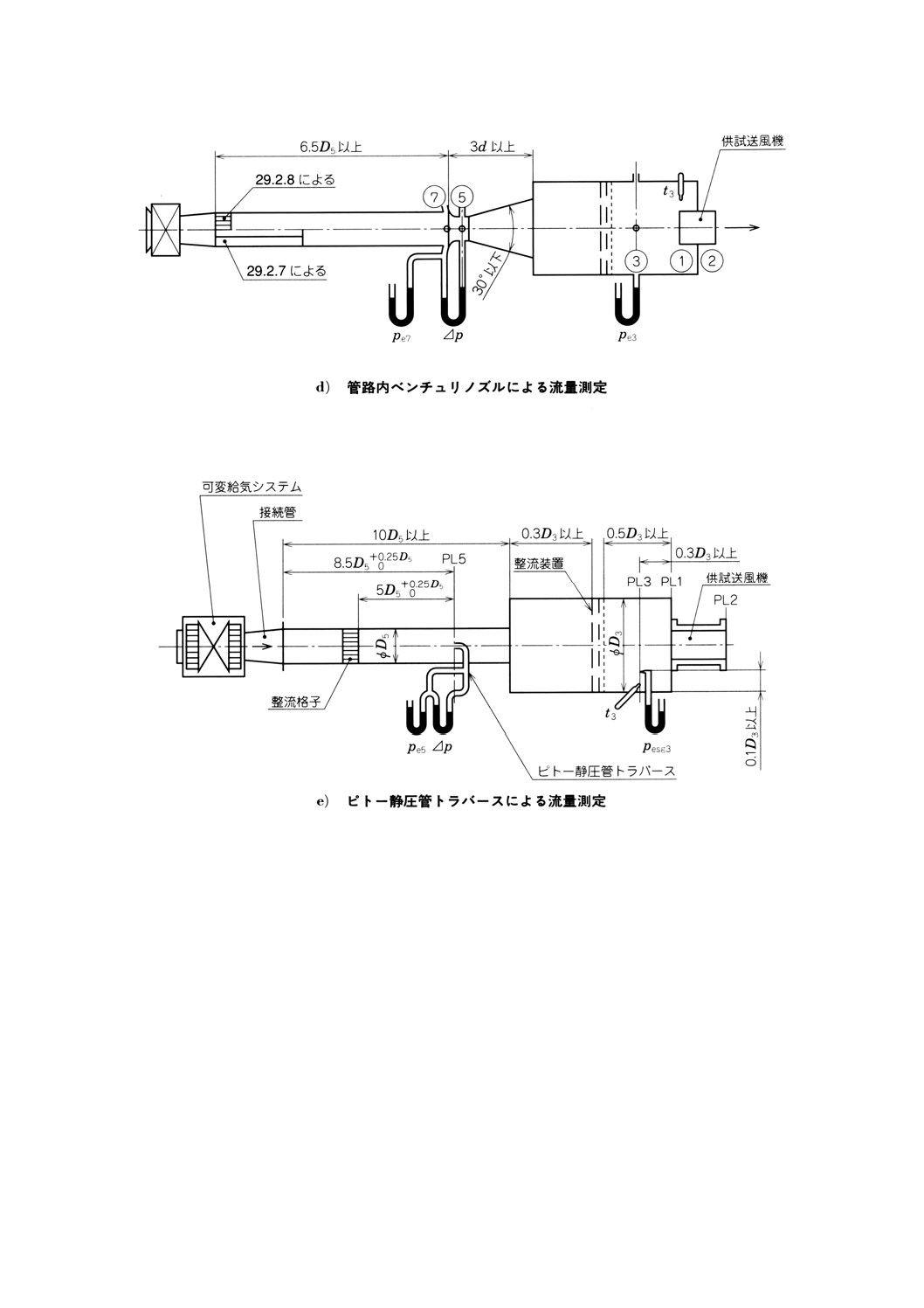
− ピトー管静圧管トラバースによる(附属書図70e)参照)
− 管路内ベンチュリノズルによる(附属書図70f)参照)
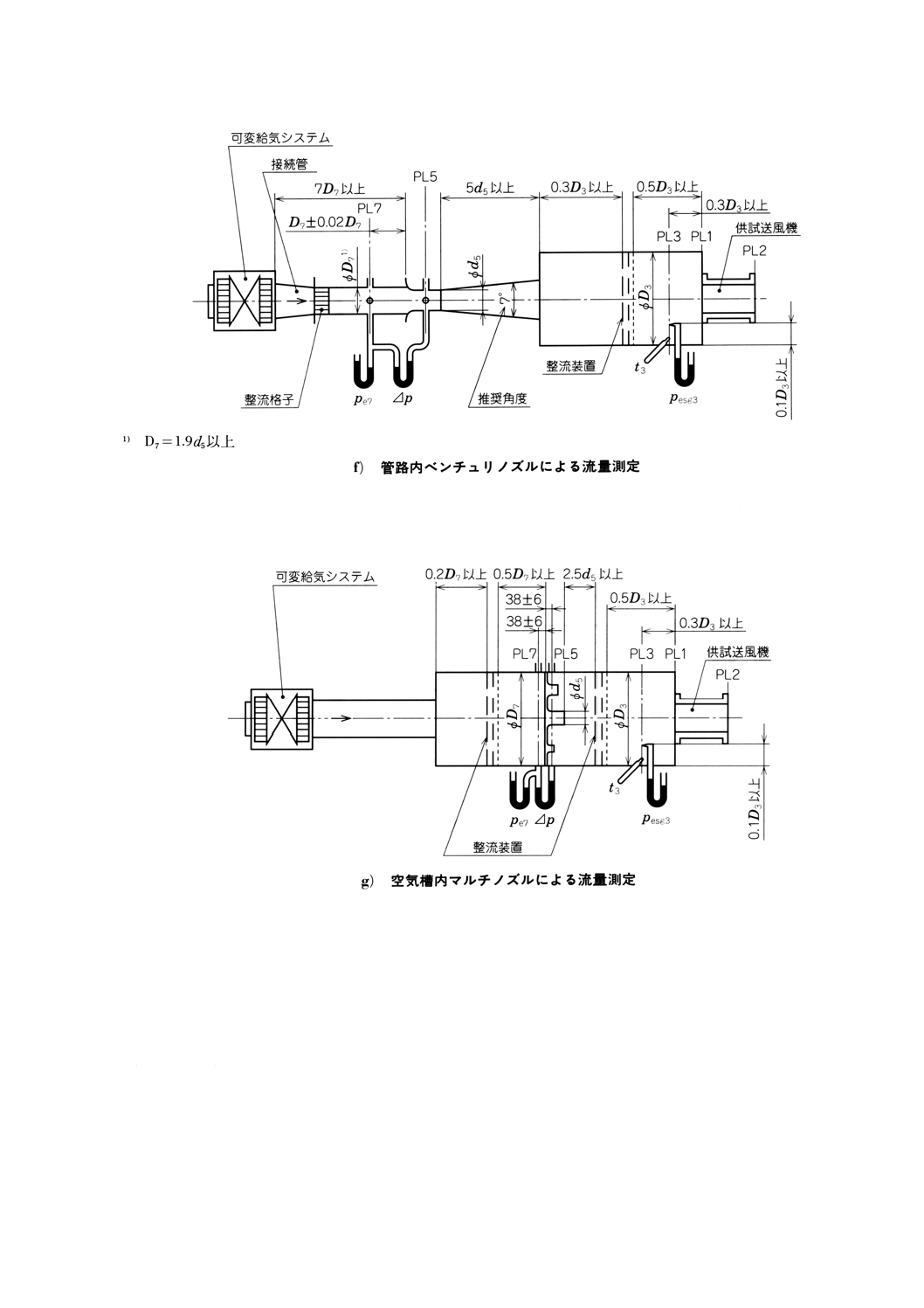
− 空気槽内マルチノズルによる(附属書図70g)参照)
− 空気槽内オリフィス板による(附属書図70g)及び23h)参照)
附属書図70 接続形式A(吸込側試験空気槽)
137
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図70 接続形式A(吸込側試験空気槽)(続き)
138
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図70 接続形式A(吸込側試験空気槽)(続き)
139
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図70 接続形式A(吸込側試験空気槽)(続き)
32.2.2 試験中に実施する測定(20.を参照)
測定項目
− 回転速度,N又は回転周波数,n
− 送風機への入力,Pa,Po又はPe,インペラ動力の推定(10.4参照)及び補助送風機の動力Pexの推定
− 流量計差圧,∆p
− 流量計の上流圧力,pe7又はpe5
− 附属書図70a)〜d)における空気槽圧力,pe3,及び附属書図70e)〜g)における空気槽のせき止め圧力
− 空気槽温度,t3
試験時の囲い内の測定項目
140
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 送風機の平均高度における大気圧,pa
− 送風機吸込口付近の周囲温度,ta
− 乾湿球温度,td及びtw
周囲の空気密度,ρa,及び湿り空気のガス定数Rwを算出する(12.参照)。
32.2.3 圧縮性流体に対する一般的な方法
この方法は,送風機の圧力比が1.02を超え,かつ基準マッハ数,Ma2ref,が0.15を超える場合に適用す
る(14.4.2参照)。
32.2.3.1 流量の算出
32.2.3.1.1 流量測定は,次による。
− 吸込側ISOベンチュリノズルによる[22.と附属書図70a)参照]
− 四分円インレットノズルによる[24.及び附属書図70a)参照]
− コニカルインレットによる,25.及び附属書図70a)参照。
− コーナタップをもつ吸込側オリフィス板による,26.10及び附属書図70b)参照。
− 管壁静圧孔をもつ吸込側オリフィス板による,26.11及び附属書図70b)参照。
インライン流量計の後ろに,調節装置又は調節装置付きの補助送風機を備える。
次のように仮定する。
p7=pa=pu
Θsg7=Θ7=ta+273.15
7
7
7
Θ
=
w
R
p
ρ
12.3によって空気の粘度を算出し,流量計に関するレイノルズ数の最初の近似を行った後で,流量係数
α及び空気の膨張による修正係数ε,又は組合せ係数αεを次によって算出してもよい。
ISOベンチュリノズルについては,22.3.2,22.3.3,22.3.4及び附属書図18。
四分円インレットノズルについては,24.4。
コニカルインレットについては,25.4と附属書図22。
コーナタップをもつ吸込側オリフィス板については,26.10,附属書図26及び附属書図28。
管壁静圧孔をもつ吸込側オリフィス板については,26.11。
質量流量は次の式による。
p
d
qm
∆
=
7
25
2
4
ρ
αεπ
αがレイノルズ数Red又はReDの関数の場合は,上式においてRed又はReDによるαの変化を考慮しなけ
ればならない。
32.2.3.1.2 流量測定は,次による。
− D・D/2タップをもつ管路内オリフィス板による,26.7及び附属書図70c)参照
− コーナタップをもつ管路内オリフィス板による,26.8及び附属書図70c)参照
− 管路内ISOベンチュリノズルによる22.及び附属書図70d)参照
流量計の上流に,調節装置又は調節装置付きの補助送風機を備える。
次のように仮定する。
p7=pe7+pa
141
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Θsg7=Θsg3=t3+273.15=Θa+
p
m
ex
rx
c
q
P
Por
p
m
sg
c
A
q
27
27
2
7
7
2
ρ
−
Θ
=
Θ
7
7
7
Θ
=
w
R
p
ρ
質量流量は次の式によって算出する。
p
d
qm
∆
=
7
25
2
4
ρ
π
αε
空気の膨張による修正係数は,22.,26.7及び26.8によって算出する。
流量計に関するレイノルズ数を次の式で推定する。
(
)
6
7
7
5
5
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
d
ρ
αε
又は,
ReD7=Red5β
その後,流量計数α又は組合せ係数αεを,次のように算出する。
D・D/2タップをもつ管路内オリフィス板については,26.7及び附属書図24
コーナタップをもつ管路内オリフィス板については,26.8及び附属書図25
管路内ISOベンチュリノズルについては,22.及び附属書図18
Θ7=Θsg7として,qmの初期値を算出してもよい。Θ7が決定されると,α及びqmの新しい値が算出される。
10−3の計算精度を得るには,2回の反復計算で十分である。
32.2.3.1.3 ピトー静圧管トラバースによる流量の算出[27.及び附属書図70e)参照]
流量測定のために,管路の上流に調節装置又は調節装置付きの補助送風機を備える。
次のように仮定する。
p5=pe5+pa
∑
=
=
n
j
j
e
e
p
n
p
1
5
5
1
Θsg5=Θsg3=t3+273.15
測定管路の温度t5を測定し,これをせき止め温度とみなしてもよい。しかし,空気槽内の温度t3を測定
する方が望ましい。
平均差圧は次の式に示す。
2
1
5.0
1
=
∆
∑
=
n
j
j
m
p
n
p
27.5参照。
また,質量流量は次の式によって算出する。
m
m
p
A
q
∆
=
5
52ρ
αε
ここに,

142
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
5
5
Θ
=
w
R
p
ρ
κ
κ1
5
5
5
5
−
∆
+
Θ
=
Θ
m
sg
p
p
p
2/1
2
2
5
6
1
2
1
1
∆
+
+
∆
−
=
s
m
m
p
p
p
p
x
κ
κ
ε
αはレイノルズ数ReD5の関数で,0.99に非常に近い値である(27.6参照)。
qmの初期値をα=0.99として算出し,αの変化に対して補正する。
32.2.3.1.4 管路内ベンチュリノズルによる流量の算出[23.及び附属書図70f)参照]
流量計の上流に,調節装値又は調節装置付きの補助送風機を備える。
次のように仮定する。
Θ3=Θsg3=Θsg7=t3+273.15=Θa+
p
m
ex
rx
c
q
P
P
or
,
p7=pe7+pa
p
m
sg
c
A
q
27
27
2
7
7
2
ρ
−
Θ
=
Θ
質量流量は,次の式で算出する。
4
7
25
7
25
1
2
4
2
4
β
α
ρ
επ
ρ
αεπ
Au
m
p
d
C
p
d
q
−
∆
=
∆
=
ここに,
εは,23.4.3及び附属書表5から算出される空気の膨張による修正係数である。
rd=1−∆p/p7
αは流量係数で,次の値に等しい。
4
1
β
αAu
C
−
Cはノズルの流出係数で,レイノルズ数Red5及びノズル形状の関数である
(23.4.2及び附属書表5参照)。
αAuは運動エネルギー係数で,空気槽進入路では1に,管路進入路では1.043に
等しい。
β=d5/D7
6
7
7
5
5
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
d
ρ
αε
初期値は
4
1
95
.0
β
α
α
Au
−
=
また,Θ7=Θsg7
143
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7
7
7
Θ
=
w
R
p
ρ
qmの初期値を算出し,この値とΘ7,ρ7,Red5及びαによって,qmの新しい値を算出することができる。
10−3の計算精度を得るには2〜3回の反復計算で十分である。
32.2.3.1.5 空気槽内マルチノズルによる流量の算出[23及び附属書図70g)参照]
空気槽の上流に,調節装置又は調節装置付きの補助送風機を備える。
次のように仮定する。
Θ3=Θsg3=Θsg7=Θ7=t3+273.15
p7=pe7+pa
7
7
7
Θ
=
w
R
p
ρ
0
7
5≈
=Dd
β
質量流量は,23.4によって次の式に示す。
p
d
C
q
n
j
j
j
m
∆
=∑
=
7
1
25
2
4
ρ
επ
ここに,
εは,23.4.3及び附属書表6による空気の膨張による修正係数である。
Cjはjthノズルの流出係数で,ノズルスロート部のレイノルズ数Red5jの関数であ
る。
β=0だからCj=αj
Cj=αjは,23.4.2及び表5によって算出される。
nはノズルの数である。
各ノズルについて,Cj=0.95としてスロート部レイノルズ数Red5を次の式によって推定する。
6
7
7
5
5
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
C
j
j
j
d
ρ
ε
質量流量の初期値を算出の後,流出係数Cjを補正する。
32.2.3.1.6 空気槽内の管壁静圧孔をもつオリフィス板による流量の算出[26.9.1並びに附属書図70g),23h),
23i)及び23j)参照]
オリフィス板が,マルチベンチュリノズルの代わりに取り付けられる。
次のように仮定する。
Θ3=Θsg3=Θsg7=Θ7=t3+273.15
p7=pe7+pa
7
7
7
Θ
=
w
R
p
ρ
.25
0
7
5≦
D
d
=
β
質量流量は,26.5によって次の式に示す。
144
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p
d
qm
∆
=
7
25
2
4
ρ
αεπ
ここに,αεは26.9及び26.9.1によって算出する。
32.2.3.2 送風機圧力の算出
32.2.3.2.1 送風機吸込口圧力
次のように仮定する。
p3=pe3+pa
Θ3=t3+273.15=Θsg3=Θsg1
3
3
3
Θ
=
w
R
p
ρ
14.5及び14.6によって
3
3
23
2
3
23
3
3
1
2
1
2
sg
m
m
sg
p
A
q
p
v
p
p
=
+
=
+
=
ρ
ρ
又は
3
3
23
2
3
23
3
3
1
2
1
2
esg
m
e
m
e
esg
p
A
q
p
v
p
p
=
+
=
+
=
ρ
ρ
これは附属書図70a)〜d)の構成に対して有効である。附属書図70e)〜g)の構成に対しては,せき止め圧
力pesg3をピトー静圧管で測定する。
psg1=pesg3+pa=psg3
pesg1=pesg3
pe3≦0及びpesg1≦0
14.4.3.2及び14.5.2によってMa1,
1
1
sg
Θ
Θ
及びp1を算出してもよい。
吸込口静圧p1は,次の式に示す。
1
2
1
1
1
1
1
1
1
2
1
M
m
sg
M
d
sg
F
A
q
p
F
p
p
p
−
=
−
=
ρ
又は
a
M
m
esg
M
d
esg
e
p
p
F
A
q
p
F
p
p
p
−
=
−
=
−
=
1
1
2
1
1
1
1
1
1
1
2
1
ρ
マッハ係数FM1は,14.5.1によって算出する。
32.2.3.2.2 送風機吐出し口圧力
送風機吐出し口において,p2は大気圧paに等しく
p
m
e
r
sg
sg
c
q
P
P又は
+
Θ
=
Θ
1
2
Ma2及びΘ2は,14.4.3.1によって算出する。
2
2
2
Θ
=
w
R
p
ρ

145
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
2
2
2
2
2
1
M
m
sg
F
A
q
p
p
+
=
ρ
FM2は,14.5.1によって算出する。
また,次のようにも表すことができる。
2
2
2
2
2
2
1
M
m
esg
F
A
q
p
=ρ
2
2
1ρ
ρ
ρ
+
=
m
m
k
ρ
ρ
ρ
1
=
32.2.3.2.3 送風機圧力
送風機静圧psFAは,次の式に示す。
psFA=p2−psg1=pa−psg1=−pesg1
また,送風機圧力pFAは,次の式に示す。
1
2
2
2
2
1
2
2
1
sg
M
m
a
sg
sg
FA
p
F
A
q
p
p
p
p
−
+
=
−
=
ρ
1
2
2
2
2
1
2
2
1
esg
M
m
esg
esg
FA
p
F
A
q
p
p
p
−
=
−
=
ρ
32.2.3.3 体積流量の算出
試験状態において,体積流量は次の式で算出する。
Θ
=
=
1
1
1
1
sg
w
sg
m
sg
m
sg
v
R
p
q
q
q
ρ
32.2.3.4 理論空気動力の算出
32.2.3.4.1 単位質量当たりの送風機仕事及び理論空気動力
14.8.1により,単位質量当たりの送風機静圧仕事は,次の式に示す。
2
1
1
1
2
1
2
1
2
2
1
2
−
−
=
−
−
=
ρ
ρ
ρ
A
q
p
p
V
p
p
y
m
m
m
m
sA
単位質量当たりの送風機仕事は,次の式に示す。
−
+
−
=
−
+
−
=
2
1
1
2
2
2
1
2
1
2
2
2
1
2
2
1
2
2
ρ
ρ
ρ
ρ
A
q
A
q
p
p
V
V
p
p
y
m
m
m
m
m
m
A
理論静圧空気動力PusA及び理論空気動力PuAは次の式に示す。
146
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
PusA=qm・ysA
PuA=qm・yA
32.2.3.4.2 理論空気動力及び圧縮性係数の算出
14.8.2によって
PusA=qvsg1・psFA・kps
PuA=qvsg1・pFA・kp
圧縮性係数kp及びkpsは,次の2種類の等価な方法で算出してもよい(14.8.2.1及び14.8.2.2参照)。
a) 第一の方法
[
])1
(
1
log
log
10
10
−
+
=
r
Z
r
Z
k
k
k
k
p
ps又は
ここに,理論静圧空気動力については,
1
1
sg
sFA
p
p
r
+
=
理論空気動力については,
1
1
sg
FA
p
p
r
+
=
また,理論静圧空気動力又は理論空気動力については,
)
(
1
1
FA
sFA
sg
v
r
k
p
p
q
P
Z
又は
κ
κ−
=
b) 第二の方法
)
1
ln(
)
1
ln(
p
p
p
ps
Z
Z
x
x
k
k
+
+
=
又は
ここに,理論静圧空気動力又は理論空気動力について
1
1
1
sg
FA
sg
sFA
p
p
p
p
r
x
又は
=
−
=
1
1
1
sg
sg
v
r
p
p
q
P
Z
κ
κ−
=
32.2.3.5 効率の算出
14.8.1によって,効率は次の式に示す。
− 送風機静圧効率;
r
usA
srA
P
P
=
η
− 送風機効率;
r
uA
rA
P
P
=
η
− 送風機静圧軸効率;
a
usA
saA
P
P
=
η
− 送風機軸効率;
147
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a
uA
aA
P
P
=
η
32.2.4 簡略方法
32.2.4.1 基準マッハ数Ma2refが0.15未満で圧力比が1.02を超える場合
せき止め温度と静温度とは等しいとみなし,マッハ係数FMは1に等しいとみなす(14.9.1参照)。
Θx=Θsgx
FM1=FM2=1
32.2.4.1.1 質量流量の算出
質量流量は,32.2.3.1に記述した方法によって算出する。
ただし,附属書図70c)〜g)の構成に対する計算では,次の簡略方法を適用することができる。
流量計上流及び空気槽内の温度は,測定してもよい。
Θu=tu+273.15=Θsgu
pu=peu+pa
u
w
u
u
R
p
Θ
=
ρ
せき止め温度と静温度の差を考慮するための逐次近似を行う必要はない。
ただし,αがレイノルズ数によって変化する場合は(32.2.3.1参照),レイノルズ数の推定が必要である。
流量は,推定したαを使用し,Θu=Θsguとして算出する。
32.2.4.1.2 送風機圧力の算出
32.2.4.1.2.1 送風機吸込口圧力
14.9.1.2及び14.9.1.3によって
2
3
3
3
3
2
3
3
3
1
2
1
2
+
=
+
=
=
A
q
p
V
p
p
p
m
m
sg
sg
ρ
ρ
又は
2
3
3
3
3
2
3
3
1
2
1
2
+
=
+
=
=
A
q
p
V
p
p
p
m
e
m
e
esg
esg
ρ
ここに,
3
3
3
3
3
Θ
+
=
Θ
=
w
a
e
w
R
p
p
R
p
ρ
せき止め圧力を測定する附属書図70e)〜g)の場合は除いて,
psg1=psg3
又は
pesg1=pesg3
2
1
1
1
1
2
1
−
=
A
q
p
p
m
sg
ρ
又は
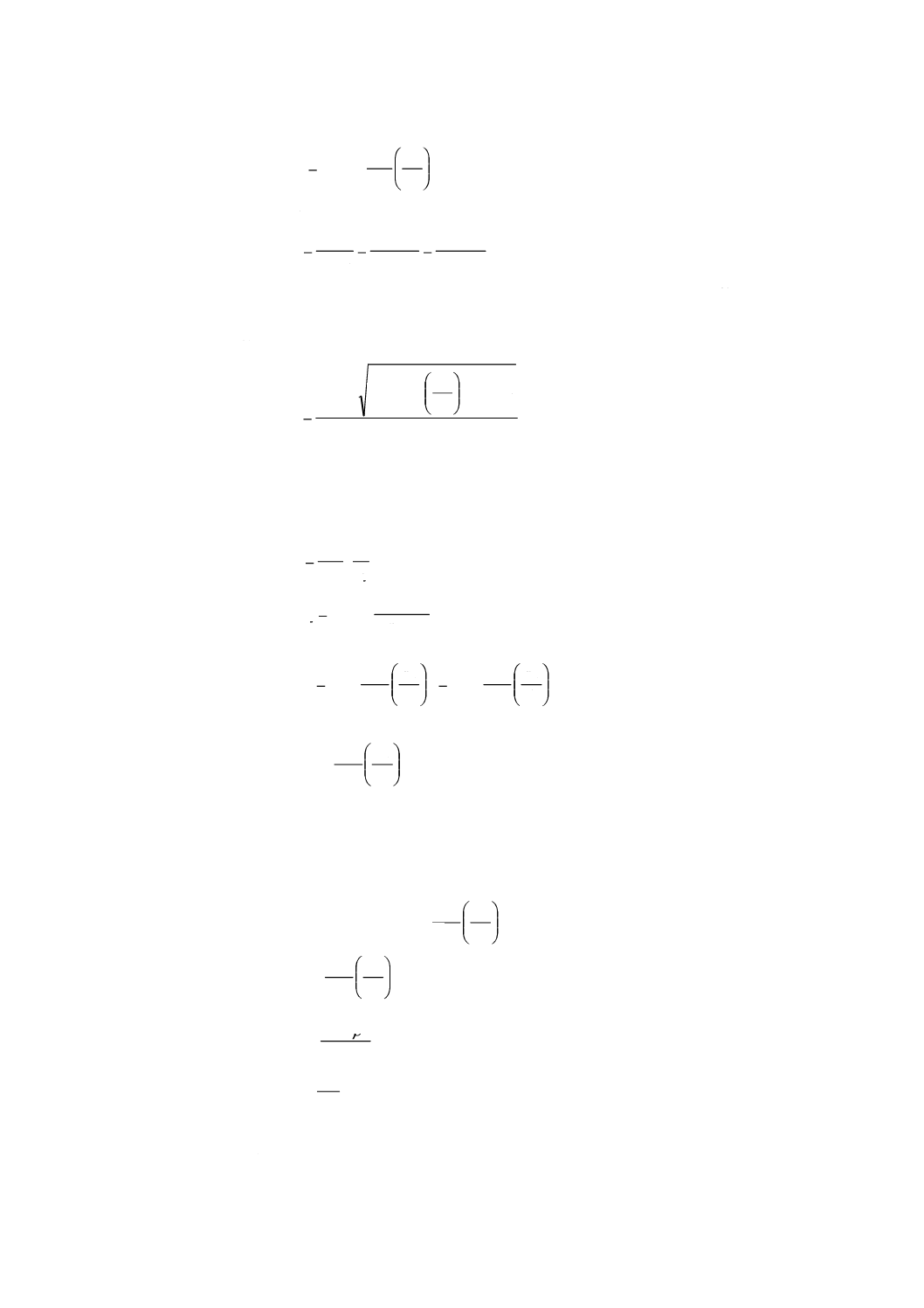
148
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
1
1
1
2
1
−
=
A
q
p
p
m
esg
e
ρ
ここに,
3
1
1
1
1
1
1
sg
w
sg
w
w
R
p
R
p
R
p
Θ
=
Θ
=
Θ
=
ρ
しかし,p1は未知であり,p1及びρ1を決定するには逐次近似を行う。2〜3回の反復計算で十分である
(14.9.1.4参照)。
圧力p1は次の式で算出してもよい(14.9.1.4参照)。
2
2
1
2
1
1
2
1
1
sg
w
m
sg
sg
R
A
q
p
p
p
Θ
−
+
=
また,
pe1=p1−pa
32.2.4.1.2.2 送風機吐出し口圧力
送風機吐出し口において,p2=pa又はpe2=0
2
2
2
sg
w
R
p
Θ
=
ρ
p
m
e
r
sg
sg
c
q
P
Por
1
2
+
Θ
=
Θ
2
2
2
2
2
2
2
2
2
1
2
1
+
=
+
=
A
q
p
A
q
p
p
m
a
m
sg
ρ
ρ
2
2
2
2
2
1
=
A
q
p
m
esg
ρ
32.2.4.1.2.3 送風機圧力
送風機静圧psFA及び送風機圧力pFAは,次の式に示す。
psFA=p2−psg1=pa−psg1=−pesg1
1
2
2
2
1
2
2
2
1
2
2
1
2
1
esg
m
sg
m
a
sg
FA
p
A
q
p
A
q
p
p
p
p
−
=
−
+
=
−
=
ρ
ρ
2
2
1ρ
ρ
ρ
+
=
m
m
p
k
ρ
ρ1
=
備考44. pesg1≦0,pe3≦0
32.2.4.1.3 体積流量の算出
149
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
体積流量は,32.2.3.3と同様に次の式に示す。
1
1
sg
m
sg
v
q
q
ρ
=
ここに,
1
1
1
sg
w
sg
sg
R
p
Θ
=
ρ
32.2.4.1.4 理論空気動力の算出
理論空気動力は,14.8.1,14.8.2,14.8.3及び32.2.3.4によって算出する。
32.2.4.1.5 送風機効率の算出
送風機効率は,14.8.1,14.8.2,14.8.3及び32.2.3.5によって算出する。
32.2.4.2 基準マッハ数Ma2refが0.15未満で圧力比が1.02未満の場合(14.9.2を参照)
送風機を通過する流れは非圧縮性とみなしてよい。
Θ1=Θsg1=Θ3=Θsg3=Θ2=Θsg2
ρ1=ρ2
FM1=FM2=1
kp=1
32.2.4.2.1 質量流量の算出
質量流量は,32.2.4.1.1によって算出する。
32.2.4.2.2 送風機圧力の算出
32.2.4.2.2.1 送風機吸込口圧力
3
3
3
1
1
Θ
=
=
=
w
sg
sg
R
p
ρ
ρ
ρ
2
3
1
3
1
2
1
+
=
A
q
p
p
m
sg
sg
ρ
2
3
1
3
1
2
1
+
=
A
q
p
p
m
e
esg
ρ
2
1
1
1
1
2
1
−
=
A
q
p
p
m
sg
ρ
又は
2
1
1
1
1
2
1
−
=
A
q
p
p
m
esg
e
ρ
例外として,附属書図70e)〜g)の場合はせき止め圧力pesg3を測定し,pesg1=pesg3又はpsg1=psg3とする。
32.2.4.2.2.2 送風機吐出し口圧力
送風機吐出し口において
p2=pa
pe2=0
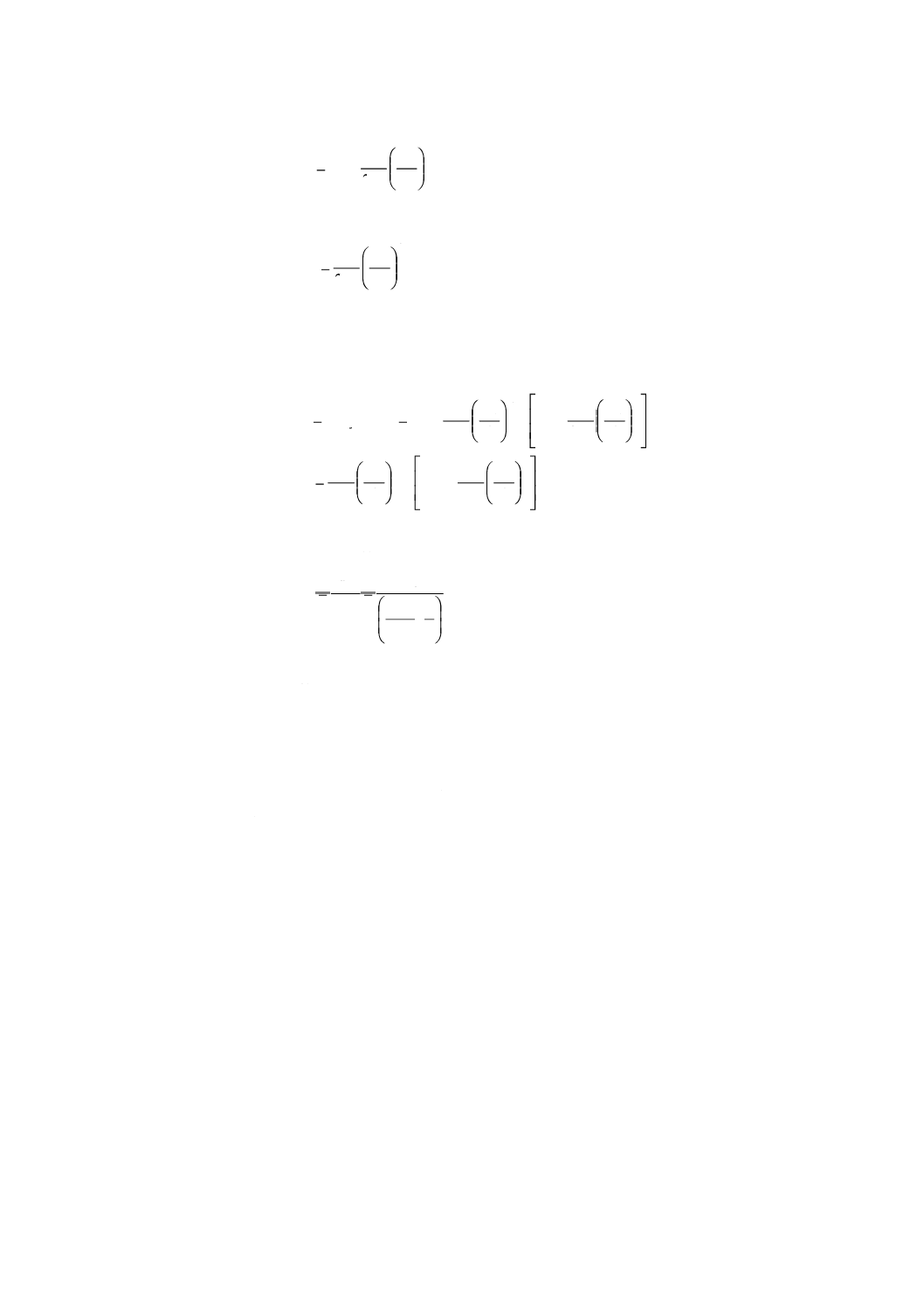
150
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
1
2
2
2
1
+
=
A
q
p
p
m
sg
ρ
又は
2
2
1
2
2
1
=
A
q
p
m
esg
ρ
32.2.4.2.2.3 送風機圧力
送風機圧力は,次の式に示す。
psFA=p2−psg1=pa−psg1=−pesg1
+
−
=
+
−
+
=
−
=
2
2
3
1
3
2
2
1
2
3
1
3
2
1
2
1
2
2
1
2
1
2
1
2
1
A
q
p
A
q
A
q
p
A
q
p
p
p
p
m
e
m
m
m
sg
sg
FA
ρ
ρ
ρ
ρ
32.2.4.2.3 体積流量の算出
吸込状態での体積流量は,次の式で算出する。
Θ
=
=
1
1
1
1
sg
w
sg
m
sg
m
sg
v
R
p
q
q
q
ρ
32.2.4.2.4 理論空気動力の算出
理論空気動力は,次の式で算出する。
PusA=qvsg1・psFA
PuA=qvsg1・pFA
32.2.4.2.5 送風機効率の算出
送風機効率は,14.8.1,及び32.2.4.1.5によって算出する。
32.2.5 試験状態での送風機の性能
試験状態での送風機の性能は,次による。
− 吸込体積流量,qvsg1
− 送風機静圧,psFA
− 送風機圧力,pFA
− 送風機効率,ηsrA又はηrA
32.3 吐出し側の試験空気槽
32.3.1 流量の測定
流量は次の方法で測定する。
− 空気槽末端のベンチュリノズルによる,23.及び附属書図71a)参照。
− 空気槽内マルチノズルによる,23.及び附属書図71b)参照。
− 空気槽内オリフィス板による,26.9.1及び附属書図71b)参照。
32.3.2 試験中に実施する測定(20.参照)
測定項目
151
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 回転速度,N,又は回転周波数,n ;
− 送風機への入力,Pa,Po又はPe及びインペラ動力の推定(10.4参照)
− 流量計差圧,∆p
− 上流圧力,pe6
− 空気槽圧力,pe4
− 空気槽温度,t4
試験時の囲い内の測定項目
− 送風機の平均高度における大気圧,pa
− 吸込口付近の周囲温度,ta
− 乾湿球温度,td及びtw
周囲の空気密度ρa及び湿り空気のガス定数Rwを12.によって算出する。
32.3.3 圧縮性流体に対する一般的な方法
この方法は,基準マッハ数Ma2refが0.15を超え,圧力比が1.02を超える場合に適用する。
32.3.3.1 質量流量の算出
32.3.3.1.1 質量流量の測定は,次による。
− ベンチュリノズルによる,23.及び附属書図71a)参照。
− 空気槽内マルチノズルによる,23.及び附属書図71b)参照。
空気槽の下流に,調節装置又は調節装置付きの補助送風機を備える。
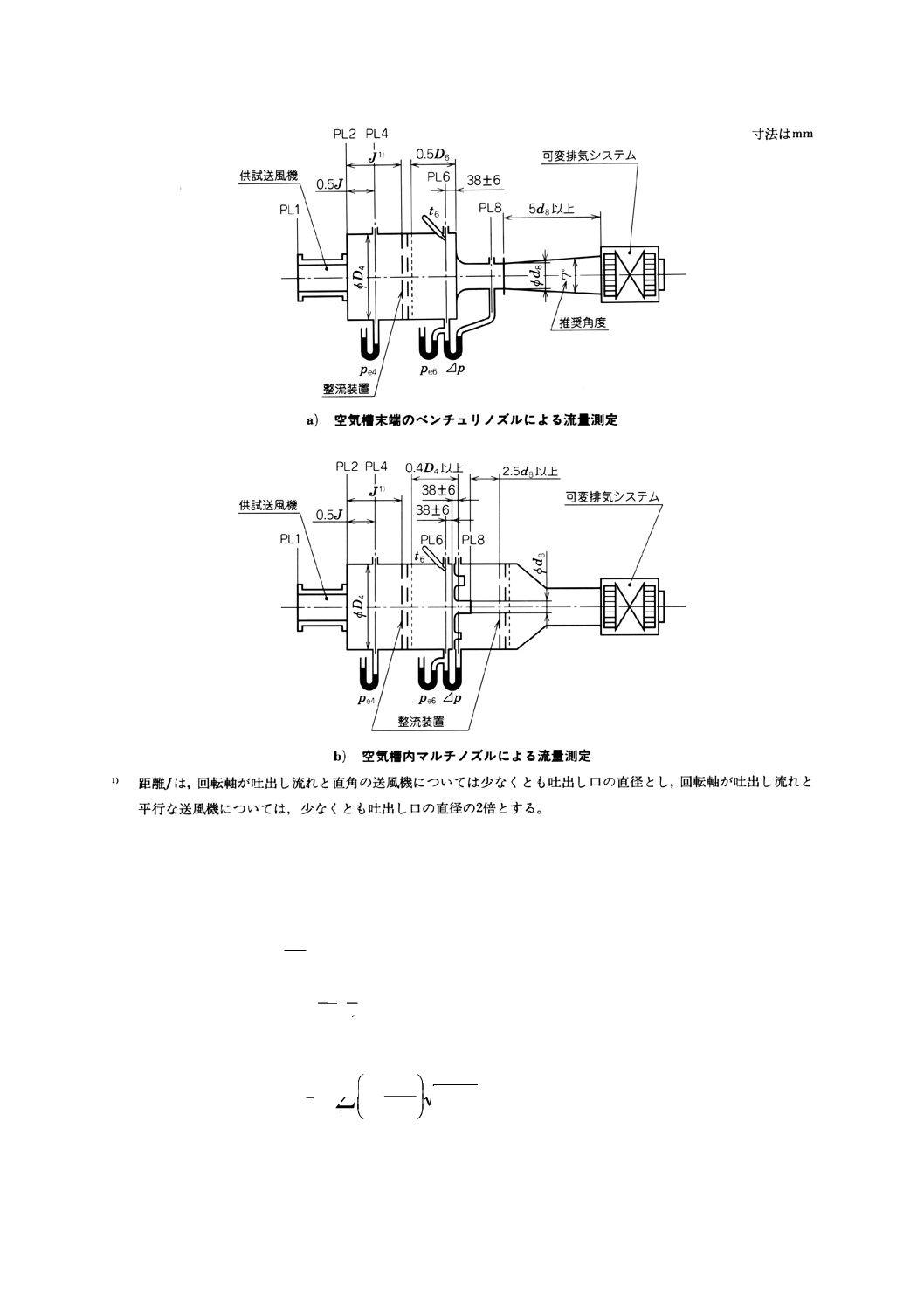
152
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図71 接続形式A(吐出し側試験空気槽)
次のように仮定する。
p6=pa+pe6
Θ6=t6+273.15=Θsg6
0
6
8
≈
=β
D
d
6
6
6
Θ
=
w
R
p
ρ
質量流量は,23.4によって次の式に示す。
p
d
C
q
n
j
j
j
m
∆
=∑
=
6
1
8
2
2
4
ρ
επ
ここに,
εは,23.4.3及び附属書表6による空気の膨張による修正係数
153
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Cjは,jthノズルの流出係数で,ノズルのスロート部レイノルズ数Red8jの関数。
23.4参照
β=0だから,Cj=α
Cj=αjは23.4及び附属書表5によって算出する。
nはノズルの数で,空気槽末端のノズルの場合は,1。
各ノズルに対し,スロート部レイノルズ数Red8jは次の式で推定する。
6
6
6
8
8
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
C
j
j
j
d
ρ
ε
ここに,Cj=0.95
質量流量の初期値を計算の後,流出係数Cjをレイノルズ数の変化に対して修正する。
32.3.3.1.2 管壁静圧孔をもつ空気槽内オリフィス板による質量の算出,[26.9.1附属書図71b)及び附属書図
23h)〜j)]
次のように仮定する。
p6=pa+pe6
Θ6=t6+273.15=Θsg6
25
.0
6
8
≦
β
=
D
d
6
6
6
Θ
=
w
R
p
ρ
質量流量は,26.5によって次の式に示す。
p
d
qm
∆
=
6
28
2
4
ρ
αεπ
ここに,αεは26.5及び26.9.1によって算出する。
32.3.3.2 送風機圧力の算出
32.3.3.2.1 送風機吐出し口圧力
p2=p4=pe4+pa
Θsg2=Θsg4=t4+273.15=Θsg6
マッハ数Ma2及び温度Θ2は,14.4.3.1及び附属書図5によって算出する。
2
2
2
2
sg
sgΘ
Θ
Θ
=
Θ
2
4
2
2
2
Θ
=
Θ
=
w
w
R
p
R
p
ρ
2
2
2
2
2
2
2
1
M
m
sg
F
A
q
p
p
+
=
ρ
又は
2
2
2
2
2
2
2
1
M
m
e
esg
F
A
q
p
p
+
=
ρ
FM2は14.5.1によって算出する。
154
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
32.3.3.2.2 送風機吸込口圧力
psg1=pa ; pesg1=0
Θsg1=ta+273.15
マッハ数Ma1比
1
1
ρ
ρsg
マッハ係数FM1は,14.4.3.2,14.4.4,及び14.5.1によって算出する。
1
2
1
1
1
1
2
1
M
m
sg
F
A
q
p
p
−
=
ρ
又は
1
2
1
1
1
2
1
M
m
e
F
A
q
p
−
=
ρ
32.3.3.2.3 送風機圧力
送風機静圧psFA及び送風機圧力pFAは,次の式に示す。
psFA=p2−psg1=p2−pa=pe2
pFA=psg2−psg1=pesg2−pesg1=pesg2
2
+
=
2
1ρ
ρ
ρm
m
p
k
ρ
ρ1
=
32.3.3.3 体積流量の算出
試験状態において,体積流量は次の式で算出する。
1
1
sg
m
sg
v
q
q
ρ
=
ここに,
1
1
sg
w
a
sg
R
p
Θ
=
ρ
32.3.3.4 理論空気動力の算出
32.3.3.4.1 単位質量当たりの送風機仕事及び理論空気動力
14.8.1によって,単位質量当たりの送風機静圧仕事及び単位質量当たりの送風機仕事は,次の式で示さ
れる。
2
1
1
1
2
1
2
1
2
2
1
2
−
−
=
−
−
=
ρ
ρ
ρ
A
q
p
p
V
p
p
y
m
m
m
m
sA
2
1
1
2
2
2
1
2
1
2
2
2
1
2
2
1
2
1
2
2
−
+
−
=
−
+
−
=
ρ
ρ
ρ
ρ
A
q
A
q
p
p
V
V
p
p
y
m
m
m
m
m
m
A
155
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
理論静圧空気動力及び理論空気動力は,次の式で示される。
PusA=qmysA
PuA=qmyA
32.3.3.4.2 理論空気動力及び圧縮性係数の算出
14.8.2によって
PusA=qvsg1psFAkps
PuA=qvsg1pFA kp
圧縮性係数kp及びkpsは,次の2種類の等価な方法で算出してもよい。(14.8.2.1及び14.8.2.2参照)。
a) 第一の方法
[
])1
(
1
log
log
10
10
−
+
=
r
Z
r
Z
k
k
k
k
p
ps又は
ここに,
kpsに対しては
1
1
sg
sFA
p
p
r
+
=
また
sFA
sg
v
r
k
p
q
P
Z
1
1
κ
κ−
=
kpに対しては
1
1
sg
FA
p
p
r
+
=
また
FA
sg
v
r
k
p
q
P
Z
1
1
κ
κ−
=
b) 第二の方法
)
1
ln(
)
1
ln(
p
p
p
ps
Z
Z
x
x
k
k
+
+
=
又は
ここに,
kpsに対しては
1
1
sg
sFA
p
p
r
x
=
−
=
kpに対しては
1
1
sg
FA
p
p
r
x
=
−
=
1
1
1
sg
sg
v
r
p
p
q
P
Z
κ
κ−
=
32.3.3.5 効率の算出
14.8.1によって,効率は,次の式で示される。
− 送風機静圧効率
r
usA
srA
P
P
=
η
− 送風機効率
r
uA
rA
P
P
=
η
32.3.4 簡略方法
32.3.4.1 基準マッハ数Ma2refが0.15未満で圧力比が1.02を超える場合
せき止め温度と静温度とは等しいとみなしてもよく,マッハ係数FMは,1に等しい(14.9.1参照)。
Θx=Θsgx
FM1=FM2=1
32.3.4.1.1 質量流量の算出
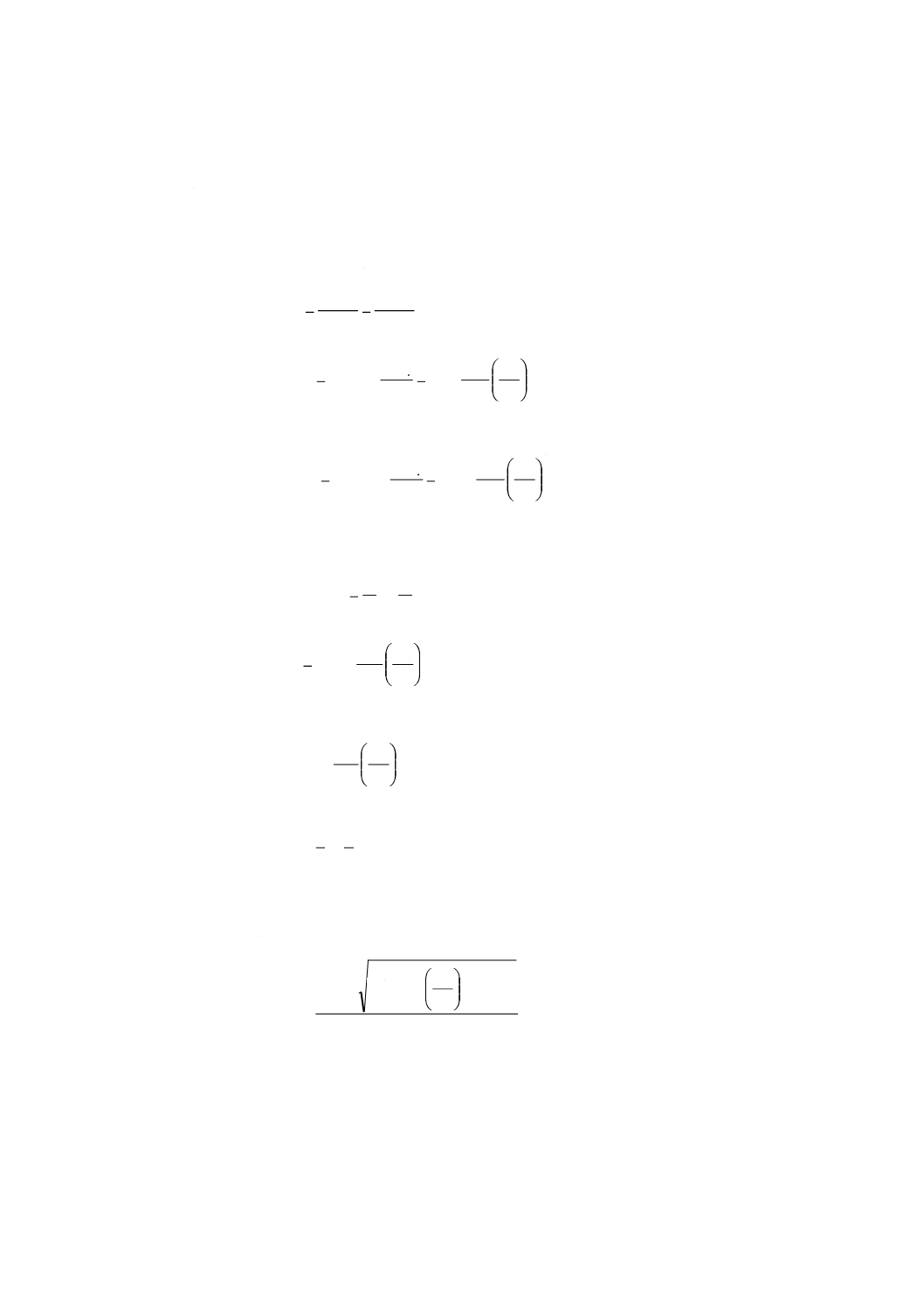
156
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
質量流量は,32.3.1に記載する方法によって算出する。
32.3.4.1.2 送風機圧力の算出
32.3.4.1.2.1 送風機吐出し口圧力
次のように仮定する。
Θ2=Θsg2=Θsg4=Θ4=t4+273.15
FM1=FM2=1
4
4
2
2
2
Θ
=
Θ
=
w
w
R
p
R
p
ρ
2
2
2
4
2
2
2
4
2
2
1
2
+
=
+
=
A
q
p
v
p
p
m
m
sg
ρ
ρ
又は
2
2
2
4
2
2
2
4
2
2
1
2
+
=
+
=
A
q
p
v
p
p
m
e
m
e
esg
ρ
ρ
32.3.4.1.2.2 送風機吸込口圧力
pa=psg1
1
1
sg
w
a
a
sg
R
p
Θ
=
=ρ
ρ
2
1
1
1
1
2
1
−
=
A
q
p
p
m
sg
ρ
又は
2
1
1
1
2
1
−
=
A
q
p
m
e
ρ
ここに,
1
1
1
Θ
=
w
R
p
ρ
しかし,p1は未知であり,逐次近似によってp1及びρ1を算出する(14.9.1.4参照)。
2〜3回の反復で十分である。
圧力p1は,次の式で算出してもよい。
2
2
1
2
1
1
2
1
1
sg
w
m
sg
sg
R
A
q
p
p
p
Θ
−
+
=
及び
pe1=p1−pa
32.3.4.1.2.3 送風機圧力
送風機静圧及び送風機圧力は,次の式に示す。
psFA=p2−psg1=p4−pa=pe4
157
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
2
4
2
2
4
1
2
2
1
2
1
+
=
−
+
=
−
=
2
A
q
p
p
A
q
p
p
p
p
m
e
a
m
sg
sg
FA
ρ
ρ
32.3.4.1.3 体積流量の算出
1
1
sg
m
sg
v
q
q
ρ
=
32.3.4.1.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,14.8.1,14.8.2及び32.3.3.4によって算出する。
32.3.4.1.5 効率の算出
効率は,32.3.3.5によって算出する。
32.3.4.2 基準マッハ数が0.15未満で圧力比が1.02未満の場合(14.9.2参照)
送風機及び試験通風路を通過する流れは,非圧縮性とみなしてよい。
Θ1=Θsg1=Θ2=Θsg2=Θ4=Θsg4=Θu=Θa=ta+273.15
ρ1=ρ2
FM1=FM2=1
kp=1
32.3.4.2.1 質量流量の算出
質量流量は,32.3.3.1によって算出する。
32.3.4.2.2 送風機圧力の算出
32.3.4.2.2.1 送風機吐出し口圧力
a
w
a
a
u
sg
sg
R
p
Θ
=
=
=
=
=
=
=
ρ
ρ
ρ
ρ
ρ
ρ
ρ
4
2
2
1
1
2
2
1
4
2
2
1
+
=
A
q
p
p
m
sg
ρ
又は
2
2
1
4
2
2
1
+
=
A
q
p
p
m
e
esg
ρ
32.3.4.2.2.2 送風機吸込口圧力
2
1
1
1
1
2
1
−
=
A
q
p
p
m
sg
ρ
2
1
1
1
2
1
−
=
A
q
p
m
e
ρ
32.3.4.2.2.3 送風機圧力
送風機圧力は,次の式に示す。
158
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
psFA=p2−psg1=p4−pa=pe4
4
2
2
1
4
2
1
4
1
2
2
1
2
1
esg
m
e
a
m
sg
sg
FA
p
A
q
p
p
A
q
p
p
p
p
=
+
=
−
+
=
−
=
2
ρ
ρ
32.3.4.2.3 体積流量の算出
1
1
sg
m
sg
v
q
q
ρ
=
32.3.4.2.4 理論空気動力の算出
理論空気動力は,次の式で算出する。
PusA=qvsg1・psFA
PuA=qvsg1・pFA
32.3.4.2.5 送風機効率の算出
送風機効率は,14.8.1,及び32.3.3.5によって算出する。
32.3.5 試験状態での送風機の性能
試験状態での送風機の性能は,下記である。
− 吸込体積流量,qvsg1
− 送風機静圧,psFA
− 送風機圧力,pFA
− 送風機効率,ηsrA又はηrA
33. 吐出し側測定管路を使用する場合の標準試験方法−接続形式B
33.1 送風機装置の形式
送風機の装置構成には,一般に次の2種類がある。
a) 旋回流防止装置を備えた吐出し側測定管路。圧力は旋回流防止装置の下流で測定する。
b) 短い吐出し管路。等価直径の2〜3倍の長さで旋回流防止装置がなく,後ろに吐出し空気槽及び流量計
が続くこの管路内では測定を行わない。この方法で得た結果は,吐出し側の標準通風路を使用して得
たものとはある程度の差が生じることがある。
測定管路の流量を調節及び測定する方法を,a)の場合で8種類,b)の場合で2種類示す。それぞれ
について流量測定方法を規定し,あわせて流量測定方法の詳細について次に示す。
接続形式Bの装置で送風機の性能試験を行う際の測定,計算などの共通する方法を33.2.3〜83.2.3.5
で示す。この方法は,この規格に従った送風機のすべてに対して概ね有効である。
ここに,次の場合は簡略方法でもよい。
− 基準マッハ数Ma2refが0.15未満で,圧力比が1.02を超える場合。
− 基準マッハ数Ma2refが0.15未満で,圧力比が1.02未満の場合。
上記の場合は,14.9.1及び14.9.2,並びに33.2.4及び33.3.4で示す方法に従ってもよい。
33.2 旋回流防止装置を備えた吐出し側測定管路
33.2.1 質量流量の算出
質量流量は,次の方法で測定する。
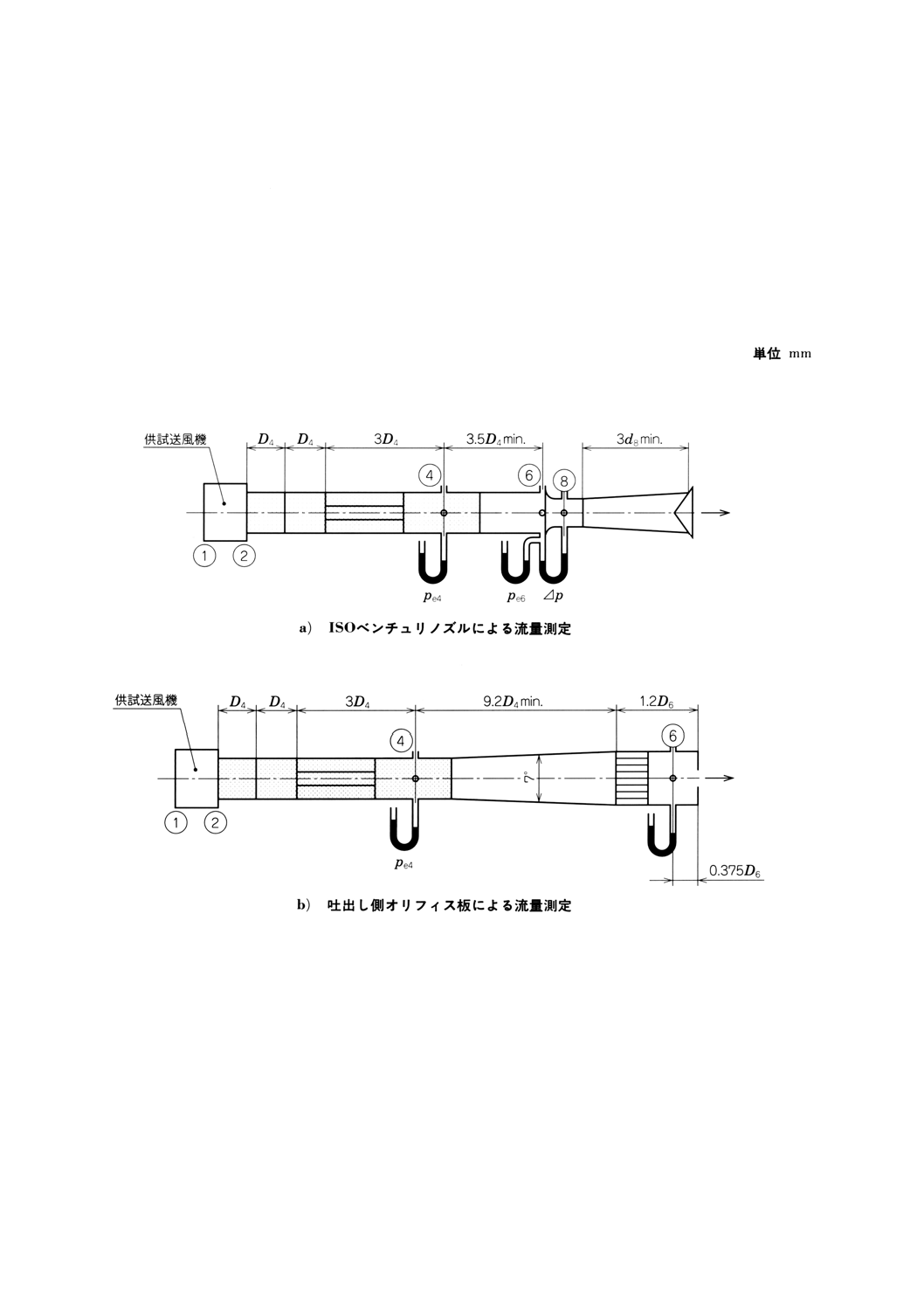
159
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 管路内のISOベンチュリノズルによる,22及び図72a)参照
− 管壁静圧孔をもつ吐出側オリフィス板による,26.9及び図72b)参照
− D・D/2タップをもつ管路内オリフィス板による,26.7及び図72c)参照
− コーナタップをもつ管路内オリフィス板による,26.8及び附属書図72c)参照。
− ピトー静圧管トラバースによる,27及び附属書図72d),e)参照。
− 管路内のベンチュリノズルによる,23及び附属書図72f)参照。
− 空気槽の出口ベンチュリノズルによる,23.及び附属書図72g)参照。
− 空気槽内のマルチノズルによる,23.及び附属書図72n)参照。
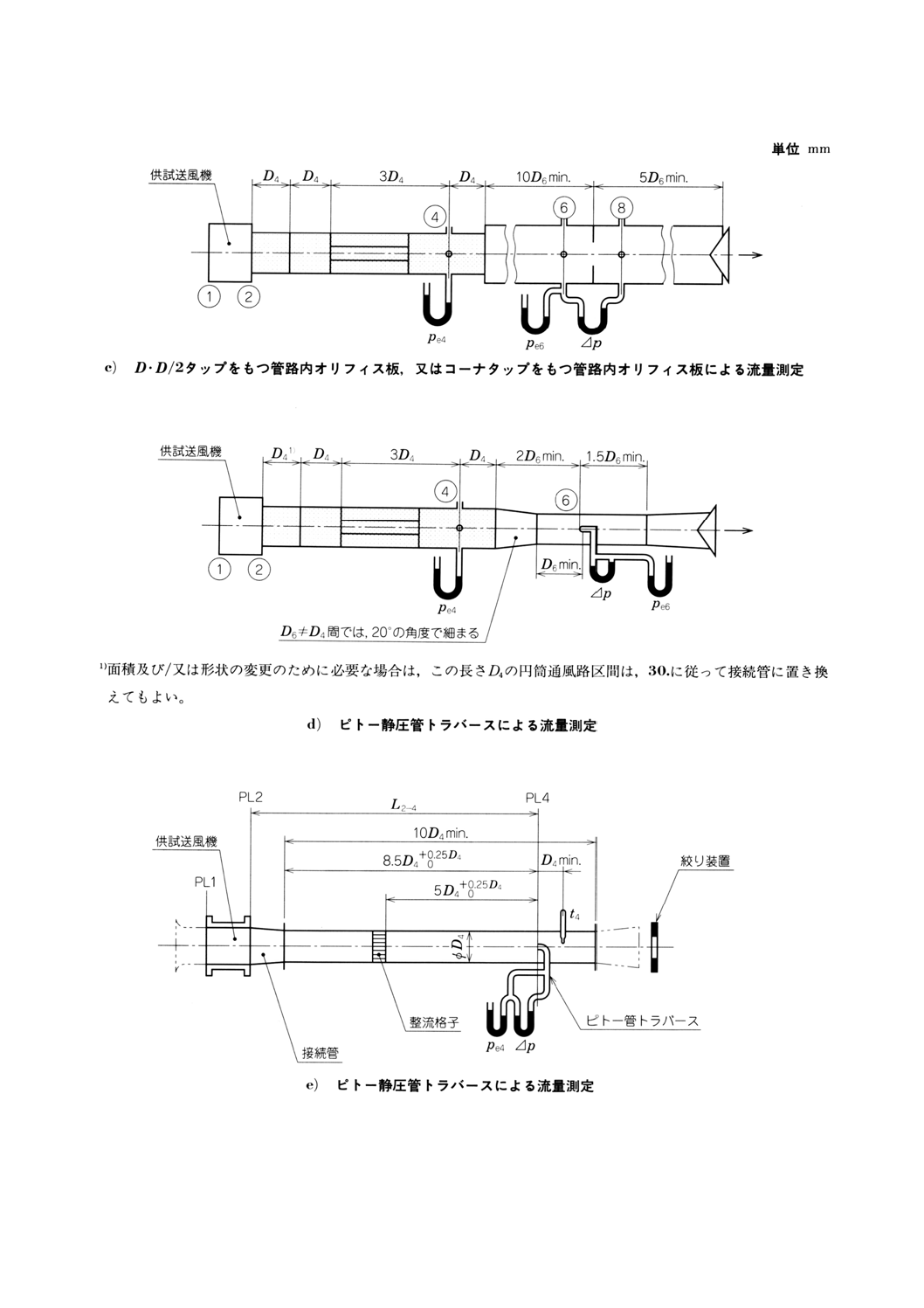
附属書図72 接続形式B(旋回流防止装置を備えた)
160
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図72 接続形式B(旋回流防止装置を備えた)(続き)
161
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
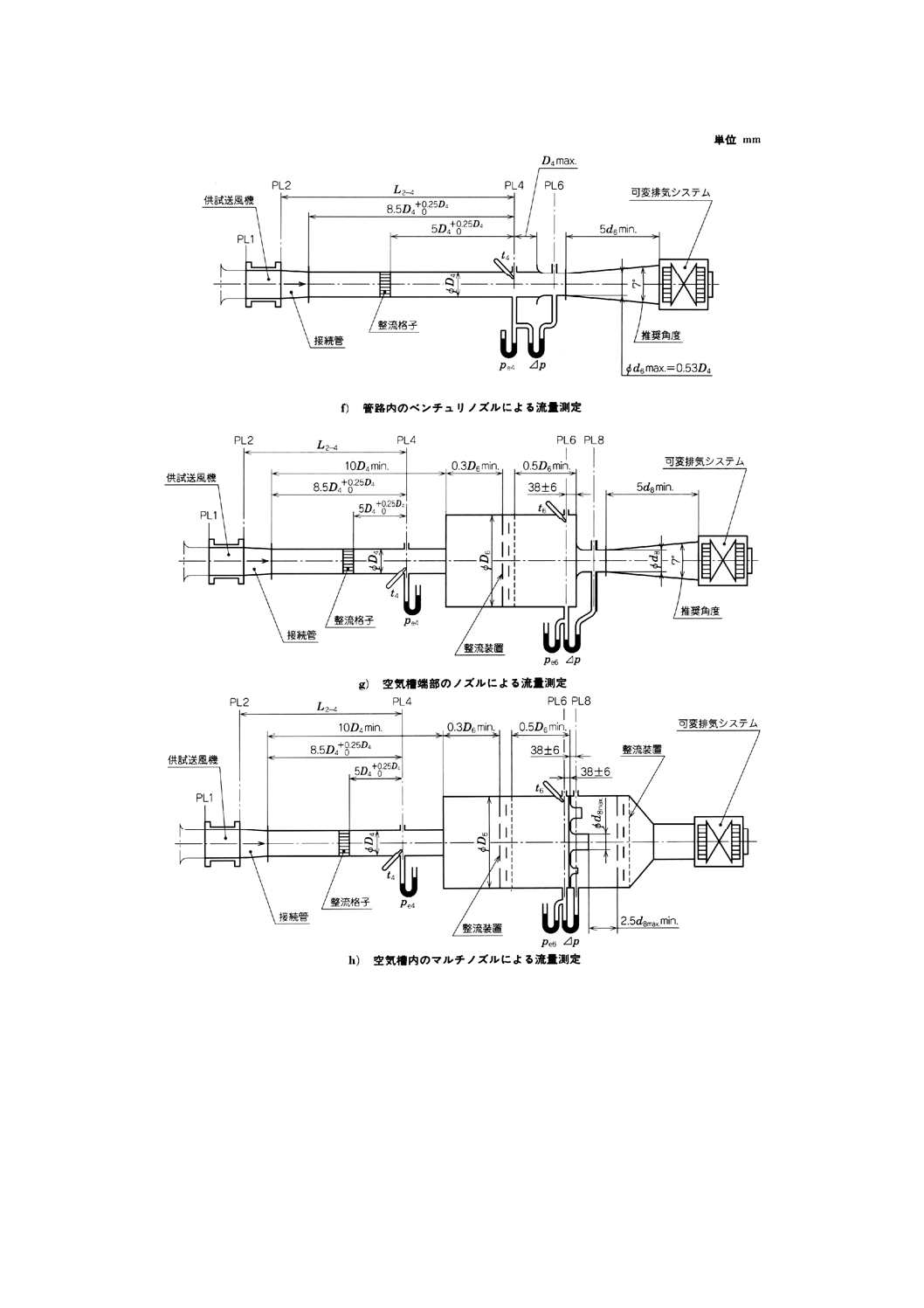
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図72 接続形式B(旋回流防止装置を備えた)(続き)
33.2.2 試験中に実施する測定(20.参照)
測定項目:
− 回転速度N又は回転周波数n
− 入力動力Pa,Po,又はPeの測定及びインペラ動力の推定(10.4参照)
− 吐出し側圧力Pe4
− 流量計の上流圧力Pe6
162
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 差圧∆p
− 空気槽温度t6
試験時の囲い内の測定項目。
− 送風機の平均高度における大気圧 Pa
− 送風機吸込口付近の周囲温度 ta
− 乾湿球温度 td及びtw
周囲の空気密度ρa及び湿り空気のガス定数Rwを算出する(12.参照)。
33.2.3 圧縮性流体に対する一般的な方法
基準マッハ数Ma2refが0.15を超え,圧力比が1.02を超える場合は,この方法を適用する。
33.2.3.1 質量流量の算出
33.2.3.1.1 質量流量の測定は,次による。
− 管路内のISOベンチュリノズルによる,22.及び附属書図72a)参照。
− 管壁静圧孔をもつ吐出側オリフィス板による,26.9及び附属書図72b)参照。
− D・D/2タップをもつ管路内オリフィス板による,26.7及び附属書図72c)参照。
− コーナタップをもつ管路内オリフィス板による,26.8及び附属書図72c)参照。
圧力及び流量測定のための吐出し側測定管路の後ろに,調節装置又は調節装置付きの補助送風機を備え
る。
a) 測定管路内の温度t4又はt6を測定しない場合
この方法が通常の方法である。
次のように仮定する。
p6=pe6+pa
Θsg1=ta+273.15
p
m
e
r
sg
sg
c
q
P
Por
1
6
+
Θ
=
Θ
p
m
p
m
e
r
sg
p
m
sg
c
A
q
c
q
P
P
c
A
q
6
2
6
2
2
1
6
2
6
2
2
6
6
2
or
2
ρ
ρ
−
+
Θ
=
−
Θ
=
Θ
6
6
6
Θ
=
w
R
p
ρ
しかし,Θ6,Θsg6,qm,は未知である。
質量流量は次の式で算出する。
p
m
d
q
∆
=
6
8
2
2
4
ρ
αεπ
ここに,
εは空気の膨張による修正係数で,22.3.3,26.7,26.8,及び26.9に従って算出
する。
αは流量係数で,レイノルズ数Red8又はReD6の関数であり,次の式で推定する。
6
6
6
8
8
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
d
ρ
αε
又は
163
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6
6
6
6
6
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
D
ρ
αεβ
α又は組合せ係数αεは,22.3,26.7,26.8,26.9,並びに附属書図18,24,25,26,及び27に従って
算出する。
Θ6,ρ6,Red8又はReD6,α,及びqaの算出には,Θ6の初期値をΘ6=Θsg6=Θsg1として,逐次近似を行
う。
qaを10−3の計算精度で得るには,3〜4回の反復計算で十分である。
b) 温度t6を測定する場合には,それはせき止め温度Θsg6とみなす。
p
m
c
A
q
t
6
2
2
2
2
6
6
2
15
.
273
ρ
−
+
=
Θ
ここに,上記の方法を適用する。
33.2.3.1.2 ピトー静圧管トラバースによる流量の算出
27.並びに附属書図72d)及び72e)参照。
備考45. 図72e)の装置において,断面4と断面6とは同一である。
圧力及び流量測定のための吐出し側管路の後ろに,調節装置又は調節装置付きの補助送風機を備える。
次のように仮定する。
∑
=
=
n
j
j
e
e
p
n
p
1
6
6
1
p6=pe6+pa
p
m
e
r
sg
sg
c
q
P
Por
1
6
+
Θ
=
Θ
κ
κ1
6
6
6
6
−
∆
+
Θ
=
Θ
m
sg
p
p
p
ここに,
2
2
1
2
1
5.0
)
...
(
1
1
∆
+
∆
+
∆
=
∆
=
∆
∑
=
n
n
j
j
m
p
p
p
n
p
n
p
6
6
6
Θ
=
w
R
p
ρ
質量流量qmは,次の式によって算出する。
m
m
p
A
q
∆
=
6
62ρ
αε
ここに,
αは流量係数で,レイノルズ数ReD6の関数であり,0.99に非常に近い値である
(27.6参照)。

164
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6
6
6
6
6
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
D
m
D
ρ
αε
εは空気の膨張による修正係数である(27.5参照)。
2/1
2
6
2
6
6
1
2
1
1
∆
+
+
∆
−
=
p
p
p
p
m
m
κ
κ
κ
ε
qmの初期値をα=0.99として算出し,εを上式によって求める。
このqmの値によって,ReD6,α及びqmの2回目の値が算出できる。
質量流量を10−3の計算精度で決定するには,2〜3回の反復計算で十分である。
33.2.3.1.3 管路内ベンチュリノズルによる質量流量の測定。23.及び附属書図72f参照。
圧力及び流量測定のための吐出し側管路の後ろに,調節装置又は調節装置付きの補助送風機を備える。
次のように仮定する。
p4=ped+pa
4
4
4
Θ
=
w
R
p
ρ
p
m
e
r
sg
sg
c
q
P
Por
1
4
+
Θ
=
Θ
p
m
p
m
e
r
sg
c
A
q
c
q
P
P
4
2
4
2
2
1
4
2
or
ρ
−
+
Θ
=
Θ
Θsg4,Θ4,qmは未知である。
4
6
D
d
=
β
質量流量qmは,次の式に示す(23.参照)。
p
d
qm
∆
=
6
6
2
2
4
ρ
αεπ
4
6
6
2
1
2
4
β
α
ρ
π
ε
AU
m
p
d
C
q
−
∆
=
ここに,
αはノズルの流量係数で,次の値に等しい。
4
1
β
αAU
C
−
Cはノズルの流出係数で,ノズルのスロート部レイノルズ数Red6の関数である(23.4.2及び表5参照)。
6
6
4
6
6
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
d
ρ
αε
αAUは運動エネルギー係数で,測定管進入路では1.043に,空気槽進入路では1に等しい。
εは空気の膨張による修正係数で,23.4.3及び附属書表6によって算出する。
初期値は,
4
1
95
.0
β
α
α
AU
−
=
165
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Θ4=Θsg1
計算されたqmによって,Θ4,ρ4,Red6,α及びqmの新しい値が算出できる。
qmの10−3の計算精度には,2〜3回の反復計算で十分である。
33.2.3.1.4 質量流量の算出
空気槽吐出し側ベンチュリノズルによる,23.及び附属書図72g),72h)参照。
空気槽内のマルチノズルによる,23.附属書図72g)及び72h)参照。
圧力及び流量測定のための吐出し側管路の後ろに,調節装置又は調節装置付きの補助送風機を備える。
空気槽の温度t6を測定する。
p6=pe6+pa
Θ6=Θsg6=t6+273.15
0
6
8=
=Dd
β
6
6
6
Θ
=
w
R
p
ρ
質量流量は次の式に示す。
∑
=
∆
=
n
j
j
j
m
p
d
C
q
1
6
8
2
2
4
ρ
επ
ここに,
εは,23.4.3及び附属書表6に従う空気の膨張による修正係数である。
Cjはjthノズルの流出係数で,ノズルのスロート部レイノルズ数Red8jに依存す
る。23.4参照。
β=0及びCj=α
Cj=αjで,23.4及び附属書表5によって算出する。
nはノズル数で,空気槽端部のノズルの場合は1である。
各ノズルに対して,ノズルのスロート部レイノルズ数Red8を次の式で推定する。
6
6
6
8
8
10
048
.0
1.
17
2
Re
×
+
∆
=
t
p
d
C
j
j
j
d
ρ
ε
ここに,Cj=0.95
質量流量の初期値を計算の後,流出係数Cjをレイノルズ数の変化に対して修正する。
33.2.3.2 送風機圧力の算出
33.2.3.2.1 送風機の吐出し口圧力
次のように仮定する。
p4=pe4+pa
15
.
273
or
6
6
1
2
4
+
=
Θ
=
+
Θ
=
Θ
=
Θ
t
c
q
P
P
sg
p
m
e
r
sg
sg
sg
断面4のマッハ数及び比Θsg4/Θ4は,14.4.3.1及び附属書図5によって算出する。
4
4
4
4
sg
sgΘ
Θ
Θ
=
Θ
166
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
4
4
Θ
=
w
R
p
ρ
600
1
40
4
1
4
6
4
4
4
2
4
Ma
Ma
Ma
FM
+
+
+
=
(14.5.1参照)
断面2と断面4との間の損失係数 (ζ2−4) 4は,30.6及び附属書図65に従って算出する。送風機の吐出し
口のせき止め圧力psg2は,次の式に示す。
]
)
(
1[
2
4
4
2
4
4
2
4
4
2
−
+
+
=
ζ
ρ
M
m
sg
F
v
p
p
又は
]
)
(
1[
2
4
4
2
4
4
2
4
4
2
−
+
+
=
ζ
ρ
M
m
e
esg
F
v
p
p
静密度ρ2及び圧力p2は,14.5.2に従って算出し,Ma2は14.4.3.2及び附属書図6に従って算出する。
2
2
2
2
2
2
2
2
2
2
2
2
1
2
M
m
sg
M
m
sg
F
A
q
p
F
v
p
p
−
=
−
=
ρ
ρ
又は
2
2
2
2
2
2
2
1
M
m
esg
F
A
q
p
p
−
=
ρ
33.2.3.2.2 送風機吸込口圧力
送風機吸込口においてpsg1=pa,Θsg1=Θa及びp1は,14.5.2及び14.4.3.2に従って算出する。
1
2
1
1
1
1
1
2
1
1
1
2
1
2
M
m
sg
M
m
sg
F
A
q
p
F
v
p
p
−
=
−
=
ρ
ρ
Ma1及びρ1は14.4.3.2,14.5.2,及び附属書図4.5.6に従って算出する。
さらに
pesg1=0
1
2
1
1
1
2
1
M
m
e
F
A
q
p
−
=
ρ
33.2.3.2.3 送風機圧力
送風機圧力pFB及び送風機静圧psFBは次の式で算出する。
pFB=psg2−psg1=pesg2
psFB=p2−psg1=pe2
2
1
2
ρ
ρ
ρ
+
=
m
及び
kp=ρ1/ρm
33.2.3.3 体積流量の算出

167
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
体積流量は次の式で算出する。
Θ
=
=
1
1
1
1
sg
w
sg
m
sg
m
sg
v
R
p
q
q
q
ρ
33.2.3.4 理論空気動力の算出
33.2.3.4.1 単位質量当たりの送風機仕事及び理論空気動力
単位質量当たりの送風機仕事y及び単位質量当たりの送風機静圧仕事ysBは,13.8.1に従って次の式に示
す。
2
2
2
1
2
1
2
2
1
2
2
2
1
2
2
1
1
2
2
2
1
2
1
2
2
2
1
2
m
m
m
e
e
m
m
m
m
m
m
B
v
v
p
p
A
q
A
q
p
p
v
v
p
p
y
−
+
−
=
−
+
−
=
−
+
−
=
ρ
ρ
ρ
ρ
ρ
2
2
1
2
1
2
1
2
2
1
1
1
2
1
2
1
2
m
m
e
e
m
m
m
m
sB
v
p
p
A
q
p
p
v
p
p
y
−
−
=
−
−
=
−
−
=
ρ
ρ
ρ
ρ
理論空気動力PuB及び理論静圧空気動力PusBは,次の式に示す。
PuB=qmyB
PusB=qmysB
33.2.3.4.2 理論空気動力及び圧縮性係数の算出
14.8.2に従って,
PuB=qvsg1pFBkp
PusB=qvsg1psFBkps
圧縮性係数kp及びkpsは,2種類の等価な方法で決められる(14.8.2.1及び14.8.2.2参照)。
a) 第一の方法
[
])1
(
1
log
log
10
10
−
+
=
r
Z
r
Z
k
k
k
k
p
ps又は
ここに,kpについては
1
1
sg
FB
p
p
r
+
=
kpsについては
1
1
sg
sFB
p
p
r
+
=
及び,kpについては
FB
sg
v
r
k
p
q
P
Z
1
1
κ
κ−
=
kpsについては
sFB
sg
v
r
k
p
q
P
Z
1
1
κ
κ−
=
168
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 第二の方法
Κps又は
)
1
ln(
)
1
ln(
p
p
p
Z
Z
x
x
k
+
+
=
ここに,
1
1
sg
FB
p
p
r
x
=
−
=
又は
1
sg
sFB
p
p
x=
及び
1
1
1
sg
sg
v
r
p
p
q
P
Z
κ
κ−
=
33.2.3.5 効率の算出
効率は,14.8.1に従って次の式に示す。
− 送風機効率
r
u
rB
P
PB
=
η
− 送風機静圧効率
r
us
srB
P
PB
=
η
− 送風機軸効率
a
us
sB
P
PB
=
η
− 送風機静圧軸効率
a
us
saB
P
PB
=
η
33.2.4 簡略方法
33.2.4.1 基準マッハ数Ma2refが0.15未満で圧力比が1.02を超える場合
測定管路の断面で,せき止め温度と静温度とは互いに等しいとみなす。
Θx=Θsgx=tx+273.15
マッハ係FM1及びFM2は1に等しい。
33.2.4.1.1 質量流量の算出
質量流量は,33.2.3.1の方法によって算出する。
ここに,次の簡略化を適用する。
流量計の上流温度を測定する。
Θu=Θsgu=tu+273.15=Θsg4=Θ4
pu=peu+pa
sgu
w
u
u
w
u
u
R
p
R
p
Θ
=
Θ
=
ρ
せき止め温度と静温度の差を考慮に入れて逐次近似を行う必要はない。ただし,α及びcへのレイノル
169
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ズ数による影響は適用すること。
33.2.4.1.2 送風機圧力の算出
33.2.4.1.2.1 送風機吐出し口圧力
14.9.1.2,14.9.1.3及び30.6に従って
]
)
(
1[
2
4
4
2
4
2
4
4
2
−
+
+
=
ζ
ρ
m
sg
v
p
p
又は
]
)
(
1[
2
4
4
2
4
2
4
4
2
−
+
+
=
ζ
ρ
m
e
esg
v
p
p
ここに,
4
4
4
4
4
sg
w
w
R
p
R
p
Θ
=
Θ
=
ρ
2
1
4
or
sg
p
m
e
r
sg
sg
c
q
P
P
Θ
=
+
Θ
=
Θ
p2は,次の方法で算出する(14.9.1.4参照)。
2
2
4
4
2
4
2
1
2
2
)
(
−
=
A
A
v
p
p
m
sg
ρ
2
1
2
1
2
)
(
)
(
sg
w
R
p
p
Θ
=
1
2
2
2
2
2
2
)
(
2
1
ρ
A
q
p
p
m
sg−
=
1
2
2
2
2
2
2
)
(
2
1
ρ
A
q
p
p
m
esg
e
−
=
2〜3回の反復計算で十分である。p2は,次の式で算出してもよい。
Θ
−
+
=
2
2
2
2
2
2
2
2
2
1
sg
w
m
sg
sg
R
A
q
p
p
p
2
2
2
sg
w
R
p
Θ
=
ρ
33.2.4.1.2.2 送風機吸込口圧力
送風機吸込口において
psg1=pa
pesg1=0
静圧p1は,33.2.4.1.2.1にある二つの方法の,どちらか一つを適用することで算出する。
33.2.4.1.2.3 送風機圧力
送風機圧力pFB及び送風機静圧psFBは,次の式に示す。
PFB=psg2−psg1=psg2−pa=pesg2
psFB=p2−psg1=p2−pa=pe2
33.2.4.1.3 体積流量の算出
170
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
体積流量は次の式に示す。
Θ
=
=
1
1
1
sg
w
a
m
sg
m
sg
v
R
p
q
q
q
ρ
33.2.4.1.4 理論空気動力の算出
理論空気動力は,14.8.1,14.8.2,14.8.3及び33.2.3.4に従って算出する。
33.2.4.1.5 送風機効率の算出
送風機効率は,14.8.1,14.8.2,14.8.3及び33.2.3.5に従って算出する。
33.2.4.2 基準マッハ数Ma2refが0.15未満で圧力比が1.02未満の場合(14.9.2参照)送風機及び測定管路
を通過する流れは非圧縮性とみなしてよい。
Θ1=Θsg1=Θ2=Θsg2=Θa=ta+273.15
a
w
a
a
R
p
Θ
=
=
=
=
=
ρ
ρ
ρ
ρ
ρ
6
4
2
1
FM1=FM2=1
kp=1
33.2.4.2.1 質量流量の算出
質量流量は,33.2.4.1.1及び
a
w
a
a
u
R
p
Θ
=
=ρ
ρ
によって算出する。
33.2.4.2.2 送風機圧力の算出
33.2.4.2.2.1 送風機吐出し口圧力
上記の仮定によって
a
w
a
a
sg
sg
R
p
Θ
=
=
=
=
=
=
=
ρ
ρ
ρ
ρ
ρ
ρ
ρ
6
4
2
2
1
1
]
)
(
1[
2
1
4
4
2
2
4
1
4
2
−
+
+
=
ζ
ρA
q
p
p
m
sg
]
)
(
1[
2
1
4
4
2
2
4
1
4
2
−
+
+
=
ζ
ρA
q
p
p
m
e
esg
2
2
1
2
2
2
1
−
=
A
q
p
p
m
sg
ρ
2
2
1
2
2
2
1
−
=
A
q
p
p
m
esg
e
ρ
33.2.4.2.2.2 送風機吸込口圧力
psg1=pa
pesg1=0
171
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
1
1
1
2
1
−
=
A
q
p
p
m
sg
ρ
2
1
1
1
2
1
−
=
A
q
p
m
e
ρ
33.2.4.2.2.3 送風機圧力
送風機圧力pFB及び送風機静圧psFBは,次の式で算出する。
pFB=psg2−psg1=psg2−pa=pesg2
psFB=p2−psg1=p2−pa=pe2
33.2.4.2.3 体積流量の算出
体積流量は,33.2.4.1.3と同様に次の式に示す。
Θ
=
=
1
1
1
sg
w
a
m
sg
m
sg
v
R
p
q
q
q
ρ
33.2.4.2.4 理論空気動力の算出
14.9.2.6に従って
PuB=qvsg1pFB
PusB=qvsg1psFB
33.2.4.2.5 送風機効率の算出
送風機効率は,33.2.3.5と同様にPuB又はPusBから算出する。
33.2.5 試験条件下の送風機の性能
試験条件下の送風機の性能は,次による。
− 吸込口体積流量 qvsg1
− 送風機圧力 pFB
− 送風機静圧 psFB
− 送風機効率 ηrs又はηars
33.3 旋回流防止装置のない吐出し側空気槽測定管路
送風機の吐出し側旋回流防止に下の装置を用いることを推奨する。
33.3.1 質量流量の算出
質量流量は次の方法で算出する。
− 空気そう末端のベンチュリノズルによる。23.及び73a)参照。
− 空気そう内のマルチノズルによる。23.及び73b)参照。
172
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 寸法Jは,流れに対して垂直な回転軸の送風機の場合は,送風機の等価直径の1.0倍以上とし,流れに平行
な回転軸の送風機の場合は,送風機の等価直径の2.0倍以上とする。
附属書図73 接続形式B(旋回流防止装置なし)
33.3.2 試験中に実施する測定(20.参照)
測定項目
− 回転速度N又は回転周波数n
− 入力動力Pa,Po,又はPeの測定及びインペラ動力の推定(10.4参照)
− 吐出し口圧力pe4
− 流量計の上流圧力pe6
− 差圧∆p
− 吐出し口温度t6
試験時の囲い内の測定項目。
− 送風機の平均高度における大気圧pa
173
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 周囲温度ta(送風機吸込口付近)
− 乾湿球温度td及びtw
周囲の空気密度ρa及び湿り空気のガス定数Rwを算出する(12.参照)。
33.3.3 圧縮性流体に対する一般的な方法
基準マッハ数Ma2refが0.15を超え,圧力比が1.02を超える場合は,この方法を適用する。
33.3.3.1 質量流量の算出
33.3.3.1.1 質量流量の測定は,次による。
− 空気そう末端部のベンチュリノズルによる。23及び附属書図73a)参照。
− 空気そう内のマルチノズルによる。23及び附属書図73b)参照。
圧力及び流量測定のための吐出し側管路の後ろに,調節装置又は調節装置付きの補助送風機を備える。
空気槽内の温度t6を測定する。
p6=pe6+pa
Θ6=Θsg6=t6+273.15
0
6
8≈
=Dd
β
6
6
6
Θ
=
w
R
p
ρ
質量流量は,次の式に示す。
p
d
C
q
n
j
j
j
m
∆
=∑
=
6
1
8
2
4
ρ
επ
ここに,
εは,23.4.3及び附属書表6に従う空気の膨張による修正係数。
Cjは,jthノズルの流出係数で,ノズルのスロート部レイノルズ数Red8jに依存す
る。
β=0及びCj=αj
Cj=αjで,23.4及び附属書表5に従って算出する。
nはノズル数で,空気そう末端部のノズルの場合は1である。
各ノズルに対して,ノズルのスロート部レイノルズ数Red8を次の式で推定する。
6
6
6
8
8
10
048
.0
1.
17
2
×
+
∆
=
t
p
d
C
e
R
j
j
j
d
ρ
ε
ここに,Cj=0.95
送風機の吐出し側旋回流防止にこれ等の装置を用いることを推奨する。
質量流量の初期値を計算後,流出係数Cjを算出及び修正する。
33.3.3.2 送風機圧力の算出
33.3.3.2.1 送風機吐出し口圧力
次のように仮定する。
p4=pe4+pa
p
m
e
r
sg
sg
sg
sg
c
q
P
P
t
or
15
.
273
1
6
6
2
4
+
Θ
=
+
=
Θ
=
Θ
=
Θ

174
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
断面2.4は,空気そう入口の吐出し側管路の断面である(吐出し側接続管路がない場合はA2.4=A2)。断
面2.4のマッハ数Ma2.4及び比Θsg4/Θ2.4は,14.4.3.1及び附属書図5に従って算出する。
4
4.2
4
4.2
sg
sg
g
Θ
Θ
Θ
=
Θ
4.2
4
4.2
Θ
=
w
sg
R
p
ρ
600
1
40
4
1
4.2
6
4.2
4
4.2
2
4.2
Ma
Ma
Ma
FM
+
+
+
=
(14.5.1及び附属書図4参照)
この測定管路では損失がなく,断面2のせき止め圧力は次の式に示す。
4.2
2
4.2
4.2
4
2
2
1
M
m
sg
F
A
q
p
p
+
=
ρ
又は
4.2
2
4.2
4.2
4
2
2
1
M
m
e
esg
F
A
q
p
p
+
=
ρ
断面2の静圧p2及び静温度Θ2は,14.5.2に従って算出する。Ma2は,14.4.3.2に従って算出する。
2
2
2
Θ
w
R
p
ρ
2
2
2
2
2
2
2
m
2
2
2
2
2
1
2
M
m
sg
M
sg
F
A
q
p
F
V
p
p
−
=
−
=
ρ
ρ
又は
2
2
2
2
2
2
2
1
M
m
esg
e
F
A
q
p
p
−
=
ρ
33.3.3.2.2 送風機吸込口圧力
送風機吸込口において
Θsg1=Θa=ta+273.15
psg1=pa
また,p1は14.5.2に従って算出され,Ma1及びΘ1は14.4.3.2に従って計算する。
1
2
1
1
1
1
2
1
M
m
sg
F
A
q
p
p
−
=
ρ
1
2
1
1
1
2
1
M
m
e
F
A
q
p =ρ
33.3.3.2.3 送風機圧力
送風機圧力pFB及び送風機静圧psFBは,次の式で算出する。
175
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
pFB=psg2−psg1=psg2−pa=psg2
psFB=p2−psg1=p2−pa=pe2
2
1
2
m
ρ
ρ
ρ
+
=
及び
m
1
ρ
ρ
ρ=
k
33.3.3.3 体積流量の算出
体積流量は次の式で算出する。
Θ
=
=
sg1
w
1
sg
m
1
sg
m
1
vsg
R
p
q
q
q
ρ
33.3.3.4 理論空気動力の算出
33.3.3.4.1 単位質量当たりの送風機仕事及び理論空気動力
単位質量当たりの送風機仕事yB及び単位質量当たりの送風機静圧仕事ysBは,14.8.1に従って次の式に
示す。
2
2
2
1
2
1
2
2
m1
2
m2
2
m
1
e
2
e
2
1
1
m
2
2
2
m
m
1
2
m1
2
m2
2
m
1
2
B
V
V
p
p
A
q
A
q
p
p
V
V
p
p
y
−
+
−
=
−
+
−
=
−
+
−
=
ρ
ρ
ρ
ρ
ρ
2
2
1
2
m1
2
m
1
e
2
e
2
1
1
m
m
1
2
m1
2
m
1
2
sB
V
p
p
A
q
p
p
V
p
p
y
−
−
=
−
−
=
−
−
=
ρ
ρ
ρ
ρ
理論空気動力PuB及び理論静圧空気動力PusBは,次の式に示す。
PuB=qmyB
PusB=qmysB
33.3.3.4.2 理論空気動力及び圧縮性係数の算出
14.8.2に従って
PuB=qvsg1pFBkp
PusB=qvsg1psFBkps
圧縮性係数kp及びkpsは,2種類の等価な方法で決められる(14.8.2.1及び14.8.2.2参照)。
a) 第一の方法
Κps又は
(
)
[
]
1
1
log
log
k
10
10
k
p
−
+
=
r
Z
r
Z
k
ここに,kpについては
sg1
FB
1
p
p
r
+
=
176
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
理論静圧空気動力については
sg1
sFB
1
p
p
r
+
=
また,理論空気動力については
FB
vsg1
r
k
1
p
q
P
Z
κ
κ−
=
理論静圧空気動力については
sFB
vsg1
r
k
1
p
q
P
Z
κ
κ−
=
b) 第二の方法
(
)(
)
p
p
p
1
ln
1
ln
Z
Z
x
x
k
+
+
=
ここに,
sg1
FB
1
p
p
r
x
=
−
=
又は
sg1
sFB
p
p
x=
及び
sg1
vsg1
r
p
1
p
q
P
Z
κ
κ−
=
33.3.3.5 効率の算出
効率は,14.8.1に従って次の式に示す。
送風機効率
r
uB
rB
P
P
=
η
送風機静圧効率
r
usB
srB
P
P
=
η
送風機軸効率
a
uB
aB
P
P
=
η
送風機静圧軸効率
a
usB
saB
P
P
=
η
33.3.4 簡略方法
33.3.4.1 基準マッハ数Ma2refが0.15未満で圧力比が1.02を超える場合
測定管路の断面では,せき止め温度と静温度とは互いに等しいとみなす。
FM1=FM2=1
Θx=Θsgx
33.3.4.1.1 質量流量の算出
177
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
質量流量は,33.3.3.1に記述した方法によって算出する。
Θu=Θsgu=t6+273.15=Θ6=Θsg6
pu=pe6+pa
6
sg
w
6
6
w
6
6
Θ
=
Θ
=
R
p
R
p
ρ
c及びαはレイノルズ数による影響についての修正を行う。
33.3.4.1.2 送風機圧力の算出
33.3.4.1.2.1 送風機吐出し口圧力
14.9.1,14.9.1.3及び33.3.3.2に従って
p4=pe4+pa
2
4.2
m
4
4
4.2
m
2
4
4
2
sg
2
1
2
+
=
+
=
A
q
p
V
p
p
ρ
ρ
又は
2
4.2
m
2
4
4
e
2
esg
V
p
p
ρ
+
=
ここに,
sg4
w
4
4
w
4
4
Θ
=
Θ
=
R
p
R
p
ρ
p2は,次の方法で算出する(14.9.1.4参照)。
()
2
2
4.2
4.2
m
2
4
sg2
1
2
2
−
=
A
A
V
p
p
ρ
(
)
()
sg2
w
1
2
21
Θ
=Rp
ρ
2
2
2
m
2
2
sg
2
2
1
ρ
A
q
p
p
−
=
2
22
m
2
2
esg
2e
2
1
ρ
A
q
p
p
−
=
2〜3回の反復計算で十分である。p2は,次の式で算出してもよい。
Θ
−
+
=
sg2
w
2
2
m
2
sg
2
2
sg
2
2
2
1
R
A
q
p
p
p
sg2
w
2
2
Θ
=Rp
ρ
33.3.4.1.2.2 送風機吸込口圧力
送風機吸込口において
psg1=pa
pesg1=0
静圧p1及び密度ρ1は,p2の計算のための2種類の方法の内の一つで算出する。
178
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
33.3.4.1.2.3 送風機圧力
送風機圧力pFB及び送風機静圧psFBは,次の式に示す。
pFB=psg2−psg1=psg2−pa=pesg2
psFB=p2−psg1=p2−pa=pe2
33.3.4.1.3 体積流量の算出
体積流量は,次の式に示す。
Θ
=
=
sg1
w
a
m
1
sg
m
1
vsg
R
p
q
q
q
ρ
33.3.4.1.4 理論空気動力の算出
理論空気動力は,14.8.1,14.8.2,14.8.3又は14.9.1.6,及び33.3.3.4に従って算出する。
33.3.4.1.5 送風機効率の算出
送風機の効率は,14.8.1,14.8.2,14.8.3,及び33.3.3.5に従って算出する。
33.3.4.2 基準マッハ数Ma2refが0.15未満で圧力比が1.02未満の場合(14.9.2参照)
送風機及び測定管路を通過する空気の流れは非圧縮性とみなしてよい。
Θ1=Θsg1=Θ2=Θsg2=Θ4=Θsg4=Θ6=Θsg6=Θa=ta+273.15
a
w
a
a
6
4
2
1
Θ
=
=
=
=
=
R
p
ρ
ρ
ρ
ρ
ρ
FM1=FM2=1
kp=1
33.3.4.2.1 質量流量の算出
質量流量は,33.3.4.1.1に従って算出する。
33.3.4.2.2 送風機圧力の算出
33.3.4.2.2.1 送風機吐出し口圧力
上記の仮定によって
ρ1=ρsg1=ρ2=ρsg2=ρa
2
2
m
1
4
2
sg
2
1
+
=
A
q
p
p
ρ
2
2
m
1
4e
2
esg
2
1
+
=
A
q
p
p
ρ
4
2
2
m
1
2
sg
2
2
1
p
A
q
p
p
=
−
=
ρ
4e
2
2
m
1
2
esg
2e
2
1
p
A
q
p
p
=
−
=
ρ
33.3.4.2.2.2 送風機吸込口圧力
psg1=pa
179
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
pesg1=0
2
1
m
1
sg1
1
2
1
−
=
A
q
p
p
ρ
2
1
m
1
1e
2
1
−
=
A
q
p
ρ
33.3.4.2.2.3 送風機圧力
送風機圧力pFB及び送風機静圧psFBは,次の式で算出する。
pFB=psg2−psg1=psg2−pa=pesg2
psFB=p2−psg1=p2−pa=pe2
33.3.4.2.3 体積流量の算出
体積流量は,33.2.4.1.3と同様に次の式に示す。
Θ
=
=
1
sg
w
a
m
1
sg
m
1
vsg
R
p
q
q
q
ρ
33.3.4.2.4 理論空気動力の算出
14.9.2.6に従って
PuB=qvsg1pFB
PusB=qvsg1psFB
33.3.4.2.5 送風機効率の算出
送風機効率は,33.2.1.1.5と同様にPuB又はPusBから算出する。
33.3.5 試験状態での送風機の性能
試験状態での送風機の性能は次による。
− 吸込体積流量 qvsg1
− 送風機圧力 pFB
− 送風機静圧 psFB
− 送風機効率 ηrB又はηsrB
34. 吸込側測定管路又は空気槽を使用する場合の標準試験方法−接続形式C
34.1 送風機装置の形式
送風機の装置構成には,一般に次の2種類がある
a) 吸込管路,吸込圧力は測定管路で測定。
b) 吸込空気そうで空気そう末端部に吸込管路模擬部分を備えているもの。吸込圧力は,空気そう内で測
定。
測定管路の流量を調節及び測定する方法を9種類示す。それぞれについて流量測定方法を規定し,あわ
せて流量測定方法の詳細を次に示す。
接続形式Cの装置で送風機の性能試験を行う際の測定及び計算などの共通する方法は,流量を算出する
9種類の方法によって,34.2.3.1.1〜34.2.3.1.3及び34.3.3.1.1〜34.3.3.1.4に示す。この方法は,この規格に準
拠する送風機のすべてに対しておおむね有効である。
180
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ただし,次の2種類の場合は簡略方法でもよい。
− 基準マッハ数が0.15未満で,圧力比が1.02を超える場合。
− 基準マッハ数が0.15未満で,圧力比が1.02未満の場合。
これらの方法は,34.2.4及び34.3.4に示す。
34.2 吸込側測定管路
34.2.1 質量流量の算出
質量流量は次の方法で測定する。
− 吸込側ISOベンチュリノズルによる,附属書図74a)参照。
− 四分円インレツトノズルによる,附属書図74a)参照。
− コニカルインレツトによる,附属書図74a)参照。
− コーナタツプをもつ吸込側オリフイス板による,附属書図74b)参照。
− 管壁静圧孔をもつ吸込側オリフイス板による,附属書図74c)参照。
− 管壁静圧孔をもつ吸込側オリフイス板による,附属書図74d)参照。
− D・D/2タツプをもつ管路内オリフイス板による,附属書図74e)参照。
− コーナタツプをもつ管路内オリフイス板による,附属書図74e)参照。
− ピトー静圧管トラバースによる,附属書図74f)参照。
− ピトー静圧管トラバースによる,附属書図74g)参照。
34.2.2 試験中に実施する測定(20.参照)
測定項目
− 回転速度,N又は回転周波数,n
− 入力動力,Pa,Po又はPe,の測定,インペラ動力の推定(10.3参照)及び補助送風機の入力動力Pex
− 流量計差圧∆p
− 流量計上流の圧力,pe7又はpe3
− 吸込側静圧pe3
試験時の囲い内の測定項目
− 送風機の平均高度における大気圧,pa
− 送風機吸込口付近の周囲温度,ta
− 乾湿球温度,td及びtw
周囲の空気密度ρa,及び湿り空気のガス定数Rwを算出する(12.参照)。
34.2.3 圧縮性流体に対する一般的な方法
基準マッハ数Ma2ref(14.4.2参照)が0.15を超え圧力比が1.02を超える場合に,この方法を適用する。
34.2.3.1 質量流量の算出
34.2.3.1.1 質量流量の測定は,次による。
− 吸込側ISOベンチュリノズル,22及び附属書図74a)参照。
− 四分円インレツトノズル,24及び附属書図74a)参照。
− コニカルインレツト,25及び附属書図74a)参照。
− コーナタップをもつ吸込側オリフイス板,26.10並びに附属書図74b)及びc)参照。
− 管壁静圧孔をもつ吸込側オリフイス板,26.11並びに附属書図74c)及びd)参照。
流量は調整可能なスクリーンの設置[附属書図74a)及び25.2参照]及びオリフィス板[附属書図74a)
及びd)参照],又は制御装置付き補助送風機[附属書図74c)参照]により制御される。
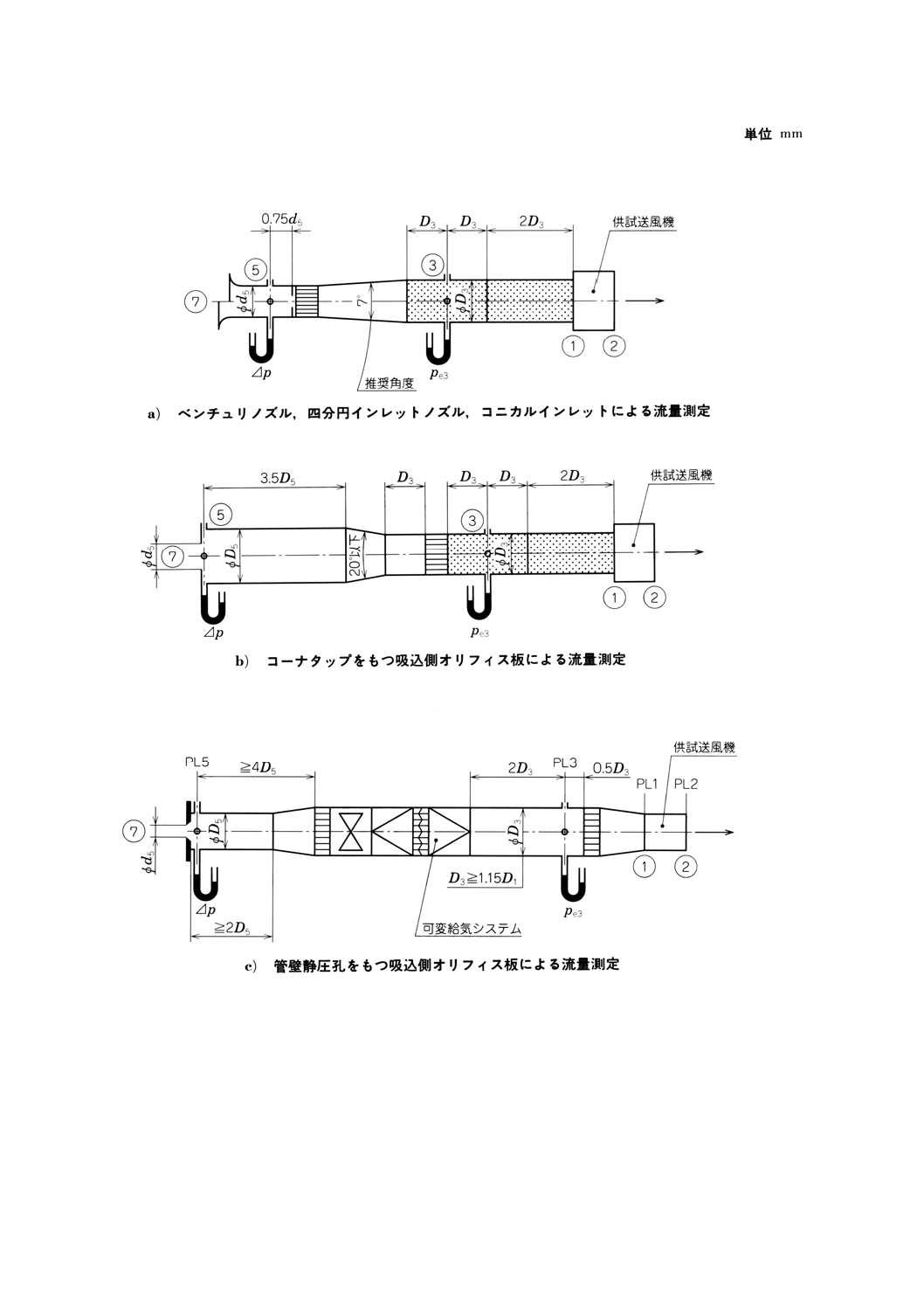
181
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図74 接続形式C(吸込側測定管路)
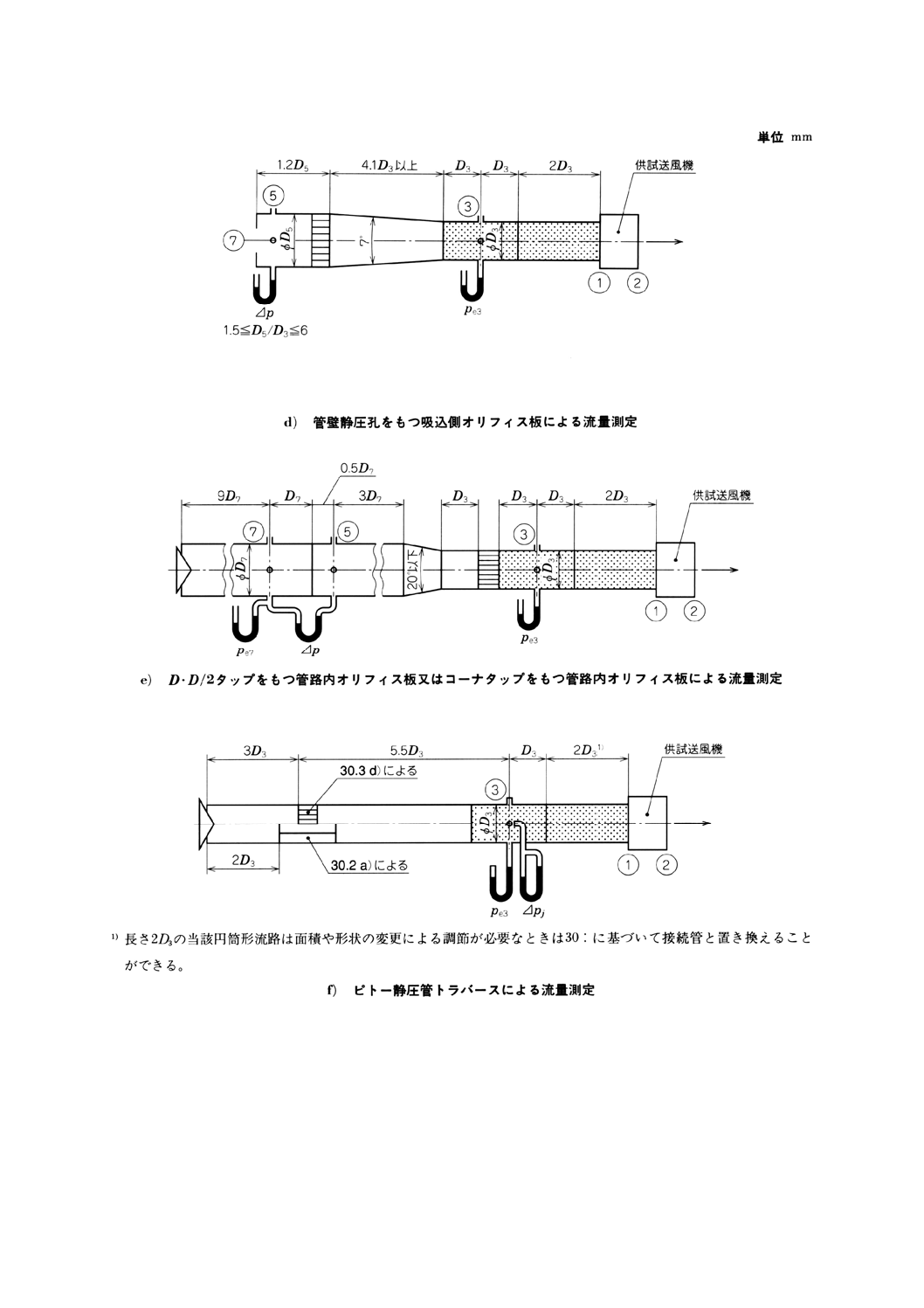
182
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図74 接続形式C(吸込側測定管路)(続き)
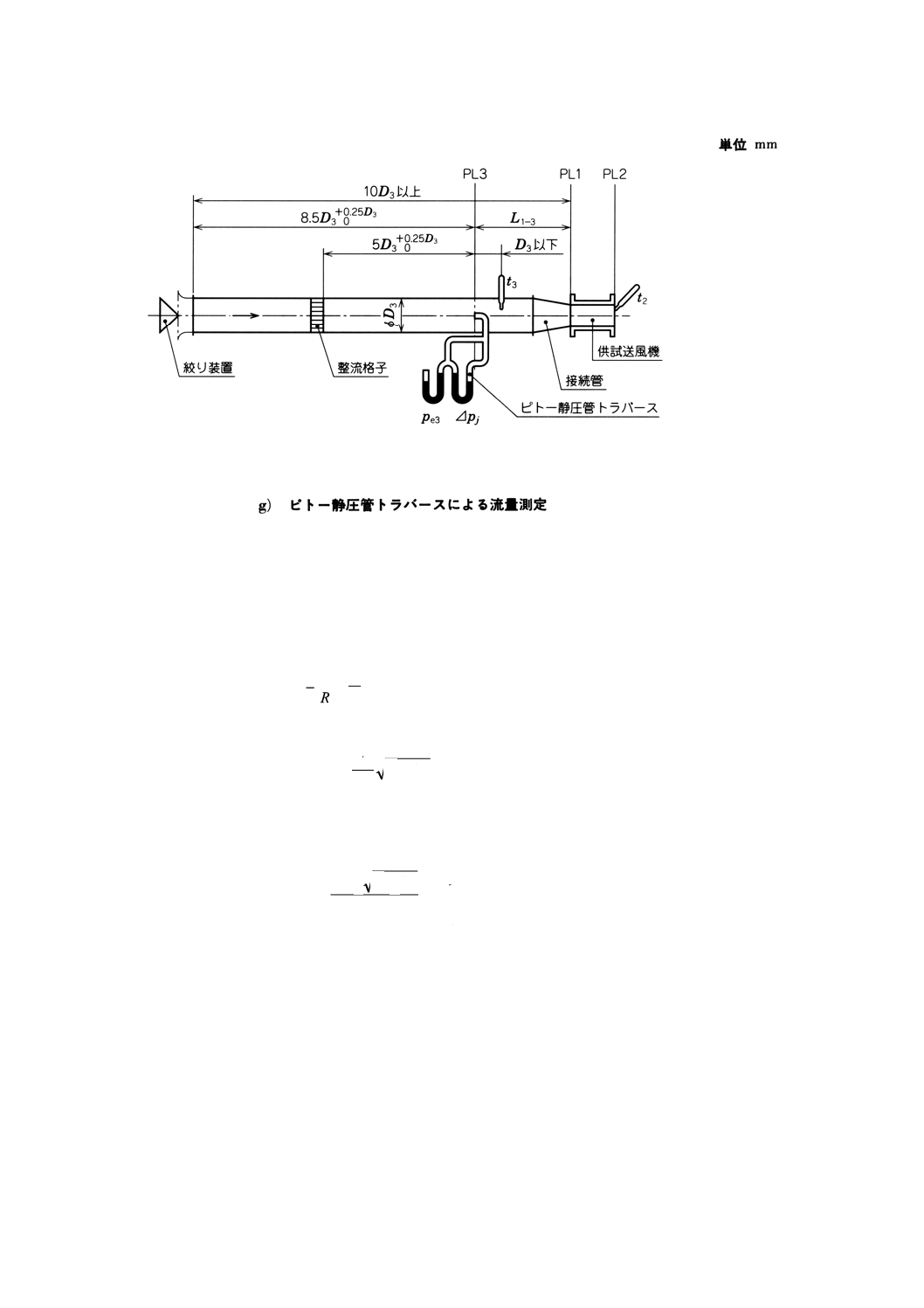
183
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図74 接続形式C(吸込側測定管路)(続き)
次のように仮定する。
pe7=0
p7=pa
Θ7=Θsg7=ta+273.15
7
w
7
7
Θ
=Rp
ρ
質量流量は次の式で算出する。
p
d
q
∆
=
7
5
2
m
2
4
ρ
αεπ
ここに,
αは,次の式で推定されるレイノルズ数Red5の関数である流量係数で,式中のα
は平均値
6
a
7
5
d5
10
048
.0
1.
17
2
×
+
∆
=
t
p
d
e
R
ρ
αε
εは,空気の膨張による修正係数
α,ε又は組み合せ係数,αεは,Red5の算出後22.3.2,22.3.3,24.4,25.4,26.10a)及びb),26.11並びに附
属書図18,22,27,28及び26により求める。
34.2.3.1.2 D・D/2タップ又は,コーナタップをもつ管路内オリフィス板による質量流量の算出[26.7,26.8
及び附属書図74e)参照]
次のように仮定する。
p7=pe7+pa
Θsg7=Θa=ta+273.15
184
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
7
7
m
sg7
7
m
2
sg7
7
2
1
2
−
Θ
=
−
Θ
=
Θ
ρ
A
q
c
c
V
p
p
7
w
7
7
Θ
=Rp
ρ
質量流量は次の式で算出する。
p
d
q
∆
=
7
5
2
m
2
4
ρ
αεπ
ここに,
εは,空気の膨張による修正係数で,比∆p/pr及びレイノルズ数ReD7の関数であ
る。
6
7
7
5
D7
10
048
.0
1.
17
2
×
+
∆
=
t
p
d
e
R
ρ
αεβ
αは次の式の値とともに変化する流量係数である。
7
5
D
d
=
β
Θ7,ρ7及びqmは,未知で,qmはΘ7=Θsg7を初期値として用い逐次近似的に算出する。
10−3の計算精度を得るには2〜3回の反復計算で十分である。
34.2.3.1.3 ピトー静圧管による質量流量の算出[27.並びに附属書図74f)及びg)参照]。
次のように仮定する。
p3=pe3+pa
圧力pe3をピトー静圧管で測定する場合
∑
=
=
n
j
p
n
p
1
e3j
e3
1
15
.
273
a
sg3
+
=
Θ
t
2
1
5.0j
m
1
∆
=
∆
∑
=
n
j
p
n
p
1
m
3
3
sg3
3
−
∆
+
Θ
=
Θ
κ
κ
p
p
p
3
w
3
3
Θ
=Rp
ρ
測定点jの位置は,27.4及び附属書図30による。
質量流量qmは,次の式で算出する(27.5参照)。
m
3
23
m
2
4
p
D
q
∆
=
ρ
αεπ
ここに,
εは,空気の膨張による修正係数(27.5参照)
185
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
αは,レイノルズ数ReD3により定まる補正係数又は流量係数(27.6参照)であ
る。
(
)
6
3
3
m
D3
10
048
.0
1.
17
4
×
+
=
t
D
q
e
R
π
αは次の2つの値の間で変化する。
ReD3=3×106の場合 0.990+0.002
又は
ReD3=3×104の場合 0.990−0.004
qmの初期値はα=0.990として計算しReD3値に対して補正する。
34.2.3.2 送風機圧力の算出
34.2.3.2.1 送風機吸込口圧力
次の二種類の場合を考慮する。
− 断面5と3の間に補助送風機がない場合
− 断面5と3の間に補助送風機がある場合
a) 断面5と3の間に補助送風機がない場合
p3=pe3+pa
Θsg3=Θsg5=Θsg7=Θa=Θsg1=ta+273.15
マッハ数Ma3及び比
sg3
3
Θ
Θ
は,14.4.3.1に従って算出する。
sg3
3
sg3
3
Θ
Θ
Θ
=
Θ
3
w
3
3
Θ
=Rp
ρ
吸込口せき止め圧力psg1は,次の式に示す(14.6.1参照)。
(
)
[
]
(
)
[
]
3
1
3
3
M
2
3
m
3
3
3
1
3
3
M
3
m
2
3
3
sg1
1
2
1
1
2
1
−
−
+
+
=
+
+
=
ξ
ρ
ρ
ξ
ρ
F
A
q
F
V
p
p
ここに,
(ζ3−1) 3≦0は,30.6.4,30.6.5及び30.6.6に従って算出される従来の係数である。
FM3は,14.5.1に従って算出するマッハ係数である。
pe3は,常に負である。
(
)
[
]
3
1
3
3
M
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
F
A
q
p
p
b) 断面5と3の間に補助送風機がある場合[附属書図74c)参照]。
この場合には (ζ3−1) 3≦0は,試験によって求めるがこの規格では定義しない。
補助送風機のインペラ動力Prx又は,補助送風機の電動機入力動力Pex(管路内に電動機が内装され
186
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る場合)を算出する場合は
sg1
p
m
ex
rx
a
p
m
ex
rx
sg7
sg3
or
or
Θ
=
+
Θ
=
+
Θ
=
Θ
c
q
P
P
c
q
P
P
その他の場合には,温度t3を測定しt3+273.15を,せき止め温度と仮定する。
静温度Θ3は,14.4.3.1に従って算出し,せき止め圧力psg1は,上記と同じ方法で算出する。
圧力p1は,マッハ数Ma1及び比。
sg1
1
Θ
Θ
を計算し14.4.3.2に従って算出する。
密度ρ1は,14.4.4に従って計算され,静圧p1は次の式で算出する(14.5.2参照)。
M1
2
1
m
1
sg1
M1
m1
2
1
sg1
1
2
1
2
1
F
A
q
p
F
V
p
p
−
=
−
=
ρ
ρ
又は
M1
2
1
m
1
esg1
M1
m1
2
1
esg1
e1
2
1
2
1
F
A
q
p
F
V
p
p
−
=
−
=
ρ
ρ
34.2.3.2.2 送風機吐出し口圧力
送風機吐出し口静圧p2は,大気圧paに等しい。
p2=pa
送風機吐出し口せき止め温度は,次の式に示す
p
m
e
r
sg3
sg2
or
c
q
P
P
+
Θ
=
Θ
マッハ数Ma2及び比
sg2
2
Θ
Θ
は,14.4.3.1に従って算出する。
sg2
2
sg2
2
Θ
Θ
Θ
=
Θ
2
w
a
2
w
2
2
Θ
=
Θ
=
R
p
R
p
ρ
psg2は,次の式に示す(14.5.1参照)。
M2
2
2
m
2
a
M2
2
2
m
2
2
sg2
2
1
2
1
F
A
q
p
F
A
q
p
p
+
=
+
=
ρ
ρ
M2
2
2
m
2
esg2
2
1
F
A
q
p
=ρ
34.2.3.2.3 送風機圧力
送風機圧力PFCは,次の式に示す。

187
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
[
]
(
)
[
]
+
+
−
=
+
+
−
+
=
−
=
−
−
3
1
3
M3
2
3
m
3
e3
M2
2
2
m
2
3
1
3
M3
2
3
m
3
3
M2
2
2
m
2
a
sg1
sg2
FC
1
2
1
2
1
1
2
1
2
1
ξ
ρ
ρ
ξ
ρ
ρ
F
A
q
p
F
A
q
F
A
q
p
F
A
q
p
p
p
p
送風機静圧psFCは,次の式で求める。
(
)
[
]
(
)
[
]
+
+
−
=
+
+
−
=
−
=
−
−
3
1
3
M3
2
3
m
3
e3
3
1
3
M3
2
3
m
3
3
a
sg1
2
sFC
1
2
1
1
2
1
ξ
ρ
ξ
ρ
F
A
q
p
F
A
q
p
p
p
p
p
2
2
1
m
ρ
ρ
ρ
+
=
m
1
ρ
ρ
ρ=
k
34.2.3.3 体積流量の算出
吸込口におけるせき止め状態の体積流量は,次の式に示す。
Θ
=
=
1
sg
w
sg1
m
1
sg
m
1
vsg
R
p
q
q
q
ρ
34.2.3.4 送風機理論空気動力の算出
34.2.3.4.1 送風機理論空気動力及び単位質量当たりの送風機仕事
14.8.1に従って,単位質量当たりの送風機仕事yc及び単位質量当たりの送風機静圧仕事yscは,次の式に
示す。
2
1
1
m
2
2
2
m
m
e1
e2
2
1
1
m
2
2
2
m
m
1
2
m1
2
m2
2
m
1
2
c
2
1
2
1
2
1
2
1
2
2
−
+
−
=
−
+
−
=
−
+
−
=
ρ
ρ
ρ
ρ
ρ
ρ
ρ
A
q
A
q
p
p
A
q
A
q
p
p
V
V
p
p
y
2
1
1
m
m
e1
e2
2
1
1
m
m
1
2
m1
2
m
1
2
sc
2
1
2
1
2
−
−
=
−
−
=
−
−
=
ρ
ρ
ρ
ρ
ρ
A
q
p
p
A
q
p
p
V
p
p
y
理論空気動力Puc及び理論静圧空気動力Puscは,次の式に示す。
Puc=ycqm
Pusc=yscqm
34.2.3.4.2 理論空気動力及び圧縮性係数の算出
14.8.2により
188
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Puc=qvsg1pFCkp
Pusc=qvsg1psFCkps
圧縮性係数kp及びkpsは,次の二種類の等価な方法で算出できる(14.8.2.1及び14.8.2.2参照)。
a) 第一の方法
(
)
[
]
1
1
log
log
or
k
10
10
k
p
ps
−
+
=
r
Z
r
Z
k
k
ここにkpに対しては
sg1
FC
1
p
p
r
+
=
またkpsに対しては
sg1
sFC
1
p
p
r
+
=
kpに対しては
FC
vsg1
r
k
1
p
q
P
Z
κ
κ−
=
また,kspに対しては
sFC
vsg1
r
k
1
p
q
P
Z
κ
κ−
=
b) 第二の方法
kps又は
(
)(
)
p
p
p
1
ln
1
ln
Z
Z
x
x
k
+
+
=
ここに,
p
sg1
FCfor
1
k
p
p
r
x
=
−
=
又は,
ps
sg1
sFCfork
p
p
x=
及び
sg1
vsg1
r
p
1
p
q
P
Z
κ
κ−
=
34.2.3.5 効率の算出
効率は,14.8.1及び14.8.2に従って,算出する。
− 送風機効率
r
UC
rc
P
P
=
η
− 送風機静圧効率
r
usC
srC
P
P
=
η
− 送風機軸効率
a
uC
aC
P
P
=
η
189
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 送風機静圧軸効率
a
usC
saC
P
P
=
η
34.2.4 簡略方法
34.2.4.1 基準マッハ数Mα2refが0.15未満で圧力比が1.02を超える場合
吸込側測定管路の断面におけるせき止め温度と静温度とは,等しいとみなしてよい。
Θ7=Θsg7=ta+273.15
マッハ係数FM1及びFM2は,それぞれ1に等しい。
34.2.4.1.1 質量流量の算出
対応する装置における方法は34.2.3.1で記述した方法に従う。
34.2.3.1.2に記述した方法において,Θ7を求めるための逐次近似を行う必要はない。
Θ7=Θsg7=t7+273.15=ta+273.15
t7は,測定管路内で測定する。
sg7
w
7
7
w
7
7
Θ
=
Θ
=
R
p
R
p
ρ
同様に34.2.3.1.3において
Θ3=Θsg3=t3+273.15ta+273.15
しかし,いずれの場合もレイノルズ数の関数としてαの補正を適用する。
34.2.4.1.2 送風機圧力の算出
34.2.4.1.2.1 送風機吸込口圧力
次のように仮定する。
補助送風機がない場合:
Θ7=Θ3=Θ1=Θsg1=Θa=ta+273.15
補助送風機がある場合:
Θ3=Θsg3=Θ1=Θsg1=t3+273.15
(ζ3−1)3は,試験によって求める。
3
w
3
3
Θ
=Rp
ρ
14.9.1に従って
(
)
[
]
(
)
[
]
3
1
3
2
3
m
3
3
3
1
3
3
m
2
3
3
sg1
1
2
1
1
2
1
−
−
+
+
=
+
+
=
ξ
ρ
ξ
ρ
A
q
p
V
p
p
又は,
(
)
[
]
3
1
3
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
ここに,
pe3及び(ζ3−1)3は,負である[34.2.3.2.1b)参照]。
圧力p1は,次の方法で算出する。

190
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
m
1
sg1
m1
2
1
sg1
1
2
1
2
−
=
−
=
A
q
p
V
p
p
ρ
ρ
ここに,
sg1
w
1
1
w
1
1
Θ
=
Θ
=
R
p
R
p
ρ
初期値 (ρ1) 1は, (ρ1) 1=ρsg1として求める。
()
1
w
sg1
1
1
Θ
=Rp
ρ
()
()
2
1
m
1
1
sg1
1
1
A
2
1
−
=
q
p
ρ
ρ
pe1=p1−pa
10−3の計算精度のpe1を得るには2〜3回の反復計算で十分である。
圧力p1は次の式でも算出できる。
Θ
−
+
=
1
sg
w
2
1
m
sg1
2
sg1
1
A
2
2
1
R
q
p
p
p
pe1=p1−pa
1
w
1
1
Θ
=Rp
ρ
34.2.4.1.2.2 送風機吐出し口圧力
送風機吐出し口においてはp2=paでせき止め圧力psg2は,次の式で算出する。
2
2
m
2
a
2
2
m
2
2
m2
2
2
2
sg2
2
1
2
1
2
1
+
=
+
=
+
=
A
q
p
A
q
p
V
p
p
ρ
ρ
ρ
2
2
m
2
esg2
2
1
=
A
q
p
ρ
2
w
2
2
Θ
=Rρ
ρ
p
m
e
r
sg1
sg2
2
or
c
q
P
P
+
Θ
=
Θ
=
Θ
34.2.4.1.2.3 送風機圧力
送風機圧力pFC及び送風機静圧p3FCは,次の式に示す。
191
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
[
]
(
)
[
]
+
+
−
=
+
+
−
+
=
−
=
−
−
3
1
3
2
3
m
3
e3
2
2
m
2
3
1
3
2
3
m
3
3
2
2
m
2
a
sg1
sg2
FC
1
2
1
2
1
1
2
1
2
1
ξ
ρ
ρ
ξ
ρ
ρ
A
q
p
A
q
A
q
p
A
q
p
p
p
p
psFC=p2−psg1=pa−psg1=−pesg1
2
2
1
m
ρ
ρ
ρ
+
=
m
1
ρ
ρ
ρ=
k
34.2.4.1.3 体積流量の算出
吸込口におけるせき止め状態の体積流量は,次の式で算出する。
sg1
m
1
vsg
ρ
q
q
=
sg1
w
sg1
sg1
Θ
=Rp
ρ
34.2.4.1.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,14.8.1,14.8.2及び34.2.3.4に従って算出する。
34.2.4.1.5 効率の算出
送風機効率は,34.2.3.5に従って算出する。
34.2.4.2 基準マッハ数Ma2refが,0.15未満で圧力比が1.02未満の場合
Θ1=Θsg1=Θ2=Θsg2=Θ3=Θsg3
測定管路内温度を測定して
FM1=FM2=FM3=1
kp=1
送風機と試験通風路間の空気の流れは,補助送風機付の場合を除いて非圧縮性とみなしてよい。
34.2.4.2.1 質量流量の算出
質量流量は,34.2.4.1.1に従いρu=ρaとして算出する。
34.2.4.2.2 送風機圧力の算出
34.2.4.2.2.1 送風機吸込口圧力
次のように仮定する
Θ1=Θsg1=Θ2=Θsg2=Θ3=Θsg3=ta+273.15
Θ3=ta+273.15
補助送風機が断面7と3の間にある場合には測定管路内の温度t3を測定する。
Θ1=Θsg1=Θ2=Θsg2=Θ3=Θsg3=t3+273.15
p3=pe3+pa
14.9に従って
192
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
[
]
(
)
[
]
3
1
3
2
3
m
3
3
3
1
3
3
m
2
3
3
sg1
1
2
1
1
2
1
−
−
+
+
=
+
+
=
ξ
ρ
ξ
ρ
A
q
p
V
p
p
(
)
[
]
3
1
3
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
ここに,
pe3及び (ζ3−1) 3≦0[34.2.3.2.1b)参照]
sg3
w
3
3
w
3
3
Θ
=
Θ
=
R
p
R
p
ρ
圧力p1は,次の式に示す。
2
1
m
3
sg1
2
1
3
2
3
m
3
sg1
1
2
1
2
1
−
=
−
=
A
q
p
A
A
A
q
p
p
ρ
ρ
2
1
m
3
esg1
e1
2
1
−
=
A
q
p
p
ρ
34.2.4.2.2.2 送風機吐出し口圧力
送風機吐出し口において
p2=pa
pe2=0
せき止め圧力psg2は,次の式に示す。
2
2
m
3
a
m2
2
3
a
sg2
2
1
2
1
+
=
+
=
A
q
p
V
p
p
ρ
ρ
2
2
m
3
esg2
2
1
=
A
q
p
ρ
34.2.4.2.2.3 送風機圧力
送風機圧力pFC及び送風機静圧psFCは,次の式に示す。
(
)
[
]
(
)
[
]
+
+
−
=
+
+
−
+
=
−
=
−
−
3
1
3
2
3
m
3
e3
2
2
m
3
3
1
3
2
3
m
3
3
2
2
m
3
a
sg1
sg2
FC
1
2
1
2
1
1
2
1
2
1
ξ
ρ
ρ
ξ
ρ
ρ
A
q
p
A
q
A
q
p
A
q
p
p
p
p
(
)
[
]
+
+
−
=
−
=
−
=
−
=
−3
1
3
2
3
m
3
e3
esg1
sg1
a
sg1
2
sFC
1
2
1
ξ
ρ A
q
p
p
p
p
p
p
p
193
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
34.2.4.2.3 体積流量の算出
吸込口におけるせき止め状態の体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
sg1
w
sg1
sg1
Θ
=Rp
ρ
34.2.4.2.4 理論空気動力の算出
14.9.2.5に従って
PuC=qvsg1pFC
PusC=qvsg1psFC
34.2.4.2.5 送風機効率の算出
効率は,14.8.1及び34.2.3.5に算出する。
34.2.5 試験状態での送風機の性能
試験状態での送風機の性能は,次による。
− 送風機圧力 pFC
− 送風機静圧 psFC
− 吸込体積流量 qvsg1
− 送風機効率 ηrC
− 送風機静圧効率 ηsrC
34.3 吸込側の試験空気槽
34.3.1 質量流量の算出
質量流量の測定は次による。
− 四分円インレットノズル,24.及び附属書図75a)参照。
− ピトー静圧管トラバース,27.及び附属書図75b)参照。
− 空気槽上流の管路内ベンチュリノズル,23.及び附属書図75c)参照。
− 空気槽内マルチノズル,23.及び附属書図75d)参照。
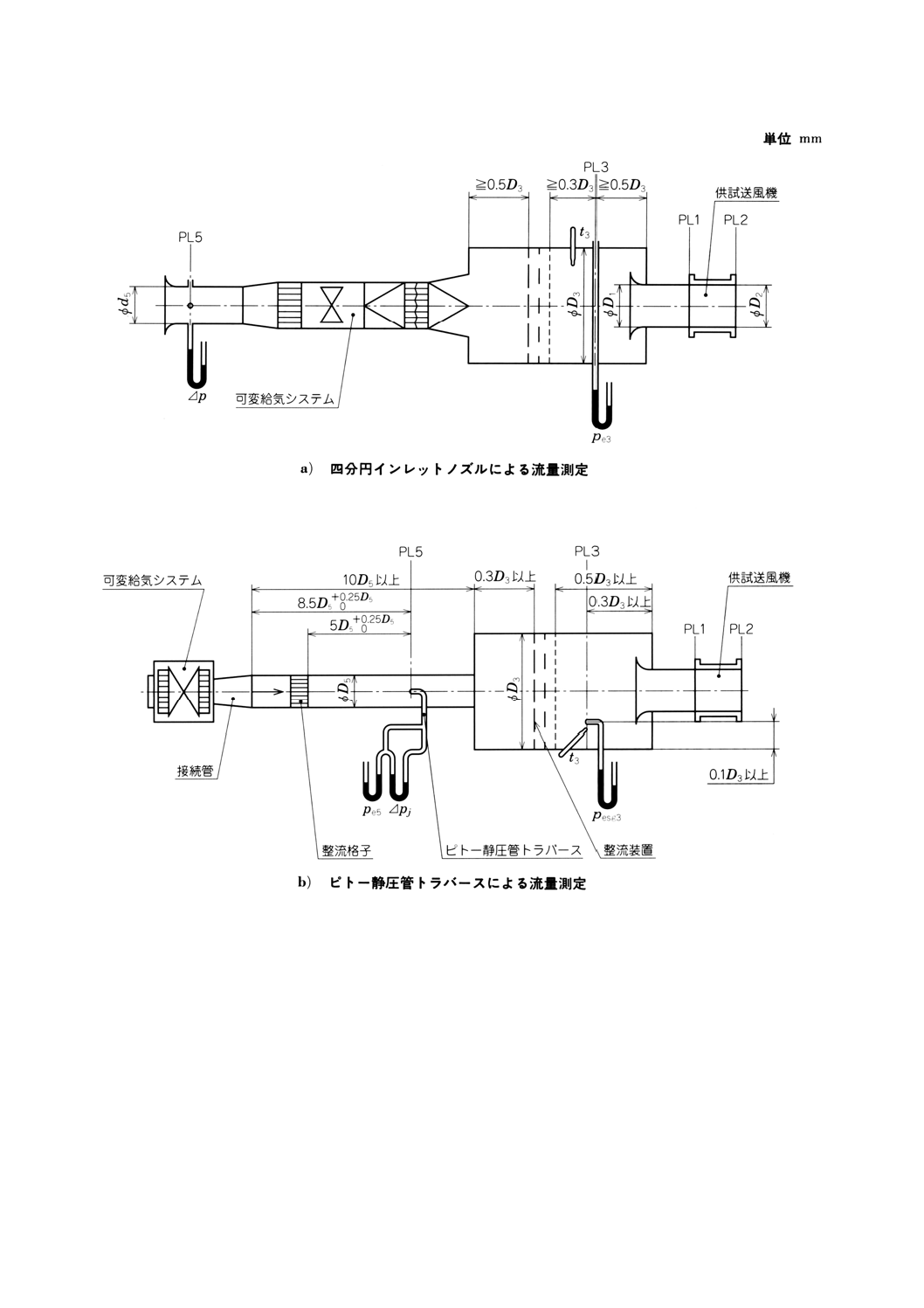
194
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図75 接続形式C(吸込側試験空気槽)
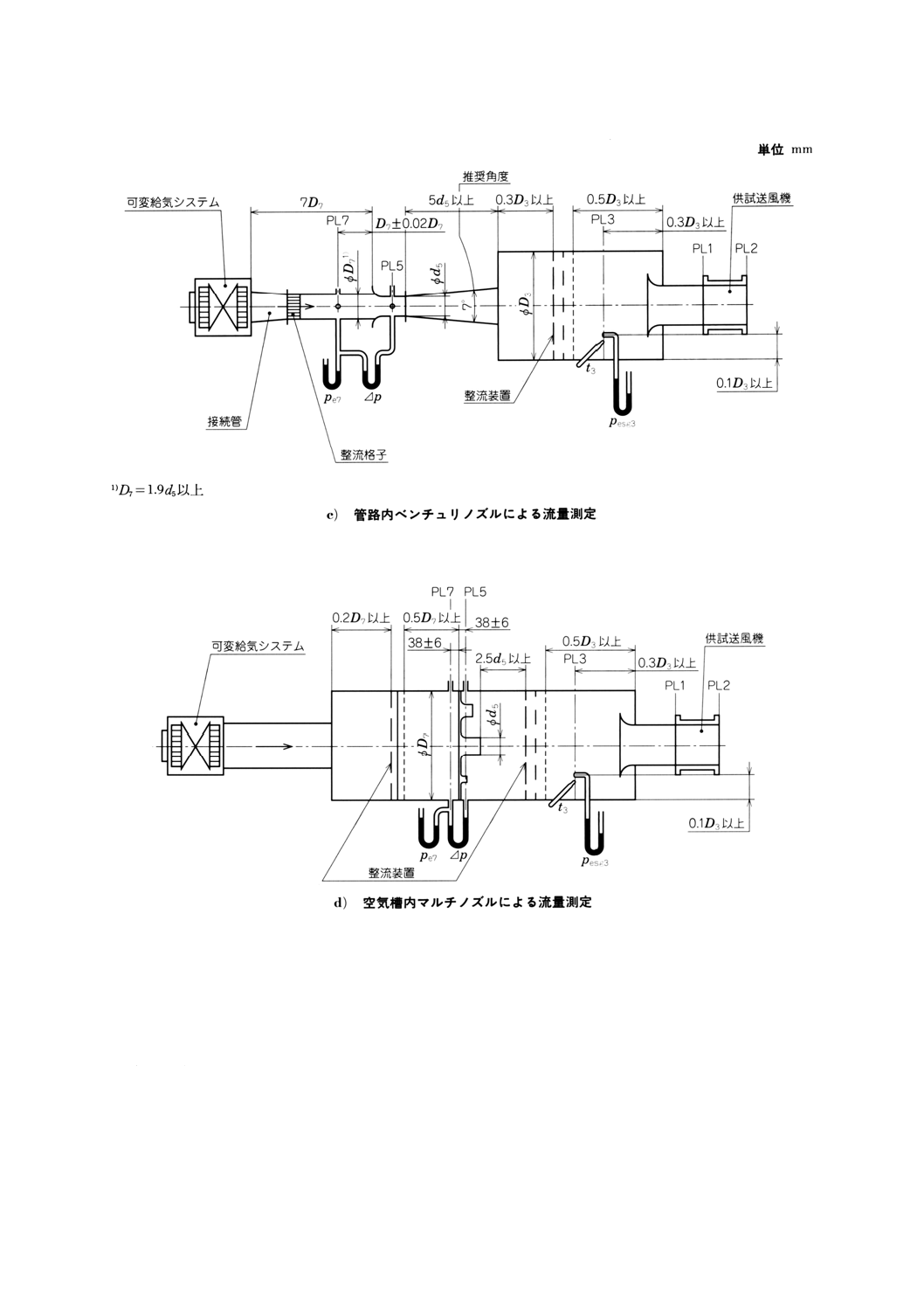
195
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図75 接続形式C(吸込側試験空気槽)(続き)
34.3.2 試験中に実施する測定(20.参照)
測定項目
− 回転速度,N,及び回転周波数,n
− 入力動力Pa,Po又は,Peの測定 インペラ動力の推定(10.4参照)及び補助送風機の入力動力Pex
− 流量計差圧,∆p
− 流量計の上流圧力,pe7又はpe5
− 空気そうせき止め圧力又は静圧pe3又はpesg3
− 空気そう温度,t3
196
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試験時の囲い内の測定項目
− 送風機平均高度における大気圧pa
− 送風機吸込口付近の周囲温度,ta
− 乾湿球温度,td及びtw
周囲の空気密度,ρa及び湿り空気のガス定数。Rwを算出する。
34.3.3 圧縮性流体に対する一般的な方法
基準マッハ数Ma2refが0.15を超え,かつ送風機圧力比が1.02を超える場合にはこの方法を適用する。
34.3.3.1 質量流量の算出
34.3.3.1.1 四分円インレットノズルによる質量流量の算出[24.及び75 a)参照]この値は,補助送風機と調
整可能なスクリーンの設置によって制御される。
次のように仮定する
pe7=0
p7=pa
Θ7=Θsg7=ta+273.15
7
w
7
7
Θ
=Rp
ρ
質量流量は次の式に示す。
p
d
q
∆
=
7
25
m
2
4
ρ
αεπ
ここに,
αは,次の式で推定するレイノルズ数Red5の関数である流量係数である。式中
のαの値は平均値で1に等しい。
6
7
7
5
d5
10
048
.0
1.
17
2
×
+
∆
=
t
p
d
e
R
ρ
αε
εは,空気の膨張による修正係数
α及びεは,24.4に従ってRed5及び∆pから算出する。
34.3.3.1.2 ピトー静圧管トラバースによる質量流量の算出[27.及び附属書図75 d)参照]
次のように仮定する
∑
=
=
n
j
p
n
p
1
e5j
5e
1
p5=pe5+pa
p
m
ex
rx
a
3
5
sg
or
15
.
273
c
q
P
P
t
+
Θ
=
+
=
Θ
2
1
5.0j
m
1
∆
=
∆
∑
=
n
j
p
n
p
κ
κ1
m
5
5
5
sg
5
−
∆
+
Θ
=
Θ
p
p
p

197
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
w
5
5
Θ
=Rp
ρ
測定点jの位置は,27.4及び附属書図30による。
質量流量は,次の式に示す(27.5参照)。
m
5
5
2
m
2
4
ρ
ρ
αεπ
∆
=
D
q
ここに,
εは,27.5による空気の膨張による修正係数
αは,補正係数又はレイノルズ数ReD5によって決まる流量係数(27.6参照)
(
)
6
5
5
m
D5
10
048
.0
1.
17
4
×
+
=
t
D
q
e
R
π
αは次の二つの値の間で変化する
ReD5=3×106の場合 0.990+0.002
ReD5=3×104の場合 0.990−0.004
qmの初期値は,α=0.990として計算しReD5の値に対して補正する(27.6参照)。
34.3.3.1.3 管路内ベンチュリノズルによる質量流量の算出 23.及び附属書図75 c)参照
次のように仮定する
p7=pe7+pa
p
m
ex
rx
a
3
sg7
or
15
.
273
c
q
P
P
t
+
Θ
=
+
=
Θ
2
7
7
m
p
sg7
7
2
1
−
Θ
=
Θ
ρ
A
q
c
質量流量qmは,次の式で算出する。
4
Au
7
5
2
7
5
2
m
1
2
4
2
4
β
α
ρ
επ
ρ
αεπ
−
∆
=
∆
=
p
d
C
p
d
q
ここに,
εは,22.4.3及び表6に従って計算される空気の膨張による修正係数
αは,ノズルの流量係数で次の値に等しい。
4
Au
1
β
α
−
C
Cは,ノズルの流出係数でスロート部レイノルズ数Red5の関数(23.4.2及び附
属書表5参照)
αAuは,運動エネルギー係数で管路進入路では1.043で,空気槽進入路では1に
等しい。
β=d5/D7
6
3
7
5
d5
10
048
.0
1.
17
2
t
p
d
e
R
+
∆
=
ρ
αε
198
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
初期値に対し
4
Au
1
95
.0
β
α
α
−
=
Θ7=Θsg7
このような条件下で求めたqmの初期値でΘ7,ρ7,Red5,αの新しい値を計算し,これからqmの新しい値
を算出。
10−3の計算精度を得るには2〜3回の反復計算で十分である。
34.3.3.1.4 空気槽内マルチノズルによる質量流量の算出 23.及び附属書図75 d)参照。
次のように仮定する。
p7=pe7+pa
Θsg7=Θ7=Θ3=Θsg3=t3+273.15
7
w
7
7
Θ
=Rp
ρ
0
7
5j=
=D
d
β
質量流量は,次の式に示す。
p
d
C
q
n
j
j
∆
=∑
=
7
1
2j
5
m
2
4
ρ
επ
ここに,
εは,23.4.3及び表6による空気の膨張による修正係数
Cjは,ノズルスロートレイノルズ数Red5jの関数であるj番目ノズルの流出係数
β=0だからCj=αj
Cj=αjは,23.4及び表5に従って算出する。
nは,ノズル数
各ノズルにおけるスロート部レイノルズ数Red5は,次の式で推定する
Cj=0.95として
6
7
7
5j
j
d5j
10
048
.0
1.
17
2
t
p
d
C
e
R
+
∆
=
ρ
ε
質量流量の初期値による計算の後で流出係数Cjを補正する。
34.3.3.2 送風機圧力の算出
34.3.3.2.1 送風機吸込口圧力
附属書図75a)〜c)には,2種類の空気槽圧力測定方法を示す。
− 空気槽圧力pe3は,ゲージ圧
− 空気槽圧力pesg3は,ゲージせき止め圧
a) 空気槽圧力が,ゲージ圧pe3の場合
次のように仮定する。
FM3=1
p3=pe3+pa
Θsg1=Θ3=Θsg3=t3+273.15
199
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3
w
3
3
Θ
=Rp
ρ
吸込口せき止め圧力psg3は,次の式に示す。
2
3
m
3
3
m3
2
3
3
sg3
2
1
2
1
+
=
+
=
A
q
p
V
p
p
ρ
ρ
2
3
m
3
e3
esg3
2
1
+
=
A
q
p
p
ρ
b) 空気槽圧力が,絶対せき止め圧pesg3の場合
次のような条件で
psg3=pesg3+pa
Θ3=Θsg3=Θsg1=t3+273.15
長さ1D1又は2D1の長さの吸込側模擬管路には摩擦損失を考慮しない。
psg1=psg3
pesg1=pesg3
1D1又は2D1よりも長い吸込側模擬管路が必要なときには摩擦損失を考慮する。
吸込側管路における吸込ベルマウスの下流では,添字3.1で
psg3.1=psg3
送風機吸込口断面1のせき止め圧力は,次の式に示す。
sg3
3.1
sg3
3.1
ρ
ρ
ρ
ρ=
(
)1
1
3
1.3
M
2
1
m
1.3
sg3
sg1
2
1
−
+
=
ξ
ρ
F
A
q
p
p
(
)1
1
3
1.3
M
2
1
m
1.3
esg3
esg1
2
1
−
+
=
ξ
ρ
F
A
q
p
p
ここに, Ma3.1ρ3.1及びFM3.1は,14.4.3.2,14.4.4及び14.5.2に従って算出する。
(ζ3−1)1≦0は,30.6による直径D1長さLの吸込側模擬管路に対しての従来の摩
擦損失
係数(
)
1
1
1
3
D
L
Λ
−
=
−
ξ
静圧p1は,次の式で算出する。
1
M
2
1
m
1
sg1
1
2
1
F
A
q
p
p
−
=
ρ
又は
1
M
2
1
m
1
esg1
e1
2
1
F
A
q
p
p
−
=
ρ
200
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに, Ma1,ρ1及びFM1は,14.4.3.2,14.4.4及び14.5.2に従って算出する。
34.3.3.2.2 送風機吐出し口圧力
送風機吐出し口において
p2=pa
p
m
e
r
sg1
sg2
or
c
q
P
P
+
Θ
=
Θ
マッハ数Ma2及び密度ρ2は,14.4.3.1及び附属書図5に従って算出する。
2
w
a
2
w
2
2
Θ
=
Θ
=
R
p
R
p
ρ
M2
2
2
m
2
a
M2
2
2
m
2
2
sg2
2
1
2
1
F
A
q
p
F
A
q
p
p
+
=
+
=
ρ
ρ
又は
M2
2
2
m
2
esg2
2
1
F
A
q
p
=ρ
34.3.3.2.3 送風機圧力
送風機圧力pFC及び送風機静圧psFCは,次の式に示す。
esg1
M2
2
2
m
2
sg1
M2
2
2
m
2
a
sg1
sg2
FC
2
1
2
1
p
F
A
q
p
F
A
q
p
p
p
p
−
=
−
+
=
−
=
ρ
ρ
psFC=p2−psg1=pa−psg1=pesg1
2
2
1
m
ρ
ρ
ρ
+
=
m
1
ρ
ρ
ρ=
k
34.3.3.3 体積流量の算出
吸込口におけるせき止め状態での体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
sg1
w
sg1
sg1
Θ
=Rp
ρ
34.3.3.4 理論空気動力の算出
34.3.3.4.1 単位質量当たりの送風機仕事及び理論空気動力
単位質量当たりの送風機仕事yc及び単位質量当たりの送風機静圧仕事yscは,次の式に示す。

201
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
1
m
2
2
2
m
m
1
2
1
m
2
2
m
2
m
1
2
C
2
1
2
1
2
2
−
+
−
=
−
+
−
=
ρ
ρ
ρ
ρ
A
q
A
q
p
p
V
V
p
p
y
2
1
1
m
m
1e
2
e
2
1
1
m
m
1
2
1
m
2
m
1
2
sC
2
1
2
1
2
−
−
=
−
−
=
−
−
=
ρ
ρ
ρ
ρ
ρ
A
q
p
p
A
q
p
p
V
p
p
y
対応する理論空気動力PuC及び理論静圧動力PusCは,次の式に示す。
PuC=ycqm
PusC=ysCqm
34.3.3.4.2 理論空気動力及び圧縮性係数の算出
14.8.2によって
PuC=qvsg1pFCkp
PusC=qvsg1psFCkps
圧縮性係数kp及びkpsは,次の2種類の等価な方法で算出する(14.8.2及び14.8.2.2参照)。
a) 第一の方法
kps又は
(
)
[
]
1
1
log
log
k
10
10
k
p
−
+
=
r
Z
r
Z
k
ここに,kpについては
1
sg
FC
1
p
p
r
+
=
kpsについては
1
sg
sFC
1
p
p
r
+
=
kpについては
FC
vsg1
r
k
1
p
q
P
Z
κ
κ−
=
kpsについては
sFC
vsg1
r
k
1
p
q
P
Z
κ
κ−
=
b) 第二の方法
kps又は
(
)(
)
p
p
p
1
ln
1
ln
Z
Z
x
x
k
+
+
=
ここに,
1
sg
FC
1
p
p
r
x
=
−
=
又は
202
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1
sg
sFC
p
p
x=
及び
sg1
vsg1
r
p
1
p
q
P
Z
κ
κ−
=
34.3.3.5 効率の算出
14.8.1に従って効率は,次の式を用いて算出する。
− 送風機効率
r
uC
rC
P
P
=
η
− 送風機静圧効率
r
usC
srC
P
P
=
η
− 送風機軸効率
a
uC
sC
P
P
=
η
− 送風機静圧軸効率
a
usC
saC
P
P
=
η
34.3.4 簡略方法
34.3.4.1 基準マッハ数Ma2refが0.15未満で圧力比が1.02を超える場合
34.3.4.1.1 流量の算出
Θx=Θsgx
FM1=FM2=FM3=1
34.3.3.1.1〜34.3.3.1.4に記述した方法を適用
試験空気槽内の温度Θ7を測定するのでΘ7を計算するための逐次近似を行う必要はない。
いずれの場合も,レイノルズ数の関数であるαの補正を適用する。
34.3.4.1.2 送風機圧力の算出
34.3.4.1.2.1 送風機吸込口圧力
空気槽内の絶対せき止め圧力pesg3を測定する。
Θsg3=Θ3=Θ1=Θsg1=t3+273.15
psg3=pesg3+pa
又は,次の式に示す。
p3=pe3+pa
3
w
3
3
Θ
=Rp
ρ
2
3
m
3
3
sg3
2
1
+
=
A
q
p
p
ρ
203
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
3
m
3
e3
esg3
2
1
+
=
A
q
p
p
ρ
通常,
psg1=psg3
pesg1=pesg3
摩擦損失の考慮を行うとき,吸込側模擬管路の圧力p3.1は,次の方法で算出する。
次のように仮定する
Θ3=Θsg3=Θsg1
2
2
m
1.3
sg3
3.1
2
1
−
=
A
q
p
p
ρ
初期値に対しては(ρ3.1)1=ρsg3
(
)
(
)
2
1
m
1
1.3
sg3
1
3.1
2
1
−
=
A
q
p
p
ρ
(
)
3
w
1
3.1
3.1
Θ
=Rp
ρ
2
1
m
1.3
sg3
3.1
2
1
−
=
A
q
p
p
ρ
2〜3回の反復計算で十分で,p3.1は,次の式でも算出できる。
Θ
−
+
=
3
sg
w
2
1
m
sg3
2
sg3
3.1
2
2
1
R
A
q
p
p
p
送風機吸込口でのせき止め圧力psgは,次の式に示す。
(
)1
1
3
2
1
m
1.3
sg3
sg1
2
1
−
+
=
ξ
ρ
A
q
p
p
又は
(
)1
1
3
2
1
m
1.3
esg3
esg1
2
1
−
+
=
ξ
ρ
A
q
p
p
ここに,(ζ3−1)1≦0は,30.6及び34.3.3.2.1による吸込側模擬管路の従来の損失係数圧力p1は,p3.1の算
出に使用した方法で算出する。
2
1
m
1
sg1
1
2
1
−
=
A
q
p
p
ρ
204
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
m
1
esg1
e1
2
1
−
=
A
q
p
p
ρ
34.3.4.1.2.2 送風機吐出し口圧力
送風機吐出し口において
p
m
e
r
sg1
sg2
2
or
c
q
P
P
+
Θ
=
Θ
=
Θ
p2=pa
2
w
2
2
Θ
=Rp
ρ
2
2
m
2
a
2
2
m
2
2
sg2
2
1
2
1
+
=
+
=
A
q
p
A
q
p
p
ρ
ρ
2
2
m
2
esg2
2
1
=
A
q
p
ρ
34.3.4.1.2.3 送風機圧力
送風機圧力pFC及び送風機静圧psFCは,次の式に示す。
pFC=psg2−psg1=pesg2−pesg1
esg1
2
2
m
2
sg1
2
2
m
2
a
2
1
2
1
p
A
q
p
A
q
p
−
=
−
+
=
ρ
ρ
psFC=p2−psg1=pa−psg1=−pesg1
ここに,
pesg1≦0
34.3.4.1.3 体積流量の算出
吸込口におけるせき止め状態の体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
1
w
sg1
sg1
w
sg1
sg1
Θ
=
Θ
=
R
p
R
p
ρ
34.3.4.1.4 理論空気動力の算出
理論空気動力は,14.8.1,14.8.2,及び34.3.3.4に従って算出する。
34.3.4.1.5 送風機効率の算出
送風機効率は,14.8.1,14.8.2,及び34.3.3.5に従って算出する。
34.3.4.2 基準マッハ数Ma2refが0.15未満で圧力比が1.02未満の場合
Θ3=Θsg3=Θ1=Θsg1=Θ2=Θsg2=t3+273.15
送風機を通過する空気の流れは,非圧縮性とみなしてよい。
ρ3=ρ1=ρ2
kp=1
205
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
34.3.4.2.1 質量流量の算出
質量流量は,34.3.4.1.1に従って算出する。
流量計の上流温度を測定する。
34.3.4.2.2 送風機圧力の算出
34.3.4.2.2.1 送風機吸込口圧力
送風機吸込口圧力は,34.3.4.1.2.1に従って算出する
測定圧力が静圧pe3の場合
p3=pe3+p2
3
3
m
3
3
sg3
2
1
+
=
A
q
p
p
ρ
2
3
m
3
e3
esg3
2
1
+
=
A
q
p
p
ρ
ここに,
sg1
3
w
3
3
ρ
ρ
Θ
=Rp
測定圧力がせき止め圧力の場合
psg3=pesg3+pa
二つの場合において
(
)1
1
3
2
1
m
3
sg3
sg1
2
1
−
+
=
ξ
ρ
A
q
p
p
又は
(
)1
1
3
2
1
m
3
esg3
esg1
2
1
−
+
=
ξ
ρ
A
q
p
p
ここに,
(ζ3−1)1≦0は,34.3.3.2.1,30.6.4,及び30.6.6に従って算出する。
2
1
m
3
sg1
1
2
1
−
=
A
q
p
p
ρ
34.3.4.2.2.2 送風機吐出し口圧力
送風機吐出し口において
p2=pa
2
2
m
3
2
sg2
2
1
+
=
A
q
p
p
ρ
2
2
m
3
esg2
2
1
=
A
q
p
ρ
206
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
34.3.4.2.2.3 送風機圧力
送風機圧pFC及び送風機静圧psFCは,次の式に示す。
pFC=psg2−psg1=pesg2−pesg1
esg1
2
2
m
3
2
1
p
A
q
−
=ρ
psFC=p2−psg1=−pesg1
34.3.4.2.3 体積流量の算出
吸込口におけるせき止め状態の体積流量は,次の式に示す。
sg3
m
1
vsg
ρ
q
q
=
3
sg
w
sg3
sg3
sg1
Θ
=
=
R
p
ρ
ρ
34.3.4.2.4 理論空気動力の算出
理論空気動力は,次の式に示す。
PuC=qvsg1pFC
PusC=qvsg1psFC
34.3.4.2.5 送風機効率の算出
送風機効率は,14.8及び34.3.3.5に従ってPuC及びPusCから算出する。
34.3.5 試験状態での送風機の性能
試験状態での送風機の性能は次による。
− 送風機圧力,pFC
− 送風機静圧,psFC
− 吸込口体積流量,qvsg1
− 送風機効率,ηrC
− 送風機静圧効率,ηsrC
35. 吸込側及び吐出し側に測定管路を使用する場合の標準試験方法−接続形式D
35.1 送風機装置の形式
接続形式Dの通常の構成:
a) 30.3〜30.5に従って吸込模擬管路を備えた接続形式B
b) 30.2〜30.4に従って吐出し模擬管路を備えた接続形式C
したがって,接続形式Dでは,次の4種類の設備について説明する。
1) 接続形式Bに,吐出し管路及び旋回流防止装置,並びに30.2,30.3及び30.5に従った吸込模擬管路
を備えたもの[附属書図76a)及びb)参照]
2) 接続形式Bに,吐出し側の旋回流防止装置を備えずに,30.2f),30.3,及び30.5に従って吸込模擬
管路を備えたもの[附属書図76d)参照]
3) 接続形式Cに,30.2 a),b),c),d),30.3, 30.4及び30.5に従って吐出し模擬管路及び旋回流防止装
置を備えたもの[附属書図76c)参照]
4) 接続形式Cに,30.2f),30.3,及び30.5に従って旋回流防止装置なしで吐出し模擬管路を備えたも
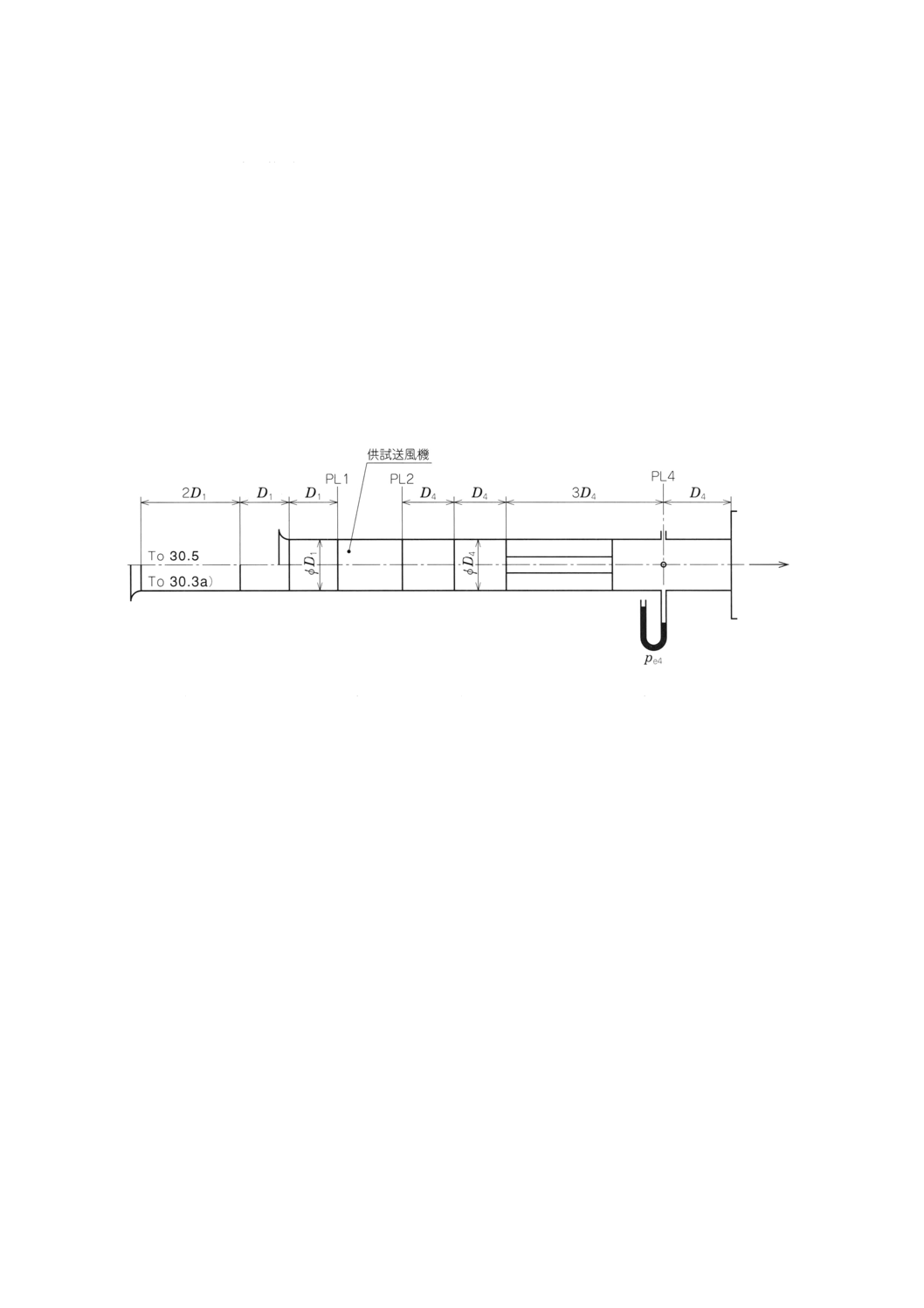
207
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の[附属書図76e),f)とg)参照]
1)及び3)の接続形式を推奨する。
2)及び4)の接続形式は認めるが,これらの設備で得た結果は,吸込側および吐出し側の両側に標準試験
通風路を使用して得た結果とは,ある程度の差が生じる。
流量測定方法は,20〜27,33.2.3.1,33.3.3.1,34.2.3.1,及び34.3.3.1に記載したものを使用する。
接続形式Dで性能試験を行う際の,測定計算などの方法を,35.2.3.1,35.3.3.1,35.4.3.1,及び35.5.3.1
に示す。
この方法は,この規格に準拠する送風機のすべてに対しておおむね有効である。
ただし,次の場合は簡略法でもよい。
− 基準マッハ数Ma2refが0.15未満で,圧力比が1.02を超える場合
− 基準マッハ数Ma2refが0.15未満で,圧力比が1.02未満の場合
後者の場合は,35.2.4,35.3.4及び35.5.4に示した方法に従ってもよい。
備考 流量の測定及び調節は33.2.3.1による。
a) 接続形式B(吐出し側測定管路),共通部分と旋回流防止装置と吸込模擬管路を備えた場合
附属書図76 接続形式D
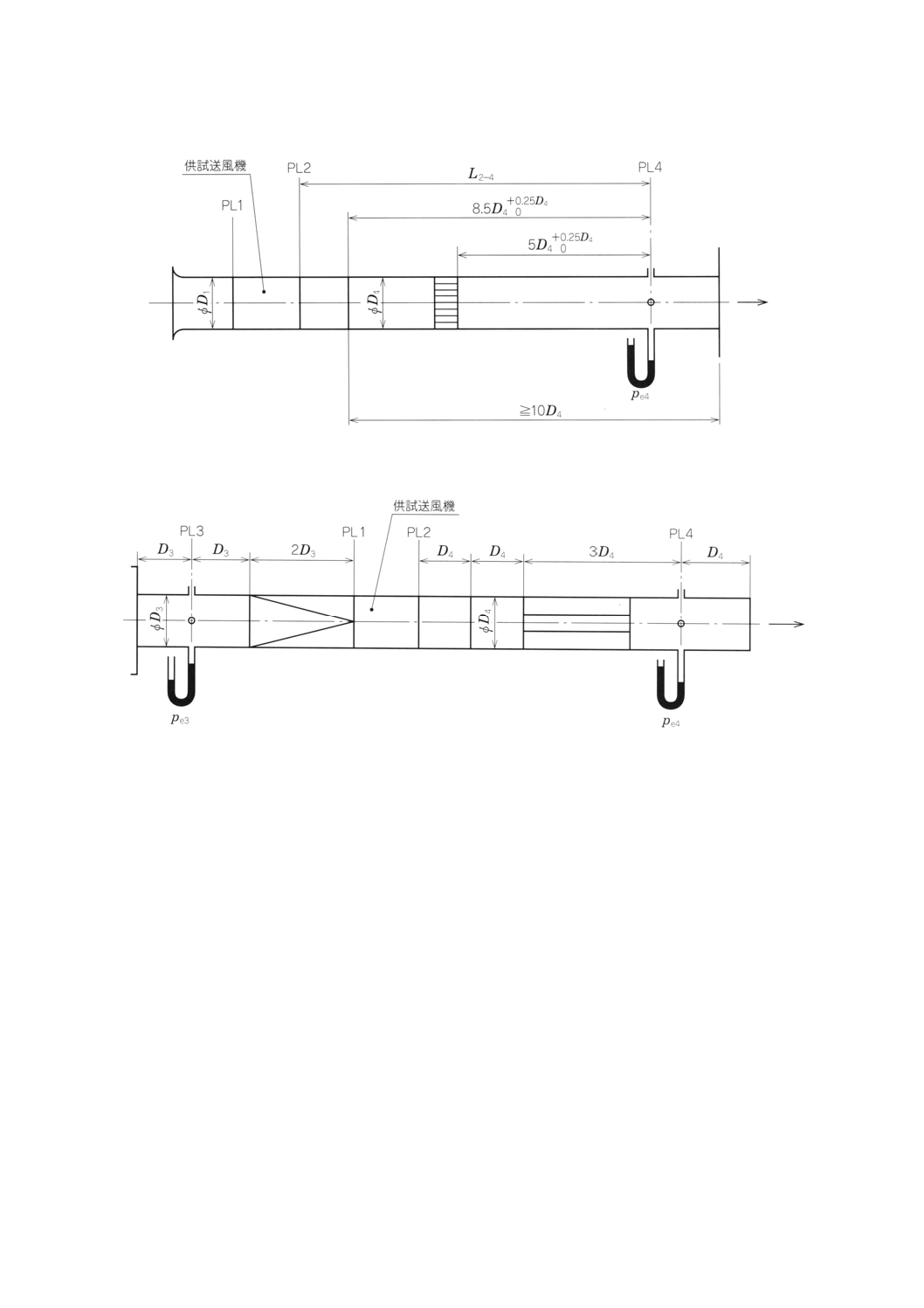
208
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 流量の測定及び調節は33.2.3.1による。
b) 接続形式B(吐出し側測定管路)共通部分,旋回流防止装置及び吸込模擬管路を備えた場合
備考 流量の測定及び調節は34.2による。
c) 接続形式C(吸込側測定管路),旋回流防止装置及び共通吸込部分を備えた場合
附属書図76 接続形式D(続き)
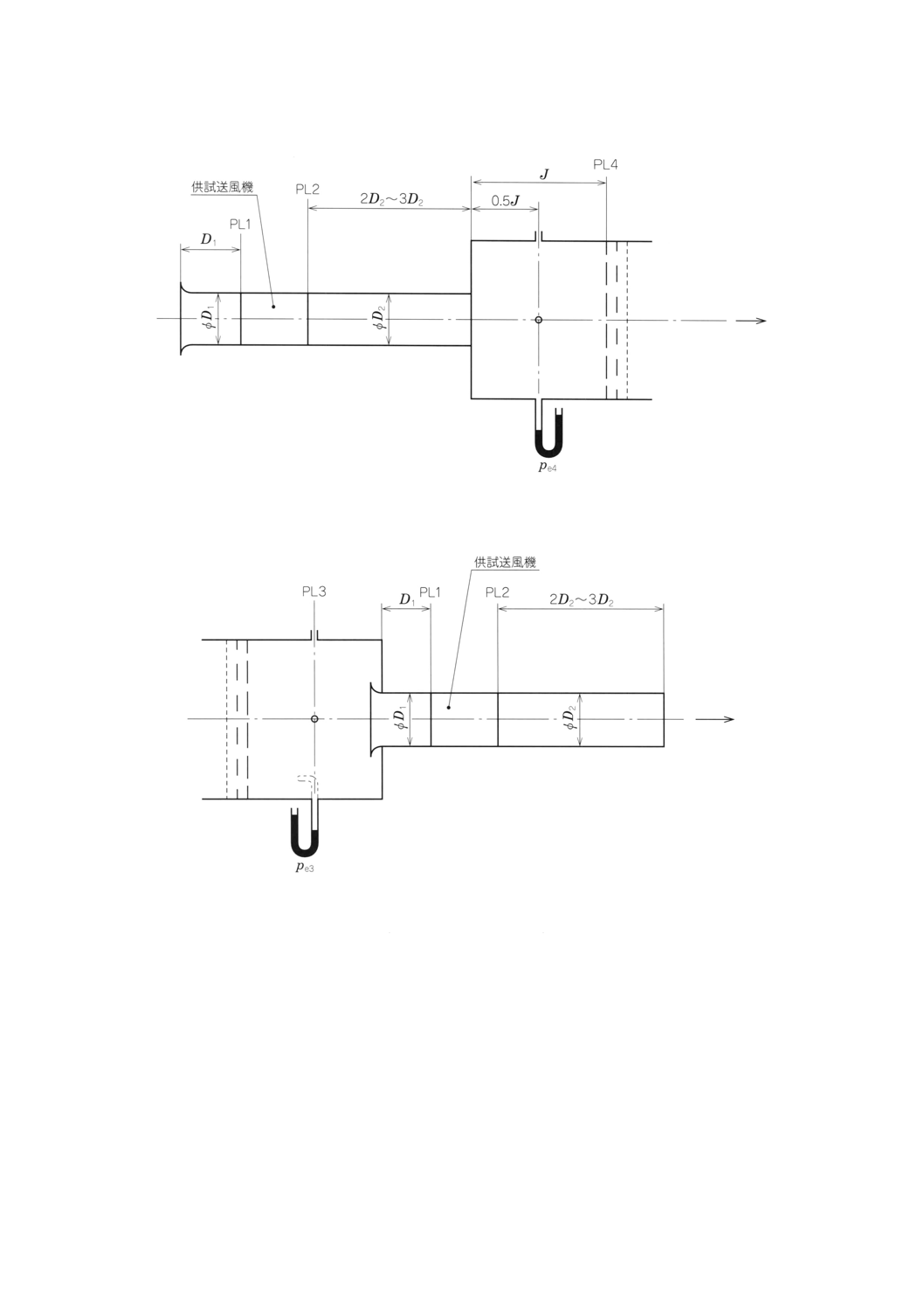
209
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 流量の測定は33.3.3.1.1並びに附属書図73a)及びb)による(吐出しに旋回流のない送風機だけに使用)。
d) 接続形式B(吐出し側測定管路),旋回流防止装置及び共通部分がなく,吸込模擬管路を備えた場合
備考 流量の測定は34.3.3.1.1,34.3.3.1.2,34.3.3.1.3,34.3.3.1.4並びに附属書図75a),b),c),d)による。(吐出
しに旋回流のない送風機だけに使用)
e) 接続形式C(吸込側測定管路)及び吐出し模擬管路をもつが,旋回流防止装置を備えない場合
附属書図76 接続形式D(続き)
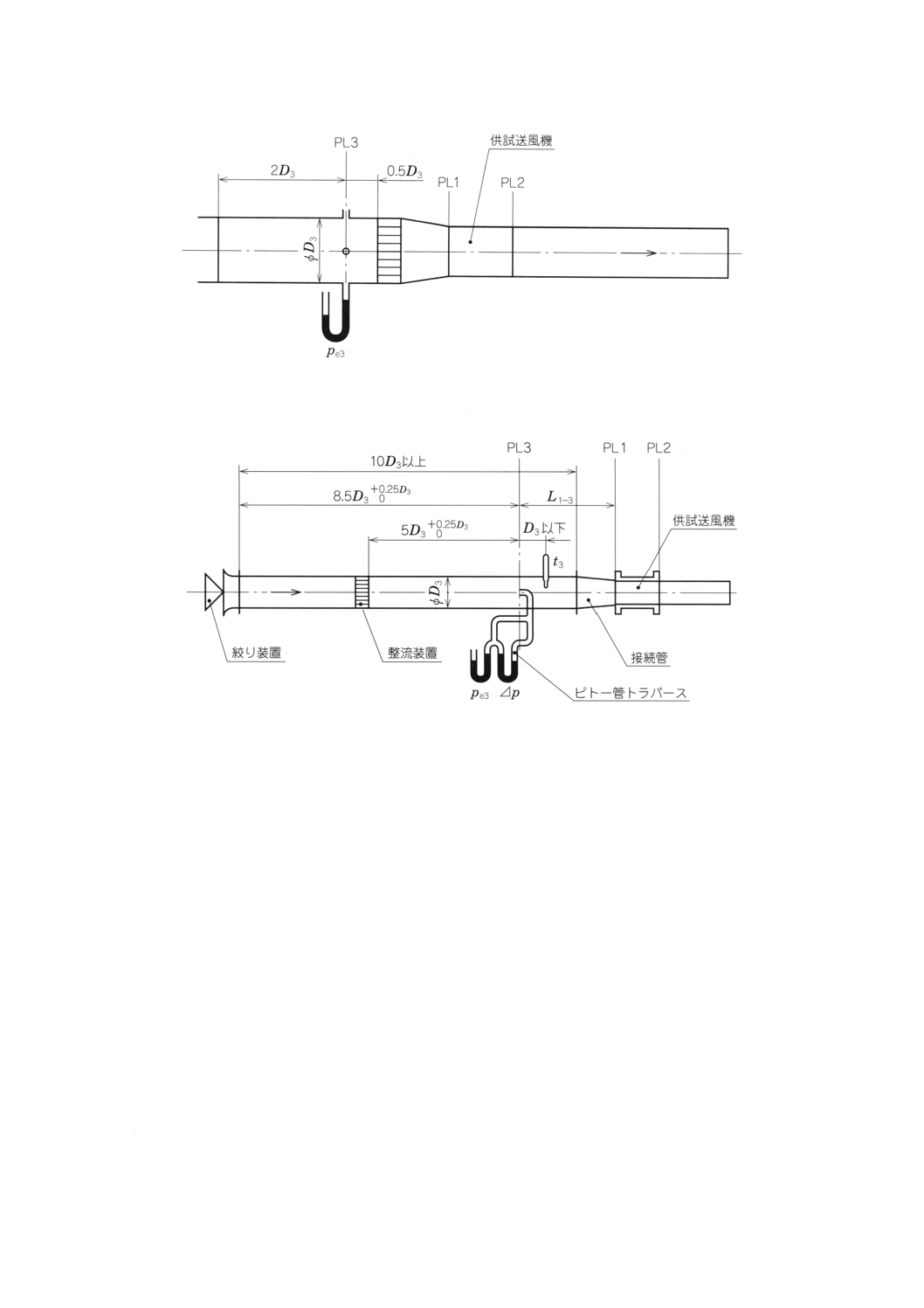
210
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
備考 流量の測定は,34.2.3.1.1及び附属書図74c)による。
f) 接続形式C(吸込側測定管路)及び吐出し模擬管路をもつが,旋回流防止装置を備えない場合
(これは大形の送風機の場合で,当事者間の協定に基づいて使用してもよい。)
備考 流量の測定は,34.2及び附属書図74g)による。
g) 接続形式C(吸込側測定管路)及び吐出し模擬管路をもつが,旋回流防止装置を備えない場合
(これは大形の送風機の場合で,当事者間の協定に基づいて使用してもよい。)
附属書図76 接続形式D(続き)
35.2 接続形式Bの装置で,吐出し側に旋回流防止装置及び吸込管路又は吸込管路模擬部分を備えた場合
35.2.1 質量流量の算出
質量流量は,次の方法で算出決定する。
− 管路内ISOベンチュリノズルによる,附属書図72a)及び附属書図76a)参照。
− 管壁静圧孔をもつオリフイス板による,附属書図72b)及び附属書図76a)参照。
− D・D/2タップをもつ管路内オリフイス板による,附属書図72c)及び附属書図76a)参照。
− コーナタップをもつ管路内オリフイス板による,附属書図72c)及び附属書図76a)参照。
− ピトー静圧管トラバースによる,附属書図72d),e)及び附属書図76a)参照。
− 管路内ベンチュリノズルによる,附属書図72f)及び附属書図76a),b)参照。
− 空気槽末端のベンチュリノズルによる,附属書図72g)及び附属書図76a),b)参照。
− 空気槽内マルチノズルによる,附属書図72h)及び附属書図76a),b)参照。
35.2.2 試験中に実施する測定(20.参照)
測定項目
− 回転速度N,又は回転周波数n
211
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 送風機への入力,Pa,Pe,Poびインペラ動力の推定(10.4参照)
− 吸込圧力,pe3
− 吐出し圧力,pe4
− 流量計の上流圧力pe6
− 差圧∆p
− 空気そう温度t6
試験時の囲い内の測定項目
− 送風機の平均高度における大気圧pa
− 周囲温度(送風機吸込口付近)ta
− 乾・湿球温度td及びtw
周囲の空気密度,ρa,及び湿り空気のガス定数Rwを算出する(12.参照)
35.2.3 圧縮性流体に対する一般的な方法
基準マッハ数Ma2refが0.15を超え,かつ圧力比が1.02を超える場合には,この方法を適用する。
35.2.3.1 質量流量の算出
35.2.3.1.1 質量流量の測定は,次による。
− 管路内ISOベンチュリノズルによる,22.及び附属書図72a)参照。
− 管壁静圧孔をもつ吐出し側オリフイス板による,26.9及び附属書図72b)参照。
− D・D/2タツプをもつ管路内オリフイス板による,26.7及び附属書図72c)参照。
− コーナタツプをもつ管路内オリフイス板による,26.8及び附属書図72c)参照。
33.2.3.1.1に記述した方法に従う。
35.2.3.1.2 ピトー静圧管トラバースによる質量流量の算出。27.並びに附属書図72d)及びe)参照。
33.2.3.1.2に記述した方法に従う。
35.2.3.1.3 管路内ベンチュリノズルによる質量流量の算出。23.及び附属書図72f)参照。
33.2.3.1.3に記述した方法に従う。
35.2.3.1.4 質量流量は次の方法を使って算出する。
− 空気槽末端のノズルによる。23.及び附属書図72g)参照。
− 空気槽内マルチノズルによる。23.及び附属書図72h)参照。
33.2.3.1.4に記述した方法に従う。
35.2.3.2 送風機圧力の算出
35.2.3.2.1 送風機吐出し口圧力
次のように仮定する(33.2.3.2.1参照)
p4=pe4+pa
又は
p
m
e
r
1
sg
2
sg
4
sg
or
c
q
P
P
+
Θ
=
Θ
=
Θ
マッハ数Ma4及び比Θsg4/Θ4は,14.4.3.1に従って算出する。
sg4
4
sg4
4
Θ
Θ
Θ
=
Θ
4
w
4
4
Θ
=Rp
ρ
212
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
600
1
40
4
1
64
44
24
4
M
Ma
Ma
Ma
F
+
+
+
=
(14.5.1参照)
送風機吐出しのせき止め圧力psg2は,次の式に示す。
(
)
[
]
(
)
[
]
4
4
2
4
M
2
4
m
4
4
4
4
2
4
M
4
m
2
4
4
2
sg
1
2
1
1
2
−
−
+
+
=
+
+
=
ξ
ρ
ξ
ρ
F
A
q
p
F
V
p
p
又は
(
)
[
]
4
4
2
4
M
2
4
m
4
e4
2
esg
1
2
1
−
+
+
=
ξ
ρ
F
A
q
p
p
(ζ2−4)4は,30.6.1又は30.6.2,及び附属書図65に従って算出する。
静圧p2は,次の式で示される。
2
M
2
2
m
2
sg2
M2
2
m
2
2
sg2
2
2
1
2
F
A
q
p
F
V
p
p
−
=
−
=
ρ
ρ
又は
2
M
2
2
m
2
esg2
2e
2
1
F
A
q
p
p
−
=
ρ
ここに,Ma2,ρ2,FM2は,14.4.3.2及び14.5に従って算出する。
35.2.3.2.2 送風機吸込口圧力
a) 30.3a),b),c),d)及びe)に従う吸込管路の場合(34.2.3.2.1参照)
吸込圧力pe3を測定する。
p3=pa+pe3
Θsg3=Θsg1=Θa=ta+273.15
マッハ数Ma3及び流体温度Θ3は,14.4.3.1に従って算出する。
3
w
3
3
Θ
=Rp
ρ
(
)
[
]
3
1
3
M3
2
3
m
3
3
sg1
1
2
1
−
+
+
=
ξ
ρ
F
A
q
p
p
又は
(
)
[
]
3
1
3
M3
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
F
A
q
p
p
(ζ3−1)3≦0は,30.6.4,30.6.5,30.6.6及び附属書図65a),b)に従って算出する。
b) 30.5又は30.3a),b),c),d),e)に従う吸込模擬管路の場合
吸込圧力pe3は,測定しない。
213
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
管路吸込口の上流のせき止め圧力は大気圧paで,送風機吸込口のせき止め温度Θsg1は周囲温度に等
しい。
Θsg1=Θa=ta+273.15
送風機の吸込せき止め圧力psg1は,次の式に示す。
(
)3
1
3
M3
2
3
m
3
a
sg1
2
1
−
+
=
ξ
ρ
F
A
q
p
p
又は
(
)3
1
3
M3
2
3
m
3
esg1
2
1
−
=
ξ
ρ
F
A
q
p
ここに,
ρ3はベルマウス下流にある管路入口の空気密度で,14.4.3.2に従ってMa3を求
めた後で,14.4.4に従って算出する。
(ζ3−1)3≦0は,断面3(吸込ベルマウスのスロート部)と送風機吸込口の断面1
との間の損失係数である。この係数は30.6.4,30.6.5,及び30.6.6に従って算出
する。
(
)
3
3
1
3
D
L
Λ
−
=
−
ξ
Lは管路の長さである(30.3及び30.5参照)
D3は管路の直径である。
Λはレイノルズ数ReD3に依存する。
圧力p1は,14.5.2に従って算出する。
M1
2
1
m
1
sg1
1
2
1
F
A
q
p
p
−
=
ρ
又は
M1
2
1
m
1
esg1
e1
2
1
F
A
q
p
p
−
=
ρ
ここに,Ma1, ρ1 and FM1は,14.4.3.2,14.4.4,及び14.5.2に従って算出する。
35.2.3.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式で算出する。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=pe2−pesg1
平均密度は次の値に等しい。
2
2
1
m
ρ
ρ
ρ
+
=
m
1
ρ
ρ
ρ=
k
35.2.3.3 体積流量の算出
214
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
体積流量は次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
ここに,
sg1
w
sg1
sg1
Θ
=Rp
ρ
35.2.3.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,14.8.1,14.8.2,及び33.2.3.4に従って算出する。
35.2.3.5 送風機効率の算出
33.2.3.5に記述した方法に従う。
35.2.4 簡略法
35.2.4.1 マッハ数 Ma2refが0.15未満で圧力比が1.02を超える場合
測定管路の断面で,せき止め温度と静温度が等しいとみなす。
FM1=FM2=1
Θx=Θsgx
よって,管路内の温度を測定し,せき止め温度とする。
35.2.4.1.1 質量流量の算出
質量流量は33.2.3.1及び35.2.3.1に記述した方法に従って算出する。
ただし,次の簡略方法を適用する。
流量計の上流温度を測定するので,質量流量の算出に流体温度の推定のための逐次近似は必要としない。
流量係数αに対するレイノルズ数の影響は,考慮する。
35.2.4.1.2 送風機圧力の算出
35.2.4.1.2.1 送風機吐出し口圧力
14.9.1.2,14.9.1.3及び33.2.4.1.2.1に従って,
(
)
[
]
4
4
2
2
4
m
4
4
sg2
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
又は
(
)
[
]
4
4
2
2
4
m
4
e4
esg2
1
2
1
−
+
+
=
ξ
ρ A
q
p
p
ここに,
sg4
w
4
4
w
4
4
Θ
=
Θ
=
R
p
R
p
ρ
p
m
e
r
sg1
sg4
or
c
q
P
P
+
Θ
=
Θ
(ζ2−4)4は,30.6.1,30.6.2及び30.6.3,並びに附属書図65に従って算出する。
圧力p2は,次の方法によって算出する(14.9.1.4参照)
()
2
2
m
2
sg
sg2
1
2
2
1
−
=
A
q
p
ρ
ρ
215
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
sg2
w
2.1
1
2
Θ
=Rp
ρ
()
2
2
m
1
2
sg2
2
2
1
−
=
A
q
p
p
ρ
()
2
2
m
1
2
esg2
e2
2
1
−
=
A
q
p
p
ρ
sg2
w
2
2
Θ
=Rp
ρ
又は,次の式による。
2
2
sg2
w
2
2
m
sg2
2
sg2
2
Θ
−
+
=
R
A
q
p
p
p
35.2.4.1.2.2 送風機吸込口圧力
a) 30.3a),b),c),d),e)及び30.5に従う吸込管路(34.2.4.1.2.1参照)
吸込圧力pe3を測定する。
Θ3=Θsg3=ta+273.15
p3=pe3+pa
3
w
3
3
Θ
=Rp
ρ
(
)
[
]
3
1
3
2
3
m
3
3
sg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
(
)
[
]
3
1
3
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
(ζ3−1)3≦0(30.6.4,30.6.5,及び30.6.6参照)
b) 30.3a),b),c),d)及び30.5に従う吸込模擬管路
吸込圧力pe3は,測定しない。
吸込ベルマウス(直径D3)のスロート部圧力p3を次の方法で算出する(14.9.1.4参照)。
()
2
3
m
a
a
1
3
2
1
−
=
A
q
p
p
ρ
()
3
w
3.1
1
3
Θ
=Rp
ρ
()
2
3
m
1
3
a
3
2
1
−
=
A
q
p
p
ρ
216
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3
w
3
3
Θ
=Rp
ρ
2〜3回の反復計算で十分である。圧力p3は次の式でも算出できる。
Θ
−
+
=
3
w
2
3
m
2a
a
3
2
2
1
R
A
q
p
p
p
送風機吸込口のせき止め圧力は,次の式に示す。
(
)
[
]
3
1
3
2
3
m
3
3
sg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
(
)3
1
3
2
3
m
3
a
sg1
2
1
−
+
=
ξ
ρ
A
q
p
p
pesg1=psg1−pa
(ζ3−1)3≦0は,30.6.4,30.6.5,30.6.6及び35.2.3.2.2に従って算出する。
圧力p1は,14.9.1.4に記述した2種類の方法のうちのどちらかで算出する。
35.2.4.1.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式で算出する。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=pe2−pesg1
送風機の取り扱う空気の平均密度は次の値に等しい。
2
2
1
m
ρ
ρ
ρ
+
=
及び
m
1
ρ
ρ
ρ=
k
35.2.4.1.3 体積流量の算出
体積流量は次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
ここに,
sg1
w
sg1
sg1
Θ
=Rp
ρ
35.2.4.1.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,14.8.1,14.8.2,14.8.3,14.9.1及び33.2.3.4に従って
算出する。
35.2.4.1.5 送風機効率の算出
14.8.1に記述した方法に従う(33.2.3.5参照)。
35.2.4.2 基準マッハ数Ma2refが0.15未満で圧力比が1.02未満の場合
測定管路の断面で,せき止め温度と静温度は等しいとみなす。
217
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Θsgx=Θx
FM1=FM2=1
ρ1=ρ2=ρ3=ρsg1=ρsg2=ρsg3=ρa=
a
w
a
Θ
R
p
Θ1=Θsg1=Θsg2=Θ2=Θsg3=Θ3=ta+273.15
試験通風路を通る流れが非圧縮性であるという仮定に基づいた方法を適用する。
35.2.4.2.1 質量流量の算出
質量流量は,33.2.3.1及び33.2.4.2.1に記述した方法で,ρu=ρsg1とおいて算出する。ただし,流量係数α
に対するレイノルズ数の影響は考慮に入れる。
35.2.4.2.2 送風機圧力の算出
35.2.4.2.2.1 送風機吐出し口圧力
せき止め圧力psg2は,次の式で示される(33.2.4.2.2.1参照)
(
)
[
]
4
4
2
2
4
m
1
4
sg2
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
ここに,(ζ2−4)4は30.6.1,30.6.2並びに附属書図65a)及びb)に従って算出する。
(
)
[
]
4
4
2
2
4
m
1
e4
esg2
1
2
1
−
+
+
=
ξ
ρA
q
p
p
2
2
m
1
sg2
2
2
1
−
=
A
q
p
p
ρ
2
2
m
1
esg2
e2
2
1
−
=
A
q
p
p
ρ
35.2.4.2.2.2 送風機吸込口圧力(34.2.4.2.2.1参照)
(
)
[
]
3
1
3
2
3
m
1
3
sg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
(pe3が測定される場合)
又は,pe3が測定されない場合
(
)3
1
3
2
3
m
1
a
sg1
2
1
−
+
=
ξ
ρ
A
q
p
p
(
)3
1
3
2
3
m
1
esg1
2
1
−
=
ξ
ρ
A
q
p
ここに,(ζ3−1)3≦0は,30.6.4,30.6.5,30.6.6,35.2.3.2.1又は35.2.3.2.2に従って
算出する。
静圧p1は次の式に示す。
218
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
1
m
1
sg1
1
2
1
−
=
A
q
p
p
ρ
35.2.4.2.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式に示す。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=pe2−pesg1
35.2.4.2.3 体積流量の算出
体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
35.2.4.2.4 理論空気動力の算出
理論空気動力puD及び理論静圧空気動力pusDは,次の式に示す。
PuD=pFDqvsg1
PusD=psFDqvsg1
35.2.4.2.5 送風機効率の算出
送風機効率は次式で算出する
r
uD
rD
P
P
=
η
r
usD
usD
P
P
=
η
35.3 接続形式Bの装置で,吐出し側に旋回流防止装置も共通部分もないが,吸込管路又は吸込模擬管路
を備えた場合
この構成は,吐出しに旋回流が小さい送風機に適用する。
35.3.1 流量の算出
流量は次の方法で測定する
− 空気槽末端のベンチュリノズルによる,23.,附属書図73a)及び附属書図76d)参照。
− 空気槽内マルチノズルによる,23.,附属書図73b)及び附属書図76d)参照。
35.3.2 試験中に実施する測定(20.参照)
測定項目
− 回転速度N又は回転周波数n
− 送風機への入力,Pa,Po,又はPeの測定及びインペラ動力の推定(10.4参照)
− 吐出し圧力,pe4
− 流量計の上流圧力,pe6
− 差圧,∆p
− 空気そう温度,t6
試験時の囲い内の測定項目
− 送風機の平均高度における大気圧pa
− 送風機吸込付近での送風機周囲温度ta
− 乾・湿球温度,td及びtw
219
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
周囲の空気密度ρa,及び湿り空気のガス定数Rwを求める(12.参照)。
35.3.3 圧縮性流体に対する一般的な方法
この方法は,基準マッハ数Ma2refが0.15を超え,かつ圧力比が1.02を超える場合に適用する。
35.3.3.1 質量流量の算出
質量流量は次の方法で求める。
− 空気槽末端のノズル,23及び附属書図73a)参照。
− 空気槽内マルチノズル,23及び附属書図73b)参照。
33.3.3.1.1に記述した方法に従う。
35.3.3.2 送風機圧力の算出
35.3.3.2.1 送風機吐出し口圧力
33.3.3.2.1に記述した方法に従う。ただし,(ζ2−4)4=0で,断面A2.4は空気槽の吐出し部に設置する測定
管路の断面積である。
35.3.3.2.2 送風機吸込口圧力
35.2.3.2.2に記述した方法に従う。
35.3.3.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,35.2.3.2.3と同様にして求める。
35.3.3.3 体積流量の算出
体積流量は,次の式に示す
sg1
m
1
vsg
ρ
q
q
=
35.3.3.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,14.8.1,14.8.2.1及び14.8.2.2に従って33.2.3.4に記述
した方法と同様にして算出する。
35.3.3.5 送風機効率の算出
33.2.3.5に記述した方法に従う。
35.3.4 簡略方法
35.3.4.1 基準マッハ数Ma3refが0.15未満であるが,圧力比が1.02を超える場合
測定管路の断面で,せき止め温度と静温度が等しいとみなす。
Θx=Θsgx
FM1=FM2=1
測定管路内の温度を測定し,せき止め温度として定義する。
35.3.4.1.1 質量流量の算出
質量流量は,23.及び33.3.4.1.1に記述した方法に従って算出する。
35.3.4.1.2 送風機圧力の算出
35.3.4.1.2.1 送風機吐出し口圧力
送風機吐出しせき止め圧力psg2及び圧力p2は,33.3.4.1.2.1と同じ方法で算出する。ただし,A2−4は空気
槽への吐出し部の測定管路断面積である。
35.3.4.1.2.2 送風機吸込口圧力
35.2.4.1.2.2に記述した方法に従う。
35.3.4.1.2.3 送風機圧力
220
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
送風機圧力pFD及び送風機静圧psFDは,35.2.4.1.2.3で用いた方法で算出する。
35.3.4.1.3 体積流量の算出
体積流量は次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
35.3.4.1.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,14.8.1,14.8.2及び33.2.3.4に従って算出する。
35.3.4.1.5 送風機効率の算出
33.2.3.5で用いた方法に従う。
35.3.4.2 基準マッハ数Ma2refが0.15未満で,かつ圧力比が1.02未満の場合
測定管路の断面で,せき止め温度と静温度とは等しいとみなす。
Θx=Θsgx
ρ1=ρsg1=ρ2=ρsg2=ρ3=ρ4=ρ6=
a
w
a
Θ
R
p
FM1=FM2=1
測定管路内の温度を測定し,試験通風路を通る流れは非圧縮性とみなす。
35.3.4.2.1 質量流量の算出
質量流量は,33.3.3.1.1に記載した方法で,ρ6=ρaとして算出する。ただし,流量係数αに対するレイノ
ルズ数の影響は考慮に入れる。
35.3.4.2.2 送風機圧力の算出
35.3.4.2.2.1 送風機吐出し口圧力
せき止め圧力psg2及び静圧p2は,33.3.4.2.2.1で使用した方法で算出する。
ここに,(ζ2−4)4=0で,A2.4は空気槽への吐出し部の測定管路断面積である。
35.3.4.2.2.2 送風機吸込圧力
せき止め圧力psg1及び静圧p1は,35.2.4.2.2.2で用いた方法で算出する。
35.3.4.2.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,35.2.4.2.2.3で用いた方法で算出する。
35.3.4.2.3 体積流量の算出
体積流量は次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
35.3.4.2.4 理論空気動力の算出
35.2.4.2.4の方法に従う。
35.3.4.2.5 送風機効率の算出
送風機効率は,35.2.4.2.5で用いた方法で算出する。
35.4 接続形式Cの装置で,吐出し管路共通部分,旋回流防止装置及び吸込管路共通部分を備えた場合
35.4.1 質量流量の算出
質量流量は次の方法で測定する
− 吸込側ISOベンチュリノズルによる,附属書図74a)及び76c)参照。
− 四分円インレツトノズルによる,附属書図74a)及び76c)参照。
221
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− コニカルインレツトによる,附属書図72a)及び76c)参照。
− コーナタツプをもつ吸込側オリフイス板による,附属書図74b)及び76c)参照。
− 管壁静圧孔をもつ吸込側オリフイス板による,附属書図74c)及び76c)参照。
− 管壁静圧孔をもつ吸込側オリフイス板による,附属書図74d)及び76c)参照。
− D・D/2タツプをもつ管路内オリフイス板による,附属書図74e)及び76c)参照。
− コーナタツプをもつ管路内オリフイス板による,附属書図74e)及び76c)参照。
− ピトー静圧管トラバースによる,附属書図74f)及び76c)参照。
− ピトー静圧管トラバースによる,附属書図74g)及び76c)参照。
35.4.2 試験中に実施する測定(20.参照)
測定項目
− 回転速度N又は回転周波数n
− 送風機への入力Pa,Po,Pe,及び,インペラ動力の推定(10.4参照)
− 流量計の差圧,∆p
− 流量計の上流圧力,pe7又は,pe3
− 吸込静圧,pe3
− 吐出し静圧,pe4
試験時の囲い内の測定項目
− 送風機の平均高度での大気圧,pa
− 管路の吸込付近の周囲温度,ta
− 乾・湿球温度,td及びtw
周囲の空気密度ρa及び湿り空気のガス定数Rwを算出する(12参照)。
35.4.3 圧縮性流体に対する一般的な方法
基準マッハ数Ma2ref(14.4.2参照)が0.15を超え,かつ圧力比が1.02を超える場合には,この方法を適
用する。
35.4.3.1 質量流量の算出
35.4.3.1.1 流量は次の方法で測定する。
− 吸込側ISOベンチュリノズルによる,22.及び附属書図74a)参照。
− 四分円インレツトノズルによる,24.及び附属書図74a)参照。
− コニカルインレツトによる,25.及び附属書図74a)参照。
− コーナタツプをもつ吸込側オリフイス板による,26.10a)及び附属書図74b)参照。
− コーナタツプをもつ吸込側オリフイス板による,26.10b)及び附属書図74b)参照。
− 管壁静圧孔をもつ吸込側オリフイス板による,26.11及び附属書図74d)参照。
34.2.3.1.1に記述した方法に従う。
35.4.3.1.2 D・D/2タップ又はコーナタップをもつ管路内オリフィス板による流量の算出,26.7,と26.8及
び附属書図74e)を参照。
34.2.3.1.2に記載した方法に従う。
35.4.3.1.3 ピトー管トラバースによる流量の算出,27.並びに附属書図74f)とg)参照。
34.2.3.1.3に記載した方法に従う。
35.4.3.2 送風機圧力の算出
35.4.3.2.1 送風機吸込圧力
222
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
せき止め圧力psg1及び静圧p1は,34.2.3.2.1に記載した方法に従って算出する。
35.4.3.2.2 送風機吐出し圧力
せき止め圧力psg2及び静圧p2は,次の方法で算出する(33.3.2.1参照)。
次のように仮定する。
p4=pe4+pa
p
m
e
r
sg1
sg2
sg4
or
c
q
P
P
+
Θ
=
Θ
=
Θ
断面4でのマッハ数及び静温度Θ4は,14.4.3.1に従って算出する。
sg4
4
sg4
4
Θ
Θ
Θ
=
Θ
4
w
4
4
Θ
=Rp
ρ
600
1
40
4
1
64
44
24
4
M
Ma
Ma
Ma
F
+
+
+
=
(14.5.1参照)
断面2と断面4との間の摩擦損失係数(ζ2−4)4は,30.6及び付属書図65に従って算出する。
せき止め圧力psg2は,次の式に示す。
(
)
[
]
(
)
[
]
4
4
2
4
M
2
4
m
4
4
4
4
2
4
M
4
m
2
4
4
sg2
1
2
1
1
2
−
−
+
+
=
+
+
=
ξ
ρ
ξ
ρ
F
A
q
p
F
V
p
p
又は
(
)
[
]
4
4
2
4
M
2
4
m
4
e4
esg2
1
2
1
−
+
+
=
ξ
ρ
F
A
q
p
p
静圧p2及び密度ρ2は,14.5.2に従って算出する。Ma2は,14.4.3.2に従って算出する。
M2
2
2
m
2
sg2
2
2
1
F
A
q
p
p
−
=
ρ
又は
M2
2
2
m
2
esg2
e2
2
1
F
A
q
p
p
−
=
ρ
35.4.3.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式に示す。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=pe2−pesg1
2
2
1
m
ρ
ρ
ρ
+
=
m
1
ρ
ρ
ρ=
k
223
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
35.4.3.3 体積流量の算出
体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
sg1
w
sg1
1
sg
Θ
=Rp
ρ
35.4.3.4 理論空気動力の算出
単位質量当たりの送風機仕事と理論空気動力は,34.2.3.4に従って算出する。
35.4.3.5 送風機効率の算出
送風機効率は,34.2.3.5に従って算出する。
35.4.4 簡略方法
35.4.4.1 基準マッハ数Ma2refが0.15未満だが,圧力比が1.02を超える場合
測定管路の断面で,せき止め温度と静温度は,等しいとみなす。
Θx=Θsgx=tx+273.15
断面xの温度を測定する。
マッハ係数FM1とFM2は1とする
35.4.4.1.1 質量流量の算出
それぞれの装置構成に応じて,34.2.3.1及び34.2.4.1.1に記述した方法に従う。
35.4.4.1.2 送風機圧力の算出
35.4.4.1.2.1 吸込圧力
せき止め圧力psg1及び静圧p1は,34.2.4.1.2.1に記載した方法に従って算出する。
35.4.4.1.2.2 送風機吐出し圧力
せき止め圧力psg2及び静圧p2は,次の方法で算出する(33.2.4.1.2.1参照)。
次のように仮定する。
p
m
e
r
sg3
sg4
4
or
c
q
p
p
+
Θ
=
Θ
=
Θ
p4=pe4+pa
4
w
4
4
Θ
=Rp
ρ
(
)
[
]
4
4
2
2
4
m
4
4
sg2
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
又は
(
)
[
]
4
4
2
2
4
m
4
e4
esg2
1
2
1
−
+
+
=
ξ
ρ A
q
p
p
p2は,次のように算出する(14.9.1.4参照)
()
2
2
m
2
sg
sg2
1
2
2
1
−
=
A
q
p
ρ
ρ
224
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
()
4
w
1
2
1
2
Θ
=Rp
ρ
()
2
2
m
1
2
sg2
2
2
1
−
=
A
q
p
p
ρ
()
2
2
m
1
2
esg2
2e
2
1
−
=
A
q
p
p
ρ
2〜3回の反復計算で十分である。
又は
2
2
sg2
w
2
2
m
sg2
2
sg2
2
Θ
−
=
R
A
q
p
p
p
2
w
2
2
Θ
=Rp
ρ
35.4.4.1.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式に示す。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=pe2−pesg1
2
2
1
m
ρ
ρ
ρ
+
=
m
1
ρ
ρ
ρ=
k
35.4.4.1.3 体積流量の算出
体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
35.4.4.1.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,14.8.1,14.8.2及び34.2.3.4又は35.2.3.4に従って算
出する。
35.4.4.1.5 送風機効率の算出
送風機効率は,14.8.1と34.2.3.5に従って算出する。
35.4.4.2 基準マッハ数Ma2refが0.15未満で,かつ圧力比が1.02未満の場合
試験通風路を通る流れは非圧縮性とみなしてよい。ただし,断面3と5との間に補助送風機のある場合
は除く[附属書図74c)を参照]
Θ3=Θsg3=Θ1=Θsg1=Θ2=Θsg2=t3+273.15
ρ1=ρ2=ρ3
FM1=FM2=1
kp=1
35.4.4.2.1 質量流量の算出
225
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
質量流量は,34.2.4.1.1に記載した方法及び34.2.4.2の仮定に従って算出する。
35.4.4.2.2 送風機圧力の算出
35.4.4.2.2.1 送風機吸込口圧力
せき止め圧力psg1及び静圧p1は,次の方法で算出する(34.2.4.2.2.1参照)。
次のように仮定する。
p3=pe3+pa
1
w
3
1
Θ
=Rp
ρ
(
)
[
]
3
1
3
2
3
m
1
3
sg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
[34.2.3.2.1b)参照]
(
)
[
]
3
1
3
2
3
m
1
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
2
1
m
1
sg1
1
2
1
−
=
A
q
p
p
ρ
2
1
m
1
esg1
1e
2
1
−
=
A
q
p
p
ρ
35.4.4.2.2.2 送風機吐出し口圧力
せき止め圧力psg2及び静圧p2は,次の式で算出する(33.2.4.2.2.1参照)。
次のように仮定する。
p4=pe4+pa
(
)
[
]
4
4
2
2
4
m
1
4
sg2
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
又は
(
)
[
]
4
4
2
2
4
m
1
e4
esg2
1
2
1
−
+
+
=
ξ
ρA
q
p
p
2
2
m
1
sg2
2
2
1
−
=
A
q
p
p
ρ
2
2
m
1
esg2
2e
2
1
−
=
A
q
p
p
ρ
35.4.4.2.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式に示す。
pFD=psg2−psg1=pesg2−pesg1
226
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
psFD=p2−psg1=pe2−pesg1
35.4.4.2.3 体積流量の算出
体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
35.4.4.2.4 理論空気動力の算出
14.9.2.6及び34.2.4.1.4に従って
PuD=qvsg1pFD
PusD=qvsg1psFD
35.4.4.2.5 送風機効率の算出
送風機効率は,34.2.4.1.5,14.8.1及び14.8.2に従って算出する。
35.5 接続形式Cの装置で,旋回流防止装置のない吐出し管路模擬部分を備えた場合
これらの構成は,吐出しに旋回流のない送風機,又は大形の送風機で使用してもよい。
これに該当して,この構成で送風機性能を試験する場合は,当事者間の協定が必要である。
この方法で得た結果は,吸込み及び吐出しの両側に標準試験通風路を使用して得た結果とある程度の差
が生じることがあり,特に吐出しに大きな旋回流を生じる送風機の場合に,この傾向が強い。
35.5.1 質量流量の算出
質量流量は,次の方法で測定する。
− 四分円インレットノズルによる,附属書図75a)及び76e)参照。
− 空気そう上流のピトー静圧管トラバースによる,附属書図75b)及び76e)参照。
− 空気そう上流の管路内ベンチュリノズルによる附属書図75c)及び76e)参照。
− 空気そう内マルチノズルによる,附属書図75d)及び76e)参照。
− ピトー静圧管トラバースによる,附属書図74g)及び76g)参照。
− コーナタップをもつ吸込側オリフィス板による,附属書図74c)及び76f)参照。
35.5.2 試験中に実施する測定(20.参照)
測定項目
− 回転速度,N又は回転周波数,n
− 送風機への入力,Pa,Po,又はPeとインペラ動力の推定(10.4参照)。
− 差圧,∆p ;
− 流量計の上流圧力,pe7又はpe5
− 空気槽のせき止め圧力,pesg3又は静圧,pe3
− 空気槽の温度,t3
− 補助送風機への入力Pex(必要な場合)
試験時の囲い内の測定項目
− 送風機の平均高度での大気圧,pa
− 送風機吸込口付近の周囲温度,ta
− 乾・湿球温度,td及びtw
周囲の空気密度ρa及び湿り空気のガス定数Rwを算出する(12.参照)。
35.5.3 圧縮性流体に対する一般的な方法
この方法は,基準マッハ数Ma2refが0.15を超え,かつ圧力比が1.02を超える場合に適用する。
227
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
35.5.3.1 質量流量の算出
35.5.3.1.1 四分円インレットノズルによる質量流量の算出,24,附属書図76e)及び75a)参照。
34.3.3.1.1 に記述した方法に従う。
35.5.3.1.2 ピトー管トラバースによる質量流量の算出,27,附属書図76e)及びg),並びに附属書図74g)及
び75b)参照。
34.3.3.1.2に記述した方法に従う。
35.5.3.1.3 管路内ベンチュリノズルによる質量流量の算出,23,附属書図76e)及び75c)参照。
34.3.3.1.3に記述し方法に従う。
35.5.3.1.4 空気そう内マルチノズルによる質量流量の算出,23,附属書図76e)及び75d)参照
34.3.3.1.4に記述した方法に従う。
35.5.3.1.5 コナタップをもつ吸込側オリフィス板による質量流量の算出,22.,24.,25.,26.7,26.8,26.10,
26.11及び附属書図76f),74a)〜74e)参照。
34.2.3.1.1〜34.2.3.1.3に記述した方法に従う。
35.5.3.2 送風機圧力の算出
35.5.3.2.1 送風機吸込口圧力
35.5.3.2.1.1 吸込圧力pe3を吸込管路で測定する場合には,附属書図74a)〜74d)及び76f)参照。
34.2.3.2.1参照。
a) 断面5と断面3との間に補助送風機がない場合
p3=pe3+pa
Θsg3=Θsg7=Θa=Θsg1=ta+273.15
マッハ数Ma3及び比
sg3
3
Θ
Θ
は,14.4.3.1に従って算出する。
sg3
3
sg3
3
Θ
Θ
Θ
=
Θ
3
w
3
3
Θ
=Rp
ρ
せき止め圧力psg1は,次の式に示す(14.5参照)
(
)
[
]
3
1
3
M3
2
3
m
3
3
sg1
1
2
1
−
+
+
=
ξ
ρ
F
A
q
p
p
(
)
[
]
3
1
3
M3
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
F
A
q
p
p
ここに,
(ζ3−1)3≦0は,断面1と3の間の損失係数で,30.6.4, 30.6.5及び30.6.6に従って
算出する(34.2.3.2.1参照)
FM3はマッハ係数である(14.5.1参照)
b) 断面5と断面3との間に補助送風機がある場合[34.2.3.2.1b)を参照]
補助送風機のインペラ動力Prx又は管路内に電動機が設置されている補助送風機の電動機動力Pexを
測定する場合
228
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
sg1
p
m
ex
rx
sg7
sg3
or
Θ
=
+
Θ
=
Θ
c
q
P
P
その他の場合は,吸込管路の温度を測定してせき止め温度tsg3と仮定する。温度Θ3は,14.4.3.1に従
って算出し,せき止め圧力psg1は上記のように算出する。
マッハ数Ma1及び比
sg1
1
Θ
Θ
をΘsg1=Θsg3として14.4.3.2に従って計算すると,圧力p1が算出される。
密度ρ1は,14.4.4に従って算出し,p1は次の式に示す。
M1
2
1
m
1
sg1
1
2
1
F
A
q
p
p
−
=
ρ
又は
M1
2
1
m
1
esg1
e1
2
1
F
A
q
p
p
−
=
ρ
35.5.3.2.1.2 吸込圧力pe3を空気槽内で測定する場合(34.3.3.2.1参照)
a) 空気槽内で測定した圧力がゲージ圧力pe3の場合
次のように仮定する。
FM31
p3=pe3+pa
Θsg1=Θsg3=Θ3=t3+273.15
3
w
3
3
Θ
=Rp
ρ
断面3のせき止め圧力,psg3は,次の式に示す。
2
3
m
3
3
sg3
2
1
+
=
A
q
p
p
ρ
b) 空気槽内で測定した圧力がゲージせき止め圧力,pesg3の場合
psg3=pesg3+pa
Θsg3=Θ3=Θsg1=t3+273.15
吸込模擬管路の長さが1D1又は2D1の場合には,損失がないとして次による。
psg1=psg3
pesg1=pesg3
吸込模擬管路の長さを1D1又は2D1より長くする必要がある場合には,管路損失を考慮する。
せき止め圧力psg1は,次の式に示す。
(
)1
1
3
M3.1
2
1
m
1.3
sg3
sg1
2
1
−
+
=
ξ
ρ
F
A
q
p
p
又は
(
)1
1
3
M3.1
2
1
m
1.3
esg3
esg1
2
1
−
+
=
ξ
ρ
F
A
q
p
p
229
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
ρ3.1はベルマウスのスロート部の空気密度で,14.4.3.2と14.4.4によって算出す
る。
FM3.1は,マッハ数Ma3.1に対応するマッハ係数である。
(ζ3−1)1は,30.6.4と30.6.5に従って算出する損失係数である。
(
)
0
1
1
1
3
≦
D
L
Λ
−
=
−
ξ
Lは直径D1の吸込模擬管路の長さである。
圧力p1は,次の式に示す。
M1
2
1
m
1
sg1
1
2
1
F
A
q
p
p
−
=
ρ
ここにMa1,ρ1及びFM1は,14.4.3.2,14.4.4及び14.5に従って算出する。
M1
2
1
m
1
esg1
e1
2
1
F
A
q
p
p
−
=
ρ
35.5.3.2.2 送風機吐出し口圧力
吐出し管路には摩擦損失がないとする。
p2=pa or pe2=0
p
m
e
r
sg1
sg2
or
c
q
P
P
+
Θ
=
Θ
せき止め圧力psg2は,次の式で示す。
M2
2
2
m
2
2
sg2
2
1
F
A
q
p
p
+
=
ρ
又は
M2
2
2
m
2
esg2
2
1
F
A
q
p
=ρ
ここに,
ρ2は送風機吐出し口の密度で次の式に示す。
2
w
2
2
Θ
=Rp
ρ
Ma2及びΘ2は,14.4.3.1に従って算出する。
35.5.3.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式で算出する。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=−pesg1
2
2
1
m
ρ
ρ
ρ
+
=
230
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
m
1
ρ
ρ
ρ=
k
35.5.3.3 体積流量の算出
体積流量は次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
ここに,
sg1
w
sg1
sg2
Θ
=Rp
ρ
35.5.3.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,34.2.3.4に記述した方法に従って算出する。
35.5.3.5 送風機効率の算出
34.2.3.5に記述した方法に従う。
35.5.4 簡略方法
35.5.4.1 基準マッハ数Ma2refが0.15未満で圧力比が1.02を超える場合
測定管路の断面で,流体のせき止め温度と静温度は等しいとみなす。
FM1=FM2=1
Θx=Θsgx
測定管路内の温度を測定し,せき止め温度と定義する。
35.5.4.1.1 質量流量の算出
質量流量は,34.2.4.1.1及び34.3.4.1.1に記述した方法に従って算出する。
ただし,次の簡略方法を適用する
流量計の上流温度を測定し,逐次近似をする必要はない。
35.5.4.1.2 送風機圧力の算出
35.5.4.1.2.1 送風機吸込口圧力
35.5.4.1.2.1.1 吸込圧力pe3を測定管路内で測定する場合(34.2.4.1.2.1参照)
p3=pe3+pa
Θ3=Θsg3=Θsg1=t3+273.15
せき止め圧力は,次の式に示す。
(
)
[
]
3
1
3
2
3
m
3
3
sg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
又は
(
)
[
]
3
1
3
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
ここに,(ζ3−1)3≦0は35.5.3.2.1.1に従って算出する[34.2.3.2.1a)及びb)参照]。
圧力p1は,次の方法で算出する。
()
2
1
m
3
sg1
1
1
2
1
−
=
A
q
p
p
ρ
231
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
()
3
w
1
1
1
1
Θ
=Rp
ρ
()
2
1
m
1
1
sg1
1
2
1
−
=
A
q
p
p
ρ
又は
()
2
1
m
1
1
esg1
e1
2
1
−
=
A
q
p
p
ρ
又は
2
2
sg1
w
2
1
m
sg1
2
sg1
1
Θ
−
+
=
R
A
q
p
p
p
pe1=p1−pa
35.5.4.1.2.1.2 吸込圧力pe3又はpesg3を空気槽内で測定する場合(34.3.4.1.2.1参照)
pe3を測定する場合は,
p3=pe3+pa
Θ3=Θsg3=Θsg1=t3+273.15
2
3
m
3
3
sg3
2
1
+
=
A
q
p
p
ρ
ここに,
3
w
3
3
Θ
=Rp
ρ
pesg3を測定する場合は,
psg3=pesg3+pa
通常の場合は,
psg1=psg3
pesg1=pesg3
管路摩擦損失を考慮する場合は次の方法を適用する。
(
)1
1
3
2
1
m
1.3
esg3
esg1
2
1
−
+
=
ξ
ρ
A
q
p
p
又は
(
)1
1
3
2
1
m
1.3
sg3
sg1
2
1
−
+
=
ξ
ρ
A
q
p
p
ここに,
(
)
0
1
1
3
≦
−
ξ
は,損失係数である(35.5.3.2.1.2参照)。
1
w
3.1
sg3
w
3.1
sg1
w
3.1
3.1
Θ
≈
Θ
=
Θ
=
R
p
R
p
R
p
ρ
232
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ベルマウスのスロート部圧力p3.1は,14.9.1.4及び34.3.4.1.2.1と同様に逐次近似によって算出する。
2
1
m
1
sg1
1
2
1
−
=
A
q
p
p
ρ
又は
2
1
m
1
esg1
e1
2
1
−
=
A
q
p
p
ρ
又は
2
2
sg1
w
2
1
m
sg1
2
sg1
1
Θ
−
+
=
R
A
q
p
p
p
35.5.4.1.2.2 送風機吐出し口圧力
p2=pa又はpe2=0
2
p
m
e
r
sg1
sg2
or
Θ
=
+
Θ
=
Θ
c
q
P
P
2
w
2
2
Θ
=Rp
ρ
2
2
m
2
2
sg2
2
1
+
=
A
q
p
p
ρ
又は
2
2
m
2
e2
esg2
2
1
+
=
A
q
p
p
ρ
35.5.4.1.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式に示す。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=−pesg1
35.5.4.1.3 体積流量の算出
体積流量は,次の式で示される。
sg1
m
1
vsg
ρ
q
q
=
35.5.4.1.4 理論空気動力の算出
単位質量当たりの送風機仕事及び理論空気動力は,34.2.3.4と同様にして算出する。
35.5.4.1.5 送風機効率
送風機効率は,34.2.3.5と同様にして算出する。
35.5.4.2 基準マッハ数Ma2refが0.15未満で,かつ圧力比が1.02未満の場合
測定管路の断面で,せき止め温度と静温度は等しいとみなす
Θ1=Θsg1=Θ3=Θsg3=Θ2=Θsg2=t3+273.15
233
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
FM1=FM2=1
kp=1
次に,試験通風路を通る流れが非圧縮性であるという仮定に基づいた方法を適用する。ただし,試験す
る送風機の上流に補助送風機がある場合は除く。
35.5.4.2.1 質量流量の算出
質量流量は,34.2.4.2.1及び34.3.4.2.1に従って算出する。
35.5.4.2.2 送風機圧力の算出
35.5.4.2.2.1 送風機吸込口圧力
35.5.4.2.2.1.1 吸込圧力pe3を測定管路内で測定する場合(34.2.4.2.2.1参照)
p3=pe3+pa
Θ3=Θsg3=Θsg1=t3+273.15
sg2
sg1
1
3
w
3
3
ρ
ρ
ρ
ρ
=
=
=
Θ
=Rp
送風機吸込口のせき止め圧力は,次の式に示す。
(
)
[
]
3
1
3
2
3
m
3
3
sg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
又は
(
)
[
]
3
1
3
2
3
m
3
e3
esg1
1
2
1
−
+
+
=
ξ
ρ
A
q
p
p
ここに,(ζ3−1)3≦0は,30.6.5に従って算出する。
圧力p1は次の式で示される。
2
1
m
3
sg1
1
2
1
−
=
A
q
p
p
ρ
又は
2
1
m
3
esg1
e1
2
1
−
=
A
q
p
p
ρ
35.5.4.2.2.1.2 吸込圧力pe3又はpesg3を空気そう内で測定する場合(34.3.4.2.2.1参照)
p3=pe3+pa
Θ3=Θsg3=Θsg1=Θ1=t3+273.15
2
3
m
3
3
sg3
2
1
+
=
A
q
p
p
ρ
又は
psg3=pesg3+pa
ρ1=ρsg1=ρ3
234
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)1
1
3
2
1
m
3
sg3
sg1
2
1
−
+
=
ξ
ρ
A
q
p
p
(
)1
1
3
2
1
m
3
esg3
esg1
2
1
−
+
=
ξ
ρ
A
q
p
p
2
1
m
3
sg1
1
2
1
−
=
A
q
p
p
ρ
2
1
m
3
esg1
e1
2
1
−
=
A
q
p
p
ρ
ここに,(ζ3−1)1≦0は,摩擦損失係数である(35.5.4.1.2.1.2参照)。
35.5.4.2.2.2 送風機吐出し口圧力
送風機吐出し口において
p2=pa又はpe2=0
2
2
m
2
2
sg2
2
1
+
=
A
q
p
p
ρ
又は
2
2
m
2
e2
esg2
2
1
+
=
A
q
p
p
ρ
ρ3=ρ2=ρ1=ρsg3
35.5.4.2.2.3 送風機圧力
送風機圧力pFD及び送風機静圧psFDは,次の式に示す。
pFD=psg2−psg1=pesg2−pesg1
psFD=p2−psg1=−psg1
35.5.4.2.3 体積流量の算出
体積流量は,次の式に示す。
sg1
m
1
vsg
ρ
q
q
=
35.5.4.2.4 理論空気動力の算出
理論空気動力は,次の式に示す。
PuD=qvsg1pFD
PusD=qvsg1psFD
35.5.4.2.5 送風機効率
送風機効率は,次の式に示す。
r
uD
rD
P
P
=
η
235
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
r
usD
srD
P
P
=
η
236
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(規定) 送風機圧力及び送風機の接続形式
附属書の18によれば,送風機の接続形式は,次の4種類に分類できる。
− 接続形式A:吸込管と吐出し管の両方をもたない場合
− 接続形式B:吸込管はもたず吐出し管だけをもっている場合
− 接続形式C:吐出し管はもたず吸込管だけをもっている場合
− 接続形式D:吸込管と吐出し管の両方をもっている場合
A.1 送風機圧力
送風機圧力は,現在国際的な合意によって,送風機吐出し口のせき止め圧力と送風機吸込口のせき止め
圧力との間の圧力差と定義される。
pF=psg2−psg1=pesg2−pesg1
吐出し管をもたない送風機における送風機吐出し口の運動エネルギーは,送風機が試験空気槽,又は仕
切られた空間に排出を行うときの損失とみなす。これは,エネルギーが送風機によって与えられていても
同様である。従って,この場合に有効な送風機圧力は,送風機静圧となる。
psF=psg2−pd2FM2−psg1=p2−psg1=pe2−pesg1
A.1.1 標準の接続形式における送風機圧力
これらは,送風機の接続形式(18.参照)により算出方法が異なり次のように定義される。
a) 接続形式A:吸込管と吐出し管の両方をもたない場合
有効な送風機圧力は,
sg1
2
M
2
m
2
2
sg2
sFA
2
p
F
V
p
p
−
−
=
ρ
また,次の式により
2
2
M
2
m
2
2
sg2
2
p
F
V
p
=
−ρ
p2−psg1
が,送風機静圧となる。
psFA=p2−psg1=pe2−pesg1
接続形式Aの場合には,送風機静圧psFAは有効送風機圧力であるが,送風機圧力pFAは,次の式で
算出してもよい。
pFA=psg2−psg1=pesg2−pesg1
b) 接続形式B:吸込管はもたず吐出し管だけをもっている場合
有効な送風機圧力は,次の式で示される送風機圧力である。
pFB=psg2−psg1=pesg2−pesg1
送風機静圧は次の式に示す。
esg1
e2
sg1
2
sg1
2
M
2
m
2
2
sg2
sFB
2
p
p
p
p
p
F
V
p
p
−
=
−
=
−
−
=
ρ
c) 接続形式C:吐出し管はもたず吸込管だけをもっている場合
有効な送風機圧力は,次のように定義される送風機静圧psFである。
237
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
esg1
e2
sg1
2
sg1
2
M
2
m
2
2
sg2
sFC
2
p
p
p
p
p
F
V
p
p
−
=
−
=
−
−
=
ρ
送風機圧力は,次の式で算出してもよい。
pFC=psg2−psg1=pesg2−pesg1
d) 接続形式D:吸込管及び吐出し管の両方をもっている場合
有効な送風機圧力は,次の式で定義される送風機圧力である。
pFD=psg2−psg1=pesg2−pesg1
送風機静圧は,次の式で算出してもよい。
psFD=p2−psg1=pe2−pesg1
A.2 算出方法
A.2.1 接続形式A
A.2.1.1 吸込側試験空気槽のある場合(附属書図66〜68参照)
この場合の有効な送風機圧力は,次の式で示される送風機静圧psFAである。
p2=pa
psFA=pa−psg1=−pesg1
ここに,
M3
m3
2
3
3
sg1
2
F
V
p
p
ρ
+
=
M3
m3
2
3
e3
esg1
2
F
V
p
p
ρ
+
=
試験空気そう内のマッハ数Ma3は,通常0.15未満で,FM3=1である。
送風機圧力pFAは,次の式で算出する。
+
−
=
+
−
+
=
2
2
2
2
m3
2
3
e3
2
M
2
m
2
2
m3
2
3
3
2
M
2
m
2
2
a
FA
V
p
F
V
V
p
F
V
p
p
ρ
ρ
ρ
ρ
ρ2,vm2,FM2,ρ3及びvm3は,附属書の14.4,14.5,14.6又は14.9によって算出する。
A.2.1.2 吐出し側試験空気槽のある場合
送風機が試験時の囲い又は開放した吸込口の周囲から空気を引き込む場合[附属書図69a)参照]
吸込み口せき止め圧力は,大気圧に等しい。
p2=p4
psg1=pa
また,有効な送風機圧力は送風機静圧である。
psFA=p4−pa=pe4
送風機圧力は次の式で
2
M
2
m
2
2
e4
a
2
M
2
m
2
2
4
FA
2
2
F
V
p
p
F
V
p
p
ρ
ρ
+
=
−
+
=
ただし,ρ2,vm2及びFM2は,附属書の14.4,14.5,14.6又は14.9によって算出する。
備考46. 吐出し側空気槽の大きさは,送風機吐出し口の大きさに比べて非常に大きいものとする(広
い開放空間に相当する)。たとえば,同じ送風機の吸込側空気槽の断面積に対して2〜3倍以上
238
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
の大きさの断面積をもつなどである。
A.2.2 接続方式B
送風機は,試験時の囲い又は開放した大気から空気を吸引する。
psg1=pa
この場合の有効な送風機圧力は,次の式に示す送風機圧力である。
pFB=psg2−psg1=psg2−pa=pesg2
また,
(
)
[
]
4
4
2
4
M
4
m
2
4
4
sg2
1
2
−
+
+
=
ξ
ρ
F
V
p
p
(
)
[
]
4
4
2
4
M
4
m
2
4
e4
esg2
1
2
−
+
+
=
ξ
ρ
F
V
p
p
送風機静圧は次の式に示す。
M2
m2
2
2
esg2
a
M2
m2
2
2
sg2
sFB
2
2
F
V
p
p
F
V
p
p
ρ
ρ
−
=
−
−
=
ρ4,vm4,FM4,ρ2,Vm2及びFM2は,附属書の14.4,14.5,14.6又は14.9によって算出する。
A.2.3 接続形式C
この場合の有効な送風機圧力は,次の式で算出する送風機静圧である。
p2=pa
(
)
[
]
(
)
[
]
+
+
−
=
+
+
−
=
−
=
−
−
3
1
3
M3
m3
2
3
e3
3
1
3
M3
m3
2
3
3
a
sg1
2
sFC
1
2
1
2
ξ
ρ
ξ
ρ
F
V
p
F
V
p
p
p
p
p
送風機圧力は,次の式で
(
)
[
]
+
+
−
+
=
−
3
1
3
M3
m3
2
3
3
M2
m2
2
2
a
FC
1
2
2
ξ
ρ
ρ
F
V
p
F
V
p
p
ρ3,,vm3,FM3,ρ2,vm2及びFM2は,附属書の14.4,14.5,14.6又は14.9により算出する。
A.2.4 接続形式D
この場合の有効な送風機圧力は,次の式に示す送風機圧力である。
(
)
[
]
(
)
[
]
(
)
[
]
(
)
[
]
+
+
−
+
+
=
+
+
−
+
+
=
−
=
−
−
−
−
3
1
3
M3
m3
2
3
e3
4
4
2
M4
m4
2
4
e4
3
1
3
M3
m3
2
3
3
4
4
2
M4
m4
2
4
4
sg1
sg2
FD
1
2
1
2
1
2
1
2
ξ
ρ
ξ
ρ
ξ
ρ
ξ
ρ
F
V
p
F
V
p
F
V
p
F
V
p
p
p
p
送風機静圧は次の式に示す。
239
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
[
]
(
)
[
]
+
+
−
−
=
+
+
−
−
=
−
=
−
−
3
1
3
M3
m3
2
3
e3
M2
m2
2
2
esg2
3
1
3
M3
m3
2
3
3
M2
m2
2
2
sg2
sg1
2
sFD
1
2
2
1
2
2
ξ
ρ
ρ
ξ
ρ
ρ
F
V
p
F
V
p
F
V
p
F
V
p
p
p
p
ρ4,vm4,FM4,ρ3,FM3,ρ2,vm2及びFM2は,附属書の14.4,14.5,14.6又は14.9によって算出する。
備考47. (ζ3−1)3及びρe3は,通常負である。
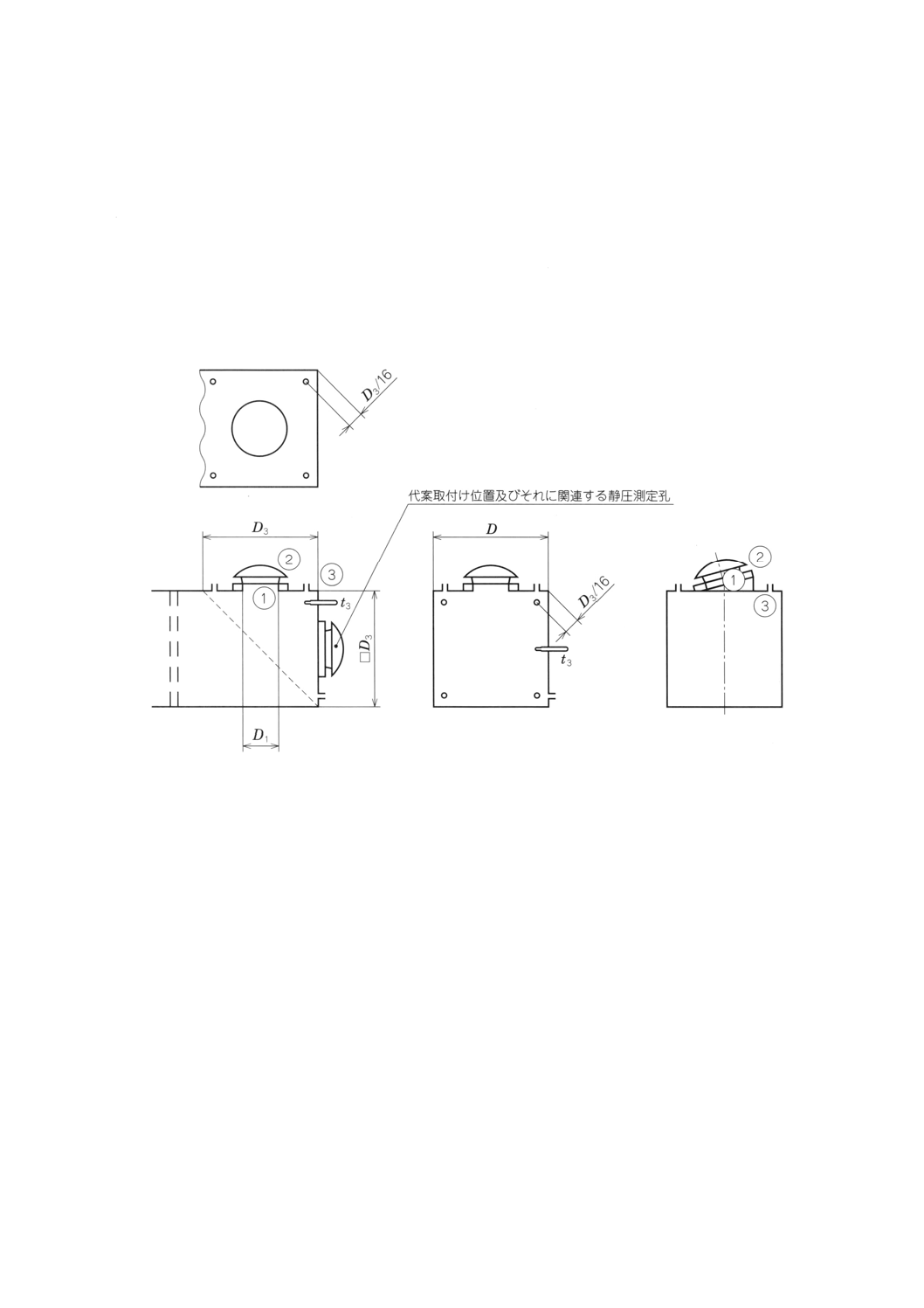
240
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(規定) 屋根強制換気扇
B.1 重力式シャッタを備えた装置を正しい取付け位置で試験するために,屋根強制換気扇を特殊な接続要
求に合致させるには,装置構成を標準から若干変更する必要がある。
B.2およびB.3に,この形の装置に限って許される2種類の代案を示す。
B.2 附属書図B.1に最大45%の自由開口面積をもつ傾斜した最終スクリーンを含む代案の一つ,及び装置
の代替取付け位置を示す。
備考1. 試験装置の残りの部分は附属書図70a)〜g)に示す。
2. D1≦0.5D3 D1は上面の開口部の直径,又は長方形開口部の長辺の長さを示す。
3. 測定及び計算は附属書の32.2による。
附属書図B.1 吸込側空気槽での屋根強制換気扇の構成
B.3 もう一つの代案は,附属書図B.2に示すように,接続形式Cに従ってインレットノズルの吐出し側端
部にスクリーンを設置することである。
空気槽へ適切に膨張させてやれば,この制御装置の位置を変えることにより,最大開口面積45%の傾斜
スクリーンが空気槽内で使用できるようになる。
傾斜スクリーンの使用が実用的でないほど空気槽が非常に大きな場合には,試験中の送風機に送り込ま
れる空気流れが十分に均一な速度分布をもち,かつ旋回流がないことが,考慮している全体積流量にわた
ってはっきりと示されれば,このスクリーンを省いてもよい。
試験装置を次の図に示す。
∆p,pe3及びt3を測定し,tu=taとおく。
pe2=0
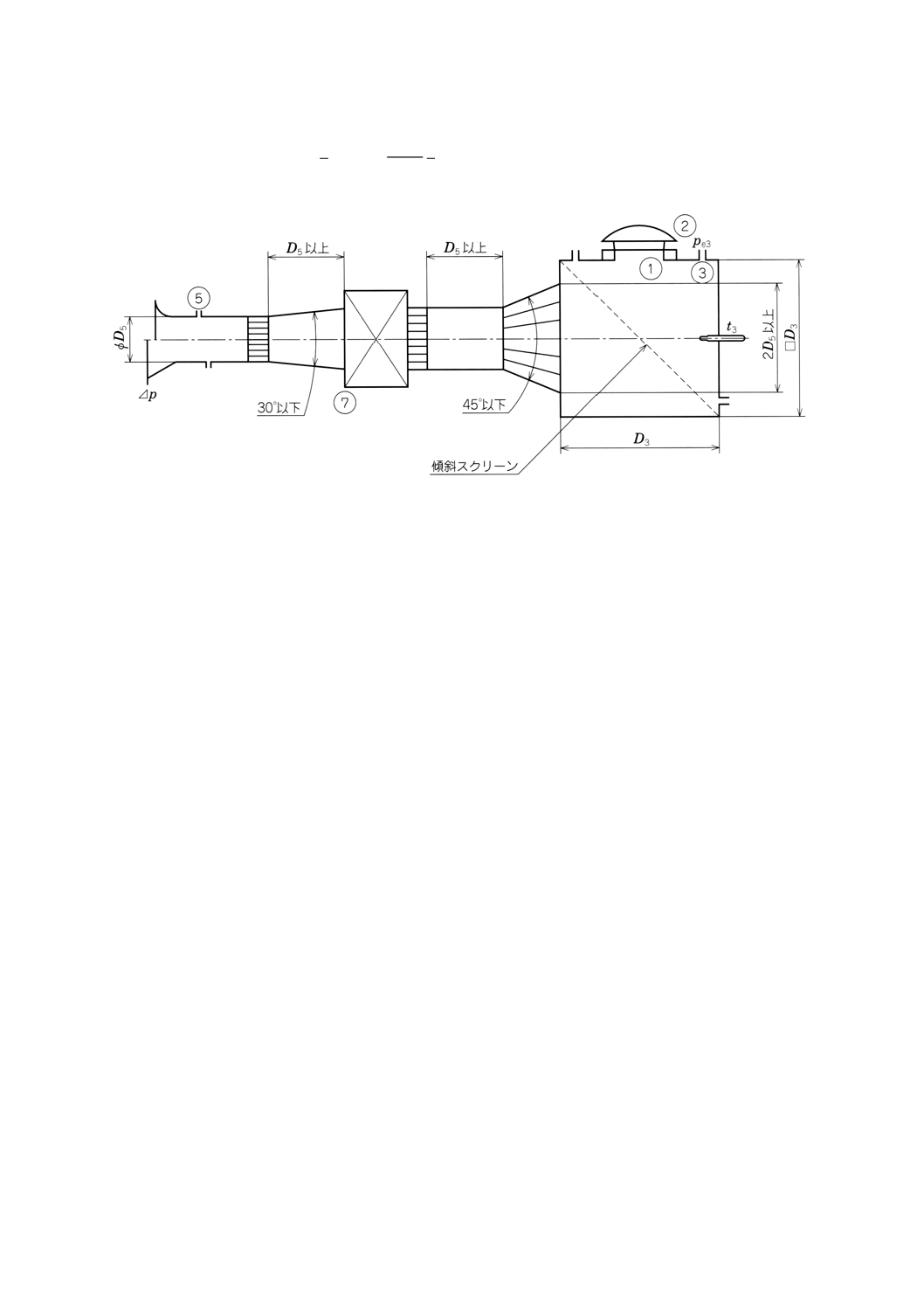
241
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
esg1
m3
2
3
e3
esg3
2
p
V
p
p
=
+
=
ρ
pe3≦0
備考 pe3は通常は負。
附属書図B.2 接続形式Cにおける屋根強制換気扇
242
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(規定)
送風機接続形式B,C及びDの断面nにおける
psgn並びにpnの直接計算法
C.1 概要
附属書の14.6で,それぞれの試験管路の断面Xで測定した静圧pexから,送風機の基準断面(1又は2)
のせき止め圧力を計算する方法を記述している。
この方法は,次の値をまず算出する必要がある。
− 断面xにおけるマッハ数Max(附属書の14.4.3.1及び14.4.3.2参照)
− 断面xの空気密度(14.4.4参照)
− マッハ係数FMx(14.5.1参照)
− 摩擦損失係数(ζn−x)x(30.6参照)
この追記で説明する直接計算の方法を使ってもよい。結果は,14.4,14.5及び14.6によって計算した送
風機圧力pFに対して,0.1%以内の差である。
C.2 せき止め圧力psgn及び圧力pnの計算
次の値は既知とする
− 質量流量qm
− 大気圧pa
− 管路の測定断面におけるゲージ圧pex
− 吸込口せき止め温度Θsg1
− インペラ動力Pr又は電動機入力Pe
− 測定断面の面積Ax
− 送風機の基準断面の面積An(n=1又は2)
せき止め温度Θsg2は次の式に示す。
p
m
e
r
sg1
sg2
or
c
q
P
P
Θ
=
Θ
14.4.3.1からΘxを算出し
px=pa+pex
x
w
x
x
Θ
=Rp
ρ
次のように仮定する。
p*=pn/px
ρ*=ρn/ρx
n1= (An/Ax) 2
x
x
x
2
m
2
1
2
1
ρ
κ
κ
γ
p
A
q
−
=
ρ*は,次の方程式の解である。
243
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
F (ρ*) =B3ρ*3−B2ρ*2+B1ρ*+B0=0
ここに,
(
)
(
)
[
]
+
−
−
+
=
x
x-n
1
1
3
1
1
2
1
1
ξ
κ
κ
γ
n
B
(
)
(
)
[
]
+
−
+
=
x
x-n
1
1
2
1
1
2
1
ξ
κ
κ
γ
n
B
(
)
−
−
=
1
2
2
1
1
κ
κ
γ
B
(
)
−
=
1
2
1
0
κ
κ
γ
B
(ζn−x)xは,断面xについて計算した断面nと断面xとの間の測定管路の摩擦損失係数である(30.6参照)。
吐出し側管路でn=2, x=4の場合は(ζn−x)x>0
吸込側管路でn=1, x=3の場合は(ζn−x)x<0
方程式F(ρ*)=0の解の計算は,ニュートン・ラフソン法による逐次近似法で行う。
次の初期値から開始する。
(ρ*)1=1
(p+1)番目の近似解は,次の式に示す。
()
()
()()p
*
p
*
p
*
1
p
*
ρ
ρ
ρ
ρ
F
F
′
−
=
+
ここに,
F'(ρ*)=3B3ρ*2−2B2ρ*+B1
通常ρ*を得るには,3回の反復計算で十分である。
係数p*は次の式に示す。
(
)
*
1
1
1
*
*
1
ρ
γ
γ
ρ
n
p
−
+
=
したがって
pn=px・p*
ρn=ρx・ρ*
せき止め圧力は次の式に示す。
1
n
n
n
2
m
2
n
sgn
2
1
1
−
−
+
=
κ
κ
ρ
κ
κ
p
A
q
p
p
C.2.1 せき止め圧力psgn,せき止め温度Θsgnは,既知である。
次のように仮定する。
sgn
sgn
n
2
m
2
2
2
1
ρ
κ
κ
p
A
q
m
−
=
n
sgn
*
Θ
Θ
=
Θ
Θ*は次の方程式の解である。
244
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
1
*
*
2
*
11
+
Θ
−
Θ
=
Θ
−+
κκ
m
F
ニュートン・ラフソン法による逐次近似法を適用する。
初期値は
(Θ*)1=1
(p+1)回目の近似解は,次の式に示す。
()(
)()
()()
*
*
p
*
1
p
*
Θ
′
Θ
−
Θ
=
Θ
+
F
F
ここに,
()
1
1
1
1
2
*
2
*
−
Θ
−
+
=
Θ
′
−
κ
κ
κ
m
F
Θ*を得るには3回の反復計算で十分である。
*
sgn
n
Θ
Θ
=
Θ
1
*
sgn
n
−
Θ
=
κκ
p
p
1
1
*
sgn
n
−
Θ
=
κ
ρ
ρ
C.2.2 圧力pn及びせき止め温度Θsgnは,既知である(14.4.3.1参照)。
次のように仮定する。
2
n
sgn
w
2
x
m
2
2
1
p
R
A
q
M
Θ
−
=
κ
κ
(
)
2
4
1
1
2
n
sgn
M
+
+
=
Θ
Θ
245
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D(参考)
吐出し口軸が水平でない場合の送風機吐出し曲管
大形の遠心送風機若しくは大出力の送風機の接続形式B又は接続形式Dにおいて,吐出し口軸が水平で
ない場合は,製造業者と購入者との間の協定によって送風機吐出し口と静圧孔をもつ標準管路間に曲管を
備え付けてもよい。
曲管は,附属書図D.1に示す仕様による。
吐出し口軸と標準の試験管路の軸との間の角度は最小限である。
曲管はA2とA4との間に位置し,一様な断面をもち,流れを転向させるスプリッタベーンを備えている。
損失係数は,次の式に示す。
()
2
c
4
6
1
4
c
2
=
A
A
b
h
x
π
ξ
ここに,
Ac 曲管の入口及び出口の断面積
x ラジアンで表した曲管の角度
(ζc)4 断面4について算出した曲管の摩擦損失係数
6
1
2
bh
x
π
は附属書図D.2に
bh及びxの関数として示される。
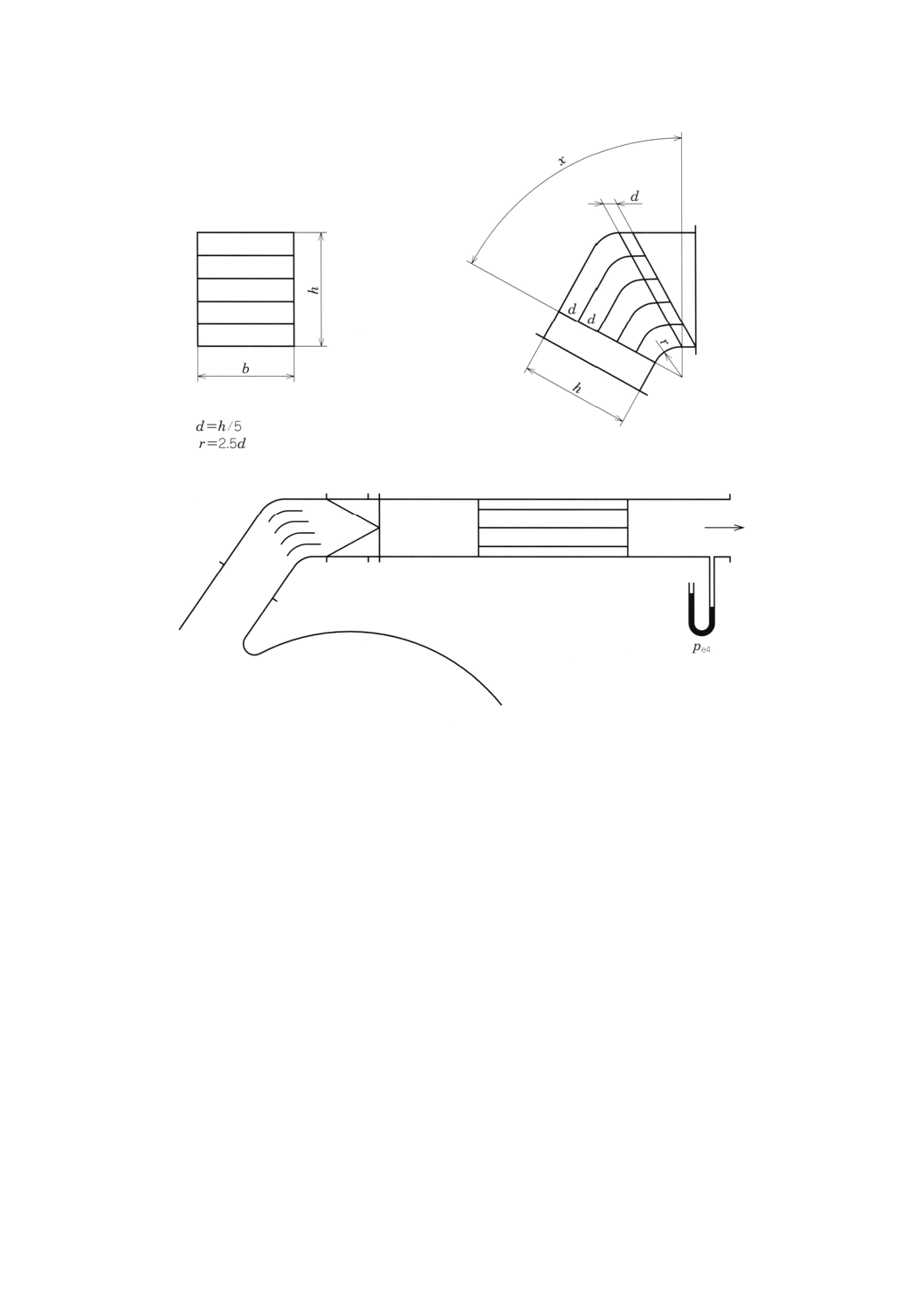
246
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図D.1 大形の遠心式送風機試験用の吐出し曲管の寸法
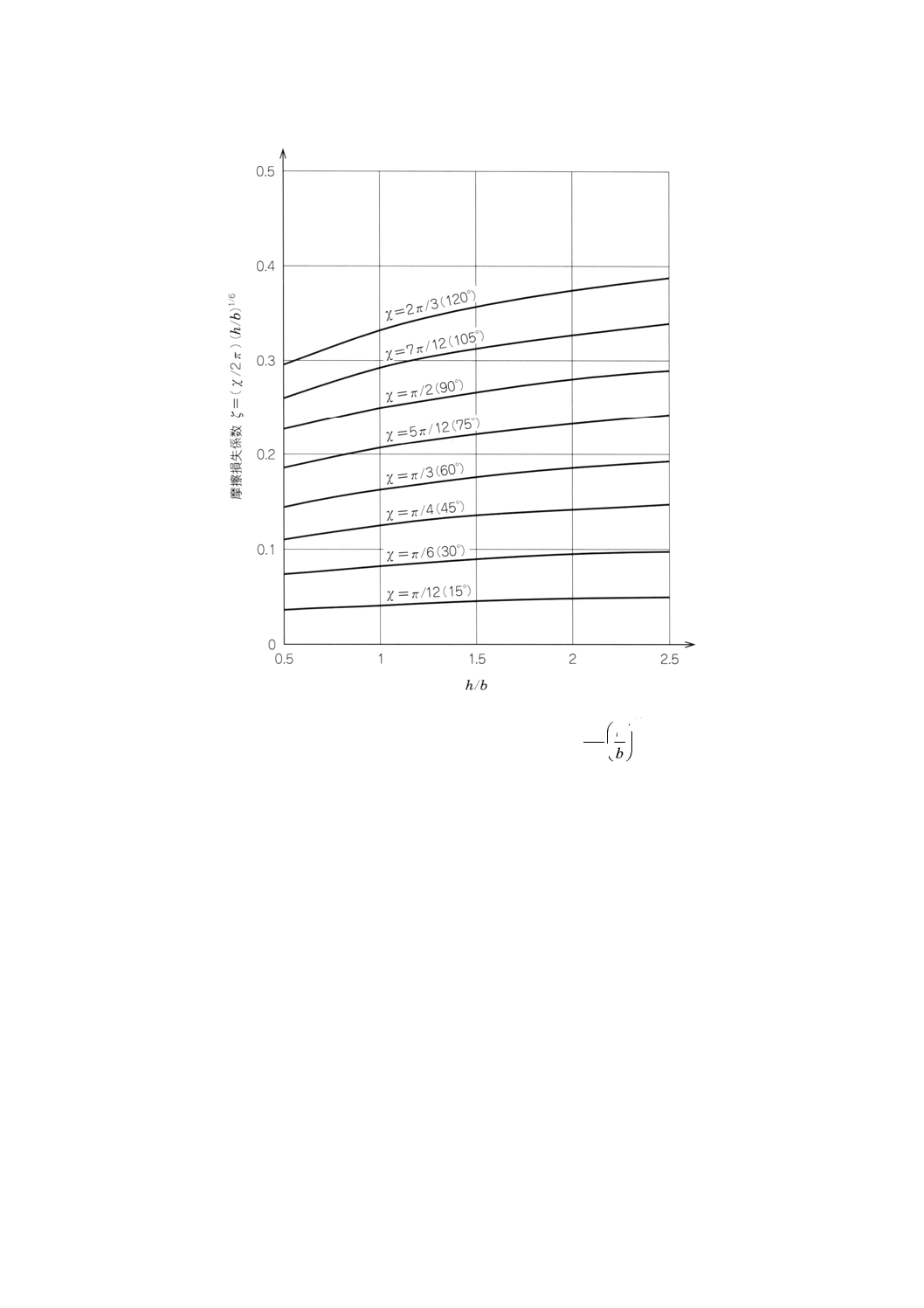
247
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書図D.2 吐出し曲管の圧力損失の計算のための
6
1
2
bh
x
π
の変化図
248
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書E(参考) 参考文献
[1] ISO/TR 8428 : −1), Influence of the compressibility of fluid on industrial fans.
[2] ANSI/AMCA 210-85 : 1985, Laboratory methods of testing fans for rating (also designated ANSI/ASHRAE
51-1985) .
[3] BS 848-1 : 1980, Fans for general purposes−Part 1 : Methods of testing performance.
[4] DIN 24163-2 : 1985, Fans−Performance testing−Part 2 : Standardized test airways.
[5] NF X 10-200 : 1986, Industrial fans−Rules for performance testing of ducted free inlet and fully ducted fans
using standardized airways− "Caisson réduit " method at the outlet.
[6] E 51-100 : 1983 (AFNOR) , Industrial fans−Compressibility effect of the fluid.
原案調査作成委員会 構成表
氏名
所属
(委員長)
中 條 徳三郎
東京理科大学
辻 茂
東京工業大学
押 田 良 輝
株式会社荏原製作所
金 田 実
株式会社ミツヤ送風機製作所
永 島 敏 雄
株式会社日立製作所
林 弘
株式会社電業社機械製作所
斎 藤 剛
石川島播磨重工業株式会社
池 田 稔
日本鋼管株式会社
古 山 雪
三菱重工業株式会社
押 田 肇
東洋エンジニアリング株式会社
山 田 信 夫
日揮株式会社
比留間 栄 二
東京電力株式会社
松 木 正 勝
航空宇宙技術研究所
山 田 益 輝
日本石炭協会
松 本 大 治
工業技術院標準部
(事務局)
和 田 帝 一
社団法人日本産業機械工業会
送風機JIS国際整合化調査研究委員会 構成表
氏名
所属
(委員長)
照 屋 仁
照屋技研
大 嶋 清 治
工業技術院標準部
本 間 清
工業技術院標準部
橋 本 繁 晴
日本規格協会技術部
(副委員長)
酒 井 潤 一
株式会社荏原製作所
(幹事)
奥 田 温 一
株式会社電業社機械製作所
(幹事)
向 林 範 久
株式会社荏原製作所
久保田 信 昭
荏原工機株式会社
斉 藤 剛
石川島播磨重工業株式会社
深 町 操
川崎重工業株式会社
高 柳 亮 昭
株式会社ミツヤ送風機製作所
中 里 勲
株式会社ツバキ・ナカシマ
1) 刊行予定
249
B 8330:2000
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
氏名
所属
高 津 恭
株式会社日立製作所
古 井 輝 武
三菱重工業株式会社
(事務局)
沖 田 宏 之
社団法人日本産業機械工業会
(事務局)
臺 健 一
社団法人日本産業機械工業会
送風機JIS改正原案作成委員会 構成表
氏名
所属
(委員長)
照 屋 仁
照屋技研
山 根 隆一郎
東京工業大学
有 賀 一 郎
千葉工業大学
中 嶋 誠
通商産業省
本 間 清
工業技術院標準部
橋 本 繁 晴
日本規格協会技術部
西 澤 滋
建設省
松 崎 章 夫
東京電力株式会社
末 広 要三郎
新日本製鐵株式会社
園 田 悟
日本石油株式会社
春 山 昭 一
日揮株式会社
細 越 幸 雄
千代田化工建設株式会社
(副委員長)
酒 井 潤 一
株式会社荏原製作所
(幹事)
奥 田 温 一
株式会社電業社機械製作所
(幹事)
向 林 範 久
株式会社荏原製作所
船 橋 俊 一
石川島播磨重工業株式会社
林 田 重 実
荏原工機株式会社
深 町 操
川崎重工業株式会社
高 津 恭
株式会社日立製作所
(事務局)
沖 田 宏 之
社団法人日本産業機械工業会
(事務局)
臺 健 一
社団法人日本産業機械工業会