B 8280:2003
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,高圧ガス保安協会
(KHK)/財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を改正すべきとの申出があ
り,日本工業標準調査会の審議を経て,厚生労働大臣及び経済産業大臣が改正した日本工業規格である。
これによって,JIS B 8280:1993は改正され,この規格に置き換えられる。
この規格の一部が,技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願公開後の
実用新案登録出願に抵触する可能性があることに注意を喚起する。厚生労働大臣,経済産業大臣及び日本
工業標準調査会は,このような技術的性質をもつ特許権,出願公開後の特許出願,実用新案権,又は出願
公開後の実用新案登録出願にかかわる確認について,責任はもたない。
JIS B 8280には,次に示す附属書がある。
附属書1(規定)フランジ付き非円形胴
附属書2(規定)検定水圧試験
この規格の一部の図・表で,†マークの付いているものは,アメリカ機械学会(The American Society of
Mechanical Engineers)によるアメリカ機械学会ボイラ圧力容器規格(ASME Boiler and Pressure Vessel Code
© 2001)から引用した資料であり,同学会Code & Standards Departmentの文書による承諾を得ている。ASME
から事前に文書による承諾を得ない限り,これらの資料を翻訳又は複製してはならない。
The figures and tables marked with † in this standard, were adapted from the ASME Boiler and Pressure Vessel
Code © 2001 by The American Society of Mechanical Engineers with the written consent of the ASME Codes &
Standards Department. No additional translation or reproduction may be made of these materials without the prior
written consent of ASME.
B 8280:2003
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
1. 適用範囲 ························································································································ 1
2. 引用規格 ························································································································ 1
3. 定義 ······························································································································ 1
4. 材料 ······························································································································ 1
5. 非円形胴の形状 ··············································································································· 1
5.1 非円形胴の横断面が長方形の胴························································································· 1
5.2 非円形胴の横断面が長円形の胴························································································· 2
5.3 円の中心を通る1枚の仕切板をもつ円筒胴 ·········································································· 2
6. 記号の意味 ····················································································································· 4
7. 非円形胴の設計 ··············································································································· 6
7.1 設計一般 ······················································································································ 6
7.2 非円形胴の横断面が長方形の胴の計算················································································ 8
7.3 非円形胴の横断面が長円形の胴の計算··············································································· 21
7.4 円の中心を通る1枚の仕切板をもつ円筒胴 ········································································· 24
8. 溶接継手の位置による分類 ······························································································· 26
附属書1(規定)フランジ付き非円形胴 ··················································································· 27
附属書2(規定)検定水圧試験 ······························································································· 34
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 8280:2003
非円形胴の圧力容器
Pressure vessels of noncircular cross section
1. 適用範囲 この規格は,横断面が長方形又は長円形の胴(以下,“非円形胴”という。)の圧力容器の
構造について規定する。その適用方法及び範囲は,次による。
a) 適用方法に関しては,適用法規,JIS B 8265又はJIS B 8266に規定がある場合には,それに従う。規
定がない場合には,受渡当事者間の協定による。
b) 非円形胴の範囲は,胴板,強め材,仕切板,ステー,胴フランジ,ノズルなどによって構成する。
2. 引用規格 次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成す
る。これらの引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0190 圧力容器の構造共通用語
JIS B 8265 圧力容器の構造−一般事項
JIS B 8266 圧力容器の構造−特定規格
JIS B 8274 圧力容器の管板
3. 定義 この規格で用いる主な用語の定義は,JIS B 0190による。
4. 材料 非円形胴の構造に使用する材料は,適用法規又は適用圧力容器規格の規定による。
5. 非円形胴の形状
5.1
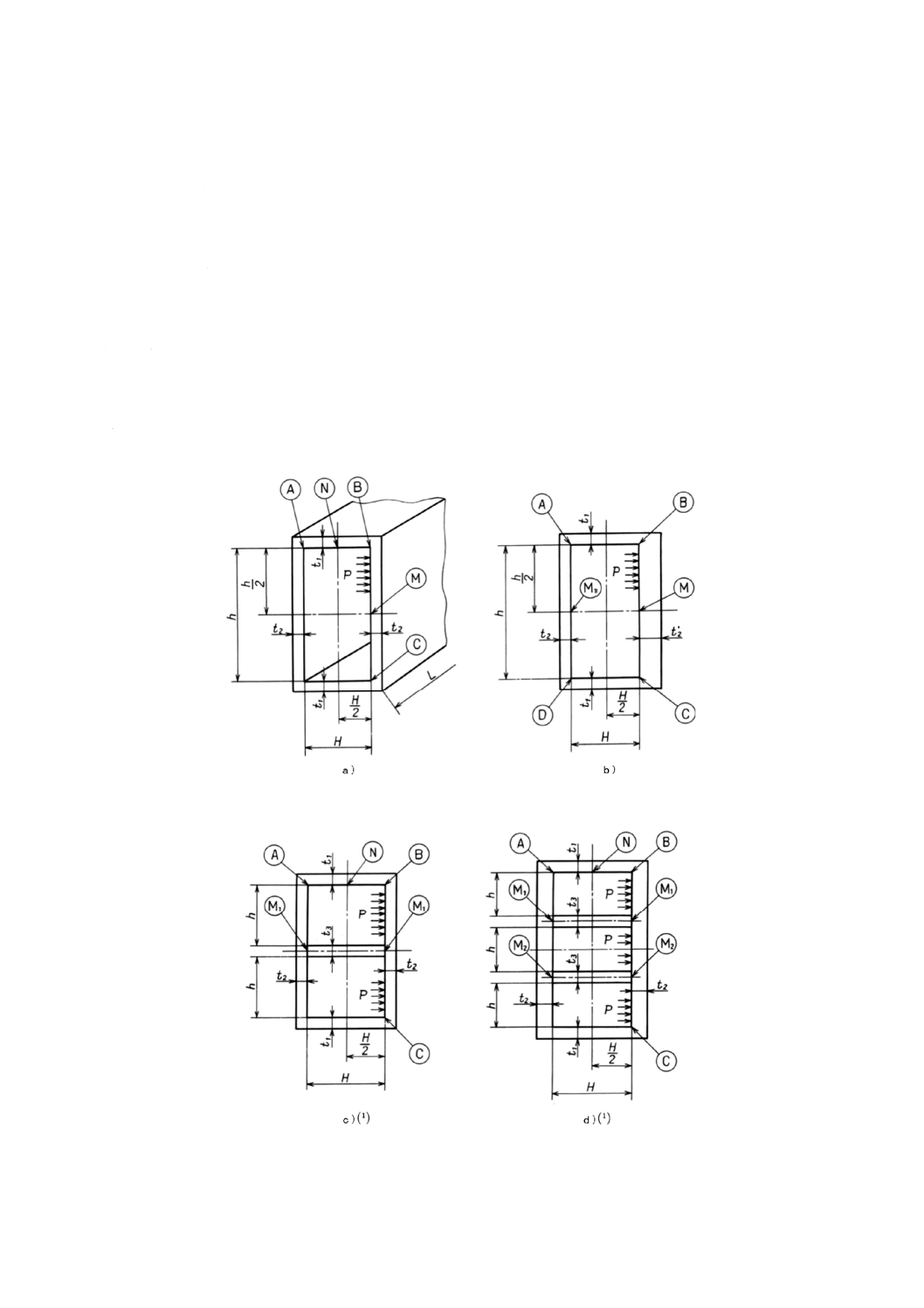
非円形胴の横断面が長方形の胴 非円形胴の横断面が長方形の胴は,次による。
a) 図1 a) の説明 相対する胴板が同じ厚さをもつ胴を示す。相対する二つの胴板の厚さが他の相対する
二つの胴板の厚さと異ってもよい。
b) 図1 b) の説明 相対する二つの胴板が同じ厚さをもち,他の相対する二つの胴板の厚さが異なる胴を
示す。
c) 図1 c) の説明 図1 a) と同じ横断面の胴の空間を一方向に2等分する仕切板又は棒ステーをもつ胴
を示す。仕切板は,圧力のかかる隔壁とならない構造とする。
d) 図1 d) の説明 図1 a) と同じ横断面の胴の空間を一方向に3等分する仕切板又は棒ステーをもつ胴
を示す。仕切板は圧力のかかる隔壁とならない構造とする。
なお,同じ横断面の胴の空間を一方向に3分割以上する仕切り板又は棒ステーをもつ胴[図1 f) を
除く。]については,その最大スパンで3等分されているものとして,当該形状によって計算してよい。
この場合,仕切り板又は棒ステーの板厚は最小のものがすべての仕切り板又はステーに用いられてい
るものとして計算する。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
e) 図1 e) の説明 図1 a) と同じ横断面の胴に空間の大きさが異なるように区切った仕切板又は棒ステ
ーをもつ胴を示す。仕切板は,圧力のかかる隔壁とならない構造とする。
f)
図1 f) の説明 図1 a) と同じ横断面の胴に上下の空間の大きさが同じで,まん中の空間の大きさが異
なるように区切った仕切板又は棒ステーをもつ胴を示す。
仕切板は圧力のかかる隔壁とならない構造とする。
g) 図1 g) の説明 全周の厚さが同じでコーナー部に同じ半径の丸みを付けた胴を示す。
h) 図1 h) の説明 図1 a) の横断面と類似で一つの胴板の両端に同じ半径の丸みを付けた胴を示す。
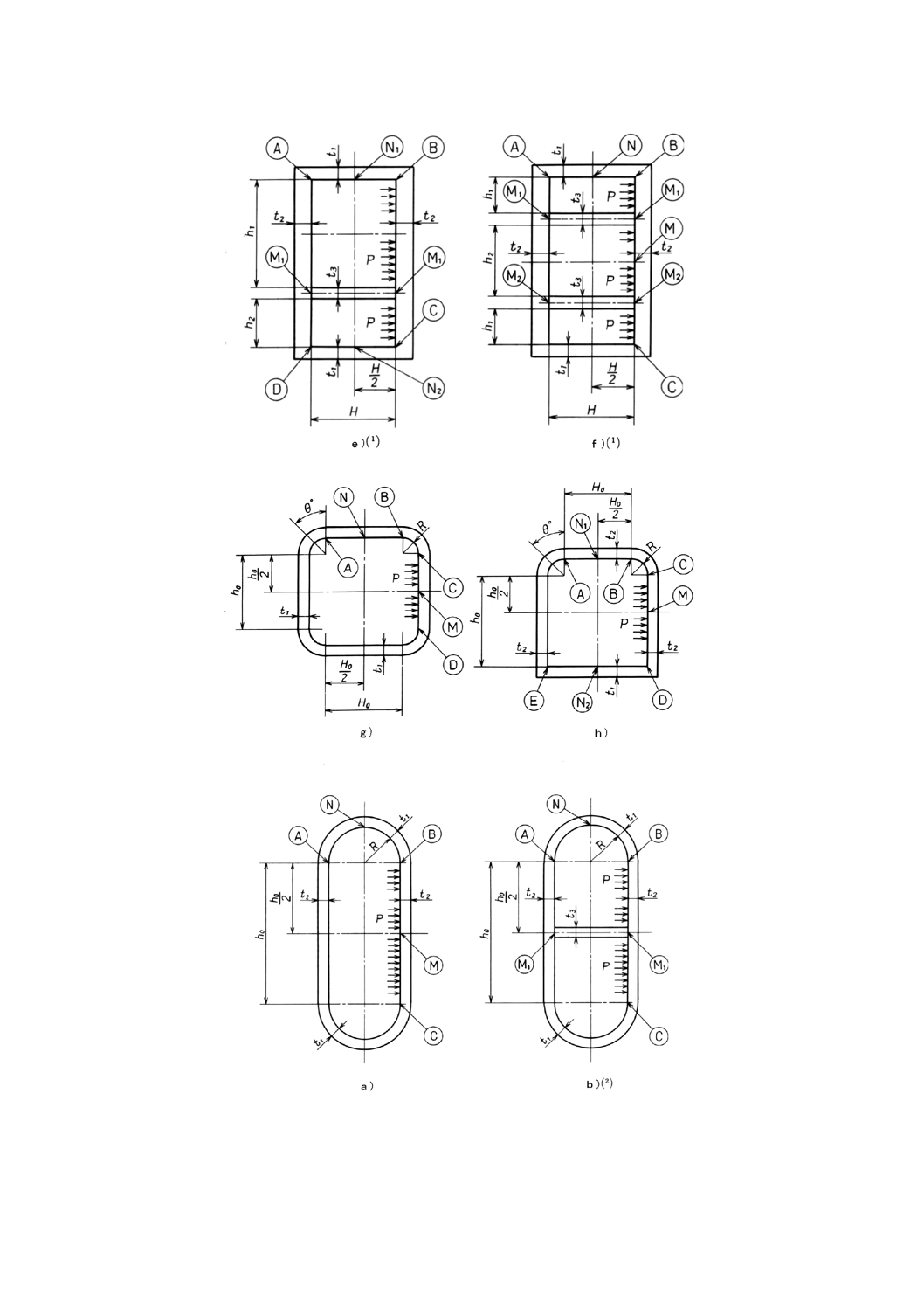
5.2
非円形胴の横断面が長円形の胴 非円形胴の横断面が長円形の胴は,次による。
a) 図2 a) の説明 相対する胴板及び半円筒部が同じ厚さをもつ長円形の胴を示す。
b) 図2 b) の説明 図2 a) と同様な長円形の胴で,胴の空間を胴板側で2等分する仕切板又は棒ステー
をもつ胴を示す。仕切板は圧力のかかる隔壁とならない構造とする。
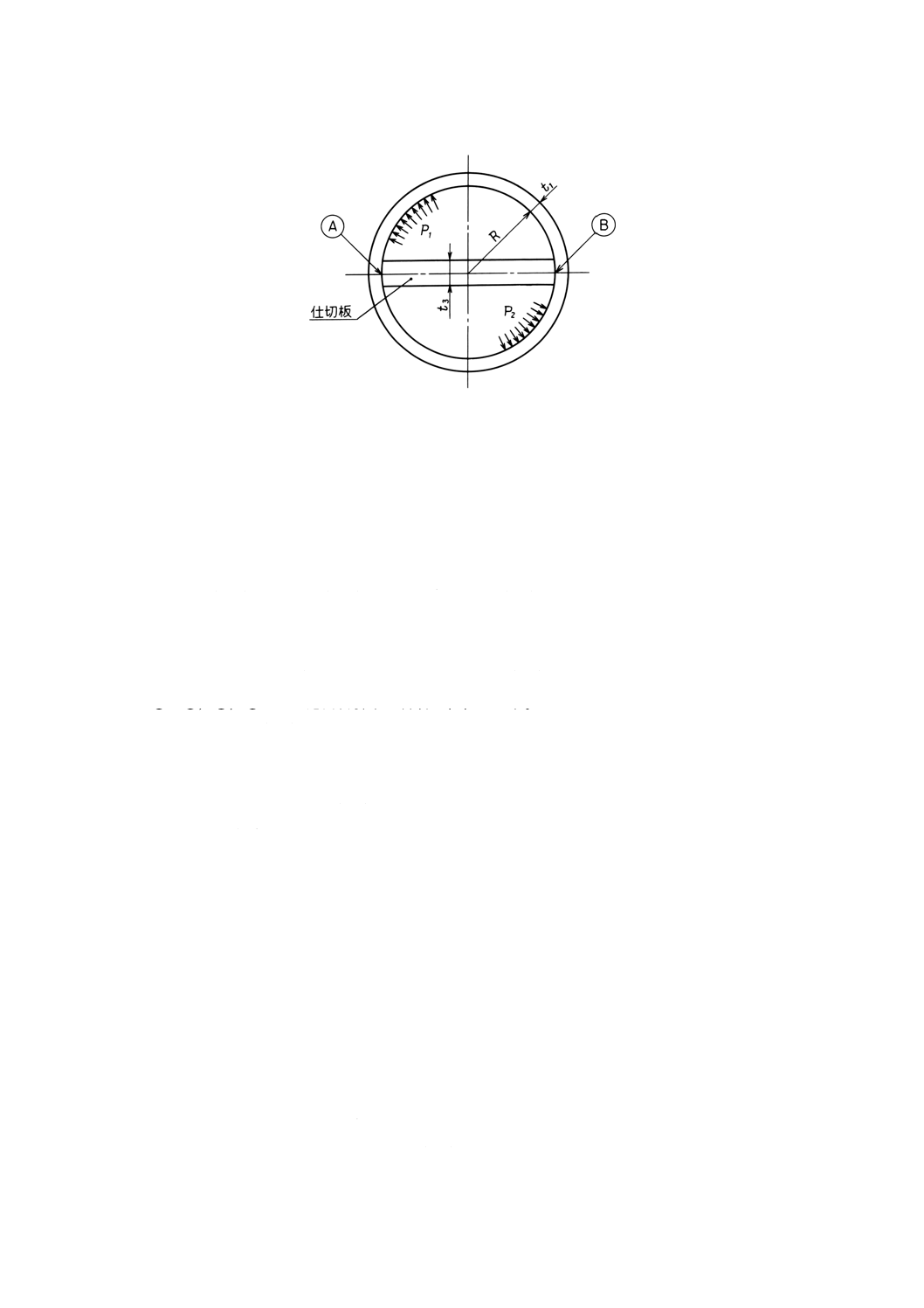
5.3
円の中心を通る1枚の仕切板をもつ円筒胴 図3に円の中心を通る1枚の仕切板をもつ円筒胴を示
す。
図 1 非円形胴の横断面が長方形の胴†
3
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注(1) 棒ステーの場合には,t3をdと読み替える。
図 1 非円形胴の横断面が長方形の胴†(続き)
注(2) 棒ステーの場合には,t3をdと読み替える。
図 2 非円形胴の横断面が長円形の胴†
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図 3 円の中心を通る1枚の仕切板をもつ円筒胴†
6. 記号の意味 この規格に用いる主な記号の意味は,次による。
P:設計圧力(内圧)(MPa)
P1,P2:仕切室の各々の設計圧力 (MPa)。P1>P2とする。(図3参照)
h:図1 a)〜d) に示す非円形胴の一辺の長さ (mm)
h1,h2:図1 e) 及びf) に示す非円形胴の一辺の長さ (mm)
h0:図1 g),h) 及び図2 a),b) に示す胴部の長さ (mm)
H:図1 a)〜f) に示す非円形胴の一辺の長さ (mm)
H0:図1 g) 及びh) に示す胴部の長さ (mm)
R:図1 g),h),図2 a),b) 及び図3に示す内半径 (mm)
◯
A〜◯
E,◯
N,◯
Mなど:応力計算する部材の位置を示す。
t:胴板の厚さ (mm)
t1,t2,t2´:図1〜3に示す胴板の厚さ (mm)
t3:図1〜3に示す仕切板の厚さ (mm)
tr:胴板の最小必要厚さ(3) (mm)
θ:図1 g) 及びh) に示す角度 (°)
η:溶接継手効率又はリガメント効率
σa:設計温度における材料の許容引張応力 (N/mm2)
σm:膜応力 (N/mm2)
σb:曲げ応力 (N/mm2)
σT:合成応力 (N/mm2)
L:非円形胴の長手方向の長さ (mm) [図1 a) 参照]
Pc:丸棒ステーの最大ピッチ (mm)
d:丸棒ステーの直径 (mm)
C:ステー取付け方による係数
DE:段付丸穴を等価の同径穴に換算した穴径 (mm)
I:断面二次モーメント (mm4)
T0:直径d0の穴の腐れ代を除いた長さ (mm)
5
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
T1:直径d1の穴の腐れ代を除いた長さ (mm)
T2:直径d2の穴の腐れ代を除いた長さ (mm)
Tn:直径dnの穴の腐れ代を除いた長さ (mm)
X:板の底辺から中立軸までの長さ (mm)
d0:長さT0の部分の穴径(ねじ穴では,ねじの有効径)(mm)
d1:長さT1の部分の穴径(ねじ穴では,ねじの有効径)(mm)
d2:長さT2の部分の穴径(ねじ穴では,ねじの有効径)(mm)
dn:長さTnの部分の穴径(ねじ穴では,ねじの有効径)(mm)
p:穴のピッチ (mm)
b0:p−d0 (mm)
b1:p−d1 (mm)
b2:p−d2 (mm)
bn:p−dn (mm)
c:部材断面の中立面から表面までの長さ (mm)
eb:曲げ応力に対するリガメント効率
em:膜応力に対するリガメント効率
注(3) 最小必要厚さは,対象としている非円形胴の応力計算式において,非円形胴,仕切板など
各部に発生する膜応力及び膜応力と曲げ応力との合成応力が各許容値以下となる最小厚さ
として算定する。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7. 非円形胴の設計
7.1
設計一般
a) 許容応力 内圧によって生じる応力に対する許容応力は,次による。
1) 膜応力に対する許容応力 膜応力に対する許容応力は,JIS B 8265の4.3.1による。
2) 膜応力と曲げ応力との合成応力に対する許容応力 膜応力と曲げ応力との合成応力に対する許容応
力は,1) に規定する値の1.5倍の値とする。
備考 この規格の算式では,内圧以外の外力及び温度差などによる熱膨張の影響は考慮されてい
ない。
b) 溶接継手効率 非円形胴の溶接継手効率は,8. に規定する継手の位置の分類によってJIS B 8265の
6.1.4(溶接継手の形式とその使用範囲)に規定する継手に応じJIS B 8265の6.2(溶接継手効率)表
6.2(4)による値とする。
注(4) 完全溶込み溶接で接合される非円形胴のコーナ継手(FP継手)はB-1継手と同等とみなしてよ
い。
c) リガメント効率 非円形胴の胴板及び仕切板に多数の穴のある場合のリガメント効率は,次による。
1) 同径穴の板のリガメント効率 膜応力及び曲げ応力に対するリガメント効率は,次の算式による。
p
D
p
e
e
b
m
0
−
=
=
ここに, D0:穴径(ねじ穴では,ねじの有効径)(mm)
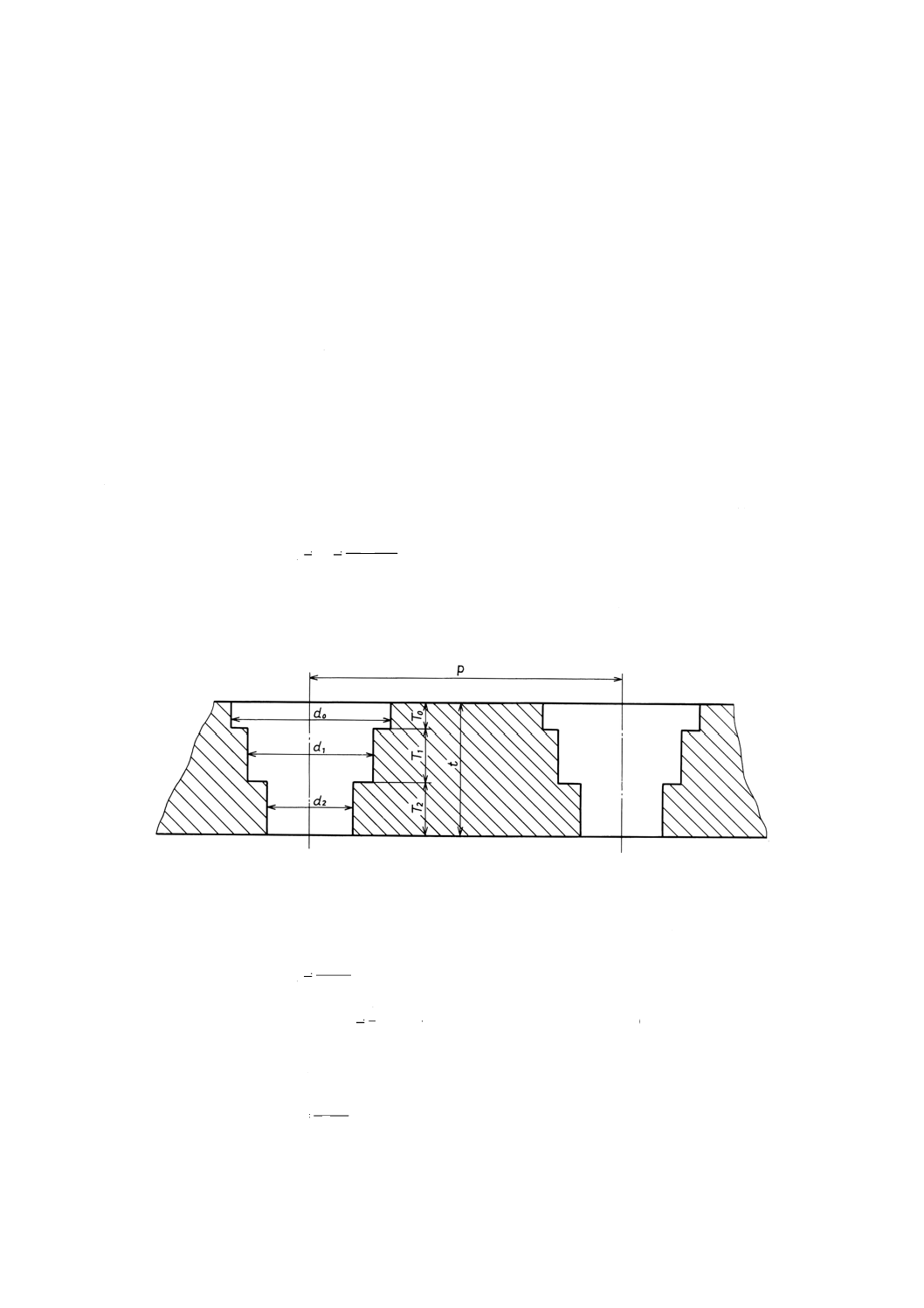
2) 段付丸穴のある板のリガメント効率 非円形胴の胴板及び仕切板に多数の段付丸穴のある場合のリ
ガメント効率は,次による。
図 4 段付丸穴のある板†
2.1) 膜応力に対するリガメント効率 膜応力に対するリガメント効率は,次の算式による。
p
D
p
e
E
m
−
=
ここに,
)
(
1
2
2
1
1
0
0
n
n
E
T
d
T
d
T
d
T
d
t
D
+
+
+
+
=
Λ
(mm)
2.2) 曲げ応力に対するリガメント効率 曲げ応力に対するリガメント効率は,次の算式による。
cp
t
I
eb
2
6
=
7
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
1
1
1
2
2
1
0
0
0
3
3
2
2
3
1
1
3
0
0
2
2
)
(
12
1
−
+
+
+
+
−
+
+
+
+
+
+
+
+
=
X
T
T
T
T
b
X
T
T
T
T
T
b
T
b
T
b
T
b
T
b
I
n
n
n
n
Λ
Λ
Λ
2
2
2
2
2
2
2
−
+
+
−
+
+
+
n
n
n
n
T
X
T
b
X
T
T
T
b
Λ
Λ
(mm4)
1
2
2
1
1
0
0
2
2
2
2
1
1
1
2
1
0
0
0
)
(
2
2
2
2
−
+
+
+
×
+
+
+
+
+
+
+
+
+
+
+
+
+
=
n
n
n
n
n
n
n
n
T
b
T
b
T
b
T
b
T
T
b
T
T
T
b
T
T
T
T
b
T
T
T
T
T
b
X
Λ
Λ
Λ
Λ
Λ
)
(
X
t
X
c
−
=
又は
のいずれか大きい方の値 (mm)
d) 非円形胴の端末ふた板 非円形胴の端末ふた板の計算は,JIS B 8265附属書1の3.6.1(平鏡板の形状
及び計算厚さ)による。ただし,いかなる場合でも係数Cの値は0.2以上とする。
なお,図1 g) 及び図1 h) に示す胴の端末ふた板は,コーナー部の丸みがない直角のものとして計
算しなければならない。図2 a) 及び図2 b) に示す胴の端末ふた板の場合には,最小スパンに直角に
測った最大スパンを用いて計算する。
e) 非円形胴に開ける穴 非円形胴に開ける穴は,次による。
1) ノズルなどを設ける場合には,JIS B 8265附属書2の4.(補強を要しない穴の規定)に該当する円
形の穴は,補強を要しない。
2) ノズルなどを設ける穴で補強を必要とする場合には,次による。
2.1) 穴径が図1,図2又は図3のH又は2Rの1/2以下の場合,穴の補強はJIS B 8265附属書2の5.6 a)
による。ただし,強め材の最小断面積AはA=dNtrとする。ここに,dNは穴径。
2.2) 穴径が2.1) より大きい場合には,次のいずれかの方法による。
なお,この方法は2.1) に該当する穴に用いてもよい。
2.2.1) ノズル部を含む確立した応力解析手法又は実験的応力解析
2.2.2) 附属書2に規定する検定水圧試験
2.2.3) 次に示す簡易補強計算
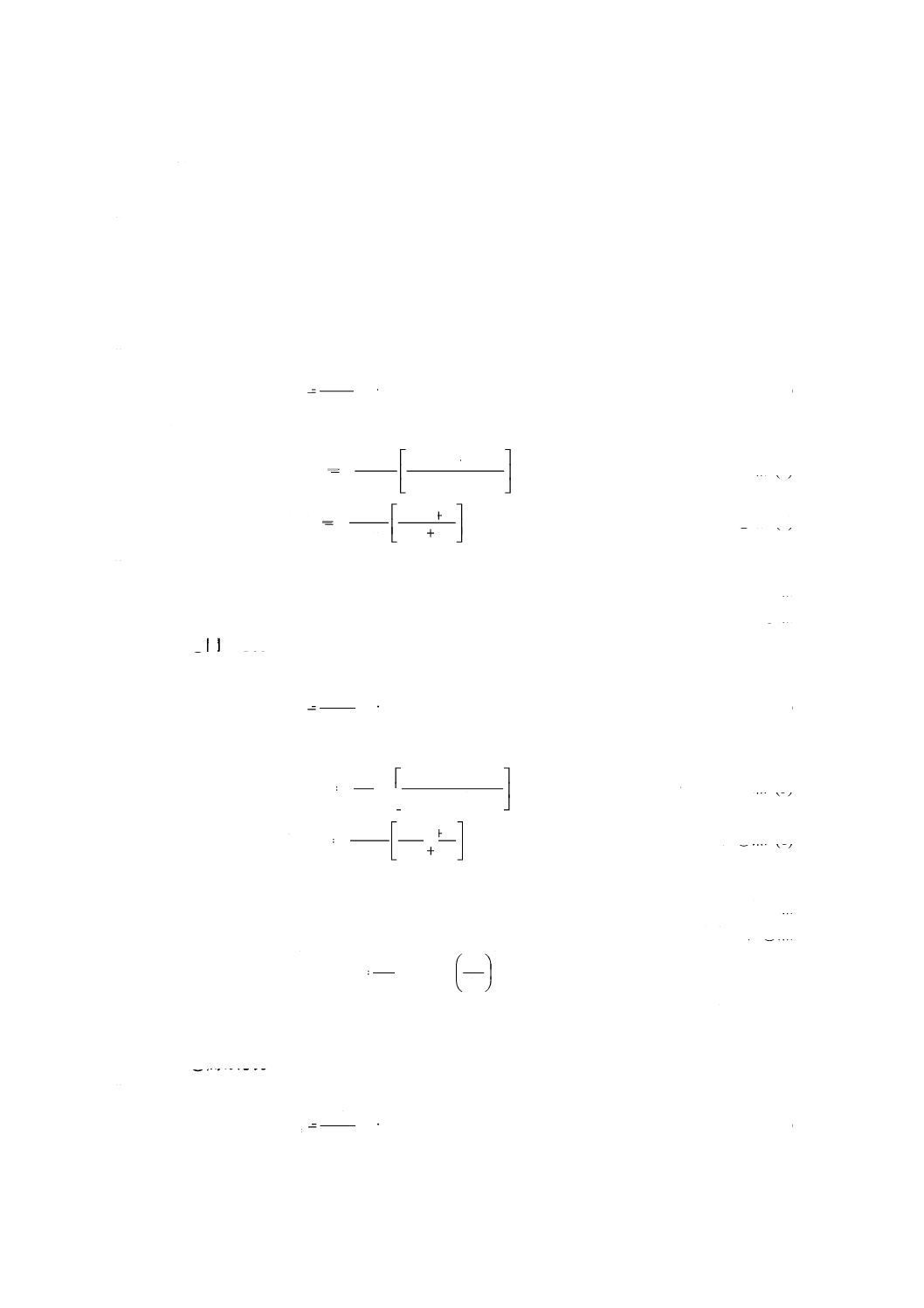
− 膜応力に対する補強計算 膜応力に対する簡易補強計算は,次による。
手順1 膜応力と曲げ応力との合成応力に対する当該穴をもつ板の最小必要厚さtrを求める。
手順2 膜応力に対する必要補強面積は,最小必要厚さに膜応力と許容引張応力との比を乗じたも
のに,穴径を乗じた面積とする。
手順3 JIS B 8265附属書2(圧力容器の穴補強)に規定する補強の有効範囲内に膜応力に対する必
要補強面積をとる。
− 曲げ応力に対する補強計算 曲げ応力に対する簡易補強計算は,次による。
手順1 最小必要厚さと穴径とからなる部材についての板厚方向に垂直な中立軸に関する断面2次
モーメントを求める。
手順2 JIS B 8265附属書2(圧力容器の穴補強)に規定する補強の有効範囲内(膜応力に対する補
強に考慮した部分以外の部分)に,手順1と同じ中立軸に関する断面2次モーメントが,
手順1で求めた必要断面2次モーメント以上となるような補強部をとる。
ここに,
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3) リガメント効率を適用する穴は,補強板を取り付ける必要はない。
f)
管穴 管穴は,JIS B 8274の4.3(管板の構造)及び4.4(伝熱管と管板の接合方法)によるほか,次
による。
1) 拡管によって胴板に管を取り付ける場合には,管穴の中心間の距離は管の外径の1.25倍以上とする。
2) 拡管によって管を取り付ける非円形胴の管板の場合には,管の取付部の厚さは,10 mm以上とする。
7.2
非円形胴の横断面が長方形の胴の計算
7.2.1
図1 a) に示す胴 図1 a) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材〜間の応力
1) 膜応力 (σm)
η
σ
1
2t
Ph
m=
············································································ (1)
2) 曲げ応力 (σb)
(
)
+
α
+
−
η
±
=
1
3
2
2
)
(
2
3
1
2
K
K
t
c
Ph
N
b
σ
··································· 中央◯
N点 (2)
++
±
=
1
1
)
(
2
3
1
2
K
K
t
c
Ph
B
b
α
η
σ
····································隅角部◯
A,◯
B点 (3)
3) 合成応力 (σT)
(σT)N=式 (1)+式 (2)························································· 中央◯
N点
(σT)B=式 (1)+式 (3) ················································ 隅角部◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
············································································ (4)
2) 曲げ応力 (σb)
+
−
−
±
=
1
1
)3
2(
2
)
(
2
3
2
2
K
K
t
c
Ph
M
b
α
η
σ
··································· 中央◯
M点 (5)
++
±
=
1
1
)
(
2
3
2
2
K
K
t
c
Ph
B
b
α
η
σ
····································隅角部◯
B,◯
C点 (6)
3) 合成応力 (σT)
(σT)M=式 (4)+式 (5) ························································ 中央◯
M点
(σT)B=式 (4)+式 (6) ················································ 隅角部◯
B,◯
C点
ここに,
3
1
2
,
=
=
t
t
K
h
H
α
α
P,H,h,t1,t2,σm,σb,σT及びηは,6. 及び図1 a) による。
7.2.2
図1 b) に示す胴 図1 b) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1
2t
Ph
m=
············································································ (7)
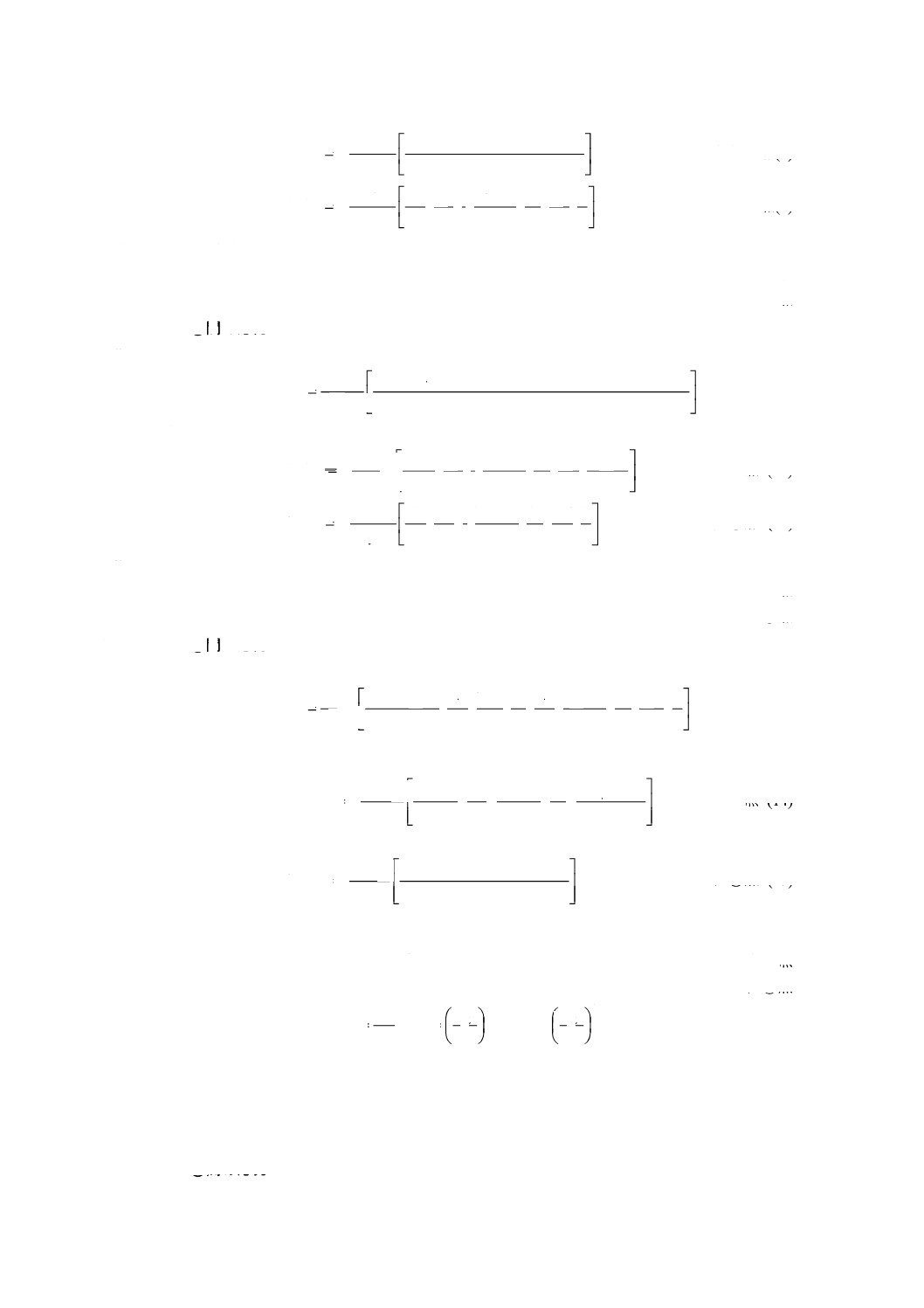
2) 曲げ応力 (σb)
9
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−
+
−
±
=
N
k
K
k
k
k
K
t
c
Ph
A
b
)
(
)
(
3
)
(
2
1
2
2
2
1
1
3
1
2
α
η
σ
··················· 隅角部◯
A点(8)
−
+
−
±
=
N
k
K
k
k
k
K
t
c
Ph
B
b
)
(
)
(
3
)
(
2
2
2
2
2
1
2
3
1
2
α
η
σ
·················· 隅角部◯
B点(9)
3) 合成応力 (σT)
(σT)A=式 (7)+式 (8) ······················································ 隅角部◯
A点
(σT)B=式 (7)+式 (9) ······················································ 隅角部◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
−
+
+
−
+
+
=
α
α
α
η
σ
N
K
K
k
k
K
k
k
K
N
t
Ph
m
)
(
)
(
)
(
2
'
4
1
2
2
2
2
1
1
2
2
2
2
··········· (10)
2) 曲げ応力 (σb)
−
−
+
−
±
=
N
N
k
K
k
k
k
K
t
c
Ph
M
b
)}
(
)
{(
2
'
2
3
)
(
2
2
2
2
2
1
2
3
2
2
α
η
σ
·········· 中央◯
M点 (11)
−
+
−
±
=
N
k
K
k
k
k
K
t
c
Ph
B
b
)
(
)
(
'
3
)
(
2
2
2
2
2
1
2
3
2
2
α
η
σ
········ 隅角部◯
B,◯
C点 (12)
3) 合成応力 (σT)
(σT) M=式 (10)+式 (11) ····················································· 中央◯
M点
(σT) B=式 (10)+式 (12) ············································ 隅角部◯
B,◯
C点
c) 部材◯
D〜◯
A間の応力
1) 膜応力 (σm)
−
−
+
+
+
−
=
α
α
α
η
σ
N
K
K
k
k
K
k
k
K
N
t
Ph
m
)
(
)
(
)
(
2
4
1
2
2
2
2
1
1
2
2
2
2
············· (13)
2) 曲げ応力 (σb)
−
−
+
−
±
=
N
N
k
K
k
k
k
K
t
c
Ph
M
b
)}
(
)
{(
2
2
3
)
(
2
1
2
2
2
1
1
3
2
2
1
α
η
σ
······· 中央◯
M1点 (14)
−
+
−
±
=
N
k
K
k
k
k
K
t
c
Ph
A
b
)
(
)
(
3
)
(
2
1
2
2
2
1
1
3
2
2
α
η
σ
············ 隅角部◯
A,◯
D点 (15)
3) 合成応力 (σT)
(σT)M1=式 (13)+式 (14) ···················································· 中央◯
M1点
(σT)A=式 (13)+式 (15) ············································· 隅角部◯
A,◯
D点
ここに,
3
1
2
2
3
2
2
1
'
,
'
,
=
=
=
t
t
k
t
t
k
h
H
α
α
K1=2k2+3,K2=3k1+2k2
N=K1K2−k22
P,H,h,t1,t2,t2´,σm,σb,σT及びηは,6. 及び図1 b) による。
7.2.3
図1 c) に示す胴 図1 c) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
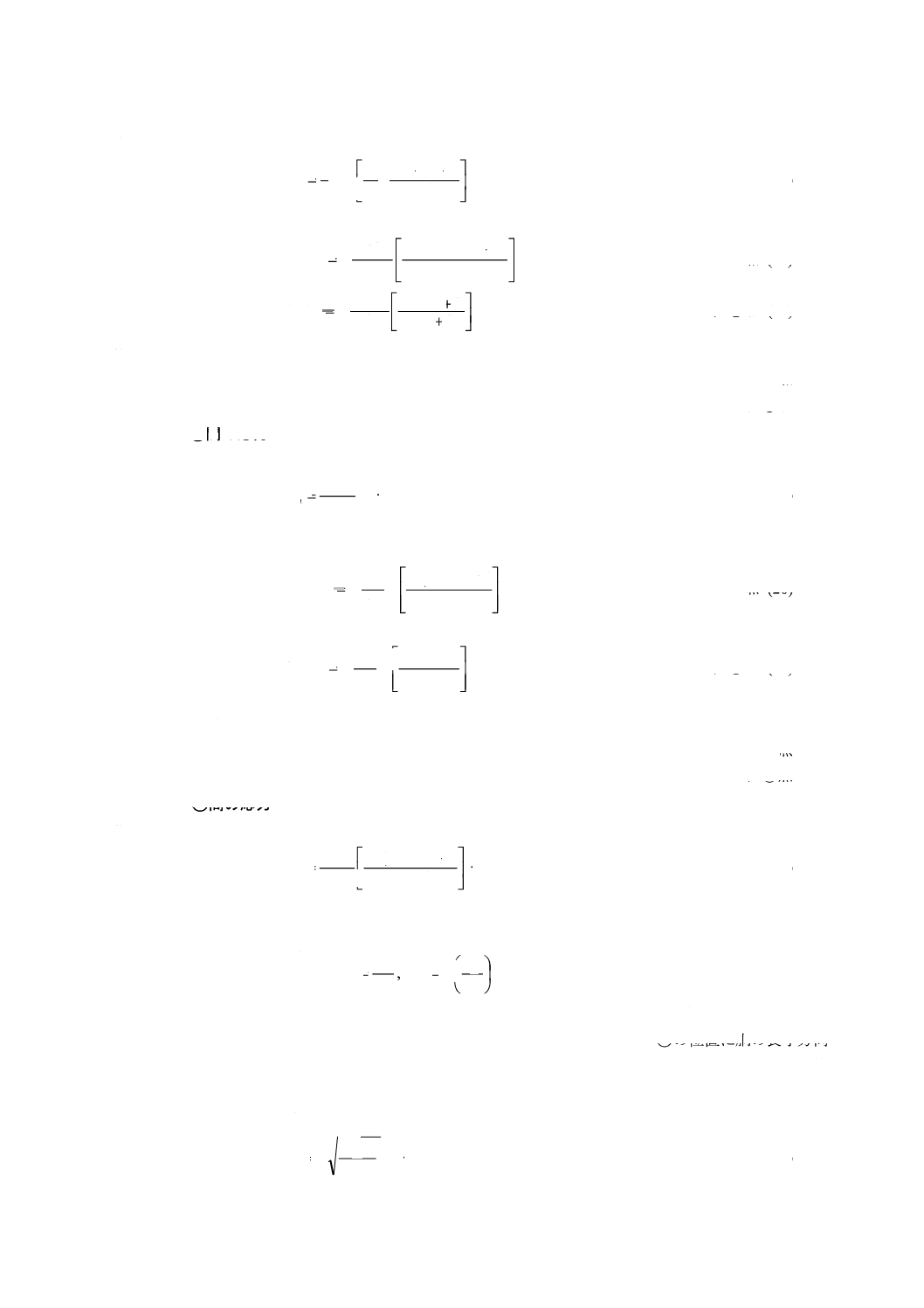
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1) 膜応力 (σm)
+
+
+
=
1
2
2
)3
(
4
2
1
K
K
t
Ph
m
α
η
σ
························································ (16)
2) 曲げ応力 (σb)
+
+
−
±
=
1
2
)3
2(
2
2
)
(
2
3
1
2
K
K
t
c
Ph
N
b
α
η
σ
································· 中央◯
N点 (17)
++
±
=
1
2
1
2
)
(
2
3
1
2
K
K
t
c
Ph
A
b
α
η
σ
································ 隅角部◯
A,◯
B点 (18)
3) 合成応力 (σT)
(σT)N=式 (16)+式 (17)······················································ 中央◯
N点
(σT)A=式 (16)+式 (18) ············································· 隅角部◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
·········································································· (19)
2) 曲げ応力 (σb)
+
+
−
±
=
1
2
1
)
3(
)
(
2
3
2
2
1
K
K
t
c
Ph
M
b
α
η
σ
································· 仕切板◯
M1点 (20)
+
+
±
=
1
2
1
2
)
(
2
3
2
2
K
K
t
c
Ph
B
b
α
η
σ
·································· 隅角部◯
B,◯
C点 (21)
3) 合成応力 (σT)
(σT)M1=式 (19)+式 (20) ················································· 仕切板◯
M1点
(σT)B=式 (19)+式 (21) ············································· 隅角部◯
B,◯
C点
c) 部材◯
M1〜◯
M1間の応力
1) 膜応力 (σm)
+
+
−
=
1
2
2
)
5(
2
2
3
K
K
t
Ph
m
α
η
σ
························································ (22)
2) 曲げ応力 (σb)
σb=0
ここに,
3
1
2
,
=
=
t
t
K
h
H
α
α
P,H,h,t1,t2,t3,σm,σb,σT及びηは,6. 及び図1 c) による。
7.2.4
図1 c) に示す胴に丸棒でステーされる胴 図1 c) に示す胴で仕切板◯
M1〜◯
M1の位置に胴の長手方向
に一定のピッチで一列の丸棒ステーで支えられる胴板に生じる膜応力,曲げ応力及び合成応力は,次の算
式による。
a) 丸棒ステーの最大ピッチ (Pc)
P
C
t
P
a
c
σ
2
=
····································································· (23)
11
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
b) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1t
Ph
m=
··········································································· (24)
2) 曲げ応力 (σb)
(σb)N=式 (17) ···························································· 中央◯
N点 (25)
(σb)A=式 (18) ··················································· 隅角部◯
A,◯
B点 (26)
3) 合成応力 (σT)
(σT)N=式 (24)+式 (25)······················································ 中央◯
N点
(σT)A=式 (24)+式 (26) ············································· 隅角部◯
A,◯
B点
c) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
········································································· (27)
2) 曲げ応力 (σb)
(σb)M1=式 (20) ··························································· 中央◯
M1点 (28)
(σb)B=式 (21) ··················································· 隅角部◯
B,◯
C点 (29)
3) 合成応力 (σT)
(σT) M1=式 (27)+式 (28)···················································· 中央◯
M1点
(σT) B=式 (27)+式 (29) ············································ 隅角部◯
B,◯
C点
d) 丸棒ステーの応力
1) 膜応力 (σm)
+
+
−
=
1
2
2
)
5(
2
2
2
K
K
d
PhPc
m
α
η
π
σ
·················································· (30)(5)
2) 曲げ応力 (σb)
σb=0
注(5) h>Pcの場合は,式(30)でPcの代わりにhを用いて計算する。
ここに,P,H,h,t1,t2,d,Pc,σa,σm,σb,σT及びηは,6. 及び図1 c) による。
h
H
t
t
K
=
=
α
α
,
3
1
2
Cはステーの取付け方による係数(JIS B 8265附属書9参照)
C=2.1 …… 厚さ11 mm以下の板に溶接したステー
C=2.2 …… 厚さ11 mmを超える板に溶接したステー
7.2.5
図1 d) に示す胴 図1 d) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
+
+
+
=
3
5
3
)4
(
2
2
1
K
K
t
Ph
m
α
η
σ
························································ (31)
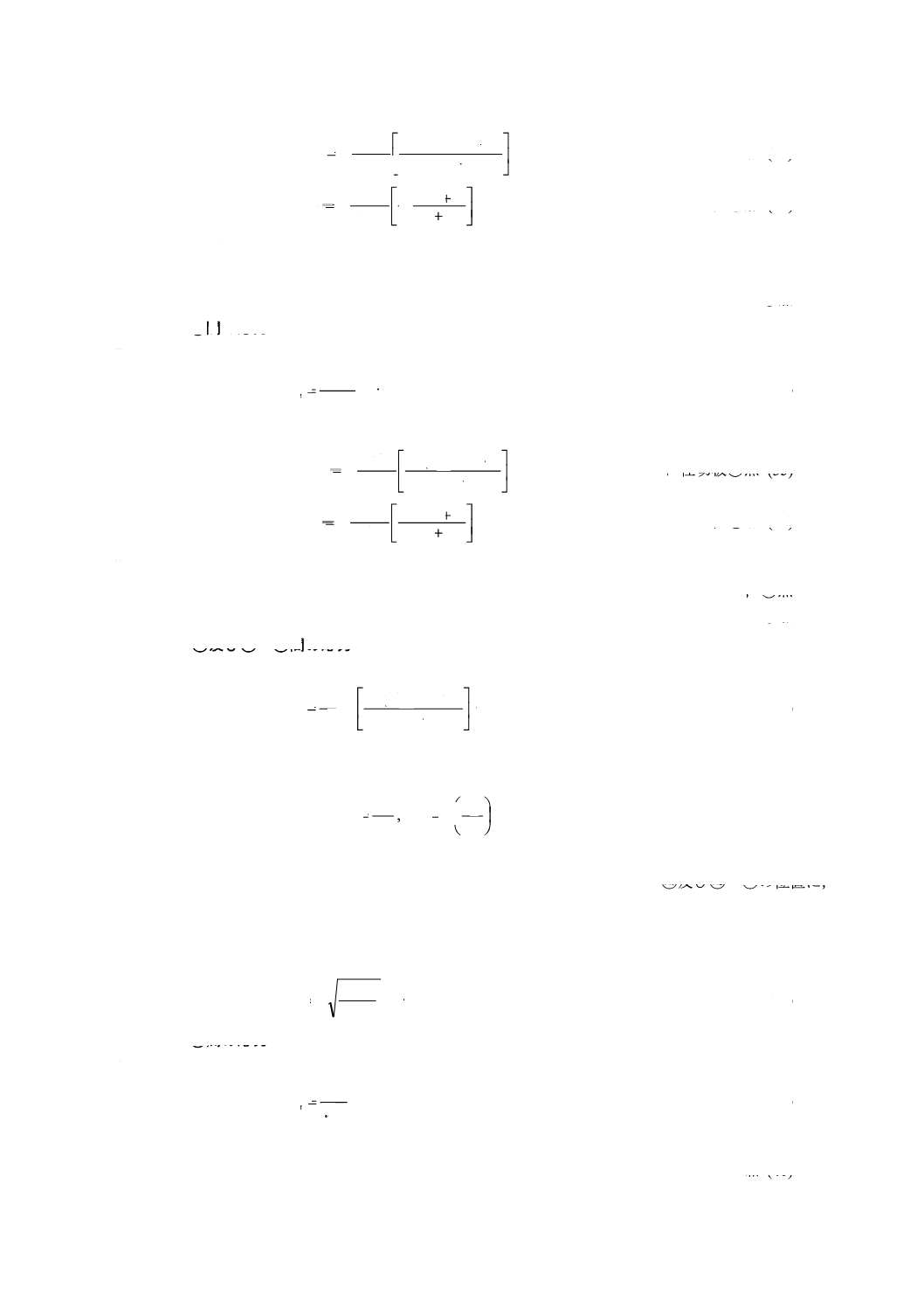
2) 曲げ応力 (σb)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
+
+
−
±
=
3
5
)9
5(
6
2
)
(
2
3
1
2
K
K
t
c
Ph
N
b
α
η
σ
·································· 中央◯
N点 (32)
++
±
=
3
5
3
5
)
(
2
3
1
2
K
K
t
c
Ph
A
b
α
η
σ
································ 隅角部◯
A,◯
B点 (33)
3) 合成応力 (σT)
(σT) N=式 (31)+式 (32) ····················································· 中央◯
N点
(σT) A=式 (31)+式 (33) ············································ 隅角部◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
·········································································· (34)
2) 曲げ応力 (σb)
+
+
−
±
=
3
5
3
)
6(
)
(
2
3
2
2
1
K
K
t
c
Ph
M
b
α
η
σ
················仕切板◯
M1,仕切板◯
M2点 (35)
++
±
=
3
5
3
5
)
(
2
3
2
2
K
K
t
c
Ph
B
b
α
η
σ
································ 隅角部◯
B,◯
C点 (36)
3) 合成応力 (σT)
(σT) M1=式 (34)+式 (35)··········································· 仕切板◯
M1,◯
M2点
(σT) B=式 (34)+式 (36) ············································ 隅角部◯
B,◯
C点
c) 部材◯
M1〜◯
M1及び◯
M2〜◯
M2間の応力
1) 膜応力 (σm)
+
+
−
=
3
5
6
)
11
(
2
2
3
K
K
t
Ph
m
α
η
σ
······················································· (37)
2) 曲げ応力 (σb)
σb=0
ここに,
3
1
2
,
=
=
t
t
K
h
H
α
α
P,H,h,t1,t2,t3,σm,σb,σT及びηは,6.及び図1 d)による。
7.2.6
図1 d) に示す胴に丸棒でステーされる胴 図1 d) に示す胴で仕切板◯
M1〜◯
M1及び◯
M2〜◯
M2の位置に,
胴の長手方向に一定のピッチで二列の丸棒ステーで支えられる胴板に生じる膜応力,曲げ応力及び合成応
力は,次の算式による。
a) 丸棒ステーの最大ピッチ (Pc)
P
C
t
P
a
c
σ
2
=
····································································· (38)
b) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1t
Ph
m=
··········································································· (39)
2) 曲げ応力 (σb)
(σb)N=式 (32) ···························································· 中央◯
N点 (40)
13
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(σb)A=式 (33) ··················································· 隅角部◯
A,◯
B点 (41)
3) 合成応力 (σT)
(σT)N=式 (39)+式 (40)······················································ 中央◯
N点
(σT)A=式 (39)+式 (41) ············································· 隅角部◯
A,◯
B点
c) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
········································································· (42)
2) 曲げ応力 (σb)
(σb)M1=式 (35) ·········································ステー取付部◯
M1,◯
M2点 (43)
(σb)B=式 (36) ··················································· 隅角部◯
B,◯
C点 (44)
3) 合成応力 (σT)
(σT)M1=式 (42)+式 (43) ·································· ステー取付部◯
M1,◯
M2点
(σT)B=式 (42)+式 (44) ············································· 隅角部◯
B,◯
C点
d) 丸棒ステーの応力
1) 膜応力 (σm)
+
+
−
=
3
5
6
)
11
(
2
2
2
K
K
d
PhPc
m
α
η
π
σ
················································· (45)(6)
2) 曲げ応力 (σb)
σb=0
注(6) h>Pcの場合は,式 (45)でPcの代わりにhを用いて計算する。
ここに,
3
1
2
,
=
=
t
t
K
h
H
α
α
Cはステーの取付け方による係数(JIS B 8265附属書9参照)
C=2.1 …… 厚さ11 mm以下の板に溶接したステー
C=2.2 …… 厚さ11 mmを超える板に溶接したステー
P,H,h,t1,t2,d,Pc,σm,σb,σT及びηは,6. 及び図1 d) による。
7.2.7
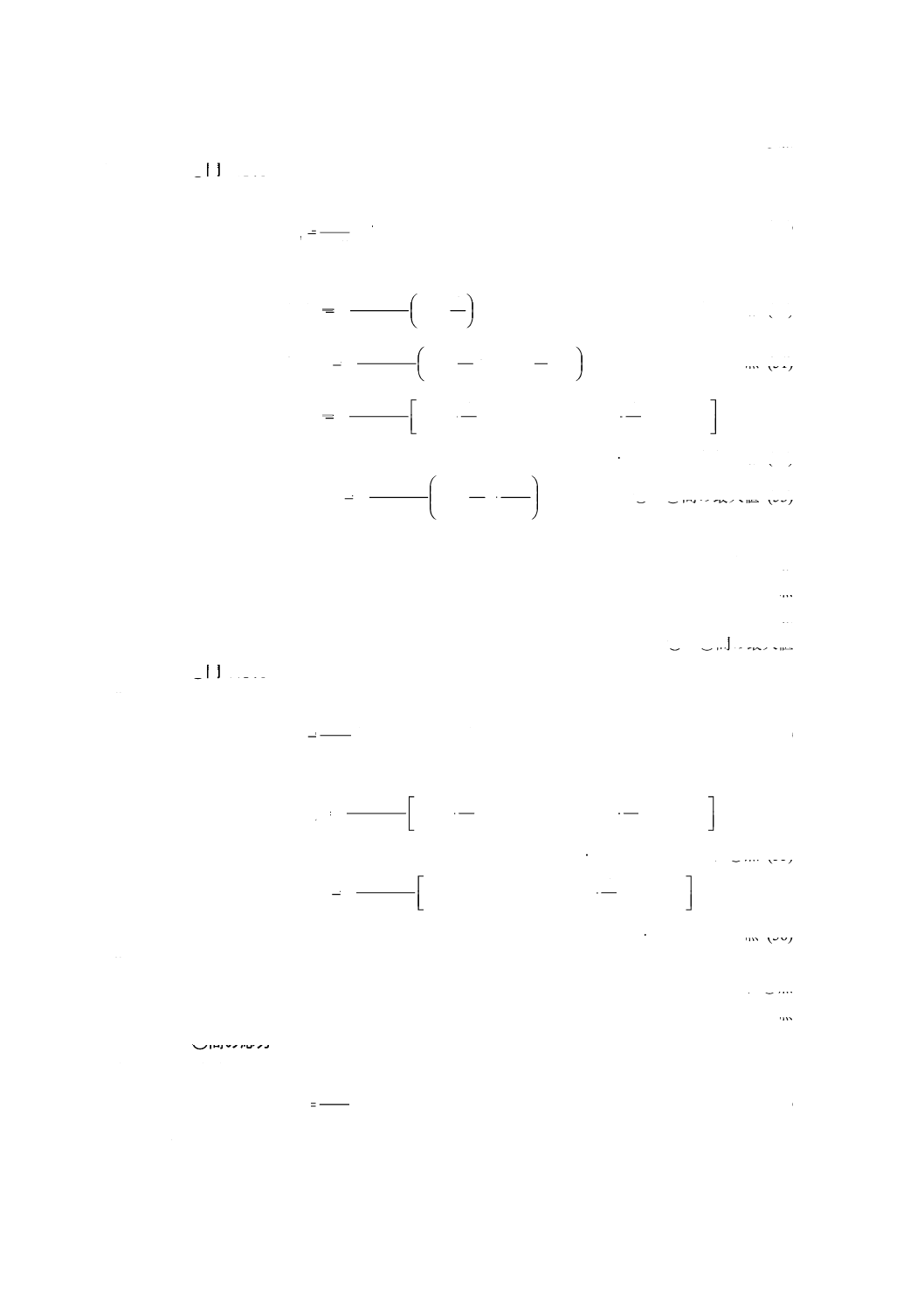
図1 e) に示す胴 図1 e) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
1
1
C
t
PH
m
η
σ=
······································································· (46)
2) 曲げ応力 (σb)
2
3
1
2
1
12
)
(
C
t
c
PH
N
b
η
σ
±
=
················································· 中央◯
N1点 (47)
+
−
±
=
8
1
12
)
(
2
3
1
2
C
t
c
PH
B
b
η
σ
······························ 隅角部◯
A,◯
B点 (48)
3) 合成応力 (σT)
(σT)N1=式 (46)+式 (47) ····················································· 中央◯
N1点
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(σT)B=式 (46)+式 (48) ············································· 隅角部◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
··········································································· (49)
2) 曲げ応力 (σb)
−
±
=
8
1
12
)
(
2
3
2
2
C
t
c
PH
B
b
η
σ
······································ 隅角部◯
B点 (50)
−
+
−
±
=
2
4
4
1
2
3
2
2
1
2
1
8
1
12
)
(
α
α
η
σ
C
C
t
c
PH
M
b
················· 仕切板◯
M1点 (51)
+
+
−
+
−
+
−
±
=
2
5
4
5
3
5
4
1
2
3
2
2
)
(
2
1
)
(
8
1
12
)
(
α
α
α
α
α
η
σ
C
C
C
t
c
PH
C
b
······························· 隅角部◯
C点 (52)
+
−
±
=
−
2
8
1
12
)
(
2
1
2
3
2
2
1
C
C
t
c
PH
M
B
b
η
σ
················· ◯
B〜◯
M1間の最大値 (53)
3) 合成応力 (σT)
(σT)B=式 (49)+式 (50) ··················································· 隅角部◯
B点
(σT)M1=式 (49)+式 (51) ················································· 仕切板◯
M1点
(σT)c=式 (49)+式 (52) ··················································· 隅角部◯
C点
(σT)B−M1=式 (49)+式 (53) ····································· ◯
B〜◯
M1間の最大値
c) 部材◯
C〜◯
D間の応力
1) 膜応力 (σm)
)
(
3
1
5
4
1
C
C
t
PH
m
−
−
+
=
α
α
η
σ
······················································ (54)
2) 曲げ応力 (σb)
+
+
−
+
−
+
−
±
=
2
5
4
5
3
5
4
1
2
3
1
2
)
(
2
1
)
(
8
1
12
)
(
α
α
α
α
α
η
σ
C
C
C
t
c
PH
c
b
························· 隅角部◯
C,◯
D点 (55)
+
+
−
+
−
−
±
=
2
5
4
5
3
5
4
1
2
3
1
2
2
)
(
2
1
)
(
12
)
(
α
α
α
α
α
η
σ
C
C
C
t
c
PH
N
b
·································· 中央◯
N2点 (56)
3) 合成応力 (σT)
(σT)c=式 (54)+式 (55) ············································· 隅角部◯
C,◯
D点
(σT)N2=式 (54)+式 (56) ····················································· 中央◯
N2点
d) 部材◯
M1〜◯
M1間の応力
1) 膜応力 (σm)
3
3
C
t
PH
m
η
σ=
······································································· (57)
2) 曲げ応力 (σb)
σb=0

15
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
+
+
+
+
−
=
12
8
24
)
(
3
3
4
4
2
2
4
2
2
4
1
α
α
α
α
α
α
C
C
7
6
5
4
2
/)
(
k
k
k
k
C
−
−
=
+
+
+
+
+
+
+
−
−
+
=
2
3
)
(
)
(
12
1
)
2
(
3
)
(
3
2
4
4
5
4
2
5
4
5
4
1
2
2
5
5
4
3
α
α
α
α
α
α
α
α
α
α
α
C
C
C
H
h
H
h
t
t
/
,
/
,
)
/
(
2
5
1
4
3
1
2
2
=
=
=
α
α
α
+
−
−
+
+
+
+
+
=
12
4
6
)
(
2
1
)
(
)
(
3
2
4
1
2
4
3
4
5
4
2
5
4
2
3
5
4
4
α
α
α
α
α
α
α
α
α
α
k
−
+
+
+
+
+
=
3
)
(
)
(
2
2
3
8
1
2
4
5
4
2
2
5
4
2
4
3
4
2
4
5
α
α
α
α
α
α
α
α
α
α
k
)
(
)
(
)
(
2
2
2
3
2
3
8
5
2
2
4
4
5
4
2
5
4
2
4
5
4
2
4
3
4
5
5
4
6
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
+
+
+
+
+
+
+
+
+
−
+
=
k
)
(
2
)
(
1
2
)
(3
3
)
(
)
(
)
(
2
3
2
2
5
2
2
4
5
4
2
4
5
5
4
2
4
5
4
2
2
5
4
2
4
2
4
2
4
5
4
7
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
+
+
+
−
+
−
−
+
+
+
+
−
+
−
+
=
k
P,H,h1,h2,t1,t2,t3,σm,σb,σT及びηは,6.及び図1 e)による。
7.2.8
図1e) に示す胴に丸棒でステーされる胴 図1e) に示す胴で仕切板◯
M1〜◯
M1の位置に胴の長手方向
に一定のピッチで一列の丸棒ステーで支えられる胴板に生じる膜応力,曲げ応力及び合成応力は,次の算
式による。
a) 丸棒ステーの最大ピッチ (Pc)
P
C
t
P
a
c
σ
2
=
····································································· (58)
b) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1
1
t
Ph
m=
·········································································· (59)
2) 曲げ応力 (σb)
(σb)N1=式 (47) ··························································· 中央◯
N1点 (60)
(σb)B=式 (48) ··················································· 隅角部◯
A,◯
B点 (61)
3) 合成応力 (σT)
(σT)N1=式 (59)+式 (60) ····················································· 中央◯
N1点
(σT)B=式 (59)+式 (61) ············································· 隅角部◯
A,◯
B点
c) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
········································································· (62)
2) 曲げ応力 (σb)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(σb)B=式 (50) ························································· 隅角部◯
B点 (63)
(σb)M1=式 (51) ··············································· ステー取付部◯
M1点 (64)
(σb)C=式 (52) ························································· 隅角部◯
C点 (65)
(σb)B−M1=式 (53) ············································ ◯
B〜◯
M1間の最大値 (66)
3) 合成応力 (σT)
(σT)B=式 (62)+式 (63) ··················································· 隅角部◯
B点
(σT)M1=式 (62)+式 (64) ········································ ステー取付部◯
M1点
(σT)C=式 (62)+式 (65)··················································· 隅角部◯
C点
(σT)B−M1=式 (62)+式 (66) ····································· ◯
B〜◯
M1間の最大値
d) 部材◯
C〜◯
D間の応力
1) 膜応力 (σm)
)
(
3
1
5
4
1
C
C
t
PH
m
−
−
+
=
α
α
η
σ
······················································ (67)
2) 曲げ応力 (σb)
(σb)c=式 (55)···················································· 隅角部◯
C,◯
D点 (68)
(σb)N2=式 (56) ··························································· 中央◯
N2点 (69)
3) 合成応力 (σT)
(σT)C=式 (67)+式 (68)············································· 隅角部◯
C,◯
D点
(σT)N2=式 (67)+式 (69) ····················································· 中央◯
N2点
e) 丸棒ステー◯
M1〜◯
M1間の応力
1) 膜応力 (σm)
3
2
4
C
d
PHPc
m
η
π
σ=
······································································ (70)
2) 曲げ応力 (σb)
σb=0
ここに,α4=h1/H,α5=h2/H
Cはステーの取付け方による係数[JIS B 8265附属書9(圧力容器のステーによって支える板)参
照]
C=2.1 ····· 厚さ11 mm以下の板に溶接したステー
C=2.2 ····· 厚さ11 mmを超える板に溶接したステー
C1,C3は7.2.7による。
P,H,h1,h2,t1,t2,d,Pc,σa,σm,σb,σT及びηは,6.及び図1 e)による。
7.2.9
図1 f) に示す胴 図1 f) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1
1
t
PHC
m=
······································································· (71)
2) 曲げ応力 (σb)
2
3
1
2
12
)
(
C
t
c
PH
N
b
η
σ
±
=
·················································· 中央◯
N点 (72)

17
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
−
η
±
=
8
1
12
)
(
2
3
1
2
C
t
c
PH
B
b
σ
······························· 隅角部◯
A,◯
B点 (73)
3) 合成応力 (σT)
(σT)N=式 (71)+式 (72)······················································ 中央◯
N点
(σT)B=式 (71)+式 (73) ············································· 隅角部◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
········································································· (74)
2) 曲げ応力 (σb)
−
±
=
8
1
12
)
(
2
3
2
2
C
t
c
PH
B
b
η
σ
······································ 隅角部◯
B点 (75)
α
−
α
+
−
η
±
=
2
4
4
1
2
3
2
2
2
1
8
1
12
)
(
1
C
C
t
c
PH
M
b
σ
········ 仕切板◯
M1,◯
M2点 (76)
[
]
+
+
−
+
+
+
±
=
2
5
4
5
3
5
4
1
2
3
2
2
)
2
(
1
8
1
2
1
)
2
(
2
1
12
)
(
α
α
α
α
α
η
σ
C
C
C
t
c
PH
M
b
·································· 中央◯
M点 (77)
3) 合成応力 (σT)
(σT)B=式 (74)+式 (75) ··················································· 隅角部◯
B点
(σT)M1=式 (74)+式 (76) ··········································· 仕切板◯
M1,◯
M2点
(σT)M=式 (74)+式 (77) ····················································· 中央◯
M点
c) 部材◯
M1〜◯
M1及び◯
M2〜◯
M2間の応力
1) 膜応力 (σm)
3
3
C
t
PH
m
η
σ=
······································································ (78)
2) 曲げ応力 (σb)
σb=0
ここに,
5
4
2
4
5
4
3
5
5
2
4
3
4
5
4
2
1
3
2
)}
(3
2
12
6
{
8
1
)
(
3
α
α
α
α
α
α
α
α
α
α
α
+
+
+
−
+
+
+
−
=
C
C
)}
3
2(
2
{
24
)
3
2(
2
6
2
6
3
5
4
2
5
4
2
4
5
4
2
3
5
4
5
3
4
4
4
5
4
2
4
2
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
+
+
+
+
+
+
−
−
+
=
C
1
5
4
3
)
2(
2
1
C
C
−
+
=
α
α
H
h
H
h
t
t
/
,
/
,
)
/
(
2
5
1
4
3
1
2
2
=
=
=
α
α
α
P,H,h1,h2,t1,t2,t3,σm,σb,σT及びηは,6. 及び図1 f) による。
7.2.10 図1 f) に示す胴に丸棒でステーされる胴 図1 f) に示す胴で仕切板◯
M1〜◯
M1及び◯
M2〜◯
M2の位置に胴
の長手方向に一定のピッチで二列の丸棒ステーで支えられる胴板に生じる膜応力,曲げ応力及び合成応力
は,次の算式による。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 丸棒ステーの最大ピッチ (Pc)
P
C
t
P
a
c
σ
2
=
····································································· (79)
b) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1
1
t
Ph
m=
··········································································· (80)
2) 曲げ応力 (σb)
(σb)N=式 (72) ···························································· 中央◯
N点 (81)
(σb)B=式 (73) ··················································· 隅角部◯
A,◯
B点 (82)
3) 合成応力 (σT)
(σT)N=式 (80)+式 (81)······················································ 中央◯
N点
(σT)B=式 (80)+式 (82) ············································· 隅角部◯
A,◯
B点
c) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2
2t
PH
m=
·········································································· (83)
2) 曲げ応力 (σb)
(σb)B=式 (75) ························································· 隅角部◯
B点 (84)
(σb)M1=式 (76) ·········································ステー取付部◯
M1,◯
M2点 (85)
(σb)M=式 (77) ···························································· 中央◯
M点 (86)
3) 合成応力 (σT)
(σT)B=式 (83)+式 (84) ··················································· 隅角部◯
B点
(σT)M1=式 (83)+式 (85) ·································· ステー取付部◯
M1,◯
M2点
(σT)M=式 (83)+式 (86) ····················································· 中央◯
M点
d) 丸棒ステー◯
M1〜◯
M1又は◯
M2〜◯
M2間の応力
1) 膜応力 (σm)
3
2
4
C
d
PHPc
m
η
π
σ=
································································ (87)(7)
2) 曲げ応力 (σb)
σb=0
注(7) h1>Pc又はh2>Pcの場合は,式 (87)でPcの代わりにh1又はh2(いずれか大きいほう)を用い
て計算する。
ここに,
Cはステーの取付け方による係数[JIS B 8265附属書9(圧力容器のステーによって支える板)
参照]
C=2.1 …… 厚さ11 mm以下の板に溶接したステー
C=2.2 …… 厚さ11 mmを超える板に溶接したステー
C3は7.2.9による。
P,H,h1,h2,t1,t2,d,Pc,σa,σm,σb,σT及びηは,6. 及び図1 f) による。
19
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.2.11 図1 g) に示す胴 図1 g) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1
0
2
)
2
(
t
R
h
P
m
+
=
································································· (88)
2) 曲げ応力 (σb)
]
2
)1
2
)(
1
(3[
2
)
(
0
0
0
3
1
2
0
K
t
c
PH
N
b
−
+
+
−
±
=
φ
α
α
η
σ
···················· 中央◯
N点 (89)
]
2
}
)1
(
2
{3[
2
)
(
0
2
0
0
3
1
2
0
K
t
c
PH
B
b
−
+
−
±
=
α
α
φ
η
σ
···· 胴板の曲がり◯
A,◯
B点 (90)
3) 合成応力 (σT)
(σT)N=式 (88)+式 (89)······················································ 中央◯
N点
(σT)B=式 (88)+式 (90) ·····································胴板の曲がり◯
A,◯
B点
b) 部材◯
C〜◯
D間の応力
1) 膜応力 (σm)
η
σ
1
0
2
)
2
(
t
R
H
P
m
+
=
································································ (91)
2) 曲げ応力 (σb)
0
3
1
2
0
)
(
K
t
c
PH
M
b
η
σ
±
=
··················································· 中央◯
M点 (92)
)
2
3(
2
)
(
0
2
0
3
1
2
0
K
t
c
PH
c
b
−
±
=
α
η
σ
······················ 胴板の曲がり◯
C,◯
D点 (93)
3) 合成応力 (σT)
(σT)M=式 (91)+式 (92) ····················································· 中央◯
M点
(σT)c=式 (91)+式 (93) ·····································胴板の曲がり◯
C,◯
D点
c) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
)
1
(
2
2
0
1
0
+
+
=
α
φ
η
σ
t
PH
m
·························································· (94)
2) 曲げ応力 (σb)
]
2
}
)
sin
1(
2
cos
2
{3[
2
)
(
0
2
0
0
3
1
2
0
K
t
c
PH
b
−
+
−
−
±
=
α
θ
φ
θ
φ
α
η
σ
···················· (95)
3) 合成応力 (σT)
(σT)=式 (94)+式 (95)
ここに,
0
0
1
0
0
0
0
tan
,
2
,
h
H
H
R
H
h
−
=
=
=
θ
φ
α
2
2
)2
3
(
)6
5.1
6(
)2
2(
3
0
2
0
3
0
2
0
0
0
2
0
+
+
−
+
+
−
+
+
+
−
=
πφ
α
α
α
πα
α
φ
π
α
φ
K
P,H0,h0,R,t1,σm,σb,σT及びηは,6. 及び図1 g) による。

2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.2.12 図1 h) に示す胴 図1 h) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
γ
σ
2
1
3
0
)
1(
t
C
Ph
m
−
+
=
···························································· (96)
2) 曲げ応力 (σb)
−
+
−
−
−
+
+
−
±
=
2
2
3
2
3
1
1
2
3
2
2
3
2
2
0
1
2
1
)
1(
2
1
)
(
2
1
12
)
(
γ
γ
γ
γ
γ
γ
η
σ
C
C
C
t
c
Ph
N
b
·································· 中央◯
N1点 (97)
+
−
−
−
+
+
−
±
=
3
2
3
1
1
2
3
2
2
3
2
2
0
)
1(
2
1
)
(
2
1
12
)
(
γ
γ
γ
γ
γ
η
σ
C
C
C
t
c
Ph
B
b
················ 胴板の曲がり◯
A,◯
B点 (98)
3) 合成応力 (σT)
(σT) N1=式 (96)+式 (97) ···················································· 中央◯
N1点
(σT) B=式 (96)+式 (98) ····································胴板の曲がり◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
)
)
1(
(
3
2
2
2
1
2
0
γ
γ
η
σ
+
+
−
=
C
t
Ph
m
················································· (99)
2) 曲げ応力 (σb)
+
−
+
+
−
+
+
−
±
=
2
2
2
1
3
3
2
1
2
3
2
2
3
2
2
0
)
1(
2
1
)
(
2
1
12
γ
γ
γ
γ
γ
γ
η
σ
C
C
C
t
c
Ph
b
(100)
3) 合成応力 (σT)
(σT)T=式 (99)+式 (100)
c) 部材◯
C〜◯
D間の応力
1) 膜応力 (σm)
)
(
3
2
2
0
γ
γ
η
σ
+
=tPh
m
······························································ (101)
2) 曲げ応力 (σb)
−
+
+
−
±
=
2
1
)
(
2
1
12
)
(
1
2
3
2
2
3
2
2
0
C
C
t
c
Ph
c
b
γ
γ
η
σ
···· 胴板の曲がり◯
C点 (102)
+
−
±
=
2
3
2
2
3
2
2
0
)
(
2
1
12
)
(
γ
γ
η
σ
C
t
c
Ph
D
b
·························隅角部◯
D点 (103)
3) 合成応力 (σT)
(σT)C=式 (101)+式 (102) ········································胴板の曲がり◯
C点
(σT)D=式 (101)+式 (103) ··············································· 隅角部◯
D点
d) 部材◯
D〜◯
E間の応力
1) 膜応力 (σm)
1
1
0C
t
Ph
m
η
σ=
······································································ (104)
21
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2) 曲げ応力 (σb)
2
3
1
2
0
2
12
)
(
C
t
c
Ph
N
b
η
σ
±
=
·············································· 中央◯
N2点(105)
3) 合成応力 (σT)
(σT) N2=式 (104)+式 (105) ················································· 中央◯
N2点
ここに,
γ2=H0/2h0,γ3=R/h0
4
4
3
2
3
4
3
3
1
2
12
2
E
A
D
B
F
A
D
C
C
−
−
=
)
6
(6
3
3
2
4
4
3
2
4
3
2
D
B
E
A
F
B
E
C
C
−
−
=
C3=2 (γ2+γ3) 3+α4 {(γ2+γ3)2 (6+3πγ3+6γ2) +3π (γ3−2γ2γ32) +12γ32 (γ2+1) +
6γ2 (1+2γ3) −12γ22γ3+2γ23+2}
A4=2 (γ2+γ3) +α4 (2+πγ3+2γ2)
B2=α4 (1+πγ3+2γ32+2γ2+2γ2γ3)
D3=1+πγ3+2γ32+2γ2 (1+γ3)
E4=4+3π (2γ3+γ33) +24γ32+12γ2 (1+γ3)2
F3=6 (γ2+γ3)2 (1+πγ3+2γ32+2γ2+2γ2γ3) +3+12γ2 (1+3γ3+4γ32−γ33) −24γ22
(γ3+γ32) +4γ23 (1+γ3) +12γ32 (3−πγ2) +6πγ3 (1+γ32)
α4=(t1/t2)3
P,H0,h0,R,t1,t2,σm,σb,σT及びηは,6. 及び図1 h) による。
7.3
非円形胴の横断面が長円形の胴の計算
7.3.1
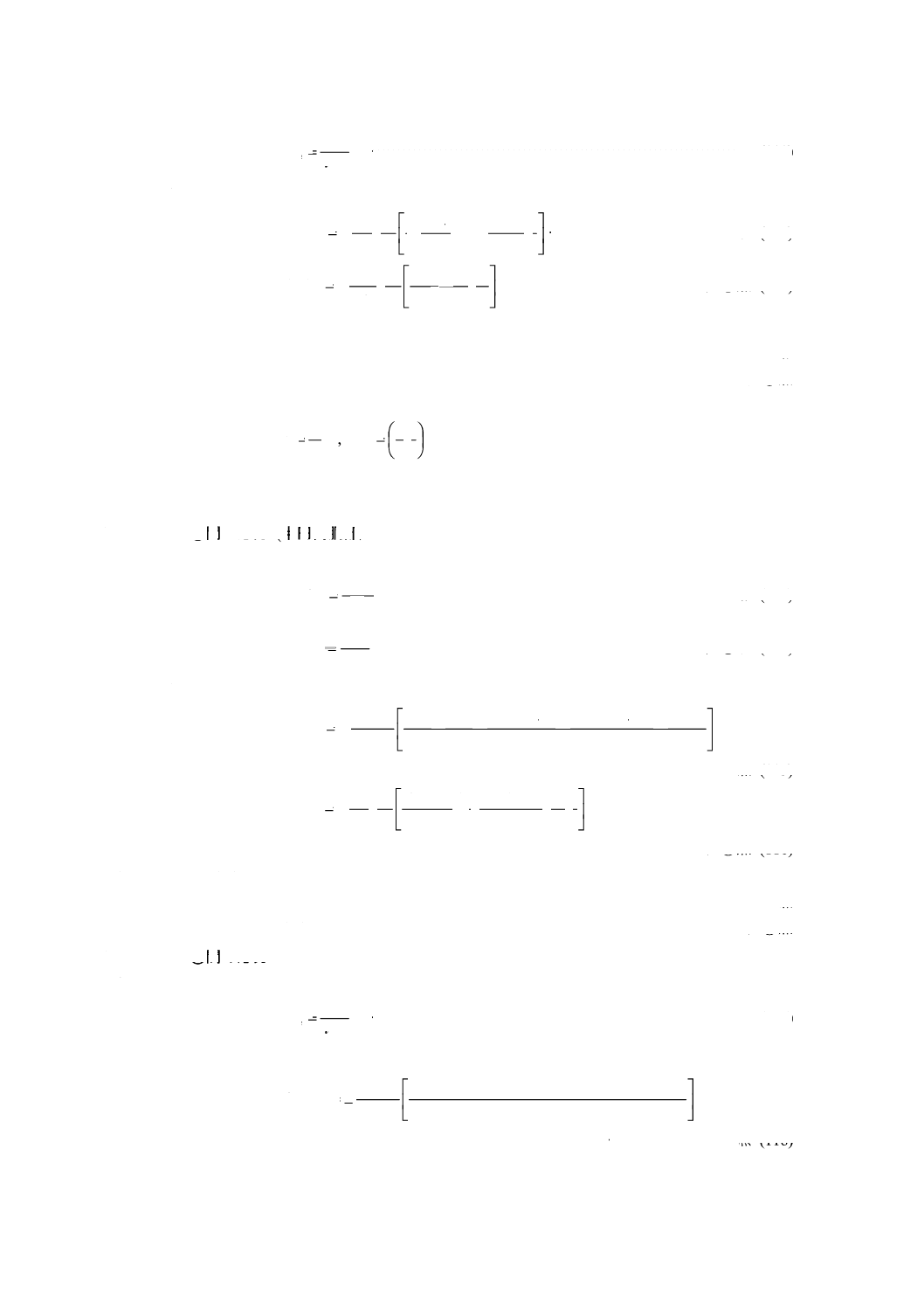
図2 a) に示す胴 図2 a) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力
1) 膜応力 (σm)
η
σ
1
0
2
)
2
(
)
(
t
R
h
P
N
m
+
=
···············································中央◯
N点 (106)
η
σ
1
)
(
t
PR
B
m
=
······································· 胴板の曲がり◯
A,◯
B点 (107)
2) 曲げ応力 (σb)
+
−
+
+
±
=
2
2
2
3
1
2
0
2
)2
(3
)3
(
2
)
(
πγα
γ
α
π
γ
γ
η
σ
t
c
Ph
N
b
·······················中央◯
N点 (108)
+
−
±
=
2
2
2
2
3
1
2
0
2
3
2
)
(
πγα
γ
α
γ
η
σ
t
c
Ph
B
b
·················· 胴板の曲がり◯
A,◯
B点 (109)
3) 合成応力 (σT)
(σT)N=式 (106)+式 (108) ··················································· 中央◯
N点
(σT)B=式 (107)+式 (109) ··································胴板の曲がり◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
η
σ
2t
PR
m=
·········································································· (110)
2) 曲げ応力 (σb)
+
+
+
±
=
2
2
2
2
2
3
2
2
0
2
12
3
2
2
)
(
πγα
γ
α
πγα
γ
η
σ
t
c
Ph
M
b
···························中央◯
M点 (111)
+
−
±
=
2
2
2
2
3
2
2
0
2
3
2
)
(
πγα
γ
α
γ
η
σ
t
c
Ph
B
b
·················· 胴板の曲がり◯
B,◯
C点 (112)
3) 合成応力 (σT)
(σT)M=式(110)+式(111)······················································ 中央◯
M点
(σT)B=式(110)+式(112) ·····································胴板の曲がり◯
B,◯
C点
ここに,
3
1
2
2
0,
2
=
=
t
t
R
h
α
γ
P,h0,R,t1,t2,σm,σb,σT及びηは,6. 及び図2 a) による。
7.3.2
図2 b) に示す胴 図2 b) に示す胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力 (半円筒胴部)
1) 膜応力 (σm)
]
2
)1
(4[
4
)
(
3
1
K
t
PR
N
m
γ
γ
η
σ
−
+
=
·······································中央◯
N点 (113)
η
σ
1
)
(
t
PR
B
m
=
······································· 胴板の曲がり◯
A,◯
B点 (114)
2) 曲げ応力 (σb)
+
−
+
−
+
−
−
±
=
2
2
3
2
3
2
3
3
1
2
0
2
)
2(6
)
3
4(
)
2
)(
2
(3
2
)
(
πγα
γ
γ
γ
α
π
η
σ
K
K
K
t
c
Ph
N
b
·································中央◯
N点 (115)
+
−
−
−
±
=
2
2
2
3
2
3
3
1
2
0
2
)
2(6
)
3
4(
2
)
(
πγα
γ
α
γ
η
σ
K
K
t
c
Ph
B
b
··············· 胴板の曲がり◯
A,◯
B点 (116)
3) 合成応力 (σT)
(σT) N=式 (113)+式 (115) ·················································· 中央◯
N点
(σT) B=式 (114)+式 (116) ·································胴板の曲がり◯
A,◯
B点
b) 部材◯
B〜◯
C間の応力
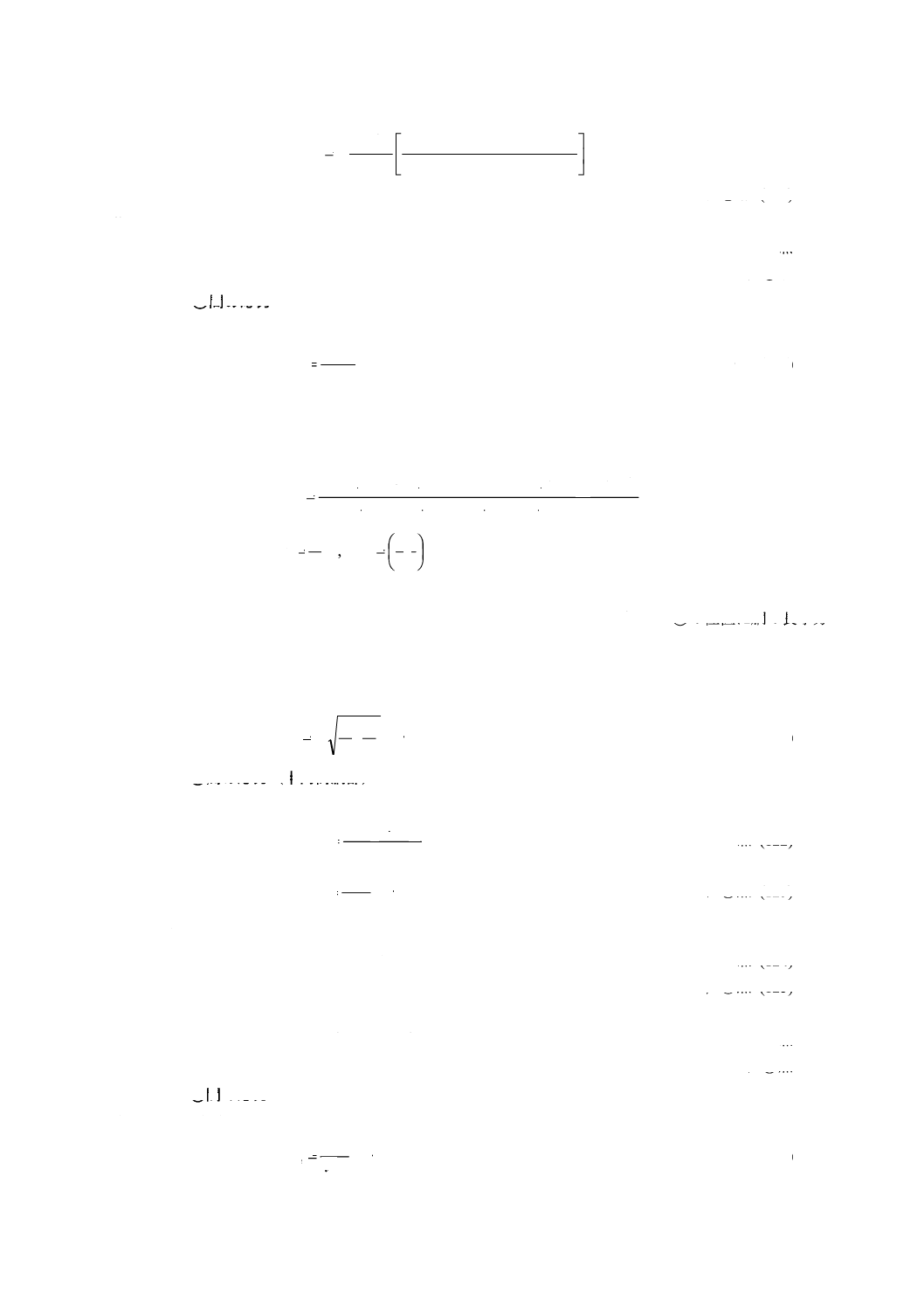
1) 膜応力 (σm)
η
σ
2t
PR
m=
·········································································· (117)
2) 曲げ応力 (σb)
+
−
−
−
−
−
±
=
2
2
2
3
2
3
2
3
3
2
2
0
1
2
)
2(6
)
1(3
)2
3(
2
)
(
πγα
γ
α
πγα
γ
η
σ
K
K
K
t
c
Ph
M
b
····························· 仕切板◯
M1点 (118)
23
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
+
−
−
−
±
=
2
2
2
3
2
3
3
2
2
0
2
)
2(6
)
3
4(
2
)
(
πγα
γ
α
γ
η
σ
K
K
t
c
Ph
B
b
··············· 胴板の曲がり◯
B,◯
C点 (119)
3) 合成応力 (σT)
(σT) M1=式 (117)+式 (118) ·············································· 仕切板◯
M1点
(σT) B=式 (117)+式 (119) ·································胴板の曲がり◯
B,◯
C点
c) 部材◯
M1〜◯
M1間の応力
1) 膜応力 (σm)
3
3
0
2
K
t
Ph
m
η
σ=
····································································· (120)
2) 曲げ応力 (σb)
σb=0
ここに,
2
2
2
2
2
2
2
3
4
2
2
2
2
2
2
2
3
4
3
)
24
3(
6
24
4
2
)
48
6(
12
40
5
2
α
π
πγα
α
γ
α
πγ
γ
α
π
πγα
α
γ
α
πγ
γ
−
+
+
+
+
−
+
+
+
+
=
K
3
1
2
2
0,
2
=
=
t
t
R
h
α
γ
P,h0,R,t1,t2,t3,σm,σb,σT及びηは,6. 及び図2 b) による。
7.3.3
図2 b) に示す胴に丸棒でステーされる胴 図2 b) に示す胴で仕切板◯
M1〜◯
M1の位置に胴の長手方
向に一定ピッチで一列の丸棒ステーで支えられる胴板に生じる膜応力,曲げ応力及び合成応力は,次の算
式による。
a) 丸棒ステーの最大ピッチ (Pc)
P
C
t
P
a
c
σ
2
=
···································································· (121)
b) 部材◯
A〜◯
B間の応力(半円筒胴部)
1) 膜応力 (σm)
η
σ
1
0
2
)
2
(
)
(
t
R
h
P
N
m
+
=
···············································中央◯
N点 (122)
η
σ
1
)
(
t
PR
B
m
=
······································· 胴板の曲がり◯
A,◯
B点 (123)
2) 曲げ応力 (σb)
(σb)N=式 (115) ··························································中央◯
N点 (124)
(σb)B=式 (116) ········································ 胴板の曲がり◯
A,◯
B点 (125)
3) 合成応力 (σT)
(σT)N=式 (122)+式 (124) ··················································· 中央◯
N点
(σT)B=式 (123)+式 (125) ··································胴板の曲がり◯
A,◯
B点
c) 部材◯
B〜◯
C間の応力
1) 膜応力 (σm)
η
σ
2t
PR
m=
·········································································· (126)

2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2) 曲げ応力 (σb)
(σb)M1=式 (118) ········································ ステー取付け部◯
M1点 (127)
(σb)B=式 (119) ········································ 胴板の曲がり◯
B,◯
C点 (128)
3) 合成応力 (σT)
(σT)M1=式 (126)+式 (127) ·································· ステー取付け部◯
M1点
(σT)B=式 (126)+式 (128) ··································胴板の曲がり◯
B,◯
C点
d) 丸棒ステーの応力
1) 膜応力 (σm)
3
2
0
2
K
P
d
Ph
c
m
η
π
σ=
······························································· (129)(8)
2) 曲げ応力 (σb)
σb=0
注(8)
2
1 (h0+R) >Pcの場合は,式 (129)でPcの代わりに21 (h0+R) を用いて計算する。
ここに,
P,h0,R,t1,t2,d,Pc,σm,σb,σT及びηは,6. 及び図2 b) による。
Cはステーの取付け方による係数(JIS B 8265附属書9参照)
C=2.1 …… 厚さ11 mm以下の板に溶接したステー
C=2.2 …… 厚さ11 mmを超える板に溶接したステー
7.4
円の中心を通る1枚の仕切板をもつ円筒胴
7.4.1
図3に示す胴で二つの仕切室の圧力が等しい場合 図3に示す胴で二つの仕切室の圧力が等しい場
合に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力(半円筒胴部)
1) 膜応力 (σm)
η
σ
1
1
t
R
P
m=
········································································· (130)
2) 曲げ応力 (σb)
η
π
σ
1
2
1
)8
(
8
t
c
P
b
−
=
································································· (131)
3) 合成応力 (σT)
σT=式(130)+式(131)
b) 部材◯
A〜◯
B間の応力 (仕切板部)
1) 膜応力 (σm)
η
π
π
σ
3
2
2
1
1
)8
(3
2
Rt
t
P
m
−
=
····························································· (132)
2) 曲げ応力 (σb)
σb=0
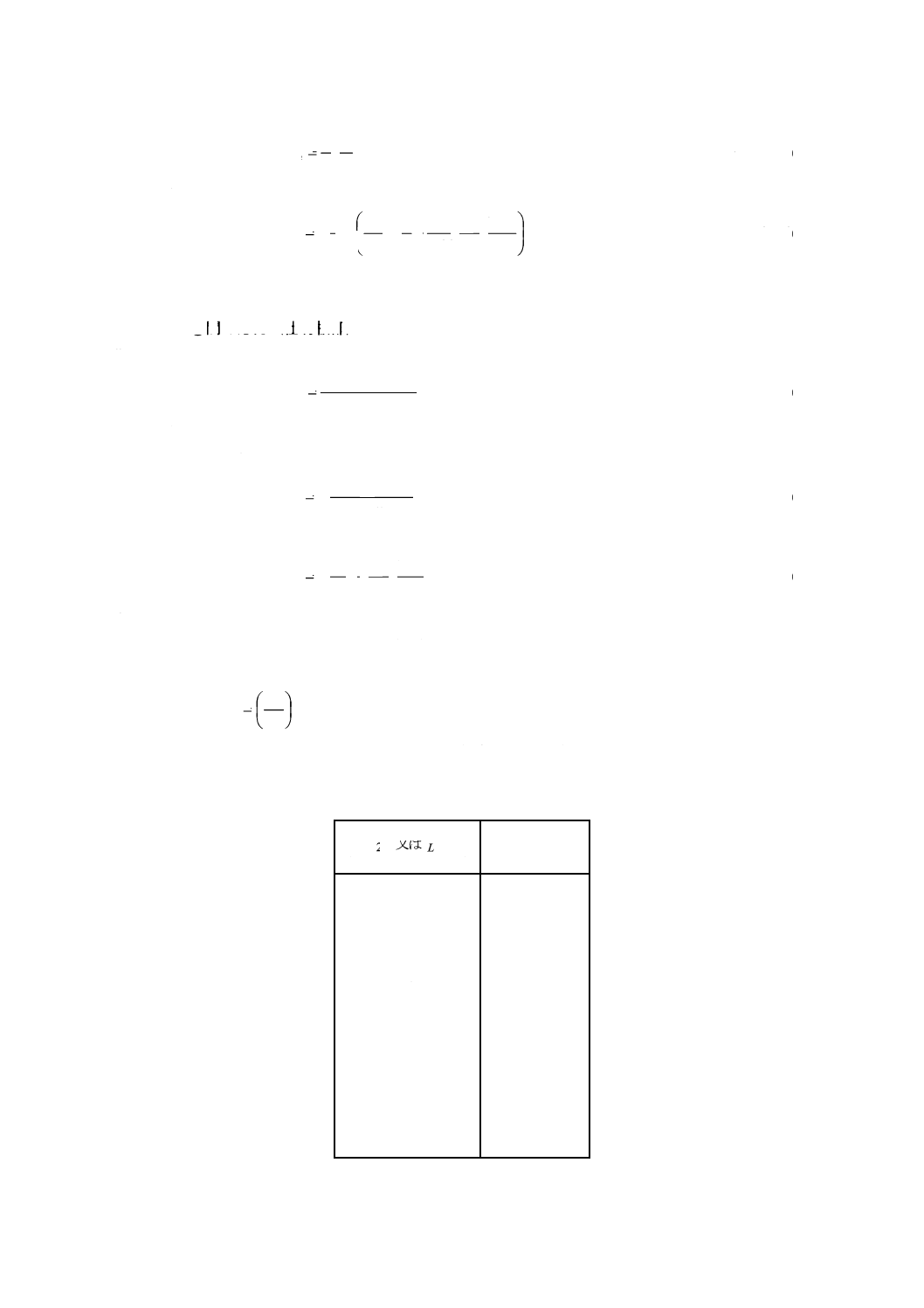
7.4.2
図3に示す胴で二つの仕切室の圧力が等しくない場合 図3に示す胴で二つの仕切室の圧力が等し
くない場合に生じる膜応力,曲げ応力及び合成応力は,次の算式による。
a) 部材◯
A〜◯
B間の応力(半円筒胴部)
1) 膜応力 (σm)
25
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
η
σ
1
1
t
R
P
m=
········································································· (133)
2) 曲げ応力 (σb)
+
−
+
−
±
=
2
1
3
2
2
1
2
1
1
)
6(
)
(6
8
4
2
t
R
P
P
P
t
c
b
α
π
η
σ
············································ (134)
3) 合成応力 (σT)
σT=式 (133)+式 (134)
b) 部材◯
A〜◯
B間の応力(仕切板部)
1) 膜応力 (σm)
η
π
π
σ
3
2
2
1
2
1
)8
(3
)
(
Rt
t
P
P
m
−
+
=
····························································· (135)
2) 曲げ応力 (σb)
L≦2Rのとき
1
2
3
2
2
1
)
(6
J
t
L
P
P
b
η
σ
−
±
=
·························································· (136)
L>2Rのとき
1
2
3
2
2
1
)
(
24
J
t
R
P
P
b
η
σ
−
±
=
························································ (137)
3) 合成応力 (σT)
L≦2Rのとき σT=式 (135)+式 (136)
L>2Rのとき σT=式 (135)+式 (137)
ここに,
3
1
3
3
=
t
t
α
P1,P2,R,L,t1,t3,η,σm,σb及びσTは,6. 及び図3による。
J1:形状係数で表1による。
表 1 形状係数J1
R
L
2又はLR
2
(いずれか大きいほう)
形状係数
J1
1.0
0.051 3
1.1
0.058 1
1.2
0.063 9
1.3
0.069 4
1.4
0.075 5
1.5
0.081 2
1.6
0.086 2
1.7
0.090 8
1.8
0.094 8
1.9
0.098 5
2.0
0.101 7
3.0
0.118 9
4.0
0.123 5
≧5.0
0.124 6
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
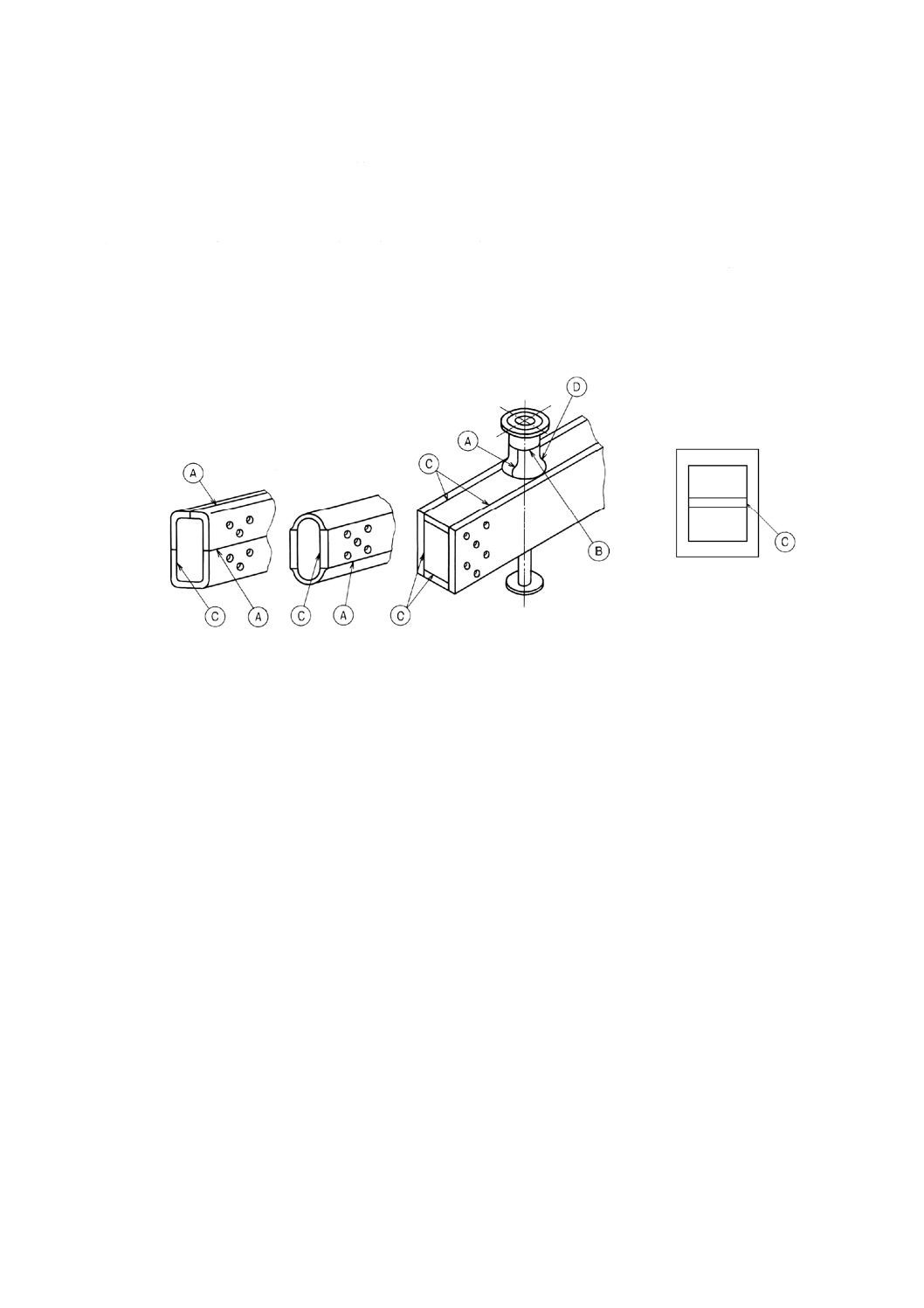
8. 溶接継手の位置による分類 非円形胴の圧力を受ける部分の溶接継手は,継手の位置によって,次の
A,B,C及びDに分類し,その代表的なものを図5に示す。
a) 分類A 非円形胴,ノズルなどの圧力を受ける部分にある長手継手をいう。ただし,分類Cに規定す
るものを除く。
b) 分類B ノズルなどの圧力を受ける部分にある周継手をいう。
c) 分類C 非円形胴のコーナー継手及び胴板と端末ふた板を取り付けるコーナー部との溶接継手,並び
に補強板又はステーと胴の溶接部をいう。
d) 分類D ドーム,サンプ,マンホール,ノズルなどを胴又は端末ふた板などに取り付ける溶接継手を
いう。
図 5 溶接継手の位置による分類
27
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1(規定)フランジ付き非円形胴
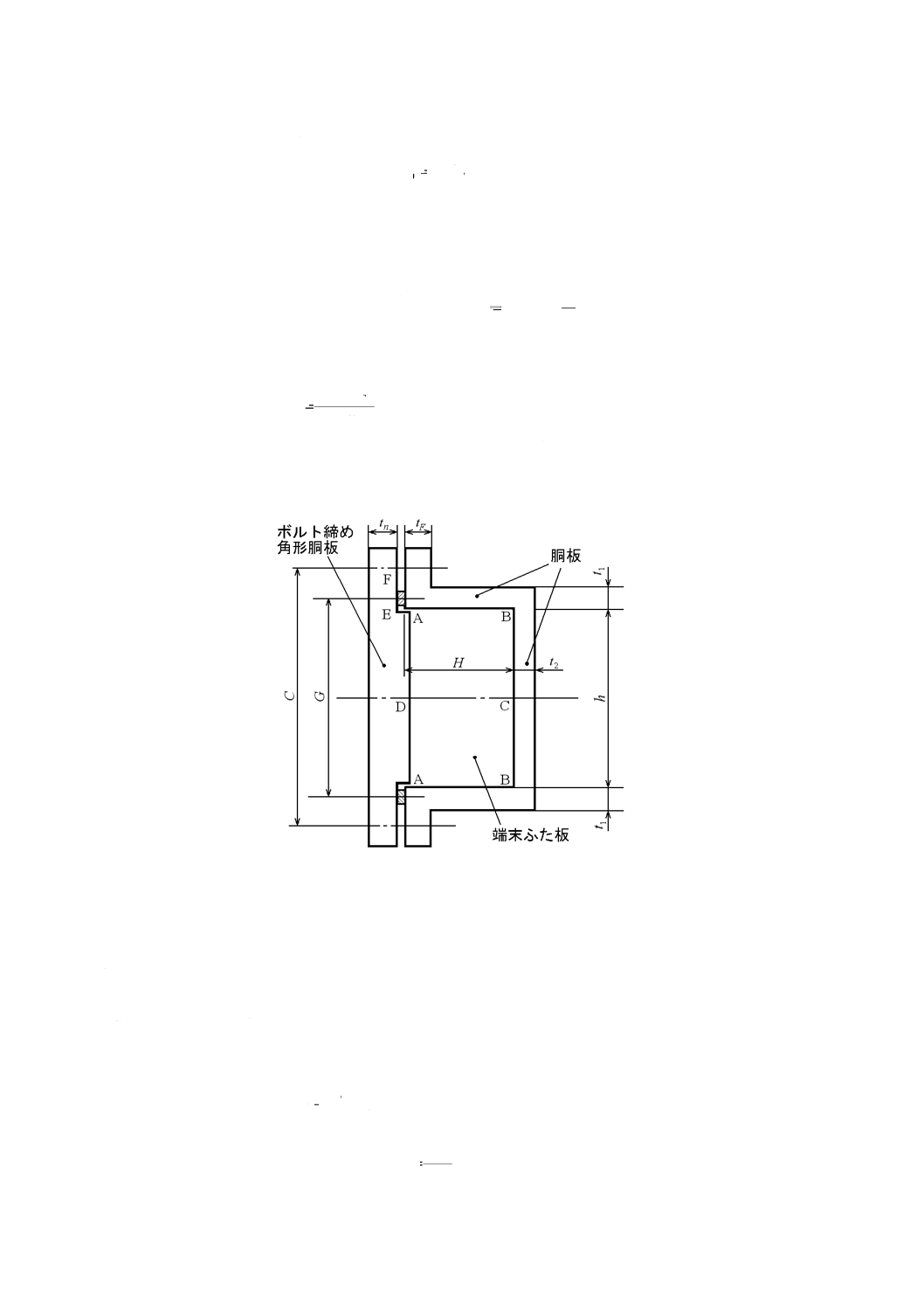
1. 適用範囲 この附属書1は,附属書1図1に示す横断面が長方形でフランジ構造をもつ非円形胴の圧
力容器の構造について規定する。この附属書1に規定のない事項については,本体による。また,記号の
意味でこの附属書の規定にないものは本体による。
2. 胴板 胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式による。ただし,応力計算は,使用
状態及びガスケット締付時の両方の場合について行う。
なお,胴板に生じる膜応力及び合成応力に対する許容応力は,本体の7.1 a) による。
a) 部材A〜B間の応力
1) 膜応力(σm)
η
σ
1
2t
Ph
m=
··············································································· (1)
ここに, P: 設計圧力(MPa)
h: 附属書1図1に示す非円形胴の内のり(mm)
t1: 附属書1図1に示す胴板の厚さ(mm)
η: 溶接継手効率又はリガメント効率の小さいほう
2) 曲げ応力(σb)
()
η
σ
21
6
t
MA
A
b
±
=
フランジ取付部A点 ···································· (2)
()
η
σ
2
1
6
t
MBj
B
b
±
=
隅角部B点 ··············································· (3)
(
)
+
±
=
−
P
R
M
t
Cj
A
B
A
b
2
6
2
21η
σ
A〜B間の最大値 ······················· (4)
ただし,(σb)A−Bは,RCj≦0の場合は考慮しなくてもよい。
ここに, MBj: 隅角部B点にかかる単位長さ当たりの曲げモーメント
(Nmm/mm)
2
1
1
2
2
2
1
3
2
)
(
4
1
Q
Q
Q
M
h
Q
H
Q
P
M
A
Bj
+
+
+
=
H: 附属書1図1に示す非円形胴の内のり(mm)
Q1: 非円形胴の内のりHを単位長さ当たりの胴板厚さt1部の断面二
次モーメントで除したもの(mm/mm3)
3
1
1
12
t
H
Q=
Q2: 非円形胴の内のりhを単位長さ当たりの胴板厚さt2部の断面二
次モーメントで除したもの(mm/mm3)
3
2
2
12
t
h
Q=
RCj: フランジ取付部A点にかかる単位長さ当たりのの反力(N/mm)
28
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
H
Q
Q
Q
Q
M
h
Q
H
Q
H
Q
P
R
A
Cj
)
3
2(
)
(
3
)
2
1
3
2
3(
2
2
1
2
1
2
2
2
2
2
1
+
+
−
−
+
=
MA: 附属書1図1に示すA点においてフランジに作用する単位長さ
当たりの曲げモーメントで,5. b) による値(Nmm/mm)
3) 合成応力(σT)
(σ T)A = (1) + (2)
(σ T)B = (1) + (3)
(σ T)A−B = (1) + (4)
b) 部材B〜C間の応力
1) 膜応力(σm)
η
σ
2t
Rtj
m=
··················································································· (5)
ここに, Rtj: 中央c点に作用する単位長さ当たりの反力(N/mm)
Cj
tj
R
PH
R
−
=
t2: 附属書1図1に示す胴板の厚さ(mm)
2) 曲げ応力(σb)
η
σ
2
)
(
I
cMBj
B
b
±
=
隅角部B点 ··············································· (6)
η
σ
2
)
(
I
cMCj
C
b
±
=
中央C点 ················································· (7)
ここに,
c: 断面の中立軸から外表面までの長さ(mm)
I2: 単位長さ当たりの胴板厚さt2部の断面2次モーメント
(mm4/mm)
12
32
2
t
I=
MCj: 中央C点に作用する単位長さ当たりの曲げモーメント
(Nmm/mm)
8
2
Ph
M
M
Bj
Cj
−
=
3) 合成応力(σT)
(σ T)B = (5) + (6)
(σ T)C = (5) + (7)
3. ボルト締め角形胴板 ボルト締め角形胴板に生じる膜応力,曲げ応力及び合成応力は,次の算式によ
る。ただし,応力計算は,使用状態及びガスケット締付時の両方の場合について行う。
a) ボルト締め角形胴板に生じる曲げ応力は,次の算式によって,その値はJIS B 8265の4.3.1(許容引張
応力)に規定する許容引張応力を超えてはならない。
η
σ
2
22
2
6
3.0
t
Wh
ZPG
G
b
+
=
ここに, G: 附属書1図1に示すガスケット反力のかかる位置を結ぶ最小ス
パン(mm)
29
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
W: 単位長さ当たりのボルト荷重で,5. a) 3) による値(N/mm)
hG: モーメントアームで,ボルト中心を結ぶ最小スパンとガスケッ
ト反力のかかる位置を結ぶ最小スパンとの差の1/2(mm)
Z: 修正係数で
D
G
Z
4.2
4.3 −
=
ただし,最大2.5とする。
D: 最小スパンGに直角に測ったガスケット反力中心の最大スパン
(mm)
t22: 附属書1図1に示すボルト締め角形胴板の厚さ(mm)
b) ボルト締め角形胴板にガスケット溝を設ける場合には,溝の深さを差し引いた部分に生じる曲げ応力
は,次の算式によって,その値はJIS B 8265の4.3.1(許容引張応力)に規定する許容引張応力を超え
てはならない。
η
σ
2
6
n
G
b
t
Wh
=
ここに, tn: 附属書1図1に示すボルト締め角形胴板のガスケット溝深さを
差し引いた部分の厚さ(mm)
c) ボルト締め角形胴板を管板として用いる場合には,次の算式による。この場合に生じる膜応力及び合
成応力に対する許容応力は,本体の7.1 a) による。
1) 膜応力(σm)
(
)
η
σ
22
t
RCj
E
D
m
=
−
D〜E間 ····················································· (8)
(
)
n
Cj
E
m
t
R
=
σ
フランジ部E点·············································· (9)
2) 曲げ応力(σb)
()
η
σ
22
2
8
I
PG
Wh
c
G
E
D
b
+
±
=
−
D〜E間 ·································· (10)
()
2
6
n
G
E
b
t
Wh
±
=
σ
フランジ部E点 ·········································(11)
ここに, I22:単位長さ当たりの胴板厚さt22部の断面2次モーメント(mm4/mm)
12
3
22
22
t
I=
3) 合成応力(σT)
(σ T)D−E = (8) + (10)
(σ T)E = (9) + (11)
4. 端末ふた板 端末ふた板に生じる曲げ応力は,次の算式による。計算で得られた端末ふた板に生じる
応力は,JIS B 8265の4.3.1(許容引張応力)に規定する許容引張応力を超えてはならない。
なお,板厚をt2以上とする場合は,計算する必要はない。
a) 使用状態
η
σ
2
0
2
6
3.0
t
M
PH
ZE
b
+
=
30
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに, M0: 単位長さ当たりの端モーメント(Nmm/mm)で,次による。
G
h
W
M
0
0=
ここに,
W0:使用状態における単位長さ当たりのボルト荷重(N/mm)
で,5. a) 3.1) による。
hG:ボルト穴の中心円からガスケット中心面までの距離(mm)
ZE: 修正係数で
h
H
ZE
4.2
4.3 −
=
ただし,最大2.5とする。
t: 端末ふた板の厚さ(mm)
b) ガスケット締付時
η
σ
2
6
t
h
W
G
g
b=
ここに, Wg: ガスケット締付時の単位長さ当たりのボルト荷重(N/mm)で,
5. a) 3.2) による。
附属書1図 1 フランジ付非円形胴
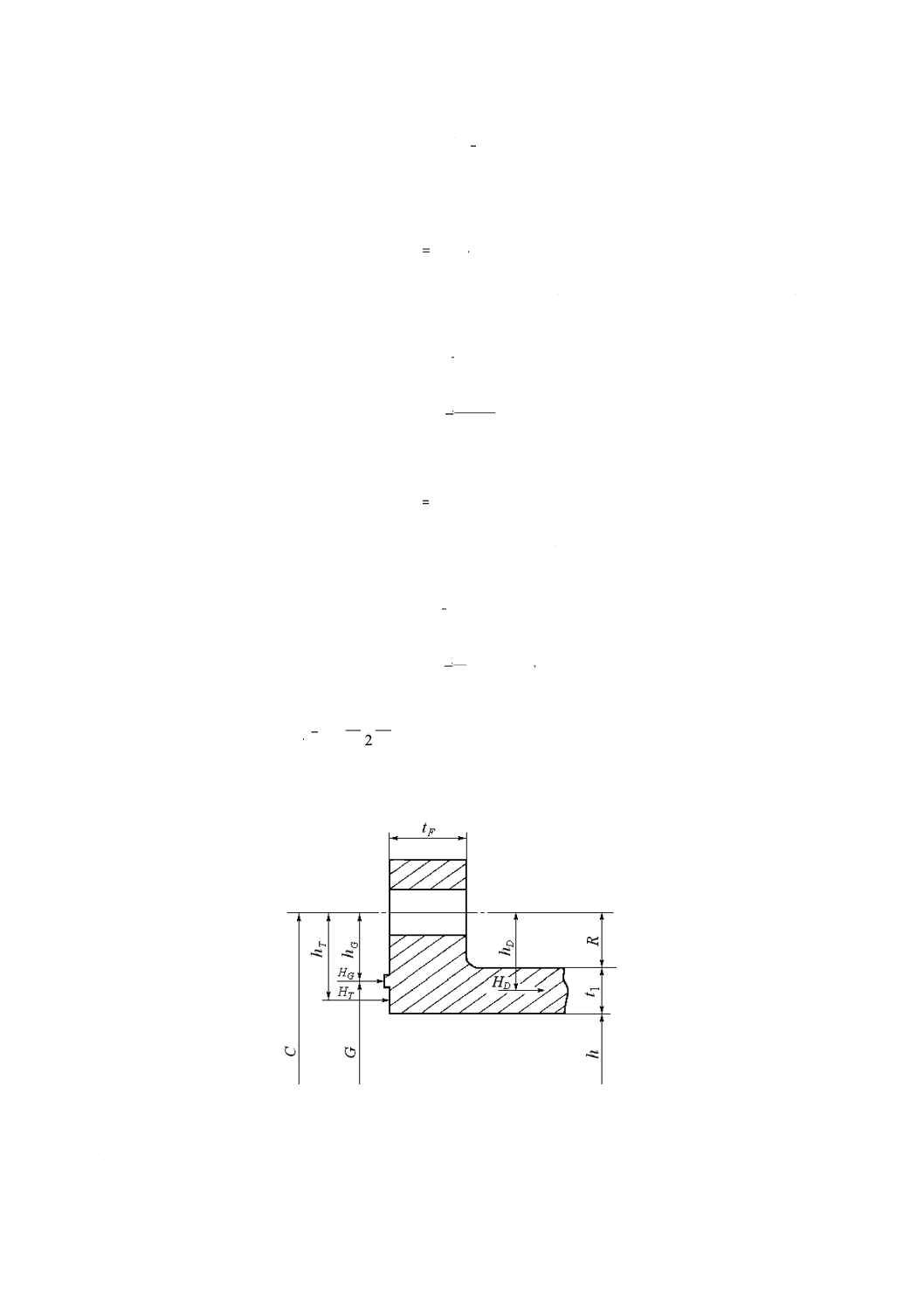
5. ボルト締め角形フランジ 附属書1図2に示すボルト締め角形フランジは,次の算式による。
a) ボルト荷重 ガスケット反力のかかる位置線上におけるフランジの単位長さ当たりのボルト荷重は,
次による。
1) 計算上必要なボルト荷重 ボルトの所要断面積の計算に用いるフランジの単位長さ当たりのボルト
荷重は,次による。
1.1) 使用状態でのボルト荷重
P
m
H
H
W
+′
=
1
ここに, H´: フランジに加わる内圧による単位長さ当たりの荷重(N/mm)
2
GP
H=′
31
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
HP: 気密を十分保つために,ガスケット又は継手接触面における単
位長さ当たりの圧縮力(N/mm)
bmP
HP
2
=
ここに,
b:ガスケット座の有効幅(mm)で,JIS B 8265附属書3によ
る。
m:ガスケット係数で,JIS B 8265附属書3表2による。
1.2) ガスケット締付時のボルト荷重
by
Wm=
2
ここに,
y: ガスケット又は継手接触面の最小設計締付圧力(N/mm2)で,
JIS B 8265附属書3表2による。
2) ボルトの所要総断面積及び実際のボルトの総断面積 使用状態及びガスケット締付時の両方に対し
て必要なフランジの単位長さ当たりのボルトの総断面積Amは,次の値のうち大きい方をとる。ただ
し,実際に使用するボルトの総断面積Abは,ボルトの所要総断面積Amより常に大きくなるように
ボルト径を定めなければならない。
0
1
1
b
m
m
W
A
σ
=
0
2
2
a
m
m
W
A
σ
=
ここに, σ b0: 使用温度におけるボルト材料の許容引張応力(N/mm2)
σ a0: 常温におけるボルト材料の許容引張応力(N/mm2)
3) フランジの計算に用いるボルト荷重 フランジの計算に用いるボルト荷重は,次の算式による。
3.1) 使用状態での単位長さ当たりのボルト荷重
1
0
m
W
W=
3.2) ガスケット締付時の単位長さ当たりのボルト荷重
0
2
a
b
m
g
A
A
W
σ
+
=
b) フランジに作用するモーメント フランジに作用するモーメントは,次の算式による。
1) 使用状態でフランジに作用する単位長さ当たりの全モーメント(Nmm/mm)
T
G
D
M
M
M
M
+
+
=
0
ここに, MD: 内圧力によってフランジの最小スパン面に加わる単位長さ当た
りのモーメント
D
D
D
h
H
M=
ここに,
HD:フランジの最小スパン面に加わる荷重(N/mm)
2
Ph
HD=
ここに,
h:附属書1図2に示す非円形胴の内のり(mm)
hD:モーメントアーム(mm)
32
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1
5.0t
R
hD
+
=
MG: ガスケット荷重によるモーメントで,フランジのボルト荷重と
フランジに加わる内圧による荷重との差による単位長さ当たり
のモーメント
G
G
G
h
H
M=
ここに,
HG:ガスケット荷重(ボルト荷重W0とフランジに加わる内圧に
よる荷重H´との差(N/mm)
H
W
HG
′
−
=
0
hG:モーメントアーム(mm)
2
G
C
hG
−
=
MT: フランジに加わる内圧による荷重とフランジの最小スパン面に
加わる荷重との差による単位長さ当たりのモーメント
T
T
T
h
H
M=
ここに,
HT:フランジに加わる内圧による荷重H´とフランジの最小スパ
ン面に加わる単位長さ当たりの荷重HDとの差(N/mm)
D
T
H
H
H
−′
=
hT:モーメントアーム(mm)
(
)
G
T
h
t
R
h
+
+
=
1
2
1
2) ガスケット締付時にフランジに作用する単位長さ当たりのモーメント(Nmm/mm)
2G
C
W
M
G
g
−
=
ここに,
C: 附属書1図1及び附属書1図2に示すボルト穴の中心を結ぶ
最小スパン(mm)
附属書1図 2 フランジ計算に用いる寸法記号
c) フランジの発生応力 フランジに発生する応力は,次の算式による。ただし,応力計算は,使用状態
33
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
及びガスケット締付時の両方の場合について行う。フランジに発生する応力は,JIS B 8265の4.3.1(許
容引張応力)に規定する許容引張応力を超えてはならない。
2
6
F
F
F
t
M
C
=
σ
ここに,
M: フランジに作用する単位長さ当たりのモーメント(Nmm/mm)
で,
使用状態 M=M0
ガスケット締付時 M=Mg
σ F: フランジに発生する応力で,
使用状態 σ F ≦σ bf
ガスケット締付時 σ F ≦σ af
ここに,σ bfは使用温度におけるフランジ材料の許容引張応力
(N/mm2)
σ afは常温におけるフランジ材料の許容引張応力
(N/mm2)
CF: 荷重修正係数で,
5.0
6
2
+
+
=
m
t
d
p
C
F
b
b
F
ただし,CF≧1.0とする。
ここに,
pb:ボルト間隔(mm)
db:ボルトのねじ部の谷の径と軸部の径の最小部のいずれか小
さいほうの径(mm)
tF:フランジの使用厚さから腐れ代を引いた値(mm)
m:ガスケット係数JIS B 8265附属書3表2による。
d) フランジ付非円形胴のフランジと胴板との取付け溶接 フランジ付非円形胴のフランジと胴板との
取付け溶接は,JIS B 8265附属書3図2に規定する6)〜10),14) 又は15) のいずれかによる。
e) フランジ付非円形胴の溶接継手の位置による分類 フランジ付非円形胴の溶接継手は次によって分
類する。
1) フランジと胴板との取付け溶接部以外の溶接部については,本体8. の規定による。
2) フランジと胴板との取付け溶接部は,JIS B 8265附属書3図2に規定する6)〜9) による場合は分類
A,10),14) 又は15) による場合は分類Cとする。
34
B 8280:2003
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2(規定)検定水圧試験
1. 適用範囲 この附属書2は,本体7.1 e) 2.2.2) に規定する大口径のノズルを取り付けるため,非円形
胴に生じる膜応力及び曲げ応力の算定が困難な場合の使用可能な圧力を求めるための検定水圧試験につい
て規定する。
2. 検定水圧試験方法 検定水圧試験の方法は,次による。
a) あらかじめ弱いと推定される箇所を数点選定し,それらの数個の点に抵抗線ひずみ計をはり付け,圧
力容器の予定する設計圧力に等しい水圧を加えて,各点に生じるひずみを計測して応力に換算し,こ
のうちの最大値(絶対値)を用いて,次の算式によって当該圧力容器の試験部分の使用可能な圧力Pa
(MPa)を算定する。
=
a
a
a
a
t
t
P
P
α
σ
σ
−
0
0
ここに,
P0: 予定する設計圧力(MPa)
σ a: 設計温度における許容引張応力(N/mm2)
σ 0: 最も弱い部分に発生した応力の最大値(N/mm2)
ta: 実際厚さ(mm)
α: 腐れ代(mm)
備考1. 水圧は設計圧力に相当する圧力まで段階的に加え,その圧力に達したときこれをゼロに戻す。
この操作を3回繰り返し,3回目にひずみの値を読み取る。
2. 最も弱いと推定されるところに降伏が発生するときは,水圧はこれを超えて上昇させてはな
らない。
3. 発生する主応力の方向が明らかな場合には,2方向の主ひずみを測定し,主ひずみの方向が
明らかでない場合には,3方向のひずみを測定して,主応力を求めなければならない。
4. Paは,P0を超えてはならない。
b) a) のほか,試験方法はJIS B 8265附属書12の圧力容器の耐圧試験の方法に準じる。


















