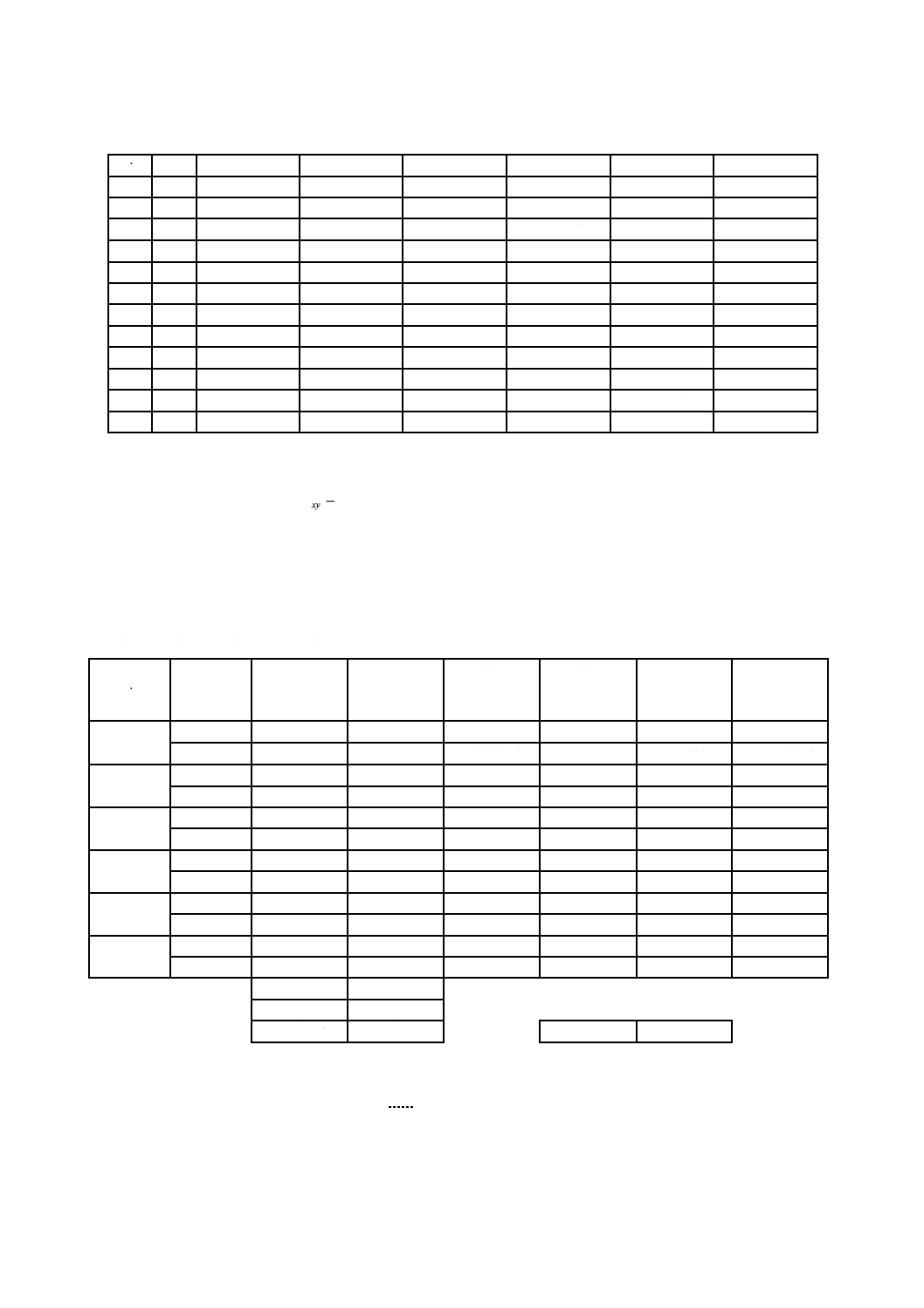B 7912-5:2016
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
4 一般······························································································································· 2
4.1 要求事項 ······················································································································ 2
4.2 試験手順1:簡易試験手順 ······························································································· 2
4.3 試験手順2:標準試験手順 ······························································································· 2
5 簡易試験手順 ··················································································································· 3
5.1 測定場所の設定 ············································································································· 3
5.2 測定 ···························································································································· 3
5.3 計算 ···························································································································· 4
6 標準試験手順 ··················································································································· 5
6.1 測定場所の設定 ············································································································· 5
6.2 測定 ···························································································································· 5
6.3 計算 ···························································································································· 6
6.4 統計的検定 ··················································································································· 9
6.5 合成標準不確かさの評価(タイプA及びタイプB) ···························································· 10
附属書A(参考)簡易試験手順の例 ························································································ 12
附属書B(参考)標準試験手順の例 ························································································ 14
附属書C(参考)不確かさバジェット表の計算例 ······································································ 18
附属書D(参考)不確かさ評価に含めなかった要因 ··································································· 20
附属書JA(参考)主な記号の解説 ·························································································· 21
参考文献 ···························································································································· 22
附属書JB(参考)JISと対応国際規格との対比表 ······································································ 24
B 7912-5:2016
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本測量機器工業会(JSIMA)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 7912の規格群には,次に示す部編成がある。
JIS B 7912-1 第1部:理論
JIS B 7912-2 第2部:レベル
JIS B 7912-3 第3部:セオドライト
JIS B 7912-4 第4部:光波測距儀
JIS B 7912-5 第5部:トータルステーション
JIS B 7912-6 第6部:回転レーザ
JIS B 7912-8 第8部:GNSS(RTK)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 7912-5:2016
測量機器の現場試験手順−
第5部:トータルステーション
Field procedures for testing geodetic and surveying instruments-
Part 5: Total stations
序文
この規格は,2012年に第2版として発行されたISO 17123-5を基とし,統計的検定についてISO 2854
及びJIS Z 9041-2の表現に合わせるため,技術的内容を変更して作成した日本工業規格である。
なお,この規格で側線又は点線の下線を施してある箇所は,対応国際規格を変更している事項である。
変更の一覧表にその説明を付けて,附属書JBに示す。
1
適用範囲
この規格は,トータルステーションによる作業を実施する前に,当該作業への適応性を確認するための
試験手順について規定する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 17123-5:2012,Optics and optical instruments−Field procedures for testing geodetic and surveying
instruments−Part 5: Total stations(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格のうちで,西暦年を付記してあるものは,記載の年の版を適用し,その後の改正版(追補を含む。)
は適用しない。西暦年の付記がない引用規格は,その最新版(追補を含む。)を適用する。
JIS B 7911:2002 測量機器用三脚
注記 対応国際規格:ISO 12858-2,Optics and optical instruments−Ancillary devices for geodetic
instruments−Part 2: Tripods(MOD)
JIS B 7912-1:2014 測量機器の現場試験手順−第1部:理論
注記 対応国際規格:ISO 17123-1:2010,Optics and optical instruments−Field procedures for testing
geodetic and surveying instruments−Part 1: Theory(MOD)
JIS Z 8101-1 統計−用語及び記号−第1部:一般統計用語及び確率で用いられる用語
注記 対応国際規格:ISO 3534-1:2006,Statistics−Vocabulary and symbols−Part 1: General statistical
terms and terms used in probability(IDT)
JIS Z 8103 計測用語
2
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ISO 4463-1,Measurement methods for building−Setting-out and measurement−Part 1: Planning and
organization, measuring procedures,acceptance criteria
ISO 7077,Measuring methods for building−General principles and procedures for the verification of
dimensional compliance
ISO 7078,Building construction−Procedures for setting out,measurement and surveying−Vocabulary and
guidance notes
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 7912-1,JIS Z 8101-1及びJIS Z 8103による。
4
一般
4.1
要求事項
トータルステーション及びその附属品は,製造業者の取扱説明書に記載されている方法によって常に調
整した状態で使用しなければならない。また,三脚及び反射プリズムは,製造業者の推奨する製品を用い
る。
トータルステーションは,座標値を求めることができるので,これを観測量とする。
全ての観測量は,同一日に求めなければならない。機器は,正しく設置し,プリズム定数も正しい値を
入力しなければならない。
試験は,気象条件,特に温度勾配の影響を受けるため,曇天下で微風のある天候において最もよい結果
が得られる。測量する場所によって,気象条件が変化する可能性があるため,測量時の実際の気象条件及
びそのときの周囲状況を記録しておくのがよい。試験時の条件は,要求された測量が実際に実行されると
きの予想される条件に合わせるのがよい(ISO 7077及びISO 7078による。)。
検査室内などで行われる試験方法は,大気の諸影響をほとんど受けないが,そのような試験は特別の装
置が必要で費用もかかるため,実用的でない。また,室内における測定は,屋外で測定した場合より通常
高い精度が得られる。
この規格は,箇条5及び箇条6に現場における二つの異なった試験手順について規定する。使用者は,
その作業の特定要求条件に最も適している試験手順を選ばなければならない。
注記1 角度測定又は距離測定を単独に評価したい場合は,JIS B 7912-3及びJIS B 7912-4を利用す
る。
注記2 主な記号の解説を,附属書JAに示す。
4.2
試験手順1:簡易試験手順
簡易試験手順は,使用する機器の精度がISO 4463-1に従った許容偏差内にあることを確認する方法であ
る。
この手順は,少数の観測で行う。この試験手順は,座標値が与えられていない測点の(x, y)座標(水平
成分)及びz座標(鉛直成分)を測定して行う。大気屈折の影響が異なるため,(x, y)座標の精度とz座
標の精度とは等しくない。したがって,精度は別々に計算する。評価は,平均値からの最大偏差を精度の
指標とする。また,観測数が限られているので,信頼性の高い標準偏差を得ることはできない。現場条件
の下で,より正確な評価が必要な場合,箇条6の標準試験手順を採用することが望ましい。
4.3
試験手順2:標準試験手順
標準試験手順は,附属品を含め現場条件下で使用するトータルステーションの精度の最も確からしい評
3
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
価値を現場条件の下で決定するために採用する。
この手順は,試験場において座標値が与えられていない測点の座標を測定することが基本である。1点
の座標値の標準偏差は,最小二乗法によって求める。
箇条6に規定する標準試験手順は,使用するトータルステーションの精度を決定することを目的として
いる。用いる測定精度は,望遠鏡正反観測による座標値の標準偏差でタイプAの標準不確かさとして次の
ように表す。
sISO-TS-XY=uISO-TS-XY
sISO-TS-Z=uISO-TS-Z
さらに,この手順は,次へも適用する。
− 一組の測量チームによる附属品などを含めた1台の機器を使用するときの測定の精密さ
− 1台の機器の測定の精密さの経時変化
− よく似た現場条件で複数の機器を用いた場合の,各々の機器が達成可能な測定の精密さの比較
統計的検定は,得られた標準偏差sが,事前に与えられている当該機器の標準偏差σ0の母集団に属する
か否か,及び二つの測定サンプルが同じ母集団に属するか否かの判定に適用する。
5
簡易試験手順
5.1
測定場所の設定
二つの目標測点(T1,T2)を設置する。プリズムなど目標物は,三脚などを使用し,しっかりと測点上
に据え付ける。2測点間の距離は,予定する作業に応じた平均距離以上(例えば,60 m)にするのが望ま
しい。2測点間の高低差は,地形上可能な範囲で大きいことが望ましい。被試験機器(以下,機器という。)
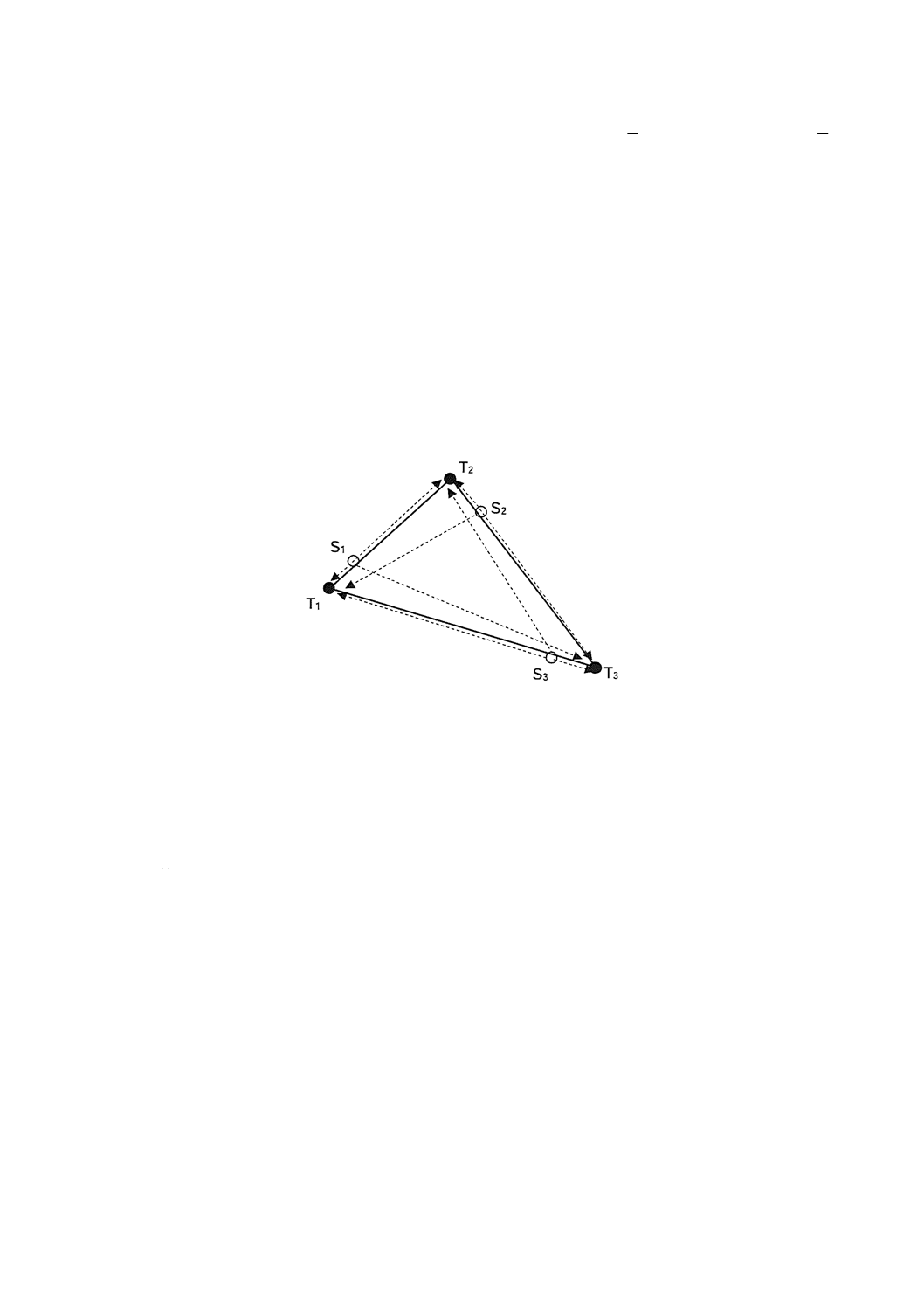
は,図1の測点(T1,T2)と機械点(S1,S2)との配置に示すように,適宜移動して設置する。
図1−測点(T1, T2)と機械点(S1, S2)との配置
機器は,S1からS2へ移動して二つの測点を測定する。機器の設置位置は各測点から5 m〜10 m離れた位
置で,S1はT1−T2の延長線近傍,S2はT1−T2線上近傍とする。
5.2
測定
測定の1セットは,各機械点から望遠鏡正又は反での二つの測点への座標測定とする。測点の座標は,
機械点S1から4セット(望遠鏡:正−反−正−反)測定する。機械点をS2に移動し同様の手順で測定す
る。機械点の座標及び方向角は任意とする。
座標計算ソフトウェアは,機器組込みソフトウェア又は外付け専用ソフトウェアを使用することも可能
であるが,実際の作業で使用するソフトウェアを使用するのが望ましい。
表1に,測定手順を示す。
T1
T2
S1
S2

4
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−測定手順
番号
機械点(T)
i
測点(S)
j
セット
k
望遠鏡
x座標
y座標
z座標
1
1
1
1
正
x1,1,1
y1,1,1
z1,1,1
2
2
x1,2,1
y1,2,1
z1,2,1
3
1
2
反
x1,1,2
y1,1,2
z1,1,2
4
2
x1,2,2
y1,2,2
z1,2,2
5
1
3
正
x1,1,3
y1,1,3
z1,1,3
6
2
x1,2,3
y1,2,3
z1,2,3
7
1
4
反
x1,1,4
y1,1,4
z1,1,4
8
2
x1,2,4
y1,2,4
z1,2,4
9
2
1
1
正
x2,1,1
y2,1,1
z2,1,1
10
2
x2,2,1
y2,2,1
z2,2,1
…
…
…
…
…
…
…
15
1
4
反
x2,1,4
y2,1,4
z2,1,4
16
2
x2,2,4
y2,2,4
z2,2,4
5.3
計算
5.3.1
x,y座標
試験結果の評価は,全x,y座標から計算した水平距離の偏差で行う。
2測点間の各測定水平距離を,式(1) によって求める。
(
)(
)
4
3
2
1
2
1
2
1
2
2
1
2
,
,
,
k
,
i
y
y
x
x
l
,k
i,
,k
i,
,k
i,
,k
i,
i,k
=
=
−
+
−
=
··················· (1)
これらの平均値Lを,式(2) によって求める。
∑∑
=
=
=
2
1
4
1
8
1
i
k
i,k
l
L
······································································· (2)
式(1)での各距離及び式(2)の平均値からの偏差を,式(3) によって求める。
ri,k=li,k−L i=1, 2 k=1, 2, 3, 4 ················································ (3)
これら偏差の最大値を次のようにdxyと定義する。
dxy=max|ri,k| i=1, 2 k=1, 2, 3, 4 ·············································· (4)
5.3.2
z座標
各セットで測定したz座標から各測点間の高低差dz,i,kを,式(5) によって求める。
dz,i,k=zi,2,k−zi,1,k i=1, 2 k=1, 2, 3, 4 ·········································· (5)
全セットの高低差の平均値azを式(6) によって求める。
∑∑
=
=
=
2
1
4
1
8
1
i
k
z,i,k
z
d
a
······································································· (6)
二つの測点間の高低差と平均値azとからの偏差rz,i,kを,式(7) によって求める。
rz,i,k=dz,i,k−az i=1, 2 k=1, 2, 3, 4 ············································ (7)
この最大値をdzとして,式(8) によって求める。
dz=max|rz,i,k| i=1, 2 k=1, 2, 3, 4 ·············································· (8)
簡易試験手順の計算例を,附属書Aに示す。
5.3.3
評価
dxy及びdzは,実施する作業であらかじめ決められた許容差pxy及びpz(ISO 4463-1の規定による。)の範
5
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
囲内でなければならない。pxy及びpzが与えられていない場合は,dxy≦2.5×2×sISO-TS-XY及びdz≦2.5×2
×sISO-TS-Zでなければならない。ただし,sISO-TS-XY及びsISO-TS-Zは,箇条6に従って得られたその機器のそれ
ぞれの標準偏差である。
簡易試験手順の例を,附属書Aに示す。
6
標準試験手順
6.1
測定場所の設定
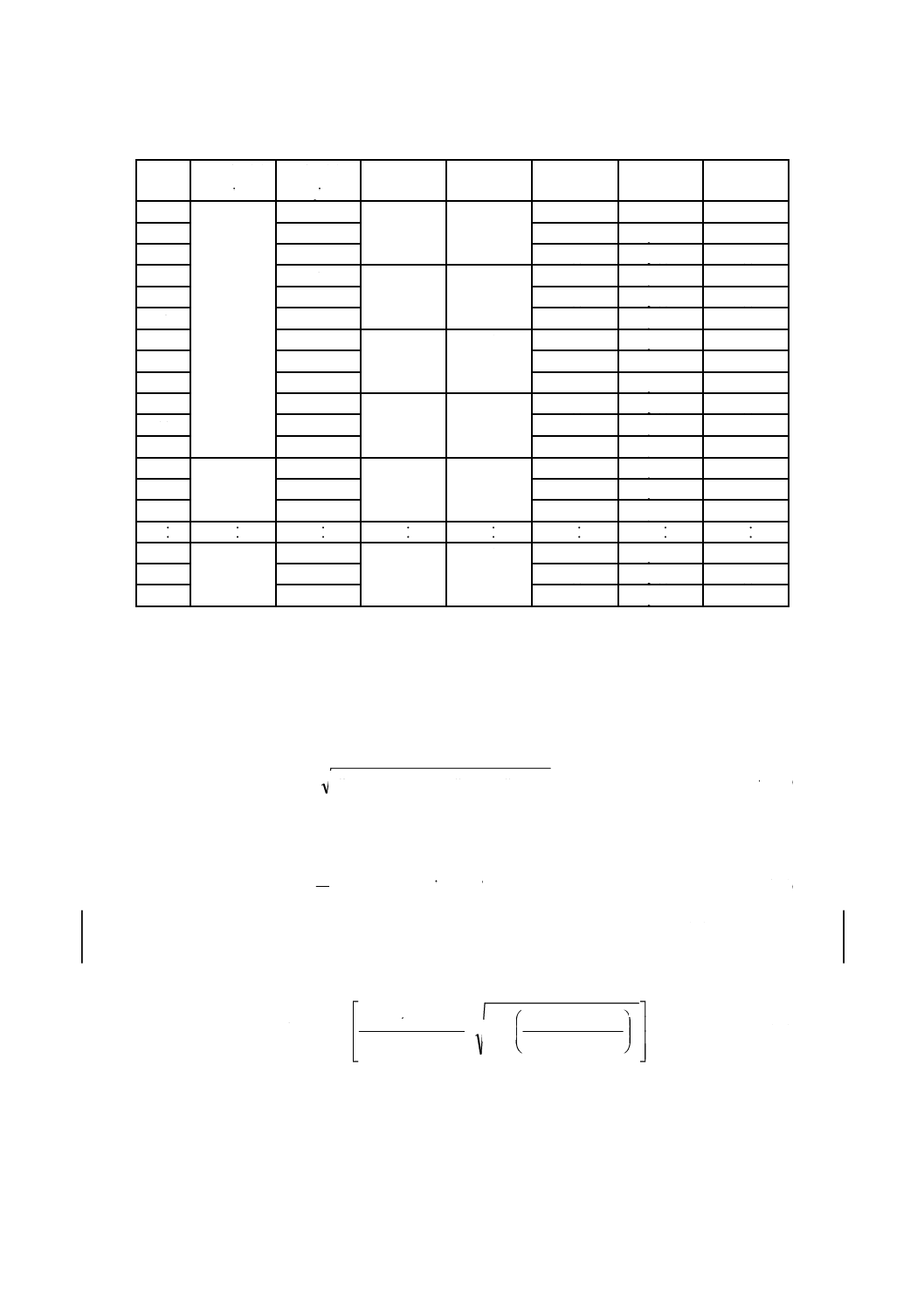
測点は,三角形の頂点(T1, T2, T3)とする(図2参照)。各測点に三脚を立てプリズムを測点上にしっか
りと設置する。測点間の距離は,少なくとも1辺が予定する測量作業での平均距離以上(例えば,60 m)
となることが望ましい。測点の高低差は,地形上可能な範囲で大きいことが望ましい。
機械点3か所(S1, S2, S3)は,できるだけ辺長上であって,一つの頂点から5 m〜10 m離れた地点に設
置する。
図2−測点(T1, T2, T3)と機械点(S1, S2, S3)との配置
6.2
測定
測定の1セットは,各機械点から,望遠鏡正又は反での片側での3測点への座標測定とする。
標準試験は,各機械点で4セット(望遠鏡:正−反−正−反)の観測を行い,機械点を移動し同様の観
測を行い,合計36回の座標測定値を得る。
機械点の座標及び方向角は任意であるが,同一機械点上での観測中は,変更してはならない。
座標計算ソフトウェアは,機器組込みソフトウェア又は外付け専用ソフトウェアを使用することも可能
であるが,実際の作業で使用するソフトウェアを使用するのが望ましい。
測定手順を,表2に示す。
6
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2−測定手順
番号
機械点(T)
i
測点(S)
j
セット
k
望遠鏡
x座標
y座標
z座標
1
1
1
1
正
x1,1,1
y1,1,1
z1,1,1
2
2
x1,2,1
y1,2,1
z1,2,1
3
3
x1,3,1
y1,3,1
z1,3,1
4
1
2
反
x1,1,2
y1,1,2
z1,1,2
5
2
x1,2,2
y1,2,2
z1,2,2
6
3
x1,3,2
y1,3,2
z1,3,2
7
1
3
正
x1,1,3
y1,1,3
z1,1,3
8
2
x1,2,3
y1,2,3
z1,2,3
9
3
x1,3,3
y1,3,3
z1,3,3
10
1
4
反
x1,1,4
y1,1,4
z1,1,4
11
2
x1,2,4
y1,2,4
z1,2,4
12
3
x1,3,4
y1,3,4
z1,3,4
13
2
1
1
正
x2,1,1
y2,1,1
z2,1,1
14
2
x2,1,2
y2,1,2
z2,1,2
15
3
x2,1,3
y2,1,3
z2,1,3
…
…
…
…
…
…
…
…
34
3
1
4
反
x3,1,4
y3,1,4
z3,1,4
35
2
x3,2,4
y3,2,4
z3,2,4
36
3
x3,3,4
y3,3,4
z3,3,4
6.3
計算
6.3.1
x,y座標
三角形の数学的モデルを構築する。
測点T1とT2間の水平距離li,3,k,T2とT3間の水平距離li,1,k及びT3とT1間の水平距離li,2,kを,それぞれ対
応する座標値(xi,j,k, yi,j,k)を用いて式(9) によって求める。
2
1
1
2
1
1
)
(
)
(
,k
i,j
,k
i,j
,k
i,j
,k
i,j
i,j,k
y
y
x
x
l
+
−
+
−
−
+
−
=
········································· (9)
ここに,i=1, 2, 3,j=1, 2, 3(j−1=0又はj+1=4なら,それぞれ3又は1とする。),k=1, 2, 3, 4
各辺の平均距離Ljを式(10) によって求める。
∑∑
=
=
=
=
3
1
4
1
3
2
1
12
1
i
k
i,j,k
j
,
,
j
l
L
···················································· (10)
この3辺によって構成される三角形をモデル三角形Mとし,頂点の座標をMi(Xi, Yi) (i=1, 2, 3)とする。
次に座標M1=(0, 0)としx軸をM2方向と決めると,
座標M2=(L3, 0)
座標
+
+
−
−
+
+
−
=
2
3
2
3
2
2
2
1
2
2
3
2
3
2
1
2
2
3
2
)
(
,
2
)
(
M
L
L
L
L
L
L
L
L
L
······················(11)
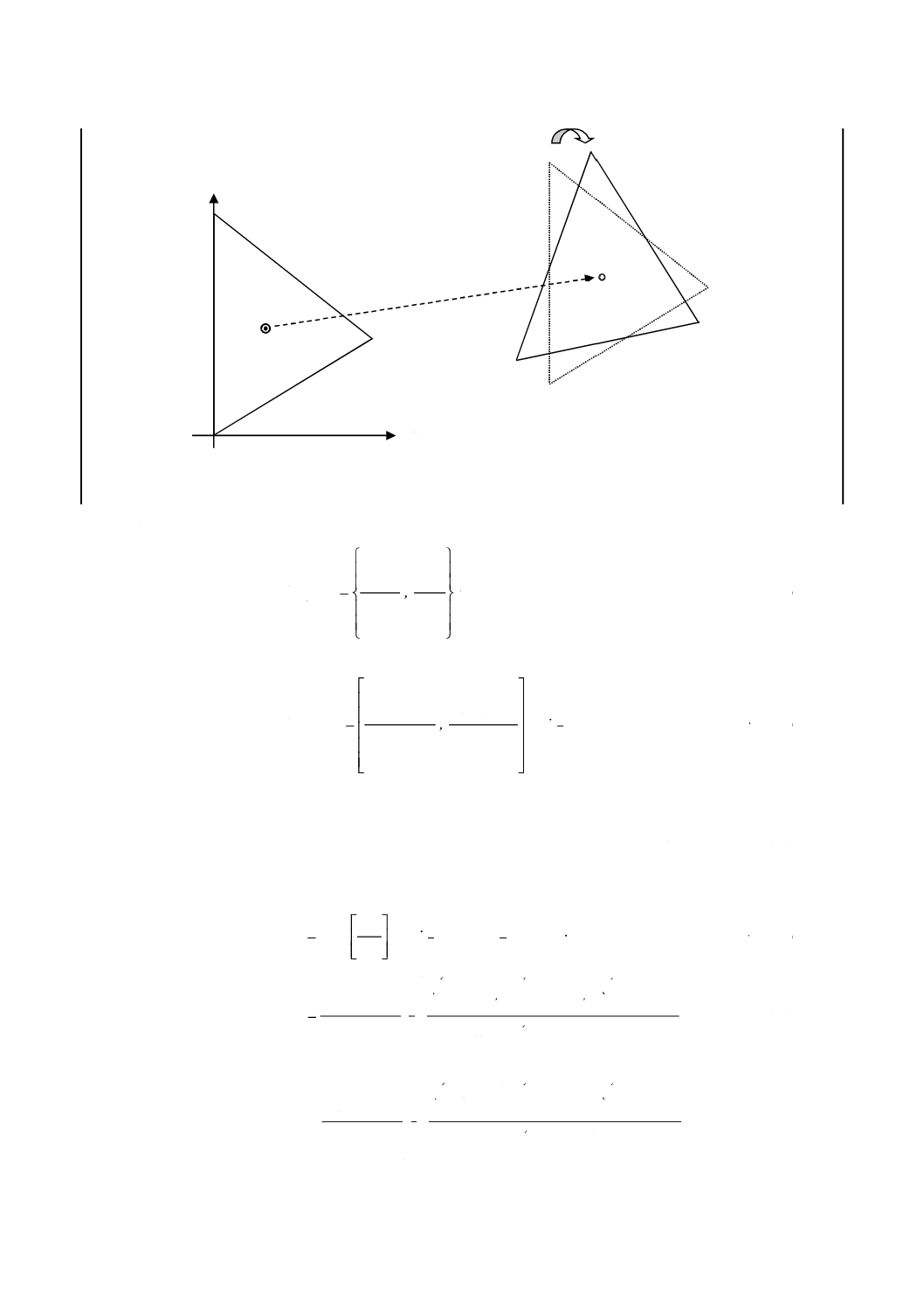
となる。図3を参照。
7
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図3−モデル三角形及び観測された三角形例
モデル三角形の重心座標(Xg, Yg)を,式(12) によって求める。
=
∑
∑
=
=
3
3
)
,
(
3
1
3
1
i
i
i
i
g
g
Y
,
X
Y
X
·························································· (12)
各機械点での観測で得られた三角形の平均重心座標(xg,i, yg,i)を,式(13) によって求める。
3
2
1
12
12
)
,
(
3
1
4
1
3
1
4
1
,
,
i
y
,
x
y
x
j
k
i,j,k
j
k
i,j,k
g,i
g,i
=
=
∑∑
∑∑
=
=
=
=
······························ (13)
モデル三角形の重心位置を,式(13) で求めたその機械点での平均三角形の重心位置まで,平行移動し,
移動後のモデル三角形の頂点座標を(Xt,i,j,k, Yt,i,j,k)とする。
Xt,i,j,k=Xi+(xg,i−Xg,i), Yt,i,j,k=Yi+(yg,i−Yg,i) i=1, 2, 3 j=1, 2, 3 k=1, 2, 3, 4 ···· (14)
移動後の重心座標を中心にして,モデル三角形の頂点座標と各セットの三角形の頂点座標との残差が最
小になるようモデル三角形を回転させるため,その回転角θi,kを求める。
4
3
2
1
3
2
1
tan1
,
,
,
k
,
,
i
p
q
θ
i,k
i,k
i,k
=
=
=
−
······································ (15)
(
)(
)(
)(
)
[
]
(
)(
)
[
]
∑
∑
=
=
−
+
−
−
×
−
−
−
×
−
=
3
1
2
2
3
1
j
g,i
i,j,k
,t
g,i
i,j,k
,t
j
g,i
i,j,k
g,i
i,j,k
,t
g,i
i,j,k
g,i
i,j,k
,t
i,k
y
Y
x
X
x
x
y
Y
y
y
x
X
q
··············· (16)
(
)(
)(
)(
)
[
]
(
)(
)
[
]
∑
∑
=
=
−
+
−
−
×
−
+
−
×
−
=
3
1
2
2
3
1
j
g,i
i,j,k
,t
g,i
i,j,k
,t
j
g,i
i,j,k
g,i
i,j,k
,t
g,i
i,j,k
g,i
i,j,k
,t
i,k
y
Y
x
X
y
y
y
Y
x
x
x
X
p
·············· (17)
(xg,i, yg,i)
(Xg, Yg)
M1(0, 0)
M3
M2
x
y
8
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
モデル三角形を式(15)で求めたθi,kだけ回転させたときの頂点座標(Xm,i,j,k, Ym,i,j,k)を,式(18) によって求
める。
(
)
(
)
(
)
(
)
4
3
2
1
3
2
1
3
2
1
cos
sin
sin
cos
,
,
,
k
,
,
j
,
,
i
y
Y
θ
x
X
θ
y
Y
y
Y
θ
x
X
θ
x
X
g,i
i,j,k
,
t
i,k
g,i
i,j,k
,
t
i,k
g,i
i,j,k
,
m
g,i
i,j,k
,
t
,k
i
g,i
i,j,k
,
t
i,k
g,i
i,j,k
,
m
=
=
=
−
×
+
−
×
+
=
−
×
−
−
×
+
=
··· (18)
各セットの頂点座標値と回転後モデル三角形の頂点座標との残差(rx,i,j,k, ry,i,j,k)を,次式で求める。
rx,i,j,k=xi,j,k−Xm,i,j,k i=1, 2, 3 j=1, 2, 3 k=1, 2, 3, 4 ···················· (19)
ry,i,j,k=yi,j,k−Ym,i,j,k i=1, 2, 3 j=1, 2, 3 k=1, 2, 3, 4 ···················· (20)
残差の二乗和を,式(21) によって求める。
(
)
∑
∑∑∑
=
=
=
+
=
3
1
3
1
4
1
2
2
2
i
j
k
i,j,k
,
y
i,j,k
,
x
xy
r
r
r
···················································· (21)
観測数72個で,モデル三角形の辺数3,モデル三角形の重心を観測三角形の重心に重ねるための移動ベ
クトル2成分×3機械点=6,及び回転パラメータ12(4セット×3機械点=12)であるので,自由度νXY
は,次のとおりである。
νXY=72−21=51 ····································································· (22)
したがって,標準偏差は,式(23)となる。
51
2
XY
∑
=
xy
r
s
········································································· (23)
最終的にx,y座標の標準不確かさは,式(24)となる。
uISO-TS-XY=sXY ·········································································· (24)
6.3.2
z座標
各機械点各セットにおける測点T1のz座標値を基準として測点2及び3のz座標値との点間高低差dz,i,2,k
及びdz,i,3,kを求める。
4
,3
,2
,1
3
,2
,1
,1,
,3,
,3,
,
,1,
,2,
,2,
,
=
=
−
=
−
=
k
i
z
z
d
z
z
d
k
i
k
i
k
i
z
k
i
k
i
k
i
z
····································· (25)
dz,i,2,k及びdz,i,3,kの全セットの平均値を,式(26) によって求める。
3
2
12
1
3
1
4
1
,
j
d
a
i
k
z,i,j,k
z,j
=
=∑∑
=
=
······················································ (26)
求められた平均値az,jとdz,i,2,k及びdz,i,3,kとの残差rz,i,j,kを,式(27) によって求める。
rz,i,j,k=dz,i,j,k−az,j i=1, 2, 3 j=2, 3 k=1, 2, 3, 4 ························· (27)
残差の二乗和を,式(28) によって求める。
∑
∑∑∑
=
=
=
=
3
1
3
2
4
1
2
2
i
j
k
i,j,k
,
z
z
r
r
······························································ (28)
自由度νZは,観測数24個で全セットの平均2個なので,次のとおりである。
νZ=24−2=22 ········································································ (29)
高低差の標準偏差sdZ及びz座標の標準偏差sZを,式(30) によって求める。
2
22
22
2
2
×
=
=
∑
∑
z
Z
z
dZ
r
s
,
r
s
························································ (30)
最後に標準不確かさは,次の式で表す。
9
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
uISO-TS-Z=sZ ············································································· (31)
標準試験手順の計算例を,附属書Bに示す。
6.4
統計的検定
6.4.1
一般
統計的検定は,標準試験手順だけに適用する。
測定結果の評価のために,試験結果として得た三角形の座標の標準偏差を用い,統計的検定を行わなけ
ればならない。
検定のための設問は,次とする(表3参照)。
a) 計算で得られた標準偏差sは,製造業者が示している値,又は事前に決めた別の値σ0より小さいか,
若しくは等しいか。
b) 二つの異なったサンプルから求めた標準偏差s及びs~は,それぞれのサンプルの自由度νが同じだと
仮定したとき,同じ母集団に属しているか。
標準偏差s及びs~は,次のいずれかから得ることができる。
1) 異なる観測者による同じ機器を用いて測定を行った二つの測定サンプル
2) 異なる時間帯に同じ機器を用いて測定を行った二つの測定サンプル
3) 異なる機器によって測定を行った二つの測定サンプル
次の検定においては,信頼水準(1−α)を0.95とし,この規格の測定手順に従い,x, y座標測定での自
由度はνXY=51,高さz座標測定での自由度はνZ=22とする。
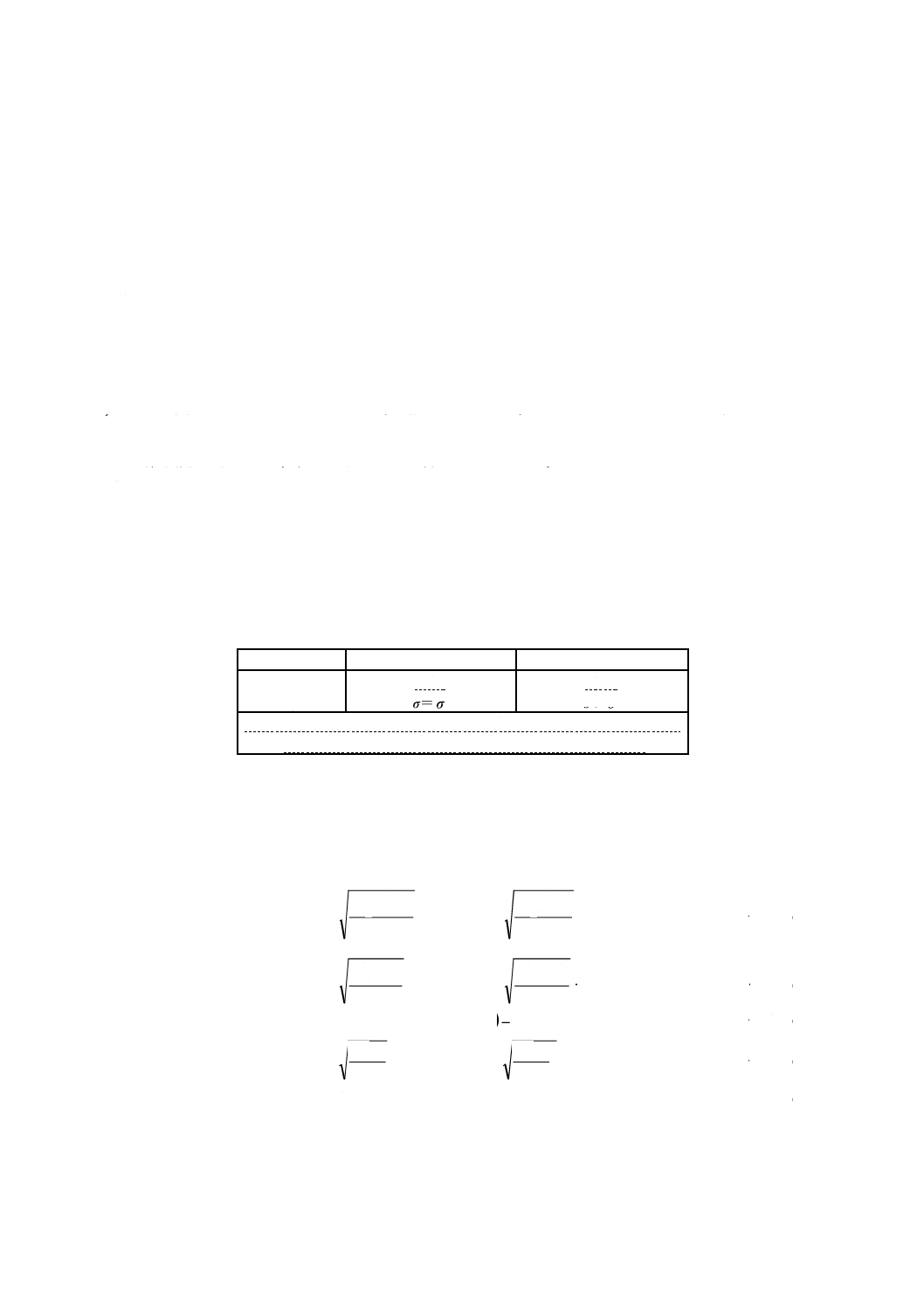
表3−統計的検定
問
帰無仮説
対立仮説
a)
σ≦σ0
σ>σ0
b)
σ=σ~
σ≠σ~
注記 帰無仮説ではサンプル測定の結果算出した標準偏差をもたらす
母集団の統計量を検証するためσをsの代わりに用いる。
6.4.2
問a)
観測して得た標準偏差sが,次の条件を満たすなら,製造業者が表明するか又は他の方法で,あらかじ
め決められた母集団の標準偏差σ0より小さいか等しいという帰無仮説は棄却することができない。
x及びyに対して zに対して
Z
Z
2
1
XY
2
1
)
(
≦
)
(
≦
0
XY
0
ν
ν
ν
ν
α
α
χ
σ
s
χ
σ
s
−
−
×
×
··································· (32)
22
)
22
(
≦
51
)
51
(
≦
2
95
0
2
95
0
0
0
.
.
χ
σ
s
χ
σ
s
×
×
···································· (33)
()
()
29
33
22
67
68
51
2
95
0
2
95
0
.
χ
.
χ
.
.
=
=
········································ (34)
22
29
33
≦
51
67
68
≦
0
0
.
σ
s
.
σ
s
×
×
······································ (35)
24
1
≦
16
1
≦
0
0
.
σ
s
.
σ
s
×
×
············································· (36)
そうでなければ,帰無仮説は棄却される。

10
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6.4.3
問b)
二つの異なったサンプルから求められた標準偏差(s及びs~)が,同じ母集団に属するかどうかを検定
する。次の条件を満たすなら,対応する帰無仮説
σ
σ~
=
は棄却することができない。
x及びyに対して zに対して
)
(
≦
~
≦
)
(
1
)
(
≦
~
≦
)
(
1
2
1
2
2
2
1
2
1
2
2
2
1
Z
Z
α/
Z
Z
α/
XY
XY
α/
XY
XY
α/
,
F
s
s
,
F
,
F
s
s
,
F
ν
ν
ν
ν
ν
ν
ν
ν
−
−
−
−
·· (37)
)
22
22
(
≦
~
≦
)
22
22
(
1
)
51
51
(
≦
~
≦
)
51
51
(
1
975
0
2
2
975
0
975
0
2
2
957
0
,
F
s
s
,
F
,
F
s
s
,
F
.
.
.
.
·· (38)
36
2
)
22
22
(
74
1
)
51
51
(
975
0
975
0
.
,
F
.
,
F
.
.
=
=
····················· (39)
36
2
≦
~
≦
42
0
74
1
≦
~
≦
57
0
2
2
2
2
.
s
s
.
.
s
s
.
······················· (40)
そうでなければ,帰無仮説は棄却される。
測定回数が異なる場合には,その自由度に対応する
()
ν
2
1α
χ−
,
(
)
ν
ν,
Fα2
1−
,
()
ν
2
1α
t−
などの値を採用しなけ
ればならない。それらの値は,JIS B 7912-1又は統計の参考書から得られる。
注記 自由度51に対するχ2分布及びF分布の値は,掲載されている数値表がないため,計算によっ
て求めた値である。
6.5
合成標準不確かさの評価(タイプA及びタイプB)
必要に応じ測定結果の信頼性評価のため,バジェット表を作成し,合成標準不確かさを評価することが
できる。
トータルステーションを用いて行う測定の不確かさの要因(影響量)の代表例を,表4に示す。
表4−トータルステーションの測定の不確かさ
不確かさ要因(影響の量)
記号
評価
分布
I. 測定の結果
x,y及びz座標値の標準偏差
uISO-TS
タイプA
正規分布
II. トータルステーション関連の要因
距離に関するカタログ表記
ur-ts
タイプB
正規分布又は製造業者の指定による。
水平角に関するカタログ表記
uφ-ts
タイプB
正規分布又は製造業者の指定による。
高度角に関するカタログ表記
uθ-ts
タイプB
正規分布又は製造業者の指定による。
最小桁表示(丸めによる不確かさ)
udisp
タイプB
一様分布
III. 機器の設置に関する要因
三脚のひねり(JIS B 7911)
utrd
タイプB
一様分布
三脚の高さ安定度(JIS B 7911)
uhs
タイプB
一様分布
IV. 大気に関する要因
気温
utemp
タイプB
正規分布
気圧
uprs
タイプB
正規分布
湿度
urh
タイプB
正規分布
極座標における不確かさ表示は,次のように表せる。
2
2
2
2
rh
prs
temp
ts
r
r
u
u
u
u
u
+
+
+
=
−
························································ (41)
2
2
trd
tsu
u
u
+
=
−
ϕ
ϕ
······································································ (42)
11
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
2
hs
ts
θ
θ
u
u
u
+
=
−
······································································· (43)
影響要因の中で距離及び角度に直接的に影響を及ぼすものについての極座標における不確かさ表示は,
次のようにまとめて表せる。
(
)
(
)(
)2
2
2
2
2
cos
sin
cos
ϕ
u
θ
r
u
θ
r
u
θ
uy
ux
θ
r
+
+
=
+
························· (44)
(
)
(
)2
2
2
cos
sin
θ
r
u
θ
r
u
θ
uz
+
=
··················································· (45)
ここに,rは斜距離,θは高度角を表す。
合成標準不確かさは,式(46) 及び式(47) によって求める。
2
2
2
XY
-
TS
-
ISO
disp
xy
u
uy
ux
u
u
+
+
+
=
················································· (46)
2
2
2
Z-
TS
-
ISO
disp
z
u
uz
u
u
+
+
=
·························································· (47)
拡張不確かさは,包含係数k=2として,式(48) 及び式(49) によって求める。
Ux,y=2×uxy············································································· (48)
Uz=2×uz ··············································································· (49)
バジェット表の例を,附属書Cに示す。
12
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
簡易試験手順の例
注記1 各例の計算は,最初から最後まで最大桁数で行っているが,中間の値及び最終結果は丸めた
値として示している。
注記2 計算結果として採用する数値を太字とし,単位記号を付記した。付記した単位記号も太字に
なっているが,これは見やすさを考えたためで,一般的なルールではない。
A.1 測定
測定条件は,次のとおりである。
観測者
日測 太郎
天候
晴れ
気温29 ℃
気圧1 006 hPa
使用機種及び機番 NN xxx 630401
測定日
2010-07-08
測定結果を,表A.1に示す。
表A.1−測定結果
番号
機械点(T)
i
測点(S)
j
セット
k
望遠鏡
x座標/m
y座標/m
z座標/m
1
1
1
1
正
6.979
4.886
9.934
2
2
59.617
25.117
6.763
3
1
2
反
6.979
4.886
9.933
4
2
59.619
25.117
6.762
5
1
1
正
6.978
4.885
9.934
6
2
59.618
25.116
6.764
7
1
2
反
6.979
4.885
9.934
8
2
59.620
25.116
6.762
9
2
1
1
正
8.344
−47.323
12.767
10
2
1.214
8.619
9.596
11
1
2
反
8.346
−47.322
12.764
12
2
1.213
8.619
9.596
13
1
1
正
8.344
−47.323
12.767
14
2
1.213
8.619
9.596
15
1
2
反
8.345
−47.324
12.766
16
2
1.213
8.619
9.596
A.2 計算結果
A.2.1 x,y座標
式(1)による。
13
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
l1,1 =56.392 0 l2,1 =56.394 5
l1,2 =56.393 8 l2,2 =56.393 9
l1,3 =56.393 8 l2,3 =56.394 7
l1,4 =56.394 8 l2,4 =56.395 8
次に式(2)による。
L=56.394 2
次に式(3)による。
r1,1 = −0.002 2 r2,1 = 0.000 4
r1,2 = −0.000 3 r2,2 = −0.000 2
r1,3 = −0.000 3 r2,3 = 0.000 5
r1,4 = 0.000 6 r2,4 = 0.001 6
最後に式(4)による。
dxy=0.002 2 m
A.2.2 z座標
式(5)による。
dz,1,1 = −3.171 dz,2,1 = −3.171
dz,1,2 = −3.171 dz,2,2 = −3.168
dz,1,3 = −3.170 dz,2,3 = −3.171
dz,1,4 = −3.172 dz,2,4 = −3.170
式(6)による。
az=−3.170 5
次に式(7)による。
rz,1,1 = −0.000 5 rz,2,1 = −0.000 5
rz,1,2 = −0.000 5 rz,2,2 = 0.002 5
rz,1,3 = −0.000 5 rz,2,3 = −0.000 5
rz,1,4 = −0.001 5 rz,2,4 = 0.001 5
最後に式(8)による。
dz=0.002 5 m
14
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
標準試験手順の例
注記1 各例の計算は,最初から最後まで最大桁数で行っているが,中間の値及び最終結果は丸めた
値として示している。
注記2 計算結果として採用する数値を太字とし,単位記号を付記した。付記した単位記号も太字に
なっているが,これは見やすさを考えたためで,一般的なルールではない。
B.1
測定
測定条件は,次のとおりである。
観測者
日測 太郎
天候
晴れ
気温29 ℃
気圧1 006 hPa
使用機種及び機番 NN xxx 630401
測定日
2010-07-08
測定結果を,表B.1に示す。
表B.1−測定結果
番号
機械点(T)
i
測点(S)
j
セット番号
k
望遠鏡
x座標/m
y座標/m
z座標/m
1
1
1
1
正
57.053
50.000
10.902
2
2
1.469
39.157
13.120
3
3
39.429
−2.997
10.641
4
1
2
反
57.053
50.001
10.902
5
2
1.470
39.159
13.121
6
3
39.426
−2.998
10.640
7
1
3
正
57.054
50.001
10.902
8
2
1.468
39.156
13.120
9
3
39.427
−2.997
10.640
10
1
4
反
57.054
50.000
10.902
11
2
1.470
39.158
13.121
12
3
39.428
−2.998
10.640
13
2
1
1
正
23.040
96.697
8.837
14
2
45.141
44.555
11.056
15
3
78.535
90.411
8.576
16
1
2
反
23.043
96.698
8.834
17
2
45.139
44.555
11.056
18
3
78.535
90.412
8.576
19
1
3
正
23.042
96.697
8.835
20
2
45.142
44.555
11.056
21
3
78.534
90.412
8.574
15
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.1−測定結果(続き)
番号
機械点(T)
i
測点(S)
j
セット番号
k
望遠鏡
x座標/m
y座標/m
z座標/m
22
2
1
4
反
23.040
96.696
8.834
23
2
45.140
44.555
11.056
24
3
78.534
90.412
8.574
25
3
1
1
正
74.685
92.755
11.703
26
2
18.066
93.974
13.922
27
3
46.198
44.716
11.442
28
1
2
反
74.686
92.752
11.703
29
2
18.068
93.975
13.922
30
3
46.198
44.715
11.442
31
1
3
正
74.687
92.752
11.703
32
2
18.068
93.976
13.922
33
3
46.199
44.715
11.442
34
1
4
反
74.689
92.751
11.701
35
2
18.068
93.975
13.923
36
3
46.199
44.715
11.442
B.2
計算
B.2.1 x, y座標
式(10) による。
L1=56.726 7
L2=55.849 9
L3=56.632 1
式(13) による。
(xg,1, yg,1)=(32.650 1, 28.720 2)
(xg,2, yg,2)=(48.905 4, 77.221 3)
(xg,3, yg,3)=(46.317 6, 77.147 6)
式(14) から求めた平行移動した数学モデルの重心座標を,次に示す。
i
k
Xt,i,1,k
Yt,i,1,k
Xt,i,2,k
Yt,i,2,k
Xt,i,3,k
Yt,i,3,k
1
1
4.624 5
12.506 3
61.256 6
12.506 3
32.069 1
61.147 9
1
2
4.624 5
12.506 3
61.256 6
12.506 3
32.069 1
61.147 9
1
3
4.624 5
12.506 3
61.256 6
12.506 3
32.069 1
61.147 9
1
4
4.624 5
12.506 3
61.256 6
12.506 3
32.069 1
61.147 9
2
1
20.879 9
61.007 4
77.512 0
61.007 4
48.324 4
109.649 0
2
2
20.879 9
61.007 4
77.512 0
61.007 4
48.324 4
109.649 0
2
3
20.879 9
61.007 4
77.512 0
61.007 4
48.324 4
109.649 0
2
4
20.879 9
61.007 4
77.512 0
61.007 4
48.324 4
109.649 0
3
1
18.292 0
60.933 7
74.924 1
60.933 7
45.736 6
109.575 3
3
2
18.292 0
60.933 7
74.924 1
60.933 7
45.736 6
109.575 3
3
3
18.292 0
60.933 7
74.924 1
60.933 7
45.736 6
109.575 3
3
4
28.292 0
60.933 7
74.924 1
60.933 7
45.736 6
109.575 3
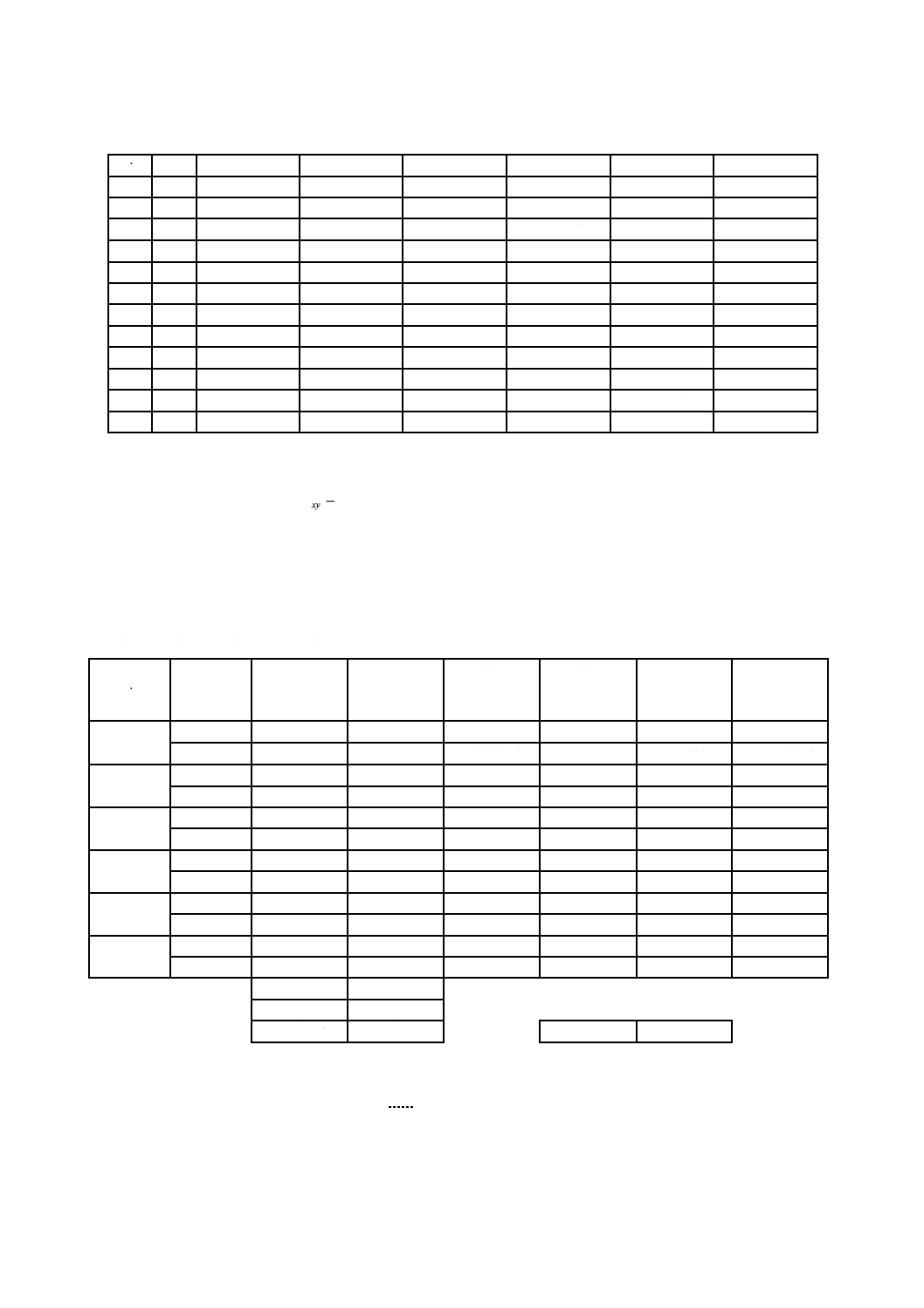
16
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
次に式(18)から求めた回転した数学モデルの頂点座標を,次に示す。
i
k
Xm,i,1,k
Ym,i,1,k
Xm,i,2,k
Ym,i,2,k
Xm,i,3,k
Ym,i,3,k
1
1
57.052 9
49.999 8
1.468 5
39.157 1
39.428 9
−2.996 4
1
2
57.053 9
49.998 7
1.469 0
39.158 6
39.424 7
−2.996 8
1
3
57.053 0
49.999 7
1.468 5
39.157 3
39.428 7
−2.996 5
1
4
57.053 6
49.999 0
1.468 8
39.158 1
39.427 9
−2.996 7
2
1
23.040 1
96.697 0
45.141 0
44.555 5
78.535 1
90.411 2
2
2
23.040 8
96.698 0
45.139 8
44.555 6
78.535 6
90.410 1
2
3
23.039 9
96.696 8
45.141 4
44.555 4
78.535 0
90.411 6
2
4
23.039 9
96.696 8
45.141 4
44.555 4
78.536 0
90.411 6
3
1
74.685 9
92.753 9
18.067 0
93.974 0
46.199 8
44.714 9
3
2
74.686 7
92.752 5
18.067 8
93.975 4
46.198 2
44.714 9
3
3
74.686 8
92.752 4
18.067 9
93.975 5
46.198 1
44.714 9
3
4
74.686 9
92.752 1
18.068 1
93.975 8
46.197 8
44.714 9
式(21)から残差の二乗和を求める。
6
061
000
0
2
.
rxy=
∑
標準偏差sXY及び標準不確かさsISO-TS-XYをそれぞれ式(22)及び式(23)から求める。
sXY=0.001 10
sISO-TS-XY=0.001 10 m
B.2.2 z座標
式(25),式(26),式(27) 及び式(28) から求めた各値を,次に示す。
機械点(S)
i
セット番
号
k
高低差2-1
dz,i,2,k
高低差3-1
dz,i,3,k
残差2-1
rz,i,2,k
残差3-1
rz,i,3,k
二乗2-1
r2z,i,2,k
二乗3-1
r2z,i,3,k
1
1
2.218
−0.261
−0.001 70
−0.000 250
0.000 003 1
0.000 000 1
2
2.219
−0.262
−0.000 70
−0.001 250
0.000 000 6
0.000 001 6
1
3
2.218
−0.262
−0.001 70
−0.001 250
0.000 003 1
0.000 001 6
4
2.219
−0.262
−0.000 70
−0.001 250
0.000 000 6
0.000 001 6
2
1
2.219
−0.261
−0.000 80
−0.000 250
0.000 000 6
0.000 000 1
2
2.222
−0.258
0.002 25
0.002 750
0.000 005 1
0.000 007 6
2
3
2.221
−0.261
0.001 25
−0.000 250
0.000 001 6
0.000 000 1
4
2.222
−0.260
0.002 25
−0.000 750
0.000 005 1
0.000 000 6
3
1
2.219
−0.261
−0.000 70
−0.000 250
0.000 000 6
0.000 000 1
2
2.219
−0.261
−0.000 70
−0.000 250
0.000 000 6
0.000 000 1
3
3
2.219
−0.261
−0.000 70
−0.000 250
0.000 000 6
0.000 000 1
4
2.222
−0.259
0.002 25
0.001 750
0.000 005 1
0.000 003 1
26.637
−3.129
az,2
az,3
2.219 8
−0.260 7
rz2
0.000 042 5
標準不確かさsISO-TS-Zを,式(31)から求める。
sISO-TS-Z=0.000 98 m
17
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.3
統計的検定
B.3.1 問a) による統計的検定
x及びy座標の検定:得られた標準偏差が事前に決めた値より小さいか等しい。
mm
8
5
≦
mm
10
1
16
1
mm
0
5
≦
mm
10
1
51
mm
10
1
mm
0
5
XY
-
TS
-
ISO
0
.
.
.
.
.
.
s
.
σ
XY
×
=
=
=
ν
上記の不等式は成立するため,観測で得た標準偏差sISO-TS-XY=1.10 mmは製造業者が示した値σ0=5.0 mm
より小さいか等しいという帰無仮説は,信頼水準95 %で棄却できない。
z座標に関する検定:得られた標準偏差が事前に決めた値より小さいか等しい。
mm
2
6
≦
mm
98
0
24
1
mm
0
5
≦
mm
98
0
22
mm
98
0
mm
0
5
Z
-
TS
-
ISO
0
.
.
.
.
.
.
s
.
σ
Z
×
=
=
=
ν
上記の不等式は成立するため,観測で得た標準偏差sISO-TS-Z=0.98 mmは製造業者が示した値σ0=5.0 mm
より小さいか等しいという帰無仮説は,信頼水準95 %で棄却できない。
B.3.2 問b) による統計的検定
x及びy座標の検定:二つの異なったサンプルから得られた標準偏差が同一母集団に属するか。
74
1
≦
92
0
≦
57
0
74
1
≦
mm
32
1
mm
21
1
≦
57
0
51
mm
15
1
~
mm
10
1
2
2
.
.
.
.
.
.
.
.
s
.
s
XY
=
=
=
ν
上記の不等式は成立するため,観測で得た標準偏差s=1.10 mm及びs~=1.15 mmは同じ母集団に属する
という帰無仮説は,信頼水準95 %で棄却できない。
z座標に関する検定:二つの異なったサンプルから得られた標準偏差が同一母集団に属するか。
36
2
≦
73
0
≦
42
0
36
2
≦
mm
32
1
mm
96
0
≦
42
0
22
mm
15
1
~
mm
98
0
2
2
.
.
.
.
.
.
.
.
s
.
s
z
=
=
=
ν
上記の不等式は成立するため,観測で得た標準偏差s=0.98 mm及びs~=1.15 mmは同じ母集団に属する
という帰無仮説は,信頼水準95 %で棄却できない。
18
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
不確かさバジェット表の計算例
注記1 各例の計算は,最初から最後まで最大桁数で行っているが,中間の値及び最終結果は丸めた
値として示している。
注記2 計算結果として採用する数値を太字とし,単位記号を付記した。付記した単位記号も太字に
なっているが,これは見やすさを考えたためで,一般的なルールではない。
C.1 不確かさバジェット表の例
標準試験手順の結果から,最長測定距離57 mにおける合成標準不確かさを次の情報を用いて見積もる。
C.1.1 不確かさの要因
a) 測定結果の解析:uISO-TS
uISO-TSは,附属書Bの値を用いる。
sISO-TS-XY=0.001 10 m
sISO-TS-Z=0.000 98 m
b) トータルステーション
製造業者の仕様を用いる。
距離測定の不確かさur−tsは,製造業者の仕様が±(3+2 ppm×D) mm,最長測定距離57 mから見積
もる。
ur−ts=3+2×57 000×10−6=3.1 mm
水平角測定の不確かさは,製造業者の仕様(JIS B 7912-3)から5''とする。
uφ−ts=5''
鉛直角測定の不確かさは,製造業者の仕様(JIS B 7912-3)から5''とする。
uθ−ts=5''
最少桁表示の不確かさは,最少桁表示1 mmとする。
mm
29
0
3
5
0
disapz
dispy
dispx
.
.
u
u
u
=
=
=
=
c) 三脚
三脚のひねりは,JIS B 7911の規格値3''から不確かさを一様分布として見積もる。
''
.
u
73
1
3
3
trd
=
=
三脚の高さの安定性は,JIS B 7911の規格値0.05 mm以下と見積もる。この値は最終結果に影響を
与えないため,不確かさの計算に算入しない。
d) 大気の状態
温度測定による不確かさutempは,経験値から1 ℃とする。
utemp=1×57 000×10−6=0.057 mm
大気圧測定による不確かさuprsは,経験値から5 hPaとする。
uprs=0.3×5×57 000×10−6=0.086 mm
19
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
湿度測定による不確かさurhは,最大距離を100 mとしても非常に小さな値のため,不確かさの計算に算
入しない。
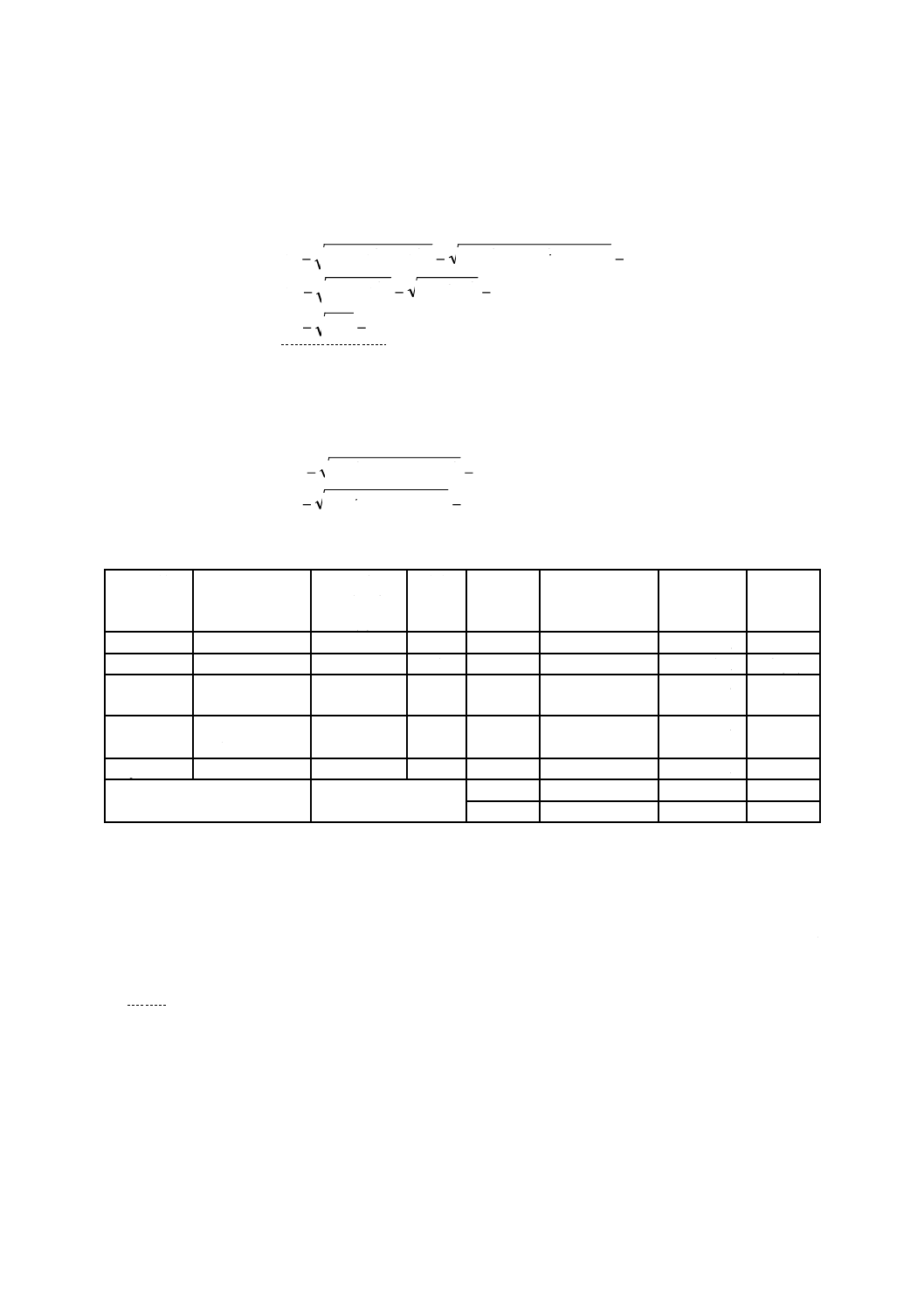
C.1.2 不確かさの計算
極座標系における不確かさは,式(41)〜式(43)参照。
9
2
5
73
1
5
mm
116
3
086
0
057
0
114
3
2
2
2
2
2
2
2
2
2
2
′′
=
+
=
+
=
=
+
+
=
+
+
=
−
−
.
.
u
u
u
.
.
.
.
u
u
u
u
trd
ts
prs
temp
ts
r
r
ϕ
ϕ
5
2
′′
=
=
−ts
θ
θ
u
u
式(44)及び式(45) に従って直角座標系における不確かさに変換する。
ux2+uy2=11.84 mm
uz2=1.91 mm
式(46)及び式(47) に従って合成標準不確かさを求める。
mm
1.72
mm
3.62
=
+
+
=
=
+
+
=
2
2
2
2
29
.0
91
.1
8
9
0.
29
.0
84
.
11
10
.1
z
xy
u
u
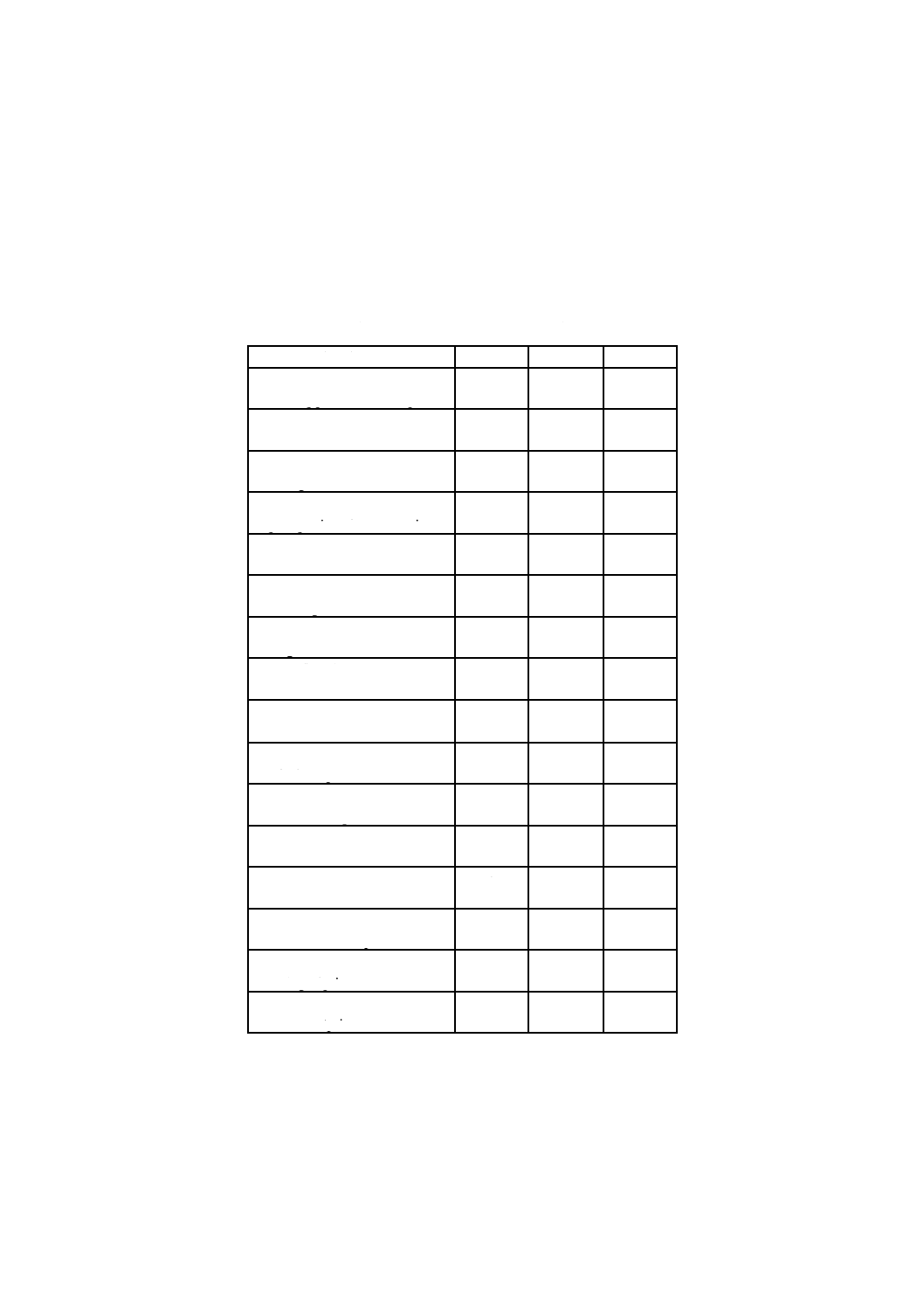
表C.1−直交座標での不確かさバジェット表
入力量
入力
推定値
標準
不確かさ
u(xi)
分布
感度係数
ci
ui(cxy)≡|ci|×u(xi)
評価
参照
uISO-TS-XY
−
1.10
正規
1
1.10
タイプA
式(24)
uISO-TS-Z
−
0.98
正規
1
0.98
タイプA
式(31)
(ux2+uy2)1/2
最長距離:57 m,
高度角 θ:1°
3.44
正規
1
3.44
タイプB
式(46)
uz
最長距離:57 m,
高度角 θ:1°
1.38
正規
1
1.38
タイプB
式(47)
udisp
0
0.29
一様
1
0.29
タイプB
最長距離:57 m,
高度角 θ:1°
最終結果
uxy
3.62
uz
1.72
C.2 拡張不確かさ
Uxy=2×3.62 ≈ 7 mm
Uz=2×1.72 ≈ 3 mm
拡張不確かさは上記となり,信頼の水準95 %に相当する区間はx,y座標で±7 mm,z座標で±3 mmと
なる。
注記 拡張不確かさの表記は,多くて2桁である。
20
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
不確かさ評価に含めなかった要因
代表的な影響要因の中に組み込まれていたり,又は影響量が小さいとして,附属書Cで不確かさ評価を
行わなかった要因を,表D.1に示す。
表D.1−不確かさ評価に含めなかった不確かさの要因
不確かさの要因
距離
高度角
水平角
望遠鏡の分解力
Resolving power of telescope
●
●
●
焦点鏡の偏差
Cross hair error
●
●
TSの致心
Centring of total station
●
●
●
視軸横軸直角度
Sighting axis and vertical axis
●
鉛直軸誤差(TS)
Vertical-axis tilt of total station
●
●
●
視軸の偏差
Line-of-sight error
●
横軸水平度
Tilting-axis error
●
水平目盛誤差
Graduation error of H circle
●
水平目盛偏心誤差
Eccentric error of H circle
●
高度角度補正誤差
Vertical compensate error
●
水平角度補正誤差
Horizontal compensate error
●
機械定数
Additional constant
●
プリズム定数の差
Prism constant error
●
気象補正式のパラメータ
Parameter of atmospheric factor
●
プリズムの致心
Centring of prism
●
プリズム面の方向
Direction of prism face
●
●
●
21
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
主な記号の解説
az
高低差の平均値
dxy
水平距離の偏差rの最大値
dz
高低差の偏差rの最大値
k
包含係数
Mi(Xi, Yi)
モデル三角形の頂点
l
2測点間の水平距離又は辺長
L
2測点間の水平距離の平均値又は辺長の平均値
pxy,pz
簡易試験のための許容差(ISO 4463-1)
pi,k
モデル三角形の回転角θを求めるためのパラメータ
qi,k
モデル三角形の回転角θを求めるためのパラメータ
r
偏差又は残差
Si
機械点
sdz
高低差の標準偏差
sXY
(x, y)座標の標準偏差
sZ
z座標の標準偏差
sISO-TS-XY
標準試験の結果の(x, y)座標の標準偏差
sISO-TS-Z
標準試験の結果のz座標の標準偏差
Ti
測点又は三角形の頂点
U
拡張不確かさ
u
標準不確かさ
uISO-TS-XY
標準試験手順で求めたx, y座標の標準不確かさ
uISO-TS-Z
標準試験手順で求めたz座標の標準不確かさ
Xg, Yg
モデル三角形の重心座標
xg,i, yg,i
観測で得られた三角形の重心座標
xi,j,k, yi,j,k
kセット目の機械点iにおける測点jの座標
Xm,i,j,k, Ym,i,j,k
回転後のモデル三角形の頂点座標
Xt,i,j,k, Yt,i,j,k
モデル三角形の重心を観測で得られた三角形の重心座標に重ね合わせたときのモデル三角
形の頂点座標
ν
自由度
θ
モデル三角形の回転角
σ
試験で得られる観測値の母集団の母標準偏差
σ0
統計的検定のために事前に決めた値

22
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] JCGM 200:2008,International vocabulary of metrology. Basic and general concepts and associated terms
(VIM)
http://www.bipm.org/utils/common/documents/jcgm/JCGM̲200̲2008.pdf
See also: Corrigendum (May 2010)
http://www.bipm.org/utils/common/documents/jcgm/JCGM̲200̲2008̲Corrigendum.pdf
[2] JCGM 100:2008,Evaluation of measurement data−Guide to the expression of uncertainty in measurement
http://www.bipm.org/utils/common/documents/jcgm/JCGM̲100̲2008̲E.pdf
[3] JCGM 104:2009,Evaluation of measurement data−An introduction to the "Guide to the expression of
uncertainty in measurement" and related documents
http://www.bipm.org/utils/common/documents/jcgm/JCGM̲104̲2009̲E.pdf
[4] NlST Technical Note 1297:1994,Guidelines for Evaluating and Expressing the Uncertainty of NlST
Measurement Results
http://physics.nist.gov/Pubs/guidelines/TN1297/tn1297s.pdf
[5] NIST SOP No29:2003,Standard Operating Procedure for the Assignment of Uncertainty
[6] JCG200 校正における測定の不確かさの評価
独立行政法人製品評価技術基盤機構認定センター
EA-4/02 Evaluation of the Uncertainty of Measurement in Calibration
[7] ISO 1101:2004,Geometrical Product Specifications (GPS)−Geometrical tolerancing−Tolerances of form,
orientation, location and run-out
[8] ISO 2854:1976,Statistical interpretation of data ‒Techniques of estimation and tests relating to means and
variances
[9] ISO 3494:1976,Statistical interpretation of data−Power of tests relating to means and variances
[10] ISO 9849,Optics and optical instruments−Geodetic and surveying instruments−Vocabulary
[11] ISO 12858-2,Optics and optical instruments−Ancillary devices for geodetic instruments−Part 2: Tripods
[12] JIS B 7912-3 測量機器の現場試験手順−第3部:セオドライト
注記 対応国際規格:ISO 17123-3,Optics and optical instruments−Field procedures for testing geodetic
and surveying instruments−Part 3: Theodolites(MOD)
[13] JIS B 7912-4 測量機器の現場試験手順−第4部:光波測距儀
注記 対応国際規格:ISO 17123-4:2012,Optics and optical instruments−Field procedures for testing
geodetic and surveying instruments−Part 4: Electro-optical distance meters (EDM measurements to
reflectors)(MOD)
[14] ISO/IEC Guide 98-3,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995)
注記 上記のガイドは,TS Z 0033:2012(測定における不確かさの表現のガイド)として公表され
ている。
[15] ISO/IEC Guide 99,International vocabulary of metrology−Basic and general concepts and associated terms
(VIM)
23
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 上記のガイドは,TS Z 0032:2012[国際計量計測用語−基本及び一般概念並びに関連用語
(VIM)]として公表されている。
[16] JIS Z 9041-2:1999 データの統計的な解釈方法−第2部:平均と分散に関する検定方法と推定方法
24
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JB
(参考)
JISと対応国際規格との対比表
JIS B 7912-5:2016 測量機器の現場試験手順−第5部:トータルステーション
ISO 17123-5:2012,Optics and optical instruments−Field procedures for testing geodetic
and surveying instruments−Part 5: Total stations
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごとの評価及びその内
容
(V)JISと国際規格との技術的
差異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
4 一般
4.2 簡易試験手順
4.2
JISに同じ
追加
水平方向と鉛直方向に分けて評価する理由を追記し
た。技術的な差異はない。
4.3 標準試験手順
4.3
JISに同じ
追加
標準偏差がタイプA標準不確かさに等しいことを追記
した。技術的な差異はない。
5 簡易試
験手順
5.3 計算
5.3.1
5.3.2
変更
変更
式(3)及び式(8)で2で除すのは適切でないことが判明
し変更した。
ISOに修正提案を行う。
6 標準試
験手順
6.3 計算
6.3.1 x,y座標
6.3.1
JISに同じ
追加
モデル三角形の頂点座標をMi(Xi,Yi)と明確に記載し
た。
JISに同じ
変更
ISO規格の式(11)及び式(12)を文章中に記述したため,
以後の式番号が変更となった。技術的な差異はない。
JISに同じ
追加
図3にモデル三角形を移動し,回転する部分を追記し
分かりやすくした。技術的な差異はない。
変更
式(12)のX,Yの添え字の誤りを修正。
ISOに修正提案を行う。
変更
重心座標2成分×3を,モデル三角形の重心を観測三
角形の重心に重ねるための移動ベクトル2成分×3に
変更した。
ISOに修正提案を行う。
6.3.2 z座標
6.3.2
JISに同じ
追加
式(25)に測点2の高低差を求める式を追記した。また
標準不確かさを表す式に式番号(31)を付け参照しやす
くした。技術的な差異はない。
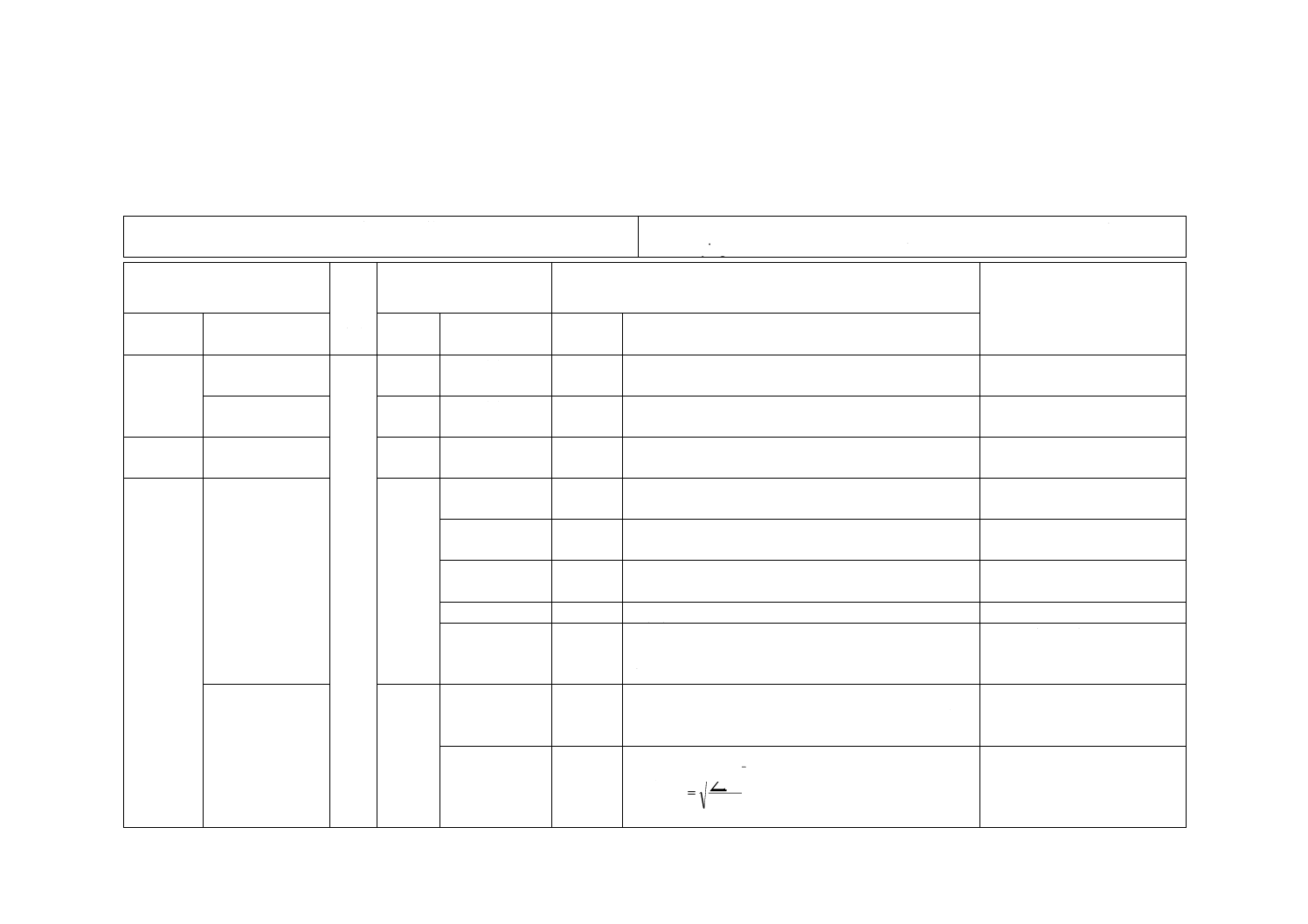
変更
z座標の評価は,高低差の評価になっているため,式
(30)に
2
22
2
×
=∑z
Z
r
s
を追記し,座標の標準偏差を算出し
た。
ISOに修正提案を行う。
2
B
7
9
1
2
-5
:
2
0
1
6
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
25
B 7912-5:2016
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごとの評価及びその内
容
(V)JISと国際規格との技術的
差異の理由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
6 標準試
験手順
(続き)
6.4 統計的検定
6.4.1 a)
JISに同じ
変更
σからσ0へ変更した。
母集団の“σ”と区別するため
表3 a)
JISに同じ
変更
σからσ0へ変更した。
母集団の“σ”と区別するため
表3
JISに同じ
追加
表3の統計的検定に注記を追加した。
帰無仮説ではサンプル測定の結果算出した標準偏差
をもたらす母集団の統計量を検証するためσをsの代
わりに使用する。
統計的検定で規定値と比較す
る試験機の標準偏差は,測定
サンプルから求められる“s”
ではなく,それをもたらした
母集団の“σ”であるべきであ
り,σとsの関係を明確にする
ため。
6.4.3問
b)
JISに同じ
追加
自由度などが異なる場合のt分布表の参照にJIS B
7912-1を追記した。
附属書A
(参考)
簡易試験手順の
例
Annex
A
附属書B
(参考)
標準試験手順の
例
Annex
B
附属書C
(参考)
不確かさバジェ
ットの表の計算
例
Annex
C
附属書JA
(参考)
主な記号の解説
−
追加
主要な記号についての解説を表にまとめ追加した。技
術的な差異はない。
JISと国際規格との対応の程度の全体評価:ISO 17123-5:2012,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 追加 ················ 国際規格にない規定項目又は規定内容を追加している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
2
B
7
9
1
2
-5
:
2
0
1
6
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。