B 7912-1:2014
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 測定の不確かさ評価 ·········································································································· 7
4.1 一般 ···························································································································· 7
4.2 標準不確かさのタイプA評価 ··························································································· 8
4.3 標準不確かさのタイプB評価 ·························································································· 13
4.4 不確かさ伝ぱ(播)の法則及び合成不確かさ ······································································ 14
4.5 拡張不確かさ ··············································································································· 15
5 不確かさの報告 ··············································································································· 16
6 不確かさ評価の要約 ········································································································· 16
7 統計的検定 ····················································································································· 17
7.1 一般 ··························································································································· 17
7.2 問a):標準偏差sは,規定の値σ0に等しい又は小さいか? ··················································· 17
7.3 問b):二つのサンプルは,同じ母集団に属しているか? ······················································ 17
7.4 問c) 及び問d):パラメータykの有意性の検定 ··································································· 18
附属書A(参考)確率分布 ···································································································· 19
附属書B(規定)χ2分布,F分布及びt分布 ············································································ 20
附属書C(参考)計算例 ······································································································· 21
参考文献 ···························································································································· 29
附属書JA(参考)JISと対応国際規格との対比表 ······································································ 30
B 7912-1:2014
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般社団法人日本
測量機器工業会(JSIMA)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業
規格を改正すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業
規格である。これによって,JIS B 7912-1:2004は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 7912の規格群には,次に示す部編成がある。
JIS B 7912-1 第1部:理論
JIS B 7912-2 第2部:レベル
JIS B 7912-3 第3部:セオドライト
JIS B 7912-4 第4部:光波測距儀
JIS B 7912-6 第6部:回転レーザ
JIS B 7912-8 第8部:GNSS(RTK)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 7912-1:2014
測量機器の現場試験手順−第1部:理論
Optics and optical instruments-Field procedures for testing geodetic and
surveying instruments-Part 1: Theory
序文
この規格は,2010年に第2版として発行されたISO 17123-1を基とし,統計的検定についてはISO 2854
及びJIS Z 9041-2の表現に合わせるため,技術的内容を変更して作成した日本工業規格である。
なお,この規格で点線の下線を施してある箇所は,対応国際規格を変更している事項である。変更の一
覧表にその説明を付けて,附属書JAに示す。
1
適用範囲
この規格は,測量機器の現場での測定精度を評価するときに用いる理論について規定する。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 17123-1:2010,Optics and optical instruments−Field procedures for testing geodetic and surveying
instruments−Part 1: Theory(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,記載の年の版を適用し,その後の改正版(追補を含む。)は適用しない。
ISO/IEC Guide 98-3:2008,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM: 1995)
ISO/IEC Guide 99:2007,International vocabulary of metrology−Basic and general concepts and associated
terms (VIM)
3
用語及び定義
この規格で用いる主な用語及び定義は,ISO/IEC Guide 99:2007によるほか,次による。
3.1
一般計測用語
3.1.1
(測定できる)量[(measurable) quantity]
数値と計量参照(reference)との組合せとして表すことができる大きさをもつ,現象又は物体若しくは
物質の性質。
例1
一般的な意味での量 長さ,時間,温度
2
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
例2
特定な意味での量 ある棒の長さ
3.1.2
値(value),量の値(value of a quantity, quantity value)
量の大きさを表現する,数値と計量参照との組合せ。
例 ある棒の長さ 3.24 m
3.1.3
真の値(true value),量の真値(true value of a quantity),真の量の値(true quantity value)
ある特定の量の定義と合致する値。
注記 これは完全な測定によって得られる量である。ただし,この値は原理的にも実際にも知ること
ができない。
3.1.4
参照値(reference value),量の参照値(reference quantity value)
同じ種類の量の値と比較する基準となる量の値。
注記 量の参照値は,通常未知である測定対象量の真値とすることができる。測定の不確かさを含む
量の参照値は,参照測定手順によって通常規定される。
3.1.5
測定(measurement)
ある量に合理的に結び付けることが可能な一つ以上の量の値を,実験的に得る手順。
注記 測定は,量の比較及び実在物の計数を含む。
3.1.6
測定原理(measurement principle)
測定の基礎となる現象(測定の科学的根拠)。
注記 測定原理とは,距離測定に適用されるドップラー効果のような物理的現象である。
3.1.7
測定方法(measurement method)
測定に用いる操作の論理的構成の一般的な記述。
注記 測定の方法は,“差動法”,“直接測定法”など様々な方法を適用することができる。
3.1.8
測定対象量(measurand)
測定によって求めたい量。
例 トータルステーションによって決定された座標x。
3.1.9
指示値(indication)
測定器又は測定システムによって与えられた量の値。
注記 指示値と測定された量とに相当する値は,同じ種類の量の値である必要はない。
3.1.10
測定結果(measurement result),測定の結果(result of measurement)
利用し得る関連情報を伴った,測定対象量に結び付けられる量の値の集合。
注記 測定結果は,指示値,補正されない結果又は補正済みの結果を表す。
測定結果は,一般に単一の測定量の値及び測定の不確かさで表される。
3
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.1.11
測定された量の値(measured quantity value)
測定結果を代表する量の値。
3.1.12
誤差(error),測定の誤差(measurement error)
測定された量の値から量の参照値を引いたもの。
3.1.13
偶然誤差(random error),偶然測定誤差(random measurement error)
複数回の測定において,予測が不可能な変化をする測定誤差の成分。
注記1 繰返し測定の集合の偶然測定誤差は,一般にゼロであるとされる期待値及びその分散によっ
て示される分布を形成する。
注記2 誤差の要因を含めてrandom effectという用語を用いることがある。
3.1.14
系統誤差(systematic error),測定の系統誤差(systematic error of measurement)
複数回の測定において,一定の,又は,予測可能な変化をする測定誤差の成分。
注記1 系統誤差及びその原因は,既知又は未知の場合がある。補正を測定の既知の系統誤差の修正
に適用することができる。
注記2 誤差の要因を含めてsystematic effectという用語を用いることがある。
3.2
この規格に特有の用語
3.2.1
測定の精確さ(accuracy of measurement)
測定された量の値と,測定対象量の真の値との一致の度合い。
注記1 “精確さ”は,定性的な概念であり,数値で表現することはできない。
注記2 “精確さ”は,系統誤差及び偶然誤差に対して正反対の関係がある。
3.2.2
標準偏差(実験標準偏差)(experimental standard deviation)
測定結果の妥当な分布の標準偏差の推定値。
注記1 実験標準偏差は,偶然の影響に起因する不確かさの尺度である。
注記2 これらの影響で生じた正確な値を知ることができない。実験標準偏差の値は,通常,統計的
手法で推定される。
注記3 測定結果から求めた標準偏差であることを明確にしたい場合,“実験標準偏差”を用いる。
3.2.3
精密さ(precision),測定の精密さ(measurement precision)
特定の条件下で,同一又は類似の対象を繰返し測定によって得られた測定量の値の密集度。
注記 測定の精密さは,通常,特定の測定条件下における実験標準偏差のような測定の不正確さとし
て表される。
3.2.4
繰返し条件(repeatability condition),測定の繰返し条件(repeatability condition of measurement)
繰返し測定を行う際の条件。
注記 同一又は類似対象の繰返し測定を短時間で行う際,考慮すべき条件は次を含む。
4
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 同一の測定手順
− 同一の測定者
− 同一の測定器
− 同一の気象条件
− 同一の場所
3.2.5
繰返し性(repeatability),測定の繰返し性(measurement repeatability)
ある測定の繰返し条件下の測定の精密さ。
3.2.6
測定の再現条件(reproducibility conditions of measurement)
再現測定を行う際の条件。
注記 同一又は類似対象の繰返し測定を行う際,考慮すべき条件は次を含む。
− 異なる場所
− 異なる観測者
− 異なる測定器
3.2.7
再現性(reproducibility),測定の再現性(measurement reproducibility)
測定の再現条件下での測定の精密さ。
3.2.8
影響量(influence quantity)
直接の測定量ではないが,測定システムの指示値と測定結果との関係に影響を与える量。
例 トータルステーションによる距離測定時の温度。
3.3
不確かさの用語
3.3.1
不確かさ(uncertainty),測定の不確かさ(uncertainty of measurement),測定不確かさ(measurement uncertainty)
用いる情報に基づき,測定対象量に属する量の値のばらつきを特徴付ける負ではないパラメータ。
注記 測定不確かさは,一般に多くの成分から成る。その一部は,測定不確かさのタイプA評価によ
って一連の測定で得られる量の値の統計分布から評価され,また実験標準偏差によっても特徴
付けることができる。その他の成分は,測定不確かさのタイプB評価によって求められ,経験
又はその他の情報に基づいて推定された確率分布から得られる標準偏差の近似によって特徴付
けられる。
3.3.2
タイプA評価(Type A evaluation),測定不確かさのタイプA評価(Type A evaluation of measurement
uncertainty)
定義された条件下で得られる測定された量の値の統計解析による測定不確かさ(標準不確かさ)の成分
の評価。
注記 統計解析に関する情報については,4.1及びISO/IEC Guide 98-3:2008を参照。
3.3.3
タイプB評価(Type B evaluation),測定不確かさのタイプB評価(Type B evaluation of measurement
uncertainty)
5
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定不確かさのタイプ A 評価以外の方法で決定される測定不確かさ(標準不確かさ)の成分の評価。
例 測定不確かさの成分は,次に基づく。
− 以前の測定データ
− 当該材料及び機器の挙動及び特性についての一般的知識及び経験
− 製造業者の仕様
− 校正又はその他の証明書から得られるデータ
− ハンドブックから得られる参照データに指定された不確かさ
− 個人的経験を通して導き出された限界
注記 その他の情報については,4.3及びISO/IEC Guide 98-3:2008を参照。
3.3.4
標準不確かさ(standard uncertainty),測定の標準不確かさ(standard uncertainty of measurement),標準測定
不確かさ(standard measurement uncertainty)
標準偏差として表した測定不確かさ。
注記 標準不確かさは,タイプ A 評価及びタイプ B 評価のいずれかによって見積もることができる。
3.3.5
合成標準不確かさ(combined standard uncertainty),合成標準測定不確かさ(combined standard measurement
uncertainty)
測定モデルの入力量に付随する個々の標準測定不確かさ(及び適切な共分散)を用いて得られる標準測
定不確かさ。
注記 合成標準不確かさの手順は,よく“不確かさの伝ぱ(播)の法則”,一般用語では,根二乗和(RSS)
法と呼ばれる。
3.3.6
包含係数(coverage factor)
拡張測定不確かさを得るために合成標準測定不確かさに乗じる,1より大きい数。
注記 包含係数は,一般に,2と3の間にあり,包含確率又は区間の必要な信頼性のレベルに基づく。
3.3.7
拡張不確かさ(expanded uncertainty),拡張測定不確かさ(expanded measurement uncertainty)
包含区間で表した測定不確かさ。
注記 合成標準不確かさに包含係数を乗じて得られる。
3.3.8
包含区間(coverage interval)
ある確率で測定対象量の真値が含まれると推定される区間。
注記 統計上の概念と混同しないように,包含区間を“信頼区間”と呼ばないようにする。区間を特
定の信頼性レベルで関連付けることは,測定結果によって特徴付けられた確率分布に関する明
示的又は暗黙的な前提条件を要求する。
3.3.9
包含確率(coverage probability)
測定対象量の真値の集合が,特定の包含区間に含まれる確率。
注記 包含確率は,ISO/IEC Guide 98-3:2008では,“信頼の水準(level of confidence)”ともいう。

6
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.3.10
不確かさバジェット(uncertainty budget)
測定不確かさ,その測定不確かさの成分,並びにそれらの計算及び合成に関する見積表。
注記 不確かさバジェットには,測定モデル,推定値と測定モデルの量に付随する測定不確かさ,共
分散,適用した確率密度関数のタイプ,自由度,測定不確かさの評価タイプ及び包含係数を含
めることが望ましい。
3.3.11
測定モデル(measurement model)
測定に関連していると考えられる全ての量の間の数学的関係。
3.4
記号
記号は,表1による。
表1−記号及び定義
a
入力量Xiのとり得る値の一様分布の幅の半分a=(a+−a−)/2
a+
入力量Xiの上限又は上側限界
a−
入力量Xiの下限又は下側限界
A
計画行列又はヤコビアン行列(N×n)
ci
偏導関数又は感度係数
(
)
N
i
i
f
ci
...,
,2,1
=
∂
∂
=
C
感度係数ベクトルci(i=1, 2, ..., N)
e
単位ベクトル
fk
測定対象量Yk及び入力量Xjの間の,並びに出力推定値yk及び入力推定値xjの関数関係
f
要素を付記したベクトルfk(xT) (k=1, 2, …, n)
F1−α/2(ν, ν)
自由度(ν, ν)及び信頼水準 (1−α) %のフィッシャーのF分布
gj
入力量の推定値xjと観測量liとの間の関数関係
k
出力推定値yの拡張不確かさU=k×uc(y) をその合成標準不確かさuc(y) から計算するのに
用いられる包含係数
li
観測量又は確率変数(i=1, 2, …, m)
m
観測量liの個数
M
不確かさをタイプA評価によって見積もることができる入力量の個数
n
出力量又は測定対象量の個数
N
入力量の個数
N-M
不確かさをタイプB評価によって見積もることができる入力量の個数
N
正規方程式行列(n×n)
pj
入力推定値xj(j=1, 2, …, N)の重み
P
重み行列pj(N×N)
Qykyk
出力推定値ykの余因子
Qy
出力推定値yk(n×n)の余因子行列
rj
入力推定値xj (j=1, 2, …, N)の残差
r
残差ベクトルrj
r(xi, xj)
入力推定値xiとxjとの相関係数
s
標準偏差(一般)
s(yk)
出力推定値ykの標準偏差
tα(ν)
自由度ν及び信頼水準(1−α) %でのスチューデントのt分布
u
標準不確かさ(一般)
u(yk)
出力推定値ykの標準不確かさ
u(xj)
入力推定値xjの標準不確かさ

7
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−記号及び定義(続き)
uc(yk)
出力推定値ykの合成標準不確かさ
U
拡張不確かさ(一般)
xj
入力量の推定値又は入力推定値(j=1, 2, …, N)
x
入力量x jの推定値ベクトル
Xj
測定対象量Ykが従属するj番目の入力量
X
入力量Xiのベクトル
yk
測定対象量Ykの推定値又は出力推定値(k=1, 2, …, n)
y
測定対象量ykの出力推定値ベクトル
Yk
k 番目の測定対象量(k=1, 2, ..., n)
Y
測定対象量Ykのベクトル
α
パーセントで表した誤りの確率
(1−α)
信頼水準
ν
自由度
σ
正規分布の標準偏差
()
ν
χα
2
1−
自由度ν及び信頼水準(1−α) %のカイ二乗分布
4
測定の不確かさ評価
4.1
一般
不確かさ評価の一般的概念は,測定における不確かさをどのように表すかを国際的見地で述べた
ISO/IEC Guide 98-3:2008に記載されている。それは,測地及び測量のデータ解析で非常に一般的な分散・
共分散法の厳密な応用である。しかしながら,この背後にある考えは,測定における偶然誤差だけではな
く,全ての測定不確かさ量における系統誤差の扱いまで拡張している。
原理的に,測定結果は,近似値又は測定に伴う特定の量,すなわち測定対象量の近似値又は推定値にす
ぎない。つまり,測定結果は,推定値の質の状態である不確かさを伴って記述されたときにだけ,完全と
いえる。
測定の不確かさは,一般に幾つかの成分から成り,これらの成分の数値を見積もる方法によって次に示
す二つのタイプに分けられる。
a) 統計的手法によって評価するもの
b) その他の方法によって評価するもの
不確かさ評価方法の基本は,測定結果の不確かさに寄与する個々の不確かさ成分を標準偏差で推定する
ことであり,これを標準不確かさと呼び,記号uで表す。
タイプAに属する不確かさ成分は,統計的評価で得られた実験標準偏差si及び関連する自由度の数νi
によって表す。このような成分に対しては,標準不確かさuiは,ui=siである。観測データから統計的解
析で得られた不確かさ成分の評価を不確かさタイプA評価という(4.2参照)。
同様にタイプBに属する不確かさ成分は,量ujで表す。この量は,相当する標準偏差の近似値として考
えられたり,有効な全ての情報に基づく確率的分布で定義されることもある。量ujは,標準偏差として取
り扱われるので,タイプBの標準不確かさは単にujである。観測データから統計的解析以外の手法で得ら
れた不確かさの評価を不確かさタイプB評価という(4.3参照)。
いずれのタイプにおいても成分間の関係は,共分散又は相関係数の推定値によって特徴付けられる。
8
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.2
標準不確かさのタイプA評価
4.2.1
一般的数学モデル
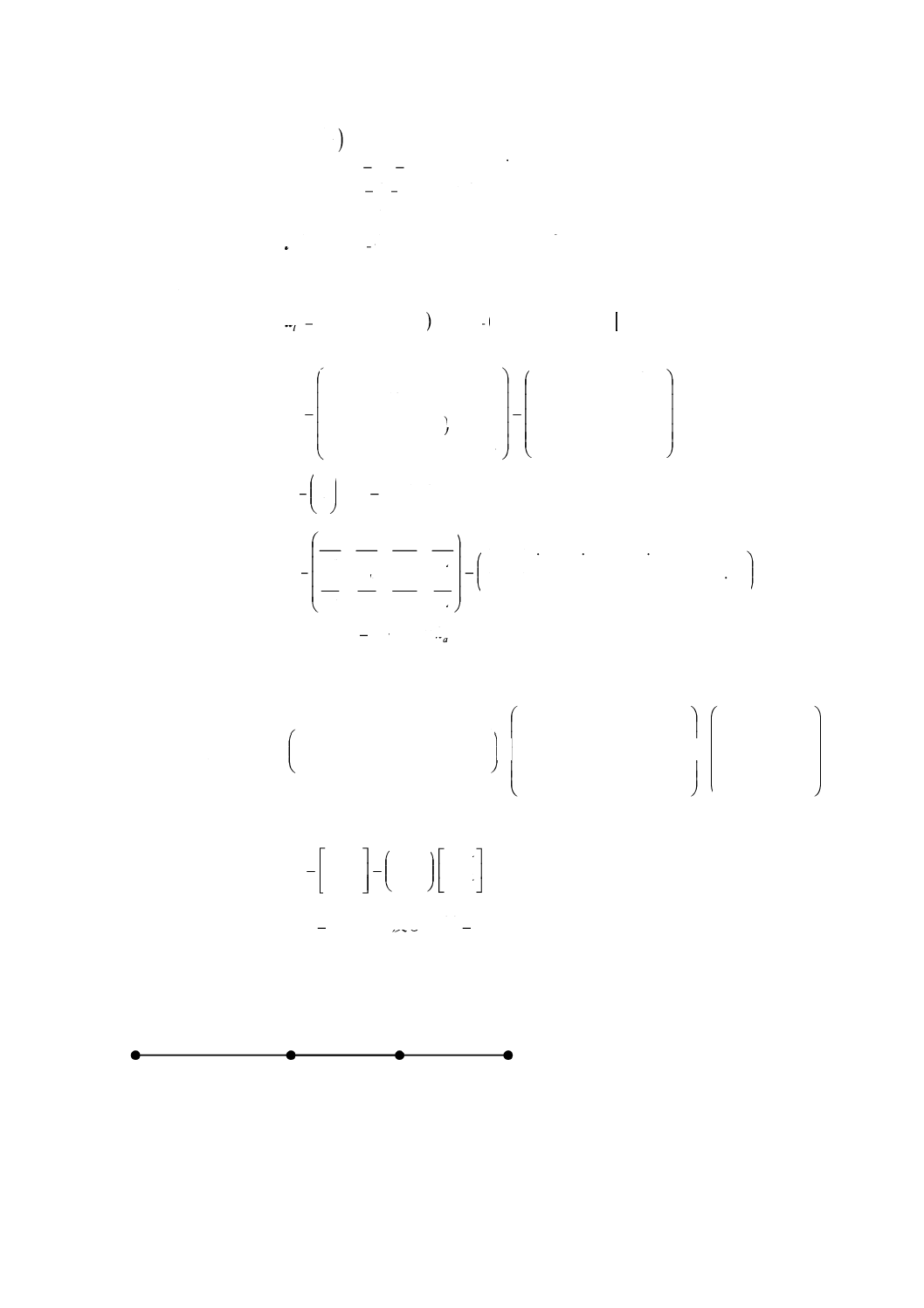
多くの場合,測定対象量Yは,直接測定ではなくN個のある入力量X1, X2, …, XNから,式(1)に示すよう
な関数関係によって決定される。 (
)
N
X
X
X
f
Y
,...,
,
2
1
=
··································································· (1)
測定対象量Yの推定値すなわち出力推定値yは,入力推定値x1, x2, …, xNを用いて次の式(2)によって求め
る。
(
)
N
x
x
x
f
y
,...,
,
2
1
=
······································································ (2)
多くの場合,測定結果,すなわち出力推定値yは,この関数関係で求まる。
しかし,ある場合,特に測地及び測量における測定結果は,複数の例えば,N個の測定値(入力推定値)
から得られる複数の出力推定値y1, y2, …, ynから成っている。
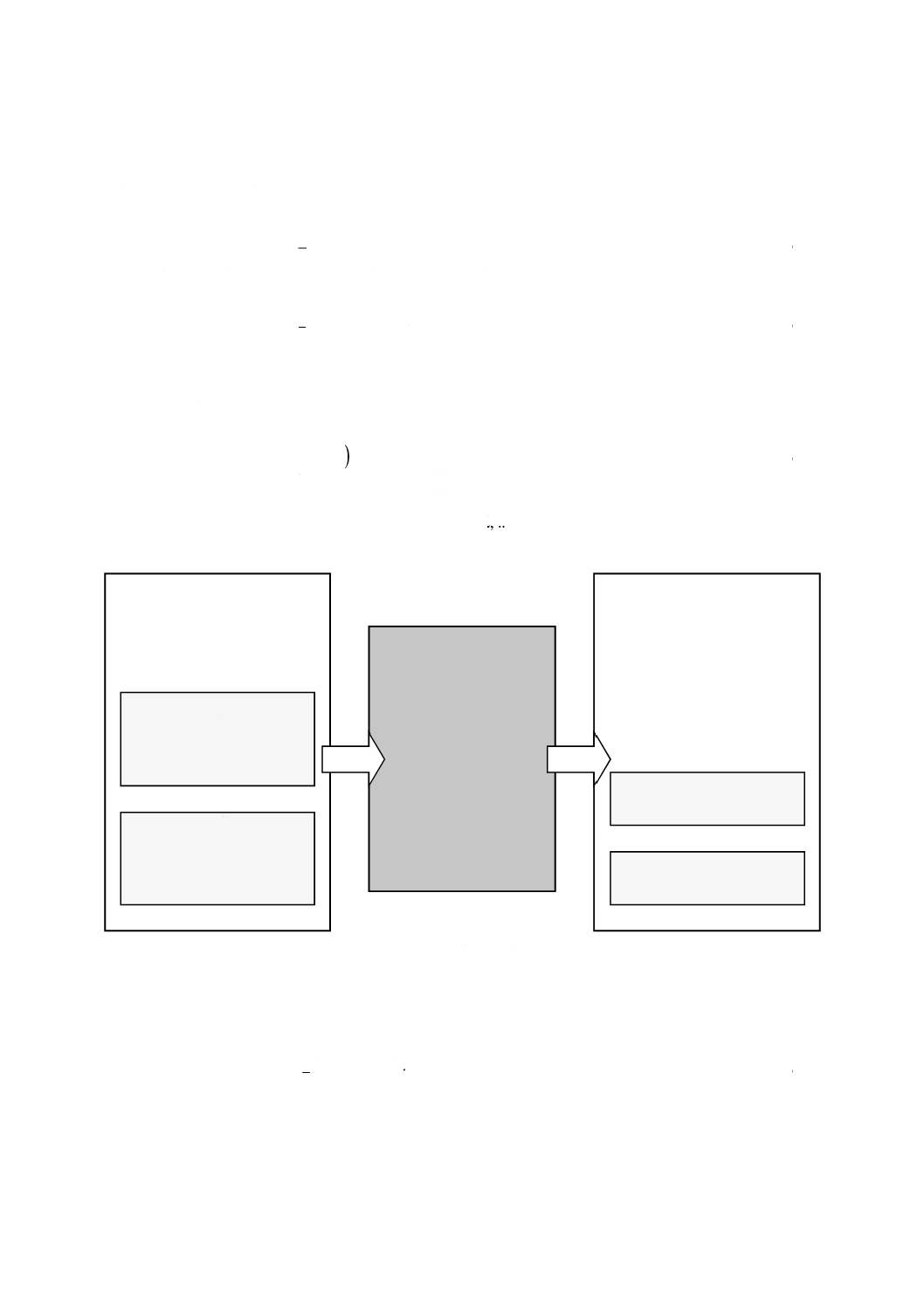
これから一般モデル関数(図1参照)は,次の式(3)となる。
()
T
x
f
y=
················································································ (3)
ここに,
x: 入力量xj (j=1, 2, ..., N)のベクトル(N×1)
y: 出力量yk (k=1, 2, ..., n)のベクトル(n×1)
f: fk (xT) (k=1, 2, ..., n)から成るベクトル(n×1)
fは,出力量yを決定するための適切なアルゴリズムと解釈できる(附属書C参照)。
図1−一般的数学モデル及び不確かさ評価
4.2.2
タイプA不確かさ伝ぱ(播)の一般法則
測地測定過程においては,多くの場合入力量xjは,幾つかの観測量又は確率変数の関数となる[式(6)]。
観測量をベクトル表現で表すと式(4)となる。
(
)
m
T
l
l
l
l
....,
,
,
3
2
1
=
l
······································································· (4)
この例として,機器の内部測定処理,校正過程で得た補正値又は同一観測における複数回測定がある。
これに対応する不確かさ行列を,次の式(5)とする。
入力:
ベクトルx, Ux
入力量xj及びその不確かさ
u(xj)
タイプA:
観測値,統計的解析で得た値
xA, Ux(A)
タイプB:
事前値,外部値など
統計的解析以外で得た値
xB, Ux(B)
評価モデル:
y=f(xT)
出力:
ベクトルy, uy
出力量yk及びその標準不確かさ
u(yk)
拡張不確かさ
U(yk)
x, Ux
y, Uy
最終結果:
yk±U(yk)
他に適用する入力量として
使用できる
9
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
=
2
2
1
0
0
m
l
u
u
Λ
Μ
Ο
Μ
Λ
U
····································································· (5)
次の一般関数を仮定する。
)
2
1
(
)
(
,....,N
,
j
g
x
j
j
=
=
l
······························································ (6)
線形化すると次の式(7)となる。
l
gTj
o
j
g
x
+
=
············································································ (7)
ここに,
(
)
∂
∂
∂
∂
∂
∂
=
=
m
j
j
j
jm
j
j
T
j
l
g
l
g
l
g
g
g
g
,...,
,
...,
,
,
2
1
2
1
g
······························· (8)
結果として入力量xjの標準不確かさu(xj)は,次の式(9)となり,
()
j
l
T
j
jx
u
g
U
g
=
········································································ (9)
観測値がランダムであるとする仮定の下では,次の式(10)となる。
()()
j
j
x
s
x
u
=
············································································ (10)
この式で,xjの標準不確かさは,その標準偏差に等しいことを示す。
相関がある場合は,uj kを式(5)の共分散として導入することができ,その場合Ulは,全要素行列となる。
C.1の数値例にタイプAの標準不確かさ評価の計算手順を示す。観測量lに全て依存するXのN個の関
数がある場合,それらは次の式(11)となる。
l
G
g
x
+
=
0
·············································································(11)
ここに,
G: ヤコビアン行列
=
Nm
N
lm
g
g
g
g
Λ
Μ
Ο
Μ
Λ
1
11
G
································································· (12)
最終的に式(9)は,次の誤差伝ぱ(播)の一般式(13)となる。
()
(
)
(
)
(
)
()
(
)
(
)
(
)
()
=
=
N
M
M
N
N
T
l
x
x
u
x
x
u
x
x
u
x
x
u
x
u
x
x
u
x
x
u
x
x
u
x
u
2
2
1
2
2
2
1
2
1
2
1
1
2
,
,
,
,
,
,
Λ
Μ
Ο
Μ
Μ
Λ
Λ
G
GU
U
·························· (13)
標準不確かさは,次の式(14)のように対角要素を用いて求まる。
()()
()
[
]T
N
x
x
u
x
u
x
u
,...,
,
2
1
=
u
·························································· (14)
対応して,実験標準偏差は,次の式(15)となる。
()()
()
[
]T
N
x
x
s
x
s
x
s
,...,
,
2
1
=
s
·························································· (15)
図1のフローチャートにある入力推定値xから得られる出力量の式を線形化すると次の式(16)となる。
()
()x
H
h
x
f
y
+
=
=
0
T
······························································· (16)
これに式(11)を代入し次の式(17)を得る。
(
)
ΗGl
h
Gl
g
H
h
y
+
=
+
+
=
0
0
0
···················································· (17)
次に,式(13)から不確かさ行列は,次の式(18)となる。
10
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
T
T
l
T
x
y
H
G
HGU
H
HU
U
=
=
······················································· (18)
行列Uyの対角要素を組み合わせて,出力推定値y1, y2, …, yNの標準不確かさベクトルは,次の式(19)とな
る。
()()
()
[
]T
N
y
y
u
y
u
y
u
,...,
,
2
1
=
u
························································· (19)
入力量がランダムに変化した場合は,式(19)の標準不確かさは,次の式(20)のとおり,出力推定値の実験
標準偏差と一致する。
y
y
s
u=
又は
)
2
1
(
)
(
)
(
,...,n
,
k
y
s
y
u
k
k
=
=
····································· (20)
式(18)の入れ子部GUlGTは,更なる適用に対して任意に拡張することができる。例えば,z=M(y)。
この場合のタイプAの標準不確かさ評価の計算手順を,C.2に記載する。
4.2.3
最小二乗法
式(3)に関連して,決定しなければならない出力量ykの数より多くのモデル式が与えられることがある。
Nがnより多い場合には,問題を最小二乗法によって解決することが適切である。このときには,観測方
程式(非線形)において,式(3)のモデル関数を次の式(21)に書き直すことが必要である。
)
(y
F
r
x
=
+
··········································································· (21)
この式を線形化し高次を無視すると次の式(22)となる。
)
(
)
(
0
0
y
y
y
F
y
F
r
x
−
∂
∂
+
=
+
························································ (22)
ここに,
x: 観測又は測定の入力量のベクトル(N×1)
r: 残差ベクトル(N×1)
y: 未知,又は推定出力値のベクトル(n×1)
y0: yの近似値ベクトル
次の式(23)及び式(24)を式(22)に代入する。
y
y
y
~
0=
−
()l
y
F
x
=
−
0
··········································································· (23)
及び
A
y
F
=
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
n
N
N
n
y
F
y
F
y
F
y
F
Λ
Μ
Ο
Μ
Λ
1
1
1
1
························································ (24)
この結果,次の式(25)となる。
l
y
A
r
−
=~
·············································································· (25)
多くの場合,測定入力量の重み行列Pによる確率モデルを導入する必要がある。
=
N
p
p
Λ
Μ
Ο
Μ
Λ
0
0
1
p
·································································· (26)
ここに,
2
2
0
j
j
s
s
p=

11
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
重みpjは,式(13)及び式(15)を考慮して決定する。
ガウス−マルコフモデルに従えば,解ベクトルは次の式(27)となる。
(
)
n
N
Pl
A
PA
A
y
1
1
~
−
−
=
=
T
T
·························································· (27)
ここに,N=ATPA及びn=ATPl
残差は,式(27)を利用して式(25)から計算する。次に分散は,次の式(28)によって求める。
ν
Pr
rT
s=
2
0
·············································································· (28)
ここに,νは,自由度であり,
ν=N−n
である。
これから,出力推定値の実験標準偏差は,よく知られた次の式(29)によって求める。
()
n
...
,
,
k
s
y
s
k
ky
y
k
,
2
1
0
=
=
Q
······················································· (29)
ここに,
y
y
y
diag
Q
k
k
Q
=
及び
1
−
=N
Qy
·········································· (30)
最後に,タイプA評価における出力推定値ykの標準不確かさは,次の式(31)となる。
y
y
s
u=
又は ()
()
n
k
y
s
y
u
k
k
,...,
2,1
=
=
········································ (31)
一方,調整された入力値は,次の式(32)となり,
r
l
x
+
=
~
················································································ (32)
x~の推定分散共分散行列は,次の式(33)となる。
T
x
s
A
AN
S
1
2
0
~
−
=
······································································· (33)
最終的に,この対角成分から,実験標準偏差は,次の式(34)によって求める。
(
)
x
n
x
x
x
x
diag
s
s
s
~
~
2
~
1
~
~
,...,
,
S
s
=
=
··················································· (34)
このようにして,調整入力値x~の標準不確かさは,次の式(35)となる。
x
x
~
~
s
u=
又は ()()(
)n
j
x
s
x
u
j
j
...,
,2,1
~
~
=
=
········································ (35)
この不確かさの計算例を,C.3に記載する。
4.2.4
特殊な場合
4.2.4.1
測定のi回シリーズにおける平均値
ixの標準不確かさ()
ix
u
の計算
独立した繰返し観測xi, j(j=1, 2, …, n)からの推定値入力量Xiを考える場合,式(27)に応じた最適な推定値
は,次の式(36)によって求める。
(
)
i
T
T
ix
Px
e
e
P
e
1
−
=
··································································· (36)
その実験標準偏差は,次の式(37)となる。
()
∑
=
=
j
i
T
i
p
s
s
x
s
0
0
e
P
e
·························································· (37)
相関がなく等しい精度をもった入力推定値xi, jの場合,平均値は次の式(38)となる。

12
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑
=
=
n
j
ij
i
x
n
x
1
1
············································································ (38)
実験標準偏差は,次の式(39)となる。
()
(
)1
0
−
=
=
n
n
n
s
x
s
T
i
r
r
······························································· (39)
ここに,
i
ix
x−
=e
r
続いて標準不確かさは,次の式(40)となる。
()
()
i
i
x
s
x
u
=
············································································ (40)
4.2.4.2
2測定のi回シリーズにおける平均値
iyの標準不確かさ()
iy
u
の計算
1組(対)測定(同一測定対象への2回の測定)の平均値から推定される出力量Yiを考える。
(
)
2
1l,
l
··················································································· (41)
ここに,
(
)T
jn
j
j
j
l
l
l
...,
,
,
2
1
=
l
2,1
=
j
出力推定値ベクトルは,次の式(42)となる。
(
)
2
1
2
1
l
l
y
+
=
·········································································· (42)
測定の過程において系統誤差は除去されるので,差分ベクトルの期待値は,次の式(43)となる。
E(d)=E(l2−l1)=0 ···································································· (43)
さらに,同じ標準不確かさが全組(対)測定に採用できると仮定すると,重みは次の式(44)となる。
P
P
P
=
=
2
1
l
l
··········································································· (44)
分散は式(45)となる。
n
s
T
2
2
0
Pd
d
=
············································································· (45)
ここに,
(
)
1
2l
l
d
-
=
全観測に同じ重みが適用できる場合,実験標準偏差は次の式(46),式(47)及び式(48)となる。
測定値lj, iに対しては,
n
s
T
l
2
d
d
=
············································································· (46)
差分値diに対しては,
n
s
T
d
d
d
=
············································································· (47)
最後に,出力推定値yiに対しては,
n
y
s
T
i
4
)
(
d
d
=
·········································································· (48)
式(43)の仮定が満足するかを確かめるには,次の式(49)を適用することが望ましい。
13
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
d
d
d
e
T
T
<
2
··········································································· (49)
これが成り立つならE(d)=0が期待できる。この場合,標準不確かさは次の式(50)となる。
()
()
i
i
y
s
y
u
=
············································································ (50)
4.2.4.3
m回シリーズ測定の全標準不確かさuの計算
m回シリーズ測定で得られたそれぞれの実験標準偏差は,全実験標準偏差の個別推定値と考えられる。
これら各々の推定値は,νi=ν1=ν2=…=νmで,同一の信頼度をもつとみなせるため,それぞれの実験標
準偏差を対等に扱い,組み合わせることで,全標準偏差は次の式(51)となる。
2
2
2
2
1
1
2
2
...
m
m
i
i
s
s
s
s
s
+
+
+
=
=
∑
∑
=
···················································· (51)
ここに,
m: 測定シリーズの回数
si: i番目シリーズの実験標準偏差
∑
2s: m回シリーズ測定での各標準偏差siの二乗和
その結果,全実験標準偏差sは,次の式(52)となる。
m
s
s∑
=
2
············································································ (52)
m回シリーズ測定の自由度の数は,次の式(53)となる。
∑
=
×
=
=
m
i
i
i
m
1
ν
ν
ν
···································································· (53)
したがって,合成不確かさuは,次の式(54)となる。
s
u= ···················································································· (54)
ここまでの数値計算例を,C.4及びC.5に記載する。
4.3
標準不確かさのタイプB評価
4.3.1
一般
入力量の個数Nの全てがタイプA評価で推定できるわけではない。タイプAで評価可能な不確かさの
数をMとすれば,N−M個の入力量からの不確かさは,タイプBと呼ばれる他の手段で決定しなければな
らない。
繰返し観測で得られたものでない入力量,又は数の少ないサンプルから得られた入力量の推定値xi, j(M
<j≦N)の場合,標準不確かさは,全ての有効な情報を利用した科学的判断に基づいて決定する。有効な情
報とは,次のようなものがある。
− 以前の測定データ
− 当該材料及び機器の挙動及び特性についての一般的知識及び経験
− 製造業者の仕様
− 校正データ
− ハンドブックから得られる参照データに指定された不確かさ
実際に使用する際に参考となるタイプB評価の例を,4.3.2〜4.3.5に示す。
4.3.2
正規分布でモデル化される入力量(附属書A参照)
− 下限及び上限の推定値:a−, a+
14
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
− 推定値:(a+−a−)/2
− 50 %確率の区間:a−〜a+
この場合の標準不確かさは,次の式(55)となる。
a
uj
48
.1
≈
·············································································· (55)
ここに,a=(a+−a−)/2
4.3.3
正規分布でモデル化される入力量(附属書A参照)
− 下限及び上限の推定値:a−, a+
− 推定値:(a+−a−)/2
− 67 %確率の区間:a−〜a+
この場合の標準不確かさは,次の式(56)となる。
a
uj=
··················································································· (56)
ここに,a=(a+−a−)/2
4.3.4
一様分布でモデル化される入力量(附属書A参照)
− 下限及び上限の推定値:a−, a+
− 推定値:(a+−a−)/2
− 100 %確率の区間:a−〜a+
この場合の標準不確かさは,次の式(57)となる。
a
a
uj
58
.0
3≈
=
······································································· (57)
ここに,a=(a+−a−)/2
4.3.5
三角分布でモデル化される入力量(附属書A参照)
− 下限及び上限の推定値:a−, a+
− 推定値:(a+−a−)/2
− 100 %確率の区間:a−〜a+
この場合の標準不確かさは,次の式(58)となる。
a
a
uj
41
.0
6≈
=
······································································ (58)
ここに,a=(a+−a−)/2
4.4
不確かさ伝ぱ(播)の法則及び合成不確かさ
測定結果ykの合成不確かさuc(yk)は,最終結果の推定標準偏差を表す。それは,タイプA評価又はタイ
プB評価にかかわらず,それから得られる入力推定値x1, x2, …, xM, xM+1, xM+2, …, xNの個々の標準不確かさ
u(xi)の合成,又は共分散u(xi, xj)との合成から得られる。この方法は,不確かさの伝ぱ(播)の法則,又は
測量用語では合成標準不確かさの二乗和平方根法と呼ばれている。
タイプA評価への入力推定値に対して次の式を考える。
(
)
T
A
M
,...,x
,x
x
x
=
2
1
································································· (59)
タイプA評価から得られる標準不確かさは,次の式(60)となる。

15
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
()
()
()
=
2
2
2
2
1
0
0
0
0
M
A
x
x
u
x
u
x
u
Λ
Ο
Μ
Μ
Λ
U
············································· (60)
タイプB評価への入力推定値は,次の式(61)となる。
(
)
T
B
N
M
M
x
x
x
x
=
+
+
...,
,
,
2
1
································································ (61)
タイプB評価から得られる標準不確かさは,次の式(62)となる。
()
(
)
(
)
()
=
+
+
2
2
2
2
1
0
0
0
0
N
M
M
B
x
x
u
x
u
x
u
Λ
Ο
Μ
Μ
Λ
U
······································· (62)
その結果
()
()
=
B
x
A
x
x
U
U
U
0
0
·································································· (63)
となり,式(7)及び式(8)によれば,次の式(64)及び式(65)が得られる。
+
=
B
A
T
k
k
c
y
x
x
c
0
······································································ (64)
(
)
kN
k
k
N
k
k
k
T
k
c
c
c
dx
df
dx
df
dx
df
...,
,
,
...,
,
,
2
1
2
1
=
=
c
········································ (65)
値cki (i=1, …, N)は,感度係数と呼ばれ,関数fkの導関数によるか又はテイラー展開の第一項についての
実験的な測定値によって決定される。
最後に式(9)から,出力推定値の合成標準不確かさuc(yk)は,次の式(66)によって求める。
()
k
c
U
c
x
T
k
k
cy
u
=
····································································· (66)
xiとxjとの共分散(
)(
)
i
j
j
i
x
x
u
x
x
u
,
,
=
が得られる場合,これらは式(60),式(62)及び式(63)の中に容易に組み
入れることができる。
この場合,相関度は推定相関係数の次の式(67)で与えられる。
(
)
(
)
()()
j
i
j
i
j
i
x
u
x
u
x
x
u
x
x
r
=
,
,
································································· (67)
ここでは,
(
)
1
,
1
+
−
≦
≦
j
ix
x
r
である。u(xi)とu(xj)とが互いに独立ならr(xi, xj)=0である。
これらの数値計算例をC.6に記載する。
4.5
拡張不確かさ
合成標準不確かさは広く利用されるが,商業上又は産業上での幾つかの適用では,しばしば測定対象量
Yの値の信頼性を反映した,測定結果yについての区間を定義する不確かさの尺度を与える必要がある。
その区間を考えた不確かさは,拡張不確かさと定義される。その記号はUとする。Uは,合成不確かさに
包含係数kを乗じたものとして次の式(68)のとおり定義される。
()y
u
k
U
c
×
=
··········································································· (68)
Yの値が合理的に信頼できる区間は,次の式(69)のとおり示すことができる。
U
y
Y
U
y
+
−
≦
≦
···································································· (69)
便宜上の表現は,次の式(70)となる。
16
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
U
y
Y
±
=
··············································································· (70)
一般に,包含係数kの値は,y−Uからy+Uの区間に要求される信頼の水準を基に選択される。一般に,
2と3の間にある。
例えば,
()y
u
U
c
×
=2
··········································································· (71)
を考えた場合,区間の信頼の水準は約p=95 %となる。この値は,正規分布する出力推定値に対しては標
準的な値である。
同様に
()y
u
U
c
×
=3
··········································································· (72)
を考えた場合,信頼の水準はp=99 %より大きくなる。
しかし,特殊な応用では,kはこの範囲外にあることがある。ある測定結果が適用されるであろう使用法
についての豊富な経験と知識があれば,kの適正な値の選定が可能となる。
これ以上の情報が必要な場合は,ISO/IEC Guide 98-3:2008の6.3及び附属書Gを参照する。
5
不確かさの報告
測定結果及びその不確かさを報告する場合,次の情報を含めることが望ましい。
− 数学モデル及び実験観測と入力データから測定結果及びその不確かさ(タイプA及びタイプB評価)
を算出するのに用いた方法の明確な記述
− 全ての不確かさ要因及びその自由度並びにその結果ucの一覧
− それぞれの標準不確かさが,どのように評価されたかの詳細な記述
− 包含係数kが2でない場合は,どのようにkを選択したかの記述
測定の不確かさがuc(y)のとき,測定結果は次のように表記することが望ましい。
D=12 345.678 m uc=9.1 mm
拡張不確かさUを報告する場合,次の表記をしてもよい。
D=12 345.678 m U=±18 mm (k=2)
又は
D=(12 345.678±0.018) m (k=2)
6
不確かさ評価の要約
次の要約は,実際に不確かさの計算を実行する際の手順である。
a) 測定対象量及び測定方法の明確な記述として,入力量と出力量との間の関係及び評価モデルを数学的
に適切に記述する。
b) 全ての補正を確認し,可能な範囲において適用することが望ましい。
c) 不確かさを評価するために全ての要因(影響量)を洗い出す。
d) 統計的手法によるタイプA評価の標準不確かさの計算をする。
e) タイプB評価の標準不確かさを決定する。このため,次の事項を引用することが望ましい。
1) 入力量の確率分布の知識
2) 入力量の推定値の分布に関する情報
3) 入力量の取り得る範囲の上限及び下限
4) その他の情報
17
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
f)
それぞれの入力量の標準不確かさの量的寄与度を計算する。すなわち,全ての感度係数は,測定モデ
ル(出力推定値を計算する数学モデル)によって決定する。
g) 不確かさ伝ぱ(播)の法則を適用し,出力推定値の合成標準不確かさを求める。
h) 合成標準不確かさに包含係数を乗じ拡張不確かさを得る。
i)
最終結果は,出力推定値,拡張不確かさ及び包含係数を提示することによって行う。
7
統計的検定
7.1
一般
測定結果の評価のための統計的検定は,標準試験手順で得られた結果にだけ適用する。統計的検定は標
準偏差s,又はタイプA評価の標準不確かさuを用いて行わなければならない。
タイプA評価の標準不確かさは,標準偏差として扱い検定できる。検定のために,次の問に答えなけれ
ばならない(表2参照)。
a) 算出した標準偏差(タイプA評価の標準不確かさ)sは,製造業者が示している値,又は事前に決め
た別の値σ0よりも小さいか?
b) 二つの異なったサンプルから求めた標準偏差(タイプA評価の標準不確かさ結果)s及びs~は,それ
ぞれのサンプルの自由度の数ν(νは,全ての組の測定の自由度の数)が同じだと仮定したとき同じ母
集団に属しているか?
c) 及びd) 調整によって得たパラメータykは,ゼロに等しいか?
表2−統計的検定
問
帰無仮説
対立仮説
a)
σ≦σ0
σ>σ0
b)
σ
σ
~
=
σ
σ
~
≠
c) 及びd)
yk=0
yk ≠ 0
注記 帰無仮説ではサンプル測定の結果算出した標準偏差をもたらす
母集団の統計量を検証するためσをsの代わりに使用する。
7.2
問a):標準偏差sは,規定の値σ0に等しい又は小さいか?
式(1)〜式(54)に従って測定の実験標準偏差s又は測定のタイプA評価の標準不確かさuを決定する。サ
ンプルサイズが小さいため,機器の製造業者が表明する,又は他の方法であらかじめ決められた母集団の
理論的標準偏差σ0とは多少異なる。
標準偏差sが1−αの信頼水準で与えられた理論的標準偏差σ0に等しい又はより小さいかどうか数学的
統計法によって検定する。
帰無仮説σ≦σ0は,次の条件が満足されるなら棄却することができない。
()
ν
ν
χ
σ
α
2
1
0
−
×
≦
s
···································································· (73)
そうでなければ,帰無仮説は棄却される。
()
ν
χα
2
1−
は附属書Bによる。
理論的標準偏差σ0は,事前に決めた値である。
7.3
問b):二つのサンプルは,同じ母集団に属しているか?
二つの異なる測定サンプルから得た標準偏差s及びs~,又はタイプA評価の標準不確かさu及びu~が,
信頼水準1−αで同じ母集団に属しているかどうか数学的統計法によって検定する。次の条件が満たされ
18
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
るなら,対応する帰無仮説
σ
σ
~
=
は棄却することができない。
(
)
(
)
ν
ν
ν
ν
α
α
,
~
,
1
2
/
1
2
2
2
/
1
−
−
F
s
s
F
≦
≦
····················································· (74)
そうでなければ,帰無仮説は棄却される。
標準偏差s及びs~を決めるために,同数
n
n~
=
の二つの測定サンプルが取られる。これらの標準偏差s及
びs~は,次のいずれからか得られる。
− 機器は同一だが,異なる観測者による二つの測定サンプル
− 異なる時間帯に同じ機器を用いて行った二つの測定サンプル
− 異なる機器による二つの測定サンプル
F1−α/2 (ν, ν) は,附属書Bによる。
7.4
問c) 及び問d):パラメータykの有意性の検定
式(21)〜式(35)に従って,最小二乗法による調整によってパラメータyk及びその標準偏差s(yk)又はタイ
プA評価の標準不確かさu(yk)を決定する。このパラメータykが信頼水準1−αで,ゼロに等しくないかど
うか数学的統計法によって検定する。帰無仮説yk=0は,次の式(75)の条件が満たされるなら棄却すること
ができない。
()
()
ν
α2/
1−
×t
y
s
y
k
k≦
································································· (75)
そうでなければ,帰無仮説は棄却される。
パラメータykは,測定の組全体で有効かどうか検定する。
m>1であれば,ykは,m組の測定で対応する値ykiによって,次の式(76)で求める。
m
y
y
m
i
i
k
k
∑
=
=
1
,
··········································································· (76)
yk,iは,標準測定手順の式によって推定する。
この場合は,次の式(77)で求める。
ν
s
y
s
k=
)
(
············································································ (77)
s(yk)は,測定の組全体で有効なパラメータykの標準偏差であり,νは標準試験手順における式で示される
定数である。m>1であれば,s(yk)は,m組の測定で対応する値s(yk,i)によって,次の式(78)で求める。
()
()
m
s
m
y
s
y
s
m
i
i
k
k
×
=
=∑
=
ν
1
,
2
····················································· (78)
t1−α/2 (ν) は,附属書Bによる。
19
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
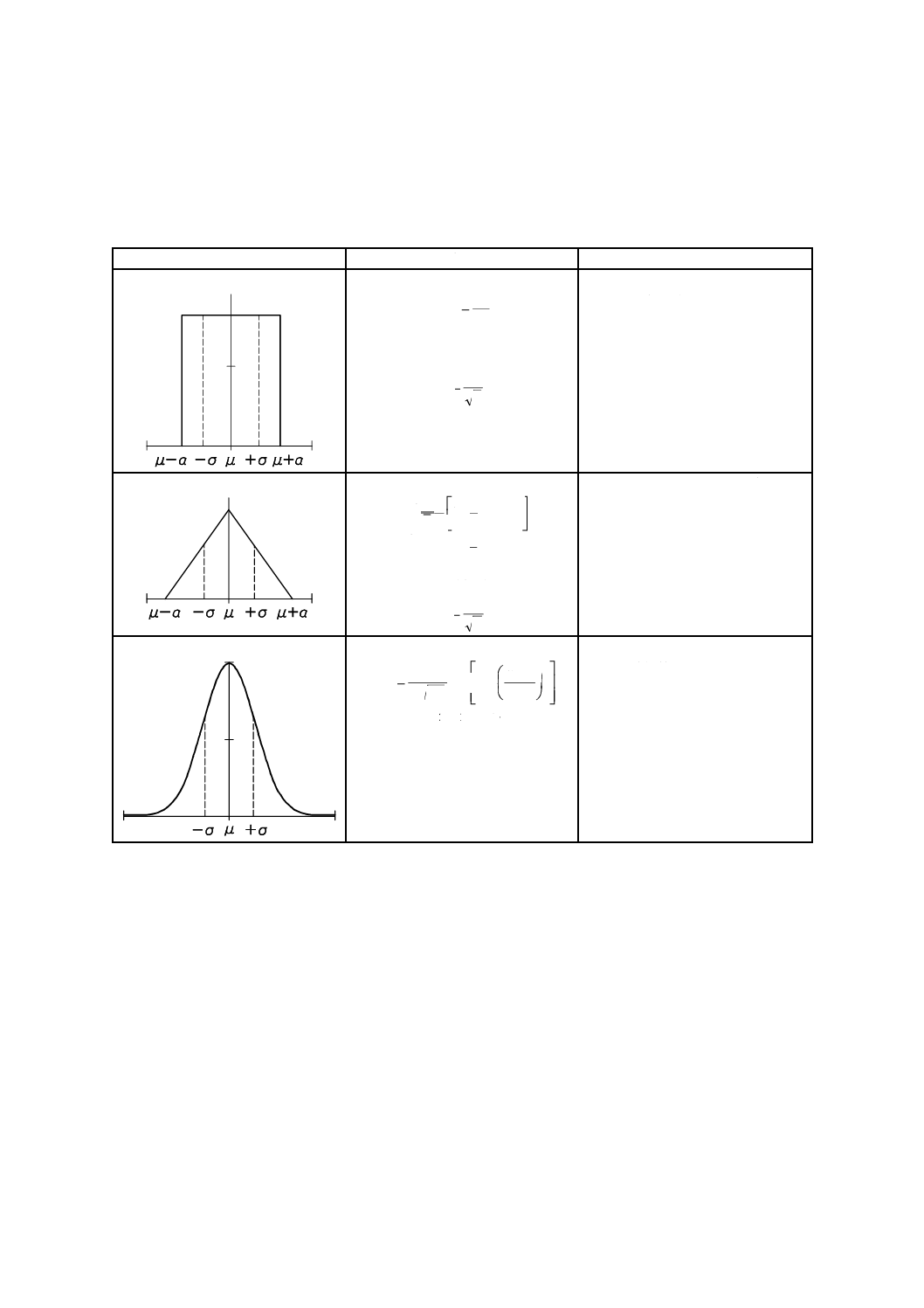
附属書A
(参考)
確率分布
確率密度分布
密度関数
応用例
一様[く(矩)形]分布
確率密度関数
()
a
x
f
2
1
=
(
)
a
x
a
+
−
μ
μ
≦
≦
標準偏差
3
a
=
σ
デジタル表示の分解能,間隔,偏差
などの許容誤差
三角分布
確率密度関数
()
(
)
−
−
=
μ
x
a
a
x
f
1
1
1
(
)
a
x
a
+
−
μ
μ
≦
≦
標準偏差
6
a
=
σ
中央が最も高く,両側に直線的に減
少する形の許容誤差
同一半値幅をもつ二つの一様分布
の合成
正規(ガウス)分布
確率密度関数
()
−
−
=
2
2
1
exp
π
2
1
σ
μ
σ
x
x
f
0
,
>
∞
<
<
−∞
σ
x
標準偏差
σ:統計的解析による。
相関のない測定サンプルから得ら
れる標準偏差
20
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(規定)
χ2分布,F分布及びt分布
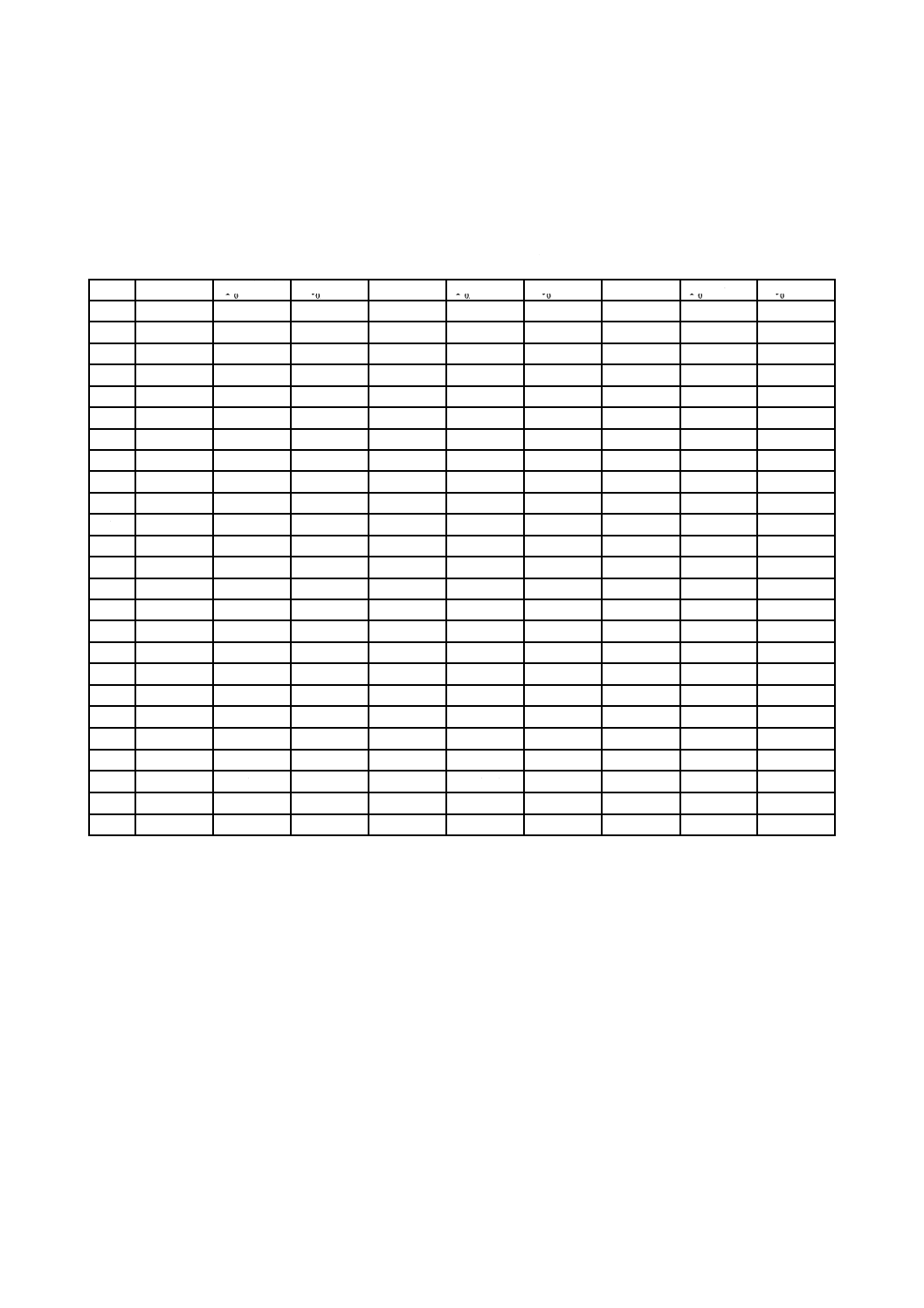
表B.1−χ2分布,F分布及びt分布
ν
()
ν
χ290
.0
(
)
ν
ν,
95
.0F
()
ν
95
.0t
()
ν
χ295
.0
(
)
ν
ν,
975
.0F
()
ν
975
.0t
()
ν
χ299
.0
(
)
ν
ν,
995
.0F
()
ν
995
.0t
2
4.61
19.00
2.92
5.99
39.00
4.30
9.21
199.01
9.92
3
6.25
9.28
2.35
7.81
15.44
3.18
11.34
47.47
5.84
4
7.78
6.39
2.13
9.49
9.60
2.78
13.28
23.15
4.60
5
9.24
5.05
2.02
11.07
7.15
2.57
15.09
14.94
4.03
6
10.64
4.28
1.94
12.59
5.82
2.45
16.81
11.07
3.71
7
12.02
3.79
1.89
14.07
4.99
2.36
16.48
8.89
3.50
8
13.36
3.44
1.86
15.51
4.43
2.31
20.09
7.50
3.36
9
14.68
3.18
1.83
16.92
4.03
2.26
21.67
6.54
3.25
10
15.99
2.98
1.81
18.31
3.72
2.23
23.21
5.85
3.17
14
21.06
2.48
1.76
23.68
2.98
2.14
29.14
4.30
2.98
15
21.31
2.40
1.75
25.00
2.86
2.13
30.58
4.07
2.95
16
23.54
2.33
1.75
26.30
2.76
2.12
32.00
3.87
2.92
18
25.99
2.22
1.73
28.87
2.60
2.10
34.81
3.56
2.88
19
27.20
2.17
1.73
30.14
2.53
2.09
36.19
3.43
2.86
24
33.20
1.98
1.71
36.42
2.27
2.06
42.98
2.97
2.80
27
36.74
1.90
1.70
40.11
2.16
2.05
46.96
2.78
2.77
28
37.92
1.88
1.70
41.34
2.13
2.05
48.28
2.72
2.76
30
40.26
1.86
1.70
43.77
2.07
2.04
50.89
2.63
2.75
32
42.58
1.80
1.69
46.19
2.02
2.04
53.49
2.54
2.74
36
47.21
1.74
1.69
51.00
1.94
2.03
58.62
2.41
2.72
38
49.51
1.72
1.69
53.38
1.91
2.02
61.16
2.35
2.71
42
54.09
1.67
1.68
58.12
1.85
2.02
66.21
2.25
2.70
54
67.67
1.57
1.67
72.15
1.71
2.00
81.07
2.04
2.67
72
87.74
1.48
1.67
92.81
1.59
1.99
102.82
1.85
2.65
108
127.21
1.37
1.66
133.26
1.46
1.98
145.10
1.65
2.62
この表の値は,JIS B 7912-2〜JIS B 7912-8の標準測定手順で使用するものである。標準測定手順におい
て測定回数を変更した場合も使用することは可能であるが,自由度も変更されるため,この表からは選択
することができないことがある。この場合,これらの値は,統計の参考書から取るのがよい。
21
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
計算例
計算例を,この附属書に記載する。
C.1 例1
測定対象量は,斜距離及び天頂角の測定による水平距離
斜距離:l1=142.432 m
標準不確かさ u1=12.0 mm
天頂角:l2=78.412°
標準不確かさ u2=0.055 mrad
入力量liの不確かさ行列Ulは,次のように表される[式(4)及び式(5)参照]。
(
)(
)
412
.
78
,
432
.
142
,2
1
=
=
l
l
Tl
[m, °]
=
=
2
2
2
2
2
1
mrad
mm
0
003
.0
0
0
144
0
0
u
u
l
U
求める水平距離及びその標準不確かさは,式(6)及び式(7)を参照し,次のようになる。
()
ο
412
.
78
sin
432
.
142
sin2
1
×
=
×
=
=
l
l
l
g
x
m
139.529
=
×
=
62
979
.0
432
.
142
x
次に式(8)〜式(10)を参照し,次のようになる。
(
)
2
1,g
g
T=
g
62
979
.0
sin2
1
1
=
=
∂
∂
=
l
l
g
g
[m]
611
.
28
87
200
.0
432
.
142
cos2
1
2
2
=
×
=
=
∂
∂
=
l
l
l
g
g
()
(
)
646
.
140
61
.
28
98
.0
003
.0
0
0
144
28.61
0.98
2
=
=
=
g
U
g
l
T
x
u
標準不確かさは,式(9)及び式(10)に従って,
()
()
mm
11.9
=
=x
s
x
u
となる。
C.2 例2
距離計の測定(測定対象量)において次の入力推定値は,測定されるか手入力される。
斜距離 :s=345.746 m
高度角 :z=70.580 8°
加数 :c=32.6 mm
大気補正:ka=12 ppm
結果として,距離計の表示の読みは,次のとおりとなる。
水平距離:D=326.111 6 m
高さ :h=114.964 9 m
図1の評価モデル(一般モデル関数)は,次のように表される。
22
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
()
Tl
g
x=
ここに,
(
)
(
)
z
k
s
c
s
h
x
z
k
s
c
s
D
x
a
a
cos
sin
2
1
×
+
+
=
=
×
+
+
=
=
さらに,D及びhの標準不確かさを評価する。このため,入力量を式(4)の表記法に従って表す。
(
)(
)[
]°
=
ppm
mm
m
8
580
.
70
12
6.
32
746
.
345
z
k
c
s
a
Tl
入力量lの不確かさは,機器の校正証明書の該当する不確かさ(タイプB評価)から取得し,次のベク
トル表記を得る。
()
()
()
()
[
](
)[
]
mrad
ppm
mm
mm
003
.0
2
5.0
3
=
=
z
u
k
u
c
u
s
u
a
T
lu
また,式(5)〜式(8)及び式(12)に従って次の式を得る。
()
()
()
()
×
=
=
−6
2
2
2
2
10
9
0
0
0
0
4
0
0
0
0
25
.0
0
0
0
0
9
0
0
0
0
0
0
0
0
0
0
0
0
z
u
k
u
c
u
s
u
a
l
U
0
,
0=
=
g
x
h
D
及び
(
)
(
)
×
−
×
+
×
×
+
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
z
s
z
s
z
z
k
z
s
z
s
z
z
k
z
h
k
h
c
h
s
h
z
D
k
D
c
D
s
D
a
a
a
a
sin
~
cos
cos
cos
1
cos
~
sin
sin
sin
1
G
ここに,
ak
s
c
s
s
×
+
+
=
~
式(13)の誤差伝ぱ(播)の法則及び式(9)から次の式を得る(結果が全てmm2となるように単位を合わせ
ている。)。
−
×
×
×
×
−
=
=
−
−
326
96
.
114
95
.
114
326
332
.0
943
.0
332
.0
943
.0
10
9
0
10
4
25
.0
0
9
326
95
.
114
332
.0
332
.0
96
.
114
326
943
.0
943
.0
6
6
T
l
x
G
GU
U
結果は
()
()
=
=
2
2
2
2
mm
mm
033
.2
772
.8
h
u
D
u
x
U
()
mm
3.0
=
D
u
及び ()
mm
1.4
=
h
u
となる。
C.3 例3
直線上の四つの測点間の水平距離を光波距離計で測定(測定対象量)
1
y1
2
y2
3
y3
4
観測量(入力量):距離x
1〜2=x1= 117.342 m
1〜3=x4=185.811 m
2〜3=x2= 68.454 m
2〜4=x5=109.707 m

23
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3〜4=x3= 41.265 m
1〜4=x6=227.058 m
(
)
x
x
x
x
x
x
T
6
5
4
3
2
1
=
x
未知量(出力量):
(
)
3
2
1
,
,
y
y
y
T=
y
式(21)に従い観測方程式は,
r1+ 117.342=y1
r2+ 68.454=
y2
r3+ 41.265=
y3
r4+ 185.811=y1+y2
r5+ 109.707=
y2+y3
r6+ 227.058=y1+y2+y3
となる。
線型方程式が成立しているので,直ちに行列を書くことができる[式(24)及び式(23)参照]。
=
1
1
1
1
1
0
0
1
1
1
0
0
0
1
0
0
0
1
A
及び
=
=
058
.
227
707
.
109
811
.
185
265
.
41
454
.
68
342
.
117
l
x
重みは等しい(P=E)として,正規行列を得る[式(27)参照]。
=
3
2
1
2
4
2
1
2
3
N
及びベクトル
=
030
.
378
030
.
591
211
.
530
n
解ベクトルは,次のようになる。
=
×
−
−
−
−
=
=
5
257
.
41
7
454
.
68
0
348
.
117
030
.
378
030
.
591
211
.
530
5.0
25
.0
0
25
.0
5.0
25
.0
0
25
.0
5
0
1
.
-n
N
y
最終的に残差は式(25)によって求めることができる。
r
x
y
A
=
−
×
++−−++
=
−
×
2
002
.0
2
005
.0
3
008
.0
5
007
.0
7
000
.0
0
006
.0
058
.
227
707
.
109
811
.
185
265
.
41
454
.
68
342
.
117
5
257
.
41
7
454
.
68
0
348
.
117
1
1
1
1
1
0
0
1
1
1
0
0
0
1
0
0
0
1
この結果から,観測の標準偏差を得る[式(28)参照]。
008
.0
3
6
10
01
.
192
6
0
=
−
×
=
=
−
ν
r
rT
s
式(29)に従い次の値を得ることができる。
24
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7
005
.0
5.0
008
.0
0
=
×
=
=
ky
ykyk
y
s
s
sk
Q
最終的に,出力推定値y1, y2, y3の標準不確かさ(タイプA評価)は,次によって得られる。
3,2,1
,
=
=
=
k
s
u
yk
yk
mm
5.7
また,
−
−
−
−
−
−
−
−
=
0.50
0.50
0.50
0.50
0.50
0.50
25
.0
25
.0
25
.0
00
.0
25
.0
25
.0
00
.0
25
.0
25
.0
25
.0
25
.0
00
.0
25
.0
25
.0
25
.0
25
.0
25
.0
25
.0
25
.0
00
.0
00
.0
25
.0
25
.0
25
.0
25
.0
25
.0
25
.0
25
.0
00
.0
25
.0
0s
x
S
及び
(
)[
]
mm
7.5
7.5
7.5
7.5
7.5
7.5
~=
T
xs
から,調整済み入力推定値x~の標準不確かさは,次によって得られる。
x
x
~s
u=
, 及び
()()
6
...,
,2,1
,
~
~
=
=
=
j
x
s
x
u
j
j
mm
5.7
C.4 例4
測定対象量(入力量)として,二つの異なる機器での複数回の角度測定
機器I:x1=124°39' 16"
機器II:x4=124°39' 13"
x2=124°39' 04"
x5=124°39' 09"
x3=124°39' 06"
x6=124°39' 08"
入力量の近似値をx0=124°39' 00"と置き入力量から近似値を引いた量Δxについて式(36)を適用する。
(
)[]
(
)
x
p
e
e
P
e
x
e
x
x
T
∆
=
∆
=
×
−
=
∆
∆
+
=
−
T
T
x
x
x
x
1
0
0
"
8
9
13
6
4
16
ここで,それぞれの機器の角測定の標準不確かさは,機器Iの仕様からuI=5",機器IIの仕様からuII=2",
として重み行列を得る。
2
2
0
3
2
1
I
u
s
p
p
p
=
=
=
,
2
2
0
6
5
4
II
u
s
p
p
p
=
=
=
2
0sの値を100として
=
25
0
25
25
4
4
0
4
P
最終的に

25
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
87
/1
1=
−
e
P
eT
及び
854
=
∆x
P
eT
その結果
[]"
8.9
87
854=
=
∆x
及び
10"
39'
124°
=
+
°
=
"8.9
"
00
'
39
124
x
その標準偏差は,式(37)及び式(28)から次によって得られる。
()
e
P
eT
s
x
s
0
=
及び
ν
r
P
rT
s=
2
0
ここで,
(
)[]"
8.1
8.0
2.3
8.3
8.5
2.6
−
−
=
Tr
及び ν=5
"8.
11
5
1.
699
0
=
=
s
及び ()
"3.1
87
8.
11
=
=
x
s
平均値xの標準不確かさは,最終的に
()
()1.3"
=
=x
s
x
u
となる。
C.5 例5
高低差測定において,測定対象量は水準標尺の前視及び後視の読みから得られる。不確かさの計算は,
式(41)〜式(50)を使うことができる。
標尺から読み取った値(高さ)は,前視及び後視をそれぞれl1,l2とする。
(
)[]
(
)[]
m
986
.6
155
.
13
732
.
12
780
.
28
211
.
15
466
.
10
m
989
.6
155
.
13
742
.
12
775
.
28
213
.
15
473
.
10
2
1
−
−
=
−
−
=
T
T
l
l
これから各々の算術平均
iy及びそのベクトルは,次のように得られる。
(
)[]
m
5
987
.6
0
155
.
13
0
737
.
12
5
777
.
28
0
212
.
15
5
469
.
10
−
−
=
Ty
高低差及びそのベクトルは,次のとおりである。
(
)[
]
mm
3
0
10
5
2
7
+
−
+
+
−
=
T
d
全ての観測量lj, j=1, 2の不確かさは同じとして,高さの標準偏差は式(46)を用いて次のようになる。
[
]
mm
9.3
12
187=
=
ls
iy, i=1, 2, …, 6の平均に対しては式(48)を用いて次が得られる。
()
[
]
mm
8.2
24
187=
=
iy
s
条件E(d)=0を確認するために,式(49)に従って計算を行う。
(7)2<187
この結果は,条件が満たされており,標準不確かさを次のように記述できることを意味する。
()
mm
3.9
=
=
l
j
s
l
u
及び ()
()
mm
2.8
=
=
i
i
y
s
y
u
26
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
C.6 例6
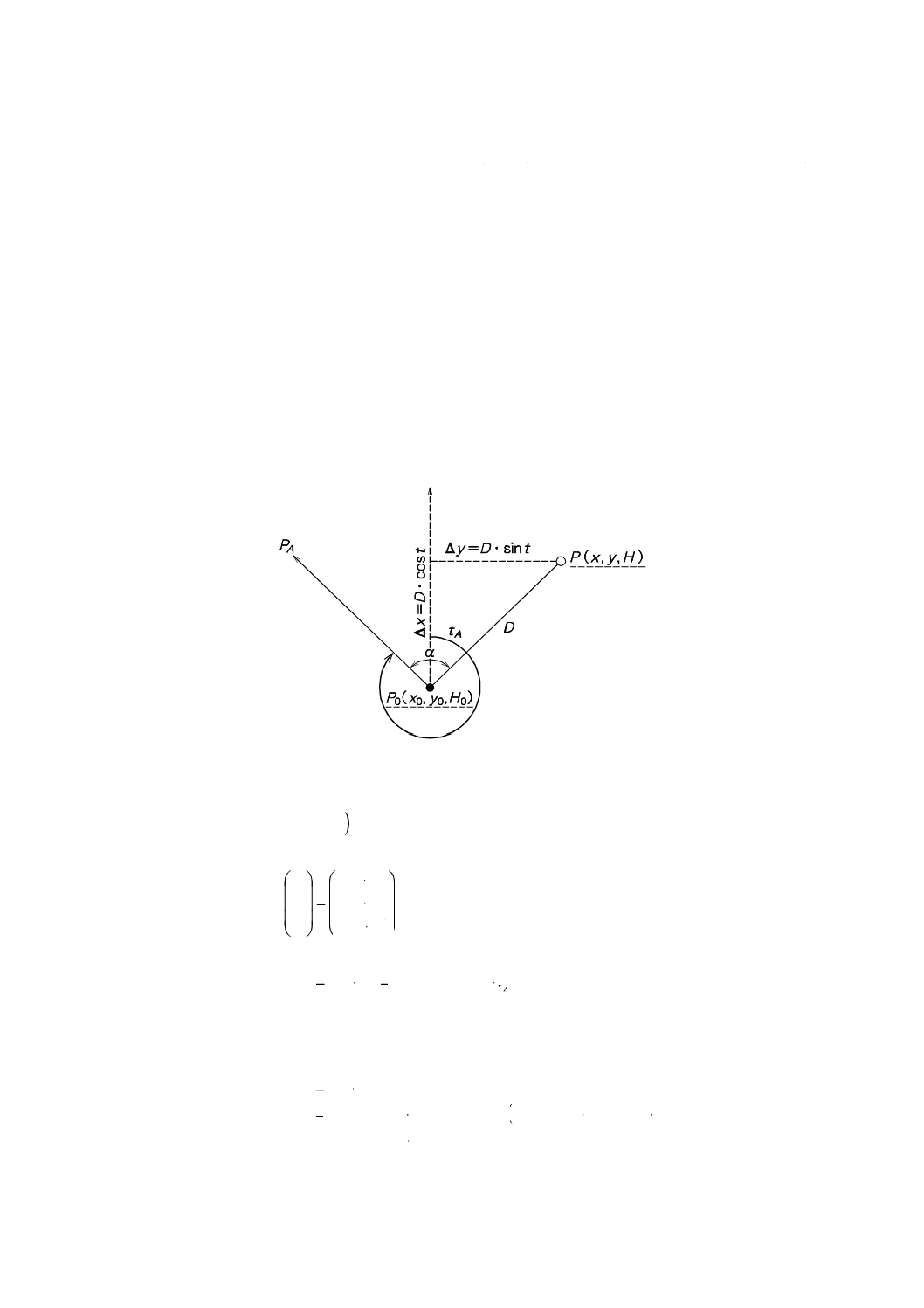
新点Pの座標x, y, H(測定対象量)は,与点P0(x0, y0, H0),片側観測だけの測距・測角法によって決定す
る(図C.1参照)。
与点P0の座標:
x0=12 345.678 m
y0=87 654.321 m
s(x0)=1.8 cm
s(y0)=1.6 cm
方位角:tA=309.090 9°
s(tA)=1.3"
観測量:
角度:α=89.999 9° s(α)=1.7"
水平距離:D=326.111 6 m
(例2の計算結果で)
u(D)=3.0 mm
図C.1−測定方法
次の数学モデルを不確かさ評価に使用する。
()
T
x
f
y=
又は,
∆
+
∆
+
∆
+
=
h
H
y
y
x
x
H
y
x
0
0
0
次にx座標についての計算例を示す。
()
(
)
At
D
x
x
x
P
x
+
×
+
=
∆
+
=
α
cos
0
0
視準軸誤差c,及び横軸誤差iを考慮して,モデルはkc及びkiを等しく補正するよう拡張しなければな
らない(ここでは,水平角αに異なる天頂角での観測による影響が直結する。)。ここでは,kc,kiにそれ
ぞれ0.003 2°,0.004 3°を与える。
()
(
)
A
i
c
t
k
k
D
x
P
x
+
+
+
×
+
=
α
cos
0
()
(
)°
+
°
+
°
+
°
×
+
=
9
090
.
309
3
004
.0
2
003
.0
9
999
.
89
cos
6
111
.
326
678
.
345
12
P
x
()
m
598.762
12
=
+
=
084
.
253
678
.
345
12
P
x
これらの不確かさの計算には,4.2.2及び4.4に対応させて表形式を用いると便利である。
27
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
さらに,追加の不確かさは,4.3に従ってタイプB評価を用いて次のように推定される。
機器の求心誤差e:
e=±3 mmとし,100 %の確率でこの区間内にあると仮定すれば,標準不確かさは一様分布の式(57)から
得られる。
()
mm
1.7
58
.0
=
×
=
e
e
u
感度係数:c7=1
水平屈折:
影響量r=±7"と見積もり,50 %の確率でこの区間内にあると仮定すれば,標準不確かさは[式(55)参照]。
()
"4.
10
48
.1
=
×
=
r
r
u
感度係数:
(
)206
sin
8
=
+
+
+
×
=
A
i
c
t
k
k
D
c
α
4.4に従い不確かさの伝ぱ(播)の法則を適用し,
()
()
()
()
()
()
()
()
()
()
=
=
2
2
2
2
2
2
2
2
0
0
0
,
0
0
r
u
e
u
k
u
k
u
u
t
u
D
u
x
u
i
c
B
x
A
A
x
α
U
U
及び
()
()
()
=
B
x
A
x
P
x
U
U
U
0
0
また,
(
)
206
1
206
206
206
206
78
.0
1
=
Tc
式(66)に従いx座標の出力推定値の合成標準不確かさは,最終的に次のように求まる。
()
[
]
mm
21.1
=
p
x
u
拡張不確かさ±U(k=2)を含めた最終結果は,
()(
)m
0.042
598.762
12
±
=
P
x
()
[
]
mm
21.1
=
p
x
uc
()
[
]
()
[
]
mm
42
2
±
=
×
=
p
x
u
p
x
U
c
となる。
不確かさバジェットを表C.1に示す。
注記 各例の計算は,最初から最後まで最大桁数で行われているが,中間の値及び最終結果は丸めた
値として示されている。
計算結果として採用する数値を太字とし,単位記号を付記した。付記した単位記号も太字に
なっているが,これは見やすさを考えたためで,一般的ルールでは太字は用いない。
28
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表C.1−不確かさバジェット
入力量
xi
入力推定値
xi
標準不確かさ
u(xj)
分布
感度係数a)
i
i
x
f
c
∂
∂
≡
/
()()
i
i
i
x
u
c
x
u
×
≡
評価のタイプ及び
不確かさ要因
[単位]
[単位]
[単位]
/mm
x0
12 345.678 m
18 mm
正規分布
1
18
A,以前の最小二乗法調
整による推定
D
326.111 6 m
3.0 mm
正規分布
0.78
2.3
A,合成標準不確かさ
α
89.999 9°
1.570 795 rad
1.7"
0.008 2 mrad
正規分布
206 m
1.7
B,偶然誤差効果,経験
値
kc
0.003 2°
0.061 mrad
1"
0.004 8 mrad
一様分布
206 m
1.0
B,一般的知識
ki
0.004 3°
0.075 mrad
1"
0.004 8 mrad
一様分布
206 m
1.0
B,一般的知識
tA
309.090 9°
5.394 654 rad
1.3"
0.006 3 mrad
正規分布
206 m
1.3
A,以前の最小二乗法調
整による推定
e
0
1.7 mm
一様分布
1
1.7
B,求心誤差
r
0
10.4"
0.050 2 mrad
正規分布
206 m
10.3
B,水平屈折
出力推定値
最終結果
12 598.762 m
21.1
注a) 式(12)又は式(17)で使用される偏導関数は,感度係数と呼ばれる。
29
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] JIS Z 8000-3 量及び単位−第3部:空間及び時間
注記 対応国際規格:ISO 80000-3,Quantities and units−Part 3: Space and time (IDT)
[2] JIS Z 8404-1:2006 測定の不確かさ−第1部:測定の不確かさの評価における併行精度,再現精度及
び真度の推定値の利用の指針
注記 対応国際規格:ISO/TS 21748:2004,Guidance for the use of repeatability, reproducibility and
trueness estimates in measurement uncertainty estimation(IDT)
[3] JIS Z 8404-2:2008 測定の不確かさ−第2部:測定の不確かさの評価における繰返し測定及び枝分か
れ実験の利用の指針
注記 対応国際規格:ISO/TS 21749:2005,Measurement uncertainty for metrological applications−
Repeated measurements and nested experiments(IDT)
[4] NIST Technical Note 1297:1994,Guidelines for Evaluating and Expressing the Uncertainty of NIST
Measurement Results
<http://physics.nist.gov/Pubs/guidelines/TN1297/tn1297s.pdf>
[5] JCG200 校正方法と不確かさに関する表現
独立行政法人製品評価技術基盤機構認定センター
<http://www.iajapan.nite.go.jp/jcss/pdf/koukaib̲f/JCG200-06.pdf>
注記 EA-4/02:1999,Expressions of the Uncertainty of Measurements in Calibration
<http://www.european-accreditation.org/publication/ea-4-02-m>
[6] TS Z 0032:2012 国際計量計測用語−基本及び一般概念並びに関連用語(VIM)
注記 対応国際規格:ISO/IEC Guide 99:2007,International vocabulary of metrology−Basic and general
concepts and associated terms (VIM)(IDT)
[7] TS Z 0033:2012 測定における不確かさの表現のガイド
注記 対応国際規格:ISO/IEC Guide 98-3:2008,Uncertainty of measurement−Part 3: Guide to the
expression of uncertainty in measurement (GUM:1995)(IDT)
[8] JIS Z 9041-2:1999 データの統計的な解釈方法−第2部:平均と分散に関する検定方法と推定方法
[9] ISO 2854:1976,Statistical interpretation of data−Techniques of estimation and tests relating to means and
variances
30
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
JISと対応国際規格との対比表
JIS B 7912-1:2014 測量機器の現場試験手順−第1部:理論
ISO 17123-1:2010 Optics and optical instruments−Field procedures for testing geodetic
and surveying instruments−Part 1: Theory
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごとの評
価及びその内容
(V)JISと国際規格との技術的差異の理
由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
3 用語及び
定義
3.1.13 偶然誤差,偶然測
定誤差
3.1.13
JISに同じ
一致
理解しやすいように注記2を追記した。
技術的差異はない。
3.1.14 系統誤差,測定の
系統誤差
3.1.14
JISに同じ
一致
理解しやすいように注記2を追記した。
技術的差異はない。
3.2.2 標準偏差(実験標
準偏差)
3.2.2
JISに同じ
変更
標準偏差と(実験標準偏差)を併記した。 規格内で標準偏差と実験標準偏差の用
語の使い分けを明確にするため。
追加
注記3を追記した。
3.3.7 拡張不確かさ,拡
張測定不確かさ
3.3.7
JISに同じ
一致
理解しやすいように簡潔にした。
技術的差異はない。
3.3.8 包含区間
3.3.8
JISに同じ
一致
理解しやすいように簡潔にした。
技術的差異はない。
4 測定の不
確かさ評価
4.2.2 タイプA不確かさ
伝ぱ(播)の一般法則
4.2.2
JISに同じ
一致
理解しやすいように“観測量をベクトル
表現で表すと式(4)となる。”を追記した。
技術的差異はない。
4.2.3 最小二乗法
4.2.3
JISに同じ
一致
理解しやすいように“ここに,N=ATPA
及びn=ATPl”を追記した。
技術的差異はない。
4.2.4.2 2測定のi回シリ
ーズにおける平均値の
標準不確かさの計算
4.2.4.2 JISに同じ
一致
E(d)=E(L2−L1)=0からE(d)=E(l2−l1)
=0へ変更した。
技術的差異はない。
ISOでの大文字表記(L)は誤記,小文
字表記(l)であるべきである。
4.2.4.3 m回シリーズ測
定の全標準不確かさの
計算
4.2.4.3 JISに同じ
一致
理解しやすいように簡潔にした。
技術的差異はない。
2
B
7
9
1
2
-1
:
2
0
1
4
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
31
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際
規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条ごとの評
価及びその内容
(V)JISと国際規格との技術的差異の理
由及び今後の対策
箇条番号
及び題名
内容
箇条
番号
内容
箇条ごと
の評価
技術的差異の内容
7 統計的検
定
7.1 一般
7.1
JISに同じ
変更
σからσ0へ変更した。
母集団の“σ”と区別するため。
JISに同じ
変更
表2 統計的検定の問a)の帰無仮説及び
対立仮説の標準偏差をsからσに,σを
σ0に変更した。
統計的検定で規定値と比較する試験機
の標準偏差は,測定サンプルから求め
られる“s”ではなく,それをもたらし
た母集団の“σ”であるべきである。
JISに同じ
変更
表2 統計的検定の注記記述を以下の記
述に変更した。
帰無仮説ではサンプル測定の結果算出
した標準偏差をもたらす母集団の統計
量を検証するためσをsの代わりに使用
する。
統計的検定で規定値と比較する試験機
の標準偏差は,測定サンプルから求め
られる“s”ではなく,それをもたらし
た母集団の“σ”であるべきであり,σ
とsとの関係を明確にするため。
7.2 問 a)
7.2
JISに同じ
変更
σからσ0へ変更した。
7.1 一般で,σをσ0に変更したため。
σからσ0へ変更した。
表2 a)の帰無仮説表現変更に合わせた。
附属書C
(参考)
C.2 例2
C.2
JISに同じ
一致
−
ppmに対する注記は不要と判断し削除
した。
JISに同じ
変更
“入力量lの不確かさは,機器の校正証
明書の該当する不確かさ(タイプA評
価)から取得し”の(タイプA評価)を
(タイプB評価)とした。
校正証明書記載の不確かさは,“タイプ
B評価”のため。
C.6 例6
図C.1 JISに同じ
変更
図内のP0の座標値(x, y, H)から(x0, y0,
H0)に変更した。
ISOの誤記を修正した。
JISに同じ
追加
図内のPに座標値(x, y, H)を追記した。 Pの座標値を明確にすることで,理解
しやすいようにした。
JISと国際規格との対応の程度の全体評価:ISO 17123-1:2010,MOD
2
B
7
9
1
2
-1
:
2
0
1
4
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。

32
B 7912-1:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 一致 ················ 技術的差異がない。
− 追加 ················ 国際規格にない規定項目又は規定内容を追加している。
− 変更 ················ 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD ··············· 国際規格を修正している。
2
B
7
9
1
2
-1
:
2
0
1
4
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
















