B 7722:2018 (ISO 148-2:2016)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 2
3.1 試験機に関する定義 ······································································································· 2
3.2 エネルギーに関する定義 ································································································· 3
3.3 試験片に関する定義 ······································································································· 3
4 記号及び意味 ··················································································································· 4
5 試験機···························································································································· 5
6 直接検証························································································································· 5
6.1 一般事項 ······················································································································ 5
6.2 基礎・据付け ················································································································ 6
6.3 機枠 ···························································································································· 6
6.4 振り子 ························································································································· 7
6.5 受け台及び載せ台 ·········································································································· 9
6.6 表示装置 ····················································································································· 10
7 基準試験片を使用する間接検証 ·························································································· 10
7.1 使用する基準試験片 ······································································································ 10
7.2 吸収エネルギーレベル ··································································································· 11
7.3 基準試験片の要件 ········································································································· 11
7.4 限定直接検証 ··············································································································· 11
7.5 繰返し性及びバイアス ··································································································· 11
8 検証の周期 ····················································································································· 11
9 検証報告書 ····················································································································· 12
9.1 一般事項 ····················································································································· 12
9.2 直接検証 ····················································································································· 12
9.3 間接検証 ····················································································································· 12
10 不確かさ ······················································································································ 12
附属書A(参考)試験機の間接検証結果の測定不確かさ ····························································· 18
附属書B(参考)試験機の直接検証結果の測定不確かさ ······························································ 22
附属書C(参考)ジグを使用した試験機の幾何学的特性の直接検証方法 ········································· 27
附属書JA(参考)試験機の検証に用いる検査具 ········································································ 32
B 7722:2018 (ISO 148-2:2016)
(2)
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,日本試験機工業会
(JTM)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を改正すべき
との申出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによって,JIS B 7722:1999は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
日本工業規格 JIS
B 7722:2018
(ISO 148-2:2016)
金属材料のシャルピー衝撃試験−試験機の検証
Metallic materials-Charpy pendulum impact test-
Verification of testing machines
序文
この規格は,2016年に第3版として発行されたISO 148-2を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,構成部品,総合的性能及び測定結果の精度に基づくシャルピー振り子式衝撃試験機(以下,
試験機という。)の検証に関するもので,例えば,JIS Z 2242によって実施するシャルピー振り子式衝撃試
験で使用する2 mm又は8 mmの衝撃刃をもつ試験機に適用する。
この規格は,次に記載する二つの検証の方法(直接検証及び間接検証)を規定する。
a) 直接検証とは,静的な方法であり,試験機がこの規格の要求事項を満たしていることを保証するため
に試験機の主要部品を測定することをいう。検証及び校正は,国内又は国際標準にトレーサブルな機
器を使用する。
b) 間接検証とは,動的な方法であり,基準試験片を使って吸収エネルギーに対する測定目盛上の測定点
を検証する。基準試験片の要求事項は,JIS B 7740による。
また,この規格は,試験片が破断するときの全吸収エネルギーを求めるための試験機の構成要素を評価
する方法を規定する。全吸収エネルギーは,次による。
− 試験片自体を破断するのに要するエネルギー
− 振り子が片振りするときの内部損失エネルギー
内部損失エネルギーは,次による。
− 直接検証(6.4.5参照)によって決まる振り子の空気抵抗,回転軸の軸受の摩擦及び置き針の摩擦
− 不適切な測定方法及び装置による基礎の衝撃,並びに機枠及び振り子の振動
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 148-2:2016,Metallic materials−Charpy pendulum impact test−Part 2: Verification of testing
machines(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
2
B 7722:2018 (ISO 148-2:2016)
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 7740 金属材料のシャルピー衝撃試験−試験機の検証用基準試験片
注記 対応国際規格:ISO 148-3:2016,Metallic materials−Charpy pendulum impact test−Part 3:
Preparation and characterization of Charpy V-notch test pieces for indirect verification of pendulum
impact machines
JIS Z 2242 金属材料のシャルピー衝撃試験方法
注記 対応国際規格:ISO 148-1:2016,Metallic materials−Charpy pendulum impact test−Part 1: Test
method
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
3.1
試験機に関する定義
3.1.1
受け台(anvil)
試験片を振り子によって打撃するとき,衝撃力を受ける左右一対の垂直な面を形成する試験機の基部の
一部。受け台の面は,載せ台の面と直角をなす(図1〜図3参照)。
3.1.2
基部(base)
載せ台の水平な面より下に位置する,試験機の機枠の部分(図1参照)。
3.1.3
打撃中心(centre of percussion)
打撃時に,振り子の全質量がその点に集中して運動しているとみなせる振り子上の点(図4参照)。
打撃中心を通る水平な線に沿って衝撃を加えたとき,振り子の回転軸に水平な反動を生じない。
3.1.4
打撃点(centre of strike)
自由につり下げた振り子の衝撃刃の垂直な刃縁と,載せ台に置いた基準寸法・形状の試験片との接触部
分(長さ10 mmの線分)の中点(図4参照)。
3.1.5
工業用試験機(industrial machine)
工業用,一般用又は試験研究用として金属材料を試験するために使用する試験機。
注記 これらの試験機は,基準試験片の値付けには使用できない。工業用試験機は,この規定に記載
した手順によって検証されている。
3.1.6
基準試験機(reference machine)
基準試験片の基準エネルギーを決定するために使用する試験機。
注記 基準試験機は,JIS B 7740に規定する手順によって検証されている。
3.1.7
衝撃刃(striker)
試験片に接して衝撃力を加える振り子の一部。
注記 試験片に接する刃先の半径は,2 mm(通常,“2 mm刃先”という。)及び8 mm(通常,“8 mm
3
B 7722:2018 (ISO 148-2:2016)
刃先”という。)がある(図2参照)。
3.1.8
載せ台(test piece supports)
試験片を置く,左右一対の水平面を形成する試験機の基部の一部。載せ台の面は,受け台の面と直角を
なす(図2及び図3参照)。
3.2
エネルギーに関する定義
3.2.1
全吸収エネルギー,KT(total absorbed energy)
試験をしたとき,試験片を破断するのに要した全てのエネルギー。
注記 全吸収エネルギーは,振り子の持上げ位置(角度)の初期位置エネルギーと,試験片が破断し
たときの最大振り上がり位置(角度)での位置エネルギーとの差に等しい(6.4参照)。
3.2.2
初期位置エネルギー,KP(initial potential energy)
直接検証によって決定した振り子の初期位置エネルギー(6.4.2参照)。
3.2.3
吸収エネルギー,K(absorbed energy)
試験をしたとき,試験片を破断するのに要した全てのエネルギーであり,損失エネルギーを補正した後
の値。
3.2.4
計算エネルギー,Kcalc(calculated energy)
直接検証によって測定した角度,長さ及び力の値から計算したエネルギー。
3.2.5
公称初期位置エネルギー,KN(nominal initial potential energy)
試験機の製造業者が指定したエネルギー。
3.2.6
表示吸収エネルギー,KS(indicated absorbed energy)
置き針又は他の読取装置が表示するエネルギー。吸収エネルギーKを決定するために摩擦損失分を補正
する場合がある。
3.2.7
基準吸収エネルギー,KR(reference absorbed energy)
基準試験機を使用して決定した基準試験片の吸収エネルギー認証値。
3.3
試験片に関する定義
3.3.1
幅,W(width)
ノッチ面とその反対面との間隔(衝撃方向の試験片の寸法)。
注記 旧規格では,“高さ”と表現していた。この寸法の表記を“幅”に変更することによって,その
他の破壊試験規格で使用されている用語と同じになる。
3.3.2
厚さ,B(thickness)
幅に垂直な相対面の間隔。

4
B 7722:2018 (ISO 148-2:2016)
注記 旧規格では,“幅”と表現していた。この寸法の表記を“厚さ”に変更することによって,その
他の破壊試験規格で使用されている用語と同じになる。
3.3.3
長さ,L(length)
ノッチに直角な相対面の間隔であり,試験片の最大寸法(幅及び厚さと直角方向の試験片の寸法)。
3.3.4
基準試験片(reference test piece)
試験機の適合性検証に用いる試験片。その試験で測定した表示吸収エネルギーを試験片群の基準吸収エ
ネルギーと比較するために使用する。
注記 基準試験片は,JIS B 7740に従って調製する。
4
記号及び意味
この規格で用いる記号及びその意味は,表1による。
表1−記号及び意味
記号a)
単位
意味
BV
J
間接検証によって決定された試験機のバイアス(偏り)
b
J
繰返し性
F
N
振り子を水平に保ちl2の距離で測定したときの振り子にかかる力
Fg
N
重力の作用によって振り子にかかる重量
g
m/s2
重力加速度
GUM
−
不確かさの表現ガイド
h
m
振り子の落下高さ
h1
m
振り子の振り上がり高さ
K
J
吸収エネルギー(特定のノッチ形状と刃先形状半径とを判別するためにKV2,KV8,
KU2,KU8と表記する。)
KT
J
全吸収エネルギー
KS
J
表示吸収エネルギー
Kcalc
J
計算エネルギー
KVR
J
間接検証に用いる基準試験片の認証値
V
KV
J
間接検証で用いる基準試験片の測定値の平均
KN
J
公称初期位置エネルギー
KP
J
初期位置エネルギー
KR
J
1セットの基準試験片の基準吸収エネルギー
K1又はβ1
J又は°
置き針の動きを伴う状態で振り子を持上げ位置から振り下ろし,反対側に振り上がっ
たときの表示吸収エネルギー又は振り上がり角度
K2又はβ2
J又は°
置き針の動きを伴わない状態で振り子を持上げ位置から振り下ろし,反対側に振り上
がったときの表示吸収エネルギー又は振り上がり角度
K3又はβ3
J又は°
振り子が11回連続片振り後(5往復後)の表示吸収エネルギー又は振り上がり角度
l
m
回転軸中心から試験片の中心(刃の中心)までの距離(振り子長さ)
l1
m
回転軸中心から打撃中心までの距離
l2
m
回転軸中心から力Fが加わる点までの距離
M
N m
F×l2で求めたモーメント
nV
−
試験機の間接検証用の基準試験片の数
p
J
置き針の摩擦によって生じるエネルギー損失
p'
J
軸受による摩擦と空気抵抗によるエネルギー損失

5
B 7722:2018 (ISO 148-2:2016)
表1−記号及び意味(続き)
記号a)
単位
意味
pβ
J
振り上がり角度βのときの,エネルギー損失の補正値
r
J又は°
目盛の分解能
RM
−
標準物質(この規格においては,基準試験片)
sV
−
nV個の基準試験片から得られたKV値の標準偏差
S
−
読取機構のバイアス
t
s
振り子の周期
T
s
振り子が100往復するのに要する時間
Tmax
s
測定したTの最大
Tmin
s
測定したTの最小
u
−
標準不確かさ
u(
V
KV)
J
V
KVの標準不確かさ
u(BV)
J
試験機のバイアスの標準不確かさ
u(F)
J
測定した力(F)の標準不確かさ
u(Fftd)
J
力測定器の標準不確かさ
u(r)
J
目盛の分解能からの標準不確かさ寄与成分
uRM
J
間接検証に用いる基準試験片の認証値の標準不確かさ
uV
J
間接検証結果の標準不確かさ
α
°
振り子の持上げ角度
β
°
振り子の振り上がり角度
νB
−
u(BV)に対応する自由度
νV
−
uVに対応する自由度
νRM
−
uRMに対応する自由度
注a) 図4参照。
5
試験機
試験機は,次の部分からなる(図1〜図3参照)。
a) 基礎・据付け
b) 機枠(基礎を除いた振り子を支える構造物)
c) ハンマ及び衝撃刃を含む振り子
d) 受け台及び載せ台(図2及び図3参照)
e) 吸収エネルギー表示装置(目盛板及び置き針又は電気的読取装置)
6
直接検証
6.1
一般事項
試験機の直接検証は,箇条5のa)〜e)に対して実施する。
測定器の不確かさは,適用した直接検証方法の精度を整合させるために必要である。直接検証の測定で
使用するダイヤルゲージ,マイクロメータ,ノギスなどの器具は,その製造業者などで一度は不確かさを
評価しなければならない。
直接検証で要求する不確かさ評価は,製品規格又は材料特性には関係しない。
直接検証の各検証項目の測定の不確かさは,それぞれの方法の妥当性確認の一部として評価する。一度
その方法の妥当性確認が完了すれば,その不確かさを日常的に用いることができる(訓練された作業者が
同じ機器を同じ手順で使用することが条件となる。)。
6
B 7722:2018 (ISO 148-2:2016)
6.2
基礎・据付け
6.2.1
試験機を据え付ける基礎,及び基礎に試験機を固定する方法に十分注意する。
6.2.2
基礎は,試験機を据え付けてしまうと検査ができないため,基礎の質量が振り子の質量の40倍以
上であることを保証する文書を据付け時に提出する。
6.2.3
据え付けた試験機の検査は,次による。
a) 据付けボルトが試験機の製造業者が定めたトルク値で締め付けられていることを確認する。トルク値
は,試験機の製造業者によって用意された書類に記録しなければならない(6.2.1参照)。所有者が他
の据付け方法を採用する場合は,据付け状態が同等であることを実証しなければならない。
b) 試験機は,衝撃試験時に外部振動の影響を受けないことを確認する。
注記 例えば,機枠の適切な位置に水の入った小さな容器を置き,衝撃試験を実施したときに水面
にさざ波が生じなければ,この要求に適合しているとみなすことができる。
6.3
機枠
6.3.1
機枠の検査は,次の項目による(図1参照)。
a) つるした状態の振り子の位置
b) 載せ台及び振り子の位置関係
c) 振り子軸受の軸方向と半径方向との遊び
d) 振り子と機枠との間隔
1998年以後に製造された試験機は,通常,水平の基準面をもつ。試験機の幾何学的特性を直接検証する
方法を,附属書Cに記載する。
6.3.2
振り子の回転軸は,基準面に対し2/1 000以内で平行とする。このことを試験機の製造業者は保証
する。
6.3.3
試験機は,基準面が,2/1 000以下で水平になっていることが検証できるように据え付ける。基準
面をもたない試験機については,回転軸が4/1 000以下で水平になるよう据え付ける,又は回転軸を検証
できる基準面がなければならない。
6.3.4
振り子を自由につり下げたとき,刃縁の位置は試験片にちょうど接触する位置から2.5 mm以内と
する。
6.3.5
振り子の運動平面は,回転軸に対して90°±0.1°とする(測定器の不確かさu<0.05°)。
6.3.6
衝撃刃の刃縁は,試験片の厚さ方向全体に接触していなければならない。これを確認するための手
法を次に示す。
55 mm×10 mm×10 mmの試験片を薄い紙でしっかり包み,載せ台に置く。刃先側にはカーボン紙をカ
ーボンを外にしてしっかり包む。その状態で振り子を僅かに持ち上げ,試験片と刃先とを衝突させる。そ
の後は,試験片に接触しないようにする。試験片を包む紙に付いたカーボンのマークで接触を確認する。
この方法は,刃先と試験片との接触角度の確認と並行して行える。
注記 カーボン紙の代わりに光明丹を使用する方法もある。
6.3.7
振り子は,衝撃刃の中心と両受け台間の中心との差が0.5 mm以内に設置する(測定器の不確かさ
u<0.1 mm)。
6.3.8
軸受の軸方向の遊びは,振り子の実際の重量Fgの約4 %の横の力を衝撃刃の中心に加えたとき,
回転軸の位置で測定して,0.25 mm以下とする(測定器の不確かさu<0.05 mm)。
6.3.9
軸受の回転軸の半径方向の遊びは,振り子の回転面に対して垂直に距離lで150 N±10 Nの力を加
えた場合,0.08 mm以下とする(測定器の不確かさu<0.02 mm)。
7
B 7722:2018 (ISO 148-2:2016)
6.3.10 試験機の基部の質量は,少なくとも振り子の質量の12倍以上であることが望ましい。
6.4
振り子
6.4.1
振り子の検証は,次の項目による。
a) 初期位置エネルギーKP
b) 表示吸収エネルギーKSのバイアス
c) 衝撃時の振り子の速度
d) 摩擦によって吸収されるエネルギー
e) 打撃中心の位置(打撃中心から回転軸中心までの距離)
f)
刃先の曲率半径
g) 刃先と試験片との接触角度
6.4.2
初期位置エネルギーKPと公称初期位置エネルギーKNとの差は,±1.0 %を超えてはならない。初期
位置エネルギーKPは,次によって決定する。
振り子のモーメントは,回転軸中心から距離l2の位置でナイフエッジを用いて振り子を保持し,回転軸
と重心とを結ぶ線が水平に対して15/1 000以下の状態において,ナイフエッジに作用する力Fをはかり又
は力検出器で測定する(測定器の不確かさu<5/1 000)。
力F及び距離l2は,いずれも±0.2 %の精度で測定する。モーメントMは,Fとl2との積である。
注記 長さl2は,長さlに等しいとすることもできる。この場合には,lの測定精度についてもl2と同
等である。
持上げ角度αは,±0.2°の精度で測定する。角度αは,90°以上でもよい。
初期位置エネルギーKPは,式(1)によって計算する。
)
cos
1(
P
α
M
K
−
×
=
···································································· (1)
6.4.3
目盛板上の公称初期位置エネルギーKNの0 %,10 %,20 %,30 %,50 %及び80 %の吸収エネルギ
ーKにほぼ対応する目盛線について検証する。
これらの目盛は,振り上がり角度βが置き針によって指示されるような機構をもち,その角度βを±0.2°
で読み取れるものとする。
計算エネルギーKcalcは,式(2)によって計算する。
)
cos
(cos
calc
α
β
M
K
−
×
=
····························································· (2)
注記1 l2,F及びβの測定の不確かさによって,Kcalcの測定不確かさは,フルスケールの約±0.3 %と
なる。
表示吸収エネルギーKSと測定値から計算された計算エネルギーKcalcとの差の絶対値は,表示吸収エネル
ギーKSの1.0 %以下,又は公称初期位置エネルギーKNの0.5 %以下でなければならない。それぞれを,式(3)
及び式(4)で表す。
0.1
100
S
S
calc
≦
×
−
K
K
K
%(KNの50 %以上80 %以下のとき) ··············· (3)
5.0
100
N
S
calc
≦
×
−
K
K
K
%(KNの50 %未満のとき) ···························· (4)
注記2 吸収エネルギーKが,公称初期位置エネルギーKNに対して小さいときほど,吸収エネルギー
Kの読取精度には注意が必要である。
注記3 エネルギー損失についての補正機能を備えた試験機の場合,結果を正しく比較するために
Kcalcの補正が必要になる。
8
B 7722:2018 (ISO 148-2:2016)
6.4.4
衝撃時の振り子の速度vは,式(5)によって求める。
)
cos
1(
2
α
l
v
−
=
g
····································································· (5)
ここに,
l: 振り子の回転軸中心から試験片中心までの距離(m)
g: 測定地における重力加速度(m/s2)。9.81 m/s2を用いてもよい。
α: 持上げ角度(°)(図4参照)
衝撃速度は,5.0 m/s〜5.5 m/sでなければならない(測定器の不確かさu<0.1 m/s)。ただし,1998年以
前に製造された試験機については,4.3 m/s〜7.0 m/sの範囲にあれば許容されるが,衝撃速度を報告書に記
載しなければならない。
6.4.5
摩擦によって吸収されるエネルギーは,空気抵抗,軸受による摩擦及び置き針による摩擦を含む。
これらの損失は,6.4.5.1及び6.4.5.2によって評価する。
6.4.5.1
置き針の摩擦による損失の評価は,次によって行う。
a) 置き針の動きを伴う状態で,振り子を持上げ位置から振り下ろし,反対側に振り上がったときの振り
上がり角度β1又は表示吸収エネルギーK1を記録する。
b) 続いて,置き針の動きを伴わない状態で同じ操作を行い,振り上がり角度β2又は表示吸収エネルギー
K2を記録する。
c) 置き針の摩擦によって生じるエネルギー損失pは,角度目盛の場合は,式(6)によって求める。また,
エネルギー目盛の場合は,式(7)によって求める。
)
cos
(cos
2
1
β
β−
=M
p
································································· (6)
2
1K
K
p
−
=
·············································································· (7)
6.4.5.2
軸受による摩擦及び空気抵抗によって生じる損失の評価は,次によって行う。
a) 6.4.5.1に従ってβ2又はK2を評価した後,振り子を持上げ位置に置く。
b) 指示機構をリセットしない状態で,振り子に衝撃及び振動を与えずに11回連続片振り後の振り上がり
角度β3又は表示吸収エネルギーK3を記録する。
c) 片振り間の軸受による摩擦及び空気抵抗によるエネルギー損失p'は,角度目盛の場合は,式(8)によっ
て求める。また,エネルギー目盛の場合は,式(9)によって求める。
)
cos
(cos
10
1
2
3
β
β
M
p'
−
=
···························································· (8)
)
(
10
1
2
3K
K
p'
−
=
······································································· (9)
注記 実際の試験において振り上がり角度βへのこれらの損失を考慮する必要がある場合,式(10)によ
って得られる値を吸収エネルギーの値から差し引くことができる。
2
1
β
β
α
β
α
p'
β
β
p
p
+
+
+
=
································································· (10)
β1及びβ2は,ほとんどαに等しいためpβは,式(11)のように近似できる。
α
β
α
p'
α
β
p
p
2
β
+
+
=
···································································(11)
エネルギー単位で目盛られた試験機のβは,式(12)によって計算できる。
−
−
=
−
M
K
K
β
T
P
11
cos
····························································· (12)
6.4.5.3
摩擦損失(p+p')の測定値は,公称初期位置エネルギーKNの0.5 %以下とする。0.5 %を超えた
9
B 7722:2018 (ISO 148-2:2016)
場合で,置き針の摩擦分を減らしても,許容値の範囲に入らないときは,軸受を洗浄するか又は交換する。
6.4.6
打撃中心から回転軸中心までの距離l1は,振り子の周期から計算し,0.995 l±0.005 lとする。計算
したl1の精度は,0.5 mm以内とする。
l1は,5°を超えない角度から振って,完全に1周期する時間t(秒)を測定することによって求め,式
(13)によって決定する。
2
2
1
π
4
t
l
g
=
················································································ (13)
ここに,
g: 重力加速度(m/s2)。9.81 m/s2を用いてもよい。
π 2: 9.87
式(13)からl1=0.248 5×t 2(m)となる。
なお,tの測定精度は,0.1 %以下とする。
約2 sの周期をもつ振り子においては,この精度を次のように求める。
100往復するのに要する時間Tを3回測定し,(Tmax−Tmin)が0.2 s以内であれば,Tの三つの値を平均し
て100で除してtとする。
6.4.7
刃先の形状・寸法は,ゲージ(附属書JA参照)によって検査する。刃先半径は2 mm及び8 mm
の二つのタイプがある。二つのタイプの刃先半径と刃先角度の寸法・形状を,表3に示す。
受け台間を通過する衝撃刃の最大幅は,10 mm以上18 mm以下でなければならない(測定器の不確かさ
u<0.2 mm)。
注記1 刃先の形状・寸法を検証する例として,検査用にレプリカをとる方法もある。
注記2 刃先半径2 mm及び8 mmの衝撃刃による試験結果は,一般に異なる。
6.4.8
刃縁と試験片の水平な面とがなす角度(刃先の方向)は,90°±2°とする(6.3.6参照)(測定器の
不確かさu<0.2°)。
6.4.9
振り子の落下機構は,初期の衝撃,遅れ又は横振れがなく振り子が自由に放たれるように操作でき
るものとする。
6.4.10 試験機に制動装置が付いている場合,偶発的に制動装置が働くことのないような安全手段を講じな
ければならない。また,例えば,周期及び摩擦損失の測定をする場合は,制動装置を切り離す手段をもつ
ものとする。
6.4.11 自動持上げ装置を備えた試験機は,直接検証もできるように,構成しなければならない。
6.5
受け台及び載せ台
6.5.1
受け台及び載せ台の検査は,次の項目による(図2,図3及び表3参照)。
a) 載せ台の配置
b) 受け台の配置
c) 受け台間の距離
d) 受け台の衝撃方向の逃げ角
e) 受け台の内角の丸み半径
f)
破断試験片が試験機から飛散するための隙間
6.5.2
左右の載せ台面は平行であり,面の食い違いは,0.1 mm(測定器の不確かさu<0.05 mm)を超え
てはならない。載せ台上の試験片の軸と回転軸とは,3/1 000以下で平行でなければならない(測定器の不
確かさu<1/1 000)。
6.5.3
左右の受け台面は,平行であり,面の食い違いは,0.1 mmを超えてはならない(測定器の不確か
10
B 7722:2018 (ISO 148-2:2016)
さu<0.05 mm)。載せ台と受け台との面は,互いに90°±0.1°でなければならない(測定器の不確かさu
<0.05°)。受け台の構成に関するその他の要件を,表3に示す。
6.5.4
破断した試験片の試験機への影響が最小となり,また振り子のスイングが終了する前に振り子に当
たることなく,試験片が試験機から自由に飛散できるように,衝撃刃と受け台との間に十分な隙間を設け
なければならない。受け台間を通過する振り子の部分は,18 mmを超えてはならない(6.4.7参照)(測定
器の不確かさu<0.2 mm)。
ハンマは,二つの基本的なタイプのいずれかであり(図1参照),Cタイプのハンマを使用する場合,試
験片の両側の隙間が13 mm以上であれば,破断試験片は振り子に跳ね返ることはない。試験片位置決めの
ためのエンドストッパーがある場合は,衝撃を加える前に取り外さなければならない。
Uタイプのハンマを使用する場合は,破断試験片が振り子に当たらないような手段を講じなければなら
ない。Uタイプのハンマを使用する試験機について,覆い(shroud)は,次の条件によって設計・装着す
る(図3参照)。
a) 厚さは,約1.5 mmとする。
b) 硬さは,45 HRC以上とする。
c) 裏面の面取りは,1.5 mm以下の半径とする。
d) 振り子との間隔が,1.5 mm以下となるよう位置を調整する。
なお,受け台にセットされた試験片の端と覆いとの隙間が13 mm以上ある場合は,a)及びd)の要求を満
足しなくてよい。
6.6
表示装置
6.6.1
アナログ表示装置の検証は,次の検査による。
a) 目盛板の検査
b) 指針の検査
目盛は角度又はエネルギーの単位とする。角度又はエネルギーの単位で目盛られた目盛板は,目盛線の
幅が均一で,指針の幅と目盛線との幅が大体等しいものとする。指針は,視差の影響を受けずに読み取れ
るものとする。
表示装置の分解能rは,指針の幅と,隣接する二つの目盛の中心から中心までの距離との比率によって
求められ,推奨する比率は,1/4,1/5又は1/10である。1目盛を1/10まで読み取るためには2.5 mm以上
の間隔が必要である。
目盛の間隔は,公称初期位置エネルギーKNの1 %より細かいものとし,公称初期位置エネルギーKNの
0.25 %又はそれ以下のエネルギー変化量を読み取れるものとする。
6.6.2
デジタル表示装置の検証は,次の検査による。
− 表示は,角度又はエネルギー単位とする。
− 表示装置の分解能は,表示の最後の数値が1増分を越えて変動しない場合は,最後の1増分を分解能
と考える。読取りが1増分を越えて変動する場合は,変動の半分を分解能とする。
− 分解能は,公称初期位置エネルギーKNの0.25 %と同じか,その値よりも少ない値でなければならない。
7
基準試験片を使用する間接検証
7.1
使用する基準試験片
間接検証では,基準試験片を使用して測定範囲内の数箇所を検証する。これらの基準試験片は,次の目
的に使用する。
11
B 7722:2018 (ISO 148-2:2016)
a) 対象とする試験機と基準試験機との比較又はJIS Z 2242に従って測定したKR値との比較
b) 他の試験機と比較することなく,ある期間にわたる試験機の性能の監視
7.2
吸収エネルギーレベル
間接検証は,試験機の使用するレンジ内の少なくとも二つの吸収エネルギーレベルで行う。各エネルギ
ーレベルで,少なくとも5本以上の基準試験片を必要とする。選択する基準試験片の吸収エネルギーレベ
ルは,使用するレンジの上限及び下限にできる限り近いものとする。3レベル以上の基準試験片を使用す
る場合は,できるだけ均等な間隔で検証することが望ましい。
7.3
基準試験片の要件
基準試験片は,JIS B 7740による。
7.4
限定直接検証
間接検証の前に少なくとも次の限定的な直接検証を行う。
a) 6.2.3 a)に基づく試験機の据付け状態の検査及び6.3.4と6.3.6とに基づく機枠の検査
b) 載せ台と受け台との過度な摩耗の有無の検査(外観検査)(表3参照)
c) 受け台間の距離の測定(表3参照)
d) 刃先,載せ台,受け台を交換した場合は,6.3.4,6.3.6,6.3.7,6.4.7,6.4.8及び6.5.2〜6.5.4の測定(表
3参照)
e) 回転軸の摩擦と空気抵抗とによる損失の測定
f)
置き針の摩擦によるエネルギー損失の測定
7.5
繰返し性及びバイアス
7.5.1
繰返し性
あるエネルギーレベルの間接検証に使用するnV個の基準吸収エネルギーを,KV1,KV2,……,KVnVと
する。その場合,試験機の繰返し性bは,式(14)によって与えられる。
min
max
KV
KV
b
−
=
····································································· (14)
繰返し性の許容値を,表2に示す。
7.5.2
バイアス(偏り)
試験機のバイアスは,式(15)によって表す。
R
V
V
KV
KV
B
−
=
······································································ (15)
ここに,
V
3
2
1
V
V
n
KV
KV
KV
KV
KV
n
+
+
+
+
=
Λ
············································· (16)
バイアスの許容値を,表2に示す。
表2−繰返し性及びバイアスの許容値
単位 J
吸収エネルギー
レベル
繰返し性
b
バイアス
V
B
<40
≦6
≦4
≧40
KVRの≦15 %
KVRの≦10 %
8
検証の周期
8.1
試験機を最初に設置した場合又は試験機を移設した後は,直接検証を実施し,引き続き間接検証を
12
B 7722:2018 (ISO 148-2:2016)
行う。
8.2
限定直接検証を含む間接検証は,12か月を超えない周期で実施する。摩耗の観察によって,より頻
繁な間接検証が必要な場合がある。
8.3
受け台及び/又は衝撃刃を交換した場合は,対応する部品の規定に従い,直接検証を実施する。ま
た,間接検証も実施する。
8.4
間接検証の結果が不満足で,装置に限定的な修理を施して再度の間接検証を行っても満足な結果に
至らない場合には,直接検証を実施する。
9
検証報告書
9.1
一般事項
検証の報告書は,少なくとも次の情報を記載する。
a) この規格への適合の明示
b) 試験機の識別に関する事項:試験機の製造業者名,形式,製造番号
c) 衝撃刃の刃先形状
d) 所有者名及び設置場所の住所
e) 検証を実施した機関の名称又は記号
f)
検証実施年月日
9.2
直接検証
試験機の直接検証を行う場合は,次の項目を含む。
a) 振り子の公称初期位置エネルギー
b) 衝撃時の振り子の速度
c) 空気抵抗及び摩擦による損失エネルギー
9.3
間接検証
試験機の間接検証を行う場合は,次の項目を含む。
a) 間接検証に用いた基準試験片の識別(記号,番号など),認証値及び実測結果
b) 間接検証の結果
1) 繰返し性
2) バイアス
3) 試験機が,この規格の要求に一致しているか否かの報告
10 不確かさ
間接検証結果の測定不確かさを決定する方法を,附属書A(参考)に示す。
直接検証結果の測定不確かさを決定する方法を,附属書B(参考)に示す。
13
B 7722:2018 (ISO 148-2:2016)
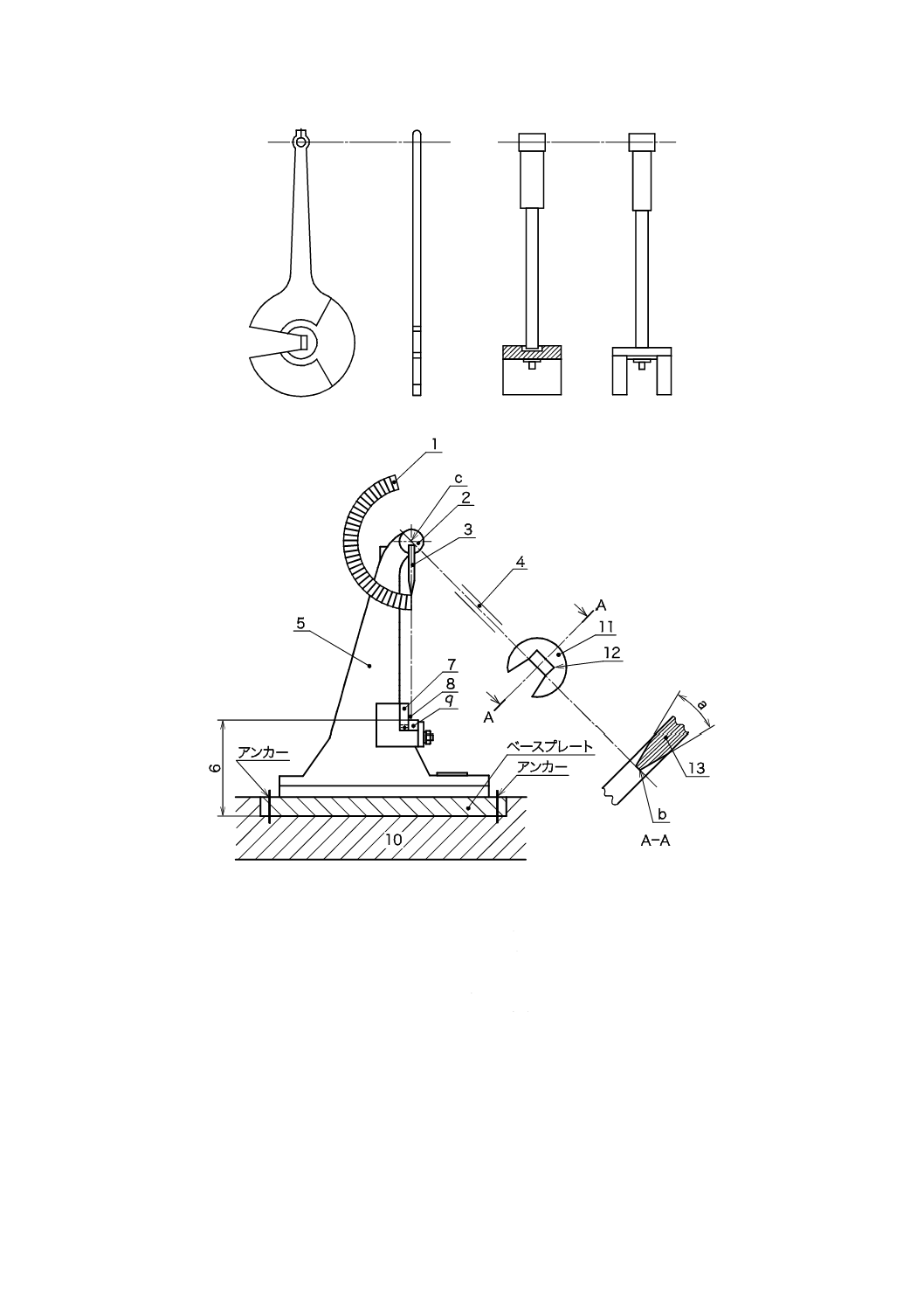
a) Cタイプハンマ
b) Uタイプハンマ
1
目盛
2
振り子軸受
3
置き針
4
振り子棒
5
機枠
6
基部の範囲
7
受け台
8
試験片
9
載せ台
10 基礎
11 Cタイプハンマ
12 衝撃刃
13 刃先
a
刃先角度
b
刃先端の曲率半径
c
回転軸
c) 試験機全体
図1−試験機
14
B 7722:2018 (ISO 148-2:2016)
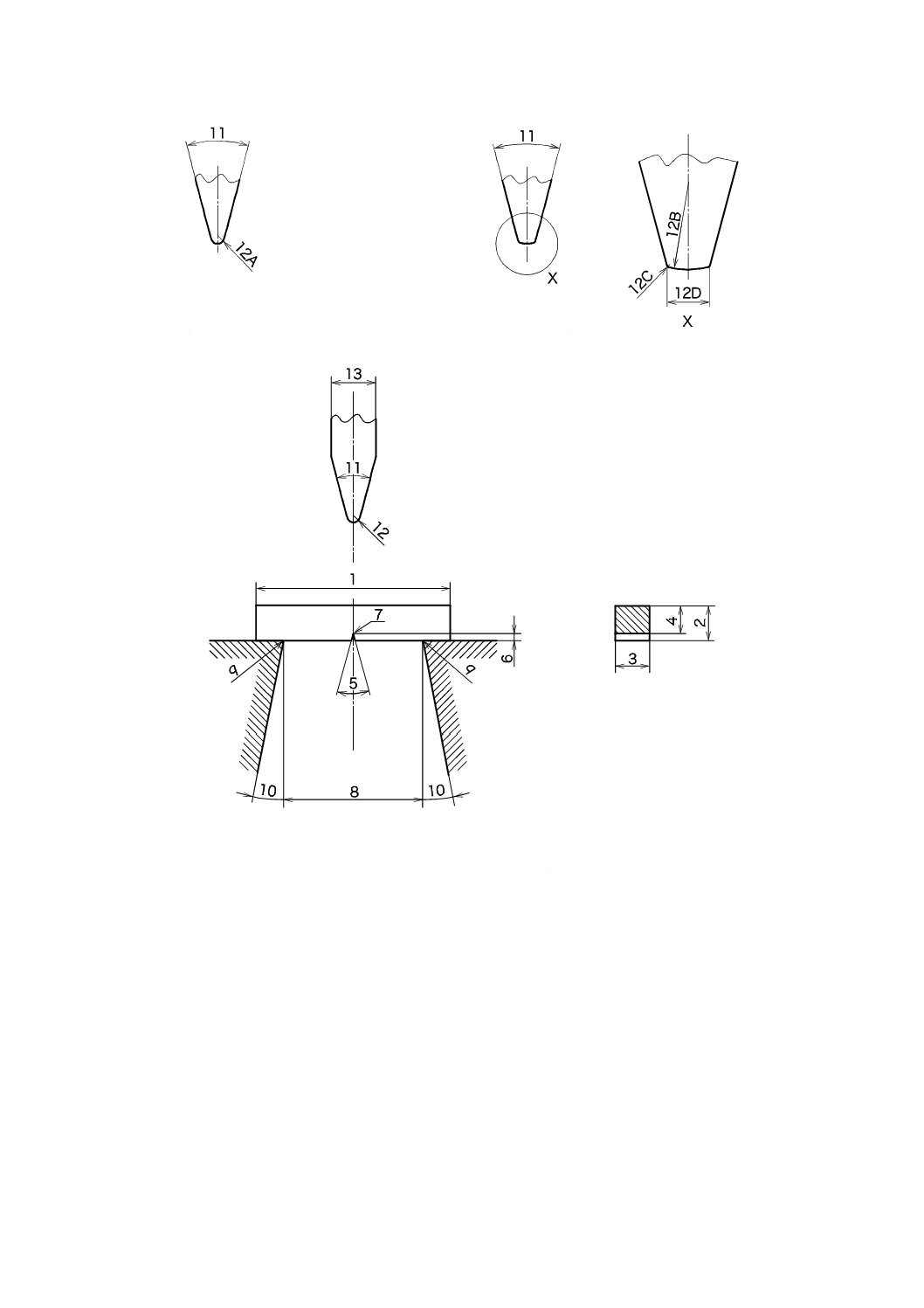
a) 2 mm刃先
b) 8 mm刃先
c) 上面図
注記 幾何学的特性については,表3を参照。
図2−試験機の刃先,載せ台及び受け台

15
B 7722:2018 (ISO 148-2:2016)
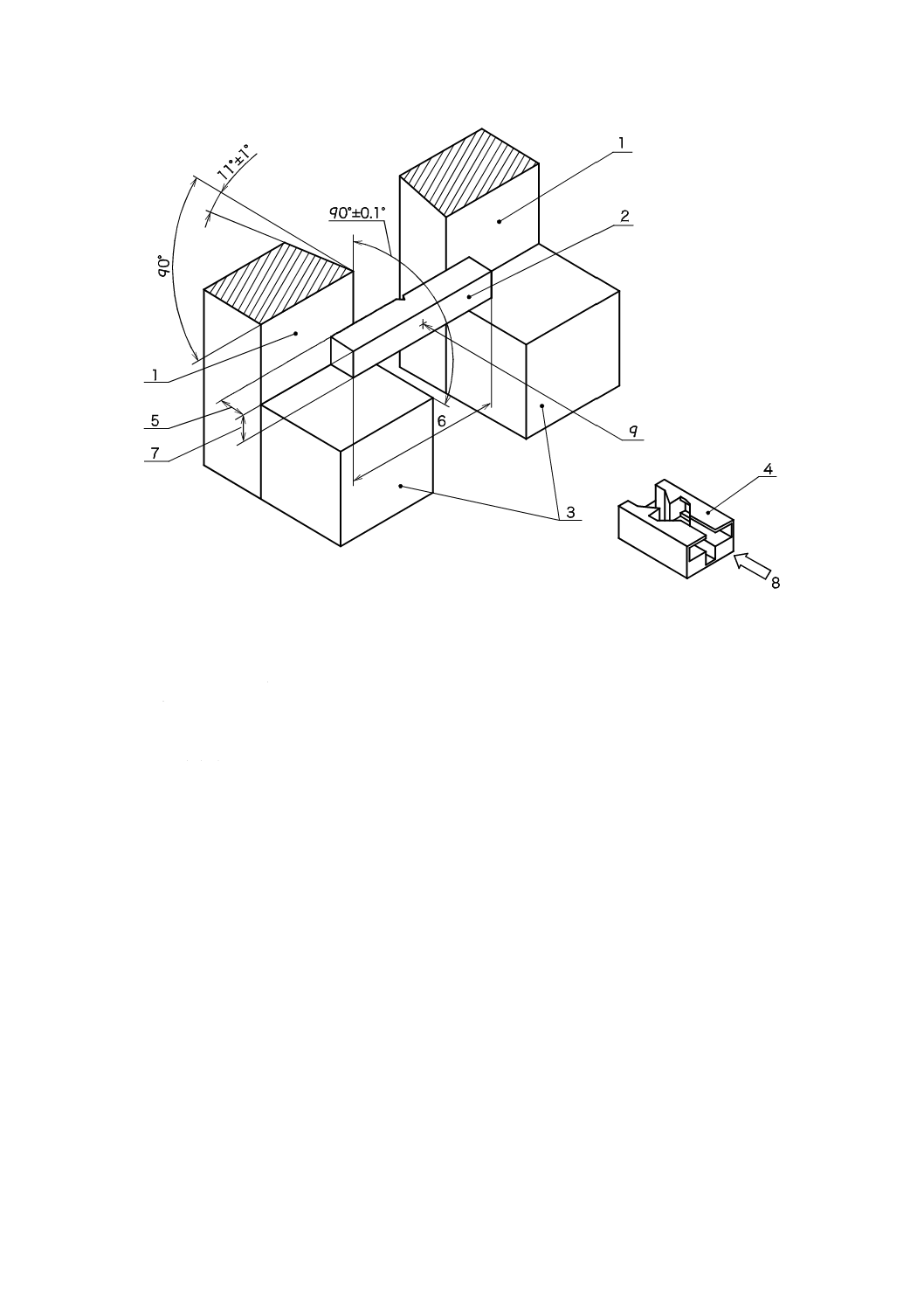
表3−衝撃刃,載せ台及び受け台の形状寸法
番号
名称
寸法
1
試験片長さL
JIS Z 2242参照
2
試験片幅 W
JIS Z 2242参照
3
試験片厚さB
JIS Z 2242参照
4
ノッチ下幅
JIS Z 2242参照
5
ノッチ角度
JIS Z 2242参照
6
ノッチ深さ
JIS Z 2242参照
7
ノッチ底半径
JIS Z 2242参照
8
受け台間の距離
0.20
00
.0
0.
40
+
mm
9
受け台の内角の丸み半径
0.50
00
.0
00
.1
+
mm
10
受け台の衝撃方向の逃げ角
11°±1°
11
刃先角度
30°±1°
12
衝撃刃の曲率半径
12A,又は12B参照
12A
2 mm衝撃刃の曲率半径
0.50
00
.0
00
.2
+
mm
12B
8 mm衝撃刃の曲率半径
8.00 mm±0.05 mm
12C
8 mm衝撃刃の肩半径
0.50
05
.0
25
.0
+
−
mm
12D
8 mm衝撃刃のエッジ幅
4.00 mm±0.05 mm
13
衝撃刃の幅
10 mm〜18 mm
16
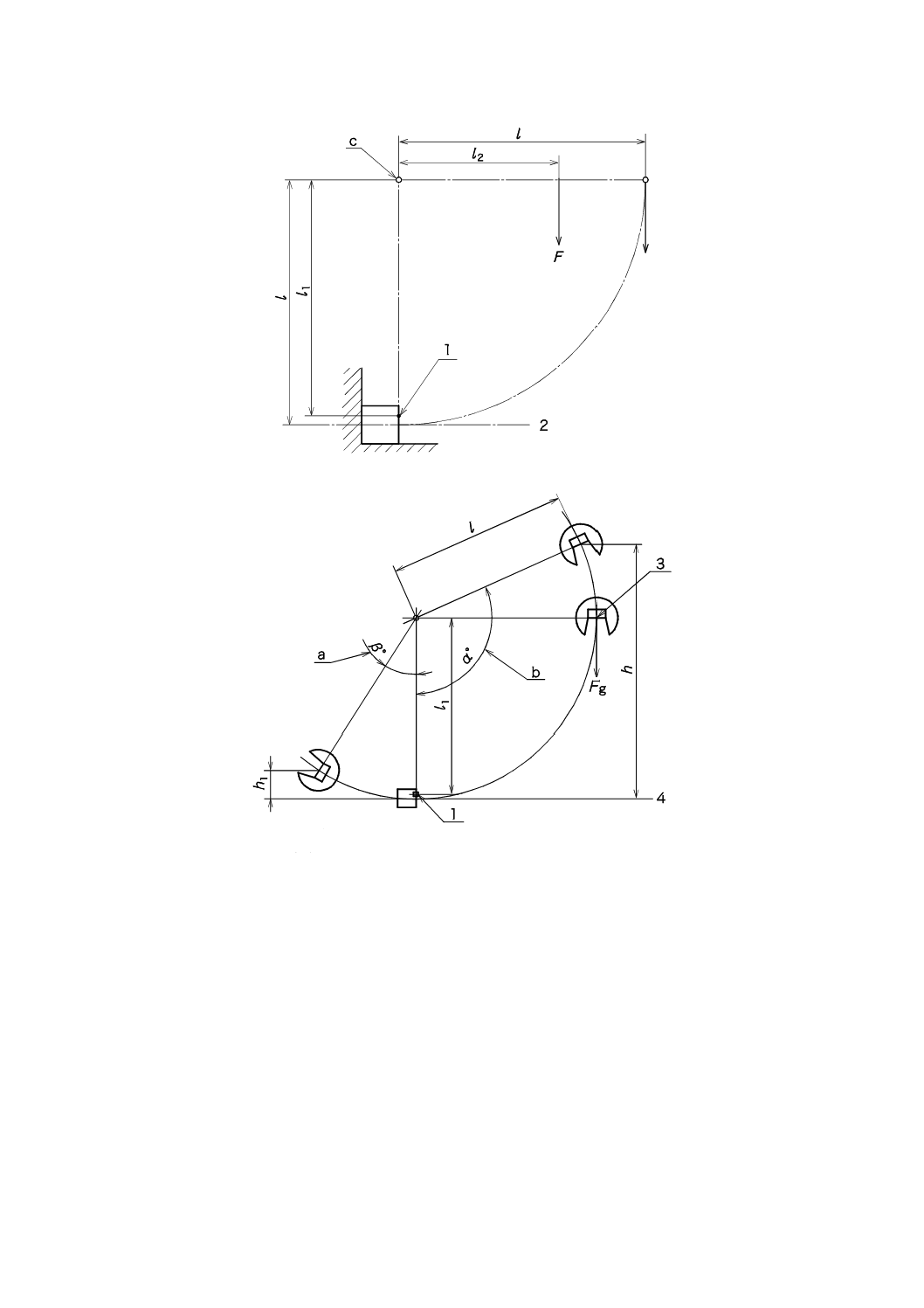
B 7722:2018 (ISO 148-2:2016)
1
受け台
2
標準サイズの試験片
3
載せ台
4
覆い(shroud)
5
試験片幅 W
6
試験片長さ L
7
試験片厚さ B
8
(振り子のスイング方向)
9
打撃点
図3−試験機の載せ台及び受け台の配置
17
B 7722:2018 (ISO 148-2:2016)
a) モーメントMの決定
b) エネルギーの決定に使用される用語の意味
1
打撃中心
2
試験片中心
3
振り子の打撃点
4
標準サイズ試験片の中心
a
振り上がり角度 β
b
持上げ角度 α
c
回転軸
図4−位置エネルギーの決定
18
B 7722:2018 (ISO 148-2:2016)
附属書A
(参考)
試験機の間接検証結果の測定不確かさ
A.1 概要及び一般要求事項
A.1.1 一般事項
この附属書は,試験機の間接検証結果に関する不確かさを決定する方法を提供する。GUM(計測におけ
る不確かさの表現ガイド)[1]の要件に適合するのであれば,その他の方法を用いてもよい。
この附属書は,BV(試験機のバイアス)及びuV(全体的な間接検証結果の不確かさ)の推測につながる
系統的なアプローチを提供する。これらのパラメータの値は,JIS Z 2242で記載されているように,検証
後の試験機で実施する試験の測定不確かさの計算に必要である。
注記 JIS Z 2242の附属書Eは,間接検証を通した,吸収エネルギーの尺度を提供するためのトレー
サビリティの方法を示す。
A.1.2 不確かさの免責事項
測定不確かさ分析は,測定結果の不一致の主な原因を特定するために有効である。
JIS B 7722の1999年版(以下,旧規格という。)に基づく製品規格及び材料特性データベースは,本質
的にこれまで考慮されていなかった測定不確かさの影響を受けている。したがって,測定不確かさを考慮
して製品の管理基準を見直すことは適切ではない。このため,特に顧客から別途指示されていない限り,
ここに記載された手順による不確かさの推定は参考情報でしかない。
この規格に定義する試験条件及び限界は,特に顧客との合意がない限り,測定不確かさを考慮して調整
するものではない。推定した測定不確かさは,特に顧客との合意がない限り,製品仕様への適合を評価す
るために測定した結果と合成するものではない。
代わりに,表示された公差を受入れの幅として考えるのがよい[2]。
このアプローチは,不確かさの概念が導入される前の測定値が暗黙のうちに認められた最大の測定不確
かさで得られていることを前提としている。この規格,JIS Z 2242及びJIS B 7740では,この最大の測定
不確かさをできる限り指定している。測定の不確かさは,記載されている値より小さい必要がある。
A.2 間接検証結果の不確かさへの寄与度
A.2.1 バイアス
間接検証の一次結果は,試験機のバイアスBV(偏り)の推定である。
R
V
V
KV
KV
B
−
=
····································································· (A.1)
ここに,
V
KV: 間接検証で用いる基準試験片の測定値の平均
KVR: 基準試験片の認証値
BVの絶対値は,7.5.2に適合しなければならない。
A.2.2 バイアスの不確かさ
バイアスの標準不確かさは,式(A.1)の二つの項の標準不確かさを組み合わせたものと等しい。
認証値KVRの標準不確かさであるuRMは,基準試験片の証明書に記載された拡張不確かさURMと同じく
証明書に記載の包含係数で除して求める。
V
KVに関わる不確かさは,次の式(A.2)によって推定する。
19
B 7722:2018 (ISO 148-2:2016)
V
V
V)
(
n
s
KV
u
=
······································································ (A.2)
ここに,
sV: nV個の基準試験片の試験結果の標準偏差
7.2は,間接検証を少なくとも5本の基準試験片で行う場合について規定している。
注記 式(A.2)は,試験片数nVが多くなれば測定不確かさを軽減できることを示している。
したがって,BVの標準不確かさであるu(BV)は,次の式(A.3)によって見積もる。
2
RM
2
V
V
V)
(
u
n
s
B
u
+
=
··························································· (A.3)
A.3 間接検証結果の合成不確かさの決定,uV
一般的に,バイアスは補正するものである。しかし,受け台とハンマ部品との摩耗によって,次回の間
接検証まで用いる一定のバイアスを定めることは難しい。これがしばしば測定されたバイアスが不確かさ
成分の一つとみなされ,間接検証結果の不確かさを求めるのに,バイアスそれ自体をバイアスの不確かさ
に合成する理由である。
2
V
V
2
V
)
(
B
B
u
u
+
=
································································· (A.4)
試験機で測定した吸収エネルギー値を補正するためには,BVを減じる。補正を行う前提として,バイア
スは厳密に求められ,その値が安定している必要がある。このためには,試験機のバイアスの安定性を証
明する必要があり,その試験機の性能に関する安定性の情報は一連の間接検証及び管理のための試験を実
施した後にだけ得ることができる。したがって,実際に補正を行うのは基準試験機に限定される可能性が
高い。
A.4 合成不確かさの拡張
JIS Z 2242の附属書Eでは,全体的な測定不確かさへの寄与成分の一つとしてuV値を使用する。合成標
準不確かさを拡張するには,個々の不確かさ寄与成分の自由度を有効自由度に合成する必要がある。uVの
自由度νVは,ウエルチ−サタスウェイトの式(Welch-Satterthwaite approximation)を用いて計算する。
B
4
V
RM
4
RM
B
V
4
4
V
V
)
(
v
B
v
u
v
KV
u
u
v
+
+
=
························································ (A.5)
ここに, νBの値: nV−1に等しい
νRMの値: 基準試験片の証明書による
検証試験片の数は,少なくとも5本であり,試験片の不均一さは無視できない。そのため,ほとんどの
場合,包含係数k=2を用いるほどに,有効自由度は大きくない。関係者の合意があればkに他の値を用い
てもよい。
A.5 BVとuVとの計算及び報告例
間接検証結果及びその分析の例を,表A.1に示す。三つの異なるエネルギーレベルの基準試験片を用い
て,直接検証後に推定される間接検証を実行した例であり,認証値KVR 123.8 J,拡張不確かさ3.4 J,自由
度30(証明書から得た値)の基準試験片が用いられている。
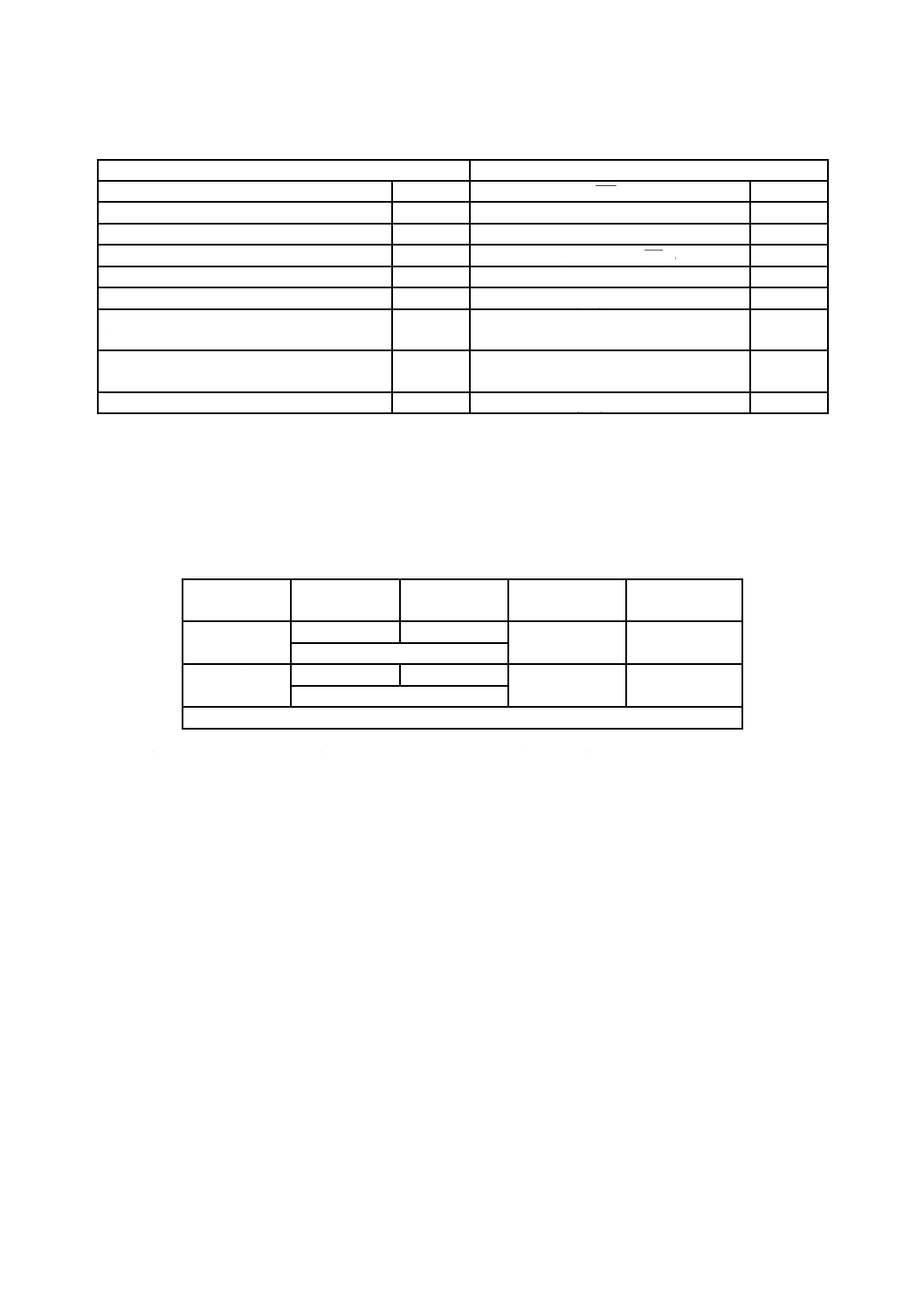
20
B 7722:2018 (ISO 148-2:2016)
表A.1−間接検証結果(例)
試験結果及び証明書のデータ
バイアスと不確かさの値の計算
試験片1
123.1 J
V
KV
119.4 J
試験片2
116.1 J
sV
4.7 J
試験片3
112.8 J
nV
5
試験片4
123.6 J
式(A.2)から:u(
V
KV)
2.1 J
試験片5
121.3 J
証明書から:自由度νRM
30
式(A.1)から:BV
−4.4 J
証明書から:
信頼の水準約95 %での拡張不確かさURM
3.4 J
式(A.3)から:u(BV)
2.7 J
vRM>10なので,標準不確かさuRMはURM/2
として計算できる。
1.7 J
式(A.4)から:uV
5.2 J
5本の試験片の自由度νB
4
式(A.5)から:vV
7
この間接検証の一次結果は,良好である。すなわち,バイアス(BV=−4.4 J)の絶対値は,7.5.2で設定
した上限を下回っている。uVを求めるのに必要なBVの値を確定できない場合には,BVの値をその不確か
さと合成する必要があるが,ここでは取り上げない。式(A.5)から,uVに対応する自由度は,7と計算され
る。検証結果は,表A.2に示すとおりに報告される。
表A.2−拡張測定不確かさU(KV)での結果KVの集計表
KVR
J
BV
J
u(BV)
J
νV
uV
J
123.8
−4.4
2.7
7
5.2
BVは確定していない
−a)
−
−
−
−
−
注a) この集計表の一行は,試験機の間接検証を行った各エネルギーレベルに対応する。
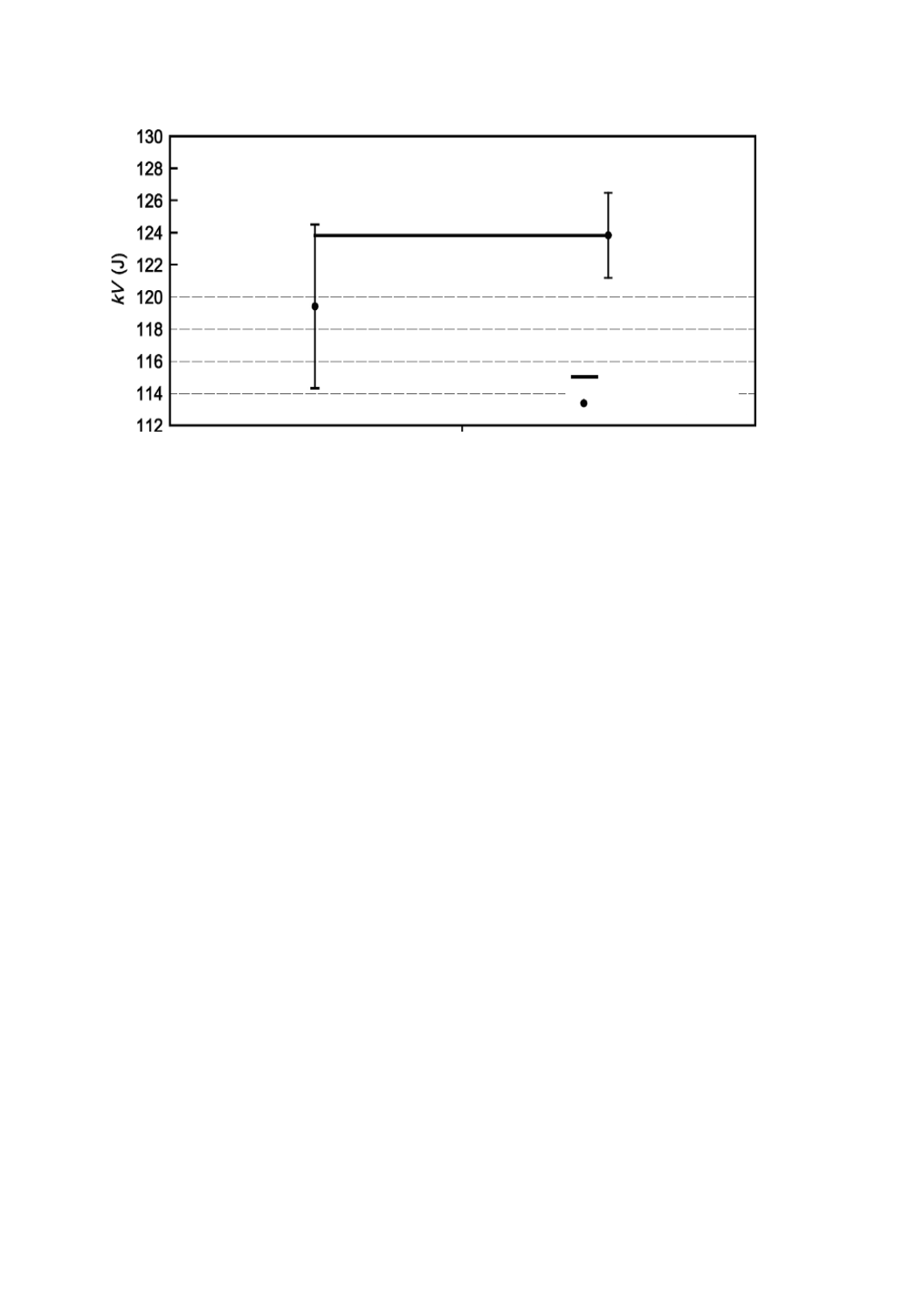
この結果の例を,測定吸収エネルギー値を測定バイアスで修正した結果とともに,図A.1に示す。間接
検証の不確かさは,u(BV)とBVの合成によるので,比較的大きい(uV=5.2 J)。バイアスが確定し,測定値
をこの値について補正するならば,不確かさは大幅に小さくなるであろう[u(BV)=2.7 J]。
21
B 7722:2018 (ISO 148-2:2016)
a) バイアスを補正していない吸収エネルギー b) バイアスを補正した吸収エネルギー
図A.1−間接検証による吸収エネルギーの測定値
認証値
測定値
22
B 7722:2018 (ISO 148-2:2016)
附属書B
(参考)
試験機の直接検証結果の測定不確かさ
B.1
適用範囲
直接検証は,試験機の一連の形状・寸法と機械的性質の確認による。これらの値の公称値との差が箇条
6の事項に完全に合致する試験機に対するバイアスに関連する。
理論的には,試験機の合成バイアスzは,式(B.1)によって見積もることができる。
S
H
l
l
V
E
C
A
R
z
+
+
−
+
+
+
+
+
=
)
(
1
··········································· (B.1)
ここに,
R: 刃先の半径ずれによる吸収エネルギーK(エネルギー単位:
以下同じ)のバイアス
A: 受け台と載せ台の形状のずれによるKのバイアス
C: 打撃中心のずれによるKのバイアス
E: 測定角度からのエネルギー計算によるKのバイアス
V: 衝撃速度のずれによるKのバイアス
(l−l1): 振り子長さと打撃中心との差異のずれによるKのバイアス
H: 摩擦損失の補正によるKのバイアス
S: アナログ目盛又はデジタル表示から読み取ったエネルギー
値のバイアスによるKのバイアス
吸収エネルギーに対する因数(R,A,C,E,V,l−l1,H及びS)の影響は,それらが直接検証の許容
値内であり(箇条6を参照),また,試験を標準的な手順(JIS Z 2242を参照)に従って実施する場合は,
小さいと推定される。しかし,zに寄与する個々の因数は不確かさを含んでいる。全ての量が独立してい
ると仮定すると,zの合成標準不確かさは,式(B.2)によって与えられる。
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
2
1
2
2
2
2
2
2
c
S
u
H
u
l
l
u
V
u
E
u
C
u
A
u
R
u
z
u
+
+
−
+
+
+
+
+
=
···· (B.2)
式(B.1)及び式(B.2)の全ての要素が確実かつ定量的に評価できるわけではない。そのためこれに代えて,
試験機の合成バイアス及び関係する不確かさを評価するために,基準試験片による間接検証を用いる。
しかし,直接検証において,異なる要素の信頼性を考慮することが重要であることに変わりはない。こ
れが,この附属書で試験機の直接検証中に実施する数多くの測定に関する不確かさを論じている理由であ
る。
通常,証明書の認証値の不確かさは,信頼の水準約95 %で規定される。したがって,合成標準不確かさ
uRMは,適切な包含係数kを用いて拡張しなければならない。使用する包含係数は,合成不確かさに関係
する自由度に左右されるが,これはウエルチ−サタスウェイトの式を用いて計算できる。典型的なケース
では,有効自由度は,20以上であり,包含係数k=2を使用できる。
注記 測定不確かさを評価するその他の方法は,それらがGUMの要求事項に適合するのであれば適
応可能であり,許容できる(参考文献[1]を参照)。
公称値と測定値の偏差との和と,この偏差の測定不確かさが箇条6で許容される公差内にあるかどうか
を,検証するために,最終的な目的は,直接的に検証された特性について信頼できる測定不確かさの推定
を行うとしている。
不確かさの免責事項に関する注記:測定不確かさ分析は,測定結果の不一致の主な原因を特定するため
に有効である。旧規格に基づく製品標準及び材料特性データベースは本質的にこれまで考慮されていなか
った測定不確かさの影響を受けている。したがって,測定不確かさを考慮して製品の管理基準を見直すこ
23
B 7722:2018 (ISO 148-2:2016)
とは適切ではない。このため,特に顧客から別途指示されていない限り,この手順による不確かさの見積
りは参考情報でしかない。
この規格に定義する試験条件及び限界(範囲)は,特に顧客との合意がない限り,測定不確かさを考慮
して調整するものではない。推定した測定不確かさは,特に顧客との合意がない限り,製品仕様への適合
を評価するために測定した結果と合成するものではない。
B.2
特定の測定項目の不確かさ
B.2.1 打撃中心
振り子は,振り子長さlが,回転軸中心から打撃中心までの距離l1と等しくなるように構成されている。
l1は,式(B.3)による。
2
2
1
π
4
t
l
g
=
················································································ (B.3)
ここに,
l1: 回転軸中心から打撃中心までの距離(m)
t: 3回の測定によって求めた平均周期
Tの測定は,手動又は校正済みの機器で実施する。スイング回数を50回の場合を例とし,現実的な測定
不確かさu(T)=0.1秒を用いるものとする。その後,l1の不確かさを,式(B.4)によって計算する。
)
(
50
)
π
4(
2
)
(
2
2
1
T
u
T
l
u
×
=
g
····························································· (B.4)
振り子長さlは,ノギス等の測長器で測定する。lは,直接的に測定できないことが多いため,3か所の
部分的な測定L1,L2及びL3で決定する。すなわち,式(B.5)による。
)
(
)
(
)
(
)
(
3
2
2
2
1
2
L
u
L
u
L
u
l
u
+
+
=
·················································· (B.5)
測定範囲の短い測長器(L1,L3などの測定)は,通常,0.1 mmの測定不確かさがある。測定範囲の長い
測長器(ここでは,L2の測定)は,通常は0.3 mmの測定不確かさがある。この場合,合成不確かさu(l)
=0.3 mmである。
注記 これらの値は,通常,使用機器の校正証明書に記載されている。
打撃中心までの長さと振り子長さとの差(l−l1)の測定不確かさは,上記の不確かさを用いて式(B.6)で
計算する。
)
(
)
(
)
(
1
2
2
1
l
u
l
u
l
l
u
+
=
−
··························································· (B.6)
例 表B.1参照。
振り子長さl=800.0 mmについて,測定値をT=89.7 s,l1=799.75 mmとして計算し,かつ,上記の長さ
と時間測定の不確かさを用いると,不確かさu(l−l1)として1.07 mmを得る。これは,許容値(0.5 %)内
である。
表B.1−打撃中心位置(距離)の測定不確かさの量
量
推定値
不確かさ
標準
不確かさ
感度係数
(l−l1)の不確かさ
への寄与成分
mm
値
分布
タイプ
l
800.0 mm
0.3 mm
正規
0.3 mm
1 mm/mm
0.3
T
89.7 s
0.1 s
く(矩)形
0.058 s
17.83 mm/s
1.03
合成不確かさu(l−l1)
1.07
信頼の水準95 %に対応するk=2を用いた拡張不確かさ
2.14
24
B 7722:2018 (ISO 148-2:2016)
B.2.2 衝撃速度
衝撃速度は,振り子長さ及び持上げ角度から計算される試験機の一般的なパラメータである。直接検証
に関する規格で規定する許容誤差は比較的大きい。衝撃速度を計算する個々の測定の相対不確かさは,極
めて小さいため,この値の不確かさの計算は必要ない。
B.2.3 吸収エネルギー計算
吸収エネルギーの計算については,式(B.7)が有効である。
)
cos
(cos
2
α
β
l
F
KV
−
×
×
=
························································ (B.7)
ここに, KV: 振り上がり角度から計算した吸収エネルギー(J)
F: 振り子を水平に保ったときl 2の位置で測定される振り子によ
って生じる力(N)
l2: 回転軸中心から力Fが加わる点までの距離(m)
α: 持上げ角度(°)
β: 振り上がり角度(°)
この規格では,上記のパラメータについて特定の公称値及び範囲を定めていない。したがって,測定値
から計算するエネルギーの不確かさは,これらのパラメータに関するバイアスはなく,測定不確かさだけ
により,式(B.8)によって表される。
)
(
)
(
)
(
)
(
2
2
2
2
2
2
2
2
2
2
2
1
α
u
α
KV
β
u
β
KV
l
u
l
KV
F
u
F
KV
u
∂∂
+
∂∂
+
∂∂
+
∂∂
=
····· (B.8)
式(B.7)から,式(B.9)〜式(B.12)が計算できる。
α
l
F
α
KV
sin
2×
×
=
∂
∂
································································· (B.9)
β
l
F
β
KV
sin
2×
×
−
=
∂
∂
······························································ (B.10)
)
cos
(cos
2
α
β
l
F
KV
−
×
=
∂
∂
························································· (B.11)
)
cos
(cos
2
α
β
F
l
KV
−
×
=
∂
∂
························································· (B.12)
個々の不確かさ寄与は,式(B.13)で与えられる。
)
(
)
(
)
(
)
(
)
(
2
2
2
ftd
2
D
u
S
u
t
u
F
u
F
u
+
+
+
=
······································· (B.13)
ここで,
3
)
(
temp
a
t
u
×
=δ
······································································· (B.14)
ここに,
δ: 力計製造業者から提供される温度係数
atemp: 基準温度との差
3
)
(
stab
a
S
u
=
··········································································· (B.15)
ここで,astabは力計の長期安定性である。
dev
-
int
)
(
a
D
u
=
········································································· (B.16)
また,aint-devは内挿誤差である。

25
B 7722:2018 (ISO 148-2:2016)
2
2
2
Δ
)
(
l
l
l
u
=
··········································································· (B.17)
ここに,
Δl2: 回転軸中心から力Fが加わる点までの距離測定の不確かさ
注記 Δl2は,l2の測定に使用する測長器の校正証明書から得る。これは,Δl2の最低限の見積りとな
る。
例 表B.2参照。
a) 力
力計の測定不確かさ
Uftd=0.12 % (k=2)
力計の長期安定性
astab=0.05 %
力計の温度係数
δ=0.01 %
基準温度からの差
atemp=5.0 ℃
力計の内挿校正式(一次)を用いたときの測定不確かさ aint-dev=0.05 %
750.1 mmの位置で測定された力 F=206.70 N
力の不確かさを合成した寄与は0.1 %に達する。そのため,206.70 Nの合成標準不確かさu(F)は,
0.21 Nである。
b) 振り子長さ
距離測定の不確かさ Δl2=0.3 mm
振り子長さ l=l2=750.1 mm
(距離l2の不確かさは,測定器を慎重に取り扱えばΔl2=±0.3 mmで適用できる。)
c) 角度
角度測定の不確かさ:Δα=Δβ=0.2°,振り上がり角度:β=120°,持上げ角度:α=160°
式に適用する前に度をラジアンに,ミリメートルをメートルに変換する点に注意が必要である。
表B.2−吸収エネルギー計算の測定不確かさの量
量
推定値
不確かさ
標準
不確かさ
感度係数
KVの不確かさ
への寄与成分
J
値
分布
タイプ
F
206.7 N
0.21 N
正規
0.21 N
0.33 J/N
0.07
l
750.1 mm
0.3 mm
く(矩)形 0.17 mm
91 J/m
0.016
β
120°
0.2°
く(矩)形
0.12°
134 J/rad
0.27
α
160°
0.2°
く(矩)形
0.12°
53 J/rad
0.11
合成不確かさ
0.30
信頼の水準95 %に対応するk=2を用いた拡張不確かさ
0.6
B.2.4 アナログ目盛又はデジタル目盛からの吸収エネルギー読取値
目盛の構造によるバイアスSは,試験機のアナログ目盛又は試験機PCに表示された式(B.18)で示すよう
に,デジタル値の吸収エネルギーと計算エネルギーとの差である。Sは,直接検証結果を用いて個々の試
験機に関して推定することができる。
calc
SK
K
S
−
=
········································································ (B.18)
このとき,Sは計算エネルギーKcalc(J)と表示吸収エネルギーKS(J)との差である。
有効不確かさu(S)は,式(B.19)によって計算する。
()
()
(
)
calc
2
S
2
K
u
K
u
S
u
+
=
························································· (B.19)

26
B 7722:2018 (ISO 148-2:2016)
ここに,
()
3
2
S
a
K
u
=
········································································· (B.20)
このとき,aは目盛の分解能である。
例 表B.3参照。
アナログ目盛の読み値
KS=68.0 J
表示器の分解能
a=0.5 J
測定角度から計算したエネルギー値
Kcalc=68.17 J
測定角度から計算したエネルギーの不確かさ u(Kcalc)=0.38 J
表B.3−表示吸収エネルギーの差の測定不確かさの量
量
推定値
不確かさ
標準
不確かさ
J
感度係数
Sの不確かさ
への寄与成分
J
値
分布
タイプ
KS
68.0 J
0.5 J
く(矩)形
0.14
1
0.14
Kcalc
68.17 J
0.3 J
正規
0.3
1
0.3
合成不確かさ
0.33
信頼の水準95 %に対応するk=2を用いた拡張不確かさ
0.7
27
B 7722:2018 (ISO 148-2:2016)
附属書C
(参考)
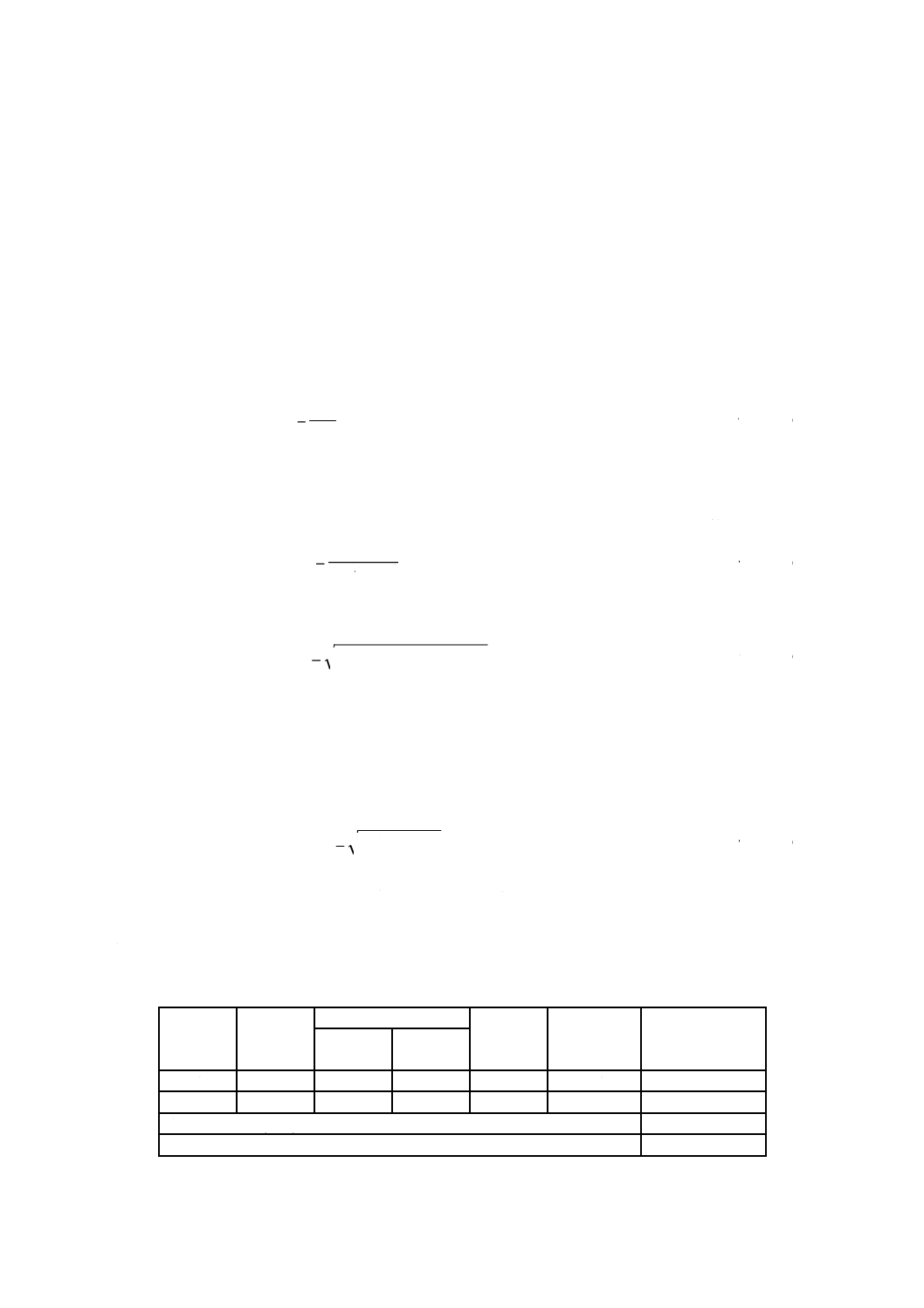
ジグを使用した試験機の幾何学的特性の直接検証方法
C.1 適用範囲
この附属書は,ジグを使用した試験機の幾何学的特性の直接検証方法を説明する。
次の特性を検証できる。
− 受け台の対称面における刃先の位置
− 振り子の回転軸の水平度
− 振り子のアームと回転軸との垂直度
− 刃先と振り子のアームのアライメント
− 刃先面と試験片との垂直度
この方法は,全ての機械,特に機枠に基準面がない試験機に適用することができる。
C.2 ジグ
ジグの形状及び寸法を図C.1に示す。ジグには,2か所の使用位置(A及びB)に対応した二つの端部
がある。
C.3 手順
ジグを使用する前に,水準器を用いて次の二つの特性を検証することが必要である。
− 載せ台面の水平度
− 受け台面と載せ台面との垂直度
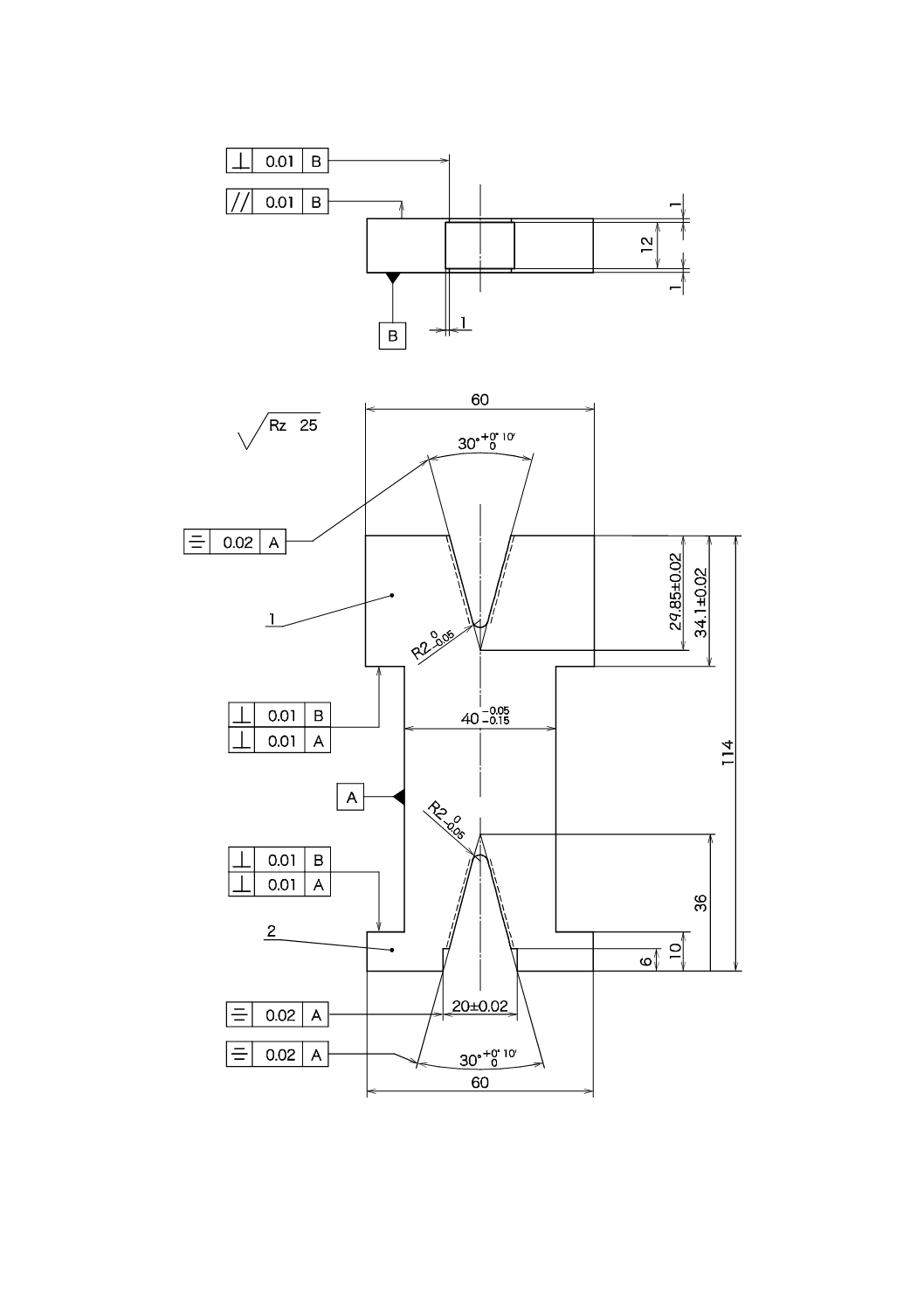
ジグは2か所(A及びB)で用いる。図C.2で示すように,位置Aから位置Bへの流れは刃先の移動30
mmに対応する。
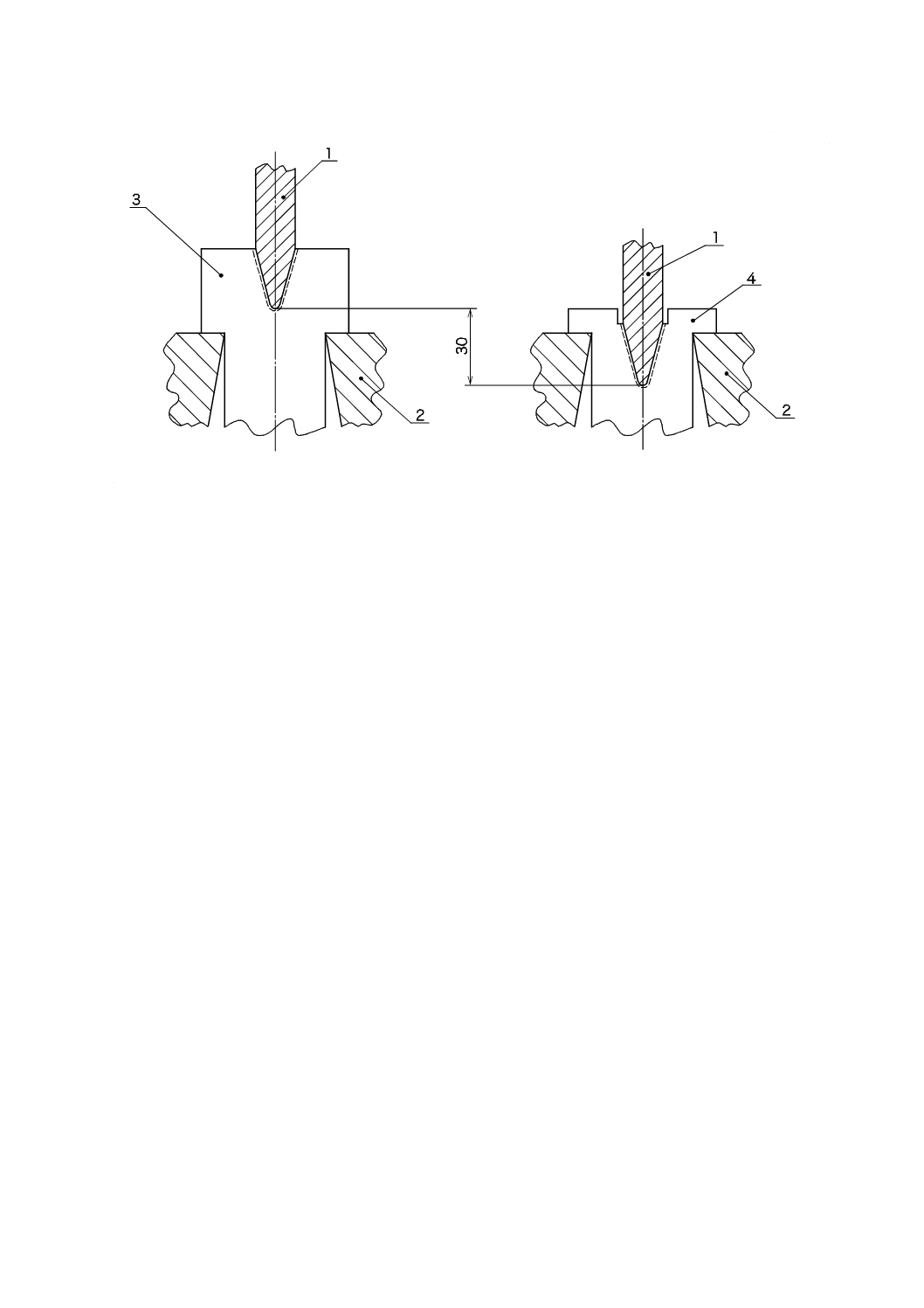
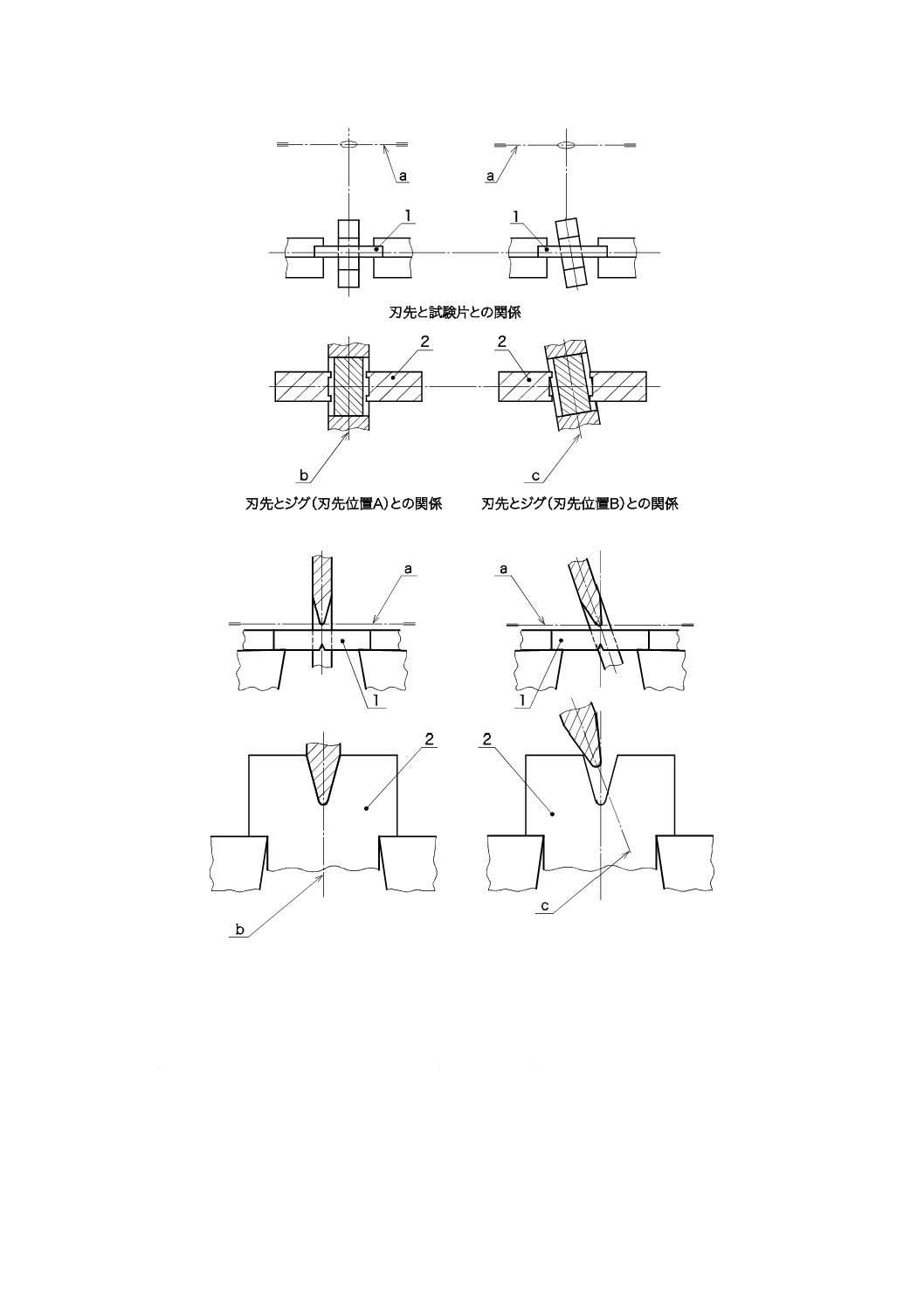
図C.3及び図C.4に,C.1で定義した特性を検証するために,ジグを使用する方法を示す。
28
B 7722:2018 (ISO 148-2:2016)
単位 mm
注記 材料は,熱膨張率の低い,ステンレス鋼又は耐食性を向上させた鋼。
例 SU420J2 (55 HRC),SUJ2 (62 HRC)
図C.1−ジグ
29
B 7722:2018 (ISO 148-2:2016)
単位 mm
a) 刃先位置A
b) 刃先位置B
1
刃先
2
アンビル
3
ジグの端部A
4
ジグの端部B
図C.2−刃先の移動30 mmに対応する位置Aから位置Bへの変化
30
B 7722:2018 (ISO 148-2:2016)
a) 刃先部の上面図
b) 刃先部の側面図
1
試験片
2
ジグ
3
端部A
4
端部B
a
振り子の軸
b
試験片の縦軸に垂直の振り子スイングの面
c
試験片の縦軸に非垂直の振り子スイングの面
注記1 振り子のスイング面は,試験片の縦軸に垂直ではない(右側の図)。
注記2 刃先がジグに片当たりしている場合には,ずれがある(ジグの端部Aの左上及び右下部分)。
図C.3−図C.1に図示したジグの適用
31
B 7722:2018 (ISO 148-2:2016)
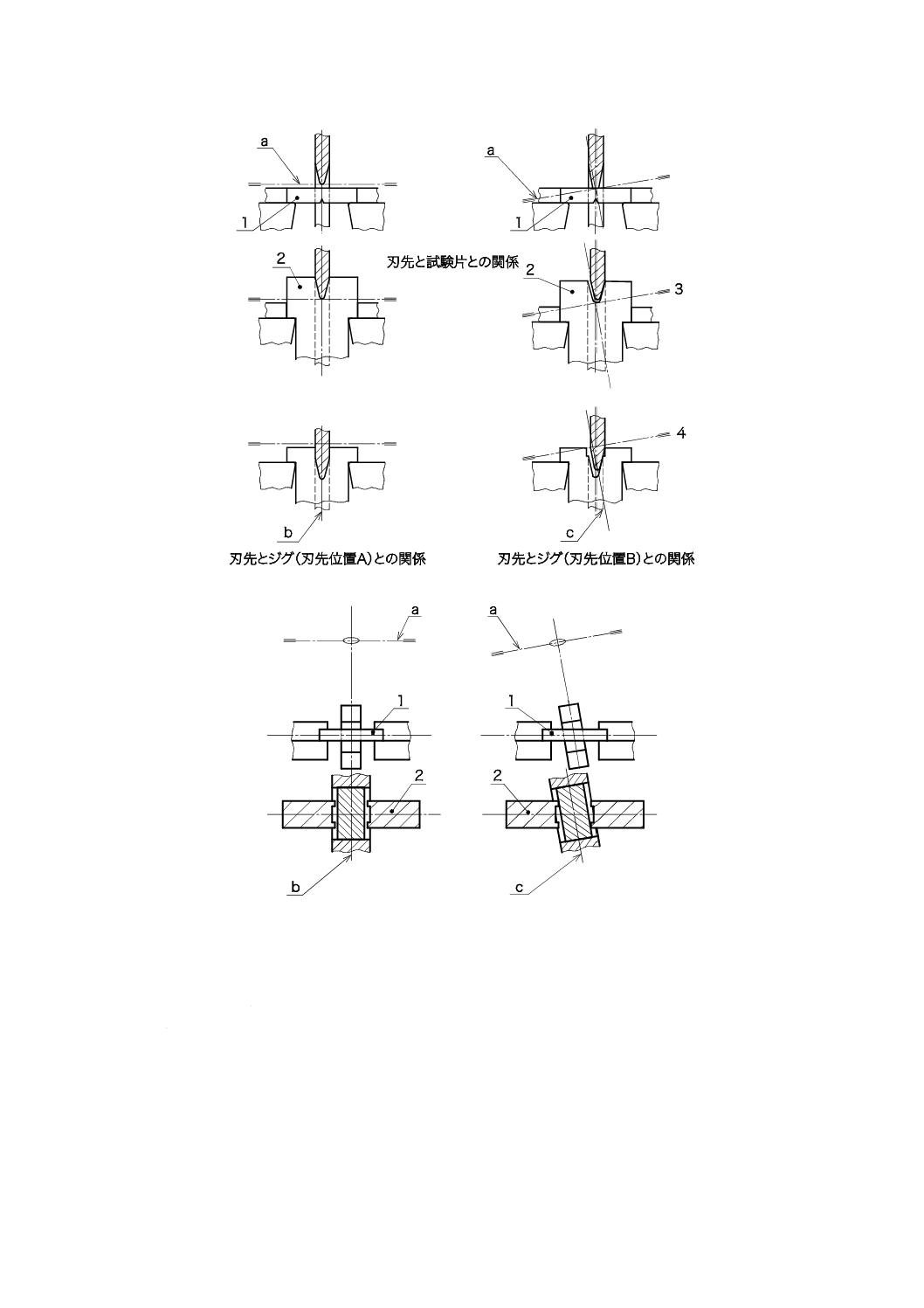
a) 刃先部の側面図
b) 刃先部の上面図
1
試験片
2
ジグ
a
振り子の軸
b
振り子のスイング面におけるハンマの対称面
c
振り子のスイング面ではないハンマの対称面
注記1 ハンマの対称面は,振り子のスイング面にはない(右側の図)。
注記2 刃先がジグに片当たりしているか,衝撃刃の先端がジグの底部に接触していない場合には,
ハンマの対称面にずれがある。
図C.4−図C.1に図示したジグの応用例
32
B 7722:2018 (ISO 148-2:2016)
附属書JA
(参考)
試験機の検証に用いる検査具
JA.1 検査具の寸法
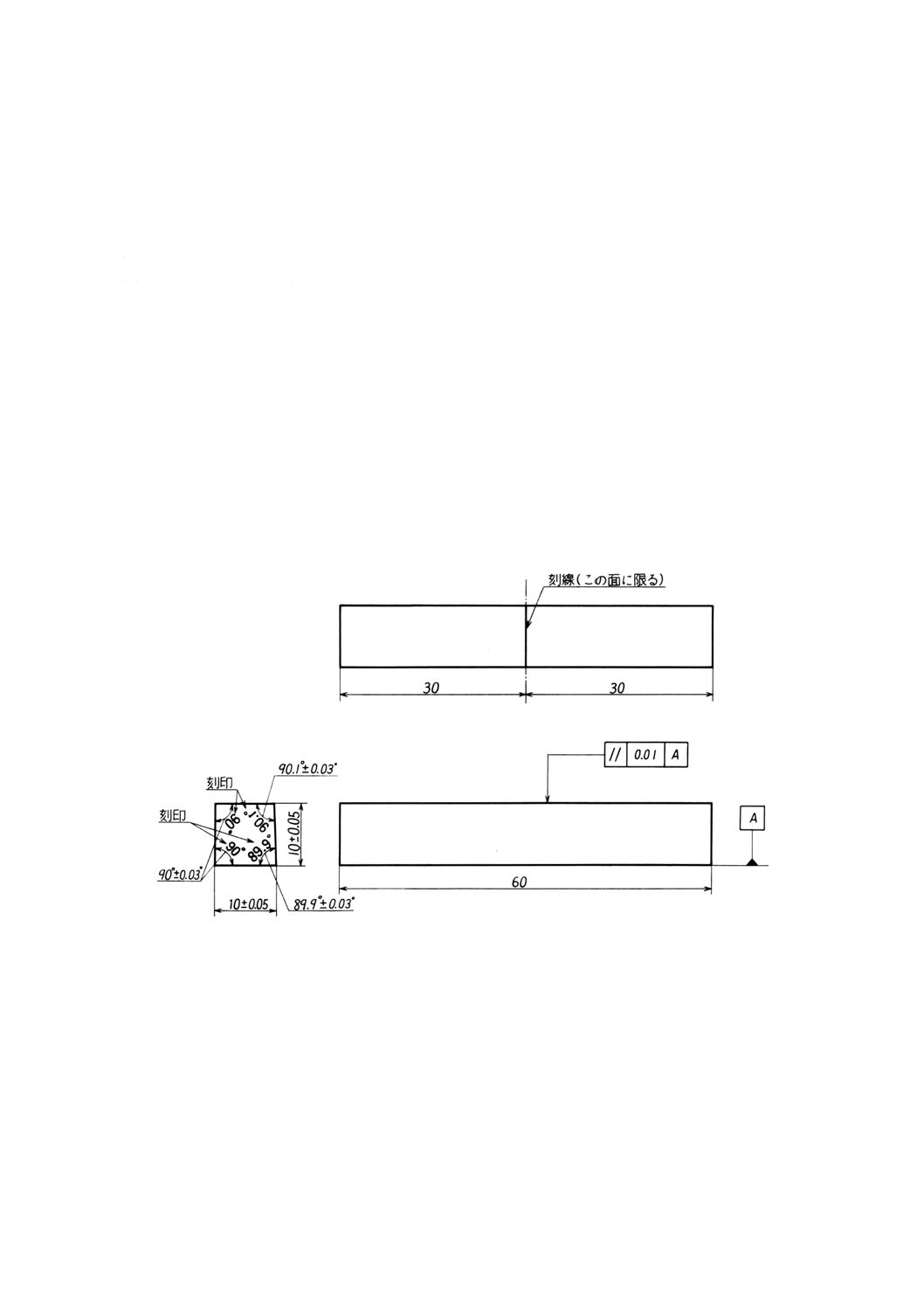
試験機の検証に用いる検査具の寸法を図JA.1〜図JA.5に示す。
a) 棒状ゲージ(図JA.1) 衝撃刃の刃縁・受け台と載せ台の検証に使用する。衝撃刃の刃縁が,試験片
の厚さ方向全体に接触することを,光明丹などを用いて検証する場合に使用する(6.3.6参照)。左右
の載せ台面の平行,左右の受け台面の平行,載せ台と受け台との面角度を,光明丹などを用いて検証
する場合に使用する(6.5.2及び6.5.3参照)。
b) 1号板状ゲージ(図JA.2) 衝撃刃の中心と両受け台間の中心との差を光明丹などを用いて検証する場
合に使用する(6.3.7参照)。受け台の距離の検証に使用する(6.5.1,図2及び表3参照)。
c) 2号板状ゲージ(図JA.3) 受け台の角度,内角の丸みの検証に使用する(図2及び表3参照)。
d) 3号板状ゲージ(図JA.4) 2 mm衝撃刃の形状の検証に使用する(図2及び表3参照)。
e) 4号板状ゲージ(図JA.5) 8 mm衝撃刃の形状の検証に使用する(図2及び表3参照)。
単位 mm
図JA.1−棒状ゲージ
33
B 7722:2018 (ISO 148-2:2016)
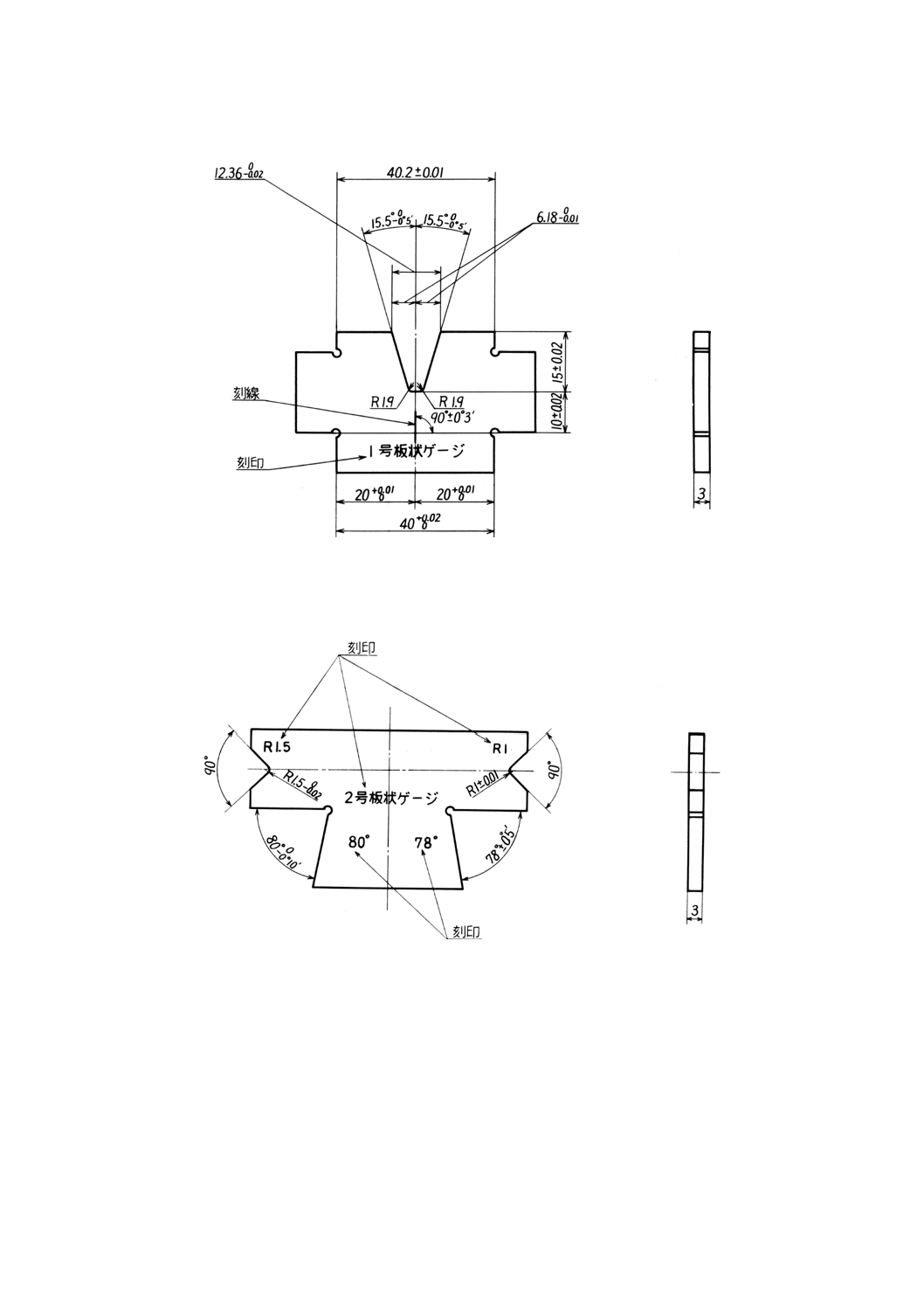
単位 mm
図JA.2−1号板状ゲージ
単位 mm
図JA.3−2号板状ゲージ
34
B 7722:2018 (ISO 148-2:2016)
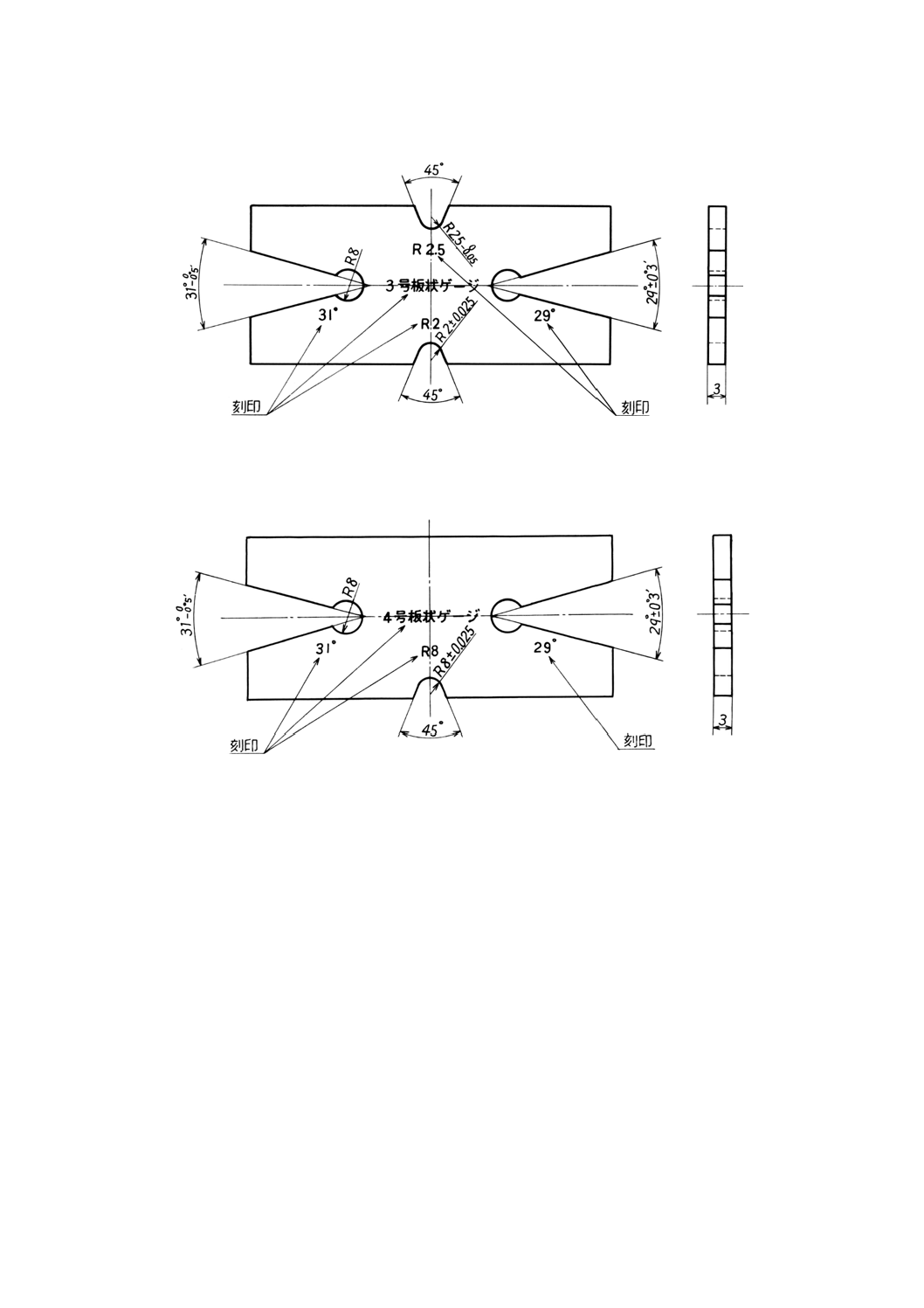
単位 mm
図JA.4−3号板状ゲージ
単位 mm
図JA.5−4号板状ゲージ
35
B 7722:2018 (ISO 148-2:2016)
参考文献
[1] ISO/IEC Guide 98-3,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995)
[2] JCGM 106,Evaluation of measurement uncertainty−The role of measurement uncertainty in conformity
assessment
[3] WEHRSTEDT A., &PATKOVSZKY I.News in the field of standardization about verification and calibration of
materials testing machines, May 2001. EMPA Academy, 2001
[4] YAMAGUCHI Y., TAKAGI S., NAKANO H. Effects of anvil configurations on absorbed energy. In: Pendulum
Impact Testing: A Century of Progress (eds.Siewert, T.A. and Manahan,M.P.), ASTM International STP 1 380,
2000年, pp. 164−180
[5] REVISE G. Influence des parametres dimensionnels du mouton pendule. Bulletin BNM. 1982, 47 pp. 29−39
[6] ISHINO J., SHIN S., NAGAI S., YANO H. Error evaluation of Charpy impact test. Keiryo Kenkyujyo Hokoku.
1992, 41(2) pp. 97−102
[7] TAKAGI S., & YAMAGUCHI Y. Uncertainty analyses of reference specimens for the verification of Charpy
impact test machines J. Material Testing Research Association of Japan. 2003, 48(4) pp. 250−254
[8] GERBER S., & HANSEL G. Determination of Uncertainty of Measurements in Calibration of Impact Testing
Machines. Proceedings of the EUROLAB International Workshop,17 to18 May 2001, Dubendorf,Switzerland
[9] GERBER S. Kalibrierung von Pendelschlagwerken und deren Messunsicherheit Werkstoffprüfung 2005
Deutscher Verband für Materialforschung und -prüfung e.V. (DVM) 1-2 December 2005 Berlin, Germany