B 7071-1:2015
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 原理······························································································································· 1
5 測定装置························································································································· 2
6 測定試料························································································································· 3
7 測定方法························································································································· 4
7.1 測定場所の状態 ············································································································· 4
7.2 測定 ···························································································································· 4
8 表示······························································································································· 6
9 試験報告書 ······················································································································ 6
附属書A(参考)主分散,アッベ数,部分分散及び部分分散比の算出方法 ······································· 7
附属書B(参考)任意波長に対する屈折率の算出方法 ·································································· 9
附属書C(参考)温度,湿度及び気圧に対する,屈折率の補正方法··············································· 11
B 7071-1:2015
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本光学硝子工業会(JOGMA)
及び一般財団法人日本規格協会(JSA)から,一般社団法人日本光学硝子工業会のJOGIS 01を基に作成し
た工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,
経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 7071の規格群には,次に示す部編成がある。
JIS B 7071-1 第1部:最小偏角法
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 7071-1:2015
光学ガラスの屈折率測定方法−第1部:最小偏角法
Measuring method for refractive index of optical glass-
Part 1: Minimum deviation method
1
適用範囲
この規格は,最小偏角法によって光学ガラスの屈折率を測定する方法について規定する。
注記 ここでの屈折率は空気中の相対屈折率をいう。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 7090 光学及び光学機器−基準波長
JIS Z 8000-1 量及び単位−第1部:一般
JIS Z 8120 光学用語
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS Z 8120及びJIS Z 8000-1による。
4
原理
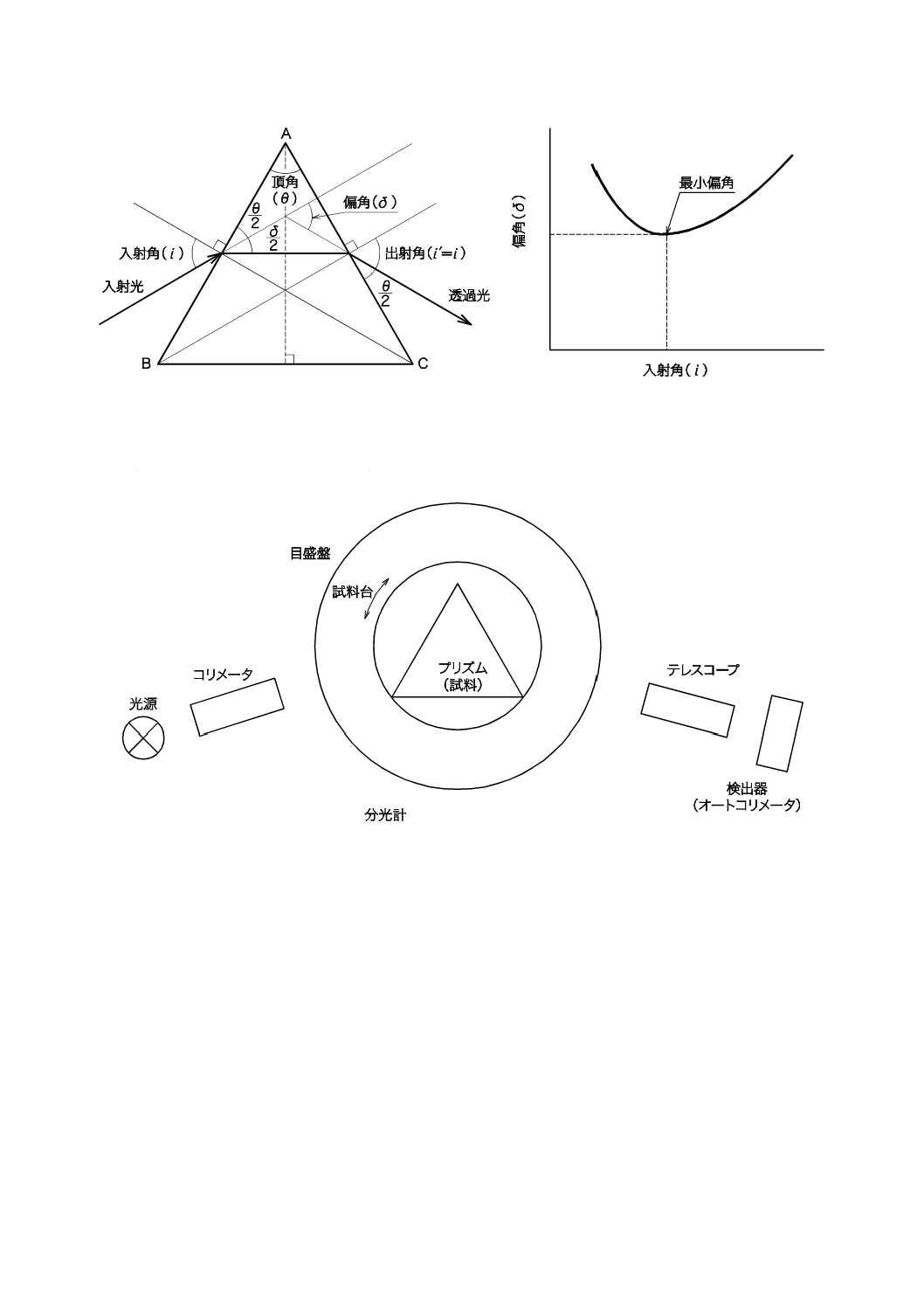
図1に示すように,光がプリズム(試料)の面ABに入射角(i)で入射し,面ACから出射角(i')で
光が透過する。この入射光と透過光とがなす角度を偏角(δ)という。偏角は,入射角を変化させると変化
し,ある入射角において,偏角が最小になる。この最小となった偏角を最小偏角という。最小偏角の場合
は,入射角(i)と出射角(i')とが等しくなる。最小偏角及びプリズム(試料)の頂角(θ)を測定し,屈
折率を算出する。
2
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1−最小偏角法原理(図は最小偏角の状態)
5
測定装置
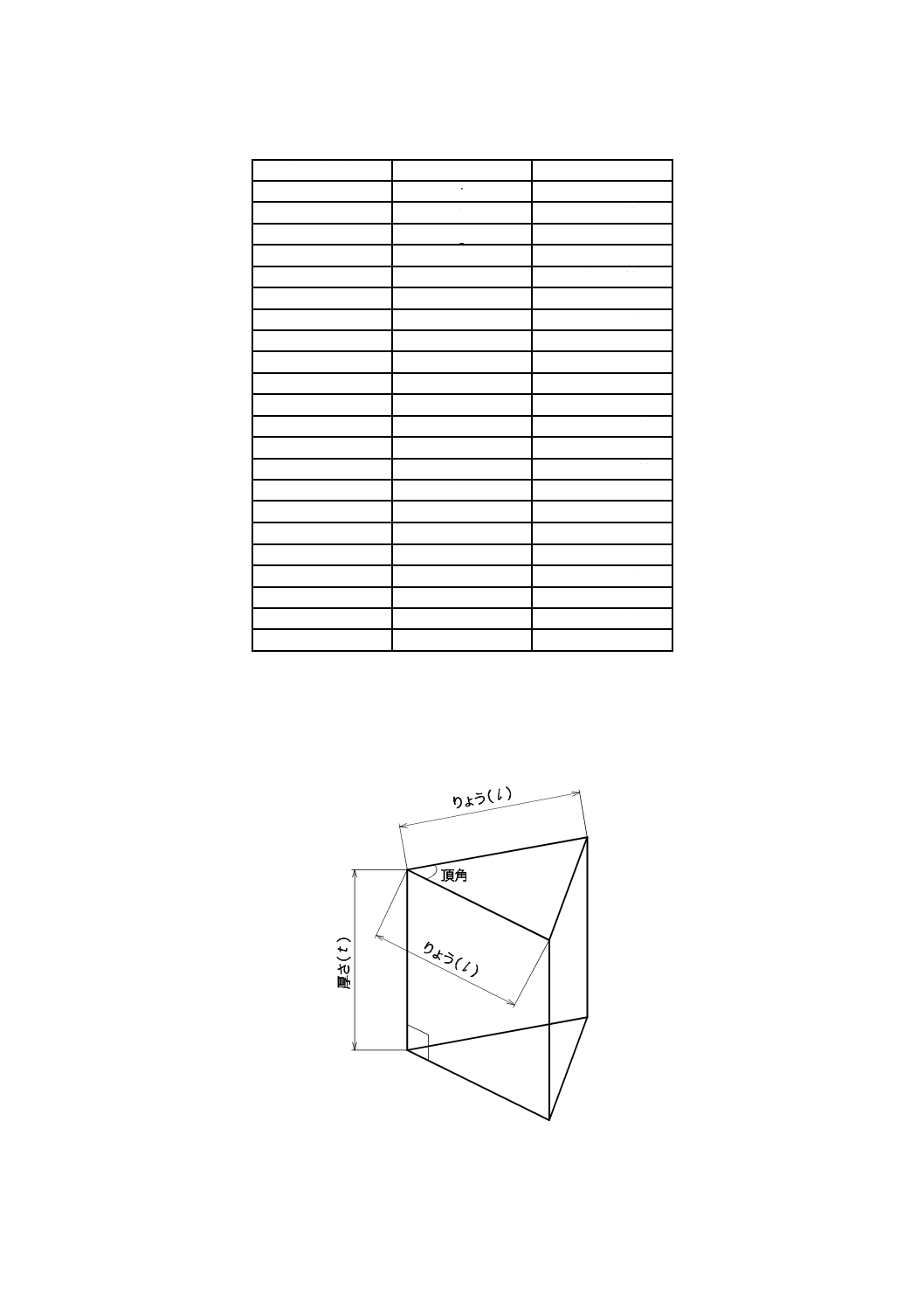
測定装置は,図2に示した機器で構成し,詳細は次による。
図2−最小偏角法測定装置
a) 分光計 分光計の角度読み取りは,目盛盤の読み取りが1秒のものを用いる。
b) 光源 光源は,JIS B 7090に規定する,水銀,水素,ヘリウム,ルビジウム,セシウム及びカドミウ
ムの各放電管,He-Neレーザ,並びにNd:YAGレーザを用い,表1に示すスペクトル線を測定波長と
することが望ましい。
なお,表1に規定していない波長の光源でも測定することは可能であるが,波長幅などによる波長
誤差を確認して使用する必要がある。
3
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−光源の波長及びスペクトル線
波長(nm)
スペクトル線
光源
365.01
i
水銀放電管
404.66
h
水銀放電管
435.83
g
水銀放電管
479.99
F'
カドミウム放電管
486.13
F
水素放電管
543.50
−
He-Neレーザ
546.07
e
水銀放電管
587.56
d
ヘリウム放電管
632.80
−
He-Neレーザ
643.85
C'
カドミウム放電管
656.27
C
水素放電管
706.52
r
ヘリウム放電管
780.00
−
ルビジウム放電管
852.11
s
セシウム放電管
1014.0
t
水銀放電管
1064.1
−
Nd:YAGレーザ
1128.7
−
水銀放電管
1395.1
−
水銀放電管
1529.6
−
水銀放電管
1813.1
−
水銀放電管
1970.1
−
水銀放電管
2325.4
−
水銀放電管
c) 検出器 検出器は,それぞれの波長を検出できる,一般的なものを用いる。
6
測定試料
測定試料は,図3のようなプリズムを用いる。試料形状,頂角及び平面度は,次による。
図3−測定試料

4
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 試料形状 試料形状は,頂角を挟むりょう(稜)の長さ(l)が15 mm〜40 mm,厚さ(t)が10 mm
〜30 mmの試料を用いることが望ましい。
注記 試料形状は,光束に合わせて,りょうの長さ(l)及び厚さ(t)を調整する。
b) 頂角 頂角は,35°〜60°の試料を用いることが望ましく,屈折率の高い試料を測定する場合は,頂
角を小さくすることが望ましい。目安を表2に示す。
表2−頂角の目安
測定波長における屈折率 頂角(°)
1.5〜1.7
60
1.7〜1.9
45
1.9〜2.1
35
c) 平面度 平面度は,光線が入射及び透過する平面が,測定する最短波長の1/4以内とする。
7
測定方法
7.1
測定場所の状態
7.1.1
測定場所の温度
測定場所の温度は, 20 ℃〜25 ℃とすることが望ましい。また,測定中の温度変化及び温度分布は,
± 0.5 ℃以下とすることが望ましい。
注記 同一試料についての各スペクトル線の測定は,同一条件で行うことが望ましい。
7.1.2
測定場所の湿度
測定場所の湿度は,相対湿度50 %〜65 %が望ましい。また,測定中の相対湿度の変化は,±3 %以下と
することが望ましい。
7.1.3
測定場所の気圧
測定場所の気圧は,86 kPa〜106 kPaが望ましい。また,測定中の変化は,±0.5 kPa以下とすることが望
ましい。
7.2
測定
7.2.1
一般
測定試料の頂角及び最小偏角を測定し,屈折率を計算によって算出する。
7.2.2
測定試料の調整
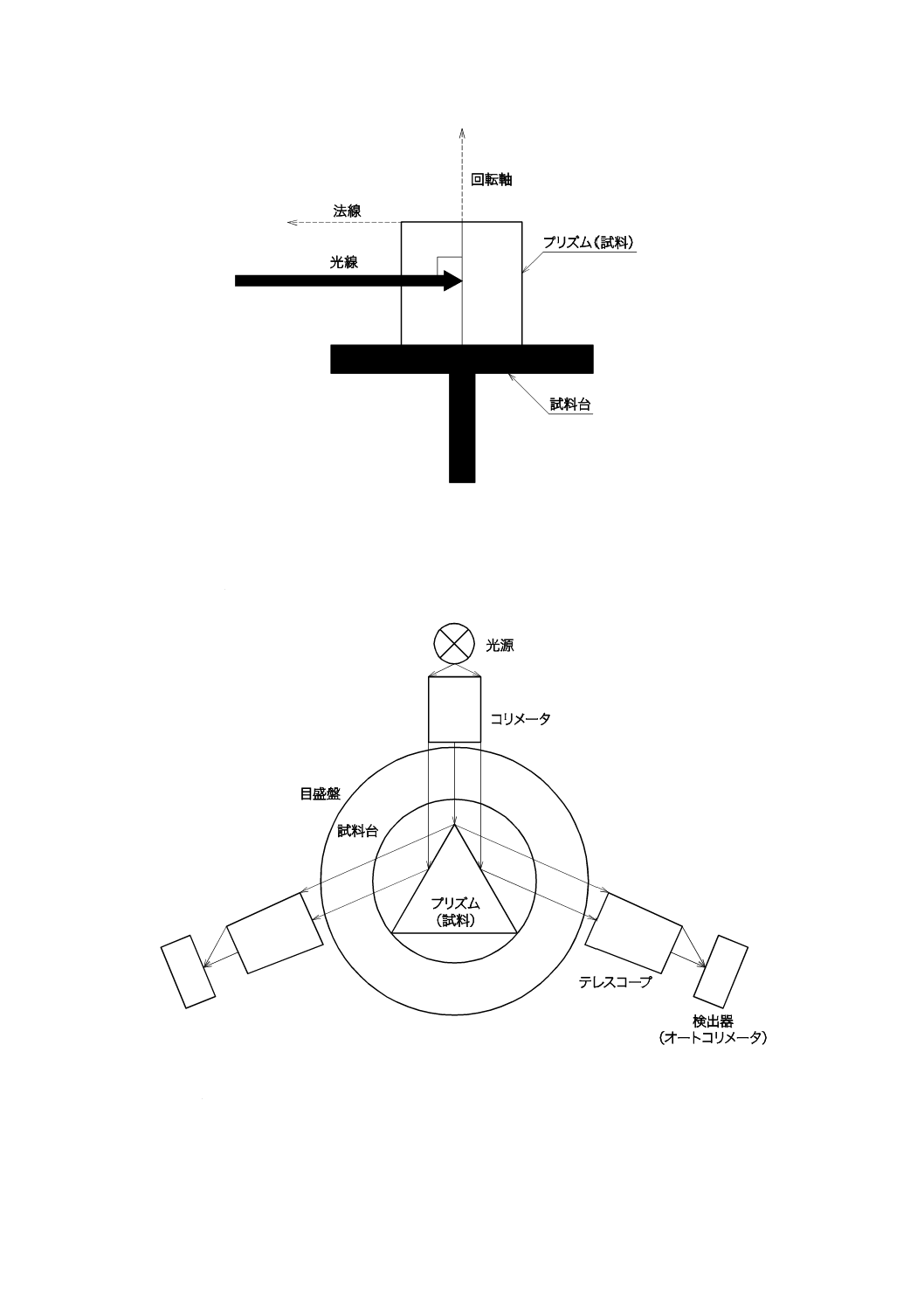
測定試料(プリズム)の調整は,図4に示すように,光線及びプリズム(試料)屈折面の法線を,プリ
ズムの回転軸に対して垂直にする。
5
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4−試料調整図
7.2.3
頂角の測定
測定する頂に向けて光源を設置し,頂を挟む面からの,反射光の検出最大値によって,目盛盤の角度を
読み取り,頂角を算出する。概略図を図5に示す。
図5−頂角測定の概略図
7.2.4
最小偏角の測定
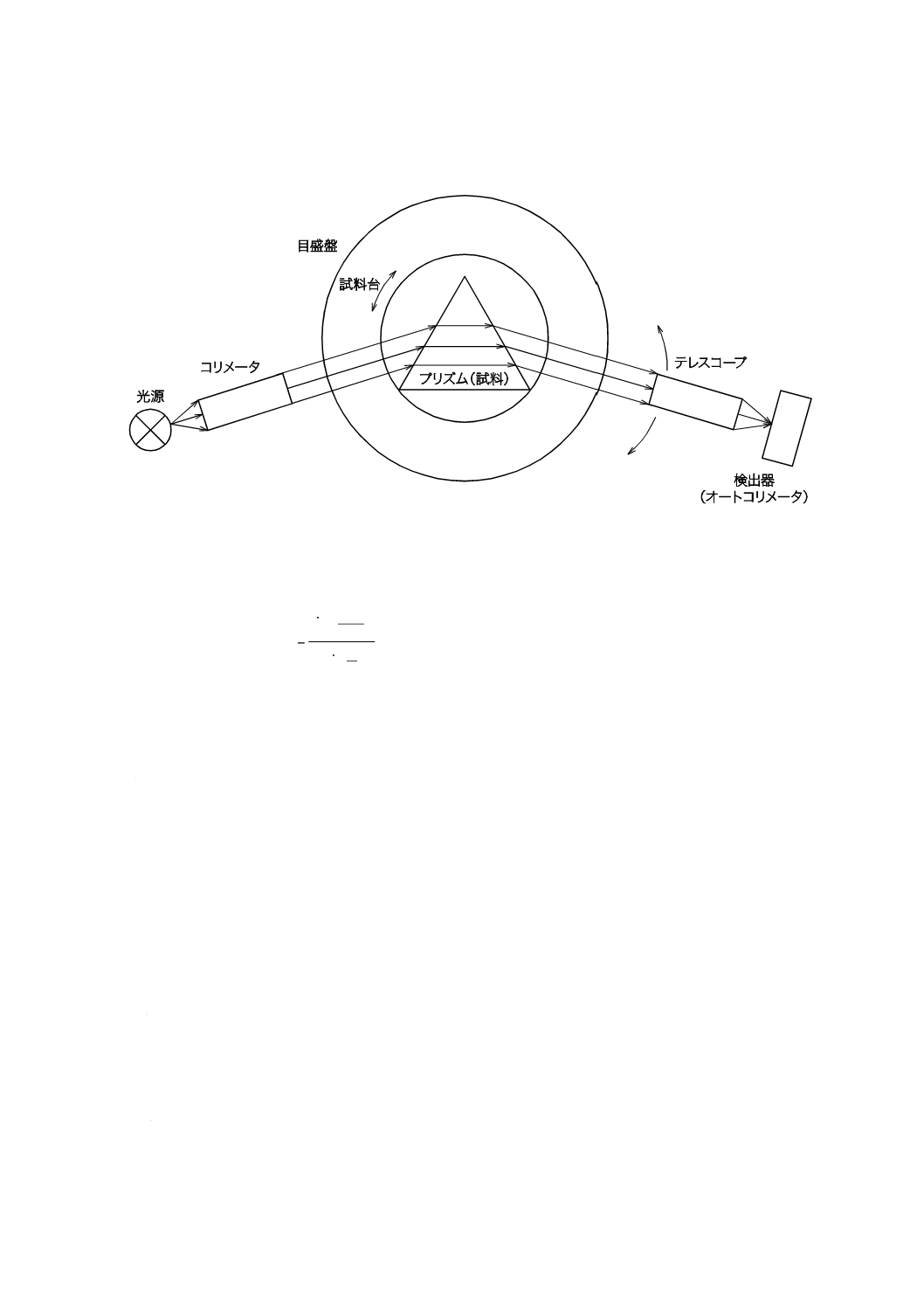
プリズム(試料)の大きさに合わせ,コリメータからの測定スペクトル光線がプリズム(試料)の入射
面に当たるように調整し,引き続き入射光と透過光との延長交点が,試料台の回転中心にくるように,プ
6
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
リズム位置を設定する。設定後,測定するスペクトル線に対して,偏角が最小となるような位置を探し,
目盛盤の角度を読み取る。概略図を図6に示す。
図6−最小偏角測定の概略図
7.2.5
屈折率の計算
屈折率は,次の式によって算出する。
(
)
2
sin
2
sin
θ
δ
θ
n
+
=
ここに,
n: 屈折率
θ: 頂角(rad)
δ: 最小偏角(rad)
また,この屈折率を用い,主分散,アッベ数,部分分散及び部分分散比を算出できる。
注記1 主分散,アッベ数,部分分散及び部分分散比の算出方法は,附属書Aに示す。
注記2 測定波長以外の波長の屈折率を算出する場合は,附属書Bに示す。
注記3 測定環境の影響を補正する場合は,附属書Cに示す。
8
表示
屈折率は,少なくとも小数点以下5位まで表示する。
9
試験報告書
報告書は,次の事項を含めなければならない。
a) 規格番号
b) 測定試料を識別する詳細
c) 測定場所の温度,気圧及び湿度
d) 光源の種類及びその波長
e) 測定屈折率
7
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
主分散,アッベ数,部分分散及び部分分散比の算出方法
A.1 一般
主分散及びアッベ数の算出方法は,JIS B 7090及びJIS Z 8120に,部分分散及び部分分散比は,JIS Z 8120
よる。したがって,この規格で測定した屈折率から,それぞれの値を算出する場合も,該当する規格を用
いることができる。
A.2 基準波長
基準波長は,d線(587.56 nm)及び/又はe線(546.07 nm)とする。
A.3 主分散の算出
A.3.1 基準波長がd線(587.56 nm)での主分散の算出
基準波長がd線での主分散の算出方法は,式(A.1)による。
nF−nC ·················································································· (A.1)
ここに,
nF: F線(486.13 nm)に対する屈折率
nC: C線(656.27 nm)に対する屈折率
A.3.2 基準波長がe線(546.07 nm)での主分散の算出
基準波長がe線での主分散の算出方法は,式(A.2)による。
nF'−nC' ················································································· (A.2)
ここに,
nF': F' 線(479.99 nm)に対する屈折率
nC': C' 線(643.85 nm)に対する屈折率
A.3.3 表示
主分散の表示は,少なくとも小数点以下5位まで表示する。
A.4 アッベ数の算出
A.4.1 基準波長がd線(587.56 nm)でのアッベ数の算出
基準波長がd線でのアッベ数の算出方法は,式(A.3)による。
C
F
d
d
1
n
n
n
ν
−
−
=
·········································································· (A.3)
ここに,
νd: d線(587.56 nm)に対するアッベ数
nd: d線(587.56 nm)に対する屈折率
nF: F線(486.13 nm)に対する屈折率
nC: C線(656.27 nm)に対する屈折率
A.4.2 基準波長がe線(546.07 nm)でのアッベ数の算出
基準波長がe線でのアッベ数の算出方法は,式(A.4)による。
'
'n
n
n
ν
C
F
e
e
1
−
−
=
·········································································· (A.4)
ここに,
νe: e線(546.07 nm)に対するアッベ数
ne: e線(546.07 nm)に対する屈折率
nF': F' 線(479.99 nm)に対する屈折率
8
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
nC': C' 線(643.85 nm)に対する屈折率
A.4.3 表示
アッベ数の表示は,少なくとも小数点以下1位まで表示する。
A.5 部分分散の算出
A.5.1 部分分散
部分分散は,異なる二つの波長に対する屈折率差である。
A.5.2 算出方法
算出方法は,式(A.5)による。
nx−ny ··················································································· (A.5)
ここに,
nx: 波長xに対する屈折率
ny: 波長yに対する屈折率
A.5.3 表示
部分分散の表示は,少なくとも小数点以下5位まで表示する。
A.6 部分分散比の算出
A.6.1 部分分散比
部分分散比は,部分分散と主分散との比で表される。
A.6.2 基準波長がd線(587.56 nm)での部分分散比の算出
基準波長がd線での部分分散比の算出方法は,式(A.6)による。
C
F
y
x
n
n
n
n
−
−
················································································ (A.6)
ここに,
nx: 波長xに対する屈折率
ny: 波長yに対する屈折率
nF: F線(486.13 nm)に対する屈折率
nC: C線(656.27 nm)に対する屈折率
A.6.3 基準波長がe線(546.07 nm)での部分分散比の算出
基準波長がe線での部分分散比の算出方法は,式(A.7)による。
'
'
n
n
n
n
C
F
y
x
−
−
··············································································· (A.7)
ここに,
nx: 波長xに対する屈折率
ny: 波長yに対する屈折率
nF': F'線(479.99 nm)に対する屈折率
nC': C'線(643.85 nm)に対する屈折率
A.6.4 表示
部分分散比の表示は,少なくとも小数点以下4位まで表示する。
9
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
任意波長に対する屈折率の算出方法
B.1
一般
任意の波長に対する屈折率は,波長分散式によって算出することができる。波長分散式は,任意の波長
に対する屈折率を算出する式である。ガラスの種類によって定まる定数を用いることで,任意の波長に対
する屈折率を算出することができる。
注記1 波長分散式によって算出された屈折率は,実測値でないため,近似値となる。したがって,
参考値として用いることが望ましい。
注記2 波長分散式によって算出された屈折率は,異なる波長分散式では,屈折率の算出値が異なる。
注記3 波長分散式によって算出される屈折率は,測定によって計算した二つの屈折率の間でだけ参
考値として有効である。
注記4 波長分散式で屈折率を算出する場合は,例えば,小数点以下5位まで屈折率を表示する場合
は,少なくとも波長は,μm表示において,小数点以下6位を使用する必要がある。
B.2
コーシーの分散式
Λ
+
+
+
+
=
6
4
2
λ
D
λ
C
λ
B
A
n
ここに,
n: 屈折率
λ: 波長(μm)
A,B,C,D…: 定数
B.3
ハルトマンの分散式
C
λ
B
A
n
−
+
=
又は,
2)
(
C
λ
B
A
n
−
+
=
ここに,
n: 屈折率
λ: 波長(μm)
A,B,C: 定数
B.4
セルマイヤーの分散式
3
2
2
3
2
2
2
2
1
2
2
1
2
1
B
λ
λ
A
B
λ
λ
A
B
λ
λ
A
n
−
+
−
+
−
=
−
ここに,
n: 屈折率
λ: 波長(μm)
A1,A2,A3,B1,B2,B3: 定数
10
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.5
ショットの分散式
8
5
6
4
4
3
2
2
2
1
0
2
−
−
−
−
+
+
+
+
+
=
λ
a
λ
a
λ
a
λ
a
λ
a
a
n
ここに,
n: 屈折率
λ: 波長(μm)
a0,a1,a2,a3,a4,a5: 定数
B.6
ヘルツベルガーの分散式
6
4
2
2
2
2
)
028
0
(
028
0
Fλ
Eλ
Dλ
.
λ
C
.
λ
B
A
n
+
+
+
−
+
−
+
=
ここに,
n: 屈折率
λ: 波長(μm)
A,B,C,D,E,F: 定数
11
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
温度,湿度及び気圧に対する,屈折率の補正方法
C.1 一般
光学ガラスの屈折率は,温度,湿度及び気圧の値によって,屈折率の測定値が変動する。この場合,空
気の屈折率を用いて補正することが可能である。また,温度による変化は,温度係数を算出してこれを補
正に用いる場合がある。
C.2 温度係数からの屈折率の補正方法
C.2.1 絶対屈折率の計算方法
種々の測定条件下で測定したガラスの屈折率に基づく,真空中でのガラスの屈折率(絶対屈折率)は,
式(C.1)によって算出する。
注記 測定条件下での空気の屈折率には,例えば参考文献[1], [2]の方法がある。
)
(
2
sin
2
)
(
sin
)
(
)
(
)
(
air
air
m
.
abs
T
n
θ
δ
θ
T
n
T
n
T
n
×
+
=
×
=
·································· (C.1)
ここに, nabs.(T): 絶対屈折率
nm(T): 測定した屈折率
nair(T): 測定場所条件下での,空気の屈折率
θ: 頂角(rad)
δ: 最小偏角(rad)
T: 試料場所温度(℃)
C.2.2 絶対屈折率の温度係数の計算方法
絶対屈折率の温度係数は,式(C.2)で算出する。
1
2
1
abs.
2
abs.
abs.
)
(
)
(
T
T
T
n
T
n
dT
dn
−
−
=
······················································· (C.2)
ここに,
abs.
dT
dn
: 絶対屈折率の温度係数(℃−1)
nabs.(T1),nabs.(T2): 試料場所温度T1及びT2のときの絶対屈折率
T1,T2: 試料場所温度(℃)
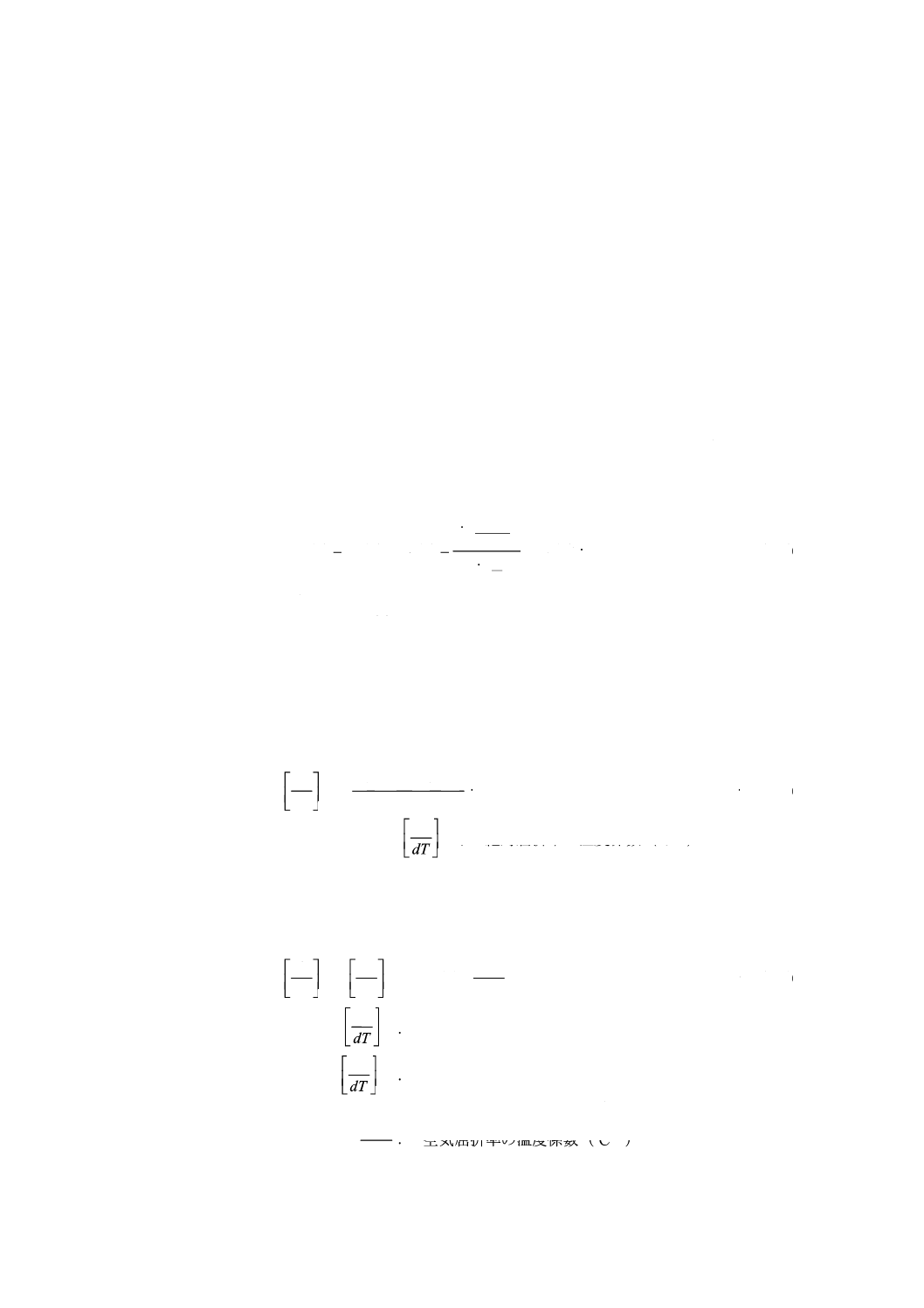
C.2.3 相対屈折率の温度係数の計算方法
相対屈折率の温度係数は,式(C.3)で算出する。
dT
dn
T
n
dT
dn
dT
dn
air
×
−
=
)
(
abs.
abs.
rel.
··············································· (C.3)
ここに,
rel.
dT
dn
: 相対屈折率の温度係数(℃−1)
.
abs
dT
dn
: 絶対屈折率の温度係数(℃−1)
nabs.(T): 試料場所温度Tのときの絶対屈折率
dT
dnair: 空気屈折率の温度係数(℃−1)
12
B 7071-1:2015
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
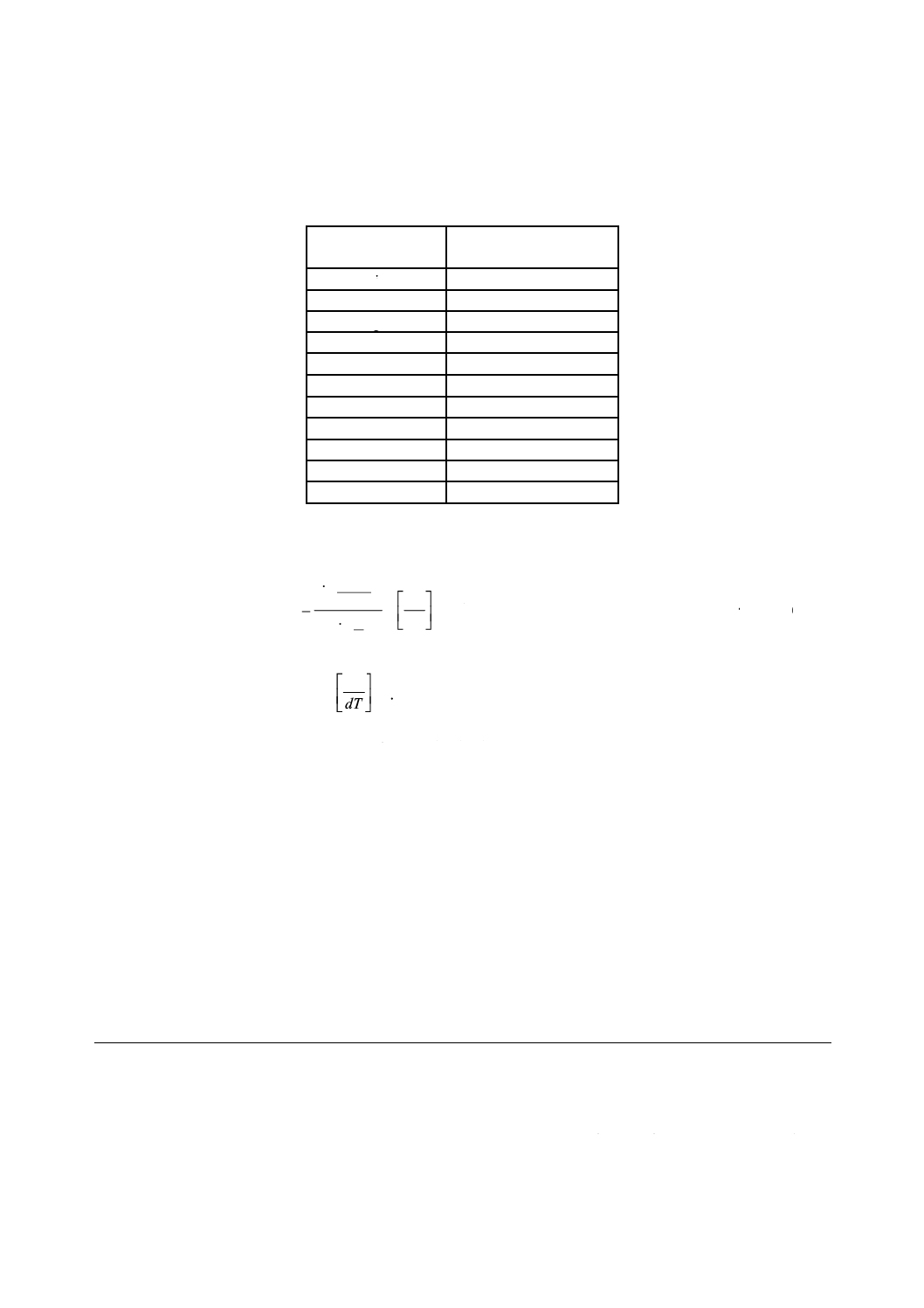
空気屈折率の温度係数は,表C.1の値を使用する。
注記 表に記載の空気屈折率の温度係数は,測定場所の温度が20 ℃〜40 ℃での係数である。
表C.1−空気屈折率の温度係数
スペクトル線
空気屈折率の温度係数
(×10−6 ℃−1)
i
−0.90
h
−0.89
g
−0.88
F'
−0.88
F
−0.87
e
−0.87
d
−0.87
C'
−0.87
C
−0.87
r
−0.87
t
−0.86
C.2.4 温度係数からの屈折率の補正方法
温度係数からの屈折率の補正は,式(C.4)で算出する。
T
dT
dn
θ
δ
θ
n
Δ
2
sin
2
)
(
sin
rel.
c
×
+
+
=
···················································· (C.4)
ここに,
nc: 補正後の屈折率
rel.
dT
dn
: 相対屈折率の温度係数(℃−1)
ΔT: 測定場所温度の設定温度との差(℃)
θ: 頂角(rad)
δ: 最小偏角(rad)
参考文献
[1] Phillip E. Ciddor, “Refractive index of air: new equations for the visible and near infrared,” Appl. Optics 35,
1566-1573 (1996).
[2] K.P. Birch and M.J. Downs, “Correction to the updated Edlén equation for the refractive index of air,”
Metrologia 31, 315-316 (1994).






