B 6190-1:2016 (ISO 230-1:2012)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲 ························································································································· 1
2 引用規格 ························································································································· 2
3 用語及び定義 ··················································································································· 3
3.1 一般 ···························································································································· 3
3.2 機械座標系及び運動の名称に関する用語 ············································································· 3
3.3 静的コンプライアンス及びヒステリシスに関する用語 ··························································· 3
3.4 直進軸に関する用語 ······································································································· 4
3.5 回転軸に関する用語 ······································································································ 10
3.6 運動軸の平行度誤差及び直角度誤差に関する用語 ································································ 14
3.7 軸平均線間の関係を表す用語··························································································· 19
3.8 多軸運動試験に関する用語······························································································ 20
3.9 機械の機能面,部品及び工作物の幾何精度に関する用語 ······················································· 23
4 許容値··························································································································· 26
4.1 一般 ··························································································································· 26
4.2 工作機械の機能面,工作機械の部品及び試験片に適用する許容値 ··········································· 30
4.3 許容値に関連する追加制限条件························································································ 30
5 測定,試験方法及び測定器の不確かさ ················································································· 31
6 試験の準備 ····················································································································· 32
6.1 試験前の機械の据付け ··································································································· 32
6.2 試験前の機械の条件 ······································································································ 32
6.3 試験装置及び測定器 ······································································································ 33
7 機械の静的コンプライアンス試験及びヒステリシス試験 ························································· 34
7.1 一般 ··························································································································· 34
7.2 外部負荷による機械の静的コンプライアンス・ヒステリシス試験 ··········································· 34
7.3 内部負荷による機械の静的コンプライアンス・ヒステリシス試験 ··········································· 36
7.4 回転軸をもつ機械の試験 ································································································ 38
8 直進軸の幾何精度試験 ······································································································ 38
8.1 一般 ··························································································································· 38
8.2 真直度誤差運動試験 ······································································································ 39
8.3 直進位置決め誤差運動試験······························································································ 43
8.4 角度誤差運動試験 ········································································································· 45
9 回転軸の幾何精度試験 ······································································································ 48
9.1 JIS B 6190-7の引用 ······································································································· 48
9.2 角度位置決め誤差運動 ··································································································· 48
B 6190-1:2016 (ISO 230-1:2012) 目次
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ページ
10 運動軸間の幾何精度−平行度,直角度,同軸度及び交差度····················································· 51
10.1 運動軸の平行度 ··········································································································· 51
10.2 軸平均線の同軸度誤差 ·································································································· 55
10.3 運動軸間の直角度誤差 ·································································································· 57
10.4 軸平均線の交差度 ········································································································ 63
11 多軸運動試験 ················································································································ 64
11.1 一般 ·························································································································· 64
11.2 直線軌跡 ···················································································································· 64
11.3 円弧軌跡 ···················································································································· 65
11.4 円すい(形状)運動 ····································································································· 70
11.5 基準球と変位計とを用いる球面補間試験 ·········································································· 71
11.6 二つの直進軸によって生成される面の平面度誤差 ······························································ 71
11.7 特殊な試験 ················································································································· 72
12 機械の機能面の幾何精度試験−真直度,平面度,直角度及び平行度 ········································· 75
12.1 機能面の真直度誤差 ····································································································· 75
12.2 テーブルの平面度 ········································································································ 81
12.3 機能面の位置及び向き ·································································································· 87
12.4 直線と平面との直角度誤差 ···························································································· 95
12.5 回転部品の振れ ··········································································································· 97
附属書A(参考)機械座標系,位置誤差及び角度誤差································································ 100
附属書B(参考)工作物の測定 ····························································································· 109
附属書C(参考)JIS B 6191:1999との対応表 ··········································································· 111
参考文献 ··························································································································· 117
B 6190-1:2016 (ISO 230-1:2012)
(3)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,一般社団法人日本工作機械工業会(JMTBA)
及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出
があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
これによって,JIS B 6191:1999は廃止され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 6190の規格群には,次に示す部編成がある。
JIS B 6190-1 第1部:幾何精度試験
JIS B 6190-2 第2部:数値制御による位置決め精度試験
JIS B 6190-3 第3部:熱変形試験
JIS B 6190-4 第4部:数値制御による円運動精度試験
JIS B 6190-7 第7部:回転軸の幾何精度試験
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 6190-1:2016
(ISO 230-1:2012)
工作機械試験方法通則−第1部:幾何精度試験
Test code for machine tools-Part 1: Geometric accuracy of machines
operating under no-load or quasi-static conditions
序文
この規格は,2012年に第3版として発行されたISO 230-1を基に,技術的内容及び構成を変更すること
なく作成した日本工業規格である。
この規格は,次の理由からISO 230-1の第2版を見直し,再構成している。
a) ISO 230-1の第2版には,新しく規定した試験方法と重複する箇条が幾つかあった。
b) 工作機械の運動を見たとき,真直度誤差を排除するために,平行度誤差及び直角度誤差の定義を,実
用的な理由から修正する必要があった。
注記 この二つの用語の定義は,部品及び形体の平行度誤差及び直角度誤差を規定するために用い
ることを意図していない。
c) 運動軌跡の精度と機能面及び工作物の幾何学的な精度とを明確に区別することが望まれていた。
d) 工作機械技術,測定技術及び測定器の進歩に対応する必要があった。
e) ISO 230-1の第2版の附属書Aは,新しい測定方法・測定器が開発され,より高精度で高速な測定が
行えるようになったことから,範囲が広くなった。そのため,その内容をISO 230-1から分離し,ISO/TR
230-11とすることとした。
f)
さらに,この規格をISO 14253(規格群)と整合させるために,測定の不確かさに関係する事項を規
定した。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,無負荷又は準静的な条件で行う工作機械の幾何精度試験方法について規定する。
この規格は,切りくずを出すか又は塑性変形によって金属,木材などを加工する,動力で駆動される機
械に適用する。加工中に手で持って操作する可搬形の機械には適用しない。
この規格は,幾何学的な精度試験だけに適用し,運転試験(振動,運動部品の動きの滑らかさなど)又
は特性試験(回転速度及び送り速度)には適用しない。
この規格は,加工力よりも明らかに慣性力が大きい高速運動の精度試験には適用しない。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 230-1:2012,Test code for machine tools−Part 1: Geometric accuracy of machines operating under
no-load or quasi-static conditions(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0021 製品の幾何特性仕様(GPS)−幾何公差表示方式−形状,姿勢,位置及び振れの公差表示
方式
注記 対応国際規格:ISO 1101:2012,Geometrical product specifications (GPS)−Geometrical tolerancing
−Tolerances of form, orientation, location and run-out
JIS B 0641-1 製品の幾何特性仕様(GPS)−製品及び測定装置の測定による検査−第1部:仕様に対
する合否判定基準
注記 対応国際規格:ISO 14253-1,Geometrical product specifications (GPS)−Inspection by
measurement of workpieces and measuring equipment−Part 1: Decision rules for proving
conformity or nonconformity with specifications(IDT)
JIS B 0680 製品の幾何特性仕様(GPS)−製品の幾何特性仕様及び検証に用いる標準温度
注記 対応国際規格:ISO 1,Geometrical Product Specifications (GPS)−Standard reference temperature
for geometrical product specification and verification(IDT)
JIS B 6190-2 工作機械試験方法通則−第2部:数値制御による位置決め精度試験
注記 対応国際規格:ISO 230-2,Test code for machine tools−Part 2: Determination of accuracy and
repeatability of positioning of numerically controlled axes(IDT)
JIS B 6190-3 工作機械試験方法通則−第3部:熱変形試験
注記 対応国際規格:ISO 230-3,Test code for machine tools−Part 3: Determination of thermal effects
(IDT)
JIS B 6190-4 工作機械試験方法通則−第4部:数値制御による円運動精度試験
注記 対応国際規格:ISO 230-4,Test code for machine tools−Part 4: Circular tests for numerically
controlled machine tools(IDT)
JIS B 6190-7 工作機械試験方法通則−第7部:回転軸の幾何精度試験
注記 対応国際規格:ISO 230-7,Test code for machine tools−Part 7: Geometric accuracy of axes of
rotation(IDT)
JIS B 6196 工作機械−対角位置決め精度試験方法通則
注記 対応国際規格:ISO 230-6,Test code for machine tools−Part 6: Determination of positioning
accuracy on body and face diagonals (Diagonal displacement tests)(IDT)
JIS B 6310 産業オートメーションシステム−機械及び装置の制御−座標系及び運動の記号
注記 対応国際規格:ISO 841,Industrial automation systems and integration−Numerical control of
machines−Coordinate system and motion nomenclature(IDT)
ISO 230-10,Test code for machine tools−Part 10: Determination of the measuring performance of probing
systems of numerically controlled machine tools
ISO 12181-1,Geometrical product specifications (GPS)−Roundness−Part 1: Vocabulary and parameters of
roundness
ISO 12780-1,Geometrical product specifications (GPS)−Straightness−Part 1: Vocabulary and parameters of
straightness
ISO 12781-1,Geometrical product specifications (GPS)−Flatness−Part 1: Vocabulary and parameters of
3
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
flatness
ISO/IEC Guide 98-3,Uncertainty of measurement−Part 3: Guide to the expression of uncertainty in
measurement (GUM:1995)
3
用語及び定義
3.1
一般
この規格で用いる主な用語及び定義は,JIS B 6190-2,JIS B 6190-4,JIS B 6190-7,JIS B 6310,ISO 12181-1,
ISO 12780-1及びISO 12781-1によるほか,次による。
この規格は,幾何精度の測定を行うときの機械構造又は測定実施上の制限を考慮し,更に測定しやすい
実際の運動並びに実際の線及び表面を考慮して計測学的な定義を用いる。
注記 この規格には,幾つかの場合に,混乱を排除し,使用する用語を明確にするための幾何学的な
定義(振れの定義など)も残している。ただし,試験方法,測定器及び許容値の説明では,計
測学的な定義を基礎としている。
3.2
機械座標系及び運動の名称に関する用語
3.2.1
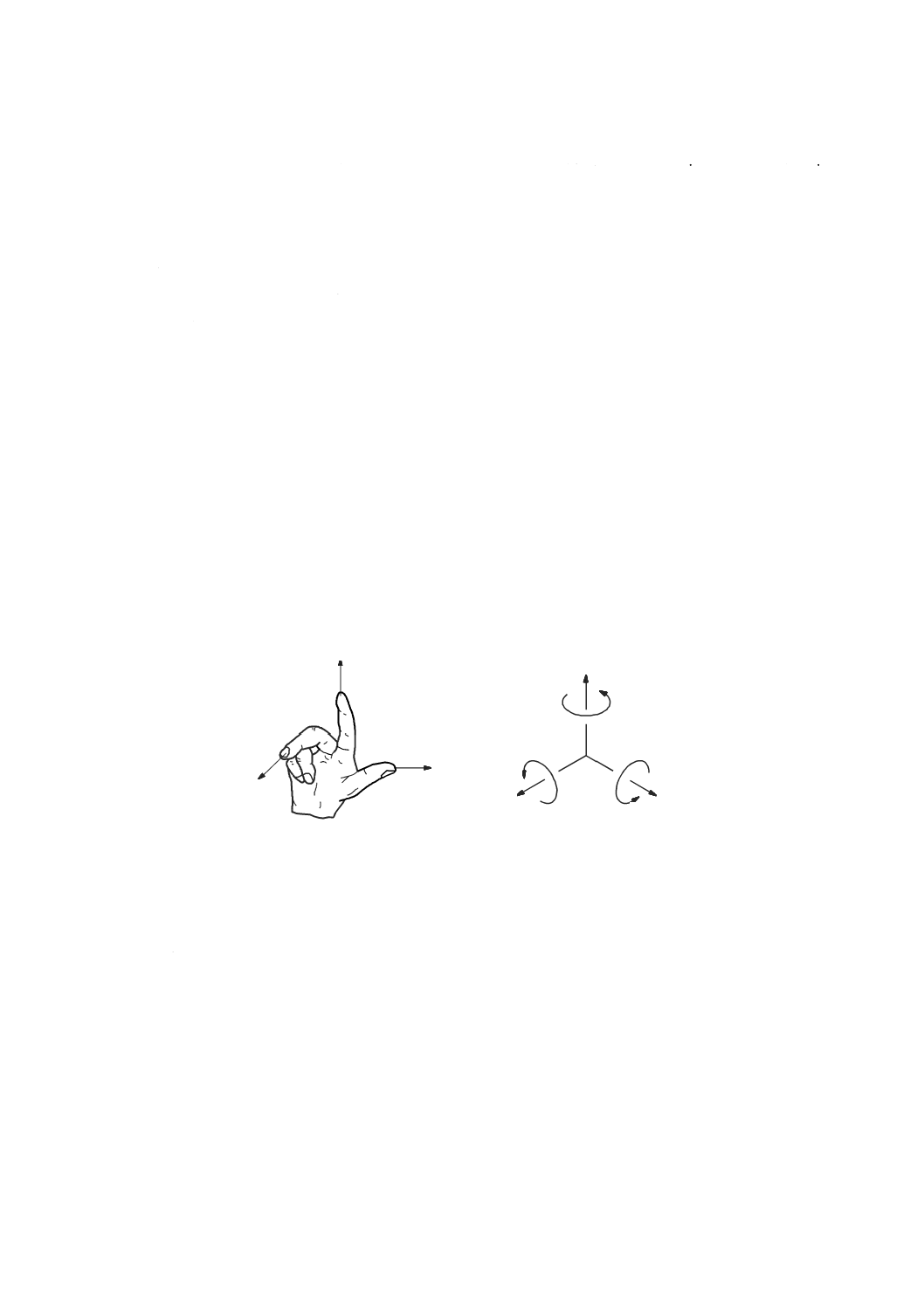
機械座標系(machine coordinate system)
X,Y及びZと名付けた三つの基本軸並びにそれぞれの軸回りのA,B及びCと名付けた三つの回転軸
をもつ右手直交座標系(図1参照)。
図1−右手直交機械座標系
3.3
静的コンプライアンス及びヒステリシスに関する用語
3.3.1
構造ループ(structural loop)
二つの指定した対象物間の相対位置を維持する要素の集合。
(JIS B 6190-7の3.1.13参照)
注記 指定した対象物の代表的な組合せは,切削工具と工作物との組合せである。構造ループは,主
軸,軸受,軸受ハウジング,主軸台,案内面,本体構造及び工具・工作物保持具を含む。大形
工作機械においては,床を構造ループの一つに含めることがある。
3.3.2
静的コンプライアンス(static compliance)
構造ループ,力の作用位置及び方向,並びに変位の測定位置及び方向について,指定した二つの対象物
+Y
+Z
+X
+Y
+B
+Z
+C
+X
+A
+Y
+Y
+B
+X
+A
+C
+X
+Z
+Z
4
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
間の静的な単位力当たりの変位(又は角度)。
注記1 静的コンプライアンスは,静剛性の逆数である。
注記2 用語“クロスコンプライアンス”は,変位と力とを同じ方向で測定しないときに用いる。
3.3.3
遊び(play)
構造ループ内の要素間の隙間に限定した変位分だけ発生する,剛性がゼロの状態。
(JIS B 6190-7の3.1.21参照)
3.3.4
ヒステリシス(hysteresis)
力(又はモーメント)を連続的に負荷し,その後に反対方向に除荷したときに生じる二つの物体間の変
位(又は角度)。
(JIS B 6190-7の3.1.22参照)
3.3.5
試験装置のヒステリシス(setup hysteresis)
通常,機械的な結合の緩みによって試験装置に発生する様々な部品のヒステリシス。
(JIS B 6190-7の3.1.22.1参照)
3.3.6
機械ヒステリシス(machine hysteresis)
特定の負荷を受けたときに発生する機械構造のヒステリシス。
(JIS B 6190-7の3.1.22.2参照)
3.4
直進軸に関する用語
3.4.1
一般
この規格の定義及び試験の多くは,工具を取り付けた運動部品と工作物を載せた運動部品との間の相対
運動の誤差について扱っている。この相対運動の誤差は,機能点の位置又は軌跡で定義し,測定する。
3.4.2
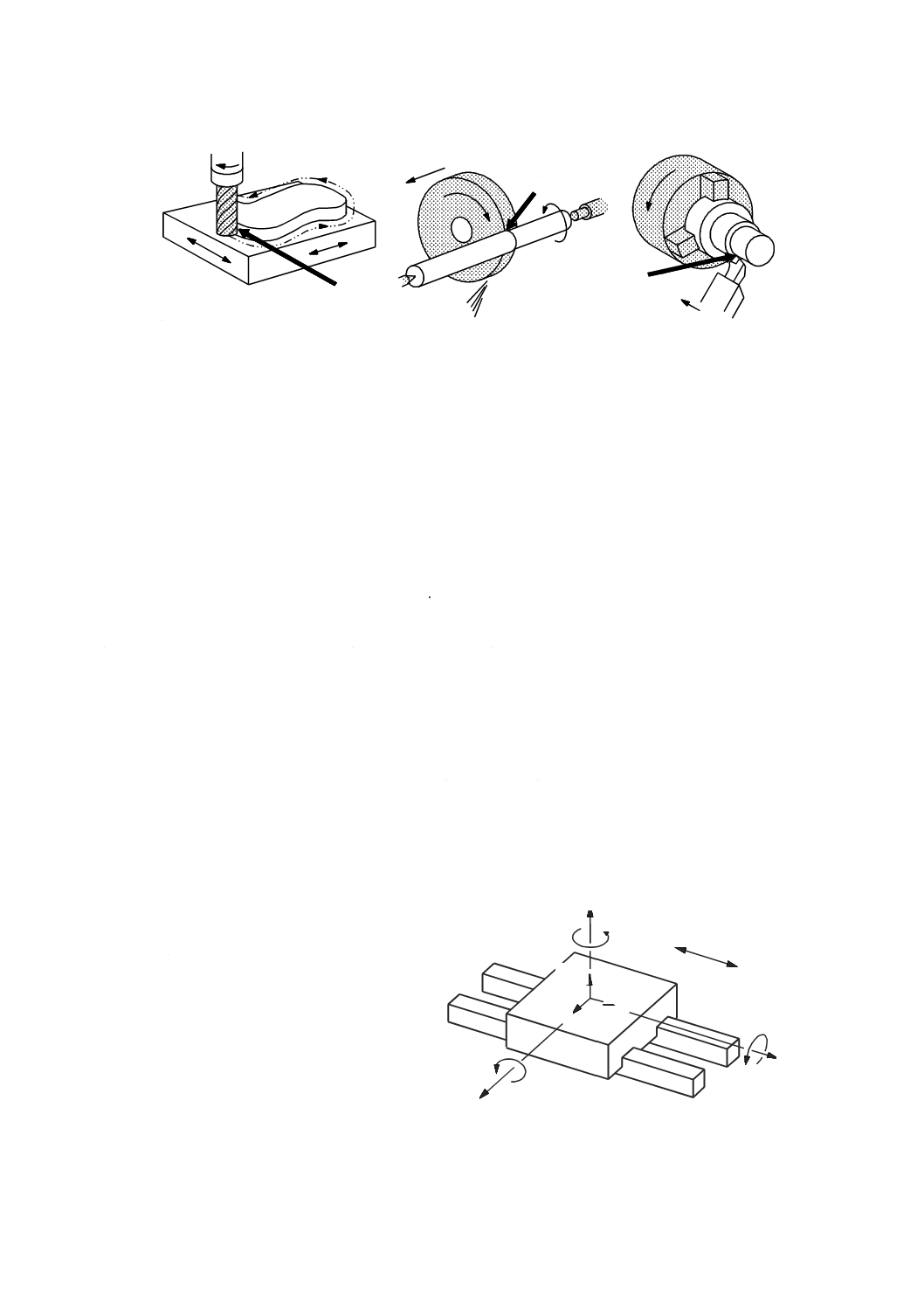
機能点(functional point)
切削工具の先端点,又は材料除去を行うために切削工具が工作物に接触する工作機械の部品と関連する
点(図2参照)。
注記1 機能点は,工作機械の作業空間内で運動できるただ一つの点である。この規格及び関連する
工作機械の機種別規格は,一般に平均的な長さの(運動する)工具と,運動軸の移動範囲の
中央近くに配置することを仮定した(運動する)工作物の仮想中心との相対位置を代表する
位置に,測定器を取り付けて幾何精度試験を行うことを推奨する。
注記2 この規格の定義及び試験では,正式にはより厳密な表現である“(運動する)工具と(運動す
る)工作物との間の相対位置を表す運動点”の代わりに,読みやすさを考慮して“運動部品
上の機能点”を用いる。
5
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2−機能点の例
3.4.3
直進軸の誤差運動(error motions of a linear axis)
直線経路に沿って運動するように指令された運動部品の不要な直進及び角度誤差運動(図3参照)。
注記1 直進軸の誤差運動は,誤差を表す文字Eの後に添え字を付けて表す。最初の添え字は,誤差
運動の向きを表し,2番目の添え字は,運動軸の名称を表す(図3及び附属書A参照)。
注記2 直進誤差運動は3.4.4に,角度誤差運動は3.4.16にそれぞれ定義している。
3.4.4
直進軸の直進誤差運動(linear error motions of a linear axis)
直線経路に沿って運動するように指令された運動部品の機能点の三つの直進誤差運動。一つは,運動の
方向に平行で,他の二つは,運動の方向に直角な二つの方向に平行である。
注記1 運動の方向に平行な直進誤差運動は,直進位置決め誤差運動(3.4.5)という。他の二つの直
進誤差運動は,真直度誤差運動(3.4.8)という。
注記2 機能点で測定された直進誤差運動は,角度誤差運動の影響を含んでいる。運動部品上の測定
点の位置が機能点と異なる場合には,角度誤差運動の影響は異なる。そのような場合は,機
能点の軌跡の偏差を求めるために角度誤差運動を考慮する。
注記3 例えば,大形のテーブルなど,運動部品が剛体とみなせない場合には,試験は,運動部品上
の2点以上について行う。
1 指令したX軸の直進運動
EAX X軸のX軸回り角度誤差運動(ロール)
EBX X軸のY軸回り角度誤差運動(ヨー)
ECX X軸のZ軸回り角度誤差運動(ピッチ)
EXX X軸の位置決め誤差運動
(X軸の位置決め偏差)
EYX X軸のY方向真直度誤差運動
EZX X軸のZ方向真直度誤差運動
図3−X軸に平行な直線経路に沿って運動するように指令した部品の直進及び角度誤差運動
1
1
1
1 機能点
EAX
ECX
EZX
EYX
EBX
EXX
1
+X
+Z
+Y
+Y
+X
+Z
6
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.4.5
直進位置決め誤差運動(linear positioning error motion)
運動部品の機能点が到達した実際の位置が,指令位置から運動方向に異なるような運動方向の不要な運
動(図4参照)。
注記1 位置決め誤差運動の正の符号は,運動の正の方向である(JIS B 6310による。)。
注記2 直進位置決め誤差運動は,運動部品及びその案内の不完全さと関係する。ただし,その誤差
運動は,運動部品及びその位置決めサーボ制御システムの動的応答とは関係しない。
3.4.6
直進位置決め偏差(linear positioning deviation)
運動部品上の機能点が到達した位置と目標位置との差。
注記1 JIS B 6190-2の2.5参照。
注記2 位置決め偏差は,JIS B 6190-2に従って,数値制御軸の位置決めの精度及び繰返し性を求め
るために規定した間隔で測定する。
注記3 JIS B 6190-2に従って測定した位置決め偏差は,限定された位置決め誤差運動を表している
(図4参照)。
X X軸の座標値(mm)
EXX X軸の位置決め偏差及び位置決め誤差
運動(μm)
1 X軸の実際の位置決め誤差運動曲線
2 X軸の測定された位置決め偏差曲線
図4−X軸に平行に直進運動させた機能点の直進位置決め誤差運動及び測定された位置決め偏差の例
3.4.7
直進位置決め誤差(linear positioning error),
直進位置決め精度(linear positioning accuracy),
直進位置決めの正確さ(accuracy of linear positioning)
正の最大位置決め偏差と負の最小位置決め偏差の絶対値との和。
注記1 この定義は,数値制御によらない軸に適用する。数値制御による直進軸の位置決め精度は,
JIS B 6190-2参照。
注記2 直進位置決め誤差の評価は,100 mmにわたって手動で前後それぞれ10回ずつ往復させて行
い,それぞれの位置決めをするたびに直進位置決め偏差を評価する。
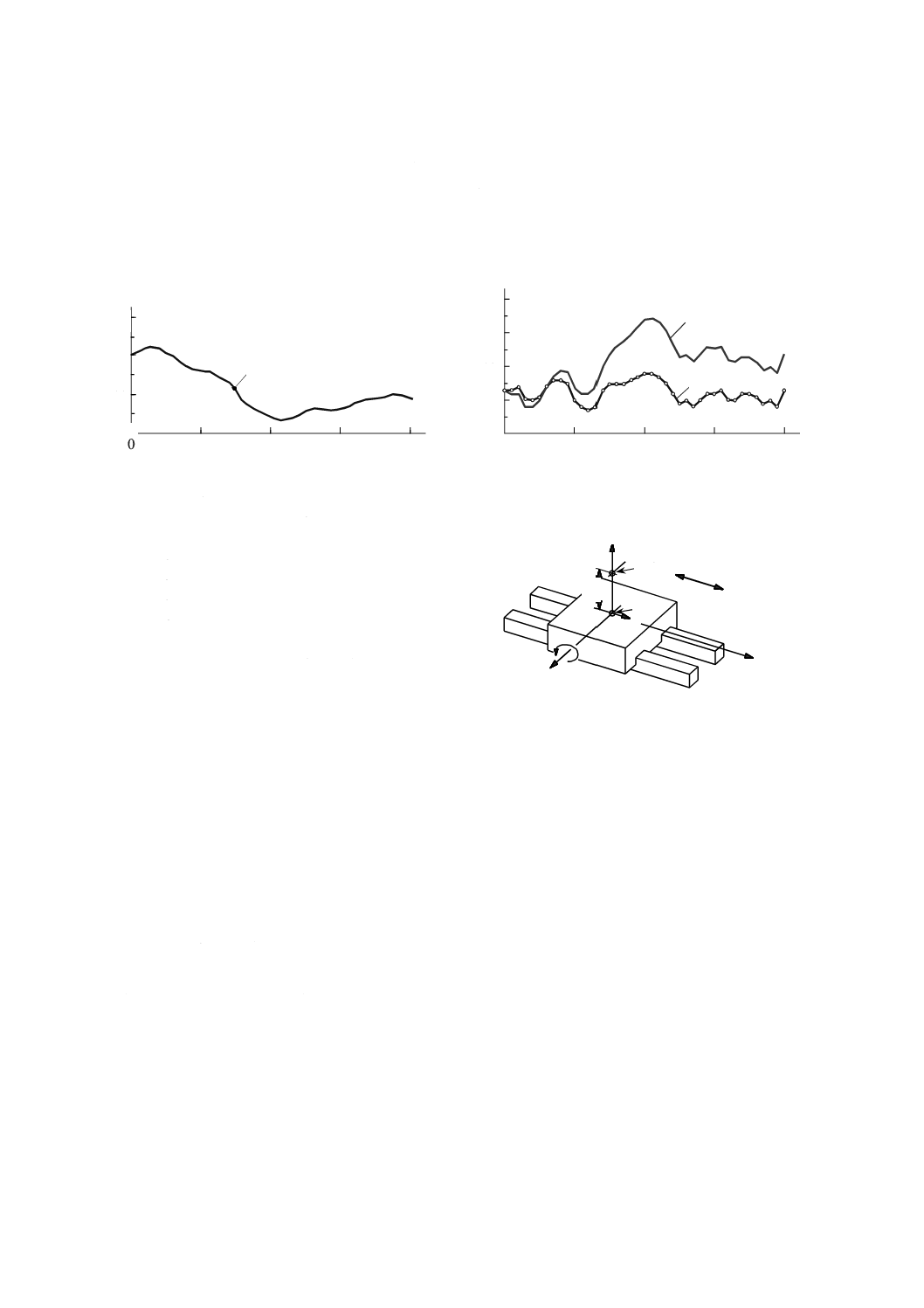
3.4.8
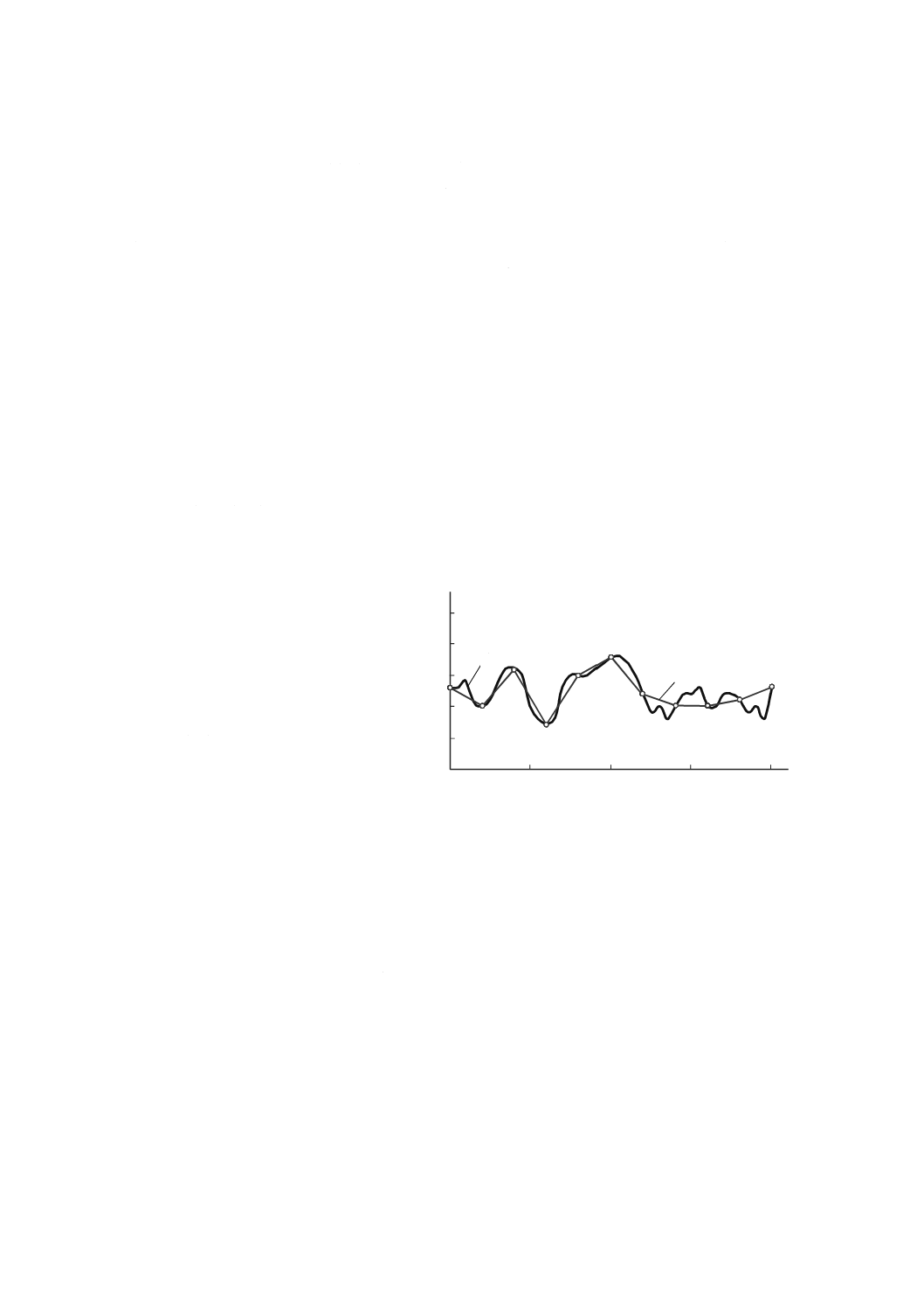
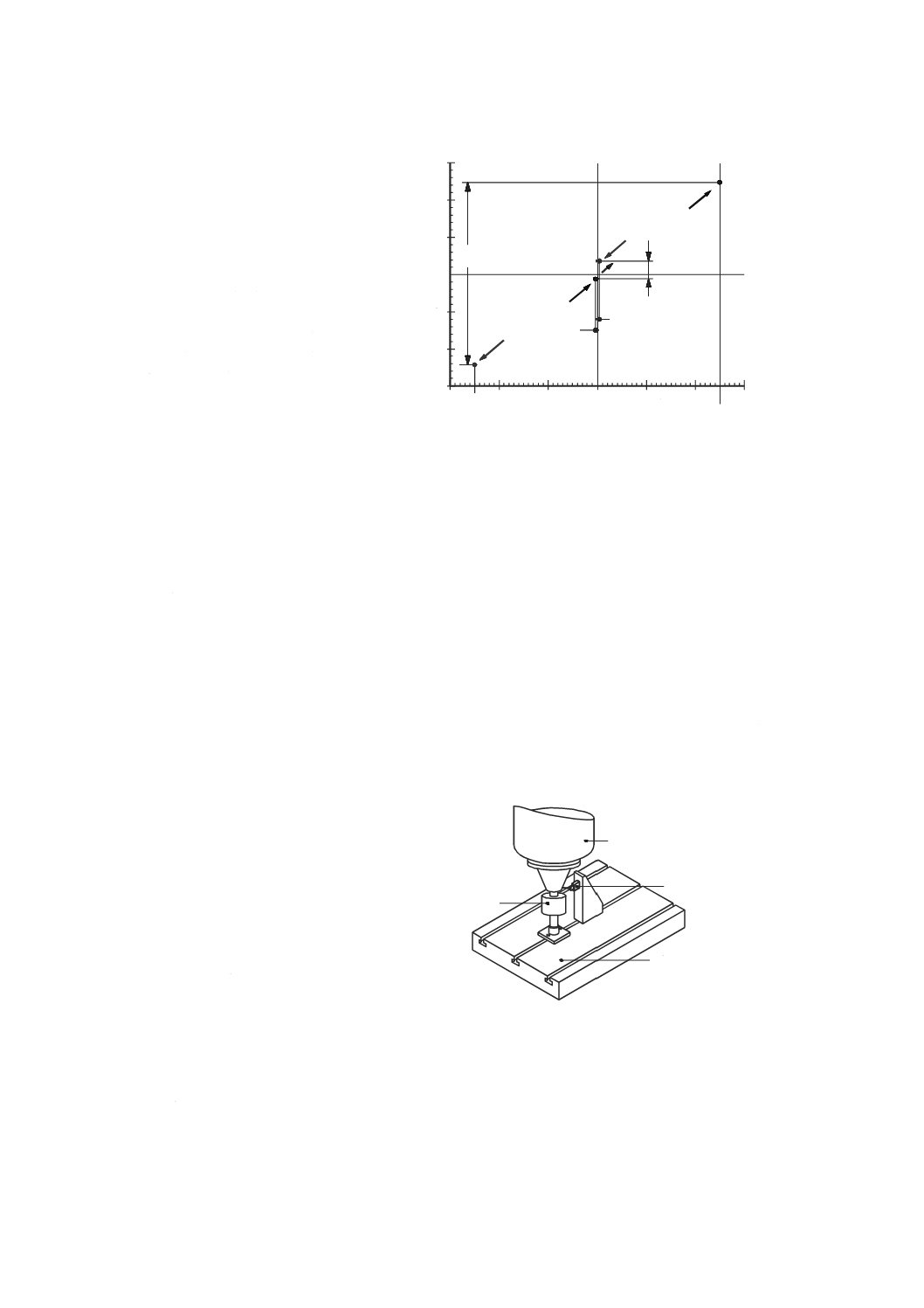
真直度誤差運動(straightness error motion)
500
-10
1000
1500
2000
-5
0
5
10
15
xx
1
2
E
0
X
1 000
1 500
2 000
−
−
7
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
直線経路に沿って運動するように指令された直進軸と直角な二方向のうちの一方向における不要な運動
(図5及び図6参照)。
X X軸の座標値(mm)
EZX X軸のZ方向真直度偏差(μm)
1 X軸の実際のZ方向真直度誤差運動
曲線
2 X軸の測定されたZ方向真直度誤差
運動曲線
3 実際の直進誤差運動の最小領域平
均基準直線
4 測定された真直度誤差運動の最小
領域平均基準直線
図5−X軸運動の機能点の軌跡のZ方向真直度誤差運動及び測定された真直度誤差運動の例
図6−X軸運動のY方向及びZ方向真直度偏差の表示
3.4.9
真直度偏差(straightness deviation)
指令された直線経路に対して直交する二方向の一つで測定した軌跡に適合させた基準直線(3.4.12)から
機能点までの距離(図6参照)。
注記1 真直度偏差は,軸間の動的な相互干渉を回避するために低速で(又は試験中に軸を停止して)
測定する。
注記2 間隔(図5の例では400 mmごと)をあけて測定した真直度偏差は,実際の真直度誤差運動
の限られた動きを代表するだけである。
注記3 真直度偏差の正の符号は,JIS B 6310に従って関係付けた基本軸の正の方向にとる。
3.4.10
直進軸の真直度誤差(straightness error of a linear axis)
(あらかじめ求めた基準直線に対する)負の最大真直度偏差の絶対値と正の最大真直度偏差との和。
注記1 真直度誤差の最小値は,最小領域基準直線を用いて求める。
注記2 真直度偏差は,測定器の読みの基準直線からの差を表し,真直度誤差は,測定された真直度
偏差の最大値と最小値との差を表す。
500
1000
1500
2000
0
4
8
-4
4
2
1
3
-80
EZX
X
1 000
1 500
2 000
EZX
−
−
EZX
+X
+Z
+Y
EYX
+X
+Z
+Y
EYX X軸のY方向真直度偏差
EZX X軸のZ方向真直度偏差
+Y
+Y
+Z
+Z
+X
+X
8
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.4.11
真直度(straightness)
直線の幾何特性。
(ISO 12780-1の3.1.1参照)
注記 直線経路に沿って移動するように指令された,運動部品の機能点の実際の軌跡は直線ではない。
3.4.12
基準直線(reference straight line)
線の総体方向。
真直度偏差及び真直度誤差の基準となる,規定に従った機能点の測定された軌跡に適合する直線。
注記1 基準直線は,測定範囲内で二つの直交平面(図6参照)において測定した偏差から算出する。
注記2 JIS B 6191:1999では,用語として“代表直線”を使用してきたが,“基準直線”の表現とし
ては適していない。
注記3 この規格では,最小領域平均基準直線(3.4.13),最小二乗基準直線(3.4.14),又は両端点基
準直線(3.4.15)のように使用している(図7,図8及び図9参照)。
注記4 最小真直度誤差は,最小領域平均基準直線を用いて得られる誤差の最小値として評価する。
ただし,最小領域計算用ソフトウェアの利用は限られているので,真直度誤差は,最小二乗
基準直線を用いるか,又は両端点基準直線を用いて最小誤差として評価する。
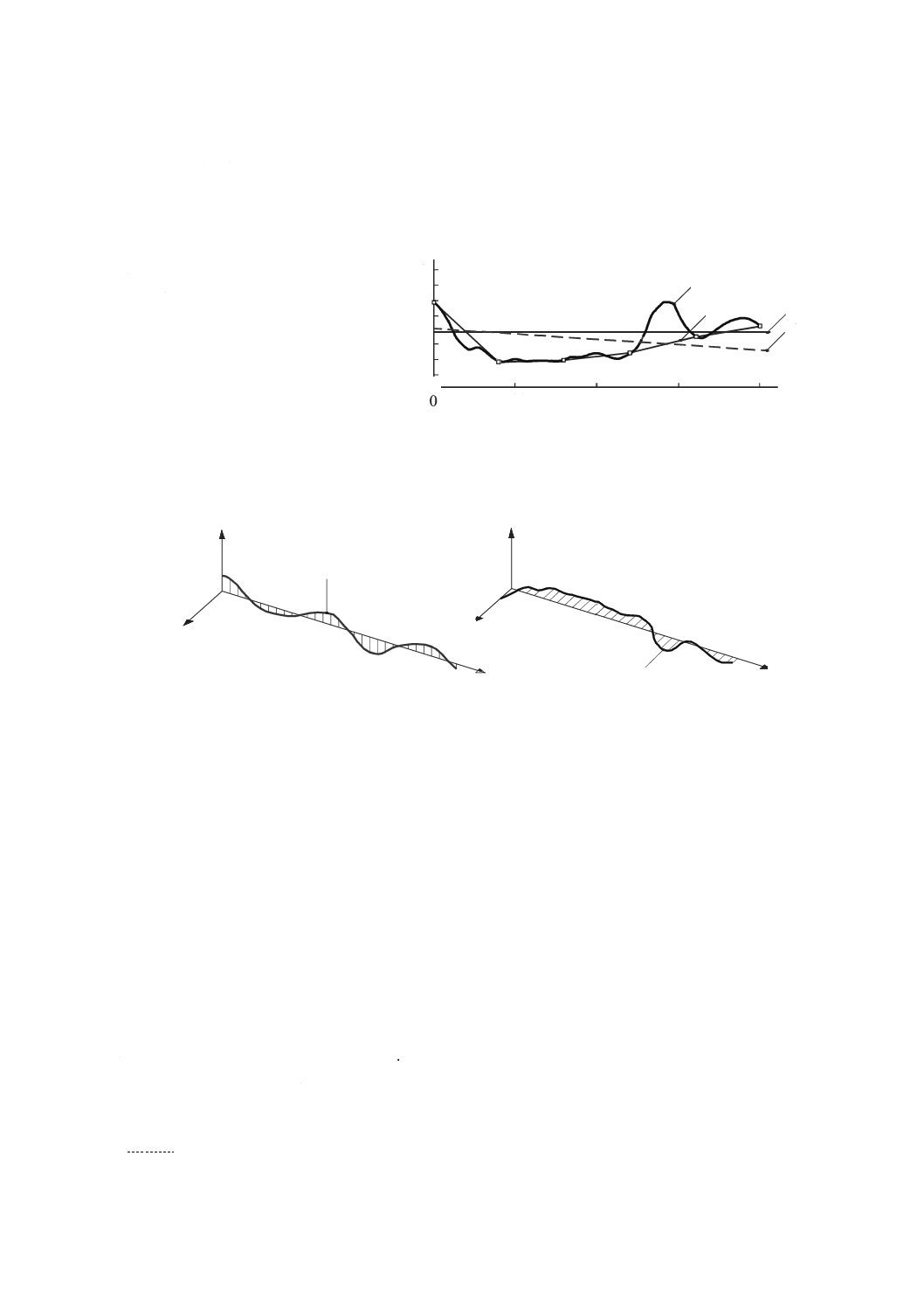
3.4.13
最小領域平均基準直線(mean minimum zone reference straight line)
測定された真直度偏差を挟み,最小間隔になる縦断面内における二つの平行な直線の算術平均(図7参
照)。
X X軸の座標値(mm)
EZX X軸のZ方向真直度偏差(μm)
1 上側の最小領域基準直線
2 最小領域平均基準直線
3 下側の最小領域基準直線
4 測定された真直度偏差
図7−ZX面内におけるX軸運動の真直度及び最小領域平均基準直線の例
3.4.14
最小二乗基準直線(least squares reference straight line)
測定された真直度偏差の二乗和が最小になる直線(図8参照)。
500
1000
1500
2000
0
4
8
-4
4
2
1
3
-80
EZX
X
1 000
1 500
2 000
EZX
−
−
9
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
X X軸の座標値(mm)
EZX X軸のZ方向真直度偏差(μm)
1 最小二乗基準直線
2 正の最大真直度偏差EZX
3 負の最大真直度偏差EZX
4 測定された真直度偏差
図8−ZX面内におけるX軸運動の真直度及び最小二乗基準直線の例
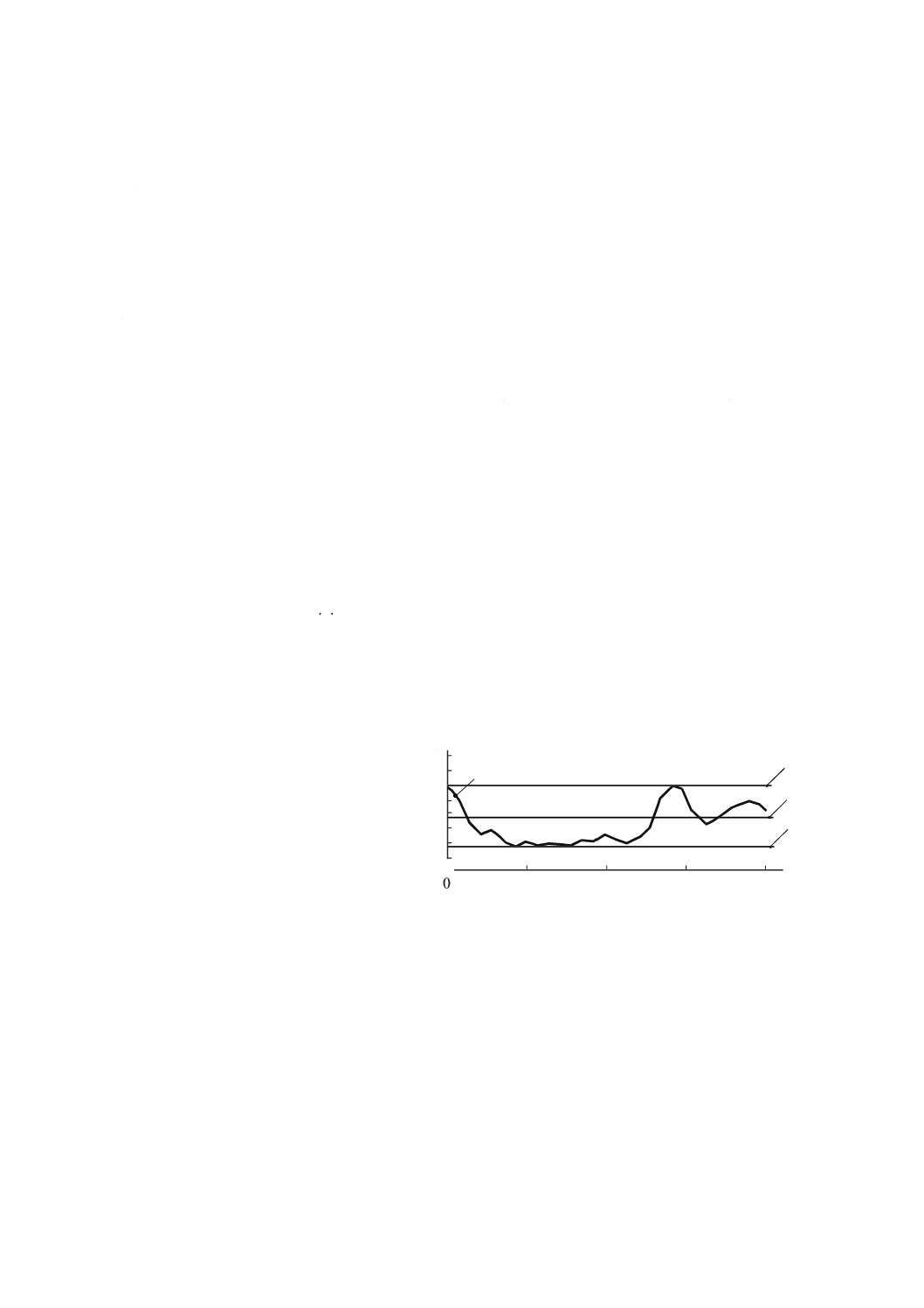
3.4.15
両端点基準直線(end-point reference straight line)
測定された真直度誤差曲線の最初の点と最後の点とを結んだ直線(図9参照)。
X X軸の座標値(mm)
EZX X軸のZ方向真直度偏差(μm)
1 両端点基準直線
2 正の最大真直度偏差EZX
3 負の最大真直度偏差EZX
4 測定された真直度偏差
a 最初の測定点
b 最後の測定点
図9−ZX面内におけるX軸運動の真直度及び両端点基準直線の例
3.4.16
直進軸の角度誤差運動(angular error motions of a linear axis)
直線経路に沿って運動するように指令された運動部品の不要な三つの回転運動。
注記1 角度誤差運動の正の符号は,JIS B 6310に規定する右手直交座標系による(図1参照)。
注記2 三つの直交軸の周りに三つの回転運動がある。運動軸の周りに一つ及び運動軸に直角な軸回
りに二つの回転運動である(図3参照)。運動方向の回転は,“ロール”という。運動方向に
垂直な軸回りの回転を“傾斜運動”といい,二つの傾斜運動がある。運動軸が水平の場合に
は,垂直な軸回りの傾斜運動を“ヨー”,水平な軸回りの傾斜運動を“ピッチ”という。
注記3 機能点の直進誤差運動は,角度誤差運動の影響を含む。運動部品上の測定点の位置が機能点
と異なる場合に,この角度誤差運動の影響は異なる(図10参照)。そのような場合に,角度
誤差運動は,機能点の軌跡の偏差を推定するために考慮する(図10参照)。
3.4.17
角度偏差(angular deviation)
運動部品の全移動範囲の間に測定された三つの直交方向のそれぞれの方向における角度測定器の読み。
500
1000
1500
2000
0
4
8
-8
-4
0
EZX
2
3
4
1
X
1 000
1 500
2 000
EZX
−
−
500
1000
1500
2000
0
4
8
-8
-4
EZX
2
3
4
b
1
a
0
X
1 000
1 500
2 000
EZX
−
−
10
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
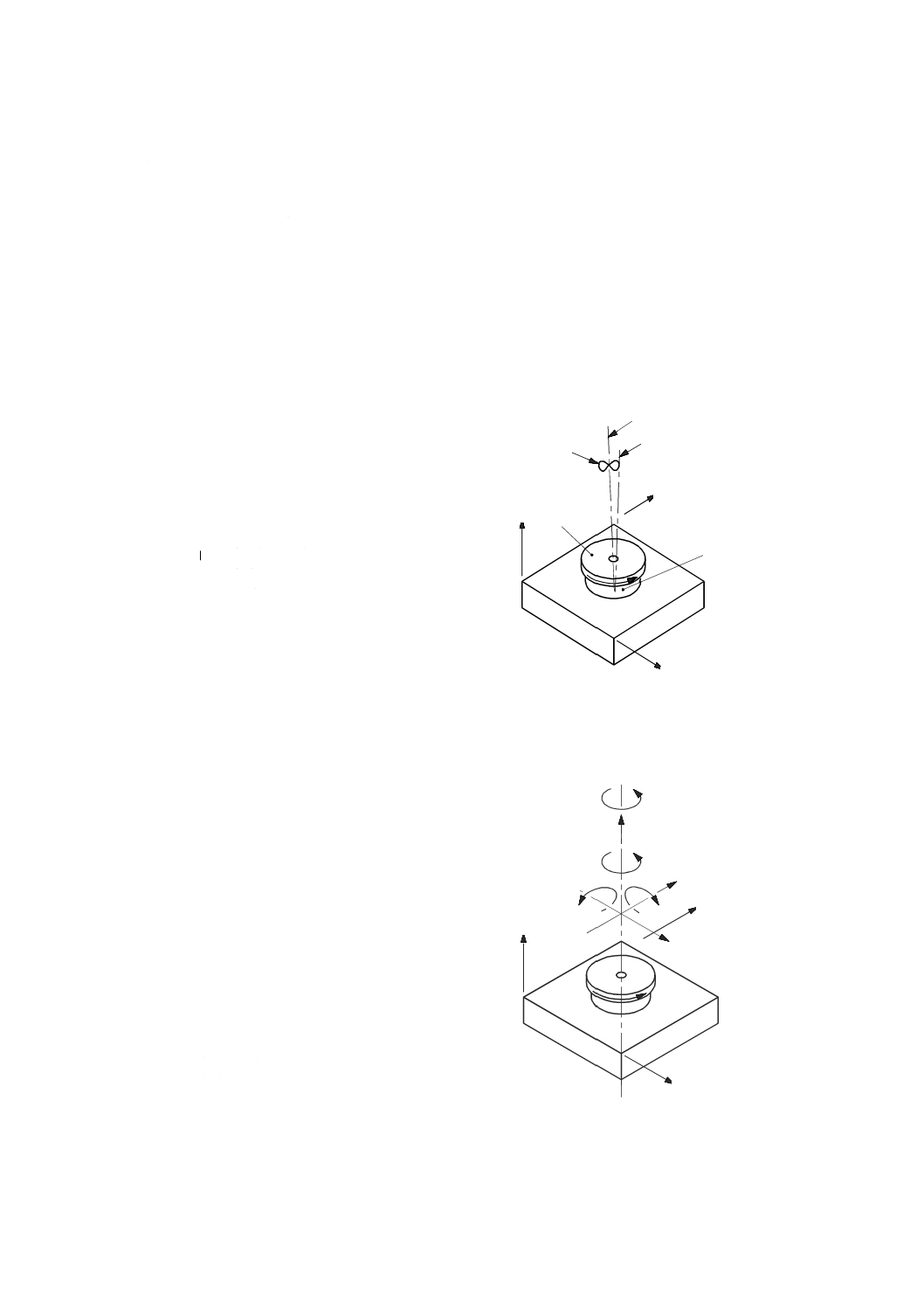
3.4.18
直進軸の角度誤差(angular error of a linear axis)
運動部品の全移動の間に測定された負の角度偏差の絶対値の最大値に最大の正の角度偏差を加えた値を
用いて,三つの直交方向のそれぞれにおいて評価する。
X X軸の座標値(mm)
ECX X軸のZ軸回り角度誤差運動(ピッチ)(μrad)
EXX X軸の位置決め誤差運動(μm)
1 指令したX軸の直進運動
2 測定された偏差ECX
3 FP1で測定された偏差EXX
4 FP2で測定された偏差EXX
(偏差ECXだけの影響を仮定している。)
d FP2とFP1とのY座標の差
(図示した例は,1 000 mm)
FP1 機能点1
FP2 機能点2
図10−EXXに及ぼすECXの影響の例
3.5
回転軸に関する用語
3.5.1
一般
回転軸(例えば,主軸,回転テーブルなどの回転軸)の幾何精度に関連する用語は,JIS B 6190-7によ
るほか,次による。
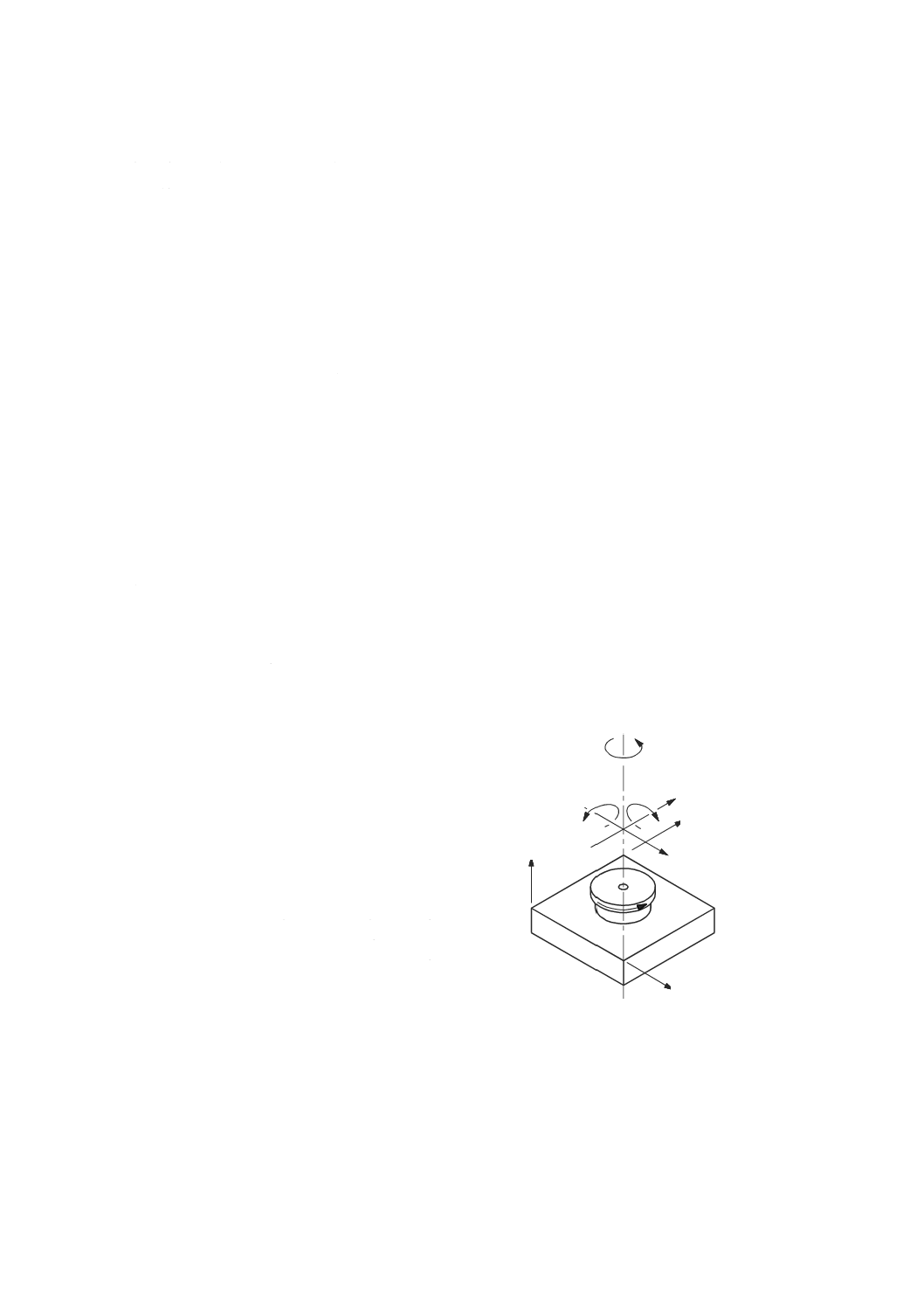
3.5.2
回転軸(axis of rotation)
回転の中心線となる線分(図11参照)。
(JIS B 6190-7の3.1.5参照)
3.5.3
軸平均線(axis average line)
基準座標系において,回転軸の平均位置を表す直線の線分。
(JIS B 6190-7の3.1.10参照)
3.5.4
回転軸誤差運動(axis of rotation error motion)
ECX
1
FP2
FP1
d
EXX
+X
+Z
+Y
+Y
+Z
+X
500
1000
1500
2000
0
0
10
20
30
-10
EXX
4
3
X
500
1000
1500
2000
2
ECX
0
10
-10
-200
X
1 000
1 500
2 000
1 000
1 500
2 000
EXX
−
−
−
11
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
回転軸の回転角度の関数として,軸平均線に対する回転軸の位置及び向きにおける変化(図11及び図
12参照)。
注記1 直進(誤差)運動の正方向は,正の位置の値を増加させるか,負の位置の値を減少させる方
向である(JIS B 6310の5.2.1参照)。角度誤差運動の正の方向(図1参照)は,直進運動の
正方向に向かって右ねじの方向である。
注記2 回転軸の誤差運動は,誤差を意味する文字Eの後ろに添え字を付けて表す。最初の添え字は,
誤差運動の向きに対応する軸の名称,2番目の添え字は,測定する回転軸の名称を表す(図
12参照)(附属書A参照)。
注記3 JIS B 6190-7の3.2.1参照。
1 主軸(ロータ)
2 回転軸の誤差運動
(角度Cの位置に到達するまでの軌跡)
3 軸平均線
4 回転軸(角度Cの位置で)
5 主軸台(ステータ)
注a) 基準軸
図11−C軸の基準座標軸,回転軸,軸平均線及び誤差運動
EXC C軸のX方向半径方向誤差運動
EYC C軸のY方向半径方向誤差運動
EZC C軸の軸方向誤差運動
EAC C軸のX軸回り角度誤差運動
EBC C軸のY軸回り角度誤差運動
ECC C軸の角度位置決め誤差
(測定された角度位置決め誤差)
注記 JIS B 6190-7参照。
注a) 基準軸
図12−回転軸の誤差運動
5
a)
a)
a)
2
3
4
1
X
Z
YY a)
Z a)
X a)
EAC
EXC
a)
a)
a)
EBC
EZC
ECC
EYC
X
Z
Y
C
Z a)
Y a)
X a)
12
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.5.5
軸方向誤差運動(axial error motion)
軸平均線と同軸方向との誤差運動。
(JIS B 6190-7の3.2.13参照)
3.5.6
半径方向誤差運動(radial error motion)
指定した軸方向位置での軸平均線に直交する方向の誤差運動。
(JIS B 6190-7の3.2.10参照)
3.5.7
傾斜方向誤差運動(tilt error motion)
軸平均線に対して,傾く方向の誤差運動。
(JIS B 6190-7の3.2.12参照)
注記 英語表記の“coning”,“wobble”,“swash”,“tumbling”,及び“towering”は,傾斜方向誤差運
動を表す用語としては不適切である。
3.5.8
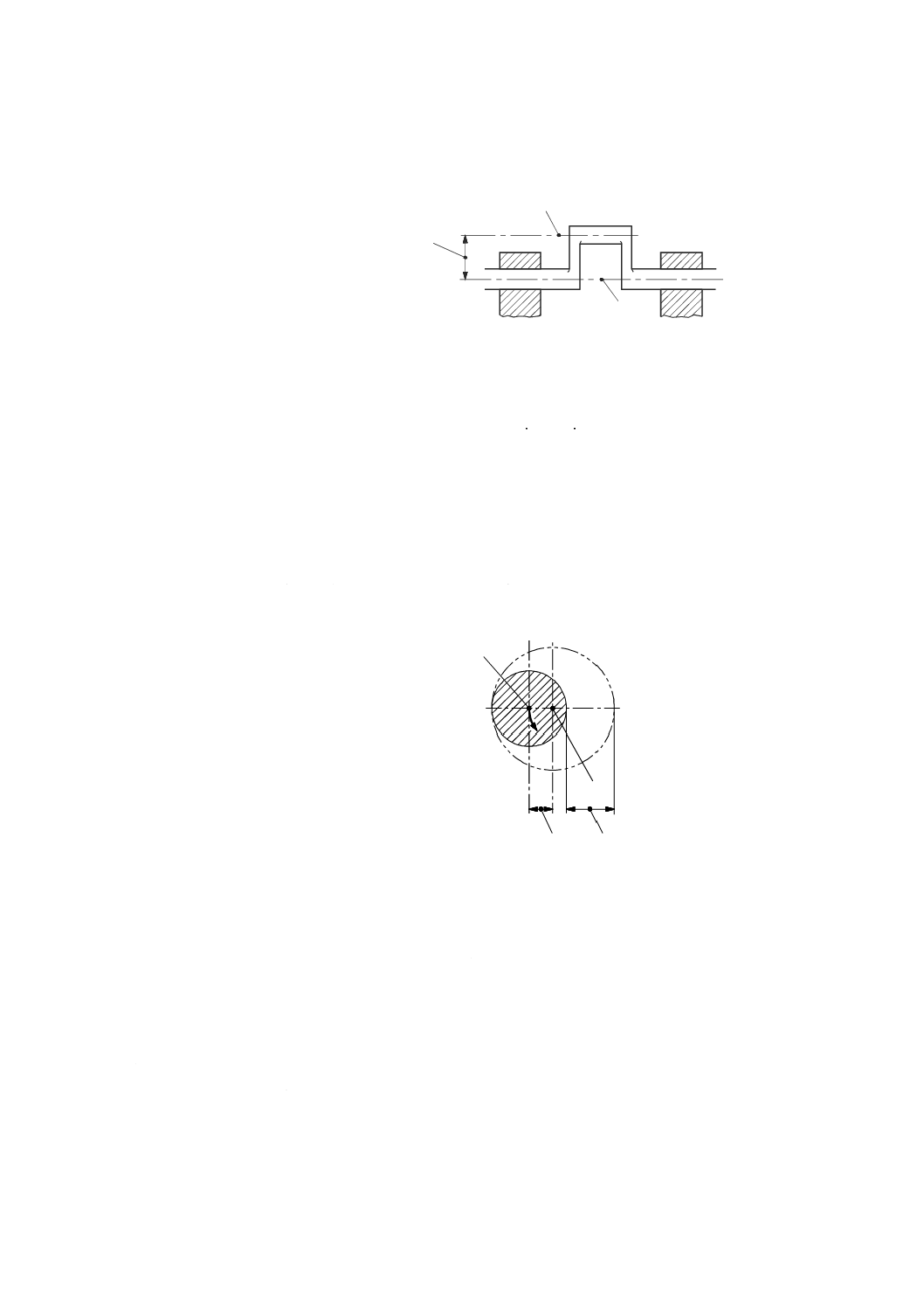
軸移動(axis shift)
状態の変化によって,軸平均線の位置と向きとに生じる(回転軸の)準静的な変化(図13参照)。
注記1 軸移動の原因には,温度ドリフト,負荷変化及び速度変化がある(JIS B 6190-7の3.7参照)。
注記2 位置及び角度の誤差は,誤差を意味する文字Eの後ろに添え字を付けて表す。最初の添え字
は,誤差の向きに対応する軸の名称,2番目の添え字として数字のゼロ(0)を付け,最後の
3番目の文字は,測定する回転軸の名称を表す(附属書A参照)。
EX0C C軸のX方向位置誤差
EY0C C軸のY方向位置誤差
EA0C C軸のX軸回り角度誤差
(Y軸に対するC軸の直角度)
EB0C C軸のY軸回り角度誤差
(X軸に対するC軸の直角度)
注a) 基準軸
図13−軸平均線の位置及び角度の誤差
3.5.9
被駆動軸の偏心量(eccentricity of a driven axis)
第一軸(駆動軸)が第二軸(被駆動軸)の回りで回転し,第二軸と平行な場合の第一軸と第二軸との距
離(図14参照)。
EB0C
EA0C
EY0C
EX0C
a)
a)
a)
X
Z
Y
CC
Y a)
Z a)
X a)
13
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 偏心量は,誤差ではなく,公差を条件とした寸法である。
1 第一軸(駆動軸)
2 第二軸(被駆動軸)
3 指定された偏心量
図14−被駆動軸と駆動軸との偏心量
3.5.10
所定の点における回転軸の半径振れ(radial throw of a rotary axis at a given point)
回転軸に接続された部品(又は測定の基準器)の幾何学的な軸線と軸平均線との距離。ただし,二つの
軸は一致しない(図15参照)。
注記1 部品(又は測定の基準器)の幾何学的な軸線は,異なる軸方向の位置で行う部品(又は測定
の基準器)の測定値から導く。
注記2 部品(又は測定の基準器)の形状誤差及び半径方向誤差運動が省略できる場合には,所定の
位置における軸の半径振れは,その位置で測定された振れの1/2である。
1 幾何学的な中心
2 回転軸
3 振れ
4 半径振れ
図15−所定の位置における軸の振れ及び半径振れ
3.5.11
角度位置決め誤差運動(angular positioning error motion)
実際に到達した回転部品の機能点の角度が,指令された角度と異なる原因になる回転方向の不要な動き
(図16参照)。
注記1 角度位置決め誤差運動の正の符号は,正の回転方向である(JIS B 6310による。)。
注記2 角度位置決め誤差運動は,回転部品の角度位置決め及びその案内の不完全さと関係している。
ただし,回転部品の動的応答及びその位置決めサーボ制御システムとは関係しない。
3.5.12
角度位置決め偏差(angular positioning deviation)
3
1
2
1
4
3
2
14
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
軸平均線に垂直な平面内において,運動部品上の機能点が到達した実際の角度と指令された角度との差。
注記1 角度位置決め偏差の正の符号は,正の回転方向である(図16参照)。
注記2 JIS B 6190-2は,数値制御軸による位置決めの正確さ及び繰返し性の試験方法及び評価方法
について規定している。
注記3 JIS B 6190-2に従って測定した角度位置決め偏差は,実際の角度位置決め誤差運動を表して
いるわけではない。
1 C軸の負の運動方向
2 目標位置
3 実際の位置
4 角度位置決め偏差(負)
図16−C軸の角度位置決め偏差
3.5.13
角度位置決め誤差(angular positioning error),
角度位置決め精度(angular positioning accuracy),
角度位置決めの正確さ(accuracy of angular positioning)
正の最大位置決め偏差と負の最小位置決め偏差の絶対値との和。
注記 この定義は,数値制御によらない軸に適用する。数値制御による回転軸の角度位置決めの精度
は,JIS B 6190-2参照。
3.5.14
角度割出しの一方向繰返し性(unidirectional repeatability of angular indexing)
一方向から同じ速度で一つの目標角度に所定の回数近づけたときの一連の測定から求めた角度位置決め
偏差の範囲。
注記1 この値は,各目標位置でクランピング(適用できる場合)及び角度遊びの影響を受ける。
注記2 数値制御による角度位置決めの繰返し性は,JIS B 6190-2参照。
3.5.15
角度割出しの両方向繰返し性(bidirectional repeatability of angular indexing)
両方向から同じ速度で一つの目標角度に所定の回数近づけたときの一連の測定から求めた角度位置決め
偏差の範囲。
注記1 この値は,各目標位置でクランピング(適用できる場合)及び角度遊びの影響を受ける。
注記2 数値制御による角度位置決めの繰返し性は,JIS B 6190-2による。
3.6
運動軸の平行度誤差及び直角度誤差に関する用語
3.6.1
一般
一般に,相対運動する運動軸の姿勢は,幾何学的に不完全な機械部品の組立の影響を受ける(例えば,
案内面,軸受のアライメント)。ただし,運動部品の直進誤差運動及び角度誤差運動は,局所的な偏差を与
1
2
4
3
+X
+Y
+X
+Y
15
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
え,相対運動する運動軸の姿勢に影響する。
したがって,直進運動部品の機能点の軌跡と次のa)〜c) との間の相対的な角度の測定においては,軌跡
自体及び基準(データム)要素に及ぼす局所的な偏差の影響は,無視する(又は避ける)必要がある。
a) 機能面(支持面又は滑り面)
b) 直線(軸平均線又は面の交線)
c) 別の直進運動部品上の機能点の軌跡
そのため,運動軸に関係する平行度誤差及び直角度誤差の定義では,直進運動の軌跡に関係する基準直
線を関連付け,かつ,基準(データム)要素に対する基準直線又は基準平面を関連付ける。したがって,
この定義には,真直度及び平面度の偏差を含まない。
直進軸及び回転軸に関係する平行度誤差の定義は,共通の座標平面の横軸に対して同じ角度をもつ二つ
の直線の特性として用語“平行度”を定義する。
直進軸及び回転軸に関係する直角度誤差の定義は,なす角度が90°である二つの直線の特性として用語
“直角度”を定義する。
注記1 平行度誤差及び直角度の定義は,JIS B 6191:1999の定義と異なる。
座標軸の直角度誤差及び平行度誤差は,誤差を意味する文字Eの後ろに添え字を付けて表す。最初の添
え字は,誤差の方向に対応する軸の名称,2番目の添え字は,選んだ基準(データム)軸を,数字のゼロ
(0)を付けて表し,最後の3番目の添え字は,測定する座標軸の名称を表す(附属書A参照)。
例1 X軸に対するZ軸の直角度誤差は,EB(0X)Zと表す。X軸が基準(データム)軸であれば,表記
は,EB0Zと簡略表記してもよい。
例2 W軸に対するZ軸の平行度誤差(ZX面内で)は,EB(0W)Zと表す。
注記2 直線経路上を動くように指令された運動部品の機能点の実際の軌跡は,直線ではない。測定
は,実際の軌跡をサンプリングしたもので,実際の軌跡を表すわけではない。直進軸及び回
転軸に関係する平行度誤差及び直角度誤差は,測定した実際の軌跡の偏差と関連する基準直
線間の角度の関係を考慮して定義する。
これらの定義は,他の規格(例えば,JIS B 0021)に規定されている平行度公差及び直角度公差と整合
する。3.9に定義する部品と機械の機能面との平行度誤差及び直角度誤差と混同してはならない。
3.6.2
二つの直進軸の平行度誤差(parallelism error between two axes of linear motion)
二つの共通の直交平面上で求めた,直進運動部品の機能点の軌跡の基準直線と(関係する)他の直進(デ
ータム)部品の基準直線(の向き)とのなす角度(図17参照)。
注記1 傾斜角度の符号は,JIS B 6310に規定する,機械座標系の軸の周りに回転する右手直交座標
系による。
注記2 平行度誤差は,基準にした軸に関連している基準直線の勾配と,データム軸と関連した基準
線の勾配との差が正であるとき,正の符号をとる。基準とした軸とデータム軸とを入れ替え
ると,平行度誤差の符号は逆になる。例えば,Z軸(基準とした軸)とW軸(データム軸)
との平行度誤差は,W軸(基準とした軸)とZ軸(データム軸)との平行度誤差とは,符号
が異なる。
注記3 基準にした軸の真直度偏差及びデータム軸の真直度偏差は,共通の物理的な真直度基準に対
して測定する。二つの座標面のそれぞれに対して,Z軸とW軸との平行度誤差は,Z軸とW
軸とを同時に反対方向に動くように指令して運動している間,テーブル上の点(静止点)に
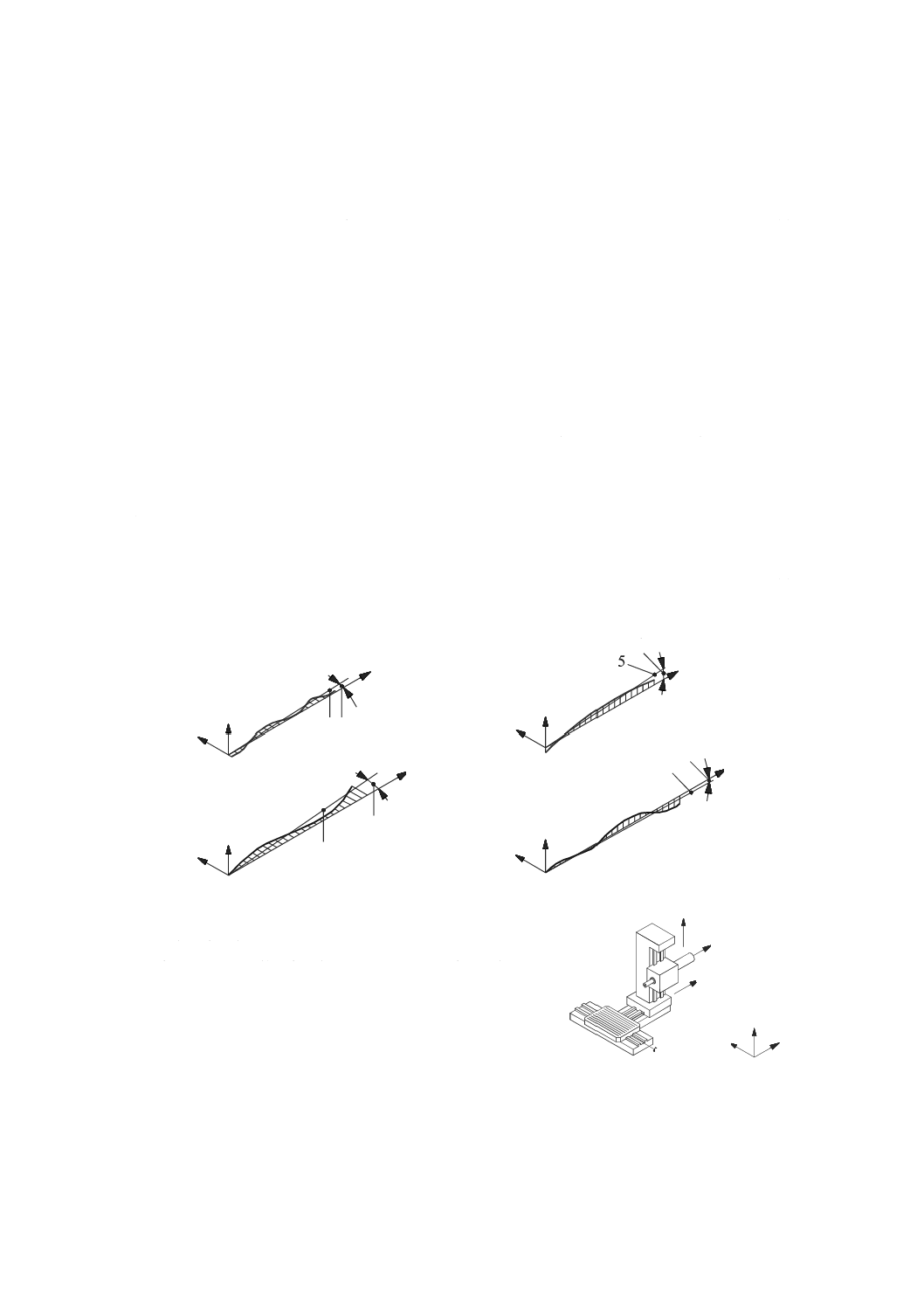
16
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
主軸台に取り付けた変位計の測定子を当てて,その読みを記録し,測定する。記録した読み
に関連している基準直線の傾斜角度は,平行度誤差となる。
注記4 図17の例については,式(1)及び式(2)を適用する。
EB(0W)Z=θ Z,ZX−θ W,ZX ·································································· (1)
EA(0W)Z=θ Z,YZ−θ W,YZ ·································································· (2)
注記5 平行度誤差の評価では,測定長さが短いと測定結果に意味がなくなることがある。
3.6.3
二つの回転軸の平行度誤差(parallelism error between two axes of rotation)
二つの直交平面上で求めた,回転部品の軸平均線(の向き)と他の(データム)回転部品の軸平均線と
のなす角度。
注記1 傾きを決定するための共通の基準は,回転軸と関連した機械の基本軸との正の方向である。
注記2 平行度誤差は,対象とした軸(図18に示す主軸の軸線)に関連した平均線の傾き角と,デー
タム軸(図18に示すC軸)と関連した平均線の傾き角との差が正であるとき,正の符号を
とる。
注記3 図18の例については,式(3)及び式(4)を適用する。
EB(0C)C1=θ C1,ZX−θ C,ZX ································································· (3)
EA(0C)C1=θ C1,YZ−θ C,YZ ································································· (4)
EXZ W軸と平行な物理的な真直度基準に対してZX面内で測定し
たZ軸の真直度偏差
EXW W軸と平行な物理的な真直度基準に対してZX面内で測定し
たW軸の真直度偏差
EYZ W軸と平行な物理的な真直度基準に対してYZ面内で測定し
たZ軸の真直度偏差
EYW W軸と平行な物理的な真直度基準に対してYZ面内で測定し
たW軸の真直度偏差
図17−ZX面及びYZ面内におけるZ軸とW軸との平行度誤差の例
+X'
+Z
+Y
+W
X
Z
Y
+Y
Y
+Z
Z
+W
X
+X'
EXW
EXZ
12
4
3
+W
+W
+Y
+Y
+W
EYZ
EYW
56
8
7
+W
+X
+X
+W
+Y
+W
+Y
+W
+X
+W
+X
17
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 EXZに関連付けた基準直線
2 基準直線EXZの傾き角,θ Z,ZX
(図示した例は,正の値)
3 EXWに関連付けた基準直線
4 基準直線EXWの傾き角,θ W,ZX
(図示した例は,正の値)
5 EYZに関連付けた基準直線
6 基準直線EYZの傾き角,θ Z,YZ
(図示した例は,負の値)
7 EYWに関連付ける基準直線
8 基準直線EYWの傾き角,θ W,YZ
(図示した例は,正の値)
注記
3.6.2の注記4参照。
図17−ZX面及びYZ面内におけるZ軸とW軸との平行度誤差の例(続き)
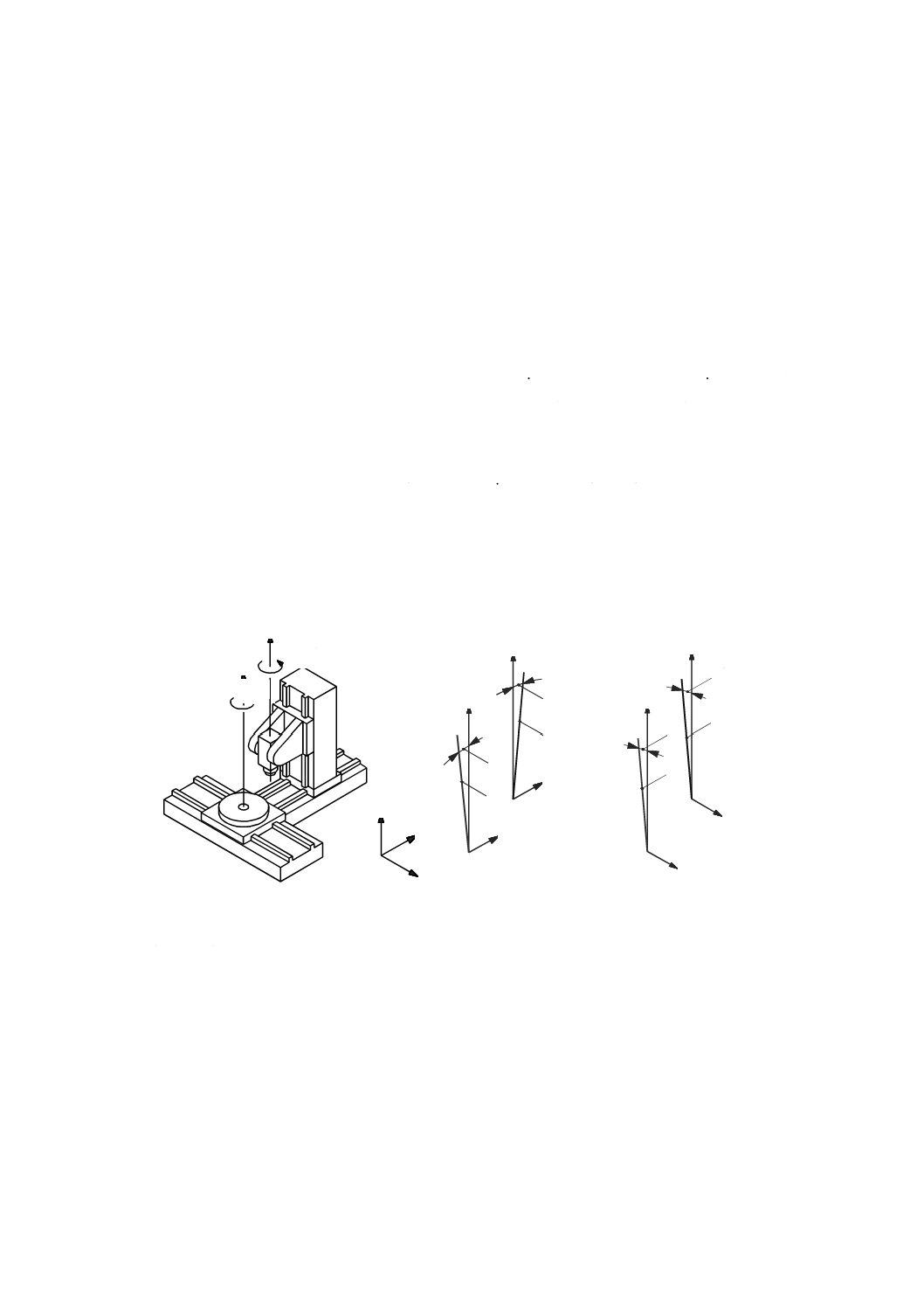
3.6.4
直進軸と回転軸との平行度誤差(parallelism error between an axis of linear motion and an axis of rotation)
二つの直交面で求めた,直進運動部品の機能点の軌跡の基準直線(の向き)と(データム)回転部品の
基準直線とのなす角度。
3.6.5
直進軸と面との平行度誤差(parallelism error between an axis of linear motion and a surface)
直進運動部品の機能点の軌跡の基準直線(の向き)と(関係する)(データム)機械の機能面とのなす角
度。
注記 傾きを決定するための共通の基準は,関連付ける機械の基本軸(共通)の正の方向である。
+C1 主軸の軸線(対象とする軸)
+C 回転テーブル(データム軸)
+Z 傾きを評価するための共通の基準
1 C軸の軸平均線
2 C1軸(主軸の軸線)の軸平均線
3 YZ面内におけるC軸の軸平均線の傾き角,θ C,YZ(図示した例は,正の値)
4 YZ面内におけるC1軸の軸平均線の傾き角,θ C1,YZ(図示した例は,負の値)
5 ZX面内におけるC軸の軸平均線の傾き角,θ C,ZX(図示した例は,負の値)
6 ZX面内におけるC1軸の軸平均線の傾き角,θ C1,ZX(図示した例は,負の値)
注記 3.6.3の注記3参照。
図18−C軸と主軸との平行度誤差の例
+C1
+Z
+Z
+C
1
5
6
2
+Z
+Z
+X
+X
+Z
+Y
+X
1
3
4
2
+Z
+Z
+Y
+Y
Z
Z
C
C
+Z
+Z
+Z
+Y
+Y
+Y
+X
+Z
+Z
+X
+X
18
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
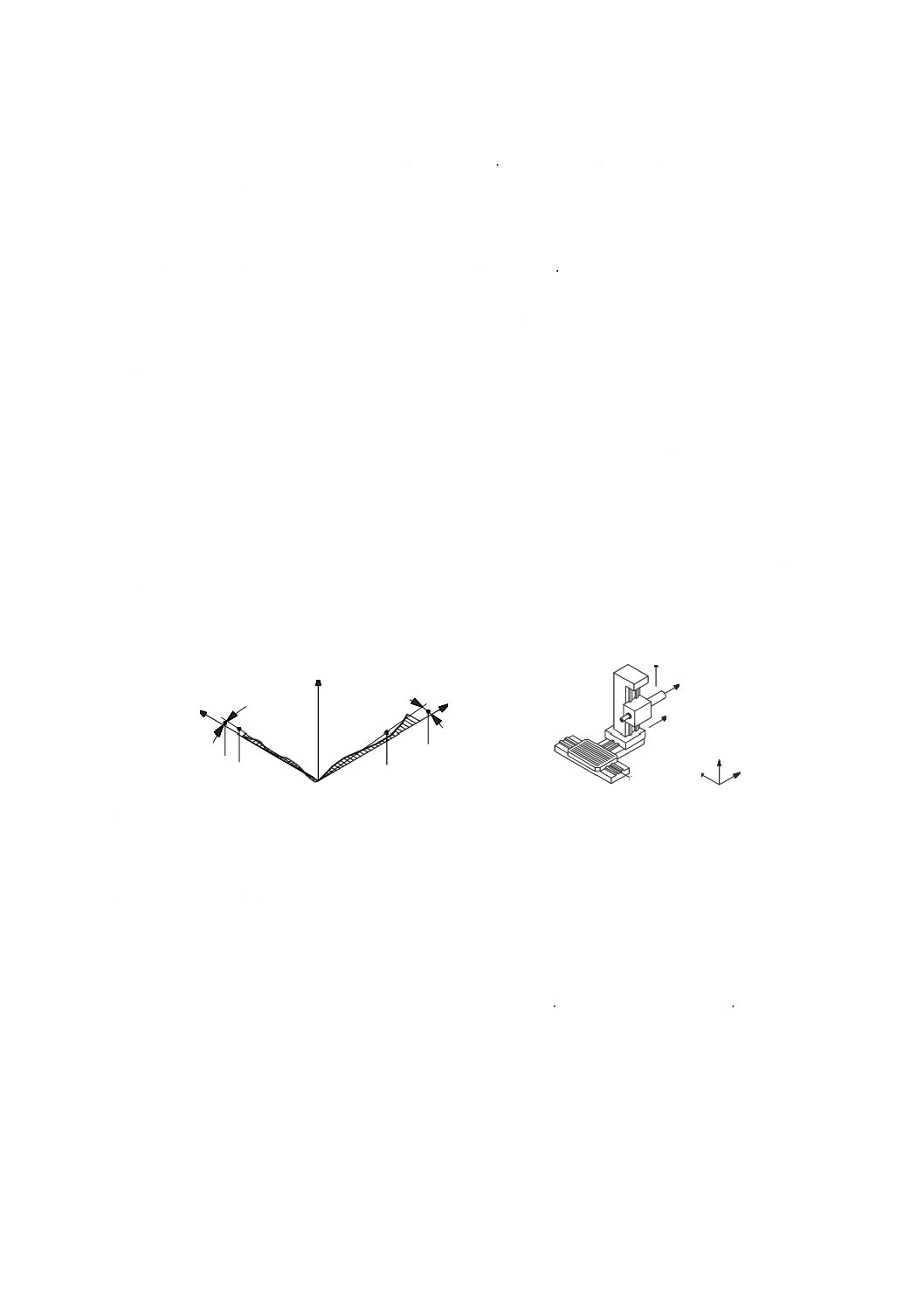
3.6.6
回転軸と面との平行度誤差(parallelism error between an axis of rotation and a surface)
回転部品の軸平均線(の向き)と機械の機能面に対応する基準平面(に関係する面)とのなす角度。
注記 傾きを決定するための共通の基準は,関連付ける機械の基本軸の正の方向である。
3.6.7
二つの直進運動の直角度誤差(squareness error between two axes of linear motion)
直進運動の基本軸に対応する直進運動部品の機能点の軌跡の基準直線の傾きと,(関係して)直進運動の
基本軸に対応する他の直進運動部品の機能点の軌跡の基準直線の傾きとの差(図19参照)。
注記1 この定義は,概念的に“二つの機能直線間の直角度誤差(3.9.5参照)”の定義とは異なる。
注記2 正の直角度誤差は,JIS B 6310に規定する,回転軸の右手直交座標系に従い,データム軸に
対する対象とした軸の向きにおける正の角度誤差に対応する。直角度誤差の符号は,対象と
した軸とデータム軸とを入れ替えると,逆になる。例えば,X軸(対象とした軸)とY軸(デ
ータム軸)との間の直角度誤差は,Y軸(対象とした軸)とX軸(データム軸)との間の直
角度誤差とは,符号が異なる。この混乱を避けるために,直角度誤差は,“90°より大きい”
又は“90°より小さい”のような記述を追加してもよい。
注記3 図19に示す例の場合には,式(5)を適用する。
EB(0Z)X=EB0X=θ X,ZX−θ Z,ZX··························································· (5)
注記4 直角度誤差の評価において,測定長さが短いと測定結果に意味がなくなることがある。
1 EXZに関係する基準直線
2 基準直線EXZの傾き,θ Z,ZX(図示した例は,正の値)
3 EZXに関係する基準直線
4 基準直線EZXの傾き,θ X,ZX(図示した例は,負の値)
注記 3.6.7の注記3参照。
図19−直進X軸とZ軸との直角度誤差の例
3.6.8
直進軸と軸の平均線との直角度誤差(squareness error between an axis of linear motion and an axis average line)
直進運動部品上の点の軌跡の基準直線と(関係する)機械の回転部品の軸の平均線との90°からの角度
偏差。
注記 回転軸と関係する正の方向は,JIS B 6310に規定する右手直交座標系に基づき直進運動の正の
方向とする。
2
1
3
4
+X
+Y
+Z
+X'
+Z
+Y
+W
X
Z
Y
+Y
+Z
+X
+Z
+Y
+W
Z
Y
+X'
X
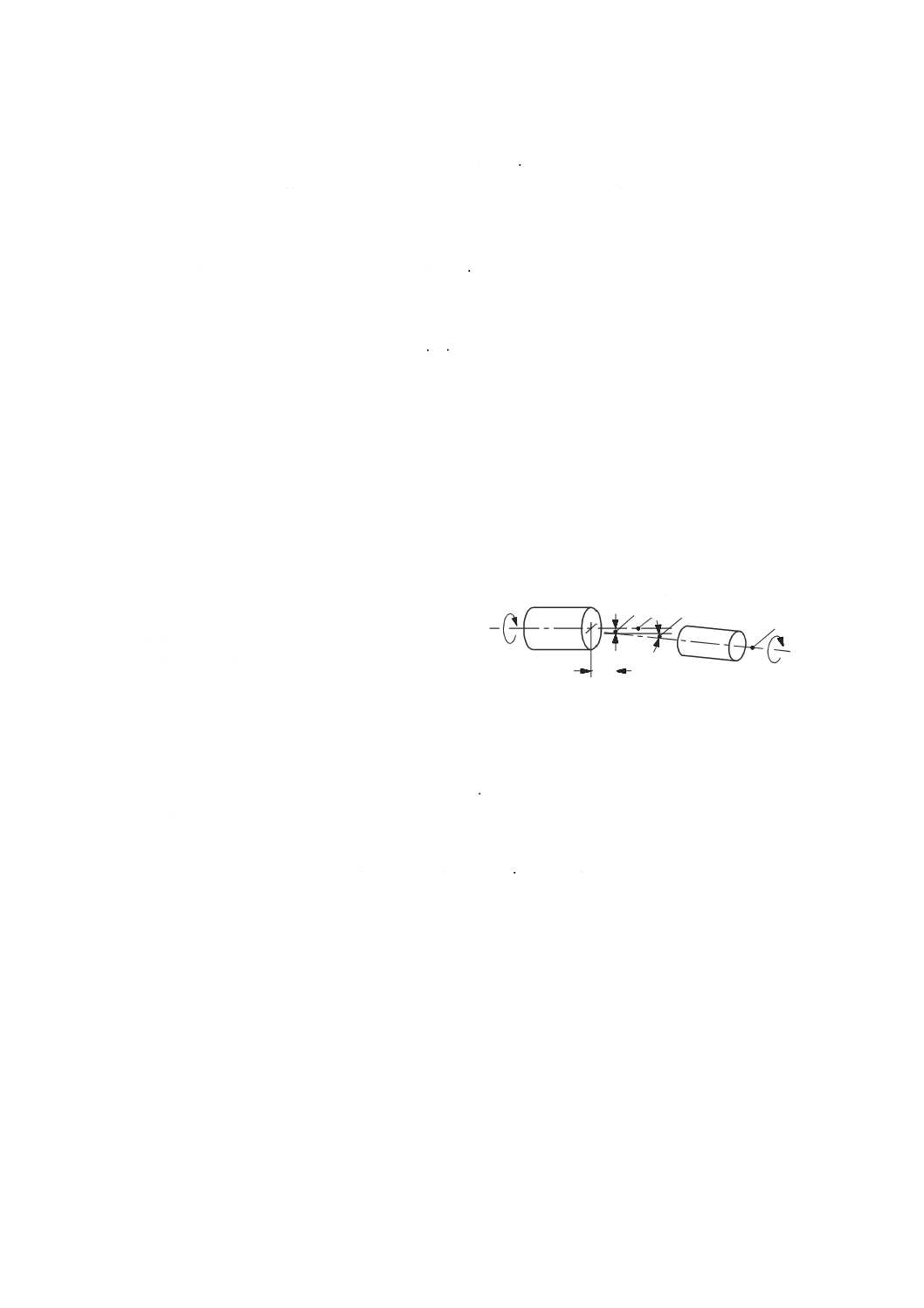
19
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.6.9
二つの軸平均線の直角度誤差(squareness error between two axis average lines)
機械の回転部品の軸平均線と(関係する)機械の他の回転部品の軸平均線との90°からの角度偏差。
3.7
軸平均線間の関係を表す用語
3.7.1
二つの軸平均線間のオフセット(offset between two axis average lines)
軸方向の指定された位置における二つの理想的には平行な軸平均線間の半径方向の距離。
3.7.2
二つの軸平均線の同軸度誤差(coaxiality error of axis average lines)
2直交平面で評価する二つの理想的には同軸平均線間の指定された位置及び角度でのオフセット(図20
参照)。
注記1 この定義は,二つの線がオフセットしていない平行な二つの直線の特性として,用語“同軸
度”を定義する。
注記2 同軸度誤差は,一つの指定された位置で2直交平面において評価した二つのオフセット及び
二つの平行度(角度)で表される。
注記3 同軸度誤差は,平行度誤差の測定と同様に二つの垂直平面において測定する。
1 軸平均線1
2 軸平均線2
3 同軸度偏差のオフセット(一つの平面で測定)
4 同軸度偏差の角度(一つの平面で測定)
L オフセット測定のために指定した距離
図20−軸平均線の同軸度誤差の例(2直交平面の一つを表示)
3.7.3
二つの軸平均線の等距離度誤差(equidistance error of axis average lines)
軸平均線と基準平面との距離と,その基準平面に対するもう一つの軸平均線との距離との差。
3.7.4
二つの軸平均線の交差度誤差(error of intersection between axis average lines)
見掛け上交わっている二つの軸平均線間の実際の最短距離(図21参照)。
注記 交差しない二つの軸平均線の投影図は,その対称面上の点で交わる。二つの軸平均線間の最短
の実際の距離は,投影図の交点に中心があって,その二つの軸平均線に接する球の直径に等し
い。
2
314
L
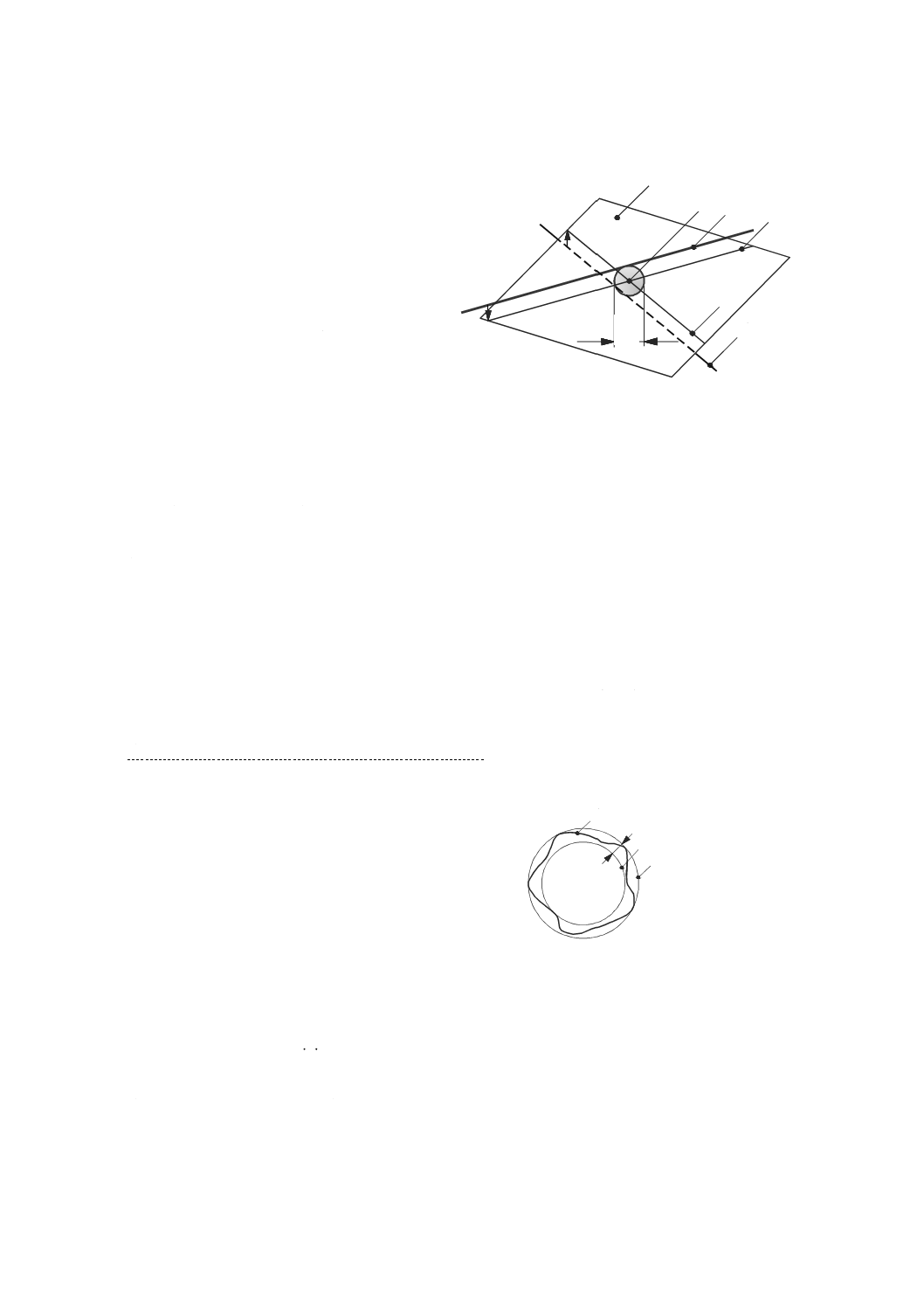
20
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 軸平均線1
2 軸平均線2
3 対称面
4 対称面上の軸平均線1の投影図
5 対称面上の軸平均線2の投影図
6 投影図4及び5の交点
d 交点6に中心があり,軸平均線1及び2に接
する球の直径(交差度誤差)
図21−二つの軸平均線間の交差度誤差
3.8
多軸運動試験に関する用語
3.8.1
同期運動(synchronous motion)
制御装置で同時に2軸以上の制御軸を同期させて,工作物及び/又は工具を空間内であらかじめ決めら
れた経路に沿って動かす運動。
3.8.2
円形誤差(circular error)
同期運動によって生成された実際の円弧軌跡を挟む二つの同心円間の半径方向の最小間隔(図22参照)。
注記1 基準円は,最小領域平均基準円(3.8.3)又は最小二乗基準円(3.8.4)である。
注記2 円形誤差は,部品及び工作機械の機能面に関係する用語“真円度”とは異なり,同期運動に
関係して用語“真円度”を用いるのは適切ではない。
注記3 二つの同心円を,最小領域基準円という。
1 円弧軌跡
2,3 最小領域基準円
4 最小半径間隔(円形誤差)
図22−円形誤差を示す円弧軌跡の例
3.8.3
最小領域平均基準円(mean minimum zone reference circle)
実円弧軌跡を含み,最小半径間隔をもつ二つの同心円の算術平均円。
注記 ISO 12181-1の3.3.1.1参照。
3.8.4
最小二乗基準円(least squares reference circle)
d
3
61
4
5
2
1
4
2
3
21
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
局所的な円形偏差の二乗の和が最小となるような実円弧軌跡に適合させた円。
注記 ISO 12181-1の3.3.1.2参照。
3.8.5
平面度(flatness)
平面の幾何特性。
3.8.6
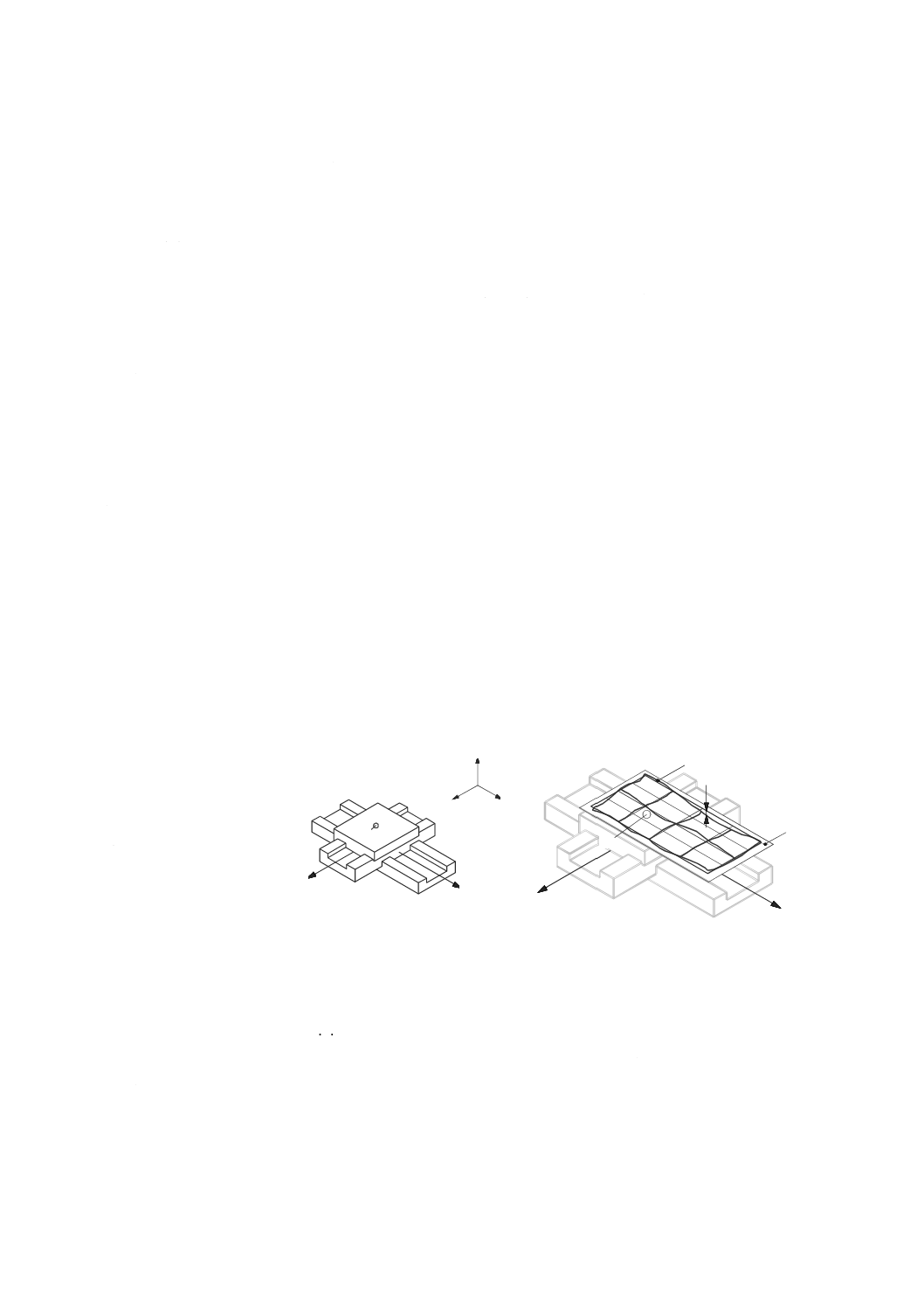
二つの直進運動によって創成された表面(surface generated by two linear motions)
仮想表面を創成する,(公称)平面上を運動するように指令された二つの直進運動部品の合成運動によっ
て得られる機能点の集合(図23参照)。
注記 “仮想表面”とは,概念的にISO 12781-1の3.2.2に定義する,実表面を表す測定平面度輪郭曲
線を意味する,“平面度輪郭曲面”に似ている。
3.8.7
平面度偏差(flatness deviation)
基準平面から(二つの直進運動によって生成された表面上の)点の偏差で,基準平面に垂直な方向の偏
差。
注記1 ISO 12781-1の3.2.3参照。
注記2 平面度偏差の正の符号は,JIS B 6310に従って正の方向。
3.8.8
基準平面(reference plane)
二つの直進運動によって創成された表面に適合させた平面で,平面度の偏差及び測定値の基準となる平
面。
注記 ISO 12781-1の3.3.1参照。
1 機能点
2 基準平面
3 機能点の軌跡
4 部分平面度偏差
図23−二つの直進運動によって決まる平面
3.8.9
最小領域平均基準平面(mean minimum zone reference plane)
二つの直進運動によって生成される面を含み,最小間隔の二つの平行平面の算術平均平面(図24参照)。
注記 ISO 12781-1の3.3.1.1.3参照。
+Z'
+X'
1
+Z'
+Y
+X'
+X'
+Z'
3
4
2
1
+Z'
+Z'
+X'
+X'
+Z'
+X'
+Y
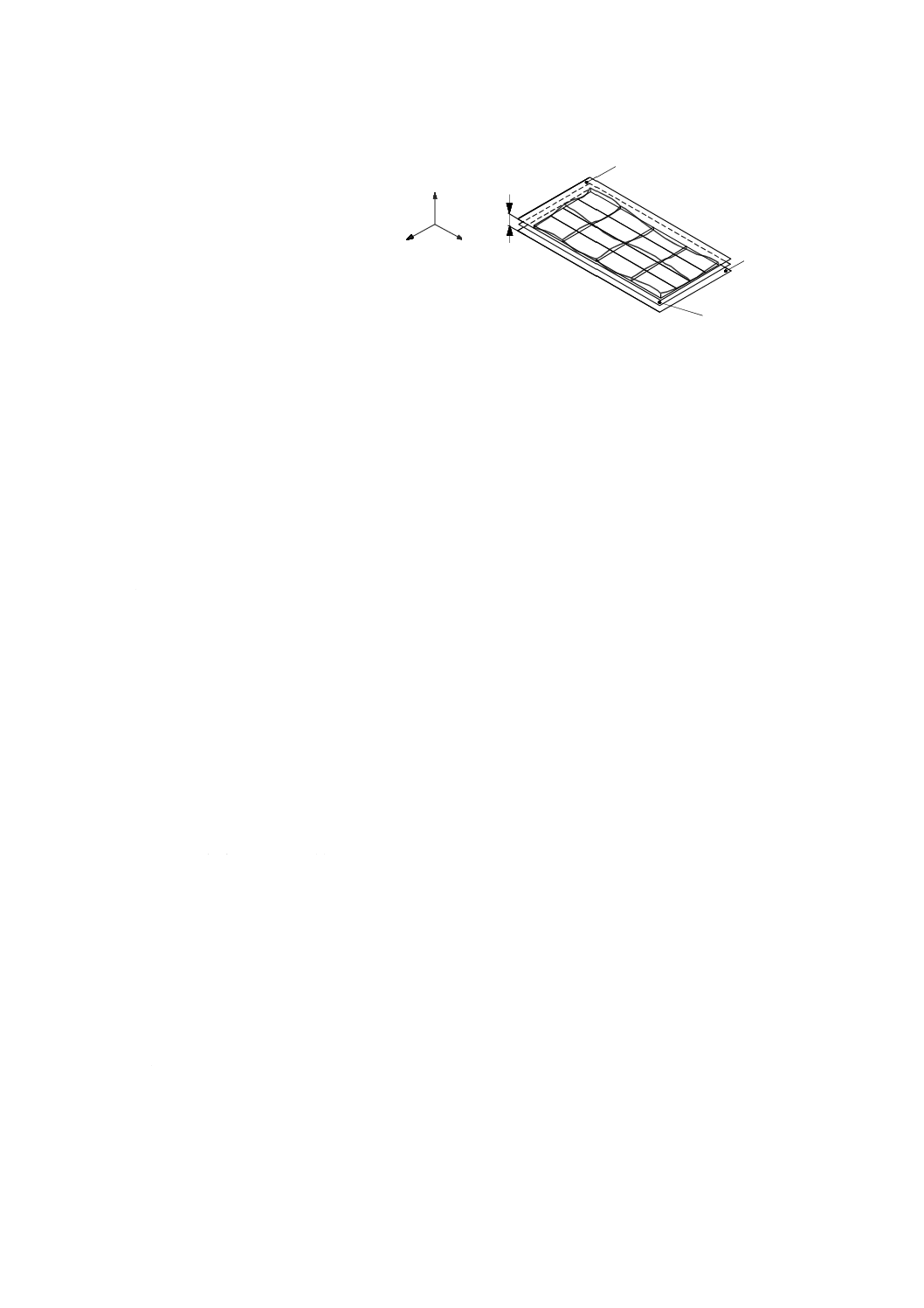
22
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 上側の最小領域基準平面
2 最小領域平均基準平面
3 下側の最小領域基準平面
d 最小間隔
図24−最小領域基準平面
3.8.10
最小二乗基準平面(least squares reference plane)
平面度偏差の二乗の和が最小になるような平面。
注記 ISO 12781-1の3.3.1.2参照。
3.8.11
二つの直進運動で決まる面の平面度誤差(flatness error of a surface defined by two linear motions)
(前もって定義した基準平面に対して)正の最大平面度偏差に負の最大平面度偏差の絶対値を加えた値。
注記 最小平面度誤差は,最小領域基準平面を用いて評価する。
3.8.12
3直進軸の空間精度,VXYZ(volumetric accuracy for three linear axes)
対象とする空間における,X,Y,Z軸運動に対する理想の位置と実際の位置とのX,Y,Z軸方向の相
対偏差の最大範囲及びA,B,C軸方向の角度偏差の最大範囲。ただし,それらの偏差は,指定された第
一軸及び第二軸に対する工作機械の工具側と工作物側との間の相対偏差(図25参照)である。
空間精度VXYZは,各直進軸及び各回転軸について,次の六つの偏差で表す。
VXYZ,X: X軸方向における最大相対偏差範囲
VXYZ,Y: Y軸方向における最大相対偏差範囲
VXYZ,Z: Z軸方向における最大相対偏差範囲
VXYZ,A: A軸方向における最大偏差範囲
VXYZ,B: B軸方向における最大偏差範囲
VXYZ,C: C軸方向における最大偏差範囲
使用した測定座標系及び次の値は,記録する。
− X,Y,Z軸方向における工具オフセット
− 関係のある空間,X×Y×Z
− 空間の中心位置,X,Y,Z
− 採用した測定座標系(附属書A参照)
注記 回転軸も機械の空間精度に影響を及ぼす。ただし,分かりやすくするためにここでは考慮し
ない。
+Z'
+Y
+X'
1
2
3
d
+Y
+Z'
+X'
23
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 X軸方向の偏差
2 Y軸方向の偏差
3 Z軸方向の偏差
4 A軸方向の偏差
5 B軸方向の偏差
6 C軸方向の偏差
AP 実際の位置
SP 開始位置
TP 目標位置
図25−目標位置の偏差
3.8.13
空間性能(volumetric performance)
工作機械の受渡当事者間で協定した全作業空間又はそれより小さな空間のどの場所でも,意図した多軸
機能を遂行できる工作機械の能力。
3.9
機械の機能面,部品及び工作物の幾何精度に関する用語
3.9.1
一般
工作機械の機能面は,実際の部品である。その部品の幾何精度に関係する用語及び定義は,JIS B 0021
による。
真直度(3.4.11),基準直線(3.4.12),平面度(3.8.5)及び基準平面(3.8.8)の用語及び定義は,部品に
も適用する。
機械の機能面間の平行度及び直角度の用語及び定義は,運動軸に関係する平行度誤差及び直角度誤差に
対する定義と概念的に異なる。“直角度”は,JIS B 0021との一貫性を保ち,かつ,運動軸に関係する幾何
学的な要素間の角度を表す用語“直角度”と区別し,機能面に関係する形体間の関係を表す用語として使
用する。
3.9.2
平面内の機能線の真直度誤差(straightness error of a functional line in a plane)
対象とする線の全ての測定点を含んだ線の総体方向に平行な二つの直線間の最小距離。
注記1 線又は基準直線の総体方向は,真直度誤差[最小領域平均基準直線(3.4.13)参照]が最小に
なるように決める。また,通常,試験する直線の両端近くの適切に選んだ2点[両端点基準
直線(3.4.15)参照],又はプロット点から計算した直線[最小二乗基準直線(3.4.14)参照]
で決めてもよい。
注記2 空間における線の真直度誤差は,直交する二つの平面に投影した線の真直度誤差によって規
定する。
3.9.3
機能線と平面との平行度誤差(parallelism error between a functional line and a plane)
対象とする線の全ての測定点を含む(データム)機能平面と関連する基準平面(3.8.8)に平行な二つの
直線間の最小距離。
TPSP
+X
+Z
+Y
AP
+Y+Z+X
TP
SP
6
AP
2
3
1
5
4
+Z
+X
+X
+Y +Z
+Y
24
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記1 JIS B 0021の18.9.3を参照。
注記2 この定義における平行度誤差は,(対象とする)線の真直度偏差を含み,直進軸と面との平行
度誤差(3.6.5)とは概念的に異なる。
3.9.4
二つの機能平面間の平行度誤差(parallelism error between two functional planes)
(対象とする)機能平面の全ての測定点を含む,(データム)機能平面と関連する基準平面(3.8.8)に平
行な二つの平面間の最小距離。
注記1 ISO 1101:2012の18.9.6を参照。
注記2 この定義による平行度誤差は,(対象とする)機能平面の平面度偏差を含む(図26参照)。
1,2 aに平行な平面
a (データム)機能平面に関連する基準平面
n,m (対象とする)機能平面の測定データ点
d 最小距離:平行度誤差
図26−二つの機能平面間の平行度誤差
3.9.5
二つの機能直線間の直角度誤差(perpendicularity error between two functional lines)
(参照する)機能直線の全ての測定点を含む,(データム)直線と関連する基準直線(3.4.8)に平行な二
つの平面間の最小距離。
注記1 JIS B 0021の18.10.1を参照。
注記2 データム直線は,回転部品の軸平均線又は二つの基準平面と交差している直線であり得る(図
27参照)。
注記3 直角度誤差は,この定義によると(対象とする)直線の真直度誤差を含んでいるが,二つの
直進軸間の直角度誤差(3.6.7)とは概念的に異なる。
1,2 aに直角な平面
a データム基準直線
n,m (参照する)機能直線の測定データ点
d 最小距離:直角度誤差
図27−二つの基準直線間の直角度誤差
2
m
1
a
n
2
m
1
a
n
25
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.9.6
二つの機能平面間の直角度誤差(perpendicularity error between two functional planes)
(参照する)機能平面の全ての測定点を含む,(データム)平面と関係する基準平面(3.8.8)に垂直な二
つの平行平面間の最小距離。図28参照。
注記1 ISO 1101:2012の18.10.5を参照。
注記2 この定義による直角度誤差は,(参照する)平面の平面度偏差を含む。
1,2 aに直角で,互いに平行な平面
a データム基準平面
n,m (参照する)機能平面の測定点
d 最小距離:直角度誤差
図28−二つの機能平面間の直角度誤差
3.9.7
一つの断面における機能面の振れ(run-out of a functional surface at a given section)
運動している表面に対して検出する変位計,又は固定した表面に対して動いて検出する変位計によって
測定された全変位。
注記1 JIS B 0021の18.15参照。
注記2 半径方向の振れは,ある一つの断面(図15参照)における一つの軸の半径振れの2倍である。
ただし,真円度誤差又は半径方向誤差運動は考慮しない。
注記3 一般に測定された振れは,次のようになる。
a) 測定点での軸の半径振れ(3.5.10)
b) 部品の真円度誤差(JIS B 0021の18.3参照)
c) 回転軸の半径方向誤差運動(JIS B 6190-7の3.2.10参照)
注記4 工作機械の幾何精度試験において,軸の半径振れは,その軸上に取り付けられた部品の振れ
を観察することによって測定する。機械の検査の担当者の混乱を避け,かつ,誤差のリスク
を取り除くために,この規格では,用語として“振れ”だけを用い,この振れに公差を系統
的に適用し,測定器の読みは2で割らない。
注記5 転がり軸受を用いる場合は,転動体と保持器とは,軸が2回転以上回転するごとに1回転す
る。軸の振れは,数回転ごとに周期的に繰り返すのが一般的である。この変化を考慮するた
めに,振れは,数回転(少なくとも2回転)にわたって測定する(JIS B 6190-7の5.4及び
5.5参照)。
注記6 (必要があれば,軸受にテストバーをはめた後に)ある長さにわたって振れを測定したとき,
各測定点での振れが所定の値を超えなければ,測定上の観点からは,円筒又は円すいころ軸
受は,回転軸と正確に一致する軸をもつという。
2
m
1
a
n

26
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.9.8
機能面の平面度誤差(flatness error of a functional surface)
全ての測定点を含み,最小の間隔をもつ,平面の総体方向に平行な2平面間の最小距離。
注記1 JIS B 0021の18.2参照。
注記2 平面又は基準平面(3.8.8)の総体方向は,平面度誤差が最小になるように定義する。すなわ
ち,通常,次のいずれかで定義する。
− 試験する平面において便宜的に選択する3点(小さな部分的欠陥をもっているエッジ近
傍は避ける。)
− 最小二乗法によってプロットした点から求めた平面(3.8.11参照)
− 最小領域平均基準平面
3.9.9
データム直線と機能円筒との同軸度誤差(coaxiality error of a functional cylinder to a datum straight line)
機能円筒の中心線とデータム直線との間の最大半径方向距離(指定した測定長さ内で評価)の2倍。
注記1 JIS B 0021の18.13.2参照。
注記2 典型的な機能円筒は,クイルである。典型的なデータム直線は,関連する主軸の軸平均線で
ある。
4
許容値
4.1
一般
許容値は,評価する工作機械の特性及び幾何精度の許容できる誤差を特定し,機能要求事項に従って規
定する。許容値を規定する場合は,製造,組立及び検査要求事項も考慮するのがよい。
許容値は,測定する特性に対応した単位で表さなければならない。
4.1.1
許容値及び適合の領域に関する基準(JIS B 0641-1参照)
許容値を規定する場合及び規定した許容値との適合を評価する場合は,測定の不確かさを考慮すること
が望ましい(箇条5及び6.3参照)。適合の領域及び不適合の領域は,JIS B 0641-1の基準に従って決定す
る[図29のa) 及びb) 参照]。
1 適合の領域
2 不適合の領域
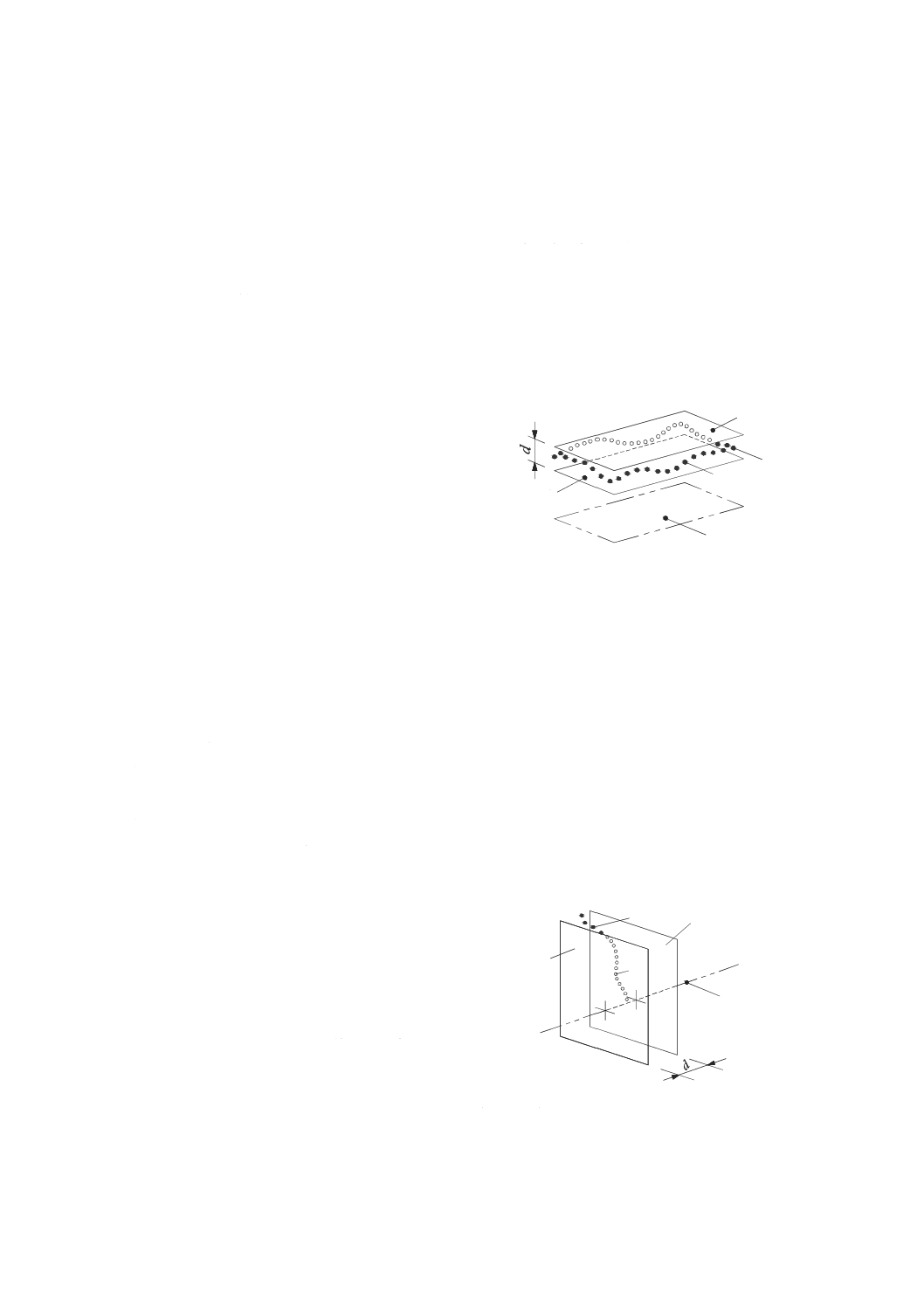
T1 片側許容値の領域。例 EZX 真直度0.012 mm
T2 両側許容値の領域。例 100 mm±0.006 mm
U 測定の不確かさ
図29−片側許容値の領域,両側許容値の領域に対する適合の領域及び不適合の領域の決定
例 振れの許容値:x mm
測定の不確かさ:y mm
試験中の読みの最大許容差:(x−y) mm(適合の領域)
U
U
T1
1
2
U
U
UU
T2
2
1
2
a) 片側許容値の領域
b) 両側許容値の領域

27
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
適合の領域のその他の定義は,受渡当事者間の協定による。
幾何精度の測定値を繰返し求める場合は,その測定値の平均をとることが望ましい。求めた測定値のば
らつきは,測定の不確かさが一因である。
4.1.2
規定された測定の限界
特に規定しない限り,この規格に規定する試験に対応する許容値は,規定された測定限界(真直度試験
の測定長さ,空間精度試験の測定体積,静的コンプライアンス,ヒステリシス試験のための加えた力の範
囲など)内において,測定対象の値について,許容できる最大値を示さなければならない。
許容値を所定の限界について規定する場合は,その限界と同等な他の限界の許容値に比例則を適用して
もよい。例えば,特定の測定長さに対して許容値がT1であり,測定長さL2に対してそれより大きな許容
値がT2である場合は,L1からL2までの測定長さに対してTLは,次の式(6)〜式(8)による比例則によって決
定する。
1L
L≦
のとき,
1
L
T
T=
·························································· (6)
2
1
L
L
L
<
<
のとき,
(
)
1
1
2
1
2
1
L
L
L
L
L
T
T
T
T
−
−
−
+
=
································ (7)
2L
L≧
のとき,
2
L
T
T=
························································· (8)
測定長さが規定する測定長さと大きく異なる場合には,(例えば,利用できる測定長さが300 mmではな
く30 mmの場合には)比例則は,適用できない。
4.1.3
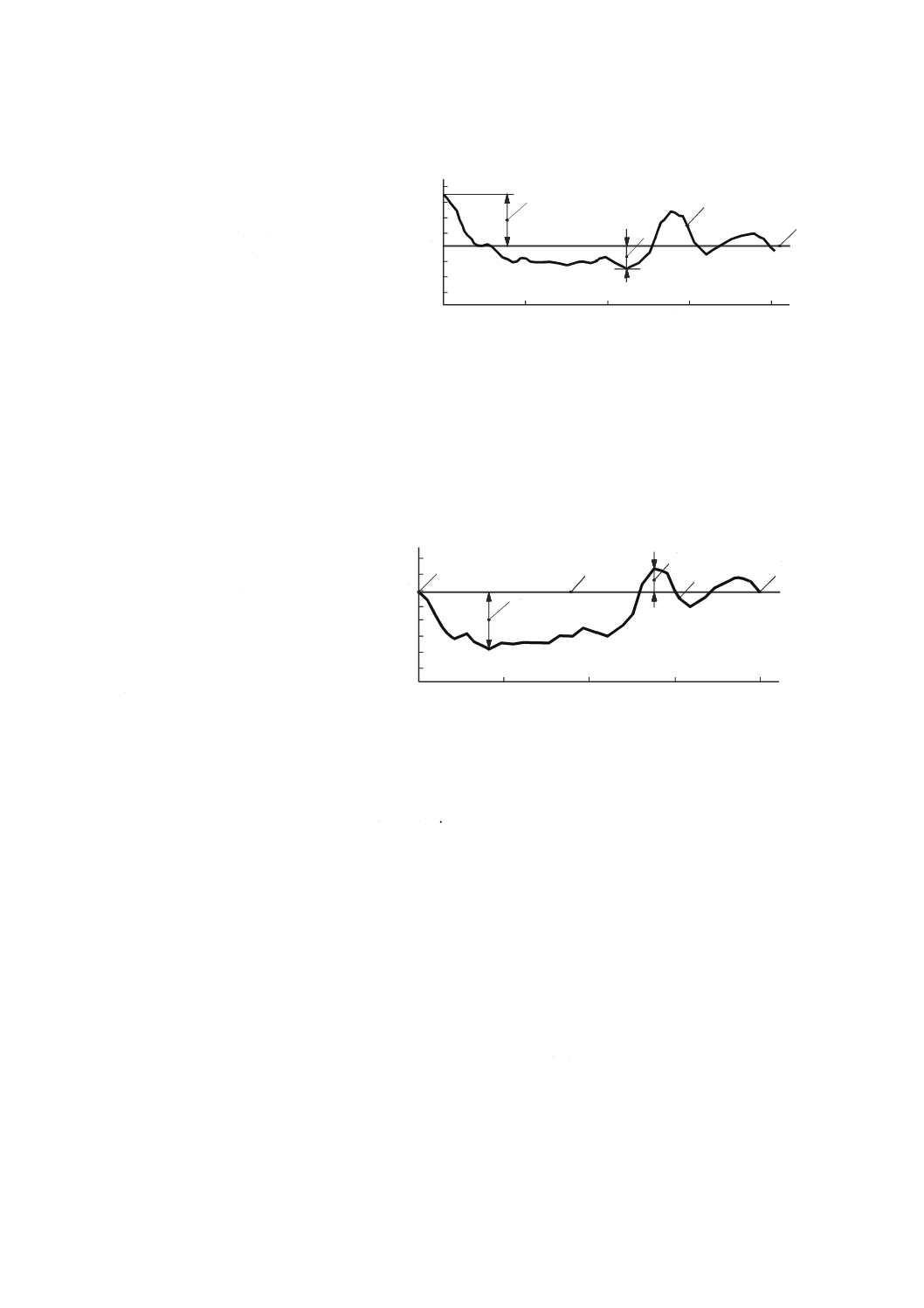
部分許容値
特に規定しない限り,許容値は,測定の限界全体にわたる測定結果に適用する。部分許容値は,部分測
定の限界を参照して規定することが望ましい。
部分許容値は,単純に比例則を適用して規定してはならない。部分許容値の規定は,試験中の特性又は
部品に関連した機能要求事項及び検査要求事項を考慮しなければならない。
直進軸の部分真直度誤差の規定は,3.4.10の定義を直接適用するが,基準直線は,部分測定長さで評価
する(図30参照)。
1 真直度誤差
2 部分測定長さ
3 部分真直度誤差
4 部分真直度の測定結果に関連する両端の点を結んだ両端点基準直線
M,N 全測定長さにわたる真直度測定値に関連する両端の点を結んだ両端点基準直線
図30−部分真直度誤差
さらに,直進軸間の平行度誤差及び直角度誤差の部分許容値は,明確に規定しなければならない。
直進軸間の平行度誤差及び直角度誤差は,参照する軸の軌跡及びデータム軸の軌跡に関連する基準直線
間の角度の関係である。
部分平行度誤差及び部分直角度誤差を規定し,試験する場合は,データム軸の軌跡に関連する基準直線
が,データム軸の全移動範囲にわたる測定から得られた結果から評価するか,又はデータム軸の部分移動
範囲にわたる測定から得られた結果から評価するかを明確に記載しなければならない(図31,図32及び
M
1
34
N
2
28
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図33参照)。
EXZ W軸に平行な物理的な真直度基準に対して,ZX平面で測定されたZ軸の真直度偏差
EXW W軸に平行な物理的な真直度基準に対して,ZX平面で測定されたW軸の真直度偏差
LZ Z軸の部分測定長さ
1 Z軸の移動範囲全体にわたるEXZの測定に関連する基準直線
2 基準直線1の傾き,θ Z1,ZX(図示した例は,正の値)
3 EXWに関連する基準直線
4 EXWの基準直線の傾き,θ W,ZX(図示した例は,正の値)
5 Z1を始点とする測定長さLZにわたるEXZの測定値に関連する基準直線
6 基準直線5の傾き,θ ZL,ZX(図示した例は,負の値)
注記 部分平行度誤差,θ Z1,ZX−θ W,ZX
図31−データムW軸の全移動範囲に対するZ軸の部分平行度誤差の評価
EXZ W軸に平行な物理的な真直度基準に対して,ZX平面で測定されたZ軸の真直度偏差
EXW W軸に平行な物理的な真直度基準に対して,ZX平面で測定されたW軸の真直度偏差
LW W軸の部分測定長さ
LZ Z軸の部分測定長さ
1 Z軸の移動範囲全体にわたるEXZの測定値に関連する基準直線
2 基準直線1の傾き:θ Z1,ZX(図示した例は,正の値)
3 EXWに関連する基準直線
4 EXWの基準直線の傾き:θ W,ZX(図示した例は,正の値)
5 Z1を始点とする測定長さLZにわたるEXZの測定値に関連する基準直線
6 基準直線5の傾き:θ ZL,ZX(図示した例は,負の値)
7 W1を始点とする測定長さLWにわたるEXWの測定値に関連する基準直線
8 基準直線7の傾き:θ ZW,ZX(図示した例は,正の値)
注記 部分平行度誤差:θ ZL,ZX−θ ZW,ZX
図32−データムW軸の部分移動範囲に対するZ軸の部分平行度誤差の評価
+W
+Y
EXW
4
3
+W
+Y
EXZ
L
12
5
6
Z
Z1
Y
W
Z
Y
W
EXZ
+W
+Y
L
12
5
6
Z
Z1
+W
+Y
EXW
4
3
W1
LW
8
7
Y
Z
W
W
W
Y

29
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
LX X軸の部分測定長さ
LZ Z軸の部分測定長さ
1 Z軸の移動範囲全体にわたって評価したEXZに関連する基準直線
2 EXZの基準直線の傾き:θ Z,ZX(図示した例は,正の値)
3 X軸の移動範囲全体にわたって評価したEZXに関連する基準直線
4 EZXの基準直線の傾き:θ X,ZX(図示した例は,負の値)
5 Z1を始点とする測定長さLZにわたるEXZの測定値に関連する基準直線
6 基準直線5の傾き:θ ZL,ZX(図示した例は,負の値)
7 X1を始点とする測定長さLXにわたるEZXの測定値に関連する基準直線
8 基準直線7の傾き:θ XL,ZX(図示した例は,正の値)
注記 部分直角度誤差:EB0X=θ X,ZX−θ ZL,ZX
図33−直進軸間の部分直角度誤差の評価
測定長さが短い場合は,直進軸間の平行度誤差及び直角度誤差の部分許容値を規定しても意味がないこ
とがある。測定結果は,可能な測定長さ全体にわたって評価した結果よりも大幅に大きくなる可能性があ
る。
例 真直度誤差,平行度誤差及び直角度誤差の許容値を規定するときには,[簡単のために,W軸(デ
ータム軸)に対するZ軸(対象とする軸)の平行度誤差の規定に関連した]次の三つの選択肢を
考慮しなければならない。
a) 部分許容値の規定なし。W軸に対するZ軸の平行度誤差を規定。
W軸の全移動範囲に対するZ軸の全移動範囲(図31における線1及び線3に対応)。
b) Z軸だけに部分許容値を規定。Z軸の300 mmごとにW軸に対するZ軸の平行度誤差を規定。
W軸については全移動範囲,Z軸については300 mmの部分測定長さ,Z軸については300
mmの測定長さごとの最大差の評価(図31において位置Z1が0から全移動範囲−300 mmま
で変化させ,線5及び線3の平行度に対応)。
c) W軸及びZ軸に部分許容値を規定。
W軸の300 mmごと及びZ軸の300 mmごとのW軸に対するZ軸の平行度誤差:W軸及
びZ軸について部分測定長さが300 mm,W軸及びZ軸の全ての取り得る300 mmの区間に
ついての最大差の評価(図32において,位置Z1が0から全移動範囲−300 mmまで変化し,
位置W1が0からW軸の全移動範囲−300 mmまで変化するとき,線1及び線7の平行度に
対応)。
部分許容値の規定は,主に機能要求事項を反映しなければならないが,工作機械の実際の性能試験つい
ても十分に考慮しなければならない。
4.1.4
総合的又は包括的な許容値
複数の幾何学的な誤差の影響による誤差を,一つの幾何学的なパラメータとして制限するために総合的
2
6
+Y
+Z
+X
1
3
4
8
5
7
X
Z
LZ
LX
1
1
+Y
+X
X
Z
+Z
30
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
又は包括的に使用する許容値がある。この許容値は,各誤差を個別に決めたり,又は測定したりすること
なく1回の測定で決定する。
例 軸の振れは,平面“ab”において,測定子が接触する点を含む円筒外周の真円度誤差,幾何学的
な軸線と回転軸との同軸度誤差,及び平面“ab”における回転軸の半径誤差及び運動誤差の合計
である(図34参照)。
1 軸平均線
2 軸の幾何学的な中心
ab 測定平面
OT 振れの許容値
図34−回転軸の振れの許容値
4.2
工作機械の機能面,工作機械の部品及び試験片に適用する許容値
JIS B 0021は,工作機械部品及び工作物特性に適用できる許容値に関する引用規格である。この規格は,
工作機械の機能面の指定及び試験に適用する。
4.3
許容値に関連する追加制限条件
特定の機能要求事項は,組立及び検査要求事項と同様に,所定の幾何学的特性又は精度パラメータに対
する許容値の規定に追加制限条件を記載する必要がある可能性がある。このような追加制限条件は,文章
で規定しなければならない。表1は,追加制限条件の例を一覧で示す。
表1−許容値に関連する追加制限条件の例
幾何精度
引用箇条
対応する許容値に対する追加制限条件
運動の平行度
3.6
一般に,誤差の方向は重要ではない。ただし,平行度誤差が一方向にだけ
許される場合には,その方向を指示しなければならない。
例1 運動軸間の角度は,ゼロよりも大きくなければならない。
直進軸間及び/又は
直進軸と回転軸の軸
平均線との直角度
3.6.7
3.6.8
3.6.9
直角度誤差が一方向にだけ許される場合には,その方向を指示しなければ
ならない。
例2 運動軸間の角度は,90°よりも大きくなければならない。
軸平均線間の交差度
3.7.4
二つの軸平均線の中の一つを,基準軸としてみなす場合は,基準軸の許容
値に追加条件を付けてもよい。
例3 軸平均線1は,軸平均線2よりも高く(又は前に)なければなら
ない。
軸平均線の等距離度
3.7.3
二つの軸の相対差が一方向だけに許される場合は,その方向を規定しなけ
ればならない。
例4 軸平均線1は,軸平均線2よりも高くなければならない。
軸平均線の同軸度
3.7.2
特別な場合には,運転条件に従って追加条件を付け加えてもよい。
例5 軸平均線1は,軸平均線2よりも高くなければならない。
例6 軸平均線の自由端は,軸平均線2に対して外側に向いていなけれ
ばならない。
機能面の真直度及び
/又は平面度
JIS B 0021
該当する場合は,追加の要求事項を規定することができる。
例7 凹面又は凸面(その実体側に対して)でなければならない。
31
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
測定,試験方法及び測定器の不確かさ
許容値を規定する場合及び規定した許容値との適合を評価する場合は,測定の不確かさを考慮すること
が望ましい。
測定結果を報告する場合に,測定結果間又は規定した値と測定結果との比較を行えるようにするために,
測定結果を定量的に表示する。このような定量的な表示は,測定の不確かさとして評価し,行う。
測定の不確かさの表現及び評価について国際的に認められた方法は,ISO/IEC Guide 98-3による。
ISO/TR 230-9は,ISO 230規格群に従った工作機械の試験における測定の不確かさの推定のための実用
的な情報を提供している。
ISO 14253-2は,不確かさの管理のための方法(PUMA)について記載している。その他の実用的な情報
は,参考文献[9]〜[11]から得られる。
検査目的のために簡略化した試験を行ったときは,測定の不確かさについて正式な報告は要求されない
ことを考慮する。ただし,ほとんどの一般的な測定(真直度,直角度,数値制御軸の位置決めの精度など)
には,利用可能な試験手順及び測定システムとともに,不確かさの見積りが利用できるようになっている。
測定の対象(測定量)の適切な定義は,不可欠である。測定は,何を測定しなければならないか,また
どのような条件下で行うかを明確に理解することなく行ってはならない。
測定の不確かさの主な要因として,次のa)〜e) を考慮しなければならない。
a) 測定器の測定の不確かさ
b) 基準器の校正の不確かさ及び偏差
c) 測定器及び基準器の利用,例えば,工作機械の軸に対する測定器及び基準器のミスアライメント,心
出しなど
d) 環境変動誤差,例えば,温度の影響及び振動
e) 測定装置を含めた測定の繰返し性
ただし,次の仮定が必要である。
− 測定器及び基準器は,製造業者の指針に従って使用する。
− 測定器及び基準器は,静的にも動的にも剛性があり,かつ,ヒステリシスがないように取り付ける(6.3.2
参照)。
− 測定器を保持する機械の部品は,断りのない場合は,剛体として扱う。
− これらの仮定を満たさない場合には,測定の不確かさには追加の要因を考慮し,報告しなければなら
ない。
− どのような測定においても,[ISO/TR 230-9:2005の式(1)に従って]合成標準不確かさを算出するのが
望ましく,測定の不確かさUは,[ISO/TR 230-9:2005の式(3)に従って]包含係数k=2として決定す
るのが望ましい。
− 幾何精度の検査は,一般に測定器,基準器及び/又は自然基準(例えば,光線,重力)を使って行う。
基準器とは,直定規,テストバーなどである。
− 測定器による測定の不正確さは,適用した測定方法と同様に試験中に考慮しなければならない。
− 測定器は,検査しようとする許容値のある割合を超えるような測定誤差を引き起こさないことが望ま
しい。校正表は,各測定器について利用できるようになっていることが望ましい。測定を行う工作機
械及び測定器は,風,及び光又は熱放射(太陽光,過度に近い電球など)から保護し,測定器の温度
は,測定を始める前に安定した状態にしておくことが望ましい。
− 測定は,できれば繰り返して行うのが望ましく,試験の結果は,測定値の平均をとることによって求
32
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
める。測定値が大きく変化する場合には,その原因が測定方法,測定器,又は工作機械のどれにある
かを探求するのが望ましい。より正確な指針については,ISO/TR 230-11を参照。
6
試験の準備
6.1
試験前の機械の据付け
6.1.1
一般
機械は,完全に組み立てられた状態で,製造業者が提供した説明書に従って運転しなければならない。
必要な全ての作業,幾何学的なアライメント調整及び機能確認は,あらかじめ全て完了し,その結果は,
試験前に文書化しておかなければならない。
工作機械は,受渡当事者間の協定に基づいて適切な基礎に据付けを行うことが望ましい。幾何精度試験
は,許容できる範囲内の振動環境の中で行わなければならない。振動問題が発生する場合は,環境振動(振
幅及び周波数)が製造業者の要求事項を満たしていることを確認することが望ましい。振動試験方法は,
ISO/TR 230-8参照。
6.1.2
水平出し
水平出しは,機械の静的に安定な条件を得るために,特にその後の測定が容易になるように,特定の部
品の真直度を基準に行う。
運動の真直度を出すために便利な方法が多くあるが,完全な水平出しを行うことは,工作機械に対する
要求事項ではない。例えば,船上で使用する工作機械は,水平出しを行うことはできないが,静止してい
る工作機械のように機能する。
6.2
試験前の機械の条件
6.2.1
特定の部品の分解
一般に,試験は,完成した機械に対して行い,特定の部品の分解(例えば,案内面を検査するためにテ
ーブルを外す。)は,製造業者の指示に従った場合だけ,例外的に行うことが望ましい。
6.2.2
試験前の特定の部品の温度条件
この規格に規定する試験の目的は,潤滑及び暖機運転に関して,通常の運転にできるだけ近い条件で機
械の精度を評価することである。幾何精度及び工作精度の試験において,主軸のように温度の影響を受け
変位しやすい部品は,製造業者による使用条件及び指示に従った暖機運転の後に行わなければならない。
JIS B 0680によると,工業製品の寸法測定に用いる標準温度は,20 ℃である。したがって,測定器及び
測定対象は,温度が20 ℃で維持された試験環境と平衡状態にあるのが望ましい。環境温度が20 ℃でない
場合は,20 ℃に対応する試験結果に補正するために測定システムと測定対象(工作機械)との間の公称熱
膨張差(NDE)補正を行わなければならない。
注記 温度変化が機械の精度に著しい影響を与える高精度機械及び数値制御機械については,特別な
条件を適用することができる。
環境温度から作業温度まで変化する通常の作業サイクルの間,機械がどの程度寸法変化するかを考慮し
なければならない。事前に行う暖機運転手順及び機械の試験を行う環境温度は,受渡当事者間で協定する
ことが望ましい。
工作機械の熱環境指針は,JIS B 6190-3の附属書Cによる。
6.2.3
事前確認
主軸速度及び送り速度は,幾何精度及び工作精度の試験に影響を及ぼすおそれがある。したがって,指
令値に対する実際の主軸速度及び送り速度の一致の程度は,これらの試験を行う前に確認するのが望まし
33
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
い。
6.2.4
運転条件
幾何精度試験は,機械が停止している状態(例えば,平面度の試験)又は無負荷の準静的運転状態の下
で行わなければならない。ただし,特別な条件下では,工作物の質量を指定して試験を実施することを受
渡当事者間で協定してもよい。
6.3
試験装置及び測定器
6.3.1
一般
この規格に規定する大部分の測定は,工作物を保持する工作機械の部品と切削工具を保持する工作機械
の部品との間の誤差運動を測定するために行う。
規定する試験装置及び測定方法は,例として示している。同じ量が測定でき,かつ,測定の不確かさが
同一又はそれ以下である他の測定器及び試験装置を用いてもよい。使用したソフトウェア補正は,全て試
験報告書に記載しなければならない。
測定器は,その製造業者の指示に従って熱的安定性に注意を払わなければならない(ISO/TR 230-11参
照)。
全ての試験装置は,通常,二つの取付具,すなわち,一方は基準点又は基準表面を与えるものであり,
もう一つは,基準点又は基準表面に対する読みを取るための測定器を保持する取付具を含んでいる。試験
球又は反射鏡は,基準点として使用できる。測定器として,差動変圧器,静電容量形変位計,渦電流形変
位計,レーザ測長器又はダイヤルゲージを使用できる。それぞれの測定を始める前には,使用する試験装
置及び測定方法が工作機械の環境内で適切に機能することを確認する。試験装置のヒステリシス及び安定
性の確認を行うために,次の二つの試験を行うことを推奨する。
6.3.2
試験装置のヒステリシス及び遊び試験
この試験の目的は,試験装置のヒステリシス又は遊びのあらゆる影響を発見することである。ヒステリ
シス又は遊びは,取り付けた試験装置におけるボルトの緩み,ブラケットの構造剛性不足などによって引
き起こされる。幾何精度試験に使用した試験装置のセットアップに関連するヒステリシスは,通常,測定
結果に繰返し性の不足として観察される。その不足は,機械の挙動による結果であると誤って理解されて
しまう可能性がある。
測定装置のヒステリシスは,二つの取付具の間で測定方向に両方向に適切な力を加え,その結果として
生じるたわみを観察することで求めることができる。一般に,このような力の大きさに対する試験結果の
感度は大きくない。力の範囲は,試験装置及び変位計の分解能に応じて,20 N〜200 Nの間に設定する。
加える力は,機械又は測定装置に損傷を与えるおそれがない程度の大きさであることが望ましい。機械ヒ
ステリシスを引き起こさないようにするために,40 N未満の力を推奨する。力は,測定する必要はない。
試験手順は,次のとおりとする。
a) 対象とする軸の性能試験の方向及び位置において,二つの取付具の間に変位センサを取り付け,読み
をゼロに設定する。
b) 基準点又は基準表面を保持する取付具に,手で力を加える。
c) 力をかけた後に,この力を徐々にゼロまで下げ,変位計の読みを取る。
d) 反対方向に手で力を加え,徐々にゼロまで力を下げて,変位計の読みを取る。
e) 読みの差は,基準点又は基準平面となる取付具のヒステリシスとなる。
f)
変位計を保持する取付具に力を加える。
g) 徐々にゼロまでこの力を減少させて,変位計の読みを取る。
34
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
h) 反対方向に手で力を加えて,徐々にゼロまで力を下げて,変位計の読みを取る。
i)
読みの差は,変位計取付具のヒステリシスである。
j)
二つの取付具のヒステリシスの値の和が,試験装置全体のヒステリシスとなる。
通常の測定では,試験装置のヒステリシスは,所望の測定の繰返し性の10 %未満である。これを著しく
超えるヒステリシスが測定された場合,及び試験装置の取付けの調整によってこのヒステリシスを小さく
することができない場合は,機械自体が引き起こしている可能性がある。このような場合には,この状態
が修正されるまで,試験を行ってはならない。
6.3.3
試験装置の安定性試験
工作機械は,内部及び外部の様々な振動源の影響を受ける。この振動の周波数と振幅とは,時間,機械
上の位置,及び機械軸の位置によって変化する。機械の剛性及び減衰特性によっては,実際の機械性能に
影響を及ぼす振動を排除できる。ただし,試験装置の取付けが適切でないと,測定器はこれらの振動を検
出してしまう可能性がある。試験装置の安定性試験は,測定器の取付けが測定の不確かさに大きく影響し
ないことを保証することを目的として行う。
試験手順は,次のとおりである。
a) 測定器は,性能試験で使用した方法で取り付ける。
b) 機械軸は,性能試験を行うための移動範囲の中央に置く。
c) 測定器をゼロに設定し,機械を動かさずに試験にかかったのと同じ時間間隔及び長さで出力を取得す
る。取得したデータの範囲は,規定した許容値の10 %を超えないのが望ましい。
7
機械の静的コンプライアンス試験及びヒステリシス試験
7.1
一般
機械の静的コンプライアンス試験及びヒステリシス試験は,工具と工作物との間又は二つの機械要素の
間に静的な負荷を加えて行い,評価することを目的とする。この試験から,より厳密な静的コンプライア
ンス試験による結果を単純化したものが得られる。静的コンプライアンスの値は,機械の軸の位置と負荷
の作用方向との関係によって変わる。軸の位置は,試験結果とともに記録することが望ましい。
静的コンプライアンスは,加工領域の中心近くで各直進位置決め軸について測定する。回転軸をもつ機
械の静的コンプライアンスは,回転軸の軸平均線からある半径離れた位置で測定する(7.4参照)。
一般に,製造業者は,最大負荷を指定し,取付具の構造についても詳細な指示をすることが望ましい。
この試験では与える負荷が大きいので,人及び機械の安全のために適切に設計された取付具が不可欠であ
る。
7.2
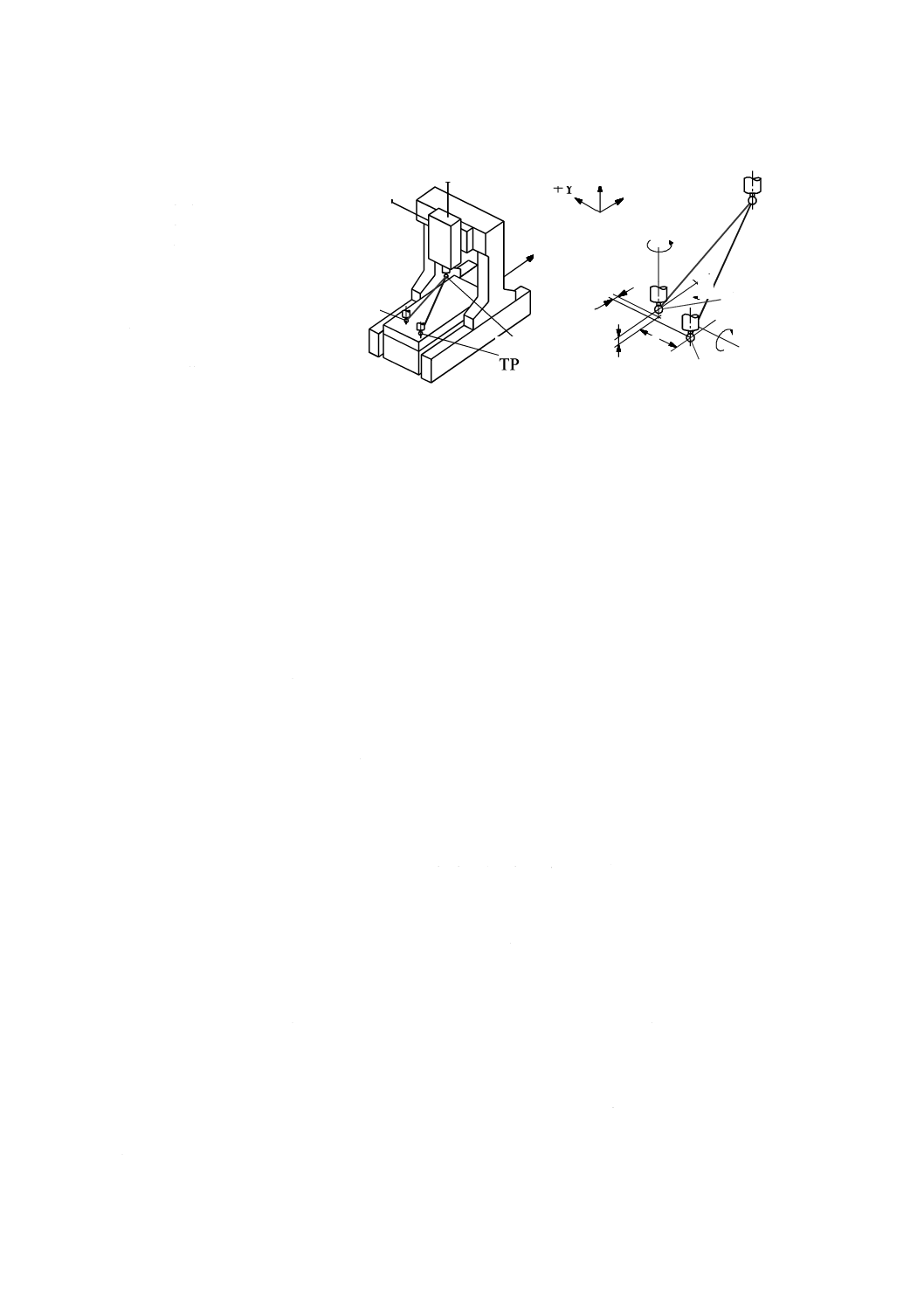
外部負荷による機械の静的コンプライアンス・ヒステリシス試験
7.2.1
一般
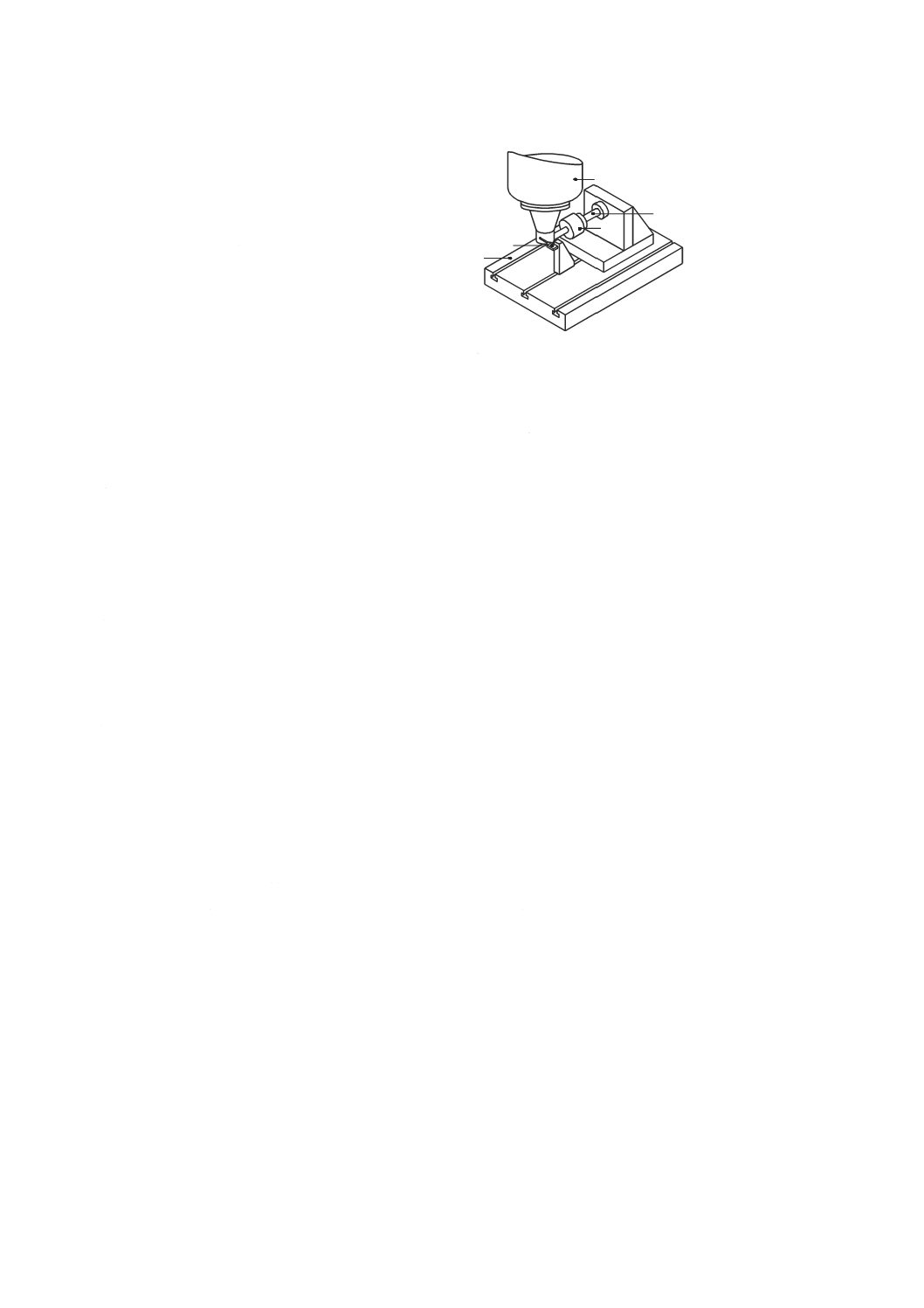
代表的な試験装置を図35に示す。負荷を与えるための機構及び力検出器(ロードセル)は,機械の工具
保持側(例えば,主軸)と,試験する直進軸に平行な方向の機械の工作物側(例えば,テーブル)との間
に直列に堅く固定する。変位計は,力検出器を移動させることによって生じた相対変位の読みを取ること
ができるように取り付ける。
静的な負荷は,ねじ機構(図35参照)又は油圧アクチュエータのようなアクチュエータを用いて与えて
もよい。試験方法及び負荷の大きさは,機種別規格に規定する。ただし,過大な負荷は機械に損傷を与え
ることがあるので,受渡当事者間で協定することが望ましい。
35
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
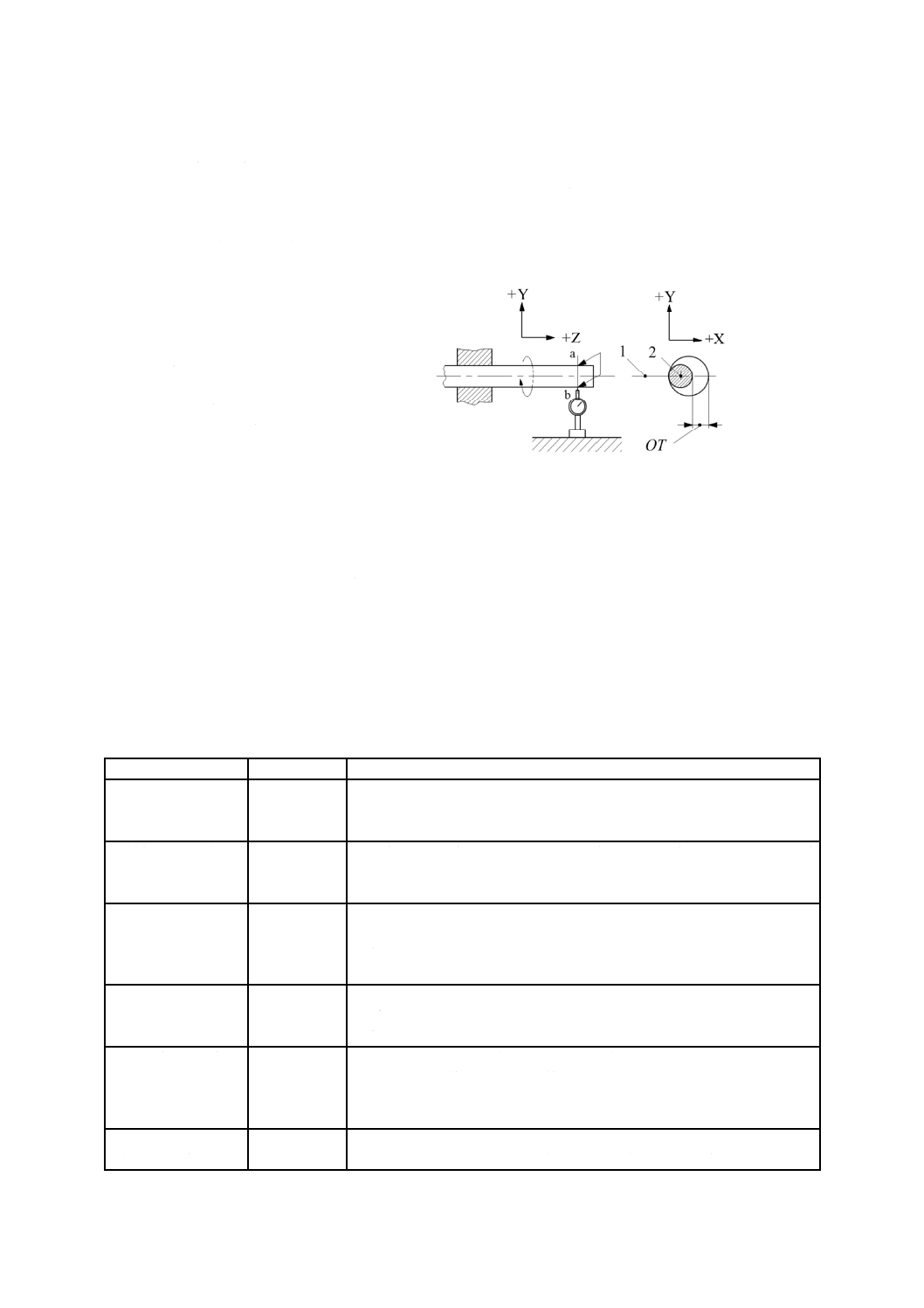
1 主軸頭
2 負荷用ねじ機構
3 力検出器
4 変位計
5 テーブル
図35−ねじ機構を用いて外部負荷を与え,静的コンプライアンス・ヒステリシスを測定するための装置
7.2.2
試験手順
別に規定がない場合には,機械の軸は,その移動範囲のほぼ中央に位置決めしなければならない。
a) 力検出器に発生する力をゼロとし,変位計をゼロに合わせる。
b) 力検出器を介して最大負荷(又は許容最大たわみ)まで力を加える。このときの負荷を与える方向を
正方向とする。
c) 負荷と変位の読みとを記録する。
d) 与える負荷が最大負荷の1 %になるまで,力検出器を反対方向(負方向)に移動させ,除荷する(正
方向負荷)。
e) 負荷と変位の読みとを記録する。
f)
負荷(又はたわみ)が負方向の最大値に達するまで,負方向に力検出器を移動させる。
g) 負荷と変位の読みとを記録する。
h) 負荷が最大負荷の1 %になるまで,力検出器を反対方向(正方向)に移動させる(負方向負荷)。
i)
負荷と変位の読みとを記録する。
7.2.3
データ解析
軸の静的コンプライアンスは,記録した全変位を記録した負荷の全範囲で除した値であり,マイクロメ
ートル毎ニュートン(μm/N)で表す。
機械のヒステリシスは,正方向負荷と負方向負荷との間の変位の差として求め,マイクロメートル(μm)
で表す。機械のヒステリシスの計算結果は,−Pと+Pとの間の機械の静的コンプライアンスを含んでお
り,したがって,この計算結果は,機械のヒステリシスの僅かではあるが過大評価になる(ただし,−P
と+Pは,最大負荷の1 %である。)。ただし,この方法は,負荷をゼロとした状態で測定を行うことが実
際には難しいことから,負荷をゼロにしたときのたわみを測定する方法として用いる。必要があり,かつ,
可能な場合には,より小さな負荷を適用してもよい。
これらの計算値を図36に示す。
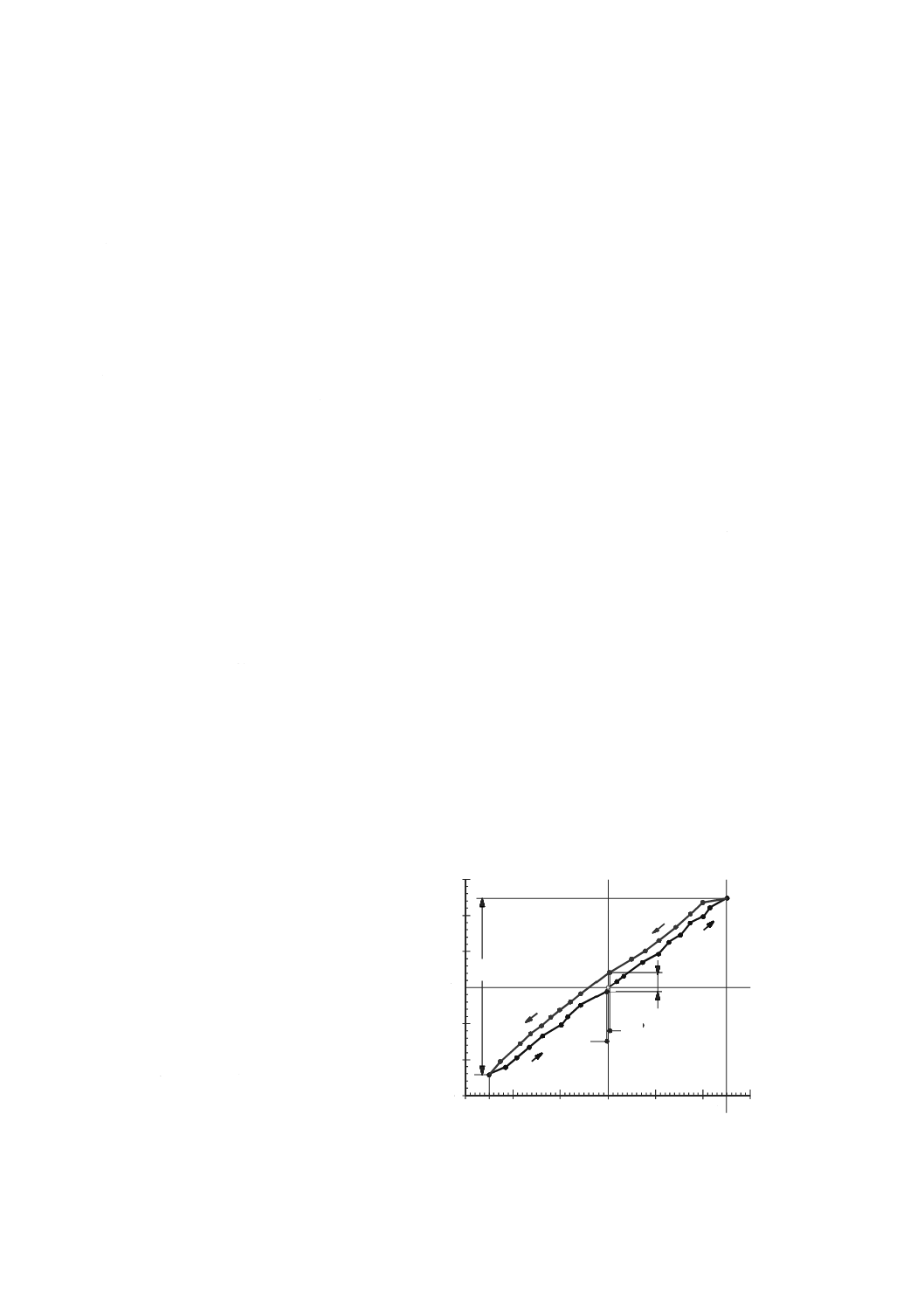
2
1
3
4
5
36
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
F 負荷(N)
D たわみ(μm)
Dtot 測定された全たわみ
+Fmax 正方向に加えた最大負荷
−Fmax 負方向に加えた最大負荷
+P 正方向負荷
−P 負方向負荷
H ヒステリシス
図36−外部負荷を与えたときに得られた機械の静的コンプライアンス・ヒステリシス試験の結果の例
7.3
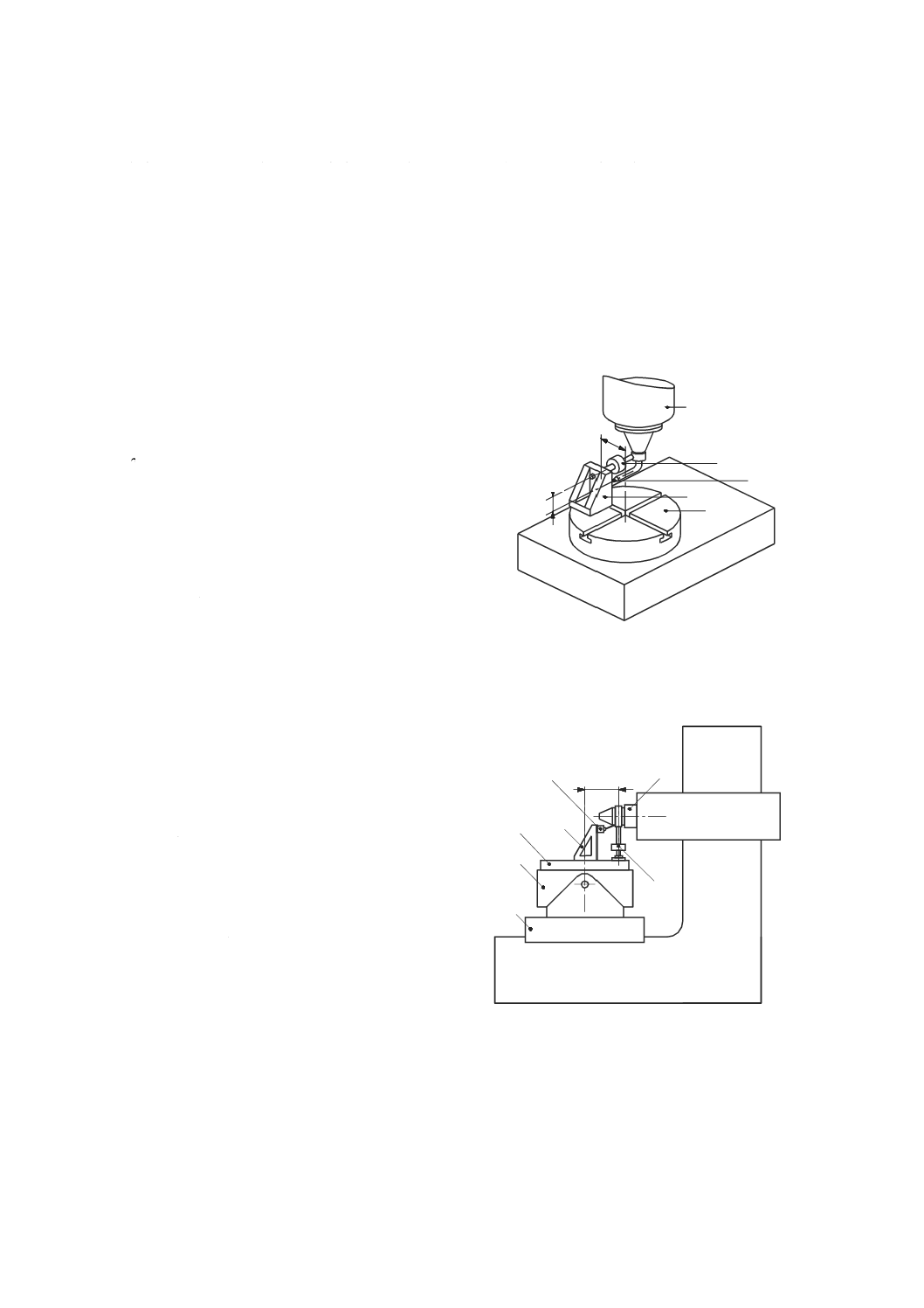
内部負荷による機械の静的コンプライアンス・ヒステリシス試験
7.3.1
一般
立て形の一般的な試験装置を図37に示す。変位計は,機械の工具側(例えば,主軸)と工作物側(例え
ば,テーブル)との間の相対変位を測定できるように試験する直進軸に平行に取り付ける。力検出器は,
試験する軸と同じ方向に,テーブルと主軸との間に堅く固定する。静的負荷は,機械の軸を移動させるこ
とによって発生させる。引張り及び圧縮の両方の負荷を測定できるように力検出器を取り付けることが望
ましい。
機械にバックラッシ補正機能が付いている場合には,この測定は,バックラッシ補正をオンにしたまま
行う。試験方法及び与える負荷の大きさは,機種別規格に規定するが,過大な負荷は機械に損傷を与える
場合があるので,受渡当事者間の協定によることが望ましい。
1 主軸頭
2 力検出器
3 変位計
4 テーブル上面
図37−主軸頭を垂直方向に移動させて内部負荷を与え,静的コンプライアンス・ヒステリシスを
測定するための装置
7.3.2
試験手順
7.3に規定する方法で試験を実施すると,取付具の隙間又は力検出器のたわみによる全ての影響を取り除
くことができる。この試験を実施することによって得られた結果は,外部負荷を加えて試験を行って得ら
D
+P
−P
H
D
F
+F
-F
0
-1000
1000
2000
3000
-2000
-3000
max
max
150
100
50
0
-50
-100
-150
tot
−
−
−
−
+
−3 000 −2 000 −1 000
0
1 000
2 000
3 000
2
1
3
4
37
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
れる結果よりも小さな機械のコンプライアンスの値を示す傾向がある。この試験は,外部負荷を加える装
置が利用できない場合に7.2に規定する試験方法の代替方法としてだけ提案されたものである。
別に規定がない場合には,機械の軸は,移動範囲のほぼ中央に位置決めしなければならない。
a) 各試験の初めに変位計の読みをゼロに設定する。
b) 指定した最大の試験負荷又は許容可能な最大たわみ(実際の変位と指令した変位との間の差)を生じ
させる負荷が発生するまで,小きざみに機械の軸を移動させる。このときの方向を正方向とする。
c) 指令した変位,変位計で測定した変位及び負荷の大きさを記録する。
d) 負荷が最大負荷の1 %になるまで,軸を反対方向(負方向)に少しずつ移動させる(正方向負荷)。
e) 指令した変位,変位計で測定した変位及び負荷を記録する。
f)
負荷(又はたわみ)がその負方向の最大値に達するまで,軸を負方向に少しずつ移動させる。
注記 機械によっては,負荷を両方向に与えることが不適切なことがある。
g) 指令した変位,変位計で測定した変位及び荷重を記録する。
h) 負荷が最大負荷の1 %になるまで,軸を正方向に少しずつ移動させる(負方向負荷)。
i)
指令した変位,変位計で測定した変位及び荷重を記録する。
7.3.3
データ解析
静的コンプライアンス・ヒステリシスを評価するために,各測定点におけるたわみ(指令した変位と実
際の変位との差)を求める。軸方向の静的コンプライアンスは,記録した全たわみを,記録した負荷の全
範囲で除した値である。マイクロメートル毎ニュートン(μm/N)で表す。
軸の機械ヒステリシスは,正方向負荷と負方向負荷との間のたわみの差として求め,マイクロメートル
(µm)で表す。機械ヒステリシスの計算結果は,−Pと+Pとの間の機械コンプライアンスを含んでおり,
したがって,この計算結果は,機械ヒステリシスの僅かではあるが過大評価になる(すなわち,−Pと+P
は最大負荷の1 %である。)。ただし,この方法は,負荷をゼロにした状態で測定を行うことが実際には難
しいことから,負荷をゼロにしたときのたわみを測定する方法として用いる。必要があり,かつ,可能な
場合には,より小さな負荷を適用してもよい。これらの計算値を図38に示す。
図38に示すように,中間位置でのたわみを記録することができる。データからは,試験した範囲での平
均コンプライアンスを得ることができる。
F 負荷(N)
D たわみ(μm)
+Fmax 正方向に加えた最大負荷
−Fmax 負方向に加えた最大負荷
Dtot 測定された全たわみ
+P 正方向負荷
−P 負方向負荷
H ヒステリシス
図38−内部負荷を与えたときに得られた機械の静的コンプライアンス・ヒステリシス試験の結果の例
D
F
+F
-F
D
+P
−P
H
0
-1000
1000
2000
3000
-2000
-3000
max
max
tot
150
100
50
0
-50
-100
-150
−3 000 −2 000 −1 000
0
1 000
2 000
3 000
−
−
−
−
+
38
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.4
回転軸をもつ機械の試験
回転軸をもつ機械の試験は,回転軸から距離Rの位置で負荷を与える点を除いて,7.2及び7.3に示した
試験と同じである。この試験では,力検出器及び変位計は,負荷の方向と同じ方向に距離Rの位置に設置
する。
回転軸をもつ機械において,内部負荷を与えることによって機械の静的コンプライアンス・ヒステリシ
スを測定するための一般的な二種類の試験装置を図39及び図40にそれぞれ示す。データ解析のための手
順は,7.2及び7.3で規定したものと同じである。静的コンプライアンスの計算結果は,距離Rにおける単
位負荷当たりの変位(μm/N)として表す。ヒステリシスは,マイクロメートル(μm)で表す。
1 主軸頭
2 力検出器
3 変位計(隠れている)
4 取付具
5 回転テーブル
h たわみ測定点と荷重が作用する点との間のオフセ
ット
R 回転テーブルの軸平均線と荷重が作用する点との
間の距離
図39−回転軸を備えた機械において,内部負荷(水平方向)を与え,機械の静的コンプライアンス・
ヒステリシスを測定するための装置
1 変位計
2 主軸頭
3 力検出器
4 取付具
5 回転テーブル
6 傾斜テーブル
7 直進テーブル
R 傾斜テーブルの軸平均線と荷重が作用する点
との間の水平面内における距離
図40−傾斜テーブルを備えた機械において,内部負荷(垂直方向)を与え,機械の静的コンプライアンス・
ヒステリシスを測定するための装置
8
直進軸の幾何精度試験
8.1
一般
全ての工作機械は,工作物と切削工具との間の相対位置を変化させるために手動又は数値制御で運動さ
2
1
4
3
5
h
R
1
2
3
4
5
6
7
R
39
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
せる刃物台,テーブル又はその他の部品から構成されている。運動する部品が剛体として振る舞う(負荷
による変形がない)ものと仮定すると,直進運動する部品は,一般にその運動に関係した次の三つの誤差
運動を示す(3.4.3参照)。
a) 移動方向に平行な一つの直線変位(位置決め)誤差運動。
b) 移動方向に対して直角な二つの方向における真直度誤差運動。
c) 三つの直交軸(X軸,Y軸及びZ軸)回りの角度誤差運動。
これらの中で,真直度及び角度誤差は,純粋な幾何誤差であるのに対して,直線変位(位置決め)誤差
は,幾何誤差と送り駆動系特性との両方が影響する。数値制御軸による位置決め(直線変位)誤差の測定
は,JIS B 6190-2による。
機械の構造構成によって幾つかの誤差運動は,感度方向に誤差を生じさせないことから,その影響が小
さいものがある(例えば,回転工具をもたないターニングセンタについては,Z軸のY方向真直度誤差は,
必ずしも重要ではない。)。
8.2
真直度誤差運動試験
8.2.1
一般
直線経路上を運動する工作機械の運動部品の真直度誤差運動は,その工作機械で加工する工作物の形体
を表す形状,位置及び姿勢だけでなく,加工面の真直度及び平面度に直接影響する。
真直度誤差運動の測定方法は,真直度基準に対して行う変位の測定を基礎としている。真直度基準は,
物理的な基準器(直定規,鋼線等)又は光学機器の光軸によって与えられる基準線である。真直度基準は,
運動部品の運動方向とほぼ平行に(運動の始点と終点とでほぼ等しい読みとなるように)定置する。測定
器は,測定長さ全体にわたって様々な位置(等間隔又は不等間隔)で真直度基準と運動軌跡との間の距離
の偏差(真直度偏差)を与える。機械の工具保持側と工作物保持側との間の相対変位を測定する。
注記 真直度誤差運動の測定は,運動部品に含まれる角度誤差運動及びブライアンオフセット(Bryan
offset)(参考文献[12])によって測定線の位置の影響を受ける(図41参照)。したがって,測定
線の位置が異なると,同じ運動を同様に測定しても,その結果が異なることがある。図41に示
す例では,角度誤差運動αの影響は,e=sin(α)・Lとして表される。ただし,Lは,オフセット
長さである。
1 直進運動
e 角度誤差運動及びオフセットによる偏差
L オフセット長さ
α 角度誤差運動
図41−真直度測定に及ぼす一つの角度誤差運動の影響
8.2.2
測定器及び測定方法
8.2.2.1
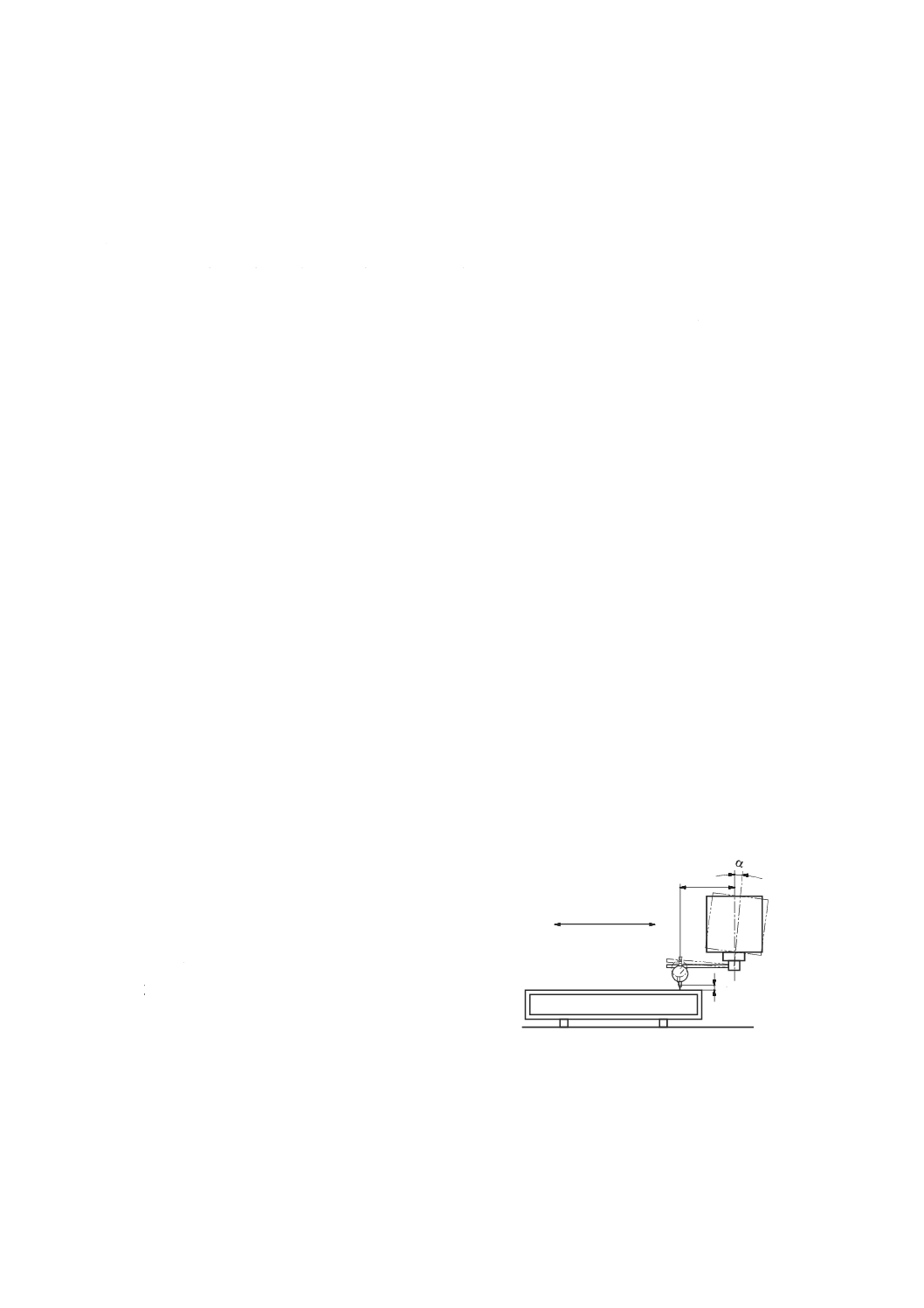
直定規と変位計とによる方法
この方法では,直定規が真直度の基準となる。この方法は,垂直及び水平方向の真直度偏差を測定の対
1
e
L
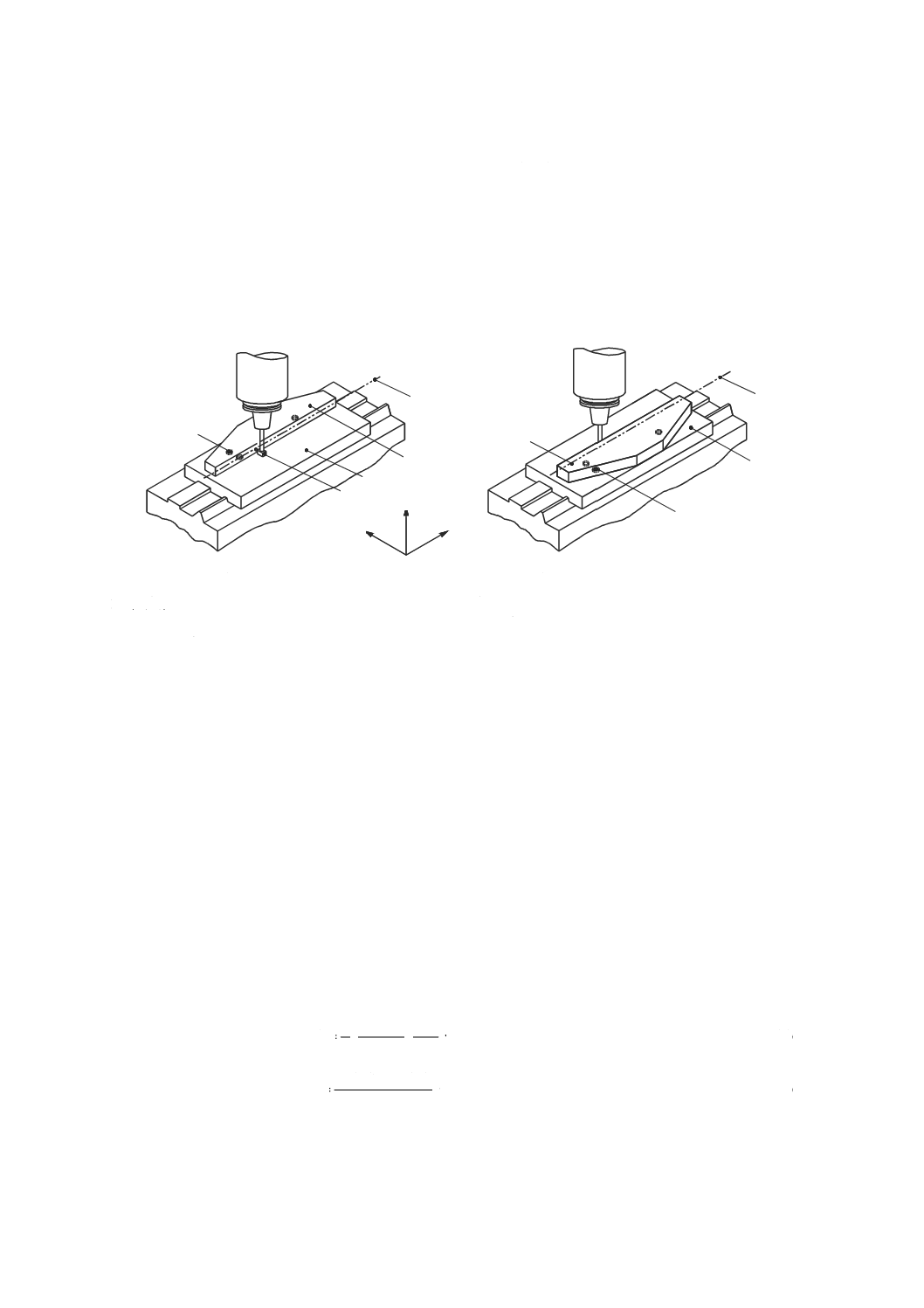
40
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
象としている。垂直方向での真直度偏差の測定では,直定規の重力によるたわみが最小となる2点でその
直定規を支持する(最適支持位置についてはISO/TR 230-11参照)。
変位計は,運動部品の機能点に可能な限り近づけて取り付ける。測定は,変位計を直定規に沿って移動
(又は直定規を移動)させて行い,読みを記録する[図42 a) 参照]。
直定規の誤差が既知の場合は,その誤差は,測定データを処理するときに考慮するのが望ましい。直定
規の誤差が既知でない場合は,8.2.2.1.1に示す水平面内における反転法を用いて誤差を求め,真直度誤差
運動の測定値から取り除く。
a) 通常の測定方法
b) 反転させた後の測定方法
1 直定規
4 変位計
2 測定線
5 テーブル
3 直定規の支持位置(両側各3点)
図42−直定規を用いた真直度測定
8.2.2.1.1
反転法による真直度運動誤差測定
水平面内において直定規を用いた真直度測定方法は,直定規基準面及び測定する直進運動の両方の真直
度誤差測定が可能である(図42及び図43参照)。
そのために,いわゆる“反転法”を用いる。 通常の測定方法で最初の測定結果を記録した後[図42 a) 及
び図43のプロットE1を参照],直定規を長手方向軸に対して180°回転させ,また,変位計も直定規の同
じ基準面[図42 b) 参照]の変位を読むために反転する。その後,テーブルを移動させ,読みを記録する
(図43のプロットE2を参照)。
二つの偏差E1及びE2は,直定規基準面の真直度誤差及び直進軸の真直度誤差運動の影響を受ける。た
だし,図42に示す二通りの測定方法によって,これらの影響を代数的に分離することができる。図43に
おいて,平均値を表す曲線Mは,直定規基準面の偏差を示す。
分離のために,次の式(9)及び式(10)を適用する。
2
)
(
)
(
)
(
2
1
X
E
X
E
X
M
+
=
······························································· (9)
2
)
(
)
(
)
(
2
1
X
E
X
E
X
S
−
=
······························································ (10)
ここに,
M(X): 測定位置Xにおける直定規基準面の真直度偏差
S(X): 測定位置Xにおける運動軸の真直度偏差
1
3
5
2
Z
Y
X
4
3
5
1
2
Z
Y
X
41
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
E1(X)及びE2(X): 通常の方法及び反転させた後の方法から得られた
測定結果
X X軸位置
EYX X軸のY方向真直度偏差
1 X軸のY方向真直度誤差[S(X)max]
2 直定規の真直度誤差
a〜h 測定位置
E1 通常の方法によって測定したときの読み
E2 反転させて測定したときの読み
M E1とE2との平均
図43−反転法による直進軸及び直定規の真直度誤差の求め方
8.2.2.2
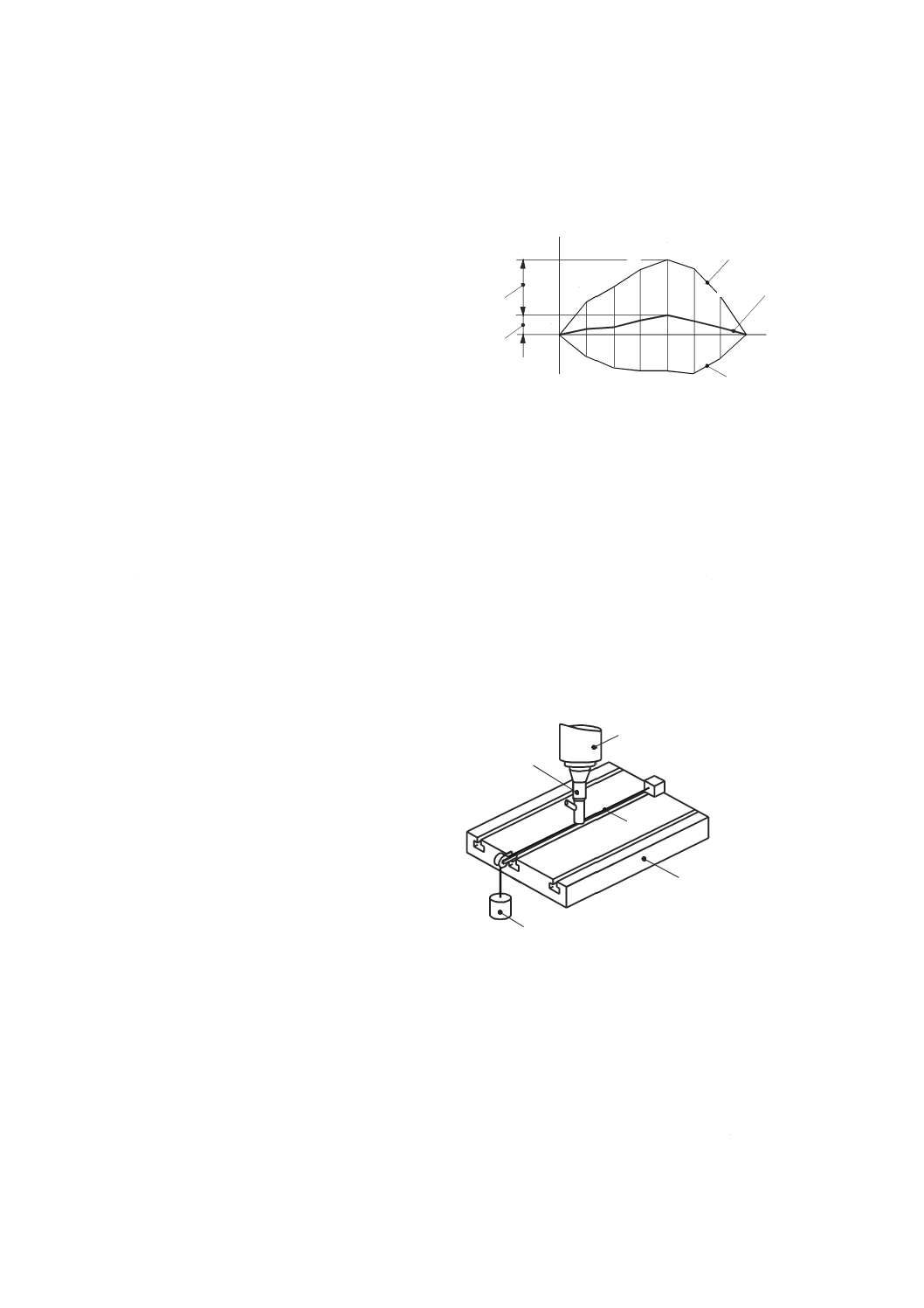
測微顕微鏡と鋼線とによる方法
直径約0.1 mmの鋼線を,試験する運動方向とほぼ平行に張る(図44参照)。鋼線に対する水平面方向
の運動の軌跡は,機械主軸に取り付けた測微顕微鏡[又は非接触変位計若しくは電荷結合素子(CCDカメ
ラ)のような光電素子]で測定する(ISO/TR 230-11参照)。
鋼線は,大形機械の水平面内における真直度偏差の測定の基準として使用することが多い。
鋼線のたわみが各位置で既知の場合は,測微顕微鏡を水平に定置し,鉛直面内における真直度誤差運動
を測定することは可能である。ただし,このたわみを適切な精度で求めることは極めて難しい。したがっ
て,一般に鋼線を鉛直面内における真直度誤差測定に使用することは推奨しない。
1 主軸
2 測微顕微鏡
3 鋼線
4 おもり
5 テーブル
図44−測微顕微鏡と鋼線とによる真直度の測定
8.2.2.3
アライメント望遠鏡による方法
アライメント望遠鏡(図45参照)を用いる場合は,望遠鏡の光軸が真直度の基準となる。測定は,工具
と工作物との相対位置を代表するように行わなければならない。望遠鏡は,工作物を取り付ける運動部品
上に定置する。測定目標は,工具を取り付ける運動部品上に,測定する運動軸に対して垂直に取り付ける。
測定目標の中心は,可能な限り機能点に近づけて取り付ける(ISO/TR 230-11参照)。望遠鏡の光軸と測定
目標の中心との間の距離は,目盛から,又は光学式マイクロメータを使って直接読み取る(ISO/TR 230-11
M
1
2
X
E
E
E
1
YX
2
a
b
c
e
d
f
g
h
X
E2
1
5
3
2
4
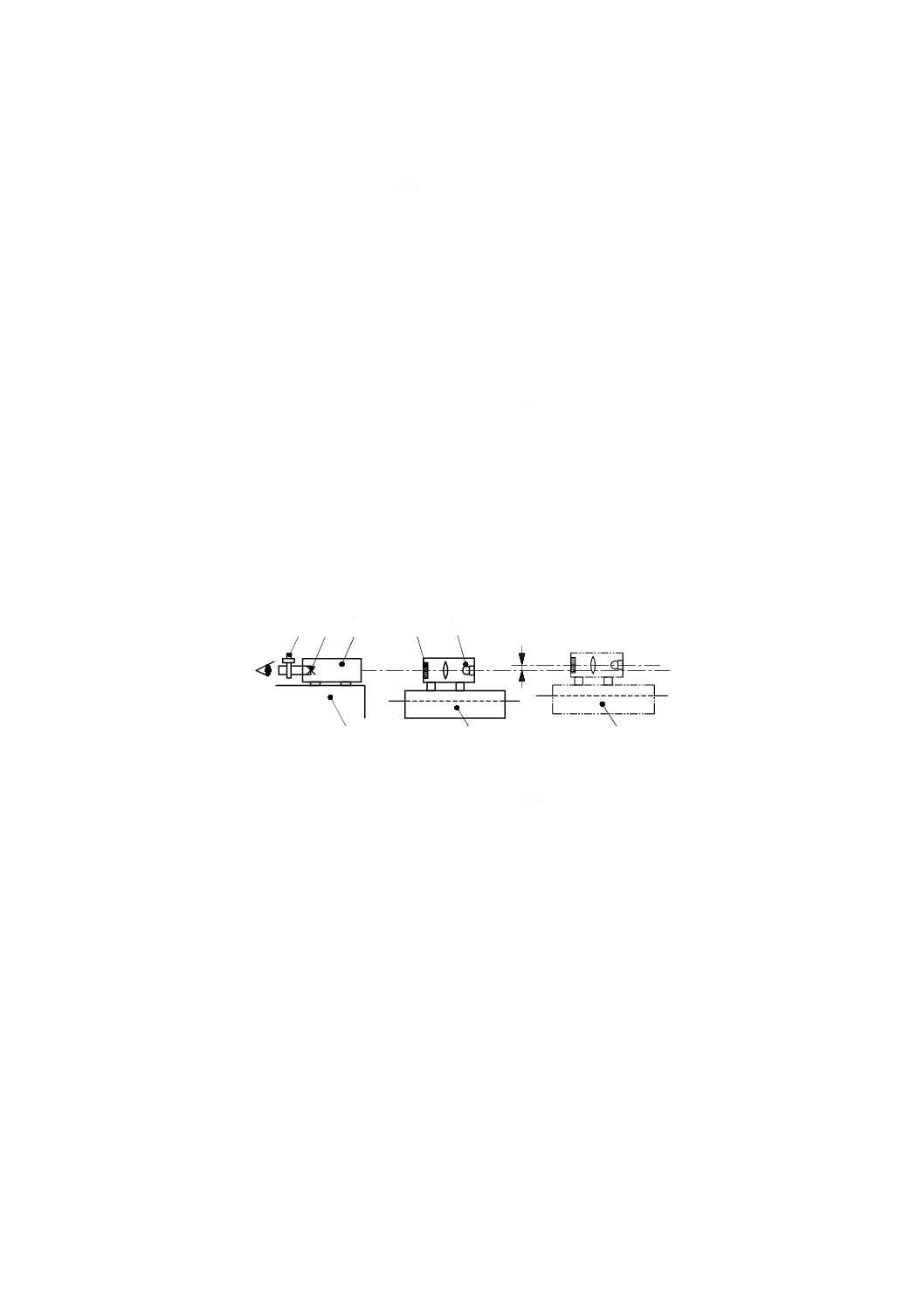
42
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参照)。
望遠鏡の光軸は,直進軸の軌跡とできるだけ平行になるように調節する。
テーブルに部分的な曲がりがあると,望遠鏡の光軸の位置を変化させる。そのような場合に得られた真
直度は,テーブル上の複数の点で固定された機械加工部品から得られる真直度を反映しない。この状況は,
運動学的に支持された台に望遠鏡を定置することによって部分的に修正することができる。特にテーブル
の曲がりが疑われる状況では,望遠鏡を固定するとき,細心の注意を払わなければならない。テーブルに
固定した(剛性の高い)工作物を模擬した支持台に望遠鏡を堅く固定すれば,最も良い結果を得ることが
できる。
注記1 移動距離が長い場合,測定の不確かさは,空気の屈折率の空間的な変化の影響を受け,空気
の屈折率は,光軸の変位に強く影響する。光軸は,垂直方向に1 ℃/mの温度勾配があると,
10 m移動させたとき直線から約46 μm偏る(参考文献[13])。最も良い結果を得るためには,
測定を適切な回数繰り返して平均をとるだけでなく,光軸回りの空気をファンでかくはんす
ることも考慮したほうがよい。
注記2 望遠鏡全体及び測定目標を光軸回りに回転させることによって任意の面内での真直度の測定
ができる。
注記3 アライメント望遠鏡の中には,直角2方向の変位を同時に測定できるものがある。この場合,
2直交面内で真直度を測定することができる。
1 工作物側(テーブル)
2 工具側(位置1)
3 工具側(位置2)
4 アライメント望遠鏡
5 読取りマイクロメータ
6 目盛
7 測定目標
8 光源
9 測定された偏差
図45−アライメント望遠鏡を用いた真直度の測定
8.2.2.4
アライメントレーザによる方法
アライメントレーザを用いる場合は,レーザ光軸が真直度の基準となる。測定は,工具と工作物との相
対位置を代表するように行わなければならない。レーザヘッドは,工作物を保持する運動部品上に定置し,
検出器である4分割フォトダイオードは,工具を保持する運動部品上に取り付けなければならない。検出
器の中心は,可能な限り機能点に近づけて取り付けなければならない(ISO/TR 230-11参照)。レーザ光軸
に対する検出器中心の水平方向及び垂直方向の偏差を記録する。
テーブルに部分的な曲がりがあると,アライメントレーザの光軸の位置を変化させる。そのような場合
に得られた真直度は,テーブル上の複数の点で固定された機械加工部品から得られる真直度を反映しない。
この状況は,運動学的に支持された台にアライメントレーザを取り付けることによって,部分的に修正で
きる。特にテーブルの曲がりが疑われる状況では,アライメントレーザを固定するとき,細心の注意を払
1
2
3
9
8
7
4
6
5
43
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
わなければならない。テーブルに固定した(剛性の高い)工作物を模擬した支持台にアライメントレーザ
を堅く固定すると,最も良い結果を得ることができる。
測定器の説明書を参照することが望ましい(ISO/TR 230-11参照)。
注記 移動距離の長い場合,測定の不確かさは,空気の屈折率の空間的な変化の影響を受ける。空気
の屈折率は,光軸の変位に強く影響する。光軸は,垂直方向に1 ℃/mの温度勾配があると,
10 m移動させたとき直線から約46 μm偏る(参考文献[13])。最も良い結果を得るためには,測
定を適切な回数繰り返して平均をとるだけでなく,光軸回りの空気をファンでかくはんするこ
とも考慮したほうがよい。
8.2.2.5
レーザ真直度干渉計による方法
最も一般に用いられているレーザ真直度干渉計は,ウォラストンプリズムと真直度反射鏡とから構成さ
れている。真直度反射鏡の中心線が真直度の基準となる。真直度反射鏡の対称軸(中心線)に対するウォ
ラストンプリズムの位置の変化を干渉法によって検出する。
測定は,工具と工作物との相対位置を代表するように行わなければならない。真直度反射鏡は,工作物
を取り付ける運動部品上に定置する。ウォラストンプリズムは,工具を取り付ける運動部品に取り付ける。
光学部品及び測定方法は一様でないので,測定器の説明書を参照することが望ましい(ISO/TR 230-11及
びISO/IEC Guide 99参照)。
テーブルに部分的な曲がりがあると,反射鏡の中心線位置を変化させる。そのような場合に得られた真
直度は,テーブル上の複数の点で固定された機械加工部品から得られる真直度を反映しない。この状況は,
運動学的に支持された台に反射鏡を定置することによって部分的に修正することができる。特に,テーブ
ルの曲がりが疑われる状況では,真直度反射鏡を固定するとき,細心の注意を払わなければならない。テ
ーブルに固定した(剛性の高い)工作物を模擬した支持台に真直度反射鏡を堅く固定すると,最も良い結
果を得ることができる。
光学式の測定器(例えば,レーザ真直度干渉計,アライメント望遠鏡)は,全て空気の特性変化に敏感
である。測定前にドリフト試験を行うことを推奨する(ISO/TR 230-11及びISO/IEC Guide 99参照)。
8.2.3
測定手順及びデータの解析
試験対象である機械部品は,関心のある移動範囲にわたって一連の目標位置まで移動させなければなら
ない。測定間隔は,移動範囲250 mm以下の軸では25 mm以下でなければならない。より長い軸において
は,測定間隔は,軸長さの1/10以下でなければならない。目標位置では,測定値を記録するのに十分な時
間だけ機械を停止させなければならない。
測定は,使用する測定器及び工作機械の使用目的によって,連続運転モードで行ってもよい。
試験するときの送り速度は,使用する測定器,測定方法及び/又は工作機械の使用目的に適した速度で
なければならない。
測定結果は,3.4.9及び3.4.10の定義に基づいて解析しなければならない。結果の表示は,グラフ形式に
よるものが望ましい。
記録した試験結果には,日付,時間,機械,使用した測定器,測定線の位置,工作物側のオフセット(始
点及び終点の座標),工具側のオフセット,解析方法(基準線の定義,測定回数及び平均値),運転モード
(連続的又は間欠的),ドウエル時間,送り速度,試験していない他の軸の位置,使用した補正,使用した
符号の決め方,及び送り方向を含めなければならない。
8.3
直進位置決め誤差運動試験
8.3.1
一般
44
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定器は,(工具と工作物との相対運動に対応する)試験中の機械の運動部品が移動する距離を測定でき
るように設置し,運動部品は,手動又は数値制御によって各目標位置に位置決めする。測定した位置の値
は,記録し,目標位置と測定値との差を直進位置決め偏差とする(JIS B 6190-2参照)。
注記 直進位置決め誤差の測定では,運動部品固有の角度誤差運動及びアッベの原理によって,測定
線の位置の影響を受ける。したがって,測定線の位置が異なると同じ運動を同様に測定しても
その結果が異なることがある。
8.3.2
測定器及び測定方法
8.3.2.1
レーザ干渉計による方法
レーザ干渉計を用いた直進位置決め誤差運動の測定においては,反射鏡及び干渉計の二つの光学部品を
使用する。このうちの一つは,工具保持部に取り付け,もう一方は,工作物保持部に取り付ける。ミスア
ライメントは,余弦誤差を引き起こすため,レーザヘッドから放射されたレーザ光軸は,可能な限り直進
運動と平行にしなければならない。加速度による振動及びたわみを避けるために,全ての光学系は,機械
部品に確実に固定しなければならない。
空気センサ(気温,大気圧及び湿度測定)は,空気の屈折率を補正するために光軸の近くに配置しなけ
ればならない。
物体温度センサ(物体の熱膨張に対するレーザ読みの補正用)は,代表的な機械温度を示す適切な機械
表面に付けなければならない。一般に,工具と工作物との間の機械の構造ループを構成する中で最も影響
する材料の線膨張係数を考慮する。また,物体温度センサは,通常,工作物を取り付ける箇所(例えば,
テーブル又はパレット)に近い位置の機械温度を測定するように取り付ける。ただし,環境温度が20 ℃
と異なり,かつ,工作物の線熱膨張係数が機械の構造ループを構成する材料と異なる場合には,機械加工
された部品の精度はその影響を受ける。また,機械(テーブル)温度ではなく機械のフィードバック用の
位置検出器の温度に,数値制御システムが影響を受けるという事実を考慮することが望ましい。環境に著
しい温度勾配が存在する場合は,予想される加工部品精度の推定においては更なる不確かさの影響因子を
検討しなければならない。
8.3.2.2
リニアスケールによる方法
リニアスケールを用いて直進位置決め誤差運動を測定する場合には,スケール及び検出器は,機械の工
具保持側と工作物保持側とに取り付ける。スケールは,ミスアライメントが余弦誤差を引き起こすことか
ら,できるだけ直進運動と平行に取り付けなければならない。基準とするリニアスケールと機械との間の
公称熱膨張差(NDE)補正を行わなければならない(6.2.2及び8.3.2.1参照)。
8.3.3
測定手順及びデータの解析
8.3.3.1
測定手順及び数値制御軸の位置決め誤差データの解析
測定手順及び数値制御軸の位置決め誤差データの解析は,JIS B 6190-2による。
8.3.3.2
周期的な直進位置決め誤差運動
機械の運動部品の位置決め誤差運動は,機械スケール又はそれと同等の部品の基本周期と一致した間隔
で周期的に変動する。例えば,角度エンコーダの付いたボールねじで駆動される機械では,変動の周期は,
通常はボールねじのピッチ(若しくは角度エンコーダのピッチ,又はそれらの両方)と同期する。リニア
スケール又は角度エンコーダの周期は,スケール又はエンコーダの格子線間隔である。レーザ干渉計の周
期は,光の波長又はその波長のてい(逓)倍長である。
測定範囲は,予想した偏差の周期の2周期以上とし,目標位置は,等間隔に少なくとも21点を選択する。
一方向位置決め測定を1回,全ての目標位置で行う。周期的な直進位置決め誤差Pは,図46に示すよう
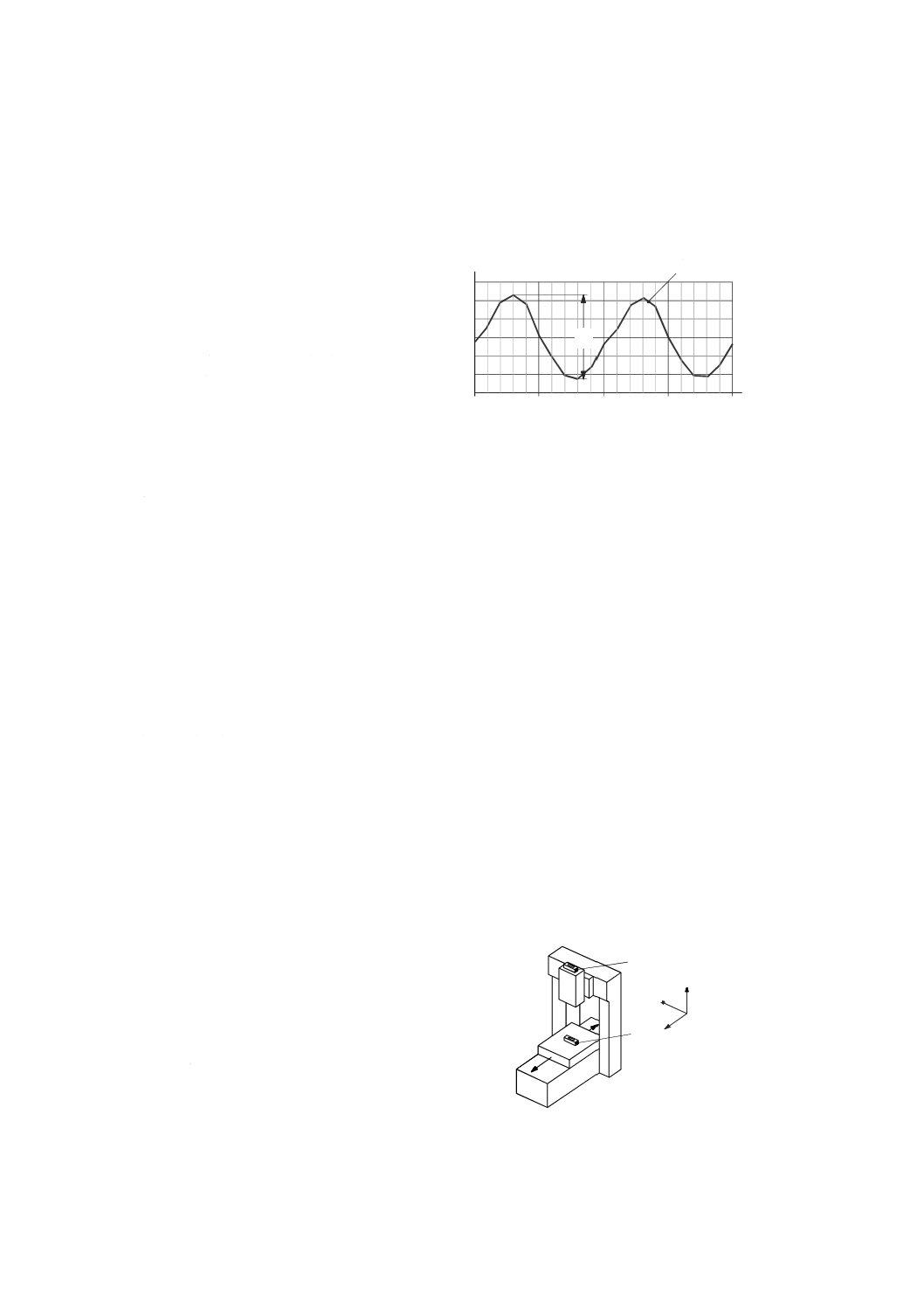
45
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
に測定した位置決め偏差の最大値と最小値との差である。
注記 直進運動の周期性のある変化は,ボールねじのミスアライメントによって起こることが多く,1
回転ごとに現れる。
X X軸の座標値(mm)
EXX 直進位置決め誤差(µm)
1 測定した偏差
P 周期的な直進位置決め誤差
図46−周期的な直進位置決め誤差
8.4
角度誤差運動試験
8.4.1
一般
運動の各直進軸の三つの直角方向角度誤差運動(一般に,ロール,ピッチ及びヨーという。)ついては,
測定することが望ましい。角度誤差測定器は,機械の運動部品が直進軸に沿って移動するとき,機械の工
具保持部と工作物保持部との間の相対的な角度誤差運動を測定するよう配置しなければならない。
8.4.2
測定器及び測定方法
一般的な角度誤差運動の測定方法は,軸のピッチ及びヨー(直進運動の軸方向と直角な軸回りの回転)
を測定するためにはレーザ角度干渉計又はオートコリメータを用い,水平軸のロール(直進運動の軸回り
の回転)を測定するためには精密水準器を用いる。 垂直軸のロールは,差分真直度測定方法によって測定
する(8.4.2.4参照)。
注記 水平面内の直進運動の場合には,精密水準器は,ピッチ及びロールを測定することができ,オ
ートコリメータ及びレーザは,ピッチ及びヨーを測定することができる。
8.4.2.1
精密水準器による方法
精密水準器を用いる場合は,その精密水準器は,移動部品上に定置する。良い結果を得るためには,二
つの精密水準器を用いて機械の工具保持部品と工作物保持部品との間の差分をとって測定を行うことが望
ましい(図47参照)。
1 測定用精密水準器
2 参照用精密水準器
図47−精密水準器によるX' 軸の角度誤差運動の測定(ロール)
1.0
-1080
-1075
-1070
-1065
-1060
0
-1.0
-2.0
-3.0
-4.0
-5.0
E
P
X
1
XX
X
−1 080
−1 075
−1 070
−1 065
−1 060
−
−
−
−
−
Z
Y
X'
1
2
Z
Y
X'

46
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8.4.2.2
オートコリメータによる方法
オートコリメータ及び反射鏡は,工作物保持部及び工具保持部との間の比較測定となるように定置する。
オートコリメータは,運動軸と同軸になるように機械の静止部品上に取り付ける(図48参照)。光軸に直
角な水平軸回りの(運動部品に取り付けた)反射鏡の回転は,焦点鏡上の標線に垂直変位となって現れる。
接眼マイクロメータによって測定した変位から,反射鏡の角度偏差を求めることができる(ISO/TR 230-11
参照)。接眼マイクロメータを90°回転させて,反射鏡の垂直軸回りの回転角を測定することができる。
両方の角度を同時に測定できる測定器も利用できる。
光電式オートコリメータは,1秒未満の分解能の必要な,より精密な測定に使用することができる。二
つの軸を同時に測定できるものもあり,二つの直交軸回りの角度(例えば,ピッチ及びヨー)を容易に測
定することができる。
注記 移動距離が長い場合,測定の不確かさは,空気の屈折率の空間的な変化の影響を受ける。空気
の屈折率は,光軸の変位に強く影響する。光軸は,垂直方向に1 ℃/mの温度勾配があると,
10 m移動させたとき,直線から約9 μrad偏る(参考文献[13])。最も良い結果を得るためには,
測定を適切な回数繰り返して平均をとるだけでなく,光軸回りの空気をファンでかくはんする
ことも考慮したほうがよい。
1 テーブル(工作物側,位置1)
2 テーブル(工作物側,位置2)
3 オートコリメータ
4 主軸(工具側)
5 反射鏡
θ 角度偏差の測定値
図48−オートコリメータによる角度誤差運動の測定
8.4.2.3
レーザ角度干渉計による方法
レーザ角度干渉計は,運動軸に直角な軸回りの回転(ピッチ及びヨー)の測定に用いる。測定器は,角
度干渉計及び反射鏡の二つの光学部品から構成する。機械の運動部品の角度誤差を測定する場合は,一方
の光学部品を工具保持部に,もう一方の光学部品を工作物保持部に取り付ける(図49参照)。主軸を固定
することができない機械においては,不安定さを防ぐために外部ブラケット又は他の適切な固定具を使用
することが望ましい。
注記1 角度干渉計では,既知の距離に分離した二つの平行光線を用いる。角度反射鏡は各光線を干
渉計へ戻す。干渉計と角度反射鏡との間の相対的な回転によって,干渉計で検出される二つ
の光路に差異が生じる。回転角度は,光路差を光路間の距離で除した値として求める。
注記2 光軸に対して光学系を90°回転させることによって別の角度誤差(ヨー又はピッチ)を測定
できる。
q
3
4
5
1
2
θ

47
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 テーブル
2 主軸
3 角度反射鏡
4 直角ミラー付干渉計
LM 直進運動方向
図49−レーザ角度干渉測長器による角度誤差運動の測定
8.4.2.4
差分真直度測定による方法
この測定は,二組の平行な真直度測定を行うことによって実行する。測定の原理は,図50に示すように,
垂直方向に移動する主軸のロールを測定するための方法で,直角定規,及び一つ又は二つの変位計を用い
る。この方法は,垂直に移動するどのような運動部品にも適用できる。他の真直度測定器も代用してもよ
い。
測定器は,運動部品の運動方向に垂直な真直度を測定するように配置する。運動部品は,真直度の測定
方向に直角な軸に沿って移動させ,真直度の読みを記録する。次に,機械主軸を位置2(図50参照)へ水
平に移動させ,再び直角定規の測定面を接触させるために,変位計を延長アーム(参照番号5)に取り付
け,直角定規の基準面に沿って同じ測定線となるよう注意しながら再び測定する。どの垂直位置における
ロール偏差も,その位置での二つの主軸位置間の距離で除した二つの局所真直度偏差の差である。
延長アームは,垂直以外の方向に取り付けるために,この測定の間に一つの運動部品(テーブル又は主
軸)を移動させる必要がある。そのために,垂直軸のロール測定は,この運動によって生じたテーブル又
は主軸の角度変化分を補正しなければならない。このような問題を回避するために,直角定規は,横に[例
えば,図50の主軸(位置2)へ]移動させて精密水準器を用いて再調整してもよい。
8.4.3
測定手順及びデータの解析
a) 機械は,試験中の運動部品を移動させて,一連の目標位置で位置決めするようプログラムしなければ
ならない。
b) 一つの目標位置で,機械は,角度偏差の値を記録するのに十分な時間停止させる。その目標位置は,
軸の関心ある移動範囲にわたって設定する必要がある。測定間隔は,移動範囲が250 mm以下の軸で
は25 mm以下でなければならない。より長い軸では,その間隔は,軸長さの1/10以下でなければな
らない。
c) 少なくとも1回の一方向測定を全ての目標位置で行う。送り速度は,受渡当事者間で協定しなければ
ならない。測定結果は,目標位置とそれに対応する測定器の読みから構成したものでなければならな
い。
角度誤差(例えば,EAX)は,測定された角度偏差の最大値と最小値との差である。角度偏差の記号の
付け方は,JIS B 6310による。
選択した目標位置での離散的な測定の代わりに,測定範囲内での連続測定を行ってもよい。
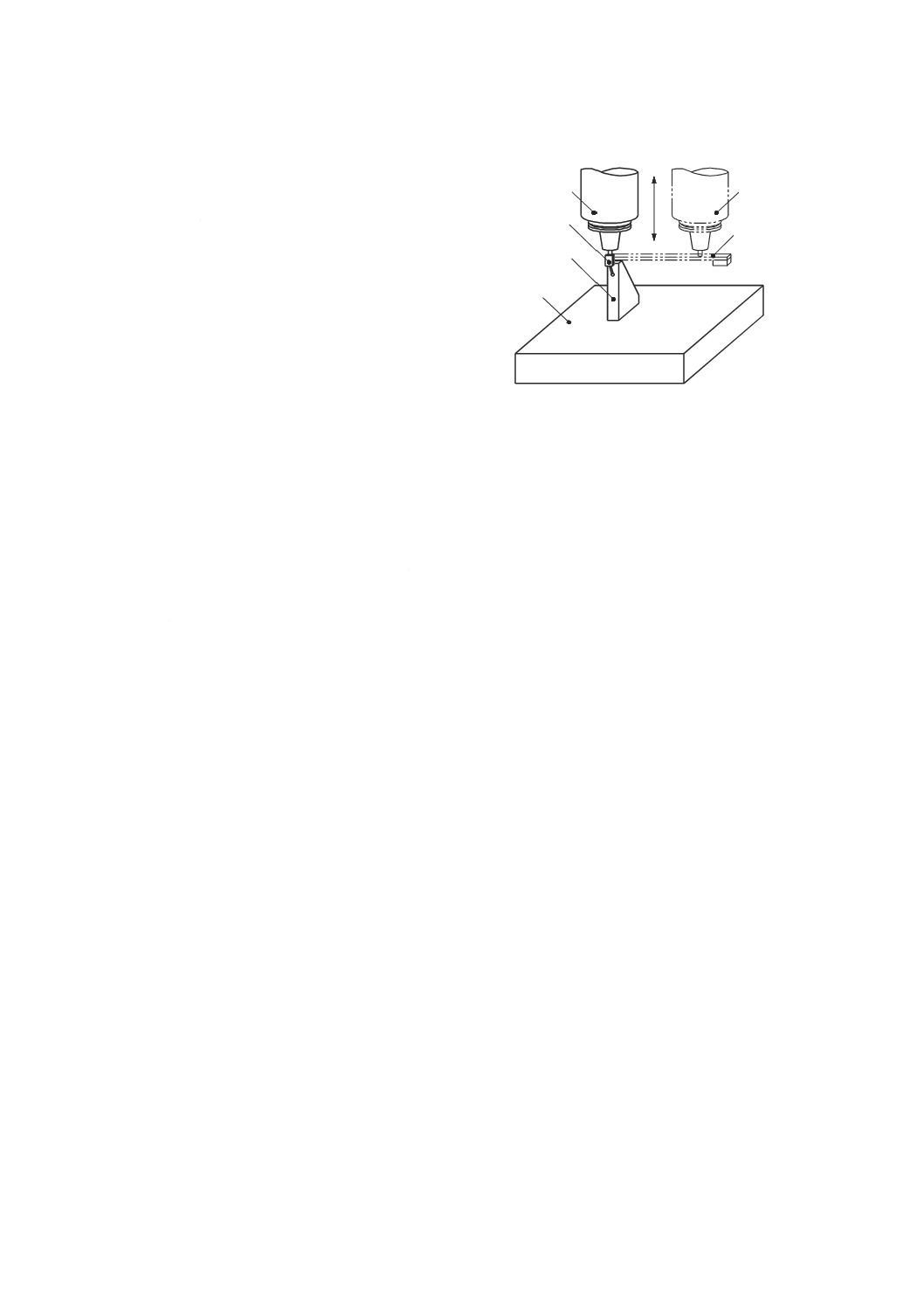
48
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 主軸(位置1)
2 主軸(位置2)
3 変位計
4 直角定規(又はテーブルに対してほぼ直角に定
置した直定規)
5 延長アーム(主軸の位置2だけ)
6 テーブル
LM 直進運動方向
図50−差分真直度測定による垂直移動方向ロールの測定
9
回転軸の幾何精度試験
9.1
JIS B 6190-7の引用
固定感度方向及び回転感度方向における回転軸の幾何精度[すなわち,半径方向誤差運動,軸方向誤差
運動,傾斜誤差運動及び端面誤差運動(3.5.5〜3.5.8参照)],並びにその同期誤差運動,非同期誤差運動な
どの構造誤差運動を評価する試験は,JIS B 6190-7に従って行わなければならない。
9.2
角度位置決め誤差運動
9.2.1
一般
工作機械には,連続又は割出位置決めが可能な回転軸(例えば,回転テーブル,割出テーブル,傾斜主
軸頭及び万能主軸頭)を備えているものが多い。連続位置決めが可能な回転軸は,数値制御(NC)される
が,割出位置決めだけが可能な回転軸は,手動,機械的,NC,プログラマブルロジックコントローラ(PLC)
などのいろいろな方法で制御される。連続位置決めが可能な回転軸の位置決め分解能は,角度フィードバ
ック用センサ及びサーボ制御装置に依存する。機械的な割出位置決めが可能な回転軸では,その位置決め
分解能(間隔)は,機械的な構造によって90°(一部のフライス盤及びボール盤用)から0.5°まで様々
である。中には,異なる割出ピッチを備えた二つの角度割出装置を組み合わせたもので最小割出角度0.02°
のものもある。
自動運転の可能な割出装置には,通常,割出動作時に回転軸の軸方向に数mmの移動を必要とするもの
がある。そのような場合には,割出動作後に再び所定の位置まで移動し固定される。
測定は,機械の工具保持部と工作物保持部との間で行うことが望ましい。
9.2.2
測定器及び測定方法
9.2.2.1
多面鏡とオートコリメータとによる方法
多面鏡は,角度基準器として,オートコリメータで測定するために回転部品とほぼ同心に取り付けるこ
とが望ましい。多面鏡の上面と回転部品の上面とは互いに平行であることが望ましく,多面鏡の上面は試
験中の回転部品の軸平均線と直角であることが望ましい。オートコリメータは,機械の非回転部分,例え
ば,主軸頭に取り付けなければならない(図51参照)。
注記 多面鏡の基準面と試験中の回転部品の軸平均線との間の平均平行度誤差は,角度位置決め精度
の測定に影響を及ぼす(360°周期の付加的な周期誤差を生じる。)。
試験中の回転部品の角度位置決め間隔は,多面鏡の基準面間のなす角度と同じか,又はその整数倍であ
1
3
4
2
5
LM
6
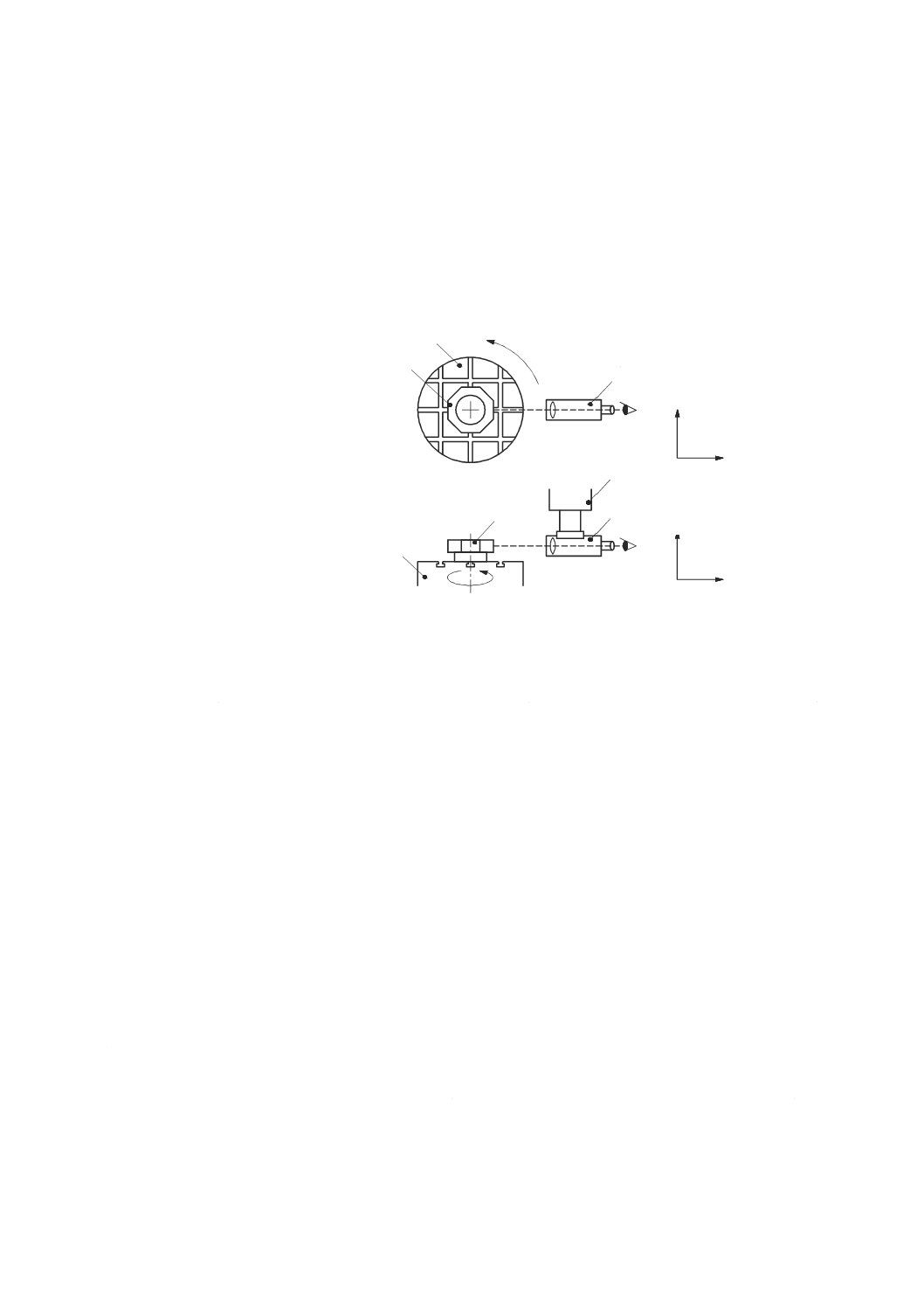
49
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ることが望ましい。例えば,12面の多面鏡を基準器として用いる場合の角度位置決め間隔は30°又は30°
の整数倍となる。多面鏡のゼロ点(0°)は,校正表に記載された誤差を補正できるようにするために,測
定開始位置として使用することが望ましい。各位置決め角度でオートコリメータを用いて測定した角度は,
その角度での角度位置決め偏差となる。
多面鏡とオートコリメータとは,多面鏡の基準面間のなす角度が試験中の割出回転軸の最小割出間隔の
整数倍である場合にも,割出回転軸の角度位置決め誤差の測定に使用してもよい。
1 多面鏡
2 オートコリメータ
3 回転テーブル
4 主軸頭
図51−オートコリメータと多面鏡とによる角度位置決め誤差の測定方法
9.2.2.2
レーザ干渉計/オートコリメータと基準割出テーブルとによる方法
基準割出テーブルは,機械の回転部品(例えば,回転テーブル)に固定しなければならない。平面反射
鏡又は角度測定光学系は,基準割出テーブル上に固定する。そのとき反射面は,光軸と垂直でなければな
らない。レーザ干渉計又はオートコリメータは,機械の非回転部分に固定する(図52参照)。基準割出テ
ーブルは,回転部品の回転運動の向きと反対の方向に回転することが望ましい。すなわち,回転部品が時
計回り(CW)に回転する場合は,基準割出テーブルは,反時計回り(CCW)に回転することが望ましい。
その結果,基準割出テーブルの上面に置かれた反射鏡(又は角度光学部品)は,常に同じ方向を維持する。
これらの測定器を用いて各位置決め角度において測定した角度は,その位置決め角度での角度位置決め偏
差となる。
基準割出テーブルとオートコリメータとは,基準割出テーブルの割出可能角度が試験中の割出回転軸の
最小割出間隔の整数倍である場合にも,割出回転軸の角度位置決め誤差の測定に使用してもよい。
レーザ干渉計を角度測定器としている場合には,おおよそ5°までの角度誤差運動を検出できる(又は
基準割出テーブルの最小割出角度以上)。したがって,連続的な角度位置決め誤差は,この方法によって測
定できる。一般に,100 μm/m(20″)より大きな角度を測定する場合は,測定の不確かさは著しく増加す
る。
割出回転軸は,通常,割出動作時にはその回転軸の軸方向に数mmの移動を必要とする。そのため,基
準割出テーブルと角度測定光学系とを備えたレーザ角度干渉計を使って試験をする場合には,レーザ光の
中断を防ぐ特別な装置が必要になる。
9.2.2.3
基準ロータリ(角度)エンコーダによる方法
Y
X
Z
X
2
3
1
4
2
1
3
Y
X
X
Z

50
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
基準(校正された)ロータリエンコーダは,エンコーダの回転部品が機械の回転部品の回転軸と一致す
るように設置しなければならない。エンコーダケース(非回転部品)は,機械の非回転部分に取り付けな
ければならない。ロータリエンコーダの取付け及びアライメントは,製造業者の推奨に従わなければなら
ない。ロータリエンコーダの読みは,実際の角変位であり,角度位置決め偏差を決定するために指令角変
位と比較するのがよい。
基準ロータリ(角度)エンコーダは,回転させるために軸方向に昇降させる必要がある割出テーブルの
角度位置決め誤差の測定に用いてはならない。
1 レーザヘッド
2 角度干渉計
3 主軸頭
4 角度測定用反射鏡
5 基準割出テーブル
6 測定対象回転軸
図52−基準割出テーブルを用いた角度位置決め誤差測定
9.2.3
測定手順及びデータの解析
数値制御(NC)によって連続的な位置決めが可能な回転軸の角度位置決めの正確さ及び繰返し性の試験
方法は,JIS B 6190-2による。
JIS B 6190-2に規定された試験方法は,割出位置決めが可能な回転軸(プログラム又は手動による操作)
の角度位置決めの正確さ及び繰返し性の測定にも適用できる。ただし,次の制限がある。
a) 目標角度位置の数は,基準器の利用可能な角度と試験する装置の最小割出間隔との組合せによって制
限されることがある。
b) 多面鏡と基準割出テーブルとを用いる場合は,目標位置決め角度を選択するときにランダム成分を適
用できない。
c) ロック形式の割出テーブルでは,ロックし終えた後に測定を行わなければならない。そのため,測定
装置を選定するときは,割出テーブル上面などが軸方向へ昇降する可能性があることを考慮しなけれ
ばならない。
9.2.3.1
周期的な角度位置決め誤差運動
機械の回転部品の周期的な角度位置決め誤差運動は,周期的な直進位置決め誤差運動の測定と同様に,2
周期分以上測定する。均等な間隔に配置された少なくとも21個の目標角度位置は,角度位置決め誤差運動
の2周期分以上の間に選択する。
一組の一方向の測定を全ての目標角度位置で行う。周期的な角度位置決め誤差Pは,測定された角度位
置決め偏差の最大差である。
1
3
2
4
5
6
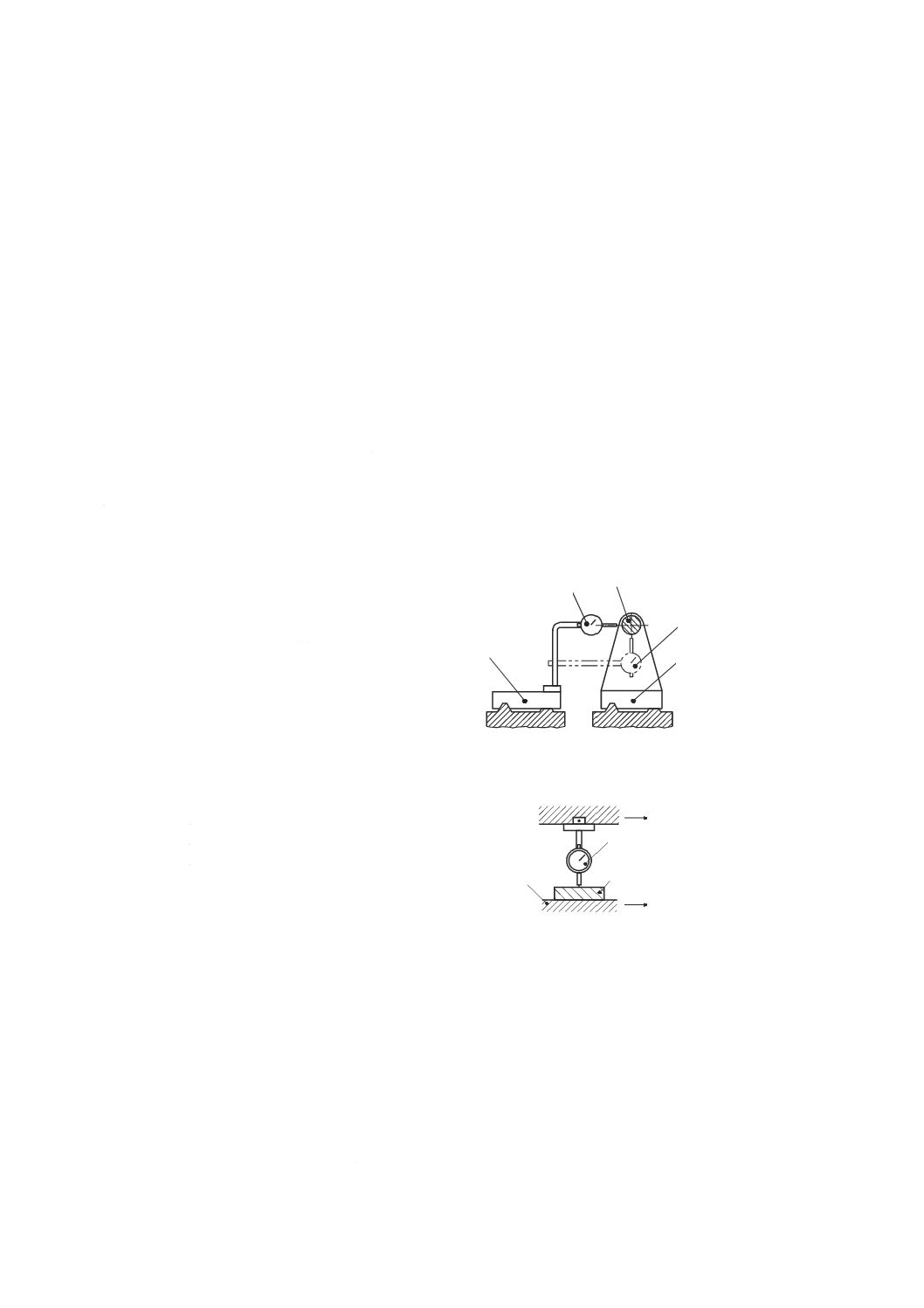
51
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
10
運動軸間の幾何精度−平行度,直角度,同軸度及び交差度
10.1
運動軸の平行度
10.1.1
一般
理想的に平行であるように設計された直進軸間の平行度誤差の測定は必要である。例えば,平行度は,
マシニングセンタにおいて繰出し主軸であるZ軸と可動テーブルであるW軸との間で検査してもよい。
また,直進軸と回転軸の軸平均線又は主軸若しくは(心押台の軸のような)固定軸の軸平均線との平行度,
又は二つの回転軸の軸平均線間の平行度誤差を測定することも必要になる。
10.1.2
二つの直進軸間の平行度誤差(二つの平面内で)
10.1.2.1 一点の振れ測定による方法
変位計は,運動部品の運動軸に垂直な方向の変位を測定するために,機械の運動部品上に取り付け,他
の運動部品に測定子を当てる。二つの運動部品は,同じ量を,同じ方向に同時に移動させ,変位計の読み
の変化としてその一点の振れを記録し(図53及び図54参照),真直度の基準線を決定するために用いる。
理想的な運動方向に対する真直度基準線の向き(傾斜角度)が平行度誤差である。
二つ目の変位計は,同時に二つの平面内における平行度を得るために,(最初の平面に垂直な)他の平面
内で用いる。
1 直進軸の運動部品
2 もう一つの直進軸の運動部品
3 テストバー
4 変位計
5 二つ目の変位計
図53−二つの直進軸間の平行度誤差
1 変位計
2 ブロックゲージ(任意)
3 テーブル
4 テーブルの直進運動方向
5 もう一つの直進軸の運動方向
図54−一点の振れの測定
10.1.2.2 二つの真直度誤差運動の測定による方法
この測定は,8.2.2に規定するいずれの真直度測定装置を用いて行ってもよい。各運動軸の真直度は,8.2.3
に規定する手順で測定しなければならない。
二つの直進軸間の平行度誤差は,互いに直交する二つの平面について計算し記録する。各平面について,
各運動部品の真直度偏差は,共通の真直度基準(例えば,基準器又は光軸)を用いて測定する。真直度偏
差のデータに関連する真直度基準線は,共通の真直度基準線と比較することが望ましい。共通の真直度基
準に対して求めた二つの真直度基準線の傾きは,二つの運動軸間の平行度誤差を得るために,その和をと
1
4
3
5
2
3
5
1
2
4
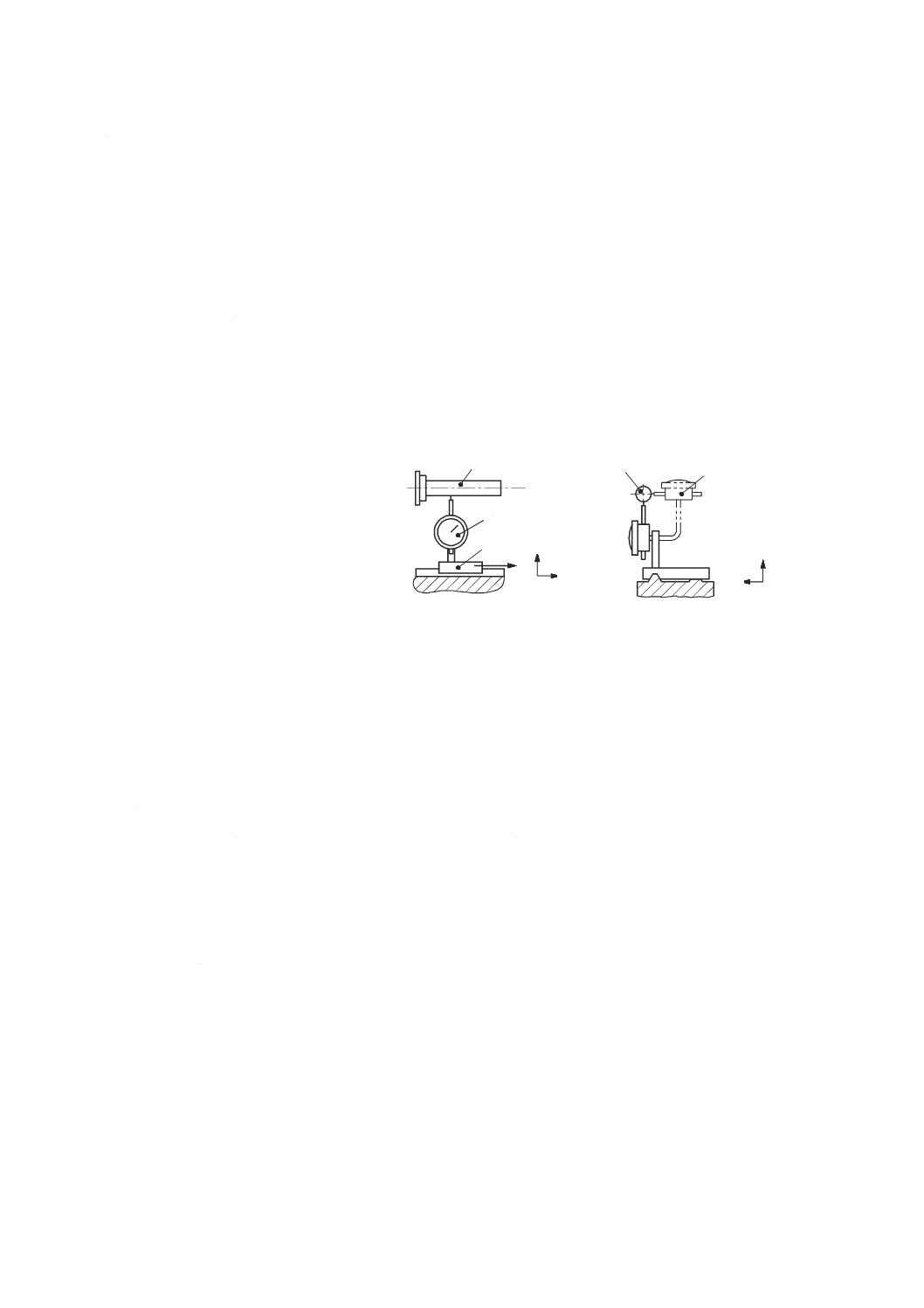
52
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
注記 平行度誤差は,マイクロメートル/メートル(μm/m)又は秒(″)で表す。
10.1.3
直進軸と静止軸との平行度誤差
テストバーは,静止軸を代表する静止部品上に取り付ける。変位計は,運動部品上に取り付け,運動方
向に対する直角方向の変位を読み取るために,その測定子はテストバーに垂直に当てなければならない(図
55参照)。運動部品は,関心ある移動範囲全体に移動させなければならない。変位計の読みの変化は,記
録し,直進運動の軌跡に対する真直度基準線を決めるために用いなければならない。理想的な運動方向に
対する真直度基準線の向き(傾斜角度)が平行度誤差になる。
注記 静止軸とは,測定中に回転しない軸である。
全ての平面が同等に重要でない限り,測定は,可能な場合には機械の使用に際して最も重要な二つの直
交した平面内において行われなければならない。
1 変位計
2 直進運動部品の軸
3 テストバー(静止軸)
4 二つ目の変位計
図55−直進軸と静止軸との平行度誤差
10.1.4
直進軸と回転軸又は機械の主軸の軸平均線との平行度誤差
10.1.4.1 一般
旋回テーブルの回転軸又は主軸の回転軸と直進軸との関係は,まず回転軸の軸平均線を決めて求める。
次に,この軸平均線に対して直進軸の運動を比較する。測定平面(回転軸及び直進軸の両方を含む平面)
内における回転の軸平均線は,回転軸の180°離れた二つの角度位置で測定した真直度の測定結果を平均
して求める。
間接的に軸平均線を表すために,回転軸と直交する基準線を定めることがある。機械的な基準器又は光
学的な基準は,回転軸の軸平均線として用いることができる。10.1.4.2〜10.1.4.4に示す測定装置は,例で
あり,測定の不確かさが同等である他の測定器を代わりに使用することができる。
10.1.4.2 レーザ真直度干渉計による方法
レーザ真直度干渉計を用いた測定方法を,図56に示す。
真直度反射鏡は,回転テーブル又は主軸に取り付け,その測定の軸が回転軸近くにあり,かつ,真直度
誤差運動の測定が試験対象とする直交平面の一つの中で行うことができるように心出しをしなければなら
ない。真直度誤差運動の測定は,まず真直度反射鏡と回転軸とを最初の角度位置に設定して行い,次に,
その反射鏡と回転軸とを180°回転させた後に再び行わなければならない。平行度誤差は,二つの角度位
置で測定した直進運動の理想的な方向に対する真直度基準線の傾きの和の1/2である。
測定の角度を90°及び270°へ変えることによってもう一つの直交平面内における平行度誤差を求める
ことができる。
Y
3
1
2
Y
Z
X
3
4
Y
Z
Y
X
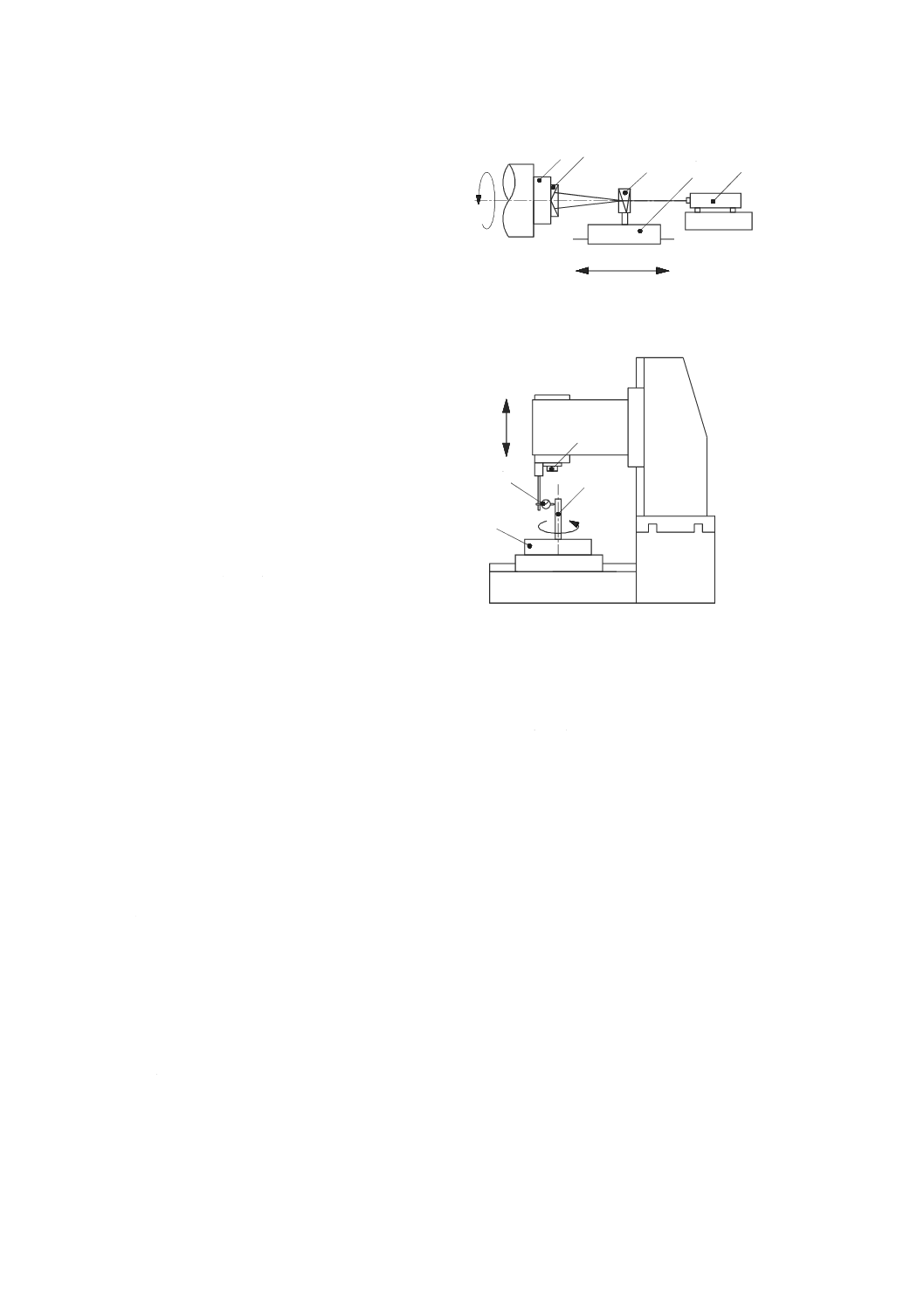
53
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 主軸又は回転軸
2 真直度反射鏡
3 ウォラストンプリズム(干渉計)
4 運動部品
5 レーザヘッド
LM 直進運動方向
図56−真直度干渉計を用いた平行度誤差測定
1 主軸
2 変位計
3 テストバー
4 回転テーブル
LM 直進運動方向
図57−テストバーを用いた平行度誤差の測定
10.1.4.3 テストバー又は直定規と変位計とによる方法
テストバーは,機械の主軸又は回転テーブルに取り付け,心出しをする。変位計は,テストバーの円筒
面に接触させるために,機械の直進運動部品上に取り付ける。真直度誤差運動の測定は,図57に示すよう
にテストバーの長手方向に沿って直進運動部品が移動する間にテストバーに対する変位を測定することに
よって行う。直進運動誤差の測定は,機械の主軸又は回転テーブルを180°回転させた後に行う。平行度
誤差は,二つの角度位置で測定した直進運動の理想的な方向に対する真直度基準線の傾きの和の1/2であ
る。
注記1 主軸又は回転テーブルを180°回転させることは,機械の主軸又は回転テーブルに対するテ
ストバーのアライメント誤差を取り除くことになる。
注記2 この方法は,直定規を反転させて測定すれば,真直度誤差及び平行度誤差の両方を求めるこ
とができる。
最初の測定値に対して90°回した位置でテストバーに対する変位計の読みを使って再びこれらの測定
を行えば,直交する方向における主軸の平行度誤差を決定できる。
10.1.4.4 基準球と変位計とによる方法
図58に示すように,基準球は,機械の直進運動部品の上に取り付け,変位計は,試験対象の回転軸(回
転テーブル又は主軸)に定置しなければならない。基準球は,回転軸又は主軸を回転させている間に,試
験対象の軸に直交した二つの機械の軸を動かすことによって回転軸の軸平均線に対して心出しをする。次
に,基準球は,直進軸(図58のh)に平行に移動させてもう一つの位置へ移動させる。変位計は,取り付
け直してこの新しい位置で基準球に当てて,読みを取る。中心位置の誤差は,二つの位置での変位計の読
LM
2
3
4
5
1
LM
4
3
1
2
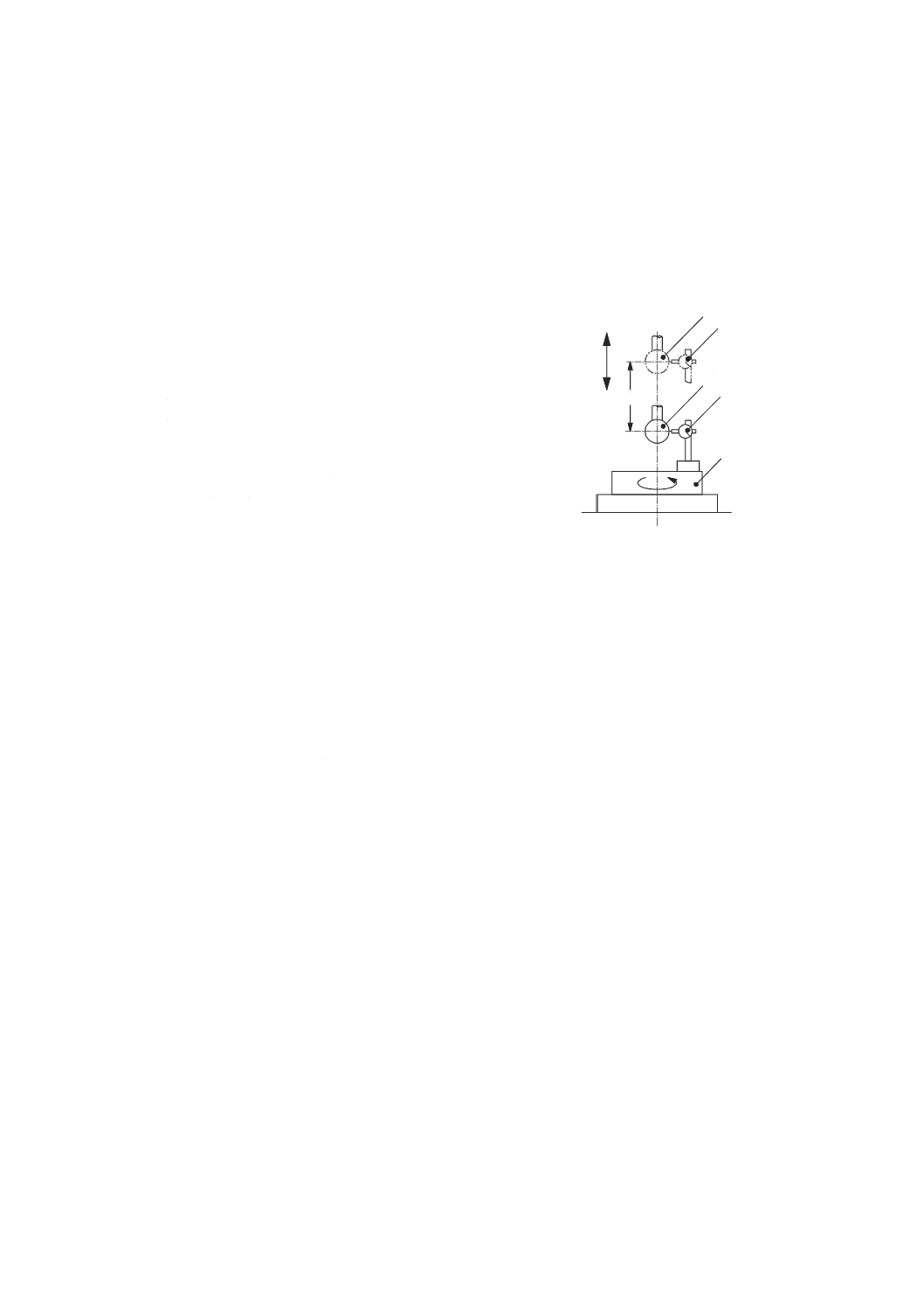
54
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
みの差の1/2として記録する。
回転軸と直進軸との平行度誤差は,二つの位置間の距離(図58のh)で,二つの位置での中心位置の差
を除して求める。
結果を改善するために(例えば,最小二乗計算を用いるために),より多くの直進軸に沿った中間位置を
選んでもよい。
1 位置1における基準球
2 位置2における基準球
3 位置1における変位計
4 試験対象の回転軸(回転テーブル又は主軸)
5 位置2における変位計
h 位置1と位置2との距離
LM 直進運動方向
図58−基準球を用いた直進軸と回転軸との平行度誤差の測定
10.1.5
二つの回転軸間の平行度誤差
10.1.5.1 一般
二つの回転軸間の関係は,まず一つ目の回転軸の軸平均線を設定してから決定する。次に二つ目の回転
軸と一つ目の軸平均線とを比較する。測定平面(両方の回転軸に見掛け上平行な機械の直交座標平面)内
の回転の軸平均線は,180°離れた一つ目の回転軸の二つの角度位置で測定値を平均して決定する。
間接的に軸平均線を表すために,回転軸と直交する基準線を定めることがある。機械的な基準器又は光
学的な基準は,回転軸の軸平均線として用いることができる。10.1.5.2及び10.1.5.3に示す二つの同軸の回
転軸間の平行度誤差の測定に使用する測定装置は,例であり,測定の不確かさが同等である他の測定器を
代わりに使用することができる。
10.1.5.2 テストバーによる方法
テストバーは,主軸(又は回転テーブル)に取り付ける。主軸が複数ある場合は,テストバーはその一
つの主軸に取り付ける。テストバーは,二つの直交する半径方向において,振れが最小になるように主軸
の回転軸に対して心出しをしなければならない。距離d(図59参照)の離れた二つの変位計を取り付ける
取付具は,もう一方の主軸に取り付ける。変位計は,テストバーの長手方向に沿った2か所で,その円筒
面に当てる。変位計は,二つ目の主軸の回転角度の関数としてテストバーに対する変位を記録するために
二つ目の主軸を使ってテストバーの周りを回転させなければならない。二つの変位計から得られたそれぞ
れの測定データに対する基準円の中心(CX,CY)は,それぞれの測定データを最小二乗基準円に適合させ
て算出する。基準円の中心座標の差(CX2−CX1)を変位計間の距離dで除した値が二つの回転軸間の水平
面内における平行度誤差になる。同様にもう一つの方向における基準円の中心座標(CY1及びCY2)を用い
て同様に求めた値が垂直面内における平行度誤差になる(図59参照)。
特に水平軸の場合には,たわみを無視できる剛性のある取付具に取り付ける必要がある。
テストバーと一つ目の主軸との心出し誤差の影響を完全に除くために,上記の測定は,一つ目の主軸を
4
3
1
5
2
LM
h
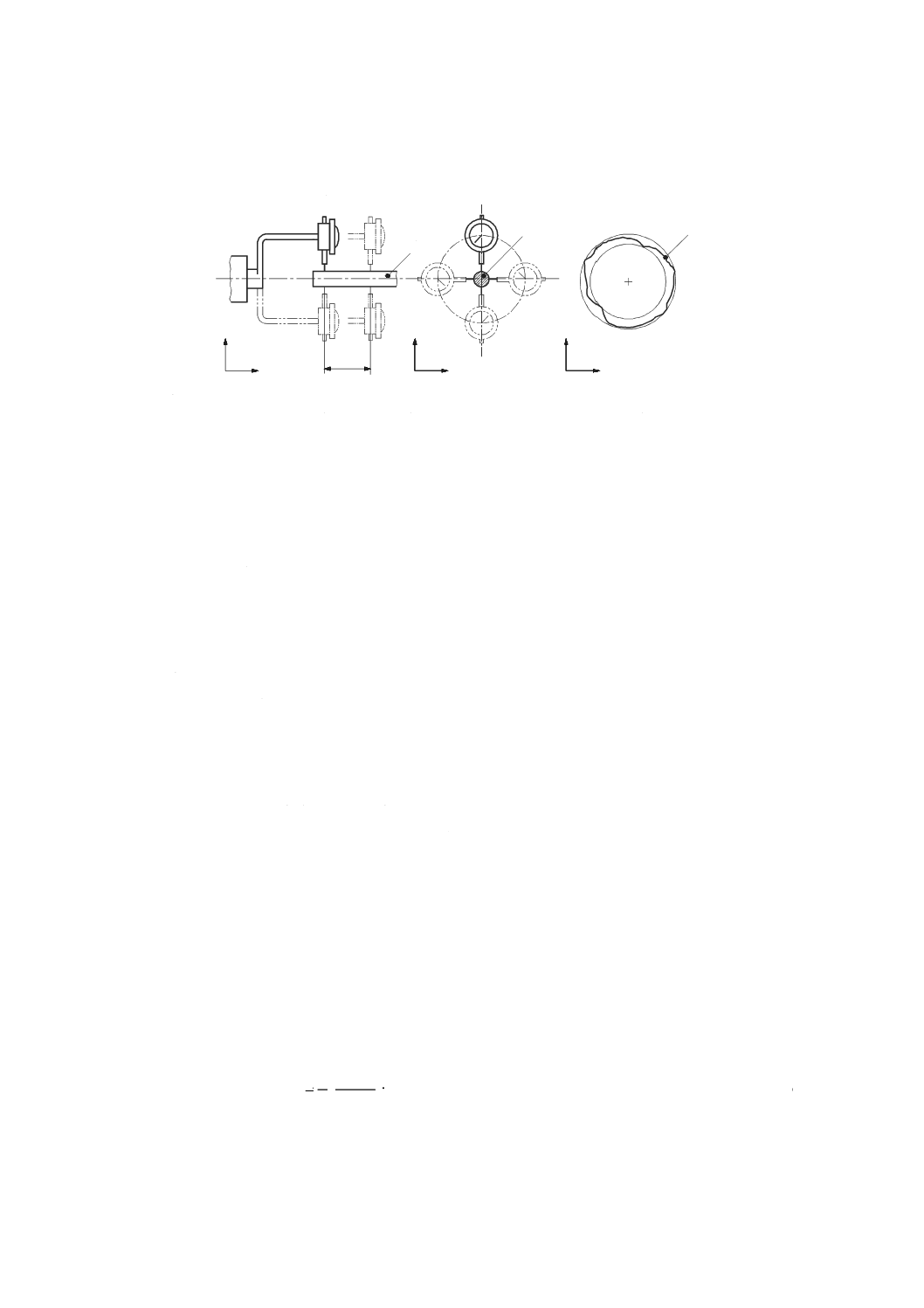
55
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
180°回転させた後に行ってもよい。この場合の平行度偏差は,求めた二つの角度の和の1/2である。
1 テストバー
2 テストバーに対する変位計の出力結果
A,B 変位計
CX 基準円中心のX軸座標
CY 基準円中心のY軸座標
d 変位計AとBとの距離
図59−テストバーを用いた二つの回転軸間の平行度誤差測定
10.1.5.3 二つの基準球による方法
直線上である距離,離れた二つの基準球は,主軸又は回転テーブルの一つに取り付ける。それぞれの球
は,回転軸の軸平均線に対して最小の振れとなるように個々に心出しをする。ある距離だけ離れた二つの
変位計を保持する取付具は,他の回転テーブル又は主軸上に取り付けなければならない。試験方法は,
10.1.5.2に規定した方法と同じである。
10.2
軸平均線の同軸度誤差
10.2.1
一般
一般に二つの軸平均線間の同軸度誤差(3.7.2参照)を規定するには,四つのパラメータが必要になる。
このうちの二つは,2軸間の平行度誤差であり,残りの二つは,二つの直交平面(例えば,水平面及び垂
直面)で規定される2軸間の心ずれである。したがって,二つの回転軸間の平行度誤差(10.1.5参照)の
測定に用いる方法は,同軸度誤差の測定にも用いることができる。同様に,同軸度誤差の測定に用いるど
のような方法も,二つの回転軸間の平行度誤差の測定に用いることができる。
10.2.2
一点の振れ測定による方法(半径方向及び軸方向の測定)
この測定方法は,精度の高い基準器を用いなくても平行度誤差及び心ずれの測定ができる実用的な方法
である。この測定方法は,図60に示すように,一方の主軸(又は回転テーブル)に二つの変位計を取り付
け,もう一方の主軸(又は回転テーブル)に取り付けた目標に変位計の測定子を当てて,半径方向(外周
部)及び軸方向(端面)変位を測定する。
二つの軸は,一緒に回転させ,0°,90°,180°及び270°の位置で変位計の読みを取る。この測定は,
温度の影響を避けるために3回行う。二つの平面内における二つの軸の同軸度誤差は,式(11)〜(14)から算
出する。
垂直方向の心ずれVO
2
180
0
O
R
R
V
−
=
··········································································(11)
X
Y
X
Y
d
A
B
CXCY
,
1
1
2
Z
YY
Z
Y
X
Y
X
56
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
垂直方向の角度VA
D
F
F
V
0
180
A
−
=
········································································· (12)
水平方向の心ずれHO
2
270
90
O
R
R
H
−
=
······································································· (13)
水平方向の角度HA
D
F
F
H
90
270
A
−
=
······································································· (14)
ここに,
R0: 0°の角度位置における半径方向の読みの平均
R90: 90°の角度位置における半径方向の読みの平均
R180: 180°の角度位置における半径方向の読みの平均
R270: 270°の角度位置における半径方向の読みの平均
F0: 0°の角度位置における軸方向の読みの平均
F90: 90°の角度位置における軸方向の読みの平均
F180: 180°の角度位置における軸方向の読みの平均
F270: 270°の角度位置における軸方向の読みの平均
D: 軸方向に当てた変位計の測定子が通る円の直径
注記 軸方向変位の測定を行うために当てた変位計の測定子の通る円の直径は,同軸度誤差を算出す
るために必要である。
測定を開始する前に目標のたわみを測定してもよい。これは,図61に示すように両センタで支持した剛
性のあるテストバーにその目標を取り付けて行う。200 mmまでの長さについては,直径50 mmの鋼製テ
ストバーで十分である(高精度な機械については,必要なテストバーの直径を計算するか又はテストバー
のたわみの補正を行うことが望ましい。)。変位計は,図61の0°位置でゼロ点に合わせ,次にテストバー
と変位計とを図61の180°位置まで回転させる。両方の変位計の読みは,それぞれの方向のたわみの影響
を表している。
二つの軸のうちの一つの軸だけが回転軸の場合には,変位計を取り付ける取付具は,回転軸(回転する
軸)を代表するテストバーに固定するのが望ましい。変位計を固定したテストバーの回りで回転させる必
要がある場合には,最小限のはめ合い隙間で回転する中空円筒に取り付けるのが望ましい。この中空円筒
は,読みがはめ合い隙間の影響を受けないような十分に長いものが望ましい。
半径方向及び軸方向測定方法で測定した平行度誤差は,測定を行う回転部品の軸方向誤差運動の影響を
受ける。この測定の不確かさの原因を排除するために測定装置の構成を図62に示すように変更してもよい。
図62に示す構成の測定装置を用いる場合は,主軸に取り付けた二つ目の半径方向変位計は,軸方向変位の
測定に使用した変位計を用いる。このとき水平方向及び垂直方向の角度の計算は,二つの変位計間の距離
で除した変位計で測定された心ずれの差に基づいて行う。
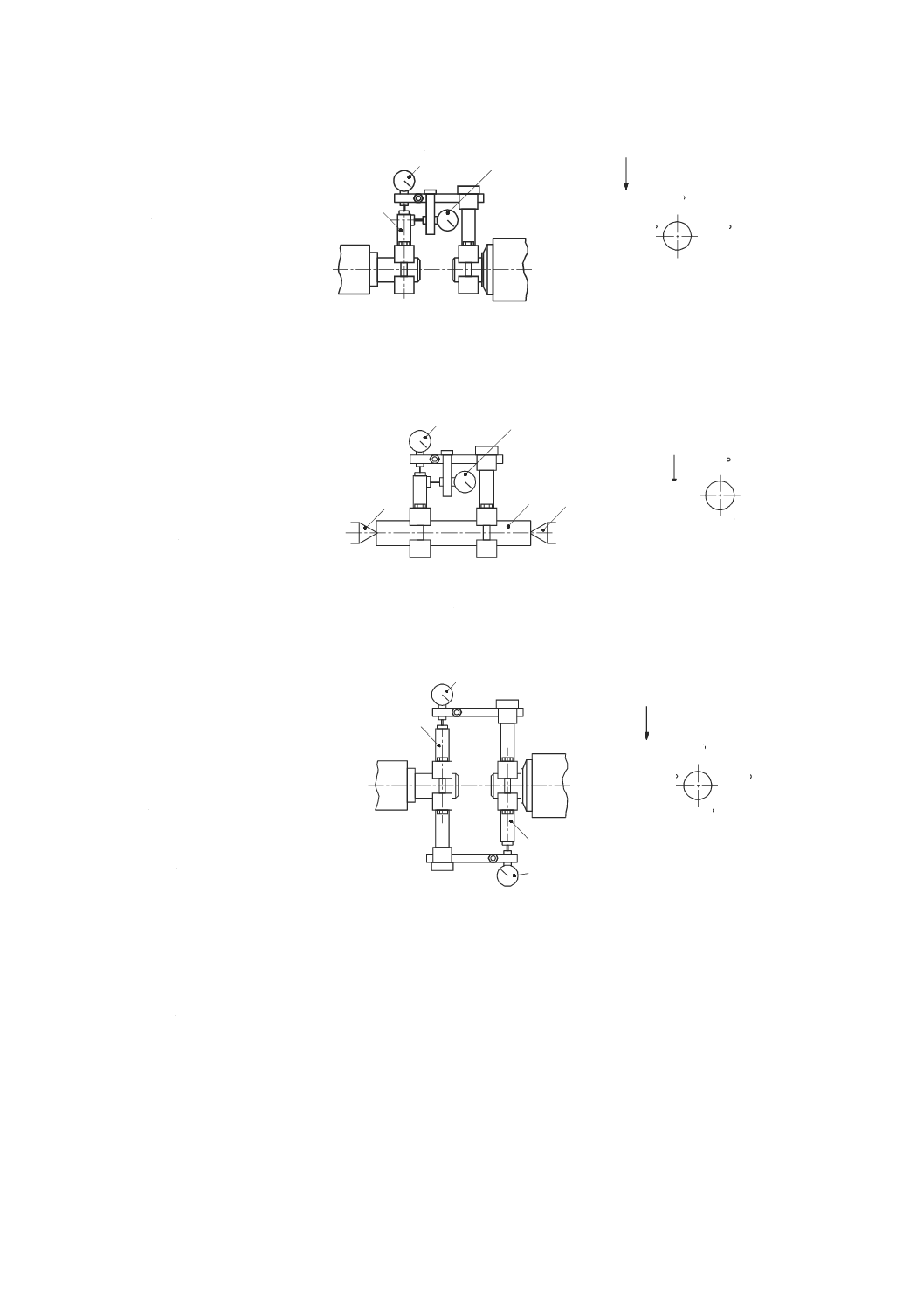
57
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 半径方向変位計
2 軸方向変位計
3 目標
g 重力
a) 測定方法図
b) 測定位置
図60−一点の振れ測定方法による同軸度誤差測定
1 半径方向変位計
2 軸方向変位計
3 テストバー
4 センタ
g 重力
a) 測定方法図
b) 測定位置
図61−取付具及び目標のたわみの校正
1 半径方向変位計
2 二つ目の半径方向変位計
3 目標
g 重力
a) 測定方法図
b) 測定位置
図62−同軸度測定における軸方向誤差運動の影響の排除
10.3
運動軸間の直角度誤差
10.3.1
一般
二つの運動軸間の直角度誤差の測定は,直進軸と静止軸との平行度誤差の測定を2回行う。ここで,静
止軸は,基準直角定規又は精密割出し盤上に定置した直定規で代表する。箇条11に規定する測定方法も,
運動軸間の直角度誤差の評価に用いる。
10.3.2
二つの直進軸間の直角度誤差
10.3.2.1 一般
1
2
3
0
270
90
g
180
g
1
2
4
3
4
g
0
180
g
3
3
2
1
0
270
90
g
180
g
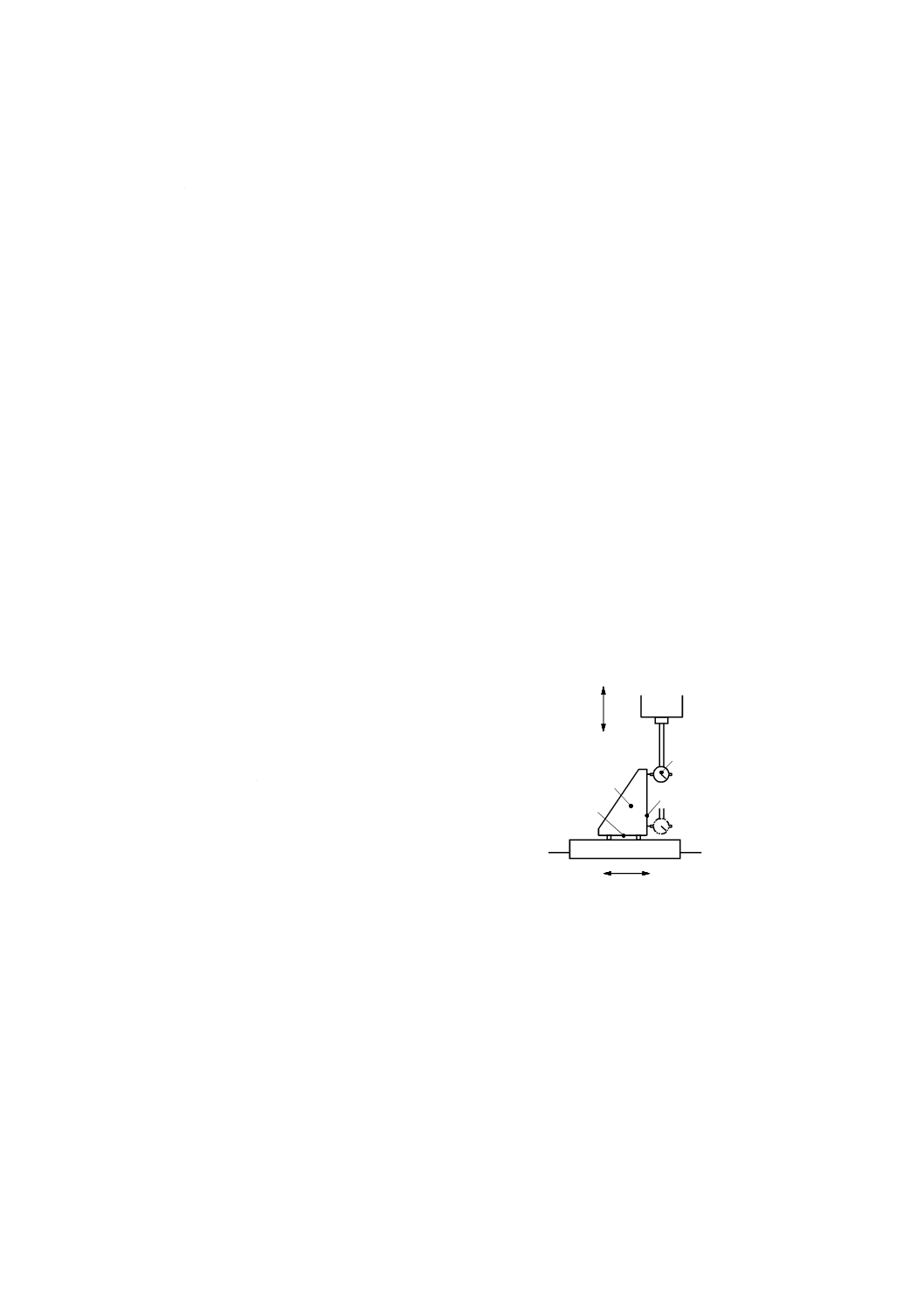
58
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
直角度誤差は,10.3.2.2〜10.3.2.5に規定するように様々な測定装置で測定することができる。その方法
は,ほとんどよく似ている。二つの直角度測定の基準線は,可能な限り作業空間の中央に設定する。その
測定の基準線は,直角度誤差を測定しようとする運動軸に平行になるように設定し,機械の直進運動部品
は,その運動軸に沿って移動させる。運動部品の機能点とこの軸に対する測定基準線との間の横方向(運
動軸に対して直交する方向)の変位(真直度偏差)を変位計で測定する。測定基準線に対する各運動軸の
平行度誤差は,10.1.3に規定するように決定する。二つの平行度誤差の和が二つの直進軸間の直角度誤差
となる。
10.3.2.2 基準直角定規と変位計とによる方法
基準直角定規の基準面を,直角度を測定しようとする二つの運動軸に平行に定置する。変位計は,直角
定規(静止軸)のもう一つの基準面に対する運動軸の平行度誤差を測定するために用いる。測定装置の例
を図63に示す。
基準直角定規の第一基準面は,変位計を使って運動経路に対して正確に平行に定置し,次に第二基準面
を10.1.3に従って測定する。また,変位計の測定子の行き戻り誤差を避けるために,ただ一方向だけに変
位するように直角定規の一辺を許容値よりも大きく傾けて定置してもよい。
基準直角定規を使う場合は,反転法(基準器の誤差を相殺するために,基準直角定規を180°回転する)
で測定することを推奨する。最初の測定と次に行う反転後の測定とで同じ軸運動及び同じ基準面になるよ
うに基準直角定規を定置し測定する。同じ軸運動でない場合には,測定結果に一つの軸の角度誤差運動の
影響が入る。このような場合に計算した直角度誤差は,二つの軸位置における直角度誤差の平均を表す(図
64参照)。二次元ボールプレートもこの測定に適用できる。
注記 定置した直定規などの負荷によって起こる部品のたわみは,考慮する必要がある可能性がある。
1 変位計
2 基準直角定規
A 基準直角定規の第一基準面
B 基準直角定規の第二基準面
LMX X軸に沿った直進運動(例)
LMZ Z軸に沿った直進運動(例)
図63−基準直角定規を用いた直角度誤差測定
1
2
A
LM
B
X
LMZ
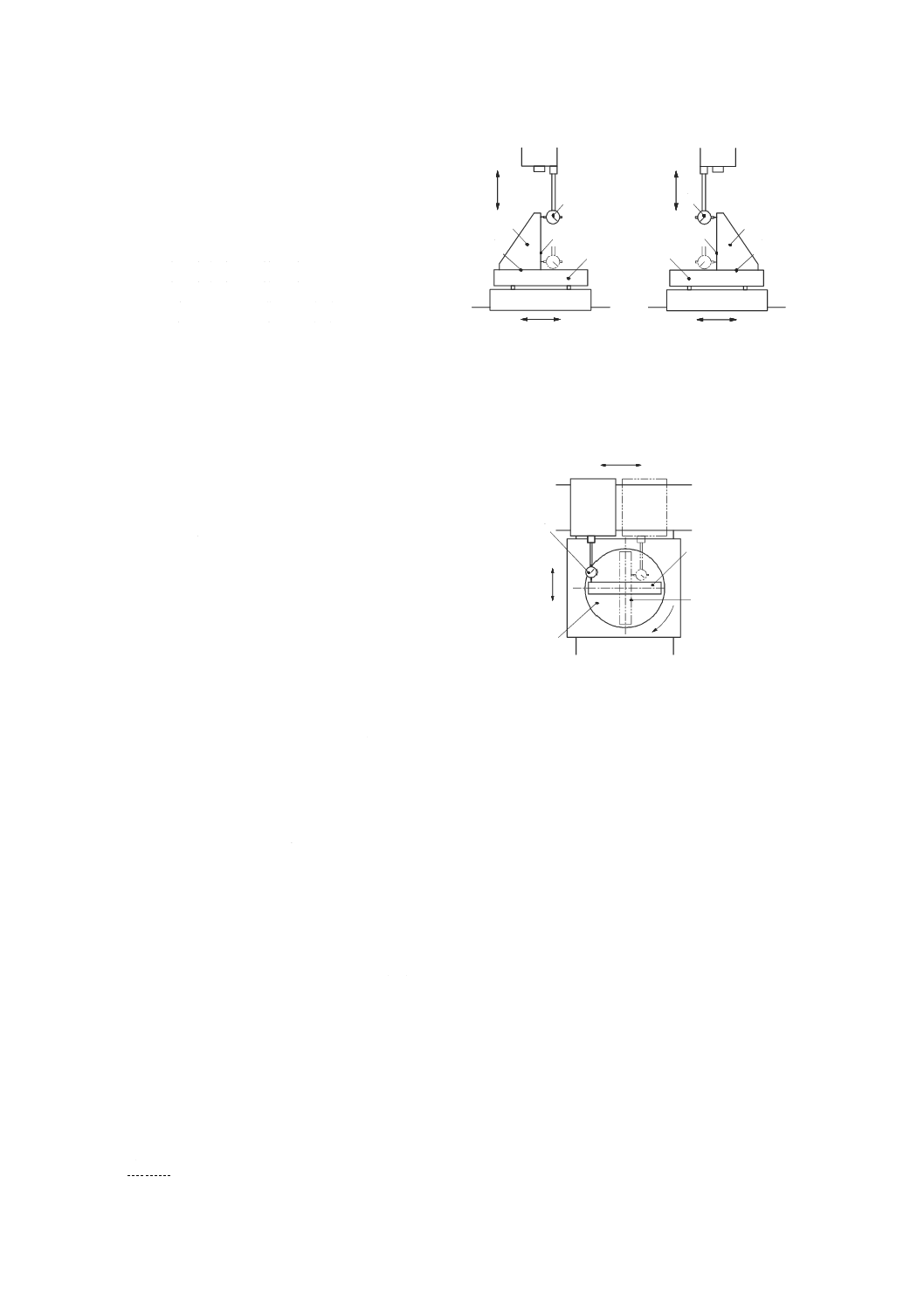
59
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 変位計
2 基準直角定規
3 直定規
A 基準直角定規の第一基準面
B 基準直角定規の第二基準面
LMX X軸に沿った直進運動(例)
LMZ Z軸に沿った直進運動(例)
a) 最初の定置状態
b) 反転後の定置状態
図64−反転法による直角度誤差測定
1 最初の位置にある直定規
2 基準割出テーブル
3 90°回転した後の直定規
4 変位計
LMX X軸に沿った直進運動(例)
LMY Y軸に沿った直進運動(例)
図65−基準割出テーブルを用いた直角度誤差測定
10.3.2.3 基準直定規と基準割出テーブルとによる方法
基準直定規は,基準割出テーブル上に定置する。この割出テーブルは,工作機械のテーブル上に堅く取
り付けなければならない。まず基準直定規を機械の一つの軸に平行になるように定置し,直進軸とその基
準面(静止軸)との平行度誤差を10.1.3に規定するようにして測定する。次に基準割出テーブルを90°回
転させて,直進軸との平行度誤差測定を測定する(図65参照)。
10.3.2.4 光学式スコヤ(五角形プリズム)とレーザ真直度干渉計とによる方法
この測定は,二つの方法で行うことができる。一つ目の方法では,最初の軌跡の真直度誤差は,光学式
スコヤを使ってレーザ光線を真直度反射鏡に位置合せをして測定する。次にウォラストンプリズムを機械
の第二の運動部品まで移動させ,第二の軌跡の真直度誤差を光学式スコヤ,真直度反射鏡,又はレーザ光
を動かすことなく測定する[図66のa) 及びb) 参照]。
二つ目の方法では,上記のように第一の軌跡の真直度誤差を測定する。次に,光学式スコヤを取り外し,
レーザ光線だけを動かして,真直度反射鏡と再度位置合せをする。真直度反射鏡は,この測定の間に動か
さずに,安定した静止台上に取り付けなければならない。
工作機械の構造形態によっては大きな反射鏡及びビームベンダを使用する必要がある可能性がある。[図
66 c) 参照]。測定装置の製造業者の説明書を参照することを強く推奨する。
環境変動誤差(EVE)試験は,この測定の前に行うことを推奨する。
注記1 環境変動誤差試験とは,空気の温度変動,環境の振動などが測定中に測定器及び/又は工作
1
2
A
3
LM
B
X
LMZ
1
2
A
3
LM
B
X
LMZ
1
2
4
3
LMY
LMX
LMX
LMY
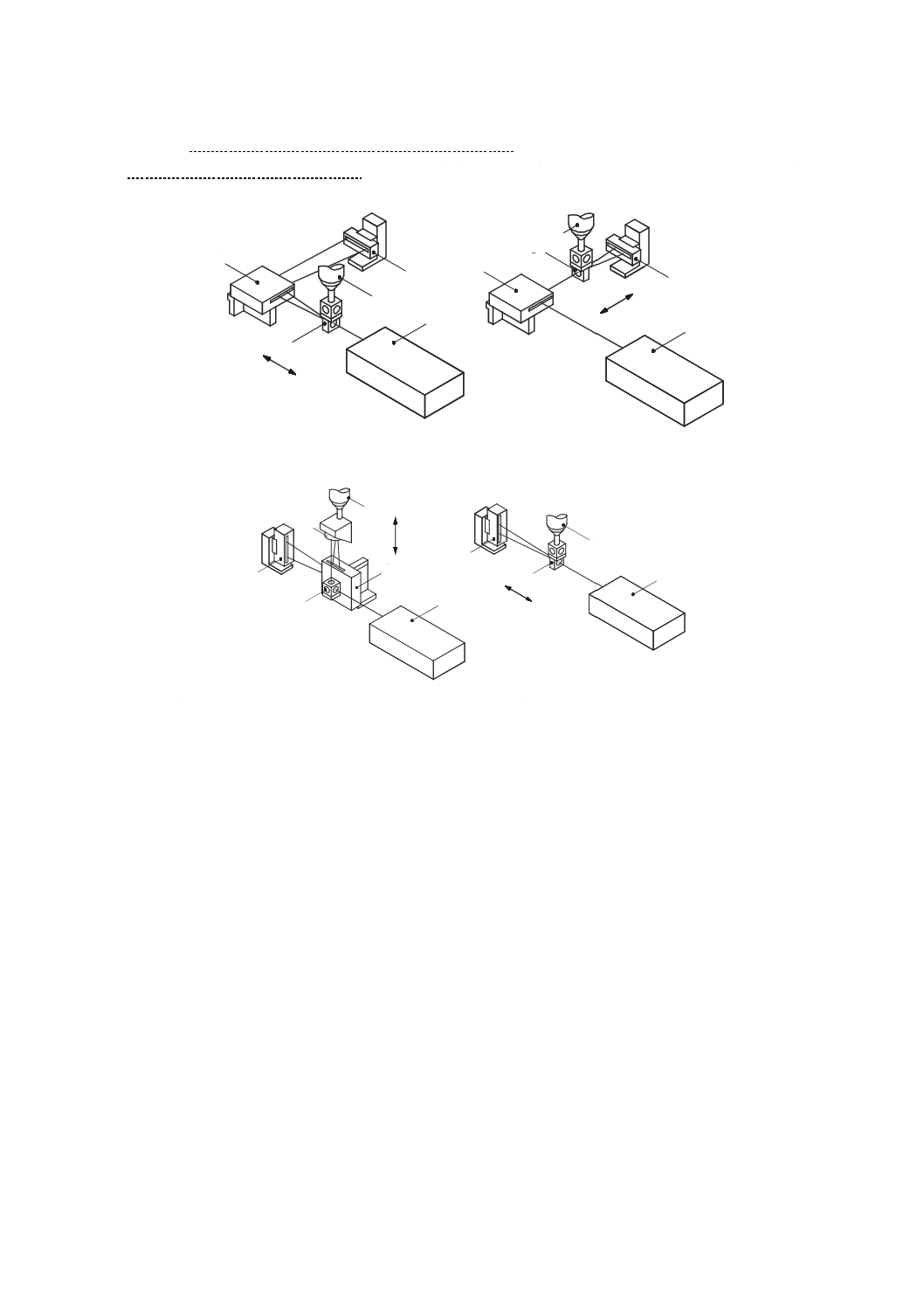
60
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
機械に与える影響の程度を調べる試験である。
注記2 温度変動についてはJIS B 6190-3の箇条5及び環境の振動についてはISO/TR 230-8を参照。
a) 例1−第一軸の測定(水平面内)
b) 例1−第二軸の測定(水平面内)
c) 例2−第一軸の測定(垂直面内)
d) 例2−第二軸の測定(垂直面内)
1 主軸
2 真直度反射鏡(2面鏡)
3 ウォラストンプリズム(干渉計)
4 光学式スコヤ(五角形プリズム)
5 レーザヘッド
6 大形反射鏡とウォラストンプリズムとの組
合せ(干渉計)
7 ビームベンダ
LM1 第一軸(直進軸)の運動
LM2 第二軸(直進軸)の運動
図66−光学式スコヤ(五角形プリズム)及びレーザ干渉計を用いた直角度誤差の測定
10.3.2.5 データの解析
得られた測定値は,まず図67に示すようにプロットする。軌跡の基準直線は,8.2.3に従って決める。
そのとき,最小二乗法を用いることを推奨する。二つの線の勾配を求める。求めた勾配が直進運動とそれ
に関係する測定基準線との間の角度誤差になる。
測定に際して選択した正負の向きに対応させて,直角度誤差を求めるために二つの角度を差をとるか,
和をとるのが望ましい。この規格では,正の直角度誤差は90°よりも大きいことを示し,負の直角度誤差
は,90°よりも小さいことを示す。
次に,基準直角定規/基準割出テーブルの直角度誤差の補正を行うことが望ましい(箇条5参照)。
加工空間内の測定基準線の位置は,算出した直角度誤差の値と一緒に報告しなければならない。
5
3
4
2
1
LM1
4
31
2
5
LM2
1
2
3
5
LM2
1
4
5
7
2
6
LM1
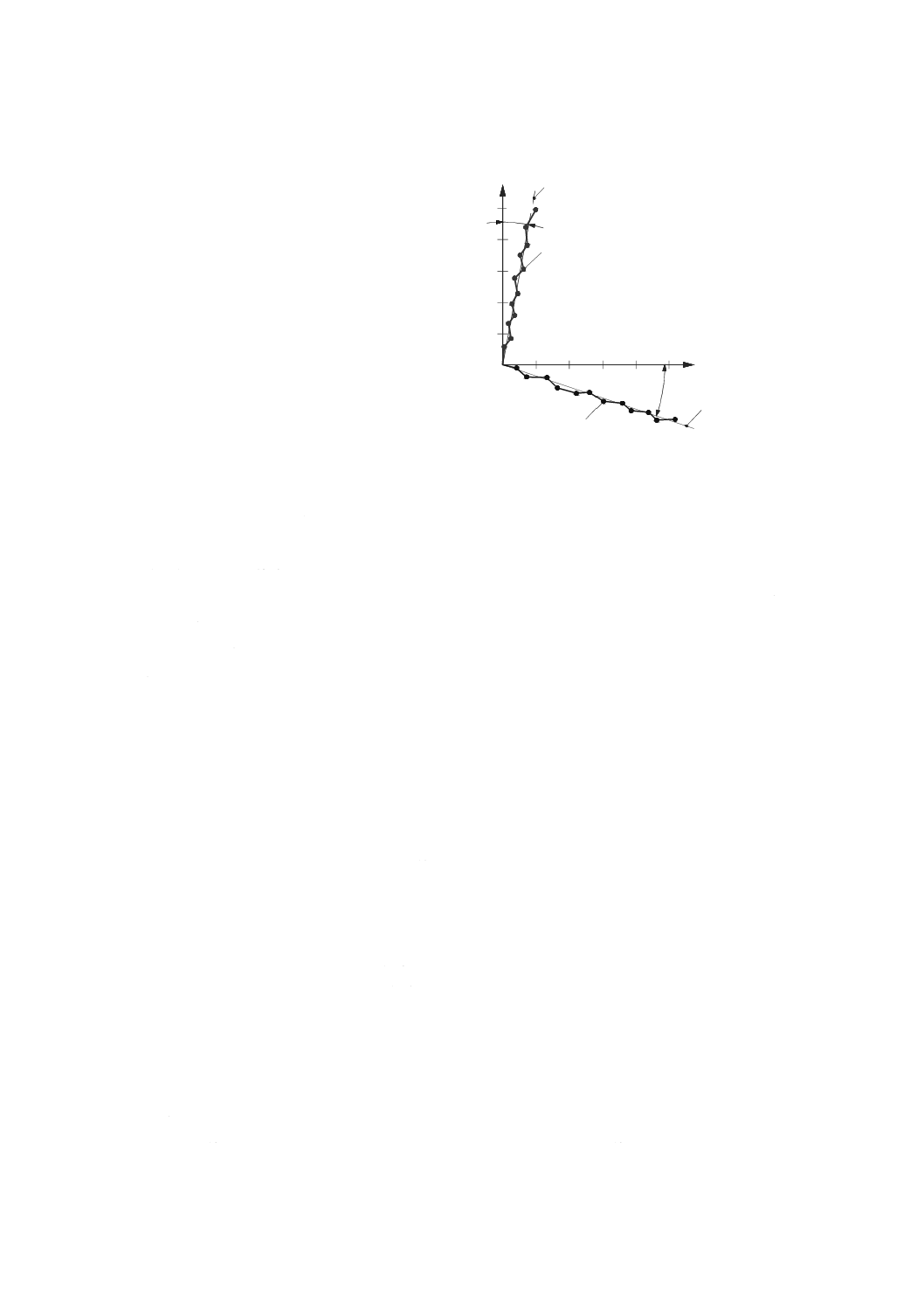
61
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
MRX X軸の測定基準線
MRY Y軸の測定基準線
1 測定したX軸運動の軌跡
2 X軸運動軌跡の基準直線
3 測定したY軸運動の軌跡
4 Y軸運動軌跡の基準直線
θX X軸軌跡の勾配
θY Y軸軌跡の勾配
図67−直角度誤差測定値のデータ解析
10.3.2.6 円運動精度試験及び対角位置決め精度試験による直角度誤差の推定(間接法)
二つの直進運動間の直角度誤差は,円運動精度試験(JIS B 6190-4参照)及び対角位置決め精度試験(JIS
B 6196参照)を用いて推定できる。
円運動試験においては,±45°における二つの直径の差ΔLを円経路の直径で除した値が直角度誤差と
なる。この場合は,比で表される。
直角度誤差に及ぼす幾何的な影響を拡大するために,円経路の直径は,できる限り大きくしたほうがよ
い(JIS B 6190-4の附属書B参照)。円経路の直径が小さいと,その結果は,局所的な直角度誤差を表すだ
けである。
直角度誤差を求める場合に,バックラッシ及び制御系に関連した影響をできる限り排除するために,最
小二乗法を用いて,低い送り速度で360°の全円を時計回り及び反時計回りの両方向のデータを使用する
ことを推奨する。
面の対角位置決め精度試験においては,45°方向の二つの対角線の長さの差ΔLを理想的な対角線の長
さDで除した値が,直角度誤差となる。この場合は,比で表される。
二つの軸の長さが同じでない場合でも,対角線を使用することができる。比として表す直角度誤差Sは,
次の式(15)によって算出する。
S=D0・(D1−D2) / (2 XY) ····························································· (15)
ここに,
D0: 理想的な対角線の長さ
D1及びD2: 測定された対角線の長さ
X及びY: それぞれの直進軸のプログラムされた移動距離
注記 アスペクト比(縦横比)が大きくなると測定の不確かさも大きくなる。
10.3.3
直進軸と回転軸又は主軸の軸平均線との直角度誤差
直進軸と回転軸又は主軸の軸平均線との関係は,まず回転軸の軸平均線を求め,次に,直進運動とその
軸平均線との比較を行う。測定平面(回転軸及び直進軸に平行な機械の直交座標平面)内における回転軸
の軸平均線は,回転軸の180°離れた二つの位置で測定した真直度誤差の平均を取ることによって求める。
回転軸の軸平均線を間接的に代表するために,回転軸に直交する測定基準線を設定することができる。機
4
3
1
2
MRY
MRX
qX
qY
θY
θX
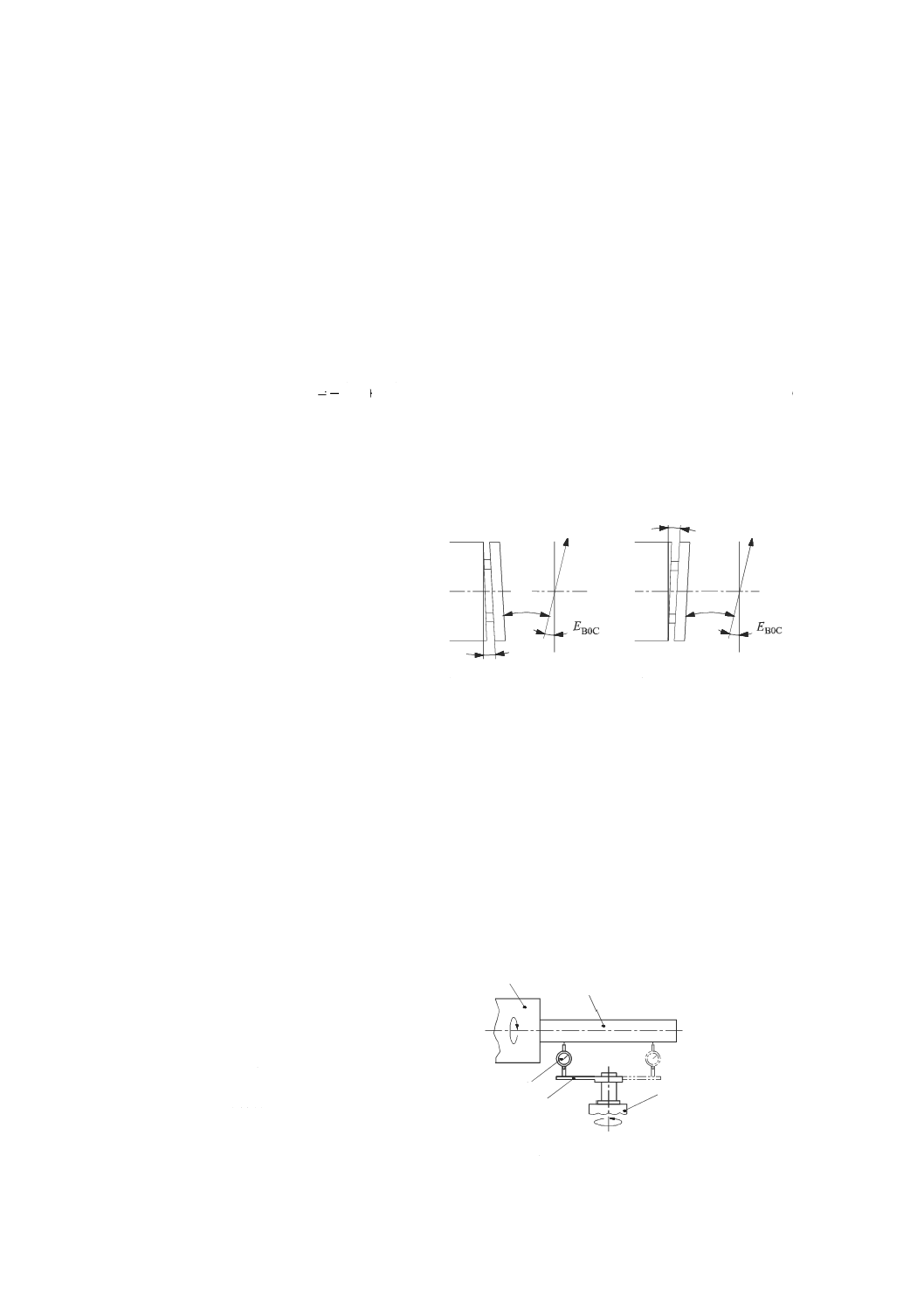
62
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
械的な基準器又は光学的な方法は,この測定基準線の代表として利用することができる。代表的な測定方
法を図68に示す。
直定規は,回転軸の中心をまたぐように取り付け,直進軸の真直度偏差は,光学式又は機械式のいずれ
かの方法で測定する。真直度基準線の勾配は,直進軸と直定規の使用面とのなす角度である。次に,回転
軸を180°回して同様の測定を行う。図68は,回転軸の任意の位置を0°にしたときの測定を“順方向”
とし,回転軸をその位置から180°回転させたときの測定を“逆方向”として表す。
図68において,角度βは,取付具に起因する回転軸と直定規との直角度誤差であり,角度EB0Cは,直
角度誤差である。測定した角度とそれぞれの向き(順方向及び逆方向)とを,φF及びφRで表すと,直角度
誤差EB0Cは,式(16)を用いて算出できる。
(
)
R
F
B0C
2
1
ϕ
ϕ+
=
E
···································································· (16)
次に,この0°の位置から回転軸を90°回した位置で,もう一つの直進軸との直角度誤差も,上記の測
定を繰り返すことによって求めることができる。
β 取付具に起因する直角度誤差
EB0C 直角度誤差
φF 測定した直角度誤差(順方向)
φR 測定した直角度誤差(逆方向)
a) 順方向:C=0°
b) 逆方向:C=180°
図68−直進軸と回転軸との直角度誤差
10.3.4
二つの軸平均線間の直角度誤差
テストバーは,第一回転軸の軸平均線に対して同軸になるように取り付ける(図69参照)。変位計は,
第二回転軸に取り付けた取付具に固定し,その測定子をテストバーに当てて第一回転軸を数回転回す。そ
の間,変位計からのデータを記録する。次に,変位計を取り付けた第二回転軸を180°回し,第一回転軸
を数回転回し,その間,変位計からのデータを記録する。この2組のデータから最小二乗基準円の中心座
標をそれぞれ算出する。この中心座標間の差を変位計の振り回し直径で除した値が二つの軸平均線間の直
角度誤差となる。
1 第一回転軸
2 第二回転軸
3 テストバー
4 変位計
5 取付具
図69−二つの軸平均線間の直角度誤差
¬
¬F
X
¬
¬R
X
β
β
C
C
X
X
φF
φR
1
3
4
5
2
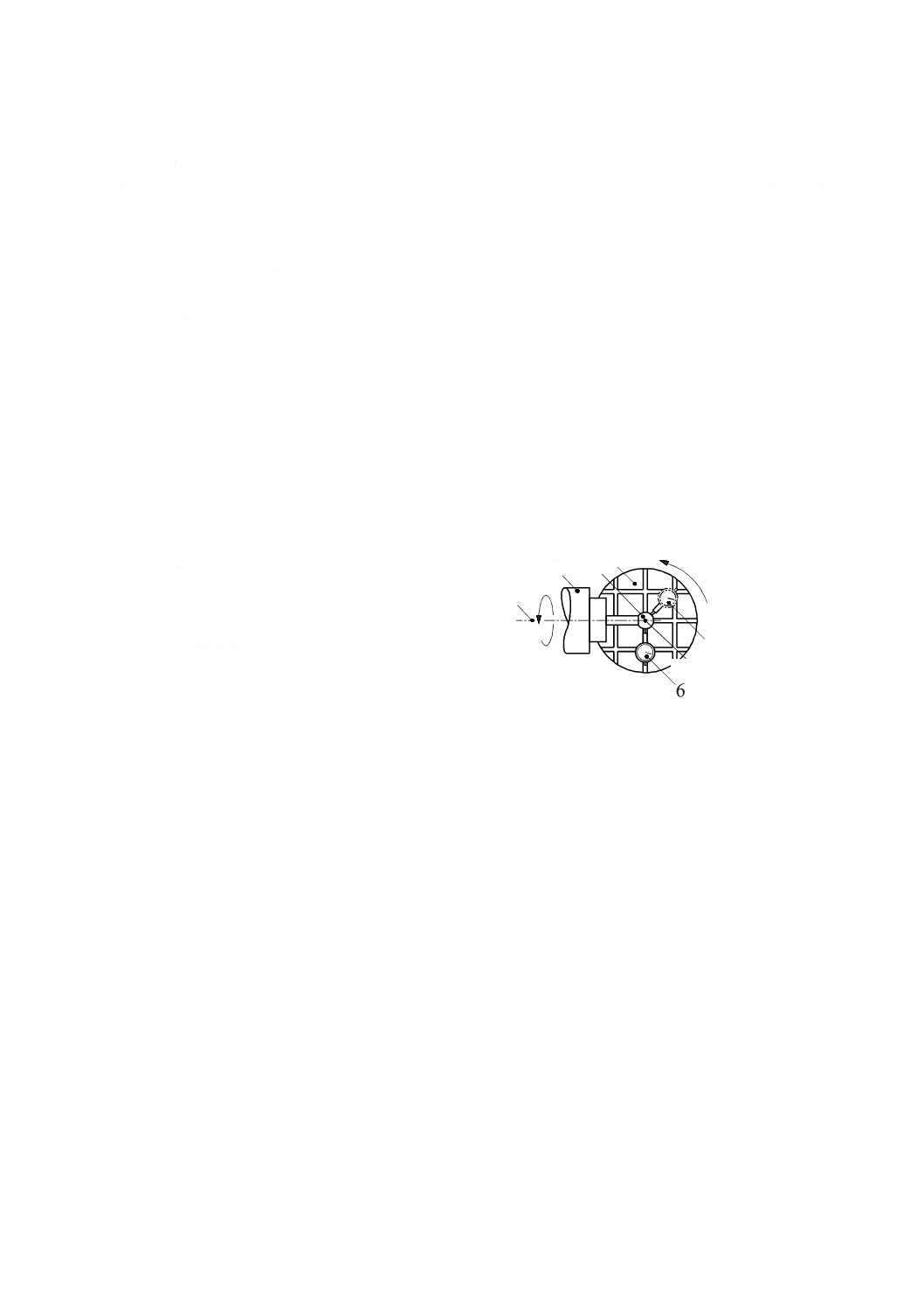
63
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
10.4
軸平均線の交差度
10.4.1
一般
複数の回転軸をもつ工作機械においては,それらの軸は,互いに平行又は直交していることが多い。複
数ある回転軸が平行でない場合は,直接的又は間接的に交差する点を測定する必要がある。直接測定する
場合は,複数の軸うち少なくとも一つの軸を代表する精密な基準器を用いる。
10.4.2
直交する軸平均線の交差度
基準球は,複数ある回転軸の一つに取り付け,もう一つの回転軸の軸平均線の所定の位置で,その回転
軸の軸平均線を代表するように調整し,心出しをする。変位計は,もう一つの回転軸に取り付け,その測
定子を基準球に当てて測定する(図70参照)。両方の軸平均線に直交した方向において変位計の読みから
得られた最良適合円の中心は,二つの回転軸間の距離を表す。
次に示す代替方法を使ってもよい。
a) 変位計を球に当てて,一つの軸を180°回転させる。
b) 次にもう一つの軸を180°回転させる。
c) 変位計は,軸平均線が交差するためには同じ値をとることが望ましい。
1 第一回転軸(主軸)
2 主軸の軸平均線
3 第二回転軸(回転テーブル)
4 第二回転軸の軸平均線
5 基準球
6 初期位置にある変位計
7 途中の位置にある変位計
図70−直交する軸平均線の交差度
10.4.3
直交しない軸平均線の交差度
平行でない(かつ,直交していない)二つの軸の交差度は,その二つの軸を代表するテストバー間で得
られた測定値を用いて求めることができる。この方法は,追加平面を用いて二つの軸の等距離度を測定す
る方法と同じである(12.3.3参照)。この測定は,テストバーを,それらの軸に平行な平面内で平らな面を
もつように適切に加工した二つの円筒と置き換えれば,より簡単になる。測定値は,交差度の誤差を求め
るために二つの平らな面間で読み取る(図71参照)。図71に表す例は,円すい研削のための旋回といし軸
頭に該当する。
10.4.4
間接測定
間接測定は,別に置いた基準面,例えば,二つの軸に平行に定置した精密定盤を用いて行ってもよい。
測定値は,基準面からそれぞれの軸について求め,比較する。
2
1
53
64
7
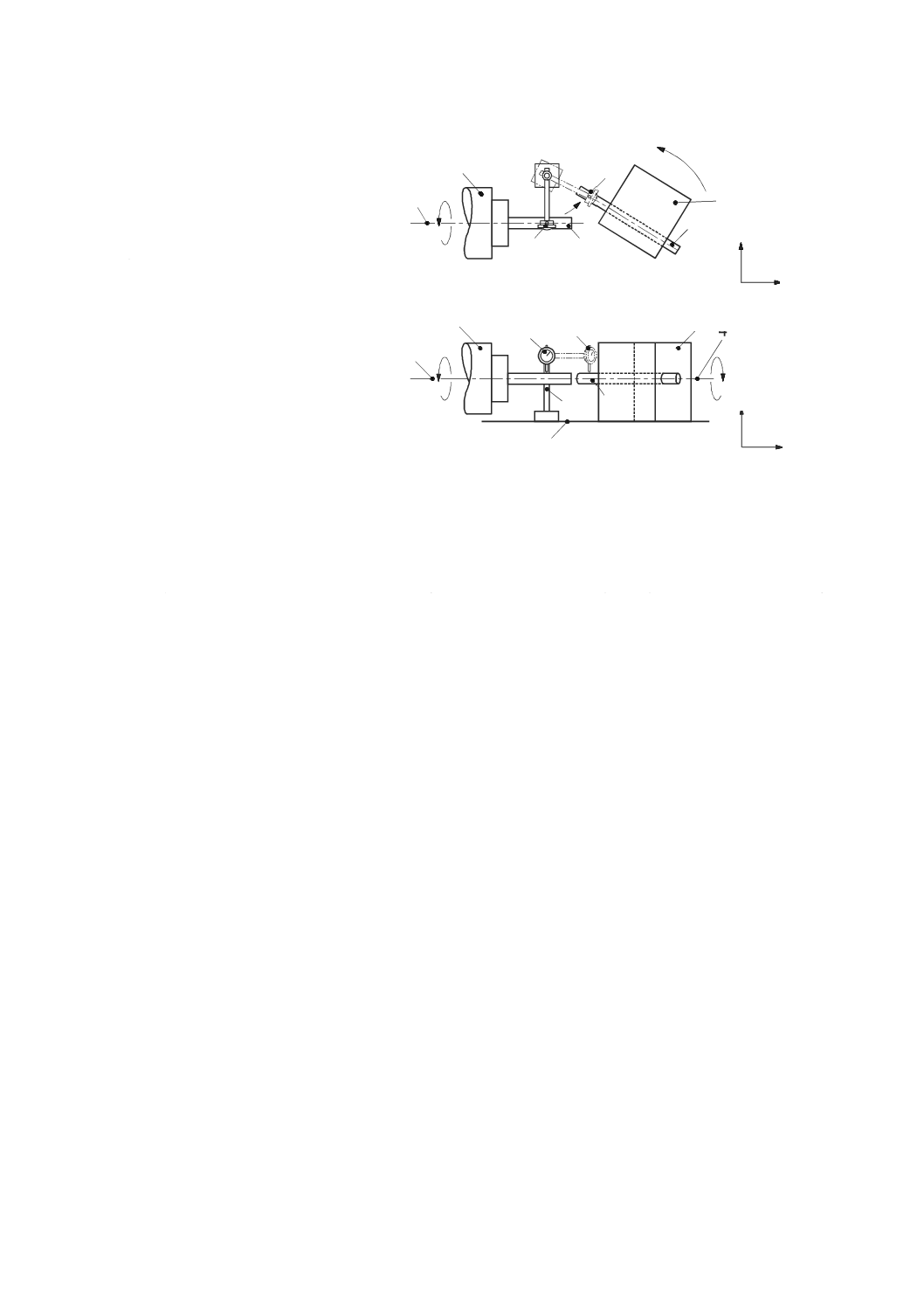
64
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 主軸1
2 主軸1の軸平均線
3 旋回ヘッド
4 旋回ヘッドの主軸の軸平均線
5 基準面
6 変位計取付具
7 テストバー1
8 テストバー2
9 測定位置1の変位計
10 測定位置2の変位計
図71−直交しない軸平均線の交差度
11
多軸運動試験
11.1
一般
この箇条は,数値制御工作機械の位置決め精度と同様に作業空間内の輪郭精度を推定し評価する,迅速
で効率的な方法について規定する。輪郭精度は,多軸運動に関連する様々な誤差要因(真直度誤差,直角
度誤差など)の影響を受ける。運動試験は,これら誤差要因が組み合わさった結果を観察する方法の一つ
である。多軸運動試験は,一度の測定で複数の軸の様々な誤差要因を観察することができ,しかも比較的
容易に実施できるために,定期的な検査及び衝突などの予期しない事象が発生した後の精度確認にも使用
できる。
11.2
直線軌跡
11.2.1
一般
二つ以上の直進軸を同時制御して,作業空間内の直方体の対角線又は面の対角線に沿って直線上を移動
運させたときの位置決め誤差又は真直度誤差運動を測定して,その偏差を記録し評価する。
11.2.2
対角位置決め試験
11.2.2.1
一般
対角位置決め試験は,数値制御工作機械の空間精度を迅速に評価するために行う。工作機械の完全な空
間精度の試験は,難しく時間のかかる作業である。 対角位置決め試験は,空間精度試験に要する時間と経
費とを低減することができる。
注記 完全な空間精度試験では,例えば,作業空間内の任意の位置での三つの位置誤差及び三つの角
度誤差の測定が必要となる。
対角位置決め試験,すなわち,作業空間における直方体又は面の対角線に沿った位置決め試験は,複数
軸の運動試験になる。測定器の構成及び評価方法は,JIS B 6196による。実際の作業空間よりも小さな縮
小空間について試験を行った場合は,測定結果に“縮小空間”で行ったことを記載しなければならない(JIS
B 6196参照)。
11.2.2.2
面の対角位置決め試験
2
1
9
10
34
5
8
6
Y
Z
1
2
9
7
10
3
4
X
Z
X
Z
Z
Y
65
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試験方法は,変位測定を直進軸と平行な方向で行うのではなく工作機械の座標面の対角線に沿って行う
こと以外,それぞれの直進軸(JIS B 6190-2参照)の位置決め試験とおおむね同じである。
11.2.2.3
直方体の対角位置決め試験
試験方法は,変位測定を直進軸と平行な方向に行うのではなく工作機械の作業空間における直方体の対
角線に沿って行うこと以外,それぞれの直進軸(JIS B 6190-2参照)の位置決め試験とおおむね同じであ
る。
11.2.3
対角線の真直度試験
11.2.3.1
一般
対角線の真直度試験は,工作機械の二つ以上の直進軸を同時制御運動して移動させたときの軌跡の真直
度を評価するために行う。
8.2に記載した試験方法は,基本的に対角線の真直度試験にも適用できる。
11.2.3.2
面の対角線の真直度試験
機能点が作業空間における四角形をした面の対角線として定義した直線経路に沿って移動するように,
二つの直進軸をプログラムする。真直度誤差の測定及び評価は,8.2による。
11.2.3.3
直方体の対角線の真直度試験
機能点が作業空間における直方体の対角線として定義した直線経路に沿って移動するように,三つの直
進軸をプログラムする。真直度誤差の測定及び評価は,8.2による。
11.3
円弧軌跡
11.3.1
一般
この箇条は,数値制御工作機械の輪郭精度の評価方法について規定する。円グラフ(図72に例示)に描
かれた円経路の誤差は,適用した送り速度における幾何誤差及び機械の動的挙動の影響を受ける。試験の
結果は,直径及び送り速度が円運動試験と実際の機械加工とが同じ場合には,理想的な加工条件で仕上げ
た工作物から得られた輪郭形状とよく一致する。円運動試験の試験条件及び結果の表示方法は,JIS B
6190-4による(典型的な測定結果を図72に示す。)。
注記1 JIS B 6190-4ではGを“真円度”(circular deviation)と定義している。この規格では,用語“偏
差”(deviation)と“誤差”(error)とを明確に区別している(箇条3参照)。したがって,図
72に示した“真円度”(circular deviation)は,3.8.2に規定する“円形誤差”(circular error)
と一致している。
注記2 実際の部品加工では,円筒内面及び外面の加工条件だけでなく,工具のたわみ,工具の直径,
工作物材料の機械的性質が輪郭誤差に影響するのに対して,円運動試験では,これらの誤差
要因は入っていない。
11.3.2
全円の軌跡
円運動試験データの評価には,装置の心出し誤差を補正し,かつ,計算誤差及びそれに関連する中心の
ずれを最小化するために最小二乗法を適用する必要があることから,全円の円経路を生成することを強く
推奨する。

66
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
0 開始点
1 最小二乗基準円
2 実円弧軌跡
G 真円度
+ 実経路に適合させた最小二乗基準円の中心
図72−円形誤差の評価
11.3.3
部分円の軌跡
円運動試験に関する軸の移動範囲又は試験に使用する測定器及び取付具が障害となって,機能点が全円
の円経路を通ることができない場合は,評価は,部分円で行ってもよい。ただし,データ処理結果が計算
誤差の影響を受けることに注意するのが望ましい。したがって,プログラムした運動に対する測定器の物
理的な心出しは,細心の注意を払って行うことを強く推奨する。部分円の軌跡については,真円度Gの代
わりに半径偏差Fを評価することを推奨する(11.3.1の注記1参照)。
11.3.4
二つ又は三つの直進軸によって生成する円弧軌跡の測定方法−二次元又は三次元円運動試験
11.3.4.1
一般
二つの直進運動軸(XY,YZ又はZX)で定義される平面内において,機能点が全円又は部分円の軌跡
となるように二つの直進軸を制御する。
円運動試験は,特にボールバー又は二次元デジタルスケールを用いて行う場合には,工作機械の基本平
面,XY面,YZ面及びZX面における試験だけに限定しない。空間内のどのような面内における円経路に
対してもX,Y及びZ軸の補間制御が可能であれば,円運動試験は,どのような面内においても実施でき
る。
11.3.4.2
回転する変位計による方法
変位計が円経路上を運動するようにプログラムする。変位計は,回転式の取付具に取り付けて回転させ,
テストバー(図73及び図74参照)又は回転式の取付具に固定した変位計とともに回転する目標との相対
変位を測定する。変位計の出力は,円グラフ上に描く(図72参照)。軌跡は,例えば,回転と同期した極
座標プロッタ,コンピュータによる解析,又は回転式の取付具に取り付けたロータリエンコーダを使って
極座標プロッタに出力することができる。
1 一次元変位計
2 回転取付具
3 テストバー
図73−一次元変位計による円運動試験
G
1
2
0
X
YY
X
G
1
2
3
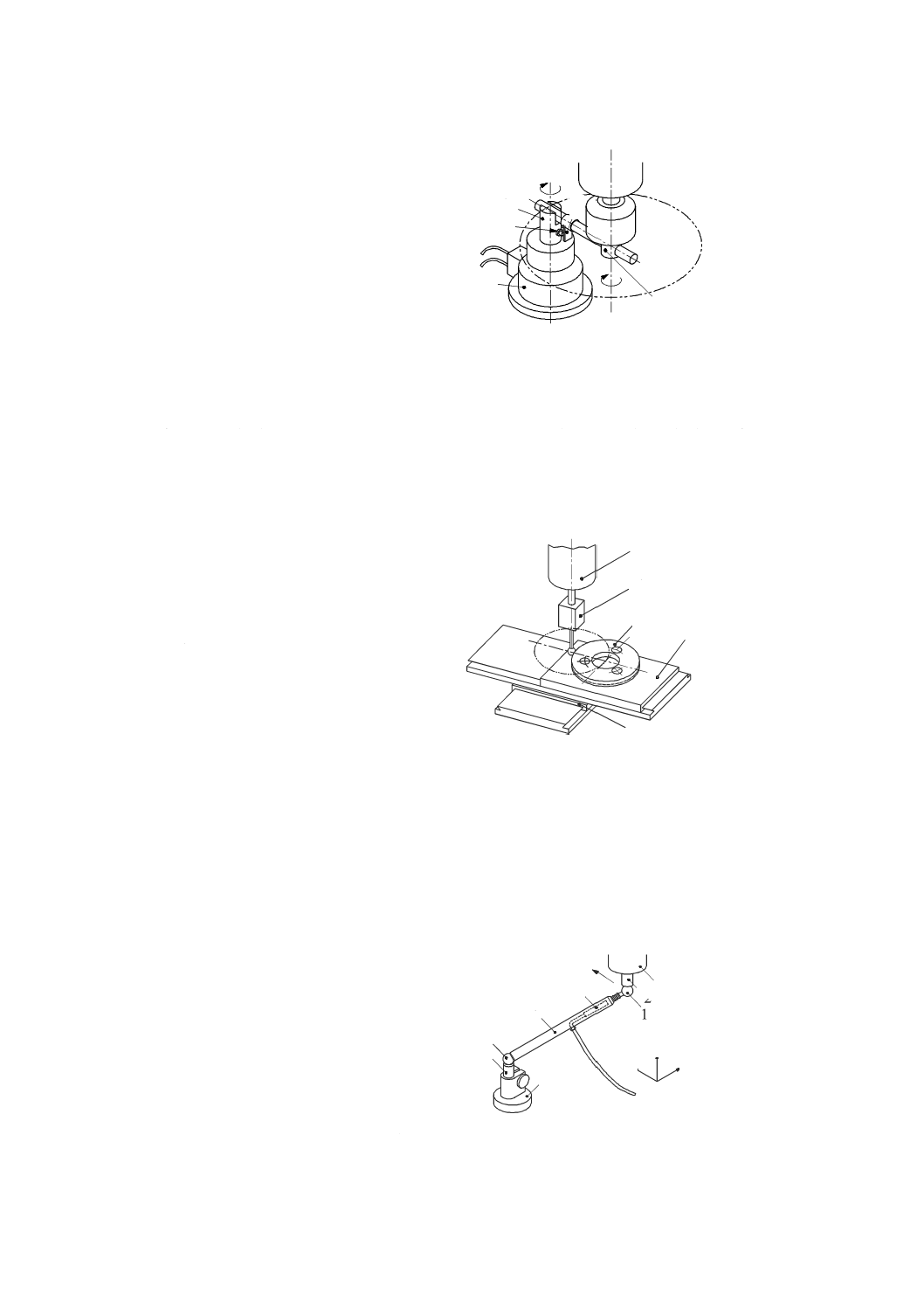
67
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 回転取付具1
2 回転取付具2
3 変位計
4 目標
5 ロータリエンコーダ
図74−ロータリエンコーダを組み込んだ測定器による円運動試験
11.3.4.3
基準円盤と二次元変位計とによる方法
二次元変位計が円経路上を運動するようにプログラミングする(図75参照)。円経路の指令直径及び中
心は,二次元変位計が基準円盤と接触を保ちながら運動するように選ぶ。変位計からの2方向(X及びY)
の出力を円グラフ上に描く(図72参照)。
1 二次元変位計
2 基準円盤
3 主軸
4 テーブル(X軸)
5 サドル(Y軸)
図75−基準円盤と二次元変位計とによる円運動試験
11.3.4.4
ボールバーによる方法
ボールバーの一方のソケット又は球を機械の工作物保持部に取り付け,他方のソケット又は球を工具保
持部に取り付ける(図76参照)。工具側と工作物側との間でボールバーの長さと等しい半径で円弧軌跡を
生成するよう指令する。2球間の距離の変化を測定する。測定信号を円グラフ上に描く(図72参照)。
1 球
2 磁気ソケット
3 変位計
4 伸縮式バー
5 主軸
6 保持具(テーブル側)
図76−ボールバーによる円運動試験
2
5
3
1
4
3
1
2
4
5
X
125
3
4
1
Z
Y
2
6
Z
X
Y
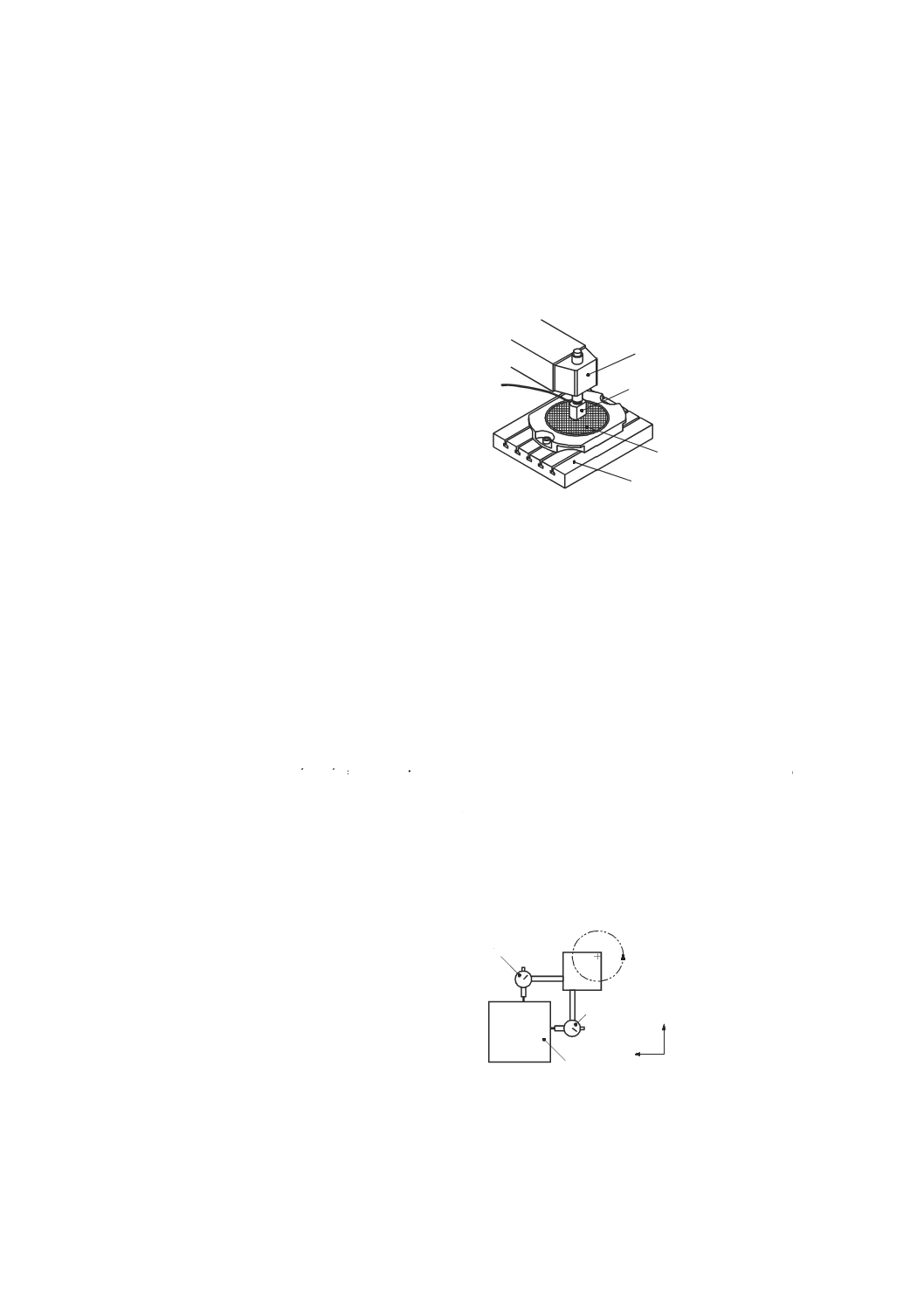
68
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
11.3.4.5
二次元スケールによる方法
二次元の座標位置を同時に検出できるデジタル式の二次元スケールは,円経路に沿った連続的な座標値
の測定に使用できる(ISO/TR 230-11参照)。位置検出器は,工具側に取り付け,二次元スケールは,工作
物側に取り付ける(図77参照)。工具側と工作物側との間の円弧経路に沿った座標値を検出し記録する。
得られた座標データを,真円度誤差を求めるために(通常,特別に作られたソフトウェアによって)処理
し,円グラフ上に描く(図72参照)。
1 二次元位置検出器
2 二次元スケール
3 主軸頭
4 テーブル
図77−二次元スケールによる円運動試験
11.3.4.6
二つの変位計と直角基準器とによる方法
直角基準器は,その基準面と二つの機械座標軸(図78に例示するX軸及びY軸)が平行になるように
テーブル上に定置する。二つの変位計は,図78に示すようにそれぞれX軸及びY軸方向に平行に工具側
に取り付け,工具側と工作物側との間の相対変位を検出する。円弧軌跡のX軸とY軸との成分は,二つの
変位計によって連続的に検出し記録する。得られた座標データ(Xn,Yn)を演算し,その偏差を円グラフ
上に描く(円グラフは,図72に示す。)。
基本的な計算は,次の式による。
(
)2
n
2
n
2
n
e
r
Y
X
+
=
+
···································································· (17)
ここに,
Xn,Yn: 位置nにおける計算値
r: 指令円の半径
en: 指令円経路からの符号付きの偏差。符号は,偏差が円弧
軌跡半径を増大させる方向にあるときが正である
互いに直角な二つの平面鏡を用いたレーザ干渉計もこの測定に使うことができる。
1 X方向変位計
2 Y方向変位計
3 直角基準器
図78−二つの変位計による小径の円運動試験
4
3
1
2
3
1
2
X
YY
X
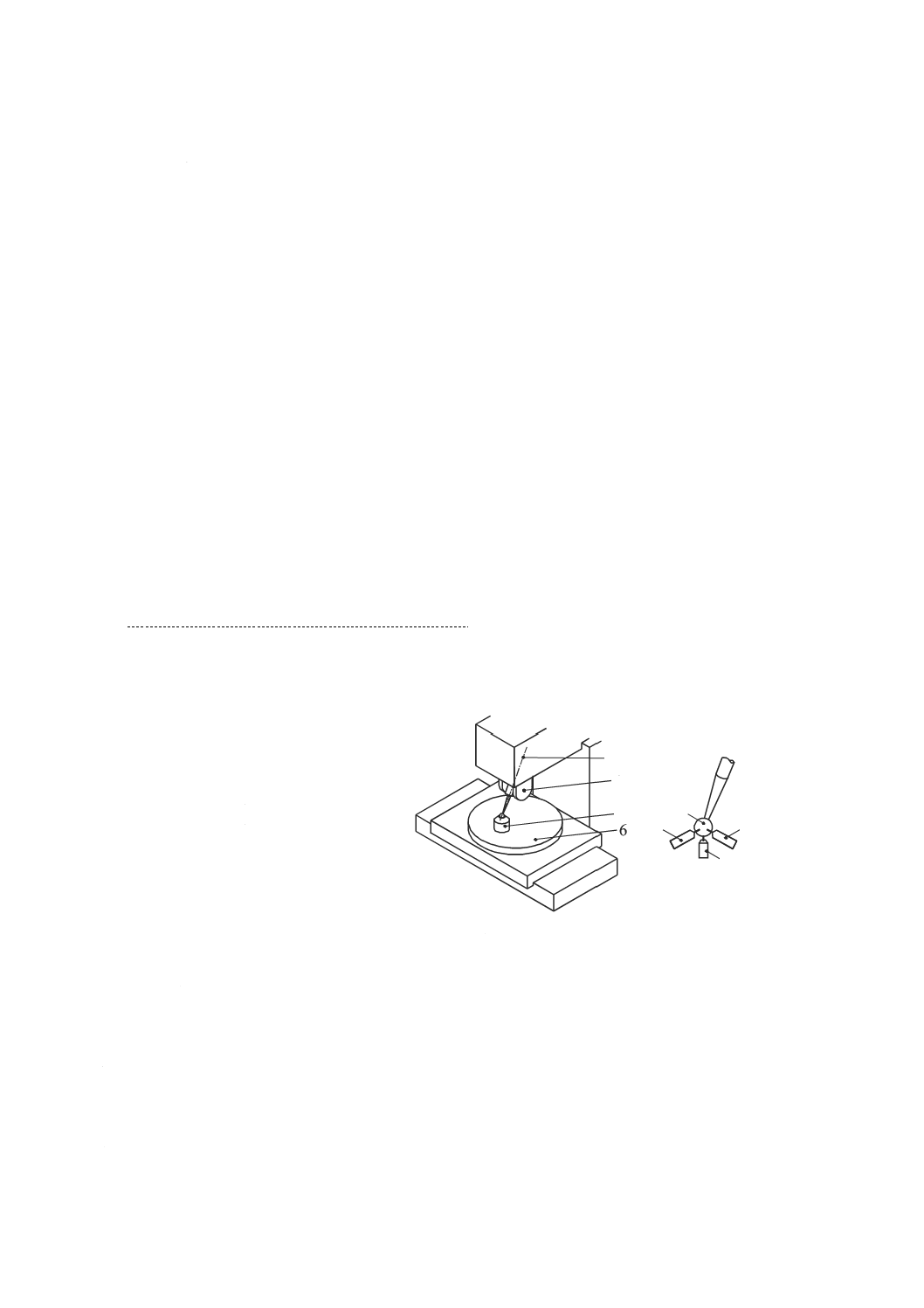
69
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
11.3.5
任意の直進軸と回転軸との組合せによる円運動
11.3.5.1
一般
この試験の目的は,同時制御(同期)された三つの直進軸及び二つの回転軸のうちの任意の軸を組み合
わせて生成される円弧軌跡又は一定半径の軌跡の偏差を調べることである。この試験の基本原理は,工具
と工作物との間の相対的な位置を一定に保持する複数の運動軸(回転軸と直進軸との組合せ)を同期させ
ることである。
この偏差は,基準球及び1個の変位計,基準球及び複数の変位計,又はボールバーを用いて測定する。
11.3.5.2
変位計と基準球とによる方法
同時制御(同期)された三つの直進軸及び二つの回転軸のうちの任意の軸を組み合わせて生成される基
準球回りの一定半径の軌跡の偏差は,1個の変位計を用いて測定する。
基準球は,工具保持側に設置し,変位計は,球面と垂直に感度方向を保つように機械の工作物保持部側
に取り付ける(図82参照)。変位計の出力は,記録計又はコンピュータに取り込む。
指令した半径rの球の中心は,基準球の中心と一致しなければならない。基準球の中心は,主軸の軸平
均線と一致するよう調整しなければならない。
11.3.5.3
三つの変位計と基準球とによる方法
工具と工作物との間の相対的な位置(運動軸を同期させて生成した経路に沿った)の偏差は,基準球に
対して三つの変位計で測定し,3直交方向(例えば,X,Y及びZ又は半径方向,軸方向及び接線方向)
に分解することができる(図79参照)。
注記 この方法を,Rテストと呼ぶことがある。
基準球は,主軸の軸平均線(工具側)に心合わせをし,三つの変位計は,工作機械の工作物側に取り付
け,基準球の中心位置の変化を測定するために0に心出しをする。
1 変位計1
2 変位計2
3 変位計3
4 主軸中心線上の基準球
5 主軸中心線
6 回転テーブル
7 変位計取付具
8 旋回主軸頭
図79−三つの変位計及び基準球による方法
11.3.5.4
ボールバーによる方法
工具と工作物との間の相対的な位置の(同期制御された運動軸によって生成された軌跡に沿った)偏差
は,ボールバー(図80参照)で測定できる。このときボールバーは,次の三つの方向に配置することがで
きる。
a) 回転軸と平行
b) 円経路の半径方向
c) 円経路の接線方向
5
8
76
4
2
3
1
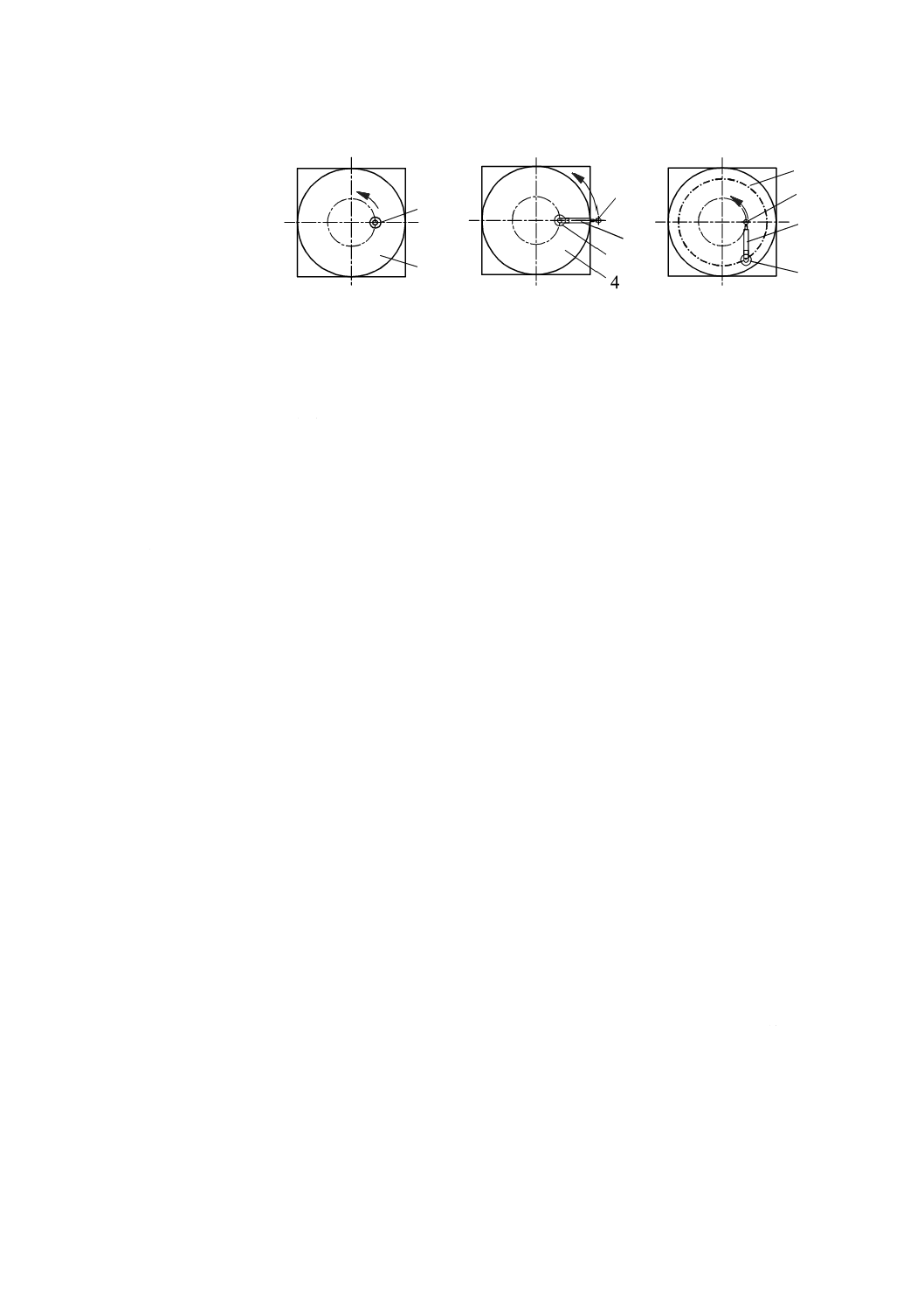
70
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 ボールバー
2 ソケット(主軸側)
3 ソケット(テーブル側)
4 回転テーブル
a) 軸方向
b) 半径方向
c) 接線方向
図80−二つの直交軸と一つの回転軸とによって生成される円運動−軸方向,半径方向,接線方向の測定
ボールバーの回転テーブル側の球は,回転テーブルの回転中心から離れた位置に置き,主軸側の球は,
主軸の回転軸上に置く。b) 及びc) ではボールバーの軸は,回転テーブル上面と平行に取り付け,a) では
回転テーブル上面に垂直に取り付ける。
ボールバーで検出する偏差は,回転軸の回転角度位置に対応させて円グラフとして描く。描いた軌跡の
円形誤差は,測定した偏差の幅である。
工具側と工作物側との間の半径方向の距離を一定に保つ測定を,他のボールバーの方向及び工具経路で
行い,多軸同時制御運動(例えば,図81に示す円すい台底面に平行な円経路に沿った運動)時の円グラフ
を描くためにも使ってもよい。
11.4
円すい(形状)運動
この試験の目的は,同時5軸制御運動(三つの直進軸及び二つの回転軸)によって生成された工具先端
点の描く円弧軌跡の偏差を測定し評価することである。この運動は,円すい状の部品を加工するときに
(CNCの工具先端点制御機能を用いて)使用するものと同じである。全ての軸を運動させるために,C軸
の軸平均線に対して円すいの軸を角度βだけ傾けなければならない。
回転テーブルをもつ機械の場合は,円すいの軸は,回転テーブルの軸平均線からオフセット距離Rだけ
離さなければならない(図81参照)。
偏差の測定は,ボールバーによる。ボールバーの主軸側球は,主軸の回転軸上に取り付け,ボールバー
のテーブル側の球は,上述したオフセット距離R離し,円すいの軸を傾き角βだけ傾くように取り付ける。
トラニオン形の回転テーブルの場合,テーブル側の球の中心位置は,A軸の中心線より高くすることが望
ましい。ボールバーの軸は,仮想の円すい面にほぼ直角に取り付ける。
輪郭送り速度は,一定でなければならない。
円経路の直径,円経路とテーブル上面とのなす傾き角,円すいの半頂角及びC軸からのオフセット量は,
記録しなければならない。
ボールバーで検出した偏差は,円弧軌跡に対応させて円グラフ上に描く。記録した値の最大値と最小値
との差を報告する。
同様な測定は,4軸運動でも実施できる。しかし,そのような場合は,回転テーブルの軸平均線と円す
いの軸との間のオフセット距離Rは,ゼロになる。
4
2
1
3
2
1
34
4
3
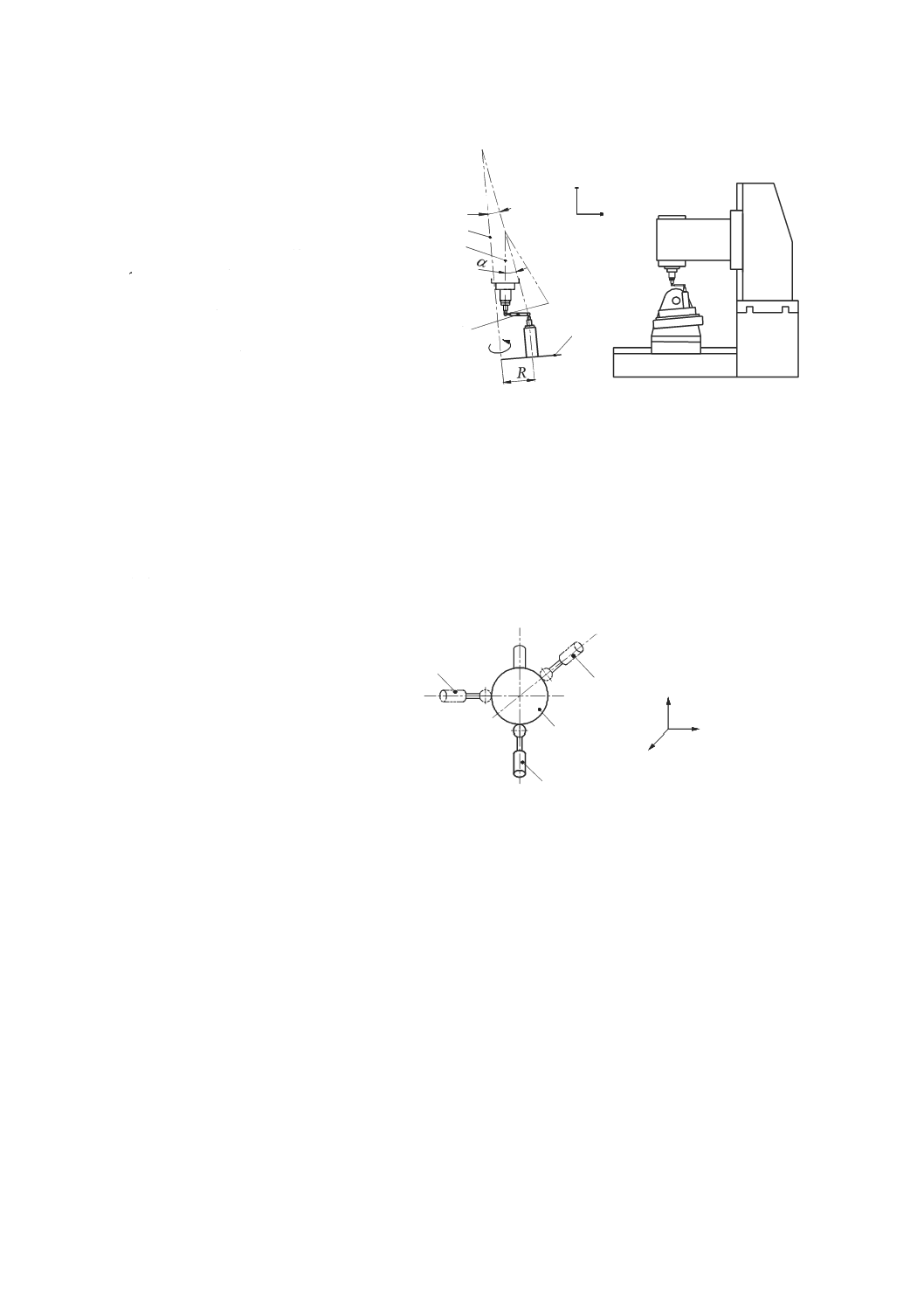
71
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 ボールバー
2 回転テーブルの軸中心線
3 主軸の中心線
4 回転テーブル上面
R C軸中心線とテーブル側球の中心位置との
間のオフセット距離
α 円すいの半頂角
β C軸中心線と円すいの軸とのなす角度
図81−直交3軸と回転2軸とを同時制御して生成される円すい(形状)運動
11.5
基準球と変位計とを用いる球面補間試験
この試験の目的は,同時5軸制御運動(三つの直進軸と二つの回転軸)によって生成された基準球回り
の複数の一定半径の経路の偏差を測定し評価することである。
この試験は,基準球と変位計(図82参照),若しくは三つの変位計(図79参照),又はボールバーを用
いて行うことができる。
1 主軸中心線上の基準球
2 変位計1
3 変位計2
4 変位計3
図82−基準球と変位計とによる方法
11.6
二つの直進軸によって生成される面の平面度誤差
11.6.1
基準定盤と変位計とによる方法
二つの直進軸で生成される仮想面の平面度は,平面基準器(定盤)(図83参照)を用いて測定できる。
変位計は,二つの直進運動によって基準とする定盤上面を掃引する。変位計で検出した偏差を,基準平面
に適合させ,部分平面度偏差(3.8.7参照)を計算するために記録し解析する(3.8.8〜3.8.10参照)。平面
度誤差は,求めた平面度偏差の最大値と最小値との差である(3.8.11参照)。
注記 最小平面度誤差は,最小領域基準平面を用いて評価する。
Z
Y
b
3
2
1
4
Z
Y
C'
2
1
3
4
Z
Y
X
Z
X
Y
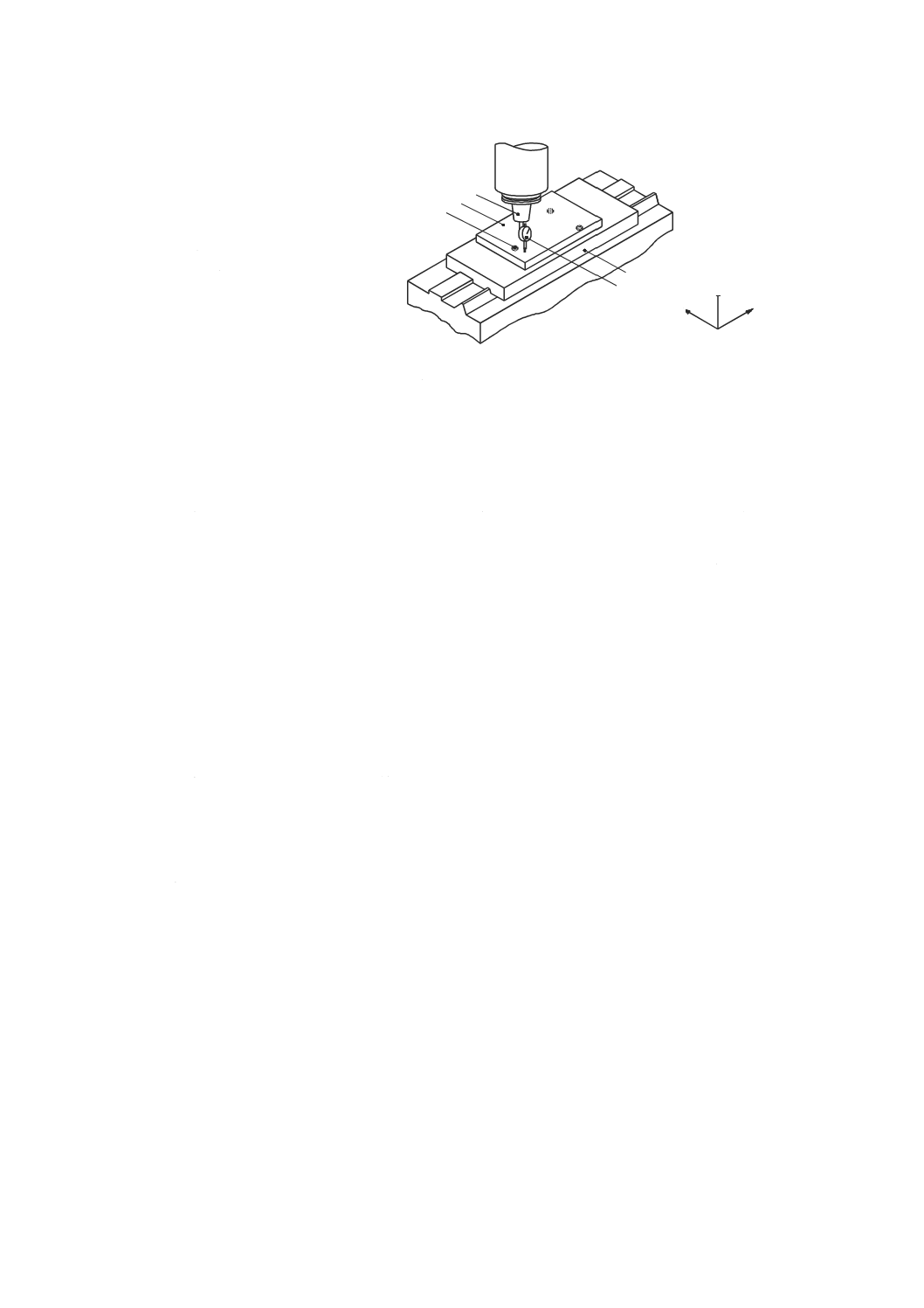
72
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 主軸
2 テーブル
3 基準定盤
4 変位計
5 支持位置(3点,裏面)
図83−基準定盤による平面度偏差の測定
11.6.2
掃引式アライメントレーザによる方法
この方法は,11.6.1に記載した方法と同様である。基準器(定盤)の基準平面を,掃引式アライメント
レーザと置き換える。ただし,レーザ光による平面を生成するために回転鏡を使ってレーザ光を掃引する。
変位計は,入射光位置の偏差を測定するためのフォトダイオードセンサ(光検出器)に置き換える。
掃引式レーザヘッドは,機械テーブル上(工作物が通常固定される位置)に取り付ける。レーザ光で形
成された平面が二つの直進軸運動によって生成される仮想平面と平行となるようにレーザヘッドの心出し
をする。光検出器は,主軸(通常工具を取り付ける位置)に取り付ける。
光検出器で検出した偏差は,基準平面(3.8.8〜3.8.10参照)に適合させ,部分平面度偏差(3.8.7参照)
を計算するために,記録し解析する。平面度誤差は,求めた平面度偏差の最大値と最小値との差である
(3.8.11参照)。
注記1 最小平面度誤差は,最小領域基準平面を用いて評価する。
注記2 移動距離が長い場合,測定の不確かさは,空気の屈折率の空間的な変化の影響を受ける。空
気の屈折率は,光軸の変位に強く影響する。光軸は,垂直方向に1 ℃/mの温度勾配がある
と,10 m移動させたとき直線から約46 μm偏る(参考文献[13]参照)。最も良い結果を得るた
めには,測定を適切な回数繰り返して平均をとるだけでなくレーザ光軸回りの空気をファン
でかくはんすることも考慮したほうがよい。
11.7
特殊な試験
11.7.1
一般
この箇条に規定する試験は,工作機械の作業空間における複数の距離測定を基礎としている。この測定
は,既知の位置に取り付けた球をもつ基準器(1-D,2-D,又は3-Dボールアレー),又は複数の方向に沿
って変位を測定するように特別に設計されたレーザ干渉計を利用する。
基準器の場合,機械座標系内の基準球の位置は,機械のスケールと連携して変位測定又は表面検出をす
るシステム(以下,プロービングシステムという。)を使って決定する。次に,基準球の測定位置は,機械
の誤差運動による偏差を決定するために基準器の座標系に対して校正した位置と比較する。
基準器に基づいた測定に用いる測定器は,タッチトリガプローブ,一つの変位計,三つの変位計(図79
参照),並びに2D及び3Dプローブである。タッチトリガプローブを用いるときは,特に測定の前に測定
システムの繰返し性の試験を行うことを推奨する。
11.7.2
一次元ボールアレイによる方法
2
1
3
4
5
Z
Y
X
Z
Y
X
73
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
球を一列に配列した基準器,すなわち,一次元ボールアレイは,測定を行う方向に球が並ぶように,テ
ーブル上に定置するのがよい(図84参照)。
ISO 230-10に従って,使用するプロービングシステムの検定を行うことを推奨する。
座標軸に対する基準器の正確な向きは,プロービングシステムで基準器の両端の球の位置を測定して決
めるのが望ましい。この両端の球の位置情報を用いて,機械座標系における基準器の全ての球の(目標)
位置を計算できる。
測定中に機械の軸をそれぞれの球の計算した位置に移動させる。機械軸の運動誤差及びミスアライメン
トに起因する偏差は,プロービングシステムを使って測定できる。
最後の球の位置を測定した後,熱変位の影響を調べるために最初の球の位置を再度プロービングするこ
とができる。
真直度誤差は,測定した偏差から決定する。位置決めの正確さ及び繰返し性は,JIS B 6190-2に従って
決定する。
図84−一次元ボールアレイ
図85−二次元ボールアレイ
11.7.3
二次元ボールアレイによる方法
校正済みのボールアレイは,球の列と行とが工作機械の二つの座標軸に平行になるように,機械のテー
ブル上に定置する(図85参照)。
ISO 230-10に従って使用するプローブビングシステムの検定を行うことを推奨する。
機械座標軸に対してボールアレイが正確に配置されているかどうかの確認は,プロービングシステムを
用いてボールアレイの三つ又は四つの隅にある球の位置を測定して行うのが望ましい。この情報を使って
機械座標系の中のボールアレイの全ての球の(目標)位置を計算する。
測定中,機械軸は,各球の計算上の位置に位置決めする。機械軸の運動誤差及びミスアライメントに起
因する偏差は,プロービングシステムを使って測定する。
最後の球の位置を測定した後に,熱変位の影響を調べるために最初の球の位置を再びプロービングする。
機械座標系における基準器の位置及びその向きは,機械偏差の二乗和が最小になるように数学的に調整
する。
代表的な機械誤差は,測定データから重複して抽出することができる。すなわち,工作機械の二つの軸
が工作物側にある場合は,使用した個々の運動軸の位置決め誤差,ボールアレイ面内の二つの運動軸の真
直度誤差,ボールアレイ面内の二つの運動軸間の直角度誤差及び二つの軸のそれぞれの角度誤差である。
垂直方向に球の座標が校正されている場合にも,二つの軸が工作機械の工作物側にあれば,ボールアレ
イの面に対する垂直方向の真直度及び運動軸回りの角度誤差(ロール)を二つの軸について測定すること
74
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ができる。
11.7.4
三次元ボールアレイによる方法
この測定は,ピラミッド形の三次元ボールアレイを使うか,又は二次元ボールアレイを機械の作業空間
内の目標基準点を与える校正された取付具を使って高さを変えて行うことができる。二次元測定の解析は,
三次元データを使って拡張できる。
11.7.5
レーザ干渉計による多辺測量法による方法
多辺測量法は,工作機械の作業空間における幾何誤差を同定するために多数の長さ又は位置の測定値を
用いる。測定値は,工作機械の工具側と工作物側との間で求める。工作機械は,一組の測定点について移
動させ(例えば,図86における二点鎖線),工作物側で選択した特定の点に対する距離又は相対的な位置
の変化を記録する。次に,工作物側の点の別の位置を選び,工作機械を再び同じ一組の測定点に移動させ,
この一組の測定点に対する距離又は相対的な位置の変化を記録する。選んだ数組の測定位置に対する数組
の測定値を記録する。測定値は,工具側の異なるオフセットについても求めることができる(図86参照)。
図86−多辺測量法による測定
全ての測定値は,その測定点でX,Y,Zの偏差を評価するために使用するか,又は位置決め誤差運動,
真直度誤差運動,直角度誤差,幾何誤差,及び角度誤差運動(ロール,ピッチ及びヨー)を評価するため
に(試験対象の工作機械の幾何誤差ソフトウェアモデルと一緒に)使用することができる。
使用する測定器は,一般に,工作機械の工具側に取り付けたターゲット(反射鏡)を自動的に追跡し,
工作機械がプログラムした測定点上を運動するときのレーザ光軸方向の変位,及び可能であれば,レーザ
光軸の角度を記録する特別な追尾式レーザ干渉計である。この干渉計に代わって,動作範囲の長いボール
バーを長さ測定に使用することもできる。
結果の不確かさは,測定器の不確かさ,環境の影響のほかに,位置決めの繰返し性,バックラッシ及び
ヒステリシス,測定条件(工作物側と工具側とで選択した位置,及び測定値の組数),並びに使用した工作
機械の幾何モデルの完全性に依存する。従来の意味での不確かさのバジェット表を設定することは,ほと
んど不可能である。したがって,多辺測量法用の評価ソフトウェアは,不確かさ推定のモンテカルロシミ
ュレーション法又は他の適切な方法を使って,全ての評価パラメータに対する不確かさの値を与えなけれ
ばならない。
75
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
12
機械の機能面の幾何精度試験−真直度,平面度,直角度及び平行度
12.1
機能面の真直度誤差
12.1.1
一般
真直度偏差の測定方法には,距離及び角度に基づく二つの方法がある。
真直度の基準には,直定規,鋼線などの有形の基準と重力(精密水準器),光(レーザ干渉計,オートコ
リメータ及びアライメント望遠鏡)などの無形の基準とがある。
12.1.2
距離の測定に基づく方法
12.1.2.1 一般
機械の機能面は,専用の測定台と基準器とを用いて測定する。変位計は,機能面に沿って動く測定台に
取り付ける。変位計は基準器に当て,真直度偏差の値を読み取る。8.2.2に規定した方法は,機能面の真直
度測定にも適用できる。
12.1.2.2 直定規による方法
8.2.2.1参照。
12.1.2.3 鋼線と測微顕微鏡とによる方法
8.2.2.2参照。
12.1.2.4 アライメント望遠鏡による方法
8.2.2.3参照。
12.1.3
角度の測定に基づく方法
12.1.3.1 一般
この方法では,専用の測定台を距離dだけ離れた2点P及びQで,試験対象とする線に当てる(図87
参照)。次に,その測定台をP0Q0からP1Q1に移動させる。このとき,P1をQ0と一致させる。試験対象と
する線及びそれに直交する面を含む面内の角度α0及びα1は,精密水準器,オートコリメータ,レーザ角
度干渉計などの適切な測定器を使って測定する。
注記1 測定台の脚間にある面は,この方法では測定することはできない。
後続の測定点と測定の基準との相対差は,式(18)によって算出する。
()
i
i
d
E
α
tan
)1
(h
×
=
+
··································································· (18)
注記2 測定の基準とは,精密水準器の水平面,又はオートコリメータ若しくはレーザ角度干渉計の
任意に設定した基準角度である。
測定点Piと測定の基準との間の距離は,式(19)によって算出する。
)1
(h
P
)1
(P
+
+
+
=
i
i
i
E
E
E
··································································· (19)
測定点Piは,図88のように図示し,測定した全ての点に対応させて基準直線を求め,真直度偏差及び
真直度誤差を評価する。
基準直線として,最小領域平均基準直線,最小二乗基準直線,又は両端点基準直線を用いることができ
る(図7,図8及び図9参照)。
測定台の支持点P及びQは,表面の小さな欠陥の影響が最小になるように十分な面積をもつことが望ま
しい。偏差を最小にするために,全体の測定結果に影響を及ぼす支持点の表面は,十分注意し,清浄にし
ておく必要がある。
この方法は,長い距離の測定にも適用できるが,その場合,dの値は,測定回数が多くなること及びそ
れに伴う累積誤差が増えることを避けるように選択するのが望ましい。
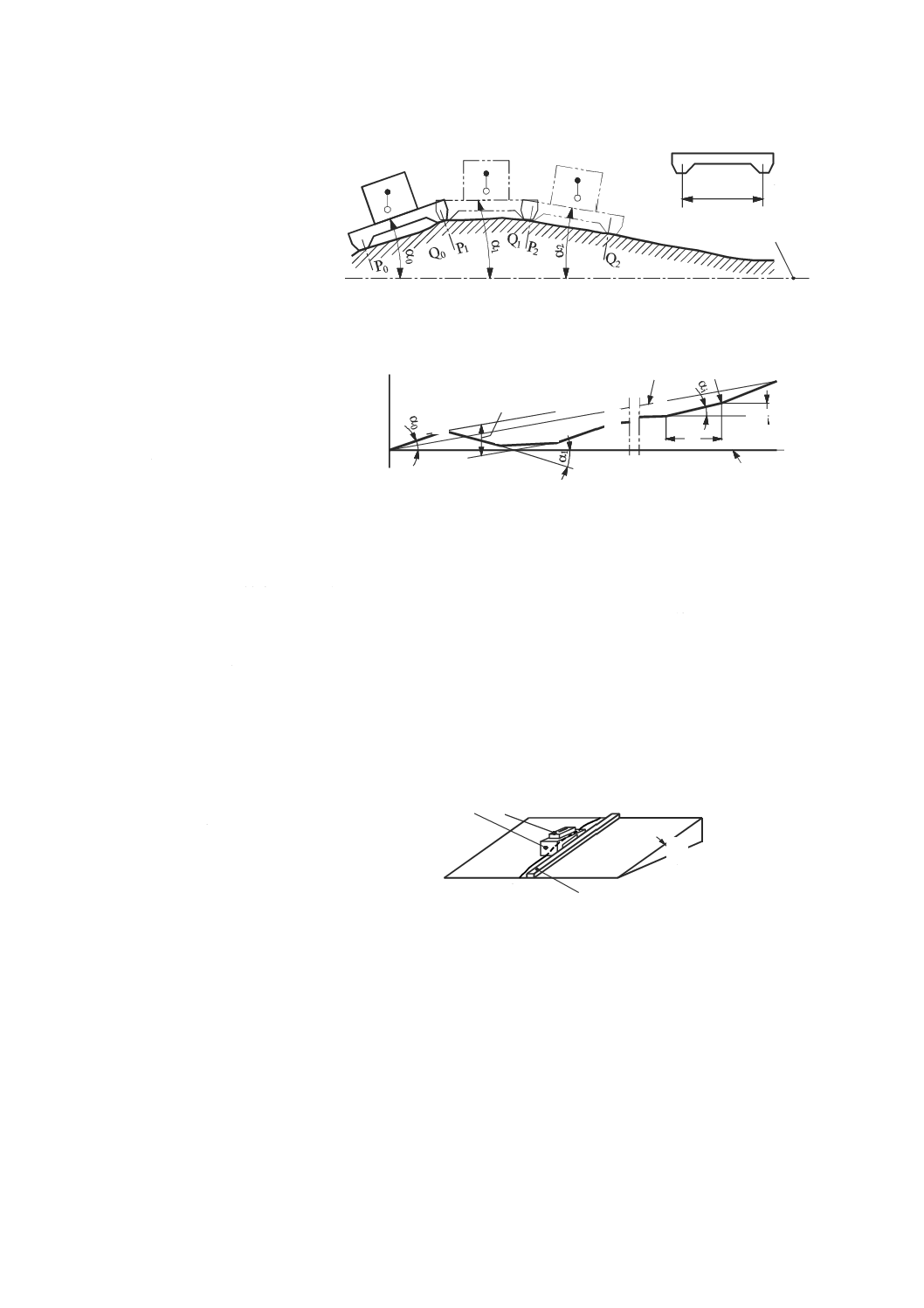
76
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 測定の基準
d 試験中に測定面に接する測
定台の接触点間距離
図87−角度の測定に基づく真直度測定
1 真直度誤差
2 両端点基準直線
3 測定基準
図88−角度の測定に基づく真直度の評価方法
12.1.3.2 精密水準器による方法
12.1.3.1に従って,精密水準器(8.4.2.1及びISO/TR 230-11参照)を試験対象とする線に沿って順次移動
させて測定する。測定の基準は,垂直面内で微小角度を測定できる精密水準器の水平線である(図87参照)。
測定対象とする線が水平でない場合には,精密水準器は,適切な角度をもった専用の傾斜支持台上に置
く(図88参照)。線ABの測定中,精密水準器はその支持台とともに一定の向きを保つようにするのが望
ましい。例えば,案内用直定規に沿わせる(図89参照)。
精密水準器は,垂直面内だけで真直度を測定できる。他の平面内での線の真直度の測定には別の方法を
用いるのがよい。例えば,鋼線と測微顕微鏡とによる方法がある。
1 精密水準器
2 専用の傾斜支持台
3 案内用直定規
α 面の水平面からの角度
図89−専用の傾斜支持台を用いた水平でない面の真直度誤差測定
12.1.3.3 オートコリメータによる方法
この方法では,同軸上に取り付けたオートコリメータ(図90参照)を用いて,光軸に直角な水平軸回り
の可動反射鏡M(測定台に定置)の回転によって生じる焦点面における標線の像の垂直方向変位を測定す
る(8.4.2.2及びISO/TR 230-11参照)。
P
Q
d
1
P0
P1
P2
P3
P4
Pi
Pi+1
Pn
3
d
2
1
E
i+
1
h
2
1
3
A
B
α
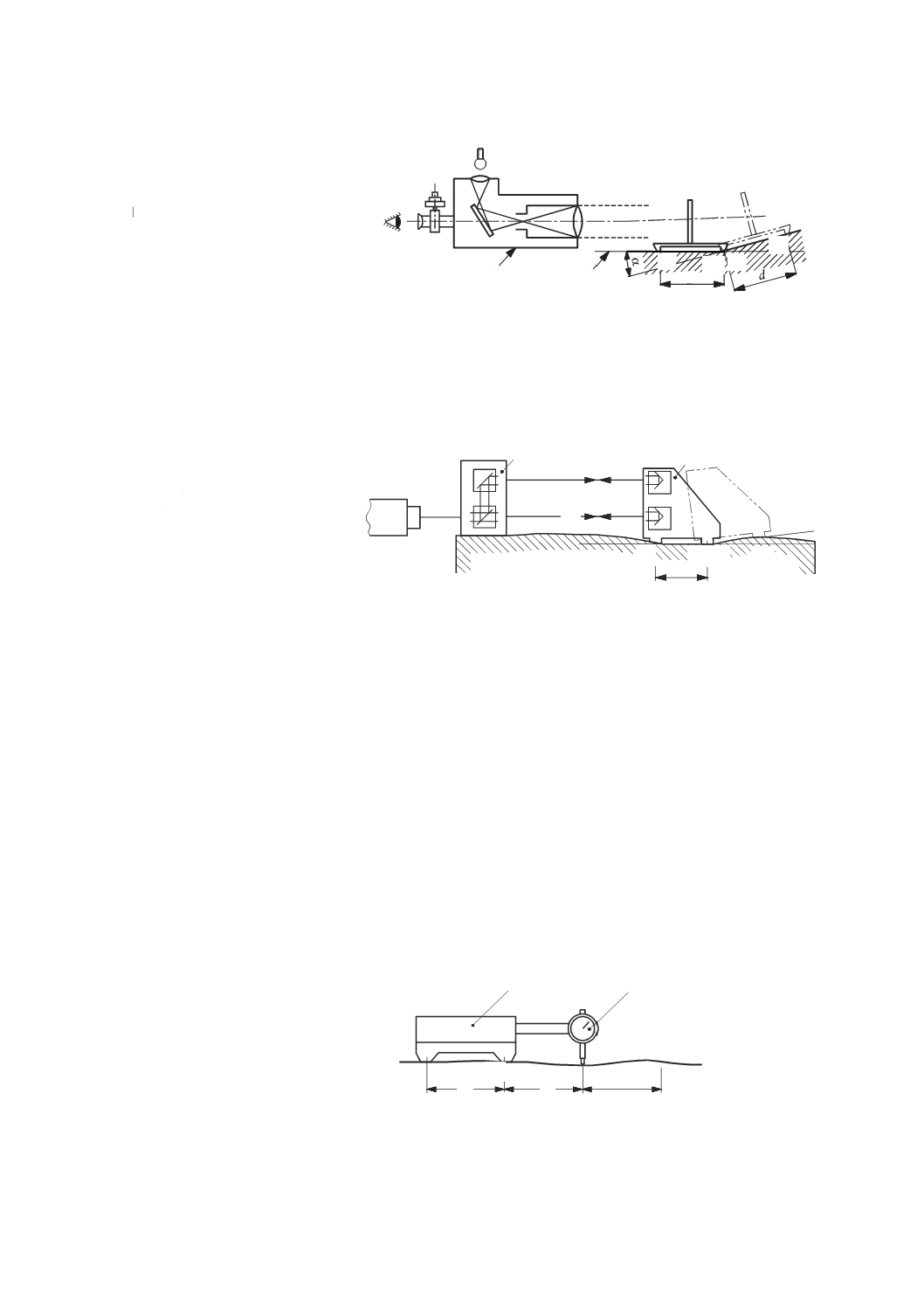
77
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 オートコリメータ
2 測定の基準
M 測定台上の移動反射鏡
d 測定台の脚間の間隔
図90−オートコリメータを用いた真直度測定
12.1.3.4 レーザ角度干渉計による方法
この方法では,干渉計を試験対象とする線がある構成要素上に堅く固定するのが望ましい(図91参照)。
1 レーザヘッド
2 角度干渉計
3 測定台上の角度測定用反射鏡
d 測定台の脚間の距離
図91−レーザ角度干渉計を用いた真直度測定
12.1.3.5 逐次3点法による方法
この方法では,測定台に固定した変位計(図92参照)を用いて,局所的な傾斜の変化を検出する。変位
計と測定台との間の距離は,測定台の二つの脚間の距離dと等しいことが望ましい。変位計は,測定対象
面に接触している測定子と同一直線上に取り付け,測定対象面に接触している測定台の二つの脚との間の
相対的な高さの変化を測定する。変位計の読みを取った後に,測定台を脚間の距離dと等しい距離だけ前
進させ,同じ測定を繰り返す。
変位計は,事実上,各測定位置における測定台の脚の下にある測定対象面と接する直線の傾きの変化を
測定することになる。測定対象面上にある各測定点間の相対高さの変化は,測定結果の二重積分によって
推定する。測定台の脚が平面上にある状態で変位計の読みが0となるように慎重に調整することが望まし
い。この調整に誤差があると,完全な平面を測定しても一定曲率半径をもつ面として測定されることにな
る。
1 測定台
2 変位計
d 接触点間の距離
図92−逐次3点法による真直度測定
1
2
M
M
d
P1
P2
Q1
Q2
F1
P1
Q1P2
Q2
F2
2
1
3
d
2
1
P0
P1
d
Q1
Q2
P2
Q0
d
d
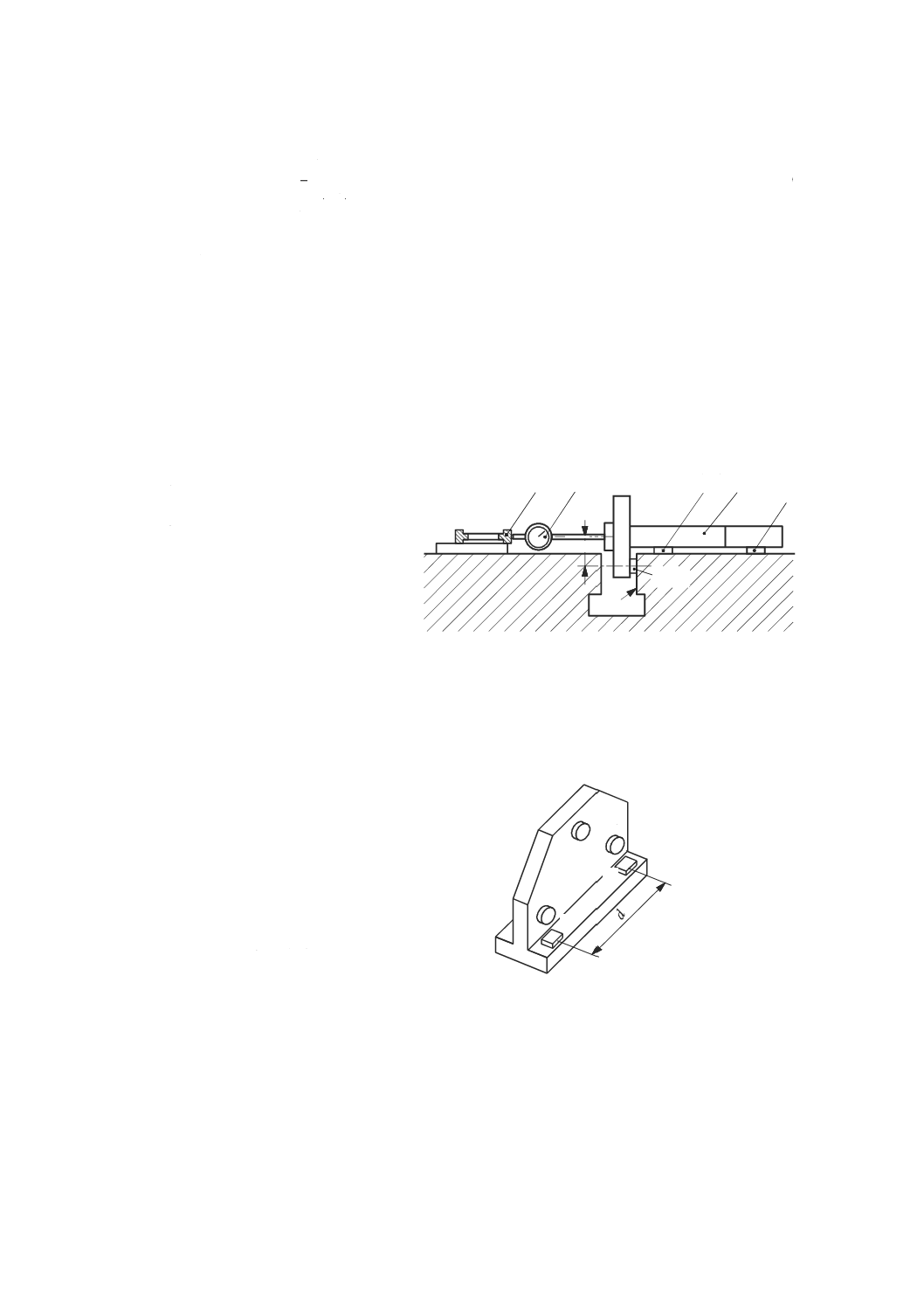
78
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
真直度を定義するための測定対象面に沿って測定した各測定点の高さ変化は,式(20)によって算出する。
∑∑
−
=
=
=
2
1
1
i
j
j
k
k
i
s
h
·········································································· (20)
ここに,
hj: 点jでの高さ変化
sj: 点jでの変位計の読み
12.1.4
テーブル基準溝又は基準面の真直度誤差
真直度誤差を直接測定する場合は,測定台を点P又はQを通る直線に垂直な面内で距離hをできるだけ
小さくなるように定置して読みを取る(図93参照)。
この測定には,図94に示す測定台を用いる。測定台は,テーブル上面に平行に置いて(全面当たりより
は,局所的に3点S1,S2及びS3で当てるほうが望ましい。),測定対象とする線上で二つの支持点P及びQ
を当てる(図93参照)。次に,変位計を直定規に当て,距離hをできるだけ小さくして測定対象面に直交
した方向の偏差を読み取る(図93参照)。
1 直定規
2 変位計
3 測定台
4 測定対象面
P,Q 接触点
S1,S2,S3 支持点
h 接触点と変位計との垂直方向の
距離
図93−テーブル基準溝の真直度測定
角度測定に基づいて真直度測定を行う場合は,距離d(図94参照)が接触点間の間隔になる(図87参
照)。
P,Q 接触点
S1,S2,S3 支持点
d 接触点間の間隔
図94−テーブル基準溝の真直度測定用測定台
より複雑な基準面(図95参照)の真直度誤差は,基準面に直角な方向ではなく,案内面の機能平面(直
線HH及びVVの方向)内で測定する。
P(Q)
1
2
S
3
S
4
(S )
3
2
1
h
P
Q
S
S
S
3
1
2
79
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 測定対象面
P,Q 接触点
S1,S2,S3 支持点
図95−傾斜した面の真直度誤差測定における機能平面HH及びVV
12.1.5
案内面の真直度誤差
案内面の検査は,真直度誤差の測定と関係しており,案内面を測定器で直接測定できる場合だけ行うこ
とができる。案内面を直接測定できない場合は,運動の真直度誤差を測定するのが望ましい(8.2参照)。
真直度誤差は,常に機能平面内で測定するのが望ましい。一般に機能平面は,水平(図95及び図96の
直線HH)又は垂直(図95及び図96の直線VV)であるが,機械構造によっては例外もある(図97参照)。
注記1 案内面の長手方向の形状は,製造業者が機能平面として特殊な形状を採用することがあるの
で,必ずしも真直であるとは限らない。
案内面は,次のように構成されている。
a) 一つの平面又は複数の小さな結合した平面
b) 複数の幅の狭い平面,円筒案内面,又はその二つの組合せ
注記2 案内は,滑り面又はより複雑な機構で構成され,取り外すと機械の幾何精度に影響を及ぼす
場合がある。
1 機能平面
図96−案内面の真直度誤差測定におけ
る機能平面HH及びVV
図97−スラントベッド構造における案内面の
機能平面
12.1.6
V形案内面の真直度誤差
測定台は,4点で接触するのが望ましい。安定のために他方の案内面上の付加支持点で支持しなければ
H
H
V
V
1
1
P, Q
S3
S1, S2
V
V
H
H
1
A
B
80
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ならない。
図98及び図99は,逃げを設けた円筒を示し,図100は,逃げを設けた逆Vを示す。
付加支持点は,運動部品に無理な位置決め力を生じさせないのが望ましい。
1 可動球
2 逃げを設けた円筒(図99参照)
図98−V形案内面の真直度測定用測定台及び逃げを設けた円筒
1 付加支持点
d 支持点間の距離
P,Q 円筒上の支持点
1 付加支持点
図99−V形案内面の真直度誤差測定において4点接触
を実現するための逃げを設けた円筒の使用方法
図100−逆Vブロックを用いた円筒
表面の真直度誤差測定用の測定台
12.1.7
円筒案内面の真直度誤差
四つの支持点をもつ測定台を円筒案内面上に置くのが望ましい。この四つの支持点は,逆Vの溝の中に
ある(図100及び図101参照)。
付加支持点は,運動部品に無理な位置決め力を生じさせないのが望ましい。
1 付加支持点
d 支持点間の距離
P,Q 支持点
図101−円筒面の真直度誤差測定用逆Vブロック
12.1.8
一つの垂直な面の真直度誤差
測定台は,測定対象とする面に点P及び点Qで接触させる。三つの付加支持点は,測定台を案内するた
めに必要である。この三つの付加支持点は,二つの測定対象面上の接触点P及び接触点Qの位置決めに影
響を及ぼさずに案内できるように設けることが望ましい(図102及び図103参照)。
1
2
Q
P
1
1
d
1
P
Q
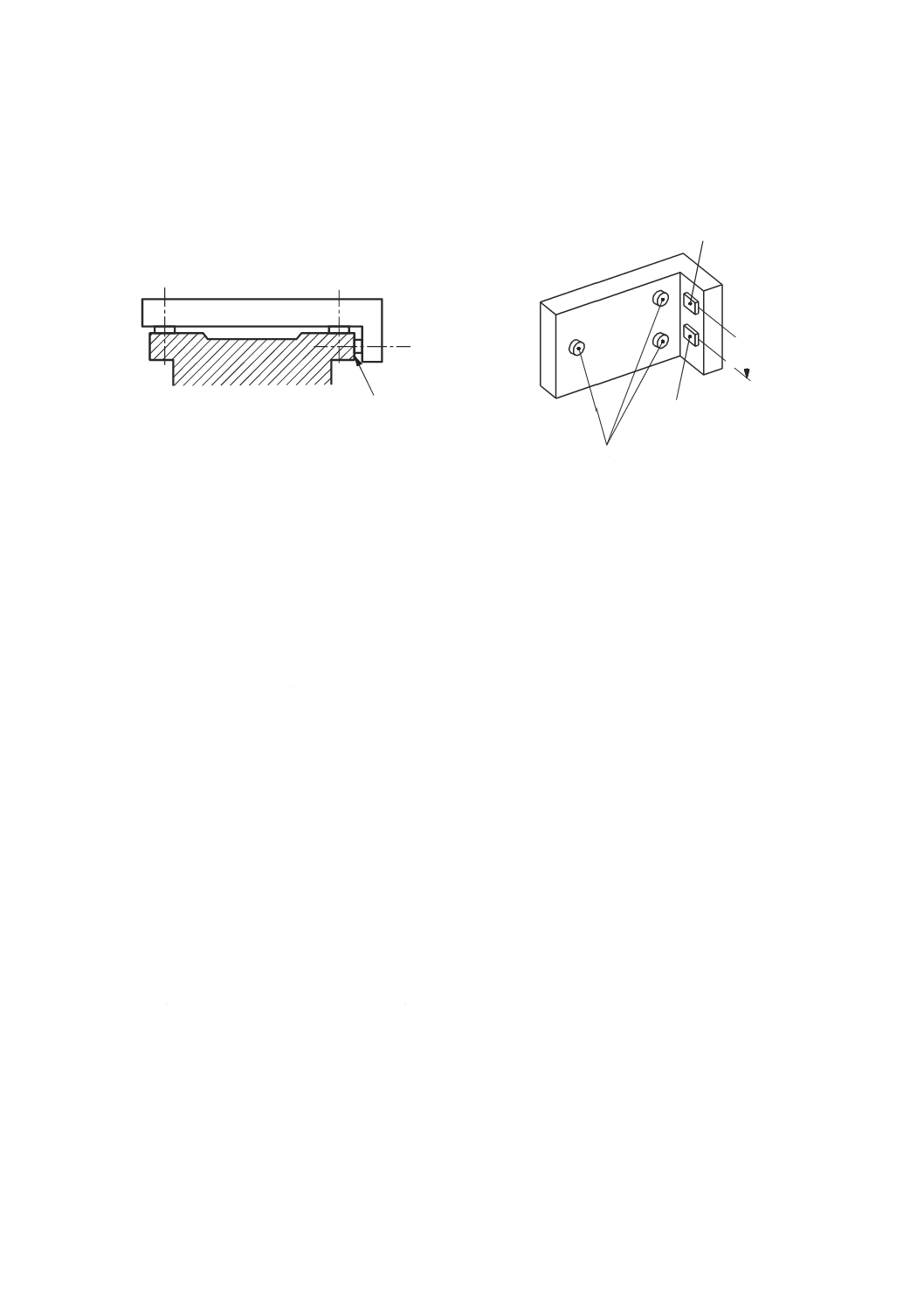
81
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
真直度偏差を直接測定するときは,測定器を測定対象面に対して垂直にし,接触点の一つを通る平面上
で測定を行うのが望ましい。また,角度偏差で測定するときは,接触点間の距離dが測定間隔を決める。
1 測定対象とする垂直な面
1 付加支持点
P,Q 接触点
d 接触点間の距離
図102−測定台を用いた垂直な面の真直度誤差測定
における測定台の使用方法
図103−垂直な面を測定するための測定台
12.1.9
スラントベッド構造における面の真直度誤差
この構造の場合,運動部品の機能平面は,水平面に対して一定の角度をなしている(図97参照)。真直
度誤差は,この機能平面(線AB)内とそれに直角な平面内とで測定する。
12.2
テーブルの平面度
12.2.1
定盤による平面度誤差の測定
定盤による平面度の評価では,定盤表面に軽油で薄めたベンガラ又は酸化クロムを塗る。その定盤を測
定対象面に載せ,軽く前後に動かす。次に,定盤を取り外して単位面積当たりの接触点の分布を記録する。
この分布は,測定対象面全域にわたって一様で,所定の単位面積当たりの接触点の数と等しいことが望ま
しい。この方法は,比較的精密な仕上げ面(きさげ面又は研削面)で,面積の小さい面に対してだけ適用
できる。
12.2.2
定盤と変位計とによる平面度誤差の測定
測定は,定盤とその定盤上に載せた研削仕上げした支持台に取り付けた変位計とによって行う。
この測定方法には,次の二通りがある。
a) 測定対象とする構成要素を定盤上に置く(定盤の寸法及び変位計の支持台の形状は,測定対象面全面
を測定するのに十分な大きさでなければならない。)(図104参照)。
b) 定盤を測定対象面に対向して置く。この場合には,定盤の寸法が測定対象面の寸法と同程度であれば
測定できる(図105参照)。
測定箇所を決めるために格子線を描く。測定対象面の不整による読取り誤差は,次の方法によって最小
化できる。
− 表面粗さの影響を受けないように測定子先端が大きな半径をもった変位計を用いる。
− 測定対象面の不整(きさげ面,平削り面など)を避けるために,測定対象面と変位計の測定子との間
1
d
1
P
Q
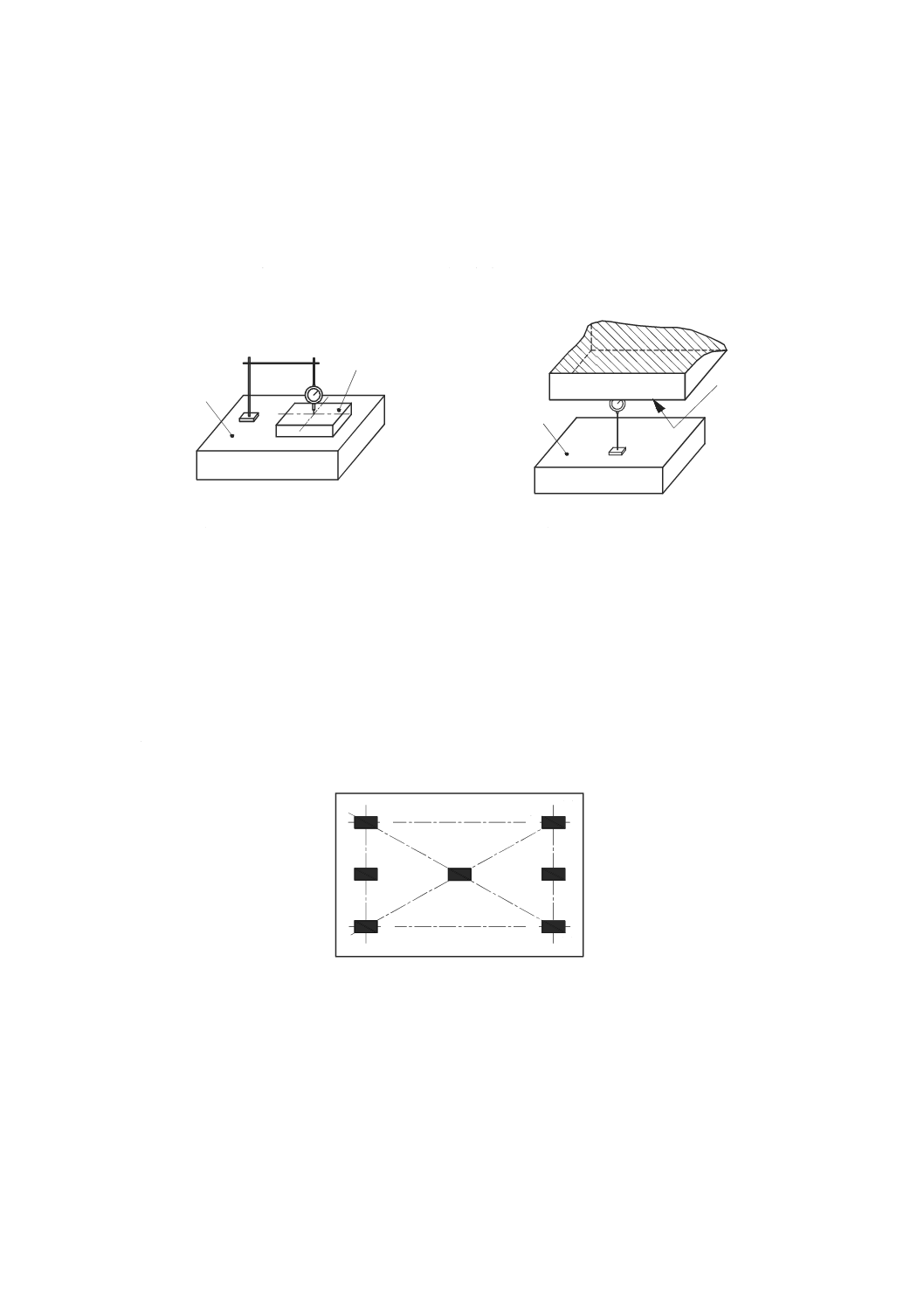
82
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
に,研削仕上げした小さな平行ブロックを置く。
定盤上に構成要素を載せる方法(図104参照)では,変位計の位置は,定盤表面の傾きの変化の影響を
受ける。この方法は,高精度な定盤を使用することが望ましい。また,この方法は,定盤表面の不整を考
慮できないため,小部品にだけ適用する。
測定対象面に対向して定盤を置く方法(図105参照)では,定盤に垂直に置いた変位計取付具を用いて
測定を行うため,測定結果の処理段階で定盤の不整を考慮することができる。
1 定盤(測定基準)
2 測定対象面
1 定盤(測定基準)
2 測定対象面
図104−定盤上に定置した部品の
平面度誤差の測定
図105−対向して定置した定盤を用いた
部品の平面度誤差の測定
12.2.3
直定規による平面度誤差の測定
12.2.3.1 直定規の変位による直線群を用いた測定
最初に,基準点が配置されている理論的な平面を決める。そのために,測定対象面上の3点a,b及びc
をゼロ点として選ぶ(図106参照)。次に,厚さの等しい3個のブロックゲージをその3点に置く。この3
個のブロックゲージの上面が比較する平面の基準平面になる。
図106−直線群による平面度誤差の測定
基準平面上に置いた第4番目の点dの高さは,次のようにして決める。まず高さを調整したブロックゲ
ージを使って,直定規を2点aとcとの上に定置し,高さ調整ブロックをその平面上の点eに置いて,直
定規の底面と接触させる。そうすると,ブロックゲージa,b,c及びeの上面は全て同一平面にそろうこ
とになる。
点dの偏差は,点b及び点e上に直定規を置くことによって分かる。高さ調整ブロックを点dに定置し,
既に配置したブロックゲージの上面によって決まる面に当てる。
1
2
2
1
a
b
g
e
f
d
c
(0)
(0)
(0)
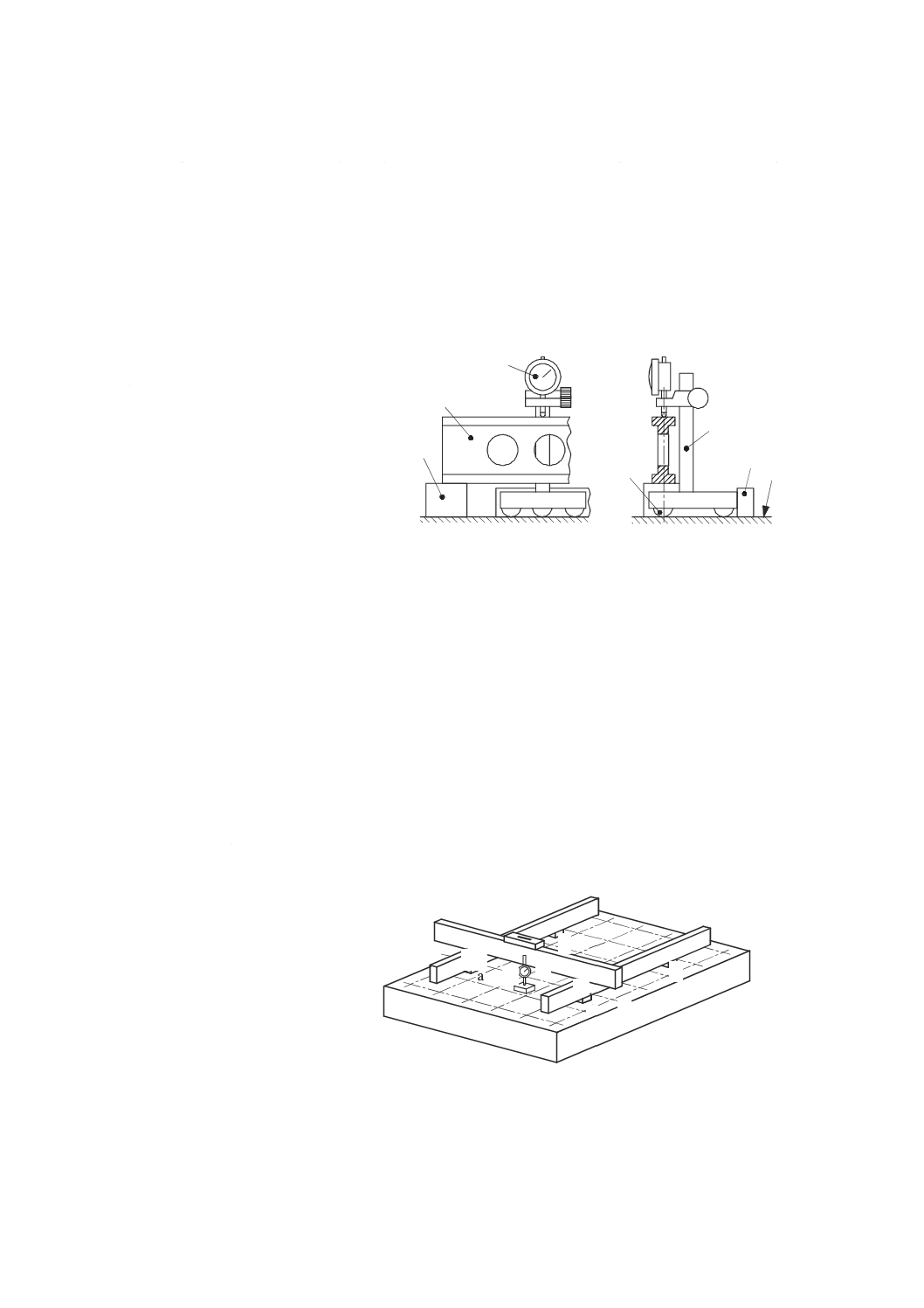
83
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
直定規をブロックゲージaとdとの上に,次いでブロックゲージbとcとの上に置くと,2点aとdと
の間及び2点bとcとの間にある全ての点の偏差が分かる。同様にして2点aとbとの間及び2点cとd
との間も分かる(直定規のたわみを考慮した許容値の設定が望ましい。)。
このようにして決めた長方形又は正方形の内側の読みを取るには,例えば,偏差が分かっている点fと
gとに正確に高さを調整したブロックゲージを置いて,直定規をこれらの点の上に定置し,ブロックゲー
ジを使って測定対象面と直定規との間の偏差を測定する。図107に例を示すような真直度の測定器を使う
こともできる。
1 変位計
2 変位計支持台
3 案内用直定規
4 測定対象面
5 平行ブロック
6 直定規
7 変位計の測定子と同一直線上にある
接触点
図107−平面度誤差測定用の真直度測定器
12.2.3.2 直定規,精密水準器及び変位計による測定
この方法では,精密水準器を使って平行に定置した二つの直定規を測定基準とする(図108参照)
(ISO/TR 230-11参照)。
高さの等しい三つの支持台a,b,c及び高さの調整できる一つの支持台d上に二つの直定規R1及びR2
を定置し,この二つの直定規の上面が平行で,かつ,同一平面になるように精密水準器を使って調整する。
直定規Rを格子線に合わせてR1とR2とに直角に定置し,変位計G(又は標準ブロックゲージ)を用いて
直定規Rに平行な直線fg上の偏差を読み取る。
直定規R1及びR2は,直定規Rの質量による変形が無視できるように十分な剛性がなければならない。
測定基準を決め,この測定基準からの偏差を測定して図示する。図示は,測定対象面全体を覆うように,
規則的な方形格子線の交点で行う(図109参照)。測定点の間隔は,使用する測定器とは無関係である。
a,b,c,d 支持台
G 変位計
L 精密水準器
R,R1,R2 直定規
fg 測定線
図108−精密水準器と直定規とによる平面度誤差の測定
1
6
5
2
3
4
7
f
Ra
G
R
R
c
d
g
1
b
L
2
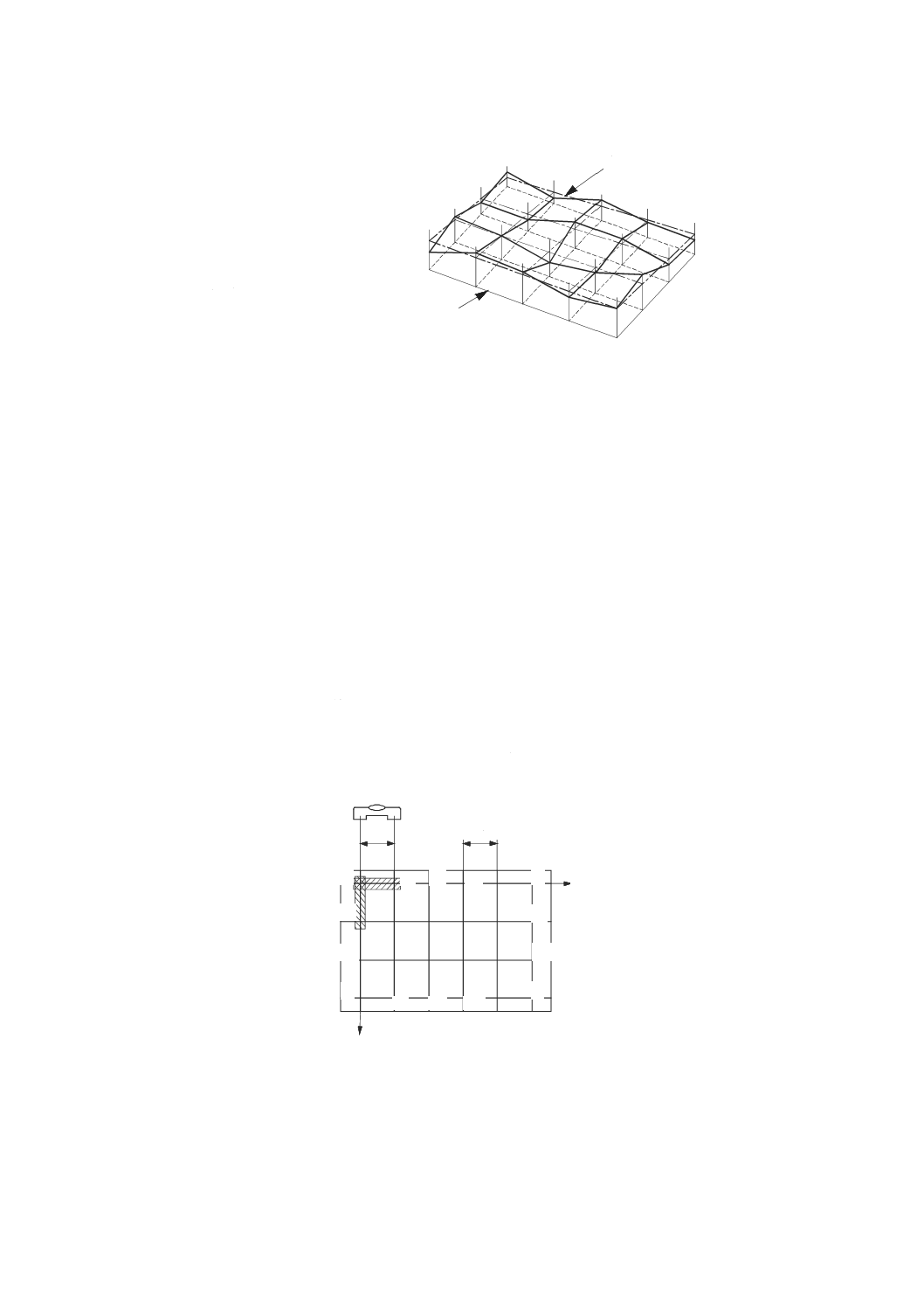
84
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 代表平面
2 測定基準面
図109−平面度偏差の表示
12.2.4
精密水準器による平面度誤差の測定
12.2.4.1 一般
精密水準器による測定方法は,測定位置を一つの位置から別の位置に変えても測定基準(水平方向)の
方向を一定に維持できる唯一の方法である。
角度の測定(12.1.3)に基づいて行う線の真直度の測定がこの測定の基本である。
移動側と固定側との二つ精密水準器の間の差分を測定することを推奨する。
12.2.4.2 長方形表面の測定
基準平面は,測定対象面上の点Oを通る二つの直線OmXとOO'Yとによって決まる。ただし,3点O,
O'及びmは,測定対象面上の点である(図110参照)。
直線OX及びOYは,互いに直角にとるのが望ましく,できれば測定対象表面の外周に平行にとる。測
定は,面の一つの隅の点OからOXの方向に行う。直線OA及びOC上の表面の輪郭を12.1.3.1に示した
方法によって求める。長手方向の線O'A',O''A''及びCBは,面全体を覆うように決める。
この測定を確認するために,mM,m'M'などについても補足的に測定を行ってもよい。
測定対象表面の幅が長さとほぼ同程度の場合には,対角線に沿った測定を行うことが望ましい。
図110−精密水準器による平面度誤差の測定
12.2.4.2.1 測定結果の処理
図87に示した手順に従って描いた線Omm'A及びOO'O''Cの結果から,Omm'A及びOO'O''Cを三次元的
1
2
X
A
A'
A"
B
m'
m"
m
O
O'
O"
d
C
M
M'
M"
Y
d
X
Y
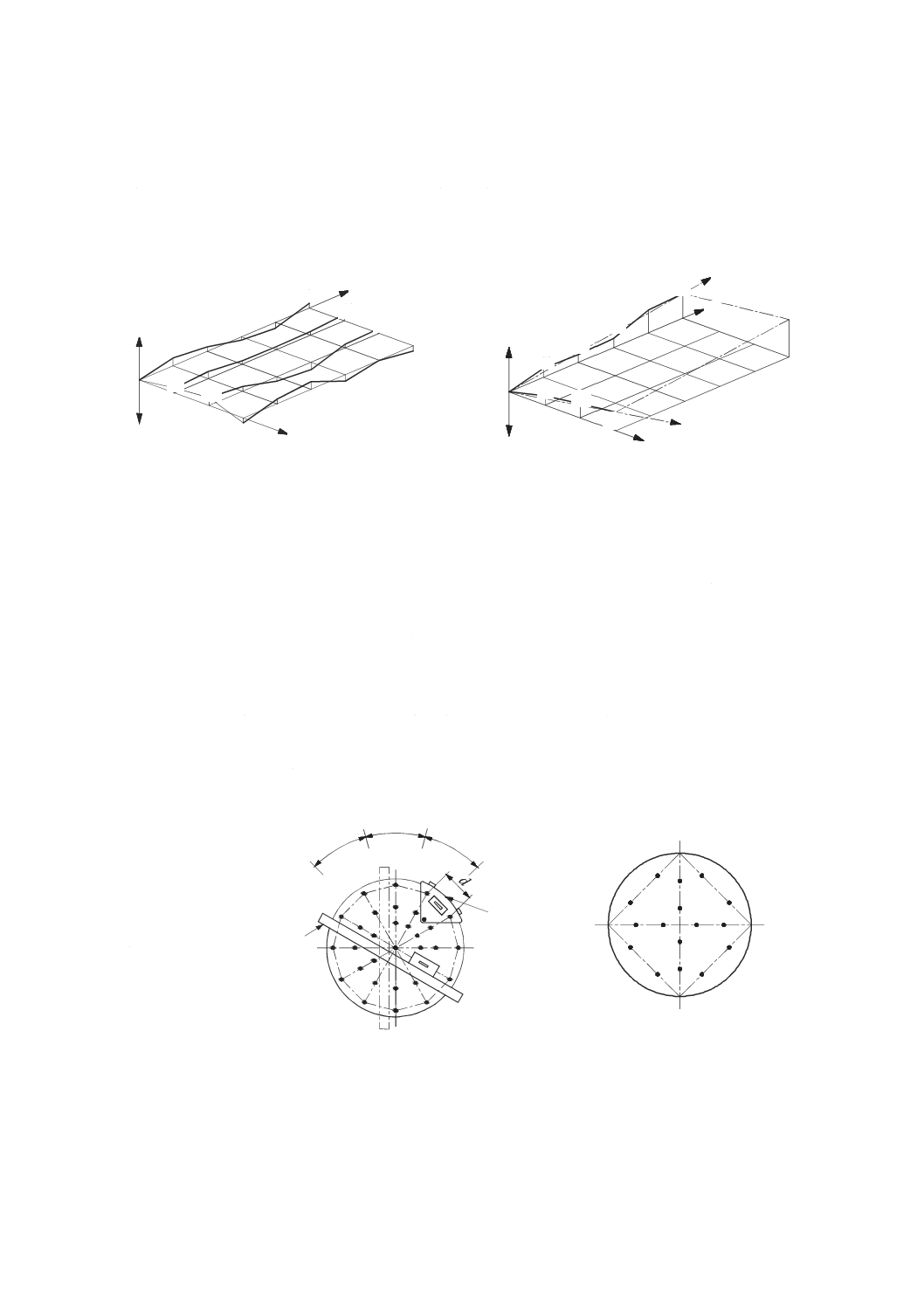
85
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
に表示する。線O'A',O''A''及びCBの始点は,それぞれO',O''及びCとする。図111に示す例では,全て
の測定値が測定基準平面に非常に近いので,その基準平面が代表平面となる。しかし,図112に示す例で
は,線Omm'A及びOO'O''Cのそれぞれの代表直線が直線OX'及びOY'の方向にあるので,代表平面はOX'
及びOY'を含む平面,すなわち,平面OABCとなる。
図111−測定基準面と代表平面とが近い場合の
平面度偏差の表示
図112−測定基準面と代表平面とが離れている
場合の平面度偏差の表示
12.2.4.3 円板平面の測定
大きな円板平面は,方形格子状に測定すると測定できない部分が残る。そのような場合は,次によって
外周円と直径とを使って測定するとよい(図113参照)。
a) 円周に沿った測定:精密水準器を測定対象表面に3点で接触する支持台Aに定置し,その支持台を円
板の外周に沿って一定間隔で移動させる。
b) 直径上の測定:機能面の真直度の測定方法による(12.1参照)。
小さな円板の平面度の測定は,次のように真直度を測定するだけの簡単な方法で行うことができる。
− 直交する2直径上の真直度の測定
− 直交する2直径を対角線とする四角形の辺上の真直度の測定(図114参照)
A 点で接触する支
持台
B 直定規
d 支持点間の距離
図113−円周に沿って測定する場合の平面度誤差の測定
図114−円板平面の平面度誤差の
測定経路
12.2.5
光学的方法による平面度の測定
12.2.5.1 オートコリメータによる測定
X
A
A'
m'
m"
m
O
O'
O"
C
Y
B
A"
-Z
+Z
+Z
−Z
X
Y
X
A
m'
m"
m
O
O'
O"
C
Y
B
-Z
+Z
X'
Y'
+Z
−Z
X'
Y'
Y
X
A
B
=
=
=
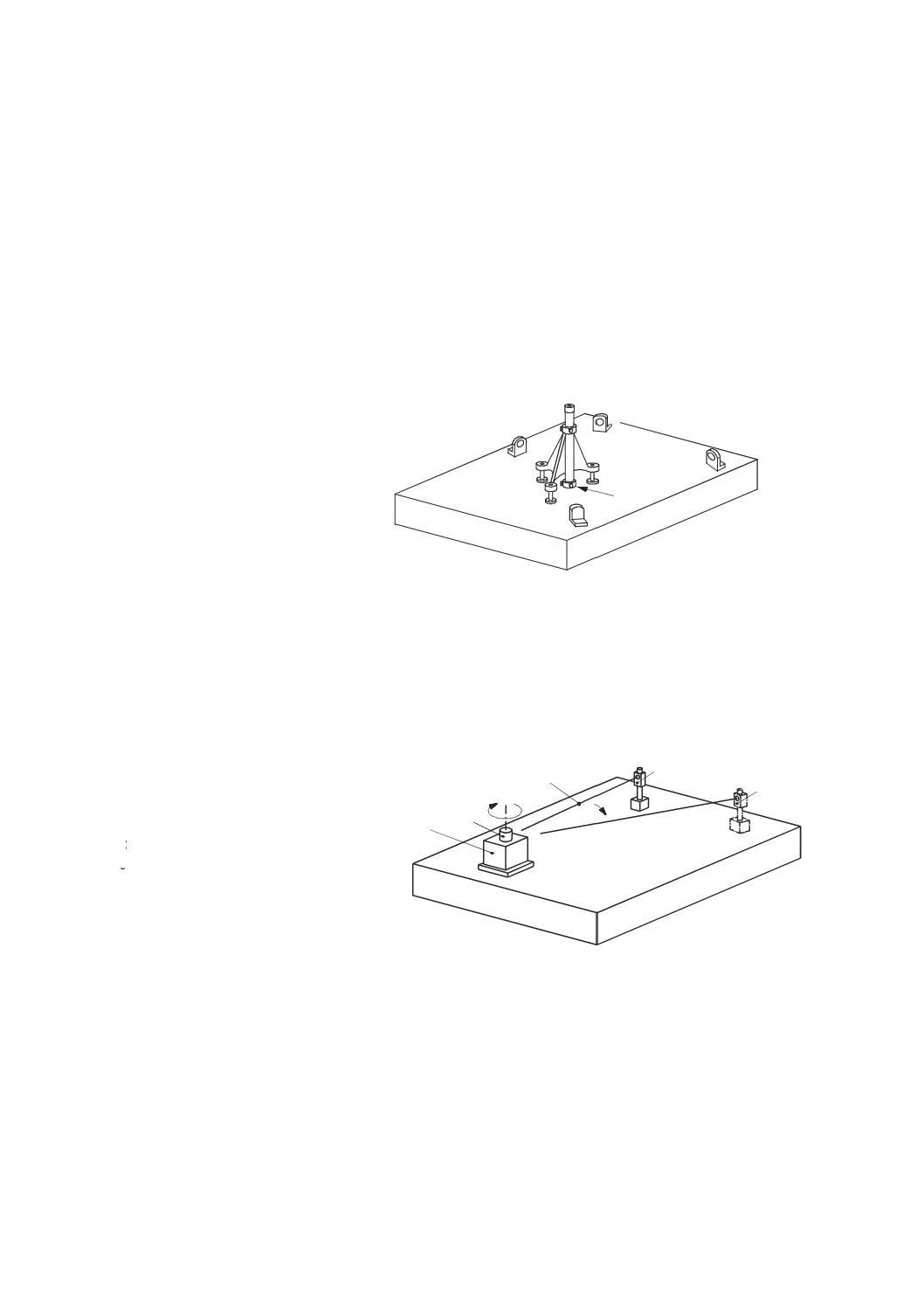
86
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
基準平面を定める直線OX及びOYは,二つの位置で,できれば互いに直角な位置で,オートコリメー
タの光軸によって決める。次いで,12.1.3.3に規定した方法で測定する。
測定の基準平面は,オートコリメータの光軸OX及びOYの方向によって決まる。したがって,O'A',
O''A''及びCBの測定では,オートコリメータの光軸は,OXに平行にしなければならない(図110参照)。
12.2.5.2 走査形光学式スコヤによる測定
走査形光学式スコヤ(五角形プリズム)も使うことができる。基準平面は,面の外周部分に定置した三
つの標点(A,B及びC)のそれぞれの中心点によって決まる(図115参照)。光学式スコヤは,望遠鏡の
光軸が基準平面と直角になるように心合わせして,第四の標点を使って面の任意の点の位置を測定する
(ISO/TR 230-11参照)。
1 第四の標点
2 走査形光学式スコヤ
(五角形プリズム)
A,B,C 標点
図115−走査形光学式スコヤによる平面度誤差の測定
12.2.5.3 走査形アライメントレーザによる測定
この方法では,同一平面上にある直線基準を使って測定のための基準平面を決めるためにアライメント
レーザと回転ユニットとを用いる(図116及びISO/TR 230-11参照)。
1 アライメントレーザヘッド
2 回転ユニット
3 走査形レーザビーム
4 測定位置nにおける光検出器
5 測定対象表面上の他の位置に定置し
た光検出器
図116−走査形アライメントレーザによる平面度誤差の測定
12.2.5.4 レーザ干渉計による測定
表面の凹凸は,測定した線の角度偏差から求めた線の真直度偏差の曲線から求めることができる
(ISO/TR 230-11参照)。
代表的な測定手順は,図117に示す1から8までの測定線で示す。
順次,測定線1から8まで測定する。データ処理によって解析した結果は,定盤の平面度を三次元的に
図示する(図118参照)。
C
1
A
B
2
4
3
1
2
5
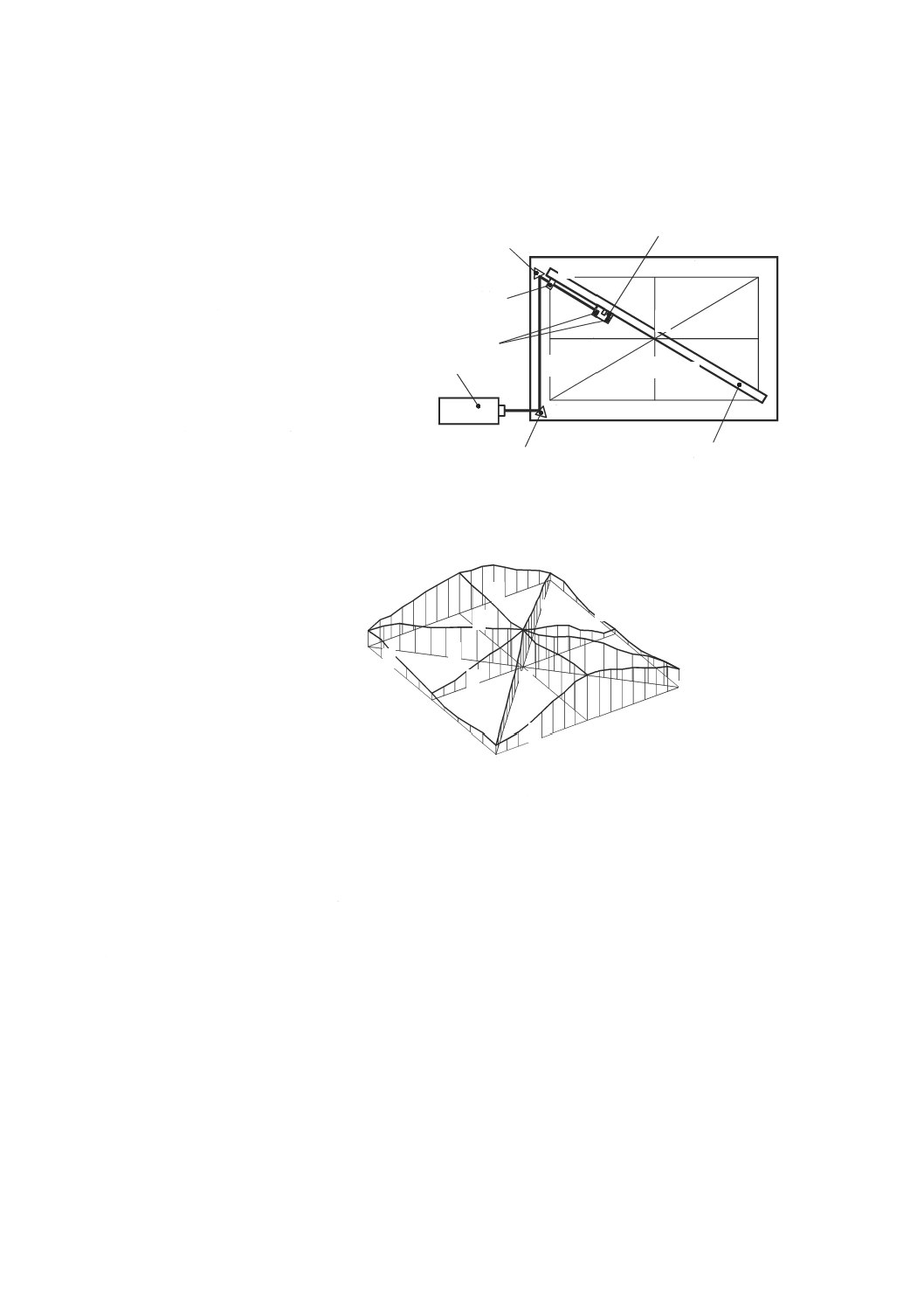
87
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
レーザ光軸は,ビームベンダを調整することによって水平面内で方向を調整できるが,垂直面内でのレ
ーザ光軸の向きに影響することがある。
1〜8 測定線
9 反射鏡取付台(反射鏡付き)
10 第二ビームベンダ
11 干渉計
12 脚
13 レーザヘッド
14 第一ビームベンダ
15 直定規
図117−レーザ干渉計による平面度誤差の測定
1〜8 測定線
図118−代表的な平面度偏差データの図示
12.3
機能面の位置及び向き
12.3.1
一般
この測定は,次の三つの幾何精度について行う。
a) 線と面との平行度:12.3.2を参照。
b) 等距離度:12.3.3を参照。
c) 同軸度:12.3.4を参照。
12.3.2
線と面との平行度
12.3.2.1 一般
平行度の測定において軸を含む場合には,測定部分の形状精度が高く,表面粗さが小さく,かつ,長さ
も十分な円筒面であれば,軸自身を直接使用してもよい。主軸の表面がこれらの条件を満たさない場合,
又は主軸穴内面で,その穴に測定子を挿入できない場合は,補助として円筒面(テストバー)を使う。
テストバーの取付け及び心出しは,工具又は他の取付具を取り付けるように設計された軸端,円筒穴又
はテーパ穴で行う。
1
2
3
4
5
8
7
6
A
D
C
B
10
9
11
12
14
13
15
E
D
A
B
C
3
6
1
7
E
2
8
4
5
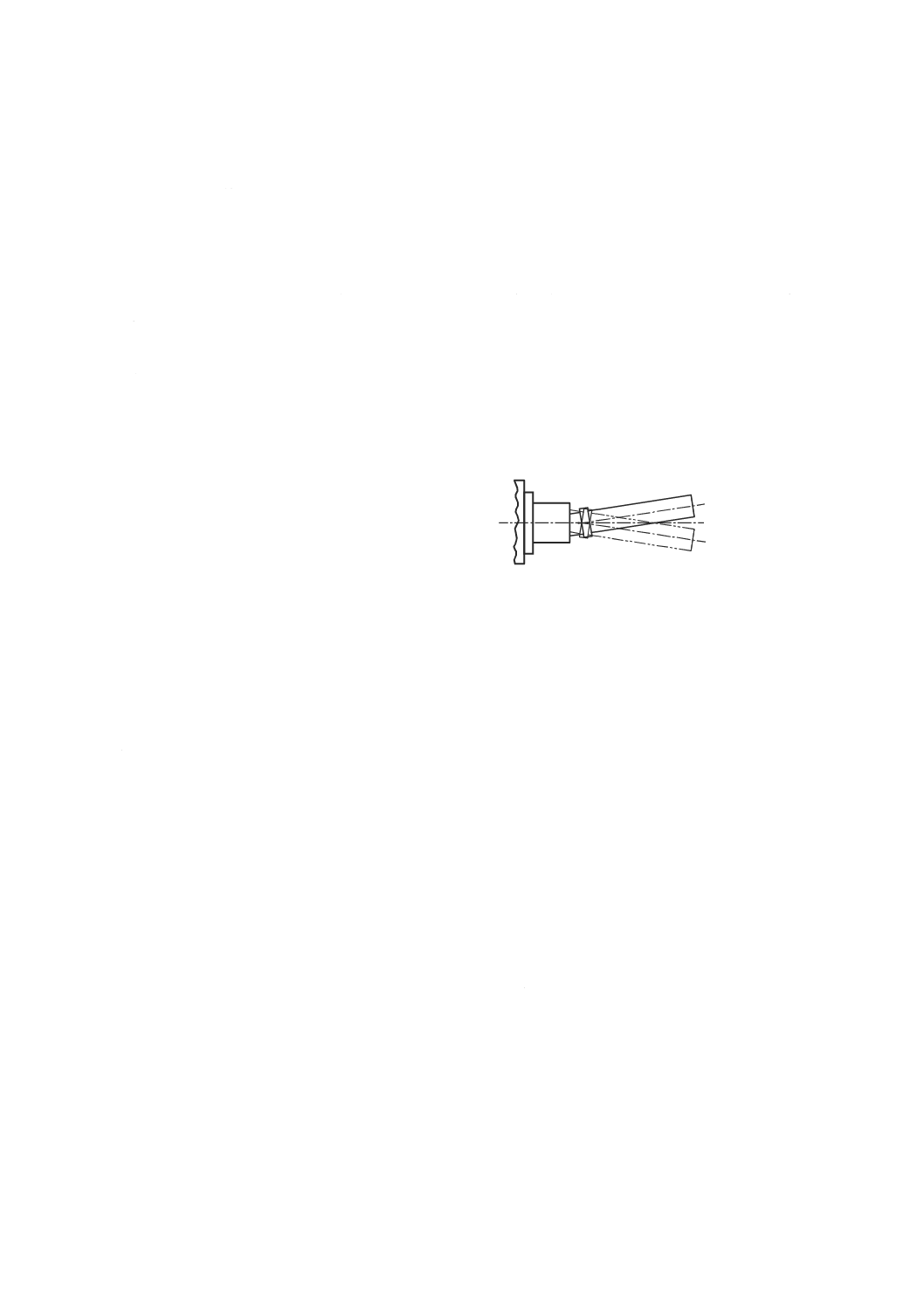
88
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
主軸穴にはめたテストバーを回転軸の代表とする場合は,回転軸にテストバーを正確に心合わせできな
いために,許容値を設けなければならない。主軸を回転させると,テストバーの軸線は,双曲線(又はテ
ストバーの回転軸線と交差するときはテーパ面)を描き,測定平面内で二つの位置B−B'を取る(図119
参照)。
平行度の測定は,これらの条件下では,主軸の回転角度位置に影響されるが,主軸を180°回転させて
から,もう一度測定を行うのがよい。二つの読みの平均が,与えられた平面における平行度の偏差を示す。
また,テストバーを平均位置A(“振れの平均位置”と呼ばれる)まで回して,この位置だけで測定を行
ってもよい。
最初の方法は,二番目の方法とほぼ同じ速さで測定できるが,それよりも精度が高い。
注記 用語“振れの平均位置”とは,変位計の測定子を測定平面内で回転軸を代表する円筒面に当て
て,回転軸をゆっくり回転させたときの変位計の読みが,最大値と最小値との平均を示すとき
の主軸の回転位置。
A 回転軸
B 0°におけるテストバーの軸線
B' 180°におけるテストバーの軸線
図119−回転軸に対するテストバーのアライメントの影響
12.3.2.2 二つの面の平行度
12.3.2.2.1
一般
二つの面の平行度の測定は,次による。測定は,2方向,できれば互いに直角な2方向について行うの
が望ましい。
線(又は面)は,与えられた長さ(又は面積)(例えば,300 mm又は300 mm×300 mm),又は面全体で
測定する。
線(又は面)の間の角度は,与えられた平面(水平,垂直,測定対象の表面と垂直,測定対象の軸と交
差など)上で評価してもよい。平行度の許容値は,異なる面であれば,違っていてもよい。
12.3.2.2.2
直定規と変位計とによる測定
変位計を平らな底面をもつ測定台に取り付け,それを直定規に接触させたまま,指定した距離だけ一つ
の面上を移動させる。測定子は,もう一つの面に沿って滑らせる(図120参照)。
読み(距離の変化)はグラフに表示し,その結果から基準直線を求める。この基準直線の傾きが与えら
れた方向における測定対象面間の角度偏差を表す。
一般に,測定は,測定範囲の両端だけで行ってもよい。角度偏差(正接)は,これら二つの読みの差及
び測定長さの両方から求める。
B
A
B'
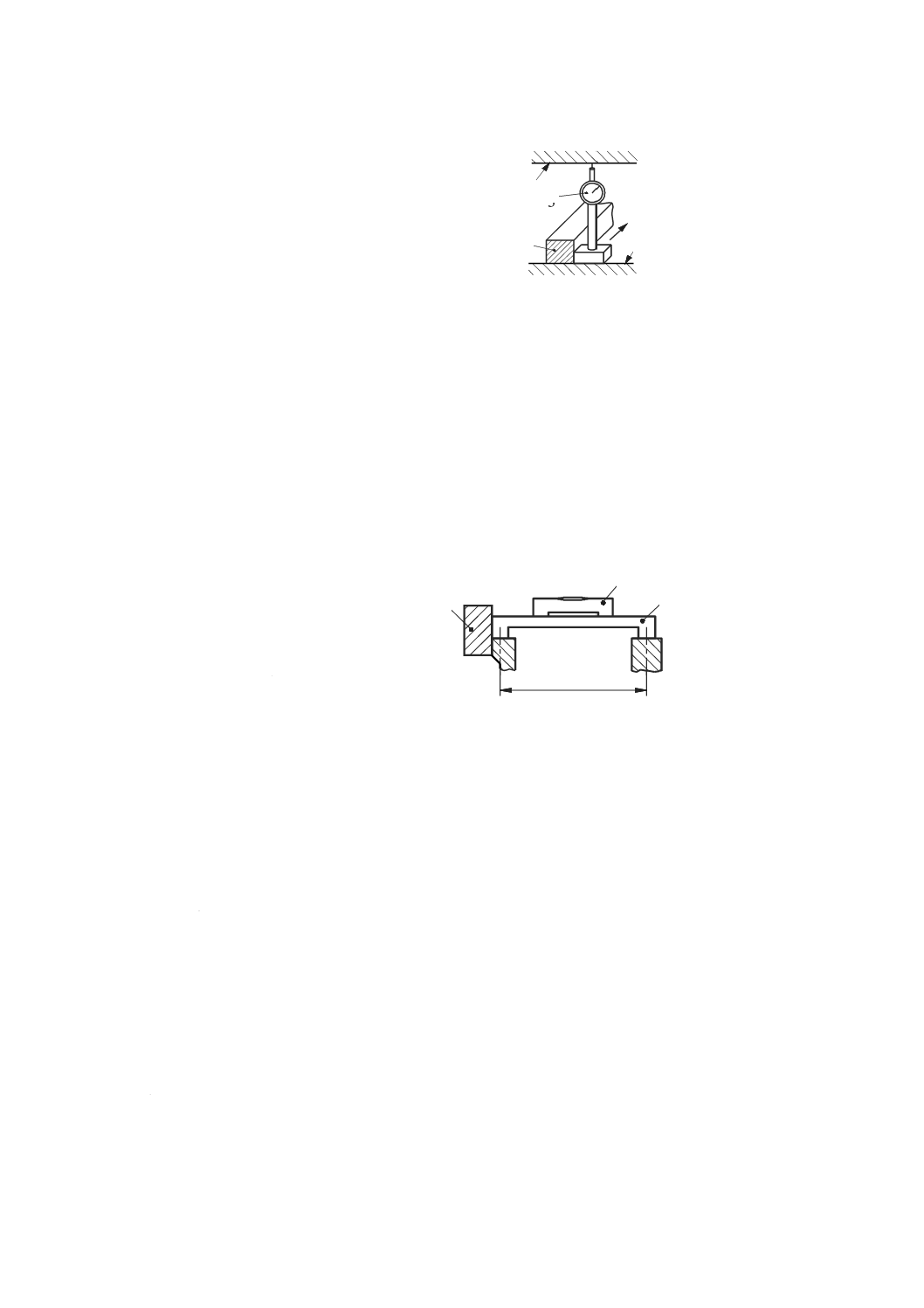
89
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 基準(データム)面
2 対象面
3 変位計
4 案内用直定規
図120−変位計と直定規とによる2平面間の平行度誤差の測定
12.3.2.2.3
精密水準器による測定
精密水準器を比較する二つの面に渡した測定台に載せる。測定台を面に沿って移動させ,次々に精密水
準器の読みを取る。d(図121参照)を乗じた読みは,基準直線を求めるために用いる2平面の相対偏差を
与える。基準直線の向き(角度)が平行度誤差になる。
二つの面に測定台を渡すことが困難な場合には,測定台を用いないで水平面を測定基準とし,各平面に
沿って読みを取る(12.1.3参照)。二つの基準直線を12.1.3に従って評価する。それらの向き(角度)の差
が平行度誤差になる。
1 案内用直定規
2 精密水準器
3 測定台
d 測定ベース長さ
図121−精密水準器による平行度誤差の測定
12.3.2.3 二つの軸の平行度
12.3.2.3.1
一般
測定は,次の二平面内で行う。
− 二つの軸を含む平面内。
注記 この表現は,二つの軸の一つを含み,もう一方の軸にできるだけ近くにとった平面を意味す
る。
− 第二の平面内。できれば,最初の平面に直角な面内。
12.3.2.3.2
二つの軸を含む平面内での平行度
測定器を適切な形状の底面をもった測定台に取り付けて,二つの軸のうちの一方の軸を代表する円筒面
に沿って滑らせる。その測定子を第二の軸を代表する円筒面に沿って滑らせる。
測定点において,2軸間の読みの最小値を求めるため,測定器を軸に直角な方向に僅かに揺り動かす(図
122参照)。必要があれば,測定台を載せる側の軸が測定中に支持している測定台の質量によって生じるた
わみを考慮する。
12.3.2.3.3
第一の平面と垂直な第二の平面内での平行度
この測定方法は,もう一つ平面を追加する必要がある。できれば二つの軸を含む平面に平行な平面を追
23
4
1
d
2
3
1
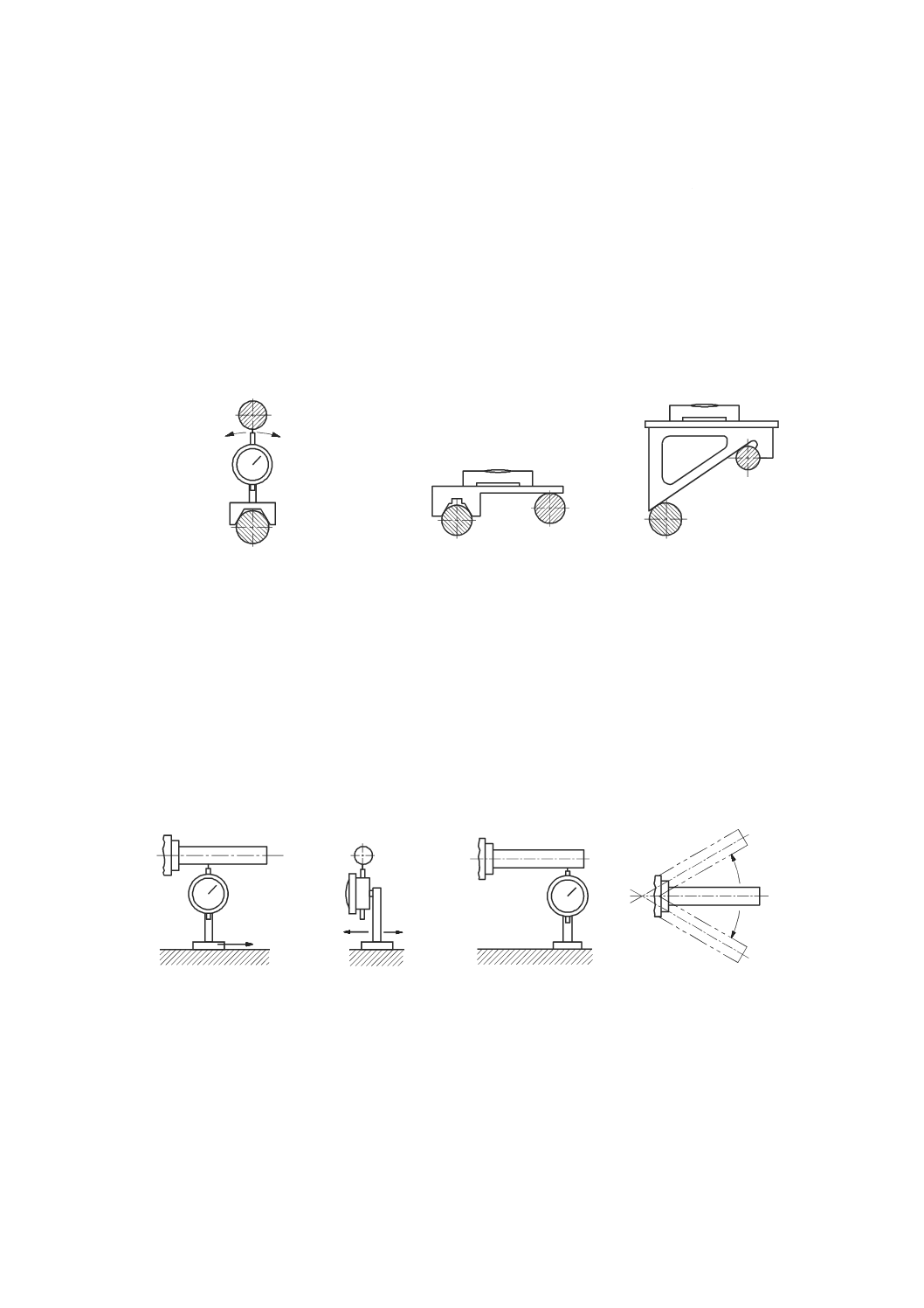
90
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
加する。
追加平面があれば,この二つの軸が機械の機能面と平行であることから,各軸のこの平面に対する平行
度は,別々に12.3.2.4に規定する方法で求める。追加平面がなければ,測定は,気泡管の調整ができる精
密水準器を用いて理論上の平面を基準として行うのが望ましい。そのためには,二つの軸を代表している
二つの円筒面上に精密水準器を置いて,その目盛を0に設定するのが望ましい。二つの軸が同一水平面内
にない場合には,補助として固定形又は調整可能な測定台を使用してもよい(図123参照)。
精密水準器を所定の距離だけ軸に沿って移動させ,読みを取る。読みに2軸間の距離を乗じる。例えば,
この距離が300 mmで,精密水準器の読みが0.06 mm/1 000 mmであれば,2軸間の相対偏差は,0.06×0.3
=0.018 mmとなる。この相対偏差から基準直線を求める。基準直線の向き(角度)が平行度誤差となる。
図122−二つの軸を含む平面内での
2軸の平行度誤差の測定
図123−二つの軸の平行度誤差の測定に
補助として用いる測定台
12.3.2.4 軸と面との平行度
測定器を平らな底面をもつ測定台に取り付けて,面に沿って所定の距離だけ動かす。その測定子は,軸
を代表する円筒面に沿って滑らせる(図124参照)。
各測定点で,測定器を軸と直角な方向に僅かに揺り動かして,読みの最小値を読み取る。
軸が旋回する場合には,中央位置と旋回の両端の位置とで測定を行えば十分である(図125参照)。
注記 円筒面で軸を代表させることについては,12.3.2.1を参照。
図124−軸と平面との平行度誤差の測定
図125−平面と旋回する軸との平行度誤差の測定
12.3.2.5 直進軸と面との平行度
12.3.2.5.1
面が運動部品上にある場合の測定
変位計を機械の固定部品に取り付け,測定子を測定対象とする面に直角に当てる。
運動部品は,例えば機種別の規格に規定された距離だけ移動させるのが望ましい。
一般に,この種の測定方法は,工作物をテーブル上に取り付けるフライス盤及び研削盤に適用する。
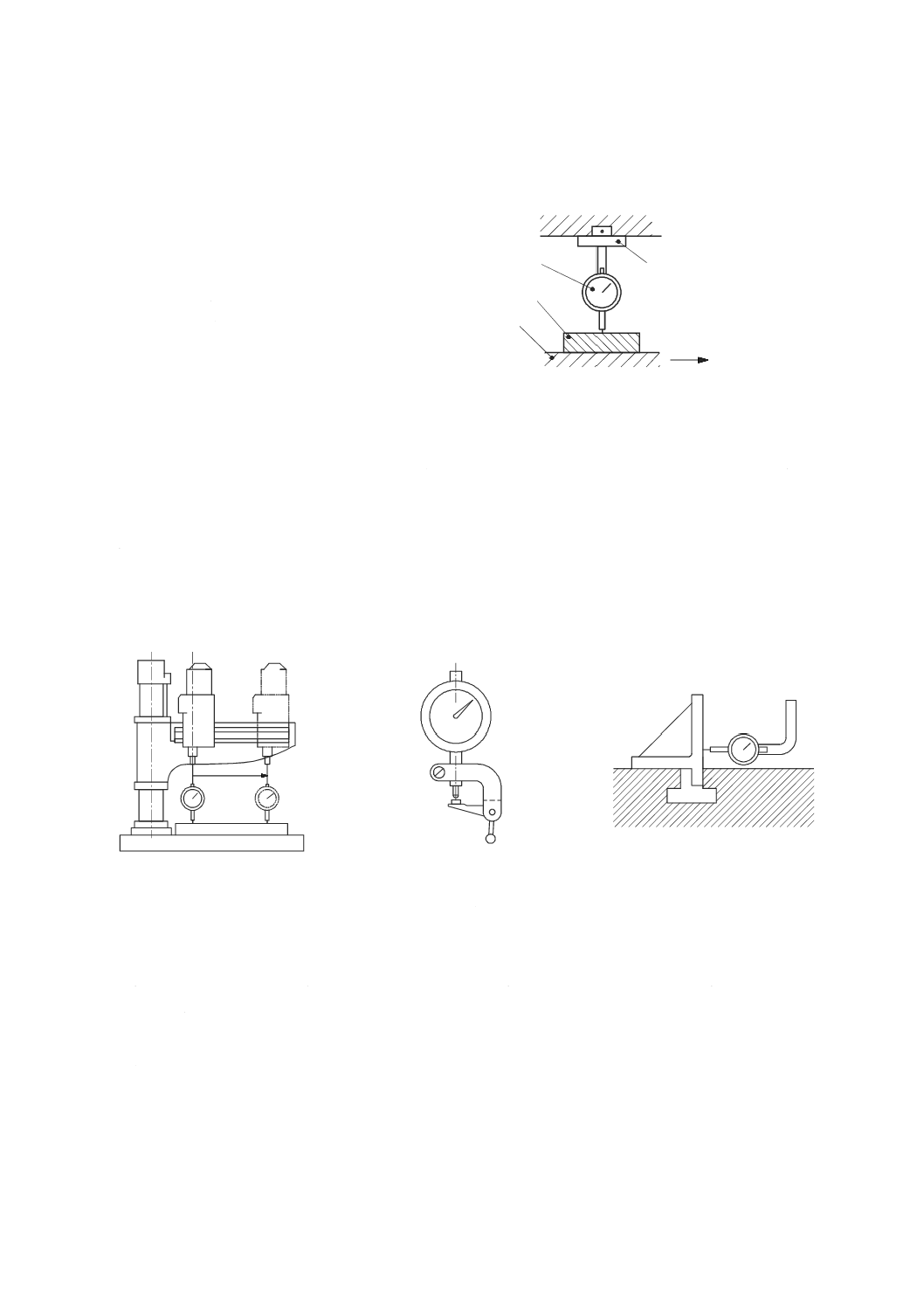
91
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
変位計は,図126に示すように主軸端に取り付け,テーブルを移動させ,読みを取る。その読みから基
準平面を決める。基準平面の向き(角度)が平行度誤差になる。
1 主軸端
2 変位計
3 ブロックゲージ(オプション)
4 運動するテーブル
図126−軸と運動する平面との平行度誤差の測定
12.3.2.5.2
面が運動部品上にない場合の測定
測定器を運動部品に取り付け,運動部品と一緒に所定の距離だけ移動させる。測定子は,測定対象とす
る面に直角に当てて,それに沿って滑らせる(図127参照)。
測定子を測定対象とする面に直接当てられない場合(例えば,狭い溝の側面)の測定は,次のいずれか
の方法によってもよい。
− アングルレバーを使用(図128参照)
− 適切な形状の基準器を使用(図129参照)
図127−軸と固定平面との
平行度誤差の測定
図128−平行度誤差の測定に
用いるアングルレバー
図129−平行度誤差の測定に
用いる特別な基準器
12.3.2.6 軸と二つの面の交線との平行度
測定器を二つの面にはまる適切な形状の底面をもった測定台に取り付ける。次に,測定器を交差する二
つの面の交線に沿って所定の距離だけ移動させ,測定子を,軸を代表する円筒面に沿って滑らす(図130
参照)。できる限り,測定は,工作機械の運転にとって最も重要な直交2平面内で行う。
注記 円筒面で軸を代表させることについては,12.3.2.1を参照。
1
2
3
4
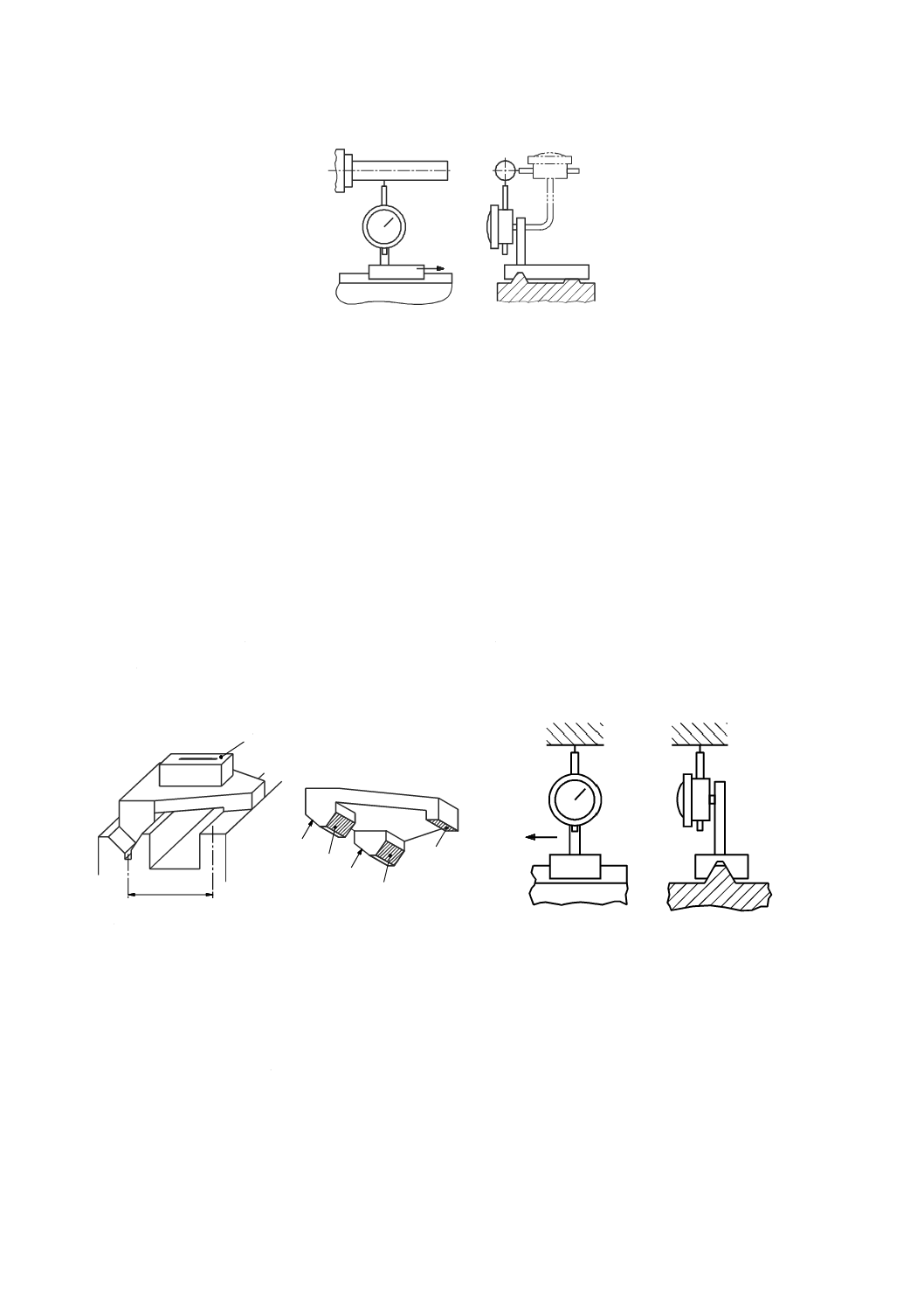
92
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図130−二つの平面の交線と軸との平行度誤差の測定
12.3.2.7 運動軸と二つの面の交線との平行度
二つの面のそれぞれと機能点の軌跡との平行度は,12.3.2.5に従って別々に測定しなければならない。交
線の位置は,平面の位置から推定する。
12.3.2.8 二つの面の交線と第三の面との平行度
交線と第三の面とが互いに測定しやすい位置に配置されている場合には,測定台及び精密水準器を使用
する(図131参照)。
精密水準器を載せた測定台を交線に沿って移動させ,角度の読みの変化にdを乗じ,偏差を算出する。
この偏差は,基準直線及び平行度誤差を求めるために用いる。平行度の評価については,12.3.2.2.3を参照。
第三の面が測定しやすい位置にない場合には,測定台と変位計とを用いる(図132参照)。その測定子を
第三の面に直角に当てて,交線に沿って次々に読みを取る。他の測定手順については,12.3.2.2.2を参照。
測定台の座面の角度は,二つの面の交差角と正確に一致していなければならない。これは,ベンガラな
どの塗布剤で確認できる。
1 精密水準器
2 座面
d 測定基準長さ
図131−二つの平面の交線と第三の面との
平行度誤差の測定
図132−二つの平面の交線とそれらと交差する
第三の面との平行度誤差の測定
12.3.2.9 二つの面の交線の平行度
この測定は,12.3.2.6と同様に行う。
測定器の測定子を一方の交線を形成する面に沿って滑るVブロックに当てる。測定は,互いに直角な2
平面について行わなければならない(図133参照)。
1
d
2
2
2
2
2
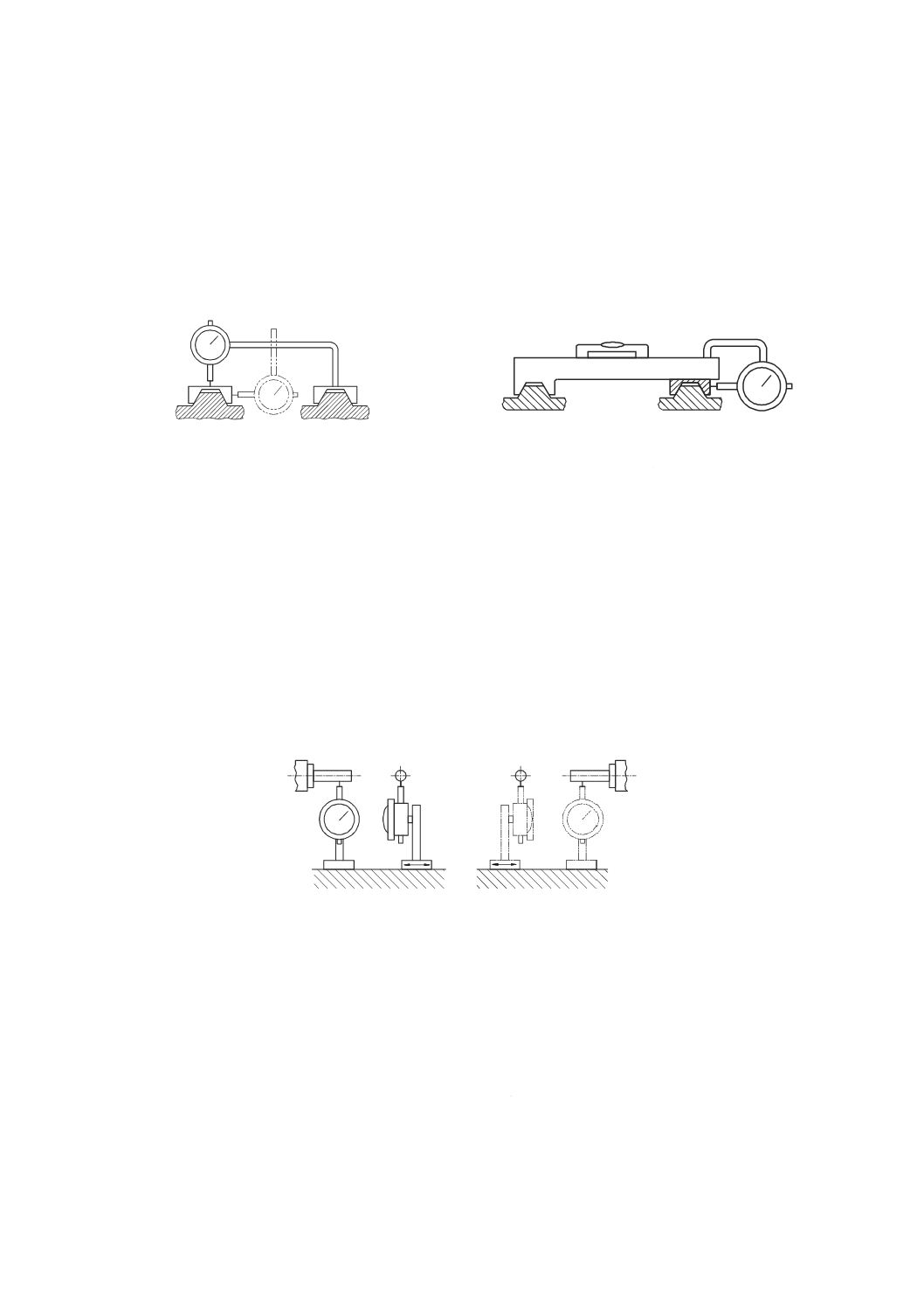
93
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この方法は,測定器を剛性の高い取付具に取り付ける必要があり,二つの交線が互いに近い場合だけに
適用できる。測定装置の剛性を上げるために,図134に示すように垂直面における平行度の測定の場合に
は,精密水準器を用いるのが望ましい。ただし,図133及び図134に示した二つの測定方法では,異なる
測定結果が得られる可能性がある。
測定領域内で工作機械の構成要素と干渉するために,測定対象の平面又は直線の直接測定が困難な場合
には,例えば,精密水準器で決まる水平面を基準平面としてもよい。
図133−二つの平面の交線の平行度誤差測定
(変位計を用いた測定)
図134−二つの平面の交線の平行度誤差測定
(垂直方向に水準器及び水平方向に変位計を用
いた測定)
12.3.3
二つの軸の等距離度
12.3.3.1 一般
等距離度は,二つの軸を含む平面と基準面との平行度と同じである。
一つの面と二つの軸又は旋回軸との等距離度の測定は,実際には平行度の測定である(12.3.2.4参照)。
まず二つの軸が基準面と平行であることを確認し,次に軸を代表する二つの円筒がこの基準面から同じ距
離にあることを同じ変位計を使って確認するのが望ましい(図135参照)。
二つの円筒が異なるときは,測定断面の半径の差を考慮するのが望ましい。
図135−二つの軸の等距離度の測定
12.3.3.2 二つの軸とその一つの軸の旋回面との等距離度(特別な場合)
一つの軸を搭載する部品の旋回面を接近させることができなくて,かつ,測定器を旋回面上で移動させ
ることができない場合には,旋回面に平行な補助平面を設ける必要がある(図136参照)。
精密水準器を補助平面上に,できれば直交する2方向に定置し,構成要素の旋回運動によってその水準
器に偏差を生じないようにこの補助平面を設定し,固定することが望ましい。次に,軸の等距離度は,(軸
の中央位置及びその両端の位置で)固定軸の測定と同様に補助平面に対して測定する。
水平又は傾斜した補助平面のいずれかを用いる場合には,旋回したときに変位計が異常な変位を起こさ
ずに元の位置に戻るように変位計を固定するのが望ましい。
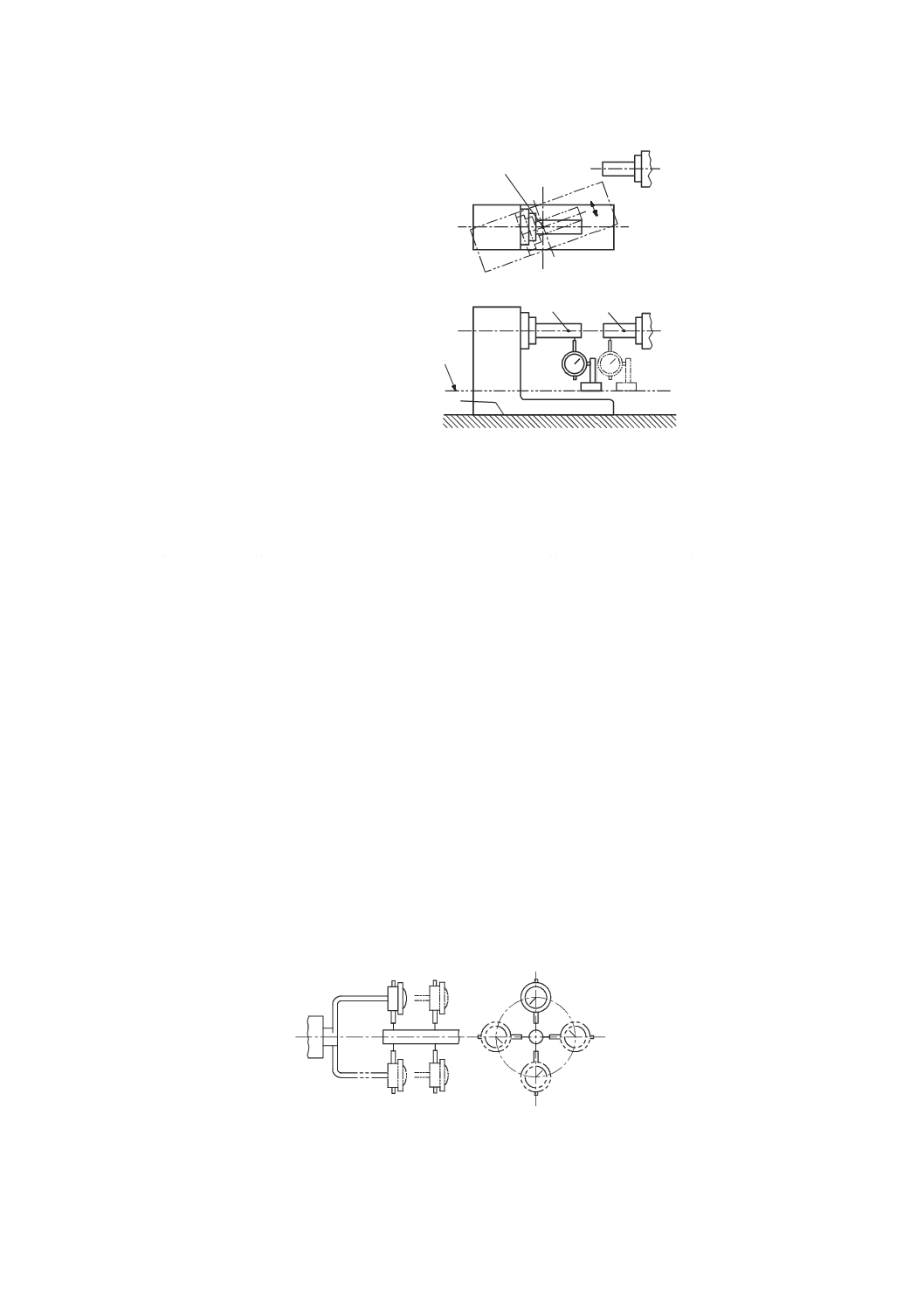
94
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 第一の軸
2 第二の軸
3 旋回面
4 補助平面
5 旋回軸
図136−軸を代表する二つのテストバーと一つの軸の旋回面との等距離度の測定
12.3.4
同軸度
一方の軸に固定した変位計をテストバーの回りに回転させる必要がある場合には,変位計は,最小限の
遊びで回転する中空円筒に取り付けるのが望ましい。この中空円筒は,読みがその円筒の遊びの影響を受
けないような十分な長さのものを使用するのがよい(図137参照)。
変位計を取付具に取り付け,一方の軸の回りで360°回転させる。変位計の測定子は,測定対象である
もう一方の軸を代表する円筒の断面Aに当てる(図137参照)。読みの変化は,同軸度の偏差の2倍を表
す。測定のために選んだ断面Aだけでは,二つの軸が交わる場合があるので,測定は,もう一つの断面B
でも行わなければならない。
所定の二つの平面上で誤差を求める場合(例えば,図137の平面H及び平面V)には,それらの二つの
平面内の偏差を別々に記録しなければならない。
特に水平軸の場合には,剛性の高い取付具が必要である。高精度な測定が必要な場合には,取付具のた
わみの影響をなくすために180°離して取り付けた二つの測定器で同時に測定しなければならない。その
代わりとして使用する変位計の質量の2倍を取り付けても,たわみを無視できる取付具を使用しなければ
ならない。
この測定では,軽量の変位計を使用する。回転に伴って,測定の方向が重力の方向に関係して変化する
ので,測定器の重力に対する感度を考慮しなければならない。
図137−2軸間の同軸度の測定
1
2
3
4
5
A
B
V
H
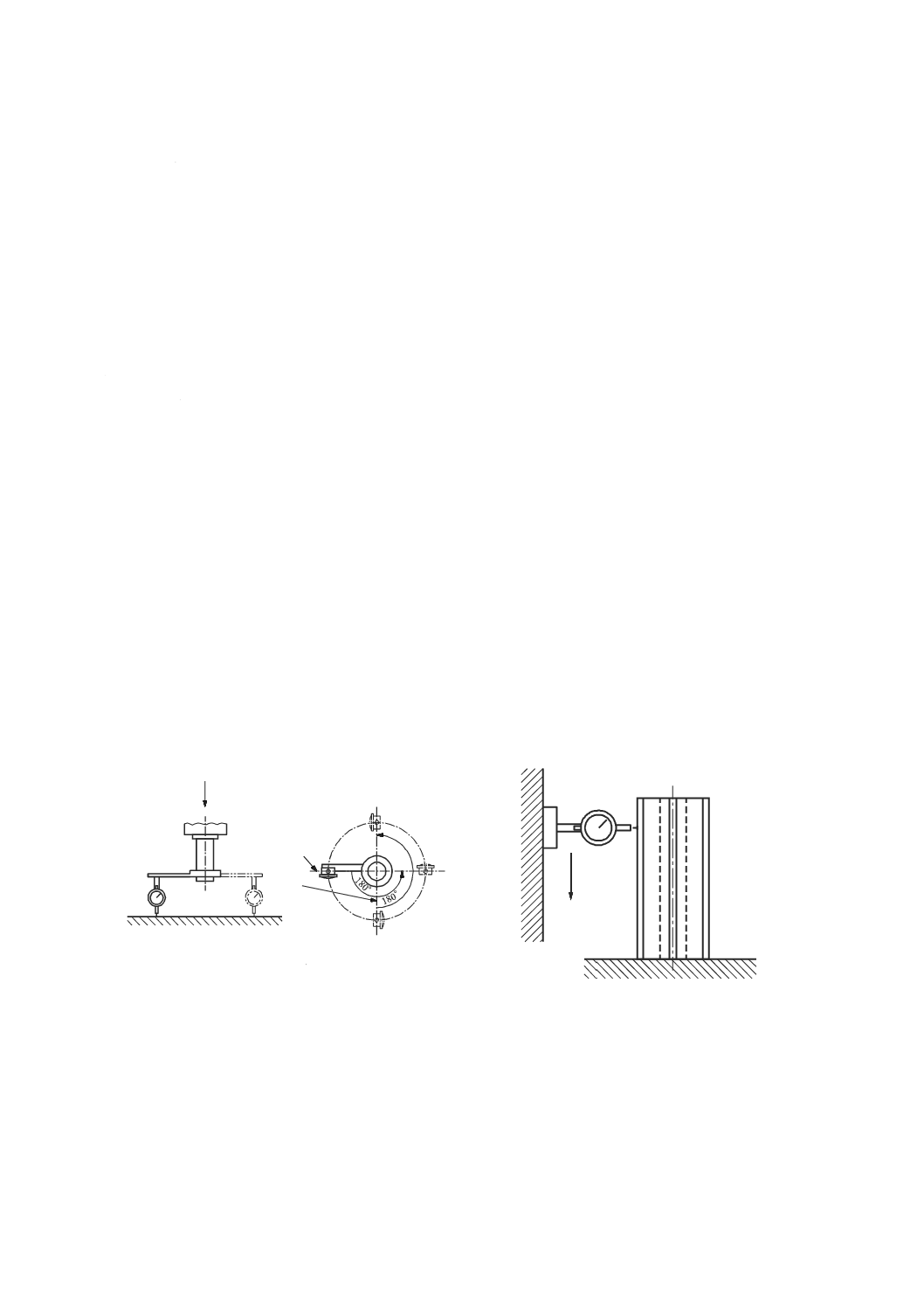
95
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
12.4
直線と平面との直角度誤差
12.4.1
一般
直進軸又は回転軸に関係する直角度誤差は,角度で表し,機能面に対する直角度誤差は,距離で表す。
直角度誤差の測定は,実際には平行度誤差の測定になる。一般に,次のように測定する。
回転軸については,次の方法を用いてよい。変位計を取り付けたアームを主軸に固定し,変位計の測定
子を回転軸に平行にする。主軸を回転させると,変位計は回転軸に直角な平面内で円を描く。この変位計
の描く円を含む平面と測定対象の平面との平行度誤差は,変位計の測定子を測定対象の平面上で移動させ
ることによって測定できる。
この誤差は,測定器の回転直径に対する値として表示する(図138参照)。
a) 測定対象の平面が規定されていない場合には,変位計を360°振り回し,読みの最大差を求める。
b) 測定対象の平面が規定されている場合(例えば,平面1及び平面2)は,180°離れた2位置で変位計
の読みの差を,それぞれの平面について記録するのが望ましい。
直角定規を用いる場合には,反転法(直角定規の誤差を相殺するために,直角定規を180°回転させる。)
を適用するのが望ましい。
測定を不正確にする可能性がある主軸の軸方向誤差運動の影響を除くために,二つの長さの等しい取付
具にそれぞれ180°離して変位計を取り付け,変位計を同じ接触点で0に合わせて,それらの読みの平均
を求めてもよい。
この測定は,一つの変位計だけを用いて行ってもよい。その場合には,最初の測定を行った後に,変位
計を主軸に対して180°移動させ,この測定を繰り返す。
12.4.2
互いに直角な二つの面
円筒スコヤを一方の面上に立て(図139参照),変位計は,他方の面に沿って移動させ,一定の間隔で読
みを取る。次に,円筒スコヤを180°回して同様の測定を行い,読みを取る。それぞれの位置における読
みから平均値を求める。
1 平面1 2 平面2
図138−平面と回転軸との直角度誤差の測定
図139−二面間の直角度誤差の測定
12.4.3
互いに直角な二つの固定軸
適切な底面をもった直角定規を,二つの軸のうちの一方を代表する円筒上に定置する(図140参照)。直
角定規の使用面ともう一つの軸との平行度は,平行度の測定に規定された方法によって測定する(12.3.2.4
参照)。
12.4.4
互いに直角な固定軸と平面
1
2
A
A
X
X
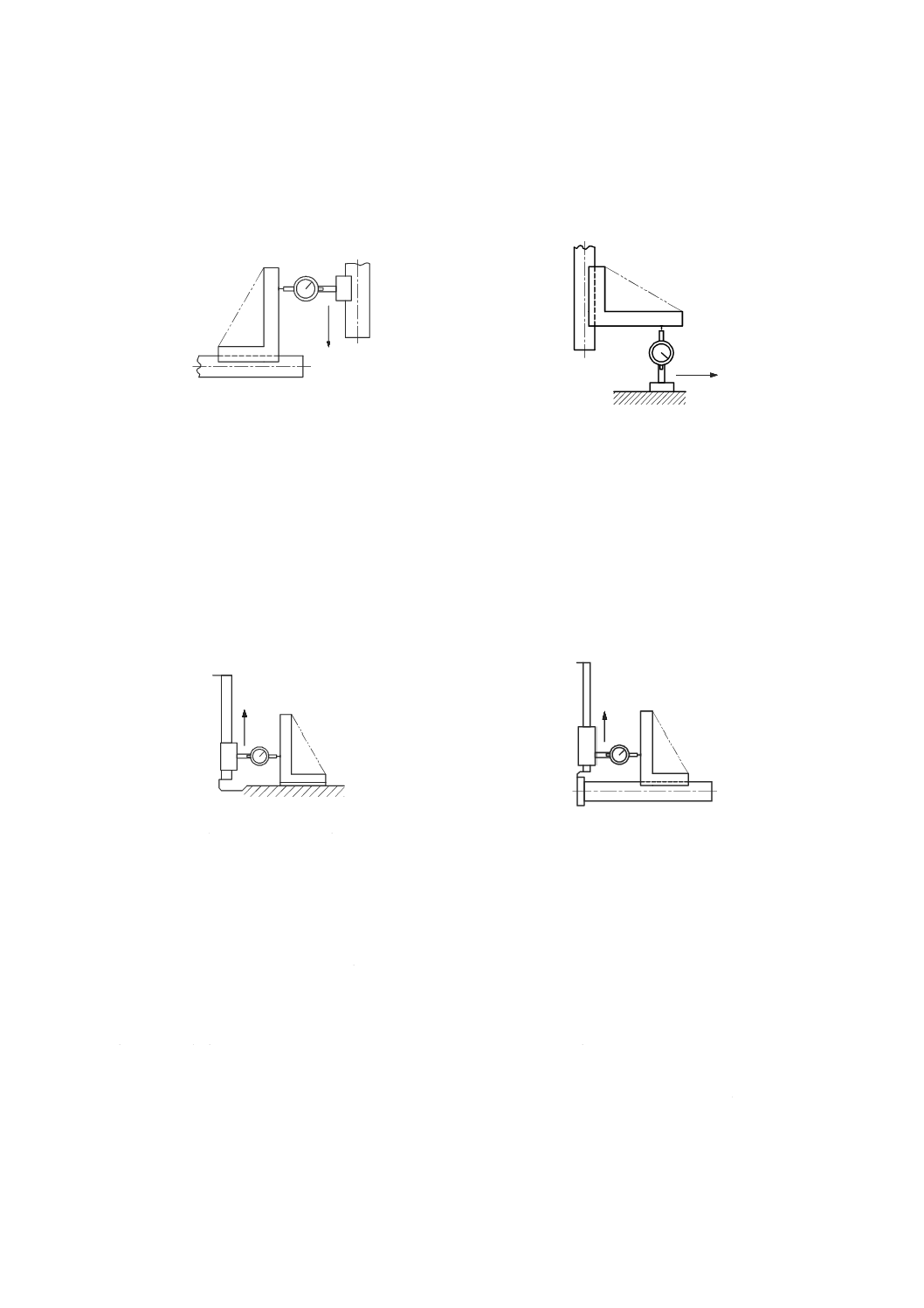
96
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
適切な底面をもった直角定規を,軸を代表する円筒に当てる(図141参照)。
直角定規の使用面と平面との平行度は,平行度の測定に規定された方法によって,軸に直角な2方向に
ついて測定する(12.3.2.2参照)。
図140−二つの固定軸間の直角度誤差の測定
図141−固定軸と平面との直角度誤差の測定
12.4.5
直進軸と平面との直角度誤差
直角定規を平面に定置する(図142参照)。運動と直角定規の使用面との平行度は,12.3.2.5.2に従って
垂直な2方向で測定する。
12.4.6
直進軸と固定軸との直角度誤差
適切な底面をもった直角定規を,軸を代表する円筒上に定置する(図143参照)。運動と直角定規の使用
面との平行度の測定は,10.1.3に従って行う。
図142−直進軸と平面との直角度誤差の測定
図143−直進軸と固定軸との直角度誤差の測定
12.4.7
回転軸と固定軸との直角度
変位計を,回転軸を代表するテストバーに固定した取付具に取り付け,その測定子をもう一方の軸を代
表する円筒上の2点A及びBに当てる(図144参照)。読みの変化は,距離ABとの関係で表す。
第二の軸も回転軸の場合は,平行度の測定(12.4.1参照)に規定する方法を用いて,第二の軸を代表す
る円筒を測定面内の振れの平均値を示すまで回す。
12.4.8
回転軸と平面との直角度
変位計を回転軸に取り付けた取付具に取り付け,12.4.1に従って測定する。
12.4.9
回転軸と二つの平面の交線との直角度
変位計を回転軸に取り付けた取付具に取り付け,測定子を二つの交差面の上に載せたVブロックに当て
る。回転軸を半回転させて,Vブロックの同じ位置に測定子が当たるように,Vブロックを移動させる(図
145参照)。
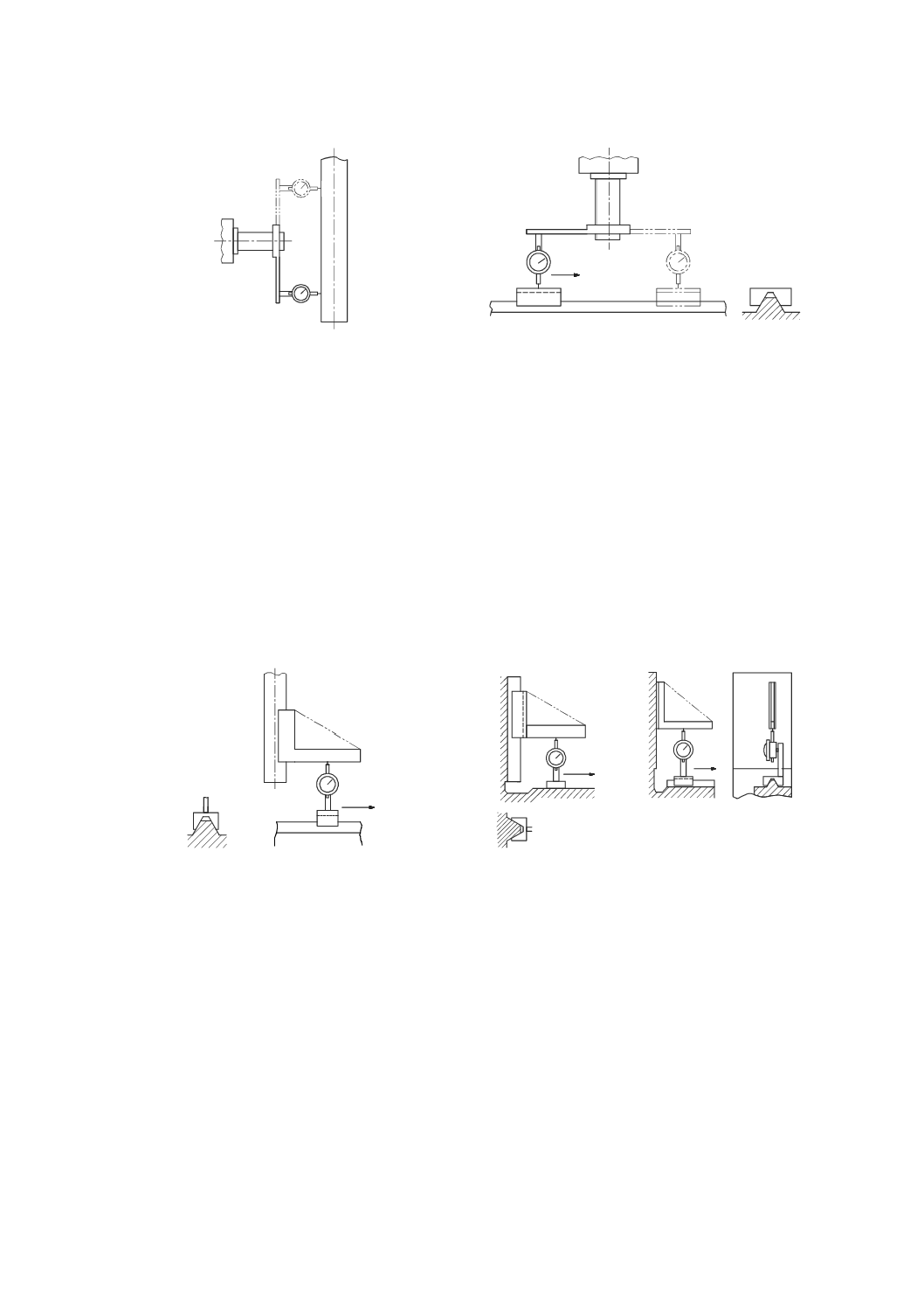
97
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図144−回転軸と固定軸との直角度誤差の測定
図145−回転軸と二つの平面の交線との
直角度誤差の測定
12.4.10
二つの平面の交線と固定軸との直角度
適切な底面をもった直角定規を,軸を代表する円筒面に当てる(図146参照)。
直角定規の使用面と交線との平行度を,平行度の測定(12.3.2.6参照)に規定する方法によって測定する。
12.4.11
二つの平面の交線と面との直角度
直角定規及び/又は変位計を,交差する平面上に載るように適切な底面をもった台に取り付ける(図147
参照)。
直角定規の使用面と第三の面又は交線との平行度は,平行度の測定(12.3.2.6又は12.3.2.8参照)に規定
された方法によって測定してもよい。測定は,できる限り二つの直交する面内で行う。
図146−固定軸と2平面の交線との
直角度誤差の測定
図147−二つの平面の交線と面との
直角度誤差の測定
12.4.12
二つの平面の交線と交線との直角度
適切な底面をもった直角定規を一方の交線上に置く。直角定規の使用面と第二の交線との平行度は,平
行度の測定(12.3.2.8参照)に規定された方法によって測定する。
測定対象となる面及び線の測定が,それらの間隔,又は構成要素による干渉のため直接できない場合に
は,測定は,基準平面に対して,例えば,精密水準器を使って行ってもよい。
12.5
回転部品の振れ
12.5.1
測定前の準備
測定を行う前に,潤滑油膜が測定中に変わらないようにし,機械の通常の運転状態の温度とみなせるよ
うに,回転軸は,十分に回転させなければならない。
A
B
98
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 回転軸の誤差運動は,ほとんどの場合,測定結果に含まれる。
12.5.2
外面
変位計の測定子を測定対象とする回転面に当てて,主軸をゆっくり回しながら読みを取る(図148参照)。
テーパ面の場合には,測定子を円すいの母線に垂直に当て,測定結果に及ぼすテーパ角度の影響を計算
する。さらに,測定する円の直径は,回転中に主軸が軸方向に変位を生じると,変化する。これは,実際
以上の振れを生じる原因になる。したがって,テーパ角度が小さいときだけに,テーパ面を振れの測定に
使うことができる。主軸の軸方向誤差運動(3.5.5参照)は,どんな場合にもあらかじめ測定しておき,そ
の軸方向誤差運動が振れの測定結果に及ぼす影響をテーパ角度に応じて計算しておく。
測定結果は,変位計の測定子に横方向から力が加わると影響されることがある。この誤差が入るのを避
けるために,測定子は,テーパ面の母線と垂直に厳密に一致させなければならない。
図148−外面の振れの測定
12.5.3
内面
変位計を円筒穴又はテーパ穴に直接当てることができない場合には,テストバーをその穴にはめる。
12.5.2に規定する方法によって,テストバーの突き出ている円筒部分を使って測定しなければならない。
しかし,テストバーの1断面だけで測定した場合は,回転軸に対する一つの円の位置だけが測定されるこ
とになる。テストバーの軸が,測定面上で回転軸と交差することもあるので,測定は,所定の距離だけ離
れた二つの断面A及びBで行うのが望ましい(図149参照)。
例えば,1回目の測定は,テストバーの口元近くで行い,2回目の測定は,そこから所定の距離だけ離れ
た位置で行うのがよい。穴にテストバーを,特にテーパ穴にはめると精度が低下する可能性があるので,
テストバーを主軸に対して90°ごとに回してはめて,少なくとも4回繰り返して測定し,読みの平均値を
求める。
いずれの場合においても,振れは,回転軸を含む垂直面内及び水平面内について測定する(図149にお
ける位置C1及びC2)。
この測定方法を適用する場合には,次の事項に留意する。
− 測定器の測定子の接線方向へのひきずりの影響を最小化するような順番で行うのが望ましい。
− テストバーを使う場合には,穴の正確な形状を知ることはできない。
円筒状の工作物を加工して,その工作物の測定から回転軸の振れを求めると,主軸の軸受の欠陥だけを
考慮することになる。
このように,実際に旋削試験を行っても,円筒又はテーパ穴の正確な形状,及び回転軸に対する穴の実
際の位置に関する情報を得られない。
99
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図149−内面の振れの測定
回転中に自動調心できる主軸(例えば,油圧を用いる静圧軸受,動圧軸受)は,通常の回転速度で運転
しているときだけ測定できる。その場合には,非接触変位計,例えば,静電容量形変位計,渦電流形変位
計,又はその他の適切な変位計を用いなければならない。
C1
C1
C1
C2
A
B
100
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
機械座標系,位置誤差及び角度誤差
A.1 一般
工作機械の運動軸の名称は,JIS B 6310による。しかし,軸の名称を定めるだけでは,機械の幾何誤差
を明らかにし,制御装置を使用してその影響を補正する目的に使用するには十分ではない。この附属書は,
工作機械の機械座標系を定義するための系統的な方法を提供し,運動軸及び関連する誤差の幾何学的関係
について明確にする。
運動軸の位置と姿勢とを一つの座標系の中に記述することで,機械の構造形態によらず,幾何精度の評
価及び/又はソフトウェアによる誤差補正に必要な運動軸間のアライメント誤差を特定することができる。
運動軸間のアライメント誤差の冗長な測定をなくすために,機械座標系の原点と向きとは,第一運動軸
(機械座標系の向きのうち,二つを定義する。)及び第二運動軸(三つ目の向きを定義する。)の向きを基に
決める。
説明をより分かりやすくするために,3軸工作機械(A.5参照),5軸工作機械(A.6参照)及び複合ター
ニングセンタ(A.7参照)の三つの例を示す。3軸工作機械の運動を完全に記述するには,五つの角度誤差
(三つの直角度及び機械座標系に対する工具の二つの角度誤差)が必要であり,5軸工作機械及び複合ター
ニングセンタを記述するには,12個の位置及び角度誤差が必要なことを示す。
A.2 直進軸の基準直線
直進軸の基準直線は,三次元座標系の中で,二つの角度誤差を用いて直線で表す。さらに,数値制御に
よる直進位置決め軸においては,図A.1に示すように,軸のゼロ点の誤差(例えば,EZ0Z)も,その軸の
誤差に含める。
XN (理想的な)X軸
YN (理想的な)Y軸
ZN (理想的な)Z軸
ZA Z軸方向へ運動する部品の実際の基準直線
EZ0Z Z軸のゼロ点の位置誤差
EA0Z Z軸のX軸回りの直角度誤差
EB0Z Z軸のY軸回りの直角度誤差
注記 一般に,工作機械の幾何精度を試験するとき,直進軸のゼロ点の位置誤差(例えば,EZ0Z)は,ゼロに設定
することができる。
図A.1−直進軸(Z軸)の位置及び角度誤差
Z
Z
Y
X
E
Z=
N
N
E
E
0
Z0Z
B0Z
A0Z
N
A
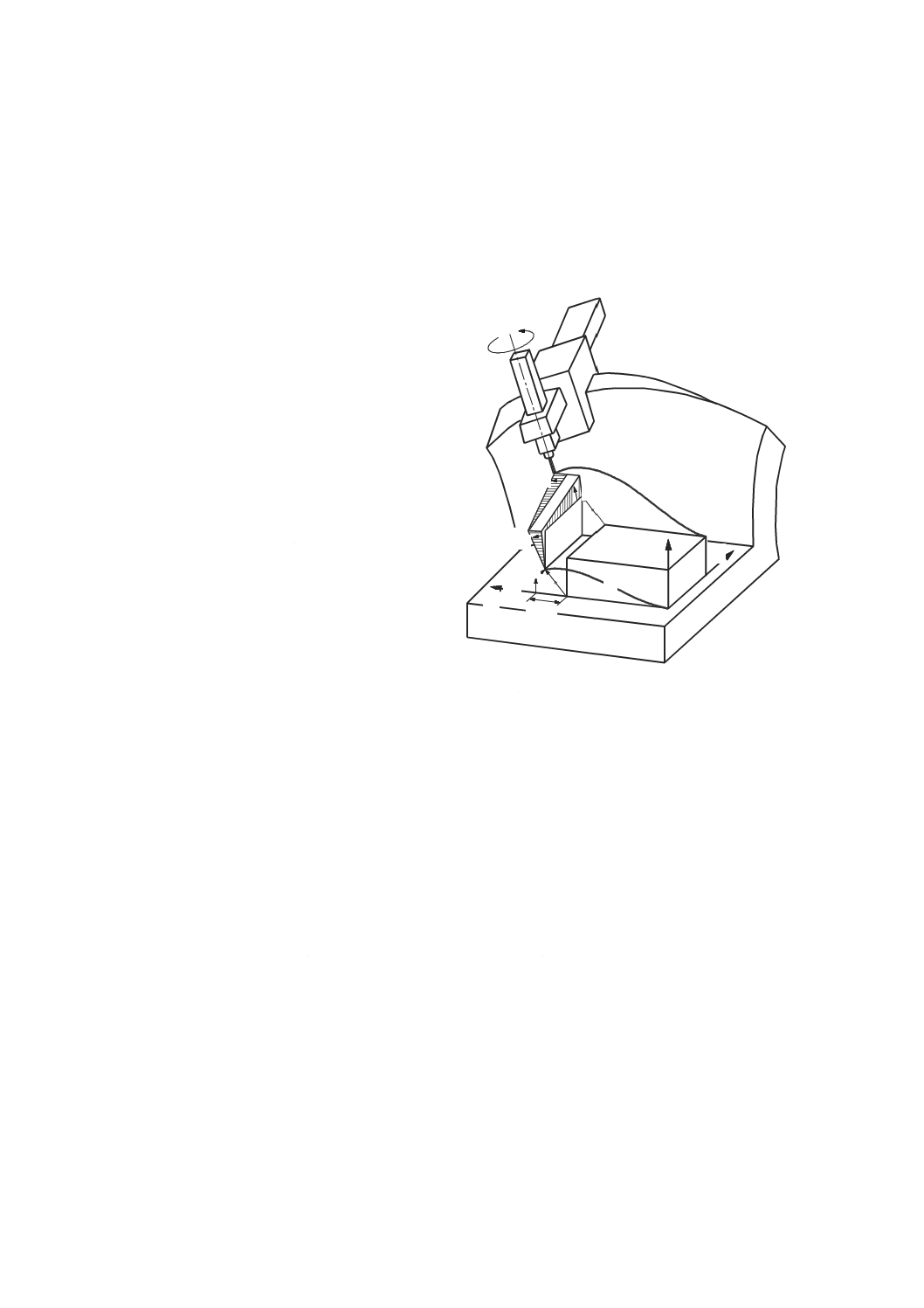
101
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
水平及び垂直方向の真直度誤差運動,並びにロール,ピッチ及びヨーの角度誤差運動によって,機械の
直進運動部品の軌跡は直線とはならず,図A.2に示す3次元空間内の軌跡“a”のようになる。この軌跡の
形状は,誤差運動の大きさ及び向きだけでなく,作業空間における軌跡の位置に関係する。例えば,軌跡
“a”は,位置を変えると図A.2に示す軌跡“b”のように変化する。直進軸の全ての誤差運動を考慮する
場合には,図A.2に示す実際の軌跡“b”は,実際の軌跡“a”から計算することができる。
X (理想的な)X軸
Y (理想的な)Y軸
Z (理想的な)Z軸
a,b (理想的な)Y軸直進運動の実際の軌跡
EAY Y軸のX軸回りの角度誤差(ピッチ)
EBY Y軸のY軸回りの角度誤差(ロール)
ECY Y軸のZ軸回りの角度誤差(ヨー)
EXY Y軸のX方向真直度誤差
EYY Y軸の位置決め誤差
EZY Y軸のZ方向真直度誤差
図A.2−Y軸に直進運動誤差がある工作機械
どの軌跡を基準軌跡とするかは,使用者が決めなければならない。この基準軌跡を用いて,直進軸の基
準直線を決める。例えば,軌跡の両端の点を結んだ直線を直進軸の基準直線と決める。この三次元空間内
の基準直線が,機械座標系の二つの角度誤差を定義する。図A.2の場合は,Y軸の基準直線を基準として,
Y軸とX軸との直角度EC0Y及びY軸とZ軸との直角度EA0Yを求める。
A.3 回転軸の基準直線
軸方向,半径方向及び傾斜方向の誤差運動をもつ回転部品の場合には,回転軸を表す基準直線は,この
回転部品の軸平均線である。
回転部品の回転軸の軸平均線は,四つのパラメータをもつ直線で表す。四つのパラメータとは,三次元
座標系において,回転軸に対して理想的な方向に直角な座標軸に沿った二つの位置誤差及び二つの角度誤
差である。回転軸が理想的には基準座標系のZ軸に平行な場合には,回転軸の二つの位置誤差及び二つの
姿勢誤差は,図13(3.5.8参照)に示すようになる。同様に,数値制御による回転位置決め軸の場合は,
回転軸のゼロ角度位置の誤差(例えば,EC0C)も回転軸の誤差に含める。
一般に,工作機械の幾何精度を試験するときには,回転軸のゼロ角度位置の誤差(例えば,EC0C)は,0
に設定することができる。
Z
BY
E
E
E
E
E
E
CY
AY
XY
ZY
X
Y
a
b
C
( )
YY
C
Z
X
Y
102
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.4 機械座標系
機械座標系は,JIS B 6310に規定する右手直交座標系とする。機械座標系の原点位置と向きとは,一般
に運動部品の運動軸を基に決める。
機械座標系の原点位置及び軸の向きは,任意に選択することができる。ただし,機械座標系の原点位置
及び向きは,工作機械運動軸の基準直線を用いて決めたほうが,工作機械の六つの位置誤差及び角度誤差
を0にすることができることから,実際的である。
まず,機械座標系の一つの座標軸と一致する基準直線をもつ第一運動軸を選び,機械座標系の二つの角
度誤差と,残りの2軸が存在する直交平面とを決める。次に,工作機械の第二運動軸を選び,その基準直
線の第一軸に垂直な平面への投影から,機械座標系の三つ目の角度誤差を決定する。最後に,三つの位置
誤差を決めて,機械座標系の原点を選ぶ。機械座標系の第一軸,第二軸及び原点の選択は,工作機械の設
計,機械的な調整の可能性,並びに機械的及び/又はソフトウェア補正の可能性による。
A.5,A.6及びA.7に示す三つの例(3軸工作機械,5軸工作機械及び複合ターニングセンタ)は,機械
座標系の選択の仕方によって,どの位置誤差と角度誤差とを測定する必要があるかを示している。
ソフトウェアによる誤差補正を行うために,使用者が定義した必要条件に基づいて最適化した機械座標
系を計算する場合がある。そのような場合には,工作機械の物理的な軸(例えば,主軸の軸線)のできる
限り近くに機械座標系の向きを合わせ,関心のある点,例えば,作業空間の中心に設定するのがよい。
A.5 3軸工作機械の機械座標系
図A.2に示す工作機械には,表A.1に示す13個の位置誤差及び角度誤差がある。
表A.1−3軸工作機械の位置誤差及び角度誤差
Y軸
X軸
Z軸
(C)主軸
−
EX0X
−
EX0(C)
EY0Y
−
−
EY0(C)
−
−
EZ0Z
−
EA0Y
−
EA0Z
EA0(C)
−
EB0X
EB0Z
EB0(C)
EC0Y
EC0X
−
−
表A.1は,機械座標系として任意の座標系を選んだときの位置誤差及び角度誤差を示す。工作機械の幾
何精度を試験するとき,直進軸ゼロ点位置は,一般に全て0にできるため,表A.1は,表A.2のように簡
略化することができる。
表A.2−簡略化した3軸工作機械の位置誤差及び角度誤差
Y軸
X軸
Z軸
(C)主軸
−
(0)
−
EX0(C)
(0)
−
−
EY0(C)
−
−
(0)
−
EA0Y
−
EA0Z
EA0(C)
−
EB0X
EB0Z
EB0(C)
EC0Y
EC0X
−
−

103
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
機械座標系の位置及び向きを工作機械の直進軸をもとに定義することで,表A.2のうちの五つの位置誤
差及び角度誤差を0(又は任意の値)に設定することができる。
次の例を考える。
− Y軸を第一軸に選んだ場合は,Y軸の基準直線は,機械座標系のY軸と一致する。このとき,EA0Y及
びEC0Yを0にできる。
− X軸を第二軸に選んだ場合は,X軸の基準直線は,機械座標系のX軸の向きを決める。このとき,EB0X
をゼロにすることができる。
− 主軸(C)の位置(主軸の軸平均線とXY面との交点)を機械座標系の原点位置と定義した場合は,EX0C
及びEX0Cを0にすることができる。
したがって,図A.2に示す工作機械に対して測定する必要のある誤差は,次の五つの角度誤差になる(表
A.3参照)。
表A.3−3軸工作機械を特徴付けるために必要な最小限の幾何誤差
Y軸
X軸
Z軸
(C)主軸
−
(0)
−
0
(0)
−
−
0
−
−
(0)
−
0
−
EA0Z
EA0(C)
−
0
EB0Z
EB0(C)
0
EC0X
−
−
工具の機能点のZ位置を,機械座標系原点のZ基準とすることができる。
注記 この手順は,ワーク座標系の定義と同様である。すなわち,基準“A”が第一軸,基準“B”が
第二軸,基準“C”がワーク座標系の原点を定義する。
3軸工作機械において,測定する必要のある幾何誤差は,次の五つの角度誤差だけとなる。
− EC0X:Y軸に対するX軸の直角度誤差
− EA0Z:Y軸に対するZ軸の直角度誤差
− EB0Z:X軸に対するZ軸の直角度誤差
− EA0(C):Y軸に対する(C)主軸の直角度誤差
− EB0(C):X軸に対する(C)主軸の直角度誤差
機械座標系を定義した後に,その機械座標系に対して機能面の位置及び姿勢(テーブルの姿勢,基準溝
の姿勢,主軸端の位置及び姿勢など)を決める。
A.6 5軸工作機械の機械座標系
図A.3に示す5軸制御工作機械では,表A.4に示す23個の位置誤差及び角度誤差がある。
104
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1 回転テーブル(C'軸)
2 テーブルサドル(X'軸)
3 ベッド
4 コラムサドル(Y軸)
5 コラム
6 ヨークサドル(Z軸)
7 ヨーク
8 旋回形主軸頭(A軸)
9 主軸(C1軸)
図A.3−5軸工作機械の構成
表A.4−5軸制御工作機械の位置誤差及び角度誤差
C軸
X軸
Y軸
Z軸
A軸
(C1)主軸
EX0C
EX0X
−
−
−
EX0(C1)
EY0C
−
EY0Y
−
EY0A
EY0(C1)
−
−
−
EZ0Z
EZ0A
−
EA0C
−
EA0Y
EA0Z
EA0A
EA0(C1)
EB0C
EB0X
−
EB0Z
EB0A
EB0(C1)
EC0C
EC0X
EC0Y
−
EC0A
−
工作機械の幾何精度を試験するとき,直進軸及び旋回軸のゼロ点位置は,一般に全て0にできるため,
表A.4は,表A.5のように簡略化できる。
表A.5−簡略化した5軸工作機械の誤差
C軸
X軸
Y軸
Z軸
A軸
(C1)主軸
EX0C
(0)
−
−
−
EX0(C1)
EY0C
−
(0)
−
EY0A
EY0(C1)
−
−
−
(0)
EZ0A
−
EA0C
−
EA0Y
EA0Z
(0)
EA0(C1)
EB0C
EB0X
−
EB0Z
EB0A
EB0(C1)
(0)
EC0X
EC0Y
−
EC0A
−
機械座標系を次のように選択する場合を考える。
− X軸を第一軸として選ぶ。
− Y軸を第二軸として選ぶ。
− 原点は,全ての軸を0に指令したときの,A軸の軸平均線とYZ平面との交点と同じ高さ(Z座標)
で,C軸の軸平均線上に選ぶ。
このように選択すると,表A.6に示す12個の幾何誤差だけが残る。
Z
Y
X
C
3
4
5
7
8
9
1
2
6
A
C
Z
Y
A
X
105
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.6−5軸工作機械を特徴付けるために必要な最小限の誤差
C軸
X軸
Y軸
Z軸
A軸
(C1)主軸
0
(0)
−
−
−
EX0(C1)
0
−
(0)
−
EY0A
EY0(C1)
−
−
−
(0)
0
−
EA0C
−
0
EA0Z
(0)
EA0(C1)
EB0C
0
−
EB0Z
EB0A
EB0(C1)
(0)
0
EC0Y
−
EC0A
−
したがって,5軸工作機械に対して測定する必要のある幾何誤差は,次の位置誤差及び角度誤差だけと
なる。
− EA0C:Y軸に対するC軸の直角度誤差
− EB0C:X軸に対するC軸の直角度誤差
− EC0Y:X軸に対するY軸の直角度誤差
− EA0Z:Y軸に対するZ軸の直角度誤差
− EB0Z:X軸に対するZ軸の直角度誤差
− EY0A:C軸に対するA軸のオフセット誤差
− EB0A:基準ZX平面内におけるX軸に対するA軸の平行度誤差
− EC0A:基準XY平面内におけるX軸に対するA軸の平行度誤差
− EX0(C1):基準XY平面内におけるC軸に対する(C1)主軸のX方向オフセット誤差
− EY0(C1):基準XY平面内におけるC軸に対する(C1)主軸のY方向オフセット誤差
− EA0(C1):Y軸に対する(C1)主軸の直角度誤差
− EB0(C1):X軸に対する(C1)主軸の直角度誤差
機械の性能を完全に評価するためには,A軸から工具の機能点までの(C1)軸(主軸)に平行な方向の距
離を測定することが望ましいことに注意する。例えば,旋回形主軸頭をもつ工作機械を,基準球と変位計
とからなる測定器又はボールバーを用いて,同時3軸運動試験のような運動試験を行うときには,この距
離を考慮することが望ましい。ただし,この誤差は,工作機械の位置誤差ではなく,工具の位置誤差であ
るとみなす。したがって,この附属書では考慮しない。
異なる機械座標系の原点,第一軸及び第二軸を選んだ場合には,幾何誤差の測定値も異なる。どのよう
に機械座標系を選ぶかにかかわらず,測定する必要のある誤差の数は,三つの位置誤差及び九つの角度誤
差の合計12個と変わらない。測定する誤差の数がこれより少ない場合には,機械の位置誤差及び角度誤差
を完全に記述していないことになる。測定する誤差の数がこれより多い場合は,冗長な誤差測定になる。
すなわち,残りの測定値の組合せで一つ以上の測定値を推定することができる。例えば,この例では,C
軸と(C1)軸(主軸)との平行度誤差は,測定する必要がない。それは,EA0C,EA0(C1),EB0C及びEB0(C1)から
計算できるからである。
注記 ある一つの軸に対して,その上に構成されているもう一つの軸の誤差運動として記載したほう
が便利な場合がある。3.6.7に示した二つの軸の直角度誤差は,相対的に表記することもできる。
例えば,図A.3に示す構造形態では,Z軸に対するA軸の軸平均線の直角度は,この“相対的”
な表記方法を使って,EB(0Z)Aと表すことができる。一方,上記の“絶対的”表記方法では,EB0A
−EB0Zとなる。この“相対的”表記方法を用いたときの最小限の誤差の導出方法については,
例えば,稲崎らの研究(参考文献[14])を参照。
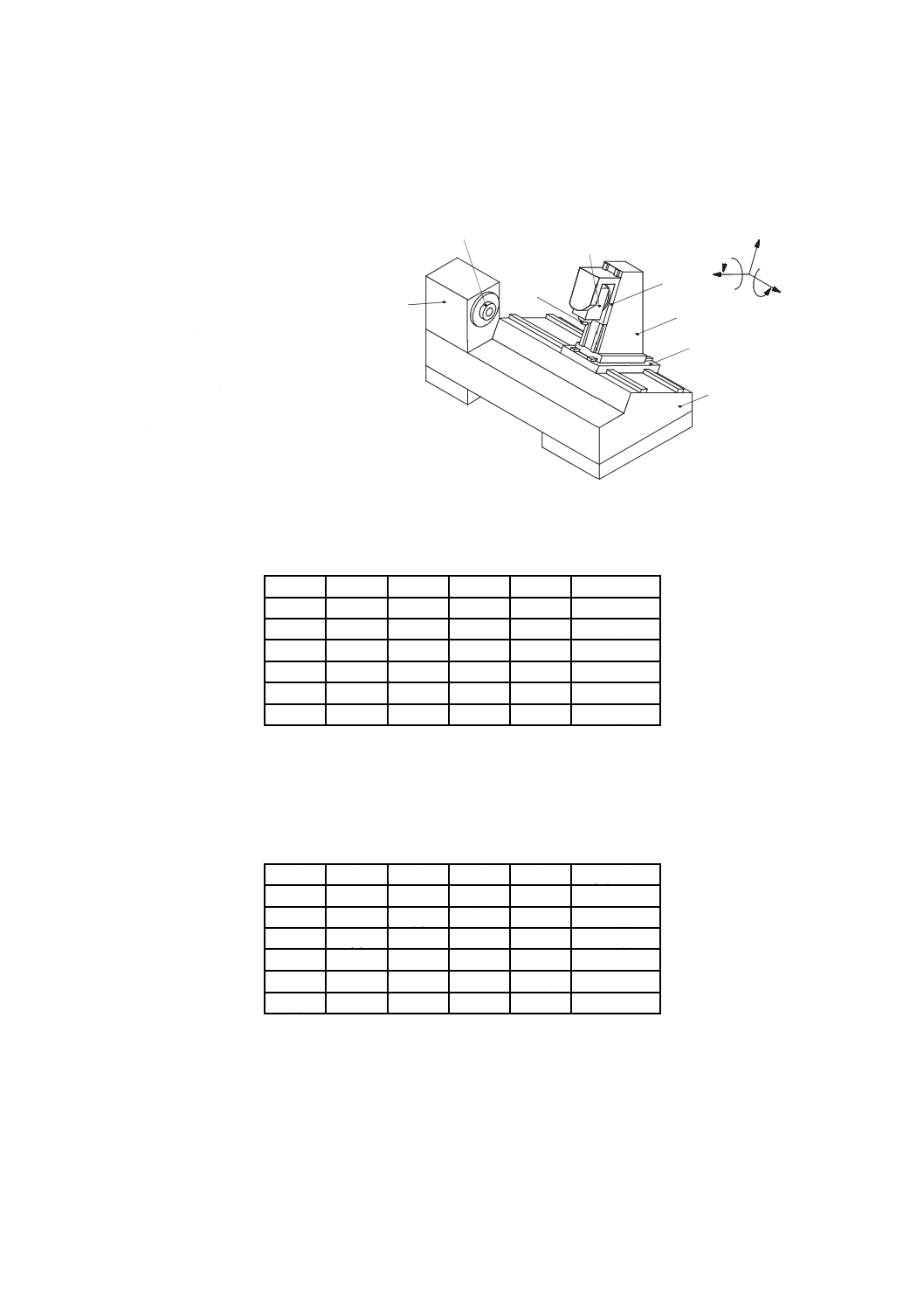
106
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.7 複合ターニングセンタの機械座標系
図A.4に示す複合ターニングセンタでは,表A.7に示す23個の位置誤差及び角度誤差がある。
1 工作主軸(C'軸)
2 工作主軸台
3 ベッド
4 コラムサドル(Z軸)
5 コラム(Y軸)
6 クロススライド(X軸)
7 旋回形主軸頭(B軸)
8 工具主軸(A軸)
図A.4−複合ターニングセンタの構造形態
表A.7−複合ターニングセンタの位置誤差及び角度誤差
C軸
Z軸
Y軸
X軸
B軸
(A)主軸
EX0C
−
−
EX0X
EX0B
−
EY0C
−
EY0Y
−
−
EY0(A)
−
EZ0Z
−
−
EZ0B
EZ0(A)
EA0C
EA0Z
EA0Y
−
EA0B
−
EB0C
EB0Z
−
EB0X
EB0B
EB0(A)
EC0C
−
EC0Y
EC0X
EC0B
EC0(A)
工作機械の幾何精度を試験するとき,直進軸及び旋回軸のゼロ点位置は,一般に全て0にできるため,
表A.7は,表A.8のように簡略化できる。
表A.8−簡略化した複合ターニングセンタの幾何誤差
C軸
Z軸
Y軸
X軸
B軸
(A)主軸
EX0C
−
−
(0)
EX0B
−
EY0C
−
(0)
−
−
EY0(A)
−
(0)
−
−
EZ0B
EZ0(A)
EA0C
EA0Z
EA0Y
−
EA0B
−
EB0C
EB0Z
−
EB0X
(0)
EB0(A)
(0)
−
EC0Y
EC0X
EC0B
EC0(A)
機械座標系を次のように選択する場合を考える。
− Z軸を第一軸として選ぶ。
− X軸を第二軸として選ぶ。
− 原点は,全ての軸を0に指令したときの,(A)主軸の軸平均線とYZ平面との交点と同じY座標で,B
軸の軸平均線上に選ぶ。
3
4
5
6
7
8
1
2
X
Z
Y
B
C
B
Y
X
Z
C

107
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
このように選択すると,表A.9に示す12個の幾何誤差だけが残る。
表A.9−複合ターニングセンタを特徴付けるために必要な最小限の幾何誤差
C軸
Z軸
Y軸
X軸
B軸
(A)主軸
EX0C
−
−
(0)
0
−
EY0C
−
(0)
−
−
0
−
(0)
−
−
0
EZ0(A)
EA0C
0
EA0Y
−
EA0B
−
EB0C
0
−
EB0X
(0)
EB0(A)
(0)
−
EC0Y
0
EC0B
EC0(A)
したがって,複合ターニングセンタに対して測定する必要のある幾何誤差は,次の位置誤差及び角度誤
差だけとなる。
− EX0C:B軸に対する基準XY平面上のC軸のX方向オフセット誤差
− EY0C:基準XY平面における(A)軸に対するC軸のX方向オフセット誤差
− EA0C:YZ平面内におけるZ軸に対するC軸の平行度誤差
− EB0C:ZX平面内におけるZ軸に対するC軸の平行度誤差
− EB0X:Z軸に対するX軸の直角度誤差
− EA0Y:Z軸に対するY軸の直角度誤差
− EC0Y:X軸に対するY軸の直角度誤差
− EA0B:Z軸に対するB軸の直角度誤差
− EC0B:X軸に対するB軸の直角度誤差
− EZ0(A):基準YZ平面内におけるB軸に対する(A)主軸のZ方向オフセット誤差
− EB0(A):Z軸に対する(A)主軸の直角度誤差
− EC0(A):基準XY平面内におけるX軸に対する(A)主軸の平行度誤差
機械の性能を完全に評価するためには,B軸から工具の先端点までの(A)軸(主軸)に平行な方向に距離
も測定することが望ましいことに注意する。例えば,旋回形主軸頭をもつ工作機械を,基準球と変位計と
からなる測定器又はボールバーを用いて,同時3軸運動試験のような運動試験を行うときには,この距離
を考慮することが望ましい。ただし,この誤差は,工作機械の位置誤差ではなく,工具の位置誤差である
とみなす。したがって,この附属書では考慮しない。
異なる機械座標系の原点,第一軸及び第二軸を選んだ場合には,幾何誤差の測定値も異なる。機械座標
系の選び方にかかわらず,測定する必要のある誤差の数は,三つの位置誤差及び九つの角度誤差の合計12
個であることは変わらない。これを示すため,異なる機械座標系の原点を選んだ例を,次に示す。
機械座標系を次のように選ぶ場合考える。
− Z軸を第一軸として選ぶ。
− X軸を第二軸として選ぶ。
− 原点は,全ての軸を0に指令したときの,B軸の軸平均線とZX平面との交点と同じZ座標で,C軸
の軸平均線上に選ぶ。
このように選択すると,表A.8に示した誤差のうち,表A.10に示す12個の誤差だけが残る。
108
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表A.10−機械座標系の原点を異なる位置に設定したときの,複合ターニングセンタを
特徴付けるために必要な最小限の幾何誤差
C軸
Z軸
Y軸
X軸
B軸
(A)主軸
0
−
−
(0)
EX0B
−
0
−
(0)
−
−
EY0(A)
−
(0)
−
−
0
EZ0(A)
EA0C
0
EA0Y
−
EA0B
−
EB0C
0
−
EB0X
(0)
EB0(A)
(0)
−
EC0Y
0
EC0B
EC0(A)
このように原点を異なる位置に設定すると,複合ターニングセンタに対して測定する必要のある幾何誤
差は,次の位置誤差及び角度誤差だけとなる。
− EA0C:YZ面内におけるZ軸に対するC軸の平行度誤差
− EB0C:ZX面内におけるZ軸に対するC軸の平行度誤差
− EB0X:Z軸に対するX軸の直角度誤差
− EA0Y:Z軸に対するY軸の直角度誤差
− EC0Y:X軸に対するY軸の直角度誤差
− EX0B:XY面内におけるC軸に対するB軸のX方向オフセット誤差
− EA0B:Z軸に対するB軸の直角度誤差
− EC0B:X軸に対するB軸の直角度誤差
− EY0(A):YZ面内におけるC軸に対する(A)主軸のY方向オフセット誤差
− EZ0(A):YZ面内におけるB軸に対する(A)主軸のZ方向オフセット誤差
− EB0(A):Z軸に対する(A)主軸の直角度誤差
− EC0(A):XY面内におけるX軸に対する(A)主軸の平行度誤差
109
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
工作物の測定
B.1
工作精度試験
B.1.1 試験
工作精度試験は,仕上げ加工によって行う。
工作精度試験を行う場合は,標準の試験片を使用することが望ましい。標準の試験片は,機種別の規格
に規定する。
工作物の数又は切削回数は,必要な精度が得られるようにすることが望ましい。必要な場合には,切削
工具の摩耗を考慮することが望ましい。
ツーリング及び取付具の条件は,必要な精度が得られるようにし,報告書にその条件を記載することが
望ましい。
B.1.2 工作精度試験における工作物の測定
工作精度試験における工作物の測定は,実施する測定の種類及び必要な測定の不確かさを考慮して選択
した測定器を用いて行うことが望ましい。
注記 測定方法は,B.2を参照。
工作物の許容値の指定及び解釈は,JIS B 0021による。
B.1.3 工作精度試験及び準静的な挙動
工作精度試験の結果を工作機械の幾何精度と関係付けるために,次の事項を考慮することが望ましい。
a) 工作機械は,低速で動かし,準静的な状態にする。すなわち,動的な影響及びサーボ(制御)の制限
のない状態にする。ただし,この条件は,工具経路と送り速度とが指定されている試験を行う場合(例
えば,5軸輪郭制御加工による工作精度試験)には,適用しない。
b) 工作機械は,ほとんどが仕上げ削りとし,切削抵抗の影響を受けないのが望ましい。
c) 工作機械は,熱負荷の影響も受けないのが望ましい。すなわち,熱的に安定した状態にするのがよい。
d) 工具及び切削条件,すなわち,送り速度,切削速度,工具形状などは,加工する工作物材料に対して
適切で,かつ,設定した値に一致することが望ましい。
e) 工作物材料は,均一であることが望ましい。すなわち,加工した表面全体の硬さ,強度などが変化し
ないものがよい。
f)
使用する工具は,摩耗していないことが望ましく,かつ,工作物を加工している間に著しい摩耗を発
生しないことが望ましい。
B.2
工作物の測定
B.2.1 一般
測定方法は,円筒部品の真円度と加工直径の一様性とを除いて,適切な方法に従うことが望ましい。三
次元測定機による測定も適用可能である。
工作物は,B.1に記載した手順に従って加工することが望ましい。
推奨する工作物上の最小測定点数は,直線の場合には10点,円の場合には15点,平面の場合には15
点,円筒の場合には25点,円すいの場合には30点とする。
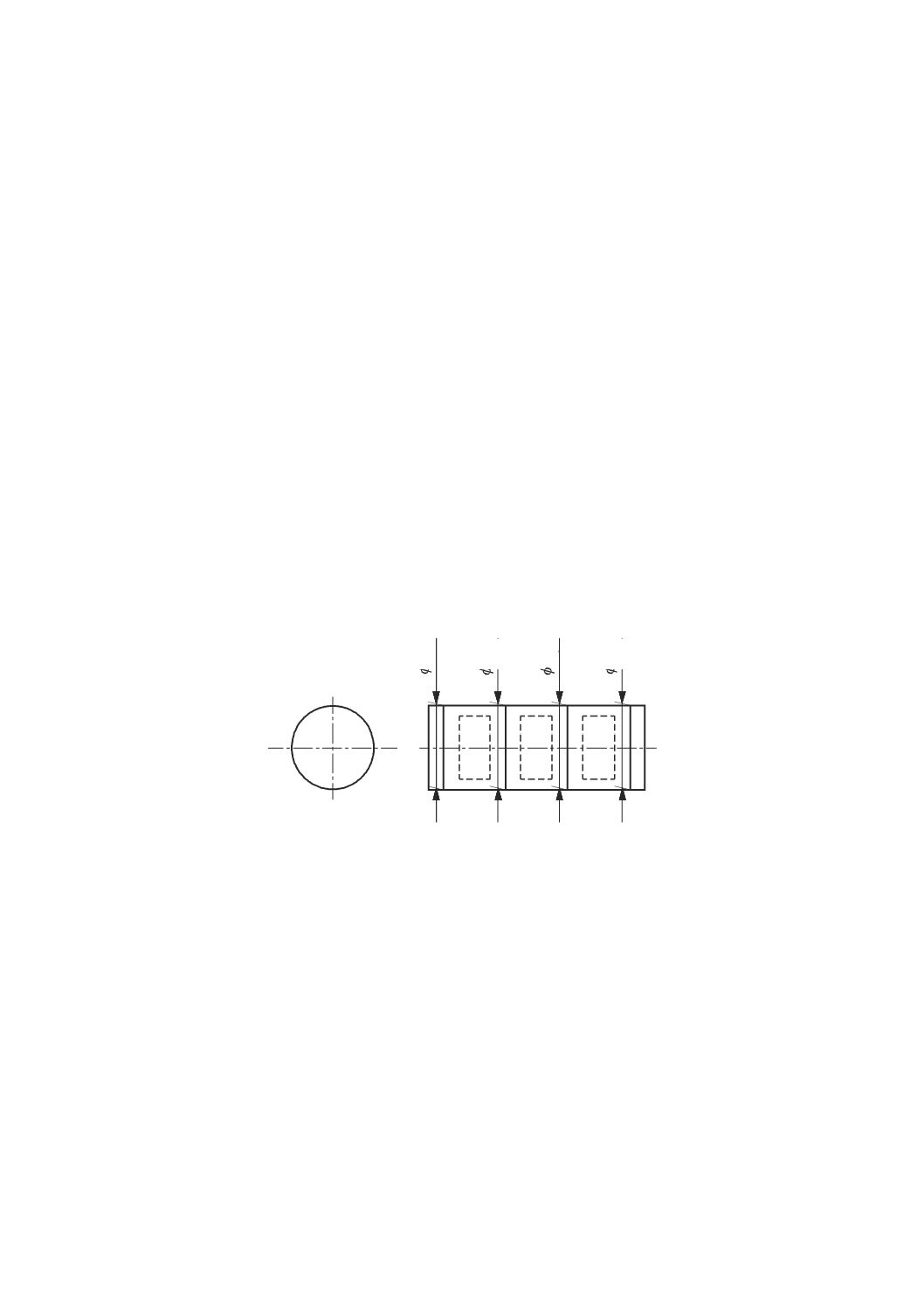
110
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
測定の基準線/基準面と加工との関係は,機械の誤差原因を特定できるように記録しておくことが望ま
しい。
B.2.2 測定の不確かさ
測定の不確かさについては,箇条5を参照。加工した工作物の幾何精度の測定に関連する不確かさは,
工作物自身又は工作機械によるものではない。
工作物の許容値を規定する場合及び規定した許容値との適合を評価する場合に,適合,不適合のもいず
れも示すことができなくなるような状況を避けるために,利用可能な測定システムの測定の不確かさを考
慮することが望ましい(4.1.1参照)。
B.2.3 加工直径の一様性
B.2.3.1 一般
機種別規格では,寸法,形状,姿勢及び振れの許容値を規定するほかに,旋盤及びターニングセンタの
検査規格では,加工した工作物直径の一様性について規定している。
工作物に沿って一定間隔で加工し,同一面内で測定した直径の最大差が許容値に適合したとき,直径は
一様であるという。
加工直径の一様性の測定方法を,次に示す。
B.2.3.2 マイクロメータ又は同等の2点接触式測定器
同一面内において,各円筒部の直径の読みを取る。
各円筒部の直径は,工作物が機械上にある間に測定することができる(図B.1参照)。
図B.1−2点接触式測定器による測定
D
1
D
2
D
3
D
4

111
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
JIS B 6191:1999との対応表
この参考は,機種別の規格で引用しているJIS B 6191:1999の箇条と,この規格に規定する箇条とを対応
させるときに用いる。
JIS B 6191:1999
JIS B 6190-1:2016
箇条・細
分箇条
項目名
箇条・細
分箇条
項目名
1.
適用範囲
箇条1
適用範囲
2.
一般事項
2.1
静的精度に関係する定義
3.1
一般
2.2
試験方法及び使用する測定器
6.3
試験装置及び測定器
2.3
許容値
箇条4
許容値
2.31
この規格で規定する許容値
4.1
一般
2.311
測定単位及び測定範囲
2.312
許容値の取扱い
4.1.1
許容値及び適合の領域に関する基準
2.32
許容値の種類
2.321
工作物及び構成要素に適用する許容値
4.2
工作機械の機能面,工作機械の部品及び試
験片に適用する許容値
2.321.1
寸法の許容値
2.321.2
形状の許容値
2.321.3
位置の許容値
2.321.4
位置の誤差を求めるときの形状誤差の影響
箇条5
測定,試験方法及び測定器の不確かさ
2.321.5
部分許容値
4.1.3
部分許容値
2.322
構成要素の運動精度の許容値
4.1
一般
2.322.1
位置決めの許容値
2.322.11
繰返し精度の許容値
2.322.2
運動軌跡の許容値
2.322.3
直進運動の相対位置の許容値
2.322.4
構成要素の運動の部分許容値
4.1.3
部分許容値
2.323
複合許容値
4.1.4
総合的又は包括的な許容値
2.324
軸,案内面などの相対角度位置に対する許容
値の符号及び位置
4.3
許容値に関連する追加制限条件
2.325
軸及び運動の従来の定義
3.2
機械座標系及び運動の名称に関する用語
3.
試験の準備
箇条6
試験の準備
3.1
試験前の機械の据付け
6.1
試験前の機械の据付け
3.11
水平出し
6.1.2
水平出し
3.2
試験前の機械の状態
6.2
試験前の機械の条件
3.21
構成要素の取外し
6.2.1
特定の部品の分解
3.22
試験前の構成要素の温度状態
6.2.2
試験前の特定の部品の温度条件
3.23
運転条件及び負荷条件
6.2.4
運転条件
4.
工作精度試験
B.1
工作精度試験
4.1
工作精度試験条件
B.1.1
試験
4.2
工作精度試験方法
B.1.2
工作精度試験における工作物の測定
5.
静的精度試験
箇条8
直進軸の幾何精度試験
5.1
一般
8.1
一般

112
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 6191:1999
JIS B 6190-1:2016
箇条・細
分箇条
項目名
箇条・細
分箇条
項目名
5.2
真直度
3.4.11
真直度
5.21
平面内又は空間内の線の真直度
3.9.2
平面内の機能線の真直度誤差
5.211
定義
5.211.1
平面内の線の真直度
5.211.2
空間内の線の真直度
5.212
測定方法
5.212.1
長さの測定による方法
12.1.2
距離の測定に基づく方法
5.212.11
直定規による方法
12.1.2.2
直定規による方法
5.212.111
垂直面内での測定
5.212.112
水平面内での測定
5.212.12
鋼線と測微顕微鏡とによる方法
12.1.2.3
鋼線と測微顕微鏡とによる方法
5.212.13
アラインメント望遠鏡による方法
12.1.2.4
アライメント望遠鏡による方法
(注記 アラインメントは,アライメントと
表記する。)
5.212.14
アラインメントレーザによる方法
5.212.15
レーザ干渉計による方法
5.212.2
角度測定による方法
12.1.3
角度の測定に基づく方法
5.212.21
精密水準器による方法
12.1.3.2
精密水準器による方法
5.212.22
オートコリメータによる方法
12.1.3.3
オートコリメータによる方法
5.212.23
レーザ干渉計による方法(角度測定)
12.1.3.4
レーザ角度干渉計による方法
5.213
許容値
箇条4
許容値
5.213.1
定義
5.213.2
許容値の決め方
5.22
構成要素の真直度
12.1
機能面の真直度誤差
5.221
定義
3.9.2
平面内の機能線の真直度誤差
5.222
測定方法
5.222.1
テーブルの基準溝又は基準面
12.1.4
テーブル基準溝又は基準面の真直度誤差
5.222.2
案内面
12.1.5
案内面の真直度誤差
5.222.21
V形案内面
12.1.6
V形案内面の真直度誤差
5.222.22
円筒案内面
12.1.7
円筒面の真直度誤差
5.222.23
一つの垂直な面
12.1.8
一つの垂直な面の真直度誤差
5.222.24
スラントベッド構造
12.1.9
スラントベッド構造における機能面の真直
度誤差
5.222.3
許容値
箇条4
許容値
5.23
直進運動
5.231
定義
3.4.3
直進軸の誤差運動
5.231.1
位置決め偏差
3.4.5
直進位置決め誤差運動
5.231.2
運動の直進偏差
3.4.4
直進軸の直進誤差運動
5.231.3
角度偏差
3.4.16
直進軸の角度誤差運動
5.232
測定方法
5.232.1
運動の直進偏差の測定方法
8.3
直進位置決め誤差運動試験
5.232.11
直定規とダイヤルゲージとによる方法
8.2.2.1
直定規と変位計とによる方法
5.232.12
測微顕微鏡と鋼線とによる方法
8.2.2.2
測微顕微鏡と鋼線とによる方法
5.232.13
アラインメント望遠鏡による方法
8.2.2.3
アライメント望遠鏡による方法
(注記 アラインメントは,アライメントと
表記する。)

113
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 6191:1999
JIS B 6190-1:2016
箇条・細
分箇条
項目名
箇条・細
分箇条
項目名
5.232.14
レーザによる方法
8.2.2.5
レーザ真直度干渉計による方法
5.232.15
角度測定による方法
5.232.2
角度偏差の測定方法
8.4
角度誤差運動試験
5.232.21
精密水準器による方法
8.4.2.1
精密水準器による方法
5.232.22
オートコリメータによる方法
8.4.2.2
オートコリメータによる方法
5.232.23
レーザによる方法
8.4.2.3
レーザ角度干渉計による方法
5.233
許容値
箇条4
許容値
5.233.1
運動の直進偏差の許容値
5.233.2
直進運動の角度偏差の許容値
5.3
平面度
5.31
定義
3.8.5
平面度
3.9.8
機能面の平面度誤差
5.32
測定方法
5.321
定盤による平面度の測定
12.2.1
定盤による平面度誤差の測定
5.321.1
定盤とダイヤルゲージとによる測定
12.2.2
定盤と変位計とによる平面度誤差の測定
5.322
直定規による平面度の測定
12.2.3
直定規による平面度誤差の測定
5.322.1
直定規の変位による直線群を用いた測定
12.2.3.1
直定規の変位による直線群を用いた測定
5.322.2
直定規,精密水準器及びダイヤルゲージによ
る測定
12.2.3.2
直定規,精密水準器及び変位計による測定
5.323
精密水準器による測定
12.2.4
精密水準器による平面度誤差の測定
5.323.1
長方形表面の測定
12.2.4.2
長方形表面の測定
5.323.2
円板平面の測定
12.2.4.3
円板平面の測定
5.324
光学的方法による平面度の測定
12.2.5
光学的方法による平面度の測定
5.324.1
オートコリメータによる測定
12.2.5.1
オートコリメータによる測定
5.324.2
走査形光学式スコヤによる測定
12.2.5.2
走査形光学式スコヤによる測定
5.324.3
アラインメントレーザによる測定
12.2.5.3
走査形アライメントレーザによる測定
5.324.4
レーザ測定システムによる測定
12.2.5.4
レーザ干渉計による測定
5.325
三次元座標測定機による測定
5.33
許容値
箇条4
許容値
5.4
平行度,等距離度及び一致度
5.41
線及び面の平行度
12.3.2
線と面との平行度
5.411
定義
3.9.3
機能線と平面との平行度誤差
3.9.4
二つの機能平面間の平行度誤差
5.412
測定方法
12.3.2
線と面との平行度
5.412.1
軸についての一般事項
12.3.2.1
一般
5.412.2
二つの面の平行度
12.3.2.2
二つの面の平行度
5.412.21
直定規とダイヤルゲージ
12.3.2.2.2
直定規と変位計とによる測定
5.412.22
精密水準器による方法
12.3.2.2.3
精密水準器による測定
5.412.3
二つの軸の平行度
12.3.2.3
二つの軸の平行度
5.412.31
二つの軸を含む平面内での平行度
12.3.2.3.2
二つの軸を含む平面内での平行度
5.412.32
第一の平面に平行な第二の平面
12.3.2.3.3
第一の平面と垂直な第二の平面内での平行
度
5.412.4
軸と面との平行度
12.3.2.4
軸と面との平行度
5.412.5
軸と二つの面の交線との平行度
12.3.2.6
軸と二つの面の交線との平行度
5.412.6
二つの面の交線と第三の面との平行度
12.3.2.8
二つの面の交線と第三の面との平行度
5.412.7
交線と交線との平行度
12.3.2.9
二つの面の交線の平行度

114
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 6191:1999
JIS B 6190-1:2016
箇条・細
分箇条
項目名
箇条・細
分箇条
項目名
5.413
許容値
箇条4
許容値
5.42
運動の平行度
10.1
運動軸の平行度
5.421
定義
3.6.1
一般
3.6.2
二つの直進軸の平行度誤差
3.6.3
二つの回転軸の平行度誤差
3.6.4
直進軸と回転軸との平行度誤差
3.6.5
直進軸と面との平行度
3.6.6
回転軸と面との平行度誤差
5.422
測定方法
5.422.1
一般事項
10.1.1
一般
5.422.2
運動の軌跡と面との平行度
12.3.2.5
直進軸と面との平行度
5.422.21
面が運動部品上にある場合
12.3.2.5.1
面が運動部品上にある場合の測定
5.422.22
面が運動部品上にない場合
12.3.2.5.2
面が運動部品上にない場合の測定
5.422.3
運転の軌跡と軸との平行度
10.1.3
直進軸と静止軸との平行度誤差
5.422.4
運動の軌跡と二つの面の交線との平行度
12.3.2.7
運動軸と二つの面の交線との平行度
5.422.5
二つの運動の軌跡の平行度
10.1.2
二つの直進軸間の平行度誤差(二つの平面
内で)
5.423
許容値
箇条4
許容値
5.43
等距離度
5.431
定義
3.7.3
二つの軸平均線の等距離度誤差
5.432
測定方法
12.3.3
二つの軸の等距離度
5.432.1
一般事項
12.3.3.1
一般
5.432.2
2軸とその1軸の旋回面との等距離度の特殊
な場合
12.3.3.2
二つの軸とその一つの軸の旋回面との等距
離度(特別な場合)
5.433
許容値
箇条4
許容値
5.44
同軸度,一致度又はアラインメント
5.441
定義
3.7.2
二つの軸平均線の同軸度誤差
3.9.9
データム直線と機能円筒との同軸度誤差
5.442
測定方法
10.2
軸平均線の同軸度誤差
12.3.4
同軸度
5.443
許容値
箇条4
許容値
5.5
直角度
5.51
直線及び面の直角度
12.4
直線と平面との直角度誤差
5.511
定義
3.9.5
二つの機能直線間の直角度誤差
3.9.6
二つの機能平面間の直角度誤差
5.512
測定方法
12.4
直線と平面との直角度誤差
5.512.1
一般事項
12.4.1
一般
5.512.2
互いに90度である二つの面
12.4.2
互いに直角な二つの面
5.512.3
二つの軸の直角度
12.4.3
互いに直角な二つの固定軸
5.512.31
二つの軸が固定軸の場合
5.512.32
軸の一つが回転軸の場合
12.4.7
回転軸と固定軸との直角度
5.512.4
軸と面との直角度
5.512.41
固定軸
12.4.4
互いに直角な固定軸と平面
5.512.42
回転軸
12.4.8
回転軸と平面との直角度
5.512.5
二つの面の交線と軸との直角度
5.512.51
固定軸
12.4.10
二つの平面の交線と固定軸との直角度

115
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 6191:1999
JIS B 6190-1:2016
箇条・細
分箇条
項目名
箇条・細
分箇条
項目名
5.512.52
回転軸
12.4.9
回転軸と二つの平面の交線との直角度
5.512.6
二つの面の交線と面との直角度
12.4.11
二つの平面の交線と面との直角度
5.512.7
交線と交線との直角度
12.4.12
二つの平面の交線と交線との直角度
5.513
許容値
箇条4
許容値
5.52
運動の直角度
5.521
定義
3.6.7
二つの直進運動の直角度誤差
3.6.8
直進軸と軸の平均線との直角度誤差
3.6.9
二つの軸平均線の直角度誤差
5.522
測定方法
10.3
運動軸間の直角度誤差
5.522.1
一般事項
10.3.1
一般
5.522.2
運動の軌跡と面との直角度
12.4.5
直進軸と平面との直角度誤差
5.522.3
運転の軌跡と軸との直角度
12.4.6
直進軸と固定軸との直角度誤差
5.522.4
互いに直角な二つの運動の軌跡
10.3.2
二つの直進軸間の直角度誤差
5.523
許容値
箇条4
許容値
5.6
回転精度
箇条9
回転軸の幾何精度試験
5.61
振れ
5.611
定義
3.9.7
一つの断面における機能面の振れ
5.611.1
直径差
5.611.2
偏心
3.5.9
被駆動軸の偏心量
5.611.3
所定の点における軸の半径振れ
3.5.10
所定の点における回転軸の半径振れ
5.611.4
所定の断面における構成要素の振れ
5.612
測定方法
12.5
回転部品の振れ
5.612.1
測定前の準備
12.5.1
測定前の準備
5.612.2
外面
12.5.2
外面
5.612.3
内面
12.5.3
内面
5.613
許容値
箇条4
許容値
5.62
周期的軸方向の動き
5.621
定義
5.621.1
最小軸方向遊び
5.621.2
周期的軸方向の動き
3.5.5
軸方向誤差運動
5.622
測定方法
9.1
JIS B 6190-7の引用
5.622.1
一般事項
5.622.2
応用
5.623
許容値
箇条4
許容値
5.63
面の振れ
9.1
JIS B 6190-7の引用
5.631
定義
5.632
測定方法
5.633
許容値
箇条4
許容値
6.
特殊な試験
6.1
分割
6.11
誤差の定義
6.111
単一分割誤差
6.112
隣接分割誤差
6.113
部分分割誤差
6.114
累積分割誤差
6.115
全分割誤差

116
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 6191:1999
JIS B 6190-1:2016
箇条・細
分箇条
項目名
箇条・細
分箇条
項目名
6.116
分割誤差の図示方法
6.12
測定方法
6.13
許容値
箇条4
許容値
6.2
ねじ送り部品の直進位置決め偏差の求め方
6.3
回転遊び
6.31
定義
6.32
測定方法(割出し装置/要素の試験)
6.33
許容値
箇条4
許容値
6.4
角度割出し装置の繰返し精度
9.1
JIS B 6190-7の引用
6.41
定義
6.42
測定方法
6.43
許容値
箇条4
許容値
6.5
軸の交差度
6.51
定義
3.7.4
二つの軸平均線の交差度誤差
6.52
測定方法
10.4
軸平均線の交差度
6.52.1
直接測定
10.4.3
直交しない軸平均線の交差度
6.52.2
間接測定
10.4.4
間接測定
6.53
許容値
箇条4
許容値
6.6
真円度
6.61
定義
3.8.2
円形誤差
6.62
試験片の測定方法
附属書B
工作物の測定
6.621
検出器回転形又は載物台回転形真円度測定
機
6.622
三次元座標測定機
6.623
輪郭の投影
6.624
Vブロックによる方法
6.63
数値制御による円運動の測定
11.3
円弧軌跡
6.631
回転形一次元変位計
11.3.4.2
回転する変位計による方法
6.632
基準円板及び二次元変位計
11.3.4.3
基準円盤と二次元変位計とによる方法
6.633
ボールバー
11.3.4.4
ボールバーによる方法
6.7
円筒度
6.71
定義
6.72
測定方法
6.721
三次元座標測定機
6.722
検出器回転形又は載物台回転形真円度測定
機
6.723
Vブロックによる方法
6.8
加工直径の一様性
B.2.3
加工直径の一様性
6.81
定義
6.82
測定方法
6.821
マイクロメータ又はこれと類似の二点式測
定器
B.2.3.2
マイクロメータ又は同等の2点接触式測定
器
6.822
ハイトゲージ
117
B 6190-1:2016 (ISO 230-1:2012)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] JIS B 6191:1999 工作機械−静的精度試験方法及び工作精度試験方法通則
[2] ISO/IEC Guide 99,International vocabulary of metrology−Basic and general concepts and associated terms
(VIM)
[3] ISO 14253-2,Geometrical product specifications (GPS)−Inspection by measurement of workpieces and
measuring equipment−Part 2: Guidance for the estimation of uncertainty in GPS measurement, in calibration
of measuring equipment and in product verification
[4] ISO 14253-3,Geometrical product specifications (GPS)−Inspection by measurement of workpieces and
measuring equipment−Part 3: Guidelines for achieving agreements on measurement uncertainty statements
[5] ISO/TS 14253-4,Geometrical product specifications (GPS)−Inspection by measurement of workpieces and
measuring equipment−Part 4: Background on functional limits and specification limits in decision rules
[6] ISO/TR 14253-6:2012,Geometrical product specifications (GPS)−Inspection by measurement of workpieces
and measuring equipment−Part 6: Generalized decision rules for the acceptance and rejection of instruments
and workpiece
[7] ISO/TR 230-8,Test code for machine tools−Part 8: Vibrations
[8] ISO/TR 230-9: 2005,Test code for machine tools−Part 9: Estimation of measurement uncertainty for machine
tool tests according to series ISO 230, basic equations
[9] ISO/TR 230-11,Test code for machine tools−Part 11: Measuring instruments suitable for machine tool
geometry tests
[10] KNAPP, W., Measurement Uncertainty and Machine Tool Testing, CIRP Annals, 51(1), 2002, pp. 459-462
[11] KNAPP, W., BRINGMANN, B., Straightness Measurements for Long Movements. Nanotechnology and
Precision Engineering 3 (2005), pp. 249-256
[12] BELL, S., A beginner's Guide to Uncertainty of Measurement. published by NPL
(see http://www.wmo.int/pages/prog/gcos/documents/gruanmanuals/UK̲NPL/mgpg11.pdf)
[13] BRYAN, J.B., The Abbé principle revisited: An updated interpretation, Precision Engineering, 1(3), 1979
[14] ESTLER, W.T., EDMUNDSON, K.L., PEGGS, G.N., PARKER, D.H., Large Scale Metrology: An Update.
CIRP Annals, 51(2), 2002, pp. 587-609
[15] 稲崎,岸浪,坂本,杉村,竹内,田中,工作機械の形状創成理論−その基礎と応用,養賢堂,東京,
(1997)