2
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
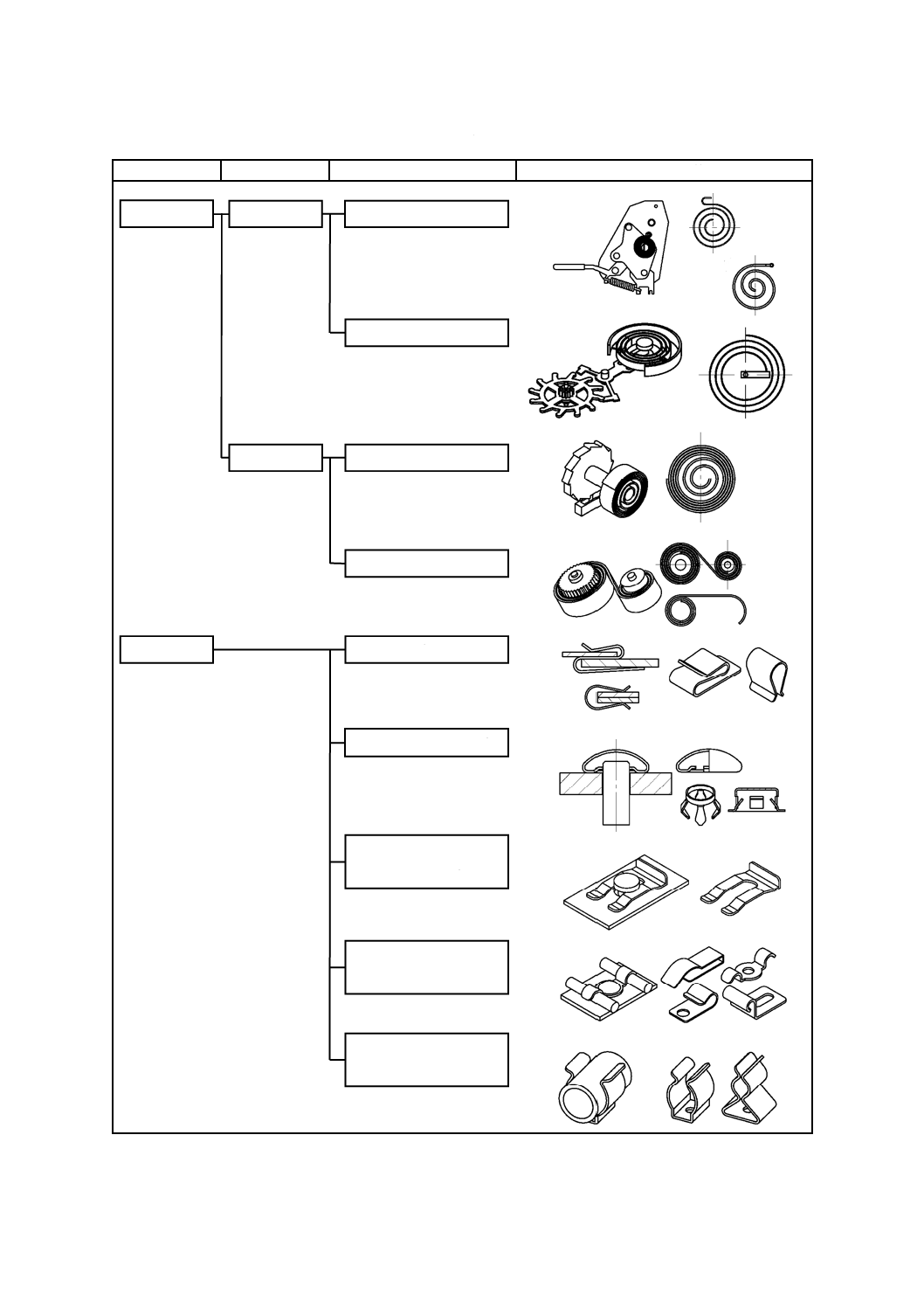
表1−薄板ばねの種類
大分類
中分類
小分類
使用例及び代表的形状
キャップスプリング
渦巻ばね
非接触形
非接触形ぜんまい
ひげぜんまい
接触形
定荷重ぜんまい
接触形ぜんまい
クリップ
バインダクリップ
シリンダロック
スプリング
ワイヤハーネス
スプリング
ロッドロック
クランプ
B 2713:2009
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 薄板ばねの種類 ················································································································ 1
5 材料······························································································································· 4
5.1 薄板ばねに用いる主な材料 ······························································································ 4
5.2 材料の特性 ··················································································································· 5
6 薄板ばねの特徴及び材料の選択 ··························································································· 8
6.1 薄板ばねの特性,種類及び特徴 ························································································ 8
6.2 材料の選択 ··················································································································· 9
7 設計計算式 ······················································································································ 9
7.1 基本設計計算式 ············································································································· 9
7.2 簡易分割形計算式(板幅変化形)····················································································· 12
7.3 典型的な形状の薄板ばねの計算式及び例············································································ 17
8 仕様の定め方 ·················································································································· 22
8.1 薄板ばねの特性 ············································································································ 22
8.2 設計応力 ····················································································································· 22
8.3 設計及び加工上の注意事項 ····························································································· 23
B 2713:2009
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,社団法人日本ばね工業会(JSMA)及び財団法
人日本規格協会(JSA)から,団体規格 (SC005:2001) を基に作成した工業標準原案を具して日本工業規格を
制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本工業規格で
ある。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格
JIS
B 2713:2009
薄板ばねの設計計算式及び仕様の定め方
The design calculating formulas and the procedures of decision of
specifications for flat springs
1
適用範囲
この規格は,一般に使用する金属製薄板ばね(以下,薄板ばねという。)の設計計算式及び仕様の定め方
について規定する。ただし,他の日本工業規格の製品規格(皿ばね,止め輪,ばね座金及びスプリングピ
ン)のばねは除く。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0103 ばね用語
JIS B 2709 ねじりコイルばね−設計・性能試験方法
JIS G 3311 みがき特殊帯鋼
JIS G 4313 ばね用ステンレス鋼帯
JIS G 4802 ばね用冷間圧延鋼帯
JIS H 3130 ばね用のベリリウム銅,チタン銅,りん青銅,ニッケル−すず銅及び洋白の板並びに条
ISO 18265 Metallic materials-Conversion of hardness values
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 0103による。
4
薄板ばねの種類
薄板ばねの種類は,表1による。

2
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−薄板ばねの種類
大分類
中分類
小分類
使用例及び代表的形状
キャップスプリング
渦巻ばね
非接触形
非接触形ぜんまい
ひげぜんまい
接触形
定荷重ぜんまい
接触形ぜんまい
クリップ
バインダクリップ
シリンダロック
スプリング
ワイヤハーネス
スプリング
ロッドロック
クランプ
3
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
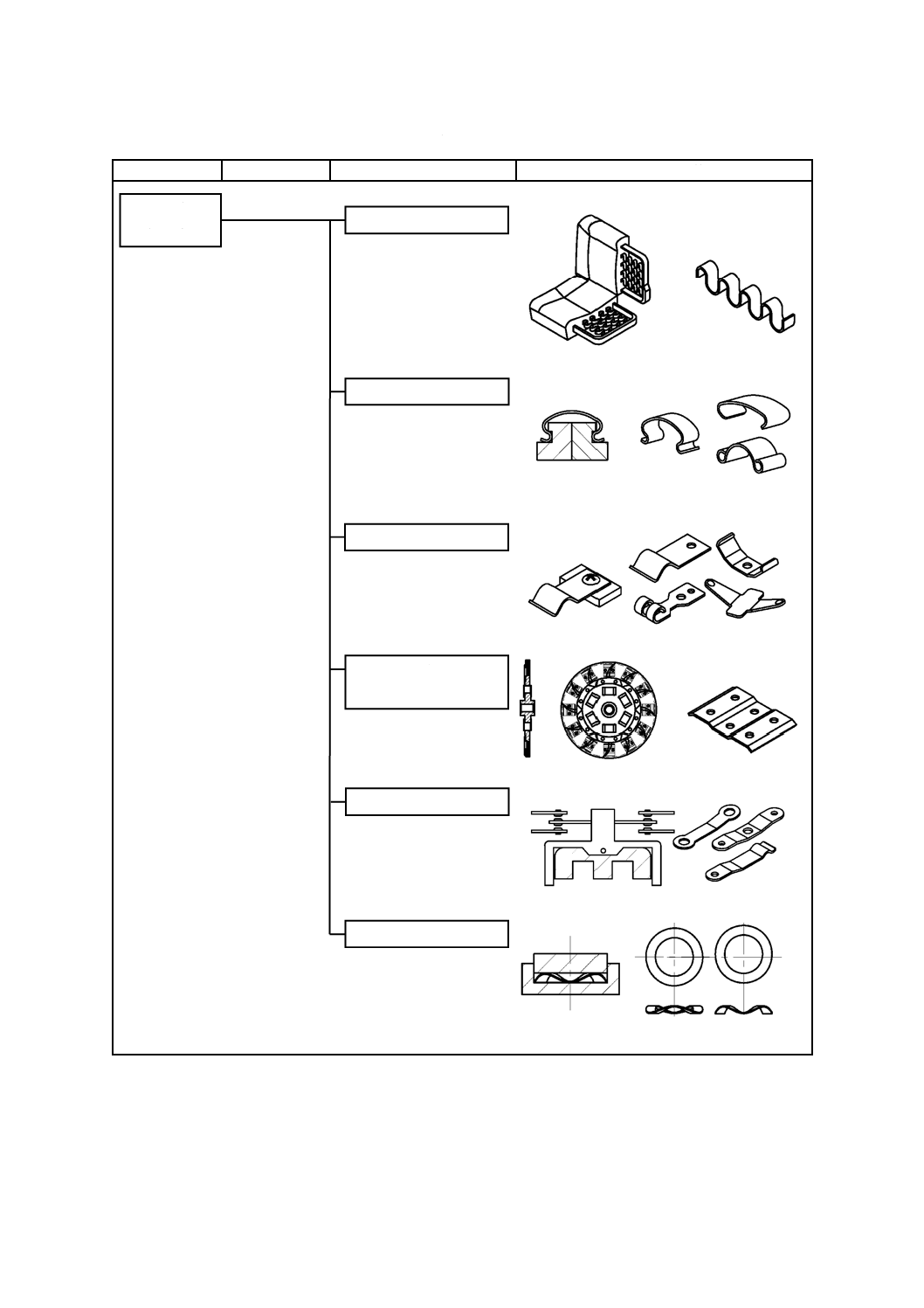
表1−薄板ばねの種類(続き)
大分類
中分類
小分類
使用例及び代表的形状
接点用ばね
その他各種
成形ばね
ジグザグばね
円弧状ばね
平たん(坦)薄板ばね
クラッチフィン
スプリング
波形ばね(3山以上)
4
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
材料
5.1
薄板ばねに用いる主な材料
薄板ばねに使用する主な材料は,鉄鋼材料と非鉄金属材料とに大別できる。これらは,更に薄板ばねと
して必要な強度を得る手段によって,次の三つに分類できる。
a) 焼入焼戻し,オーステンパなどの熱処理によって強度を得るもの。
b) 冷間圧延によって強度を得るもの。
c) 冷間圧延と熱処理との組合せによって強度を得るもの。
薄板ばね用材料として,JIS G 3311,JIS G 4313,JIS G 4802及びJIS H 3130の規格がある。薄板ばねに
用いる主な材料とその特徴を,表2に示す。
表2−薄板ばねに用いる主な材料
熱処理の有無
材料規格
代表鋼種
特徴
鉄
鋼
材
料
熱処理によっ
て強度を得る
材料
JIS G 3311
S60CM,S70CM及びSK85M
ばね加工後熱処理(焼入焼戻し,オ
ーステンパなど)によって強度を得
る。複雑な形状の加工が可能。
JIS G 4802のうち調質
の記号A及びRのもの
S60C-CSPA及びS60C-CSPR
JIS G 4802のうち調質
記号H及びBのもの
S60C-CSPH及びS60C-CSPB
S70C-CSPH及びS70C-CSPB
SK85-CSPH及びSK85-CSPB
材料の状態で熱処理を行い強度を得
ているため,複雑な加工に適さない。
JIS G 4313
SUS420J2-CSP(調質記号O) マルテンサイト系:ばね加工後,焼
入焼戻しによって強度を得る。すべ
ての状態で磁性をもつ。
冷間圧延によ
って強度を得
る材料
SUS301-CSP(調質記号1/2H,
3/4H,H,EH及びSEH)及び
SUS304-CSP(調質記号1/2H,
3/4H及びH)
オーステナイト系:調質の記号を指
定することで硬さ指定可能。耐食性
がよい。硬さによっては複雑な形状
に加工可能。固溶化熱処理状態では
非磁性,強加工によって弱い磁性を
もつ。同一硬さではSUS304より
SUS301のほうが成形性がよい。
冷間圧延と熱
処理とによっ
て強度を得る
材料
SUS631-CSP(調質記号O,
1/2H,3/4H及びH)及び
SUS632J1-CSP(調質記号1/2H
及び3/4H)
析出硬化系:ばね加工後,析出硬化
処理を施し強度を得る。調質の記号
を指定することで硬さ指定可能。
SUS301及びSUS304よりも高価。析
出硬化後は強磁性をもつ。
非
鉄
金
属
材
料
冷間圧延と熱
処理とによっ
て強度を得る
材料
JIS H 3130
ばね用ベリリウム銅及びばね
用低ベリリウム銅
C1700P(板),C1700R(条),
C1720P(板),C1720R(条),
C1751P(板),C1751R(条)(質
別 O,1/2H及びH)
ばね加工後に時効硬化処理を施し強
度を得る。質別を指定することで硬
さ指定可能。非鉄金属の中では強度
最大。耐食性がよい。複雑形状に成
形可能。非常に高価である。
ばね用りん青銅
C5210P(板)及びC5210R(条)
(質別1/2H,H,EH,SH及び
ESH)
非鉄金属材料では,最も代表的な材
料。質別を指定することで硬さ指定
可能。耐食性がよい。硬さによって
は複雑な加工が可能。
ばね用洋白C7701P(板)及び
C7701R(条)(質別1/2H,H,
EH及びSH)
りん青銅と比較すると導電率は劣る
が,耐食性はよい。
5
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2
材料の特性
薄板ばねに用いる主な材料の特性値は,次による。
a) 縦弾性係数 曲げ,引張り及び圧縮にかかわる縦弾性係数は,表3を参照する。
表3−縦弾性係数
単位 MPa
材料
縦弾性係数E
鉄鋼材料a)
2.06×105
ばね用ステンレス鋼
SUS301-CSP
SUS304-CSP
1.86×105
SUS420J2-CSP
SUS631-CSP
SUS632J1-CSP
1.96×105
ばね用ベリリウム銅
1.27×105
ばね用りん青銅
0.98×105
ばね用洋白
1.08×105
注a) ステンレス鋼を除く。
b) 密度 薄板ばねの質量計算などに用いる主な材料の密度は,表4による。
表4−主な材料の密度
単位 kg/mm3
材料
密度
鉄鋼材料a)
7.85×10−6
ばね用ステンレス鋼
7.90×10−6
ばね用ベリリウム銅
8.20×10−6
ばね用りん青銅
8.80×10−6
ばね用洋白
8.70×10−6
注a) ステンレス鋼を除く。
c) 硬さ 薄板ばねの設計では,材料の硬さから引張強さを換算して寿命を予測する場合がある。主な材
料の硬さは,表5〜表9による。
表5−ばね用冷間圧延鋼帯の調質の記号H及びBの硬さ(中心値)の指定してよい範囲
種類の記号
H(ビッカース硬さHV)
B(ビッカース硬さHV)
S60C-CSP
350〜500
360〜440
S70C-CSP
350〜550
−
SK85-CSP
350〜600
−
硬さの許容差は,±25HVとする。ただし,鋼帯1条内のばらつきは,30HV以内とする。
6
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表6−ばね用ステンレス鋼帯の硬さ
種類の記号
調質の
記号
冷間圧延又は固溶化熱処理
若しくは焼きなまし状態
析出硬化熱処理状態
ビッカース硬さ HV
熱処理記号
ビッカース硬さ HV
SUS301-CSP
1/2H
310以上
−
−
3/4H
370以上
−
−
H
430以上
−
−
EH
490以上
−
−
SEH a)
530以上
−
−
SUS304-CSP
1/2H
250以上
−
−
3/4H
310以上
−
−
H
370以上
−
−
SUS420J2-CSP
O
247以下
−
−
SUS631-CSP
O
200以下
TH1050
RH950
345以上
392以上
1/2H
350以上
CH
380以上
3/4H
400以上
CH
450以上
H
450以上
CH
530以上
SUS632J1-CSP
1/2H
350以下
CH
400以上
3/4H
420以下
CH
480以上
注a) 調質の記号SEHは,調質の記号EH区分の範囲で,特に注文者の指定がある場合に適用する。
表7−合金番号C1700・C1720・C5210・C7701の板及び条の硬さ
合金番号
質別
記号
硬さ
厚さ mm
ビッカース硬さ HV
C1700
O
C1700 P-O
C1700 R-O
0.10以上
1.6 以下
90〜160
1/4H
C1700 P-1/4H
C1700 R-1/4H
0.10以上
1.6 以下
145〜220
1/2H
C1700 P-1/2H
C1700 R-1/2H
0.10以上
1.6 以下
180〜240
H
C1700 P-H
C1700 R-H
0.10以上
1.6 以下
210〜270
C1720
O
C1720 P-O
C1720 R-O
0.10以上
1.6 以下
90〜160
1/4H
C1720 P-1/4H
C1720 R-1/4H
0.10以上
1.6 以下
145〜220
1/2H
C1720 P-1/2H
C1720 R-1/2H
0.10以上
1.6 以下
180〜240
H
C1720 P-H
C1720 R-H
0.10以上
1.6 以下
210〜270
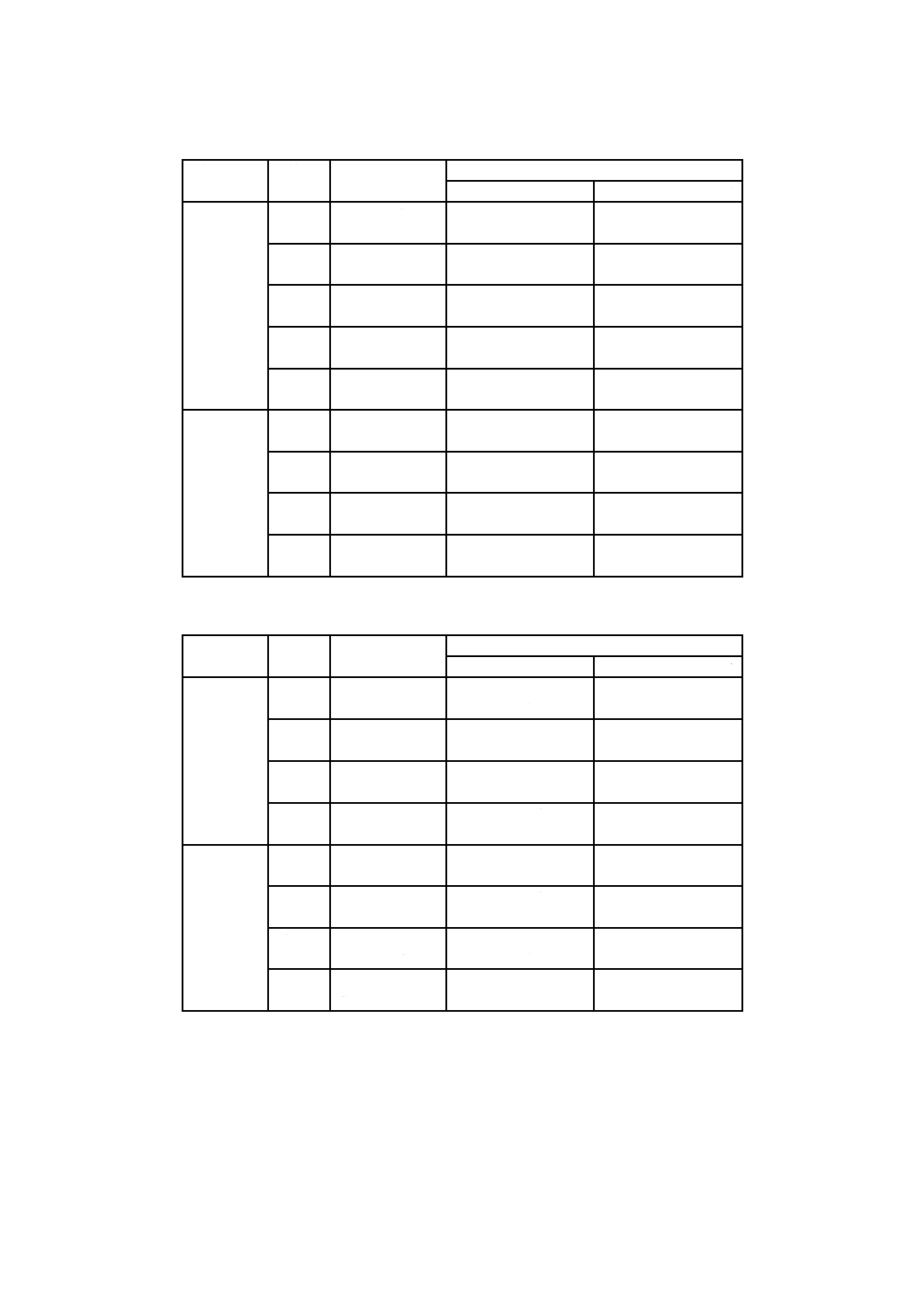
7
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表7−合金番号C1700・C1720・C5210・C7701の板及び条の硬さ(続き)
合金番号
質別
記号
硬さ
厚さ mm
ビッカース硬さ HV
C5210
1/2H
C5210 P-1/2H
C5210 R-1/2H
0.10以上
140〜205
H
C5210 P-H
C5210 R-H
0.10以上
185〜235
EH
C5210 P-EH
C5210 R-EH
0.10以上
210〜260
SH
C5210 P-SH
C5210 R-SH
0.10以上
230〜270
ESH
C5210 P-ESH
C5210 R-ESH
0.10以上
245〜285
C7701
1/2H
C7701 P-1/2H
C7701 R-1/2H
0.10以上
150〜210
H
C7701 P-H
C7701 R-H
0.10以上
180〜240
EH
C7701 P-EH
C7701 R-EH
0.10以上
210〜260
SH
C7701 P-SH
C7701 R-SH
0.10以上
230〜270
表8−合金番号C1700・C1720の板及び条の時効処理後の硬さ
合金番号
質別
記号
硬さ
厚さ mm
ビッカース硬さ HV
C1700
O
C1700 P-O
C1700 R-O
0.10以上
1.6 以下
310〜370
1/4H
C1700 P-1/4H
C1700 R-1/4H
0.10以上
1.6 以下
330〜410
1/2H
C1700 P-1/2H
C1700 R-1/2H
0.10以上
1.6 以下
345〜420
H
C1700 P-H
C1700 R-H
0.10以上
1.6 以下
360〜430
C1720
O
C1720 P-O
C1720 R-O
0.10以上
1.6 以下
325〜400
1/4H
C1720 P-1/4H
C1720 R-1/4H
0.10以上
1.6 以下
350〜430
1/2H
C1720 P-1/2H
C1720 R-1/2H
0.10以上
1.6 以下
360〜440
H
C1720 P-H
C1720 R-H
0.10以上
1.6 以下
380〜450
8
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表9−合金番号C1720・C1751の板及び条の硬さ(ミルハードン材)
合金番号
質別
記号
硬さ
厚さ mm
ビッカース硬さ HV
C1720
OM
C1720 P-OM
C1720 R-OM
0.10以上
1.6 以下
200以上
1/4HM
C1720 P-1/4HM
C1720 R-1/4HM
0.10以上
1.6 以下
210以上
1/2HM
C1720 P-1/2HM
C1720 R-1/2HM
0.10以上
1.6 以下
240以上
HM
C1720 P-HM
C1720 R-HM
0.10以上
1.6 以下
270以上
C1751
OM
C1751 P-OM
C1751 R-OM
0.10以上
1.6 以下
210〜260
HM
C1751 P-HM
C1751 R-HM
0.10以上
1.6 以下
230〜280
注記 ミルハードン材とは,製造業者が適切な冷間加工及び時効硬化処理を施し,規定
された機械的性質を付与したものをいう。
6
薄板ばねの特徴及び材料の選択
6.1
薄板ばねの特性,種類及び特徴
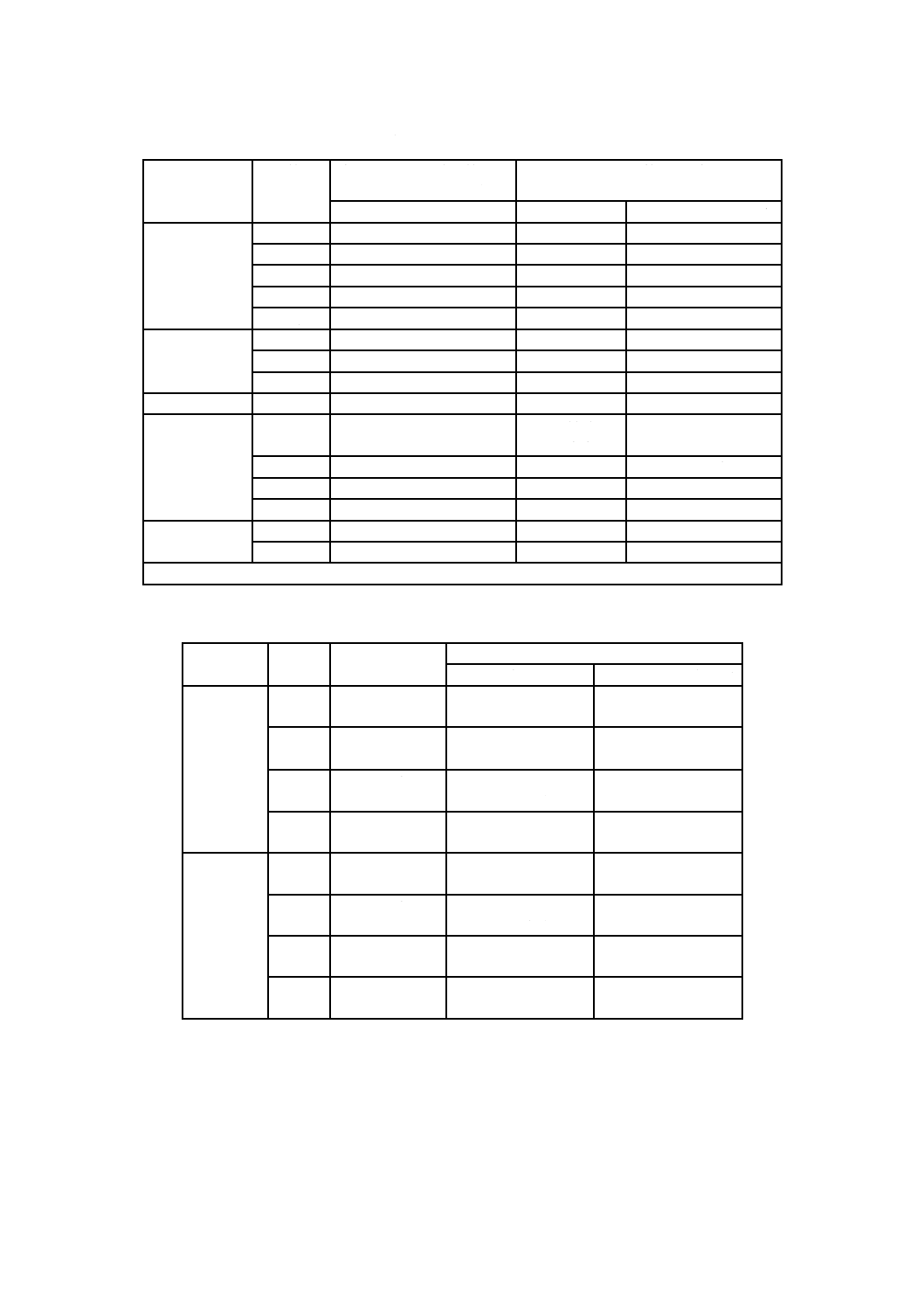
薄板ばねは,その形状及び使い方によって,荷重P又はトルクMとばねたわみδとが比例する線形特性
のほかに,各種の非線形特性が得られる。また,ぜんまいばねには,限られた空間で大きなたわみ(変位)
のもとに比較的大きなエネルギーを蓄積でき,ばねの成形がその他のばねに比べ簡単であるという特徴が
ある。基本的なばねの特性,種類及び特徴を,薄板ばねとぜんまいばねとについて表10及び表11に示す。
表10−薄板ばねの基本的な特性,種類及び特徴
番号
ばね特性
ばねの種類
特徴
1
線形特性
バインダクリップ,キャップス
プリング,ロッドロッククラン
プ,波形ばねなどの片持ちは
り,両端支持はり及び曲がりは
りのばね
形状の設計自由度が高い。
波形ばねは,軸方向の空間
に対し大きな荷重が得ら
れ,支持方法によって支点
が移動し,ばね定数が高く
なり非線形特性となる場
合もある。
2
非線形特性
平たん(坦)薄板ばね及び波形
ばね
9
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表11−ぜんまいばねの基本的な特性,種類及び特徴
番号
ばね特性
ばねの種類
特徴
1
線形特性
非接触形ぜんまい及びひげぜ
んまい
振動周期の等時性を重視する
点で特異性がある。
2
非線形特性
接触形ぜんまい
巻き始めは板間摩擦の影響に
よって高いばね定数となる
が,たわみが大きくなると,
非接触となるため,低いばね
定数が得られる。
3
定荷重特性
定荷重ぜんまい
渦巻が解けるときの荷重は,
たわみにほとんど無関係で一
定となり,ばね自身の寸法の
数倍にも達するたわみが得ら
れる。
6.2
材料の選択
多くの場合,既存の用途ごとに使用材料の種類が大まかに知られているので,それらを参考にするとよ
い(例えば,自動車部品:みがき特殊帯鋼,電気関係のスイッチ類:ばね用のベリリウム銅,チタン銅,
りん青銅,ニッケル−すず銅及び洋白の板及び条)。一般的には,材料を選択するときには,表1及び表
12を参照し,次の項目を考慮して選択する。
a) 薄板ばねの使用環境 許容される薄板ばねの占める体積,寸法,使用温度,雰囲気など。
b) 要求性能 荷重,たわみ,必要とされる耐久性など。また,前記のほかに次のような点も考慮する必
要がある。
c) 材料の入手性(市場性)。
d) 材料及びばね加工工程の経済性。
e) 廃棄の容易性,再資源化(リサイクル)までの無公害性,安全性,及び法規制の遵守。
表12−材料選択の目安
材料
材質区分
弾性限
加工性
導電性
耐食性
耐熱性
経済性
冷間圧延鋼帯(ばね加工後熱処理)
◎
○
○
◎
冷間圧延鋼帯(熱処理をした材料)
◎
○
○
ばね用ステンレス鋼帯
○
◎
◎
○
ばね用ベリリウム銅
○
◎
◎
○
○
ばね用りん青銅
◎
○
○
○
ばね用洋白
◎
○
○
○
注記 ◎:非常に良好 ○:良好
7
設計計算式
7.1
基本設計計算式
薄板ばねの形状は,表1に示したように多種多様であり,また使われ方も様々であるから,すべての場
10
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
合について規定することはできないので,ここでは,基本的なものについて規定する。
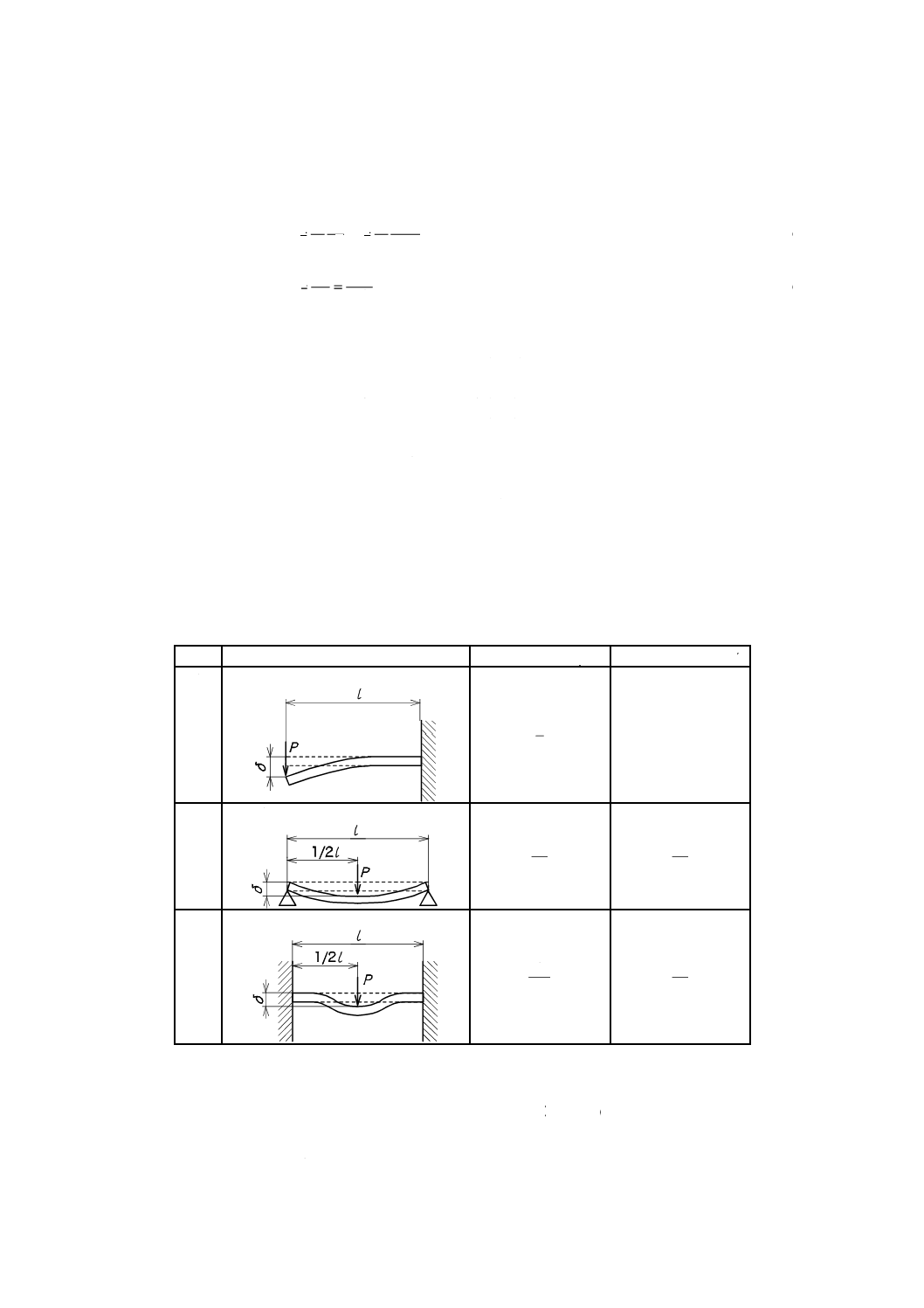
a) 真直はり 表13に示す,板厚t及び板幅bが一定で長さがlのはりの荷重P及び応力σは,それぞれ
式 (1) 及び式 (2) によって求める。
δ
β
δ
β
3
3
3
12
1
1
l
Ebt
l
EI
P
=
=
······························································· (1)
2
6
bt
M
Z
M=
=
σ
··········································································· (2)
ここに,
P: ばねにかかる荷重 (N)
β: たわみの係数
E: 縦弾性係数 (MPa)
I: 断面二次モーメント (mm4)
b: 材料の板幅 (mm)
t: 材料の板厚 (mm)
l: はりの長さ (mm)
δ: ばねのたわみ (mm)
σ: 曲げ応力 (MPa)
M: 曲げモーメント (N・mm)
Z: 断面係数 (mm3)
ただし,たわみの係数β及び曲げモーメントMは,はりの種類によって決まる係数であり,表13
による。
表13−はりの種類,たわみの係数及び曲げモーメント
番号
はりの種類
たわみの係数β
曲げモーメントM
1
片持ちはり
3
1
Pl
2
両端支持はり
48
1
4
Pl
3
両端固定はり
192
1
8
Pl
例1 数値を代入した計算例として,次のときの荷重と応力とを求める。
b:3 (mm) t:0.1 (mm) l:10 (mm)
E:1.86×105 (MPa)
となる片持ちはりを考えると,たわみの係数βは1/3となり,ばねのたわみδを1とすると,荷
11
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
重Pは次の式による。
1
10
12
1.0
3
10
86
.1
3
3
3
5
×
×
×
×
×
×
=
P
= 0.140 (N)
また,片持ちはりのため,曲げモーメントMはPlとなり,応力σは次の式による。
2
2
2
1.0
3
10
140
.0
6
6
6
×
×
×
=
=
=
bt
Pl
bt
M
σ
= 280 (MPa)
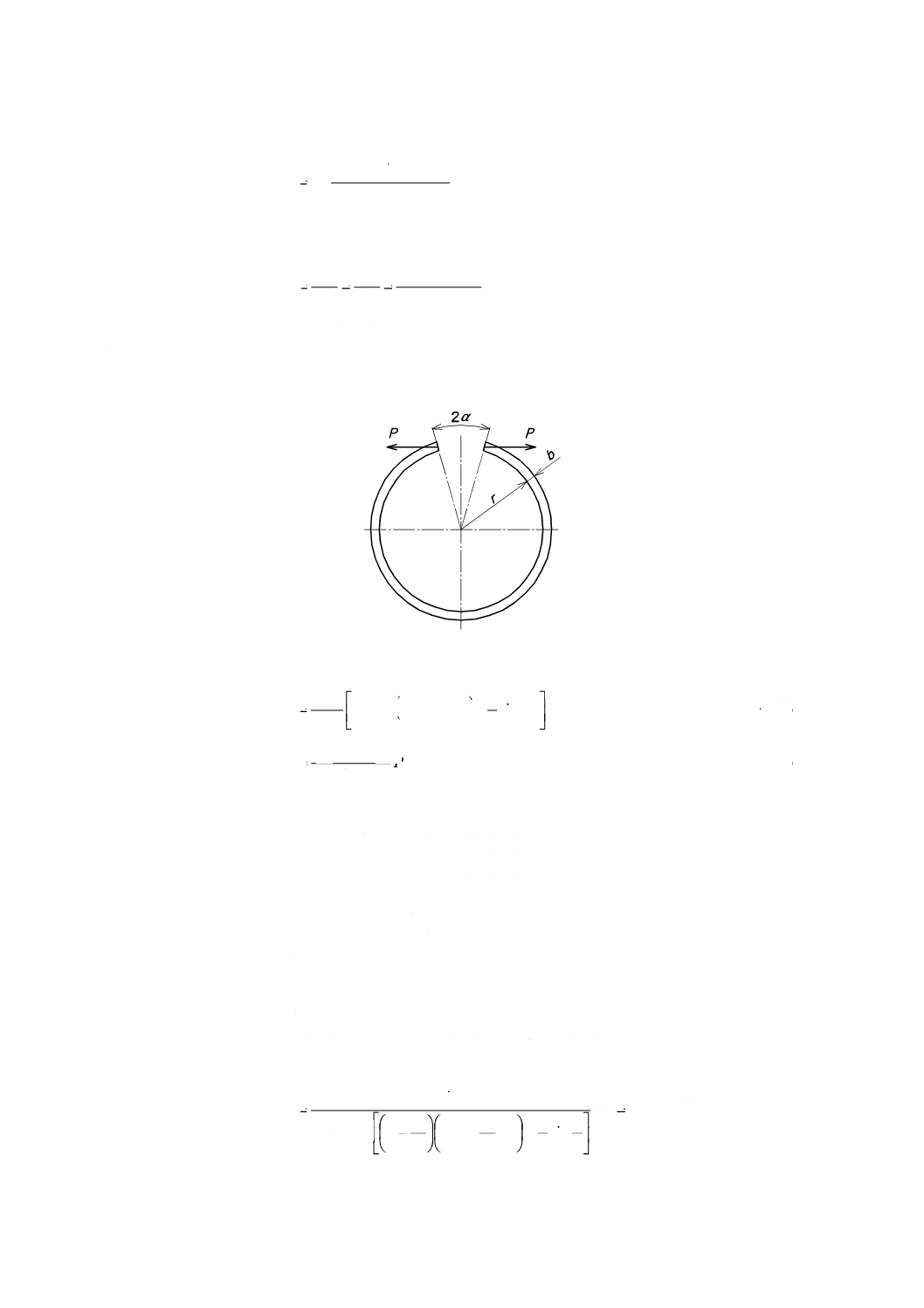
b) 円弧状はり 図1に示す,板厚tの円弧状はりの荷重P及び応力σは,式 (3) 及び式 (4) によって求
める。
図1−円弧状はりのモデル
(
)(
)
δ
α
α
α
1
2
3
3
2
sin
2
3
1
cos
2
π
12
−
+
+
−
=
r
Ebt
P
······································ (3)
(
)P
bt
r
2
1
cos
6
+
=
α
σ
····································································· (4)
ここに,
P: ばねにかかる荷重 (N)
E: 縦弾性係数 (MPa)
b: 材料の板幅 (mm)
t: 材料の板厚 (mm)
r: 円弧の半径 (mm)
α: 開口部角度(図1参照)(rad)
δ: ばねのたわみ (mm)
σ: 曲げ応力 (MPa)
例2 数値を代入した計算例として,次のときの荷重と応力とを求める。
E:1.86×105 (MPa)
r:10 (mm)
α:π/12 (rad)
b:3 (mm)
t:0.1 (mm)
δ:4 (mm)
とすると,荷重P及び応力σは次の式による。
(N)
7
0.020
4
6
π
sin
2
3
1
12
π
cos
2
12
π
π
10
12
1.0
3
10
86
.1
2
3
3
5
=
×
+
+
−
×
×
×
×
×
=
P
12
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(MPa)
81.4
7
0.020
1.0
3
1
12
π
cos
10
6
2
=
×
×
+
×
×
=
σ
7.2
簡易分割形計算式(板幅変化形)
7.2.1
一般
直線と円弧とを組み合わせた薄板ばね,直線と円弧以外の曲線とを組み合わせた薄板ばねなどの複雑な
形状をもつものについては,計算が煩雑になり,厳密な荷重及び応力の計算が困難な場合がある。
近年は有限要素法(FEM)などの活用によって,計算ができるようになってきているが,従来とは異な
った力量が必要となる。また,概略設計及び幾つかの類似形状を比較する場合などにはあまり適していな
い。そのような場合の薄板ばねの設計には,簡易分割計算法が活用でき,有用である。
7.2.2
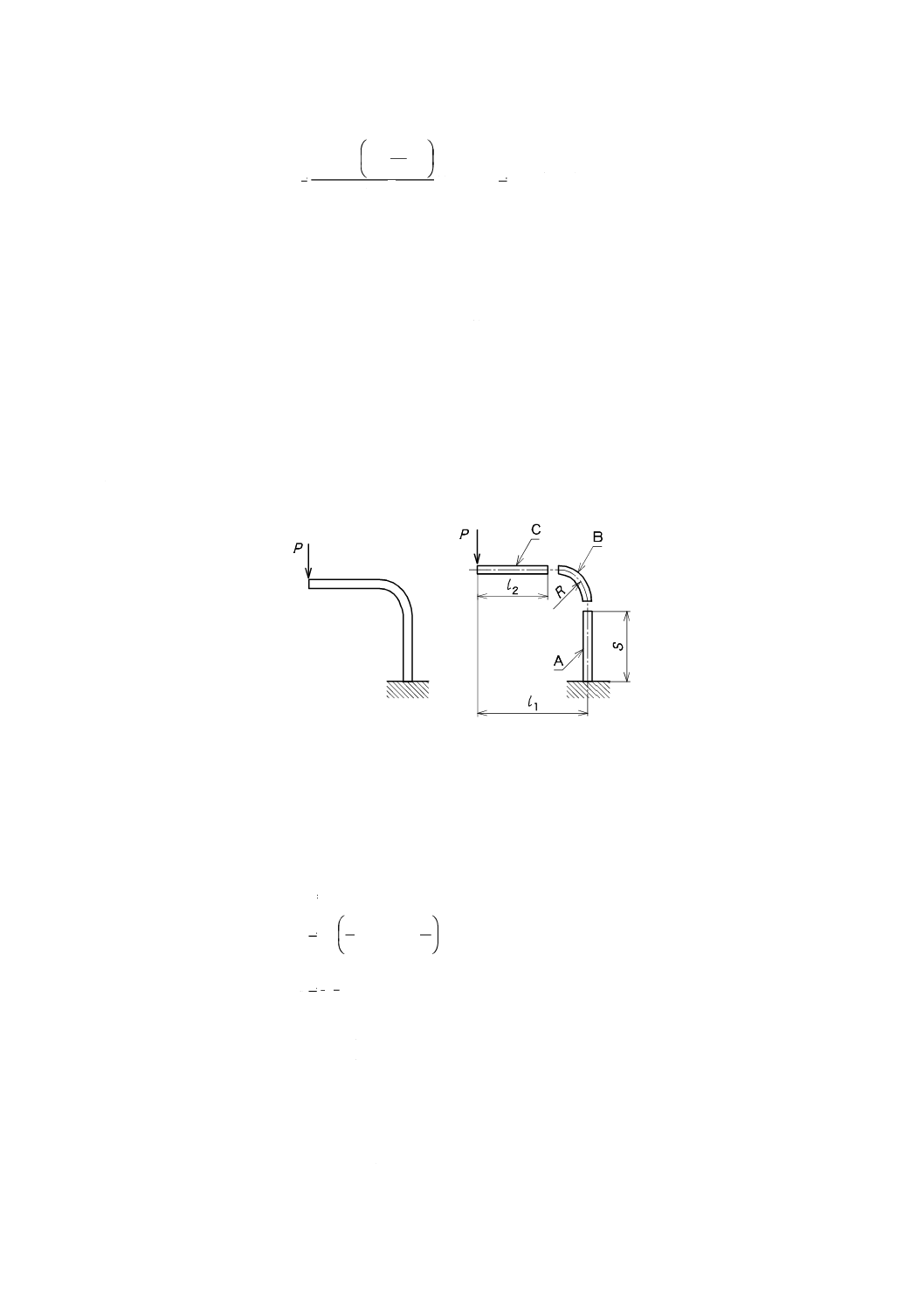
基本的な使い方
図2に示す,板厚t及び板幅bが一定の薄板ばねの一端を固定し他端に荷重Pを加える場合は,次の手
順によって荷重及び応力を求める。
a) 薄板ばねの軸線方向の形状を,図2のように直線及び円弧の要素に分割する。
図2−要素分割例
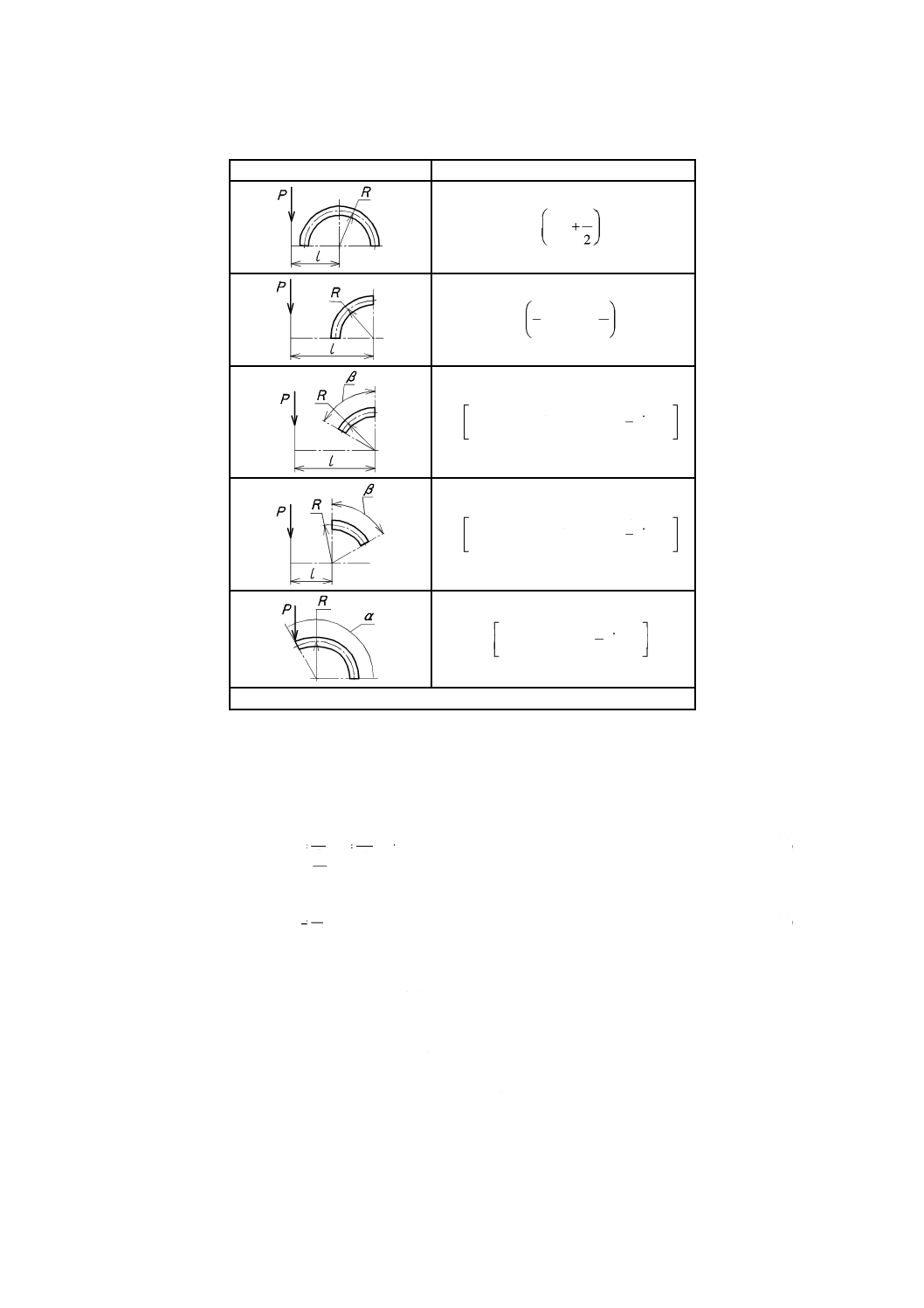
b) 各要素の形状による係数Λを計算する。Λは,薄板ばねの軸線の,荷重作用点に対する2次モーメン
トであり,たわみの係数βと形状とによって決まる係数である。直線及び円弧要素のΛは,表14及
び表15を参照するのがよい。ここで,Sは軸線の長さであり,lは荷重作用点に対する直角方向の長
さである。図2のA,B及びCの各要素の形状による係数Λは,次の式による。
2
1
A
Λ
Sl
=
+
+
=
4
π
2
2
π
Λ
2
3
B
n
n
R
3
Λ
3
2
C
l
=
ここに,
ΛA: 要素Aの形状による係数 (mm3)
ΛB: 要素Bの形状による係数 (mm3)
ΛC: 要素Cの形状による係数 (mm3)
S: 要素Aの長さ (mm)
l1: 要素Aの荷重点からの距離 (mm)
l2: 要素Cの長さ (mm)
R: 要素Bの半径 (mm)
n: l2/R
13
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表14−直線要素のΛ
形状
形状による係数 Λ
3
3l
3
2
Sl 又は
3
3
ml
ここに,
l
S
m=
Sl2
(
)
3
A
3
B
3
1
l
l −
(
)
3
A
3
B
3
l
l
m
−
ここに,
A
Bl
l
S
m
−
=
表15−円弧要素のΛ
形状
形状による係数 Λ
(
)
+
+
+
α
α
α
2
sin
4
1
sin
2
5.0
2
3
n
n
R
上記の場合のΛをΛ(α)と表して,
Λ(α1)+Λ(α2)
Λ(α2)−Λ(α1)
+
+
4
π
2
2
π
2
3
n
n
R
14
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表15−円弧要素のΛ(続き)
形状
形状による係数 Λ
+2π
π
2
3
n
R
+
−
4
π
2
2
π
2
3
n
n
R
(
)
(
)
−
−
−
+
β
β
β
2
sin
4
1
cos
1
2
5.0
2
3
n
n
R
(
)
(
)
−
−
+
+
β
β
β
2
sin
4
1
cos
1
2
5.0
2
3
n
n
R
(
)
−
+
α
α
α
2
sin
4
3
5.0
cos2
3
R
注記 n=1/R
c) 各要素のΛを加算して全体のΛ(ΛA+ΛB+ΛC)を求める。
d) 荷重P及び応力σは,断面二次モーメントをI,断面係数をZとすると,このΛを用いて,式 (5) 及
び式 (6)によって求める。
δ
δ
Λ
Λ
EI
I
E
P
=
=
········································································· (5)
P
Z
l1
=
σ
·················································································· (6)
ここに,
P: ばねにかかる荷重 (N)
E: 縦弾性係数 (MPa)
Λ: 全体の形状による係数 (mm3)
I: 断面二次モーメント (mm4)
δ: ばねのたわみ (mm)
σ: 曲げ応力 (MPa)
l1: 要素Aの荷重点からの距離 (mm)
Z: 断面係数 (mm3)
7.2.3
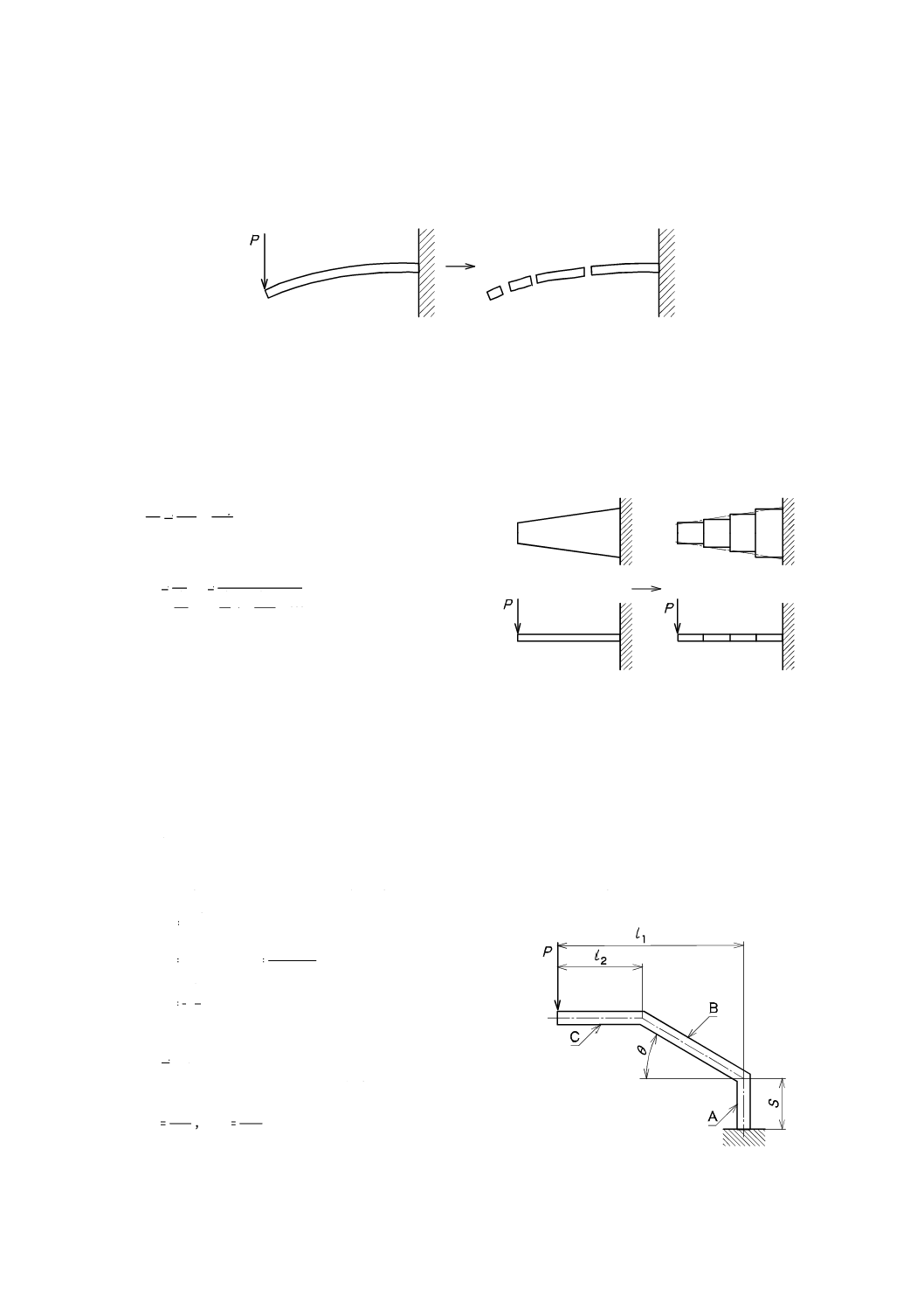
応用的な使い方
円弧以外の薄板ばねの一端を固定し,他端に荷重Pを加える場合で,曲線形状と板幅とが変化する場合
15
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
は,次の手順によって荷重及び応力を求める。
a) 図3に示す円弧以外の曲線形状の場合には,その部分を幾つかに分割して,直線の折線で形状を近似
すると基本的な使い方が応用できる。
図3−円弧以外の曲線形状
b) 図4に示す,板厚tが一定で板幅bが変化する場合には,その形状を幾つかの均一な板幅の要素に近
似して分割すると基本的な使い方が応用できる。ただし,この場合は,断面二次モーメントIも各要
素で変化するので,それぞれ要素ごとに計算する必要がある。すなわち,各要素のΛとIとをΛ1,Λ2
…,I1,I2…,とすると,Λ/I及び荷重Pは,次の式によって求める。
Λ
+
+
=
2
2
1
1
Λ
Λ
Λ
I
I
I
δ
δ
Λ
+
+
=
=
2
2
1
1
Λ
Λ
Λ
I
I
E
I
E
P
図4−板幅が変化する形状
7.2.4
計算例
理解を深めるため,幾つかの例題を示す。厳密な計算手法ではないために,たわみの小さいときには,
適用できるが,たわみの大きいときには,適用できない。概略的ではあるが,材料力学の原理原則に基づ
いた手法であり,複雑な形状を設計的に把握することができるため,補助的な使い方であっても,活用す
ることが望ましい。
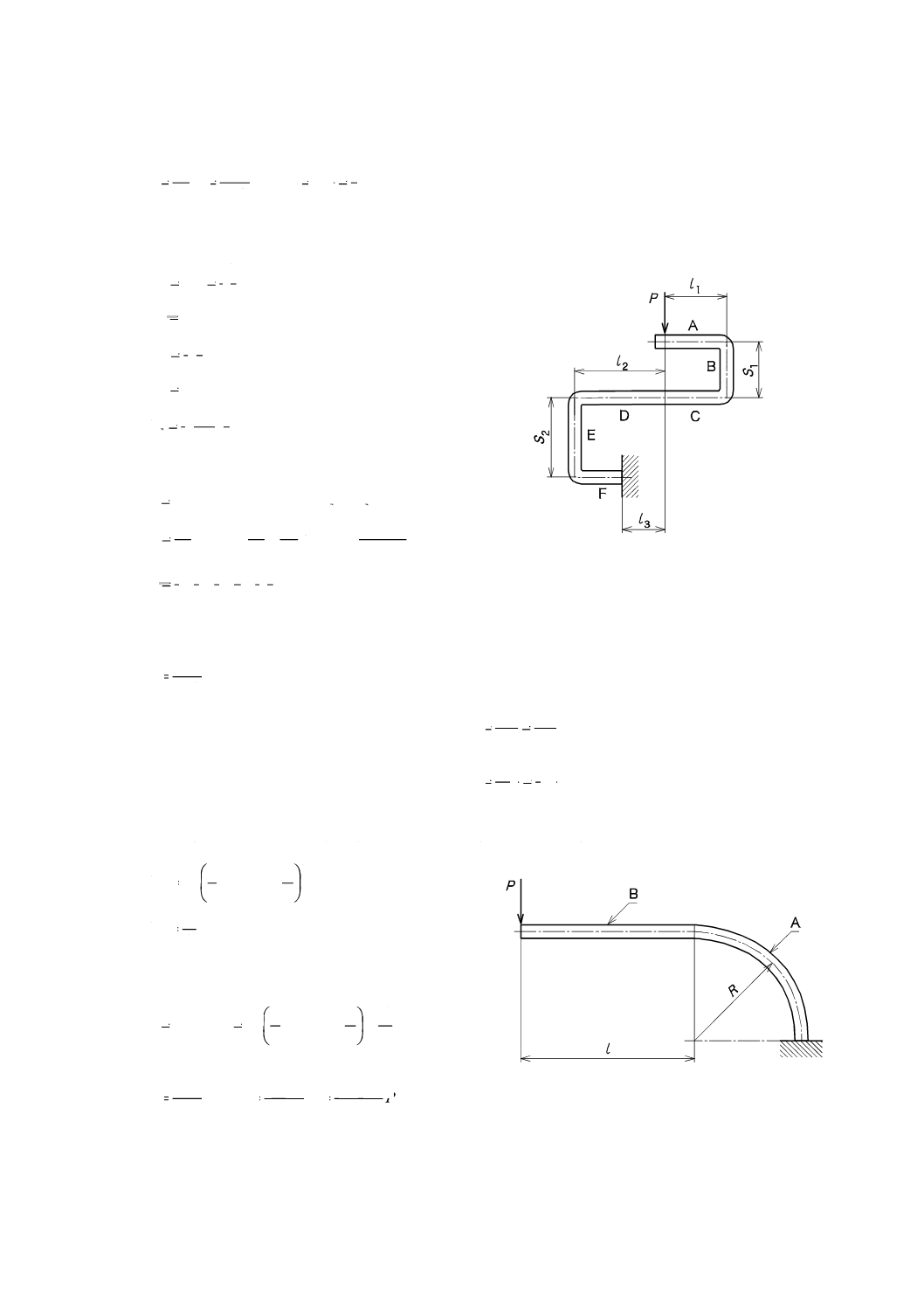
例1 図5に示す,板厚t及び板幅bが一定の薄板ばねの一端を固定し他端に荷重Pを加える場合は,
分割したA,B及びCの各要素の形状による係数Λは,次の式による。
2
1
A
Λ
Sl
=
(
)
θ
cos
3
3
Λ
3
2
3
1
3
2
3
1
B
l
l
l
l
m
−
=
−
=
3
Λ
3
2
C
l
=
全体の形状による係数Λは,次の式による。
C
B
A
Λ
Λ
Λ
Λ
+
+
=
断面二次モーメントI及び断面係数Zを
12
3
bt
I=
,
6
2
bt
Z=
図5−例1の形状
16
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とすると,荷重P及び応力σは,次の式による。
δ
δ
Λ
12
Λ
3
Ebt
EI
P
=
=
,
P
bt
l
Z
Pl
2
1
1
6
=
=
σ
例2 図6に示す,板厚t及び板幅bが一定の薄板ばねの一端を固定し他端に荷重Pを加える場合は,
分割したA,B,C,D,E及びFの各要素の形状による係数Λは,次の式による。
3
Λ
Λ
3
1
C
A
l
=
=
2
1
1
B
Λ
l
S
=
3
Λ
3
2
D
l
=
2
2
2
E
Λ
l
S
=
3
Λ
3
3
3
2
F
l
l−
=
全体の形状による係数Λは,次の式による。
F
E
D
C
B
A
Λ
Λ
Λ
Λ
Λ
Λ
Λ
+
+
+
+
+
=
3
3
3
3
3
3
3
2
2
2
2
3
2
3
1
2
1
1
3
1
l
l
l
S
l
l
l
S
l
−
+
+
+
+
+
=
2
2
2
2
1
1
3
3
3
2
3
1
3
3
2
3
2
l
S
l
S
l
l
l
+
+
−
+
=
図6−例2の形状
例1と同様に,荷重P及び応力σは,次の式による。
δ
Λ
12
3
Ebt
P=
l1及びl2>l3であることから,l1>l2のときは,
P
bt
l
Z
Pl
2
1
1
6
=
=
σ
l1>l2のときは,
P
bt
l
Z
Pl
2
2
2
6
=
=
σ
例3 図7に示す,板厚t及び板幅bが一定の薄板ばねの一端を固定し他端に荷重Pを加える場合は,
分割したA及びBの各要素の形状による係数Λは,次の式による。
+
+
=
4
π
2
2
π
Λ
2
3
A
n
n
R
3
Λ
3
B
l
=
全体の形状による係数Λは,次の式による。
3
4
π
2
2
π
Λ
Λ
Λ
3
2
3
B
A
l
n
n
R
+
+
+
=
+
=
例1と同様に,荷重P及び応力σは,次の式による。
δ
Λ
12
3
Ebt
P=
,
(
)
(
)P
bt
R
l
P
Z
R
l
2
6+
=
+
=
σ
図7−例3の形状
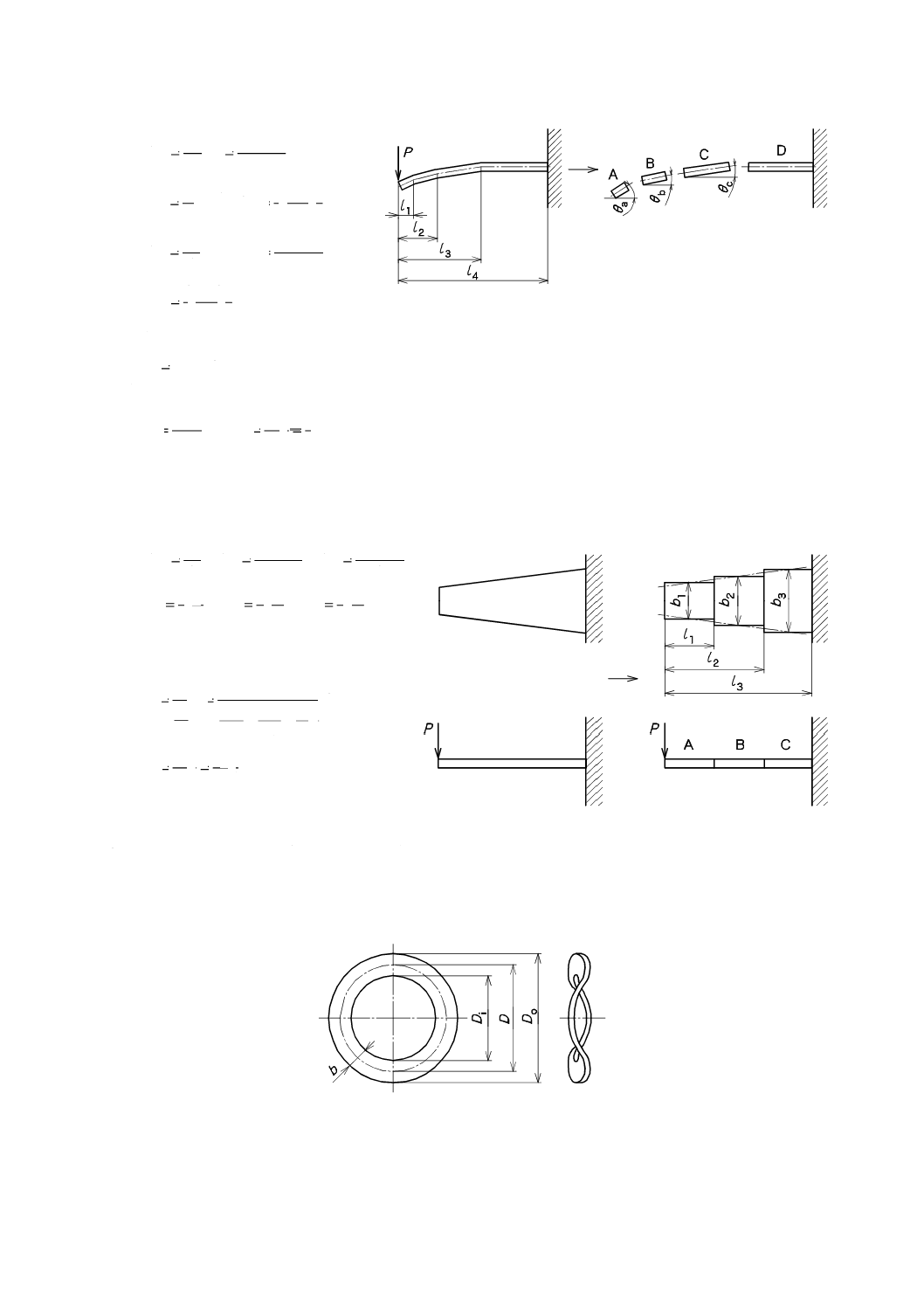
例4 図8に示す,板厚t及び板幅bが一定の薄板ばねで一端を固定し他端に荷重Pを加える場合は,
分割したA,B,C及びDの各要素の形状による係数Λは,次の式による。
17
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a
3
1
3
1
a
A
cos
3
3
Λ
θ
l
l
m
=
=
(
)
b
3
1
3
2
3
1
3
2
b
B
cos
3
3
Λ
θ
l
l
l
l
m
−
=
−
=
(
)
c
3
2
3
3
3
2
3
3
c
C
cos
3
3
Λ
θ
l
l
l
l
m
−
=
−
=
3
Λ
3
3
3
4
D
l
l−
=
図8−例4の形状
全体の形状による係数Λは,次の式による。
D
C
B
A
Λ
Λ
Λ
Λ
Λ
+
+
+
=
例1と同様に,荷重P及び応力σは,次の式による。
δ
Λ
12
3
Ebt
P=
,
P
bt
l
Z
Pl
2
4
4
6
=
=
σ
例5 図9に示す,板厚tが一定で,板幅bが変化する薄板ばねの一端を固定し他端に荷重Pを加え
る場合は,A,B及びCのそれぞれ均一な板幅の三つの要素に近似して分割すると,各要素の
形状による係数Λ及び断面二次モーメントIは,次の式による。
3
Λ
3
1
A
l
=
,
3
Λ
3
1
3
2
B
l
l−
=
,
3
Λ
3
2
3
3
C
l
l−
=
12
3
1
A
t
b
I=
,
12
3
2
B
t
b
I=
,
12
3
3
C
t
b
I=
このときの,荷重P及び応力σは,
次の式による。
δ
δ
C
C
B
B
A
A
Λ
Λ
Λ
Λ
I
I
I
E
I
E
P
+
+
=
=
P
t
b
l
Z
Pl
2
3
3
3
6
=
=
σ
図9−例5の形状
7.3
典型的な形状の薄板ばねの計算式及び例
7.3.1
波形ばね(3山以上)
図10に示す,板厚がt,板幅がbの波形ばねの荷重P及び応力σは,式 (7) 及び式 (8) によって求める。
図10−波形ばねのモデル
18
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
δ
κ
δ
3
4
3
94
.1 D
N
Ebt
k
P
=
=
···································································· (7)
δ
σ
2
2
2
π
12
D
EtN
=
·········································································· (8)
ここに,
P: ばねにかかる荷重 (N)
k: ばね定数 (N/mm)
δ: ばねのたわみ (mm)
κ: 修正係数
E: 縦弾性係数 (MPa)
b: 材料の板幅 (mm)
t: 材料の板厚 (mm)
N: 波の山数
D: 平均直径 (mm)
σ: 曲げ応力 (MPa)
波の山数Nは,製品の大きさにもよるが最大でも8山程度とし,修正係数κは,内径をDi,外径をD0
としたとき,Di/D0の比によって,次の式による。
Di/D0=0.5〜0.777のときは,κ=[1.35−1.45(Di/D0)]/(1−Di/D0)
Di/D0≧0.777のときは,κ=1とする。
例 数値を代入した計算例として,次のときの荷重と応力とを求める。
D0:50 (mm)
Di:42 (mm)
E:2.06×105 (MPa)
t:0.5 (mm)
b:4 (mm)
N:6
δ:0.3 (mm)
としたとき,修正係数κは,
Di/D0=0.84>0.777であるから,κ=1となる。
また,平均直径Dは,
D=(D0+Di)/2=46 (mm) となる。
以上によって,荷重Pは,次の式による。
(N)
212
0.3
46
94
.1
6
5.0
4
10
06
.2
1
3
4
3
5
=
×
×
×
×
×
×
×
=
P
また,このときの応力σは,次の式による。
(MPa)
640
3.0
46
π
6
5.0
10
06
.2
12
2
2
2
5
=
×
×
×
×
×
×
=
σ
7.3.2
接触形ぜんまい
図11に示す,接触形ぜんまいのトルクM及び応力σは,式 (9) 及び式 (10) によって求める。
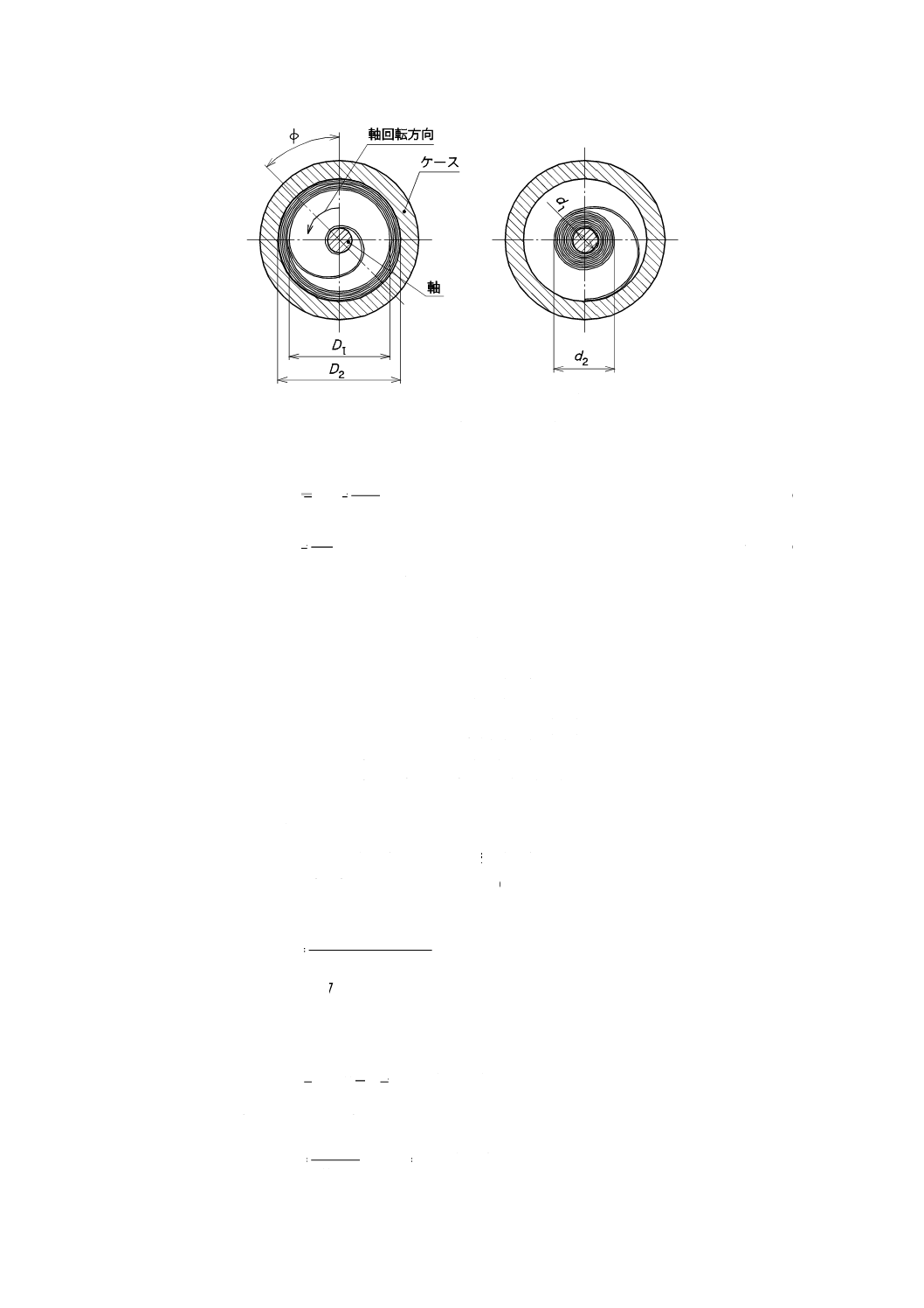
19
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 巻き戻しの状態
b) 巻き締めの状態
図11−接触形ぜんまいのモデル
φ
φ
l
Ebt
k
M
12
3
=
=
······································································· (9)
M
bt2
6
=
σ
·············································································· (10)
ここに,
M: トルク (N・mm)
k: ばね定数 (N・mm/rad)
E: 縦弾性係数 (MPa)
b: 材料の板幅 (mm)
t: 材料の板厚 (mm)
l: ばねの展開長 (mm)
σ: 曲げ応力 (MPa)
D1: 解かれたばねの内径 (mm)
D2: ケースの内径 (mm)
d1: 軸の外径 (mm)
d2: 巻いたばねの外径 (mm)
φ: 変位角 (rad)
例 数値を代入した計算例として,次のときのトルクと応力とを求める。
E:2.06×105 (MPa)
b:5 (mm)
t:0.2 (mm)
l:500 (mm)
のとき,ばね定数kは次の式による。
500
12
2.0
5
10
06
.2
3
5
×
×
×
×
=
k
=1.37 (N・mm/rad)
したがって,3/4巻(270°)巻いたときのトルクMは,270°を3/2 π radと表して,次の式によ
る。
mm)
(N
45
.6
π
2
3
37
.1
・
=
×
=
M
このときの応力σは,次の式による。
)
(MPa
194
45
.6
2.0
5
6
2
=
×
×
=
σ
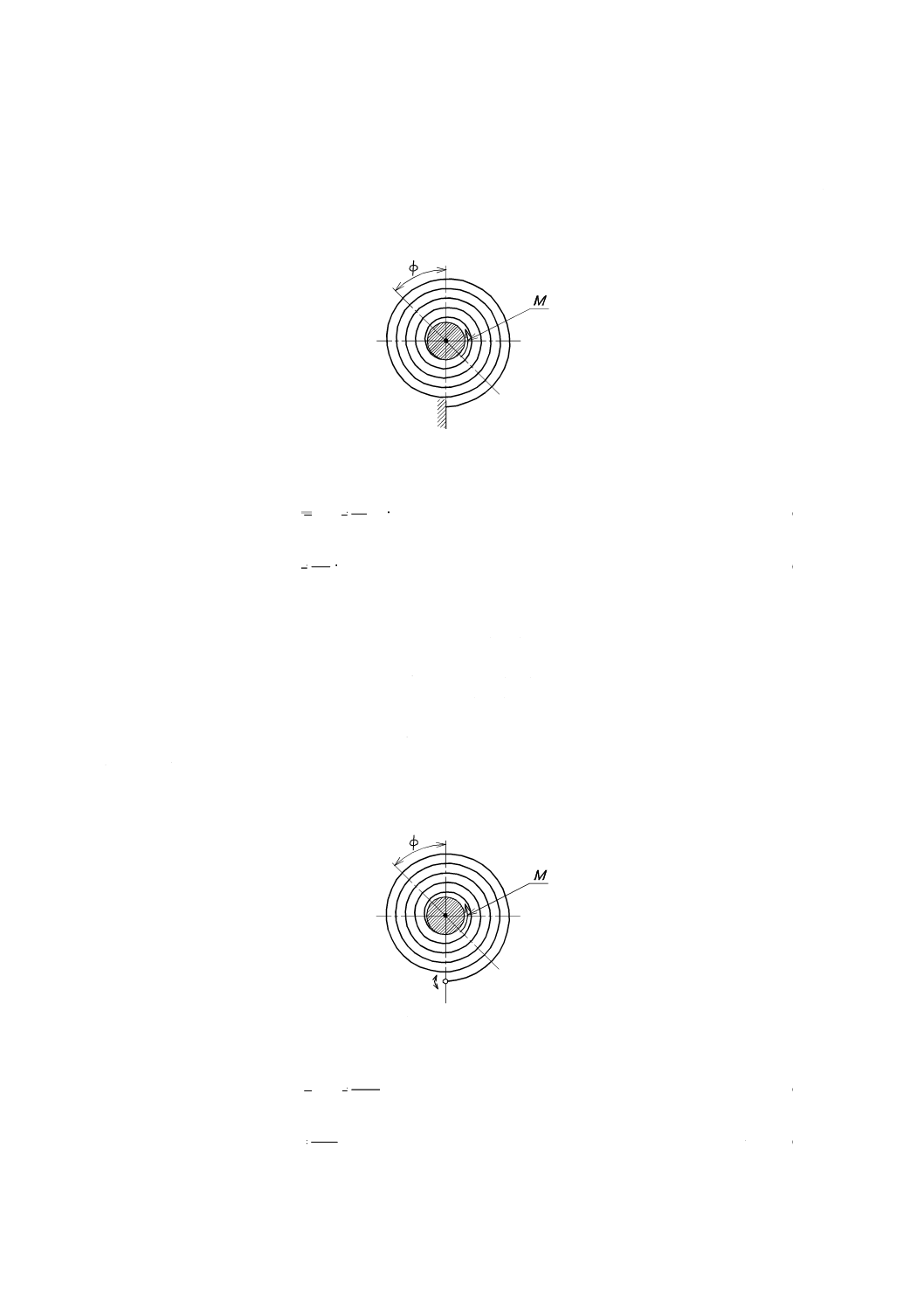
20
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7.3.3
非接触形ぜんまい
非接触形ぜんまいばねは,次の二つの場合による。
a) 巻数が多く外端固定支持の場合 図12に示す非接触形ぜんまいのトルクM及び応力σは,式 (11) 及
び式 (12) によって求める。
図12−非接触形ぜんまい(外端固定支持)のモデル
φ
φ
l
EI
k
M
=
=
·········································································(11)
Z
M
=
σ
·················································································· (12)
ここに,
M: トルク (N・mm)
k: ばね定数 (N・mm/rad)
E: 縦弾性係数 (MPa)
I: 断面二次モーメント (mm4)
l: ばねの展開長 (mm)
σ: 曲げ応力 (MPa)
Z: 断面係数 (mm3)
φ: 変位角 (rad)
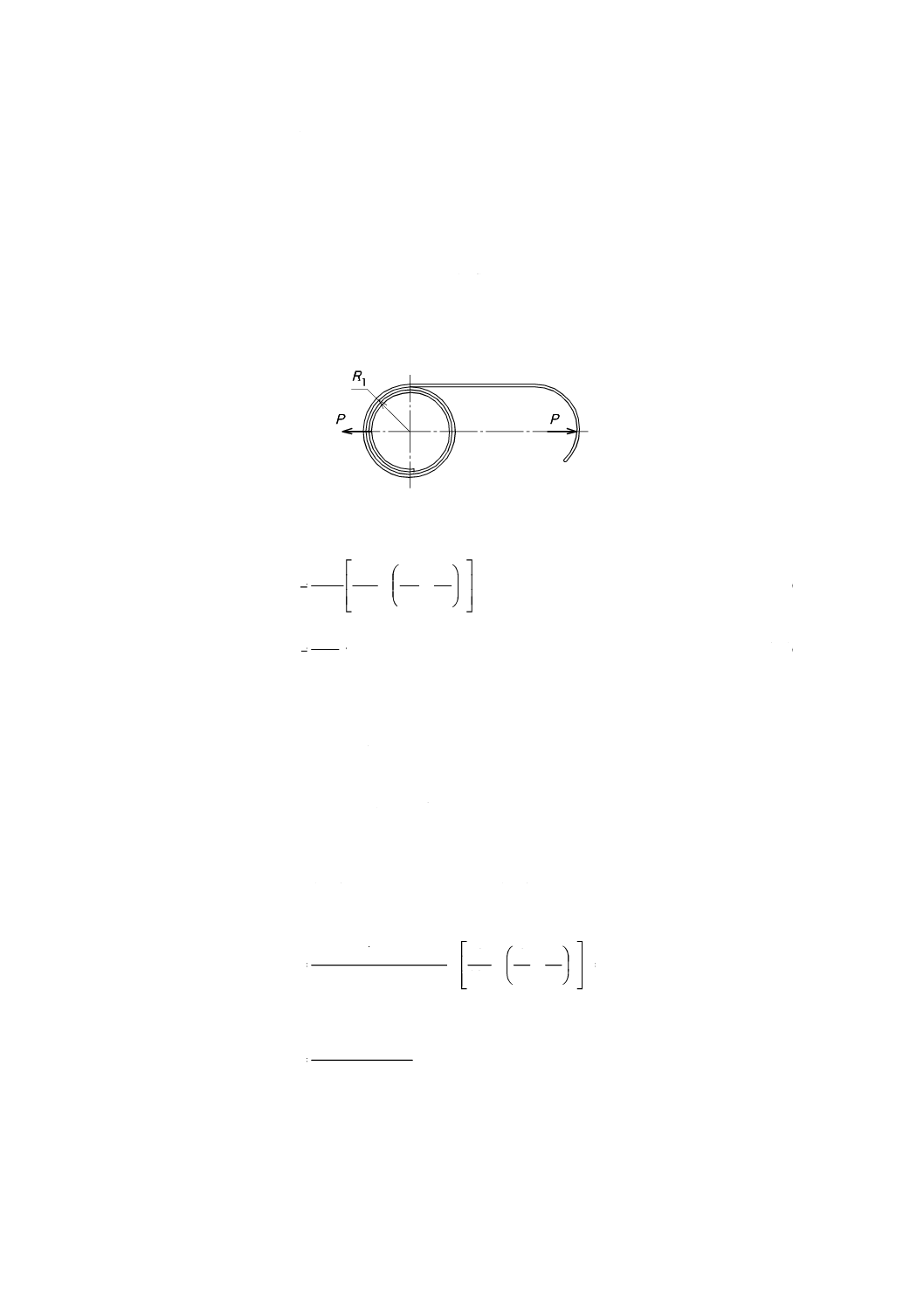
b) 巻数が多く外端自由支持の場合 図13に示す,非接触形ぜんまいのトルクM及び応力σは,式 (13) 及
び式 (14) によって求める。
図13−非接触形ぜんまい(外端自由支持)のモデル
φ
φ
l
EI
k
M
25
.1
=
=
····································································· (13)
Z
M
2
=
σ
················································································ (14)
21
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
M: トルク (N・mm)
k: ばね定数 (N・mm/rad)
E: 縦弾性係数 (MPa)
I: 断面二次モーメント (mm4)
l: ばねの展開長 (mm)
σ: 曲げ応力 (MPa)
Z: 断面係数 (mm3)
φ: 変位角 (rad)
7.3.4
定荷重ぜんまい
図14に示す,定荷重ぜんまいの荷重P及び応力σは,式 (15) 及び式 (16) によって求める。
図14−定荷重ぜんまいのモデル
−
−
=
2
1
n
2
n
3
1
1
1
4.
26
R
R
R
Ebt
P
······················································ (15)
n
2R
Et
=
σ
················································································ (16)
ここに,
P: ばねにかかる荷重 (N)
E: 縦弾性係数 (MPa)
b: 材料の板幅 (mm)
t: 材料の板厚 (mm)
Rn: コイルの最小自然半径 (mm)
R1: コイル外半径 (mm)
σ: 曲げ応力 (MPa)
例 数値を代入した計算例として,次のときの荷重と応力とを求める。
E:1.86×105 (MPa)
b:25 (mm)
t:0.15 (mm)
Rn:10 (mm)
R1:12 (mm)
のとき,荷重Pは次の式による。
)
(N
78
.5
12
1
10
1
10
1
4.
26
15
.0
25
10
86
.1
2
2
3
5
=
−
−
×
×
×
×
=
P
また,応力σは次の式による。
(MPa)
10
40
.1
10
2
15
.0
10
86
.1
3
5
×
=
×
×
×
=
σ
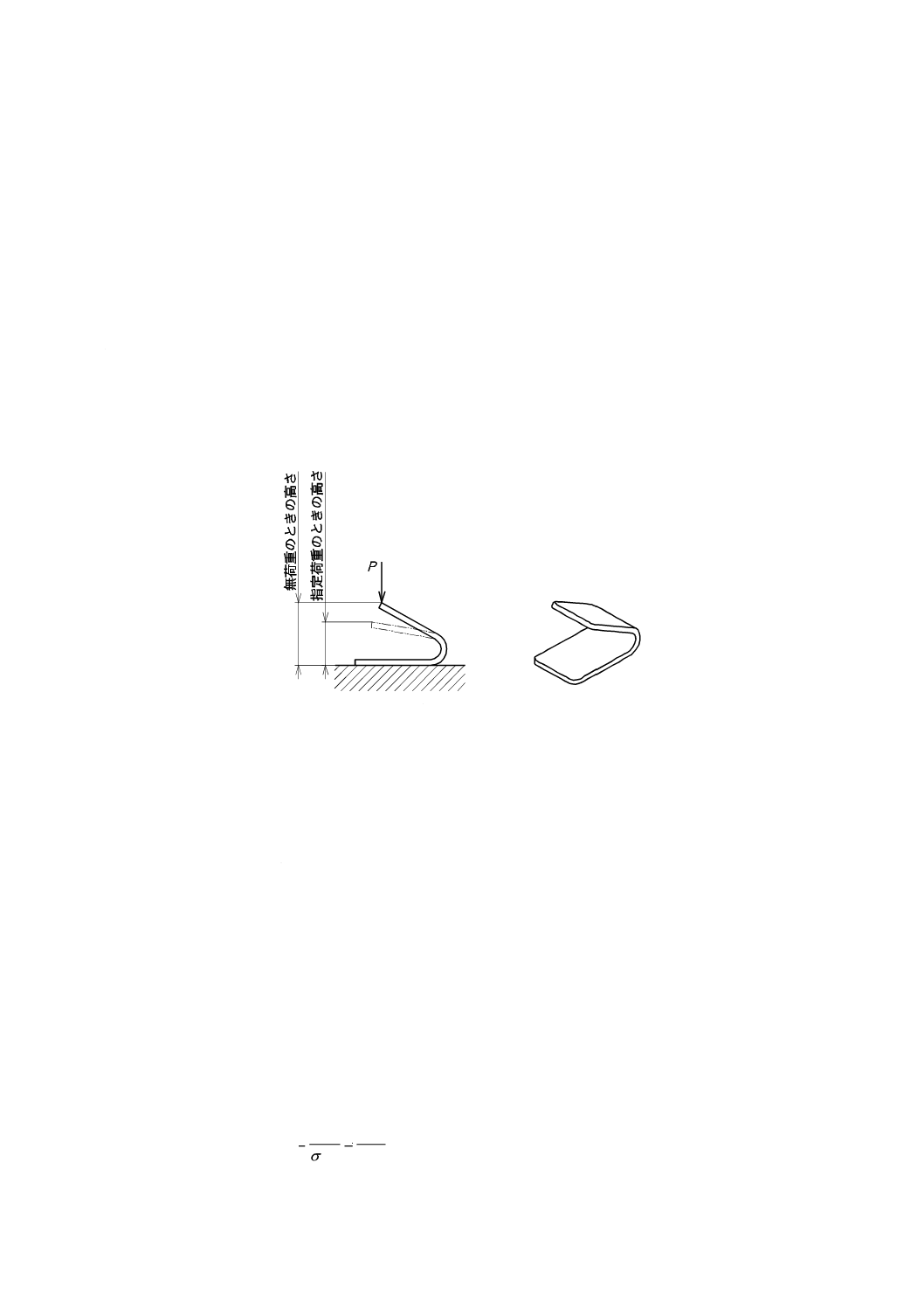
22
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
8
仕様の定め方
8.1
薄板ばねの特性
薄板ばねの使用方法によって,要求のばね特性に適した形状を選定する。ばね特性の代用として,寸法
許容差を指定する場合が一般的であるが,機能上の理由などで,ばね特性を指定する場合には,次に規定
する項目から選択して仕様を決める。高さ又は荷重を指定するときは,図15を参照する。
a) 指定高さのときの荷重 指定高さのときの荷重は,そのときのたわみが全たわみ1) の20〜80 %にな
るように決める。
注1) 全たわみとは,無荷重時から最大荷重時までのばねのたわみをいう。
b) 指定荷重のときの高さ 指定荷重のときの高さは,そのときのたわみが全たわみの20〜80 %になる
ように決める。
c) ばね定数 ばね定数は,全たわみの30〜70 %にある二つの荷重点における荷重の差及びたわみの差
によって決める。
図15−ばね特性の指定の仕方
8.2
設計応力
薄板ばねの設計応力は,箇条7の各種の設計計算式から求める。設計応力は,使用条件,表面状態,硬
さ,切欠き部形状,加工欠陥の有無,端面の処理方法など,多くの事項を考慮する必要があるが,大まか
には,次に規定する方法で目安をつけることができる。
a) 静荷重を受ける薄板ばね 静荷重又は低レベルの繰返し荷重を受ける薄板ばねの許容曲げ応力は,鉄
鋼材料の場合は,材料の引張強さの70 %以下とするのが望ましい。
b) 繰返し荷重を受ける薄板ばね 繰返し荷重を受ける薄板ばねの許容曲げ応力は,薄板ばねを使用する
ときの下限応力と上限応力との関係,繰返し回数,材料の表面状態などの疲れ強さに影響を及ぼす諸
因子を考慮して,適切な値を選ばなければならない。
薄板ばね寿命を予測する方法の一例を,次に示す。図16の疲れ強さ線図を用いて,繰返し荷重を受
ける薄板ばねの寿命を推定することができる。
なお,図16はJIS B 2709による寿命予測を容易にするために,最小荷重Pminを最大荷重Pmaxで除
した値をγとすると,通常,γは設計の当初において分かっていることが多いので,図16にγの斜線
を併記した。γは,次の式で表す。
max
min
max
min
P
P
=
=σσ
γ
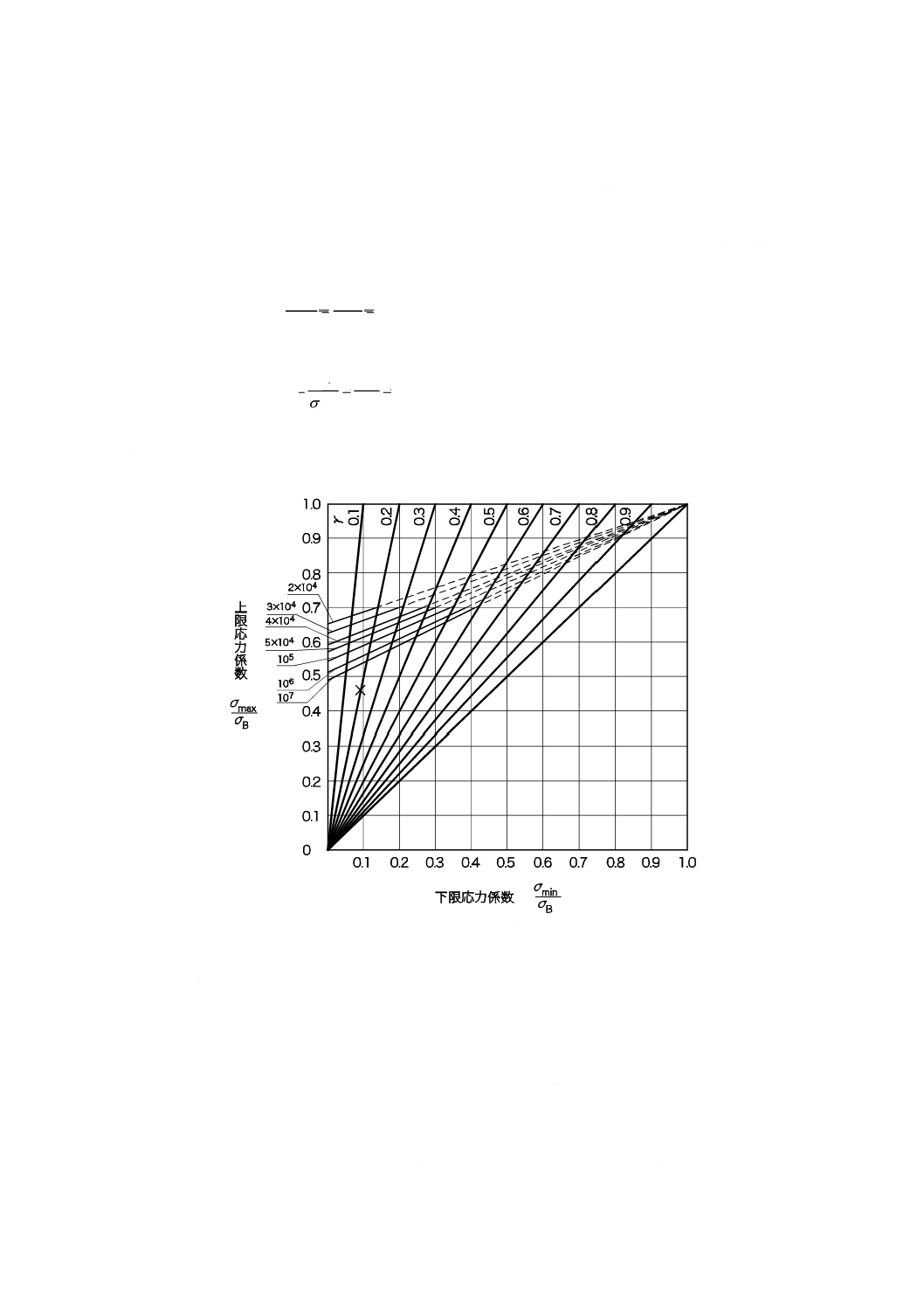
23
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
上限応力係数又は下限応力係数のいずれかと,このγとで寿命予測は容易に行うことができる。薄
板ばねの材料では,引張強さの規定がないものがあり,薄板ばねの硬さから引張強さを換算し求めな
ければならない場合がある。表16を参照して硬さから引張強さに換算する。
材料にビッカース硬さが450HVのSK85Mを用いた薄板ばねにσmax=630 (MPa)及びσmin=126 (MPa)
の応力が作用する場合の寿命回数を推定する。σB値は,表16の換算表から1401 (MPa) を得る。上限
応力係数σmax/σBは,次の式による。
45
.0
1401
630
B
max
=
=
σ
σ
ここに,σBは,材料の硬さから換算した引張強さである。また,γは,次の式となり,
20
.0
630
126
max
min
=
=
=σσ
γ
図16に示す×印の点を得る。この点は,図から明らかなように107回以上の寿命を期待することがで
きる。
図16−疲れ強さ線図
8.3
設計及び加工上の注意事項
8.3.1
設計上の注意事項
薄板ばねの設計に当たっては,次に規定する事項に注意する。
a) 接触形ぜんまい
1) 接触形ぜんまいは,板同士のしゅう(摺)動に伴い生じる摩擦のために,巻き戻すときのトルクが
巻き上げるときのトルクを下回る,いわゆるヒステリシス特性を示す。過大な摩擦を避け,安定し
たトルク特性を得るために,ばねの長さは,板厚の15 000倍までとする。
2) ばね板の曲率半径が小さい部分に応力集中が生じ,耐久性の低下につな(繋)がることから,応力
24
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
集中を避けるために,軸径は,板厚の20倍以上とする。
b) 定荷重ぜんまい 定荷重ぜんまいは,コイル状に加工した薄板を直線にまで引き伸ばして使用するた
めに,コイル径が小さい場合は,直線に引き伸ばすと塑性変形が生じる。そのため,製造可能なコイ
ル内径にはおのずと限界がある。引き伸ばしたときの塑性変形を避けるために,コイル内径は,板厚
の80倍以上とする。
c) その他の薄板ばね
1) 応力集中する部位は,曲げ半径をできる限り大きく取り,応力集中の軽減をはかる。
2) 相手部品との摩擦によって,ばねと相手部品とに摩耗が生じ,問題が発生することもあるために,
ばり及びだれ面の方向は,使用方法及び相手部品によって決定する。
8.3.2
加工上の注意事項
薄板ばねの加工に当たっては,次に規定する事項に注意する。
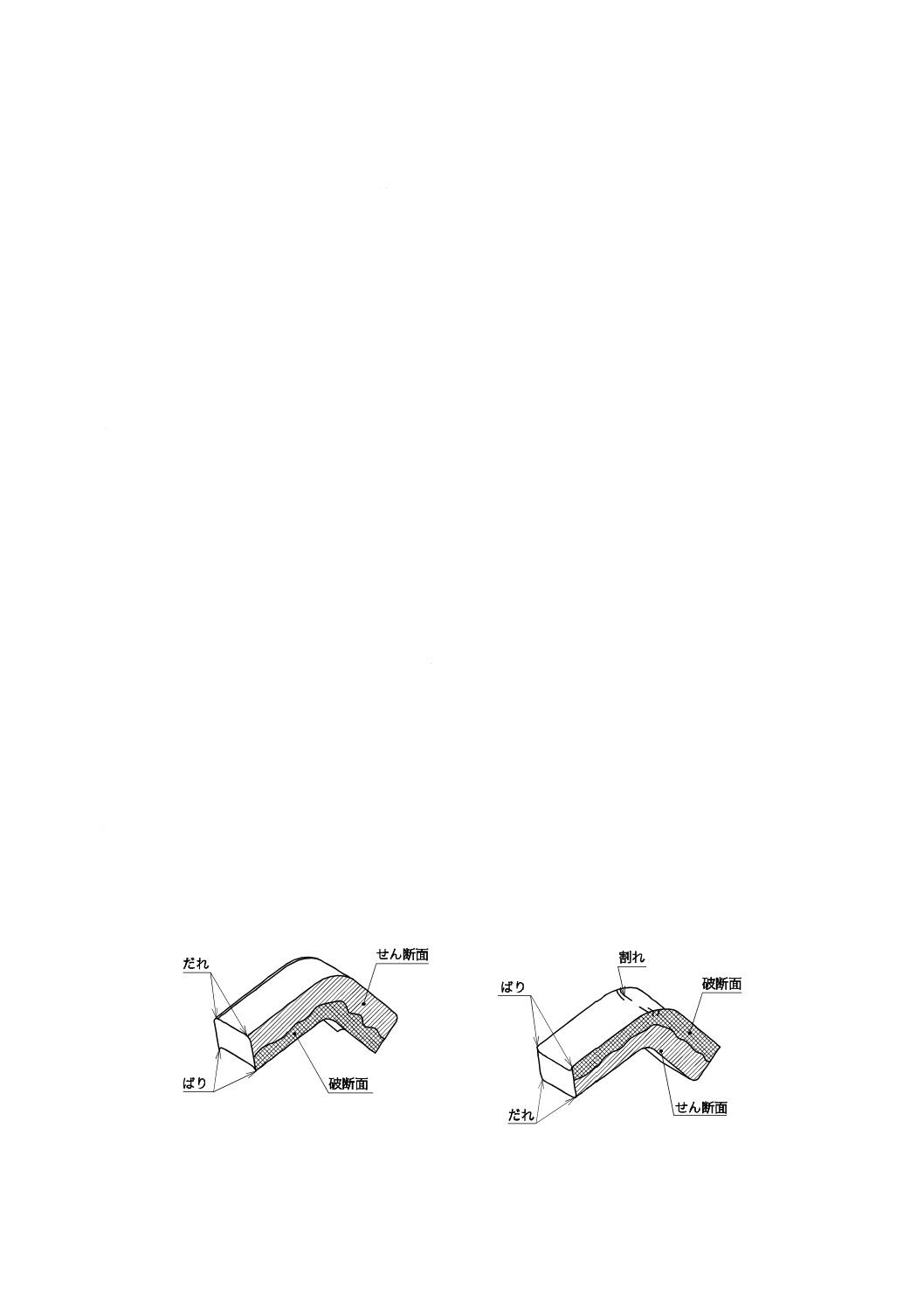
a) 金属材料に切断,孔あけなどのプレス加工を行うと,破断面の縁にばりと称するまくれあがったよう
な形の余肉が生じる。このばりは,曲げ加工によって割れにつな(繋)がることもあるために,次の
事項に注意する。曲げ方向と割れとの関係については,図17を参照する。
1) 曲げ部は,できる限り曲げの外側が抜きだれ側になるように加工する。
2) プレス加工の都合によって,すべての抜きだれ側を外側となるように加工することができない場合
がある。その場合は,応力が集中しやすい部位を優先的にだれが外側となるように加工し,残りの
ばりは,ばりを少なくする工程とする。
3) ばりを少なくするには,バレル研摩の施工,パンチとダイとのすき間を小さく設定するなどの方法
がある。
b) 材料の圧延方向は,機械的性質に影響を及ぼすため,材料の異方性を調査し,用途及び働きに応じて,
圧延方向に対する製品の材料取りの方向を指定する。
c) 製品の形状から,熱処理変形及び加工の容易さなどを考慮し,熱処理をした材料を使用するか,又は
加工後に熱処理を行うかを決める。
d) 複雑な形状の製品は,表面処理などの中間工程で製品同士のからみ合いによって,変形が生じやすい
ので,1回の処理数量を少なくするなどの対応をするのがよい。
e) 板ばねでは,特に耐久性が要求される場合には,ショットピーニングを行うが,薄板ばねは,変形し
やすいので,ショットピーニングは行わない。
f)
ぜんまいばねでは,材料断面の角部に応力集中が生じやすいので,角部をできる限り滑らかな円弧状
の形状とする。
図17−曲げ方向と割れとの関係
25
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表16−鋼の焼入焼戻し後の硬さと引張強さの換算表
(出典 ISO 18265による。)
650
79.9
―
57.5
88.9
75.0
62.8
―
650
640
79.7
―
57.1
88.7
74.6
62.3
―
640
630
79.4
―
56.6
88.5
74.2
61.7
―
630
620
79.2
―
56.1
88.2
73.7
61.2
―
620
610
78.9
―
55.6
88.0
73.3
60.6
―
610
600
78.7
―
55.1
87.7
72.8
60.0
―
600
590
78.4
―
54.6
87.5
72.4
59.4
―
590
580
78.2
―
54.0
87.2
71.9
58.8
―
580
570
77.9
―
53.5
86.9
71.4
58.2
―
570
560
77.6
―
52.9
86.6
70.9
57.5
―
560
550
77.3
―
52.4
86.4
70.4
56.8
―
550
540
77.0
―
51.8
86.1
69.9
56.2
―
540
530
76.7
―
51.2
85.8
69.3
55.5
―
530
520
76.4
―
50.5
85.4
68.8
54.8
―
520
510
76.0
―
49.9
85.1
68.2
54.0
―
510
500
75.7
―
49.2
84.8
67.6
53.2
―
500
490
75.4
―
48.6
84.4
67.0
52.5
―
490
480
75.0
―
47.9
84.1
66.4
51.7
―
480
470
74.6
―
47.2
83.7
65.8
50.8
1460
470
460
74.3
―
46.4
83.3
65.1
50.0
1430
460
450
73.9
―
45.7
82.9
64.4
49.1
1401
450
440
73.5
―
44.9
82.5
63.7
48.2
1371
440
430
73.0
―
44.1
82.1
63.0
47.2
1341
430
420
72.6
―
43.2
81.8
62.2
46.3
1311
420
410
72.2
(113.6)
42.4
81.2
61.4
45.3
1281
410
400
71.7
(113.1)
41.5
80.7
60.6
44.2
1250
400
390
71.2
(112.7)
40.6
80.2
59.8
43.2
1220
390
380
70.7
(112.2)
39.6
79.7
58.9
42.0
1189
380
370
70.2
(111.7)
38.6
79.1
58.0
40.9
1159
370
360
69.6
(111.1)
37.6
78.6
57.1
39.7
1128
360
350
69.1
(110.5)
36.5
78.0
56.1
38.4
1097
350
340
68.5
(109.9)
35.4
77.3
55.1
37.2
1070
340
330
67.8
(109.2)
34.3
76.7
54.0
35.8
1035
330
320
67.2
(108.5)
33.1
76.0
52.9
34.4
1003
320
310
66.5
(107.7)
31.8
75.3
51.8
32.9
972
310
Aスケール
全試験力588.4N
円すい形
ダイヤモンド圧子
ビッカ
ース
硬さ
ビッカ
ース
硬さ
引張強さ
(近似値)
MPa
45Nスケール
全試験力
441.3N
ロックウェル硬さ
ロックウェルスーパーフィシャル硬さ
円すい形ダイヤモンド圧子
15Nスケール
全試験力
147.1N
30Nスケール
全試験力
294.2N
Bスケール
全試験力988.7N
円すい形
ダイヤモンド圧子
Cスケール
全試験力1471N
円すい形
ダイヤモンド圧子
26
B 2713:2009
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表16−鋼の焼入焼戻し後の硬さと引張強さの換算表(続き)
(出典 ISO 18265による。)
300
65.8
(106.9)
30.5
74.5
50.5
31.4
940
300
290
65.0
(106.0)
29.1
73.7
49.3
29.8
909
290
280
64.3
(105.0)
27.7
72.9
47.9
28.1
877
280
270
63.4
(103.9)
26.2
72.0
46.5
26.3
845
270
260
62.5
(102.7)
24.6
71.0
45.0
24.4
813
260
250
61.6
(101.4)
22.9
70.0
43.4
22.5
781
250
240
60.6
100.0
21.2
68.9
41.8
20.4
748
240
230
59.6
98.4
(19.3)
67.8
40.4
18.2
716
230
220
58.4
96.7
(17.4)
66.5
38.1
15.9
683
220
210
57.2
94.8
(15.3)
65.2
36.1
13.4
651
210
注記 表中括弧 ( ) 内の数値は,参考として示したものである。
引張強さ
(近似値)
MPa
ビッカ
ース
硬さ
ビッカ
ース
硬さ
ロックウェル硬さ
ロックウェルスーパーフィシャル硬さ
円すい形ダイヤモンド圧子
30Nスケール
全試験力
294.2N
45Nスケール
全試験力
441.3N
Aスケール
全試験力588.4N
円すい形
ダイヤモンド圧子
Bスケール
全試験力988.7N
円すい形
ダイヤモンド圧子
Cスケール
全試験力1471N
円すい形
ダイヤモンド圧子
15Nスケール
全試験力
147.1N