B 2710-2:2020
(1)
目 次
ページ
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義··················································································································· 1
4 記号······························································································································· 1
5 設計の基本概念················································································································ 2
5.1 設計の原理 ··················································································································· 2
5.2 設計方法の種類 ············································································································· 2
5.3 設計の手順 ··················································································································· 2
5.4 留意事項 ······················································································································ 3
6 マルチリーフスプリングの設計 ··························································································· 3
6.1 展開法による設計 ·········································································································· 3
6.2 板端法による設計 ·········································································································· 5
7 テーパリーフスプリングの設計 ··························································································· 7
7.1 設計の原理 ··················································································································· 7
7.2 テーパリーフのモデル及び計算式 ····················································································· 7
8 非対称ばねの設計············································································································ 10
8.1 設計の原理 ·················································································································· 10
8.2 ばね定数及び曲げ応力 ··································································································· 10
9 トレーリングリーフの設計 ································································································ 11
10 設計における考慮事項 ···································································································· 11
10.1 中央部締付けによる無効長さ ························································································· 11
10.2 たわみによるスパンの変化 ···························································································· 12
10.3 ワインドアップ ··········································································································· 13
10.4 板間摩擦及び動ばね定数 ······························································································· 14
10.5 フレッティング ··········································································································· 14
附属書A(参考)重ね板ばねの疲労設計 ·················································································· 15
附属書B(参考)設計計算例 ································································································· 20
附属書C(規定)設計に用いる係数の線図 ··············································································· 23
B 2710-2:2020
(2)
まえがき
この規格は,産業標準化法第16条において準用する同法第12条第1項の規定に基づき,一般社団法人
日本ばね工業会(JSMA)及び一般財団法人日本規格協会(JSA)から,産業標準原案を添えて日本産業規
格を改正すべきとの申出があり,日本産業標準調査会の審議を経て,経済産業大臣が改正した日本産業規
格である。これによって,JIS B 2710-2:2008は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本産業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 2710の規格群には,次に示す部編成がある。
JIS B 2710-1 第1部:用語
JIS B 2710-2 第2部:設計方法
JIS B 2710-3 第3部:試験方法
JIS B 2710-4 第4部:製品仕様

日本産業規格 JIS
B 2710-2:2020
重ね板ばね−第2部:設計方法
Leaf springs-Part 2: Design method
1
適用範囲
この規格は,主に自動車,鉄道車両,産業機械に使用する重ね板ばねの設計方法について規定する。
なお,この規格でいう重ね板ばねには,ばね板が1枚だけの場合も含む。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0103 ばね用語
JIS B 0156 ばね記号
JIS B 2710-1 重ね板ばね−第1部:用語
JIS B 2710-3 重ね板ばね−第3部:試験方法
JIS B 2710-4 重ね板ばね−第4部:製品仕様
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 0103及びJIS B 2710-1による。
4
記号
この規格で用いる主な記号及び定義は,JIS B 0156の規定に基づき,表1による。
表1−記号及び定義
記号
定義
単位
b
板幅
mm
C
反り
mm
E
縦弾性係数,E=206×103
N/mm2
e
目玉半径
mm
2F
重ね板ばねに対する作用力
N
I
リーフの断面二次モーメント
mm4
l
重ね板ばねのハーフスパン,2lはスパン
mm
lA
非対称ばねの固定側スパン
mm
lB
非対称ばねのシャックル又はスライド側スパン
mm
lST
ハーフストレートスパン,2lSTはストレートスパン
mm
lST,A
非対称ばねの固定側ストレートスパン
mm
lST,B
非対称ばねのシャックル又はスライド側ストレートスパン
mm
n
リーフの総数,又は親板を表す添え字
−
2
B 2710-2:2020
表1−記号及び定義(続き)
記号
定義
単位
nf
全長板の数
−
R
ばね定数,R=2F/s
N/mm
RT
ワインドアップ剛性,RT=T/θ
N mm/rad
RU
Uボルト締付時のばね定数
N/mm
s
たわみ
mm
T
ワインドアップトルク
N mm
t
板厚
mm
U
Uボルト間距離(図10参照)
mm
Z
リーフの断面係数
mm3
η
リーフの総数に対する全長板の比率,η=nf/n
−
θ
ワインドアップによる回転角
rad
σ
リーフの曲げ応力
N/mm2
σR
ワインドアップによる1番リーフの曲げ応力
N/mm2
5
設計の基本概念
5.1
設計の原理
重ね板ばねの設計においては,ばね定数及び強度耐久性を重視する。例えば,マルチリーフスプリング
の各リーフは,力学的には中央固定で両端自由の片もちはりと同等と考えられる。一般の重ね板ばねは,
形状及び寸法の異なる複数のリーフを束ねた構造体であるが,全体に作用する力とたわみとの関係が一義
的に決まる限り,個別のリーフに作用する力とたわみとの関係を解析することができる。ただし,たわみ
によるスパンの変化は,通常,無視する。すなわち,ばね全体にたわみを与えると,それから個々のリー
フのたわみが決定でき,個別のリーフが及ぼす力の総和としてばね全体の力が定まり,ばね定数を決定す
ることができる。また,各リーフに作用する力に応じて,リーフ内の応力分布を求め,強度耐久性を検討
することができる。
5.2
設計方法の種類
重ね板ばねの設計方法の種類は,表2による。
表2−設計方法の種類
ばねの種類
設計方法
摘要
細分箇条
マルチリーフスプリング
展開法
隣接リーフが全面で接触して力を伝達すると仮定
し,各リーフを同一平面に展開した広幅の一枚板と
みなして設計計算を行う。
6.1
板端法
隣接リーフがリーフの端部だけで接触して力を伝達
すると仮定して設計計算を行う。
6.2
テーパリーフスプリング
直線テーパ法
テーパ部の板厚を直線状に漸減させて設計する。
7.2.2
放物線テーパ法
テーパ部の応力分布がより均一となるように板厚を
放物線状に漸減させて設計する。
7.2.3
非対称ばねの設計方法は,ばねの片側ずつこの表のいずれかの方法を用い,その手順は,箇条8による。
5.3
設計の手順
重ね板ばねの設計においては,ばねを組み込む装置及び機器の要求に合わせ,あらかじめばねの諸元を
設定する。ここでいう諸元には,通常,ばねの種類,ストレートスパン,リーフの形状,板幅,板厚,枚
数などを含む。その上で,これら諸元に基づき算定したばね定数及びリーフの曲げ応力が要求に対して適
3
B 2710-2:2020
切な範囲にあるかどうかを評価する。結果が十分でなければ,ばねの種類及び諸元に戻って見直しを行う。
すなわち,重ね板ばねの設計には,要求仕様に対する提案,評価及び見直しという,繰返し過程を含む。
附属書Aに代表的なばね材料に用いる常用曲げ応力と最大作用曲げ応力との関係,疲労強度及び時間強度
線図を示す。また,附属書Bに設計計算例を示す。
なお,形状寸法の詳細,処理方法及び部品を含めた製品仕様については,JIS B 2710-4による。また,
設計した製品を検証するための試験方法は,JIS B 2710-3による。
5.4
留意事項
重ね板ばねは,ばね力を利用して振動吸収及び緩衝の役に立てるばかりでなく,それ自体が構造部材と
して他の部材の位置決め及び連結機能を担うことが可能である。重ね板ばねの特性は,このほかに板間摩
擦によるエネルギー吸収の効果,ワインドアップトルクの作用による付加的な応力及び変形の発生,フレ
ッティング摩耗による耐久性低下などの問題があり,特に自動車用ばねでは,腐食疲労の問題も重視する。
設計においては,これらを考慮した対策も十分に行うことが望ましい。
6
マルチリーフスプリングの設計
6.1
展開法による設計
6.1.1
展開法の原理
展開法では,中心穴から等距離にある点の各リーフの曲率が全て等しいと仮定し,隣接する各リーフが
互いに全面で接触して力を伝達すると考える。その場合,マルチリーフスプリングは同一平面上に展開し
た1枚の広幅のばね板と力学的に等価になる。展開法は,ばね定数及び曲げ応力の計算が比較的簡単なた
め,ばねの概略設計及び疲労強度の評価に用いることが多い。全長板が2枚以上あるばねの場合には,通
常,展開法で計算する。
なお,展開法には,台形モデルを用いる場合及び階段モデルを用いる場合がある。
6.1.2
適用対象
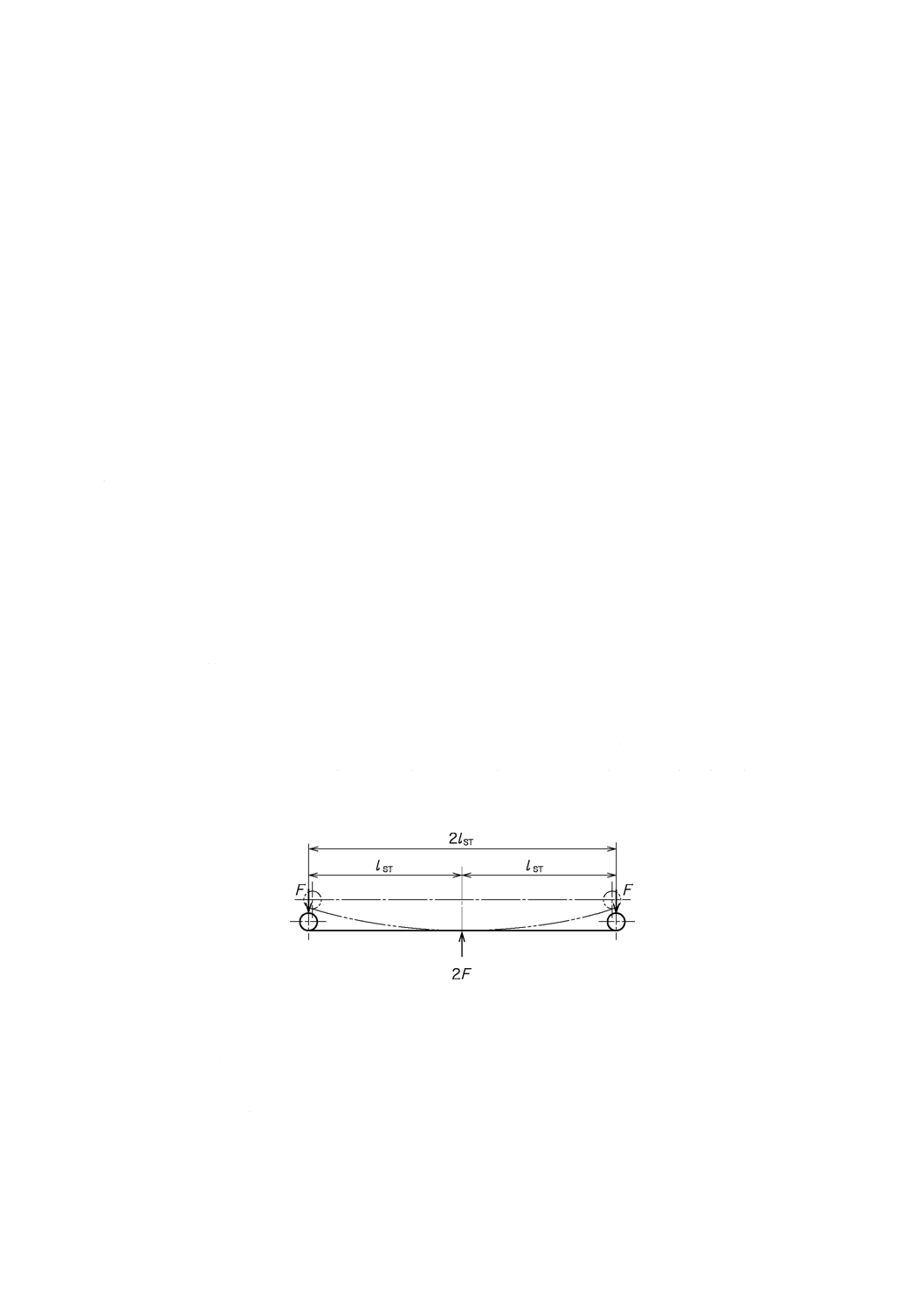
展開法によるマルチリーフスプリングの解析は,図1に示す対称ばねに適用する。ここでは基本的なマ
ルチリーフスプリングについて規定するが,親子重ね板ばね及びまくらばねにこの考え方を適用してもよ
い。
図1−対称ばねのモデル
6.1.3
台形モデルによる方法
6.1.3.1
台形モデル
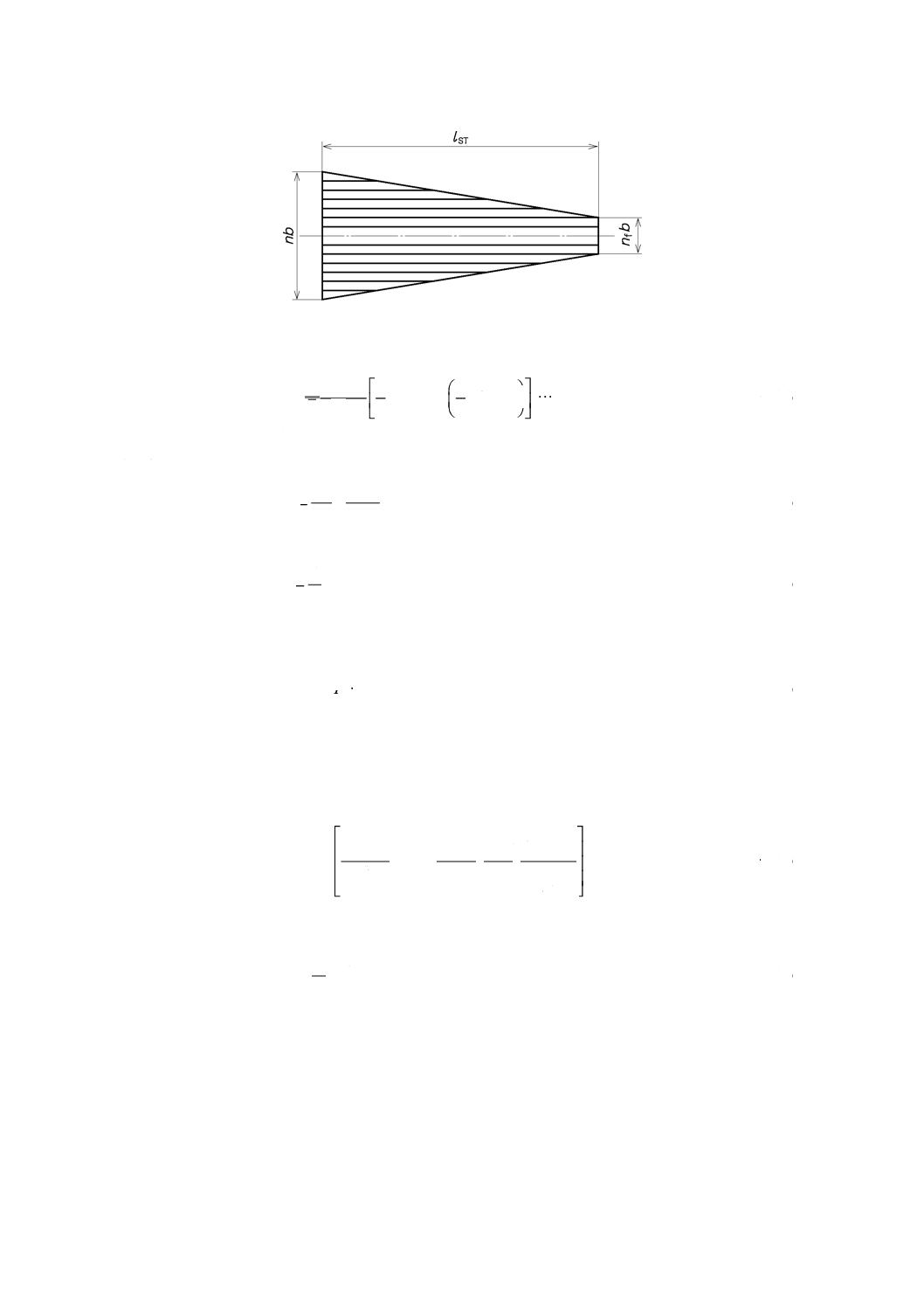
各リーフの厚さが全て等しい場合には,リーフの開先形状及び長さの違いによるステップの違いを無視
して,図2の台形モデルで近似する。
4
B 2710-2:2020
図2−台形モデル
台形の形状に基づく係数KTは,式(1)による。KTは,C.1から読み取ってもよい。
2
T
3
3
1
3
2
log
2
2
(1
)
e
K
ηη
η
η
=
−
+
−
−
············································· (1)
6.1.3.2
ばね定数及び曲げ応力
ばね定数Rは,式(2)による。
3
T
ST
1
6nEI
R
K
l
=
×
·········································································· (2)
Iは,リーフの断面二次モーメントで,長方形断面リーフの場合は,式(3)による。
3
1
12
I
bt
=
················································································· (3)
各リーフの長さ中央(センタ穴位置)における曲げ応力は等しく,式(4)による。長方形断面の場合は,
Z=2I/tである。
ST
lF
nZ
σ=
················································································· (4)
6.1.4
階段モデルによる方法
6.1.4.1
階段モデル
リーフごとに厚さが異なる場合には,開先形状によらず,図3の階段モデルで近似する。階段モデルを
用いるときの係数KSは,式(5)による。
(
)(
)
f
3
S
1
1
+1
(1
)
1
nn
i
i
n
n
n
n
i
i
j
j
i
ji
ji
I
K
I
I
I
I
λ
−
=
=
=
=
−
=
+
×
∑
∑
∑
∑
··································· (5)
ここに,
λi: 短い方からi番目のリーフの相対長さ比,λi=li/lST
Iiは,同じくi番目のリーフの断面二次モーメントで,長方形断面リーフの場合は,式(6)による。
3
1
12
i
ii
I
bt
=
················································································ (6)

5
B 2710-2:2020
図3−階段モデル
6.1.4.2
ばね定数及び曲げ応力
ばね定数Rは,式(7)による。
3
S
ST
6
1
n
EI
R
K
l
=
×
··········································································· (7)
各リーフの長さ中央(センタ穴位置)における曲げ応力σiは,式(8)による。
ST
1
2
i
i
n
j
j
tl
F
I
σ
=
=∑
········································································ (8)
6.2
板端法による設計
6.2.1
板端法の原理
板端法では,隣接するリーフ間での力の伝達が,リーフの先端だけで行われると仮定する。したがって,
各リーフの板厚,開先形状及びステップがどのような寸法であっても適用可能である。
板端法によるばね定数は,一般に実測値とよく一致するほか,各リーフ内の応力分布が容易に計算可能
なため,ばねの詳細設計に用いることが多い。
6.2.2
適用対象
板端法によるマルチリーフスプリングの解析は,対称ばねについて適用する(図1参照)。ここでは基本
的なマルチリーフスプリングについて規定するが,親子重ね板ばね及びまくらばねにこの考え方を適用し
てもよい。
6.2.3
板端形状係数
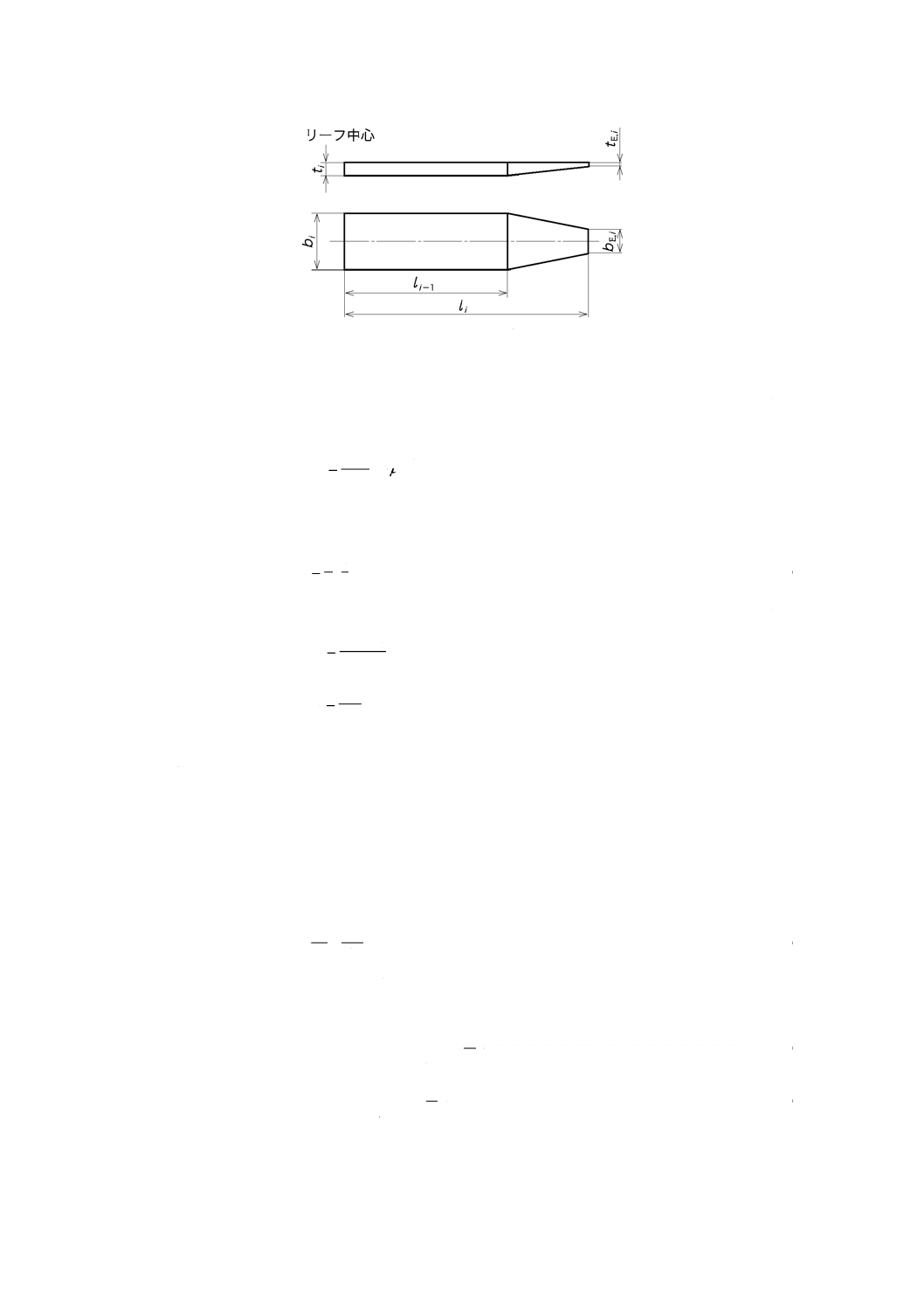
リーフの開先形状は,図4のモデルによって近似する。まず,短い方からi番目のリーフの開先につい
て,板端形状係数Kiは,式(9)による。Kiは,C.2から読み取ってもよい。
2
3
2
3
3(
3)
log
1
(
)
2(
)
i
i
i
i
i
e
i
i
i
i
i
K
β
ξ
ξ
β
β
ξβ
ξβ
−
=
+
−
−
−
··············································· (9)
ただし,リーフ端の相対幅をβi=bE,i/bi,相対厚さをξi=tE,i/tiとする(図4参照)。
6
B 2710-2:2020
図4−開先のモデル
ばね定数を求めるための係数ηiは,式(10)による。
ηi=Bi−αi−1×Γi−1 ···································································· (10)
Bi=1+(1−μi−1)3Ki
2
1
1
1
3
2
i
i
i
Γ
μμ
−
−
−
−
=
式中,αi−1は,i−1番目のリーフ端での作用力と,i番目のリーフ端での作用力との比で,式(11)及び式
(12)による。
1
1
1
1
i
i
i
i
A
D
α
ϕ
−
−
−
−
=
··········································································(11)
Di−1=ϕi−1+ηi−1 ······································································ (12)
1
1
1
3
2
i
i
i
A
μ
μ
−
−
−
−
=
1
1
i
i
i
I
I
ϕ
−
−=
また,μは力の入力位置で,μi−1=li−1/liである。
以上の計算において,Ai−1,Bi,Γi−1,ϕi−1及びμi−1は,ばね諸元に応じて決まるため,初めに求めてお
くとよい。その場合は,A0=Γ0=ϕ0=0とする。
その上で,まず式(10)によってi=1としてη1を求め,これを式(12)に代入してD1を求めれば,式(11)か
らα1が求まる。これを再び式(10)に入れると,η2を得る。次に,同じように繰り返すと,最後にηnを得る。
6.2.4
ばね定数及び曲げ応力
ばね定数Rは,式(13)による。
3
ST
6
1
n
n
EI
R
l
η
=
×
········································································· (13)
i番目のリーフにおいて,中央部の曲げ応力σioは,式(14)に,i−1番目のリーフとの接触点の曲げ応力
σicは,式(15)による。
1
1
o
1
1
1
(1
)
n
i
i
i
j
i
j
Fl
Z
σ
σ
μ
α
−
−
−
=
=
−
×
×
∏
···················································· (14)
1
1
c
1
1
(1
)
n
i
i
j
i
j
Fl
Z
σ
μ
α
−
−
=
=
−
×
∏
··························································· (15)
7
B 2710-2:2020
7
テーパリーフスプリングの設計
7.1
設計の原理
テーパリーフスプリングは,ばね中心から長手方向の先端部にかけて板厚が漸減するテーパ形状をもつ
リーフを重ねて構成したばねである。
図5−テーパリーフスプリングの例
図5に示すような対称ばねにおいて,ばね全体のたわみ変化と,各リーフのたわみ変化とが等しいため,
各リーフはそのばね定数に応じた力を分担する。したがって,全体のばね定数は個々のリーフのばね定数
の総和に等しい。すなわち,設計は個別のリーフについて行えばよい。
注記 テーパリーフスプリングは,マルチリーフスプリングに比べリーフの長さ方向応力分布を均等
化しやすいため,軽量化に有利である。
7.2
テーパリーフのモデル及び計算式
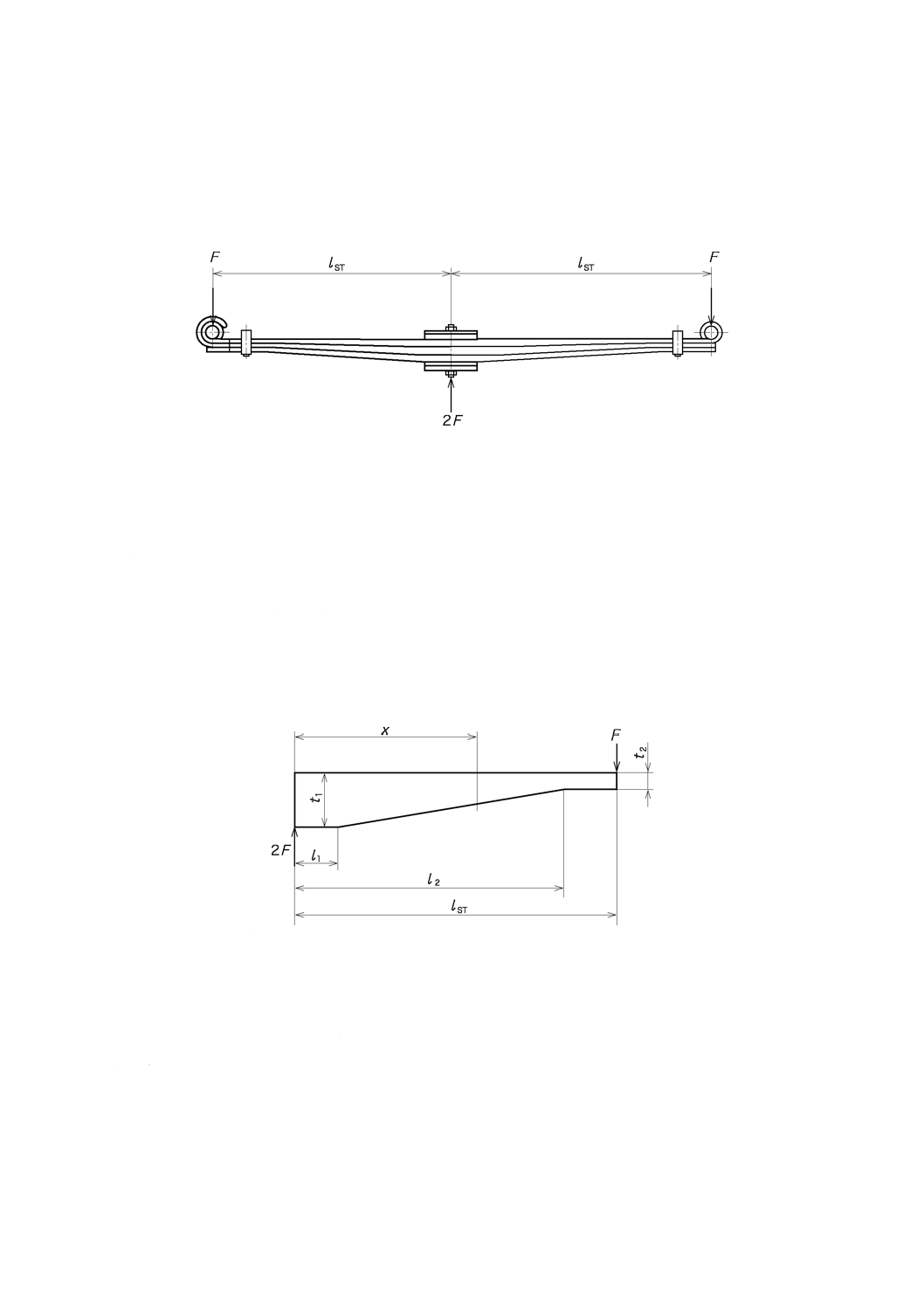
7.2.1
テーパリーフのモデル
リーフの板幅bが一定で,リーフの板厚tがt1〜t2まで漸減する対称形のテーパリーフについて,そのハ
ーフストレートスパン分をモデル化して図6に示す。
注記 x:中心穴からの距離(mm)
図6−テーパリーフのモデル
7.2.2
直線テーパ法の場合のばね定数及び曲げ応力
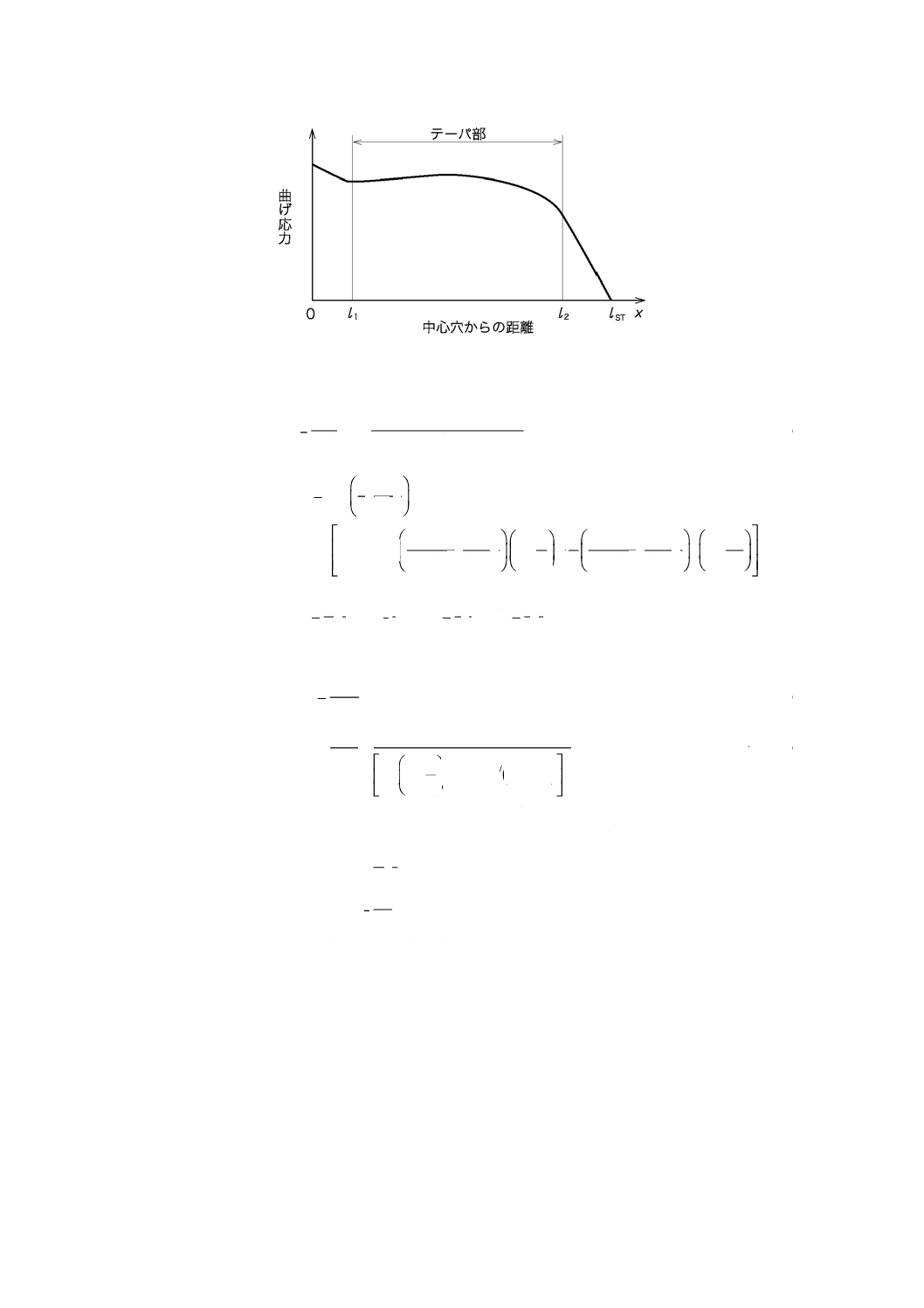
図6で示すテーパ部の板厚が直線状に変化する場合のリーフの曲げ応力分布を模式的に表すと,図7の
ようになる。
8
B 2710-2:2020
図7−直線テーパ法の場合の曲げ応力分布図
ばね定数は,式(16)による。
3
3
3
3
ST
1
2
6
1
1(1
)
(1
)
EI
R
l
J
λ
η
λ
=
×−
−
+
−
+
············································· (16)
3
3
2
1
2
1
2
1
2
2
2
1
2
1
3
1
1
1
1
1
1
log
2
1
1
2
e
J
λλ
η
η
ηληλ
ηληλ
η
λλ
η
λλ
η
−
=
−
−−
+
−−
+
−
−
+
−
−
−
3
1
1
1
2
1
2
2
ST
ST
12
bt
t
l
l
I
t
l
l
η
λ
λ
=
=
=
=
,
,
,
曲げ応力は,式(17)及び式(18)による。
ST
(0)
Fl
Z
σ
=
············································································ (17)
(
)(
)
ST
2
1
2
1
1
()
1
1
1
Fl
x
Z
μ
σ
μλ
λλ
η
−
=
×
−
−
−
−
··································· (18)
ここに, σ(0): 中心穴位置の曲げ応力
σ(x): テーパ部の座標xにおける曲げ応力
2
1
ST
6
bt
Z
x
l
μ
=
=
7.2.3
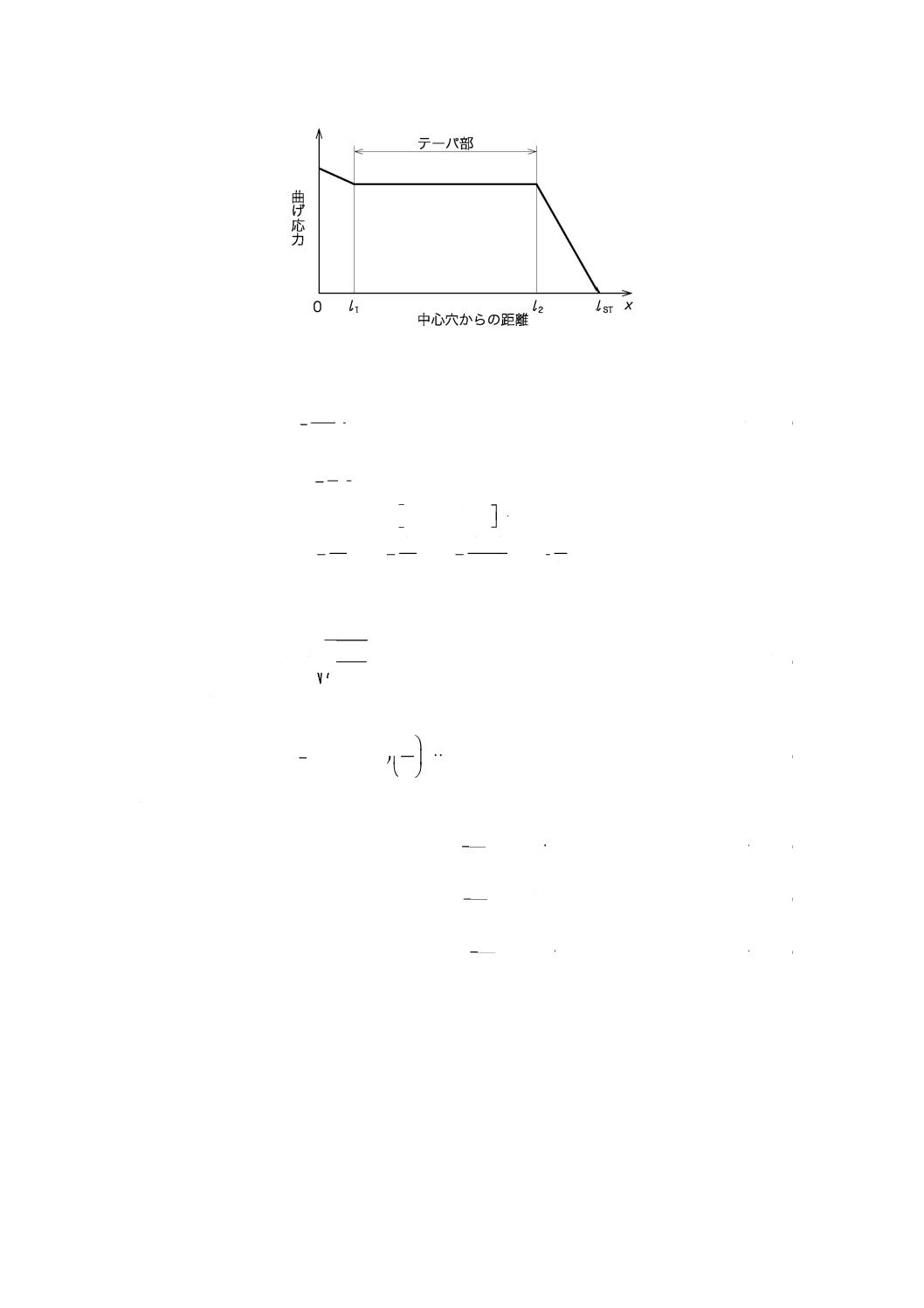
放物線テーパ法の場合のばね定数及び曲げ応力
図6に示すテーパ部の板厚が放物線状に変化する場合のリーフの曲げ応力分布を模式的に表すと,図8
に示すようにテーパ部の曲げ応力が均一な分布となる。
9
B 2710-2:2020
図8−放物線テーパ法の場合の曲げ応力分布図
ばね定数は,式(19)による。
1
3
ST
6EI
R
Kl
=
·············································································· (19)
3
1
1
3
3/2
3
1
1
2
1
2
2
1
1
1
2
1
ST
ST
ST
1
2
12
1(1
)12(1
)
(1
)
bt
I
K
l
l
l
l
t
l
l
l
l
t
λ
ζ
λη
λ
λ
ζ
η
=
=+
−
−
−
+
−
−
=
=
=
=
−
,
,
,
ただし,板厚は中心穴からの距離l1〜l2の位置まで放物線状に変化し,中心穴から任意の距離xにおけ
る板厚は,式(20)による。
ST
1
ST
1
l
x
ttl
l
−
=
−
·········································································· (20)
また,l2は,式(21)による。
2
2
2
ST
ST
1
1
(
)t
l
l
l
l
t
=
−
−
······························································· (21)
曲げ応力は,式(22)〜式(24)による。
0≦x≦l1の範囲では,
ST
2
1
6
(
)
Fl
x
bt
σ=
−
·········································· (22)
l1≦x≦l2の範囲では,
ST
1
2
1
6
(
)
Fl
l
bt
σ=
−
········································· (23)
l2≦x≦lSTの範囲では,
ST
2
2
6
(
)
Fl
x
bt
σ=
−
········································ (24)
7.2.4
テーパリーフを重ね合わせた場合のばね定数及び曲げ応力
ばね全体のたわみ変化が,個々のリーフのたわみ変化と等しいばねにおいては,全体のばね定数は各リ
ーフのばね定数の総和となり,図5に示すような3枚重ねのテーパリーフスプリングの場合,ばね定数は,
式(25)による。
R=R1+R2+R3 ········································································ (25)
ここに,
R1: 1番リーフのばね定数
R2: 2番リーフのばね定数
R3: 3番リーフのばね定数
10
B 2710-2:2020
各リーフの曲げ応力は,各リーフの分担力を割り出すことによって求められる。各リーフの分担力は,
式(26)〜式(28)による。
1
1
R
F
F
R
=
··············································································· (26)
2
2
R
F
F
R
=
·············································································· (27)
3
3
R
F
F
R
=
·············································································· (28)
ここに,
F1: 1番リーフの分担力
F2: 2番リーフの分担力
F3: 3番リーフの分担力
8
非対称ばねの設計
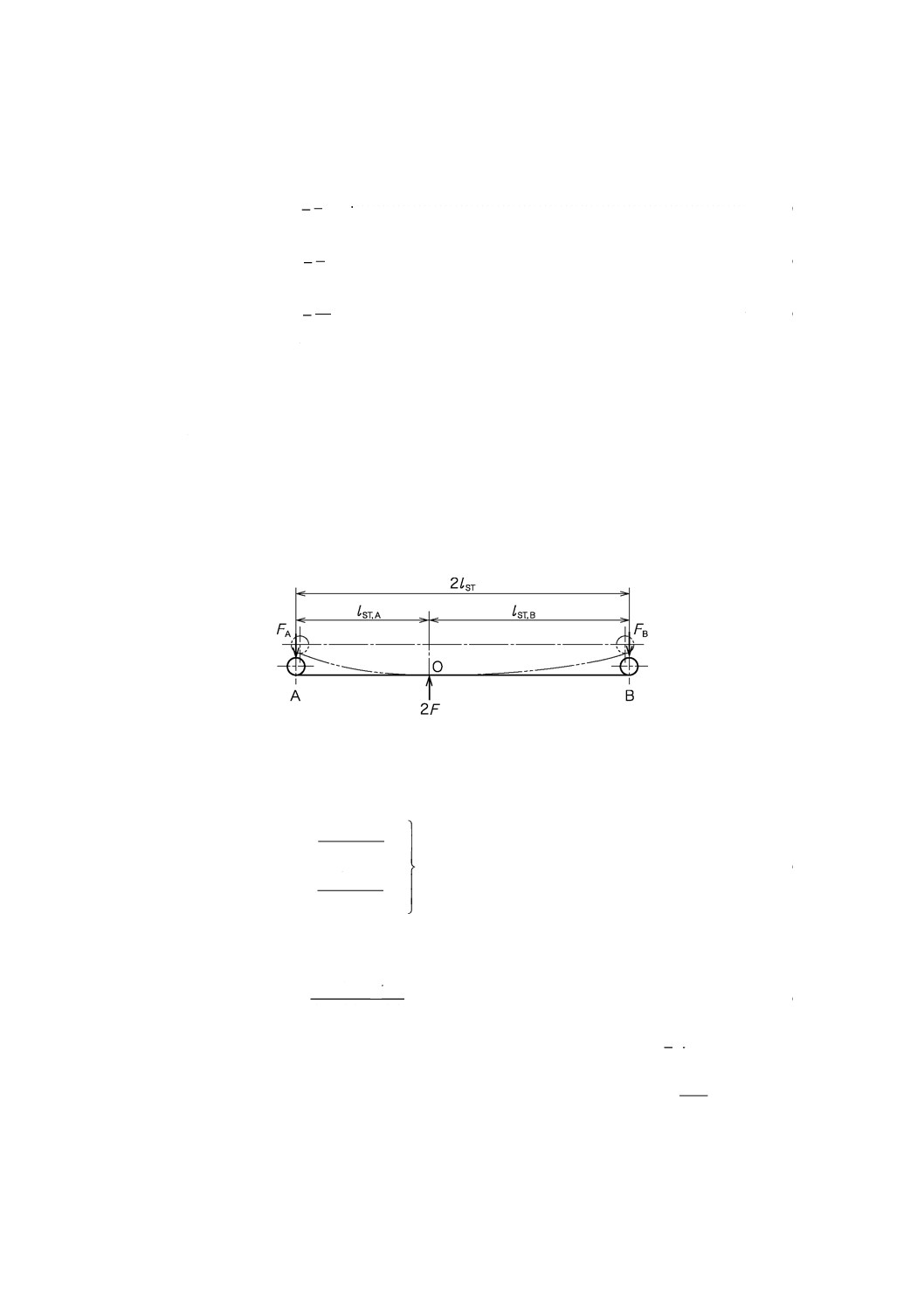
8.1
設計の原理
非対称ばねは,図9のようにモデル化できる。この場合,力2Fの作用点Oにおいて,ばねは自由に回
転可能と仮定する。設計においては,これをストレートスパン2lST,Aの対称ばねの半分と,ストレートス
パン2lST,Bの対称ばねの半分とを加え合わせたものと考え,箇条6又は箇条7の設計方法を適用する。
図9−非対称ばねのモデル
図9のモデルにおいて,作用力2Fによって作用点A及び作用点Bでの作用力の大きさFA及びFBは,
式(29)による。
ST,B
A
ST,A
ST,B
ST,A
B
ST,A
ST,B
2
2
l
F
F
l
l
l
F
F
l
l
=
+
=
+
································································· (29)
8.2
ばね定数及び曲げ応力
ばね定数Rは,式(30)による。
2
A
B
2
(1
)
(
)
(1
)(1
)
R
R
R
κ
λ
κ
κλ
+
=
+
+
+
······················································· (30)
ここに,
κ: A側とB側とのばね定数の比で,
A
B
R
R
κ=
λ: A側とB側との非対称長さの比で,
ST,A
ST,B
l
l
λ=
特に,各リーフでA側とB側との長さの比が等しい場合には,式(31)による。また,C.3から数値を読
み取って求めてもよい。
11
B 2710-2:2020
A
A
B
3
(1
)
(1
)
(
)
1
R
R
R
R
λ
λ
λ
λ
λ
+
=
+
=
+
+
················································ (31)
式(30)及び式(31)に用いるばね定数RA及びRBは,台形モデルの展開法においては式(2),階段モデルの展
開法においては式(7),板端法においては式(13),及びテーパリーフにおいては式(16)又は式(19)による。
各リーフの曲げ応力は,式(29)による作用力を用い,台形モデルの展開法においては式(4),階段モデル
の展開法においては式(8),板端法においては式(14)及び式(15),テーパリーフにおいては式(17)及び式(18),
又は式(22)〜式(24)による。
9
トレーリングリーフの設計
JIS B 2710-4によるタイプ1及びタイプ2のトレーリングリーフの設計原理は,非対称テーパリーフス
プリングと同等である。したがって,まず各リーフの固定側ストレートスパン及び空気ばね側ハーフスパ
ン(JIS B 2710-1参照)について,それぞれ式(16)又は式(19)によって個別のばね定数を求め,次いで非対
称ばねとして,式(30)によって全体のばね定数を求めればよい。ただし,空気ばね側ハーフスパンのばね
定数は,リーフを剛体とみなして省略することも可能である。
10 設計における考慮事項
10.1 中央部締付けによる無効長さ
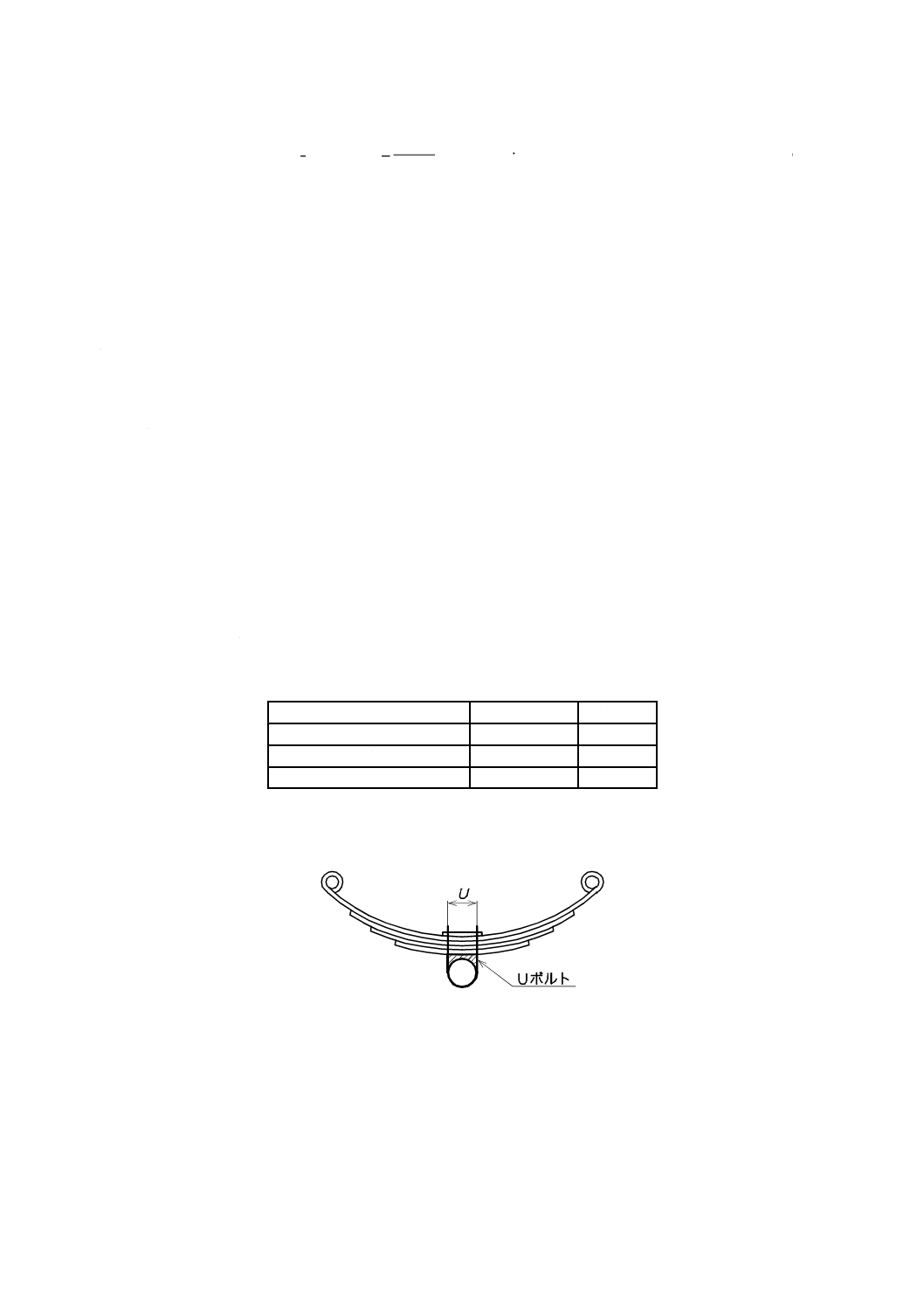
重ね板ばねは,中央部をUボルトなどで締め付けたり,胴締めによって固定したりするため,スパンの
一部にばね作用をしない無効部分が含まれることがある。設計における無効長さは,表3による。図10
〜図12に,中央部締付けの例を示す。
表3−締付けによる無効長さ
締付方法
無効長さ
説明図
Uボルトのリジッドクランプ
0.4 U〜0.8 U
図10
アイソクランプ
0〜0.2 U
図11
胴締め
0.6 B
図12
なお,無効長さが大きくなると,ばね定数は大きくなる。例えば,無効長さが0.6 Uのリジッドクラン
プでは,ばね定数は,RU=[2lST/(2lST−0.6U)]3Rとなる。
図10−自動車用ばねのUボルトによるリジッドクランプの例
12
B 2710-2:2020
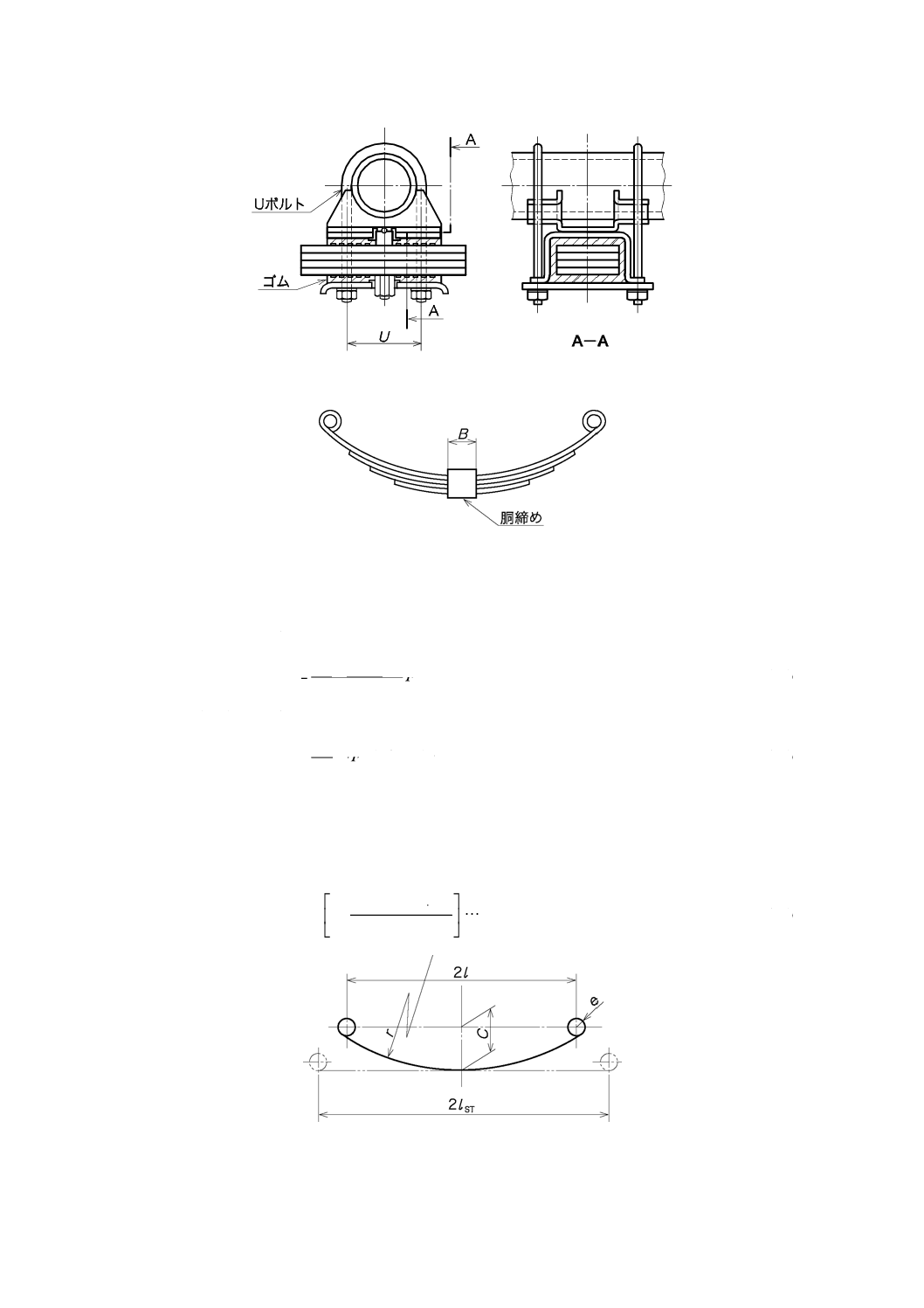
図11−自動車用ばねのアイソクランプの例
図12−鉄道車両用ばねの胴締めの例
胴締めのあるマルチリーフスプリングの曲げ応力は,式(32)又は式(33)による。Bは,胴締めの長さ(mm)
である。
a) lST/n<80(mm)の場合
2
ST
2
5.5(
0.3)
(N/mm)
l
BF
nbt
σ
−
=
····················································· (32)
b) lST/n≧80(mm)の場合
2
ST
2
5.3
(N/mm)
lF
nbt
σ=
······························································· (33)
10.2 たわみによるスパンの変化
重ね板ばねは,たわみによってスパンが変化し,取付機構への影響があるため,その関係特性を知るこ
とが必要である。図13に示すマルチリーフスプリングのモデルでは,ハーフスパンlと反りCとの関係は,
式(34)による。lは,C.4から数値を読み取って求めてもよい。
ST
2
ST
2(
)(
2)
1
3
CeC
e
ll
l
−
+
=
−
························································· (34)
図13−たわみによるスパンの変化
13
B 2710-2:2020
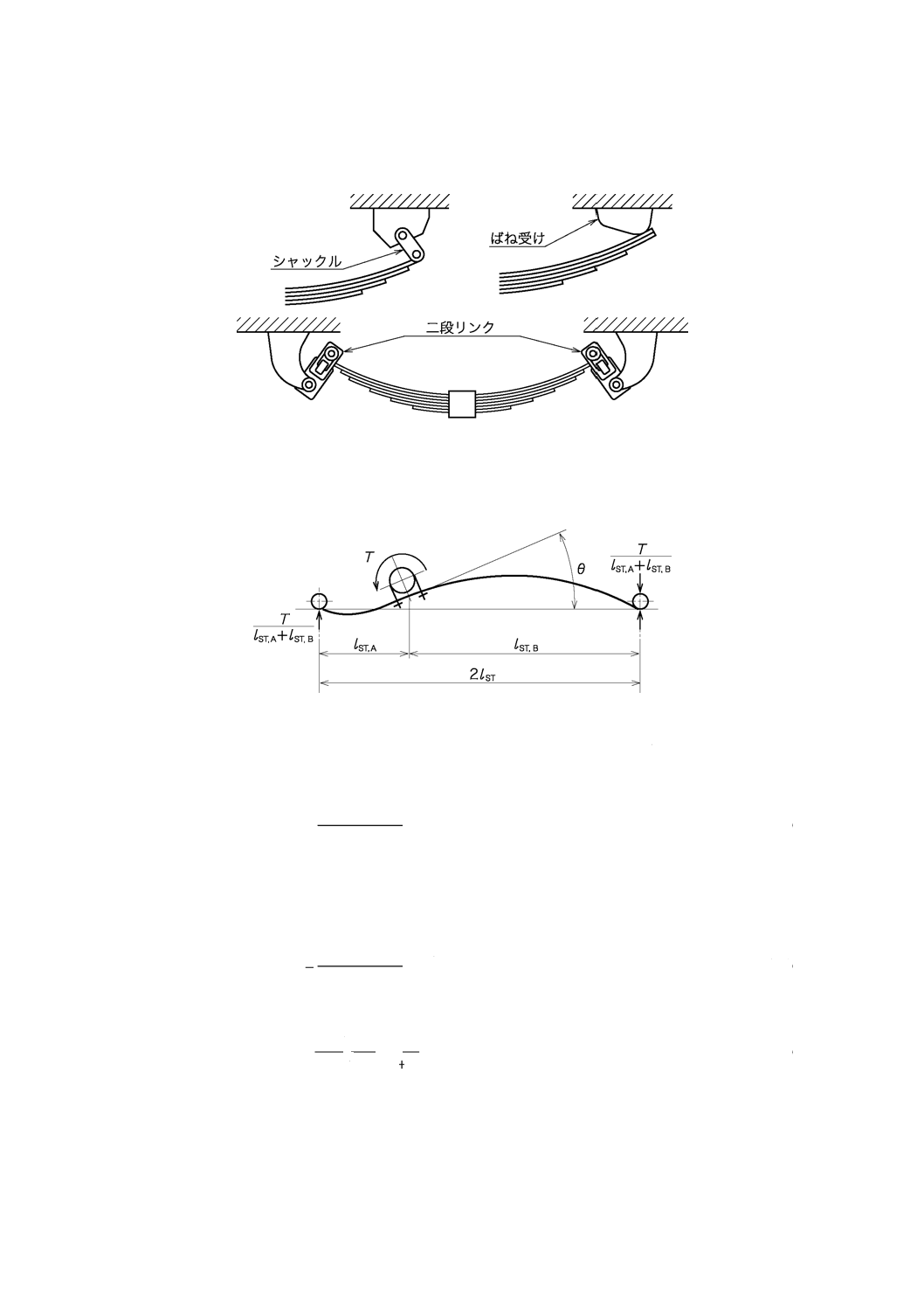
反りの変化によるスパンの変化を逃がすために,目玉にシャックル又は二段リンクを取り付ける方法,
目玉を付けずにばね受けで支持する方法など,何らかの対策を施す(図14参照)。
図14−スパンの変化の逃がし方の例
10.3 ワインドアップ
ワインドアップトルクTが作用すると,ばねは図15のように回転変形する。
注記 この図は,制動時トルクが作用した状態を示す。
図15−ワインドアップトルクT及び中心部の回転角θ
この場合のワインドアップ剛性RTは,式(35)による。RTは,C.5から数値を読み取って求めてもよい。
2
2
T
ST
2
4(1
)
(1
)(1
)
R
Rl
κλ
κ
λ
+
=
+
+
····························································· (35)
ここに,
λ: A側とB側との非対称長さの比で,λ=lST,A/lST,B
κ: A側とB側とのばね定数の比で,κ=RA/RB
RA,RB及びR: A側,B側,及び全体のばね定数
特に,A側とB側とのばね板の枚数及び長さの比が等しい場合には,RTは,式(36)による。
2
2
T
ST
3
4
(1
)(1
)
R
Rl
λ
λ
λ
=
+
+
····························································· (36)
短い方からi番目のリーフに作用する応力は,長さlST,A又はlST,Bの間で一定で,式(37)による。
1
1
2
i
i
n
j
j
t
T
I
σ
λ
=
=
×+
∑
································································ (37)
ワインドアップトルクは,通常の作用力に重畳して作用し,トルクの向きによってリーフの応力が増減
するので,ばねの耐久性評価においては注意しなければならない。
A
B

14
B 2710-2:2020
10.4 板間摩擦及び動ばね定数
重ね板ばねは,リーフ間の摩擦のため,図16に示すように,力とたわみとの関係が加力時と減力時とで
異なり,ヒステリシス特性を示す。
図16−板間摩擦によるヒステリシス
その結果,動ばね定数は静ばね定数より高めとなり,無視できない影響を及ぼすことがある。一方では,
板間摩擦による制振効果を期待することも多い。したがって,設計では板間摩擦の程度を考慮する必要が
ある。
板間摩擦を減少するためには,リーフ数を少なくする,板端に摩擦係数の低いスペーサを挟むなどの方
策があり,板間摩擦を増加するためには,リーフ数を多くする,リーフを締め付けるなどの方策がある。
板間摩擦による動ばね定数の変化は,ばねのたわみが小さい範囲で特に大きく,そのためばねを含む振
動系の共振周波数が変化して,他の防振対策などの効果を損ねることがあるので注意が必要である。
なお,潤滑による板間摩擦の低減策は,効果の持続性が期待できない。
10.5 フレッティング
重ね板ばねの中央締付部は,フレッティングによる摩耗を生じやすいので,リーフ間に樹脂又は軟鋼の
センタスペーサを挟むなど,対策を工夫することが望ましい。
フレッティングを起こす箇所の作用応力が高いと,疲労破壊を起こしやすい。例えば,Uボルトによる
締付部では,Uボルトの締付け境界部から折損することがある。
15
B 2710-2:2020
附属書A
(参考)
重ね板ばねの疲労設計
A.1 重ね板ばねの強度耐久性
重ね板ばねの強度耐久性は,実際の使用環境における種々の作用応力の大きさ及びその変動条件の影響
を強く受ける。しかし,それら応力条件の詳細は,個別のばねによって大きく異なり,一定の基準を示す
ことは困難である。この附属書は,過去の経験に基づく応力条件の実態を示す重ね板ばねの疲労設計に関
する資料について記載している。
なお,この附属書に示すデータは,トラック,バスなどに用いる線形特性ばねの設計において,国内の
製造業者が考慮している応力条件の調査結果をまとめたもので,2000年当時のものである。ばねには,シ
ョットピーニング施工ばね,ストレスピーニング施工ばね,モディファイドオースフォーミングなどの高
強度ばねを含んでいる。
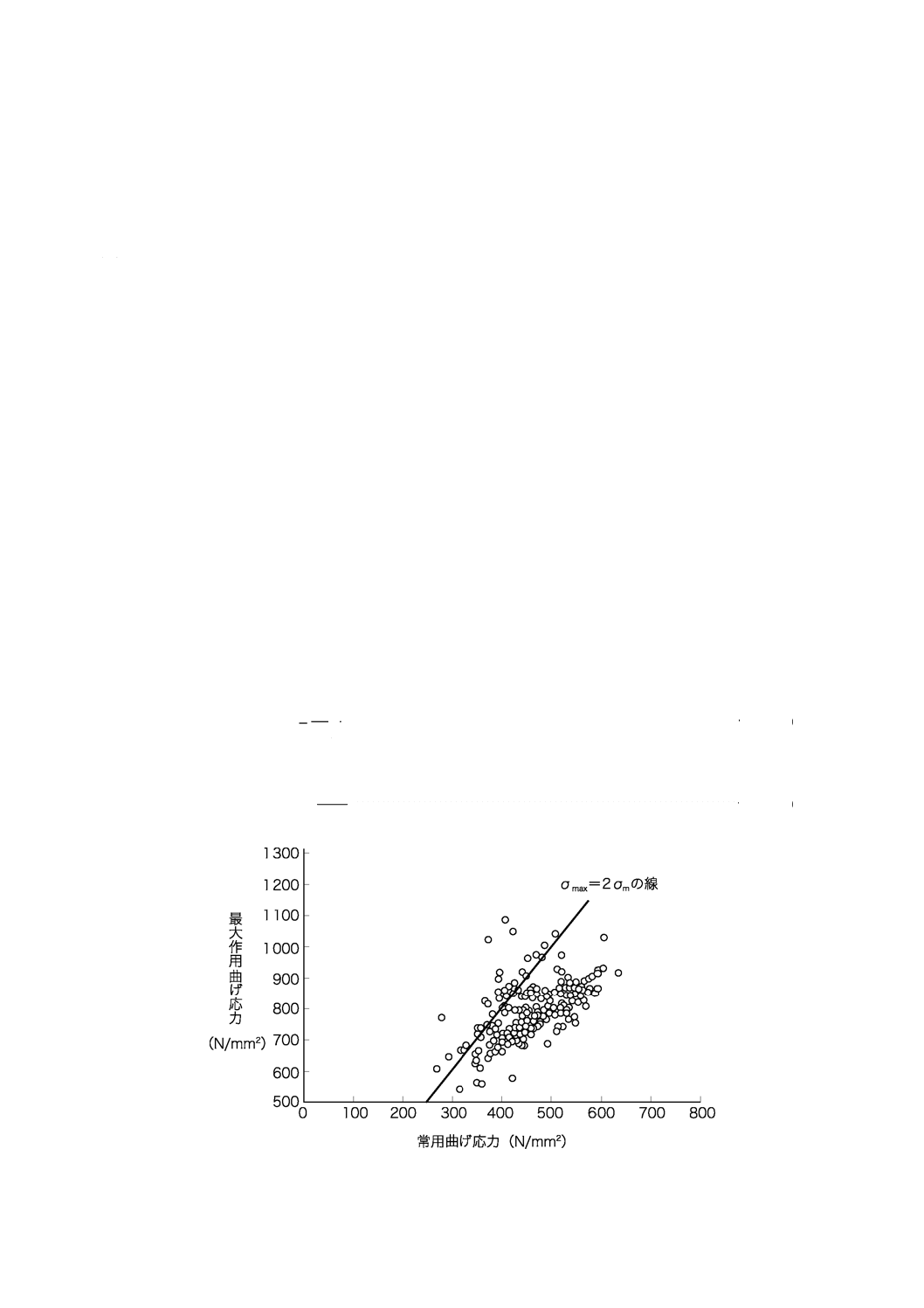
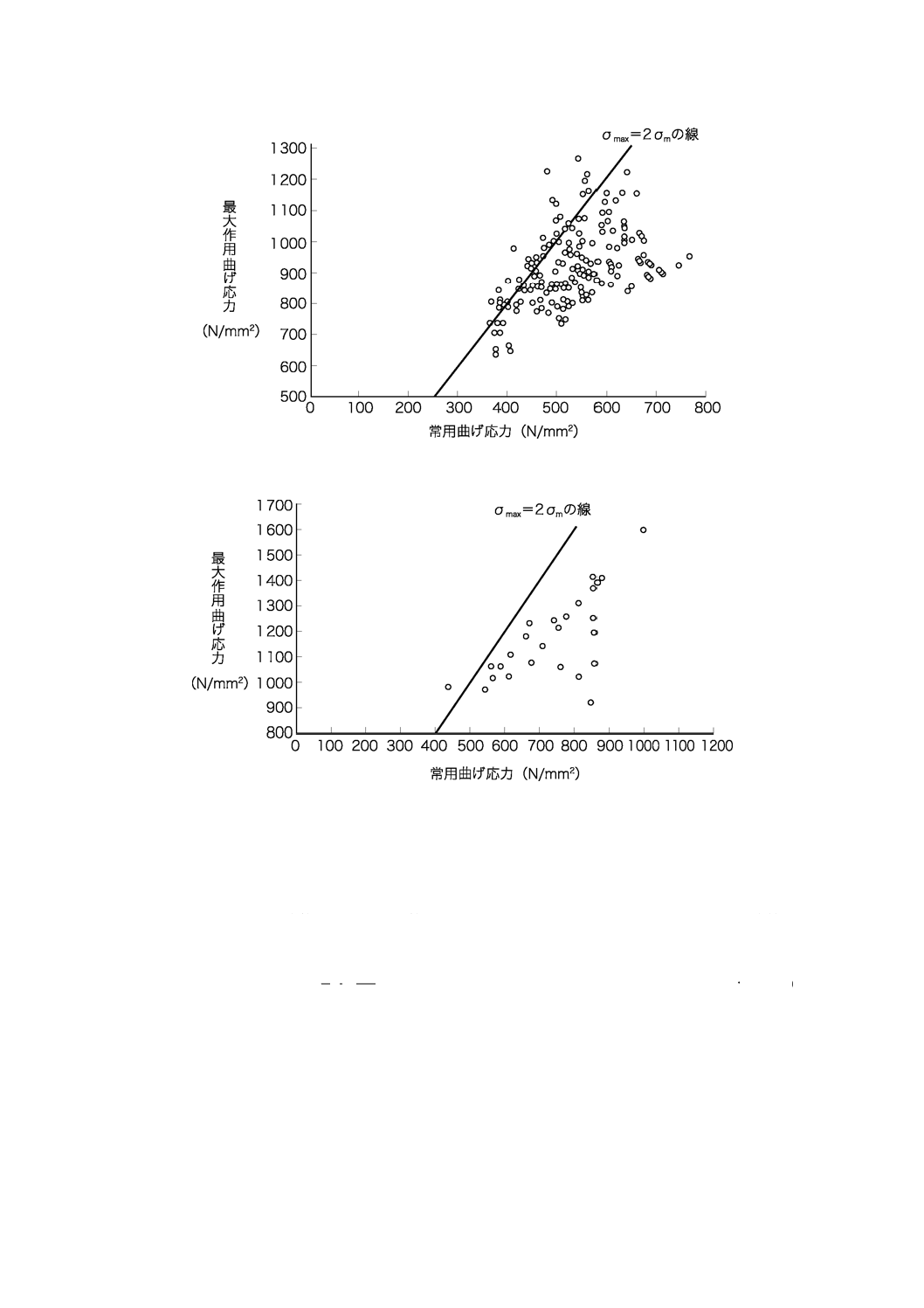
A.2 常用曲げ応力と最大作用曲げ応力との関係
ばねの常用曲げ応力と最大作用曲げ応力との関係について,図A.1〜図A.3に例を示す。疲労設計にお
いては,常用曲げ応力を平均応力σm,最大作用曲げ応力を最大応力σmaxと考えると,応力振幅σaは,式(A.1)
及び式(A.3)で表される。
a) σmax<2σmの場合:
σa=σmax−σm ·········································································· (A.1)
このとき,最小最大応力比Vは,式(A.2)で表される。
m
max
2
1
V
σ
σ
=
− ··········································································· (A.2)
b) σmax≧2σmの場合は,V=0と考えて,
max
a
2
σ
σ=
············································································· (A.3)
図A.1−ショットピーニング施工ばねにおける常用曲げ応力と最大作用曲げ応力との関係
16
B 2710-2:2020
図A.2−ストレスピーニング施工ばねにおける常用曲げ応力と最大作用曲げ応力との関係
図A.3−高強度ばねにおける常用曲げ応力と最大作用曲げ応力との関係
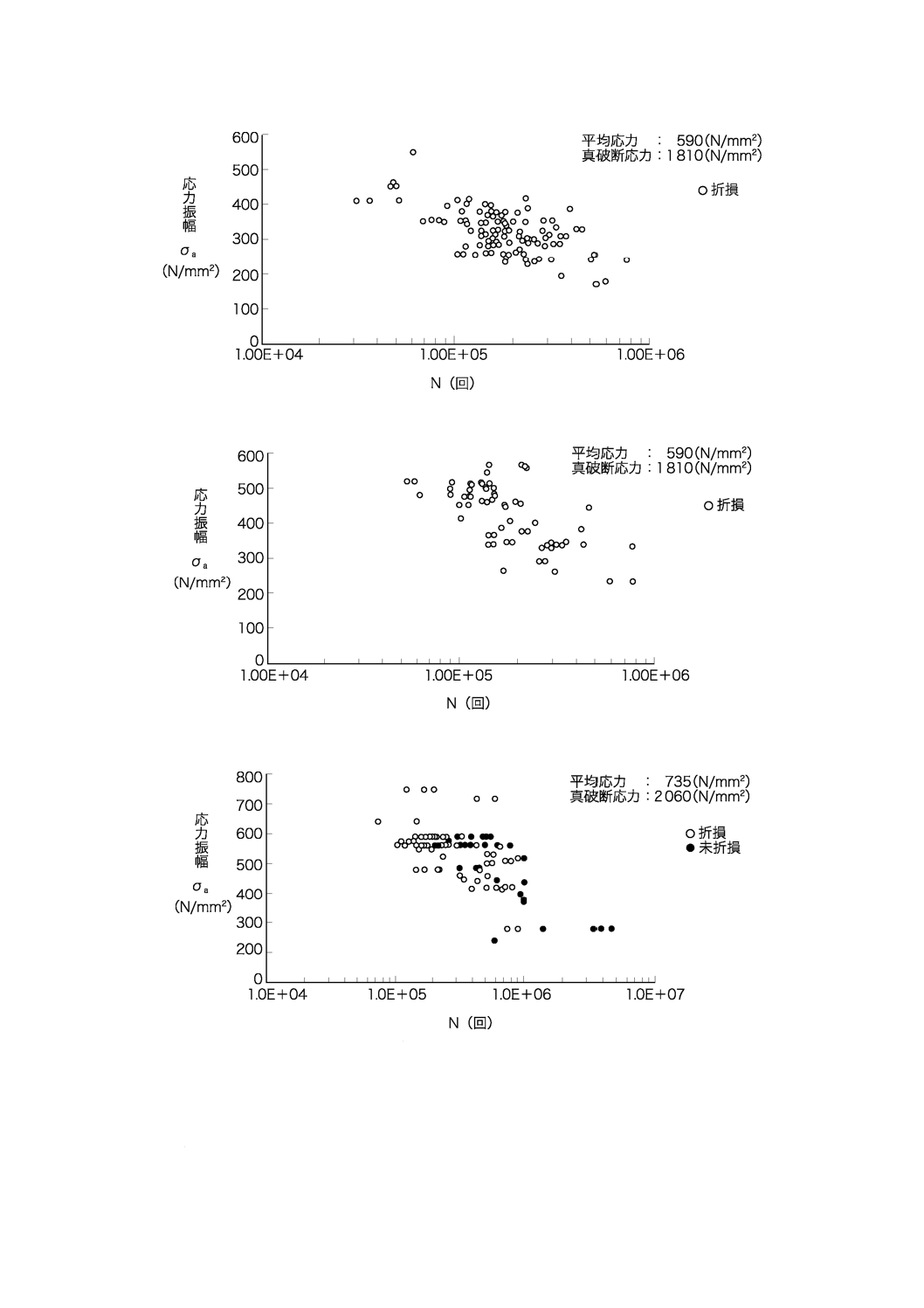
A.3 疲労強度
平均応力を基準値σm0にとったときのばねの疲労強度の例を,図A.4〜図A.6に示す。
ここで,実際のデータは種々の異なる平均応力σmの下での応力振幅σaなので,真破断応力σTを用いて
σm0に対する応力振幅σa0に換算している。計算に用いたσm0及びσTの値は,各図中に示した。換算の方法
は,式(A.4)で表される。
T
m0
a0
a
T
m
σ σ
σ
σ
σ σ
−
=
−
···································································· (A.4)
曲げ応力の計算は展開法又は板端法によって,マルチリーフスプリングでは中心穴位置,テーパリーフ
スプリングでは曲げ応力が最大となる位置について求めている。
17
B 2710-2:2020
図A.4−ショットピーニング施工ばねの応力振幅と折損回数との関係
図A.5−ストレスピーニング施工ばねの応力振幅と折損回数との関係
図A.6−高強度ばねの応力振幅と折損回数との関係
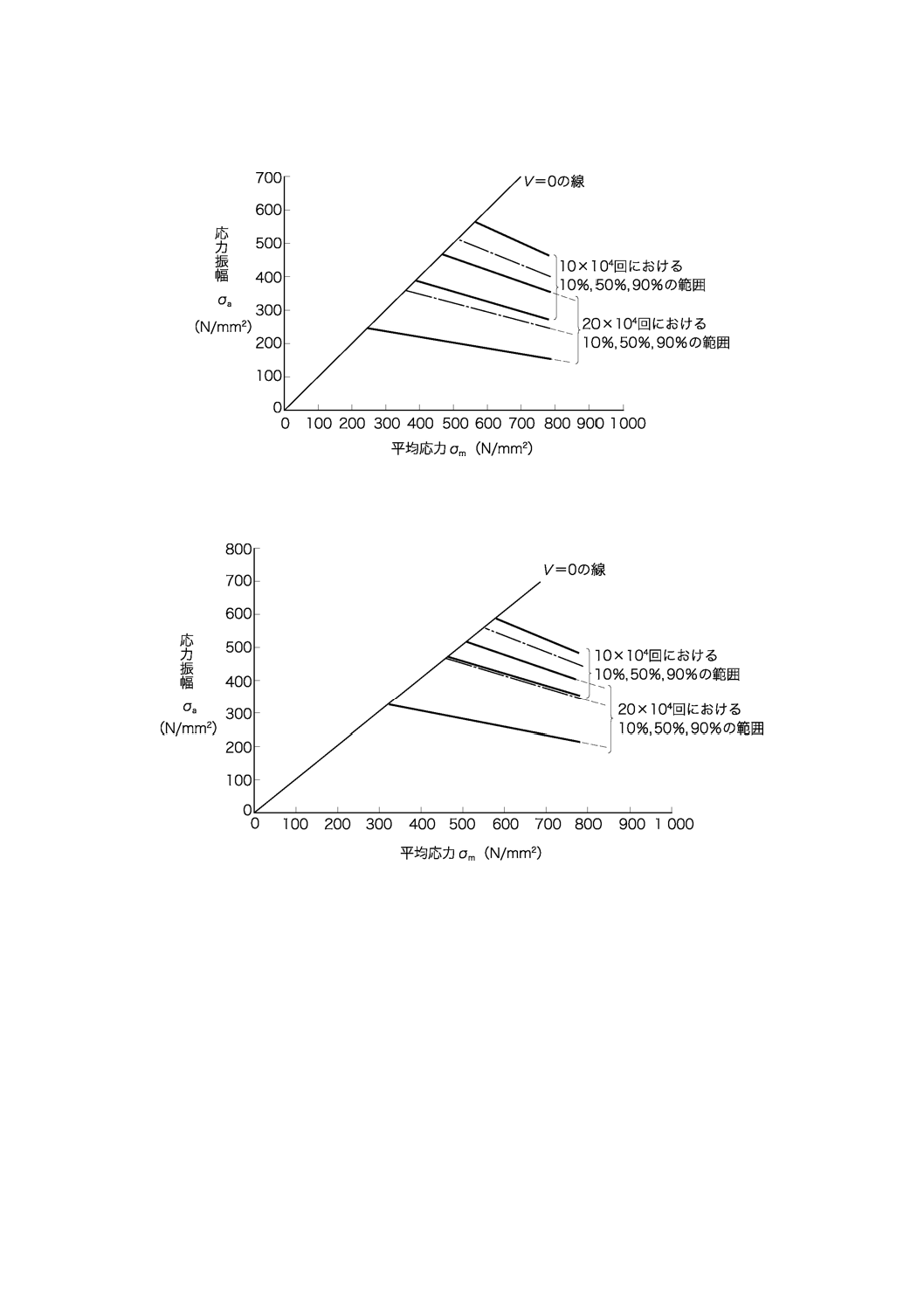
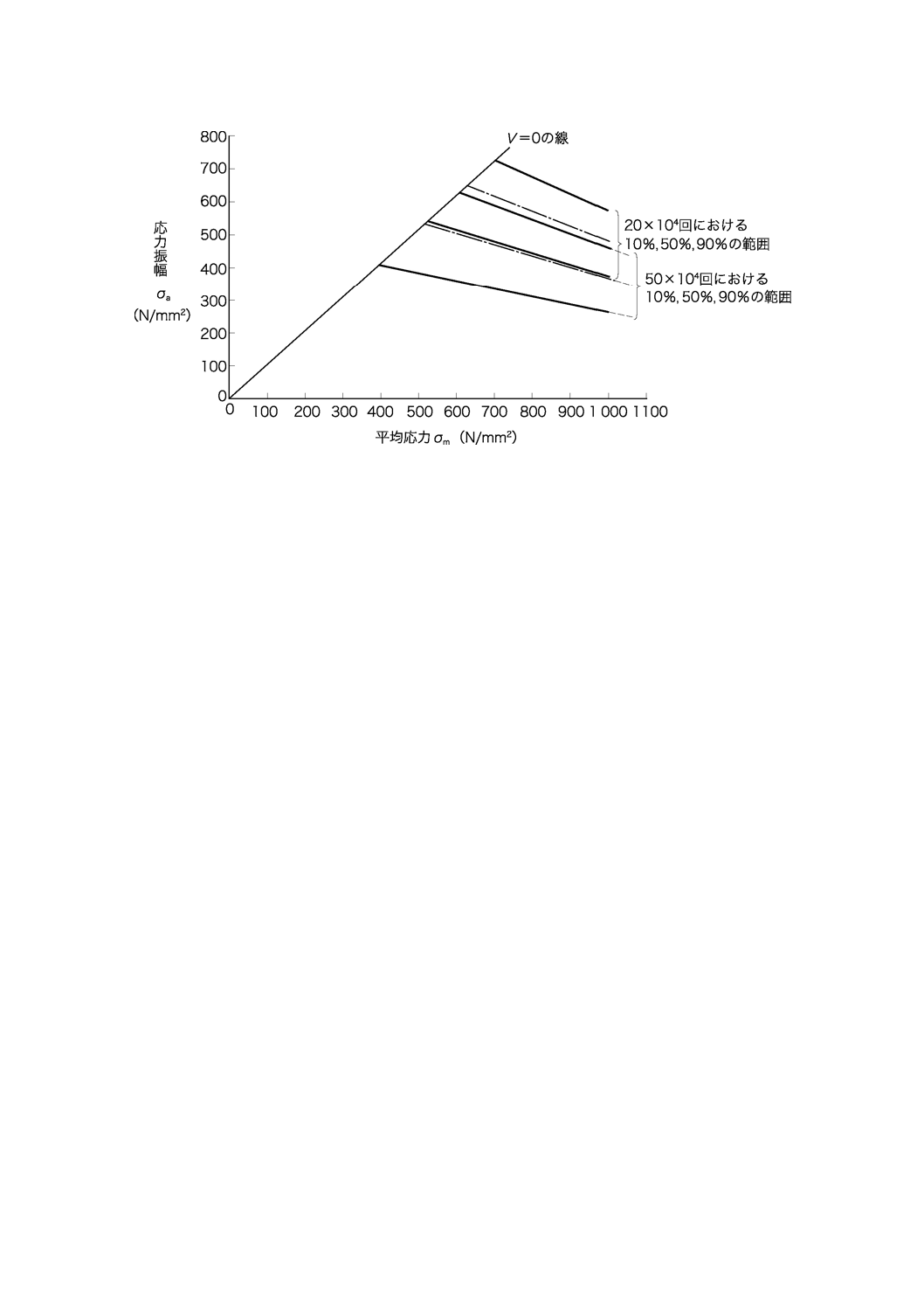
A.4 時間強度線図
ばねの設計に用いる時間強度線図の例を,図A.7〜図A.9に示す。
時間強度線図は,A.3に示した応力振幅及び折損回数から求めている。このとき,時間強度のばらつき
18
B 2710-2:2020
は寿命によらず一定とし,かつ,正規分布に従うと仮定している。
図A.7−ショットピーニング施工ばねの時間強度線図
図A.8−ストレスピーニング施工ばねの時間強度線図
19
B 2710-2:2020
図A.9−高強度ばねの時間強度線図
20
B 2710-2:2020
附属書B
(参考)
設計計算例
B.1
マルチリーフスプリングの設計計算例
マルチリーフスプリングの板端法による設計計算例を,次に示す。
a) 計算式 式(9)〜式(15)を使用。
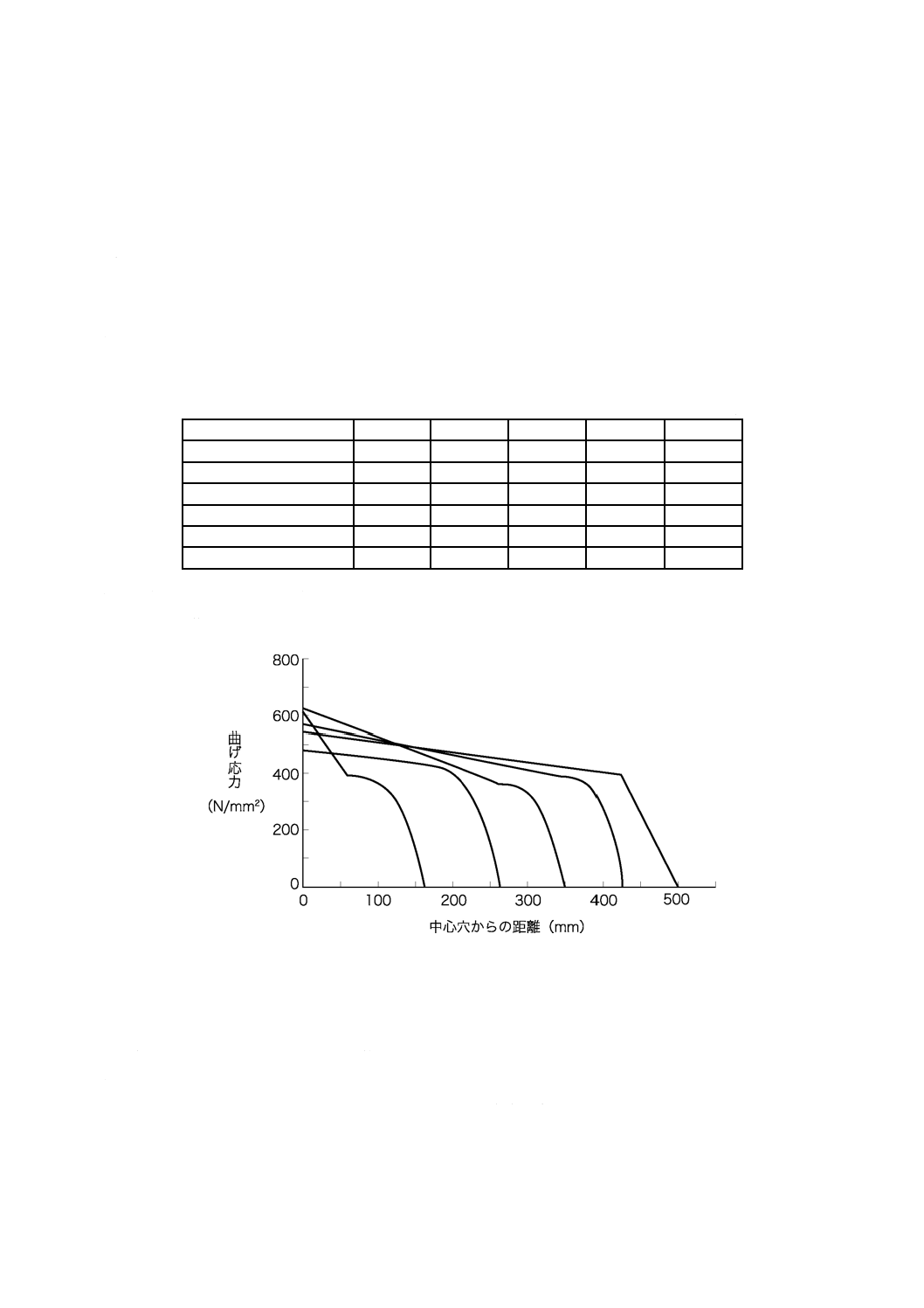
b) ばね諸元 ばね諸元を,表B.1に示す。
表B.1−板端法による計算例のばね諸元
単位 mm
リーフNo.
1
2
3
4
5
ハーフストレートスパン
500
425
345
260
160
板幅
70
70
70
70
70
板厚
7
7
7
7
7
テーパ長さ
0
80
85
100
100
先端板幅
70
56
56
56
56
先端板厚
7
4.2
4.2
3.6
3.6
c) 計算結果 ばね定数の計算結果は,R=70.14 N/mmとなる。
なお,作用力2 F=5 884 Nでの応力分布図を,図B.1に示す。
図B.1−板端法によるマルチリーフスプリングの応力分布図
B.2
テーパリーフスプリング
B.2.1 直線テーパ法によるリーフの設計計算例
直線テーパ法によるリーフの設計計算例を,次に示す。
a) 計算式 式(16)〜式(18)を使用。
b) ばね諸元 板幅70 mm,スパン1 250 mm及びリーフ枚数3枚とする。テーパ形状を,図B.2に示す。
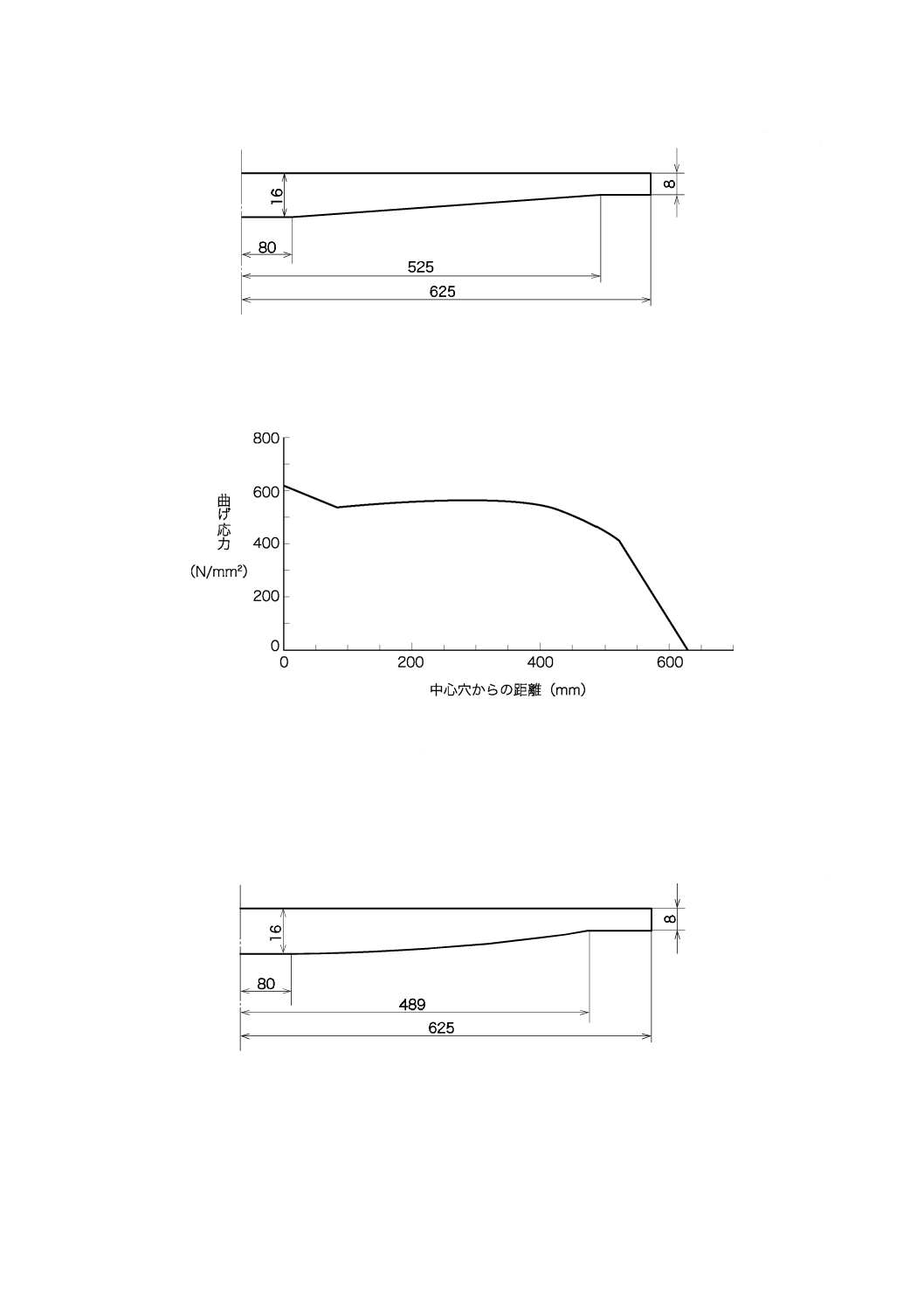
21
B 2710-2:2020
単位 mm
図B.2−直線テーパ法によるリーフ板厚形状
c) 計算結果 ばね定数の計算結果は,R=225 N/mmとなる。
なお,作用力2 F=17 652 Nでの曲げ応力分布図を,図B.3に示す。
図B.3−直線テーパによる曲げ応力分布図
B.2.2 放物線テーパ法によるリーフの設計計算例
放物線テーパ法によるリーフの設計計算例を,次に示す。
a) 計算式 式(19)〜式(24)を使用。
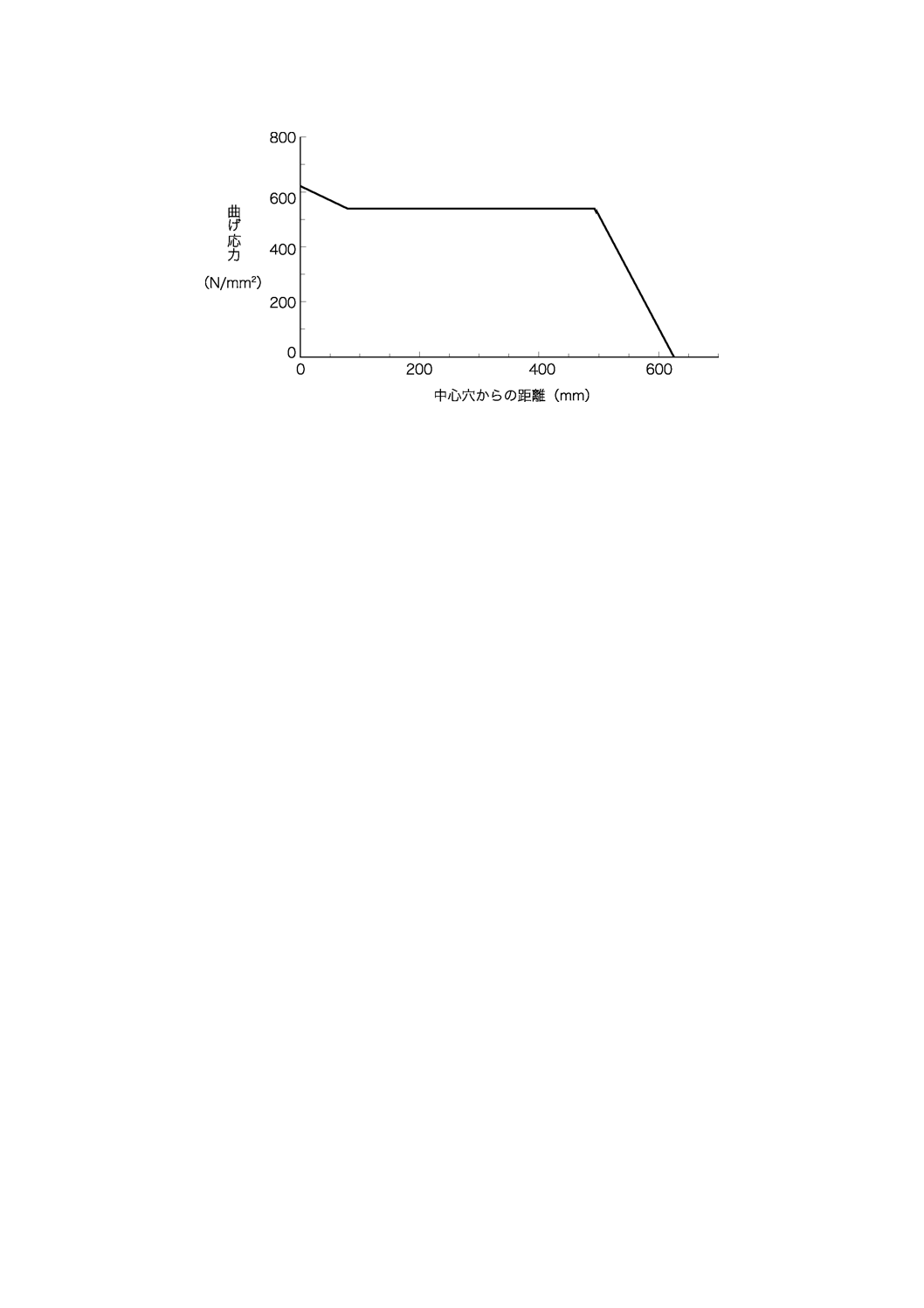
b) ばね諸元 幅70 mm,スパン1 250 mm及びリーフ枚数3枚とする。テーパ形状を,図B.4に示す。
単位 mm
図B.4−放物線テーパ法によるリーフ板厚形状
c) 計算結果 ばね定数の計算結果は,R=230 N/mmとなる。
なお,作用力2 F=17 652 Nでの曲げ応力分布図を,図B.5に示す。
22
B 2710-2:2020
図B.5−放物線テーパ法によるリーフの曲げ応力分布図
23
B 2710-2:2020
附属書C
(規定)
設計に用いる係数の線図
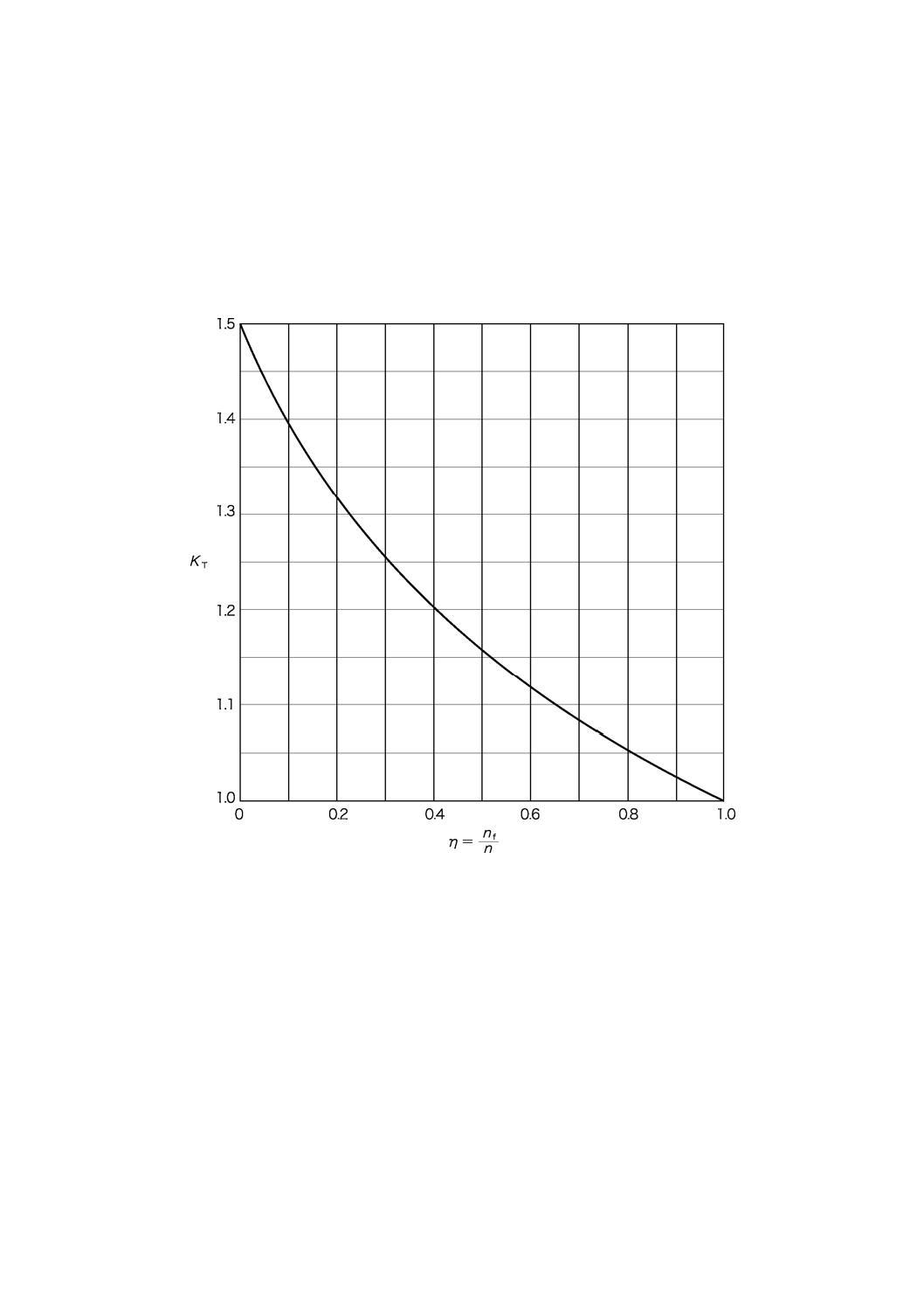
C.1 展開法の台形モデルにおける展開ばねの台形の形状に基づく係数
展開法の台形モデルにおける展開ばねの台形の形状に基づく係数を,図C.1に示す。
図C.1−台形モデルの台形の形状に基づく係数
24
B 2710-2:2020
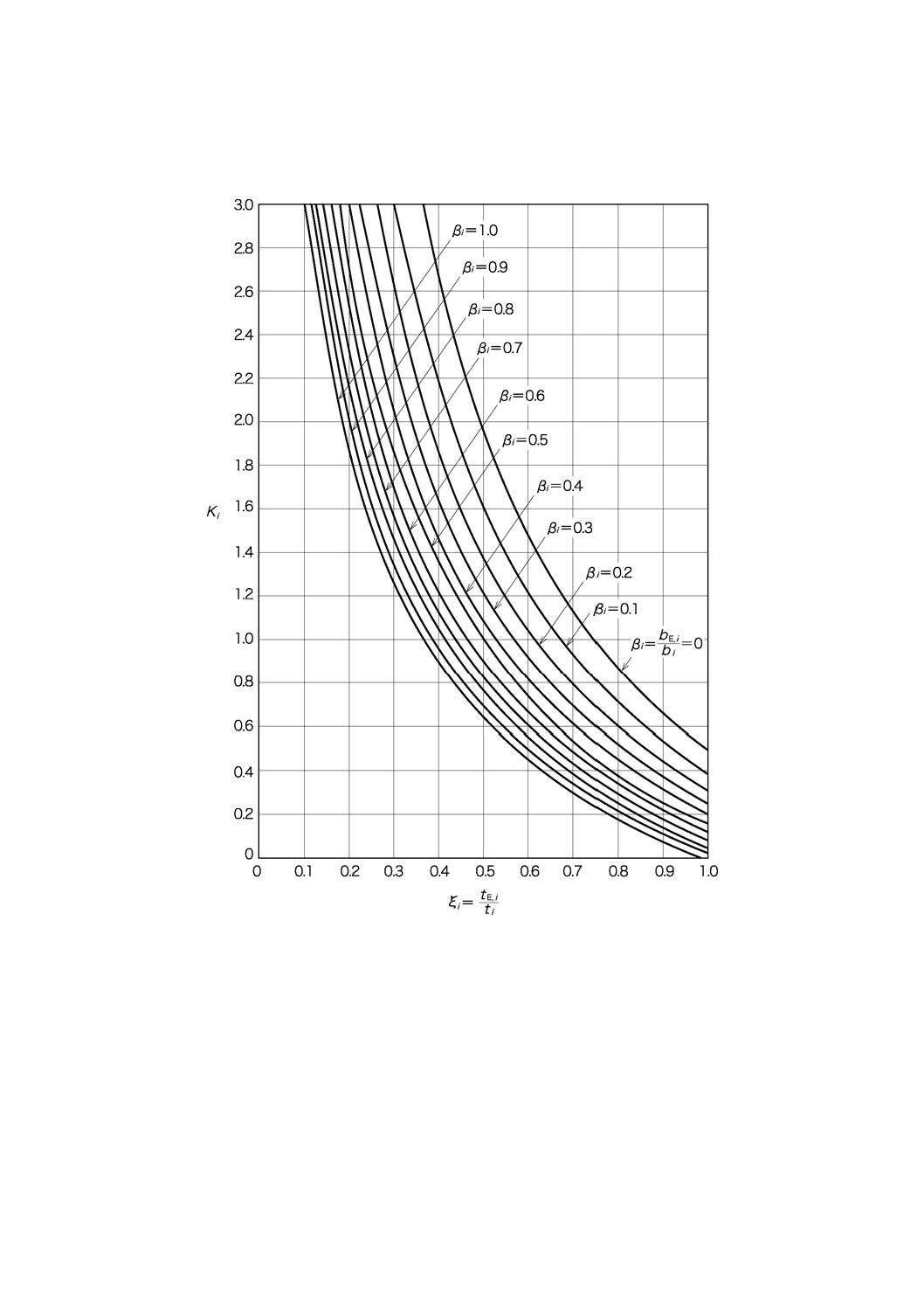
C.2 板端法における板端形状係数
板端法における板端形状係数を,図C.2に示す。
図C.2−板端形状係数
25
B 2710-2:2020
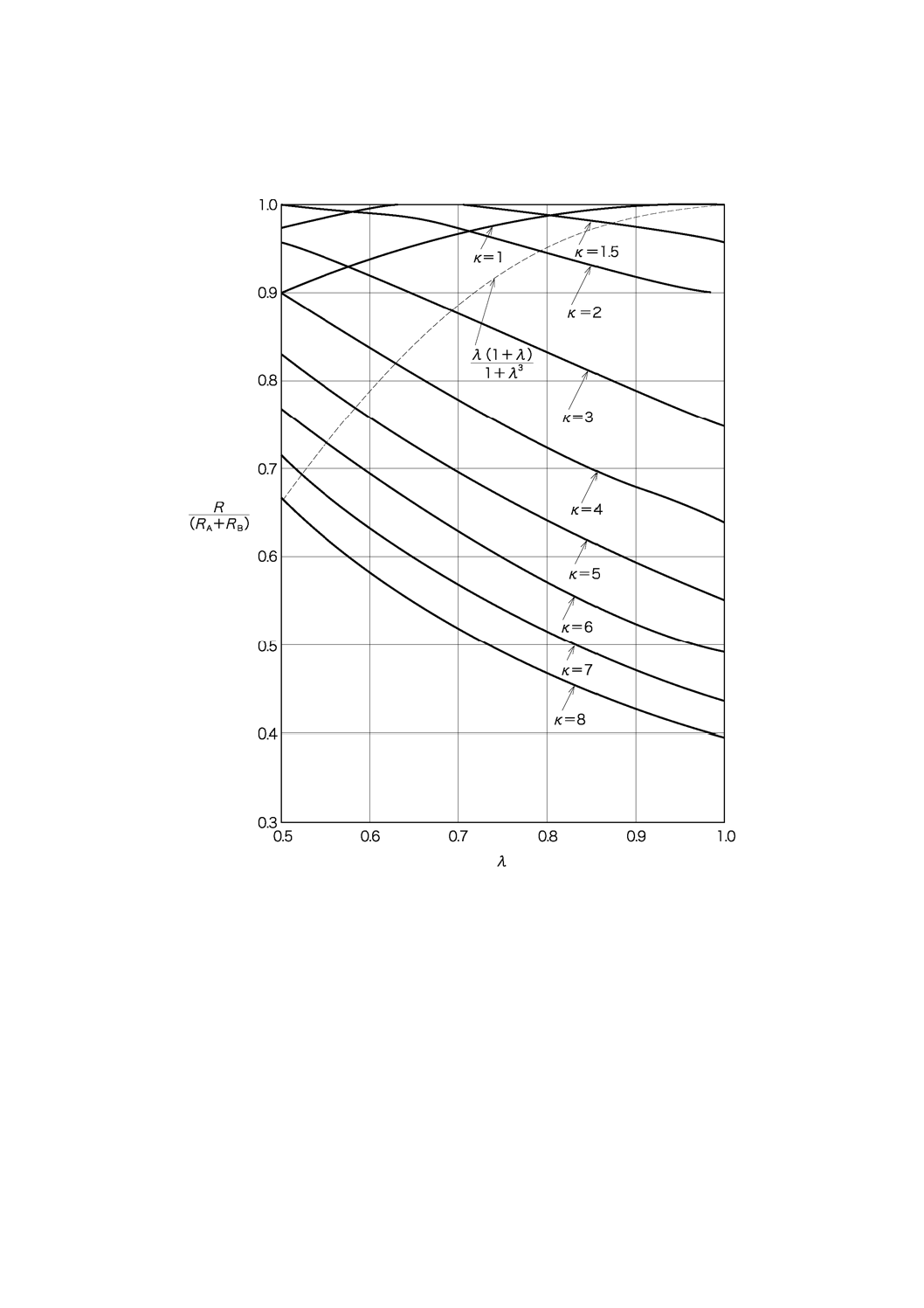
C.3 非対称ばねのばね定数
両側のリーフ長さ分布が比例関係にある場合の非対称長さ比とばね定数との関係を,図C.3に示す。
図C.3−非対称長さ比λとばね定数Rとの関係線図
26
B 2710-2:2020
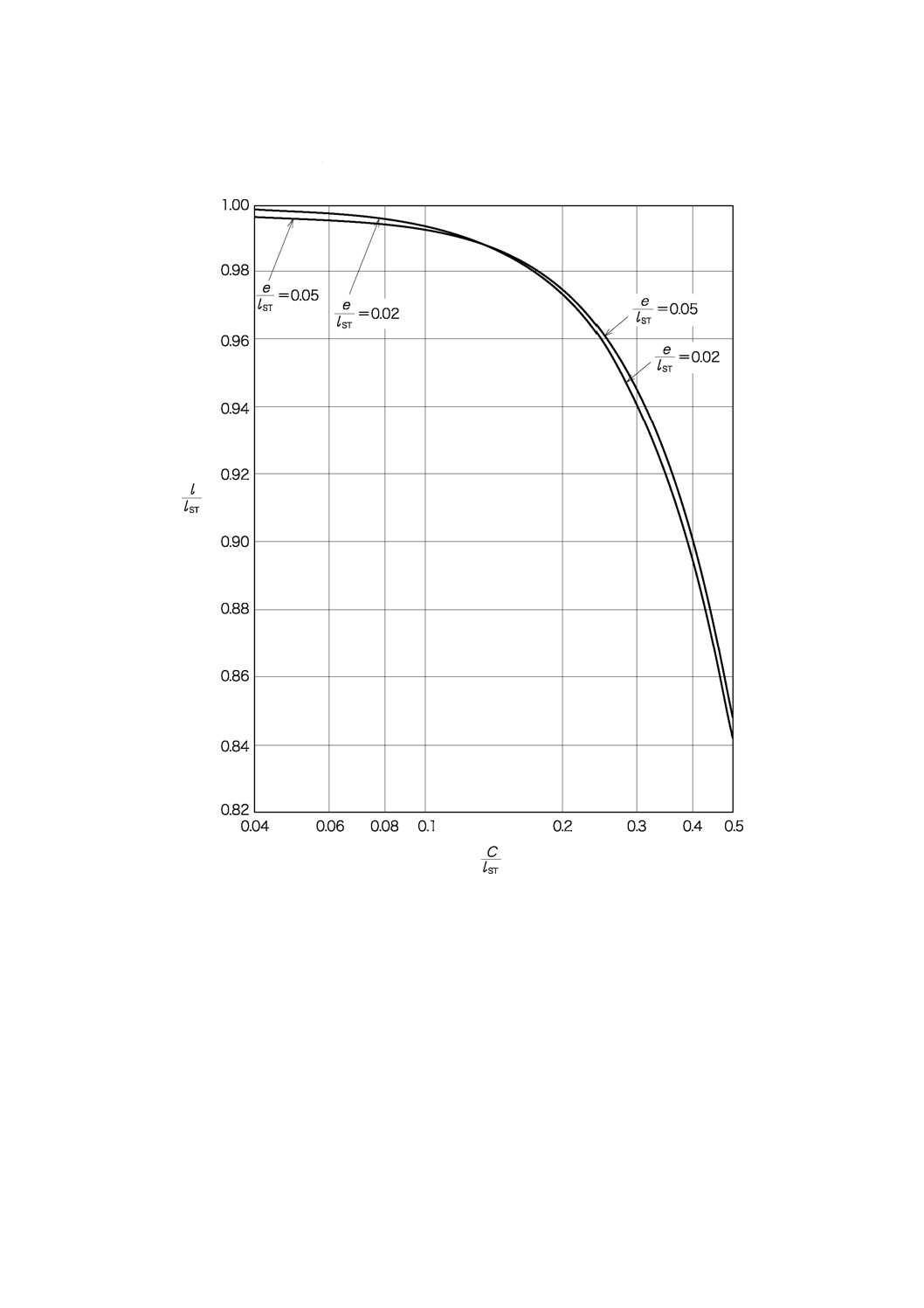
C.4 たわみによるスパンの変化
たわみによる反りとスパンの変化との関係を,図C.4に示す。
図C.4−反りCとハーフスパンlとの関係
27
B 2710-2:2020
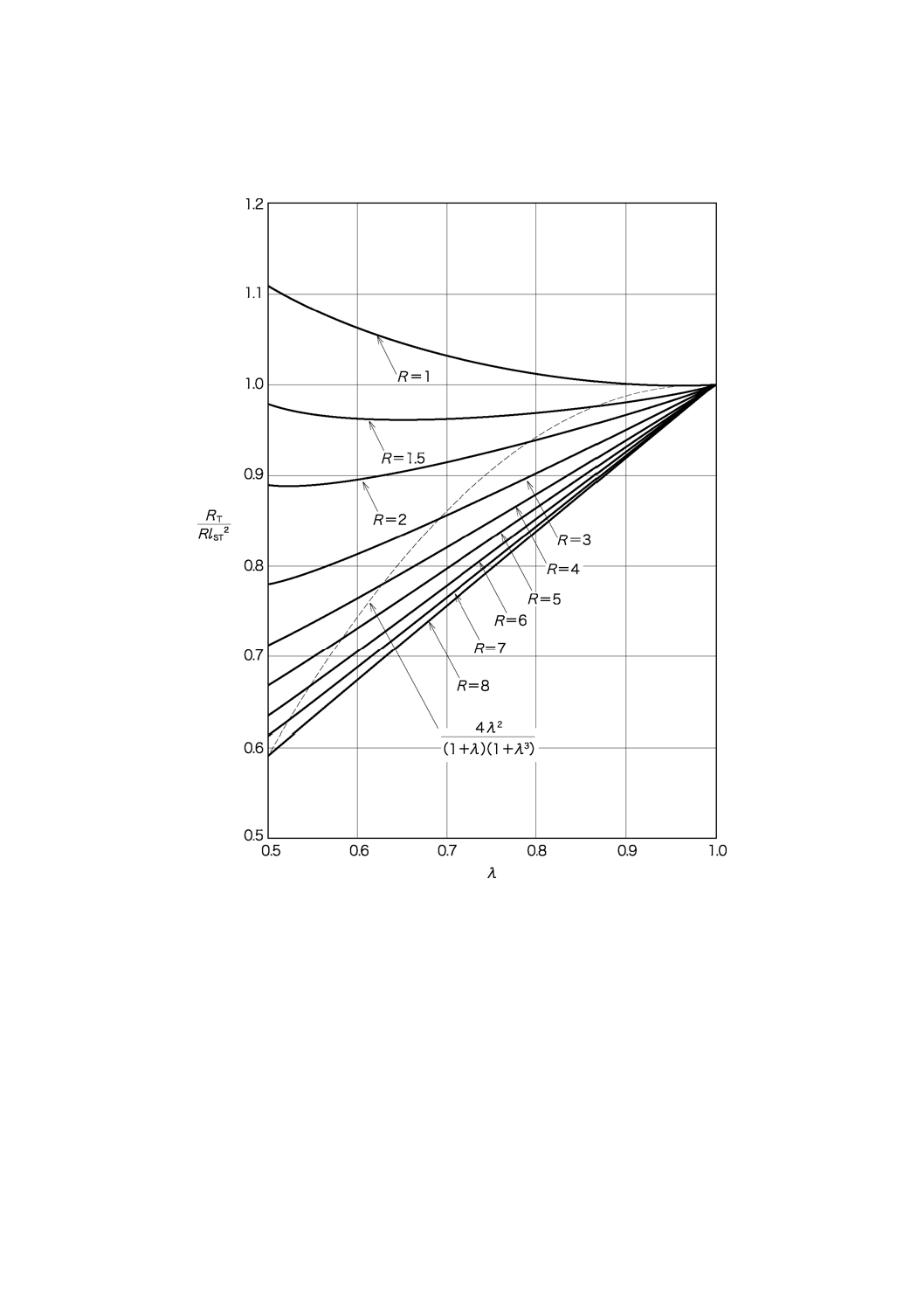
C.5 ワインドアップ剛性
非対称長さ比とワインドアップ剛性との関係を,図C.5に示す。
図C.5−非対称長さ比λとワインドアップ剛性RTとの関係


























