B 2005-8-3:2008(IEC 60534-8-3:2000)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲及び制限事項 ······································································································· 2
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 3
4 記号及び単位 ··················································································································· 4
5 標準トリムバルブ ············································································································· 6
5.1 圧力及び圧力比 ············································································································· 6
5.2 状態の定義 ··················································································································· 7
5.3 予備的計算 ··················································································································· 7
5.4 状態Ⅰ(亜音速流) ······································································································· 9
5.5 状態Ⅱ〜Ⅴ(共通の計算) ····························································································· 10
5.6 騒音の計算 ·················································································································· 11
5.7 計算の手順 ·················································································································· 13
6 騒音低減トリムバルブ ······································································································ 13
6.1 適用範囲 ····················································································································· 13
6.2 単段多流路トリム ········································································································· 13
6.3 多段単一流路減圧トリム(二つ以上の絞りステップ) ·························································· 14
6.4 多段多流路トリム(二つ以上の流路及び二つ以上の減圧段) ················································· 15
6.5 この規格で取り上げないバルブ類····················································································· 16
7 より高い出口マッハ数のバルブ類 ······················································································· 17
7.1 適用範囲 ····················································································································· 17
7.2 計算の手順 ·················································································································· 17
附属書A(参考)計算例題 ···································································································· 19
附属書B(参考)参考文献 ···································································································· 45
B 2005-8-3:2008(IEC 60534-8-3:2000)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,社団法人日本バルブ工業会(JVMA)から,工
業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済
産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に係る確認について,責任は
もたない。
JIS B 2005の規格群には,次に示す部編成がある。
JIS B 2005-1 第1部:調節弁用語及び一般的必要条件
JIS B 2005-2-1 第2部:流れの容量−第1節:取付け状態における流れのサイジング式
JIS B 2005-2-3 第2部:流れの容量−第3節:試験手順
JIS B 2005-2-4 第2部:流れの容量−第4節:固有流量特性及びレンジアビリティ
JIS B 2005-3-1 第3部:寸法−第1節:フランジ形二方ストレート形グローブ調節弁の面間寸法及び
アングル形グローブ調節弁の中心−面間寸法
JIS B 2005-3-2 第3部:寸法−第2節:バタフライ弁を除く回転形調節弁の面間寸法
JIS B 2005-3-3 第3部:寸法−第3節:突合せ溶接形二方ストレート形グローブ調節弁の面間寸法
JIS B 2005-4 第4部:検査及び試験
JIS B 2005-5 第5部:表示
JIS B 2005-6-1 第6部:調節弁へのポジショナの取付けの詳細−第1節:直線運動駆動部へのポジ
ショナの取付け
JIS B 2005-6-2 第6部:調節弁へのポジショナの取付けの詳細−第2節:回転運動駆動部へのポジ
ショナの取付け
JIS B 2005-7 第7部:調節弁データシート
JIS B 2005-8-1 第8部:騒音−第1節:調節弁の空気力学的流動騒音の実験室における測定
JIS B 2005-8-2 第8部:騒音−第2節:調節弁の液体流動騒音の実験室における測定
JIS B 2005-8-3 第8部:騒音−第3節:調節弁の空気力学的流動騒音の予測方法
JIS B 2005-8-4 第8部:騒音−第4節:調節弁の液体流動騒音の予測方法
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 2005-8-3:2008
(IEC 60534-8-3:2000)
工業プロセス用調節弁−
第8部:騒音−第3節:調節弁の空気力学的
流動騒音の予測方法
Industrial-process control valves-Part 8-3: Noise considerations-
Control valve aerodynamic noise prediction method
序文
この規格は,2000年に第2版として発行されたIEC 60534-8-3を基に,技術的内容及び対応国際規格の
構成を変更することなく作成した日本工業規格である。
ここでは,音響効率係数だけでなく,流れの機械的パワーをいろいろな流れの状態に対して計算する。
これらの音響効率係数は,配管内の音響パワーに変換される流れの機械的パワーの割合を示す。また,こ
の手法では,配管内音圧及びその音圧のピーク周波数も計算する。これらは,配管の透過損失を計算する
のに特に重要である。
現時点では,配管外の音圧レベルを知ることは,バルブ使用者の一般的な要求事項である。通常,これ
は,バルブ又はエキスパンダから下流に1 mで,かつ,配管壁から1 mの位置の音圧レベルを指す。
この規格は,この位置の音圧レベルを求めるための手法を示す。
この規格の式には,JIS B 2005-1及びJIS B 2005-2-1で使われているサイジング係数を使用する。
通常の調節弁では,バルブの壁面を透過する騒音はわずかである。対象とする騒音は,バルブの下流へ
配管内を伝ぱし,配管壁を透過する騒音だけである。この騒音は,一般的には,バルブ本体から下流1 m
で,かつ,配管外表面から1 m離れた位置で測定する。
2番目の騒音源は,高マッハ数で排出されるバルブ出口部で発生し,バルブ内部で発生する音圧レベル
に対数的に加算できる。これらの付加的音圧レベルの予測も,この手法で行える。マッハ数が0.3以下の
場合は,箇条5及び箇条6を適用し,マッハ数が0.3より大きい場合は,箇条7を適用する。
この予測手法は,現場における実測値を保証するものではない。実験室環境(JIS B 2005-8-1参照)で
の試験による大部分の騒音データに対し,5 dB (A) 以内の予測値を求めることを意味している。
この予測手法の検証のために行った大部分の試験データは,中レベルの圧力及び温度における空気を用
いたものである。この手法は,他の気体及び蒸気並びに更に高い圧力に対しても,一般的に適用できると
考えられる。しかし,極度の高温の場合,下流圧力が大気圧と大きく異なる場合,臨界点の近傍など完全
気体の条件から外れるにつれて,不確かさは増大する。騒音予測式は,流体密度及び比熱比を考慮する項
を含んでいる。
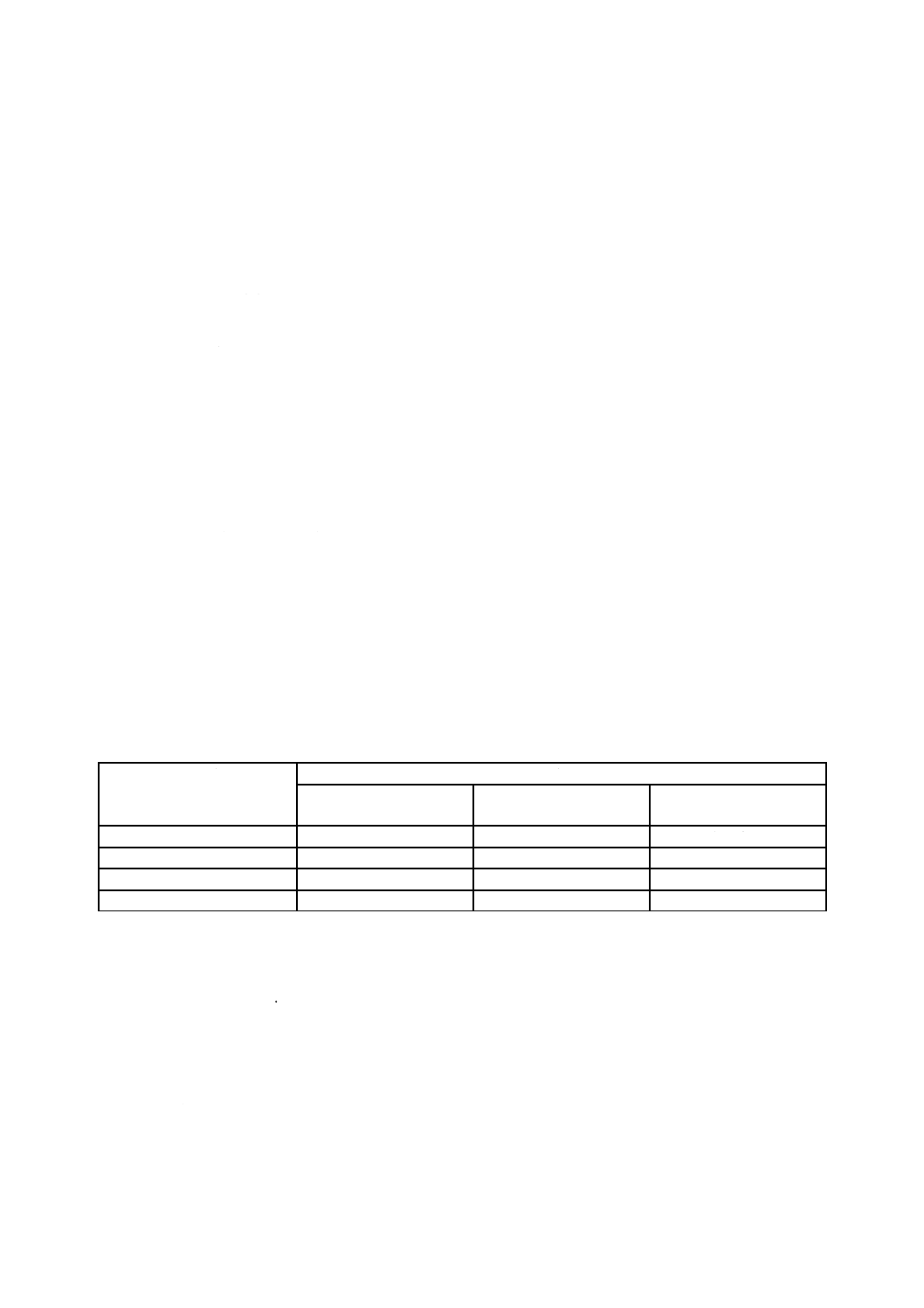
2
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 上流圧力1 830 kPa(18.3 bar)以下,かつ,下流圧力1 600 kPa(16.0 bar)以下の実験室空気試
験,及び225 ℃以下の蒸気試験では,予測計算値とよく一致する。
透過損失の式は,配管内に生成する音波と,配管壁の複数のコインシデンス周波数との相互作用の厳密
な解析を基にしている。商取引される配管の厚さには大きな公差があり,これが厳密な解析に必要な非常
に複雑な数学的方法を大きく制限する。したがって,この規格では簡略手法を使用している。
計算例を,附属書Aに示す。
この予測手法は,箇条2に示すJIS B 2005規格群及び附属書Bに基づいている。
1
適用範囲及び制限事項
この規格は,圧縮性流体の流れによって,調節弁及び隣接した配管エキスパンダ内に発生する外部音圧
レベルを予測する理論的手法について規定する。
この手法は,単相の乾燥気体及び蒸気だけを考え,完全気体の法則に基づいている。
この規格は,空気力学的プロセスによって,バルブ内及び接続配管内に発生する騒音だけを扱う。反射,
機械的振動,不安定な流れのパターン及び他の予測できない挙動によって発生する騒音は,扱わない。
下流側配管は,騒音測定点から少なくとも長さ2 mの直管を想定している。
この手法は,鋼管及び合金鋼管にだけ有効である[5.6の式(38)及び式(40)を参照]。
この手法は,単段のバルブ,すなわち,グローブ(ストレート形及びアングル形),バタフライ,回転プ
ラグ(偏心形及び球形),ボール及びケージトリム付きバルブに適用できる。
特記事項として,FpCが定格容量係数の50 %を超えるフルボアのボール弁は除く。
この規格で取り扱わない特殊な低騒音トリムに関する制限事項については,6.5を参照する。バルブ出口
のマッハ数が,標準トリムで0.3を超えるか,又は低騒音トリムで0.2を超えるときは,箇条7に示す手順
による。
この規格のマッハ数の制限は,次による。
マッハ数
マッハ数の制限
箇条5
標準トリム
箇条6
騒音低減トリム
箇条7
高マッハ数の適用
自由膨張噴流Mj
制限なし
制限なし
制限なし
バルブ出口Mo
0.3
0.2
1.0
下流レジューサ入口Mr
不適用
不適用
1.0
下流配管M2
0.3
0.2
0.8
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 60534-8-3: 2000,Industrial-process control valves−Part 8-3: Noise considerations−Control valve
aerodynamic noise prediction method(IDT)
なお,対応の程度を表す記号(IDT)は,ISO/IEC Guide 21に基づき,一致していることを
示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。その最新
版(追補を含む。)を適用する。
3
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 2005(規格群) 工業プロセス用調節弁
注記 対応国際規格:IEC 60534 (all parts), Industrial-process control valves(IDT)
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 2005規格群によるほか,次による。
3.1
音響効率(acoustical efficiency)
音響パワーに変換した流れのパワーの,質量流量の流れのパワーに対する比。
3.2
外部コインシデンス周波数(external coincidence frequency)
外部の空気中を伝わる音波の伝ぱ速度と,配管壁と等しい肉厚の平板内の屈曲波の伝ぱ速度とが等しい
ときの周波数。
3.3
内部コインシデンス周波数(internal coincidence frequency)
音響的,かつ,構造的な軸方向周波数が,与えられた円周方向モードに関して等しく,したがって,最
小の透過損失を生じるような最低の周波数。
3.4
溝付ベーンバタフライ弁(fluted vane butterfly valve)
ベーンの片面又は両面上に複数の溝があるバタフライ弁。これらの溝は,着座線又は着座表面を変えな
いで流れを形作るために考えられている。
3.5
独立流路(independent flow passage)
出て行く流れが,隣接した流路から出て行く流れに影響されないような流路。
3.6
ピーク周波数(peak frequency)
内部の音圧が最大である周波数。
3.7
バルブ形状修正係数Fd(valve style modifier)
単一流路の水力学的直径と環状オリフィスの直径との比。環状オリフィスの面積は,使用するトラベル
におけるすべての同一流路の面積の和に等しい。

4
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
記号及び単位
この規格で用いる記号及び単位は,表1による。
表1−記号及び単位
記号
説明
単位
A
単一の流路の面積
m2
An
n段の多段トリムの,使用するトラベルでの最終段の全流路面積
m2
C
容量係数(Kv 及び Cv)
多種(JIS B 2005-1を参照)
Cn
n段の多段トリムの最終段に対する容量係数
多種(JIS B 2005-1を参照)
cvc
亜音速の流動条件における縮流部での音速
m/s
cvcc
閉そく流状態における縮流部での音速
m/s
c2
下流条件での音速
m/s
D
バルブ出口の直径
m
d
流路の直径(円形以外に対しては,dHを使用)
m
dH
単一の流路の水力学的直径
m
di
バルブ出口又はエキスパンダ入口の小さいほうの内径
m
Di
下流配管の内径
m
Dj
縮流部における噴流の直径
m
do
使用するトラベルでの流路面積の和に等しい面積をもつ,環状オリフィスの直径
m
Fd
バルブ形状修正係数
無名数の1
FL
継手を接続しない場合のバルブの液体圧力回復係数
無名数の1 d)
FLn
低騒音トリムの最終段の液体圧力回復係数
無名数の1
FLP
継手を接続する場合の,バルブの液体圧力回復係数と配管形状係数との組合せ係数
無名数の1 d)
Fp
配管形状係数
無名数の1
fg
外部コインシデンス周波数
Hz
fo
内部コインシデンス周波数
Hz
fp
発生ピーク周波数
Hz
fpR
バルブ出口又はエキスパンダの縮小された直径での発生ピーク周波数
Hz
fr
リング周波数
Hz
Gx,Gy 周波数係数(表5参照)
無名数の1
l
放射状流路の長さ
m
lw
単一の流路のぬれ縁の長さ
m
LpeR
配管エキスパンダで引き起こされた気体の乱れによって生じる,配管壁から
1 mでのA特性音圧レベル
dB(A)(Po 基準)
Lg
マッハ数の補正
dB (Po 基準)
LpAe
配管外部でのA特性音圧レベル
dB(A)(Po 基準)
LpAe, 1m 配管壁から1 mでのA特性音圧レベル
dB(A)(Po 基準)
Lpi
配管壁での内部音圧レベル(5.6参照)
dB (Po 基準)
LpiR
下流配管の内部音圧レベル(7.2参照)
dB (Po 基準)
LpS
バルブトリムとエキスパンダとで生じた,配管壁から1 mでの組合せ
A特性音圧レベル
dB(A)(Po 基準)
Lwi
全内部音響パワーレベル
dB (Wo 基準)
M
流れている流体のモル質量
kg/kmol
Mj
状態ⅡからⅣまでにおける自由膨張噴流のマッハ数
無名数の1
Mjn
n段の多段弁での最終段の自由膨張噴流のマッハ数
無名数の1
Mj5
状態Ⅴにおける自由膨張噴流のマッハ数
無名数の1
Mo
バルブ出口におけるマッハ数
無名数の1
MR
エキスパンダ入口におけるマッハ数
無名数の1

5
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−記号及び単位(続き)
記号
説明
単位
Mvc
縮流部におけるマッハ数
無名数の1
M2
下流配管におけるマッハ数
無名数の1
m&
質量流量
kg/s
s
m&
音速における質量流量
kg/s
N
数値定数(表2参照)
多種
No
バルブトリムにおける独立した同一の流路数
無名数の1
pa
配管外部の実際の大気圧
Pa c)
pn
n段の多段弁の最終段におけるよどみ点絶対圧力
Pa
Po
基準音圧=2×10−5 e)
Pa
ps
標準大気圧 a)
Pa
pvc
亜音速の流動条件における縮流部の絶対圧力
Pa
pvcc
閉そく流状態における縮流部の絶対圧力
Pa
p1
バルブ入口の絶対圧力
Pa
p2
バルブ出口の絶対圧力
Pa
p2B
ブレークポイントにおけるバルブ出口の絶対圧力
Pa
p2C
閉そく流状態におけるバルブ出口の絶対圧力
Pa
p2CE
一定の音響効率の状態が始まる点でのバルブ出口の絶対圧力
Pa
R
気体定数=8 314
J/(kmol・K)
rw
音響パワー比(表4参照)
無名数の1
Tn
n段の多段弁の最終段における入口の絶対温度
K
Tvc
亜音速の流動条件における縮流部の絶対温度
K
Tvcc
閉そく流状態における縮流部の絶対温度
K
T1
入口の絶対温度
K
T2
出口の絶対温度
K
TL
透過損失
dB
TLR
下流配管における透過損失
dB
tp
配管壁の厚さ
m
Up
下流配管における気体の速度
m/s
UR
エキスパンダの入口における気体の速度
m/s
Uvc
亜音速の流動条件における縮流部の速度
m/s
Wa
音響パワー
W
WaR
バルブ出口又はエキスパンダの縮小された直径での音響パワー
W
Wm
質量流量の流れパワー
W
WmR バルブ出口又はエキスパンダの縮小された直径での質量流量の流れのパワー
W
Wms
音速での質量流量の流れのパワー
W
Wo
基準音響パワー=10−12 e)
W
α
回復補正係数
無名数の1
β
バルブ出口又はエキスパンダ入口における収縮係数
無名数の1
γ
比熱比
無名数の1
η
音響効率係数 b)
無名数の1
1ρ
p1及びT1における流体の密度
kg/m3
2
ρ
p2及びT2における流体の密度
kg/m3
n
ρ
n段の多段弁の最終段のpn及びTnにおける流体の密度
kg/m3
Φ
相対容量係数
無名数の1
添字
e
外部を表す。

6
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表1−記号及び単位(続き)
添字
i
内部を表す。
n
トリムの最終段を表す。
R
下流配管又は管エキスパンダにおける条件を表す。
注a) 標準大気圧は,101.325 kPa 又は1.013 25 bar 。
b) 添字1,2,3,4及び5は,それぞれ状態Ⅰ,Ⅱ,Ⅲ,Ⅳ及びⅤを示す。
c) 1 bar =102 kPa =105 Pa 。
d) 縮流部の圧力,したがって,速度を計算するために,この規格では,気体に対する圧力回復は,液体のそれと同
一であると仮定している。
e) 音響パワー及び音圧は,慣例上デシベルスケールとして知られている対数スケールを用いて表す。このスケール
は,ある標準の基準値と対数的な関係がある。この標準の基準値は,音圧に対して2×10−5 Pa及び音響パワーに
対して10−12 Wである。
5
標準トリムバルブ
5.1
圧力及び圧力比
騒音の予測手順においては,幾つかの圧力及び圧力比が必要である。これらを,次に示す。
縮流部は,流体の最高速度及び最低圧力の領域である。この最低圧力は,絶対圧0より小さくなること
はないが,式 (1) によって求める。
2
L
2
1
1
vc
F
p
p
p
p
−
−
=
····································································· (1)
注記1 この式は,亜音速条件に対するFLの定義である。
注記2 バルブに継手類が取り付けてあるときは,FLをFLP / Fpと入れ換える。
注記3 係数FLは,縮流部の圧力の計算に必要である。縮流部の圧力は,次に速度を計算するのに用
いるが,この速度は音響効率係数を求めるのに必要となる。
閉そく流状態では,縮流部の圧力は,式 (2) によって求める。
(
)1
/
1
vcc
1
2
−
+
=
γ
γ
γ
p
p
·································································· (2)
縮流部で音速流が始まる臨界下流圧力は,式 (3) によって計算する。
(
)
vcc
1
2
L
1
2C
p
p
F
p
p
−
−
=
······························································ (3)
注記4 バルブに継手類が取り付けてあるときは,FLをFLP / Fpと入れ換える。
補正係数αは,次の二つの圧力比の比である。
a) 閉そく流状態での入口圧力の出口圧力に対する比。
b) 閉そく流状態での入口圧力の縮流部の圧力に対する比。
αは,式 (4) で定義する。
C
2
vcc
vcc
1
C
2
1
p
p
p
p
p
p
=
≡
α
······································································ (4)
衝撃セル−乱流の相互作用機構(状態Ⅳ)が,乱流−せん断機構(状態Ⅲ)を上回って騒音スペクトル
を支配し始める点は,ブレークポイントとして知られている。これらの状態の説明については,5.2を参照。
7
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ブレークポイントでの下流圧力は,式 (5) によって計算する。
(
)1
/
1
2B
1
−
=
γ
γ
γ
α
p
p
······································································ (5)
一定の音響効率の領域(状態Ⅴ)が始まる点の下流圧力は,式 (6) によって計算する。
α
22
1
2CE
p
p
=
············································································· (6)
5.2
状態の定義
調節弁は,ポテンシャル(圧力)のエネルギーを乱流に変換することによって流れを制御する。調節弁
内の騒音は,このエネルギーのわずかの部分が音へ変換することから生じる。大部分のエネルギーは,熱
に変換される。
音響の現象が多様であること,又は気体分子と音速衝撃セルとの間の干渉の結果,騒音の発生は,複数
の状態に分類できる。状態Ⅰでは,流れは亜音速であって,気体は部分的に再圧縮され,したがって,係
数FLが深く関与している。この状態での騒音発生は,主として双極子的である。
状態Ⅱでは,音速流が衝撃セル間の相互作用及び閉そく流の乱流混合を伴いながら存在している。状態
Ⅱの限界に近づくにつれて,再圧縮の程度が低下してくる。
状態Ⅲでは,等エントロピーの再圧縮は存在しない。流れは超音速となり,乱流−せん断機構が支配的
となる。
状態Ⅳでは,マッハディスクが形成されるにつれて衝撃セル構造が弱まり,これに代わって衝撃セル−
乱流相互作用が支配的となる。
状態Ⅴでは,一定の音響効率が存在し,更にp2が減少しても騒音は,増加しない。
流れの各状態は,与えられる一連の運転条件によって,次のように場合分けできる。
状態Ⅰ p2 ≧ p2C の場合
状態Ⅱ p2C > p2 ≧ pvcc の場合
状態Ⅲ pvcc > p2 ≧ p2B の場合
状態Ⅳ p2B > p2 ≧ p2CE の場合
状態Ⅴ p2CE > p2
の場合
5.3 予備的計算
5.3.1
バルブ形状修正係数 Fd
多段弁の場合,Fdは最終段だけ適用する。
バルブ形状修正係数は,式 (7a) によって計算する。
o
H
d
d
d
F=
················································································· (7a)
単一流路の水力学的直径dHは,式 (7b) によって求める。
W
H
4
l
A
d=
··············································································· (7b)
全流れ面積の等価円の直径doは,式 (7c) による。
π
A
N
d
o
o
4
=
·········································································· (7c)
Fdの代表的な値を,表3に規定する。
8
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.3.2
噴流の直径 Dj
噴流の直径は,式 (8) による。
L
d
14
j
CF
F
N
D=
······································································ (8)
注記1 N14は,数値定数である。使用する容量係数(Kv又はCv)によって決まる。定数の値は,表
2による。
注記2 バルブの定格Cの値ではなく,所要のCの値を使用する。
注記3 バルブに継手類が取り付けてあるときは,FLをFLP/Fpと入れ換える。
5.3.3
音響パワー比 rw
音響パワー比は,下流側配管へ放射する音響パワーと運動エネルギーの割合を表す。種々のバルブ及び
継手類に対する係数を,表4に規定する。
表2−数値定数 N
定数
容量係数
Kv
Cv
N14
4.9×10−3
4.6×10−3
N16
4.23×104
4.89×104
注記 表にない数値定数は,この規格に用いない。
表3−バルブ形状修正係数Fdの代表的な値(フルサイズトリム)
バルブ形状
流れ方向
相対容量係数Φ
0.10
0.20
0.40
0.60
0.80
1.00
グローブ,パラボリックプラグ
オープン
クローズ
0.10
0.20
0.15
0.30
0.25
0.50
0.31
0.60
0.39
0.80
0.46
1.00
グローブ,3V‐ポートプラグ
両方向 a)
0.29
0.40
0.42
0.43
0.45
0.48
グローブ,4V‐ポートプラグ
両方向 a)
0.25
0.35
0.36
0.37
0.39
0.41
グローブ,6V‐ポートプラグ
両方向 a)
0.17
0.23
0.24
0.26
0.28
0.30
グローブ,60同径ドリル孔ケージ
両方向 a)
0.40
0.29
0.20
0.17
0.14
0.13
グローブ,120同径ドリル孔ケージ
両方向 a)
0.29
0.20
0.14
0.12
0.10
0.09
バタフライ,スイングスルー(同心軸),70°
両方向
0.26
0.34
0.42
0.50
0.53
0.57
バタフライ溝付きベーン,70°
両方向
0.08
0.10
0.15
0.20
0.24
0.30
バタフライ,60°平円板
両方向
0.50
偏心回転プラグ
両方向
0.12
0.18
0.22
0.30
0.36
0.42
セグメント ボール,90°
両方向
0.60
0.65
0.70
0.75
0.78
0.98
注記 これらの値は代表的な値である。実際の値は製造業者による。
注a) フロー ツー クローズ方向の流れに対しては,弁差圧(p1−p2 )の制限がある。
表4−音響パワー比 rw
バルブ又は接手
rw
グローブ,パラボリックプラグ
0.25
グローブ,3 V‐ポートプラグ
0.25
グローブ,4 V‐ポートプラグ
0.25
グローブ,6 V‐ポートプラグ
0.25
グローブ,60同径ドリル孔ケージ
0.25
9
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表4−音響パワー比 rw(続き)
バルブ又は接手
rw
グローブ,120同径ドリル孔ケージ
0.25
バタフライ,スイングスルー(同心軸),70°
0.5
バタフライ,溝付きベーン,70°
0.5
バタフライ,60°平円板
0.5
偏心回転プラグ
0.25
セグメントボール,90°
0.25
エキスパンダ
1
5.4
状態Ⅰ(亜音速流)
縮流部における気体の速度は,式 (9) による。
1
1
/)1
(
1
vc
vc
1
1
2
ρ
γ
γ
γ
γ
p
p
p
U
−
−
=
−
············································· (9)
質量流の流れのパワーは,式 (10) によって計算する。
2
)
(
2
vc
m
U
m
W
&
=
······································································· (10)
亜音速に対する縮流部の温度は,式 (11) によって計算する。
γ
γ /)1
(
1
vc
1
vc
−
=
p
p
T
T
·································································· (11)
縮流部における音速は,式 (12) によって計算する。
M
RT
c
vc
vc
γ
=
········································································· (12)
縮流部におけるマッハ数は,式 (13) によって計算する。
vc
vc
vc
c
U
M
=
············································································· (13)
状態Ⅰに対する音響効率係数は,式 (14) によって計算する。
(
)
6.3
vc
4
1
10
1
M
−
×
=
η
································································ (14)
したがって,状態Ⅰで発生し,下流側配管に放射される音響パワーは,式 (15) による。
2
L
m
w
1
a
F
W
r
W
η
=
····································································· (15)
注記 バルブに継手類が取り付けてあるときは,FLをFLP/Fpと入れ換える。
この方法には不必要であるが,全内部音響パワーレベルは,式 (16) によって計算する。
o
a
10
wi
log
10
W
W
L=
···································································· (16)
配管内部の音響パワーを計算するときには,Lwiから6 dBを減じる。
発生した騒音のピーク周波数は,式 (17) によって計算する。
10
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
j
vc
p
2.0
D
U
f=
·········································································· (17)
5.5
状態Ⅱ〜Ⅴ(共通の計算)
式 (18) 〜 (21) は,状態ⅡからⅤまで共通である。これらの状態は,音速以上である。
音速(又は臨界)流については,縮流部の温度は,式 (18) による。
1
21
vcc
+
=γT
T
············································································· (18)
縮流部における音速は,式 (19) によって計算する。
M
RT
c
vcc
vcc
γ
=
······································································· (19)
したがって,流れのパワーは,式 (20) によって求める。
2
2
vcc
ms
c
m
W
&
=
········································································· (20)
この方法には不必要であるが,内部音響パワーレベルは,式 (16) 及び式 (23),式 (26),式 (28) 又は
式 (32) を使って計算する。
自由膨張する噴流部では,マッハ数は状態ⅡからⅣまでについて,式 (21) によって計算する。
(
)
−
−
=
−
1
1
2
/
1
2
1
j
γ
γ
α
γ
p
p
M
··················································· (21)
5.5.1
状態Ⅱ
状態Ⅱに対する音響効率係数は,式 (22) によって計算する。
(
)
2
L
6.6
j
4
2
10
1
F
M
−
×
=
η
······························································ (22)
注記 バルブに継手類が取付けてあるときは,FLをFLP/Fpと入れ換える。
状態Ⅱで発生し,下流側配管に放射される音響パワーは,式 (23) によって計算する。
−
−
=
vcc
1
2
1
ms
w
2
a
p
p
p
p
W
r
W
η
·························································· (23)
したがって,ピーク周波数は,式 (24) によって求める。
j
vcc
j
p
2.0
D
c
M
f=
······································································ (24)
5.5.2
状態Ⅲ
状態Ⅲに対する音響効率係数は,式 (25) によって計算する。
(
)
2
L
6.6
j
4
3
10
1
F
M
−
×
=
η
······························································ (25)
注記 バルブに継手類が取り付けてあるときは,FLをFLP/Fpと入れ換える。
状態Ⅲで発生し,下流側配管に放射される音響パワーは,式 (26) によって計算する。
ms
w
3
a
W
r
W
η
=
········································································· (26)
ピーク周波数は,式 (24) から計算する。
5.5.3
状態Ⅳ
状態Ⅳでの音響効率係数は,式 (27) によって計算する。

11
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
()
2
L
6.6
2
j
4
4
2
2
10
1
F
M
×
=
−
η
··················································· (27)
注記 バルブに継手類が取り付けてあるときは,FLをFLP/Fpと入れ換える。
状態Ⅳで発生し,下流側配管に放射された音響パワーは,式 (28) によって計算する。
ms
w
4
a
W
r
W
η
=
········································································· (28)
状態Ⅳに対するピーク周波数は,式 (29) によって求める。
1
25
.1
35
.0
2
j
j
vcc
p
−
=
M
D
c
f
······························································ (29)
5.5.4
状態Ⅴ
状態Ⅴでは,噴流のマッハ数は,式 (30) によって計算する。
()(
)
[
]1
22
1
2
/
1
j5
−
−
=
−
γ
γ
γ
M
······················································· (30)
一定の音響効率係数は,式 (31) によって求める。
()
×
=
−
2
L
6.6
2
5j
4
5
2
2
10
1
F
M
η
··················································· (31)
注記 バルブに継手類が取り付けてあるときは,FLをFLP/Fpと入れ換える。
したがって,状態Ⅴで発生し,下流側配管に放射される音響パワーは,式 (32) によって計算する。
ms
w
5
a
W
r
W
η
=
········································································· (32)
状態Ⅴに対するピーク周波数は,Mjの代わりにMj5を用いて式 (29) から計算する。
5.6
騒音の計算
下流の密度は,式 (33) によって計算する。
=
1
2
1
2
p
p
ρ
ρ
········································································· (33)
下流側温度T2は,必要な流体の性質が分かれば,熱力学的等エンタルピーの関係を使うことによって,
求めることができる。ただし,流体の性質が分かっていない場合は,T2はほぼT1に等しいとすることがで
きる。
式 (34) から,下流の音速を計算する。
M
RT
c
2
2
γ
=
·········································································· (34)
バルブ出口でのマッハ数は,式 (35) によって計算する。
2
2
2
o
4
c
D
m
M
ρ
π
&
=
····································································· (35)
注記1 Moは,0.3を超えてはならない。0.3を超える場合は,正確さを保つことができないので,箇
条7の手順による。
Poを基準にした内部音圧レベルは,式 (36) による。
(
)
×
=
2
i
2
2
a
9
10
pi
10
2.3
log
10
D
c
W
L
ρ
·············································· (36)
12
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
配管壁の透過損失は,式 (37) によって計算する。
(
)
+
×
=
−
s
a
y
2
2
x
2
p
p
2
7
10
1
415
10
6.7
log
10
p
p
G
c
G
f
t
c
TL
ρ
····················· (37)
注記2 Gx 及びGyは,表5による。
注記3 比pa /ps は,局所気圧に対する補正である。
注記4 透過損失モデルは,6 dB/オクターブ減衰の内部周波数分布を基にしている。
周波数fr fo 及びfgは,それぞれ式 (38),式 (39) 及び式 (40) によって計算する。
i
r
000
5
D
f
π
=
············································································· (38)
=
343
4
2
r
o
c
f
f
········································································ (39)
(
)
(
)
000
5
343
3
p
2
t
f
π
=
g
······································································ (40)
注記5 式 (39) 及び式 (40) で,定数343は空気中の音速 (m/s) である。
注記6 式 (38) 及び式 (40) で,定数5 000は鋼に対する配管壁中の音速 (m/s) である。
注記7 最小の透過損失は,配管の第一のコインシデンス周波数で起こることに注意する。
表5−周波数係数 Gx 及びGy
o
p
f
f<
o
p
f
f≥
4
o
p
3/
2
r
x
=
f
f
f
f
G
o
3/
2
r
p
x
=
f
f
G
r
p
f
f<
のとき
1
x=
G
r
p
f
f≥
のとき
=
gf
f
G
o
y
gf
f<
o
のとき
1
y=
G
gf
f≥
o
のとき
=
r
p
y
f
f
G
gf
f<
p
のとき
1
y=
G
gf
f≥
p
のとき
下流側配管の速度補正は,近似的に式 (41) 及び式 (42) による。
−
=
2
101
1
log
16
M
Lg
······························································· (41)
2
2
2
i
2
4
c
D
m
M
ρ
π
&
=
····································································· (42)
注記8 Lgを計算するときは,M2は0.3までとする。
配管の外径のところで放射されるA特性音圧レベルは,式 (43) によって求める。
gL
TL
L
L
+
+
+
=
pi
pAe
5
······························································ (43)
注記9 式 (43) で,最初の項5 dBは,周波数ピークのすべてに対応するための平均補正である。
最後に,管壁から1 mのところでのA特性音圧レベルは,式 (44) によって計算する。
+
+
+
−
=
p
i
p
i
10
pAe
pAe,1m
2
2
2
log
10
t
D
t
D
L
L
·········································· (44)
13
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.7
計算の手順
次に示す手順は,前記の式を用いて音圧レベルを計算するための,論理的な順序を示す。
5.1,5.2及び5.3から開始する。
状態Ⅰの場合は,5.4及び5.6を使用する。
状態Ⅱの場合は,5.5,5.5.1及び5.6を使用する。
状態Ⅲの場合は,5.5,5.5.2及び5.6を使用する。
状態Ⅳの場合は,5.5,5.5.3及び5.6を使用する。
状態Ⅴの場合は,5.5,5.5.4及び5.6を使用する。
注記 計算例を,附属書Aに示す。
6
騒音低減トリムバルブ
6.1
適用範囲
この箇条は,騒音低減トリムバルブに適用する。ここでは多くの手順を箇条5から引用するが,これら
のトリムには特別な配慮が必要であるため,別の箇条として設ける。
6.2
単段多流路トリム
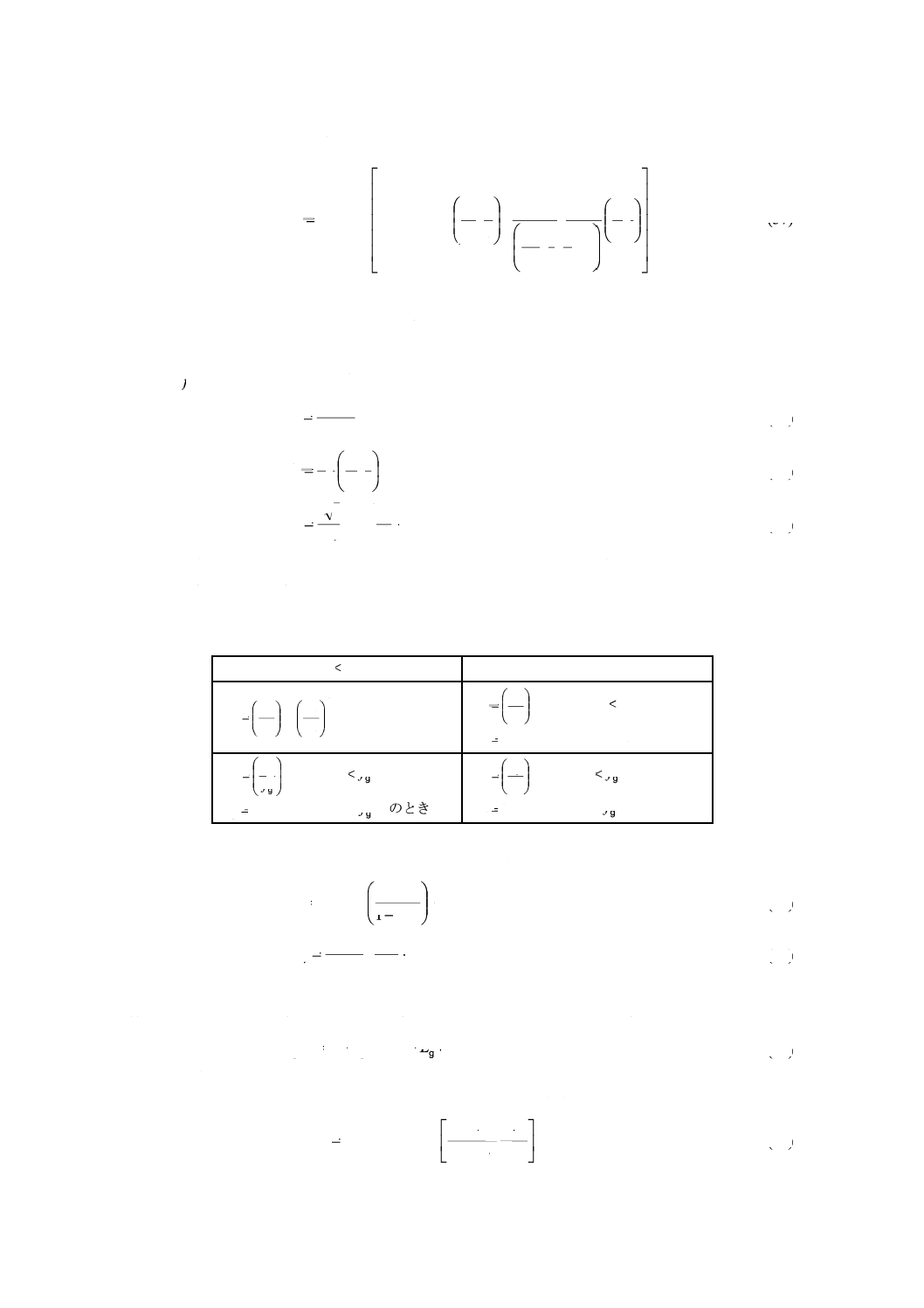
単段多流路トリム付きバルブ(多くの実用例がある騒音低減トリムの一例を,図1に示す。)については,
次に規定する手順を除き,箇条5の手順による。
注記 多くの実用例がある騒音低減トリムの一例
図1−単段多流路トリムの例
14
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
流路は,すべて同じ水力学的直径をもち,これらの流路間の距離は,噴流の相互作用を防ぐのに十分な
距離がなければならない。
バルブ形状修正係数は箇条5と同じである。その適用例を,次に示す。
例 幅0.010 m,高さ0.002 mの48個の長方形流路をもつトリムを想定する。各流路の面積Aは,0.010
× 0.002 = 0.000 02 m2である。ぬれ縁の長さlw = (2×0.010) + (2×0.002) = 0.024 m,do = 0.035 m,
dH = 0.003 3 mから,Fd = 0.003 3 / 0.035 = 0.094となる。
噴流の直径Djは,式 (45) によって計算する。
(
)
[
]
d
l
C
F
N
D
/
06
.0
9.0
d
14
j
−
=
··················································· (45)
注記1 Djの計算式で,式中FLnは [0.9−0.06 (l/d)] に置き換えてあり,l/dの最大値は4である。
FLnの代わりに [0.9−0.06(l/d)] を使用する結果,状態Ⅰ,Ⅱ及びⅢにおいて,一般に透過損失が最大5 dB
増大する。
バルブ出口におけるマッハ数は,式 (35) を用いて計算する。
注記2 圧力比p1/p2 > 4の場合,Fdの計算に用いる式 (7a) は,流路同士の壁面間隔が0.7dを超える
場合にだけ使用できる。式 (7a) は,バルブ出口におけるマッハ数Moが0.2を超えると妥当
性を失う。
6.3
多段単一流路減圧トリム(二つ以上の絞りステップ)
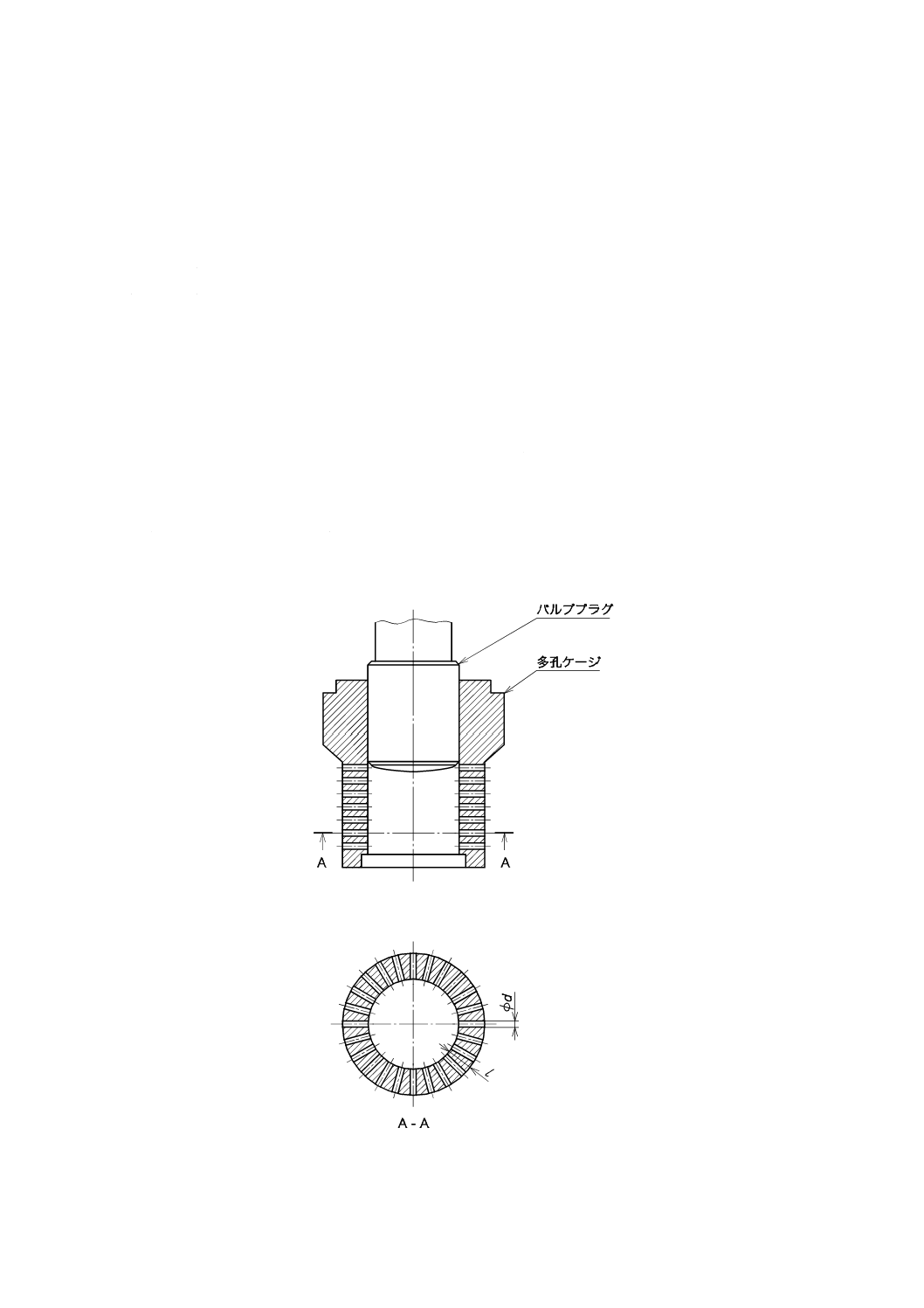
多段単一流路弁の場合(多くの実用例がある騒音低減トリムの一例を,図2に示す。),次のことを除き,
箇条5による。
注記 多くの実用例がある騒音低減トリムの一例
図2−多段単一流路減圧トリムの例
注記1 最終段には,6.3の計算のすべてが適用できる。
15
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
容量係数Cnは,Cの代わりに用いることとする。これは,多段トリムの最終段に適用できる。
バルブ製造業者からCnの値が得られない場合は,式 (46) を用いる。
n
16
n
A
N
C=
············································································ (46)
注記2 N16は数値定数で,使用する容量係数 (Kv又はCv) によって,定数の値が決まる。これらの
定数の値は,表2による。
p1の代わりに最終段のよどみ点圧力pnを用い,密度ρnはρ1の代わりに用いる。
これらの値は,式 (47a),式 (47b),式 (47c) 及び式 (48) によって求める。
注記3 p1 / p2 ≧ 2の場合,まずpn / p2 < 2と仮定して式 (47a) からpnを計算する。pnの計算値が
pn ≧ 2 p2ならば,式 (47b) からpnを計算して,この手順を続ける。
p1 / p2 ≧ 2,かつ,pn / p2 < 2ならば
2
2
2
n
1
n
155
.1
p
C
C
p
p
+
=
························································· (47a)
p1 / p2 ≧ 2,かつ,pn / p2 ≧ 2ならば
=
n
1
n
C
C
p
p
········································································ (47b)
p1 / p2 < 2ならば
(
)
2
2
2
2
2
1
2
n
n
p
p
p
C
C
p
+
−
=
·················································· (47c)
=
1
n
1
n
p
p
ρ
ρ
·········································································· (48)
ピーク周波数の計算式に用いる最終段の噴流の直径は,式 (49) によって求める。
L
n
d
14
j
F
C
F
N
D=
·································································· (49)
注記4 この式 (49) に対しては,最終段のFdを用いる。
最後に,配管の外径部から放射されるA特性音圧レベルは,式 (50) によって求める。
gL
TL
p
p
L
L
+
+
+
+
=
n
1
10
pi
pAe
log
10
5
········································· (50)
注記5 最終段の騒音寄与は,Lpiによって与えられる。式中の項10 log10(p1/pn) は,他の段の減圧に
よる音圧レベルを含む。
6.4
多段多流路トリム(二つ以上の流路及び二つ以上の減圧段)
注記1 この細分箇条は,リニアトラベルのバルブにだけ適用する。
注記2 最終段には,6.4の計算がすべて適用できる。
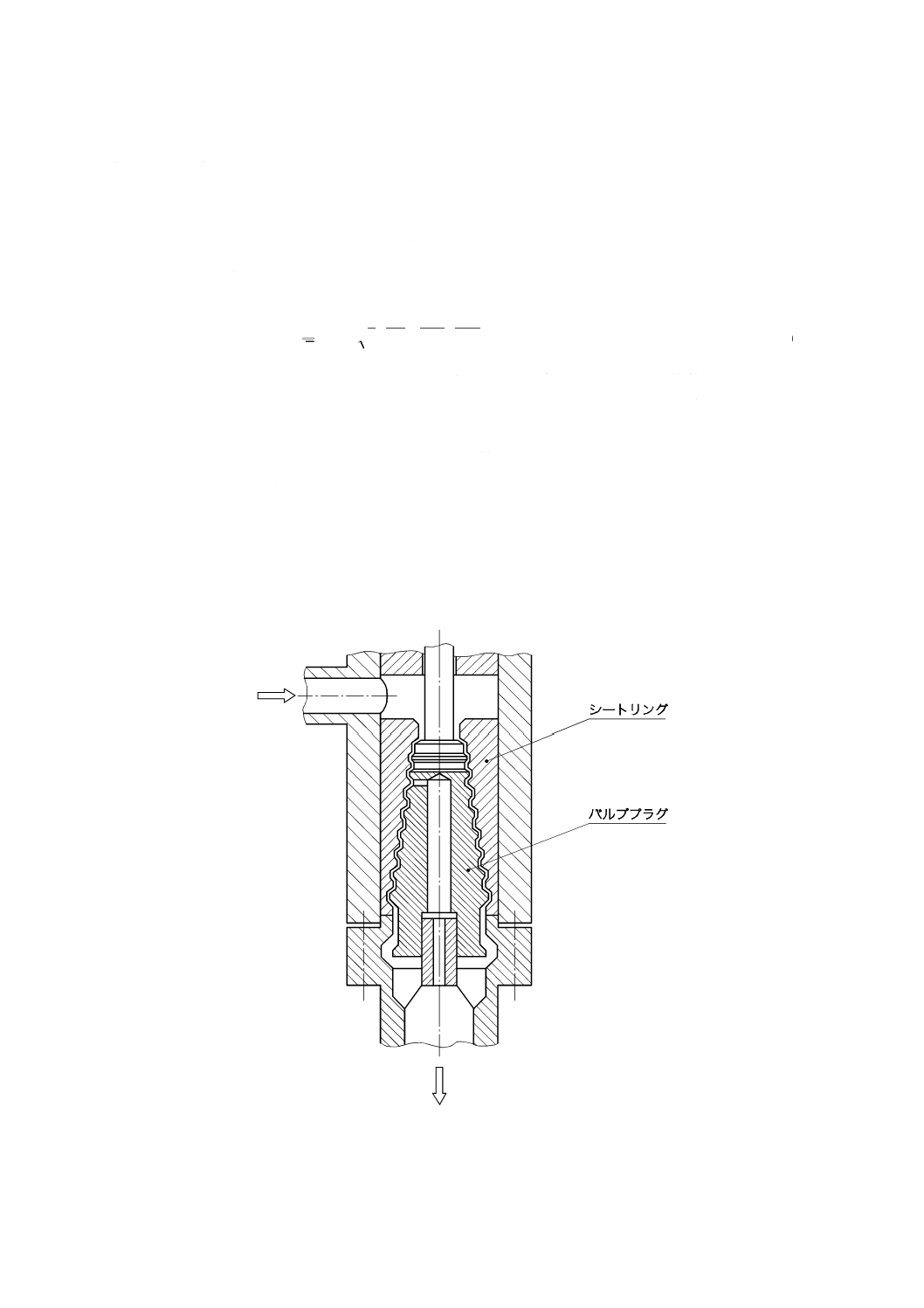
多段多流路トリムに対しては(多くの実用例がある騒音低減トリムの一例を,図3に示す。),次のこと
を除き,箇条5による。
16
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記 多くの実用例がある騒音低減トリムの一例
図3−多段多流路トリム(二つ以上の流路及び二つ以上の減圧段)の例
流路はすべて同じ水力学的直径をもち,かつ,これら流路間は,噴流の相互作用を防ぐのに十分な距離
とする。各段の流路面積は,入口と出口との間で増大するものとする。
縮流部の圧力pvcは,式 (1) のFLの代わりにFLnを用いて計算する。容量係数Cの代わりに式 (46) の
Cnを用い,p1の代わりに式 (47) の最終段のよどみ点圧力pnを用い,かつ,密度ρ1の代わりに式 (48) の
ρnを用いる。
噴流マッハ数は,式 (51) によって計算する。
vc
vc
jn
c
U
M
=
············································································· (51)
ここに,最終段の速度Uvcは,p1の代わりにpnを,及びρ1の代わりにρnを用いて,式 (9) によって求
める。
ピーク周波数fpは,式 (49) から得られる最終段の噴流の直径Djを用いて,式 (52) によって計算する。
j
vc
jn
p
2.0
D
c
M
f=
····································································· (52)
最後に,A特性音圧レベルLpAeは,式 (50) を用いて計算する。
注記3 6.4の手法は,バルブ出口のマッハ数Moが0.2を超える場合は正確ではない。Moの計算につ
いては,式 (35) を参照する。マッハ数が0.3の場合は,誤差が5 dBを超える場合がある。
より高いマッハ数に対する手順については,箇条7を参照する。
注記4 計算例を,附属書Aに示す。
6.5
この規格で取り上げないバルブ類
箇条6に示す以外の低騒音トリムは,この規格の適用範囲外とする。しかし,このようなトリムであっ
ても,バルブ製造業者が,この規格の箇条5の適用可能な各条項を用いて得られる音圧レベルに加え,ト
ラベル及び/又はバルブ圧力比の関数として付随する音圧レベルの変化について,その裏付けとなる値を
提供してくれる場合は,この規格の手法を使ってよい。
17
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7
より高い出口マッハ数のバルブ類
7.1
適用範囲
この箇条は,バルブが出口エキスパンダに接続され,かつ,箇条5及び箇条6に規定する制限を超える
マッハ数のとき,音圧レベルを予測する方法を規定する。注記の箇所を除いて,箇条5及び箇条6の式を
用いる。また,この方法は,バルブ呼び径が配管呼び径に等しいときも適用する。
7.2
計算の手順
下流側配管において,速度は,マッハ数0.8以下に制限され,式 (53) によって計算する。
2i
2
p
4
D
m
U
ρ
π
&
=
········································································ (53)
エキスパンダの入口における気体速度URは,音速c2以下に制限され,式 (54) によって計算する。
2
i
2
i
p
R
d
D
U
U
β
=
·········································································· (54)
注記1 バルブ出口における速度分布が,すべての場合に一様でないこと,及び収縮係数を使用しな
ければならないことに留意する。この係数βは,式 (54) に算入されている。βの値は,バ
ルブ出口において,閉そく流れの点がマッハ数1であることを用いて,試験データから求め
ることができる。正味の面積は,質量流量を密度と音速との積で除したものに等しい。また,
解析的手法で決めることができる。β= 0.93の値は,ストレート形グローブ弁に適用できる。
他のバルブ形式に対するデータは,現時点では整理されていないが,あるバルブに対しては
この値は低く,0.7程度である。
エキスパンダ内の変換された流れのパワーは,式 (55) によって求める。
+
−
=
2.0
1
2
2
2
i
2
i
2
R
mR
D
d
U
m
W
&
················································· (55)
発生した騒音のピーク周波数は,式 (56) によって求める。
i
R
pR
2.0
d
U
f
=
········································································· (56)
音響効率係数は式 (57) 及び式 (58) によって計算する。
(
)
3
R
3
R
10
1
M
−
×
=
η
································································· (57)
ここに,
2
R
R
c
U
M=
·············································································· (58)
発生した音響パワー,式 (59) によって決める。
mR
R
aR
W
W
η
=
·········································································· (59)
ここでの手順では必要はないが,全内部音響パワーは式 (16) を用いて計算する。
Poを基準にした内部音圧レベルは,式 (60) による。
18
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
×
=
2
i
2
2
aR
9
10
piR
10
2.3
log
10
D
c
W
L
ρ
········································· (60)
透過損失TLRは,式 (61) によって計算する。
(
)
+
×
=
−
s
a
y
2
2
x
2
pR
p
2
7
10
R
1
415
10
6.7
log
10
p
p
G
c
G
f
t
c
TL
ρ
··················· (61)
注記2 Gx及びGyは,表5による。表5で,fpの代わりにfpRとする。
下流側配管の速度補正は,式 (41) 及び式 (42) によって計算する。
配管の外径部において放射されるA特性音圧レベルは,式 (62) によって,配管の壁から1 mの距離の
ところで計算する。Lgは,M2が0.8で制限されることを除いて,式 (41) によって計算する。
+
+
+
−
+
+
+
=
p
i
p
i
10
R
piR
peR
2
2
2
log
10
5
t
D
t
D
L
TL
L
L
g
··························· (62)
バルブトリムLpAe及びエキスパンダLpeRの両者を組み合わせた音圧レベルは,式 (63) によって算出す
る。
(
)
10
/
10
/
10
pS
peR
pAe,1m
10
10
log
10
L
L
L
+
=
············································· (63)
19
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
計算例題
この附属書は,本体に関連する事柄を補足するもので,規定の一部ではない。
例題1:状態Ⅰの場合
与えられたデータ:
バルブ
バルブの種類:
フロー ツー オープンに取り付けられた単座グローブ弁(ケージ付き)
バルブ呼び径:
DN 100
バルブ出口の直径D:
100 mm = 0.100 m
定格Cv:
195
要求Cv:
90
液体圧力回復係数と配管形状係数との組合せ係数: FLP = 0.792
入口呼び径:
DN 200
出口呼び径:
DN 200
管壁の厚さ:
tp = 8 mm = 0.008 m
配管の内径:
Di = 203.1 mm = 0.203 1 m
ケージ開口部の数:
No = 6
単一流路のぬれ縁の長さ:lw = 181 mm = 0.181 m
単一流路の面積:
A = 0.001 37 m2
差圧比係数:
xT = 0.75
流体
流体の種類:
蒸気
入口絶対圧力:
p1 = 10 bar = 1.0×106 Pa
出口絶対圧力:
p2 = 7.2 bar = 7.2×105 Pa
入口密度:
1
ρ = 5.30 kg/m3
入口温度:
T1 = 177 ℃ = 450 K
比熱比:
γ = 1.22
モル質量:
M = 19.8 kg/kmol
その他
実際の大気:
pa = 1.013 25 bar = 1.013 25×105 Pa
標準大気圧:
ps = 1.013 25 bar = 1.013 25×105 Pa
20
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
次の値は,JIS B 2005-2-1に基づく計算に用いる値,又はJIS B 2005-2-1の計算によって求められる値で
ある。
速度水頭の損失係数: Σζ= 0.86
入口側の速度水頭損失係数:ζi = 1.2
配管形状係数: Fp = 0.98,FLP / Fp = 0.8
質量流量: m& = 2.22 kg/s
計算:
Pa
10
7.5
5
2
L
2
1
1
vc
×
=
−
−
=
F
p
p
p
p
·················································· (1)
ここに,
p1 = 1.0×106 Pa
p2 = 7.2×105 Pa
FLP / Fp = 0.80(継手類が付いているためFLP / Fpを使用。)
(
)
Pa
10
6.5
1
2
5
1
/
1
vcc
×
=
+
=
−
γ
γ
γ
p
p
·············································· (2)
ここに,
p1 = 1.0×106 Pa
γ = 1.22
(
)
Pa
10
2.7
5
vcc
1
2
L
1
2C
×
=
−
−
=
p
p
F
p
p
·········································· (3)
ここに,
p1 = 1.0×106 Pa
pvcc = 5.6×105 Pa
FLP / Fp = 0.80(継手類が付いているためFLP / Fpを使用。)
78
.0
2C
vcc=
=pp
α
········································································ (4)
ここに,
vcc
p= 5.6×105 Pa
2c
p= 7.2×105 Pa
(
)
Pa
10
2.4
1
5
1
/
1
2B
×
=
=
−
γ
γ
γ
α
p
p
··················································· (5)
ここに,
p1 = 1.0×106 Pa
α = 0.78
γ = 1.22
21
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Pa
10
8
5
22
4
1
2CE
×
=
=
.
p
p
α
······························································ (6)
ここに,
p1 = 1.0×106 Pa
α = 0.78
p2 ≧ p2Cならば,状態はⅠである。7.2×105 ≧ 7.2×105であるから,状態はⅠである。
Fdの計算手順は,次による。
m
030
.0
4
w
H
=
=lA
d
·································································· (7b)
ここに,
A = 0.001 37 m2
lw = 0.181 m
m
10
.0
4
o
o
=
=
π
A
N
d
······························································ (7c)
ここに,
No = 6
A = 0.001 37 m2
30
.0
o
H
d
=
=dd
F
······································································· (7a)
ここに,
dH = 0.030 m
do = 0.102 m
通常,製造業者がFdの値を提供する。この例では,0.30とする。
m
012
.0
L
d
14
j
=
=
CF
F
N
D
························································ (8)
ここに,
N14 = 4.6×10−3(表2から)
Fd = 0.30
C = Cv = 90
FLP / Fp = 0.80(継手類が付いているためFLP / Fpを使用。)
(
)
m/s
450
1
1
2
1
1
/
1
1
vc
vc
=
−
−
=
−
ρ
γ
γ
γ
γ
p
p
p
U
······························· (9)
ここに,
γ = 1.22
pvc = 5.7×105 Pa
p1 = 1.0×106 Pa
1ρ= 5.30 kg/m3
22
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
W
10
3.2
2
5
2
vc
m
×
=
=
U
m
W
&
····················································· (10)
ここに,
m& = 2.22 kg/s
Uvc = 450 m/s
(
)
K
410
/
1
1
vc
1
vc
=
=
−
γ
γ
p
p
T
T
······················································· (11)
ここに,
T1 = 450 K
pvc = 5.7×105 Pa
p1 = 1.0×106 Pa
γ = 1.22
m/s
460
vc
vc
=
=
M
RT
c
γ
·························································· (12)
ここに,
γ = 1.22
R = 8 314 J/(kmol・K)
Tvc = 410 K
M = 19.8 kg/kmol
99
.0
vc
vc
vc
=
=cU
M
···································································· (13)
ここに,
Uvc = 450 m/s
cvc = 460 m/s
(
)
5
6.3
vc
4
1
10
6.9
10
1
−
−
×
=
×
=
M
η
·················································· (14)
ここに,
Mvc = 0.99
W
5.3
2
L
m
w
1
a
=
=
F
W
r
W
η
························································· (15)
ここに,
1η = 9.6×10−5
rw = 0.25(表4から)
Wm = 2.23×105 W
FLP / Fp = 0.80(継手類が付いているためFLP / Fp使用。)
z
D
U
f
H
700
7
2.0
j
vc
p
=
=
···························································· (17)
23
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
Uvc = 450 m/s
Dj = 0.012 m
3
1
2
1
2
kg/m
8.3
=
=
p
p
ρ
ρ
·························································· (33)
ここに,
1ρ= 5.30 kg/m3
p2 = 7.2×105 Pa
p1 = 1.0×106 Pa
m/s
480
2
2
=
=
M
RT
c
γ
····························································· (34)
ここに,
γ = 1.22
R = 8 314 J/(kmol・K)
T2 = 450 K
M = 19.8 kg/kmol
15
.0
4
2
2
2
o
=
=
c
D
m
M
ρ
π
&
····························································· (35)
ここに,
m&= 2.22 kg/s
D = 0.100 m
2ρ= 3.8 kg/m3
c2 = 480 m/s
注記 Moは0.3を超えていないので,これらの計算は適切である。
(
)
dB
147
10
2.3
log
10
2
i
2
2
a
9
10
pi
=
×
=
D
c
W
L
ρ
··································· (36)
ここに,
a
W= 3.5 W
2ρ= 3.8 kg/m3
C2 = 480 m/s
Di = 0.203 1 m
Hz
800
7
000
5
i
r
=
=
D
f
π
······························································ (38)
ここに,
Di = 0.203 1 m
Hz
700
2
343
4
2
r
o
=
=
c
f
f
·························································· (39)
ここに,
f r = 7 800 Hz
c2 = 480 m/s

24
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(
)
(
)
Hz
600
1
000
5
343
3
p
2
=
=
t
f
π
g
························································ (40)
ここに,
tp = 0.008 m
(
)
dB
51
1
G
415
10
6.7
log
10
s
a
y
2
2
x
2
p
p
2
7
10
−
=
+
×
=
−
p
p
c
G
f
t
c
TL
ρ
······· (37)
ここに,
c2 = 480 m/s
tp = 0.008 m
fp = 7 700 Hz
2ρ= 3.8 kg/m3
Gx = (fp / fr ) 2/3 = 0.99(表5から)
Gy = 1(表5から)
pa = 1.013 25×105 Pa
ps = 1.013 25×105 Pa
037
.0
4
2
2
2i
2
=
=
c
D
m
M
ρ
π
&
·························································· (42)
ここに,
m&= 2.22 kg/s
Di = 0.203 1 m
2ρ= 3.8 kg/m3
c2 = 480 m/s
dB
26
.0
1
1
log
16
2
10
=
−
=
M
Lg
·················································· (41)
ここに,
M2 = 0.037 m
dB(A)
101
5
pi
pAe
=
+
+
+
=
gL
TL
L
L
············································ (43)
ここに,
Lpi = 147 dB
TL = −51 dB
Lg = 0.26 dB
dB(A)
91
2
2
2
log
10
p
i
p
i
10
pAe
pAe,1m
=
+
+
+
−
=
t
D
t
D
L
L
···························· (44)
ここに,
LpAe = 101 dB(A)
Di = 0.203 1 m
25
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
tp = 0.008 m
結論:91 dB(A)を使用。
例題2:状態Ⅱの場合
与えられたデータは,次の点を除き例題1と同じである。
出口絶対圧力 p2 = 6.9 bar = 6.9×105 Pa
質量流量 m& = 2.29 kg/s
計算は,次の点を除き状態Ⅰの場合の例題1と同じである。
pvcc = 5.6×105 Pa(例題1から)
p2C = 7.2×105 Pa(例題1から)
p2C > p2≥pvccならば,状態Ⅱである。
5
5
5
10
6.5
10
9.6
10
2.7
×
≥
×
>
×
であるから,状態Ⅱである。
K
410
1
21
vcc
=
+
=γT
T
································································· (18)
ここに,
T1 = 450 K
γ = 1.22
m/s
456
vcc
vcc
=
=
M
RT
c
γ
·························································· (19)
ここに,
γ = 1.22
R = 8 314 J/(kmol・K)
Tvcc = 410 K
M = 19.8 kg/kmol
W
10
4.2
2
5
2
vcc
ms
×
=
=
c
m
W
&
······················································· (20)
ここに,
m&= 2.59 kg/s
cvcc = 460 m/s
(
)
0.1
1
1
2
/
1
2
1
j
=
−
−
=
−
γ
γ
α
γ
p
p
M
············································ (21)
ここに,
γ = 1.22
p1 = 1.0×106 Pa
α = 0.78
p2 = 6.9×105 Pa
(
)
4
6.6
j
4
2
10
1.1
10
1
2
L
−
−
×
=
×
=
F
M
η
················································ (22)
26
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
Mj = 1.0
FLP / Fp = 0.80(継手類が付いているためFLP / Fpを使用。)
W
8.4
vcc
1
2
1
ms
w
2
a
=
−
−
=
p
p
p
p
W
r
W
η
·············································· (23)
ここに,
2η= 1.1×10−4
rw = 0.25(表4から)
Wms = 2.4×105 W
p1 = 1.0×106 Pa
p2 = 6.9×105 Pa
pvcc = 5.6×105 Pa
Hz
000
8
D
2.0
j
vcc
j
p
=
=
c
M
f
························································· (24)
ここに,
Mj = 1.0
cvcc = 460 m/s
Dj = 0.012 m
3
1
2
1
2
kg/m
7.3
=
=
p
p
ρ
ρ
·························································· (33)
ここに,
1ρ= 5.30 kg/m3
p2 = 6.9×105 Pa
p1 = 1.0×106 Pa
c2 = 480 m/s(例題1から)
17
.0
4
2
2
2
o
=
=
c
D
m
M
ρ
π
&
···························································· (35)
ここに,
m&= 2.29 kg/s
D = 0.100 m
2ρ= 3.7 kg/m3
c2 = 480 m/s
注記 Moは0.3を超えていないので,これらの計算は適切である。
(
)
dB
148
10
2.3
log
10
2
i
2
2
a
9
10
pi
=
×
=
D
c
W
L
ρ
·································· (36)
ここに,
Wa = 4.8 W
2ρ= 3.7 kg/m3
c2 = 480 m/s
27
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Di = 0.203 1 m
fr = 7 800 Hz(例題1から)
fo = 2 700 Hz(例題1から)
fg = 1 600 Hz(例題1から)
(
)
dB
51
1
415
10
6.7
log
10
s
a
y
2
2
x
2
p
p
2
7
10
−
=
+
×
=
−
p
p
G
c
G
f
t
c
TL
ρ
·········· (37)
ここに,
c2 = 480 m/s
tp = 0.008 m
fp = 8 000 Hz
2ρ= 3.7 kg/m3
Gx = 1(表5から)
Gy = 1(表5から)
pa = 1.013 25×105 Pa
ps = 1.013 25×105 Pa
040
.0
4
2
2
2
2
=
=
c
D
m
M
ρ
i
π
&
··························································· (42)
ここに,
m&= 2.29 kg/s
Di = 0.203 1 m
2ρ= 3.7 kg/m3
c2 = 480 m/s
dB
29
.0
1
1
log
16
2
10
=
−
=
M
Lg
················································· (41)
ここに,
M2 = 0.040
dB(A)
103
5
pi
pAe
=
+
+
+
=
g
L
TL
L
L
············································· (43)
ここに,
Lpi = 148 dB
TL = −51 dB
Lg = 0.29 dB
dB(A)
93
2
2
2
10
p
i
p
i
10
pAe
pAe,1m
=
+
+
+
+
=
t
D
t
D
log
L
L
········································ (44)
ここに,
LpAe = 103 dB(A)
Di = 0.203 1 m
tp = 0.008 m
28
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
結論:93 dB(A)を用いる。
例題3:状態Ⅲの場合
与えられたデータは,次の点を除き例題1と同じである。
出口絶対圧力 p2 = 4.8 bar = 4.8×105 Pa
質量流量 m&= 2.59 kg/s
計算は,次の点を除き状態Ⅰの場合の例題1と同じである。
pvcc = 5.6×105 Pa(例題1から)
p2C = 7.2×105 Pa(例題1から)
p2B = 4.2×105 Pa(例題1から)
pvcc > p2 ≧ p2Bならば,状態Ⅲである。
5
5
5
10
2
4
10
8
4
10
6
5
×
×
>
×
.
.
.
≧
であるから,状態Ⅲである。
Fd = 0.30(例題1から)
Tvcc = 410 K(例題2から)
cvcc = 460 m/s(例題2から)
W
10
7.2
2
5
2
vcc
ms
×
=
=
c
m
W
&
······················································· (20)
ここに,
m&= 2.59 kg/s
cvcc = 460 m/s
(
)
3.1
1
1
2
/
1
2
1
j
=
−
−
=
−
γ
γ
α
γ
p
p
M
············································· (21)
ここに,
γ = 1.22
p1 = 1.0×106 P
α = 0.78
p2 = 4.8×105 Pa
(
)
4
6.6
j
4
3
10
3.3
10
1
2
L
−
−
×
=
×
=
F
M
η
··············································· (25)
ここに,
Mj = 1.3
FLP / Fp = 0.80(継手類が付いているためFLP / Fpを使用。)
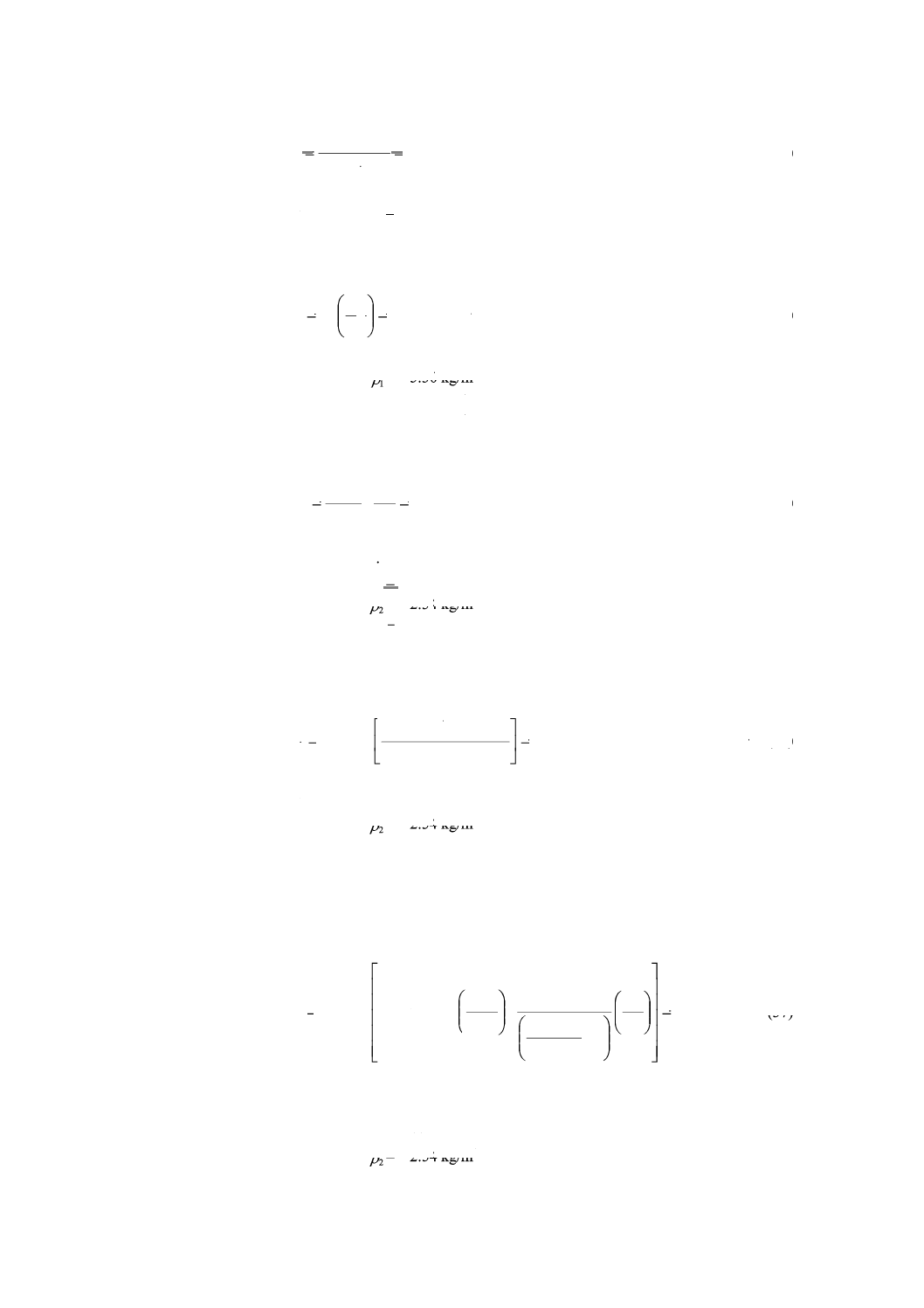
W
22
ms
w
3
a
=
=
W
r
W
η
······························································ (26)
ここに,
3η= 3.3×10−4
rw = 0.25(表4から)
Wms = 2.7×105 W
29
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Hz
000
10
D
2.0
j
vcc
j
p
=
=
c
M
f
······················································ (24)
ここに,
Mj = 1.3
cvcc = 460 m/s
Dj = 0.012 m
3
1
2
1
2
kg/m
54
.2
=
=
p
p
ρ
ρ
························································ (33)
ここに,
1ρ= 5.30 kg/m3
p2 = 4.8×105 Pa
p1 = 1.0×106 Pa
c2 = 480 m/s(例題1から)
27
.0
4
2
2
2
o
=
=
c
D
m
M
ρ
π
&
···························································· (35)
ここに,
m&= 2.59 kg/s
D = 0.100 m
2ρ= 2.54 kg/m3
c2 = 480 m/s
注記 Moは0.3を超えていないので,これらの計算は適切である。
(
)
dB
153
10
2.3
log
10
2
i
2
2
a
9
10
pi
=
×
=
D
c
W
L
ρ
·································· (36)
ここに,
Wa = 22 W
2ρ= 2.54 kg/m3
c2 = 480 m/s
Di = 0.203 1 m
fr = 7 800 Hz(例題1から)
fo = 2 700 Hz(例題1から)
fg = 1 600 Hz(例題1から)
(
)
dB
52
1
415
10
6.7
log
10
s
a
y
2
2
x
2
p
p
2
7
10
−
=
+
×
=
−
p
p
G
c
G
f
t
c
TL
ρ
······· (37)
ここに,
c2 = 480 m/s
tp = 0.008 m
fp = 10 000 Hz
2ρ= 2.54 kg/m3
30
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Gx = 1(表5から)
Gy = 1(表5から)
pa = 1.013 25×105 Pa
ps = 1.013 25×105 Pa
065
.0
4
2
2
2
i
2
=
=
c
D
m
M
ρ
π
&
··························································· (42)
ここに,
m&= 2.59 kg/s
Di = 0.203 1 m
2ρ= 2.54 kg/m3
c2 = 480 m/s
dB
47
.0
1
1
log
16
2
10
=
−
=
M
Lg
·················································· (41)
ここに,
M2 = 0.065
dB(A)
107
5
pi
pAe
=
+
+
+
=
g
L
TL
L
L
············································· (43)
ここに,
Lpi = 153 dB
TL = −52 dB
Lg = 0.47 dB
dB(A)
97
2
2
2
10
p
i
p
i
10
pAe
pAe,1m
=
+
+
+
−
=
t
D
t
D
log
L
L
····································· (44)
ここに,
LpAe = 107 dB(A)
Di = 0.203 1 m
tp = 0.008 m
結論:97 dB(A)を用いる。
例題4:状態Ⅳの場合
与えられたデータは,次の点を除き例題1と同じである。
出口絶対圧力
p2 = 4.2 bar = 4.2×105 Pa
バルブ出口の直径
D = 0.203 1 m
液体圧力回復係数
FL = 0.80
C = Cv = 40
質量流量 m& = 1.18 kg/s
計算は,次の点を除き状態Ⅰの場合の例題1と同じである。
p2B = 4.2×105 Pa(例題1から)
31
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
p2C = 7.2×105 Pa
pvc = 1.0×105 Pa
α = 0.78
p2CE = 5.8 × 104 Pa(例題1から)
p2B > p2 ≧ p2CEならば,状態Ⅳである。4.2×105 > 4.2×105≧5.8×104であるから,状態Ⅳである。
Dj = 7.8 × 10-3 m
Tvcc = 410 K(例題2から)
cvcc = 460 m/s(例題2から)
W
10
2.1
2
5
2
vcc
ms
×
=
=
c
m
W
&
······················································· (20)
ここに,
m&= 1.18 kg/s
cvcc = 460 m/s
(
)
4.1
1
1
2
/
1
2
1
j
=
−
−
=
−
γ
γ
α
γ
p
p
M
············································· (21)
ここに,
γ = 1.22
p1 = 1.0×106 Pa
α = 0.78
p2 = 4.2×105 Pa
(
)
()
4
6.6
2
j
4
4
10
4.4
2
2
10
1
2
L
−
−
×
=
×
=
F
M
η
······································ (27)
ここに,
Mj = 1.4
FL = 0.80
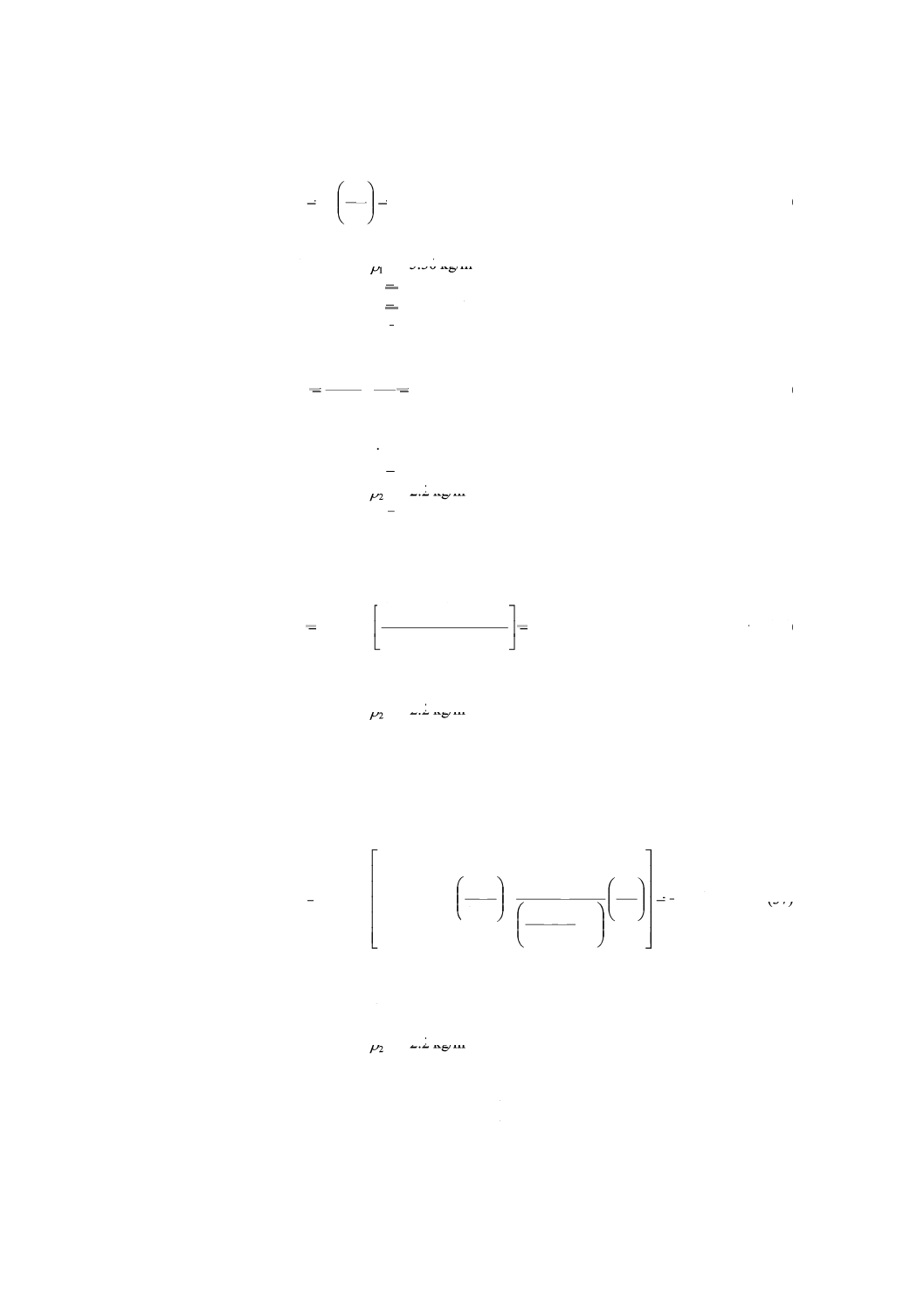
W
14
ms
w
4
a
=
=
W
r
W
η
······························································· (28)
ここに,
4η= 4.4×10−4
rw = 0.25(表4から)
Wms = 1.2×105 W
Hz
000
16
1
1.25
35
.0
2
j
j
vcc
p
=
−
=
M
D
c
f
·············································· (29)
ここに,
Mj = 1.4
cvcc = 460 m/s
32
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Dj = 7.8×10−3 m
3
1
2
1
2
kg/m
2.2
=
=
p
p
ρ
ρ
·························································· (33)
ここに,
1ρ= 5.30 kg/m3
p2 = 4.2×105 Pa
p1 = 1.0×106 Pa
c2 = 480 m/s(例題1から)
14
.0
4
2
2
2
o
=
=
c
D
m
M
ρ
π
&
···························································· (35)
ここに,
m&= 1.18 kg/s
D = 0.100 m
2ρ= 2.2 kg/m3
c2 = 480 m/s
注記 Moは0.3を超えていないので,これらの計算は適切である。
(
)
dB
151
10
2.3
log
10
2
i
2
2
a
9
10
pi
=
×
=
D
c
W
L
ρ
·································· (36)
ここに,
Wa = 14 W
2ρ= 2.2 kg/m3
c2 = 480 m/s
Di = 0.203 1 m
fr = 7 800 Hz(例題1から)
fo = 2 700 Hz(例題1から)
fg = 1 600 Hz(例題1から)
(
)
dB
55
1
415
10
6.7
log
10
s
a
y
2
2
x
2
p
p
2
7
10
−
=
+
×
=
−
p
p
G
c
G
f
t
c
TL
ρ
········ (37)
ここに,
c2 = 480 m/s
tp = 0.008 m
fp = 16 000 Hz
2ρ= 2.2 kg/m3
Gx = 1(表5から)
Gy = 1(表5から)
pa = 1.013 25×105 Pa
ps = 1.013 25×105 Pa
33
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
034
.0
4
2
2
2
i
2
=
=
c
D
m
M
ρ
π
&
·························································· (42)
ここに,
m&= 1.18 kg/s
Di = 0.203 1 m
2ρ= 2.2 kg/m3
c2 = 480 m/s
dB
24
.0
1
1
log
16
2
10
=
−
=
M
Lg
·················································· (41)
ここに,
M2 = 0.034
dB(A)
100
5
pi
pAe
=
+
+
+
=
g
L
TL
L
L
·············································· (43)
ここに,
Lpi = 151 dB
TL = −55 dB
Lg = 0.24 dB
dB(A)
90
2
2
2
10
p
i
p
i
10
pAe
pAe,1m
=
+
+
+
−
=
t
D
t
D
log
L
L
····································· (44)
ここに,
LpAe = 100 dB(A)
Di = 0.203 1 m
tp = 0.008 m
結論:90 dB(A)を用いる。
例題5:状態Ⅴの場合
与えられたデータは,次の点を除き例題1と同じである。
出口絶対圧力
p2 = 0.50 bar = 5.0×104 Pa
質量流量
m&= 1.19 kg/s
バルブ出口の直径
D = 0.203 1 m
液体圧力回復係数
FL= 0.80
C = Cv = 40
計算は,次の点を除き状態Ⅰの場合の例題1と同じである。
p2CE = 5.8×104 Pa(例題1から)
2
CE
2
p
p>
ならば,状態Ⅴである。
4
4
10
0.5
10
80
.5
×
>
×
であるから,状態Ⅴである。
Dj = 7.8×10−3 m(例題4から)
Tvcc = 410 K(例題2から)
cvcc = 460 m/s(例題2から)。
34
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
W
10
2.1
2
5
2
vcc
ms
×
=
=
c
m
W
&
······················································· (20)
ここに,
m&= 1.19 kg/s
cvcc = 460 m/s
()(
)
[
]
6.2
1
22
1
2
/
1
j5
=
−
−
=
−
γ
γ
γ
M
················································ (30)
ここに,
γ = 1.22
()
3
6.6
2
j5
4
5
10
5.1
2
2
10
1
2
L
−
−
×
=
×
=
F
M
η
··································· (31)
ここに,
Mj5 = 2.6
FL = 0.80
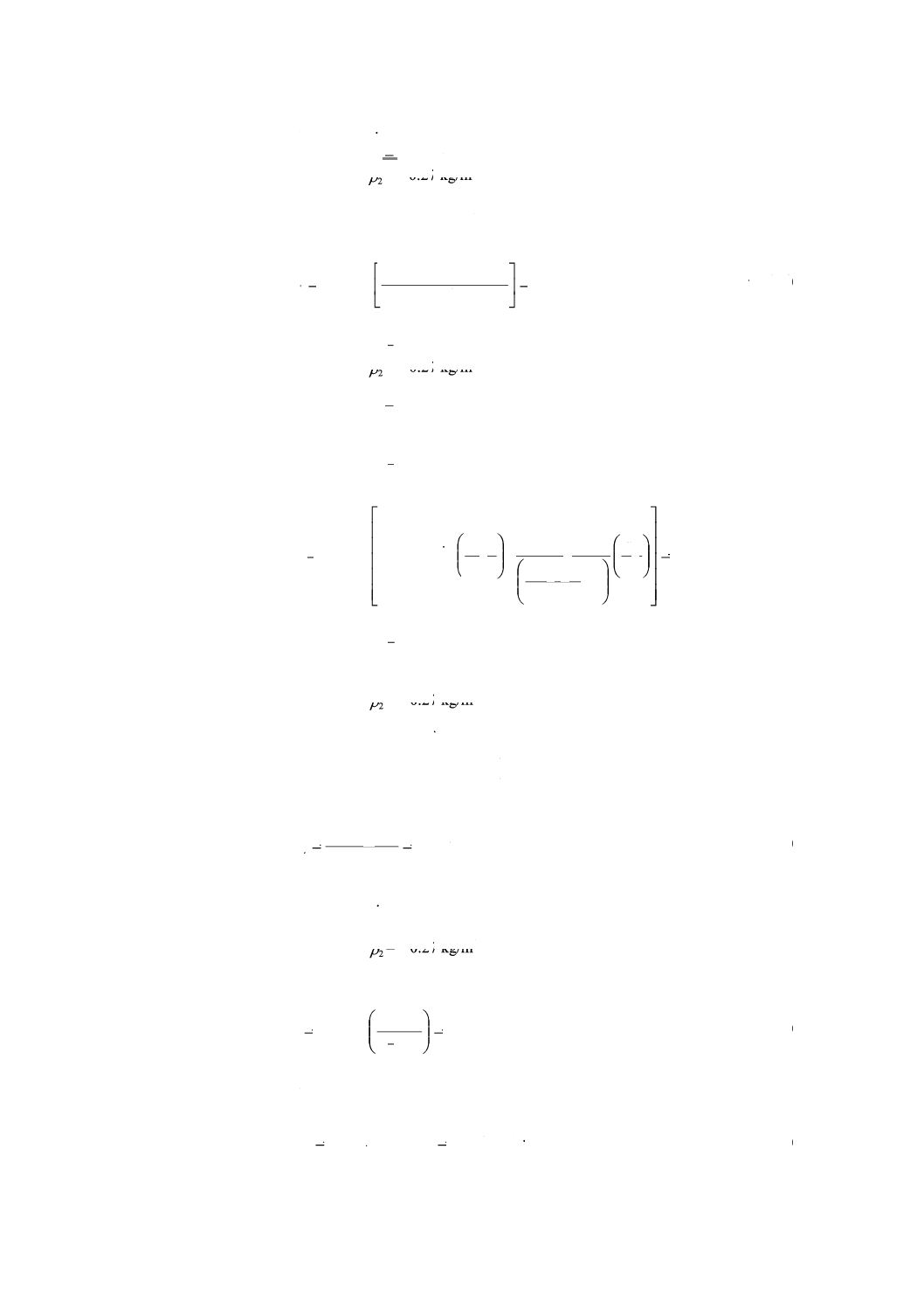
W
46
ms
w
5
a
=
=
W
r
W
η
······························································· (32)
ここに,
5η= 1.5×10−3
rw = 0.25(表4から)
Wms = 1.2×105 W
Hz
800
6
1
1.25
35
.0
2
j
j
vcc
p
=
−
=
M
D
c
f
················································ (29)
ここに,
Mj = Mj5 = 2.6
cvcc = 460 m/s
Dj = 7.8×10−3 m
3
1
2
1
2
kg/m
27
.0
=
=
p
p
ρ
ρ
························································ (33)
ここに,
1ρ= 5.30 kg/m3
p2 = 5.0×104 Pa
p1 = 1.0×106 Pa
c2 = 480 m/s(例題1から)
30
.0
4
2
2
2
o
=
=
c
D
m
M
ρ
π
&
···························································· (35)
35
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
m&= 1.19 kg/s
D = 0.200 m
2ρ= 0.27 kg/m3
c2 = 480 m/s
注記 Moは0.3を超えていないので,これらの計算は適切である。
(
)
dB
147
10
2.3
log
10
2
i
2
2
a
9
10
pi
=
×
=
D
c
W
L
ρ
·································· (36)
ここに,
Wa = 46 W
2ρ= 0.27 kg/m3
c2 = 480 m/s
Di = 0.203 1 m
fr = 7 800 Hz(例題1から)
fo = 2 700 Hz(例題1から)
fg = 1 600 Hz(例題1から)
(
)
dB
44
1
415
10
6.7
log
10
s
a
y
2
2
x
2
p
p
2
7
10
−
=
+
×
=
−
p
p
G
c
G
f
t
c
TL
ρ
······· (37)
ここに,
c2 = 480 m/s
tp = 0.008 m
fp = 6 800 Hz
2ρ= 0.27 kg/m3
Gx = (fp / fr ) 2/3 = 0.91(表5から)
Gy = 1(表5から)
pa = 1.013 25×105 Pa
ps = 1.013 25×105 Pa
29
.0
4
2
2
2
i
2
=
=
c
D
m
M
ρ
π
&
···························································· (42)
ここに,
m&= 1.19 kg/s
Di = 0.203 1 m
2ρ= 0.27 kg/m3
c2 = 480 m/s
dB
4.2
1
1
log
16
2
10
=
−
=
M
Lg
··················································· (41)
ここに,
M2 = 0.29
dB(A)
110
5
pi
pAe
=
+
+
+
=
g
L
TL
L
L
·············································· (43)
36
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
Lpi = 147 dB
TL = −44 dB
Lg = 2.4 dB
dB(A)
100
2
2
2
10
p
i
p
i
10
pAe
pAe,1m
=
+
+
+
−
=
t
D
t
D
log
L
L
···································· (44)
ここに,
LpAe = 110 dB(A)
Di = 0.203 1 m
tp = 0.008 m
結論:100 dB(A)を用いる。
例題6:エキスパンダに接続され,かつ,より高いマッハ数のバルブの場合(状態Ⅴ)
与えられたデータは,次の点を除き例題1と同じである。
出口絶対圧力
p2 = 0.50 bar = 5.0×104 Pa
質量流量
m& = 0.89 kg/s
C = Cv = 30
Di = 0.150 m
Dj = 6.8×10−3 m
計算は,次の点を除き状態Ⅰの場合の例題1と同じである。
p2CE = 5.8×104 Pa(例題4から)
p2CE > p2ならば,状態Ⅴである。
4
4
10
0.5
10
80
.5
×
>
×
であるから,状態Ⅴである。
Tvcc = 410 K(例題2から)
cvcc = 460 m/s(例題2から)
W
10
2.9
2
4
2
vcc
ms
×
=
=
c
m
W
&
······················································· (20)
ここに,
m&= 0.89 kg/s
cvcc = 460 m/s
()(
)
[
]
6.2
1
22
1
2
/
1
j5
=
−
−
=
−
γ
γ
γ
M
················································ (30)
ここに,
γ = 1.22
()
3
6.6
2
j5
4
5
10
5.1
2
2
10
1
2
L
−
−
×
=
×
=
F
M
η
··································· (31)
37
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
Mj5 = 2.6
FL = 0.804
W
34
ms
w
5
a
=
=
W
r
W
η
······························································· (32)
ここに,
5η= 1.5×10−3
rw = 0.25(表4から)
Wms = 9.2×104 W
Hz
800
7
1
1.25
35
.0
2
j
j
vcc
p
=
−
=
M
D
c
f
··············································· (29)
ここに,
Mj = Mj5 = 2.6
cvcc = 460 m/s
Dj = 6.8×10−3 m
3
1
2
1
2
kg/m
27
.0
=
=
p
p
ρ
ρ
························································ (33)
ここに,
1ρ= 5.30 kg/m3
p1 = 1.0×106 Pa
p2 = 5.0×104 Pa
89
.0
4
2
2
2
o
=
=
c
D
m
M
ρ
π
&
····························································· (35)
ここに,
m&= 0.89 kg/s
D = 0.100 m
2ρ= 0.27 kg/m3
c2 = 480 m/s
注記 Moは0.30を超えるので,LpAe,1mを決めるための計算をする。これは箇条7の計算による。
(
)
dB
148
10
2.3
log
10
2
i
2
2
a
9
10
pi
=
×
=
D
c
W
L
ρ
·································· (36)
ここに,
Wa = 34 W
2ρ= 0.27 kg/m3
c2 = 480 m/s
Di = 0.150 m
fr = 10 600 Hz
fo = 3 700 Hz
fg = 1 600 Hz(例題1から)
Gx = (fp / fr ) 2/3 = 0.82(表5から)

38
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Gy = 1(表5から)
(
)
dB
46
1
415
10
6.7
log
10
s
a
y
2
2
x
2
p
p
2
7
10
−
=
+
×
=
−
p
p
G
c
G
f
t
c
TL
ρ
········· (37)
ここに,
c2 = 480 m/s
tp = 0.008 m
fp = 7 800 Hz
2ρ= 0.27 kg/m3
Gx = 0.82
Gy = 1
pa = 1.013 25×105 Pa
ps = 1.013 25×105 Pa
40
.0
4
2
2
2
i
2
=
=
c
D
m
M
ρ
π
&
···························································· (42)
ここに,
m&= 0.89 kg/s
Di = 0.150 m
2ρ= 0.27 kg/m3
c2 = 480 m/s
5.3
1
1
log
16
2
10
=
−
=
M
Lg
······················································ (41)
ここに,
M2 = 0.40
dB(A)
111
5
pi
pAe
=
+
+
+
=
g
L
TL
L
L
·············································· (43)
ここに,
Lpi = 148 dB(A)
TL = −46 dB
Lg = 3.5 dB
dB(A)
100
2
2
2
10
p
i
p
i
10
pAe
pAe,1m
=
+
+
+
−
=
t
D
t
D
log
L
L
··································· (44)
ここに,
LpAe = 111 dB(A)
Di = 0.150 m
tp = 0.008 m
m/s
190
4
2
i
2
p
=
=
D
m
U
ρ
π
&
···························································· (53)
39
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
m&= 0.89 kg/s
2ρ= 0.27 kg/m3
Di = 0.150 m
m/s
460
2
i
2
i
p
R
=
=
d
D
U
U
β
····························································· (54)
ここに,
Up = 190 m/s
Di = 0.150 m
β = 0.93(仮定する)
di = 0.100 m
96
.0
2
R
R
=
=c
U
M
····································································· (58)
ここに,
UR = 460 m/s
c2 = 480 m/s
W
10
8.4
2.0
1
2
4
2
2
i
2
i
2
R
mR
×
=
+
−
=
D
d
U
m
W
&
······························· (55)
ここに,
m&= 0.89 kg/s
UR = 460 m/s
di = 0.100 m
Di = 0.150 m
Hz
920
2.0
i
R
pR
=
=
d
U
f
····························································· (56)
ここに,
UR = 460 m/s
di = 0.100 m
(
)
4
3
R
3
R
10
8.8
10
1
−
−
×
=
×
=
M
η
··················································· (57)
ここに,
MR = 0.96
W
42
mR
R
aR
=
=
W
W
η
······························································· (59)
ここに,
R
η= 8.8×10−4
WmR = 4.8×104
(
)
B
d
149
10
2.3
log
10
2
i
2
2
aR
9
10
piR
=
×
=
D
c
W
L
ρ
································· (60)
40
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
WaR = 42 W
2ρ= 0.27 kg/m3
c2 = 480 m/s
Di = 0.150 m
dB
53
1
415
10
6
7
10
s
a
y
2
2
x
2
pR
p
2
7
10
R
−
=
+
×
=
−
p
p
G
c
G
f
t
c
.
log
TL
ρ
····················· (61)
ここに,
c2 = 480 m/s
tp = 0.008 m
fpR = 920 Hz
Gx = (fo / fr ) 2/3 (fpR / fo ) 4 = 1.9×10−3(表5から)
Gy = 1(表5から)
2ρ= 0.27 kg/m3
pa = 1.013 25×105 Pa
ps = 1.013 25×105 Pa
dB(A)
93
2
2
2
log
10
5
p
i
p
i
10
R
piR
peR
=
+
+
+
−
+
+
+
=
t
D
t
D
L
TL
L
L
g
············· (62)
ここに,
LpiR = 149 dB
TLR = −53 dB
Lg = 3.5 dB
Di = 0.150 m
tp = 0.008 m
(
)
dB(A)
101
10
10
log
10
10
/
10
/
10
pS
peR
pAe,1m
=
+
=
L
L
L
······························ (63)
ここに,
LpAe,1m = 100 dB(A)
LpeR = 93 dB(A)
結論:101 dB(A)を用いる。
例題7:多段多流路トリム弁
与えられたデータ:
バルブ
バルブの種類:DN 200の多段多流路トリムグローブ弁
バルブ出口の直径:
D = 0.200 m
41
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
入口呼び径:
DN 200
出口呼び径:
DN 200
配管の内径:
Di = 0.200 m
管壁の厚さ:
tp = 0.008 m
独立した全く同じ流路数: No = 432
最終の段の全流路面積: An = 6.44×10−3 m2
水力学的直径:
dH = 0.002 5 m
容量係数Cの計算値:
Cv = 81.5
最終の段の液体圧力回復係数:FLn = 0.98
流体
流体の種類:
気体
質量流量:
m& = 23.1 kg/s
比熱比:
γ = 1.31
入口絶対圧力:
p1 = 70 bar = 7×106 Pa
出口絶対圧力:
p2 = 14 bar = 1.4×106 Pa
入口温度:
T1 = 290 K
入口密度:
1ρ = 55.3 kg/m3
モル質量:
M = 19.0 kg/kmol
その他
実際の大気:
pa = 1.013 25 bar = 1.013 25×105 Pa
標準大気圧:
ps = 1.013 25 bar = 1.013 25×105 Pa
計算:
このバルブに用いられる手順は,次の点を除き例題1の手順と同じである。
Cの代わりにCnを用いる。
310
n
16
n
=
=
A
N
C
···································································· (46)
ここに,
N16 = 4.89×104(表2から)
An = 6.44×10−3 m2
p1の代わりに最後の段のよどみ点圧力pnを用いる。
p1 / p2≥2ならば,まずpn / p2 < 2と仮定する。
ここで,p1 / p2 = 5であるからpn / p2 < 2と仮定する。
p1 / p2≥2かつpn / p2 < 2ならば,式 (47a) を用いる。
Pa
10
1.2
155
.1
6
2
2
2
n
1
n
×
=
+
=
p
C
C
p
p
········································ (47a)
42
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ここに,
p1 = 7.0×106 Pa
C = Cv = 81.5
Cn = 310
p2 = 1.4×106 Pa
pnは2p2より小さいので,式 (47a) を用いることは適切である。
Pa
10
14
.1
6
vcc
×
=
p
···································································· (2)
Pa
10
2.1
6
2C
×
=
p
······································································ (3)
97
.0
=
α
·················································································· (4)
Pa
10
9.6
5
2B
×
=
p
······································································ (5)
Pa
10
9.9
4
2CE
×
=
p
···································································· (6)
2C
2
p
p≥
ならば,状態Ⅰである。
6
6
10
2
1
10
4
1
×
×
.
.
≧
であるから,状態はⅠである。
m
5
002
.0
H=
d
······································································· (7b)
2
5
o
n
m
10
5.1
−
×
=
=NA
A
ここに,
A n = 6.44×10−3 m2
No = 432
m
091
.0
4
o
o
=
=
π
A
N
d
···························································· (7c)
028
.0
d=
F
·············································································· (7a)
m
2
002
.0
L
n
d
14
j
=
=
F
C
F
N
D
··················································· (49)
ここに,
N 14 = 4.6×10−3(表2から)
Fd = 0.028
Cn = 310
FLn = 0.98
圧力p2をpvcの代わりに用いる。
密度ρnをρ1の代わりに用いる。
3
1
n
1
n
kg/m
17
=
=
p
p
ρ
ρ
··························································· (48)
ここに,
1ρ= 55.3 kg/ m3
pn = 2.1×106 Pa
p1 = 7.0×106 Pa
m/s
310
VC=
U
·········································································· (9)
W
10
1.1
6
m
×
=
W
····································································· (10)
43
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
K
260
VC=
T
··········································································· (11)
m/s
390
VC=
c
········································································· (12)
81
.0
jn=
M
············································································· (51)
5
1
10
6.4
−
×
=
η
········································································ (14)
W
13
a=
W
············································································· (15)
Hz
000
28
p=
f
······································································· (52)
3
1
2
1
2
kg/m
11
=
=
p
p
ρ
ρ
··························································· (33)
ここに,
1ρ= 55.3 kg/ m3
p2 = 1.4×106 Pa
p1 = 7.0×106 Pa
m/s
410
2=
c
·········································································· (34)
16
.0
4
2
2
2
o
=
=
c
D
m
M
ρ
π
&
···························································· (35)
ここに,
m&= 23.1 kg/s
D = 0.200 m
2ρ= 11 kg/m3
c2 = 410 m/s
注記 Moは0.2より小さいので,これらの計算は適切である。
dB
157
pi=
L
··········································································· (36)
dB
67
−
=
TL
··········································································· (37)
Hz
000
8
r=
f
········································································· (38)
Hz
400
2
o=
f
········································································· (39)
Hz
600
1
=
gf
········································································· (40)
16
.0
4
2
2
2
i
2
=
=
c
D
m
M
ρ
π
&
···························································· (42)
ここに,
m&= 23.1 kg/s
Di = 0.200 m
2ρ= 11 kg/m3
c2 = 410 m/s
dB
2.1
1
1
log
16
2
10
=
−
=
M
Lg
··················································· (41)
ここに,
M2 = 0.16
dB(A)
101
pAe=
L
····································································· (50)
44
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
dB(A)
91
pAe,1m=
L
···································································· (44)
結論:91 dB(A)を用いる。
45
B 2005-8-3:2008(IEC 60534-8-3:2000)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
参考文献
[1]
BAUMANN, H. D., Determination of Peak Internal Sound Frequency Generated by Throttling Valves for the
Calculation of Pipe Transmission Losses, Noise Control Engineering Journal, Vol. 36, No. 2, March-April
1991, p. 75-82
[2]
BAUMANN, H. D., Predicting Control Valve Noise at High Exit Velocities, INTECH, February 1997, p.
56-59
[3]
REETHOF, G. and WARD W. C., A Theoretically Based Valve Noise Prediction Method for Compressible
Fluids, Journal of Vibrations, Acoustics, Stress, and Reliability in Design, ASME, Vol.108,July 1986, p.329