B 2005-2-1:2019 (IEC 60534-2-1:2011)
(1)
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義 ··················································································································· 2
4 記号······························································································································· 2
5 取付け···························································································································· 3
6 非圧縮性流体に対するサイジング式 ····················································································· 4
6.1 乱流 ···························································································································· 4
6.2 差圧 ···························································································································· 5
6.3 非乱流(層流及び遷移領域での流れ)················································································ 5
7 圧縮性流体に対するサイジング式 ························································································ 5
7.1 一般 ···························································································································· 5
7.2 差圧 ···························································································································· 6
7.3 比熱比係数,Fγ ············································································································· 6
7.4 膨張係数,Y·················································································································· 6
7.5 圧縮係数,Z·················································································································· 7
7.6 非乱流(層流及び遷移領域での流れ)················································································ 7
8 非圧縮性及び圧縮性流れに共通の補正係数 ············································································ 7
8.1 種々の配管形状係数,(FP,FLP及びxTP) ·········································································· 7
8.2 配管形状係数,FP ·········································································································· 8
8.3 継手を接続する場合の液体圧力回復係数と配管形状係数との組合せ係数,FLP ··························· 8
8.4 継手を接続する場合の差圧比係数,xTP··············································································· 9
9 バルブレイノルズ数,Rev ·································································································· 9
附属書A(規定)非乱流サイジング式の分類 ············································································ 11
附属書B(規定)多段調節弁のサイジング計算式 ······································································· 14
附属書C(参考)配管係数計算の検討 ····················································································· 21
附属書D(参考)エンジニアリング資料 ·················································································· 26
附属書E(参考)計算例 ······································································································· 32
参考文献 ···························································································································· 44
B 2005-2-1:2019 (IEC 60534-2-1:2011)
(2)
まえがき
この規格は,工業標準化法第14条によって準用する第12条第1項の規定に基づき,一般社団法人日本
バルブ工業会(JVMA)から,工業標準原案を具して日本工業規格を改正すべきとの申出があり,日本工
業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによって,JIS B 2005-2-1:2005は改正され,この規格に置き換えられた。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 2005の規格群には,次に示す部編成がある。
JIS B 2005-1 第1部:調節弁用語及び一般的必要条件
JIS B 2005-2-1 第2部:流れの容量−第1節:取付け状態における流れのサイジング式
JIS B 2005-2-3 第2部:流れの容量−第3節:試験手順
JIS B 2005-2-4 第2部:流れの容量−第4節:固有流量特性及びレンジアビリティ
JIS B 2005-3-1 第3部:寸法−第1節:フランジ形二方ストレート形グローブ調節弁の面間寸法及び
アングル形グローブ調節弁の中心-面間寸法
JIS B 2005-3-2 第3部:寸法−第2節:バタフライ弁を除く回転形調節弁の面間寸法
JIS B 2005-3-3 第3部:寸法−第3節:突合せ溶接形二方ストレート形グローブ調節弁の面間寸法
JIS B 2005-4 第4部:検査及び試験
JIS B 2005-5 第5部:表示
JIS B 2005-6-1 第6部:調節弁へのポジショナの取付けの詳細−第1節:直線運動駆動部へのポジシ
ョナの取付け
JIS B 2005-6-2 第6部:調節弁へのポジショナの取付けの詳細−第2節:回転運動駆動部へのポジシ
ョナの取付け
JIS B 2005-7 第7部:調節弁データシート
JIS B 2005-8-1 第8部:騒音−第1節:調節弁の空気力学的流動騒音の実験室における測定
JIS B 2005-8-2 第8部:騒音−第2節:調節弁の液体流動騒音の実験室における測定
JIS B 2005-8-3 第8部:騒音−第3節:調節弁の空気力学的流動騒音の予測方法
JIS B 2005-8-4 第8部:騒音−第4節:調節弁の液体流動騒音の予測方法
日本工業規格 JIS
B 2005-2-1:2019
(IEC 60534-2-1:2011)
工業プロセス用調節弁−第2部:流れの容量−
第1節:取付け状態における流れのサイジング式
Industrial-process control valves-Part 2-1: Flow capacity-Sizing equations
for fluid flow under installed conditions
序文
この規格は,2011年に第2版として発行されたIEC 60534-2-1を基に,技術的内容及び構成を変更する
ことなく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,調節弁を流れる圧縮性流体及び非圧縮性流体の流れを予測する式について規定する。
非圧縮性流体の式は,非圧縮性ニュートン流体についての基本的な水力学の式に基づいている。これら
の式は,非ニュートン流体,混合流体,スラリー及び固液輸送系については適用しない。これらの式は,
非蒸発の多成分混合液へ適用してもよい。箇条6に追加の説明式を規定する。
入口絶対圧力に対する差圧の比(Δp/p1)がごく小さい場合には,圧縮性流体は,非圧縮性流体と同様の
流れとなる。そのような場合には,圧縮性流体のサイジング式は,非圧縮性ニュートン流体の基本的な水
力学の式と同様として扱うことができる。Δp/p1が増加するとともに圧縮性の影響が現れるため,適切な補
正係数を用いて基本式を修正する必要がある。圧縮性流体の式は,理想気体又は蒸気に対して使用し,気
体−液体,蒸気−液体又は気体−固体の多相流体に対しては使用することはできない。比熱比γが,1.08
<γ<1.65の場合には,その精度は妥当である。
圧縮性流体の場合には,この規格は,xT≦0.84のバルブに対して有効である(表D.2参照)。xT>0.84の
バルブ[例えば,多段減圧弁(附属書B参照)など]に対しては,サイジング予測によって大きな誤差が
見込まれる。
次の条件の場合には,調節弁の計算精度は妥当である。
047
.0
2
18
<
d
N
C
この規格において使用している数式の構造は旧規格から大きく変わっているが,基本的な計算方法は,
ほぼ同じである。種々の式の表示方法を簡素化し,文書を読みやすくするために表示形式を改正した。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
IEC 60534-2-1:2011,Industrial-process control valves−Part 2-1: Flow capacity−Sizing equations for
fluid flow under installed conditions(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。

2
B 2005-2-1:2019 (IEC 60534-2-1:2011)
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 2005-1 工業プロセス用調節弁−第1部:調節弁用語及び一般的必要条件
注記 対応国際規格:IEC 60534-1,Industrial-process control valves−Part 1: Control valve terminology
and general considerations
JIS B 2005-2-3 工業プロセス用調節弁−第2部:流れの容量−第3節:試験手順
注記 対応国際規格:IEC 60534-2-3,Industrial-process control valves−Part 2-3: Flow capacity−Test
procedures
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 2005-1によるほか,次による。
3.1
バルブ形状修正係数,Fd(valve style modifier)
単一流路の水力学的直径に対する円形オリフィスの直径との比。円形オリフィスの面積は使用する弁開
度における,同じ特性をもつ全ての流路の面積の総和に等しい。この係数は,製造業者によって弁開度の
関数として示すことが望ましい(附属書D参照)。
3.2
標準体積流量,Qs(standard volumetric flowrates)
単位時間当たりの体積(m3/h)で表す圧縮性流体の体積流量(記号Qsによって表す。)。次のいずれかに
対応して決まる。
a) 標準気体状態,絶対圧力101.325 kPa(1 013.25 mbar),温度288 K
b) 標準大気条件,絶対圧力101.325 kPa(1 013.25 mbar),温度273 K
これら二つの基準条件に対して流量方程式で使用する数値定数を決めている(表2参照)。
4
記号
この規格で用いる記号は,表1による。
表1−記号
記号
意味
単位
C
容量係数(Kv,Cv)
多種(JIS B 2005-1参照)d)
d
バルブ呼び径
mm
D
配管の内径
mm
D1
上流配管の内径
mm
D2
下流配管の内径
mm
Do
オリフィス径
mm
Fd
バルブ形状修正係数(附属書D参照)
無次元数d)
FF
液体臨界圧力比係数
無次元数
FL
継手を接続しない場合の調節弁の液体圧力回復係数
無次元数d)
FLP
継手を接続する場合の調節弁の液体圧力回復係数と配管形状係数との組
合せ係数
無次元数
FP
配管形状係数
無次元数

3
B 2005-2-1:2019 (IEC 60534-2-1:2011)
表1−記号(続き)
記号
意味
単位
FR
レイノルズ数係数
無次元数
Fγ
比熱比係数
無次元数
M
流体のモル質量
kg/kmol
N
数値定数(表2参照)
多種a)
p1
A点で測定した入口絶対静圧(図1参照)
kPa又はbarb)
p2
B点で測定した出口絶対静圧(図1参照)
kPa又はbar
pc
熱力学的臨界絶対圧力
kPa又はbar
pr
換算圧力(p1/pc)
無次元数
pv
入口温度における液体の絶対蒸気圧
kPa又はbar
Δpactual
上流圧力タップと下流圧力タップとの間の差圧(p1−p2)
kPa又はbar
Δpchoked 閉塞状態での差圧(非圧縮性流れに対する限界差圧の計算値)
kPa又はbar
Δpsizing
サイジング差圧(非圧縮性流れについて,流れの計算又は必要容量係数に
用いる圧力差の値)
kPa又はbar
Q
実体積流量
m3/h
Qs
標準体積流量(3.2参照)
m3/h
Rev
バルブレイノルズ数
無次元数
T1
入口絶対温度
K
Tc
熱力学的絶対臨界温度
K
Tr
換算温度(T1/Tc)
無次元数
ts
標準状態における参照温度
K
W
質量流量
kg/h
x
入口絶対圧力に対する差圧比(Δp/p1)
無次元数
xchoked
閉塞圧力降下比(圧縮性流れに対する閉塞圧力降下比)
無次元数
xsizing
サイジング圧力降下比(圧縮性流れについて流れ又は必要容量係数に用い
る圧力降下比)
無次元数
xT
閉塞流れにおいて継手を接続しない場合の調節弁の差圧比係数
無次元数d)
xTP
閉塞流れにおいて継手を接続する場合の調節弁の差圧比係数
無次元数
Y
膨張係数
無次元数
Z1
入口条件における圧縮係数
無次元数
ν
動粘度
m2/sc)
ρ1
p1及びT1における流体密度
kg/m3
ρ1/ρ0
相対密度(水の場合は,15 ℃においてρ1/ρ0=1.0)
無次元数
γ
比熱比
無次元数
ζ
調節弁に接続するレデューサ,エクスパンダ又はその他継手の速度水頭損
失係数
無次元数
ζ1
上流継手の速度水頭損失係数
無次元数
ζ2
下流継手の速度水頭損失係数
無次元数
ζB1
入口ベルヌーイ係数
無次元数
ζB2
出口ベルヌーイ係数
無次元数
注a) 数値定数の単位を決めるために,表2の単位を用いて,適合する式で次元解析を行う。
b) 1 bar=102 kPa=105 Pa
c) 1 cSt=10−6 m2/s
d) これらの値は,開度と関係があり,製造業者が示すことが望ましい。
5
取付け
多くの工業用途では,レデューサ,その他の継手などを調節弁に接続する。これらの継手が調節弁の公
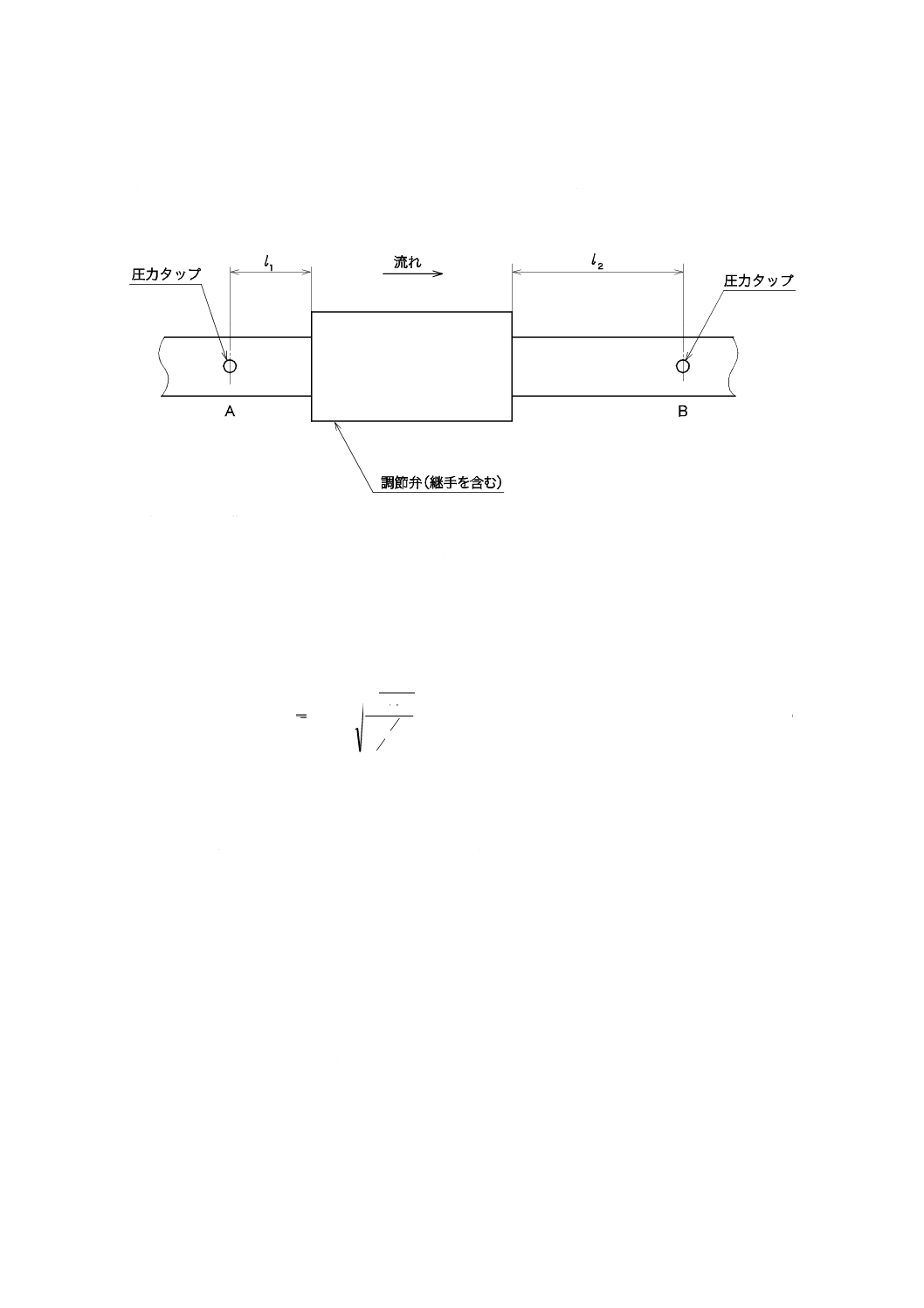
4
B 2005-2-1:2019 (IEC 60534-2-1:2011)
称容量係数に及ぼす影響は重要になる。この影響を明確に説明するために補正係数を導入する。さらに,
係数は,調節弁の流れの容量に影響を及ぼす流体の物性を考慮した幾つかの係数を導入する。
調節弁のサイジングにおいて,この規格に規定する関係式を用いて算出する容量係数は,図1に示すAB
間の全てのヘッド損失を含むものと仮定する。
l1=配管呼び径の2倍
l2=配管呼び径の6倍
図1−サイジングのための基準配管区間
6
非圧縮性流体に対するサイジング式
6.1
乱流
非圧縮性流体の乱流領域での基本的な流れのモデルは,式(1)による。
0
1
sizing
P
1
ρ
ρ
p
F
CN
Q
∆
=
··································································· (1)
注記1 数値定数N1は,一般的サイジング式に用いる単位及び容量係数であるKv又はCvによる。
注記2 バルブに隣接した配管の径が同じ場合,配管形状係数FPは1とする。評価及び追加情報は,
8.1を参照。
この流れのモデルによって,非圧縮性流体を扱う調節弁に対する流量,容量係数,流体の物性,関連す
る取付けの係数及び流体条件の間での関係が明確になる。式(1)は,Q,C,Δpのうち与えられた二つを使
って,Q,C,Δpのいずれかを計算するために使用する。
この流れのモデルは,厳密には単一成分,単相流(多相混合流でなく,多成分の混合流でもない。)に限
って適用する。ただし,ある条件下では,この流れのモデルを,液相の多成分の混合流に対しても使用し
てもよい。次の条件に合う液−液混合流体が,この流れのモデルの基礎になる前提を満足するためである。
・ 均質な混合物
・ 化学的及び熱力学的に平衡な混合物
・ 流れの全プロセスの状態は,多相状態から十分に離れて発生している。
これらの条件を満足したとき,流体密度ρ1を混合流の密度に置き換えることで式(1)が適用できる。
5
B 2005-2-1:2019 (IEC 60534-2-1:2011)
6.2
差圧
6.2.1
サイジング差圧,Δpsizing
流量の予測又は必要容量係数の計算では,式(1)で使用する差圧の値は,実際の差圧又は閉塞差圧の小さ
い方の値とする。
∆
∆
∆
∆
∆
∆
=
∆
choked
choked
choked
sizing
p
p
if
p
p
p
if
p
p
≧
<
··············································· (2)
6.2.2
閉塞状態での差圧,Δpchoked
上流圧力が一定の下で,差圧が更に増加しても,調節弁を通過する流量が増加しない状態を“閉塞流れ”
と呼ぶ。このような現象が起こる場合の圧力降下を,閉塞差圧と定義し,式(3)による。
(
)
v
F
1
2
P
LP
choked
p
F
p
F
F
p
−
=
∆
························································ (3)
注記 バルブ径と隣接した配管径が同一の場合,
2
P
LP
F
F
は,FL2となる。詳しくは8.1参照。
6.2.3
液体臨界圧力比係数,FF
FFは,液体臨界圧力に対する補正係数である。この補正係数は,入口温度における液体の蒸気圧に対す
る閉塞流れ条件での見掛けの最縮流部圧力の比である。蒸気圧が0に近い場合,この補正係数は0.96であ
る。既知のFFの値は,ユーザが与えてもよい。単一成分の流体においては,FFの値は図D.3の曲線から求
めるか,又は式(4)で近似してもよい。
c
v
F
28
.0
96
.0
p
p
F
−
=
··································································· (4)
多成分混合流れの閉塞の初生を表すために式(4)を使用するには,フラッシングモデルに現れる適切な状
態パラメータを適用できるかどうかで決まる。
6.3
非乱流(層流及び遷移領域での流れ)
式(1)で表した流れのモデルは,完全に発達した乱流に限って適用する。特に流量がかなり少ないか,又
は,流体粘度がかなり大きい場合には,非乱流条件になる。式(1)の適用可能性を確認するためには,バル
ブレイノルズ数[式(23)参照]の値を計算する。Rev≧10 000で式(1)を適用する。非乱流状態の場合,附属
書Aに基づき計算する。
7
圧縮性流体に対するサイジング式
7.1
一般
圧縮性流体の乱流領域での基本的な流れモデルは,次の式で与える。
1
1
sizing
P
6
ρ
p
x
Y
F
CN
W=
······························································ (5)
このモデルは,圧縮性流体を扱う調節弁について,流量,容量係数,流体の物性,関連する取付けの要
因及び流体条件の関係を定めている。従来使用しているデータ形式に適応するように,式(5)に等価な二つ
の式を示す。
6
B 2005-2-1:2019 (IEC 60534-2-1:2011)
1
1
sizing
1
P
8
Z
T
M
x
Y
p
F
CN
W=
······························································ (6)
1
1
sizing
1
P
9
s
Z
MT
x
Y
p
F
CN
Q=
······························································· (7)
注記 Mの値は,附属書Dを参照。
式(6)は,理想気体の状態方程式から計算した流体密度を式(5)に代入して導く。式(7)は,標準容積単位で
の流量を表す。式(5)〜式(7)は,三つの量のうちいずれか二つを与えて,必要な容量係数,流量又は動作差
圧の計算に使用する。
7.2
差圧
7.2.1
サイジング圧力降下比,xsizing
流量を予測し,又は要求する容量係数を計算するには,式(5)〜式(7)の中で使用する圧力降下比の値とし
て,実際の圧力降下比と閉塞圧力降下比とのうちで小さい方の値を使用する。
=
choked
choked
choked
sizing
x
x
if
x
x
x
if
x
x
≧
<
······················································ (8)
ここに,
1p
p
x
∆
=
···················································································· (9)
7.2.2
閉塞圧力降下比,xchoked
閉塞圧力降下比は,圧力降下比を増加しても流量が増加しなくなる圧力降下比であり,次の式で与える。
xchoked=FγxTP ··········································································· (10)
注記 弁呼び径及び接続配管呼び径が同一の場合,xTPはxTとなる。詳細は8.1参照。
7.3
比熱比係数,Fγ
係数xTは,比熱比1.40の流動流体として大気圧に近い空気を基準としている。流体の比熱比が1.40で
ない場合には,係数Fγを用いてxTを補正する。比熱比係数は,次の式を用いて計算する。
1.40
γ
γ
=
F
················································································(11)
注記 γ及びFγの値については,附属書Dを参照。
式(11)は,完全気体の状態変化を仮定し,空気及び蒸気試験に基づくオリフィスプレートのモデルを調
節弁に拡張して,創出した式である。1.08<γ<1.65の範囲での前述モデルの解析によって,式(11)が表す
線形モデルを得る。この範囲内では,元来のオリフィスモデル及び他の理論モデルと式(11)との差は小さ
い。しかし,この範囲外では,式(11)の誤差が大きくなる。最大の精度を得るためには,このモデルに基
づく流れ計算は,比熱比をこの範囲に限定し理想気体の状態変化に限って適用するのがよい。
7.4
膨張係数,Y
膨張係数Yは,流体がバルブの入口からベナコントラクタ(噴流面積が最小となるオリフィスのすぐ下
流側に位置する。以下,縮流部という。)まで通過するときの密度の変化を表す。Yは,また,差圧が変化
したときの縮流部面積の変化を表している。
理論的には,Yは次の全ての事項の影響を受ける。
a) ボディ入口面積に対するポート面積比
7
B 2005-2-1:2019 (IEC 60534-2-1:2011)
b) 流路の形状
c) 差圧比x
d) バルブレイノルズ数Rev
e) 比熱比γ
上記a),b),c)及びe)による影響は,空気試験によって確定する差圧比係数xTで表す。このxTについて
は,8.4に規定する(JIS B 2005-2-3参照)。
レイノルズ数は,調節弁最縮流部での流体の慣性力と粘性力との比である。圧縮性流体の場合には,ほ
とんど常に乱流であるために,レイノルズ数は膨張係数に影響を及ぼさない。
差圧比係数xTは,流体の比熱比の影響を受ける。
Yは,式(12)による。
choked
sizing
3
1
x
x
Y
−
=
········································································ (12)
注記 膨張係数Yは,閉塞流状態で2/3の極限値をとる。
7.5
圧縮係数,Z
サイジング式の幾つかは,上流側条件における実際の流体密度の項を含んでいない。その代わりに,理
想気体法則に基づいて入口圧力及び温度から密度が推定できる。ある条件下では,実在気体の変化は,理
想状態から大きく変わる場合がある。このような場合,圧縮係数Zを導入して,その差を補償しなければ
ならない。Zは,換算圧力及び換算温度の関数である。換算圧力prは,該当する流体の熱力学的臨界絶対
圧力に対する実際の入口絶対圧力の比として定義する。換算温度Trも同様に定義する。
c
1
r
p
p
p=
················································································· (13)
c
1
r
T
T
T=
·················································································· (14)
注記 pc及びTc値については,附属書Dを参照。
7.6
非乱流(層流及び遷移領域での流れ)
式(5)〜式(7)によって表す流れのモデルは,完全に発達した乱流に限って使用する。特に流量が非常に少
なく又は流体の粘性がかなり大きい場合には,非乱流の条件になることがある。この乱流モデルを適用で
きるかどうかを確認するために,バルブレイノルズ数[式(23)参照]を計算するのがよい。Rev≧10 000の
場合には,この乱流モデルを適用する。
8
非圧縮性及び圧縮性流れに共通の補正係数
8.1
種々の配管形状係数,(FP,FLP及びxTP)
種々の配管形状係数(FP,FLP及びxTP)は,調節弁本体の上流及び/又は下流に設置した継手による影
響を評価するために必要となる。係数FPは,閉塞流れが生じない同一条件において,継手を接続した調節
弁を通る流量と,調節継手を接続していない調節弁を通る流量との比である(図1参照)。指定した流量
精度±5 %を満足するためには,全ての配管形状係数を,JIS B 2005-2-3の試験によって決定する。
配管形状係数の予測値を使用することを許容する場合,調節弁に直結した同心レデューサ及びエクスパ
ンダについては,8.2以降に示す式を用いてもよい。これらの式は,継手によって生じる付加的な抵抗及び
静圧と動圧との配分変更を解析的に考慮して得る。
この方法の有効性は,バルブ及び附属品が,水力学的又は空気力学的にどの程度独立かによって決まる。
8
B 2005-2-1:2019 (IEC 60534-2-1:2011)
すなわち,それぞれの累積的効果が加算で表すことがきる範囲が有効である。この状態は,多くの実際の
運用に対して適用できる。しかしながら,バタフライ弁,ボール弁などの一部の形式においては,バルブ
ボディの内部よりも主として下流配管において圧力回復が起こりやすい。下流配管部を任意の配管継手と
交換することによって,回復域が変わる場合がある。このような条件では,単純な流れ抵抗の修正法によ
ってこの方法の有効性を適正に表すことはできない。
8.2
配管形状係数,FP
係数FPは,継手が接続された調節弁を流れる流量と,閉塞流れが生じない同一条件において,継手を接
続した調節弁を通る流量と調節継手を接続していない調節弁を通る流量との比である(図1参照)。
計算値を使用することを許す場合,式(15)を用いる。
2
2
2
P
1
1
+
=
∑
d
C
N
ζ
F
······························································· (15)
この式において,係数Σζは,調節弁に取り付けられている全ての継手の有効速度水頭損失係数の代数和
である。調節弁自体の速度水頭損失係数は含まれない。
Σζ=ζ1+ζ2+ζB1−ζB2 ································································· (16)
調節弁の上流と下流との配管径が異なる場合,係数ζBは,式(17)で計算する。
4
B1
−
=
D
d
ζ
·········································································· (17)
入口及び出口の継手が短い市販の同心円状のレデューサである場合,係数ζ1及びζ2は,式(18)及び式(19)
で近似できる。
入口レデューサ
2
2
1
1
1
0.5 −
=
D
d
ζ
··································································· (18)
出口レデューサ(エクスパンダ)
2
2
2
2
1
1.0 −
=
D
d
ζ
·································································· (19)
同一寸法の入口及び出口レデューサ
2
2
2
1
1
1.5 −
=
+
D
d
ζ
ζ
······························································ (20)
上記の係数ζによって計算したFPの値を用いると,一般には,必要とする容量係数より大きめのバルブ
を選ぶことになる。附属書Cに計算方法を示す。FPの図式近似については,図D.1 a)及び図D.1 b)を参照。
8.3
継手を接続する場合の液体圧力回復係数と配管形状係数との組合せ係数,FLP
FLは,継手を接続しない場合の調節弁の液体圧力回復係数である。この係数は,閉塞流れにおいてバル
ブ内部形状がバルブ容量に与える影響を計算に入れるものである。この係数は,理論非閉塞流量に対する
閉塞状態実最大流量の比で定義し,この理論非閉塞流量は適用する圧力差が弁入口圧力と閉塞状態にある
見掛けの縮流部圧力との差であるとして計算した流量である。係数FLは,JIS B 2005-2-3に基づく試験に
9
B 2005-2-1:2019 (IEC 60534-2-1:2011)
よって決定する。定格容量の百分率に対する代表的なFL値を図D.2に示す。
FLPは,継手を接続する場合の調節弁に対する,液体圧力回復係数と配管形状係数との複合係数である。
この係数は,FLと同様の方法で求める。
FLPが偏差±5 %を満たすには,FLPは,JIS B 2005-2-3が規定する試験によって決定しなければならない。
許容する予測値を使用する場合には,式(21)による。
(
)
2
2
1
2
2
L
L
LP
1+
=
∑
d
C
ζ
N
F
F
F
······················································· (21)
ここで,Σζ1は,バルブの上流側に接続した継手の速度水頭損失係数ζ1+ζB1で,上流圧力タップと調節
弁本体入口との間で測定した損失係数である。
8.4
継手を接続する場合の差圧比係数,xTP
xTは,レデューサ又はその他の継手を接続しない場合の調節弁の差圧比係数である。入口圧力p1を一定
に保ちながら出口圧力p2を徐々に下げると,調節弁を通過する質量流量は増加して最大極限に達し,閉塞
流れを示す条件となる。さらに,p2を下げても流量はそれ以上には増加しない。
この流量極限は,差圧比xがFγxTの値になったときに到達する。xの極限値を,臨界差圧比として定義
する。サイジング式でも,また,Y[式(12)]の式にも用いるxの値は,実際の差圧比が大きい場合でも,
この極限値に抑えられる。したがって,Yの数値は,x=FγxTとなる場合の値0.667から極めて低い差圧の
場合の1.0までの間にある。
xTの値は,空気試験によって求める。この値を決定するための試験方法は,JIS B 2005-2-3で規定して
いる。
注記1 幾つかの形式の調節弁について,フルサイズのトリムでバルブ全開状態における代表的な値
xTを表D.2に示す。これらの資料の使用に際しては,注意を要する。正確な値が必要な場合
は,JIS B 2005-2-3の試験によって求めるのがよい。
継手が接続される調節弁では,xTの値は影響を受ける。
xTPは,継手が接続した調節弁の閉塞流れにおける差圧比係数である。xTPの偏差±5 %を満足するために
は,バルブと継手とを一体として試験しなければならない。予測値を使う場合は,式(22)を用いる。
2
2
5
i
T
2
P
T
TP
1 +
=
d
C
N
ζ
x
F
x
x
·································································· (22)
注記2 N5の値は,表2による。
上記の式においてxTは,レデューサもその他の継手も接続していない調節弁の差圧比係数である。ζiは,
バルブ入口に接続するレデューサ又はその他の継手の入口速度水頭損失係数の和(ζ1+ζB1)である。
入口継手が短い市販のレデューサである場合には,ζ1の値は,式(18)を用いて推定する。
9
バルブレイノルズ数,Rev
先の箇条に示した非圧縮性及び圧縮性流れモデルは,完全に発達した乱流に対するモデルである。低差
圧,高粘度,微少容量係数又はこれらの複合した要因によって,調節弁内の流れが非乱流状態にある場合
には別の流れモデルが必要となる。
バルブレイノルズ数Revは,流れが完全な乱流であるか否かを判断するために採用する。試験によって,
10
B 2005-2-1:2019 (IEC 60534-2-1:2011)
バルブレイノルズ数がRev≧10 000となる場合,流れが完全な乱流となることが分かる。バルブレイノル
ズ数は,式(23)によって計算する。
1/4
4
2
2
2
L
L
d
4
v
1
+
=
d
N
C
F
F
C
ν
Q
F
N
Re
······················································· (23)
注記1 式(23)中の流量は,非圧縮性及び圧縮性流れの両方について実体積流量単位で表したもので
ある。
注記2 動粘度vは,流れ条件によって決めるのがよい。
Rev<10 000となる場合,附属書Aで提示した式を用いる。
バルブレイノルズ数は,流量とバルブ容量係数との関数である。したがって,これら二つの変数のうち
いずれか一方を解く場合,各変数の毎回の値を逐次に修正することが確実な反復解法を使わなければなら
ない。
注記3 バルブレイノルズ数は,流量とバルブ流量係数とによって決まることから一種の反復解法が
必要となる。
バルブ形状修正係数Fdによって,オリフィス(単一,複数)の形状は等価な円形の単一流路に置き換え
る。代表的な値は表D.2を,詳細は附属書Dを参照。Fdが偏差±5 %を満足するためには,係数FdをJIS B
2005-2-3に基づく試験によって決定する。
注記4 FPを含む方程式は適用できない。
表2−数値定数N
定数
容量係数C
式に用いる単位
Kv
Cv
W
Q
p×Δp
Ρ
T
d,D
ν
N1
1×10−1
1
8.65×10−2
8.65×10−1
−
−
m3/h
m3/h
kPa
bar
kg/m3
kg/m3
−
−
−
−
−
−
N2
1.60×10−3
2.14×10−3
−
−
−
−
−
mm
−
N4
7.07×10−2
7.60×10−2
−
m3/h
−
−
−
−
m2/s
N5
1.80×10−3
2.41×10−3
−
−
−
−
−
mm
−
N6
3.16
3.16×101
2.73
2.73×101
kg/h
kg/h
−
−
kPa
bar
kg/m3
kg/m3
−
−
−
−
−
−
N8
1.10
1.10×102
9.48×10−1
9.48×101
kg/h
kg/h
−
−
kPa
bar
−
−
K
K
−
−
−
−
N9
(ts=0 ℃)
2.46×101
2.46×103
2.12×101
2.12×103
−
−
m3/h
m3/h
kPa
bar
−
−
K
K
−
−
−
−
N9
(ts=15 ℃)
2.60×101
2.60×103
2.25×101
2.25×103
−
−
m3/h
m3/h
kPa
bar
−
−
K
K
−
−
−
−
N17
1.05×10−3
1.21×10−3
−
−
−
−
−
mm
−
N18
8.65×10−1
1.00
−
−
−
−
−
mm
−
N19
2.5
2.3
−
−
−
−
−
mm
−
N22
(ts=0 ℃)
1.73×101
1.73×103
1.50×101
1.50×103
−
−
m3/h
m3/h
kPa
bar
−
−
K
K
−
−
−
−
N22
(ts=15 ℃)
1.84×101
1.84×103
1.59×101
1.59×103
−
−
m3/h
m3/h
kPa
bar
−
−
K
K
−
−
−
−
N27
7.75×10−1
7.75×101
6.70×10−1
6.70×101
kg/h
kg/h
−
−
kPa
bar
−
−
K
K
−
−
−
−
N32
1.40×102
1.27×102
−
−
−
−
−
Mm
−
注記 この表で与えられる数値定数と,表示の実用メートル単位系とを組み合わせて使用することによって,定義
された単位における容量係数を求めることができる。
11
B 2005-2-1:2019 (IEC 60534-2-1:2011)
附属書A
(規定)
非乱流サイジング式の分類
A.1 一般
この附属書は,非乱流における非圧縮性流体及び圧縮性流体を扱う調節弁について現在使用しているサ
イジング式を提示する。
この工業的方法は,一般的には,十分に発達した乱流の場合に比べて不明な点もあり,バルブの幾何学
的形状に更に強く依存している。したがって,各バルブ製造業者は個々のバルブの設計の技術データによ
ってこの方法を拡張してもよい。
A.2 記号
表A.1の係数は,この附属書に独自のものである。他の記号の全ては,この規格の本体で定義されてい
る。
表A.1−記号
記号
意味
単位
Crated
FR
n
定格トラベルにおける容量係数
レイノルズ数係数
中間係数[式(A.8a)及び式(A.8b)]
多種
無次元数
無次元数
A.3 非乱流状態の判定
箇条9に記載するように,バルブレイノルズ数Revは,十分に発達した乱流であるか否かを決定するた
めに使用する。バルブレイノルズ数は式(23)によって,ここでも使用する。
1/4
4
2
2
2
L
L
d
4
v
1
+
=
d
N
C
F
F
C
ν
Q
F
N
Re
······················································ (A.1)
注記1 式(A.1)中の流量Qには,非圧縮性及び圧縮性流れの両方に対して実体積流量を用いる。
注記2 圧縮性流体の場合,動粘度νの値は平均圧力(P1+P2)/2に対して求めるのがよい。
注記3 流量と容量係数とによって変わるバルブレイノルズ数の計算には,反復法が必要になる。
バルブレイノルズ数Rev≧10 000のときは,流れが完全に乱流と考える。バルブレイノルズ数Rev<10 000
のときは,この附属書に示す式を適用する必要がある。
A.4 技術的適用範囲
非乱流におけるサイジング式には,次の制限がある。
1) ここに記載する方法は,ニュートン流体のレオロジーの範囲に限定する。非ニュートン流体では,
粘度はせん断速度の関数で著しく変わる。そのせん断速度は,流量に比例する。
2) この方法は,蒸発しない流体に限定する。
3)
047
.0
2
18
≦
d
N
C

12
B 2005-2-1:2019 (IEC 60534-2-1:2011)
さらに,近接するレデューサ又はその他の流れを乱す継手による非乱流への影響は,よく知られていな
い。配管レデューサの間に取り付けた調節弁の層流又は遷移領域での流動現象についての情報はないが,
このような調節弁の使用に際して,係数FRの計算には,配管径と同径の調節弁に対して適合する式の使用
を推奨する。その結果,控え目に見積もった容量係数となるが,それは,レデューサ及びエクスパンダに
よって発生する不可的乱れが層流の生成を更に遅延するからである。したがって,設定したバルブレイノ
ルズ数に対するそれぞれの係数FRは,大きくなる傾向がある。
A.5 非圧縮性流体に対するサイジング式
非圧縮性流体に対する非乱流領域での基本的な流れのモデルは,次の式で表す。
0
1
actual
R
1
ρ
ρ
P
F
CN
Q
∆
=
································································· (A.2)
このモデルは,非圧縮性流体を扱う調節弁について流量,容量係数,流体物性及び運転条件の間の関係
を確定している。式(A.2)は,三つの流体量のうち二つを与えた場合に,必要容量係数,流量又は実圧力差
を計算するために使用してもよい。
A.6 圧縮性流体に対するサイジング式
圧縮性流体に対する非乱流領域での基本的な流れのモデルは,式(A.3)で表される。
(
)
1
2
1
R
27
T
M
p
p
p
Y
F
CN
W
+
∆
=
···················································· (A.3)
このモデルは,圧縮性流体を扱う調節弁について流量,容量係数,流体物性及び運転条件の間の関係を
確定している。
式(A.3)の代替式(A.4)は,従来の有用なデータ形式に対応する。
(
)
1
2
1
R
22
s
MT
p
p
p
Y
F
CN
Q
+
∆
=
······················································· (A.4)
注記 Mの値は,附属書Dを参照。
ここに,
−
−
+
−
−
−
−
=
000
1
Re
2
1
000
1
Re
000
10
2
1
2
1
3
1
000
9
000
1
Re
v
v
choked
sizing
v
<
≧
>
if
x
if
x
x
x
x
Y
························· (A.5)
式(A.4)は,標準気体状態における体積単位での流量を表す。式(A.3)又は(A.4)は,必要容量係数,流量又
は実圧力差の三つの流体量のうちいずれか二つが与えられた場合,残りの一つを計算するために使用して
もよい。
A.7 レイノルズ数係数FRに対する式
レイノルズ数係数FRは,次の式で計算する。
流れが層流(Rev<10)の場合

13
B 2005-2-1:2019 (IEC 60534-2-1:2011)
=
00
.1
026
.0
Min
v
L
R
Re
n
F
F
·························································· (A.6)
注記 関数“Min”は,括弧内の引数の最小値を表す。
遷移領域(Rev≧10)の場合
+
=
00
.1
026
.0
000
10
10
log
33
.0
1
Min
v
L
v
4
1
2
1
L
R
Re
n
F
Re
n
F
F
······································· (A.7)
定数の値nは,トリム形状に基づいて決定する。
フルサイズトリム
016
.0
18
2
rated
≧
N
d
C
の場合,
2
2
2
=
d
C
N
n
········································································· (A.8a)
レデュースドトリム
016
.0
18
2
rated
<
N
d
C
の場合,
3
2
2
32
1 +
=
d
C
N
n
·································································(A.8b)
14
B 2005-2-1:2019 (IEC 60534-2-1:2011)
附属書B
(規定)
多段調節弁のサイジング計算式
B.1
一般
この附属書は,多段調節弁を流れる圧縮性流体の流れの予測式を提示する。流れの基本式は,次の相異
点を除いてこの規格の本文に示す式に一致する。
− 膨張係数Yの計算式[式(B.3)]
− ステージ相互作用係数k及び再加熱係数rの算入
− 多段弁に対するFL及びxT値の表を追加(表D.2)
この方法は,多段多流路調節弁,多段単一流路調節弁及び連続抵抗トリム調節弁の設計に適用できる。
それぞれの調節弁形式の定義及び説明についてはB.3を参照。
多段単一流路及び多流路(1段〜5段)に対してのサイジング手法を検証するために使われた試験データ
は,試験媒体に5×105 Paから13.5×105 Paまでの圧力範囲で温度約300 Kの空気を使用し,JIS B 2005-2-3
に従って実施するサイズ別試験によって得られたものである。幾つかのデータは,12×105 Pa から110×
105 Paまでの様々な圧力及び温度460 Kから750 Kまでの蒸気を使用して,プラント運転条件で確認した。
したがって,この規定は流路数にかかわらず適用でき,5段流路まで実証されている。
曲がり回数(4〜30)の連続する抵抗をもつトリムに対する規定の有効性確認に使用する試験データは,
試験媒体に5×105 Pa以上の圧力範囲及び温度約300 Kの空気を使用し,JIS B 2005-2-3に従ってサイズ別
の試験によってこの規定を実証した。幾つかのデータは,24×105 Pa以上の圧力範囲及び温度500 Kから
720 Kまでのプラント運転条件で確認した。この規定は,いかなる曲がり数に対しても使用でき,曲がり
回数30まで実証している。
バルブの特性係数(Kv,Cv,FL,xTなど)がJIS B 2005-2-3に示す適切な試験手順によっては決定でき
ない場合,製造業者から提示された値を使用するのが望ましい。
この規格の本文に示す従来の単段弁は次の場合,式を多段調節弁に使用してもよい。
− この文書に示す形状の範囲を外れた弁構造である場合,及び/又は,
− 単段弁の表式が検討中の設計形状に適用できることを示す場合
B.2
記号
表B.1の記号は,この附属書特有の変数である。その他の全ては,表1で定義される。
表B.1−記号
記号
意味
単位
AHT
定格トラベルでの上流に隣接した減圧段の総孔面積
mm2
A0
単一流路の出口面積(途中で流路が分岐する場合は,その全ての面積)
mm2
A1
単一流路の入口面積
mm2
Ds
上流に隣接した減圧段の外径
mm
k
減圧段相互作用係数
無次元数
l
トラベル
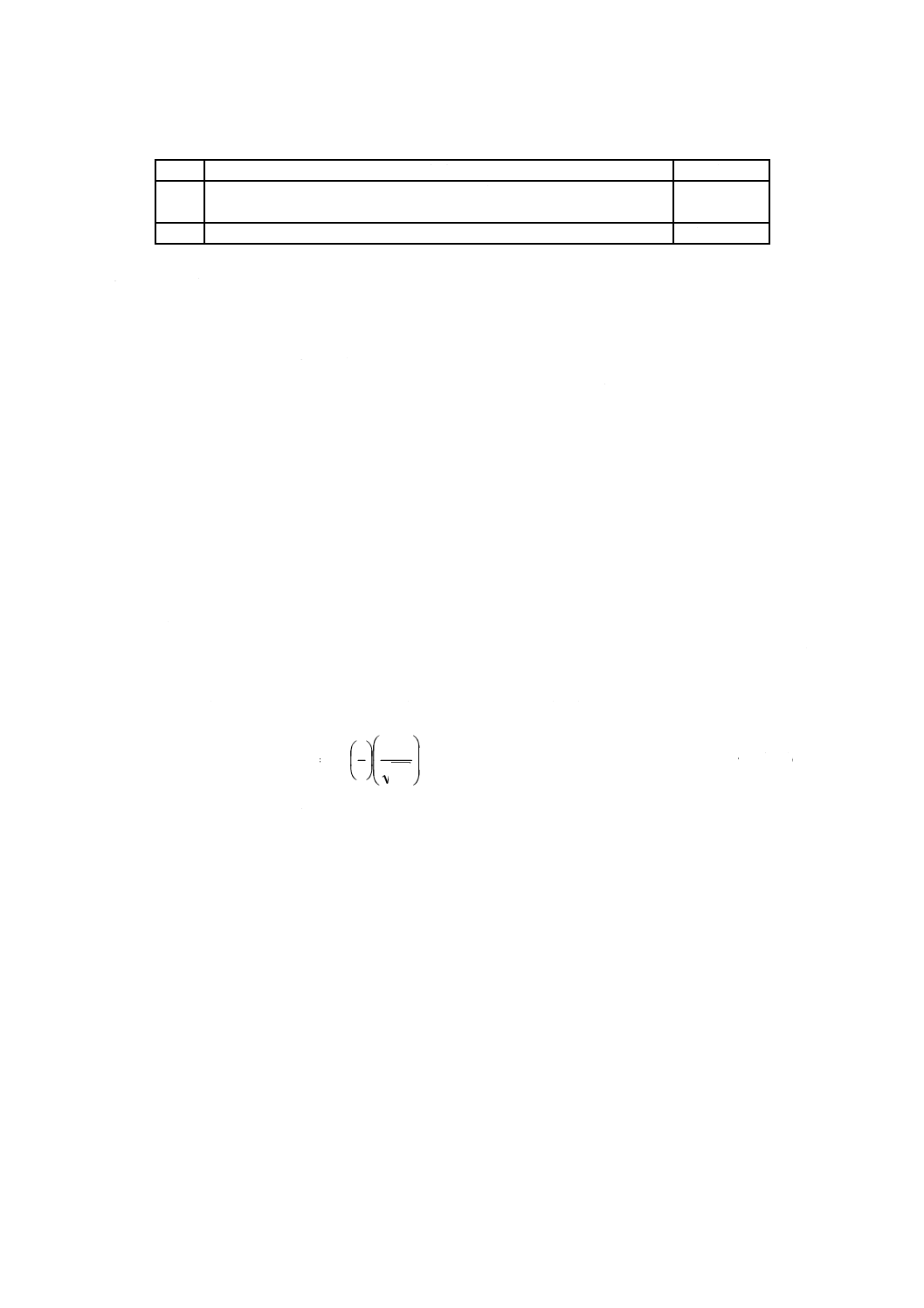
mm
15
B 2005-2-1:2019 (IEC 60534-2-1:2011)
表B.1−記号(続き)
記号
意味
単位
n
単一流路の曲がり(又はステージ)の数。多流路に分岐する流れの場合
は一つの流路に限って考慮する。
無次元数
r
再熱係数
無次元数
B.3
用語及び定義
この附属書で用いる主な用語及び定数は,JIS B 2005-1によるほか,次による。
B.3.1
多段調節弁(multistage control valves)
隙間で隔てた幾つかの減圧段をもつトリムが組み込まれたグローブ調節弁(図B.1及びB.2を参照)。絞
りの幾何学的な形状は,全ての段で相似であることが望ましい。1段目の容量係数Cに対する2段目の容
量係数Cの比率は1.8を超えないほうがよい。前段に対する他の段の容量係数Cの比率は,1.55を超えな
いで±9 %の範囲で一様なほうがよい。非圧縮性流体に対しては,通常各段の容量係数Cは,およそ等し
く,より大きな圧力降下が必要な場合に限っては,特定の段について僅かに小さい容量係数を設定する。
B.3.2
間隙(gap)
隣接する段の間の距離。
B.3.3
多段多流路調節弁(multistage multipath control valves)
ある間隙で隔てられた幾つかの減圧段をもつ複数の流路をもったトリムを組み込んだグローブ調節弁
(図B.1を参照)。この附属書の予測式が適切であるためには,間隙は,次の式で計算する値の+15 %か
ら−10 %までの範囲にあることが望ましい(図B.1及び図B.2を参照)。
=
s
HT
6.1
1
D
l
A
gap
································································ (B.1)
ここに,4 mm≦gap≦44 mm
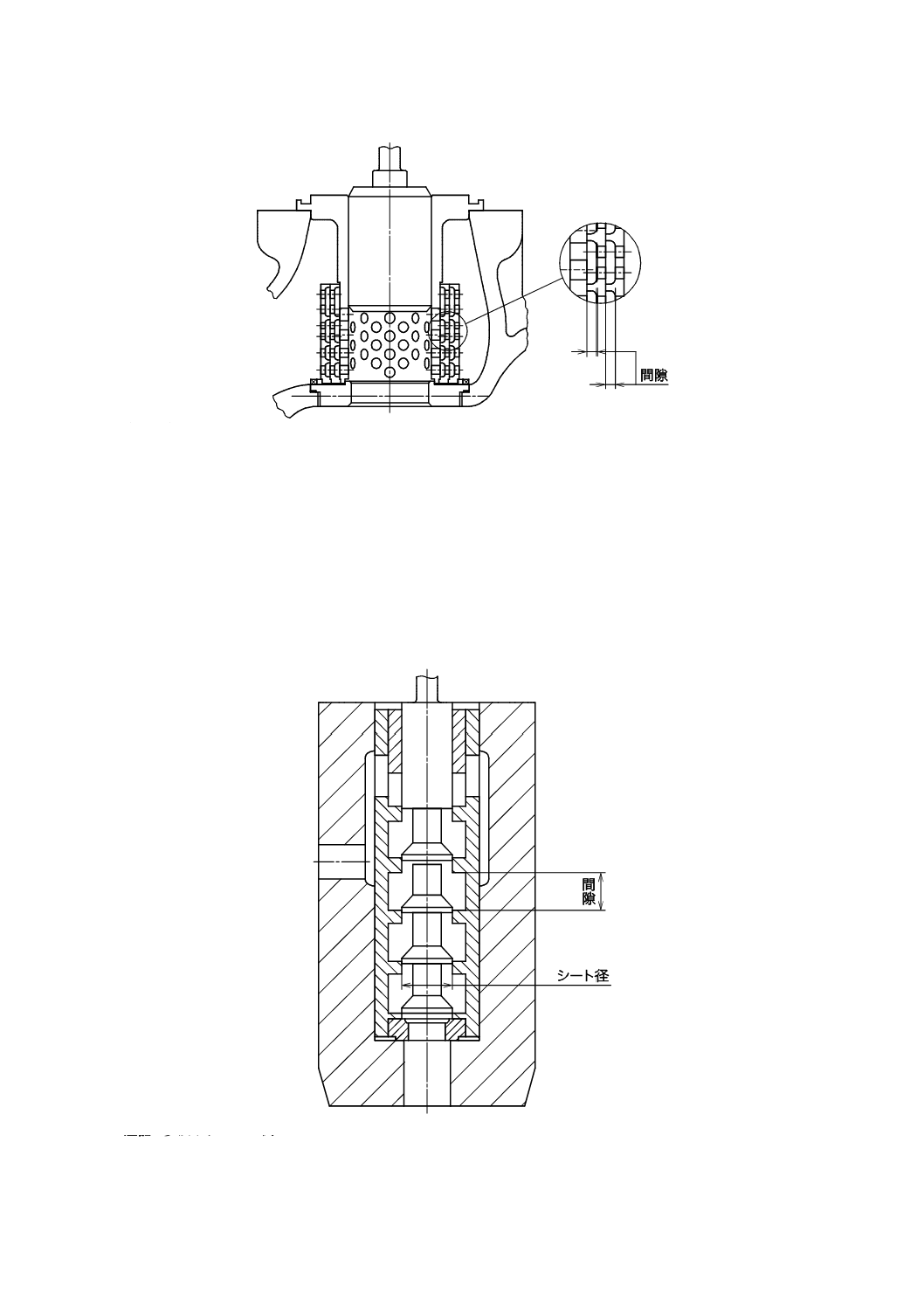
16
B 2005-2-1:2019 (IEC 60534-2-1:2011)
注記 多段トリムの一例
図B.1−多段多流路トリム
B.3.4
多段単一流路調節弁(multistage single path control valves)
ある間隙で隔てられた幾つかの減圧段をもつ単一の流路をもつトリムが組み込まれたグローブ調節弁
(図B.2を参照)。間隙間隔は,次の最小と最大との限度内にあることが望ましい。
最小間隙=前段のバルブシート径の0.6倍
最大間隙=前段のバルブシート径の1.1倍
注記 多段トリムの一例
図B.2−多段単一流路トリム

17
B 2005-2-1:2019 (IEC 60534-2-1:2011)
B.3.5
連続抵抗トリム調節弁(continuous resistance trim control valves)
連続抵抗形の絞りを調整する多段で相互に連結しない多流路で構成するトリムを組み込んだグローブ弁
で,通常,ラビリンス弁という(図B.3及びB.4を参照)。各流路は幾何学的に類似していて流路相互には
合流しないほうがよいが,あるところで複数路に分岐してもよい。非圧縮性流体に対しては,それぞれ流
路断面積は一定で差し支えないが,非常に高減圧の場合には,出口流速を低く抑えるためにそれぞれの流
路の面積が増加してもよい。圧縮性流体に対しては,面積が流れ方向に沿って拡大することが望ましい。
その拡大率は,次の範囲内であることが望ましい。
A1×(1.12)n≦A0≦A1×(1.23)n ······················································ (B.2)
各々の流路の長さに対する各々の流路における曲がりの数の関係は,次の式で計算する最大値と最小値
との間にあることが望ましい。
lp,max=n×10.50
lp,min=n×7.00(最小流路長さは25 mmを下回ってはならない。)
ここに,
lp: 各々の流路の長さで,分割された複数流路の場合,一つの流
路だけをlに含める(mm)。
図B.3−連続抵抗トリムのディスク
(全体トリムは多数のこれらのディスクを積層して構成される。)
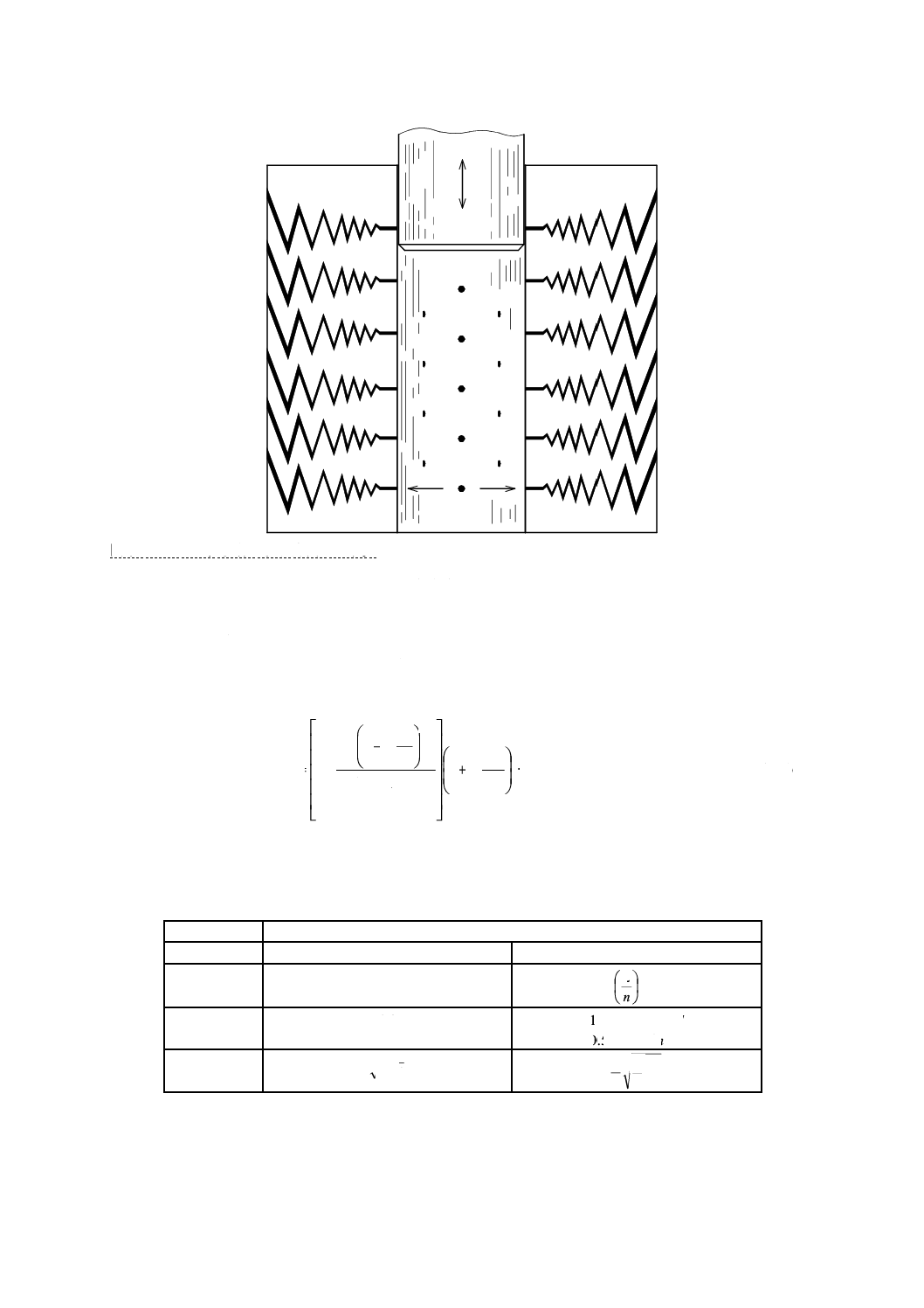
18
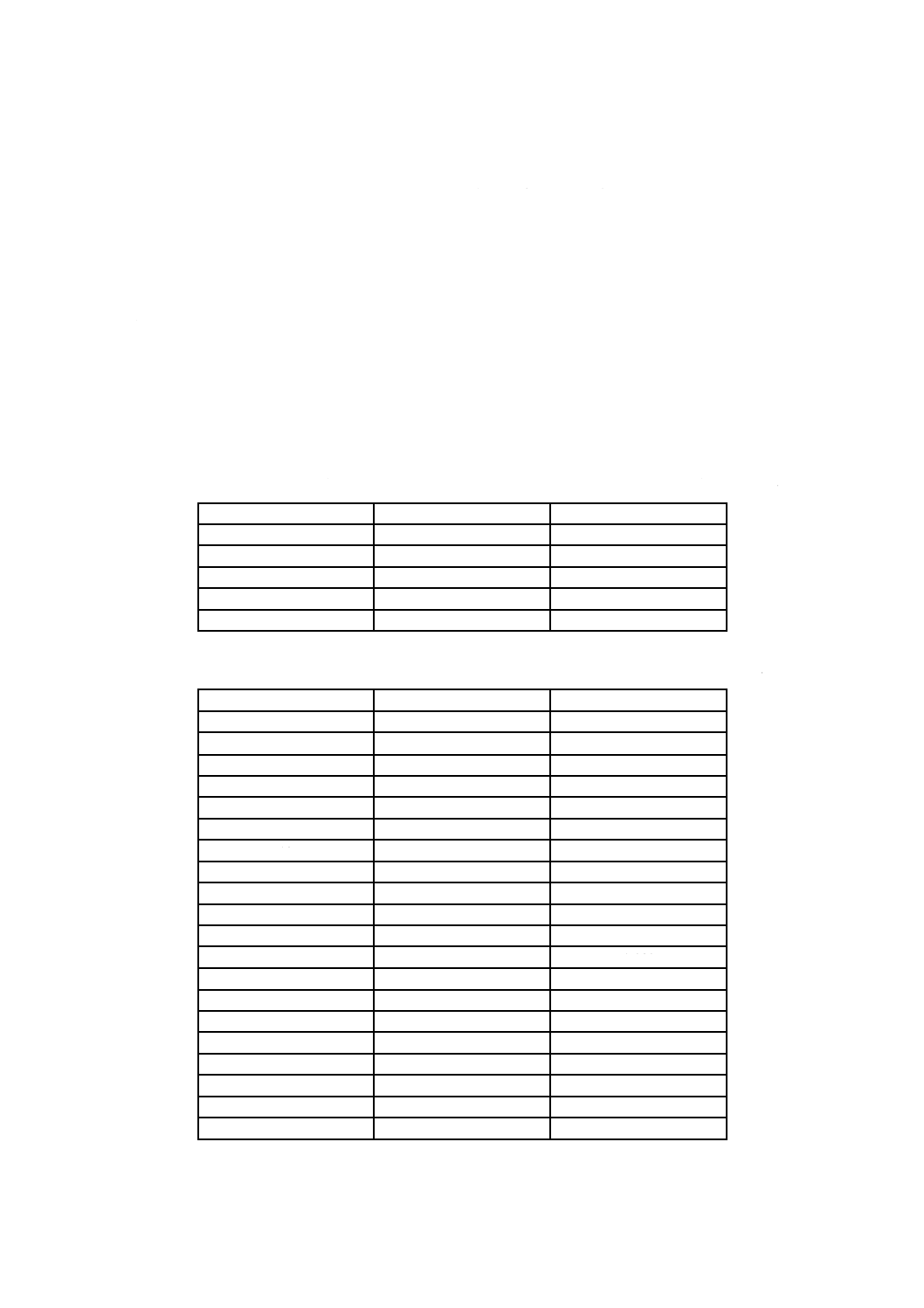
B 2005-2-1:2019 (IEC 60534-2-1:2011)
図中の“→”は,流体の流れ方向を示す。
図B.4−軸方向に複数のジグザグ流路をもつ連続抵抗トリムの断面図
B.4
膨張係数,Y
膨張係数の用語及び役割を7.4に示す。多段弁に対して,減圧段の間での再加熱の影響を考慮するため
の膨張係数を,次の式を使用して評価するとよい。
+
−
−
−
=
γ
γ
T
3
2
1
1
212
.1
1
1
1
F
x
r
F
x
x
k
Y
β
β
β
·············································· (B.3)
ここに,指数を表B.2に定義する。
表B.2−調節弁トリム形式
圧力回復形式(図B.1,図B.2)
連続抵抗形式(図B.3,図B.4)
β1
0.5
333
.0
2 n
β2
1.0
1.0 2≦n≦7
0.5 8≦n
β3
1
−
n
1
2
2
1
−
n
式(B.3)のxの値は,FγxTを超えないほうがよい。式(B.3)におけるこの項の最大値は,0.963である。さ
らに,式(B.3)のxTの値はFγで補正することはできない。
19
B 2005-2-1:2019 (IEC 60534-2-1:2011)
B.5
減圧段相互作用係数,k
式(B.3)のY式に含まれるこの係数は,バルブ差圧比xを縮流部差圧比に変えるために必要な係数を導入
し,それは減圧段間と最終減圧段出口での圧力回復の違いの補正係数を含む。各減圧段数によるkの固有
の値を表B.3及び表B.4に示す。
B.6
再熱係数,r
式(B.3)のY式の第一因子は各減圧段間で流体を完全に再加熱するという理論に基づいている(膨張過程
の熱降下に続くエンタルピの完全回復)。これは実際には起こらない。減圧段間では部分的な再加熱しかな
いので,流体は理論的比容積まで膨張しない。減圧段数が4以上の場合,減圧段数による摩擦加熱の増加
のため,この部分的な再加熱の影響は徐々に逆転する。式(B.3)のY式の第二因子は,これらの影響を表し
ており,理論的なYの値を適切な量だけ修正する。係数rによって,バルブ差圧比に基づく計算から補正
することができる。異なる段数に対して特有なrの値があり,それらを表B.3及び表B.4に示す。
表B.3−多段単一流路及び多流路の調節弁に対する減圧段の相互作用係数k及び再熱係数r
減圧段数
k
r
1
0.404
0
2
0.673
0.215
3
0.825
0.316
4
0.885
0.335
5
0.915
0.310
表B.4−連続抵抗形の調節弁トリムに対する減圧段間の相互作用係数k及び再熱係数r
曲がり数
k
r
2
0.420a)
0.066
4
0.510a)
0.130
6
0.600
0.153
7
0.624
0.156
8
0.652
0.152
10
0.700
0.147
12
0.722
0.122
14
0.740
0.106
16
0.752
0.095
18
0.769
0.091
20
0.780
0.087
22
0.795
0.083
24
0.800
0.078
26
0.812
0.073
28
0.820
0.067
30
0.830
0.062
34
0.852
0.049
38
0.880
0.040
42
0.905
0.032
46
0.927
0.024

20
B 2005-2-1:2019 (IEC 60534-2-1:2011)
表B.4−連続抵抗形の調節弁トリムに対する減圧段間の相互作用係数k及び再熱係数r(続き)
曲がり数
k
r
50
0.950
0.019
注a) 2段〜4段に対してxが0.35以下の場合は,表中のkの値を1.3倍すること
が望ましい。
21
B 2005-2-1:2019 (IEC 60534-2-1:2011)
附属書C
(参考)
配管係数計算の検討
C.1 解法
FP,FLPなど配管系の形状係数を推定する式は,容量係数Cの関数である。これらの式に実際の絞り過
程の流れの容量係数を使用すると,これらの形状係数を最も正確に推定することができる。しかし,この
推定法では代数的に解くのが不可能な連立方程式となり,反復解法を選択することになる。定格容量係数
(JIS B 2005-1を参照)を用いて代数式から単純に必要容量係数を求めることができるが,その値は過大
な値となり,実際の運用では補正が必要となろう。この状況は,通常,制御弁及び接続継手の合成抵抗が
大きいため,必要流量を流すことができないことを表している。この場合,より大きいバルブ口径を選択
するのがよい。
可能性のある解決案を次の各項に示すが,それらの項は一つのこれまでに提示した流量方程式の各々に
対して採用してもよい。
C.2 反復解法
C.2.1 概要
次の数値解は,単純な反復二分割法を用いて関数の根を見つけるという考え方に基づいている。この方
法は直接的で,安定性が強く,更に精度が予測可能な範囲に設定されるという利点をもつ。他の数値解法
も可能であるが,実際の解が得られるように,配慮するのがよい。
二分割法の考え方では,関数の根を含む初回区間を確定することが中心となる。効果的に根を算定する
ために根を含む区間が十分に小さくなるまで,この区間を繰り返し二分割する。この解法全体にわたる論
理を,図C.1及び図C.2に示し,C.2.2〜C.2.7で解説する。
C.2.2 ステップ1−流動関数の定義
この規格の本文に示される全ての流動方程式は,容量係数(C)を独立変数として,次の関数形式で表
すことができる。
F(C)=[流量]−[流量方程式の定義] ············································· (C.1)
例えば,非圧縮性流量方程式(1)は,次の関数形で表される。
0
1
sizing
P
1
)
(
ρ
ρ
p
F
CN
Q
C
F
∆
−
=
······················································· (C.2)
この関数表式に含まれる幾つかの項は,容量係数(C)によって決まることに注意する。例えば,式(C.2)
の例では,これらの項には,配管補正項FP,及びサイジング差圧Δpsizingが含まれる。与えられた運転条件
に関係する容量係数は,この関数の根を見つけることで決まる。すなわち,Cの値は,次の方程式の根と
して定まる。
F(C)=0 ················································································ (C.3)
C.2.3 ステップ2−流量区間下限の設定
解を含む区間の下限の初期値を,ゼロに設定する。Cに従属する係数FL及びxTの適切に対応する値は,
22
B 2005-2-1:2019 (IEC 60534-2-1:2011)
設計対象の調節弁について決定するのがよい(例えば,低開度での値を採用する。)。各々の配管補正係数
項,FP,FLP及びxTPは,C,FL及びxTの値を用いて求める。流量関数F(C)は,独立変数の最新の値に
基づいて計算する。
C.2.4 ステップ3−流量区間上限の設定
この解区間上限の初期値を設定する場合には,ある条件を考慮する必要がある。第一に,その区間の間
に根が含まれていることを確かにするために,上限は十分に大きい値に設定する。例えば,任意に大きく
選んだ式(C.4)の値を推奨する。
CUpper=0.075d2N18 ···································································· (C.4)
この値は,実際にはこの規格の範囲外に相当する値であるが,有意の実在する根を補足するために,上
限値は十分に大きくとるのが望ましい。
第二の論点は,容量係数(C)が大きい値をとる場合に関係する。容量係数が非常に大きな場合,下流
での流れの大きな拡大流と組み合わさって,式(15)に関して数学的特異性が生じる場合がある。この特異
性が生じることを防ぐために,式(15)の根号内にある数式を用いて上限を設定することができる。すなわ
ち,
ζ
Σ
−
=
2
2
Upper
99
.0
N
d
C
····························································· (C.5)
流量区間の上限値は,これら二つの値の小さい方に設定することが望ましい。さらに,また,CUpperに関
連するFL及びxTの値を決定して,FP,FLP及びxTPの値を計算する。その上で,流れの流量関数を,これ
ら独立変数の最新の値を使って計算する。
C.2.5 ステップ4−解が区間に含まれることの確認
解の関数F(C)は,確定したこの区間の中で単調である。したがって,根が区間の中に存在する場合,
区間の両側境界における関数値は異符号となる。それらの関数値が同じ符号である場合,その区間には実
解は含まれない。このことは,選択された容量係数範囲は,流れが通過するために十分な容量をもってい
ないことを示す。より大きい弁サイズを選んで,再計算する。
関数の値が異符号の場合,解は区間内に存在する。次のステップに進み,区間が解に収束するように反
復を進める。
C.2.6 ステップ5−区間の更新
区間の中間点を計算して,容量係数に従属する全てのパラメータ(FL,XT,FP,xTP及びFLPlp)を計算す
る。この初回区間を二つの小区間に分割し,そのうちの一つが関数の根を含む。いずれの区間に根が含ま
れるかについて判断するために,中間点及び区間上限における流量関数の値について符号を比較する。同
符号である場合は,下限側の小区間に根が含まれている。区間の上限を現在の中間点に再定義する。関数
の値が異符号である場合,上限側区間に根が含まれている。区間の下限を現在の中間点に再定義する。
C.2.7 ステップ6−収束の確認
根を含む区間の上限と下限とが互いに近づいて目標精度に合うようになったとき,根の値が得られ,反
復が中止されることになる。その収束条件を式(C.6)に示す。
ε
≦
Lower
UpperC
C
−
································································· (C.6)
ここで,収束許容差εの推奨値は,0.000 01である。この求解過程が適切に収束した場合には,最終的
23
B 2005-2-1:2019 (IEC 60534-2-1:2011)
な今の値を区間の中間点に設定するのがよい。
2
Lower
Upper
C
C
C
+
=
·································································· (C.7)
24
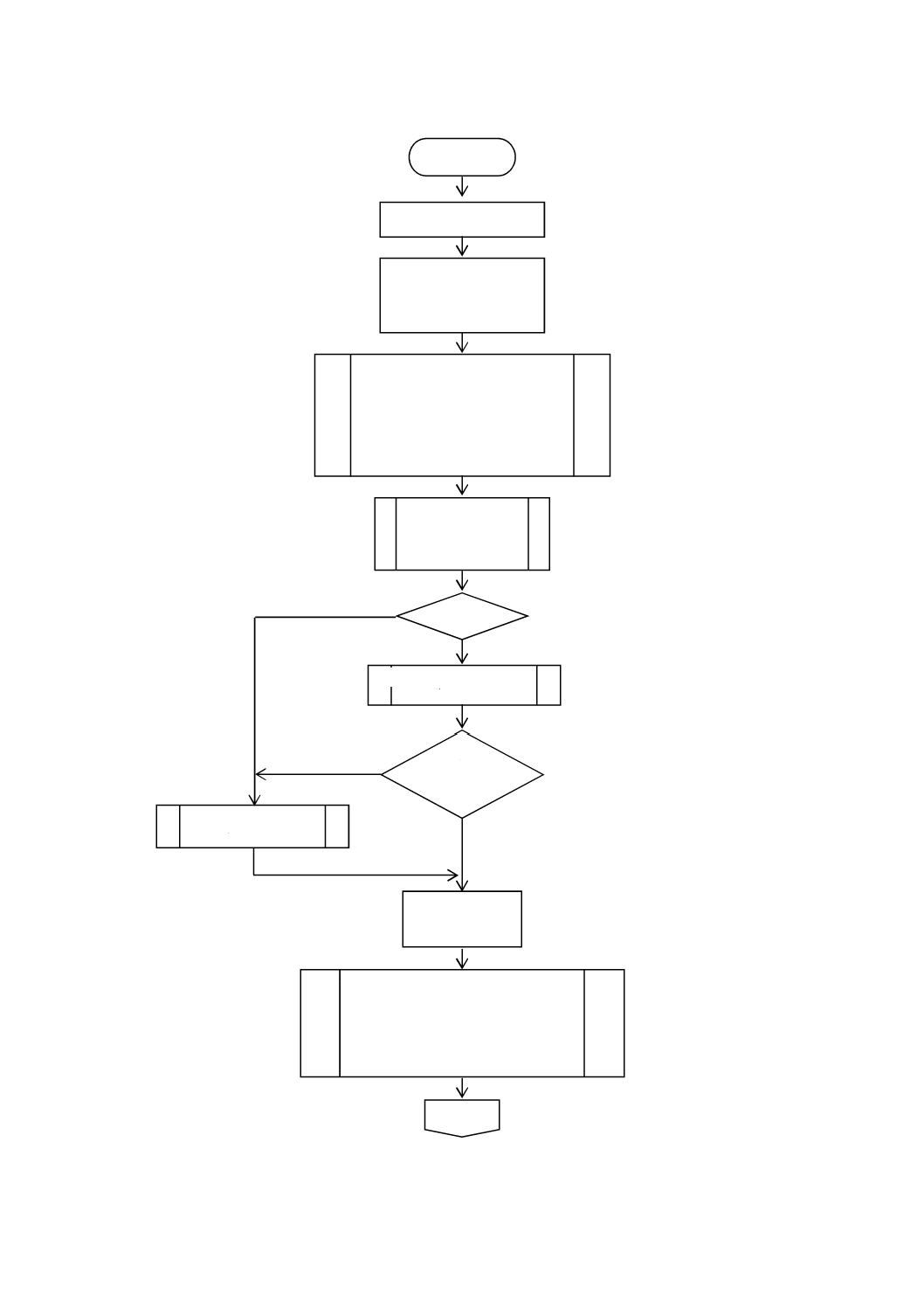
B 2005-2-1:2019 (IEC 60534-2-1:2011)
図C.1−反復法による容量係数Cの上限値の決定
開始
CLow=0.0
決定:
xT
FL
計算:
FpLow
XtpLow
FlpLow
FLow=F(CvLow,FPLow,xtpLow,FlpLow)
計算:
Σζ (eqn. 16)
Σζ<0 ?
No
計算:
CUpper (eqn. C.5)
CMax<
0.075d2N18 ?
計算:
CUpper (eqn. C.4)
C-1
決定:
xT
FL
Yes
No
Yes
計算:
FpUpper
xtpUpper
FlpUpper
FUpper=F(CUpper,FPUpper,xtpUpper,FlpUpper)
25
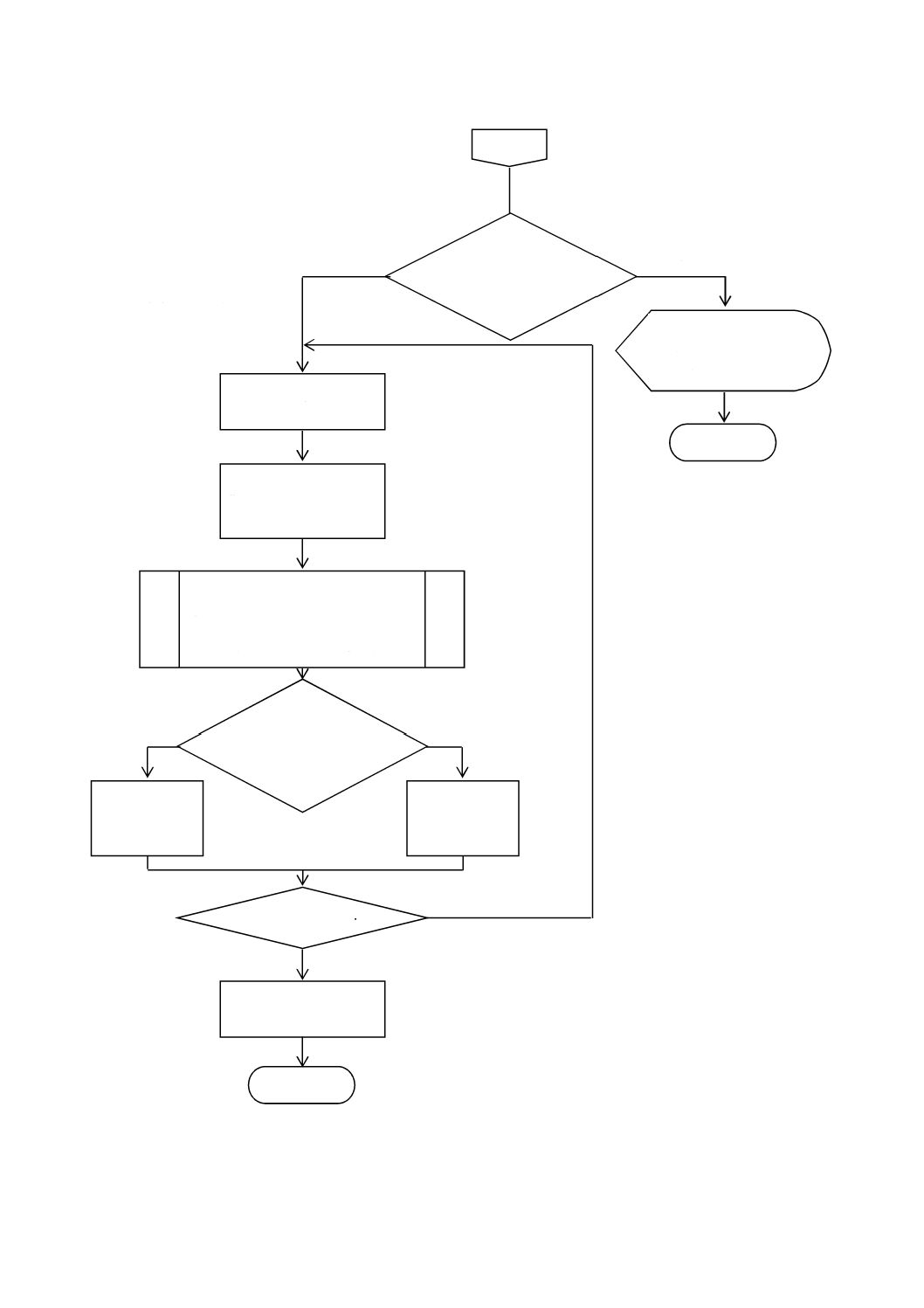
B 2005-2-1:2019 (IEC 60534-2-1:2011)
図C.2−反復法による最終容量係数Cの決定
区間両端で計算された流
量関数値が,異符号でない
場合,設定した区間には,
実解は含まれない。
No
Yes
中間値を計算:
CMid=(CLow+CUpper)/2
C-1
Sign
FLow×FUpper ?
不十分な配管継手容量
である。より大きなバ
ルブサイズを選定しな
ければならない。
中止
決定:
xT
FL
計算:
FpMid
xtpMid
FlpMid
FMid=F(CMid,FPMid,xtpMid,FlpMid)
Sign
FMid×FUpper ?
(-)
CLow=CMid
FpLow=FpMid
FLow=FMid
CUpper=CMid
FpUpper=FpMid
FUpper=FMid
|CUpper−CLow |<ε ?
計算:
CMid=(CLow+CUpper)/2
終了
(+)
(+)
(-)
26
B 2005-2-1:2019 (IEC 60534-2-1:2011)
附属書D
(参考)
エンジニアリング資料
D.1 物理定数
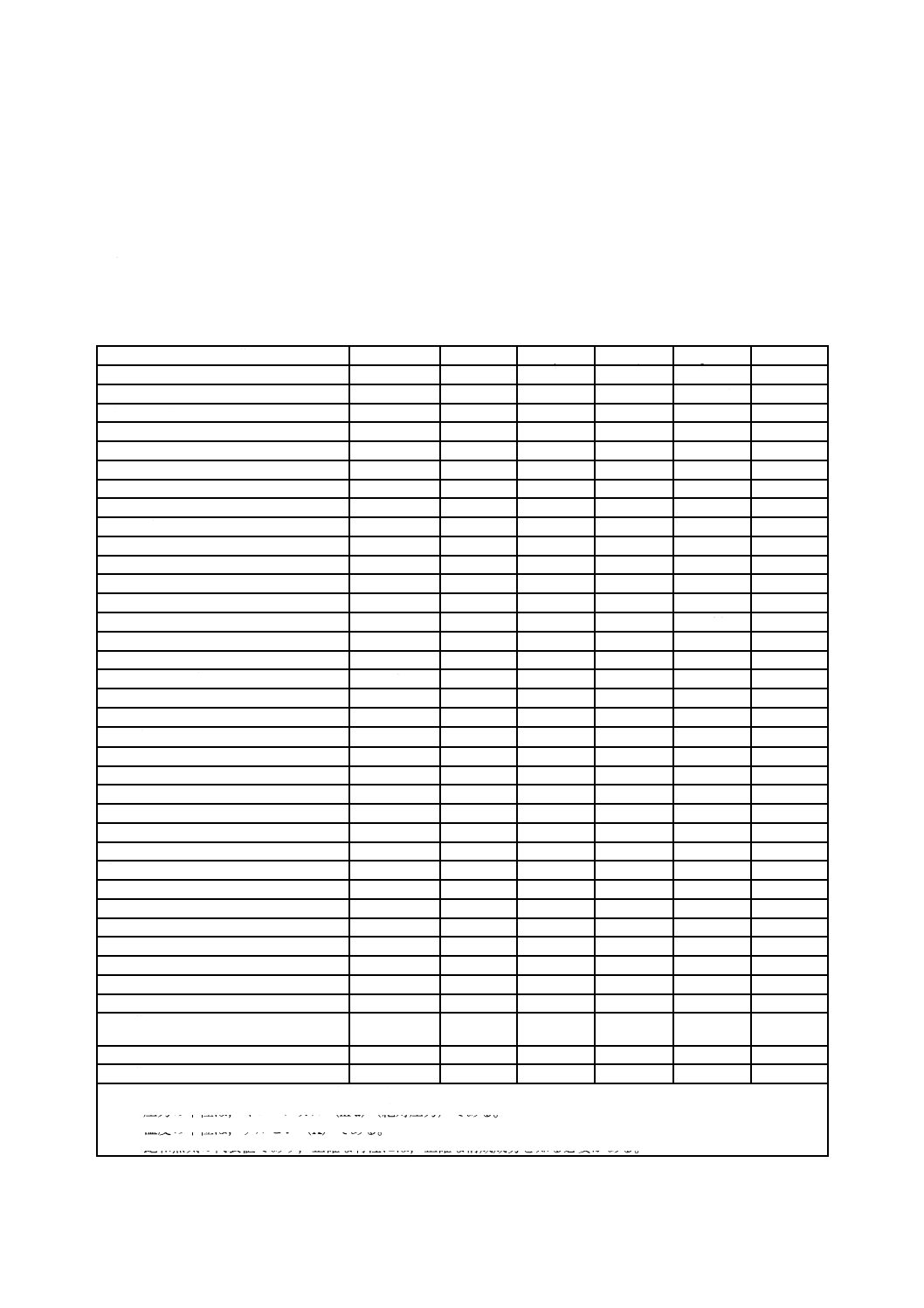
物理定数は表D.1を用いる。
表D.1−ガス及び蒸気の物理定数a)
ガス又は蒸気
分子式記号
M
γ
Fγ
pcb)
Tcc)
アセチレン
C2H2
26.04
1.30
0.929
6 140
309
空気
−
28.97
1.40
1.000
3 771
133
アンモニア
NH3
17.03
1.32
0.943
11 400
406
アルゴン
Ar
39.948
1.67
1.191
4 870
151
ベンゼン
C6H6
78.11
1.12
0.800
4 924
562
イソブタン
C4H10
58.12
1.10
0.784
3 638
408
n-ブタン
C4H10
58.12
1.11
0.793
3 800
425
イソブチレン
C4H8
56.11
1.11
0.790
4 000
418
二酸化炭素
CO2
44.01
1.30
0.929
7 387
304
一酸化炭素
CO
28.01
1.40
1.000
3 496
133
塩素
Cl2
70.906
1.31
0.934
7 980
417
エタン
C2H6
30.07
1.22
0.871
4 884
305
エチレン
C2H4
28.05
1.22
0.871
5 040
283
ふっ素
F2
18.998
1.36
0.970
5 215
144
フレオン11(3塩化1ふっ化メタン)
CCl3F
137.37
1.14
0.811
4 409
471
フレオン12(2塩化2ふっ化メタン)
CCl2F2
120.91
1.13
0.807
4 114
385
フレオン13(塩化3ふっ化メタン)
CClF3
104.46
1.14
0.814
3 869
302
フレオン22(塩化2ふっ化メタン)
CHClF2
80.47
1.18
0.846
4 977
369
ヘリウム
He
4.003
1.66
1.186
229
5.25
n-ヘプタン
C7H16
100.20
1.05
0.750
2 736
540
水素
H2
2.016
1.41
1.007
1 297
33.25
塩化水素
HCl
36.46
1.41
1.007
8 319
325
ふっ化水素
HF
20.01
0.97
0.691
6 485
461
メタン
CH4
16.04
1.32
0.943
4 600
191
塩化メチル
CH3Cl
50.49
1.24
0.889
6 677
417
天然ガスd)
−
17.74
1.27
0.907
4 634
203
ネオン
Ne
20.179
1.64
1.171
2 726
44.45
一酸化窒素
NO
63.01
1.40
1.000
6 485
180
窒素
N2
28.013
1.40
1.000
3 394
126
オクタン
C8H18
114.23
1.66
1.186
2 513
569
酸素
O2
32.000
1.40
1.000
5 040
155
ペンタン
C5H12
72.15
1.06
0.757
3 374
470
プロパン
C3H8
44.10
1.15
0.821
4 256
370
プロピレン
C3H6
42.08
1.14
0.814
4 600
365
飽和蒸気
−
18.016
1.25〜
1.32d)
0.893〜
0.943d)
22 119
647
二酸化硫黄
SO2
64.06
1.26
0.900
7 822
430
過熱蒸気
−
18.016
1.315
0.939
22 119
647
注a) 定数は,外気温度(288 K)で大気圧(101.3 kPa)の流体(蒸気を除く。)における値である。
b) 圧力の単位は,キロパスカル(kPa)(絶対圧力)である。
c) 温度の単位は,ケルビン(K)である。
d) 飽和蒸気の代表値であり,正確な特性には,正確な構成成分を知る必要がある。

27
B 2005-2-1:2019 (IEC 60534-2-1:2011)
D.2 バルブ諸係数の代表値
表D.2−全開定格トラベルにおけるバルブ形状修正係数Fd,液体圧力回復係数FL及び差圧比係数xTの
代表的値
バルブ形式
トリム形式
流れ方向a)
FL
xT
Fd
グローブ
(単座形)
3 V−ポート プラグ
オープン又はクローズ
0.9
0.70
0.48
4 V−ポート プラグ
オープン又はクローズ
0.9
0.70
0.41
6 V−ポート プラグ
オープン又はクローズ
0.9
0.70
0.30
コンタード プラグ
(リニア及びイコールパー
センテージ)
オープン
クローズ
0.9
0.8
0.72
0.55
0.46
1.00
60同径ドリル孔ケージ
アウトワードb)又は
インワードb)
0.9
0.68
0.13
120同径ドリル孔ケージ
アウトワードb)又は
インワードb)
0.9
0.68
0.09
特性ケージ,4ポート
アウトワードb)
インワードb)
0.9
0.85
0.75
0.70
0.41
0.41
グローブ
(複座形)
ポーテッド プラグ
入口はシート間
0.9
0.75
0.28
コンタード プラグ
両方向
0.85
0.70
0.32
グローブ
(アングル
形)
コンタード プラグ
(リニア及びイコールパー
センテージ)
オープン
クローズ
0.9
0.8
0.72
0.65
0.46
1.00
特性ケージ,4ポート
アウトワードb)
インワードb)
0.9
0.85
0.65
0.60
0.41
0.41
ベンチュリ
クローズ
0.5
0.20
1.00
グローブ,
微少流量トリ
ム
V−ノッチ
オープン
0.98
0.84
0.70
平面シート(小トラベル)
クローズ
0.85
0.70
0.30
テーパ形ニードル
オープン
0.95
0.84
0
L
19
D
F
C
N
×
回転
偏心形球面プラグ
オープン
クローズ
0.85
0.68
0.60
0.40
0.42
0.42
偏心形円すいプラグ
オープン
クローズ
0.77
0.79
0.54
0.55
0.44
0.44
バタフライ
(同心軸)
スイングスルー(70°)
両方向
0.62
0.35
0.57
スイングスルー(60°)
両方向
0.70
0.42
0.50
溝付きベーン(70°)
両方向
0.67
0.38
0.30
バタフライ
(偏心軸)
オフセット シート(70°) 両方向
0.67
0.35
0.57
ボール
フル ボア(70°)
両方向
0.74
0.42
0.99
セグメント ボール
両方向
0.60
0.30
0.98
グローブ
多段多流路
2
両方向
0.97
0.812
3
0.99
0.888
4
0.99
0.925
5
0.99
0.950
多段単一流路
2
両方向
0.97
0.896
3
0.99
0.935
4
0.99
0.960
28
B 2005-2-1:2019 (IEC 60534-2-1:2011)
表D.2−全開定格トラベルにおけるバルブ形状修正係数Fd,液体圧力回復係数FL及び差圧比係数xTの
代表的値(続き)
注記 これらの値は,代表的な値である。実際の値は,製造業者による。
注a) オープンとは流れが閉止部品をシートから押し離す方向であり,クローズとは流れが閉止部品をシートに向
けて押し付ける方向を意味する。
b) アウトワードとはケージの中心から外側への流れを意味し,インワードとはケージの外側から中心への流れ
を意味する。
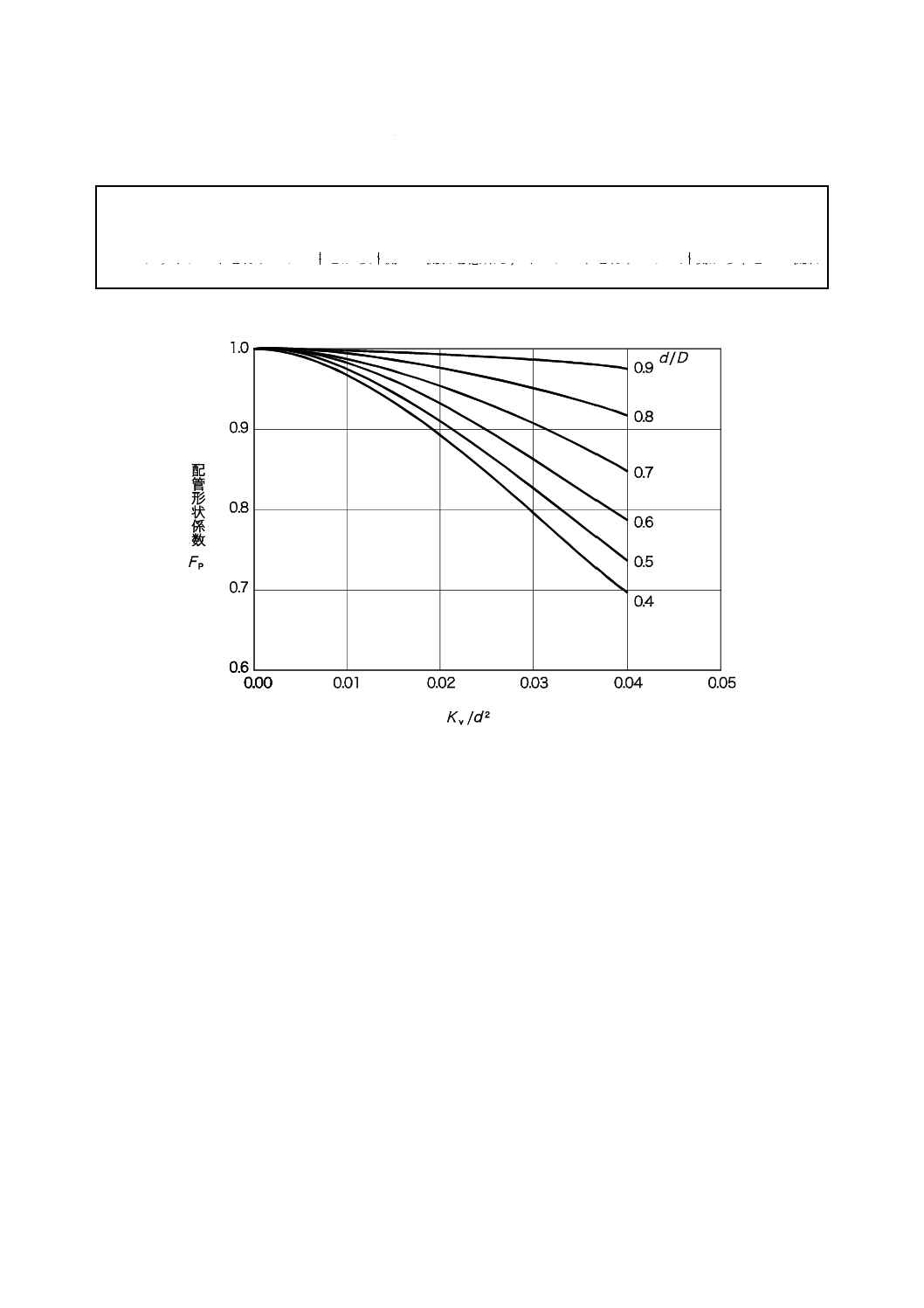
注記1 配管の径Dは,バルブの両端で同じ径である[式(20)を参照]。
注記2 これらの曲線の使用例は,附属書Eを参照。
a) Kv/d2に対する配管形状係数FP
図D.1−配管形状係数
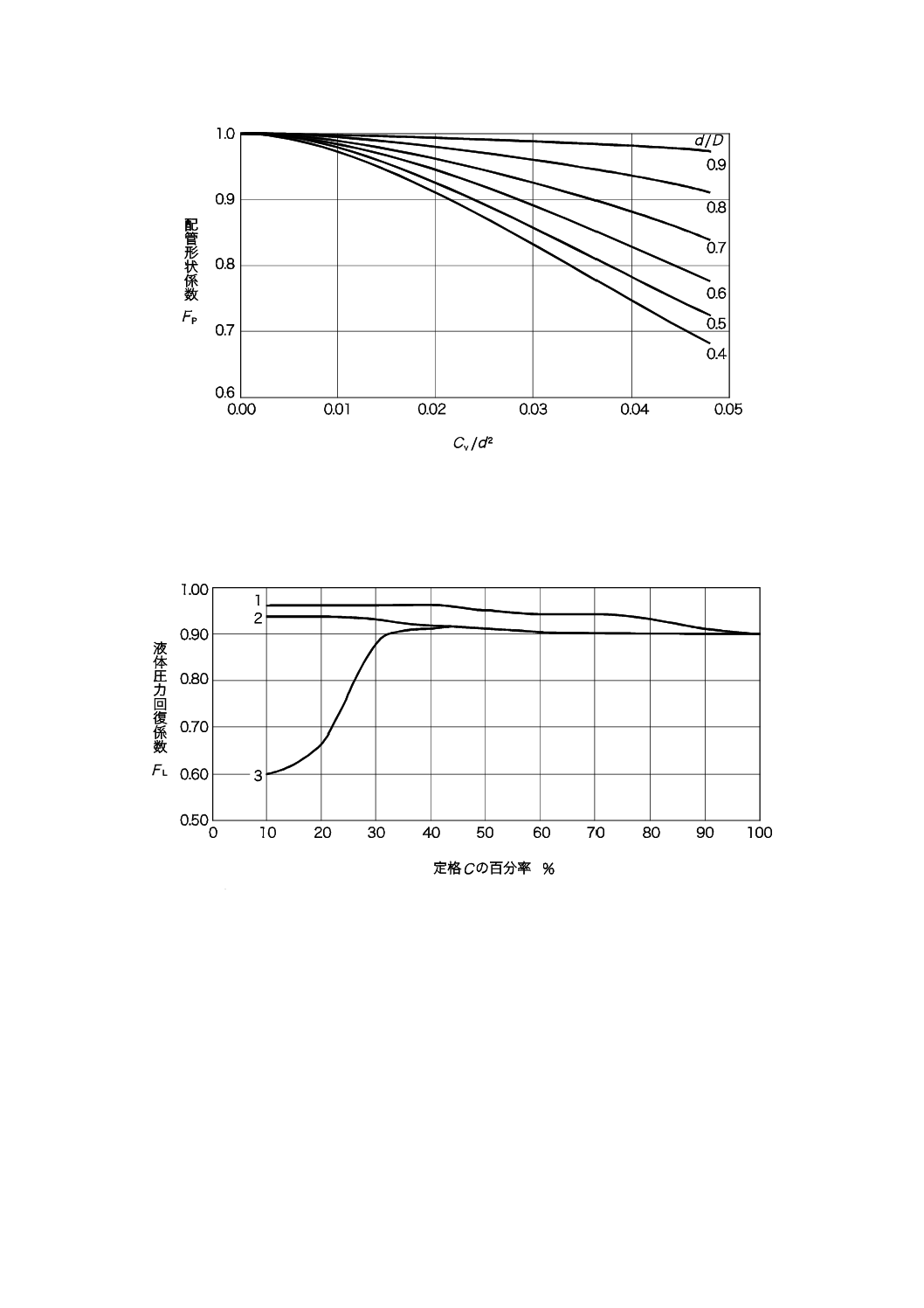
29
B 2005-2-1:2019 (IEC 60534-2-1:2011)
注記1 配管の径Dは,バルブの両端で同じ径である[式(20)を参照]。
注記2 これらの曲線の使用例は,附属書Eを参照。
b) Cv/d2に対する配管形状係数FP
図D.1−配管形状係数(続き)
a) 複座グローブ弁及びケージ ガイド グローブ弁(識別数字は記号表参照)
図D.2−圧力回復係数
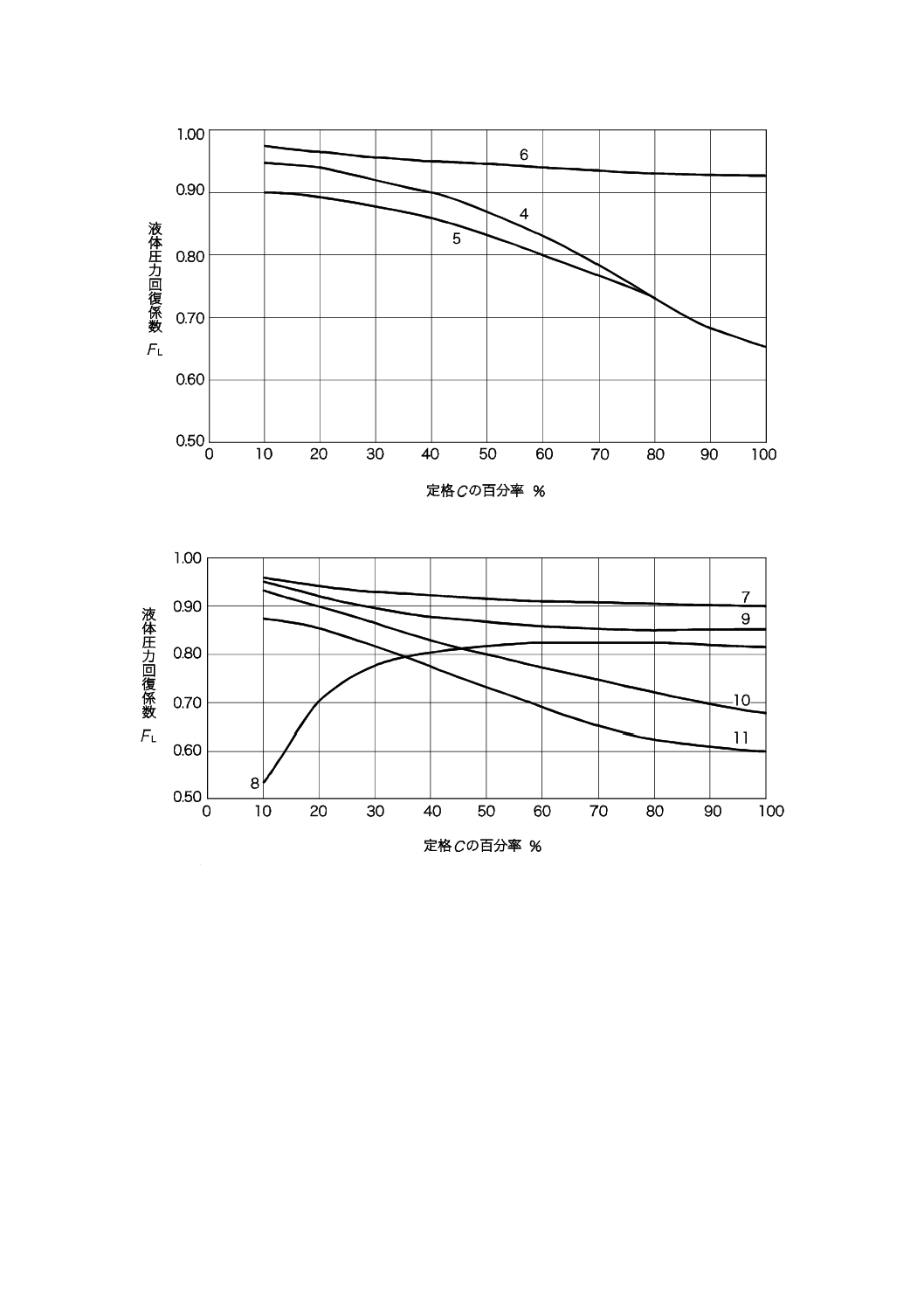
30
B 2005-2-1:2019 (IEC 60534-2-1:2011)
b) バタフライ弁及びコンタード微小流量弁(識別数字は記号表参照)
c) コンタード グローブ弁,偏心形球面プラグ弁及びセグメント ボール弁(識別数字は記号表参照)
図D.2−圧力回復係数(続き)
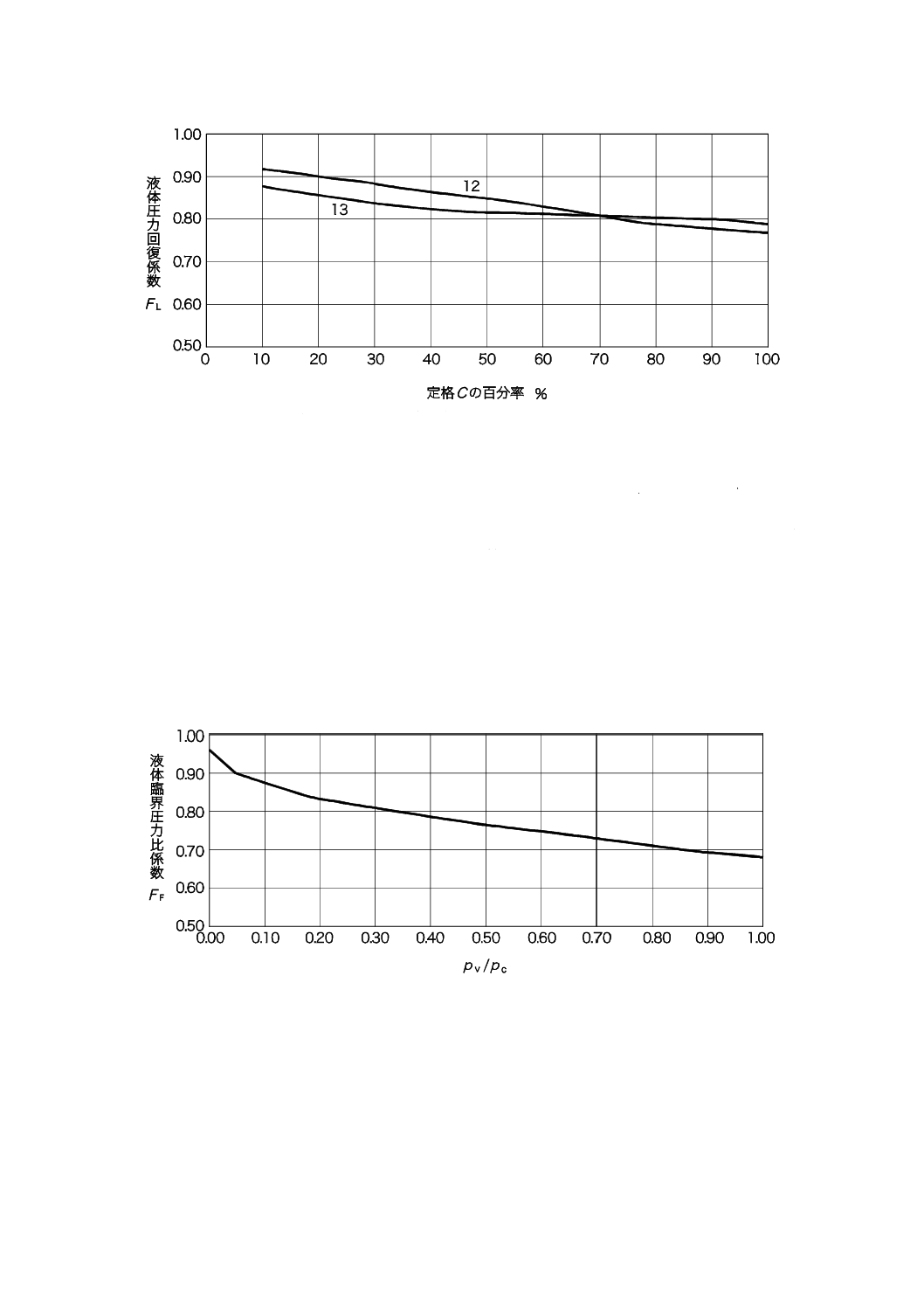
31
B 2005-2-1:2019 (IEC 60534-2-1:2011)
d) 偏心形円すいプラグ弁(識別数字は記号表参照)
記号表
1 複座グローブ弁,V−ポート プラグ
8 単座,イコール パーセンテージ,コンタード
2 ポーテッド ケージ ガイド グローブ弁(フロー トゥ
グローブ弁,フロー トゥ クローズ
オープン及びフロー トゥ クローズ)
9 偏心形球面プラグ弁,開方向流れ
3 複座グローブ弁,コンタード プラグ
10 偏心形球面プラグ弁,フロー トゥ クローズ
4 オフセット シート バタフライ弁
11 セグメント ボール弁
5 スイングスルー バタフライ弁
12 偏心形円すいプラグ弁,開方向流れ
6 コンタード微少流量弁
13 偏心形円すいプラグ弁,フロー トゥ クローズ
7 単座,イコール パーセンテージ,
コンタードグローブ弁,開方向流れ
注記 これらの値は代表的な値であり,実際の値は製造業者による。
図D.2−圧力回復係数(続き)
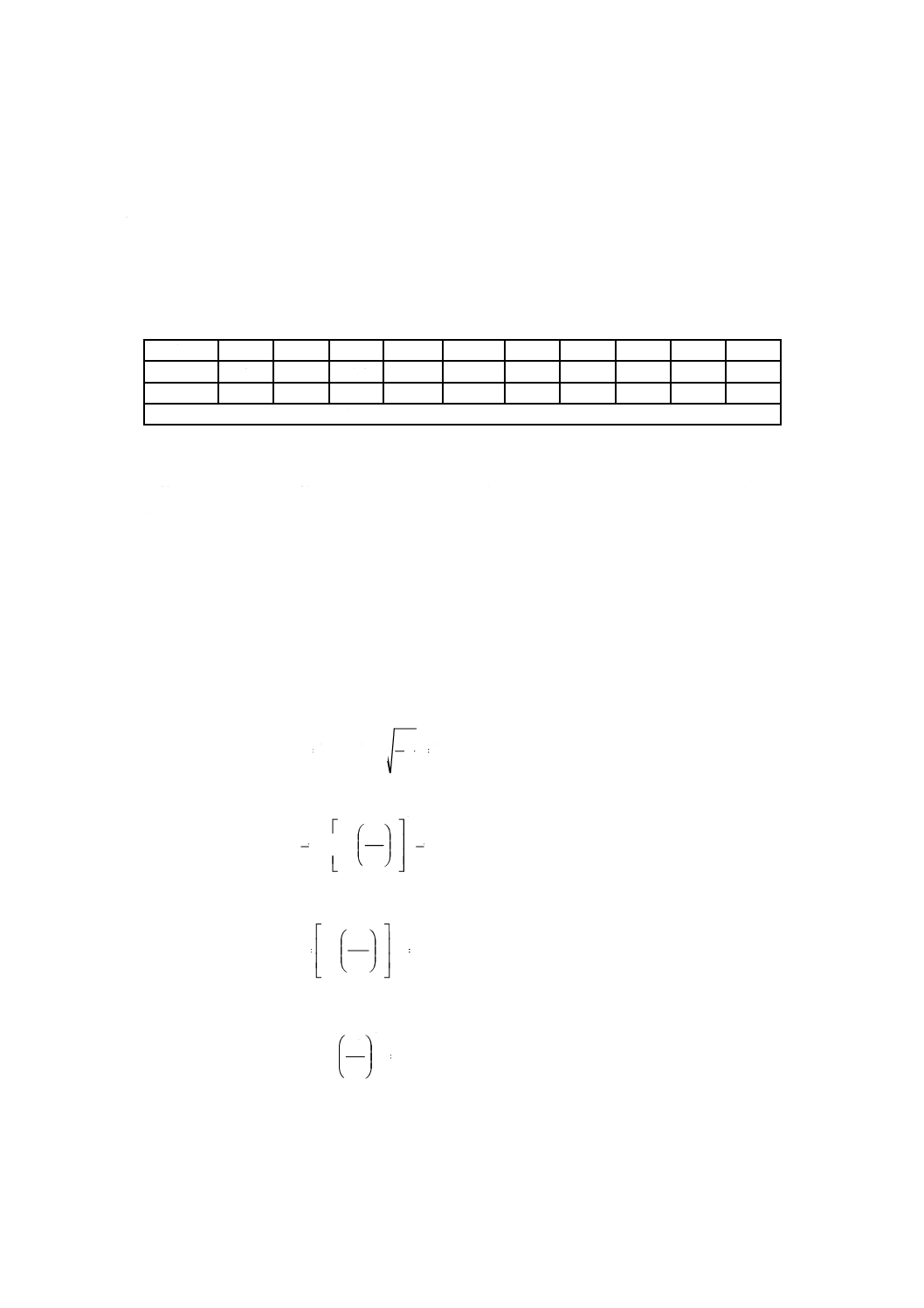
図D.3−液体臨界圧力比係数FF
32
B 2005-2-1:2019 (IEC 60534-2-1:2011)
附属書E
(参考)
計算例
E.1
例題1:非圧縮性流体−継手を接続しない場合の非閉塞乱流,容量係数Kvの計算例
E.1.1 プロセス データ:
流体
:水
入口温度
: T1 =363 K
密度
: ρ1 =965.4 kg/m3
蒸気圧
: pv =70.1 kPa
熱力学的臨界圧力
: pc =22 120 kPa
動粘度
: ν =3.26×10−7 m2/s
入口絶対圧力
: p1 =680 kPa
出口絶対圧力
: p2 =220 kPa
流量
: Q =360 m3/h
配管の内径
: D1=D2=150 mm
E.1.2 バルブ データ:
バルブ形式
: グローブ
トリム
: パラボリック プラグ
流れ方向
: フロー トゥ オープン
呼び径
: d =150 mm
液体圧力回復係数
: FL =0.90(表D.2から)
バルブ形状修正係数 : Fd =0.46(表D.2から)
E.1.3 計算:
乱流域における非圧縮性流体に適用できる流れのモデルに式(1)を用いる。
0
1
sizing
P
1
ρ
ρ
p
F
CN
Q
∆
=
表2から,これらのプロセスデータで使用する数値定数は,
N1
=1×10−1
N2
=1.60×10−3
N4
=7.07×10−2
N18
=8.65×10−1
液体臨界圧力比係数FFを,式(4)によって求める。
944
.0
28
.0
96
.0
c
v
F
=
−
=
p
p
F
33
B 2005-2-1:2019 (IEC 60534-2-1:2011)
ここで,バルブは配管径と同じ口径なので,FP=1及びFLP=FLとなる。
閉塞差圧Δpchokedを,式(3)によって求める。
(
)
kPa
497
v
F
1
2
P
LP
choked
=
−
=
∆
p
F
p
F
F
p
次に,サイジング差圧比Δpsizingを,式(2)によって求める。
kPa
460
kPa
460
sizing
choked
choked
choked
sizing
2
1
=
∆
∆
∆
∆
∆
∆
∆
=
∆
=
−
=
∆
p
p
p
if
p
p
p
if
p
p
p
p
p
≧
<
式(1)を変形してKvを求める。
sizing
0
1
P
1
v
p
F
N
Q
K
C
∆
=
=
ρ
ρ
ここに, ρ0は15 ℃における水の密度である。
h/
m
165
3
v=
K
次に,式(23)によってバルブレイノルズ数Revを計算して流れが乱流であることを確認する。
6
4
/1
4
2
2
2
L
L
d
4
v
10
97
.2
1
×
=
+
=
d
N
C
F
F
C
v
Q
F
N
Re
ここに, Rev≧10 000であり,流れは乱流となる。
結果がこの規格の適用範囲内であることを確認する。
047
.0
5
008
.0
2
18
<
=
d
N
C
E.2
例題2:非圧縮性流体−継手を接続しない場合の閉塞流れ,容量係数Kvの計算例
E.2.1 プロセスデータ:
流体
: 水
入口温度
: T1 =363 K
密度
: ρ1 =965.4 kg/m3
蒸気圧
: pv =70.1 kPa
熱力学的臨界圧力
: pc =22 120 kPa
動粘度
: ν =3.26×10−7 m2/s
入口絶対圧力
: p1 =680 kPa
出口絶対圧力
: p2 =220 kPa
流量
: Q = 360 m3/h
配管の内径
: D1=D2=100 mm
34
B 2005-2-1:2019 (IEC 60534-2-1:2011)
E.2.2 バルブ データ:
バルブ形式
: ボール弁
トリム
: セグメント ボール
流れ方向
: フロー トゥ オープン
呼び径
: d =100 mm
液体圧力回復係数
: FL =0.60(表D.2から)
バルブ形状修正係数 : Fd =0.98(表D.2から)
E.2.3 計算:
乱流域における非圧縮性流体に適用できる流れのモデルは,式(1)で与えられる。
0
1
sizing
P
1
ρ
ρ
p
F
CN
Q
∆
=
表2から,これらのプロセスデータで使用する数値定数は,
N1
=1×10−1
N2
=1.60×10−3
N4
=7.07×10−2
N18
=8.65×10−1
液体臨界圧力比係数FFは,式(4)によって求める。
944
.0
28
.0
96
.0
c
v
F
=
−
=
p
p
F
ここで,バルブは配管径と同じ口径なので,FP=1及びFLP=FLとなる。
閉塞差圧Δpchokedを,式(3)によって求める。
(
)
kPa
221
v
F
1
2
P
LP
choked
=
−
=
∆
p
F
p
F
F
p
次に,サイジングの差圧Δpsizingを,式(2)によって求める。
kPa
221
kPa
460
sizing
choked
choked
choked
sizing
2
1
=
∆
∆
∆
∆
∆
∆
∆
=
∆
=
−
=
∆
p
p
p
if
p
p
p
if
p
p
p
p
p
≧
<
式(1)を変形してKvを求める。
sizing
0
1
P
1
v
p
F
N
Q
K
C
∆
=
=
ρ
ρ
ここで, ρ0は15 ℃における水の密度である。
Kv=238 m3/h
次に,式(23)によってバルブレイノルズ数Revを計算して流れが乱流であることを確認する。
35
B 2005-2-1:2019 (IEC 60534-2-1:2011)
6
4
/1
4
2
2
2
L
L
d
4
v
10
60
.6
1
×
=
+
=
d
N
C
F
F
C
v
Q
F
N
Re
ここで, Rev≧10 000であり,流れは乱流となる。
結果がこの規格の適用範囲内であることを確認する。
047
.0
028
.0
2
18
<
=
d
N
C
E.3
例題3:圧縮性流体−非閉塞流れ,容量係数Kvの計算例
E.3.1 プロセス データ:
流体
: 二酸化炭素
入口温度
: T1 =433 K
入口絶対圧力
: p1 =680 kPa
出口絶対圧力
: p2 =450 kPa
動粘度
: ν =2.526×10−6 m2/s(680 kPa及び433 Kのとき)
流量
: Qs =3 800 m3/h(101.325 kPa及び273 Kのとき)
密度
: ρ1 =8.389 kg/m3(680 kPa及び433 Kのとき)
圧縮係数
: Z1 =0.991(680 kPa及び 433 Kのとき)
標準状態における圧縮係数 : ZS =0.994(101.325 kPa及び273 Kのとき)
モル質量
: M =44.01 kg/kmol
比熱比
: γ =1.30
配管の内径
: D1 =D2=100 mm
E.3.2 バルブ データ:
バルブ形式
: 回転
トリム
: 偏心球形プラグ
流れ方向
: フロー トゥ オープン
呼び径
: d =100 mm
差圧比係数
: xT =0.60(表D.2から)
液体圧力回復係数
: FL =0.85(表D.2から)
バルブ形状修正係数
: Fd =0.42(表D.2から)
E.3.3 計算:
乱流域における圧縮性流体に適用できる流れのモデルに式(7)を用いる。
1
1
sizing
1
P
9
s
Z
MT
x
Y
p
F
CN
Q=
表2から,これらのプロセスデータで使用する数値定数は,
36
B 2005-2-1:2019 (IEC 60534-2-1:2011)
N2
=1.60×10−3
N4
=7.07×10−2
N9
=2.46×101
N18
=8.65×10−1
ここで,バルブは配管径と同じ口径なので,FP=1及びxTP=xTとなる。
比熱比係数Fγは,式(11)によって求める。
929
.0
40
.1
γ
=
=γ
F
閉塞差圧比xchokedを,式(10)によって求める。
xchoked=FγxTP=0.557
次に,サイジング差圧比xsizingを式(8)及び式(9)によって求める。
338
.0
338
.0
sizing
choked
choked
choked
sizing
1
2
1
=
=
=
−
=
x
x
x
if
x
x
x
if
x
x
p
p
p
x
≧
<
膨張係数Yを,式(12)によって求める。
798
.0
3
1
choked
sizing=
−
=
x
x
Y
式(7)を変形してKvを求める。
h/
m
2.
67
3
v
sizing
1
1
1
P
9
s
v
=
=
=
K
x
Z
MT
Y
p
F
N
Q
K
C
実体積流量を求める。
h
/
m
4.
895
3
1
1
1
s
s
s
s
=
=
p
T
Z
T
Z
p
Q
Q
次に,式(23)によってバルブレイノルズ数Revを計算して流れが乱流であることを確認する。
6
4
/1
4
2
2
2
L
L
d
4
v
10
40
.1
1
×
=
+
=
d
N
C
F
F
C
v
Q
F
N
Re
ここで, Rev≧10 000であり,流れは乱流となる。
結果がこの規格の適用範囲内であることを確認する。
047
.0
8
007
.0
2
18
<
=
d
N
C
37
B 2005-2-1:2019 (IEC 60534-2-1:2011)
E.4
例題4:圧縮性流体−閉塞流れ,容量係数Kvの計算例
E.4.1 プロセス データ:
流体
: 二酸化炭素ガス
入口温度
: T1 =433 K
入口絶対圧力
: p1 =680 kPa
出口絶対圧力
: p2 =250 kPa
動粘度
: ν =2.526×10-6 m2/s(680 kPa及び433 Kのとき)
流量
: Qs =3 800 標準m3/h(101.325 kPa及び273 Kのとき)
密度
: ρ1 =8.389 kg/m3(680 kPa及び433 Kのとき)
標準状態における密度
: ρ2 =1.978 kg/m3(101.325 kPa及び273 Kのとき)
圧縮係数
: Z1 =0.991(680 kPa及び433 Kのとき)
標準状態における圧縮係数 : ZS =0.994(101.325 kPa及び273 Kのとき)
モル質量
: M =44.01 kg/kmol
比熱比
: γ =1.30
配管の内径
: D1 =D2=100 mm
E.4.2 バルブ データ:
バルブ形式
: 回転
トリム
: 偏心球形プラグ
流れ方向
: フロー トゥ オープン
呼び径
: d =100 mm
差圧比係数
: xT =0.60(表D.2から)
液体圧力回復係数
: FL =0.85(表D.2から)
バルブ形状修正係数
: Fd =0.42(表D.2から)
E.4.3 計算:
乱流域における圧縮性流体に適用できる流れのモデルに式(7)を用いる。
1
1
sizing
1
P
9
s
Z
MT
x
Y
p
F
CN
Q=
表2から,これらのプロセスデータで使用する数値定数は,
N2
=1.60×10−3
N4
=7.07×10−2
N9
=2.46×101
N18
=8.65×10−1
ここで,バルブは配管径と同じ口径なので,FP=1及びxTP=xTとなる。
比熱比係数Fγは,式(11)を用いて決定する。
929
.0
40
.1
γ
=
=γ
F
38
B 2005-2-1:2019 (IEC 60534-2-1:2011)
閉塞差圧比xchokedは,式(10)を用いて決定する。
xchoked=FγxTP=0.557
次に,サイジング差圧比xsizingは式(8)及び式(9)を用いて決定する。
557
.0
632
.0
sizing
choked
choked
choked
sizing
1
2
1
=
=
=
−
=
x
x
x
if
x
x
x
if
x
x
p
p
p
x
≧
<
膨張係数Yは,式(12)を用いて決定する。
667
.0
3
1
choked
sizing=
−
=
x
x
Y
式(7)を変形してKvを求める。
h/
m
6.
62
3
v
sizing
1
1
1
P
9
s
v
=
=
=
K
x
Z
MT
Y
p
F
N
Q
K
C
実体積流量を求める。
h
/
m
4.
895
3
1
1
1
s
s
s
s
=
=
p
T
Z
T
Z
p
Q
Q
次に,式(23)によってバルブレイノルズ数Revを計算して,流れが乱流であることを確認する。
6
4
/1
4
2
2
2
L
L
d
4
v
10
45
.1
1
×
=
+
=
d
N
C
F
F
C
v
Q
F
N
Re
ここで, Rev≧10 000であり,流れは乱流となる。
結果がこの規格の適用範囲内であることを確認する。
047
.0
3
007
.0
2
18
<
=
d
N
C
E.5
例題5:非圧縮性流体−継手を接続する場合の閉塞流れ
E.5.1 プロセス データ:
流体
: 特に想定せず
密度
: ρ1 =780 kg/m3
蒸気圧
: pv =4 kPa
熱力学的臨界圧力
: pc =22 120 kPa
入口絶対圧力
: p1 =3 550 kPa
出口絶対圧力
: p2 =1 310 kPa(Δp=2 240 kPa)
流量
: Q =750 m3/h
39
B 2005-2-1:2019 (IEC 60534-2-1:2011)
上流配管の内径
: D1 =154.1 mm
下流配管の内径
: D2 =202.7 mm
E.5.2 バルブ データ:
バルブ形式
: バタフライ
呼び径
: d=101.6 mm
流量係数データ
:
回転角
0
10
20
30
40
50
60
70
80
90
Cv
0
17.2
50.2
87.8
146
206
285
365
465
521
FL
0.85a)
0.85
0.84
0.79
0.75
0.71
0.63
0.58
0.56
0.54
注a) 0度〜10度の間では,計算の便宜上FL値は固定した。
E.5.3 計算:
次の計算は,C.2の反復計算法に基づいている。流れ解析の方程式は,構成する変数の直前回の数値を
基に計算した結果を用いて表される。
定数:
次の変数及び項は一定か,又は上記の条件下では一定のままである。
N1
=0.086 5
N2
=0.002 14
N18
=1.00
式(4)を用いて:
956
.0
28
.0
96
.0
c
v
F
=
−
=
p
p
F
式(18)を用いて:
160
.0
1
0.5
2
2
1
1
=
−
=
D
d
ζ
式(19)を用いて:
561
.0
1
2
2
2
2
=
−
=
D
d
ζ
式(17)を用いて:
811
.0
1
4
1
B1
=
−
=
D
d
ζ
式(17)を用いて:
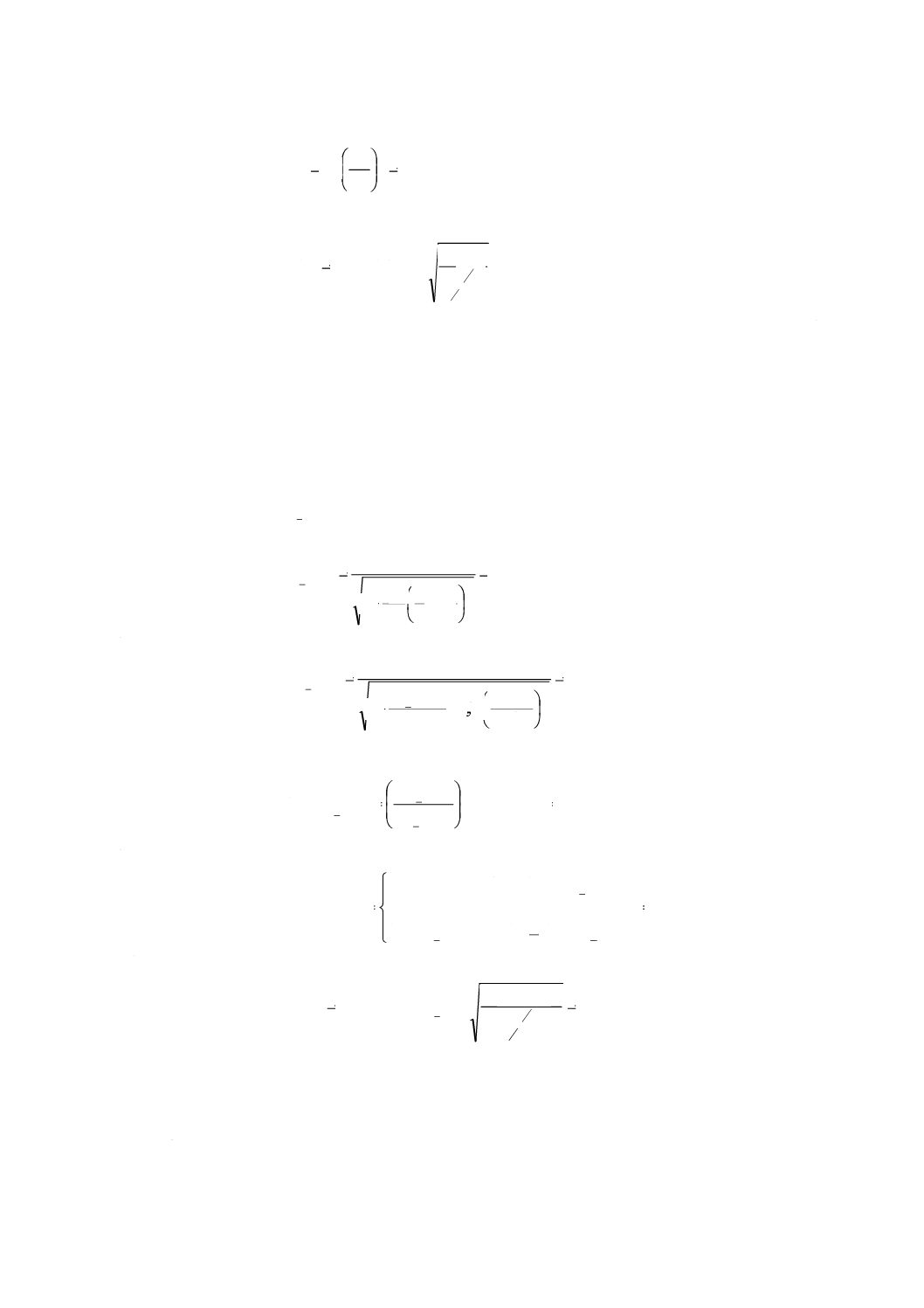
40
B 2005-2-1:2019 (IEC 60534-2-1:2011)
937
.0
1
4
2
B2
=
−
=
D
d
ζ
ステップ1:式(C.2)によって流量関数を定義:
0
1
sizing
P
1
)
(
750
)
(
ρ
ρ
p
F
N
C
C
F
∆
−
=
この関数の根Cは,与えられた引数に対する解に相当する。FP及びΔpsizingの値は,それぞれの反復計算
によって変わるので留意する。
ステップ2:C.2.3による流量区間下限の設定:
下限の設定:
CLower=0
バルブデータから:
FL̲Lower=0.85
式(15)を用いて:
0.1
1
1
2
2
Lower
2
P̲Lower
=
Σ
+
=
d
C
N
F
ζ
式(21)を用いて:
(
)
85
.0
1
1
2
2
Lower
1
2
2
L̲Lower
LP̲Lower
=
Σ
+
=
d
C
N
F
F
ζ
式(3)を用いて:
(
)
418
2
v
F
1
2
P̲Lower
LP̲Lower
̲Lower
choked
=
−
=
∆
p
F
p
F
F
p
式(2)を用いて:
=
∆
∆
∆
∆
∆
∆
=
∆
240
2
er
choked̲Low
er
choked̲Low
er
choked̲Low
er
sizing̲Low
p
p
if
p
p
p
if
p
p
≧
<
ゆえに,FLowerは
750
0
1
er
sizing̲Low
P̲Lower
1
Lower
Lower
=
∆
−
=
ρ
ρ
p
F
N
C
Q
F
ステップ3:C.2.4による流量区間上限値の設定
上限の設定:
CUpper=0.075d2N18=774.192
バルブデータから:
FL̲Upper=0.54
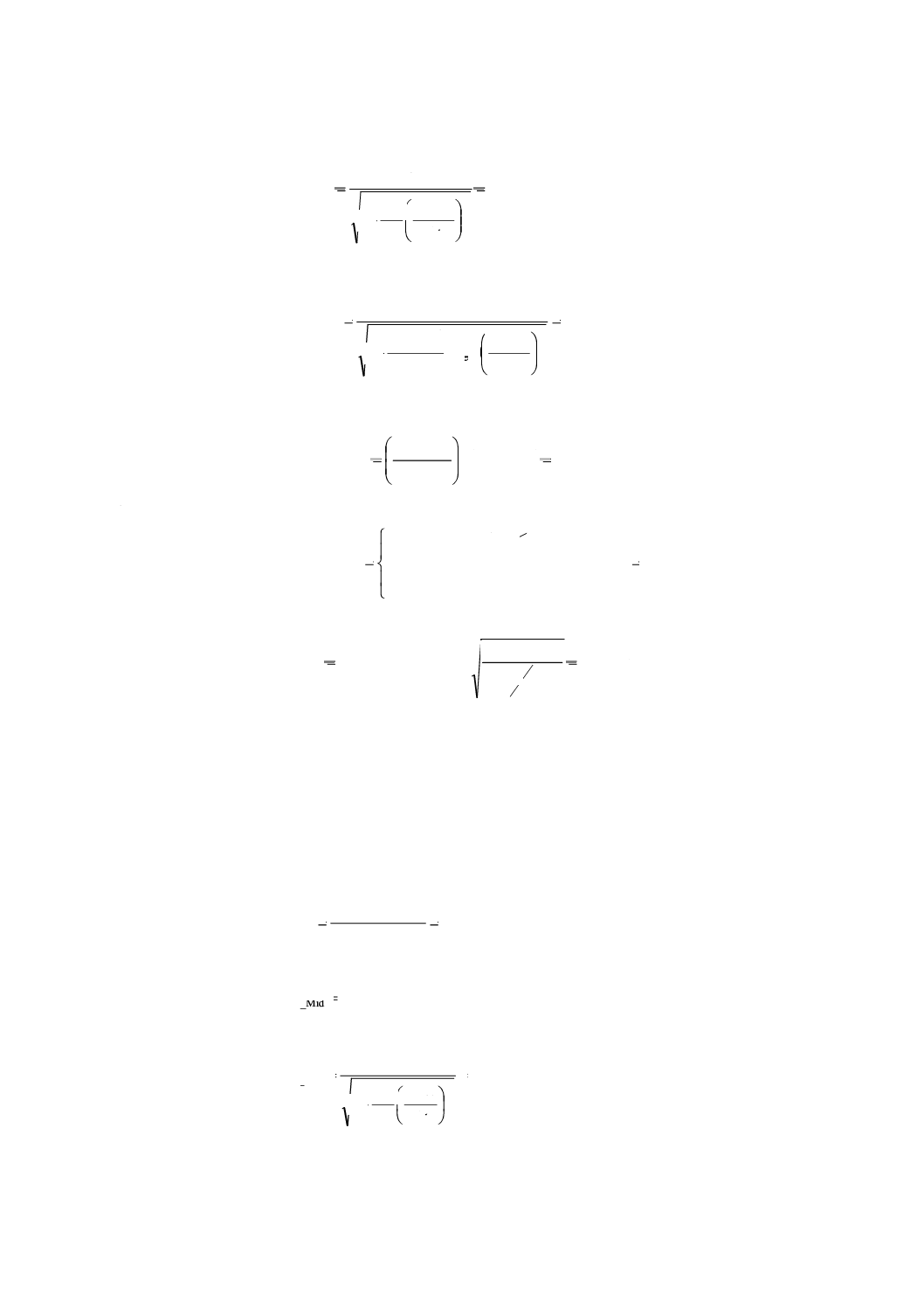
41
B 2005-2-1:2019 (IEC 60534-2-1:2011)
式(15)を用いて:
625
.0
1
1
2
2
Upper
2
p̲Upper
=
Σ
+
=
d
C
N
F
ζ
式(21)を用いて:
(
)
409
.0
1
2
2
Upper
1
2
2
L̲Upper
L̲Upper
LP̲Upper
=
Σ
+
=
d
C
N
F
F
F
ζ
式(3)を用いて:
(
)
520
1
v
F
1
2
P̲Upper
LP̲Upper
̲Upper
choked
=
−
=
∆
p
F
p
F
F
p
式(2)を用いて:
=
∆
∆
∆
∆
∆
∆
=
∆
520
1
er
choked̲Upp
er
choked̲Upp
er
choked̲Upp
er
sizing̲Upp
p
p
if
p
p
p
if
p
p
≧
<
関数:
3
0
1
er
sizing̲Upp
P̲Upper
1
Upper
Upper
10
096
.1
×
−
=
∆
−
=
ρ
ρ
p
F
N
C
Q
F
ステップ4:この区間にC.2.5による解が含まれることの確認
FUpper=−1.096×103
FLower=750
FUpper及びFLowerは,異符号であるため,選択された区間限界値は問題への解決策となる。
ステップ5:区間の中間点及び関係する値の計算
中間値の計算:
096
.
387
2
Lower
Upper
Mid
=
+
=
C
C
C
バルブデータから:
576
.0
L̲Mid=
F
式(15)を用いて:
848
.0
1
1
2
2
Mid
2
p̲Mid
=
Σ
+
=
d
C
N
F
ζ
式(21)を用いて:
42
B 2005-2-1:2019 (IEC 60534-2-1:2011)
(
)
523
.0
1
2
2
Mid
1
2
2
L̲Mid
L̲Mid
LP̲Mid
=
Σ
+
=
d
C
N
F
F
F
ζ
式(3)を用いて:
(
)
349
1
v
F
1
2
P̲Mid
LP̲Mid
̲Mid
choked
=
−
=
∆
p
F
p
F
F
p
式(2)を用いて:
=
∆
∆
∆
∆
∆
∆
=
∆
349
1
choked̲Mid
choked̲Mid
choked̲Mid
sizing̲Mid
p
p
if
p
p
p
if
p
p
≧
<
関数:
7.
430
0
1
sizing̲Mid
P̲Mid
1
Mid
Mid
−
=
∆
−
=
ρ
ρ
p
F
N
C
Q
F
ステップ6:区間の設定をC.2.6によって修正する(収束条件を満たすまで反復計算を行う。)。
FUpper=−1.096×103
FMid=−430.7
FLower=750
上限及び中間の関数は,値同符号であるので,区間の上限値は,区間の中間値と同じ値を設定し,関連
する項目に当てはめる。
CUpper=CMid=387.096
FL̲Upper=FL̲Mid=0.576
FP̲Upper=FP̲Mid=0.848
FLP̲Upper=FLP̲Mid=0.523
Δpchoked̲Upper=Δpchoked̲Mid=1 349
Δpsizing̲Upper=Δpsizing̲Mid=1 349
FUpper=FMid=−430.7
収束解が得られるまでステップ5及びステップ6を繰り返す。
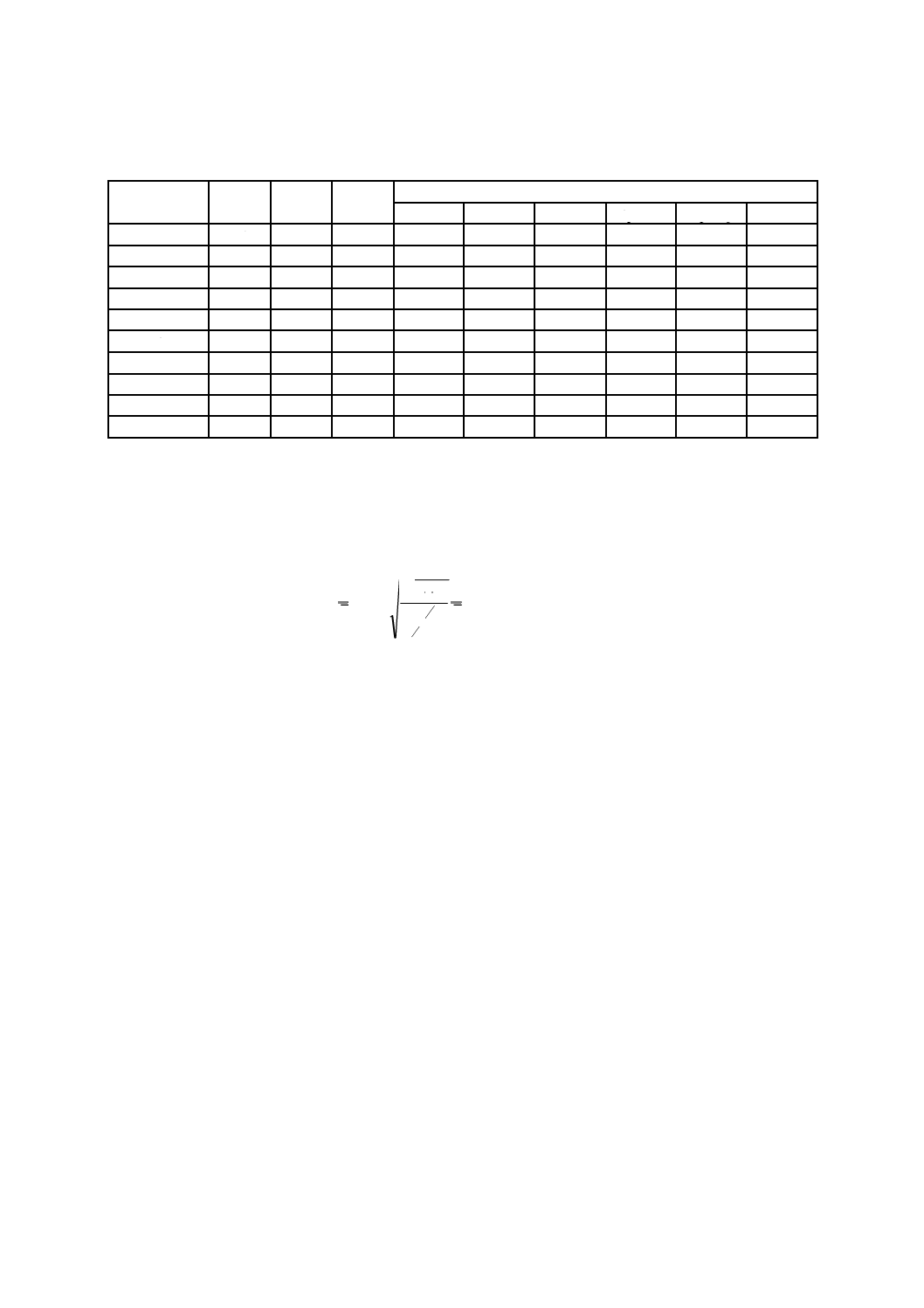
43
B 2005-2-1:2019 (IEC 60534-2-1:2011)
繰返し計算の概要:
繰返し数
CLower
CMid
CUpper
中間値
FL
Fp
FLP
Δpchoked
Δpsizing
FMid
1
0
387
774
0.576
0.848
0.523
1 349
1 349
−431
2
0
194
387
0.718
0.954
0.690
1 856
1 856
−29.4
3
0
96.8
194
0.784
0.988
0.774
2 179
2 179
313
4
96.8
145
194
0.751
0.974
0.732
2 006
2 006
130
5
130
169
194
0.734
0.965
0.711
1 929
1 929
47.3
6
169
181
194
0.726
0.960
0.701
1 892
1 892
8.23
7
181
188
194
0.722
0.957
0.696
1 874
1 874
−10.8
8
181
184
188
0.724
0.958
0.698
1 883
1 883
−1.32
9
181
183
184
0.725
0.959
0.700
1 887
1 887
3.44
10
183
183.7
184
0.725
0.959
0.699
1 885
1 885
1.06
最終値:C=183.7
ステップ7:解の確認:
容量係数の計算値を用いて予測流量を計算し,与えられた流量と比較する。
749
0
1
sizing
1
predicted
=
∆
=
ρ
ρ
p
F
CN
Q
予測流量は,設定した流量750 m3/hと同等である。
44
B 2005-2-1:2019 (IEC 60534-2-1:2011)
参考文献
[1] BAUMANN, H.D., A Unifying Method for Sizing Throttling Valves Under Laminar or Transitional Flow
Conditions, Journal of Fluids Engineering, Vol. 115, No. 1, March 1993, pp.166-168.
[2] BAUMANN, H.D. Effect of Pipe Reducers on Control Valve Sizing, Instruments and Control Systems,
December 1968, pp 99-102.
[3] STILES, G.F. Liquid Viscosity Effects on Control Valve Sizing, Technical Manual TM 17A,October 1967,
Fisher Governor Co., Marshalltown.
[4] BAUMANN, H.D. Whatʼs New in Valve Sizing, Chemical Engineering, June 1996.
[5] BOGER, H.W. Recent Trends in Sizing Control Valves, Instruments and Control Systems,1991, pp 117-121.
[6] SINGLETON, E.W. Adapting Single Stage Sizing Standards for Multistage Control Valves,Intech, August 1997.
[7] SINGLETON, E.W. The Calculation of the Expansion Factor “Y” for Multistage Control Valves,Valve World,
Vol 6, Issue 2, April 2001.
[8] BOGER, H.W. The Control Valve Body−a Variable Flow Restrictor, ISA Preprint No 11, 11-2-66.
[9] BAUMANN, H.D. The Introduction of a Critical Flow Factor for Valve Sizing, ISA Transactions,Vol 2, pp
107-111.

























