2
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a)
b)
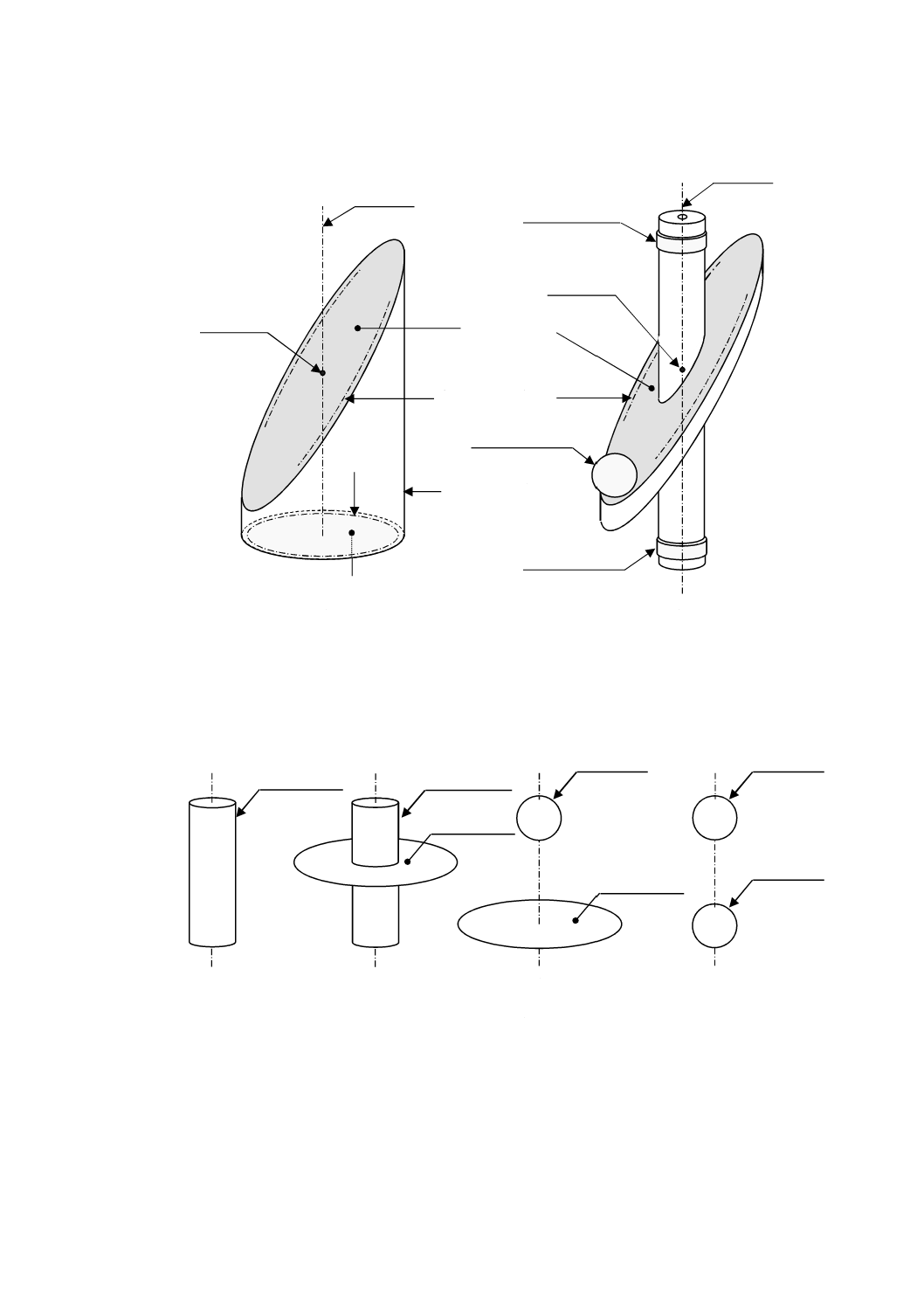
図1−平面基準器の例
図2−基準軸の定義
測定用平面
基準軸用円筒
基準軸用円筒
原点参照用球
測定円
歯すじ測定箇所
基準軸
基準軸
座標原点
座標原点
基準軸用円筒
原点参照用平面
a)
b)
c)
d)
軸心用球
軸心用球
軸心用球
データム面
データム面
軸心用円筒
軸心用円筒
B 1757-3:2013
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
4 記号······························································································································· 7
5 測定······························································································································· 8
5.1 測定環境 ······················································································································ 8
5.2 基準器 ························································································································· 8
5.3 測定子先端形状 ············································································································· 8
5.4 諸元の設定 ··················································································································· 8
5.5 基準器の取付け ············································································································· 8
5.6 平面基準器原点の設定 ··································································································· 11
5.7 測定子位置の初期設定 ··································································································· 11
5.8 検出器の押込み量の設定 ································································································ 11
5.9 測定子の測定開始位置への移動 ······················································································· 13
5.10 歯すじ測定の実施 ········································································································ 13
6 評価······························································································································ 15
6.1 理論曲線の計算 ············································································································ 15
6.2 実測曲線の導出 ············································································································ 16
6.3 精度評価対象範囲 ········································································································· 17
6.4 偏差曲線の計算 ············································································································ 17
6.5 評価項目 ····················································································································· 18
附属書A(参考)平面基準器の設計 ························································································ 19
附属書B(参考)取付け誤差を考慮した形状偏差の計算方法 ························································ 23
附属書C(参考)S字曲線に影響を及ぼす主要な要因 ································································· 30
附属書D(参考)形状偏差の実測例 ························································································ 38
参考文献 ···························································································································· 40
B 1757-3:2013
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,社団法人日本歯車工業会(JGMA),独立行
政法人産業技術総合研究所(AIST)及び一般財団法人日本規格協会(JSA)から,工業標準原案を具して
日本工業規格を制定すべきとの申出があり,日本工業標準調査会の審議を経て,経済産業大臣が制定した
日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
JIS B 1757の規格群には,次に示す部編成がある。
JIS B 1757-1 第1部:歯車形の基準器を用いる方法
JIS B 1757-2 第2部:球基準器又は円筒基準器を用いた歯形測定
JIS B 1757-3 第3部:平面基準器を用いた歯すじ測定
JIS B 1757-4 第4部:球基準器を用いたピッチ測定
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 1757-3:2013
歯車測定機の評価方法−第3部:
平面基準器を用いた歯すじ測定
Evaluation of instruments for the measurement of individual gears-
Part 3: Helix measurement using plane artifacts
1
適用範囲
この規格は,インボリュート円筒歯車の歯すじ精度を検査する測定機の歯すじ測定の精度を,平面基準
器を用いて評価する方法について規定する。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。この引用
規格は,その最新版(追補を含む。)を適用する。
JIS B 0102 歯車用語−幾何学的定義
3
用語及び定義
この規格で用いる主な用語及び定義は,JIS B 0102によるほか,次による。
3.1
平面基準器
平面を歯車の歯面とみなして歯すじ形状を測定することによって,その測定機の歯すじ測定の精度を評
価するための基準器(図1参照)。基準軸と一定の角度をなす測定用平面,及び原点参照用基準によって
構成する。
平面基準器の設計方法については,附属書Aを参照。
3.2
基準軸
平面基準器の基準軸であって,次の四つのいずれかで定義する軸(図2参照)。
a) 軸心用円筒の中心軸
b) データム面に垂直な軸で,その軸と直角な円筒のある断面円の中心を通る軸
c) 軸心用球の中心を通りデータム面に垂直な軸
d) 二つの軸心用球の中心を通る軸

2
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a)
b)
図1−平面基準器の例
図2−基準軸の定義
測定用平面
基準軸用円筒
基準軸用円筒
原点参照用球
測定円
歯すじ測定箇所
基準軸
基準軸
座標原点
座標原点
基準軸用円筒
原点参照用平面
a)
b)
c)
d)
軸心用球
軸心用球
軸心用球
データム面
データム面
軸心用円筒
軸心用円筒
3
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.3
測定用平面
平面基準器の基準軸と一定の角度をなす平面で,歯すじ測定を行う平面。
3.4
原点参照用基準
平面基準器の座標原点の基準軸方向位置を決定するためのもので,平面基準器に固定されているもの。
被評価装置の測定子を用いて測定できるもの。図1 a)の例では,平面を原点参照用基準としている。図
1 b)の例では,球を原点参照用基準としている。
3.5
平面基準器の座標系
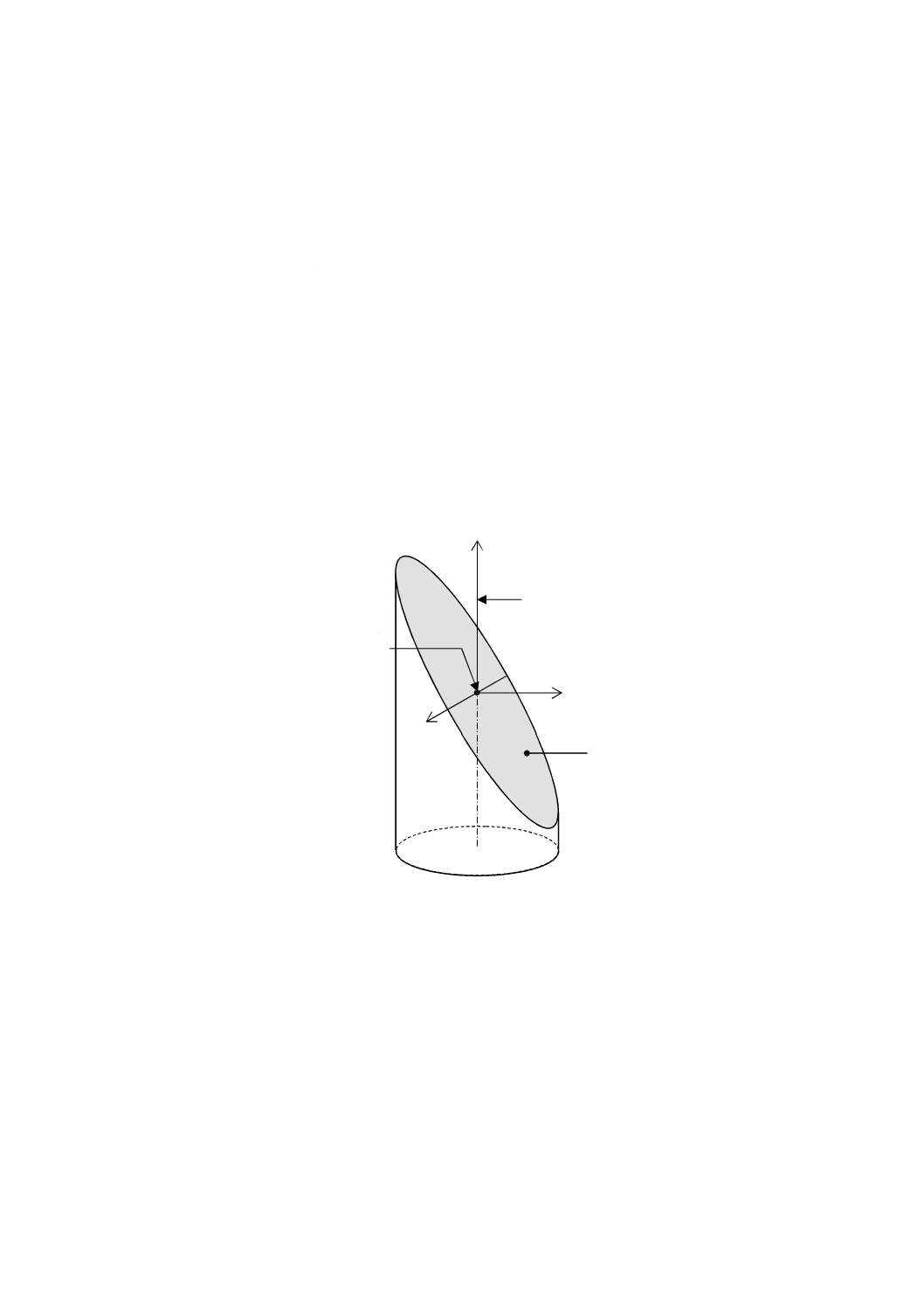
基準軸をζ軸とするξ,η及びζ の三つの軸をもつ右手直交座標系(図3参照)。
座標原点は,測定用平面と基準軸との交点とする。ξ軸は,測定用平面上に置く。+η軸方向は,測定用
平面の実体側から空間側に向かう方向とする。+ζ軸方向は,測定用平面の実体側から空間側に向かう方
向とする。
図3−平面基準器の座標系
3.6
被評価装置の測定座標系
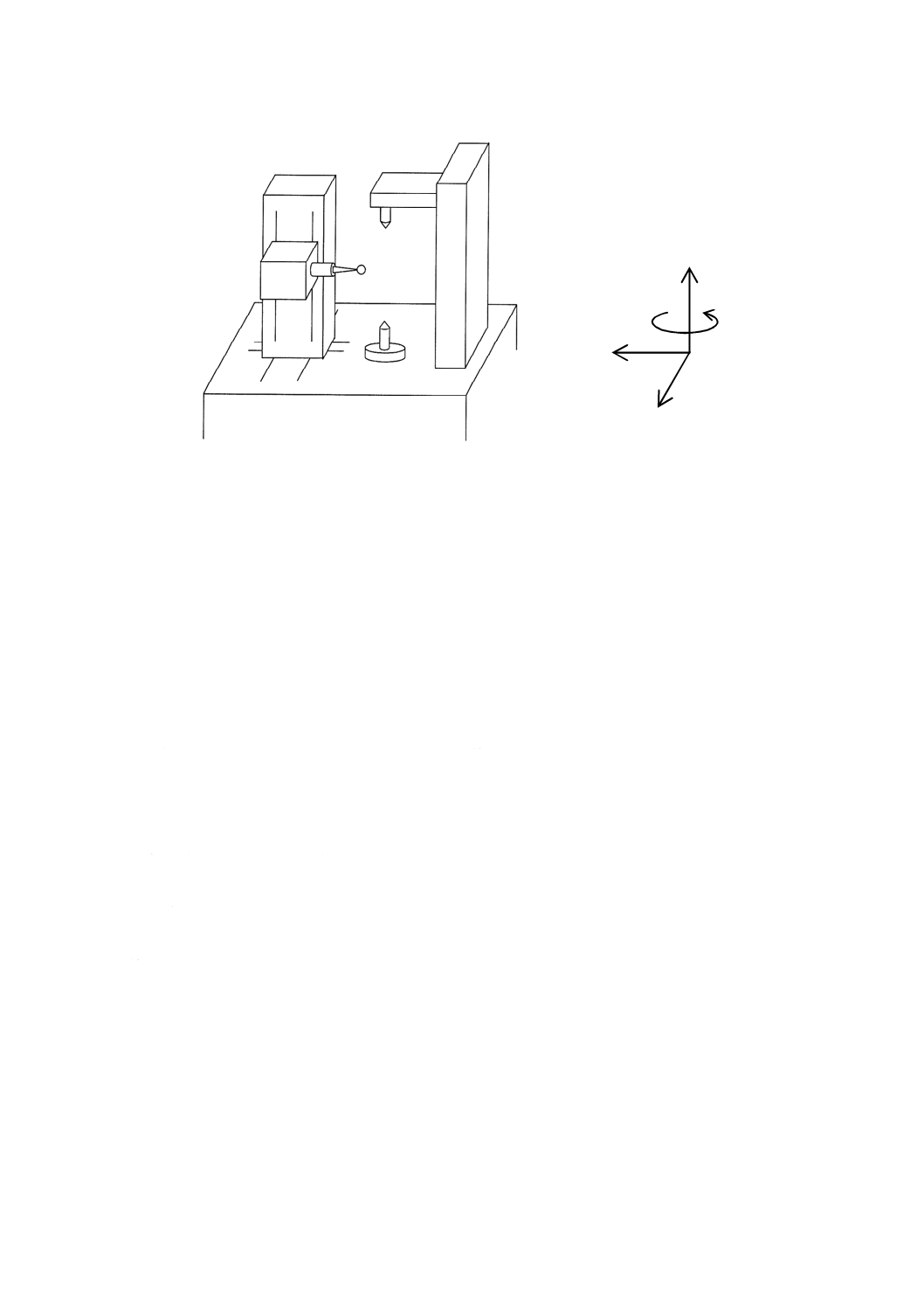
歯車の回転軸をZ軸とするX,Y及びZの三つの軸をもつ右手直交座標系(図4参照)。
平面基準器の基準軸(ζ軸)と被評価装置の回転軸(Z軸)とが一致するように平面基準器を被評価装
置に取り付けたとき,平面基準器の座標原点を,測定座標系の座標原点とする。
+X軸は,Z軸から測定子の側にとる。Y軸は基礎円接線(作用線ともいう。)に平行で,+Y軸の方向
は右手直交座標系の方向に従うものとする。+Z軸の方向は,鉛直上方とする。回転角θ の正の向きは,Z
軸の正の方向に右ねじが進む方向とする。
測定用平面
ξ
η
ζ
基準軸
座標原点
4
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図4−被評価装置の測定座標系
3.7
測定円
測定機の回転軸(Z軸)を中心とするZ軸に直角な面上の円で,歯すじ測定対象の点をZ軸方向に投影
した点が含まれる円(図8,図9,図10及び図11参照)。
3.8
原点断面
平面基準器の座標原点を通り,Z軸に直角な断面。
3.9
仮想インボリュートヘリコイド
測定対象とする歯車の基礎円筒に接する平面上の直線で創成される仮想のインボリュートヘリコイド。
3.10
仮想インボリュート歯形
仮想インボリュートへリコイドを,測定子先端球の中心を通りZ軸に直角な面で切断したときの切り口
が描く歯形(図8及び図11参照)。
3.11
仮想インボリュート歯形と平面との形状偏差
測定子先端球の中心を通りZ軸に直角な面において,仮想インボリュート歯形と測定子先端球表面との
作用線方向偏差(δH)。この規格では,単に“形状偏差”とも呼ぶ。形状偏差の符号は,測定子先端が測定
用平面の空間側に向かう方向を正とする(図11参照)。
3.12
歯幅方向位置
測定子先端球中心のZ軸方向位置。原点断面において,歯幅方向位置をゼロとする。
3.13
初期設定
平面基準器の測定開始に先立って,測定子先端球中心の座標を設定すること。
+Y
+Z
+X
+θ
+θ
5
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.14
S字曲線
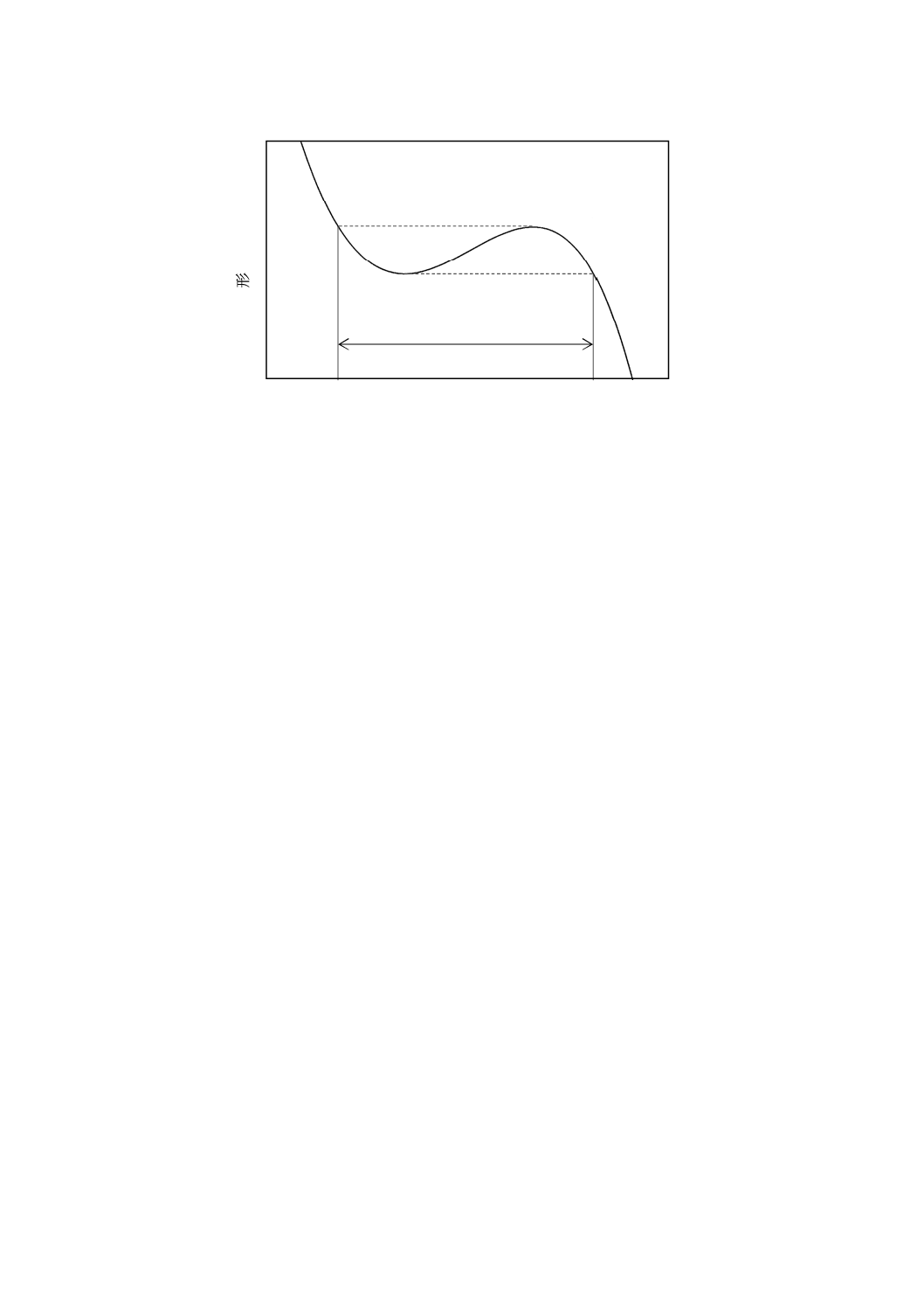
測定子先端球中心の歯幅方向位置を横軸とし,その位置における形状偏差を縦軸として描いた曲線(図
5参照)。
3.15
理論曲線
測定対象とする歯車の諸元,測定用平面と基準軸とのなす角度,測定子先端球半径,及び測定子先端球
の歯幅方向位置から計算で求めたS字曲線。
3.16
実測曲線
測定した測定子先端球の歯幅方向位置と,その歯幅方向位置における形状偏差の実測値とから求めたS
字曲線。
3.17
フィッティング
実測曲線と理論曲線とを重ね合わせて比較すること。
3.18
偏差曲線
実測曲線と理論曲線とを重ね合わせ,実測曲線の形状偏差と理論曲線の形状偏差との差を,歯幅方向位
置を横軸としてグラフに表したもの。
3.19
精度評価対象範囲
歯すじ測定の精度を評価する平面基準器の,Z軸方向の範囲(図5及び図14参照)。
3.20
全歯すじ測定誤差
精度評価対象範囲で,偏差曲線の縦軸の最大値と最小値との差(fβ1)。歯車の全歯すじ誤差の許容値(Fβ)
に相当する(図14参照)。
3.21
歯すじ傾斜測定誤差
偏差曲線を直線近似したとき,その直線の精度評価対象範囲の両端における上下の差(fβ2)。歯車の歯す
じ傾斜測定誤差の許容値(fHβ)に相当する(図14参照)。
3.22
平均曲線
偏差曲線の輪郭を,2次式,3次式,4次式などで表した曲線(図14参照)。
3.23
高次歯すじ測定誤差
精度評価対象範囲で,偏差曲線を挟むように平均曲線を上下に平行移動して得られる二つの曲線の縦軸
の差(fβ3)(図14参照)。
6
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図5−S字曲線の例
歯幅方向位置
形
状
偏
差
δ
H
Zmin
Zmax
Le(精度評価対象範囲)
7
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
記号
この規格で用いる主な記号は,表1による。
表1−記号
記号
記号の意味
e1,e2
基準軸を定義した2か所における,Z軸に対するζ軸の偏心量
eh
基準軸を定義した平面の,Z軸方向の振れの片振幅
fβ1
精度評価対象範囲における偏差曲線の,縦軸の最大値と最小値との差
fβ2
歯すじ偏差曲線を直線近似したときの,直線の上下端の差
fβ3
精度評価対象範囲で,偏差曲線を挟むように平均曲線を上下に平行移動して得られる二つの曲線
の,縦軸の差
c
S字曲線の谷と頂点に関連した指数で式(17)で表現されるもの
Le
精度評価対象範囲
mn
歯直角モジュール
mt
正面モジュール
O
平面基準器の座標原点
r
測定円半径
rb
インボリュート基礎円半径
rp
測定子先端球の半径
Rh
基準軸を定義した平面の,振れ測定点の半径
X
被評価装置の測定座標系の軸
Y
被評価装置の測定座標系の軸
Y'
Y軸に平行で,歯車の基礎円に接する軸(作用線)
Y0
原点断面において,歯車の基礎円とX軸との交点から,測定子先端球中心までの作用線上の距離
Z
歯数
Z
被評価装置の測定座標系の軸(歯車の回転軸)
Zmin
精度評価対象範囲における歯幅方向位置の最小値
Zmax
精度評価対象範囲における歯幅方向位置の最大値
Zw
歯すじ測定時の,測定子先端球中心と原点断面とのZ軸方向の距離
αn
歯直角圧力角
αt
正面圧力角
Β
測定円筒上ねじれ角
βb
基礎円筒上ねじれ角
δH
形状偏差で,仮想インボリュート歯形と測定子先端球表面との作用線方向偏差
ε0
初期設定状態での,平面基準器のZ軸回りの回転角
ε0'
右ねじれの測定の際の初期設定状態を表現するための,平面基準器のZ軸回りの回転角に相当する
量
εm
歯すじ測定時の,平面基準器のZ軸回りの回転角
Ζ
平面基準器座標系の軸で基準軸と一致
Η
平面基準器座標系の軸
η0
平面基準器の初期設定において,平面基準器の座標原点から測定子先端球中心までの距離で,η軸
方向の距離
ηm
測定子先端球中心が初期設定時からZ軸方向にZwだけ移動したとき,平面基準器の座標原点から
測定子先端球中心までの距離の,η軸方向成分
θ
Z軸回りの回転角
ξ
平面基準器座標系の軸で,測定用平面上の軸
Ω
平面基準器の測定用平面と基準軸とのなす角度
8
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5
測定
5.1
測定環境
被評価装置を,測定機製造業者が精度保証する環境(温度,振動など)下に置く。この被評価装置に平
面基準器を設置し,被評価装置及び平面基準器が環境に十分順応した後,測定を行う。
5.2
基準器
基準軸の定義を明確にする。基準軸の定義に円筒又は球を用いる場合,その円筒又は球の測定断面にお
ける真円度を校正する。基準軸の定義に平面を用いる場合,その測定面の平面度を校正する。これら校正
箇所は,明記しなければならない。その精度が測定精度に影響を及ぼすので,基準軸を定義した円筒,球
及び平面は,被評価装置の評価に適した高精度なものが望ましい。
測定用平面については,その平面度,及び平面と基準軸とのなす角度を校正する。歯すじの測定箇所は
平面基準器の外周に近いので,その外周端部近くまで校正する必要がある。測定用平面は,その精度が測
定精度に直接影響を及ぼすので,被評価装置の評価に適した高精度なものが望ましい。
基準器原点については,平面基準器の座標原点と原点参照用基準との,基準軸上の距離を校正する。原
点参照用基準の校正箇所は,明記しなければならない。
全ての校正は,国家計量標準へのトレーサビリティを確保しなければならない。平面基準器を校正した
ときの温度と,被評価装置での測定したときの温度とが異なる場合は,校正値を,測定したときの温度に
補正してもよいし,測定値を,校正したときの温度に補正してもよい。
平面基準器の設計に関しては,附属書Aを参照。
5.3
測定子先端形状
平面基準器を測定する測定子先端は球状とし,その半径を記録する。測定子先端は,その精度が測定精
度に直接影響を及ぼすので,高精度なものでなければならない。摩耗によって球の形状が変化することが
あるので注意を要する。そろばん玉形状の測定子は,歯車の測定に使用してもよいが,平面基準器の測定
に使用してはならない。測定子先端球の大きさが歯すじ測定結果に及ぼす影響については,附属書Cを参
照。
5.4
諸元の設定
仮想インボリュート歯形と平面との形状偏差を描いた理論曲線が,一つの谷と一つの頂点とをもつよう
に基準器の諸元及び歯車諸元を設定する。このとき,式(17)のc>0が成立するように諸元を設定しなけれ
ばならない(図5,箇条6及び附属書Aを参照)。測定者は,測定円の大きさを任意に定めることができる
が,設定した測定円の大きさを明確にしなければならない。
5.5
基準器の取付け
5.5.1
一般事項
平面基準器の基準軸(ζ軸)が被評価装置の回転軸(Z軸)と一致するように,平面基準器を被評価装
置に設置する。
回転軸に対する基準軸の取付け誤差は,被評価装置の精度評価に大きな影響を与えるので,取付け誤差
をできるだけ小さくすることが望ましい。基準軸の取付け誤差の扱い方には,次の二つの方法がある。
a) 基準軸の取付け誤差の影響を,被評価装置の評価に含める。
b) 基準軸の取付け誤差から計算して,平面基準器の測定データを補正する(附属書B参照)。
この規格は,a)の場合について規定する。
5.5.2
両センタ支持
平面基準器が両センタ支持構造の場合,基準器の取付けは容易である。しかし,両センタを結ぶ軸を基
9
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
準軸として測定すると,測定不確かさ要因が多くなるので注意を要する。
5.5.3
センタなし
基準軸を,被評価装置の回転軸に近づけることが可能である。必要ならば取付けジグを用いる。基準軸
の偏心量をソフトウェアで補正するシステムの測定機では,仮想的に取付け誤差ゼロとすることも可能で
ある。
5.5.4
取付け誤差の測定
この規格では,基準軸の取付け誤差による仮想インボリュート歯形と平面との形状偏差の変化量が,対
象とする歯車の全歯すじ誤差の許容値(Fβ)を超えないように,基準軸を取り付ける方法を示す。
基準軸の定義によって,次のような方法がある。
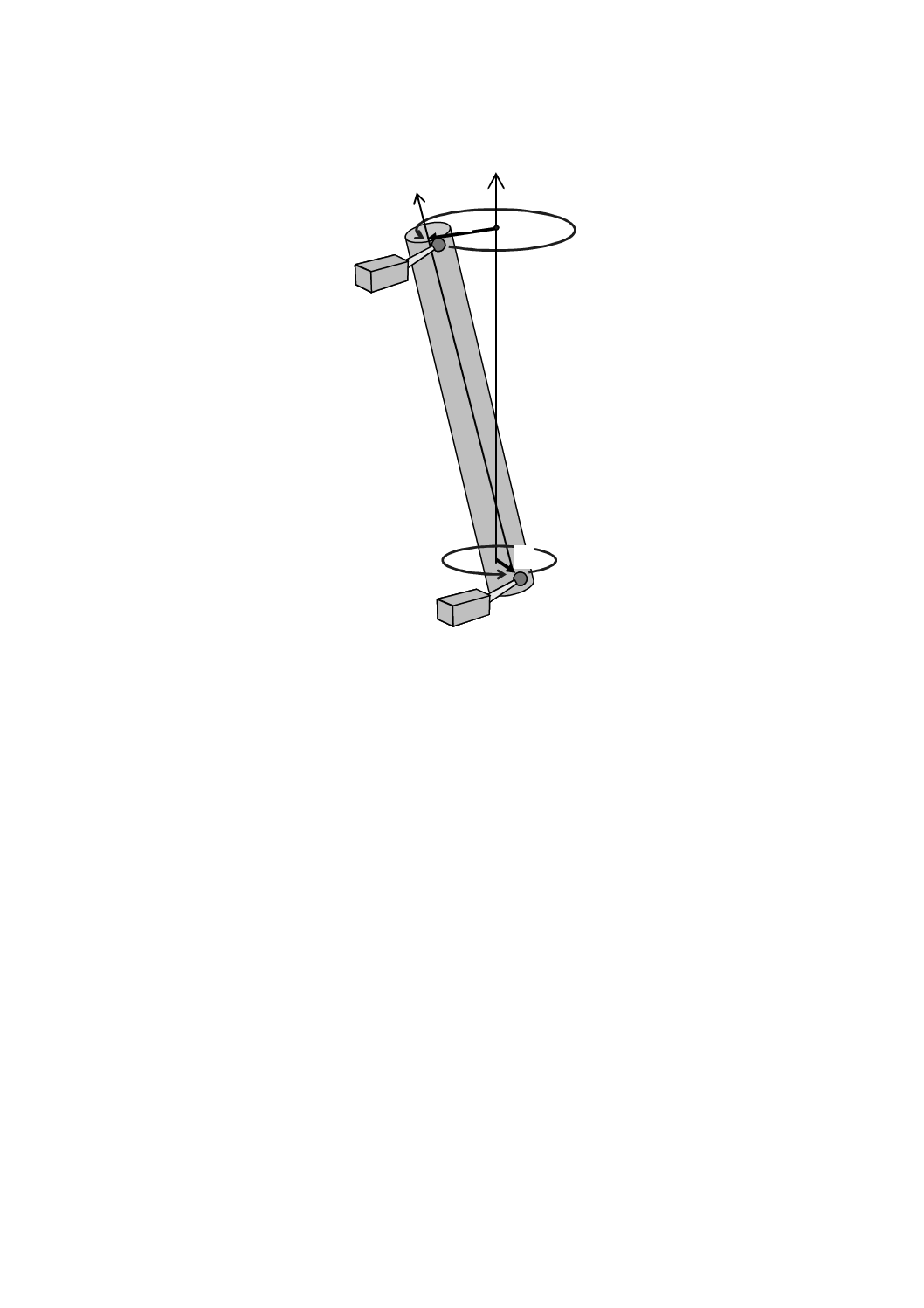
a) 円筒,又は球と球とで基準軸を定義した場合,基準軸を定義した軸方向2か所で,基準軸の偏心量を
測定する(図6参照)。測定する2か所のZ軸方向距離は,精度評価対象範囲と同程度又はそれ以上
とする。測定した2か所の偏心量をe1,e2として,式(1)が成り立つように取付け調整を行う。
なお,偏心量は,振れの最大値と最小値との差の1/2である。
t
2
β
2
1
cos
cos
)
(
α
Ω
F
e
e
<
+
·························································· (1)
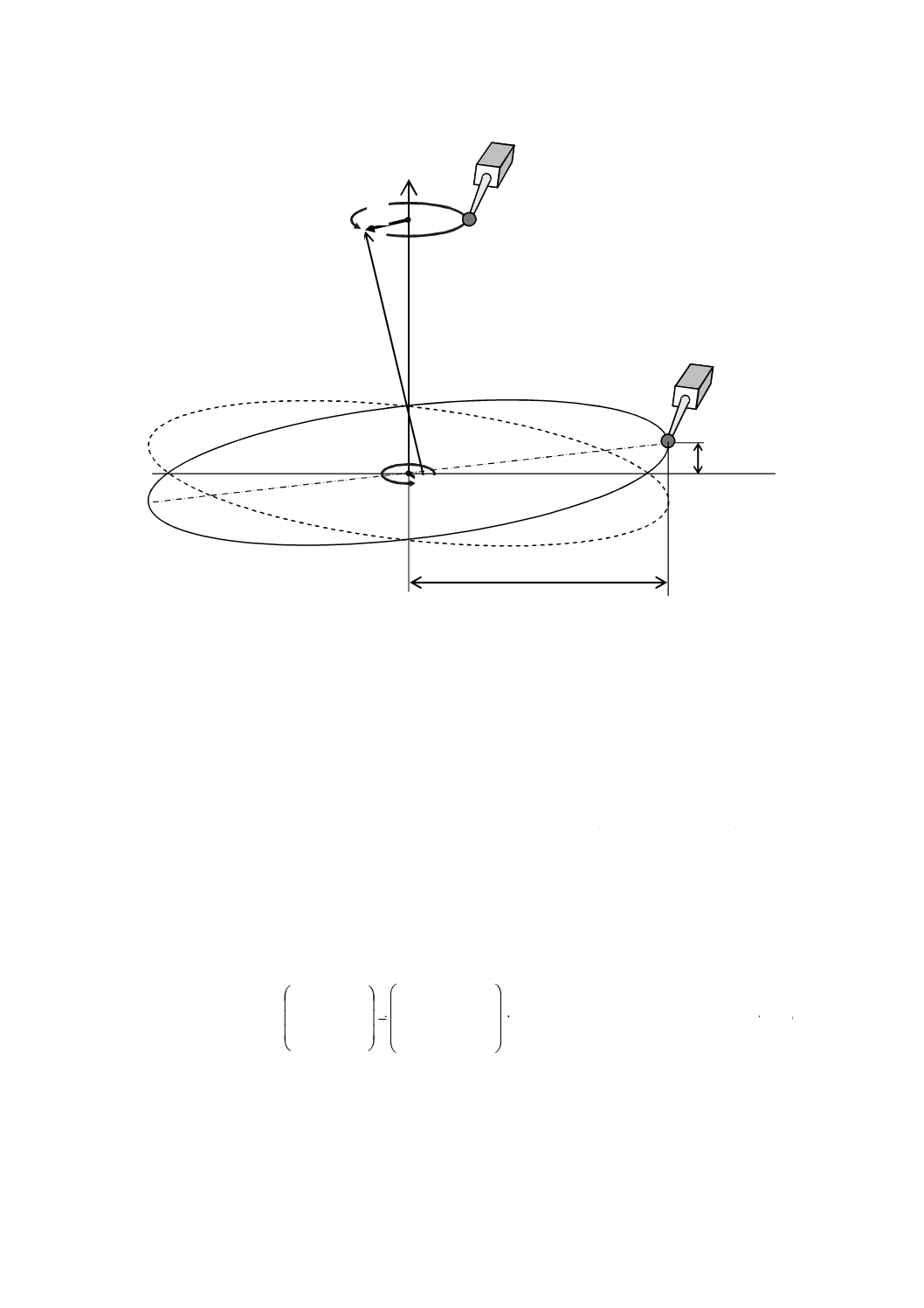
b) 球と平面とで基準軸を定義した場合,基準軸を定義した平面の振れ及び球の偏心を測定する(図7参
照)。
平面の測定において,測定点の半径の大きさは,精度評価対象範囲の大きさと同程度又はそれ以上
とする。平面の測定点の振れの片振幅をehとして,式(2)が成り立つように取付け調整を行う。片振幅
は,振れの最大値と最小値との差の1/2である。これによって,基準軸の傾きを調整することができ
る。
球の測定においては,偏心量をe1とすると,式(3)が成り立つように取付け調整を行う。
t
2
β
h
cos
cos
α
Ω
F
e<
·································································· (2)
β
1
F
e≦
··················································································· (3)
測定対象とする歯車の大きさは,測定円の直径を基準円直径とし,平面基準器の精度評価対象範囲を歯
幅とする。
具体例について計算すると,Ω=30°,r=55 mm,β=29.85°,αn=20°,αt=22.765 1°の場合,精度
評価対象範囲は約40 mmであり,0級の歯車はFβ=1.6 μmとなる。したがって,Fβ cos2Ω cosαt=1.1 μmで
あり,0級の歯車を評価するならば,40 mm以上離れた2か所の点のζ軸の偏心量の和が,(e1+e2)<1.1
μmとなるように,又は半径40 mm以上の点における平面の片振幅がeh<1.1 μmとなり,基準軸を定義し
た球の偏心がe1<1.6 μmとなるように,平面基準器を取り付けるとよい。
全歯すじ誤差の1/10の精度を要求するならば,上記の値の1/10の取付け精度が必要となる。
10
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図6−基準軸を円筒で定義した2か所の偏心量の測定
Z
e1
ζ
e2
11
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図7−基準軸を定義した平面の振れの測定
5.6
平面基準器原点の設定
被評価装置の測定子を用いて原点参照用基準の校正された基準軸方向位置を測定し,その測定位置から
計算して,平面基準器の座標原点位置を設定する。原点参照用基準と平面基準器の座標原点との基準軸方
向距離は,校正値を用いる。
5.7
測定子位置の初期設定
測定子先端球が,原点断面上の仮想インボリュート歯形と接触するようにする。そのために,測定子先
端球の中心を,式(4)の測定座標位置に移動する(図8参照)。ただし,複号は,(+)が左歯面の測定に,
(−)が右歯面の測定に対応する。
なお,測定子の位置は,測定圧がかかった状態での座標位置とする。正面圧力角αtは,図8のように正
の値が普通であるが,図9のように負の値にすることもできる。
右ねじれの歯すじ測定及び左ねじれの歯すじ測定では,平面基準器の回転の向き,及び初期設定におけ
る測定子のY軸方向位置を変えなければならない。
+
±
=
0
)
tan
(
p
t
b
b
r
r
r
α
··················································· (4)
5.8
検出器の押込み量の設定
式(4)の初期設定位置に測定子を停止させた状態で,平面基準器だけを回転させ,測定用平面を測定子先
端球に当て,検出器出力が測定レンジの中央となる状態にする。
X座標位置
Y座標位置
Z座標位置
ζ
Rh
eh
Z
e2
e1
12
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
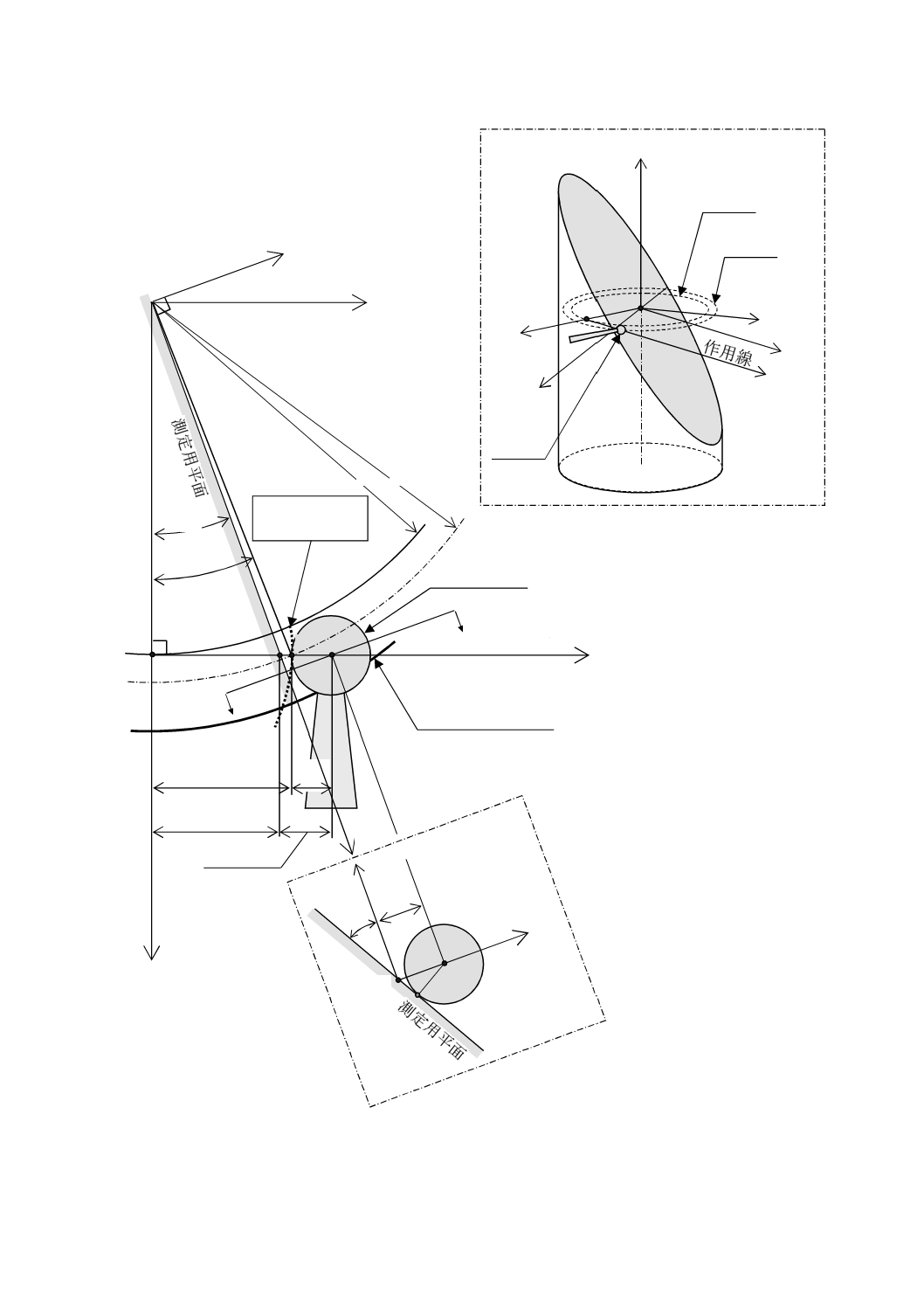
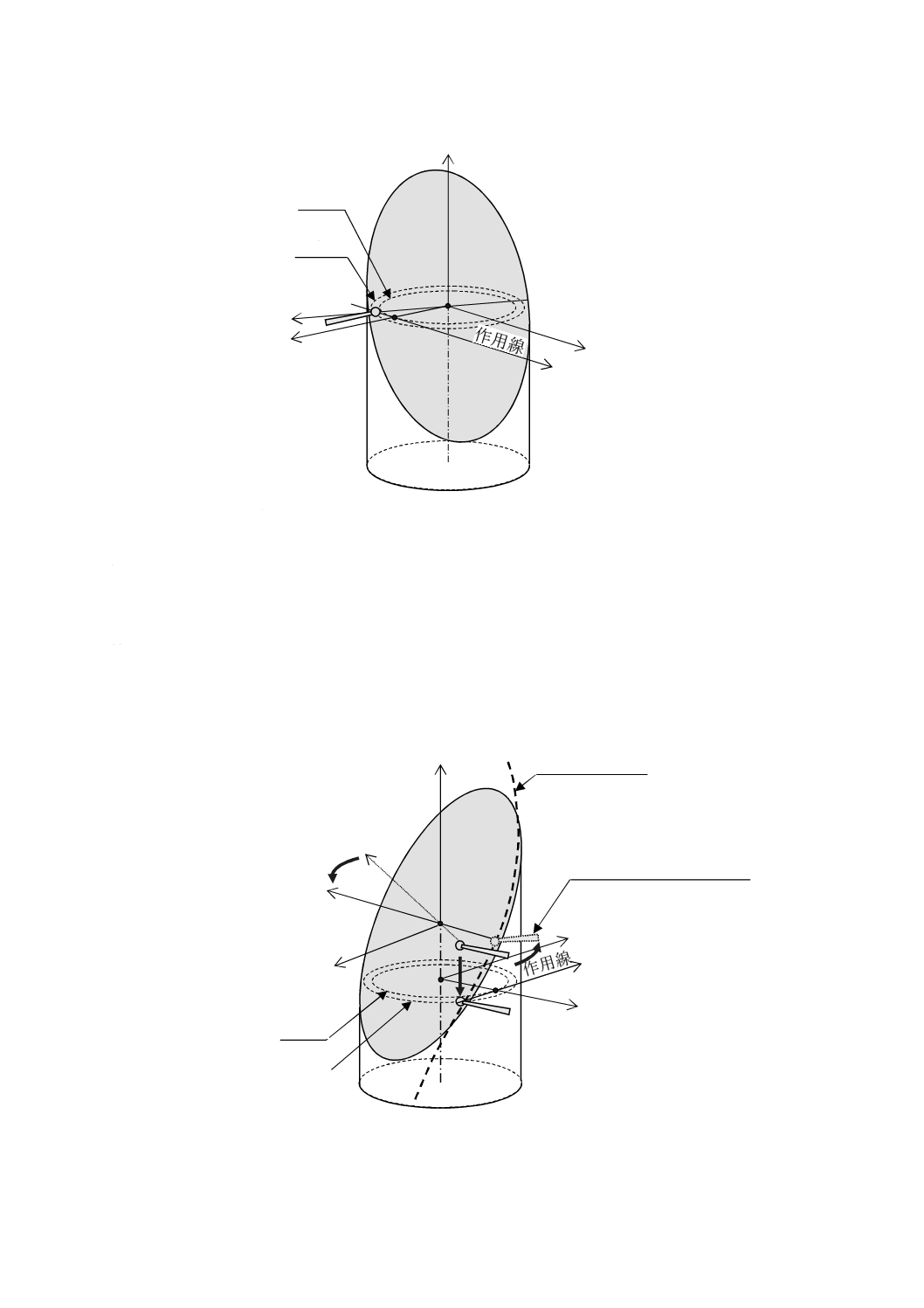
図8−仮想インボリュート歯形と測定子とが接触している初期設定状態の図(左ねじれ左歯面測定の例)
η0/cosε0
測定子
先端球
ξ
ζ
X
Z
Y
測定円
基礎円
η
立体図
η0
η
Ω
rp
O
ζ
ε0
ξ
Y
X
αt
rbtanε0
rp
r btanαt
作用線
仮想インボ
リュート歯形
rb
η
r
測定子先端球
A-A
O
Z
A
A
I
平面基準器の外径
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
13
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図9−αtが負の初期設定における測定子先端位置(左ねじれ左歯面測定の例)
5.9
測定子の測定開始位置への移動
測定子を測定開始位置まで移動させる。このとき,歯すじ測定と同じ運動で,平面基準器を回転させな
がら測定子を軸方向に移動させる。
5.10 歯すじ測定の実施
インボリュート円筒歯車の歯すじ測定手順に従って,測定用平面の歯すじ測定を行う(図10及び図11
参照)。
図10−右ねじれ右歯面測定の例
ξ
X
Z
Y
測定円
基礎円
ξ
ζ
X
Z
Y
測定円
基礎円
測定円筒周りの
ヘリコイド曲線
初期設定位置の測定子を
平面基準器と共に
回転させた仮想の位置
η
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
14
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
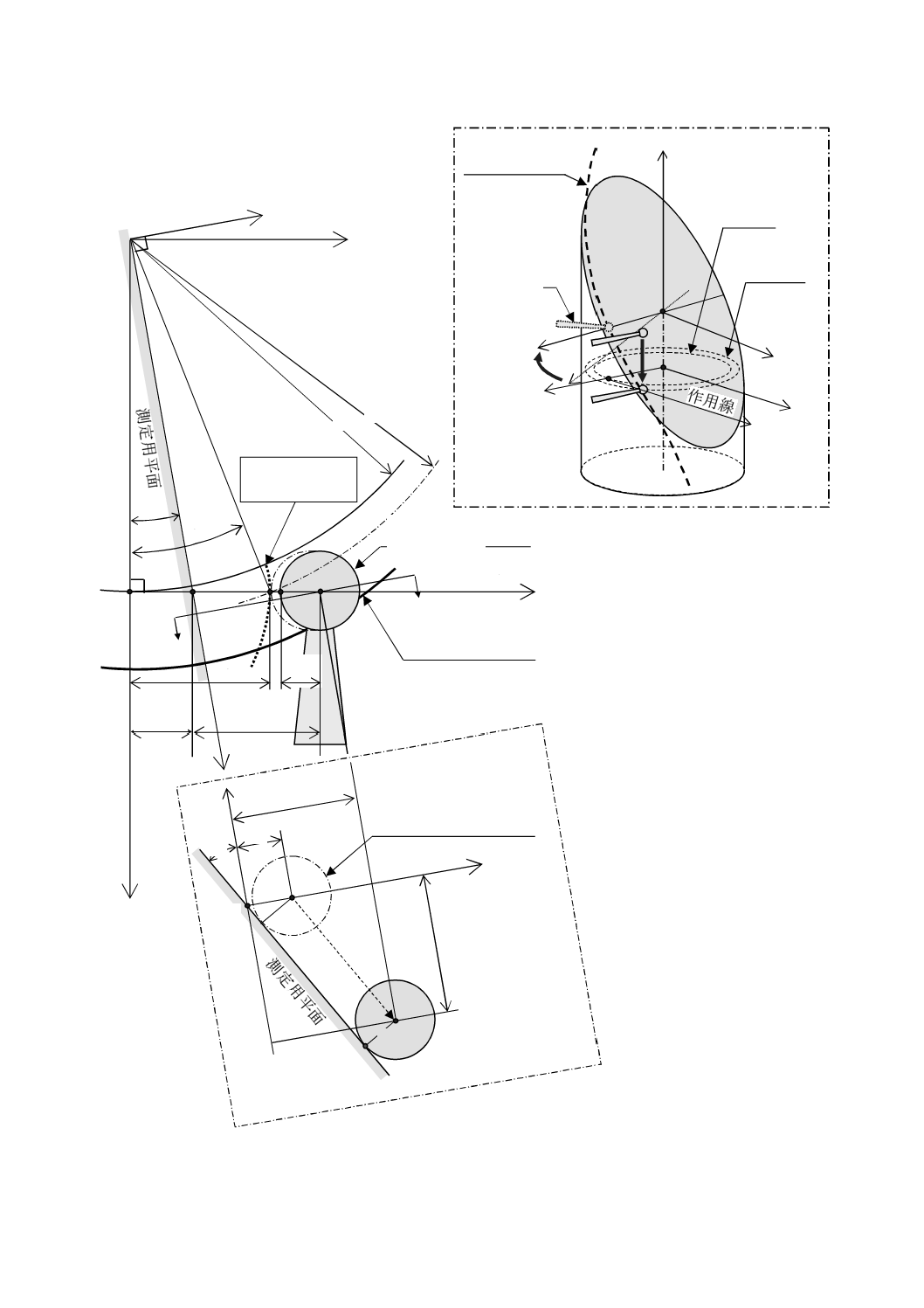
図11−左ねじれ左歯面測定状態の図(測定子はZ軸方向にZwの位置にあり,δHが形状偏差)
立体図
ξ
ζ
X
Z
Y
測定円
基礎円
測定円筒周りの
ヘリコイド曲線
初期位置の
測定子を
平面基準器と
共に回転させた
仮想の位置
η
η
rp
εm
ξ
X
αt
rbtanεm
ηm/cosεm
δH
rp
rbtanαt
rb
η
r
原点断面に投影した
測定子先端球
Y
Y'
Ω
ζ
O
Zw
η0
ηm
初期位置の測定子先端を
平面基準器と共に
回転させた仮想の位置
Z
O
A
A
A-A
I
作用線
仮想インボ
リュート歯形
平面基準器の外周
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
15
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6
評価
6.1
理論曲線の計算
式(5)〜式(15)に従って形状偏差δHを計算する(図12参照)。δH及び歯幅方向位置ZwからS字曲線を求
め,これを理論曲線とする。平面基準器の座標原点位置において,理論曲線の形状偏差はゼロとなる。複
号は,(+)が左歯面の測定,(−)が右歯面の測定に対応する。左歯面と右歯面とでは,形状偏差の符号
が逆になる。
なお,測定する面が左ねじれで左歯面の場合及び右ねじれで右歯面の場合は,同じようなS字曲線が得
られ,測定する面が左ねじれで右歯面の場合及び右ねじれで左歯面の場合は,同じようなS字曲線が得ら
れる(図13参照)。
Ω
r
cos
p
0=
η
················································································ (5)
(
)
p
t
b
0
tan
r
r
Y
+
±
=
α
····································································· (6)
a) 左ねじれの測定の場合
2
0
2
b
2
0
2
0
2
b
0
0
b
0
tan
η
η
η
ε
−
−
+
=
r
Y
r
Y
r
μ
····················································· (7)
b
b
w
0
w
0
m
tan
tan
r
Z
r
Z
β
ε
β
ε
ε
+
=
+
=
··············································· (8)
Ω
Ztan
w
0
m
μ
η
η=
······································································ (9)
0
m
m
m
b
H
cos
tan
Y
r
−
+
±
=
ε
η
ε
δ
························································ (10)
b) 右ねじれの測定の場合
2
0
2
b
2
0
2
0
2
b
0
0
b
0
tan
η
η
η
ε
−
−
+
±
−
=
r
Y
r
Y
r
'
··················································(11)
'
0
0
πε
ε
−
=
·············································································· (12)
b
b
w
0
w
0
m
tan
tan
r
Z
r
Z
β
ε
β
ε
ε
−
=
−
=
·············································· (13)
Ω
Ztan
w
0
m
±
=η
η
···································································· (14)
0
m
m
m
b
H
cos
tan
Y
r
−
−
±
=
ε
η
ε
δ
························································ (15)
16
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
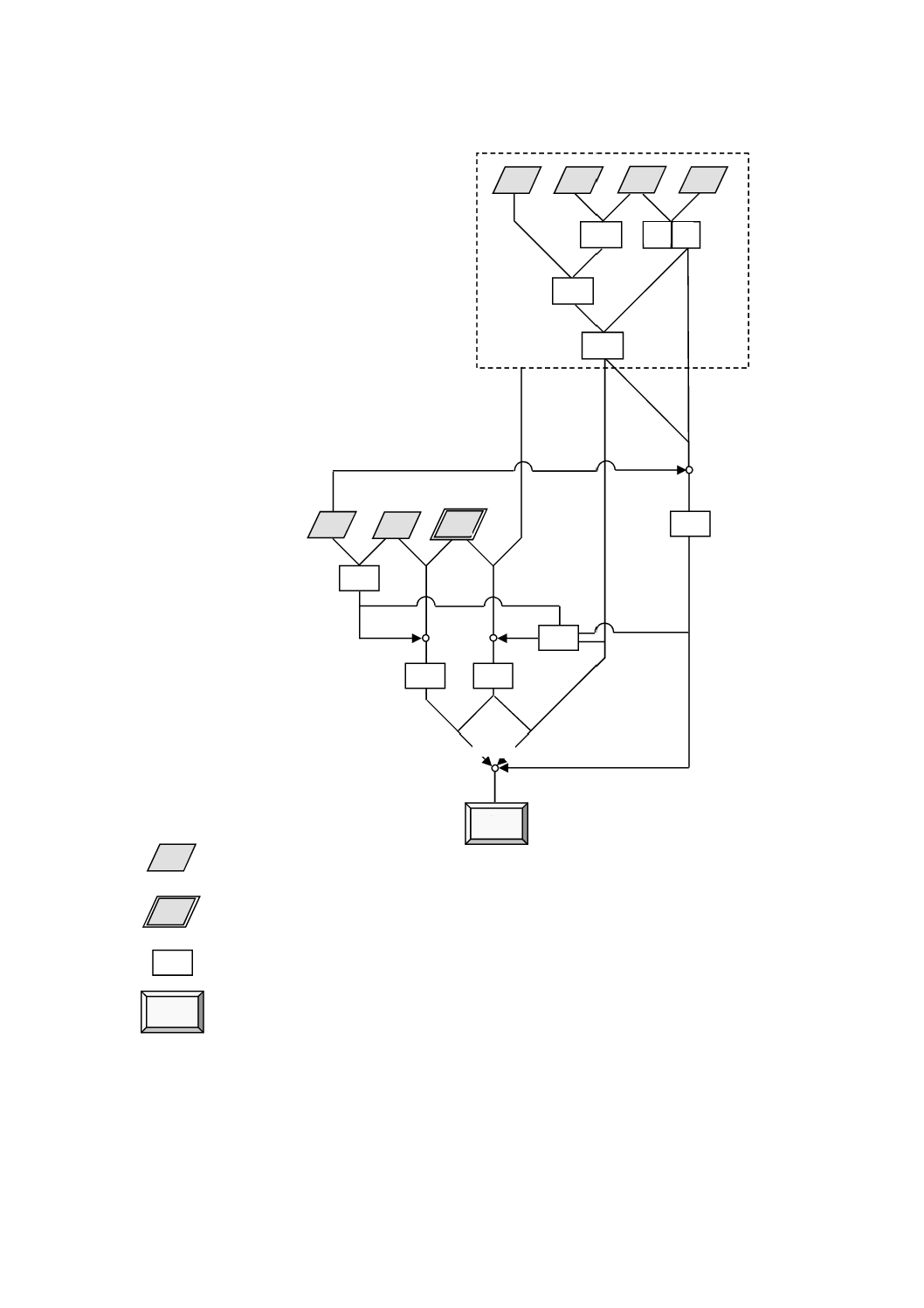
図12−形状偏差δHの計算フローチャート
6.2
実測曲線の導出
測定して得られた測定子の歯幅方向位置の実測値,及びその歯幅方向位置における形状偏差の実測値に
歯車諸元
z
mn
mt
βb αt
r
rb
+
+
+
±
−
rp
η0
ηm
Y0
β
αn
δH
ε0
入力(定数)
入力(変数)
計算結果
形状偏差
εm
Zw
Ω
±
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
17
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
よってS字曲線を求め,これを実測曲線とする。
6.3
精度評価対象範囲
S字曲線の頂点における形状偏差と同じ形状偏差の歯幅方向位置から,S字曲線の谷における形状偏差
と同じ形状偏差の歯幅方向位置までの範囲を,精度評価対象範囲Leとする(図13参照)。精度評価対象範
囲の下限Zmin及び上限Zmaxは,測定する面によってS字曲線の頂点に対応する場合と谷に対応する場合と
がある。
なお,Le,Zmax及びZminは,近似的に,次の式で求めることができる。
c
r
r
L
2
tan
4
sin
p
e
β
Ω+
=
······························································ (16)
ただし,
1
sin
1
tan
tan
t
p
−
+
=
r
r
c
α
Ω
β
·························································· (17)
a) 左ねじれ左歯面,右ねじれ右歯面の場合
+
≈
c
r
Ω
r
Z
2
tan
2
sin
2p
max
β
························································· (18)
−
≈
c
r
Ω
r
Z
2
tan
2
sin
p
min
β
························································· (19)
b) 左ねじれ右歯面,右ねじれ左歯面の場合
−
−
≈
c
r
Ω
r
Z
2
tan
2
sin
p
max
β
······················································· (20)
+
−
≈
c
r
Ω
r
Z
2
tan
2
sin
2p
min
β
························································ (21)
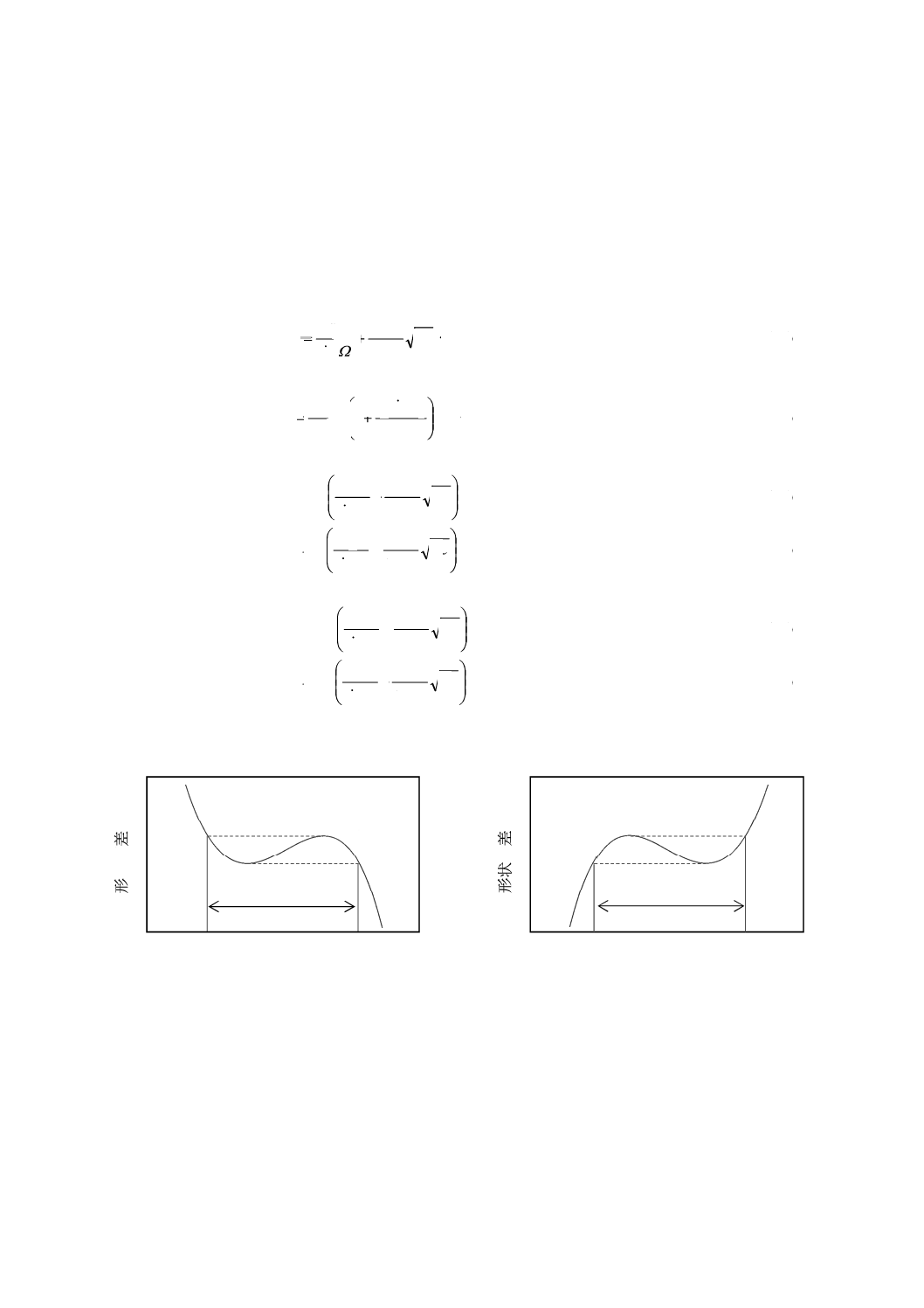
図13−精度評価対象範囲の上限及び下限
6.4
偏差曲線の計算
理論曲線及び実測曲線を,その形状を変えることなく平行移動させ,フィッティングを行う(附属書D
参照)。このとき,理論曲線のグラフ上で実測曲線を平行移動させる。理論曲線と実測曲線との縦軸方向の
残差平方和を,精度評価対象範囲で計算し,残差平方和が最小になるよう平行移動量の補正を行い偏差曲
歯幅方向位置
形
状
偏
差
δ
H
Zmin
Zmax
Le
形
状
偏
差
δ
H
Zmin
Zmax
Le
歯幅方向位置
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
18
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
線を得る(図14参照)。
6.5
評価項目
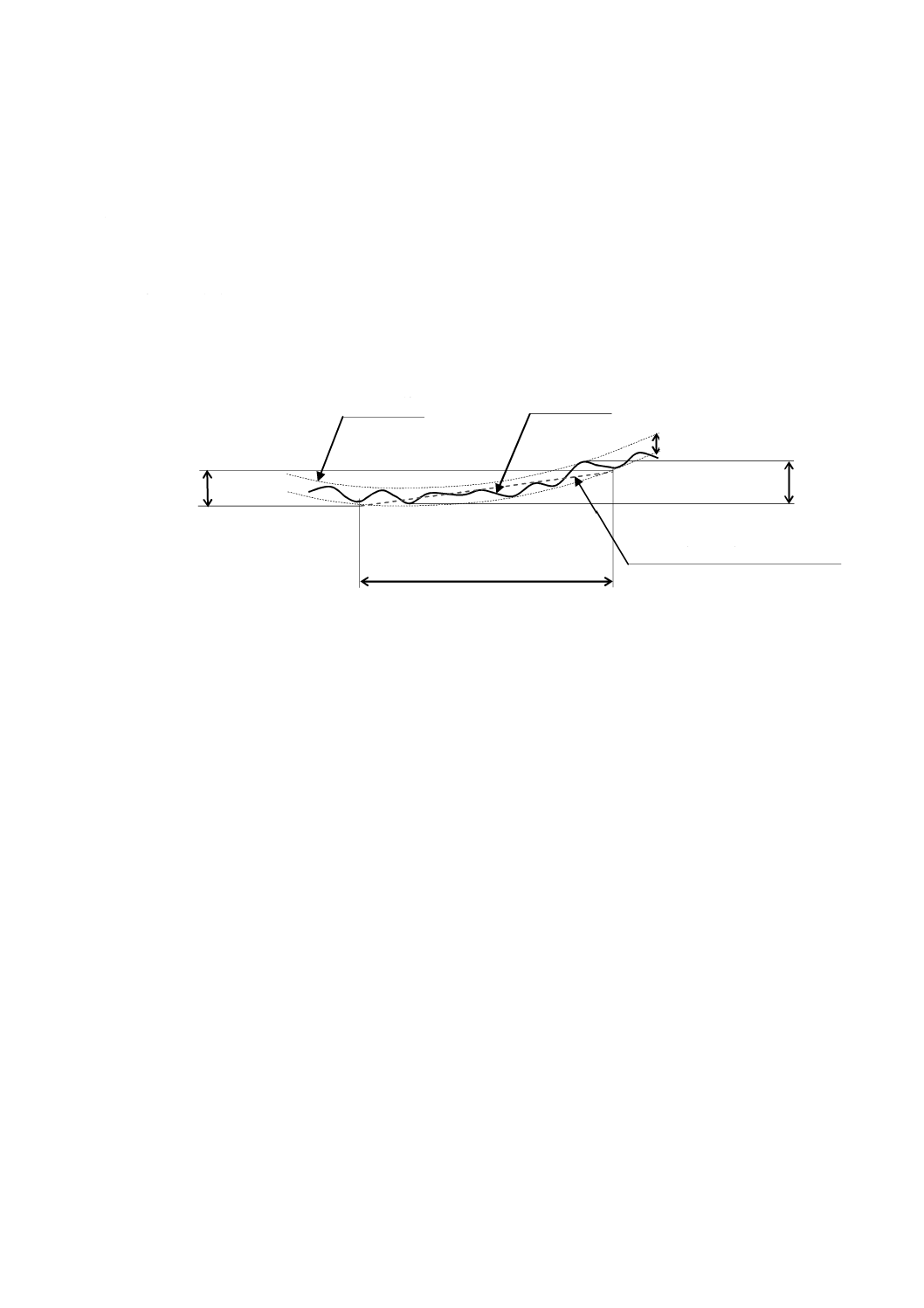
次の評価項目について測定精度を評価する(図14参照)。
a) 精度評価対象範囲における偏差曲線の,縦軸の最大値と最小値との差(fβ1)
b) 歯すじ偏差曲線を直線近似したときの,直線の上下端の差(fβ2)
c) 精度評価対象範囲で,偏差曲線を挟むように平均曲線を上下に平行移動して得られる二つの曲線の,
縦軸の差(fβ3)
この値は,被評価装置の出力が示す細かい出力の凹凸の信頼性を示す。その定量的な値に言及する場合
には,採用した平均曲線の定義を記録するとよい。
図14−歯すじ偏差曲線の例
偏差曲線
fβ3
精度評価対象範囲
fβ2
fβ1
平均曲線
偏差曲線を直線近似したもの
19
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
平面基準器の設計
A.1 設計に必要な仕様
測定円の大きさが分かっているものとすると,平面基準器の主な設計仕様は,次の3点である。平面基
準器が製作された後でも,測定円の大きさを変更することは可能である。
a) 測定用平面と基準軸とのなす角度
b) 平面基準器の外径
c) 平面基準器の高さ
A.2 測定用平面と基準軸とのなす角度
測定用平面と基準軸とのなす角度は,歯車のねじれ角とほぼ等しくする。しかし,僅かな角度の違いに
よってS字曲線は大きく変化するので,図12の計算フローチャートに従ってS字曲線を求め,形状偏差
が測定可能な範囲に入るかどうかを確認する必要がある。
a) 測定用平面と基準軸とのなす角Ωの簡易計算法
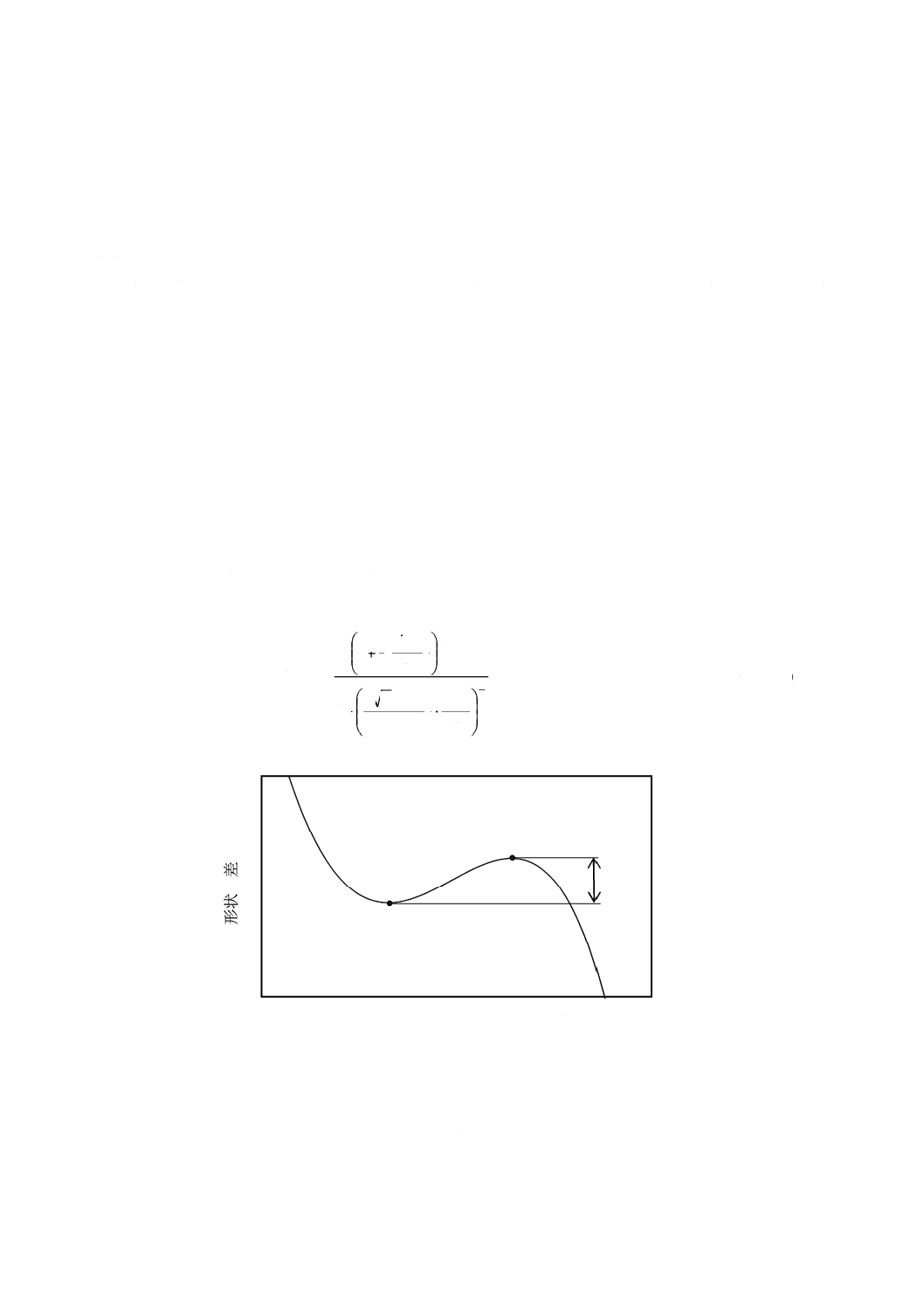
図A.1のS字曲線に示すように,曲線の頂点と谷との差δHppが与えられたとき,測定用平面と基準軸と
のなす角Ωは,式(A.1)で近似的に求めることができる。
3
2
Hpp
t
t
p
8
cos
2
3
1
tan
sin
1
tan
+
+
≈
r
r
r
Ω
δ
α
β
α
·················································· (A.1)
図A.1−S字曲線の頂点と谷との差
b) 歯車の設定ねじれ角βの簡易計算法
平面基準器が既に製作されているときは,S字曲線の頂点と谷との差δHpp,測定円半径r,及び測定子先
端球の半径rpを与えれば,設定する歯車の測定円上ねじれ角βを,式(A.2)及び式(A.3)で近似的に求めるこ
歯幅方向位置 (mm)
形
状
偏
差
(μ
m
)
δHpp
20
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
とができる。
r
r
Ω
r
t
p
3
2
Hpp
t
sin
1
tan
8
cos
2
3
1
tan
α
δ
α
β
′
+
′
+
≈
········································ (A.2)
ただし,
Ω
cos
tan
n
t
α
α=
′
··········································································· (A.3)
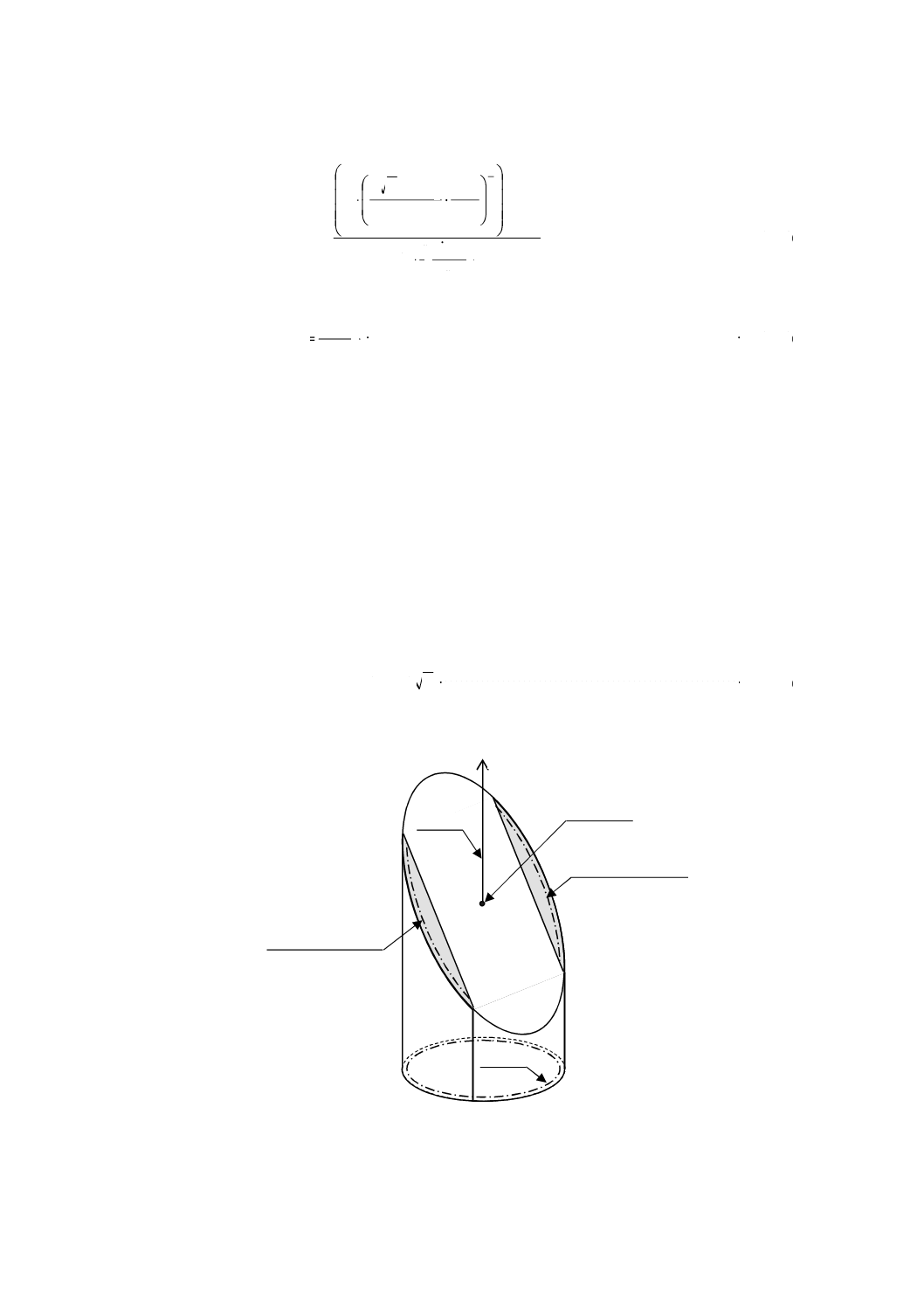
A.3 平面基準器の外径
平面基準器の外径は,(測定円の直径+測定子の直径)とすればよい。この場合,外周近くの測定用平面
は,だれないように加工することが望ましい。測定円が非常に大きいとき,歯すじ測定部分だけを切り出
したブロック状の平面基準器としてもよい(図A.2参照)。この場合,右ねじれ及び左ねじれに対応したも
のが必要である。また,基準軸を定義するためのもの,及び基準軸と測定用平面との交点である座標原点
位置を測定するためのものも,一体として備わっていることが望ましい。
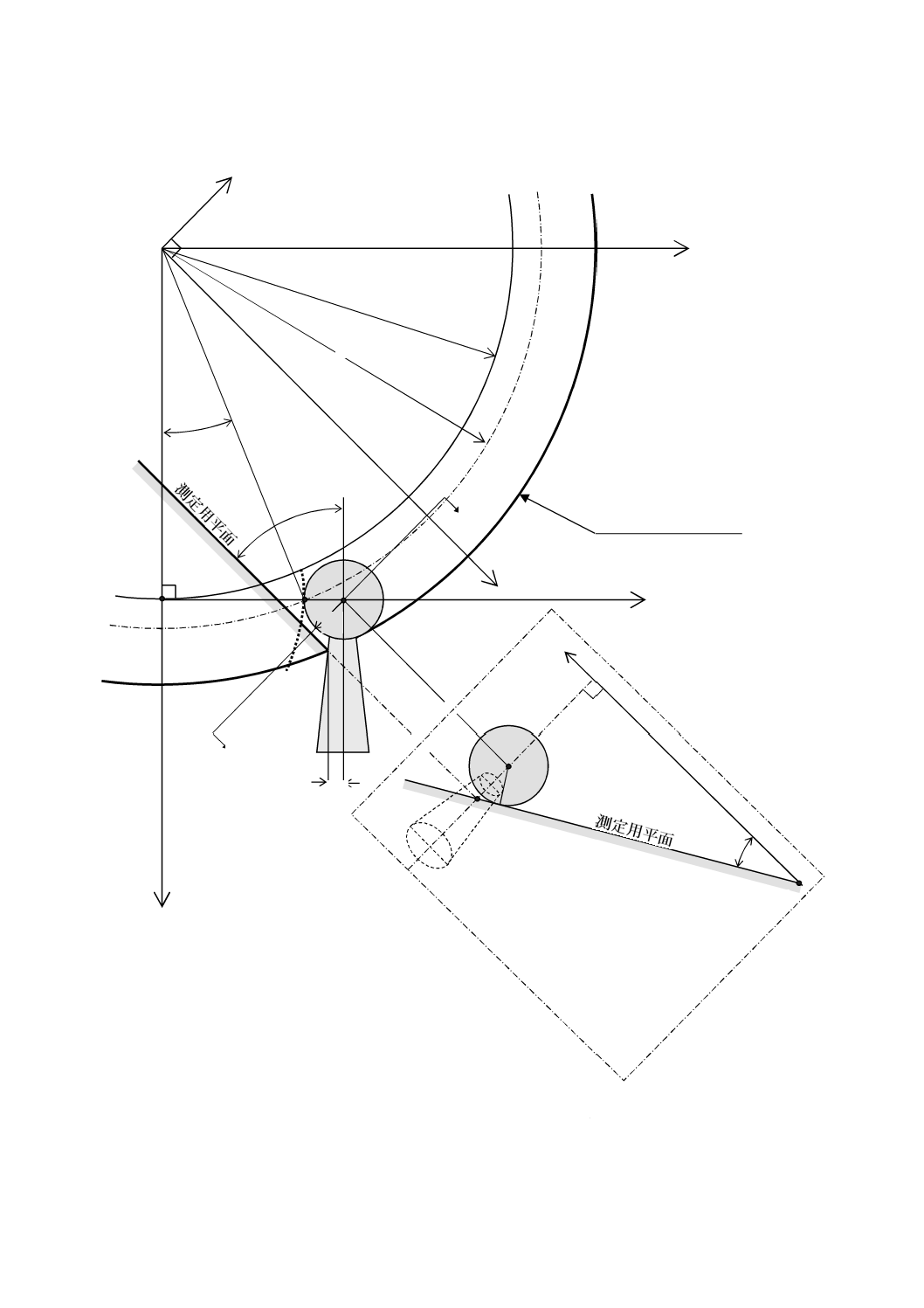
なお,測定子の軸が被評価装置のX軸方向にある場合,測定用平面の回転位置によっては平面基準器の
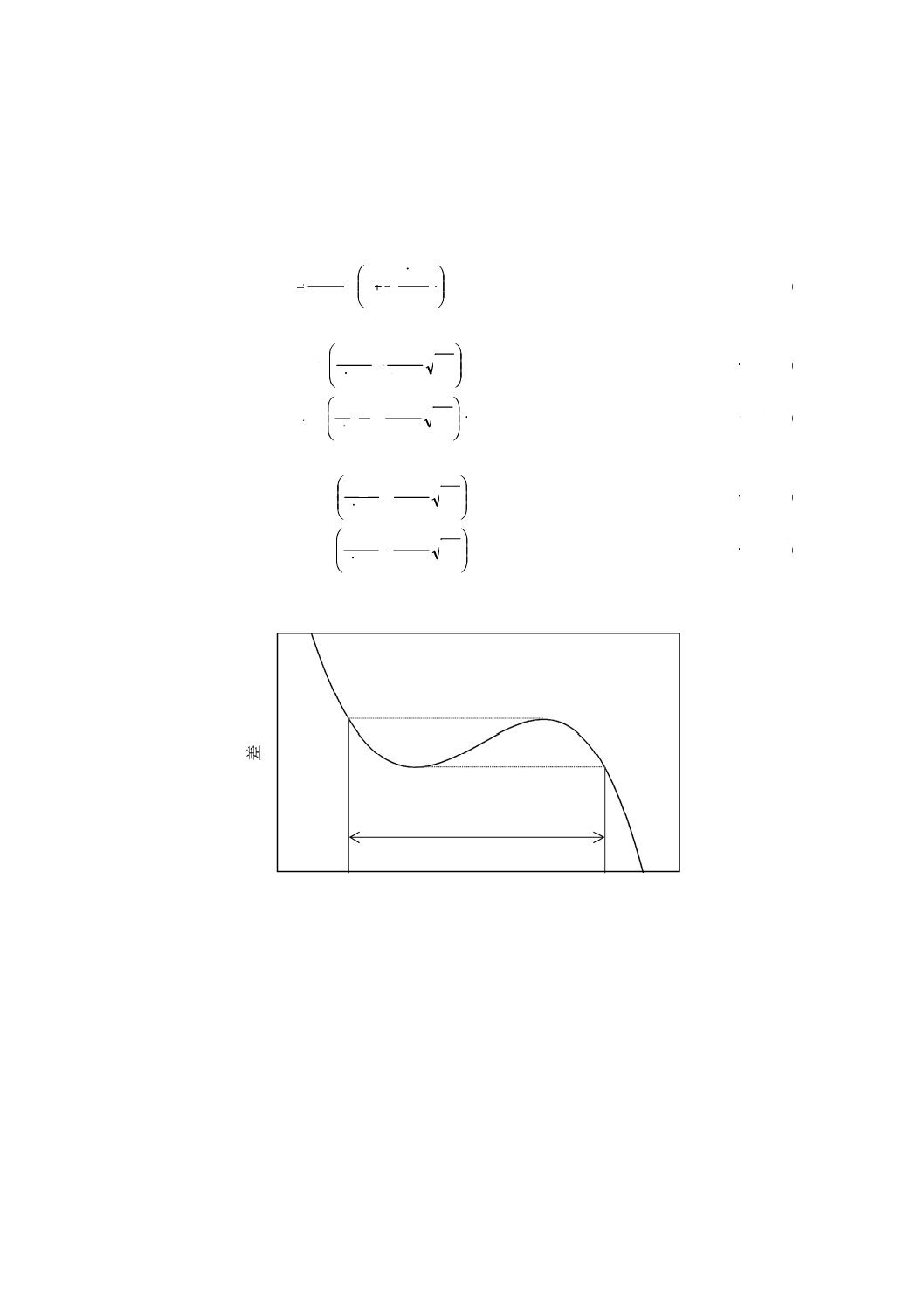
外周が測定子の柄に接触することもあるので,注意が必要である。測定子の柄の中心軸と測定用平面との
角度λが最大で45°と仮定すると,平面基準器の外径Ro,測定子先端球の半径rp,及び測定子の柄の先端
近くの半径rsは,式(A.4)の関係を満足するとよい(図A.3参照)。
Ro < 2r+
2
)
(2
s
p
r
r−
····························································· (A.4)
図A.2−部分的に切り出した平面基準器
歯すじ測定部分
歯すじ測定部分
測定円
ζ
基準軸
座標原点
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
21
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.3−測定子のシャフト柄と平面基準器の外周とが接触している図
ξ
αt
作用線
rb
η
r
Y
Y'
X
Ω
O
Z
λ
平面基準器の外周
rs
rp
O
A
A-A
A
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
22
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.4 平面基準器の高さ
平面基準器の歯すじ測定部分の歯幅方向高さは,精度評価対象範囲で歯すじ測定ができればよいが,多
少の余裕をもたせることが望ましい(図A.4参照)。
精度評価対象範囲の上限Zmax及び下限Zminは,近似的に次の式で求めることができる。厳密には,S字
曲線を求め,精度評価ができる十分な高さを計算することが望ましい。
0
1
sin
1
tan
tan
t
p
>
−
+
×
=
r
r
Ω
c
α
β
··········································· (A.5)
a) 左ねじれ左歯面,右ねじれ右歯面の測定の場合
+
≈
c
r
Ω
r
Z
2
tan
2
sin
2p
max
β
······················································· (A.6)
−
≈
c
r
Ω
r
Z
2
tan
2
sin
p
min
β
························································ (A.7)
b) 左ねじれ右歯面,右ねじれ左歯面の測定の場合
−
−
≈
c
r
Ω
r
Z
2
tan
2
sin
p
max
β
······················································ (A.8)
+
−
≈
c
r
Ω
r
Z
2
tan
2
sin
2p
min
β
······················································ (A.9)
図A.4−精度評価対象範囲
歯幅方向位置 Z (mm)
形
状
偏
差
δ
H
(μ
m
)
Zmin
Zmax
Le(精度評価対象範囲)
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
23
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B
(参考)
取付け誤差を考慮した形状偏差の計算方法
B.1
取付け誤差の扱い
平面基準器の基準軸を定義した軸方向2か所で基準軸の偏心を測定し,それぞれ軸心の偏心量及び位相
を求める。そして,取付け誤差によって変化した座標原点位置,及び回転軸に対する測定用平面の角度を
求め,この変化した座標原点,及び変化した傾斜角度で設定した新たな座標系を,取付け誤差のない元の
座標系と同様に扱うことによって,形状偏差を計算することができる。球の中心と球の中心とを結ぶ軸で
基準軸を定義したものは,円筒の中心軸で定義したものと同様に扱うことができる。
B.2
円筒の中心軸で定義した基準軸の場合
B.2.1 取付け誤差の測定
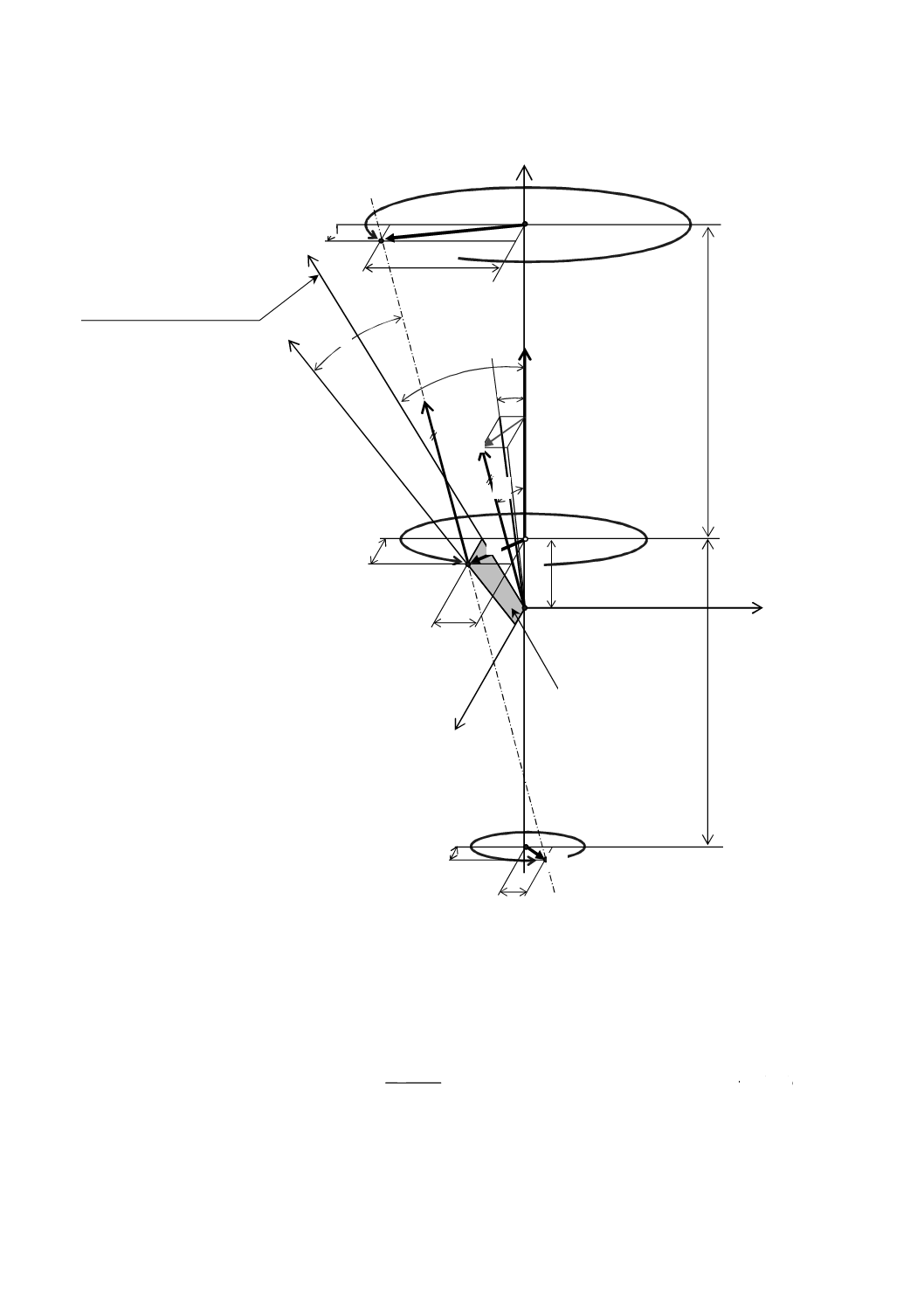
図B.1において,Z軸は被評価装置の回転軸である。ζ軸は平面基準器の基準軸で,Oが平面基準器の座
標原点である。いま,ζ軸がZ軸に対して平行に偏心し,更に傾斜しているとして,測定用平面はZ軸と
点O'とで交差するものとする。基準軸を定義した2か所,すなわち,座標原点からZ軸方向にZ1及びZ2
だけ離れた点での基準軸の偏心量及び位相を測定する。
B.2.2 新しい座標系
O'を座標原点とする平面基準器の直交座標系(ξ',η',ζ')を新たに設定する。ζ' 軸はZ軸に一致し,ξ' 軸
は測定用平面上にあるものとする。η' 軸は測定用平面の実体側から空間側に向かう方向を+とする。この
新しい座標系では,測定用平面とZ軸とのなす角度がΩ' に変化している。
B.2.3 偏心量,傾き及び原点移動量
Z軸方向Z1及びZ2において,(ξ',η')面における基準軸の偏心をe1(e1ξ',e1η')及びe2(e2ξ',e2η')とし,
座標原点Oにおいて,(ξ',η')面における基準軸の偏心をe(eξ',eη),及び座標原点の軸方向移動量をeζ'
とすると,次の式が得られる。
)
(/)
(
2
1
ξ
1
2
ξ
2
1
ξ
Z
Z
e
Z
e
Z
e
+
+
=
′
′
′
·················································· (B.1)
)
(/)
(
2
1
η
1
2
η
2
1
η
Z
Z
e
Z
e
Z
e
+
+
=
′
′
′
·················································· (B.2)
Ω
e
e
tan
/
η
ς
′
′=
········································································· (B.3)
ただし,
)
cos
tan
(sin
cos
sin
ξ
Ω
Ω
Ω
′
−
′
=
′
ω
ω
·············································· (B.4)
2
1
η
1
η
2
ξ
tan
Z
Z
e
e
+
−
=
′
′
′
ω
··································································· (B.5)
2
2
1
2
η
1
η
2
2
ξ1
ξ2
2
1
)
(
)
(
)
(
cos
Z
Z
e
e
e
e
Z
Z
+
+
−
+
−
+
=
′
′
′
′
ω
································ (B.6)
24
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.1−円筒の中心軸で定義された基準軸が偏心している図
式(B.1)〜式(B.6)によってΩ' を求めることができるが,基準軸の偏心量はZ1,Z2に比べて非常に小さい
と考えると,角度変化も非常に小さいと考えられるので,式(B.7)によってΩ' の近似値が得られる。
2
1
η
1
η
2
ξ
Z
Z
e
e
Ω
Ω
+
−
≈
≈
−
′
′
′
′
ω
··························································· (B.7)
Ω' が得られると,座標原点の軸方向移動量eζ' は,式(B.2)及び式(B.3)によって,η' 軸方向だけの偏心量
から求められる。Z1及びZ2は,基準軸の偏心量及び傾斜角度の変化が非常に小さいので,元の座標系(ξ,
ζ' 軸とη' 軸を通る平面
及び測定用平面との交線
Z
e2
ξ'
e1
e
η'
ζ
Z2
Z=0
Z1
O'
ζ'(Z軸と一致)
O
Ω
Ω'
eξ'
eη'
ζ"
ωξ'
測定用平面(一部)
ω
e1ξ'
e1η'
e2ξ'
e2η'
eζ'=eη'/tanΩ'
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
25
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
η,ζ)で考えて差し支えない。
なお,e1η' 及びe2η' は,符号を含んでいることに注意する必要がある。座標原点Oにおける偏心eがゼ
ロの場合,(e2η'−e1η')の絶対値は,e1η' 及びe2η' の絶対値の和となる。
B.3
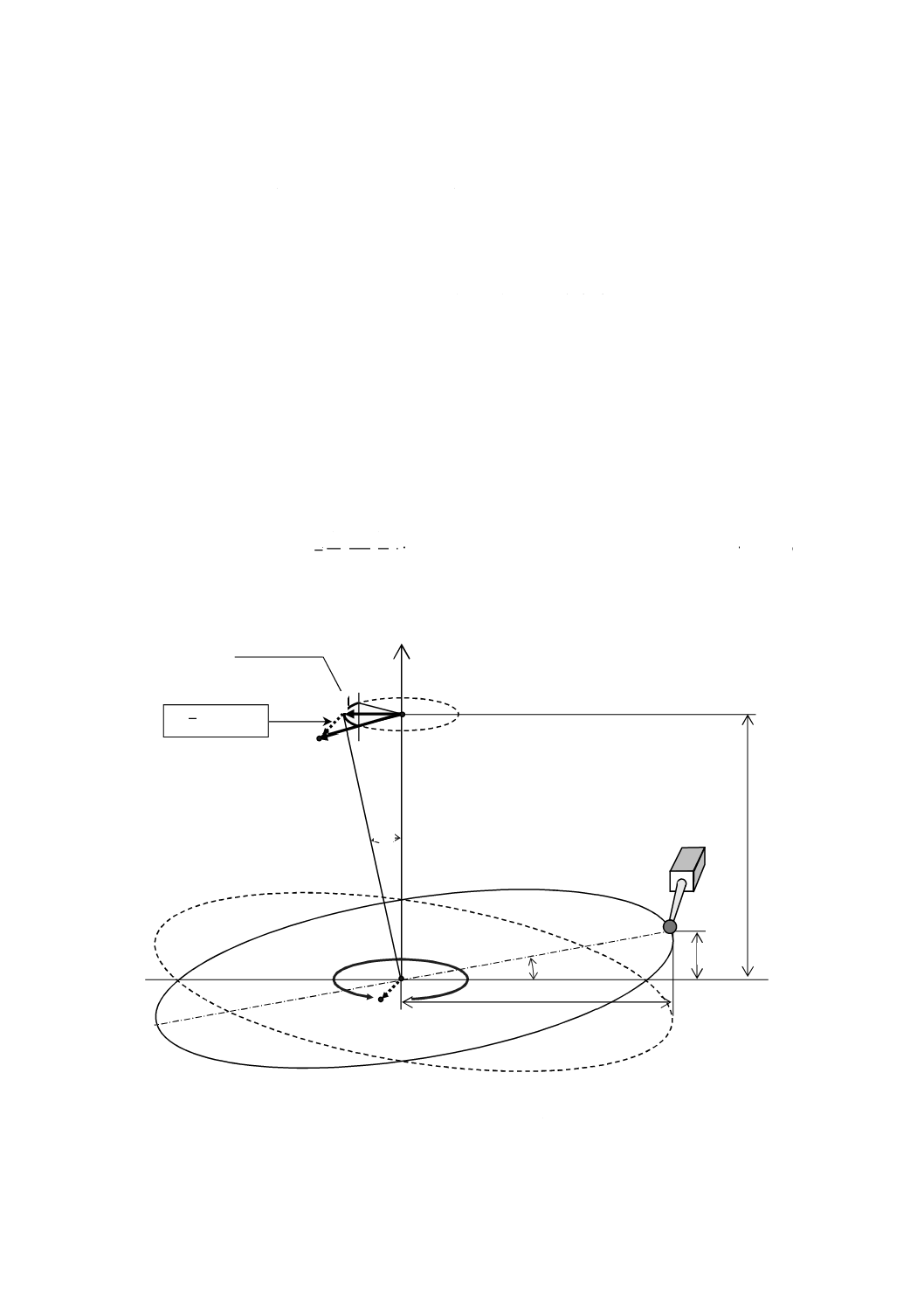
球と平面とで定義した基準軸の場合
図B.2は,球と面とで定義した基準軸が回転軸に対して傾斜している図で,半径Rhだけ離れた点で測定
した面の振れの片振幅をehとする。面の中心から(Z1+Z2)だけ回転軸方向に離れた位置にある球の中心
は,面が傾斜している方向に偏心し,回転軸に直角な方向の偏心量をepeakとすると,epeakは式(B.8)のよう
に計算される。
基準軸が傾斜し,更に回転軸と平行に偏心した場合,回転軸に直角な方向に測定したときの球の中心の
偏心ベクトルをe1とすると,回転軸と平行な偏心ベクトルe2は,ベクトルe1とベクトルepeakとの差(e1
−epeak)として表される。このe1及びe2を用いて,B.2と同様に,座標原点及び測定用平面の傾斜角度の
変化を求めることができる。
なお,面の振れの測定において,面の最大傾斜方向と直角な方向の角度測定精度は低いので,ベクトル
epeakの精度も低いことに注意する必要がある。
h
h
2
1
peak
)
(
R
e
Z
Z
e
+
=
···································································· (B.8)
図B.2−球と平面とで定義した基準軸が偏心している図
Rh
eh
(Z1+Z2)
ω'
Z
e1
e2
ω'
不確かな領域
epeak
e2 = e1−epeak
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
26
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.4
取付け誤差があるときの形状偏差
取付け誤差があるときの形状偏差は,式(5)〜式(15)において,変化した傾斜角度Ω' をΩとして,変化
した座標原点に対する式(B.9)のη0を用いて計算すればよい。
なお,式(B.9)の中の符号は,図B.1のように左ねじれの左歯面に対応している。
η
p
ς
p
0
cos
tan
cos
′
′
−
′
=
′
−
′
=
e
Ω
r
Ω
e
Ω
r
η
······································· (B.9)
B.5
偏心による形状偏差の変化の近似式
基準軸(ζ軸)が回転軸(Z軸)と平行に偏心したとき(図B.3参照),ζ軸がξ軸方向に偏心しても,δH
は変化しない。偏心のη軸方向の成分が,δHの変化に関係する。η軸方向の偏心を考慮した式(B.9),又は
歯面のねじれ方向に対応した式を用い,式(10)又は式(15)のδHを,η軸方向の偏心量で偏微分すると,高次
の項を無視すれば,次の式が得られる。
2
w
t
η
H
tan
cos
2
3
×
−
−
≈
∂
∂
r
Z
e
β
α
δ
············································· (B.10)
式(B.10)はZ軸座標Zwの2次関数となり,精度評価対象範囲の端部で最大となる。式(B.10)のZwに,式
(18)又は式(21)の歯幅方向位置を代入し,更に近似計算を行うと,
η
H/e
∂
∂δ
の最大値は式(B.11)のようにな
る。測定子の先端半径rpは測定円半径rに比べて非常に小さいので,
η
H/e
∂
∂δ
の最大値は小さく,回転軸
と平行な基準軸の偏心が形状偏差δHに及ぼす影響は,小さいことが分かる。
t
p
t
max
η
H
tan
cos
2
3
8
α
α
δ
×
−
×
≈
∂
∂
r
r
e
≪ 1.0 ························· (B.11)
B.6
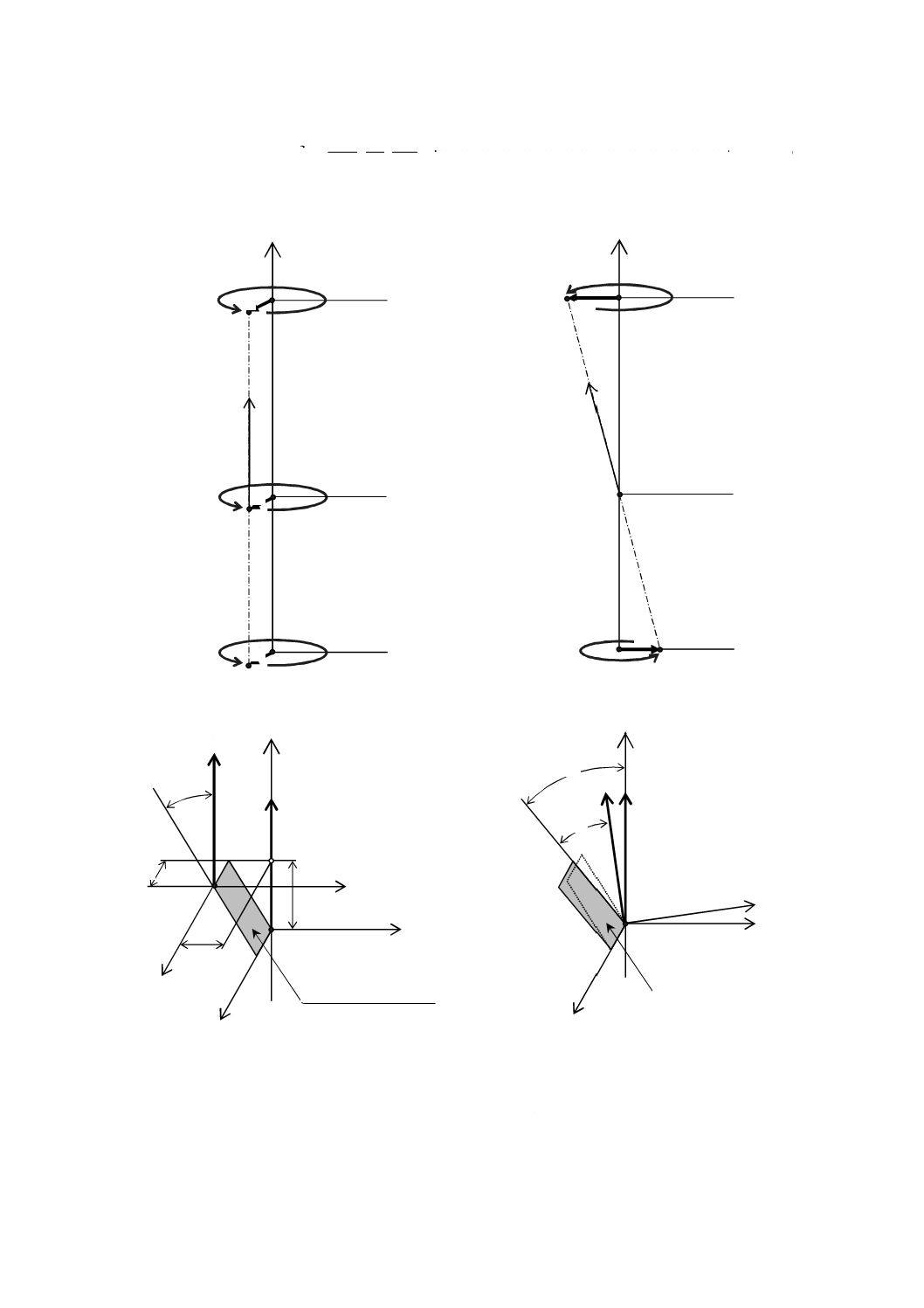
傾きによる形状偏差の変化の近似式
基準軸(ζ軸)が回転軸(Z軸)に対して傾斜したとき(図B.3参照),ζ軸が測定用平面上の軸(ξ軸)
の方向に傾いても,δHはほとんど変化しない。ζ軸の傾きの,η軸方向の成分(ξ軸回りの回転)がδHの
変化に関係する。すなわち,平面基準器の傾斜角Ωの変化に対するδHの変化を求めればよい。
ζ軸の傾きによる形状偏差の変化を求めるため,式(10)又は式(15)のδHをΩで偏微分すると,高次の項
を無視すれば,式(B.12)が得られる。式(B.12)はZ軸方向の座標Zwの1次関数となる。
t
2
w
H
cos
cos
α
δ
≈
∂
∂
Ω
Z
Ω
······························································· (B.12)
角度Ωの変化を,Zwの位置におけるζ軸の半径方向の偏心量として表し,これをeΩとすると,式(B.12)
は,式(B.13)のように表される。式(B.13)によって,ζ軸の傾斜が形状偏差δHに及ぼす影響は,大きいこと
が分かる。
0.1
cos
cos
1
t
2
Ω
H
>
≈
∂
∂
α
δ
Ω
e
················································ (B.13)
精度評価対象範囲の端部での基準軸の偏心量の最大値をe1及びe2とすると,振れの位相が180°反対な
ので,精度評価範囲の両端における偏心量の差の最大値は(e1+e2)となり,形状偏差δHの変化
H
δ
Δ
は,
式(B.14)のように表される。
27
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
t
2
2
1
H
cos
cos
)
(
α
δ
+
≈
Ω
e
e
Δ
····························································· (B.14)
a) 回転軸に平行な偏心
b) 傾き
図B.3−基準軸の偏心及び傾き
Z
ζ
Z=0
O
Ω
eξ
eη
測定用平面(一部)
eζ =eη/tanΩ
ξ
η
Z
ξ
ζ
O
Ω
測定用平面(一部)
η
Ω'
Z
e
e
e
ζ
Z= Zmax
O
Z= 0
Z= Zmin
Z
e2
e1
ζ
O
Z= Zmax
Z= 0
Z= Zmin
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
28
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
B.7
計算例
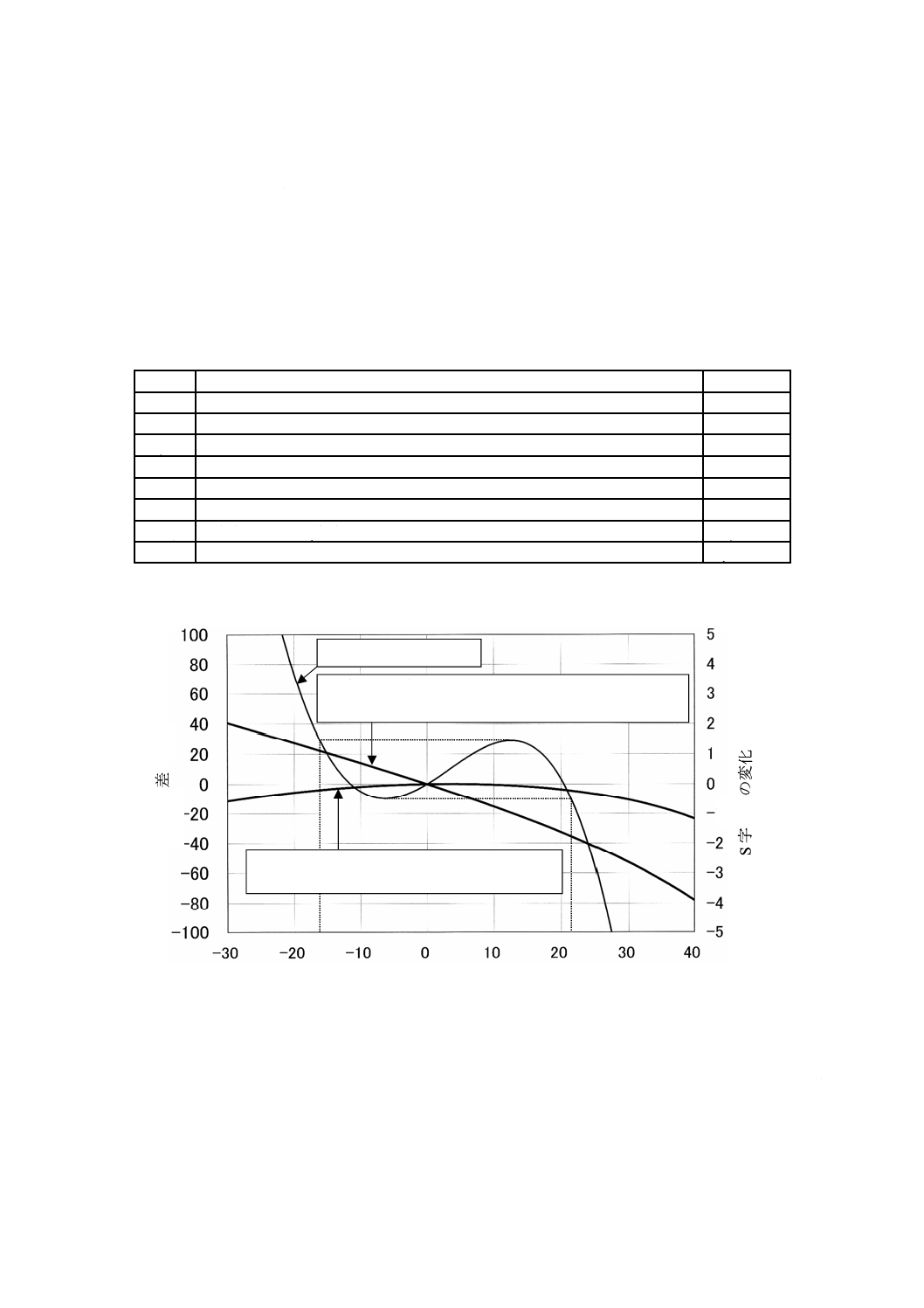
表B.1に示す諸元及び基準軸の偏心量並びに傾きの大きさに対する形状偏差δHの変化(S字曲線の変化
量)を,式(5)〜式(15)で計算すると図B.4のようになる。
表B.1において,Δeηは,式(B.9)のeη'と同じものである。図B.4のグラフは,式(B.7)で求めた測定用平
面の角度Ω',及び式(B.9)で求めたη0を用いて計算した結果である。
計算結果から分かるように,基準軸の偏心による形状偏差δHの変化は,基準軸の傾きによる形状偏差δH
の変化に比べると小さく,平面基準器の取付けは,主に,基準軸の傾きに注意すればよいことが分かる。
表B.1−計算例
記号
記号の意味
計算条件
Ω
測定用平面と基準軸とのなす角度
30°
r
測定円半径
55 mm
β
測定円筒上ねじれ角
29.85°
αn
歯直角圧力角
20°
αt
正面圧力角
22.765 1°
rp
測定子先端球の半径
1.5 mm
Δeη
回転軸に平行なη軸方向の偏心量
10 μm
ΔeΩ
傾きによる精度評価対象範囲の上端Zmaxと下端Zminとの偏心量の差
2 μm
図B.4−基準軸の偏心及び傾きによるS字曲線の変化
表B.1に示す諸元及び基準軸の偏心量並びに傾きの大きさに対する形状偏差δHの変化を,近似的な計算
式で求めると表B.2のようになる。表B.2に示す計算結果を図B.4のグラフと比較すると,よく一致して
いる。
歯幅方向位置 (mm)
形
状
偏
差
(μ
m
)
S
字
曲
線
の
変
化
(μ
m
)
S字曲線(左目盛)
η軸方向に+10 μmだけ基準軸が平行に偏心
したときのS字曲線の変化量(右目盛)
精度評価対象範囲の両端が2 μmの差をもつように
基準軸が傾いたときのS字曲線の変化量(右目盛)
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
29
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表B.2−基準軸の偏心及び傾きによる形状偏差の変化
計算例
計算条件
計算結果
軸方向位置
Zmax
精度評価対象範囲の上端位置
23 mm
Zmin
精度評価対象範囲の下端位置
−17 mm
軸の偏心
η
Δe
回転軸に平行な基準軸の偏心量
10 μm
η
η
H
)
/
(
Δe
e×
∂
∂δ
Zmaxにおける形状偏差の変化を式(B.10)で計算
−0.33 μm
η
η
H
)
/
(
Δe
e×
∂
∂δ
Zminにおける形状偏差の変化を式(B.10)で計算
−0.18 μm
η
η
H
)
/
(
Δe
e×
∂
∂δ
式(B.11)で計算
−0.53 μm
軸の傾き
Ω
Δe
基準軸のZmaxとZminとにおける偏心量の差
2 μm
Ω
Ω×
∂
∂
e
Δ
e)
/
(
H
δ
形状偏差の変化の差を式(B.13)で計算
2.9 μm
30
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C
(参考)
S字曲線に影響を及ぼす主要な要因
C.1 要因
この附属書では,主要な要因がS字曲線に及ぼす影響の大きさを,具体的計算例によって示す。多くの
要因を全て組み合わせることは不可能なので,表C.1に示す要因について,値を変化させたときのS字曲
線の変化を図C.1から図C.9に示す。測定子先端球の中心の座標位置は,5.7の式(4)と同じ条件である。
表C.1−S字曲線に影響を及ぼす主要な要因
記号
要因
Ω
測定用平面と基準軸とのなす角度
r
測定円半径
β
測定円筒上ねじれ角
αn
歯直角圧力角
rp
測定子先端球の半径
eg
検出器出力のゲイン誤差
ey
測定子のX軸方向オフセット
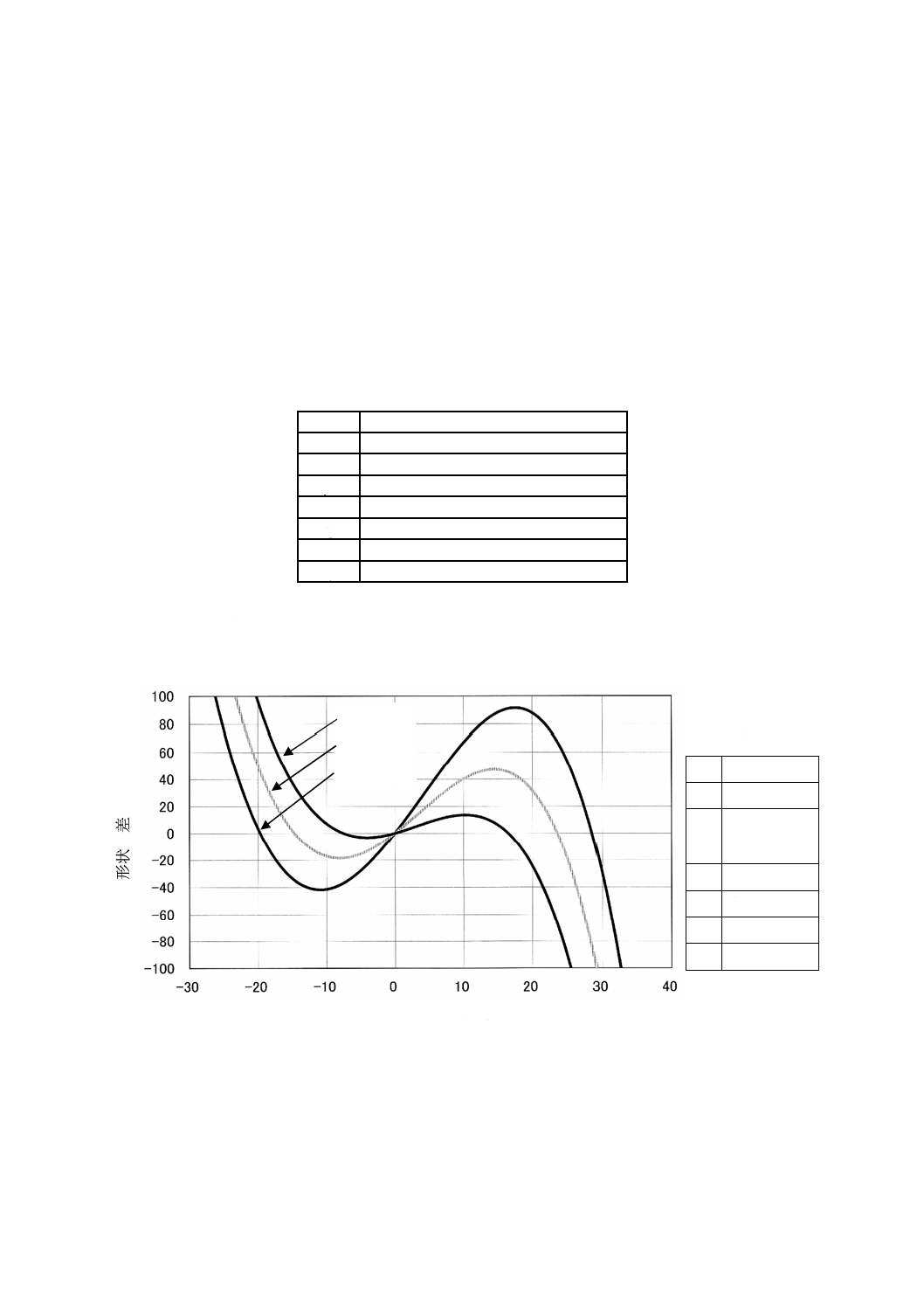
C.2 ねじれ角の影響
測定円におけるねじれ角βを変化させたときの計算結果を,図C.1及び図C.2に示す。
図C.1−測定円上ねじれ角を変化させたときの計算結果
計算条件
Ω
30°
r
55 mm
β
29.8°, 29.9°,
30.0°
αn
20°
rp
1.5 mm
eg
0 %
ey
0 mm
歯幅方向位置 (mm)
β =29.8°
β =29.9°
β =30.0°
形
状
偏
差
(μ
m
)
31
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
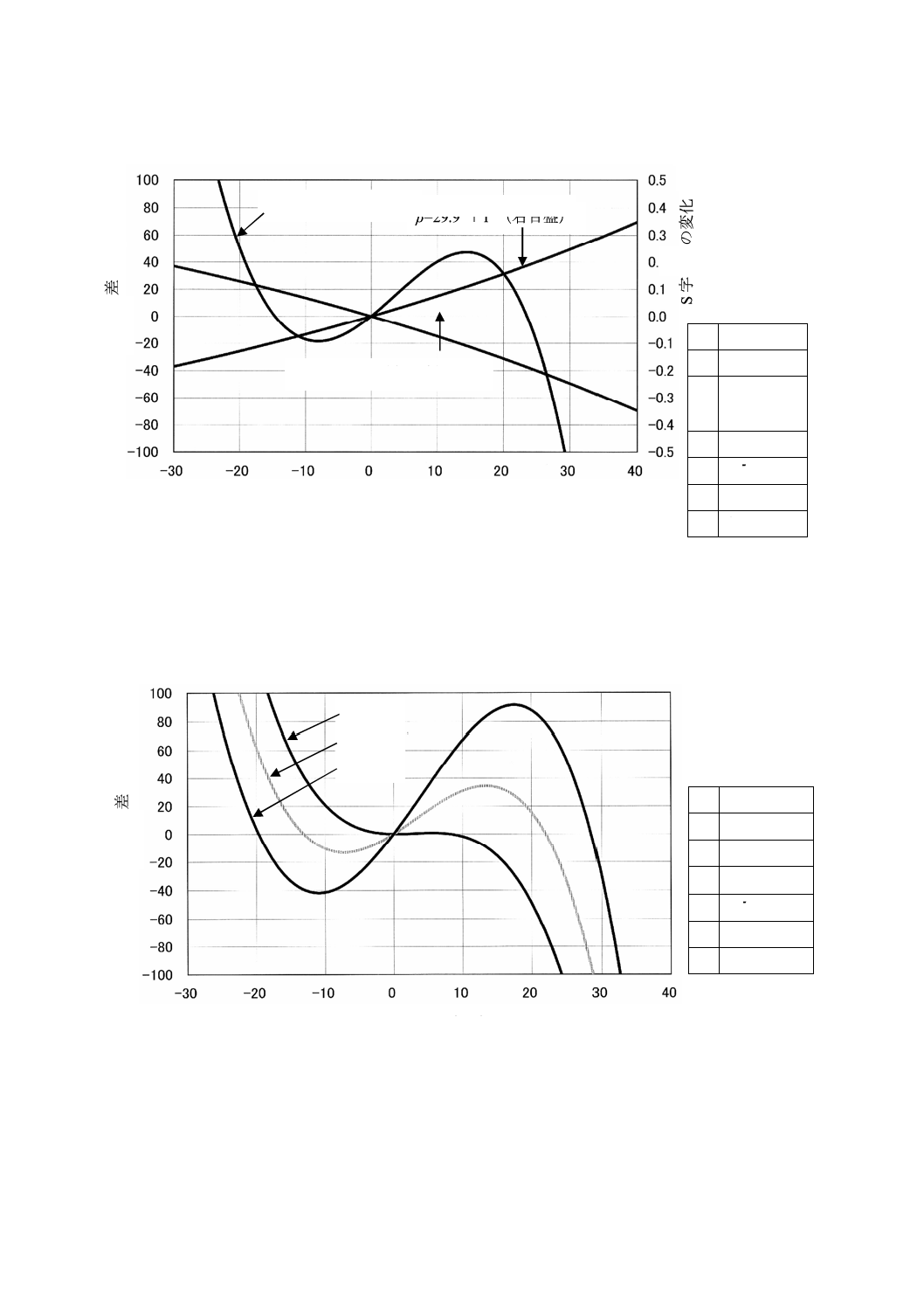
図C.2−測定円上ねじれ角を僅かに変化させたときの計算結果
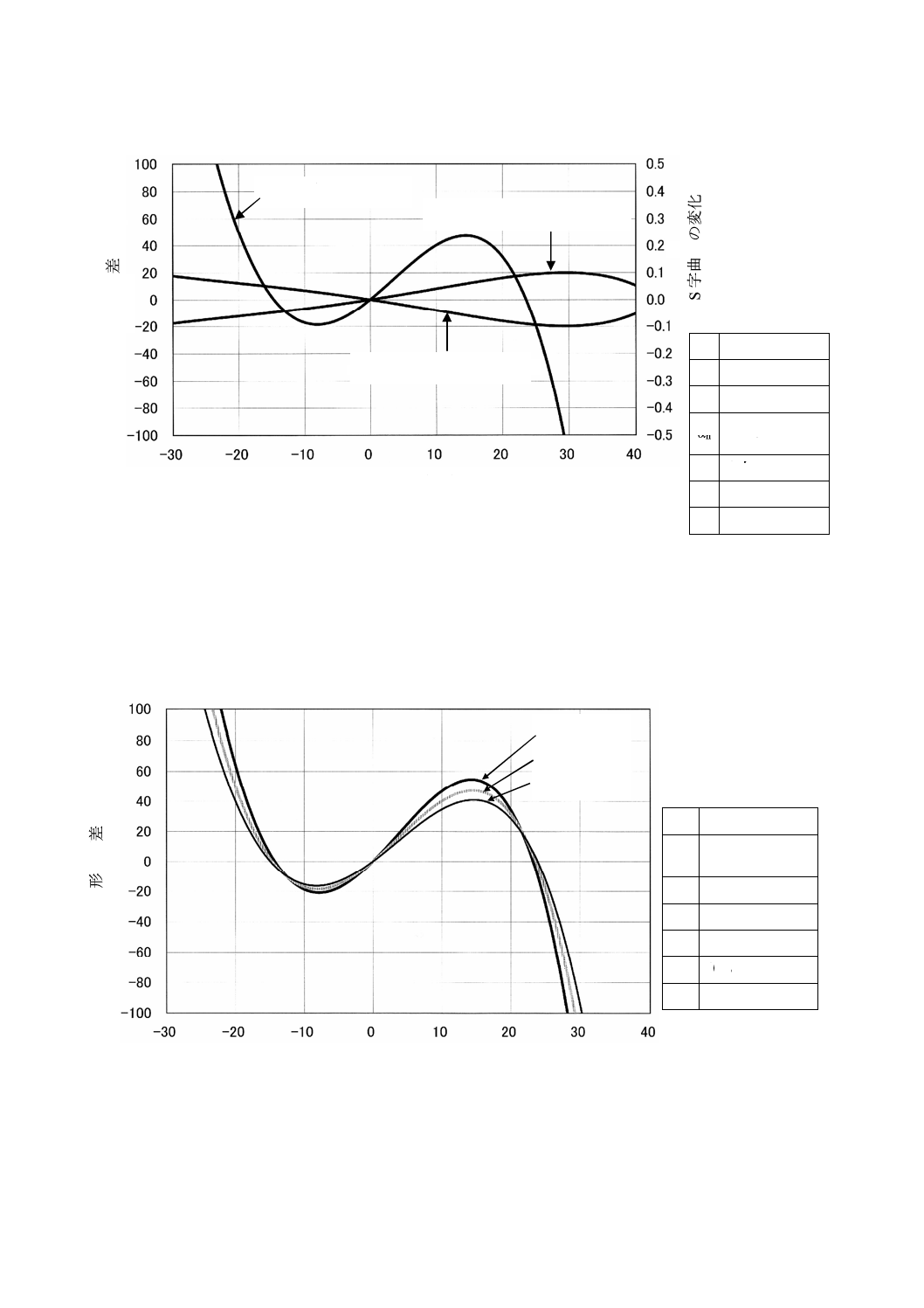
C.3 歯直角圧力角の影響
歯直角圧力角αnを変化させたときの計算結果を,図C.3及び図C.4に示す。
図C.3−歯直角圧力角を変化させたときの計算結果
形
状
偏
差
(μ
m
)
S
字
曲
線
の
変
化
(μ
m
)
計算条件
Ω 30°
r
55 mm
β
29.9°−1'',
29.9°+1''
αn 20°
rp 1.5 mm
eg 0 %
ey 0 mm
S字曲線(左目盛) β=29.9°+1''(右目盛)
β=29.9°−1''(右目盛)
歯幅方向位置 (mm)
形
状
偏
差
(μ
m
)
歯幅方向位置 (mm)
αn=0°
αn=10°
αn=20°
計算条件
Ω 30°
r
55 mm
β 30°
αn 0°, 10°, 20°
rp 1.5 mm
eg 0 %
ey 0 mm
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
32
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図C.4−歯直角圧力角を僅かに変化させたときの計算結果
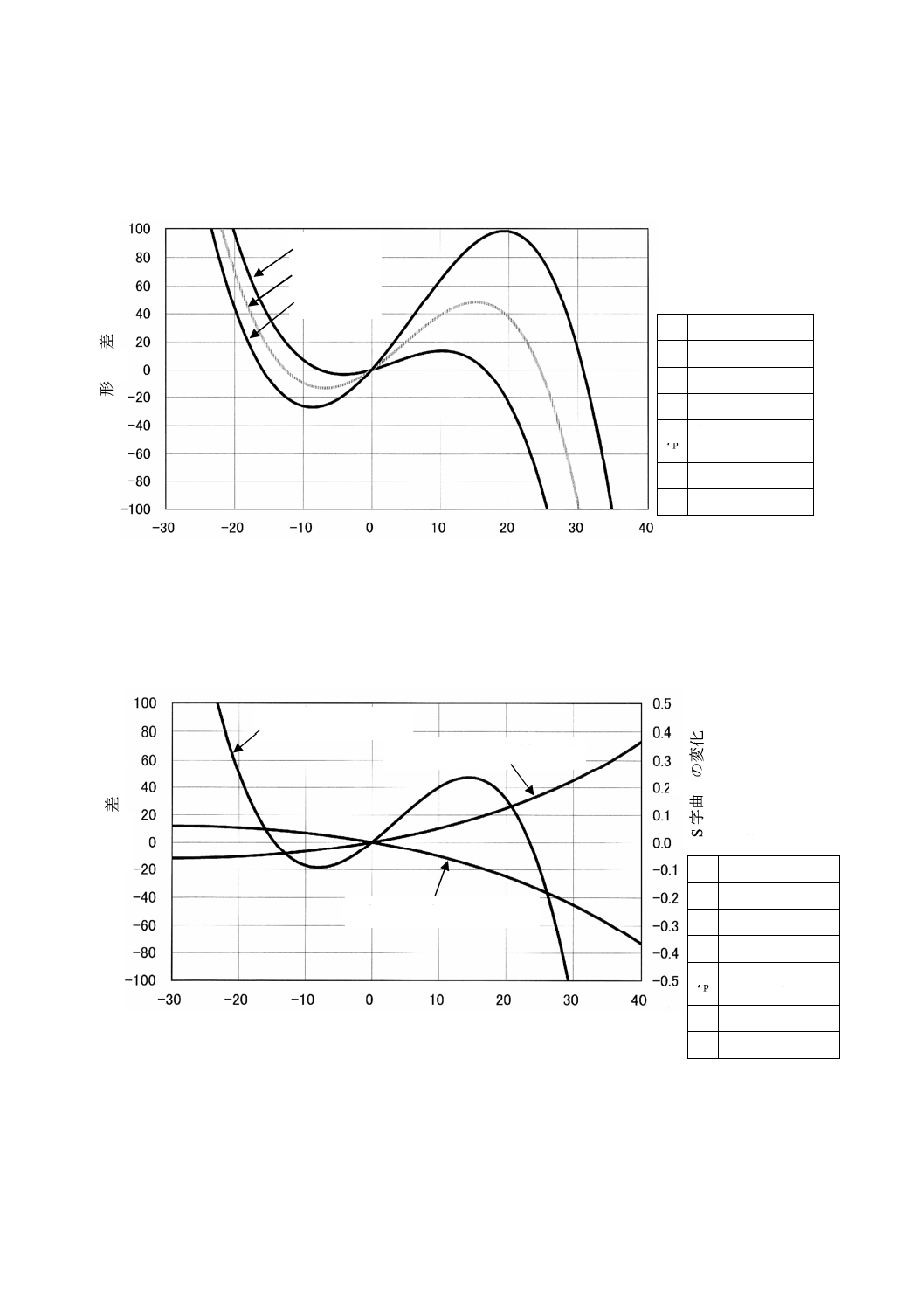
C.4 測定円半径の影響
測定円半径rを変化させたときの計算結果を,図C.5に示す。
図C.5−測定円半径を変化させたときの計算結果
形
状
偏
差
(μ
m
)
S
字
曲
線
の
変
化
(μ
m
)
歯幅方向位置 (mm)
S字曲線(左目盛)
αn =20°+0.011 3°(右目盛)
計算条件
Ω 30°
r 55 mm
β 30°
αn 20°−0.011 3°,
20°+0.011 3°
rp 1.5 mm
eg 0 %
ey 0 mm
αn =20°−0.011 3°(右目盛)
αn±0.011 3°は,作用線方向±10 μmに相当する。
形
状
偏
差
(μ
m
)
r =50 mm
r =55 mm
r =60 mm
歯幅方向位置 (mm)
計算条件
Ω 30°
r
50 mm, 55 mm,
60 mm
β
29.9°
αn 20°
rp 1.5 mm
eg 0 %
ey
0 mm
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
33
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
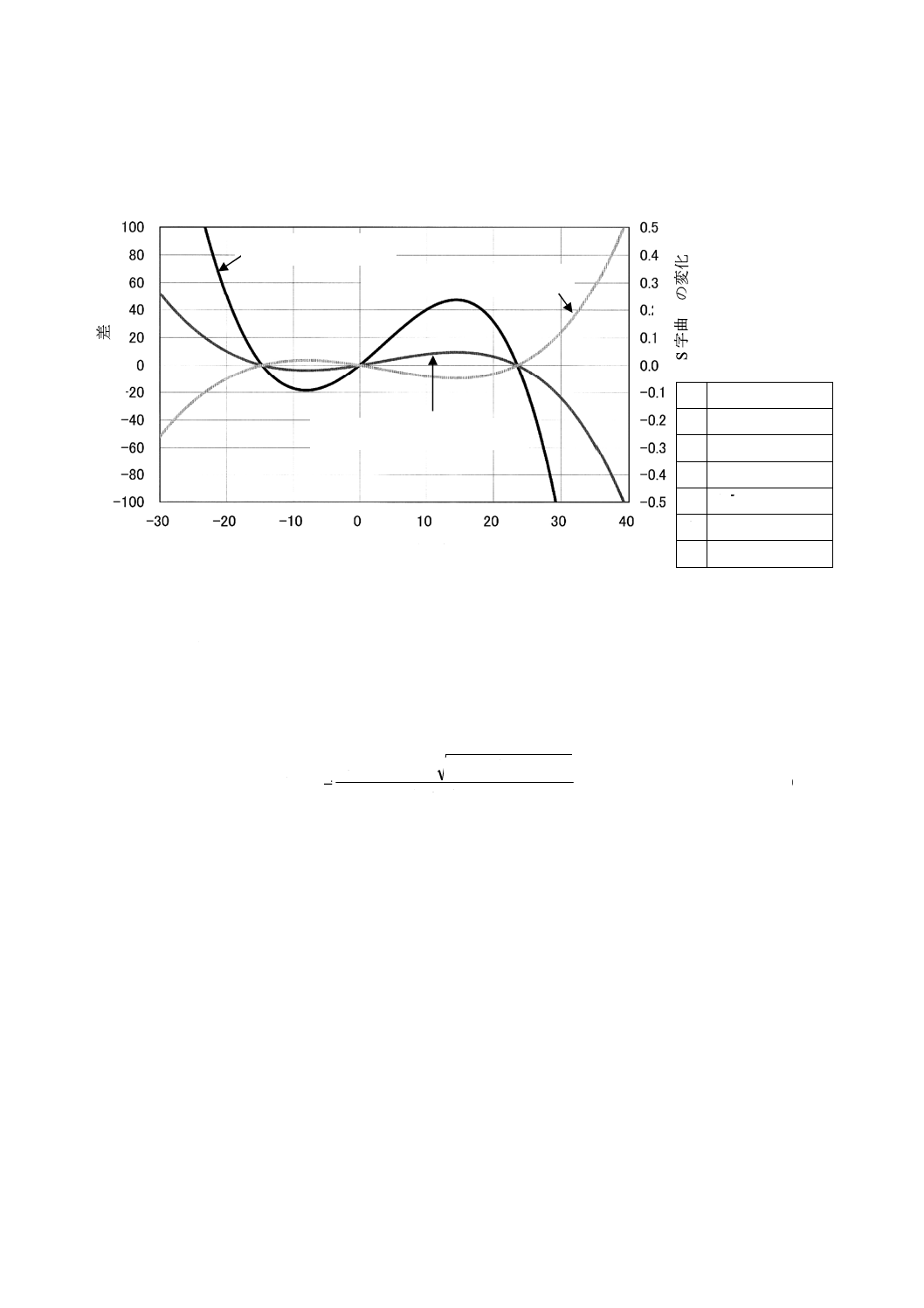
C.5 測定子先端球の半径の影響
測定子先端球の半径rpを変化させたときの計算結果を,図C.6及び図C.7に示す。
図C.6−測定子先端球の半径を変化させたときの計算結果
図C.7−測定子先端球の半径を僅かに変化させたときの計算結果
形
状
偏
差
(μ
m
)
歯幅方向位置 (mm)
rp=1.5 mm
rp=2.0 mm
rp=2.5 mm
計算条件
Ω 30°
r
55 mm
β
29.8°
αn 20°
rp 1.5 mm, 2.0 mm,
2.5 mm
eg 0 %
ey 0 mm
形
状
偏
差
(μ
m
)
S字曲線(左目盛)
計算条件
Ω 30°
r
55 mm
β
29.9°
αn 20°
rp 1.5 mm−1 μm,
1.5 mm+1 μm
eg 0 %
ey 0 mm
rp =1.5 mm+1 μm(右目盛)
rp=1.5 mm−1 μm(右目盛)
S
字
曲
線
の
変
化
(μ
m
)
歯幅方向位置 (mm)
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
34
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
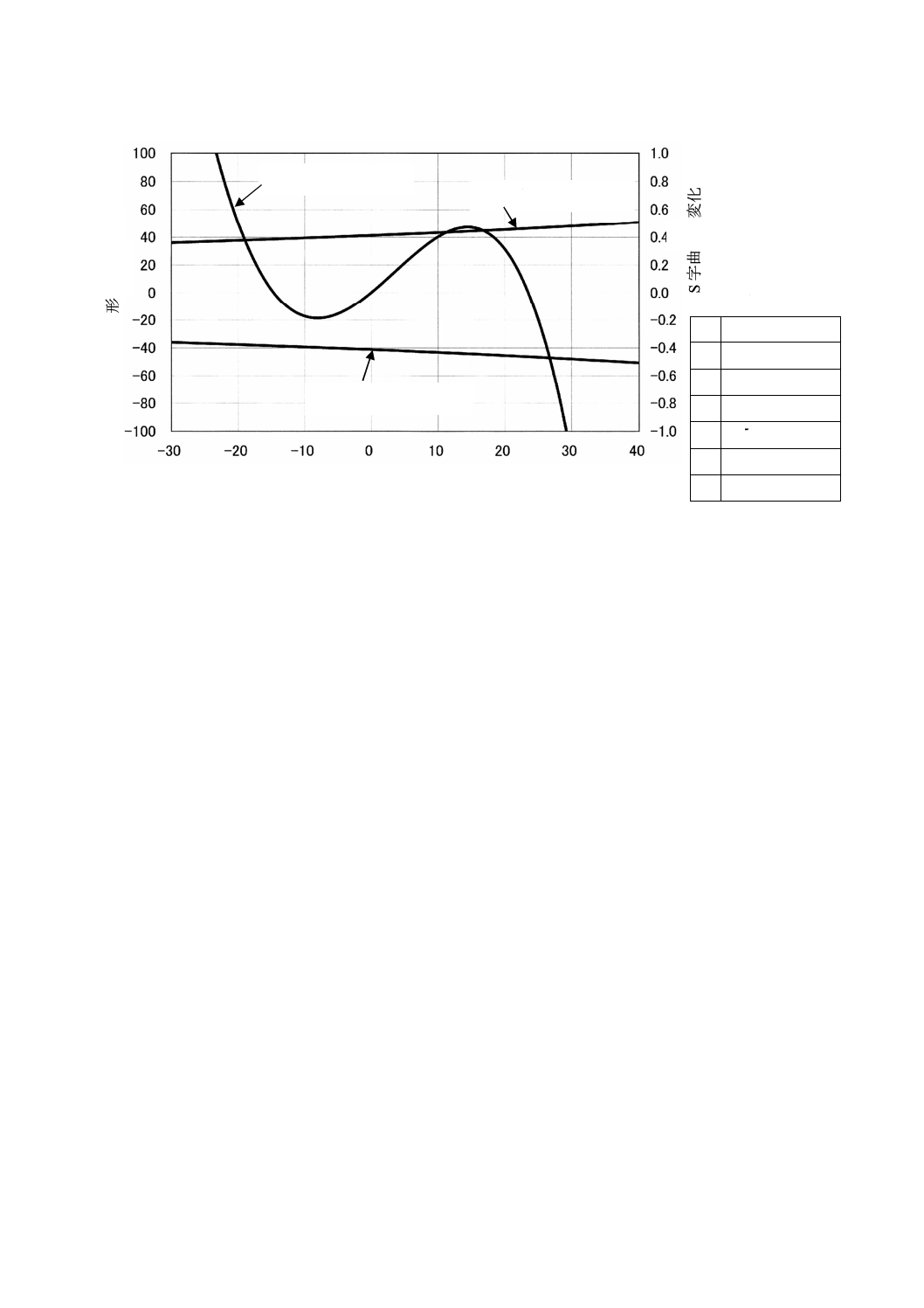
C.6 検出器出力にゲイン誤差があるとき
検出器出力にゲイン誤差があるときの計算結果を,図C.8に示す。
図C.8−検出器出力にゲイン誤差があるときの計算結果
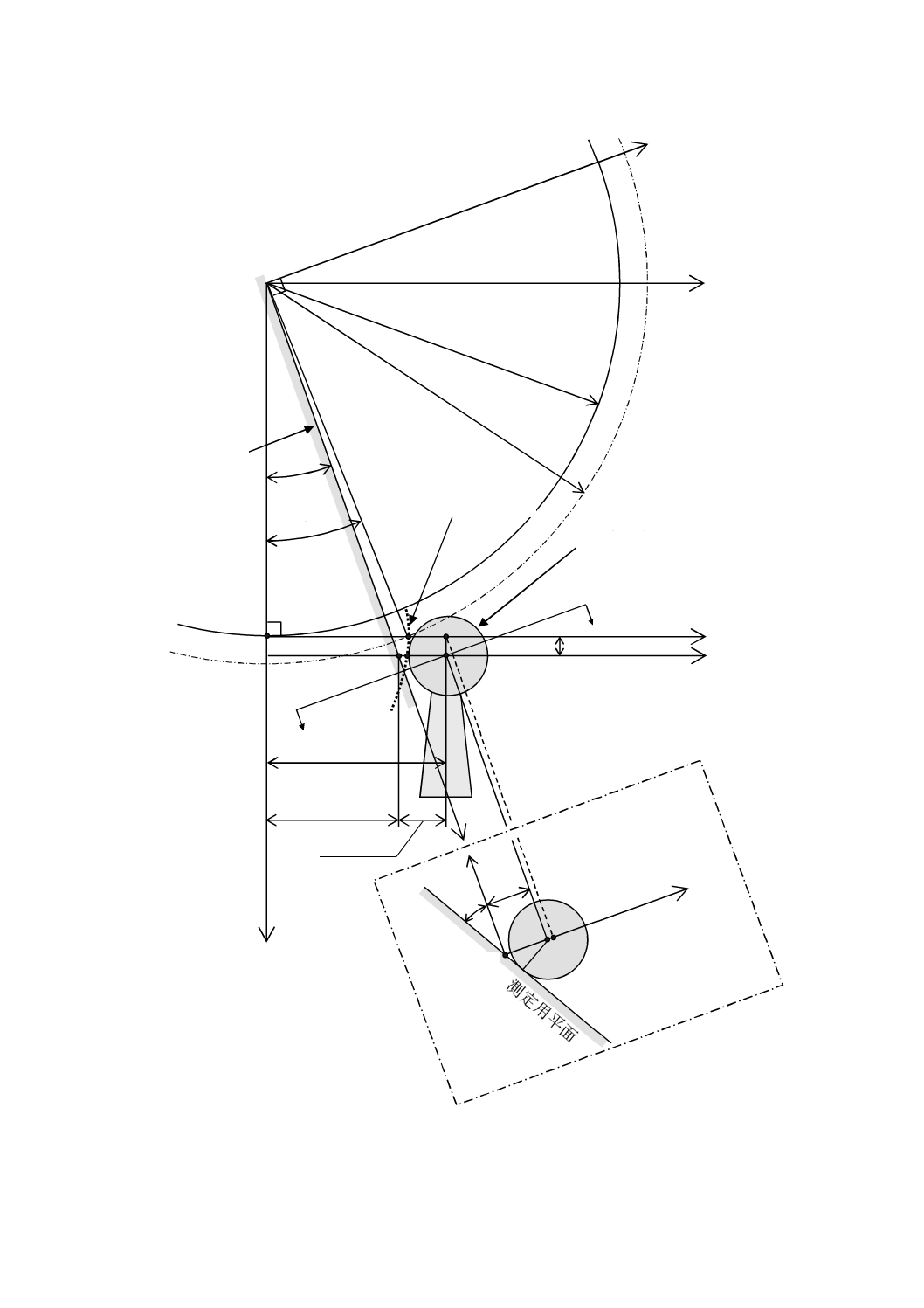
C.7 測定子がX軸方向にオフセットしたとき
測定子先端球の曲率中心がX軸方向にepオフセットしたときの形状偏差は(図C.10及び図C.11参照),
Y' 軸(作用線)と平行でepだけ離れたY''上において仮想インボリュートを測定していると考え,6.1の計
算式においてtanε0を式(C.1)のように置き換えることによって計算することができる。
2
0
2
p
b
2
0
2
0
2
p
b
0
0
p
b
0
)
(
)
(
)
(
tan
η
η
η
ε
−
+
−
+
+
−
+
=
e
r
Y
e
r
Y
e
r
·································· (C.1)
epが±1 μmのときの計算結果を,図C.9に示す。
形
状
偏
差
(μ
m
)
S
字
曲
線
の
変
化
(μ
m
)
S字曲線(左目盛)
ゲイン誤差−0.1 %(右目盛)
ゲイン誤差+0.1 %(右目盛)
歯幅方向位置 (mm)
計算条件
Ω 30°
r
55 mm
β
29.9°
αn 20°
rp 1.5 mm
eg −0.1 %,+0.1 %
ey 0 mm
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
35
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図C.9−測定子がX軸方向にオフセットしたときの計算結果
形
状
偏
差
(μ
m
)
S字曲線(左目盛)
S
字
曲
線
の
変
化
(μ
m
)
計算条件
Ω 30°
r
55 mm
β
29.9°
αn 20°
rp 1.5 mm
eg 0 %
ep −1 μm,+1 μm
歯幅方向位置 (mm)
ep =−1 μm(右目盛)
ep =+1 μm(右目盛)
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
36
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図C.10−測定子がX軸方向にオフセットしているときの初期設定状態の図
η0
η
Ω
rp
O
ζ
ε0
ξ
Y
X
αt
(rb+ep)tanε0
η0/cosε0
(rbtanαt+ rp)
作用線
仮想インボリュート曲線
rb
η
r
A-A
O
Y'
Z
Y''
ep
原点断面における
測定用平面
原点断面における
測定子先端球
A
A
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
37
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
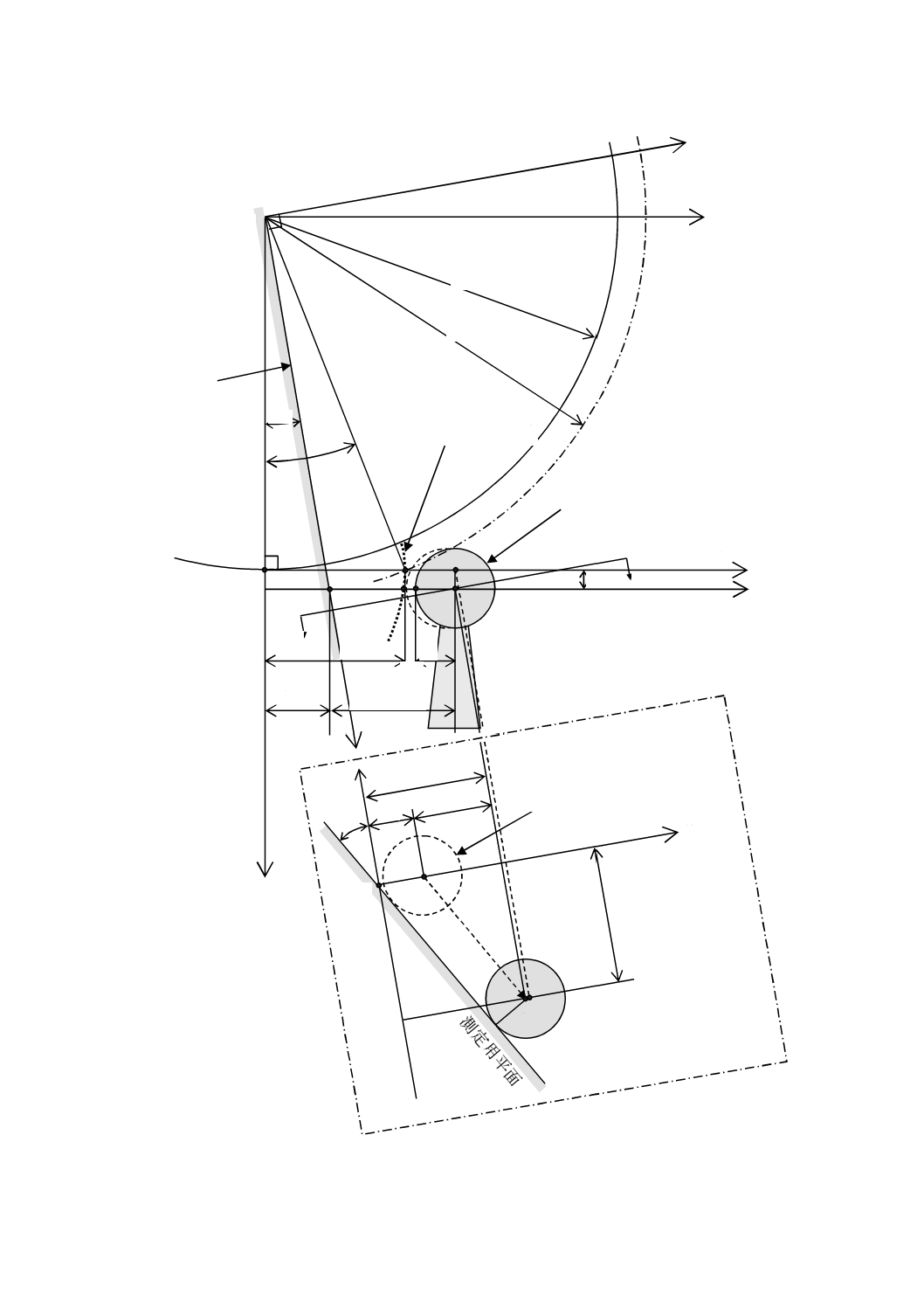
図C.11−測定子がX軸方向にオフセットしているときの歯すじ測定状態の図
ηw
η
rp
εm
ξ
X
αt
rbtanεm
ηm/cosεm
δH
rp
rbtanαt
作用線
仮想インボリュート曲線
rb
η
r
原点断面に投影した
測定子先端球
Y
Y'
Ω
ζ
O
Zw
η0
ηm
Z
A-A
O
ep
Y''
A
A
原点断面における
測定用平面
初期位置の測定子先端を
平面基準器と共に
回転させた位置
2019年7月1日の法改正により名称が変わりました。まえがきを除き、本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
38
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書D
(参考)
形状偏差の実測例
D.1 実測例
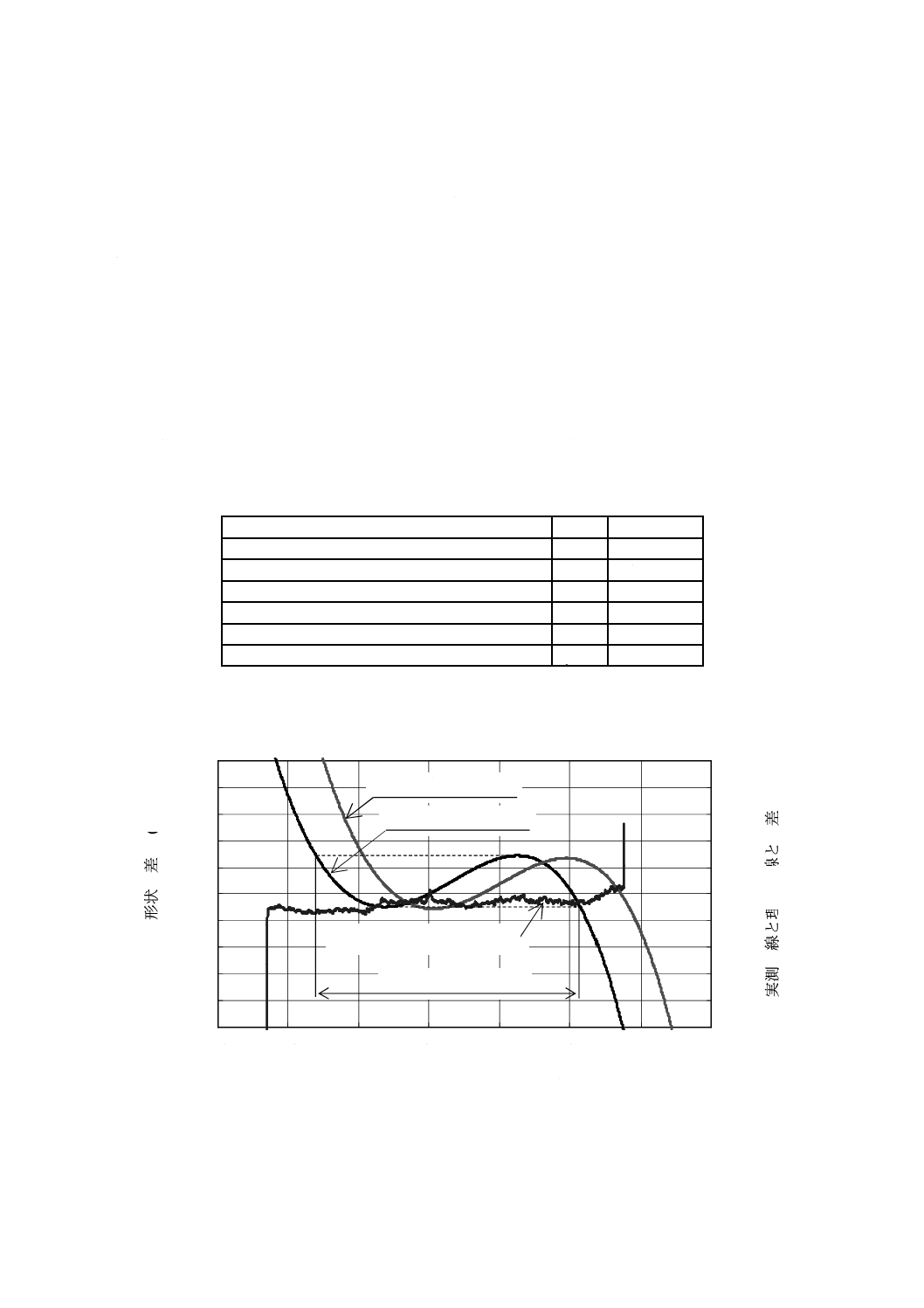
測定に用いた平面基準器及び対象とした歯車の諸元を表D.1に,平面基準器の歯すじ測定例を図D.1に
示す。測定子先端球中心の座標位置は,5.7と同じ条件である。このときの理論形状偏差の計算値を,表
D.2に示す。
実測曲線の歯幅方向の位置は,初期設定位置の歯幅方向の座標をゼロとして出力されない場合がある。
このとき,実測曲線を,理論曲線のグラフ上でその形状を変えることなく平行移動させ,フィッティング
を行う。フィッティングは,理論曲線と実測曲線との縦軸方向の残差平方和を,理論曲線の精度評価対象
範囲で計算し,残差平方和が最小になるよう平行移動を行い偏差曲線を得る。
表D.1−実測例の諸元
平面基準器の直径
114 mm
平面基準器の高さ
183 mm
基準軸と測定用平面とのなす角度
Ω
30°
測定円半径
r
55 mm
測定円半径におけるねじれ角
β
29.85°
歯直角圧力角
αn
20°
測定子先端球の半径
rp
1.5 mm
-100
-80
-60
-40
-20
0
20
40
60
80
100
-30
-20
-10
0
10
20
30
40
-2.0
-1.6
-1.2
-0.8
-0.4
0.0
0.4
0.8
1.2
1.6
2.0
図D.1−平面基準器の歯すじ測定例
形
状
偏
差
(μ
m
)
実
測
曲
線
と理
論
曲線
と
の
差
(μ
m
)
精度評価対象範囲
実測曲線(左目盛)
理論曲線(左目盛)
歯すじ偏差曲線(右目盛)
歯幅方向位置 Zw (mm)
39
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
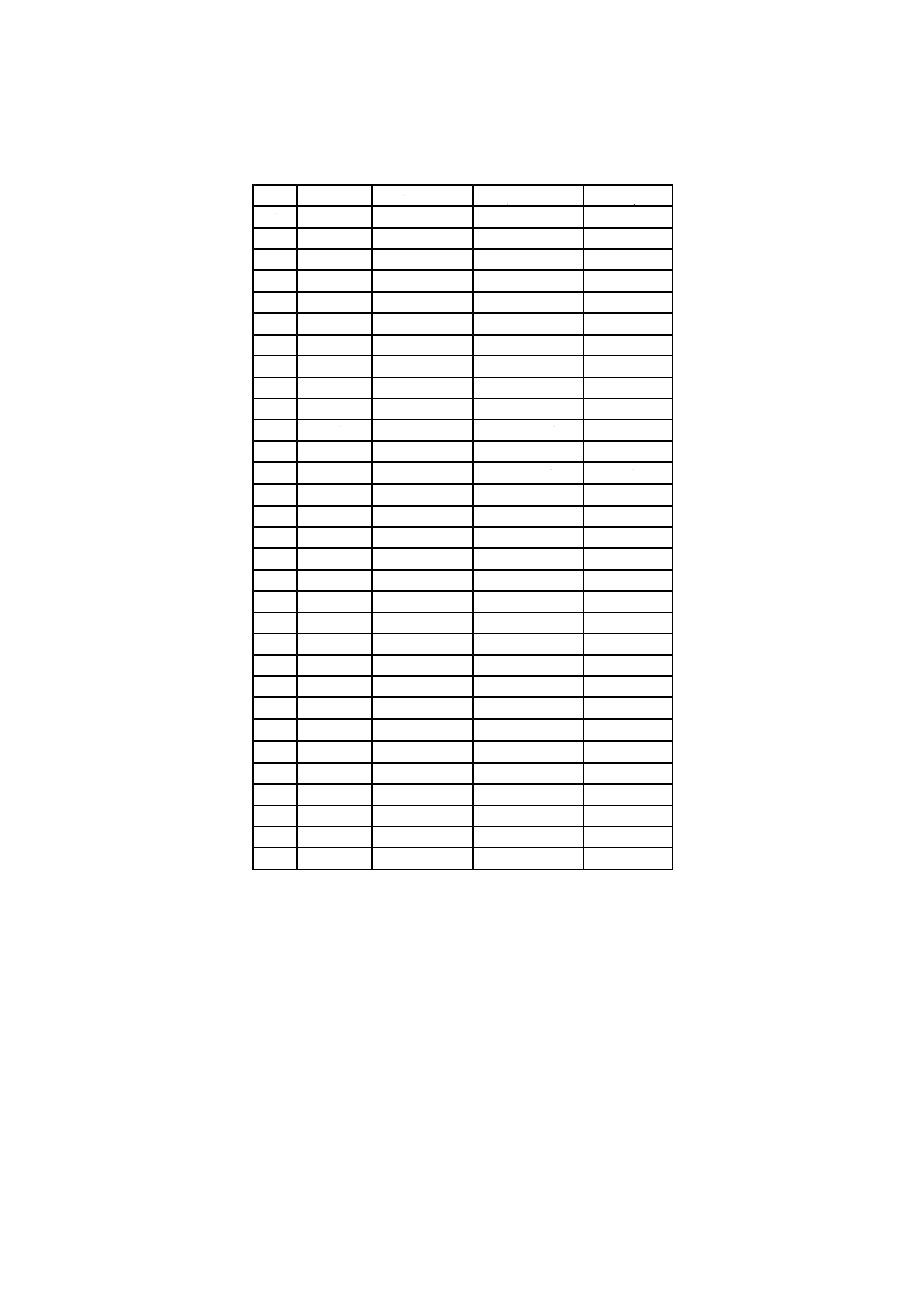
表D.2−形状偏差δHの計算例
η0=1.732 1 mm,Y0=22.782 4 mm,tanε0=0.412 28
Zw mm
εm rad
ηm mm
δH μm
1
−30
0.078 030
19.052 6
293.7
2
−28
0.098 898
17.897 9
235.4
3
−26
0.119 766
16.743 2
184.7
4
−24
0.140 633
15.588 5
141.1
5
−22
0.161 501
14.433 8
104.2
6
−20
0.182 369
13.279 1
73.4
7
−18
0.203 237
12.124 4
48.3
8
−16
0.224 105
10.969 7
28.3
9
−14
0.244 972
9.815 0
13.1
10
−12
0.265 840
8.660 3
2.2
11
−10
0.286 708
7.505 6
−5.0
12
−8
0.307 576
6.350 9
−8.7
13
−6
0.328 444
5.196 2
−9.7
14
−4
0.349 312
4.041 5
−8.2
15
−2
0.370 179
2.886 8
−4.8
16
0
0.391 047
1.732 1
0.0
17
2
0.411 915
0.577 4
5.7
18
4
0.432 783
−0.577 4
11.8
19
6
0.453 651
−1.732 1
17.7
20
8
0.474 518
−2.886 8
22.9
21
10
0.495 386
−4.041 5
26.8
22
12
0.516 254
−5.196 2
28.8
23
14
0.537 122
−6.350 9
28.1
24
16
0.557 990
−7.505 6
24.2
25
18
0.578 858
−8.660 3
16.3
26
20
0.599 725
−9.815 0
3.6
27
22
0.620 593
−10.969 7
−14.7
28
24
0.641 461
−12.124 4
−39.6
29
26
0.662 329
−13.279 1
−71.9
30
28
0.683 197
−14.433 8
−112.8
31
30
0.704 064
−15.588 5
−163.3
40
B 1757-3:2013
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考文献
[1] ISO 1328-1,Cylindrical gears−ISO system of accuracy−Part 1: Definitions and allowable values of
deviations relevant to corresponding flanks of gear teeth
[2] ISO 18653,Gears−Evaluation of instruments for the measurement of individual gears
[3] ISO/TR 10064-5,Cylindrical gears−Code of inspection practice−Part 5: Recommendations relative to
evaluation of gear measuring instruments
[4] Masaharu Komori, Fumi Takeoka, Aizoh Kubo, Kazuhiko Okamoto, Sonko Osawa, Osamu Sato and Toshiyuki
Takatsuji, Evaluation method of lead measurement accuracy of gears using a wedge artefact, Measurement
Science and Technology, Volume 20, Number 2, February 2009, 025109.
[5] Masaharu Komori, Fumi Takeoka, Aizoh Kubo, Kazuhiko Okamoto, Sonko Osawa, Osamu Sato, Toshiyuki
Takatsuji, and Yohan Kondo, Artifact Design and Measurement Error Analysis in the Evaluation of Lead
Measurement Accuracy of Helical Gear Using Wedge Artifact, Journal of Mechanical Design, Vol. 132, Issue 7,
071006-1-11, 2010-7.
[6] Yohan Kondo, Koshi Kondo, Sonko Osawa, Osamu Sato, Masaharu Komori, Fumi Takeoka, Aizo Kubo,
Kazuhiko Okamoto and Kazuyuki Sasajima “Evaluation of instruments for helix measurement using wedge
artifact” Precision Engineering, 34, 667-674,2010