2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 0621-1984
幾何偏差の定義及び表示
Definitions and Designations of Geometrical Deviations
1. 適用範囲 この規格は,対象物の形状偏差,姿勢偏差,位置偏差及び振れ(以下,これらを総称して
幾何偏差という。)の定義及び表示について規定する。
備考 幾何偏差の許容値である幾何公差の記号による表示及びそれらの図示方法については,JIS B
0021(幾何公差の図示方法)による。
引用規格:
JIS B 0021 幾何公差の図示方法
JIS B 0022 幾何公差のためのデータム
2. 用語の意味 この規格で用いる主な用語の意味は,次による。
(1) 形体 幾何偏差の対象となる点,線,軸線,面又は中心面。
(2) 単独形体 データムに関連なく,幾何偏差が決められる形体。
(3) 関連形体 データムに関連して,幾何偏差が決められる形体。
(4) データム 形体の姿勢偏差,位置偏差,振れなどを決めるために設定した理論的に正確な幾何学的基
準。例えば,幾何学的基準が点,直線,軸直線(1),平面及び中心平面の場合には,それぞれデータム
点,データム直線,データム軸直線,データム平面及びデータム中心平面という。
注(1) 軸直線とは,形状偏差がない軸線,すなわち,幾何学的に正しい直線である軸線をいう。
備考 データムに関する詳細は,JIS B 0022(幾何公差のためのデータム)による。
(5) 直線形体 機能上直線であるように指定した形体。例えば,平面形体をそれに垂直な平面で切断した
ときに切り口に現れる断面輪郭線,軸線,円筒の母線,ナイフエッジの先端など。
(6) 軸線 直線形体のうち,円筒又は直方体であるように指定した対象物の各横断面における断面輪郭線
の中心(2)を結ぶ線。
注(2) 断面輪郭線の中心とは,円筒であるように指定した対象物では,その断面輪郭線に外接する最
小の幾何学的に正しい円(軸の場合)又は内接する最大の幾何学的に正しい円(穴の場合)の
中心をいう。
また,直方体であるように指定した対象物では,その断面輪郭線に外接する最小の幾何学的
に正しい長方形(軸の場合)又は内接する最大の幾何学的に正しい長方形(穴の場合)の中心
をいう。
(7) 平面形体 機能上平面であるように指定した形体。
(8) 中心面 平面形体のうち,互いに面対称であるべき二つの面上の対応する二つの点を結ぶ直線の中点
を含む面。
(9) 円形形体 機能上円であるように指定した形体。例えば,平面図形としての円や回転面の円形断面。
2
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(10) 円筒形体 機能上円筒面であるように指定した形体。
(11) 線の輪郭 機能上定められた形状をもつように指定した表面の要素としての外形線。
(12) 面の輪郭 機能上定められた形状をもつように指定した表面。
3. 幾何偏差の種類 幾何偏差の種類は,表による。
表 幾何偏差の種類
種類
適用する形体
形状偏差
真直度
平面度
真円度
円筒度
単独形体
線の輪郭度
面の輪郭度
単独形体又は
関連形体
姿勢偏差
平行度
直角度
傾斜度
位置偏差
位置度
同軸度及び同心度
対称度
関連形体
振れ
円周振れ
全振れ
4. 定義
4.1
真直度 真直度とは,直線形体の幾何学的に正しい直線(以下,幾何学的直線という。)からの狂い
の大きさをいう。
4.2
平面度 平面度とは,平面形体の幾何学的に正しい平面(以下,幾何学的平面という。)からの狂い
の大きさをいう。
4.3
真円度 真円度とは,円形形体の幾何学的に正しい円(以下,幾何学的円という。)からの狂いの大
きさをいう。
4.4
円筒度 円筒度とは,円筒形体の幾何学的に正しい円筒(以下,幾何学的円筒という。)からの狂い
の大きさをいう。
4.5
線の輪郭度 線の輪郭度とは,理論的に正確な寸法によって定められた幾何学的に正しい輪郭(以
下,幾何学的輪郭という。)からの線の輪郭の狂いの大きさをいう。
なお,データムに関連する場合と関連しない場合とがある。
4.6
面の輪郭度 面の輪郭度とは,理論的に正確な寸法によって定められた幾何学的輪郭からの面の輪
郭の狂いの大きさをいう。
なお,データムに関連する場合と関連しない場合とがある。
4.7
平行度 平行度とは,データム直線又はデータム平面に対して平行な幾何学的直線又は幾何学的平
面からの平行であるべき直線形体又は平面形体の狂いの大きさをいう。
4.8
直角度 直角度とは,データム直線又はデータム平面に対して直角な幾可学的直線又は幾何学的平
面からの直角であるべき直線形体又は平面形体の狂いの大きさをいう。
4.9
傾斜度 傾斜度とは,データム直線又はデータム平面に対して理論的に正確な角度をもつ幾何学的
直線又は幾何学的平面からの理論的に正確な角度をもつべき直線形体又は平面形体の狂いの大きさをいう。
3
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.10 位置度 位置度とは,データム又は他の形体に関連して定められた理論的に正確な位置からの点,
直線形体又は平面形体の狂いの大きさをいう。
4.11 同軸度 同軸度とは,データム軸直線と同一直線上にあるべき軸線のデータム軸直線からの狂いの
大きさをいう。
備考 平面図形の場合には.データム円の中心に対する他の円形形体の中心の位置の狂いの大きさを
同心度という。
4.12 対称度 対称度とは,データム軸直線又はデータム中心平面に関して互いに対称であるべき形体の
対称位置からの狂いの大きさをいう。
4.13 円周振れ 円周振れとは,データム軸直線を軸とする回転面をもつべき対象物又はデータム軸直線
に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき,その表面が指定した
位置又は任意の位置で指定した方向(3)に変位する大きさをいう。
注(3) 指定した方向とは,データム軸直線と交わりデータム軸直線に対して垂直な方向(半径方向),
データム軸直線に平行な方向(軸方向)又はデータム軸直線と交わりデータム軸直線に対して
斜めの方向(斜め法線方向及び斜め指定方向)をいう。
4.14 全振れ 全振れとは,データム軸直線を軸とする円筒面をもつべき対象物又はデータム軸直線に対
して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき,その表面が指定した方向
(4)に変位する大きさをいう。
注(4) 指定した方向とは,データム軸直線と交わりデータム軸直線に対して垂直な方向(半径方向)
又はデータム軸直線に平行な方向(軸方向)をいう。
5. 表示
5.1
真直度 真直度は,直線形体が占める領域の大きさによって,次に示すように表し,真直度_mm又
は真直度_μmと表示する。
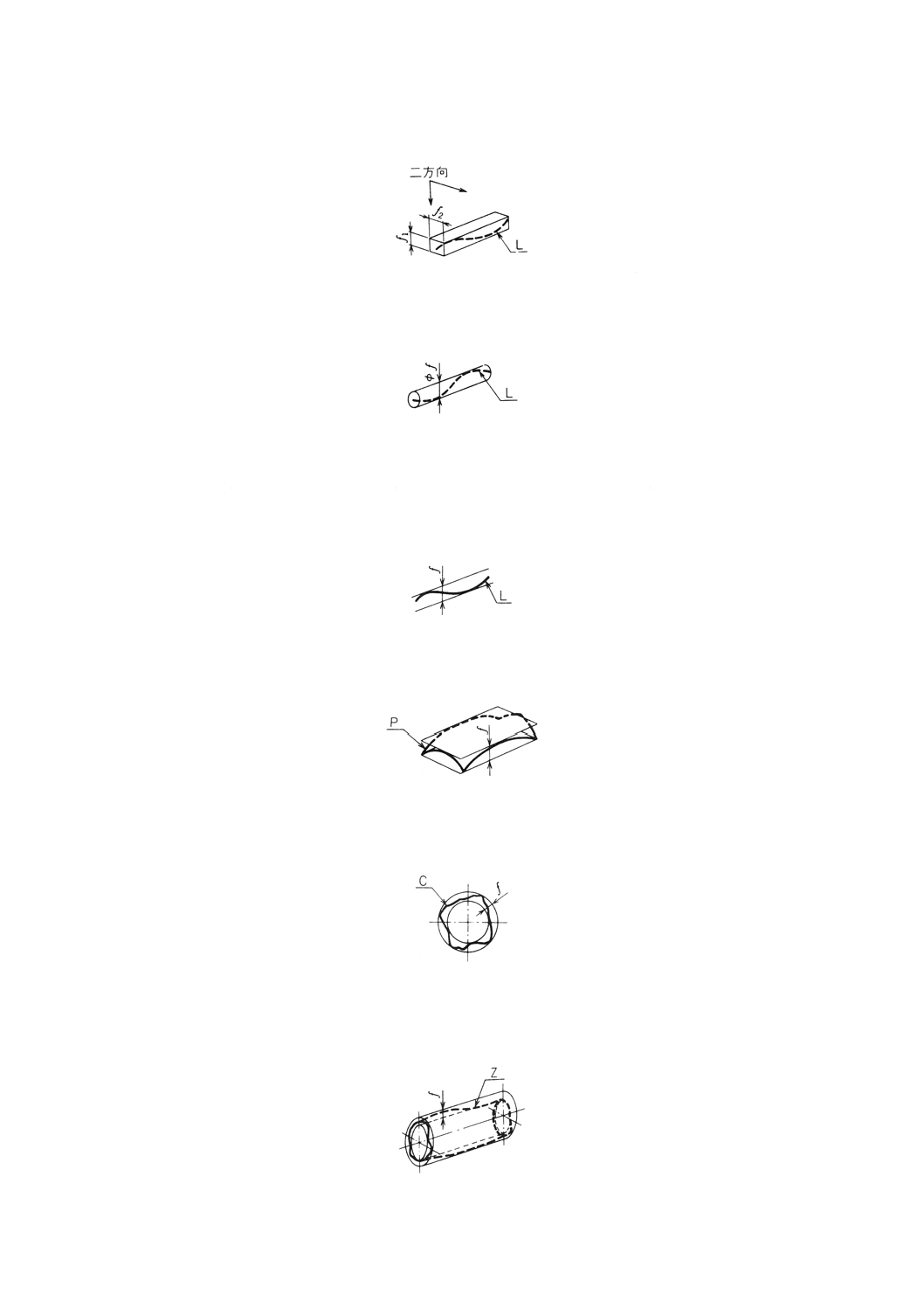
(1) 一方向の真直度 一方向の真直度は,その方向に垂直な幾何学的に正しい平行な二平面(以下,幾何
学的平行二平面という。)でその直線形体 (L) を挟んだとき,平行二平面の間隔が最小となる場合の
二平面の間隔 (f) で表す(図1)。
図1
備考 その方向が,例えば水平方向又は鉛直方向の場合には,それぞれを水平方向の真直度又は鉛直方向の
真直度という。
(2) 互いに直角な二方向の真直度 互いに直角な二方向[例えば5.1(1)の備考の水平方向及び鉛直方向]
の真直度は,その二方向にそれぞれ垂直な二組の幾何学的平行二平面でその直線形体 (L) を挟んだと
き,二組の平行二平面の各々の間隔が最小となる場合の,二平面の間隔 (f1,f2) (すなわち,二組の
平行二平面で区切られる直方体の二辺の長さ)で表す(図2)。
4
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図2
(3) 方向を定めない場合の真直度 方向を定めない場合(例えば,円筒の軸線など)の真直度は,その直
線形体 (L) をすべて含む幾何学的円筒のうち,最も径の小さい円筒の直径 (f) で表す(図3)。
図3
(4) 表面の要素としての直線形体の真直度 表面の要素としての直線形体(回転面の母線や,平面形体の
表面に垂直な平面による断面輪郭線など)の真直度は,幾何学的に正しい平行な二直線(以下,幾何
学的平行二直線という。)で,その直線形体 (L) を挟んだとき,平行二直線の間隔が最小になる場合
の,二直線の間隔 (f) で表す(図4)。
図4
5.2
平面度 平面度は,平面形体 (P) を幾何学的平行二平面で挟んだとき,平行二平面の間隔が最小と
なる場合の,二平面の間隔 (f) で表し(図5),平面度_mm又は平面度_μmと表示する。
図5
5.3
真円度 真円度は,円形形体 (C) を二つの同心の幾何学的円で挟んだとき,同心二円の間隔が最小
となる場合の,二円の半径の差 (f) で表し(図6),真円度_mm又は真円度_μmと表示する。
図6
5.4
円筒度 円筒度は,円筒形体 (Z) を二つの同軸の幾何学的円筒で挟んだとき,同軸二円筒の間隔が
最小となる場合の,二円筒の半径の差 (f) で表し(図7),円筒度_mm又は円筒度̲μmと表示する。
図7
5
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考 円筒形体の幾何偏差は,軸線に直角な断面における輪郭線の偏差(真円度)と,軸線を含む断
面における輪郭線の偏差(母線の真直度と平行度)とに分けて考えることもできる。
5.5
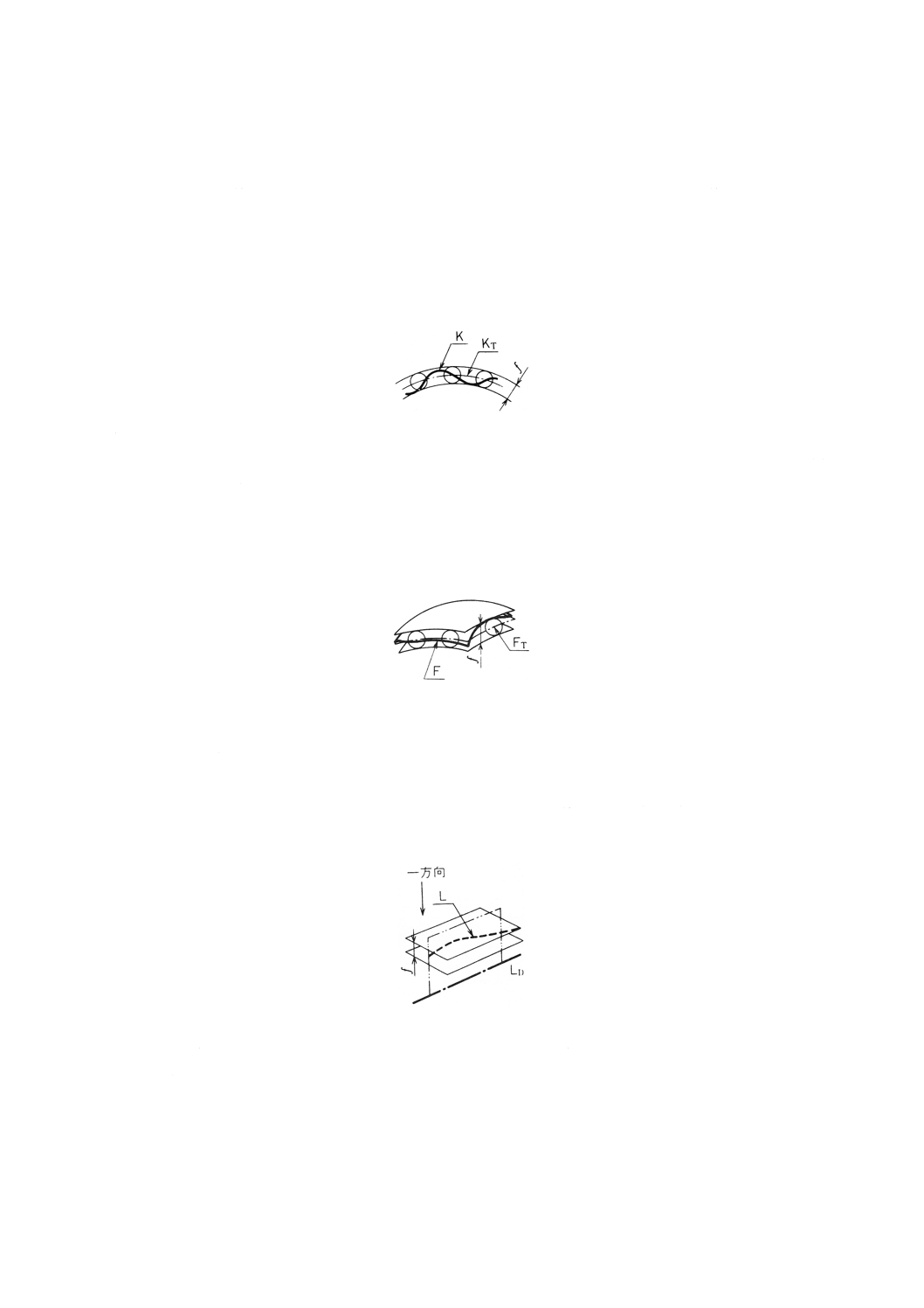
線の輪郭度 線の輪郭度は,理論的に正確な寸法によって定められた幾何学的輪郭線 (KT) 上に中心
をもつ同一の直径の幾何学的円の二つの包絡線で,その線の輪郭 (K) を挟んだときの,二包絡線の間隔 (f)
(円の直径)で表し(図8),線の輪郭度_mm又は線の輪郭度_μmと表示する。ただし,理論的に正確
な寸法は,データム線又はデータム面に関して与える場合と,それらと関係しないで与える場合とがある。
図8
5.6
面の輪郭度 面の輪郭度は,理論的に正確な寸法によって定められる幾何学的輪郭面 (FT) 上に中心
をもつ同一の直径の幾何学的に正しい球(以下,幾何学的球という。)の二つの包絡面でその面の輪郭 (F)
を挟んだときの,二包絡面の間隔 (f) (球の直径)で表し(図9),面の輪郭度_mm又は面の輪郭度_μm
と表示する。ただし,理論的に正確な寸法は,データム線又はデータム面に関して与える場合と,それら
と関係しないで与える場合とがある。
図9
5.7
平行度 平行度は,直線形体又は平面形体が,データム直線又はデータム平面に対して垂直な方向
において占める領域の大きさによって,次に示すように表し,平行度_mm又は平行度_μmと表示する。
(1) 直線形体のデータム直線に対する平行度
(a) 一方向の平行度 一方向の平行度は,その方向に垂直でデータム直線 (LD) に平行な幾何学的平行
二平面でその直線形体 (L) を挟んだときの,二平面の間隔 (f) で表す(図10)。
図10
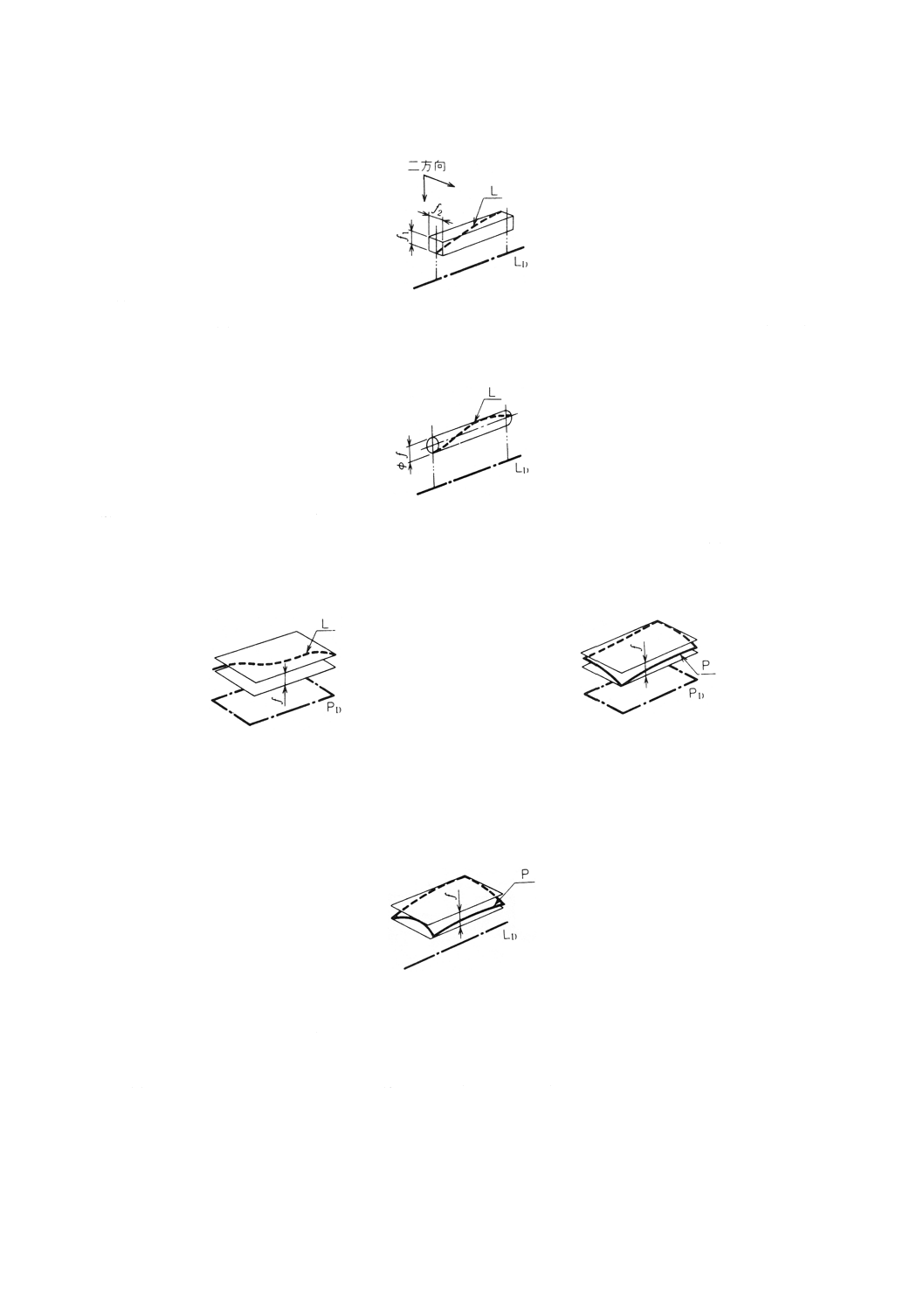
(b) 互いに直角な二方向の平行度 互いに直角な二方向の平行度は,その二方向にそれぞれ垂直でデー
タム直線 (LD) に平行な二組の幾何学的平行二平面でその直線形体 (L) を挟んだときの,二平面の
間隔 (f1,f2) (すなわち,二組の平行二平面で区切られる直方体の二辺の長さ)で表す(図11)。
6
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図11
(c) 方向を定めない場合の平行度 方向を定めない場合の平行度は,データム直線 (LD) に平行でその
直線形体 (L) をすべて含む幾何学的円筒のうち,最も小さい径の円筒の直径 (f) で表す(図12)。
図12
(2) 直線形体又は平面形体のデータム平面に対する平行度 直線形体又は平面形体のデータム平面に対
する平行度は,データム平面 (PD) に平行な幾何学的平行二平面でその直線形体 (L) 又は平面形体
(P) を挟んだときの,二平面の間隔 (f) で表す(図13,図14)。
図13
図14
(3) 平面形体のデータム直線に対する平行度 平面形体のデータム直線に対する平行度は,データム直線
(LD) に平行な幾何学的平行二平面でその平面形体 (P) を挟んだとき,平行二平面の間隔が最小となる
場合の二平面の間隔 (f) で表す(図15)。
図15
5.8
直角度 直角度は,直線形体又は平面形体がデータム直線又はデータム平面に対して平行な方向で
占める領域の大きさによって,次に示すように表し,直角度_mm又は直角度_μmと表示する。
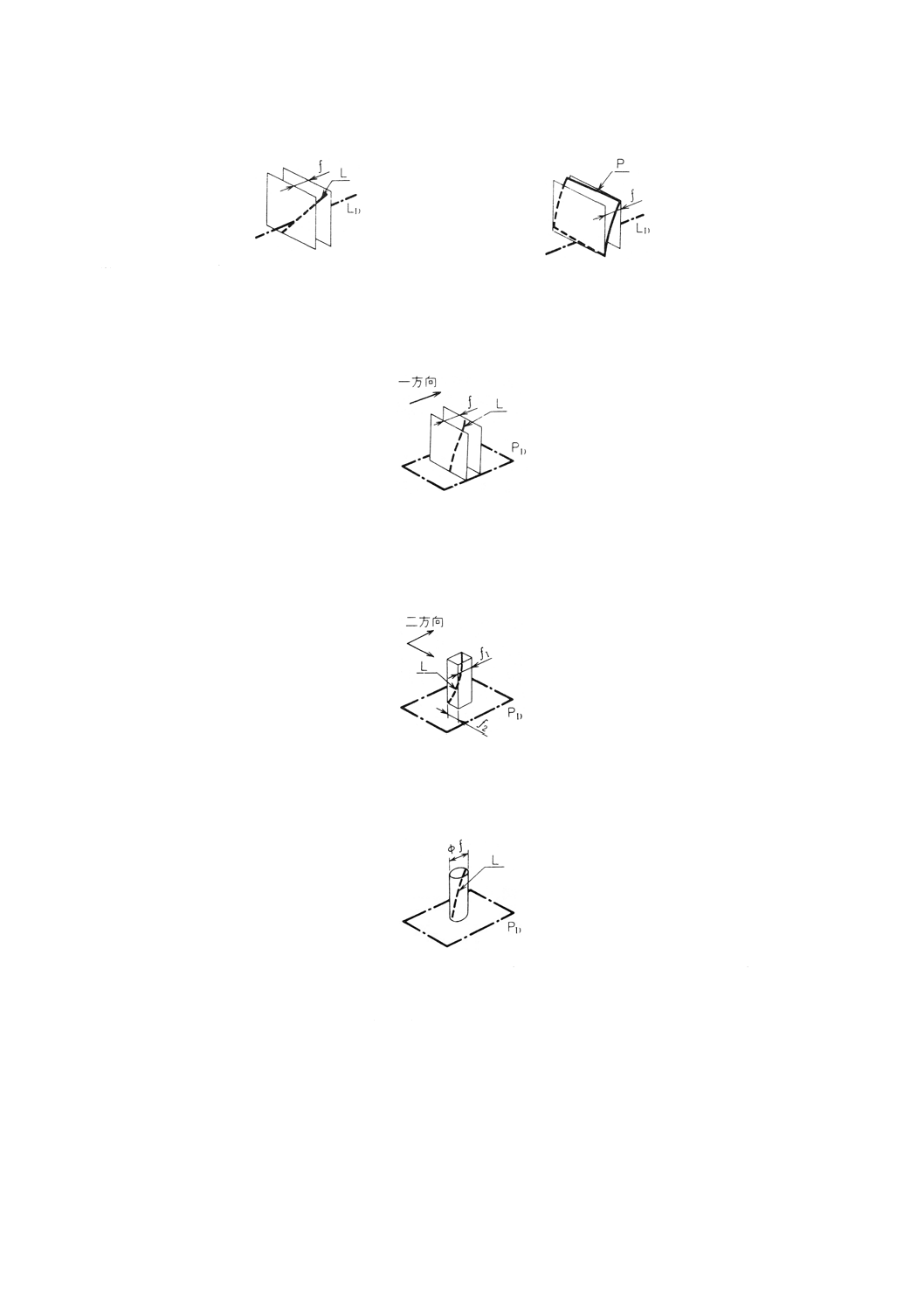
(1) 直線形体又は平面形体のデータム直線に対する直角度 直線形体又は平面形体のデータム直線に対
する直角度は,データム直線 (LD) に垂直な幾何学的平行二平面でその直線形体 (L) 又は平面形体
(P) を挟んだときの,二平面の間隔 (f) で表す(図16,図17)。
7
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図16
図17
(2) 直線形体のデータム平面に対する直角度
(a) 一方向の直角度 一方向の直角度は,その方向とデータム平面 (PD) に垂直な幾何学的平行二平面
でその直線形体 (L) を挟んだときの,二平面の間隔 (f) で表す(図18)。
図18
(b) 互いに直角な二方向の直角度 互いに直角な二方向の直角度は,その二方向とデータム平面 (PD)
にそれぞれ垂直な二組の幾何学的平行二平面でその直線形体 (L) を挟んだときの,二平面の間隔
(f1,f2) (すなわち,二組の平行二平面で区切られる直方体の二辺の長さ)で表す(図19)。
図19
(c) 方向を定めない場合の直角度 方向を定めない場合の直角度は,データム平面 (PD) に垂直でその
直線形体 (L) をすべて含む幾何学的円筒のうち,最も小さい径の円筒の直径 (f) で表す(図20)。
図20
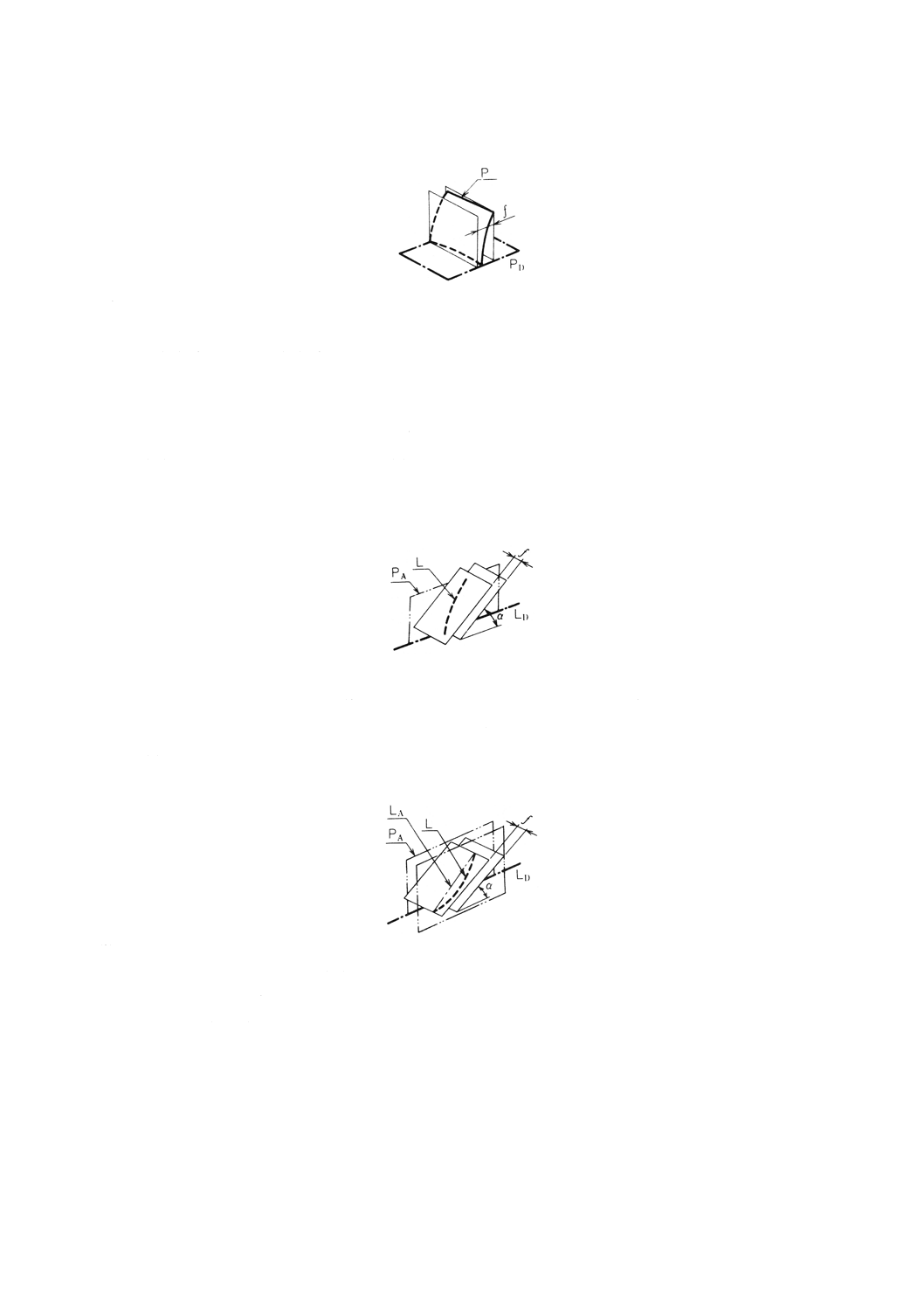
(3) 平面形体のデータム平面に対する直角度 平面形体のデータム平面に対する直角度は,データム平面
(PD) に垂直な幾何学的平行二平面でその平面形体 (P) を挟んだとき,平行二平面の間隔が最小となる
場合の,二平面の間隔 (f) で表す(図21)。
8
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図21
5.9
傾斜度 傾斜度は,直線形体又は平面形体がデータム直線又はデータム平面に対して理論的に正確
な角度をもつ幾何学的直線又は幾何学的平面に垂直な方向で占める領域の大きさによって,次に示すよう
に表し,傾斜度_mm又は傾斜度_μmと表示する。
(1) 直線形体のデータム直線に対する傾斜度
(a) 同一平面上にある場合 同一平面上にあるべき直線形体のデータム直線に対する傾斜度は,直線形
体 (L) のいずれか一端とデータム直線 (LD) とを含む幾何学的平面 (PA) に垂直で,データム直線
(LD) に対して理論的に正確な角度 (α) をなす幾何学的平行二平面で直線形体 (L) を挟んだときの,
二平面の間隔 (f) で表す(図22)。
図22
(b) 同一平面上にない場合 同一平面上にない直線形体のデータム直線に対する傾斜度は,直線形体
(L) の両端を結ぶ幾何学的直線 (LA) に平行で,データム直線 (LD) を含む幾何学的平面 (PA) に垂
直で,データム直線 (LD) に理論的に正確な角度 (α) をなす幾何学的平行二平面でその直線形体
(L) を挟んだときの,二平面の間隔 (f) で表す(図23)。
図23
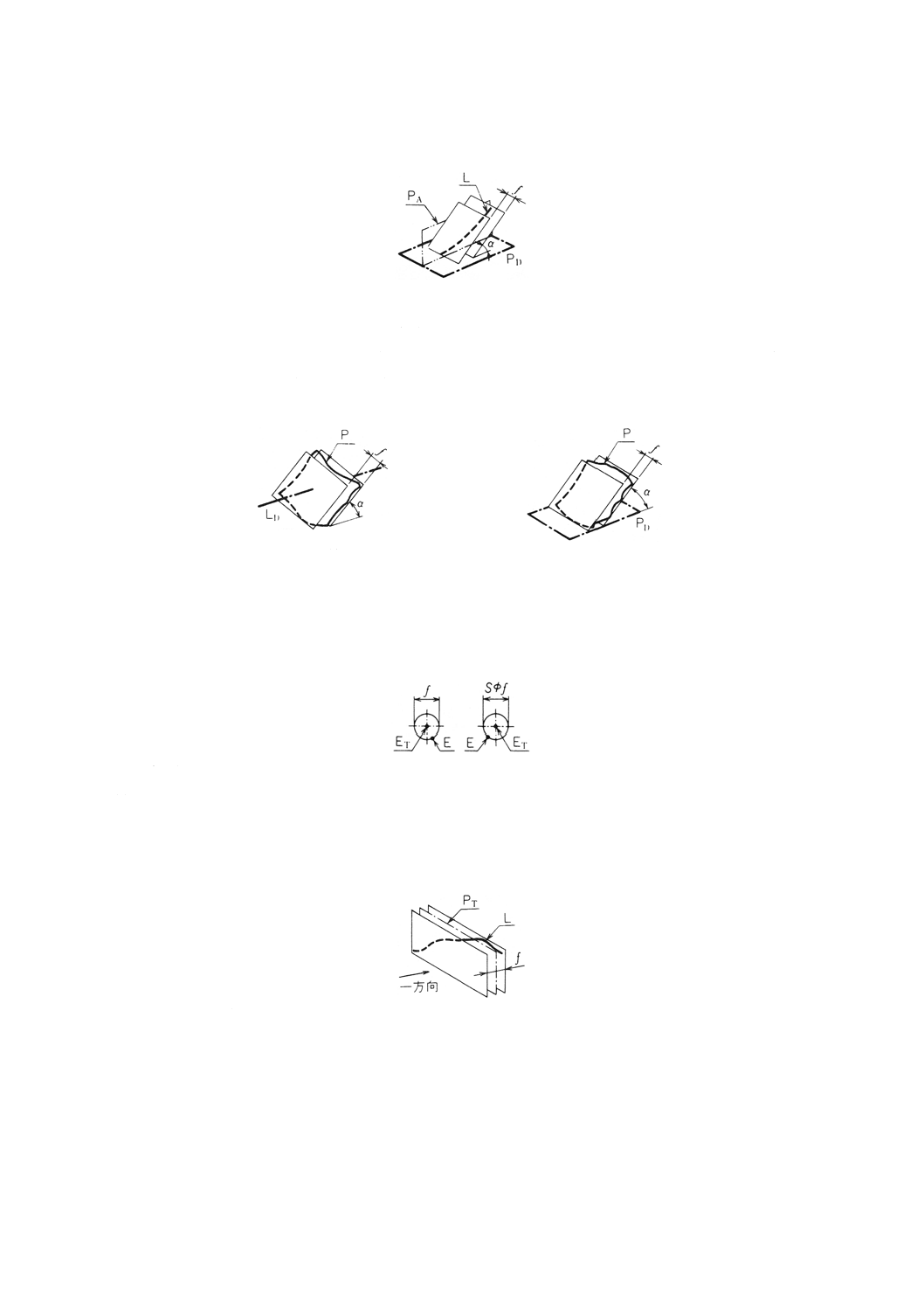
(2) 直線形体のデータム平面に対する傾斜度 直線形体のデータム平面に対する傾斜度は,直線形体 (L)
の両端を含みデータム平面 (PD) に垂直な幾何学的平面 (PA) に垂直で,データム平面 (PD) に対して
理論的に正確な角度 (α) をなす幾何学的平行二平面で直線形体 (L) を挟んだときの,二平面の間隔
(f) で表す(図24)。
9
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図24
(3) 平面形体のデータム直線又はデータム平面に対する傾斜度 平面形体のデータム直線又はデータム
平面に対する傾斜度は,データム直線 (LD) 又はデータム平面 (PD) に対して理論的に正確な角度 (α)
をなす幾何学的平行二平面で平面形体 (P) を挟んだとき,平行二平面の間隔が最小となる場合の,二
平面の間隔 (f) で表す(図25,図26)。
図25
図26
5.10 位置度 位置度は,点,直線形体又は平面形体が理論的に正確な位置に対して占める領域の大きさ
によって,次に示すように表し,位置度_mm又は位置度_μmと表示する。
(1) 点の位置度 点の位置度は,理論的に正確な位置にある点 (ET) を中心とし,対象としている点 (E) を
通る幾何学的円又は幾何学的球の直径 (f) で表す(図27)。
図27
(2) 直線形体の位置度
(a) 一方向の位置度 一方向の位置度は,その方向に垂直で理論的に正確な位置にある幾何学的直線(5)
に対して対称な幾何学的平行二平面でその直線形体 (L) を挟んだときの,二平面の間隔 (f) で表す
(図28)。
図28
注(5) 図28の平面 (PT) は,理論的に正確な位置にある幾何学的直線を含み,その方向に垂直な平面を
示す。
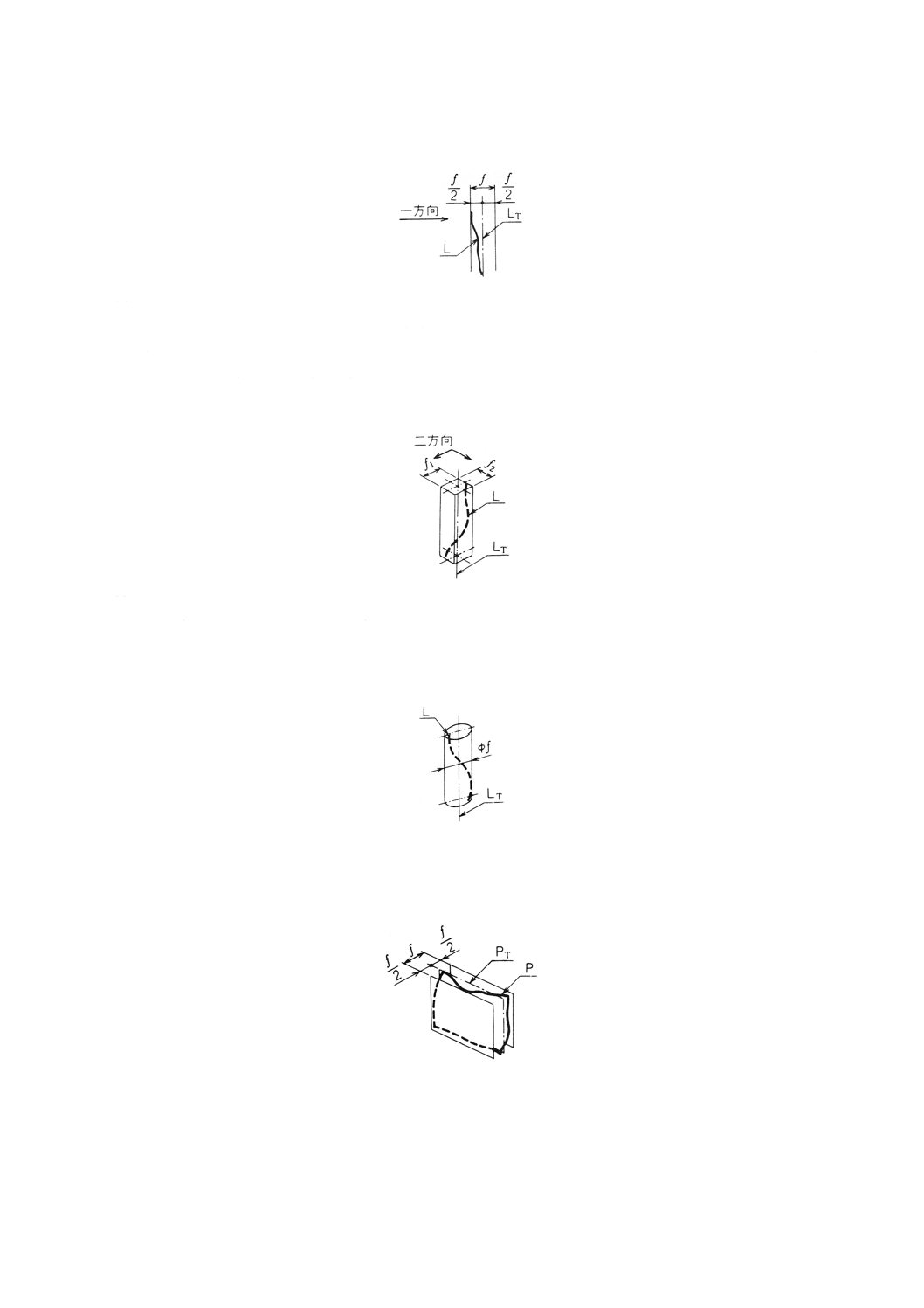
参考 直線形体が一平面上にある場合の直線形体の位置度は,理論的に正確な位置にある幾何学的直
線 (LT) に対して対称な幾何学的平行二直線でその直線形体 (L) を挟んだときの,二直線の間
隔 (f) で表す(参考図1)。
10
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考図1
(b) 互いに直角な二方向の位置度 互いに直角な二方向の位置度は,その二方向にそれぞれ垂直で理論
的に正確な位置にある幾何学的直線 (LT) に対して対称な二組の幾何学的平行二平面でその直線形
体 (L) を挟んだときの,二平面の間隔 (f1,f2) (すなわち,二組の平行二平面で区切られる直方体
の二辺の長さ)で表す(図29)。
図29
(c) 方向を定めない場合の位置度 方向を定めない場合の位置度は,理論的に正確な位置にある幾何学
的直線 (LT) を軸とし,その直線形体 (L) をすべて含む幾何学的円筒のうち最も径の小さい円筒の
直径 (f) で表す(図30)。
図30
(3) 平面形体の位置度 平面形体の位置度は,理論的に正確な位置にある幾何学的平面 (PT) に対して
対称な幾何学的平行二平面でその平面形体 (P) を挟んだときの,二平面の間隔 (f) で表す(図31)。
図31
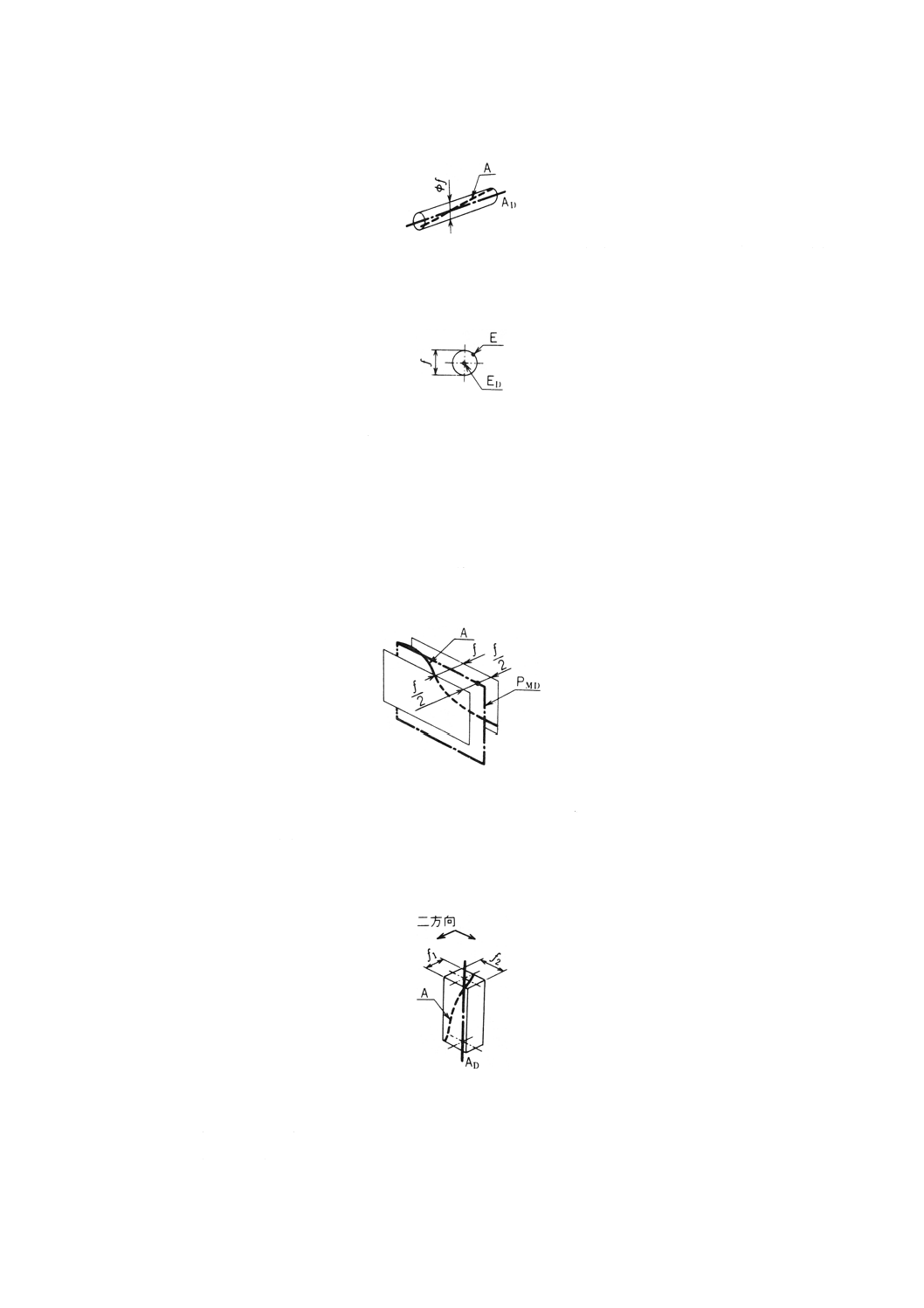
5.11 同軸度 軸線のデータム軸直線に対する同軸度は,その軸線 (A) をすべて含みデータム軸直線 (AD)
と同軸の幾何学的円筒のうち,最も径の小さい円筒の直径 (f) で表し(図32),同軸度_mm又は同軸度_
μmと表示する。
11
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図32
参考 平面図形としての二つの円の同心度は,データム円の中心 (ED) と同心で,円形形体の中心 (E)
を通る幾何学的円の直径 (f) で表す(参考図2)。
参考図2
ここに,円形形体の中心とは,二つの同心の幾何学的円でその円形形体を挟んだとき,二円
の半径の差が最小となる場合の同心円の中心をいう。
5.12 対称度 対称度は,軸線又は中心面がデータム軸直線又はデータム中心平面に対して垂直な方向で
占める領域の大きさによって,(1)又は(2)に示すように表し,対称度_mm又は対称度_μmと表示する。
(1) 軸線の対称度
(a) データム中心平面に対する対称度 データム中心平面に対する対称度は,データム中心平面 (PMD)
に対して対称な幾何学的平行二平面でその軸線を挟んだときの,二平面の間隔 (f) で表す(図33)。
図33
(b) データム軸直線に対する互いに直角な二方向の対称度 データム軸直線に対する互いに直角な二方
向の対称度は,その二方向にそれぞれ垂直で,データム軸直線 (AD) に対して対称な幾何学的平行
二平面でその軸線 (A) を挟んだときの,二平面の間隔 (f1,f2) (すなわち,二組の平行二平面で区
切られる直方体の二辺の長さ)で表す(図34)。
図34
(2) 中心面の対称度
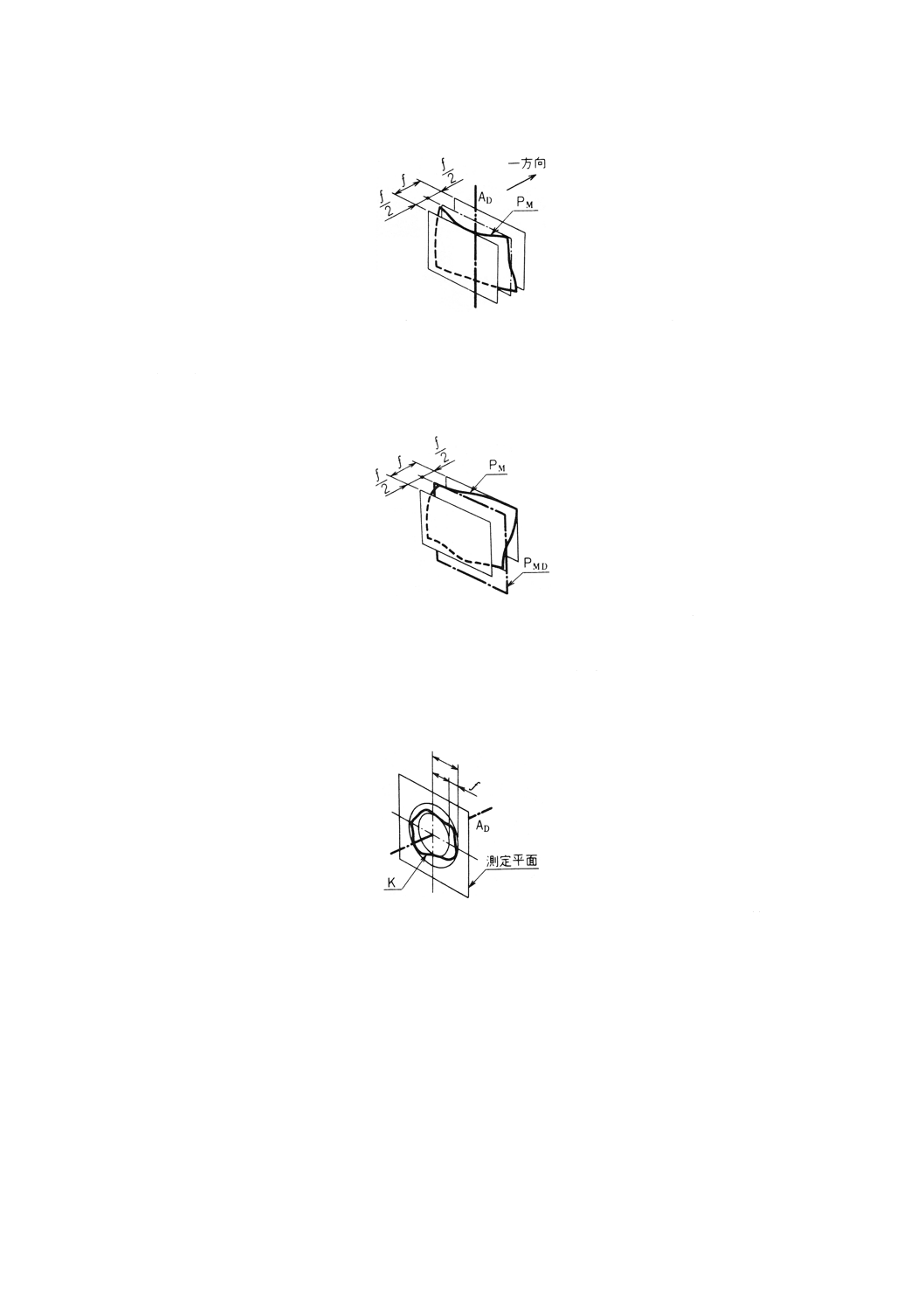
(a) データム軸直線に対する一方向の対称度 データム軸直線に対する一方向の対称度は,その方向に
垂直でデータム軸直線 (AD) に対して対称な幾何学的平行二平面でその中心面 (PM) を挟んだとき
の,二平面の間隔 (f) で表す(図35)。
12
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図35
(b) データム中心平面に対する対称度 データム中心平面に対する対称度は,データム中心平面 (PMD)
に対して対称な幾何学的平行二平面でその中心面 (PM) を挟んだときの,二平面の間隔 (f) で表す
(図36)。
図36
5.13 円周振れ 円周振れは,指定した方向によって,それぞれ次に示すような,対象物の表面上の各位
置における振れのうち,その最大値で表すことを原則とし,円周振れ_mm又は円周振れ_μmと表示する。
(1) 半径方向の円周振れ 半径方向の円周振れは,データム軸直線 (AD) に垂直な一平面(測定平面)内
で,データム軸直線から対象とした表面 (K) までの距離の最大値と最小値との差 (f) で表す(図37)。
図37
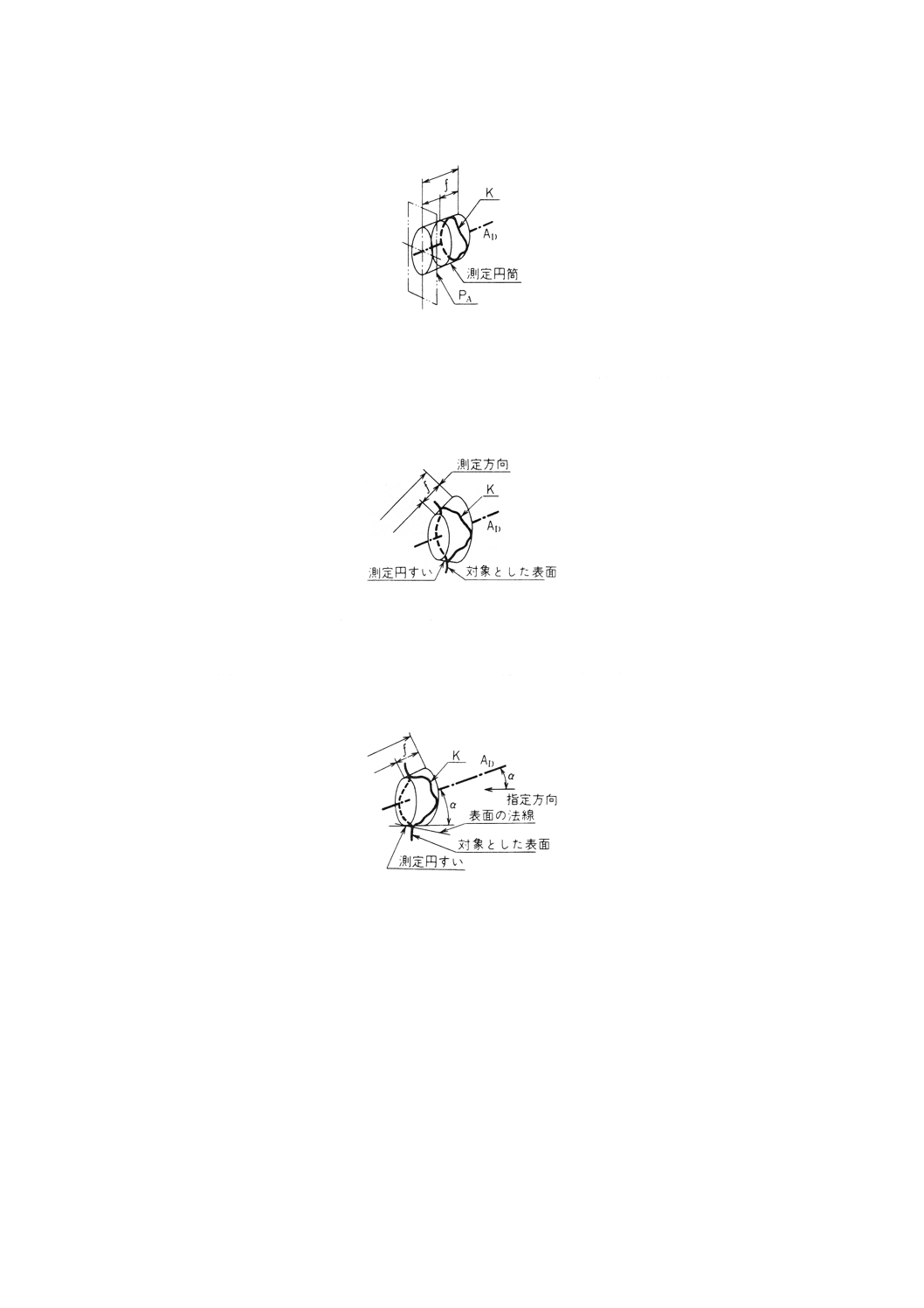
(2) 軸方向の円周振れ 軸方向の円周振れは,データム軸直線 (AD) から一定の距離にある円筒面(測定
円筒)上で,データム軸直線に垂直な一つの幾何学的平面 (PA) から対象とした表面 (K) までの距離
の最大値と最小値との差 (f) で表す(図38)。
13
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図38
(3) 斜め法線方向の円周振れ 斜め法線方向の円周振れは,対象とした表面に対する法線がデータム軸直
線に対してある角度をもつ場合,その法線を母線とし,データム軸直線 (AD) を軸とする一つの円す
い面(測定円すい)上で頂点から対象とした表面 (K) までの距離の最大値と最小値との差 (f) で表す
(図39)。
図39
(4) 斜め指定方向の円周振れ 斜め指定方向の円周振れは,指定した方向が対象とした表面の法線方向に
かかわりなく一定で,かつ,データム軸直線 (AD) に対してある角度 (α) をもつ場合,その方向を与
える直線を母線とし,データム軸直線を軸とする一つの円すい面(測定円すい)上で,頂点から対象
とした表面 (K) までの距離の最大値と最小値との差 (f) で表す(図40)。
図40
5.14 全振れ 全振れは,指定した方向によって,それぞれ(1)又は(2)に示すように表し,全振れ_mm又
は全振れ_μmと表示する。
(1) 半径方向の全振れ 半径方向の全振れは,データム軸直線に垂直な方向で,データム軸直線から対象
とした表面までの距離の最大値と最小値との差で表す。
(2) 軸方向の全振れ 軸方向の全振れは,データム軸直線に平行な方向で,データム軸直線に垂直な一つ
の幾何学的平面から対象とした表面までの距離の最大値と最小値との差で表す。
14
B 0621-1984
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
機械要素部会 幾何学的公差専門委員会 構成表
氏名
所属
(委員会長)
青 木 保 雄
千葉工業大学
大 園 成 夫
東京大学
佐 藤 豪
慶応義塾大学
福 永 太 郎
東京都立工科短期大学
吉 本 勇
東京工業大学精密工学研究所
加 藤 敬
工業技術院計量研究所
小 栁 武 昭
工業技術院標準部
野 上 昭 三
株式会社アマダ
杉 浦 守 彦
石川島播磨重工業株式会社
中 込 常 雄
社団法人自動車技術会
前 田 祥 彦
キャタピラー三菱株式会社
佐々木 茂 夫
東京芝浦電気株式会社生産技術研究所
矢 島 宣 明
株式会社東京精密八王子工場
桑 田 浩 志
トヨタ自動車株式会社
江 守 忠 哉
財団法人日本規格協会
西 村 伸 二
財団法人日本規格協会
津 川 浩 造
日本精工株式会社製品技術研究所
山 崎 隆
株式会社日立製作所土浦工場
広 瀬 藤 司
株式会社三豊製作所
浜 野 徹
三菱重工業株式会社相模原工場
松 本 美 韶
NTN東洋ベアリング株式会社
(専門委員)
沢 辺 雅 二
株式会社三豊製作所
(事務局)
中 谷 節 男
工業技術院標準部機械規格課
根 岸 喜代春
工業技術院標準部機械規格課