2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 0419-1991
(ISO 2768-2 : 1989)
普通公差−第2部:
個々に公差の指示がない形体
に対する幾何公差
General tolerances−Part 2 : Geometrical tolerances
for features without individual tolerance indications
日本工業規格としてのまえがき
この規格は,1989年第1版として発行されたISO 2768-2 (General tolerances−Part 2 : Geometrical tolerances
for features without individual tolerance indications) を翻訳し,技術的内容及び規格票の様式を変更すること
なく作成した日本工業規格である。
なお,この規格の中で点線の下線を施してある“参考”は,原国際規格にはない事項である。
序文 すべての構成部品の形体は,常に寸法及び幾何形状をもっている。寸法の偏差及び幾何特性(形状,
姿勢及び位置)の偏差がある限界を超えると,部品の機能を損なうので,それらの偏差の制限を必要とす
る。
図面上の公差表示は,すべての形体の寸法と幾何特性の要素を確実に規制するために完全でなければなら
ない。すなわち,工場又は検査部門において,採否判定が暗黙の了解のもとに任されることがないように
しなければならない。
寸法及び幾何特性に対する普通公差の使用によって,この必要条件を満たしていることを確認する業務を
簡単にすることができる。
1. 適用範囲 この規格は,図面指示を簡単にすることを意図し,個々に幾何公差の指示がない形体を規
制するための三つの公差等級の普通幾何公差 (general geometrical tolerance) について規定する。
この規格は,主として除去加工 (removal of material) によって製作した形体に適用する。他の加工方法
によって製作した形体にこれを適用することができるが,通常の工場で得られる加工精度がこの規格に規
定された普通幾何公差内にあるかどうかについて確認することが必要である。
2. 一般事項 公差等級を選ぶ場合,個々の工場で通常に得られる加工精度を考慮しなければならない。
個々の形体に対して,より小さな公差が要求される場合,又はより大きな公差が許容され,かつ,それが
より経済的である場合には,そのような公差をISO 1101によって,直接指示するのがよい(附属書A.2
参照)。
参考 ISO 1101の規定内容は,JIS B 0021-1984(幾何公差の図示方法)と同等である。
この規格が6.に従って図面又は関連文書に引用されるときに,この規格による普通幾何公差を適用する。
2
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
この普通幾何公差は,個々に幾何公差が指示されていない形体に適用する。
普通幾何公差は,円筒度,線の輪郭度,面の輪郭度,傾斜度,同軸度,位置度及び全振れを除くすべて
の幾何特性に適用する。
いずれにしても,この規格による普通幾何公差は,JIS B 0024による公差表示方式の基本原則が使用さ
れ,図面上に指示されたときに用いる(附属書B.1参照)。
3. 引用規格 次に掲げる国際規格は,この規格に引用されたことによって,この規格の規定を構成する。
出版の時点では,表示された版が有効である。すべての規格は,改正されるものであり,この規格に基づ
くことに合意した関係者は,次に列挙する規格の最新版を適用する可能性を調べることに努めるのがよい。
IEC及びISOの会員は,現行の国際規格の登録簿を維持管理している。
ISO 1101 : 1983 Technical drawings−Geometrical tolerancing−Tolerancing of form, orientation, location
and run-out−Generalities, definitions, symbols, indications on drawings
ISO 2768-1 : 1989 General tolerances−Part 1 : Tolerances for linear and angular dimensions without
individual tolerance indications
備考 JIS B 0405-1991(普通公差−第1部:個々に公差の指示がない長さ寸法及び角度寸法に対す
る公差)がこの国際規格と一致している。
ISO 5459 : 1981 Technical drawings−Geometrical tolerancing−Datums and datum-systems for geometrical
tolerances
ISO 8015 : 1985 Technical drawings−Fundamental tolerancing principle
備考 JIS B 0024-1988(製図−公差表示方式の基本原則)がこの国際規格と一致している。
4. 用語の定義 この規格の目的に対して,幾何公差の用語の定義は,ISO 1101及びISO 5459による。
参考 ISO 1101及びISO 5459の規定内容は,それぞれJIS B 0021-1984及びJIS B 0022-1984(幾何公
差のためのデータム)と同等である。
5. 普通幾何公差 (附属書B.1参照)
5.1
単独形体に対する普通公差
5.1.1
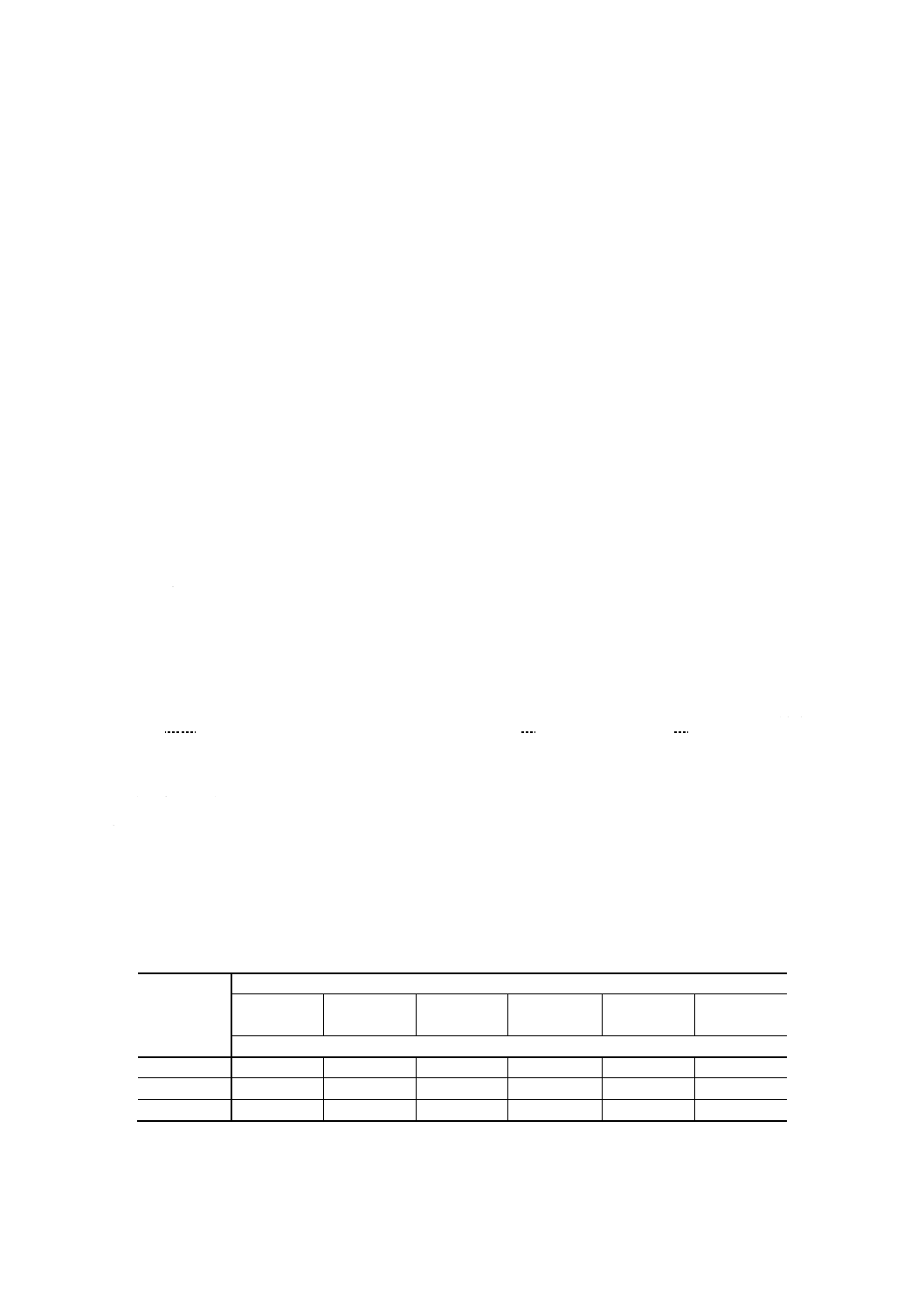
真直度及び平面度 真直度及び平面度の普通公差は,表1による。公差をこの表から選ぶときには,
真直度は該当する線の長さを,平面度は長方形の場合には長い方の辺の長さを,円形の場合には直径をそ
れぞれ基準とする。
表1 真直度及び平面度の普通公差
単位 mm
公差等級
呼び長さの区分
10以下
10を超え
30以下
30を超え
100以下
100を超え
300以下
300を超え
1 000以下
1 000を超え
3 000以下
真直度公差及び平面度公差
H
0.02
0.05
0.1
0.2
0.3
0.4
K
0.05
0.1
0.2
0.4
0.6
0.8
L
0.1
0.2
0.4
0.8
1.2
1.6
5.1.2
真円度 真円度の普通公差は直径の寸法公差の値に等しくとるが,表4の半径方向の円周振れ公差
の値を超えてはならない(附属書B.2の例参照)。
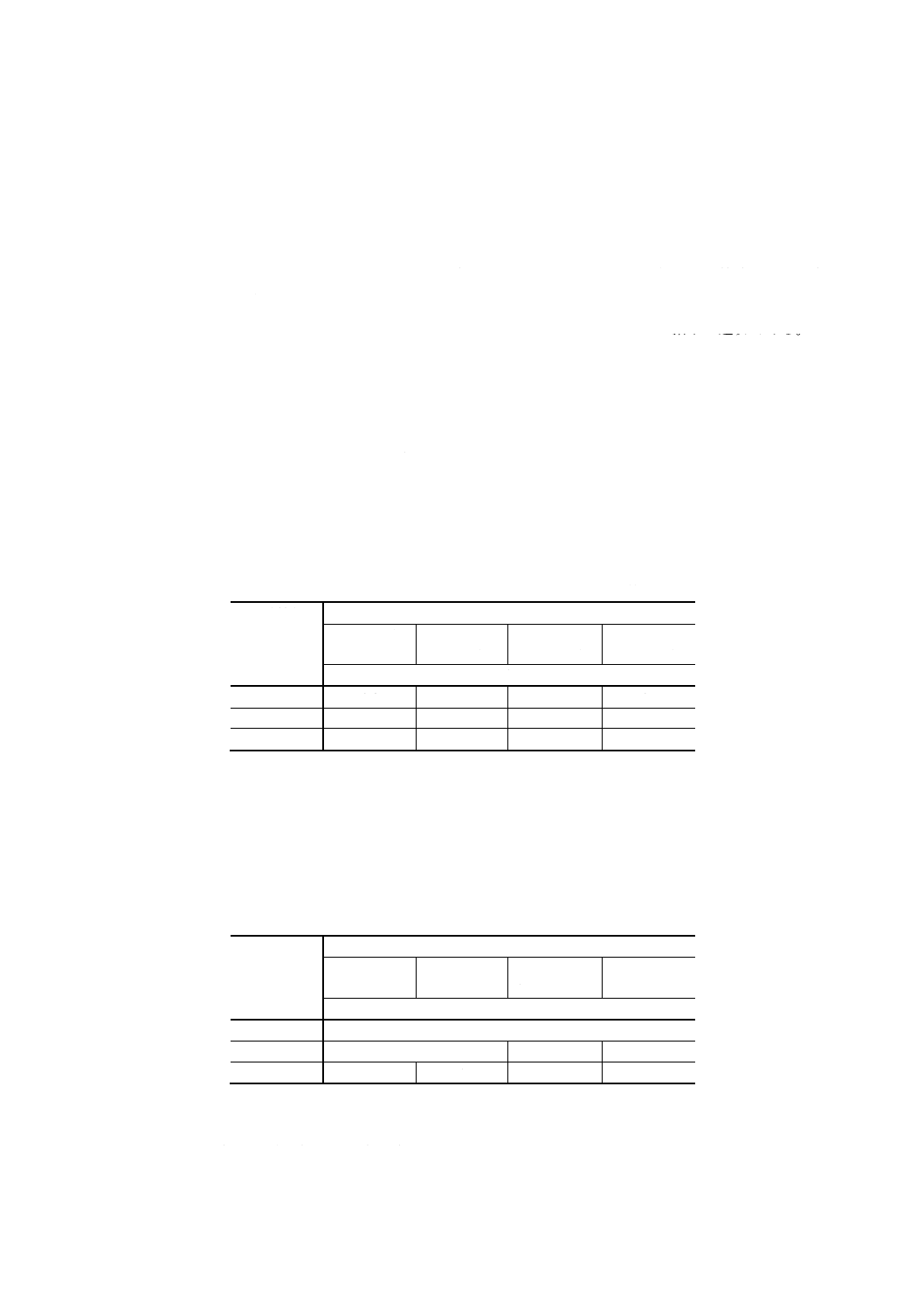
3
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.1.3
円筒度 円筒度の普通公差は,規定しない。
備考1. 円筒度は,三つの構成要素,すなわち,真円度,真直度及び相対向する母線の平行度からな
る。これらの構成要素のそれぞれは,個々に指示した公差又はその普通公差によって規制さ
れる。
2. 機能的理由から,円筒度が真円度,真直度及び平行度の普通公差の複合効果(附属書B.3参
照)よりも小さくなければならない場合には,ISO 1101によって,個々に円筒度公差を対象
とする形体に指示するのがよい。
場合によっては,(例えば,はめあいの場合には),包絡の条件◯
Eの指示が適切である。
5.2
関連形体に対する普通公差
5.2.1
一般事項 5.2.2〜5.2.6に規定する公差は,互いに関連する形体で,幾何公差が個々に指示されて
いないすべての形体に適用する。
5.2.2
平行度 平行度の普通公差は,寸法公差と平面度公差・真直度公差とのいずれか大きいほうの値に
等しくとる。二つの形体のうち長いほうをデータムとする。それらの形体が等しい呼び長さの場合には,
いずれの形体をデータムとしてもよい(附属書B.4参照)。
5.2.3
直角度 直角度の普通公差は,表2による。直角を形成する二辺のうち長い方の辺をデータムとす
る。二つの辺が等しい呼び長さの場合には,いずれの辺をデータムとしてもよい。
表2 直角度の普通公差
単位 mm
公差等級
短い方の辺の呼び長さの区分
100以下
100を超え
300以下
300を超え
1 000以下
1 000を超え
3 000以下
直角度公差
H
0.2
0.3
0.4
0.5
K
0.4
0.6
0.8
1
L
0.6
1
1.5
2
5.2.4
対称度 対称度の普通公差は,表3による。二つの形体のうち長いほうをデータムとする。これら
の形体が等しい呼び長さの場合には,いずれの形体をデータムとしてもよい。
備考 対称度の普通公差は,次の場合に適用する(附属書B.5の例参照)。
・ 少なくとも二つの形体の一つが中心平面をもつとき。
・ 二つの形体の軸線が互いに直角であるとき。
表3 対称度の普通公差
単位 mm
公差等級
呼び長さの区分
100以下
100を超え
300以下
300を超え
1 000以下
1 000を超え
3 000以下
対称度公差
H
0.5
K
0.6
0.8
1
L
0.6
1
1.5
2
5.2.5
同軸度 同軸度の普通公差は,規定しない。
備考 同軸度は,半径方向の円周振れが同軸度と真円度とからなるので,極端な場合には,表4に示
す円周振れ公差の値と同じ大きさでよい。

4
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2.6
円周振れ 円周振れ(半径方向,軸方向及び斜め法線方向)の普通公差は,表4による。
円周振れの普通公差に対しては,図面上に支持面が指定されている場合には,その面をデータムとする。
支持面が指定されていない場合には,半径方向の円周振れに対して,二つの形体のうち長いほうをデータ
ムとする。二つの形体の呼び長さが等しい場合には,いずれの形体をデータムとしてもよい。
表4 円周振れの普通公差
単位 mm
公差等級
円周振れ公差
H
0.1
K
0.2
L
0.5
6. 図面上の指示
6.1
この規格による普通公差を,JIS B 0405による普通公差とともに適用する場合には,次の事項を表
題欄の中又はその付近に指示する。
a) “JIS B 0419”
b) JIS B 0405による公差等級
c) この規格による公差等級
例 JIS B 0419-mK
参考 ISO 2768-2では,“JIS B 0419”を“ISO 2768”と表示している。
この場合,暗示されてはいるが,角度数値が指示されていない直角 (90°) に対しては,JIS B 0405に
よる角度寸法に対する普通公差は適用しない。
6.2
普通寸法公差(公差等級m)を適用しない場合には,図面上に指示する表示からその記号を除く。
例 JIS B 0419-K
6.3
すべての単一のサイズ形体1) (feature of size) に包絡の条件◯
Eを適用する場合には,6.1に規定した表
示に記号“E”を追加する。
例 JIS B 0419-mK-E
備考 包絡の条件◯
Eは,形体の寸法公差よりも大きい真直度公差を個々に指示した形体,例えば,素
形材 (stock material) には適用できない。
7. 採否 特に明示した場合を除いて,普通幾何公差を超えた工作物でも,工作物の機能が損なわれない
場合には,自動的に不採用としてはならない(附属書A.4参照)。
1) この規格では,単一のサイズ形体は,一つの円筒面又は平行二平面からなるものとする。
5
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A 幾何特性に対する普通公差表示方式の背景にある概念(参考)
A.1 普通公差は,本体6.に基づき,この規格を引用することによって,図面上に指示するのがよい。
普通公差の値は,工場の通常の加工精度の程度に対応したものであり,適切な公差等級を選び,図面上
に指示される。
A.2 工場の通常の加工精度に対応する公差値を超えて公差を大きくしても,通常,生産の経済性における
利益は得られない。いずれにしても,工場の機械及び普通の技能によれば,通常,大きな偏差をもつ形体
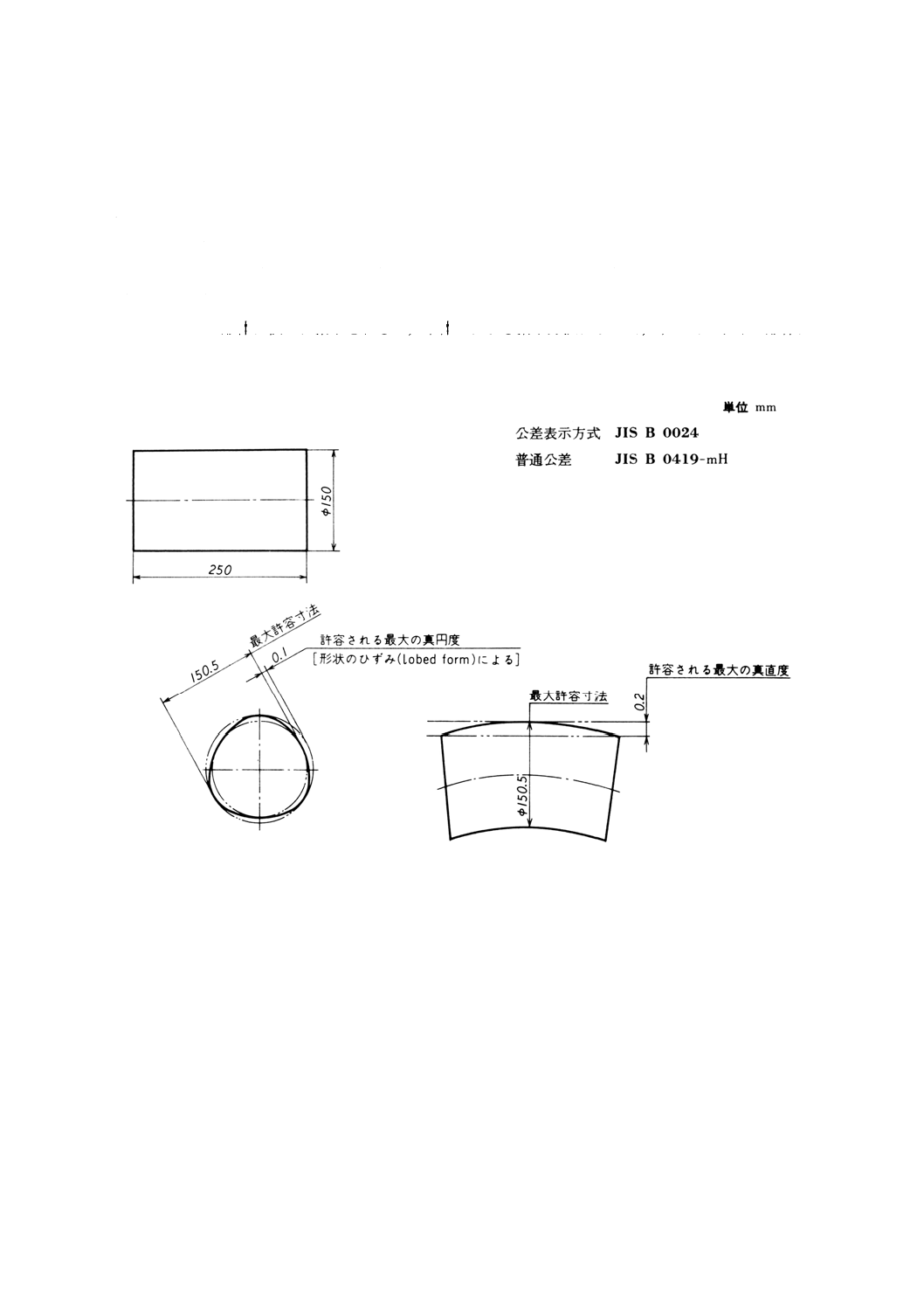
を製造することはない。例えば,JIS B 0419-mHに等しいか,又はそれより良い,通常の加工精度をもつ
工場で製造した長さ80mmで,直径25mm±0.1mmの形体は,幾何偏差が真円度に対しては0.1mm以内に,
母線の真直度に対しては0.1mm以内に,半径方向の円周振れに対しては0.1mm以内によく入っている(こ
れらの数値は,この規格から採用している)。より大きな公差を指示したとしても,その特定の工場に利益
をもたらすことはない。
しかし,機能的理由によって,形体に“普通公差”よりも小さい公差値を要求する場合には,その特定
の形体に対して,個々に隣接して,より小さな公差を指示する。この種の公差は,普通公差の適用範囲外
である。
形体の機能が普通公差の値に等しいか,又はそれより大きい幾何公差を許容する場合には,公差を個々
に指示しないで,本体6.に規定したように図面上に明示するのがよい。この種の公差は,普通幾何公差方
式の概念を最大限に使用できる。
機能が普通公差よりも大きな公差を許容し,かつ,より大きな公差が生産上の経済性をもたらす場合に
は,“規則の例外”がある。これらの特別な場合には,より大きな幾何公差をその特定の形体に隣接して個々
に指示するのがよい。例えば,大きい直径で薄いリングの真円度公差がその例である。
A.3 普通幾何公差の適用には,次の利点がある。
a) 図面が容易に読め,情報伝達が図面の使用者に,より効果的になる。
b) 製図者は,機能が普通公差と等しいか,又はそれより大きい公差を許容することだけを知れば十分で
あるので,詳細な公差の算定を避けることによって時間を節約できる。
c) 図面は,どの形体が通常の工程能力 (normal process capability) によって生産できるかを容易に指示で
き,それはまた,検査水準を下げることによって品質管理業務を助ける。
d) 個々に指示した幾何公差をもつ残りの形体は,大部分はその機能上相対的に小さい公差が要求され,
それゆえ製造において特別な努力が要求される形体を規制するものである。これは製造計画に役立ち,
検査要求事項を解析する際に品質管理業務に役立つものである。
e) 発注及び受注契約の技術者は,契約が成立する前に“工場の通常の加工精度”が分かるので,容易に
注文を取り決めることができる。これはまた,図面が完全であることを期待しているから,受渡当事
者間の引渡しにおいて,争いを避けることができる。
これらの利点は,普通公差を超えないという十分な信頼性があるとき,すなわち,特定の工場の通常の
加工精度が図面上に指示された普通公差に等しいか,又はそれより加工精度がよいときにだけ得られる。
そのためには,工場では次のことを行うのがよい。
・ 測定によって,工場の通常の加工精度をつかむ。
6
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
・ 普通公差が工場の通常の加工精度に等しいか,又はそれより公差の大きい図面だけを受け入れる。
・ 工場の通常の加工精度が低下していないことを抜取りによって調べておく。
すべての不確定さ及び思い違いがある,漠然とした“良い技能” (good workmanship) を頼みにすること
は,普通幾何公差の概念によって,もはや不要になる。普通幾何公差は,“良い技能”が要求される精度を
明らかにしている。
A.4 機能によって許容される公差は,普通公差よりも大きいことがしばしばある。そのため,工作物のい
ずれかの形体で普通公差を(ときおり)超えても,部品の機能が必ずしも損なわれるとは限らない。普通
公差から逸脱し,機能を損なうときだけ,その工作物を不採用にする。
7
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B 追加情報(参考)
B.1 普通幾何公差(本体5.参照)
独立の原則(JIS B 0024参照)によって,普通幾何公差は工作物の形体の個々の実寸法とは関係なく適
用する。したがって,普通幾何公差は形体がどこにおいても,その最大実体寸法にあるときでも用いてよ
い(図B.1参照)。
包絡の条件◯
Eが形体に個々に指示されるか,本体6.による指示方法によって,すべてのサイズ形体に一
括して指示される場合には,この要求にも従うのがよい。
図B.1 独立の原則,同一形体上の許容される最大の形状偏差
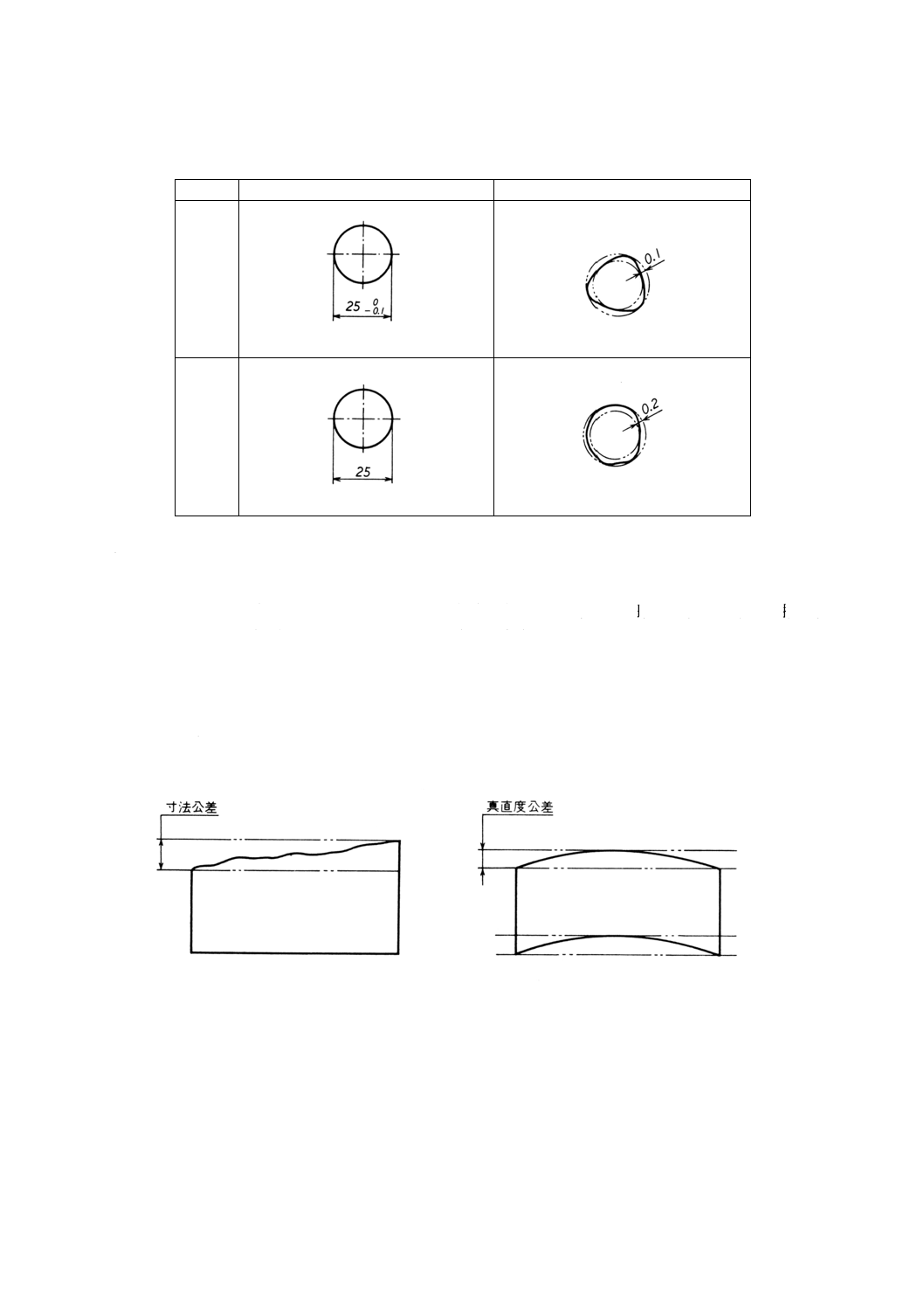
B.2 真円度(本体5.1.2参照)−適用例
例1. (図B.2参照)
直径の寸法許容差を図面に直接指示する。真円度に関する普通公差は,直径公差の値に等しい。
例2. (図B.2参照)
JIS B 0419-mKという指示による普通公差を適用する。25mmの直径に対する許容差は±0.2mmである。
この許容差から,公差は本体表4の値0.2mmよりも大きい値0.4mmになる。したがって,その値0.2mm
を真円度公差に対して適用する。
8
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.2 真円度の普通公差の例
単位 mm
例
図面上の指示
真円度の公差域
1
JIS B 0419-K
2
JIS B 0419-mK
B.3 円筒度(本体5.1.3の備考2.参照)
真円度,真直度及び平行度の普通公差の複合効果は,寸法公差によるある制限があるので,幾何学的理
由のため三つの公差の合計よりも小さい。しかし,包絡の条件◯
E又は個々の円筒度公差のいずれを指示す
るかを決めるために,簡単化のために三つの公差の合計を考慮に入れることができる。
B.4 平行度(本体5.2.2参照)
形体の偏差の形によって,平行度は寸法公差の値によって制限されるか(図B.3参照),又は真直度公差
若しくは平面度公差の値によって制限される(図B.4参照)。
図B.3 寸法公差の値に等しい平行度
図B.4 真直度公差の値に等しい平行度
9
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
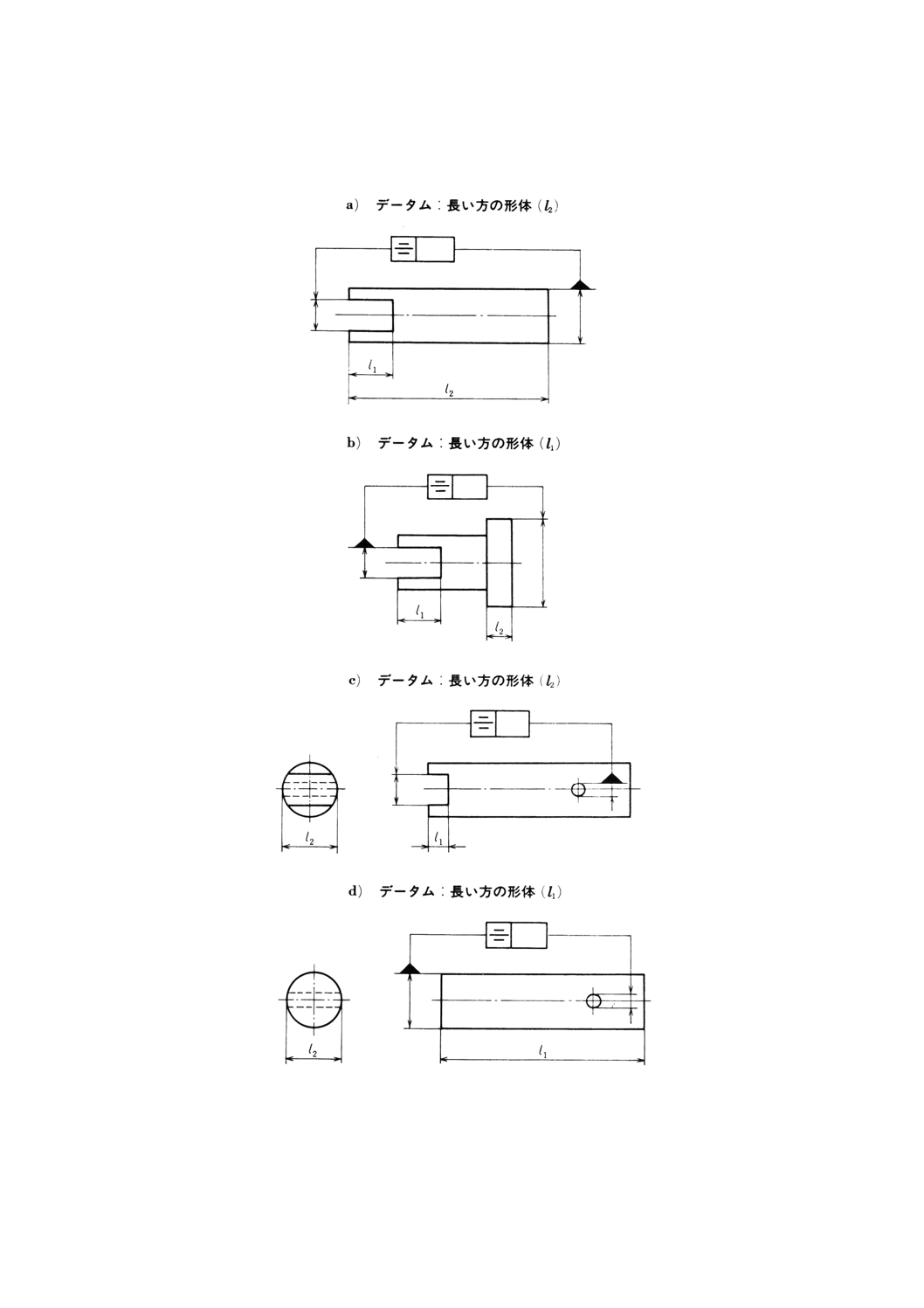
B.5 対称度(本体5.2.4参照)−例
図B.5 対称度の普通公差の例(本体5.2.4によって規定されたデータム)
10
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
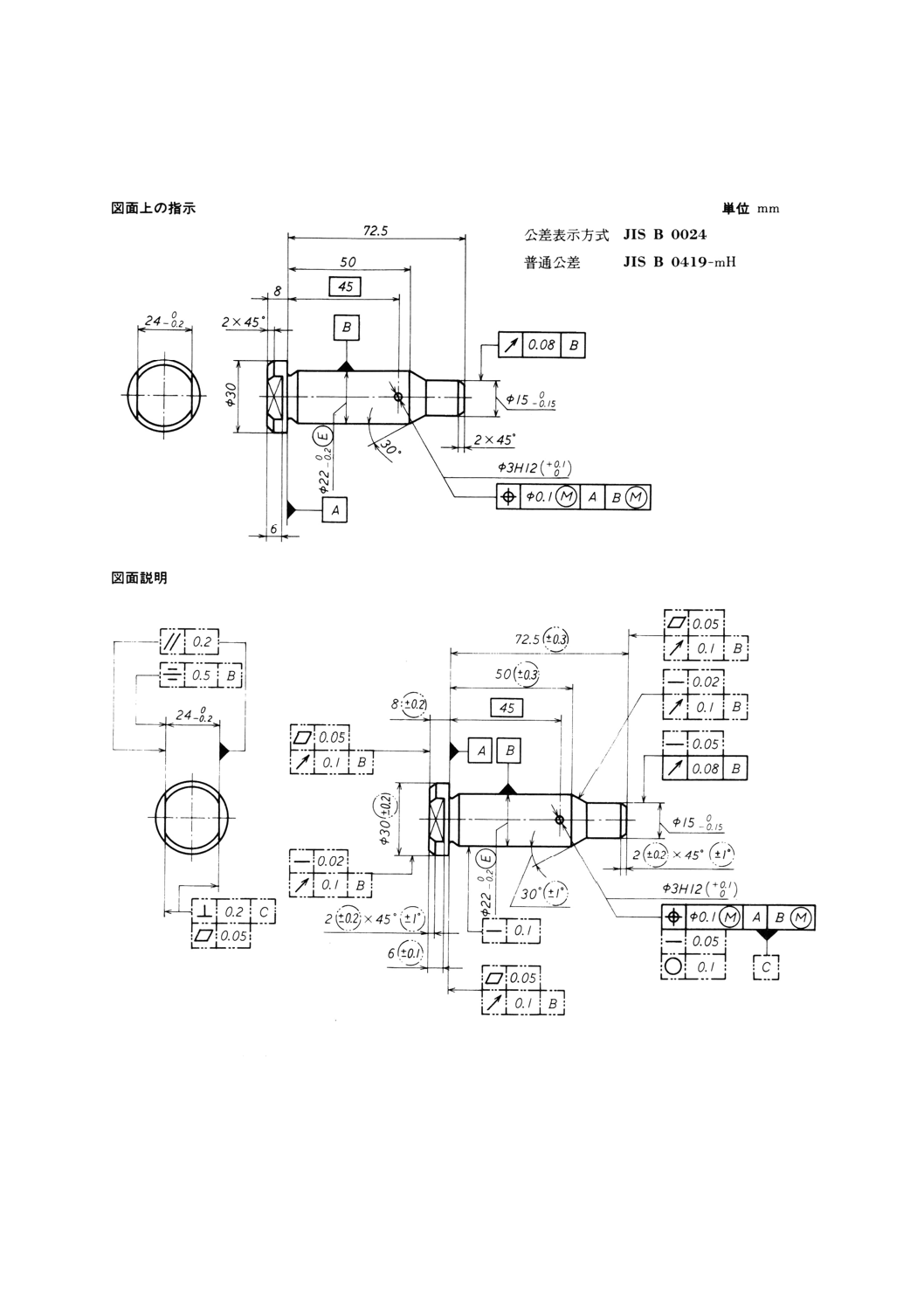
B.6 図面例
図B.6 図面上の普通公差の例
備考1. 細い二点鎖線(枠又は円)で囲んで示した公差は,普通公差である。これらの公
差の値は,JIS B 0419-mHに等しいか,又はそれより良い通常の加工精度をもつ
工場で機械加工することによって自動的に満足され,したがって,一般には検査
は要求されない。
2. ある公差は同じ形体の別の種類の偏差も制限する(例えば,直角度公差が真直度
も制限する)ので,すべての普通公差が上記の図面の説明の中に示されているわ
けではない。
11
B 0419-1991 (ISO 2768-2 : 1989)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
機械要素部会 公差専門委員会 構成表
氏名
所属
(委員会長)
吉 本 勇
拓殖大学工学部
青 木 保 雄
東京大学名誉教授
石 井 章 夫
NTN株式会社
大 園 成 夫
東京大学工学部
桑 田 浩 志
トヨタ自動車株式会社
沢 辺 雅 二
株式会社三豊製作所
下河辺 明
東京工業大学精密工学研究所
菅 原 淳 夫
財団法人日本規格協会
佐々木 茂 夫
株式会社東芝生産技術研究所
中 込 常 雄
財団法人日本規格協会(嘱託)
奈 良 治 郎
宇都宮大学工学部
福 永 太 郎
東京都立工科短期大学名誉教授
亀 井 明 敏
株式会社東京精密
伊佐山 建 志
通商産業省機械情報産業局
吉 田 藤 夫
工業技術院標準部
(事務局)
時 山 聖 司
工業技術院標準部機械規格課
原案作成委員会 委員構成表
氏名
所属
(委員長)
吉 本 勇
拓殖大学(東京工業大学名誉教授)
(幹事)
桑 田 浩 志
トヨタ自動車株式会社設計管理部
鈴 木 茂 光
工業技術院標準部
前 田 禎 三
東京電機大学(東京大学名誉教授)
藤 原 孝 誌
工業技術院機械技術研究所
大 園 茂 夫
東京大学
杉 浦 守 彦
石川島播磨重工業株式会社技術本部
三 町 勲
日立精機株式会社我孫子工場
渡 辺 昭 俊
新技術コンサルタント
黒 柳 啓太郎
三菱重工業株式会社技術管理部
佐々木 茂 夫
株式会社東芝生産技術研究所
金 子 昌 雄
社団法人日本ダイカスト協会
天 野 健 郎
株式会社北沢バルブ技術本部
中 鏡 肇
社団法人日本塑性加工学会(日本電気オートメーション株式会社)
川 崎 陽 康
社団法人日本金属プレス工業協会(株式会社川崎精工所)
田 仁 哲
社団法人日本工作機械工業会
中 込 常 雄
財団法人日本規格協会
(事務局)
大 熊 敬 尚
財団法人日本規格協会