B 0153 : 2001
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化第14条によって準用する第12条第1項の規定に基づき,社団法人日本機械学
会 (JSME) /財団法人日本規格協会 (JSA) から,工業標準原案を具して日本工業規格を改正すべきとの申
出があり,日本工業標準調査会の審議を経て,経済産業大臣が改正した日本工業規格である。
これによってJIS B 0153-1995は改正され,この規格に置き換えられる。
旧JIS B 0153の対応国際規格はISO 2041とともに,ISO 1925(釣り合わせ用語)及びISO 5805(人体
関連振動及び衝撃用語)をも含んでいた。今回の改正では,ISO/IEC Guide 21 : 1999に基づき,JIS B 0153
をISO 2041-1990の翻訳JISとすることに努めた。その結果,規格本体及び附属書A,附属書B,附属書C
の番号並びに用語は,ISO 2041のそれらに完全に一致しており,定義説明もわずかの例外を除きISO 2041
の翻訳となっている。ただし重要な用語で工業的に必要とされるものは,その一部を関連する用語の備考
として追加し,備考に入れがたい用語は附属書1とした。
JIS B 0153には,次に示す附属書がある。
附属書A(参考) 数学的用語
附属書B(参考) 補足的用語
附属書C(参考) 振動用語の体系
附属書1(規定) 機械振動用語(追加)
附属書2(参考) JISと対応する国際規格との対比表
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 0153 : 2001
機械振動・衝撃用語
Glossary of terms used in mechanical vibration and shock
序文 この規格は,1990年に第2版として発行されたISO 2041, Vibration and shock−Vocabularyに対応す
る日本工業規格である。旧JIS B 0153 : 1985の中で規定されていた用語などで,今後国際規格としてISO
で採用すべきと考えられる用語は,その一部を関連する用語の定義の備考に点線の下線を付けて示し,備
考に入れがたい用語は附属書1に示した。なお,この規格で点線の下線を施してある箇所は,原国際規格
にない事項である。
1. 適用範囲 この規格は,鉱工業において,機械振動及び衝撃に関して用いる主な用語及び定義につい
て規定する。
備考 この規格の対応国際規格を,次に示す。
なお,対応の程度を示す記号は,ISO/IEC Guide 21に基づき,IDT(一致している),MOD
(修正している),NEQ(同等でない)とする。
ISO 2041 : 1990 Vibration and shock−Vocabulary (MOD)
2. 分類 用語は,次の分類による。
a) 一般
b) 振動
c) 機械衝撃
d) 衝撃・振動計測用変換器
e) データ処理
3. 用語及び定義 用語及び定義は,次による。
なお,参考のために対応英語を示す。
備考1. 二つ以上の用語を並べてある場合は,その順位に従って優先的に使用する。
2. 定義にa),b),c)とあるのは,a),b)及びc)の三とおりの定義があることを示す。
3. 用語の一部に括弧を付けてある場合は,括弧の中の用字を含める用語及び括弧の中の用字を
省略する用語の場合又は前の用語を置き換える場合の二とおりである。
2
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
a) 一般
番号
用語
定義
対応英語(参考)
1.1
変位,
相対変異
ある座標系に対して物体又は質点の位置の変化を表すベクトル量。
備考1. 座標系は,普通,平均位置又は静止位置を原点とする
複数の座標軸の組合せからなる。一般に,変位は,回
転ベクトル,並進ベクトル又はこの両方によって表す
ことができる。
2. はじめに定義された座標系以外の座標系で測定される
変位は,相対変位と呼ばれる。2点間の相対変位は,こ
の2点の変位のベクトル差である。
displacement ;
relative
displacement
1.2
速度,
相対速度
変位の時間微分で規定されるベクトル。
備考1. 座標系は,普通,平均位置又は静止位置を原点とする
複数の座標軸の組合せからなる。一般に,速度は,回
転ベクトル,並進ベクトル又はこの両方によって表す
ことができる。
2. はじめに定義された座標系以外の座標系で測定される
速度は,相対速度と呼ばれる。2点間の相対速度は,こ
の2点の速度のベクトル差である。
velocity ;
relative velocity
1.3
加速度
速度の時間微分で規定されるベクトル。
備考1. 座標系は,普通,平均位置又は静止位置を原点とする
複数の座標軸の組合せからなる。一般に,加速度は,
回転ベクトル,並進ベクトル又はこの両方によって表
すことができる。
2. はじめに定義された座標系以外の座標系で測定される
加速度は,相対加速度と呼ばれる。2点間の相対加速度
は,この2点の加速度のベクトル差である。
3. 変動する加速度は,ピーク,平均及びrms(二乗平均平
方根)といった様々な処理がよく行われる。平均及び
二乗平均平方根では評価時間を示しておくべきであ
る。
4. 加速度が周期的であれば,その調和波形成分を振幅と
周波数で定義できる。ランダムな加速度は,ある範囲
の値をもつ確率を定義するのに加速度rms(及びバンド
幅又は確率密度分布)を用いることができる。継続期
間の短い加速度は,過渡的加速度 (transient acceleration)
という。非周期的加速度は,長期間であれば継続的加
速度 (sustained acceleration),短期間であれば加速度パ
ルスという。
acceleration
1.4
重力加速度,g
重力によって生ずる地球の表面での加速度。観測点の緯度及び高さ
によって変化する。
備考1. 国際的には重力加速度の標準値として,9.806 65m/s2
(=980.665cm/s2=386.089inch/s2=32.174 0ft/s2) が用い
られている。
2. 加速度値は,gの比率として表されることも多い。
acceleration of
gravity, g
1.5
ジャーク
加速度の時間微分で規定されるベクトル。
jerk
1.6
慣性座標系
慣性の法則(古典力学)が成り立つ座標系。
備考 慣性座標系は,空間的に固定されているか,加速しない
等速座標系を意味する。
inertial reference
system ;
inertial reference
frame
1.7
慣性力
物体を加速するときその質量から受ける力。
備考 質量とその運動加速度との積の大きさをもつ力。
inertia force ;
inertial force

3
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
1.8
振動
ある座標系に関する量の大きさが平均値より交互に大きくなった
り小さくなったりするような変動。通常は時間的変動である。
oscillation ;
vibration
1.9
音
a) 音波によって引き起こされる聴感覚。
b) 聴感覚を引き起こす可能性のある音波。
c) 内力が働いている媒体中における圧力,応力,粒子速度などの
振動。
sound
1.10
音響学
音の発生,伝達及び影響に関する科学・技術。
acoustics
1.11
環境
ある時点で系が従属させられている外的条件と影響の総称[誘導環
境(1.12),及び自然環境(1.13) 参照]。
environment
1.12
誘導環境
系が作用した結果として発生する系の外部の状況。
induced
environment
1.13
自然環境
自然外力によって引き起こされる状況。その効果は,系が動いてい
るときはもちろん,静止しているときも系に影響する。
natural
environment
1.14
事前調整
ある定義された状態を達成するため,ある特定な系に対し規定され
る気候的,機械的及び電気的な処理手続き。
preconditioning
1.15
調整
系への影響を決定する気候的,機械的及び電気的調整。
conditioning
1.16
加振,
励振,
外乱
応答を引き起こす,系に加えられる外力又は入力。
備考 時間の調和関数で表される外力又は入力を調和励振又は
調和加振 (harmonic excitation) という。
excitation ;
stimules
1.17
(系の)応答
系の出力の量的な表現。
response (of a
system)
1.18
伝達率
定常強制振動において加振振幅に対する系の応答振幅の無次元比。
この比には力,変位,速度又は加速度がある。
transmissibility
1.19
行過ぎ
(負の行過ぎ)
系の出力を定常値Aから定常値Bまで入力によって変化させると
き,BがAよりも大きい(小さい)場合で,最大(最小)過渡応答
がBを超える(下回る)とき,その応答を行過ぎ(負の行過ぎ)と
呼ぶ。
備考 最大(最小)の過渡応答とBの値との差を行過ぎ量(負
の行過ぎ量)という。
overshoot
(undershoot)
1.20
系
装置の関連又は構成する部分の集合体。
system
1.21
線形系
応答が励振の大きさに比例する系。
備考 この定義によれば系の各要素の動的特性が一連の線形微
分方程式で表され,重ね合わせの原理を適用できる。
linear system
1.22
機械系
質量,剛性及び減衰の組合せによって構成される系の総称。
備考 ばね及び質量によって構成される機械系をばね・質量系
(spring-mass system) という。
mechanical system
1.23
基礎
機械系を支持している構造体。構造体は,指定された座標系に固定
されているか,又は支持されている系を励振する運動をしている。
foundation
1.24
サイズモ系
1個又はそれ以上のばね要素を介して基礎枠に取り付けられている
一つの質量からなる系。一般に,減衰要素も含まれている。
備考1. サイズモ系は,普通,粘性減衰をもつ1自由度系として
理想化されている。
2. 変位又は速度ピックアップとしてサイズモ系を用いる
とき,その固有振動数は,測定する振動数より低く,
加速度ピックアップとして用いるとき,その固有振動
数は,高く選ぶ。
3. サイズモ系の固有振動数が測定対象の振動数より低い
とき,サイズモ系の質点は,静止しているとみなせる。
seismic system
4
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
1.25
等価系
解析の便宜のために等価的に置き換えられた系。
備考 振動と衝撃を光学的に扱うとき,次のような種々の等価
な系に置き換えられる。
a) 等価剛性
b) 等価減衰
c) 並進系に等価なねじれ系
d) 機械系に等価な電気系,音響系など。
equivalent system
1.26
自由度
任意の時刻において,機械系のすべての部分の位置を完全に決定す
るのに必要な独立座標の最小の数。
degrees of freedom
1.27
1自由度系
任意の時刻における系の形態を完全に決定するのに必要な座標が
一つである系。
single
degree-of-freedom
system
1.28
多自由度系
任意の時刻における系の形態を完全に決定するのに必要な座標が
二つ以上の系。
multi-degree-of-free
dom system
1.29
連続系,
分布系
無限個の独立した形態をとることができる系。
備考 連続系の形態は,連続した空間的変数の関数によって決
定される。一方,離散系 (discrete system) 又は集中系
(lumped parameter system) では,その形態が有限個の座標
で決定される。
continuous
system ;
distributed system
1.30
重心
重力場において物体のどの方向に対してもその構成部分の重量の
合力が通る点。
備考 場が一様ならば,重心と質量中心[(1.31)参照]とは一致
する。
centre of gravity
1.31
質量中心
与えられた物質系の質量に等しい仮想の質点を考えると,その点を
通る任意の平面に関する1次モーメントが系の対応する1次モーメ
ントに等しくなるような点。
centre of mass
1.32
慣性主軸
一般に,与えられた点における直交座標系の各軸に対する物体の六
つの慣性モーメントIxixj (i, j=1, 2, 3) は,等しくない。ある一つの
座標系に対し,慣性の積Ixixj (i≠j ) は0となる。この特定の座標系
に対するIxixj (i=j ) の値を主慣性モーメントと呼び,対応する座標
方向を,慣性主軸と呼ぶ。
備考1.
)
(
j
i
dm
x
x
I
j
i
x
xj
i
≠
=∫
(
)
)
(
2
2
j
i
dm
x
r
I
i
x
xj
i
=
−
=∫
ここに,
∑
=
=
3
1
2
2
i
ix
r
, xi及びxjは,直交座標。
2. 座標の原点が物体の質量中心(重心)にあるとき,そ
の座標軸とモーメントを,それぞれ重心慣性主軸と重
心主慣性モーメントと呼ぶ。
3. 釣合わせに関しては,“慣性主軸”という用語は,三つ
ある重心慣性主軸のうちロータの軸中心線に最も近い
ものを指し,釣合軸又は質量軸と呼ばれることもある。
principal axes of
inertia
1.33
剛性,
こわさ,k
弾性要素の並進(又は回転)変位の変化に対する力(又はトルク)
の変化の比。
備考1. ばね定数 (spring constant) 又は弾性係数 (elastic
coefficient) ともいう。
2. 機械系のばねが変形することによって生じる力を復原
力 (restoring force) という。線形系では,復原力は,剛
性とばねのたわみとの積の大きさをもつ力。
stiffness, k

5
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
1.34
コンプライアン
ス
剛性の逆数。
compliance
1.35
[単純曲げを受
けるはり(梁)の]
中立面
はり(梁)の曲げ変形において,軸方向の応力が生じない面。
備考 中立面が曲げだけの結果か,又は曲げと他の荷重との組
合せの結果によるのかを示しておくべきである。
neutral surface (of
a beam in simple
flexure)
1.36
[単純曲げを受
けるはり(梁)の]
中立軸
はり(梁)断面に現れる中立面の位置。
neutral axis (of a
beam in simple
flexure)
1.37
(系の)伝達関数 系の出力(又は応答)と入力(又は励振)との数学的関係。
備考 通常,振動数の関数として与えられ,複素関数であるこ
とが多い[応答(1.17),伝達率(1.18),伝達インピーダン
ス(1.44) 及び周波数応答(B.13) 参照]。
transfer function
(of a system)
1.38
複素励振
実部と虚部をもつ励振。
備考1. 複素励振及び複素応答の概念は,歴史的に計算を簡略
化するために導き出されてきたものである。実際の励
振及び応答は,複素励振と複素応答の実部である。も
し,系が線形ならば,重ね合わせの原理が成り立つの
で,この手法を適用できる。
2. 複素励振 (complex excitation) を複合振動 (complex
vibration)又は複雑な波形の振動による励振と混同すべ
きでない。この意味での“複合振動 (complex vibration)”
という用語の使用は,好ましくない[単振動 (2.3) の
備考2参照]。
complex excitation
1.39
複素応答
複素励振に対する線形系の応答[複素励振(1.38)の備考参照]。
備考 実部と虚部をもつ振幅を複素振幅 (complex amplitude)
といい,複素応答は,定量的に複素振幅で表される。
complex response
1.40
複素系のパラメ
ータ
複素応答に対する複素励振の比,又はその比から導かれる複素量。
備考 電気的及び機械的インピーダンスは,複素系のパラメー
タの例である。
complex system
parameter
1.41
インピーダンス
(同じ単位系で)系の励振の応答に対する比。その両方とも複素量
で,その両方の偏角は,時間とともに直線的に同じ割合で増加する。
この用語は,線形系に対してだけ適用される[機械インピーダンス
(1.42)参照]。
備考1. この概念は,非線形系にも拡張され,増加インピーダ
ンス (incremental impedance) という用語が類似の量を
記述するために用いられる。
2. インピーダンスに関連する用語及び定義は,正弦振動
だけを受けている系に対し適用する。
impedance
1.42
機械インピーダ
ンス
単振動している機械系において,ある点の速度の複素振幅に対す
る,同じ点又は異なる点に作用している力の複素振幅比。
備考 ねじれ機械インピーダンスの場合,“力”及び“速度”は,
それぞれ“トルク”及び“角速度”に置き換える。
mechanical
impedance
1.43
自己インピーダ
ンス,
駆動点インピー
ダンス
単振動している機械系において,ある点の速度に対する,同じ点に
作用をしている力の複素振幅比[インピーダンス (1.41) 及び機械イ
ンピーダンス (1.42) の備考参照]。
direct impedance ;
driving-point
impedance
1.44
伝達インピーダ
ンス
単振動しているある機械系において,ある点の速度に対する,異な
る点に作用している力の複素振幅比[インピーダンス(1.41)及び機械
インピーダンス(1.42)の備考参照]。
transfer impedance

6
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
1.45
自由インピーダ
ンス
他の系へのすべての接続点が自由で,拘束力が作用しないとき,複
素励振力の速度複素振幅に対する比。自由インピーダンスは,モビ
リティマトリックスの単一要素の数学的逆数。
備考1. 古くは,固定インピーダンスと自由インピーダンスと
を区別しないことが多かった。このため古い資料を解
釈するときは注意が必要である。
2. 実験的に決定された自由インピーダンスをマトリック
スに組み込むことはできるが,このマトリックスは,
構造の数学的モデルから生じる固定インピーダンスマ
トリックスとは全く違うものである。したがって,こ
のマトリックスを系全体の理論解析の際に機械インピ
ーダンスとして用いることはできない。
free impedance
1.46
負荷時インピー
ダンス
変換器の負荷時電気的インピーダンス,又は構造物の負荷時駆動点
機械インピーダンス。これらは,出力側に通常の負荷,又は構造物
が接続されたときの入力側でのインピーダンスである。
loaded impedance
1.47
固定インピーダ
ンス,Zij
変換器の固定電気的インピーダンス,又は構造物の駆動点機械イン
ピーダンス。これらは,出力側が無限の機械インピーダンスをもつ
負荷に接続されたときの入力側のインピーダンスである。
備考1. 固定インピーダンスは,j点に加えられた励振速度の複
素振幅に対するi点における固定,又は駆動点力応答
の複素振幅の比によって作られる周波数応答関数であ
る。このとき,構造物のほかのすべての測定点は,“固
定”すなわち速度0に拘束される。構造体の解析対象と
するすべての点を完全に拘束するのに必要なすべての
力とモーメントは,固定インピーダンスマトリックス
を得るために測定されなければならない。
2. 測定点の数又は場所のどんな変化も,すべての測定点
での固定インピーダンスを変化させる。
3. 構造物を質点,剛性及び減衰要素で数学的にモデル化
する場合,又は有限要素でモデル化する場合,固定イ
ンピーダンスが有効である。そのような数学的モデル
と実験的モビリティデータとを統合又は比較すると
き,解析的な固定インピーダンスマトリックスをモビ
リティマトリックスに,又はその逆に変換する必要が
ある。
blocked impedance,
Zij
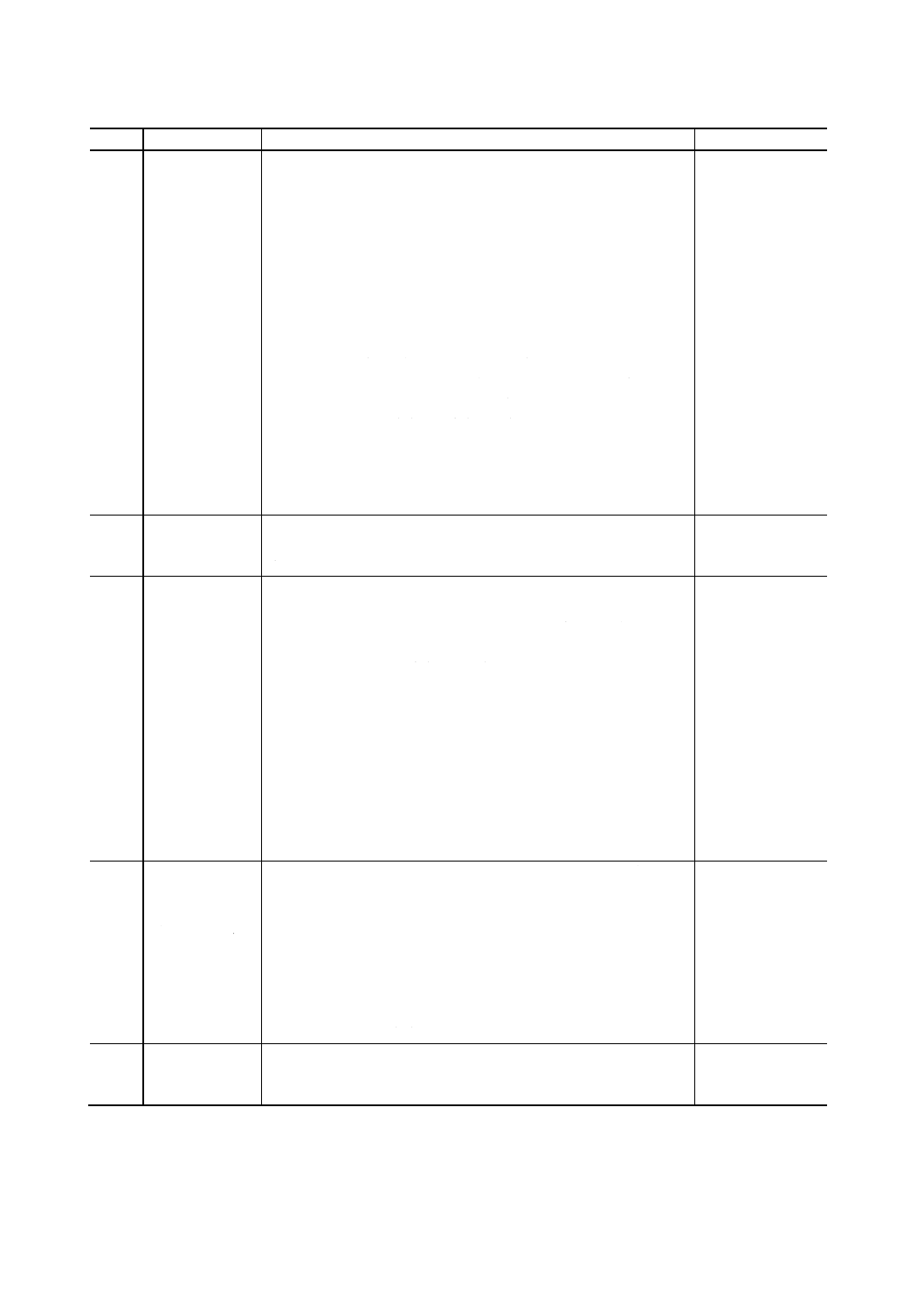
7
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
1.48
周波数応答関数
複素調和励振力の振幅に対する複素応答の比の周波数依存性。
備考1. 周波数応答関数は,励振関数の形に依存しない線形動
的システムの特性である。励振は,時間的に調和,ラ
ンダム又は過渡的関数であり得る。ある励振によって
得られた実験結果は,別の励振に対する系の応答を予
測するのに使用される。
2. 系の線形性は,系のタイプ及び入力の大きさに依存し,
実際は近似に過ぎない。特に衝撃励振を適用する場合,
非線形の影響を避けるのに注意をはらうべきである。
非線形として知られている構造体(例えば,リベット
接合構造)は,衝撃励振で試験されるべきでなく,ま
た,そのような構造体の試験に対し,ランダム励振を
用いるときには十分な注意を払うべきである。
3. 運動が速度,加速度又は変位で表現されるとき,対応
する周波数応答関数の名称は,それぞれ,モビリティ,
アクセレランス及び動コンプライアンス,又はインピ
ーダンス,有効質量及び動剛性と呼ばれる(付表1参
照)。
frequency-response
function
1.49
解析周波数範囲
最低周波数から最高周波数までの範囲で,単位は,ヘルツで表す。
例えば,モビリティデータは,一連の試験においてその範囲で取得
される。
frequency range of
interest
1.50
(機械)モビリテ
ィ,Yij
単振動をする機械系のある点の速度の,その系の同じ点又は別の点
に作用している力に対する複素振幅比。
備考1. 機械モビリティは,機械インピーダンスの逆数である。
2. モビリティは,点jにおける励振力の複素振幅に対す
る点iの速度応答の複素振幅比によって表される周波
数応答関数。ここで点j以外のすべての点は,構造体
を使用するための通常の支持以外に拘束されず,自由
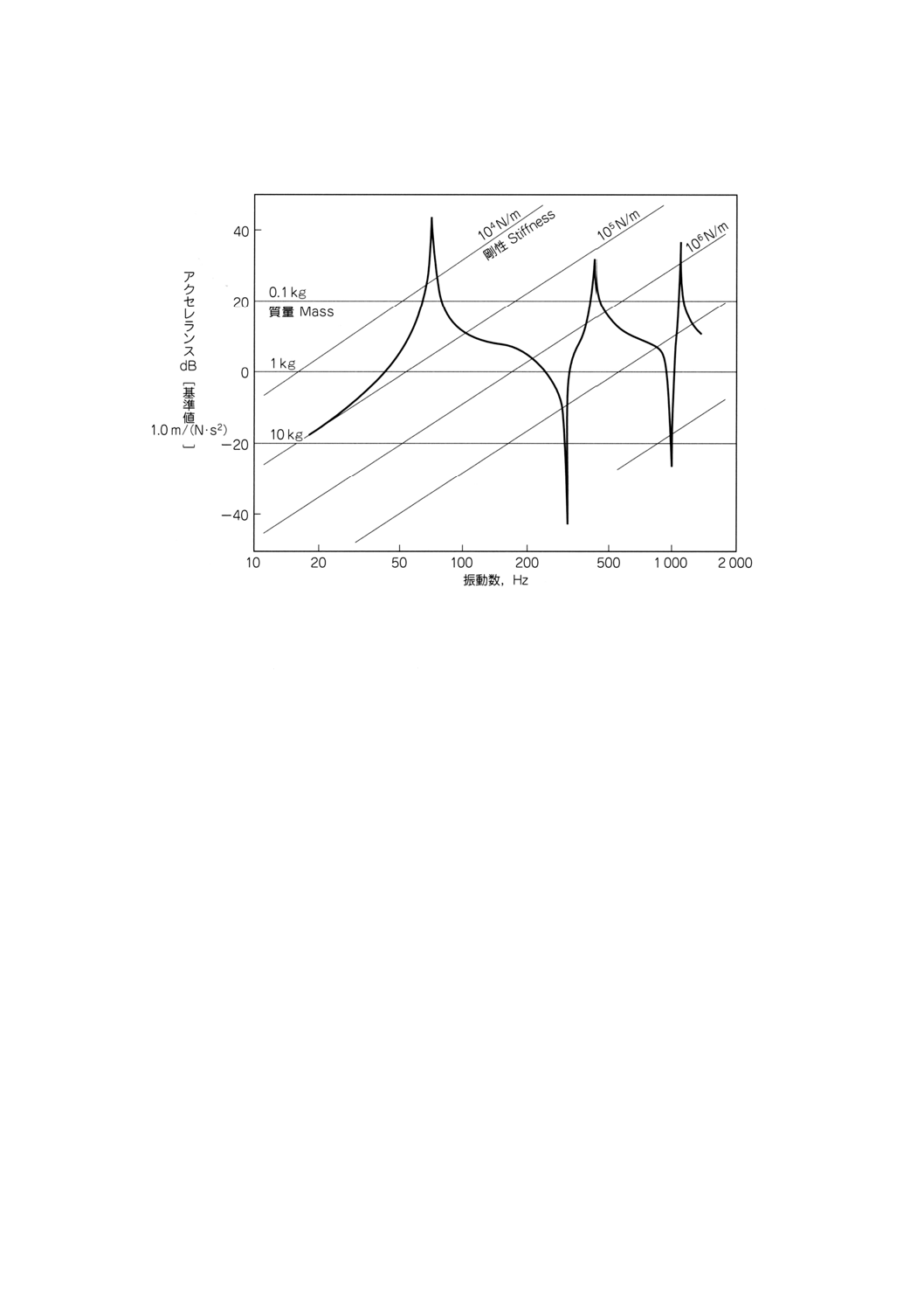
に応答できる状態にある。典型的なプロットを付図1
に示す。
3. 速度応答は,並進,回転のどちらでも表され,対応す
る励振力は,並進力又はモーメントで表される。
4. 測定される速度応答が並進であり,外力が直線的に作
用するなら,モビリティの単位は,SI単位でm/N・sに
なる。
(mechanical)
mobility, Yij
1.51
自己(機械)モビ
リティ,
駆動点(機械)モ
ビリティ,Yjj
単振動をしている機械系で同一点における速度と力との複素振幅
比。
備考1. 駆動点モビリティは,点jにおける励振力の複素振幅
に対する同じ点における速度応答の複素振幅の比を
m/N・sで表現した周波数応答関数である。ここで点j
以外のすべての点は,構造体を使用するための通常の
支持以外に拘束されず,自由に応答できる状態にある。
2. 用語“点”は,場所と方向を示す。用語“座標”も,“点”
と同じ意味で用いられる。
direct (mechanical)
mobility,
driving-point
(mechanical)
mobility, Yjj
1.52
周波数平均モビ
リティ量
指定された周波数範囲で平均された点iでの励振力の大きさに対す
る,同じ点での速度応答の大きさの比のrms値で,単位はm/N・s。
frequency-averaged
mobility
magnitude

8
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
1.53
伝達(機械)モビ
リティ
単振動をしている機械系のある点における力に対する同じ系の別
の点での速度の複素振幅比。
備考 伝達モビリティは,点jにおける励振力に対する点iにお
ける速度応答の複素振幅の比をm/N・sで表現した周波数
応答関数である。ここで点j以外のすべての点は,構造
体を使用するための通常の支持以外に拘束されず,自由
に応答できる状態にある。
transfer
(mechanical)
mobility
1.54
動剛性,
動こわさ,
動弾性係数,
動ばね定数,k*
a) 動的な状態における,変位の変化に対する力の変化の比。
b) 単振動をしている状態で変位に対する力の複素振幅比。
備考1. 動剛性は,ひずみ(振幅及びスペクトル),ひずみ速度,
温度,その他の条件に依存することがある。
2. 次の式で表される線形並進1自由度系
F
kx
dt
dx
c
dt
x
d
m
=
+
+
=
2
2
において,x=xoe iωt,F=F0e iωtとすると動剛性k*は,次の
式に等しい。
c
i
m
k
x
F
k
ω
ω+
−
=
=
2
0
0
*
これらの式で,
m:質量,x:変位,t:時間,c:線形(粘性)減衰係数,k:
剛性(弾性係数),F0:力振幅,e:自然対数の底,i=
1
−,
ω:角振動数,x0:変位振幅
dynamic stiffness,
dynamic elastic
constant,
dynamic spring
constant, k*
1.55
みかけの質量,
有効質量
単振動において加速度に対する力の複素振幅比。
備考 加速度に対する力の比は,加速度がgで与えられるとき,
有効重量又は有効荷重と呼ばれることもある。
apparent mass,
effective mass
1.56
スペクトル
ある量の周波数又は波長の関数としての記述。
備考 スペクトルという用語は,通常広範囲にわたり連続する
成分を示すのに使用される(例えば,音響周波数スペク
トル)。
spectrum
9
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
1.57
(ある量の)レベ
ル
ある量の同種の基準量に対する比の対数。対数の底,基準量及びレ
ベルの種類を表示する必要がある。
備考1. 一般に使用されるレベルの種類の例として,電気パワ
ーレベル,音圧レベル,電圧の二乗などがある。
2. この国際基準で定義するレベルは,基準量に対する比
が対数の底と等しいときを基準比と呼び,これの対数
を単位として測定されている。
3. この定義を数式化すると
=
0
log
q
q
L
r
ここに,
L:log r rを単位として測定されるレベル
r:対数の底であり基準比である。
q:対象とする量
qO:同じ種類の基準量
4. q1とq2の二つのレベルの差は,対数の定理から基準値
が相殺され,次の式のように同じ式で表される。
=
−
2
1
0
2
0
1
log
log
log
q
q
q
q
q
q
r
r
r
5. 振動用語では,レベルという用語は,振幅,平均値,
rms値又はこれらの値の比を示すことがあるが,このよ
うな使い方は,好ましくない。
level (of a quantity)
1.58
ベル
対数の底が10のときのレベルの単位。ベルの使用は,パワーに比
例した量のレベルに制限される[レベル(1.57)及びデシベル(1.59)の
備考参照]。
bel
1.59
デシベル (dB)
ベルの1/10。
備考1. デシベル単位のレベル量は,10を底にしたパワーに類
する量の比の対数を10倍したものである。すなわち,
=
=
0
10
20
2
10
log
20
log
10
X
X
X
X
Lp
2. パワーに類する量として,音圧の二乗,粒子速度の二
乗,音の強さ,音響エネルギ密度,電圧の二乗などが
ある。このようにデシベルは,音圧の二乗のレベルの
単位であるが,短くしてもあいまいにならないので,
普通これを音圧レベルと呼んでいる。
decibel (dB)
b) 振動
番号
用語
定義
対応英語(参考)
2.1
振動
機械系の運動又は位置を表す量の大きさが平均値又は基準値より
も大きい状態と小さい状態とを交互に繰り返す時間的変化[振動
(1.8)参照]。
vibration
2.2
周期振動
独立変数が一定量増加するごとに同じ値を繰り返すような周期量。
備考1. 時間tの関数として示される周期量yは,次のように
表される。
)
(
)
(
τ
n
t
f
t
f
y
±
=
=
ここに,
n:整数,τ:定数,t:独立変数
2. 準周期(概周期)振動は,周期振動からごくわずかだ
け逸脱する振動である。
periodic vibration

10
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.3
単振動,
正弦振動
独立変数の正弦関数で表される周期振動。次のように表される。
)
sin(
φ
ω+
=
t
A
y
ここに,
y:単振動,A:振幅,ω:角振動数,t:独立変数,
φ:振動の位相角
備考1. 単振動の極大値は,振幅Aである。
2. 二つ以上の正弦量の総和からなり,それらの振動数が
基本振動数の倍数である振動は,しばしば,複合振動
(complex vibration) ,多正弦振動と称される。この意味
で “complex vibration” という用語の使用は,好ましく
ない。
3. 準正弦振動は,見かけは正弦量であるが,振動数と振
幅の両方又は一方が,比較的緩やかに変化する。
simple harmonic
vibration ;
sinusoidal vibration
2.4
不規則振動
任意の時刻における大きさが正確に予測できない振動[不規則雑音
(2.7)参照]。
備考 不規則振動の大きさが与えられた範囲内にある確率は,
確率分布関数によって表される。
random vibration
2.5
非定常振動
定常的でない不規則振動。
non-stationary
vibration
2.6
雑音,
ノイズ
a) 不愉快な,望ましくない音。
b) 一般に不規則な性質をもち,そのスペクトルが明確な振動数成
分をもたない音又は信号。
備考 上記の定義を拡張して,雑音は,望ましくない,又は不
規則な性質の電気的な振動を含むことがある。もし,雑
音の性質があいまいならば,音響雑音,電気雑音のよう
な用語が使われるべきである。
noise
2.7
不規則雑音
任意の時刻における大きさが正確に予測できない雑音[不規則振動
(2.4)とその備考参照]。
random noise
2.8
ガウス雑音
瞬時値がガウス分布をもつような不規則雑音[ガウス分布(A.32)参
照]。
Gaussian random
noise
2.9
ホワイトノイズ,
白色雑音,
白色不規則振動
問題としているスペクトルの全域にわたって,一定の周波数帯域幅
(又は単位帯域幅)当たり,等しいエネルギをもつような雑音。
備考 白色不規則振動は,問題にしている周波数全域にわたっ
て,一定の二乗平均スペクトル密度をもつ[パワースペ
クトル密度(5.1)参照]。
white noise ;
white random
vibration
2.10
ピンクノイズ,
ピンク不規則振
動
帯域幅をその中心周波数に比例するようにとったとき,その帯域幅
当たり一定のエネルギをもつような雑音。
備考 オクターブ帯域幅(又は1/nオクターブ帯域幅)のフィ
ルタを通してピンクノイズのエネルギスペクトルを作る
と振動数に無関係な一定値をとる。
pink noise ;
pink random
vibration
2.11
狭帯域不規則振
動
ある狭い帯域幅の周波数成分だけをもつ不規則振動[不規則振動
(2.4) 参照]。
備考1. 帯域幅が“狭い”という意味は,問題に応じて相対的
に決まるが,通常1/3オクターブ以下である。
2. 狭帯域不規則振動の波形は,振幅と位相とが不規則に
変化する正弦波の様相を呈する。
narrow-band
random vibration
2.12
広帯域不規則振
動
振動数成分が広い周波数帯域に広がっているような不規則振動[不
規則振動(2.4)参照]。
備考 帯域幅が“広い”という意味は,問題に応じて相対的に
決まるが,通常1オクターブ以上である。
broad-band random
vibration
11
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.13
卓越振動数
スペクトル密度曲線において,最大値を示す振動数。
dominant frequency
2.14
定常振動
継続的な周期振動。
steady-state
vibration
2.15
過渡振動
定常又は不規則ではない振動。定常状態でない振動。
備考 この用語は,基本的に機械衝撃(3.1)と関連している。
transient vibration
2.16
強制振動
定常的な励振によって引き起こされる定常振動。
備考1. 強制振動は,(線形系の場合)励振と同じ振動数をも
つ。
2. 過渡振動は,強制振動と考えられていない。
forced vibration
[oscillation]
2.17
自由振動
励振又は拘束を除いた後に生じる振動。
備考1. 系は,その固有振動数で振動する。
2. 多自由度系では,空間的に特定の固有振動モード(2.49
参照)の振幅分布で,また時間的には固有振動数(2.80
参照)で正弦振動する性質があり,これを“固有振動
(natural vibration) ”という。ただし1自由度系は,1質
点の運動なので,その固有振動は,固有振動数で正弦
振動するだけである。1自由度系の自由振動では,外乱
に応じてこの固有振動が現れる。線形多自由度系の自
由振動では,初期外乱の分布と時間変動に近い固有振
動モード及び固有振動数をもつ,一つ又は複数の固有
振動が重ね合わされて現れる。
3. 減衰をもつ振動系の自由振動を減衰自由振動 (damped
free vibration) という。
free vibration ;
free oscillation
2.18
自励振動
系の内部において,非振動的なエネルギが振動的エネルギへ変換さ
れておこる機械系の振動。
備考 一般に系がもつ固有振動数に近い振動数で振動する。
self-induced
vibration ;
self-excited
vibration
2.19
周囲振動
与えられた環境に関連するすべてを包含する振動。通常,遠く及び
近くの多くの振動源からの振動の合成である。
ambient vibration
2.20
外来振動
問題としている主要な振動とは異なるすべての振動。
備考 周囲振動は,外来振動の大きさに影響する。
extraneous vibration
2.21
非周期運動
周期的ではない振動。
aperiodic motion
2.22
サイクル(名詞) 周期的な現象又は関数が,全く同じ状態を繰り返すまでにたどる状
態又は値の全範囲[サイクル(動詞)(2.101)参照]。
cycle (noun)
2.23
基本周期,
周期
周期関数が同じ状態を繰り返すのに必要な独立変数の最小増加分
[周期振動(2.2)参照]。
備考 あいまいさがなければ基本周期は,単に周期と呼ばれる。
fundamental
period ;
period
2.24
振動数,
周波数
周期の逆数。
備考 振動数の単位は,ヘルツ (Hz) であり,1秒当たり1サイ
クルに相当する。
(cyclic) frequency
2.25
基本振動数
a) 周期量については,基本周期の逆数。
b) 振動系については,最も低い固有振動数。この振動数に対応す
る正規モードを,基本固有モードという。
fundamental
frequency

12
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.26
(周期量の)調波 基本振動数の整倍数の振動数をもつ正弦量。
備考1. 倍音という用語は,しばしば調波の代わりに使われ,n
番目の調波は, (n−1) 倍音と呼ばれる。
2. 英語では,第1倍音及び第2調波は,基本振動数の2
倍の振動数をもつ。フランス語では,調波と倍音とを
区別せず,第2調波は,基本振動数の2倍の振動数を
もつ。“倍音”という用語は,周期量の成分を数える上
であいまいなため好ましくない。
harmonic (of a
periodic quantity)
2.27
分数調波
関係している量の基本周期の1/n(nは整数)の周期をもつ正弦量。 subharmonic
2.28
うなり
振動数がわずかに異なる二つの単振動を組み合わせたときに生じ
る振幅の周期的な変化。うなりは,振動数の差で起こる。
beats
2.29
うなり振動数
振動数がわずかに異なる二つの振動の振動数の差の絶対値。
beat frequency
2.30
角振動数,
円振動数
振動数の2π倍の量。
備考 角振動数の単位は,単位時間当たりのラジアンである。
angular frequency ;
circular frequency
2.31
位相角,
(正弦振動の)位
相
独立変数のある値を基準として測られた,正弦振動の進み角。
phase angle ;
phase (of a
sinusoidal
vibration)
2.32
位相差,
位相角差
振動数が等しい二つの周期振動の間のそれぞれの位相の差。正弦振
動の場合には同じ原点から測った位相角の差。
phase difference ;
phase angle
difference
2.33
振幅
正弦振動の極大値。
備考1. この“振幅”という用語は,他の意味と区別するため
ベクトル振幅と呼ばれ,また全振幅と区別するため,
片振幅又は最大振幅と呼ばれることがある。全振幅は,
調和振動の全行程(変位の概念)又はp-p値と等しい。
“全振幅”と“片振幅”という用語の使用は,好まし
くない。
2. 振動理論では,正弦量の極大値を示す以外の目的で“振
幅”が使われることは,好ましくない。
amplitude
2.34
ピーク値,
正(負)のピーク
値
振動量の与えられた時間の範囲における極大値[極大値(2.40)も参
照]。
備考 通常,振動する量のピーク値は,平均値からのその振動
の最大変化量をいう。正のピーク値は,正の最大変化量
であり,負のピーク値は,負の最大変化量である。
peak value ;
peak magnitude ;
positive (negative)
peak value
2.35
(振動の)p-p値 振動の与えられた区間内の極大極小間の代数差。
peak-to-peak value
(of a vibration)
2.36
行程,
(振動の)全行程
変位のp-p値。
excursion ;
total excursion (of a
vibration)
2.37
(振動の)クレス
トファクタ,
波高率,
ピーク−rms比
ピーク値のrms値に対する比[附属書A,A.37 : rms値参照]。
備考1. 正弦波の波高率は,2である。
2. ピークファクタ (peak factor) ともいう。
crest factor (of a
vibration) ;
peak-to-r. m. s. ratio
2.38
(振動の)波形率 二つの連続したゼロ点を通る半サイクルの平均値に対するrms値の
比。
備考 正弦波の波形率は,
2
2/
π
=1.111である。
form factor (of a
vibration)
2.39
瞬時値,
値
ある時刻における変化量の値。
instantaneous
value ;
value
13
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.40
極大値
関数の値が独立変数のいかなる小さな変化によってでも減少する
とき,その関数の値。
maximum value
2.41
最大値
独立変数のある与えられた区間において,関数の値が二つ以上の極
大値を含むとき,最も大きい極大値。
maximum
2.42
振動シビアリテ
ィ
振動の大きさを記述する極大値,平均値,rms値又は他のパラメー
タで表されるような値,若しくは一連の値の包括的な用語である。
瞬時値又は平均値に対しても使用できる。
備考1. 機械の振動シビアリティは,軸受又は取付台のような
機械の重要な点で測られた振動速度の最大のrms値で
定義される。
2. 振動の暴露時間が,振動のシビアリティを記述するパ
ラメータとして使われることがあるが,この用法は好
ましくない。
vibration severity
2.43
だ円振動
振動している点の軌跡がだ円の形である振動。
elliptical vibration
2.44
直線振動
振動している点の軌跡が直線である振動。
rectilinear
vibration ;
linear vibration
2.45
円振動
振動している点の軌跡が円の形である振動。これは,だ円振動の特
別な場合である。
circular vibration
2.46
節(ふし,せつ) 定在波の特性を表す量の振幅がゼロとなる点,線又は面。
備考1. 節の性質が明らかでない場合,適切な修飾語が使われ
るべきである。例えば,変位の節,圧力の節など。
2. 定在波の特性を表す量の振幅がゼロとなる点を節点
(nodal point) ,線を節線 (nodal line) ,面を節面 (nodal
surface) という。
node
2.47
腹(はら)
定在波の振幅が極大値であるような点,線又は面。
備考 腹の性質が明らかでない場合,適切な修飾語が使われる
べきである。例えば,変位の腹,圧力の腹など。
antinode ;
loop
2.48
振動モード
振動している系内の各点が特定の振動数に対して単振動(線形系の
場合)している場合,節及び腹からなる特有のパターン。
備考 多自由度系では,同時に二つ以上の固有振動モードが含
まれることがある。
mode of vibration
2.49
固有振動モード
系が一つの固有振動数で自由振動するときに現れる振動モード。
備考1. 系の固有振動がもつ振動振幅の空間的分布。
2. 系に減衰がなければ,固有振動モードは,正規モード
と等しい[正規モード(2.55)参照]。
3. 固有振動モードは,系の自由度の数だけ存在する。
4. 固有振動モードはしばしば単に固有モード (natural
mode, eigen mode) ともよばれる。
natural mode of
vibration
2.50
基本固有振動モ
ード
系の最も低い固有振動数をもつ固有振動モード[基本振動数(2.25)
参照]。
fundamental
natural mode of
vibration
2.51
モード形
機械系のある特定の振動モードの形は,振動の変位が最大になった
ときの変位分布によって与えられる。通常,モード形は,ある特定
の点における変位の大きさが特定の値をもつように正規化される。
備考 振動モード(2.48)と同じ意味で使われる場合が多い。
mode shape
2.52
モード数
系の正規モードがひと続きの整数で定義されるとき,これらの整数
は,モード数と呼ばれる。
model numbers
14
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.53
連成モード
一方の振動モードから他の振動モードへエネルギが移動できるよ
うな,互いに独立でなく影響し合う振動モード。
備考1. 線形系では各固有振動モードは,独立で連成しない。
系のパラメータが変化すると,変化後の固有振動モー
ドは,変化前の固有振動モードが連成し合うように観
測される。
2. 二つ以上の振動系が結合されることによって,互いに
影響し合う振動を連成振動 (coupled vibration) という。
coupled modes
2.54
非連成モード
一方の振動モードから他の振動モードへエネルギが移動すること
がなく,他のモードと同時に,互いに独立系に存在することができ
る振動モード。
uncoupled modes
2.55
正規モード
不減衰機械系の固有振動モード。
備考1. 系の運動は,関係するそれぞれの正規モードの運動の
総和からなる。
2. natural mode,characterstic mode及びeigen modeという
用語は,不減衰系においては正規モードと同義である。
normal mode
2.56
波動,
波
媒体の物理的状態の変化で,それは媒体の物理的特性によって媒体
に伝搬される。
備考 変動を表す量は,媒体の任意の点においては時間の関数
であり,また任意の時間において,位置の関数で表され
る量。
wave
2.57
波列
通常ほぼ周期的で,同じ(又はほぼ同じ)速度で移動している,限
られた数の連続した波。
wave train
2.58
(周期的な波の)
波長
1周期離れた相次ぐ2点間を波面に対して垂直な伝搬方向に測った
距離。
wavelenghth (of a
periodic wave)
2.59
圧縮波
弾性媒体に伝搬される圧縮又は引張応力の波動。
備考 圧縮波は,通常縦波である[縦波(2.60)参照]。
compressional wave
2.60
縦波
波の運動によって引き起こされる変位の方向が,伝搬の方向と平行
な波動。
longitudinal wave
2.61
せん断波
弾性媒体を伝搬するせん断応力の波動。
備考1. せん断波は,通常横波である[横波(2.62)参照]。
2. せん断波は,体積の変化を伴わない。
shear wave
2.62
横波
波面に対して垂直に伝搬される,媒体の要素の変位の方向が伝搬の
方向と垂直な波動。
transverse wave
2.63
波面,
波先
a) 空間における進行波では,ある瞬間に同じで位相をもつ点の軌
跡からなる連続した面。
b) 進行している表面波では,ある瞬間に同じで位相をもつ点の軌
跡からなる連続した線。
wave front
2.64
平面波
波面が平行な平面になっている波動。
plane wave
2.65
球面波
波面が同心球面となっている波動。
spherical wave
2.66
定在波
空間的に固定された一定の振幅分布をもつ周期的な波動で,同じ振
動数とで同じ種類の進行波の干渉の結果生じる。
備考1. 定在波は,同じ振動数と種類の逆方向に進行する波の
重ね合せの結果であると考えることができる。
2. 定在波は,節及び腹の位置が固定されていることが特
徴である。
standing wave
2.67
可聴周波数,
AF
通常,可聴音波のあらゆる周波数。
備考 一般に可聴周波数は,20〜20 000Hz。
audio frequency

15
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.68
超音波周波数,
超音波
可聴周波数範囲より高い周波数。
備考 “超音波”という用語は,超音波振動を利用した装置を
示すため使われることがある
ultrasonic
frequency ;
ultrasonic
2.69
超低周波数
可聴周波数範囲より低い周波数。
備考 “超低周波”という用語は,超低周波振動を利用した装
置を示すために使われることがある。
infrasonic
frequency ;
infrasonic
2.70
残響
音源が止まった後,閉空間内で反射と散乱とが繰り返されて持続す
る音。
reverberation
2.71
エコー,
反響,
こだま
十分な大きさと遅れをもって反射したり往復することによって,直
接伝わってきた波とは異なり,その繰り返しとして識別される波
動。
echo
2.72
共振,
共鳴
強制振動における系の共振とは,励振振動数の微小変化によって,
系の応答が減少するような状態をいう。
resonance
2.73
共振振動数,
共鳴周波数
共振している振動数。
備考1. 共振振動数は,測定される変数によることががある,
例えば,速度共振は,変位共振とは,異なる振動数で
起こることがある。(付表2参照)
2. 混乱しやすい場合には,例えば速度共振振動数などの
ように共振のタイプを示す必要がある[付表2参照]。
resonance frequency
2.74
反共振
強制振動における系の反共振とは,励振振動数の微小な変化によっ
て,この点での応答が増加するような状態をいう。
antiresonance
2.75
反共振振動数,
反共鳴周波数
反共振している振動数。
備考1. 反共振振動数は,測定される変数によることがあり,
例えば,速度反共振は,変位反共振とは異なる振動数
で起こる。
2. 混乱しやすい場合には,例えば速度反共振振動数など
のように,反共振の量を示す必要がある。
antiresonance
frequency
2.76
基礎固定時固有
振動数
装置が取り付けられる基礎が剛で無限の質量をもつときに,系がも
つ固有振動数。
備考 付表2で与えられた振動方程式及び固有振動数は,基礎
固定時の状態に対するものである。
fixed-base natural
frequency
2.77
危険速度
系の共振が励振されている特有の速度。
備考1. 回転機械系の危険速度は,その系の共振振動数(共振
振動数の倍数及び約数も含むことがある。)に等しい回
転系の速度である,例えば,単位時間当たりの回転系
の回転速度は,共振振動数に等しい。
2. 幾つかの回転系がある場合,全体系の各モードに対応
するいくつかの危険速度がある。
critical speed
2.78
分数調波応答,
分数調波共振応
答
励振の周期の整数倍の周期をもつ振動数において,共振の性質を表
す機械系の応答。
subharmonic
response ;
subharmonic
resonance
response

16
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.79
減衰
距離又は時間の変化に伴うエネルギ消費。
備考1. 振動・衝撃の分野では,減衰は,時間に伴い振幅が減
少することである。
2. 減衰による抵抗力を減衰力 (damping force) という。
3. 物体の変形に伴いその内部まで費やされるエネルギ損
失に伴って発生する減衰を内部減衰 (internal damping)
という。
4. 物体の運動に対する抵抗力によって失われるエネルギ
損失に伴って発生する減衰を外部減衰 (external
damping) という。
damping
2.80
(機械系の)不減
衰固有振動数
系の弾性力と慣性力だけによって生じる自由振動の振動数。
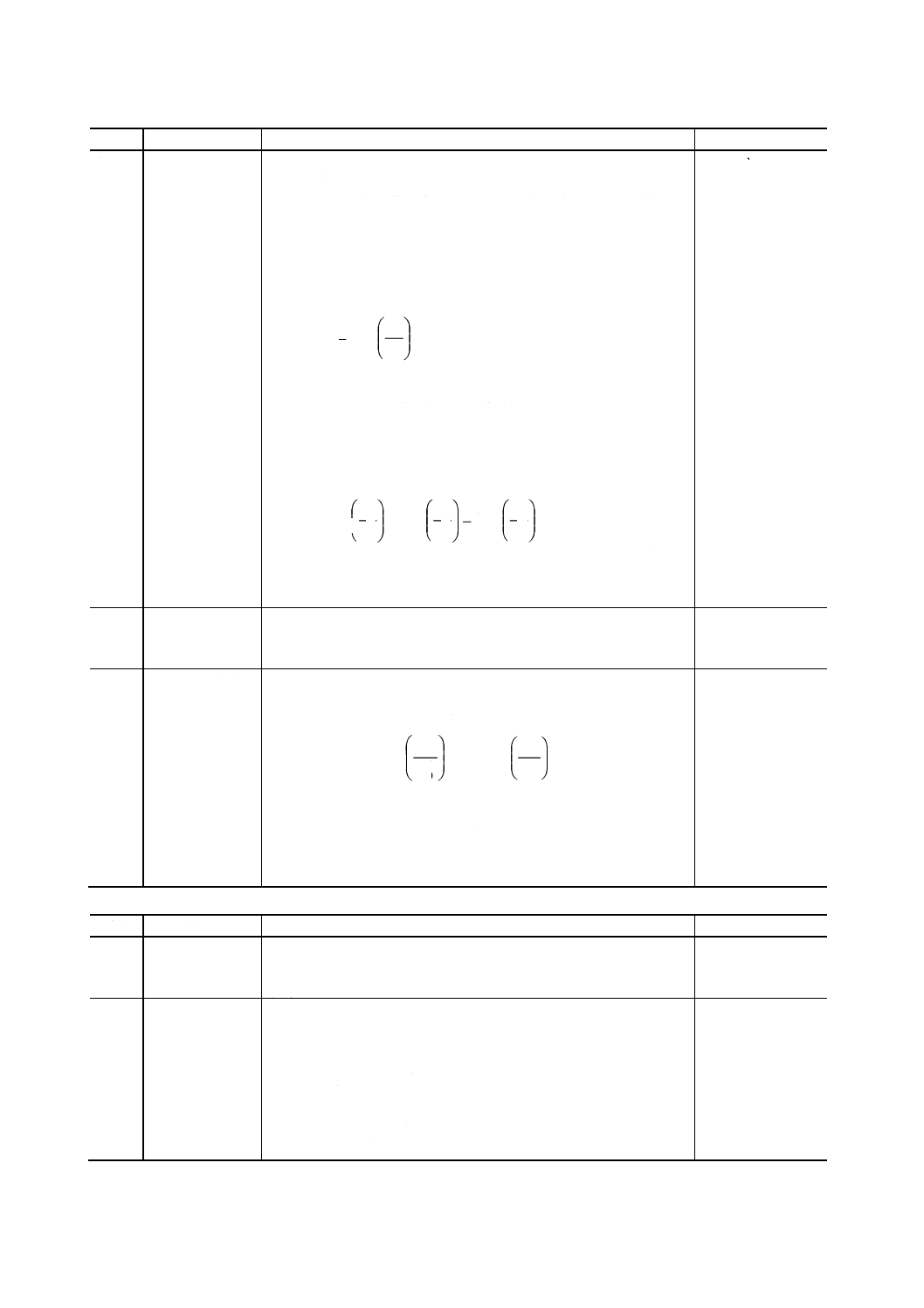
備考1. 付表2の振動方程式に対しては,不減衰固有振動数は,
m
k/
)
2
/1(
π
Hzである。
2. 単に固有振動数ともいう。
3. n自由度系では,一般にn個の固有振動数が存在する。
undamped natural
frequency (of a
mechanical
system)
2.81
減衰固有振動数
線形系の減衰する自由振動の振動数(付表2参照)。
damped natural
frequency
2.82
粘性減衰,
線形粘性減衰
振動系の要素又は一部が,要素の速度に比例する大きさで,速度と
は反対の方向の抵抗力をうけるときに生じる,エネルギの消費。
備考 線形粘性減衰を発生する要素をダシュポットという。
viscous damping ;
linear viscous
damping
2.83
等価粘性減衰
振動を解析するために,共振におけるサイクル当たりのエネルギ消
費が,実際の減衰力と等しくなるように仮定された線形粘性減衰の
値。
equivalent viscous
damping
2.84
線形粘性減衰係
数,
粘性減衰係数
線形粘性減衰において,速度に対する減衰力の比[線形粘性減衰
(2.82)参照]。
linear viscous
damping
coefficient ;
viscous damping
coefficient
2.85
臨界減衰,
臨界粘性減衰
1自由度系において,自由振動が振動的になるか非振動的になるか
の境界状態に対応する粘性減衰の大きさ。
備考 付表2の方程式によって表される1自由度系に対する臨
界線形粘性減衰係数ccは,次のようになる。
0
2
2
ω
m
mk
cc
=
=
ここに,ω0は,不減衰固有角振動数である[不減衰固有振動
数(2.80)参照]。
critical damping ;
critical viscious
damping
2.86
減衰比
線形粘性減衰をもつ系において,臨界減衰係数に対する実際の減衰
係数の比[線形粘性減衰係数(2.84)及び臨界減衰(2.85)参照]。
備考1. 減衰比は,臨界減衰に対する百分率として表されるこ
ともある。
2. 減衰比が1より小さな減衰を不足減衰 (under damping)
という。
3. 減衰比が1より大きな減衰を過減衰 (over damping) と
いう。
4. 振動の固有振動モードごとの減衰比をモード減衰比
(modal damping ratio) という。
damping ratio ;
fraction of critical
damping
2.87
対数減衰率
単一振動数の振動の減衰において,同じ符号の二つの連続した振幅
の比の自然対数。
logarithmic
decrement
2.88
非線形減衰
系の運動が定数係数の線形微分,積分又は積微分方程式によって表
現できない系のエネルギ損失に関連する現象。
non-linear damping
17
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.89
Q(キュー)値,
Qファクタ
機械系又は電気系のいずれにおいても,1自由度をもつ共振振動系
の,共振の鋭さ又は振動数の卓越さを表す量。
備考1. Q値の大きさは,減衰比の逆数の1/2に等しい。すなわ
ち,
c
c
c
Q
/
2
1
=
2. 振動系の共振の鋭さを表す量。共振振動数において,
振動系のエネルギ(機械振動系では運動エネルギと位
置エネルギとの和。)と,一定振幅を持続するために外
部から与えられる1サイクル当たりのエネルギとの比
の2π倍で定義する。対数減衰率の逆数のπ倍に等しい。
Q ;
Q factor
2.90
振動発生機,
加振機
振動を発生し,それを他の構造物又は装置に伝えられるように特別
に設計された機械。
備考 試験される装置は,発生機の上のテーブルに取り付けら
れるか,又はテーブルを使わずスタッドによって,発生
機で装置を励振するように用いられる。
vibration
generator ;
vibration machine
2.91
振動発生装置,
加振機システム
振動発生機とその操作に必要な周辺装置。
vibration generator
system
2.92
動電型振動発生
機,
動電型加振機
一定の値の磁界及び交流電流によって励振されるコイルとの相互
作用によって,コイルに生じる加振力を生じさせる振動発生機。
備考 動電型振動発生機の運動要素は,振動台,ムービングコ
イル及び振動するすべての部分を含んでいる。
electrodynamic
vibration
generator ;
electro-dynamic
vibration machine
2.93
電磁型振動発生
機
加振力を電磁石と磁気を帯びた素材との相互作用から引き出して
いる振動発生機。
electromagnetic
vibration
generator
2.94
機械直動型振動
発生機,
直動型振動発生
機
振動台が荷重又は振動数にかかわらず,直動リンクによって一定の
変位振幅で励振される振動発生機。
mechanical direct
drive vibration
generator ;
direct-drive
vibration
generator
2.95
油圧振動発生機
適切な運転操作によって,液体の圧力を利用して加振力を生じさせ
ている振動発生機。
hydraulic vibration
generator
2.96
機械回転型振動
発生機,
不平衡質量型振
動発生機
加振力が,偏芯した質量の回転又は往復運動によって引き起こされ
る加振機。
mechanical reaction
type vibration
generator ;
unbalanced mass
vibration
generator
2.97
共振型振動発生
機
共振振動数において励振される振動系を含む振動発生機。
resonance vibration
generator
2.98
圧電型振動発生
機
力を発生する要素として,圧電型トランスデューサをもつ振動発生
機。
piezoelectric
vibration
generator
2.99
磁わい(歪)型振
動発生機
力を発生する要素として,磁わい(歪)型トランスデューサをもつ
振動発生機。
magnetostrictive
vibration
generator
18
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.100
死荷重,
純質量,
集中質量
対象とする振動数領域にわたって完全に剛な性質をもつ質量。
deadweight ;
pure mass ;
lumped mass
2.101
繰り返し,
サイクル(動詞)
ある装置が,振動数のような変数を一定の範囲で制御し繰り返して
操作されるとき,装置は繰り返されているという[サイクル(名詞)
(2.22)参照]。
cycle (verb)
2.102
繰り返し周期
すべての制御変数を制御範囲で変化させて,装置が繰り返すのに要
する時間。
cycle period
2.103
繰り返し範囲
繰り返し範囲は,装置が繰り返す間に変化させた,振動数のような
制御変数の最大値と最小値とで定義される。
cycle range
2.104
掃引
独立変数(通常は振動数)をある範囲内で連続的に変化させる過程。 sweep (as applied
to the operation
of a vibration
generator)
2.105
掃引速度
独立変数(通常は振動数)の変化率。例えば,df / dt,ここに,f:
振動数,t:時間
sweep rate
2.106
一様掃引速度,
線形掃引速度
掃引に対する独立変数(通常は振動数)の変化率が一定のとき,す
なわちdf / dt=一定のときの掃引速度[掃引速度(2.105)参照]。
uniform sweep
rate ;
linear sweep rate
2.107
対数掃引速度
ある振動数に対する振動数の変化率が一定のとき,すなわち (df / f)
/ dt=一定のときの掃引速度[掃引速度(2.105)参照]。
備考1. 対数掃引速度に対しては,同じ比率の二つの振動数の
間を掃引する時間は一定である。
2. 対数掃引速度は,1分間当たりのオクターブ数で表すの
がよい。
logarithmic
frequency sweep
rate
2.108
(振動環境試験
における)クロス
オーバ振動数
振動性状が,ある関係から別の関係へ変化するときの振動数。
備考 クロスオーバ振動数は,例えば振動振幅又はrms値が,
振動数に対して変位一定から加速度一定に変化するとき
の振動数である。
cross-over
frequency (in
vibration
environmental
testing)
2.109
絶縁装置
衝撃と振動の一方又は両方の伝達を低減する機能をもつ,通常弾性
体から構成される支持装置。
備考1. 絶縁装置は,弾性要素の代用として,又は弾性要素に
加えて,破壊要素,サーボ機構及びそのほかの装置を
含むことがある。
2. ある振動数範囲において生じる振動の伝達を妨げる機
能,すなわち振動伝達率を1未満にする機能を振動絶
縁 (vibration isolation) 又は防振という。
isolator
2.110
振動絶縁装置
ある振動数範囲において振動の伝達を低減するために設計された
絶縁装置。
vibration isolator
2.111
衝撃絶縁装置
ある範囲の衝撃運動又は衝撃力から系を守るために設計された絶
縁装置。
shock isolator
19
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
2.112
重心支持系
支持装置が並進運動によってその平衡位置から変位するとき,重心
を通るどの軸まわりにも合力モーメントが生じないような支持系。
備考1. 装置が重心支持系によって支持されるなら,支持装置
の並進振動と回転振動とは,連成しない。励振の並進
運動は,回転振動を励振せず,その逆もまた成り立つ。
実際にはこれを実現するのは非常に難しい。
2. 振動系のばねに,ある一方向に力を加えたとき,力の
方向と作用点の変位の方向とが等しく,かつ,作用点
を含むばねの面が回転しないような軸を弾性主軸
(principal elastic axes) という。
3. 互いに直交する3本の弾性主軸の交点を弾性中心
(elastic centre) という。重心支持系は,重心と弾性中心
とが一致している系である。
centre-of-gravity
mounting system
2.113
緩衝装置
加えられた衝撃に対する機械系の応答を低減するためにエネルギ
を消費させる装置。
shock absorber
2.114
ダンパ
振動の応用において,エネルギを消費させる方法によって振動又は
衝撃の大きさを減らすために使われる装置。
damper,
absorber
2.115
スナッバ
変位が特定の値よりも大きくなるようなとき,系の弾性要素の剛性
を(通常は飛躍的に大きな率で)増加することによって,機械系の
相対的な変位を制限するために使われる装置。
snubber
2.116
動吸振器
共振によって,主振動系に働く力に対して逆位相の力が働くように
調整された補助系へのエネルギの伝達によって,対象とする振動数
範囲で主振動系の振動を低減するための装置。
備考 動吸振器は,減衰をもつことも,不減衰なこともあるが,
対象とする振動数範囲が広い場合は減衰が必要である。
dynamic vibration
absorber
2.117
ディチューナ
振動系の振動特性を変えるために主振動系に取り付けられた振幅
依存形の振動数特性をもつ補助の振動系。
備考 一つの例は,非線形のばねによって制御された補助の質
量である。
detuner
c) 機械衝撃
番号
用語
定義
対応英語(参考)
3.1
衝撃
系に過渡的変化をもたらす力,位置,速度又は加速度の突然な変化。
備考1. 変化が固有周期に比べ短時間に起こるならば,突然の
変化と見なされる。
2. 突然の非振動性の速度変化によって生じる衝撃を速度
衝撃という。
3. 突然の比振動性の加速度によって生じる衝撃を加速度
衝撃という。
mechanical shock ;
shock
3.2
衝撃パルス
(運動,力又は速度のような)時間的に変化する量の急激な上昇,
又は急激な下降によって特徴づけられる衝撃励振の形。
備考 例えば,加速度衝撃パルスのように記述的機械用語とし
て用いられる。
shock pulse
3.3
衝撃励振
機械的衝撃を系に生じさせるような励振。
applied shock ;
shock excitation
3.4
衝撃運動
衝撃励振を引き起こす過渡運動又は衝撃励振によって引き起こさ
れる過渡運動。
shock motion
3.5
衝突
一つの質点と他の質点との1回のぶつかりあい。
impact

20
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
3.6
インパルス(力
積)
a) 力が加えられている時間にわたる力の時間積分。
b) 一定の力の場合,力と力が作用している時間との積。
備考1. 衝撃として用いられる場合,時間間隔は,比較的短い。
2. 瞬間的な外力又は入力による励振をインパルス励振又
は打撃加振という。
impulse
3.7
バンプ
試験のために何回も繰り返される衝撃の形。
bump
3.8
理想衝撃パルス
例えば3.9〜3.15に定義されるような単純な時間関数で表される衝
撃パルス。
ideal shock pulse
3.9
正弦半波衝撃パ
ルス
正弦波の1サイクル中の正(又は負)の部分の時刻歴をもつ理想衝
撃パルス
half-sine shock pulse
3.10
のこぎり波衝撃
パルス
直線的に最大値まで増加し,その後瞬時にゼロとなる三角波形の時
刻歴をもつ理想衝撃パルス。
final peak
sawtooth shock
pulse ;
terminal peak
sawtooth shock
pulse
3.11
逆のこぎり波衝
撃パルス
瞬時に最大値に達し,その後直線的に減衰してゼロとなる時刻歴を
もつ理想衝撃パルス。
initial peak sawtooth
shock pulse
3.12
三角波衝撃パル
ス
時間履歴曲線が二等辺三角形の時刻歴をもつ理想衝撃パルス。
symmetrical
triangular shock
pulse
3.13
バーサイン衝撃
パルス
ゼロから始まるバーサイン曲線(サイン自乗曲線)の1サイクルの
時刻歴をもつ理想衝撃パルス。
versine shock
pulse ;
haversine shock
pulse
3.14
方形波衝撃パル
ス
時刻歴が瞬時にある値に達し,パルスが持続している間一定の値を
とり,瞬時にゼロとなる理想衝撃パルス。
rectangular shock
pulse
3.15
台形波衝撃パル
ス
時刻歴が直線的にある値まで増加し,その後ある時間内は一定の値
を取り,その後直線的に減少してゼロとなる理想衝撃パルス。
trapezoidal shock
pulse
3.16
公称衝撃パルス
理想衝撃パルスからの許容偏差が指定された衝撃パルス。
備考1. “公称衝撃パルス”は,総称的な用語である。例えば,
公称正弦半波衝撃パルス,公称のこぎり波衝撃パルス
などの修飾語を追加し,その意味を明確にする必要が
ある。
2. 理想パルスに対する公称パルスの偏差の許容幅は,パ
ルスの形(面積を含む。),又はこれに対応するスペク
トルを用いて表すことができる。
nominal shock
pulse ;
nominal pulse
3.17
衝撃パルスの公
称値
許容偏差を含むピーク値,継続時間などの指定値。
nominal value of a
shock pulse
3.18
衝撃パルス作用
時間
運動が最大値に対してある指定された割合を超えた瞬間から,それ
以下になる瞬間までの時間幅。
備考1. この定義は,単純な形のパルスに限定される。
2. 測定されたパルスではこの“指定された割合”は,通
常1/10を用い,理想衝撃パルスではゼロを用いる。
duration of shock
pulse
3.19
立上がり時間,
ライズタイム
パルスの値が最大値に対して指定された小さな割合から,ある指定
された大きな割合まで上昇するのに必要な時間幅。
備考 実測衝撃パルスでは,“指定された小さな割合”は,一般
的に1/10を用い,“指定された大きな割合”は9/10を用
いる。理想パルスでは,0と1.0を用いる。
rise time ;
pulse rise time
21
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
3.20
下降時間
パルスの値が最大値のある指定された大きな割合から,指定された
小さな割合まで低下するのに要する時間幅。
備考 3.19の備考を参照。
pulse drop-off
time ;
pulse decay time
3.21
爆風,
水中爆発
大気又は水中における爆発,若しくは,その他の圧力の突然の変化
によって生じる圧力パルス及びこれに付随する空気又は水の運動。
blast ;
air blast ;
underwater blast
3.22
衝撃波
ある媒体又は構造体を衝撃が伝搬するのに伴う衝撃時刻歴(変位,
圧力又はその他の変数)。
備考 液体及び気体中では,衝撃波は通常,圧力が比較的大き
な値に突然上昇する波先によって特徴づけられる。
shock wave
3.23
衝撃試験機
系に制御された再現性のある機械衝撃を与える装置。
shock testing
machine ;
shock machine
3.24
衝撃応答スペク
トル
a) ある衝撃に対する特定の一連の系の応答を,その系の固有振動
数の関数として表現したもの。
b) 機械衝撃の分野で用いられているように,ある与えられた衝撃
に対する線形一自由度系の最大応答(変位,速度又は加速度)
を,その固有振動数の関数として近似的に表したもの。
備考1. “衝撃応答スペクトル”は,総称的な用語である。例
えば,加速度,速度,変位衝撃応答スペクトルなどの
修飾語を追加し,その意味を具体的にする必要がある。
2. 系の減衰のタイプ及び減衰量が与えられていない場合
は,それらをゼロとみなしてよい。特に指示のないと
きは,応答は符号又は最大となる時間にかかわらず絶
対値の最大値を意味する。これはしばしば最大衝撃応
答スペクトルと呼ばれる。もし他の種類の衝撃応答ス
ペクトルの場合は,その旨明記する必要がある。
3. 衝撃応答スペクトルの概念は,スペクトルの定義と完
全には整合していないことに注意すべきである(1.56参
照)。
4. 構造物上に設置された質量の小さい付加構造物の地震
応答倍率を求めるため,あらかじめ各床面に伝達され
る地震波を想定し,これによって作成された,付加構
造物の応答スペクトルを床応答スペクトル (floor
response spectrum) という。
shock response
spectrum
d) 衝撃・振動計測用変換器
番号
用語
定義
対応英語(参考)
4.1
変換器
a) ある系からエネルギを受け取り,同種又は異種のエネルギとし
て他の系に供給し,入力エネルギの所望の特性が出力側に現れ
るように設計された装置。
b) 信号又は量を,それに対応する同種若しくは異種の信号又は量
に変換するための器具。
transducer
22
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
4.2
機械−電気式ピ
ックアツプ
機械系からのエネルギ(ひずみ,力,運動など)によって作動し,
電気系にエネルギを供給するか,又はその逆を行う変換器。
備考 振動及び衝撃で用いられる変換器の主なタイプは,次の
ようなものがある。
a) 圧電型加速度計
b) 圧電抵抗型加速度計
c) ひずみゲージ式加速度計
d) 可変抵抗変換器
e) 静電容量変換器
f) ひずみゲージ
g) 可変リアクタンス変換器
h) 磁わい(歪)変換器
i) 渦電流型変換器
j) 動電型変換器
k) 誘導変換器
l) 電子式変換器
m) レーザドップラ速度振動計
electromechanical
pick-up
4.3
サイズモ式ピッ
クアップ
サイズモ系からなり,系の質量と基礎との間の相対運動によって電
気的出力を生じる変換器。
備考 加速度ピックアップは,サイズモ系に現れる固有振動数
より低い振動数範囲で作動する。速度及び変位ピックア
ップは,サイズモ系の固有振動数より高い振動数範囲で
作動する。
seismic pick-up
4.4
線形変換器
一定振動数及び振幅の範囲内で出力と入力とが比例する変換器。
linear
transducer
4.5
非可逆変換器
出力側に信号を加えることによって,入力側に信号を加えたときの
ような動作を行わせることが不可能な変換器。
unilateral transducer
4.6
可逆変換器
入出力端の間で,どちらの方向にも伝送できる変換器。
備考 可逆変換器は,通常相反性の原理を満たす。
bilateral transducer
4.7
変換素子
入力の励振によって駆動され出力信号を発生する変換器の要素。
sensing element
4.8
並進変換器
並進運動の特性を測定するように設計された変換器。
備考 修飾語“並進”は,このタイプの変換器を回転運動を測
定するタイプと区別することが必要な場合に限り用いら
れる。
rectilinear
transducer
4.9
角変換器
回転運動の特性を測定するように設計された変換器。
angular transducer
4.10
加速度計,
加速度ピックア
ップ
入力加速度をそれに比例する出力(通常電気的)に変換するピック
アップ。
accelerometer ;
acceleration pick-up
4.11
速度計
入力速度をそれに比例する出力(通常電気的)に変換するピックア
ップ。
velocity pick-up
4.12
変位計
入力変位をそれに比例する出力(通常電気的)に変換するピックア
ップ。
displacement
pick-up
4.13
振動記録計
電気的・機械的に作動し,振動波形のオシログラム記録が可能な測
定器。
vibrograph
4.14
振動指示計
振動の大きさの何らかの尺度,例えばピーク速度,rms加速度など
を目盛上に表示できる装置。
vibrometer
4.15
(変換器の)感度 ある入力量に対する出力量の比。
備考 変換器の感度は,一般に正弦波励振によって決定される。
sensitivity
(of a transducer)
4.16
(変換器の)校正
係数
ある一定振動数範囲内の平均の感度[感度(4.15)参照]。
calibration factor (of
a transducer)

23
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
4.17
(並進変換器の)
受感軸
並進変換器が最大の感度をもつ方向。
sensitive axis (of a
rectilinear
transducer)
4.18
(変換器の)横感
軸
受感軸と直交する方向。
transverse axis (of
a transducer)
4.19
(並進変換器の)
横感度
受感軸と直交する方向での励振に対する感度。
備考 横感度は,通常選んだ軸の方向の関数である。
transverse
sensitivity (of a
rectilinear
transducer) ;
cross-sensitivity
4.20
(並進変換器の)
横感度
変換器の横感度の受感軸方向の感度に対する比。
transverse
sensitivity ratio
(of a rectilinear
transducer) ;
cross-sensitivity
ratio
4.21
変換器位相変化
正弦波励振での変換器出力と入力との間の位相変化。
transducer phase
shift
4.22
変換器ひずみ
変換器の出力が入力に比例しないときに起こるひずみ。
transducer
distortion
4.23
(変換器の)増幅
ひずみ
ある振動数で変換器の入力に対する出力の比が入力振幅によって
変わるときに起こるひずみ。
amplitude distortion
(of a transducer)
4.24
周波数ひずみ,
周波数応答
ある振動数範囲内で,ある励振振幅に対する変換器の増幅感度が,
その振動数範囲にわたって一定でないときに起こるひずみ又は応
答。
frequency
distortion ;
frequency response
4.25
位相ひずみ
ある変換器の出力と入力との間の位相角が振動数に対して線形関
数でないときに起こるひずみ。
phase distortion

24
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
e) データ処理
番号
用語
定義
対応英語(参考)
5.1
パワースペクト
ル密度,
自己スペクトル
密度,
自己スペクトル
ξ (t) なる量のパワースペクトル密度G (f ) は,単位帯域幅ごとに中
心周波数fの狭帯域フィルタを通過するξ (t) の二乗平均値で,帯域
幅→0,平均時間→∞の極限値とする。
備考1. パワースペクトル密度は,次の式で表される。
∫
∞
→→
=
T
TB
dt
B
t
f
BT
f
G
0
2
0
)
,,
(
1
lim
)
(
ξ
ここに,
ξ 2(f, t, B) は,中心周波数f,帯域幅Bの狭帯域フィ
ルタを通過するξ(t) の二乗,Tは平均時間。
フーリエ変換を用いるとG(f) は,次の式で表され
る。
2)
,
(
2
lim
)
(
T
f
F
T
f
G
T
∞
→
=
ここに,
0
≥
f
;
∫
−
=
T
t
f
i
dt
e
t
T
f
F
0
2
)(
)
,
(
π
ξ
2. パワースペクトル密度は,時刻歴で表される物理量の
種類に関係なく用いられる一般用語である。例えば,
加速度スペクトルを表現する場合,単にパワースペク
トル密度というのでなく加速度パワースペクトル密度
又は加速度スペクトル密度という用語が用いられる。
3. 定常過程の場合,パワースペクトル密度は,自己相関
関数[(5.36)参照]のフーリエ変換(A.20参照)の2
倍として,次の式にように表される。
∫
∫
∞
∞
∞
−
−
≥
=
=
0
2
)0
(
)
2
cos(
)
(
4
)
(
2
)
(
f
dt
t
f
t
R
dt
e
t
R
f
G
t
f
i
π
π
power spectral
density ;
auto-spectral
density ;
auto-spectrum
5.2
パワースペクト
ル
時間的又は空間的に変動する量の二乗平均値を振動数成分の分布
として表したもの。
power spectrum

25
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
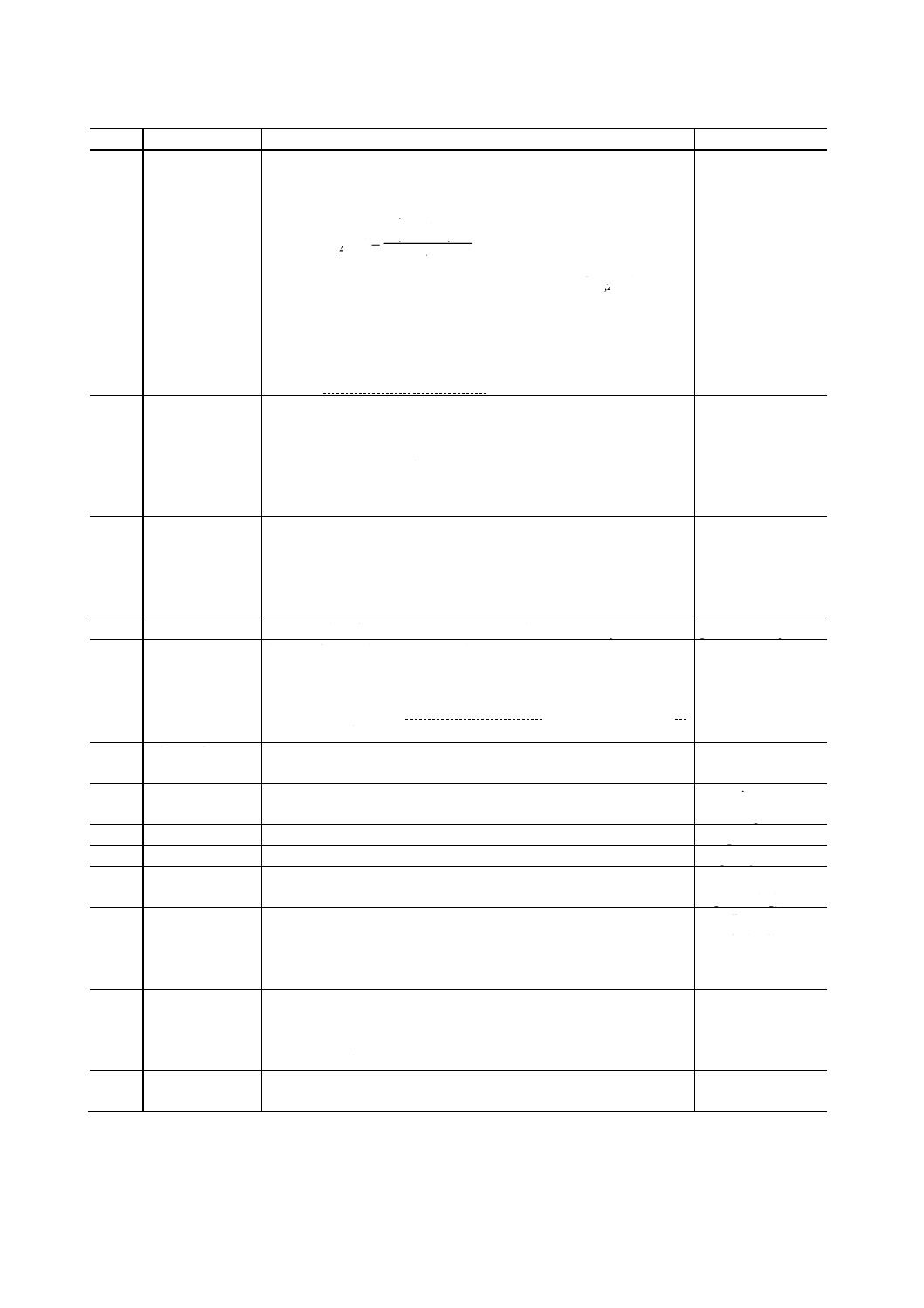
5.3
クロススペクト
ル密度,
クロススペクト
ル
ξ1(t),ξ2(t)なる二つの量の,周波数fに関する複素関数で,次の式で
表される。
G1, 2(f ) =C1, 2(f ) −iQ1, 2(f )
ここに,
実数部C1, 2(f );同時スペクトル密度関数又はコ・スペクトルと呼ば
れる。周波数fの単位帯域幅におけるξ1(t) とξ2(t) との積の適切な帯
域幅B及び平均時間Tについての平均値として表される。すなわち,
実数部C1,2(f ) は,次の式で表される。
∫
∞
→→
=
T
TB
dt
B
t
f
B
t
f
f
C
0
2
1
0
2,1
)
,,
(
)
,,
(
lim
)
(
ξ
ξ
ここに,
ξ1(f, t, B),ξ2(f, t, B) は,それぞれξ1(t),ξ2(t) のうち中心周波数f,帯
域幅Bの同一の狭帯域フィルタを通過する成分。
虚数部Q1, 2(f ):クォドラスペクトル密度関数又はクォドスペクトラ
ムと呼ばれる。ξ2(t) が位相を90度ずらせたものである点を除いて,
これも,周波数fの単位帯域幅におけるξ1(t) とξ2(t) との積の平均と
して表される。すなわち,虚数部Q1, 2(f ) は,次の式で示される。
∫
∞
→→
=
dt
B
t
f
B
t
f
BT
f
Q
TB
)
,,
(
)
,,
(
1
lim
)
(
02
1
0
2,1
ξ
ξ
ここに,
ξ1(f, t, B) は,ξ1(t) のうち中心周波数f,帯域幅Bの狭帯域フィルタ
を通過する成分。
また,
02
ξ(f, t, B) は,ξ2(t) のうち中心周波数f,帯域幅Bの狭帯域
フィルタを通過する成分ξ2(f, t, B) から90度の位相ずれがあるもの。
備考1. G(f ) の定義については,パワースペクトル密度(5.1)の
注釈を参照。
2. C1, 2(f ),Q1, 2(f ) は,フーリエ変換を用いて次の式で表
される。
[
]
[
])
,
(
)
,
(
Im
2
lim
)
(
)
,
(
)
,
(
Re
2
lim
)
(
2
*1
0
2,1
2
*1
0
2,1
T
f
F
T
f
F
T
f
Q
T
f
F
T
f
F
T
f
C
T
T
=
=
→
→
ここに,
0
≥
f
;
∫
=
T
t
f
i
dt
e
t
T
f
F
0
2
1
*1
)
(
)
,
(
π
ξ
;
∫
−
=
T
t
f
i
dt
e
t
T
f
F
0
2
2
*2
)
(
)
,
(
π
ξ
;
Re […] 及びIm […] は,それぞれ括弧内の関数の実数部及び
虚数部を示す。
3. 有限フーリエ変換を用いて,G1, 2(f ) は,次の式で表さ
れる。
[
])
(
)
,
(
2
lim
)
(
2
2
*1
2,1
T
f
F
T
f
F
T
f
G
T
∞
→
=
4. 相互相関関数 (R1, 2) のフーリエ変換を用いて,G1, 2は,
次の式で表される。
dt
e
t
R
f
G
t
f
i
∫∞∞
−
−
=
π
2
2,1
2.1
)
(
2
)
(
cross-spectral
density ;
cross-spectrum
26
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
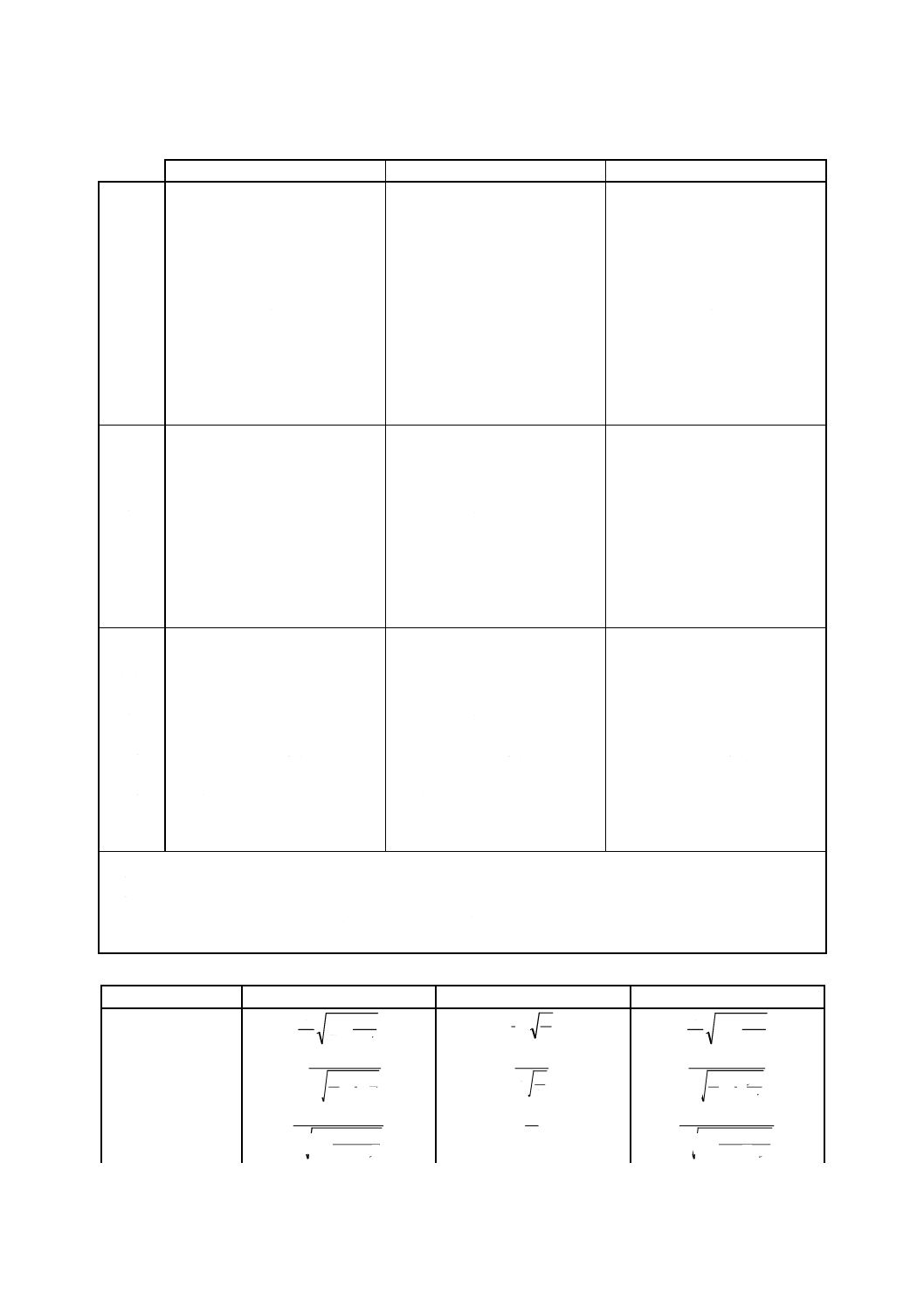
5.4
コヒーレンス関
数
ξ1(t),ξ2(t) のクロススペクトル密度関数の絶対値の二乗と,ξ1(t) 及
びξ2(t) 各々のスペクトル密度関数の積との比。コヒーレンス関数
は,次の式で表される。
)
(
)
(
)
(
)
(
2
1
2
2,1
22,1
f
G
f
G
f
G
f =
γ
任意の周波数fにおいてコヒーレンス関数は,
1
)
(
0
22,1
≤
≤
f
γ
を満
足する。
備考1. G1, 2(f ),G1(f ) 及びG2(f ) の定義は,パワースペクトル
密度(5.1)及びクロススペクトル密度(5.3)の注釈を参
照。
2. 関連度関数ともいう。
coherence function
5.5
統計的な自由度
ある量を推定する際の独立変数の数。
備考1. 自由度の数は,ある量を推定する際の統計的な正確さ
を決定する。
2. ランダムデータを解析する際に,時間平均を行う場合,
統計的な自由度の有効数nは,フィルタの有効帯域幅
をB,平均時間をTとして,n=2BTとなる。
statistical degrees of
freedom
5.6
(1自由度系に
対する)等価(定
常)加速度
動的励振において,励振によるものと同じ最大相対変位を生じるよ
うな,定常的に加えられる加速度。
equivalent (static)
acceleration (for a
single
degree-of-freedom
system)
5.7
疑似速度
不減衰1自由度系の最大相対変位と,固有角振動数2π f nとの積。 pseudovelocity
5.8
折り返し誤差,
エイリアシング
誤差
信号のデジタル解析において,信号の最大周波数がサンプリング周
波数(5.15参照)の1/2を超えることによって生じる誤差。
備考 サンプリング周波数の半分を折りたたみ周波数 (folding
frequency) 又はナイキスト周波数 (Nyquist frequency) と
いう。
aliasing error
5.9
データブロック
一つの記録時間において,デジタルコンピュータのメモリに記録さ
れたデータ群。
data block
5.10
ブロックサイズ,
ブロック長
ブロック内のレコード数,ワード数又は文字数。
block size ;
block length
5.11
標本値群
アナログ信号を変換した結果得られるデジタル値。
data points
5.12
周波数分解能
記録時間の逆数(5.13参照)。
frequency resolution
5.13
記録時間
データブロックの記録時間。
total time (in data
processing)
5.14
サンプリング標
本化
規則的又は不規則に離散化された変数に対する関数値を抽出する
こと。
備考 特定の分野,例えば統計の分野などではこの用語が他の
意味で使われることがある。
sampling ;
sample (verb)
5.15
サンプリング周
波数
1秒間に取得する標本値の数。
備考 与えられた信号をエリアシング誤差なく取得できるサン
プリング周波数は,信号が含む最大の周波数の2倍以上
である。
sampling frequency
5.16
サンプリング周
期
二つのサンプリング間の時間間隔。
sampling interval

27
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
5.17
平滑化,スムージ
ング
データブロックの移動平均。
備考 例えば,三つの標本値の平滑化は,次の関係で特徴づけ
られる。
3/)
(
1
1
+
−
+
+
=
k
k
k
k
x
x
x
x
平滑化は,時間領域,周波数領域及びヒストグラムにおいて
行うことができる。
smoothing
5.18
トランケーショ
ン
信号を正確に定義するには短すぎる記録長さを適用すること。
truncation (in
vibration
analysis)
5.19
データ処理
原情報を電気的又は機械的に処理することを意味する一般用語。
data processing
5.20
データの前処理
原情報に変化をもたらさないデータ処理。例えば,カードソーティ
ング,作表,保管,検索,座標変換など。
data handling
5.21
データの変換
原情報に変化をもたらすデータ処理。例えば,アナログからデジタ
ルへの変換又はその逆,関数の反転,平均化など。
data reduction
5.22
実時間解析,
リアルタイム解
析
パラメータを実時間で解析する信号処理法。
real-time analysis
5.23
高速フーリエ変
換 (FFT)
フーリエ変換を行う際,複素数の演算時間(掛け算及び足し算)を
大幅に低減させる処理法。
Fast Fourier
Transform
(FFT)
5.24
量子化
サンプリングしたアナログ信号を有限個のレベルに対応させデジ
タル信号に変換すること。
quantizing
5.25
ウィンドウ関数,
窓関数
記録時間内で現象が終了しない又は周期的とならない信号のデー
タを処理する際の誤差を低減するために用いられる打切り関数。
備考 記録時間の前後で信号が不連続となるために生じるスペ
クトルの誤差を漏れ誤差又はリーケージエラー (leakage
error) という。
window function
5.26
確定的な振動
ある時刻における瞬間的な値が,それまでの時刻歴から予測できる
ような振動。
備考 数学的な表現では,t > t0のf (t) がt<t0のf (t) から予測で
きる場合には,f (t) は,確定的であるという。
deterministic
vibration
5.27
時刻歴
ある量の時間の関数としての表現。
time history
5.28
定常過程
統計的な性質が時間の移動に対して不変であるような時刻歴の母
集団。
stationary process
5.29
強い自己定常
標本値を有限の時間にわたって平均することによって求まるすべ
ての統計的な性質が,サンプリングした時刻に無関係であるような
ランダム信号を記述するのに用いられる用語。
strongly
self-stationary
5.30
弱い自己定常
標本値を有限の時間にわたって平均することによって求める平均
値及び自己相関関数が,サンプリングした時刻に無関係であるよう
なランダム信号を記述するのに用いられる用語。
weakly
self-stationary
5.31
エルゴード過程
すべての時刻歴に対して時間平均が等しくなるような時刻歴の母
集団からなる定常過程。
備考 任意の時刻歴の時間平均は,母集団にわたっての統計的
平均に等しいことになる。
ergodic process
5.32
不規則過程,
確率過程
統計的性質によって特徴づけることができる時間関数の集合(母集
団)。
random process ;
stochastic process
5.33
母集団,集合
信号の集合。
ensemble ;
set

28
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
5.34
自己相関関数
x (t) なる量についての,時刻tにおける値と時刻t+rにおける値と
の積の平均値。
備考1. 自己相関関数は,数学的に次の式で表される。
[
][
]
∫
+
=
+
=
T
dt
t
x
t
x
T
t
x
t
x
R
0
)
(
)
(
1
)
(
)
(
)
(
τ
τ
τ
2. 常に継続するような定常不規則量x(t) では,Tは無限
大となる。すなわち,
∫
+
=
∞
→
T
T
dt
t
x
t
x
T
R
0
)
(
)
(
1
lim
)
(
τ
τ
実際には,Tは有限で,備考1.に示される式は,Tの
減少に従って増大するような,ある統計的な不確実性
を伴う評価を与える。
autocorrelation
function
5.35
相互相関関数
二つの量x (t) とy (t) についての,時刻tにおける一方の関数値と,
時刻t+τにおけるもう一方の関数値との積の平均値。
備考1. 相互相関関数は,数学的に次の式で表される。
[
][
]
∫
+
=
+
=
T
y
x
dt
t
y
t
x
T
t
y
t
x
R
0
,
)
(
)
(
1
)
(
)
(
)
(
τ
τ
τ
2. 自己相関関数 (5.34) の備考2.を参照。
cross-correlation
function
5.36
自己相関係数
x (t) なる量についての自己相関関数の二乗平均値に対する比。
備考 自己相関関数は,数学的に次の式で表される。
[
][
]
)
(
)
(
)(
)0(
)
(
)
(
2t
x
t
x
t
x
R
R
τ
τ
τ
ρ
+
=
=
autocorrelation
coefficient
5.37
相互相関係数
二つの量x (t) とy (t) についての,相互相関関数とそれぞれの量の
二乗平均値の積の平方根との比。
備考 これは,数学的に次の式で表される。
)0(
)0(
)
(
)
(
,
,
y
x
y
x
y
x
R
R
R
τ
τ
ρ
=
ここに,
)
(
)0(
2t
x
Rx
=
;
)
(
)0(
2t
y
Rx
=
;
)
(
,τ
y
x
R
は,5.35の定義による。
任意の時間遅れτについて相互相関係数は,次の式を満た
す。
1
)
(
1
,
≤
≤
−
τ
ρy
x
cross-correlation
coefficient
5.38
(指定された帯
域通過フィルタ
の)有効帯域幅
通過帯域の応答が平坦で,二つのフィルタが同じ白色雑音入力信号
を受けたときに指定されたフィルタと同じパワーを伝達するよう
な理想的なフィルタの帯域幅。
備考 有効帯域幅は,白色雑音励振に対するフィルタの二乗平
均応答を励振スペクトル密度と最大送信 (maximum
transmission) の二乗との積で除することによって評価で
きる。
effective bandwidth
(of a specified
band-pass filter)
5.39
有効平均時間
理想的な積分器が,使用されている平均化器と同じパラメータの評
価値を与えるのに必要な時間。
effective averaging
time
5.40
信頼区間
測定データが正規分布の場合,ある値が与えられた確率で存在し得
る範囲。
confidence interval
29
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
付表1 様々な種類の計測された出力/入力比の等価な定義
変位で表現された運動
速度で表現された運動
加速度で表現された運動
用語
動コンプライアンス(1)
モビリティ(2)
アクセレランス(3)
記号
xi/Fj
Yij=vi/Fj
ai/Fj
単位
m/N
m/ (N・S)
m/ (N・s2) =kg−1
境界条件
Fk=0 ; k≠j
Fk=0 ; k≠j
Fk=0 ; k≠j
参照図番
3
1
2
備考
境界条件を実験的に達成すること
は容易。
境界条件を実験的に達成すること
は容易。
境界条件を実験的に達成すること
は容易。
用語
動剛性
固定インピーダンス
固定有効質量
記号
Fi/xj
Zij=Fi/vj
Fi/aj
単位
N/m
(N・s) /m
(N・s2) /m=kg
xk=0 ; k≠j
vk=0 ; k≠j
ak=0 ; k≠j
備考
境界条件を実験的に達成すること
は非常に困難か不可能。
境界条件を実験的に達成すること
は非常に困難か不可能。
境界条件を実験的に達成すること
は非常に困難か不可能。
用語
自由動剛性
自由インピーダンス
有効質量
(自由有効質量)
記号
Fj/xi
Fj/vi=1/Yij
Fj/ai
単位
N/m
(N・s) /m
(N・s2) /m=kg
境界条件
Fk=0 ; k≠j
Fk=0 ; k≠j
Fk=0 ; k≠j
備考
境界条件を達成することは容易で
あるが,系のモデル化に結果を用
いる際は十分注意を払う。
境界条件を達成することは容易で
あるが,系のモデル化に結果を用
いる際は十分注意を払う。
境界条件を達成することは容易で
あるが,系のモデル化に結果を用
いる際は十分注意を払う。
注(1) “動コンプライアンス”は,“レセプタンス”と呼ばれることがある。
(2) “モビリティ”はときに“メカニカルアドミッタンス”と呼ばれることもある。付図1参照。
(3) “アクセレランス”は幾つかの出版物では“イナータンス”と呼ばれることがあるが望ましくない。イナータ
ンスは標準的な用語ではなく,普通に使われている音響イナータンスと矛盾し,また,“イナータンス”が本
来もっている意味とは逆なので好ましくない。
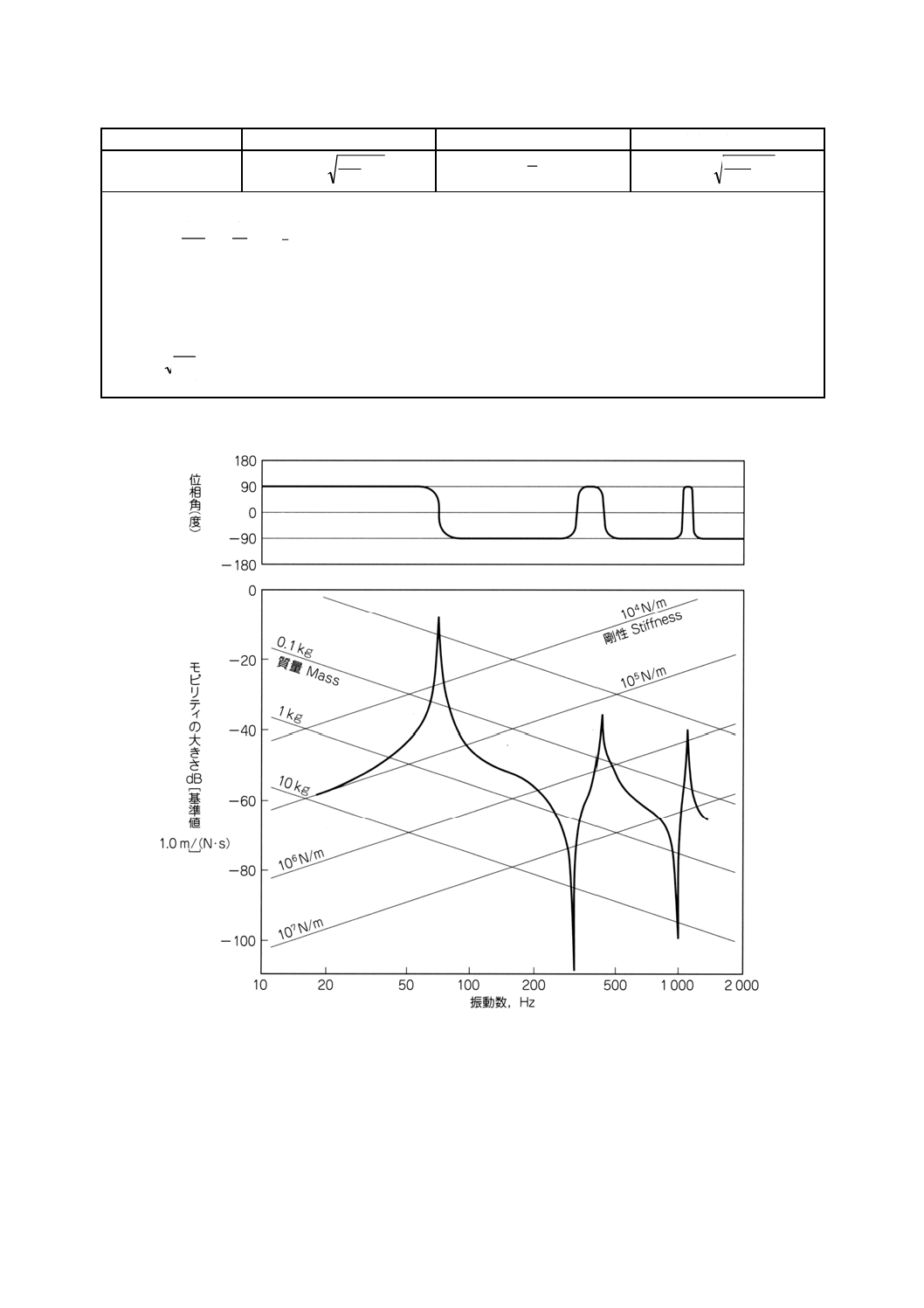
付表2 共振関係
特性
変位共振
速度共振
減衰固有振動数
振動数,Hz
2
2
2
2
1
m
c
m
k−
π
m
k
π
2
1
2
2
4
2
1
m
c
m
k−
π
変位振幅
2
2
4m
c
m
k
c
A
−
m
k
c
A
2
2
16
3
m
c
m
k
c
A
−
速度振幅
2
2
2
4
1
c
mk
c
c
A
−
+
c
A
2
2
4
16
1
c
mk
c
c
A
−
+
30
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
特性
変位共振
速度共振
減衰固有振動数
作用力に関する変
位の位相
2
tan
2
4
1
−
−
c
mk
2
π
4
tan
2
16
1
−
−
c
mk
備考1. 線形1自由度系の場合,運動方程式は次の式で表される。
t
A
kx
dt
dx
c
dt
x
d
m
ω
cos
2
2
=
+
+
ここに,
xは,変位
ωは,角振動数
m,c及びkは,定数
上の式の定数によって表される種々の共振の特性は,表に示すとおりである。
2.
mkに比べてcの値が小さいときには,三つの場合で差異は小さい。速度共振の振動数は,(系の)不減
衰固有振動数に等しい。電気共振では他の記号が使われる。
付図1 モビリティ
31
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
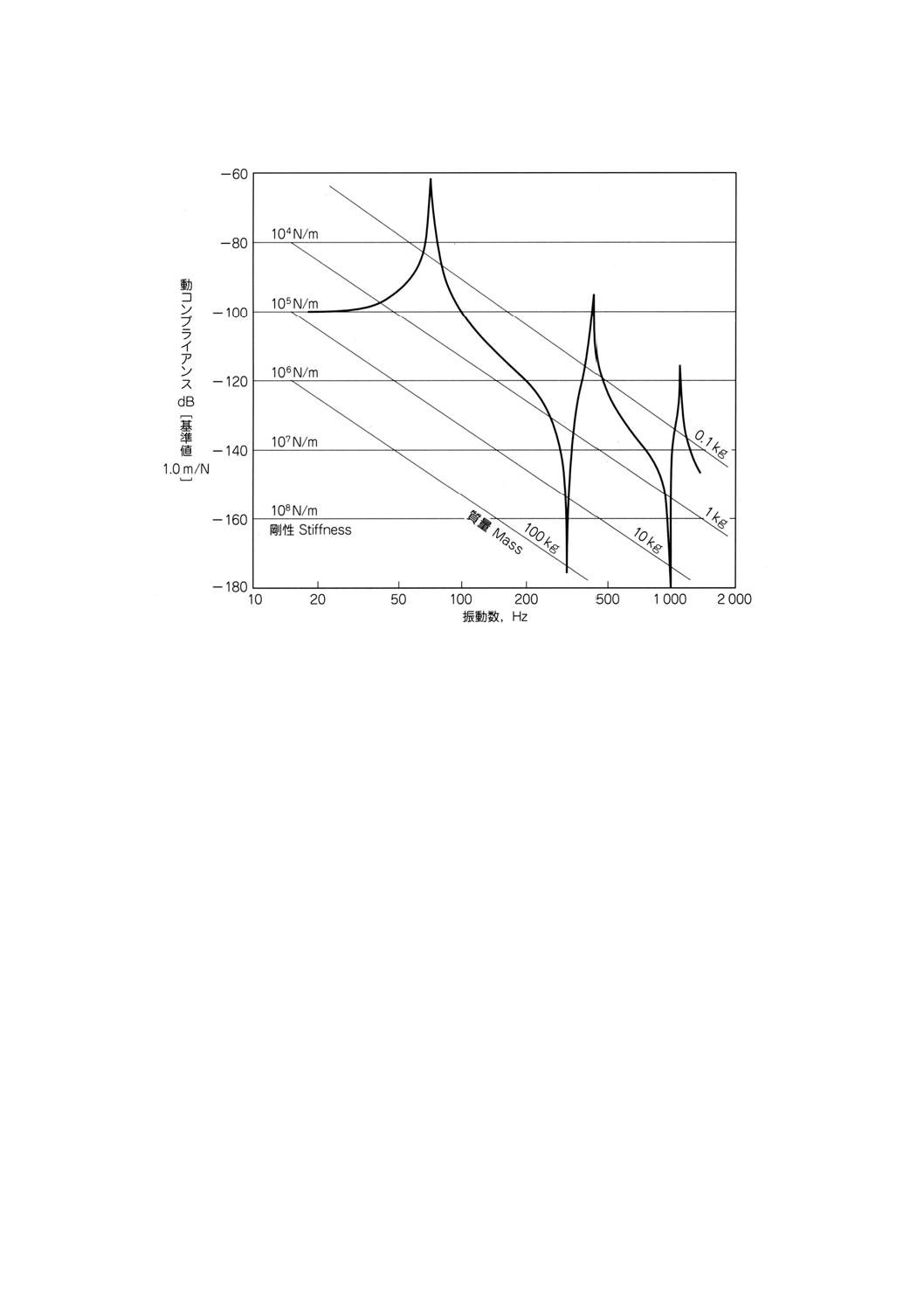
付図2 付図1のモビリティに対応するアクセレランス
32
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
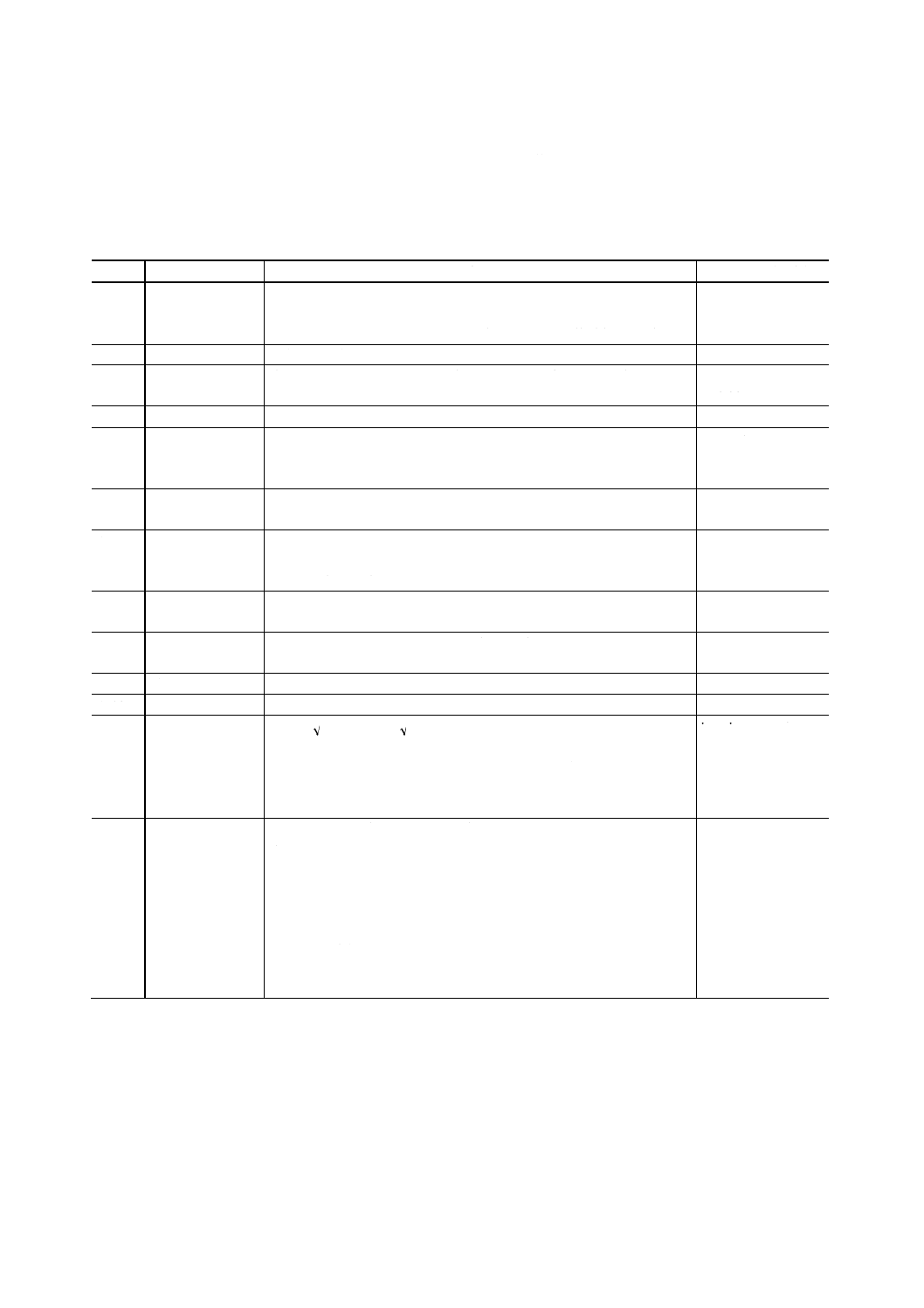
付図3 付図1のモビリティに対応する動コンプライアンス
33
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A(参考) 数学的用語
この附属書に含まれる定義は,振動及び衝撃の分野では必須の事項である。しかしながら,他の分野に
も関係するため,これらの定義は,規定の一部ではない。
番号
用語
定義
対応英語(参考)
A.1
基準値
要素又は系のある点における量で,この点から,又はこの点を基準
として,他の同種の量が測定される。もし,同じ基準値が系全体に
わたって,共通に用いられるならば,それは共通基準値と呼ばれる。
reference
A.2
変数
(有限又は無限の)継続する値をとることができる量。
variable
A.3
独立変数
時間のように,その値が他の変数によって決定されない変数。
independent
variable
A.4
従属変数
その値が,独立変数及びパラメータとの値によって決定される変数。 dependent variable
A.5
パラメータ
数学の分野では,システムの特性を記述する量をいう。パラメータ
は,方程式中の変数であったり,又は異なる値を与えることができ
る定数であったりする。
parameter
A.6
関数
一つの従属変数(関数の値)と,一つ又はそれ以上の独立変数及び
定数との関係を表現するもの。例えば,y,z及びtの関係。
function
A.7
比例
ある変数の値と他の変数の値との比が一定であるとき,正比例であ
るという。また,ある変数の逆数と他の変数との比が一定であると
き,反比例という。
proportional
A.8
線形関数
ある変数の変化が,他のある変数の変化と正比例の関係があるとき,
前者の変数は,後者の変数の線形関数であるという。
linear function
A.9
一般座標
互いに独立で,必要十分に系の形態を記述することができる量。
generalized
coordinates
A.10
ベクトル
大きさと方向とによって完全に決定できる量。
vector
A.11
スカラー
大きさによって完全に決定できる量。
scalar
A.12
虚数
実数と
1
−との積。
1
−は,一般にj又iはで表される。
備考1. この平方根は,正の値を意味している。
2. ベクトル又は幾何学的な解釈では,複素数とiとの積は,
原点に関して半時計回りに90°回転し,−iとの積は,
時計回りに90°回転する。
imaginary number
A.13
複素数
a) 実数部及び虚数部の両方を含む数。
b) 2次元の座標系において原点からのベクトルを表す数。
備考 もし,複素数がz=x+iyで与えられているとき,虚数部
は,iyで,xとyは,二つの直交するxとiy軸上のベクト
ル成分を表している。ベクトルの大きさ(複素数の絶対値)
は,Z= (x2+y2)1/2であり,ベクトルの方向(複素数の偏
角)は,φ=arctany/xである。
複素数は,次のようにも表される。
z=Z (cosφ+i sinφ) =Zeiφ
complex number
34
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
A.14
複素振幅
大きさが振動の振幅,角度が位相を表す複素数。例えば,調和振動Y
(t) =Y0cos (ωt+φ) を複素数で表示する場合,次のように表される。
Y (t) =Re(Y1e i ω t)
ここに,
Y1は,複素振幅と呼ばれる複素量で,その大きさはY0に等しく,そ
の偏角は位相角φに等しい。すなわち,
∠Y1=φ
Reは,実数部を意味するが一般には周知のものとして省略される。
Y1は,次のように表される。
Y0cosφ+iY0sinφ
ここに,
1
−
=
i
である。
Y1は,
Y1=Y0e i Φ
とも書ける。
phasor
A.15
(複素数の)偏角 複素数(ベクトル)の方向を決める角度[複素数(A.13)の備考参照]。 argument (of a
complex number)
A.16
(複素数の)大き
さ
複素数の絶対値[複素数(A.13)の備考参照]。
modulus (of a
complex number)
A.17
絶対値
a) 実数の絶対値は,正負のいずれかの符号をもつ実数と同じ数値
をもつ正の数。
b) 複素数の絶対値は,実数部と虚数部の二乗の和の正の平方根[複
素数(A.13)の備考参照]。
absolute value

35
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
A.18
フーリエ級数
互いに調和的な関係をもつ離散的な周波数成分によって,周期的な
関数の値を表す級数。
備考1. 非周期的な関数は,その関数が定義されている間隔を,
級数の基本周期とみなすならば,フーリエ級数で表すこ
とができる。
2. f (t) のフーリエ級数への展開は,次のように与えられ
る。
∑
∞
=
+
+
=
1
)
sin
cos
(
)
(
n
n
n
o
t
n
b
t
n
a
a
t
f
ω
ω
f (t) の複素フーリエ級数への展開は,次のように与えら
れる。
∑
∞
=
=
1
)
(
n
t
in
ne
c
t
f
ω
ここに,
anとbnは,フーリエ係数
cnは,複素フーリエ係数
wは,角振動数で2π/Tに等しい。ここに,Tは,基
本周期,nは,整数値だけが割り当てられる。
フーリエ係数の値は,
∫
=
T
dt
t
f
T
a
0
0
)
(
1
∫
=
T
n
tdt
n
t
f
T
a
0
cos
)
(
2
ω
(n=1, 2, 3, …)
∫
=
T
n
tdt
n
t
f
T
b
0
sin
)
(
2
ω
(n=1, 2, 3, …)
∫
−
=
T
t
n
i
n
dt
e
t
f
T
c
0
)
(
1
ω
(n=0, ±1, ±2, ±3, …)
これは,次のように示される。
2
0
0
2
n
n
n
n
ib
a
n
ib
a
n
c
a
c
c
+
−
−
+
=
=
=
,
,
各々のフーリエ離散周波数に対する振幅は,
2
2
n
n
n
b
a
A
+
=
フーリエ位相角は,
)
arctan(nn
a
b
n=
φ
Fourier series
A.19
フーリエ係数
フーリエ級数の離散調和成分の係数[フーリエ級数(A.18)備考2参
照]。
Fourier coefficients
36
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
A.20
フーリエ変換,
フーリエ積分方
程式
a) フーリエ変換:非周期的な時間関数(又は距離のような他の変
数に関する関数)を周波数の連続関数(又は波数のような他の
変数に関する関数)に変換すること。
b) 逆フーリエ変換:周波数に関する連続関数(又は波数のような
他の変数に関する関数)を対応する時間関数(又は距離のよう
な他の変数に関する関数)に変換すること。
備考 もしf (t) が時間に関する非周期関数であるとき,複素フ
ーリエ変換は,
dt
e
t
f
F
t
i
∫+∞∞
−
−
=
ω
ω
)(
)
(
時間関数f (t) は,F (w) から次のような積分(逆フーリエ変換)
によって得られる。
∫+∞∞
−
=
ω
ω
ω
π
d
e
F
t
f
t
i
)
(
)
(
2
1
(1/2πを使っているが,これは幾つかある一対の変換公式のう
ちの一つの表し方である。他の公式では,1/2πが,逆変換では
なく,正変換のほうに現れることもあれば,両方に
π
2
/1
が
現れることもある。)
F (ω) は,一般に複素数なので,実数部と虚数部とに分けて書
くことができる。
F (ω) =Re [F (ω)] +i Im [F (ω)]
ここに,
[
]∫+∞∞
−
=
tdt
t
f
F
ω
ω
cos
)
(
)
(
Re
[
]∫+∞∞
−
=
tdt
t
f
F
ω
ω
sin
)
(
)
(
Im
一方,フーリエ変換は,絶対値と位相角とで定義できる。
)
(ω
F
と
)
(ω
φ
は,それぞれ
)
(
)
(
)
(
ω
φ
ω
ω
ie
F
F
=
ここに,
[
]
[
])
(
Im
)
(
Re
)
(
2
2
ω
ω
ω
F
F
F
+
=
[
]
[
]
=
)
(
Re
)
(
Im
arctan
)
(
ω
ω
ω
φ
F
F
Fourier transform ;
Fourier integral
equation
A.21
フーリエスペク
トル
フーリエ係数を周波数の関数として表したもの。
備考 関数を定義するには二つのフーリエスペクトルが必要で
ある。すなわち,フーリエ係数のcos関数成分の係数とsin
関数の係数である。これらをそれぞれフーリエ変換に対応
させて実数部と虚数部として表す場合もある。また,振幅
の絶対値のスペクトルとフーリエ位相角のスペクトルと
して表すこともできる[フーリエ級数(A.18)の備考及びフ
ーリエ変換(A.20)の備考参照]。
Fourier spectrum
A.22
フーリエ位相ス
ペクトル,
位相スペクトル
周波数の関数として,フーリエ位相角を表したもの[フーリエ級数
(A.18)の備考及びフーリエ(A.20)備考参照]。
Fourier phase
spectrum ;
phase spectrum
A.23
線スペクトル
スペクトルの成分が,一つ又はそれ以上の離散的な周波数でしか生
じていないようなスペクトル。
line spectrum
A.24
連続スペクトル
スペクトルの成分が,ある周波数範囲にわたって,連続的に分布し
ているスペクトル。
continuous
spectrum

37
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
A.25
直交関数
0≤x≤Xの範囲で定義されている関数群φn (x) が,次のような関係が
あるならばこの関数群は,直交しているという。
∫
≠
=
x
m
n
m
n
dx
0
*
0,
φ
φ
ここに,
*m
φは,m
φの共役複素数である。
orthogonal
functions
A.26
確定関数
それ以前の挙動がわかっていれば,値を予測することができる関数。 deterministic
function
A.27
重ね合わせの原
理
複数の励振に対する系の応答は,一つ一つを足し合わせて求めるこ
とができるという原理。重ね合わせの原理は,線形システムに対し
てだけ有効である。
superposition
principle
A.28
過程
信号の集まり。信号が集合としてのある特性をもつ又はもたないと
いうことを強調したい場合には,“アンサンブル”という用語よりも
“過程”という用語が通常用いられる。したがって,定常アンサン
ブルというより定常過程という。
process
A.29
確率
ある事象が起こる可能性。ある特定の事象の発生確率は,考えられ
るすべての事象の発生数に対する,その特定の事象の発生数の割合
として一般に評価される。定常不規則振動では,振動の大きさがあ
る範囲内に存在する確率は,その範囲内に存在する時間の,総観測
時間に対する割合に等しい。
備考1. 確率を決定するためには,多くの事象又は長い観測時間
が必要である。
2. 確率1というのは,ある特定の事象が必ず起こることを
意味する。確率0というのは,起こらないことを意味す
る。
3. 振動の大きさがある範囲内に存在する確率は,その振動
の確率密度関数を,その範囲にわたって積分したものに
等しい[確率密度(A.30)参照]。
probability
A.30
確率密度
特定の振動の大きさにおいて,振動の大きさがある増分幅内に収ま
っている確率を,その増分幅で割り,増分幅を0に近づけて極限を
とったもの。
備考1. 確率密度は,数学的に次のように表される。
m
m
x
m
x
x
P
x
p
m
∆
∆
=
→
∆
)
(
lim
)
(
0
又は
dx
x
dP
x
p
)
(
)
(
=
ここに,
p (xm) は,xmにおける確率密度,
∆ xmは,振幅xmからの増分変化量,
p (∆ xm) は,振幅がxmからxm+∆xmの間にある確率
である。
2. 確率密度p (x) は,xに関する累積確率分布関数P (x) の
導関数である[(A.34)参照]。
probability density
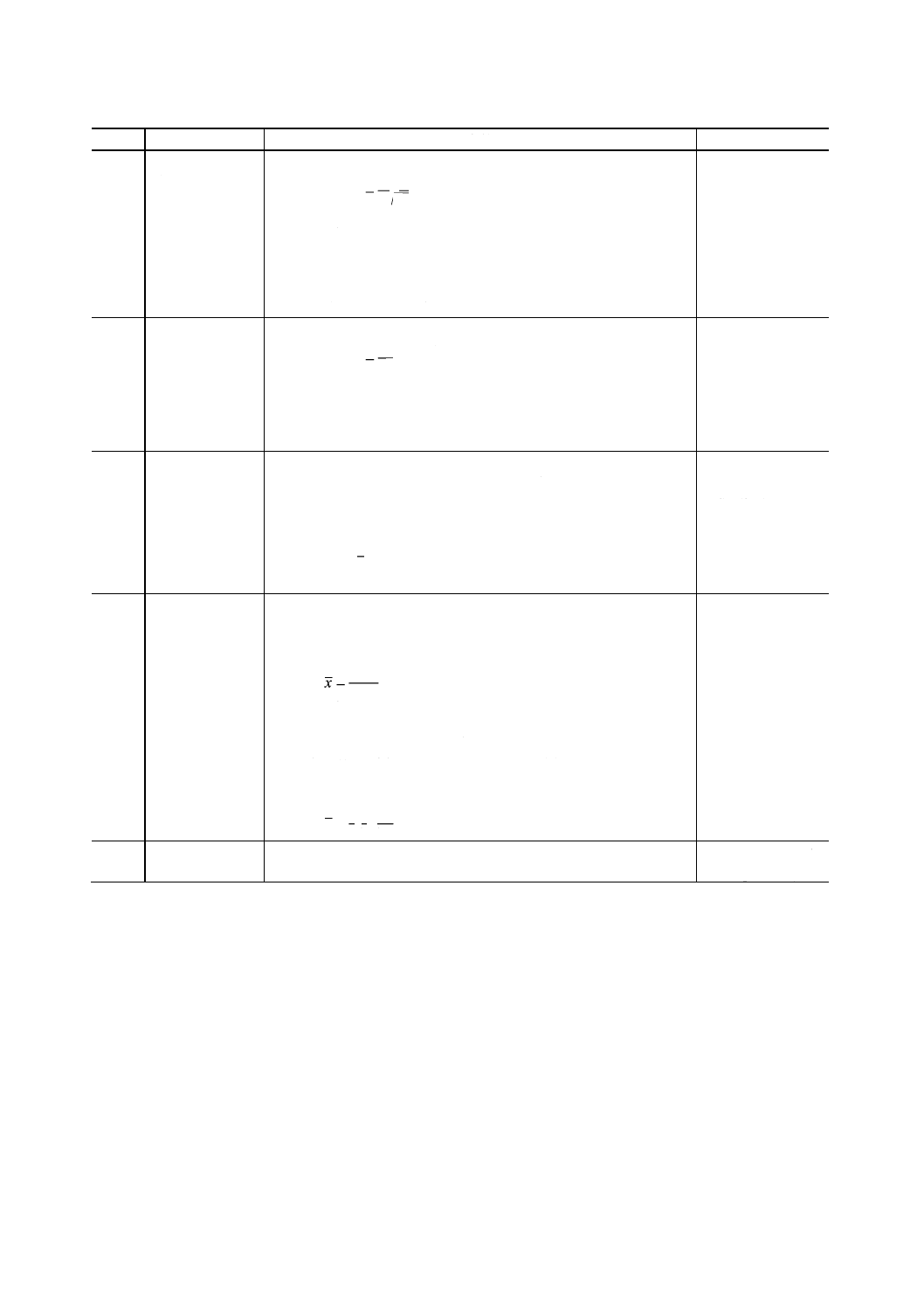
A.31
確率密度関数,
確率密度分布曲
線
確率密度関数は,ある振動に関連した確率密度の表現である。確率
密度曲線は,確率密度関数を図示したものである。
備考1. 確率密度(A.30)で与えられた関数p (x),正規分布(A.32)
及びレイリー分布(A.33)は,確率密度関数である。
2. 確率密度曲線で囲まれた全面積は,1に等しい。
probability density
function ;
probability density
distribution curve
38
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
A.32
正規分布,
ガウス分布,
正規確率密度分
布
正規分布又はガウス分布は,次のような確率密度関数をもつ。
)
2
/(
2
1
2
2
)
(
σ
π
σ
p
x
p
e
x
p
−
=
ここに,
σは,例えば振動の大きさのrms値[標準偏差(A.37)
参照]
xpは,振動の大きさの瞬時の値である。
振動の平均値は,0と仮定した。
normal
distribution ;
Gaussian
distribution ;
normal probability
density
distribution
A.33
レイリー分布
レイリー分布は,次のような確率密度関数をもつ。
)
2
/(
2
2
2
)
(
σ
σ
p
p
x
x
p
e
x
p
−
=
ここに,
σ:rms値,xp:正の極大値
狭帯域ガウス性不規則振動の極大値(ピーク値)は,レイリー分布
をもつ。
Rayleigh
distribution
A.34
累積確率分布関
数,
確率分布関数
累積確率分布関数P (x) は,変数xの大きさ(不規則振動の振幅)が
ある値を超えない確率を表す。すなわち,変数xが特定の値Xより
小さい確率である。
備考 累積確率分布関数は,次のように表される。
∫∞
−
=
x
du
u
p
x
P
)
(
)
(
ここに,uは,xに関する積分の仮変数である。
cumulative
probability
distribution
function ;
probability
distribution
function
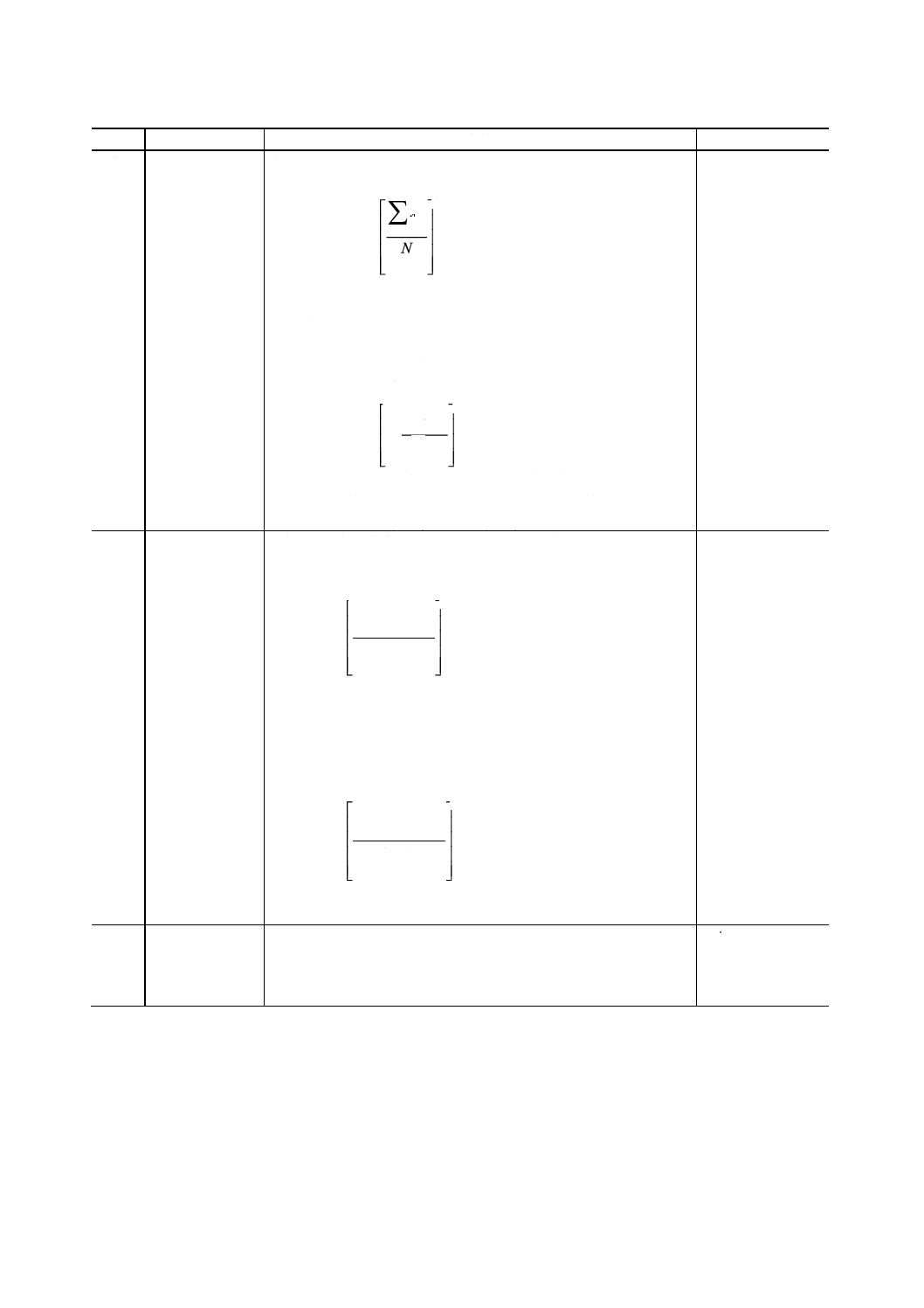
A.35
平均値,算術平均 a) 多数の離数値の平均値は,離散値の代数和を個数で除したもの
に等しい。
備考 平均値xは,次のように表される。
N
x
n
n
x∑
=
ここに,
xnは,n番目のデータの値
Nは,離散値の個数
b) 関数x (t) の時刻t1からt2までの間の平均値xは,次のように表
される。
1
2
2
1
)
(
t
t
dt
t
x
t
t
x
−
∫
=
mean value ;
arithmetic mean
A.36
(二つの量の)幾
何平均
二つの量の積の平方根。
geometric mean (of
two quantities)
39
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
A.37
実効値(二乗平均
の平方根),
rms値(あーるえ
むえすち)
a) データの二乗平均値の平方根。
備考 実効値は,次のように表すことができる。
実効値=
2
/
1
2
∑Nx
n
n
ここに,添字のnは,総数N個のデータのうち,n番目のも
のであることを表す。
b) 一価関数f (t) の時刻t1からt2までの間の実効値は,その時間内
におけるf (t) の二乗平均値の平方根である。
備考1. 一価関数f (t) の時刻t1からt2までの間の実効値は,次の
ようになる。
実効値=
2/1
1
2
2)
(
−
∫
t
t
dt
t
f
2. 振動の平均値を0とみなす場合,実効値は,標準偏差に
等しく,二乗平均値は,分散 (σ2) に等しくなる。[標
準偏差(A.38)及び分散(A.39)参照]。
root-mean-square
valuer ;
r. m. s. value
A.38
標準偏差
関数(又は数の集合)の平均値からの偏差の実効値。
備考1. 標準偏差を表す記号としてσが一般的に用いられる。
2. 数の集合に対して標準偏差は,次のようになる。
2
/1
2)
(
−
∑
N
x
x
n
n
=
σ
ここに,
添字nは,n番目のデータであることを表す。
Nはデータの総数である。
xは,平均値である[平均値(A.35)参照]。
3. もし,xがtに関する一価関数であるならば,xの時刻
t1からt2までの間の標準偏差は,次のように表される。
2/1
1
2
2
2
1
)
(
−
−
∫
t
t
dt
x
x
t
t
n
=
σ
4. 平均値xを0とみなす場合,標準偏差は,実効値に等し
い。
standard deviation
A.39
分散
標準偏差の二乗。
備考 平均値を0とみなす場合,分散は,振動の大きさを表す変
数の二乗平均値に等しい[二乗平均値(A.40)の備考3参
照]。
variance

40
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
A.40
二乗平均値
ある与えられた区間にわたる関数(又は数の集合)の二乗平均値は,
その区間にわたって関数(又は数の集合)の二乗値を平均したもの
である。
備考1. 二乗平均値は,rms値の二乗である。
2. 平均値を0とみなす場合,二乗平均値は,分散に等しい
[分散(A.39)参照]。
3. もし,平均値が0でない場合は
ψ2=σ2+
2x
ここに,
ψ2:二乗平均値,σ2:分散,x:平均値
mean-square value
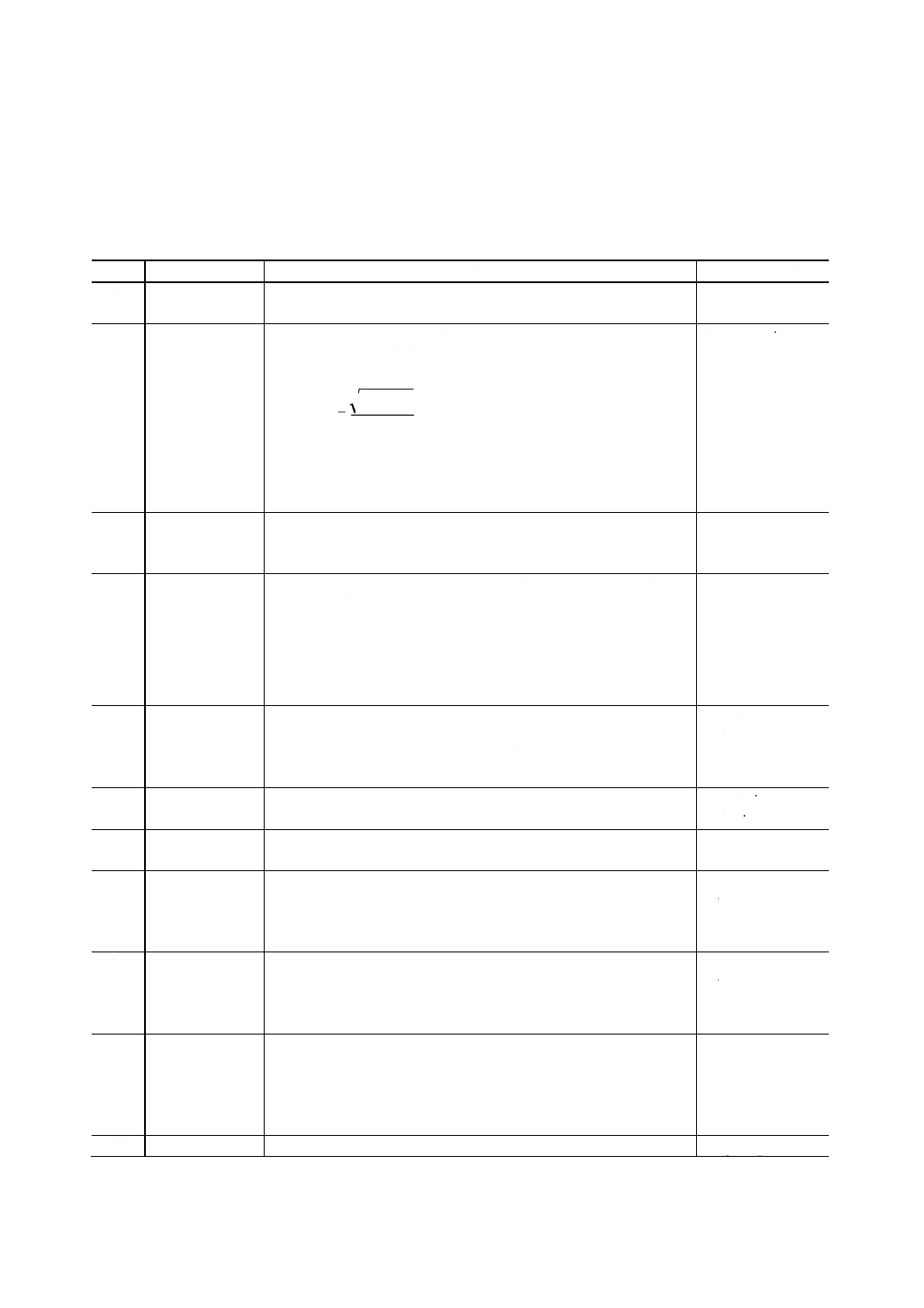
41
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書B(参考)補足的用語
この附属書に含まれる定義は,振動及び衝撃の分野では必須の事項である。しかしながら,他の分野に
も関係するため,これらの定義は,規定の一部ではない。
番号
用語
定義
対応英語(参考)
B.1
信号
a) 情報を含む物理量。
b) 伝達システムを介して伝えられる情報。
signal
B.2
(信号の)ひずみ 波形における好ましくない変化。
備考 例えば加速度においては,ひずみdはパーセント量とし
て,通常次のように表される。
100
1
21
2
×
−
a
a
a
d
tot
=
ここに,
a1は,加振された振動数での加速度実効値
atotは,与えられた加速度の総合実効値(a1の値を含
む。)。
distortion (of a
signal)
B.3
分解能
運動を計測するシステムの分解能は,出力の変化が識別できる,最
も小さい入力(変位,速度,加速度,ひずみ,その他の入力量)の
変化。
resolution
B.4
時定数,
緩和時間
ある量が指数関数的に1/e=0.367 9まで減少するのに要する時間。
備考 抵抗を通して電気容量から放出される電荷は,次の式に比
例する。
e-t/RC
ここに,
t:時間,R:抵抗 (Ω),C:容量 (F),e:自然対数の
底,RC:時定数又は緩和時間
time constant ;
relaxation time
B.5
接地,
アース
a) 大地の伝導マス又は非常に小さい抵抗を通して大地に結ばれた
伝導体。
b) 電気的ポテンシャルをもたないと考えられる伝導体。大地の電
気的ポテンシャルは,通常ゼロとみなす。
ground ;
earth
B.6
接地線,
アース線
接地極に結ばれた導体。
ground wire ;
earth wire
B.7
接地ループ,
アースループ
異なる場所のいくつかの接地極に接地線を結ぶことによって作られ
る閉電気回路。
ground loop ;
earth loop
B.8
(電気的アンプ
の)入力インピー
ダ
入力端子間の電気的インピーダンス。
備考 入力インピーダンスは,出力負荷によって影響されること
がある。そのような場合には,出力負荷を指定する必要が
ある。
input impedance
(of an electronic
amplifier)
B.9
(電気的アンプ
の)出力インピー
ダンス
出力端子間の電気的インピーダンス。
備考 出力インピーダンスは,入力におけるソースインピーダン
スによって影響されることがある。そのような場合には,
ソースインピーダンスを指定する必要がある。
output impedance
(of an electronic
amplifier)
B.10
オペアンプ(オペ
レーショナルア
ンプ)
出力端子と入力端子間にある関係が保たれるフィードバックループ
(帰還)をもつアンプ。
備考 フィードバック又は他の付加回路の種類によって,アンプ
は,積分,微分,増幅などの様々な機能を行うことができ
る。
operational
amplifier
B.11
チャージアンプ
入力された全電荷に比例した量を出力するアンプ。
charge amplifier
42
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
B.12
クロストーク
他のチャンネルの信号の影響によって,あるチャンネルで観測され
る信号。
cross-talk
B.13
周波数応答
入力信号の周波数の関数として表現された出力信号。周波数応答は,
通常,出力信号の関係を,場合によっては位相のずれ又は位相角の
関係をも周波数の関数として図示したものである。
frequency response
B.14
フィルタ,
波形フィルタ
周波数に応じて振動を分離するための装置。一つ又はそれ以上の周
波数帯域に対して振動をあまり減衰させず,その他の周波数の振動
を比較的大きく減衰させるもの。
備考 電気的フィルタと共振を利用した幾つかの機械的フィル
タは,選択する周波数帯域を増幅し,それがフィルタの役
割をしている。
filter ;
wave filter
B.15
(帯域通過フィ
ルタの)通過帯域
上限及び下限カットオフ周波数に挟まれた周波数帯域。
pass-band (of a
band-pass filter)
B.16
低減通過フィル
タ
ゼロからある周波数までの連続した通過帯域をもつフィルタ。
low-pass filter
B.17
高域通過フィル
タ
ゼロでないあるカットオフ周波数から無限大の周波数。実際上は対
象とする最高周波数より高い周波数までの連続した通過帯域をもつ
フィルタ。
high-pass filter
B.18
帯域通過フィル
タ
ゼロより大きい下限のカットオフ周波数から,ある上限のカットオ
フ周波数までの連続した通過帯域をもつフィルタ。
band-pass filter
B.19
(フィルタの)公
称帯域幅,
バンド幅
上限と下限の公称カットオフ周波数の差。この差は,次のように表
すことができる。
a) Hz単位で。
b) 通過帯域の中心周波数の百分率として。
c) オクターブにおける上限と下限の公称カットオフ周波数の区間
として。
nominal bandwidth
(of a filter) ;
bandwidth
B.20
(フィルタ通過
帯域の)公称上限
及び下限カット
オフ周波数,
カットオフ周波
数
フィルタの最大応答の周波数より高いか低いカットオフ周波数では
正弦信号の応答は,最大応答より3dB低くなる。
nominal upper and
lower cut-off
frequencies (of a
filter pass-band) ;
cut-off frequency
B.21
定帯域幅フィル
タ
Hz単位で一定の帯域幅をもつフィルタ。定帯域幅フィルタの帯域幅
は,フィルタの中心周波数の値に依存しない。
constant-bandwidth
filter
B.22
比例帯域幅フィ
ルタ
中心周波数に比例した帯域幅をもつフィルタ。
備考 オクターブ帯域,1/3オクターブ帯域などは,典型的な比
例帯域幅フィルタである。
proportional-bandwid
th filter
B.23
オクターブ
2倍の周波数比をもつ二つの周波数の区間。
備考 オクターブにおいては,どんな二つの周波数の区間も周波
数比の2を底とする対数(又は10を底とする対数の3.322
倍)である。
octave
B.24
1/2オクターブ
(ハーフオクタ
ーブ)
21/2又は1.414の周波数比となる二つの周波数の区間[オクターブ
(B.23)の備考参照。]
one-half octave ;
half octave

43
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
B.25
1/3オクターブ
(サードオクタ
ーブ)
21/3又は1.2599の周波数比となる二つの周波数の区間[オクターブ
(B.23)の備考参照]。
備考 ある音響計測では1/3オクターブ単位で周波数を分ける
のが便利である。しかし,低周波及び超音波領域に対象を
広げると10のべき乗を使うのが便利である。これら二つ
の相対する条件は,ほとんどの目的に対して満たされる。
なぜならば,21/3=1.259 9は101/10=1.258 9とほとんど等
しく,その差は0.1%以下であるからである。これは1/3
オクターブの連続的な10個分の間隔が周波数の10倍にほ
とんど等しいことを意味する。
one-third octave ;
third octave
B.26
1/10ディケード
101/10又は1.258 9の周波数比となる二つの周波数の区間。
備考1. 1/10ディケードと1/3オクターブバンドの違いは,0.1%
以下である[1/3オクターブバンド (B.25) の備考参照]。
したがって,二つの帯域幅は,実用的な目的に対して等
価と考えられる。
2. ディケードでは,どんな二つの周波数の区間も周波数比
の10を底とする対数である。
one-tenth decade
B.27
オクターブ帯域
幅フィルタ
通過帯域が1オクターブのバンドパスフィルタ。すなわち,上限及
び下限のカットオフ周波数の差が1オクターブである[比例帯域幅
フィルタ(B.22)を参照]。
octave-bandwidth
filter
B.28
1/3オクターブ帯
域幅フィルタ
上限及び下限のカットオフ周波数の差が1/3オクターブであるバン
ドパスフィルタ[比例帯域幅フィルタ(B.22)と1/3オクターブバンド
(B.25)の備考を参照]。
one-third-octave
filter ;
third-octave filter
B.29
狭帯域フィルタ
通過帯域幅が比較的狭いバンドパスフィルタ。
備考 帯域幅が狭いか否かは対象による。例えば,衝撃・振動で
は,通常は1/3オクターブ又はそれ以下のものをいう。
narrow-band filter
B.30
広帯域フィルタ
通過帯域幅が比較的広いバンドパスフィルタ。
備考 帯域幅が広いか否かは対象による。例えば,衝撃・振動で
は,通常1オクターブより大きいものをいう。
wide-band filter
B.31
中心周波数,公称
通過帯域中心周
波数
帯域幅の公称カットオフ周波数の幾何平均。
備考 幾何平均は
2
1f
fと等しい。ここに,f1, f2はカットオフ周波
数である。
centre frequency ;
nominal pass-band
centre frequency
B.32
帯域阻止フィル
タ
ある周波数帯域で大きな減衰を与え,それ以外の周波数ではほとん
ど損失を与えないフィルタ。
band-elimination
filter ;
band-reject filter
B.33
トラッキングフ
ィルタ
周波数が変化する準正弦振動に追従するような中心周波数をもつ
(通常狭帯域の)帯域通過フィルタ。
tracking filter
B.34
クリスタルフィ
ルタ
共振周波数で作動する圧電クリスタルがフィルタの主な要素である
狭帯域フィルタ。
crystal filter
B.35
磁わい(歪)フィ
ルタ
共振周波数での磁わい(歪)要素がフィルタの主な要素である狭帯
域フィルタ。
magnetostrictive
filter
B.36
ピークノッチフ
ィルタ
発生器出力のスペクトルに現れる相対的な最大値と最小値を除去す
るように,動電型振動発生器を駆動するパワーアンプへ加える信号
を変えるように調整された電気的フィルタ。
備考 スペクトルにおける相対的な最大値と最小値は通常加振
される機械的弾性システムの反作用によって生じる。
peak-notch filter
B.37
(動電型振動発
生システムの)均
等化(イコライ
ザ)
電気的アンプのゲイン及び制御システムの調整を意味し,それによ
って入力信号の振幅に対する出力の振動振幅の比を,求める周波数
スペクトルに対して一定値(又は規定値)にすること。
equalization (of an
electrodynamic
vibraion
generator system)
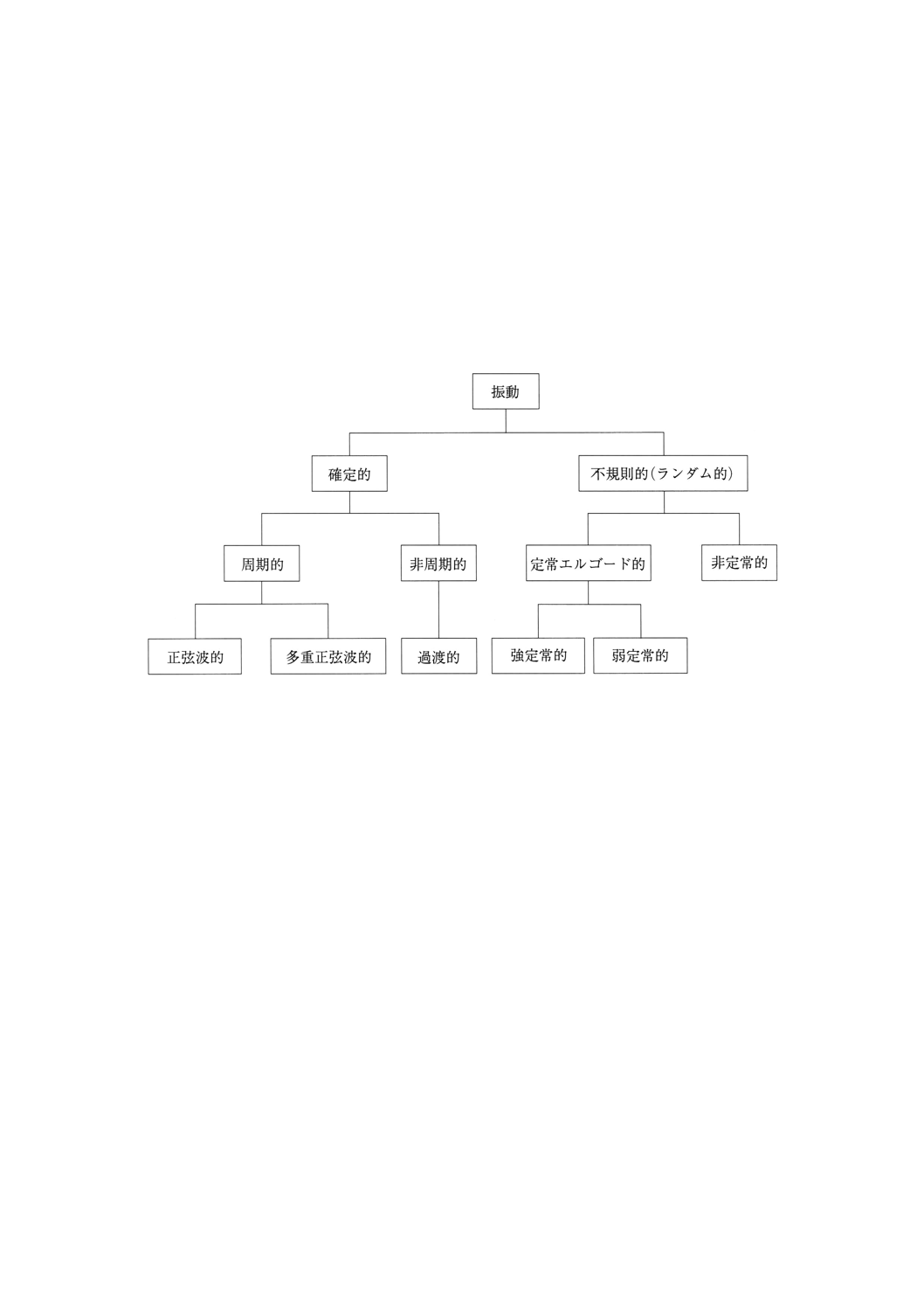
44
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書C(参考) 振動用語の体系
この振動用語における用語は付図C.1のように整理される。この図は,理論的考察よりむしろ実用性す
なわち集められた振動の記録(時刻歴)の収集及び記録データから抽出された情報の取扱い方法に基づい
ている。振動は,基本的に確定的か不規則かで二つに分類される。
確定的な振動は,ある時刻における振動の瞬時値がその時刻以前の時刻歴(その瞬時値の記録)によっ
て正確に決定される振動である。不規則振動は,ある時刻の振動の瞬時値がそれまでの時刻歴によって決
定できない振動である。
図C.1 振動の分類

45
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書1(規定) 機械振動用語(追加)
この附属書は,機械振動用語について,ISO規格にはないが,JISとして必要な用語の定義を規定した
ものである。
番号
用語
定義
対応英語(参考)
1
曲げ振動
弾性体の曲げの変化として現れる振動。
flexural vibration,
bending vibration
2
ねじり振動
弾性体のねじりの変化として現れる振動。
torsional vibration
3
ふれまわり
軸中心線の旋回運動。
whirling
4
オイルホイ
ップ
十分に潤滑されたジャーナル軸受の油膜の性質のために起こるジ
ャーナルの自励的な振れ回り。
oil-whip
5
サージング
a) 流体機械で,配管を含めた系が一種の自励振動を起こし,特有
の定まった周期で吐出し圧力及び吐出し量が変動する現象。
b) コイルばねなどにおける軸方向の,分布系としての共振。
surging
6
フラッタ
液体の流れの中の翼など,弾性体の流力弾性的自励振動。
flutter
7
スロッシン
グ
自由表面をもつ容器内の液体の液面揺動。
sloshing
8
流体励起振
動
流体の流れが原因となって発生する振動。
flow-induced
vibration
9
非線形振動
系の運動が定係数の線形微分方程式で記述できない振動。
nonlinear vibration
10
高調波共振
振動数fの励振が振動系に働くとき,nを2以上の正整数としてnf
が系の固有振動数に近いために起こる共振。
備考 優勢なn次高調波を含む周期1/fの振動が起こり,これ
をn次高調波共振という。
higher harmonic
resonance
11
振動履歴
過去における励振の経過によって,系に生じる振動の状態が異なる
現象。
oscillation hysteresis
12
し(弛)緩振
動
変位及び速度が小さいときには,負減衰が作用して振幅を増大さ
せ,それらが大きくなると減衰が働いて振幅の増大を制限するよう
な非線形減衰をもつ振動系で,慣性力に比べ非線形減衰力が大きい
ときに生じ,方形波に近い波形を示す振動。
relaxation vibration
13
跳躍現象
質量,ばねなどの要素又は外部からの励振の連続的な変化に対し
て,応答が不連続的に変化する現象。
jumping phenomena
14
リミットサ
イクル
自励振動で,それに近い振動がすべて収束していく極限の周期振
動。
limit cycle
15
パラメータ
励振
質量,ばねなどの要素が時間的に変化することによる励振。
parametric
excitation
16
周波数分析
振動現象のスペクトル分析[スペクトル(1.56)参照]。
frequency analysis
17
調波分析,
フーリエ解
析
複雑な波形の中に含まれる,各振動成分の振幅と位相の大きさを求
めること。
harmonic analysis

46
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
番号
用語
定義
対応英語(参考)
18
モード解析
a) 多自由度機械系又は連続体の応答を複数の固有振動モードの
応答の重ね合わせとみなし,実験的に計測した振動の振幅分布
から各固有振動モードを求めること。
b) 多自由度振動系又は連続体の固有振動モードを解析すること。
また系全体の応答を,まず各固有振動モードごとに分解して求
め,次にそれを加算することによって求めること。
備考 多自由度系又は連続体の応答を求める手法であって,そ
の固有モードが互いに独立であるとして扱える系に適用
する。
modal analysis
19
モードパラ
メータ
固有振動数,固有モード,モード質量,モード減衰及びモード剛性
の総称。多自由度系の振動を主座標について記述するときの各固有
振動の特性を表すために用いられるパラメータ。
modal parameter
20
モード行列,
モードマト
リックス
n自由度系におけるn個の固有モードの形を列とする,n行n列の
正方行列。
modal matrix
21
主座標
(しゅざひ
ょう)
互いに独立な一般座標を,モード行列によって一次変換した座標。
各固有振動の変位を意味し,モード座標とも呼ぶ。
principal coordinate
22
主質量,
モード質量
多自由度系における振動を,固有振動ごとに分けて論じる場合,あ
る固有振動に対応する質量。モード行列の選び方によって値が異な
る。
principal mass,
modal mass
23
主剛性,
モード剛性
多自由度系における振動を,固有振動ごとに分けて論じる場合,あ
る固有振動に対応する剛性。モード行列の選び方によって値が異な
る。
principal stiffness,
modal stiffness
24
質量行列,
質量マトリ
ックス
n自由度系の力の平衡を表す運動方程式を,n個の互いに独立な一
般座標を用いて記述するときの,加速度ベクトルにかかる係数行
列。
mass matrix
25
剛性行列,
剛性マトリ
ックス
n自由度系の力の平衡を表す運動方程式を,n個の互いに独立な一
般座標を用いて記述するときの,変位ベクトルにかかる係数行列。
stiffness matrix
4
7
B
0
1
5
3
:
2
0
0
1
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書2(参考) JISと対応する国際規格との対比表
JIS B 0153 : 2001
機械振動・衝撃用語
ISO 2041 : 1990
振動及び衝撃−用語
(I) JISの規定
(II) 国際規
格番号
(III) 国際規格の規定
(IV) JISと国際規格との技術的差異の項目ごと
の評価及びその内容
表示箇所:本体及び附属書
表示方法:側線又は点線の下線
(V) JISと国際規格との技術的差異
の理由及び今後の対策
項目番号
内容
項目
番号
内容
項目ごとの評価
技術的差異の内容
1.適用範囲 機械振動及び衝撃に関
する用語を定義
1.
JISに同じ。
IDT
−
2.分類
用語の分類
−
−
MOD/追加
分かりやすくするため,項目を設け
た。
3.用語及び
定義
用語の定義
2.
用語の定義。
用語の数及び番号は,JISに
同じ。
MOD/追加
一部の用語について,定義を
備考に追加。
JISとして必要な定義を追加。
ISOに追加を提案する予定。
附属書1
(規定)
機械振動に関する用語
(追加)の定義
−
−
MOD/追加
ISO規格にない用語を追加。 JISとして必要な用語を追加。
ISOに追加を提案する予定。
JISと国際規格との対応の程度の全体評価:MOD
備考1. 項目ごとの評価欄の記号の意味は,次のとおりである。
− IDT ············· 技術的差異がない。
− MOD/追加 ··· 国際規格にない規定項目又は規定内容を追加している。
2. JISと国際規格との対応の程度の全体評価欄の記号の意味は,次のとおりである。
− MOD ··········· 国際規格を修正している。
48
B 0153 : 2001
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JIS B 0153機械振動・衝撃用語改正原案作成分科会 構成表
氏名
所属
(主査)
小 野 京 右
東京工業大学工学部機械科学科
(幹事)
佐 藤 勇 一
埼玉大学工学部機械工学科
(委員)
井 下 芳 雄
エミック株式会社技術部
今 泉 八 郎
株式会社小野測器マーケティング本部
岩 壷 卓 三
神戸大学工学部機械工学科
金 子 成 彦
東京大学大学院工学系研究科機械工学専攻
黒 澤 富 蔵
通商産業省工業技術院計量研究所力学部機械計測研究室
榊 田 均
株式会社東芝電力システム社電力・産業システム技術開発
センター
篠 田 東洋児
株式会社共和電業マーケティング本部
鈴 木 雅 靖
鹿島建設株式会社技術研究所先端技術研究部
高 木 亨 之
株式会社日立製作所機械研究所第四部第45研究室
長 松 昭 男
東京工業大学工学部機械科学科
藤 田 隆 史
東京大学生産技術研究所
藤 本 裕
財団法人鉄道総合技術研究所基礎研究部
二 井 義 則
通商産業省工業技術院機械技術研究所極限技術部
松 下 修 己
防衛大学校機械工学教室
屋 代 春 樹
日産自動車株式会社総合研究所車両研究所
安 田 千 秋
三菱重工業株式会社高砂研究所振動・騒音研究室
山 川 宏
早稲田大学理工学部機械工学科
吉 田 和 夫
慶應義塾大学理工学部システムデザイン工学科
米 川 善 晴
労働省産業医学総合研究所人間工学特性研究部
穐 山 貞 治
通商産業省工業技術院標準部標準業務課産業基盤標準化推
進室
橋 本 進
財団法人日本規格協会技術部規格開発課
(事務局)
中 嶌 勉
社団法人日本機械学会事業課