B 0091:2010 (ISO 14999-4:2007)
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 1
3 用語及び定義 ··················································································································· 1
3.1 数学的定義 ··················································································································· 2
3.2 光学関数の定義 ············································································································· 2
3.3 3.2で定義した光学関数に関連する値の定義 ········································································ 3
4 干渉計測と表面形状偏差又は透過波面形状との関係 ································································ 5
4.1 被検領域 ······················································································································ 5
4.2 量(大きさ) ················································································································ 5
4.3 シングルパス(片道)透過波面 ························································································ 5
4.4 ダブルパス(往復)透過波面 ··························································································· 5
4.5 表面形状偏差 ················································································································ 5
4.6 他波長への変換 ············································································································· 5
附属書A(規定)視覚的方法による干渉図形解析 ······································································· 6
B 0091:2010 (ISO 14999-4:2007)
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法第12条第1項の規定に基づき,日本光学工業協会(JOIA)及び財団法人日
本規格協会(JSA)から,工業標準原案を具して日本工業規格を制定すべきとの申出があり,日本工業標
準調査会の審議を経て,経済産業大臣が制定した日本工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願,実用新案権又は出願公開後の実用新案登録出願に
抵触する可能性があることに注意を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許
権,出願公開後の特許出願,実用新案権及び出願公開後の実用新案登録出願にかかわる確認について,責
任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 0091:2010
(ISO 14999-4:2007)
光学素子及び光学システムの干渉測定−
表面形状及び波面形状公差の用語及び定義
Interferometric measurement of optical elements and systems-
Terms and definitions of suface form and wavefront deformation tolerances
序文
この規格は,2007年に第1版として発行されたISO 14999-4を基に,技術的内容及び構成を変更するこ
となく作成した日本工業規格である。
なお,この規格で点線の下線を施してある参考事項は,対応国際規格にはない事項である。
1
適用範囲
この規格は,JIS B 0090規格群で使用される光学素子及び光学システムの公差の中で,干渉測定に関す
る用語及び定義について規定する。この規格は,光学素子及び光学システム用の製図手法における光学関
数の定義についても規定する。附属書Aは,視覚的解析方法による干渉じま評価のための手引きとして,
JIS B 0090-5及び/又はJIS B 0090-14に準拠している。
注記 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 14999-4:2007,Optics and photonics−Interferometric measurement of optical elements and optical
systems−Part 4: Interpretation and evaluation of tolerances specified in ISO 10110(IDT)
なお,対応の程度を表す記号“IDT”は,ISO/IEC Guide 21-1に基づき,“一致している”こ
とを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS B 0090-5 光学素子及び光学システム用の製図手法−第5部:表面形状公差
注記 対応国際規格:ISO 10110-5:2007,Optics and photonics−Preparation of drawings for optical
elements and systems−Part 5:Surface form tolerances(IDT)
JIS B 0090-14 光学素子及び光学システム用の製図手法−第14部:波面形状公差
注記 対応国際規格:ISO 10110-14:2007,Optics and photonics−Preparation of drawings for optical
elements and systems−Part 14:Wavefront deformation tolerance(IDT)
3
用語及び定義
この規格で用いる主な用語及び定義は,次による。
2
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.1
数学的定義
3.1.1
関数(function)
測定波面形状及びその成分へ分解するための数学的表現。
注記 この規格で用いる関数は,スカラー関数とする。
3.1.2
最大高低値(peak-to-valley value),PV (f)
関数fについて,評価対象領域内での関数の最大値から関数の最小値を引いた値。
3.1.3
二乗平均平方根(root mean square value),rms (f)
領域Aにわたる関数fについて,次の積分式のどちらかで与えられる値。
a) 直交座標系の変数x,y
[
]
2
/
1
2
d
d
d
d
)
,
(
)
(
rms
=
∫∫
∫∫
xy
xy
y
x
y
x
y
x
f
f
ここに, (x, y)∈A
b) 極座標系の変数r,θ
[
]
2
/
1
2
d
d
d
d
)
,
(
)
(
rms
=
∫∫
∫∫
θr
θr
θ
r
r
θ
r
r
θ
r
f
f
ここに, (r, θ)∈A
注記 測定分解能が明示されて,それが十分な場合には,この積分は標準偏差で近似できる。
3.2
光学関数の定義
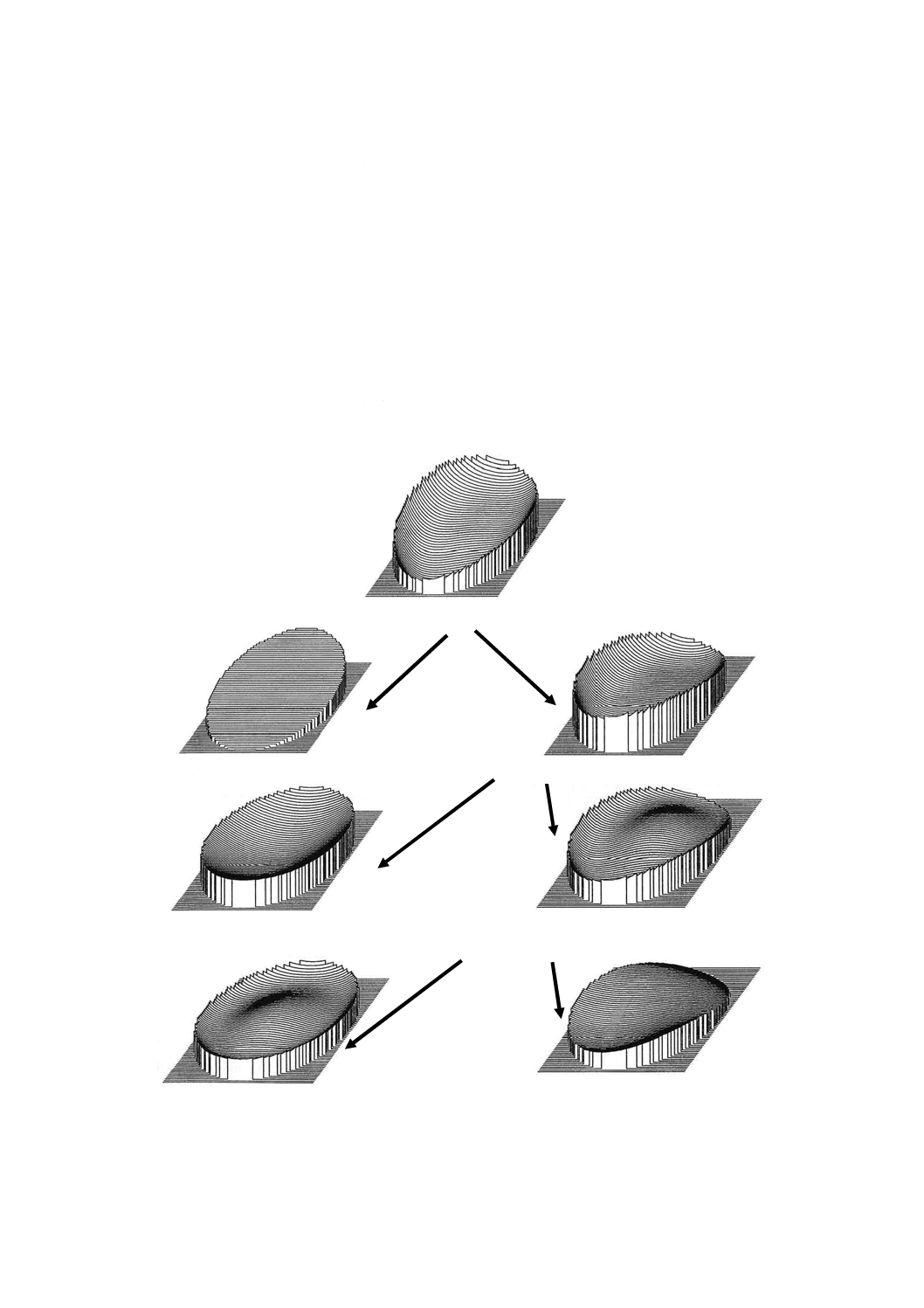
次に定義する光学関数を図1に示す。表面形状偏差と透過波面形状の干渉測定との関係については,箇
条4を参照。
3.2.1
測定波面形状(measured wavefront deformation),fMWD
名目上の理論波面に対して垂直に測定した,測定波面と名目上の理論波面との間の距離を表す関数[図
1 a)参照]。
3.2.2
チルト(傾き)(tilt),fTLT
測定波面形状fMWDに対して最適の(rmsが最小という意味の)線形近似する平面関数[図1 b)参照]。
3.2.3
波面形状(wavefront deformation),fWD
測定波面形状fMWDからチルト(傾き)fTLTを引いた関数[図1 c)参照]。
fWD=fMWD−fTLT
3
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.2.4
波面の球面近似(wavefront spherical approximation),fWS
波面形状fWDを最適の(rmsが最小という意味の)近似する球面の関数[図1 d)参照]。
3.2.5
波面イレギュラリティ(wavefront irregularity),fWI
波面形状fWDから波面の球面近似fWSを引いた関数[図1 e)参照]。
fWI=fWD−fWS
3.2.6
波面の非球面近似(wavefront aspheric approximation),fWRI
波面イレギュラリティfWIを最適の(rmsが最小という意味の)近似する回転対称な非球面関数[図1 f)
参照]。
3.2.7
回転非対称な波面形状偏差(rotationally varying wavefront deviation),fWRV
波面イレギュラリティfWIから波面の非球面近似fWRIを引いた関数[図1 g)参照]。
fWRV=fWI−fWRI
3.3
3.2で定義した光学関数に関連する値の定義
3.3.1
サジッタ偏差(sagitta deviation),PV(fWS)
球面波で近似した最大高低差。
注記1 PV(fWS)は,JIS B 0090-5及びJIS B 0090-14の量Aに相当する。
注記2 サジッタ偏差は,“ニュートン”,“ニュートンじま”,又は単に“しま”ともいう。
3.3.2
イレギュラリティ(irregularity),PV(fWI)
波面イレギュラリティの最大高低差。
注記1 PV(fWI)は,JIS B 0090-5及びJIS B 0090-14の量Bに相当する。
注記2 イレギュラリティを“アス・クセ”ともいう。
3.3.3
回転対称なイレギュラリティ(rotationally invariant irregularity),PV(fWRI)
波面の非球面近似の最大高低差。
注記1 PV (fWRI)は,JIS B 0090-5及びJIS B 0090-14の量Cに相当する。
注記2 回転対称なイレギュラリティを“クセ”ともいう。
3.3.4
回転非対称なイレギュラリティ(rotationally varying irregularity),PV(fWRV)
回転非対称な波面形状偏差の最大高低差。
注記 回転非対称なイレギュラリティを“アス”ともいう。
3.3.5
全rms(rms total),rms (fWD)
波面形状の二乗平均平方根。
注記 rms(fWD)は,JIS B 0090-5及びJIS B 0090-14の量RMStに相当する。
4
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.3.6
rmsイレギュラリティ(rms irregularity),rms(fWI)
波面イレギュラリティの二乗平均平方根。
注記 rms(fWI)は,JIS B 0090-5及びJIS B 0090-14の量RMSiに相当する。
3.3.7
rms回転対称なイレギュラリティ(rms rotationally invariant irregularity),rms(fWRI)
波面の非球面近似の二乗平均平方根。
3.3.8
rms回転非対称なイレギュラリティ(rms rotationally varying irregularity),rms(fWRV)
回転非対称な波面形状の二乗平均平方根。
注記 rms(fWRV)は,JIS B 0090-5及びJIS B 0090-14の量RMSaに相当する。
a) 測定波面形状(fMWD)
b) チルト(傾き)(fTLT)
c) RMStを決定する波面形状(fWD)
d) サジッタ偏差Aを決定する波面の球面近似(fWS)
e) イレギュラリティB及びRMSiを決定する波面イレ
ギュラリティ(fWI)
f) 回転対称イレギュラリティCを決定する回転対称な
波面の非球面近似(fWRI)
g) RMSaを決定する回転非対称な波面形状偏差(fWRV)
図1−測定波面形状,及び各種波面形状成分への分解
5
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
干渉計測と表面形状偏差又は透過波面形状との関係
4.1
被検領域
3.2で定義した光学関数の定義域は,指定の被検領域内である。
注記 被検領域が円形でない場合は,波面形状をゼルニケ多項式に展開することはできない。
4.2
量(大きさ)
3.3で定義した量は,JIS B 0090-5及びJIS B 0090-14の指示に従い,しまの本数,波長又はナノメート
ルを単位として用いる。JIS B 0090-5又はJIS B 0090-14を参照。
垂直入射で1回反射の場合には,波面1波長の光路差は半波長の表面形状偏差に相当する。
4.3
シングルパス(片道)透過波面
JIS B 0090-14で定義しているように,干渉計の波長が指定波長と同一である場合には,透過波面形状は
マッハ・ツエンダ干渉計のようなシングルパスの配置で直接計測することができる。
4.4
ダブルパス(往復)透過波面
コモンパス(共通光路)の装置で光学素子の透過波面形状を計測する場合は,ダブルパスの配置をよく
用いる。この場合には,干渉計測の感度はおよそ2倍となる。透過波面形状の近似値を求めるためには,
干渉計測値を2で除しなければならない。
注記 被検物通過のときは,往復で回折が生じ,また復路の被検物による波面形状は往路で生じる波
面形状にわずかに依存するので,ダブルパスの配置で計測した透過波面形状は干渉計計測値の
およそ半分である。
4.5
表面形状偏差
通常,表面形状偏差は,被検面からの1回反射波面の干渉計測によって計測する。
垂直入射で1回反射の場合には,波面1波長の光路差は半波長の表面形状偏差に相当する。
4.6
他波長への変換
検査波長が指定波長と異なる場合は,干渉検査の値を次の式で変換することができる。
2
1
1
2
λ
λ
N
N
λ
λ
×
=
ここに,
Nλ1: (波長)λ1のしまの本数
Nλ2: (波長)λ2のしまの本数
6
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(規定)
視覚的方法による干渉図形解析
A.1 一般
A.1.1 一般事項
この附属書は,JIS B 0090-5及びJIS B 0090-14の理解を助けることを意図している。この附属書は,干
渉図形(ニュートンゲージを用いたとき観察されるしまパターンを含む。)の解釈に有益である。表面形状
測定において,表面形状は,波面形状によって表す。この附属書は,種々の波面形状の量の評価を示すも
のであって,波面形状タイプを定義するものではない。
この附属書の目的は,様々な波面形状が干渉図形の中に視覚的にどのように現れるかを示すことにある。
この附属書は,次のタイプの波面形状に限って取り扱う。
− サジッタ偏差
− イレギュラリティ
− 回転対称なイレギュラリティ
rms偏差タイプの波面形状(3.3参照)は,視覚的検査では正確に求められない。
A.2及びA.3は,円形被検領域における解析を示す。A.4は,非円形被検領域の特殊条件を示す。
干渉図形解析については,様々な文献でより詳しく取り扱われている。例えば,文献 [1] を参照。
A.1.2 干渉計的チルト(傾き)
サジッタ偏差及びイレギュラリティの量を評価するために,被検波面と参照波面との間の相対的傾き量
に応じた二つの方法が用いられている。傾きなしによる方法は,主に波面形状偏差が大きいときに使われ
る。傾きありを利用した方法は,一般的に,より高精度となる。
二つの波面の相対的な傾きは,波面形状偏差の大きさと無関係である。
A.1.3 形状の符号の決定
干渉計のテストアーム(被検面側の光路)をわずかに縮めたり伸ばしたりするとき,又は被検面と参照
面との間隔をわずかに変化させたときの干渉じまの挙動を観察することで,波面形状の符号又は波面の領
域を決定することができる。
A.2 サジッタ偏差及びイレギュラリティの評価
A.2.1 一般
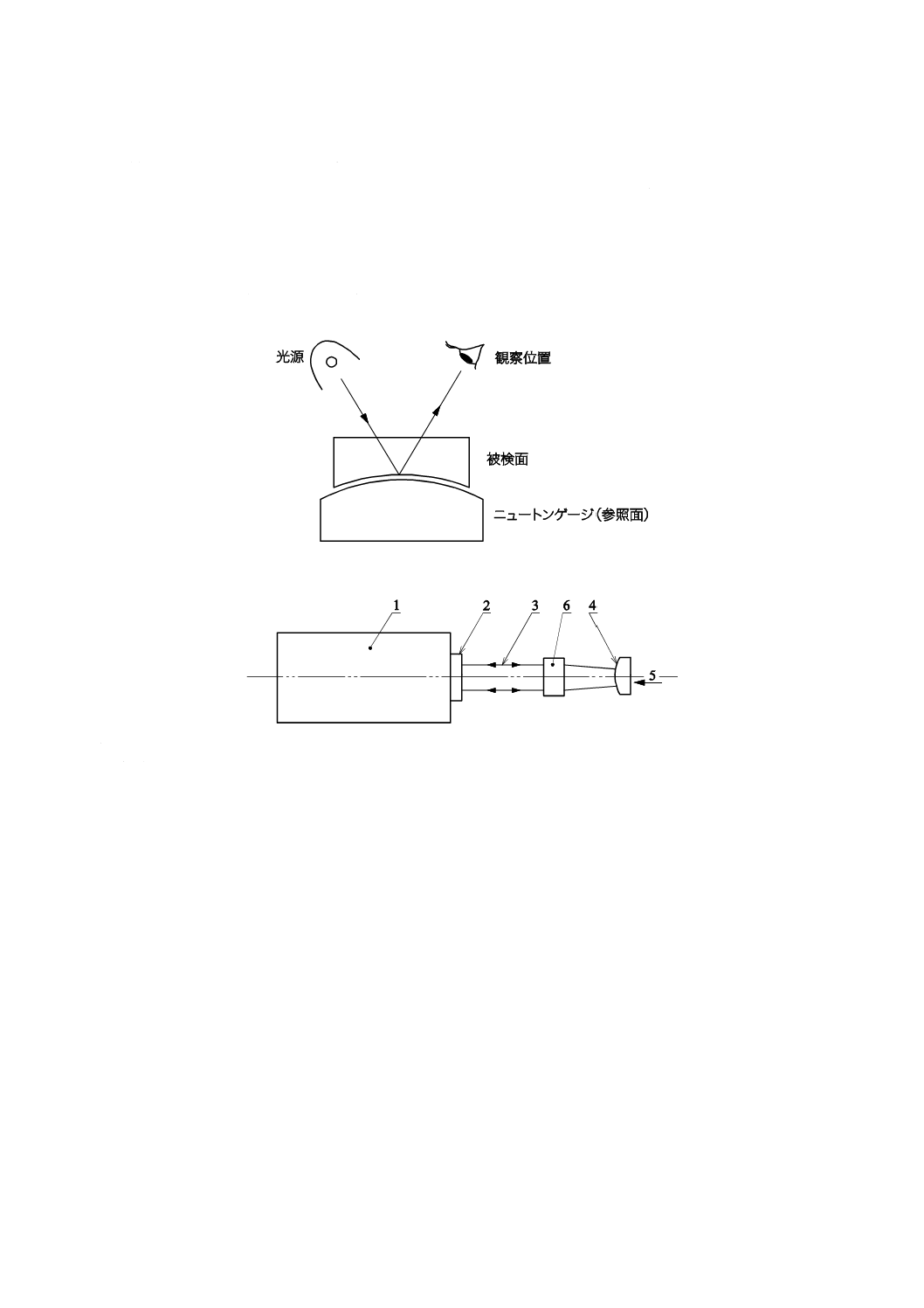
サジッタ偏差は,参照面の曲率半径が知られているときだけ決定できる。ニュートンゲージを用いると
きには,参照面の曲率半径はニュートンゲージの曲率半径に等しい(図A.0A)。干渉計の場合は(図A.0B
及び図A.0C),物点と像点との両方の位置が特定できる場合に限り,サジッタ偏差は決定できる。光学素
子及び光学系を干渉計で検査するとき,しばしばこの二つの点の一つしか位置が分からない場合がある。
そのような場合には,サジッタ偏差は決定できない。ただし,イレギュラリティはそのような場合でも決
定できる。
サジッタ偏差の決定は,干渉計の点光源が指示された物点に位置し,干渉計側に光を戻すミラーが,指
示された像点との同心位置におかれるとき,最も簡単になる。次に,これらが同心位置に置かれた場合を
仮定する。同心位置に置かれていないときは,物点と像点との間の距離を計算に入れなければならない。
7
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
寸法公差が物点と像点との位置の指示で関連付けられている場合には,光源及び反射表面は,サジッタ偏
差を最小にするためにこの許容量内で動かしてもよい。
通常,波面形状は,サジッタ偏差,及び/又はある種の非対称成分によって多く占められている。非対
称の場合には,異なる方向の波面の断面で異なるサジッタ偏差量を示す。他の種類のイレギュラリティも
あり得るが,その量の評価はより難しい。典型的な場合のサジッタ偏差及びイレギュラリティ量の評価は,
A.2.2及びA.2.3に示す。通常でないタイプのイレギュラリティに対するより一般的な手法については,
A.2.4に示す。より詳細な干渉図形の解析は,文献[1]に記述されている。
図A.0A−ニュートンゲージによる検査例
1 フィゾー干渉計[内部に参照アーム(光路)あり]
2 参照面
3 テストアーム(被検面側の光路)
4 反射面
5 ここを押してテストアーム(被検面側の光路)を短くする。
6 被検レンズ
図A.0B−ダブルパス干渉計による検査例
8
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
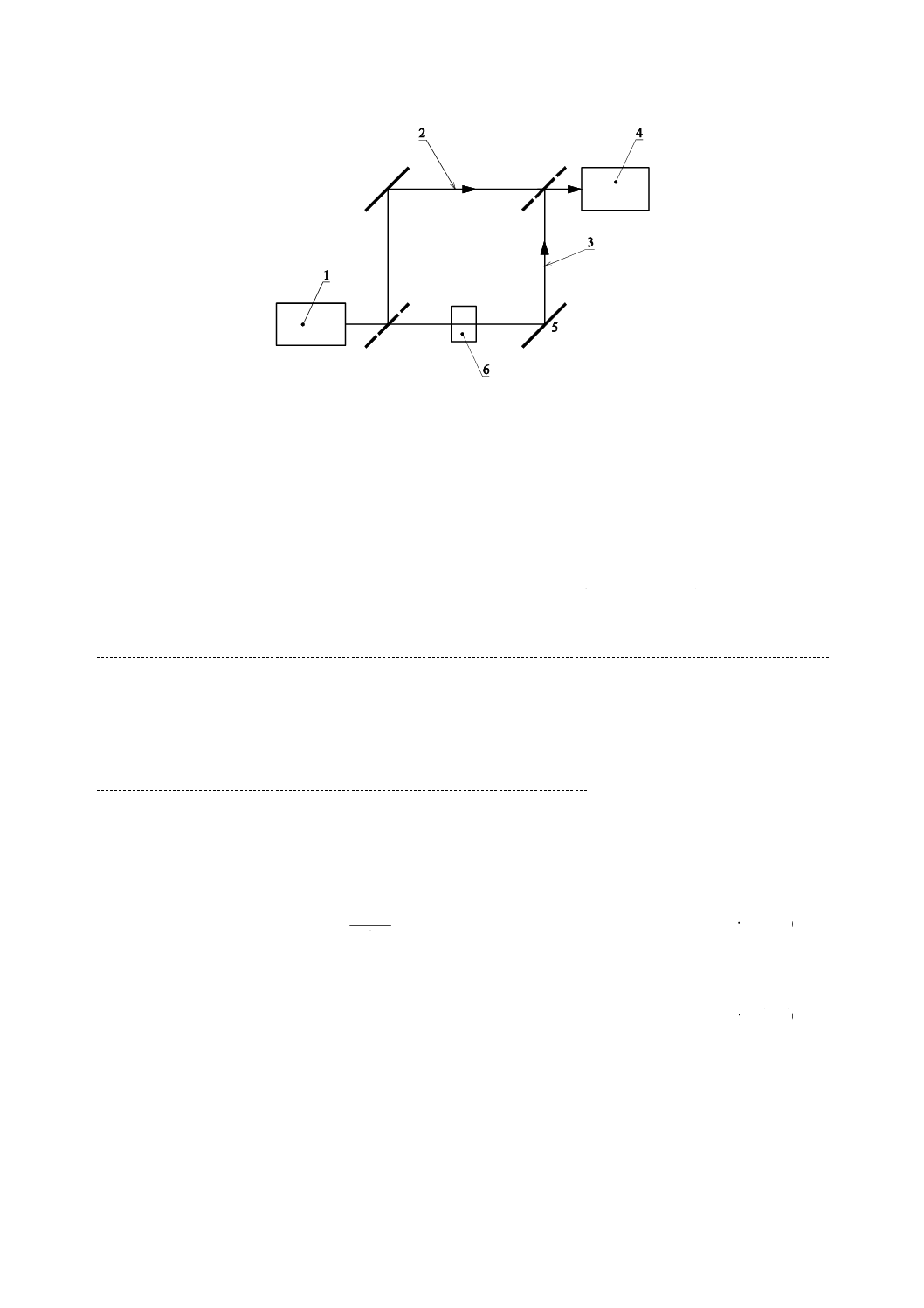
1 光源
2 参照アーム(光路)
3 テストアーム(被検面側の光路)
4 ディテクター
5 ここを押してテストアーム(被検面側の光路)を短くする。
6 被検レンズ
図A.0C−シングルパス干渉計による検査例
A.2.2 チルト(傾き)をもたない干渉図形の解析
他のタイプの波面形状偏差がすべて存在しない場合には,サジッタ偏差は,同心円じまの干渉パターン
を生じる。しまの半径は,干渉図形の中心から数えたしまの本数の平方根に比例して増加する。
ニュートンゲージの場合には,参照面に対し,被検面を参照面側にわずかに近づけたとき,被検面の中
心部分より先に周辺部分が接すると,しまが中心に向かって移動する。また逆に,被検面の周辺部分より
先に中心部分が接すると,しまが外に向かって移動する。干渉計の場合には,干渉計のテストアーム(被
検波面側の光路)を短くなるよう動かすと,被検波面の曲率が参照波面と比較して光を受ける側から見た
ときに凹面であれば,(参照波面に対し被検波面の周辺部分が中心部分より先に近づくので),しまが中心
に向かって移動する。逆に被検波面が参照波面と比較して光を受ける側から見たときに凸面であれば(参
照波面に対し,被検波面の周辺部分が中心部分より遅れているので),しまが外に向かって移動する。
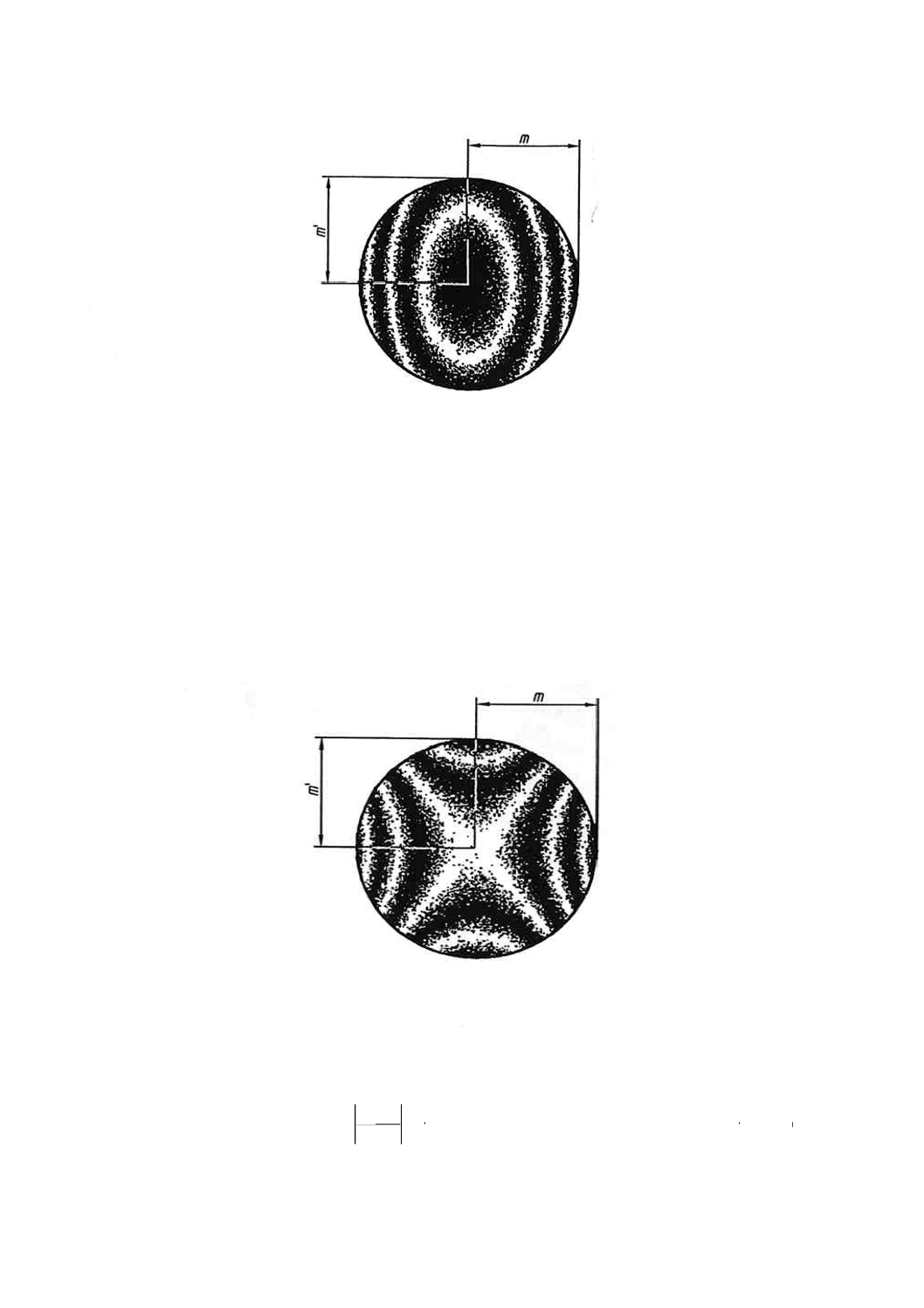
少量の非対称形状が現れると,図A.1のように円がだ円にひずむ。
サジッタ偏差及びイレギュラリティの量の評価は,次のように行う。しまパターンの中央から周辺まで
のしまの本数を数え,その数が最大となる方向のしまの本数をmとし,最小となる方向のしまの本数を
m'とする。だ円じまの場合のサジッタ偏差PV(fWS)は,mとm'との平均で与えられる。
2
)
PV(
WS
m'
m
f
+
=
·································································· (A.1)
だ円じまの場合の波面イレギュラリティPV(fWI)は,mとm'との差の絶対値に等しくなる。これは“アス”
ともいう。
m'
m
f
−
=
)
PV(
WI
·································································· (A.2)
9
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
m=3.0
m'=1.0
図A.1−2本のサジッタ偏差及び2本のイレギュラリティを示す干渉図形の例(例1の評価)
例1 図A.1の光学素子干渉図形で,m及びm'の値は,それぞれ3本と1本である。したがって,サ
ジッタ偏差[式(A.1)]は,(3+1)/2=2本であり,イレギュラリティ[式(A.2)]は,|3−1|=2
本である。
大きな非対称形状が現れた場合,だ円じまは,図A.2のように双曲線じまになる場合がある。この場合
には,被検波面が参照波面に向かって動くとき,一部のしまはパターンの中心に向かって動き,一部のし
まは外に逃げるように動く。
m=2.5
m'=1.5
図A.2−0.5本のサジッタ偏差及び4本のイレギュラリティを示す干渉図形の例(例2の評価)
双曲線じまの場合のサジッタ偏差PV(fWS)は,しまの本数の差の半分に等しい。
2
)
PV(WS
m'
m
f
−
=
································································ (A.3)
双曲線じまの場合のイレギュラリティPV(fWI)は,しまの本数の和で与えられる。

10
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
m'
m
f
+
=
)
PV(
WI
································································· (A.4)
例2 図A.2の光学素子干渉図形で,m及びm'の値は,それぞれ2.5本と1.5本である。したがって,
サジッタ偏差[式(A.3)]は,|2.5−1.5|/2=0.5本であり,イレギュラリティ[式(A.4)]は,2.5
+1.5=4本である。
A.2.3 チルト(傾き)をもったしまパターンの解析
この方法では,干渉じまが二つの異なる方向に向くように被検波面と参照波面との間の傾きを2回調整
して干渉じまを観測する必要がある。
参照面が被検面に対して傾いているとき,しまは図A.3のように現れる。サジッタ誤差だけが存在する
と,しまは同心円の一部として現れる。しまの半径は,しまパターンの見掛けの中心から数えたしまの本
数の平方根に比例して増加する。他のタイプの表面形状偏差が存在すると,しまは同心円の一部ではなく
なる。
a)
b)
m=h/s
m'=h'/s'
矢印:テストアーム(被検面側の光路)を短くするか,又は被検面を参照面側にわずかに移動させたとき,
しまが矢印方向へ移動する。
図A.3−参照面が2方向に向いた場合の0.3本のサジッタ偏差及び
1.8本のイレギュラリティを示す例(例3の評価)
サジッタ偏差及びイレギュラリティを評価するためには,しまの湾曲が最大及び最小となる二つの傾き
方向に対し,しまに平行な断面内の面の湾曲を評価する必要がある[図A.3 a)及び図A.3 b)参照]。各々の
場合において,しまの本数mは,干渉図形の中心に最も近いしまの湾曲hを可能な限り被検領域の中心近
くで測定したしまの間隔sで除した値に等しい。
さらに,(両方向の傾きについて)干渉計のテストアーム(被検面側の光路)を短くしたとき,又は被検
面を参照面側にわずかに移動させたときのしまの移動方向に注意する必要がある。
両方向の傾きについて,しまがしまの見掛け上の曲率半径中心方向に動くとき,又は見掛け上の中心か
ら離れる方向に動くとき,サジッタ偏差はイレギュラリティより大きく,サジッタ偏差及びイレギュラリ
ティの評価には,それぞれ式(A.1)及び式(A.2)を用いる。
テストアーム(被検面側の光路)を短くしたとき,又は被検面を参照面側にわずかに移動させたとき,
一方の傾きの場合の一連のしまが見掛け上の曲率中心に向かって移動し,他方の傾きの場合のしまパター
'

11
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ンが見かけ上の中心から離れるように移動する場合は,イレギュラリティはサジッタ偏差より大きく,サ
ジッタ偏差とイレギュラリティの評価には,それぞれ式(A.3)及び式(A.4)を用いる。
例3 図A.3は,光学素子の傾きによる検査の干渉図形である。図A.3 a)では,テストアーム(被検
面側の光路)を短くしたとき,又は被検面を参照面側にわずかに移動させたとき,しまは見か
けの中心方向へ移動し,図A.3 b)では,見かけの中心から離れる方向へ移動する。このときの
評価には,式(A.3)及び式(A.4)を用いる。図A.3 a)の湾曲hは,しま間隔sの約1.2倍であり,m
=1.2となる。図A.3 b)では,湾曲h'はしま間隔s'の60 %であり,m'=0.6となる。式(A.3)によ
って,サジッタ偏差は0.3本となる。同様に,式(A.4)によってイレギュラリティは1.8本とな
る。
A.2.4 イレギュラリティの異常形
波面形状偏差が,被検領域周辺ではなく被検領域内のある点で最大になることがある。参照波面と被検
波面との間で傾きなしで検査するとき,図A.4に示すように,検査領域の中心に対して同心ではない閉じ
た一連のしまになることがある。このような場合は,干渉計のテストアーム(被検面側の光路)を短くし
たとき,又は被検面を参照面側にわずかに移動させたとき,どのしま群が中心から離れ,どのしま群が中
心方向に移動するかに注意する必要がある。中心方向へ移動するしまは“正”,他は“負”とみなす。
矢印:移動方向
図A.4−干渉計のテストアーム(被検面側の光路)を短くしたとき,又は被検面を参照面側に
わずかに移動させたときの,しまの移動方向を示す異常なしまパターンの例(例4の評価)
例4 サジッタ偏差は,式(A.1)によって求める。ここに,m及びm'は二つの代表的な方向で測定され
たしまの本数の加算数を表す。図A.4の縦断面において,負方向に4本,続いて正方向に4本
のしまが存在する。したがって,mは0となる。横方向においては,二つの負と二つの正のし
まの本数があり,やはりm'=0である。したがって,式(A.1)からサジッタ誤差は,(0+0)/2=0
となる。
イレギュラリティは,しまの半径がしまの本数の平方根に比例して大きくなる同心円となるような理論
的に予測されるしまパターンからの最大外れ及び最小外れを見いだすことによって求める。イレギュラリ
ティはしまの本数単位で測定したその最大外れと最小外れとの絶対値の和である。図A.4のパターンに対
しては,サジッタ偏差0本であるので,理論的に期待されるしまパターンは0本である。これらの最小外
れは,外側の二つの卵形パターンの中心で−4本,最大外れは0本である。したがって,式(A.2)からイレ
ギュラリティは,|0|+|−4|=4本となる。

12
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
A.3 回転対称なイレギュラリティの評価
視覚的方法によるこの偏差の評価は,他のタイプの波面形状偏差が大きいときには困難である。そのた
めに,干渉図形解析はデジタル的方法によって行うことを推奨する。回転対称なイレギュラリティは“ク
セ”ともいう。
被検波面と参照波面との間に傾きが存在しなければ,しまパターンは同心円として現れるが,その半径
はサジッタ偏差の場合とは異なり,しまの本数の平方根に比例しては増加しない。この性質を視覚的に観
察するのは難しく,偏差が小さく,不正確になる。したがって,このタイプの波面形状の評価は傾きが存
在するときに限って実用的である。
傾きが存在する場合,しまは傾きの方向によって,W字又はM字形状になる。サジッタ偏差が存在し
なければ,しまパターンの中心に最も近いしまの両端と中心は直線で結ぶことができる。この場合には,
イレギュラリティはしまパターンにおけるしまの直線からの偏差として示される。波面にサジッタ偏差が
含まれている場合には,しまは図A.5に示すように曲がっており,イレギュラリティは中央じまの中心と
両端を結ぶ円弧からのしまの偏差とみなすことができる。
図A.5−0.3本の回転対称なイレギュラリティを示すしまパターンの例(例5の評価)
イレギュラリティは,円弧からのしまの最大偏差hをしま間隔sで除した量に等しい。最大偏差hは,
しまとの最大ずれ位置で円弧に垂直に計測する。
回転対称なイレギュラリティPV(fWRI)は,式(A.5)によって求める。
s
h
f
=
)
PV(
WRI
········································································ (A.5)
例5 図A.5において,中央部のしまの円弧からの偏差hは,しま間隔sの30 %である。したがって,
回転対称なイレギュラリティは0.3本となる[式(A.5)による]。
波面形状が回転対称である程度は,しまが別の方向に対して向くように傾きを調節し,検査を繰り返す
ことによって観察できる。しまの乱れ方がすべてのしま方向に対して同じであれば,波面の形状は回転対
称である。回転対称なイレギュラリティは,すべてのしま方向に対して同じで変らない偏差の一部である。
A.4 非円形被検領域
サジッタ偏差の定義(3.3.1参照)によると,サジッタ偏差は,被検波面を最もよく近似できる球面波を
基にしている。視覚的な解析方法を用いるとき,波面の球面近似(3.2.4参照)は,波面イレギュラリティ
13
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(3.2.5参照)が被検領域の境界周辺に均等に分布するように選んでもよい。これは,m及びm′を測定する
2断面方向の被検領域の大きさを考慮して計算しなければならない場合を別として,サジッタ偏差及びイ
レギュラリティは,A.2で示した方法と類似の方法で評価しなければならないことを意味している。
この方法は,波面形状が単純な形(すなわち,x,yについて2次のもの)に対してはおおむね正確であ
る。より複雑な形の正確な評価には,デジタル的な方法を用いる必要がある。
非円形被検領域に対しては,被検領域の“中心”はその図心(“重心”)を指しており,その“半径”は,
中心から被検領域のうちで最も遠い点までの距離に等しい。
断面湾曲m及びm'は,傾きがある場合とない場合との記述を適宜使用し,A.2と同様の方法で決定する。
m及びm'を決定する方向は,波面形状の対称性によって決まる。これらの方向は,必ずしも被検領域の
形状に関係しない。
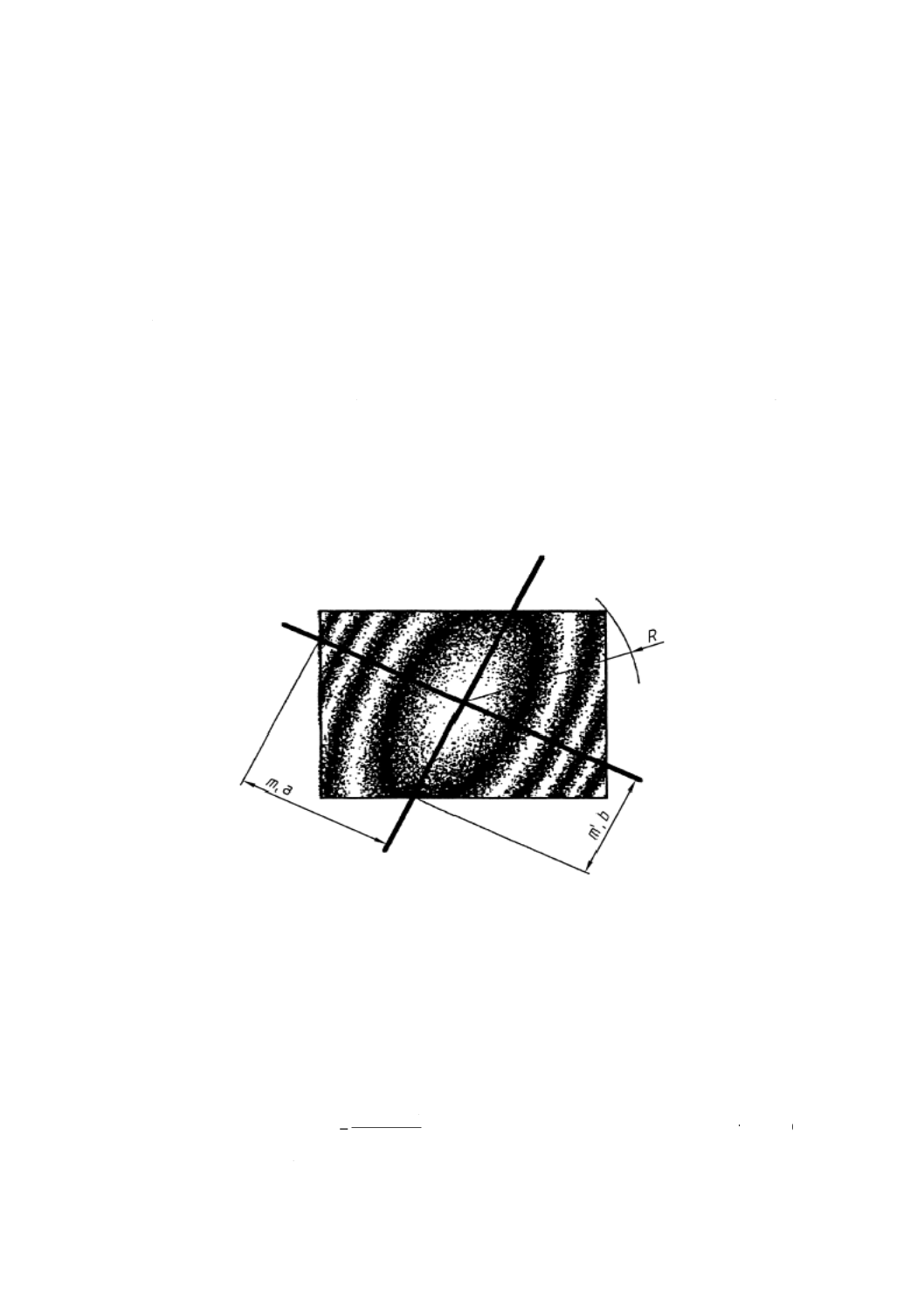
m及びm′は,図A.6に示すような被検領域の中心から周縁までの,対称性をもつ2方向の断面湾曲とす
る。aは,湾曲mが測定される方向での被検領域の中心から周縁までの距離とする。同様にbは,湾曲m'
が測定される方向での被検域の中心から周縁までの距離とする。また,Rは上記で定義した被検領域の半
径とする。
R
36 mm
m
3.6
a
33 mm
m'
0.4
b
23 mm
図A.6−サジッタ偏差3.2本,イレギュラリティ2.2本を
もつ非円形被検領域の干渉図形の例(例6の評価)
だ円じま,かつ,非円形被検領域の場合,サジッタ偏差PV(fWS)は,式(A.6)によって求める。
2
2
2
WS
)
(
)
PV(
b
a
m
m
R
f
+
′
+
=
······························································· (A.6)
だ円じま,かつ,非円形被検領域の場合,イレギュラリティPV(fWI)は,式(A.7)によって求める。
14
B 0091:2010 (ISO 14999-4:2007)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
)
(
)
(
2
)
PV(
2
2
2
2
2
2
WI
b
a
a
m
b
m
a
R
f
+
−
′
=
························································ (A.7)
例6 図A.6では,それぞれ33 mmと23 mmとの範囲で測定されるm及びm′の値は,3.6本及び0.4
本である。被検領域の半径は36 mmである。式(A.6)及び式(A.7)の結果は,それぞれ3.2本,2.16
本である。このようにして,サジッタ偏差とイレギュラリティは,3.2本と2.16本であること
が分かる。
双曲線じまの場合,サジッタ偏差PV(fWS)は,式(A.8)によって求める。
2
2
2
WS
)
(
)
PV(
b
a
m
m
R
f
+
′
−
=
······························································· (A.8)
双曲線じまの場合,イレギュラリティPV(fWI)は,式(A.9)によって求める。
)
(
)
(
2
)
PV(
2
2
2
2
2
2
WI
b
a
a
m
b
m
a
R
f
+
+
′
=
························································· (A.9)
参照波面と被検波面との間に傾きが存在する場合には,(両方向の傾きに対し)干渉計のテストアーム
(被検面側の光路)が短くなるとき,又は被検面を参照面側にわずかに移動させたときのしまの移動方向
に注意する必要がある。
両方向の傾きに対し,しまがしまパターンの見掛け上の中心に向かって動く場合,又は,その中心から
離れるように動く場合,サジッタ偏差はイレギュラリティより大きく,サジッタ偏差及びイレギュラリテ
ィの評価に式(A.6)及び式(A.7)を用いる。
一方の傾きの場合の一連のしまが見掛け上の中心に向かって動き,他方の傾きの場合のしまパターンが
見掛け上の中心から離れるように動く場合,イレギュラリティがサジッタ偏差より大きく,サジッタ偏差
とイレギュラリティの評価に式(A.8)及び式(A.9)を用いる。
A.5 目標収差
目標収差が明記されているときには,干渉図形の視覚による解析は,困難であり推奨しない。通常,目
標収差に一致する干渉じまパターンを描画するか,又はそうでなければ生成し,これと実際の干渉図形と
の違いを検査することは可能である。しかし,実際の干渉図形の視覚的外観は,傾きが存在するときには大
きさと方向に依存する。同様に,しばしば大きな許容誤差をもっている参照球面の半径の正確な選択は,
干渉じまの視覚的外観に影響を及ぼす。このような理由から,実際の干渉図形が比較できる理論的干渉パ
ターンの正確な生成は,一般的に不可能である。この場合,デジタル解析技術を用いることによってだけ,
正確な評価を得ることができる。
参考文献 [1] Malacara, D. (ed.), Optical shop testing, Wiley, New York, 2nd edition 1992.







