4
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
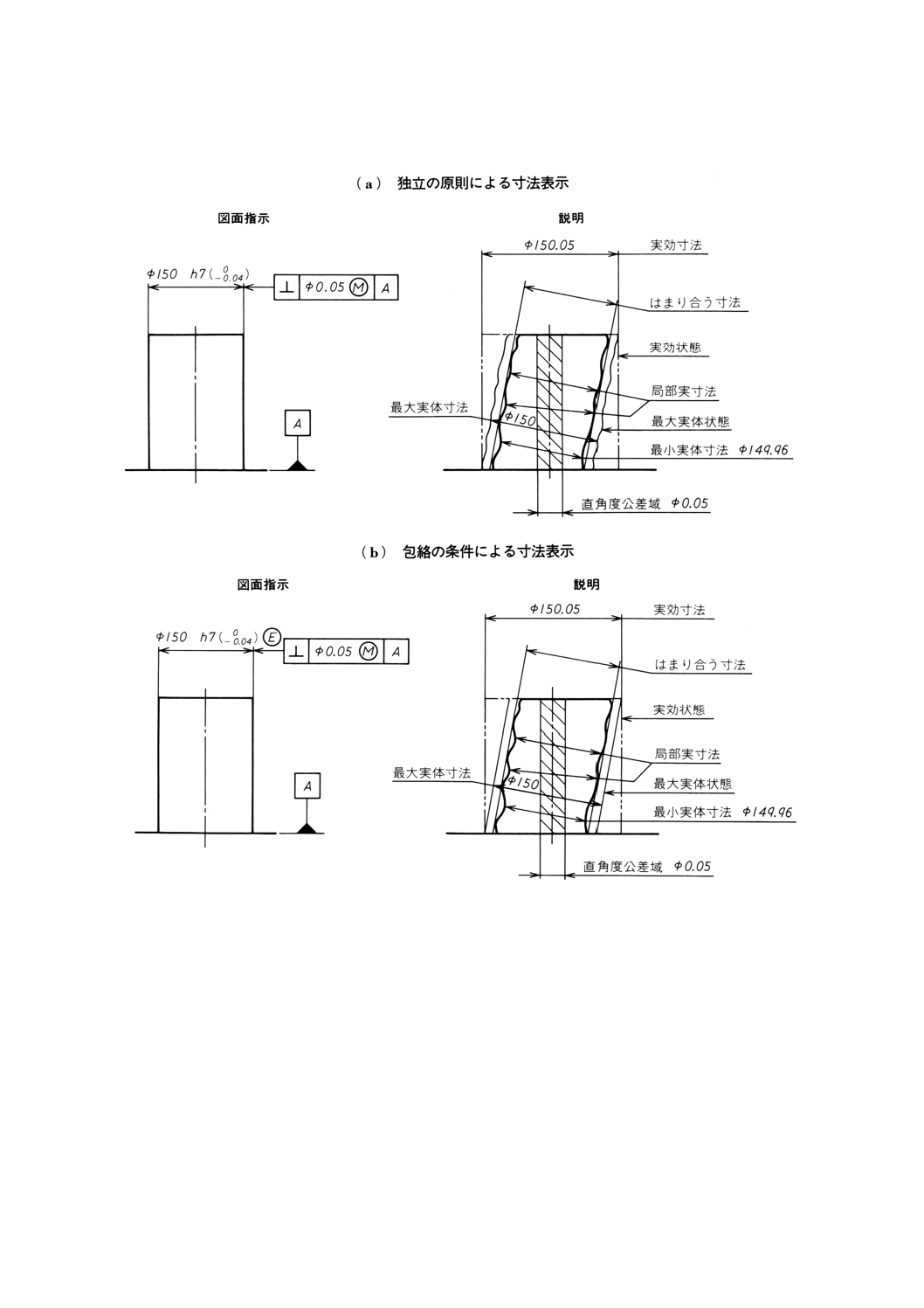
図1
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
B 0023-1996
製図−幾何公差表示方式−
最大実体公差方式及び最小実体公差方式
Technical drawings−Geometrical tolerancing−
Maximum material requirement and least material requirement
日本工業規格としてのまえがき
この規格は,1988年第1版として発行されたISO 2692 (Technical drawings−Geometrical tolerancing−
Maximum material principle) 及び1992年に発行されたISO 2692追加版1 (Technical drawings−Geometrical
tolerancing−Maximum material principle Amendment 1 : Least material requirement) を翻訳して,前者を第1部,
後者を第2部とし,技術的内容を変更することなく作成した日本工業規格である。
なお,この規格の中で点線の下線を施してある箇所は,原国際規格の規定内容を変更した事項又は原国際
規格にはない事項である。
第1部 最大実体公差方式
0. 序文
0.1
二つのフランジのボルト穴とそれらを締め付けるボルトとのように,部品の組立は,互いにはめ合
わされる形体の実寸法と実際の幾何偏差との間の関係に依存する。
組み付ける形体のそれぞれがその最大実体寸法(例えば,最大許容限界寸法の軸及び最小許容限界寸法
の穴)であり,かつ,それらの幾何偏差(例えば,位置偏差)も最大であるときに,組立すきまは最小に
なる。
組み付けられた形体の実寸法がそれらの最大実体寸法から最も離れ(例えば,最小許容限界寸法の軸及
び最大許容限界寸法の穴),かつ,それらの幾何偏差(例えば,位置偏差)がゼロのときに,組立すきまは
最大になる。
以上から,はまり合う部品の実寸法が両許容限界寸法内で,それらの最大実体寸法にない場合には,指
示した幾何公差を増加させても組立に支障をきたすことはない。
これを“最大実体公差方式”といい,記号◯
Mによって図面上に指示する。
この規格の中の図は,最大実体公差方式の理解を助けるためにだけ示すものであり,寸法及び公差の値
は,説明の目的のためにだけ示してある。
さらに,簡略化のために,図示例は単純形状を用いている。
0.2
この規格のすべての図は,統一するために,第三角法で示す。
参考 ISO 2692では,すべての図を第一角法で示している。
第一角法による場合にも,規定された原則を損なうことなく,そのまま使用できるものと理解するのが
2
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
よい。
幾何公差表示方式に使用する記号(字体及び寸法)の一義性を図るために,ISO 7083を参照されたい。
参考 ISO 7083の内容については,JIS B 0021を参照のこと。
1. 適用範囲 この規格は,最大実体公差方式及びその適用について規定する。
最大実体公差方式の使用は,寸法公差と幾何公差とが相互に依存する部品同士の組付けを妨げることな
く,製造を容易にすることができる。
備考 単独形体に用いる包絡の条件(5.2.2参照)は,記号◯
Eによって指示しても(JIS B 0024参照),
包絡の条件を規定する適切な国家規格を引用して指示してもよい。
2. 引用規格
ISO 1101 Technical drawings−Geometrical tolerancing−Tolerancing of form, orientation, location and
run-out−Generalities, definitions, symbols, indications on drawings
参考 JIS B 0021-1984(幾何公差の図示方法)が,この国際規格と同等である。
ISO 5458 Technical drawings−Geometrical tolerancing−Positional tolerancing
備考 JIS B 0025-1991(製図−幾何公差表示方式−位置度公差方式)が,この国際規格と一致して
いる。
ISO 5459 Technical drawings−Geometrical tolerancing−Datums and datum-systems for geometrical
tolerances
参考 JIS B 0022-1984(幾何公差のためのデータム)が,この国際規格と同等である。
ISO/TR 5460 Technical drawings−Geometrical tolerancing−Tolerancing of form, orientation, location and
run-out−Verification principles and methods−Guidelines
参考 JIS B 0021の参考を参照のこと。
ISO 7083 Technical drawings−Symbols for geometrical tolerancing−Proportions and dimensions
ISO 8015 Technical drawings−Fundamental tolerancing principle
備考 JIS B 0024-1988(製図−公差表示方式の基本原則)が,この規格と一致している。
3. 定義
3.1
局部実寸法 形体の任意の断面における個々の距離,すなわち,任意の相対する2点間で測定した
寸法[図1,図12(b)及び図13(b)参照]。
3.2
はまり合う寸法
3.2.1
外側形体のはまり合う寸法 形体の表面の最も高い点で接触して,その形体に外接する最小の完全
形体の寸法。
備考 例えば,表面の最も高い点に接触する,完全形状の最小円筒の寸法,又は完全形状の二つの平
行平面間の最短距離(図1参照)。
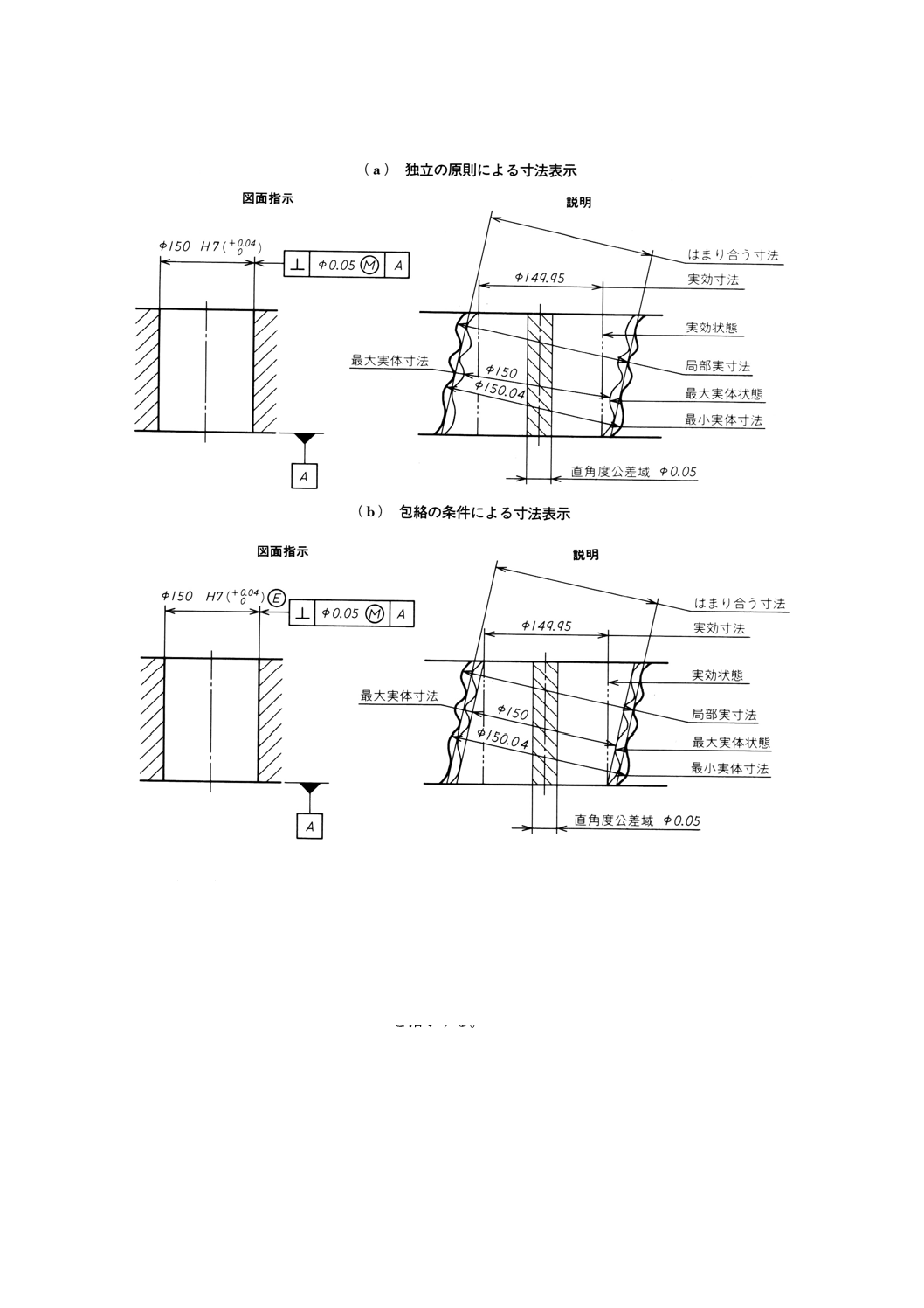
3.2.2
内側形体のはまり合う寸法 形体の表面の最も高い点で接触して,その形体に内接する最大の完全
形体の寸法(参考図1参照)。
備考 例えば,表面の最も高い点に接触する,完全形状の最大円筒の寸法,又は完全形状の二つの平
行平面間の最長距離(図1及び参考図1参照)。
3
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.3
最大実体状態 (maximum material condition) (MMC) 形体のどこにおいても,その形体の実体が最大
となるような許容限界寸法,例えば,最小の穴径,最大の軸径をもつ形体の状態(図1参照)。
備考 形体の軸線は,真直である必要はない。
3.4
最大実体寸法 (maximum material size) (MMS) 形体の最大実体状態を決める寸法(図1参照)。
3.5
最小実体状態 (least material condition) (LMC) 形体のどこにおいても,その形体の実体が最小とな
るような許容限界寸法,例えば,最大の穴径,最小の軸径をもつ形体の状態(図1参照)。
3.6
最小実体寸法 (least material size) (LMS) 形体の最小実体状態を決める寸法(図1参照)。
3.7
実効状態 (virtual condition) (VC) 図面指示によってその形体に許容される完全形状の限界であり,
この状態は,最大実体寸法と幾何公差との総合効果によって生じる。
最大実体公差方式を適用する場合には,記号◯
Mを付記した幾何公差にだけ実効状態を考慮しなければな
らない(図1参照)。
参考 穴については,参考図1を参照。
備考 実効状態は,機能ゲージ (functional gauge) の理論的な設計寸法を表す。
3.8
実効寸法 (VS) 形体の実効状態を決める寸法。

4
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図1
5
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
参考図1
4. 最大実体公差方式
4.1
一般 最大実体公差方式は,公差付き形体に対する実効状態を越えないことを,そして,もしデー
タムに対しても指示されるならば,データム形体に対する完全形状の最大実体状態を越えないことを要求
する公差方式である。
この公差方式は,軸線又は中心平面に適用し,寸法と幾何公差との間の相互依存関係を考慮している。
この公差方式を適用する場合には,記号◯
Mを指示する。
4.2 公差付き形体への最大実体公差方式の適用 最大実体公差方式を公差付き形体に適用する場合には,
対象とする公差付き形体が両許容限界寸法内でその最大実体状態から離れていると,形体が実効状態を越
えないという条件で,指示した幾何公差を増加させることができる。
6
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4.3 データム形体への最大実体公差方式の適用 最大実体公差方式をデータム形体に適用する場合には,
データム軸直線又は中心平面は,データム形体が両許容限界寸法内で最大実体状態から離れていると,公
差付き形体に関連して浮動 (floating) してもよい。浮動の値は,その最大実体寸法とデータム形体のはま
り合う寸法との差に等しい[図27(b)及び図27(c)参照]。
備考 データム形体がその最大実体寸法から離れた寸法分は,関連する公差付き形体の公差に加えな
い。
5. 最大実体公差方式の適用 設計者は,常に対象とする公差に最大実体公差方式の適用ができるかどう
かを決めなければならない。
備考 運動学的リンク機構,歯車中心,ねじ穴,しまりばめの穴など,公差を増加することによって
機能が損なわれる場合には,最大実体公差方式を適用しないほうがよい。
5.1
一群の穴に対する位置度公差 最大実体公差方式は,位置度公差とともに用いるのが最も一般的で
あるので,この項における説明のために位置度公差方式を用いる。
備考 実効寸法の計算には,ピン及び穴が最大実体寸法であり,かつ,完全形状であると仮定する。
5.1.1
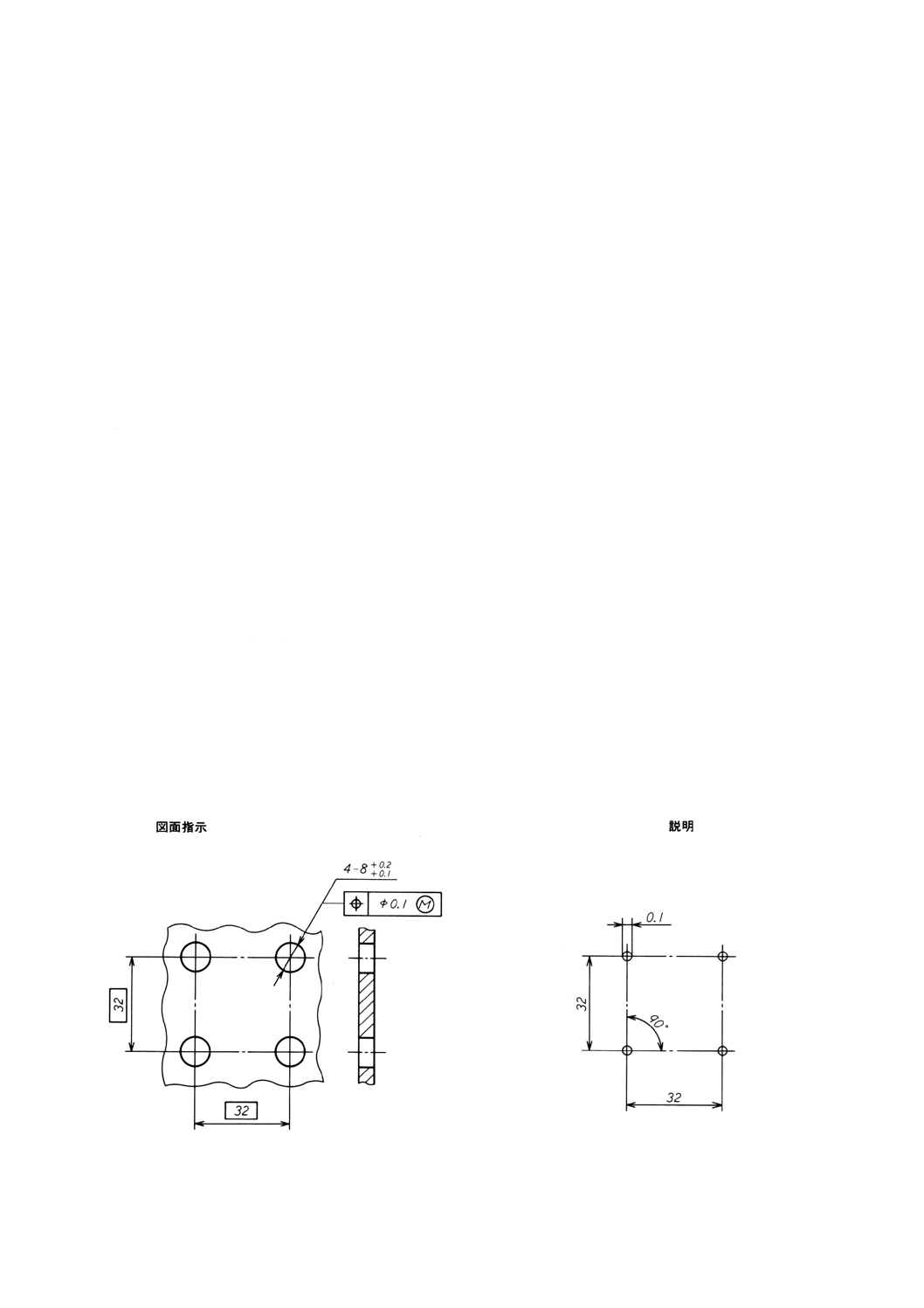
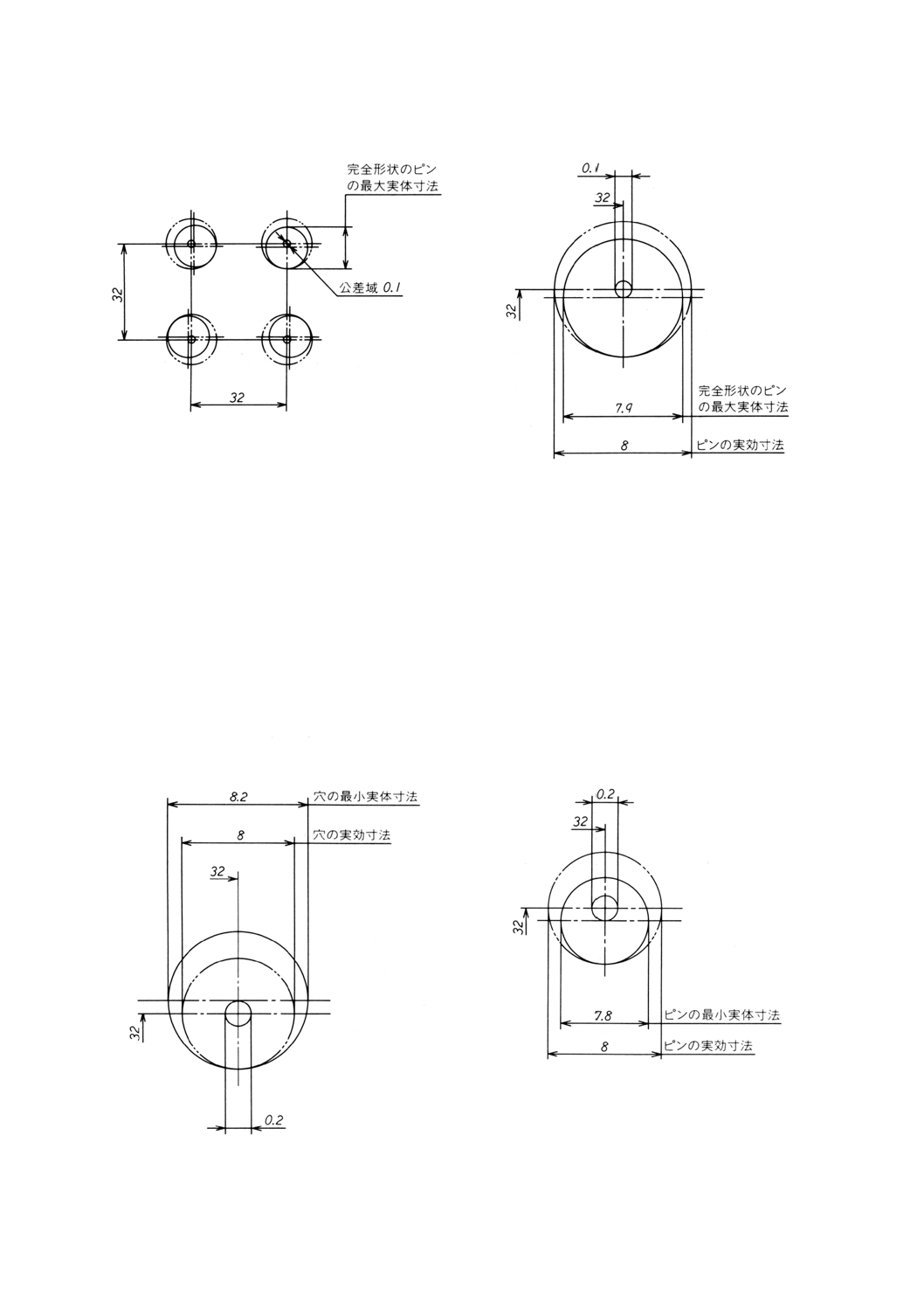
一群の四つの穴に対する位置度公差の図面指示を図2に示す。
この穴のグループにはまり合う一群の四つの固定ピンのグループに対する位置度公差の図面指示を図4
に示す。
四つの穴の最小寸法はφ8.1であり,これは最大実体寸法である。
四つのピンの最大寸法はφ7.9であり,これは最大実体寸法である。
5.1.2
穴及びピンの最大実体寸法の差は,8.1−7.9=0.2である。
穴及びピンに対する位置度公差の合計は,この差 (0.2) を超えてはならない。この例において,この公
差は,穴及びピンに等しく配分される。すなわち,穴に対する位置度公差はφ0.1であり(図2参照),そ
してピンに対する位置度公差はφ0.1である(図4参照)。
φ0.1の公差域は,それらの理論的に正確な位置に置かれる(図3及び図5参照)。
位置度公差の増加は,個々の形体の実寸法に依存するので,個々の形体で異なってよい。
図2
図3
7
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
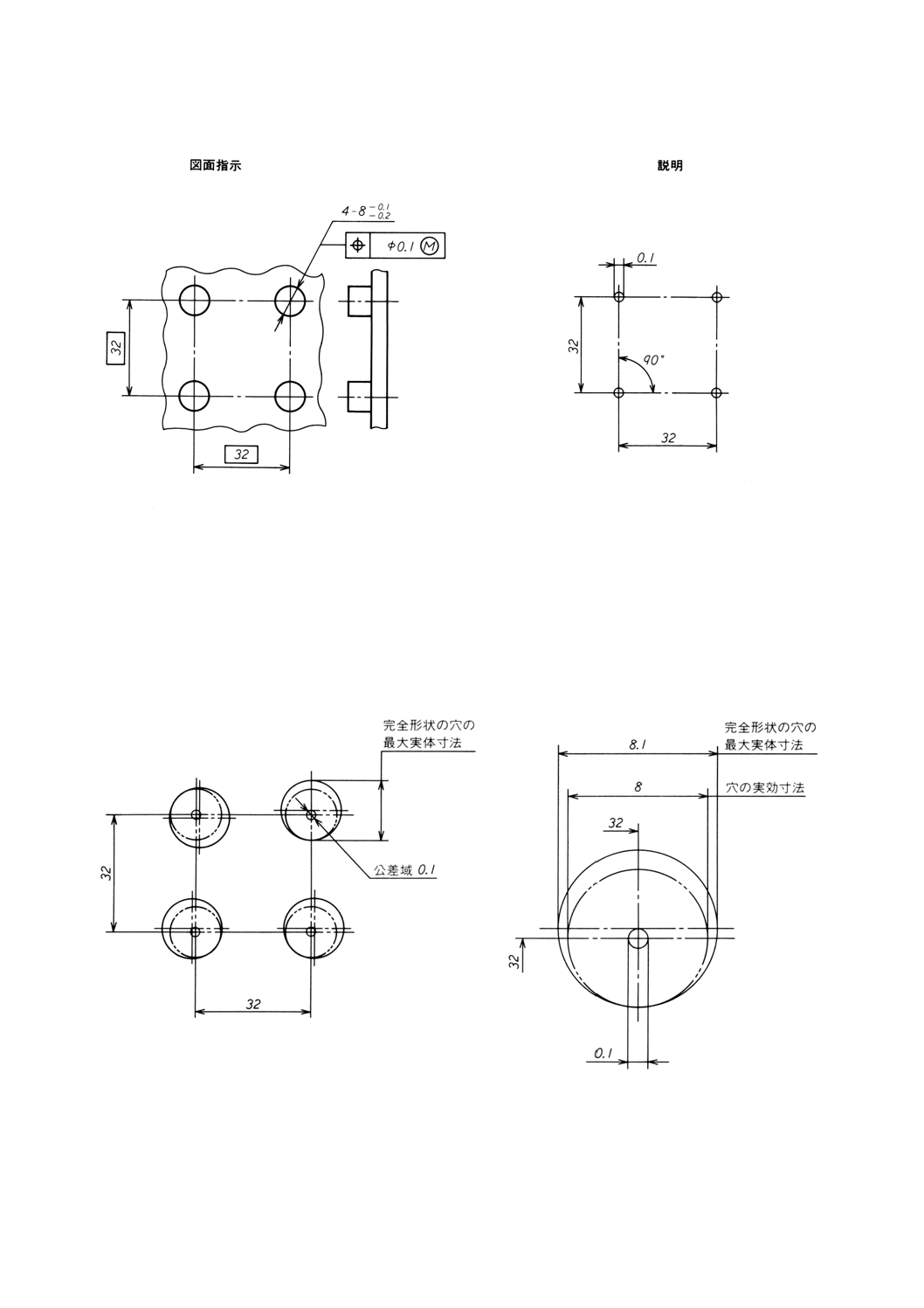
図4
図5
5.1.3
図6は,それらのすべてが最大実体寸法であり,かつ,完全形状である四つの穴の円筒面を示す。
その軸線は,公差域内で極限の位置にある。
図8は,最大実体寸法にある対応するピンを示す。部品の組付けが最も好ましくない状態のもとで可能
であるということが図6〜9から分かる。
5.1.3.1
図6の穴の一つを図7に拡大して示す。軸線に対する公差域は,φ0.1である。穴の最大実体寸法
は,φ8.1である。φ8.1のすべての円の軸線は,φ0.1の公差域の極限の位置にあり,φ8の内接する包絡円筒
を形成している。このφ8に内接する包絡円筒は,理論的に正確な位置にあり,穴の表面に対して機能上の
境界を形成する。
図6
図7
5.1.3.2
図8のピンの一つを図9に拡大して示す。軸線に対する公差域は,φ0.1である。ピンの最大実体
寸法は,φ7.9である。φ7.9のすべての円筒の軸線は,φ0.1の公差域の極限の位置にあり,φ8の外接する包
絡円筒を形成している。このφ8の外接する包絡円筒は,ピンの実効状態である。
8
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図8
図9
5.1.4
穴の寸法がその最大実体寸法よりも大きいとき,ピンの寸法がその最大実体寸法よりも小さいとき
に生じるすきまは,ピン・穴の位置度公差を増やすために使用される。ピンと穴との間にすきまが増加し,
個々の形体の実寸法によって,位置度公差の増加分はそれぞれ異なってもよい。
極限状態は,穴が最小実体寸法,すなわち,φ8.2のときである。図10は,穴の表面が実効寸法の円筒
を越えなければ,その穴の軸線はφ0.2の公差域内にあればよいことを示している。
図11は,ピンに関して同様の内容を示している。ピンが最小実体寸法,すなわち,φ7.8であるときに,
位置度公差の公差域の直径は,φ0.2である。
5.1.5
幾何公差の増加は,はまり合う相手部品に関係なく組付けの一つの部品に対して適用される。はま
り合う相手部品が組付けに最も不利な方向に,公差の極限の値で製作されたときでも,常に組付けは可能
である。なぜならば,はまり合う双方の部品のいずれも寸法と幾何公差との複合した公差を超えない,す
なわち,それらの実効状態を越えないからである。
図10
図11
9
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
5.2
データム平面に関連する軸の直角度公差
5.2.1
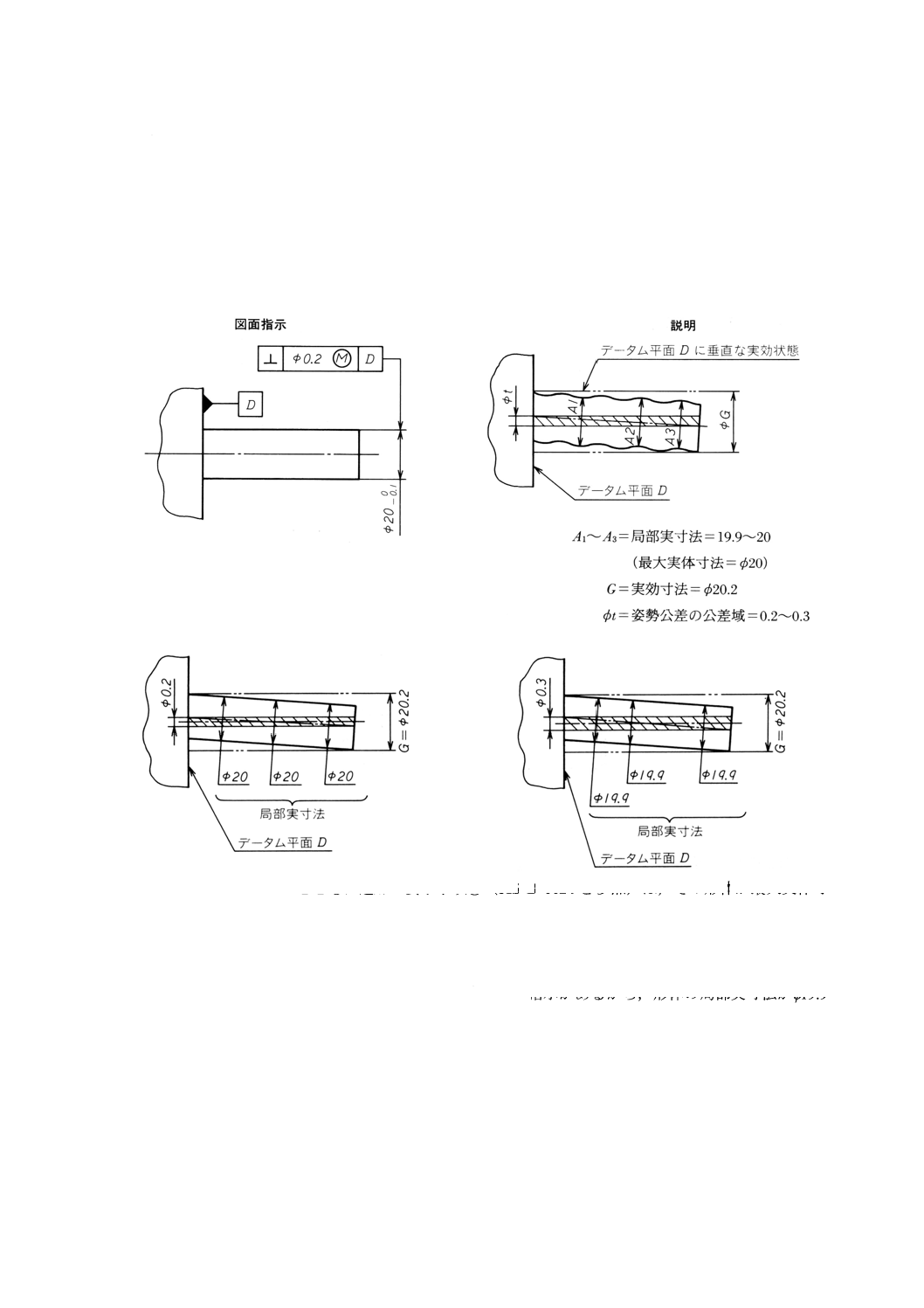
図12(a)の公差付き形体は,図12(b)に示す状態を満たさなければならない。すなわち,形体は実効
状態,φ20.2 (φ20+0.2) を超えてはならない。さらに,すべての局部実寸法はφ19.9とφ20との間にあり,
母線又は軸線の真直度は局部実寸法に応じて,0.2…0.3を超えることはできない。例えば,すべての局部
実寸法がφ20であれば,真直度は0.2[図12(c)参照],すべての局部実寸法がφ19.9であれば,真直度は0.3
[図12(d)参照]である。
図12(a)
図12(b)
図12(c)
図12(d)
5.2.2
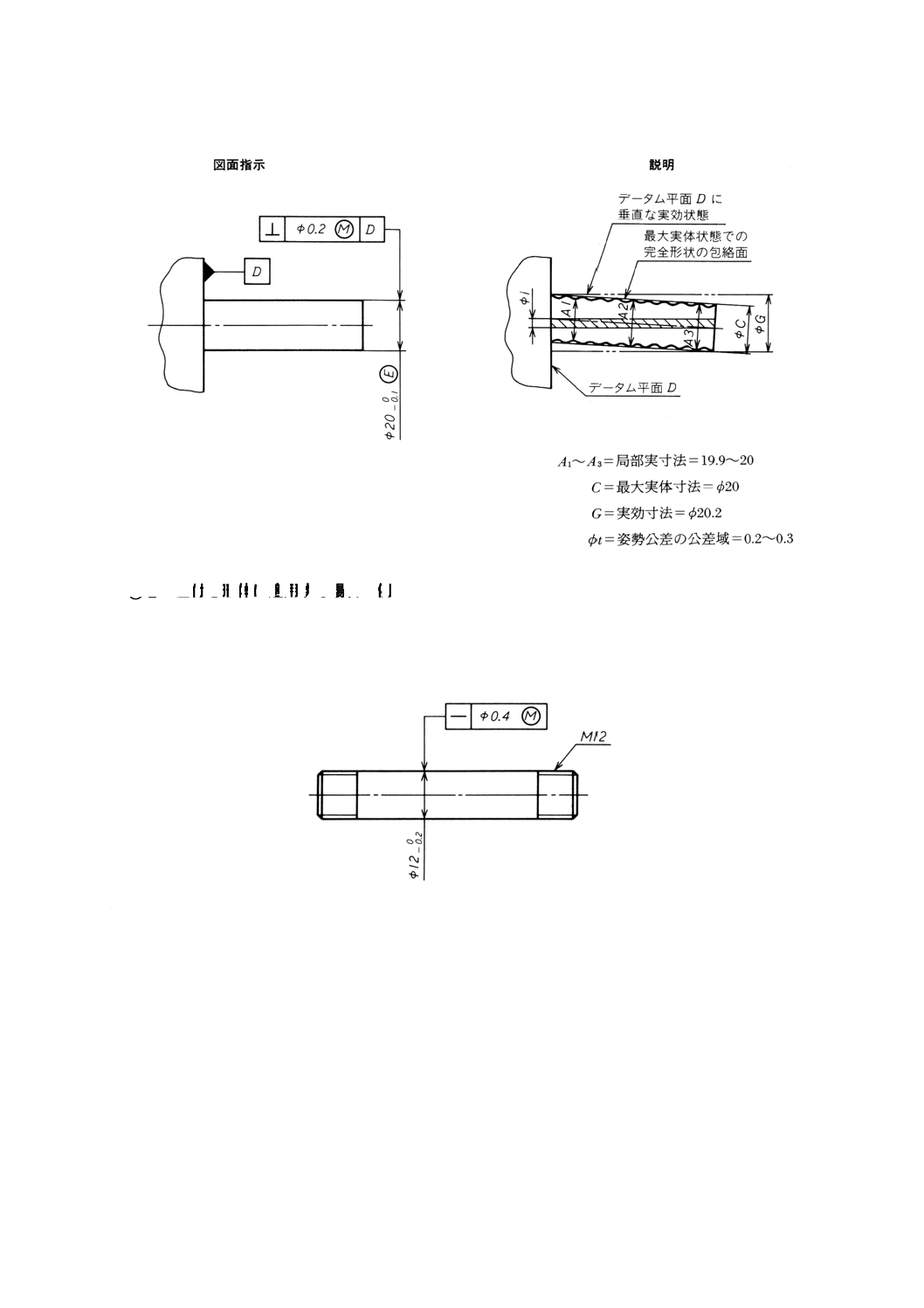
図13(a)において,◯
Mとともに追加の要求事項◯
E(JIS B 0024を参照)は,その形体が最大実体寸
法φ20[図13(b)]で完全形状の包絡面内になければならないことを要求している。この例において,局部
実寸法は,φ19.9とφ20との間になければならず,かつ,真直度と真円度との複合された効果によって得ら
れた形体は包絡の条件を侵害することはない。例えば,母線又は軸線の真直度は,局部実寸法に応じて,0
…0.1を超えることはできない。しかしながら,直角度は,◯
M指示があるから,形体の局部実寸法がφ19.9
であるときには[図13(b)参照],0.3(実効寸法=φ20.2)に増加させてもよい[図13(b)参照]。
10
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図13(a)
>
図13(b)
6. ◯
Mを公差付き形体に適用する場合の例
6.1
軸線の真直度公差
(a) 図面指示
図14(a)
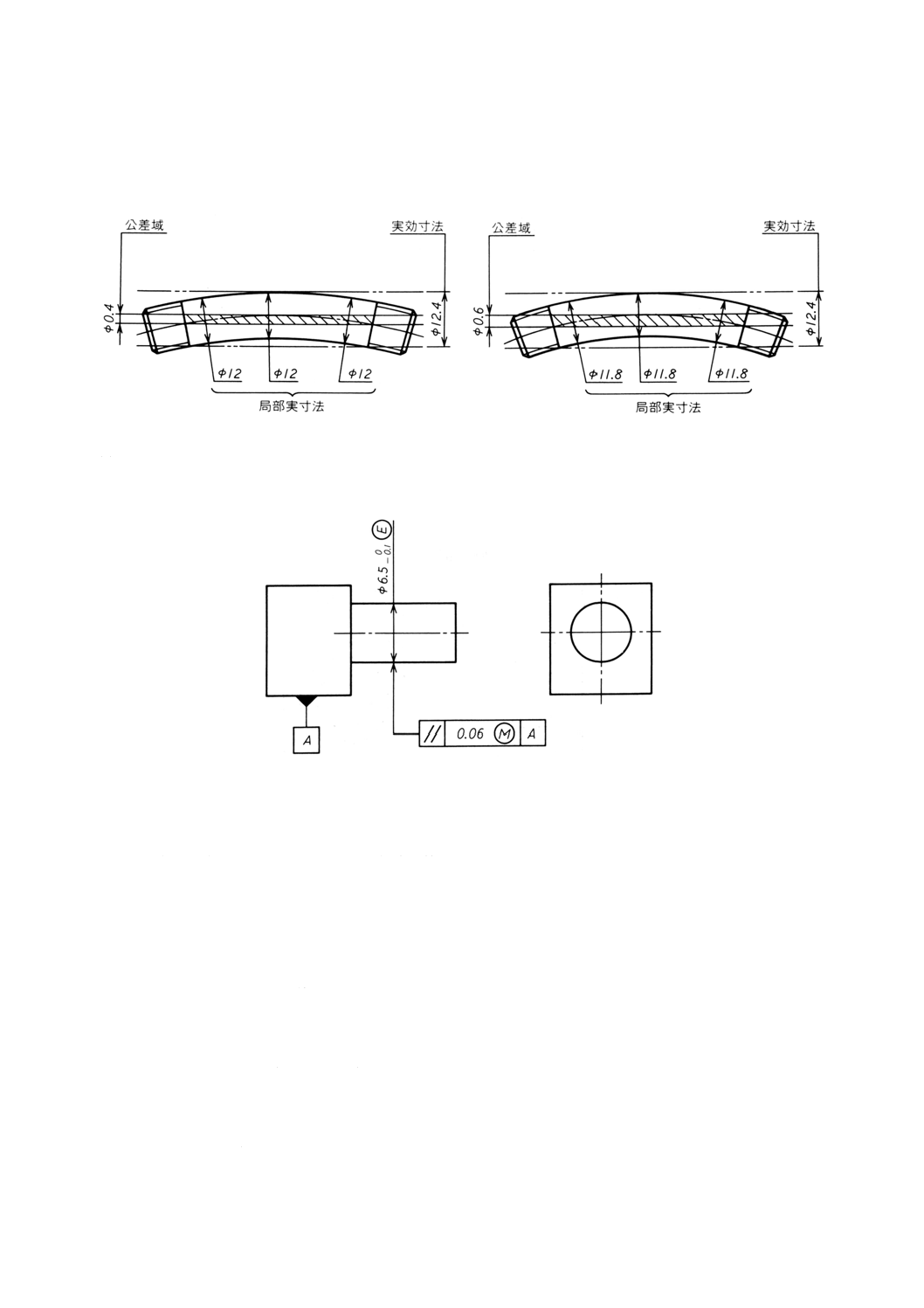
(b) 機能上の要求事項 公差付き形体は,次の要求事項を満たさなければならない。
− 形体の個々の局部実寸法は,0.2の寸法公差内になければならず,したがって,φ12とφ11.8との間
を変動してもよい。
− 公差付き形体は,実効状態,すなわち,φ12.4 (=φ12+φ0.4) の完全形状の包絡円筒内になければな
らない[図14(b)及び図14(c)参照]。
したがって,軸線は,形体のすべての直径が最大実体寸法φ12であるときには,φ0.4の真直度公差の公
差域内になければならないが[図14(b)参照],形体のすべての寸法が最小実体寸法φ11.8であるときには,
φ0.6の公差域内で変動してもよい[図14(c)参照]。
備考1. 図14(b)及び図14(c)は,形体の寸法の極限の場合を説明している。実際には,形体は異なった
局部実寸法をもち,極限状態の間のどこかにある。
11
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
2. この指示[図14(a)参照]は,直径公差が大きくて,包絡の条件が適用できない場合に適して
いる。例えば,ボルトの場合である。
図14(b)
図14(c)
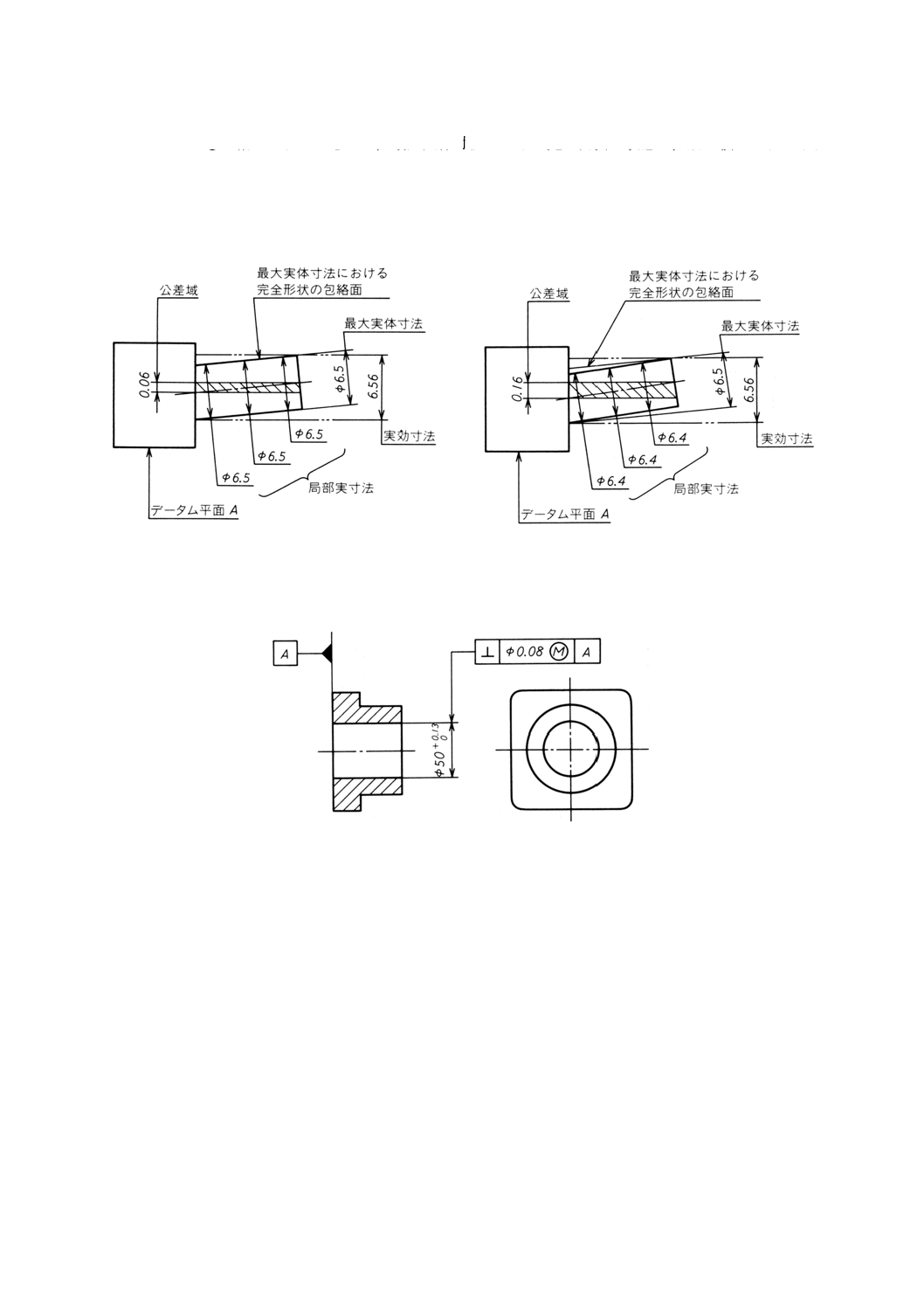
6.2
データム平面に関連する軸の平行度公差
(a) 図面指示
図15(a)
(b) 機能上の要求事項 公差付き形体は,次の要求事項を満たさなければならない。
− 形体の個々の局部実寸法は,0.1の公差内になければならず,したがって,φ6.5とφ6.4との間を変
動してもよい。
− 全体の形体は,φ6.5の完全形状の包絡円筒の境界内になければならない。
− 公差付き形体は,データム平面Aに平行で,6.56 (=6.5+0.06) 離れた2平行平面によって設定され
た実効状態内になければならない[図15(b)及び図15(c)参照]。
したがって,形体のすべての直径がφ6.5の最大実体寸法であるときには[図15(b)参照],軸線はデータ
ム平面Aに平行で,0.06離れた2平行平面の間になければならないが,形体のすべての直径がφ6.4の最小
実体寸法であるときには,軸線は0.16(2平行平面の間の距離)までの公差域内で変動してもよい[図15(c)
参照]。
備考1. データム平面に対する軸線の平行度公差の場合には,公差域は2平行平面の間で,円筒公差域
ではない領域になければならない。
2. 平行度公差の公差域が2平行平面の間の領域にあるときには,実効状態は2平行平面の間の
領域である。それらの間の距離は,最大実体寸法6.5と平行度公差0.06との和,すなわち,
6.56である。
12
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
◯
Eが指示されたときには,最大実体寸法における完全円筒の状態は,別に検査されなけれ
ばならない。
3. 図15(b)及び図15(c)は,形体が理論的に正確な形状を示したものであり,実際には,形体は
異なった局部実寸法をもつ極限の状態の間のどこかにある。
図15(b)
図15(c)
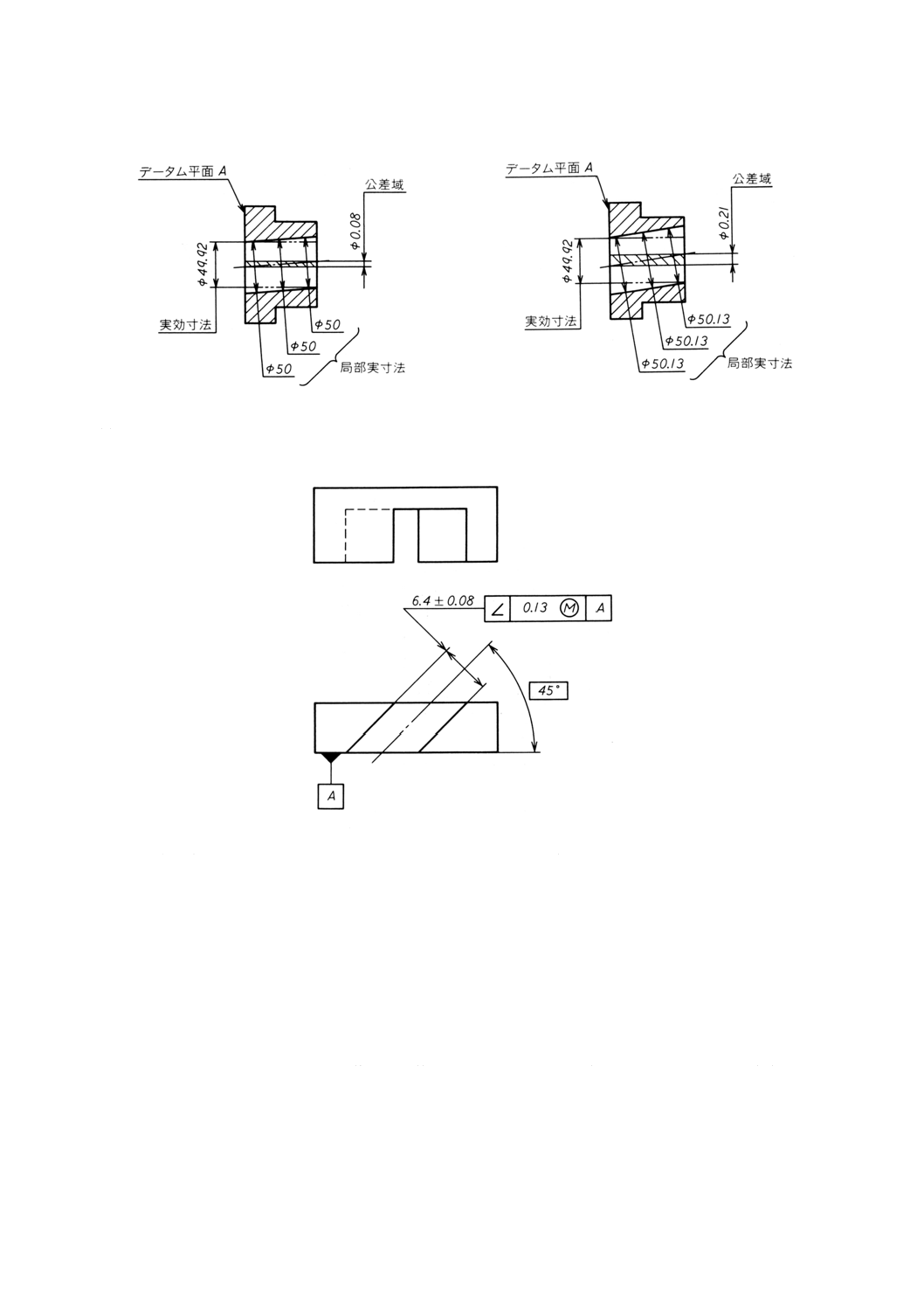
6.3
データム平面に関連する穴の直角度公差
(a) 図面指示
図16(a)
(b) 機能上の要求事項 公差付き形体は,次の要求事項を満たさなければならない。
− 形体の個々の局部実寸法は,0.13の寸法公差内になければならず,したがって,φ50とφ50.13との
間を変動してもよい。
− 公差付き形体は,実効状態の境界外,すなわち,データム平面Aに直角で,φ49.92 (=φ50−φ0.08) の
完全形状の内接円筒外になければならない[図16(b)及び図16(c)参照]。
したがって,形体のすべての直径がφ50の最大実体寸法であるときには,軸線はデータム平面Aに直角
で,φ0.08の公差内になければならないが[図16(b)参照],形体のすべての直径がφ50.13の最小実体寸法
であるときには,φ0.21までの公差域内で変動してもよい[図16(c)参照]。
備考 図16(b)及び図16(c)は,形体が理論的に正確な形状にある場合を示したものであり,実際には,
形体は異なった局部実寸法をもつ極限の状態の間のどこかにある。
13
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図16(b)
図16(c)
6.4
データム平面に関連する溝の傾斜度公差
(a) 図面指示
図17(a)
(b) 機能上の要求事項 公差付き形体は,次の要求事項を満たさなければならない。
− 形体の個々の局部実寸法は,0.16の寸法公差の中になければならず,したがって,6.32と6.48との
間を変動してもよい。
− 公差付き形体は,データム平面Aに対して45°の指定した角度で,6.19 (=6.32−0.13) 離れた2平
行平面によって設定された実効状態の境界外になければならない[図17(b)及び図17(c)参照]。
したがって,形体の中心平面は,形体のすべての幅が6.32の最大実体寸法であるときには,データム平
面Aに対して45°指定した角度で傾斜し,0.13だけ離れた2平行平面の間になければならない[図17(b)
参照]。形体の中心平面は,形体のすべての幅が6.48の最小実体寸法であるときには,0.29までの公差域
内で変動してもよい[図17(c)参照]。
備考 図17(b)及び図17(c)は,形体が理論的に正確な形状にある場合を示したものであり,実際には,
形体は異なった局部実寸法をもつ極限の状態の間のどこかにある。
14
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図17(b)
図17(c)
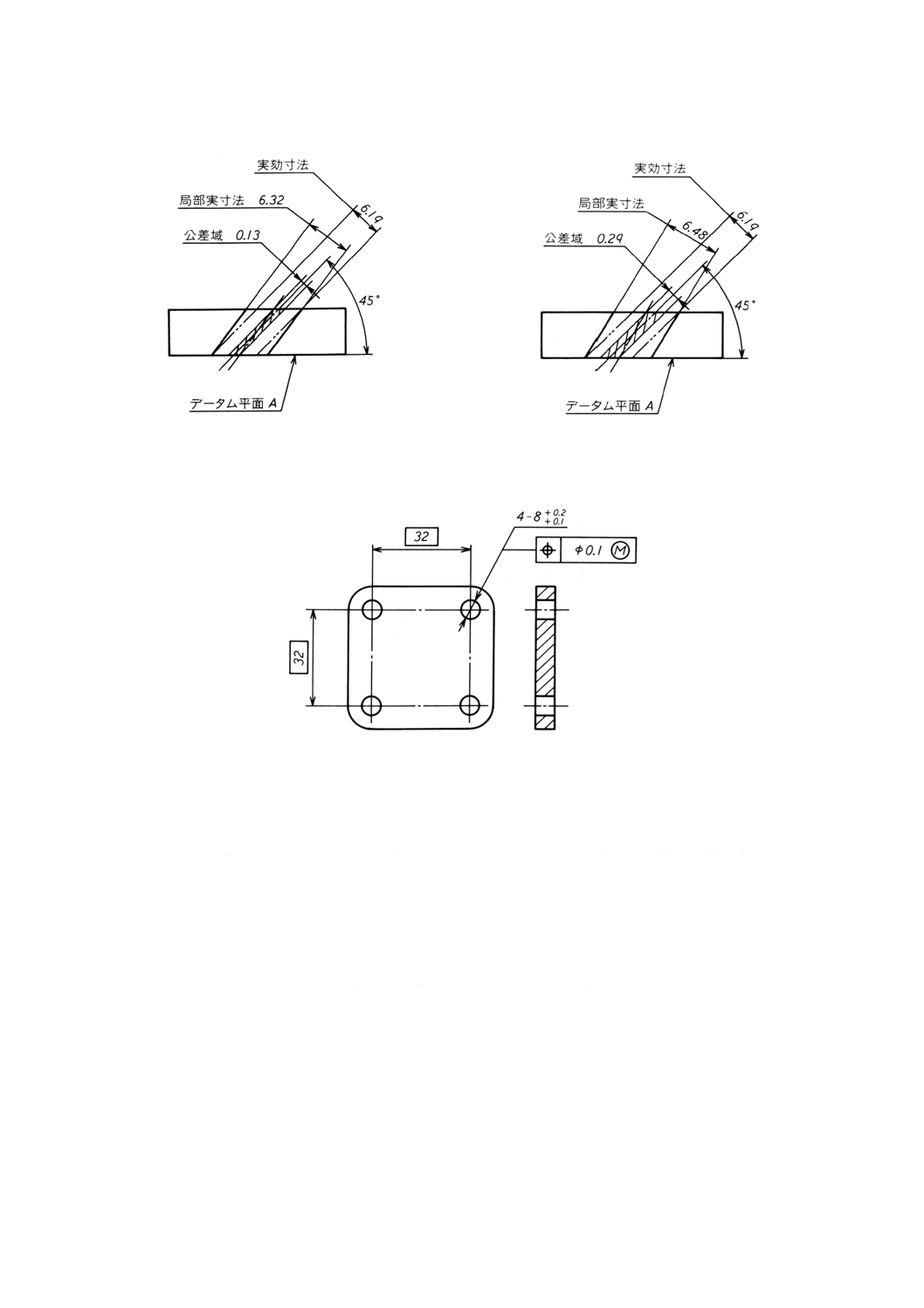
6.5
互いに関連する四つの穴の位置度公差
(a) 図面指示
図18(a)
(b) 機能上の要求事項 公差付き形体は,次の要求事項を満たさなければならない。
− 形体の個々の局部実寸法は,φ0.1の寸法公差内になければならず,したがって,φ8.1とφ8.2との間
を変動してもよい。
− すべての公差付き形体は,それぞれが他の円筒(正確に90°に配置された形体,間隔32で)に対
して,理論的に正確な位置にある場合に,φ8 (=φ8.1−φ0.1) の完全形状の内接円筒の境界外になけ
ればならない[図18(a)参照]。
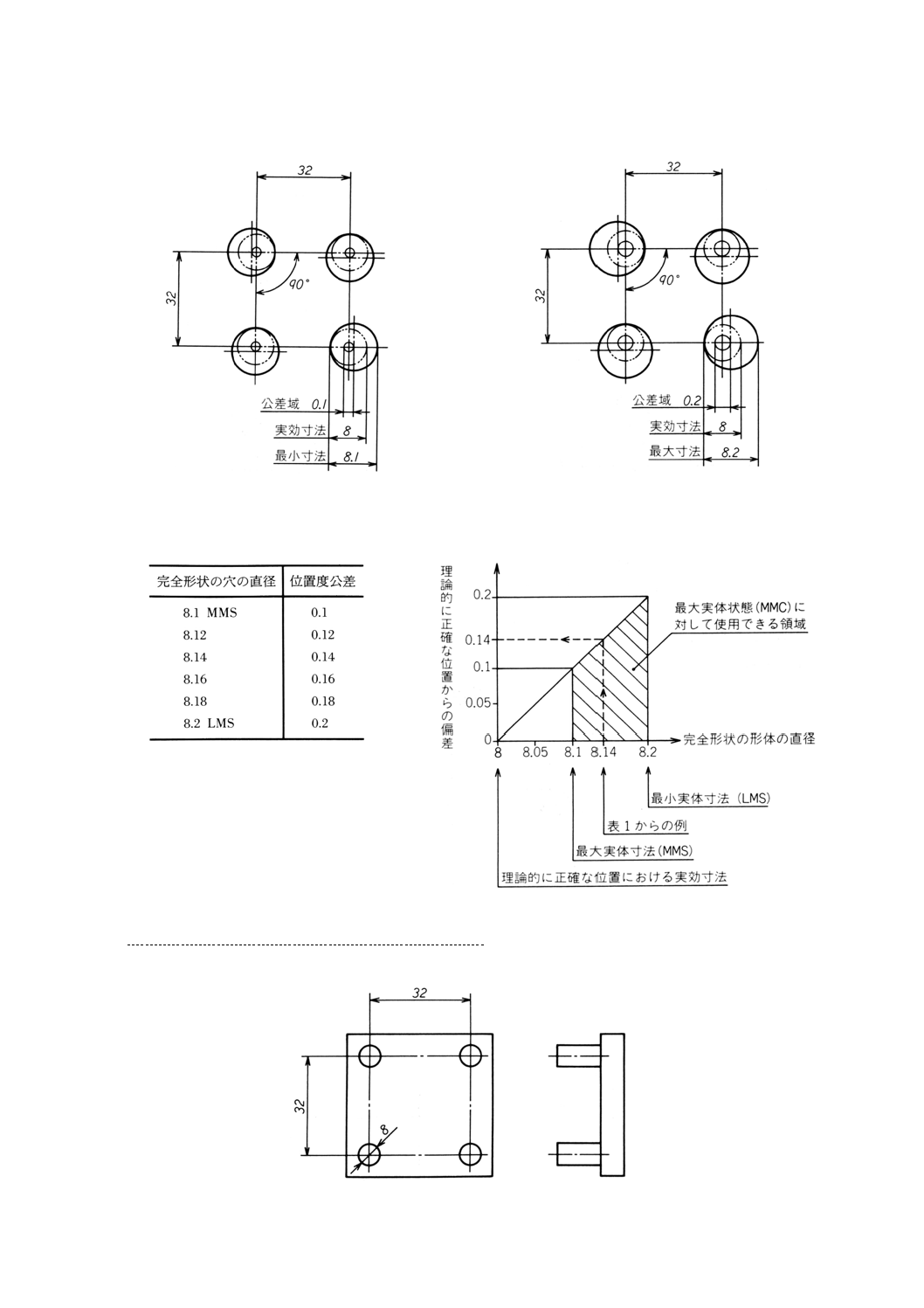
したがって,形体の軸線は,形体のそれぞれの直径がφ8.1の最大実体寸法であるときには,φ0.1の位置
度公差の公差域内になければならないが[図18(b)参照],形体のそれぞれの直径がφ8.2の最小実体寸法で
あるときには,φ0.2までの位置度公差の公差内で変動してもよい[図18(c)参照]。
備考 図18(b)及び図18(c)は,形体が理論的に正確な形状にある場合を示したものであり,実際には,
形体は異なった局部実寸法をもつ極限の状態の間のどこかにある。
15
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図18(b)
図18(c)
動的公差線図(図19参照)は,表1に示すように形体の寸法と理論的に正確な位置からの許容偏差との
間の相互関係を示している。
表1
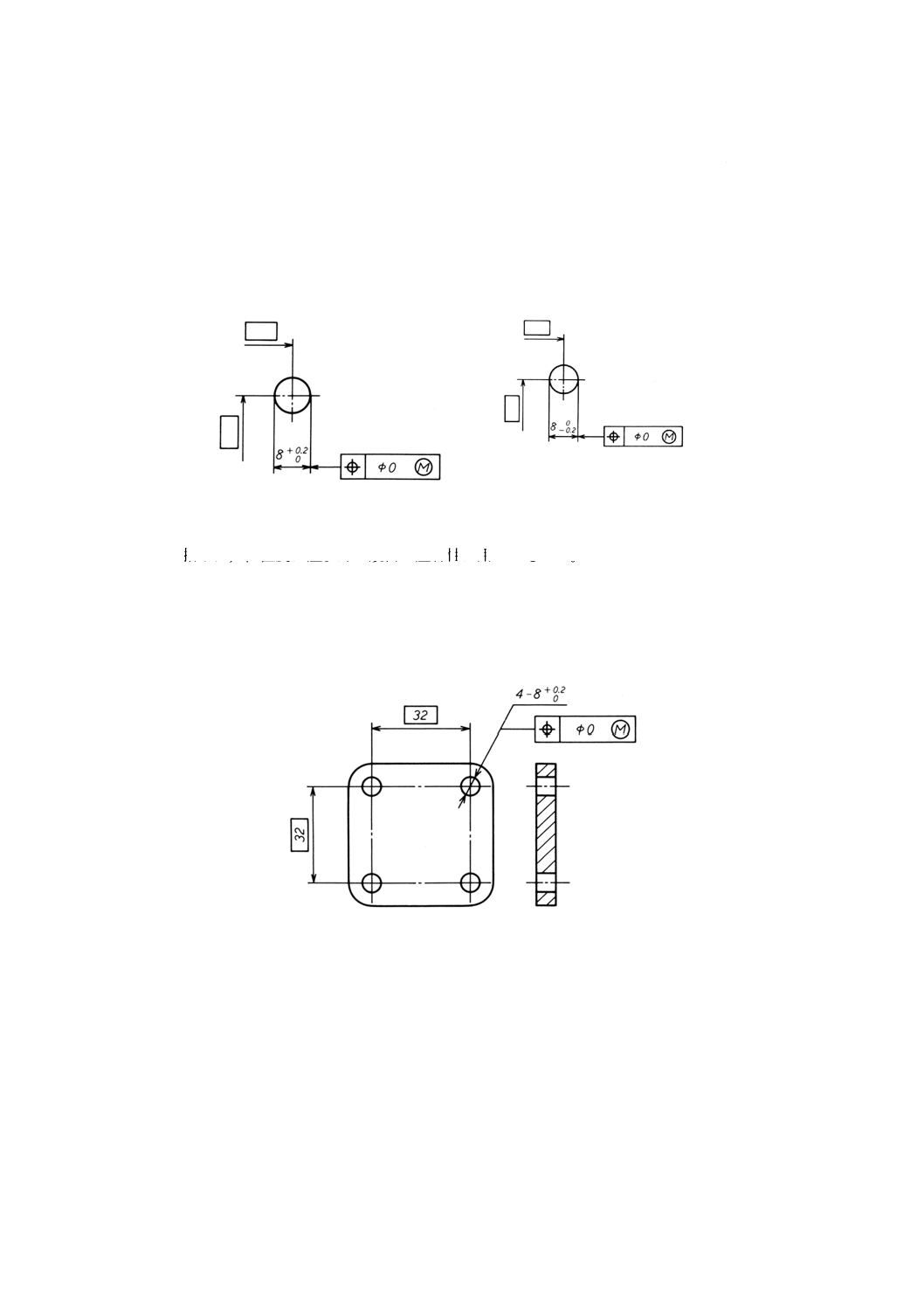
図19
図20は,実効状態を表す機能ゲージを示す。
参考 機能ゲージの製作公差は,含まれていない。
図20
16
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
7. ゼロ幾何公差方式
7.1
一般 5.1及び6.5に示す例では,公差は寸法と位置とに配分されている。特別の場合として,寸法
に対する全公差を割り当てて,ゼロ位置度公差を指示する。この場合には,寸法公差は増加され,前述の
寸法と位置公差との和になる。
したがって,図2の穴に対する図面指示は,図21(a)に示すようになり,図4のピンに対する図面指示は,
図21(b)に示すようになる。
図21(a)
図21(b)
図21(a)及び図21(b)の図面指示によれば,実寸法が最大許容寸法と最小許容寸法との間を変動するとき
には,位置度公差はφ0とφ0.2との間を変動してもよい。
“0◯
M”の指示は,位置度公差以外の幾何公差特性に用いてもよい。
7.2
図面指示例
7.2.1
互いに関連する四つ穴
(a) 図面指示
図22
(b) 解釈 図22の図面指示によって,実効寸法は,最大実体寸法(穴の最小径)から与えられた位置度公
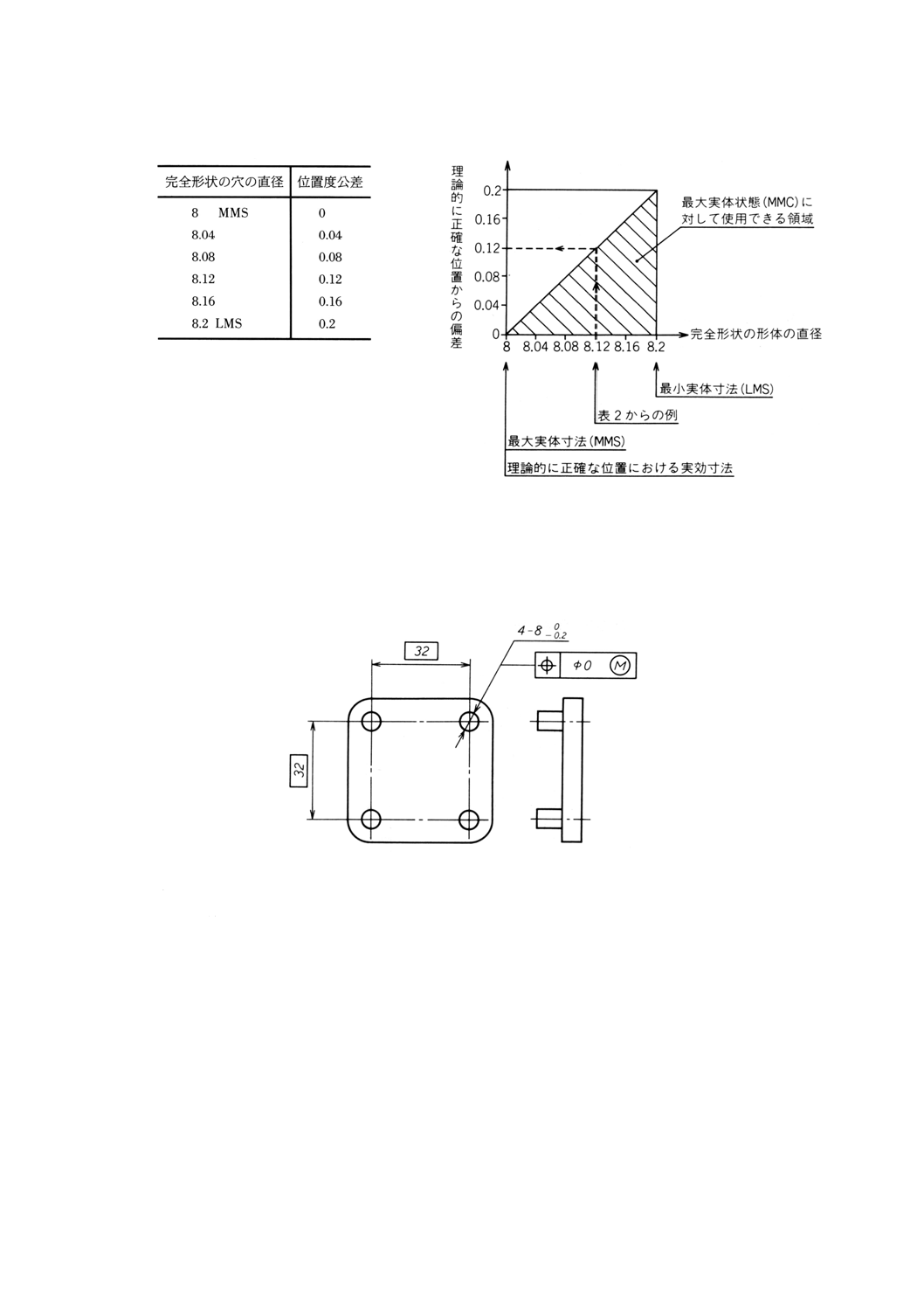
差を差し引いたものである。すなわち,φ8−φ0=φ8である。
動的公差線図(図23参照)は,表2に示すように,形体寸法と理論的に正確な位置からの許容偏差
との間の関係を説明している。
17
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表2
図23
図20に関する機能ゲージは,図22に示した部品の実効状態をも示す。両方の場合とも,形体の直
径は,それらの異なった寸法公差に応じて,別々に検査されなければならない。
7.2.2
互いに関連する四本のピン
(a) 図面指示
図24
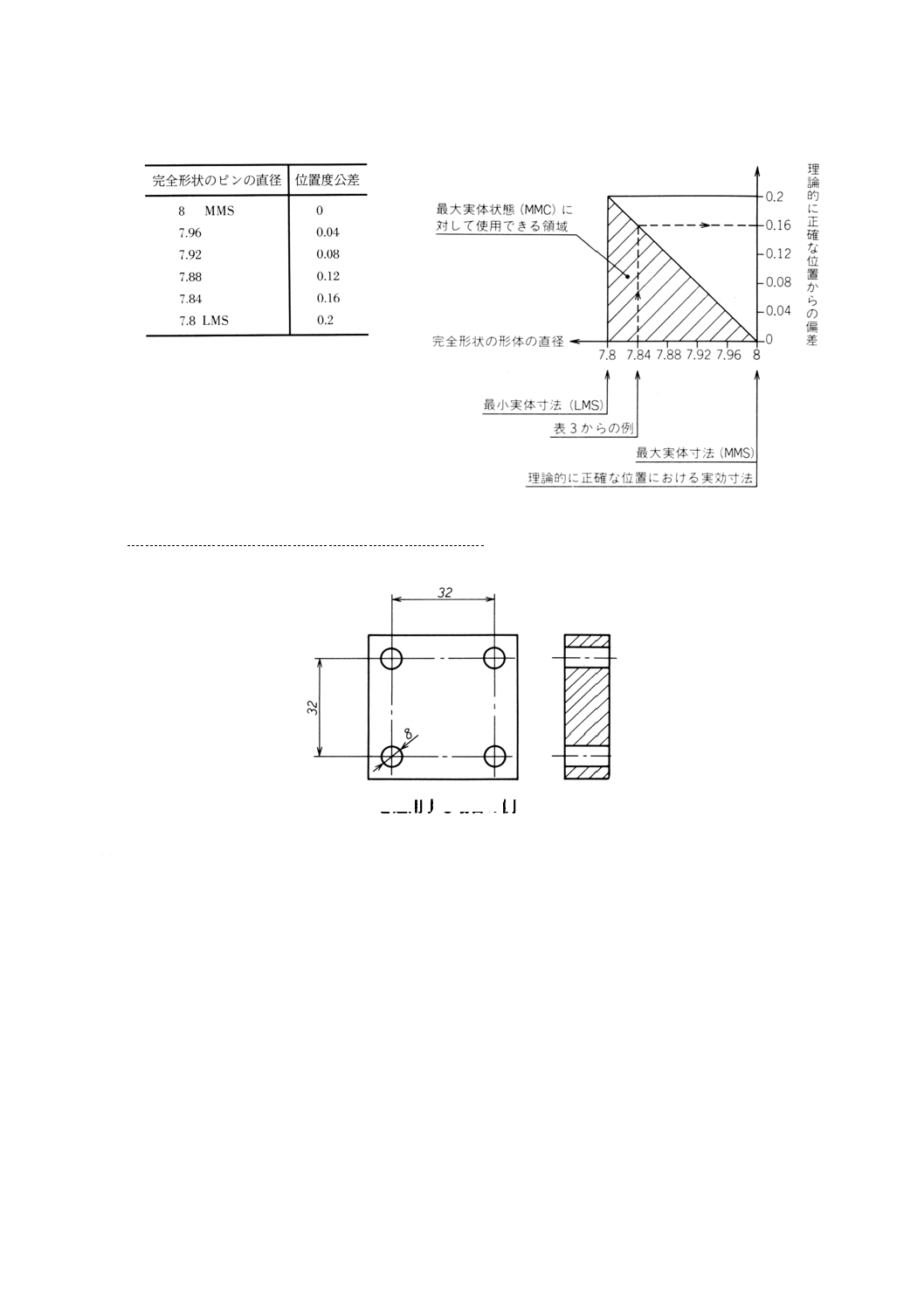
(b) 解釈 図24の図面指示によって,実効寸法は,最大実体寸法(ピンの最大径)に与えられた位置度公
差を加えたものである。すなわち,φ8+φ0=φ8である。
動的公差線図(図25参照)は,表3に示すように,形体の寸法と理論的に正確な位置からの許容偏
差との間の関係を説明している。
18
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表3
図25
図26は,実効状態を表す機能ゲージを示す。
参考 機能ゲージの製作公差は,含まれていない。
図26
8. 公差付き形体及びデータム形体に◯
Mを適用する場合の例
8.1
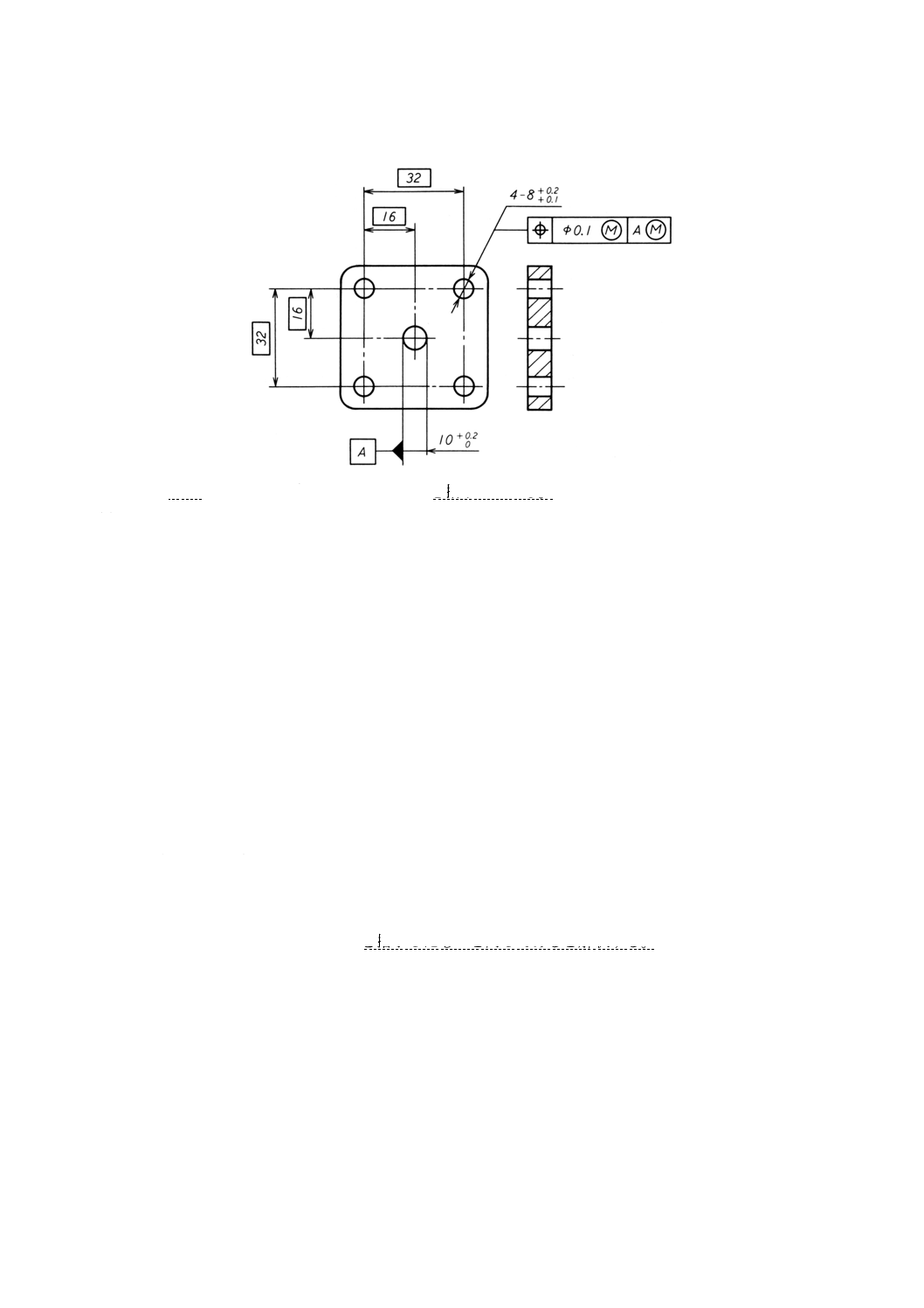
データム穴に関連する四つの穴の位置度公差
(a) 図面指示
19
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図27(a)
参考 ISO 2692では,データムAに記号◯
Eを指示している。
(b) 機能上の要求事項 公差付き形体は,次の要求事項を満たさなければならない。
− 個々の形体の局部実寸法は,0.1の寸法公差内になければならず,したがって,φ8.1とφ8.2との間
を変動してもよい[図27(b)及び図27(c)参照]。
− すべての公差付き形体は,実効状態の境界外,すなわち,これらの円筒のそれぞれが他の円筒に対
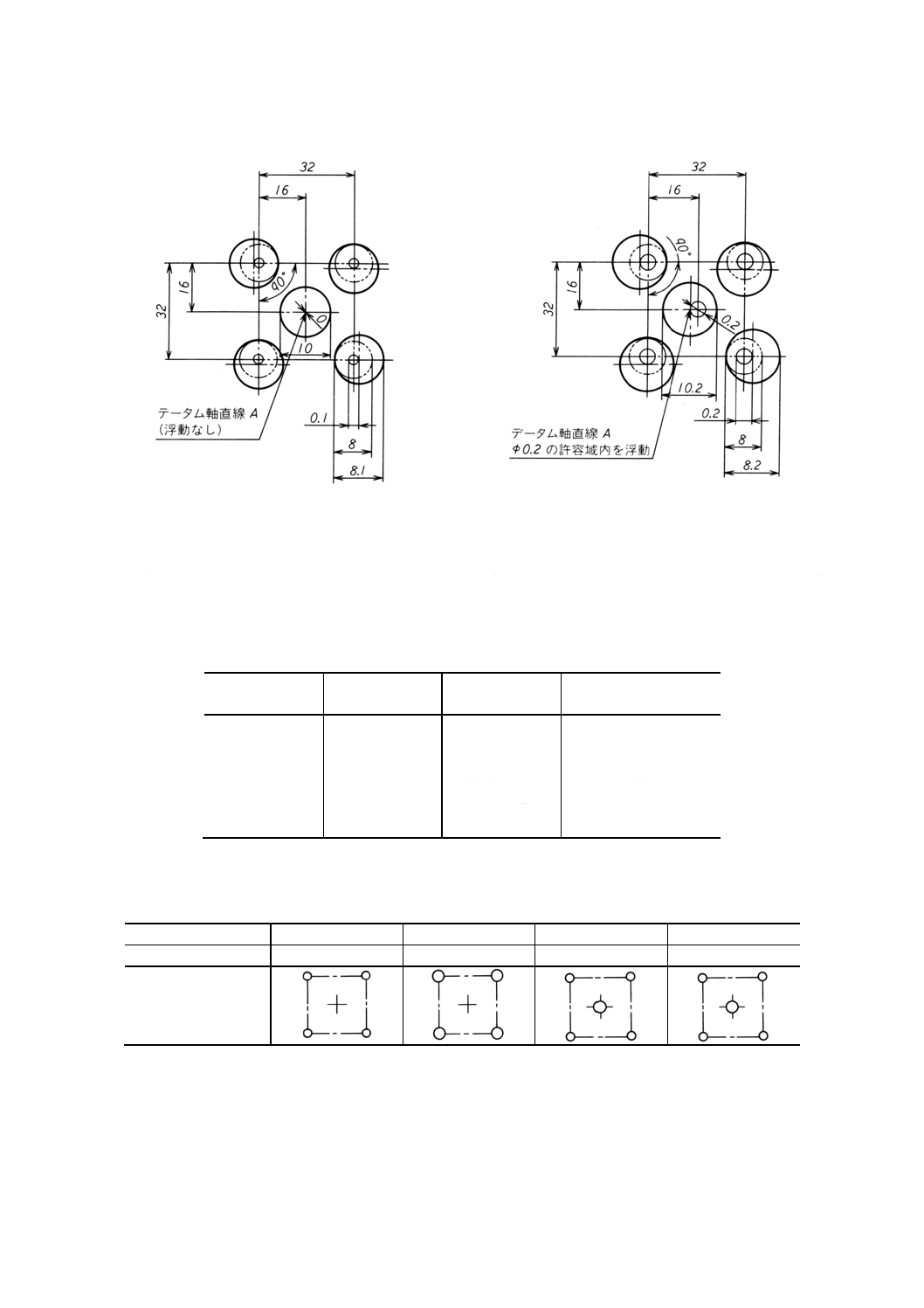
して理論的に正確な位置[正確に90°に,間隔32のパターンで配置された形,図27(b)及び図27(c)
参照]にあり,かつ,データムAの穴のはまり合う寸法がφ10の最大実体寸法であるときには[図
27(b)参照],データム軸直線に対して,理論的に正確な位置にある状態で,φ8 (=φ8.1−φ0.1) の完
全形状の内接円筒外になければならない。
したがって,特別な場合には,個々の形体の軸線は,直径がその最大実体寸法φ8.1であるときに
は,φ0.1の位置度の公差域内になければならないが[図27(b)参照],それぞれの形体の直径がその
最小実体寸法φ8.2であるときには,φ0.2の公差域内で変動してもよい[図27(c)参照]。
− データム形体Aの実際の軸線は,データム形体の最大実体寸法から離れているときには,四つの形
体の位置の実効状態に関連して浮動してもよい。この浮動の値は,その最大実体寸法からデータム
形体のはまり合う寸法の離れた寸法分に等しい[図27(b)及び図27(c)参照]。
したがって,特別な場合には,データム形体Aの実際の軸線は,データム形体Aが完全形状の,最小実
体寸法φ10.2のときには,φ0.2の公差域内を浮動してもよい[図27(c)参照]。
参考 データム形体には,記号◯
Eを指示したものと同じであると解釈する。
20
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図27(b)
図27(c)
位置度公差は,データム形体に関連するだけでなく,互いに関連した四つの公差付き形体に適用する。
与えられた数値は,表4の第2欄に示す離れた量に等しい量が増加される。
データム形体の寸法に依存する付加的な位置度公差は(データムについての最大実体状態のため),デー
タム形体に関連するグループ公差として公差付き形体に適用するが,互いに関連する公差付き形体には適
用しない。すなわち,データムは,公差付き形体に関連して浮動してもよい(数値については,表4参照)。
表4
単位 mm
公差付き穴の直径 個々の公差付き
形体の位置度公差
データム穴の直径 データム形体の浮動領域
8.1 MMS
0.1
10
MMS
0
8.12
0.12
10.05
0.05
8.14
0.14
10.1
0.1
8.16
0.16
10.15
0.15
8.18
0.18
10.2 LMS
0.2
8.2 LMS
0.2
表4の第2欄及び第4欄の値の幾つかの組合せが生じる。第2欄及び第4欄の値は,それぞれ意味が異
なるので,単純に加算することはできない。特別の組合せの例を表5に示す。
表5
公差付き形体の公差域
0.1
0.2
0.1
0.2
データム形体の公差域
0
0
0.2
0.2
公差域図
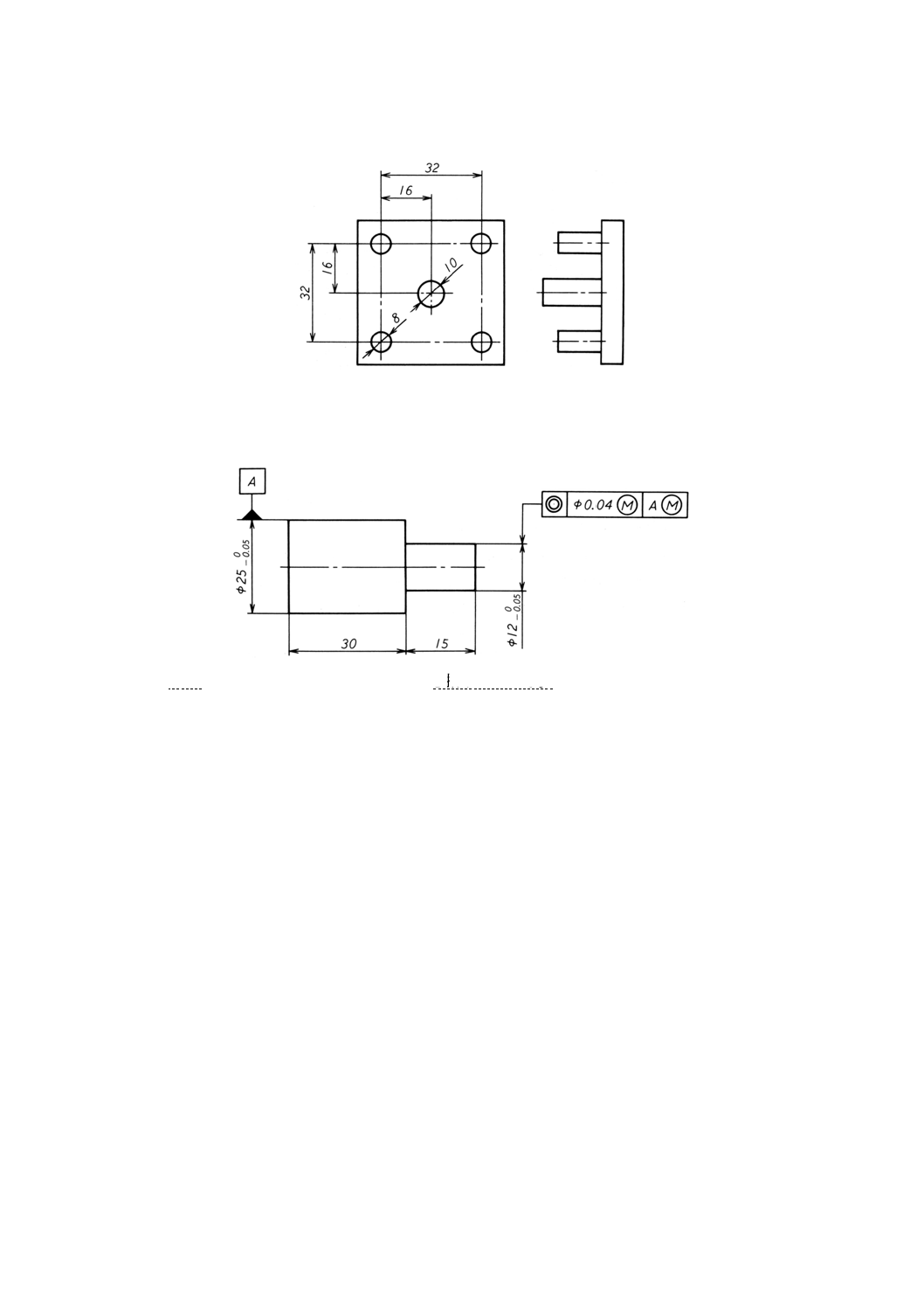
図28は,実効状態を表す機能ゲージを示す。
参考 機能ゲージの製作公差は,含まれていない。
21
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図28
8.2
同軸度公差
(a) 図面指示
図29(a)
参考 ISO 2692では,データムAに記号◯
Eを指示している。
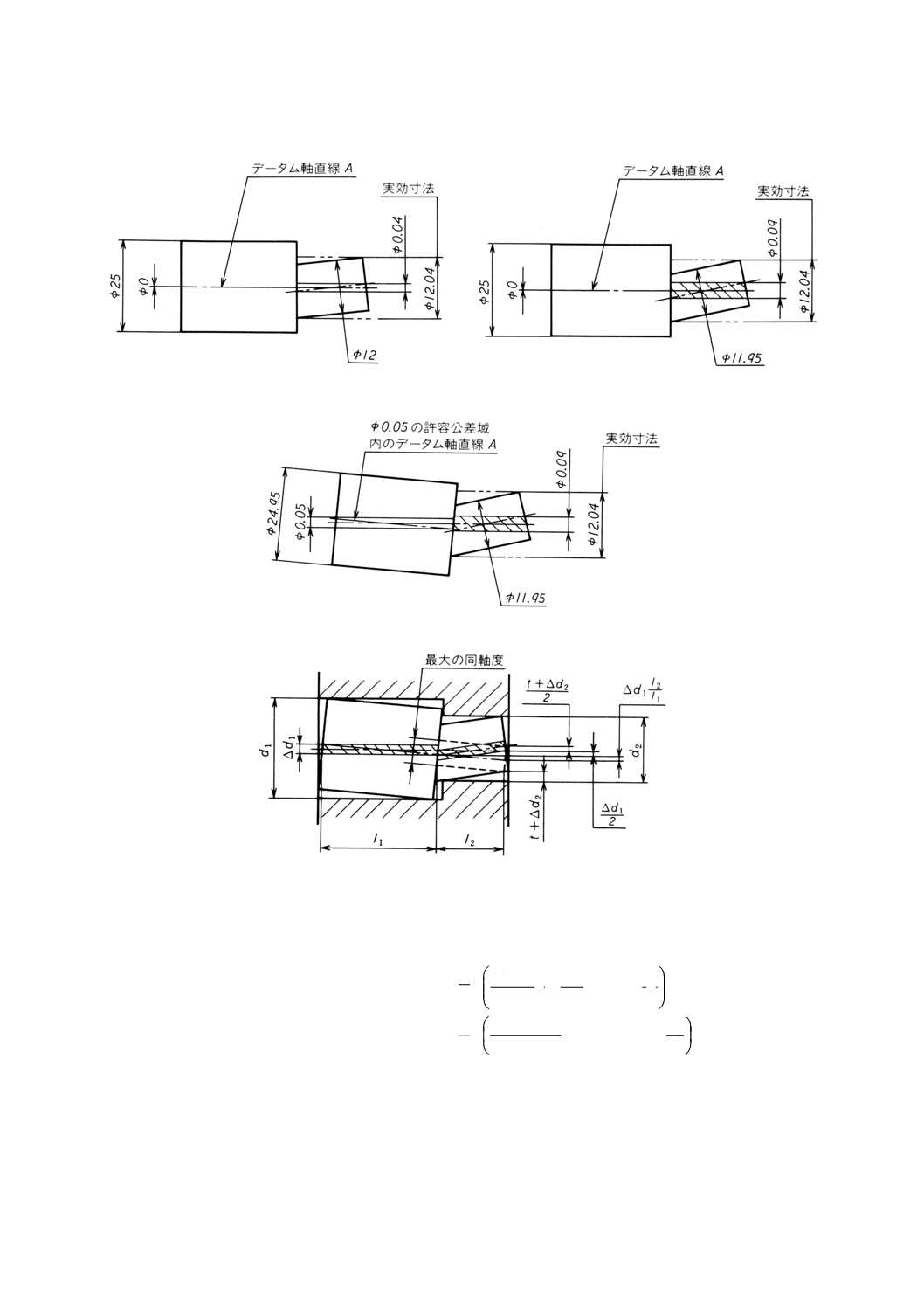
(b) 機能上の要求事項 実際の公差付き形体は,次の要求事項を満たさなければならない。
− 形体の個々の局部実寸法は,0.05の寸法公差内になければならず,したがって,φ12とφ11.95との
間を変動してもよい[図29(b)及び図29(c)参照]。
− 全体の形体は,実効状態,すなわち,データム形体Aのはまり合う寸法がその最大実体寸法である
ときに,データム形体Aに同軸で,かつ,φ12.04 (=φ12+φ0.04) の完全形状の包絡円筒内になけれ
ばならない[図29(b)及び図29(c)参照]。
− データム形体Aの実際の軸線は,データム形体の最大実体寸法から離れていると,実効状態に関連
して浮動してもよい。浮動の値は,その最大実体寸法からデータム形体のはまり合う寸法の離れた
量に等しい[図29(d)参照]。
したがって,形体の軸線は,形体のすべての直径が最大実体寸法φ12であるときには,φ0.04の同軸度公
差の公差域内になければならないが[図29(b)参照],公差付き形体のすべての直径がφ11.95の最小実体寸
法であり,かつ,データム形体のはまり合う寸法がφ25の最大実体寸法であるときには,φ0.09までの公差
域内で変動してもよい[図29(c)参照]。データム形体Aの実際の軸線は,データム形体Aのはまり合う寸
法がφ24.95の最小実体寸法であるときには,φ0.05の領域の中で浮動してもよい[図29(d)参照]。この場
合には,一つの形体だけがデータムに関連しているので,データムの浮動は,図29(e)に示すように,同軸
度公差が増加するという効果がある。
22
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図29(b)
図29(c)
図29(d)
図29(e)
ここに,
d1: データム形体の最大実体寸法
d2: 公差付き形体の実効寸法
t: 幾何公差
∆d1= d1−[データム形体のはまり合う寸法]
t+∆d2= d2−[公差付き形体のはまり合う寸法]
最大の同軸度 =
+
+
+
1
2
1
1
2
2
2
2
l
l
d
d
d
t
⊿
⊿
⊿
=
×
+
+
+
30
15
05
.0
025
.0
2
05
.0
04
.0
2
=0.19
23
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
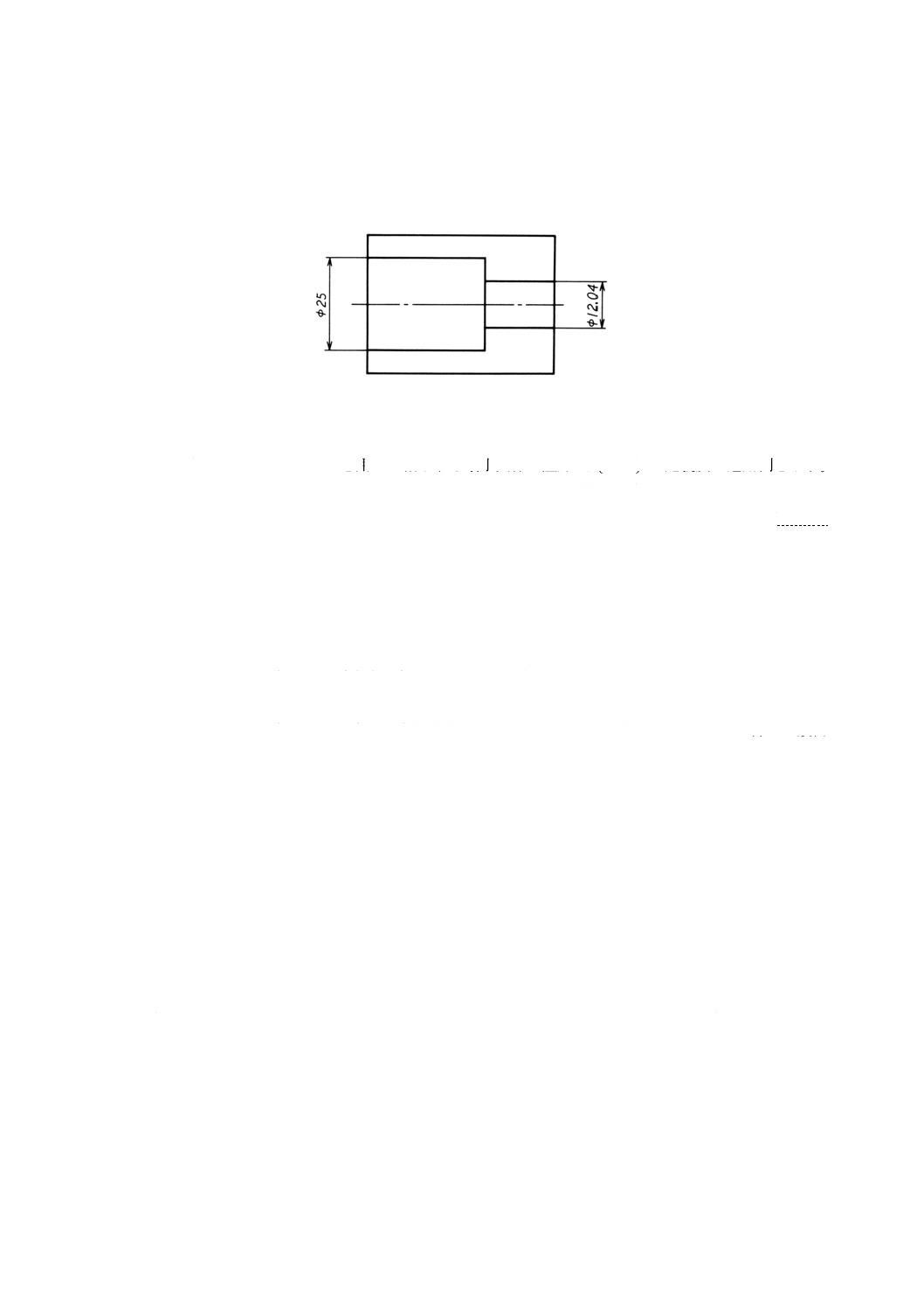
図30は,実効状態を表す機能ゲージを示す。
参考 機能ゲージの製作公差は,含まれていない。
図30
第2部 最小実体公差方式
序文 この規格は,図面上に記号◯
Lを用いて指示する最小実体公差方式 (LMR) の定義及び適用例を示す。
最小実体公差方式は,最大実体公差方式に密接に関係し,最小厚さの管理,破断防止などに用いられる。
参考 この規格のこの部分は,ISO 2692-1988に追加する技術的事項を日本工業規格として,JIS B 0023
の規定事項として追加するものである。
1. 適用範囲 この規格は,最小実体公差方式とその適用について規定する。
2. 定義 用語の定義は,この規格の第1部によるほか,次による。
2.1
最小実体実効状態 (least material virtual condition) (LMVC) 完全形状で,最小実体実効寸法の境界の
状態。
2.2
最小実体実効寸法 (least material virtual size) (LMVS) 最小実体寸法 (LMS) と記号◯
Lが付いた幾何
公差との総合効果によって得られる寸法。
備考1. 軸に対して:LMVS=LMS−[幾何公差]
穴に対して:LMVS=LMS+[幾何公差]
3. 最小実体公差方式 (LMR) 最小実体公差方式は,対象とする形体がその最小実体状態 (LMC) から
離れるときに,指示した幾何公差を増加させることができる(附属書A参照)。
最小実体公差方式は,公差枠の中の公差付き形体の公差の後,又はデータム文字記号の後に付ける記号◯
L
によって図面上に指示され,次の事項が指定される。
− 公差付き形体に適用する場合には,最小実体実効状態 (LMVC) は,実際の公差付き形体の実体の
中に完全に含まれなければならない。
− データムに適用する場合には,最小実体寸法における完全形状の境界は,(実際のデータム形体の表
面に干渉することなく)実際のデータム形体の実体の中で浮動してもよい。
4. 適用例 最小実体公差方式 (LMR) の適用例を,附属書Bに示す。
24
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
第2部 附属書A
(参考)
最小実体公差方式の説明
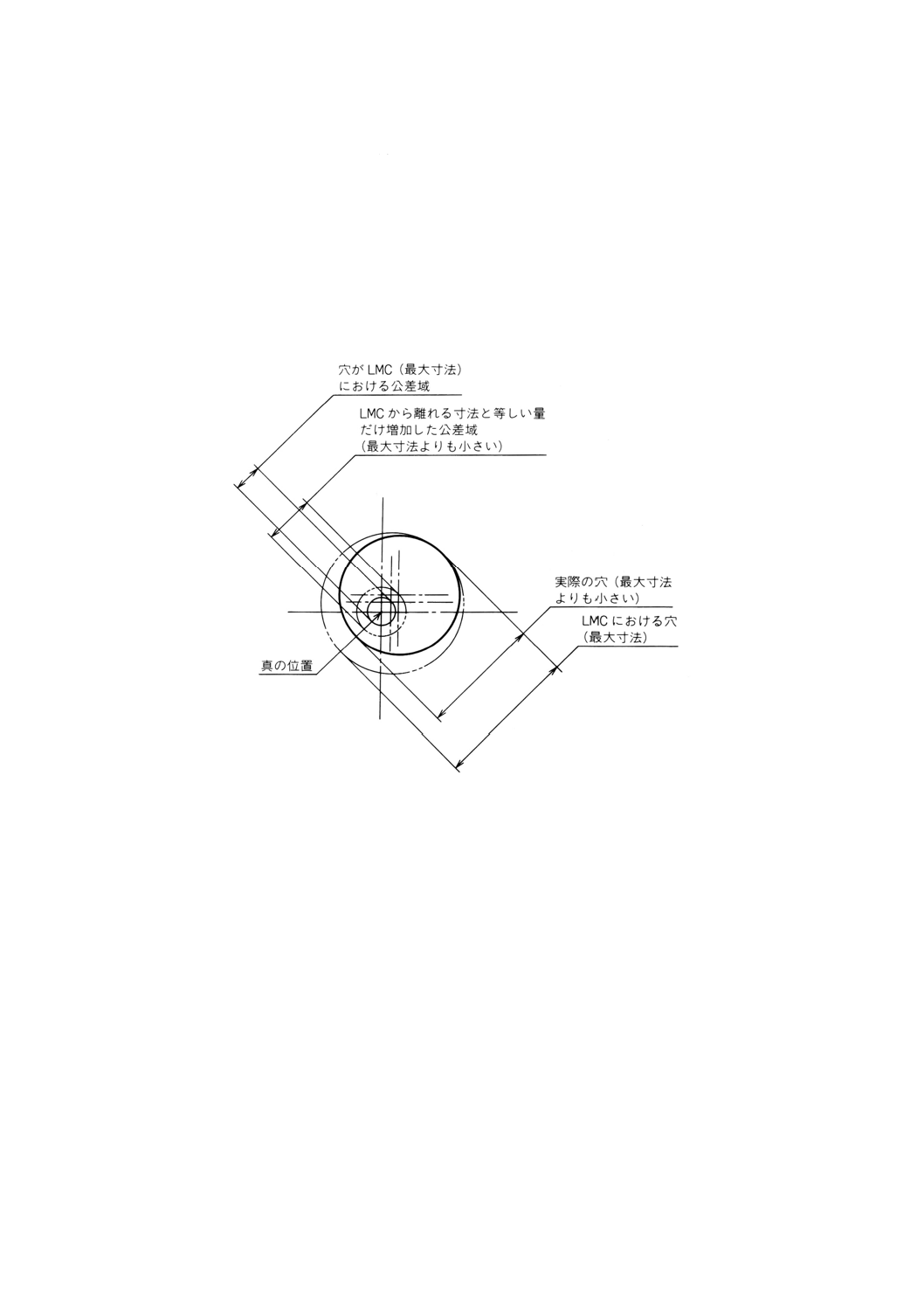
最小実体公差方式を,図A.1によって説明する。完全形状の形体がその最小実体寸法から離れたときに
は,その離れた寸法分に等しく位置度公差を増加することが許容される。
図A.1
25
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
第2部 附属書B
(参考)
図示例及び説明
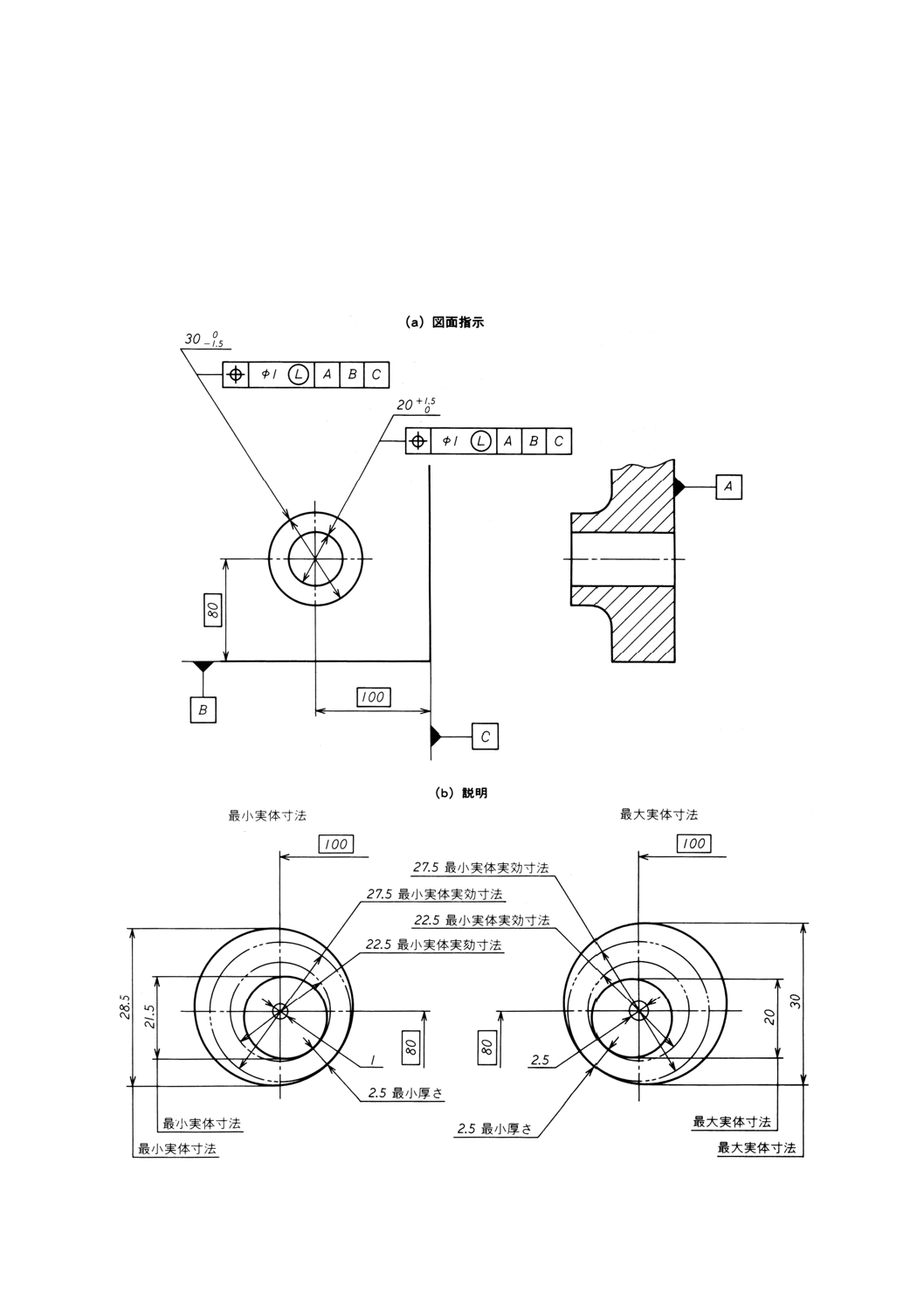
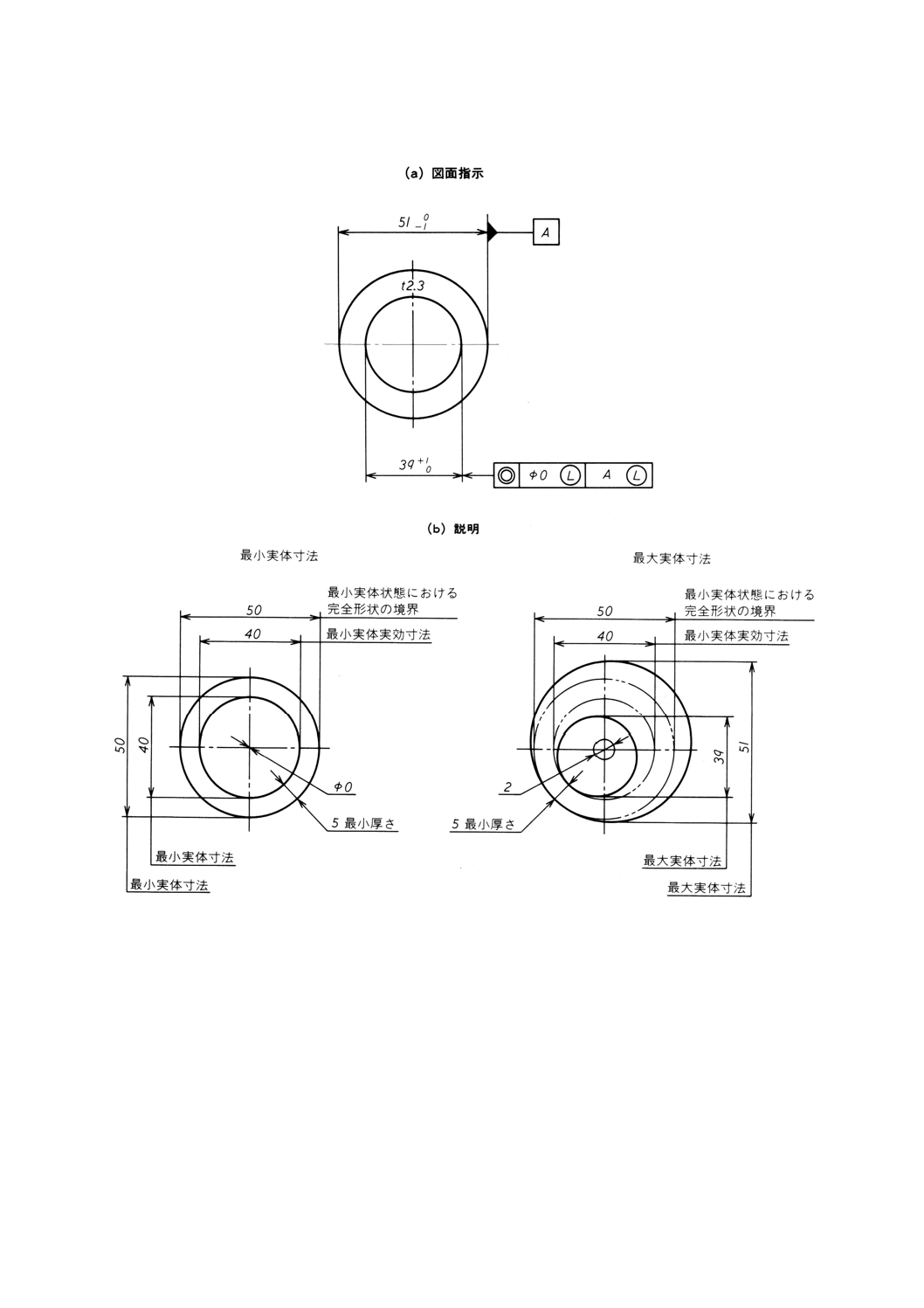
図B.1 最小実体公差方式,最小厚さ
26
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
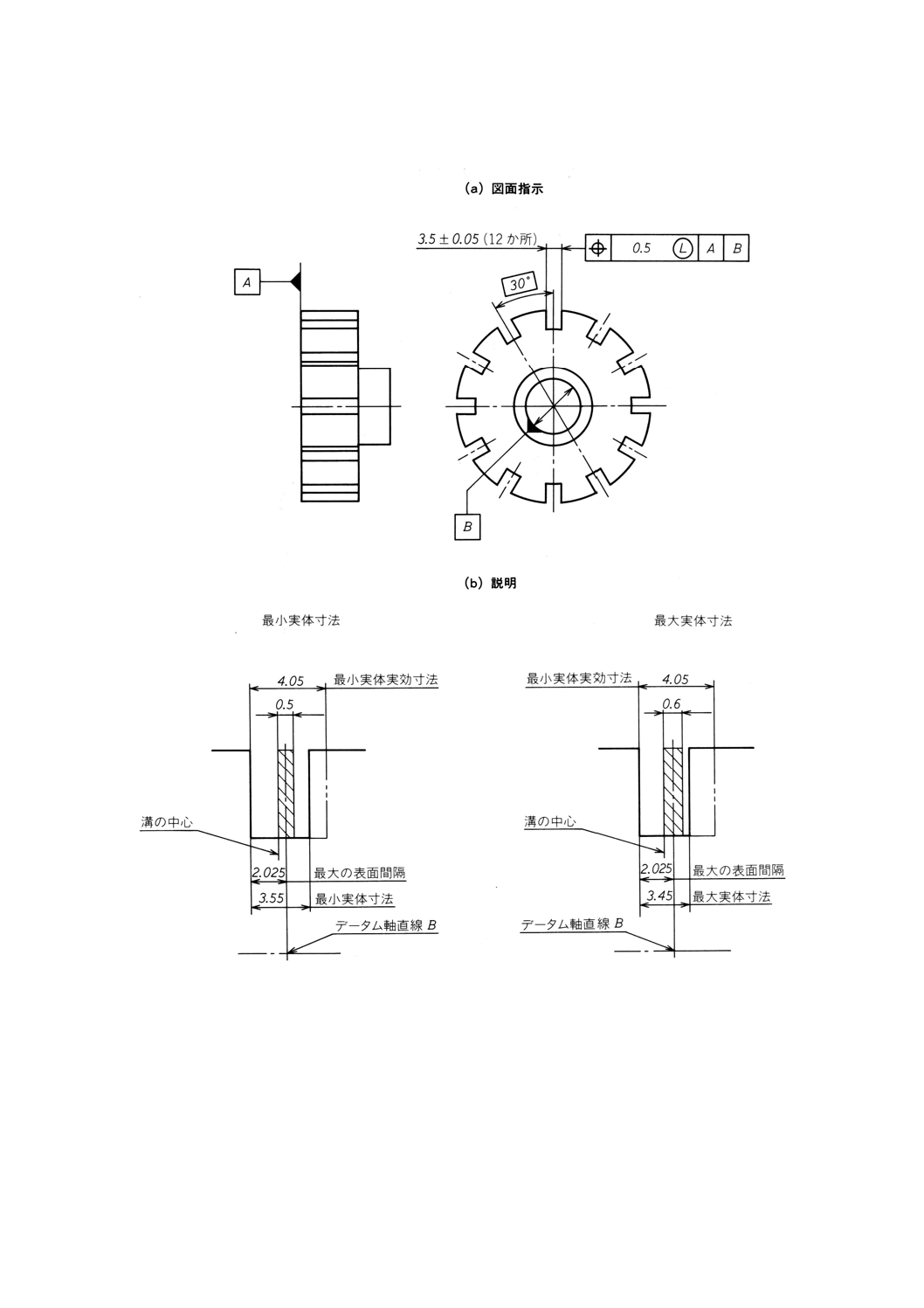
図B.2 最小実体公差方式,理論的に正確な位置から溝表面までの最大距離
27
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
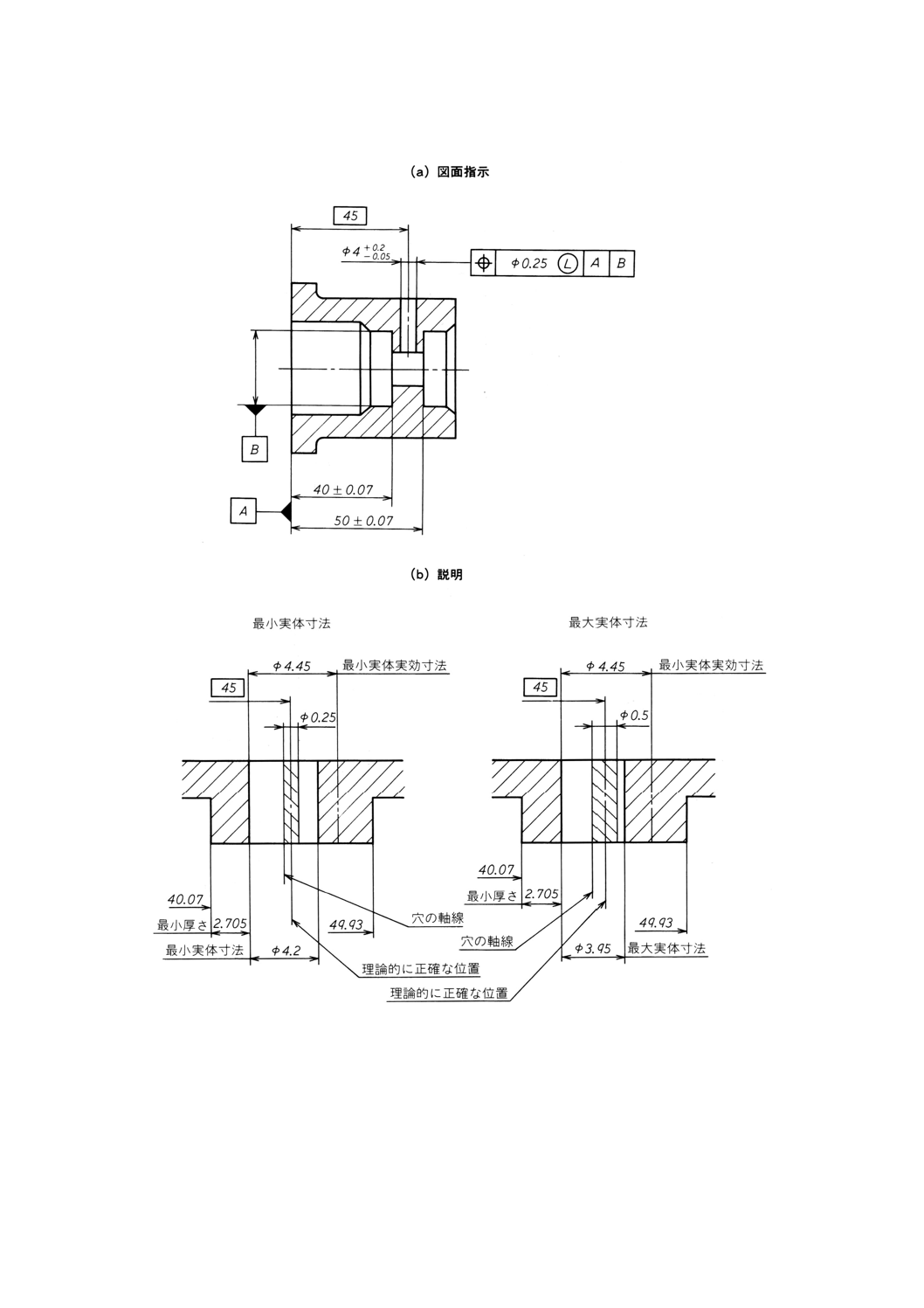
図B.3 最小実体公差方式,最小厚さ
28
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図B.4 最小実体公差方式,最小実体状態における完全形状の最小厚さ
29
B 0023-1996
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
原案作成委員会 構成表
氏名
所属
(委員長)
塚 田 忠 夫
東京工業大学工学部
(幹事)
◎ 桑 田 浩 志
トヨタ自動車株式会社
○ 竹田原 昇 治
通商産業省工業技術院標準部
豊 田 幸 司
通商産業省工業技術院計量研究所
○ 徳 岡 直 静
慶応義塾大学工学部
○ 野 上 昭 三
株式会社アマダ
○ 沢 辺 雅 二
株式会社ミツトヨ
高 木 誠
株式会社小松製作所
吉 田 育 夫
株式会社東芝京浜事業所
○ 安 藤 弘 之
株式会社日立製作所
○ 荒 井 正 敏
株式会社東京精密
平 田 幸 雄
日本精工株式会社
加 山 英 男
財団法人日本規格協会
(事務局)
岡 本 裕
財団法人日本規格協会
◎印:小委員会主査,○印:小委員会委員を兼ねる。