A 1486:2014
(1)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
目 次
ページ
序文 ··································································································································· 1
1 適用範囲························································································································· 1
2 引用規格························································································································· 2
3 用語及び定義並びに記号及び単位 ························································································ 2
4 一般事項························································································································· 5
4.1 適用条件 ······················································································································ 5
4.2 結果に影響を与える要因 ································································································· 5
5 試験方法························································································································· 5
5.1 試験方法A−芯材の断熱性の経時変化を測定するための試験方法 ············································ 5
5.2 試験方法B−被覆層のない製品の設計耐用期間における熱抵抗を測定するための簡易試験方法 ····· 7
6 報告事項························································································································· 8
附属書A(参考)解析モデル ·································································································· 9
附属書JA(参考)被覆層がある場合の解析モデル−断熱材内分圧の簡易計算法に基づく
熱伝導率変化量 ············································································································· 15
附属書JB(参考)簡易計算に基づく熱伝導率変化量の計算例 ······················································ 23
附属書JC(参考)被覆層の拡散抵抗を測定又は同定する方法 ······················································ 25
附属書JD(参考)被覆層の拡散抵抗を直接測定する方法 ···························································· 26
附属書JE(参考)被覆層の拡散抵抗を熱伝導率の経時変化から同定する方法 ································· 27
附属書JF(参考)JISと対応国際規格との対比表 ······································································ 28
A 1486:2014
(2)
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
まえがき
この規格は,工業標準化法に基づき,日本工業標準調査会の審議を経て,経済産業大臣が制定した日本
工業規格である。
この規格は,著作権法で保護対象となっている著作物である。
この規格の一部が,特許権,出願公開後の特許出願又は実用新案権に抵触する可能性があることに注意
を喚起する。経済産業大臣及び日本工業標準調査会は,このような特許権,出願公開後の特許出願及び実
用新案権に関わる確認について,責任はもたない。
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
日本工業規格 JIS
A 1486:2014
発泡プラスチック系断熱材の熱抵抗の長期変化
促進試験方法
Accelerated test method for long-term change in thermal resistance
of rigid cellular plastics
序文
この規格は,1999年に第1版として発行されたISO 11561を基とし,技術的内容を変更して作成した日
本工業規格である。
熱抵抗の長期変化は,使用条件下における熱性能の設計値を設定する場合及び耐用期間でのエネルギー
消費量を推定する場合に必要な一つの特性である。熱抵抗及びその変化の程度は,使用条件(温度)及び
厚さ,又は製品のばらつきによって変わる。また,内部の気泡の分布状態,及び被覆層の影響によっても
変わる。この規格の目的は,発泡ガスの放散に起因して性能が変化する発泡プラスチック系断熱材の熱抵
抗の長期変化を促進試験によって求める方法を示すことである。
なお,この規格で点線の下線を施してある箇所は,対応国際規格を変更している事項である。変更の一
覧表にその説明を付けて,附属書JFに示す。また,附属書JA〜附属書JEは,対応国際規格にはない事
項である。
1
適用範囲
この規格は,主に常温で使用される発泡プラスチック系断熱材の熱抵抗の長期的な変化を試験室におい
て測定するための二つの方法(試験方法A及び試験方法B)について規定する。
なお,この規格は発泡ガスの放散による熱抵抗の長期変化を促進試験によって求める方法を示すもので
あり,これ以外の要因は含まない。
熱抵抗の測定は,次のいずれかの方法で行う。
試験方法A(5.1)は,一定の周囲温度に状態調節したスライスした試験片に対する短期間の測定方法で
ある。測定した経時変化のデータを処理して,より厚い材料の熱抵抗の時間変化を算定する。
試験方法B(5.2)は,被覆層のない発泡プラスチック系断熱材を安全側の設計耐用期間の概算値(25
年以上)として測定する簡易試験方法である。この方法は被覆層のない均質な材料に限り適用できる。た
だし,材料の芯材及び被覆層からなる試料においては,経年変化の一次段階(通常5年以内)における熱
伝導抵抗と時間との関係の傾きのばらつきが一つの試料内で10 %未満の場合,均質とみなすことができる。
一般に,そのような製品は,成形スキン層,面材又は密度の分布がある場合においても,試験方法Bによ
って試験することが可能である。
注記1 断熱材の表面を覆う被覆層によって発泡ガス放散抑制効果が期待できる材料では,附属書
JC,及び附属書JD又は附属書JEによって被覆層の拡散抵抗を測定し,附属書JA及び附属
書JBによって長期的な変化を知ることができる。
2
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
注記2 厚さが通常の製品と同等の試料を対象とした場合,熱抵抗の長期変化のデータを得るには長
期間の測定が必要となる。したがって,この促進試験方法の精度に関しては確定的なことは
いえない。
注記3 この規格の対応国際規格及びその対応の程度を表す記号を,次に示す。
ISO 11561:1999,Ageing of thermal insulation materials−Determination of the long-term change in
thermal resistance of closed-cell plastics (accelerated laboratory test methods)(MOD)
なお,対応の程度を表す記号“MOD”は,ISO/IEC Guide 21-1に基づき,“修正している”
ことを示す。
2
引用規格
次に掲げる規格は,この規格に引用されることによって,この規格の規定の一部を構成する。これらの
引用規格は,その最新版(追補を含む。)を適用する。
JIS A 0202 断熱用語
注記 対応国際規格:ISO 7345,Thermal insulation−Physical quantities and definitions及びISO 9346,
Hygrothermal performance of buildings and building materials−Physical quantities for mass transfer
−Vocabulary(MOD)
JIS A 1412-1 熱絶縁材の熱抵抗及び熱伝導率の測定方法−第1部:保護熱板法(GHP法)
注記 対応国際規格:ISO 8302,Thermal insulation−Determination of steady-state thermal resistance and
related properties−Guarded hot plate apparatus(MOD)
JIS A 1412-2 熱絶縁材の熱抵抗及び熱伝導率の測定方法−第2部:熱流計法(HFM法)
注記 対応国際規格:ISO 8301,Thermal insulation−Determination of steady-state thermal resistance and
related properties−Heat flow meter apparatus(MOD)
JIS A 9511 発泡プラスチック保温材
JIS A 9526 建築物断熱用吹付け硬質ウレタンフォーム
3
用語及び定義並びに記号及び単位
この規格で用いる主な用語及び定義は,JIS A 0202によるほか,次による。また,この規格で用いる主
な記号及びその単位は,表1による。
3.1
経年変化(ageing)
材料,製品又はシステムの物理,機械又は熱特性の経時変化。この規格では,発泡ガスの放散による熱
抵抗の数年〜数十年にわたる変化をいう。
注記1 促進試験は,自然の状態での経年変化では起こり得ない影響を及ぼすことがある。したがっ
て,促進試験方法及び結果の判断には注意が必要である。
注記2 経年変化の要因として,一部の低密度繊維系材料の沈下,発泡プラスチックのガス拡散など
がある。
注記3 経年変化は,材料,製品又はシステムが暴露される環境,使用条件,形状,寸法又は仕上げ
に大きく影響される。経年変化への影響を正確に予測するためには,これらの要素の考慮が
必要となる。
3
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.2
経年変化後の値(aged value)
特定の期間,ある環境条件下に暴露した後の材料,製品又はシステムの特性値。
3.3
促進経年変化後の値(accelerated aged value)
一般的な使用状態を再現することを目的とした特定の期間及び環境条件下での試験室における試験,又
は信頼性のある予測モデルによって得られた経年変化後の値。
注記 促進経年変化後の値の定義における寸法,使用環境及び推定耐用年数は,実際のそれらとの対
応関係を注意深く検討することが望ましい。
3.4
設計耐用年数(design life-time)
施工された材料,製品又はシステムが,設計性能を維持すべき年数。
注記 耐用年数は,使用目的などで決まる。
3.5
有効拡散係数(effective diffusion coefficient)
ある温度の材料内のガスの分圧勾配とガス移動速度との関係を示す材料特性。
3.6
経年変化の一次段階(primary stage)
発泡プラスチック系断熱材の内外に窒素,酸素など空気中のガス成分が拡散することで,断熱性の変化
に影響を与える経年変化プロセスの部分。
3.7
スケーリング係数(scaling factor)
製品厚さの二乗と試料厚さの二乗との比。
注記 この値は,厚さが異なることによる発泡プラスチックの経年変化への影響を表し,この規格で
規定する促進試験における促進率を表す。
3.8
経年変化の二次段階(secondary stage)
発泡ガスが独立気泡材の外部へ拡散することで,断熱性の変化に影響を与える経年変化プロセスの部分。
3.9
損傷表面層の厚さ,TDSL(thickness of damaged surface layer)
試験片の作製中に破裂又はダメージを受けた気泡の片側表面における平均厚さ。
3.10
遷移点(transition point)
経年変化プロセスが一次段階から二次段階に変化する時点における発泡プラスチック系断熱材の推定経
過時間。
注記 遷移点は,移行点ともいう。
3.11
被覆層
断熱材の表面を覆う層。被覆層は,成形スキン層と面材とに分類される。

4
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
3.12
成形スキン層
原材料を発泡したとき,表面に成形される発泡倍率の低い樹脂層。
3.13
面材
断熱材とは別の材料で断熱材の表面に貼り付けたもの。
3.14
試料
試験対象とする厚さが25 mm以上の発泡プラスチック系断熱材製品。
3.15
スライスした試験片
試料(断熱材製品)を約10 mm(6 mm以上)の均一な厚さに切り分けたもの。この規格では,単に試
験片ともいう。
表1−記号及び単位
記号
量
単位
a
温度拡散係数(温度拡散率)
m2/s
λ
熱伝導率
W/(m・K)
ρ
密度
kg/m3
cp
定圧比熱
J/(kg・K)
D
有効拡散係数
m2/s
D0
基準板の有効拡散係数
m2/s
d
スライスした試験片の厚さ
m
d0
基準試料の厚さ
m
F
数値係数
−
F0
フーリエ数
−
i
経年変化期間における第i日
日
n
経年変化期間
日数
r
熱伝導抵抗
m・K/W
r0
初期熱伝導抵抗
m・K/W
rt
t日後の試験片の熱伝導抵抗
m・K/W
R
熱抵抗
m2・K/W
Rav
経年変化期間中の平均熱抵抗
m2・K/W
R0
初期熱抵抗
m2・K/W
Rt
t日後の試験片の熱抵抗
m2・K/W
Rn
経年変化期間最終日の熱抵抗
m2・K/W
S
スケーリング係数
−
t
日
日
t0
開始日
日
T
温度
K
T1,T2
加熱又は冷却された基準板の表面温度
K
Tm
基準試料の平均温度
K
TDSL
損傷表面層の厚さ
m
5
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
4
一般事項
4.1
適用条件
この規格の基になる解析モデルの概要を,参考として附属書Aに示す。この試験手順は,スライスした
試験片の材料特性が試験対象の材料と同一であるとの前提に基づく。すなわち,スライスした試験片は,
元の厚さの材料と有効拡散係数及び初期の気泡ガスの量が等しく,一次元拡散が支配的要因であるとの仮
定に基づいている。
通常の厚さの試料を対象とすると,25年以上の値を得るためには,非常に長い試験期間が必要である。
4.2
結果に影響を与える要因
経年変化プロセスに影響を与える要因は,次のとおりであり,その詳細を附属書Aに示す。
− 用いた厚さが薄いことが原因の誤差
− 損傷表面層の厚さ
− 試料作成前の経年変化
− 材料の不均質性
− 連続気泡率が高いか又は連続気泡が不均一に存在
5
試験方法
5.1
試験方法A−芯材の断熱性の経時変化を測定するための試験方法
5.1.1
一般
試験方法Aは,状態調節の期間を短くし,各時点における熱抵抗の変化を測定するための一般的な手順
である。無作為に採取した厚さが25 mm以上の発泡プラスチック系断熱材を試料とし,それぞれ約10 mm
(6 mm以上)の均一な厚さの試験片に切り分ける。この場合,切断面の気泡の損傷を考慮する。試験片
の熱抵抗の測定は,製造後可能な限り速やかに開始し,初期の熱抵抗に対する測定時点の熱抵抗の比が,
経年変化プロセスの一次段階から二次段階に十分に移行していることを示すまで,一定の時間間隔で実施
する。製品の経年変化後の熱抵抗は,スケーリング係数を用いて算出する。
注記 試験片の作製が断熱性に与える影響を最小にするために,TDSLは,試験片の厚さの5 %以下
とすることが望ましい。
5.1.2
試料採取
試料の採取方法は,JIS A 9511の5.2(試料及び試験片),又はJIS A 9526の6.2.2(試料の状態調節)に
よる。
5.1.3
試験片の準備
試験片の準備は,次による。
a) 試験片の状態調節及び試験場所は,JIS A 9511の5.1(試験片の状態調節及び試験場所),又はJIS A 9526
の6.2.4(試験場所)による。
b) 試料の元の厚さに応じて,各試料を均等な厚さにスライスする。表面に何らかの被覆膜がある場合,
表面から1枚目の試験片は破棄する。試験片全体の面積は,試験装置の最小測定可能面積を下回らな
いものとする。試験装置の総面積が大きい場合,試験片の過度の反りを防止するため,試験片を試験
装置の測定面積より少し大きい中央部分と,それを取り巻く同一厚さの周囲部分との二つの部分に分
ける必要がある。
c) 複数の試験片を積み重ねて測定を行う場合,切り出し後,状態調節後又は試験後において正確に元の
状態に重ね合わすことができるように,各側面に印を付ける。
6
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
試料を旋盤に載せ,所定位置に保持する。
注記1 試料を研削盤の真空吸着テーブルに載せ,空気吸引によって所定位置に固定し,歯の細かい
バンドソーを用いて所定の幅にスライスするとよい。
注記2 二重反転式の食品調理用のミートスライサーで,各面に複数の切削を行ってスライスしても
よい。
5.1.4
試験片の寸法測定
試験片の寸法測定は,次による。
a) 各試験片の長さと幅を2 mm単位の精度で測定する。
b) 各試験片の厚さを±0.02 mmの精度で測定する。試験片を積み重ねた場合,厚さを±0.2 mmの精度で
測定する。
c) 熱伝導抵抗を求める場合,b)で得た値から,測定で得たTDSLの値,又は二つの気泡の直径に等しい
数値を差し引くことによって,有効厚さを計算する。
注記 寸法その他の変化が試験期間中に発生しなかったことを確認するため,熱抵抗の測定の後,1
枚の試験片に対してa)及びb)の手順を再度行うことを推奨する。
5.1.5
試験片の熱抵抗及び熱伝導抵抗の測定
試験片の熱抵抗及び熱伝導抵抗の測定は,次による。
a) 測定は,一つの選択温度において,恒温室でJIS A 1412-1又はJIS A 1412-2のいずれかに従って行わ
なければならない。スライスした試験片を積み重ねた試験片を測定する場合,十分な数のスライスし
た試験片を積み重ね,厚さに依存しない熱伝導率を得られるようにしなければならない。
b) 熱抵抗及び熱伝導抵抗の測定時のスライスした試験片の平均温度は23
2
3
+
− ℃とする。
c) 単一の試験片又は積み重ねた試験片の初期熱抵抗R0(さらに,必要がある場合,初期熱伝導抵抗r0
も求める。)を,選択した方法に基づき,スライス後1日以内に測定する。
d) 各試験片を個別に状態調節した上で,一定の時間間隔で熱抵抗Rtを測定する。相対熱抵抗比Rt/R0を
計算した上,その数値と時間の対数との関係をグラフ化する(必要がある場合,相対熱伝導抵抗比を
用いてもよい。)。状態調節の条件は,温度23±2 ℃,相対湿度(50±5)%RHとする。ただし,相対
湿度は(50
20
10
+
−)%としてもよい。
e) Rt/R0又はrt/r0の数値が遷移点を超えた経年変化の二次段階において,グラフが線形関係を示す(図
A.1参照)までd)の手順を繰り返し実施する。
5.1.6
製品における長期熱抵抗の計算
製品における長期熱抵抗の計算は,次による。
a) 厚さが10 mmでない試験片を使用することができるが,結果の比較検討ができるように,標準値又は
基準値として10 mmの厚さとすることを推奨する。
b) 試験片の厚さが10 mmでない場合,試験片の平均熱抵抗を求め,附属書Aに示すスケーリング係数
の概念を利用して,5.1.5で得た試験結果から成る曲線を,式(1)によって厚さが10 mmである場合の
曲線に変換する。
r = F(log t) ············································································ (1)
c) b)において,スケーリング係数によって得た数値を用いて,要求された特定時間に試験した試験片の
元の厚さの熱抵抗を推定する。
d) 一例として,厚さが50 mmの製品の場合,25年後の熱抵抗(R25)と同一期間における平均値Rav.25は,
次のとおり導き出すことができる。
7
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
1) 厚さ50 mmの製品の25年後における熱抵抗 期間25年は,9 125日となる。したがって,厚さが
10 mmの場合,式(A.11)に基づき,これは,次の式(2)の期間に相当する。
日
365
50
10
125
9
125
9
2=
=
=
S
t
···················································· (2)
厚さ10 mmの試験片の場合に得た曲線から,365日目における熱伝導抵抗r(10,365)を求める。
したがって,次の式(3)及び式(4)となる。
r(50,9 125)= r(10,365) ······················································ (3)
R25 = 0.05 r(50,9 125) ····························································· (4)
2) 厚さ50 mmの製品の25年間における平均熱抵抗 式(5)に基づき,25年(9 125日)間における平
均熱伝導抵抗は,9 125/10= 2 886日後の熱伝導抵抗に等しくなる。
10
/n
t=
················································································ (5)
したがって,厚さ10 mmの試験片の場合,この期間は,次の式(6)の期間に等しい。
日
115
50
10
886
2
886
2
2=
=
=
S
t
···················································· (6)
この厚さ10 mmの試験片の場合に得た曲線から,115日目における熱伝導抵抗r(10,115)を求
める。したがって,次の式(7)及び式(8)となる。
rav(50,9 125)= r(50,2 886)= r(10,115) ··························· (7)
Rav.25 = 0.05 rav(50,9 125) ························································· (8)
e) 必要に応じて,スケーリング係数を用いて,製品の経年変化後の熱抵抗値を求めることができる。
5.2
試験方法B−被覆層のない製品の設計耐用期間における熱抵抗を測定するための簡易試験方法
5.2.1
一般
試験方法Bは,箇条4及び5.1に基づく。この試験方法では,元の製品から切り出した厚さ約10 mmの
複数の試験片を重ねず状態調節した後,これらを積み重ねて熱抵抗を測定する方法を規定する。試験方法
Bでは,厚さ100 mmの場合の,25±2年後の値を得ることが実証されている。その他の厚さにおいても,
当該ガスの拡散係数と熱伝導率の関数として,若干の誤差が生じ得る。
5.2.2
手順
手順は,次による。
a) 5.1.1に基づき試料を採取する。製造から試料作製までの期間は,1年を超えてはならない。
b) 切り出し後及び状態調節後において,正確に元の状態に重ね合わすことができるように,各側面に印
を付ける。
c) 各試料を厚さ方向にスライスして分割する。この時,各試験片の厚さは原則10±1 mmとして,可能
な限り表面層を保持する。
d) 状態調節の前後において,スライスした試験片の厚さ及び元の状態に積み重ねた試験片の厚さを測定
する。
e) スライスした試験片を温度23±2 ℃,相対湿度(50±5)% RHで,91±7日間,個々に状態調節する。
この状態調節後,スライスした試験片を積み重ね直して,元の状態とする。
f)
積み重ねた試験片の熱抵抗をJIS A 1412-1又はJIS A 1412-2に基づき,平均温度23
2
3
+
− ℃,温度差25 ℃
以内で測定する。
8
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
6
報告事項
試験報告書には,次の情報を記載しなければならない。
a) 材料の名称及び商品名
b) 試験期間
c) 製造日(発泡日,成形日及び出荷日)
d) 試験片の作製日及び作製の詳細
e) 採用した試験方法(試験方法A又は試験方法B)
f)
試験片の採取方法
g) 寸法,質量及びかさ密度
h) 試験片の有効厚さ(ただし,必要がある場合だけ)
i)
熱伝導率試験装置の説明
j)
平均温度及び温度差
k) 単一の試験片に対する初期試験日又は積み重ねた試験片の状態調節開始日,及びその後の単一の試験
片又は積み重ねた試験片の熱抵抗試験日
l)
試験方法Aで測定した場合,試験片の1枚又はそれ以上のスライスした試験片における結果の平均と,
適切なスケーリング係数を利用して得た,要求された期間における長期熱抵抗値又は熱伝導率
m) 試験方法Bで測定した場合,簡易測定法を用いて,複数の試験片を積み重ねた試験片の平均値測定か
ら得られる,設計耐用年数(3.4)における長期熱抵抗値
また,試験報告書には,必要に応じて次の情報を記載する。
n) 被覆層の拡散係数を測定又は同定した方法(附属書JD又は附属書JE)
o) 附属書JAでの解析によって予測した場合は,設定した経過年数,及び対応する長期熱抵抗値又は熱
伝導率
p) 被覆層の材質,種類及び厚さ
q) 計算に用いた発泡ガスの種類及び物性値
r) 養生条件(シールの有無及び周囲の温湿度)
9
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書A
(参考)
解析モデル
A.1 促進経年変化
長期断熱性能の測定を目的として,幾つかの促進試験方法が何年かにわたり開発されてきた。このよう
な試験方法の一部は,国によっては国内規格に既に組み込まれている。一般に,こうした試験方法では,
一定に制御された高温又は室温で状態調節した均一な厚さ(25 mm以上)の試験片の熱抵抗を,初期,す
なわち,ゼロ時点から一定の時間間隔で測定を行う。昇温する場合,温度は規格によって異なり,60 ℃〜
100 ℃の幅をもち,試験期間も10日〜90日と異なる。また,室温で180日以上の測定を条件とする規格
もある。
試験片の長期熱抵抗は,幾つかの数学モデルを基に熱抵抗の経時変化の曲線を外挿して算出する。特に,
この10年間に,様々な複雑なモデルが開発されてきた。そうしたモデルは,経年変化プロセスに対する理
解を深めるとともに,求めた長期熱抵抗値の不確実さをある程度解消する点でも役立ってきた。
これらの手順は,いずれも全面的に満足のいくものではなく,一般に認められた手順には至っていない。
ある材料の場合は,一定の高温に長期間暴露すること[すなわち,実用されている材料が通常ではさら(曝)
されない条件]は,ガス放散を加速化することに加え,経年変化プロセスとは関係のない材質の変化を引
き起こす原因となり,結果的に不正確なデータを得る可能性がある。また,最近はクロロフルオロカーボ
ン(CFC)に代わる代替発泡剤に関する研究が活発になっており,より迅速な試験方法を提供することが
求められている。
このため,最適な試験方法を実現するには,状態調節を高温ではなく室温又はそれに近い温度で実施す
ることが要求される。これを実現するためには,期間を長期化するか,厚さを薄くするかのいずれかが必
要である。各種の発泡プラスチックに対して,10 mm以下の均等な厚さをもつ試験片を用いて,短期間で
断熱性の変化の測定法に関する重要かつ有望な研究が,様々な国で行われている。
この試験方法は,上記の考え方,すなわち,一般に,スライシング・スケーリング手法と呼ばれている
方法に基づいている。
A.2 平均熱抵抗値の算出
多くの場合,発泡プラスチックの経年変化の研究では,熱伝導抵抗r(熱伝導率の逆数)は,時間の対
数関数として式(A.1)で表される。
r = F (log t) ··········································································· (A.1)
また,試験結果は,初期“ゼロ”時点(通常,数日)におけるr値を基準値として用いて,無次元化し
た熱伝導抵抗で示される[式(A.2)参照]。
rt/r0 = F (log t) ······································································· (A.2)
これによって,経年変化プロセスの一般的特性を,絶対値に注意を払わなくても理解できる。
Rtを期間t日後の熱抵抗とし,Rav,nをn日間の平均熱抵抗とすれば,次の式(A.3)で表される。
Rav,n = ΣRt/n··········································································· (A.3)
Rが時間に対数依存すると仮定すれば,式(A.1)及び式(A.2)は,次の式(A.4)で表される。
10
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(Ri−Rn) / (R0−Rn) = 1−log i/log n ················································ (A.4)
ここに,R0及びRnは,経年変化期間の初期及びn日後における熱抵抗である。
したがって,n日間における平均熱抵抗Ravは,t日後における熱抵抗Rtに相当するので,
10
/
n
t=
············································································· (A.5)
期間25年(9 125日)をスライスされていない発泡プラスチックの耐用期間と考えると,平均熱抵抗値
を得るには,期間9 125/3.16日,すなわち2 886日を要する。
A.3 熱移動及び物質移動の相似
窒素及び酸素の発泡プラスチック板内部への侵入並びに発泡剤の発泡プラスチックからの放散は,いず
れも発泡プラスチック板の加熱又は冷却と同様に記載することができる。
均一な温度T1のある板の表面温度をT2に冷却する場合,ある板の平均温度Tmは次の式(A.6)で与えられ
る。
Tm= (T0−T2) / (T1−T2) = 8π2Σ1/ (2n+l) exp[−F0 (2n+l) 2π2] (n = 0) ··············· (A.6)
ここに,F0 = a・t/d 2 = λ/(ρ・cp) ·················································· (A.7)
F0の値が大きい場合(要するに,期間が長い又は厚さが薄い場合),式(A.6)の級数は急速に収れんする。
したがって,式(A.6)は,次のように簡略化できる。
(Tm−T2) / (T1−T2) = 8π2exp (−F0π2) ··········································· (A.8)
これは,特定の期間における値(厚さと温度拡散率とが一定)の場合,拡散プロセスは,厳密に指数関
数的であることを示している。これは,十分に進展した段階での拡散プロセスと呼ばれている。ガスの移
動も拡散プロセスと同様に扱うことができる。ガスの分圧が温度に,圧力変化が温度変化に,有効ガス拡
散係数が温度拡散係数にそれぞれ対応している。
したがって,ガス移動現象も,式(A.6)及び式(A.8)によって同様に解析することができる。式(A.8)は,
F0の値が大きい場合,相対(無次元)圧力の対数がF0に線形依存することを示している。一方,式(A.6)
は,相対(無次元)圧力の対数は常に,F0に比例することを示している。F0が一定の場合,ガス移動プロ
セスを式(A.6)が表している限り,ガス移動プロセスのスケーリングは,薄い試料の拡散速度を求め,この
求めた拡散速度と厚い試料の拡散速度との関係を求めることによって行う。したがって,任意の一連の特
性(d及びD)をもつ板について測定した拡散速度を基準板(d0,D0)の場合と比較検討するには,測定
時間に,スケーリング係数を乗じなければならない。
t=t0S ··················································································· (A.9)
S=(d02D/d2D0) ···································································(A.10)
試験材料についてD = D0(すなわち,均質である。)と仮定すれば,スケーリング係数は厚さだけの比
で表すことができる。すなわち,次の式(A.11)となる[例の式(A.12)を参照。]。
S = d02/d2 ············································································ (A.11)
例 t10 =t100・(d10)2/(d100)2 = 25×365・(0.01)2 / (0.1)2 = 91日 ·········································(A.12)
A.4 経年変化プロセスのモデル化及びスケーリング係数の利用
経年変化プロセスにおいて発生する代表的な変化を説明するために,各種モデルを利用することができ
る。気泡ガスの熱伝導抵抗は,板内における位置と経年変化状態(経過時間,温度並びに気泡ガス組成に
影響を与える窒素,酸素及び分子量が大きい発泡剤のそれぞれの有効拡散係数)の関数として変化する。
11
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
与えられた変数を理想的な材料に適用することで,モデルを用いて経年変化特性を計算することができ
る。気泡内の各ガスの拡散は独立に扱うことができる。他のガスがもし存在しなければ,発泡剤のセル内
モル濃度は変化しないため,発泡剤による熱性能への影響はほとんどないこととなる。酸素の拡散速度は
窒素の6倍であるが,窒素の濃度が酸素の4倍であるため,窒素ガスが支配的な役割を果たす。空気が気
泡セルに入ることで,発泡剤の濃度を相対的に引き下げるため,断熱性の変化は非常にはっきりとしてい
る。
ある理想的な材料の三つの厚さについて,計算で求めた代表的な経年変化曲線を図A.1に示す。経年変
化は,一次段階及び二次段階に当てはめた個別の直線で近似的に示すことが可能である。遷移点(実質的
には遷移区間)は,拡散プロセスの進行速度の変化点と一致するため,発泡プラスチックの断熱性の分析
において重要な役割を果たす。
厚さが経年変化曲線の特性に与える影響は,非常にはっきりとしている。厚さが薄くなると,熱伝導抵
抗が時間の指数関数になるまでの期間も減少する。
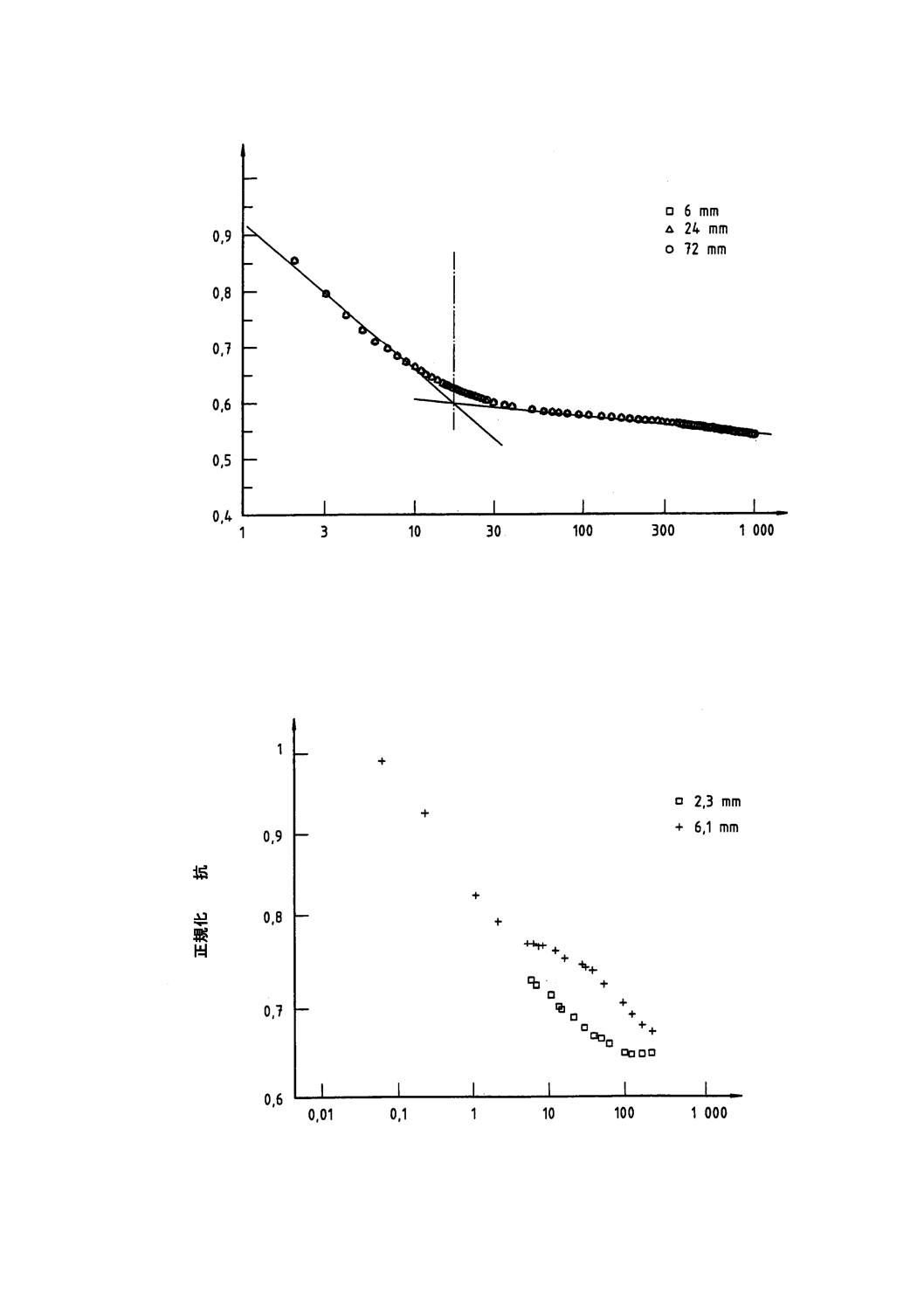
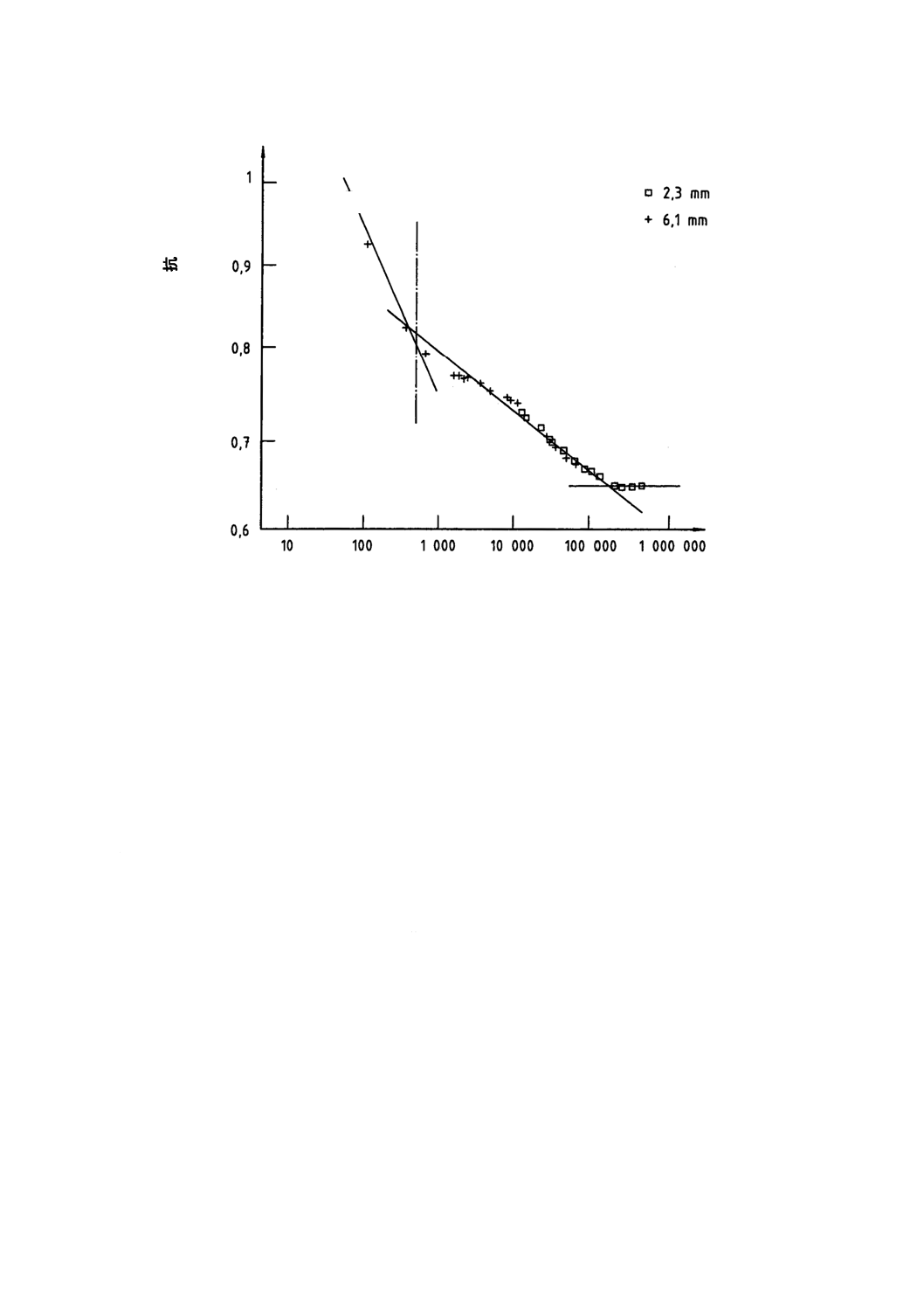
二つの材料厚さを用いた試験で得た結果を図A.2では実時間で示し,図A.3ではスケーリング係数適用
後の時間で示している。図A.2は実時間の関数としての2種類の厚さの硬質独立気泡プラスチックの正規
化熱抵抗を,図A.3はスケーリング係数適用後の2種類の厚さの硬質独立気泡プラスチックの正規化熱抵
抗を示している。図に示すように,スケーリング係数Sを用いると,全てのデータが一つの曲線に沿うよ
うになる。したがって,薄い試料を測定すれば,それと同材質の厚い試料の,対応する挙動を知ることが
可能なデータを得られる。
A.5 結果に影響を与えうる要因
スライスした試験片及びスケーリング係数を利用する手法の利点は,高分子ポリマーのガス含有量,拡
散係数,気泡サイズ及び放射特性に関係なく適応できる比較的単純な手法であるという点にある。ただし,
この手法を適用する際には,幾つかの要素について注意を要する。特に,二つの変数,すなわち,厚さの
二乗の比及び有効拡散係数の比に依存するスケーリング係数の適用には,注意しなければならない。した
がって,“正確な”有効厚さの測定は,非常に重要である。また,試験する材料又は製品は,厚さ方向の特
性が均一であるべきである。すなわち,表面層と中心層との拡散係数は,大きく異ならないことが必要で
ある。
A.5.1 厚さの誤差
通常,試験片の厚さは10 mm程度である。現在,熱抵抗の測定に適した面積をもつ試験片を作製するた
めの各種方法を用いれば,最大誤差±10 %で均等な厚さを得ることが可能である。通常は,これよりはる
かに小さい誤差である。
12
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.2−実時間の関数としての2種類の厚さの硬質独立気泡プラスチックの正規化熱抵抗
図A.1−スケーリング係数適用後の3種類の厚さの硬質独立気泡プラスチックの正規化熱抵抗
正
規
化
熱
抵
抗
実時間(日)
正
規
化
熱
抵
抗
相対時間(日)
一次段階
遷移点
ニ次段階
13
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
図A.3−スケーリング係数適用後の2種類の厚さの硬質独立気泡プラスチックの正規化熱抵抗
A.5.2 損傷表面層
試料を切断することで連続気泡の部分が増え,試験片の“有効”厚さが減少する。これは,厚さが薄く
なるほど著しくなる。この厚さの減少を補正するために,TDSLという考え方が導入された。
試験片の有効体積をガスビュレット又は空気比較比重瓶のいずれかを用いて測定し,これを幾何学的体
積の測定値と比較する方法で,最も高い精度で有効厚さを求めることができる。ガスビュレットは,試験
片の表面積と体積との比が大きい場合に最も適した精度の高い方法であるが,標準的な試験方法はまだ開
発されていない。
一般に,この損傷表面層は,各切断面について最大で一つの気泡径に等しいことが明らかになっている。
損傷表面層の測定に適した試験方法が開発されるまでは,この値を適用することが望ましい。
表面の損傷した気泡の影響は,近似的に次の式(A.13)で排除できる。
λ= (ds−2x) / (ds/λs−2x/λair) ·····················································(A.13)
ここに,λairは,一定の気泡径xをもつ,損傷を受けて空気で満たされた場合の発泡プラスチックの熱伝
導率である。気泡径が0.5 mmの場合,λは0.038 W/(m・K)となる(この値は,製品ごとに異なる。)。λsは,
この測定法で測定された熱伝導率,dsは試験片の厚さである。
したがって,気泡径が0.5 mm,厚さ100 mmの製品の場合,式(A.14)になる。
λ= (0.01−0.001) / (0.01/0.028−0.001/0.038) = 0.027 2 W/(m・K) ··········(A.14)
これに対応する測定値は,0.028 W/(m・K)であった。
A.5.3 試験片作製前の経年変化
これまで行われてきた経年変化現象の様々な研究においては,試験は製造“直後”(通常,5日未満)に
作製された試験片について実施されてきた。しかし,実際には,製造から試験片作製までの期間は,それ
相対時間(日)
正
規
化
熱
抵
抗
一次段階
遷移点
ニ次段階
14
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
よりはるかに長くなることもあると考えられる。このことが,変数として状態調節期間の長さに影響を与
える場合がある。
A.5.4 不均質な材料
実際には,“均質な”発泡プラスチック材料の多くは,密度が比較的均一な独立気泡構造の芯材と,それ
を囲む密度が高い表面層とで構成される。連続気泡率が10 %を超える場合又は,連続芯材気泡の不均質部
分があることもある。また,発泡プラスチック製品は,経年変化の影響を減少させることが目的で,様々
な種類のスキン層及び面材で被覆される。
こうしたスキン層及び面材が拡散係数に対して与える影響は,芯材が拡散係数に対して与える影響とは
異なる。したがって,この試験方法は,芯材だけに適用される。また,芯材と表面層との拡散速度が類似
(10 %未満)しており,平均値を用いることが可能な材料には適用できる。材料の不均質部分に補正を加
えることを検討してもよい。
15
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JA
(参考)
被覆層がある場合の解析モデル−
断熱材内分圧の簡易計算法に基づく熱伝導率変化量
この附属書では,被覆層がある場合の解析モデルを示す。
なお,この附属書における記号は,本体とは異なり,JA.7に示す。
JA.1
概要
発泡プラスチック系断熱材内部の発泡ガスの放散及び断熱材外部の空気の侵入によって変化する,断熱
材内分圧に基づいて,製造からt時間経過した発泡プラスチック系断熱材の熱伝導率を算出する方法を示
す。
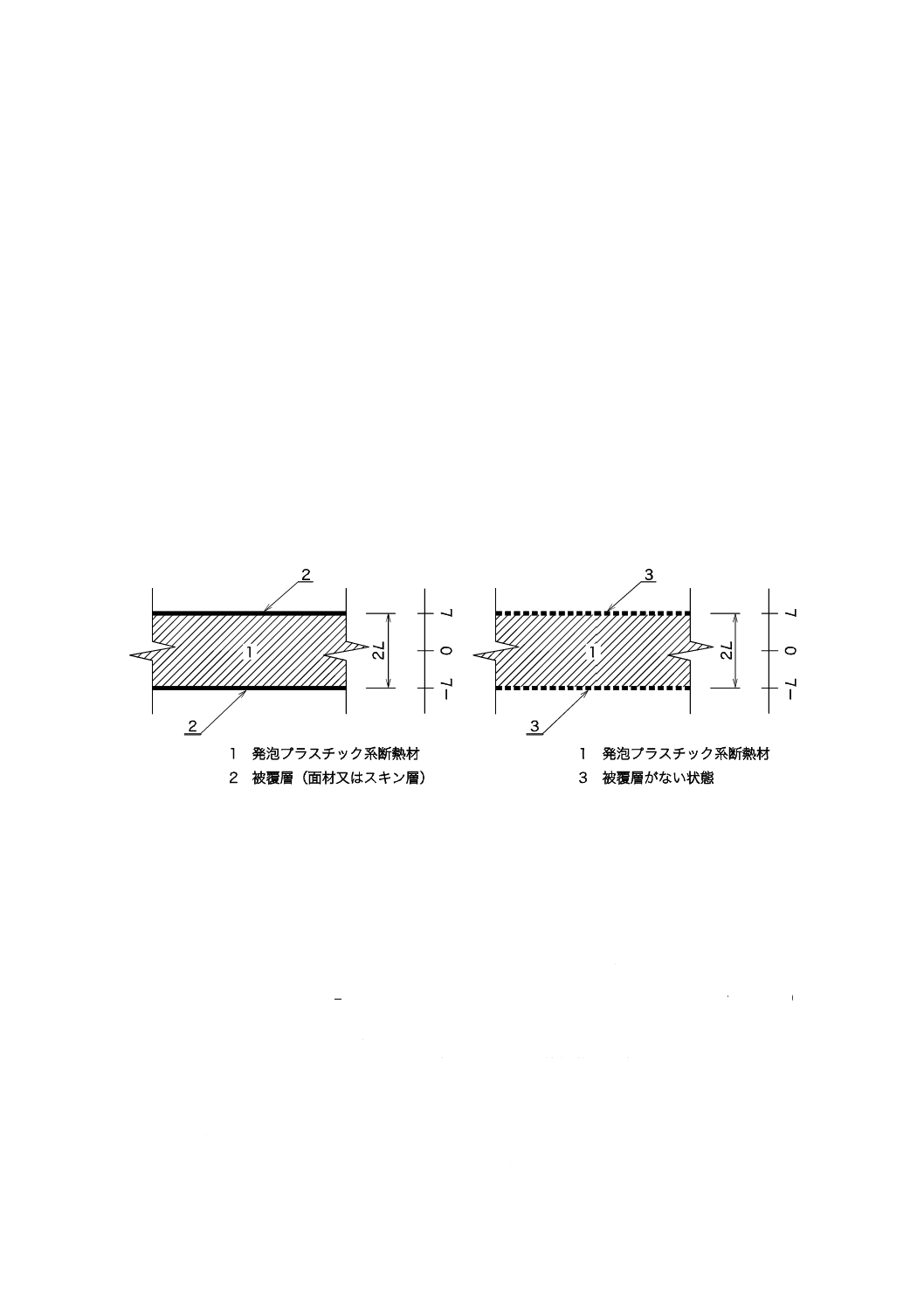
計算によって熱伝導率を求める際の解析モデルを図JA.1に示す。解析モデルでは,熱伝導率変化の主な
原因である発泡ガスと周囲空気が移動(放散又は侵入)する方向は,厚さに対する方向(一次元方向)で
ある。
a) 被覆層がある場合
b) 被覆層がない場合
図JA.1−発泡プラスチック系断熱材の解析モデル(断面)
JA.2 断熱材の熱伝導率
製造からt時間経過した発泡プラスチック系断熱材の熱伝導率[λfoam(t)]は,式(JA.1)によって表現でき
る。また,製造直後の熱伝導率(λfoam, ini)は,JA.3に従って測定又は計算する。
なお,時間経過に伴う熱伝導率の変化量[λaging(t)]は,JA.4に従って計算する。
)
(
)
(
t
t
aging
foam,ini
foam
λ
λ
λ
+
=
························································· (JA.1)
ここに,
λfoam(t): 製造からt時間経過した熱伝導率[W/(m・K)]
λfoam, ini: 製造直後(t=0)の熱伝導率[W/(m・K)]
λaging(t): 時間経過に伴う熱伝導率の変化量[W/(m・K)]
JA.3 製造直後の熱伝導率
JA.3.1 製造直後の熱伝導率の測定
製造直後の発泡プラスチック系断熱材の熱伝導率(λfoam, ini)は,JIS A 1412-2に従って測定した値を用い
16
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
る。
JA.3.2 製造直後の熱伝導率の計算
JIS A 1412-2に従って測定された熱伝導率がない場合,製造直後の発泡プラスチック系断熱材の熱伝導
率(λfoam, ini)は,式(JA.2)によって計算する。
)0(
,
gas
solid
radiation
ini
foam
λ
λ
λ
λ
+
+
=
·················································· (JA.2)
ここに,
λfoam, ini: 製造直後(t=0)の発泡プラスチック系断熱材の
熱伝導率[W/(m・K)]
λradiation: 気泡セル膜間の放射熱伝達による伝熱成分
[W/(m・K)]
λsolid: 樹脂部分(気泡セル膜及びポリマー支柱)の熱伝
導による伝熱成分[W/(m・K)]
λgas(0): 製造直後(t=0)の気泡セル内気体の熱伝導によ
る伝熱成分[W/(m・K)]
式(JA.2)における気泡セル膜間の放射熱伝達による伝熱成分(λradiation),樹脂部分(気泡セル膜及びポリ
マー支柱)の熱伝導による伝熱成分(λsolid)は,それぞれ式(JA.3),式(JA.4)によって計算する。また,製
造直後の気泡セル内気体の熱伝導による伝熱成分[λgas(0)]は,式(JA.5)によって計算する。
φ
ρ
ρ
σ
λ
polymer
foam
strut
radiation
V
T
×
×
=
1.4
3
16
3
··················································· (JA.3)
ここに,
σ: ステファン・ボルツマン定数(=5.67×10−8)
[W/(m2・K4)]
T: 温度(K)
Vstrut: 支柱ポリマー体積率
ρfoam: 断熱材密度(kg/m3)
ρpolymer: 気泡セル膜を構成するポリマー密度(kg/m3)
φ: 気泡セルの直径(μm)
(
)
polymer
polymer
foam
strut
solid
V
λ
ρ
ρ
λ
−
=
2
3
1
················································· (JA.4)
ここに,
λpolymer: 気泡セル膜を構成するポリマー熱伝導率[W/(m・K)]
∑
=
=
n
i
i
i
gas
1
)0(
)0(
λ
ω
λ
······························································· (JA.5)
ここに,
ωi(0): 断熱材内の空気及び発泡ガスの熱伝導率に対す
る重み係数
λi: 空気及び発泡ガスの熱伝導率[W/(m・K)]
i: 断熱材内気体の種類(1:空気,2〜:発泡ガス)
式(JA.5)における断熱材内の空気及び発泡ガスの熱伝導率に対する重み係数[ωi(0)]は,式(JA.6)によっ
て計算する。
なお,式(JA.6)におけるxi(0)及びAijは,それぞれ式(JA.7)又は式(JA.8)によって計算する。
∑
=
=
n
j
ij
j
i
i
A
x
x
1
)0(
)0(
)0(
ω
································································ (JA.6)
ここに,
xi(0): 製造直後(t=0)の断熱材内空気及び発泡ガスのモ
17
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
ル分率
Aij: 断熱材内空気及び発泡ガスに対する結合係数
∑
=
=
n
i
i
i
i
P
P
x
1
)0(
)0(
)0(
····································································· (JA.7)
ここに,
Pi(0): 製造直後(t=0)の断熱材内空気及び発泡ガスの
分圧(MPa)
(
)
ij
ij
ij
b
a
A
+
=
2
1
25
.0
···························································· (JA.8)
j
i
i
j
j
i
ij
S
T
S
T
M
M
n
n
a
+
+
=
4/3
j
ij
ij
S
T
S
T
b
+
+
=
i
b
i
T
S
,
5.1
=
j
i
ij
S
S
S =
ここに,
ni: 断熱材内空気及び発泡ガスの粘性係数(μPa・s)
Mi: 断熱材内空気及び発泡ガスの分子量(g/mol)
T: 温度(K)
Tb, i: 断熱材内空気及び発泡ガスの沸点(K)
i: 断熱材内気体の種類(1:空気,2〜:発泡ガス)
j: 断熱材内気体の種類(1:空気,2〜:発泡ガス)
空気及び主な発泡ガスの物性値は,表JA.1に示すとおりである。
なお,この値を用いて,対象とする気体が空気(i=1)及び1種類の発泡ガス(i=2)である場合には,
表JA.2に示す値を用いることができる。
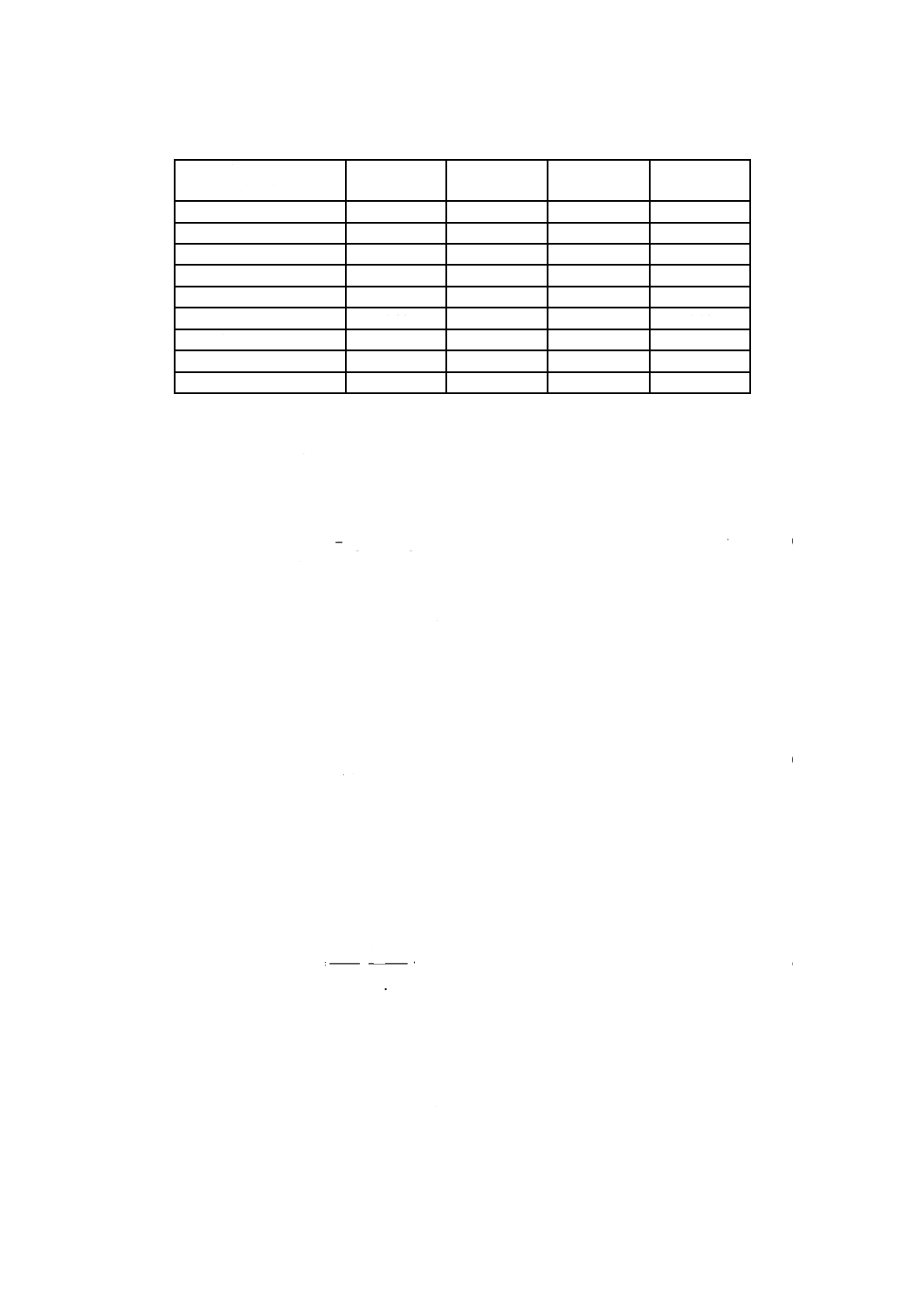
表JA.1−各種気体の物性値{熱伝導率[296 K(23 ℃)],分子量,粘性係数,沸点}
気体名
熱伝導率λi
W/(m・K)
分子量Mi
g/mol
粘性係数ni
μPa・s
沸点Tb, i
K
空気
25.54
29.0
18.2
80.3
HFC134a
13.42
102.0
12.2
246.7
HFC152a
13.29
66.0
10.3
248.3
HFC245fa
12.07
134.0
9.4
288.5
HFC365mfc
10.73
148.0
8.4
313.2
ノルマルペンタン(nC5)
14.91
72.0
6.9
309.2
シクロペンタン(cC5)
11.84
70.0
7.4
322.2
イソブタン(iC4)
15.89
58.1
7.4
261.5
ノルマルブタン(nC4)
16.23
58.1
7.4
272.5
二酸化炭素(CO2)
16.45
44.0
14.7
194.6
18
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
表JA.2−各種気体の結合係数(Aij)(空気i=1,発泡ガスi=2)
発泡ガスの種類
(i=2)
A11
A12
A21
A22
HFC134a
1.00
1.98
0.51
1.00
HFC152a
1.00
1.80
0.55
1.00
HFC245fa
1.00
2.59
0.42
1.00
HFC365mfc
1.00
2.89
0.39
1.00
ノルマルペンタン(nC5)
1.00
2.33
0.44
1.00
シクロペンタン(cC5)
1.00
2.18
0.46
1.00
イソブタン(iC4)
1.00
2.06
0.50
1.00
ノルマルブタン(nC4)
1.00
2.05
0.49
1.00
二酸化炭素(CO2)
1.00
1.27
0.75
1.00
JA.4 熱伝導率変化量
JA.4.1 時間経過に伴う発泡プラスチック系断熱材の熱伝導率変化量
JA.2に記載した式(JA.1)における時間経過に伴う発泡プラスチック系断熱材の熱伝導率変化量[λaging(t)]
は,式(JA.9)によって計算する。
)0(
)
(
)
(
gas
gas
aging
t
t
λ
λ
λ
−
=
·························································· (JA.9)
ここに,
λaging(t): 時間経過に伴う熱伝導率の変化量[W/(m・K)]
λgas(t): 時刻tにおける気泡セル内気体の熱伝導による伝
熱成分[W/(m・K)]
λgas(0): 製造直後(t=0)における気泡セル内気体の熱伝
導による伝熱成分[W/(m・K)]
JA.4.2 時間経過後の気泡セル内気体の熱伝導による伝熱成分
時間経過後の気泡セル内気体の熱伝導による伝熱成分[λgas(t)]は,式(JA.10)によって計算する。
∑
=
=
n
i
i
i
gas
t
t
1
)(
)(
λ
ω
λ
······························································· (JA.10)
ここに,
ωi(t): 断熱材内の空気及び発泡ガスの熱伝導率に対する
重み係数
λi: 空気及び発泡ガスの熱伝導率[W/(m・K)]
i: 断熱材内気体の種類(1:空気,2〜:発泡ガス)
式(JA.10)における断熱材内空気及び発泡ガスの熱伝導率に対する重み係数[ωi(t)]は,式(JA.11)によっ
て計算する。
∑
=
=
n
j
ij
j
i
i
A
t
x
t
x
t
1
)
(
)
(
)
(
ω
······························································· (JA.11)
ここに,
xi(t): 時刻tにおける断熱材内空気及び発泡ガスのモル
分率
Aij: 断熱材内空気及び発泡ガスに対する結合係数
式(JA.11)におけるxi(t)は,式(JA.12)によって計算する。また,式(JA.11)における結合係数(Aij)は,JA.3.2
に示す式(JA.8)によって計算する。
19
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
∑
=
=
n
i
i
i
i
t
P
t
P
t
x
1
)(
)(
)(
···································································· (JA.12)
ここに,
Pi(t): 時間経過後の断熱材内空気及び発泡ガスの分圧
(MPa)
JA.4.3 製造直後の気泡セル内気体の熱伝導による伝熱成分
製造直後の気泡セル内気体の熱伝導による伝熱成分[λgas(0)]は,JA.3.2に示す式(JA.5)によって計算す
る。
JA.5 時刻tにおける断熱材内の空気及び発泡ガスの分圧
JA.5.1 断熱材表面に被覆層がある場合
断熱材表面に被覆層がある場合[図JA.1 a)]には,空気及び発泡ガスの無次元断熱材内分圧は,式(JA.13)
によって計算する。
∑
∞
=
+
+
−
=
−
−
1
2
2
2
2
,
2
2
,
,
}
{
exp
2
)0(
)
(
n
i
i
n
n
i
eff
n
i
out
i
i
out
i
i
L
t
D
P
P
P
t
P
μ
μ
β
β
β
μ
·································· (JA.13)
β
β
μ
tan
=
i
i
eff
i
i
D
L
,
α
μ
=
ここに,
Pi(t): 時刻tにおける断熱材内の空気及び発泡ガスの分圧
(Pa)
Pi, out: 断熱材外部の空気及び発泡ガスの分圧(Pa)
Pi(0): 製造直後(t=0)の断熱材内の空気及び発泡ガスの
分圧(Pa)
Deff, i: 断熱材内部における空気又は発泡ガスの有効拡散
係数(m2/s)
αi: 断熱材表面における空気又は発泡ガスの物質移動
係数(m/s)
t: 時間(s)
L: 断熱材中心から断熱材表面までの距離(m)
JA.5.2 断熱材表面に被覆層がない場合
断熱材表面に被覆層がない場合[図JA.1 b)]には,空気及び発泡ガスの無次元断熱材内分圧は,式(JA.14)
によって計算する。
(
)
∑
∞
=
−
−
=
−
−
1
2
,
2
,
,
exp
)1
2(
1
π
8
)0(
)
(
n
i
eff
out
i
i
out
i
i
t
D
n
P
P
P
t
P
μ
····························· (JA.14)
L
n
2
π)1
2( −
=
μ
ここに,
Pi(t): 時刻tにおける空気及び発泡ガスの断熱材内分圧
(Pa)
Pi, out: 断熱材外部の空気及び発泡ガスの分圧(Pa)
Pi(0): 製造直後(t=0)の断熱材内の空気及び発泡ガスの
20
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
分圧(Pa)
Deff, i: 空気又は発泡ガスの有効拡散係数(m2/s)
t: 時間(s)
L: 断熱材中心から断熱材表面までの距離(m)
なお,式(JA.13)又は式(JA.14)によって計算する時刻tにおける断熱材内の空気及び発泡ガスの分圧は,
JA.6に記載する簡易計算法によって計算することができる。
JA.6 断熱材内分圧の簡易計算法
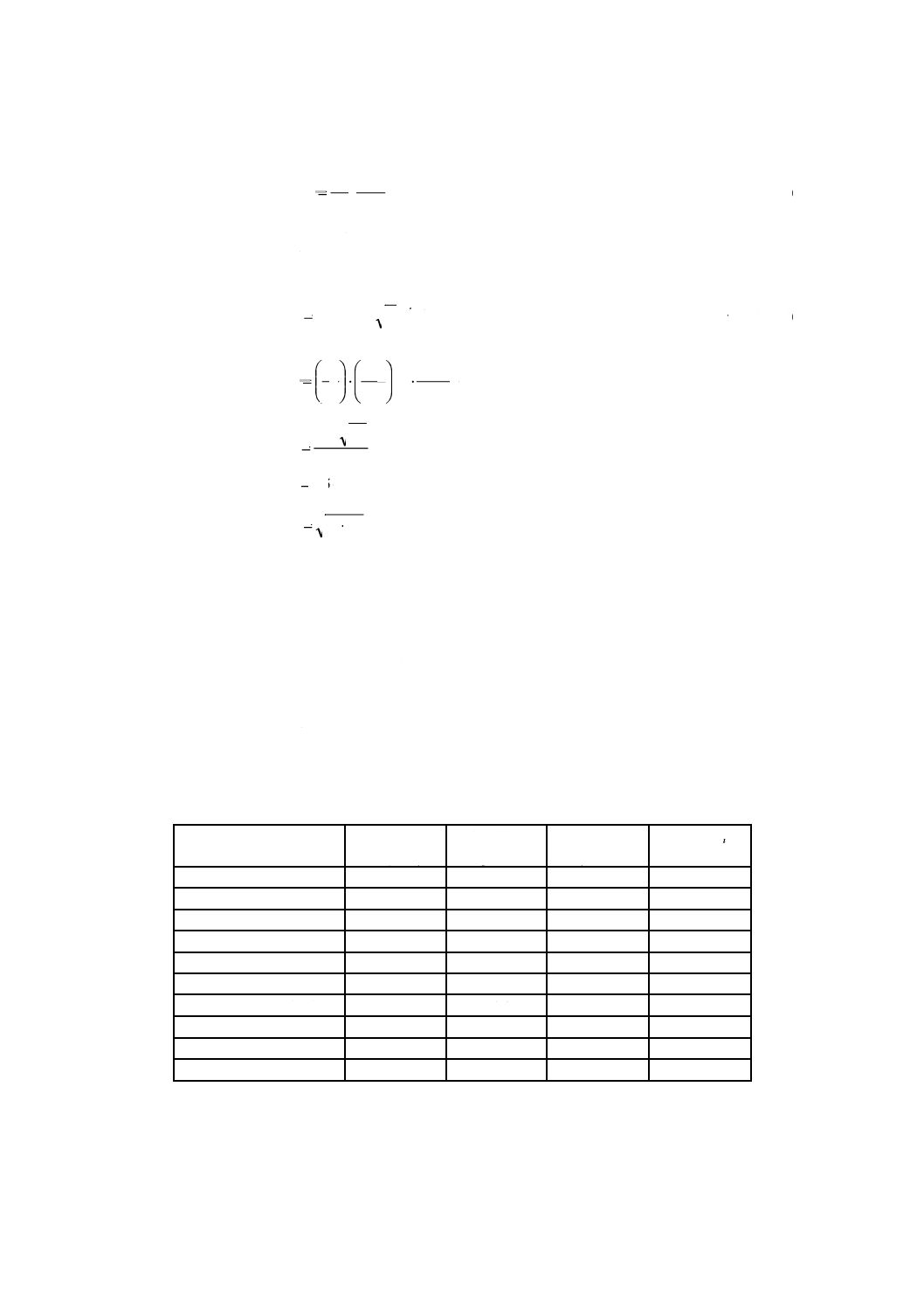
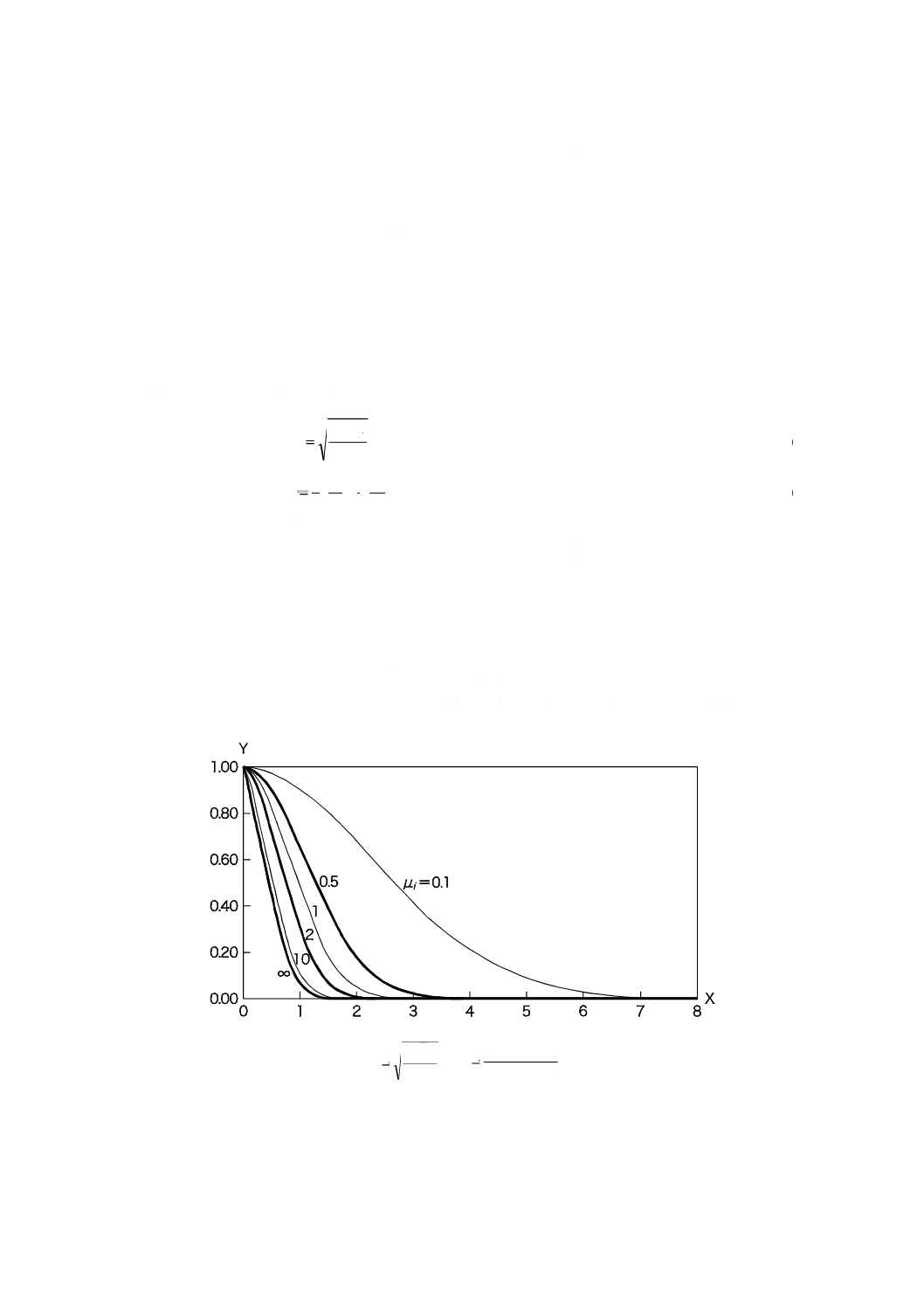
JA.6.1 無次元時間と無次元断熱材内分圧との関係
式(JA.15)に示す無次元時間と,式(JA.16)に示す無次元断熱材内分圧[=式(JA.13)及び式(JA.14)の左辺]
との関係は,図JA.2のように示される。
2
,
L
t
D
X
i
eff
i=
······································································ (JA.15)
out
i
i
out
i
i
i
P
P
P
t
P
Y
,
,
)0(
)(
−
−
=
··································································· (JA.16)
ここに,
Xi: 空気又は発泡ガスの無次元時間
Yi: 空気又は発泡ガスの無次元断熱材内分圧
Deff, i: 空気又は発泡ガスの有効拡散係数(m2/s)
t: 時間(s)
L: 断熱材中心から断熱材表面までの距離(m)
Pi(0): 製造直後(t=0)の断熱材内の空気及び発泡ガ
スの分圧(Pa)
Pi(t): 時刻tにおける断熱材内の空気及び発泡ガスの
分圧(Pa)
Pi, out: 断熱材外部の空気及び発泡ガスの分圧(Pa)
2
,
L
t
D
X
i
eff
=
,
out
i
i
out
i
i
P
P
P
t
P
Y
,
,
)0(
)
(
−
−
=
図JA.2−無次元時間と無次元断熱材内分圧との関係
JA.5において求める時刻tにおける断熱材内の空気及び発泡ガスの分圧は,図JA.2を用いることによっ
21
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
て計算することができる。
JA.6.2 断熱材表面に被覆層がある場合
被覆層がある場合には,図JA.2における曲線群の中から,式(JA.17)によって計算する無次元物質移動係
数(μi)に対応する曲線を選択する。
i
eff
i
i
D
L
,
α
μ=
·········································································· (JA.17)
ここに,
μi: 無次元物質移動係数
αi: 断熱材表面における空気又は発泡ガスの物質
移動係数{g/[m2・s・(g/m3)]}[=(m/s)]
L: 断熱材中心から断熱材表面までの距離(m)
Deff, i: 断熱材内部における空気又は発泡ガスの有効
拡散係数(m2/s)
次に,式(JA.15)によって得られる対象時刻の無次元時間から,その時の無次元断熱材内分圧を求める。
さらに,対象とする気体の製造直後(t=0)における断熱材内分圧[Pi(0)],断熱材外部の分圧(Pi, out)に
よって,時刻tにおける断熱材内分圧[Pi(t)]を求める。
JA.6.3 断熱材表面に被覆層がない場合
被覆層がない場合には,図JA.2における曲線群の中から,無次元物質移動係数(μi)が∞に対応する曲
線を選択する。
次に,JA.6.1と同様に,式(JA.15)によって得られる対象時刻の無次元時間から,その時の無次元断熱材
内分圧を求める。さらに,対象とする気体の製造直後(t=0)の断熱材内分圧[Pi(0)],断熱材外部の分圧
(Pi, out)によって,時刻tにおける断熱材内分圧[Pi(t)]を求める。
JA.7 記号一覧
Aij:
断熱材内空気及び発泡ガスに対する結合係数
Deff, i:
空気又は発泡ガスの有効拡散係数(m2/s)
i:
断熱材内気体の種類(1:空気,2〜:発泡ガス)
j:
断熱材内気体の種類(1:空気,2〜:発泡ガス)
L:
断熱材中心から断熱材表面までの距離(m)
Mi:
断熱材内空気及び発泡ガスの分子量(g/mol)
ni:
断熱材内空気及び発泡ガスの粘性係数(μPa・s)
Pi(0):
製造直後(t=0)における断熱材内空気及び発泡ガスの分圧(MPa)
Pi(t):
時刻tにおける断熱材内の空気及び発泡ガスの分圧(Pa)
Pi, out:
断熱材外部の空気及び発泡ガスの分圧(Pa)
Tb, i:
断熱材内空気及び発泡ガスの沸点(K)
T:
温度(K)
t:
時間(s)
Vstrut:
支柱ポリマー体積率
X:
無次元時間
xi(0):
製造直後(t=0)における断熱材内空気及び発泡ガスのモル分率
xi(t):
時刻tにおける断熱材内空気及び発泡ガスのモル分率
22
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
Y:
無次元断熱材内分圧
αi:
空気又は発泡ガスの物質移動係数{g/[m2・s・(g/m3)]}[=(m/s)]
λaging(t): 時間経過に伴う熱伝導率の変化量[W/(m・K)]
λfoam, ini: 製造直後(t=0)の熱伝導率[W/(m・K)]
λfoam(t): 製造からt時間経過した熱伝導率[W/(m・K)]
λgas(0): 製造直後(t=0)における気泡セル内気体の熱伝導による伝熱成分[W/(m・K)]
λgas(t): 時刻tにおける気泡セル内気体の熱伝導による伝熱成分[W/(m・K)]
λi:
空気及び発泡ガスの熱伝導率[W/(m・K)]
λpolymer: 気泡セル膜を構成するポリマー熱伝導率[W/(m・K)]
λradiation: 気泡セル膜間の放射熱伝達による伝熱成分[W/(m・K)]
λsolid:
樹脂部分(気泡セル膜及びポリマー支柱)の熱伝導による伝熱成分[W/(m・K)]
μi:
無次元物質移動係数
ρfoam:
断熱材密度(kg/m3)
ρpolymer: 気泡セル膜を構成するポリマー密度(kg/m3)
σ:
ステファン・ボルツマン定数(=5.67×10−8)[W/(m2・K4)]
φ:
気泡セルの直径(μm)
ωi(0):
断熱材内の空気及び発泡ガスの熱伝導率に対する重み係数
ωi(t):
断熱材内の空気及び発泡ガスの熱伝導率に対する重み係数
23
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JB
(参考)
簡易計算に基づく熱伝導率変化量の計算例
JB.1 概要
この附属書では,JA.4に示す断熱材の熱伝導率の変化量である式(JA.9)を計算する際に必要となる式
(JA.13)及び式(JA.14)に示す断熱材内分圧をJA.6に示す簡易計算法に従って計算した結果を示す。さらに,
この値に基づいて熱伝導率変化量を計算した結果を示す。
JB.2 計算対象断熱材及び対象気体の物性値など
表JB.1に示す断熱材(厚さ20 mm,被覆層あり)を対象に,製造後3年が経過した時点の断熱材内分圧
を簡易計算法によって計算する。計算の際に対象とする気体は,空気(i=1)及び1種類の発泡ガス(i=
2)として,空気及び発泡ガスの物性値などは,表JB.2に示す値を用いる。
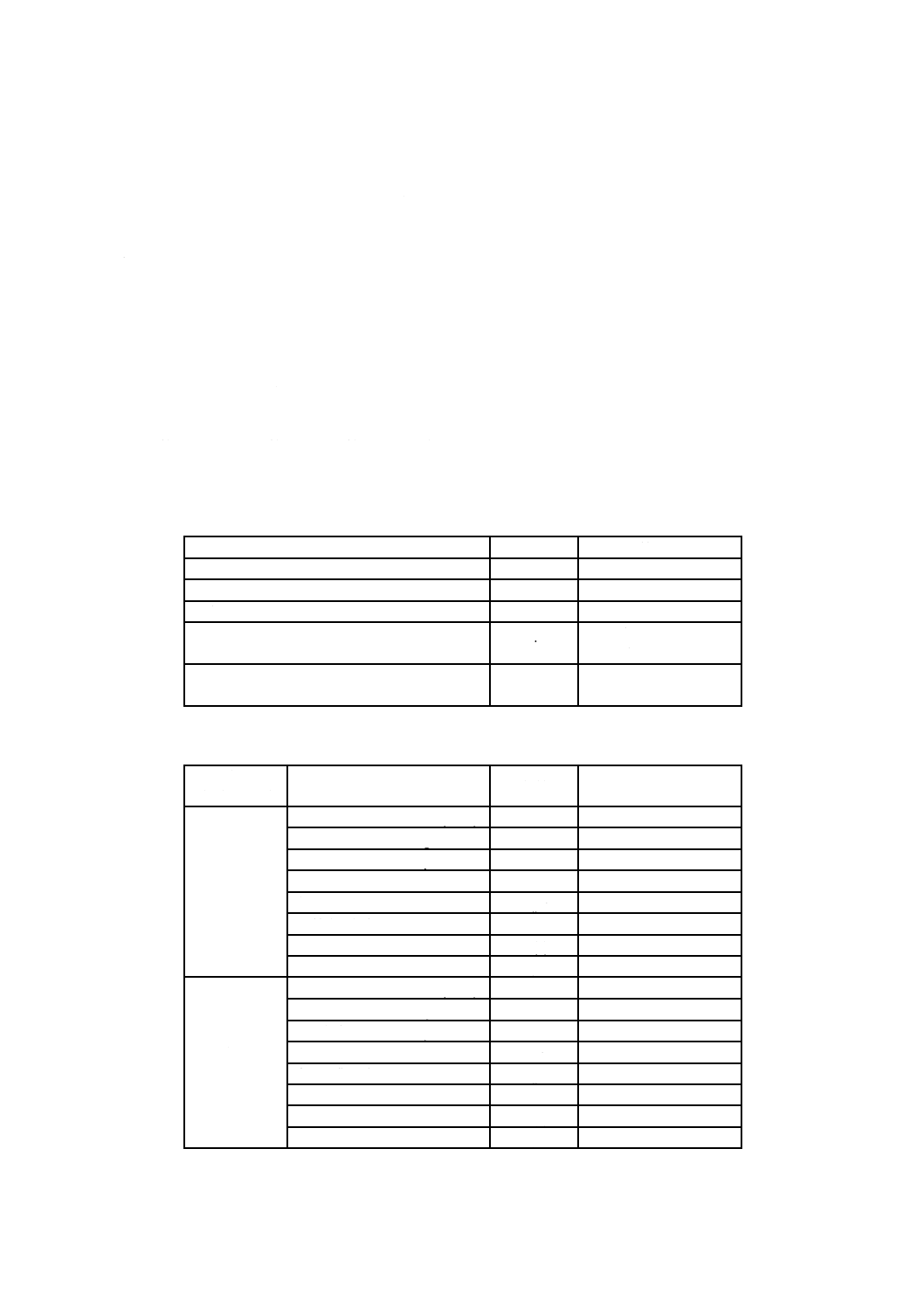
表JB.1−対象断熱材の概要
計算条件
記号
値など
断熱材厚さ
m
L
0.020
被覆層の有無
−
被覆層あり
温度
℃
T
23.0
対象気体名
i
1:空気
2:発泡ガス
計算対象時刻
t
製造後3年経過時
(=9.46×107秒)
表JB.2−対象気体の物性値など
気体名
(気体番号i)
物性値
記号
値
空気
(i=1)
熱伝導率
W/(m・K)
λ1
1.76
分子量
g/mol
M1
29.0
粘性係数
μPa・s
n1
18.2
沸点
K
Tb, 1
80.3
有効拡散係数
m2/s
Deff, 1
2.0×10−11
物質移動係数
m/s
α1
1.0×10−10
初期断熱材内分圧 MPa
P1(0)
0.000
断熱材外部分圧
MPa
P1, out
0.101
発泡ガス
(i=2)
熱伝導率
W/(m・K)
λ2
15.89
分子量
g/mol
M2
58.1
粘性係数
μPa・s
n2
7.4
沸点
K
Tb, 2
261.5
有効拡散係数
m2/s
Deff, 2
2.0×10−12
物質移動係数
m/s
α2
1.0×10−10
初期断熱材内分圧 MPa
P2(0)
0.080
断熱材外部分圧
MPa
P2, out
0.000
24
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
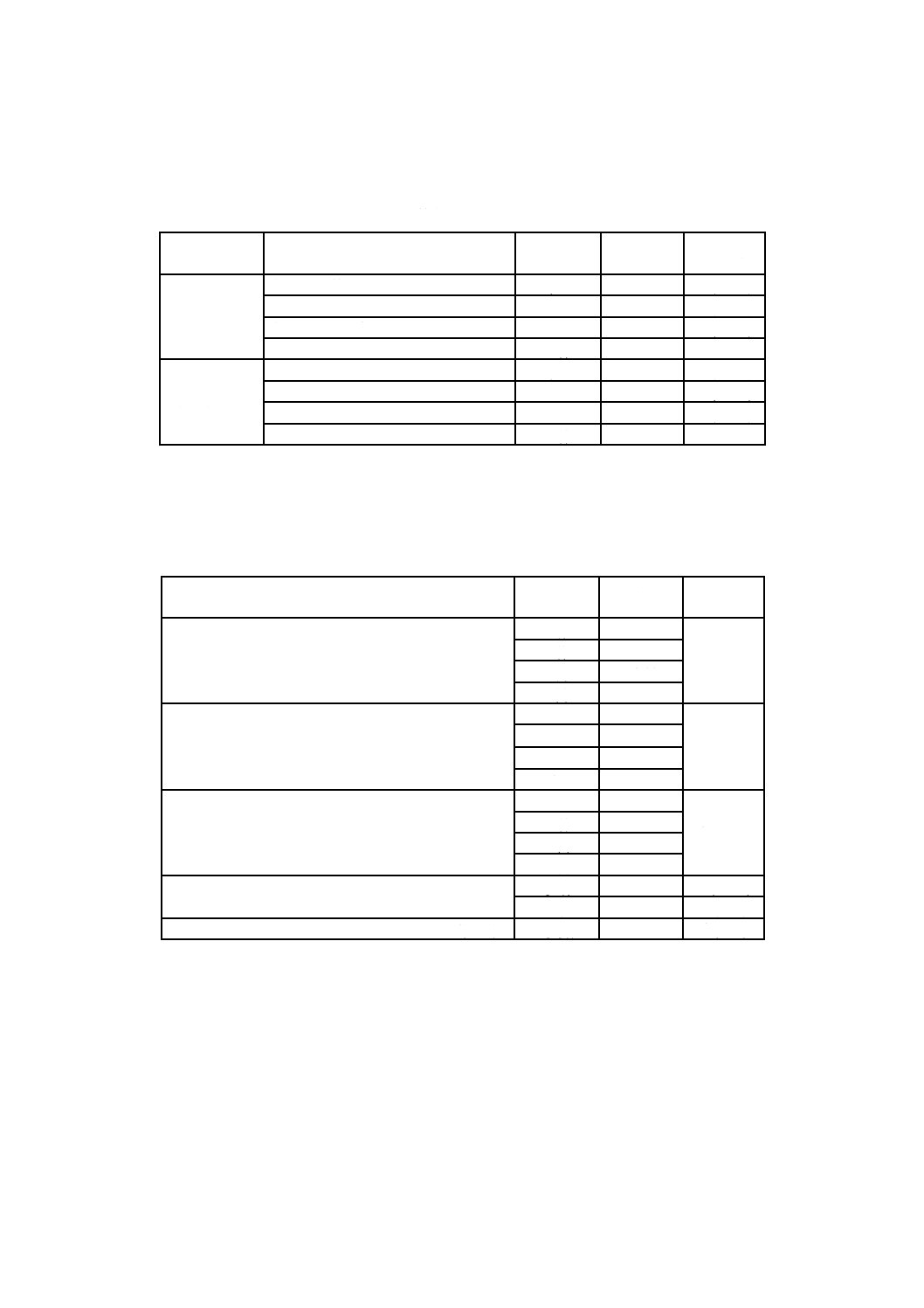
JB.3 結果(断熱材内分圧)
断熱材内分圧の計算結果を,表JB.3に示す。
表JB.3−計算結果(断熱材内分圧)
気体名
(気体番号i)
計算項目
記号
値
式番号
図番号
空気
(i=1)
無次元物質移動係数
μ1
0.10
式(JA.17)
無次元時間
X1
2.18
式(JA.15)
無次元断熱材内分圧
Y1
0.63
式(JA.16)
対象時刻tの断熱材内分圧
MPa
P1(t)
0.037
図JA.2
発泡ガス
(i=2)
無次元物質移動係数
μ2
1.00
式(JA.17)
無次元時間
X2
0.69
式(JA.15)
無次元断熱材内分圧
Y2
0.68
式(JA.16)
対象時刻tの断熱材内分圧
MPa
P2(t)
0.054
図JA.2
JB.4 結果(熱伝導率変化量)
熱伝導率変化量の計算結果を,表JB.4に示す。
表JB.4−計算結果(熱伝導率変化量)
計算項目
記号
値
式番号
表番号
モル分率
x1(t)
0.40
式(JA.12)
x2(t)
0.60
x1(0)
0.00
x2(0)
1.00
結合係数
A11
1.00
式(JA.8)
又は
表JA.2
A12
2.06
A21
0.50
A22
1.00
熱伝導率に対する重み係数
ω1(t)
0.24
式(JA.11)
ω2(t)
0.75
ω1(0)
0.00
ω2(0)
1.00
断熱材内気体の熱伝導による伝熱成分
W/(m・K)
λgas(t)
18.05
式(JA.10)
λgas(0)
15.89
式(JA.5)
時間経過に伴う熱伝導率変化量
W/(m・K)
λaging(t)
2.16
式(JA.9)
25
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JC
(参考)
被覆層の拡散抵抗を測定又は同定する方法
JC.1 概要
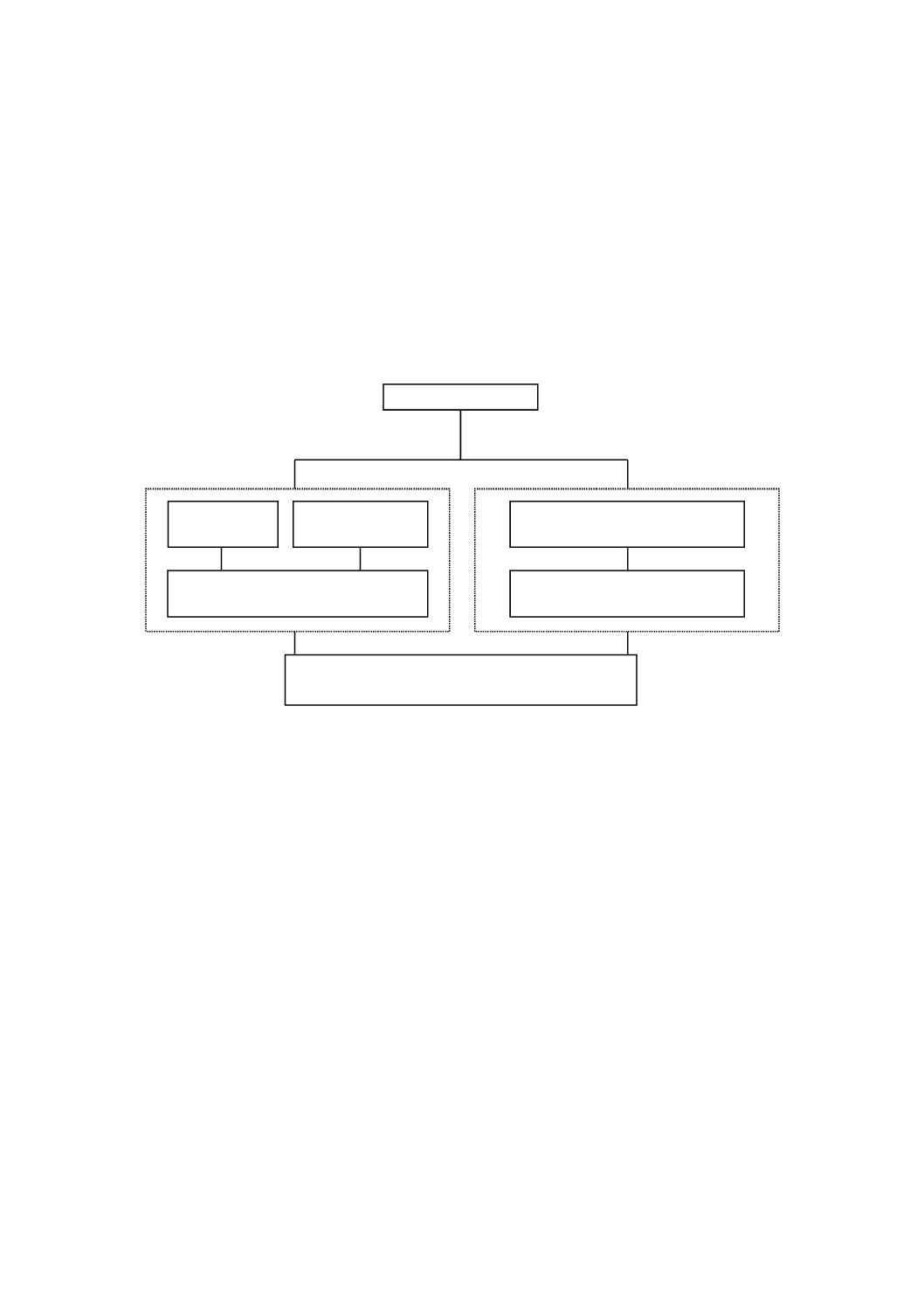
この附属書では,被覆層の拡散抵抗を測定又は同定する方法のフローを示す。
JC.2 解析フロー
図JC.1−解析フロー
被覆層あり
ガスの場合
(JD.2)
揮発性物質の場合
(JD.3)
熱伝導率経時変化の測定
(JE.2及びJE.3)
物質移動係数の算出
(JD.4)
拡散抵抗の同定
(JE.4)
数値解析による熱伝導率変化の予測
(附属書JA)
拡散抵抗を直接測定する方法
(附属書JD)
熱伝導率の経時変化から同定する方法
(附属書JE)
26
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JD
(参考)
被覆層の拡散抵抗を直接測定する方法
JD.1 概要
この附属書では,被覆層の拡散抵抗を直接測定する方法を示す。
JD.2 ガス透過度(GTR)の測定
ガス透過度(GTR)の測定は,次による。
a) 被覆層に対する気体iの気体透過度GTRi[mol/(m2・s・Pa)]をJIS K 7126-1又はJIS K 7126-2に代表さ
れる方法によって測定する。
注記1 装置を汚染するガス及び腐食性ガスは測定することができない。
注記2 試験ガスの透過方向によって気体透過度(GTR)が異なる場合があるので,結果の取扱いに
は注意を要する。GTRが異なる原因は,試験片のガス透過面以外からの大気の漏れ込みなど
が挙げられる。断面からの漏れ込みへの対策として,適切な接着剤などによるコーティング
処理,ガス透過面以外の面をアルミ材で被覆などの処置を行うことがある。
b) 試験は,一般的条件として,室温23±1 ℃の室内で行う。
注記 試験温度を可変できる試験機では,必要に応じて条件設定を変更することができる。
JD.3 揮発性物質透過度の測定
揮発性物質透過度の測定は,次による。
a) 被覆層に対する揮発性物質の透過度をISO 6179に代表される方法によって測定する。
b) 試験は,一般的条件として,室温23±1 ℃の室内で行う。
JD.4 物質移動係数(αi)の算出
式(JD.1)によって,物質移動係数αi{g/[(m2・s)・(g/m3)]}を算出する。
i
i
i
i
i
i
GTR
RT
M
RT
M
M
GTR
2
=
×
×
=
α
················································· (JD.1)
ここに,
Mi: 分子量(g/mol)
R: 気体定数(m3・Pa/mol・K)[=8.314 m3・Pa/(mol・K)]
T: 絶対温度(K)
27
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JE
(参考)
被覆層の拡散抵抗を熱伝導率の経時変化から同定する方法
JE.1 概要
この附属書では,被覆層の拡散抵抗を試験片の熱伝導率の経時変化から同定する方法を示す。
JE.2 試験片の作製
試験片の作製は,次による。
a) 同一の試料から熱伝導率測定用の試験片を2枚切り出す。このとき,表面の被覆層はそのままとする。
b) a)で切り出した2枚の試験片のうち1枚の被覆層を取り除き芯材だけの状態とし,被覆層試験片及び
芯材試験片を作製し,それぞれの初期熱伝導率を測定する。熱伝導率の測定方法及び測定条件は5.1.5
のa)及びb)による。
c) 初期熱伝導率測定後,被覆層試験片は発泡ガス放散面[表面(1面)又は表裏面(2面)]を除く面を
ガス透過性のない材料でシールし,解放面以外の面から材料内部のガスの拡散がないようにする。芯
材試験片も被覆層試験片と同様の面をシールする。シールした2種類の試験片は,5.1.5のd)の条件で
状態調節を行う。
JE.3 測定
適切な時間間隔で2種類の試験片の熱伝導率を測定する。2種類の試験片は,通常,同じ周期で測定を
行う。
注記 シール材にアルミニウム製テープなどの金属材料を用いると,熱伝導率測定方法によってはシ
ール材が測定結果に影響を与える場合がある。このため,熱伝導率測定に際してはシール材の
影響がない状態で測定を行う。
JE.4 拡散抵抗の同定
拡散抵抗の同定は,次による。
a) 芯材試験片の熱伝導率の経時変化測定結果から附属書JAの解析モデルを用いて断熱材内気体の有効
拡散係数Deff, iを同定する。
b) 被覆層試験片の熱伝導率の経時変化測定結果から附属書JAの解析モデルを用いて被覆層の拡散抵抗
Riを同定する。
参考文献 JIS K 7126-1 プラスチック−フィルム及びシート−ガス透過度試験方法−第1部:差圧法
JIS K 7126-2 プラスチック−フィルム及びシート−ガス透過度試験方法−第2部:等圧法
ISO 6179,Rubber, vulcanized or thermoplastic−Rubber sheets and rubber-coated fabrics−
Determination of transmission rate of volatile liquids (gravimetric technique)
28
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
附属書JF
(参考)
JISと対応国際規格との対比表
JIS A 1486:2014 発泡プラスチック系断熱材の熱抵抗の長期変化促進試験方法
ISO 11561:1999 Ageing of thermal insulation materials−Determination of the
long-term change in thermal resistance of closed-cell plastics (accelerated laboratory
test methods)
(I)JISの規定
(II)
国際規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
1 適用範
囲
適用範囲
1
JISとほぼ同じ
追加
JISでは被覆層による発泡ガス
放散抑制効果を期待する場合,
任意で附属書JC及び附属書JD
又は附属書JEによって被覆層
の拡散抵抗を測定し,附属書JA
及び附属書JBによって長期的
な変化を知ることができること
を追加。また,“主に常温で使用
される”を追加した。
国内の生産者側のニーズに対応
した。JISとして運用し国内での
実績を踏んだ上でISO規格への
追加を提案する。
2 引用規
格
3 用語及
び定義並
びに記号
及び単位
用語及び定義
3
JISとほぼ同じ
追加
附属書JA〜附属書JEを追加し
たことによって新たに定義が必
要となった用語及び定義を追加
した。
国内の生産者側のニーズに対応
した。JISとして運用し国内での
実績を踏んだ上でISO規格への
追加を提案する。
5.1.2
試
料採取
試料の採取方法につ
いて規定
5.2
標準的な採取手順によ
る。
変更
JISは,JIS A 9511又はJIS A
9526の該当箇条を適用するこ
ととした。
ISO規格は,標準的な採取手順と
しか規定されていないため,国内
で運用している製品規格を引用
した。実質的な差異はない。
5.1.3
試
験片の準
備
試験片の準備につい
て規定
5.3
JISとほぼ同じ
変更
JISは,JIS A 9511又はJIS A
9526の該当箇条を適用するこ
ととした。
国内で運用している製品規格を
引用した。実質的な差異はない。
6
A
1
4
8
6
:
2
0
1
4
29
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
(I)JISの規定
(II)
国際規格
番号
(III)国際規格の規定
(IV)JISと国際規格との技術的差異の箇条
ごとの評価及びその内容
(V)JISと国際規格との技術的差
異の理由及び今後の対策
箇条番号
及び題名
内容
箇条番号
内容
箇条ごと
の評価
技術的差異の内容
5.1.5
試
験片の熱
抵抗及び
熱伝導抵
抗の測定
b) 熱抵抗及び熱伝
導抵抗測定時の試験
片の平均温度
5.5.2
推奨試験温度は10±2 ℃
又は23±2 ℃のいずれか
とする。
変更
JISは,熱抵抗及び熱伝導抵抗
測定時の試験片の平均温度を
2
3
23+
− ℃とした。
国内での使用環境及び試験環境
を考慮した。WTO/TBT協定の例
外事項であるため特に提案はし
ない。
d) 状態調節の条件
5.5.4
温度23±2 ℃,相対湿度
(50±5)%RH
変更
原則温度23±2 ℃,相対湿度
(50±5)%RHだが,相対湿度
は(
20
10
50+
−)%とすることができ
る緩和条件を追記した。
国内での使用環境及び試験環境
を考慮した。WTO/TBT協定の例
外事項であるため特に提案はし
ない。
5.2.2
手
順
試験方法Bの手順に
ついて規定
6.2
JISとほぼ同じ
変更
JISは,熱抵抗及び熱伝導抵抗
測定時の試験片の平均温度を
2
3
23+
− ℃,温度差25 ℃以内とし
た。
国内での使用環境及び試験環境
を考慮した。WTO/TBT協定の例
外事項であるため特に提案はし
ない。
6 報告事
項
報告事項について規
定
8
JISとほぼ同じ
追加
試験報告書に,必要に応じて記
載する事項を追加した。
附属書JA〜附属書JEの追加に伴
い,必要に応じて記載する事項を
追加した。JISとして運用し国内
での実績を踏んだ上でISO規格
への追加を提案する。
附属書JA
(参考)
−
附属書JB
(参考)
−
附属書JC
(参考)
−
附属書JD
(参考)
−
附属書JE
(参考)
−
6
A
1
4
8
6
:
2
0
1
4

30
A 1486:2014
2019年7月1日の法改正により名称が変わりました。まえがきを除き,本規格中の「日本工業規格」を「日本産業規格」に読み替えてください。
JISと国際規格との対応の程度の全体評価:ISO 11561:1999,MOD
注記1 箇条ごとの評価欄の用語の意味は,次による。
− 追加……………… 国際規格にない規定項目又は規定内容を追加している。
− 変更……………… 国際規格の規定内容を変更している。
注記2 JISと国際規格との対応の程度の全体評価欄の記号の意味は,次による。
− MOD…………… 国際規格を修正している。
6
A
1
4
8
6
:
2
0
1
4












